(Refer Slide Time: 03:41)
|
|
|
- Willis Webster
- 5 years ago
- Views:
Transcription
1 Solid State Devices Dr. S. Karmalkar Department of Electronics and Communication Engineering Indian Institute of Technology, Madras Lecture - 25 PN Junction (Contd ) This is the 25th lecture of this course and the 7th lecture on PN junction. In the previous lecture we have seen the reverse current voltage characteristics of a diode. In this lecture we will see the equivalent circuit of the diode under small signal conditions. So let us look at the slide which is related to this particular topic. (Refer Slide Time: 03:41) This is the biasing arrangement in which we measure the characteristics. You have a DC voltage applied across a diode. Although the circuit shows a forward bias the DC voltage V a could as well be a reverse bias. Over and above this DC voltage is an AC voltage which is super imposed so this is the AC voltage. The magnitude of this voltage is small and that is why the term V m is set to be very small compared to the thermal voltage V t. Now why the V n should be much less than V t? At this point this is not clear but it will become clear when we take up the details. The frequency of the signal is omega as shown by the equation v is equal to V suffix m into sin of omega t. If this is the applied voltage we will find that there will be a small signal current I as shown here in addition to the DC current capital I. And this small signal current I will have amplitude and also there may be a phase difference between the current and the voltage. We would like to find out what kind of an equivalent circuit will explain this phase difference and will also help us to calculate the amplitude of the current for a given voltage. So the equivalent circuit of the diode will look like this. So
2 we would like to explain how you obtain the diode equivalent circuit as a parallel combination of a resistance and capacitance. Now, the approach for this is called the quasi-static approach. This means we will try to derive the formulae for AC conditions from the DC characteristics or static characteristics. This is an important point to remember that this approach gives you only approximate estimates of the capacitance and resistance of the equivalent circuit. To see the difference between the quasi-static approach or non-quasi-static approach in detail I would suggest that you look into the reference material that is given in this particular slide. This is an article published in IEEE transaction on education in November (Refer Slide Time: 05:02) The page numbers are 328 to 330. The title of the article is Appealing analogies for aiding student s assimilation of some key physical concepts related to semiconductor devices. Here with the help of an analogy the difference between the quasi-static and the rigorous approach of estimating the capacitance has been given. In this course we will only do the quasi-static approach. Now let us understand what is meant by the quasistatic approach in a little bit detail. This is a PN junction across which a bias has been applied, let us assume a forward bias. We will derive the family of a forward bias and we will show that the formulae will also enable us to get the parameters for the reverse bias. Now what we do is we change the voltage V by a small amount as a result of which the current I will also change by small amount. Now when we make the change we wait until in the new voltage the conditions in the diode has stabilized and you are getting a new current. That is to say: for voltage V you get a current I then you change the voltage to v plus dv and then you give sufficient time so that the current stabilizes at I plus di. So, just as I is a DC current corresponding to the voltage V, I plus di is the steady state or DC current corresponding to the voltage V plus dv. Now, when the current changes from I to
3 I plus di the charges inside the device also will change. For example, you find that a certain charge Q is stored in the device for a voltage V. (Refer Slide Time: 13:34) We will shortly see what is it that is responsible for storing a charge Q. As of now let us just assume that if a charge Q is stored for v and when you change the voltage to v plus dv this charge increases to Q plus dq. Then from these conditions now one can obtain the resistance and capacitance as follows. So you can get a resistance r is equal to dv by di. So dv is increment in voltage and corresponding increment in the DC or static current is di so it is dv by di. And you can define the capacitance C as this change dq in the charge because of the change dv in the voltage. So this is the meaning of the quasi-static approach. We are making a change in the voltage and we are estimating the changes in the current and charges because of the change in voltage but we give sufficient time for the effects of the change to stabilize. For example this resistance equal to dv by di you can represent drastically as follows. This is your forward current voltage characteristics where I is on a linear scale and voltage is also on a linear scale. At some voltage V you make a change dv so this is the change dv and the corresponding change in current is di. So you note this change in current di and this dv by di is the resistance. So basically it is a slope of this DC curve at any point. Similarly, one can sketch this charge Q as a function of voltage V and then one can take the slope of that and one can obtain the capacitance dq by dv. This is the quasi-static approach of determining the resistance and capacitance. Now we can quickly estimate the resistance using this formula because we know that the ideal diode equation is given by I is equal to I 0 exponential of V by V t minus 1. So, differentiating this we get di by dv is equal to I 0 exponential V by V t by V t which we can write as the numerator I 0 exponential V by V t is I plus I 0 from this equation. So this is I plus I 0 by V t. So di by dv is nothing
4 but one by small signal resistance r. This is the formula for small signal resistance. Now for forward bias generally the current I is much greater than I 0 so we can write r is approximately equal to V t by I for forward bias. On the other hand, what you see is that for reverse bias the current I will saturate to minus I 0 which is more than 3V t. And therefore you find from the formula that the small signal resistance of the diode for reverse bias more than 3V t would be infinity because the numerator is 0. So we can write r tends to infinity for reverse bias VR greater than 3V t. Now this is true for an ideal diode, please note that we are deriving this for an ideal diode. In a real diode you will find that this r will not be infinity because the reverse current increases with voltage because the reverse current in practical silicon diodes is because of generation within the depletion layer which goes on increasing because of the increase in depletion width with voltage. So in that case you will have a finite non-zero conductance or nonzero di by dv on the reverse side therefore resistance will not be infinity but it will be of the order of hundreds of kilo ohms or higher. What we are doing here is for ideal diode characteristics. Now how do we determine the capacitance of this particular diode under small signal conditions? Before doing this let me explain why the capacitance and the resistance both should be regarded as in parallel. Please note that the voltage V that is responsible for the current I and the charge Q is the same. Since the resistance and the capacitance are due to a common voltage V that is the voltage across both the resistance and capacitance is the same and therefore it follows that the resistance and capacitance should be shown to be in parallel. Now, determining the estimation of the capacitance we need to derive a relation for charge Q as a function of voltage V in the same way as we have a relation between the current I in response to V. Let us see how we determine the charge Q. Here we have shown the conditions in a PN junction under forward bias. This is the space charge region and these are the conditions in the neutral region. This is the first time we have shown both the electron and hole concentrations in the neutral regions on a linear scale and that is why you will find a cut shown here. If we use the same scale we cannot show both majority and minority carriers. The reason we have shown both electrons and holes in a given-region on linear scale is that we must recognize that the excess hole concentration which is shown by this shaded area in the n- region is exactly compensated by the excess electron concentration which is the area under this portion. So, when the p-region injects holes into n-region these are the injected holes the negative terminal injects electrons to compensate for the holes so that charge neutrality is maintained. So this equality in the holes and electrons is clearly seen when you plot it on a linear scale and similar conditions exist here also. These are the injected electrons from the p-side and to compensate for this you have holes injected from the positive contact. We will be shading the positive charges in the device, these are the extra positive chargers, excess holes on the p-side. The dotted lines here show the equilibrium condition.
5 Now, come back to the space charge region. Here corresponding to the equilibrium condition the space charge region would look like this. The width of the space charge region would have been longer. So the distance between this dotted line and this dotted line shows the space charge region width under equilibrium and the solid line shows the conditions for the applied voltage V which is the forward voltage. Here this is for V and this is for V is equal to 0. (Refer Slide Time: 16:21) We find that the depletion-region has shrunk for the forward bias V. Or in other words, the width of the quasi-neutral region has increased on either side. This is the shrunk wing of the depletion-region which represents also the extension of the quasi-neutral n-region. So equilibrium quasi-neutral region was between this dotted line and this end whereas for applied bias it is between the solid line and this end. So we can say that the swing in of the depletion layer has cost expansion of the quasi-neutral regions and in other words therefore what has happened is that extra electrons have been introduced in this n-region and extra holes have been introduced in this p-region. So as to compensate for the ionized impurities here and as well as there to create charge neutrality. When you have extra electrons in the quasi-neutral regions obviously some holes will be there which are minority carriers and similarly some electrons will also be there. But we neglect the effect of the electrons on the p-side and holes and the n-side because they are minority carriers as far as the depletion layers are concerned. So we can say the expansion of the quasi-neutral region has been because of injection of electrons from the negative terminal. And exactly equal number of holes has been injected from the positive terminal so as to extend the quasi-neutral region on the p-side. So this area represents the extra holes which have come in at the forward bias voltage V as compared to the equilibrium condition. And obviously this area is equal to this area and this represents the extra electrons. These are the extra electrons.
6 What one can say is that, as compared to the equilibrium condition because of forward bias there has been a change in the concentration of holes and concentration of electrons. So we can write it down as follows. In the PN junction you have charges which are because of impurities which are bound charges and you have free charges which are electrons or holes. And now the electrons and holes change when a voltage is applied so the free carrier chargers change due to change in this space charge width and due to change in the excess charge in the neutral regions or quasi-neutral region. Therefore the electrons and holes change in the number. But these impurities the bound charges do not change so we need not take the effect of this into account because we are defining the capacitance as dq by dv. So, only the change in the charge is of interest to us because of dv and not the absolute magnitude of charges. Since a bound charger or impurities do not change with voltage we do not consider the effect of the impurities in estimation of the capacitance. (Refer Slide Time: 21:21) The changes in the free carrier charge are indicated here in the diagram. The shaded area shows the excess holes which are coming because of the applied voltage V as compared to the equilibrium conditions. Now we can estimate the capacitance by taking the some of these hole concentrations and then dividing by the incremental voltage. So in this case the incremental voltage is v itself because we are comparing it with respect to equilibrium condition. Alternately we could write down an expression for these excess holes and we could differentiate this expression with respect to voltage. Now there is one point you must remember that while estimating the capacitance you can either take the change in the positive charge or the change in the negative charge so the term dq here represents either the positive or the negative component. That is why we normally put a modulus on this particular term to represent the capacitance.
7 The capacitance is always positive so you can either take the positive component or the negative component. If you take the negative component this term will be negative so you have to take the magnitude to take the capacitance. So we will take the positive component of this charge for estimating the capacitance. And for any capacitance the positive and negative component will always be equal because the device as a whole is charge neutral. Now let us write down the expressions for this excess hole charge. We will take the space charge region and the quasi-neutral region separately. Let us take this space charge region first. What is the formula for these excess holes as compared to the equilibrium condition can be written as follows. Let us represent the excess hole concentration in the space charge region as Q p suffix d where d stands for depletion. So we are calling this either space charge or depletion-region. So Q p is excess hole concentration that has come in at voltage V because of change in the depletion-region. So Q p d is this particular shaded area and we can write that as the depletion-region width on the p-side that is X p minus X p0 the change in the depletion-region into Q into the acceptor impurity concentration there N a into the area of the junction. So this area of the junction is a cross-sectional area in direction perpendicular to the board. In this case here this width is X p and this width is X p0. In fact this formula should be written X p0 minus X p because X p0 is more than X p and this is the Q p hole charge. Now what one can do is one can differentiate this with respective tp voltage. The voltage dependence comes because of the dependence of X p on voltage the depletion width on the p-side on the voltage. So you can differentiate dq pd by dv and we can write this as q times and we have to take a modulus so q N a into a into d Xp by dv, there is a negative sign here because this is minus X p. So this would represent the capacitance contribution due to the space charge region. Normally this contribution is shown using a symbol C suffix depletion because this is a capacitance due to changes in the depletion layer. So, one can evaluate this by substituting the expression for X p. I will leave it an exercise for you to derive the expression for the capacitance C depletion by substituting the expression for X p and differentiating with respect to the applied voltage. What I will do here is I will derive the final expression by a different method which is much simpler and which is more physical rather than mathematical. Now this method can be understood as follows: You take only the increments and let us see how the incremental picture of this charge looks like. The incremental picture can be drawn as follows. This is the p plus side and this is the n plus side and this is the PN junction, this is incremental hole charge and this is incremental electron charge so this is the so called Q p d. Now, if you take this increment between any two voltages that is this edge corresponds to voltage V and this edge corresponds to V plus dv. Therefore this is the increment dq pd because of increment dv then this thickness of these regions will be very small. So here we have shown these changes with reference to the equilibrium condition. So this is v and this is equilibrium.
8 Supposing this V is very small as compared to equilibrium then this V is nothing but the incremental voltage dv. Or alternately we can draw the picture for any two voltages which are different only by an incremental voltage dv and that is what we have done here. So, for one voltage V this is the picture and for another voltage V plus dv depletion has shrunk and this is the picture, dv is very small so this thickness is very small. And this is the corresponding picture on the p-side. Now this picture corresponds to that of a parallelepiped capacitor, you can very easily see this like a parallel plate capacitor whose distance is between the charges which is nothing but the depletion-region X d and the charges around this side. This is an incremental picture and we are interested in the incremental capacitance which is dq by dv. So, the incremental picture of the changes of in charges at the edges of the depletion layer is similar to that of a parallel plate capacitor, the distance between the plates being X d. We can very simply write this particular capacitance that is the depletion capacitance. We can show that this will be equal to epsilon into A by X d. This is a capacitance because of a parallel plate capacitor plate separation X d. This is the physical approach to determine the equation. You can mathematically do this expression, work out and then show that this is nothing but epsilon A by X d. Oone clarification is, this is the change in the depletion layer charge so it is shown on a negative side because on the p-side the space charge is negative and on the n-side the space charge is positive. (Refer Slide Time: 30:52) Now one might wonder that how the change in the negative side has been shown as the hole dq pd change in the positive charge. Here what you are seeing is the magnitude of the change in the positive charge so the negative charge is decreasing in magnitude. In this previous figure this is the negative charge and when you apply more and more forward voltage the negative charge decreases so what is shown is the change in the negative charge. So the decrease in negative charge means increase in positive charge so if you
9 want to show that more accurately then you must show the dq pd as a rectangle on this side. And dq n is the change in electron charge on this side as a rectangle here. Here we are discussing about the magnitude of dq pd. So this shaded area is the magnitude and we do not care about the sign when you are talking of the magnitudes. This is how one can estimate what is called the depletion component of the incremental capacitance of a diode. Now we should see how we can determine the diffusion component of the capacitance. That is, the capacitance or incremental capacitance because of charges in the quasi-neutral regions. This particular capacitance is called diffusion capacitance because these chargers in the neutral region contribute to the diffusion current of the diode. Now you might have a doubt, how does this charge contribute to diffusion current? This is the majority carrier charge. This is an important point you must note that this charge is equal to this charge because this region should be quasi-neutral. So, the sum of these two charges which are the excess holes in the neutral regions is equal to the sum of these two charges which are these areas. And you know that the excess minority carrier charge contributes to the diffusion current on the p-sides just as the excess minority carrier charger or hole charge contributes to the diffusion current on the n-side. That is why we can estimate the capacitance by summing up these two areas. And therefore this capacitance is referred to as the diffusion capacitance. Now let us discuss the estimation of the diffusion capacitance. The diffusion capacitance can be written as differential of the sum Q p plus Q n by dv where Q p is this charge which is the excess charge due to minority carrier stored on the n-side and Q n is this charge the area under this excess carrier concentration stored on the p-side and this is excess electron charge stored on the p-side. Here we want to find out the total number of excess holes because of voltage V which is this plus this. But since this area is equal to this area and we know that distribution of minority carriers can be solved very simply using the continuity equation so instead of summing up these two we are summing up these two. One should not think why are we summing up the electron charge and the hole charge. Electrons are negatively charged and holes are positively charged. So we are not summing up negative and positive charges but we are summing up magnitudes. Actually we are summing up the hole charges on the two sides of the quasi-neutral region. But since the magnitude of excess hole charge on the p-side is same as the magnitude of the excess electron charge on the p-side we are summing up these two and these two can be written down easily. This is where you must understand the quasi-static approach and why the word quasi-static is being used is because this distribution which I have drawn here is known for this static or steady state condition and they are exponentials, therefore the area can be easily determined once you know the distribution. In steady state conditions the distribution is exponential because you take the continuity equation for the minority carriers and then you set the rate of change of the minority carrier concentration as 0. For example, if you want to get this exponential distribution then you take the continuity equation for holes and you are going to set dow p by dow t in the continuity equation to be 0. Let me write that equation here to show this.
10 So dow p by dow t is equal to minus 1 by q dow Jp by dow x minus delta p by tau. This is the continuity equation for holes on the n-side. To get the distribution of holes you are going to set this equal to 0 under steady state conditions. Now you are going to use this exponential distribution update under steady state conditions to estimate the changes in the charges also under non steady state or time varying conditions or the voltage varying with time conditions. This means you are setting this dow p by dow t not exactly equal to 0 but approximately equal to 0 so that you can still use the continuity equation setting these terms equal to 0 and get the exponential distribution and then work with that. So approximately equal to 0 means quasi-static. And for dow p by dow t when the conditions are varying with time it is not equal to 0. That is why strictly speaking the distribution of the holes will not be exponential. So, coming back to the estimation of Q p and Q n we can easily write the expressions for Q p and Q n by looking at this diagram and our knowledge of the distribution of holes and electrons. So we write Q p is equal to Q(delta p) into diffusion length L p into the area A of the cross section of the diode. This is your excess carrier distribution delta p, this is diffusion length L p and here the area under this rectangle is same as the area under this exponential. Here this is the area that we are interested in. Now similarly one can write down the expression for Q n also. Now what we will do is since we are considering a one sided junction the p-side doping is much more than n-side therefore we will neglect Q n compared to Q p which will help as to get a simple equation for the diffusion capacitance. So we assume Q n less than Q p since p to the power plus n junction. With this approximation and this equation you get the equation for C diffusion as d by dv of Delta p into q L p into A. Now we know the expression for delta p as a function of v that is delta p is equal to p n0 exponential of V by V t minus 1. So, if you differentiate this with respect to V you will get p n0 exponential of V by V t by V t which you can write as delta p plus p n0 by V t. This term is nothing but p n0 exponential V by V t so you shift this minus 1 on this side and that is how you get this equal to this from this equation. So we can write this here as this is equal to qa L p into delta p plus p n0 by V t. Now, when you are talking about forward voltages this delta p is much greater than p n0.
11 (Refer Slide Time: 40:53) So we can approximate for forward voltage conditions or for forward bias the diffusion capacitance C dif approximately equal to qa L p delta p by V t since we have neglected p n0. Now, we can write this term very simply in terms of the current. We know from our diode theory that for p to the power plus n junction the forward current I is approximately equal to qa delta p into Dp by L p. This is the diffusion current and we are neglecting the diffusion current because of electrons. So look back into the forward diode equation which we have derived and you will find this equation. We can write this equation by multiplying by lifetime tau and divide by lifetime tau and then we can identify this term as L p square. Now this L p square will cancel with L p, one of this L p terms will cancel and so this is equal to qa delta p L p by tau. So from this equation of a forward current it is clear that you can write the numerator qa L p delta p as I into tau. So this is equal to I tau by V t. This is the formula for the diffusion capacitance. This is very easy to remember because current into time is charge and charge by voltage is the capacitance. So the characteristic voltage is the thermal voltage and here this is the characteristic time that is that the lifetime.
12 (Refer Slide Time: 43:26) So this enables you to write down an expression for the diffusion capacitance very simply in terms of the forward current. Please note that this is derived under the condition that it is a one sided junction when we neglect the electron charge on the p-side. Now what happens under the reverse bias? In the reverse bias this excess carrier concentration Delta p is negative of p n0 because you have depletion of carriers in the neutral regions. So delta p is minus (p n0 ) so these two terms cancel and the diffusion capacitance goes to 0. Now this will happen for reverse bias voltages more than 3V t. For reverse bias voltages less than 3V t there will be some small diffusion capacitance. But generally we operate in reverse bias voltages more than 3V t therefore diffusion capacitance is taken to be negligible under these conditions. Now we can summarize the results of our small signal analysis as follows. From the DC current voltage characteristics where in the current is proportional to exponential V by V t minus 1 we get the small signal resistance r of the diode that is shown here. So this is the equivalent circuit under forward bias. This r is V t by I where the I 0 term has been neglected as compared to I.
13 (Refer Slide Time: 48:10) Now this is obtained as the slope of this particular curve so it is di by dv is equal to 1 by r. Now consider this stored charge in the neutral regions taking only the store charge in the lightly doped region for a p to the power plus n junction. This Q p varies with V in the same way as the current so this is also exponential behavior and this is also an exponential behavior. You can check this from the formula that we have derived for Q p which was Q p is equal to Q Delta p L p into A. So you can write expression for Delta p and you can show that the Q p will be proportional to exponential of V by V t minus 1. Then you take the slope of this curve and this gives you the diffusion capacitance. So dq p by dv is the diffusion capacitance. Similarly, you take the hole charge that is injected into the device because of shrinking of the depletion layer in the forward bias and that follows this particular behavior as shown in this graph. Here this particular quantity is proportion to square root of psi 0 minus V minus square root of psi 0. This is because of the change in the depletion layer width. Here Q p d is negative for reverse bias because here when you apply a reverse bias this is positive with respect to this and then the depletion-region expands so the quasi-neutral region shrinks and therefore you are extracting holes from this side and electrons from the other side. So the extracted holes are what are represented here for reverse bias. So you take the slope of this and then you get the depletion capacitance. The depletion and diffusion capacitances are shown here. The results are that C diffusion is current into lifetime by thermal voltage and depletion capacitance equal to epsilon A by X d where X d is the depletion width. The depletion capacitance can be seen physically as a parallel plate capacitor. This is an incremental capacitance and it is like a parallel plate capacitor so the incremental charges are separated by the distance X d. For reverse bias you should put equal to sign exactly and the depletion capacitance is again given by epsilon A by X d and here X d goes on expanding so depletion capacitance falls. We do not show any diffusion capacitance or resistance in reverse bias because as we have said the
14 diffusion capacitance is negligible and resistance is very high so those two elements do not exist for reverse bias. For moderate forward bias where the devices are operated generally the diffusion capacitance dominates over the depletion capacitance. So this quantity is negligible for moderate forward biases. Now it is of interest to look at the reverse bias capacitance or depletion capacitance for reverse bias in a little bit detail as this quantity is useful in several applications. Since the reverse bias diode is almost like a pure capacitor without any parallel resistive component or loss component and this capacitance varies with voltage an important application of a reverse bias diode is that of a voltage Variable capacitor. Now, another application of diode in reverse bias is, we can show that we can extract the doping level in the lighted dope region from the measurement of the reverse bias diode capacitance. To see this let us expand the formula; C depletion is equal to epsilon A by X d. We write X d is equal to 2 epsilon V R plus psi 0 where V R is the reverse bias upon q into 1 by N d plus 1 by N a. Then here we recognize that, since N a is much greater than N d this quantity can be neglected the one sided junction. We should put a square root here. Now, for the one sided junction we can substitute for X d here and then we can simplify and you can show that 1 by C depletion square can be written as 2 by epsilon A square q into 1 by N d approximately equal to this quantity. Here we are assuming that N d is much less than N a. Of course we should write the V R plus psi 0. And what we find from here is 1 by C depletion square versus the reverse bias V R is a straight line whose slope gives you N d. So slope of 1 by C depletion square versus V R is equal to 2 by epsilon A square Q n d. So, if you know the area A and you measure 1 by C depletion square and plot it on the function of V R then you can get the N d. Let us look at the measured characteristics of reverse bias capacitance. This is shown in this slide.
15 (Refer Slide Time: 51:44) You can see that it is almost a straight line. Here CJ indicates the junction capacitance, this is another symbol used normally for the capacitance. This is a function of applied bias and that is why it is shown on the negative access so these are reverse voltages. These are the values for a typical silicon diode of area 0.32 mm by 0.32 mm. (Refer Slide Time: 52:10) Now the intercept here if you extend this solid line and then allow it to intersect the voltage access the intercept gives you the quantity psi 0 and this can be seen from this particular equation. So V R is minus psi 0 or if you are writing instead of V R minus V if you write V R plus psi 0 as psi 0 minus V then v is equal to psi 0 when the 1 by C depletion is
16 0. So the intercept this quantity here on this slide shows psi 0 which is this distance so you can extract an approximate value of psi 0 also. The slide also shows the typical values of the capacitances for the area considered. So the capacitances are of the order of Pico farads. What you see here is square of Pico farads but you can always estimate these values from here and you can see that they are of the order of Pico farads. Now for information if you take the equivalent circuit for the forward bias here since these capacitances are of the order of Pico farads for areas of 0.3 mm by 0.32 mm we have considered the moderate forward bias the diffusion capacitance will be of the order of Nano farads. It can go up to micro facts for larger forward bias. What about the small signal resistance? For the small signal resistance see if the currents are in the ma range since V t at room temperature is of the order of 25 or 26 mv this is of the order of ohms so for 10 ma current 26 mv by 10 ma about 2.6 ohms is the kind of small signal resistance that you get for the diode. Now, before summarizing our discussion on the PN junction if there are any questions I would like to take them. (Refer Slide Time: 54:44) Here is a question regarding the reverse saturation current I 0. For the measured I-V characteristics at room temperature we calculated I 0 to be of the order of 10 to the power minus 13 amperes but the reverse characteristics at the room temperature show a much larger reverse current below breakdown that is of the order of 10 to the power minus 9 amperes, why it is so? To explain this forward characteristic we found that the I 0 was of the order of 10 to the power minus 13 amperes. But if you see the reverse characteristics here what you are saying is this current is of the order of 10 to the power minus 9 at room temperature
17 somewhere around this. Now this is because the forward characteristics where explained using the diffusion current and I 0 calculated there was the diffusion current. As we have pointed out in silicon diode the generation current dominates on the reverse side as compared to the diffusion current. So, though the diffusion current saturates the generation current within the depletion layer dominates the diffusion current which goes on increasing with voltage. Now this generation current within the depletion layer is of the order of 10 to the power minus 9 and that is why you are getting the reverse current of the order of 10 to the power minus 9 amperes instead of the 10 to the power minus 13 ampere current we used for calculating the forward characteristics. Since you have asked a question about the reverse characteristics let me tell you another important aspect of the reverse saturation current. It is found that the reverse saturation current in a silicon diode doubles for every 10 degree C raise in temperature. And for germanium diodes in which the energy gap of the germanium material is less than silicon in fact it doubles for as small as about 4 to 5 degree C change in temperature. Now how to get this behavior that the current doubles for 10 degree C raise in temperature in a silicon diode? What you should do is, write the expression for generation current and then for diffusion current and you sum it up. The total reverse current is because of generation in the depletion layer plus diffusion. Now, around room temperature generation current will dominate over diffusion current and the generation current is proportional to n i. If you take the ratio of n i at two temperatures differing by 10 degree C around room temperature you will find it is close to 2. At higher temperatures diffusion current dominates over the generation current and the diffusion current is proportional to n i square at higher temperatures around 100 degree C for example. If you take the ratio of n i square for two different temperatures differing by 10 degree C for silicon you will find that this quantity will again turn out to be close to about two. This is how the combination of generation and diffusion currents gives rise to this kind of a behavior of doubling the reverse current for every 10 degree C rise in temperature.
18 (Refer Slide Time: 58:28) Now I would like to summarize the discussion on the PN junctions: We covered the following topics in the last seven lectures. First we discussed device structure and fabrication. Then we idealized this structure and used the approximate in the structure for analysis. First we discussed the equilibrium picture in which we gave the distributions of n, p, J n, J p and E and we also considered the variation of energy bands. Then we considered the ideal current voltage characteristics for forward and reverse bias. We derived the characteristics based on spatial distribution of n, p, J n, J p and E. We showed how the analysis can be done without the aid of energy bands using the five basic equations. We also drew the energy band diagram for forward and reverse bias to show the advantage you gain in terms of getting information and details using the energy band diagram. Then we explained the non-idealities in real current voltage characteristics namely the ideality factors, series resistance, depletion layer generation current and breakdown. Finally we considered the small signal characteristics where we gave the equivalent circuit of the diode consisting of resistance and capacitance for forward and reverse bias.
This is the 15th lecture of this course in which we begin a new topic, Excess Carriers. This topic will be covered in two lectures.
 Solid State Devices Dr. S. Karmalkar Department of Electronics and Communication Engineering Indian Institute of Technology, Madras Lecture - 15 Excess Carriers This is the 15th lecture of this course
Solid State Devices Dr. S. Karmalkar Department of Electronics and Communication Engineering Indian Institute of Technology, Madras Lecture - 15 Excess Carriers This is the 15th lecture of this course
Today we begin the first technical topic related directly to the course that is: Equilibrium Carrier Concentration.
 Solid State Devices Dr. S. Karmalkar Department of Electronics and Communication Engineering Indian Institute of Technology, Madras Lecture - 3 Equilibrium and Carrier Concentration Today we begin the
Solid State Devices Dr. S. Karmalkar Department of Electronics and Communication Engineering Indian Institute of Technology, Madras Lecture - 3 Equilibrium and Carrier Concentration Today we begin the
Semiconductor Physics fall 2012 problems
 Semiconductor Physics fall 2012 problems 1. An n-type sample of silicon has a uniform density N D = 10 16 atoms cm -3 of arsenic, and a p-type silicon sample has N A = 10 15 atoms cm -3 of boron. For each
Semiconductor Physics fall 2012 problems 1. An n-type sample of silicon has a uniform density N D = 10 16 atoms cm -3 of arsenic, and a p-type silicon sample has N A = 10 15 atoms cm -3 of boron. For each
Session 6: Solid State Physics. Diode
 Session 6: Solid State Physics Diode 1 Outline A B C D E F G H I J 2 Definitions / Assumptions Homojunction: the junction is between two regions of the same material Heterojunction: the junction is between
Session 6: Solid State Physics Diode 1 Outline A B C D E F G H I J 2 Definitions / Assumptions Homojunction: the junction is between two regions of the same material Heterojunction: the junction is between
Electronics Fets and Mosfets Prof D C Dube Department of Physics Indian Institute of Technology, Delhi
 Electronics Fets and Mosfets Prof D C Dube Department of Physics Indian Institute of Technology, Delhi Module No. #05 Lecture No. #02 FETS and MOSFETS (contd.) In the previous lecture, we studied the working
Electronics Fets and Mosfets Prof D C Dube Department of Physics Indian Institute of Technology, Delhi Module No. #05 Lecture No. #02 FETS and MOSFETS (contd.) In the previous lecture, we studied the working
Semiconductor Physics fall 2012 problems
 Semiconductor Physics fall 2012 problems 1. An n-type sample of silicon has a uniform density N D = 10 16 atoms cm -3 of arsenic, and a p-type silicon sample has N A = 10 15 atoms cm -3 of boron. For each
Semiconductor Physics fall 2012 problems 1. An n-type sample of silicon has a uniform density N D = 10 16 atoms cm -3 of arsenic, and a p-type silicon sample has N A = 10 15 atoms cm -3 of boron. For each
Lecture 16 - The pn Junction Diode (II) Equivalent Circuit Model. April 8, 2003
 6.012 - Microelectronic Devices and Circuits - Spring 2003 Lecture 16-1 Lecture 16 - The pn Junction Diode (II) Equivalent Circuit Model April 8, 2003 Contents: 1. I-V characteristics (cont.) 2. Small-signal
6.012 - Microelectronic Devices and Circuits - Spring 2003 Lecture 16-1 Lecture 16 - The pn Junction Diode (II) Equivalent Circuit Model April 8, 2003 Contents: 1. I-V characteristics (cont.) 2. Small-signal
Electronics Prof. D C Dube Department of Physics Indian Institute of Technology Delhi
 Electronics Prof. D C Dube Department of Physics Indian Institute of Technology Delhi Module No. 07 Differential and Operational Amplifiers Lecture No. 39 Summing, Scaling and Averaging Amplifiers (Refer
Electronics Prof. D C Dube Department of Physics Indian Institute of Technology Delhi Module No. 07 Differential and Operational Amplifiers Lecture No. 39 Summing, Scaling and Averaging Amplifiers (Refer
Final Examination EE 130 December 16, 1997 Time allotted: 180 minutes
 Final Examination EE 130 December 16, 1997 Time allotted: 180 minutes Problem 1: Semiconductor Fundamentals [30 points] A uniformly doped silicon sample of length 100µm and cross-sectional area 100µm 2
Final Examination EE 130 December 16, 1997 Time allotted: 180 minutes Problem 1: Semiconductor Fundamentals [30 points] A uniformly doped silicon sample of length 100µm and cross-sectional area 100µm 2
ECE 340 Lecture 27 : Junction Capacitance Class Outline:
 ECE 340 Lecture 27 : Junction Capacitance Class Outline: Breakdown Review Junction Capacitance Things you should know when you leave M.J. Gilbert ECE 340 Lecture 27 10/24/11 Key Questions What types of
ECE 340 Lecture 27 : Junction Capacitance Class Outline: Breakdown Review Junction Capacitance Things you should know when you leave M.J. Gilbert ECE 340 Lecture 27 10/24/11 Key Questions What types of
Semiconductor Physics and Devices
 The pn Junction 1) Charge carriers crossing the junction. 3) Barrier potential Semiconductor Physics and Devices Chapter 8. The pn Junction Diode 2) Formation of positive and negative ions. 4) Formation
The pn Junction 1) Charge carriers crossing the junction. 3) Barrier potential Semiconductor Physics and Devices Chapter 8. The pn Junction Diode 2) Formation of positive and negative ions. 4) Formation
Lecture-4 Junction Diode Characteristics
 1 Lecture-4 Junction Diode Characteristics Part-II Q: Aluminum is alloyed into n-type Si sample (N D = 10 16 cm 3 ) forming an abrupt junction of circular cross-section, with an diameter of 0.02 in. Assume
1 Lecture-4 Junction Diode Characteristics Part-II Q: Aluminum is alloyed into n-type Si sample (N D = 10 16 cm 3 ) forming an abrupt junction of circular cross-section, with an diameter of 0.02 in. Assume
6.012 Electronic Devices and Circuits
 Page 1 of 1 YOUR NAME Department of Electrical Engineering and Computer Science Massachusetts Institute of Technology 6.12 Electronic Devices and Circuits Exam No. 1 Wednesday, October 7, 29 7:3 to 9:3
Page 1 of 1 YOUR NAME Department of Electrical Engineering and Computer Science Massachusetts Institute of Technology 6.12 Electronic Devices and Circuits Exam No. 1 Wednesday, October 7, 29 7:3 to 9:3
(Refer Time Slide: 1:35)
 Analog Electronic Circuits Prof. S. C. Dutta Roy Department of Electrical Engineering. Indian Institute of Technology Delhi Lecture No 04 Problem Session 1 On DC Analysis of BJT Circuits This is the fourth
Analog Electronic Circuits Prof. S. C. Dutta Roy Department of Electrical Engineering. Indian Institute of Technology Delhi Lecture No 04 Problem Session 1 On DC Analysis of BJT Circuits This is the fourth
Lecture 16 The pn Junction Diode (III)
 Lecture 16 The pn Junction iode (III) Outline I V Characteristics (Review) Small signal equivalent circuit model Carrier charge storage iffusion capacitance Reading Assignment: Howe and Sodini; Chapter
Lecture 16 The pn Junction iode (III) Outline I V Characteristics (Review) Small signal equivalent circuit model Carrier charge storage iffusion capacitance Reading Assignment: Howe and Sodini; Chapter
Diodes. anode. cathode. cut-off. Can be approximated by a piecewise-linear-like characteristic. Lecture 9-1
 Diodes mplest nonlinear circuit element Basic operation sets the foundation for Bipolar Junction Transistors (BJTs) Also present in Field Effect Transistors (FETs) Ideal diode characteristic anode cathode
Diodes mplest nonlinear circuit element Basic operation sets the foundation for Bipolar Junction Transistors (BJTs) Also present in Field Effect Transistors (FETs) Ideal diode characteristic anode cathode
Higher Physics. Electricity. Summary Notes. Monitoring and measuring a.c. Current, potential difference, power and resistance
 Higher Physics Electricity Summary Notes Monitoring and measuring a.c. Current, potential difference, power and resistance Electrical sources and internal resistance Capacitors Conductors, semiconductors
Higher Physics Electricity Summary Notes Monitoring and measuring a.c. Current, potential difference, power and resistance Electrical sources and internal resistance Capacitors Conductors, semiconductors
Networks and Systems Prof. V. G. K. Murti Department of Electrical Engineering Indian Institution of Technology, Madras
 Networks and Systems Prof. V. G. K. Murti Department of Electrical Engineering Indian Institution of Technology, Madras Lecture - 32 Network Function (3) 2-port networks: Symmetry Equivalent networks Examples
Networks and Systems Prof. V. G. K. Murti Department of Electrical Engineering Indian Institution of Technology, Madras Lecture - 32 Network Function (3) 2-port networks: Symmetry Equivalent networks Examples
PN Junction
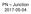 P Junction 2017-05-04 Definition Power Electronics = semiconductor switches are used Analogue amplifier = high power loss 250 200 u x 150 100 u Udc i 50 0 0 50 100 150 200 250 300 350 400 i,u dc i,u u
P Junction 2017-05-04 Definition Power Electronics = semiconductor switches are used Analogue amplifier = high power loss 250 200 u x 150 100 u Udc i 50 0 0 50 100 150 200 250 300 350 400 i,u dc i,u u
ECE 340 Lecture 31 : Narrow Base Diode Class Outline:
 ECE 340 Lecture 31 : Narrow Base Diode Class Outline: Narrow-Base Diodes Things you should know when you leave Key Questions What is a narrow-base diode? How does current flow in a narrow-base diode? Quick
ECE 340 Lecture 31 : Narrow Base Diode Class Outline: Narrow-Base Diodes Things you should know when you leave Key Questions What is a narrow-base diode? How does current flow in a narrow-base diode? Quick
EE105 Fall 2015 Microelectronic Devices and Circuits: Semiconductor Fabrication and PN Junctions
 EE105 Fall 2015 Microelectronic Devices and Circuits: Semiconductor Fabrication and PN Junctions Prof. Ming C. Wu wu@eecs.berkeley.edu 511 Sutardja Dai Hall (SDH) 1 pn Junction p-type semiconductor in
EE105 Fall 2015 Microelectronic Devices and Circuits: Semiconductor Fabrication and PN Junctions Prof. Ming C. Wu wu@eecs.berkeley.edu 511 Sutardja Dai Hall (SDH) 1 pn Junction p-type semiconductor in
Semiconductor Physics Problems 2015
 Semiconductor Physics Problems 2015 Page and figure numbers refer to Semiconductor Devices Physics and Technology, 3rd edition, by SM Sze and M-K Lee 1. The purest semiconductor crystals it is possible
Semiconductor Physics Problems 2015 Page and figure numbers refer to Semiconductor Devices Physics and Technology, 3rd edition, by SM Sze and M-K Lee 1. The purest semiconductor crystals it is possible
(Refer Slide Time: 01:30)
 Networks and Systems Prof V.G K.Murti Department of Electrical Engineering Indian Institute of Technology, Madras Lecture - 11 Fourier Series (5) Continuing our discussion of Fourier series today, we will
Networks and Systems Prof V.G K.Murti Department of Electrical Engineering Indian Institute of Technology, Madras Lecture - 11 Fourier Series (5) Continuing our discussion of Fourier series today, we will
Fundamentals of Semiconductor Devices Prof. Digbijoy N. Nath Centre for Nano Science and Engineering Indian Institute of Science, Bangalore
 Fundamentals of Semiconductor Devices Prof. Digbijoy N. Nath Centre for Nano Science and Engineering Indian Institute of Science, Bangalore Lecture - 05 Density of states Welcome back. So, today is the
Fundamentals of Semiconductor Devices Prof. Digbijoy N. Nath Centre for Nano Science and Engineering Indian Institute of Science, Bangalore Lecture - 05 Density of states Welcome back. So, today is the
Electronic PRINCIPLES
 MALVINO & BATES Electronic PRINCIPLES SEVENTH EDITION Chapter 2 Semiconductors Topics Covered in Chapter 2 Conductors Semiconductors Silicon crystals Intrinsic semiconductors Two types of flow Doping a
MALVINO & BATES Electronic PRINCIPLES SEVENTH EDITION Chapter 2 Semiconductors Topics Covered in Chapter 2 Conductors Semiconductors Silicon crystals Intrinsic semiconductors Two types of flow Doping a
Spring Semester 2012 Final Exam
 Spring Semester 2012 Final Exam Note: Show your work, underline results, and always show units. Official exam time: 2.0 hours; an extension of at least 1.0 hour will be granted to anyone. Materials parameters
Spring Semester 2012 Final Exam Note: Show your work, underline results, and always show units. Official exam time: 2.0 hours; an extension of at least 1.0 hour will be granted to anyone. Materials parameters
Electronic Circuits for Mechatronics ELCT 609 Lecture 2: PN Junctions (1)
 Electronic Circuits for Mechatronics ELCT 609 Lecture 2: PN Junctions (1) Assistant Professor Office: C3.315 E-mail: eman.azab@guc.edu.eg 1 Electronic (Semiconductor) Devices P-N Junctions (Diodes): Physical
Electronic Circuits for Mechatronics ELCT 609 Lecture 2: PN Junctions (1) Assistant Professor Office: C3.315 E-mail: eman.azab@guc.edu.eg 1 Electronic (Semiconductor) Devices P-N Junctions (Diodes): Physical
Introductory Quantum Chemistry Prof. K. L. Sebastian Department of Inorganic and Physical Chemistry Indian Institute of Science, Bangalore
 Introductory Quantum Chemistry Prof. K. L. Sebastian Department of Inorganic and Physical Chemistry Indian Institute of Science, Bangalore Lecture - 4 Postulates Part 1 (Refer Slide Time: 00:59) So, I
Introductory Quantum Chemistry Prof. K. L. Sebastian Department of Inorganic and Physical Chemistry Indian Institute of Science, Bangalore Lecture - 4 Postulates Part 1 (Refer Slide Time: 00:59) So, I
Low Power VLSI Circuits and Systems Prof. Ajit Pal Department of Computer Science and Engineering Indian Institute of Technology, Kharagpur
 Low Power VLSI Circuits and Systems Prof. Ajit Pal Department of Computer Science and Engineering Indian Institute of Technology, Kharagpur Lecture No. # 08 MOS Inverters - III Hello, and welcome to today
Low Power VLSI Circuits and Systems Prof. Ajit Pal Department of Computer Science and Engineering Indian Institute of Technology, Kharagpur Lecture No. # 08 MOS Inverters - III Hello, and welcome to today
REVISED HIGHER PHYSICS REVISION BOOKLET ELECTRONS AND ENERGY
 REVSED HGHER PHYSCS REVSON BOOKLET ELECTRONS AND ENERGY Kinross High School Monitoring and measuring a.c. Alternating current: Mains supply a.c.; batteries/cells supply d.c. Electrons moving back and forth,
REVSED HGHER PHYSCS REVSON BOOKLET ELECTRONS AND ENERGY Kinross High School Monitoring and measuring a.c. Alternating current: Mains supply a.c.; batteries/cells supply d.c. Electrons moving back and forth,
1st Year-Computer Communication Engineering-RUC. 4- P-N Junction
 4- P-N Junction We begin our study of semiconductor devices with the junction for three reasons. (1) The device finds application in many electronic systems, e.g., in adapters that charge the batteries
4- P-N Junction We begin our study of semiconductor devices with the junction for three reasons. (1) The device finds application in many electronic systems, e.g., in adapters that charge the batteries
Processing of Semiconducting Materials Prof. Pallab Banerji Department of Material Science Indian Institute of Technology, Kharagpur
 Processing of Semiconducting Materials Prof. Pallab Banerji Department of Material Science Indian Institute of Technology, Kharagpur Lecture - 4 Doping in Semiconductors Good morning. Let us start with
Processing of Semiconducting Materials Prof. Pallab Banerji Department of Material Science Indian Institute of Technology, Kharagpur Lecture - 4 Doping in Semiconductors Good morning. Let us start with
Department of Electrical and Computer Engineering, Cornell University. ECE 3150: Microelectronics. Spring Due on Feb. 15, 2018 by 7:00 PM
 Department of Electrical and Computer Engineering, Cornell University ECE 3150: Microelectronics Spring 018 Homework 3 Due on Feb. 15, 018 by 7:00 PM Suggested Readings: a) Lecture notes Important Note:
Department of Electrical and Computer Engineering, Cornell University ECE 3150: Microelectronics Spring 018 Homework 3 Due on Feb. 15, 018 by 7:00 PM Suggested Readings: a) Lecture notes Important Note:
Lecture (02) PN Junctions and Diodes
 Lecture (02) PN Junctions and Diodes By: Dr. Ahmed ElShafee ١ I Agenda N type, P type semiconductors N Type Semiconductor P Type Semiconductor PN junction Energy Diagrams of the PN Junction and Depletion
Lecture (02) PN Junctions and Diodes By: Dr. Ahmed ElShafee ١ I Agenda N type, P type semiconductors N Type Semiconductor P Type Semiconductor PN junction Energy Diagrams of the PN Junction and Depletion
Electronic Devices and Circuits Lecture 5 - p-n Junction Injection and Flow - Outline
 6.012 - Electronic Devices and Circuits Lecture 5 - p-n Junction Injection and Flow - Outline Review Depletion approimation for an abrupt p-n junction Depletion charge storage and depletion capacitance
6.012 - Electronic Devices and Circuits Lecture 5 - p-n Junction Injection and Flow - Outline Review Depletion approimation for an abrupt p-n junction Depletion charge storage and depletion capacitance
Lecture Number - 01 Metals, Semiconductors and Insulators
 Electronic Materials, Devices and Fabrication Dr. S. Parasuraman Department of Metallurgical and Materials Engineering Indian Institute of Technology, Madras Lecture Number - 01 Metals, Semiconductors
Electronic Materials, Devices and Fabrication Dr. S. Parasuraman Department of Metallurgical and Materials Engineering Indian Institute of Technology, Madras Lecture Number - 01 Metals, Semiconductors
CHAPTER 4: P-N P N JUNCTION Part 2. M.N.A. Halif & S.N. Sabki
 CHAPTER 4: P-N P N JUNCTION Part 2 Part 2 Charge Storage & Transient Behavior Junction Breakdown Heterojunction CHARGE STORAGE & TRANSIENT BEHAVIOR Once injected across the junction, the minority carriers
CHAPTER 4: P-N P N JUNCTION Part 2 Part 2 Charge Storage & Transient Behavior Junction Breakdown Heterojunction CHARGE STORAGE & TRANSIENT BEHAVIOR Once injected across the junction, the minority carriers
Electromagnetic Theory Prof. D. K. Ghosh Department of Physics Indian Institute of Technology, Bombay
 Electromagnetic Theory Prof. D. K. Ghosh Department of Physics Indian Institute of Technology, Bombay Module -4 Time Varying Lecture - 29 Faraday s Law and Inductance In the previous lecture, we had started
Electromagnetic Theory Prof. D. K. Ghosh Department of Physics Indian Institute of Technology, Bombay Module -4 Time Varying Lecture - 29 Faraday s Law and Inductance In the previous lecture, we had started
Diodes. EE223 Digital & Analogue Electronics Derek Molloy 2012/2013.
 Diodes EE223 Digital & Analogue Electronics Derek Molloy 2012/2013 Derek.Molloy@dcu.ie Diodes: A Semiconductor? Conductors Such as copper, aluminium have a cloud of free electrons weak bound valence electrons
Diodes EE223 Digital & Analogue Electronics Derek Molloy 2012/2013 Derek.Molloy@dcu.ie Diodes: A Semiconductor? Conductors Such as copper, aluminium have a cloud of free electrons weak bound valence electrons
BJT - Mode of Operations
 JT - Mode of Operations JTs can be modeled by two back-to-back diodes. N+ P N- N+ JTs are operated in four modes. HO #6: LN 251 - JT M Models Page 1 1) Forward active / normal junction forward biased junction
JT - Mode of Operations JTs can be modeled by two back-to-back diodes. N+ P N- N+ JTs are operated in four modes. HO #6: LN 251 - JT M Models Page 1 1) Forward active / normal junction forward biased junction
Solid State Electronics. Final Examination
 The University of Toledo EECS:4400/5400/7400 Solid State Electronic Section elssf08fs.fm - 1 Solid State Electronics Final Examination Problems Points 1. 1. 14 3. 14 Total 40 Was the exam fair? yes no
The University of Toledo EECS:4400/5400/7400 Solid State Electronic Section elssf08fs.fm - 1 Solid State Electronics Final Examination Problems Points 1. 1. 14 3. 14 Total 40 Was the exam fair? yes no
Chapter 1 The Electric Force
 Chapter 1 The Electric Force 1. Properties of the Electric Charges 1- There are two kinds of the electric charges in the nature, which are positive and negative charges. - The charges of opposite sign
Chapter 1 The Electric Force 1. Properties of the Electric Charges 1- There are two kinds of the electric charges in the nature, which are positive and negative charges. - The charges of opposite sign
Midterm I - Solutions
 UNIVERSITY OF CALIFORNIA College of Engineering Department of Electrical Engineering and Computer Sciences EECS 130 Spring 2008 Professor Chenming Hu Midterm I - Solutions Name: SID: Grad/Undergrad: Closed
UNIVERSITY OF CALIFORNIA College of Engineering Department of Electrical Engineering and Computer Sciences EECS 130 Spring 2008 Professor Chenming Hu Midterm I - Solutions Name: SID: Grad/Undergrad: Closed
UNIVERSITY OF CALIFORNIA College of Engineering Department of Electrical Engineering and Computer Sciences. EECS 130 Professor Ali Javey Fall 2006
 UNIVERSITY OF CALIFORNIA College of Engineering Department of Electrical Engineering and Computer Sciences EECS 130 Professor Ali Javey Fall 2006 Midterm I Name: Closed book. One sheet of notes is allowed.
UNIVERSITY OF CALIFORNIA College of Engineering Department of Electrical Engineering and Computer Sciences EECS 130 Professor Ali Javey Fall 2006 Midterm I Name: Closed book. One sheet of notes is allowed.
Electro - Principles I
 Electro - Principles I Page 10-1 Atomic Theory It is necessary to know what goes on at the atomic level of a semiconductor so the characteristics of the semiconductor can be understood. In many cases a
Electro - Principles I Page 10-1 Atomic Theory It is necessary to know what goes on at the atomic level of a semiconductor so the characteristics of the semiconductor can be understood. In many cases a
For the following statements, mark ( ) for true statement and (X) for wrong statement and correct it.
 Benha University Faculty of Engineering Shoubra Electrical Engineering Department First Year communications. Answer all the following questions Illustrate your answers with sketches when necessary. The
Benha University Faculty of Engineering Shoubra Electrical Engineering Department First Year communications. Answer all the following questions Illustrate your answers with sketches when necessary. The
Lecture - 11 Bendixson and Poincare Bendixson Criteria Van der Pol Oscillator
 Nonlinear Dynamical Systems Prof. Madhu. N. Belur and Prof. Harish. K. Pillai Department of Electrical Engineering Indian Institute of Technology, Bombay Lecture - 11 Bendixson and Poincare Bendixson Criteria
Nonlinear Dynamical Systems Prof. Madhu. N. Belur and Prof. Harish. K. Pillai Department of Electrical Engineering Indian Institute of Technology, Bombay Lecture - 11 Bendixson and Poincare Bendixson Criteria
Circuits for Analog System Design Prof. Gunashekaran M K Center for Electronics Design and Technology Indian Institute of Science, Bangalore
 Circuits for Analog System Design Prof. Gunashekaran M K Center for Electronics Design and Technology Indian Institute of Science, Bangalore Lecture No. # 08 Temperature Indicator Design Using Op-amp Today,
Circuits for Analog System Design Prof. Gunashekaran M K Center for Electronics Design and Technology Indian Institute of Science, Bangalore Lecture No. # 08 Temperature Indicator Design Using Op-amp Today,
Junction Diodes. Tim Sumner, Imperial College, Rm: 1009, x /18/2006
 Junction Diodes Most elementary solid state junction electronic devices. They conduct in one direction (almost correct). Useful when one converts from AC to DC (rectifier). But today diodes have a wide
Junction Diodes Most elementary solid state junction electronic devices. They conduct in one direction (almost correct). Useful when one converts from AC to DC (rectifier). But today diodes have a wide
ECE-342 Test 2 Solutions, Nov 4, :00-8:00pm, Closed Book (one page of notes allowed)
 ECE-342 Test 2 Solutions, Nov 4, 2008 6:00-8:00pm, Closed Book (one page of notes allowed) Please use the following physical constants in your calculations: Boltzmann s Constant: Electron Charge: Free
ECE-342 Test 2 Solutions, Nov 4, 2008 6:00-8:00pm, Closed Book (one page of notes allowed) Please use the following physical constants in your calculations: Boltzmann s Constant: Electron Charge: Free
Semiconductor Physics. Lecture 6
 Semiconductor Physics Lecture 6 Recap pn junction and the depletion region Driven by the need to have no gradient in the fermi level free carriers migrate across the pn junction leaving a region with few
Semiconductor Physics Lecture 6 Recap pn junction and the depletion region Driven by the need to have no gradient in the fermi level free carriers migrate across the pn junction leaving a region with few
Electronic Circuits 1. Transistor Devices. Contents BJT and FET Characteristics Operations. Prof. C.K. Tse: Transistor devices
 Electronic Circuits 1 Transistor Devices Contents BJT and FET Characteristics Operations 1 What is a transistor? Three-terminal device whose voltage-current relationship is controlled by a third voltage
Electronic Circuits 1 Transistor Devices Contents BJT and FET Characteristics Operations 1 What is a transistor? Three-terminal device whose voltage-current relationship is controlled by a third voltage
Power System Analysis Prof. A. K. Sinha Department of Electrical Engineering Indian Institute of Technology, Kharagpur
 Power System Analysis Prof. A. K. Sinha Department of Electrical Engineering Indian Institute of Technology, Kharagpur Lecture - 9 Transmission Line Steady State Operation Welcome to lesson 9, in Power
Power System Analysis Prof. A. K. Sinha Department of Electrical Engineering Indian Institute of Technology, Kharagpur Lecture - 9 Transmission Line Steady State Operation Welcome to lesson 9, in Power
The pn junction. [Fonstad, Ghione]
![The pn junction. [Fonstad, Ghione] The pn junction. [Fonstad, Ghione]](/thumbs/93/112370833.jpg) The pn junction [Fonstad, Ghione] Band diagram On the vertical axis: potential energy of the electrons On the horizontal axis: now there is nothing: later we ll put the position qf s : work function (F
The pn junction [Fonstad, Ghione] Band diagram On the vertical axis: potential energy of the electrons On the horizontal axis: now there is nothing: later we ll put the position qf s : work function (F
Lecture 12: MOS Capacitors, transistors. Context
 Lecture 12: MOS Capacitors, transistors Context In the last lecture, we discussed PN diodes, and the depletion layer into semiconductor surfaces. Small signal models In this lecture, we will apply those
Lecture 12: MOS Capacitors, transistors Context In the last lecture, we discussed PN diodes, and the depletion layer into semiconductor surfaces. Small signal models In this lecture, we will apply those
p-n junction biasing, p-n I-V characteristics, p-n currents Norlaili Mohd. Noh EEE /09
 CLASS 6&7 p-n junction biasing, p-n I-V characteristics, p-n currents 1 p-n junction biasing Unbiased p-n junction: the potential barrier is 0.7 V for Si and 0.3 V for Ge. Nett current across the p-n junction
CLASS 6&7 p-n junction biasing, p-n I-V characteristics, p-n currents 1 p-n junction biasing Unbiased p-n junction: the potential barrier is 0.7 V for Si and 0.3 V for Ge. Nett current across the p-n junction
Electromagnetic Theory Prof. D. K. Ghosh Department of Physics Indian Institute of Technology, Bombay
 Electromagnetic Theory Prof. D. K. Ghosh Department of Physics Indian Institute of Technology, Bombay Lecture -1 Element of vector calculus: Scalar Field and its Gradient This is going to be about one
Electromagnetic Theory Prof. D. K. Ghosh Department of Physics Indian Institute of Technology, Bombay Lecture -1 Element of vector calculus: Scalar Field and its Gradient This is going to be about one
ECE PN Junctions and Diodes
 ECE 342 2. PN Junctions and iodes Jose E. Schutt-Aine Electrical & Computer Engineering University of Illinois jschutt@emlab.uiuc.edu ECE 342 Jose Schutt Aine 1 B: material dependent parameter = 5.4 10
ECE 342 2. PN Junctions and iodes Jose E. Schutt-Aine Electrical & Computer Engineering University of Illinois jschutt@emlab.uiuc.edu ECE 342 Jose Schutt Aine 1 B: material dependent parameter = 5.4 10
n i exp E g 2kT lnn i E g 2kT
 HOMEWORK #10 12.19 For intrinsic semiconductors, the intrinsic carrier concentration n i depends on temperature as follows: n i exp E g 2kT (28.35a) or taking natural logarithms, lnn i E g 2kT (12.35b)
HOMEWORK #10 12.19 For intrinsic semiconductors, the intrinsic carrier concentration n i depends on temperature as follows: n i exp E g 2kT (28.35a) or taking natural logarithms, lnn i E g 2kT (12.35b)
ITT Technical Institute ET215 Devices I Unit 1
 ITT Technical Institute ET215 Devices I Unit 1 Chapter 1 Chapter 2, Sections 2.1-2.4 Chapter 1 Basic Concepts of Analog Circuits Recall ET115 & ET145 Ohms Law I = V/R If voltage across a resistor increases
ITT Technical Institute ET215 Devices I Unit 1 Chapter 1 Chapter 2, Sections 2.1-2.4 Chapter 1 Basic Concepts of Analog Circuits Recall ET115 & ET145 Ohms Law I = V/R If voltage across a resistor increases
Lecture 15 - The pn Junction Diode (I) I-V Characteristics. November 1, 2005
 6.012 - Microelectronic Devices and Circuits - Fall 2005 Lecture 15-1 Lecture 15 - The pn Junction Diode (I) I-V Characteristics November 1, 2005 Contents: 1. pn junction under bias 2. I-V characteristics
6.012 - Microelectronic Devices and Circuits - Fall 2005 Lecture 15-1 Lecture 15 - The pn Junction Diode (I) I-V Characteristics November 1, 2005 Contents: 1. pn junction under bias 2. I-V characteristics
PN Junction and MOS structure
 PN Junction and MOS structure Basic electrostatic equations We will use simple one-dimensional electrostatic equations to develop insight and basic understanding of how semiconductor devices operate Gauss's
PN Junction and MOS structure Basic electrostatic equations We will use simple one-dimensional electrostatic equations to develop insight and basic understanding of how semiconductor devices operate Gauss's
BASIC ELECTRONICS PROF. T.S. NATARAJAN DEPT OF PHYSICS IIT MADRAS LECTURE-3 ELECTRONIC DEVICES -II RESISTOR SERIES & PARALLEL
 BASIC ELECTRONICS PROF. T.S. NATARAJAN DEPT OF PHYSICS IIT MADRAS LECTURE-3 ELECTRONIC DEVICES -II RESISTOR SERIES & PARALLEL Hello everybody we are doing a course on basic electronics by the method of
BASIC ELECTRONICS PROF. T.S. NATARAJAN DEPT OF PHYSICS IIT MADRAS LECTURE-3 ELECTRONIC DEVICES -II RESISTOR SERIES & PARALLEL Hello everybody we are doing a course on basic electronics by the method of
Semiconductor Devices and Circuits Fall Midterm Exam. Instructor: Dr. Dietmar Knipp, Professor of Electrical Engineering. Name: Mat. -Nr.
 Semiconductor Devices and Circuits Fall 2003 Midterm Exam Instructor: Dr. Dietmar Knipp, Professor of Electrical Engineering Name: Mat. -Nr.: Guidelines: Duration of the Midterm: 1 hour The exam is a closed
Semiconductor Devices and Circuits Fall 2003 Midterm Exam Instructor: Dr. Dietmar Knipp, Professor of Electrical Engineering Name: Mat. -Nr.: Guidelines: Duration of the Midterm: 1 hour The exam is a closed
SRI VIDYA COLLEGE OF ENGINEERING AND TECHNOLOGY VIRUDHUNAGAR Department of Electronics and Communication Engineering
 SRI VIDYA COLLEGE OF ENGINEERING AND TECHNOLOGY VIRUDHUNAGAR Department of Electronics and Communication Engineering Class/Sem:I ECE/II Question Bank for EC6201-ELECTRONIC DEVICES 1.What do u meant by
SRI VIDYA COLLEGE OF ENGINEERING AND TECHNOLOGY VIRUDHUNAGAR Department of Electronics and Communication Engineering Class/Sem:I ECE/II Question Bank for EC6201-ELECTRONIC DEVICES 1.What do u meant by
Mechanics, Heat, Oscillations and Waves Prof. V. Balakrishnan Department of Physics Indian Institute of Technology, Madras
 Mechanics, Heat, Oscillations and Waves Prof. V. Balakrishnan Department of Physics Indian Institute of Technology, Madras Lecture - 21 Central Potential and Central Force Ready now to take up the idea
Mechanics, Heat, Oscillations and Waves Prof. V. Balakrishnan Department of Physics Indian Institute of Technology, Madras Lecture - 21 Central Potential and Central Force Ready now to take up the idea
EECS130 Integrated Circuit Devices
 EECS130 Integrated Circuit Devices Professor Ali Javey 9/18/2007 P Junctions Lecture 1 Reading: Chapter 5 Announcements For THIS WEEK OLY, Prof. Javey's office hours will be held on Tuesday, Sept 18 3:30-4:30
EECS130 Integrated Circuit Devices Professor Ali Javey 9/18/2007 P Junctions Lecture 1 Reading: Chapter 5 Announcements For THIS WEEK OLY, Prof. Javey's office hours will be held on Tuesday, Sept 18 3:30-4:30
Forward-Active Terminal Currents
 Forward-Active Terminal Currents Collector current: (electron diffusion current density) x (emitter area) diff J n AE qd n n po A E V E V th ------------------------------ e W (why minus sign? is by def.
Forward-Active Terminal Currents Collector current: (electron diffusion current density) x (emitter area) diff J n AE qd n n po A E V E V th ------------------------------ e W (why minus sign? is by def.
Lecture 19 - p-n Junction (cont.) October 18, Ideal p-n junction out of equilibrium (cont.) 2. pn junction diode: parasitics, dynamics
 6.720J/3.43J - Integrated Microelectronic Devices - Fall 2002 Lecture 19-1 Lecture 19 - p-n Junction (cont.) October 18, 2002 Contents: 1. Ideal p-n junction out of equilibrium (cont.) 2. pn junction diode:
6.720J/3.43J - Integrated Microelectronic Devices - Fall 2002 Lecture 19-1 Lecture 19 - p-n Junction (cont.) October 18, 2002 Contents: 1. Ideal p-n junction out of equilibrium (cont.) 2. pn junction diode:
SEMICONDUCTORS. Conductivity lies between conductors and insulators. The flow of charge in a metal results from the
 SEMICONDUCTORS Conductivity lies between conductors and insulators The flow of charge in a metal results from the movement of electrons Electros are negatively charged particles (q=1.60x10-19 C ) The outermost
SEMICONDUCTORS Conductivity lies between conductors and insulators The flow of charge in a metal results from the movement of electrons Electros are negatively charged particles (q=1.60x10-19 C ) The outermost
Module - 01 Assignment - 02 Intrinsic Semiconductors. In today's assignment class, we will be looking fully at intrinsic semiconductors.
 Electronic Materials, Devices and Fabrication Dr. S. Parasuraman Department of Metallurgical and Materials Engineering Indian Institute of Technology, Madras Module - 01 Assignment - 02 Intrinsic Semiconductors
Electronic Materials, Devices and Fabrication Dr. S. Parasuraman Department of Metallurgical and Materials Engineering Indian Institute of Technology, Madras Module - 01 Assignment - 02 Intrinsic Semiconductors
(Refer Slide Time: 1:49)
 Analog Electronic Circuits Professor S. C. Dutta Roy Department of Electrical Engineering Indian Institute of Technology Delhi Lecture no 14 Module no 01 Midband analysis of FET Amplifiers (Refer Slide
Analog Electronic Circuits Professor S. C. Dutta Roy Department of Electrical Engineering Indian Institute of Technology Delhi Lecture no 14 Module no 01 Midband analysis of FET Amplifiers (Refer Slide
FREQUENTLY ASKED QUESTIONS February 21, 2017
 FREQUENTLY ASKED QUESTIONS February 21, 2017 Content Questions How do you place a single arsenic atom with the ratio 1 in 100 million? Sounds difficult to get evenly spread throughout. Yes, techniques
FREQUENTLY ASKED QUESTIONS February 21, 2017 Content Questions How do you place a single arsenic atom with the ratio 1 in 100 million? Sounds difficult to get evenly spread throughout. Yes, techniques
Holes (10x larger). Diode currents proportional to minority carrier densities on each side of the depletion region: J n n p0 = n i 2
 Part V. (40 pts.) A diode is composed of an abrupt PN junction with N D = 10 16 /cm 3 and N A =10 17 /cm 3. The diode is very long so you can assume the ends are at x =positive and negative infinity. 1.
Part V. (40 pts.) A diode is composed of an abrupt PN junction with N D = 10 16 /cm 3 and N A =10 17 /cm 3. The diode is very long so you can assume the ends are at x =positive and negative infinity. 1.
Process Control and Instrumentation Prof. A. K. Jana Department of Chemical Engineering Indian Institute of Technology, Kharagpur
 Process Control and Instrumentation Prof. A. K. Jana Department of Chemical Engineering Indian Institute of Technology, Kharagpur Lecture - 10 Dynamic Behavior of Chemical Processes (Contd.) (Refer Slide
Process Control and Instrumentation Prof. A. K. Jana Department of Chemical Engineering Indian Institute of Technology, Kharagpur Lecture - 10 Dynamic Behavior of Chemical Processes (Contd.) (Refer Slide
16EC401 BASIC ELECTRONIC DEVICES UNIT I PN JUNCTION DIODE. Energy Band Diagram of Conductor, Insulator and Semiconductor:
 16EC401 BASIC ELECTRONIC DEVICES UNIT I PN JUNCTION DIODE Energy bands in Intrinsic and Extrinsic silicon: Energy Band Diagram of Conductor, Insulator and Semiconductor: 1 2 Carrier transport: Any motion
16EC401 BASIC ELECTRONIC DEVICES UNIT I PN JUNCTION DIODE Energy bands in Intrinsic and Extrinsic silicon: Energy Band Diagram of Conductor, Insulator and Semiconductor: 1 2 Carrier transport: Any motion
A SEMICONDUCTOR DIODE. P-N Junction
 A SEMICONDUCTOR DIODE P-N Junction Analog Electronics Pujianto Department of Physics Edu. State University of Yogyakarta A Semiconductor Devices A Semiconductor devices can be defined as a unit which consists,
A SEMICONDUCTOR DIODE P-N Junction Analog Electronics Pujianto Department of Physics Edu. State University of Yogyakarta A Semiconductor Devices A Semiconductor devices can be defined as a unit which consists,
L03: pn Junctions, Diodes
 8/30/2012 Page 1 of 5 Reference:C:\Users\Bernhard Boser\Documents\Files\Lib\MathCAD\Default\defaults.mcd L03: pn Junctions, Diodes Intrinsic Si Q: What are n, p? Q: Is the Si charged? Q: How could we make
8/30/2012 Page 1 of 5 Reference:C:\Users\Bernhard Boser\Documents\Files\Lib\MathCAD\Default\defaults.mcd L03: pn Junctions, Diodes Intrinsic Si Q: What are n, p? Q: Is the Si charged? Q: How could we make
Electronics The basics of semiconductor physics
 Electronics The basics of semiconductor physics Prof. Márta Rencz, Gergely Nagy BME DED September 16, 2013 The basic properties of semiconductors Semiconductors conductance is between that of conductors
Electronics The basics of semiconductor physics Prof. Márta Rencz, Gergely Nagy BME DED September 16, 2013 The basic properties of semiconductors Semiconductors conductance is between that of conductors
Peak Electric Field. Junction breakdown occurs when the peak electric field in the PN junction reaches a critical value. For the N + P junction,
 Peak Electric Field Junction breakdown occurs when the peak electric field in the P junction reaches a critical value. For the + P junction, qa E ( x) ( xp x), s W dep 2 s ( bi Vr ) 2 s potential barrier
Peak Electric Field Junction breakdown occurs when the peak electric field in the P junction reaches a critical value. For the + P junction, qa E ( x) ( xp x), s W dep 2 s ( bi Vr ) 2 s potential barrier
What happens when things change. Transient current and voltage relationships in a simple resistive circuit.
 Module 4 AC Theory What happens when things change. What you'll learn in Module 4. 4.1 Resistors in DC Circuits Transient events in DC circuits. The difference between Ideal and Practical circuits Transient
Module 4 AC Theory What happens when things change. What you'll learn in Module 4. 4.1 Resistors in DC Circuits Transient events in DC circuits. The difference between Ideal and Practical circuits Transient
ECE 440 Lecture 20 : PN Junction Electrostatics II Class Outline:
 ECE 440 Lecture 20 : PN Junction Electrostatics II Class Outline: Depletion Approximation Step Junction Things you should know when you leave Key Questions What is the space charge region? What are the
ECE 440 Lecture 20 : PN Junction Electrostatics II Class Outline: Depletion Approximation Step Junction Things you should know when you leave Key Questions What is the space charge region? What are the
Analog Integrated Circuit Design Prof. Nagendra Krishnapura Department of Electrical Engineering Indian Institute of Technology, Madras
 Analog Integrated Circuit Design Prof. Nagendra Krishnapura Department of Electrical Engineering Indian Institute of Technology, Madras Lecture No - 42 Fully Differential Single Stage Opamp Hello and welcome
Analog Integrated Circuit Design Prof. Nagendra Krishnapura Department of Electrical Engineering Indian Institute of Technology, Madras Lecture No - 42 Fully Differential Single Stage Opamp Hello and welcome
Semiconductor Optoelectronics Prof. M. R. Shenoy Department of physics Indian Institute of Technology, Delhi
 Semiconductor Optoelectronics Prof. M. R. Shenoy Department of physics Indian Institute of Technology, Delhi Lecture - 18 Optical Joint Density of States So, today we will discuss the concept of optical
Semiconductor Optoelectronics Prof. M. R. Shenoy Department of physics Indian Institute of Technology, Delhi Lecture - 18 Optical Joint Density of States So, today we will discuss the concept of optical
ECE 305 Exam 2: Spring 2017 March 10, 2017 Muhammad Alam Purdue University
 NAME: PUID: : ECE 305 Exam 2: Spring 2017 March 10, 2017 Muhammad Alam Purdue University This is a closed book exam You may use a calculator and the formula sheet Following the ECE policy, the calculator
NAME: PUID: : ECE 305 Exam 2: Spring 2017 March 10, 2017 Muhammad Alam Purdue University This is a closed book exam You may use a calculator and the formula sheet Following the ECE policy, the calculator
Lecture (02) Introduction to Electronics II, PN Junction and Diodes I
 Lecture (02) Introduction to Electronics II, PN Junction and Diodes I By: Dr. Ahmed ElShafee ١ Agenda Current in semiconductors/conductors N type, P type semiconductors N Type Semiconductor P Type Semiconductor
Lecture (02) Introduction to Electronics II, PN Junction and Diodes I By: Dr. Ahmed ElShafee ١ Agenda Current in semiconductors/conductors N type, P type semiconductors N Type Semiconductor P Type Semiconductor
( )! N D ( x) ) and equilibrium
 ECE 66: SOLUTIONS: ECE 66 Homework Week 8 Mark Lundstrom March 7, 13 1) The doping profile for an n- type silicon wafer ( N D = 1 15 cm - 3 ) with a heavily doped thin layer at the surface (surface concentration,
ECE 66: SOLUTIONS: ECE 66 Homework Week 8 Mark Lundstrom March 7, 13 1) The doping profile for an n- type silicon wafer ( N D = 1 15 cm - 3 ) with a heavily doped thin layer at the surface (surface concentration,
PHYSICAL ELECTRONICS(ECE3540) CHAPTER 9 METAL SEMICONDUCTOR AND SEMICONDUCTOR HETERO-JUNCTIONS
 PHYSICAL ELECTRONICS(ECE3540) CHAPTER 9 METAL SEMICONDUCTOR AND SEMICONDUCTOR HETERO-JUNCTIONS Tennessee Technological University Monday, November 11, 013 1 Introduction Chapter 4: we considered the semiconductor
PHYSICAL ELECTRONICS(ECE3540) CHAPTER 9 METAL SEMICONDUCTOR AND SEMICONDUCTOR HETERO-JUNCTIONS Tennessee Technological University Monday, November 11, 013 1 Introduction Chapter 4: we considered the semiconductor
figure shows a pnp transistor biased to operate in the active mode
 Lecture 10b EE-215 Electronic Devices and Circuits Asst Prof Muhammad Anis Chaudhary BJT: Device Structure and Physical Operation The pnp Transistor figure shows a pnp transistor biased to operate in the
Lecture 10b EE-215 Electronic Devices and Circuits Asst Prof Muhammad Anis Chaudhary BJT: Device Structure and Physical Operation The pnp Transistor figure shows a pnp transistor biased to operate in the
CLASS 12th. Semiconductors
 CLASS 12th Semiconductors 01. Distinction Between Metals, Insulators and Semi-Conductors Metals are good conductors of electricity, insulators do not conduct electricity, while the semiconductors have
CLASS 12th Semiconductors 01. Distinction Between Metals, Insulators and Semi-Conductors Metals are good conductors of electricity, insulators do not conduct electricity, while the semiconductors have
Lecture 04 Review of MOSFET
 ECE 541/ME 541 Microelectronic Fabrication Techniques Lecture 04 Review of MOSFET Zheng Yang (ERF 3017, email: yangzhen@uic.edu) What is a Transistor? A Switch! An MOS Transistor V GS V T V GS S Ron D
ECE 541/ME 541 Microelectronic Fabrication Techniques Lecture 04 Review of MOSFET Zheng Yang (ERF 3017, email: yangzhen@uic.edu) What is a Transistor? A Switch! An MOS Transistor V GS V T V GS S Ron D
Fundamentals of the Metal Oxide Semiconductor Field-Effect Transistor
 Triode Working FET Fundamentals of the Metal Oxide Semiconductor Field-Effect Transistor The characteristics of energy bands as a function of applied voltage. Surface inversion. The expression for the
Triode Working FET Fundamentals of the Metal Oxide Semiconductor Field-Effect Transistor The characteristics of energy bands as a function of applied voltage. Surface inversion. The expression for the
n N D n p = n i p N A
 Summary of electron and hole concentration in semiconductors Intrinsic semiconductor: E G n kt i = pi = N e 2 0 Donor-doped semiconductor: n N D where N D is the concentration of donor impurity Acceptor-doped
Summary of electron and hole concentration in semiconductors Intrinsic semiconductor: E G n kt i = pi = N e 2 0 Donor-doped semiconductor: n N D where N D is the concentration of donor impurity Acceptor-doped
Antennas Prof. Girish Kumar Department of Electrical Engineering Indian Institute of Technology, Bombay. Module 02 Lecture 08 Dipole Antennas-I
 Antennas Prof. Girish Kumar Department of Electrical Engineering Indian Institute of Technology, Bombay Module 02 Lecture 08 Dipole Antennas-I Hello, and welcome to today s lecture. Now in the last lecture
Antennas Prof. Girish Kumar Department of Electrical Engineering Indian Institute of Technology, Bombay Module 02 Lecture 08 Dipole Antennas-I Hello, and welcome to today s lecture. Now in the last lecture
Engineering 2000 Chapter 8 Semiconductors. ENG2000: R.I. Hornsey Semi: 1
 Engineering 2000 Chapter 8 Semiconductors ENG2000: R.I. Hornsey Semi: 1 Overview We need to know the electrical properties of Si To do this, we must also draw on some of the physical properties and we
Engineering 2000 Chapter 8 Semiconductors ENG2000: R.I. Hornsey Semi: 1 Overview We need to know the electrical properties of Si To do this, we must also draw on some of the physical properties and we
4. I-V characteristics of electric
 KL 4. - characteristics of electric conductors 4.1 ntroduction f an electric conductor is connected to a voltage source with voltage a current is produced. We define resistance being the ratio of the voltage
KL 4. - characteristics of electric conductors 4.1 ntroduction f an electric conductor is connected to a voltage source with voltage a current is produced. We define resistance being the ratio of the voltage
Key Questions. ECE 340 Lecture 27 : Junction Capacitance 4/6/14. Class Outline: Breakdown Review Junction Capacitance
 ECE 340 Lecture 27 : Junction Capacitance Breakdown Reiew Class Outline: Things you should know when you leae Key Questions What types of capacitance are prealent in p-n junctions? Which is important in
ECE 340 Lecture 27 : Junction Capacitance Breakdown Reiew Class Outline: Things you should know when you leae Key Questions What types of capacitance are prealent in p-n junctions? Which is important in
Plasma Physics Prof. V. K. Tripathi Department of Physics Indian Institute of Technology, Delhi
 Plasma Physics Prof. V. K. Tripathi Department of Physics Indian Institute of Technology, Delhi Lecture No. # 03 DC Conductivity and Negative Differential Conductivity Well friends, in this lecture, I
Plasma Physics Prof. V. K. Tripathi Department of Physics Indian Institute of Technology, Delhi Lecture No. # 03 DC Conductivity and Negative Differential Conductivity Well friends, in this lecture, I
Power System Operations and Control Prof. S.N. Singh Department of Electrical Engineering Indian Institute of Technology, Kanpur. Module 3 Lecture 8
 Power System Operations and Control Prof. S.N. Singh Department of Electrical Engineering Indian Institute of Technology, Kanpur Module 3 Lecture 8 Welcome to lecture number 8 of module 3. In the previous
Power System Operations and Control Prof. S.N. Singh Department of Electrical Engineering Indian Institute of Technology, Kanpur Module 3 Lecture 8 Welcome to lecture number 8 of module 3. In the previous
Charge Storage in the MOS Structure. The Inverted MOS Capacitor (V GB > V Tn )
 The Inverted MO Capacitor (V > V Tn ) We consider the surface potential as Þxed (ÒpinnedÓ) at φ s,max = - φ p φ(x).5 V. V V ox Charge torage in the MO tructure Three regions of operation: Accumulation:
The Inverted MO Capacitor (V > V Tn ) We consider the surface potential as Þxed (ÒpinnedÓ) at φ s,max = - φ p φ(x).5 V. V V ox Charge torage in the MO tructure Three regions of operation: Accumulation:
