This is the 15th lecture of this course in which we begin a new topic, Excess Carriers. This topic will be covered in two lectures.
|
|
|
- Berenice Wilkins
- 5 years ago
- Views:
Transcription
1 Solid State Devices Dr. S. Karmalkar Department of Electronics and Communication Engineering Indian Institute of Technology, Madras Lecture - 15 Excess Carriers This is the 15th lecture of this course in which we begin a new topic, Excess Carriers. This topic will be covered in two lectures. (Refer Slide Time: 01:13) (Refer Slide Time: 01:28)
2 First we will discuss the methods of generating excess carriers and then we will discuss the concept of injection level, and the concept of Quasi Fermi-level. We will then discuss an important parameter namely: the lifetime. Like the energy gap and mobility this is an important parameter associated with any semiconductor. We will then discuss about the direct and indirect recombination phenomena which govern the lifetime and finally we will discuss surface recombination. Let us begin by discussing the methods of generating excess carriers. The first method is the method of impact ionization. (Refer Slide Time: 02:10) Let us say we have an n-type semiconductor and we apply an electric field to this semiconductor, there is a current I flowing through this and we will assume that the semiconductor is uniform. We have already shown that if you plot the current as a function of voltage the picture would look as something like this. That is the current will increase linearly for small voltages but for large voltages it will saturate and this is because the drift velocity saturates. If you increase the voltage further in the saturation region, it is found that beyond a critical voltage a very high the current starts rapidly increasing again. Since the velocity of carriers has saturated in this range of voltages the increase in current here can only be attributed to change in the carrier concentration or increase in the carrier concentration because the current depends on the carrier concentration and the velocity. So here the carriers are increasing in number beyond this limit because between any two collisions the carriers are gaining energy from the electric field that we have applied and the energy gained is so large that when the carrier collides with the silicon atom it can break a bond and it can generate excess electron hole pairs. So the energy gained by the carrier between two collisions is more than the energy gap. This is the situation of impact ionization. The field involved here are of the order of 100KV by cm so E is greater than 100KV by cm whereas the fields involved here are of the order of about 20KV by cm which means if this silicon sample is 100mu in length where 100mu is 1 by 100th of a cm
3 then this voltage would correspond to 20KV by cm that is 20 into 10 cube V by cm into 100mu that is 10 to the power minus 2 cm which amounts to 200V whereas this point is 100KV by cm which could be about 1000V. It is beyond such high voltages you are going to see this kind of excess carrier generation. In practice, please note that the power dissipated in the sample for such high voltages and these currents is so high that the sample will melt unless you do the experiment in which this high voltage is applied for a short time so that the total energy generated or dissipated is small and the particular phenomenon of excess carrier generation due to impact ionization can be observed. This is one way you create excess carriers. Please note that excess carriers means carriers over and above the equilibrium value. So if this an n-type sample and doping is 10 to the power 15 by cm cube of phosphorous atoms then under equilibrium conditions it will have about 10 to the power 15 by cm cube of electrons and about 10 to the power 5 by cm cube of holes of that order. The exact value of hole concentration of holes is (n i ) whole square by 10 to the power 15. So over and above this we are creating carriers and those are excess carriers. Generally excess carriers are created in pairs that are for every excess electron that is created you have an excess hole. Let us discuss another method of generating excess carriers that is photo ionization or photo generation. (Refer Slide Time: 07:56) In this case you have a sample which is very thin. Let us assume that you have applied a small voltage to this so that a current flows. We will assume that this sample is n-type and the thickness of the sample is about 3mu. Obviously this is an imaginary sample because you cannot handle a 3mu thin sample of semiconductor. We will assume that this is the third experiment. We will not discuss about the practical aspects of how you can have a 3mu thin silicon sample. Now let us also assume that its doping is as low as possible so that its resistivity is high. If light is shown on this sample and the frequency
4 of light is such that hmu is greater than the energy gap of the sample and if the condition is satisfied where the frequency is greater than E g by h then what we will see is the following: Here I am sketching the current I as a function of the frequency of the light and we will assume that the intensity is kept constant so we are varying the frequency and the voltage also is kept constant. Now if you see the current picture would look something like this. This is the point where the frequency is exactly equal to E g by h this is a critical frequency. We can call this current as a dark current i 0 because in this type of current even when the light is falling, its frequency is very small, so no electron hole pairs are being generated. Strictly speaking dark means that the intensity of light is 0 but here we are keeping the intensity of light constant but the frequency is small so that no electron hole pairs can be really generated. When the frequency exceeds this E g by h the energy of the photons which is incident on the sample is more than the energy gap then each photon can participate in breaking of the silicon bond and creating an excess electron hole pair. If the energy is more than E g by h that is if your frequency is more then the number of electron hole pairs will not increase but what will happen is that the extra energy over and above the energy gap that the photon has will be dissipated as heat. So you look at the energy band diagram, this is E c and this is E v the energy required for an electron to jump from valance band to conduction band and created an electron pair is E g so if E g is energy of the photon the entire energy is used for creating the electron hole pair. If however the energy of the photon is more than E g then the electron is going to jump up to some other energy here. But the difference between this energy and this energy is the energy given by the photon. Then this free electron to this particular energy state close to the E c and this energy will be dissipated as heat. Please note that this is E g and if the energy is more than E g then the extra energy hmu minus E g this energy is dissipated as heat. You do not get extra electron hole pairs because of the extra energy and it is energy dissipated as heat. Therefore you note that if you have some way of removing the heat from the sample so that the sample is kept at uniform temperature then this is the picture that you will get. There are a certain number of excess electron hole pairs created which are going to increase the conductivity of the sample and therefore the current is increasing to this value. If the intensity of the sample is less then this final current that you are getting will be less so this is increasing intensity. Please understand the difference between intensity and frequency. Intensity of light means how many of photons are falling on this sample per unit time per unit area. In other words it can also be regarded as incident power. Another point to note is that all the photons which are falling on the sample will not create electron hole pairs because some of the light is going to be reflected and not the entire light is going to be absorbed. Another point to note is that the light which is absorbed within a micron or so of this surface which is being illuminated. So within a couple of microns the intensity of light is going to fall to 0. That is why only a thin layer
5 near the surface is going to absorb the light and create the excess electron hole pairs. This is the method of creating excess electron hole pairs by photo generation or photo ionization. Let us look at the third method of generating electron hole pairs called injection. (Refer Slide Time: 15:31) Consider a PN junction and supposing we apply a voltage a forward bias to this. In this case what happens is the p-region will inject extra holes into n-region and the n-region will inject extra electrons into the p-region. This is because this terminal is positive and this is negative. This positive terminal attracts electrons from here and these electrons injected into this region are excess electrons, over and above the equilibrium value of electrons in the p-region. Similarly, this negative terminal attracts these holes and p- region therefore creates holes in this n-region which are over and above the equilibrium value. Of course the sample as a hole will remain charge neutral because the holes which are being injected from p to n will be neutralized by electrons which are injected from these terminals. Now it is important to note that by neutralization we do not mean that the holes and electrons are annihilated or it means the charge is 0. So this is a unique situation that can happen in a semiconductor where you have excess electrons and equal number of excess holes which together gives rise to 0 charges but both excess electrons and holes are present. This is the method called as injection across a forward bias junction. We will show the injection as something like this. If we slightly make the diagram bigger to show this the p-region is injecting holes and the n-region is injecting electrons in this region. The holes which are injected are recombining with electrons which are injected from this terminal and these electrons are recombining with holes which are injected here so the sample is charge neutral. So this is the picture. You see how excess electrons and holes have been created by the application of a voltage or they are being injected from an
6 external contact. So this is the process of injection and this is the reason why you get a large current in the forward bias junction. If you sketch the current voltage characteristics of this diode then the forward bias you get a large current; this is the origin. If you reverse the voltage polarity then there is a small current flowing and beyond a certain critical voltage what happens is that the current increases rapidly. This increase in current for reverse voltages also signifies generation of excess carriers. This is in the breakdown region. Now these excess carriers either is created by impact ionization, a process where high field is created in very narrow region called the depletion region at the junction. The details of the operation of the PN junction will be discussed later elaborately. Now we are just mentioning the method of excess carrier creation. So, for this reverse voltage a high electric field is created near the junction which may give rise to excess electron hole pairs because of impact ionization or it could also be what is called tunneling. Tunneling is another method by which excess carriers can be created. So an example of excess carrier creation by tunneling is in a tunnel diode. We can probably show it here as band to band tunneling. (Refer Slide Time: 20:19) So here you have a PN junction where this side is heavily doped and this side also is very heavily doped. When you forward bias is junction it turns out that the characteristic looks something like this. This is the curve if there is no tunneling and this portion of the curve is because of tunneling. What is happening is that because of tunneling a current starts increasing very rapidly but the tunneling phenomenon drops off beyond a certain voltage. This entire current is because of tunneling and then the normal process of injection that we have discussed takes over. In fact this portion is nothing but this portion here which is expanded. So in
7 the reverse direction in such diodes again the current starts increasing rapidly because of tunneling. There is excess carrier generation because of tunneling. We will not discuss the details of how this tunneling occurs but we just want to mention that this is one method of generation of excess carriers. To summarize; excess carriers can be generated by impact ionization as discussed here that is under the influence of high electric fields the excess carriers can be generated by photo ionization that is illumination or with the help of photons. It can be generated by band to band tunneling or it can be generated by injection. Excess carriers can be generated by injection mechanism. Having discussed the various methods of generating excess carriers how do you analyze the devices in the presence of excess carriers? That is the topic that we must consider. In this context the first important idea we discuss is the concept of injection level. (Refer Slide Time: 23:14) The word injection is used in semiconductor devices to mean any method of generating excess carriers. In our earlier discussion so far we used the word injection to denote creation of excess carriers within a device because of contacts which are injecting the excess carriers. So injection so far meant injection from outside into a semiconductor device. But here after the word injection will be used to denote any method of generating excess carriers. So the injection level refers to the extent to which the semiconductor is disturbed from equilibrium because of excess carriers. Now here the first point to note is the excess carriers are created in pairs. So this can be understood by the equation like this, you write the charge balance equation we have p plus N d to the power plus minus n minus N a to the power minus is equal to 0 this is the picture under equilibrium. Let us assume that you have some donor type impurities and some acceptor type impurities. So under equilibrium this is the charge balance equation. Now if you create excess carriers then the
8 changed delta is equal to 0. Therefore what it means is delta p minus delta n is equal to N a to the power minus N d to the power plus. If we assume that the change in the ionization of the impurities is 0 the impurity ionization state does not change which is a reasonable assumption. Then the left hand side can be equated to 0 so this means delta p can be assumed to be equal to delta n so this is the situation in most semiconductors. Here these impurities may mean deep levels or shallow levels and although we have shown only two types of impurities one type of donor and other type of acceptor in principle there can be several different impurities. All this will mean is the change in the ionization of impurities is negligible. So in such a situation we can very easily see that delta p is equal to delta n. So this means excess carriers are generated in pairs. Therefore what we will do is we will assume that the symbol delta represents the excess carriers over and above the equilibrium value either electrons or holes since they are equal in number we use only a single symbol delta. In other words concentration p in the presence of excess carriers is equal to p 0, which is the equilibrium concentration plus delta (p is equal to p 0 plus delta) and concentration of electrons is equal to equilibrium concentration of electrons plus delta (n is equal to n 0 plus delta). (Refer Slide Time: 26:59) Now how do you classify the disturbance from equilibrium because of excess carriers? Supposing we show the concentration delta on a log scale then this particular point shows that if delta is less than 1 by 10 of the majority carrier concentration where this is majority carrier concentration by 10. So if delta is less than 1 by 10 of the majority carrier concentration it is clear that the concentration of carriers which refer to the majority carriers the n-type semiconductor which is the electron concentration then for delta less than majority carrier concentration by 10 we have n is equal to n 0 plus delta which is quantity less than n 0 by 10 because n 0 is a majority carrier concentration which is equal to
9 approximately n 0 itself. For delta less than majority carrier concentration by 10 the majority carrier concentration is not disturbed at all. However, the minority carrier concentration is disturbed because the minority concentration is very small. For this case minority carrier concentration will definitely be disturbed. Whenever you have excess carrier creation minority carrier concentration will definitely be disturbed. Therefore, depending on whether the majority carrier concentration is disturbed or not we classify the injection level into several parts. This particular region is called low level or low injection level when the majority carrier concentration is not disturbed. On the other hand, if delta greater than 10 into the majority carrier concentration at this point, if delta is here in this region then both majority and minority carrier concentrations are disturbed and what you will find is that the concentration of electrons and holes will tend to become almost equal. So for delta greater than majority carrier concentration into 10 you have n is equal to n 0 plus a quantity greater than 10 into n 0 is equal to delta so delta is a quantity approximately equal to delta itself. Here n delta because delta is more than 10 into n 0 so this plus this is this quantity itself. Now (p is equal to p 0 plus delta) delta because p 0 is much less than n 0 in an n-type semiconductor. This plus this would be again this itself. What is happening is n p. It is because of excess carrier creation the excess carriers created as so large that the number of electrons and number of holes in any unit volume are almost same. This particular condition is classified as high injection level or high level. This region will be the intermediate injection level region which is neither high nor low. It turns out that the device analysis is simple either under low level conditions or under high level conditions. In both these extreme cases simplifications are possible as when the majority carrier concentration is not disturbed at all or when the electron and hole concentrations in the device almost become equal and these are the two extremes. So under these conditions the device can be analyzed in a simple way and that is why these two regions are defined. Now let us consider this particular concept of this injection level with a numerical example.
10 (Refer Slide Time: 32:19) Let us assume an n-type semiconductor with a doping level of 10 to the power 15 atoms of phosphorous by cm cube. Let us show the conditions of electrons and holes on a log scale. This is a concentration on a log scale. Under equilibrium the majority carrier concentration is 10 to the power 15 by cm cube and the minority carrier would be n i square by 10 to the power 15 by cm cube. I am not considering the multiplication constant because when you take n i square by 10 to the power 15 then your n i square is equal to 10 to the power 20 into 2.25 so the 2.25 factor I am just ignoring here for simplicity just to show this particular scale in a simple manner. So n i would be somewhere here exactly in the middle and on a log scale n i is exactly in the middle so this is of the order of 10 to the power 10 by cm cube and for simplicity I am ignoring the constant. This is the picture under equilibrium 10 to the power 15 and this is n 0, 10 to the power 5 this is p 0 and this is n i. Now let us take low level injection. Supposing you assume delta is equal to 10 to the power 12 by cm cube because of photo ionization or any other means. Supposing you have excess electron and hole concentration or 10 to the power 12 by cm cube then the hole concentration would be 10 to the power 5 plus 10 to the power 12 which is 10 to the power 12 itself so excess carrier concentration is equal to the minority carrier concentration. Now let us locate at 10 to the power 12 on this so it is 1 by 5 of this and each of this is a factor of 10 so this is 10 to the power 10, 10 to the power 11, 10 to the power 12, this is the concentration p delta for low level conditions. Now what is the majority carrier concentration? The majority carrier concentration is 10 to the power 12 plus 10 to the power 15 which is 10 to the power 15 itself so the majority carrier concentration is the same here. Now this is your n so let us call this delta 1 because this is one particular condition we are considering. Here this is delta 1, p 1 and this is n 1. This is the so-called low level condition so therefore p 1 delta 1 and n 1 n 0 so here it is n 1 n 0 which is the equilibrium concentration.
11 Let us consider another case that is the high level. This means you have an excess carrier concentration delta 2 which is 10 to the power 16 by cm cube or 10 to the power 17 by cm cube. Now what are the electron and hole concentrations? So the hole concentration is 10 to the power 17 plus 10 to the power 5 which is 10 to the power 17 and the electron concentration is 10 to the power 17 plus 10 to the power 15 which is again 10 to the power 17 itself because 10 to the power 15 is much less than 10 to the power 17 so what you find is electron and hole concentrations both are almost the same and this is 10 to the power 17 so the value is in cm cube and here you have this is n 2 p 2 delta 2 which is the high level injection. A log scale very clearly shows both the hole and electron concentrations for low and high level. For the low level the minority carrier concentration is disturbed but majority carrier concentration is almost same as under equilibrium. But for the high level both majority and both electron and hole concentrations are almost the same and both are disturbed. So, that is the concept of low and injection level. In this course we will be considering the devices under low injection level because the analysis in that condition is very simple. After this concept of injection level we need to consider the concept of the Quasi Fermilevel. (Refer Slide Time: 39:00) How do you show the effect on the energy band diagram of the excess carriers? Quasi Fermi-level: Now recall that we said the electron concentration in a semiconductor can be written in terms of the following equation n 0 is equal to N c exponential minus (E c minus E f by kt). And the hole concentration under equilibrium can be written as p 0 is equal to N v exponential minus (E f minus E v by kt). Now both n 0 and p 0 are characterized by the same Fermi-level. The same Fermi-level E f comes into both these formulae.
12 You can also write the electron and hole concentrations in terms of the deviation from the intrinsic semiconductor. For example I could write n 0 is equal to n i exponential (E f minus E i ) by kt. And p 0 is equal to n i exponential (E i minus E f ) by kt is another way of writing the same concentration. Now here the Fermi-level is again the same that is used in both formulae and the diagram is as follows. (Refer Slide Time: 40:52) E c E v that is we are drawing the energy band diagram and this is E i. And let us assume an n-type semiconductor so this is E f. So here E f will be more than E i, E f greater than E i. (Refer Slide Time: 41:22)
13 Can we use similar equations also under non equilibrium conditions when excess carriers are present. There is nothing that prevents us from using similar equations that is to relate the electron concentration to the difference between the conduction band edge and a Fermi-level. We can always use similar equations under non equilibrium conditions. What will happen now is that instead of n 0 you will have n which will be greater than n 0. (Refer Slide Time: 41:54) Therefore the difference E c minus E f should reduce. If your left hand side increases the right hand side should also increase which means the difference should reduce. The E f will have to therefore change to a new value that is E fn this is called the Quasi Fermilevel for electrons. It is that Fermi-level which when you substitute in this formula which is similar to that under equilibrium you will get the concentration of the electrons and similarly we can get the concentration of holes also as will see. So n is equal to N c exp minus (E c minus E fn ) into kt or if you were to substitute here you will get n 0 is equal to n i exp (Quasi Fermi-level of electrons minus e i) by kt. Fermi-level under non equilibrium conditions is called Quasi Fermi-level. One important point is to be noted. When you want to express the hole concentration you will note that since left hand side has increased the hole concentration is more because of the presence of excess carriers because it is p 0 plus delta then the right hand side should also increase which means that this different should decrease. You have a new Fermilevel for holes which is different from the Fermi-level under equilibrium. This means that the Fermi-level should move closer to the valance band edge to have increased hole concentration. But in the same semiconductor for increase electron concentration the Fermi-level should move closer to the conduction band to have the higher concentration because this difference should decrease. Obviously the same Fermilevel cannot move close to the conduction band as well as to the valance band so this is
14 what is important to note under non equilibrium. The Quasi Fermi-levels for electrons and for holes are not the same they are different. The Quasi Fermi-levels for the electrons moves closer to the conduction band edge as compared to the equilibrium whereas Quasi Fermi-level for holes moves closer to the valance band edge as compared to equilibrium, this is an important difference. Similarly, we substitute E fp here instead of E f and we will get the hole concentration, this is the concept of Quasi Fermi-level, determining the concentrations in terms of a new Fermilevel. Now what is the advantage of this? The advantage will be seen later in analysis that many forms of equations under non equilibrium conditions for devices gets simplified if you use this kind of representation or formula to relate the energy band parameters and the concentrations. This point will be clear in the subsequent lectures when we take up analysis of devices. The Quasi Fermi-level also has lot of physical significance. Now before leaving this concept of Quasi Fermi-level let us see what is the Quasi Fermi-level picture under low injection level and under high injection level? We will be assuming n-type semiconductor in this example. Under low injection level the concentration of majority carriers the electrons will not change significantly but it remains equal to the equilibrium value. Therefore the Quasi Fermi-level for electrons remains equal to the equilibrium Fermilevel. (Refer Slide Time: 45:37) So if you take low injection level the E fn is equal to E f. However the Quasi Fermi-level for holes cannot be the same as under equilibrium because definitely even if it is low injection level the minority carrier concentration is always disturbed. So E fp will be closer to the valance band edge as it depends on how much is your excess carrier concentration.
15 If excess carrier concentration is 10 to the power 12 as we considered in this example for low level then the Fermi-level would be definitely below E i because when you have Fermi-level at E i the concentration is n i which in silicon is 10 to the power 10. So if you want 10 to the power 12 then it will be below this which is the Quasi Fermi-level for holes. You see E fp and E fn are different so Fermi-level has split. And further E fp minus E i will be less than E fn minus E i because this deviation represents 10 to the power 12 while this deviation from E i represents 10 to the power 15. We are assuming an n-type semiconductor doping 10 to the power 15. So low level delta is equal to 10 to the power 12 therefore the Fermi-level splits into two Quasi Fermilevels. Now, what about high injection level? Under high injection level the excess hole concentration will be same as excess electron concentration. (Refer Slide Time: 47:51) So if you take 10 to the power 17 as we have discussed in this example here as delta 2 then the picture can be shown separately to avoid confusion this is E c, this is E c, this is E i and this is E f corresponding to equilibrium. The majority carrier concentration has increased to 10 to the power 17 so you will have a new Quasi Fermi-level for electrons which is E fn. And you will have a new Quasi Fermi-level for holes exactly at the same distance below so this is E fp which is for delta 10 to the power 17 by cm cube high level. So E fn minus E i E fp minus E i or E c minus E fn is equal to E v minus E fp the condition at high level. Therefore the Quasi Fermi-levels are situated symmetrically about E i under high injection level conditions. With this we have completed the discussion on Quasi Fermi-level. Next we must consider the important parameter of lifetime which describes the transient phenomena related to excess carriers. Let us discuss this concept with the help of this figure of photo ionization.
16 (Refer Slide Time: 49:22) Generation of excess carriers is because of light and we keep the voltage constant and you have a current flowing. Supposing you switch on the light at some instant of time how long does it take for the excess carriers to increase to their steady state value? And when you switch off the impulse how long does the sample take to come back to equilibrium conditions? We can show it on a graph. (Refer Slide Time: 49:57) We will plot the current I as a function of time. We will assume that it is the intensity that we are changing suddenly, the intensity of the light is being changed suddenly. I am going to plot the intensity here. Let us assume the intensity is 0 to start with and at some
17 instant it has suddenly increased so the light is switched on. It is maintained on for sometime and then it is suddenly switched off. Here you have on and here you have off and these are the instants. How do we sketch I as a function of T, the observed current? We will find that you will have a small current called the dark current i 0. This is the dark current and at this instant the current will start rising and will slowly reach the steady state value something like charging of a capacitor, something similar to that. Then after it reaches the steady state let us assume that the light is kept on until a steady state is reached. It is for a sufficiently long duration it is on. Now at this instant when it is switched off you find that the current will come back to its dark current value slowly after decay. In other words, your change in current will not be instantaneous. The current will not reach a new steady state value instantaneously when the intensity has increased so there is a delay and there is a time which elapses before the sample can respond so excess carriers are not generated instantaneously. The excess carriers are generated and their concentration starts increasing and then reaches a steady state after sometime. It is this time that is of interest in the switching performance of devices. We will show that these delays associated with the on-transient and off-transient are related to an important parameter called the lifetime. Let us discuss this situation further. What is the reason for these transient durations? What is happening here is that the moment we switch on the light the generation rate has changed suddenly but the recombination rate has not changed at this instant. Since the generation rate is more than recombination rate the carriers are being generated. Excess carriers are being generated and the carrier concentration is rising. As the excess carrier concentration rises the recombination rate also goes on rising because recombination rate depends on the hole and electron concentrations. Here we can say in this region G is equal to G 0 plus G prime which is the excess generation rate but r which is equal to R 0 plus R prime this r is less than g because R prime less than G prime in this region. I want to emphasize this fact that we are assuming that this particular sample is absorbing the light in a uniform manner so that excess carrier concentration throughout the sample is uniform so the generation rate is also said to be uniform. So this is the third experiment it may not be actually true but in this experiment we are assuming uniform conditions. So that any of these transients you see here are simply because of the differences between the generation and recombination rates and not because of any carrier movement. Since the carrier concentration is uniform carriers do not move from a one region to another. Now in this portion what has happened is G is equal to G 0 because G prime has become 0 because the light has been switched off and therefore generation rate has dropped to 0. Recombination rate however cannot drop to 0 immediately. So this is R 0 plus R prime but as the excess carrier concentration starts falling R prime also starts falling. So in the steady state beyond this you have R prime is equal to 0, G prime is anyway 0 here so that is equilibrium condition.
18 In this region you have R prime greater than G prime. Since recombination rate is more than the generation rate you have a decay in excess carrier population. Whereas here the generation rate is more than the recombination rate so you have a rise. So in the steady state portion you have G prime is equal to R prime so no change in carrier concentration is seen because the recombination rate has risen and has become equal to the excess generation rate. However, this is not equilibrium because G prime and R prime both are non zero. Both G prime and R prime are non zero whereas here R prime is 0 and G prime is 0 and that is why this is in equilibrium state which is the condition. The rate of increase of carrier concentration in this region here we can write ddelta by dt the rate of increase of excess carrier concentration is related to G prime minus R prime. The difference G prime minus R prime is causing this. On the other hand, in this region you have ddelta into dt equal to minus r because G prime has become 0 and there is an excess recombination here and that is why carrier concentration is falling. So here carrier concentration is rising. This is the situation from which we need to develop the concept of lifetime. We will do this in the next class.
(Refer Slide Time: 03:41)
 Solid State Devices Dr. S. Karmalkar Department of Electronics and Communication Engineering Indian Institute of Technology, Madras Lecture - 25 PN Junction (Contd ) This is the 25th lecture of this course
Solid State Devices Dr. S. Karmalkar Department of Electronics and Communication Engineering Indian Institute of Technology, Madras Lecture - 25 PN Junction (Contd ) This is the 25th lecture of this course
Today we begin the first technical topic related directly to the course that is: Equilibrium Carrier Concentration.
 Solid State Devices Dr. S. Karmalkar Department of Electronics and Communication Engineering Indian Institute of Technology, Madras Lecture - 3 Equilibrium and Carrier Concentration Today we begin the
Solid State Devices Dr. S. Karmalkar Department of Electronics and Communication Engineering Indian Institute of Technology, Madras Lecture - 3 Equilibrium and Carrier Concentration Today we begin the
Semiconductor Physics fall 2012 problems
 Semiconductor Physics fall 2012 problems 1. An n-type sample of silicon has a uniform density N D = 10 16 atoms cm -3 of arsenic, and a p-type silicon sample has N A = 10 15 atoms cm -3 of boron. For each
Semiconductor Physics fall 2012 problems 1. An n-type sample of silicon has a uniform density N D = 10 16 atoms cm -3 of arsenic, and a p-type silicon sample has N A = 10 15 atoms cm -3 of boron. For each
n N D n p = n i p N A
 Summary of electron and hole concentration in semiconductors Intrinsic semiconductor: E G n kt i = pi = N e 2 0 Donor-doped semiconductor: n N D where N D is the concentration of donor impurity Acceptor-doped
Summary of electron and hole concentration in semiconductors Intrinsic semiconductor: E G n kt i = pi = N e 2 0 Donor-doped semiconductor: n N D where N D is the concentration of donor impurity Acceptor-doped
Semiconductor Physics fall 2012 problems
 Semiconductor Physics fall 2012 problems 1. An n-type sample of silicon has a uniform density N D = 10 16 atoms cm -3 of arsenic, and a p-type silicon sample has N A = 10 15 atoms cm -3 of boron. For each
Semiconductor Physics fall 2012 problems 1. An n-type sample of silicon has a uniform density N D = 10 16 atoms cm -3 of arsenic, and a p-type silicon sample has N A = 10 15 atoms cm -3 of boron. For each
Engineering 2000 Chapter 8 Semiconductors. ENG2000: R.I. Hornsey Semi: 1
 Engineering 2000 Chapter 8 Semiconductors ENG2000: R.I. Hornsey Semi: 1 Overview We need to know the electrical properties of Si To do this, we must also draw on some of the physical properties and we
Engineering 2000 Chapter 8 Semiconductors ENG2000: R.I. Hornsey Semi: 1 Overview We need to know the electrical properties of Si To do this, we must also draw on some of the physical properties and we
Processing of Semiconducting Materials Prof. Pallab Banerji Department of Material Science Indian Institute of Technology, Kharagpur
 Processing of Semiconducting Materials Prof. Pallab Banerji Department of Material Science Indian Institute of Technology, Kharagpur Lecture - 4 Doping in Semiconductors Good morning. Let us start with
Processing of Semiconducting Materials Prof. Pallab Banerji Department of Material Science Indian Institute of Technology, Kharagpur Lecture - 4 Doping in Semiconductors Good morning. Let us start with
ITT Technical Institute ET215 Devices I Unit 1
 ITT Technical Institute ET215 Devices I Unit 1 Chapter 1 Chapter 2, Sections 2.1-2.4 Chapter 1 Basic Concepts of Analog Circuits Recall ET115 & ET145 Ohms Law I = V/R If voltage across a resistor increases
ITT Technical Institute ET215 Devices I Unit 1 Chapter 1 Chapter 2, Sections 2.1-2.4 Chapter 1 Basic Concepts of Analog Circuits Recall ET115 & ET145 Ohms Law I = V/R If voltage across a resistor increases
Session 6: Solid State Physics. Diode
 Session 6: Solid State Physics Diode 1 Outline A B C D E F G H I J 2 Definitions / Assumptions Homojunction: the junction is between two regions of the same material Heterojunction: the junction is between
Session 6: Solid State Physics Diode 1 Outline A B C D E F G H I J 2 Definitions / Assumptions Homojunction: the junction is between two regions of the same material Heterojunction: the junction is between
Lecture 15: Optoelectronic devices: Introduction
 Lecture 15: Optoelectronic devices: Introduction Contents 1 Optical absorption 1 1.1 Absorption coefficient....................... 2 2 Optical recombination 5 3 Recombination and carrier lifetime 6 3.1
Lecture 15: Optoelectronic devices: Introduction Contents 1 Optical absorption 1 1.1 Absorption coefficient....................... 2 2 Optical recombination 5 3 Recombination and carrier lifetime 6 3.1
Semiconductor Physics and Devices
 The pn Junction 1) Charge carriers crossing the junction. 3) Barrier potential Semiconductor Physics and Devices Chapter 8. The pn Junction Diode 2) Formation of positive and negative ions. 4) Formation
The pn Junction 1) Charge carriers crossing the junction. 3) Barrier potential Semiconductor Physics and Devices Chapter 8. The pn Junction Diode 2) Formation of positive and negative ions. 4) Formation
Electro - Principles I
 Electro - Principles I Page 10-1 Atomic Theory It is necessary to know what goes on at the atomic level of a semiconductor so the characteristics of the semiconductor can be understood. In many cases a
Electro - Principles I Page 10-1 Atomic Theory It is necessary to know what goes on at the atomic level of a semiconductor so the characteristics of the semiconductor can be understood. In many cases a
PN Junction
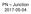 P Junction 2017-05-04 Definition Power Electronics = semiconductor switches are used Analogue amplifier = high power loss 250 200 u x 150 100 u Udc i 50 0 0 50 100 150 200 250 300 350 400 i,u dc i,u u
P Junction 2017-05-04 Definition Power Electronics = semiconductor switches are used Analogue amplifier = high power loss 250 200 u x 150 100 u Udc i 50 0 0 50 100 150 200 250 300 350 400 i,u dc i,u u
Semiconductor Devices and Circuits Fall Midterm Exam. Instructor: Dr. Dietmar Knipp, Professor of Electrical Engineering. Name: Mat. -Nr.
 Semiconductor Devices and Circuits Fall 2003 Midterm Exam Instructor: Dr. Dietmar Knipp, Professor of Electrical Engineering Name: Mat. -Nr.: Guidelines: Duration of the Midterm: 1 hour The exam is a closed
Semiconductor Devices and Circuits Fall 2003 Midterm Exam Instructor: Dr. Dietmar Knipp, Professor of Electrical Engineering Name: Mat. -Nr.: Guidelines: Duration of the Midterm: 1 hour The exam is a closed
Effective masses in semiconductors
 Effective masses in semiconductors The effective mass is defined as: In a solid, the electron (hole) effective mass represents how electrons move in an applied field. The effective mass reflects the inverse
Effective masses in semiconductors The effective mass is defined as: In a solid, the electron (hole) effective mass represents how electrons move in an applied field. The effective mass reflects the inverse
The German University in Cairo. Faculty of Information Engineering & Technology Semiconductors (Elct 503) Electronics Department Fall 2014
 The German University in Cairo th Electronics 5 Semester Faculty of Information Engineering & Technology Semiconductors (Elct 503) Electronics Department Fall 2014 Problem Set 3 1- a) Find the resistivity
The German University in Cairo th Electronics 5 Semester Faculty of Information Engineering & Technology Semiconductors (Elct 503) Electronics Department Fall 2014 Problem Set 3 1- a) Find the resistivity
ECE 340 Lecture 27 : Junction Capacitance Class Outline:
 ECE 340 Lecture 27 : Junction Capacitance Class Outline: Breakdown Review Junction Capacitance Things you should know when you leave M.J. Gilbert ECE 340 Lecture 27 10/24/11 Key Questions What types of
ECE 340 Lecture 27 : Junction Capacitance Class Outline: Breakdown Review Junction Capacitance Things you should know when you leave M.J. Gilbert ECE 340 Lecture 27 10/24/11 Key Questions What types of
Peak Electric Field. Junction breakdown occurs when the peak electric field in the PN junction reaches a critical value. For the N + P junction,
 Peak Electric Field Junction breakdown occurs when the peak electric field in the P junction reaches a critical value. For the + P junction, qa E ( x) ( xp x), s W dep 2 s ( bi Vr ) 2 s potential barrier
Peak Electric Field Junction breakdown occurs when the peak electric field in the P junction reaches a critical value. For the + P junction, qa E ( x) ( xp x), s W dep 2 s ( bi Vr ) 2 s potential barrier
Semiconductor Physics. Lecture 6
 Semiconductor Physics Lecture 6 Recap pn junction and the depletion region Driven by the need to have no gradient in the fermi level free carriers migrate across the pn junction leaving a region with few
Semiconductor Physics Lecture 6 Recap pn junction and the depletion region Driven by the need to have no gradient in the fermi level free carriers migrate across the pn junction leaving a region with few
ESE 372 / Spring 2013 / Lecture 5 Metal Oxide Semiconductor Field Effect Transistor
 Metal Oxide Semiconductor Field Effect Transistor V G V G 1 Metal Oxide Semiconductor Field Effect Transistor We will need to understand how this current flows through Si What is electric current? 2 Back
Metal Oxide Semiconductor Field Effect Transistor V G V G 1 Metal Oxide Semiconductor Field Effect Transistor We will need to understand how this current flows through Si What is electric current? 2 Back
UNIVERSITY OF CALIFORNIA College of Engineering Department of Electrical Engineering and Computer Sciences. EECS 130 Professor Ali Javey Fall 2006
 UNIVERSITY OF CALIFORNIA College of Engineering Department of Electrical Engineering and Computer Sciences EECS 130 Professor Ali Javey Fall 2006 Midterm I Name: Closed book. One sheet of notes is allowed.
UNIVERSITY OF CALIFORNIA College of Engineering Department of Electrical Engineering and Computer Sciences EECS 130 Professor Ali Javey Fall 2006 Midterm I Name: Closed book. One sheet of notes is allowed.
KATIHAL FİZİĞİ MNT-510
 KATIHAL FİZİĞİ MNT-510 YARIİLETKENLER Kaynaklar: Katıhal Fiziği, Prof. Dr. Mustafa Dikici, Seçkin Yayıncılık Katıhal Fiziği, Şakir Aydoğan, Nobel Yayıncılık, Physics for Computer Science Students: With
KATIHAL FİZİĞİ MNT-510 YARIİLETKENLER Kaynaklar: Katıhal Fiziği, Prof. Dr. Mustafa Dikici, Seçkin Yayıncılık Katıhal Fiziği, Şakir Aydoğan, Nobel Yayıncılık, Physics for Computer Science Students: With
Carriers Concentration and Current in Semiconductors
 Carriers Concentration and Current in Semiconductors Carrier Transport Two driving forces for carrier transport: electric field and spatial variation of the carrier concentration. Both driving forces lead
Carriers Concentration and Current in Semiconductors Carrier Transport Two driving forces for carrier transport: electric field and spatial variation of the carrier concentration. Both driving forces lead
Session 5: Solid State Physics. Charge Mobility Drift Diffusion Recombination-Generation
 Session 5: Solid State Physics Charge Mobility Drift Diffusion Recombination-Generation 1 Outline A B C D E F G H I J 2 Mobile Charge Carriers in Semiconductors Three primary types of carrier action occur
Session 5: Solid State Physics Charge Mobility Drift Diffusion Recombination-Generation 1 Outline A B C D E F G H I J 2 Mobile Charge Carriers in Semiconductors Three primary types of carrier action occur
Unit IV Semiconductors Engineering Physics
 Introduction A semiconductor is a material that has a resistivity lies between that of a conductor and an insulator. The conductivity of a semiconductor material can be varied under an external electrical
Introduction A semiconductor is a material that has a resistivity lies between that of a conductor and an insulator. The conductivity of a semiconductor material can be varied under an external electrical
3.1 Introduction to Semiconductors. Y. Baghzouz ECE Department UNLV
 3.1 Introduction to Semiconductors Y. Baghzouz ECE Department UNLV Introduction In this lecture, we will cover the basic aspects of semiconductor materials, and the physical mechanisms which are at the
3.1 Introduction to Semiconductors Y. Baghzouz ECE Department UNLV Introduction In this lecture, we will cover the basic aspects of semiconductor materials, and the physical mechanisms which are at the
Schottky Rectifiers Zheng Yang (ERF 3017,
 ECE442 Power Semiconductor Devices and Integrated Circuits Schottky Rectifiers Zheng Yang (ERF 3017, email: yangzhen@uic.edu) Power Schottky Rectifier Structure 2 Metal-Semiconductor Contact The work function
ECE442 Power Semiconductor Devices and Integrated Circuits Schottky Rectifiers Zheng Yang (ERF 3017, email: yangzhen@uic.edu) Power Schottky Rectifier Structure 2 Metal-Semiconductor Contact The work function
Semiconductor Physics. Lecture 3
 Semiconductor Physics Lecture 3 Intrinsic carrier density Intrinsic carrier density Law of mass action Valid also if we add an impurity which either donates extra electrons or holes the number of carriers
Semiconductor Physics Lecture 3 Intrinsic carrier density Intrinsic carrier density Law of mass action Valid also if we add an impurity which either donates extra electrons or holes the number of carriers
Solid State Electronics. Final Examination
 The University of Toledo EECS:4400/5400/7400 Solid State Electronic Section elssf08fs.fm - 1 Solid State Electronics Final Examination Problems Points 1. 1. 14 3. 14 Total 40 Was the exam fair? yes no
The University of Toledo EECS:4400/5400/7400 Solid State Electronic Section elssf08fs.fm - 1 Solid State Electronics Final Examination Problems Points 1. 1. 14 3. 14 Total 40 Was the exam fair? yes no
Chapter 7. The pn Junction
 Chapter 7 The pn Junction Chapter 7 PN Junction PN junction can be fabricated by implanting or diffusing donors into a P-type substrate such that a layer of semiconductor is converted into N type. Converting
Chapter 7 The pn Junction Chapter 7 PN Junction PN junction can be fabricated by implanting or diffusing donors into a P-type substrate such that a layer of semiconductor is converted into N type. Converting
Due to the quantum nature of electrons, one energy state can be occupied only by one electron.
 In crystalline solids, not all values of the electron energy are possible. The allowed intervals of energy are called allowed bands (shown as blue and chess-board blue). The forbidden intervals are called
In crystalline solids, not all values of the electron energy are possible. The allowed intervals of energy are called allowed bands (shown as blue and chess-board blue). The forbidden intervals are called
Lecture 15 - The pn Junction Diode (I) I-V Characteristics. November 1, 2005
 6.012 - Microelectronic Devices and Circuits - Fall 2005 Lecture 15-1 Lecture 15 - The pn Junction Diode (I) I-V Characteristics November 1, 2005 Contents: 1. pn junction under bias 2. I-V characteristics
6.012 - Microelectronic Devices and Circuits - Fall 2005 Lecture 15-1 Lecture 15 - The pn Junction Diode (I) I-V Characteristics November 1, 2005 Contents: 1. pn junction under bias 2. I-V characteristics
Lecture 2. Semiconductor Physics. Sunday 4/10/2015 Semiconductor Physics 1-1
 Lecture 2 Semiconductor Physics Sunday 4/10/2015 Semiconductor Physics 1-1 Outline Intrinsic bond model: electrons and holes Charge carrier generation and recombination Intrinsic semiconductor Doping:
Lecture 2 Semiconductor Physics Sunday 4/10/2015 Semiconductor Physics 1-1 Outline Intrinsic bond model: electrons and holes Charge carrier generation and recombination Intrinsic semiconductor Doping:
Charge Carriers in Semiconductor
 Charge Carriers in Semiconductor To understand PN junction s IV characteristics, it is important to understand charge carriers behavior in solids, how to modify carrier densities, and different mechanisms
Charge Carriers in Semiconductor To understand PN junction s IV characteristics, it is important to understand charge carriers behavior in solids, how to modify carrier densities, and different mechanisms
Diodes. anode. cathode. cut-off. Can be approximated by a piecewise-linear-like characteristic. Lecture 9-1
 Diodes mplest nonlinear circuit element Basic operation sets the foundation for Bipolar Junction Transistors (BJTs) Also present in Field Effect Transistors (FETs) Ideal diode characteristic anode cathode
Diodes mplest nonlinear circuit element Basic operation sets the foundation for Bipolar Junction Transistors (BJTs) Also present in Field Effect Transistors (FETs) Ideal diode characteristic anode cathode
collisions of electrons. In semiconductor, in certain temperature ranges the conductivity increases rapidly by increasing temperature
 1.9. Temperature Dependence of Semiconductor Conductivity Such dependence is one most important in semiconductor. In metals, Conductivity decreases by increasing temperature due to greater frequency of
1.9. Temperature Dependence of Semiconductor Conductivity Such dependence is one most important in semiconductor. In metals, Conductivity decreases by increasing temperature due to greater frequency of
Lecture 1. OUTLINE Basic Semiconductor Physics. Reading: Chapter 2.1. Semiconductors Intrinsic (undoped) silicon Doping Carrier concentrations
 Lecture 1 OUTLINE Basic Semiconductor Physics Semiconductors Intrinsic (undoped) silicon Doping Carrier concentrations Reading: Chapter 2.1 EE105 Fall 2007 Lecture 1, Slide 1 What is a Semiconductor? Low
Lecture 1 OUTLINE Basic Semiconductor Physics Semiconductors Intrinsic (undoped) silicon Doping Carrier concentrations Reading: Chapter 2.1 EE105 Fall 2007 Lecture 1, Slide 1 What is a Semiconductor? Low
Lecture (02) PN Junctions and Diodes
 Lecture (02) PN Junctions and Diodes By: Dr. Ahmed ElShafee ١ I Agenda N type, P type semiconductors N Type Semiconductor P Type Semiconductor PN junction Energy Diagrams of the PN Junction and Depletion
Lecture (02) PN Junctions and Diodes By: Dr. Ahmed ElShafee ١ I Agenda N type, P type semiconductors N Type Semiconductor P Type Semiconductor PN junction Energy Diagrams of the PN Junction and Depletion
Fundamentals of Semiconductor Physics
 Fall 2007 Fundamentals of Semiconductor Physics 万 歆 Zhejiang Institute of Modern Physics xinwan@zimp.zju.edu.cn http://zimp.zju.edu.cn/~xinwan/ Transistor technology evokes new physics The objective of
Fall 2007 Fundamentals of Semiconductor Physics 万 歆 Zhejiang Institute of Modern Physics xinwan@zimp.zju.edu.cn http://zimp.zju.edu.cn/~xinwan/ Transistor technology evokes new physics The objective of
The pn junction. [Fonstad, Ghione]
![The pn junction. [Fonstad, Ghione] The pn junction. [Fonstad, Ghione]](/thumbs/93/112370833.jpg) The pn junction [Fonstad, Ghione] Band diagram On the vertical axis: potential energy of the electrons On the horizontal axis: now there is nothing: later we ll put the position qf s : work function (F
The pn junction [Fonstad, Ghione] Band diagram On the vertical axis: potential energy of the electrons On the horizontal axis: now there is nothing: later we ll put the position qf s : work function (F
Semi-Conductors insulators semi-conductors N-type Semi-Conductors P-type Semi-Conductors
 Semi-Conductors In the metal materials considered earlier, the coupling of the atoms together to form the material decouples an electron from each atom setting it free to roam around inside the material.
Semi-Conductors In the metal materials considered earlier, the coupling of the atoms together to form the material decouples an electron from each atom setting it free to roam around inside the material.
1 Name: Student number: DEPARTMENT OF PHYSICS AND PHYSICAL OCEANOGRAPHY MEMORIAL UNIVERSITY OF NEWFOUNDLAND. Fall :00-11:00
 1 Name: DEPARTMENT OF PHYSICS AND PHYSICAL OCEANOGRAPHY MEMORIAL UNIVERSITY OF NEWFOUNDLAND Final Exam Physics 3000 December 11, 2012 Fall 2012 9:00-11:00 INSTRUCTIONS: 1. Answer all seven (7) questions.
1 Name: DEPARTMENT OF PHYSICS AND PHYSICAL OCEANOGRAPHY MEMORIAL UNIVERSITY OF NEWFOUNDLAND Final Exam Physics 3000 December 11, 2012 Fall 2012 9:00-11:00 INSTRUCTIONS: 1. Answer all seven (7) questions.
Concept of Core IENGINEERS- CONSULTANTS LECTURE NOTES SERIES ELECTRONICS ENGINEERING 1 YEAR UPTU. Page 1
 Concept of Core Conductivity of conductor and semiconductor can also be explained by concept of Core. Core: Core is a part of an atom other than its valence electrons. Core consists of all inner shells
Concept of Core Conductivity of conductor and semiconductor can also be explained by concept of Core. Core: Core is a part of an atom other than its valence electrons. Core consists of all inner shells
Consider a uniformly doped PN junction, in which one region of the semiconductor is uniformly doped with acceptor atoms and the adjacent region is
 CHAPTER 7 The PN Junction Consider a uniformly doped PN junction, in which one region of the semiconductor is uniformly doped with acceptor atoms and the adjacent region is uniformly doped with donor atoms.
CHAPTER 7 The PN Junction Consider a uniformly doped PN junction, in which one region of the semiconductor is uniformly doped with acceptor atoms and the adjacent region is uniformly doped with donor atoms.
electronics fundamentals
 electronics fundamentals circuits, devices, and applications THOMAS L. FLOYD DAVID M. BUCHLA Lesson 1: Diodes and Applications Semiconductors Figure 1-1 The Bohr model of an atom showing electrons in orbits
electronics fundamentals circuits, devices, and applications THOMAS L. FLOYD DAVID M. BUCHLA Lesson 1: Diodes and Applications Semiconductors Figure 1-1 The Bohr model of an atom showing electrons in orbits
Electronic PRINCIPLES
 MALVINO & BATES Electronic PRINCIPLES SEVENTH EDITION Chapter 2 Semiconductors Topics Covered in Chapter 2 Conductors Semiconductors Silicon crystals Intrinsic semiconductors Two types of flow Doping a
MALVINO & BATES Electronic PRINCIPLES SEVENTH EDITION Chapter 2 Semiconductors Topics Covered in Chapter 2 Conductors Semiconductors Silicon crystals Intrinsic semiconductors Two types of flow Doping a
Semiconductor Optoelectronics Prof. M. R. Shenoy Department of physics Indian Institute of Technology, Delhi
 Semiconductor Optoelectronics Prof. M. R. Shenoy Department of physics Indian Institute of Technology, Delhi Lecture - 18 Optical Joint Density of States So, today we will discuss the concept of optical
Semiconductor Optoelectronics Prof. M. R. Shenoy Department of physics Indian Institute of Technology, Delhi Lecture - 18 Optical Joint Density of States So, today we will discuss the concept of optical
B12: Semiconductor Devices
 B12: Semiconductor Devices Example Sheet 2: Solutions Question 1 To get from eq. (5.70) of the notes to the expression given in the examples sheet, we simply invoke the relations n 0 p 0, n 0 n 0. In this
B12: Semiconductor Devices Example Sheet 2: Solutions Question 1 To get from eq. (5.70) of the notes to the expression given in the examples sheet, we simply invoke the relations n 0 p 0, n 0 n 0. In this
ECE 606 Homework Week 7 Mark Lundstrom Purdue University (revised 2/25/13) e E i! E T
 ECE 606 Homework Week 7 Mark Lundstrom Purdue University (revised 2/25/13) 1) Consider an n- type semiconductor for which the only states in the bandgap are donor levels (i.e. ( E T = E D ). Begin with
ECE 606 Homework Week 7 Mark Lundstrom Purdue University (revised 2/25/13) 1) Consider an n- type semiconductor for which the only states in the bandgap are donor levels (i.e. ( E T = E D ). Begin with
Semiconductor Physics
 Semiconductor Physics Motivation Is it possible that there might be current flowing in a conductor (or a semiconductor) even when there is no potential difference supplied across its ends? Look at the
Semiconductor Physics Motivation Is it possible that there might be current flowing in a conductor (or a semiconductor) even when there is no potential difference supplied across its ends? Look at the
Lecture (02) Introduction to Electronics II, PN Junction and Diodes I
 Lecture (02) Introduction to Electronics II, PN Junction and Diodes I By: Dr. Ahmed ElShafee ١ Agenda Current in semiconductors/conductors N type, P type semiconductors N Type Semiconductor P Type Semiconductor
Lecture (02) Introduction to Electronics II, PN Junction and Diodes I By: Dr. Ahmed ElShafee ١ Agenda Current in semiconductors/conductors N type, P type semiconductors N Type Semiconductor P Type Semiconductor
Electronics The basics of semiconductor physics
 Electronics The basics of semiconductor physics Prof. Márta Rencz, Gergely Nagy BME DED September 16, 2013 The basic properties of semiconductors Semiconductors conductance is between that of conductors
Electronics The basics of semiconductor physics Prof. Márta Rencz, Gergely Nagy BME DED September 16, 2013 The basic properties of semiconductors Semiconductors conductance is between that of conductors
Spring Semester 2012 Final Exam
 Spring Semester 2012 Final Exam Note: Show your work, underline results, and always show units. Official exam time: 2.0 hours; an extension of at least 1.0 hour will be granted to anyone. Materials parameters
Spring Semester 2012 Final Exam Note: Show your work, underline results, and always show units. Official exam time: 2.0 hours; an extension of at least 1.0 hour will be granted to anyone. Materials parameters
Semiconductor Physics Problems 2015
 Semiconductor Physics Problems 2015 Page and figure numbers refer to Semiconductor Devices Physics and Technology, 3rd edition, by SM Sze and M-K Lee 1. The purest semiconductor crystals it is possible
Semiconductor Physics Problems 2015 Page and figure numbers refer to Semiconductor Devices Physics and Technology, 3rd edition, by SM Sze and M-K Lee 1. The purest semiconductor crystals it is possible
junctions produce nonlinear current voltage characteristics which can be exploited
 Chapter 6 P-N DODES Junctions between n-and p-type semiconductors are extremely important foravariety of devices. Diodes based on p-n junctions produce nonlinear current voltage characteristics which can
Chapter 6 P-N DODES Junctions between n-and p-type semiconductors are extremely important foravariety of devices. Diodes based on p-n junctions produce nonlinear current voltage characteristics which can
For the following statements, mark ( ) for true statement and (X) for wrong statement and correct it.
 Benha University Faculty of Engineering Shoubra Electrical Engineering Department First Year communications. Answer all the following questions Illustrate your answers with sketches when necessary. The
Benha University Faculty of Engineering Shoubra Electrical Engineering Department First Year communications. Answer all the following questions Illustrate your answers with sketches when necessary. The
( )! N D ( x) ) and equilibrium
 ECE 66: SOLUTIONS: ECE 66 Homework Week 8 Mark Lundstrom March 7, 13 1) The doping profile for an n- type silicon wafer ( N D = 1 15 cm - 3 ) with a heavily doped thin layer at the surface (surface concentration,
ECE 66: SOLUTIONS: ECE 66 Homework Week 8 Mark Lundstrom March 7, 13 1) The doping profile for an n- type silicon wafer ( N D = 1 15 cm - 3 ) with a heavily doped thin layer at the surface (surface concentration,
Basic Physics of Semiconductors
 Basic Physics of Semiconductors Semiconductor materials and their properties PN-junction diodes Reverse Breakdown EEM 205 Electronics I Dicle University, EEE Dr. Mehmet Siraç ÖZERDEM Semiconductor Physics
Basic Physics of Semiconductors Semiconductor materials and their properties PN-junction diodes Reverse Breakdown EEM 205 Electronics I Dicle University, EEE Dr. Mehmet Siraç ÖZERDEM Semiconductor Physics
SRI VIDYA COLLEGE OF ENGINEERING AND TECHNOLOGY VIRUDHUNAGAR Department of Electronics and Communication Engineering
 SRI VIDYA COLLEGE OF ENGINEERING AND TECHNOLOGY VIRUDHUNAGAR Department of Electronics and Communication Engineering Class/Sem:I ECE/II Question Bank for EC6201-ELECTRONIC DEVICES 1.What do u meant by
SRI VIDYA COLLEGE OF ENGINEERING AND TECHNOLOGY VIRUDHUNAGAR Department of Electronics and Communication Engineering Class/Sem:I ECE/II Question Bank for EC6201-ELECTRONIC DEVICES 1.What do u meant by
Electronic Circuits for Mechatronics ELCT 609 Lecture 2: PN Junctions (1)
 Electronic Circuits for Mechatronics ELCT 609 Lecture 2: PN Junctions (1) Assistant Professor Office: C3.315 E-mail: eman.azab@guc.edu.eg 1 Electronic (Semiconductor) Devices P-N Junctions (Diodes): Physical
Electronic Circuits for Mechatronics ELCT 609 Lecture 2: PN Junctions (1) Assistant Professor Office: C3.315 E-mail: eman.azab@guc.edu.eg 1 Electronic (Semiconductor) Devices P-N Junctions (Diodes): Physical
Electronics Fets and Mosfets Prof D C Dube Department of Physics Indian Institute of Technology, Delhi
 Electronics Fets and Mosfets Prof D C Dube Department of Physics Indian Institute of Technology, Delhi Module No. #05 Lecture No. #02 FETS and MOSFETS (contd.) In the previous lecture, we studied the working
Electronics Fets and Mosfets Prof D C Dube Department of Physics Indian Institute of Technology, Delhi Module No. #05 Lecture No. #02 FETS and MOSFETS (contd.) In the previous lecture, we studied the working
4. I-V characteristics of electric
 KL 4. - characteristics of electric conductors 4.1 ntroduction f an electric conductor is connected to a voltage source with voltage a current is produced. We define resistance being the ratio of the voltage
KL 4. - characteristics of electric conductors 4.1 ntroduction f an electric conductor is connected to a voltage source with voltage a current is produced. We define resistance being the ratio of the voltage
The Three terminal MOS structure. Semiconductor Devices: Operation and Modeling 115
 The Three terminal MOS structure 115 Introduction MOS transistor two terminal MOS with another two opposite terminal (back to back of inversion layer). Theses two new terminal make the current flow if
The Three terminal MOS structure 115 Introduction MOS transistor two terminal MOS with another two opposite terminal (back to back of inversion layer). Theses two new terminal make the current flow if
Review Energy Bands Carrier Density & Mobility Carrier Transport Generation and Recombination
 Review Energy Bands Carrier Density & Mobility Carrier Transport Generation and Recombination The Metal-Semiconductor Junction: Review Energy band diagram of the metal and the semiconductor before (a)
Review Energy Bands Carrier Density & Mobility Carrier Transport Generation and Recombination The Metal-Semiconductor Junction: Review Energy band diagram of the metal and the semiconductor before (a)
Classification of Solids
 Classification of Solids Classification by conductivity, which is related to the band structure: (Filled bands are shown dark; D(E) = Density of states) Class Electron Density Density of States D(E) Examples
Classification of Solids Classification by conductivity, which is related to the band structure: (Filled bands are shown dark; D(E) = Density of states) Class Electron Density Density of States D(E) Examples
The photovoltaic effect occurs in semiconductors where there are distinct valence and
 How a Photovoltaic Cell Works The photovoltaic effect occurs in semiconductors where there are distinct valence and conduction bands. (There are energies at which electrons can not exist within the solid)
How a Photovoltaic Cell Works The photovoltaic effect occurs in semiconductors where there are distinct valence and conduction bands. (There are energies at which electrons can not exist within the solid)
Lecture 2. Introduction to semiconductors Structures and characteristics in semiconductors
 Lecture 2 Introduction to semiconductors Structures and characteristics in semiconductors Semiconductor p-n junction Metal Oxide Silicon structure Semiconductor contact Literature Glen F. Knoll, Radiation
Lecture 2 Introduction to semiconductors Structures and characteristics in semiconductors Semiconductor p-n junction Metal Oxide Silicon structure Semiconductor contact Literature Glen F. Knoll, Radiation
L03: pn Junctions, Diodes
 8/30/2012 Page 1 of 5 Reference:C:\Users\Bernhard Boser\Documents\Files\Lib\MathCAD\Default\defaults.mcd L03: pn Junctions, Diodes Intrinsic Si Q: What are n, p? Q: Is the Si charged? Q: How could we make
8/30/2012 Page 1 of 5 Reference:C:\Users\Bernhard Boser\Documents\Files\Lib\MathCAD\Default\defaults.mcd L03: pn Junctions, Diodes Intrinsic Si Q: What are n, p? Q: Is the Si charged? Q: How could we make
EE495/695 Introduction to Semiconductors I. Y. Baghzouz ECE Department UNLV
 EE495/695 Introduction to Semiconductors I Y. Baghzouz ECE Department UNLV Introduction Solar cells have always been aligned closely with other electronic devices. We will cover the basic aspects of semiconductor
EE495/695 Introduction to Semiconductors I Y. Baghzouz ECE Department UNLV Introduction Solar cells have always been aligned closely with other electronic devices. We will cover the basic aspects of semiconductor
Solid State Physics SEMICONDUCTORS - IV. Lecture 25. A.H. Harker. Physics and Astronomy UCL
 Solid State Physics SEMICONDUCTORS - IV Lecture 25 A.H. Harker Physics and Astronomy UCL 9.9 Carrier diffusion and recombination Suppose we have a p-type semiconductor, i.e. n h >> n e. (1) Create a local
Solid State Physics SEMICONDUCTORS - IV Lecture 25 A.H. Harker Physics and Astronomy UCL 9.9 Carrier diffusion and recombination Suppose we have a p-type semiconductor, i.e. n h >> n e. (1) Create a local
Metal Semiconductor Contacts
 Metal Semiconductor Contacts The investigation of rectification in metal-semiconductor contacts was first described by Braun [33-35], who discovered in 1874 the asymmetric nature of electrical conduction
Metal Semiconductor Contacts The investigation of rectification in metal-semiconductor contacts was first described by Braun [33-35], who discovered in 1874 the asymmetric nature of electrical conduction
Recombination: Depletion. Auger, and Tunnelling
 Recombination: Depletion Region, Bulk, Radiative, Auger, and Tunnelling Ch 140 Lecture Notes #13 Prepared by David Gleason We assume: Review of Depletion Region Recombination Flat Quantum Fermi Levels
Recombination: Depletion Region, Bulk, Radiative, Auger, and Tunnelling Ch 140 Lecture Notes #13 Prepared by David Gleason We assume: Review of Depletion Region Recombination Flat Quantum Fermi Levels
Semiconductor Junctions
 8 Semiconductor Junctions Almost all solar cells contain junctions between different materials of different doping. Since these junctions are crucial to the operation of the solar cell, we will discuss
8 Semiconductor Junctions Almost all solar cells contain junctions between different materials of different doping. Since these junctions are crucial to the operation of the solar cell, we will discuss
ECE 440 Lecture 20 : PN Junction Electrostatics II Class Outline:
 ECE 440 Lecture 20 : PN Junction Electrostatics II Class Outline: Depletion Approximation Step Junction Things you should know when you leave Key Questions What is the space charge region? What are the
ECE 440 Lecture 20 : PN Junction Electrostatics II Class Outline: Depletion Approximation Step Junction Things you should know when you leave Key Questions What is the space charge region? What are the
Qualitative Picture of the Ideal Diode. G.R. Tynan UC San Diego MAE 119 Lecture Notes
 Qualitative Picture of the Ideal Diode G.R. Tynan UC San Diego MAE 119 Lecture Notes Band Theory of Solids: From Single Attoms to Solid Crystals Isolated Li atom (conducting metal) Has well-defined, isolated
Qualitative Picture of the Ideal Diode G.R. Tynan UC San Diego MAE 119 Lecture Notes Band Theory of Solids: From Single Attoms to Solid Crystals Isolated Li atom (conducting metal) Has well-defined, isolated
Semiconductor device structures are traditionally divided into homojunction devices
 0. Introduction: Semiconductor device structures are traditionally divided into homojunction devices (devices consisting of only one type of semiconductor material) and heterojunction devices (consisting
0. Introduction: Semiconductor device structures are traditionally divided into homojunction devices (devices consisting of only one type of semiconductor material) and heterojunction devices (consisting
Misan University College of Engineering Electrical Engineering Department. Exam: Final semester Date: 17/6/2017
 Misan University College of Engineering Electrical Engineering Department Subject: Electronic I Class: 1 st stage Exam: Final semester Date: 17/6/2017 Examiner: Dr. Baqer. O. TH. Time: 3 hr. Note: Answer
Misan University College of Engineering Electrical Engineering Department Subject: Electronic I Class: 1 st stage Exam: Final semester Date: 17/6/2017 Examiner: Dr. Baqer. O. TH. Time: 3 hr. Note: Answer
EE 446/646 Photovoltaic Devices I. Y. Baghzouz
 EE 446/646 Photovoltaic Devices I Y. Baghzouz What is Photovoltaics? First used in about 1890, the word has two parts: photo, derived from the Greek word for light, volt, relating to electricity pioneer
EE 446/646 Photovoltaic Devices I Y. Baghzouz What is Photovoltaics? First used in about 1890, the word has two parts: photo, derived from the Greek word for light, volt, relating to electricity pioneer
6.012 Electronic Devices and Circuits
 Page 1 of 1 YOUR NAME Department of Electrical Engineering and Computer Science Massachusetts Institute of Technology 6.12 Electronic Devices and Circuits Exam No. 1 Wednesday, October 7, 29 7:3 to 9:3
Page 1 of 1 YOUR NAME Department of Electrical Engineering and Computer Science Massachusetts Institute of Technology 6.12 Electronic Devices and Circuits Exam No. 1 Wednesday, October 7, 29 7:3 to 9:3
3.1 Absorption and Transparency
 3.1 Absorption and Transparency 3.1.1 Optical Devices (definitions) 3.1.2 Photon and Semiconductor Interactions 3.1.3 Photon Intensity 3.1.4 Absorption 3.1 Absorption and Transparency Objective 1: Recall
3.1 Absorption and Transparency 3.1.1 Optical Devices (definitions) 3.1.2 Photon and Semiconductor Interactions 3.1.3 Photon Intensity 3.1.4 Absorption 3.1 Absorption and Transparency Objective 1: Recall
FIBER OPTICS. Prof. R.K. Shevgaonkar. Department of Electrical Engineering. Indian Institute of Technology, Bombay. Lecture: 12.
 FIBER OPTICS Prof. R.K. Shevgaonkar Department of Electrical Engineering Indian Institute of Technology, Bombay Lecture: 12 Optical Sources Fiber Optics, Prof. R.K. Shevgaonkar, Dept. of Electrical Engineering,
FIBER OPTICS Prof. R.K. Shevgaonkar Department of Electrical Engineering Indian Institute of Technology, Bombay Lecture: 12 Optical Sources Fiber Optics, Prof. R.K. Shevgaonkar, Dept. of Electrical Engineering,
Final Examination EE 130 December 16, 1997 Time allotted: 180 minutes
 Final Examination EE 130 December 16, 1997 Time allotted: 180 minutes Problem 1: Semiconductor Fundamentals [30 points] A uniformly doped silicon sample of length 100µm and cross-sectional area 100µm 2
Final Examination EE 130 December 16, 1997 Time allotted: 180 minutes Problem 1: Semiconductor Fundamentals [30 points] A uniformly doped silicon sample of length 100µm and cross-sectional area 100µm 2
Electronic Circuits 1. Transistor Devices. Contents BJT and FET Characteristics Operations. Prof. C.K. Tse: Transistor devices
 Electronic Circuits 1 Transistor Devices Contents BJT and FET Characteristics Operations 1 What is a transistor? Three-terminal device whose voltage-current relationship is controlled by a third voltage
Electronic Circuits 1 Transistor Devices Contents BJT and FET Characteristics Operations 1 What is a transistor? Three-terminal device whose voltage-current relationship is controlled by a third voltage
16EC401 BASIC ELECTRONIC DEVICES UNIT I PN JUNCTION DIODE. Energy Band Diagram of Conductor, Insulator and Semiconductor:
 16EC401 BASIC ELECTRONIC DEVICES UNIT I PN JUNCTION DIODE Energy bands in Intrinsic and Extrinsic silicon: Energy Band Diagram of Conductor, Insulator and Semiconductor: 1 2 Carrier transport: Any motion
16EC401 BASIC ELECTRONIC DEVICES UNIT I PN JUNCTION DIODE Energy bands in Intrinsic and Extrinsic silicon: Energy Band Diagram of Conductor, Insulator and Semiconductor: 1 2 Carrier transport: Any motion
Semiconductor Detectors
 Semiconductor Detectors Summary of Last Lecture Band structure in Solids: Conduction band Conduction band thermal conductivity: E g > 5 ev Valence band Insulator Charge carrier in conductor: e - Charge
Semiconductor Detectors Summary of Last Lecture Band structure in Solids: Conduction band Conduction band thermal conductivity: E g > 5 ev Valence band Insulator Charge carrier in conductor: e - Charge
ECE 250 Electronic Devices 1. Electronic Device Modeling
 ECE 250 Electronic Devices 1 ECE 250 Electronic Device Modeling ECE 250 Electronic Devices 2 Introduction to Semiconductor Physics You should really take a semiconductor device physics course. We can only
ECE 250 Electronic Devices 1 ECE 250 Electronic Device Modeling ECE 250 Electronic Devices 2 Introduction to Semiconductor Physics You should really take a semiconductor device physics course. We can only
Lecture 16 - The pn Junction Diode (II) Equivalent Circuit Model. April 8, 2003
 6.012 - Microelectronic Devices and Circuits - Spring 2003 Lecture 16-1 Lecture 16 - The pn Junction Diode (II) Equivalent Circuit Model April 8, 2003 Contents: 1. I-V characteristics (cont.) 2. Small-signal
6.012 - Microelectronic Devices and Circuits - Spring 2003 Lecture 16-1 Lecture 16 - The pn Junction Diode (II) Equivalent Circuit Model April 8, 2003 Contents: 1. I-V characteristics (cont.) 2. Small-signal
Lecture-4 Junction Diode Characteristics
 1 Lecture-4 Junction Diode Characteristics Part-II Q: Aluminum is alloyed into n-type Si sample (N D = 10 16 cm 3 ) forming an abrupt junction of circular cross-section, with an diameter of 0.02 in. Assume
1 Lecture-4 Junction Diode Characteristics Part-II Q: Aluminum is alloyed into n-type Si sample (N D = 10 16 cm 3 ) forming an abrupt junction of circular cross-section, with an diameter of 0.02 in. Assume
Junction Diodes. Tim Sumner, Imperial College, Rm: 1009, x /18/2006
 Junction Diodes Most elementary solid state junction electronic devices. They conduct in one direction (almost correct). Useful when one converts from AC to DC (rectifier). But today diodes have a wide
Junction Diodes Most elementary solid state junction electronic devices. They conduct in one direction (almost correct). Useful when one converts from AC to DC (rectifier). But today diodes have a wide
Chemistry Instrumental Analysis Lecture 8. Chem 4631
 Chemistry 4631 Instrumental Analysis Lecture 8 UV to IR Components of Optical Basic components of spectroscopic instruments: stable source of radiant energy transparent container to hold sample device
Chemistry 4631 Instrumental Analysis Lecture 8 UV to IR Components of Optical Basic components of spectroscopic instruments: stable source of radiant energy transparent container to hold sample device
Energetic particles and their detection in situ (particle detectors) Part II. George Gloeckler
 Energetic particles and their detection in situ (particle detectors) Part II George Gloeckler University of Michigan, Ann Arbor, MI University of Maryland, College Park, MD Simple particle detectors Gas-filled
Energetic particles and their detection in situ (particle detectors) Part II George Gloeckler University of Michigan, Ann Arbor, MI University of Maryland, College Park, MD Simple particle detectors Gas-filled
Diodes. EE223 Digital & Analogue Electronics Derek Molloy 2012/2013.
 Diodes EE223 Digital & Analogue Electronics Derek Molloy 2012/2013 Derek.Molloy@dcu.ie Diodes: A Semiconductor? Conductors Such as copper, aluminium have a cloud of free electrons weak bound valence electrons
Diodes EE223 Digital & Analogue Electronics Derek Molloy 2012/2013 Derek.Molloy@dcu.ie Diodes: A Semiconductor? Conductors Such as copper, aluminium have a cloud of free electrons weak bound valence electrons
A SEMICONDUCTOR DIODE. P-N Junction
 A SEMICONDUCTOR DIODE P-N Junction Analog Electronics Pujianto Department of Physics Edu. State University of Yogyakarta A Semiconductor Devices A Semiconductor devices can be defined as a unit which consists,
A SEMICONDUCTOR DIODE P-N Junction Analog Electronics Pujianto Department of Physics Edu. State University of Yogyakarta A Semiconductor Devices A Semiconductor devices can be defined as a unit which consists,
PN Junction and MOS structure
 PN Junction and MOS structure Basic electrostatic equations We will use simple one-dimensional electrostatic equations to develop insight and basic understanding of how semiconductor devices operate Gauss's
PN Junction and MOS structure Basic electrostatic equations We will use simple one-dimensional electrostatic equations to develop insight and basic understanding of how semiconductor devices operate Gauss's
Quiz #1 Practice Problem Set
 Name: Student Number: ELEC 3908 Physical Electronics Quiz #1 Practice Problem Set? Minutes January 22, 2016 - No aids except a non-programmable calculator - All questions must be answered - All questions
Name: Student Number: ELEC 3908 Physical Electronics Quiz #1 Practice Problem Set? Minutes January 22, 2016 - No aids except a non-programmable calculator - All questions must be answered - All questions
Lecture 2. Introduction to semiconductors Structures and characteristics in semiconductors
 Lecture 2 Introduction to semiconductors Structures and characteristics in semiconductors Semiconductor p-n junction Metal Oxide Silicon structure Semiconductor contact Literature Glen F. Knoll, Radiation
Lecture 2 Introduction to semiconductors Structures and characteristics in semiconductors Semiconductor p-n junction Metal Oxide Silicon structure Semiconductor contact Literature Glen F. Knoll, Radiation
Module - 01 Assignment - 02 Intrinsic Semiconductors. In today's assignment class, we will be looking fully at intrinsic semiconductors.
 Electronic Materials, Devices and Fabrication Dr. S. Parasuraman Department of Metallurgical and Materials Engineering Indian Institute of Technology, Madras Module - 01 Assignment - 02 Intrinsic Semiconductors
Electronic Materials, Devices and Fabrication Dr. S. Parasuraman Department of Metallurgical and Materials Engineering Indian Institute of Technology, Madras Module - 01 Assignment - 02 Intrinsic Semiconductors
5. Semiconductors and P-N junction
 5. Semiconductors and P-N junction Thomas Zimmer, University of Bordeaux, France Summary Learning Outcomes... 2 Physical background of semiconductors... 2 The silicon crystal... 2 The energy bands... 3
5. Semiconductors and P-N junction Thomas Zimmer, University of Bordeaux, France Summary Learning Outcomes... 2 Physical background of semiconductors... 2 The silicon crystal... 2 The energy bands... 3
Semiconductor Optoelectronics Prof. M. R. Shenoy Department of Physics Indian Institute of Technology, Delhi. Lecture - 13 Band gap Engineering
 Semiconductor Optoelectronics Prof. M. R. Shenoy Department of Physics Indian Institute of Technology, Delhi Lecture - 13 Band gap Engineering (Refer Slide Time: 00:38) Let us continue with the lectures,
Semiconductor Optoelectronics Prof. M. R. Shenoy Department of Physics Indian Institute of Technology, Delhi Lecture - 13 Band gap Engineering (Refer Slide Time: 00:38) Let us continue with the lectures,
PHYSICAL ELECTRONICS(ECE3540) CHAPTER 9 METAL SEMICONDUCTOR AND SEMICONDUCTOR HETERO-JUNCTIONS
 PHYSICAL ELECTRONICS(ECE3540) CHAPTER 9 METAL SEMICONDUCTOR AND SEMICONDUCTOR HETERO-JUNCTIONS Tennessee Technological University Monday, November 11, 013 1 Introduction Chapter 4: we considered the semiconductor
PHYSICAL ELECTRONICS(ECE3540) CHAPTER 9 METAL SEMICONDUCTOR AND SEMICONDUCTOR HETERO-JUNCTIONS Tennessee Technological University Monday, November 11, 013 1 Introduction Chapter 4: we considered the semiconductor
