3.4 Conic sections. Such type of curves are called conics, because they arise from different slices through a cone
|
|
|
- Berniece Parsons
- 5 years ago
- Views:
Transcription
1 3.4 Conic sections Next we consider the objects resulting from ax 2 + bxy + cy ey + f = 0. Such type of curves are called conics, because they arise from different slices through a cone Circles belong to a special class of curves called conic sections. Other such curves are the ellipse, parabola, and hyperbola. Andreas Fring (City University London) AS1051 Lecture Autumn / 40 In polar coordinates (r, θ) conics are parameterized as 0 = r k 1 e cosθ k > 0, e 0 e is called the eccentricity k is an overall constant Transform into Cartesian coordinates: With x = r cosθ and y = r sinθ r = k + e r cosθ r 2 = (k + e r cosθ) 2 x 2 + y 2 = (k + ex) 2 = e 2 (k/e + x) 2 Andreas Fring (City University London) AS1051 Lecture Autumn / 40
2 Geometrical interpretation of x 2 + y 2 = e 2 (k/e + x) 2 : D P(x, y) F(0, 0) FP = x 2 + y 2 DP = x + k e x = k e FP = edp Thus a conic is described by all the points P, such that the distance to a fixed point F is a fixed ratio to a line x = k e, called the directrix. Andreas Fring (City University London) AS1051 Lecture Autumn / The ellipse (e < 1) Manipulating x 2 + y 2 = e 2 (k/e + x) 2 gives Transforming the variables: (1 e 2 )(x ke 1 e 2 )2 + y 2 = k 2 1 e 2 x X = x yields the normal form of the ellipse ke 1 e 2 y Y X 2 a 2 + Y 2 b 2 = 1 with a := k and b := k 1 e 2 1 e. 2 We can also express k, e in terms of a, b We shifted the focus by k = b2 a e = 1 b2 a 2 ke 1 e 2 =: c = e a. e = 0 is a circle of radius k. Andreas Fring (City University London) AS1051 Lecture Autumn / 40
3 Collecting everything gives ae ae 2b a/e 2a a/e The distance 2a is called the major axis and the distance 2b is called the minor axis.the foci are at ±e a. The two directrices are at ±a/e. We can parametrise the ellipse by or with rational function by X(φ) = acosφ Y (φ) = bsinφ X(t) = a 1 t2 1 + t 2 Y (t) = b 2t 1 + t 2. Andreas Fring (City University London) AS1051 Lecture Autumn / The hyperbola (e > 1) Similarly as for the ellipse but now (1 e 2 ) < 0. (1 e 2 ) 2 k 2 X 2 + (1 e2 ) k 2 Y 2 = 1 Therefore the normal form of the hyperbola becomes X 2 a 2 Y 2 b 2 = 1 with a := k and b := k 1 e 2 e. 2 1 Expressing k, e in terms of a, b k = b2 a e = 1 + b2 a 2 Andreas Fring (City University London) AS1051 Lecture Autumn / 40
4 ae a 2a a ae a/e a/e The shortest distance between the two sections of the curve is called the major axis, equalling 2a. The two directrices are at ±a/e. We can parametrise the hyperbola by X ± (φ) = ±acoshφ Y (φ) = bsinhφ Andreas Fring (City University London) AS1051 Lecture Autumn / The parabola (e = 1) Now we have x 2 + y 2 = (k + x) 2 such that y 2 = 2kx + k 2 Transforming the variables: x X = x + k 2 y Y yields the normal form of the parabola with a := k/2. Y 2 = 4aX Andreas Fring (City University London) AS1051 Lecture Autumn / 40
5 a a Now we have only one focus at The directrix is at x = a. (a, 0) The curve parabola can be parameterised by X = at 2 Y = 2at Andreas Fring (City University London) AS1051 Lecture Autumn / 40 Example 3.4.1: Determine the foci and directices of the ellipse (x 2) (y + 3)2 16 We compare with X 2 a 2 + Y 2 b 2 = 1. To transform in this way we must have = 1. X = x 2 Y = y + 3 a = 5 b = 4. Also b 2 = a 2 (1 e 2 ) implies that e = 3 5. Therefore the centre of the ellipse is at (2, 3), the major axis has length 2a = 10 and the minor axis has length 2b = 8. Andreas Fring (City University London) AS1051 Lecture Autumn / 40
6 The foci lie on the major axis at distance ae = 3 from the centre. So the foci are (5, 3) ( 1, 3). Directrices are perpendicular to the major axis and at distance a e = 25 3 from the centre. So the directrices are x = 31 3 x = Andreas Fring (City University London) AS1051 Lecture Autumn / 40 Example 3.4.2: An ellipse has foci at (2, 5) and (8, 5) and eccentricity e = 1 4. Find its Cartesian equation. The centre is midway between the foci, so lies at (5, 5). The distance from the centre to each focus is ae = 3, and so a = 12. Therefore b 2 = a 2 (1 e 2 ) = 135. From this we see that the equation is given by (x 5) (y 5)2 135 = 1. Andreas Fring (City University London) AS1051 Lecture Autumn / 40
7 Lecture Calculus I: Differentiation 4.1 The derivative of a function Suppose we are given a curve with a point A lying on it. If the curve is smooth at A then we can find a unique tangent to the curve at A: a b c A A A Here the curve in (a) is smooth at A, but the curves in (b) and (c) are not. Andreas Fring (City University London) AS1051 Lecture Autumn / 40 If the tangent is unique then the gradient of the curve at A is defined to be the gradient of the tangent to the curve at A. The process of finding the general gradient function for a curve is called differentiation. B Consider the chord AB. As B gets closer to A, the gradient of the chord gets closer to the gradient of the tangent at A. A Andreas Fring (City University London) AS1051 Lecture Autumn / 40
8 For y = f (x), the gradient function is defined by ( ) ( ) δy f (x + ) f (x) lim = lim. 0 0 (x+,y+ δy) (x,y) δy We denote the gradient function by or f (x), and call it the derivative of f. This is not the formal definition of the derivative, as we have not explained exactly what we mean by the limit as 0. But this intuitive definition will be sufficient for the basic functions which we consider. Andreas Fring (City University London) AS1051 Lecture Autumn / 40 Example 4.1.1: Take f (x) = c, a constant function. At every x the gradient is 0, so f (x) = 0 for all x. Or f (x + ) f (x) = c c = 0. Example 4.1.2: Take f (x) = ax. At every x the gradient is a, so f (x) = a for all x. Or f (x + ) f (x) a(x + ) ax = = a = a. Andreas Fring (City University London) AS1051 Lecture Autumn / 40
9 Example 4.1.3: Take f (x) = x 2. Now we need to consider the second formulation, as we cannot simply read the gradient off from the graph. f (x + ) f (x) = (x + )2 x 2 = x 2 + 2x + () 2 x 2 (2x + ) = = 2x +. The limit as tends to 0 is 2x, so f (x) = 2x. Andreas Fring (City University London) AS1051 Lecture Autumn / 40 Example 4.1.4: Take f (x) = 1 x. f (x + ) f (x) = 1 ( 1 x + 1 ) x x (x + ) = ()(x + )x = ()(x + )x = 1 (x + )x. The limit as tends to 0 is 1 x 2, so f (x) = 1 x 2. Andreas Fring (City University London) AS1051 Lecture Autumn / 40
10 Example 4.1.5: Take f (x) = x n with n N and n > 1. Recall that and so a n b n = (a b)(a n 1 + a n 2 b + a n 3 b b n 1 ) a n b n a b = an 1 + a n 2 b + a n 3 b b n 1 where the sum has n terms. As a b we have ( a n b n ) lim a b a b = lim a b (a n 1 + a n 2 b + a n 3 b b n 1 ) = nb n 1. If a = x + and b = x then ( ) f (x + ) f (x) lim 0 ( a n b n ) = lim = nb n 1 = nx n 1. a b a b Hence f (x) = nx n 1. Andreas Fring (City University London) AS1051 Lecture Autumn / 40 Example 4.1.6: f (x) = sin x. We use the identity for sin A + sin B. and so f (x + ) f (x) = 2 sin f (x + ) f (x) ( 2 ) cos = sin ( ) 2 cos 2 ( x + 2 ( x + 2 ) ). We need the following fact (which we will not prove here): sin θ lim θ 0 θ = 1 and so f (x) = lim ( sin ) cos ( x + 2 ) = cos(x). Andreas Fring (City University London) AS1051 Lecture Autumn / 40
11 Some standard derivatives, which must be memorised: f (x) f (x) x k e x kx k 1 e x 1 ln x x sin x cos x cos x sin x tan x sec 2 x cosec x cosec x cot x sec x sec x tan x cot x cosec 2 x Some of these results can be derived from the results in the following sections, or from first principles. However it is much more efficient to know them. Andreas Fring (City University London) AS1051 Lecture Autumn / 40 Lecture Differentiation of compound functions Once we know a few basic derivatives, we can determine many others using the following rules: Let u(x) and v(x) be functions of x, and a and b be constants. Function Derivative Sum and difference au ± bv a du ± b dv Product uv v du + u dv u v Quotient dv u v v du 2 Composite u(v(x)) dz. dz where z = v(x). The final rule above is known as the chain rule and has the following special case u(ax + b) a du (ax + b) For example, the derivative of sin(ax + b) is a cos(ax + b). Andreas Fring (City University London) AS1051 Lecture Autumn / 40
12 Example 4.2.1: Differentiate y = 2x 5 3x x 2. = 10x 4 9x 2 8 x 3. Example 4.2.2: Differentiate y = x 2 1 x = (x 2 + 1)2x (x 2 1)2x (x 2 + 1) 2 = 4x (x 2 + 1) 2. Andreas Fring (City University London) AS1051 Lecture Autumn / 40 Example 4.2.3: Differentiate y = x 2 ln(x + 3). = 2x ln(x + 3) + x 2 x + 3. Example 4.2.4: Differentiate y = e 5x. Set z = 5x, then = dz dz = ez 5 = 5e 5x. Andreas Fring (City University London) AS1051 Lecture Autumn / 40
13 Example 4.2.5: Differentiate y = 4 sin(2x + 3). Set z = 2x + 3, then = dz dz = 4 cos(z)2 = 8 cos(2x + 3). As we have alrea noted, some of the standard derivatives can be deduced from the others. Example 4.2.6: Differentiate y = tan x = sin x cos x. = cos x cos x sin x( sin x) cos 2 x = cos2 x + sin 2 x cos 2 x = 1 cos 2 x = sec2 x. Andreas Fring (City University London) AS1051 Lecture Autumn / 40 Example 4.2.7: y = cosec x = 1 sin x. = sin x.(0) 1. cos x sin 2 x = cos x sin 2 x = cosec x cot x. Example 4.2.8: y = ln(x + x 2 + 1), i.e. y = ln u where u = x + x so = 1 du u ( = 1 x x = and ) x x x + x du = 1 + (x 2 + 1) 2 ( x x x ).2x = 1 x Andreas Fring (City University London) AS1051 Lecture Autumn / 40
14 Example 4.2.9: y = x x. We have y = (e ln x ) x = e (x ln x), i.e. y = e u where u = x ln x. = eu du = ex ln x (ln(x) + 1) = x x (ln(x) + 1). 4.3 Higher derivatives The derivative is itself a function, so we can consider its derivative. If y = f (x) then we denote the second derivative, i.e. the derivative of with respect to x, by d2 y or f (x). We can also calculate the higher 2 derivatives dn y or f (n) (x). n Andreas Fring (City University London) AS1051 Lecture Autumn / 40 Example 4.3.1: y = ln(1 + x 2 ). Let z = = 2x 1+x 2. d 2 y 2 = dz = (1 + x 2 ).2 2x(2x) (1 + x 2 ) 2 = 2(1 x 2 ) (1 + x 2 ) 2. Example 4.3.2: Show that y = e x sin(2x) satisfies d 2 y y = 0. = e x sin 2x + 2e x cos 2x = e x (2 cos 2x sin 2x) d 2 y 2 = e x (2 cos 2x sin 2x) + e x ( 4 sin 2x 2 cos 2x) = e x ( 3 sin 2x 4 cos 2x). Andreas Fring (City University London) AS1051 Lecture Autumn / 40
15 Writing s for sin 2x and c for cos 2x we have y + 2y + 5y = e x ( 3s 4c 2s + 4c + 5s) = 0. Example 4.3.3: Evaluate at x = 0. d 3 3 ( 1 + 3x 2 ) (1 + x) 2 (1 + 3x) We could use the quotient rule, but this will get complicated. Instead we use partial fractions. y = 1 + 3x 2 (1 + x) 2 (1 + 3x) = A 1 + x + B (1 + x) 2 + C 1 + 3x. We obtain (check!) A = 0, B = 2, and C = 3. Andreas Fring (City University London) AS1051 Lecture Autumn / 40 Now = 4 (1 + x) 3 9 (1 + 3x) 2 d 2 y 2 = 12 (1 + x) (1 + 3x) 3 d 3 y 3 = 48 (1 + x) (1 + 3x) 4 and substituting x = 0 we obtain that d 3 y (0) = = Andreas Fring (City University London) AS1051 Lecture Autumn / 40
16 Lecture 16 Generally it is hard to give a simple formula for the nth derivative of a function. However, in some cases it is possible. The following can be proved by induction. Example 4.3.4: y = e ax. = aeax and d 2 y 2 = a2 e ax. We can show that d n y n = an e ax. Andreas Fring (City University London) AS1051 Lecture Autumn / 40 Example 4.3.5: y = sin(ax). y = a cos(ax) = a sin(ax + π 2 ) y = a 2 sin(ax) = a 2 sin(ax + π) y = a 3 cos(ax) = a 3 sin(ax + 3π 2 ) y (iv) = a 4 sin(ax) = a 4 sin(ax + 2π). We can show that d n y n = an sin(ax + nπ 2 ). Andreas Fring (City University London) AS1051 Lecture Autumn / 40
17 4.4 Differentiating implicit functions Sometimes we cannot rearrange a function into the form y = f (x), or we may wish to consider the original form anyway (for example, because it is simpler). However, we may still wish to differentiate with respect to x. Given a function g(y) we have from the chain rule d (g(y)) = d (g(y)). Andreas Fring (City University London) AS1051 Lecture Autumn / 40 Example 4.4.1: x 2 + 3xy 2 y 4 = 2. Therefore we have d (x 2 + 3xy 2 y 4 ) = d (2) = 0. 2x + d (3xy 2 ) d (y 4 ) = 0 2x + 3y 2 + 3x d (y 2 ) 4y 3 2x + 3y 2 + 6xy 4y 3 = 0 = 0. Andreas Fring (City University London) AS1051 Lecture Autumn / 40
18 Example 4.4.2: 2 x y 2 = 1 2. d ( 2 x y 2 ) = d (1 2 ) = 0. Therefore we have 4 x 3 + d ( ) 3 y 2 4 x 3 6 y 3 = 0 = 0. Andreas Fring (City University London) AS1051 Lecture Autumn / Differentiating parametric equations Sometimes there is no easy way to express the relationship between x and y directly in a single equation. In such cases it may be possible to express the relationship between them by writing each in terms of a third variable. We call such equations parametric equations as both x and y depend on a common parameter. Example 4.5.1: x = t 3 y = t 2 4t + 2. Although we can write this in the form y = x 2 3 4x the parametric version is easier to work with. Andreas Fring (City University London) AS1051 Lecture Autumn / 40
19 To differentiate a parametric equation in the variable t we use = dt dt and dt = 1. dt Example 4.5.1: (Continued.) dt = 2t 4 dt = 3t 2 and so = 2t 4 3t 2. Andreas Fring (City University London) AS1051 Lecture Autumn / 40 Example 4.5.2: Find the second derivative with respect to x of x = sin θ y = cos 2θ. We have Therefore Now d 2 y 2 = d dθ = cos θ dθ = 2 sin 2θ cos θ ( ) = d ( 4 sin θ) = d dθ = 2 sin 2θ. = 4 sin θ. ( 4 sin θ) dθ = 4 cos θ cos θ = 4. Andreas Fring (City University London) AS1051 Lecture Autumn / 40
20 Note: The rules so far may suggest that derivatives can be treated just like fractions. However d 2 y 2 d2 y d 2 t dt 2 2 in general. Moreover d 2 ( y d 2 ) 1 2 x 2. Andreas Fring (City University London) AS1051 Lecture Autumn / 40 Example 4.5.2: (Continued.) We have and Therefore d 2 θ 2 = d d 2 y dθ 2 = 4 cos 2θ = 4(sin2 θ cos 2 θ) ( ) dθ = d ( ) dθ dθ (sec θ) = sec 2 θ tan θ. d 2 y d 2 θ dθ 2 2 = 4 tan3 θ 4 tan θ 4 = d2 y 2. Andreas Fring (City University London) AS1051 Lecture Autumn / 40
x n cos 2x dx. dx = nx n 1 and v = 1 2 sin(2x). Andreas Fring (City University London) AS1051 Lecture Autumn / 36
 We saw in Example 5.4. that we sometimes need to apply integration by parts several times in the course of a single calculation. Example 5.4.4: For n let S n = x n cos x dx. Find an expression for S n
We saw in Example 5.4. that we sometimes need to apply integration by parts several times in the course of a single calculation. Example 5.4.4: For n let S n = x n cos x dx. Find an expression for S n
3.4 Conic sections. In polar coordinates (r, θ) conics are parameterized as. Next we consider the objects resulting from
 3.4 Conic sections Net we consier the objects resulting from + by + cy + + ey + f 0. Such type of cures re clle conics, becuse they rise from ifferent slices through cone In polr coorintes r, θ) conics
3.4 Conic sections Net we consier the objects resulting from + by + cy + + ey + f 0. Such type of cures re clle conics, becuse they rise from ifferent slices through cone In polr coorintes r, θ) conics
ECM Calculus and Geometry. Revision Notes
 ECM1702 - Calculus and Geometry Revision Notes Joshua Byrne Autumn 2011 Contents 1 The Real Numbers 1 1.1 Notation.................................................. 1 1.2 Set Notation...............................................
ECM1702 - Calculus and Geometry Revision Notes Joshua Byrne Autumn 2011 Contents 1 The Real Numbers 1 1.1 Notation.................................................. 1 1.2 Set Notation...............................................
(x,y) 4. Calculus I: Differentiation
 4. Calculus I: Differentiation 4. The eriatie of a function Suppose we are gien a cure with a point lying on it. If the cure is smooth at then we can fin a unique tangent to the cure at : If the tangent
4. Calculus I: Differentiation 4. The eriatie of a function Suppose we are gien a cure with a point lying on it. If the cure is smooth at then we can fin a unique tangent to the cure at : If the tangent
1.7 Sums of series Example 1.7.1: 2. Real functions of one variable Example 1.7.2: 2.1 General definitions Example 2.1.3: Example 2.1.
 7 Sums of series We often want to sum a series of terms, for example when we look at polynomials As we already saw, we abbreviate a sum of the form For example and u + u + + u r by r u i i= a n x n + a
7 Sums of series We often want to sum a series of terms, for example when we look at polynomials As we already saw, we abbreviate a sum of the form For example and u + u + + u r by r u i i= a n x n + a
PRACTICE PAPER 6 SOLUTIONS
 PRACTICE PAPER 6 SOLUTIONS SECTION A I.. Find the value of k if the points (, ) and (k, 3) are conjugate points with respect to the circle + y 5 + 8y + 6. Sol. Equation of the circle is + y 5 + 8y + 6
PRACTICE PAPER 6 SOLUTIONS SECTION A I.. Find the value of k if the points (, ) and (k, 3) are conjugate points with respect to the circle + y 5 + 8y + 6. Sol. Equation of the circle is + y 5 + 8y + 6
Mathematical Techniques: Revision Notes
 Differentiation Dr A. J. Bevan October 20, 200 Mathematical Techniques: Revision Notes Dr A. J. Bevan, These notes contain the core of the information conveed in the lectures. The are not a substitute
Differentiation Dr A. J. Bevan October 20, 200 Mathematical Techniques: Revision Notes Dr A. J. Bevan, These notes contain the core of the information conveed in the lectures. The are not a substitute
Conic section. Ans: c. Ans: a. Ans: c. Episode:43 Faculty: Prof. A. NAGARAJ. 1. A circle
 Episode:43 Faculty: Prof. A. NAGARAJ Conic section 1. A circle gx fy c 0 is said to be imaginary circle if a) g + f = c b) g + f > c c) g + f < c d) g = f. If (1,-3) is the centre of the circle x y ax
Episode:43 Faculty: Prof. A. NAGARAJ Conic section 1. A circle gx fy c 0 is said to be imaginary circle if a) g + f = c b) g + f > c c) g + f < c d) g = f. If (1,-3) is the centre of the circle x y ax
School of Distance Education UNIVERSITY OF CALICUT SCHOOL OF DISTANCE EDUCATION. B Sc Mathematics. (2011 Admission Onwards) IV Semester.
 School of Dtance Education UNIVERSITY OF CALICUT SCHOOL OF DISTANCE EDUCATION B Sc Mathematics 0 Admsion Onwards IV Semester Core Course CALCULUS AND ANALYTIC GEOMETRY QUESTION BANK The natural logarithm
School of Dtance Education UNIVERSITY OF CALICUT SCHOOL OF DISTANCE EDUCATION B Sc Mathematics 0 Admsion Onwards IV Semester Core Course CALCULUS AND ANALYTIC GEOMETRY QUESTION BANK The natural logarithm
The Distance Formula. The Midpoint Formula
 Math 120 Intermediate Algebra Sec 9.1: Distance Midpoint Formulas The Distance Formula The distance between two points P 1 = (x 1, y 1 ) P 2 = (x 1, y 1 ), denoted by d(p 1, P 2 ), is d(p 1, P 2 ) = (x
Math 120 Intermediate Algebra Sec 9.1: Distance Midpoint Formulas The Distance Formula The distance between two points P 1 = (x 1, y 1 ) P 2 = (x 1, y 1 ), denoted by d(p 1, P 2 ), is d(p 1, P 2 ) = (x
Extra FP3 past paper - A
 Mark schemes for these "Extra FP3" papers at https://mathsmartinthomas.files.wordpress.com/04//extra_fp3_markscheme.pdf Extra FP3 past paper - A More FP3 practice papers, with mark schemes, compiled from
Mark schemes for these "Extra FP3" papers at https://mathsmartinthomas.files.wordpress.com/04//extra_fp3_markscheme.pdf Extra FP3 past paper - A More FP3 practice papers, with mark schemes, compiled from
Lecture 17. Implicit differentiation. Making y the subject: If xy =1,y= x 1 & dy. changed to the subject of y. Note: Example 1.
 Implicit differentiation. Lecture 17 Making y the subject: If xy 1,y x 1 & dy dx x 2. But xy y 2 1 is harder to be changed to the subject of y. Note: d dx (f(y)) f (y) dy dx Example 1. Find dy dx given
Implicit differentiation. Lecture 17 Making y the subject: If xy 1,y x 1 & dy dx x 2. But xy y 2 1 is harder to be changed to the subject of y. Note: d dx (f(y)) f (y) dy dx Example 1. Find dy dx given
CO-ORDINATE GEOMETRY
 CO-ORDINATE GEOMETRY 1 To change from Cartesian coordinates to polar coordinates, for X write r cos θ and for y write r sin θ. 2 To change from polar coordinates to cartesian coordinates, for r 2 write
CO-ORDINATE GEOMETRY 1 To change from Cartesian coordinates to polar coordinates, for X write r cos θ and for y write r sin θ. 2 To change from polar coordinates to cartesian coordinates, for r 2 write
Math 250 Skills Assessment Test
 Math 5 Skills Assessment Test Page Math 5 Skills Assessment Test The purpose of this test is purely diagnostic (before beginning your review, it will be helpful to assess both strengths and weaknesses).
Math 5 Skills Assessment Test Page Math 5 Skills Assessment Test The purpose of this test is purely diagnostic (before beginning your review, it will be helpful to assess both strengths and weaknesses).
Mathematics Extension 1
 009 HIGHER SCHOOL CERTIFICATE EXAMINATION Mathematics Extension General Instructions Reading time 5 minutes Working time hours Write using black or blue pen Board-approved calculators may be used A table
009 HIGHER SCHOOL CERTIFICATE EXAMINATION Mathematics Extension General Instructions Reading time 5 minutes Working time hours Write using black or blue pen Board-approved calculators may be used A table
MATHEMATICS FOR ENGINEERING DIFFERENTIATION TUTORIAL 2 ADVANCED DIFFERENTIATION
 MATHEMATICS FOR ENGINEERING DIFFERENTIATION TUTORIAL ADVANCED DIFFERENTIATION CONTENTS Function of a Function Differentiation of a Sum Differentiation of a Proct Differentiation of a Quotient Turning Points
MATHEMATICS FOR ENGINEERING DIFFERENTIATION TUTORIAL ADVANCED DIFFERENTIATION CONTENTS Function of a Function Differentiation of a Sum Differentiation of a Proct Differentiation of a Quotient Turning Points
2.2 The derivative as a Function
 2.2 The derivative as a Function Recall: The derivative of a function f at a fixed number a: f a f a+h f(a) = lim h 0 h Definition (Derivative of f) For any number x, the derivative of f is f x f x+h f(x)
2.2 The derivative as a Function Recall: The derivative of a function f at a fixed number a: f a f a+h f(a) = lim h 0 h Definition (Derivative of f) For any number x, the derivative of f is f x f x+h f(x)
Distance and Midpoint Formula 7.1
 Distance and Midpoint Formula 7.1 Distance Formula d ( x - x ) ( y - y ) 1 1 Example 1 Find the distance between the points (4, 4) and (-6, -). Example Find the value of a to make the distance = 10 units
Distance and Midpoint Formula 7.1 Distance Formula d ( x - x ) ( y - y ) 1 1 Example 1 Find the distance between the points (4, 4) and (-6, -). Example Find the value of a to make the distance = 10 units
Honors Precalculus Chapter 8 Summary Conic Sections- Parabola
 Honors Precalculus Chapter 8 Summary Conic Sections- Parabola Definition: Focal length: y- axis P(x, y) Focal chord: focus Vertex x-axis directrix Focal width/ Latus Rectum: Derivation of equation of parabola:
Honors Precalculus Chapter 8 Summary Conic Sections- Parabola Definition: Focal length: y- axis P(x, y) Focal chord: focus Vertex x-axis directrix Focal width/ Latus Rectum: Derivation of equation of parabola:
3. On the grid below, sketch and label graphs of the following functions: y = sin x, y = cos x, and y = sin(x π/2). π/2 π 3π/2 2π 5π/2
 AP Physics C Calculus C.1 Name Trigonometric Functions 1. Consider the right triangle to the right. In terms of a, b, and c, write the expressions for the following: c a sin θ = cos θ = tan θ =. Using
AP Physics C Calculus C.1 Name Trigonometric Functions 1. Consider the right triangle to the right. In terms of a, b, and c, write the expressions for the following: c a sin θ = cos θ = tan θ =. Using
Chapter 3. Integration. 3.1 Indefinite Integration
 Chapter 3 Integration 3. Indefinite Integration Integration is the reverse of differentiation. Consider a function f(x) and suppose that there exists another function F (x) such that df f(x). (3.) For
Chapter 3 Integration 3. Indefinite Integration Integration is the reverse of differentiation. Consider a function f(x) and suppose that there exists another function F (x) such that df f(x). (3.) For
a Write down the coordinates of the point on the curve where t = 2. b Find the value of t at the point on the curve with coordinates ( 5 4, 8).
 Worksheet A 1 A curve is given by the parametric equations x = t + 1, y = 4 t. a Write down the coordinates of the point on the curve where t =. b Find the value of t at the point on the curve with coordinates
Worksheet A 1 A curve is given by the parametric equations x = t + 1, y = 4 t. a Write down the coordinates of the point on the curve where t =. b Find the value of t at the point on the curve with coordinates
Introduction to conic sections. Author: Eduard Ortega
 Introduction to conic sections Author: Eduard Ortega 1 Introduction A conic is a two-dimensional figure created by the intersection of a plane and a right circular cone. All conics can be written in terms
Introduction to conic sections Author: Eduard Ortega 1 Introduction A conic is a two-dimensional figure created by the intersection of a plane and a right circular cone. All conics can be written in terms
THE NATIONAL UNIVERSITY OF IRELAND, CORK COLÁISTE NA hollscoile, CORCAIGH UNIVERSITY COLLEGE, CORK. Summer Examination 2009.
 OLLSCOIL NA héireann, CORCAIGH THE NATIONAL UNIVERSITY OF IRELAND, CORK COLÁISTE NA hollscoile, CORCAIGH UNIVERSITY COLLEGE, CORK Summer Examination 2009 First Engineering MA008 Calculus and Linear Algebra
OLLSCOIL NA héireann, CORCAIGH THE NATIONAL UNIVERSITY OF IRELAND, CORK COLÁISTE NA hollscoile, CORCAIGH UNIVERSITY COLLEGE, CORK Summer Examination 2009 First Engineering MA008 Calculus and Linear Algebra
Functions, Graphs, Equations and Inequalities
 CAEM DPP Learning Outcomes per Module Module Functions, Graphs, Equations and Inequalities Learning Outcomes 1. Functions, inverse functions and composite functions 1.1. concepts of function, domain and
CAEM DPP Learning Outcomes per Module Module Functions, Graphs, Equations and Inequalities Learning Outcomes 1. Functions, inverse functions and composite functions 1.1. concepts of function, domain and
Conic Sections and Polar Graphing Lab Part 1 - Circles
 MAC 1114 Name Conic Sections and Polar Graphing Lab Part 1 - Circles 1. What is the standard equation for a circle with center at the origin and a radius of k? 3. Consider the circle x + y = 9. a. What
MAC 1114 Name Conic Sections and Polar Graphing Lab Part 1 - Circles 1. What is the standard equation for a circle with center at the origin and a radius of k? 3. Consider the circle x + y = 9. a. What
Chapter 10: Conic Sections; Polar Coordinates; Parametric Equations
 Chapter 10: Conic Sections; Polar Coordinates; Parametric Equations Section 10.1 Geometry of Parabola, Ellipse, Hyperbola a. Geometric Definition b. Parabola c. Ellipse d. Hyperbola e. Translations f.
Chapter 10: Conic Sections; Polar Coordinates; Parametric Equations Section 10.1 Geometry of Parabola, Ellipse, Hyperbola a. Geometric Definition b. Parabola c. Ellipse d. Hyperbola e. Translations f.
A-Level Mathematics DIFFERENTIATION I. G. David Boswell - Math Camp Typeset 1.1 DIFFERENTIATION OF POLYNOMIALS. d dx axn = nax n 1, n!
 A-Level Mathematics DIFFERENTIATION I G. David Boswell - Math Camp Typeset 1.1 SET C Review ~ If a and n are real constants, then! DIFFERENTIATION OF POLYNOMIALS Problems ~ Find the first derivative of
A-Level Mathematics DIFFERENTIATION I G. David Boswell - Math Camp Typeset 1.1 SET C Review ~ If a and n are real constants, then! DIFFERENTIATION OF POLYNOMIALS Problems ~ Find the first derivative of
10.1 Review of Parametric Equations
 10.1 Review of Parametric Equations Recall that often, instead of representing a curve using just x and y (called a Cartesian equation), it is more convenient to define x and y using parametric equations
10.1 Review of Parametric Equations Recall that often, instead of representing a curve using just x and y (called a Cartesian equation), it is more convenient to define x and y using parametric equations
MathsGeeks. Everything You Need to Know A Level Edexcel C4. March 2014 MathsGeeks Copyright 2014 Elite Learning Limited
 Everything You Need to Know A Level Edexcel C4 March 4 Copyright 4 Elite Learning Limited Page of 4 Further Binomial Expansion: Make sure it starts with a e.g. for ( x) ( x ) then use ( + x) n + nx + n(n
Everything You Need to Know A Level Edexcel C4 March 4 Copyright 4 Elite Learning Limited Page of 4 Further Binomial Expansion: Make sure it starts with a e.g. for ( x) ( x ) then use ( + x) n + nx + n(n
Circles. Example 2: Write an equation for a circle if the enpoints of a diameter are at ( 4,5) and (6, 3).
 Conics Unit Ch. 8 Circles Equations of Circles The equation of a circle with center ( hk, ) and radius r units is ( x h) ( y k) r. Example 1: Write an equation of circle with center (8, 3) and radius 6.
Conics Unit Ch. 8 Circles Equations of Circles The equation of a circle with center ( hk, ) and radius r units is ( x h) ( y k) r. Example 1: Write an equation of circle with center (8, 3) and radius 6.
Level 3, Calculus
 Level, 4 Calculus Differentiate and use derivatives to solve problems (965) Integrate functions and solve problems by integration, differential equations or numerical methods (966) Manipulate real and
Level, 4 Calculus Differentiate and use derivatives to solve problems (965) Integrate functions and solve problems by integration, differential equations or numerical methods (966) Manipulate real and
Calculus & Analytic Geometry I
 TQS 124 Autumn 2008 Quinn Calculus & Analytic Geometry I The Derivative: Analytic Viewpoint Derivative of a Constant Function. For c a constant, the derivative of f(x) = c equals f (x) = Derivative of
TQS 124 Autumn 2008 Quinn Calculus & Analytic Geometry I The Derivative: Analytic Viewpoint Derivative of a Constant Function. For c a constant, the derivative of f(x) = c equals f (x) = Derivative of
e x3 dx dy. 0 y x 2, 0 x 1.
 Problem 1. Evaluate by changing the order of integration y e x3 dx dy. Solution:We change the order of integration over the region y x 1. We find and x e x3 dy dx = y x, x 1. x e x3 dx = 1 x=1 3 ex3 x=
Problem 1. Evaluate by changing the order of integration y e x3 dx dy. Solution:We change the order of integration over the region y x 1. We find and x e x3 dy dx = y x, x 1. x e x3 dx = 1 x=1 3 ex3 x=
M GENERAL MATHEMATICS -2- Dr. Tariq A. AlFadhel 1 Solution of the First Mid-Term Exam First semester H
 M 4 - GENERAL MATHEMATICS -- Dr. Tariq A. AlFadhel Solution of the First Mid-Term Exam First semester 435-436 H Q. Let A ( ) 4 and B 3 3 Compute (if possible) : AB and BA ( ) 4 AB 3 3 ( ) ( ) ++ 4+4+ 4
M 4 - GENERAL MATHEMATICS -- Dr. Tariq A. AlFadhel Solution of the First Mid-Term Exam First semester 435-436 H Q. Let A ( ) 4 and B 3 3 Compute (if possible) : AB and BA ( ) 4 AB 3 3 ( ) ( ) ++ 4+4+ 4
AP Calculus Chapter 3 Testbank (Mr. Surowski)
 AP Calculus Chapter 3 Testbank (Mr. Surowski) Part I. Multiple-Choice Questions (5 points each; please circle the correct answer.). If f(x) = 0x 4 3 + x, then f (8) = (A) (B) 4 3 (C) 83 3 (D) 2 3 (E) 2
AP Calculus Chapter 3 Testbank (Mr. Surowski) Part I. Multiple-Choice Questions (5 points each; please circle the correct answer.). If f(x) = 0x 4 3 + x, then f (8) = (A) (B) 4 3 (C) 83 3 (D) 2 3 (E) 2
When e = 0 we obtain the case of a circle.
 3.4 Conic sections Circles belong to specil clss of cures clle conic sections. Other such cures re the ellipse, prbol, n hyperbol. We will briefly escribe the stnr conics. These re chosen to he simple
3.4 Conic sections Circles belong to specil clss of cures clle conic sections. Other such cures re the ellipse, prbol, n hyperbol. We will briefly escribe the stnr conics. These re chosen to he simple
Pure Further Mathematics 3. Revision Notes
 Pure Further Mathematics Revision Notes February 6 FP FEB 6 SDB Hyperbolic functions... Definitions and graphs... Addition formulae, double angle formulae etc.... Osborne s rule... Inverse hyperbolic functions...
Pure Further Mathematics Revision Notes February 6 FP FEB 6 SDB Hyperbolic functions... Definitions and graphs... Addition formulae, double angle formulae etc.... Osborne s rule... Inverse hyperbolic functions...
Math 190 (Calculus II) Final Review
 Math 90 (Calculus II) Final Review. Sketch the region enclosed by the given curves and find the area of the region. a. y = 7 x, y = x + 4 b. y = cos ( πx ), y = x. Use the specified method to find the
Math 90 (Calculus II) Final Review. Sketch the region enclosed by the given curves and find the area of the region. a. y = 7 x, y = x + 4 b. y = cos ( πx ), y = x. Use the specified method to find the
Mathematics Extension 2
 00 HIGHER SCHOOL CERTIFICATE EXAMINATION Mathematics Extension General Instructions Reading time 5 minutes Working time hours Write using black or blue pen Board-approved calculators may be used A table
00 HIGHER SCHOOL CERTIFICATE EXAMINATION Mathematics Extension General Instructions Reading time 5 minutes Working time hours Write using black or blue pen Board-approved calculators may be used A table
JUST THE MATHS UNIT NUMBER INTEGRATION APPLICATIONS 10 (Second moments of an arc) A.J.Hobson
 JUST THE MATHS UNIT NUMBER 13.1 INTEGRATION APPLICATIONS 1 (Second moments of an arc) by A.J.Hobson 13.1.1 Introduction 13.1. The second moment of an arc about the y-axis 13.1.3 The second moment of an
JUST THE MATHS UNIT NUMBER 13.1 INTEGRATION APPLICATIONS 1 (Second moments of an arc) by A.J.Hobson 13.1.1 Introduction 13.1. The second moment of an arc about the y-axis 13.1.3 The second moment of an
2. Determine the domain of the function. Verify your result with a graph. f(x) = 25 x 2
 29 April PreCalculus Final Review 1. Find the slope and y-intercept (if possible) of the equation of the line. Sketch the line: y = 3x + 13 2. Determine the domain of the function. Verify your result with
29 April PreCalculus Final Review 1. Find the slope and y-intercept (if possible) of the equation of the line. Sketch the line: y = 3x + 13 2. Determine the domain of the function. Verify your result with
THE KING S SCHOOL. Mathematics Extension Higher School Certificate Trial Examination
 THE KING S SCHOOL 2009 Higher School Certificate Trial Examination Mathematics Extension 1 General Instructions Reading time 5 minutes Working time 2 hours Write using black or blue pen Board-approved
THE KING S SCHOOL 2009 Higher School Certificate Trial Examination Mathematics Extension 1 General Instructions Reading time 5 minutes Working time 2 hours Write using black or blue pen Board-approved
Brief answers to assigned even numbered problems that were not to be turned in
 Brief answers to assigned even numbered problems that were not to be turned in Section 2.2 2. At point (x 0, x 2 0) on the curve the slope is 2x 0. The point-slope equation of the tangent line to the curve
Brief answers to assigned even numbered problems that were not to be turned in Section 2.2 2. At point (x 0, x 2 0) on the curve the slope is 2x 0. The point-slope equation of the tangent line to the curve
Conic Sections. Geometry - Conics ~1~ NJCTL.org. Write the following equations in standard form.
 Conic Sections Midpoint and Distance Formula M is the midpoint of A and B. Use the given information to find the missing point. 1. A(, 2) and B(3, -), find M 2. A(5, 7) and B( -2, -), find M 3. A( 2,0)
Conic Sections Midpoint and Distance Formula M is the midpoint of A and B. Use the given information to find the missing point. 1. A(, 2) and B(3, -), find M 2. A(5, 7) and B( -2, -), find M 3. A( 2,0)
Mth Review Problems for Test 2 Stewart 8e Chapter 3. For Test #2 study these problems, the examples in your notes, and the homework.
 For Test # study these problems, the examples in your notes, and the homework. Derivative Rules D [u n ] = nu n 1 du D [ln u] = du u D [log b u] = du u ln b D [e u ] = e u du D [a u ] = a u ln a du D [sin
For Test # study these problems, the examples in your notes, and the homework. Derivative Rules D [u n ] = nu n 1 du D [ln u] = du u D [log b u] = du u ln b D [e u ] = e u du D [a u ] = a u ln a du D [sin
Edexcel GCE A Level Maths. Further Maths 3 Coordinate Systems
 Edecel GCE A Level Maths Further Maths 3 Coordinate Sstems Edited b: K V Kumaran kumarmaths.weebl.com 1 kumarmaths.weebl.com kumarmaths.weebl.com 3 kumarmaths.weebl.com 4 kumarmaths.weebl.com 5 1. An ellipse
Edecel GCE A Level Maths Further Maths 3 Coordinate Sstems Edited b: K V Kumaran kumarmaths.weebl.com 1 kumarmaths.weebl.com kumarmaths.weebl.com 3 kumarmaths.weebl.com 4 kumarmaths.weebl.com 5 1. An ellipse
JUST THE MATHS UNIT NUMBER DIFFERENTIATION 4 (Products and quotients) & (Logarithmic differentiation) A.J.Hobson
 JUST THE MATHS UNIT NUMBER 104 DIFFERENTIATION 4 (Products and quotients) & (Logarithmic differentiation) by AJHobson 1041 Products 1042 Quotients 1043 Logarithmic differentiation 1044 Exercises 1045 Answers
JUST THE MATHS UNIT NUMBER 104 DIFFERENTIATION 4 (Products and quotients) & (Logarithmic differentiation) by AJHobson 1041 Products 1042 Quotients 1043 Logarithmic differentiation 1044 Exercises 1045 Answers
Power Series. x n. Using the ratio test. n n + 1. x n+1 n 3. = lim x. lim n + 1. = 1 < x < 1. Then r = 1 and I = ( 1, 1) ( 1) n 1 x n.
 .8 Power Series. n x n x n n Using the ratio test. lim x n+ n n + lim x n n + so r and I (, ). By the ratio test. n Then r and I (, ). n x < ( ) n x n < x < n lim x n+ n (n + ) x n lim xn n (n + ) x
.8 Power Series. n x n x n n Using the ratio test. lim x n+ n n + lim x n n + so r and I (, ). By the ratio test. n Then r and I (, ). n x < ( ) n x n < x < n lim x n+ n (n + ) x n lim xn n (n + ) x
Conic Sections Session 2: Ellipse
 Conic Sections Session 2: Ellipse Toh Pee Choon NIE Oct 2017 Toh Pee Choon (NIE) Session 2: Ellipse Oct 2017 1 / 24 Introduction Problem 2.1 Let A, F 1 and F 2 be three points that form a triangle F 2
Conic Sections Session 2: Ellipse Toh Pee Choon NIE Oct 2017 Toh Pee Choon (NIE) Session 2: Ellipse Oct 2017 1 / 24 Introduction Problem 2.1 Let A, F 1 and F 2 be three points that form a triangle F 2
Outline schemes of work A-level Mathematics 6360
 Outline schemes of work A-level Mathematics 6360 Version.0, Autumn 013 Introduction These outline schemes of work are intended to help teachers plan and implement the teaching of the AQA A-level Mathematics
Outline schemes of work A-level Mathematics 6360 Version.0, Autumn 013 Introduction These outline schemes of work are intended to help teachers plan and implement the teaching of the AQA A-level Mathematics
Questions Q1. The function f is defined by. (a) Show that (5) The function g is defined by. (b) Differentiate g(x) to show that g '(x) = (3)
 Questions Q1. The function f is defined by (a) Show that The function g is defined by (b) Differentiate g(x) to show that g '(x) = (c) Find the exact values of x for which g '(x) = 1 (Total 12 marks) Q2.
Questions Q1. The function f is defined by (a) Show that The function g is defined by (b) Differentiate g(x) to show that g '(x) = (c) Find the exact values of x for which g '(x) = 1 (Total 12 marks) Q2.
cosh 2 x sinh 2 x = 1 sin 2 x = 1 2 cos 2 x = 1 2 dx = dt r 2 = x 2 + y 2 L =
 Integrals Volume: Suppose A(x) is the cross-sectional area of the solid S perpendicular to the x-axis, then the volume of S is given by V = b a A(x) dx Work: Suppose f(x) is a force function. The work
Integrals Volume: Suppose A(x) is the cross-sectional area of the solid S perpendicular to the x-axis, then the volume of S is given by V = b a A(x) dx Work: Suppose f(x) is a force function. The work
Ch 4 Differentiation
 Ch 1 Partial fractions Ch 6 Integration Ch 2 Coordinate geometry C4 Ch 5 Vectors Ch 3 The binomial expansion Ch 4 Differentiation Chapter 1 Partial fractions We can add (or take away) two fractions only
Ch 1 Partial fractions Ch 6 Integration Ch 2 Coordinate geometry C4 Ch 5 Vectors Ch 3 The binomial expansion Ch 4 Differentiation Chapter 1 Partial fractions We can add (or take away) two fractions only
Further Pure Mathematics 3 GCE Further Mathematics GCE Pure Mathematics and Further Mathematics (Additional) A2 optional unit
 Unit FP3 Further Pure Mathematics 3 GCE Further Mathematics GCE Pure Mathematics and Further Mathematics (Additional) A optional unit FP3.1 Unit description Further matrix algebra; vectors, hyperbolic
Unit FP3 Further Pure Mathematics 3 GCE Further Mathematics GCE Pure Mathematics and Further Mathematics (Additional) A optional unit FP3.1 Unit description Further matrix algebra; vectors, hyperbolic
Derivatives and Integrals
 Derivatives and Integrals Definition 1: Derivative Formulas d dx (c) = 0 d dx (f ± g) = f ± g d dx (kx) = k d dx (xn ) = nx n 1 (f g) = f g + fg ( ) f = f g fg g g 2 (f(g(x))) = f (g(x)) g (x) d dx (ax
Derivatives and Integrals Definition 1: Derivative Formulas d dx (c) = 0 d dx (f ± g) = f ± g d dx (kx) = k d dx (xn ) = nx n 1 (f g) = f g + fg ( ) f = f g fg g g 2 (f(g(x))) = f (g(x)) g (x) d dx (ax
Foundations of Calculus. November 18, 2014
 Foundations of Calculus November 18, 2014 Contents 1 Conic Sections 3 11 A review of the coordinate system 3 12 Conic Sections 4 121 Circle 4 122 Parabola 5 123 Ellipse 5 124 Hyperbola 6 2 Review of Functions
Foundations of Calculus November 18, 2014 Contents 1 Conic Sections 3 11 A review of the coordinate system 3 12 Conic Sections 4 121 Circle 4 122 Parabola 5 123 Ellipse 5 124 Hyperbola 6 2 Review of Functions
Core Mathematics 3 Differentiation
 http://kumarmaths.weebly.com/ Core Mathematics Differentiation C differentiation Page Differentiation C Specifications. By the end of this unit you should be able to : Use chain rule to find the derivative
http://kumarmaths.weebly.com/ Core Mathematics Differentiation C differentiation Page Differentiation C Specifications. By the end of this unit you should be able to : Use chain rule to find the derivative
Chapter 1 Analytic geometry in the plane
 3110 General Mathematics 1 31 10 General Mathematics For the students from Pharmaceutical Faculty 1/004 Instructor: Dr Wattana Toutip (ดร.ว ฒนา เถาว ท พย ) Chapter 1 Analytic geometry in the plane Overview:
3110 General Mathematics 1 31 10 General Mathematics For the students from Pharmaceutical Faculty 1/004 Instructor: Dr Wattana Toutip (ดร.ว ฒนา เถาว ท พย ) Chapter 1 Analytic geometry in the plane Overview:
Week beginning Videos Page
 1 M Week beginning Videos Page June/July C3 Algebraic Fractions 3 June/July C3 Algebraic Division 4 June/July C3 Reciprocal Trig Functions 5 June/July C3 Pythagorean Identities 6 June/July C3 Trig Consolidation
1 M Week beginning Videos Page June/July C3 Algebraic Fractions 3 June/July C3 Algebraic Division 4 June/July C3 Reciprocal Trig Functions 5 June/July C3 Pythagorean Identities 6 June/July C3 Trig Consolidation
18.02 Multivariable Calculus Fall 2007
 MIT OpenourseWare http://ocw.mit.edu 8.02 Multivariable alculus Fall 2007 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 8.02 Lecture 8. hange of variables.
MIT OpenourseWare http://ocw.mit.edu 8.02 Multivariable alculus Fall 2007 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 8.02 Lecture 8. hange of variables.
Rotation of Axes. By: OpenStaxCollege
 Rotation of Axes By: OpenStaxCollege As we have seen, conic sections are formed when a plane intersects two right circular cones aligned tip to tip and extending infinitely far in opposite directions,
Rotation of Axes By: OpenStaxCollege As we have seen, conic sections are formed when a plane intersects two right circular cones aligned tip to tip and extending infinitely far in opposite directions,
MATH1013 Calculus I. Derivatives II (Chap. 3) 1
 MATH1013 Calculus I Derivatives II (Chap. 3) 1 Edmund Y. M. Chiang Department of Mathematics Hong Kong University of Science & Technology October 16, 2013 2013 1 Based on Briggs, Cochran and Gillett: Calculus
MATH1013 Calculus I Derivatives II (Chap. 3) 1 Edmund Y. M. Chiang Department of Mathematics Hong Kong University of Science & Technology October 16, 2013 2013 1 Based on Briggs, Cochran and Gillett: Calculus
MATH 1080 Test 2 -Version A-SOLUTIONS Fall a. (8 pts) Find the exact length of the curve on the given interval.
 MATH 8 Test -Version A-SOLUTIONS Fall 4. Consider the curve defined by y = ln( sec x), x. a. (8 pts) Find the exact length of the curve on the given interval. sec x tan x = = tan x sec x L = + tan x =
MATH 8 Test -Version A-SOLUTIONS Fall 4. Consider the curve defined by y = ln( sec x), x. a. (8 pts) Find the exact length of the curve on the given interval. sec x tan x = = tan x sec x L = + tan x =
MA 162 FINAL EXAM PRACTICE PROBLEMS Spring Find the angle between the vectors v = 2i + 2j + k and w = 2i + 2j k. C.
 MA 6 FINAL EXAM PRACTICE PROBLEMS Spring. Find the angle between the vectors v = i + j + k and w = i + j k. cos 8 cos 5 cos D. cos 7 E. cos. Find a such that u = i j + ak and v = i + j + k are perpendicular.
MA 6 FINAL EXAM PRACTICE PROBLEMS Spring. Find the angle between the vectors v = i + j + k and w = i + j k. cos 8 cos 5 cos D. cos 7 E. cos. Find a such that u = i j + ak and v = i + j + k are perpendicular.
Some commonly encountered sets and their notations
 NATIONAL UNIVERSITY OF SINGAPORE DEPARTMENT OF MATHEMATICS (This notes are based on the book Introductory Mathematics by Ng Wee Seng ) LECTURE SETS & FUNCTIONS Some commonly encountered sets and their
NATIONAL UNIVERSITY OF SINGAPORE DEPARTMENT OF MATHEMATICS (This notes are based on the book Introductory Mathematics by Ng Wee Seng ) LECTURE SETS & FUNCTIONS Some commonly encountered sets and their
CRASH COURSE IN PRECALCULUS
 CRASH COURSE IN PRECALCULUS Shiah-Sen Wang The graphs are prepared by Chien-Lun Lai Based on : Precalculus: Mathematics for Calculus by J. Stuwart, L. Redin & S. Watson, 6th edition, 2012, Brooks/Cole
CRASH COURSE IN PRECALCULUS Shiah-Sen Wang The graphs are prepared by Chien-Lun Lai Based on : Precalculus: Mathematics for Calculus by J. Stuwart, L. Redin & S. Watson, 6th edition, 2012, Brooks/Cole
SOLUTIONS FOR PRACTICE FINAL EXAM
 SOLUTIONS FOR PRACTICE FINAL EXAM ANDREW J. BLUMBERG. Solutions () Short answer questions: (a) State the mean value theorem. Proof. The mean value theorem says that if f is continuous on (a, b) and differentiable
SOLUTIONS FOR PRACTICE FINAL EXAM ANDREW J. BLUMBERG. Solutions () Short answer questions: (a) State the mean value theorem. Proof. The mean value theorem says that if f is continuous on (a, b) and differentiable
Core A-level mathematics reproduced from the QCA s Subject criteria for Mathematics document
 Core A-level mathematics reproduced from the QCA s Subject criteria for Mathematics document Background knowledge: (a) The arithmetic of integers (including HCFs and LCMs), of fractions, and of real numbers.
Core A-level mathematics reproduced from the QCA s Subject criteria for Mathematics document Background knowledge: (a) The arithmetic of integers (including HCFs and LCMs), of fractions, and of real numbers.
You can learn more about the services offered by the teaching center by visiting
 MAC 232 Exam 3 Review Spring 209 This review, produced by the Broward Teaching Center, contains a collection of questions which are representative of the type you may encounter on the exam. Other resources
MAC 232 Exam 3 Review Spring 209 This review, produced by the Broward Teaching Center, contains a collection of questions which are representative of the type you may encounter on the exam. Other resources
Calculus III. George Voutsadakis 1. LSSU Math 251. Lake Superior State University. 1 Mathematics and Computer Science
 Calculus III George Voutsadakis 1 1 Mathematics and Computer Science Lake Superior State University LSSU Math 251 George Voutsadakis (LSSU) Calculus III January 2016 1 / 76 Outline 1 Parametric Equations,
Calculus III George Voutsadakis 1 1 Mathematics and Computer Science Lake Superior State University LSSU Math 251 George Voutsadakis (LSSU) Calculus III January 2016 1 / 76 Outline 1 Parametric Equations,
Introduction to Computer Graphics (Lecture No 07) Ellipse and Other Curves
 Introduction to Computer Graphics (Lecture No 07) Ellipse and Other Curves 7.1 Ellipse An ellipse is a curve that is the locus of all points in the plane the sum of whose distances r1 and r from two fixed
Introduction to Computer Graphics (Lecture No 07) Ellipse and Other Curves 7.1 Ellipse An ellipse is a curve that is the locus of all points in the plane the sum of whose distances r1 and r from two fixed
Mathematics 104 Fall Term 2006 Solutions to Final Exam. sin(ln t) dt = e x sin(x) dx.
 Mathematics 14 Fall Term 26 Solutions to Final Exam 1. Evaluate sin(ln t) dt. Solution. We first make the substitution t = e x, for which dt = e x. This gives sin(ln t) dt = e x sin(x). To evaluate the
Mathematics 14 Fall Term 26 Solutions to Final Exam 1. Evaluate sin(ln t) dt. Solution. We first make the substitution t = e x, for which dt = e x. This gives sin(ln t) dt = e x sin(x). To evaluate the
x n+1 = ( x n + ) converges, then it converges to α. [2]
![x n+1 = ( x n + ) converges, then it converges to α. [2] x n+1 = ( x n + ) converges, then it converges to α. [2]](/thumbs/92/110299841.jpg) 1 A Level - Mathematics P 3 ITERATION ( With references and answers) [ Numerical Solution of Equation] Q1. The equation x 3 - x 2 6 = 0 has one real root, denoted by α. i) Find by calculation the pair
1 A Level - Mathematics P 3 ITERATION ( With references and answers) [ Numerical Solution of Equation] Q1. The equation x 3 - x 2 6 = 0 has one real root, denoted by α. i) Find by calculation the pair
3.4 The Chain Rule. F (x) = f (g(x))g (x) Alternate way of thinking about it: If y = f(u) and u = g(x) where both are differentiable functions, then
 3.4 The Chain Rule To find the derivative of a function that is the composition of two functions for which we already know the derivatives, we can use the Chain Rule. The Chain Rule: Suppose F (x) = f(g(x)).
3.4 The Chain Rule To find the derivative of a function that is the composition of two functions for which we already know the derivatives, we can use the Chain Rule. The Chain Rule: Suppose F (x) = f(g(x)).
Pre-Calculus Final Exam Review Name: May June Use the following schedule to complete the final exam review.
 Pre-Calculus Final Exam Review Name: May June 2015 Use the following schedule to complete the final exam review. Homework will be checked in every day. Late work will NOT be accepted. Homework answers
Pre-Calculus Final Exam Review Name: May June 2015 Use the following schedule to complete the final exam review. Homework will be checked in every day. Late work will NOT be accepted. Homework answers
TRIAL HIGHER SCHOOL CERTIFICATE EXAMINATION. Ext II Mathematics
 00 TRIAL HIGHER SCHOOL CERTIFICATE EXAMINATION Ext II Mathematics General Instructions Reading time 5 minutes Working time 3 hours Write using black or blue pen Approved calculators may be used A table
00 TRIAL HIGHER SCHOOL CERTIFICATE EXAMINATION Ext II Mathematics General Instructions Reading time 5 minutes Working time 3 hours Write using black or blue pen Approved calculators may be used A table
MATH 32A: MIDTERM 2 REVIEW. sin 2 u du z(t) = sin 2 t + cos 2 2
 MATH 3A: MIDTERM REVIEW JOE HUGHES 1. Curvature 1. Consider the curve r(t) = x(t), y(t), z(t), where x(t) = t Find the curvature κ(t). 0 cos(u) sin(u) du y(t) = Solution: The formula for curvature is t
MATH 3A: MIDTERM REVIEW JOE HUGHES 1. Curvature 1. Consider the curve r(t) = x(t), y(t), z(t), where x(t) = t Find the curvature κ(t). 0 cos(u) sin(u) du y(t) = Solution: The formula for curvature is t
KEMATH1 Calculus for Chemistry and Biochemistry Students. Francis Joseph H. Campeña, De La Salle University Manila
 KEMATH1 Calculus for Chemistry and Biochemistry Students Francis Joseph H Campeña, De La Salle University Manila February 9, 2015 Contents 1 Conic Sections 2 11 A review of the coordinate system 2 12 Conic
KEMATH1 Calculus for Chemistry and Biochemistry Students Francis Joseph H Campeña, De La Salle University Manila February 9, 2015 Contents 1 Conic Sections 2 11 A review of the coordinate system 2 12 Conic
FINAL EXAM CALCULUS 2. Name PRACTICE EXAM SOLUTIONS
 FINAL EXAM CALCULUS MATH 00 FALL 08 Name PRACTICE EXAM SOLUTIONS Please answer all of the questions, and show your work. You must explain your answers to get credit. You will be graded on the clarity of
FINAL EXAM CALCULUS MATH 00 FALL 08 Name PRACTICE EXAM SOLUTIONS Please answer all of the questions, and show your work. You must explain your answers to get credit. You will be graded on the clarity of
Revision Checklist. Unit FP3: Further Pure Mathematics 3. Assessment information
 Revision Checklist Unit FP3: Further Pure Mathematics 3 Unit description Further matrix algebra; vectors, hyperbolic functions; differentiation; integration, further coordinate systems Assessment information
Revision Checklist Unit FP3: Further Pure Mathematics 3 Unit description Further matrix algebra; vectors, hyperbolic functions; differentiation; integration, further coordinate systems Assessment information
UNIVERSITY OF CAMBRIDGE Faculty of Mathematics MATHEMATICS WORKBOOK
 UNIVERSITY OF CAMBRIDGE Faculty of Mathematics MATHEMATICS WORKBOOK August, 07 Introduction The Mathematical Tripos is designed to be accessible to students who are familiar with the the core A-level syllabus
UNIVERSITY OF CAMBRIDGE Faculty of Mathematics MATHEMATICS WORKBOOK August, 07 Introduction The Mathematical Tripos is designed to be accessible to students who are familiar with the the core A-level syllabus
CALCULUS. Berkant Ustaoğlu CRYPTOLOUNGE.NET
 CALCULUS Berkant Ustaoğlu CRYPTOLOUNGE.NET Secant 1 Definition Let f be defined over an interval I containing u. If x u and x I then f (x) f (u) Q = x u is the difference quotient. Also if h 0, such that
CALCULUS Berkant Ustaoğlu CRYPTOLOUNGE.NET Secant 1 Definition Let f be defined over an interval I containing u. If x u and x I then f (x) f (u) Q = x u is the difference quotient. Also if h 0, such that
Math Final Exam Review
 Math - Final Exam Review. Find dx x + 6x +. Name: Solution: We complete the square to see if this function has a nice form. Note we have: x + 6x + (x + + dx x + 6x + dx (x + + Note that this looks a lot
Math - Final Exam Review. Find dx x + 6x +. Name: Solution: We complete the square to see if this function has a nice form. Note we have: x + 6x + (x + + dx x + 6x + dx (x + + Note that this looks a lot
Conic Sections Session 3: Hyperbola
 Conic Sections Session 3: Hyperbola Toh Pee Choon NIE Oct 2017 Toh Pee Choon (NIE) Session 3: Hyperbola Oct 2017 1 / 16 Problem 3.1 1 Recall that an ellipse is defined as the locus of points P such that
Conic Sections Session 3: Hyperbola Toh Pee Choon NIE Oct 2017 Toh Pee Choon (NIE) Session 3: Hyperbola Oct 2017 1 / 16 Problem 3.1 1 Recall that an ellipse is defined as the locus of points P such that
Lone Star College-CyFair Formula Sheet
 Lone Star College-CyFair Formula Sheet The following formulas are critical for success in the indicated course. Student CANNOT bring these formulas on a formula sheet or card to tests and instructors MUST
Lone Star College-CyFair Formula Sheet The following formulas are critical for success in the indicated course. Student CANNOT bring these formulas on a formula sheet or card to tests and instructors MUST
MATH10000 Mathematical Workshop Project 2 Part 1 Conic Sections
 MATH10000 Mathematical Workshop Project 2 Part 1 Conic Sections The aim of this project is to introduce you to an area of geometry known as the theory of conic sections, which is one of the most famous
MATH10000 Mathematical Workshop Project 2 Part 1 Conic Sections The aim of this project is to introduce you to an area of geometry known as the theory of conic sections, which is one of the most famous
Precalculus Table of Contents Unit 1 : Algebra Review Lesson 1: (For worksheet #1) Factoring Review Factoring Using the Distributive Laws Factoring
 Unit 1 : Algebra Review Factoring Review Factoring Using the Distributive Laws Factoring Trinomials Factoring the Difference of Two Squares Factoring Perfect Square Trinomials Factoring the Sum and Difference
Unit 1 : Algebra Review Factoring Review Factoring Using the Distributive Laws Factoring Trinomials Factoring the Difference of Two Squares Factoring Perfect Square Trinomials Factoring the Sum and Difference
Chapter 2: Differentiation
 Chapter 2: Differentiation Spring 2018 Department of Mathematics Hong Kong Baptist University 1 / 82 2.1 Tangent Lines and Their Slopes This section deals with the problem of finding a straight line L
Chapter 2: Differentiation Spring 2018 Department of Mathematics Hong Kong Baptist University 1 / 82 2.1 Tangent Lines and Their Slopes This section deals with the problem of finding a straight line L
Parametric Equations and Polar Coordinates
 Parametric Equations and Polar Coordinates Parametrizations of Plane Curves In previous chapters, we have studied curves as the graphs of functions or equations involving the two variables x and y. Another
Parametric Equations and Polar Coordinates Parametrizations of Plane Curves In previous chapters, we have studied curves as the graphs of functions or equations involving the two variables x and y. Another
Conic Sections in Polar Coordinates
 Conic Sections in Polar Coordinates MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction We have develop the familiar formulas for the parabola, ellipse, and hyperbola
Conic Sections in Polar Coordinates MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction We have develop the familiar formulas for the parabola, ellipse, and hyperbola
Time : 3 hours 02 - Mathematics - July 2006 Marks : 100 Pg - 1 Instructions : S E CT I O N - A
 Time : 3 hours 0 Mathematics July 006 Marks : 00 Pg Instructions :. Answer all questions.. Write your answers according to the instructions given below with the questions. 3. Begin each section on a new
Time : 3 hours 0 Mathematics July 006 Marks : 00 Pg Instructions :. Answer all questions.. Write your answers according to the instructions given below with the questions. 3. Begin each section on a new
M GENERAL MATHEMATICS -2- Dr. Tariq A. AlFadhel 1 Solution of the First Mid-Term Exam First semester H
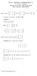 M - GENERAL MATHEMATICS -- Dr. Tariq A. AlFadhel Solution of the First Mid-Term Exam First semester 38-39 H 3 Q. Let A =, B = and C = 3 Compute (if possible) : A+B and BC A+B is impossible. ( ) BC = 3
M - GENERAL MATHEMATICS -- Dr. Tariq A. AlFadhel Solution of the First Mid-Term Exam First semester 38-39 H 3 Q. Let A =, B = and C = 3 Compute (if possible) : A+B and BC A+B is impossible. ( ) BC = 3
Practice Final Exam Solutions
 Important Notice: To prepare for the final exam, study past exams and practice exams, and homeworks, quizzes, and worksheets, not just this practice final. A topic not being on the practice final does
Important Notice: To prepare for the final exam, study past exams and practice exams, and homeworks, quizzes, and worksheets, not just this practice final. A topic not being on the practice final does
Chapter 2: Differentiation
 Chapter 2: Differentiation Winter 2016 Department of Mathematics Hong Kong Baptist University 1 / 75 2.1 Tangent Lines and Their Slopes This section deals with the problem of finding a straight line L
Chapter 2: Differentiation Winter 2016 Department of Mathematics Hong Kong Baptist University 1 / 75 2.1 Tangent Lines and Their Slopes This section deals with the problem of finding a straight line L
Note: Final Exam is at 10:45 on Tuesday, 5/3/11 (This is the Final Exam time reserved for our labs). From Practice Test I
 MA Practice Final Answers in Red 4/8/ and 4/9/ Name Note: Final Exam is at :45 on Tuesday, 5// (This is the Final Exam time reserved for our labs). From Practice Test I Consider the integral 5 x dx. Sketch
MA Practice Final Answers in Red 4/8/ and 4/9/ Name Note: Final Exam is at :45 on Tuesday, 5// (This is the Final Exam time reserved for our labs). From Practice Test I Consider the integral 5 x dx. Sketch
IIT JEE Maths Paper 2
 IIT JEE - 009 Maths Paper A. Question paper format: 1. The question paper consists of 4 sections.. Section I contains 4 multiple choice questions. Each question has 4 choices (A), (B), (C) and (D) for
IIT JEE - 009 Maths Paper A. Question paper format: 1. The question paper consists of 4 sections.. Section I contains 4 multiple choice questions. Each question has 4 choices (A), (B), (C) and (D) for
Learning Objectives for Math 166
 Learning Objectives for Math 166 Chapter 6 Applications of Definite Integrals Section 6.1: Volumes Using Cross-Sections Draw and label both 2-dimensional perspectives and 3-dimensional sketches of the
Learning Objectives for Math 166 Chapter 6 Applications of Definite Integrals Section 6.1: Volumes Using Cross-Sections Draw and label both 2-dimensional perspectives and 3-dimensional sketches of the
Preliminaries Lectures. Dr. Abdulla Eid. Department of Mathematics MATHS 101: Calculus I
 Preliminaries 2 1 2 Lectures Department of Mathematics http://www.abdullaeid.net/maths101 MATHS 101: Calculus I (University of Bahrain) Prelim 1 / 35 Pre Calculus MATHS 101: Calculus MATHS 101 is all about
Preliminaries 2 1 2 Lectures Department of Mathematics http://www.abdullaeid.net/maths101 MATHS 101: Calculus I (University of Bahrain) Prelim 1 / 35 Pre Calculus MATHS 101: Calculus MATHS 101 is all about
IYGB Mathematical Methods 1
 IYGB Mathematical Methods Practice Paper B Time: 3 hours Candidates may use any non programmable, non graphical calculator which does not have the capability of storing data or manipulating algebraic expressions
IYGB Mathematical Methods Practice Paper B Time: 3 hours Candidates may use any non programmable, non graphical calculator which does not have the capability of storing data or manipulating algebraic expressions
