Does modeling a structural break improve forecast accuracy?
|
|
|
- Charleen Dorsey
- 5 years ago
- Views:
Transcription
1 Does modeling a structural break improve forecast accuracy? Tom Boot Andreas Pick December 3, 27 Abstract Mean square forecast error loss implies a bias-variance trade-off that suggests that structural breaks of small magnitude should be ignored. In this paper, we provide a test to determine whether modeling a break improves forecast accuracy. The test is near optimal even when the date of a local-to-zero break is not consistently estimable. The results extend to forecast combinations that weight the post-break sample and the full sample forecasts by our test statistic. In a large number of macroeconomic time series, we find that structural breaks that are relevant for forecasting occur much less frequently than existing tests indicate. JEL codes: C2, C53 Keywords: structural break test, forecasting, squared error loss University of Groningen, t.boot@rug.nl Erasmus University Rotterdam, Tinbergen Institute, De Nederlandsche Bank, and CESifo Institute, andreas.pick@cantab.net. We thank Graham Elliott, Bart Keijsers, Alex Koning, Robin Lumsdaine, Agnieszka Markiewicz, Michael McCracken, Allan Timmermann, participants of seminars at CESifo Institute, Tinbergen Institute, University of Nottingham, and conference participants at BGSE summer forum, ESEM, IAAE annual conference, NESG meeting, RMSE workshop, and SNDE conference for helpful comments. The paper previously circulated under the title A near optimal test for structural breaks when forecasting under square error loss.
2 Introduction Many macroeconomic and financial time series contain structural breaks as documented by Stock and Watson 996. Yet, Stock and Watson also find that forecasts are not substantially affected by the presence of structural breaks. Estimates for break dates and post-break parameters can often be estimated only imprecisely Elliott and Müller, 27, 24 and the implicit deterioration of the forecast may offset any gains from modeling a structural break. Additionally, forecasts are typically evaluated using mean square forecast error loss, which implies a bias-variance trade-off. Ignoring rather than modeling small breaks may therefore lead to more accurate forecasts Pesaran and Timmermann, 25. If sufficiently small breaks can be ignored, the question is: what constitutes sufficiently small? In this paper, we develop a real-time test for equal forecast accuracy that compares the expected mean square forecast error MSFE of a forecast from the post-break sample to that from the full sample. The difference in MSFE is a standardized, linear combination of pre- and post-break parameters with weights that depend on the regressors in the forecast period. As a result, breaks in the parameter vector, which are the focus of the extant literature on structural breaks, do not necessarily imply a break in the forecast. Full sample and post-break sample forecasts achieve equal forecast accuracy at a critical magnitude of the break. The bias-variance trade-off implies that this critical magnitude is non-zero. The null of our test therefore differs from the null of existing tests where the focus is on testing the absence of any parameter instability, such as Ploberger et al. 989, Andrews 993, Andrews and Ploberger 994, and Dufour et al Additionally, the critical magnitude of the break under the null depends on the unknown break date, which under local breaks is not consistently estimable. Using results from Andrews 993 and Piterbarg 996, we show that our test is optimal as the size of the test tends to zero. We provide evidence that the power of test remains close to that of the optimal test for conventional choices of the nominal size. The reason is that critical magnitudes that follow from the MSFE loss function are relatively large, which result in accurate estimates of the break date. This near optimality does not depend on whether our Wald-statistic is used in its homoskedastic form or whether a heteroskedastic version is used, as long as the estimator of the variance is consistent. The competing forecasts in our test are from the full sample and from the post-break sample. Yet, Pesaran et al. 23 show that forecasts based on post-break samples can be improved by using all observations and weighting them such that the MSFE is minimized. We show that this forecast can be written as a combination of the forecasts based on the post-break sample and the full sample. The relative weight is a function of the test statistic introduced in this paper. This approach is similar to that proposed by Hansen 29, who minimizes the in-sample mean square error using weights based on the Mallows criterion. We find that for small break magnitudes, where the break date is not accurately identified, the combined forecast is less accurate than the full sample forecast. However, compared 2
3 to the post-break sample forecast, we find that the combined forecast is more accurate for a large area of the parameter space. We therefore propose a second version of our test that compares the forecast accuracy of the combined forecast to the full sample forecast. More generally, we propose a testing framework that incorporates the loss function, here the mean square forecast error, into the test. Similar to the work of Trenkler and Toutenburg 992 and Clark and McCracken 22, our test is inspired by the in-sample MSE test of Toro-Vizcarrondo and Wallace 968 and Wallace 972. However, compared to the tests of Trenkler and Toutenburg 992 and Clark and McCracken 22, our testing framework is much simpler in that, under a known break date, our test statistic has a known distribution that is free of nuisance parameters. Our test shares some similarity with the work of Dette and Wied 26, who consider CUSUM tests in the spirit of Brown et al. 975 but allow for a constant parameter differences under the null. They do, however, not consider local-to-zero breaks, which would eliminate break date uncertainty in our asymptotic framework. Also, we show that the critical magnitude of the break depends on the break date and is therefore not identical across samples. Forecast accuracy tests of the kind suggested by Diebold and Mariano 995 and Clark and McCracken 2 assess forecast accuracy ex post see Clark and McCracken 23 for a review. In contrast, the test we propose in this paper is a real-time test of the accuracy of forecasts of models that do or do not account for breaks. Giacomini and Rossi 29 assess forecast breakdowns by comparing the in-sample fit and out-of-sample forecast accuracy of a given model. The main focus of their work is on assessing pseudo-out-of-sample forecasts. However, they also consider forecasting the loss differential of in-sample and out-of-sample forecast performance by modeling it with additional regressors. This contrasts with our approach, which targets the out-of-sample period directly in the construction of the test statistic. Of interest for our work is that, while a structural break is only one possible source of forecast breakdowns, Giacomini and Rossi find that it is a major contributor to forecast breakdowns in predicting US inflation using the Phillips curve. Similiary, Giacomini and Rossi 2 use a pseudo-out-of-sample period to assess competing models in the presence of instability. Our test, in contrast, does not require a pseudo-out-of-sample period but is a real-time test. Substantial evidence for structural breaks has been found in macroeconomic and financial time series by, for example, Pastor and Stambaugh 2, Paye and Timmermann 26, Pesaran and Timmermann 22, Pettenuzzo and Timmermann 2, Rapach and Wohar 26, Rossi 26, and Stock and Watson 996, 27. We apply our test to macroeconomic and financial time series in the FRED-MD data set of McCracken and Ng 26. We find that breaks that are important for forecasting under MSFE loss are between a factor two to three less frequent than the sup-wald test by Andrews 993 would indicate. Incorporating only the breaks suggested by our test substantially reduces the average MSFE 3
4 in this data set compared to the forecasts that take the breaks suggested by Andrews sup- Wald test into account. Our paper, therefore, provides theoretical support for the finding of Stock and Watson 996 that many breaks do not appear to have a substantial effect on forecast accuracy even though they are a prominent feature of macroeconomic data. The paper is structured as follows. In Section 2, we start with a motivating example using the linear regression model with a break of known timing. The model is generalized in Section 3 using the framework of Andrews 993. In Section 4, we derive the test, show its near optimality, and extend the test to cover the forecast that combines the full-sample and post-break forecasts based on the derived test statistic. Simulation results in Section 5 shows that the near optimality of the test is in fact quite strong, with power very close to the optimal, but infeasible, test conditional on the true break date. Finally, the application of our tests to the large set of time series in the FRED-MD data set is presented in Section 6. 2 Motivating example In order to gain intuition, initially consider a linear regression model with a structural break that is know to be at time T b y t = x tβ t + ε t, ε t iid, σ 2 where { β if t T b β t = β 2 if t > T b x t is a k vector of exogenous regressors, and β i a k vector of parameters. parameter vectors β and β 2 can be estimated by OLS in the two subsamples. If the break is ignored, a single vector of parameter estimates, ˆβ F, can be obtained via OLS using the full sample. Denote V i = T i T i Varˆβ i, for i =, 2, T =, T = T b, T 2 = T and V F = T Varˆβ F as the covariance matrices of the vectors of coefficient estimates. Initially, assume these matrices to be known; later they will be replaced by their probability limits. In this paper, we would like to test whether the expected mean squared forecast error MSFE from the h-step ahead forecast using the full sample, ŷ F T +h = x T +h ˆβ F, is smaller or equal to that of the post-break sample, ŷ P T +h = x T +h ˆβ 2. In this motivating example, we consider h =, and extend the results to the more general case in Section 4. The MSFE for the forecast from the post-break sample estimate, ˆβ2, conditional on x T +, is [ MSFEx ˆβ T + 2 = E x T ˆβ ] x T +β 2 ε T + = T T b x T + V 2 x T + + σ 2 The 2 4
5 where the first term in the second line represents the estimation uncertainty in the shorter post-break sample and the second term the uncertainty of the disturbance term in the forecast period. Using the full sample estimate, ˆβ F, we have [ MSFEx ˆβ T + F = E x T ˆβ ] 2 + F x T +β 2 ε T + [ = E x ˆβ ] 2 T + F x T +β 2 + T x T +V F x T + + σ 2 [ ] 2 Tb = T x T +V F V β β 2 + T x T +V F x T + + σ 2 where, in the last line of the equation, the first term is the square bias that arises from estimating the parameter vector over the two sub-periods, the second term represents the estimation uncertainty in the full sample, and the final term is the uncertainty of the disturbance term in the forecast period. Comparing 2 and 3, we see that the full sample forecast is at least as accurate as the post-break sample forecast if 3 [ x ζ = T τb 2 T + V F V β β 2 ] 2 x V 2 T + τ b V F x T + [ p x T τ b τ b T + β β 2 ] 2 x T + V x T + 4 where τ b = T b /T and the second line assumes that the covariance matrices asymptotically satisfy plim T V i = V for i =, 2, F. To test H : ζ = note that W τ b = T τ 2 b p [ x T + V F V ] 2 ˆβ ˆβ 2 x T + x V 2 T + τ V F [ x T + ˆβ F ˆβ ] 2 2 x T + Varˆβ F ˆβ χ 2, ζ 2 x T + Furthermore, given that we are interested in the null of ζ =, the test statistic has a χ 2, -distribution under the null, which is free of nuisance parameters. A more conventional and asymptotically equivalent form of the test statistic is W τ b = T [ x T + ˆβ ˆβ ] χ 2, ζ 6 x V T + τ b + V 2 τ b x T + 5
6 which can be recognized as a Wald test statistic with the regressors at T + as weights. The results of the test will, in general, differ from the outcomes of the classical Wald test on the difference between the parameter vectors β and β 2 for two reasons. The first is that the multiplication by x T + can render large breaks irrelevant. Alternatively, it can increase the importance of small breaks in the coefficient vector for forecasting. The second reason is that under H : ζ =, we compare the test statistic against the critical values of the non-central χ 2 -distribution, instead of the central χ 2 -distribution. The critical values of these distributions differ substantially: the α =.5 critical value of the χ 2 is 3.84 and that of the χ 2, is 7.. As is clear from 4, if the difference in the parameters, β β 2, converges to zero at a rate T /2+ɛ for some ɛ >, then the test statistic diverges to infinity as T, which is unlikely to reflect the uncertainty surrounding the break date in empirical applications. In the remainder of the paper, we will therefore consider breaks that are local in nature, i.e. β 2 = β + T η, rendering a finite test statistic in the asymptotic limit. Local breaks have been intensively studied in the recent literature, see for example Elliott and Müller 27, 24 and Elliott et al. 25. An implication of local breaks is that no consistent estimator for the break date is available. A consequence is that post-break parameters cannot be consistently estimated. This will deteriorate the accuracy of the post-break window forecast compared the full sample forecast, which, in turn, increases the break magnitude that yields equal forecasting performance between full and post-break sample estimation windows. 3 Model and estimation We consider a possibly non-linear, parametric model, where parameters are estimated using the generalized method of moments. The general estimation framework is that of Andrews 993. The observed data are given by a triangular array of random variables {W t = Y t, X t : t T }, Y t = y, y 2,... y t, and X t = x, x 2,..., x t. Assumptions can be made with regard to the dependence structure of W t such that the results below apply to a range of time series models. We make the following additional assumption on the noise and the relation between y t, lagged values of y t and exogenous regressors x t. Assumption The model for the dependent variable y t consists of a signal and additive noise y t = f t β t, δ; X t, Y t + ε t 7 where the function f t is fixed and differentiable with respect to the parameter vector θ t = β t, δ. In 7, while the parameter vector δ is constant for all t, the parameter vector β t could be subject to a structural break. When ignoring the break, parameters are estimated by 6
7 minimizing the sample analogue of the population moment conditions which requires solving T T E[mW t, β, δ] = t= T T mw t, ˆβ F, ˆδ ˆγ T t= inf β, δ T T mw t, ˆβ F, ˆδ = t= T mw t, β, δ ˆγ T t= T mw t, β, δ t= 8 where ˆβ F is estimator based on the full estimation window. Throughout we set the weighting matrix γ = S and S = lim T Var T T t= mw t, β, δ for which a consistent estimator is assumed to be available. As discussed above, we consider a null hypothesis that allows for local breaks, β t = β + T ητ where ητ = b Iτ < τ b, IA is the indicator function, which is unity if A is true and zero otherwise, b is a vector of constants, and τ = t/t. The partial sample parameter vectors β and β 2 satisfy the partial sample moment conditions τt τt t= mw t, β, δ =, and τt T t=t τ+ mw t, β 2, δ = Define mβ, β 2, δ, τ = τt τt t= mw t, β, δ + τt T t=t τ+ mw t, β 2, δ Then, the partial sum GMM estimators can be obtained by solving 8 with m replaced by m and ˆγ replaced by ˆγτ = τ Ŝ τ Ŝ 7
8 Forecasts are constructed as ŷ F T +h = f T +h ˆβ F, ˆδ; I T 9 ŷ P T +h = f T +h ˆβ 2, ˆδ; I T where I T is the information set at time T and includes any exogenous and lagged dependent variables that are needed to construct the forecast. If h >, the forecasts can be iterated or direct forecasts and the function f T +h will depend on which type of forecast is chosen. As the function f T +h can be non-linear in the parameters, iterated forecasts are covered by our analysis. Direct forecasts, in contrast, leads to residual autocorrelation, which can be addressed using a robust covariance matrix Pesaran et al. 2. In order not to complicate the notation further, we do not distinguish between the different forecasts for h >. The comparison between ŷt F +h and ŷp T +h is, however, non-standard as, under a local break, even the parameter estimates of the model that incorporates the break may not be unbiased. Our aim is to determine whether the full sample forecast 9 is more precise in the MSFE sense than the post-break sample forecast. We start by providing the asymptotic properties of the estimators in a model that incorporates the break and in a model that ignores the break. The asymptotic distributions derived by Andrews 993 depend on the following matrices, for which consistent estimators are assumed to be available, M = lim T T T [ ] mw t, β, δ E, M δ = lim β T T t= To simplify the notation, define X = M S /2 Z = M δ S /2 T [ ] mw t, β, δ E δ t= Partial sample estimator The partial sample estimators converge to the following Gaussian process indexed by τ ˆβ τ β 2 τ T ˆβ 2 τ β 2 X X τ X Z τ X X τ X Z ˆδ δ τ Z X τ Z X Z Z X Bτ + X τ X ηsds X [B Bτ] + X X τ ηsds Z B + Z X ηsds where Bτ is a Brownian motion defined on the interval [, ] and denotes weak convergence. We subtract β 2 from both estimators ˆβ and ˆβ 2 as our interest is in forecasting future observations, which are functions of β 2. The remainder that arises if τ τ b is absorbed in 8
9 the integral on the right hand side. Define the projection matrix P X = X X X X, its orthogonal complement as M X = I P X, and V = X X H = Z M X Z L = X X X Z Z M X Z H = LHL 2 The inverse in yields the asymptotic variance covariance matrix of ˆβ τ, ˆβ 2 τ, ˆδ Σ P = τ V + H H L H τ V + H L L L H Hence, T ˆβ τ β 2 τ [ X X X Bτ + τ ] ηsds X X X Z Z M X Z Z M XB T ˆβ2 τ β 2 ] [ τ X X X B Bτ + ηsds X X X Z Z M X Z Z M XB T ˆδ δ Z M X Z Z M XB τ 3 where the convergence occurs jointly. These expressions are analogous to those resulting from the Frisch-Waugh-Lovell theorem in a multivariate regression problem. Full sample estimator T ˆβF β 2 ˆδ δ For estimators that ignore the break, we have [ X X X Z Z X Z X ] [ X B + X X ηsds ] Z B + Z X ηsds 4 Using the notation defined in 2, the inverse in 4 is Σ F = V + H L L H 9
10 and, therefore, T ˆβF β 2 X X X B + ηsds X X X Z Z M X Z Z M XB T ˆδ δ Z M X Z Z M XB 5 Note that for the parameters ˆδ, the expression is identical to partial sample estimator. Later results require the asymptotic covariance between the estimators from the full sample and the break model, which is plim T Covˆβ 2 τ, ˆβ F = V + H = plim T Varˆβ F T T which corresponds to the results by Hausman 978 that, under the null of no misspecification, a consistent and asymptotically efficient estimator should have zero covariance with its difference from an consistent but asymptotically inefficient estimator, i.e. plim T T Covˆβ F, ˆβ F ˆβ 2 τ =. A difference here is that, under a local structural break, ˆβ F and ˆβ 2 τ are both inconsistent. 4 Testing for a break In this section, we apply the estimation framework in the previous section to generalize the motivating example from Section 2. We briefly consider the case of a known break date and then proceed to the case of an unknown break date. A complication in the testing procedure arises when mapping the null hypothesis of equal predictive accuracy to one based on the break magnitude because the latter varies with the unknown break date. Nevertheless, a test which has correct size and near optimal power can be established. 4. A local break of known timing Conditional on the information set I T, which contains the regressor set necessary to construct the forecast, the h-step-ahead forecast is ŷ T +h = f T +h ˆβ 2, ˆδ I T Denote the derivative of f T +h with respect to a parameter vector θ as f θ, where we drop the time subscript for notational convenience. Equal predictive accuracy is obtained when the break magnitude satisfies [ f β2 β β 2 ] 2 ζ = T τ b τ b f = 6 β 2
11 Details of the derivation can be found in Appendix A.. As in the motivating example of Section 2, the null hypothesis of equal mean squared forecast error maps into a hypothesis on the standardized break magnitude, ζ /2. A test for H : ζ = can be derived by noting that, asymptotically, T Varˆβ ˆβ 2 p τ b τ b V and, therefore, W τ b = T τ b τ b [ f β 2 ˆβ ˆβ ] 2 2 ˆω a χ 2, ζ 7 where ˆω is any consistent estimator of f β 2. The test statistic, W τ b, can be compared against the critical values of the χ 2, distribution to test for equal forecast performance. 4.2 A local break of unknown timing The preceding section motivates the use of the Wald-type test statistic 7 to test for equal predictive accuracy between a full-sample and post-break forecast. In this section, we adjust the test statistic to a local-to-zero break of unknown date and provide its asymptotic distribution. When the break date is unknown, we consider the following test statistic sup τ I W τ = sup τ I T ττ [ f β 2 ˆβ τ ˆβ 2 τ ˆω ] 2 8 with I = [τ min, τ max ]. Since the function f β 2 in 8 is fixed, the results in Andrews 993 and the continuous mapping theorem show that, under local alternatives and as T, W τ in 8 weakly converges to Q τ = [ Bτ τb τ τ τ + ηsds τ τ τ τ τ ηsds = [Zτ + µτ; θ τb ] 2 9 where Zτ = Bτ τb is a self-normalized Brownian bridge with expectation zero and τ τ variance equal to one, and [ ] τ τ µτ; θ τb = θ τb τ b Iτ b < τ + τ τ τ biτ b τ arises when a structural break is present. For a fixed break date, Q τ follows a non-central χ 2 -distribution with one degree of freedom and non-centrality parameter µτ; θ τb 2. ] 2 2
12 Throughout, we use the following estimate of the break date ˆτ = arg sup τ I 4.2. MSFE under an unknown break date W τ arg sup Q τ 2 τ I The difference between the expected asymptotic MSFE of the partial sample forecast based on the true break date and that of the full sample forecast, standardized by the variance of the post-break forecast, is { τ b = lim MSFEˆβ 2 ˆτ, ˆδ MSFEˆβ F, ˆδ } /f β T 2 where MSFEˆθ is the asymptotic MSFE under parameter estimates ˆθ. Lemma If the break date is estimated using 2 then difference in the standardized mean squared forecast error, τ, is { [ τ b = lim T E f T +h ˆβ 2 ˆτ, ˆδ I ] } 2 T f T +h β 2, δ I T T { [ E f T +h ˆβ F, ˆδ I ] } 2 T f T +h β 2, δ I T /f β 2 22 = lim T T E { [ ] } 2 f β 2 ˆβ 2 ˆτ β 2 E { [ ] } 2 f β 2 ˆβ F β 2 /f β 2 The proof is provided in Appendix A.2. Lemma shows that the difference in the MSFE is not affected by the estimation of the parameter vector δ, which is constant over the sample. Note that if instead of estimating the break date, one considers a fixed value τ, then Lemma holds with ˆτ replaced by the fixed value τ. The difference in the standardized mean squared forecast error is then a function of both τ b and τ. Using 3 and 5 in 22 yields τ b = E ˆτ f β 2 V X B Bˆτ + f β 2 V f ˆτ ˆτ β2 f β 2 ηs ds f β2 2 f β 2 2 ηs ds f V f β2 β2 23 The results in 23 are valid for a general form of instability ητ. Define Jτ = τ f β 2 /2 f β 2 ηsds and note that, for fixed f β 2, f β 2 /2 f β 2 V X [B Bˆτ] = B Bˆτ 2
13 where B is a one-dimensional Brownian motion. Then τ b = E { [ ] } 2 B Bˆτ + ˆτ ˆτ Jˆτ J 2 which could be used to test whether the use of a partial sample will improve forecast accuracy compared to the full sample under various forms of parameter instability. The expectation can be evaluated analytically if the size of the partial sample is exogenously set to some fraction of the total number of observations. Under a structural break, ητ = biτ < τ b, where b = T β 2 β, and 23 becomes τ b = E { [ ] } ˆτ B Bˆτ + θ τ b ˆτ 2 τ b ˆτ I[ˆτ < τ b] θτ 2 b τb 2 24 where θ τb = f β 2 b f β2 = ζ/τ b τ b. If the break date is known, then ˆτ = τ b and the critical break magnitude of the previous section is obtained. If τ b is estimated, then the expectation in 24 has to be taken with respect to both the stochastic process B and the distribution of the estimate ˆτ. The distribution of ˆτ is not analytically tractable and we evaluate 24 for different values of τ b and θ τb via simulation. Since τ b > for θ τb =, and τ b < when θ τb, there is a value of θ τb and thus for ζ τb for which τ b = for each τ b. Numerical results in Appendix A.8 show that τ b is a monotonically decreasing function of θ τb, which implies that τ b = for a unique value of θ τb. This supports the use of 8 to test τ b =. The break magnitude θ τb that yields τ b = depends on the unknown break date, τ b. This implies that critical values u = uτ b will differ across different values of the unknown break date. However, as we will show, our testing framework remains valid when the critical value uτ b is replaced with uˆτ Testing under unknown break date While the structural break case is our main focus, the results in this section hold for a general form of structural change as long as the change point is identified. Assumption 2 The function µτ; θ τb has a unique extremum at τ = τ b. For the structural break model it is easy to verify that Assumption 2 holds. The extremum value of 2 is given by µτ b ; θ τb = θ τb τb τ b = ζ /2 τ b. Under Assumption 2, and for a small nominal size, we show below that rejections are found only for break locations that are close to τ b. The following theorem shows that the estimated location of the break is close to the true break date. 3
14 Theorem Location concentration Suppose Q τ = [Zτ + µτ; θ τb ] 2 where Zτ is a zero mean Gaussian process with variance equal to one and µτ; θ τb satisfies Assumption 2, then as u P sup Q τ > u 2 = P [Zτ > u µτ; θ τb for some τ I ] [ + o] τ I where I = [τ min, τ max ], I = [τ b δu, τ b + δu] and δu = u log 2 u. The proof is presented in Appendix A.3. The location concentration is necessary to show that the proposed test controls size and has near optimal power. Close inspection of the proof of Theorem reveals that for the break magnitudes we find when solving 24 the concentration is expected to hold for conventional choices of the level of the test. This is indeed confirmed by the simulation results in Section 5. For each break date τ b and corresponding break magnitude θ τb for which 24 equals zero, we can obtain a critical value uτ b such that P sup τ I Q τ > uτ b 2 = α. This yields a sequence of critical values uτ b that depend on the unknown break date τ b. Assumption 3 Slowly varying critical values Suppose that uτ b is a differentiable function with respect to τ b, then the critical values are slowly varying with τ b in comparison to the derivative of the function µτ; θ τb with respect to τ on the interval I, i.e. uτ b τ b < µτ; θ τb τ < In the structural break model, the derivative γ = µτ;θτ b τ = θ τb [τ b τ b ] /2. The assumptions that critical values vary slowly relates the dependence of the critical values on τ b to the identification strength of the break date as the derivative of µτ; θ τb with respect to τ scales linearly with the break magnitude. It was shown in Section 2 that θ τb τb τ b, where the equality holds if the break date is known with certainty. Therefore, γ = θ τb τb τ b τ b τ b A sufficient condition for the slowly varying assumption is therefore uτ b τ b τ b τ b 25 This inequality can be verified once critical values are obtained. In Appendix A.7 we show that the inequality holds for the case of the structural break model. Under the assumptions above, the following theorem guarantees that the size of the test is controlled at the desired level once the critical value uτ b is replaced by the critical value uˆτ. 4
15 Theorem 2 Size Suppose uτ b is a sequence of critical values such that, for a break of magnitude θ τb at time τ b, we have that P sup Q τ > uτ b 2 = α 26 τ I Then as uτ b where ˆτ is given in 2. P sup Q τ > uˆτ 2 = α 27 τ I The proof is in Appendix A.4. Using critical values uˆτ, we can also establish that the test is near optimal in the sense that the power converges to the power of a test conditional on τ b. Suppose the critical values for the latter test are given by vτ b such that P H Q τ b > vτ b 2 = α, then we can establish the following theorem. Theorem 3 Near optimal power Suppose Assumption 3 holds, then ] P Ha [sup Q τ > uˆτ 2 [ P Ha Q τ b > vτ b 2] τ [ P Ha Q τ b > uτ b 2] [ P Ha Q τ b > vτ b 2] = 28 where ˆτ = arg sup τ Q τ and P Ha denotes the crossing probability under the alternative. Appendix A.5 contains the proof. A test based on the Wald statistic 8 uses critical values that depend on the estimated break date. The following corollary provides a test statistic with critical values that are independent of the break date in the limit where u. Corollary A test statistic with critical values that are independent of τ b for u is given by f β2 ˆβ2 τ ˆβ τ Sˆτ = sup T µˆτ; θˆτ 29 τ I f ˆV β 2 τ + ˆV 2 τ f β2 where ˆτ maximizes the first term of S or, equivalently, the Wald statistic 8. The proof is presented in Appendix A.6. Finally, following from the location concentration established in Theorem, in the limit where α, inference following a rejection is standard. Corollary 2 Corollary 8. of Piterbarg 996 As u, the distribution of the break location denoted by D converges converges to a delta function located at τ = τ b for 5
16 excesses over the boundary u 2, i.e. D ˆτ : Q ˆτ = sup τ I Testing procedure Q τ sup τ I Q τ > u 2 a δ τb as u To summarize, we use the following steps to make the test for τ b = in 24 operational. Using 2, evaluate 24 by simulation to find the break magnitude θ τb that yields τ b = for each τ b. 2. For each τ b and corresponding θ τb obtain a critical value uτ b such that P sup τ I Q τ b > uτ b 2 = α. 3. Now the test statistic sup τ I Q τ or its finite sample analogue can be compared to the critical value uˆτ 2 with ˆτ from 2. This test controls size P sup τ I Q τ > uˆτ 2 = α when α is sufficiently small per Theorem 2. The power of this test approaches that of the infeasible test P Q τ b > vτ b 2 per Theorem 3. The above procedure can also be performed to operationalize test statistic 29, which leads to critical values that are independent of the unknown break date for sufficiently small size. We will present critical values for both test statistics in Section Combining post-break and full sample forecasts Pesaran et al. 23 derive optimal weights for observations in an estimation sample such that, in the presence of a structural break, the MSFE of the one-step-ahead forecast is minimized. Conditional on the break date, the optimal weights take one value for observations in the pre-break regime and one value for observations in the post-break regime. This implies that we can write the optimally weighted forecast as a convex combination of the forecasts from pre-break observations and post-break observations ŷt c +h τ = ωf T +hˆβ + ωf T +h ˆβ 2 where the optimal forecast is denoted with superscript c. This forecast can be rewritten as a combination of the post-break sample forecast and the full sample forecast forecast as follows. For ease of exposition, we assume here that all parameters break. The asymptotic, expected mean square forecast error minus the variance of the forecast 6
17 period s error is [ lim E T = lim T E T ŷt c +h f T +hβ 2 ] 2 = [ T ωf β 2 ˆβ ˆβ ] f β 2 ˆβ 2 β 2 = ω 2 T [ f β 2 β β 2 ] 2 + ω 2 f β 2 τ b + τ b 2ω τ b f β 2 + τ b f β 2 + o + o 3 where f β2 = f T +hβ 2 β and the first equality relies on a Taylor expansion and the local-tozero nature of the breaks. See Appendix A.9 for 2 details. Maximizing 3 with respect to ω and ignoring the lower order term, yields ω = τ b + T [ f β2 β β 2 ] 2 f β 2 τ b + τ b V f β 2 where the denominator contains the Wald statistic, W τ b, derived above. Alternatively, we can combine the full sample forecast and the post-break sample forecast. Since, ˆβ F = τ b ˆβ + τ b ˆβ 2 + o p T /2, ŷt c +h = ωf T +hˆβ + ωf T +h ˆβ 2 + o p T /2 = ω f T +h ˆβ τ F + ωτb f T +h ˆβ 2 + o p T /2 b 3 and after applying a Taylor expansion of the forecast function f T +h, the optimal weight on the full sample forecast is given by ω F = ω τ b = + W τ b 32 The forecast ŷt c +h is therefore a convex combination of the full sample and post-break sample forecast with weights that are determined by our Wald test statistic. The empirical results in Pesaran et al. 23 suggest that uncertainty around the break date substantially deteriorates the accuracy of the optimal weights forecast. As a consequence, Pesaran et al. 23 derive robust optimal weights by integrating over the break dates, which yield substantially more accurate forecasts in their application. Given the impact that break date uncertainty has on choosing between the post-break and the full sample forecasts, it is not surprising that the same uncertainty should affect the weights. If this uncertainty is not taken into account, the weight on the post-break forecast will be too high. It will therefore be useful to test whether the break date uncertainty is small enough to justify using the combined forecast. As the Wald statistic in 32 is conditional on the true break date, consider the combined 7
18 forecast for a general value of τ ŷ c T +h τ = + W τ f T +hˆβ F + W τ + W τ f T +hˆβ 2 τ + Q τ f T +hˆβ F + Q τ + Q τ f T +hˆβ 2 τ 33 where the last line holds by the continuous mapping theorem. The asymptotic expressions for ˆβ 2 and ˆβ F are provided in 3 and 5. The difference in MSFE between the combined forecast and the full sample forecast, after applying a Taylor expansion on the forecast function f T +h, is given by [ ] c = T E + Q ˆτ f β 2 ˆβ F β 2 + Q ˆτ 2 + Q ˆτ f β 2 ˆβ 2 ˆτ β 2 [ ] 2 T E f β 2 ˆβ F β 2 + o 34 where we solve for c = numerically to obtain the break magnitude that corresponds to equal predictive accuracy. Numerical results in Appendix A.8 show that equal predictive accuracy is associated with a unique break magnitude for each τ b. The testing procedure outlined in Section can be applied to find the appropriate critical values. 5 Simulations 5. Asymptotic analysis for standard size The theoretical results of the previous section are derived under the assumption that the nominal size tends to zero. In this section, we investigate the properties of our tests using simulations under conventional choices for nominal size, α = {.,.5,.}, while maintaining the assumption that T. We will study for which break magnitude the MSFE from the post-break forecast equals that of the full sample forecast. Conditional on this break magnitude, we use simulation to obtain critical values. Finally, we study the size and power properties of the resulting tests. 5.. Implementation We simulate 9 with 2 for different combinations of break date and magnitude {τ b, θ τb }. Here, we focus on τ b = {τ min, τ min + δ τ,..., τ max } where τ min =.5, τ max = τ min and δ τ =.. Additionally, we ran simulations for τ min = τ max =.5 and those results are reported in Appendix B. For the break magnitude, θ τb, we consider θ τb = {,.5,..., 2}. The Brownian motion is approximated by dividing the [, ] interval in n = equally spaced parts, generating ɛ i N, and Bτ = nτ n i= ɛ i, see Bai and Perron 998. By maximizing 9 we obtain a distribution of the estimated break date ˆτ that can 8
19 Figure : Break magnitude for equal predictive accuracy between post-break and full sample forecasts ζ / τ b Note: The graph shows the standardized break magnitude, ζ /2, in 35 for which forecasts from post-break and full sample achieve the same MSFE, that is, in 23 equals zero. be used to evaluate 23. To approximate the expectation, we use 5, repetitions for each break date and break magnitude. For each value of τ b, we obtain the θ τb that yields equal predictive accuracy in 23 for full sample and post-break forecasts. This translates the null hypothesis of equal predictive accuracy into a null hypothesis regarding the break magnitude conditional of the break date τ b. By simulating under the null hypothesis for each τ b, we obtain critical values that are conditional on τ b. Accurate estimation of the break date implies that these critical values can be used for testing without correction. The magnitude of the breaks that we find under the null hypothesis suggest that the estimated break date will, in fact, be quite accurate Post-break versus full-sample forecast: break magnitude for equal forecast accuracy Using 23, we simulate the break magnitude for which the full sample and the post-break sample achieve equal predictive accuracy. Figure shows the combinations of break magnitude and break date for which equal predictive accuracy is obtained. The break magnitude is given in units of the standardized break magnitude, ζ /2 = T τ b τ b f β 2 β β 2 f β2 35 so that it can be interpreted as a standard deviations from a standard normal. The figure shows that for each break date τ b, the break magnitude of equal forecast accuracy is substantially larger than that under a known break date, which is ζ /2 =, 9
20 because the uncertainty of the break date estimation increases the MSFE of the post-break sample forecast. If a break occurs early the sample, τ =.5, then the post-break forecast is more precise only if the break magnitude is larger than three standard deviations. The break magnitude uniformly decreases as the break date, τ, increases and reaches about.2 standard deviations at τ =.85. The intuition for the downward sloping nature of the break magnitude of equal forecast accuracy is as follows. The local-to-zero nature of the break implies that, even asymptotically, the break date is estimated with uncertainty and has a non-degenerate distribution around the true break date. The uncertainty surrounding the break date implies that estimated post-break samples may be too short, increasing the forecast variance, or too long and include a pre-break sample, introducing a forecast bias. The former leads to an increase in MSFE. The latter can reduce the MSFE as it trades off the increase in the bias for a reduction in variance Pesaran and Timmermann, 27. However, this benefit decreases as the post-break sample increases. Additionally, supremum type test statistics require a trimming of dates over which breaks are allowed. Trimming leads to a truncation of the distribution of break dates at both ends of the sample. From a forecasting perspective, the effect of this truncation is not symmetric over the break dates. If the true break is early in the sample, the distribution is left truncated and the break date is likely to be, on average, estimated too late. The forecasts are therefore less likely to benefit from the MSFE reduction of a longer sample and more likely to have an estimation sample that is too short, which implies a larger variance without the benefit of a bias reduction. If, in contrast, the true break date is late in the sample, the distribution will be right truncated and therefore lead to an estimated break date that is, on average, too early. The estimation window will likely contain a short pre-break sample that reduces the MSFE and is less likely to be inefficiently short. Therefore, if the break is late, the break magnitude for which the post-break forecast is preferred over the full-sample forecast is smaller compared to the case when the break is early. This is reflected in the downward slope of the critical break magnitude observed in Figure Critical values, size, and power After finding the break magnitude for which post-break sample and full sample forecasts yield equal predictive accuracy, we can compute critical values for both the Wald-type test statistic in 8, which we will denote as W for simplicity from here, and the α-asymptotic statistic in 29, denoted as S, for a grid of break dates, τ b. Condition 25, which is required for the near optimality result does hold for all τ b details are available in Appendix A.7. The first line of the right panel of Table shows that the test has the correct size for α =.. For α =.5 and. size is still very close to the asymptotic size. At the beginning and the end of the sample, however, some size distortion occurs. Using the corrected test statistic 29 largely remedies these size distortions. 2
21 Table : Critical values and size of the ζ and S test statistics Critical values Size Test α W S Note: Reported are critical values and size for, first, W, the Wald test statistic 8 and, second, S, the test statistic 29, which is independent of τ b when the nominal size tends to zero. The critical values are given in the left panel of Table. Critical values for a finer grid of the true break date can be found in Appendix B. The large break magnitude that yields equal forecast accuracy implies a major increase in critical values when using the Wald test statistic 8, compared to the standard values of Andrews 993. For a nominal size of [.,.5,.] the critical values in Andrews are equal to [7.7, 8.85, 2.35]. The critical values for the α-asymptotic test statistic, S, in 29 are independent of ˆτ in the limit where α. Under a known break date, critical values would be from a one-sided normal distribution, that is, they would be [.64, 2.33, 2.58] for nominal size of [.,.5,.]. The critical values for the corrected test, S, vary substantially less over ˆτ than those for the Wald statistic, W. The results in Section suggest that the differences to the critical values that would be used if the break date is known diminish as α and this can be observed in Table. Given that the break magnitudes that lead to equal forecast performance are reasonably large, we expect the tests to have relatively good power properties. The power curves in Figure 2 show that the power of both tests is close to the power of the optimal test which uses the known break date to test whether the break magnitude exceeds the boundary depicted in Figure. The good power properties are true for all break dates. This confirms that the theoretical results for vanishing nominal size extend to conventional choices of the nominal size Forecast combination versus full-sample forecast Figure 3 shows the combination of τ b and break magnitude for which the forecast combination of Section 4.3 and the full sample forecast that weights observations equally have the same MSFE, which is represented by the solid line in the graph. For comparison, the dashed line gives the combination of post-break and full sample forecasts that have the same MSFE, that is, the line from Figure. It can be seen that the break magnitude of equal forecast performance for the combined forecast is lower than for the post-break sample forecast. This 2
22 Figure 2: Asymptotic power when testing between a post-break and full-sample forecast at α = W S Known τ b = τ b = ζ /2 τ b = ζ /2 τ b = ζ /2 ζ /2 Note: The plots show the power for tests at a nominal size of α =.5 with the null hypothesis given by the break magnitude depicted in Figure. The panels show power for different values of the unknown break date. The power of infeasible test conditional on the true break date is given as the dashed line, that of the test statistic W as the solid line with stars, and that of the test statistic S as the dashed line with diamonds. The solid horizontal line indicates the nominal size, and the vertical solid line indicates the break magnitude at which equal predictive accuracy is achieved corresponding to Figure. implies that combining the post-break and full sample forecasts offers improvements over the post-break forecast for smaller break magnitudes for a given break date. However, the difference is relatively small and breaks need to be quite large before the combined forecast is more precise than the full sample forecast. In order to determine whether to use the combined forecast, critical values can be obtained as before and are presented in Table 2. Again, the size is close to the theoretical size with small size distortions when using W, which are largely remedied when using S. Critical values on a finer grid of the true break date are presented in Appendix B. Figure 4 displays the power curves of the tests that compare the combined forecast and the full sample, equal weights forecast. Since, the break magnitudes for equal forecast performance are similar to the post-break sample forecast, it is not surprising that the properties in terms of size and power of the tests for the combined forecast are largely the same as those for the post-break forecast. 22
23 Figure 3: Break magnitude for equal predictive accuracy of forecast combination and full sample forecasts ζ / Note: The solid line shows the standardized break magnitude for which the forecast combination 33 achieves the same MSFE as the full sample forecast, in which case 34 equals zero. For comparison, the dashed line shows the break magnitude for which the post-break forecast and the full sample forecast achieve equal MSFE. τ b 5..5 Forecast combination versus the post-break forecast Finally, we investigate the break magnitudes that leads to equal forecast performance of the post-break forecast and the forecast that combines the post-break with the full sample forecast. Figure 5 plots the ratio of the MSFE of the combined forecast over that of the post-break forecast. For nearly all break magnitudes and dates, the combined forecast outperforms the post-break forecast. Only when the break occurs at the end of the sample and is relatively large, the post-break forecast is slightly more accurate. 5.2 Finite sample analysis 5.2. Set up of the Monte Carlo experiments We analyze the performance of the tests in finite sample for an AR model with varying degree of persistence. We consider the two tests for equal predictive accuracy between the post-break forecast and the full-sample forecast based on the Wald statistic 8 and on the S-statistic 29. Next, we consider the same test statistics but now test for equal predictive accuracy between the forecast combination 33 and the full-sample, equal weighted forecast. All tests are carried out at a nominal size α =.5, using sample sizes of T = {2, 24, 48} and break dates τ b = [.5,.25,.5,.75,.85]. While the sample sizes may appear large, note that τ b =.5 and T = 2 yield only 8 post-break observations. Parameter estimates are obtained by least squares, and the results are based on, repetitions. 23
24 Table 2: Critical values and size: forecast combination versus full sample forecasts Critical values Size Test α W S Note: Reported are critical values and size when testing for equal MSFE of the forecast combination 33 and the full sample forecast using, first, W, the Wald test statistic in 8 and, second, S, the test statistic 29 that is independent of τ b when the nominal size tends to zero. The data generating process DGP is given by y t = µ t + ρy t + ε t, ε t N, σ 2 36 where σ 2 = and µ t = { µ if t τ b T µ 2 if t > τ b T T τb τ b We set µ = µ 2 and µ = 2 T ζ/2 τ b + λ 2. When λ = the experiments deliver the finite sample size, whereas λ = {, 2} shows the power of the tests. The influence of the degree of persistence on the results is analyzed by varying ρ = {.,.3,.6,.9} Results The results in Table 3 show that for models with low and moderate persistence, ρ =. and.3, the size of the W and S tests are extremely close to the nominal size irrespective of the sample size and the break date. As persistent increases to ρ =.9, some size distortions become apparent for T = 2. Those do, however, diminish as T increases. These size distortions are similar for W and S and are the result of the small effective sample size in this setting. Power increases with λ. For T = 2 it is slightly larger when the break is in the middle of the sample but this effect disappears with increasing T. Overall, differences between W and S are small. The results for the tests that compare the forecast combination against the full sample, equal weights forecast in Table 4 are very similar to the results for the test with the postbreak sample forecast under the alternative. Size is very close to the nominal size for large effective sample sizes and power increases in λ and, mildly, in T. Overall, the results suggest that the W and S tests have good size and power properties 24
25 Figure 4: Asymptotic power when testing at α =.5 between forecast combination and full-sample forecast W S Known τ b = τ b = ζ /2 τ b = ζ /2 τ b = ζ /2 ζ /2 Note: The plots show asymptotic power curves when testing for equal predictive accuracy between the forecast combination 33 and the full-sample forecast using the break magnitude depicted in Figure 3 for different values of the break date τ b. For more information, see the footnote of Figure 2. unless the persistence of the time series is very high and this is combined with a small effective T. 6 Application We investigate the importance of structural breaks for 3 macroeconomic and financial time series from the St. Louis Federal Reserve FRED-MD database, which is a monthly updated database. We use the vintage from May 26. The data are described by McCracken and Ng 26, who suggest various transformations to render the series stationary and to deal with discontinued series or changes in classification. In the vintage used here, the data start in January 959 and end in April 26. After the transformations, all 3 series are available from January 96 until October 25. Our first forecast is for July 97 and we recursively construct one-step ahead forecasts until the end of the sample. The data are split into 8 groups: output and income OI, 7 series, labor market LM, 32 series, consumption and orders CO, series, orders and inventories OrdInv, series, money and credit MC, 4 series, interest rates and exchange rates IRER, 2 series, prices 25
A near optimal test for structural breaks when forecasting under square error loss
 A near optimal test for structural breaks when forecasting under square error loss Tom Boot Andreas Pick December 22, 26 Abstract We propose a near optimal test for structural breaks of unknown timing
A near optimal test for structural breaks when forecasting under square error loss Tom Boot Andreas Pick December 22, 26 Abstract We propose a near optimal test for structural breaks of unknown timing
A near optimal test for structural breaks when forecasting under squared error loss
 A near optimal test for structural breaks when forecasting under squared error loss Tom Boot Andreas Pick February 5, 26 Abstract We propose a near optimal test for local structural breaks of unknown timing
A near optimal test for structural breaks when forecasting under squared error loss Tom Boot Andreas Pick February 5, 26 Abstract We propose a near optimal test for local structural breaks of unknown timing
Does modeling a structural break improve forecast accuracy?
 Does modeling a structural break improve forecast accuracy? Tom Boot University of Groningen Andreas Pick Erasmus University Rotterdam Tinbergen Institute De Nederlandsche Bank 10th ECB Workshop on Forecasting
Does modeling a structural break improve forecast accuracy? Tom Boot University of Groningen Andreas Pick Erasmus University Rotterdam Tinbergen Institute De Nederlandsche Bank 10th ECB Workshop on Forecasting
Using all observations when forecasting under structural breaks
 Using all observations when forecasting under structural breaks Stanislav Anatolyev New Economic School Victor Kitov Moscow State University December 2007 Abstract We extend the idea of the trade-off window
Using all observations when forecasting under structural breaks Stanislav Anatolyev New Economic School Victor Kitov Moscow State University December 2007 Abstract We extend the idea of the trade-off window
Central Bank of Chile October 29-31, 2013 Bruce Hansen (University of Wisconsin) Structural Breaks October 29-31, / 91. Bruce E.
 Forecasting Lecture 3 Structural Breaks Central Bank of Chile October 29-31, 2013 Bruce Hansen (University of Wisconsin) Structural Breaks October 29-31, 2013 1 / 91 Bruce E. Hansen Organization Detection
Forecasting Lecture 3 Structural Breaks Central Bank of Chile October 29-31, 2013 Bruce Hansen (University of Wisconsin) Structural Breaks October 29-31, 2013 1 / 91 Bruce E. Hansen Organization Detection
Econometrics of Panel Data
 Econometrics of Panel Data Jakub Mućk Meeting # 6 Jakub Mućk Econometrics of Panel Data Meeting # 6 1 / 36 Outline 1 The First-Difference (FD) estimator 2 Dynamic panel data models 3 The Anderson and Hsiao
Econometrics of Panel Data Jakub Mućk Meeting # 6 Jakub Mućk Econometrics of Panel Data Meeting # 6 1 / 36 Outline 1 The First-Difference (FD) estimator 2 Dynamic panel data models 3 The Anderson and Hsiao
Non-nested model selection. in unstable environments
 Non-nested model selection in unstable environments Raffaella Giacomini UCLA (with Barbara Rossi, Duke) Motivation The problem: select between two competing models, based on how well they fit thedata Both
Non-nested model selection in unstable environments Raffaella Giacomini UCLA (with Barbara Rossi, Duke) Motivation The problem: select between two competing models, based on how well they fit thedata Both
Bootstrapping Heteroskedasticity Consistent Covariance Matrix Estimator
 Bootstrapping Heteroskedasticity Consistent Covariance Matrix Estimator by Emmanuel Flachaire Eurequa, University Paris I Panthéon-Sorbonne December 2001 Abstract Recent results of Cribari-Neto and Zarkos
Bootstrapping Heteroskedasticity Consistent Covariance Matrix Estimator by Emmanuel Flachaire Eurequa, University Paris I Panthéon-Sorbonne December 2001 Abstract Recent results of Cribari-Neto and Zarkos
On the Power of Tests for Regime Switching
 On the Power of Tests for Regime Switching joint work with Drew Carter and Ben Hansen Douglas G. Steigerwald UC Santa Barbara May 2015 D. Steigerwald (UCSB) Regime Switching May 2015 1 / 42 Motivating
On the Power of Tests for Regime Switching joint work with Drew Carter and Ben Hansen Douglas G. Steigerwald UC Santa Barbara May 2015 D. Steigerwald (UCSB) Regime Switching May 2015 1 / 42 Motivating
LECTURE ON HAC COVARIANCE MATRIX ESTIMATION AND THE KVB APPROACH
 LECURE ON HAC COVARIANCE MARIX ESIMAION AND HE KVB APPROACH CHUNG-MING KUAN Institute of Economics Academia Sinica October 20, 2006 ckuan@econ.sinica.edu.tw www.sinica.edu.tw/ ckuan Outline C.-M. Kuan,
LECURE ON HAC COVARIANCE MARIX ESIMAION AND HE KVB APPROACH CHUNG-MING KUAN Institute of Economics Academia Sinica October 20, 2006 ckuan@econ.sinica.edu.tw www.sinica.edu.tw/ ckuan Outline C.-M. Kuan,
Long-Run Covariability
 Long-Run Covariability Ulrich K. Müller and Mark W. Watson Princeton University October 2016 Motivation Study the long-run covariability/relationship between economic variables great ratios, long-run Phillips
Long-Run Covariability Ulrich K. Müller and Mark W. Watson Princeton University October 2016 Motivation Study the long-run covariability/relationship between economic variables great ratios, long-run Phillips
Economics 582 Random Effects Estimation
 Economics 582 Random Effects Estimation Eric Zivot May 29, 2013 Random Effects Model Hence, the model can be re-written as = x 0 β + + [x ] = 0 (no endogeneity) [ x ] = = + x 0 β + + [x ] = 0 [ x ] = 0
Economics 582 Random Effects Estimation Eric Zivot May 29, 2013 Random Effects Model Hence, the model can be re-written as = x 0 β + + [x ] = 0 (no endogeneity) [ x ] = = + x 0 β + + [x ] = 0 [ x ] = 0
Forecasting Under Structural Break Uncertainty
 ISSN 1440-771X Australia Department of Econometrics and Business Statistics http://www.buseco.monash.edu.au/depts/ebs/pubs/wpapers/ Forecasting Under Structural Break Uncertainty Jing Tian and Heather
ISSN 1440-771X Australia Department of Econometrics and Business Statistics http://www.buseco.monash.edu.au/depts/ebs/pubs/wpapers/ Forecasting Under Structural Break Uncertainty Jing Tian and Heather
Single Equation Linear GMM with Serially Correlated Moment Conditions
 Single Equation Linear GMM with Serially Correlated Moment Conditions Eric Zivot October 28, 2009 Univariate Time Series Let {y t } be an ergodic-stationary time series with E[y t ]=μ and var(y t )
Single Equation Linear GMM with Serially Correlated Moment Conditions Eric Zivot October 28, 2009 Univariate Time Series Let {y t } be an ergodic-stationary time series with E[y t ]=μ and var(y t )
Understanding Regressions with Observations Collected at High Frequency over Long Span
 Understanding Regressions with Observations Collected at High Frequency over Long Span Yoosoon Chang Department of Economics, Indiana University Joon Y. Park Department of Economics, Indiana University
Understanding Regressions with Observations Collected at High Frequency over Long Span Yoosoon Chang Department of Economics, Indiana University Joon Y. Park Department of Economics, Indiana University
Introduction to Econometrics
 Introduction to Econometrics T H I R D E D I T I O N Global Edition James H. Stock Harvard University Mark W. Watson Princeton University Boston Columbus Indianapolis New York San Francisco Upper Saddle
Introduction to Econometrics T H I R D E D I T I O N Global Edition James H. Stock Harvard University Mark W. Watson Princeton University Boston Columbus Indianapolis New York San Francisco Upper Saddle
Inference about Clustering and Parametric. Assumptions in Covariance Matrix Estimation
 Inference about Clustering and Parametric Assumptions in Covariance Matrix Estimation Mikko Packalen y Tony Wirjanto z 26 November 2010 Abstract Selecting an estimator for the variance covariance matrix
Inference about Clustering and Parametric Assumptions in Covariance Matrix Estimation Mikko Packalen y Tony Wirjanto z 26 November 2010 Abstract Selecting an estimator for the variance covariance matrix
A better way to bootstrap pairs
 A better way to bootstrap pairs Emmanuel Flachaire GREQAM - Université de la Méditerranée CORE - Université Catholique de Louvain April 999 Abstract In this paper we are interested in heteroskedastic regression
A better way to bootstrap pairs Emmanuel Flachaire GREQAM - Université de la Méditerranée CORE - Université Catholique de Louvain April 999 Abstract In this paper we are interested in heteroskedastic regression
Testing for structural breaks in discrete choice models
 19th International Congress on Modelling and Simulation, Perth, Australia, 12 16 December 2011 http://mssanz.org.au/modsim2011 Testing for structural breaks in discrete choice models Johnathan Wongsosaputro
19th International Congress on Modelling and Simulation, Perth, Australia, 12 16 December 2011 http://mssanz.org.au/modsim2011 Testing for structural breaks in discrete choice models Johnathan Wongsosaputro
Averaging Estimators for Regressions with a Possible Structural Break
 Averaging Estimators for Regressions with a Possible Structural Break Bruce E. Hansen University of Wisconsin y www.ssc.wisc.edu/~bhansen September 2007 Preliminary Abstract This paper investigates selection
Averaging Estimators for Regressions with a Possible Structural Break Bruce E. Hansen University of Wisconsin y www.ssc.wisc.edu/~bhansen September 2007 Preliminary Abstract This paper investigates selection
The Bootstrap: Theory and Applications. Biing-Shen Kuo National Chengchi University
 The Bootstrap: Theory and Applications Biing-Shen Kuo National Chengchi University Motivation: Poor Asymptotic Approximation Most of statistical inference relies on asymptotic theory. Motivation: Poor
The Bootstrap: Theory and Applications Biing-Shen Kuo National Chengchi University Motivation: Poor Asymptotic Approximation Most of statistical inference relies on asymptotic theory. Motivation: Poor
E 4101/5101 Lecture 9: Non-stationarity
 E 4101/5101 Lecture 9: Non-stationarity Ragnar Nymoen 30 March 2011 Introduction I Main references: Hamilton Ch 15,16 and 17. Davidson and MacKinnon Ch 14.3 and 14.4 Also read Ch 2.4 and Ch 2.5 in Davidson
E 4101/5101 Lecture 9: Non-stationarity Ragnar Nymoen 30 March 2011 Introduction I Main references: Hamilton Ch 15,16 and 17. Davidson and MacKinnon Ch 14.3 and 14.4 Also read Ch 2.4 and Ch 2.5 in Davidson
VAR-based Granger-causality Test in the Presence of Instabilities
 VAR-based Granger-causality Test in the Presence of Instabilities Barbara Rossi ICREA Professor at University of Pompeu Fabra Barcelona Graduate School of Economics, and CREI Barcelona, Spain. barbara.rossi@upf.edu
VAR-based Granger-causality Test in the Presence of Instabilities Barbara Rossi ICREA Professor at University of Pompeu Fabra Barcelona Graduate School of Economics, and CREI Barcelona, Spain. barbara.rossi@upf.edu
Nonstationary Time Series:
 Nonstationary Time Series: Unit Roots Egon Zakrajšek Division of Monetary Affairs Federal Reserve Board Summer School in Financial Mathematics Faculty of Mathematics & Physics University of Ljubljana September
Nonstationary Time Series: Unit Roots Egon Zakrajšek Division of Monetary Affairs Federal Reserve Board Summer School in Financial Mathematics Faculty of Mathematics & Physics University of Ljubljana September
Discussion of Tests of Equal Predictive Ability with Real-Time Data by T. E. Clark and M.W. McCracken
 Discussion of Tests of Equal Predictive Ability with Real-Time Data by T. E. Clark and M.W. McCracken Juri Marcucci Bank of Italy 5 th ECB Workshop on Forecasting Techniques Forecast Uncertainty in Macroeconomics
Discussion of Tests of Equal Predictive Ability with Real-Time Data by T. E. Clark and M.W. McCracken Juri Marcucci Bank of Italy 5 th ECB Workshop on Forecasting Techniques Forecast Uncertainty in Macroeconomics
Economics Division University of Southampton Southampton SO17 1BJ, UK. Title Overlapping Sub-sampling and invariance to initial conditions
 Economics Division University of Southampton Southampton SO17 1BJ, UK Discussion Papers in Economics and Econometrics Title Overlapping Sub-sampling and invariance to initial conditions By Maria Kyriacou
Economics Division University of Southampton Southampton SO17 1BJ, UK Discussion Papers in Economics and Econometrics Title Overlapping Sub-sampling and invariance to initial conditions By Maria Kyriacou
Estimation of Threshold Cointegration
 Estimation of Myung Hwan London School of Economics December 2006 Outline Model Asymptotics Inference Conclusion 1 Model Estimation Methods Literature 2 Asymptotics Consistency Convergence Rates Asymptotic
Estimation of Myung Hwan London School of Economics December 2006 Outline Model Asymptotics Inference Conclusion 1 Model Estimation Methods Literature 2 Asymptotics Consistency Convergence Rates Asymptotic
A Test for State-Dependent Predictive Ability based on a Markov-Switching Framework
 A Test for State-Dependent Predictive Ability based on a Markov-Switching Framework Sebastian Fossati University of Alberta This version: May 17, 2018 Abstract This paper proposes a new test for comparing
A Test for State-Dependent Predictive Ability based on a Markov-Switching Framework Sebastian Fossati University of Alberta This version: May 17, 2018 Abstract This paper proposes a new test for comparing
E 4160 Autumn term Lecture 9: Deterministic trends vs integrated series; Spurious regression; Dickey-Fuller distribution and test
 E 4160 Autumn term 2016. Lecture 9: Deterministic trends vs integrated series; Spurious regression; Dickey-Fuller distribution and test Ragnar Nymoen Department of Economics, University of Oslo 24 October
E 4160 Autumn term 2016. Lecture 9: Deterministic trends vs integrated series; Spurious regression; Dickey-Fuller distribution and test Ragnar Nymoen Department of Economics, University of Oslo 24 October
Testing an Autoregressive Structure in Binary Time Series Models
 ömmföäflsäafaäsflassflassflas ffffffffffffffffffffffffffffffffffff Discussion Papers Testing an Autoregressive Structure in Binary Time Series Models Henri Nyberg University of Helsinki and HECER Discussion
ömmföäflsäafaäsflassflassflas ffffffffffffffffffffffffffffffffffff Discussion Papers Testing an Autoregressive Structure in Binary Time Series Models Henri Nyberg University of Helsinki and HECER Discussion
Chapter 6. Panel Data. Joan Llull. Quantitative Statistical Methods II Barcelona GSE
 Chapter 6. Panel Data Joan Llull Quantitative Statistical Methods II Barcelona GSE Introduction Chapter 6. Panel Data 2 Panel data The term panel data refers to data sets with repeated observations over
Chapter 6. Panel Data Joan Llull Quantitative Statistical Methods II Barcelona GSE Introduction Chapter 6. Panel Data 2 Panel data The term panel data refers to data sets with repeated observations over
Economic modelling and forecasting
 Economic modelling and forecasting 2-6 February 2015 Bank of England he generalised method of moments Ole Rummel Adviser, CCBS at the Bank of England ole.rummel@bankofengland.co.uk Outline Classical estimation
Economic modelling and forecasting 2-6 February 2015 Bank of England he generalised method of moments Ole Rummel Adviser, CCBS at the Bank of England ole.rummel@bankofengland.co.uk Outline Classical estimation
Discussion of Bootstrap prediction intervals for linear, nonlinear, and nonparametric autoregressions, by Li Pan and Dimitris Politis
 Discussion of Bootstrap prediction intervals for linear, nonlinear, and nonparametric autoregressions, by Li Pan and Dimitris Politis Sílvia Gonçalves and Benoit Perron Département de sciences économiques,
Discussion of Bootstrap prediction intervals for linear, nonlinear, and nonparametric autoregressions, by Li Pan and Dimitris Politis Sílvia Gonçalves and Benoit Perron Département de sciences économiques,
Econ 423 Lecture Notes: Additional Topics in Time Series 1
 Econ 423 Lecture Notes: Additional Topics in Time Series 1 John C. Chao April 25, 2017 1 These notes are based in large part on Chapter 16 of Stock and Watson (2011). They are for instructional purposes
Econ 423 Lecture Notes: Additional Topics in Time Series 1 John C. Chao April 25, 2017 1 These notes are based in large part on Chapter 16 of Stock and Watson (2011). They are for instructional purposes
Forecasting in the presence of recent structural breaks
 Forecasting in the presence of recent structural breaks Second International Conference in memory of Carlo Giannini Jana Eklund 1, George Kapetanios 1,2 and Simon Price 1,3 1 Bank of England, 2 Queen Mary
Forecasting in the presence of recent structural breaks Second International Conference in memory of Carlo Giannini Jana Eklund 1, George Kapetanios 1,2 and Simon Price 1,3 1 Bank of England, 2 Queen Mary
Monitoring Forecasting Performance
 Monitoring Forecasting Performance Identifying when and why return prediction models work Allan Timmermann and Yinchu Zhu University of California, San Diego June 21, 2015 Outline Testing for time-varying
Monitoring Forecasting Performance Identifying when and why return prediction models work Allan Timmermann and Yinchu Zhu University of California, San Diego June 21, 2015 Outline Testing for time-varying
Are Forecast Updates Progressive?
 CIRJE-F-736 Are Forecast Updates Progressive? Chia-Lin Chang National Chung Hsing University Philip Hans Franses Erasmus University Rotterdam Michael McAleer Erasmus University Rotterdam and Tinbergen
CIRJE-F-736 Are Forecast Updates Progressive? Chia-Lin Chang National Chung Hsing University Philip Hans Franses Erasmus University Rotterdam Michael McAleer Erasmus University Rotterdam and Tinbergen
Econ 510 B. Brown Spring 2014 Final Exam Answers
 Econ 510 B. Brown Spring 2014 Final Exam Answers Answer five of the following questions. You must answer question 7. The question are weighted equally. You have 2.5 hours. You may use a calculator. Brevity
Econ 510 B. Brown Spring 2014 Final Exam Answers Answer five of the following questions. You must answer question 7. The question are weighted equally. You have 2.5 hours. You may use a calculator. Brevity
Forecasting the term structure interest rate of government bond yields
 Forecasting the term structure interest rate of government bond yields Bachelor Thesis Econometrics & Operational Research Joost van Esch (419617) Erasmus School of Economics, Erasmus University Rotterdam
Forecasting the term structure interest rate of government bond yields Bachelor Thesis Econometrics & Operational Research Joost van Esch (419617) Erasmus School of Economics, Erasmus University Rotterdam
A Non-Parametric Approach of Heteroskedasticity Robust Estimation of Vector-Autoregressive (VAR) Models
 Journal of Finance and Investment Analysis, vol.1, no.1, 2012, 55-67 ISSN: 2241-0988 (print version), 2241-0996 (online) International Scientific Press, 2012 A Non-Parametric Approach of Heteroskedasticity
Journal of Finance and Investment Analysis, vol.1, no.1, 2012, 55-67 ISSN: 2241-0988 (print version), 2241-0996 (online) International Scientific Press, 2012 A Non-Parametric Approach of Heteroskedasticity
Testing for Anomalous Periods in Time Series Data. Graham Elliott
 Testing for Anomalous Periods in Time Series Data Graham Elliott 1 Introduction The Motivating Problem There are reasons to expect that for a time series model that an anomalous period might occur where
Testing for Anomalous Periods in Time Series Data Graham Elliott 1 Introduction The Motivating Problem There are reasons to expect that for a time series model that an anomalous period might occur where
The Functional Central Limit Theorem and Testing for Time Varying Parameters
 NBER Summer Institute Minicourse What s New in Econometrics: ime Series Lecture : July 4, 008 he Functional Central Limit heorem and esting for ime Varying Parameters Lecture -, July, 008 Outline. FCL.
NBER Summer Institute Minicourse What s New in Econometrics: ime Series Lecture : July 4, 008 he Functional Central Limit heorem and esting for ime Varying Parameters Lecture -, July, 008 Outline. FCL.
Single Equation Linear GMM with Serially Correlated Moment Conditions
 Single Equation Linear GMM with Serially Correlated Moment Conditions Eric Zivot November 2, 2011 Univariate Time Series Let {y t } be an ergodic-stationary time series with E[y t ]=μ and var(y t )
Single Equation Linear GMM with Serially Correlated Moment Conditions Eric Zivot November 2, 2011 Univariate Time Series Let {y t } be an ergodic-stationary time series with E[y t ]=μ and var(y t )
FORECAST-BASED MODEL SELECTION
 FORECAST-ASED MODEL SELECTION IN THE PRESENCE OF STRUCTURAL REAKS Todd E. Clark Michael W. McCracken AUGUST 2002 RWP 02-05 Research Division Federal Reserve ank of Kansas City Todd E. Clark is an assistant
FORECAST-ASED MODEL SELECTION IN THE PRESENCE OF STRUCTURAL REAKS Todd E. Clark Michael W. McCracken AUGUST 2002 RWP 02-05 Research Division Federal Reserve ank of Kansas City Todd E. Clark is an assistant
Lectures on Structural Change
 Lectures on Structural Change Eric Zivot Department of Economics, University of Washington April5,2003 1 Overview of Testing for and Estimating Structural Change in Econometric Models 1. Day 1: Tests of
Lectures on Structural Change Eric Zivot Department of Economics, University of Washington April5,2003 1 Overview of Testing for and Estimating Structural Change in Econometric Models 1. Day 1: Tests of
Testing for a Trend with Persistent Errors
 Testing for a Trend with Persistent Errors Graham Elliott UCSD August 2017 Abstract We develop new tests for the coe cient on a time trend in a regression of a variable on a constant and time trend where
Testing for a Trend with Persistent Errors Graham Elliott UCSD August 2017 Abstract We develop new tests for the coe cient on a time trend in a regression of a variable on a constant and time trend where
Department of Economics, Vanderbilt University While it is known that pseudo-out-of-sample methods are not optimal for
 Comment Atsushi Inoue Department of Economics, Vanderbilt University (atsushi.inoue@vanderbilt.edu) While it is known that pseudo-out-of-sample methods are not optimal for comparing models, they are nevertheless
Comment Atsushi Inoue Department of Economics, Vanderbilt University (atsushi.inoue@vanderbilt.edu) While it is known that pseudo-out-of-sample methods are not optimal for comparing models, they are nevertheless
Forecasting the unemployment rate when the forecast loss function is asymmetric. Jing Tian
 Forecasting the unemployment rate when the forecast loss function is asymmetric Jing Tian This version: 27 May 2009 Abstract This paper studies forecasts when the forecast loss function is asymmetric,
Forecasting the unemployment rate when the forecast loss function is asymmetric Jing Tian This version: 27 May 2009 Abstract This paper studies forecasts when the forecast loss function is asymmetric,
Casuality and Programme Evaluation
 Casuality and Programme Evaluation Lecture V: Difference-in-Differences II Dr Martin Karlsson University of Duisburg-Essen Summer Semester 2017 M Karlsson (University of Duisburg-Essen) Casuality and Programme
Casuality and Programme Evaluation Lecture V: Difference-in-Differences II Dr Martin Karlsson University of Duisburg-Essen Summer Semester 2017 M Karlsson (University of Duisburg-Essen) Casuality and Programme
Supplement to Quantile-Based Nonparametric Inference for First-Price Auctions
 Supplement to Quantile-Based Nonparametric Inference for First-Price Auctions Vadim Marmer University of British Columbia Artyom Shneyerov CIRANO, CIREQ, and Concordia University August 30, 2010 Abstract
Supplement to Quantile-Based Nonparametric Inference for First-Price Auctions Vadim Marmer University of British Columbia Artyom Shneyerov CIRANO, CIREQ, and Concordia University August 30, 2010 Abstract
10. Time series regression and forecasting
 10. Time series regression and forecasting Key feature of this section: Analysis of data on a single entity observed at multiple points in time (time series data) Typical research questions: What is the
10. Time series regression and forecasting Key feature of this section: Analysis of data on a single entity observed at multiple points in time (time series data) Typical research questions: What is the
A TIME SERIES PARADOX: UNIT ROOT TESTS PERFORM POORLY WHEN DATA ARE COINTEGRATED
 A TIME SERIES PARADOX: UNIT ROOT TESTS PERFORM POORLY WHEN DATA ARE COINTEGRATED by W. Robert Reed Department of Economics and Finance University of Canterbury, New Zealand Email: bob.reed@canterbury.ac.nz
A TIME SERIES PARADOX: UNIT ROOT TESTS PERFORM POORLY WHEN DATA ARE COINTEGRATED by W. Robert Reed Department of Economics and Finance University of Canterbury, New Zealand Email: bob.reed@canterbury.ac.nz
Econ 583 Final Exam Fall 2008
 Econ 583 Final Exam Fall 2008 Eric Zivot December 11, 2008 Exam is due at 9:00 am in my office on Friday, December 12. 1 Maximum Likelihood Estimation and Asymptotic Theory Let X 1,...,X n be iid random
Econ 583 Final Exam Fall 2008 Eric Zivot December 11, 2008 Exam is due at 9:00 am in my office on Friday, December 12. 1 Maximum Likelihood Estimation and Asymptotic Theory Let X 1,...,X n be iid random
Missing dependent variables in panel data models
 Missing dependent variables in panel data models Jason Abrevaya Abstract This paper considers estimation of a fixed-effects model in which the dependent variable may be missing. For cross-sectional units
Missing dependent variables in panel data models Jason Abrevaya Abstract This paper considers estimation of a fixed-effects model in which the dependent variable may be missing. For cross-sectional units
Econometrics II - EXAM Outline Solutions All questions have 25pts Answer each question in separate sheets
 Econometrics II - EXAM Outline Solutions All questions hae 5pts Answer each question in separate sheets. Consider the two linear simultaneous equations G with two exogeneous ariables K, y γ + y γ + x δ
Econometrics II - EXAM Outline Solutions All questions hae 5pts Answer each question in separate sheets. Consider the two linear simultaneous equations G with two exogeneous ariables K, y γ + y γ + x δ
Inflation Revisited: New Evidence from Modified Unit Root Tests
 1 Inflation Revisited: New Evidence from Modified Unit Root Tests Walter Enders and Yu Liu * University of Alabama in Tuscaloosa and University of Texas at El Paso Abstract: We propose a simple modification
1 Inflation Revisited: New Evidence from Modified Unit Root Tests Walter Enders and Yu Liu * University of Alabama in Tuscaloosa and University of Texas at El Paso Abstract: We propose a simple modification
Tests of the Co-integration Rank in VAR Models in the Presence of a Possible Break in Trend at an Unknown Point
 Tests of the Co-integration Rank in VAR Models in the Presence of a Possible Break in Trend at an Unknown Point David Harris, Steve Leybourne, Robert Taylor Monash U., U. of Nottingam, U. of Essex Economics
Tests of the Co-integration Rank in VAR Models in the Presence of a Possible Break in Trend at an Unknown Point David Harris, Steve Leybourne, Robert Taylor Monash U., U. of Nottingam, U. of Essex Economics
An estimate of the long-run covariance matrix, Ω, is necessary to calculate asymptotic
 Chapter 6 ESTIMATION OF THE LONG-RUN COVARIANCE MATRIX An estimate of the long-run covariance matrix, Ω, is necessary to calculate asymptotic standard errors for the OLS and linear IV estimators presented
Chapter 6 ESTIMATION OF THE LONG-RUN COVARIANCE MATRIX An estimate of the long-run covariance matrix, Ω, is necessary to calculate asymptotic standard errors for the OLS and linear IV estimators presented
Linear Regression with Time Series Data
 u n i v e r s i t y o f c o p e n h a g e n d e p a r t m e n t o f e c o n o m i c s Econometrics II Linear Regression with Time Series Data Morten Nyboe Tabor u n i v e r s i t y o f c o p e n h a g
u n i v e r s i t y o f c o p e n h a g e n d e p a r t m e n t o f e c o n o m i c s Econometrics II Linear Regression with Time Series Data Morten Nyboe Tabor u n i v e r s i t y o f c o p e n h a g
Panel Threshold Regression Models with Endogenous Threshold Variables
 Panel Threshold Regression Models with Endogenous Threshold Variables Chien-Ho Wang National Taipei University Eric S. Lin National Tsing Hua University This Version: June 29, 2010 Abstract This paper
Panel Threshold Regression Models with Endogenous Threshold Variables Chien-Ho Wang National Taipei University Eric S. Lin National Tsing Hua University This Version: June 29, 2010 Abstract This paper
What s New in Econometrics. Lecture 13
 What s New in Econometrics Lecture 13 Weak Instruments and Many Instruments Guido Imbens NBER Summer Institute, 2007 Outline 1. Introduction 2. Motivation 3. Weak Instruments 4. Many Weak) Instruments
What s New in Econometrics Lecture 13 Weak Instruments and Many Instruments Guido Imbens NBER Summer Institute, 2007 Outline 1. Introduction 2. Motivation 3. Weak Instruments 4. Many Weak) Instruments
Econometrics II - EXAM Answer each question in separate sheets in three hours
 Econometrics II - EXAM Answer each question in separate sheets in three hours. Let u and u be jointly Gaussian and independent of z in all the equations. a Investigate the identification of the following
Econometrics II - EXAM Answer each question in separate sheets in three hours. Let u and u be jointly Gaussian and independent of z in all the equations. a Investigate the identification of the following
Has U.S. Labor Productivity Undergone High-Frequency Changes?
 Has U.S. Labor Productivity Undergone High-Frequency Changes? Luiggi Donayre Department of Economics University of Minnesota-Duluth Neil A. Wilmot Department of Economics University of Minnesota-Duluth
Has U.S. Labor Productivity Undergone High-Frequency Changes? Luiggi Donayre Department of Economics University of Minnesota-Duluth Neil A. Wilmot Department of Economics University of Minnesota-Duluth
Wooldridge, Introductory Econometrics, 4th ed. Chapter 15: Instrumental variables and two stage least squares
 Wooldridge, Introductory Econometrics, 4th ed. Chapter 15: Instrumental variables and two stage least squares Many economic models involve endogeneity: that is, a theoretical relationship does not fit
Wooldridge, Introductory Econometrics, 4th ed. Chapter 15: Instrumental variables and two stage least squares Many economic models involve endogeneity: that is, a theoretical relationship does not fit
A Forecast Rationality Test that Allows for Loss Function Asymmetries
 A Forecast Rationality Test that Allows for Loss Function Asymmetries Andrea A. Naghi First Draft: May, 2013 This Draft: August 21, 2014 Abstract In this paper, we propose a conditional moment type test
A Forecast Rationality Test that Allows for Loss Function Asymmetries Andrea A. Naghi First Draft: May, 2013 This Draft: August 21, 2014 Abstract In this paper, we propose a conditional moment type test
2.5 Forecasting and Impulse Response Functions
 2.5 Forecasting and Impulse Response Functions Principles of forecasting Forecast based on conditional expectations Suppose we are interested in forecasting the value of y t+1 based on a set of variables
2.5 Forecasting and Impulse Response Functions Principles of forecasting Forecast based on conditional expectations Suppose we are interested in forecasting the value of y t+1 based on a set of variables
Obtaining Critical Values for Test of Markov Regime Switching
 University of California, Santa Barbara From the SelectedWorks of Douglas G. Steigerwald November 1, 01 Obtaining Critical Values for Test of Markov Regime Switching Douglas G Steigerwald, University of
University of California, Santa Barbara From the SelectedWorks of Douglas G. Steigerwald November 1, 01 Obtaining Critical Values for Test of Markov Regime Switching Douglas G Steigerwald, University of
Robust Backtesting Tests for Value-at-Risk Models
 Robust Backtesting Tests for Value-at-Risk Models Jose Olmo City University London (joint work with Juan Carlos Escanciano, Indiana University) Far East and South Asia Meeting of the Econometric Society
Robust Backtesting Tests for Value-at-Risk Models Jose Olmo City University London (joint work with Juan Carlos Escanciano, Indiana University) Far East and South Asia Meeting of the Econometric Society
Økonomisk Kandidateksamen 2004 (I) Econometrics 2. Rettevejledning
 Økonomisk Kandidateksamen 2004 (I) Econometrics 2 Rettevejledning This is a closed-book exam (uden hjælpemidler). Answer all questions! The group of questions 1 to 4 have equal weight. Within each group,
Økonomisk Kandidateksamen 2004 (I) Econometrics 2 Rettevejledning This is a closed-book exam (uden hjælpemidler). Answer all questions! The group of questions 1 to 4 have equal weight. Within each group,
Comparing Forecast Accuracy of Different Models for Prices of Metal Commodities
 Comparing Forecast Accuracy of Different Models for Prices of Metal Commodities João Victor Issler (FGV) and Claudia F. Rodrigues (VALE) August, 2012 J.V. Issler and C.F. Rodrigues () Forecast Models for
Comparing Forecast Accuracy of Different Models for Prices of Metal Commodities João Victor Issler (FGV) and Claudia F. Rodrigues (VALE) August, 2012 J.V. Issler and C.F. Rodrigues () Forecast Models for
Density Forecast Evaluation in Unstable Environments 1
 Density Forecast Evaluation in Unstable Environments 1 GORIA GONZÁEZ-RIVERA Department of Economics University of alifornia, Riverside, A, USA YINGYING SUN Bank of the West San Francisco, A, USA April
Density Forecast Evaluation in Unstable Environments 1 GORIA GONZÁEZ-RIVERA Department of Economics University of alifornia, Riverside, A, USA YINGYING SUN Bank of the West San Francisco, A, USA April
Regime switching models
 Regime switching models Structural change and nonlinearities Matthieu Stigler Matthieu.Stigler at gmail.com April 30, 2009 Version 1.1 This document is released under the Creative Commons Attribution-Noncommercial
Regime switching models Structural change and nonlinearities Matthieu Stigler Matthieu.Stigler at gmail.com April 30, 2009 Version 1.1 This document is released under the Creative Commons Attribution-Noncommercial
Specification Test for Instrumental Variables Regression with Many Instruments
 Specification Test for Instrumental Variables Regression with Many Instruments Yoonseok Lee and Ryo Okui April 009 Preliminary; comments are welcome Abstract This paper considers specification testing
Specification Test for Instrumental Variables Regression with Many Instruments Yoonseok Lee and Ryo Okui April 009 Preliminary; comments are welcome Abstract This paper considers specification testing
Linear Regression with Time Series Data
 Econometrics 2 Linear Regression with Time Series Data Heino Bohn Nielsen 1of21 Outline (1) The linear regression model, identification and estimation. (2) Assumptions and results: (a) Consistency. (b)
Econometrics 2 Linear Regression with Time Series Data Heino Bohn Nielsen 1of21 Outline (1) The linear regression model, identification and estimation. (2) Assumptions and results: (a) Consistency. (b)
A Practitioner s Guide to Cluster-Robust Inference
 A Practitioner s Guide to Cluster-Robust Inference A. C. Cameron and D. L. Miller presented by Federico Curci March 4, 2015 Cameron Miller Cluster Clinic II March 4, 2015 1 / 20 In the previous episode
A Practitioner s Guide to Cluster-Robust Inference A. C. Cameron and D. L. Miller presented by Federico Curci March 4, 2015 Cameron Miller Cluster Clinic II March 4, 2015 1 / 20 In the previous episode
GMM-based inference in the AR(1) panel data model for parameter values where local identi cation fails
 GMM-based inference in the AR() panel data model for parameter values where local identi cation fails Edith Madsen entre for Applied Microeconometrics (AM) Department of Economics, University of openhagen,
GMM-based inference in the AR() panel data model for parameter values where local identi cation fails Edith Madsen entre for Applied Microeconometrics (AM) Department of Economics, University of openhagen,
Multiple Equation GMM with Common Coefficients: Panel Data
 Multiple Equation GMM with Common Coefficients: Panel Data Eric Zivot Winter 2013 Multi-equation GMM with common coefficients Example (panel wage equation) 69 = + 69 + + 69 + 1 80 = + 80 + + 80 + 2 Note:
Multiple Equation GMM with Common Coefficients: Panel Data Eric Zivot Winter 2013 Multi-equation GMM with common coefficients Example (panel wage equation) 69 = + 69 + + 69 + 1 80 = + 80 + + 80 + 2 Note:
Multivariate Out-of-Sample Tests for Granger Causality
 Multivariate Out-of-Sample Tests for Granger Causality Sarah Gelper and Christophe Croux K.U.Leuven, Faculty of Economics and Applied Economics, Naamsestraat 69, 3000 Leuven, Belgium Abstract A time series
Multivariate Out-of-Sample Tests for Granger Causality Sarah Gelper and Christophe Croux K.U.Leuven, Faculty of Economics and Applied Economics, Naamsestraat 69, 3000 Leuven, Belgium Abstract A time series
The Slow Convergence of OLS Estimators of α, β and Portfolio. β and Portfolio Weights under Long Memory Stochastic Volatility
 The Slow Convergence of OLS Estimators of α, β and Portfolio Weights under Long Memory Stochastic Volatility New York University Stern School of Business June 21, 2018 Introduction Bivariate long memory
The Slow Convergence of OLS Estimators of α, β and Portfolio Weights under Long Memory Stochastic Volatility New York University Stern School of Business June 21, 2018 Introduction Bivariate long memory
On Perron s Unit Root Tests in the Presence. of an Innovation Variance Break
 Applied Mathematical Sciences, Vol. 3, 2009, no. 27, 1341-1360 On Perron s Unit Root ests in the Presence of an Innovation Variance Break Amit Sen Department of Economics, 3800 Victory Parkway Xavier University,
Applied Mathematical Sciences, Vol. 3, 2009, no. 27, 1341-1360 On Perron s Unit Root ests in the Presence of an Innovation Variance Break Amit Sen Department of Economics, 3800 Victory Parkway Xavier University,
G. S. Maddala Kajal Lahiri. WILEY A John Wiley and Sons, Ltd., Publication
 G. S. Maddala Kajal Lahiri WILEY A John Wiley and Sons, Ltd., Publication TEMT Foreword Preface to the Fourth Edition xvii xix Part I Introduction and the Linear Regression Model 1 CHAPTER 1 What is Econometrics?
G. S. Maddala Kajal Lahiri WILEY A John Wiley and Sons, Ltd., Publication TEMT Foreword Preface to the Fourth Edition xvii xix Part I Introduction and the Linear Regression Model 1 CHAPTER 1 What is Econometrics?
Introductory Econometrics
 Based on the textbook by Wooldridge: : A Modern Approach Robert M. Kunst robert.kunst@univie.ac.at University of Vienna and Institute for Advanced Studies Vienna November 23, 2013 Outline Introduction
Based on the textbook by Wooldridge: : A Modern Approach Robert M. Kunst robert.kunst@univie.ac.at University of Vienna and Institute for Advanced Studies Vienna November 23, 2013 Outline Introduction
MFE Financial Econometrics 2018 Final Exam Model Solutions
 MFE Financial Econometrics 2018 Final Exam Model Solutions Tuesday 12 th March, 2019 1. If (X, ε) N (0, I 2 ) what is the distribution of Y = µ + β X + ε? Y N ( µ, β 2 + 1 ) 2. What is the Cramer-Rao lower
MFE Financial Econometrics 2018 Final Exam Model Solutions Tuesday 12 th March, 2019 1. If (X, ε) N (0, I 2 ) what is the distribution of Y = µ + β X + ε? Y N ( µ, β 2 + 1 ) 2. What is the Cramer-Rao lower
Econometrics of Panel Data
 Econometrics of Panel Data Jakub Mućk Meeting # 4 Jakub Mućk Econometrics of Panel Data Meeting # 4 1 / 30 Outline 1 Two-way Error Component Model Fixed effects model Random effects model 2 Non-spherical
Econometrics of Panel Data Jakub Mućk Meeting # 4 Jakub Mućk Econometrics of Panel Data Meeting # 4 1 / 30 Outline 1 Two-way Error Component Model Fixed effects model Random effects model 2 Non-spherical
Labor-Supply Shifts and Economic Fluctuations. Technical Appendix
 Labor-Supply Shifts and Economic Fluctuations Technical Appendix Yongsung Chang Department of Economics University of Pennsylvania Frank Schorfheide Department of Economics University of Pennsylvania January
Labor-Supply Shifts and Economic Fluctuations Technical Appendix Yongsung Chang Department of Economics University of Pennsylvania Frank Schorfheide Department of Economics University of Pennsylvania January
Intermediate Econometrics
 Intermediate Econometrics Heteroskedasticity Text: Wooldridge, 8 July 17, 2011 Heteroskedasticity Assumption of homoskedasticity, Var(u i x i1,..., x ik ) = E(u 2 i x i1,..., x ik ) = σ 2. That is, the
Intermediate Econometrics Heteroskedasticity Text: Wooldridge, 8 July 17, 2011 Heteroskedasticity Assumption of homoskedasticity, Var(u i x i1,..., x ik ) = E(u 2 i x i1,..., x ik ) = σ 2. That is, the
Discussion of Sensitivity and Informativeness under Local Misspecification
 Discussion of Sensitivity and Informativeness under Local Misspecification Jinyong Hahn April 4, 2019 Jinyong Hahn () Discussion of Sensitivity and Informativeness under Local Misspecification April 4,
Discussion of Sensitivity and Informativeness under Local Misspecification Jinyong Hahn April 4, 2019 Jinyong Hahn () Discussion of Sensitivity and Informativeness under Local Misspecification April 4,
May 2, Why do nonlinear models provide poor. macroeconomic forecasts? Graham Elliott (UCSD) Gray Calhoun (Iowa State) Motivating Problem
 (UCSD) Gray with May 2, 2012 The with (a) Typical comments about future of forecasting imply a large role for. (b) Many studies show a limited role in providing forecasts from. (c) Reviews of forecasting
(UCSD) Gray with May 2, 2012 The with (a) Typical comments about future of forecasting imply a large role for. (b) Many studies show a limited role in providing forecasts from. (c) Reviews of forecasting
Heteroskedasticity and Autocorrelation Consistent Standard Errors
 NBER Summer Institute Minicourse What s New in Econometrics: ime Series Lecture 9 July 6, 008 Heteroskedasticity and Autocorrelation Consistent Standard Errors Lecture 9, July, 008 Outline. What are HAC
NBER Summer Institute Minicourse What s New in Econometrics: ime Series Lecture 9 July 6, 008 Heteroskedasticity and Autocorrelation Consistent Standard Errors Lecture 9, July, 008 Outline. What are HAC
Advanced Econometrics
 Based on the textbook by Verbeek: A Guide to Modern Econometrics Robert M. Kunst robert.kunst@univie.ac.at University of Vienna and Institute for Advanced Studies Vienna May 16, 2013 Outline Univariate
Based on the textbook by Verbeek: A Guide to Modern Econometrics Robert M. Kunst robert.kunst@univie.ac.at University of Vienna and Institute for Advanced Studies Vienna May 16, 2013 Outline Univariate
Bayesian Compressed Vector Autoregressions
 Bayesian Compressed Vector Autoregressions Gary Koop a, Dimitris Korobilis b, and Davide Pettenuzzo c a University of Strathclyde b University of Glasgow c Brandeis University 9th ECB Workshop on Forecasting
Bayesian Compressed Vector Autoregressions Gary Koop a, Dimitris Korobilis b, and Davide Pettenuzzo c a University of Strathclyde b University of Glasgow c Brandeis University 9th ECB Workshop on Forecasting
This chapter reviews properties of regression estimators and test statistics based on
 Chapter 12 COINTEGRATING AND SPURIOUS REGRESSIONS This chapter reviews properties of regression estimators and test statistics based on the estimators when the regressors and regressant are difference
Chapter 12 COINTEGRATING AND SPURIOUS REGRESSIONS This chapter reviews properties of regression estimators and test statistics based on the estimators when the regressors and regressant are difference
Bias Correction and Out of Sample Forecast Accuracy
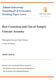 Auburn University Department of Economics Working Paper Series Bias Correction and Out of Sample Forecast Accuracy Hyeongwoo Kim and Nazif Durmaz Auburn University AUWP 2010 02 This paper can be downloaded
Auburn University Department of Economics Working Paper Series Bias Correction and Out of Sample Forecast Accuracy Hyeongwoo Kim and Nazif Durmaz Auburn University AUWP 2010 02 This paper can be downloaded
Bias-Correction in Vector Autoregressive Models: A Simulation Study
 Econometrics 2014, 2, 45-71; doi:10.3390/econometrics2010045 OPEN ACCESS econometrics ISSN 2225-1146 www.mdpi.com/journal/econometrics Article Bias-Correction in Vector Autoregressive Models: A Simulation
Econometrics 2014, 2, 45-71; doi:10.3390/econometrics2010045 OPEN ACCESS econometrics ISSN 2225-1146 www.mdpi.com/journal/econometrics Article Bias-Correction in Vector Autoregressive Models: A Simulation
Econometrics. Week 4. Fall Institute of Economic Studies Faculty of Social Sciences Charles University in Prague
 Econometrics Week 4 Institute of Economic Studies Faculty of Social Sciences Charles University in Prague Fall 2012 1 / 23 Recommended Reading For the today Serial correlation and heteroskedasticity in
Econometrics Week 4 Institute of Economic Studies Faculty of Social Sciences Charles University in Prague Fall 2012 1 / 23 Recommended Reading For the today Serial correlation and heteroskedasticity in
Choice of Spectral Density Estimator in Ng-Perron Test: Comparative Analysis
 MPRA Munich Personal RePEc Archive Choice of Spectral Density Estimator in Ng-Perron Test: Comparative Analysis Muhammad Irfan Malik and Atiq-ur- Rehman International Institute of Islamic Economics, International
MPRA Munich Personal RePEc Archive Choice of Spectral Density Estimator in Ng-Perron Test: Comparative Analysis Muhammad Irfan Malik and Atiq-ur- Rehman International Institute of Islamic Economics, International
B y t = γ 0 + Γ 1 y t + ε t B(L) y t = γ 0 + ε t ε t iid (0, D) D is diagonal
 Structural VAR Modeling for I(1) Data that is Not Cointegrated Assume y t =(y 1t,y 2t ) 0 be I(1) and not cointegrated. That is, y 1t and y 2t are both I(1) and there is no linear combination of y 1t and
Structural VAR Modeling for I(1) Data that is Not Cointegrated Assume y t =(y 1t,y 2t ) 0 be I(1) and not cointegrated. That is, y 1t and y 2t are both I(1) and there is no linear combination of y 1t and
Augmenting our AR(4) Model of Inflation. The Autoregressive Distributed Lag (ADL) Model
 Augmenting our AR(4) Model of Inflation Adding lagged unemployment to our model of inflationary change, we get: Inf t =1.28 (0.31) Inf t 1 (0.39) Inf t 2 +(0.09) Inf t 3 (0.53) (0.09) (0.09) (0.08) (0.08)
Augmenting our AR(4) Model of Inflation Adding lagged unemployment to our model of inflationary change, we get: Inf t =1.28 (0.31) Inf t 1 (0.39) Inf t 2 +(0.09) Inf t 3 (0.53) (0.09) (0.09) (0.08) (0.08)
Least Squares Estimation of a Panel Data Model with Multifactor Error Structure and Endogenous Covariates
 Least Squares Estimation of a Panel Data Model with Multifactor Error Structure and Endogenous Covariates Matthew Harding and Carlos Lamarche January 12, 2011 Abstract We propose a method for estimating
Least Squares Estimation of a Panel Data Model with Multifactor Error Structure and Endogenous Covariates Matthew Harding and Carlos Lamarche January 12, 2011 Abstract We propose a method for estimating
Principles of forecasting
 2.5 Forecasting Principles of forecasting Forecast based on conditional expectations Suppose we are interested in forecasting the value of y t+1 based on a set of variables X t (m 1 vector). Let y t+1
2.5 Forecasting Principles of forecasting Forecast based on conditional expectations Suppose we are interested in forecasting the value of y t+1 based on a set of variables X t (m 1 vector). Let y t+1
