A third-order unconditionally positivity-preserving scheme for. production-destruction equations with applications to non-equilibrium flows.
|
|
|
- Elwin Pope
- 5 years ago
- Views:
Transcription
1 A thrd-order ucodtoally postvty-preservg scheme for producto-destructo equatos wth applcatos to o-equlbrum flows Jutao Huag 1, Wefeg Zhao 2 ad Ch-Wag Shu 3 Abstract I ths paper, we exted our prevous work [10] ad develop a thrd-order ucodtoally postvty-preservg modfed Patakar Ruge-Kutta MPRK method for productodestructo equatos. The ecessary ad suffcet codtos for the method to be of thrd-order accuracy are derved. Wth the same approach as [10], ths tme tegrato method s the geeralzed to solve a class of ODEs arsg from sem-dscrete schemes for PDEs ad coupled wth the postvty-preservg fte dfferece weghted essetally ooscllatory WENO schemes for o-equlbrum flows. Numercal expermets are provded to demostrate the performace of our proposed scheme. Keywords: Compressble Euler equatos; postvty-preservg; chemcal reactos; producto-destructo equatos; fte dfferece; thrd-order accuracy 1 Zhou Pe-Yua Ceter for Appled Mathematcs, Tsghua Uversty, Bejg , Cha. E-mal: huagjt13@mals.tsghua.edu.c 2 Departmet of Appled Mathematcs, Uversty of Scece ad Techology Bejg, Bejg , Cha. E-mal: wfzhao@ustb.edu.c 3 Dvso of Appled Mathematcs, Brow Uversty, Provdece, RI 02912, USA. E-mal: shu@dam.brow.edu. Research supported by ARO grat W911NF ad NSF grat DMS
2 1 Itroducto Ths paper s cocered wth postvty-preservg umercal methods for o-equlbrum flow models wthout coducto or radato [17], a system of hyperbolc balace laws U t + FU x = SU. 1.1 Here U, FU ad SU are vectors wth m = s + 2 compoets where s s the umber of speces: U = ρ 1,, ρ s, ρu, ρe 0 T, FU = ρ 1 u,, ρ s u, ρu 2 + p, ρue 0 + up T, SU = s 1,, s s, 0, 0 T, where ρ s the desty of the -th speces, = 1, 2,, s, u s the velocty ad e 0 s the total eergy per ut mass of mxture. The total desty s defed as ρ = s =1 ρ ad the pressure p s gve by p = RT s where R s the uversal gas costat ad M s the molar mass of the -th speces. The total eergy has the expresso: =1 ρ M, s s ρe 0 = ρ e, T + ρ h ρu2, =1 where e, T = C T s the teral eergy of the -th speces wth C = 3R/2M ad =1 5R/2M for mooatomc speces ad datomc speces, respectvely, ad the ethalpes h 0 are costats. The source term SU descrbes the chemcal reactos occurrg gas flows whch result chages the amout of mass of each chemcal speces. It s assumed that there are J reactos of the form ν 1,j X 1 + ν 2,j X ν s,j X s ν 1,j X 1 + ν 2,j X ν s,j X s, j = 1,, J, 2
3 where ν,j ad ν,j are respectvely the stochometrc coeffcets of the reactats ad products of the -th speces the j-th reacto. For o-equlbrum chemstry, the rate of producto of speces due to chemcal reacto, may be wrtte as J s = M ν,j ν,j s k f,j ρ s s ν s,j kb,j ρ s ν s,j, = 1,, s. M s M s j=1 s=1 For each reacto j, the forward ad backward reacto rates, k f,j ad k b,j are gve fuctos of the temperature. Notce that the reactve Euler equatos, whch are ofte used to model detoato waves [16], ca also be wrtte ths form 1.1. For more detals, please refer to our prevous work [10]. Physcally, the desty ad the pressure should both be postve. I practcal computato, the falure of preservg postvty of such quattes may cause blow-ups of the computato because the learzed system may become ll-posed. I recet years, there have bee sgfcat progresses developg hgh-order postvty-preservg schemes for hyperbolc systems sce the poeerg works by Zhag ad Shu [19, 20, 21, 22]. Readers are referred to the revew papers [18, 14] for detals. We remark that almost all these works rely o the strog-stablty-preservg SSP tme tegrato [4], whch could be take as a covex combato of Euler forward method ad thus aturally preserve the postvty of umercal solutos. However, for equatos wth stff chemcal reacto sources 1.1, the explct tme tegrato may suffer from very severe restrcto o the tme step ad thus causes large computatoal cost. Recetly, there are a few works o postvty-preservg tme dscretzatos for PDEs wth stff source terms. A famly of sem-mplct schemes for a partcular class of ODEs wth stff terms were proposed [2] ad further adapted to shallow water equatos wth frcto terms [3]. We developed a class of mplct-explct IMEX RK methods for the systems of ODEs arsg from the sem-dscretzato of the Kerr-Debye model [8]. I [9], a class of expoetal SSP hgh order tme tegrato wth boud-preservg property was costructed ad appled to scalar hyperbolc equatos wth stff dsspatve source terms. Most recetly, Hu et al. proposed IMEX RK schemes [7] ad expoetal RK schemes [6] 3 s=1
4 for ketc equatos, whch share both the asymptotc-preservg ad postvty-preservg propertes. Ths paper s devoted to the dervato of postvty-preservg schemes for ths class of hyperbolc equatos 1.1. Followg our prevous work [10], we frst gore the covecto terms 1.1 ad move to a larger class of ODEs called producto-destructo equatos whch have the form: wth ad dc dt = P c D c, = 1, 2,, N, 1.2 P c = N p j c, D c = j=1 N d j c, j=1 p j c = d j c 0. Here c = c 1, c 2,, c N T ad c = c t 0 deotes the cocetrato of the -th compoet. The producto fucto p j c deotes the rate at whch the j-th compoet trasforms to the -th compoet, whle the destructo fucto d j c deotes the rate at whch the -th compoet trasforms to the j-th compoet. The exact solutos to 1.2 share the coservato property,.e., N =1 c t remas uchaged wth respect to tme t. Also, the postvty of the soluto s guarateed as log as the tal codto s postve ad d j c = 0 for c = 0 [1]. There have bee may lteratures o developg umercal methods for 1.2 whch ucodtoally preserve the coservato ad the postvty of the solutos. Here we oly commet o the most recet works by Kopecz ad Mester [13, 12] where they formulated a class of modfed Patakar-Ruge-Kutta MPRK methods. The methods adapt explct Ruge-Kutta schemes a way to esure the coservato ad the postvty of the soluto depedet of the tme step sze. Ispred by ther work, we modfy the explct RK scheme Shu-Osher form [15] stead of the classcal form ad develop aother class of secodorder MPRK schemes whch are the successfully appled to sem-dscrete schemes arsg from PDEs [10]. Combg wth the postvty-preservg fte-dfferece WENO schemes, 4
5 we obta a postvty-preservg WENO scheme for o-equlbrum flows 1.1. For more detaled revews, please refer to our prevous work [10]. I ths paper, we cotue our work [10] ad costruct a thrd-order MPRK scheme for producto-destructo equatos 1.2 ad a class of sem-dscrete schemes for PDEs. Followg the les of [13, 12, 10], the MPRK scheme s appled to a specal class of ODEs ad thus the ecessary codto for thrd order accuracy s derved. By drect Taylor expaso, we fd that the ecessary codto s ot a suffcet codto. For elmatg the redudat terms, a addtoal costrat o the coeffcets of the method s proposed. The MPRK scheme s the exteded to solve sem-dscrete schemes arsg from PDEs after dscretzato space ad the order of accuracy s valdated. The paper s orgazed as follows. I secto 2, we formulate a class of MPRK scheme the Shu-Osher form ad the derve the ecessary ad suffcet codtos for the scheme to be thrd-order accurate. I secto 3, the explct form of udetermed fucto the scheme s costructed to satsfy the suffcet codto. The scheme s the exteded to sem-dscrete schemes arsg from PDEs after dscretzato space. Numercal results for the ODEs ad PDEs are preseted secto 4. Some cocludg remarks are gve secto 5. 2 The ODE solver I ths part, we frst formulate a class of modfed Patakar RK scheme the Shu-Osher form. Followg the procedures [13], we apply t to a specal class of ODEs ad derve the ecessary codto for ths solver to be thrd-order accurate. However, we further fd that ths ecessary codto s ot a suffcet codto. By elmatg the redudat terms Taylor expasos, the suffcet codto s obtaed. The three-stage explct RK scheme the Shu-Osher form s c 0 = c, 2.1a 5
6 c 1 = α 10 c 0 + t j c 2 = α 20 c 0 + α 21 c 1 + t j β 10 p 0 j β 10 d 0 j, 2.1b β 20 p 0 j + β 21 p 1 j β 20d 0 j + β 21 d 1 j, 2.1c c +1 = α 30 c 0 + α 31 c 1 + α 32 c 2 + t β 30 p 0 j + β 31 p 1 j + β 32 p 2 j β 30d 0 j + β 31 d 1 j + β 32 d 2 j. 2.1d j Here ad afterwards, the summato s from 1 to N, uless otherwse stated. The superscrpt deotes the stage whch the fucto evaluates, e.g., p k j = p j c k for k = 0, 1, 2. Followg the modfcato [10], the explct RK scheme 2.1 becomes c 0 = c, c 1 = α 10 c 0 + t j β 10 p 0 j c 2 = α 20 c 0 + α 21 c 1 + t j 2.2a β 10 d 0 c 1 j π j π, 2.2b c 1 j β 20 p 0 j + β 21 p 1 c2 j j β 20 d 0 j + β 21 d 1 ρ j c2 j ρ c +1 = α 30 c 0 + α 31 c 1 + α 32 c 2 c+1 β 30 p 0 j + β 31 p 1 j + β 32 p 2 j β 30 d jσ 0 j + β 31 d 1 j + β 32 d 2 j + t j c+1 j σ, 2.2c. 2.2d Here π, ρ ad σ are fuctos of c k, k = 0, 1, 2 ad wll be determed later. The coeffcets are assumed to be postve ad satsfy the order codtos for the explct RK scheme 2.1: α 10 = 1, α 20 + α 21 = 1, α 30 + α 31 + α 32 = 1, α 31 β 10 + α 32 α 21 β 10 + β 20 + β 21 + β 30 + β 31 + β 32 = 1, β 10 α 32 β 21 + β 31 + β 32 α 21 β 10 + β 20 + β 21 = 1 2, β10 2 α 32β 21 + β 31 + β 32 α 21 β 10 + β 20 + β 21 2 = 1 3, β 10 β 21 β 32 =
7 Sce 2.2 s oly a modfcato of 2.1, t s atural to assume that 2.1 Necessary codtos π = c 1 ρ = c 2 σ = c +1 + O t, + O t, + O t. To derve the ecessary codtos for 2.2 to be thrd-order accurate, we cosder a specfc class of ODEs wth the source to be of lear ad quadratc forms [12]: For I, J {1, 2,, N} ad I J, ad wth costat µ > 0 ad κ = 1, 2. µc κ I, = J, j = I, p j c = 0, otherwse, µc κ I, = I, j = J, d j c = 0, otherwse, We splt our procedure to three steps: 1. Frst, by Taylor expasos, we express the exact soluto c t +1 terms of c ad other quattes at tme level up to O t 4. Smplfy the fal stage 2.2d for the specfc class of ODEs; 2. Secod, derve the expressos of c 1 ad c 2 ad 2.2c. by the frst ad the secod stage 2.2b 3. Fally, obta the ecessary codtos terms of c1 π, c2 ρ ad c+1 σ. We start wth the frst step. Step 1: By takg the dervatve wth respect to t o the ODEs 1.2, we have d 2 c dt 2 = d dt P c D c = k P D P k D k = P D P D, c k c 7
8 wth the vector P = P 1, P 2,, P N T ad D = D 1, D 2,, D N T, ad furthermore, d 3 c dt 3 = k,l 2 P D c k c l P l D l P k D k + P D c k P k D k c l P l D l = P D T H P D P D + k P D P k D k P D, c k c where H φ deotes the Hessa matrx of some fucto φ = φc. Therefore, by Taylor expasos, we obta c t +1 = c + tdc dt + t2 d 2 c 2 dt + t3 d 3 c 2 6 dt + 3 O t4 = c + tp D + t2 P D P D 2 c + t3 6 P D T H P D P D + k Substtutg the above expresso to the fal stage 2.2d yelds α 30 c + α 31c 1 + α 32 c 2 + t j c tp D t2 P D P D 2 c t3 6 P D T H P D P D + k P D Pk D k P D + O t 4. c k c 2.5 β 30 p j + β 31p 1 j + β 32 p 2 j c+1 jσ j β 30 d j + β 31d 1 j + β 32 d 2 P D c+1 j Pk D k P D = O t 4. c k c By takg = I, rememberg that p Ij c = 0 for ay j, ad rewrtg I as, we have α 31 c 1 c + α 32 c 2 c tβ 30 D + β 31 D 1 + td t2 2 + β 32 D 2 c+1 σ D D c + t3 2 D D 6 c t3 6 D 2 D = O t 4, 2.6 c where we used the relato α 30 + α 31 + α 32 = 1. Note that the above equato holds for ay, sce I could be ay umber from 1 to N. Expad D k = D c k = µc k κ for k = 1, 2 at c : σ D k = D + D c k c D c k c 2 c 2 c 2, 2.7 8
9 where the hgher order terms vash due to the fact that D k s a lear or quadratc fucto of c k. Thus, the lear combato β 30 D + β 31D 1 + β 32 D 2 s smplfed as follows: β 30 D + β 31 D 1 + β 32 D 2 = β 30 D + β 31D + D c 1 c c D 2 c 2 c 1 c 2 + β 32 D + D c 2 c c D c 2 2 c 2 c 2 = β 30 + β 31 + β 32 D + D β 31 c 1 c + β 32 c 2 c D β c 2 c 2 31 c 1 c 2 + β 32 c 2 c 2 By substtutg the above relato to 2.6 ad rearragg the terms, we obta: α 31 c 1 c + α 32c 2 t 2 D c t 2 D 2 c 2 c + td 2 D + tβ 31c 1 c + β 32c 2 β 31 c 1 c 2 + β 32 c 2 1 β 30 + β 31 + β 32 c+1 c 2 c+1 σ c+1 c σ σ + t3 6 D 2 D c = O t t2 3 D 2 Step 2: I the ext, we expad c 1 ad c 2 the frst stage 2.2b ad the secod stage 2.2c. By the frst stage 2.2b, we mmedately get c 1 = α 10 c tβ 10D c 1 π = c tβ 10D c 1 π. 2.9 By the secod stage 2.2c, we obta c 2 = α 20 c + α 21 c 1 Substtute 2.7 for k = 1 ad 2.9 to 2.10: c 2 tβ 20 D + β 21 D 1 = α 20 c + α 21c tβ 10D c 1 π t β 20 D + β 21 D + D c 1 c D c 1 c 2 c 2 c 2 = α 20 + α 21 c tα 21 β 10 D c 1 π t β 20 + β 21 D + β 21 D c tβ 10 D c ρ c 2 ρ c π 2 β 2 D 21 tβ c 2 10 D c 1 2 π c 2 ρ 9
10 = c tα 21β 10 D t c2 ρ c 1 π β 20 + β 21 D + β 21 D c tβ 10 D = c td α c 1 21β 10 + β 20 + β 21 c2 + t 2 β 21 β 10 D π ρ t 31 2 β 21β 2 10 D 2 2 D c 2 c1 c π 2 β 2 D 21 tβ c 2 10 D D c 1 c 2 c π ρ c 1 2 π 2c π ρ Step 3: I ths step, we wll substtute the expressos of c ad c to 2.8, ad derve the ecessary codtos. We frst focus o the case κ = 1,.e., the ODEs wth lear source terms. I ths case, the followg equalty holds: 2 D c 2 = 0, ad the 2.8 s smplfed as follows: α 31 tβ 10 D c 1 + α 32 td c 1 α 21 β 10 π + td D c tβ 32 1 β 30 + β 31 + β 32 c+1 σ + β 20 + β 21 c2 + t 2 β 21 β 10 D π ρ D c t 2 2 D D c tβ 31 tβ 10 D td c 1 α 21 β 10 + β 20 + β 21 c2 + t 2 β 21 β 10 D π ρ D c 1 c 2 c π D c 1 c+1 π σ c 1 c 2 c +1 c π ρ σ + t3 6 D c 2 D = O t O left had sde of 2.12, the O t term s D c 1 c 1 α 31 β 10 + α 32 α 21 β 10 + β 20 + β 21 c2 + β 30 + β 31 + β 32 c+1 1 t π π ρ σ = µc c 1 α 31 + α 32 α 21 β 10 + α 32 β 20 + β 21 c2 + β 30 + β 31 + β 32 c+1 1 t. π ρ σ The O t 2 term s α 32 β 21 β 10 D D c 1 c 2 1 c π ρ 2 + D c +1 β 31 β 10 D c σ c 1 D c D + β 32 D π α c 1 21β 10 + β 20 + β 21 c2 t 2 π ρ 10 ρ
11 = D D c = µ 2 c c 1 c 2 α 32 β 21 β 10 + β 31 β 10 + β 32 α 21 β 10 c1 c +1 π ρ π c 1 c 2 α 32 β 21 β 10 + β 31 β 10 + β 32 α 21 β 10 c1 c +1 π ρ π The O t 3 term s σ σ + β 32 β 20 + β 21 c2 + β 32 β 20 + β 21 c2 D c +1 β 32 β 21 β 10 D D c 1 c c σ c π ρ 6 D 2 D t 3 c = D D 2 c 1 c 2 c +1 β 32 β 21 β t 3 c π ρ σ 6 = µ 3 c c 1 c 2 c +1 β 32 β 21 β t 3. π ρ σ 6 Sce the costat µ s arbtrary, we have c 1 α 31 + α 32 α 21 β 10 + α 32 β 20 + β 21 c2 + β 30 + β 31 + β 32 c+1 π ρ c 1 c 2 c 1 c +1 α 32 β 21 β 10 + β 31 + β 32 α 21 β 10 π ρ π c 1 c 2 c +1 β 32 β 21 β 10 = 1 π ρ σ 6 σ σ + β 32 β 20 + β 21 c2 c +1 1 t 2 ρ σ 2 c +1 1 t 2. ρ σ 2 = 1 + O t 3, 2.13a c +1 = 1 ρ σ 2 + O t2, 2.13b + O t. 2.13c I the ext, we set κ = 2. Note that the terms 2.8, whch do ot volve 2 D c 2 are balaced as log as the codto 2.13 holds. We oly focus o the terms whch are relevat to 2 D c 2. O the left had sde of 2.8, the term c 1 The term c 2 c has t3 1β 2 21β10 2 D 2 2 D c 2 sde of 2.8, we have β 31 c 1 c 2 + β 32 c 2 c 2 = β 31 tβ 10 D = t 2 D 2 c 1 c1 π 2 c2 c does ot volve 2 D c 2 ρ. For the last term o the left had 2 + β 32 td π α c 1 21β 10 + β 20 + β 21 c2 2 π ρ β 31 β10 2 c1 2 c 1 + β 32 α 21 β 10 + β 20 + β 21 c2 2 π π ρ.,. Therefore, the O t 3 term volvg 2 D c 2 α β 21β10 2 D D 2 2 c1 2c2 c 2 π ρ s 11
12 1 2 D 2 c 2 = 1 2 D 2 2 D c 2 D 2 β 31 β10 2 c1 2 c 1 + β 32 α 21 β 10 + β 20 + β 21 c2 2 c+1 π π ρ σ 1 3 D 2 β 31 β10 2 c1 2 c 1 + β 32 α 21 β 10 + β 20 + β 21 c2 2 c+1 π π ρ ad thus the codto s derved: σ + α 32 β 21 β10 2 c1 2c2 1 π ρ 3 β 31 β10 2 c1 2 c 1 + β 32 α 21 β 10 + β 20 + β 21 c2 2 c+1 π π ρ σ c1 + α 32 β 21 β10 2 2c2 π ρ = O t By the order codtos for the coeffcets, 2.13c ad 2.14 are automatcally satsfed. Therefore, we oly cosder the frst two codtos 2.13a ad 2.13b afterwards. We summarze the above results the followg theorem: Theorem 2.1 ecessary codto. The ecessary codto for 2.2 to be thrd-order accurate s c 1 α 31 + α 32 α 21 β 10 + α 32 β 20 + β 21 c2 + β 30 + β 31 + β 32 c+1 π ρ c 1 c 2 c 1 c +1 α 32 β 21 β 10 + β 31 + β 32 α 21 β 10 π ρ π σ σ + β 32 β 20 + β 21 c2 = 1 + O t 3, 2.15a c +1 = 1 ρ σ 2 + O t b Remark 2.1. If restrctg to the case of classcal RK form,.e., α 21 = α 31 = α 32 = 0, the ecessary codtos 2.15 reduce to the codtos gve Theorem 2.6 [12]. 2.2 Suffcet codto I ths part, we try to derve the suffcet codto for 2.2 to be thrd-order accurate. Dfferet from the works [13, 12, 10], the ecessary codto s o loger a suffcet codto. For smplcty, we take π = c. The procedure s splt to three steps: 1. Expad c 1 2. Expad c 2 the frst stage 2.2b; the secod stage 2.2c; 12
13 3. Expad c +1 the fal stage 2.2d. c 1 Step 1: By the frst stage 2.2b, we have the expresso of c 1 = c + tβ 10P D + t2 β t 3 β10 3 p j p jk j,k P k D k c k c j j P p j Dj j c j d Pj D j jk c j To smplfy the dervato, we troduce some otatos: d P D j c d j p Pk D k k c k c by teratos: d P D k c + O t R := j,k p j p jk Q := j P k D k c k S := P Q, P p j Dj j c j c j d Pj D j jk c j d P D j c d j p Pk D k k c k, c d P D k c, wth the vector S = S 1, S 2,, S N T, Q = Q 1, Q 2,, Q N T ad R = R 1, R 2,, R N T. The 2.16 s rewrtte as c 1 = c + tβ 10S + t 2 β 2 10 Q + t 3 β 3 10 R + O t Now we trasfer the ecessary codto 2.15 to a equvalet form. Assume c 2 /ρ ad c +1 /σ have the expaso: c 2 ρ = 1 + X t + T t 2 + O t 3, c +1 σ = 1 + Y t + N t 2 + O t 3. Substtutg ths to the ecessary codto 2.15 gves α 31 + α 32 α 21 β10 2 S + α c 32 β 20 + β 21 X + β 30 + β 31 + β 32 Y = a α 32 β 21 β 10 β 10 S c + X + β 31 + β 32 α 21 β 10 β 10 S c + Y + β 32 β 20 + β 21 Y + X = 0, 2.18b α 31 + α 32 α 21 β10 3 Q + α c 32 β 20 + β 21 T + β 30 + β 31 + β 32 N = c 13
14 From 2.18a ad 2.18b, we solve out wth x, y beg costats satsfyg X = x S c, Y = y S, c α 31 + α 32 α 21 β α 32β 20 + β 21 x + β 30 + β 31 + β 32 y = a α 32 β 21 β 10 β 10 + x + β 31 + β 32 α 21 β 10 β 10 + y + β 32 β 20 + β 21 x + y = b Note that the codtos 2.15 are equvalet to 2.18c-2.19a-2.19b. Gve the coeffcets 2.2, the costats x ad y are uquely determed ad ca be solved out by I the followg, we wll focus o the equvalet codtos 2.18c-2.19a-2.19b. Step 2: We proceed to derve the expaso of c 2 φ k = φc k at c wth k = 1, 2 ad φ = p j, d j : by the secod stage 2.2c. Expad φ k = φc k = φ + φ c ck c ck c T H φ ck c + O t Takg k = ad substtutg 2.17 to 2.20, we have wth φ = p j, d j. φ 1 = φ + tβ 10 φ c S + t2 β 2 10 φ c Q β2 10 t2 S T H φ S + O t3,
15 Now by the secod stage 2.2c, the expaso of c 2 s smplfed as follows: c 2 = α 20 c + α 21c 1 + t j β 20 p j + β 21p 1 c2 j j ρ j t j β 20 d j + β 21d 1 c2 j ρ = c + α 21 β 10 ts + α 21 β 2 10 t 2 Q + α 21 β 3 10 t 3 R + β 20 t j p j1 + X j t + T j t 2 β 20 t j d j1 + X t + T t 2 + β 21 t j p j + β 21 β 10 t 2 j p j c S + β 21β 2 10 t 3 j p j c Q β 21β 2 10 t 3 j S T H p j S + β 21 t 2 j p jx j + β 21 β 10 t 3 j p j c SX j + β 21 t 3 j p jt j β 21 t j d j β 21 β 10 t 2 j d j c S β 21β 2 10 t 3 j d j c Q 1 2 β 21β 2 10 t 3 j S T H d j S β 21 t 2 j d jx β 21 β 10 t 3 j d j c SX β 21 t 3 j d jt + O t 4 = c + α 21 β 10 + β 20 + β 21 ts + β 21 β 10 t 2 S c S + α 21β β 20 + β 21 x t 2 Q + α 21 β 3 10 t 3 R + β 20 + β 21 t 3 j β 21β 2 10 t 3 j Step 3: We expad c +1 p jt j j S T H p j H d j S + β 21 β 10 x t 3 j the fal stage 2.2d ths step. d jt + β 21 β 2 10 t 3 S c Q p j c SS j c j Takg k = ad substtutg 2.22 to 2.20, we have φ 2 = φ + tα 21 β 10 + β 20 + β 21 φ c S + β 21β 10 t 2 k φ c k S k c S j d j c SS + O t 4. c α 21 β β 20 + β 21 x t 2 φ c Q α 21β 10 + β 20 + β 21 2 t 2 S T H φs + O t 3 wth φ = p j, d j. It mmedately follows that β 30 φ + β 31 φ 1 + β 32 φ 2 = β 30 + β 31 + β 32 φ + t[β 31 β 10 + β 32 α 21 β 10 + β 20 + β 21 ] φ c S + β 32β 21 β 10 t 2 k φ c k S k c S + t 2 β 31 β β 32 α 21 β β 32 β 20 + β 21 x φ c Q β 31β β 32 α 21 β 10 + β 20 + β 21 2 t 2 S T H φs + O t 3. 15
16 The the lear combato terms 2.2d are smplfed: α 30 c + α 31c 1 + α 32 c 2 = c + tα 31 β 10 + α 32 α 21 β 10 + β 20 + β 21 S + α 32 β 21 β 10 t 2 S c S ad + α 31 β α 32 α 21 β α 32 β 20 + β 21 x t 2 Q + α 31 + α 32 α 21 β10 t 3 3 R + t 3 α 32 β 20 + β 21 p jt j d jt + α 32 β 21 β10 t 2 3 S c Q j α 32β 21 β10 t 2 3 S T H p j H d j S + α 32 β 21 β 10 x t p 3 j c SS j d j c j j j c SS + O t 4 c t j β 30 p j + β 31p 1 j + β 32 p 2 c+1 j j σ j t j β 30 d j + β 31d 1 j + β 32 d 2 c+1 j σ = β 30 + β 31 + β 32 ts + t 2 β 31 β 10 + β 32 α 21 β 10 + β 20 + β 21 S c S + β 32 β 21 β 10 t 3 S S k c k c S + t3 β 31 β β 32 α 21 β β 32 β 20 + β 21 x S c Q k β 31β β 32 α 21 β 10 + β 20 + β 21 2 t 3 j S T H p j H d j S + β 30 + β 31 + β 32 y t 2 Q + t 3 β 31 β 10 + β 32 α 21 β 10 + β 20 + β 21 y j p j c SS j c j d j c SS c + t 3 β 30 + β 31 + β 32 j p jn j d jn + O t 4. 16
17 Now we have the expaso of c +1 : c +1 = α 30 c + α 31c 1 + α 32 c 2 + t j β 30 p j + β 31p 1 j + β 32 p 2 c+1 j j σ j t j β 30 d j + β 31d 1 j + β 32 d 2 c+1 j σ = c + t[α 31 β 10 + α 32 α 21 β 10 + β 20 + β 21 + β 30 + β 31 + β 32 ]S + α 32 β 21 β 10 + β 31 β 10 + β 32 α 21 β 10 + β 20 + β 21 t 2 S c S + β 32β 21 β 10 t 3 k S c k S k c S + α 31 β α 32α 21 β α 32β 20 + β 21 x + β 30 + β 31 + β 32 y t 2 Q + t 3 α 31 + α 32 α 21 β 3 10 R + t 3 α 32 β 20 + β 21 j p j T j d j T + t 3 β 30 + β 31 + β 32 j p j N j d j N t3 β 31 β β 32α 21 β 10 + β 20 + β α 32 β 21 β 2 10 j S T H p j H d j S + t 3 β 31 β β 32α 21 β β 32β 20 + β 21 x + α 32 β 21 β10 2 S c Q + t 3 α 32 β 21 β 10 x + β 31 β 10 y + β 32 α 21 β 10 + β 20 + β 21 y p j c SS j c j j d j c SS + O t 4. c By the order codtos for the thrd-order explct RK scheme ad the codto 2.18c, the above expaso ca be smplfed as follows: c +1 = c + ts t2 S c S t3 k S c k S k c S t3 j S T H p j H d j S + t 3 β 31 β β 32α 21 β β 32β 20 + β 21 x + α 32 β 21 β10 2 S c Q + t 3 α 32 β 21 β 10 x + β 31 β 10 y + β 32 α 21 β 10 + β 20 + β 21 y p j c SS j c j j d j c SS + O t 4 c = c + ts t2 S c S t3 k S c k S k c S t3 j + t 3 β 31 β β 32α 21 β β 32β 20 + β 21 x + α 32 β 21 β10 2 [ S c Q p ] j c SS j d j c j j c SS + O t 4. c S T H p j H d j S 2.23 I the last equalty, we used the relato α 32 β 21 β 10 x + β 31 β 10 y + β 32 α 21 β 10 + β 20 + β 21 y = [α 32 β 21 β β 31 + β 32 α 21 β β 32β 20 + β 21 x], 17
18 whch s derved from 2.19b. It s observed 2.23 that, the expaso of c +1 cocde wth that of the exact soluto 2.5, besdes the last term. The last addtoal term does ot vash for the geeral case. However, t vashes for ODEs wth oly oe compoet, amely, fc, = J, j = I, fc, = I, j = J, p j c = d j c = 0, otherwse, 0, otherwse, where fc s some fucto of c. It s easly valdated by the followg computato: S c Q p j c SS j d j c j j c SS c = j,k,l p j d j c k p Pl Dl kl c l d Pk D k kl c k j p j c SP j D j c j j 2.24 d j c SP D c = p JI d IJ d IJ c I c I p JI c I d IJ d IJ c I = 0. I the geeral case, to acheve thrd order accuracy, t s requred that 2.25 β 31 β β 32α 21 β β 32β 20 + β 21 x + α 32 β 21 β10 2 = Ths relato s automatcally satsfed by the RK scheme classcal form α 21 = α 31 = α 32 = 0 sce y = 0 ad β 31 β β 32β 20 + β 21 x = 0. For the SSP RK3 scheme wth the optmal coeffcets [4], t s deduced from 2.19 that y = 0 ad x = 1 ad thereby β 31 β β 32α 21 β β 32β 20 + β 21 x + α 32 β 21 β10 2 = 1 6. Thus the scheme wth the coeffcets the optmal SSP RK3 scheme s ot thrd order accurate. Moreover, we pot out that, the valdato 2.25 dcates that the addtoal relato 2.26 caot be obtaed by testg the specal class of ODEs wth polyomals of hgh degree 2.3 ad 2.4. By expressg x terms of α ad β from 2.19 ad substtutg t to 2.26, we fally arrve at 0 =β 32 β 20 + β 21 α 31 + α 32 α 21 α 32 β 21 β [α 32 β 20 + β 21 α 32 β 21 β β 30 + β 31 + β 32 α 32 β 21 β 10 ]β 31 + β 32 α 21 + α 32 β
19 Ths s the addtoal codto for the scheme to be thrd order accurate. The above result s summarzed the followg theorem: Theorem 2.2 suffcet codto. A suffcet codto for the scheme 2.2 to be thrdorder accurate s c 1 α 31 + α 32 α 21 β 10 + α 32 β 20 + β 21 c2 + β 30 + β 31 + β 32 c+1 π ρ c 1 c 2 c 1 c +1 α 32 β 21 β 10 + β 31 + β 32 α 21 β 10 π ρ π σ σ + β 32 β 20 + β 21 c2 = 1 + O t 3, 2.27a c +1 = 1 ρ σ 2 + O t2, β 32 β 20 + β 21 α 31 + α 32 α 21 α 32 β 21 β α 32β 20 + β 21 α 32 β 21 β b + β 30 + β 31 + β 32 α 32 β 21 β 10 β 31 + β 32 α 21 + α 32 β 21 = c 3 MPRK schemes I ths secto, we frst focus o the MPRK scheme wth the coeffcets the SSP RK3 method, whch s thrd-order accurate for ODEs wth oly oe compoet, see Next, we move to the suffcet codtos the geeral case. We wll fd the optmal coeffcets such that the thrd codto 2.27c s fulflled. The, we try to costruct the explct form of ρ ad σ such that the frst two suffcet codtos 2.27a ad 2.27b are satsfed. Lastly, we exted the MPRK scheme to sem-dscrete schemes arsg from PDEs after dscretzato space ad valdate the order of accuracy. 3.1 Optmal RK3 method For the optmal SSP RK3 method wth coeffcets α 10 = β 10 = 1, α 20 = 3 4, α 21 = β 21 = 1 4, β 20 = 0, α 30 = 1 3, α 32 = β 32 = 2 3, α 31 = β 30 = β 31 = 0, 19
20 the frst two codtos 2.27 reduce to 1 6 c 1 c 1 π c 2 ρ c 2 + c1 c +1 π ρ π σ c +1 σ = 1 + O t 3, + c2 c +1 = 3 + O t 2. ρ σ To smplfy the above codto, we gve the followg lemma: Lemma 3.1. Cosder three fuctos y = y t for = 1, 2, 3. Assume that y = 1 + O t, = 1, 2, 3, ad y 1 + y 2 + 4y 3 = 6 + O t 3. The y 1 y 2 + y 2 y 3 + y 3 y 1 = 3 + O t 2 s equvalet to y 1 + y 2 = 2 + O t 2. Proof. y 1 y 2 + y 2 y 3 + y 3 y 1 = 3 + O t 2, y 1 y 2 + y 1 + y 2 y 3 = 3 + O t 2, y 1 y 2 + y 1 + y y 1 y 2 + O t 3 = 3 + O t 2, 6y 1 + y 2 y 1 y = O t 2, 6y 1 + y 2 12 = O t 2. By the lemma, we have the equvalet order codtos c 1 + c2 + 4 c+1 = 6 + O t 3, 3.1a π ρ σ 20
21 c 1 Take π = c ad recall from 2.16 ad 2.22 that c 1 π c 2 c + c2 = 2 + O t b π ρ = c1 c = 1 + t S c = ts c Wth these relatos, we have c c 2 c 2 c Accordg to 3.1b, c2 ρ ad the = ts c c 1 c t2 S c ca be expaded as c 2 ρ = 1 t S c + t 2 Q + O t 3, t2 S c S c t2 S c c 2 ρ = 1 + t 2 Q + T t 2 It follows from above expasos of c1 π σ c = 1 + t S c ad c2 ρ Combg ths wth 3.2 ad 3.4, we take σ c = 4 c2 c + O t 3. c 2 4 c S c + O t T t 2 + O t S c ad 3.1a that t2 Q + T t2 S c c2 c 2 + O t S c c c 4 + O t 3. c 1 c c 2 ρ. 3.5 Its valdty does ot deped o the specfc expresso of ρ. O the other had, from 3.3 we have Thus ρ ca be take as ρ = 1 2 c ρ c c 1 c = ts c + c1 2 c + O t 2. or c c c Wth the coeffcets for the optmal RK3 method ad the expressos of σ ad ρ 3.5 ad 3.6, the scheme 2.2 s thrd-order accurate for ODEs wth oly oe compoet. 21
22 3.2 Optmal coeffcets Next we focus o the thrd codto 2.27c ad try to fd the optmal coeffcets. To ths ed, oe eeds to solve the optmzato problem maxmze m{ α 10 β 10, α 20 β 20, α 21 β 21, α 30 β 30, α 31 β 31, α 32 β 32 }, s.t. α 10, β 10, α 20, β 20, α 21, β 21, α 30, β 30, α 31, β 31, α 32, β 32 0, α 10 = 1, α 20 + α 21 = 1, α 30 + α 31 + α 32 = 1, α 31 β 10 + α 32 α 21 β 10 + β 20 + β 21 + β 30 + β 31 + β 32 = 1, β 10 α 32 β 21 + β 31 + β 32 α 21 β 10 + β 20 + β 21 = 1 2, β 2 10 α 32β 21 + β 31 + β 32 α 21 β 10 + β 20 + β 21 2 = 1 3, β 10β 21 β 32 = 1 6, β 32 β 20 + β 21 α 31 + α 32 α 21 α 32 β 21 β α 32β 20 + β 21 α 32 β 21 β β 30 + β 31 + β 32 α 32 β 21 β 10 β 31 + β 32 α 21 + α 32 β 21 = 0. We use the MATLAB fucto fmco to solve the above optmzato problem. It s easy to verfy that α 10 = 1, β 10 = 2 3, α 20 = 35 36, α 21 = 1 36, β 20 = , β 21 = 3 8, α 30 = , α 31 = , α 32 = 1 9, β 30 = , β 31 = 1 24, β 32 = 2 3, satsfy all the codtos the optmzato problem. We take these as the tal data for terato fmco. The fal result s α 10 = 1, α 20 = E-01, α 21 = E-02, α 31 = E-10, β 10 = E-01, β 21 = E-01, β 31 = E-10, α 30 = E-01, α 32 = E-01, β 20 = E-02, β 30 = E-01, β 32 = E wth m{ α 10 β 10, α 20 β 20, α 21 β 21, α 30 β 30, α 31 β 31, α 32 β 32 } =
23 The above results may be locally optmal sce t s dffcult to solve the global optmzato problem. I the followg, we fx the coeffcets 3.7 ad try to fd the explct form of ρ ad σ such that the suffcet codtos 2.27a ad 2.27b are satsfed. 3.3 Costructo of ρ ad σ Note that the suffcet codtos 2.27a ad 2.27b are equvalet to Also, gve α ad β, the values of x ad y are determed by We splt the procedure to several steps. Frst, we calculate the expaso of ρ ad try to approxmate ρ by approprate combatos of c 1 ad c. Step 1: Note that ρ c = c2 /c = c 2 /ρ Wth the coeffcets 3.7, we have 1 + α 21 β 10 + β 20 + β 21 t S c 1 + x t S + O t c 2 = 1 + α 21 β 10 + β 20 + β 21 x t S c + O t 2. + O t 2 β 10 < α 21 β 10 + β 20 + β 21 x < 2β Thus, we try to take ρ c the form wth 1 ad 2 are gve by ρ c c 1 = 1 c + 2 c c 1 = α 21β 10 β 20 β 21 + x + 2β 10 β 10 > 0, 2 = 1 1 = α 21β 10 + β 20 + β 21 x β 10 β 10 > 0. Remark 3.1. Note that we ca also take other forms of combato, such as ρ c m 2 c1 3 as log as the coeffcet m c 1 ad m 2 are o-egatve c = m 1 1 c + Gve the explct expresso of ρ 3.9, we proceed to hgher order expaso of ρ. Recall from 2.17 that c 1 c P D = 1 + β 10 t + β c 10 2 Q t 2 + O t 3. 23
24 Wth ths, 3.9 ca be expaded to hgher order as ρ c c 1 = 1 c + 2 c1 2 c = 1 + α 21 β 10 + β 20 + β 21 x t S c + α 21 β 10 + β 20 + β 21 xβ 10 Q t 2 Thus, wth the expaso + α 21 β 10 + β 20 + β 21 x β 10 β 10 S c 2 t 2 + O t 3. c 2 ρ = c2 /c ρ /c = 1 + x S t + T c t 2 + O t 3 we have T = β 20 β 10 β 21 β 10 + β 10 + β 20 + β 21 xq + β 21 β 10 S c α 21 β 10 + β 20 + β 21 x β 10 β 10 + xα 21 β 10 + β 20 + β 21 x S c S c O the other had, t follows from 2.18c that N = α 31 + α 32 α 21 β 3 10 β 30 + β 31 + β 32 Q α 32β 20 + β 21 β 30 + β 31 + β 32 T
25 3.12 Step 2: The we have the expaso of σ σ c = c+1 /c c +1 = 1 + /σ S t + 1 S c 2 c S t 2 + O t 3 c 1 + y S t + N c t 2 + O t 3 = y S t N c t 2 y1 y S c 2 t S 2 c S t 2 + O t 3 = y S t + α 31 + α 32 α 21 β10 3 Q c t 2 + α 32β 20 + β 21 T t 2 β 30 + β 31 + β 32 β 30 + β 31 + β 32 2 S y1 y t S S t 2 + O t 3 2 c 3.11 c = y S t c c + α 31 + α 32 α 21 β α 32β 20 + β 21 β 20 β 10 β 21 β 10 + β 10 x + β 20 x + β 21 x Q t 2 β 30 + β 31 + β 32 y1 y + α 32β 20 + β 21 α 21 β 10 + β 20 + β 21 x β 10 β 10 + xα 21 β 10 + β 20 + β 21 x β 30 + β 31 + β 32 2 S t 2 c α 32β 21 β 10 β 20 + β 21 S S t 2 + O t 3. β 30 + β 31 + β 32 c c 3.13 Note that there exsts S c 2 the above equalty. It seems mpossble to geerate approxmatos to ths term. Here, we use c2 ρ to elmate S c c Deote z := y1 y + α 32β 20+β 21 β 30 +β 31 +β 32 α 21 β 10 + β 20 + β 21 x β 10 β 10 + xα 21 β 10 + β 20 + β 21 x α 21 β 10 + β 20 + β 21 x β 10 β 10 + xα 21 β 10 + β 20 + β 21 x y1 y = α 21 β 10 + β 20 + β 21 x β 10 β 10 + xα 21 β 10 + β 20 + β 21 x + α 32β 20 + β 21 > 0 β 30 + β 31 + β ad take a c = σ c z c ρ Sce z s postve, σ determed by 3.15 s postve f so s a. Such a expresso of a 25
26 wll be costructed as follows. Before that, we use 3.15 to gve the expaso of a : where a c = 1 z + 1 y zx S t c + M β 20 β 10 β 21 β 10 + β 10 + β 20 + β 21 xz Q t α 32β 21 β 10 β 20 + β 21 S S β 21 β 10 z t 2 + O t 3, β 30 + β 31 + β 32 c M = α 31 + α 32 α 21 β α 32 β 20 + β 21 β 20 β 10 β 21 β 10 + β 10 x + β 20 x + β 21 x β 30 + β 31 + β 32. For the sake of coveece, we rewrte the above expaso as a c S = r 1 + r 2 t + r c 3 Q t 2 S + r 4 c where the costats r, = 1, 2, 3, 4 are gve by r 1 = 1 z, r 2 = 1 y xz, r 3 = M [ β 20 β 10 β 21 β 10 + β 10 + β 20 + β 21 x] z, r 4 = α 32β 21 β 10 β 20 + β 21 β 30 + β 31 + β 32 β 21 β 10 z. c S t 2 + O t Step 3: Now we follow the dea [12] ad sert a addtoal stage to costruct a. c Set ad costruct aother stage: a = η 1 c + η 2 c 1 + t j µ = c c1 s. c η 3 p j + η 4 p 1 j a j η 3 d j + η 4 d 1 j µ a j µ 3.17 wth coeffcets η k > 0, k = 1, 2, 3, 4 to be determed. It follows from the above equato that ad thus a c a a µ = η 1 + η 2 + O t = η 1 + η 2 + [η 2 β 10 + η 1 + η 2 η 3 + η 4 ] S t + O t 2, c = η 1 + η 2 + [η 2 β 10 + η 1 + η 2 η 3 + η 4 sβ 10 ] S t + O t 2. µ c 26
27 Wth ths ad 2.21, we proceed to hgher order expaso: a c = η 1 + η 2 + [η 2 β 10 + η 1 + η 2 η 3 + η 4 ] S t c + {η 2 β [η 2β 10 + η 1 + η 2 η 3 + η 4 sβ 10 ]η 3 + η 4 }Q t 2 + η 4 β 10 η 1 + η 2 S c S t 2 + O t 3. c 3.18 Comparg 3.18 ad 3.16 gves r 1 = η 1 + η 2, r 2 = η 2 β 10 + η 1 + η 2 η 3 + η 4 = η 2 β 10 + r 1 η 3 + η 4, r 3 = η 2 β [η 2β 10 + η 1 + η 2 η 3 + η 4 sβ 10 ]η 3 + η 4, r 4 = η 4 β 10 η 1 + η 2 = η 4 β 10 r 1, from whch η 1, η 3, η 4 ad s ca be expressed terms of η 2 : η 1 = r 1 η 2, η 3 = r 2 η 2 β 10 r 1 r 4 β 10 r 1, η 4 = r 4 β 10 r 1, s = r 2 β 10 r 1 r 3 η 2 β 2 10 β 10 r 2 β 10 η To esure the postvty of η k, t s requred that 0 < η 2 < m{r 1, r 2 r 4 }, 3.20 β 10 β10 2 I summary, the fal scheme for the geeral ODEs 1.2 s c 0 = c c 1 = α 10 c 0 + t j ρ = 1 c 1 c 2 = α 20 c 0 + t j c1 + 2 c 2, c + α 21 c 1 β 10 p 0 c 1 j j c 0 j β 20 p 0 j + β 21 p 1 d 0 j c2 j j c 1 c a, 3.21b β 20 d 0 j + β 21 d 1 ρ j c2 j ρ, 3.21c 27
28 c µ = c c1 s, a = η 1 c + η 2 c 1 + t j η 3 p j + η 4 p 1 j a j η 3 d j + η 4 d 1 j µ a, 3.21d j µ σ = a + Zc c 2 ρ, c +1 = α 30 c 0 + α 31 c 1 + α 32 c 2 c+1 β 30 p 0 j + β 31 p 1 j + β 32 p 2 j β 30 d jσ 0 j + β 31 d 1 j + β 32 d 2 j + t j c+1 j σ, 3.21e where the coeffcets α j ad β j are gve by 3.7, 1, 2 are gve by 3.10, η 1, η 3, η 4, s are gve by 3.19, ad z s gve by The parameter η 2 s a free parameter satsfyg the costrat I partcular, we take η 2 = 1/3 satsfyg the codto 3.20 ad the other parameters are gve by 1 = E-01, 2 = E-01, Z = E-01, η 1 = E-02, η 2 = 1/3, η 3 = E-01, η 4 = , s = Ths scheme s of thrd-order accuracy ad ucodtoally postvty-preservg for Exteso to sem-dscrete scheme Followg our prevous work [10], we formulate a system of ODEs the followg form, to cover the sem-dscrete scheme for the PDEs: dc k, dt = F k, c + P k, c D k, c, k = 1,, M, = 1,, N Here c k, = c k, t deotes the cocetrato of the -th speces at the k-th grd pot, N ad M deote the umber of speces ad odes, respectvely. The vector c s the collecto of all ukow varables wth the form c := c 11, c 12,, c 1N,, c M1, c M2,, c MN T ad s of legth M N. F k, = F k, c deotes the cotrbutos of the covecto terms after spatal 28
29 dscretzatos the PDEs. The producto ad destructo terms are P k, = P k, c = N j=1 p k,,jc ad D k, = D k, c = N j=1 d k,,jc whch satsfy p k,,j c = d k,j, c,, j, k ad c 0. We make the followg assumpto o 3.23: Assumpto 3.1. The Euler forward method for the covecto term satsfes the postvtypreservg property: f c k, 0 for all k,, the c k, + tf k,c 0, for all k, ad t t 0. Remark 3.2. Ths famly of ODEs 3.23 covers the sem-dscrete fte dfferece WENO scheme for chemcal reactg flows 1.1 by settg the producto ad destructo terms to be zero the mometum ad eergy equatos. The varable c k, does ot ecessarly deote the cocetrato or desty ths case. We geeralze the MPRK scheme 3.21 by corporatg the covecto term F k, usg the Euler forward each stage ad arrve at c 0 k, = c k, c 1 k, = α 10c 0 k, + tβ 10F k, c 0 + t j β 10 p 0 c 1 k,j k,j c k,j d 0 k,j 3.24a c 1 k,, 3.24b c k, c1 ρ k, = 1 c 1 k, + 2c k, k, 2, 3.24c c k, c 2 k, = α 20c 0 k, + α 21c 1 k, + tβ 20F k, c 0 + tβ 21 F k, c 1 + t j β 20 p 0 k,j + β 21p 1 c2 k,j k,j β 20 d 0 k,j ρ + β 21d 1 k,j c2 k, k,j ρ k,, 3.24d µ k, = c k, c1 k, s, c k, a k, = η 1 c k, + η 2c 1 k, + tη 3η 1 + η 2 F k, c 0 + tη 4 η 1 + η 2 F k, c e 29
30 + t j η 3 p k,j + η 4p 1 k,j a k,j µ k,j t j η 3 d k,j + η 4d 1 k,j a k, µ k,, 3.24f σ k, = a k, + Zc 0 c 2 k, k,, ρ k, c +1 k, = α 30 c 0 k, + α 31c 1 k, + α 32c 2 k, + tβ 30F k, c 0 + tβ 31 F k, c 1 + tβ 32 F k, c 2 + t j β 30 p 0 k,j + β 31p 1 k,j + β 32p 2 c+1 k,j k,j β 30 d 0 k,j σ + β 31d 1 k,j + β 32d 2 k,j c+1 k, k,j σ k, 3.24g. 3.24h Except for the stage 3.24f, the other steps are oly drect extesos of those The thrd-order accuracy of ths scheme s show the appedx. We summarze the result the followg theorem. Theorem 3.1. The MPRK scheme 3.24 s thrd-order accurate for the system of ODEs It s coservatve: k, k, k, c 1 k, = k, c 2 k, = α 20 c +1 k, c k, + tβ 10 F k, c, k, c k, + α 21 k, k, = α 30 c k, + α 31 k, k, c 1 k, + t β 20 F k, c + β 21 F k, c 1, k, c 1 k, + α 32 k, c 2 k, + t β 30 F k, c + β 31 F k, c 1 + β 32 F k, c 2, k, where the summato of the covecto terms wll vash wth perodc boudary codtos. It s postvty-preservg: f c k, 0 for all k,, the c1 k, k, ad t m{ α 10 β 10, α 20 β 20, α 21 β 21, α 30 β 30, α 31 β 31, α 32 β 32 } t 0. 0, c2 k, 0 ad c+1 k, 0 for all 4 Numercal tests I ths part, the umercal results wll be preseted. We frst dscuss the covergece order for the o-stff problems ad the performace o the stff problems solvg the ODEs. The we move to reactve Euler equatos ad Euler equatos wth three speces reactos ad geeral equato of state. The ffth-order fte-dfferece WENO spatal dscretzato [11] s appled here. For the mplemetato detals of our tme tegrato ad the postvtypreservg WENO schemes ad the lmter, please refer to our prevous work [10]. 30
31 4.1 ODEs Example 4.1 lear case. The lear test case s wth costat a > 0, ad tal value dc 1 dt = c 2 ac 1, dc 2 dt = ac 1 c 2, c 1 0 = c 0 1, c 20 = c 0 2. The exact soluto s c 1 t = 1 + b exp a + 1tc 1, c 2t = c c0 2 c 1t, wth the parameters c 1 ad b determed by c 1 = c0 1 + c0 2 a + 1, b = c0 1 c 1 1. I the umercal expermet, we take c 0 1 = 4.5, c 0 2 = 3.2, a = 2.7 ad the fal tme t = 1. The errors betwee umercal solutos ad exact solutos at the fal tme are lsted Table 4.1. The thrd-order accuracy s clearly observed. Table 4.1: Example 4.1: Error table for lear ODEs. t error order 1/ e-04-1/ e / e / e / e Example 4.2 olear case. To test the accuracy of our solver 3.21, we make up a o-stff olear problem: dc 1 dt = F 1c c 1c 2 c 1 + 1, 4.1a 31
32 dc 2 dt = F 2c + c 1c 2 c ac 2, dc 3 dt = F 3c + ac b 4.1c where F 1 c, F 2 c, F 3 c deotes covecto terms. To express ths system of ODEs the form of producto-destructo equatos, we set p 21 c = d 21 c = c 1c 2 c 1 + 1, p 32c = d 32 c = ac 2, ad p j = d j = 0 for other sets of, j. I the umercal examples, the tal codtos are set as c 0 1 = 9.98, c 2 = 0.01 ad c 3 = The covecto terms are F 1 c, F 2 c, F 3 c = c 1 c 2 c 3, c 3 c 2, c 1 c 2 c 2 3. The fal tme s t = 1 ad the parameter a = 1. The errors are lsted Table 4.2, whch shows thrd-order accuracy. Table 4.2: Example 4.2: Error table for olear ODEs 4.1. t error order 1/ e-04-1/ e / e / e / e To test our solver 2.2 wth optmal RK3 coeffcets whch s thrd-order accuracy for ODEs wth oly oe compoet, we take the ODEs to be dc 1 dt = c 1c 2 c 1 + 1, dc 2 dt = c 1c 2 c 1 + 1, dc 3 dt = a 4.2b 4.2c The results are lsted Table 4.3, where the thrd-order accuracy s observed. Moreover, the errors wth optmal SSP RK3 coeffcets are much smaller tha those wth optmal coeffcets
33 Example 4.3 stff case. Oe of the most promet examples of the stff ODEs s the Robertso test case, whch descrbes the chemcal reactos [5]: wth tal values c 0 = c 0 for = 1, 2, 3. dc 1 dt = 104 c 2 c c 1, dc 2 dt = c c 2 c c 2 2, dc 3 dt = c 2 2, I ths problem, the producto ad destructo terms are p 12 c = d 21 c = 10 4 c 2 c 3, p 21 c = d 21 c = c 1, p 32 c = d 23 c = c 2 2, ad p j = d j = 0 for other sets of, j. I the umercal smulatos, we take c 0 1 = 1 ad c 0 2 = c 0 3 = 0. Followg [13], the tme step sze the k-th tme step s chose as t k = 2 k 1 t 1 wth the tal tme step sze t 1 = The small tal tme step was set to obta a adequate resoluto of the compoet c 2 the startg tme terval. To vsualze the evoluto of c 2, t s multpled by 10 4 Fg From Fg. 4.1, we observe the excellet accuracy of our scheme the case of a hghly stff problem. 4.2 Reactve Euler equatos We cosder the reactve Euler equatos whch are ofte used to model the detoato waves [16] 2D case: U t + FU x + GU y = SU, 4.3 Table 4.3: Example 4.2: Error table for olear ODEs wth oly oe compoet 4.2. The SSP RK3 coeffcets vs. coeffcets 3.7. t error SSP RK3 order error optmal order 1/ e e-08-1/ e e / e e / e e / e e
34 c 1 exa c 1 um 10 4 c 2 exa 10 4 c 2 um c 3 exa c 3 um Fgure 4.1: Example 4.3: Tme evoluto of c, = 1, 2, 3. wth U = ρ, m,, E, ρy, FU = m, ρu 2 + p, ρuv, E + pu, ρuy, GU =, ρuv, ρv 2 + p, E + pu, ρvy, SU = 0, 0, 0, 0, ω, ad m = ρu, = ρv, E = 1 2 ρu2 + v 2 + p + ρqy. 4.4 γ 1 Here q > 0 s the heat release of reacto, γ s the specfc heat rato ad 0 Y 1 deotes the reactat mass fracto. The source term s assumed to be a Arrheus form ω = KρY e T/T, 4.5 where T = p/ρ s the temperature, T > 0 s the actvato costat temperature ad K > 0 s a costat. To ft to our framework, we rewrte 4.3 a equvalet form the same approach [10]. Here, we omt the detals for savg space ad preset the umercal results the followg part. 34
35 y 1.00 ρ x x y p x x a b Fgure 4.2: Example 4.4: Numercal covergece study. Left: colored cotour map of desty ad pressure of our scheme; rght: cut alog y = 0. Up: desty; dow: pressure. The symbols ad the sold les represet the results of our scheme ad the SSP RK3 method, respectvely. Example 4.4 Numercal covergece study. We study the umercal covergece of our scheme ths test. The same parameters ad tal ad boudary codtos wth Example 4.4 [16] are appled here. The tal codto s, f x 2 + y , the ρ, u, v, p, Y = 1, 0, 0, 80, 0; otherwse, ρ, u, v, p, Y = 1, 0, 0, 10 9, 1. The boudary codtos for the bottom ad the left are reflectve. The termal tme s t = 0.2. The mesh s uformly rectagular. The umercal results wth our tme tegrato ad the SSP RK3 method are show Fg The mesh szes are x = y = 1/120. We observe the good agreemet. Example 4.5 Detoato dffracto problems. We test the detoato dffracto ths example. The same parameters ad tal codtos wth [16] are appled here. 35
36 y 6 y x x y 25 y x x a b Fgure 4.3: Example 4.5: Detoato dffracto problems. Top: colored cotour map ad cotour le of desty; bottom: colored cotour map ad cotour le of pressure. The tal codtos are, f x < 0.5, the ρ, u, v, E, Y = 11, 6.18, 0, 970, 1; otherwse, ρ, u, v, E, Y = 1, 0, 0, 55, 1. The boudary codtos are reflectve except that at x = 0, ρ, u, v, E, Y = 11, 6.18, 0, 970, 1. The termal tme s t = 0.6. The parameters are γ = 1.2, q = 50, T = 50 ad K = The umercal results wth x = y = 1/48 are show Fgure 4.3, whch are comparable to the results [16]. 4.3 Euler equatos wth three speces reactos ad geeral equato of state We cosder the three speces model wth a more geeral equato of state [17] U = ρ 1, ρ 2, ρ 3, ρu, E T, 36
37 FU = ρ 1 u, ρ 2 u, ρ 3 u, ρu 2 + p, E + pu T, SU = 2M 1 ω, M 2 ω, 0, 0, 0. ad ρ = 3 ρ s, s=1 p = RT 3 s=1 ρ s M s, E = 3 ρ s e s T + ρ 1 h ρu the teral eergy e s T = 3RT/2M s ad 5RT/2M s for mooatomc ad datomc speces s=1 respectvely. The rate of chemcal reacto s gve by ω = k f T ρ 2 k b T ρ ρ s 4.7 M 2 M 1 M s k f = CT 2 e E/T, k b = k f / expb 1 + b 2 log z + b 3 z + b 4 z 2 + b 5 z 3, z = 10000/T 4.8 where b, C ad E are costats whch ca be foud [21]. s=1 Example 4.6. We take the same parameters as [17, 22]. The parameters are M 1 = 0.016, M 2 = 0.032, M 3 = 0.028, h 0 1 = , R = , C 0 = m 3, E 0 = K, ad b 1 = 2.855, b 2 = 0.988, b 3 = 6.181, b 4 = 0.023, b 5 = The tal codtos are: the destes ρ 1, ρ 2 ad ρ 3 are , , o the left, ad , , o the rght. The veloctes are zero. The pressures are 1000 o the left ad 1 o the rght. The fal tme s t = ad the mesh sze s x = 1/4000. The profles of desty, velocty ad pressure are preseted Fgure. 4.4, where good agreemet of our scheme ad the SSP RK3 method s observed. 5 Cocludg remarks I ths paper, a thrd-order tme tegrato method for the producto-destructo equatos, whch s coservatve ad ucodtoally postvty-preservg, s costructed. The ecessary ad suffcet codtos for the methods to be thrd-order accurate are derved. Ths ODE solver s the exteded to cover a class of sem-dscrete schemes for PDEs ad 37
38 ρ1 um ρ1 exa ρ2 um ρ2 exa x ρ3 um ρ3 exa x x u um u exa x p um p exa x Fgure 4.4: Example 4.6: Three speces reacto problem at t = Fte dfferece. The sold les are the referece solutos geerated wth SSP-RK3 whle the symbols are the umercal solutos wth our scheme. 38
39 successfully appled to fte dfferece WENO schemes for o-equlbrum flows. A varety of umercal examples are coducted to valdate the performace of the tme tegrato method coupled wth the ffth-order WENO scheme ad the postvty-preservg lmter. Ackowledgemets We would lke to thak Xagxog Zhag from Purdue Uversty for may frutful dscussos. A Proof of accuracy for the MPRK scheme 3.24 I ths appedx, we show that the MPRK scheme 3.24 s thrd-order accurate for the system of ODEs Accordg to 3.24a ad 3.24b, c 1 k, ca be expaded as c 1 k, = c k, + tβ 10S k, + t 2 β 2 10 Q k, + t 3 β 3 10 R k, + O t 4, A.1 wth S k, := F k, + P k, D k,, Q k, := j R k, := j,r F p k,j + P k,j D k,j k,j c k,j j d k,j p k,j p Fk,r +P k,r D k,r k,jr d c k,jr k,r j,r c k,j Fk, + P k, D k,, c k, Fk,j +P k,j D k,j c k,j d k,j p Fk,r +P k,r D k,r k,r d c k,r k,r c k, F k, +P k, D k, c k,. Thus ρ k, c k, = 1 c 1 k, c k, + 2 c1 k, 2 c k, = 1 + α 21 β 10 + β 20 + β 21 x t S k, + α c 21 β 10 + β 20 + β 21 xβ 10 Q k, t 2 k, 2 S k, + α 21 β 10 + β 20 + β 21 x β 10 β 10 t 2 + O t 3. c k, A.2 39
40 Recall from 2.20 that φ l wth l = 1, 2 ad φ = p k,j, d k,j, F k, ca be expaded as φ l = φc l = φ + φ c cl c cl c T H φc l c + O t 3. A.3 Takg l = 1 ad substtutg A.1 to the above equato, we have φ 1 = φ + tβ 10 φ c S + t2 β 2 10 φ c Q β2 10 t2 S T H φ S + O t3 A.4 wth φ = p k,j, d k,j, F k,. It follows from ths, 3.24d ad A.2 that ad c 2 k, =α 20c 0 k, + α 21c 1 k, + tβ 20F k, c 0 + tβ 21 F k, c 1 + t j β 20 p 0 k,j + β 21p 1 c2 k,j k,j =c k, + α 21 β 10 + β 20 + β 21 S k, t + O t 2 The above two equatos further yeld c 2 k, ρ k, = c k, + xs k, t + O t 2. β 20 d 0 k,j ρ + β 21d 1 k,j c2 k, k,j ρ k, c 2 k, = c k,+α 21 β 10 +β 20 +β 21 ts k, +β 21 β 10 t 2 S k, c S+ t2 [α 21 β 2 10+β 20 +β 21 x]q k, +O t 3 ad wth c 2 k, ρ k, = c k, + xs k, t + T k, t 2 + O t 3 T k, = [ β 20 β 10 β 21 β 10 + β 10 + β 20 + β 21 x] Q k, + β 21 β 10 S k, c [α 21 β 10 + β 20 + β 21 x β 10 β 10 + xα 21 β 10 + β 20 + β 21 x] S c k, S k, c k, 2. A.5 Furthermore, we deote X k, := x S k, c k, 40
41 ad have the expaso of c 2 k, : c 2 k, =α 20c 0 k, + α 21c 1 k, + tβ 20F k, c 0 + tβ 21 F k, c 1 + t j β 20 p 0 k,j + β 21p 1 c2 k,j k,j β 20 d 0 k,j ρ + β 21d 1 k,j =c k, + tα 21β 10 S k, + t 2 α 21 β 2 10 Q k, + t 3 α 21 β 3 10 R k, c2 k, k,j ρ k, + tβ 20 + β 21 Fk, + F t2 k, β 10 β 21 c S + t3 β10 2 β Fk, 21 c Q β2 10 β 21 t 3 S T H F k, S + β 20 t j p k,j 1 + X k,j t + T k,j t 2 β 20 t j d k,j 1 + X k, t + T k, t 2 + β 21 t j p k,j + β 21 β 10 t 2 j p k,j c S + β 21β 2 10 t 3 j p k,j c Q β 21β 2 10 t 3 j S T H p k,j S + β 21 t 2 j p k,jx k,j + β 21 β 10 t 3 j p k,j c SX k,j + β 21 t 3 j p k,jt k,j β 21 t j d k,j + β 21β 10 t 2 j d k,j c S β 21β 2 10 t3 j d k,j c Q 1 2 β 21β 2 10 t3 j S T H d k,j S β 21 t 2 j d k,j X k, + β 21 β 10 t 3 j d k,j c SX k, + β 21 t 3 j d k,j T k, + O t 4 =c k, + α 21β 10 + β 20 + β 21 ts k, + β 21 β 10 t 2 S k, c S + [α 21β β 20 + β 21 x] t 2 Q k, + t 3 α 21 β 3 10 R k, + t 3 β 20 + β 21 j p k,j T k,j j d k,j T k, + β 21 β 2 10 t3 S k, c Q β 21β10 2 t3 S T H Fk, + H p k,j H d k,j S j j + β 21 β 10 x t p 3 k,j c SS k,j d k,j c j k,j c SS k, + O t 4. c k, A.6 Next we expad a k, accordg to 3.24e ad 3.24f. Note that µ k, = c k, c1 k, s = c c k, + sβ 10 S k, t + O t 2 k, 41
42 ad thereby a k, =η 1 c k, + η 2 c 1 k, + tη 3η 1 + η 2 F k, c 0 + tη 4 η 1 + η 2 F k, c 1 + t j η 3 p k,j + η 4p 1 k,j a k,j µ k,j t j η 3 d k,j + η 4d 1 k,j a k, µ k,, a k, =η 1 + η 2 c k, + tη 2 β 10 S k, + tη 1 + η 2 η 3 + η 4 F k, + η 1 + η 2 η 3 + η 4 P k, D k, t + O t 2 =η 1 + η 2 c k, + [η 2β 10 + η 1 + η 2 η 3 + η 4 ]S k, t + O t 2, =η 1 + η 2 + [η 2 β 10 + η 1 + η 2 η 3 + η 4 sβ 10 ] S k, t + O t 2. µ k, Wth these, we further expad a k, c k, as c,k a k, c k, =η 1 + η 2 + [η 2 β 10 + η 1 + η 2 η 3 + η 4 ] S k, t c,k + {η 2 β [η 2β 10 + η 1 + η 2 η 3 + η 4 sβ 10 ]η 3 + η 4 }Q k, t 2 + η 4 β 10 η 1 + η 2 S k, c S c k, t 2 + O t 3 S k, =r 1 + r 2 t + r c 3 Q k, t 2 S k, + r 4,k c S c k, t 2 + O t 3, A.7 where r, = 1, 2, 3, 4 are defed below It follows from ths ad 3.13 that σ k, =a k, + zc 0 c 2 k, k, ρ k, =1 + 1 ys k, t + α 31 + α 32 α 21 β10 3 Q k, t 2 + α 32β 20 + β 21 T k, t 2 β 30 + β 31 + β 32 β 30 + β 31 + β 32 2 y1 yc S k, k, t S k, c k, 2 c S t2 + O t 3. A.8 Moreover, we substtute expaso A.6 to A.3 wth l = 2 ad obta φ 2 =φ + tα 21 β 10 + β 20 + β 21 φ c S + β 21β 10 t 2 m,r φ c m,r S m,r c S + t 2 [α 21 β β 20 + β 21 x] φ c Q α 21β 10 + β 20 + β 21 2 t 2 S T H φ S + O t3 A.9 42
Derivation of 3-Point Block Method Formula for Solving First Order Stiff Ordinary Differential Equations
 Dervato of -Pot Block Method Formula for Solvg Frst Order Stff Ordary Dfferetal Equatos Kharul Hamd Kharul Auar, Kharl Iskadar Othma, Zara Bb Ibrahm Abstract Dervato of pot block method formula wth costat
Dervato of -Pot Block Method Formula for Solvg Frst Order Stff Ordary Dfferetal Equatos Kharul Hamd Kharul Auar, Kharl Iskadar Othma, Zara Bb Ibrahm Abstract Dervato of pot block method formula wth costat
Cubic Nonpolynomial Spline Approach to the Solution of a Second Order Two-Point Boundary Value Problem
 Joural of Amerca Scece ;6( Cubc Nopolyomal Sple Approach to the Soluto of a Secod Order Two-Pot Boudary Value Problem W.K. Zahra, F.A. Abd El-Salam, A.A. El-Sabbagh ad Z.A. ZAk * Departmet of Egeerg athematcs
Joural of Amerca Scece ;6( Cubc Nopolyomal Sple Approach to the Soluto of a Secod Order Two-Pot Boudary Value Problem W.K. Zahra, F.A. Abd El-Salam, A.A. El-Sabbagh ad Z.A. ZAk * Departmet of Egeerg athematcs
MOLECULAR VIBRATIONS
 MOLECULAR VIBRATIONS Here we wsh to vestgate molecular vbratos ad draw a smlarty betwee the theory of molecular vbratos ad Hückel theory. 1. Smple Harmoc Oscllator Recall that the eergy of a oe-dmesoal
MOLECULAR VIBRATIONS Here we wsh to vestgate molecular vbratos ad draw a smlarty betwee the theory of molecular vbratos ad Hückel theory. 1. Smple Harmoc Oscllator Recall that the eergy of a oe-dmesoal
We have already referred to a certain reaction, which takes place at high temperature after rich combustion.
 ME 41 Day 13 Topcs Chemcal Equlbrum - Theory Chemcal Equlbrum Example #1 Equlbrum Costats Chemcal Equlbrum Example #2 Chemcal Equlbrum of Hot Bured Gas 1. Chemcal Equlbrum We have already referred to a
ME 41 Day 13 Topcs Chemcal Equlbrum - Theory Chemcal Equlbrum Example #1 Equlbrum Costats Chemcal Equlbrum Example #2 Chemcal Equlbrum of Hot Bured Gas 1. Chemcal Equlbrum We have already referred to a
CHAPTER 4 RADICAL EXPRESSIONS
 6 CHAPTER RADICAL EXPRESSIONS. The th Root of a Real Number A real umber a s called the th root of a real umber b f Thus, for example: s a square root of sce. s also a square root of sce ( ). s a cube
6 CHAPTER RADICAL EXPRESSIONS. The th Root of a Real Number A real umber a s called the th root of a real umber b f Thus, for example: s a square root of sce. s also a square root of sce ( ). s a cube
d dt d d dt dt Also recall that by Taylor series, / 2 (enables use of sin instead of cos-see p.27 of A&F) dsin
 Learzato of the Swg Equato We wll cover sectos.5.-.6 ad begg of Secto 3.3 these otes. 1. Sgle mache-fte bus case Cosder a sgle mache coected to a fte bus, as show Fg. 1 below. E y1 V=1./_ Fg. 1 The admttace
Learzato of the Swg Equato We wll cover sectos.5.-.6 ad begg of Secto 3.3 these otes. 1. Sgle mache-fte bus case Cosder a sgle mache coected to a fte bus, as show Fg. 1 below. E y1 V=1./_ Fg. 1 The admttace
Functions of Random Variables
 Fuctos of Radom Varables Chapter Fve Fuctos of Radom Varables 5. Itroducto A geeral egeerg aalyss model s show Fg. 5.. The model output (respose) cotas the performaces of a system or product, such as weght,
Fuctos of Radom Varables Chapter Fve Fuctos of Radom Varables 5. Itroducto A geeral egeerg aalyss model s show Fg. 5.. The model output (respose) cotas the performaces of a system or product, such as weght,
Beam Warming Second-Order Upwind Method
 Beam Warmg Secod-Order Upwd Method Petr Valeta Jauary 6, 015 Ths documet s a part of the assessmet work for the subject 1DRP Dfferetal Equatos o Computer lectured o FNSPE CTU Prague. Abstract Ths documet
Beam Warmg Secod-Order Upwd Method Petr Valeta Jauary 6, 015 Ths documet s a part of the assessmet work for the subject 1DRP Dfferetal Equatos o Computer lectured o FNSPE CTU Prague. Abstract Ths documet
Part 4b Asymptotic Results for MRR2 using PRESS. Recall that the PRESS statistic is a special type of cross validation procedure (see Allen (1971))
 art 4b Asymptotc Results for MRR usg RESS Recall that the RESS statstc s a specal type of cross valdato procedure (see Alle (97)) partcular to the regresso problem ad volves fdg Y $,, the estmate at the
art 4b Asymptotc Results for MRR usg RESS Recall that the RESS statstc s a specal type of cross valdato procedure (see Alle (97)) partcular to the regresso problem ad volves fdg Y $,, the estmate at the
Q-analogue of a Linear Transformation Preserving Log-concavity
 Iteratoal Joural of Algebra, Vol. 1, 2007, o. 2, 87-94 Q-aalogue of a Lear Trasformato Preservg Log-cocavty Daozhog Luo Departmet of Mathematcs, Huaqao Uversty Quazhou, Fua 362021, P. R. Cha ldzblue@163.com
Iteratoal Joural of Algebra, Vol. 1, 2007, o. 2, 87-94 Q-aalogue of a Lear Trasformato Preservg Log-cocavty Daozhog Luo Departmet of Mathematcs, Huaqao Uversty Quazhou, Fua 362021, P. R. Cha ldzblue@163.com
Fourth Order Four-Stage Diagonally Implicit Runge-Kutta Method for Linear Ordinary Differential Equations ABSTRACT INTRODUCTION
 Malasa Joural of Mathematcal Sceces (): 95-05 (00) Fourth Order Four-Stage Dagoall Implct Ruge-Kutta Method for Lear Ordar Dfferetal Equatos Nur Izzat Che Jawas, Fudzah Ismal, Mohamed Sulema, 3 Azm Jaafar
Malasa Joural of Mathematcal Sceces (): 95-05 (00) Fourth Order Four-Stage Dagoall Implct Ruge-Kutta Method for Lear Ordar Dfferetal Equatos Nur Izzat Che Jawas, Fudzah Ismal, Mohamed Sulema, 3 Azm Jaafar
Lecture 12 APPROXIMATION OF FIRST ORDER DERIVATIVES
 FDM: Appromato of Frst Order Dervatves Lecture APPROXIMATION OF FIRST ORDER DERIVATIVES. INTRODUCTION Covectve term coservato equatos volve frst order dervatves. The smplest possble approach for dscretzato
FDM: Appromato of Frst Order Dervatves Lecture APPROXIMATION OF FIRST ORDER DERIVATIVES. INTRODUCTION Covectve term coservato equatos volve frst order dervatves. The smplest possble approach for dscretzato
ECE 595, Section 10 Numerical Simulations Lecture 19: FEM for Electronic Transport. Prof. Peter Bermel February 22, 2013
 ECE 595, Secto 0 Numercal Smulatos Lecture 9: FEM for Electroc Trasport Prof. Peter Bermel February, 03 Outle Recap from Wedesday Physcs-based devce modelg Electroc trasport theory FEM electroc trasport
ECE 595, Secto 0 Numercal Smulatos Lecture 9: FEM for Electroc Trasport Prof. Peter Bermel February, 03 Outle Recap from Wedesday Physcs-based devce modelg Electroc trasport theory FEM electroc trasport
Numerical Analysis Formulae Booklet
 Numercal Aalyss Formulae Booklet. Iteratve Scemes for Systems of Lear Algebrac Equatos:.... Taylor Seres... 3. Fte Dfferece Approxmatos... 3 4. Egevalues ad Egevectors of Matrces.... 3 5. Vector ad Matrx
Numercal Aalyss Formulae Booklet. Iteratve Scemes for Systems of Lear Algebrac Equatos:.... Taylor Seres... 3. Fte Dfferece Approxmatos... 3 4. Egevalues ad Egevectors of Matrces.... 3 5. Vector ad Matrx
Lecture 07: Poles and Zeros
 Lecture 07: Poles ad Zeros Defto of poles ad zeros The trasfer fucto provdes a bass for determg mportat system respose characterstcs wthout solvg the complete dfferetal equato. As defed, the trasfer fucto
Lecture 07: Poles ad Zeros Defto of poles ad zeros The trasfer fucto provdes a bass for determg mportat system respose characterstcs wthout solvg the complete dfferetal equato. As defed, the trasfer fucto
BERNSTEIN COLLOCATION METHOD FOR SOLVING NONLINEAR DIFFERENTIAL EQUATIONS. Aysegul Akyuz Dascioglu and Nese Isler
 Mathematcal ad Computatoal Applcatos, Vol. 8, No. 3, pp. 293-300, 203 BERNSTEIN COLLOCATION METHOD FOR SOLVING NONLINEAR DIFFERENTIAL EQUATIONS Aysegul Ayuz Dascoglu ad Nese Isler Departmet of Mathematcs,
Mathematcal ad Computatoal Applcatos, Vol. 8, No. 3, pp. 293-300, 203 BERNSTEIN COLLOCATION METHOD FOR SOLVING NONLINEAR DIFFERENTIAL EQUATIONS Aysegul Ayuz Dascoglu ad Nese Isler Departmet of Mathematcs,
Towards developing a reacting- DNS code Design and numerical issues
 Towards developg a reactg- DNS code Desg ad umercal ssues Rx Yu 20-03-09 20-03-09 FM teral semar Motvatos Why we eed a Reactg DNS code No model for both flow (turbulece) ad combusto Study applcatos of
Towards developg a reactg- DNS code Desg ad umercal ssues Rx Yu 20-03-09 20-03-09 FM teral semar Motvatos Why we eed a Reactg DNS code No model for both flow (turbulece) ad combusto Study applcatos of
CS286.2 Lecture 4: Dinur s Proof of the PCP Theorem
 CS86. Lecture 4: Dur s Proof of the PCP Theorem Scrbe: Thom Bohdaowcz Prevously, we have prove a weak verso of the PCP theorem: NP PCP 1,1/ (r = poly, q = O(1)). Wth ths result we have the desred costat
CS86. Lecture 4: Dur s Proof of the PCP Theorem Scrbe: Thom Bohdaowcz Prevously, we have prove a weak verso of the PCP theorem: NP PCP 1,1/ (r = poly, q = O(1)). Wth ths result we have the desred costat
Applying the condition for equilibrium to this equilibrium, we get (1) n i i =, r G and 5 i
 CHEMICAL EQUILIBRIA The Thermodyamc Equlbrum Costat Cosder a reversble reacto of the type 1 A 1 + 2 A 2 + W m A m + m+1 A m+1 + Assgg postve values to the stochometrc coeffcets o the rght had sde ad egatve
CHEMICAL EQUILIBRIA The Thermodyamc Equlbrum Costat Cosder a reversble reacto of the type 1 A 1 + 2 A 2 + W m A m + m+1 A m+1 + Assgg postve values to the stochometrc coeffcets o the rght had sde ad egatve
Estimation of Stress- Strength Reliability model using finite mixture of exponential distributions
 Iteratoal Joural of Computatoal Egeerg Research Vol, 0 Issue, Estmato of Stress- Stregth Relablty model usg fte mxture of expoetal dstrbutos K.Sadhya, T.S.Umamaheswar Departmet of Mathematcs, Lal Bhadur
Iteratoal Joural of Computatoal Egeerg Research Vol, 0 Issue, Estmato of Stress- Stregth Relablty model usg fte mxture of expoetal dstrbutos K.Sadhya, T.S.Umamaheswar Departmet of Mathematcs, Lal Bhadur
Chapter 5 Properties of a Random Sample
 Lecture 6 o BST 63: Statstcal Theory I Ku Zhag, /0/008 Revew for the prevous lecture Cocepts: t-dstrbuto, F-dstrbuto Theorems: Dstrbutos of sample mea ad sample varace, relatoshp betwee sample mea ad sample
Lecture 6 o BST 63: Statstcal Theory I Ku Zhag, /0/008 Revew for the prevous lecture Cocepts: t-dstrbuto, F-dstrbuto Theorems: Dstrbutos of sample mea ad sample varace, relatoshp betwee sample mea ad sample
Numerical Simulations of the Complex Modied Korteweg-de Vries Equation. Thiab R. Taha. The University of Georgia. Abstract
 Numercal Smulatos of the Complex Moded Korteweg-de Vres Equato Thab R. Taha Computer Scece Departmet The Uversty of Georga Athes, GA 002 USA Tel 0-542-2911 e-mal thab@cs.uga.edu Abstract I ths paper mplemetatos
Numercal Smulatos of the Complex Moded Korteweg-de Vres Equato Thab R. Taha Computer Scece Departmet The Uversty of Georga Athes, GA 002 USA Tel 0-542-2911 e-mal thab@cs.uga.edu Abstract I ths paper mplemetatos
Bounds on the expected entropy and KL-divergence of sampled multinomial distributions. Brandon C. Roy
 Bouds o the expected etropy ad KL-dvergece of sampled multomal dstrbutos Brado C. Roy bcroy@meda.mt.edu Orgal: May 18, 2011 Revsed: Jue 6, 2011 Abstract Iformato theoretc quattes calculated from a sampled
Bouds o the expected etropy ad KL-dvergece of sampled multomal dstrbutos Brado C. Roy bcroy@meda.mt.edu Orgal: May 18, 2011 Revsed: Jue 6, 2011 Abstract Iformato theoretc quattes calculated from a sampled
Solving Constrained Flow-Shop Scheduling. Problems with Three Machines
 It J Cotemp Math Sceces, Vol 5, 2010, o 19, 921-929 Solvg Costraed Flow-Shop Schedulg Problems wth Three Maches P Pada ad P Rajedra Departmet of Mathematcs, School of Advaced Sceces, VIT Uversty, Vellore-632
It J Cotemp Math Sceces, Vol 5, 2010, o 19, 921-929 Solvg Costraed Flow-Shop Schedulg Problems wth Three Maches P Pada ad P Rajedra Departmet of Mathematcs, School of Advaced Sceces, VIT Uversty, Vellore-632
PGE 310: Formulation and Solution in Geosystems Engineering. Dr. Balhoff. Interpolation
 PGE 30: Formulato ad Soluto Geosystems Egeerg Dr. Balhoff Iterpolato Numercal Methods wth MATLAB, Recktewald, Chapter 0 ad Numercal Methods for Egeers, Chapra ad Caale, 5 th Ed., Part Fve, Chapter 8 ad
PGE 30: Formulato ad Soluto Geosystems Egeerg Dr. Balhoff Iterpolato Numercal Methods wth MATLAB, Recktewald, Chapter 0 ad Numercal Methods for Egeers, Chapra ad Caale, 5 th Ed., Part Fve, Chapter 8 ad
UNIT 2 SOLUTION OF ALGEBRAIC AND TRANSCENDENTAL EQUATIONS
 Numercal Computg -I UNIT SOLUTION OF ALGEBRAIC AND TRANSCENDENTAL EQUATIONS Structure Page Nos..0 Itroducto 6. Objectves 7. Ital Approxmato to a Root 7. Bsecto Method 8.. Error Aalyss 9.4 Regula Fals Method
Numercal Computg -I UNIT SOLUTION OF ALGEBRAIC AND TRANSCENDENTAL EQUATIONS Structure Page Nos..0 Itroducto 6. Objectves 7. Ital Approxmato to a Root 7. Bsecto Method 8.. Error Aalyss 9.4 Regula Fals Method
Introduction to local (nonparametric) density estimation. methods
 Itroducto to local (oparametrc) desty estmato methods A slecture by Yu Lu for ECE 66 Sprg 014 1. Itroducto Ths slecture troduces two local desty estmato methods whch are Parze desty estmato ad k-earest
Itroducto to local (oparametrc) desty estmato methods A slecture by Yu Lu for ECE 66 Sprg 014 1. Itroducto Ths slecture troduces two local desty estmato methods whch are Parze desty estmato ad k-earest
1 Lyapunov Stability Theory
 Lyapuov Stablty heory I ths secto we cosder proofs of stablty of equlbra of autoomous systems. hs s stadard theory for olear systems, ad oe of the most mportat tools the aalyss of olear systems. It may
Lyapuov Stablty heory I ths secto we cosder proofs of stablty of equlbra of autoomous systems. hs s stadard theory for olear systems, ad oe of the most mportat tools the aalyss of olear systems. It may
Analysis of Lagrange Interpolation Formula
 P IJISET - Iteratoal Joural of Iovatve Scece, Egeerg & Techology, Vol. Issue, December 4. www.jset.com ISS 348 7968 Aalyss of Lagrage Iterpolato Formula Vjay Dahya PDepartmet of MathematcsMaharaja Surajmal
P IJISET - Iteratoal Joural of Iovatve Scece, Egeerg & Techology, Vol. Issue, December 4. www.jset.com ISS 348 7968 Aalyss of Lagrage Iterpolato Formula Vjay Dahya PDepartmet of MathematcsMaharaja Surajmal
Strong Convergence of Weighted Averaged Approximants of Asymptotically Nonexpansive Mappings in Banach Spaces without Uniform Convexity
 BULLETIN of the MALAYSIAN MATHEMATICAL SCIENCES SOCIETY Bull. Malays. Math. Sc. Soc. () 7 (004), 5 35 Strog Covergece of Weghted Averaged Appromats of Asymptotcally Noepasve Mappgs Baach Spaces wthout
BULLETIN of the MALAYSIAN MATHEMATICAL SCIENCES SOCIETY Bull. Malays. Math. Sc. Soc. () 7 (004), 5 35 Strog Covergece of Weghted Averaged Appromats of Asymptotcally Noepasve Mappgs Baach Spaces wthout
Journal of Mathematical Analysis and Applications
 J. Math. Aal. Appl. 365 200) 358 362 Cotets lsts avalable at SceceDrect Joural of Mathematcal Aalyss ad Applcatos www.elsever.com/locate/maa Asymptotc behavor of termedate pots the dfferetal mea value
J. Math. Aal. Appl. 365 200) 358 362 Cotets lsts avalable at SceceDrect Joural of Mathematcal Aalyss ad Applcatos www.elsever.com/locate/maa Asymptotc behavor of termedate pots the dfferetal mea value
LINEAR RECURRENT SEQUENCES AND POWERS OF A SQUARE MATRIX
 INTEGERS: ELECTRONIC JOURNAL OF COMBINATORIAL NUMBER THEORY 6 2006, #A12 LINEAR RECURRENT SEQUENCES AND POWERS OF A SQUARE MATRIX Hacèe Belbachr 1 USTHB, Departmet of Mathematcs, POBox 32 El Ala, 16111,
INTEGERS: ELECTRONIC JOURNAL OF COMBINATORIAL NUMBER THEORY 6 2006, #A12 LINEAR RECURRENT SEQUENCES AND POWERS OF A SQUARE MATRIX Hacèe Belbachr 1 USTHB, Departmet of Mathematcs, POBox 32 El Ala, 16111,
Point Estimation: definition of estimators
 Pot Estmato: defto of estmators Pot estmator: ay fucto W (X,..., X ) of a data sample. The exercse of pot estmato s to use partcular fuctos of the data order to estmate certa ukow populato parameters.
Pot Estmato: defto of estmators Pot estmator: ay fucto W (X,..., X ) of a data sample. The exercse of pot estmato s to use partcular fuctos of the data order to estmate certa ukow populato parameters.
{ }{ ( )} (, ) = ( ) ( ) ( ) Chapter 14 Exercises in Sampling Theory. Exercise 1 (Simple random sampling): Solution:
 Chapter 4 Exercses Samplg Theory Exercse (Smple radom samplg: Let there be two correlated radom varables X ad A sample of sze s draw from a populato by smple radom samplg wthout replacemet The observed
Chapter 4 Exercses Samplg Theory Exercse (Smple radom samplg: Let there be two correlated radom varables X ad A sample of sze s draw from a populato by smple radom samplg wthout replacemet The observed
5 Short Proofs of Simplified Stirling s Approximation
 5 Short Proofs of Smplfed Strlg s Approxmato Ofr Gorodetsky, drtymaths.wordpress.com Jue, 20 0 Itroducto Strlg s approxmato s the followg (somewhat surprsg) approxmato of the factoral,, usg elemetary fuctos:
5 Short Proofs of Smplfed Strlg s Approxmato Ofr Gorodetsky, drtymaths.wordpress.com Jue, 20 0 Itroducto Strlg s approxmato s the followg (somewhat surprsg) approxmato of the factoral,, usg elemetary fuctos:
Block-Based Compact Thermal Modeling of Semiconductor Integrated Circuits
 Block-Based Compact hermal Modelg of Semcoductor Itegrated Crcuts Master s hess Defese Caddate: Jg Ba Commttee Members: Dr. Mg-Cheg Cheg Dr. Daqg Hou Dr. Robert Schllg July 27, 2009 Outle Itroducto Backgroud
Block-Based Compact hermal Modelg of Semcoductor Itegrated Crcuts Master s hess Defese Caddate: Jg Ba Commttee Members: Dr. Mg-Cheg Cheg Dr. Daqg Hou Dr. Robert Schllg July 27, 2009 Outle Itroducto Backgroud
A tighter lower bound on the circuit size of the hardest Boolean functions
 Electroc Colloquum o Computatoal Complexty, Report No. 86 2011) A tghter lower boud o the crcut sze of the hardest Boolea fuctos Masak Yamamoto Abstract I [IPL2005], Fradse ad Mlterse mproved bouds o the
Electroc Colloquum o Computatoal Complexty, Report No. 86 2011) A tghter lower boud o the crcut sze of the hardest Boolea fuctos Masak Yamamoto Abstract I [IPL2005], Fradse ad Mlterse mproved bouds o the
C-1: Aerodynamics of Airfoils 1 C-2: Aerodynamics of Airfoils 2 C-3: Panel Methods C-4: Thin Airfoil Theory
 ROAD MAP... AE301 Aerodyamcs I UNIT C: 2-D Arfols C-1: Aerodyamcs of Arfols 1 C-2: Aerodyamcs of Arfols 2 C-3: Pael Methods C-4: Th Arfol Theory AE301 Aerodyamcs I Ut C-3: Lst of Subects Problem Solutos?
ROAD MAP... AE301 Aerodyamcs I UNIT C: 2-D Arfols C-1: Aerodyamcs of Arfols 1 C-2: Aerodyamcs of Arfols 2 C-3: Pael Methods C-4: Th Arfol Theory AE301 Aerodyamcs I Ut C-3: Lst of Subects Problem Solutos?
Lecture 3 Probability review (cont d)
 STATS 00: Itroducto to Statstcal Iferece Autum 06 Lecture 3 Probablty revew (cot d) 3. Jot dstrbutos If radom varables X,..., X k are depedet, the ther dstrbuto may be specfed by specfyg the dvdual dstrbuto
STATS 00: Itroducto to Statstcal Iferece Autum 06 Lecture 3 Probablty revew (cot d) 3. Jot dstrbutos If radom varables X,..., X k are depedet, the ther dstrbuto may be specfed by specfyg the dvdual dstrbuto
2006 Jamie Trahan, Autar Kaw, Kevin Martin University of South Florida United States of America
 SOLUTION OF SYSTEMS OF SIMULTANEOUS LINEAR EQUATIONS Gauss-Sedel Method 006 Jame Traha, Autar Kaw, Kev Mart Uversty of South Florda Uted States of Amerca kaw@eg.usf.edu Itroducto Ths worksheet demostrates
SOLUTION OF SYSTEMS OF SIMULTANEOUS LINEAR EQUATIONS Gauss-Sedel Method 006 Jame Traha, Autar Kaw, Kev Mart Uversty of South Florda Uted States of Amerca kaw@eg.usf.edu Itroducto Ths worksheet demostrates
Comparing Different Estimators of three Parameters for Transmuted Weibull Distribution
 Global Joural of Pure ad Appled Mathematcs. ISSN 0973-768 Volume 3, Number 9 (207), pp. 55-528 Research Ida Publcatos http://www.rpublcato.com Comparg Dfferet Estmators of three Parameters for Trasmuted
Global Joural of Pure ad Appled Mathematcs. ISSN 0973-768 Volume 3, Number 9 (207), pp. 55-528 Research Ida Publcatos http://www.rpublcato.com Comparg Dfferet Estmators of three Parameters for Trasmuted
ESS Line Fitting
 ESS 5 014 17. Le Fttg A very commo problem data aalyss s lookg for relatoshpetwee dfferet parameters ad fttg les or surfaces to data. The smplest example s fttg a straght le ad we wll dscuss that here
ESS 5 014 17. Le Fttg A very commo problem data aalyss s lookg for relatoshpetwee dfferet parameters ad fttg les or surfaces to data. The smplest example s fttg a straght le ad we wll dscuss that here
ENGI 4421 Joint Probability Distributions Page Joint Probability Distributions [Navidi sections 2.5 and 2.6; Devore sections
 ENGI 441 Jot Probablty Dstrbutos Page 7-01 Jot Probablty Dstrbutos [Navd sectos.5 ad.6; Devore sectos 5.1-5.] The jot probablty mass fucto of two dscrete radom quattes, s, P ad p x y x y The margal probablty
ENGI 441 Jot Probablty Dstrbutos Page 7-01 Jot Probablty Dstrbutos [Navd sectos.5 ad.6; Devore sectos 5.1-5.] The jot probablty mass fucto of two dscrete radom quattes, s, P ad p x y x y The margal probablty
UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS
 UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS Postpoed exam: ECON430 Statstcs Date of exam: Jauary 0, 0 Tme for exam: 09:00 a.m. :00 oo The problem set covers 5 pages Resources allowed: All wrtte ad prted
UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS Postpoed exam: ECON430 Statstcs Date of exam: Jauary 0, 0 Tme for exam: 09:00 a.m. :00 oo The problem set covers 5 pages Resources allowed: All wrtte ad prted
Laboratory I.10 It All Adds Up
 Laboratory I. It All Adds Up Goals The studet wll work wth Rema sums ad evaluate them usg Derve. The studet wll see applcatos of tegrals as accumulatos of chages. The studet wll revew curve fttg sklls.
Laboratory I. It All Adds Up Goals The studet wll work wth Rema sums ad evaluate them usg Derve. The studet wll see applcatos of tegrals as accumulatos of chages. The studet wll revew curve fttg sklls.
Lecture 7. Confidence Intervals and Hypothesis Tests in the Simple CLR Model
 Lecture 7. Cofdece Itervals ad Hypothess Tests the Smple CLR Model I lecture 6 we troduced the Classcal Lear Regresso (CLR) model that s the radom expermet of whch the data Y,,, K, are the outcomes. The
Lecture 7. Cofdece Itervals ad Hypothess Tests the Smple CLR Model I lecture 6 we troduced the Classcal Lear Regresso (CLR) model that s the radom expermet of whch the data Y,,, K, are the outcomes. The
Aitken delta-squared generalized Juncgk-type iterative procedure
 Atke delta-squared geeralzed Jucgk-type teratve procedure M. De la Se Isttute of Research ad Developmet of Processes. Uversty of Basque Coutry Campus of Leoa (Bzkaa) PO Box. 644- Blbao, 488- Blbao. SPAIN
Atke delta-squared geeralzed Jucgk-type teratve procedure M. De la Se Isttute of Research ad Developmet of Processes. Uversty of Basque Coutry Campus of Leoa (Bzkaa) PO Box. 644- Blbao, 488- Blbao. SPAIN
Chapter 9 Jordan Block Matrices
 Chapter 9 Jorda Block atrces I ths chapter we wll solve the followg problem. Gve a lear operator T fd a bass R of F such that the matrx R (T) s as smple as possble. f course smple s a matter of taste.
Chapter 9 Jorda Block atrces I ths chapter we wll solve the followg problem. Gve a lear operator T fd a bass R of F such that the matrx R (T) s as smple as possble. f course smple s a matter of taste.
Module 1 : The equation of continuity. Lecture 5: Conservation of Mass for each species. & Fick s Law
 Module : The equato of cotuty Lecture 5: Coservato of Mass for each speces & Fck s Law NPTEL, IIT Kharagpur, Prof. Sakat Chakraborty, Departmet of Chemcal Egeerg 2 Basc Deftos I Mass Trasfer, we usually
Module : The equato of cotuty Lecture 5: Coservato of Mass for each speces & Fck s Law NPTEL, IIT Kharagpur, Prof. Sakat Chakraborty, Departmet of Chemcal Egeerg 2 Basc Deftos I Mass Trasfer, we usually
CH E 374 Computational Methods in Engineering Fall 2007
 CH E 7 Computatoal Methods Egeerg Fall 007 Sample Soluto 5. The data o the varato of the rato of stagato pressure to statc pressure (r ) wth Mach umber ( M ) for the flow through a duct are as follows:
CH E 7 Computatoal Methods Egeerg Fall 007 Sample Soluto 5. The data o the varato of the rato of stagato pressure to statc pressure (r ) wth Mach umber ( M ) for the flow through a duct are as follows:
best estimate (mean) for X uncertainty or error in the measurement (systematic, random or statistical) best
 Error Aalyss Preamble Wheever a measuremet s made, the result followg from that measuremet s always subject to ucertaty The ucertaty ca be reduced by makg several measuremets of the same quatty or by mprovg
Error Aalyss Preamble Wheever a measuremet s made, the result followg from that measuremet s always subject to ucertaty The ucertaty ca be reduced by makg several measuremets of the same quatty or by mprovg
General Method for Calculating Chemical Equilibrium Composition
 AE 6766/Setzma Sprg 004 Geeral Metod for Calculatg Cemcal Equlbrum Composto For gve tal codtos (e.g., for gve reactats, coose te speces to be cluded te products. As a example, for combusto of ydroge wt
AE 6766/Setzma Sprg 004 Geeral Metod for Calculatg Cemcal Equlbrum Composto For gve tal codtos (e.g., for gve reactats, coose te speces to be cluded te products. As a example, for combusto of ydroge wt
ENGI 4421 Propagation of Error Page 8-01
 ENGI 441 Propagato of Error Page 8-01 Propagato of Error [Navd Chapter 3; ot Devore] Ay realstc measuremet procedure cotas error. Ay calculatos based o that measuremet wll therefore also cota a error.
ENGI 441 Propagato of Error Page 8-01 Propagato of Error [Navd Chapter 3; ot Devore] Ay realstc measuremet procedure cotas error. Ay calculatos based o that measuremet wll therefore also cota a error.
Mu Sequences/Series Solutions National Convention 2014
 Mu Sequeces/Seres Solutos Natoal Coveto 04 C 6 E A 6C A 6 B B 7 A D 7 D C 7 A B 8 A B 8 A C 8 E 4 B 9 B 4 E 9 B 4 C 9 E C 0 A A 0 D B 0 C C Usg basc propertes of arthmetc sequeces, we fd a ad bm m We eed
Mu Sequeces/Seres Solutos Natoal Coveto 04 C 6 E A 6C A 6 B B 7 A D 7 D C 7 A B 8 A B 8 A C 8 E 4 B 9 B 4 E 9 B 4 C 9 E C 0 A A 0 D B 0 C C Usg basc propertes of arthmetc sequeces, we fd a ad bm m We eed
PTAS for Bin-Packing
 CS 663: Patter Matchg Algorthms Scrbe: Che Jag /9/00. Itroducto PTAS for B-Packg The B-Packg problem s NP-hard. If we use approxmato algorthms, the B-Packg problem could be solved polyomal tme. For example,
CS 663: Patter Matchg Algorthms Scrbe: Che Jag /9/00. Itroducto PTAS for B-Packg The B-Packg problem s NP-hard. If we use approxmato algorthms, the B-Packg problem could be solved polyomal tme. For example,
arxiv:math/ v1 [math.gm] 8 Dec 2005
![arxiv:math/ v1 [math.gm] 8 Dec 2005 arxiv:math/ v1 [math.gm] 8 Dec 2005](/thumbs/94/118250722.jpg) arxv:math/05272v [math.gm] 8 Dec 2005 A GENERALIZATION OF AN INEQUALITY FROM IMO 2005 NIKOLAI NIKOLOV The preset paper was spred by the thrd problem from the IMO 2005. A specal award was gve to Yure Boreko
arxv:math/05272v [math.gm] 8 Dec 2005 A GENERALIZATION OF AN INEQUALITY FROM IMO 2005 NIKOLAI NIKOLOV The preset paper was spred by the thrd problem from the IMO 2005. A specal award was gve to Yure Boreko
Lecture Note to Rice Chapter 8
 ECON 430 HG revsed Nov 06 Lecture Note to Rce Chapter 8 Radom matrces Let Y, =,,, m, =,,, be radom varables (r.v. s). The matrx Y Y Y Y Y Y Y Y Y Y = m m m s called a radom matrx ( wth a ot m-dmesoal dstrbuto,
ECON 430 HG revsed Nov 06 Lecture Note to Rce Chapter 8 Radom matrces Let Y, =,,, m, =,,, be radom varables (r.v. s). The matrx Y Y Y Y Y Y Y Y Y Y = m m m s called a radom matrx ( wth a ot m-dmesoal dstrbuto,
1 Convergence of the Arnoldi method for eigenvalue problems
 Lecture otes umercal lear algebra Arold method covergece Covergece of the Arold method for egevalue problems Recall that, uless t breaks dow, k steps of the Arold method geerates a orthogoal bass of a
Lecture otes umercal lear algebra Arold method covergece Covergece of the Arold method for egevalue problems Recall that, uless t breaks dow, k steps of the Arold method geerates a orthogoal bass of a
7.0 Equality Contraints: Lagrange Multipliers
 Systes Optzato 7.0 Equalty Cotrats: Lagrage Multplers Cosder the zato of a o-lear fucto subject to equalty costrats: g f() R ( ) 0 ( ) (7.) where the g ( ) are possbly also olear fuctos, ad < otherwse
Systes Optzato 7.0 Equalty Cotrats: Lagrage Multplers Cosder the zato of a o-lear fucto subject to equalty costrats: g f() R ( ) 0 ( ) (7.) where the g ( ) are possbly also olear fuctos, ad < otherwse
Uniform asymptotical stability of almost periodic solution of a discrete multispecies Lotka-Volterra competition system
 Iteratoal Joural of Egeerg ad Advaced Research Techology (IJEART) ISSN: 2454-9290, Volume-2, Issue-1, Jauary 2016 Uform asymptotcal stablty of almost perodc soluto of a dscrete multspeces Lotka-Volterra
Iteratoal Joural of Egeerg ad Advaced Research Techology (IJEART) ISSN: 2454-9290, Volume-2, Issue-1, Jauary 2016 Uform asymptotcal stablty of almost perodc soluto of a dscrete multspeces Lotka-Volterra
Chapter 14 Logistic Regression Models
 Chapter 4 Logstc Regresso Models I the lear regresso model X β + ε, there are two types of varables explaatory varables X, X,, X k ad study varable y These varables ca be measured o a cotuous scale as
Chapter 4 Logstc Regresso Models I the lear regresso model X β + ε, there are two types of varables explaatory varables X, X,, X k ad study varable y These varables ca be measured o a cotuous scale as
Chapter 4 (Part 1): Non-Parametric Classification (Sections ) Pattern Classification 4.3) Announcements
 Aoucemets No-Parametrc Desty Estmato Techques HW assged Most of ths lecture was o the blacboard. These sldes cover the same materal as preseted DHS Bometrcs CSE 90-a Lecture 7 CSE90a Fall 06 CSE90a Fall
Aoucemets No-Parametrc Desty Estmato Techques HW assged Most of ths lecture was o the blacboard. These sldes cover the same materal as preseted DHS Bometrcs CSE 90-a Lecture 7 CSE90a Fall 06 CSE90a Fall
End of Finite Volume Methods Cartesian grids. Solution of the Navier-Stokes Equations. REVIEW Lecture 17: Higher order (interpolation) schemes
 REVIEW Lecture 17: Numercal Flud Mechacs Sprg 2015 Lecture 18 Ed of Fte Volume Methods Cartesa grds Hgher order (terpolato) schemes Soluto of the Naver-Stokes Equatos Dscretzato of the covectve ad vscous
REVIEW Lecture 17: Numercal Flud Mechacs Sprg 2015 Lecture 18 Ed of Fte Volume Methods Cartesa grds Hgher order (terpolato) schemes Soluto of the Naver-Stokes Equatos Dscretzato of the covectve ad vscous
16 Homework lecture 16
 Quees College, CUNY, Departmet of Computer Scece Numercal Methods CSCI 361 / 761 Fall 2018 Istructor: Dr. Sateesh Mae c Sateesh R. Mae 2018 16 Homework lecture 16 Please emal your soluto, as a fle attachmet,
Quees College, CUNY, Departmet of Computer Scece Numercal Methods CSCI 361 / 761 Fall 2018 Istructor: Dr. Sateesh Mae c Sateesh R. Mae 2018 16 Homework lecture 16 Please emal your soluto, as a fle attachmet,
Lecture 9: Tolerant Testing
 Lecture 9: Tolerat Testg Dael Kae Scrbe: Sakeerth Rao Aprl 4, 07 Abstract I ths lecture we prove a quas lear lower boud o the umber of samples eeded to do tolerat testg for L dstace. Tolerat Testg We have
Lecture 9: Tolerat Testg Dael Kae Scrbe: Sakeerth Rao Aprl 4, 07 Abstract I ths lecture we prove a quas lear lower boud o the umber of samples eeded to do tolerat testg for L dstace. Tolerat Testg We have
EVALUATION OF FUNCTIONAL INTEGRALS BY MEANS OF A SERIES AND THE METHOD OF BOREL TRANSFORM
 EVALUATION OF FUNCTIONAL INTEGRALS BY MEANS OF A SERIES AND THE METHOD OF BOREL TRANSFORM Jose Javer Garca Moreta Ph. D research studet at the UPV/EHU (Uversty of Basque coutry) Departmet of Theoretcal
EVALUATION OF FUNCTIONAL INTEGRALS BY MEANS OF A SERIES AND THE METHOD OF BOREL TRANSFORM Jose Javer Garca Moreta Ph. D research studet at the UPV/EHU (Uversty of Basque coutry) Departmet of Theoretcal
ECE606: Solid State Devices Lecture 13 Solutions of the Continuity Eqs. Analytical & Numerical
 ECE66: Sold State Devces Lecture 13 Solutos of the Cotuty Eqs. Aalytcal & Numercal Gerhard Klmeck gekco@purdue.edu Outle Aalytcal Solutos to the Cotuty Equatos 1) Example problems ) Summary Numercal Solutos
ECE66: Sold State Devces Lecture 13 Solutos of the Cotuty Eqs. Aalytcal & Numercal Gerhard Klmeck gekco@purdue.edu Outle Aalytcal Solutos to the Cotuty Equatos 1) Example problems ) Summary Numercal Solutos
CIS 800/002 The Algorithmic Foundations of Data Privacy October 13, Lecture 9. Database Update Algorithms: Multiplicative Weights
 CIS 800/002 The Algorthmc Foudatos of Data Prvacy October 13, 2011 Lecturer: Aaro Roth Lecture 9 Scrbe: Aaro Roth Database Update Algorthms: Multplcatve Weghts We ll recall aga) some deftos from last tme:
CIS 800/002 The Algorthmc Foudatos of Data Prvacy October 13, 2011 Lecturer: Aaro Roth Lecture 9 Scrbe: Aaro Roth Database Update Algorthms: Multplcatve Weghts We ll recall aga) some deftos from last tme:
Complete Convergence and Some Maximal Inequalities for Weighted Sums of Random Variables
 Joural of Sceces, Islamc Republc of Ira 8(4): -6 (007) Uversty of Tehra, ISSN 06-04 http://sceces.ut.ac.r Complete Covergece ad Some Maxmal Iequaltes for Weghted Sums of Radom Varables M. Am,,* H.R. Nl
Joural of Sceces, Islamc Republc of Ira 8(4): -6 (007) Uversty of Tehra, ISSN 06-04 http://sceces.ut.ac.r Complete Covergece ad Some Maxmal Iequaltes for Weghted Sums of Radom Varables M. Am,,* H.R. Nl
DIFFERENTIAL GEOMETRIC APPROACH TO HAMILTONIAN MECHANICS
 DIFFERENTIAL GEOMETRIC APPROACH TO HAMILTONIAN MECHANICS Course Project: Classcal Mechacs (PHY 40) Suja Dabholkar (Y430) Sul Yeshwath (Y444). Itroducto Hamltoa mechacs s geometry phase space. It deals
DIFFERENTIAL GEOMETRIC APPROACH TO HAMILTONIAN MECHANICS Course Project: Classcal Mechacs (PHY 40) Suja Dabholkar (Y430) Sul Yeshwath (Y444). Itroducto Hamltoa mechacs s geometry phase space. It deals
A Collocation Method for Solving Abel s Integral Equations of First and Second Kinds
 A Collocato Method for Solvg Abel s Itegral Equatos of Frst ad Secod Kds Abbas Saadatmad a ad Mehd Dehgha b a Departmet of Mathematcs, Uversty of Kasha, Kasha, Ira b Departmet of Appled Mathematcs, Faculty
A Collocato Method for Solvg Abel s Itegral Equatos of Frst ad Secod Kds Abbas Saadatmad a ad Mehd Dehgha b a Departmet of Mathematcs, Uversty of Kasha, Kasha, Ira b Departmet of Appled Mathematcs, Faculty
Stability For a stable numerical scheme, the errors in the initial condition will not grow unboundedly with time.
 .3.5. Stablty Aalyss Readg: Taehll et al. Secto 3.6. Stablty For a stable umercal scheme, the errors the tal codto wll ot grow uboudedly wth tme. I ths secto, we dscuss the methods for determg the stablty
.3.5. Stablty Aalyss Readg: Taehll et al. Secto 3.6. Stablty For a stable umercal scheme, the errors the tal codto wll ot grow uboudedly wth tme. I ths secto, we dscuss the methods for determg the stablty
Generalized One-Step Third Derivative Implicit Hybrid Block Method for the Direct Solution of Second Order Ordinary Differential Equation
 Appled Mathematcal Sceces, Vol. 1, 16, o. 9, 417-4 HIKARI Ltd, www.m-hkar.com http://dx.do.org/1.1988/ams.16.51667 Geeralzed Oe-Step Thrd Dervatve Implct Hybrd Block Method for the Drect Soluto of Secod
Appled Mathematcal Sceces, Vol. 1, 16, o. 9, 417-4 HIKARI Ltd, www.m-hkar.com http://dx.do.org/1.1988/ams.16.51667 Geeralzed Oe-Step Thrd Dervatve Implct Hybrd Block Method for the Drect Soluto of Secod
Analysis of Variance with Weibull Data
 Aalyss of Varace wth Webull Data Lahaa Watthaacheewaul Abstract I statstcal data aalyss by aalyss of varace, the usual basc assumptos are that the model s addtve ad the errors are radomly, depedetly, ad
Aalyss of Varace wth Webull Data Lahaa Watthaacheewaul Abstract I statstcal data aalyss by aalyss of varace, the usual basc assumptos are that the model s addtve ad the errors are radomly, depedetly, ad
C.11 Bang-bang Control
 Itroucto to Cotrol heory Iclug Optmal Cotrol Nguye a e -.5 C. Bag-bag Cotrol. Itroucto hs chapter eals wth the cotrol wth restrctos: s boue a mght well be possble to have scotutes. o llustrate some of
Itroucto to Cotrol heory Iclug Optmal Cotrol Nguye a e -.5 C. Bag-bag Cotrol. Itroucto hs chapter eals wth the cotrol wth restrctos: s boue a mght well be possble to have scotutes. o llustrate some of
Overview of the weighting constants and the points where we evaluate the function for The Gaussian quadrature Project two
 Overvew of the weghtg costats ad the pots where we evaluate the fucto for The Gaussa quadrature Project two By Ashraf Marzouk ChE 505 Fall 005 Departmet of Mechacal Egeerg Uversty of Teessee Koxvlle, TN
Overvew of the weghtg costats ad the pots where we evaluate the fucto for The Gaussa quadrature Project two By Ashraf Marzouk ChE 505 Fall 005 Departmet of Mechacal Egeerg Uversty of Teessee Koxvlle, TN
ECON 5360 Class Notes GMM
 ECON 560 Class Notes GMM Geeralzed Method of Momets (GMM) I beg by outlg the classcal method of momets techque (Fsher, 95) ad the proceed to geeralzed method of momets (Hase, 98).. radtoal Method of Momets
ECON 560 Class Notes GMM Geeralzed Method of Momets (GMM) I beg by outlg the classcal method of momets techque (Fsher, 95) ad the proceed to geeralzed method of momets (Hase, 98).. radtoal Method of Momets
Arithmetic Mean and Geometric Mean
 Acta Mathematca Ntresa Vol, No, p 43 48 ISSN 453-6083 Arthmetc Mea ad Geometrc Mea Mare Varga a * Peter Mchalča b a Departmet of Mathematcs, Faculty of Natural Sceces, Costate the Phlosopher Uversty Ntra,
Acta Mathematca Ntresa Vol, No, p 43 48 ISSN 453-6083 Arthmetc Mea ad Geometrc Mea Mare Varga a * Peter Mchalča b a Departmet of Mathematcs, Faculty of Natural Sceces, Costate the Phlosopher Uversty Ntra,
X ε ) = 0, or equivalently, lim
 Revew for the prevous lecture Cocepts: order statstcs Theorems: Dstrbutos of order statstcs Examples: How to get the dstrbuto of order statstcs Chapter 5 Propertes of a Radom Sample Secto 55 Covergece
Revew for the prevous lecture Cocepts: order statstcs Theorems: Dstrbutos of order statstcs Examples: How to get the dstrbuto of order statstcs Chapter 5 Propertes of a Radom Sample Secto 55 Covergece
Summary of the lecture in Biostatistics
 Summary of the lecture Bostatstcs Probablty Desty Fucto For a cotuos radom varable, a probablty desty fucto s a fucto such that: 0 dx a b) b a dx A probablty desty fucto provdes a smple descrpto of the
Summary of the lecture Bostatstcs Probablty Desty Fucto For a cotuos radom varable, a probablty desty fucto s a fucto such that: 0 dx a b) b a dx A probablty desty fucto provdes a smple descrpto of the
A unified matrix representation for degree reduction of Bézier curves
 Computer Aded Geometrc Desg 21 2004 151 164 wwwelsevercom/locate/cagd A ufed matrx represetato for degree reducto of Bézer curves Hask Suwoo a,,1, Namyog Lee b a Departmet of Mathematcs, Kokuk Uversty,
Computer Aded Geometrc Desg 21 2004 151 164 wwwelsevercom/locate/cagd A ufed matrx represetato for degree reducto of Bézer curves Hask Suwoo a,,1, Namyog Lee b a Departmet of Mathematcs, Kokuk Uversty,
On the convergence of derivatives of Bernstein approximation
 O the covergece of dervatves of Berste approxmato Mchael S. Floater Abstract: By dfferetatg a remader formula of Stacu, we derve both a error boud ad a asymptotc formula for the dervatves of Berste approxmato.
O the covergece of dervatves of Berste approxmato Mchael S. Floater Abstract: By dfferetatg a remader formula of Stacu, we derve both a error boud ad a asymptotc formula for the dervatves of Berste approxmato.
18.413: Error Correcting Codes Lab March 2, Lecture 8
 18.413: Error Correctg Codes Lab March 2, 2004 Lecturer: Dael A. Spelma Lecture 8 8.1 Vector Spaces A set C {0, 1} s a vector space f for x all C ad y C, x + y C, where we take addto to be compoet wse
18.413: Error Correctg Codes Lab March 2, 2004 Lecturer: Dael A. Spelma Lecture 8 8.1 Vector Spaces A set C {0, 1} s a vector space f for x all C ad y C, x + y C, where we take addto to be compoet wse
Extreme Value Theory: An Introduction
 (correcto d Extreme Value Theory: A Itroducto by Laures de Haa ad Aa Ferrera Wth ths webpage the authors ted to form the readers of errors or mstakes foud the book after publcato. We also gve extesos for
(correcto d Extreme Value Theory: A Itroducto by Laures de Haa ad Aa Ferrera Wth ths webpage the authors ted to form the readers of errors or mstakes foud the book after publcato. We also gve extesos for
1. A real number x is represented approximately by , and we are told that the relative error is 0.1 %. What is x? Note: There are two answers.
 PROBLEMS A real umber s represeted appromately by 63, ad we are told that the relatve error s % What s? Note: There are two aswers Ht : Recall that % relatve error s What s the relatve error volved roudg
PROBLEMS A real umber s represeted appromately by 63, ad we are told that the relatve error s % What s? Note: There are two aswers Ht : Recall that % relatve error s What s the relatve error volved roudg
Econometric Methods. Review of Estimation
 Ecoometrc Methods Revew of Estmato Estmatg the populato mea Radom samplg Pot ad terval estmators Lear estmators Ubased estmators Lear Ubased Estmators (LUEs) Effcecy (mmum varace) ad Best Lear Ubased Estmators
Ecoometrc Methods Revew of Estmato Estmatg the populato mea Radom samplg Pot ad terval estmators Lear estmators Ubased estmators Lear Ubased Estmators (LUEs) Effcecy (mmum varace) ad Best Lear Ubased Estmators
Maximum Likelihood Estimation
 Marquette Uverst Maxmum Lkelhood Estmato Dael B. Rowe, Ph.D. Professor Departmet of Mathematcs, Statstcs, ad Computer Scece Coprght 08 b Marquette Uverst Maxmum Lkelhood Estmato We have bee sag that ~
Marquette Uverst Maxmum Lkelhood Estmato Dael B. Rowe, Ph.D. Professor Departmet of Mathematcs, Statstcs, ad Computer Scece Coprght 08 b Marquette Uverst Maxmum Lkelhood Estmato We have bee sag that ~
[ L] υ = (3) [ L] n. Q: What are the units of K in Eq. (3)? (Why is units placed in quotations.) What is the relationship to K in Eq. (1)?
![[ L] υ = (3) [ L] n. Q: What are the units of K in Eq. (3)? (Why is units placed in quotations.) What is the relationship to K in Eq. (1)? [ L] υ = (3) [ L] n. Q: What are the units of K in Eq. (3)? (Why is units placed in quotations.) What is the relationship to K in Eq. (1)?](/thumbs/87/96901092.jpg) Chem 78 Spr. M. Wes Bdg Polyomals Bdg Polyomals We ve looked at three cases of lgad bdg so far: The sgle set of depedet stes (ss[]s [ ] [ ] Multple sets of depedet stes (ms[]s, or m[]ss All or oe, or two-state
Chem 78 Spr. M. Wes Bdg Polyomals Bdg Polyomals We ve looked at three cases of lgad bdg so far: The sgle set of depedet stes (ss[]s [ ] [ ] Multple sets of depedet stes (ms[]s, or m[]ss All or oe, or two-state
å 1 13 Practice Final Examination Solutions - = CS109 Dec 5, 2018
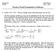 Chrs Pech Fal Practce CS09 Dec 5, 08 Practce Fal Examato Solutos. Aswer: 4/5 8/7. There are multle ways to obta ths aswer; here are two: The frst commo method s to sum over all ossbltes for the rak of
Chrs Pech Fal Practce CS09 Dec 5, 08 Practce Fal Examato Solutos. Aswer: 4/5 8/7. There are multle ways to obta ths aswer; here are two: The frst commo method s to sum over all ossbltes for the rak of
means the first term, a2 means the term, etc. Infinite Sequences: follow the same pattern forever.
 9.4 Sequeces ad Seres Pre Calculus 9.4 SEQUENCES AND SERIES Learg Targets:. Wrte the terms of a explctly defed sequece.. Wrte the terms of a recursvely defed sequece. 3. Determe whether a sequece s arthmetc,
9.4 Sequeces ad Seres Pre Calculus 9.4 SEQUENCES AND SERIES Learg Targets:. Wrte the terms of a explctly defed sequece.. Wrte the terms of a recursvely defed sequece. 3. Determe whether a sequece s arthmetc,
MATH 247/Winter Notes on the adjoint and on normal operators.
 MATH 47/Wter 00 Notes o the adjot ad o ormal operators I these otes, V s a fte dmesoal er product space over, wth gve er * product uv, T, S, T, are lear operators o V U, W are subspaces of V Whe we say
MATH 47/Wter 00 Notes o the adjot ad o ormal operators I these otes, V s a fte dmesoal er product space over, wth gve er * product uv, T, S, T, are lear operators o V U, W are subspaces of V Whe we say
A FINITE DIFFERENCE SCHEME FOR A FLUID DYNAMIC TRAFFIC FLOW MODEL APPENDED WITH TWO-POINT BOUNDARY CONDITION
 GANIT J. Bagladesh Math. Soc. (ISSN 66-3694 3 ( 43-5 A FINITE DIFFERENCE SCHEME FOR A FLUID DYNAMIC TRAFFIC FLOW MODEL APPENDED WITH TWO-POINT BOUNDARY CONDITION M. O. Ga, M. M. Hossa ad L. S. Adallah
GANIT J. Bagladesh Math. Soc. (ISSN 66-3694 3 ( 43-5 A FINITE DIFFERENCE SCHEME FOR A FLUID DYNAMIC TRAFFIC FLOW MODEL APPENDED WITH TWO-POINT BOUNDARY CONDITION M. O. Ga, M. M. Hossa ad L. S. Adallah
Unsupervised Learning and Other Neural Networks
 CSE 53 Soft Computg NOT PART OF THE FINAL Usupervsed Learg ad Other Neural Networs Itroducto Mture Destes ad Idetfablty ML Estmates Applcato to Normal Mtures Other Neural Networs Itroducto Prevously, all
CSE 53 Soft Computg NOT PART OF THE FINAL Usupervsed Learg ad Other Neural Networs Itroducto Mture Destes ad Idetfablty ML Estmates Applcato to Normal Mtures Other Neural Networs Itroducto Prevously, all
UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS
 UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS Exam: ECON430 Statstcs Date of exam: Frday, December 8, 07 Grades are gve: Jauary 4, 08 Tme for exam: 0900 am 00 oo The problem set covers 5 pages Resources allowed:
UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS Exam: ECON430 Statstcs Date of exam: Frday, December 8, 07 Grades are gve: Jauary 4, 08 Tme for exam: 0900 am 00 oo The problem set covers 5 pages Resources allowed:
Simulation Output Analysis
 Smulato Output Aalyss Summary Examples Parameter Estmato Sample Mea ad Varace Pot ad Iterval Estmato ermatg ad o-ermatg Smulato Mea Square Errors Example: Sgle Server Queueg System x(t) S 4 S 4 S 3 S 5
Smulato Output Aalyss Summary Examples Parameter Estmato Sample Mea ad Varace Pot ad Iterval Estmato ermatg ad o-ermatg Smulato Mea Square Errors Example: Sgle Server Queueg System x(t) S 4 S 4 S 3 S 5
TESTS BASED ON MAXIMUM LIKELIHOOD
 ESE 5 Toy E. Smth. The Basc Example. TESTS BASED ON MAXIMUM LIKELIHOOD To llustrate the propertes of maxmum lkelhood estmates ad tests, we cosder the smplest possble case of estmatg the mea of the ormal
ESE 5 Toy E. Smth. The Basc Example. TESTS BASED ON MAXIMUM LIKELIHOOD To llustrate the propertes of maxmum lkelhood estmates ad tests, we cosder the smplest possble case of estmatg the mea of the ormal
MA 524 Homework 6 Solutions
 MA 524 Homework 6 Solutos. Sce S(, s the umber of ways to partto [] to k oempty blocks, ad c(, s the umber of ways to partto to k oempty blocks ad also the arrage each block to a cycle, we must have S(,
MA 524 Homework 6 Solutos. Sce S(, s the umber of ways to partto [] to k oempty blocks, ad c(, s the umber of ways to partto to k oempty blocks ad also the arrage each block to a cycle, we must have S(,
Multivariate Transformation of Variables and Maximum Likelihood Estimation
 Marquette Uversty Multvarate Trasformato of Varables ad Maxmum Lkelhood Estmato Dael B. Rowe, Ph.D. Assocate Professor Departmet of Mathematcs, Statstcs, ad Computer Scece Copyrght 03 by Marquette Uversty
Marquette Uversty Multvarate Trasformato of Varables ad Maxmum Lkelhood Estmato Dael B. Rowe, Ph.D. Assocate Professor Departmet of Mathematcs, Statstcs, ad Computer Scece Copyrght 03 by Marquette Uversty
8.1 Hashing Algorithms
 CS787: Advaced Algorthms Scrbe: Mayak Maheshwar, Chrs Hrchs Lecturer: Shuch Chawla Topc: Hashg ad NP-Completeess Date: September 21 2007 Prevously we looked at applcatos of radomzed algorthms, ad bega
CS787: Advaced Algorthms Scrbe: Mayak Maheshwar, Chrs Hrchs Lecturer: Shuch Chawla Topc: Hashg ad NP-Completeess Date: September 21 2007 Prevously we looked at applcatos of radomzed algorthms, ad bega
Bayes (Naïve or not) Classifiers: Generative Approach
 Logstc regresso Bayes (Naïve or ot) Classfers: Geeratve Approach What do we mea by Geeratve approach: Lear p(y), p(x y) ad the apply bayes rule to compute p(y x) for makg predctos Ths s essetally makg
Logstc regresso Bayes (Naïve or ot) Classfers: Geeratve Approach What do we mea by Geeratve approach: Lear p(y), p(x y) ad the apply bayes rule to compute p(y x) for makg predctos Ths s essetally makg
