Optimal Switching of One-Dimensional Reflected BSDEs, and Associated Multi-Dimensional BSDEs with Oblique Reflection
|
|
|
- Mavis Bennett
- 5 years ago
- Views:
Transcription
1 arxv: v1 [mah.pr] 17 Oc 28 Opmal Swchng of One-Dmenonal Refleced BSDE, and Aocaed Mul-Dmenonal BSDE wh Oblque Reflecon Shanjan Tang We Zhong Ocober 17, 28 Abrac In h paper, he opmal wchng problem propoed for one-dmenonal refleced backward ochac dfferenal equaon (BSDE, for hor) where he generaor, he ermnal value, and he barrer are all wched wh pove co. The value proce characerzed by a yem of mul-dmenonal refleced BSDE wh oblque reflecon, whoe exence and unquene by no mean rval and herefore carefully examned. Exence hown ung boh mehod of he Pcard eraon and penalzaon, bu under ome dfferen condon. Unquene proved by repreenaon eher a he equlbrum value proce o a ochac mxed game of wchng and oppng, or a he value proce o our opmal wchng problem for one-dmenonal refleced BSDE. Keyword. Refleced backward ochac dfferenal equaon, oblque reflecon, opmal wchng, ochac game. MR(2) Subjec Clafcaon. 93E2, 6H1, 9A15 1 Inroducon Le {W(), T } be a d-dmenonal andard Brownan moon defned on ome complee probably pace (Ω, F,P). {F, T } he naural flraon of he Brownan moon {W(), T }, augmened by all he P-null e of F. The followng noaon wll be ued n he equel. { φ : φ an {F, T }-adaped r.c.l.l. proce..e[ up φ() 2 ] < T S 2 {φ S 2 : φ connuou}, N 2 {φ S 2 : φ ncreang and φ() = }, N 2 {φ N 2 : φ connuou}, M 2 {φ : φ {F, T }-predcable and quare-negrable on [,T] Ω}. S 2 }, Deparmen of Fnance and Conrol Scence, School of Mahemacal Scence, Fudan Unvery, Shangha 2433, Chna. Th auhor uppored n par by NSFC Gran , Bac Reearch Program of Chna (973 Program) Gran 27CB81494, and Chang Jang Scholar Programme. E-mal addre: jang@fudan.edu.cn Inue of Mahemac and Deparmen of Fnance and Conrol Scence, School of Mahemacal Scence, Fudan Unvery,Shangha 2433, Chna. E-mal addre: zhongwe@fudan.edu.cn
2 Le {θ j } j= be an ncreang equence of oppng me wh value n [,T]. j, α j an F θj -meaurable random varable wh value n Λ. Aume ha a..ω, here ex an neger N(ω) < uch ha θ N = T. Then we defne a wchng raegy a: N 1 a() = α χ [θ, θ 1 ]() + α j χ (θj, θ j+1 ](). Denoe by A all he wchng raege wh nal daa α = Λ, θ =. For gven a A,ξ L 2 (Ω, F T,P;R m ), and S (S 2 ) m, conder he followng wched refleced backward ochac dfferenal equaon (abbrevaed a RBSDE): U a () = ξ a(t) + ψ(r,u a (r),v a (r),a(r))dr (L a (T) L a ()) N 1 j=1 [U a (θ j ) h αj 1, α j (θ j,u a (θ j ))]χ (,T] (θ j ) j=1 V a (r)dw(r), U a () S a() (), [,T]; [,T]; (U a () S a() ())dl a () =. (1.1) Here and n he followng χ an ndcaor funcon. The generaor ψ, he ermnal condon ξ, and he upper barrer S of RBSDE (1.1) are all wched by a. A each wchng me θ j before ermnaon, he value of U a wll jump by an amoun of U a (θ j ) h αj 1, α j (θ j,u a (θ j )) whch can be regarded a a penaly or co for he wchng. RBSDE (1.1) can be olved n a backwardly recurve way n he ubnerval [θ N 1,T] and [θ j 1,θ j ) for j = N 1,,2,1. To be prece, RBSDE (1.1) n he la ubnerval [θ N 1,T] read: U a () = ξ αn 1 + ψ(r,u a (r),v a (r),α N 1 )dr (L a (T) L a ()) V a (r)dw(r), U a () S αn 1 (), [θ N 1,T]; (U a () S αn 1 ())dl a () =. θ N 1 [θ N 1,T]; (1.2) From [3, Theorem 5.2], RBSDE (1.2) ha a unque adaped oluon on [θ N 1,T] under Hypohe 1 (ee Secon 2 below). Then we have U a (θ N 1 ) = h αn 2,α N 1 (θ N 1,U a (θ N 1 )), whch erve a he ermnal value of RBSDE (1.1) n [θ N 2,θ N 1 ). In general, n
3 he ubnerval [θ j 1,θ j ), RBSDE (1.1) read θj U a () = h αj 1, α j (θ j,u a (θ j )) + ψ(r,u a (r),v a (r),α j 1 )dr (L a (θ j ) L a ()) θj U a () S αj 1 (), [θ j 1,θ j ); θj (U a () S αj 1 ())dl a () = θ j 1 V a (r)dw(r), [θ j 1,θ j ); (1.3) for j = N 1,,2,1. Here U a (θ j ) pecfed n he nerval [θ j,θ j+1 ) and we have he followng relaon: h αj 1, α j (θ j,u a (θ j )) U a (θ j ) S αj 1 (θ j ). The exence and unquene of an adaped oluon o RBSDE (1.1) n he nerval [,T] obaned n an obvou way from he exence and unquene of an adaped oluon o RBSDE (1.1) n all he ubnerval [θ N 1,T] and [θ j 1,θ j ) for j = N 1,,2,1. In h paper, we udy he opmal wchng problem for one-dmenonal RB- SDE (1.1), where he generaor, he ermnal value, and he upper barrer are all wched wh pove co. One-dmenonal RBSDE wh fxed ngle reflecng barrer are a generalzaon of radonal opmal oppng problem, and hey were nroduced by El Karou e al.[3], who gave he fr exence and unquene reul for RBSDE. Cvanc and Karaza[1] generalzed he work of El Karou e al.[3] o he cae of fxed double reflecng barrer and lnked he oluon of one-dmenonal RBSDE wh double barrer o he well-known Dynkn game. The opmal wchng problem for RBSDE (1.1) o maxmze U a () over a A, Λ. The value proce urn ou o be decrbed by he followng yem of mul-dmenonal RBSDE wh double reflecng barrer: for Λ {1,,m}, Y () = ξ + + ψ(,y (),Z (),)d dk () dk + () Z ()dw(), [,T]; S () Y () max h,j(,y j ()), [,T]; j,j Λ ( ) Y () max h,j(,y j ()) dk + () =, j,j Λ (Y () S ()) dk () =. (1.4) The la wo equale are repecvely called he lower and he upper mnmal condon. Soluon of he above RBSDE (1.4) by no mean rval, and wll be examned carefully n h paper. The unuual feaure here ha for RBSDE (1.4), he upper barrer a fxed proce, whle he lower barrer depend on he unknown proce and herefore mplc, whch dfferen from one-dmenonal RBSDE wh fxed double barrer. In conra o RBSDE wh oblque reflecon nroduced n Hu and Tang [1], here an addonal fxed upper barrer. Th dfference wll complcae he analy of he exence and unquene for oluon o
4 RBSDE (1.4). For [,T], defne Q() {(y 1,,y m ) T R m : h,j (,y j ) y S (),,j Λ,j }. Then he ae proce Y ( ) of (1.4) forced o evolve n he me-dependen e Q( ), hank o he accumulave acon of wo ncreang procee K + and K. Exence of he oluon of RBSDE (1.4) proved by wo dfferen mehod. Aumng ha he fxed barrer uper-regular, we frly prove exence of he oluon by he mehod of a Pcard eraon, nvokng a generalzed monoonc lm heorem. A a key condon of he generalzed monoonc lm heorem, he comparon of he dfferenal of he ncreang proce neceary, whch formulaed a our Lemma 2.2. In addon, he proof of he mnmal boundary condon complcaed by he appearance of he addonal fxed barrer, and our mehod very echncal and novel. Secondly we conder he cae where he ner-conneced barrer ake a parcular form, and oban an exence reul by a penaly mehod. A pror emae play a crucal role heren. Unquene of he oluon o RBSDE (1.4) proved n Secon 5 by lnkng eher o he value proce for our opmal wchng of one-dmenonal RBSDE, or o a ochac game nvolvng boh wchng and oppng raege for onedmenonal BSDE. Recenly, Hu and Tang [1] nally formulaed and dcued he opmal wchng problem for general one-dmenonal BSDE. The value proce characerzed by he oluon of mul-dmenonal BSDE wh oblque reflecon. Laer, Hamadene and Zhang [8] generalzed he precedng work o a general form of pove co for wchng, wh a dfferen mehod of Pcard eraon. The paper a naural connuaon of he wo work. The re of he paper organzed a follow: In Secon 2, we formulae our problem, nroduce he generalzed monoonc heorem and gve ome prelmnary reul on RBSDE, whch wll be ued n ubequen argumen. In Secon 3, we prove exence of he oluon by he mehod of Pcard eraon. In Secon 4, exence of he oluon hown by he penaly mehod. Unquene of he oluon hown n Secon 5. 2 Prelmnare We make he followng aumpon on he generaor {ψ(,,,), Λ}. Hypohe 1. The generaor ψ afe he followng: () The proce ψ(,y,z,) M 2 for any (y,z,) R R d Λ. () There a conan C > uch ha for (y,y,z,z ) R R R d R d and (,) [,T] Λ, we have ψ(,y,z,) ψ(,y,z,) C( y y + z z ). We make he followng aumpon on he funcon {h,j,,j Λ}. Hypohe 2. For any (,j) Λ Λ, he funcon h,j (,y) connuou n (,y), ncreang n y, and h,j (,y) y. Hypohe 3. For any y n R and any loop { k Λ, k = 1,,n} uch ha 1 = n and k k+1 for k = 1,2,...,n 1, defne y k h k, k+1 (,y k+1 ) for k = 1,,n 1. Then y 1 < y n.
5 In Secon 4, we hall pecalze he funcon h,j o he form: h,j (,y) = y k(,j) for ome povely valued funcon k defned on Λ Λ. We hall make he followng aumpon on k, whch andard n he leraure. Hypohe 3. The funcon k : Λ Λ R afe he followng: (),j Λ, k(,j) > for j, and k(,) =. (),j,l Λ uch ha j, j l, k(,j) + k(j,l) k(,l). Remark 2.1. Hypohe 3 mean ha here no free loop of nananeou wchng. Hypohee 2 and 3 are afed when h,j (,y) = y k(,j) for (,y) [, T] R and, j Λ wh he funcon k afyng Hypohe 3 (). Defnon 2.1. An adaped oluon of yem (1.4) a quadruple (Y,Z,K +,K ) {Y (),Z(),K + (),K (); T } (S 2 ) m (M 2 ) m (N 2 ) m (N 2 ) m, akng value n R m R m d R m R m and afyng (1.4). We recall here he generalzed monoonc lm heorem [14, Theorem 3.1], whch wll be ued n our mehod of Pcard eraon. Lemma 2.1. (generalzed monoonc heorem) We aume he followng equence of Iô procee: y () = y () + g ()d K +, () + K, () + z ()dw(), = 1,2, afy () for each, g M 2,K +, N 2,K, N 2 ; () K,j () K,j () K, () K, (), T, j; () For each [,T], {K, ()} =1 ncreangly converge o K () wh E K (T) 2 < ; (v) (g,z ) =1 converge o (g,z) weakly n M2 ; (v) For each [,T], {y ()} =1 ncreangly converge o y() wh E up y() 2 <. T Then he lm y of {y } =1 ha he followng form y() = y() + g()d K + () + K () + z()dw() where K + (rep. K ) he weak (rep. rong) lm of {K +, } =1 (rep. {K, } =1 ) n M 2 and K +,K N 2. Moreover, for any p [,2), lm E z () z() p d =. If furhermore, K + connuou, hen we have lm E z () z() 2 d =.
6 When we apply he above generalzed monoonc heorem o RBSDE (1.4), we need o compare he dfferenal of he ncreang proce K for Λ. However, uch a knd of conderaon doe no eem o be avalable n he leraure due o he appearance of he lower barrer, whch mplc and hu varyng wh he fr unknown varable. The followng lemma fll n uch a gap, whch wll be ued n Secon 3. Aume ha ξ L 2 (Ω, F T,P) and L and U are {F, T }-adaped connuou procee afyng E[ up { L() U() 2 }] <, L() U(), [,T]. T Conder he followng one-dmenonal RBSDE wh fxed double reflecng barrer: Ŷ () = ξ + L() + ψ(,ŷ (),Ẑ())d d ˆK () d ˆK + () Ŷ () U(), [,T]; (Ŷ () L())d ˆK + () =, Ẑ()dW(), [,T]; (Ŷ () U())d ˆK () =. (2.1) Defnon 2.2. A barrer U called uper-regular f here ex a equence of procee {U n } n=1 uch ha () U n () U n+1 () and lm Un () = U() for [,T]; () For n 1 and [,T], we have du n () = u n ()d + v n ()dw() where u n an {F, T }-adaped proce uch ha up up n 1 T u n () < and v n M 2. A barrer V called ub-regular f he barrer V uper-regular. Noe ha he concep of our uper-regular barrer dencal o he defnon of he regular upper barrer by Hamadène e al. [5]. Lemma 2.2. Aume ha ψ 1 and ψ 2 afy Hypohe 1 and ha he barrer U uper-regular. Aume ha ξ 1,ξ 2 L 2 (Ω, F T,P), and L 1,L 2, and U are {F, T }-adaped connuou procee afyng E[ up { L j () U() 2 }] <, L j () U(), [,T], j = 1,2. T For j = 1,2, le (Ŷ j,ẑj, ˆK +,j, ˆK,j ) be he unque adaped oluon of RBSDE (2.1) aocaed wh daa (ξ j,ψ j,l j,u). Moreover, aume ha () ξ 1 ξ 2 ; () ψ 1 (,y,z) ψ 2 (,y,z), (y,z) R R d ; () L 1 L 2. Then we have (1) Ŷ 1 () Ŷ 2 (), ˆK,1 () ˆK,2 (), T; (2) ˆK,1 (r) ˆK,1 () ˆK,2 (r) ˆK,2 (), r T.
7 Proof. For j = 1,2, and n 1, he followng penalzed RBSDE wh a ngle reflecng barrer: Ŷ j,n () = ξ j + ψ j (,Ŷ j,n (),Ẑj,n ())d n (Ŷ j,n () U()) + d + d ˆK j,n () Ŷ j,n () L j (), [,T]; (Ŷ j,n () L j ())d ˆK j,n () = Ẑ j,n ()dw(), [,T]; ha a unque adaped oluon, denoed by (Ŷ j,n,ẑj,n, ˆK j,n ). In vew of he comparon heorem [3, Theorem 4.1], we have Ŷ 1,n () Ŷ 2,n (), T. Nong ha he barrer U uper-regular, by he proof of [5, Theorem 42.2 and Remark 42.3], we have Ŷ j () = lm Ŷ j,n (), The dered reul hen follow. ˆK,j () = lm n (Ŷ j,n () U()) + d, [,T]. Remark 2.2. In a ymmerc way, aumng ha he lower barrer ub-regular and fxed, we can compare he ncremen of ˆK+ when he upper barrer vare. The followng lemma gve he connuou dependency of RBSDE wh one r.c.l.l. (rgh connuou and lef lmed) reflecng barrer, whch wll be ued o prove he lower mnmal boundary condon. Lemma 2.3. Aume ha ξ j L 2 (Ω, F T,P), ψ j afe Hypohe 1, and L j S 2 for j = 1,2. For j = 1,2, denoe by (Y j,z j,k j ) S 2 M 2 N 2 he unque adaped oluon of he followng RBSDE: Se Y j () = ξ j + T ψ j (,Y j (),Z j ())d + Z j ()dw(), Y j () L j (), [,T]; (Y j ( ) L j ( ))dk j () =. Y j () Y j () Y j ( ), [,T]; [,T] for j = 1,2. Then here a conan c > uch ha ( ) E up Y 1 () Y 2 () 2 + Z 1 () Z 2 () 2 d T +E ( K 1 (T) K 2 (T) 2 + Y 1 () Y 2 () 2) T dk j () ( ) ce ξ 1 ξ ψ 1 (,Y 1 (),Z 1 ()) ψ 2 (,Y 1 (),Z 1 ()) 2 d +c(e[ up L 1 () L 2 () 2 ]) 2Φ(T) T
8 where Φ(T) [ 2 E ξ j 2 + j=1 ] ψ j (,,) 2 d + up L j () + 2. T Remark 2.3. Lemma 2.3 can be exended o he mul-dmenonal cae where for j = 1,2, Y j,ξ j,ψ j,k j,s j, and L j are all R m -valued, Z j R m d -valued, and z race(zz T ) for z R m d. The proof mlar o [3, Propoon 3.6] and omed. 3 Exence: he mehod of Pcard eraon We have he followng exence reul for RBSDE (1.4). Theorem 3.1. Le Hypohee 1, 2 and 3 be afed. Aume ha he upper barrer S uper-regular wh S() Q() for [,T], and ha he ermnal value ξ L 2 (Ω, F T,P;R m ) ake value n Q(T). Then RBSDE (1.4) ha an adaped oluon (Y,Z,K +,K ). Proof. We ue he mehod of Pcard eraon. The whole proof dvded no he followng x ep. Sep 1. Conrucon of Pcard equence of oluon {Y n,zn,kn ; Λ} n. For Λ, he followng RBSDE wh ngle reflecng barrer: Y () = ξ + Y ψ(,y (),Z (),)d dk () Z ()dw(), () S (), [,T]; (Y () S ())dk () = [,T]; (3.1) ha a unque adaped oluon, denoed by (Y,Z,K ). For n 1 and Λ, conder he followng RBSDE: Noe ha Y n () = ξ + S () () () + ψ(,y n (),Zn (),)d dk +,n () Z n ()dw(), dk,n () [,T]; Y n() max h,j(,yj n 1 ()), [,T]; j,j Λ max h,j(,yj n 1 ()))dk +,n () =, j,j Λ S ())dk,n () =. (3.2) max h,j(,yj n 1 ()) max h,j(,s j ()) S (), j,j Λ j,j Λ [,T]
9 due o Hypohe 2 and he aumpon ha S() Q() for [,T]. In vew of [5, Theorem 42.2 and Remark 42.3], RBSDE (3.2) ha a unque oluon,zn,k+,n,k,n ) S 2 M 2 N 2 N 2. Sep 2. Convergence of {Y n,k,n ; Λ} n 1. Snce h j (, ) ncreang, he lower barrer of RBSDE (3.1) ncreang wh n by nducon. RBSDE (3.1) can be vewed a havng he lower barrer. Then from Lemma 2.2, we have Y () Y 1 (), T. Snce h,j (,y) ncreang n y, ung Lemma 2.2 agan, we have for n 1 and Λ, Y n n+1 () Y K,n (), K,n () K,n+1 (), T; (r) K,n () K,n+1 (r) K,n+1 (), r T. Hence, he equence {(),K,n ())} n=1 ha a lm, denoed by (Y (),K ()). Snce Y () Y n () S (), T, Λ, we have upe[ up Y n () 2 ] E up ( Y () 2 + S() 2 ) <, Λ. (3.3) n 1 T T Applyng Faou lemma and he domnaed convergence heorem, we have E[ up Y () 2 ] <, lm E Y T n () Y () 2 d =, Λ. (3.4) For Λ, he followng RBSDE Ỹ () = ξ + + ψ(,ỹ(), Z (),)d d K + () Z ()dw(), S () Ỹ() max j,j Λ h,j(,s j ()), (Ỹ() max j,j Λ h,j(,s()))d K + (Ỹ() S ())d K () = () =, [,T]; d K () [,T]; (3.5) ha a unque adaped oluon, denoed by (Ỹ, Z, K +, K ) S2 M 2 N 2 N 2. By Lemma 2.2, we know ha for n 1 and Λ, K,n () K n+1 () K K,n Then, K (r) K,n upe[ up n 1 T (), T, () K,n+1 (r) K,n+1 () K (r) K (), r T. connuou for Λ. Hence, K,n () 2 ] E[ up T K () 2 ] E[ up T K () 2 ] <, Λ. (3.6)
10 From Dn heorem, we have lm up T K,n () K () 2 =, Λ. From he domnaed convergence heorem, we have lm E[ up K,n () K () 2 ] =, Λ. (3.7) T Sep 3. Unform boundedne of {ψ(,y n,zn,),zn,k+,n ; Λ} n 1 n M 2 M 2 N 2. Applyng Iô lemma o Y n() 2, we have for Λ, Y n () 2 + Z n () 2 d = ξ Y n ()ψ(,y n (),Zn (),)d + 2 Y n ()dk+,n () 2 Y n ()dk,n () 2 Y n ()Z n ()dw(). Ung he Lpchz propery of ψ, he upper mnmal boundary condon n (3.2) and he elemenary nequaly: ab 1 α a2 + αb 2, we have for any arbrary pove real number α, E Y n () 2 + E[ ( E ξ ( +E 2 ( E ξ E( α [ up Y n T Z n () 2 d] ) Y n ()(ψ(,,,) + C Y n () + C Z n () )d Y n ()dk+,n () 2 ψ(,,,) 2 d + c () 2 ] + α K +,n ) S ()dk,n () Y n () 2 d ) Z n () 2 d (T) 2 + up S () 2 + K,n (T) 2). T (3.8) Here and n he equel, c a pove conan whoe value only depend on he Lpchz coeffcen C and may change from lne o lne. From RBSDE (3.2), we know ha for Λ, K +,n (T) = Y n () ξ ψ(,y n (),Zn (),)d + K,n (T) + Z n ()dw(). Hence, ( E K +,n (T) 2 c 1+E Subung (3.9) no (3.8) and leng α = 1 3c ( Y n () 2 + Z n () 2 )d+e K,n (T) 2), Λ. (3.9) and =, we have ( E Z n () 2 d ce 1 + up Y n () 2 + Y n () 2 d + K,n (T) 2), Λ. T
11 From (3.3) and (3.6), we know Then from (3.9), we know upe n 1 Z n () 2 d <, Λ. (3.1) upe K +,n (T) 2 <, Λ. (3.11) n 1 From (3.3), (3.1) and he Lpchz propery of ψ, we know upe n 1 ψ(,y n (),) 2 d <, Λ. Therefore, whou lo of generaly, we can aume ha for Λ, {ψ(,y n,zn,)} n, {Z n} n, and {K +,n } n converge weakly n M 2 o ψ,z, and K +, repecvely. Sep 4. Verfcaon of he fr equaon of RBSDE (1.4). From he fr equaon of (3.2), we have Y n () = Y n () ψ(,y n (),Zn (),)d K+,n ()+K,n ()+ Z n ()dw(). All he aumpon of he generalzed monoonc lm heorem (ee Lemma 2.1) are hown o be afed n prevou ep. Therefore, for Λ, he lm Y r.c.l.l. and ha he form: Y () = ξ + ψ ()d and K + N 2. Moreover, for any p [,2), Hence, we have for Λ, dk () + dk + () Z ()dw(), lm E Z n () Z () p d =, Λ. lm E ψ(,y n (),Z n (),) ψ(,y (),Z (),) p d = ; Y () = ξ + ψ () = ψ(,y (),Z (),), + a.e.,a..; ψ(,y (),Z (),)d dk + () Z ()dw(). dk () (3.12) Sep 5. The mnmal boundary condon. In vew of RBSDE (3.2), we have max {h,j(,yj n 1 ())} Y n () S (), [,T], Λ. j,j Λ Pang o he lm, we have max {h,j(,y j ())} Y () S (), [,T], Λ. (3.13) j,j Λ
12 Snce T we have = Hence, () S ())dk,n () = and Y n () = Y n ( ) Y ( ) S (), () S ())dk,n () On he oher hand, for Λ, Snce we have (Y ( ) S ())dk,n (), Λ. (Y ( ) S ())dk,n () =, Λ. (S () Y ( ))d(k () K,n ()) up (S () Y ( ))[K (T) K,n (T)]. T (Y ( ) S ())dk lm K,n (T) = K () = lm (T), Λ, (Y ( ) S ())dk,n () =, Λ. We have ju proved he upper mnmal boundary condon. I reman o prove he lower mnmal boundary condon. The echnque ued n [8] found dffcul o be drecly appled o our cae nce he correpondng argumen on he malle ψ-upermarngale no rue n he cae of double barrer. We hall vew he RBSDE wh double barrer a RBSDE wh ngle lower barrer by akng he ncreang procee K,n a gven. For Λ and n 1, he followng RBSDE Ȳ n () = ξ + Ȳ n () (Ȳ n ( ) +K,n () + ψ(,ȳ n (), Z n (),)d K,n (T) d +,n K () h () max j,j Λ h,j(,y j ()), h ( ))d K +,n () = ha a unque adaped oluon, denoed by (Ȳ n, Z n Defne Then ( X n, Z n, K +,n ). Z n ()dw(), [,T], X n Ȳ n K,n, ψ n (,y,z,) ψ(,y + K,n (),z,), Λ., K +,n ) afe he followng RBSDE: X n() = (ξ K,n (T)) + +,n + d K () ψ n (, X n (), Z n (),)d Z n ()dw(), X n() h () K,n (), [,T], ( Xn ( ) h ) ( ) + K,n +,n () d K () =. (3.14) (3.15)
13 For Λ, le (Ȳ, Z, K + ) be he oluon of he followng RBSDE: Ȳ () = ξ + ψ(,ȳ(), Z (),)d K (T) + K () + d K + () Ȳ () h (), [,T]; Z ()dw(), [,T]; (3.16) Defne (Ȳ( ) h ( ))d K + () =. X Ȳ K, ψ (,y,z,) ψ(,y + K (),z,), Λ. Then ( X, Z, K + ) afe he followng RBSDE: X () = (ξ K (T)) + ψ (, X (), Z (),)d + d K + () Z ()dw(), X () h () K (), [,T], ( X ( ) h ) ( ) + K () d K + () =. Snce ψ n (,y,z,) ψ (,y,z,) (3.17) = ψ(,y + K,n (),z,) ψ(,y + K (),z,) n vew of Lemma 2.3, we have C K,n () K (), E[ up T ( c E( K +c(e[ up K T X n () X () 2 ] (T) K,n (T) 2 ) + C K () K,n () 2 ]) 1 2 (Φ n (T)) 1 2, ) () K,n () 2 d (3.18) where Snce ( ) Φ n (T) E (ξ K,n (T)) 2 + ψ K n(,,,) 2 d +E[ up (( h () K,n ()) + ) 2 ] +E T ( (ξ K (T))2 + +E[ up (( h () K ())+ ) 2 ]. T ) ψ K (,,,) 2 d ψ n (,,,) ψ(,,,) + CK,n (), ψ (,,,) ψ(,,,) + CK (),
14 up (( h () K,n ()) + ) 2 up (( h ()) + ) 2 T T up (( max Y j()) + ) 2 j,j Λ T j Λ up T Y j () 2, and up () K T(( h ())+ ) 2 j Λ up T Y j () 2, we have Φ n (T) 4E(ξ 2 + ψ(,,,) 2 d) + 2 E[ up Y j () 2 ] j Λ T +2(C 2 T + 1)E( K,n (T) 2 + K (T) 2 ). From (3.3) and (3.6), we ee From (3.7), (3.18) and (3.19), we ee upφ n (T) <. (3.19) n 1 lm E[ up X n () X () 2 ] =, Λ. T So here a ubequence of { X n } n 1 convergng o X,a.e.,a.. Whou lo of generaly, aume ha Se lm X n = X, a.e.,a.., Λ. (3.2) X n Y n K,n, Λ. Then from refleced BSDE (3.2) we know ha (X n,zn,k+,n ) he oluon of he followng refleced BSDE wh ngle reflecng barrer: X n() = (ξ K,n (T)) + ψ K n(,x n (),Zn (),)d + dk +,n () Z n ()dw(), [,T]; (3.21) X n() max h,j(,yj n 1 ()) K,n (), [,T]; j,j Λ ( ) X n () max h,j(,yj n 1 ()) + K,n () dk +,n () =. j,j Λ Comparng wh refleced BSDE (3.15) and ung he comparon heorem for r.c.l.l. reflecng barrer [6, Theorem 1.5], we know ha In vew of (3.2), we have X n () X n () = Y n () K,n (), (,) [,T] Λ. X () Y () K (), (,) [,T] Λ. (3.22) Noe ha due o he appearance of he addonal fxed upper barrer, no clear wheher he lower barrer of (3.17) no le han ha of (3.21). Such a dffculy go around by comparng (3.21) and (3.15).
15 On he oher hand, from (3.17) and [11, Theorem 2.1], we know ha X ( ) he malle ψ -upermarngale wh he lower barrer { h () K (), T }. From (3.12) and (3.13), can be ealy obaned ha {Y () K (), T } a ψ -upermarngale wh he ame lower barrer and ermnal value. Hence, Togeher wh (3.22), we have Then X () Y () K X () = Y () K (), T, Λ. (), T, Λ. Ȳ () = Y (), T, Λ. From he unquene of he Doob-Meyer Decompoon, follow ha Z () = Z (), K+ () = K + (), T, Λ. Hence, for Λ, (Y,Z,K +,K ) almo afe RBSDE (1.4) excep ha boh mnmal boundary condon are replaced by ( Y ( ) max h,j(,y j ( )) )dk + () =, (Y ( ) S())dK () =. j,j Λ If we furher prove he connuy of Y, hen we know {(Y,Z,K +,K ), Λ} an adaped oluon of RBSDE (1.4). Sep 6. The connuy of Y and K + for Λ. Snce K connuou, we know Y () = K + (). Suppoe Y 1 ( ) < for ome 1 Λ and ome [,T], hen K + 1 ( ) >. From he mnmal boundary condon of (4.2), we know Y 1 ( ) = max j 1,j Λ h 1,j(,Y j ( )). The ndex aanng he maxmum denoed by 2 and 2 1. Hence, h 1, 2 (,Y 2 ( )) = Y 1 ( ) > Y 1 ( ) h 1, 2 (,Y 2 ( )). I follow ha Y 2 ( ) <. Repeang hee argumen, we can oban ha Y k ( ) = h k, k+1 (,Y k+1 ( )), k = 2,3,. Snce Λ a fne e, here mu be a loop n Λ, whou lo of generaly, we aume ha 1 = n. Then for he loop { n, n 1,, 1 }, we have Y n 1 ( ) = h n 1, n (,Y n ( )),,Y 1 ( ) = h 1, 2 (,Y 2 ( )), and Y n ( ) = Y 1 ( ). Th conradc Hypohe 3. Therefore, Y () =, T, Λ. So K +. 4 Exence: he penaly mehod In Theorem 3.1, every componen of he upper barrer S aumed o be uperregular. Le k(,j) be he wchng co from ae o ae j n he opmal wchng problem (ee Hu and Tang [1]) afyng Hypohe 3, and le he funcon h,j nroduced n he precedng econ ake he parcular form h,j (,y) = y k(,j). Then we can prove by a penaly mehod he exence of an adaped oluon o RBSDE (1.4) whou he uper-regulary aumpon on he upper barrer S.
16 4.1 Mul-dmenonal RBSDE wh fxed ngle reflecng barrer. In wha follow, we conder he mul-dmenonal RBSDE wh fxed ngle reflecng barrer, how he exence and unquene by a penaly mehod, and gve a comparon heorem. For wo m-dmenonal vecor x (x 1,,x m ) T and y (y 1,,y m ) T, we mean by x y ha x y for Λ. For a vecor x (x 1,,x m ) T, x + defned a he m-dmenonal vecor (x + 1,,x+ m )T. Conder he followng mul-dmenonal RBSDE wh fxed ngle reflecng barrer: Y () = ξ + φ(,y (),Z())d dk() Z()dW(), [,T]; (4.1) Y () S(), [,T]; (Y () S ())dk () =, Λ. We make he followng aumpon on he generaor φ, he ermnal value ξ (ξ 1,,ξ m ) T, and he barrer S (S 1,,S m ) T. Hypohe 4. () The proce φ(,,) (M 2 ) m. For Λ, ξ L 2 (Ω, F T,P) and S S 2 wh ξ S (T). () There a conan C > uch ha for any (,y,y,z,z ) [,T] (R m ) 2 (R m d ) 2, we have φ(,y,z) φ(,y,z ) C( y y + z z ), 4 y,φ(,y + + y,z) φ(,y,z ) 2 χ {y <} z z 2 + C y 2. =1 (4.2) We have Theorem 4.1. Le Hypohe 4 be afed. Then RBSDE (4.1) ha a unque adaped oluon (Y,Z,K) (S 2 ) m (M 2 ) m d (N 2 ) m. Proof. For any pove neger n, conder he followng penalzed BSDE: Y n () = ξ + φ(,y n (),Z n ())d n Z n ()dw(), [,T]. () S()) + d (4.3) From Pardoux and Peng [13], we know ha for each n, BSDE (4.3) ha a unque adaped oluon,z n ) (S 2 ) m (M 2 ) m d. Defne for (,y,z) [,T] R m R m d, φ n (,y,z) φ(,y,z) n(y S()) + and K n () n () S()) + d.
17 In vew of Hypohe 4 (), we have for all y R m, 4 y,φ n (,y + + y,z) φ n+1 (,y,z ) 4 y,φ(,y + + y,z) φ(,y,z ) + (y S()) + 4 y,φ(,y + + y,z) φ(,y,z ) 2 χ {y <} z z 2 + C y 2. =1 Applyng he comparon heorem of mul-dmenonal BSDE (ee [9, Theorem 2.1]), we deduce ha Y n+1 () Y n (), T. For [,1], he equence {Y n ()} n 1 almo urely adm a lm, whch denoed by Y () below. Applyng Iô lemma o compue Y n () 2, we have Y n () 2 + = ξ Z n () 2 d Y n (),φ(,y n (),Z n ()) d Y n (),dk n () Y n (),Z n ()dw(). Takng expecaon on boh de, n vew of he followng nequaly we have E Y n () 2 + E E ξ 2 + 2E E E ξ 2 + E E S(),dK n () Y n (),dk n () Z n () 2 d S(),dK n (), [ φ(,,) + C( Y n () + Z n () )] Y n () d φ(,,) 2 d + (3C 2 + 2C + 1)E Y n () 2 d Z n () 2 d + m E( up S () 2 ) + αe K n (T) K n () 2 α T (4.4) (4.5) for an arbrary pove real number α. From (4.3), we have K n (T) K n () = ξ Y n () + φ(,y n (),Z n ())d Z n ()dw(). (4.6) Furher, we have E K n (T) K n () 2 4E( Y n () 2 + ξ 2 ) + 4(3TC 2 + 1)E +12TE ( φ(,,) 2 + C 2 Y n () 2 )d. Z n () 2 d (4.7)
18 Seng n (4.5), n vew of (4.7), we have α = 1 12(3TC 2 + 1) 2 3 E Y n () E Z n () 2 d c(1 + E Y n () 2 )d for a conan c whch doe no dependen on n. I hen follow from Gronwall nequaly ha whch mple ha up E Y n () 2 + E Z n () 2 d c, n = 1,2, T E K n (T) 2 c, n = 1,2, (4.8) In vew of (4.4), applyng he Burkholder-Dav-Gundy nequaly, we have E up Y n () 2 + E Z n () 2 d + E K n (T) 2 c, n = 1,2, T Recallng ha Y () = lm Y n (), ung Faou lemma, we have E up Y () 2 c. T I hen follow from Lebegue domnaed convergence heorem ha lm E Y n () Y () 2 d =. For pove neger n 1 and n 2, applyng Iô lemma o compue Y n 1 () Y n 2 () 2, we have for [,T], = 2 Y n 1 () Y n 2 () Z n 1 () Z n 2 () 2 d Y n 1 () Y n 2 (),φ(,y n 1 (),Z n 1 ()) φ(,y n 2 (),Z n 2 ()) d Y n 1 () Y n 2 (),d(k n 1 () K n 2 ()) Y n 1 () Y n 2 (),(Z n 1 () Z n 2 ())dw(). Takng expecaon and leng =, we have E Y n 1 () Y n 2 () 2 + E 2C(C + 1)E +2E Z n 1 () Z n 2 () 2 d Y n 1 () Y n 2 () 2 d E Z n 1 () Z n 2 () 2 d 2 () S()) +,dk n 1 () + 2E (4.9) 1 () S()) +,dk n 2 ().
19 A a conequence, E Z n 1 () Z n 2 () 2 d 4C(C + 1)E +4E +4E Y n 1 () Y n 2 () 2 d 2 () S()) +,dk n 1 () 1 () S()) +,dk n 2 (). (4.1) Followng almo he ame argumen a n he proof of [3, Lemma 6.1], we have E up () S()) + 2 a. (4.11) T Then from (4.8) and (4.11), we know ha a n 1,n 2, E 2 () S()) +,dk n 1 () + E Togeher wh (4.1), we oban lm E Z n 1 () Z n 2 () 2 d =. n 1,n 2 1 () S()) +,dk n 2 (). In vew of (4.9), ung he Burkholder-Dav-Gundy nequaly, we conclude lm E up Y n 1 () Y n 2 () 2 =. n 1,n 2 T In vew of (4.3) and he defnon of K n, we know lm E up K n 1 () K n 2 () 2 =. n 1,n 2 T From he above convergence, we conclude ha here ex (Z,K) (M 2 ) m d (N 2 ) m, afyng lm E Z n () Z() 2 d = and lm E up K n () K() 2 =. T Pang o lm n equaon (4.3), we know ha afe he followng equaon: (Y,Z,K) (S 2 ) m (M 2 ) m d (N 2 ) m Y () = ξ + φ(,y (),Z())d dk() Z()dW(). From (4.11), ung Faou lemma, we know ha E up (Y () S()) + 2 lm E up () S()) + 2 =, T T whch mple ha Y () S(), T. (4.12)
20 Therefore, (Y () S ())dk (), Λ. (4.13) Snce,K n ) end o (Y,K) n (S 2 ) 2m, we have for Λ, Thu, (Y () S ())dk () = lm () S ())dk n () = lm n () S ()) () S ()) + d. (4.14) (Y () S ())dk () =, Λ. (4.15) We conclude ha (Y,Z,K) an adaped oluon o RBSDE (4.1). Unquene of he oluon follow from Lemma 2.3 and Remark 2.3. Remark 4.1. For he exence and unquene for mul-dmenonal RBSDE, we refer he reader o Gegou-Pe and Pardoux [4]. Remark 4.2. The comparon heorem of mul-dmenonal BSDE fr eablhed by Hu and Peng [9] under he ronger condon on he generaor φ ha φ(,y,z) connuou for any fxed (y,z) and φ(,,) (S 2 ) m. By he mehod of approxmaon, can be hown ha he comparon heorem ll hold f Hypohe 4 () afed. Thank o he above exence and unquene reul, we can prove he followng comparon heorem for mul-dmenonal RBSDE wh a fxed ngle reflecng barrer. Theorem 4.2. Aume ha (φ 1,ξ 1 ),(φ 2,ξ 2 ), and S afy Hypohe 4. Furher, aume ha () ξ 1 ξ 2 ; () There a pove conan C uch ha for (y,y ) (R m ) 2,(z,z ) (R m d ) 2, and [,T], 4 y,φ 1 (,y + + y,z) φ 2 (,y,z ) 2 χ {y <} z z 2 + C y 2. (4.16) For j = 1,2, denoe by (Y j,z j,k j ) he adaped oluon of RBSDE (4.1) aocae wh he daa (ξ j,φ j,s). Then, we have (1) Y 1 () Y 2 (), K 1 () K 2 (), T; (2) K 1 (r) K 1 () K 2 (r) K 2 (), r T. Proof. For j = 1,2 and pove neger n, he followng BSDE: Y j,n () = ξ j + =1 φ j (,Y j,n (),Z j,n ())d n Z j,n ()dw(), [,T] (Y j,n () S j ()) + d (4.17)
21 ha a unque adaped oluon, denoed by (Y j,n,z j,n,k j,n ). In vew of (4.16), we have 4 y,(φ 1 (,y + + y,z) n(y + + y S()) + ) (φ 2 (,y,z ) n(y S()) + ) 4 y,φ 1 (,y + + y,z) φ 2 (,y,z ) ny + 2 χ {y <} z z 2 + C y 2. =1 By he comparon heorem of mul-dmenonal BSDE (ee [9, Theorem 2.1]), follow ha Y 1,n () Y 2,n (), [,T],n = 1,2,. (4.18) Then from he proof of Theorem 4.1, we know ha for [,T] and j = 1,2, Y j () = K j () = lm Y j,n (), lm n (Y j,n () S()) + d. (4.19) The dered reul hen follow from (4.18) and (4.19). 4.2 Mul-dmenonal RBSDE wh oblque reflecon. Conder he followng RBSDE: for Λ, Y () = ξ + ψ(,y (),Z (),)d dk () + dk + () Z ()dw(), [,T]; S () Y () max {Y j() k(,j)}, [,T]; j,j Λ ( ) Y () max {Y j() k(,j)} dk + () =, j,j Λ (Y () S ())dk () =. (4.2) The followng heorem preen he exence of he oluon whou uperregulary aumpon on S. Theorem 4.3. Le Hypohee 1 and 3 be afed. Aume ha S (S 2 ) m wh S() Q() for [,T] and ξ L 2 (Ω, F T,P;R m ) wh ξ(ω) Q(T). Here we have defned for [,T], Q() {(y 1,,y m ) T R m : y j k(,j) y S (),,j Λ,j }. Then RBSDE (4.2) ha an adaped oluon (Y,Z,K +,K ) (S 2 ) m (M 2 ) m d (N 2 ) 2m. Proof. The proof dvded no four ep. Sep 1. The approxmang equence of penalzed RBSDE.
22 For any pove neger n, conder he followng RBSDE: Λ, Y n() = ξ + Y n +n T ψ(,y n (),Z n (),)d () Y n l () + k(,l)) d Z n ()dw(), () S (), [,T]; () S ())dk,n () =. [,T]; dk,n () They urn ou o be RBSDE well uded n he precedng ubecon. Defne for (,y,z,) [,T] R m R m d Λ, (4.21) ψ n (,y,z,) ψ(,y,z,) + n (y y l + k(,l)), ψ n (,y,z) ( ψ n (,y,z,1),, ψ n (,y,z,m)) T. Snce y,(y+ + y y+ l y l + k(,l)) (y y l + k(,l)) = y,(y y+ l y l + k(,l)) (y y l + k(,l)) (4.22) for y,y R m and,l Λ, and ψ n (,y,z,) doe no depend on z j for j, we have for (y,y ) (R m ) 2,(z,z ) (R m d ) 2, and (,l) (Λ) 2, 4 y, ψ n (,y + + y,z) ψ n (,y,z ) = 4 y,ψ(,y+ + y,z,) ψ(,y,z,) 4n =1 y,(y+ + y y+ l y l + k(,l)) (y y l + k(,l)), 4 y,ψ(,y+ + y,z,) ψ(,y,z,) 2 =1 χ {y <} z z 2 + 2C 2 y 2. =1 (4.23) I eay o check ha ψ n (,y,z) alo Lpchz connuou n (y,z). From Theorem 4.1, we know ha RBSDE (4.21) ha a unque adaped oluon,z n,k,n ) wh Y n 1,,Y n m) T (S 2 ) m, Z n (Z n 1,,Z n m) T (M 2 ) m d, and K,n (K,n 1,,K,n m ) T (N 2 ) m.
23 Moreover, we have from (4.23) ha for (y,y ) (R m ) 2,(z,z ) (R m d ) 2, and (,l) (Λ) 2, 4 y, ψ n+1 (,y + + y,z) ψ n (,y,z ) = 4 y, ψ n (,y + + y,z) ψ n (,y,z ) 4 4 y, ψ n (,y + + y,z) ψ n (,y,z ) 2 χ {y <} z z 2 + 2C 2 y 2. =1 From Theorem 4.2, we know y,(y+ + y y+ l y l + k(,l)), Y n () Y n+1 (), K,n () K,n+1 (), T. (4.24) The equence { (),K,n ())} n 1 adm a lm, whch denoed by (Y (),K ()) below wh Y () (Y 1 (),,Y m ()) T and K () (K 1 (),,K m()) T, for [,T]. Sep 2. A pror emae. The followng lemma he key o our ubequen argumen. Lemma 4.1. There a pove conan c whch ndependen of n, uch ha E up T Y n () 2 + E K,n (T) 2 + E n 2 E Z n () 2 d c, () Y n j () + k(,j)) 2 d c, Λ. I proof follow. Applyng Iô-Meyer formula [12] o compue () Y n j ()+ k(,j)) 2, we have = 2 where () Y n +2n n j () + k(,j)) 2 + () Y n j () + k(,j)) 2 d χ L () Z n () Zj n () 2 d,j,n () Y n j () + k(,j)) [ψ(,y n j (),Z n j (),j) ψ(,y n (),Z n (),)]d +2n () Y n j () + k(,j)) (Z n () Zn j ())dw() () Yj n () + k(,j)) d(k,n l, l j () Y n j () + k(,j)) j () Y n () K,n j ()) () + k(j,)) d () Y n j () + k(,j)) [ j () Y n l () + k(j,l)) () Yl n () + k(,l)) ]d L,j,n n {(,ω) : Y () Y j n () + k(,j) < }. (4.25)
24 We clam ha he la hree erm of (4.25) are all equal o or le han. In fac, due o (4.21), we have and Y n j () k(,j) S j() k(,j) S () (nong S() Q()) (4.26) = () Y n () Y n j () + k(,j)) d(k,n j () + k(,j)) dk,n () () S ()) dk,n () In vew of Hypohe 3 (), we have (S () Y n ())dk,n () =. () K,n j ()) {(y 1,,y m ) T R m : y y j + k(,j) <,y j y + k(j,) < } = whch mmedaely gve () Y n j () + k(,j)) j () Y n () + k(j,)) =. From Hypohe 3 (), ung he propery ha x 1 x 2 (x 1 x 2 ), we have () Y n j () + k(,j)) [ j () Y n l () + k(j,l)) () Y n l () + k(,l)) ] () Y j n() + k(,j)) (Yj n() Y n () + k(j,l) k(,l)) () Y j n() + k(,j)) (Yj n() Y n () k(,j)) = () Y n j () + k(,j)) () Y n j () + k(,j))+ =. Takng expecaon on boh de of (4.25), we have Nong ha E () Yj n () + k(,j)) 2 + E +2nE 2E () Y n j () + k(,j)) 2 d χ L () Z n () Zj n () 2 d,j,n ( () Y n j () + k(,j)) ψ(,y n (),Z n (),) ψ(,yj n(),zn j (),j) d. (4.27) ψ(,y n(),zn (),) ψ(,y n j (),Zn j (),j) ψ(,y n(),zn (),) ψ(,y n (),Zn (),j) + ψ(,y n(),zn (),j) ψ(,y n j (),Zn j (),j) c( ψ(,,) + Y n() + Zn () + Y n () Y j n() + Zn () Zn j () ) ( c 1 + ψ(,,) + Y n() + Zn () + Y n () Y j n () + k(,j) ) + Z n() Zn j ()
25 for a pove conan c (ndependen of n and pobly varyng from lne o lne), n vew of (4.27), we have E () Yj n () + k(,j)) 2 + E +2nE () Y n j () + k(,j)) 2 d χ L () Z n () Zj n () 2 d,j,n ( n 2 + 2c)E () Y j n () + k(,j)) 2 d + 2c2 n E χ L (),j,n ( 1 + ψ(,,) 2 + Y n () 2 + Z n () 2 + Z n () Zn j () 2) d. So for uffcenly large n, n 2 E ( () Y j n () + k(,j)) 2 d c 1 + E Applyng Iô lemma o compue Y n() 2, we have ) ( Y n () 2 + Z n () 2 )d. (4.28) Y n () 2 + Z n () 2 d ( = 2 Y n () ψ(,y n (),Zn (),) + n m () Y l n () + k(,l)) ) d T +ξ 2 2 Y n ()dk,n () 2 Y n ()Zn ()dw(). (4.29) Ung he elemenary nequaly: we oban ha 2 Y n ()dk,n 2ab 1 α a2 + αb 2 for a,b,α >, () = 2 1 α up T S ()dk,n () S () 2 + α K,n (T) K,n () 2 (4.3) for an arbrary pove real number α. Then akng expecaon on boh de of (4.29), we have E Y n () 2 + E 2E Z n () 2 d m Y n () ( ψ(,y n (),Zn (),) + n () Y j n () + k(,l)) )d +E(ξ 2 ) 2E Y n ()dk,n () c ε E Y n () 2 d + ε n 2 E +εe Z n () 2 d + 1 α E up T () Y n l () + k(,l)) 2 d + E(ξ ) 2 S () 2 + αe K,n (T) K,n () 2 (4.31)
26 for arbrary pove real number ε,α, and a conan c ε dependng on ε. On he oher hand, from equaon (4.21), we have K,n (T) K,n () = ξ Y n () + +n In vew of (4.28), we have ψ(,y n (),Zn (),)d () Y n l () + k(,l)) d Z n ()dw(). E K,n (T) K,n () 2 ( c Eξ 2 + E Y n () 2 + E +c [ c ) ( Y n () 2 + Z n () 2 )d n 2 E Y n () Yl n () + k(,l)) 2 d 1 + E Y n () 2 + E ( Y n () 2 + Z n () 2 )d ]. (4.32) Furher, n vew of (4.31), we have E Y n () 2 + E c ε,α (1 + E +(ε + α)ce Z n () 2 d Y n () 2 d) + αce Y n () α E up Z n () 2 d T S () 2 for any pove number ε,α, and a conan c ε,α dependng on ε,α. Seng α = ε = 1 3c, we have from Gronwall nequaly ha From (4.28) and (4.32), we have E Y n () 2 + E Z n () 2 d c. n 2 E () Yj n () + k(,j)) 2 d c, E K +,n (T) 2 c. Moreover, n vew of (4.29), applyng he Burkholder-Dav-Gundy nequaly, we have E up Y n () 2 c. T The proof of Lemma 4.1 hen complee. Sep 3. The convergence of penalzed BSDE. In vew of Lemma 4.1, ung Faou lemma, we have E[ up ( Y () 2 + K () 2 )]. T
27 Then applyng Lebegue domnaed convergence heorem, we have E Y n () Y () 2 d + E K,n () K () 2 d a. (4.33) For pove neger n 1 and n 2, applyng Iô lemma o Y n 1 () Y n 2 () 2, we have Y n 1 () Y n 2 () 2 + Z n 1 () Z n 2 () 2 d Snce = 2 = (ψ(,y n 1 (),Z n 1 (),) ψ(,y n 2 (),Z n 2 (),)) 1 () Y n 2())d +2n 1 m 2n 2 m 2 2 T 1 () Y n 1 l () + k(,l)) 1 2 () Y n 2 l () + k(,l)) 1 1 () Y n 2 ())d(k,n 1 () K,n 2 ()) () Y n 2())d () Y n 2())d 1 () Y n 2 ())(Z n 1 () Z n 2 ())dw(), Λ. 1 () Y n 2 ())d(k,n 1 (S () Y n 2 ())dk,n 1 () + n vew of (4.34), we have for Λ, () K,n 2 ()) E Y n 1 () Y n 2 () 2 + E Z n 1 () Z n 2 () 2 d = 2E m +2n 1 E (4.34) (S () Y n 1 ())dk,n 2 ()), Λ, (4.35) (ψ(,y n 1 (),Z n 1 (),) ψ(,y n 2 (),Z n 2 (),)) 1 () Y n 2())d m 2n 2 E 2C(C + 1)E +2(E +2(E 1 () Y n 1 l () + k(,l)) 1 2 () Y n 2 l () + k(,l)) 1 Y n 1 () Y n 2() 2 d E Y n 1 () Y n 2 () 2 d) 1 2 Y n 1 () Y n 2 () 2 d) 1 2 (n 2 1 E (n 2 2E () Y n 2())d () Y n 2())d Seng =, n vew of (4.33) and Lemma 4.1, we have Z n 1 () Z n 2 () 2 d ( 1 () Y n 1 l () + k(,l)) ) 2 d) 1 2 ( 2 () Y n 2 l () + k(,l)) ) 2 d) 1 2. E Z n 1 () Z n 2 () 2 d, Λ, a n 1,n 2. (4.36)
28 So here ex Z (Z 1,,Z m ) T (M 2 ) m d uch ha lm E Z n () Z () 2 d =, Λ. In vew of (4.34), applyng he Burkholder-Dav-Gundy nequaly, we have E( up Y n 1 () Y n 2 () 2 ), Λ a n 1,n 2. (4.37) T From (4.21), we have d(k,n 1 () K,n 2 ()) = (ψ(,y n 1 (),Z n 1 (),) ψ(,y n 2 (),Z n 2 (),))d +d 1 () Y n 2 ()) + n 1 1 () Y n 1() + k(,l)) d m n 2 2 () Y n 2 l () + k(,l)) d (Z n 1 () Z n 2 ())dw(). Snce he proce {(K,n 1 () K,n 2 ()), [,T]} of fne varaon, quadrac varaon. By Iô lemma follow ha = 2 (K,n 1 () K,n 2 ()) (K,n 1 () K,n 2 ())(ψ(,y n 1 (),Z n 1 (),) ψ(,y n 2 (),Z n 2 (K,n 1 () K,n 2 ())(n 1 (K,n 1 () K,n 2 ())(n 2 l 1 () Y n 1() + k(,l)) )d l 2 () Y n 2() + k(,l)) )d (K,n 1 () K,n 2 ())d 1 (K,n 1 () K,n 2 ())(Z,n 1 () Y n 2()) () Z,n 2())dW(). Applyng he Burkholder-Dav-Gundy nequaly, we have l (),))d E up c(e T +2(E +2(E +E up {2 T K,n 1 () K,n 2 () 2 ( K,n 1 () K,n 2 () 2 + Y n 1 () Y n 2 () 2 + Z n 1 () Z n 2 K,n 1 () K,n 2 () 2 d) 1 2 K,n 1 () K,n 2 () 2 d) 1 2 () 2 )d (n 2 1 E ( 1 () Y n 1 l () + k(,l) ) 2 d) 1 2 (n 2 2 E ( 2 () Y n 2 l () + k(,l) ) 2 d) 1 2 (K,n 1 () K,n 2 ())d 1 () Y n 2())} E up K,n 1 () K,n 2 T () 2 (4.38)
29 for a pove conan c ndependen of n 1 and n 2. Idencal o he proof of (4.35), we have Hence by Iô lemma, 1 () Y n 2 ())d(k,n 1 () K,n 2 ()). 2 (K,n 1 () K,n 2 ())d 1 () Y n 2 ()) = 2((K,n 1 () K,n 2 ()) 1 () Y n 2 ())) 2 Then a a conequence, { E up 2 T ( 2E up 1 () Y n 2 ())d(k,n 1 () K,n 2()) 2 K,n 1 () K,n 2 () Y n 1 () Y n 2(). T 1 3 E up K,n 1 T (K,n 1 () K,n 2 ())d 1 K,n 1 () K,n 2 () Y n 1 () K,n 2 () Y n 2 ) () Y n 2() Togeher wh (4.33), (4.38), and Lemma 4.1, we have E( up ce T +ce up T From (4.36) and (4.37), we have Se and } ()) () 2 + 3E up Y n 1 () Y n 2 () 2. T K,n 1 () K,n 2 () 2 ) ( Y n 1 () Y n 2 () 2 + Z n 1 () Z n 2 () 2 )d Y n 1 () Y n 2 () 2. E up K,n 1 () K,n 2 () 2, Λ, a n 1,n 2. T K +,n () n K + () Y () Y () We have K +,n () = Y n () Y n () and =. () Y n l () + k(,l)) d ψ(,y (),Z (),)d + ψ(,y n (),Z n (),)d+ (4.39) dk () + Z ()dw(). dk,n ()+ lm E( up K +,n () K + () 2 ) T ( lm ce up { Y n () Y () 2 + K,n () K () 2 } T ) + Z n () Z () 2 d Z n ()dw()
30 Hence, K (K 1 +,,K+ m) (N 2 ) m, and (Y,Z,K +,K ) afe he fr equaon of (4.2). By Lemma 4.1 and Faou lemma, we oban ha E lm E lm whch mple mmedaely ha (Y () Y l () + k(,l)) 2 d c n 2 =, () Y n l () + k(,l)) 2 d Y () Y l () + k(,l), T. (4.4) Snce Y n () S() for any n and [,T], we have Hence, Y () S(), T. Y () Q(), T. Sep 4. The lower mnmal boundary condon. For,j,l Λ, j,l =, obvou ha () Y n j () + k(,j)) + () Y n l () + k(,l)) =. For,j,l Λ, j,l, we have Hence, = n. =. mn j () Y n j () + k(,j))+ () Y n l () + k(,l)) () Y n l () + k(,l)) + () Y n l () + k(,l)) () max j {Y n j () k(,j)}) + dk +,n () mn {(Y n () Yj n () + k(,j)) + () Yl n () + k(,j)) }d j On he oher hand, nce K +,n ( ) ncreang, we have Therefore, () max {Y j n () j k(,j)})+ dk +,n (). () max j {Y n j () k(,j)}) + dk +,n () =. Followng he ame argumen a n he proof of (4.14) and applyng [4, Lemma 5.8], we have In vew of (4.4), we have (Y () max j {Y j() k(,j)}) + dk + (Y () max j {Y j() k(,j)})dk + () =. () =.
31 5 Unquene The unquene of oluon defned n he followng ene: f (Y,Z,K +,K ) anoher oluon, hen Y () Y (), Z () Z(), K + () K () K + () K (), T,a.. The followng Sronger aumpon on h,j needed n our proof of he unquene reul. Hypohe 5.,j,l Λ uch ha j, j l, y R, h,j (,h j,l (,y)) < h,l (,y). Remark 5.1. I eay o check ha Hypohe 5 mple Hypohe 3. If h,j (,y) y k(,j), hen Hypohe 5 reduce o he nequaly: k(,j) + k(j,l) > k(,l) for j and j l. Le {θ j } j= be an ncreang equence of oppng me wh value n [,T]. j, α j an F θj -meaurable random varable wh value n Λ. Aume ha a..ω, here ex an neger N(ω) < uch ha θ N = T. Then we defne a wchng raegy a: N 1 a() = α χ [θ, θ 1 ]() + α j χ (θj, θ j+1 ](). We denoe by A all he wchng raege wh nal daa (α,θ ) = (,) Λ [,T]. For gven a A, conder he followng RBSDE: U a () = ξ a(t) + ψ(r,u a (r),v a (r),a(r))dr (L a (T) L a ()) N 1 j=1 [U a (θ j ) h αj 1, α j (θ j,u a (θ j ))]χ (,T] (θ j ) j=1 V a (r)dw(r), U a () S a() (), [,T]; [,T]; (5.1) (U a () S a() ())dl a () =. The generaor ψ of RBSDE (5.1) depend on he conrol a and a each wchng me θ j before ermnaon, he value of U a wll jump by an amoun of U a (θ j ) h αj 1, α j (θ j,u a (θ j )) whch can be regarded a a penaly or co for he wchng. In each ubnerval dvded by he wchng me, RBSDE (5.1) evolve a a andard RBSDE wh ngle barrer, whch can be olved n a backwardly nducve way. The opmal conrol problem for RBSDE (5.1) o maxmze U a () over a A. The oluon of RBSDE (1.4) cloely conneced wh h conrol problem. Bede, alo conneced o he ochac game conruced below. Le τ be a oppng me wh value n [,T]. For gven a A and oppng
32 me τ, conder he followng BSDE: U a,τ () = S a(τ) (τ)χ {τ<t } + ξ a(τ) χ {τ=t } + N 1 τ [U a,τ (θ j ) h αj 1, α j (θ j,u a,τ (θ j ))]χ (,τ] (θ j ) j=1 τ V a,τ (r)dw(r), [,τ]. ψ(r,u a,τ (r),v a,τ (r),a(r))dr (5.2) The ermnal value S a(τ) (τ)χ {τ<t } + ξ a(τ) χ {τ=t } of BSDE (5.2) depend on he ermnal me τ. And he value U a,τ () depend on boh he wchng raegy a and ermnal me τ. Ung he ame argumen a n RBSDE (5.1), we know ha BSDE (5.2) well defned and ha a unque oluon. Baed on ha, we conruc a zero-um ochac game a follow. Suppoe here are wo player A and B whoe benef are anagonc. The payoff U a,τ () whch afe BSDE (5.2) a reward for player A and a co for player B. Player A chooe a wchng raegy a A o a o maxmze he reward U a,τ (). Player B chooe he me τ o ermnae he game and re o mnmze he co U a,τ (). The followng heorem reveal he connecon among he oluon of he yem (1.4), he above conrol problem and ochac game. Theorem 5.1. Le Hypohee 1 and 5 be afed. Aume ha (U a,v a,l a ) he unque adaped oluon of RBSDE (5.1) for a A and (U a,τ,v a,τ ) he unque oluon of BSDE (5.2) for a A and oppng me τ. Then f (Y,Z,K +,K ) an adaped oluon of RBSDE (1.4), we have Y () = eup a A U a () = eupenf U a,τ () = enf a A τ τ eupu a,τ (), a A [,T]. Le ˆθ = and ˆα =. Defne he equence {ˆθ j, ˆα j } j=1 follow: n an nducve way a ˆθ j = nf{ ˆθ j 1 : Yˆαj 1 () = max k ˆα j 1,k Λ hˆα j 1,k(,Y k ())} T. And f ˆθ j < T, e ˆα j be he malle ndex n Λ uch ha Oherwe, e ˆα j be an arbrary ndex. Defne Yˆαj 1 (ˆθ j ) = hˆαj 1,ˆα j (ˆθ j,yˆαj (ˆθ j )). (5.3) ˆN 1 â() ˆα χ [ˆθ, ˆθ 1 ] () + j=1 ˆα j χ (ˆθj, ˆθ j+1 ] () and τ nf{ [,T) : Uâ() = Sâ() ()} T, wh he convenon ha nf +. Then, we have â A and Y () = Uâ() and Y () = Uâ,τ (), [,T]. (5.4)
33 Proof. For [,T],a A, and [,θ N ], defne Y a () Z a () K +,a () K,a () N Y αj 1 ()χ [θj 1, θ j )() + ξ αn 1 χ {=T }, j=1 N Z αj 1 ()χ [θj 1, θ j )(), j=1 N (K α + j 1 (θ j ) K α + j 1 (θ j 1 )), j=1 N (Kα j 1 (θ j ) Kα j 1 (θ j 1 )). j=1 (5.5) In vew of he jump Y αj (θ j ) Y αj 1 (θ j ) = Y a (θ j ) Y a (θ j ) a each oppng me θ j, j = 1,,N 1, we know ha (Y a,z a,k +,a,k,a ) afe he followng RBSDE: Y a () = ξ a(t) + Y a () N 1 ψ(r,y a (r),z a (r),a(r))dr (Y a (θ j ) Y a (θ j ))χ (,T] (θ j ) + K +,a (T) K +,a () j=1 (K,a (T) K,a ()) S a() () Z a (r)dw(r), (Y a () S a() ())dk,a () =, [,T]. (5.6) And for any oppng me τ, (Y a,z a,k +,a,k,a ) alo afe he followng BSDE: and Y a () = Y a (τ) + N 1 τ ψ(r,y a (r),z a (r),a(r))dr (Y a (θ j ) Y a (θ j ))χ (,τ] (θ j ) + K +,a (τ) K +,a () j=1 (K,a (τ) K,a ()) τ Z a (r)dw(r), Comparng RBSDE (5.1) wh (5.6), n vew of he fac ha [,τ]. Y a (θ j ) = Y αj 1 (θ j ) h αj 1,α j (θ j,y αj (θ j )) = h αj 1,α j (θ j,y a (θ j )) K +,a (T) K +,a (), we deduce from he comparon heorem [3, Theorem 4.1] ha From he defnon n (5.5), Hence, Y a () U a (), T. Y a () = Y (). (5.7) Y () U a (), a A. (5.8)
34 For he equence {ˆθ j } j=1, we clam ha for a..ω, here ex an neger ˆN(ω) < uch ha ˆθ ˆN = T. Oherwe, defne B j=1 {ω : ˆθ j (ω) < T } F T, hen P(B) >. For j = 1,2,, we have Yˆαj 1 (ˆθ j ) = hˆαj 1,ˆα j (ˆθ j,yˆαj (ˆθ j )), Yˆαj (ˆθ j+1 ) = hˆαj,ˆα j+1 (ˆθ j+1,yˆαj+1 (ˆθ j+1 )), on B. (5.9) Snce he equence {(ˆα j 1, ˆα j, ˆα j+1 )} j=1 ake value n Λ3, whch a fne e, here are a rple ( 1, 2, 3 ) and a ubequence j k uch ha for k = 1,2, (ˆα jk 1, ˆα jk, ˆα jk +1) = ( 1, 2, 3 ). Snce he equence {ˆθ j } j=1 ncreang and bounded by T, here a lm ˆθ. Pang o he lm n (5.9) for he ubequence {j k }, we have Y 1 (ˆθ ) = h 1, 2 (ˆθ,Y 2 (ˆθ )), Y 2 (ˆθ ) = h 2, 3 (ˆθ,Y 3 (ˆθ )), on B. (5.1) From Hypohe 5, we have Th conradc o he fac ha Th how â A. I eay o ee ha Y 1 (ˆθ ) = h 1, 2 (ˆθ,h 2, 3 (ˆθ,Y 3 (ˆθ ))) < h 1, 3 (ˆθ,Y 3 (ˆθ )) on B. Y 1 (ˆθ ) max h 1,j(ˆθ,Y j (ˆθ )). (5.11) j 1,j Λ Y â(ˆθ j ) = hˆαj 1,ˆα j (ˆθ j,y â(ˆθ j )), K +,â (T) K +,â () =. (5.12) Then (Y â,zâ,k,â ) afe RBSDE (5.1). By he unquene of he oluon of RBSDE (5.1), we have Y â() = Uâ(), T. Hence, Nong (5.8), we know Y () = Uâ(). Y () = eupu (), [,T]. (5.13) a A In vew of (5.7), follow from (5.12) ha Y â() = Y â(τ) + ˆN 1 τ ψ(r,y â(r),zâ(r),â(r))dr (Y â(ˆθ j ) hˆαj 1,ˆα j (ˆθ j,y â(ˆθ j )))χ (,τ] (ˆθ j ) j=1 (K,â (τ) K,â ()) τ Zâ(r)dW(r). (5.14)
35 For any wchng raegy a, defne ˆτ nf{ [,T) : Y a () = S a() ()} T, wh he convenon ha nf +. From he upper mnmal boundary condon n (1.4), we know ha K,a (ˆτ) K,a () =, Y a (ˆτ) = S a(ˆτ) (ˆτ)χ {ˆτ<T } + ξ a(ˆτ) χ {ˆτ=T }. (5.15) In vew of (5.7) and (5.14), we have from (5.15) ha and ˆτ Y a () = S a(ˆτ) (ˆτ)χ {ˆτ<T } + ξ a(ˆτ) χ {ˆτ=T } + N 1 ψ(r,y a (r),z a (r),a(r))dr (Y a (θ j ) Y a (θ j ))χ (,ˆτ] (θ j ) + K +,a (ˆτ) K +,a () j=1 ˆτ Z a (r)dw(r), [, ˆτ];a A. Y â() = Sâ(ˆτ) (ˆτ)χ {ˆτ<T } + ξâ(ˆτ) χ {ˆτ=T } + ˆN j=1 ˆτ ˆτ (Y â(ˆθ j ) hˆαj 1,ˆα j (ˆθ j,y â(ˆθ j )))χ (,ˆτ] (ˆθ j ) Zâ(r)dW(r), [, ˆτ]. ψ(r,y â(r),zâ(r),â(r))dr (5.16) (5.17) Comparng BSDE (5.2) wh (5.16), (5.14) and (5.17), repecvely, n vew of he fac ha Y a (θ j ) = Y αj 1 (θ j ) h αj 1,α j (θ j,y αj (θ j )) = h αj 1,α j (θ j,y a (θ j )), Y â(τ) Sâ(τ) (τ)χ {τ<t } + ξâ(τ) χ {τ=t }, and K +,a and K,â are ncreang procee, we have Y a () U a,ˆτ (), Y â() Uâ,τ (), Y â() = Uâ,ˆτ (), [,T]. Nong by defnon ha (5.18) Y a () = Y â() = Y (), [,T], we have Y () = Uâ,ˆτ (), U a,ˆτ () Uâ,ˆτ () Uâ,τ () [,T]. (5.19) Th how ha (â, ˆτ) a addle pon for he funconal U a,τ () a a funconal of (a,τ) A T, wh T beng he oaly of oppng me whch ake value n [,T]; or equvalenly, Y () = Uâ,ˆτ () = eupenf U a,τ () = enf a A τ τ eupu a,τ (), [,T]. (5.2) a A
36 Theorem 5.1 gve he unquene of Y. The unquene of oher componen (Z,K +,K ) of he oluon (Y,Z,K +,K ) a conequence of Doob-Meyer decompoon of Y. We conclude he followng reul. Theorem 5.2. Le Hypohee 1, 2 and 5 be afed. Aume ha he upper barrer S uper-regular wh S() Q() for [,T], and ha he ermnal value ξ L 2 (Ω, F T,P;R m ) ake value n Q(T). Then RBSDE (1.4) ha a unque adaped oluon (Y,Z,K +,K ). Theorem 5.3. Le Hypohee 1 and 3 () be afed. Aume ha he upper barrer S (S 2 ) m wh S() Q() for [,T], ha he ermnal value ξ L 2 (Ω, F T,P;R m ) ake value n Q(T), and ha k(,j) + k(j,l) > k(,l) for j, j l,,j,l Λ. Then RBSDE (4.2) ha a unque adaped oluon. Reference [1] Cvanc, J. and I. Karaza (1996): Backward SDE wh reflecon and Dynkn game. Annal of Probably 24 (4), [2] Dellachere, C. and P. A. Meyer (198): Probablé e Poenel, I-IV. Hermann, Par. [3] El Karou, N., C. Kapoudjan, E. Pardoux, S. Peng and M. C. Quenez (1997): Refleced oluon of backward SDE and relaed obacle problem for PDE. Annal of Probably 25 (2), [4] Gegou-Pe, A. and E. Pardoux (1996): Equaon dfférenelle ochaque rérograde réfléche dan un convexe. Sochac Rep. 57, [5] Hamadene, S., J.-P. Lepeler and A. Maou (1997): Double barrer backward SDE wh connuou coeffcen. In El Karou, N. and L. Mazlak (Ed) Backward ochac dfferenal equaon, Pman Reearch Noe n Mahemac Sere 364, [6] Hamadene, S. (22): Refleced BSDE wh dconnuou barrer and applcaon. Sochac Sochac Rep. 74(3-4), [7] Hamadene, S. and M. Haan (25): BSDE wh wo reflecng barrer: he general reul. Probab. Theory Rela. Feld 132, [8] Hamadene, S. and J. Zhang (27): The Sarng and Soppng Problem under Knghan Uncerany and Relaed Syem of Refleced BSDE. arxv:mah.pr/ [9] Hu, Y. and S. Peng (26): On he comparon heorem for mul-dmenonal BSDE. C.R.Mah Acad.Sc.Par 343, [1] Hu, Y. and S. Tang (27): Mul-dmenonal BSDE wh oblque reflecon and opmal wchng. arxv:mah.pr/ [11] Lepeler, J.-P. and M. Xu (25): Penalzaon mehod for refleced backward ochac dfferenal equaon wh one r.c.l.l. barrer. Sac Probably Leer 75, [12] Meyer, P.A. (1976): Un cour ur le négrale ochaque, Sémnare de Probablé X. Lecure Noe n. Mah. 511, Sprnger, Berln. [13] Pardoux, E. and S. Peng (199): Adaped oluon of a backward ochac dfferenal equaon. Syem Conrol Le. 14,
37 [14] Peng, S. and M. Xu (25): The malle g-upermarngale and refleced BSDE wh ngle and double L 2 obacle, Ann. I. H. Poncare. PR 41,
Research Article A Two-Mode Mean-Field Optimal Switching Problem for the Full Balance Sheet
 Hndaw Publhng Corporaon Inernaonal Journal of Sochac Analy Volume 14 Arcle ID 159519 16 page hp://dx.do.org/1.1155/14/159519 Reearch Arcle A wo-mode Mean-Feld Opmal Swchng Problem for he Full Balance Shee
Hndaw Publhng Corporaon Inernaonal Journal of Sochac Analy Volume 14 Arcle ID 159519 16 page hp://dx.do.org/1.1155/14/159519 Reearch Arcle A wo-mode Mean-Feld Opmal Swchng Problem for he Full Balance Shee
(,,, ) (,,, ). In addition, there are three other consumers, -2, -1, and 0. Consumer -2 has the utility function
 MACROECONOMIC THEORY T J KEHOE ECON 87 SPRING 5 PROBLEM SET # Conder an overlappng generaon economy le ha n queon 5 on problem e n whch conumer lve for perod The uly funcon of he conumer born n perod,
MACROECONOMIC THEORY T J KEHOE ECON 87 SPRING 5 PROBLEM SET # Conder an overlappng generaon economy le ha n queon 5 on problem e n whch conumer lve for perod The uly funcon of he conumer born n perod,
Matrix reconstruction with the local max norm
 Marx reconrucon wh he local max norm Rna oygel Deparmen of Sac Sanford Unvery rnafb@anfordedu Nahan Srebro Toyoa Technologcal Inue a Chcago na@cedu Rulan Salakhudnov Dep of Sac and Dep of Compuer Scence
Marx reconrucon wh he local max norm Rna oygel Deparmen of Sac Sanford Unvery rnafb@anfordedu Nahan Srebro Toyoa Technologcal Inue a Chcago na@cedu Rulan Salakhudnov Dep of Sac and Dep of Compuer Scence
Epistemic Game Theory: Online Appendix
 Epsemc Game Theory: Onlne Appendx Edde Dekel Lucano Pomao Marcano Snscalch July 18, 2014 Prelmnares Fx a fne ype srucure T I, S, T, β I and a probably µ S T. Le T µ I, S, T µ, βµ I be a ype srucure ha
Epsemc Game Theory: Onlne Appendx Edde Dekel Lucano Pomao Marcano Snscalch July 18, 2014 Prelmnares Fx a fne ype srucure T I, S, T, β I and a probably µ S T. Le T µ I, S, T µ, βµ I be a ype srucure ha
ELIMINATION OF DOMINATED STRATEGIES AND INESSENTIAL PLAYERS
 OPERATIONS RESEARCH AND DECISIONS No. 1 215 DOI: 1.5277/ord1513 Mamoru KANEKO 1 Shuge LIU 1 ELIMINATION OF DOMINATED STRATEGIES AND INESSENTIAL PLAYERS We udy he proce, called he IEDI proce, of eraed elmnaon
OPERATIONS RESEARCH AND DECISIONS No. 1 215 DOI: 1.5277/ord1513 Mamoru KANEKO 1 Shuge LIU 1 ELIMINATION OF DOMINATED STRATEGIES AND INESSENTIAL PLAYERS We udy he proce, called he IEDI proce, of eraed elmnaon
L N O Q. l q l q. I. A General Case. l q RANDOM LAGRANGE MULTIPLIERS AND TRANSVERSALITY. Econ. 511b Spring 1998 C. Sims
 Econ. 511b Sprng 1998 C. Sm RAD AGRAGE UPERS AD RASVERSAY agrange mulpler mehod are andard fare n elemenary calculu coure, and hey play a cenral role n economc applcaon of calculu becaue hey ofen urn ou
Econ. 511b Sprng 1998 C. Sm RAD AGRAGE UPERS AD RASVERSAY agrange mulpler mehod are andard fare n elemenary calculu coure, and hey play a cenral role n economc applcaon of calculu becaue hey ofen urn ou
Part II CONTINUOUS TIME STOCHASTIC PROCESSES
 Par II CONTINUOUS TIME STOCHASTIC PROCESSES 4 Chaper 4 For an advanced analyss of he properes of he Wener process, see: Revus D and Yor M: Connuous marngales and Brownan Moon Karazas I and Shreve S E:
Par II CONTINUOUS TIME STOCHASTIC PROCESSES 4 Chaper 4 For an advanced analyss of he properes of he Wener process, see: Revus D and Yor M: Connuous marngales and Brownan Moon Karazas I and Shreve S E:
A Weak Dynamic Programming Principle for Zero-Sum Stochastic Differential Games with Unbounded Controls
 A Weak Dynac Prograng Prncple for Zero-Su Sochac Dfferenal Gae wh Unbounded Conrol rhan Bayrakar, Song Yao Abrac We analyze a zero-u ochac dfferenal gae beween wo copeng player who can chooe unbounded
A Weak Dynac Prograng Prncple for Zero-Su Sochac Dfferenal Gae wh Unbounded Conrol rhan Bayrakar, Song Yao Abrac We analyze a zero-u ochac dfferenal gae beween wo copeng player who can chooe unbounded
Control Systems. Mathematical Modeling of Control Systems.
 Conrol Syem Mahemacal Modelng of Conrol Syem chbum@eoulech.ac.kr Oulne Mahemacal model and model ype. Tranfer funcon model Syem pole and zero Chbum Lee -Seoulech Conrol Syem Mahemacal Model Model are key
Conrol Syem Mahemacal Modelng of Conrol Syem chbum@eoulech.ac.kr Oulne Mahemacal model and model ype. Tranfer funcon model Syem pole and zero Chbum Lee -Seoulech Conrol Syem Mahemacal Model Model are key
GENERATING CERTAIN QUINTIC IRREDUCIBLE POLYNOMIALS OVER FINITE FIELDS. Youngwoo Ahn and Kitae Kim
 Korean J. Mah. 19 (2011), No. 3, pp. 263 272 GENERATING CERTAIN QUINTIC IRREDUCIBLE POLYNOMIALS OVER FINITE FIELDS Youngwoo Ahn and Kae Km Absrac. In he paper [1], an explc correspondence beween ceran
Korean J. Mah. 19 (2011), No. 3, pp. 263 272 GENERATING CERTAIN QUINTIC IRREDUCIBLE POLYNOMIALS OVER FINITE FIELDS Youngwoo Ahn and Kae Km Absrac. In he paper [1], an explc correspondence beween ceran
A. Inventory model. Why are we interested in it? What do we really study in such cases.
 Some general yem model.. Inenory model. Why are we nereed n? Wha do we really udy n uch cae. General raegy of machng wo dmlar procee, ay, machng a fa proce wh a low one. We need an nenory or a buffer or
Some general yem model.. Inenory model. Why are we nereed n? Wha do we really udy n uch cae. General raegy of machng wo dmlar procee, ay, machng a fa proce wh a low one. We need an nenory or a buffer or
V.Abramov - FURTHER ANALYSIS OF CONFIDENCE INTERVALS FOR LARGE CLIENT/SERVER COMPUTER NETWORKS
 R&RATA # Vol.) 8, March FURTHER AALYSIS OF COFIDECE ITERVALS FOR LARGE CLIET/SERVER COMPUTER ETWORKS Vyacheslav Abramov School of Mahemacal Scences, Monash Unversy, Buldng 8, Level 4, Clayon Campus, Wellngon
R&RATA # Vol.) 8, March FURTHER AALYSIS OF COFIDECE ITERVALS FOR LARGE CLIET/SERVER COMPUTER ETWORKS Vyacheslav Abramov School of Mahemacal Scences, Monash Unversy, Buldng 8, Level 4, Clayon Campus, Wellngon
Existence and Uniqueness Results for Random Impulsive Integro-Differential Equation
 Global Journal of Pure and Appled Mahemacs. ISSN 973-768 Volume 4, Number 6 (8), pp. 89-87 Research Inda Publcaons hp://www.rpublcaon.com Exsence and Unqueness Resuls for Random Impulsve Inegro-Dfferenal
Global Journal of Pure and Appled Mahemacs. ISSN 973-768 Volume 4, Number 6 (8), pp. 89-87 Research Inda Publcaons hp://www.rpublcaon.com Exsence and Unqueness Resuls for Random Impulsve Inegro-Dfferenal
H = d d q 1 d d q N d d p 1 d d p N exp
 8333: Sacal Mechanc I roblem Se # 7 Soluon Fall 3 Canoncal Enemble Non-harmonc Ga: The Hamlonan for a ga of N non neracng parcle n a d dmenonal box ha he form H A p a The paron funcon gven by ZN T d d
8333: Sacal Mechanc I roblem Se # 7 Soluon Fall 3 Canoncal Enemble Non-harmonc Ga: The Hamlonan for a ga of N non neracng parcle n a d dmenonal box ha he form H A p a The paron funcon gven by ZN T d d
Downloaded 10/13/16 to Redistribution subject to SIAM license or copyright; see
 SIAM J. CONTROL OPTIM. Vol. 52, No. 5, pp. 335 375 c 204 Socey for Indural and Appled Mahemac Downloaded 0/3/6 o 36.42.24.99. Redrbuon ubec o SIAM lcene or copyrgh; ee hp://www.am.org/ournal/oa.php ON
SIAM J. CONTROL OPTIM. Vol. 52, No. 5, pp. 335 375 c 204 Socey for Indural and Appled Mahemac Downloaded 0/3/6 o 36.42.24.99. Redrbuon ubec o SIAM lcene or copyrgh; ee hp://www.am.org/ournal/oa.php ON
( ) () we define the interaction representation by the unitary transformation () = ()
 Hgher Order Perurbaon Theory Mchael Fowler 3/7/6 The neracon Represenaon Recall ha n he frs par of hs course sequence, we dscussed he chrödnger and Hesenberg represenaons of quanum mechancs here n he chrödnger
Hgher Order Perurbaon Theory Mchael Fowler 3/7/6 The neracon Represenaon Recall ha n he frs par of hs course sequence, we dscussed he chrödnger and Hesenberg represenaons of quanum mechancs here n he chrödnger
Online Appendix for. Strategic safety stocks in supply chains with evolving forecasts
 Onlne Appendx for Sraegc safey socs n supply chans wh evolvng forecass Tor Schoenmeyr Sephen C. Graves Opsolar, Inc. 332 Hunwood Avenue Hayward, CA 94544 A. P. Sloan School of Managemen Massachuses Insue
Onlne Appendx for Sraegc safey socs n supply chans wh evolvng forecass Tor Schoenmeyr Sephen C. Graves Opsolar, Inc. 332 Hunwood Avenue Hayward, CA 94544 A. P. Sloan School of Managemen Massachuses Insue
Dynamic Team Decision Theory. EECS 558 Project Shrutivandana Sharma and David Shuman December 10, 2005
 Dynamc Team Decson Theory EECS 558 Proec Shruvandana Sharma and Davd Shuman December 0, 005 Oulne Inroducon o Team Decson Theory Decomposon of he Dynamc Team Decson Problem Equvalence of Sac and Dynamc
Dynamc Team Decson Theory EECS 558 Proec Shruvandana Sharma and Davd Shuman December 0, 005 Oulne Inroducon o Team Decson Theory Decomposon of he Dynamc Team Decson Problem Equvalence of Sac and Dynamc
Cooling of a hot metal forging. , dt dt
 Tranen Conducon Uneady Analy - Lumped Thermal Capacy Model Performed when; Hea ranfer whn a yem produced a unform emperaure drbuon n he yem (mall emperaure graden). The emperaure change whn he yem condered
Tranen Conducon Uneady Analy - Lumped Thermal Capacy Model Performed when; Hea ranfer whn a yem produced a unform emperaure drbuon n he yem (mall emperaure graden). The emperaure change whn he yem condered
CH.3. COMPATIBILITY EQUATIONS. Continuum Mechanics Course (MMC) - ETSECCPB - UPC
 CH.3. COMPATIBILITY EQUATIONS Connuum Mechancs Course (MMC) - ETSECCPB - UPC Overvew Compably Condons Compably Equaons of a Poenal Vecor Feld Compably Condons for Infnesmal Srans Inegraon of he Infnesmal
CH.3. COMPATIBILITY EQUATIONS Connuum Mechancs Course (MMC) - ETSECCPB - UPC Overvew Compably Condons Compably Equaons of a Poenal Vecor Feld Compably Condons for Infnesmal Srans Inegraon of he Infnesmal
Comparison of Differences between Power Means 1
 In. Journal of Mah. Analyss, Vol. 7, 203, no., 5-55 Comparson of Dfferences beween Power Means Chang-An Tan, Guanghua Sh and Fe Zuo College of Mahemacs and Informaon Scence Henan Normal Unversy, 453007,
In. Journal of Mah. Analyss, Vol. 7, 203, no., 5-55 Comparson of Dfferences beween Power Means Chang-An Tan, Guanghua Sh and Fe Zuo College of Mahemacs and Informaon Scence Henan Normal Unversy, 453007,
CS286.2 Lecture 14: Quantum de Finetti Theorems II
 CS286.2 Lecure 14: Quanum de Fne Theorems II Scrbe: Mara Okounkova 1 Saemen of he heorem Recall he las saemen of he quanum de Fne heorem from he prevous lecure. Theorem 1 Quanum de Fne). Le ρ Dens C 2
CS286.2 Lecure 14: Quanum de Fne Theorems II Scrbe: Mara Okounkova 1 Saemen of he heorem Recall he las saemen of he quanum de Fne heorem from he prevous lecure. Theorem 1 Quanum de Fne). Le ρ Dens C 2
A NUMERICAL SCHEME FOR BSDES. BY JIANFENG ZHANG University of Southern California, Los Angeles
 The Annals of Appled Probably 24, Vol. 14, No. 1, 459 488 Insue of Mahemacal Sascs, 24 A NUMERICAL SCHEME FOR BSDES BY JIANFENG ZHANG Unversy of Souhern Calforna, Los Angeles In hs paper we propose a numercal
The Annals of Appled Probably 24, Vol. 14, No. 1, 459 488 Insue of Mahemacal Sascs, 24 A NUMERICAL SCHEME FOR BSDES BY JIANFENG ZHANG Unversy of Souhern Calforna, Los Angeles In hs paper we propose a numercal
arxiv: v5 [math.pr] 31 Mar 2015
![arxiv: v5 [math.pr] 31 Mar 2015 arxiv: v5 [math.pr] 31 Mar 2015](/thumbs/94/118302367.jpg) STOCHASTIC CONTROL REPRESENTATIONS FOR PENALIZED BACKWARD STOCHASTIC DIFFERENTIAL EQUATIONS GECHUN LIANG arxv:132.48v5 [mah.pr 31 Mar 215 Absrac. Ths paper shows ha penalzed backward sochasc dfferenal
STOCHASTIC CONTROL REPRESENTATIONS FOR PENALIZED BACKWARD STOCHASTIC DIFFERENTIAL EQUATIONS GECHUN LIANG arxv:132.48v5 [mah.pr 31 Mar 215 Absrac. Ths paper shows ha penalzed backward sochasc dfferenal
Available online at J. Nonlinear Sci. Appl. 9 (2016), Research Article
 Avalable onlne a www.jna.com J. Nonlnear Sc. Appl. 9 06, 76 756 Reearch Arcle Aympoc behavor and a poeror error emae n Sobolev pace for he generalzed overlappng doman decompoon mehod for evoluonary HJB
Avalable onlne a www.jna.com J. Nonlnear Sc. Appl. 9 06, 76 756 Reearch Arcle Aympoc behavor and a poeror error emae n Sobolev pace for he generalzed overlappng doman decompoon mehod for evoluonary HJB
ON THE WEAK LIMITS OF SMOOTH MAPS FOR THE DIRICHLET ENERGY BETWEEN MANIFOLDS
 ON THE WEA LIMITS OF SMOOTH MAPS FOR THE DIRICHLET ENERGY BETWEEN MANIFOLDS FENGBO HANG Absrac. We denfy all he weak sequenal lms of smooh maps n W (M N). In parcular, hs mples a necessary su cen opologcal
ON THE WEA LIMITS OF SMOOTH MAPS FOR THE DIRICHLET ENERGY BETWEEN MANIFOLDS FENGBO HANG Absrac. We denfy all he weak sequenal lms of smooh maps n W (M N). In parcular, hs mples a necessary su cen opologcal
A-posteriori estimates for backward SDEs
 A-poseror esmaes for backward SDEs Chrsan Bender 1, Jessca Sener 1 Aprl 4, 01 Suppose an approxmaon o he soluon of a backward SDE s pre-compued by some numercal algorhm. In hs paper we provde a-poseror
A-poseror esmaes for backward SDEs Chrsan Bender 1, Jessca Sener 1 Aprl 4, 01 Suppose an approxmaon o he soluon of a backward SDE s pre-compued by some numercal algorhm. In hs paper we provde a-poseror
Online Supplement for Dynamic Multi-Technology. Production-Inventory Problem with Emissions Trading
 Onlne Supplemen for Dynamc Mul-Technology Producon-Invenory Problem wh Emssons Tradng by We Zhang Zhongsheng Hua Yu Xa and Baofeng Huo Proof of Lemma For any ( qr ) Θ s easy o verfy ha he lnear programmng
Onlne Supplemen for Dynamc Mul-Technology Producon-Invenory Problem wh Emssons Tradng by We Zhang Zhongsheng Hua Yu Xa and Baofeng Huo Proof of Lemma For any ( qr ) Θ s easy o verfy ha he lnear programmng
A Nonlinear ILC Schemes for Nonlinear Dynamic Systems To Improve Convergence Speed
 IJCSI Inernaonal Journal of Compuer Scence Iue, Vol. 9, Iue 3, No, ay ISSN (Onlne): 694-84 www.ijcsi.org 8 A Nonlnear ILC Scheme for Nonlnear Dynamc Syem o Improve Convergence Speed Hoen Babaee, Alreza
IJCSI Inernaonal Journal of Compuer Scence Iue, Vol. 9, Iue 3, No, ay ISSN (Onlne): 694-84 www.ijcsi.org 8 A Nonlnear ILC Scheme for Nonlnear Dynamc Syem o Improve Convergence Speed Hoen Babaee, Alreza
Wissal SABBAGH. Some Contributions on Probabilistic Interpretation For Nonlinear Stochastic PDEs JURY
 Wal SABBAGH Mémore préené en vue de l obenon du grade de Doceur de l Unveré du Mane ou le label de L Unveré Nane Anger Le Man e de l'ecole Naonale d'ingéneur de Tun ou le label de L Unveré de Tun EL Manar
Wal SABBAGH Mémore préené en vue de l obenon du grade de Doceur de l Unveré du Mane ou le label de L Unveré Nane Anger Le Man e de l'ecole Naonale d'ingéneur de Tun ou le label de L Unveré de Tun EL Manar
Method of upper lower solutions for nonlinear system of fractional differential equations and applications
 Malaya Journal of Maemak, Vol. 6, No. 3, 467-472, 218 hps://do.org/1.26637/mjm63/1 Mehod of upper lower soluons for nonlnear sysem of fraconal dfferenal equaons and applcaons D.B. Dhagude1 *, N.B. Jadhav2
Malaya Journal of Maemak, Vol. 6, No. 3, 467-472, 218 hps://do.org/1.26637/mjm63/1 Mehod of upper lower soluons for nonlnear sysem of fraconal dfferenal equaons and applcaons D.B. Dhagude1 *, N.B. Jadhav2
Dual Representation as Stochastic Differential Games of Backward Stochastic Differential Equations and Dynamic Evaluations
 arxiv:mah/0602323v1 [mah.pr] 15 Feb 2006 Dual Represenaion as Sochasic Differenial Games of Backward Sochasic Differenial Equaions and Dynamic Evaluaions Shanjian Tang Absrac In his Noe, assuming ha he
arxiv:mah/0602323v1 [mah.pr] 15 Feb 2006 Dual Represenaion as Sochasic Differenial Games of Backward Sochasic Differenial Equaions and Dynamic Evaluaions Shanjian Tang Absrac In his Noe, assuming ha he
SOME NOISELESS CODING THEOREMS OF INACCURACY MEASURE OF ORDER α AND TYPE β
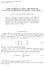 SARAJEVO JOURNAL OF MATHEMATICS Vol.3 (15) (2007), 137 143 SOME NOISELESS CODING THEOREMS OF INACCURACY MEASURE OF ORDER α AND TYPE β M. A. K. BAIG AND RAYEES AHMAD DAR Absrac. In hs paper, we propose
SARAJEVO JOURNAL OF MATHEMATICS Vol.3 (15) (2007), 137 143 SOME NOISELESS CODING THEOREMS OF INACCURACY MEASURE OF ORDER α AND TYPE β M. A. K. BAIG AND RAYEES AHMAD DAR Absrac. In hs paper, we propose
Relative controllability of nonlinear systems with delays in control
 Relave conrollably o nonlnear sysems wh delays n conrol Jerzy Klamka Insue o Conrol Engneerng, Slesan Techncal Unversy, 44- Glwce, Poland. phone/ax : 48 32 37227, {jklamka}@a.polsl.glwce.pl Keywor: Conrollably.
Relave conrollably o nonlnear sysems wh delays n conrol Jerzy Klamka Insue o Conrol Engneerng, Slesan Techncal Unversy, 44- Glwce, Poland. phone/ax : 48 32 37227, {jklamka}@a.polsl.glwce.pl Keywor: Conrollably.
Approximate Analytic Solution of (2+1) - Dimensional Zakharov-Kuznetsov(Zk) Equations Using Homotopy
 Arcle Inernaonal Journal of Modern Mahemacal Scences, 4, (): - Inernaonal Journal of Modern Mahemacal Scences Journal homepage: www.modernscenfcpress.com/journals/jmms.aspx ISSN: 66-86X Florda, USA Approxmae
Arcle Inernaonal Journal of Modern Mahemacal Scences, 4, (): - Inernaonal Journal of Modern Mahemacal Scences Journal homepage: www.modernscenfcpress.com/journals/jmms.aspx ISSN: 66-86X Florda, USA Approxmae
Solution in semi infinite diffusion couples (error function analysis)
 Soluon n sem nfne dffuson couples (error funcon analyss) Le us consder now he sem nfne dffuson couple of wo blocks wh concenraon of and I means ha, n a A- bnary sysem, s bondng beween wo blocks made of
Soluon n sem nfne dffuson couples (error funcon analyss) Le us consder now he sem nfne dffuson couple of wo blocks wh concenraon of and I means ha, n a A- bnary sysem, s bondng beween wo blocks made of
A Demand System for Input Factors when there are Technological Changes in Production
 A Demand Syem for Inpu Facor when here are Technologcal Change n Producon Movaon Due o (e.g.) echnologcal change here mgh no be a aonary relaonhp for he co hare of each npu facor. When emang demand yem
A Demand Syem for Inpu Facor when here are Technologcal Change n Producon Movaon Due o (e.g.) echnologcal change here mgh no be a aonary relaonhp for he co hare of each npu facor. When emang demand yem
Linear Response Theory: The connection between QFT and experiments
 Phys540.nb 39 3 Lnear Response Theory: The connecon beween QFT and expermens 3.1. Basc conceps and deas Q: ow do we measure he conducvy of a meal? A: we frs nroduce a weak elecrc feld E, and hen measure
Phys540.nb 39 3 Lnear Response Theory: The connecon beween QFT and expermens 3.1. Basc conceps and deas Q: ow do we measure he conducvy of a meal? A: we frs nroduce a weak elecrc feld E, and hen measure
Track Properities of Normal Chain
 In. J. Conemp. Mah. Scences, Vol. 8, 213, no. 4, 163-171 HIKARI Ld, www.m-har.com rac Propes of Normal Chan L Chen School of Mahemacs and Sascs, Zhengzhou Normal Unversy Zhengzhou Cy, Hennan Provnce, 4544,
In. J. Conemp. Mah. Scences, Vol. 8, 213, no. 4, 163-171 HIKARI Ld, www.m-har.com rac Propes of Normal Chan L Chen School of Mahemacs and Sascs, Zhengzhou Normal Unversy Zhengzhou Cy, Hennan Provnce, 4544,
, the. L and the L. x x. max. i n. It is easy to show that these two norms satisfy the following relation: x x n x = (17.3) max
 ecure 8 7. Sabiliy Analyi For an n dimenional vecor R n, he and he vecor norm are defined a: = T = i n i (7.) I i eay o how ha hee wo norm aify he following relaion: n (7.) If a vecor i ime-dependen, hen
ecure 8 7. Sabiliy Analyi For an n dimenional vecor R n, he and he vecor norm are defined a: = T = i n i (7.) I i eay o how ha hee wo norm aify he following relaion: n (7.) If a vecor i ime-dependen, hen
Survival Analysis and Reliability. A Note on the Mean Residual Life Function of a Parallel System
 Communcaons n Sascs Theory and Mehods, 34: 475 484, 2005 Copyrgh Taylor & Francs, Inc. ISSN: 0361-0926 prn/1532-415x onlne DOI: 10.1081/STA-200047430 Survval Analyss and Relably A Noe on he Mean Resdual
Communcaons n Sascs Theory and Mehods, 34: 475 484, 2005 Copyrgh Taylor & Francs, Inc. ISSN: 0361-0926 prn/1532-415x onlne DOI: 10.1081/STA-200047430 Survval Analyss and Relably A Noe on he Mean Resdual
Mechanics Physics 151
 Mechancs Physcs 5 Lecure 9 Hamlonan Equaons of Moon (Chaper 8) Wha We Dd Las Tme Consruced Hamlonan formalsm H ( q, p, ) = q p L( q, q, ) H p = q H q = p H = L Equvalen o Lagrangan formalsm Smpler, bu
Mechancs Physcs 5 Lecure 9 Hamlonan Equaons of Moon (Chaper 8) Wha We Dd Las Tme Consruced Hamlonan formalsm H ( q, p, ) = q p L( q, q, ) H p = q H q = p H = L Equvalen o Lagrangan formalsm Smpler, bu
Lecture 18: The Laplace Transform (See Sections and 14.7 in Boas)
 Lecure 8: The Lalace Transform (See Secons 88- and 47 n Boas) Recall ha our bg-cure goal s he analyss of he dfferenal equaon, ax bx cx F, where we emloy varous exansons for he drvng funcon F deendng on
Lecure 8: The Lalace Transform (See Secons 88- and 47 n Boas) Recall ha our bg-cure goal s he analyss of he dfferenal equaon, ax bx cx F, where we emloy varous exansons for he drvng funcon F deendng on
Let s treat the problem of the response of a system to an applied external force. Again,
 Page 33 QUANTUM LNEAR RESPONSE FUNCTON Le s rea he problem of he response of a sysem o an appled exernal force. Agan, H() H f () A H + V () Exernal agen acng on nernal varable Hamlonan for equlbrum sysem
Page 33 QUANTUM LNEAR RESPONSE FUNCTON Le s rea he problem of he response of a sysem o an appled exernal force. Agan, H() H f () A H + V () Exernal agen acng on nernal varable Hamlonan for equlbrum sysem
Laplace Transformation of Linear Time-Varying Systems
 Laplace Tranformaon of Lnear Tme-Varyng Syem Shervn Erfan Reearch Cenre for Inegraed Mcroelecronc Elecrcal and Compuer Engneerng Deparmen Unvery of Wndor Wndor, Onaro N9B 3P4, Canada Aug. 4, 9 Oulne of
Laplace Tranformaon of Lnear Tme-Varyng Syem Shervn Erfan Reearch Cenre for Inegraed Mcroelecronc Elecrcal and Compuer Engneerng Deparmen Unvery of Wndor Wndor, Onaro N9B 3P4, Canada Aug. 4, 9 Oulne of
Mechanics Physics 151
 Mechancs Physcs 5 Lecure 9 Hamlonan Equaons of Moon (Chaper 8) Wha We Dd Las Tme Consruced Hamlonan formalsm Hqp (,,) = qp Lqq (,,) H p = q H q = p H L = Equvalen o Lagrangan formalsm Smpler, bu wce as
Mechancs Physcs 5 Lecure 9 Hamlonan Equaons of Moon (Chaper 8) Wha We Dd Las Tme Consruced Hamlonan formalsm Hqp (,,) = qp Lqq (,,) H p = q H q = p H L = Equvalen o Lagrangan formalsm Smpler, bu wce as
Randomized Perfect Bipartite Matching
 Inenive Algorihm Lecure 24 Randomized Perfec Biparie Maching Lecurer: Daniel A. Spielman April 9, 208 24. Inroducion We explain a randomized algorihm by Ahih Goel, Michael Kapralov and Sanjeev Khanna for
Inenive Algorihm Lecure 24 Randomized Perfec Biparie Maching Lecurer: Daniel A. Spielman April 9, 208 24. Inroducion We explain a randomized algorihm by Ahih Goel, Michael Kapralov and Sanjeev Khanna for
Appendix H: Rarefaction and extrapolation of Hill numbers for incidence data
 Anne Chao Ncholas J Goell C seh lzabeh L ander K Ma Rober K Colwell and Aaron M llson 03 Rarefacon and erapolaon wh ll numbers: a framewor for samplng and esmaon n speces dversy sudes cology Monographs
Anne Chao Ncholas J Goell C seh lzabeh L ander K Ma Rober K Colwell and Aaron M llson 03 Rarefacon and erapolaon wh ll numbers: a framewor for samplng and esmaon n speces dversy sudes cology Monographs
Notes on the stability of dynamic systems and the use of Eigen Values.
 Noes on he sabl of dnamc ssems and he use of Egen Values. Source: Macro II course noes, Dr. Davd Bessler s Tme Seres course noes, zarads (999) Ineremporal Macroeconomcs chaper 4 & Techncal ppend, and Hamlon
Noes on he sabl of dnamc ssems and he use of Egen Values. Source: Macro II course noes, Dr. Davd Bessler s Tme Seres course noes, zarads (999) Ineremporal Macroeconomcs chaper 4 & Techncal ppend, and Hamlon
Chapter 6: AC Circuits
 Chaper 6: AC Crcus Chaper 6: Oulne Phasors and he AC Seady Sae AC Crcus A sable, lnear crcu operang n he seady sae wh snusodal excaon (.e., snusodal seady sae. Complee response forced response naural response.
Chaper 6: AC Crcus Chaper 6: Oulne Phasors and he AC Seady Sae AC Crcus A sable, lnear crcu operang n he seady sae wh snusodal excaon (.e., snusodal seady sae. Complee response forced response naural response.
CS434a/541a: Pattern Recognition Prof. Olga Veksler. Lecture 4
 CS434a/54a: Paern Recognon Prof. Olga Veksler Lecure 4 Oulne Normal Random Varable Properes Dscrmnan funcons Why Normal Random Varables? Analycally racable Works well when observaon comes form a corruped
CS434a/54a: Paern Recognon Prof. Olga Veksler Lecure 4 Oulne Normal Random Varable Properes Dscrmnan funcons Why Normal Random Varables? Analycally racable Works well when observaon comes form a corruped
( ) [ ] MAP Decision Rule
![( ) [ ] MAP Decision Rule ( ) [ ] MAP Decision Rule](/thumbs/82/84970741.jpg) Announcemens Bayes Decson Theory wh Normal Dsrbuons HW0 due oday HW o be assgned soon Proec descrpon posed Bomercs CSE 90 Lecure 4 CSE90, Sprng 04 CSE90, Sprng 04 Key Probables 4 ω class label X feaure
Announcemens Bayes Decson Theory wh Normal Dsrbuons HW0 due oday HW o be assgned soon Proec descrpon posed Bomercs CSE 90 Lecure 4 CSE90, Sprng 04 CSE90, Sprng 04 Key Probables 4 ω class label X feaure
Lecture 11: Stereo and Surface Estimation
 Lecure : Sereo and Surface Emaon When camera poon have been deermned, ung rucure from moon, we would lke o compue a dene urface model of he cene. In h lecure we wll udy he o called Sereo Problem, where
Lecure : Sereo and Surface Emaon When camera poon have been deermned, ung rucure from moon, we would lke o compue a dene urface model of he cene. In h lecure we wll udy he o called Sereo Problem, where
NONLOCAL BOUNDARY VALUE PROBLEM FOR SECOND ORDER ANTI-PERIODIC NONLINEAR IMPULSIVE q k INTEGRODIFFERENCE EQUATION
 Euroean Journal of ahemac an Comuer Scence Vol No 7 ISSN 59-995 NONLOCAL BOUNDARY VALUE PROBLE FOR SECOND ORDER ANTI-PERIODIC NONLINEAR IPULSIVE - INTEGRODIFFERENCE EQUATION Hao Wang Yuhang Zhang ngyang
Euroean Journal of ahemac an Comuer Scence Vol No 7 ISSN 59-995 NONLOCAL BOUNDARY VALUE PROBLE FOR SECOND ORDER ANTI-PERIODIC NONLINEAR IPULSIVE - INTEGRODIFFERENCE EQUATION Hao Wang Yuhang Zhang ngyang
Mechanics Physics 151
 Mechancs Physcs 5 Lecure 0 Canoncal Transformaons (Chaper 9) Wha We Dd Las Tme Hamlon s Prncple n he Hamlonan formalsm Dervaon was smple δi δ Addonal end-pon consrans pq H( q, p, ) d 0 δ q ( ) δq ( ) δ
Mechancs Physcs 5 Lecure 0 Canoncal Transformaons (Chaper 9) Wha We Dd Las Tme Hamlon s Prncple n he Hamlonan formalsm Dervaon was smple δi δ Addonal end-pon consrans pq H( q, p, ) d 0 δ q ( ) δq ( ) δ
Scattering at an Interface: Oblique Incidence
 Course Insrucor Dr. Raymond C. Rumpf Offce: A 337 Phone: (915) 747 6958 E Mal: rcrumpf@uep.edu EE 4347 Appled Elecromagnecs Topc 3g Scaerng a an Inerface: Oblque Incdence Scaerng These Oblque noes may
Course Insrucor Dr. Raymond C. Rumpf Offce: A 337 Phone: (915) 747 6958 E Mal: rcrumpf@uep.edu EE 4347 Appled Elecromagnecs Topc 3g Scaerng a an Inerface: Oblque Incdence Scaerng These Oblque noes may
John Geweke a and Gianni Amisano b a Departments of Economics and Statistics, University of Iowa, USA b European Central Bank, Frankfurt, Germany
 Herarchcal Markov Normal Mxure models wh Applcaons o Fnancal Asse Reurns Appendx: Proofs of Theorems and Condonal Poseror Dsrbuons John Geweke a and Gann Amsano b a Deparmens of Economcs and Sascs, Unversy
Herarchcal Markov Normal Mxure models wh Applcaons o Fnancal Asse Reurns Appendx: Proofs of Theorems and Condonal Poseror Dsrbuons John Geweke a and Gann Amsano b a Deparmens of Economcs and Sascs, Unversy
Discrete time approximation of decoupled Forward-Backward SDE with jumps
 Dscree me approxmaon of decoupled Forward-Backward SD wh jumps Bruno Bouchard, Romuald le To ce hs verson: Bruno Bouchard, Romuald le Dscree me approxmaon of decoupled Forward-Backward SD wh jumps Sochasc
Dscree me approxmaon of decoupled Forward-Backward SD wh jumps Bruno Bouchard, Romuald le To ce hs verson: Bruno Bouchard, Romuald le Dscree me approxmaon of decoupled Forward-Backward SD wh jumps Sochasc
Discrete Time Approximation and Monte-Carlo Simulation of Backward Stochastic Differential Equations
 Dscree Tme Approxmaon and Mone-Carlo Smulaon of Backward Sochasc Dfferenal Equaons Bruno Bouchard Unversé Pars VI, PMA, and CREST Pars, France bouchard@ccrjusseufr Nzar Touz CREST Pars, France ouz@ensaefr
Dscree Tme Approxmaon and Mone-Carlo Smulaon of Backward Sochasc Dfferenal Equaons Bruno Bouchard Unversé Pars VI, PMA, and CREST Pars, France bouchard@ccrjusseufr Nzar Touz CREST Pars, France ouz@ensaefr
Graduate Macroeconomics 2 Problem set 5. - Solutions
 Graduae Macroeconomcs 2 Problem se. - Soluons Queson 1 To answer hs queson we need he frms frs order condons and he equaon ha deermnes he number of frms n equlbrum. The frms frs order condons are: F K
Graduae Macroeconomcs 2 Problem se. - Soluons Queson 1 To answer hs queson we need he frms frs order condons and he equaon ha deermnes he number of frms n equlbrum. The frms frs order condons are: F K
Testing a new idea to solve the P = NP problem with mathematical induction
 Tesng a new dea o solve he P = NP problem wh mahemacal nducon Bacground P and NP are wo classes (ses) of languages n Compuer Scence An open problem s wheher P = NP Ths paper ess a new dea o compare he
Tesng a new dea o solve he P = NP problem wh mahemacal nducon Bacground P and NP are wo classes (ses) of languages n Compuer Scence An open problem s wheher P = NP Ths paper ess a new dea o compare he
New Oscillation Results for Forced Second Order Differential Equations with Mixed Nonlinearities
 Appled Maheac,, 3, 47-53 hp://dxdoorg/436/a33 Publhed Onlne February (hp://wwwscrporg/ournal/a) New Ocllaon Reul for Forced Second Order Dfferenal Equaon wh Mxed Nonlneare Ercan Tunç, Adl Kayaz Deparen
Appled Maheac,, 3, 47-53 hp://dxdoorg/436/a33 Publhed Onlne February (hp://wwwscrporg/ournal/a) New Ocllaon Reul for Forced Second Order Dfferenal Equaon wh Mxed Nonlneare Ercan Tunç, Adl Kayaz Deparen
Variants of Pegasos. December 11, 2009
 Inroducon Varans of Pegasos SooWoong Ryu bshboy@sanford.edu December, 009 Youngsoo Cho yc344@sanford.edu Developng a new SVM algorhm s ongong research opc. Among many exng SVM algorhms, we wll focus on
Inroducon Varans of Pegasos SooWoong Ryu bshboy@sanford.edu December, 009 Youngsoo Cho yc344@sanford.edu Developng a new SVM algorhm s ongong research opc. Among many exng SVM algorhms, we wll focus on
Existence of Time Periodic Solutions for the Ginzburg-Landau Equations. model of superconductivity
 Journal of Mahemacal Analyss and Applcaons 3, 3944 999 Arcle ID jmaa.999.683, avalable onlne a hp:www.dealbrary.com on Exsence of me Perodc Soluons for he Gnzburg-Landau Equaons of Superconducvy Bxang
Journal of Mahemacal Analyss and Applcaons 3, 3944 999 Arcle ID jmaa.999.683, avalable onlne a hp:www.dealbrary.com on Exsence of me Perodc Soluons for he Gnzburg-Landau Equaons of Superconducvy Bxang
. The geometric multiplicity is dim[ker( λi. number of linearly independent eigenvectors associated with this eigenvalue.
 Lnear Algebra Lecure # Noes We connue wh he dscusson of egenvalues, egenvecors, and dagonalzably of marces We wan o know, n parcular wha condons wll assure ha a marx can be dagonalzed and wha he obsrucons
Lnear Algebra Lecure # Noes We connue wh he dscusson of egenvalues, egenvecors, and dagonalzably of marces We wan o know, n parcular wha condons wll assure ha a marx can be dagonalzed and wha he obsrucons
HEAT CONDUCTION PROBLEM IN A TWO-LAYERED HOLLOW CYLINDER BY USING THE GREEN S FUNCTION METHOD
 Journal of Appled Mahemacs and Compuaonal Mechancs 3, (), 45-5 HEAT CONDUCTION PROBLEM IN A TWO-LAYERED HOLLOW CYLINDER BY USING THE GREEN S FUNCTION METHOD Sansław Kukla, Urszula Sedlecka Insue of Mahemacs,
Journal of Appled Mahemacs and Compuaonal Mechancs 3, (), 45-5 HEAT CONDUCTION PROBLEM IN A TWO-LAYERED HOLLOW CYLINDER BY USING THE GREEN S FUNCTION METHOD Sansław Kukla, Urszula Sedlecka Insue of Mahemacs,
On One Analytic Method of. Constructing Program Controls
 Appled Mahemacal Scences, Vol. 9, 05, no. 8, 409-407 HIKARI Ld, www.m-hkar.com hp://dx.do.org/0.988/ams.05.54349 On One Analyc Mehod of Consrucng Program Conrols A. N. Kvko, S. V. Chsyakov and Yu. E. Balyna
Appled Mahemacal Scences, Vol. 9, 05, no. 8, 409-407 HIKARI Ld, www.m-hkar.com hp://dx.do.org/0.988/ams.05.54349 On One Analyc Mehod of Consrucng Program Conrols A. N. Kvko, S. V. Chsyakov and Yu. E. Balyna
. The geometric multiplicity is dim[ker( λi. A )], i.e. the number of linearly independent eigenvectors associated with this eigenvalue.
![. The geometric multiplicity is dim[ker( λi. A )], i.e. the number of linearly independent eigenvectors associated with this eigenvalue. . The geometric multiplicity is dim[ker( λi. A )], i.e. the number of linearly independent eigenvectors associated with this eigenvalue.](/thumbs/78/77822798.jpg) Mah E-b Lecure #0 Noes We connue wh he dscusson of egenvalues, egenvecors, and dagonalzably of marces We wan o know, n parcular wha condons wll assure ha a marx can be dagonalzed and wha he obsrucons are
Mah E-b Lecure #0 Noes We connue wh he dscusson of egenvalues, egenvecors, and dagonalzably of marces We wan o know, n parcular wha condons wll assure ha a marx can be dagonalzed and wha he obsrucons are
Lecture 6: Learning for Control (Generalised Linear Regression)
 Lecure 6: Learnng for Conrol (Generalsed Lnear Regresson) Conens: Lnear Mehods for Regresson Leas Squares, Gauss Markov heorem Recursve Leas Squares Lecure 6: RLSC - Prof. Sehu Vjayakumar Lnear Regresson
Lecure 6: Learnng for Conrol (Generalsed Lnear Regresson) Conens: Lnear Mehods for Regresson Leas Squares, Gauss Markov heorem Recursve Leas Squares Lecure 6: RLSC - Prof. Sehu Vjayakumar Lnear Regresson
@FMI c Kyung Moon Sa Co.
 Annals of Fuzzy Mahemacs and Informacs Volume 8, No. 2, (Augus 2014), pp. 245 257 ISSN: 2093 9310 (prn verson) ISSN: 2287 6235 (elecronc verson) hp://www.afm.or.kr @FMI c Kyung Moon Sa Co. hp://www.kyungmoon.com
Annals of Fuzzy Mahemacs and Informacs Volume 8, No. 2, (Augus 2014), pp. 245 257 ISSN: 2093 9310 (prn verson) ISSN: 2287 6235 (elecronc verson) hp://www.afm.or.kr @FMI c Kyung Moon Sa Co. hp://www.kyungmoon.com
Optimal Filtering for Linear Discrete-Time Systems with Single Delayed Measurement
 378 Hong-Guo Inernaonal Zhao, Journal Huan-Shu of Conrol, Zhang, Auomaon, Cheng-Hu an Zhang, Syem, an vol. Xn-Mn 6, no. Song 3, pp. 378-385, June 28 Opmal Flerng for Lnear Dcree-me Syem h Sngle Delaye
378 Hong-Guo Inernaonal Zhao, Journal Huan-Shu of Conrol, Zhang, Auomaon, Cheng-Hu an Zhang, Syem, an vol. Xn-Mn 6, no. Song 3, pp. 378-385, June 28 Opmal Flerng for Lnear Dcree-me Syem h Sngle Delaye
In the complete model, these slopes are ANALYSIS OF VARIANCE FOR THE COMPLETE TWO-WAY MODEL. (! i+1 -! i ) + [(!") i+1,q - [(!
 ANALYSIS OF VARIANCE FOR THE COMPLETE TWO-WAY MODEL The frs hng o es n wo-way ANOVA: Is here neracon? "No neracon" means: The man effecs model would f. Ths n urn means: In he neracon plo (wh A on he horzonal
ANALYSIS OF VARIANCE FOR THE COMPLETE TWO-WAY MODEL The frs hng o es n wo-way ANOVA: Is here neracon? "No neracon" means: The man effecs model would f. Ths n urn means: In he neracon plo (wh A on he horzonal
Robustness Experiments with Two Variance Components
 Naonal Insue of Sandards and Technology (NIST) Informaon Technology Laboraory (ITL) Sascal Engneerng Dvson (SED) Robusness Expermens wh Two Varance Componens by Ana Ivelsse Avlés avles@ns.gov Conference
Naonal Insue of Sandards and Technology (NIST) Informaon Technology Laboraory (ITL) Sascal Engneerng Dvson (SED) Robusness Expermens wh Two Varance Componens by Ana Ivelsse Avlés avles@ns.gov Conference
2/20/2013. EE 101 Midterm 2 Review
 //3 EE Mderm eew //3 Volage-mplfer Model The npu ressance s he equalen ressance see when lookng no he npu ermnals of he amplfer. o s he oupu ressance. I causes he oupu olage o decrease as he load ressance
//3 EE Mderm eew //3 Volage-mplfer Model The npu ressance s he equalen ressance see when lookng no he npu ermnals of he amplfer. o s he oupu ressance. I causes he oupu olage o decrease as he load ressance
NON-HOMOGENEOUS SEMI-MARKOV REWARD PROCESS FOR THE MANAGEMENT OF HEALTH INSURANCE MODELS.
 NON-HOOGENEOU EI-AKO EWA POCE FO THE ANAGEENT OF HEATH INUANCE OE. Jacque Janen CEIAF ld Paul Janon 84 e 9 6 Charlero EGIU Fax: 32735877 E-mal: ceaf@elgacom.ne and amondo anca Unverà a apenza parmeno d
NON-HOOGENEOU EI-AKO EWA POCE FO THE ANAGEENT OF HEATH INUANCE OE. Jacque Janen CEIAF ld Paul Janon 84 e 9 6 Charlero EGIU Fax: 32735877 E-mal: ceaf@elgacom.ne and amondo anca Unverà a apenza parmeno d
UNIVERSITAT AUTÒNOMA DE BARCELONA MARCH 2017 EXAMINATION
 INTERNATIONAL TRADE T. J. KEHOE UNIVERSITAT AUTÒNOMA DE BARCELONA MARCH 27 EXAMINATION Please answer wo of he hree quesons. You can consul class noes, workng papers, and arcles whle you are workng on he
INTERNATIONAL TRADE T. J. KEHOE UNIVERSITAT AUTÒNOMA DE BARCELONA MARCH 27 EXAMINATION Please answer wo of he hree quesons. You can consul class noes, workng papers, and arcles whle you are workng on he
Should Exact Index Numbers have Standard Errors? Theory and Application to Asian Growth
 Should Exac Index umbers have Sandard Errors? Theory and Applcaon o Asan Growh Rober C. Feensra Marshall B. Rensdorf ovember 003 Proof of Proposon APPEDIX () Frs, we wll derve he convenonal Sao-Vara prce
Should Exac Index umbers have Sandard Errors? Theory and Applcaon o Asan Growh Rober C. Feensra Marshall B. Rensdorf ovember 003 Proof of Proposon APPEDIX () Frs, we wll derve he convenonal Sao-Vara prce
China s Model of Managing the Financial System
 Chna odel of anagng he Fnancal Syem arku K Brunnermeer chael Sockn We Xong Inerne Appendx Th nerne appendx preen proof of he propoon n he man paper Proof of Propoon A We dere he perfec nformaon equlbrum
Chna odel of anagng he Fnancal Syem arku K Brunnermeer chael Sockn We Xong Inerne Appendx Th nerne appendx preen proof of he propoon n he man paper Proof of Propoon A We dere he perfec nformaon equlbrum
Ordinary Differential Equations in Neuroscience with Matlab examples. Aim 1- Gain understanding of how to set up and solve ODE s
 Ordnary Dfferenal Equaons n Neuroscence wh Malab eamples. Am - Gan undersandng of how o se up and solve ODE s Am Undersand how o se up an solve a smple eample of he Hebb rule n D Our goal a end of class
Ordnary Dfferenal Equaons n Neuroscence wh Malab eamples. Am - Gan undersandng of how o se up and solve ODE s Am Undersand how o se up an solve a smple eample of he Hebb rule n D Our goal a end of class
Generalized Snell envelope and BSDE With Two general Reflecting Barriers
 1/22 Generalized Snell envelope and BSDE Wih Two general Reflecing Barriers EL HASSAN ESSAKY Cadi ayyad Universiy Poly-disciplinary Faculy Safi Work in progress wih : M. Hassani and Y. Ouknine Iasi, July
1/22 Generalized Snell envelope and BSDE Wih Two general Reflecing Barriers EL HASSAN ESSAKY Cadi ayyad Universiy Poly-disciplinary Faculy Safi Work in progress wih : M. Hassani and Y. Ouknine Iasi, July
Performance Analysis for a Network having Standby Redundant Unit with Waiting in Repair
 TECHNI Inernaonal Journal of Compung Scence Communcaon Technologes VOL.5 NO. July 22 (ISSN 974-3375 erformance nalyss for a Nework havng Sby edundan Un wh ang n epar Jendra Sngh 2 abns orwal 2 Deparmen
TECHNI Inernaonal Journal of Compung Scence Communcaon Technologes VOL.5 NO. July 22 (ISSN 974-3375 erformance nalyss for a Nework havng Sby edundan Un wh ang n epar Jendra Sngh 2 abns orwal 2 Deparmen
Density Matrix Description of NMR BCMB/CHEM 8190
 Densy Marx Descrpon of NMR BCMBCHEM 89 Operaors n Marx Noaon Alernae approach o second order specra: ask abou x magnezaon nsead of energes and ranson probables. If we say wh one bass se, properes vary
Densy Marx Descrpon of NMR BCMBCHEM 89 Operaors n Marx Noaon Alernae approach o second order specra: ask abou x magnezaon nsead of energes and ranson probables. If we say wh one bass se, properes vary
Multiple Failures. Diverse Routing for Maximizing Survivability. Maximum Survivability Models. Minimum-Color (SRLG) Diverse Routing
 Mulple Falure Dvere Roung for Maxmzng Survvably One-falure aumpon n prevou work Mulple falure Hard o provde 100% proecon Maxmum urvvably Maxmum Survvably Model Mnmum-Color (SRLG) Dvere Roung Each lnk ha
Mulple Falure Dvere Roung for Maxmzng Survvably One-falure aumpon n prevou work Mulple falure Hard o provde 100% proecon Maxmum urvvably Maxmum Survvably Model Mnmum-Color (SRLG) Dvere Roung Each lnk ha
Density Matrix Description of NMR BCMB/CHEM 8190
 Densy Marx Descrpon of NMR BCMBCHEM 89 Operaors n Marx Noaon If we say wh one bass se, properes vary only because of changes n he coeffcens weghng each bass se funcon x = h< Ix > - hs s how we calculae
Densy Marx Descrpon of NMR BCMBCHEM 89 Operaors n Marx Noaon If we say wh one bass se, properes vary only because of changes n he coeffcens weghng each bass se funcon x = h< Ix > - hs s how we calculae
FUZZY n-inner PRODUCT SPACE
 Bull. Korean Mah. Soc. 43 (2007), No. 3, pp. 447 459 FUZZY n-inner PRODUCT SPACE Srinivaan Vijayabalaji and Naean Thillaigovindan Reprined from he Bullein of he Korean Mahemaical Sociey Vol. 43, No. 3,
Bull. Korean Mah. Soc. 43 (2007), No. 3, pp. 447 459 FUZZY n-inner PRODUCT SPACE Srinivaan Vijayabalaji and Naean Thillaigovindan Reprined from he Bullein of he Korean Mahemaical Sociey Vol. 43, No. 3,
How about the more general "linear" scalar functions of scalars (i.e., a 1st degree polynomial of the following form with a constant term )?
 lmcd Lnear ransformaon of a vecor he deas presened here are que general hey go beyond he radonal mar-vecor ype seen n lnear algebra Furhermore, hey do no deal wh bass and are equally vald for any se of
lmcd Lnear ransformaon of a vecor he deas presened here are que general hey go beyond he radonal mar-vecor ype seen n lnear algebra Furhermore, hey do no deal wh bass and are equally vald for any se of
Lecture VI Regression
 Lecure VI Regresson (Lnear Mehods for Regresson) Conens: Lnear Mehods for Regresson Leas Squares, Gauss Markov heorem Recursve Leas Squares Lecure VI: MLSC - Dr. Sehu Vjayakumar Lnear Regresson Model M
Lecure VI Regresson (Lnear Mehods for Regresson) Conens: Lnear Mehods for Regresson Leas Squares, Gauss Markov heorem Recursve Leas Squares Lecure VI: MLSC - Dr. Sehu Vjayakumar Lnear Regresson Model M
[ ] 2. [ ]3 + (Δx i + Δx i 1 ) / 2. Δx i-1 Δx i Δx i+1. TPG4160 Reservoir Simulation 2018 Lecture note 3. page 1 of 5
![[ ] 2. [ ]3 + (Δx i + Δx i 1 ) / 2. Δx i-1 Δx i Δx i+1. TPG4160 Reservoir Simulation 2018 Lecture note 3. page 1 of 5 [ ] 2. [ ]3 + (Δx i + Δx i 1 ) / 2. Δx i-1 Δx i Δx i+1. TPG4160 Reservoir Simulation 2018 Lecture note 3. page 1 of 5](/thumbs/85/92299540.jpg) TPG460 Reservor Smulaon 08 page of 5 DISCRETIZATIO OF THE FOW EQUATIOS As we already have seen, fne dfference appromaons of he paral dervaves appearng n he flow equaons may be obaned from Taylor seres
TPG460 Reservor Smulaon 08 page of 5 DISCRETIZATIO OF THE FOW EQUATIOS As we already have seen, fne dfference appromaons of he paral dervaves appearng n he flow equaons may be obaned from Taylor seres
FLAT CYCLOTOMIC POLYNOMIALS OF ORDER FOUR AND HIGHER
 #A30 INTEGERS 10 (010), 357-363 FLAT CYCLOTOMIC POLYNOMIALS OF ORDER FOUR AND HIGHER Nahan Kaplan Deparmen of Mahemaic, Harvard Univeriy, Cambridge, MA nkaplan@mah.harvard.edu Received: 7/15/09, Revied:
#A30 INTEGERS 10 (010), 357-363 FLAT CYCLOTOMIC POLYNOMIALS OF ORDER FOUR AND HIGHER Nahan Kaplan Deparmen of Mahemaic, Harvard Univeriy, Cambridge, MA nkaplan@mah.harvard.edu Received: 7/15/09, Revied:
Chapter Lagrangian Interpolation
 Chaper 5.4 agrangan Inerpolaon Afer readng hs chaper you should be able o:. dere agrangan mehod of nerpolaon. sole problems usng agrangan mehod of nerpolaon and. use agrangan nerpolans o fnd deraes and
Chaper 5.4 agrangan Inerpolaon Afer readng hs chaper you should be able o:. dere agrangan mehod of nerpolaon. sole problems usng agrangan mehod of nerpolaon and. use agrangan nerpolans o fnd deraes and
This article appeared in a journal published by Elsevier. The attached copy is furnished to the author for internal non-commercial research and
 hs arcle appeared n a journal publshed by Elsever. he aached copy s furnshed o he auhor for nernal non-commercal research and educaon use, ncludng for nsrucon a he auhors nsuon and sharng wh colleagues.
hs arcle appeared n a journal publshed by Elsever. he aached copy s furnshed o he auhor for nernal non-commercal research and educaon use, ncludng for nsrucon a he auhors nsuon and sharng wh colleagues.
TSS = SST + SSE An orthogonal partition of the total SS
 ANOVA: Topc 4. Orhogonal conrass [ST&D p. 183] H 0 : µ 1 = µ =... = µ H 1 : The mean of a leas one reamen group s dfferen To es hs hypohess, a basc ANOVA allocaes he varaon among reamen means (SST) equally
ANOVA: Topc 4. Orhogonal conrass [ST&D p. 183] H 0 : µ 1 = µ =... = µ H 1 : The mean of a leas one reamen group s dfferen To es hs hypohess, a basc ANOVA allocaes he varaon among reamen means (SST) equally
Fundamentals of PLLs (I)
 Phae-Locked Loop Fundamenal of PLL (I) Chng-Yuan Yang Naonal Chung-Hng Unvery Deparmen of Elecrcal Engneerng Why phae-lock? - Jer Supreon - Frequency Synhe T T + 1 - Skew Reducon T + 2 T + 3 PLL fou =
Phae-Locked Loop Fundamenal of PLL (I) Chng-Yuan Yang Naonal Chung-Hng Unvery Deparmen of Elecrcal Engneerng Why phae-lock? - Jer Supreon - Frequency Synhe T T + 1 - Skew Reducon T + 2 T + 3 PLL fou =
SSRG International Journal of Thermal Engineering (SSRG-IJTE) Volume 4 Issue 1 January to April 2018
 SSRG Inernaonal Journal of Thermal Engneerng (SSRG-IJTE) Volume 4 Iue 1 January o Aprl 18 Opmal Conrol for a Drbued Parameer Syem wh Tme-Delay, Non-Lnear Ung he Numercal Mehod. Applcaon o One- Sded Hea
SSRG Inernaonal Journal of Thermal Engneerng (SSRG-IJTE) Volume 4 Iue 1 January o Aprl 18 Opmal Conrol for a Drbued Parameer Syem wh Tme-Delay, Non-Lnear Ung he Numercal Mehod. Applcaon o One- Sded Hea
A New Generalized Gronwall-Bellman Type Inequality
 22 Inernaonal Conference on Image, Vson and Comung (ICIVC 22) IPCSIT vol. 5 (22) (22) IACSIT Press, Sngaore DOI:.7763/IPCSIT.22.V5.46 A New Generalzed Gronwall-Bellman Tye Ineualy Qnghua Feng School of
22 Inernaonal Conference on Image, Vson and Comung (ICIVC 22) IPCSIT vol. 5 (22) (22) IACSIT Press, Sngaore DOI:.7763/IPCSIT.22.V5.46 A New Generalzed Gronwall-Bellman Tye Ineualy Qnghua Feng School of
SELFSIMILAR PROCESSES WITH STATIONARY INCREMENTS IN THE SECOND WIENER CHAOS
 POBABILITY AD MATEMATICAL STATISTICS Vol., Fasc., pp. SELFSIMILA POCESSES WIT STATIOAY ICEMETS I TE SECOD WIEE CAOS BY M. M A E J I M A YOKOAMA AD C. A. T U D O LILLE Absrac. We sudy selfsmlar processes
POBABILITY AD MATEMATICAL STATISTICS Vol., Fasc., pp. SELFSIMILA POCESSES WIT STATIOAY ICEMETS I TE SECOD WIEE CAOS BY M. M A E J I M A YOKOAMA AD C. A. T U D O LILLE Absrac. We sudy selfsmlar processes
Robust and Accurate Cancer Classification with Gene Expression Profiling
 Robus and Accurae Cancer Classfcaon wh Gene Expresson Proflng (Compuaonal ysems Bology, 2005) Auhor: Hafeng L, Keshu Zhang, ao Jang Oulne Background LDA (lnear dscrmnan analyss) and small sample sze problem
Robus and Accurae Cancer Classfcaon wh Gene Expresson Proflng (Compuaonal ysems Bology, 2005) Auhor: Hafeng L, Keshu Zhang, ao Jang Oulne Background LDA (lnear dscrmnan analyss) and small sample sze problem
Explicit form of global solution to stochastic logistic differential equation and related topics
 SAISICS, OPIMIZAION AND INFOMAION COMPUING Sa., Opim. Inf. Compu., Vol. 5, March 17, pp 58 64. Publihed online in Inernaional Academic Pre (www.iapre.org) Explici form of global oluion o ochaic logiic
SAISICS, OPIMIZAION AND INFOMAION COMPUING Sa., Opim. Inf. Compu., Vol. 5, March 17, pp 58 64. Publihed online in Inernaional Academic Pre (www.iapre.org) Explici form of global oluion o ochaic logiic
Lecture 11 SVM cont
 Lecure SVM con. 0 008 Wha we have done so far We have esalshed ha we wan o fnd a lnear decson oundary whose margn s he larges We know how o measure he margn of a lnear decson oundary Tha s: he mnmum geomerc
Lecure SVM con. 0 008 Wha we have done so far We have esalshed ha we wan o fnd a lnear decson oundary whose margn s he larges We know how o measure he margn of a lnear decson oundary Tha s: he mnmum geomerc
Cubic Bezier Homotopy Function for Solving Exponential Equations
 Penerb Journal of Advanced Research n Compung and Applcaons ISSN (onlne: 46-97 Vol. 4, No.. Pages -8, 6 omoopy Funcon for Solvng Eponenal Equaons S. S. Raml *,,. Mohamad Nor,a, N. S. Saharzan,b and M.
Penerb Journal of Advanced Research n Compung and Applcaons ISSN (onlne: 46-97 Vol. 4, No.. Pages -8, 6 omoopy Funcon for Solvng Eponenal Equaons S. S. Raml *,,. Mohamad Nor,a, N. S. Saharzan,b and M.
