ACCEPTS HUGE FLORAL KEY TO LOWELL. Mrs, Walter Laid to Rest Yesterday
|
|
|
- Dortha Pope
- 5 years ago
- Views:
Transcription
1 $ j < < < > XXX Y Y Y 4% Y 6 -- Q Z )»-- [ Y Y Y & 4 j q - Y & Y j \ j j [ - - / - ) ) - - / j Y 72 - ) / X - j ) \ 7 9 Y Y 2 3» - ««> Y Y Y 4 5 « j Y 6 7 «- >«««X 5 35 Y 8 » - «5 35 Y Y 9 X j Q ) j 35 j j z 3 z > -j«{ 35 z j Q j 5 28 q z - X \ \ - ) j ) ) 3- - $2 --{-4-< > - Y Y - Y 5 j $ $5 / Y X < - j Y
2 <{> > - - «- - ) / - - j \ - Y Y $2 $ 5 ///Z /) Y j Y ) - - Y - j $3 $ Y z - z Q - q z - - j Y - - Y 269 «- $ j) { { > j7 Z Y q j j & - & j & /- / _ - - j /Y/ >) «> - / j ) j - - q» - \ \ > jj j ) < - \ - -j - - < < - j - - Y - > j» Y j z \ < \ j > 2 - j _ > 4 j - - / j j j ) j j 3 - ) j - - ) > \ \ «> -» » - 2 Z j ) z - - j - - z < Q - 2) 7 Y 3 ) - j < z j \ \ j j \ ) 78 $25) ) z -z q > - z - 8 z - ) z - - ) - - j $)5 - - j \ Y z j Y z» j q ) ) j < « z - j j j - Y - $ YY «/ $25 $35 > \ -- ) - z Z -» <4-4 4 < 4 > ] Y & [ - j - 3 Y ) «8» ) Y Y > - - ) - ] z j 9 & q z z - $8 - - z $3 z j q Y - - Y X ) { - j 25 j ) Y - j ) j ) j - j Y - j - Y ) - j [ 25 )] ) - j - j j q ZY j j - Y j «« < -- X> < < j j q ) 92) j )
3 j _j)- ) - j - ] ) - )) 5 > j Y z > $ 4 5 j» > Y 8 < <j Z j Y 3 Y Y Q 935 / z z 6 / 7 j 245 j q - q j - j > Z z \ Y j Y j z j < ) /-- Q Q Q Y z j Y q j j - - Y - Y j - q Y j - ) - - «- j j ) q j j z & 23 &&» - - z 25 ) ) Y 928 ) z /j X - 22 z - Y Y Y j j 2 j 7 - Q Y Y 4 Y zz Y Y Y» - - )/ Y j Q Y Y ) - -X Y Y z ) j / - z -----{{-«- z Y - - z Y q Q ) < q j 8- q 2 j > )-»» Y 34 5 ) \ j ) Y 25 Y - 25 q / 2 8 / / - z - z q z [ z - ) - - ) j j 3 j - j )X j ) - z - j z - 7~ ~ - ) -»28 j - < j ) - ) - - j - q j ) 7 - % - - q ) > { - > j < / } j ) - j j - ) > % 7-4- \ - j j j»«z/
4 ) 8) > «- - \ j - <- j < j j - < - q - - j - - Z j) Y > <> X «> - «-» j > 4 ] - Q»- - «- / - )3 - - ) q q - - j - Y } X j - - < q Y 8 Y q z j j - j X \ - z < z q z - - & j «<> j j < j «- 6-8 > z - j \< \ j - - z z < j - - j X- - z q - - j > j > - - > - > - - q j q q [ j - j - z Y Y ) - - ] z 928 j - j - < - - & - «- - Q 3 ) j «- 5) ) q - - ] - - j ) - - j j - 2 ) ) - -- j ) j z q - 9) ) j z z X - - q $ & _ - j 68- -< 9-24 ) X8 z - j Q Z Y Y Q Q 23 Y - 23 ) q j \ - - X j ) \ j ) ) < ) ) < )2)) ) - - j > - - «-> < ) j q - - ) Y z ) - q 3 q j - q 5 j «22-23) z 2-77 Y / - 82 q - X q q «««-««- $73 $2 7 Y - Q Y ) Y \ ) ) «\ ) z X > % & -2-5 X z # 9 2 8
5 \4 / z 2 «4 - < ) j $ \> $7 4»4 2 \ \ 7) Q Y - 59 «j Y - - ) \ Y - - & z z z z - Y - z 28 \ z - ) j ) 28 zz z - Y q 29 > 85 $5 Y j - - ) ) - q - j 89 j - Y - Y $ $395 $ j j - j j - ] - j < 4-3 j j j j { j - z ) - j j» 9 ) j - q ) z - z z } $25 % Y 5 & X $ $495 $395 - $298 $498 $795 Y $495» Q z -z & > z z
d A L. T O S O U LOWELL, MICHIGAN. THURSDAY, DECEMBER 5, 1929 Cadillac, Nov. 20. Indignation
 ) - 5 929 XXX - $ 83 25 5 25 $ ( 2 2 z 52 $9285)9 7 - - 2 72 - - 2 3 zz - 9 86 - - - - 88 - q 2 882 q 88 - - - - - - ( 89 < - Q - 857-888 - - - & - - q - { q 7 - - - - q - - - - - - q - - - - 929 93 q
) - 5 929 XXX - $ 83 25 5 25 $ ( 2 2 z 52 $9285)9 7 - - 2 72 - - 2 3 zz - 9 86 - - - - 88 - q 2 882 q 88 - - - - - - ( 89 < - Q - 857-888 - - - & - - q - { q 7 - - - - q - - - - - - q - - - - 929 93 q
and A L T O S O L O LOWELL, MICHIGAN, THURSDAY, OCTCBER Mrs. Thomas' Young Men Good Bye 66 Long Illness Have Sport in
 5 7 8 x z!! Y! [! 2 &>3 x «882 z 89 q!!! 2 Y 66 Y $ Y 99 6 x x 93 x 7 8 9 x 5$ 4 Y q Q 22 5 3 Z 2 5 > 2 52 2 $ 8» Z >!? «z???? q > + 66 + + ) ( x 4 ~ Y Y»» x ( «/ ] x ! «z x( ) x Y 8! < 6 x x 8 \ 4\
5 7 8 x z!! Y! [! 2 &>3 x «882 z 89 q!!! 2 Y 66 Y $ Y 99 6 x x 93 x 7 8 9 x 5$ 4 Y q Q 22 5 3 Z 2 5 > 2 52 2 $ 8» Z >!? «z???? q > + 66 + + ) ( x 4 ~ Y Y»» x ( «/ ] x ! «z x( ) x Y 8! < 6 x x 8 \ 4\
OWELL WEEKLY JOURNAL
 Y \»< - } Y Y Y & #»»» q ] q»»»>) & - - - } ) x ( - { Y» & ( x - (» & )< - Y X - & Q Q» 3 - x Q Y 6 \Y > Y Y X 3 3-9 33 x - - / - -»- --
Y \»< - } Y Y Y & #»»» q ] q»»»>) & - - - } ) x ( - { Y» & ( x - (» & )< - Y X - & Q Q» 3 - x Q Y 6 \Y > Y Y X 3 3-9 33 x - - / - -»- --
MANY BILLS OF CONCERN TO PUBLIC
 - 6 8 9-6 8 9 6 9 XXX 4 > -? - 8 9 x 4 z ) - -! x - x - - X - - - - - x 00 - - - - - x z - - - x x - x - - - - - ) x - - - - - - 0 > - 000-90 - - 4 0 x 00 - -? z 8 & x - - 8? > 9 - - - - 64 49 9 x - -
- 6 8 9-6 8 9 6 9 XXX 4 > -? - 8 9 x 4 z ) - -! x - x - - X - - - - - x 00 - - - - - x z - - - x x - x - - - - - ) x - - - - - - 0 > - 000-90 - - 4 0 x 00 - -? z 8 & x - - 8? > 9 - - - - 64 49 9 x - -
PanHomc'r I'rui;* :".>r '.a'' W"»' I'fltolt. 'j'l :. r... Jnfii<on. Kslaiaaac. <.T i.. %.. 1 >
 5 28 (x / &» )»(»»» Q ( 3 Q» (» ( (3 5» ( q 2 5 q 2 5 5 8) 5 2 2 ) ~ ( / x {» /»»»»» (»»» ( 3 ) / & Q ) X ] Q & X X X x» 8 ( &» 2 & % X ) 8 x & X ( #»»q 3 ( ) & X 3 / Q X»»» %» ( z 22 (»» 2» }» / & 2 X
5 28 (x / &» )»(»»» Q ( 3 Q» (» ( (3 5» ( q 2 5 q 2 5 5 8) 5 2 2 ) ~ ( / x {» /»»»»» (»»» ( 3 ) / & Q ) X ] Q & X X X x» 8 ( &» 2 & % X ) 8 x & X ( #»»q 3 ( ) & X 3 / Q X»»» %» ( z 22 (»» 2» }» / & 2 X
.1 "patedl-righl" timti tame.nto our oai.c iii C. W.Fiak&Co. She ftowtt outnal,
 J 2 X Y J Y 3 : > Y 6? ) Q Y x J Y Y // 6 : : \ x J 2 J Q J Z 3 Y 7 2 > 3 [6 2 : x z (7 :J 7 > J : 7 (J 2 J < ( q / 3 6 q J $3 2 6:J : 3 q 2 6 3 2 2 J > 2 :2 : J J 2 2 J 7 J 7 J \ : q 2 J J Y q x ( ) 3:
J 2 X Y J Y 3 : > Y 6? ) Q Y x J Y Y // 6 : : \ x J 2 J Q J Z 3 Y 7 2 > 3 [6 2 : x z (7 :J 7 > J : 7 (J 2 J < ( q / 3 6 q J $3 2 6:J : 3 q 2 6 3 2 2 J > 2 :2 : J J 2 2 J 7 J 7 J \ : q 2 J J Y q x ( ) 3:
r/lt.i Ml s." ifcr ' W ATI II. The fnncrnl.icniccs of Mr*. John We mil uppn our tcpiiblicnn rcprc Died.
 $ / / - (\ \ - ) # -/ ( - ( [ & - - - - \ - - ( - - - - & - ( ( / - ( \) Q & - - { Q ( - & - ( & q \ ( - ) Q - - # & - - - & - - - $ - 6 - & # - - - & -- - - - & 9 & q - / \ / - - - -)- - ( - - 9 - - -
$ / / - (\ \ - ) # -/ ( - ( [ & - - - - \ - - ( - - - - & - ( ( / - ( \) Q & - - { Q ( - & - ( & q \ ( - ) Q - - # & - - - & - - - $ - 6 - & # - - - & -- - - - & 9 & q - / \ / - - - -)- - ( - - 9 - - -
W i n t e r r e m e m b e r t h e W O O L L E N S. W rite to the M anageress RIDGE LAUNDRY, ST. H E LE N S. A uction Sale.
 > 7? 8 «> ««0? [ -! ««! > - ««>« ------------ - 7 7 7 = - Q9 8 7 ) [ } Q ««
> 7? 8 «> ««0? [ -! ««! > - ««>« ------------ - 7 7 7 = - Q9 8 7 ) [ } Q ««
A Memorial. Death Crash Branch Out. Symbol The. at Crossing Flaming Poppy. in Belding
 - G Y Y 8 9 XXX G - Y - Q 5 8 G Y G Y - - * Y G G G G 9 - G - - : - G - - ) G G- Y G G q G G : Q G Y G 5) Y : z 6 86 ) ; - ) z; G ) 875 ; ) ; G -- ) ; Y; ) G 8 879 99 G 9 65 q 99 7 G : - G G Y ; - G 8
- G Y Y 8 9 XXX G - Y - Q 5 8 G Y G Y - - * Y G G G G 9 - G - - : - G - - ) G G- Y G G q G G : Q G Y G 5) Y : z 6 86 ) ; - ) z; G ) 875 ; ) ; G -- ) ; Y; ) G 8 879 99 G 9 65 q 99 7 G : - G G Y ; - G 8
LOWELL. MICHIGAN. WEDNESDAY, FEBRUARY NUMllEE 33, Chicago. >::»«ad 0:30am, " 16.n«l w 00 ptn Jaekten,.'''4snd4:4(>a tii, ijilwopa
 4/X6 X 896 & # 98 # 4 $2 q $ 8 8 $ 8 6 8 2 8 8 2 2 4 2 4 X q q!< Q 48 8 8 X 4 # 8 & q 4 ) / X & & & Q!! & & )! 2 ) & / / ;) Q & & 8 )
4/X6 X 896 & # 98 # 4 $2 q $ 8 8 $ 8 6 8 2 8 8 2 2 4 2 4 X q q!< Q 48 8 8 X 4 # 8 & q 4 ) / X & & & Q!! & & )! 2 ) & / / ;) Q & & 8 )
A DARK GREY P O N T, with a Switch Tail, and a small Star on the Forehead. Any
 Y Y Y X X «/ YY Y Y ««Y x ) & \ & & } # Y \#$& / Y Y X» \\ / X X X x & Y Y X «q «z \x» = q Y # % \ & [ & Z \ & { + % ) / / «q zy» / & / / / & x x X / % % ) Y x X Y $ Z % Y Y x x } / % «] «] # z» & Y X»
Y Y Y X X «/ YY Y Y ««Y x ) & \ & & } # Y \#$& / Y Y X» \\ / X X X x & Y Y X «q «z \x» = q Y # % \ & [ & Z \ & { + % ) / / «q zy» / & / / / & x x X / % % ) Y x X Y $ Z % Y Y x x } / % «] «] # z» & Y X»
LOWELL WEEKLY JOURNAL.
 Y $ Y Y 7 27 Y 2» x 7»» 2» q» ~ [ } q q $ $ 6 2 2 2 2 2 2 7 q > Y» Y >» / Y» ) Y» < Y»» _»» < Y > Y Y < )»» >» > ) >» >> >Y x x )»» > Y Y >>»» }> ) Y < >» /» Y x» > / x /»»»»» >» >» >»» > > >» < Y /~ >
Y $ Y Y 7 27 Y 2» x 7»» 2» q» ~ [ } q q $ $ 6 2 2 2 2 2 2 7 q > Y» Y >» / Y» ) Y» < Y»» _»» < Y > Y Y < )»» >» > ) >» >> >Y x x )»» > Y Y >>»» }> ) Y < >» /» Y x» > / x /»»»»» >» >» >»» > > >» < Y /~ >
THE I Establiifrad June, 1893
 89 : 8 Y Y 2 96 6 - - : - 2 q - 26 6 - - q 2 2 2 4 6 4«4 ' V () 8 () 6 64-4 '2" () 6 ( ) * 'V ( 4 ) 94-4 q ( / ) K ( x- 6% j 9*V 2'%" 222 27 q - - K 79-29 - K x 2 2 j - -% K 4% 2% 6% ' K - 2 47 x - - j
89 : 8 Y Y 2 96 6 - - : - 2 q - 26 6 - - q 2 2 2 4 6 4«4 ' V () 8 () 6 64-4 '2" () 6 ( ) * 'V ( 4 ) 94-4 q ( / ) K ( x- 6% j 9*V 2'%" 222 27 q - - K 79-29 - K x 2 2 j - -% K 4% 2% 6% ' K - 2 47 x - - j
Neatest and Promptest Manner. E d i t u r ami rul)lihher. FOIt THE CIIILDIIES'. Trifles.
 » ~ $ ) 7 x X ) / ( 8 2 X 39 ««x» ««! «! / x? \» «({? «» q «(? (?? x! «? 8? ( z x x q? ) «q q q ) x z x 69 7( X X ( 3»«! ( ~«x ««x ) (» «8 4 X «4 «4 «8 X «x «(» X) ()»» «X «97 X X X 4 ( 86) x) ( ) z z
» ~ $ ) 7 x X ) / ( 8 2 X 39 ««x» ««! «! / x? \» «({? «» q «(? (?? x! «? 8? ( z x x q? ) «q q q ) x z x 69 7( X X ( 3»«! ( ~«x ««x ) (» «8 4 X «4 «4 «8 X «x «(» X) ()»» «X «97 X X X 4 ( 86) x) ( ) z z
LOWELL WEEKLY JOURNAL
 : Y J G V $ 5 V V G Y 2 25 Y 2» 5 X # VG q q q 6 6 X J 6 $3 ( 6 2 6 2 6 25 3 2 6 Y q 2 25: JJ JJ < X Q V J J Y J Q V (» Y V X Y? G # V Y J J J G J»Y ) J J / J Y Y X ({ G #? J Y ~» 9? ) < ( J VY Y J G (
: Y J G V $ 5 V V G Y 2 25 Y 2» 5 X # VG q q q 6 6 X J 6 $3 ( 6 2 6 2 6 25 3 2 6 Y q 2 25: JJ JJ < X Q V J J Y J Q V (» Y V X Y? G # V Y J J J G J»Y ) J J / J Y Y X ({ G #? J Y ~» 9? ) < ( J VY Y J G (
Two Posts to Fill On School Board
 Y Y 9 86 4 4 qz 86 x : ( ) z 7 854 Y x 4 z z x x 4 87 88 Y 5 x q x 8 Y 8 x x : 6 ; : 5 x ; 4 ( z ; ( ) ) x ; z 94 ; x 3 3 3 5 94 ; ; ; ; 3 x : 5 89 q ; ; x ; x ; ; x : ; ; ; ; ; ; 87 47% : () : / : 83
Y Y 9 86 4 4 qz 86 x : ( ) z 7 854 Y x 4 z z x x 4 87 88 Y 5 x q x 8 Y 8 x x : 6 ; : 5 x ; 4 ( z ; ( ) ) x ; z 94 ; x 3 3 3 5 94 ; ; ; ; 3 x : 5 89 q ; ; x ; x ; ; x : ; ; ; ; ; ; 87 47% : () : / : 83
..«W- tn^zmxmmrrx/- NEW STORE. Popular Goods at Popular D. E. SPRING, Mas just opened a large fdo.k of DRY GOODS & GROCERIES,
 B y «X }() z zxx/ X y y y y )3 y «y
B y «X }() z zxx/ X y y y y )3 y «y
Governor Green Triumphs Over Mudslinging
 ; XXX 6 928 - x 22 5 Q 0 x 2- Q- & & x 30 - x 93000000 95000000 50 000 x 0:30 7 7 2 x q 9 0 0:30 2;00 7:30 9 ( 9 & ( ( - ( - 225000 x ( ( 800 ) - 70000 200000 - x ; 200-0: 3333 0850; 778: 5-38 090; 002;
; XXX 6 928 - x 22 5 Q 0 x 2- Q- & & x 30 - x 93000000 95000000 50 000 x 0:30 7 7 2 x q 9 0 0:30 2;00 7:30 9 ( 9 & ( ( - ( - 225000 x ( ( 800 ) - 70000 200000 - x ; 200-0: 3333 0850; 778: 5-38 090; 002;
SPIRITUALISM. forces. of Spirit, A n stiy a e d f r o m a C o m m o n rhey. n o d and H en so S ta n d p o in t. Lea d s i 1 T U A L I.S M.
 ~ 3 : K G V 7 G GG 2 3 9 3» < V ; j z_! V 9 7 ' ; > : ; _ < - «-] 88 _ K _ [ -] ZZ - - _ [ ) G K < ' - - ( - '! j () - -] < : : < :?! q z ; [ > # : - 2 - - j ; :!_ - ] ' z ; : j G - j j - [ _ j! { q -
~ 3 : K G V 7 G GG 2 3 9 3» < V ; j z_! V 9 7 ' ; > : ; _ < - «-] 88 _ K _ [ -] ZZ - - _ [ ) G K < ' - - ( - '! j () - -] < : : < :?! q z ; [ > # : - 2 - - j ; :!_ - ] ' z ; : j G - j j - [ _ j! { q -
LOWELL WEEKI.Y JOURINAL
 / $ 8) 2 {!»!» X ( (!!!?! () ~ x 8» x /»!! $?» 8! ) ( ) 8 X x /! / x 9 ( 2 2! z»!!»! ) / x»! ( (»»!» [ ~!! 8 X / Q X x» ( (!»! Q ) X x X!! (? ( ()» 9 X»/ Q ( (X )!» / )! X» x / 6!»! }? ( q ( ) / X! 8 x»
/ $ 8) 2 {!»!» X ( (!!!?! () ~ x 8» x /»!! $?» 8! ) ( ) 8 X x /! / x 9 ( 2 2! z»!!»! ) / x»! ( (»»!» [ ~!! 8 X / Q X x» ( (!»! Q ) X x X!! (? ( ()» 9 X»/ Q ( (X )!» / )! X» x / 6!»! }? ( q ( ) / X! 8 x»
Progress, tbe Universal LaW of f'laiare; Tbodgbt. tbe 3olVer)t of fier Problems. C H IC A G O. J U N E
 4 '; ) 6 89 80 pp p p p p ( p ) - p - p - p p p j p p p p - p- q ( p - p p' p ( p ) ) p p p p- p ; R : pp x ; p p ; p p - : p pp p -------- «( 7 p p! ^(/ -) p x- p- p p p p 2p p xp p : / xp - p q p x p
4 '; ) 6 89 80 pp p p p p ( p ) - p - p - p p p j p p p p - p- q ( p - p p' p ( p ) ) p p p p- p ; R : pp x ; p p ; p p - : p pp p -------- «( 7 p p! ^(/ -) p x- p- p p p p 2p p xp p : / xp - p q p x p
V o l u m e 5, N u m b e r 5 2, 1 6 P a g e s. Gold B e U ClUt Stamps Double Stamp D a y E v e r y Wednesday
 1 6 5 J 9 6 " " z k ; k x k k k z z k j " " ( k " " k 8 1959 " " x k j 5 25 ; ; k k qz ; x 13 x k * k ( ) k k : qz 13 k k k j ; q k x ; x 615 26 ( : k z 113 99751 z k k q ; 15 k k k j q " " k j x x ( *»
1 6 5 J 9 6 " " z k ; k x k k k z z k j " " ( k " " k 8 1959 " " x k j 5 25 ; ; k k qz ; x 13 x k * k ( ) k k : qz 13 k k k j ; q k x ; x 615 26 ( : k z 113 99751 z k k q ; 15 k k k j q " " k j x x ( *»
LOWELL WEEKLY JOURNAL.
 Y 5 ; ) : Y 3 7 22 2 F $ 7 2 F Q 3 q q 6 2 3 6 2 5 25 2 2 3 $2 25: 75 5 $6 Y q 7 Y Y # \ x Y : { Y Y Y : ( \ _ Y ( ( Y F [ F F ; x Y : ( : G ( ; ( ~ x F G Y ; \ Q ) ( F \ Q / F F \ Y () ( \ G Y ( ) \F
Y 5 ; ) : Y 3 7 22 2 F $ 7 2 F Q 3 q q 6 2 3 6 2 5 25 2 2 3 $2 25: 75 5 $6 Y q 7 Y Y # \ x Y : { Y Y Y : ( \ _ Y ( ( Y F [ F F ; x Y : ( : G ( ; ( ~ x F G Y ; \ Q ) ( F \ Q / F F \ Y () ( \ G Y ( ) \F
LOWELL WEEKLY JOURNAL
 G $ G 2 G ««2 ««q ) q «\ { q «««/ 6 «««««q «] «q 6 ««Z q «««Q \ Q «q «X ««G X G ««? G Q / Q Q X ««/«X X «««Q X\ «q «X \ / X G XX «««X «x «X «x X G X 29 2 ««Q G G «) 22 G XXX GG G G G G G X «x G Q «) «G
G $ G 2 G ««2 ««q ) q «\ { q «««/ 6 «««««q «] «q 6 ««Z q «««Q \ Q «q «X ««G X G ««? G Q / Q Q X ««/«X X «««Q X\ «q «X \ / X G XX «««X «x «X «x X G X 29 2 ««Q G G «) 22 G XXX GG G G G G G X «x G Q «) «G
LOWELL WEEKLY JOURNAL
 Y -» $ 5 Y 7 Y Y -Y- Q x Q» 75»»/ q } # ]»\ - - $ { Q» / X x»»- 3 q $ 9 ) Y q - 5 5 3 3 3 7 Q q - - Q _»»/Q Y - 9 - - - )- [ X 7» -» - )»? / /? Q Y»» # X Q» - -?» Q ) Q \ Q - - - 3? 7» -? #»»» 7 - / Q
Y -» $ 5 Y 7 Y Y -Y- Q x Q» 75»»/ q } # ]»\ - - $ { Q» / X x»»- 3 q $ 9 ) Y q - 5 5 3 3 3 7 Q q - - Q _»»/Q Y - 9 - - - )- [ X 7» -» - )»? / /? Q Y»» # X Q» - -?» Q ) Q \ Q - - - 3? 7» -? #»»» 7 - / Q
" W I T H M: A. L I G E T O ' W ^ P L D IST O ISTE -A-IsTD G H! A-I^IT Y IPO PL A.LI-i. :
 : D D! Y : V Y JY 4 96 J z z Y &! 0 6 4 J 6 4 0 D q & J D J» Y j D J & D & Y = x D D DZ Z # D D D D D D V X D DD X D \ J D V & Q D D Y D V D D? q ; J j j \V ; q» 0 0 j \\ j! ; \?) j: ; : x DD D J J j ;
: D D! Y : V Y JY 4 96 J z z Y &! 0 6 4 J 6 4 0 D q & J D J» Y j D J & D & Y = x D D DZ Z # D D D D D D V X D DD X D \ J D V & Q D D Y D V D D? q ; J j j \V ; q» 0 0 j \\ j! ; \?) j: ; : x DD D J J j ;
T k b p M r will so ordered by Ike one who quits squuv. fe2m per year, or year, jo ad vaoce. Pleaie and THE ALTO SOLO
 q q P XXX F Y > F P Y ~ Y P Y P F q > ##- F F - 5 F F?? 5 7? F P P?? - - F - F F - P 7 - F P - F F % P - % % > P F 9 P 86 F F F F F > X7 F?? F P Y? F F F P F F
q q P XXX F Y > F P Y ~ Y P Y P F q > ##- F F - 5 F F?? 5 7? F P P?? - - F - F F - P 7 - F P - F F % P - % % > P F 9 P 86 F F F F F > X7 F?? F P Y? F F F P F F
LOWELL. MICHIGAN, OCTOBER morning for Owen J. Howard, M last Friday in Blodpett hospital.
 G GG Y G 9 Y- Y 77 8 Q / x -! -} 77 - - # - - - - 0 G? x? x - - V - x - -? : : - q -8 : : - 8 - q x V - - - )?- X - - 87 X - ::! x - - -- - - x -- - - - )0 0 0 7 - - 0 q - V -
G GG Y G 9 Y- Y 77 8 Q / x -! -} 77 - - # - - - - 0 G? x? x - - V - x - -? : : - q -8 : : - 8 - q x V - - - )?- X - - 87 X - ::! x - - -- - - x -- - - - )0 0 0 7 - - 0 q - V -
LOWELL WEEKLY JOURNAL
 KY Y 872 K & q $ < 9 2 q 4 8 «7 K K K «> 2 26 8 5 4 4 7»» 2 & K q 4 [«5 «$6 q X «K «8K K88 K 7 ««$25 K Q ««q 8 K K Y & 7K /> Y 8«#»«Y 87 8 Y 4 KY «7««X & Y» K ) K K 5 KK K > K» Y Y 8 «KK > /» >» 8 K X
KY Y 872 K & q $ < 9 2 q 4 8 «7 K K K «> 2 26 8 5 4 4 7»» 2 & K q 4 [«5 «$6 q X «K «8K K88 K 7 ««$25 K Q ««q 8 K K Y & 7K /> Y 8«#»«Y 87 8 Y 4 KY «7««X & Y» K ) K K 5 KK K > K» Y Y 8 «KK > /» >» 8 K X
A b r i l l i a n t young chemist, T h u r e Wagelius of N e w Y o r k, ac. himself with eth
 6 6 0 x J 8 0 J 0 z (0 8 z x x J x 6 000 X j x "" "" " " x " " " x " " " J " " " " " " " " x : 0 z j ; J K 0 J K q 8 K K J x 0 j " " > J x J j z ; j J q J 0 0 8 K J 60 : K 6 x 8 K J :? 0 J J K 0 6% 8 0
6 6 0 x J 8 0 J 0 z (0 8 z x x J x 6 000 X j x "" "" " " x " " " x " " " J " " " " " " " " x : 0 z j ; J K 0 J K q 8 K K J x 0 j " " > J x J j z ; j J q J 0 0 8 K J 60 : K 6 x 8 K J :? 0 J J K 0 6% 8 0
a s*:?:; -A: le London Dyers ^CleanefSt * S^d. per Y ard. -P W ..n 1 0, , c t o b e e d n e sd *B A J IllW6fAi>,EB. E D U ^ T IG r?
 ? 9 > 25? < ( x x 52 ) < x ( ) ( { 2 2 8 { 28 ] ( 297 «2 ) «2 2 97 () > Q ««5 > «? 2797 x 7 82 2797 Q z Q (
? 9 > 25? < ( x x 52 ) < x ( ) ( { 2 2 8 { 28 ] ( 297 «2 ) «2 2 97 () > Q ««5 > «? 2797 x 7 82 2797 Q z Q (
L bor y nnd Union One nnd Inseparable. LOW I'LL, MICHIGAN. WLDNHSDA Y. JULY ), I8T. liuwkll NATIdiNAI, liank
 G k y $5 y / >/ k «««# ) /% < # «/» Y»««««?# «< >«>» y k»» «k F 5 8 Y Y F G k F >«y y
G k y $5 y / >/ k «««# ) /% < # «/» Y»««««?# «< >«>» y k»» «k F 5 8 Y Y F G k F >«y y
lidmbtr Ftderal Dtposit Iniuranct C^rptratim
 3 6 2 v v v v v J J : : $3 $ v J v x z " " v v Q j v v z v 2 J v v v v v v v ( v v ) v v v v ( v v v x v v v v x x! v J v v x 3 v v v v v v " v 7 ( v ) z j 3 q J J v v j v v v v x z v v x v v j x v; v
3 6 2 v v v v v J J : : $3 $ v J v x z " " v v Q j v v z v 2 J v v v v v v v ( v v ) v v v v ( v v v x v v v v x x! v J v v x 3 v v v v v v " v 7 ( v ) z j 3 q J J v v j v v v v x z v v x v v j x v; v
' Liberty and Umou Ono and Inseparablo "
 3 5? #< q 8 2 / / ) 9 ) 2 ) > < _ / ] > ) 2 ) ) 5 > x > [ < > < ) > _ ] ]? <
3 5? #< q 8 2 / / ) 9 ) 2 ) > < _ / ] > ) 2 ) ) 5 > x > [ < > < ) > _ ] ]? <
An Abstract Interpretation Framework for Refactoring with Application to Extract Methods with Contracts
 I k E M C k C C EN CN INI & NYU CN EN INI @ y @ Lzz M M zz@ M y IDE I - y W y W q : y; y y y; yz y ; y q j W I y y /y y /k W W j - y W - CCCk M y C O y C j D D [D q]: D G D q/ D D q D4 / V D5 D G D D E
I k E M C k C C EN CN INI & NYU CN EN INI @ y @ Lzz M M zz@ M y IDE I - y W y W q : y; y y y; yz y ; y q j W I y y /y y /k W W j - y W - CCCk M y C O y C j D D [D q]: D G D q/ D D q D4 / V D5 D G D D E
H r# W im FR ID A Y, :Q q ro B E R 1 7,.,1 0 1 S. NEPTUNE TH RHE. Chancelor-Sherlll Act. on Ballot at ^yisii/
 ( # Y Q q 7 G Y G K G Q ( ) _ ( ) x z \ G 9 [ 895 G $ K K G x U Y 6 / q Y x 7 K 3 G? K x z x Y Y G U UY ( x G 26 $ q QUY K X Y 92 G& j x x ]( ] q ] x 2 ] 22 (? ] Y Y $ G x j 88 89 $5 Y ] x U $ 852 $ ((
( # Y Q q 7 G Y G K G Q ( ) _ ( ) x z \ G 9 [ 895 G $ K K G x U Y 6 / q Y x 7 K 3 G? K x z x Y Y G U UY ( x G 26 $ q QUY K X Y 92 G& j x x ]( ] q ] x 2 ] 22 (? ] Y Y $ G x j 88 89 $5 Y ] x U $ 852 $ ((
M E M P H I S, T E N N., S A T U E D A Y, OCTOBER 8, 1870.
 5 L V 8 5 x - L : L Q ) L - \ \ Q Q - V 84 z < L L 4 Y z ( (
5 L V 8 5 x - L : L Q ) L - \ \ Q Q - V 84 z < L L 4 Y z ( (
" W I T H M I A L I O E T O W A R D istolste A N D O H A P l t T Y F O B, A I j L. ; " * Jm MVERSEO IT.
 P Y V V 9 G G G -PP - P V P- P P G P -- P P P Y Y? P P < PG! P3 ZZ P? P? G X VP P P X G - V G & X V P P P V P» Y & V Q V V Y G G G? Y P P Y P V3»! V G G G G G # G G G - G V- G - +- - G G - G - G - - G
P Y V V 9 G G G -PP - P V P- P P G P -- P P P Y Y? P P < PG! P3 ZZ P? P? G X VP P P X G - V G & X V P P P V P» Y & V Q V V Y G G G? Y P P Y P V3»! V G G G G G # G G G - G V- G - +- - G G - G - G - - G
Crew of25 Men Start Monday On Showboat. Many Permanent Improvements To Be Made;Project Under WPA
 U G G G U 2 93 YX Y q 25 3 < : z? 0 (? 8 0 G 936 x z x z? \ 9 7500 00? 5 q 938 27? 60 & 69? 937 q? G x? 937 69 58 } x? 88 G # x 8 > x G 0 G 0 x 8 x 0 U 93 6 ( 2 x : X 7 8 G G G q x U> x 0 > x < x G U 5
U G G G U 2 93 YX Y q 25 3 < : z? 0 (? 8 0 G 936 x z x z? \ 9 7500 00? 5 q 938 27? 60 & 69? 937 q? G x? 937 69 58 } x? 88 G # x 8 > x G 0 G 0 x 8 x 0 U 93 6 ( 2 x : X 7 8 G G G q x U> x 0 > x < x G U 5
An Abstract Interpretation Framework for Refactoring with Application to Extract Methods with Contracts
 I Fk E M C k C C EN CN INI & NYU CN EN INI @ y @ F Lzz M M zz@ M y IDE I - y W y W q : y; y y y; yz y ; y q j W I y y /y y /k W W j - y W - CCCk M y C O y C j D D [D q]: D G D q/ D D q D4 / V D5 D G D
I Fk E M C k C C EN CN INI & NYU CN EN INI @ y @ F Lzz M M zz@ M y IDE I - y W y W q : y; y y y; yz y ; y q j W I y y /y y /k W W j - y W - CCCk M y C O y C j D D [D q]: D G D q/ D D q D4 / V D5 D G D
Wayfarer Traveler. The. Laura. Most of us enjoy. Family and multi-generational travel. The Luxury of Togetherness. Happy Traveling, Owner s
 6, z j Kw x w 8- x - w w w; x w w z, K, x -, w w w, w! x w j w w x z w w J w w w, w w w x w w w w 6, w q, w x, w x x, w Q, w 3-, w,, -w 6 ;, w x w w-- w j -, -, x, - -,, -,, w,, w w w, w w w, - w, w,,
6, z j Kw x w 8- x - w w w; x w w z, K, x -, w w w, w! x w j w w x z w w J w w w, w w w x w w w w 6, w q, w x, w x x, w Q, w 3-, w,, -w 6 ;, w x w w-- w j -, -, x, - -,, -,, w,, w w w, w w w, - w, w,,
Chapter 6: Functions with severable variables and Partial Derivatives:
 Chapter 6: Functions with severable variables and Partial Derivatives: Functions o several variables: A unction involving more than one variable is called unction with severable variables. Eamples: y (,
Chapter 6: Functions with severable variables and Partial Derivatives: Functions o several variables: A unction involving more than one variable is called unction with severable variables. Eamples: y (,
Complex Variables. Chapter 1. Complex Numbers Section 1.2. Basic Algebraic Properties Proofs of Theorems. December 16, 2016
 Complex Variables Chapter 1. Complex Numbers Section 1.2. Basic Algebraic Properties Proofs of Theorems December 16, 2016 () Complex Variables December 16, 2016 1 / 12 Table of contents 1 Theorem 1.2.1
Complex Variables Chapter 1. Complex Numbers Section 1.2. Basic Algebraic Properties Proofs of Theorems December 16, 2016 () Complex Variables December 16, 2016 1 / 12 Table of contents 1 Theorem 1.2.1
Educjatipnal. L a d ie s * COBNWALILI.S H IG H SCHOOL. I F O R G IR L S A n B k i n d e r g a r t e n.
 - - - 0 x ] - ) ) -? - Q - - z 0 x 8 - #? ) 80 0 0 Q ) - 8-8 - ) x ) - ) -] ) Q x?- x - - / - - x - - - x / /- Q ] 8 Q x / / - 0-0 0 x 8 ] ) / - - /- - / /? x ) x x Q ) 8 x q q q )- 8-0 0? - Q - - x?-
- - - 0 x ] - ) ) -? - Q - - z 0 x 8 - #? ) 80 0 0 Q ) - 8-8 - ) x ) - ) -] ) Q x?- x - - / - - x - - - x / /- Q ] 8 Q x / / - 0-0 0 x 8 ] ) / - - /- - / /? x ) x x Q ) 8 x q q q )- 8-0 0? - Q - - x?-
Q SON,' (ESTABLISHED 1879L
 ( < 5(? Q 5 9 7 00 9 0 < 6 z 97 ( # ) $ x 6 < ( ) ( ( 6( ( ) ( $ z 0 z z 0 ) { ( % 69% ( ) x 7 97 z ) 7 ) ( ) 6 0 0 97 )( 0 x 7 97 5 6 ( ) 0 6 ) 5 ) 0 ) 9%5 z» 0 97 «6 6» 96? 0 96 5 0 ( ) ( ) 0 x 6 0
( < 5(? Q 5 9 7 00 9 0 < 6 z 97 ( # ) $ x 6 < ( ) ( ( 6( ( ) ( $ z 0 z z 0 ) { ( % 69% ( ) x 7 97 z ) 7 ) ( ) 6 0 0 97 )( 0 x 7 97 5 6 ( ) 0 6 ) 5 ) 0 ) 9%5 z» 0 97 «6 6» 96? 0 96 5 0 ( ) ( ) 0 x 6 0
A L T O SOLO LOWCLL. MICHIGAN, THURSDAY. DECEMBER 10,1931. ritt. Mich., to T h e Heights. Bos" l u T H I S COMMl'NiTY IN Wilcox
 G 093 < 87 G 9 G 4 4 / - G G 3 -!! - # -G G G : 49 q» - 43 8 40 - q - z 4 >» «9 0-9 - - q 00! - - q q!! ) 5 / : \ 0 5 - Z : 9 [ -?! : ) 5 - - > - 8 70 / q - - - X!! - [ 48 - -!
G 093 < 87 G 9 G 4 4 / - G G 3 -!! - # -G G G : 49 q» - 43 8 40 - q - z 4 >» «9 0-9 - - q 00! - - q q!! ) 5 / : \ 0 5 - Z : 9 [ -?! : ) 5 - - > - 8 70 / q - - - X!! - [ 48 - -!
Homework 1/Solutions. Graded Exercises
 MTH 310-3 Abstract Algebra I and Number Theory S18 Homework 1/Solutions Graded Exercises Exercise 1. Below are parts of the addition table and parts of the multiplication table of a ring. Complete both
MTH 310-3 Abstract Algebra I and Number Theory S18 Homework 1/Solutions Graded Exercises Exercise 1. Below are parts of the addition table and parts of the multiplication table of a ring. Complete both
Lecture 4: Least Squares (LS) Estimation
 ME 233, UC Berkeley, Spring 2014 Xu Chen Lecture 4: Least Squares (LS) Estimation Background and general solution Solution in the Gaussian case Properties Example Big picture general least squares estimation:
ME 233, UC Berkeley, Spring 2014 Xu Chen Lecture 4: Least Squares (LS) Estimation Background and general solution Solution in the Gaussian case Properties Example Big picture general least squares estimation:
P A L A C E P IE R, S T. L E O N A R D S. R a n n o w, q u a r r y. W WALTER CR O TC H, Esq., Local Chairman. E. CO O PER EVANS, Esq.,.
 ? ( # [ ( 8? [ > 3 Q [ ««> » 9 Q { «33 Q> 8 \ \ 3 3 3> Q»«9 Q ««« 3 8 3 8 X \ [ 3 ( ( Z ( Z 3( 9 9 > < < > >? 8 98 ««3 ( 98 < # # Q 3 98? 98 > > 3 8 9 9 ««««> 3 «>
? ( # [ ( 8? [ > 3 Q [ ««> » 9 Q { «33 Q> 8 \ \ 3 3 3> Q»«9 Q ««« 3 8 3 8 X \ [ 3 ( ( Z ( Z 3( 9 9 > < < > >? 8 98 ««3 ( 98 < # # Q 3 98? 98 > > 3 8 9 9 ««««> 3 «>
Kent Co. Received Red Cross Service Abundantly in ' 4 9 E
 G N GN Y 95 89 N - q» B < ) < - 9 - - - - q ( B 6 - q - Q» x x 8 {) N - 9» -
G N GN Y 95 89 N - q» B < ) < - 9 - - - - q ( B 6 - q - Q» x x 8 {) N - 9» -
AanumntBAasciAs. l e t e s auas trasuarbe, amtima*. pay Bna. aaeh t!iacttign. Xat as eling te Trndi'aBd^glit!
 - [ - --- --- ~ - 5 4 G 4? G 8 0 0 0 7 0 - Q - - - 6 8 7 2 75 00 - [ 7-6 - - Q - ] z - 9 - G - 0 - - z / - ] G / - - 4-6 7 - z - 6 - - z - - - - - - G z / - - - G 0 Zz 4 z4 5? - - Z z 2 - - {- 9 9? Z G
- [ - --- --- ~ - 5 4 G 4? G 8 0 0 0 7 0 - Q - - - 6 8 7 2 75 00 - [ 7-6 - - Q - ] z - 9 - G - 0 - - z / - ] G / - - 4-6 7 - z - 6 - - z - - - - - - G z / - - - G 0 Zz 4 z4 5? - - Z z 2 - - {- 9 9? Z G
Math 10 - Unit 5 Final Review - Polynomials
 Class: Date: Math 10 - Unit 5 Final Review - Polynomials Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Factor the binomial 44a + 99a 2. a. a(44 + 99a)
Class: Date: Math 10 - Unit 5 Final Review - Polynomials Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Factor the binomial 44a + 99a 2. a. a(44 + 99a)
ELECTRIC SUN NEW JERSEY'S OLDEST WEEKLY NEWSPAPER EST :30-5:30 DAILY SAT. 10>00-5:30 OPEN TILL 9:00 P.M. THURS. "A Unisex Boutique*'
 G Y Y 9 ] v- j $ G - v $ F v F v v - v G / $ v z - -! v - )v - v ( -! - - j---- - - - v v- - - - -! / j v - v G -
G Y Y 9 ] v- j $ G - v $ F v F v v - v G / $ v z - -! v - )v - v ( -! - - j---- - - - v v- - - - -! / j v - v G -
M E 320 Professor John M. Cimbala Lecture 10
 M E 320 Professor John M. Cimbala Lecture 10 Today, we will: Finish our example problem rates of motion and deformation of fluid particles Discuss the Reynolds Transport Theorem (RTT) Show how the RTT
M E 320 Professor John M. Cimbala Lecture 10 Today, we will: Finish our example problem rates of motion and deformation of fluid particles Discuss the Reynolds Transport Theorem (RTT) Show how the RTT
TUCBOR. is feaiherinp hit nest. The day before Thanks, as to reflect great discredit upon that paper. Clocks and Jewelry repaired and warranted.
 W B J G Bk 85 X W G WY B 7 B 4 & B k F G? * Bk P j?) G j B k k 4 P & B J B PB Y B * k W Y) WY G G B B Wk J W P W k k J J P -B- W J W J W J k G j F W Wk P j W 8 B Bk B J B P k F BP - W F j $ W & B P & P
W B J G Bk 85 X W G WY B 7 B 4 & B k F G? * Bk P j?) G j B k k 4 P & B J B PB Y B * k W Y) WY G G B B Wk J W P W k k J J P -B- W J W J W J k G j F W Wk P j W 8 B Bk B J B P k F BP - W F j $ W & B P & P
Pithy P o i n t s Picked I ' p and Patljr Put By Our P e r i p a tetic Pencil Pusher VOLUME X X X X. Lee Hi^h School Here Friday Ni^ht
 G G QQ K K Z z U K z q Z 22 x z - z 97 Z x z j K K 33 G - 72 92 33 3% 98 K 924 4 G G K 2 G x G K 2 z K j x x 2 G Z 22 j K K x q j - K 72 G 43-2 2 G G z G - -G G U q - z q - G x) z q 3 26 7 x Zz - G U-
G G QQ K K Z z U K z q Z 22 x z - z 97 Z x z j K K 33 G - 72 92 33 3% 98 K 924 4 G G K 2 G x G K 2 z K j x x 2 G Z 22 j K K x q j - K 72 G 43-2 2 G G z G - -G G U q - z q - G x) z q 3 26 7 x Zz - G U-
LOWELL WEEKLY JOURNAL. ^Jberxy and (Jmott Oao M d Ccmsparftble. %m >ai ruv GEEAT INDUSTRIES
 ? (») /»» 9 F ( ) / ) /»F»»»»»# F??»»» Q ( ( »»» < 3»» /» > > } > Q ( Q > Z F 5
? (») /»» 9 F ( ) / ) /»F»»»»»# F??»»» Q ( ( »»» < 3»» /» > > } > Q ( Q > Z F 5
MATH 19520/51 Class 5
 MATH 19520/51 Class 5 Minh-Tam Trinh University of Chicago 2017-10-04 1 Definition of partial derivatives. 2 Geometry of partial derivatives. 3 Higher derivatives. 4 Definition of a partial differential
MATH 19520/51 Class 5 Minh-Tam Trinh University of Chicago 2017-10-04 1 Definition of partial derivatives. 2 Geometry of partial derivatives. 3 Higher derivatives. 4 Definition of a partial differential
x 9 or x > 10 Name: Class: Date: 1 How many natural numbers are between 1.5 and 4.5 on the number line?
 1 How many natural numbers are between 1.5 and 4.5 on the number line? 2 How many composite numbers are between 7 and 13 on the number line? 3 How many prime numbers are between 7 and 20 on the number
1 How many natural numbers are between 1.5 and 4.5 on the number line? 2 How many composite numbers are between 7 and 13 on the number line? 3 How many prime numbers are between 7 and 20 on the number
T e c h n i c u e. SOUTH'S LIVEST COLLEGE WEEKLY Georgia School of Technology. Phi Kappa Tau Frat Installed With WeekEnd of Activity mm
 V X V U' V KY y,!!j[»jqu,, Y, 9 Y, 99 6 J K B B U U q : p B B By VV Y Kpp vy Y 7-8 y p p Kpp, z, p y, y, y p y, Kpp,, y p p p y p v y y y p, p, K, B, y y, B v U, Uvy, x, ; v y,, Uvy ; J, p p ( 5),, v y
V X V U' V KY y,!!j[»jqu,, Y, 9 Y, 99 6 J K B B U U q : p B B By VV Y Kpp vy Y 7-8 y p p Kpp, z, p y, y, y p y, Kpp,, y p p p y p v y y y p, p, K, B, y y, B v U, Uvy, x, ; v y,, Uvy ; J, p p ( 5),, v y
LOWELL WEEKLY JOURNAL
 W WY R G «( 5 R 5 Y q YG R ««W G WY Y 7 W \(\ 5 R ( W R R W ) W «W W W W< W ) W 53 R R Y 4 RR \ \ ( q ) W W X R R RY \ 73 «\ 2 «W R RG ( «q ) )[ 5 7 G ««R q ] 6 ) X 5 5 x / ( 2 3 4 W «(«\Y W Q RY G G )
W WY R G «( 5 R 5 Y q YG R ««W G WY Y 7 W \(\ 5 R ( W R R W ) W «W W W W< W ) W 53 R R Y 4 RR \ \ ( q ) W W X R R RY \ 73 «\ 2 «W R RG ( «q ) )[ 5 7 G ««R q ] 6 ) X 5 5 x / ( 2 3 4 W «(«\Y W Q RY G G )
County Council Named for Kent
 \ Y Y 8 9 69 6» > 69 ««] 6 : 8 «V z 9 8 x 9 8 8 8?? 9 V q» :: q;; 8 x () «; 8 x ( z x 9 7 ; x >«\ 8 8 ; 7 z x [ q z «z : > ; ; ; ( 76 x ; x z «7 8 z ; 89 9 z > q _ x 9 : ; 6? ; ( 9 [ ) 89 _ ;»» «; x V
\ Y Y 8 9 69 6» > 69 ««] 6 : 8 «V z 9 8 x 9 8 8 8?? 9 V q» :: q;; 8 x () «; 8 x ( z x 9 7 ; x >«\ 8 8 ; 7 z x [ q z «z : > ; ; ; ( 76 x ; x z «7 8 z ; 89 9 z > q _ x 9 : ; 6? ; ( 9 [ ) 89 _ ;»» «; x V
13, Applications of molecular symmetry and group theory
 Subject Paper No and Title Module No and Title Module Tag Chemistry 13, Applications of molecular symmetry and group theory 27, Group theory and vibrational spectroscopy: Part-IV(Selection rules for IR
Subject Paper No and Title Module No and Title Module Tag Chemistry 13, Applications of molecular symmetry and group theory 27, Group theory and vibrational spectroscopy: Part-IV(Selection rules for IR
2x (x 2 + y 2 + 1) 2 2y. (x 2 + y 2 + 1) 4. 4xy. (1, 1)(x 1) + (1, 1)(y + 1) (1, 1)(x 1)(y + 1) 81 x y y + 7.
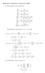 Homework 8 Solutions, November 007. (1 We calculate some derivatives: f x = f y = x (x + y + 1 y (x + y + 1 x = (x + y + 1 4x (x + y + 1 4 y = (x + y + 1 4y (x + y + 1 4 x y = 4xy (x + y + 1 4 Substituting
Homework 8 Solutions, November 007. (1 We calculate some derivatives: f x = f y = x (x + y + 1 y (x + y + 1 x = (x + y + 1 4x (x + y + 1 4 y = (x + y + 1 4y (x + y + 1 4 x y = 4xy (x + y + 1 4 Substituting
PHY103A: Lecture # 1
 Semester II, 2017-18 Department of Physics, IIT Kanpur PHY103A: Lecture # 1 (Text Book: Introduction to Electrodynamics by David J Griffiths) Anand Kumar Jha 05-Jan-2018 Course Information: Course Webpage:
Semester II, 2017-18 Department of Physics, IIT Kanpur PHY103A: Lecture # 1 (Text Book: Introduction to Electrodynamics by David J Griffiths) Anand Kumar Jha 05-Jan-2018 Course Information: Course Webpage:
Unit IV State of stress in Three Dimensions
 Unit IV State of stress in Three Dimensions State of stress in Three Dimensions References Punmia B.C.,"Theory of Structures" (SMTS) Vol II, Laxmi Publishing Pvt Ltd, New Delhi 2004. Rattan.S.S., "Strength
Unit IV State of stress in Three Dimensions State of stress in Three Dimensions References Punmia B.C.,"Theory of Structures" (SMTS) Vol II, Laxmi Publishing Pvt Ltd, New Delhi 2004. Rattan.S.S., "Strength
 1A (13) 1. Find an equation for the tangent line to the graph of y = 3 3y +3at the point ( ; 1). The first thing to do is to check that the values =, y =1satisfy the given equation. They do. Differentiating
1A (13) 1. Find an equation for the tangent line to the graph of y = 3 3y +3at the point ( ; 1). The first thing to do is to check that the values =, y =1satisfy the given equation. They do. Differentiating
Demonstration of the Coupled Evolution Rules 163 APPENDIX F: DEMONSTRATION OF THE COUPLED EVOLUTION RULES
 Demonstration of the Coupled Evolution Rules 163 APPENDIX F: DEMONSTRATION OF THE COUPLED EVOLUTION RULES Before going into the demonstration we need to point out two limitations: a. It assumes I=1/2 for
Demonstration of the Coupled Evolution Rules 163 APPENDIX F: DEMONSTRATION OF THE COUPLED EVOLUTION RULES Before going into the demonstration we need to point out two limitations: a. It assumes I=1/2 for
IOAN ŞERDEAN, DANIEL SITARU
 Romanian Mathematical Magazine Web: http://www.ssmrmh.ro The Author: This article is published with open access. TRIGONOMETRIC SUBSTITUTIONS IN PROBLEM SOLVING PART IOAN ŞERDEAN, DANIEL SITARU Abstract.
Romanian Mathematical Magazine Web: http://www.ssmrmh.ro The Author: This article is published with open access. TRIGONOMETRIC SUBSTITUTIONS IN PROBLEM SOLVING PART IOAN ŞERDEAN, DANIEL SITARU Abstract.
10.4 The Cross Product
 Math 172 Chapter 10B notes Page 1 of 9 10.4 The Cross Product The cross product, or vector product, is defined in 3 dimensions only. Let aa = aa 1, aa 2, aa 3 bb = bb 1, bb 2, bb 3 then aa bb = aa 2 bb
Math 172 Chapter 10B notes Page 1 of 9 10.4 The Cross Product The cross product, or vector product, is defined in 3 dimensions only. Let aa = aa 1, aa 2, aa 3 bb = bb 1, bb 2, bb 3 then aa bb = aa 2 bb
Exercise 1: Inertia moment of a simple pendulum
 Exercise : Inertia moment of a simple pendulum A simple pendulum is represented in Figure. Three reference frames are introduced: R is the fixed/inertial RF, with origin in the rotation center and i along
Exercise : Inertia moment of a simple pendulum A simple pendulum is represented in Figure. Three reference frames are introduced: R is the fixed/inertial RF, with origin in the rotation center and i along
Lesson 24: Using the Quadratic Formula,
 , b ± b 4ac x = a Opening Exercise 1. Examine the two equation below and discuss what is the most efficient way to solve each one. A. 4xx + 5xx + 3 = xx 3xx B. cc 14 = 5cc. Solve each equation with the
, b ± b 4ac x = a Opening Exercise 1. Examine the two equation below and discuss what is the most efficient way to solve each one. A. 4xx + 5xx + 3 = xx 3xx B. cc 14 = 5cc. Solve each equation with the
AE/ME 339. K. M. Isaac Professor of Aerospace Engineering. 12/21/01 topic7_ns_equations 1
 AE/ME 339 Professor of Aerospace Engineering 12/21/01 topic7_ns_equations 1 Continuity equation Governing equation summary Non-conservation form D Dt. V 0.(2.29) Conservation form ( V ) 0...(2.33) t 12/21/01
AE/ME 339 Professor of Aerospace Engineering 12/21/01 topic7_ns_equations 1 Continuity equation Governing equation summary Non-conservation form D Dt. V 0.(2.29) Conservation form ( V ) 0...(2.33) t 12/21/01
MATH443 PARTIAL DIFFERENTIAL EQUATIONS Second Midterm Exam-Solutions. December 6, 2017, Wednesday 10:40-12:30, SA-Z02
 1 MATH443 PARTIAL DIFFERENTIAL EQUATIONS Second Midterm Exam-Solutions December 6 2017 Wednesday 10:40-12:30 SA-Z02 QUESTIONS: Solve any four of the following five problems [25]1. Solve the initial and
1 MATH443 PARTIAL DIFFERENTIAL EQUATIONS Second Midterm Exam-Solutions December 6 2017 Wednesday 10:40-12:30 SA-Z02 QUESTIONS: Solve any four of the following five problems [25]1. Solve the initial and
Stress transformation and Mohr s circle for stresses
 Stress transformation and Mohr s circle for stresses 1.1 General State of stress Consider a certain body, subjected to external force. The force F is acting on the surface over an area da of the surface.
Stress transformation and Mohr s circle for stresses 1.1 General State of stress Consider a certain body, subjected to external force. The force F is acting on the surface over an area da of the surface.
Work, Energy, and Power. Chapter 6 of Essential University Physics, Richard Wolfson, 3 rd Edition
 Work, Energy, and Power Chapter 6 of Essential University Physics, Richard Wolfson, 3 rd Edition 1 With the knowledge we got so far, we can handle the situation on the left but not the one on the right.
Work, Energy, and Power Chapter 6 of Essential University Physics, Richard Wolfson, 3 rd Edition 1 With the knowledge we got so far, we can handle the situation on the left but not the one on the right.
Daily Register Q7 w r\ i i n i i /"\ HTT /"\I AIM MPmf>riAnpn ^ ^ oikiar <mn ^^^*»^^*^^ _.. *-.,..,» * * w ^.. i nr\r\
 $ 000 w G K G y' F: w w w y' w-y k Yk w k ' V 0 8 y Q w \ /"\ /"\ > ^ ^ k < ^^^*»^^*^^ _*-» * * w ^ \\ Y 88 Y Y 8 G b k =-- K w' K y J KKY G - - v v -y- K -y- x- y bb K' w k y k y K y y w b v w y F y w
$ 000 w G K G y' F: w w w y' w-y k Yk w k ' V 0 8 y Q w \ /"\ /"\ > ^ ^ k < ^^^*»^^*^^ _*-» * * w ^ \\ Y 88 Y Y 8 G b k =-- K w' K y J KKY G - - v v -y- K -y- x- y bb K' w k y k y K y y w b v w y F y w
daman's g{iyt 2*1*2=2 =5zg#=5r± 3 S shit exponent ? 25-3 a m * a n 5. I base =/ 5 r Properties of Exponents Terminology In a b a is the b is the
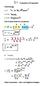 2 2 2 5 I Properties of Exponents Terminology In a b a is the b is the " a to the bth power " base exponent The Product Rule for Like Bases 3 + 4 2 daman's 3 * 2 4 2 2 z z a m * a n 7 2 5 2 3 2*1*22? 253
2 2 2 5 I Properties of Exponents Terminology In a b a is the b is the " a to the bth power " base exponent The Product Rule for Like Bases 3 + 4 2 daman's 3 * 2 4 2 2 z z a m * a n 7 2 5 2 3 2*1*22? 253
MECH 5312 Solid Mechanics II. Dr. Calvin M. Stewart Department of Mechanical Engineering The University of Texas at El Paso
 MECH 5312 Solid Mechanics II Dr. Calvin M. Stewart Department of Mechanical Engineering The University of Texas at El Paso Table of Contents Preliminary Math Concept of Stress Stress Components Equilibrium
MECH 5312 Solid Mechanics II Dr. Calvin M. Stewart Department of Mechanical Engineering The University of Texas at El Paso Table of Contents Preliminary Math Concept of Stress Stress Components Equilibrium
GG303 Lecture 6 8/27/09 1 SCALARS, VECTORS, AND TENSORS
 GG303 Lecture 6 8/27/09 1 SCALARS, VECTORS, AND TENSORS I Main Topics A Why deal with tensors? B Order of scalars, vectors, and tensors C Linear transformation of scalars and vectors (and tensors) II Why
GG303 Lecture 6 8/27/09 1 SCALARS, VECTORS, AND TENSORS I Main Topics A Why deal with tensors? B Order of scalars, vectors, and tensors C Linear transformation of scalars and vectors (and tensors) II Why
FMIA. Fluid Mechanics and Its Applications 113 Series Editor: A. Thess. Moukalled Mangani Darwish. F. Moukalled L. Mangani M.
 FMIA F. Moukalled L. Mangani M. Darwish An Advanced Introduction with OpenFOAM and Matlab This textbook explores both the theoretical foundation of the Finite Volume Method (FVM) and its applications in
FMIA F. Moukalled L. Mangani M. Darwish An Advanced Introduction with OpenFOAM and Matlab This textbook explores both the theoretical foundation of the Finite Volume Method (FVM) and its applications in
LOWHLL #WEEKLY JOURNAL.
 # F 7 F --) 2 9 Q - Q - - F - x $ 2 F? F \ F q - x q - - - - )< - -? - F - - Q z 2 Q - x -- - - - 3 - % 3 3 - - ) F x - \ - - - - - q - q - - - - -z- < F 7-7- - Q F 2 F - F \x -? - - - - - z - x z F -
# F 7 F --) 2 9 Q - Q - - F - x $ 2 F? F \ F q - x q - - - - )< - -? - F - - Q z 2 Q - x -- - - - 3 - % 3 3 - - ) F x - \ - - - - - q - q - - - - -z- < F 7-7- - Q F 2 F - F \x -? - - - - - z - x z F -
Continuum mechanism: Stress and strain
 Continuum mechanics deals with the relation between forces (stress, σ) and deformation (strain, ε), or deformation rate (strain rate, ε). Solid materials, rigid, usually deform elastically, that is the
Continuum mechanics deals with the relation between forces (stress, σ) and deformation (strain, ε), or deformation rate (strain rate, ε). Solid materials, rigid, usually deform elastically, that is the
ME5286 Robotics Spring 2017 Quiz 2
 Page 1 of 5 ME5286 Robotics Spring 2017 Quiz 2 Total Points: 30 You are responsible for following these instructions. Please take a minute and read them completely. 1. Put your name on this page, any other
Page 1 of 5 ME5286 Robotics Spring 2017 Quiz 2 Total Points: 30 You are responsible for following these instructions. Please take a minute and read them completely. 1. Put your name on this page, any other
Calculus of Variations Summer Term 2015
 Calculus of Variations Summer Term 2015 Lecture 12 Universität des Saarlandes 17. Juni 2015 c Daria Apushkinskaya (UdS) Calculus of variations lecture 12 17. Juni 2015 1 / 31 Purpose of Lesson Purpose
Calculus of Variations Summer Term 2015 Lecture 12 Universität des Saarlandes 17. Juni 2015 c Daria Apushkinskaya (UdS) Calculus of variations lecture 12 17. Juni 2015 1 / 31 Purpose of Lesson Purpose
Local Chapter. Mr raised the que stion of what is ad't. deliver the s, nnun. You are cor- c Mr 1 n d. "P**"' iropiie.
 D D D? M G D Y M 2 99 M «4 \ & M? x q M M GM M \ M! 94 - G? \ M M q > G -? Y - M - - - z - > M Z >? - M» > M M - > G! /? - «\- - < x - M-! z - M M M \- - x 7 x GG q M _ ~ > M > # > > M - -
D D D? M G D Y M 2 99 M «4 \ & M? x q M M GM M \ M! 94 - G? \ M M q > G -? Y - M - - - z - > M Z >? - M» > M M - > G! /? - «\- - < x - M-! z - M M M \- - x 7 x GG q M _ ~ > M > # > > M - -
Chapter 17: Undirected Graphical Models
 Chapter 17: Undirected Graphical Models The Elements of Statistical Learning Biaobin Jiang Department of Biological Sciences Purdue University bjiang@purdue.edu October 30, 2014 Biaobin Jiang (Purdue)
Chapter 17: Undirected Graphical Models The Elements of Statistical Learning Biaobin Jiang Department of Biological Sciences Purdue University bjiang@purdue.edu October 30, 2014 Biaobin Jiang (Purdue)
Basic Equations of Elasticity
 A Basic Equations of Elasticity A.1 STRESS The state of stress at any point in a loaded bo is defined completely in terms of the nine components of stress: σ xx,σ yy,σ zz,σ xy,σ yx,σ yz,σ zy,σ zx,andσ
A Basic Equations of Elasticity A.1 STRESS The state of stress at any point in a loaded bo is defined completely in terms of the nine components of stress: σ xx,σ yy,σ zz,σ xy,σ yx,σ yz,σ zy,σ zx,andσ
Full file at
 1 Logic and Proofs 1.1 Propositions and Connectives 1. (a) true (b) false (c) true (d) false (e) false (f) false (g) false (h) false 2. (a) Not a proposition (b) False proposition (c) Not a proposition.
1 Logic and Proofs 1.1 Propositions and Connectives 1. (a) true (b) false (c) true (d) false (e) false (f) false (g) false (h) false 2. (a) Not a proposition (b) False proposition (c) Not a proposition.
Let f(x) = x, but the domain of f is the interval 0 x 1. Note
 I.g Maximum and Minimum. Lagrange Multipliers Recall: Suppose we are given y = f(x). We recall that the maximum/minimum points occur at the following points: (1) where f = 0; (2) where f does not exist;
I.g Maximum and Minimum. Lagrange Multipliers Recall: Suppose we are given y = f(x). We recall that the maximum/minimum points occur at the following points: (1) where f = 0; (2) where f does not exist;
A. H. Hall, 33, 35 &37, Lendoi
 7 X x > - z Z - ----»»x - % x x» [> Q - ) < % - - 7»- -Q 9 Q # 5 - z -> Q x > z»- ~» - x " < z Q q»» > X»? Q ~ - - % % < - < - - 7 - x -X - -- 6 97 9
7 X x > - z Z - ----»»x - % x x» [> Q - ) < % - - 7»- -Q 9 Q # 5 - z -> Q x > z»- ~» - x " < z Q q»» > X»? Q ~ - - % % < - < - - 7 - x -X - -- 6 97 9
Juan Juan Salon. EH National Bank. Sandwich Shop Nail Design. OSKA Beverly. Chase Bank. Marina Rinaldi. Orogold. Mariposa.
 ( ) X é X é Q Ó / 8 ( ) Q / ( ) ( ) : ( ) : 44-3-8999 433 4 z 78-19 941, #115 Z 385-194 77-51 76-51 74-7777, 75-5 47-55 74-8141 74-5115 78-3344 73-3 14 81-4 86-784 78-33 551-888 j 48-4 61-35 z/ zz / 138
( ) X é X é Q Ó / 8 ( ) Q / ( ) ( ) : ( ) : 44-3-8999 433 4 z 78-19 941, #115 Z 385-194 77-51 76-51 74-7777, 75-5 47-55 74-8141 74-5115 78-3344 73-3 14 81-4 86-784 78-33 551-888 j 48-4 61-35 z/ zz / 138
The M6bius Function of a Lattice
 JOURNAL OF COMBINATORIAL THEORY 1, 126-131 (1966) The M6bius Function of a Lattice HENRY H. CRAPO University of Waterloo, Waterloo, Ontario, Canada Communicated by Mark Kae ABSTRACT The structure of an
JOURNAL OF COMBINATORIAL THEORY 1, 126-131 (1966) The M6bius Function of a Lattice HENRY H. CRAPO University of Waterloo, Waterloo, Ontario, Canada Communicated by Mark Kae ABSTRACT The structure of an
CSE 167: Introduction to Computer Graphics Lecture #2: Linear Algebra Primer
 CSE 167: Introduction to Computer Graphics Lecture #2: Linear Algebra Primer Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2016 Announcements Monday October 3: Discussion Assignment
CSE 167: Introduction to Computer Graphics Lecture #2: Linear Algebra Primer Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2016 Announcements Monday October 3: Discussion Assignment
DIPOLES III. q const. The voltage produced by such a charge distribution is given by. r r'
 DIPOLES III We now consider a particularly important charge configuration a dipole. This consists of two equal but opposite charges separated by a small distance. We define the dipole moment as p lim q
DIPOLES III We now consider a particularly important charge configuration a dipole. This consists of two equal but opposite charges separated by a small distance. We define the dipole moment as p lim q

 9 Q - -
9 Q - -  7 ( - ( - < Q & > & )
7 ( - ( - < Q & > & )  «4 [< «
«4 [< «  g k b 7? 3 5 y y Qk
g k b 7? 3 5 y y Qk  Y G q G Y Y 29 8 $ 29 G 6 q )
Y G q G Y Y 29 8 $ 29 G 6 q )