Quadratic Functions. Before we start looking at polynomials, we should know some common terminology.
|
|
|
- Merryl Small
- 5 years ago
- Views:
Transcription
1 Quadratic Fuctios I this sectio we begi the study of fuctios defied by polyomial expressios. Polyomial ad ratioal fuctios are the most commo fuctios used to model data, ad are used extesively i mathematical models of productio costs, cosumer demads, wildlife maagemet, biological processes, ad may other scietific studies. Usig these fuctios ad their graphs, predictios regardig future treds ca be made. Polyomial Fuctios ad Their Graphs: Before we start lookig at polyomials, we should kow some commo termiology. Defiitio: A polyomial of degree is a fuctio of the form 1 1 ( )... P x = a x + a x + + a x + a where a 0. The umbers a0, a1, a,..., a are called the coefficiets of the polyomial. The umber a 0 is the costat coefficiet or costat term. The umber a, the coefficiet of the highest power is the leadig coefficiet, ad the term ax is the leadig term. Notice that a polyomial is usually writte i descedig powers of the variable, ad the degree of a polyomial is the power of the leadig term. For istace ( ) 3 P x = 4x x + 5 is a polyomial of degree 3. Also, if a polyomial cosists of just a sigle term, such as Q x = 7x, the it is called a moomial. ( ) 4 Polyomials of degree 0 are costat fuctios ad polyomials of degree 1 are liear fuctios, whose graphs are both straight lies. Polyomials of degree are quadratic equatios, ad their graphs are parabolas. As the degree of the polyomial icreases beyod, the umber of possible shapes the graph ca be icreases. However, the graph of a polyomial fuctio is always a smooth cotiuous curve (o breaks, gaps, or sharp corers). ( ) Moomials of the form P x = x are the simplest polyomials.
2 As the figure suggest, the graph of P(x) = x has the same geeral shape as y = x whe is eve, ad the same geeral shape as y = x 3 whe is odd. However, as the degree becomes larger, the graphs become flatter aroud the origi ad steeper elsewhere. To this poit, we have had some experiece with quadratic equatios. We kow that the graph of a quadratic equatio gives us a parabola. I this sectio, we will see how quadratic equatios (ad their correspodig parabolas) ca give us some valuable iformatio i real-life situatios. If a parabola opes upward, the we kow that there is a poit at which the graph reaches its miimum value. Likewise, if we have a parabola that opes dowward, we kow that there must be a maximum value for that fuctio. These maximum ad miimum values are referred to as extreme values. There are may practical situatios, which ca be represeted by such fuctios. I these situatios, the extreme values ca ofte give us valuable pieces of iformatio. For example, the ower of a clothig store might be iterested i kowig her maximum profit or miimum cost. As review, we will look at the defiitio of a quadratic fuctio. Def: A quadratic fuctio is a fuctio f of the form = ax + bx + c where a, b, ad c are real umbers ad a 0. Stadard Form ad Completig the Square: I determiig extreme values, it is very helpful to put the quadratic fuctio ito stadard form. This ca be doe by completig the square. Now, I ca already hear the collective groa at the metio of completig the square, but it is a very ecessary skill i determiig extreme values. I am cofidet that you ca lear it well if you just take it step-by-step. First, let s take a look at stadard form.
3 Def: A quadratic fuctio ca be expressed i the stadard form = a( x h) + k by completig the square. The graph of f is a parabola with vertex (h,k); the parabola opes upward if a > 0 or dowward if a < 0. If a > 0, the the miimum value of f occurs at x = h ad this value is words, the poit with coordiates (h,k). f ( h) = k, i other If a < 0, the the maximum value of f occurs at x = h ad this value is also the poit (h,k). f ( h) = k,
4 Example 1: Sketch the graph of the fuctio = x + 10x 0 ad state the vertex. Begi by completig the square. Solutio: Comparig this with the form a = 1 b = 10 c = 0 = ax + bx + c, we ca see that Example 1 (Cotiued): Step 1: Group the x ad x terms, ad factor out ay a value. I this case, sice a = 1, we simply have to group the first two terms. = ( x + 10x) 0 Step : After groupig the first two terms ad factorig out a, cosider the coefficiet of x, i this case 10. Divide this value by ad take the square. 10 = 5 = 5 Step 3: Complete the square by addig the above value iside the paretheses. Note: Ay value that is added to oe side of the equatio must also be subtracted from that side of the equatio i order to keep from chagig the value. i.e.- add a value of zero to the equatio. Therefore, we must subtract the total value outside the paretheses. (Here is where you must be careful to pay attetio to ay commo value that has bee factored out. We will see this i the ext example.) = ( x + 10x + 5) 0 5 Step 4: Factor the portio of the equatio i paretheses ad combie ay other like terms. = ( x + 10x + 5) 0 5 = ( x + 10x + 5) 45 = ( x + 5) 45 OR = ( x ( 5)) 45 (which will be helpful, as you will see ow)
5 The fuctio should be i the form = a( x h) + k. I this case, a = 1 h = 5 k = 45 Example 1 (Cotiued): Notice: You must pay special attetio to the sig of h. Rewritig the equatio as we did above will be helpful i seeig the sig of h more clearly. Now that we have completed the square, the remaider of the solutio is very simple. By defiitio, we kow the parabola opes upward, sice a > 0, ad we have a miimum value at the poit (-5,-45) which is also the vertex of the parabola. We are simply asked to sketch the parabola, so it is ot ecessary i this case to fid multiple poits o the graph. We ca simply sketch the graph usig what we kow. Let s look at oe more example. Example : For the fuctio = x 16x + 1 (a) Express the fuctio i stadard form. (b) Sketch its graph. (c) Fid its maximum or miimum value.
6 Solutio: (a) We ca put the fuctio ito stadard form by completig the square. Step 1: Group the x ad x terms, ad factor out ay a value. = (x 16x) + 1 = ( x 8x) + 1 Example (Cotiued): Step : After groupig the first two terms ad factorig out a, cosider the coefficiet of x, i this case ( 8). Divide this value by ad take the square. 8 = ( 4) = 16 (Notice that the sig of the x coefficiet does ot really matter at this poit, because after squarig the term, you will always have a positive umber.) Step 3: Complete the square by addig the above value iside the paretheses ad subtractig the total value outside the paretheses. = ( x 8x + 16) Note: Special attetio must be give to the value that was factored out. This will affect the value which is subtracted outside the paretheses. i.e.- (16)=3 Step 4: Factor the portio of the equatio i paretheses ad combie ay other like terms. = ( x 8x + 16) = ( x 8x + 16) 0 = ( x 4) 0 So, we have the graph i stadard form. (b) To sketch the graph, let s combie the iformatio we have from the stadard form of the equatio.
7 a = h = 4 k = 0 Sice a > 0, the parabola opes upward; therefore, we have a miimum value at x = 4. This value occurs at the poit (4,-0) which is also the vertex. With this iformatio, we ca easily sketch the graph. Example (Cotiued): (c) The miimum value of the graph occurs at x = 4, ad the value there is ( 0). This is the value f ( h) = k. Maximum or Miimum Value of a Quadratic Equatio: I the examples so far, we have bee asked to graph the fuctio, etc. Sometimes is simply ecessary to kow the maximum or miimum value. I this case, you do ot eed to complete the square, because you do ot eed the equatio to be i stadard form. Def: The maximum or miimum value of a quadratic fuctio = ax + bx + c occurs at x = b a If a > 0, the the miimum value is f b a.
8 b If a < 0, the the maximum value is f. a
9 Example 3: A coffee shop o the SAC campus has a sales aalyst cosider the store s sales records for a moth. The aalyst produces a formula i order to help the store geerate more profit. He fids that if the shop cells l orders of latte i oe day, the profit (i dollars) is give by the followig fuctio 1 P ( l) = x + 3x What is the maximum profit possible for the store i oe day, ad how may lattes must they sell i order to reach this maximum? Solutio: First, it is importat to otice that they asked for a maximum profit. We kow we will have a maximum istead of a miimum, because a < 0. Usig the defiitio above, the maximum occurs at b a l = = 3 ( 1 ) (1000) = ( 1) = 3000 = 1500 This meas that i order to receive a maximum profit, the coffee shop must sell 1500 lattes per day. I order to fid out what the maximum profit actually is (i dollars), we have to evaluate the fuctio at this value, l. b 1 P = P (1500) = (1500) a = = = 450 The maximum profit would be $ (1500) 1800
Polynomial Functions and Their Graphs
 Polyomial Fuctios ad Their Graphs I this sectio we begi the study of fuctios defied by polyomial expressios. Polyomial ad ratioal fuctios are the most commo fuctios used to model data, ad are used extesively
Polyomial Fuctios ad Their Graphs I this sectio we begi the study of fuctios defied by polyomial expressios. Polyomial ad ratioal fuctios are the most commo fuctios used to model data, ad are used extesively
Polynomial Functions. New Section 1 Page 1. A Polynomial function of degree n is written is the form:
 New Sectio 1 Page 1 A Polyomial fuctio of degree is writte is the form: 1 P x a x a x a x a x a x a 1 1 0 where is a o-egative iteger expoet ad a 0 ca oly take o values where a, a, a,..., a, a. 0 1 1.
New Sectio 1 Page 1 A Polyomial fuctio of degree is writte is the form: 1 P x a x a x a x a x a x a 1 1 0 where is a o-egative iteger expoet ad a 0 ca oly take o values where a, a, a,..., a, a. 0 1 1.
Properties and Tests of Zeros of Polynomial Functions
 Properties ad Tests of Zeros of Polyomial Fuctios The Remaider ad Factor Theorems: Sythetic divisio ca be used to fid the values of polyomials i a sometimes easier way tha substitutio. This is show by
Properties ad Tests of Zeros of Polyomial Fuctios The Remaider ad Factor Theorems: Sythetic divisio ca be used to fid the values of polyomials i a sometimes easier way tha substitutio. This is show by
Zeros of Polynomials
 Math 160 www.timetodare.com 4.5 4.6 Zeros of Polyomials I these sectios we will study polyomials algebraically. Most of our work will be cocered with fidig the solutios of polyomial equatios of ay degree
Math 160 www.timetodare.com 4.5 4.6 Zeros of Polyomials I these sectios we will study polyomials algebraically. Most of our work will be cocered with fidig the solutios of polyomial equatios of ay degree
Unit 4: Polynomial and Rational Functions
 48 Uit 4: Polyomial ad Ratioal Fuctios Polyomial Fuctios A polyomial fuctio y px ( ) is a fuctio of the form p( x) ax + a x + a x +... + ax + ax+ a 1 1 1 0 where a, a 1,..., a, a1, a0are real costats ad
48 Uit 4: Polyomial ad Ratioal Fuctios Polyomial Fuctios A polyomial fuctio y px ( ) is a fuctio of the form p( x) ax + a x + a x +... + ax + ax+ a 1 1 1 0 where a, a 1,..., a, a1, a0are real costats ad
3.2 Properties of Division 3.3 Zeros of Polynomials 3.4 Complex and Rational Zeros of Polynomials
 Math 60 www.timetodare.com 3. Properties of Divisio 3.3 Zeros of Polyomials 3.4 Complex ad Ratioal Zeros of Polyomials I these sectios we will study polyomials algebraically. Most of our work will be cocered
Math 60 www.timetodare.com 3. Properties of Divisio 3.3 Zeros of Polyomials 3.4 Complex ad Ratioal Zeros of Polyomials I these sectios we will study polyomials algebraically. Most of our work will be cocered
x c the remainder is Pc ().
 Algebra, Polyomial ad Ratioal Fuctios Page 1 K.Paulk Notes Chapter 3, Sectio 3.1 to 3.4 Summary Sectio Theorem Notes 3.1 Zeros of a Fuctio Set the fuctio to zero ad solve for x. The fuctio is zero at these
Algebra, Polyomial ad Ratioal Fuctios Page 1 K.Paulk Notes Chapter 3, Sectio 3.1 to 3.4 Summary Sectio Theorem Notes 3.1 Zeros of a Fuctio Set the fuctio to zero ad solve for x. The fuctio is zero at these
SNAP Centre Workshop. Basic Algebraic Manipulation
 SNAP Cetre Workshop Basic Algebraic Maipulatio 8 Simplifyig Algebraic Expressios Whe a expressio is writte i the most compact maer possible, it is cosidered to be simplified. Not Simplified: x(x + 4x)
SNAP Cetre Workshop Basic Algebraic Maipulatio 8 Simplifyig Algebraic Expressios Whe a expressio is writte i the most compact maer possible, it is cosidered to be simplified. Not Simplified: x(x + 4x)
The picture in figure 1.1 helps us to see that the area represents the distance traveled. Figure 1: Area represents distance travelled
 1 Lecture : Area Area ad distace traveled Approximatig area by rectagles Summatio The area uder a parabola 1.1 Area ad distace Suppose we have the followig iformatio about the velocity of a particle, how
1 Lecture : Area Area ad distace traveled Approximatig area by rectagles Summatio The area uder a parabola 1.1 Area ad distace Suppose we have the followig iformatio about the velocity of a particle, how
CALCULUS BASIC SUMMER REVIEW
 CALCULUS BASIC SUMMER REVIEW NAME rise y y y Slope of a o vertical lie: m ru Poit Slope Equatio: y y m( ) The slope is m ad a poit o your lie is, ). ( y Slope-Itercept Equatio: y m b slope= m y-itercept=
CALCULUS BASIC SUMMER REVIEW NAME rise y y y Slope of a o vertical lie: m ru Poit Slope Equatio: y y m( ) The slope is m ad a poit o your lie is, ). ( y Slope-Itercept Equatio: y m b slope= m y-itercept=
TEACHER CERTIFICATION STUDY GUIDE
 COMPETENCY 1. ALGEBRA SKILL 1.1 1.1a. ALGEBRAIC STRUCTURES Kow why the real ad complex umbers are each a field, ad that particular rigs are ot fields (e.g., itegers, polyomial rigs, matrix rigs) Algebra
COMPETENCY 1. ALGEBRA SKILL 1.1 1.1a. ALGEBRAIC STRUCTURES Kow why the real ad complex umbers are each a field, ad that particular rigs are ot fields (e.g., itegers, polyomial rigs, matrix rigs) Algebra
Continuous Functions
 Cotiuous Fuctios Q What does it mea for a fuctio to be cotiuous at a poit? Aswer- I mathematics, we have a defiitio that cosists of three cocepts that are liked i a special way Cosider the followig defiitio
Cotiuous Fuctios Q What does it mea for a fuctio to be cotiuous at a poit? Aswer- I mathematics, we have a defiitio that cosists of three cocepts that are liked i a special way Cosider the followig defiitio
We are mainly going to be concerned with power series in x, such as. (x)} converges - that is, lims N n
 Review of Power Series, Power Series Solutios A power series i x - a is a ifiite series of the form c (x a) =c +c (x a)+(x a) +... We also call this a power series cetered at a. Ex. (x+) is cetered at
Review of Power Series, Power Series Solutios A power series i x - a is a ifiite series of the form c (x a) =c +c (x a)+(x a) +... We also call this a power series cetered at a. Ex. (x+) is cetered at
September 2012 C1 Note. C1 Notes (Edexcel) Copyright - For AS, A2 notes and IGCSE / GCSE worksheets 1
 September 0 s (Edecel) Copyright www.pgmaths.co.uk - For AS, A otes ad IGCSE / GCSE worksheets September 0 Copyright www.pgmaths.co.uk - For AS, A otes ad IGCSE / GCSE worksheets September 0 Copyright
September 0 s (Edecel) Copyright www.pgmaths.co.uk - For AS, A otes ad IGCSE / GCSE worksheets September 0 Copyright www.pgmaths.co.uk - For AS, A otes ad IGCSE / GCSE worksheets September 0 Copyright
Recurrence Relations
 Recurrece Relatios Aalysis of recursive algorithms, such as: it factorial (it ) { if (==0) retur ; else retur ( * factorial(-)); } Let t be the umber of multiplicatios eeded to calculate factorial(). The
Recurrece Relatios Aalysis of recursive algorithms, such as: it factorial (it ) { if (==0) retur ; else retur ( * factorial(-)); } Let t be the umber of multiplicatios eeded to calculate factorial(). The
INTEGRATION BY PARTS (TABLE METHOD)
 INTEGRATION BY PARTS (TABLE METHOD) Suppose you wat to evaluate cos d usig itegratio by parts. Usig the u dv otatio, we get So, u dv d cos du d v si cos d si si d or si si d We see that it is ecessary
INTEGRATION BY PARTS (TABLE METHOD) Suppose you wat to evaluate cos d usig itegratio by parts. Usig the u dv otatio, we get So, u dv d cos du d v si cos d si si d or si si d We see that it is ecessary
P.3 Polynomials and Special products
 Precalc Fall 2016 Sectios P.3, 1.2, 1.3, P.4, 1.4, P.2 (radicals/ratioal expoets), 1.5, 1.6, 1.7, 1.8, 1.1, 2.1, 2.2 I Polyomial defiitio (p. 28) a x + a x +... + a x + a x 1 1 0 1 1 0 a x + a x +... +
Precalc Fall 2016 Sectios P.3, 1.2, 1.3, P.4, 1.4, P.2 (radicals/ratioal expoets), 1.5, 1.6, 1.7, 1.8, 1.1, 2.1, 2.2 I Polyomial defiitio (p. 28) a x + a x +... + a x + a x 1 1 0 1 1 0 a x + a x +... +
FLC Ch 8 & 9. Evaluate. Check work. a) b) c) d) e) f) g) h) i) j) k) l) m) n) o) 3. p) q) r) s) t) 3.
 Math 100 Elemetary Algebra Sec 8.1: Radical Expressios List perfect squares ad evaluate their square root. Kow these perfect squares for test. Def The positive (pricipal) square root of x, writte x, is
Math 100 Elemetary Algebra Sec 8.1: Radical Expressios List perfect squares ad evaluate their square root. Kow these perfect squares for test. Def The positive (pricipal) square root of x, writte x, is
Some examples of vector spaces
 Roberto s Notes o Liear Algebra Chapter 11: Vector spaces Sectio 2 Some examples of vector spaces What you eed to kow already: The te axioms eeded to idetify a vector space. What you ca lear here: Some
Roberto s Notes o Liear Algebra Chapter 11: Vector spaces Sectio 2 Some examples of vector spaces What you eed to kow already: The te axioms eeded to idetify a vector space. What you ca lear here: Some
A sequence of numbers is a function whose domain is the positive integers. We can see that the sequence
 Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece,, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet as
Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece,, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet as
x x x Using a second Taylor polynomial with remainder, find the best constant C so that for x 0,
 Math Activity 9( Due with Fial Eam) Usig first ad secod Taylor polyomials with remaider, show that for, 8 Usig a secod Taylor polyomial with remaider, fid the best costat C so that for, C 9 The th Derivative
Math Activity 9( Due with Fial Eam) Usig first ad secod Taylor polyomials with remaider, show that for, 8 Usig a secod Taylor polyomial with remaider, fid the best costat C so that for, C 9 The th Derivative
CHAPTER 10 INFINITE SEQUENCES AND SERIES
 CHAPTER 10 INFINITE SEQUENCES AND SERIES 10.1 Sequeces 10.2 Ifiite Series 10.3 The Itegral Tests 10.4 Compariso Tests 10.5 The Ratio ad Root Tests 10.6 Alteratig Series: Absolute ad Coditioal Covergece
CHAPTER 10 INFINITE SEQUENCES AND SERIES 10.1 Sequeces 10.2 Ifiite Series 10.3 The Itegral Tests 10.4 Compariso Tests 10.5 The Ratio ad Root Tests 10.6 Alteratig Series: Absolute ad Coditioal Covergece
Lesson 10: Limits and Continuity
 www.scimsacademy.com Lesso 10: Limits ad Cotiuity SCIMS Academy 1 Limit of a fuctio The cocept of limit of a fuctio is cetral to all other cocepts i calculus (like cotiuity, derivative, defiite itegrals
www.scimsacademy.com Lesso 10: Limits ad Cotiuity SCIMS Academy 1 Limit of a fuctio The cocept of limit of a fuctio is cetral to all other cocepts i calculus (like cotiuity, derivative, defiite itegrals
NAME: ALGEBRA 350 BLOCK 7. Simplifying Radicals Packet PART 1: ROOTS
 NAME: ALGEBRA 50 BLOCK 7 DATE: Simplifyig Radicals Packet PART 1: ROOTS READ: A square root of a umber b is a solutio of the equatio x = b. Every positive umber b has two square roots, deoted b ad b or
NAME: ALGEBRA 50 BLOCK 7 DATE: Simplifyig Radicals Packet PART 1: ROOTS READ: A square root of a umber b is a solutio of the equatio x = b. Every positive umber b has two square roots, deoted b ad b or
In algebra one spends much time finding common denominators and thus simplifying rational expressions. For example:
 74 The Method of Partial Fractios I algebra oe speds much time fidig commo deomiators ad thus simplifyig ratioal epressios For eample: + + + 6 5 + = + = = + + + + + ( )( ) 5 It may the seem odd to be watig
74 The Method of Partial Fractios I algebra oe speds much time fidig commo deomiators ad thus simplifyig ratioal epressios For eample: + + + 6 5 + = + = = + + + + + ( )( ) 5 It may the seem odd to be watig
Section 11.8: Power Series
 Sectio 11.8: Power Series 1. Power Series I this sectio, we cosider geeralizig the cocept of a series. Recall that a series is a ifiite sum of umbers a. We ca talk about whether or ot it coverges ad i
Sectio 11.8: Power Series 1. Power Series I this sectio, we cosider geeralizig the cocept of a series. Recall that a series is a ifiite sum of umbers a. We ca talk about whether or ot it coverges ad i
Sequences A sequence of numbers is a function whose domain is the positive integers. We can see that the sequence
 Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece 1, 1, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet
Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece 1, 1, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet
11. FINITE FIELDS. Example 1: The following tables define addition and multiplication for a field of order 4.
 11. FINITE FIELDS 11.1. A Field With 4 Elemets Probably the oly fiite fields which you ll kow about at this stage are the fields of itegers modulo a prime p, deoted by Z p. But there are others. Now although
11. FINITE FIELDS 11.1. A Field With 4 Elemets Probably the oly fiite fields which you ll kow about at this stage are the fields of itegers modulo a prime p, deoted by Z p. But there are others. Now although
a is some real number (called the coefficient) other
 Precalculus Notes for Sectio.1 Liear/Quadratic Fuctios ad Modelig http://www.schooltube.com/video/77e0a939a3344194bb4f Defiitios: A moomial is a term of the form tha zero ad is a oegative iteger. a where
Precalculus Notes for Sectio.1 Liear/Quadratic Fuctios ad Modelig http://www.schooltube.com/video/77e0a939a3344194bb4f Defiitios: A moomial is a term of the form tha zero ad is a oegative iteger. a where
A.1 Algebra Review: Polynomials/Rationals. Definitions:
 MATH 040 Notes: Uit 0 Page 1 A.1 Algera Review: Polyomials/Ratioals Defiitios: A polyomial is a sum of polyomial terms. Polyomial terms are epressios formed y products of costats ad variales with whole
MATH 040 Notes: Uit 0 Page 1 A.1 Algera Review: Polyomials/Ratioals Defiitios: A polyomial is a sum of polyomial terms. Polyomial terms are epressios formed y products of costats ad variales with whole
Recursive Algorithms. Recurrences. Recursive Algorithms Analysis
 Recursive Algorithms Recurreces Computer Sciece & Egieerig 35: Discrete Mathematics Christopher M Bourke cbourke@cseuledu A recursive algorithm is oe i which objects are defied i terms of other objects
Recursive Algorithms Recurreces Computer Sciece & Egieerig 35: Discrete Mathematics Christopher M Bourke cbourke@cseuledu A recursive algorithm is oe i which objects are defied i terms of other objects
1 Generating functions for balls in boxes
 Math 566 Fall 05 Some otes o geeratig fuctios Give a sequece a 0, a, a,..., a,..., a geeratig fuctio some way of represetig the sequece as a fuctio. There are may ways to do this, with the most commo ways
Math 566 Fall 05 Some otes o geeratig fuctios Give a sequece a 0, a, a,..., a,..., a geeratig fuctio some way of represetig the sequece as a fuctio. There are may ways to do this, with the most commo ways
MAT 271 Project: Partial Fractions for certain rational functions
 MAT 7 Project: Partial Fractios for certai ratioal fuctios Prerequisite kowledge: partial fractios from MAT 7, a very good commad of factorig ad complex umbers from Precalculus. To complete this project,
MAT 7 Project: Partial Fractios for certai ratioal fuctios Prerequisite kowledge: partial fractios from MAT 7, a very good commad of factorig ad complex umbers from Precalculus. To complete this project,
Algebra 1 Hour Final Exam Review Days
 Semester Fial Eam Review Packet Name Algebra 1 Hour Fial Eam Review Days Assiged o Assigmet 6/6 Fial Eam Review Chapters 11 ad 1 Problems 54 7 6/7 Fial Eam Review Chapters 10 Problems 44 5 6/8 Fial Eam
Semester Fial Eam Review Packet Name Algebra 1 Hour Fial Eam Review Days Assiged o Assigmet 6/6 Fial Eam Review Chapters 11 ad 1 Problems 54 7 6/7 Fial Eam Review Chapters 10 Problems 44 5 6/8 Fial Eam
Northwest High School s Algebra 2/Honors Algebra 2 Summer Review Packet
 Northwest High School s Algebra /Hoors Algebra Summer Review Packet This packet is optioal! It will NOT be collected for a grade et school year! This packet has bee desiged to help you review various mathematical
Northwest High School s Algebra /Hoors Algebra Summer Review Packet This packet is optioal! It will NOT be collected for a grade et school year! This packet has bee desiged to help you review various mathematical
CHAPTER I: Vector Spaces
 CHAPTER I: Vector Spaces Sectio 1: Itroductio ad Examples This first chapter is largely a review of topics you probably saw i your liear algebra course. So why cover it? (1) Not everyoe remembers everythig
CHAPTER I: Vector Spaces Sectio 1: Itroductio ad Examples This first chapter is largely a review of topics you probably saw i your liear algebra course. So why cover it? (1) Not everyoe remembers everythig
Curve Sketching Handout #5 Topic Interpretation Rational Functions
 Curve Sketchig Hadout #5 Topic Iterpretatio Ratioal Fuctios A ratioal fuctio is a fuctio f that is a quotiet of two polyomials. I other words, p ( ) ( ) f is a ratioal fuctio if p ( ) ad q ( ) are polyomials
Curve Sketchig Hadout #5 Topic Iterpretatio Ratioal Fuctios A ratioal fuctio is a fuctio f that is a quotiet of two polyomials. I other words, p ( ) ( ) f is a ratioal fuctio if p ( ) ad q ( ) are polyomials
multiplies all measures of center and the standard deviation and range by k, while the variance is multiplied by k 2.
 Lesso 3- Lesso 3- Scale Chages of Data Vocabulary scale chage of a data set scale factor scale image BIG IDEA Multiplyig every umber i a data set by k multiplies all measures of ceter ad the stadard deviatio
Lesso 3- Lesso 3- Scale Chages of Data Vocabulary scale chage of a data set scale factor scale image BIG IDEA Multiplyig every umber i a data set by k multiplies all measures of ceter ad the stadard deviatio
62. Power series Definition 16. (Power series) Given a sequence {c n }, the series. c n x n = c 0 + c 1 x + c 2 x 2 + c 3 x 3 +
 62. Power series Defiitio 16. (Power series) Give a sequece {c }, the series c x = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + is called a power series i the variable x. The umbers c are called the coefficiets of
62. Power series Defiitio 16. (Power series) Give a sequece {c }, the series c x = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + is called a power series i the variable x. The umbers c are called the coefficiets of
RADICAL EXPRESSION. If a and x are real numbers and n is a positive integer, then x is an. n th root theorems: Example 1 Simplify
 Example 1 Simplify 1.2A Radical Operatios a) 4 2 b) 16 1 2 c) 16 d) 2 e) 8 1 f) 8 What is the relatioship betwee a, b, c? What is the relatioship betwee d, e, f? If x = a, the x = = th root theorems: RADICAL
Example 1 Simplify 1.2A Radical Operatios a) 4 2 b) 16 1 2 c) 16 d) 2 e) 8 1 f) 8 What is the relatioship betwee a, b, c? What is the relatioship betwee d, e, f? If x = a, the x = = th root theorems: RADICAL
[ 11 ] z of degree 2 as both degree 2 each. The degree of a polynomial in n variables is the maximum of the degrees of its terms.
![[ 11 ] z of degree 2 as both degree 2 each. The degree of a polynomial in n variables is the maximum of the degrees of its terms. [ 11 ] z of degree 2 as both degree 2 each. The degree of a polynomial in n variables is the maximum of the degrees of its terms.](/thumbs/82/84777652.jpg) [ 11 ] 1 1.1 Polyomial Fuctios 1 Algebra Ay fuctio f ( x) ax a1x... a1x a0 is a polyomial fuctio if ai ( i 0,1,,,..., ) is a costat which belogs to the set of real umbers ad the idices,, 1,...,1 are atural
[ 11 ] 1 1.1 Polyomial Fuctios 1 Algebra Ay fuctio f ( x) ax a1x... a1x a0 is a polyomial fuctio if ai ( i 0,1,,,..., ) is a costat which belogs to the set of real umbers ad the idices,, 1,...,1 are atural
, then cv V. Differential Equations Elements of Lineaer Algebra Name: Consider the differential equation. and y2 cos( kx)
 Cosider the differetial equatio y '' k y 0 has particular solutios y1 si( kx) ad y cos( kx) I geeral, ay liear combiatio of y1 ad y, cy 1 1 cy where c1, c is also a solutio to the equatio above The reaso
Cosider the differetial equatio y '' k y 0 has particular solutios y1 si( kx) ad y cos( kx) I geeral, ay liear combiatio of y1 ad y, cy 1 1 cy where c1, c is also a solutio to the equatio above The reaso
Linear Regression Analysis. Analysis of paired data and using a given value of one variable to predict the value of the other
 Liear Regressio Aalysis Aalysis of paired data ad usig a give value of oe variable to predict the value of the other 5 5 15 15 1 1 5 5 1 3 4 5 6 7 8 1 3 4 5 6 7 8 Liear Regressio Aalysis E: The chirp rate
Liear Regressio Aalysis Aalysis of paired data ad usig a give value of oe variable to predict the value of the other 5 5 15 15 1 1 5 5 1 3 4 5 6 7 8 1 3 4 5 6 7 8 Liear Regressio Aalysis E: The chirp rate
Ma 530 Introduction to Power Series
 Ma 530 Itroductio to Power Series Please ote that there is material o power series at Visual Calculus. Some of this material was used as part of the presetatio of the topics that follow. What is a Power
Ma 530 Itroductio to Power Series Please ote that there is material o power series at Visual Calculus. Some of this material was used as part of the presetatio of the topics that follow. What is a Power
Chapter 9 - CD companion 1. A Generic Implementation; The Common-Merge Amplifier. 1 τ is. ω ch. τ io
 Chapter 9 - CD compaio CHAPTER NINE CD-9.2 CD-9.2. Stages With Voltage ad Curret Gai A Geeric Implemetatio; The Commo-Merge Amplifier The advaced method preseted i the text for approximatig cutoff frequecies
Chapter 9 - CD compaio CHAPTER NINE CD-9.2 CD-9.2. Stages With Voltage ad Curret Gai A Geeric Implemetatio; The Commo-Merge Amplifier The advaced method preseted i the text for approximatig cutoff frequecies
Slide 1. Slide 2. Slide 3. Solids of Rotation:
 Slide 1 Solids of Rotatio: The Eggplat Experiece Suz Atik Palo Alto High School Palo Alto, Ca EdD; NBCT, AYA Math satik@pausd.org May thaks to my colleague, Kathy Weiss, NBCT, AYA Math, who origially desiged
Slide 1 Solids of Rotatio: The Eggplat Experiece Suz Atik Palo Alto High School Palo Alto, Ca EdD; NBCT, AYA Math satik@pausd.org May thaks to my colleague, Kathy Weiss, NBCT, AYA Math, who origially desiged
Most text will write ordinary derivatives using either Leibniz notation 2 3. y + 5y= e and y y. xx tt t
 Itroductio to Differetial Equatios Defiitios ad Termiolog Differetial Equatio: A equatio cotaiig the derivatives of oe or more depedet variables, with respect to oe or more idepedet variables, is said
Itroductio to Differetial Equatios Defiitios ad Termiolog Differetial Equatio: A equatio cotaiig the derivatives of oe or more depedet variables, with respect to oe or more idepedet variables, is said
Exponents. Learning Objectives. Pre-Activity
 Sectio. Pre-Activity Preparatio Epoets A Chai Letter Chai letters are geerated every day. If you sed a chai letter to three frieds ad they each sed it o to three frieds, who each sed it o to three frieds,
Sectio. Pre-Activity Preparatio Epoets A Chai Letter Chai letters are geerated every day. If you sed a chai letter to three frieds ad they each sed it o to three frieds, who each sed it o to three frieds,
Math 113, Calculus II Winter 2007 Final Exam Solutions
 Math, Calculus II Witer 7 Fial Exam Solutios (5 poits) Use the limit defiitio of the defiite itegral ad the sum formulas to compute x x + dx The check your aswer usig the Evaluatio Theorem Solutio: I this
Math, Calculus II Witer 7 Fial Exam Solutios (5 poits) Use the limit defiitio of the defiite itegral ad the sum formulas to compute x x + dx The check your aswer usig the Evaluatio Theorem Solutio: I this
Mth 138 College Algebra Review Guide for Exam III
 Mth 138 College Algebra Review Guide for Exam III Thomas W. Judso Stephe F. Austi State Uiversity Sprig 2018 Exam III Details Exam III will be o Thursday, April 19 ad will cover material up to Chapter
Mth 138 College Algebra Review Guide for Exam III Thomas W. Judso Stephe F. Austi State Uiversity Sprig 2018 Exam III Details Exam III will be o Thursday, April 19 ad will cover material up to Chapter
Section 1.1. Calculus: Areas And Tangents. Difference Equations to Differential Equations
 Differece Equatios to Differetial Equatios Sectio. Calculus: Areas Ad Tagets The study of calculus begis with questios about chage. What happes to the velocity of a swigig pedulum as its positio chages?
Differece Equatios to Differetial Equatios Sectio. Calculus: Areas Ad Tagets The study of calculus begis with questios about chage. What happes to the velocity of a swigig pedulum as its positio chages?
Problem Cosider the curve give parametrically as x = si t ad y = + cos t for» t» ß: (a) Describe the path this traverses: Where does it start (whe t =
 Mathematics Summer Wilso Fial Exam August 8, ANSWERS Problem 1 (a) Fid the solutio to y +x y = e x x that satisfies y() = 5 : This is already i the form we used for a first order liear differetial equatio,
Mathematics Summer Wilso Fial Exam August 8, ANSWERS Problem 1 (a) Fid the solutio to y +x y = e x x that satisfies y() = 5 : This is already i the form we used for a first order liear differetial equatio,
Definitions and Theorems. where x are the decision variables. c, b, and a are constant coefficients.
 Defiitios ad Theorems Remember the scalar form of the liear programmig problem, Miimize, Subject to, f(x) = c i x i a 1i x i = b 1 a mi x i = b m x i 0 i = 1,2,, where x are the decisio variables. c, b,
Defiitios ad Theorems Remember the scalar form of the liear programmig problem, Miimize, Subject to, f(x) = c i x i a 1i x i = b 1 a mi x i = b m x i 0 i = 1,2,, where x are the decisio variables. c, b,
x a x a Lecture 2 Series (See Chapter 1 in Boas)
 Lecture Series (See Chapter i Boas) A basic ad very powerful (if pedestria, recall we are lazy AD smart) way to solve ay differetial (or itegral) equatio is via a series expasio of the correspodig solutio
Lecture Series (See Chapter i Boas) A basic ad very powerful (if pedestria, recall we are lazy AD smart) way to solve ay differetial (or itegral) equatio is via a series expasio of the correspodig solutio
ACCESS TO SCIENCE, ENGINEERING AND AGRICULTURE: MATHEMATICS 1 MATH00030 SEMESTER / Statistics
 ACCESS TO SCIENCE, ENGINEERING AND AGRICULTURE: MATHEMATICS 1 MATH00030 SEMESTER 1 018/019 DR. ANTHONY BROWN 8. Statistics 8.1. Measures of Cetre: Mea, Media ad Mode. If we have a series of umbers the
ACCESS TO SCIENCE, ENGINEERING AND AGRICULTURE: MATHEMATICS 1 MATH00030 SEMESTER 1 018/019 DR. ANTHONY BROWN 8. Statistics 8.1. Measures of Cetre: Mea, Media ad Mode. If we have a series of umbers the
Topic 9 - Taylor and MacLaurin Series
 Topic 9 - Taylor ad MacLauri Series A. Taylors Theorem. The use o power series is very commo i uctioal aalysis i act may useul ad commoly used uctios ca be writte as a power series ad this remarkable result
Topic 9 - Taylor ad MacLauri Series A. Taylors Theorem. The use o power series is very commo i uctioal aalysis i act may useul ad commoly used uctios ca be writte as a power series ad this remarkable result
( ) 2 + k The vertex is ( h, k) ( )( x q) The x-intercepts are x = p and x = q.
 A Referece Sheet Number Sets Quadratic Fuctios Forms Form Equatio Stadard Form Vertex Form Itercept Form y ax + bx + c The x-coordiate of the vertex is x b a y a x h The axis of symmetry is x b a + k The
A Referece Sheet Number Sets Quadratic Fuctios Forms Form Equatio Stadard Form Vertex Form Itercept Form y ax + bx + c The x-coordiate of the vertex is x b a y a x h The axis of symmetry is x b a + k The
U8L1: Sec Equations of Lines in R 2
 MCVU U8L: Sec. 8.9. Equatios of Lies i R Review of Equatios of a Straight Lie (-D) Cosider the lie passig through A (-,) with slope, as show i the diagram below. I poit slope form, the equatio of the lie
MCVU U8L: Sec. 8.9. Equatios of Lies i R Review of Equatios of a Straight Lie (-D) Cosider the lie passig through A (-,) with slope, as show i the diagram below. I poit slope form, the equatio of the lie
( a) ( ) 1 ( ) 2 ( ) ( ) 3 3 ( ) =!
 .8,.9: Taylor ad Maclauri Series.8. Although we were able to fid power series represetatios for a limited group of fuctios i the previous sectio, it is ot immediately obvious whether ay give fuctio has
.8,.9: Taylor ad Maclauri Series.8. Although we were able to fid power series represetatios for a limited group of fuctios i the previous sectio, it is ot immediately obvious whether ay give fuctio has
The Method of Least Squares. To understand least squares fitting of data.
 The Method of Least Squares KEY WORDS Curve fittig, least square GOAL To uderstad least squares fittig of data To uderstad the least squares solutio of icosistet systems of liear equatios 1 Motivatio Curve
The Method of Least Squares KEY WORDS Curve fittig, least square GOAL To uderstad least squares fittig of data To uderstad the least squares solutio of icosistet systems of liear equatios 1 Motivatio Curve
Infinite Sequences and Series
 Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
Rearranging the Alternating Harmonic Series
 Rearragig the Alteratig Harmoic Series Da Teague C School of Sciece ad Mathematics teague@cssm.edu 00 TCM Coferece CSSM, Durham, C Regroupig Ifiite Sums We kow that the Taylor series for l( x + ) is x
Rearragig the Alteratig Harmoic Series Da Teague C School of Sciece ad Mathematics teague@cssm.edu 00 TCM Coferece CSSM, Durham, C Regroupig Ifiite Sums We kow that the Taylor series for l( x + ) is x
Solving equations (incl. radical equations) involving these skills, but ultimately solvable by factoring/quadratic formula (no complex roots)
 Evet A: Fuctios ad Algebraic Maipulatio Factorig Square of a sum: ( a + b) = a + ab + b Square of a differece: ( a b) = a ab + b Differece of squares: a b = ( a b )(a + b ) Differece of cubes: a 3 b 3
Evet A: Fuctios ad Algebraic Maipulatio Factorig Square of a sum: ( a + b) = a + ab + b Square of a differece: ( a b) = a ab + b Differece of squares: a b = ( a b )(a + b ) Differece of cubes: a 3 b 3
PROBLEM SET 5 SOLUTIONS 126 = , 37 = , 15 = , 7 = 7 1.
 Math 7 Sprig 06 PROBLEM SET 5 SOLUTIONS Notatios. Give a real umber x, we will defie sequeces (a k ), (x k ), (p k ), (q k ) as i lecture.. (a) (5 pts) Fid the simple cotiued fractio represetatios of 6
Math 7 Sprig 06 PROBLEM SET 5 SOLUTIONS Notatios. Give a real umber x, we will defie sequeces (a k ), (x k ), (p k ), (q k ) as i lecture.. (a) (5 pts) Fid the simple cotiued fractio represetatios of 6
Chapter 6 Infinite Series
 Chapter 6 Ifiite Series I the previous chapter we cosidered itegrals which were improper i the sese that the iterval of itegratio was ubouded. I this chapter we are goig to discuss a topic which is somewhat
Chapter 6 Ifiite Series I the previous chapter we cosidered itegrals which were improper i the sese that the iterval of itegratio was ubouded. I this chapter we are goig to discuss a topic which is somewhat
Math 113 Exam 3 Practice
 Math Exam Practice Exam 4 will cover.-., 0. ad 0.. Note that eve though. was tested i exam, questios from that sectios may also be o this exam. For practice problems o., refer to the last review. This
Math Exam Practice Exam 4 will cover.-., 0. ad 0.. Note that eve though. was tested i exam, questios from that sectios may also be o this exam. For practice problems o., refer to the last review. This
1.3 Convergence Theorems of Fourier Series. k k k k. N N k 1. With this in mind, we state (without proof) the convergence of Fourier series.
 .3 Covergece Theorems of Fourier Series I this sectio, we preset the covergece of Fourier series. A ifiite sum is, by defiitio, a limit of partial sums, that is, a cos( kx) b si( kx) lim a cos( kx) b si(
.3 Covergece Theorems of Fourier Series I this sectio, we preset the covergece of Fourier series. A ifiite sum is, by defiitio, a limit of partial sums, that is, a cos( kx) b si( kx) lim a cos( kx) b si(
We will conclude the chapter with the study a few methods and techniques which are useful
 Chapter : Coordiate geometry: I this chapter we will lear about the mai priciples of graphig i a dimesioal (D) Cartesia system of coordiates. We will focus o drawig lies ad the characteristics of the graphs
Chapter : Coordiate geometry: I this chapter we will lear about the mai priciples of graphig i a dimesioal (D) Cartesia system of coordiates. We will focus o drawig lies ad the characteristics of the graphs
Chapter Vectors
 Chapter 4. Vectors fter readig this chapter you should be able to:. defie a vector. add ad subtract vectors. fid liear combiatios of vectors ad their relatioship to a set of equatios 4. explai what it
Chapter 4. Vectors fter readig this chapter you should be able to:. defie a vector. add ad subtract vectors. fid liear combiatios of vectors ad their relatioship to a set of equatios 4. explai what it
G r a d e 1 1 P r e - C a l c u l u s M a t h e m a t i c s ( 3 0 S )
 G r a d e 1 1 P r e - C a l c u l u s M a t h e m a t i c s ( 3 0 S ) Grade 11 Pre-Calculus Mathematics (30S) is desiged for studets who ited to study calculus ad related mathematics as part of post-secodary
G r a d e 1 1 P r e - C a l c u l u s M a t h e m a t i c s ( 3 0 S ) Grade 11 Pre-Calculus Mathematics (30S) is desiged for studets who ited to study calculus ad related mathematics as part of post-secodary
REVISION SHEET FP1 (MEI) ALGEBRA. Identities In mathematics, an identity is a statement which is true for all values of the variables it contains.
 The mai ideas are: Idetities REVISION SHEET FP (MEI) ALGEBRA Before the exam you should kow: If a expressio is a idetity the it is true for all values of the variable it cotais The relatioships betwee
The mai ideas are: Idetities REVISION SHEET FP (MEI) ALGEBRA Before the exam you should kow: If a expressio is a idetity the it is true for all values of the variable it cotais The relatioships betwee
Once we have a sequence of numbers, the next thing to do is to sum them up. Given a sequence (a n ) n=1
 . Ifiite Series Oce we have a sequece of umbers, the ext thig to do is to sum them up. Give a sequece a be a sequece: ca we give a sesible meaig to the followig expressio? a = a a a a While summig ifiitely
. Ifiite Series Oce we have a sequece of umbers, the ext thig to do is to sum them up. Give a sequece a be a sequece: ca we give a sesible meaig to the followig expressio? a = a a a a While summig ifiitely
U8L1: Sec Equations of Lines in R 2
 MCVU Thursda Ma, Review of Equatios of a Straight Lie (-D) U8L Sec. 8.9. Equatios of Lies i R Cosider the lie passig through A (-,) with slope, as show i the diagram below. I poit slope form, the equatio
MCVU Thursda Ma, Review of Equatios of a Straight Lie (-D) U8L Sec. 8.9. Equatios of Lies i R Cosider the lie passig through A (-,) with slope, as show i the diagram below. I poit slope form, the equatio
Essential Question How can you recognize an arithmetic sequence from its graph?
 . Aalyzig Arithmetic Sequeces ad Series COMMON CORE Learig Stadards HSF-IF.A.3 HSF-BF.A. HSF-LE.A. Essetial Questio How ca you recogize a arithmetic sequece from its graph? I a arithmetic sequece, the
. Aalyzig Arithmetic Sequeces ad Series COMMON CORE Learig Stadards HSF-IF.A.3 HSF-BF.A. HSF-LE.A. Essetial Questio How ca you recogize a arithmetic sequece from its graph? I a arithmetic sequece, the
II. Descriptive Statistics D. Linear Correlation and Regression. 1. Linear Correlation
 II. Descriptive Statistics D. Liear Correlatio ad Regressio I this sectio Liear Correlatio Cause ad Effect Liear Regressio 1. Liear Correlatio Quatifyig Liear Correlatio The Pearso product-momet correlatio
II. Descriptive Statistics D. Liear Correlatio ad Regressio I this sectio Liear Correlatio Cause ad Effect Liear Regressio 1. Liear Correlatio Quatifyig Liear Correlatio The Pearso product-momet correlatio
Linear Regression Demystified
 Liear Regressio Demystified Liear regressio is a importat subject i statistics. I elemetary statistics courses, formulae related to liear regressio are ofte stated without derivatio. This ote iteds to
Liear Regressio Demystified Liear regressio is a importat subject i statistics. I elemetary statistics courses, formulae related to liear regressio are ofte stated without derivatio. This ote iteds to
4x 2. (n+1) x 3 n+1. = lim. 4x 2 n+1 n3 n. n 4x 2 = lim = 3
 Exam Problems (x. Give the series (, fid the values of x for which this power series coverges. Also =0 state clearly what the radius of covergece is. We start by settig up the Ratio Test: x ( x x ( x x
Exam Problems (x. Give the series (, fid the values of x for which this power series coverges. Also =0 state clearly what the radius of covergece is. We start by settig up the Ratio Test: x ( x x ( x x
1 Approximating Integrals using Taylor Polynomials
 Seughee Ye Ma 8: Week 7 Nov Week 7 Summary This week, we will lear how we ca approximate itegrals usig Taylor series ad umerical methods. Topics Page Approximatig Itegrals usig Taylor Polyomials. Defiitios................................................
Seughee Ye Ma 8: Week 7 Nov Week 7 Summary This week, we will lear how we ca approximate itegrals usig Taylor series ad umerical methods. Topics Page Approximatig Itegrals usig Taylor Polyomials. Defiitios................................................
REGRESSION (Physics 1210 Notes, Partial Modified Appendix A)
 REGRESSION (Physics 0 Notes, Partial Modified Appedix A) HOW TO PERFORM A LINEAR REGRESSION Cosider the followig data poits ad their graph (Table I ad Figure ): X Y 0 3 5 3 7 4 9 5 Table : Example Data
REGRESSION (Physics 0 Notes, Partial Modified Appedix A) HOW TO PERFORM A LINEAR REGRESSION Cosider the followig data poits ad their graph (Table I ad Figure ): X Y 0 3 5 3 7 4 9 5 Table : Example Data
= 4 and 4 is the principal cube root of 64.
 Chapter Real Numbers ad Radicals Day 1: Roots ad Radicals A2TH SWBAT evaluate radicals of ay idex Do Now: Simplify the followig: a) 2 2 b) (-2) 2 c) -2 2 d) 8 2 e) (-8) 2 f) 5 g)(-5) Based o parts a ad
Chapter Real Numbers ad Radicals Day 1: Roots ad Radicals A2TH SWBAT evaluate radicals of ay idex Do Now: Simplify the followig: a) 2 2 b) (-2) 2 c) -2 2 d) 8 2 e) (-8) 2 f) 5 g)(-5) Based o parts a ad
Castiel, Supernatural, Season 6, Episode 18
 13 Differetial Equatios the aswer to your questio ca best be epressed as a series of partial differetial equatios... Castiel, Superatural, Seaso 6, Episode 18 A differetial equatio is a mathematical equatio
13 Differetial Equatios the aswer to your questio ca best be epressed as a series of partial differetial equatios... Castiel, Superatural, Seaso 6, Episode 18 A differetial equatio is a mathematical equatio
Mini Lecture 10.1 Radical Expressions and Functions. 81x d. x 4x 4
 Mii Lecture 0. Radical Expressios ad Fuctios Learig Objectives:. Evaluate square roots.. Evaluate square root fuctios.. Fid the domai of square root fuctios.. Use models that are square root fuctios. 5.
Mii Lecture 0. Radical Expressios ad Fuctios Learig Objectives:. Evaluate square roots.. Evaluate square root fuctios.. Fid the domai of square root fuctios.. Use models that are square root fuctios. 5.
MATH 304: MIDTERM EXAM SOLUTIONS
 MATH 304: MIDTERM EXAM SOLUTIONS [The problems are each worth five poits, except for problem 8, which is worth 8 poits. Thus there are 43 possible poits.] 1. Use the Euclidea algorithm to fid the greatest
MATH 304: MIDTERM EXAM SOLUTIONS [The problems are each worth five poits, except for problem 8, which is worth 8 poits. Thus there are 43 possible poits.] 1. Use the Euclidea algorithm to fid the greatest
TR/46 OCTOBER THE ZEROS OF PARTIAL SUMS OF A MACLAURIN EXPANSION A. TALBOT
 TR/46 OCTOBER 974 THE ZEROS OF PARTIAL SUMS OF A MACLAURIN EXPANSION by A. TALBOT .. Itroductio. A problem i approximatio theory o which I have recetly worked [] required for its solutio a proof that the
TR/46 OCTOBER 974 THE ZEROS OF PARTIAL SUMS OF A MACLAURIN EXPANSION by A. TALBOT .. Itroductio. A problem i approximatio theory o which I have recetly worked [] required for its solutio a proof that the
(b) What is the probability that a particle reaches the upper boundary n before the lower boundary m?
 MATH 529 The Boudary Problem The drukard s walk (or boudary problem) is oe of the most famous problems i the theory of radom walks. Oe versio of the problem is described as follows: Suppose a particle
MATH 529 The Boudary Problem The drukard s walk (or boudary problem) is oe of the most famous problems i the theory of radom walks. Oe versio of the problem is described as follows: Suppose a particle
It is often useful to approximate complicated functions using simpler ones. We consider the task of approximating a function by a polynomial.
 Taylor Polyomials ad Taylor Series It is ofte useful to approximate complicated fuctios usig simpler oes We cosider the task of approximatig a fuctio by a polyomial If f is at least -times differetiable
Taylor Polyomials ad Taylor Series It is ofte useful to approximate complicated fuctios usig simpler oes We cosider the task of approximatig a fuctio by a polyomial If f is at least -times differetiable
7.1 Finding Rational Solutions of Polynomial Equations
 Name Class Date 7.1 Fidig Ratioal Solutios of Polyomial Equatios Essetial Questio: How do you fid the ratioal roots of a polyomial equatio? Resource Locker Explore Relatig Zeros ad Coefficiets of Polyomial
Name Class Date 7.1 Fidig Ratioal Solutios of Polyomial Equatios Essetial Questio: How do you fid the ratioal roots of a polyomial equatio? Resource Locker Explore Relatig Zeros ad Coefficiets of Polyomial
Sail into Summer with Math!
 Sail ito Summer with Math! For Studets Eterig Hoors Geometry This summer math booklet was developed to provide studets i kidergarte through the eighth grade a opportuity to review grade level math objectives
Sail ito Summer with Math! For Studets Eterig Hoors Geometry This summer math booklet was developed to provide studets i kidergarte through the eighth grade a opportuity to review grade level math objectives
(3) If you replace row i of A by its sum with a multiple of another row, then the determinant is unchanged! Expand across the i th row:
 Math 5-4 Tue Feb 4 Cotiue with sectio 36 Determiats The effective way to compute determiats for larger-sized matrices without lots of zeroes is to ot use the defiitio, but rather to use the followig facts,
Math 5-4 Tue Feb 4 Cotiue with sectio 36 Determiats The effective way to compute determiats for larger-sized matrices without lots of zeroes is to ot use the defiitio, but rather to use the followig facts,
Notes on iteration and Newton s method. Iteration
 Notes o iteratio ad Newto s method Iteratio Iteratio meas doig somethig over ad over. I our cotet, a iteratio is a sequece of umbers, vectors, fuctios, etc. geerated by a iteratio rule of the type 1 f
Notes o iteratio ad Newto s method Iteratio Iteratio meas doig somethig over ad over. I our cotet, a iteratio is a sequece of umbers, vectors, fuctios, etc. geerated by a iteratio rule of the type 1 f
Chapter 4. Fourier Series
 Chapter 4. Fourier Series At this poit we are ready to ow cosider the caoical equatios. Cosider, for eample the heat equatio u t = u, < (4.) subject to u(, ) = si, u(, t) = u(, t) =. (4.) Here,
Chapter 4. Fourier Series At this poit we are ready to ow cosider the caoical equatios. Cosider, for eample the heat equatio u t = u, < (4.) subject to u(, ) = si, u(, t) = u(, t) =. (4.) Here,
Math 61CM - Solutions to homework 3
 Math 6CM - Solutios to homework 3 Cédric De Groote October 2 th, 208 Problem : Let F be a field, m 0 a fixed oegative iteger ad let V = {a 0 + a x + + a m x m a 0,, a m F} be the vector space cosistig
Math 6CM - Solutios to homework 3 Cédric De Groote October 2 th, 208 Problem : Let F be a field, m 0 a fixed oegative iteger ad let V = {a 0 + a x + + a m x m a 0,, a m F} be the vector space cosistig
Math 120 Answers for Homework 23
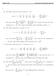 Math 0 Aswers for Homewor. (a) The Taylor series for cos(x) aroud a 0 is cos(x) x! + x4 4! x6 6! + x8 8! x0 0! + ( ) ()! x ( ) π ( ) ad so the series ()! ()! (π) is just the series for cos(x) evaluated
Math 0 Aswers for Homewor. (a) The Taylor series for cos(x) aroud a 0 is cos(x) x! + x4 4! x6 6! + x8 8! x0 0! + ( ) ()! x ( ) π ( ) ad so the series ()! ()! (π) is just the series for cos(x) evaluated
Section 6.4: Series. Section 6.4 Series 413
 ectio 64 eries 4 ectio 64: eries A couple decides to start a college fud for their daughter They pla to ivest $50 i the fud each moth The fud pays 6% aual iterest, compouded mothly How much moey will they
ectio 64 eries 4 ectio 64: eries A couple decides to start a college fud for their daughter They pla to ivest $50 i the fud each moth The fud pays 6% aual iterest, compouded mothly How much moey will they
AP Calculus BC Review Applications of Derivatives (Chapter 4) and f,
 AP alculus B Review Applicatios of Derivatives (hapter ) Thigs to Kow ad Be Able to Do Defiitios of the followig i terms of derivatives, ad how to fid them: critical poit, global miima/maima, local (relative)
AP alculus B Review Applicatios of Derivatives (hapter ) Thigs to Kow ad Be Able to Do Defiitios of the followig i terms of derivatives, ad how to fid them: critical poit, global miima/maima, local (relative)
Statistics 511 Additional Materials
 Cofidece Itervals o mu Statistics 511 Additioal Materials This topic officially moves us from probability to statistics. We begi to discuss makig ifereces about the populatio. Oe way to differetiate probability
Cofidece Itervals o mu Statistics 511 Additioal Materials This topic officially moves us from probability to statistics. We begi to discuss makig ifereces about the populatio. Oe way to differetiate probability
 1 of 7 7/16/2009 6:06 AM Virtual Laboratories > 6. Radom Samples > 1 2 3 4 5 6 7 6. Order Statistics Defiitios Suppose agai that we have a basic radom experimet, ad that X is a real-valued radom variable
1 of 7 7/16/2009 6:06 AM Virtual Laboratories > 6. Radom Samples > 1 2 3 4 5 6 7 6. Order Statistics Defiitios Suppose agai that we have a basic radom experimet, ad that X is a real-valued radom variable
SECTION 1.5 : SUMMATION NOTATION + WORK WITH SEQUENCES
 SECTION 1.5 : SUMMATION NOTATION + WORK WITH SEQUENCES Read Sectio 1.5 (pages 5 9) Overview I Sectio 1.5 we lear to work with summatio otatio ad formulas. We will also itroduce a brief overview of sequeces,
SECTION 1.5 : SUMMATION NOTATION + WORK WITH SEQUENCES Read Sectio 1.5 (pages 5 9) Overview I Sectio 1.5 we lear to work with summatio otatio ad formulas. We will also itroduce a brief overview of sequeces,
Exponential and Trigonometric Functions Lesson #1
 Epoetial ad Trigoometric Fuctios Lesso # Itroductio To Epoetial Fuctios Cosider a populatio of 00 mice which is growig uder plague coditios. If the mouse populatio doubles each week we ca costruct a table
Epoetial ad Trigoometric Fuctios Lesso # Itroductio To Epoetial Fuctios Cosider a populatio of 00 mice which is growig uder plague coditios. If the mouse populatio doubles each week we ca costruct a table
Ma 4121: Introduction to Lebesgue Integration Solutions to Homework Assignment 5
 Ma 42: Itroductio to Lebesgue Itegratio Solutios to Homework Assigmet 5 Prof. Wickerhauser Due Thursday, April th, 23 Please retur your solutios to the istructor by the ed of class o the due date. You
Ma 42: Itroductio to Lebesgue Itegratio Solutios to Homework Assigmet 5 Prof. Wickerhauser Due Thursday, April th, 23 Please retur your solutios to the istructor by the ed of class o the due date. You
