Problem Set 6: Trees Spring 2018
|
|
|
- Roland Clark
- 5 years ago
- Views:
Transcription
1 Problem Set 6: Trees 1-29 Sprng 2018 A Average dstance Gven a tree, calculate the average dstance between two vertces n the tree. For example, the average dstance between two vertces n the followng tree s (d 01 + d 02 + d 03 + d 04 + d 12 + d 13 + d 14 + d 23 + d 24 + d 34 )/10 = ( )/10 = 8.6. Fgure 1: The frst sample case On the frst lne an nteger t (1 t 100): the number of test cases. Then for each test case: One lne wth an nteger n (2 n ): the number of nodes n the tree. The nodes are numbered from 0 to n 1. n 1lnes,eachwththreentegersa (0 a<n), b (0 b<n)andd (1 d 1000). There s an edge between the nodes wth numbers a and b of length d. The resultng graph wll be a tree. For each testcase: One lne wth the average dstance between two vertces. ether an absolute or a relatve error of at most Ths valueshouldhave Sample n- and
2 B. Duff n the Army tme lmt per test: 4 seconds memory lmt per test: 12 megabytes nput: standard nput : standard Recently Duff has been a solder n the army. Malek s her commander. Ther country, Andarz Gu has n ctes (numbered from 1 to n) and n - 1 bdrectonal roads. Each road connects two dfferent ctes. There exst a unque path between any two ctes. There are also m people lvng n Andarz Gu (numbered from 1 to m). Each person has and ID number. ID number of - th person s and he/she lves n cty number c. Note that there may be more than one person n a cty, also there may be no people lvng n the cty. Malek loves to order. That's why he asks Duff to answer to q queres. In each query, he gves her numbers v, u and a. To answer a query: Assume there are x people lvng n the ctes lyng on the path from cty v to cty u. Assume these people's IDs are p, p,..., p n ncreasng order. x If k = mn(x, a), then Duff should tell Malek numbers k, p, p,..., p n ths order. In the other words, Malek wants to k know a mnmums on that path (or less, f there are less than a people). Duff s very busy at the moment, so she asked you to help her and answer the queres. The frst lne of nput contans three ntegers, n, m and q (1 n, m, q 10 ). The next n - 1 lnes contan the roads. Each lne contans two ntegers v and u, endponts of a road (1 v, u n, v u). Next lne contans m ntegers c, c,..., c separated by spaces (1 c n for each 1 m). m Next q lnes contan the queres. Each of them contans three ntegers, v, u and a (1 v, u n and 1 a 10). For each query, prnt numbers k, p, p,..., p separated by spaces n one lne. k
3 Examples nput Note Graph of Andarz Gu n the sample case s as follows (ID of people n each cty are wrtten next to them):
4 C. New Year Santa Network tme lmt per test: 2 seconds memory lmt per test: 26 megabytes nput: standard nput : standard New Year s comng n Tree World! In ths world, as the name mples, there are n ctes connected by n - 1 roads, and for any two dstnct ctes there always exsts a path between them. The ctes are numbered by ntegers from 1 to n, and the roads are numbered by ntegers from 1 to n - 1. Let's defne d(u, v) as total length of roads on the path between cty u and cty v. As an annual event, people n Tree World repars exactly one road per year. As a result, the length of one road decreases. It s already known that n the -th year, the length of the r -th road s gong to become w, whch s shorter than ts length before. Assume that the current year s year 1. Three Santas are plannng to gve presents annually to all the chldren n Tree World. In order to do that, they need some preparaton, so they are gong to choose three dstnct ctes c, c, c and make exactly one warehouse n each cty. The k-th (1 k 3) Santa wll take charge of the warehouse n cty c. It s really borng for the three Santas to keep a warehouse alone. So, they decded to buld an only-for-santa network! The cost needed to buld ths network equals to d(c, c ) + d(c, c ) + d(c, c ) dollars. Santas are too busy to fnd the best place, so they decded to choose c, c, c randomly unformly over all trples of dstnct 3 numbers from 1 to n. Santas would lke to know the expected value of the cost needed to buld the network. However, as mentoned, each year, the length of exactly one road decreases. So, the Santas want to calculate the expected after each length change. Help them to calculate the value. The frst lne contans an nteger n (3 n 10 ) the number of ctes n Tree World. Next n - 1 lnes descrbe the roads. The -th lne of them (1 n - 1) contans three space-separated ntegers a, b, l (1 a, b n, a b, 1 l 103 ), denotng that the -th road connects ctes a and b, and the length of -th road s l. The next lne contans an nteger q (1 q 10 ) the number of road length changes. Next q lnes descrbe the length changes. The j-th lne of them (1 j q) contans two space-separated ntegers r j, w (1 r n - 1, 1 w 103 j j j ). It means that n the j-th repar, the length of the rj-th road becomes w j. It s guaranteed that w s smaller than the current length of the r -th road. The same road can be repared several tmes. j q numbers. For each gven change, prnt a lne contanng the expected cost needed to buld the network n - 6 Tree World. The answer wll be consdered correct f ts absolute and relatve error doesn't exceed 10. j k
5 Examples nput nput Note Consder the frst sample. There are 6 trples: (1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), (3, 2, 1). Because n = 3, the cost needed to buld the network s always d(1, 2) + d(2, 3) + d(3, 1) for all the trples. So, the expected cost equals to d(1, 2) + d(2, 3) + d(3, 1).
6 D. Book of Evl tme lmt per test: 2 seconds memory lmt per test: 26 megabytes nput: standard nput : standard Paladn Manao caught the tral of the ancent Book of Evl n a swampy area. Ths area contans n settlements numbered from 1 to n. Movng through the swamp s very dffcult, so people tramped exactly n - 1 paths. Each of these paths connects some par of settlements and s bdrectonal. Moreover, t s possble to reach any settlement from any other one by traversng one or several paths. The dstance between two settlements s the mnmum number of paths that have to be crossed to get from one settlement to the other one. Manao knows that the Book of Evl has got a damage range d. Ths means that f the Book of Evl s located n some settlement, ts damage (for example, emergence of ghosts and werewolves) affects other settlements at dstance d or less from the settlement where the Book resdes. Manao has heard of m settlements affected by the Book of Evl. Ther numbers are p, p,..., p. Note that the Book m may be affectng other settlements as well, but ths has not been detected yet. Manao wants to determne whch settlements may contan the Book. Help hm wth ths dffcult task. The frst lne contans three space-separated ntegers n, m and d (1 m n ; 0 d n - 1). The second lne contans m dstnct space-separated ntegers p, p,..., p (1 p n). Then n - 1 lnes follow, each lne descrbes a path made n the area. A path s descrbed by a par of space-separated ntegers a and b representng the ends of ths path. m Prnt a sngle number the number of settlements that may contan the Book of Evl. It s possble that Manao receved some controversal nformaton and there s no settlement that may contan the Book. In such case, prnt 0. Examples nput Note Sample 1. The damage range of the Book of Evl equals 3 and ts effects have been notced n settlements 1 and 2. Thus, t can be n settlements 3, 4 or.
7 Andrew plays a game called "Cvlzaton". Dma helps hm. E. Cvlzaton tme lmt per test: 1 second memory lmt per test: 26 megabytes nput: standard nput : standard The game has n ctes and m bdrectonal roads. The ctes are numbered from 1 to n. Between any par of ctes there ether s a sngle (unque) path, or there s no path at all. A path s such a sequence of dstnct ctes v 1, v 2,..., v k, that there s a road between any contguous ctes v and v + 1 (1 < k). The length of the descrbed path equals to (k - 1). We assume that two ctes le n the same regon f and only f, there s a path connectng these two ctes. Durng the game events of two types take place: 1. Andrew asks Dma about the length of the longest path n the regon where cty x les. 2. Andrew asks Dma to merge the regon where cty x les wth the regon where cty y les. If the ctes le n the same regon, then no mergng s needed. Otherwse, you need to merge the regons as follows: choose a cty from the frst regon, a cty from the second regon and connect them by a road so as to mnmze the length of the longest path n the resultng regon. If there are multple ways to do so, you are allowed to choose any of them. Dma fnds t hard to execute Andrew's queres, so he asks you to help hm. Help Dma. The frst lne contans three ntegers n, m, q (1 n 3 10 ; 0 m < n; 1 q 3 10 ) the number of ctes, the number of the roads we already have and the number of queres, correspondngly. Each of the followng m lnes contans two ntegers, a and b (a b ; 1 a, b n). These numbers represent the road between ctes a and b. There can be at most one road between two ctes. Each of the followng q lnes contans one of the two events n the followng format: 1 x. It s the request Andrew gves to Dma to fnd the length of the maxmum path n the regon that contans cty x (1 x n). 2 x y. It s the request Andrew gves to Dma to merge the regon that contans cty x and the regon that contans cty y (1 x, y n). Note, that x can be equal to y. For each event of the frst type prnt the answer on a separate lne. Examples nput
8 F. A and B and Lecture Rooms tme lmt per test: 2 seconds memory lmt per test: 26 megabytes nput: standard nput : standard A and B are preparng themselves for programmng contests. The Unversty where A and B study s a set of rooms connected by corrdors. Overall, the Unversty has n rooms connected by n - 1 corrdors so that you can get from any room to any other one by movng along the corrdors. The rooms are numbered from 1 to n. Every day А and B wrte contests n some rooms of ther unversty, and after each contest they gather together n the same room and dscuss problems. A and B want the dstance from the rooms where problems are dscussed to the rooms where contests are wrtten to be equal. The dstance between two rooms s the number of edges on the shortest path between them. As they wrte contests n new rooms every day, they asked you to help them fnd the number of possble rooms to dscuss problems for each of the followng m days. The frst lne contans nteger n (1 n 10 ) the number of rooms n the Unversty. The next n - 1 lnes descrbe the corrdors. The -th of these lnes (1 n - 1) contans two ntegers a and b (1 a, b n), showng that the -th corrdor connects rooms a and b. The next lne contans nteger m (1 m 10 ) the number of queres. Next m lnes descrbe the queres. The j-th of these lnes (1 j m) contans two ntegers x and y (1 x, y n) that means that on the j-th day A wll wrte the contest n the room x, B wll wrte n the room y. In the -th (1 m) lne prnt the number of rooms that are equdstant from the rooms where A and B wrte contest on the -th day. j j j j j j Examples nput nput Note n the frst sample there s only one room at the same dstance from rooms number 2 and 3 room number 1.
Problem Set 9 Solutions
 Desgn and Analyss of Algorthms May 4, 2015 Massachusetts Insttute of Technology 6.046J/18.410J Profs. Erk Demane, Srn Devadas, and Nancy Lynch Problem Set 9 Solutons Problem Set 9 Solutons Ths problem
Desgn and Analyss of Algorthms May 4, 2015 Massachusetts Insttute of Technology 6.046J/18.410J Profs. Erk Demane, Srn Devadas, and Nancy Lynch Problem Set 9 Solutons Problem Set 9 Solutons Ths problem
Complex Numbers Alpha, Round 1 Test #123
 Complex Numbers Alpha, Round Test #3. Wrte your 6-dgt ID# n the I.D. NUMBER grd, left-justfed, and bubble. Check that each column has only one number darkened.. In the EXAM NO. grd, wrte the 3-dgt Test
Complex Numbers Alpha, Round Test #3. Wrte your 6-dgt ID# n the I.D. NUMBER grd, left-justfed, and bubble. Check that each column has only one number darkened.. In the EXAM NO. grd, wrte the 3-dgt Test
Calculation of time complexity (3%)
 Problem 1. (30%) Calculaton of tme complexty (3%) Gven n ctes, usng exhaust search to see every result takes O(n!). Calculaton of tme needed to solve the problem (2%) 40 ctes:40! dfferent tours 40 add
Problem 1. (30%) Calculaton of tme complexty (3%) Gven n ctes, usng exhaust search to see every result takes O(n!). Calculaton of tme needed to solve the problem (2%) 40 ctes:40! dfferent tours 40 add
Affine transformations and convexity
 Affne transformatons and convexty The purpose of ths document s to prove some basc propertes of affne transformatons nvolvng convex sets. Here are a few onlne references for background nformaton: http://math.ucr.edu/
Affne transformatons and convexty The purpose of ths document s to prove some basc propertes of affne transformatons nvolvng convex sets. Here are a few onlne references for background nformaton: http://math.ucr.edu/
Math1110 (Spring 2009) Prelim 3 - Solutions
 Math 1110 (Sprng 2009) Solutons to Prelm 3 (04/21/2009) 1 Queston 1. (16 ponts) Short answer. Math1110 (Sprng 2009) Prelm 3 - Solutons x a 1 (a) (4 ponts) Please evaluate lm, where a and b are postve numbers.
Math 1110 (Sprng 2009) Solutons to Prelm 3 (04/21/2009) 1 Queston 1. (16 ponts) Short answer. Math1110 (Sprng 2009) Prelm 3 - Solutons x a 1 (a) (4 ponts) Please evaluate lm, where a and b are postve numbers.
Complete subgraphs in multipartite graphs
 Complete subgraphs n multpartte graphs FLORIAN PFENDER Unverstät Rostock, Insttut für Mathematk D-18057 Rostock, Germany Floran.Pfender@un-rostock.de Abstract Turán s Theorem states that every graph G
Complete subgraphs n multpartte graphs FLORIAN PFENDER Unverstät Rostock, Insttut für Mathematk D-18057 Rostock, Germany Floran.Pfender@un-rostock.de Abstract Turán s Theorem states that every graph G
Société de Calcul Mathématique SA
 Socété de Calcul Mathématque SA Outls d'ade à la décson Tools for decson help Probablstc Studes: Normalzng the Hstograms Bernard Beauzamy December, 202 I. General constructon of the hstogram Any probablstc
Socété de Calcul Mathématque SA Outls d'ade à la décson Tools for decson help Probablstc Studes: Normalzng the Hstograms Bernard Beauzamy December, 202 I. General constructon of the hstogram Any probablstc
Chapter 3 Describing Data Using Numerical Measures
 Chapter 3 Student Lecture Notes 3-1 Chapter 3 Descrbng Data Usng Numercal Measures Fall 2006 Fundamentals of Busness Statstcs 1 Chapter Goals To establsh the usefulness of summary measures of data. The
Chapter 3 Student Lecture Notes 3-1 Chapter 3 Descrbng Data Usng Numercal Measures Fall 2006 Fundamentals of Busness Statstcs 1 Chapter Goals To establsh the usefulness of summary measures of data. The
Min Cut, Fast Cut, Polynomial Identities
 Randomzed Algorthms, Summer 016 Mn Cut, Fast Cut, Polynomal Identtes Instructor: Thomas Kesselhem and Kurt Mehlhorn 1 Mn Cuts n Graphs Lecture (5 pages) Throughout ths secton, G = (V, E) s a mult-graph.
Randomzed Algorthms, Summer 016 Mn Cut, Fast Cut, Polynomal Identtes Instructor: Thomas Kesselhem and Kurt Mehlhorn 1 Mn Cuts n Graphs Lecture (5 pages) Throughout ths secton, G = (V, E) s a mult-graph.
Dynamic Programming. Preview. Dynamic Programming. Dynamic Programming. Dynamic Programming (Example: Fibonacci Sequence)
 /24/27 Prevew Fbonacc Sequence Longest Common Subsequence Dynamc programmng s a method for solvng complex problems by breakng them down nto smpler sub-problems. It s applcable to problems exhbtng the propertes
/24/27 Prevew Fbonacc Sequence Longest Common Subsequence Dynamc programmng s a method for solvng complex problems by breakng them down nto smpler sub-problems. It s applcable to problems exhbtng the propertes
Problem Do any of the following determine homomorphisms from GL n (C) to GL n (C)?
 Homework 8 solutons. Problem 16.1. Whch of the followng defne homomomorphsms from C\{0} to C\{0}? Answer. a) f 1 : z z Yes, f 1 s a homomorphsm. We have that z s the complex conjugate of z. If z 1,z 2
Homework 8 solutons. Problem 16.1. Whch of the followng defne homomomorphsms from C\{0} to C\{0}? Answer. a) f 1 : z z Yes, f 1 s a homomorphsm. We have that z s the complex conjugate of z. If z 1,z 2
Finding Dense Subgraphs in G(n, 1/2)
 Fndng Dense Subgraphs n Gn, 1/ Atsh Das Sarma 1, Amt Deshpande, and Rav Kannan 1 Georga Insttute of Technology,atsh@cc.gatech.edu Mcrosoft Research-Bangalore,amtdesh,annan@mcrosoft.com Abstract. Fndng
Fndng Dense Subgraphs n Gn, 1/ Atsh Das Sarma 1, Amt Deshpande, and Rav Kannan 1 Georga Insttute of Technology,atsh@cc.gatech.edu Mcrosoft Research-Bangalore,amtdesh,annan@mcrosoft.com Abstract. Fndng
HMMT February 2016 February 20, 2016
 HMMT February 016 February 0, 016 Combnatorcs 1. For postve ntegers n, let S n be the set of ntegers x such that n dstnct lnes, no three concurrent, can dvde a plane nto x regons (for example, S = {3,
HMMT February 016 February 0, 016 Combnatorcs 1. For postve ntegers n, let S n be the set of ntegers x such that n dstnct lnes, no three concurrent, can dvde a plane nto x regons (for example, S = {3,
find (x): given element x, return the canonical element of the set containing x;
 COS 43 Sprng, 009 Dsjont Set Unon Problem: Mantan a collecton of dsjont sets. Two operatons: fnd the set contanng a gven element; unte two sets nto one (destructvely). Approach: Canoncal element method:
COS 43 Sprng, 009 Dsjont Set Unon Problem: Mantan a collecton of dsjont sets. Two operatons: fnd the set contanng a gven element; unte two sets nto one (destructvely). Approach: Canoncal element method:
Lecture 4: Universal Hash Functions/Streaming Cont d
 CSE 5: Desgn and Analyss of Algorthms I Sprng 06 Lecture 4: Unversal Hash Functons/Streamng Cont d Lecturer: Shayan Oves Gharan Aprl 6th Scrbe: Jacob Schreber Dsclamer: These notes have not been subjected
CSE 5: Desgn and Analyss of Algorthms I Sprng 06 Lecture 4: Unversal Hash Functons/Streamng Cont d Lecturer: Shayan Oves Gharan Aprl 6th Scrbe: Jacob Schreber Dsclamer: These notes have not been subjected
8.6 The Complex Number System
 8.6 The Complex Number System Earler n the chapter, we mentoned that we cannot have a negatve under a square root, snce the square of any postve or negatve number s always postve. In ths secton we want
8.6 The Complex Number System Earler n the chapter, we mentoned that we cannot have a negatve under a square root, snce the square of any postve or negatve number s always postve. In ths secton we want
College of Computer & Information Science Fall 2009 Northeastern University 20 October 2009
 College of Computer & Informaton Scence Fall 2009 Northeastern Unversty 20 October 2009 CS7880: Algorthmc Power Tools Scrbe: Jan Wen and Laura Poplawsk Lecture Outlne: Prmal-dual schema Network Desgn:
College of Computer & Informaton Scence Fall 2009 Northeastern Unversty 20 October 2009 CS7880: Algorthmc Power Tools Scrbe: Jan Wen and Laura Poplawsk Lecture Outlne: Prmal-dual schema Network Desgn:
Kernel Methods and SVMs Extension
 Kernel Methods and SVMs Extenson The purpose of ths document s to revew materal covered n Machne Learnng 1 Supervsed Learnng regardng support vector machnes (SVMs). Ths document also provdes a general
Kernel Methods and SVMs Extenson The purpose of ths document s to revew materal covered n Machne Learnng 1 Supervsed Learnng regardng support vector machnes (SVMs). Ths document also provdes a general
A 2D Bounded Linear Program (H,c) 2D Linear Programming
 A 2D Bounded Lnear Program (H,c) h 3 v h 8 h 5 c h 4 h h 6 h 7 h 2 2D Lnear Programmng C s a polygonal regon, the ntersecton of n halfplanes. (H, c) s nfeasble, as C s empty. Feasble regon C s unbounded
A 2D Bounded Lnear Program (H,c) h 3 v h 8 h 5 c h 4 h h 6 h 7 h 2 2D Lnear Programmng C s a polygonal regon, the ntersecton of n halfplanes. (H, c) s nfeasble, as C s empty. Feasble regon C s unbounded
Lecture 3: Probability Distributions
 Lecture 3: Probablty Dstrbutons Random Varables Let us begn by defnng a sample space as a set of outcomes from an experment. We denote ths by S. A random varable s a functon whch maps outcomes nto the
Lecture 3: Probablty Dstrbutons Random Varables Let us begn by defnng a sample space as a set of outcomes from an experment. We denote ths by S. A random varable s a functon whch maps outcomes nto the
Expected Value and Variance
 MATH 38 Expected Value and Varance Dr. Neal, WKU We now shall dscuss how to fnd the average and standard devaton of a random varable X. Expected Value Defnton. The expected value (or average value, or
MATH 38 Expected Value and Varance Dr. Neal, WKU We now shall dscuss how to fnd the average and standard devaton of a random varable X. Expected Value Defnton. The expected value (or average value, or
CS 331 DESIGN AND ANALYSIS OF ALGORITHMS DYNAMIC PROGRAMMING. Dr. Daisy Tang
 CS DESIGN ND NLYSIS OF LGORITHMS DYNMIC PROGRMMING Dr. Dasy Tang Dynamc Programmng Idea: Problems can be dvded nto stages Soluton s a sequence o decsons and the decson at the current stage s based on the
CS DESIGN ND NLYSIS OF LGORITHMS DYNMIC PROGRMMING Dr. Dasy Tang Dynamc Programmng Idea: Problems can be dvded nto stages Soluton s a sequence o decsons and the decson at the current stage s based on the
NP-Completeness : Proofs
 NP-Completeness : Proofs Proof Methods A method to show a decson problem Π NP-complete s as follows. (1) Show Π NP. (2) Choose an NP-complete problem Π. (3) Show Π Π. A method to show an optmzaton problem
NP-Completeness : Proofs Proof Methods A method to show a decson problem Π NP-complete s as follows. (1) Show Π NP. (2) Choose an NP-complete problem Π. (3) Show Π Π. A method to show an optmzaton problem
Turing Machines (intro)
 CHAPTER 3 The Church-Turng Thess Contents Turng Machnes defntons, examples, Turng-recognzable and Turng-decdable languages Varants of Turng Machne Multtape Turng machnes, non-determnstc Turng Machnes,
CHAPTER 3 The Church-Turng Thess Contents Turng Machnes defntons, examples, Turng-recognzable and Turng-decdable languages Varants of Turng Machne Multtape Turng machnes, non-determnstc Turng Machnes,
Simultaneous Optimization of Berth Allocation, Quay Crane Assignment and Quay Crane Scheduling Problems in Container Terminals
 Smultaneous Optmzaton of Berth Allocaton, Quay Crane Assgnment and Quay Crane Schedulng Problems n Contaner Termnals Necat Aras, Yavuz Türkoğulları, Z. Caner Taşkın, Kuban Altınel Abstract In ths work,
Smultaneous Optmzaton of Berth Allocaton, Quay Crane Assgnment and Quay Crane Schedulng Problems n Contaner Termnals Necat Aras, Yavuz Türkoğulları, Z. Caner Taşkın, Kuban Altınel Abstract In ths work,
Graph Reconstruction by Permutations
 Graph Reconstructon by Permutatons Perre Ille and Wllam Kocay* Insttut de Mathémathques de Lumny CNRS UMR 6206 163 avenue de Lumny, Case 907 13288 Marselle Cedex 9, France e-mal: lle@ml.unv-mrs.fr Computer
Graph Reconstructon by Permutatons Perre Ille and Wllam Kocay* Insttut de Mathémathques de Lumny CNRS UMR 6206 163 avenue de Lumny, Case 907 13288 Marselle Cedex 9, France e-mal: lle@ml.unv-mrs.fr Computer
3.1 Expectation of Functions of Several Random Variables. )' be a k-dimensional discrete or continuous random vector, with joint PMF p (, E X E X1 E X
 Statstcs 1: Probablty Theory II 37 3 EPECTATION OF SEVERAL RANDOM VARIABLES As n Probablty Theory I, the nterest n most stuatons les not on the actual dstrbuton of a random vector, but rather on a number
Statstcs 1: Probablty Theory II 37 3 EPECTATION OF SEVERAL RANDOM VARIABLES As n Probablty Theory I, the nterest n most stuatons les not on the actual dstrbuton of a random vector, but rather on a number
MTH 263 Practice Test #1 Spring 1999
 Pat Ross MTH 6 Practce Test # Sprng 999 Name. Fnd the area of the regon bounded by the graph r =acos (θ). Observe: Ths s a crcle of radus a, for r =acos (θ) r =a ³ x r r =ax x + y =ax x ax + y =0 x ax
Pat Ross MTH 6 Practce Test # Sprng 999 Name. Fnd the area of the regon bounded by the graph r =acos (θ). Observe: Ths s a crcle of radus a, for r =acos (θ) r =a ³ x r r =ax x + y =ax x ax + y =0 x ax
Lectures - Week 4 Matrix norms, Conditioning, Vector Spaces, Linear Independence, Spanning sets and Basis, Null space and Range of a Matrix
 Lectures - Week 4 Matrx norms, Condtonng, Vector Spaces, Lnear Independence, Spannng sets and Bass, Null space and Range of a Matrx Matrx Norms Now we turn to assocatng a number to each matrx. We could
Lectures - Week 4 Matrx norms, Condtonng, Vector Spaces, Lnear Independence, Spannng sets and Bass, Null space and Range of a Matrx Matrx Norms Now we turn to assocatng a number to each matrx. We could
On quasiperfect numbers
 Notes on Number Theory and Dscrete Mathematcs Prnt ISSN 1310 5132, Onlne ISSN 2367 8275 Vol. 23, 2017, No. 3, 73 78 On quasperfect numbers V. Sva Rama Prasad 1 and C. Suntha 2 1 Nalla Malla Reddy Engneerng
Notes on Number Theory and Dscrete Mathematcs Prnt ISSN 1310 5132, Onlne ISSN 2367 8275 Vol. 23, 2017, No. 3, 73 78 On quasperfect numbers V. Sva Rama Prasad 1 and C. Suntha 2 1 Nalla Malla Reddy Engneerng
On the Multicriteria Integer Network Flow Problem
 BULGARIAN ACADEMY OF SCIENCES CYBERNETICS AND INFORMATION TECHNOLOGIES Volume 5, No 2 Sofa 2005 On the Multcrtera Integer Network Flow Problem Vassl Vasslev, Marana Nkolova, Maryana Vassleva Insttute of
BULGARIAN ACADEMY OF SCIENCES CYBERNETICS AND INFORMATION TECHNOLOGIES Volume 5, No 2 Sofa 2005 On the Multcrtera Integer Network Flow Problem Vassl Vasslev, Marana Nkolova, Maryana Vassleva Insttute of
Exercises. 18 Algorithms
 18 Algorthms Exercses 0.1. In each of the followng stuatons, ndcate whether f = O(g), or f = Ω(g), or both (n whch case f = Θ(g)). f(n) g(n) (a) n 100 n 200 (b) n 1/2 n 2/3 (c) 100n + log n n + (log n)
18 Algorthms Exercses 0.1. In each of the followng stuatons, ndcate whether f = O(g), or f = Ω(g), or both (n whch case f = Θ(g)). f(n) g(n) (a) n 100 n 200 (b) n 1/2 n 2/3 (c) 100n + log n n + (log n)
Caps and Colouring Steiner Triple Systems
 Desgns, Codes and Cryptography, 13, 51 55 (1998) c 1998 Kluwer Academc Publshers, Boston. Manufactured n The Netherlands. Caps and Colourng Stener Trple Systems AIDEN BRUEN* Department of Mathematcs, Unversty
Desgns, Codes and Cryptography, 13, 51 55 (1998) c 1998 Kluwer Academc Publshers, Boston. Manufactured n The Netherlands. Caps and Colourng Stener Trple Systems AIDEN BRUEN* Department of Mathematcs, Unversty
EEL 6266 Power System Operation and Control. Chapter 3 Economic Dispatch Using Dynamic Programming
 EEL 6266 Power System Operaton and Control Chapter 3 Economc Dspatch Usng Dynamc Programmng Pecewse Lnear Cost Functons Common practce many utltes prefer to represent ther generator cost functons as sngle-
EEL 6266 Power System Operaton and Control Chapter 3 Economc Dspatch Usng Dynamc Programmng Pecewse Lnear Cost Functons Common practce many utltes prefer to represent ther generator cost functons as sngle-
n α j x j = 0 j=1 has a nontrivial solution. Here A is the n k matrix whose jth column is the vector for all t j=0
 MODULE 2 Topcs: Lnear ndependence, bass and dmenson We have seen that f n a set of vectors one vector s a lnear combnaton of the remanng vectors n the set then the span of the set s unchanged f that vector
MODULE 2 Topcs: Lnear ndependence, bass and dmenson We have seen that f n a set of vectors one vector s a lnear combnaton of the remanng vectors n the set then the span of the set s unchanged f that vector
= z 20 z n. (k 20) + 4 z k = 4
 Problem Set #7 solutons 7.2.. (a Fnd the coeffcent of z k n (z + z 5 + z 6 + z 7 + 5, k 20. We use the known seres expanson ( n+l ( z l l z n below: (z + z 5 + z 6 + z 7 + 5 (z 5 ( + z + z 2 + z + 5 5
Problem Set #7 solutons 7.2.. (a Fnd the coeffcent of z k n (z + z 5 + z 6 + z 7 + 5, k 20. We use the known seres expanson ( n+l ( z l l z n below: (z + z 5 + z 6 + z 7 + 5 (z 5 ( + z + z 2 + z + 5 5
Volume 18 Figure 1. Notation 1. Notation 2. Observation 1. Remark 1. Remark 2. Remark 3. Remark 4. Remark 5. Remark 6. Theorem A [2]. Theorem B [2].
![Volume 18 Figure 1. Notation 1. Notation 2. Observation 1. Remark 1. Remark 2. Remark 3. Remark 4. Remark 5. Remark 6. Theorem A [2]. Theorem B [2]. Volume 18 Figure 1. Notation 1. Notation 2. Observation 1. Remark 1. Remark 2. Remark 3. Remark 4. Remark 5. Remark 6. Theorem A [2]. Theorem B [2].](/thumbs/87/96503364.jpg) Bulletn of Mathematcal Scences and Applcatons Submtted: 016-04-07 ISSN: 78-9634, Vol. 18, pp 1-10 Revsed: 016-09-08 do:10.1805/www.scpress.com/bmsa.18.1 Accepted: 016-10-13 017 ScPress Ltd., Swtzerland
Bulletn of Mathematcal Scences and Applcatons Submtted: 016-04-07 ISSN: 78-9634, Vol. 18, pp 1-10 Revsed: 016-09-08 do:10.1805/www.scpress.com/bmsa.18.1 Accepted: 016-10-13 017 ScPress Ltd., Swtzerland
Problem Solving in Math (Math 43900) Fall 2013
 Problem Solvng n Math (Math 43900) Fall 2013 Week four (September 17) solutons Instructor: Davd Galvn 1. Let a and b be two nteger for whch a b s dvsble by 3. Prove that a 3 b 3 s dvsble by 9. Soluton:
Problem Solvng n Math (Math 43900) Fall 2013 Week four (September 17) solutons Instructor: Davd Galvn 1. Let a and b be two nteger for whch a b s dvsble by 3. Prove that a 3 b 3 s dvsble by 9. Soluton:
Week3, Chapter 4. Position and Displacement. Motion in Two Dimensions. Instantaneous Velocity. Average Velocity
 Week3, Chapter 4 Moton n Two Dmensons Lecture Quz A partcle confned to moton along the x axs moves wth constant acceleraton from x =.0 m to x = 8.0 m durng a 1-s tme nterval. The velocty of the partcle
Week3, Chapter 4 Moton n Two Dmensons Lecture Quz A partcle confned to moton along the x axs moves wth constant acceleraton from x =.0 m to x = 8.0 m durng a 1-s tme nterval. The velocty of the partcle
Linear Regression Analysis: Terminology and Notation
 ECON 35* -- Secton : Basc Concepts of Regresson Analyss (Page ) Lnear Regresson Analyss: Termnology and Notaton Consder the generc verson of the smple (two-varable) lnear regresson model. It s represented
ECON 35* -- Secton : Basc Concepts of Regresson Analyss (Page ) Lnear Regresson Analyss: Termnology and Notaton Consder the generc verson of the smple (two-varable) lnear regresson model. It s represented
Chapter 5. Solution of System of Linear Equations. Module No. 6. Solution of Inconsistent and Ill Conditioned Systems
 Numercal Analyss by Dr. Anta Pal Assstant Professor Department of Mathematcs Natonal Insttute of Technology Durgapur Durgapur-713209 emal: anta.bue@gmal.com 1 . Chapter 5 Soluton of System of Lnear Equatons
Numercal Analyss by Dr. Anta Pal Assstant Professor Department of Mathematcs Natonal Insttute of Technology Durgapur Durgapur-713209 emal: anta.bue@gmal.com 1 . Chapter 5 Soluton of System of Lnear Equatons
Module 9. Lecture 6. Duality in Assignment Problems
 Module 9 1 Lecture 6 Dualty n Assgnment Problems In ths lecture we attempt to answer few other mportant questons posed n earler lecture for (AP) and see how some of them can be explaned through the concept
Module 9 1 Lecture 6 Dualty n Assgnment Problems In ths lecture we attempt to answer few other mportant questons posed n earler lecture for (AP) and see how some of them can be explaned through the concept
Introduction to Vapor/Liquid Equilibrium, part 2. Raoult s Law:
 CE304, Sprng 2004 Lecture 4 Introducton to Vapor/Lqud Equlbrum, part 2 Raoult s Law: The smplest model that allows us do VLE calculatons s obtaned when we assume that the vapor phase s an deal gas, and
CE304, Sprng 2004 Lecture 4 Introducton to Vapor/Lqud Equlbrum, part 2 Raoult s Law: The smplest model that allows us do VLE calculatons s obtaned when we assume that the vapor phase s an deal gas, and
2E Pattern Recognition Solutions to Introduction to Pattern Recognition, Chapter 2: Bayesian pattern classification
 E395 - Pattern Recognton Solutons to Introducton to Pattern Recognton, Chapter : Bayesan pattern classfcaton Preface Ths document s a soluton manual for selected exercses from Introducton to Pattern Recognton
E395 - Pattern Recognton Solutons to Introducton to Pattern Recognton, Chapter : Bayesan pattern classfcaton Preface Ths document s a soluton manual for selected exercses from Introducton to Pattern Recognton
U.C. Berkeley CS294: Beyond Worst-Case Analysis Handout 6 Luca Trevisan September 12, 2017
 U.C. Berkeley CS94: Beyond Worst-Case Analyss Handout 6 Luca Trevsan September, 07 Scrbed by Theo McKenze Lecture 6 In whch we study the spectrum of random graphs. Overvew When attemptng to fnd n polynomal
U.C. Berkeley CS94: Beyond Worst-Case Analyss Handout 6 Luca Trevsan September, 07 Scrbed by Theo McKenze Lecture 6 In whch we study the spectrum of random graphs. Overvew When attemptng to fnd n polynomal
Lecture 5 Decoding Binary BCH Codes
 Lecture 5 Decodng Bnary BCH Codes In ths class, we wll ntroduce dfferent methods for decodng BCH codes 51 Decodng the [15, 7, 5] 2 -BCH Code Consder the [15, 7, 5] 2 -code C we ntroduced n the last lecture
Lecture 5 Decodng Bnary BCH Codes In ths class, we wll ntroduce dfferent methods for decodng BCH codes 51 Decodng the [15, 7, 5] 2 -BCH Code Consder the [15, 7, 5] 2 -code C we ntroduced n the last lecture
Generalized Linear Methods
 Generalzed Lnear Methods 1 Introducton In the Ensemble Methods the general dea s that usng a combnaton of several weak learner one could make a better learner. More formally, assume that we have a set
Generalzed Lnear Methods 1 Introducton In the Ensemble Methods the general dea s that usng a combnaton of several weak learner one could make a better learner. More formally, assume that we have a set
APPENDIX 2 FITTING A STRAIGHT LINE TO OBSERVATIONS
 Unversty of Oulu Student Laboratory n Physcs Laboratory Exercses n Physcs 1 1 APPEDIX FITTIG A STRAIGHT LIE TO OBSERVATIOS In the physcal measurements we often make a seres of measurements of the dependent
Unversty of Oulu Student Laboratory n Physcs Laboratory Exercses n Physcs 1 1 APPEDIX FITTIG A STRAIGHT LIE TO OBSERVATIOS In the physcal measurements we often make a seres of measurements of the dependent
U.C. Berkeley CS294: Beyond Worst-Case Analysis Luca Trevisan September 5, 2017
 U.C. Berkeley CS94: Beyond Worst-Case Analyss Handout 4s Luca Trevsan September 5, 07 Summary of Lecture 4 In whch we ntroduce semdefnte programmng and apply t to Max Cut. Semdefnte Programmng Recall that
U.C. Berkeley CS94: Beyond Worst-Case Analyss Handout 4s Luca Trevsan September 5, 07 Summary of Lecture 4 In whch we ntroduce semdefnte programmng and apply t to Max Cut. Semdefnte Programmng Recall that
ACTM State Calculus Competition Saturday April 30, 2011
 ACTM State Calculus Competton Saturday Aprl 30, 2011 ACTM State Calculus Competton Sprng 2011 Page 1 Instructons: For questons 1 through 25, mark the best answer choce on the answer sheet provde Afterward
ACTM State Calculus Competton Saturday Aprl 30, 2011 ACTM State Calculus Competton Sprng 2011 Page 1 Instructons: For questons 1 through 25, mark the best answer choce on the answer sheet provde Afterward
Difference Equations
 Dfference Equatons c Jan Vrbk 1 Bascs Suppose a sequence of numbers, say a 0,a 1,a,a 3,... s defned by a certan general relatonshp between, say, three consecutve values of the sequence, e.g. a + +3a +1
Dfference Equatons c Jan Vrbk 1 Bascs Suppose a sequence of numbers, say a 0,a 1,a,a 3,... s defned by a certan general relatonshp between, say, three consecutve values of the sequence, e.g. a + +3a +1
6. Stochastic processes (2)
 Contents Markov processes Brth-death processes Lect6.ppt S-38.45 - Introducton to Teletraffc Theory Sprng 5 Markov process Consder a contnuous-tme and dscrete-state stochastc process X(t) wth state space
Contents Markov processes Brth-death processes Lect6.ppt S-38.45 - Introducton to Teletraffc Theory Sprng 5 Markov process Consder a contnuous-tme and dscrete-state stochastc process X(t) wth state space
a. (All your answers should be in the letter!
 Econ 301 Blkent Unversty Taskn Econometrcs Department of Economcs Md Term Exam I November 8, 015 Name For each hypothess testng n the exam complete the followng steps: Indcate the test statstc, ts crtcal
Econ 301 Blkent Unversty Taskn Econometrcs Department of Economcs Md Term Exam I November 8, 015 Name For each hypothess testng n the exam complete the followng steps: Indcate the test statstc, ts crtcal
6. Stochastic processes (2)
 6. Stochastc processes () Lect6.ppt S-38.45 - Introducton to Teletraffc Theory Sprng 5 6. Stochastc processes () Contents Markov processes Brth-death processes 6. Stochastc processes () Markov process
6. Stochastc processes () Lect6.ppt S-38.45 - Introducton to Teletraffc Theory Sprng 5 6. Stochastc processes () Contents Markov processes Brth-death processes 6. Stochastc processes () Markov process
Multilayer Perceptron (MLP)
 Multlayer Perceptron (MLP) Seungjn Cho Department of Computer Scence and Engneerng Pohang Unversty of Scence and Technology 77 Cheongam-ro, Nam-gu, Pohang 37673, Korea seungjn@postech.ac.kr 1 / 20 Outlne
Multlayer Perceptron (MLP) Seungjn Cho Department of Computer Scence and Engneerng Pohang Unversty of Scence and Technology 77 Cheongam-ro, Nam-gu, Pohang 37673, Korea seungjn@postech.ac.kr 1 / 20 Outlne
Chapter 8. Potential Energy and Conservation of Energy
 Chapter 8 Potental Energy and Conservaton of Energy In ths chapter we wll ntroduce the followng concepts: Potental Energy Conservatve and non-conservatve forces Mechancal Energy Conservaton of Mechancal
Chapter 8 Potental Energy and Conservaton of Energy In ths chapter we wll ntroduce the followng concepts: Potental Energy Conservatve and non-conservatve forces Mechancal Energy Conservaton of Mechancal
Exercises of Chapter 2
 Exercses of Chapter Chuang-Cheh Ln Department of Computer Scence and Informaton Engneerng, Natonal Chung Cheng Unversty, Mng-Hsung, Chay 61, Tawan. Exercse.6. Suppose that we ndependently roll two standard
Exercses of Chapter Chuang-Cheh Ln Department of Computer Scence and Informaton Engneerng, Natonal Chung Cheng Unversty, Mng-Hsung, Chay 61, Tawan. Exercse.6. Suppose that we ndependently roll two standard
PhysicsAndMathsTutor.com
 PhscsAndMathsTutor.com phscsandmathstutor.com June 005 5. The random varable X has probablt functon k, = 1,, 3, P( X = ) = k ( + 1), = 4, 5, where k s a constant. (a) Fnd the value of k. (b) Fnd the eact
PhscsAndMathsTutor.com phscsandmathstutor.com June 005 5. The random varable X has probablt functon k, = 1,, 3, P( X = ) = k ( + 1), = 4, 5, where k s a constant. (a) Fnd the value of k. (b) Fnd the eact
COMPLEX NUMBERS AND QUADRATIC EQUATIONS
 COMPLEX NUMBERS AND QUADRATIC EQUATIONS INTRODUCTION We know that x 0 for all x R e the square of a real number (whether postve, negatve or ero) s non-negatve Hence the equatons x, x, x + 7 0 etc are not
COMPLEX NUMBERS AND QUADRATIC EQUATIONS INTRODUCTION We know that x 0 for all x R e the square of a real number (whether postve, negatve or ero) s non-negatve Hence the equatons x, x, x + 7 0 etc are not
Introduction to Information Theory, Data Compression,
 Introducton to Informaton Theory, Data Compresson, Codng Mehd Ibm Brahm, Laura Mnkova Aprl 5, 208 Ths s the augmented transcrpt of a lecture gven by Luc Devroye on the 3th of March 208 for a Data Structures
Introducton to Informaton Theory, Data Compresson, Codng Mehd Ibm Brahm, Laura Mnkova Aprl 5, 208 Ths s the augmented transcrpt of a lecture gven by Luc Devroye on the 3th of March 208 for a Data Structures
763622S ADVANCED QUANTUM MECHANICS Solution Set 1 Spring c n a n. c n 2 = 1.
 7636S ADVANCED QUANTUM MECHANICS Soluton Set 1 Sprng 013 1 Warm-up Show that the egenvalues of a Hermtan operator  are real and that the egenkets correspondng to dfferent egenvalues are orthogonal (b)
7636S ADVANCED QUANTUM MECHANICS Soluton Set 1 Sprng 013 1 Warm-up Show that the egenvalues of a Hermtan operator  are real and that the egenkets correspondng to dfferent egenvalues are orthogonal (b)
20. Mon, Oct. 13 What we have done so far corresponds roughly to Chapters 2 & 3 of Lee. Now we turn to Chapter 4. The first idea is connectedness.
 20. Mon, Oct. 13 What we have done so far corresponds roughly to Chapters 2 & 3 of Lee. Now we turn to Chapter 4. The frst dea s connectedness. Essentally, we want to say that a space cannot be decomposed
20. Mon, Oct. 13 What we have done so far corresponds roughly to Chapters 2 & 3 of Lee. Now we turn to Chapter 4. The frst dea s connectedness. Essentally, we want to say that a space cannot be decomposed
NUMERICAL DIFFERENTIATION
 NUMERICAL DIFFERENTIATION 1 Introducton Dfferentaton s a method to compute the rate at whch a dependent output y changes wth respect to the change n the ndependent nput x. Ths rate of change s called the
NUMERICAL DIFFERENTIATION 1 Introducton Dfferentaton s a method to compute the rate at whch a dependent output y changes wth respect to the change n the ndependent nput x. Ths rate of change s called the
First Year Examination Department of Statistics, University of Florida
 Frst Year Examnaton Department of Statstcs, Unversty of Florda May 7, 010, 8:00 am - 1:00 noon Instructons: 1. You have four hours to answer questons n ths examnaton.. You must show your work to receve
Frst Year Examnaton Department of Statstcs, Unversty of Florda May 7, 010, 8:00 am - 1:00 noon Instructons: 1. You have four hours to answer questons n ths examnaton.. You must show your work to receve
Homework 9 Solutions. 1. (Exercises from the book, 6 th edition, 6.6, 1-3.) Determine the number of distinct orderings of the letters given:
 Homework 9 Solutons PROBLEM ONE 1 (Exercses from the book, th edton,, 1-) Determne the number of dstnct orderngs of the letters gven: (a) GUIDE Soluton: 5! (b) SCHOOL Soluton:! (c) SALESPERSONS Soluton:
Homework 9 Solutons PROBLEM ONE 1 (Exercses from the book, th edton,, 1-) Determne the number of dstnct orderngs of the letters gven: (a) GUIDE Soluton: 5! (b) SCHOOL Soluton:! (c) SALESPERSONS Soluton:
Maximizing the number of nonnegative subsets
 Maxmzng the number of nonnegatve subsets Noga Alon Hao Huang December 1, 213 Abstract Gven a set of n real numbers, f the sum of elements of every subset of sze larger than k s negatve, what s the maxmum
Maxmzng the number of nonnegatve subsets Noga Alon Hao Huang December 1, 213 Abstract Gven a set of n real numbers, f the sum of elements of every subset of sze larger than k s negatve, what s the maxmum
8.1 Arc Length. What is the length of a curve? How can we approximate it? We could do it following the pattern we ve used before
 .1 Arc Length hat s the length of a curve? How can we approxmate t? e could do t followng the pattern we ve used before Use a sequence of ncreasngly short segments to approxmate the curve: As the segments
.1 Arc Length hat s the length of a curve? How can we approxmate t? e could do t followng the pattern we ve used before Use a sequence of ncreasngly short segments to approxmate the curve: As the segments
STAT 511 FINAL EXAM NAME Spring 2001
 STAT 5 FINAL EXAM NAME Sprng Instructons: Ths s a closed book exam. No notes or books are allowed. ou may use a calculator but you are not allowed to store notes or formulas n the calculator. Please wrte
STAT 5 FINAL EXAM NAME Sprng Instructons: Ths s a closed book exam. No notes or books are allowed. ou may use a calculator but you are not allowed to store notes or formulas n the calculator. Please wrte
THE CHINESE REMAINDER THEOREM. We should thank the Chinese for their wonderful remainder theorem. Glenn Stevens
 THE CHINESE REMAINDER THEOREM KEITH CONRAD We should thank the Chnese for ther wonderful remander theorem. Glenn Stevens 1. Introducton The Chnese remander theorem says we can unquely solve any par of
THE CHINESE REMAINDER THEOREM KEITH CONRAD We should thank the Chnese for ther wonderful remander theorem. Glenn Stevens 1. Introducton The Chnese remander theorem says we can unquely solve any par of
Chapter 8 SCALAR QUANTIZATION
 Outlne Chapter 8 SCALAR QUANTIZATION Yeuan-Kuen Lee [ CU, CSIE ] 8.1 Overvew 8. Introducton 8.4 Unform Quantzer 8.5 Adaptve Quantzaton 8.6 Nonunform Quantzaton 8.7 Entropy-Coded Quantzaton Ch 8 Scalar
Outlne Chapter 8 SCALAR QUANTIZATION Yeuan-Kuen Lee [ CU, CSIE ] 8.1 Overvew 8. Introducton 8.4 Unform Quantzer 8.5 Adaptve Quantzaton 8.6 Nonunform Quantzaton 8.7 Entropy-Coded Quantzaton Ch 8 Scalar
On cyclic of Steiner system (v); V=2,3,5,7,11,13
 On cyclc of Stener system (v); V=,3,5,7,,3 Prof. Dr. Adl M. Ahmed Rana A. Ibraham Abstract: A stener system can be defned by the trple S(t,k,v), where every block B, (=,,,b) contans exactly K-elementes
On cyclc of Stener system (v); V=,3,5,7,,3 Prof. Dr. Adl M. Ahmed Rana A. Ibraham Abstract: A stener system can be defned by the trple S(t,k,v), where every block B, (=,,,b) contans exactly K-elementes
More metrics on cartesian products
 More metrcs on cartesan products If (X, d ) are metrc spaces for 1 n, then n Secton II4 of the lecture notes we defned three metrcs on X whose underlyng topologes are the product topology The purpose of
More metrcs on cartesan products If (X, d ) are metrc spaces for 1 n, then n Secton II4 of the lecture notes we defned three metrcs on X whose underlyng topologes are the product topology The purpose of
Foundations of Arithmetic
 Foundatons of Arthmetc Notaton We shall denote the sum and product of numbers n the usual notaton as a 2 + a 2 + a 3 + + a = a, a 1 a 2 a 3 a = a The notaton a b means a dvdes b,.e. ac = b where c s an
Foundatons of Arthmetc Notaton We shall denote the sum and product of numbers n the usual notaton as a 2 + a 2 + a 3 + + a = a, a 1 a 2 a 3 a = a The notaton a b means a dvdes b,.e. ac = b where c s an
Statistics MINITAB - Lab 2
 Statstcs 20080 MINITAB - Lab 2 1. Smple Lnear Regresson In smple lnear regresson we attempt to model a lnear relatonshp between two varables wth a straght lne and make statstcal nferences concernng that
Statstcs 20080 MINITAB - Lab 2 1. Smple Lnear Regresson In smple lnear regresson we attempt to model a lnear relatonshp between two varables wth a straght lne and make statstcal nferences concernng that
Analytical Chemistry Calibration Curve Handout
 I. Quck-and Drty Excel Tutoral Analytcal Chemstry Calbraton Curve Handout For those of you wth lttle experence wth Excel, I ve provded some key technques that should help you use the program both for problem
I. Quck-and Drty Excel Tutoral Analytcal Chemstry Calbraton Curve Handout For those of you wth lttle experence wth Excel, I ve provded some key technques that should help you use the program both for problem
Case A. P k = Ni ( 2L i k 1 ) + (# big cells) 10d 2 P k.
 THE CELLULAR METHOD In ths lecture, we ntroduce the cellular method as an approach to ncdence geometry theorems lke the Szemeréd-Trotter theorem. The method was ntroduced n the paper Combnatoral complexty
THE CELLULAR METHOD In ths lecture, we ntroduce the cellular method as an approach to ncdence geometry theorems lke the Szemeréd-Trotter theorem. The method was ntroduced n the paper Combnatoral complexty
Edge Isoperimetric Inequalities
 November 7, 2005 Ross M. Rchardson Edge Isopermetrc Inequaltes 1 Four Questons Recall that n the last lecture we looked at the problem of sopermetrc nequaltes n the hypercube, Q n. Our noton of boundary
November 7, 2005 Ross M. Rchardson Edge Isopermetrc Inequaltes 1 Four Questons Recall that n the last lecture we looked at the problem of sopermetrc nequaltes n the hypercube, Q n. Our noton of boundary
Subset Topological Spaces and Kakutani s Theorem
 MOD Natural Neutrosophc Subset Topologcal Spaces and Kakutan s Theorem W. B. Vasantha Kandasamy lanthenral K Florentn Smarandache 1 Copyrght 1 by EuropaNova ASBL and the Authors Ths book can be ordered
MOD Natural Neutrosophc Subset Topologcal Spaces and Kakutan s Theorem W. B. Vasantha Kandasamy lanthenral K Florentn Smarandache 1 Copyrght 1 by EuropaNova ASBL and the Authors Ths book can be ordered
LECTURE V. 1. More on the Chinese Remainder Theorem We begin by recalling this theorem, proven in the preceeding lecture.
 LECTURE V EDWIN SPARK 1. More on the Chnese Remander Theorem We begn by recallng ths theorem, proven n the preceedng lecture. Theorem 1.1 (Chnese Remander Theorem). Let R be a rng wth deals I 1, I 2,...,
LECTURE V EDWIN SPARK 1. More on the Chnese Remander Theorem We begn by recallng ths theorem, proven n the preceedng lecture. Theorem 1.1 (Chnese Remander Theorem). Let R be a rng wth deals I 1, I 2,...,
Structure and Drive Paul A. Jensen Copyright July 20, 2003
 Structure and Drve Paul A. Jensen Copyrght July 20, 2003 A system s made up of several operatons wth flow passng between them. The structure of the system descrbes the flow paths from nputs to outputs.
Structure and Drve Paul A. Jensen Copyrght July 20, 2003 A system s made up of several operatons wth flow passng between them. The structure of the system descrbes the flow paths from nputs to outputs.
arxiv: v2 [cs.ds] 1 Feb 2017
![arxiv: v2 [cs.ds] 1 Feb 2017 arxiv: v2 [cs.ds] 1 Feb 2017](/thumbs/93/113731213.jpg) Polynomal-tme Algorthms for the Subset Feedback Vertex Set Problem on Interval Graphs and Permutaton Graphs Chars Papadopoulos Spyrdon Tzmas arxv:170104634v2 [csds] 1 Feb 2017 Abstract Gven a vertex-weghted
Polynomal-tme Algorthms for the Subset Feedback Vertex Set Problem on Interval Graphs and Permutaton Graphs Chars Papadopoulos Spyrdon Tzmas arxv:170104634v2 [csds] 1 Feb 2017 Abstract Gven a vertex-weghted
Ph 219a/CS 219a. Exercises Due: Wednesday 23 October 2013
 1 Ph 219a/CS 219a Exercses Due: Wednesday 23 October 2013 1.1 How far apart are two quantum states? Consder two quantum states descrbed by densty operators ρ and ρ n an N-dmensonal Hlbert space, and consder
1 Ph 219a/CS 219a Exercses Due: Wednesday 23 October 2013 1.1 How far apart are two quantum states? Consder two quantum states descrbed by densty operators ρ and ρ n an N-dmensonal Hlbert space, and consder
PHYSICS - CLUTCH CH 28: INDUCTION AND INDUCTANCE.
 !! www.clutchprep.com CONCEPT: ELECTROMAGNETIC INDUCTION A col of wre wth a VOLTAGE across each end wll have a current n t - Wre doesn t HAVE to have voltage source, voltage can be INDUCED V Common ways
!! www.clutchprep.com CONCEPT: ELECTROMAGNETIC INDUCTION A col of wre wth a VOLTAGE across each end wll have a current n t - Wre doesn t HAVE to have voltage source, voltage can be INDUCED V Common ways
Module 2. Random Processes. Version 2 ECE IIT, Kharagpur
 Module Random Processes Lesson 6 Functons of Random Varables After readng ths lesson, ou wll learn about cdf of functon of a random varable. Formula for determnng the pdf of a random varable. Let, X be
Module Random Processes Lesson 6 Functons of Random Varables After readng ths lesson, ou wll learn about cdf of functon of a random varable. Formula for determnng the pdf of a random varable. Let, X be
2.3 Nilpotent endomorphisms
 s a block dagonal matrx, wth A Mat dm U (C) In fact, we can assume that B = B 1 B k, wth B an ordered bass of U, and that A = [f U ] B, where f U : U U s the restrcton of f to U 40 23 Nlpotent endomorphsms
s a block dagonal matrx, wth A Mat dm U (C) In fact, we can assume that B = B 1 B k, wth B an ordered bass of U, and that A = [f U ] B, where f U : U U s the restrcton of f to U 40 23 Nlpotent endomorphsms
Please initial the statement below to show that you have read it
 EN0: Structural nalyss Exam I Wednesday, March 2, 2005 Dvson of Engneerng rown Unversty NME: General Instructons No collaboraton of any nd s permtted on ths examnaton. You may consult your own wrtten lecture
EN0: Structural nalyss Exam I Wednesday, March 2, 2005 Dvson of Engneerng rown Unversty NME: General Instructons No collaboraton of any nd s permtted on ths examnaton. You may consult your own wrtten lecture
Learning Theory: Lecture Notes
 Learnng Theory: Lecture Notes Lecturer: Kamalka Chaudhur Scrbe: Qush Wang October 27, 2012 1 The Agnostc PAC Model Recall that one of the constrants of the PAC model s that the data dstrbuton has to be
Learnng Theory: Lecture Notes Lecturer: Kamalka Chaudhur Scrbe: Qush Wang October 27, 2012 1 The Agnostc PAC Model Recall that one of the constrants of the PAC model s that the data dstrbuton has to be
Section 8.1 Exercises
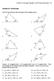 Secton 8.1 Non-rght Trangles: Law of Snes and Cosnes 519 Secton 8.1 Exercses Solve for the unknown sdes and angles of the trangles shown. 10 70 50 1.. 18 40 110 45 5 6 3. 10 4. 75 15 5 6 90 70 65 5. 6.
Secton 8.1 Non-rght Trangles: Law of Snes and Cosnes 519 Secton 8.1 Exercses Solve for the unknown sdes and angles of the trangles shown. 10 70 50 1.. 18 40 110 45 5 6 3. 10 4. 75 15 5 6 90 70 65 5. 6.
Lecture 4: November 17, Part 1 Single Buffer Management
 Lecturer: Ad Rosén Algorthms for the anagement of Networs Fall 2003-2004 Lecture 4: November 7, 2003 Scrbe: Guy Grebla Part Sngle Buffer anagement In the prevous lecture we taled about the Combned Input
Lecturer: Ad Rosén Algorthms for the anagement of Networs Fall 2003-2004 Lecture 4: November 7, 2003 Scrbe: Guy Grebla Part Sngle Buffer anagement In the prevous lecture we taled about the Combned Input
Stanford University CS359G: Graph Partitioning and Expanders Handout 4 Luca Trevisan January 13, 2011
 Stanford Unversty CS359G: Graph Parttonng and Expanders Handout 4 Luca Trevsan January 3, 0 Lecture 4 In whch we prove the dffcult drecton of Cheeger s nequalty. As n the past lectures, consder an undrected
Stanford Unversty CS359G: Graph Parttonng and Expanders Handout 4 Luca Trevsan January 3, 0 Lecture 4 In whch we prove the dffcult drecton of Cheeger s nequalty. As n the past lectures, consder an undrected
CHAPTER 13. Exercises. E13.1 The emitter current is given by the Shockley equation:
 HPT 3 xercses 3. The emtter current s gen by the Shockley equaton: S exp VT For operaton wth, we hae exp >> S >>, and we can wrte VT S exp VT Solng for, we hae 3. 0 6ln 78.4 mv 0 0.784 5 4.86 V VT ln 4
HPT 3 xercses 3. The emtter current s gen by the Shockley equaton: S exp VT For operaton wth, we hae exp >> S >>, and we can wrte VT S exp VT Solng for, we hae 3. 0 6ln 78.4 mv 0 0.784 5 4.86 V VT ln 4
Lecture Notes 7: The Unruh Effect
 Quantum Feld Theory for Leg Spnners 17/1/11 Lecture Notes 7: The Unruh Effect Lecturer: Prakash Panangaden Scrbe: Shane Mansfeld 1 Defnng the Vacuum Recall from the last lecture that choosng a complex
Quantum Feld Theory for Leg Spnners 17/1/11 Lecture Notes 7: The Unruh Effect Lecturer: Prakash Panangaden Scrbe: Shane Mansfeld 1 Defnng the Vacuum Recall from the last lecture that choosng a complex
Errors for Linear Systems
 Errors for Lnear Systems When we solve a lnear system Ax b we often do not know A and b exactly, but have only approxmatons  and ˆb avalable. Then the best thng we can do s to solve ˆx ˆb exactly whch
Errors for Lnear Systems When we solve a lnear system Ax b we often do not know A and b exactly, but have only approxmatons  and ˆb avalable. Then the best thng we can do s to solve ˆx ˆb exactly whch
Prof. Dr. I. Nasser Phys 630, T Aug-15 One_dimensional_Ising_Model
 EXACT OE-DIMESIOAL ISIG MODEL The one-dmensonal Isng model conssts of a chan of spns, each spn nteractng only wth ts two nearest neghbors. The smple Isng problem n one dmenson can be solved drectly n several
EXACT OE-DIMESIOAL ISIG MODEL The one-dmensonal Isng model conssts of a chan of spns, each spn nteractng only wth ts two nearest neghbors. The smple Isng problem n one dmenson can be solved drectly n several
a b a In case b 0, a being divisible by b is the same as to say that
 Secton 6.2 Dvsblty among the ntegers An nteger a ε s dvsble by b ε f there s an nteger c ε such that a = bc. Note that s dvsble by any nteger b, snce = b. On the other hand, a s dvsble by only f a = :
Secton 6.2 Dvsblty among the ntegers An nteger a ε s dvsble by b ε f there s an nteger c ε such that a = bc. Note that s dvsble by any nteger b, snce = b. On the other hand, a s dvsble by only f a = :
The path of ants Dragos Crisan, Andrei Petridean, 11 th grade. Colegiul National "Emil Racovita", Cluj-Napoca
 Ths artcle s wrtten by students. It may nclude omssons and mperfectons, whch were dentfed and reported as mnutely as possble by our revewers n the edtoral notes. The path of ants 07-08 Students names and
Ths artcle s wrtten by students. It may nclude omssons and mperfectons, whch were dentfed and reported as mnutely as possble by our revewers n the edtoral notes. The path of ants 07-08 Students names and
Spectral Graph Theory and its Applications September 16, Lecture 5
 Spectral Graph Theory and ts Applcatons September 16, 2004 Lecturer: Danel A. Spelman Lecture 5 5.1 Introducton In ths lecture, we wll prove the followng theorem: Theorem 5.1.1. Let G be a planar graph
Spectral Graph Theory and ts Applcatons September 16, 2004 Lecturer: Danel A. Spelman Lecture 5 5.1 Introducton In ths lecture, we wll prove the followng theorem: Theorem 5.1.1. Let G be a planar graph
Self-complementing permutations of k-uniform hypergraphs
 Dscrete Mathematcs Theoretcal Computer Scence DMTCS vol. 11:1, 2009, 117 124 Self-complementng permutatons of k-unform hypergraphs Artur Szymańsk A. Paweł Wojda Faculty of Appled Mathematcs, AGH Unversty
Dscrete Mathematcs Theoretcal Computer Scence DMTCS vol. 11:1, 2009, 117 124 Self-complementng permutatons of k-unform hypergraphs Artur Szymańsk A. Paweł Wojda Faculty of Appled Mathematcs, AGH Unversty
DEMO #8 - GAUSSIAN ELIMINATION USING MATHEMATICA. 1. Matrices in Mathematica
 demo8.nb 1 DEMO #8 - GAUSSIAN ELIMINATION USING MATHEMATICA Obectves: - defne matrces n Mathematca - format the output of matrces - appl lnear algebra to solve a real problem - Use Mathematca to perform
demo8.nb 1 DEMO #8 - GAUSSIAN ELIMINATION USING MATHEMATICA Obectves: - defne matrces n Mathematca - format the output of matrces - appl lnear algebra to solve a real problem - Use Mathematca to perform
PHYS 705: Classical Mechanics. Newtonian Mechanics
 1 PHYS 705: Classcal Mechancs Newtonan Mechancs Quck Revew of Newtonan Mechancs Basc Descrpton: -An dealzed pont partcle or a system of pont partcles n an nertal reference frame [Rgd bodes (ch. 5 later)]
1 PHYS 705: Classcal Mechancs Newtonan Mechancs Quck Revew of Newtonan Mechancs Basc Descrpton: -An dealzed pont partcle or a system of pont partcles n an nertal reference frame [Rgd bodes (ch. 5 later)]
