Matrices and vectors A matrix is a rectangular array of numbers. Here s an example: A =
|
|
|
- Spencer Hines
- 5 years ago
- Views:
Transcription
1 Matrices and vectors A matrix is a rectangular array of numbers Here s an example: A = This matrix has dimensions 2 3 The number of rows is first, then the number of columns We can write the n p matrix X abstractly as x 11 x 12 x 13 x 1p x 21 x 22 x 23 x 2p X = x 31 x 32 x 33 x 3p x n1 x n2 x n3 x np 1
2 Another notation that is common is A = [a ij ] n m for an n m matrix A with element a ij in the i th row and j th column The matrix X on the previous page would then be written X = [x ij ] n p If two matrices A = [a ij ] n m and B = [b ij ] n m have the same dimensions, you can add them together, element by element, to get a new matrix C = [c ij ] n m That is, C = A + B is the matrix with elements c ij = a ij + b ij For example, = =
3 Multiplying a matrix A = [a ij ] n m by a number b yields the matrix C = Ab with elements c ij = a ij b For example, 1 2 1( 2) 2( 2) 2 4 ( 2) 5 7 = 5( 2) 7( 2) = ( 2) 20( 2) The transpose of a matrix A takes the matrix A and makes the rows the columns and the columns the rows Precisely, if A = [a ij ] n m then A is the m n matrix with elements a ij = a ji For example: If A = Question: what is (A )? , then A =
4 A vector is a matrix with only one column or row, called a column vector or row vector respectively Here s an example of each: 1 x = 1, y = [ ] 14 Note that for these vectors, x = y and y = x The product of an 1 n row vector and a n 1 column vector is the sum of the pairwise products of elements So if x = [x i ] 1 n and y = [y i ] n 1 then xy = n i=1 x iy i 4
5 For example, if x = [ 1 2 ] and y = xy = [ 1 2 ] then = 1(10) + 2( 5) = 20 The inner product of two n 1 column vectors x and y is the product x y = [ x 1 x 2 x 3 x n ] y 1 y 2 y 3 y n = n x i y i i=1 5
6 Note that if x = x 1 x 2 is a point in the plane R 2, then x x = x x 2 2 is the square of the length of x That is, x = x x We are now ready to define general matrix multiplication The product of an n p matrix A and a p m matrix B is the n m matrix C with elements c ij = p k=1 a ikb kj Let A be comprised of n 1 p row vectors a 1,,a n and let B be comprised of m p 1 column vectors b 1,,b m like A = a 1 a 2 a n n p and B = b 1 b 2 b m p m 6
7 Then c ij = a i b j : C = For example, let A = Then a 1 b 1 a 1 b 2 a 1 b m a 2 b 1 a 2 b 2 a 2 b m a n b 1 a n b 2 a n b m and B = AB = = 1(2) 1(0) 2(1) 1(0) 1( 5) 2(05) 1( 2) 1(7) 2( 4) 1(0) + 5(1) 3(2) 3(0) 1( 5) + 5(05) 3( 2) 1(7) + 5( 4)
8 On the previous slide, does BA make sense? No The rows of the first matrix must be the same length as the columns of the second Note that, in general, AB BA Define I n n as Then I = A n p I p p = A n p and I n n A n p = A n p, for any A n p The matrix I n n is called the n n identity matrix 8
9 For example, = and =
10 The inverse of a square (p p) matrix A is the p p matrix A 1 such that A 1 A = AA 1 = I p p For example, if A = 1 1, then 0 2 and so A 1 = as well = Note that we must have = , 10
11 There is an algorithm for finding the inverse of any size matrix but it is very computationally intensive, except for 2 2 matrices Let A = a 11 a 12 a 21 a 22 Then A 1 = 1 a 11 a 22 a 12 a 21 a 22 a 12 a 21 a 11 That is, switch the diagonal entries, multiply the off-diagonals by 1, and divide the works by a 11 a 22 a 12 a 21 We can show that this is the inverse in class Try it out on A on the previous slide 11
12 Not every square matrix has an inverse For example A = 1 2, 2 4 does not Try the formula on the previous slide out on this matrix What happens? Square matrices that do not have an inverse are said to be singular 12
13 The two sample problem in terms of matrices Recall the two-sample normal model with equal variances: Y 11, Y 12,,Y 1n1 iid N(µ 1, σ 2 ), Y 21, Y 22,,Y 2n2 iid N(µ 2, σ 2 ) We can rewrite this as where Y ij = µ i + e ij, e ij iid N(0, σ 2 ), where i = 1, 2 indexes the group (1 or 2) and j = 1,,n i is the observation within the group 13
14 Each piece of data Y ij follows: Y 11 = µ 1 + e 11 Y 12 = µ 1 + e 12 Y 13 = µ 1 + e 13 Y 1n1 = µ 1 + e 1n1 Y 21 = µ 2 + e 21 Y 22 = µ 2 + e 22 Y 23 = µ 2 + e 23 Y 2n2 = µ 2 + e 2n2 14
15 Define the following vectors and matrices: Y = Y 11 Y 12 Y 1n2 Y 21 Y 22 Y 2n2, X = , µ = µ 1 µ 2, and e = e 11 e 12 e 1n2 e 21 e 22 e 2n2 15
16 Then we can write the model succinctly as Y = Xµ + e We ll show this on the board for n 1 = n 2 = 3 It turns out the the MLE s for µ 1 and µ 2, namely ˆµ 1 = n 1 n1 1 j=1 y 1j = ȳ 1 and ˆµ 2 = n 1 n2 2 j=1 y 2j = ȳ 2 are obtained in matrix terms as ˆµ = ˆµ 1 ˆµ 2 = (X X) 1 X y 16
17 We ll show part of this: X X = = n n 2 17
18 And so Also, X y = (X X) 1 = n n = 1 n n 2 y 11 y 12 y 1n2 y 21 y 22 = n1 j=1 y 1j n2 j=1 y 2j y 2n2 18
19 Then (X X) 1 X y = 1 n n 2 n1 j=1 y 1j n2 j=1 y 2j = ȳ1 ȳ 2 = ˆµ 1 ˆµ 2, as promised The MLE of σ 2 in terms of matrices is ˆσ 2 = (y Xˆµ) (y Xˆµ)/(n 1 + n 2 ) = y Xˆµ 2 /(n 1 + n 2 ) What is the point? Although the two-sample normal model is fairly simple, very complex models with multiple predictors, both categorical and continuous, can be written as Y = Xβ + e, including the simple linear regression model, multiple regression models, oneway and multiway ANOVA models, and ANCOVA models 19
20 In Y = Xβ + e, Y is the n 1 data vector X is the n p design matrix Often the i th row of X is comprised of p 1 measurements taken on the i th subject in a study, eg the i th row of an Excel spreadsheet, and an intercept term β is the p 1 coefficient vector For the two-sample model, p = 2 and β = (µ 1, µ 2 ) e is the n 1 error vector All the elements of e are assumed to be iid N(0, σ 2 ) 20
21 The j th residual in group i is defined to be r ij = y ij Ê(Y ij) = y ij ˆµ i These can be plotted versus the group number i = 1, 2 to assess whether constant variance across groups is reasonable A histogram of all n = n 1 + n 2 residuals can be used to assess the normality assumption There are formal tests for both constant variance and for normality > skull <- c(english,celt) > group <- c(rep("english",length(english)),rep("celt",length(celt))) > group <- factor(group) > ttest(skull~group,varequal=t) Two Sample t-test data: skull by group t = , df = 32, p-value = 9003e-09 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval:
22 sample estimates: mean in group Celt mean in group English > fit1 <- lm(skull~group) #lm() is "linear model" > summary(fit1) Call: lm(formula = skull ~ group) Residuals: Min 1Q Median 3Q Max Coefficients: Estimate Std Error t value Pr(> t ) (Intercept) <2e-16 *** groupenglish e-09 *** --- F-statistic: 5922 on 1 and 32 DF, p-value: 9003e-09 > r <- fit1$residuals # get residuals > plot(group,r) # gives boxplots instead of scatterplot > hist(r) # looks roughly normal 22
23 Histogram of r Frequency Celt English r Figure 1: Boxplots show roughly the same spread; histogram is roughly normal looking 23
24 The lm() fit to the data fits a different, but equivalent model: Celts : Y 1,1,,Y 1,16 iid N(µ, σ 2 ), English : Y 2,1,,Y 2,18 iid N(µ + δ, σ 2 ), reports estimates of the mean Celtic headbreadth µ, and the mean difference for Englishmen δ Of interest in this reparameterized model is H 0 : δ = 0, which is the same as testing H 0 : µ 1 = µ 2 in the two-sample model 24
25 The simple linear regression model stipulates Y i = β 0 + β 1 x i + e i, where i = 1,,n Here we can write Y = Y 1 Y 2, X = 1 x 1 1 x 2, β = β 0 β 1, and e = e 1 e 2 Y n 1 x n e n The model is succinctly written Y = Xβ + e 25
26 As in the two-sample model, the MLE s ˆβ = (ˆβ 0, ˆβ 1 ) are given by ˆβ = ˆβ 0 ˆβ 1 = (X X) 1 X y The MLE for σ 2 is ˆσ 2 = (y Xˆβ) (y Xˆβ) n = 1 n n (y i [ˆβ 0 + ˆβ 1 x i ]) 2 i=1 For the i th observation, the fitted value ŷ i is the point on the line at x i, namely ˆβ 0 + ˆβ 1 x i So at value x i we see the observed value y i, but estimate the underlying mean ŷ i = Ê(Y i) = ˆβ 0 + ˆβ 1 x i Since the MLE s ˆβ 0 and ˆβ 1 are unbiased, E(ˆβ 0 + ˆβ 1 x i ) = E(ˆβ 0 ) + E(ˆβ 1 )x i = β 0 + β 1 x i 26
27 That is, E(ŷ i ) = β 0 + β 1 x i The i th residual r i estimates the unknown e i = y i [β 0 + β 1 x i ] by r i = y i [ˆβ 0 + ˆβ 1 x i ] = y i Ê(Y i) These are used to check model assumptions: (1) that the e 1,,e n iid N(0, σ 2 ), and (2) that the mean changes linearly with x: E(Y i ) = β 0 + β 1 x i A histogram of r 1,,r n should be roughly symmetric and unimodal, ie normal looking A plot of r i versus x i should show no discernable pattern and roughly constant spread 27
28 > fit2 <- lm(score~ses) > plot(fit2) # get a variety of diagnostic plots automatically > r <- fit2$residuals > plot(ses,r) > hist(r) r ses Figure 2: Residual plot shows no discernable pattern 28
29 Histogram of r Frequency r Figure 3: Histogram of residuals is roughly normal looking 29
. a m1 a mn. a 1 a 2 a = a n
 Biostat 140655, 2008: Matrix Algebra Review 1 Definition: An m n matrix, A m n, is a rectangular array of real numbers with m rows and n columns Element in the i th row and the j th column is denoted by
Biostat 140655, 2008: Matrix Algebra Review 1 Definition: An m n matrix, A m n, is a rectangular array of real numbers with m rows and n columns Element in the i th row and the j th column is denoted by
14 Multiple Linear Regression
 B.Sc./Cert./M.Sc. Qualif. - Statistics: Theory and Practice 14 Multiple Linear Regression 14.1 The multiple linear regression model In simple linear regression, the response variable y is expressed in
B.Sc./Cert./M.Sc. Qualif. - Statistics: Theory and Practice 14 Multiple Linear Regression 14.1 The multiple linear regression model In simple linear regression, the response variable y is expressed in
Lecture 2. The Simple Linear Regression Model: Matrix Approach
 Lecture 2 The Simple Linear Regression Model: Matrix Approach Matrix algebra Matrix representation of simple linear regression model 1 Vectors and Matrices Where it is necessary to consider a distribution
Lecture 2 The Simple Linear Regression Model: Matrix Approach Matrix algebra Matrix representation of simple linear regression model 1 Vectors and Matrices Where it is necessary to consider a distribution
Ch 2: Simple Linear Regression
 Ch 2: Simple Linear Regression 1. Simple Linear Regression Model A simple regression model with a single regressor x is y = β 0 + β 1 x + ɛ, where we assume that the error ɛ is independent random component
Ch 2: Simple Linear Regression 1. Simple Linear Regression Model A simple regression model with a single regressor x is y = β 0 + β 1 x + ɛ, where we assume that the error ɛ is independent random component
Chapter 5 Matrix Approach to Simple Linear Regression
 STAT 525 SPRING 2018 Chapter 5 Matrix Approach to Simple Linear Regression Professor Min Zhang Matrix Collection of elements arranged in rows and columns Elements will be numbers or symbols For example:
STAT 525 SPRING 2018 Chapter 5 Matrix Approach to Simple Linear Regression Professor Min Zhang Matrix Collection of elements arranged in rows and columns Elements will be numbers or symbols For example:
Ch 3: Multiple Linear Regression
 Ch 3: Multiple Linear Regression 1. Multiple Linear Regression Model Multiple regression model has more than one regressor. For example, we have one response variable and two regressor variables: 1. delivery
Ch 3: Multiple Linear Regression 1. Multiple Linear Regression Model Multiple regression model has more than one regressor. For example, we have one response variable and two regressor variables: 1. delivery
Multiple Linear Regression
 Multiple Linear Regression Simple linear regression tries to fit a simple line between two variables Y and X. If X is linearly related to Y this explains some of the variability in Y. In most cases, there
Multiple Linear Regression Simple linear regression tries to fit a simple line between two variables Y and X. If X is linearly related to Y this explains some of the variability in Y. In most cases, there
Linear Regression. In this lecture we will study a particular type of regression model: the linear regression model
 1 Linear Regression 2 Linear Regression In this lecture we will study a particular type of regression model: the linear regression model We will first consider the case of the model with one predictor
1 Linear Regression 2 Linear Regression In this lecture we will study a particular type of regression model: the linear regression model We will first consider the case of the model with one predictor
MATH 644: Regression Analysis Methods
 MATH 644: Regression Analysis Methods FINAL EXAM Fall, 2012 INSTRUCTIONS TO STUDENTS: 1. This test contains SIX questions. It comprises ELEVEN printed pages. 2. Answer ALL questions for a total of 100
MATH 644: Regression Analysis Methods FINAL EXAM Fall, 2012 INSTRUCTIONS TO STUDENTS: 1. This test contains SIX questions. It comprises ELEVEN printed pages. 2. Answer ALL questions for a total of 100
K. Model Diagnostics. residuals ˆɛ ij = Y ij ˆµ i N = Y ij Ȳ i semi-studentized residuals ω ij = ˆɛ ij. studentized deleted residuals ɛ ij =
 K. Model Diagnostics We ve already seen how to check model assumptions prior to fitting a one-way ANOVA. Diagnostics carried out after model fitting by using residuals are more informative for assessing
K. Model Diagnostics We ve already seen how to check model assumptions prior to fitting a one-way ANOVA. Diagnostics carried out after model fitting by using residuals are more informative for assessing
Lecture 1: Linear Models and Applications
 Lecture 1: Linear Models and Applications Claudia Czado TU München c (Claudia Czado, TU Munich) ZFS/IMS Göttingen 2004 0 Overview Introduction to linear models Exploratory data analysis (EDA) Estimation
Lecture 1: Linear Models and Applications Claudia Czado TU München c (Claudia Czado, TU Munich) ZFS/IMS Göttingen 2004 0 Overview Introduction to linear models Exploratory data analysis (EDA) Estimation
Simple and Multiple Linear Regression
 Sta. 113 Chapter 12 and 13 of Devore March 12, 2010 Table of contents 1 Simple Linear Regression 2 Model Simple Linear Regression A simple linear regression model is given by Y = β 0 + β 1 x + ɛ where
Sta. 113 Chapter 12 and 13 of Devore March 12, 2010 Table of contents 1 Simple Linear Regression 2 Model Simple Linear Regression A simple linear regression model is given by Y = β 0 + β 1 x + ɛ where
Regression Review. Statistics 149. Spring Copyright c 2006 by Mark E. Irwin
 Regression Review Statistics 149 Spring 2006 Copyright c 2006 by Mark E. Irwin Matrix Approach to Regression Linear Model: Y i = β 0 + β 1 X i1 +... + β p X ip + ɛ i ; ɛ i iid N(0, σ 2 ), i = 1,..., n
Regression Review Statistics 149 Spring 2006 Copyright c 2006 by Mark E. Irwin Matrix Approach to Regression Linear Model: Y i = β 0 + β 1 X i1 +... + β p X ip + ɛ i ; ɛ i iid N(0, σ 2 ), i = 1,..., n
Linear Regression. In this problem sheet, we consider the problem of linear regression with p predictors and one intercept,
 Linear Regression In this problem sheet, we consider the problem of linear regression with p predictors and one intercept, y = Xβ + ɛ, where y t = (y 1,..., y n ) is the column vector of target values,
Linear Regression In this problem sheet, we consider the problem of linear regression with p predictors and one intercept, y = Xβ + ɛ, where y t = (y 1,..., y n ) is the column vector of target values,
Linear Regression. 1 Introduction. 2 Least Squares
 Linear Regression 1 Introduction It is often interesting to study the effect of a variable on a response. In ANOVA, the response is a continuous variable and the variables are discrete / categorical. What
Linear Regression 1 Introduction It is often interesting to study the effect of a variable on a response. In ANOVA, the response is a continuous variable and the variables are discrete / categorical. What
Weighted Least Squares
 Weighted Least Squares The standard linear model assumes that Var(ε i ) = σ 2 for i = 1,..., n. As we have seen, however, there are instances where Var(Y X = x i ) = Var(ε i ) = σ2 w i. Here w 1,..., w
Weighted Least Squares The standard linear model assumes that Var(ε i ) = σ 2 for i = 1,..., n. As we have seen, however, there are instances where Var(Y X = x i ) = Var(ε i ) = σ2 w i. Here w 1,..., w
Multiple Linear Regression
 Multiple Linear Regression ST 430/514 Recall: a regression model describes how a dependent variable (or response) Y is affected, on average, by one or more independent variables (or factors, or covariates).
Multiple Linear Regression ST 430/514 Recall: a regression model describes how a dependent variable (or response) Y is affected, on average, by one or more independent variables (or factors, or covariates).
Density Temp vs Ratio. temp
 Temp Ratio Density 0.00 0.02 0.04 0.06 0.08 0.10 0.12 Density 0.0 0.2 0.4 0.6 0.8 1.0 1. (a) 170 175 180 185 temp 1.0 1.5 2.0 2.5 3.0 ratio The histogram shows that the temperature measures have two peaks,
Temp Ratio Density 0.00 0.02 0.04 0.06 0.08 0.10 0.12 Density 0.0 0.2 0.4 0.6 0.8 1.0 1. (a) 170 175 180 185 temp 1.0 1.5 2.0 2.5 3.0 ratio The histogram shows that the temperature measures have two peaks,
Business Statistics. Tommaso Proietti. Linear Regression. DEF - Università di Roma 'Tor Vergata'
 Business Statistics Tommaso Proietti DEF - Università di Roma 'Tor Vergata' Linear Regression Specication Let Y be a univariate quantitative response variable. We model Y as follows: Y = f(x) + ε where
Business Statistics Tommaso Proietti DEF - Università di Roma 'Tor Vergata' Linear Regression Specication Let Y be a univariate quantitative response variable. We model Y as follows: Y = f(x) + ε where
Simple Linear Regression
 Simple Linear Regression In simple linear regression we are concerned about the relationship between two variables, X and Y. There are two components to such a relationship. 1. The strength of the relationship.
Simple Linear Regression In simple linear regression we are concerned about the relationship between two variables, X and Y. There are two components to such a relationship. 1. The strength of the relationship.
Peter Hoff Linear and multilinear models April 3, GLS for multivariate regression 5. 3 Covariance estimation for the GLM 8
 Contents 1 Linear model 1 2 GLS for multivariate regression 5 3 Covariance estimation for the GLM 8 4 Testing the GLH 11 A reference for some of this material can be found somewhere. 1 Linear model Recall
Contents 1 Linear model 1 2 GLS for multivariate regression 5 3 Covariance estimation for the GLM 8 4 Testing the GLH 11 A reference for some of this material can be found somewhere. 1 Linear model Recall
Statistics for Engineers Lecture 9 Linear Regression
 Statistics for Engineers Lecture 9 Linear Regression Chong Ma Department of Statistics University of South Carolina chongm@email.sc.edu April 17, 2017 Chong Ma (Statistics, USC) STAT 509 Spring 2017 April
Statistics for Engineers Lecture 9 Linear Regression Chong Ma Department of Statistics University of South Carolina chongm@email.sc.edu April 17, 2017 Chong Ma (Statistics, USC) STAT 509 Spring 2017 April
MAT2377. Rafa l Kulik. Version 2015/November/26. Rafa l Kulik
 MAT2377 Rafa l Kulik Version 2015/November/26 Rafa l Kulik Bivariate data and scatterplot Data: Hydrocarbon level (x) and Oxygen level (y): x: 0.99, 1.02, 1.15, 1.29, 1.46, 1.36, 0.87, 1.23, 1.55, 1.40,
MAT2377 Rafa l Kulik Version 2015/November/26 Rafa l Kulik Bivariate data and scatterplot Data: Hydrocarbon level (x) and Oxygen level (y): x: 0.99, 1.02, 1.15, 1.29, 1.46, 1.36, 0.87, 1.23, 1.55, 1.40,
22s:152 Applied Linear Regression. Take random samples from each of m populations.
 22s:152 Applied Linear Regression Chapter 8: ANOVA NOTE: We will meet in the lab on Monday October 10. One-way ANOVA Focuses on testing for differences among group means. Take random samples from each
22s:152 Applied Linear Regression Chapter 8: ANOVA NOTE: We will meet in the lab on Monday October 10. One-way ANOVA Focuses on testing for differences among group means. Take random samples from each
Lecture 18: Simple Linear Regression
 Lecture 18: Simple Linear Regression BIOS 553 Department of Biostatistics University of Michigan Fall 2004 The Correlation Coefficient: r The correlation coefficient (r) is a number that measures the strength
Lecture 18: Simple Linear Regression BIOS 553 Department of Biostatistics University of Michigan Fall 2004 The Correlation Coefficient: r The correlation coefficient (r) is a number that measures the strength
Lecture 6: Geometry of OLS Estimation of Linear Regession
 Lecture 6: Geometry of OLS Estimation of Linear Regession Xuexin Wang WISE Oct 2013 1 / 22 Matrix Algebra An n m matrix A is a rectangular array that consists of nm elements arranged in n rows and m columns
Lecture 6: Geometry of OLS Estimation of Linear Regession Xuexin Wang WISE Oct 2013 1 / 22 Matrix Algebra An n m matrix A is a rectangular array that consists of nm elements arranged in n rows and m columns
Chapter 12: Multiple Linear Regression
 Chapter 12: Multiple Linear Regression Seungchul Baek Department of Statistics, University of South Carolina STAT 509: Statistics for Engineers 1 / 55 Introduction A regression model can be expressed as
Chapter 12: Multiple Linear Regression Seungchul Baek Department of Statistics, University of South Carolina STAT 509: Statistics for Engineers 1 / 55 Introduction A regression model can be expressed as
[y i α βx i ] 2 (2) Q = i=1
![[y i α βx i ] 2 (2) Q = i=1 [y i α βx i ] 2 (2) Q = i=1](/thumbs/75/72005858.jpg) Least squares fits This section has no probability in it. There are no random variables. We are given n points (x i, y i ) and want to find the equation of the line that best fits them. We take the equation
Least squares fits This section has no probability in it. There are no random variables. We are given n points (x i, y i ) and want to find the equation of the line that best fits them. We take the equation
22s:152 Applied Linear Regression. There are a couple commonly used models for a one-way ANOVA with m groups. Chapter 8: ANOVA
 22s:152 Applied Linear Regression Chapter 8: ANOVA NOTE: We will meet in the lab on Monday October 10. One-way ANOVA Focuses on testing for differences among group means. Take random samples from each
22s:152 Applied Linear Regression Chapter 8: ANOVA NOTE: We will meet in the lab on Monday October 10. One-way ANOVA Focuses on testing for differences among group means. Take random samples from each
CAS MA575 Linear Models
 CAS MA575 Linear Models Boston University, Fall 2013 Midterm Exam (Correction) Instructor: Cedric Ginestet Date: 22 Oct 2013. Maximal Score: 200pts. Please Note: You will only be graded on work and answers
CAS MA575 Linear Models Boston University, Fall 2013 Midterm Exam (Correction) Instructor: Cedric Ginestet Date: 22 Oct 2013. Maximal Score: 200pts. Please Note: You will only be graded on work and answers
Inference for Regression
 Inference for Regression Section 9.4 Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Lecture 13b - 3339 Cathy Poliak, Ph.D. cathy@math.uh.edu
Inference for Regression Section 9.4 Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Lecture 13b - 3339 Cathy Poliak, Ph.D. cathy@math.uh.edu
11 Hypothesis Testing
 28 11 Hypothesis Testing 111 Introduction Suppose we want to test the hypothesis: H : A q p β p 1 q 1 In terms of the rows of A this can be written as a 1 a q β, ie a i β for each row of A (here a i denotes
28 11 Hypothesis Testing 111 Introduction Suppose we want to test the hypothesis: H : A q p β p 1 q 1 In terms of the rows of A this can be written as a 1 a q β, ie a i β for each row of A (here a i denotes
Lecture 4 Multiple linear regression
 Lecture 4 Multiple linear regression BIOST 515 January 15, 2004 Outline 1 Motivation for the multiple regression model Multiple regression in matrix notation Least squares estimation of model parameters
Lecture 4 Multiple linear regression BIOST 515 January 15, 2004 Outline 1 Motivation for the multiple regression model Multiple regression in matrix notation Least squares estimation of model parameters
Chapter 3: Multiple Regression. August 14, 2018
 Chapter 3: Multiple Regression August 14, 2018 1 The multiple linear regression model The model y = β 0 +β 1 x 1 + +β k x k +ǫ (1) is called a multiple linear regression model with k regressors. The parametersβ
Chapter 3: Multiple Regression August 14, 2018 1 The multiple linear regression model The model y = β 0 +β 1 x 1 + +β k x k +ǫ (1) is called a multiple linear regression model with k regressors. The parametersβ
Homoskedasticity. Var (u X) = σ 2. (23)
 Homoskedasticity How big is the difference between the OLS estimator and the true parameter? To answer this question, we make an additional assumption called homoskedasticity: Var (u X) = σ 2. (23) This
Homoskedasticity How big is the difference between the OLS estimator and the true parameter? To answer this question, we make an additional assumption called homoskedasticity: Var (u X) = σ 2. (23) This
Random vectors X 1 X 2. Recall that a random vector X = is made up of, say, k. X k. random variables.
 Random vectors Recall that a random vector X = X X 2 is made up of, say, k random variables X k A random vector has a joint distribution, eg a density f(x), that gives probabilities P(X A) = f(x)dx Just
Random vectors Recall that a random vector X = X X 2 is made up of, say, k random variables X k A random vector has a joint distribution, eg a density f(x), that gives probabilities P(X A) = f(x)dx Just
Statistics - Lecture Three. Linear Models. Charlotte Wickham 1.
 Statistics - Lecture Three Charlotte Wickham wickham@stat.berkeley.edu http://www.stat.berkeley.edu/~wickham/ Linear Models 1. The Theory 2. Practical Use 3. How to do it in R 4. An example 5. Extensions
Statistics - Lecture Three Charlotte Wickham wickham@stat.berkeley.edu http://www.stat.berkeley.edu/~wickham/ Linear Models 1. The Theory 2. Practical Use 3. How to do it in R 4. An example 5. Extensions
Lecture 15. Hypothesis testing in the linear model
 14. Lecture 15. Hypothesis testing in the linear model Lecture 15. Hypothesis testing in the linear model 1 (1 1) Preliminary lemma 15. Hypothesis testing in the linear model 15.1. Preliminary lemma Lemma
14. Lecture 15. Hypothesis testing in the linear model Lecture 15. Hypothesis testing in the linear model 1 (1 1) Preliminary lemma 15. Hypothesis testing in the linear model 15.1. Preliminary lemma Lemma
Chaper 5: Matrix Approach to Simple Linear Regression. Matrix: A m by n matrix B is a grid of numbers with m rows and n columns. B = b 11 b m1 ...
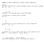 Chaper 5: Matrix Approach to Simple Linear Regression Matrix: A m by n matrix B is a grid of numbers with m rows and n columns B = b 11 b 1n b m1 b mn Element b ik is from the ith row and kth column A
Chaper 5: Matrix Approach to Simple Linear Regression Matrix: A m by n matrix B is a grid of numbers with m rows and n columns B = b 11 b 1n b m1 b mn Element b ik is from the ith row and kth column A
Simple Linear Regression
 Simple Linear Regression September 24, 2008 Reading HH 8, GIll 4 Simple Linear Regression p.1/20 Problem Data: Observe pairs (Y i,x i ),i = 1,...n Response or dependent variable Y Predictor or independent
Simple Linear Regression September 24, 2008 Reading HH 8, GIll 4 Simple Linear Regression p.1/20 Problem Data: Observe pairs (Y i,x i ),i = 1,...n Response or dependent variable Y Predictor or independent
Linear models and their mathematical foundations: Simple linear regression
 Linear models and their mathematical foundations: Simple linear regression Steffen Unkel Department of Medical Statistics University Medical Center Göttingen, Germany Winter term 2018/19 1/21 Introduction
Linear models and their mathematical foundations: Simple linear regression Steffen Unkel Department of Medical Statistics University Medical Center Göttingen, Germany Winter term 2018/19 1/21 Introduction
Topic 7 - Matrix Approach to Simple Linear Regression. Outline. Matrix. Matrix. Review of Matrices. Regression model in matrix form
 Topic 7 - Matrix Approach to Simple Linear Regression Review of Matrices Outline Regression model in matrix form - Fall 03 Calculations using matrices Topic 7 Matrix Collection of elements arranged in
Topic 7 - Matrix Approach to Simple Linear Regression Review of Matrices Outline Regression model in matrix form - Fall 03 Calculations using matrices Topic 7 Matrix Collection of elements arranged in
Applied Regression Analysis
 Applied Regression Analysis Chapter 3 Multiple Linear Regression Hongcheng Li April, 6, 2013 Recall simple linear regression 1 Recall simple linear regression 2 Parameter Estimation 3 Interpretations of
Applied Regression Analysis Chapter 3 Multiple Linear Regression Hongcheng Li April, 6, 2013 Recall simple linear regression 1 Recall simple linear regression 2 Parameter Estimation 3 Interpretations of
Lecture 6 Multiple Linear Regression, cont.
 Lecture 6 Multiple Linear Regression, cont. BIOST 515 January 22, 2004 BIOST 515, Lecture 6 Testing general linear hypotheses Suppose we are interested in testing linear combinations of the regression
Lecture 6 Multiple Linear Regression, cont. BIOST 515 January 22, 2004 BIOST 515, Lecture 6 Testing general linear hypotheses Suppose we are interested in testing linear combinations of the regression
Matrices: 2.1 Operations with Matrices
 Goals In this chapter and section we study matrix operations: Define matrix addition Define multiplication of matrix by a scalar, to be called scalar multiplication. Define multiplication of two matrices,
Goals In this chapter and section we study matrix operations: Define matrix addition Define multiplication of matrix by a scalar, to be called scalar multiplication. Define multiplication of two matrices,
Properties of Matrices and Operations on Matrices
 Properties of Matrices and Operations on Matrices A common data structure for statistical analysis is a rectangular array or matris. Rows represent individual observational units, or just observations,
Properties of Matrices and Operations on Matrices A common data structure for statistical analysis is a rectangular array or matris. Rows represent individual observational units, or just observations,
Simple Linear Regression
 Simple Linear Regression MATH 282A Introduction to Computational Statistics University of California, San Diego Instructor: Ery Arias-Castro http://math.ucsd.edu/ eariasca/math282a.html MATH 282A University
Simple Linear Regression MATH 282A Introduction to Computational Statistics University of California, San Diego Instructor: Ery Arias-Castro http://math.ucsd.edu/ eariasca/math282a.html MATH 282A University
POL 213: Research Methods
 Brad 1 1 Department of Political Science University of California, Davis April 15, 2008 Some Matrix Basics What is a matrix? A rectangular array of elements arranged in rows and columns. 55 900 0 67 1112
Brad 1 1 Department of Political Science University of California, Davis April 15, 2008 Some Matrix Basics What is a matrix? A rectangular array of elements arranged in rows and columns. 55 900 0 67 1112
Weighted Least Squares
 Weighted Least Squares The standard linear model assumes that Var(ε i ) = σ 2 for i = 1,..., n. As we have seen, however, there are instances where Var(Y X = x i ) = Var(ε i ) = σ2 w i. Here w 1,..., w
Weighted Least Squares The standard linear model assumes that Var(ε i ) = σ 2 for i = 1,..., n. As we have seen, however, there are instances where Var(Y X = x i ) = Var(ε i ) = σ2 w i. Here w 1,..., w
UNIVERSITY OF MASSACHUSETTS. Department of Mathematics and Statistics. Basic Exam - Applied Statistics. Tuesday, January 17, 2017
 UNIVERSITY OF MASSACHUSETTS Department of Mathematics and Statistics Basic Exam - Applied Statistics Tuesday, January 17, 2017 Work all problems 60 points are needed to pass at the Masters Level and 75
UNIVERSITY OF MASSACHUSETTS Department of Mathematics and Statistics Basic Exam - Applied Statistics Tuesday, January 17, 2017 Work all problems 60 points are needed to pass at the Masters Level and 75
20.1. Balanced One-Way Classification Cell means parametrization: ε 1. ε I. + ˆɛ 2 ij =
 20. ONE-WAY ANALYSIS OF VARIANCE 1 20.1. Balanced One-Way Classification Cell means parametrization: Y ij = µ i + ε ij, i = 1,..., I; j = 1,..., J, ε ij N(0, σ 2 ), In matrix form, Y = Xβ + ε, or 1 Y J
20. ONE-WAY ANALYSIS OF VARIANCE 1 20.1. Balanced One-Way Classification Cell means parametrization: Y ij = µ i + ε ij, i = 1,..., I; j = 1,..., J, ε ij N(0, σ 2 ), In matrix form, Y = Xβ + ε, or 1 Y J
Math 3330: Solution to midterm Exam
 Math 3330: Solution to midterm Exam Question 1: (14 marks) Suppose the regression model is y i = β 0 + β 1 x i + ε i, i = 1,, n, where ε i are iid Normal distribution N(0, σ 2 ). a. (2 marks) Compute the
Math 3330: Solution to midterm Exam Question 1: (14 marks) Suppose the regression model is y i = β 0 + β 1 x i + ε i, i = 1,, n, where ε i are iid Normal distribution N(0, σ 2 ). a. (2 marks) Compute the
Matrices. Chapter Definitions and Notations
 Chapter 3 Matrices 3. Definitions and Notations Matrices are yet another mathematical object. Learning about matrices means learning what they are, how they are represented, the types of operations which
Chapter 3 Matrices 3. Definitions and Notations Matrices are yet another mathematical object. Learning about matrices means learning what they are, how they are represented, the types of operations which
13 Simple Linear Regression
 B.Sc./Cert./M.Sc. Qualif. - Statistics: Theory and Practice 3 Simple Linear Regression 3. An industrial example A study was undertaken to determine the effect of stirring rate on the amount of impurity
B.Sc./Cert./M.Sc. Qualif. - Statistics: Theory and Practice 3 Simple Linear Regression 3. An industrial example A study was undertaken to determine the effect of stirring rate on the amount of impurity
Categorical Predictor Variables
 Categorical Predictor Variables We often wish to use categorical (or qualitative) variables as covariates in a regression model. For binary variables (taking on only 2 values, e.g. sex), it is relatively
Categorical Predictor Variables We often wish to use categorical (or qualitative) variables as covariates in a regression model. For binary variables (taking on only 2 values, e.g. sex), it is relatively
Matrix Approach to Simple Linear Regression: An Overview
 Matrix Approach to Simple Linear Regression: An Overview Aspects of matrices that you should know: Definition of a matrix Addition/subtraction/multiplication of matrices Symmetric/diagonal/identity matrix
Matrix Approach to Simple Linear Regression: An Overview Aspects of matrices that you should know: Definition of a matrix Addition/subtraction/multiplication of matrices Symmetric/diagonal/identity matrix
Probability and Statistics Notes
 Probability and Statistics Notes Chapter Seven Jesse Crawford Department of Mathematics Tarleton State University Spring 2011 (Tarleton State University) Chapter Seven Notes Spring 2011 1 / 42 Outline
Probability and Statistics Notes Chapter Seven Jesse Crawford Department of Mathematics Tarleton State University Spring 2011 (Tarleton State University) Chapter Seven Notes Spring 2011 1 / 42 Outline
Simple Linear Regression
 Simple Linear Regression ST 430/514 Recall: A regression model describes how a dependent variable (or response) Y is affected, on average, by one or more independent variables (or factors, or covariates)
Simple Linear Regression ST 430/514 Recall: A regression model describes how a dependent variable (or response) Y is affected, on average, by one or more independent variables (or factors, or covariates)
Swarthmore Honors Exam 2012: Statistics
 Swarthmore Honors Exam 2012: Statistics 1 Swarthmore Honors Exam 2012: Statistics John W. Emerson, Yale University NAME: Instructions: This is a closed-book three-hour exam having six questions. You may
Swarthmore Honors Exam 2012: Statistics 1 Swarthmore Honors Exam 2012: Statistics John W. Emerson, Yale University NAME: Instructions: This is a closed-book three-hour exam having six questions. You may
ST430 Exam 2 Solutions
 ST430 Exam 2 Solutions Date: November 9, 2015 Name: Guideline: You may use one-page (front and back of a standard A4 paper) of notes. No laptop or textbook are permitted but you may use a calculator. Giving
ST430 Exam 2 Solutions Date: November 9, 2015 Name: Guideline: You may use one-page (front and back of a standard A4 paper) of notes. No laptop or textbook are permitted but you may use a calculator. Giving
AMS-207: Bayesian Statistics
 Linear Regression How does a quantity y, vary as a function of another quantity, or vector of quantities x? We are interested in p(y θ, x) under a model in which n observations (x i, y i ) are exchangeable.
Linear Regression How does a quantity y, vary as a function of another quantity, or vector of quantities x? We are interested in p(y θ, x) under a model in which n observations (x i, y i ) are exchangeable.
Data Mining Stat 588
 Data Mining Stat 588 Lecture 02: Linear Methods for Regression Department of Statistics & Biostatistics Rutgers University September 13 2011 Regression Problem Quantitative generic output variable Y. Generic
Data Mining Stat 588 Lecture 02: Linear Methods for Regression Department of Statistics & Biostatistics Rutgers University September 13 2011 Regression Problem Quantitative generic output variable Y. Generic
F3: Classical normal linear rgression model distribution, interval estimation and hypothesis testing
 F3: Classical normal linear rgression model distribution, interval estimation and hypothesis testing Feng Li Department of Statistics, Stockholm University What we have learned last time... 1 Estimating
F3: Classical normal linear rgression model distribution, interval estimation and hypothesis testing Feng Li Department of Statistics, Stockholm University What we have learned last time... 1 Estimating
Linear Algebra Review
 Linear Algebra Review Yang Feng http://www.stat.columbia.edu/~yangfeng Yang Feng (Columbia University) Linear Algebra Review 1 / 45 Definition of Matrix Rectangular array of elements arranged in rows and
Linear Algebra Review Yang Feng http://www.stat.columbia.edu/~yangfeng Yang Feng (Columbia University) Linear Algebra Review 1 / 45 Definition of Matrix Rectangular array of elements arranged in rows and
Confidence Intervals, Testing and ANOVA Summary
 Confidence Intervals, Testing and ANOVA Summary 1 One Sample Tests 1.1 One Sample z test: Mean (σ known) Let X 1,, X n a r.s. from N(µ, σ) or n > 30. Let The test statistic is H 0 : µ = µ 0. z = x µ 0
Confidence Intervals, Testing and ANOVA Summary 1 One Sample Tests 1.1 One Sample z test: Mean (σ known) Let X 1,, X n a r.s. from N(µ, σ) or n > 30. Let The test statistic is H 0 : µ = µ 0. z = x µ 0
Biostatistics 380 Multiple Regression 1. Multiple Regression
 Biostatistics 0 Multiple Regression ORIGIN 0 Multiple Regression Multiple Regression is an extension of the technique of linear regression to describe the relationship between a single dependent (response)
Biostatistics 0 Multiple Regression ORIGIN 0 Multiple Regression Multiple Regression is an extension of the technique of linear regression to describe the relationship between a single dependent (response)
Summer School in Statistics for Astronomers V June 1 - June 6, Regression. Mosuk Chow Statistics Department Penn State University.
 Summer School in Statistics for Astronomers V June 1 - June 6, 2009 Regression Mosuk Chow Statistics Department Penn State University. Adapted from notes prepared by RL Karandikar Mean and variance Recall
Summer School in Statistics for Astronomers V June 1 - June 6, 2009 Regression Mosuk Chow Statistics Department Penn State University. Adapted from notes prepared by RL Karandikar Mean and variance Recall
Problems. Suppose both models are fitted to the same data. Show that SS Res, A SS Res, B
 Simple Linear Regression 35 Problems 1 Consider a set of data (x i, y i ), i =1, 2,,n, and the following two regression models: y i = β 0 + β 1 x i + ε, (i =1, 2,,n), Model A y i = γ 0 + γ 1 x i + γ 2
Simple Linear Regression 35 Problems 1 Consider a set of data (x i, y i ), i =1, 2,,n, and the following two regression models: y i = β 0 + β 1 x i + ε, (i =1, 2,,n), Model A y i = γ 0 + γ 1 x i + γ 2
1 The Classic Bivariate Least Squares Model
 Review of Bivariate Linear Regression Contents 1 The Classic Bivariate Least Squares Model 1 1.1 The Setup............................... 1 1.2 An Example Predicting Kids IQ................. 1 2 Evaluating
Review of Bivariate Linear Regression Contents 1 The Classic Bivariate Least Squares Model 1 1.1 The Setup............................... 1 1.2 An Example Predicting Kids IQ................. 1 2 Evaluating
Example: Poisondata. 22s:152 Applied Linear Regression. Chapter 8: ANOVA
 s:5 Applied Linear Regression Chapter 8: ANOVA Two-way ANOVA Used to compare populations means when the populations are classified by two factors (or categorical variables) For example sex and occupation
s:5 Applied Linear Regression Chapter 8: ANOVA Two-way ANOVA Used to compare populations means when the populations are classified by two factors (or categorical variables) For example sex and occupation
ST430 Exam 1 with Answers
 ST430 Exam 1 with Answers Date: October 5, 2015 Name: Guideline: You may use one-page (front and back of a standard A4 paper) of notes. No laptop or textook are permitted but you may use a calculator.
ST430 Exam 1 with Answers Date: October 5, 2015 Name: Guideline: You may use one-page (front and back of a standard A4 paper) of notes. No laptop or textook are permitted but you may use a calculator.
MS&E 226: Small Data
 MS&E 226: Small Data Lecture 15: Examples of hypothesis tests (v5) Ramesh Johari ramesh.johari@stanford.edu 1 / 32 The recipe 2 / 32 The hypothesis testing recipe In this lecture we repeatedly apply the
MS&E 226: Small Data Lecture 15: Examples of hypothesis tests (v5) Ramesh Johari ramesh.johari@stanford.edu 1 / 32 The recipe 2 / 32 The hypothesis testing recipe In this lecture we repeatedly apply the
ML and REML Variance Component Estimation. Copyright c 2012 Dan Nettleton (Iowa State University) Statistics / 58
 ML and REML Variance Component Estimation Copyright c 2012 Dan Nettleton (Iowa State University) Statistics 611 1 / 58 Suppose y = Xβ + ε, where ε N(0, Σ) for some positive definite, symmetric matrix Σ.
ML and REML Variance Component Estimation Copyright c 2012 Dan Nettleton (Iowa State University) Statistics 611 1 / 58 Suppose y = Xβ + ε, where ε N(0, Σ) for some positive definite, symmetric matrix Σ.
401 Review. 6. Power analysis for one/two-sample hypothesis tests and for correlation analysis.
 401 Review Major topics of the course 1. Univariate analysis 2. Bivariate analysis 3. Simple linear regression 4. Linear algebra 5. Multiple regression analysis Major analysis methods 1. Graphical analysis
401 Review Major topics of the course 1. Univariate analysis 2. Bivariate analysis 3. Simple linear regression 4. Linear algebra 5. Multiple regression analysis Major analysis methods 1. Graphical analysis
Lecture 9: Linear Regression
 Lecture 9: Linear Regression Goals Develop basic concepts of linear regression from a probabilistic framework Estimating parameters and hypothesis testing with linear models Linear regression in R Regression
Lecture 9: Linear Regression Goals Develop basic concepts of linear regression from a probabilistic framework Estimating parameters and hypothesis testing with linear models Linear regression in R Regression
STAT 705 Chapter 16: One-way ANOVA
 STAT 705 Chapter 16: One-way ANOVA Timothy Hanson Department of Statistics, University of South Carolina Stat 705: Data Analysis II 1 / 21 What is ANOVA? Analysis of variance (ANOVA) models are regression
STAT 705 Chapter 16: One-way ANOVA Timothy Hanson Department of Statistics, University of South Carolina Stat 705: Data Analysis II 1 / 21 What is ANOVA? Analysis of variance (ANOVA) models are regression
LAB 5 INSTRUCTIONS LINEAR REGRESSION AND CORRELATION
 LAB 5 INSTRUCTIONS LINEAR REGRESSION AND CORRELATION In this lab you will learn how to use Excel to display the relationship between two quantitative variables, measure the strength and direction of the
LAB 5 INSTRUCTIONS LINEAR REGRESSION AND CORRELATION In this lab you will learn how to use Excel to display the relationship between two quantitative variables, measure the strength and direction of the
One-Way ANOVA Model. group 1 y 11, y 12 y 13 y 1n1. group 2 y 21, y 22 y 2n2. group g y g1, y g2, y gng. g is # of groups,
 One-Way ANOVA Model group 1 y 11, y 12 y 13 y 1n1 group 2 y 21, y 22 y 2n2 group g y g1, y g2, y gng g is # of groups, n i denotes # of obs in the i-th group, and the total sample size n = g i=1 n i. 1
One-Way ANOVA Model group 1 y 11, y 12 y 13 y 1n1 group 2 y 21, y 22 y 2n2 group g y g1, y g2, y gng g is # of groups, n i denotes # of obs in the i-th group, and the total sample size n = g i=1 n i. 1
20. REML Estimation of Variance Components. Copyright c 2018 (Iowa State University) 20. Statistics / 36
 20. REML Estimation of Variance Components Copyright c 2018 (Iowa State University) 20. Statistics 510 1 / 36 Consider the General Linear Model y = Xβ + ɛ, where ɛ N(0, Σ) and Σ is an n n positive definite
20. REML Estimation of Variance Components Copyright c 2018 (Iowa State University) 20. Statistics 510 1 / 36 Consider the General Linear Model y = Xβ + ɛ, where ɛ N(0, Σ) and Σ is an n n positive definite
CS 246 Review of Linear Algebra 01/17/19
 1 Linear algebra In this section we will discuss vectors and matrices. We denote the (i, j)th entry of a matrix A as A ij, and the ith entry of a vector as v i. 1.1 Vectors and vector operations A vector
1 Linear algebra In this section we will discuss vectors and matrices. We denote the (i, j)th entry of a matrix A as A ij, and the ith entry of a vector as v i. 1.1 Vectors and vector operations A vector
4 Multiple Linear Regression
 4 Multiple Linear Regression 4. The Model Definition 4.. random variable Y fits a Multiple Linear Regression Model, iff there exist β, β,..., β k R so that for all (x, x 2,..., x k ) R k where ε N (, σ
4 Multiple Linear Regression 4. The Model Definition 4.. random variable Y fits a Multiple Linear Regression Model, iff there exist β, β,..., β k R so that for all (x, x 2,..., x k ) R k where ε N (, σ
Linear Regression Model. Badr Missaoui
 Linear Regression Model Badr Missaoui Introduction What is this course about? It is a course on applied statistics. It comprises 2 hours lectures each week and 1 hour lab sessions/tutorials. We will focus
Linear Regression Model Badr Missaoui Introduction What is this course about? It is a course on applied statistics. It comprises 2 hours lectures each week and 1 hour lab sessions/tutorials. We will focus
STAT 350: Geometry of Least Squares
 The Geometry of Least Squares Mathematical Basics Inner / dot product: a and b column vectors a b = a T b = a i b i a b a T b = 0 Matrix Product: A is r s B is s t (AB) rt = s A rs B st Partitioned Matrices
The Geometry of Least Squares Mathematical Basics Inner / dot product: a and b column vectors a b = a T b = a i b i a b a T b = 0 Matrix Product: A is r s B is s t (AB) rt = s A rs B st Partitioned Matrices
Oct Simple linear regression. Minimum mean square error prediction. Univariate. regression. Calculating intercept and slope
 Oct 2017 1 / 28 Minimum MSE Y is the response variable, X the predictor variable, E(X) = E(Y) = 0. BLUP of Y minimizes average discrepancy var (Y ux) = C YY 2u C XY + u 2 C XX This is minimized when u
Oct 2017 1 / 28 Minimum MSE Y is the response variable, X the predictor variable, E(X) = E(Y) = 0. BLUP of Y minimizes average discrepancy var (Y ux) = C YY 2u C XY + u 2 C XX This is minimized when u
Dealing with Heteroskedasticity
 Dealing with Heteroskedasticity James H. Steiger Department of Psychology and Human Development Vanderbilt University James H. Steiger (Vanderbilt University) Dealing with Heteroskedasticity 1 / 27 Dealing
Dealing with Heteroskedasticity James H. Steiger Department of Psychology and Human Development Vanderbilt University James H. Steiger (Vanderbilt University) Dealing with Heteroskedasticity 1 / 27 Dealing
Statistics 203 Introduction to Regression Models and ANOVA Practice Exam
 Statistics 203 Introduction to Regression Models and ANOVA Practice Exam Prof. J. Taylor You may use your 4 single-sided pages of notes This exam is 7 pages long. There are 4 questions, first 3 worth 10
Statistics 203 Introduction to Regression Models and ANOVA Practice Exam Prof. J. Taylor You may use your 4 single-sided pages of notes This exam is 7 pages long. There are 4 questions, first 3 worth 10
Figure 1: The fitted line using the shipment route-number of ampules data. STAT5044: Regression and ANOVA The Solution of Homework #2 Inyoung Kim
 0.0 1.0 1.5 2.0 2.5 3.0 8 10 12 14 16 18 20 22 y x Figure 1: The fitted line using the shipment route-number of ampules data STAT5044: Regression and ANOVA The Solution of Homework #2 Inyoung Kim Problem#
0.0 1.0 1.5 2.0 2.5 3.0 8 10 12 14 16 18 20 22 y x Figure 1: The fitted line using the shipment route-number of ampules data STAT5044: Regression and ANOVA The Solution of Homework #2 Inyoung Kim Problem#
Bayesian Linear Regression
 Bayesian Linear Regression Sudipto Banerjee 1 Biostatistics, School of Public Health, University of Minnesota, Minneapolis, Minnesota, U.S.A. September 15, 2010 1 Linear regression models: a Bayesian perspective
Bayesian Linear Regression Sudipto Banerjee 1 Biostatistics, School of Public Health, University of Minnesota, Minneapolis, Minnesota, U.S.A. September 15, 2010 1 Linear regression models: a Bayesian perspective
Stat 101 Exam 1 Important Formulas and Concepts 1
 1 Chapter 1 1.1 Definitions Stat 101 Exam 1 Important Formulas and Concepts 1 1. Data Any collection of numbers, characters, images, or other items that provide information about something. 2. Categorical/Qualitative
1 Chapter 1 1.1 Definitions Stat 101 Exam 1 Important Formulas and Concepts 1 1. Data Any collection of numbers, characters, images, or other items that provide information about something. 2. Categorical/Qualitative
STAT 540: Data Analysis and Regression
 STAT 540: Data Analysis and Regression Wen Zhou http://www.stat.colostate.edu/~riczw/ Email: riczw@stat.colostate.edu Department of Statistics Colorado State University Fall 205 W. Zhou (Colorado State
STAT 540: Data Analysis and Regression Wen Zhou http://www.stat.colostate.edu/~riczw/ Email: riczw@stat.colostate.edu Department of Statistics Colorado State University Fall 205 W. Zhou (Colorado State
Linear Algebra V = T = ( 4 3 ).
 Linear Algebra Vectors A column vector is a list of numbers stored vertically The dimension of a column vector is the number of values in the vector W is a -dimensional column vector and V is a 5-dimensional
Linear Algebra Vectors A column vector is a list of numbers stored vertically The dimension of a column vector is the number of values in the vector W is a -dimensional column vector and V is a 5-dimensional
Comparing Nested Models
 Comparing Nested Models ST 370 Two regression models are called nested if one contains all the predictors of the other, and some additional predictors. For example, the first-order model in two independent
Comparing Nested Models ST 370 Two regression models are called nested if one contains all the predictors of the other, and some additional predictors. For example, the first-order model in two independent
Section 4.6 Simple Linear Regression
 Section 4.6 Simple Linear Regression Objectives ˆ Basic philosophy of SLR and the regression assumptions ˆ Point & interval estimation of the model parameters, and how to make predictions ˆ Point and interval
Section 4.6 Simple Linear Regression Objectives ˆ Basic philosophy of SLR and the regression assumptions ˆ Point & interval estimation of the model parameters, and how to make predictions ˆ Point and interval
Linear Modelling: Simple Regression
 Linear Modelling: Simple Regression 10 th of Ma 2018 R. Nicholls / D.-L. Couturier / M. Fernandes Introduction: ANOVA Used for testing hpotheses regarding differences between groups Considers the variation
Linear Modelling: Simple Regression 10 th of Ma 2018 R. Nicholls / D.-L. Couturier / M. Fernandes Introduction: ANOVA Used for testing hpotheses regarding differences between groups Considers the variation
Homework 2: Simple Linear Regression
 STAT 4385 Applied Regression Analysis Homework : Simple Linear Regression (Simple Linear Regression) Thirty (n = 30) College graduates who have recently entered the job market. For each student, the CGPA
STAT 4385 Applied Regression Analysis Homework : Simple Linear Regression (Simple Linear Regression) Thirty (n = 30) College graduates who have recently entered the job market. For each student, the CGPA
Review: General Approach to Hypothesis Testing. 1. Define the research question and formulate the appropriate null and alternative hypotheses.
 1 Review: Let X 1, X,..., X n denote n independent random variables sampled from some distribution might not be normal!) with mean µ) and standard deviation σ). Then X µ σ n In other words, X is approximately
1 Review: Let X 1, X,..., X n denote n independent random variables sampled from some distribution might not be normal!) with mean µ) and standard deviation σ). Then X µ σ n In other words, X is approximately
Coefficient of Determination
 Coefficient of Determination ST 430/514 The coefficient of determination, R 2, is defined as before: R 2 = 1 SS E (yi ŷ i ) = 1 2 SS yy (yi ȳ) 2 The interpretation of R 2 is still the fraction of variance
Coefficient of Determination ST 430/514 The coefficient of determination, R 2, is defined as before: R 2 = 1 SS E (yi ŷ i ) = 1 2 SS yy (yi ȳ) 2 The interpretation of R 2 is still the fraction of variance
Well-developed and understood properties
 1 INTRODUCTION TO LINEAR MODELS 1 THE CLASSICAL LINEAR MODEL Most commonly used statistical models Flexible models Well-developed and understood properties Ease of interpretation Building block for more
1 INTRODUCTION TO LINEAR MODELS 1 THE CLASSICAL LINEAR MODEL Most commonly used statistical models Flexible models Well-developed and understood properties Ease of interpretation Building block for more
Linear Models and Estimation by Least Squares
 Linear Models and Estimation by Least Squares Jin-Lung Lin 1 Introduction Causal relation investigation lies in the heart of economics. Effect (Dependent variable) cause (Independent variable) Example:
Linear Models and Estimation by Least Squares Jin-Lung Lin 1 Introduction Causal relation investigation lies in the heart of economics. Effect (Dependent variable) cause (Independent variable) Example:
CS100: DISCRETE STRUCTURES. Lecture 3 Matrices Ch 3 Pages:
 CS100: DISCRETE STRUCTURES Lecture 3 Matrices Ch 3 Pages: 246-262 Matrices 2 Introduction DEFINITION 1: A matrix is a rectangular array of numbers. A matrix with m rows and n columns is called an m x n
CS100: DISCRETE STRUCTURES Lecture 3 Matrices Ch 3 Pages: 246-262 Matrices 2 Introduction DEFINITION 1: A matrix is a rectangular array of numbers. A matrix with m rows and n columns is called an m x n
