APPLİCATION OF BOOLEAN ALGEABRA
|
|
|
- Jerome Brown
- 5 years ago
- Views:
Transcription
1 APPLİCATION OF BOOLEAN ALGEABRA CHAPTER 4 Prof. Dr. Mehmet Akbaba Prof. Mehmet Akbaba Digital Logic 1
2 Multiplying Out and Factoring Expressions Given an expression in product-of-sums form, the corresponding sum-of-products expression can be obtained by multiplying out, using the two distributive laws: X(Y + Z) = XY + XZ (X + Y)(X + Z) = X + YZ (4-1) (4-2) In addition, the following theorem is very useful for factoring and multiplying out (X + Y)(X' +Z) = XZ + X'Y (4.3) Note that the variable that is paired with X on one side of the equation is paired with X' on the other side, and vice versa. Prof. Mehmet Akbaba Digital Logic 2
3 Proof: If X = 0, (3-3) reduces to Y(1 + Z) = Y or Y = Y If X = 1, (3-3) reduces to (1 + Y)Z = Z + 0. Y or Z = Z. Because the equation is valid for both X = 0 and X = 1, it is always valid. The following example illustrates the use of Theorem (3-3) for factoring: AB+A'C = (A + C)(A' + B) Note that the theorem can be applied when we have two terms, one which contains a variable and another which contains its complement. Prof. Mehmet Akbaba Digital Logic 3
4 Theorem (3-3) is very useful for multiplying out expressions. In the following example, we can apply (3-3) because one factor contains the variable Q, and the other factor contains Q'. (Q + AB')(CD+ Q') = QCD + Q'AB' If we simply multiplied out by using the distributive law, we would get four terms instead of two: (Q + AB')(CD + Q') = QCD + QQ' + AB'CD + AB'Q' Because the term A B' C D is difficult to eliminate, it is much better to use (3-3)instead of the distributive law. Prof. Mehmet Akbaba Digital Logic 4
5 In general, when we multiply out an expression, we should use (4-3) along with (4-1) and (4-2). To avoid generating unnecessary terms when multiplying out, (4-2) and (4-3) should generally be applied before (4-1), and terms should be grouped to expedite their application. [(X+A)(X+B)=X+AB, (X+A)(X +A)=XA+X A] What theorem was used to eliminate ABC? (Hint: let X = AC.) Prof. Mehmet Akbaba Digital Logic 5
6 In this example, if the ordinary distributive law (4-1) had been used to multiply out the expression by brute force, 162 terms would have been generated, and 158 of these terms would then have to be eliminated. Prof. Mehmet Akbaba Digital Logic 6
7 Example of Factoring The same theorems that are useful for multiplying out expressions are useful for factoring. By repeatedly applying (4-1), (4-2), and (4-3), any expression can be converted to a product-of-sums (POS) form. Prof. Mehmet Akbaba Digital Logic 7
8 = (A + B + C DE)(A + C DE + D' + E)(A' + C) =(A+B+C )(A+B+DE)(A+D +E)(A +C) = (A + B + C )(A + B + D)(A + B + E)(A + D' + E)(A' + C) (4-5; This is the same expression we started with in (4-4). Prof. Mehmet Akbaba Digital Logic 8
9 Exclusive-OR (EX-OR) Operations or EX-OR GATE The exclusive-or operation ( ) is defined as follows: 0 0=0 0 1=1 1 1=0 1 0=1 The truth table for X Y is Prof. Mehmet Akbaba Digital Logic 9
10 The truth table for X Y is X Y X Y EX-OR GATE SYMBOL Prof. Mehmet Akbaba Digital Logic 10
11 Prof. Mehmet Akbaba Digital Logic 11
12 From this table, we can see that X Y = 1 iff X = 1 anad Y=0 or X=0 and Y = 1, but not both =1. The ordinary OR operation, which we have previously defined, is sometimes called inclusive OR because X + Y = 1 iff X = 1 or Y = 1, or both. Exclusive OR can be expressed in terms of AND and OR. Because X Y = 1 iff X is 0 and Y is 1 or X is 1 and Y is 0, we can write, X Y = X' Y + XY' (4.6) Prof. Mehmet Akbaba Digital Logic 12
13 X Y = (X + Y)(XY)' = (X + Y)(X' + Y') = X' Y + XY' (4.7) In (4-7), note that (X Y)' = 1 if X and Y are not both 1. We will use the following symbol for an exclusive-or gate: Prof. Mehmet Akbaba Digital Logic 13
14 The following theorems apply to exclusive OR X 0=X X X=0 X Y=Y X 1=X X X =1 X (commutative law) (X Y) Z = X (Y Z)=X Y Z (Associative law) X(Y Z)= XY XZ (Distributive law) (X Y) =X Y =X Y=X Y +XY Prof. Mehmet Akbaba Digital Logic 14
15 Any of these theorems can be proved by using a truth table or by replacing X Y with one of the equivalent expressions from Equation (4-7). Proof of the distributive law follows: XY XZ=XY(XZ) +(XY) XZ=XY(X +Z )+(X +Y )XZ =XYZ +XY Z =X(YZ +Y Z)=X(Y Z) Prof. Mehmet Akbaba Digital Logic 15
16 EQUIVALENT OR EX-NOR OPERATION OR EX-NOR GATE The equivalence operation ( ) or EX-NOR operation (or EX-NOR GATE) is defined by truth table: EX-NOR=(EX-OR) (4.8) Therefore EX-NOR is defined As complement (NOT) of EX-OR Prof. Mehmet Akbaba Digital Logic 16
17 (4.9) Prof. Mehmet Akbaba Digital Logic 17
18 Prof. Mehmet Akbaba Digital Logic 18
19 Just as for exclusive-or, the equivalence (EX-NOR ) operation is commutative and associative. We will use the following symbol for an equivalence gate: Or another notation is EX-NOR GATE shown below A B Prof. Mehmet Akbaba Digital Logic 19
20 Because equivalence is the complement of exclusive-or, an alternate symbol for the equivalence gate is an exclusive-or gate with a complemented output: (A B) =(A B) F=(A B C)+(B AC ) Prof. Mehmet Akbaba Digital Logic 20
21 EX-NOR=(EX-OR) A B= (A B) =(AB +A B) = (A +B)(A+B ) =A A+A B +AB+BB = A B +AB Prof. Mehmet Akbaba Digital Logic 21
22 Example 1 (Örnek 1) Open the following expression (Aşağıdaki ifadeyi açınız) F=(A B C)+(B AC ) = Prof. Mehmet Akbaba Digital Logic 22
23 Example 2 (Örnek 2) Open the following expression (Aşağıdaki ifadeyi açınız) A B C=[A B +AB] C =(A B +AB)C +(A B +AB) C =(A B +AB)C +((A+B).(A +B ))C =A B C +ABC +A BC+AB C =A(BC +B C)+A (B C +BC) =A(B C)+A (B C) =B(A C)+B (A C) =C(A B)+C (A B) Prof. Mehmet Akbaba Digital Logic 23
24 CONSENSUS THEOREM The consensus theorem is very useful in simplifying Boolean expressions. Given an expression of the form XY + X' Z + YZ, the term YZ is redundant and can be eliminated to form the equivalent expression XY + X' Z. The term that was eliminated is referred to as the consensus term. Given a pair of terms for which a variable appears in one term and the complement of that variable in another, the consensus term is formed by multiplying the two original terms together, leaving out the selected variable and its complement. Prof. Mehmet Akbaba Digital Logic 24
25 For example, the consensus of ab and a' c is bc. Also the consensus of abd and b'de' is (ad)(de') = ade'. The consensus of terms ab'd and a' bd' is 0. The consensus theorem can be stated as follows: XY + X'Z + YZ = XY + X'Z Proof: XY + X'Z + YZ = XY + X'Z + (X + X')YZ = (XY + XYZ) + (X'Z + X'YZ) = XY(1 + Z) + X'Z(1 + Y) = XY + X'Z Prof. Mehmet Akbaba Digital Logic 25
26 The consensus theorem can be used to eliminate redundant terms from Boolean expressions. For example, in the following expression, b' c is the consensus of a' b' and ac, and ab is the consensus of ac and bc', so both consensus terms can be eliminated: (a b +ac+b c=a b +ac and ac+bc +ab=ac+bc ) Prof. Mehmet Akbaba Digital Logic 26
27 The brackets indicate how the consensus terms are formed. The dual form of the consensus theorem is: (X+Y)(X +Z)(Y+Z)=(X+Y)(X +Z) (4.9) Note again that the key to recognizing the consensus term is to first find a pair of terms, one of which contains a variable and the other its complement. In this case, the consensus is formed by adding this pair of terms together leaving out the selected variable and its complement. In the following expression, (a + b + d') is a consensus term and can be eliminated by using the dual consensus theorem: Prof. Mehmet Akbaba Digital Logic 27
28 The final result obtained by application of the consensus theorem may depend on the order in which terms are eliminated. Example: First, we eliminate BCD as shown. (Why can it be eliminated?) Now that BCD has been eliminated, it is no longer there, and it cannot be used to eliminate another term. Checking all pairs of terms shows that no additional terms can be eliminated by the consensus theorem. (4.10) Prof. Mehmet Akbaba Digital Logic 28
29 This time, we do not eliminate BCD; instead we eliminate two other terms by the consensus theorem. After doing this, observe that BCD can no longer be eliminated. Note that the expression reduces to four terms if BCD is eliminated first, but that it can be reduced to three terms if BCD is not eliminated. (C and C also D and D is considered) (4.11) Prof. Mehmet Akbaba Digital Logic 29
30 Sometimes it is impossible to directly reduce an expression to a minimum number of terms by simply eliminating terms. It may be necessary to first add a term using the consensus theorem and then use the added term to eliminate other terms. For example, consider the expression F=ABCD+B CDE+A B +BCE Consensus of ABCD+B CDE (choosing variable B) is ACDE. Adding this term gives: F=ABCD+B CDE+A B +BCE +ACDE Prof. Mehmet Akbaba Digital Logic 30
31 Now we can see that ABCD and B CDE are consensus terms they can be eliminated. Then, we can eliminate ABCD and B'CDE using the consensus theorem, and F reduces to: F=A B +BCE +ACDE The term ACDE is no longer redundant and cannot be eliminated from the final expression. Prof. Mehmet Akbaba Digital Logic 31
32 Algebraic Simplification of Switching Expressions In this section we review and summarize methods for simplifying switching expressions, using the laws and theorems of Boolean algebra. This is important because simplifying an expression reduces the cost of realizing the expression using gates. Later, we will learn graphical methods for simplifying switching functions, but we will learn algebraic methods first. In addition to multiplying out and factoring, three basic ways of simplifying switching functions are combining terms, eliminating terms, and eliminating literals. Prof. Mehmet Akbaba Digital Logic 32
33 1. Combining terms. Use the theorem XY + XY' = X to combine two terms. For example, abc d +abcd =abd (X=abd, Y=c) (4.12) When combining terms by this theorem, the two terms to be combined should contain exactly the same variables, and exactly one of the variables should appear complemented in one term and not in the other. Because X + X = X, a given term may be duplicated and combined with two or more other terms. For example, ab c+abc+a bc=ab c+abc+abc+a bc=ac+bc (=ac( b +b )+bc( a+a )=ac+bc) Prof. Mehmet Akbaba Digital Logic 33
34 The theorem still can be used, of course, when X and Y are replaced with more complicated expressions. For example, (Notice that (a+bc) =a (b +c ) X=a+bc X =a (b +c ) X+X =1 has been used) (a+bc)(d+e )+a (b +c )(d+e )=d+e =(d+e )[(a+bc)+a (b +c )]=d+e 2. Eliminating terms. Use the theorem X + XY = X to eliminate redundant terms if possible; then try to apply the consensus theorem (XY + X' Z + YZ = XY + X' Z) to eliminate any consensus terms. For example, Prof. Mehmet Akbaba Digital Logic 34
35 a b+a bc=a b (X=a b) a bc +bcd+a bd=a bc +bcd (X=c, Y=bd, Z=a b) (consensus theorem) [=a b c +b c d + a bbd = a bc +bcd)] (b=bb) Prof. Mehmet Akbaba Digital Logic 35
36 Eliminating literals. Use the theorem X + X' Y = X + Y to eliminate redundant literals. Simple factoring may be necessary before the theorem is applied. Example: (B+B C D =(B+B )(B+C D )=B+C D) A B+A B C +ABCD =A (B+B C )+ABCD =A (B+C D )+ABCD =B(A +ACD )+A C D =B(A +CD )+A C D =A B+BCD +A C D Prof. Mehmet Akbaba Digital Logic 36
37 The expression obtained after applying steps 1, 2, and 3 will not necessarily have a minimum number of terms or a minimum number of literals. If it does not and no further simplification can be made using steps 1,2, and 3, the deliberate introduction of redundant terms may be necessary before further simplification can be made. 4. Adding redundant terms. Redundant terms can be introduced in several ways such as adding xx', multiplying by (x + x'), adding yz to xy + x' Z, or adding xy to x. When possible, the added terms should be chosen so that they will combine with or eliminate other terms. Prof. Mehmet Akbaba Digital Logic 37
38 Example (4.13) The following comprehensive example illustrates the use of all four methods: Prof. Mehmet Akbaba Digital Logic 38
39 ACD (4.14) What theorems were used in steps 1,2,3, and 4 Prof. Mehmet Akbaba Digital Logic 39
40 If the simplified expression is to be left in a product-ofsums form instead of a sum-of-products form, the duals of the preceding theorems should be applied. (4.15) What theorems were used in steps 1,2, and 3? In general, there is no easy way of determining when a Boolean expression has a minimum number of terms or a minimum number of literals. Systematic methods for finding minimum sum-of-products and minimum productof-sums expressions will be discussed in coming chapters. Prof. Mehmet Akbaba Digital Logic 40
41 REFEENCES» 1. Prof. M. Akbaba Mantık Devreleri Notları 2. Hüseyin EKİZ, Mantık Devreleri, Değişim Yayınları, 4. Baskı, Thomas L. Floyd, Digital Fundamentals, Prentice-Hall Inc. New Jersey, M. Morris Mano, Michael D. Ciletti, Digital Design, Prentice-Hall, Inc.,New Jersey, /25/2015
UNIT 3 BOOLEAN ALGEBRA (CONT D)
 UNIT 3 BOOLEAN ALGEBRA (CONT D) Spring 2011 Boolean Algebra (cont d) 2 Contents Multiplying out and factoring expressions Exclusive-OR and Exclusive-NOR operations The consensus theorem Summary of algebraic
UNIT 3 BOOLEAN ALGEBRA (CONT D) Spring 2011 Boolean Algebra (cont d) 2 Contents Multiplying out and factoring expressions Exclusive-OR and Exclusive-NOR operations The consensus theorem Summary of algebraic
CHAPTER 3 BOOLEAN ALGEBRA
 CHAPTER 3 BOOLEAN ALGEBRA (continued) This chapter in the book includes: Objectives Study Guide 3.1 Multiplying Out and Factoring Expressions 3.2 Exclusive-OR and Equivalence Operations 3.3 The Consensus
CHAPTER 3 BOOLEAN ALGEBRA (continued) This chapter in the book includes: Objectives Study Guide 3.1 Multiplying Out and Factoring Expressions 3.2 Exclusive-OR and Equivalence Operations 3.3 The Consensus
CHAPTER 2 BOOLEAN ALGEBRA
 CHAPTER 2 BOOLEAN ALGEBRA This chapter in the book includes: Objectives Study Guide 2.1 Introduction 2.2 Basic Operations 2.3 Boolean Expressions and Truth Tables 2.4 Basic Theorems 2.5 Commutative, Associative,
CHAPTER 2 BOOLEAN ALGEBRA This chapter in the book includes: Objectives Study Guide 2.1 Introduction 2.2 Basic Operations 2.3 Boolean Expressions and Truth Tables 2.4 Basic Theorems 2.5 Commutative, Associative,
Chapter 3. Boolean Algebra. (continued)
 Chapter 3. Boolean Algebra (continued) Algebraic structure consisting of: set of elements B binary operations {+, -} unary operation {'} Boolean Algebra such that the following axioms hold:. B contains
Chapter 3. Boolean Algebra (continued) Algebraic structure consisting of: set of elements B binary operations {+, -} unary operation {'} Boolean Algebra such that the following axioms hold:. B contains
MULTI-LEVEL GATE CIRCUITS NAND AND NOR GATES
 CHAPTER 7 MULTI-LEVEL GATE CIRCUITS NAND AND NOR GATES 7.1 Multi-Level Gate Circuits 11/20/2014 Prof. M. Akbaba Digital Logic 1 Figure 7-1: Four-Level Realization of Z 11/20/2014 Prof. M. Akbaba Digital
CHAPTER 7 MULTI-LEVEL GATE CIRCUITS NAND AND NOR GATES 7.1 Multi-Level Gate Circuits 11/20/2014 Prof. M. Akbaba Digital Logic 1 Figure 7-1: Four-Level Realization of Z 11/20/2014 Prof. M. Akbaba Digital
Unit 2 Boolean Algebra
 Unit 2 Boolean Algebra 1. Developed by George Boole in 1847 2. Applied to the Design of Switching Circuit by Claude Shannon in 1939 Department of Communication Engineering, NCTU 1 2.1 Basic Operations
Unit 2 Boolean Algebra 1. Developed by George Boole in 1847 2. Applied to the Design of Switching Circuit by Claude Shannon in 1939 Department of Communication Engineering, NCTU 1 2.1 Basic Operations
DIGITAL CIRCUIT LOGIC BOOLEAN ALGEBRA (CONT.)
 DIGITAL CIRCUIT LOGIC BOOLEAN ALGEBRA (CONT.) 1 Learning Objectives 1. Apply the laws and theorems of Boolean algebra to to the manipulation of algebraic expressions to simplifying an expression, finding
DIGITAL CIRCUIT LOGIC BOOLEAN ALGEBRA (CONT.) 1 Learning Objectives 1. Apply the laws and theorems of Boolean algebra to to the manipulation of algebraic expressions to simplifying an expression, finding
Chapter 2 Combinational Logic Circuits
 Logic and Computer Design Fundamentals Chapter 2 Combinational Logic Circuits Part 1 Gate Circuits and Boolean Equations Chapter 2 - Part 1 2 Chapter 2 - Part 1 3 Chapter 2 - Part 1 4 Chapter 2 - Part
Logic and Computer Design Fundamentals Chapter 2 Combinational Logic Circuits Part 1 Gate Circuits and Boolean Equations Chapter 2 - Part 1 2 Chapter 2 - Part 1 3 Chapter 2 - Part 1 4 Chapter 2 - Part
Unit 2 Boolean Algebra
 Unit 2 Boolean Algebra 2.1 Introduction We will use variables like x or y to represent inputs and outputs (I/O) of a switching circuit. Since most switching circuits are 2 state devices (having only 2
Unit 2 Boolean Algebra 2.1 Introduction We will use variables like x or y to represent inputs and outputs (I/O) of a switching circuit. Since most switching circuits are 2 state devices (having only 2
ECE 238L Boolean Algebra - Part I
 ECE 238L Boolean Algebra - Part I August 29, 2008 Typeset by FoilTEX Understand basic Boolean Algebra Boolean Algebra Objectives Relate Boolean Algebra to Logic Networks Prove Laws using Truth Tables Understand
ECE 238L Boolean Algebra - Part I August 29, 2008 Typeset by FoilTEX Understand basic Boolean Algebra Boolean Algebra Objectives Relate Boolean Algebra to Logic Networks Prove Laws using Truth Tables Understand
DIGITAL ELECTRONICS & it0203 Semester 3
 DIGITAL ELECTRONICS & it0203 Semester 3 P.Rajasekar & C.M.T.Karthigeyan Asst.Professor SRM University, Kattankulathur School of Computing, Department of IT 8/22/2011 1 Disclaimer The contents of the slides
DIGITAL ELECTRONICS & it0203 Semester 3 P.Rajasekar & C.M.T.Karthigeyan Asst.Professor SRM University, Kattankulathur School of Computing, Department of IT 8/22/2011 1 Disclaimer The contents of the slides
Chapter 2 Combinational Logic Circuits
 Logic and Computer Design Fundamentals Chapter 2 Combinational Logic Circuits Part 1 Gate Circuits and Boolean Equations Charles Kime & Thomas Kaminski 2008 Pearson Education, Inc. (Hyperlinks are active
Logic and Computer Design Fundamentals Chapter 2 Combinational Logic Circuits Part 1 Gate Circuits and Boolean Equations Charles Kime & Thomas Kaminski 2008 Pearson Education, Inc. (Hyperlinks are active
Chapter 2 Boolean Algebra and Logic Gates
 Ch1: Digital Systems and Binary Numbers Ch2: Ch3: Gate-Level Minimization Ch4: Combinational Logic Ch5: Synchronous Sequential Logic Ch6: Registers and Counters Switching Theory & Logic Design Prof. Adnan
Ch1: Digital Systems and Binary Numbers Ch2: Ch3: Gate-Level Minimization Ch4: Combinational Logic Ch5: Synchronous Sequential Logic Ch6: Registers and Counters Switching Theory & Logic Design Prof. Adnan
Lecture 6: Manipulation of Algebraic Functions, Boolean Algebra, Karnaugh Maps
 EE210: Switching Systems Lecture 6: Manipulation of Algebraic Functions, Boolean Algebra, Karnaugh Maps Prof. YingLi Tian Feb. 21/26, 2019 Department of Electrical Engineering The City College of New York
EE210: Switching Systems Lecture 6: Manipulation of Algebraic Functions, Boolean Algebra, Karnaugh Maps Prof. YingLi Tian Feb. 21/26, 2019 Department of Electrical Engineering The City College of New York
CHAPTER III BOOLEAN ALGEBRA
 CHAPTER III- CHAPTER III CHAPTER III R.M. Dansereau; v.. CHAPTER III-2 BOOLEAN VALUES INTRODUCTION BOOLEAN VALUES Boolean algebra is a form of algebra that deals with single digit binary values and variables.
CHAPTER III- CHAPTER III CHAPTER III R.M. Dansereau; v.. CHAPTER III-2 BOOLEAN VALUES INTRODUCTION BOOLEAN VALUES Boolean algebra is a form of algebra that deals with single digit binary values and variables.
CHAPTER III BOOLEAN ALGEBRA
 CHAPTER III- CHAPTER III CHAPTER III R.M. Dansereau; v.. CHAPTER III-2 BOOLEAN VALUES INTRODUCTION BOOLEAN VALUES Boolean algebra is a form of algebra that deals with single digit binary values and variables.
CHAPTER III- CHAPTER III CHAPTER III R.M. Dansereau; v.. CHAPTER III-2 BOOLEAN VALUES INTRODUCTION BOOLEAN VALUES Boolean algebra is a form of algebra that deals with single digit binary values and variables.
UNIT 5 KARNAUGH MAPS Spring 2011
 UNIT 5 KRNUGH MPS Spring 2 Karnaugh Maps 2 Contents Minimum forms of switching functions Two- and three-variable Four-variable Determination of minimum expressions using essential prime implicants Five-variable
UNIT 5 KRNUGH MPS Spring 2 Karnaugh Maps 2 Contents Minimum forms of switching functions Two- and three-variable Four-variable Determination of minimum expressions using essential prime implicants Five-variable
Lecture 5: NAND, NOR and XOR Gates, Simplification of Algebraic Expressions
 EE210: Switching Systems Lecture 5: NAND, NOR and XOR Gates, Simplification of Algebraic Expressions Prof. YingLi Tian Feb. 15, 2018 Department of Electrical Engineering The City College of New York The
EE210: Switching Systems Lecture 5: NAND, NOR and XOR Gates, Simplification of Algebraic Expressions Prof. YingLi Tian Feb. 15, 2018 Department of Electrical Engineering The City College of New York The
MC9211 Computer Organization
 MC92 Computer Organization Unit : Digital Fundamentals Lesson2 : Boolean Algebra and Simplification (KSB) (MCA) (29-2/ODD) (29 - / A&B) Coverage Lesson2 Introduces the basic postulates of Boolean Algebra
MC92 Computer Organization Unit : Digital Fundamentals Lesson2 : Boolean Algebra and Simplification (KSB) (MCA) (29-2/ODD) (29 - / A&B) Coverage Lesson2 Introduces the basic postulates of Boolean Algebra
Boolean Algebra & Logic Gates. By : Ali Mustafa
 Boolean Algebra & Logic Gates By : Ali Mustafa Digital Logic Gates There are three fundamental logical operations, from which all other functions, no matter how complex, can be derived. These Basic functions
Boolean Algebra & Logic Gates By : Ali Mustafa Digital Logic Gates There are three fundamental logical operations, from which all other functions, no matter how complex, can be derived. These Basic functions
CHAPTER 5 KARNAUGH MAPS
 CHAPTER 5 1/36 KARNAUGH MAPS This chapter in the book includes: Objectives Study Guide 5.1 Minimum Forms of Switching Functions 5.2 Two- and Three-Variable Karnaugh Maps 5.3 Four-Variable Karnaugh Maps
CHAPTER 5 1/36 KARNAUGH MAPS This chapter in the book includes: Objectives Study Guide 5.1 Minimum Forms of Switching Functions 5.2 Two- and Three-Variable Karnaugh Maps 5.3 Four-Variable Karnaugh Maps
BOOLEAN ALGEBRA. Introduction. 1854: Logical algebra was published by George Boole known today as Boolean Algebra
 BOOLEAN ALGEBRA Introduction 1854: Logical algebra was published by George Boole known today as Boolean Algebra It s a convenient way and systematic way of expressing and analyzing the operation of logic
BOOLEAN ALGEBRA Introduction 1854: Logical algebra was published by George Boole known today as Boolean Algebra It s a convenient way and systematic way of expressing and analyzing the operation of logic
Chap 2. Combinational Logic Circuits
 Overview 2 Chap 2. Combinational Logic Circuits Spring 24 Part Gate Circuits and Boolean Equations Binary Logic and Gates Boolean Algebra Standard Forms Part 2 Circuit Optimization Two-Level Optimization
Overview 2 Chap 2. Combinational Logic Circuits Spring 24 Part Gate Circuits and Boolean Equations Binary Logic and Gates Boolean Algebra Standard Forms Part 2 Circuit Optimization Two-Level Optimization
T9: Covering. Prove true by: Method 1: Perfect induction Method 2: Using other theorems and axioms. Number Theorem. T9 B (B+C) = B Covering
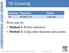 T9: Covering Number Theorem Name T9 B (B+C) = B Covering Prove true by: Method 1: Perfect induction Method 2: Using other theorems and axioms Chapter 2 T9: Covering Number Theorem Name T9 B (B+C)
T9: Covering Number Theorem Name T9 B (B+C) = B Covering Prove true by: Method 1: Perfect induction Method 2: Using other theorems and axioms Chapter 2 T9: Covering Number Theorem Name T9 B (B+C)
Digital Logic Design. Combinational Logic
 Digital Logic Design Combinational Logic Minterms A product term is a term where literals are ANDed. Example: x y, xz, xyz, A minterm is a product term in which all variables appear exactly once, in normal
Digital Logic Design Combinational Logic Minterms A product term is a term where literals are ANDed. Example: x y, xz, xyz, A minterm is a product term in which all variables appear exactly once, in normal
Boolean Algebra. Boolean Variables, Functions. NOT operation. AND operation. AND operation (cont). OR operation
 oolean lgebra asic mathematics for the study of logic design is oolean lgebra asic laws of oolean lgebra will be implemented as switching devices called logic gates. Networks of Logic gates allow us to
oolean lgebra asic mathematics for the study of logic design is oolean lgebra asic laws of oolean lgebra will be implemented as switching devices called logic gates. Networks of Logic gates allow us to
Chapter 2 Combinational
 Computer Engineering 1 (ECE290) Chapter 2 Combinational Logic Circuits Part 1 Gate Circuits and Boolean Equations HOANG Trang Reference: 2008 Pearson Education, Inc. Overview Part 1 Gate Circuits and Boolean
Computer Engineering 1 (ECE290) Chapter 2 Combinational Logic Circuits Part 1 Gate Circuits and Boolean Equations HOANG Trang Reference: 2008 Pearson Education, Inc. Overview Part 1 Gate Circuits and Boolean
Homework Solution #1. Chapter 2 2.6, 2.17, 2.24, 2.30, 2.39, 2.42, Grading policy is as follows: - Total 100
 Homework Solution #1 Chapter 2 2.6, 2.17, 2.24, 2.30, 2.39, 2.42, 2.48 Grading policy is as follows: - Total 100 Exercise 2.6 (total 10) - Column 3 : 5 point - Column 4 : 5 point Exercise 2.17 (total 25)
Homework Solution #1 Chapter 2 2.6, 2.17, 2.24, 2.30, 2.39, 2.42, 2.48 Grading policy is as follows: - Total 100 Exercise 2.6 (total 10) - Column 3 : 5 point - Column 4 : 5 point Exercise 2.17 (total 25)
Boolean algebra. Examples of these individual laws of Boolean, rules and theorems for Boolean algebra are given in the following table.
 The Laws of Boolean Boolean algebra As well as the logic symbols 0 and 1 being used to represent a digital input or output, we can also use them as constants for a permanently Open or Closed circuit or
The Laws of Boolean Boolean algebra As well as the logic symbols 0 and 1 being used to represent a digital input or output, we can also use them as constants for a permanently Open or Closed circuit or
Advanced Digital Design with the Verilog HDL, Second Edition Michael D. Ciletti Prentice Hall, Pearson Education, 2011
 Problem 2-1 Recall that a minterm is a cube in which every variable appears. A Boolean expression in SOP form is canonical if every cube in the expression has a unique representation in which all of the
Problem 2-1 Recall that a minterm is a cube in which every variable appears. A Boolean expression in SOP form is canonical if every cube in the expression has a unique representation in which all of the
Binary Logic and Gates
 1 COE 202- Digital Logic Binary Logic and Gates Dr. Abdulaziz Y. Barnawi COE Department KFUPM 2 Outline Introduction Boolean Algebra Elements of Boolean Algebra (Binary Logic) Logic Operations & Logic
1 COE 202- Digital Logic Binary Logic and Gates Dr. Abdulaziz Y. Barnawi COE Department KFUPM 2 Outline Introduction Boolean Algebra Elements of Boolean Algebra (Binary Logic) Logic Operations & Logic
Chapter 2 Combinational Logic Circuits
 Logic and Computer Design Fundamentals Chapter 2 Combinational Logic Circuits Part 1 Gate Circuits and Boolean Equations Charles Kime & Thomas Kaminski 2008 Pearson Education, Inc. Overview Part 1 Gate
Logic and Computer Design Fundamentals Chapter 2 Combinational Logic Circuits Part 1 Gate Circuits and Boolean Equations Charles Kime & Thomas Kaminski 2008 Pearson Education, Inc. Overview Part 1 Gate
Boolean Algebra and Logic Design (Class 2.2 1/24/2013) CSE 2441 Introduction to Digital Logic Spring 2013 Instructor Bill Carroll, Professor of CSE
 Boolean Algebra and Logic Design (Class 2.2 1/24/2013) CSE 2441 Introduction to Digital Logic Spring 2013 Instructor Bill Carroll, Professor of CSE Today s Topics Boolean algebra applications in logic
Boolean Algebra and Logic Design (Class 2.2 1/24/2013) CSE 2441 Introduction to Digital Logic Spring 2013 Instructor Bill Carroll, Professor of CSE Today s Topics Boolean algebra applications in logic
Number System conversions
 Number System conversions Number Systems The system used to count discrete units is called number system. There are four systems of arithmetic which are often used in digital electronics. Decimal Number
Number System conversions Number Systems The system used to count discrete units is called number system. There are four systems of arithmetic which are often used in digital electronics. Decimal Number
Gate-Level Minimization
 Gate-Level Minimization Dr. Bassem A. Abdullah Computer and Systems Department Lectures Prepared by Dr.Mona Safar, Edited and Lectured by Dr.Bassem A. Abdullah Outline 1. The Map Method 2. Four-variable
Gate-Level Minimization Dr. Bassem A. Abdullah Computer and Systems Department Lectures Prepared by Dr.Mona Safar, Edited and Lectured by Dr.Bassem A. Abdullah Outline 1. The Map Method 2. Four-variable
CS 121 Digital Logic Design. Chapter 2. Teacher Assistant. Hanin Abdulrahman
 CS 121 Digital Logic Design Chapter 2 Teacher Assistant Hanin Abdulrahman 1 2 Outline 2.2 Basic Definitions 2.3 Axiomatic Definition of Boolean Algebra. 2.4 Basic Theorems and Properties 2.5 Boolean Functions
CS 121 Digital Logic Design Chapter 2 Teacher Assistant Hanin Abdulrahman 1 2 Outline 2.2 Basic Definitions 2.3 Axiomatic Definition of Boolean Algebra. 2.4 Basic Theorems and Properties 2.5 Boolean Functions
Logic and Computer Design Fundamentals. Chapter 2 Combinational Logic Circuits. Part 1 Gate Circuits and Boolean Equations
 Logic and Computer Design Fundamentals Chapter 2 Combinational Logic Circuits Part Gate Circuits and Boolean Equations Charles Kime & Thomas Kaminski 28 Pearson Education, Inc. (Hperlinks are active in
Logic and Computer Design Fundamentals Chapter 2 Combinational Logic Circuits Part Gate Circuits and Boolean Equations Charles Kime & Thomas Kaminski 28 Pearson Education, Inc. (Hperlinks are active in
Boolean Algebra, Gates and Circuits
 Boolean Algebra, Gates and Circuits Kasper Brink November 21, 2017 (Images taken from Tanenbaum, Structured Computer Organization, Fifth Edition, (c) 2006 Pearson Education, Inc.) Outline Last week: Von
Boolean Algebra, Gates and Circuits Kasper Brink November 21, 2017 (Images taken from Tanenbaum, Structured Computer Organization, Fifth Edition, (c) 2006 Pearson Education, Inc.) Outline Last week: Von
In Module 3, we have learned about Exclusive OR (XOR) gate. Boolean Expression AB + A B = Y also A B = Y. Logic Gate. Truth table
 Module 8 In Module 3, we have learned about Exclusive OR (XOR) gate. Boolean Expression AB + A B = Y also A B = Y Logic Gate Truth table A B Y 0 0 0 0 1 1 1 0 1 1 1 0 In Module 3, we have learned about
Module 8 In Module 3, we have learned about Exclusive OR (XOR) gate. Boolean Expression AB + A B = Y also A B = Y Logic Gate Truth table A B Y 0 0 0 0 1 1 1 0 1 1 1 0 In Module 3, we have learned about
Binary Logic and Gates. Our objective is to learn how to design digital circuits.
 Binary Logic and Gates Introduction Our objective is to learn how to design digital circuits. These circuits use binary systems. Signals in such binary systems may represent only one of 2 possible values
Binary Logic and Gates Introduction Our objective is to learn how to design digital circuits. These circuits use binary systems. Signals in such binary systems may represent only one of 2 possible values
UNIT 4 MINTERM AND MAXTERM EXPANSIONS
 UNIT 4 MINTERM AND MAXTERM EXPANSIONS Spring 2 Minterm and Maxterm Expansions 2 Contents Conversion of English sentences to Boolean equations Combinational logic design using a truth table Minterm and
UNIT 4 MINTERM AND MAXTERM EXPANSIONS Spring 2 Minterm and Maxterm Expansions 2 Contents Conversion of English sentences to Boolean equations Combinational logic design using a truth table Minterm and
CDA 3200 Digital Systems. Instructor: Dr. Janusz Zalewski Developed by: Dr. Dahai Guo Spring 2012
 CDA 3200 Digital Systems Instructor: Dr. Janusz Zalewski Developed by: Dr. Dahai Guo Spring 2012 Outline Combinational Logic Design Using a Truth Table Minterm and Maxterm Expansions General Minterm and
CDA 3200 Digital Systems Instructor: Dr. Janusz Zalewski Developed by: Dr. Dahai Guo Spring 2012 Outline Combinational Logic Design Using a Truth Table Minterm and Maxterm Expansions General Minterm and
ECE380 Digital Logic. Axioms of Boolean algebra
 ECE380 Digital Logic Introduction to Logic Circuits: Boolean algebra Dr. D. J. Jackson Lecture 3-1 Axioms of Boolean algebra Boolean algebra: based on a set of rules derived from a small number of basic
ECE380 Digital Logic Introduction to Logic Circuits: Boolean algebra Dr. D. J. Jackson Lecture 3-1 Axioms of Boolean algebra Boolean algebra: based on a set of rules derived from a small number of basic
Signals and Systems Digital Logic System
 Signals and Systems Digital Logic System Prof. Wonhee Kim Chapter 2 Design Process for Combinational Systems Step 1: Represent each of the inputs and outputs in binary Step 1.5: If necessary, break the
Signals and Systems Digital Logic System Prof. Wonhee Kim Chapter 2 Design Process for Combinational Systems Step 1: Represent each of the inputs and outputs in binary Step 1.5: If necessary, break the
Midterm1 Review. Jan 24 Armita
 Midterm1 Review Jan 24 Armita Outline Boolean Algebra Axioms closure, Identity elements, complements, commutativity, distributivity theorems Associativity, Duality, De Morgan, Consensus theorem Shannon
Midterm1 Review Jan 24 Armita Outline Boolean Algebra Axioms closure, Identity elements, complements, commutativity, distributivity theorems Associativity, Duality, De Morgan, Consensus theorem Shannon
EC-121 Digital Logic Design
 EC-121 Digital Logic Design Lecture 2 [Updated on 02-04-18] Boolean Algebra and Logic Gates Dr Hashim Ali Spring 2018 Department of Computer Science and Engineering HITEC University Taxila!1 Overview What
EC-121 Digital Logic Design Lecture 2 [Updated on 02-04-18] Boolean Algebra and Logic Gates Dr Hashim Ali Spring 2018 Department of Computer Science and Engineering HITEC University Taxila!1 Overview What
Chapter 2 Combinational Logic Circuits
 Logic and Computer Design Fundamentals Chapter 2 Combinational Logic Circuits Part 2 Circuit Optimization Goal: To obtain the simplest implementation for a given function Optimization is a more formal
Logic and Computer Design Fundamentals Chapter 2 Combinational Logic Circuits Part 2 Circuit Optimization Goal: To obtain the simplest implementation for a given function Optimization is a more formal
ENG2410 Digital Design Combinational Logic Circuits
 ENG240 Digital Design Combinational Logic Circuits Fall 207 S. Areibi School of Engineering University of Guelph Binary variables Binary Logic Can be 0 or (T or F, low or high) Variables named with single
ENG240 Digital Design Combinational Logic Circuits Fall 207 S. Areibi School of Engineering University of Guelph Binary variables Binary Logic Can be 0 or (T or F, low or high) Variables named with single
2 Application of Boolean Algebra Theorems (15 Points - graded for completion only)
 CSE140 HW1 Solution (100 Points) 1 Introduction The purpose of this assignment is three-fold. First, it aims to help you practice the application of Boolean Algebra theorems to transform and reduce Boolean
CSE140 HW1 Solution (100 Points) 1 Introduction The purpose of this assignment is three-fold. First, it aims to help you practice the application of Boolean Algebra theorems to transform and reduce Boolean
Chapter 2 : Boolean Algebra and Logic Gates
 Chapter 2 : Boolean Algebra and Logic Gates By Electrical Engineering Department College of Engineering King Saud University 1431-1432 2.1. Basic Definitions 2.2. Basic Theorems and Properties of Boolean
Chapter 2 : Boolean Algebra and Logic Gates By Electrical Engineering Department College of Engineering King Saud University 1431-1432 2.1. Basic Definitions 2.2. Basic Theorems and Properties of Boolean
Logic Design I (17.341) Fall Lecture Outline
 Logic Design I (17.341) Fall 2011 Lecture Outline Class # 06 October 24, 2011 Dohn Bowden 1 Today s Lecture Administrative Main Logic Topic Homework 2 Course Admin 3 Administrative Admin for tonight Syllabus
Logic Design I (17.341) Fall 2011 Lecture Outline Class # 06 October 24, 2011 Dohn Bowden 1 Today s Lecture Administrative Main Logic Topic Homework 2 Course Admin 3 Administrative Admin for tonight Syllabus
ECEN 248: INTRODUCTION TO DIGITAL SYSTEMS DESIGN. Week 2 Dr. Srinivas Shakkottai Dept. of Electrical and Computer Engineering
 ECEN 248: INTRODUCTION TO DIGITAL SYSTEMS DESIGN Week 2 Dr. Srinivas Shakkottai Dept. of Electrical and Computer Engineering Boolean Algebra Boolean Algebra A Boolean algebra is defined with: A set of
ECEN 248: INTRODUCTION TO DIGITAL SYSTEMS DESIGN Week 2 Dr. Srinivas Shakkottai Dept. of Electrical and Computer Engineering Boolean Algebra Boolean Algebra A Boolean algebra is defined with: A set of
E&CE 223 Digital Circuits & Systems. Lecture Transparencies (Boolean Algebra & Logic Gates) M. Sachdev
 E&CE 223 Digital Circuits & Systems Lecture Transparencies (Boolean Algebra & Logic Gates) M. Sachdev 4 of 92 Section 2: Boolean Algebra & Logic Gates Major topics Boolean algebra NAND & NOR gates Boolean
E&CE 223 Digital Circuits & Systems Lecture Transparencies (Boolean Algebra & Logic Gates) M. Sachdev 4 of 92 Section 2: Boolean Algebra & Logic Gates Major topics Boolean algebra NAND & NOR gates Boolean
Chapter 2: Boolean Algebra and Logic Gates
 Chapter 2: Boolean Algebra and Logic Gates Mathematical methods that simplify binary logics or circuits rely primarily on Boolean algebra. Boolean algebra: a set of elements, a set of operators, and a
Chapter 2: Boolean Algebra and Logic Gates Mathematical methods that simplify binary logics or circuits rely primarily on Boolean algebra. Boolean algebra: a set of elements, a set of operators, and a
CHAPTER 7 MULTI-LEVEL GATE CIRCUITS NAND AND NOR GATES
 CHAPTER 7 MULTI-LEVEL GATE CIRCUITS NAND AND NOR GATES This chapter in the book includes: Objectives Study Guide 7.1 Multi-Level Gate Circuits 7.2 NAND and NOR Gates 7.3 Design of Two-Level Circuits Using
CHAPTER 7 MULTI-LEVEL GATE CIRCUITS NAND AND NOR GATES This chapter in the book includes: Objectives Study Guide 7.1 Multi-Level Gate Circuits 7.2 NAND and NOR Gates 7.3 Design of Two-Level Circuits Using
Chapter 2: Switching Algebra and Logic Circuits
 Chapter 2: Switching Algebra and Logic Circuits Formal Foundation of Digital Design In 1854 George Boole published An investigation into the Laws of Thoughts Algebraic system with two values 0 and 1 Used
Chapter 2: Switching Algebra and Logic Circuits Formal Foundation of Digital Design In 1854 George Boole published An investigation into the Laws of Thoughts Algebraic system with two values 0 and 1 Used
Chapter-2 BOOLEAN ALGEBRA
 Chapter-2 BOOLEAN ALGEBRA Introduction: An algebra that deals with binary number system is called Boolean Algebra. It is very power in designing logic circuits used by the processor of computer system.
Chapter-2 BOOLEAN ALGEBRA Introduction: An algebra that deals with binary number system is called Boolean Algebra. It is very power in designing logic circuits used by the processor of computer system.
Chapter 2 Boolean Algebra and Logic Gates
 Chapter 2 Boolean Algebra and Logic Gates Huntington Postulates 1. (a) Closure w.r.t. +. (b) Closure w.r.t.. 2. (a) Identity element 0 w.r.t. +. x + 0 = 0 + x = x. (b) Identity element 1 w.r.t.. x 1 =
Chapter 2 Boolean Algebra and Logic Gates Huntington Postulates 1. (a) Closure w.r.t. +. (b) Closure w.r.t.. 2. (a) Identity element 0 w.r.t. +. x + 0 = 0 + x = x. (b) Identity element 1 w.r.t.. x 1 =
 / M Morris Mano Digital Design Ahmad_911@hotmailcom / / / / wwwuqucscom Binary Systems Introduction - Digital Systems - The Conversion Between Numbering Systems - From Binary To Decimal - Octet To Decimal
/ M Morris Mano Digital Design Ahmad_911@hotmailcom / / / / wwwuqucscom Binary Systems Introduction - Digital Systems - The Conversion Between Numbering Systems - From Binary To Decimal - Octet To Decimal
E&CE 223 Digital Circuits & Systems. Lecture Transparencies (Boolean Algebra & Logic Gates) M. Sachdev. Section 2: Boolean Algebra & Logic Gates
 Digital Circuits & Systems Lecture Transparencies (Boolean lgebra & Logic Gates) M. Sachdev 4 of 92 Section 2: Boolean lgebra & Logic Gates Major topics Boolean algebra NND & NOR gates Boolean algebra
Digital Circuits & Systems Lecture Transparencies (Boolean lgebra & Logic Gates) M. Sachdev 4 of 92 Section 2: Boolean lgebra & Logic Gates Major topics Boolean algebra NND & NOR gates Boolean algebra
EEE130 Digital Electronics I Lecture #4
 EEE130 Digital Electronics I Lecture #4 - Boolean Algebra and Logic Simplification - By Dr. Shahrel A. Suandi Topics to be discussed 4-1 Boolean Operations and Expressions 4-2 Laws and Rules of Boolean
EEE130 Digital Electronics I Lecture #4 - Boolean Algebra and Logic Simplification - By Dr. Shahrel A. Suandi Topics to be discussed 4-1 Boolean Operations and Expressions 4-2 Laws and Rules of Boolean
Logic Design. Chapter 2: Introduction to Logic Circuits
 Logic Design Chapter 2: Introduction to Logic Circuits Introduction Logic circuits perform operation on digital signal Digital signal: signal values are restricted to a few discrete values Binary logic
Logic Design Chapter 2: Introduction to Logic Circuits Introduction Logic circuits perform operation on digital signal Digital signal: signal values are restricted to a few discrete values Binary logic
Digital Techniques. Figure 1: Block diagram of digital computer. Processor or Arithmetic logic unit ALU. Control Unit. Storage or memory unit
 Digital Techniques 1. Binary System The digital computer is the best example of a digital system. A main characteristic of digital system is its ability to manipulate discrete elements of information.
Digital Techniques 1. Binary System The digital computer is the best example of a digital system. A main characteristic of digital system is its ability to manipulate discrete elements of information.
INTRO TO I & CT. (Boolean Algebra and Logic Simplification.) Lecture # By: Department of CS & IT.
 INTRO TO I & CT. (Boolean Algebra and Logic Simplification.) Lecture # 13-14 By: M.Nadeem Akhtar. Department of CS & IT. URL: https://sites.google.com/site/nadeemcsuoliict/home/lectures 1 Boolean Algebra
INTRO TO I & CT. (Boolean Algebra and Logic Simplification.) Lecture # 13-14 By: M.Nadeem Akhtar. Department of CS & IT. URL: https://sites.google.com/site/nadeemcsuoliict/home/lectures 1 Boolean Algebra
Chapter 2. Digital Logic Basics
 Chapter 2 Digital Logic Basics 1 2 Chapter 2 2 1 Implementation using NND gates: We can write the XOR logical expression B + B using double negation as B+ B = B+B = B B From this logical expression, we
Chapter 2 Digital Logic Basics 1 2 Chapter 2 2 1 Implementation using NND gates: We can write the XOR logical expression B + B using double negation as B+ B = B+B = B B From this logical expression, we
Solutions to Assignment No 5 Digital Techniques Fall 2007
 Solutions to Assignment No 5 Digital Techniques Fall 2007 André Deutz October 19, 2007 1 Simplifying and Manipulating Boolean Expressions 1. Simplification (a) Simplify each of the following expressions,
Solutions to Assignment No 5 Digital Techniques Fall 2007 André Deutz October 19, 2007 1 Simplifying and Manipulating Boolean Expressions 1. Simplification (a) Simplify each of the following expressions,
Lecture 7: Karnaugh Map, Don t Cares
 EE210: Switching Systems Lecture 7: Karnaugh Map, Don t Cares Prof. YingLi Tian Feb. 28, 2019 Department of Electrical Engineering The City College of New York The City University of New York (CUNY) 1
EE210: Switching Systems Lecture 7: Karnaugh Map, Don t Cares Prof. YingLi Tian Feb. 28, 2019 Department of Electrical Engineering The City College of New York The City University of New York (CUNY) 1
DIGITAL CIRCUIT LOGIC BOOLEAN ALGEBRA
 DIGITAL CIRCUIT LOGIC BOOLEAN ALGEBRA 1 Learning Objectives Understand the basic operations and laws of Boolean algebra. Relate these operations and laws to circuits composed of AND gates, OR gates, INVERTERS
DIGITAL CIRCUIT LOGIC BOOLEAN ALGEBRA 1 Learning Objectives Understand the basic operations and laws of Boolean algebra. Relate these operations and laws to circuits composed of AND gates, OR gates, INVERTERS
BOOLEAN ALGEBRA TRUTH TABLE
 BOOLEAN ALGEBRA TRUTH TABLE Truth table is a table which represents all the possible values of logical variables / statements along with all the possible results of the given combinations of values. Eg:
BOOLEAN ALGEBRA TRUTH TABLE Truth table is a table which represents all the possible values of logical variables / statements along with all the possible results of the given combinations of values. Eg:
Boolean Algebra and Logic Gates
 Boolean Algebra and Logic Gates ( 范倫達 ), Ph. D. Department of Computer Science National Chiao Tung University Taiwan, R.O.C. Fall, 2017 ldvan@cs.nctu.edu.tw http://www.cs.nctu.edu.tw/~ldvan/ Outlines Basic
Boolean Algebra and Logic Gates ( 范倫達 ), Ph. D. Department of Computer Science National Chiao Tung University Taiwan, R.O.C. Fall, 2017 ldvan@cs.nctu.edu.tw http://www.cs.nctu.edu.tw/~ldvan/ Outlines Basic
Week-I. Combinational Logic & Circuits
 Week-I Combinational Logic & Circuits Overview Binary logic operations and gates Switching algebra Algebraic Minimization Standard forms Karnaugh Map Minimization Other logic operators IC families and
Week-I Combinational Logic & Circuits Overview Binary logic operations and gates Switching algebra Algebraic Minimization Standard forms Karnaugh Map Minimization Other logic operators IC families and
Circuits & Boolean algebra.
 Circuits & Boolean algebra http://xkcd.com/730/ CSCI 255: Introduction to Embedded Systems Keith Vertanen Copyright 2011 Digital circuits Overview How a switch works Building basic gates from switches
Circuits & Boolean algebra http://xkcd.com/730/ CSCI 255: Introduction to Embedded Systems Keith Vertanen Copyright 2011 Digital circuits Overview How a switch works Building basic gates from switches
Chapter 2 Boolean Algebra and Logic Gates
 Chapter 2 Boolean Algebra and Logic Gates The most common postulates used to formulate various algebraic structures are: 1. Closure. N={1,2,3,4 }, for any a,b N we obtain a unique c N by the operation
Chapter 2 Boolean Algebra and Logic Gates The most common postulates used to formulate various algebraic structures are: 1. Closure. N={1,2,3,4 }, for any a,b N we obtain a unique c N by the operation
EECS150 - Digital Design Lecture 19 - Combinational Logic Circuits : A Deep Dive
 EECS150 - Digital Design Lecture 19 - Combinational Logic Circuits : A Deep Dive March 30, 2010 John Wawrzynek Spring 2010 EECS150 - Lec19-cl1 Page 1 Boolean Algebra I (Representations of Combinational
EECS150 - Digital Design Lecture 19 - Combinational Logic Circuits : A Deep Dive March 30, 2010 John Wawrzynek Spring 2010 EECS150 - Lec19-cl1 Page 1 Boolean Algebra I (Representations of Combinational
Hardware Design I Chap. 2 Basis of logical circuit, logical expression, and logical function
 Hardware Design I Chap. 2 Basis of logical circuit, logical expression, and logical function E-mail: shimada@is.naist.jp Outline Combinational logical circuit Logic gate (logic element) Definition of combinational
Hardware Design I Chap. 2 Basis of logical circuit, logical expression, and logical function E-mail: shimada@is.naist.jp Outline Combinational logical circuit Logic gate (logic element) Definition of combinational
ECE 20B, Winter 2003 Introduction to Electrical Engineering, II LECTURE NOTES #2
 ECE 20B, Winter 2003 Introduction to Electrical Engineering, II LECTURE NOTES #2 Instructor: Andrew B. Kahng (lecture) Email: abk@ucsd.edu Telephone: 858-822-4884 office, 858-353-0550 cell Office: 3802
ECE 20B, Winter 2003 Introduction to Electrical Engineering, II LECTURE NOTES #2 Instructor: Andrew B. Kahng (lecture) Email: abk@ucsd.edu Telephone: 858-822-4884 office, 858-353-0550 cell Office: 3802
Boolean Algebra. Sungho Kang. Yonsei University
 Boolean Algebra Sungho Kang Yonsei University Outline Set, Relations, and Functions Partial Orders Boolean Functions Don t Care Conditions Incomplete Specifications 2 Set Notation $09,3/#0,9 438 v V Element
Boolean Algebra Sungho Kang Yonsei University Outline Set, Relations, and Functions Partial Orders Boolean Functions Don t Care Conditions Incomplete Specifications 2 Set Notation $09,3/#0,9 438 v V Element
Combinational Logic Design Principles
 Combinational Logic Design Principles Switching algebra Doru Todinca Department of Computers Politehnica University of Timisoara Outline Introduction Switching algebra Axioms of switching algebra Theorems
Combinational Logic Design Principles Switching algebra Doru Todinca Department of Computers Politehnica University of Timisoara Outline Introduction Switching algebra Axioms of switching algebra Theorems
CHAPTER 7. Exercises 17/ / /2 2 0
 CHAPTER 7 Exercises E7. (a) For the whole part, we have: Quotient Remainders 23/2 /2 5 5/2 2 2/2 0 /2 0 Reading the remainders in reverse order, we obtain: 23 0 = 0 2 For the fractional part we have 2
CHAPTER 7 Exercises E7. (a) For the whole part, we have: Quotient Remainders 23/2 /2 5 5/2 2 2/2 0 /2 0 Reading the remainders in reverse order, we obtain: 23 0 = 0 2 For the fractional part we have 2
CPE100: Digital Logic Design I
 Chapter 2 Professor Brendan Morris, SEB 326, brendan.morris@unlv.edu http://www.ee.unlv.edu/~bmorris/cpe/ CPE: Digital Logic Design I Section 4: Dr. Morris Combinational Logic Design Chapter 2 Chapter
Chapter 2 Professor Brendan Morris, SEB 326, brendan.morris@unlv.edu http://www.ee.unlv.edu/~bmorris/cpe/ CPE: Digital Logic Design I Section 4: Dr. Morris Combinational Logic Design Chapter 2 Chapter
ELCT201: DIGITAL LOGIC DESIGN
 ELCT2: DIGITAL LOGIC DESIGN Dr. Eng. Haitham Omran, haitham.omran@guc.edu.eg Dr. Eng. Wassim Alexan, wassim.joseph@guc.edu.eg Lecture 4 Following the slides of Dr. Ahmed H. Madian محرم 439 ه Winter 28
ELCT2: DIGITAL LOGIC DESIGN Dr. Eng. Haitham Omran, haitham.omran@guc.edu.eg Dr. Eng. Wassim Alexan, wassim.joseph@guc.edu.eg Lecture 4 Following the slides of Dr. Ahmed H. Madian محرم 439 ه Winter 28
12/31/2010. Overview. 05-Boolean Algebra Part 3 Text: Unit 3, 7. DeMorgan s Law. Example. Example. DeMorgan s Law
 Overview 05-oolean lgebra Part 3 Text: Unit 3, 7 EEGR/ISS 201 Digital Operations and omputations Winter 2011 DeMorgan s Laws lgebraic Simplifications Exclusive-OR and Equivalence Functionally omplete NND-NOR
Overview 05-oolean lgebra Part 3 Text: Unit 3, 7 EEGR/ISS 201 Digital Operations and omputations Winter 2011 DeMorgan s Laws lgebraic Simplifications Exclusive-OR and Equivalence Functionally omplete NND-NOR
Digital Circuit And Logic Design I. Lecture 3
 Digital Circuit And Logic Design I Lecture 3 Outline Combinational Logic Design Principles (). Introduction 2. Switching algebra 3. Combinational-circuit analysis 4. Combinational-circuit synthesis Panupong
Digital Circuit And Logic Design I Lecture 3 Outline Combinational Logic Design Principles (). Introduction 2. Switching algebra 3. Combinational-circuit analysis 4. Combinational-circuit synthesis Panupong
II. COMBINATIONAL LOGIC DESIGN. - algebra defined on a set of 2 elements, {0, 1}, with binary operators multiply (AND), add (OR), and invert (NOT):
 ENGI 386 Digital Logic II. COMBINATIONAL LOGIC DESIGN Combinational Logic output of digital system is only dependent on current inputs (i.e., no memory) (a) Boolean Algebra - developed by George Boole
ENGI 386 Digital Logic II. COMBINATIONAL LOGIC DESIGN Combinational Logic output of digital system is only dependent on current inputs (i.e., no memory) (a) Boolean Algebra - developed by George Boole
12/31/2010. Overview. 04-Boolean Algebra Part 2 Text: Unit 2. Basic Theorems. Basic Theorems. Basic Theorems. Examples
 Overview 04-Boolean lgebra Part 2 Text: Unit 2 Basic Theorems Multiplying and Factoring ECEGR/ISSC 201 Digital Operations and Computations Winter 2011 Dr. Louie 2 Basic Theorems Basic Theorems Basic laws
Overview 04-Boolean lgebra Part 2 Text: Unit 2 Basic Theorems Multiplying and Factoring ECEGR/ISSC 201 Digital Operations and Computations Winter 2011 Dr. Louie 2 Basic Theorems Basic Theorems Basic laws
Administrative Notes. Chapter 2 <9>
 Administrative Notes Note: New homework instructions starting with HW03 Homework is due at the beginning of class Homework must be organized, legible (messy is not), and stapled to be graded Chapter 2
Administrative Notes Note: New homework instructions starting with HW03 Homework is due at the beginning of class Homework must be organized, legible (messy is not), and stapled to be graded Chapter 2
Combinational Logic Fundamentals
 Topic 3: Combinational Logic Fundamentals In this note we will study combinational logic, which is the part of digital logic that uses Boolean algebra. All the concepts presented in combinational logic
Topic 3: Combinational Logic Fundamentals In this note we will study combinational logic, which is the part of digital logic that uses Boolean algebra. All the concepts presented in combinational logic
Karnaugh Maps Objectives
 Karnaugh Maps Objectives For Karnaugh Maps of up to 5 variables Plot a function from algebraic, minterm or maxterm form Obtain minimum Sum of Products and Product of Sums Understand the relationship between
Karnaugh Maps Objectives For Karnaugh Maps of up to 5 variables Plot a function from algebraic, minterm or maxterm form Obtain minimum Sum of Products and Product of Sums Understand the relationship between
ELC224C. Karnaugh Maps
 KARNAUGH MAPS Function Simplification Algebraic Simplification Half Adder Introduction to K-maps How to use K-maps Converting to Minterms Form Prime Implicants and Essential Prime Implicants Example on
KARNAUGH MAPS Function Simplification Algebraic Simplification Half Adder Introduction to K-maps How to use K-maps Converting to Minterms Form Prime Implicants and Essential Prime Implicants Example on
CSC9R6 Computer Design. Practical Digital Logic
 CSC9R6 Computer Design Practical Digital Logic 1 References (for this part of CSC9R6) Hamacher et al: Computer Organization App A. In library Floyd: Digital Fundamentals Ch 1, 3-6, 8-10 web page: www.prenhall.com/floyd/
CSC9R6 Computer Design Practical Digital Logic 1 References (for this part of CSC9R6) Hamacher et al: Computer Organization App A. In library Floyd: Digital Fundamentals Ch 1, 3-6, 8-10 web page: www.prenhall.com/floyd/
Digital Logic Design. Malik Najmus Siraj
 Digital Logic Design Malik Najmus Siraj siraj@case.edu.pkedu LECTURE 4 Today s Agenda Recap 2 s complement Binary Logic Boolean algebra Recap Computer Arithmetic Signed numbers Radix and diminished radix
Digital Logic Design Malik Najmus Siraj siraj@case.edu.pkedu LECTURE 4 Today s Agenda Recap 2 s complement Binary Logic Boolean algebra Recap Computer Arithmetic Signed numbers Radix and diminished radix
Chapter 7 Logic Circuits
 Chapter 7 Logic Circuits Goal. Advantages of digital technology compared to analog technology. 2. Terminology of Digital Circuits. 3. Convert Numbers between Decimal, Binary and Other forms. 5. Binary
Chapter 7 Logic Circuits Goal. Advantages of digital technology compared to analog technology. 2. Terminology of Digital Circuits. 3. Convert Numbers between Decimal, Binary and Other forms. 5. Binary
Ex: Boolean expression for majority function F = A'BC + AB'C + ABC ' + ABC.
 Boolean Expression Forms: Sum-of-products (SOP) Write an AND term for each input combination that produces a 1 output. Write the input variable if its value is 1; write its complement otherwise. OR the
Boolean Expression Forms: Sum-of-products (SOP) Write an AND term for each input combination that produces a 1 output. Write the input variable if its value is 1; write its complement otherwise. OR the
Chapter 2. Boolean Algebra and Logic Gates
 Chapter 2 Boolean Algebra and Logic Gates Basic Definitions A binary operator defined on a set S of elements is a rule that assigns, to each pair of elements from S, a unique element from S. The most common
Chapter 2 Boolean Algebra and Logic Gates Basic Definitions A binary operator defined on a set S of elements is a rule that assigns, to each pair of elements from S, a unique element from S. The most common
Chapter 2 Combinational Logic Circuits
 Logic and Computer Design Fundamentals Chapter 2 Combinational Logic Circuits Part 2 Circuit Optimization Charles Kime & Thomas Kaminski 2004 Pearson Education, Inc. Terms of Use (Hyperlinks are active
Logic and Computer Design Fundamentals Chapter 2 Combinational Logic Circuits Part 2 Circuit Optimization Charles Kime & Thomas Kaminski 2004 Pearson Education, Inc. Terms of Use (Hyperlinks are active
Chapter 4: Combinational Logic Solutions to Problems: [1, 5, 9, 12, 19, 23, 30, 33]
![Chapter 4: Combinational Logic Solutions to Problems: [1, 5, 9, 12, 19, 23, 30, 33] Chapter 4: Combinational Logic Solutions to Problems: [1, 5, 9, 12, 19, 23, 30, 33]](/thumbs/81/84077758.jpg) Chapter 4: Combinational Logic Solutions to Problems: [, 5, 9, 2, 9, 23, 3, 33] Problem: 4- Consider the combinational circuit shown in Fig. P4-. (a) Derive the Boolean expressions for T through T 4. Evaluate
Chapter 4: Combinational Logic Solutions to Problems: [, 5, 9, 2, 9, 23, 3, 33] Problem: 4- Consider the combinational circuit shown in Fig. P4-. (a) Derive the Boolean expressions for T through T 4. Evaluate
If f = ABC + ABC + A B C then f = AB C + A BC + AB C + A BC + A B C
 Examples: If f 5 = AB + AB then f 5 = A B + A B = f 10 If f = ABC + ABC + A B C then f = AB C + A BC + AB C + A BC + A B C In terms of a truth table, if f is the sum (OR) of all the minterms with a 1 in
Examples: If f 5 = AB + AB then f 5 = A B + A B = f 10 If f = ABC + ABC + A B C then f = AB C + A BC + AB C + A BC + A B C In terms of a truth table, if f is the sum (OR) of all the minterms with a 1 in
Lab 1 starts this week: go to your session
 Lecture 3: Boolean Algebra Logistics Class email sign up Homework 1 due on Wednesday Lab 1 starts this week: go to your session Last lecture --- Numbers Binary numbers Base conversion Number systems for
Lecture 3: Boolean Algebra Logistics Class email sign up Homework 1 due on Wednesday Lab 1 starts this week: go to your session Last lecture --- Numbers Binary numbers Base conversion Number systems for
EECS150 - Digital Design Lecture 4 - Boolean Algebra I (Representations of Combinational Logic Circuits)
 EECS150 - Digital Design Lecture 4 - Boolean Algebra I (Representations of Combinational Logic Circuits) September 5, 2002 John Wawrzynek Fall 2002 EECS150 Lec4-bool1 Page 1, 9/5 9am Outline Review of
EECS150 - Digital Design Lecture 4 - Boolean Algebra I (Representations of Combinational Logic Circuits) September 5, 2002 John Wawrzynek Fall 2002 EECS150 Lec4-bool1 Page 1, 9/5 9am Outline Review of
Digital System Design Combinational Logic. Assoc. Prof. Pradondet Nilagupta
 Digital System Design Combinational Logic Assoc. Prof. Pradondet Nilagupta pom@ku.ac.th Acknowledgement This lecture note is modified from Engin112: Digital Design by Prof. Maciej Ciesielski, Prof. Tilman
Digital System Design Combinational Logic Assoc. Prof. Pradondet Nilagupta pom@ku.ac.th Acknowledgement This lecture note is modified from Engin112: Digital Design by Prof. Maciej Ciesielski, Prof. Tilman
