Stat 8053 Lecture Notes An Example that Shows that Statistical Obnoxiousness is not Related to Dimension Charles J. Geyer November 17, 2014
|
|
|
- Lester Byrd
- 5 years ago
- Views:
Transcription
1 Stat 8053 Lecture Notes An Example that Shows that Statistical Obnoxiousness is not Related to Dimension Charles J. Geyer November 17, 2014 We are all familiar with the usual mathematics of maximum likelihood. Under the usual regularity conditions the MLE is consistent and asymptotically normal, and the inverse of the Fisher information matrix estimates the asymptotic variance of the MLE. The phrase usual regularity conditions sweeps a lot under the rug, since every theory book seems to have slightly different regularity conditions and each list of regularity conditions is too complicated and technical to provide any insight into what is going on. But it gets worse. One can radically weaken the usual regularity conditions and get the same asymptotics for some estimators other than the MLE. The main source for this is Lucian Le Cam (Le Cam and Yang, 2000). His theory is notoriously hard to read and far beyond the scope of this course. The purpose of this note is just to present one concrete example. The integral 0 e xα dx is evaluated using the change of variable which gives 0 y = x α x = y 1/α dx = 1 α y1/α 1 dy e xα dx = 1 α 0 y 1/α 1 e y dy = 1 α Γ ( 1 α Hence for any real θ, the function f θ defined by ) ( = Γ ) α f θ (x) = e x θ α 2Γ ( ), < x < (1) α is a probability density and the family of densities { f θ : θ R } is a statistical model (a location family). Having derived this density, we see that it can be derived from the gamma distribution by change of variable. Suppose X is a random variable with 1
2 density (1), then, defining Y = X θ α, we see that the distribution of Y does not depend on θ and has density g(y) = e y Γ ( α ) 1 α y1/α 1 that is, Y Gamma(1/α), and X = θ + SY 1/α, where S is a random sign (equal to 1 or +1 with equal probabilities). > set.seed(42) > n <- 1e2 > alpha <- 3 / 4 > theta <- 0 > y <- rgamma(n, shape = 1 / alpha) > x <- theta + y^(1 / alpha) * sample(c(-1, 1), n, replace = TRUE) If we treat α as a known constant, so θ is the only unknown parameter, the log likelihood is n l n (θ) = x i θ α (2) i=1 If we choose α < 1, then the log likelihood has a cusp at every x i. And the usual notions of maximum likelihood go out the window. But Le Cam and Yang (2000) assert that for 1/2 < α the log likelihood is asymptotically quadratic at a root n rate. The MLE is useless, but other likelihood-based estimators keep going. Evaluate the log likelihood at a prespecified finite set of points ( prespecified meaning specified before any data are observed). Fit a quadratic function to this log likelihood evaluated on a grid by any reasonable method, say robust regression, take the maximum of the quadratic approximation as the parameter estimate, and take the inverse of minus the second derivative of the quadratic approximation evaluated at the maximum, that is, we replace the actual log likelihood with a good quadratic approximation and then proceed to do likelihood inference as if the quadratic approximation were a log likelihood satisfying the usual regularity conditions. > xgrid <- pretty(x, n = 20) > l <- function(theta) sum(- abs(x - theta)^alpha) > vl <- Vectorize(l) > lgrid <- vl(xgrid) > # xgrid > # lgrid 2
3 > library(mass) > rout <- rlm(lgrid ~ xgrid + I(xgrid^2)) > beta <- rout$coefficients > theta.hat <- as.numeric(- beta[2] / (2 * beta[3])) > theta.hat [1] > fish.hat <- as.numeric(- 2 * beta[3]) > theta.hat + c(- 1, 1) * qnorm(0.975) * sqrt(1 / fish.hat) [1] Now we try to picture what is going on. The picture (Figure 1) is given by the following code > plot(xgrid, lgrid, ylab = "log likelihood", xlab = "theta") > curve(predict(rout, newdata = data.frame(xgrid = x)), + add = TRUE, lty = "dashed") > # and now for actual log likelihood > foo <- par("usr") > xgrid2 <- seq(foo[1], foo[2], length = 10001) > xgrid2 <- sort(c(x, xgrid2)) > lgrid2 <- vl(xgrid2) > lines(xgrid2, lgrid2) Perhaps we should have fit the quadratic just to the middle part of the curve. > xgrid <- theta.hat + c(- 1, 1) * qnorm(0.995) * sqrt(1 / fish.hat) > lgrid <- vl(xgrid) > xgrid <- pretty(xgrid2[min(lgrid) <= lgrid2], n = 20) > lgrid <- vl(xgrid) > rout <- rlm(lgrid ~ xgrid + I(xgrid^2)) > beta <- rout$coefficients > theta.hat <- as.numeric(- beta[2] / (2 * beta[3])) > theta.hat [1] > fish.hat <- as.numeric(- 2 * beta[3]) > theta.hat + c(- 1, 1) * qnorm(0.975) * sqrt(1 / fish.hat) 3
4 log likelihood theta Figure 1: Log likelihood and quadratic approximation. 4
5 [1] Of course, this is not what the theory says to do. We were suppose to choose the points where the log likelihood is evaluated before we saw the data, but this is impossible in practice. We would need more complicated theory to say that what we are doing here is o. k. Since this method is not used by applied people (only by theoreticians), there is no theory (AFAIK) that justifies what we have to do to get a practical method. Now the picture (Figure 2) is given by the following code > plot(xgrid, lgrid, ylab = "log likelihood", xlab = "theta", + xlim = range(xgrid)) > curve(predict(rout, newdata = data.frame(xgrid = x)), + add = TRUE, lty = "dashed") > foo <- par("usr") > xgrid2 <- seq(foo[1], foo[2], length = 10001) > xgrid2 <- sort(c(x, xgrid2)) > xgrid2 <- xgrid2[foo[1] < xgrid2 & xgrid2 < foo[2]] > lgrid2 <- vl(xgrid2) > lines(xgrid2, lgrid2) References Le Cam, L. and Yang, G. L. (2000). Asymptotics in Statistics: Some Basic Concepts, 2nd ed. Springer-Verlag, New York. 5
6 log likelihood theta Figure 2: Log likelihood and quadratic approximation. 6
Stat 5421 Lecture Notes Likelihood Inference Charles J. Geyer March 12, Likelihood
 Stat 5421 Lecture Notes Likelihood Inference Charles J. Geyer March 12, 2016 1 Likelihood In statistics, the word likelihood has a technical meaning, given it by Fisher (1912). The likelihood for a statistical
Stat 5421 Lecture Notes Likelihood Inference Charles J. Geyer March 12, 2016 1 Likelihood In statistics, the word likelihood has a technical meaning, given it by Fisher (1912). The likelihood for a statistical
5601 Notes: The Subsampling Bootstrap
 5601 Notes: The Subsampling Bootstrap Charles J. Geyer April 13, 2006 1 Web Pages This handout accompanies the web pages http://www.stat.umn.edu/geyer/5601/examp/subboot.html http://www.stat.umn.edu/geyer/5601/examp/subtoot.html
5601 Notes: The Subsampling Bootstrap Charles J. Geyer April 13, 2006 1 Web Pages This handout accompanies the web pages http://www.stat.umn.edu/geyer/5601/examp/subboot.html http://www.stat.umn.edu/geyer/5601/examp/subtoot.html
Stat 5101 Lecture Notes
 Stat 5101 Lecture Notes Charles J. Geyer Copyright 1998, 1999, 2000, 2001 by Charles J. Geyer May 7, 2001 ii Stat 5101 (Geyer) Course Notes Contents 1 Random Variables and Change of Variables 1 1.1 Random
Stat 5101 Lecture Notes Charles J. Geyer Copyright 1998, 1999, 2000, 2001 by Charles J. Geyer May 7, 2001 ii Stat 5101 (Geyer) Course Notes Contents 1 Random Variables and Change of Variables 1 1.1 Random
CS 361: Probability & Statistics
 October 17, 2017 CS 361: Probability & Statistics Inference Maximum likelihood: drawbacks A couple of things might trip up max likelihood estimation: 1) Finding the maximum of some functions can be quite
October 17, 2017 CS 361: Probability & Statistics Inference Maximum likelihood: drawbacks A couple of things might trip up max likelihood estimation: 1) Finding the maximum of some functions can be quite
Yet More Supporting Data Analysis for Unifying Life History Analysis for Inference of Fitness and Population Growth By Ruth G. Shaw, Charles J.
 Yet More Supporting Data Analysis for Unifying Life History Analysis for Inference of Fitness and Population Growth By Ruth G. Shaw, Charles J. Geyer, Stuart Wagenius, Helen H. Hangelbroek, and Julie R.
Yet More Supporting Data Analysis for Unifying Life History Analysis for Inference of Fitness and Population Growth By Ruth G. Shaw, Charles J. Geyer, Stuart Wagenius, Helen H. Hangelbroek, and Julie R.
Later in the same chapter (page 45) he asserted that
 Chapter 7 Randomization 7 Randomization 1 1 Fisher on randomization..................... 1 2 Shoes: a paired comparison................... 2 3 The randomization distribution................. 4 4 Theoretical
Chapter 7 Randomization 7 Randomization 1 1 Fisher on randomization..................... 1 2 Shoes: a paired comparison................... 2 3 The randomization distribution................. 4 4 Theoretical
Package bpp. December 13, 2016
 Type Package Package bpp December 13, 2016 Title Computations Around Bayesian Predictive Power Version 1.0.0 Date 2016-12-13 Author Kaspar Rufibach, Paul Jordan, Markus Abt Maintainer Kaspar Rufibach Depends
Type Package Package bpp December 13, 2016 Title Computations Around Bayesian Predictive Power Version 1.0.0 Date 2016-12-13 Author Kaspar Rufibach, Paul Jordan, Markus Abt Maintainer Kaspar Rufibach Depends
Aster Models and Lande-Arnold Beta By Charles J. Geyer and Ruth G. Shaw Technical Report No. 675 School of Statistics University of Minnesota January
 Aster Models and Lande-Arnold Beta By Charles J. Geyer and Ruth G. Shaw Technical Report No. 675 School of Statistics University of Minnesota January 9, 2010 Abstract Lande and Arnold (1983) proposed an
Aster Models and Lande-Arnold Beta By Charles J. Geyer and Ruth G. Shaw Technical Report No. 675 School of Statistics University of Minnesota January 9, 2010 Abstract Lande and Arnold (1983) proposed an
CS 361: Probability & Statistics
 March 14, 2018 CS 361: Probability & Statistics Inference The prior From Bayes rule, we know that we can express our function of interest as Likelihood Prior Posterior The right hand side contains the
March 14, 2018 CS 361: Probability & Statistics Inference The prior From Bayes rule, we know that we can express our function of interest as Likelihood Prior Posterior The right hand side contains the
Chapter 5 Exercises 1
 Chapter 5 Exercises 1 Data Analysis & Graphics Using R, 2 nd edn Solutions to Exercises (December 13, 2006) Preliminaries > library(daag) Exercise 2 For each of the data sets elastic1 and elastic2, determine
Chapter 5 Exercises 1 Data Analysis & Graphics Using R, 2 nd edn Solutions to Exercises (December 13, 2006) Preliminaries > library(daag) Exercise 2 For each of the data sets elastic1 and elastic2, determine
Stat260: Bayesian Modeling and Inference Lecture Date: February 10th, Jeffreys priors. exp 1 ) p 2
 Stat260: Bayesian Modeling and Inference Lecture Date: February 10th, 2010 Jeffreys priors Lecturer: Michael I. Jordan Scribe: Timothy Hunter 1 Priors for the multivariate Gaussian Consider a multivariate
Stat260: Bayesian Modeling and Inference Lecture Date: February 10th, 2010 Jeffreys priors Lecturer: Michael I. Jordan Scribe: Timothy Hunter 1 Priors for the multivariate Gaussian Consider a multivariate
Stat 5102 Notes: Markov Chain Monte Carlo and Bayesian Inference
 Stat 5102 Notes: Markov Chain Monte Carlo and Bayesian Inference Charles J. Geyer April 6, 2009 1 The Problem This is an example of an application of Bayes rule that requires some form of computer analysis.
Stat 5102 Notes: Markov Chain Monte Carlo and Bayesian Inference Charles J. Geyer April 6, 2009 1 The Problem This is an example of an application of Bayes rule that requires some form of computer analysis.
i=1 h n (ˆθ n ) = 0. (2)
 Stat 8112 Lecture Notes Unbiased Estimating Equations Charles J. Geyer April 29, 2012 1 Introduction In this handout we generalize the notion of maximum likelihood estimation to solution of unbiased estimating
Stat 8112 Lecture Notes Unbiased Estimating Equations Charles J. Geyer April 29, 2012 1 Introduction In this handout we generalize the notion of maximum likelihood estimation to solution of unbiased estimating
 Additional Problems Additional Problem 1 Like the http://www.stat.umn.edu/geyer/5102/examp/rlike.html#lmax example of maximum likelihood done by computer except instead of the gamma shape model, we will
Additional Problems Additional Problem 1 Like the http://www.stat.umn.edu/geyer/5102/examp/rlike.html#lmax example of maximum likelihood done by computer except instead of the gamma shape model, we will
Using R in Undergraduate Probability and Mathematical Statistics Courses. Amy G. Froelich Department of Statistics Iowa State University
 Using R in Undergraduate Probability and Mathematical Statistics Courses Amy G. Froelich Department of Statistics Iowa State University Undergraduate Probability and Mathematical Statistics at Iowa State
Using R in Undergraduate Probability and Mathematical Statistics Courses Amy G. Froelich Department of Statistics Iowa State University Undergraduate Probability and Mathematical Statistics at Iowa State
Prof. Thistleton MAT 505 Introduction to Probability Lecture 13
 Prof. Thistleton MAT 55 Introduction to Probability Lecture 3 Sections from Text and MIT Video Lecture: Sections 5.4, 5.6 http://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-4- probabilisticsystems-analysis-and-applied-probability-fall-2/video-lectures/lecture-8-continuousrandomvariables/
Prof. Thistleton MAT 55 Introduction to Probability Lecture 3 Sections from Text and MIT Video Lecture: Sections 5.4, 5.6 http://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-4- probabilisticsystems-analysis-and-applied-probability-fall-2/video-lectures/lecture-8-continuousrandomvariables/
Hypothesis Tests and Confidence Intervals Involving Fitness Landscapes fit by Aster Models By Charles J. Geyer and Ruth G. Shaw Technical Report No.
 Hypothesis Tests and Confidence Intervals Involving Fitness Landscapes fit by Aster Models By Charles J. Geyer and Ruth G. Shaw Technical Report No. 674 revised School of Statistics University of Minnesota
Hypothesis Tests and Confidence Intervals Involving Fitness Landscapes fit by Aster Models By Charles J. Geyer and Ruth G. Shaw Technical Report No. 674 revised School of Statistics University of Minnesota
Optimization. Charles J. Geyer School of Statistics University of Minnesota. Stat 8054 Lecture Notes
 Optimization Charles J. Geyer School of Statistics University of Minnesota Stat 8054 Lecture Notes 1 One-Dimensional Optimization Look at a graph. Grid search. 2 One-Dimensional Zero Finding Zero finding
Optimization Charles J. Geyer School of Statistics University of Minnesota Stat 8054 Lecture Notes 1 One-Dimensional Optimization Look at a graph. Grid search. 2 One-Dimensional Zero Finding Zero finding
R-companion to: Estimation of the Thurstonian model for the 2-AC protocol
 R-companion to: Estimation of the Thurstonian model for the 2-AC protocol Rune Haubo Bojesen Christensen, Hye-Seong Lee & Per Bruun Brockhoff August 24, 2017 This document describes how the examples in
R-companion to: Estimation of the Thurstonian model for the 2-AC protocol Rune Haubo Bojesen Christensen, Hye-Seong Lee & Per Bruun Brockhoff August 24, 2017 This document describes how the examples in
Hypothesis Tests and Confidence Intervals Involving Fitness Landscapes fit by Aster Models By Charles J. Geyer and Ruth G. Shaw Technical Report No.
 Hypothesis Tests and Confidence Intervals Involving Fitness Landscapes fit by Aster Models By Charles J. Geyer and Ruth G. Shaw Technical Report No. 674 School of Statistics University of Minnesota March
Hypothesis Tests and Confidence Intervals Involving Fitness Landscapes fit by Aster Models By Charles J. Geyer and Ruth G. Shaw Technical Report No. 674 School of Statistics University of Minnesota March
Weak convergence of Markov chain Monte Carlo II
 Weak convergence of Markov chain Monte Carlo II KAMATANI, Kengo Mar 2011 at Le Mans Background Markov chain Monte Carlo (MCMC) method is widely used in Statistical Science. It is easy to use, but difficult
Weak convergence of Markov chain Monte Carlo II KAMATANI, Kengo Mar 2011 at Le Mans Background Markov chain Monte Carlo (MCMC) method is widely used in Statistical Science. It is easy to use, but difficult
Stat 5102 Notes: Markov Chain Monte Carlo and Bayesian Inference
 Stat 5102 Notes: Markov Chain Monte Carlo and Bayesian Inference Charles J. Geyer March 30, 2012 1 The Problem This is an example of an application of Bayes rule that requires some form of computer analysis.
Stat 5102 Notes: Markov Chain Monte Carlo and Bayesian Inference Charles J. Geyer March 30, 2012 1 The Problem This is an example of an application of Bayes rule that requires some form of computer analysis.
Chapter 5 Exercises 1. Data Analysis & Graphics Using R Solutions to Exercises (April 24, 2004)
 Chapter 5 Exercises 1 Data Analysis & Graphics Using R Solutions to Exercises (April 24, 2004) Preliminaries > library(daag) Exercise 2 The final three sentences have been reworded For each of the data
Chapter 5 Exercises 1 Data Analysis & Graphics Using R Solutions to Exercises (April 24, 2004) Preliminaries > library(daag) Exercise 2 The final three sentences have been reworded For each of the data
Mathematical statistics
 October 1 st, 2018 Lecture 11: Sufficient statistic Where are we? Week 1 Week 2 Week 4 Week 7 Week 10 Week 14 Probability reviews Chapter 6: Statistics and Sampling Distributions Chapter 7: Point Estimation
October 1 st, 2018 Lecture 11: Sufficient statistic Where are we? Week 1 Week 2 Week 4 Week 7 Week 10 Week 14 Probability reviews Chapter 6: Statistics and Sampling Distributions Chapter 7: Point Estimation
Stat 5421 Lecture Notes Proper Conjugate Priors for Exponential Families Charles J. Geyer March 28, 2016
 Stat 5421 Lecture Notes Proper Conjugate Priors for Exponential Families Charles J. Geyer March 28, 2016 1 Theory This section explains the theory of conjugate priors for exponential families of distributions,
Stat 5421 Lecture Notes Proper Conjugate Priors for Exponential Families Charles J. Geyer March 28, 2016 1 Theory This section explains the theory of conjugate priors for exponential families of distributions,
Maximum-Likelihood Estimation: Basic Ideas
 Sociology 740 John Fox Lecture Notes Maximum-Likelihood Estimation: Basic Ideas Copyright 2014 by John Fox Maximum-Likelihood Estimation: Basic Ideas 1 I The method of maximum likelihood provides estimators
Sociology 740 John Fox Lecture Notes Maximum-Likelihood Estimation: Basic Ideas Copyright 2014 by John Fox Maximum-Likelihood Estimation: Basic Ideas 1 I The method of maximum likelihood provides estimators
Stat 8931 (Aster Models) Lecture Slides Deck 8
 Stat 8931 (Aster Models) Lecture Slides Deck 8 Charles J. Geyer School of Statistics University of Minnesota June 7, 2015 Conditional Aster Models A conditional aster model is a submodel parameterized
Stat 8931 (Aster Models) Lecture Slides Deck 8 Charles J. Geyer School of Statistics University of Minnesota June 7, 2015 Conditional Aster Models A conditional aster model is a submodel parameterized
Stat 3701 Lecture Notes: Bootstrap Charles J. Geyer April 17, 2017
 Stat 3701 Lecture Notes: Bootstrap Charles J. Geyer April 17, 2017 1 License This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License (http: //creativecommons.org/licenses/by-sa/4.0/).
Stat 3701 Lecture Notes: Bootstrap Charles J. Geyer April 17, 2017 1 License This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License (http: //creativecommons.org/licenses/by-sa/4.0/).
Fisher Example for Le Cam Made Simple
 Fisher Example for Le Cam Made Simple Charles J. Geyer May 20, 2005 1 Introduction 1.1 Model We do, rather inefficiently, an example from quantitative genetics, using a model originally proposed by Fisher
Fisher Example for Le Cam Made Simple Charles J. Geyer May 20, 2005 1 Introduction 1.1 Model We do, rather inefficiently, an example from quantitative genetics, using a model originally proposed by Fisher
Package pearson7. June 22, 2016
 Version 1.0-2 Date 2016-06-21 Package pearson7 June 22, 2016 Title Maximum Likelihood Inference for the Pearson VII Distribution with Shape Parameter 3/2 Author John Hughes Maintainer John Hughes
Version 1.0-2 Date 2016-06-21 Package pearson7 June 22, 2016 Title Maximum Likelihood Inference for the Pearson VII Distribution with Shape Parameter 3/2 Author John Hughes Maintainer John Hughes
Introduction 1. STA442/2101 Fall See last slide for copyright information. 1 / 33
 Introduction 1 STA442/2101 Fall 2016 1 See last slide for copyright information. 1 / 33 Background Reading Optional Chapter 1 of Linear models with R Chapter 1 of Davison s Statistical models: Data, and
Introduction 1 STA442/2101 Fall 2016 1 See last slide for copyright information. 1 / 33 Background Reading Optional Chapter 1 of Linear models with R Chapter 1 of Davison s Statistical models: Data, and
Lecture 17: The Exponential and Some Related Distributions
 Lecture 7: The Exponential and Some Related Distributions. Definition Definition: A continuous random variable X is said to have the exponential distribution with parameter if the density of X is e x if
Lecture 7: The Exponential and Some Related Distributions. Definition Definition: A continuous random variable X is said to have the exponential distribution with parameter if the density of X is e x if
Probability and Estimation. Alan Moses
 Probability and Estimation Alan Moses Random variables and probability A random variable is like a variable in algebra (e.g., y=e x ), but where at least part of the variability is taken to be stochastic.
Probability and Estimation Alan Moses Random variables and probability A random variable is like a variable in algebra (e.g., y=e x ), but where at least part of the variability is taken to be stochastic.
MS&E 226: Small Data
 MS&E 226: Small Data Lecture 12: Frequentist properties of estimators (v4) Ramesh Johari ramesh.johari@stanford.edu 1 / 39 Frequentist inference 2 / 39 Thinking like a frequentist Suppose that for some
MS&E 226: Small Data Lecture 12: Frequentist properties of estimators (v4) Ramesh Johari ramesh.johari@stanford.edu 1 / 39 Frequentist inference 2 / 39 Thinking like a frequentist Suppose that for some
Stat 5101 Lecture Slides: Deck 8 Dirichlet Distribution. Charles J. Geyer School of Statistics University of Minnesota
 Stat 5101 Lecture Slides: Deck 8 Dirichlet Distribution Charles J. Geyer School of Statistics University of Minnesota 1 The Dirichlet Distribution The Dirichlet Distribution is to the beta distribution
Stat 5101 Lecture Slides: Deck 8 Dirichlet Distribution Charles J. Geyer School of Statistics University of Minnesota 1 The Dirichlet Distribution The Dirichlet Distribution is to the beta distribution
Statistics/Mathematics 310 Larget April 14, Solution to Assignment #9
 Solution to Assignment #9 1. A sample s = (753.0, 1396.9, 1528.2, 1646.9, 717.6, 446.5, 848.0, 1222.0, 748.5, 610.1) is modeled as an i.i.d sample from a Gamma(α, λ) distribution. You may think of this
Solution to Assignment #9 1. A sample s = (753.0, 1396.9, 1528.2, 1646.9, 717.6, 446.5, 848.0, 1222.0, 748.5, 610.1) is modeled as an i.i.d sample from a Gamma(α, λ) distribution. You may think of this
Stat 451 Homework 04 Solutions 1
 Stat 45 Homewor 04 Solutions. (a) Let Z Gamma( ν, ) and, given Z z, X N(0, ν ). Note that z gamma RATE parameter in this case. The joint density of (X, Z) is is the f Z (z)f X Z (x z) z ν e z (z/ν) / e
Stat 45 Homewor 04 Solutions. (a) Let Z Gamma( ν, ) and, given Z z, X N(0, ν ). Note that z gamma RATE parameter in this case. The joint density of (X, Z) is is the f Z (z)f X Z (x z) z ν e z (z/ν) / e
Math 70 Homework 8 Michael Downs. and, given n iid observations, has log-likelihood function: k i n (2) = 1 n
 1. (a) The poisson distribution has density function f(k; λ) = λk e λ k! and, given n iid observations, has log-likelihood function: l(λ; k 1,..., k n ) = ln(λ) k i nλ ln(k i!) (1) and score equation:
1. (a) The poisson distribution has density function f(k; λ) = λk e λ k! and, given n iid observations, has log-likelihood function: l(λ; k 1,..., k n ) = ln(λ) k i nλ ln(k i!) (1) and score equation:
BUGS Bayesian inference Using Gibbs Sampling
 BUGS Bayesian inference Using Gibbs Sampling Glen DePalma Department of Statistics May 30, 2013 www.stat.purdue.edu/~gdepalma 1 / 20 Bayesian Philosophy I [Pearl] turned Bayesian in 1971, as soon as I
BUGS Bayesian inference Using Gibbs Sampling Glen DePalma Department of Statistics May 30, 2013 www.stat.purdue.edu/~gdepalma 1 / 20 Bayesian Philosophy I [Pearl] turned Bayesian in 1971, as soon as I
Statistics II: Estimating simple parametric models
 Statistics II: Estimating simple parametric models Richard Gill March 6, 2009 First of all we look at a normal plot of a sample from the t distribution with 9 degrees of freedom (and before that, we set
Statistics II: Estimating simple parametric models Richard Gill March 6, 2009 First of all we look at a normal plot of a sample from the t distribution with 9 degrees of freedom (and before that, we set
Likelihoods. P (Y = y) = f(y). For example, suppose Y has a geometric distribution on 1, 2,... with parameter p. Then the pmf is
 Likelihoods The distribution of a random variable Y with a discrete sample space (e.g. a finite sample space or the integers) can be characterized by its probability mass function (pmf): P (Y = y) = f(y).
Likelihoods The distribution of a random variable Y with a discrete sample space (e.g. a finite sample space or the integers) can be characterized by its probability mass function (pmf): P (Y = y) = f(y).
Inference for a Population Proportion
 Al Nosedal. University of Toronto. November 11, 2015 Statistical inference is drawing conclusions about an entire population based on data in a sample drawn from that population. From both frequentist
Al Nosedal. University of Toronto. November 11, 2015 Statistical inference is drawing conclusions about an entire population based on data in a sample drawn from that population. From both frequentist
Lecture 3 September 1
 STAT 383C: Statistical Modeling I Fall 2016 Lecture 3 September 1 Lecturer: Purnamrita Sarkar Scribe: Giorgio Paulon, Carlos Zanini Disclaimer: These scribe notes have been slightly proofread and may have
STAT 383C: Statistical Modeling I Fall 2016 Lecture 3 September 1 Lecturer: Purnamrita Sarkar Scribe: Giorgio Paulon, Carlos Zanini Disclaimer: These scribe notes have been slightly proofread and may have
At the end, f(m) 0. We can see how this works with a plot using the objective function f(x) = 1/2 e x2 :
 Root finding algorithms Consider a function f(x) for x (a, b). A root of f is a number x such that f(x ) = 0. Many computational problems can be viewed as a root finding problem, in particular optimums
Root finding algorithms Consider a function f(x) for x (a, b). A root of f is a number x such that f(x ) = 0. Many computational problems can be viewed as a root finding problem, in particular optimums
GOV 2001/ 1002/ E-2001 Section 3 Theories of Inference
 GOV 2001/ 1002/ E-2001 Section 3 Theories of Inference Solé Prillaman Harvard University February 11, 2015 1 / 48 LOGISTICS Reading Assignment- Unifying Political Methodology chs 2 and 4. Problem Set 3-
GOV 2001/ 1002/ E-2001 Section 3 Theories of Inference Solé Prillaman Harvard University February 11, 2015 1 / 48 LOGISTICS Reading Assignment- Unifying Political Methodology chs 2 and 4. Problem Set 3-
Mathematical statistics
 October 4 th, 2018 Lecture 12: Information Where are we? Week 1 Week 2 Week 4 Week 7 Week 10 Week 14 Probability reviews Chapter 6: Statistics and Sampling Distributions Chapter 7: Point Estimation Chapter
October 4 th, 2018 Lecture 12: Information Where are we? Week 1 Week 2 Week 4 Week 7 Week 10 Week 14 Probability reviews Chapter 6: Statistics and Sampling Distributions Chapter 7: Point Estimation Chapter
An exponential family of distributions is a parametric statistical model having densities with respect to some positive measure λ of the form.
 Stat 8112 Lecture Notes Asymptotics of Exponential Families Charles J. Geyer January 23, 2013 1 Exponential Families An exponential family of distributions is a parametric statistical model having densities
Stat 8112 Lecture Notes Asymptotics of Exponential Families Charles J. Geyer January 23, 2013 1 Exponential Families An exponential family of distributions is a parametric statistical model having densities
Chapter 8: Sampling distributions of estimators Sections
 Chapter 8: Sampling distributions of estimators Sections 8.1 Sampling distribution of a statistic 8.2 The Chi-square distributions 8.3 Joint Distribution of the sample mean and sample variance Skip: p.
Chapter 8: Sampling distributions of estimators Sections 8.1 Sampling distribution of a statistic 8.2 The Chi-square distributions 8.3 Joint Distribution of the sample mean and sample variance Skip: p.
5601 Notes: The Sandwich Estimator
 560 Notes: The Sandwich Estimator Charles J. Geyer December 6, 2003 Contents Maximum Likelihood Estimation 2. Likelihood for One Observation................... 2.2 Likelihood for Many IID Observations...............
560 Notes: The Sandwich Estimator Charles J. Geyer December 6, 2003 Contents Maximum Likelihood Estimation 2. Likelihood for One Observation................... 2.2 Likelihood for Many IID Observations...............
Statistical modelling: Theory and practice
 Statistical modelling: Theory and practice Introduction Gilles Guillot gigu@dtu.dk August 27, 2013 Gilles Guillot (gigu@dtu.dk) Stat. modelling August 27, 2013 1 / 6 Schedule 13 weeks weekly time slot:
Statistical modelling: Theory and practice Introduction Gilles Guillot gigu@dtu.dk August 27, 2013 Gilles Guillot (gigu@dtu.dk) Stat. modelling August 27, 2013 1 / 6 Schedule 13 weeks weekly time slot:
Lecture 16 Solving GLMs via IRWLS
 Lecture 16 Solving GLMs via IRWLS 09 November 2015 Taylor B. Arnold Yale Statistics STAT 312/612 Notes problem set 5 posted; due next class problem set 6, November 18th Goals for today fixed PCA example
Lecture 16 Solving GLMs via IRWLS 09 November 2015 Taylor B. Arnold Yale Statistics STAT 312/612 Notes problem set 5 posted; due next class problem set 6, November 18th Goals for today fixed PCA example
Lecture 10: Generalized likelihood ratio test
 Stat 200: Introduction to Statistical Inference Autumn 2018/19 Lecture 10: Generalized likelihood ratio test Lecturer: Art B. Owen October 25 Disclaimer: These notes have not been subjected to the usual
Stat 200: Introduction to Statistical Inference Autumn 2018/19 Lecture 10: Generalized likelihood ratio test Lecturer: Art B. Owen October 25 Disclaimer: These notes have not been subjected to the usual
Stat 451 Lecture Notes Simulating Random Variables
 Stat 451 Lecture Notes 05 12 Simulating Random Variables Ryan Martin UIC www.math.uic.edu/~rgmartin 1 Based on Chapter 6 in Givens & Hoeting, Chapter 22 in Lange, and Chapter 2 in Robert & Casella 2 Updated:
Stat 451 Lecture Notes 05 12 Simulating Random Variables Ryan Martin UIC www.math.uic.edu/~rgmartin 1 Based on Chapter 6 in Givens & Hoeting, Chapter 22 in Lange, and Chapter 2 in Robert & Casella 2 Updated:
Introduction to Machine Learning Prof. Sudeshna Sarkar Department of Computer Science and Engineering Indian Institute of Technology, Kharagpur
 Introduction to Machine Learning Prof. Sudeshna Sarkar Department of Computer Science and Engineering Indian Institute of Technology, Kharagpur Module 2 Lecture 05 Linear Regression Good morning, welcome
Introduction to Machine Learning Prof. Sudeshna Sarkar Department of Computer Science and Engineering Indian Institute of Technology, Kharagpur Module 2 Lecture 05 Linear Regression Good morning, welcome
P n. This is called the law of large numbers but it comes in two forms: Strong and Weak.
 Large Sample Theory Large Sample Theory is a name given to the search for approximations to the behaviour of statistical procedures which are derived by computing limits as the sample size, n, tends to
Large Sample Theory Large Sample Theory is a name given to the search for approximations to the behaviour of statistical procedures which are derived by computing limits as the sample size, n, tends to
GENERALIZED ERROR DISTRIBUTION
 CHAPTER 21 GENERALIZED ERROR DISTRIBUTION 21.1 ASSIGNMENT Write R functions for the Generalized Error Distribution, GED. Nelson [1991] introduced the Generalized Error Distribution for modeling GARCH time
CHAPTER 21 GENERALIZED ERROR DISTRIBUTION 21.1 ASSIGNMENT Write R functions for the Generalized Error Distribution, GED. Nelson [1991] introduced the Generalized Error Distribution for modeling GARCH time
Maximum Likelihood Estimation
 Maximum Likelihood Estimation Guy Lebanon February 19, 2011 Maximum likelihood estimation is the most popular general purpose method for obtaining estimating a distribution from a finite sample. It was
Maximum Likelihood Estimation Guy Lebanon February 19, 2011 Maximum likelihood estimation is the most popular general purpose method for obtaining estimating a distribution from a finite sample. It was
Copula Regression RAHUL A. PARSA DRAKE UNIVERSITY & STUART A. KLUGMAN SOCIETY OF ACTUARIES CASUALTY ACTUARIAL SOCIETY MAY 18,2011
 Copula Regression RAHUL A. PARSA DRAKE UNIVERSITY & STUART A. KLUGMAN SOCIETY OF ACTUARIES CASUALTY ACTUARIAL SOCIETY MAY 18,2011 Outline Ordinary Least Squares (OLS) Regression Generalized Linear Models
Copula Regression RAHUL A. PARSA DRAKE UNIVERSITY & STUART A. KLUGMAN SOCIETY OF ACTUARIES CASUALTY ACTUARIAL SOCIETY MAY 18,2011 Outline Ordinary Least Squares (OLS) Regression Generalized Linear Models
All other items including (and especially) CELL PHONES must be left at the front of the room.
 TEST #2 / STA 5327 (Inference) / Spring 2017 (April 24, 2017) Name: Directions This exam is closed book and closed notes. You will be supplied with scratch paper, and a copy of the Table of Common Distributions
TEST #2 / STA 5327 (Inference) / Spring 2017 (April 24, 2017) Name: Directions This exam is closed book and closed notes. You will be supplied with scratch paper, and a copy of the Table of Common Distributions
STATS 200: Introduction to Statistical Inference. Lecture 29: Course review
 STATS 200: Introduction to Statistical Inference Lecture 29: Course review Course review We started in Lecture 1 with a fundamental assumption: Data is a realization of a random process. The goal throughout
STATS 200: Introduction to Statistical Inference Lecture 29: Course review Course review We started in Lecture 1 with a fundamental assumption: Data is a realization of a random process. The goal throughout
For iid Y i the stronger conclusion holds; for our heuristics ignore differences between these notions.
 Large Sample Theory Study approximate behaviour of ˆθ by studying the function U. Notice U is sum of independent random variables. Theorem: If Y 1, Y 2,... are iid with mean µ then Yi n µ Called law of
Large Sample Theory Study approximate behaviour of ˆθ by studying the function U. Notice U is sum of independent random variables. Theorem: If Y 1, Y 2,... are iid with mean µ then Yi n µ Called law of
Linear Methods for Prediction
 Chapter 5 Linear Methods for Prediction 5.1 Introduction We now revisit the classification problem and focus on linear methods. Since our prediction Ĝ(x) will always take values in the discrete set G we
Chapter 5 Linear Methods for Prediction 5.1 Introduction We now revisit the classification problem and focus on linear methods. Since our prediction Ĝ(x) will always take values in the discrete set G we
Theory of Inference: Homework 4
 Theory of Inference: Homework 4 1. Here is a slightly technical question about hypothesis tests. Suppose that Y 1,..., Y n iid Poisson(λ) λ > 0. The two competing hypotheses are H 0 : λ = λ 0 versus H
Theory of Inference: Homework 4 1. Here is a slightly technical question about hypothesis tests. Suppose that Y 1,..., Y n iid Poisson(λ) λ > 0. The two competing hypotheses are H 0 : λ = λ 0 versus H
Example of MC for Continuous State Space
 Example of MC for Continuous State Space Notes 2, Sta624 The MC we discussed so far are discrete state space, i.e. the random variable take values in a discrete space. We shall discuss here briefl MC with
Example of MC for Continuous State Space Notes 2, Sta624 The MC we discussed so far are discrete state space, i.e. the random variable take values in a discrete space. We shall discuss here briefl MC with
Covariance function estimation in Gaussian process regression
 Covariance function estimation in Gaussian process regression François Bachoc Department of Statistics and Operations Research, University of Vienna WU Research Seminar - May 2015 François Bachoc Gaussian
Covariance function estimation in Gaussian process regression François Bachoc Department of Statistics and Operations Research, University of Vienna WU Research Seminar - May 2015 François Bachoc Gaussian
BIO5312 Biostatistics Lecture 13: Maximum Likelihood Estimation
 BIO5312 Biostatistics Lecture 13: Maximum Likelihood Estimation Yujin Chung November 29th, 2016 Fall 2016 Yujin Chung Lec13: MLE Fall 2016 1/24 Previous Parametric tests Mean comparisons (normality assumption)
BIO5312 Biostatistics Lecture 13: Maximum Likelihood Estimation Yujin Chung November 29th, 2016 Fall 2016 Yujin Chung Lec13: MLE Fall 2016 1/24 Previous Parametric tests Mean comparisons (normality assumption)
When is MLE appropriate
 When is MLE appropriate As a rule of thumb the following to assumptions need to be fulfilled to make MLE the appropriate method for estimation: The model is adequate. That is, we trust that one of the
When is MLE appropriate As a rule of thumb the following to assumptions need to be fulfilled to make MLE the appropriate method for estimation: The model is adequate. That is, we trust that one of the
Maximum Likelihood. F θ, θ Θ. X 1,..., X n. L(θ) = f(x i ; θ) l(θ) = ln L(θ) = i.i.d. i=1. n ln f(x i ; θ) Sometimes
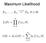 Maximum Likelihood X 1,..., X n i.i.d. F θ, θ Θ L(θ) = n i=1 f(x i ; θ) l(θ) = ln L(θ) = Sometimes n i=1 ln f(x i ; θ) Close your eyes and differentiate? Let X 1,..., X n be a random sample from a Gamma
Maximum Likelihood X 1,..., X n i.i.d. F θ, θ Θ L(θ) = n i=1 f(x i ; θ) l(θ) = ln L(θ) = Sometimes n i=1 ln f(x i ; θ) Close your eyes and differentiate? Let X 1,..., X n be a random sample from a Gamma
Probability Methods in Civil Engineering Prof. Rajib Maity Department of Civil Engineering Indian Institute of Technology, Kharagpur
 Probability Methods in Civil Engineering Prof. Rajib Maity Department of Civil Engineering Indian Institute of Technology, Kharagpur Lecture No. # 12 Probability Distribution of Continuous RVs (Contd.)
Probability Methods in Civil Engineering Prof. Rajib Maity Department of Civil Engineering Indian Institute of Technology, Kharagpur Lecture No. # 12 Probability Distribution of Continuous RVs (Contd.)
Stat 5031 Quadratic Response Surface Methods (QRSM) Sanford Weisberg November 30, 2015
 Stat 5031 Quadratic Response Surface Methods (QRSM) Sanford Weisberg November 30, 2015 One Variable x = spacing of plants (either 4, 8 12 or 16 inches), and y = plant yield (bushels per acre). Each condition
Stat 5031 Quadratic Response Surface Methods (QRSM) Sanford Weisberg November 30, 2015 One Variable x = spacing of plants (either 4, 8 12 or 16 inches), and y = plant yield (bushels per acre). Each condition
Logistic regression: Miscellaneous topics
 Logistic regression: Miscellaneous topics April 11 Introduction We have covered two approaches to inference for GLMs: the Wald approach and the likelihood ratio approach I claimed that the likelihood ratio
Logistic regression: Miscellaneous topics April 11 Introduction We have covered two approaches to inference for GLMs: the Wald approach and the likelihood ratio approach I claimed that the likelihood ratio
Lecture notes on statistical decision theory Econ 2110, fall 2013
 Lecture notes on statistical decision theory Econ 2110, fall 2013 Maximilian Kasy March 10, 2014 These lecture notes are roughly based on Robert, C. (2007). The Bayesian choice: from decision-theoretic
Lecture notes on statistical decision theory Econ 2110, fall 2013 Maximilian Kasy March 10, 2014 These lecture notes are roughly based on Robert, C. (2007). The Bayesian choice: from decision-theoretic
ACTEX CAS EXAM 3 STUDY GUIDE FOR MATHEMATICAL STATISTICS
 ACTEX CAS EXAM 3 STUDY GUIDE FOR MATHEMATICAL STATISTICS TABLE OF CONTENTS INTRODUCTORY NOTE NOTES AND PROBLEM SETS Section 1 - Point Estimation 1 Problem Set 1 15 Section 2 - Confidence Intervals and
ACTEX CAS EXAM 3 STUDY GUIDE FOR MATHEMATICAL STATISTICS TABLE OF CONTENTS INTRODUCTORY NOTE NOTES AND PROBLEM SETS Section 1 - Point Estimation 1 Problem Set 1 15 Section 2 - Confidence Intervals and
Interpreting Regression
 Interpreting Regression January 10, 2018 Contents Standard error of the estimate Homoscedasticity Using R to make interpretations about regresssion Questions In the tutorial on prediction we used the regression
Interpreting Regression January 10, 2018 Contents Standard error of the estimate Homoscedasticity Using R to make interpretations about regresssion Questions In the tutorial on prediction we used the regression
Bayesian inference. Rasmus Waagepetersen Department of Mathematics Aalborg University Denmark. April 10, 2017
 Bayesian inference Rasmus Waagepetersen Department of Mathematics Aalborg University Denmark April 10, 2017 1 / 22 Outline for today A genetic example Bayes theorem Examples Priors Posterior summaries
Bayesian inference Rasmus Waagepetersen Department of Mathematics Aalborg University Denmark April 10, 2017 1 / 22 Outline for today A genetic example Bayes theorem Examples Priors Posterior summaries
Beta statistics. Keywords. Bayes theorem. Bayes rule
 Keywords Beta statistics Tommy Norberg tommy@chalmers.se Mathematical Sciences Chalmers University of Technology Gothenburg, SWEDEN Bayes s formula Prior density Likelihood Posterior density Conjugate
Keywords Beta statistics Tommy Norberg tommy@chalmers.se Mathematical Sciences Chalmers University of Technology Gothenburg, SWEDEN Bayes s formula Prior density Likelihood Posterior density Conjugate
Advanced Statistical Modelling Statistical Modelling for Researchers
 161.304 - Advanced Statistical Modelling 161.776 - Statistical Modelling for Researchers Lecture 7 - Gradients, Hessian, Standard Errors, and Correlations Semester One - 2010 Project The are two new models
161.304 - Advanced Statistical Modelling 161.776 - Statistical Modelling for Researchers Lecture 7 - Gradients, Hessian, Standard Errors, and Correlations Semester One - 2010 Project The are two new models
On the Expected Absolute Value of a Bivariate Normal Distribution
 Journal of Statistical Theory and Applications Volume, Number 4, 0, pp. 37-377 ISSN 538-7887 On the Expected Absolute Value of a Bivariate Normal Distribution S. Reza H. Shojaie, Mina Aminghafari and Adel
Journal of Statistical Theory and Applications Volume, Number 4, 0, pp. 37-377 ISSN 538-7887 On the Expected Absolute Value of a Bivariate Normal Distribution S. Reza H. Shojaie, Mina Aminghafari and Adel
1 Introduction. P (n = 1 red ball drawn) =
 Introduction Exercises and outline solutions. Y has a pack of 4 cards (Ace and Queen of clubs, Ace and Queen of Hearts) from which he deals a random of selection 2 to player X. What is the probability
Introduction Exercises and outline solutions. Y has a pack of 4 cards (Ace and Queen of clubs, Ace and Queen of Hearts) from which he deals a random of selection 2 to player X. What is the probability
Statistics Ph.D. Qualifying Exam: Part I October 18, 2003
 Statistics Ph.D. Qualifying Exam: Part I October 18, 2003 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your answer
Statistics Ph.D. Qualifying Exam: Part I October 18, 2003 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your answer
Statistical Simulation An Introduction
 James H. Steiger Department of Psychology and Human Development Vanderbilt University Regression Modeling, 2009 Simulation Through Bootstrapping Introduction 1 Introduction When We Don t Need Simulation
James H. Steiger Department of Psychology and Human Development Vanderbilt University Regression Modeling, 2009 Simulation Through Bootstrapping Introduction 1 Introduction When We Don t Need Simulation
(Riemann) Integration Sucks!!!
 (Riemann) Integration Sucks!!! Peyam Ryan Tabrizian Friday, November 8th, 2 Are all functions integrable? Unfortunately not! Look at the handout Solutions to 5.2.67, 5.2.68, we get two examples of functions
(Riemann) Integration Sucks!!! Peyam Ryan Tabrizian Friday, November 8th, 2 Are all functions integrable? Unfortunately not! Look at the handout Solutions to 5.2.67, 5.2.68, we get two examples of functions
STAT 135 Lab 3 Asymptotic MLE and the Method of Moments
 STAT 135 Lab 3 Asymptotic MLE and the Method of Moments Rebecca Barter February 9, 2015 Maximum likelihood estimation (a reminder) Maximum likelihood estimation Suppose that we have a sample, X 1, X 2,...,
STAT 135 Lab 3 Asymptotic MLE and the Method of Moments Rebecca Barter February 9, 2015 Maximum likelihood estimation (a reminder) Maximum likelihood estimation Suppose that we have a sample, X 1, X 2,...,
Logistic Regression. Will Monroe CS 109. Lecture Notes #22 August 14, 2017
 1 Will Monroe CS 109 Logistic Regression Lecture Notes #22 August 14, 2017 Based on a chapter by Chris Piech Logistic regression is a classification algorithm1 that works by trying to learn a function
1 Will Monroe CS 109 Logistic Regression Lecture Notes #22 August 14, 2017 Based on a chapter by Chris Piech Logistic regression is a classification algorithm1 that works by trying to learn a function
Foundations of Statistical Inference
 Foundations of Statistical Inference Julien Berestycki Department of Statistics University of Oxford MT 2016 Julien Berestycki (University of Oxford) SB2a MT 2016 1 / 20 Lecture 6 : Bayesian Inference
Foundations of Statistical Inference Julien Berestycki Department of Statistics University of Oxford MT 2016 Julien Berestycki (University of Oxford) SB2a MT 2016 1 / 20 Lecture 6 : Bayesian Inference
hoa: An R Package Bundle for Higher Order Likelihood Inference
 hoa: An R Package Bundle for Higher Order Likelihood Inference by Alessandra R. Brazzale Rnews, 5/1 May 2005, pp. 20 27 Introduction The likelihood function represents the basic ingredient of many commonly
hoa: An R Package Bundle for Higher Order Likelihood Inference by Alessandra R. Brazzale Rnews, 5/1 May 2005, pp. 20 27 Introduction The likelihood function represents the basic ingredient of many commonly
Linear Systems of ODE: Nullclines, Eigenvector lines and trajectories
 Linear Systems of ODE: Nullclines, Eigenvector lines and trajectories James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University October 6, 203 Outline
Linear Systems of ODE: Nullclines, Eigenvector lines and trajectories James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University October 6, 203 Outline
Variations. ECE 6540, Lecture 10 Maximum Likelihood Estimation
 Variations ECE 6540, Lecture 10 Last Time BLUE (Best Linear Unbiased Estimator) Formulation Advantages Disadvantages 2 The BLUE A simplification Assume the estimator is a linear system For a single parameter
Variations ECE 6540, Lecture 10 Last Time BLUE (Best Linear Unbiased Estimator) Formulation Advantages Disadvantages 2 The BLUE A simplification Assume the estimator is a linear system For a single parameter
Previous lecture. Single variant association. Use genome-wide SNPs to account for confounding (population substructure)
 Previous lecture Single variant association Use genome-wide SNPs to account for confounding (population substructure) Estimation of effect size and winner s curse Meta-Analysis Today s outline P-value
Previous lecture Single variant association Use genome-wide SNPs to account for confounding (population substructure) Estimation of effect size and winner s curse Meta-Analysis Today s outline P-value
Stat 5421 Lecture Notes Fuzzy P-Values and Confidence Intervals Charles J. Geyer March 12, Discreteness versus Hypothesis Tests
 Stat 5421 Lecture Notes Fuzzy P-Values and Confidence Intervals Charles J. Geyer March 12, 2016 1 Discreteness versus Hypothesis Tests You cannot do an exact level α test for any α when the data are discrete.
Stat 5421 Lecture Notes Fuzzy P-Values and Confidence Intervals Charles J. Geyer March 12, 2016 1 Discreteness versus Hypothesis Tests You cannot do an exact level α test for any α when the data are discrete.
Conjugate Predictive Distributions and Generalized Entropies
 Conjugate Predictive Distributions and Generalized Entropies Eduardo Gutiérrez-Peña Department of Probability and Statistics IIMAS-UNAM, Mexico Padova, Italy. 21-23 March, 2013 Menu 1 Antipasto/Appetizer
Conjugate Predictive Distributions and Generalized Entropies Eduardo Gutiérrez-Peña Department of Probability and Statistics IIMAS-UNAM, Mexico Padova, Italy. 21-23 March, 2013 Menu 1 Antipasto/Appetizer
Bayesian Inference. STA 121: Regression Analysis Artin Armagan
 Bayesian Inference STA 121: Regression Analysis Artin Armagan Bayes Rule...s! Reverend Thomas Bayes Posterior Prior p(θ y) = p(y θ)p(θ)/p(y) Likelihood - Sampling Distribution Normalizing Constant: p(y
Bayesian Inference STA 121: Regression Analysis Artin Armagan Bayes Rule...s! Reverend Thomas Bayes Posterior Prior p(θ y) = p(y θ)p(θ)/p(y) Likelihood - Sampling Distribution Normalizing Constant: p(y
Fall 2017 STAT 532 Homework Peter Hoff. 1. Let P be a probability measure on a collection of sets A.
 1. Let P be a probability measure on a collection of sets A. (a) For each n N, let H n be a set in A such that H n H n+1. Show that P (H n ) monotonically converges to P ( k=1 H k) as n. (b) For each n
1. Let P be a probability measure on a collection of sets A. (a) For each n N, let H n be a set in A such that H n H n+1. Show that P (H n ) monotonically converges to P ( k=1 H k) as n. (b) For each n
Topic 17: Simple Hypotheses
 Topic 17: November, 2011 1 Overview and Terminology Statistical hypothesis testing is designed to address the question: Do the data provide sufficient evidence to conclude that we must depart from our
Topic 17: November, 2011 1 Overview and Terminology Statistical hypothesis testing is designed to address the question: Do the data provide sufficient evidence to conclude that we must depart from our
A Bayesian perspective on GMM and IV
 A Bayesian perspective on GMM and IV Christopher A. Sims Princeton University sims@princeton.edu November 26, 2013 What is a Bayesian perspective? A Bayesian perspective on scientific reporting views all
A Bayesian perspective on GMM and IV Christopher A. Sims Princeton University sims@princeton.edu November 26, 2013 What is a Bayesian perspective? A Bayesian perspective on scientific reporting views all
Exam 2 Practice Questions, 18.05, Spring 2014
 Exam 2 Practice Questions, 18.05, Spring 2014 Note: This is a set of practice problems for exam 2. The actual exam will be much shorter. Within each section we ve arranged the problems roughly in order
Exam 2 Practice Questions, 18.05, Spring 2014 Note: This is a set of practice problems for exam 2. The actual exam will be much shorter. Within each section we ve arranged the problems roughly in order
Non-Conjugate Models and Grid Approximations. Patrick Lam
 Non-Conjugate Models and Grid Approximations Patrick Lam Outline The Binomial Model with a Non-Conjugate Prior Bayesian Regression with Grid Approximations Outline The Binomial Model with a Non-Conjugate
Non-Conjugate Models and Grid Approximations Patrick Lam Outline The Binomial Model with a Non-Conjugate Prior Bayesian Regression with Grid Approximations Outline The Binomial Model with a Non-Conjugate
Statistics & Data Sciences: First Year Prelim Exam May 2018
 Statistics & Data Sciences: First Year Prelim Exam May 2018 Instructions: 1. Do not turn this page until instructed to do so. 2. Start each new question on a new sheet of paper. 3. This is a closed book
Statistics & Data Sciences: First Year Prelim Exam May 2018 Instructions: 1. Do not turn this page until instructed to do so. 2. Start each new question on a new sheet of paper. 3. This is a closed book
2017 SISG Bayesian Statistics for Genetics R Notes: Generalized Linear Modeling
 2017 SISG Bayesian Statistics for Genetics R Notes: Generalized Linear Modeling Jon Wakefield Departments of Statistics and Biostatistics, University of Washington 2017-09-05 Overview In this set of notes
2017 SISG Bayesian Statistics for Genetics R Notes: Generalized Linear Modeling Jon Wakefield Departments of Statistics and Biostatistics, University of Washington 2017-09-05 Overview In this set of notes
Introduction to Rare Event Simulation
 Introduction to Rare Event Simulation Brown University: Summer School on Rare Event Simulation Jose Blanchet Columbia University. Department of Statistics, Department of IEOR. Blanchet (Columbia) 1 / 31
Introduction to Rare Event Simulation Brown University: Summer School on Rare Event Simulation Jose Blanchet Columbia University. Department of Statistics, Department of IEOR. Blanchet (Columbia) 1 / 31
