Matrix Inequalities by Means of Block Matrices 1
|
|
|
- Kristian Thomas
- 6 years ago
- Views:
Transcription
1 Mathematical Inequalities & Applications, Vol. 4, No. 4, 200, pp Matrix Inequalities by Means of Block Matrices Fuzhen Zhang 2 Department of Math, Science and Technology Nova Southeastern University, Fort Lauderdale, Florida 3334, USA We first show a weak log-majorization inequality of singular values for partitioned positive semidefinite matrices which will imply some existing results of a number of authors, then present some basic matrix inequalities and apply them to obtain a number of matrix inequalities involving sum, ordinary product and Hadamard product. AMS classification: 5A45 Keywords: Eigenvalue inequality; Hadamard (Schur product; matrix inequality; positive semidefinite matrix; singular value inequality; unitarily invariant norm; weak log-majorization. INTRODUCTION One of the most useful tools for deriving matrix inequalities is to utilize block matrices; usually they are 2 2 in most applications. In this paper, we shall show a weak log-majorization inequality of singular values for partitioned positive semidefinite matrices, from which some classical and recent results of Bhatia and Kittaneh [4], Wang, Xi and Zhang [2], and Zhan [3] will follow. We shall also develop a new technique that is complementary to the Schur complement; while by making use of Schur complements, a number of determinantal, trace, and other inequalities are exhibited in [6]. With the new technique we add more inequalities to these in [6]. We denote the eigenvalues of an n n complex matrix X by λ i (X, i =, 2,...,n, and arrange them in modulus decreasing order λ (X λ 2 (X λ n (X. The singular values of an m n matrix X are denoted by σ (X,...,σ n (X and are also arranged in decreasing order. Note that σ i (X =λ i ( X foreachi, where X =(X X 2.Wefurtherwrite λ(x =(λ (X,λ 2 (X,...,λ n (X, σ(x =(σ (X,σ 2 (X,...,σ n (X. The leading principal k k submatrix of a matrix X is denoted by [X] k. The work was supported in part by the Nova Faculty Development Funds. 2 zhang@nova.edu
2 Write X 0ifX is a positive semidefinite matrix and X Y if X and Y are Hermitian matrices such that X Y 0. The strict inequality X > 0 denotes the positive definiteness of X. LetX Y =(x ij y ij be the Hadamard (Schur product of matrices X and Y of the same size and X the conjugate transpose of X. For complex vector x =(x,x 2,...,x n, we denote x =( x, x 2,..., x n, and for vectors x =(x,x 2,...,x n andy =(y,y 2,...,y n with nonnegative components in decreasing order, we write log x w log y to mean k k x i y i, i= i= k =, 2,...,n. As is well known, log x w log y yields x w y (see, e.g., [3, p. 42]. The latter means k k x i y i, k =, 2,...,n. i= i= The subscript w is dropped off in either w if equality holds when k = n. 2. A WEAK LOG-MAJORIZATION INEQUALITY Theorem Let A, B, and C be complex matrices such that A B B 0, C where A is m m, C is n n, andb is m n. Letrank (B =r. Then log σ(b w log µ, ( where µ =(µ,µ 2,...,µ n with µ i =max{λ i (A,λ i (C} if i r, 0 otherwise. Thus And if A, B, and C are all square of the same size, then σ(b w µ. (2 log λ(b w log µ. (3 Proof. We may assume that B 0. LetB = UDV be a singular value decomposition of the matrix B, whered = diag(σ (B,...,σ r (B, and U and V are m r and n r partial unitary matrices, respectively, i.e., U U = V V = I r.then U 0 A B U 0 U 0 V B = AU D C 0 V D V 0. CV 2
3 Taking the leading principal k k submatrix of each block, k r, wehave [U AU] k [D] k [D] k [V 0. CV ] k It follows that, by taking determinant for each block, Or equivalently, for each k r, det[d] 2 k det([u AU] k det([v CV ] k. k σ i (B 2 i= k λ i ([U AU] k λ i ([V CV ] k. i= By the eigenvalue interlacing theorem (see, e.g., [7, p ], we arrive at k σ i (B 2 i= k λ i (Aλ i (C i= k µ 2 i. The desired inequality (, thus (2, follows immediately by taking square roots. (3 is similarly obtained by letting B = WTW,whereT is an upper triangular matrix with diagonal entries λ (B,λ 2 (B,...,λ n (B andw is unitary. Corollary Let A 0, B 0 be of size n n. Then for any z C log σ(a z B w log σ(a + zb w log σ(a + z B. (4 Proof. For the second part, by (, it is sufficient to notice that A + z B A+ zb A + z 0; B A+ z B whereas the first part is proven by using the elementary inequality (see [2] or [3] z z + z. (4 is to appear in [3]. It refines the majorization inequality [2] i= log σ(a B w log σ(a + B and implies the weaker inequality for unitarily invariant norms ui [4] A z B ui A + zb ui A + z B ui. We note that the following matrix inequalities do not hold in general: A z B A zb A + z B. 3
4 For a counterexample, take z = i, 4 2 A = 2 and B = ( Then λ( A B =(3, 3, λ( A + ib =(6.95,.294, and λ(a + B =(9,. Corollary 2 Let A be any n n complex matrix. Then Proof. By (3, it is sufficient to notice that A A A 0. A log λ(a log σ(a. (5 Inequality (5 is the well known Weyl s inequality (see, e.g., [7, p. 7]. Remark 2.: Note that µ in ( and (3 cannot be replaced by σ(a orσ(c. Remark 2.2: In the proof of the theorem, we used the result [9, p. 42] that A B 0 det(b C B det A det C, B where A, B, and C square matrices of the same size. (This does not hold in general if B is rectangular. Using this result, one can also give a very simple proof to the determinantal inequality [9, p. 44]: Let λ i be complex numbers and A i 0. Then det(λ A + + λ k A k det( λ A + + λ k A k. This is because k i= ( λi A i λ i A i λ i A i λ i A i SOME BASIC INEQUALITIES H K Block matrices in the form have played a pivotal role in proving some K H matrix inequalities. We shall give some elementary matrix inequalities by applying a result on the block matrix to some partitioned positive semidefinite matrices and then to further derive inequalities on sum, ordinary and Hadamard products. Let H and K be (complex Hermitian matrices of the same size. Then H K 0 H ±K. (6 K H 4
5 This is seen by noticing the matrix identity via nonsingular congruence (similarity [ ] [ ] I I H K I I H K =. I I K H I I 0 H + K Obviously the eigenvalues of the block matrix in (6 are those of H ± K. Aproof of (6 for the real case is given in [5] via quadratic forms, and a characterization of the matrices K, which comprise a convex set, for the given H by trace inequalities is presented in [2]. A majorization inequality of the eigenvalues of the matrices H and K in (6 is seen in [4]: λ(k w λ(h, (7 which is strengthened as, by Theorem, log λ(k w log λ(h, (8 while the (stronger eigenvalue pairwise dominant inequalities λ i (K λ i (H do not hold for all i, though λ (K λ (H. (Thus H ±K H K. Moreover, by using the block matrix in (6 and the Albert theorem [], one has H ±K K = HH + K = KH + H, where H + is the Moore-Penrose generalized inverse of H. We now give our basic inequalities that easily follow from (6. Theorem 2 Let A, B, and C be n-square complex matrices such that A B 0. C B Then, with for + or, and, if AB = BA, A C ±(B B (9 A 2 CA 2 B B. (0 Proof. Since the block matrix via a permutation congruence is also positive semidefinite, we have (by the Schur Hadamard product theorem; see, e.g., [7, p. 92] A B C B A C B B = B C B A B 0. B A C (9 thus follows from (6. For (0, notice that if B commutes with A, thenb commutes with A 2 (see, e.g., [6, p. 322] or [7, p. 65]. Let A be nonsingular. Then C B A B = B A 2 A 2 B = A 2 B BA 2, 5
6 from which, by pre- and post-multiplying both sides by A 2, we arrive at the desired inequality. The singular case of A follows from a continuity argument. With the assumption of the theorem, we note the following. Remark 3.: For the sum in (9, the inequality A + C ±(B + B isalsoproven by observing A B I (I,±I B = A ± (B + B C ±I +C 0. Remark 3.2: Applying (8 to (9, we have explicitly and In particular, log λ(b + B w log λ(a + C log λ(b B w log λ(a C. det(b + B det(a + C and det(b B det(a C. Remark 3.3: The condition AB = BA for (0 is not removable in general, and B and B on the right hand side cannot be switched. It is easy to find an example that I B 0 C B C B, but C BB. B Remark 3.4: If the matrices B and C in the theorem commute, then C 2 AC 2 BB. 4. APPLICATIONS Applications of Theorem 2 to some frequently used 2 2 block positive semidefinite matrices result in some interesting inequalities. We present some as examples. Assume in the following that matrices A, B, andc are all n-square (some results also hold for the rectangular case. We itemize with the block positive semidefinite matrices followed by immediate inequalities and comments. Inequalities of one matrix: A I. I A 0, for any A>0, gives 6
7 i. 2I A + A ; ii. I A A. Comments: These are existing inequalities. Alternative proof of the first one is by a unitary diagonalization of A, while the second one s proof does not come that easy; it usually needs to prove A A (A A first (see, e.g, [8]. If A and B are both positive definite and n-square, by noticing that A I B I A B I I A = I B I A 0, B we obtain a result of Visick ([0, Theorem 5 ii]: 2. ( σ I A A σ I A B + B A 2I. 0, where σ is the largest singular value of (any A, implies 3. 2i. A + A 2σ I; 2ii. A A σ 2I. Comments: A direct proof for 2i and 2ii without using the theorem may not work out as smoothly, though they are weaker than the following inequality 3i. ( A 2α A A A 2( α 3i. A A A 2α A 2( α. 0, for any A and α [0, ], gives Comments: Taking α =, we have the comparison of sum and ordinary product A + A A A + I and the comparison of the Hadamard product and ordinary product A A A A I. In particular, if A is positive semidefinite, with the above A replaced by A 2, 2A 2 A + I, A 2 A 2 A I = diag(a. And taking α = 2, we have the inequalities involving sum and the two products A + A A + A, A A A A. (Note: Neither A + B A + B nor A B A B holds in general. 7
8 Inequalities of two or three matrices: A B 4. B A 0, for any A>0andanyB, gives B B 4i. ±(B B A (B A B. Comments: If B = I, then the block matrix is the same as the one in. Taking B = J, the all one matrix, and switching A and A, one obtains a lower bound for the inverse of A: Σ(A J A, where Σ(A = a ij is the sum of all entries of A. Note also that for any A>0 A J J Σ(A 0. J With a similar block matrix for B>0, one obtains a lower bound for A B: A B Σ(A Σ(B J. 5. ( A A 2 CB 2 B 2 C A 2 B 0, for A, B 0 and any contraction matrix C, gives 5i. (A 2 CB 2 (B 2 C A 2 A B. 6. Comments: Taking B = C = I for the Hadamard product yields A 2 A 2 A I as seen in 3. 5i is equivalent to (ACB (BCA A 2 B 2. Setting C = I gives AB + BA A 2 + B 2 and its Hadamard companion AB BA A 2 B 2. A A A B B A B 0, for any A and B, gives B 7. 6i. ±(A B B A A A B B. Comments: The Hadamard product case of 6i is seen in [0, Corollary 2]. In particular, if we take B = I for the Hadamard product, then ±(A A A A I. Letting A>0 and setting B = A results in ii. I + A A A + B A + B I + BB 0, for any A and B, gives 7i. (A + B (A + B (I + A A (I + BB. 8
9 Comments: This Hadamard product matrix inequality is compared to the conventional product matrix inequality (by taking Schur complement 8. (A + B(I + A A (A + B I + BB. AA I A B A B B 0, for any A and B, gives B I 8i. A B + A B AA I + B B I; 8ii. A A B B AA B B I. Comments: For A 0 and B 0, 8i gives the inequality of means for Hadamard product A B A2 + B 2 I. 2 It follows that for any correlation matrices A and B (with diagonal entries A 2 B 2 I. Notice that AA σ I. We put B = A t, the transpose of A in 8ii. Then 9. ( AA BB A B A B I A A A t A σ 4 I. 0, for any A and B, gives 9i. (A B(A B AA BB. 0. Comments: This has appeared in [5] and in a recent paper [0, Theorem 4]. A B A B A B A B 0, for any A and B, gives 0i. A B + A B A B + A B ; 0ii. A A B B A A B B. Comments: By taking B to be a matrix of 0 and, one can get the inequalities for the specified entries of A. For example, if B is a permutation matrix, then B = B = I and one gets the inequalities that compare any diagonal (entries of A to the diagonals of A and A. And one may also obtain inequalities for submatrices of A by setting B = ( 0 0 J 0. 9
10 ( A AB. B A B AB 0, for any A 0andanyn m matrix B, implies i. B A + AB A + B AB; ii. B A AB A (B AB. Comments: Setting B = A k yields the inequalities of shifting A 2A k+ A + A 2k+, k =, 2,..., and A k+ A k+ A A 2k+, k =, 2,... Inequalities of generalized inverses: A AA + 2. A + A A + 0, for any A 0, gives 2i. A A + A + A AA + ; 2ii. A + A + A + A + AA +. Comments: These are compared to the inequality of Visick in [, p. 282]: A A + (AA + AA + (A A + + (AA + AA +. Combining the above block matrices via sum or Hadamard product, one may get more block positive semidefinite matrices and thus more inequalities. For instance, if A 0andB>0, both n-square, then I A A A 2 ( B I I B = I B I A I A A 2 B 0. Thus A 2 B (I A(I B (I A =(diaga 2 (diag B. Note that the right hand side involves only the diagonal entries of A and B. addition, for any correlation matrix A and nonsingular correlation matrix B In A 2 B I. More inequalities are available by substituting the above matrices with matrices involving Kronecker product and by using the fact that the Hadamard product is a principal submatrix of the Kronecker product when the matrices are square. One also gets majorization inequalities by applying Theorem to the above block matrices. 0
11 References [] A. Albert, Conditions for positive and nonnegative definiteness in terms of pseudoinverses, SIAM J. Appl. Math, Vol. 7, No. 2, March 969. [2] P.A. Bekker, The positive semidefiniteness of partitioned matrices, Linear Algebra and Its Applications :26-278(988. [3] R. Bhatia, Matrix Analysis, Springer-Verlag, New York, 997. [4] R. Bhatia and F. Kittaneh, Norm Inequalities for Positive Operators, Letters in Math Phys. 43: (998. [5] C.H. FitzGerald and R.A. Horn, On fractional Hadamard powers of positive definite matrices, J. of Math Analysis and Appl. 6, pp (977. [6] P.R. Halmos, Linear Algebra Problem Book, Mathematical Association of America, Washington, DC, 995. [7] R.A. Horn and C.R. Johnson, Topics in Matrix Analysis, Cambridge University Press, New York, 99. [8] C.R. Johnson, Partitioned and Hadamard product matrix inequalities, J. Res. Nat. Bur. Standards, 83:585 59(978. [9] V.V. Prasolov, Problems and Theorems in Linear Algebra, American Mathematical Society, Providence, RI, 994. [0] G. Visick, A quantitative version of the observation that the Hadamard product is a principal submatrix of the Kronecker product, Linear Algebra and Its Applications 304( [] G. Visick, An algebra relationship between the Hadamard and Kronecker product with some applications, Bull.Soc.Math.Belg.42(990, 3, Ser. B, pp [2] B.-Y. Wang, B.-Y. Xi and F. Zhang, Some inequalities for sum and product of positive semidefinite matrices, Linear Algebra and Its Applications, 293( [3] X.-Z. Zhan, Singular values of differences of positive semidefinite matrices, SIAM Matrix Analysis and Appl., Vol. 22, No. 3, pp [4] F. Zhang, Another Proof of a Singular Value Inequality Concerning Hadamard Products of Matrices, Linear and Multilinear Algebra, Vol. 22 (988, pp [5] F. Zhang, Notes on Hadamard products of matrices, Linear and Multilinear Algebra, Vol. 25, pp , 989. [6] F. Zhang, Schur complements and matrix inequalities in the Löwner ordering, Linear Algebra and Its Applications, 32( [7] F. Zhang, Matrix Theory: Basic Results and Techniques, Springer-Verlag, New York, 999.
Some inequalities for sum and product of positive semide nite matrices
 Linear Algebra and its Applications 293 (1999) 39±49 www.elsevier.com/locate/laa Some inequalities for sum and product of positive semide nite matrices Bo-Ying Wang a,1,2, Bo-Yan Xi a, Fuzhen Zhang b,
Linear Algebra and its Applications 293 (1999) 39±49 www.elsevier.com/locate/laa Some inequalities for sum and product of positive semide nite matrices Bo-Ying Wang a,1,2, Bo-Yan Xi a, Fuzhen Zhang b,
Spectral inequalities and equalities involving products of matrices
 Spectral inequalities and equalities involving products of matrices Chi-Kwong Li 1 Department of Mathematics, College of William & Mary, Williamsburg, Virginia 23187 (ckli@math.wm.edu) Yiu-Tung Poon Department
Spectral inequalities and equalities involving products of matrices Chi-Kwong Li 1 Department of Mathematics, College of William & Mary, Williamsburg, Virginia 23187 (ckli@math.wm.edu) Yiu-Tung Poon Department
Trace Inequalities for a Block Hadamard Product
 Filomat 32:1 2018), 285 292 https://doiorg/102298/fil1801285p Published by Faculty of Sciences and Mathematics, University of Niš, Serbia Available at: http://wwwpmfniacrs/filomat Trace Inequalities for
Filomat 32:1 2018), 285 292 https://doiorg/102298/fil1801285p Published by Faculty of Sciences and Mathematics, University of Niš, Serbia Available at: http://wwwpmfniacrs/filomat Trace Inequalities for
Abstract. In this article, several matrix norm inequalities are proved by making use of the Hiroshima 2003 result on majorization relations.
 HIROSHIMA S THEOREM AND MATRIX NORM INEQUALITIES MINGHUA LIN AND HENRY WOLKOWICZ Abstract. In this article, several matrix norm inequalities are proved by making use of the Hiroshima 2003 result on majorization
HIROSHIMA S THEOREM AND MATRIX NORM INEQUALITIES MINGHUA LIN AND HENRY WOLKOWICZ Abstract. In this article, several matrix norm inequalities are proved by making use of the Hiroshima 2003 result on majorization
ELA ON A SCHUR COMPLEMENT INEQUALITY FOR THE HADAMARD PRODUCT OF CERTAIN TOTALLY NONNEGATIVE MATRICES
 ON A SCHUR COMPLEMENT INEQUALITY FOR THE HADAMARD PRODUCT OF CERTAIN TOTALLY NONNEGATIVE MATRICES ZHONGPENG YANG AND XIAOXIA FENG Abstract. Under the entrywise dominance partial ordering, T.L. Markham
ON A SCHUR COMPLEMENT INEQUALITY FOR THE HADAMARD PRODUCT OF CERTAIN TOTALLY NONNEGATIVE MATRICES ZHONGPENG YANG AND XIAOXIA FENG Abstract. Under the entrywise dominance partial ordering, T.L. Markham
Singular Value and Norm Inequalities Associated with 2 x 2 Positive Semidefinite Block Matrices
 Electronic Journal of Linear Algebra Volume 32 Volume 32 (2017) Article 8 2017 Singular Value Norm Inequalities Associated with 2 x 2 Positive Semidefinite Block Matrices Aliaa Burqan Zarqa University,
Electronic Journal of Linear Algebra Volume 32 Volume 32 (2017) Article 8 2017 Singular Value Norm Inequalities Associated with 2 x 2 Positive Semidefinite Block Matrices Aliaa Burqan Zarqa University,
Singular Value Inequalities for Real and Imaginary Parts of Matrices
 Filomat 3:1 16, 63 69 DOI 1.98/FIL16163C Published by Faculty of Sciences Mathematics, University of Niš, Serbia Available at: http://www.pmf.ni.ac.rs/filomat Singular Value Inequalities for Real Imaginary
Filomat 3:1 16, 63 69 DOI 1.98/FIL16163C Published by Faculty of Sciences Mathematics, University of Niš, Serbia Available at: http://www.pmf.ni.ac.rs/filomat Singular Value Inequalities for Real Imaginary
arxiv: v1 [math.ra] 8 Apr 2016
![arxiv: v1 [math.ra] 8 Apr 2016 arxiv: v1 [math.ra] 8 Apr 2016](/thumbs/94/121659101.jpg) ON A DETERMINANTAL INEQUALITY ARISING FROM DIFFUSION TENSOR IMAGING MINGHUA LIN arxiv:1604.04141v1 [math.ra] 8 Apr 2016 Abstract. In comparing geodesics induced by different metrics, Audenaert formulated
ON A DETERMINANTAL INEQUALITY ARISING FROM DIFFUSION TENSOR IMAGING MINGHUA LIN arxiv:1604.04141v1 [math.ra] 8 Apr 2016 Abstract. In comparing geodesics induced by different metrics, Audenaert formulated
On the Schur Complement of Diagonally Dominant Matrices
 On the Schur Complement of Diagonally Dominant Matrices T.-G. Lei, C.-W. Woo,J.-Z.Liu, and F. Zhang 1 Introduction In 1979, Carlson and Markham proved that the Schur complements of strictly diagonally
On the Schur Complement of Diagonally Dominant Matrices T.-G. Lei, C.-W. Woo,J.-Z.Liu, and F. Zhang 1 Introduction In 1979, Carlson and Markham proved that the Schur complements of strictly diagonally
Schur complements and matrix inequalities in the Löwner ordering
 Linear Algebra and its Applications 321 (2000) 399 410 www.elsevier.com/locate/laa Schur complements and matrix inequalities in the Löwner ordering Fuzhen Zhang Department of Mathematics, Sciences and
Linear Algebra and its Applications 321 (2000) 399 410 www.elsevier.com/locate/laa Schur complements and matrix inequalities in the Löwner ordering Fuzhen Zhang Department of Mathematics, Sciences and
InequalitiesInvolvingHadamardProductsof HermitianMatrices y
 AppliedMathematics E-Notes, 1(2001), 91-96 c Availablefreeatmirrorsites ofhttp://math2.math.nthu.edu.tw/»amen/ InequalitiesInvolvingHadamardProductsof HermitianMatrices y Zhong-pengYang z,xianzhangchong-guangcao
AppliedMathematics E-Notes, 1(2001), 91-96 c Availablefreeatmirrorsites ofhttp://math2.math.nthu.edu.tw/»amen/ InequalitiesInvolvingHadamardProductsof HermitianMatrices y Zhong-pengYang z,xianzhangchong-guangcao
arxiv: v3 [math.ra] 22 Aug 2014
![arxiv: v3 [math.ra] 22 Aug 2014 arxiv: v3 [math.ra] 22 Aug 2014](/thumbs/91/105622575.jpg) arxiv:1407.0331v3 [math.ra] 22 Aug 2014 Positivity of Partitioned Hermitian Matrices with Unitarily Invariant Norms Abstract Chi-Kwong Li a, Fuzhen Zhang b a Department of Mathematics, College of William
arxiv:1407.0331v3 [math.ra] 22 Aug 2014 Positivity of Partitioned Hermitian Matrices with Unitarily Invariant Norms Abstract Chi-Kwong Li a, Fuzhen Zhang b a Department of Mathematics, College of William
Jordan Canonical Form of A Partitioned Complex Matrix and Its Application to Real Quaternion Matrices
 COMMUNICATIONS IN ALGEBRA, 29(6, 2363-2375(200 Jordan Canonical Form of A Partitioned Complex Matrix and Its Application to Real Quaternion Matrices Fuzhen Zhang Department of Math Science and Technology
COMMUNICATIONS IN ALGEBRA, 29(6, 2363-2375(200 Jordan Canonical Form of A Partitioned Complex Matrix and Its Application to Real Quaternion Matrices Fuzhen Zhang Department of Math Science and Technology
Foundations of Matrix Analysis
 1 Foundations of Matrix Analysis In this chapter we recall the basic elements of linear algebra which will be employed in the remainder of the text For most of the proofs as well as for the details, the
1 Foundations of Matrix Analysis In this chapter we recall the basic elements of linear algebra which will be employed in the remainder of the text For most of the proofs as well as for the details, the
University, Fort Lauderdale, FL, USA. Published online: 30 Jun To link to this article:
 This article was downloaded by: [172.4.212.45] On: 12 August 2014, At: 11:32 Publisher: Taylor & Francis Informa Ltd Registered in England and Wales Registered Number: 1072954 Registered office: Mortimer
This article was downloaded by: [172.4.212.45] On: 12 August 2014, At: 11:32 Publisher: Taylor & Francis Informa Ltd Registered in England and Wales Registered Number: 1072954 Registered office: Mortimer
Math Camp Lecture 4: Linear Algebra. Xiao Yu Wang. Aug 2010 MIT. Xiao Yu Wang (MIT) Math Camp /10 1 / 88
 Math Camp 2010 Lecture 4: Linear Algebra Xiao Yu Wang MIT Aug 2010 Xiao Yu Wang (MIT) Math Camp 2010 08/10 1 / 88 Linear Algebra Game Plan Vector Spaces Linear Transformations and Matrices Determinant
Math Camp 2010 Lecture 4: Linear Algebra Xiao Yu Wang MIT Aug 2010 Xiao Yu Wang (MIT) Math Camp 2010 08/10 1 / 88 Linear Algebra Game Plan Vector Spaces Linear Transformations and Matrices Determinant
Multiplicative Perturbation Bounds of the Group Inverse and Oblique Projection
 Filomat 30: 06, 37 375 DOI 0.98/FIL67M Published by Faculty of Sciences Mathematics, University of Niš, Serbia Available at: http://www.pmf.ni.ac.rs/filomat Multiplicative Perturbation Bounds of the Group
Filomat 30: 06, 37 375 DOI 0.98/FIL67M Published by Faculty of Sciences Mathematics, University of Niš, Serbia Available at: http://www.pmf.ni.ac.rs/filomat Multiplicative Perturbation Bounds of the Group
CHARACTERIZATIONS. is pd/psd. Possible for all pd/psd matrices! Generating a pd/psd matrix: Choose any B Mn, then
 LECTURE 6: POSITIVE DEFINITE MATRICES Definition: A Hermitian matrix A Mn is positive definite (pd) if x Ax > 0 x C n,x 0 A is positive semidefinite (psd) if x Ax 0. Definition: A Mn is negative (semi)definite
LECTURE 6: POSITIVE DEFINITE MATRICES Definition: A Hermitian matrix A Mn is positive definite (pd) if x Ax > 0 x C n,x 0 A is positive semidefinite (psd) if x Ax 0. Definition: A Mn is negative (semi)definite
ETNA Kent State University
 Electronic Transactions on Numerical Analysis. Volume 1, pp. 1-11, 8. Copyright 8,. ISSN 168-961. MAJORIZATION BOUNDS FOR RITZ VALUES OF HERMITIAN MATRICES CHRISTOPHER C. PAIGE AND IVO PANAYOTOV Abstract.
Electronic Transactions on Numerical Analysis. Volume 1, pp. 1-11, 8. Copyright 8,. ISSN 168-961. MAJORIZATION BOUNDS FOR RITZ VALUES OF HERMITIAN MATRICES CHRISTOPHER C. PAIGE AND IVO PANAYOTOV Abstract.
Journal of Inequalities in Pure and Applied Mathematics
 Journal of Inequalities in Pure and Applied Mathematics http://jipam.vu.edu.au/ Volume 7, Issue 1, Article 34, 2006 MATRIX EQUALITIES AND INEQUALITIES INVOLVING KHATRI-RAO AND TRACY-SINGH SUMS ZEYAD AL
Journal of Inequalities in Pure and Applied Mathematics http://jipam.vu.edu.au/ Volume 7, Issue 1, Article 34, 2006 MATRIX EQUALITIES AND INEQUALITIES INVOLVING KHATRI-RAO AND TRACY-SINGH SUMS ZEYAD AL
Generalized Schur complements of matrices and compound matrices
 Electronic Journal of Linear Algebra Volume 2 Volume 2 (200 Article 3 200 Generalized Schur complements of matrices and compound matrices Jianzhou Liu Rong Huang Follow this and additional wors at: http://repository.uwyo.edu/ela
Electronic Journal of Linear Algebra Volume 2 Volume 2 (200 Article 3 200 Generalized Schur complements of matrices and compound matrices Jianzhou Liu Rong Huang Follow this and additional wors at: http://repository.uwyo.edu/ela
A note on an unusual type of polar decomposition
 A note on an unusual type of polar decomposition H. Faßbender a, Kh. D. Ikramov b,,1 a Institut Computational Mathematics, TU Braunschweig, Pockelsstr. 14, D-38023 Braunschweig, Germany. b Faculty of Computational
A note on an unusual type of polar decomposition H. Faßbender a, Kh. D. Ikramov b,,1 a Institut Computational Mathematics, TU Braunschweig, Pockelsstr. 14, D-38023 Braunschweig, Germany. b Faculty of Computational
MINIMAL NORMAL AND COMMUTING COMPLETIONS
 INTERNATIONAL JOURNAL OF INFORMATION AND SYSTEMS SCIENCES Volume 4, Number 1, Pages 5 59 c 8 Institute for Scientific Computing and Information MINIMAL NORMAL AND COMMUTING COMPLETIONS DAVID P KIMSEY AND
INTERNATIONAL JOURNAL OF INFORMATION AND SYSTEMS SCIENCES Volume 4, Number 1, Pages 5 59 c 8 Institute for Scientific Computing and Information MINIMAL NORMAL AND COMMUTING COMPLETIONS DAVID P KIMSEY AND
Inequalities For Spreads Of Matrix Sums And Products
 Applied Mathematics E-Notes, 4(004), 150-159 c ISSN 1607-510 Available free at mirror sites of http://www.math.nthu.edu.tw/ amen/ Inequalities For Spreads Of Matrix Sums And Products Jorma K. Meriosi,
Applied Mathematics E-Notes, 4(004), 150-159 c ISSN 1607-510 Available free at mirror sites of http://www.math.nthu.edu.tw/ amen/ Inequalities For Spreads Of Matrix Sums And Products Jorma K. Meriosi,
A norm inequality for pairs of commuting positive semidefinite matrices
 Electronic Journal of Linear Algebra Volume 30 Volume 30 (205) Article 5 205 A norm inequality for pairs of commuting positive semidefinite matrices Koenraad MR Audenaert Royal Holloway University of London,
Electronic Journal of Linear Algebra Volume 30 Volume 30 (205) Article 5 205 A norm inequality for pairs of commuting positive semidefinite matrices Koenraad MR Audenaert Royal Holloway University of London,
Two Results About The Matrix Exponential
 Two Results About The Matrix Exponential Hongguo Xu Abstract Two results about the matrix exponential are given. One is to characterize the matrices A which satisfy e A e AH = e AH e A, another is about
Two Results About The Matrix Exponential Hongguo Xu Abstract Two results about the matrix exponential are given. One is to characterize the matrices A which satisfy e A e AH = e AH e A, another is about
ON WEIGHTED PARTIAL ORDERINGS ON THE SET OF RECTANGULAR COMPLEX MATRICES
 ON WEIGHTED PARTIAL ORDERINGS ON THE SET OF RECTANGULAR COMPLEX MATRICES HANYU LI, HU YANG College of Mathematics and Physics Chongqing University Chongqing, 400030, P.R. China EMail: lihy.hy@gmail.com,
ON WEIGHTED PARTIAL ORDERINGS ON THE SET OF RECTANGULAR COMPLEX MATRICES HANYU LI, HU YANG College of Mathematics and Physics Chongqing University Chongqing, 400030, P.R. China EMail: lihy.hy@gmail.com,
ON WEIGHTED PARTIAL ORDERINGS ON THE SET OF RECTANGULAR COMPLEX MATRICES
 olume 10 2009, Issue 2, Article 41, 10 pp. ON WEIGHTED PARTIAL ORDERINGS ON THE SET OF RECTANGULAR COMPLEX MATRICES HANYU LI, HU YANG, AND HUA SHAO COLLEGE OF MATHEMATICS AND PHYSICS CHONGQING UNIERSITY
olume 10 2009, Issue 2, Article 41, 10 pp. ON WEIGHTED PARTIAL ORDERINGS ON THE SET OF RECTANGULAR COMPLEX MATRICES HANYU LI, HU YANG, AND HUA SHAO COLLEGE OF MATHEMATICS AND PHYSICS CHONGQING UNIERSITY
Norm inequalities related to the matrix geometric mean
 isid/ms/2012/07 April 20, 2012 http://www.isid.ac.in/ statmath/eprints Norm inequalities related to the matrix geometric mean RAJENDRA BHATIA PRIYANKA GROVER Indian Statistical Institute, Delhi Centre
isid/ms/2012/07 April 20, 2012 http://www.isid.ac.in/ statmath/eprints Norm inequalities related to the matrix geometric mean RAJENDRA BHATIA PRIYANKA GROVER Indian Statistical Institute, Delhi Centre
Generalized Numerical Radius Inequalities for Operator Matrices
 International Mathematical Forum, Vol. 6, 011, no. 48, 379-385 Generalized Numerical Radius Inequalities for Operator Matrices Wathiq Bani-Domi Department of Mathematics Yarmouk University, Irbed, Jordan
International Mathematical Forum, Vol. 6, 011, no. 48, 379-385 Generalized Numerical Radius Inequalities for Operator Matrices Wathiq Bani-Domi Department of Mathematics Yarmouk University, Irbed, Jordan
MAPPING AND PRESERVER PROPERTIES OF THE PRINCIPAL PIVOT TRANSFORM
 MAPPING AND PRESERVER PROPERTIES OF THE PRINCIPAL PIVOT TRANSFORM OLGA SLYUSAREVA AND MICHAEL TSATSOMEROS Abstract. The principal pivot transform (PPT) is a transformation of a matrix A tantamount to exchanging
MAPPING AND PRESERVER PROPERTIES OF THE PRINCIPAL PIVOT TRANSFORM OLGA SLYUSAREVA AND MICHAEL TSATSOMEROS Abstract. The principal pivot transform (PPT) is a transformation of a matrix A tantamount to exchanging
Analytical formulas for calculating extremal ranks and inertias of quadratic matrix-valued functions and their applications
 Analytical formulas for calculating extremal ranks and inertias of quadratic matrix-valued functions and their applications Yongge Tian CEMA, Central University of Finance and Economics, Beijing 100081,
Analytical formulas for calculating extremal ranks and inertias of quadratic matrix-valued functions and their applications Yongge Tian CEMA, Central University of Finance and Economics, Beijing 100081,
2. Linear algebra. matrices and vectors. linear equations. range and nullspace of matrices. function of vectors, gradient and Hessian
 FE661 - Statistical Methods for Financial Engineering 2. Linear algebra Jitkomut Songsiri matrices and vectors linear equations range and nullspace of matrices function of vectors, gradient and Hessian
FE661 - Statistical Methods for Financial Engineering 2. Linear algebra Jitkomut Songsiri matrices and vectors linear equations range and nullspace of matrices function of vectors, gradient and Hessian
MATRIX ALGEBRA AND SYSTEMS OF EQUATIONS. + + x 1 x 2. x n 8 (4) 3 4 2
 MATRIX ALGEBRA AND SYSTEMS OF EQUATIONS SYSTEMS OF EQUATIONS AND MATRICES Representation of a linear system The general system of m equations in n unknowns can be written a x + a 2 x 2 + + a n x n b a
MATRIX ALGEBRA AND SYSTEMS OF EQUATIONS SYSTEMS OF EQUATIONS AND MATRICES Representation of a linear system The general system of m equations in n unknowns can be written a x + a 2 x 2 + + a n x n b a
STAT 309: MATHEMATICAL COMPUTATIONS I FALL 2017 LECTURE 5
 STAT 39: MATHEMATICAL COMPUTATIONS I FALL 17 LECTURE 5 1 existence of svd Theorem 1 (Existence of SVD) Every matrix has a singular value decomposition (condensed version) Proof Let A C m n and for simplicity
STAT 39: MATHEMATICAL COMPUTATIONS I FALL 17 LECTURE 5 1 existence of svd Theorem 1 (Existence of SVD) Every matrix has a singular value decomposition (condensed version) Proof Let A C m n and for simplicity
Some bounds for the spectral radius of the Hadamard product of matrices
 Some bounds for the spectral radius of the Hadamard product of matrices Guang-Hui Cheng, Xiao-Yu Cheng, Ting-Zhu Huang, Tin-Yau Tam. June 1, 2004 Abstract Some bounds for the spectral radius of the Hadamard
Some bounds for the spectral radius of the Hadamard product of matrices Guang-Hui Cheng, Xiao-Yu Cheng, Ting-Zhu Huang, Tin-Yau Tam. June 1, 2004 Abstract Some bounds for the spectral radius of the Hadamard
OHSx XM511 Linear Algebra: Solutions to Online True/False Exercises
 This document gives the solutions to all of the online exercises for OHSx XM511. The section ( ) numbers refer to the textbook. TYPE I are True/False. Answers are in square brackets [. Lecture 02 ( 1.1)
This document gives the solutions to all of the online exercises for OHSx XM511. The section ( ) numbers refer to the textbook. TYPE I are True/False. Answers are in square brackets [. Lecture 02 ( 1.1)
Taxonomy of n n Matrices. Complex. Integer. Real. diagonalizable. Real. Doubly stochastic. Unimodular. Invertible. Permutation. Orthogonal.
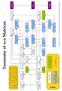 Doubly stochastic Taxonomy of n n Matrices Each rectangle represents one class of complex n n matrices. Arrows indicate subset relations. Classes in green are closed under multiplication. Classes in blue
Doubly stochastic Taxonomy of n n Matrices Each rectangle represents one class of complex n n matrices. Arrows indicate subset relations. Classes in green are closed under multiplication. Classes in blue
Matrices. Chapter What is a Matrix? We review the basic matrix operations. An array of numbers a a 1n A = a m1...
 Chapter Matrices We review the basic matrix operations What is a Matrix? An array of numbers a a n A = a m a mn with m rows and n columns is a m n matrix Element a ij in located in position (i, j The elements
Chapter Matrices We review the basic matrix operations What is a Matrix? An array of numbers a a n A = a m a mn with m rows and n columns is a m n matrix Element a ij in located in position (i, j The elements
Chapter 1. Matrix Algebra
 ST4233, Linear Models, Semester 1 2008-2009 Chapter 1. Matrix Algebra 1 Matrix and vector notation Definition 1.1 A matrix is a rectangular or square array of numbers of variables. We use uppercase boldface
ST4233, Linear Models, Semester 1 2008-2009 Chapter 1. Matrix Algebra 1 Matrix and vector notation Definition 1.1 A matrix is a rectangular or square array of numbers of variables. We use uppercase boldface
Matrix Mathematics. Theory, Facts, and Formulas with Application to Linear Systems Theory. Dennis S. Bernstein
 Matrix Mathematics Theory, Facts, and Formulas with Application to Linear Systems Theory Dennis S. Bernstein PRINCETON UNIVERSITY PRESS PRINCETON AND OXFORD Contents Special Symbols xv Conventions, Notation,
Matrix Mathematics Theory, Facts, and Formulas with Application to Linear Systems Theory Dennis S. Bernstein PRINCETON UNIVERSITY PRESS PRINCETON AND OXFORD Contents Special Symbols xv Conventions, Notation,
SCHUR IDEALS AND HOMOMORPHISMS OF THE SEMIDEFINITE CONE
 SCHUR IDEALS AND HOMOMORPHISMS OF THE SEMIDEFINITE CONE BABHRU JOSHI AND M. SEETHARAMA GOWDA Abstract. We consider the semidefinite cone K n consisting of all n n real symmetric positive semidefinite matrices.
SCHUR IDEALS AND HOMOMORPHISMS OF THE SEMIDEFINITE CONE BABHRU JOSHI AND M. SEETHARAMA GOWDA Abstract. We consider the semidefinite cone K n consisting of all n n real symmetric positive semidefinite matrices.
Notes on Linear Algebra and Matrix Analysis
 Notes on Linear Algebra and Matrix Analysis Maxim Neumann May 2006, Version 0.1.1 1 Matrix Basics Literature to this topic: [1 4]. x y < y,x >: standard inner product. x x = 1 : x is normalized x y = 0
Notes on Linear Algebra and Matrix Analysis Maxim Neumann May 2006, Version 0.1.1 1 Matrix Basics Literature to this topic: [1 4]. x y < y,x >: standard inner product. x x = 1 : x is normalized x y = 0
HUA S MATRIX EQUALITY AND SCHUR COMPLEMENTS
 INTERNATIONAL JOURNAL OF INFORMATION AND SYSTEMS SCIENCES Volume 3, Number 1, Pages 1 18 c 2007 Institute for Scientific Computing and Information HUA S MATRIX EQUALITY AND SCHUR COMPLEMENTS CHRIS PAGE,
INTERNATIONAL JOURNAL OF INFORMATION AND SYSTEMS SCIENCES Volume 3, Number 1, Pages 1 18 c 2007 Institute for Scientific Computing and Information HUA S MATRIX EQUALITY AND SCHUR COMPLEMENTS CHRIS PAGE,
Interpolating the arithmetic geometric mean inequality and its operator version
 Linear Algebra and its Applications 413 (006) 355 363 www.elsevier.com/locate/laa Interpolating the arithmetic geometric mean inequality and its operator version Rajendra Bhatia Indian Statistical Institute,
Linear Algebra and its Applications 413 (006) 355 363 www.elsevier.com/locate/laa Interpolating the arithmetic geometric mean inequality and its operator version Rajendra Bhatia Indian Statistical Institute,
Moore Penrose inverses and commuting elements of C -algebras
 Moore Penrose inverses and commuting elements of C -algebras Julio Benítez Abstract Let a be an element of a C -algebra A satisfying aa = a a, where a is the Moore Penrose inverse of a and let b A. We
Moore Penrose inverses and commuting elements of C -algebras Julio Benítez Abstract Let a be an element of a C -algebra A satisfying aa = a a, where a is the Moore Penrose inverse of a and let b A. We
Mathematical Foundations of Applied Statistics: Matrix Algebra
 Mathematical Foundations of Applied Statistics: Matrix Algebra Steffen Unkel Department of Medical Statistics University Medical Center Göttingen, Germany Winter term 2018/19 1/105 Literature Seber, G.
Mathematical Foundations of Applied Statistics: Matrix Algebra Steffen Unkel Department of Medical Statistics University Medical Center Göttingen, Germany Winter term 2018/19 1/105 Literature Seber, G.
EE/ACM Applications of Convex Optimization in Signal Processing and Communications Lecture 2
 EE/ACM 150 - Applications of Convex Optimization in Signal Processing and Communications Lecture 2 Andre Tkacenko Signal Processing Research Group Jet Propulsion Laboratory April 5, 2012 Andre Tkacenko
EE/ACM 150 - Applications of Convex Optimization in Signal Processing and Communications Lecture 2 Andre Tkacenko Signal Processing Research Group Jet Propulsion Laboratory April 5, 2012 Andre Tkacenko
Symmetric Norm Inequalities And Positive Semi-Definite Block-Matrices
 Symmetric Norm Inequalities And Positive Semi-Definite lock-matrices Antoine Mhanna To cite this version: Antoine Mhanna Symmetric Norm Inequalities And Positive Semi-Definite lock-matrices 15
Symmetric Norm Inequalities And Positive Semi-Definite lock-matrices Antoine Mhanna To cite this version: Antoine Mhanna Symmetric Norm Inequalities And Positive Semi-Definite lock-matrices 15
Chapter 2. Ma 322 Fall Ma 322. Sept 23-27
 Chapter 2 Ma 322 Fall 2013 Ma 322 Sept 23-27 Summary ˆ Matrices and their Operations. ˆ Special matrices: Zero, Square, Identity. ˆ Elementary Matrices, Permutation Matrices. ˆ Voodoo Principle. What is
Chapter 2 Ma 322 Fall 2013 Ma 322 Sept 23-27 Summary ˆ Matrices and their Operations. ˆ Special matrices: Zero, Square, Identity. ˆ Elementary Matrices, Permutation Matrices. ˆ Voodoo Principle. What is
Determinants Chapter 3 of Lay
 Determinants Chapter of Lay Dr. Doreen De Leon Math 152, Fall 201 1 Introduction to Determinants Section.1 of Lay Given a square matrix A = [a ij, the determinant of A is denoted by det A or a 11 a 1j
Determinants Chapter of Lay Dr. Doreen De Leon Math 152, Fall 201 1 Introduction to Determinants Section.1 of Lay Given a square matrix A = [a ij, the determinant of A is denoted by det A or a 11 a 1j
Clarkson Inequalities With Several Operators
 isid/ms/2003/23 August 14, 2003 http://www.isid.ac.in/ statmath/eprints Clarkson Inequalities With Several Operators Rajendra Bhatia Fuad Kittaneh Indian Statistical Institute, Delhi Centre 7, SJSS Marg,
isid/ms/2003/23 August 14, 2003 http://www.isid.ac.in/ statmath/eprints Clarkson Inequalities With Several Operators Rajendra Bhatia Fuad Kittaneh Indian Statistical Institute, Delhi Centre 7, SJSS Marg,
Compound matrices and some classical inequalities
 Compound matrices and some classical inequalities Tin-Yau Tam Mathematics & Statistics Auburn University Dec. 3, 04 We discuss some elegant proofs of several classical inequalities of matrices by using
Compound matrices and some classical inequalities Tin-Yau Tam Mathematics & Statistics Auburn University Dec. 3, 04 We discuss some elegant proofs of several classical inequalities of matrices by using
On the Hermitian solutions of the
 Journal of Applied Mathematics & Bioinformatics vol.1 no.2 2011 109-129 ISSN: 1792-7625 (print) 1792-8850 (online) International Scientific Press 2011 On the Hermitian solutions of the matrix equation
Journal of Applied Mathematics & Bioinformatics vol.1 no.2 2011 109-129 ISSN: 1792-7625 (print) 1792-8850 (online) International Scientific Press 2011 On the Hermitian solutions of the matrix equation
G1110 & 852G1 Numerical Linear Algebra
 The University of Sussex Department of Mathematics G & 85G Numerical Linear Algebra Lecture Notes Autumn Term Kerstin Hesse (w aw S w a w w (w aw H(wa = (w aw + w Figure : Geometric explanation of the
The University of Sussex Department of Mathematics G & 85G Numerical Linear Algebra Lecture Notes Autumn Term Kerstin Hesse (w aw S w a w w (w aw H(wa = (w aw + w Figure : Geometric explanation of the
There are six more problems on the next two pages
 Math 435 bg & bu: Topics in linear algebra Summer 25 Final exam Wed., 8/3/5. Justify all your work to receive full credit. Name:. Let A 3 2 5 Find a permutation matrix P, a lower triangular matrix L with
Math 435 bg & bu: Topics in linear algebra Summer 25 Final exam Wed., 8/3/5. Justify all your work to receive full credit. Name:. Let A 3 2 5 Find a permutation matrix P, a lower triangular matrix L with
The matrix arithmetic-geometric mean inequality revisited
 isid/ms/007/11 November 1 007 http://wwwisidacin/ statmath/eprints The matrix arithmetic-geometric mean inequality revisited Rajendra Bhatia Fuad Kittaneh Indian Statistical Institute Delhi Centre 7 SJSS
isid/ms/007/11 November 1 007 http://wwwisidacin/ statmath/eprints The matrix arithmetic-geometric mean inequality revisited Rajendra Bhatia Fuad Kittaneh Indian Statistical Institute Delhi Centre 7 SJSS
arxiv: v3 [math.ra] 10 Jun 2016
![arxiv: v3 [math.ra] 10 Jun 2016 arxiv: v3 [math.ra] 10 Jun 2016](/thumbs/89/98896853.jpg) To appear in Linear and Multilinear Algebra Vol. 00, No. 00, Month 0XX, 1 10 The critical exponent for generalized doubly nonnegative matrices arxiv:1407.7059v3 [math.ra] 10 Jun 016 Xuchen Han a, Charles
To appear in Linear and Multilinear Algebra Vol. 00, No. 00, Month 0XX, 1 10 The critical exponent for generalized doubly nonnegative matrices arxiv:1407.7059v3 [math.ra] 10 Jun 016 Xuchen Han a, Charles
RITZ VALUE BOUNDS THAT EXPLOIT QUASI-SPARSITY
 RITZ VALUE BOUNDS THAT EXPLOIT QUASI-SPARSITY ILSE C.F. IPSEN Abstract. Absolute and relative perturbation bounds for Ritz values of complex square matrices are presented. The bounds exploit quasi-sparsity
RITZ VALUE BOUNDS THAT EXPLOIT QUASI-SPARSITY ILSE C.F. IPSEN Abstract. Absolute and relative perturbation bounds for Ritz values of complex square matrices are presented. The bounds exploit quasi-sparsity
1 Multiply Eq. E i by λ 0: (λe i ) (E i ) 2 Multiply Eq. E j by λ and add to Eq. E i : (E i + λe j ) (E i )
 Direct Methods for Linear Systems Chapter Direct Methods for Solving Linear Systems Per-Olof Persson persson@berkeleyedu Department of Mathematics University of California, Berkeley Math 18A Numerical
Direct Methods for Linear Systems Chapter Direct Methods for Solving Linear Systems Per-Olof Persson persson@berkeleyedu Department of Mathematics University of California, Berkeley Math 18A Numerical
Banach Journal of Mathematical Analysis ISSN: (electronic)
 Banach J. Math. Anal. 6 (2012), no. 1, 139 146 Banach Journal of Mathematical Analysis ISSN: 1735-8787 (electronic) www.emis.de/journals/bjma/ AN EXTENSION OF KY FAN S DOMINANCE THEOREM RAHIM ALIZADEH
Banach J. Math. Anal. 6 (2012), no. 1, 139 146 Banach Journal of Mathematical Analysis ISSN: 1735-8787 (electronic) www.emis.de/journals/bjma/ AN EXTENSION OF KY FAN S DOMINANCE THEOREM RAHIM ALIZADEH
Math 408 Advanced Linear Algebra
 Math 408 Advanced Linear Algebra Chi-Kwong Li Chapter 4 Hermitian and symmetric matrices Basic properties Theorem Let A M n. The following are equivalent. Remark (a) A is Hermitian, i.e., A = A. (b) x
Math 408 Advanced Linear Algebra Chi-Kwong Li Chapter 4 Hermitian and symmetric matrices Basic properties Theorem Let A M n. The following are equivalent. Remark (a) A is Hermitian, i.e., A = A. (b) x
arxiv: v1 [math.na] 1 Sep 2018
![arxiv: v1 [math.na] 1 Sep 2018 arxiv: v1 [math.na] 1 Sep 2018](/thumbs/85/92407263.jpg) On the perturbation of an L -orthogonal projection Xuefeng Xu arxiv:18090000v1 [mathna] 1 Sep 018 September 5 018 Abstract The L -orthogonal projection is an important mathematical tool in scientific computing
On the perturbation of an L -orthogonal projection Xuefeng Xu arxiv:18090000v1 [mathna] 1 Sep 018 September 5 018 Abstract The L -orthogonal projection is an important mathematical tool in scientific computing
Some inequalities for unitarily invariant norms of matrices
 Wang et al Journal of Inequalities and Applications 011, 011:10 http://wwwjournalofinequalitiesandapplicationscom/content/011/1/10 RESEARCH Open Access Some inequalities for unitarily invariant norms of
Wang et al Journal of Inequalities and Applications 011, 011:10 http://wwwjournalofinequalitiesandapplicationscom/content/011/1/10 RESEARCH Open Access Some inequalities for unitarily invariant norms of
Some Inequalities for Commutators of Bounded Linear Operators in Hilbert Spaces
 Some Inequalities for Commutators of Bounded Linear Operators in Hilbert Spaces S.S. Dragomir Abstract. Some new inequalities for commutators that complement and in some instances improve recent results
Some Inequalities for Commutators of Bounded Linear Operators in Hilbert Spaces S.S. Dragomir Abstract. Some new inequalities for commutators that complement and in some instances improve recent results
Some New Results on Lyapunov-Type Diagonal Stability
 Some New Results on Lyapunov-Type Diagonal Stability Mehmet Gumus (Joint work with Dr. Jianhong Xu) Department of Mathematics Southern Illinois University Carbondale 12/01/2016 mgumus@siu.edu (SIUC) Lyapunov-Type
Some New Results on Lyapunov-Type Diagonal Stability Mehmet Gumus (Joint work with Dr. Jianhong Xu) Department of Mathematics Southern Illinois University Carbondale 12/01/2016 mgumus@siu.edu (SIUC) Lyapunov-Type
Interlacing Inequalities for Totally Nonnegative Matrices
 Interlacing Inequalities for Totally Nonnegative Matrices Chi-Kwong Li and Roy Mathias October 26, 2004 Dedicated to Professor T. Ando on the occasion of his 70th birthday. Abstract Suppose λ 1 λ n 0 are
Interlacing Inequalities for Totally Nonnegative Matrices Chi-Kwong Li and Roy Mathias October 26, 2004 Dedicated to Professor T. Ando on the occasion of his 70th birthday. Abstract Suppose λ 1 λ n 0 are
b jσ(j), Keywords: Decomposable numerical range, principal character AMS Subject Classification: 15A60
 On the Hu-Hurley-Tam Conjecture Concerning The Generalized Numerical Range Che-Man Cheng Faculty of Science and Technology, University of Macau, Macau. E-mail: fstcmc@umac.mo and Chi-Kwong Li Department
On the Hu-Hurley-Tam Conjecture Concerning The Generalized Numerical Range Che-Man Cheng Faculty of Science and Technology, University of Macau, Macau. E-mail: fstcmc@umac.mo and Chi-Kwong Li Department
Universitext. Series Editors: Sheldon Axler San Francisco State University. Vincenzo Capasso Università degli Studi di Milano
 Universitext Universitext Series Editors: Sheldon Axler San Francisco State University Vincenzo Capasso Università degli Studi di Milano Carles Casacuberta Universitat de Barcelona Angus J. MacIntyre Queen
Universitext Universitext Series Editors: Sheldon Axler San Francisco State University Vincenzo Capasso Università degli Studi di Milano Carles Casacuberta Universitat de Barcelona Angus J. MacIntyre Queen
Throughout these notes we assume V, W are finite dimensional inner product spaces over C.
 Math 342 - Linear Algebra II Notes Throughout these notes we assume V, W are finite dimensional inner product spaces over C 1 Upper Triangular Representation Proposition: Let T L(V ) There exists an orthonormal
Math 342 - Linear Algebra II Notes Throughout these notes we assume V, W are finite dimensional inner product spaces over C 1 Upper Triangular Representation Proposition: Let T L(V ) There exists an orthonormal
MATH2210 Notebook 2 Spring 2018
 MATH2210 Notebook 2 Spring 2018 prepared by Professor Jenny Baglivo c Copyright 2009 2018 by Jenny A. Baglivo. All Rights Reserved. 2 MATH2210 Notebook 2 3 2.1 Matrices and Their Operations................................
MATH2210 Notebook 2 Spring 2018 prepared by Professor Jenny Baglivo c Copyright 2009 2018 by Jenny A. Baglivo. All Rights Reserved. 2 MATH2210 Notebook 2 3 2.1 Matrices and Their Operations................................
MATH 511 ADVANCED LINEAR ALGEBRA SPRING 2006
 MATH 511 ADVANCED LINEAR ALGEBRA SPRING 2006 Sherod Eubanks HOMEWORK 2 2.1 : 2, 5, 9, 12 2.3 : 3, 6 2.4 : 2, 4, 5, 9, 11 Section 2.1: Unitary Matrices Problem 2 If λ σ(u) and U M n is unitary, show that
MATH 511 ADVANCED LINEAR ALGEBRA SPRING 2006 Sherod Eubanks HOMEWORK 2 2.1 : 2, 5, 9, 12 2.3 : 3, 6 2.4 : 2, 4, 5, 9, 11 Section 2.1: Unitary Matrices Problem 2 If λ σ(u) and U M n is unitary, show that
Diagonal and Monomial Solutions of the Matrix Equation AXB = C
 Iranian Journal of Mathematical Sciences and Informatics Vol. 9, No. 1 (2014), pp 31-42 Diagonal and Monomial Solutions of the Matrix Equation AXB = C Massoud Aman Department of Mathematics, Faculty of
Iranian Journal of Mathematical Sciences and Informatics Vol. 9, No. 1 (2014), pp 31-42 Diagonal and Monomial Solutions of the Matrix Equation AXB = C Massoud Aman Department of Mathematics, Faculty of
MATH 5720: Unconstrained Optimization Hung Phan, UMass Lowell September 13, 2018
 MATH 57: Unconstrained Optimization Hung Phan, UMass Lowell September 13, 18 1 Global and Local Optima Let a function f : S R be defined on a set S R n Definition 1 (minimizers and maximizers) (i) x S
MATH 57: Unconstrained Optimization Hung Phan, UMass Lowell September 13, 18 1 Global and Local Optima Let a function f : S R be defined on a set S R n Definition 1 (minimizers and maximizers) (i) x S
Math 102, Winter Final Exam Review. Chapter 1. Matrices and Gaussian Elimination
 Math 0, Winter 07 Final Exam Review Chapter. Matrices and Gaussian Elimination { x + x =,. Different forms of a system of linear equations. Example: The x + 4x = 4. [ ] [ ] [ ] vector form (or the column
Math 0, Winter 07 Final Exam Review Chapter. Matrices and Gaussian Elimination { x + x =,. Different forms of a system of linear equations. Example: The x + 4x = 4. [ ] [ ] [ ] vector form (or the column
QUASI-DIAGONALIZABLE AND CONGRUENCE-NORMAL MATRICES. 1. Introduction. A matrix A C n n is normal if AA = A A. A is said to be conjugate-normal if
 QUASI-DIAGONALIZABLE AND CONGRUENCE-NORMAL MATRICES H. FAßBENDER AND KH. D. IKRAMOV Abstract. A matrix A C n n is unitarily quasi-diagonalizable if A can be brought by a unitary similarity transformation
QUASI-DIAGONALIZABLE AND CONGRUENCE-NORMAL MATRICES H. FAßBENDER AND KH. D. IKRAMOV Abstract. A matrix A C n n is unitarily quasi-diagonalizable if A can be brought by a unitary similarity transformation
Maths for Signals and Systems Linear Algebra in Engineering
 Maths for Signals and Systems Linear Algebra in Engineering Lectures 13 15, Tuesday 8 th and Friday 11 th November 016 DR TANIA STATHAKI READER (ASSOCIATE PROFFESOR) IN SIGNAL PROCESSING IMPERIAL COLLEGE
Maths for Signals and Systems Linear Algebra in Engineering Lectures 13 15, Tuesday 8 th and Friday 11 th November 016 DR TANIA STATHAKI READER (ASSOCIATE PROFFESOR) IN SIGNAL PROCESSING IMPERIAL COLLEGE
Matrices and Determinants
 Chapter1 Matrices and Determinants 11 INTRODUCTION Matrix means an arrangement or array Matrices (plural of matrix) were introduced by Cayley in 1860 A matrix A is rectangular array of m n numbers (or
Chapter1 Matrices and Determinants 11 INTRODUCTION Matrix means an arrangement or array Matrices (plural of matrix) were introduced by Cayley in 1860 A matrix A is rectangular array of m n numbers (or
New insights into best linear unbiased estimation and the optimality of least-squares
 Journal of Multivariate Analysis 97 (2006) 575 585 www.elsevier.com/locate/jmva New insights into best linear unbiased estimation and the optimality of least-squares Mario Faliva, Maria Grazia Zoia Istituto
Journal of Multivariate Analysis 97 (2006) 575 585 www.elsevier.com/locate/jmva New insights into best linear unbiased estimation and the optimality of least-squares Mario Faliva, Maria Grazia Zoia Istituto
A Note on Eigenvalues of Perturbed Hermitian Matrices
 A Note on Eigenvalues of Perturbed Hermitian Matrices Chi-Kwong Li Ren-Cang Li July 2004 Let ( H1 E A = E H 2 Abstract and à = ( H1 H 2 be Hermitian matrices with eigenvalues λ 1 λ k and λ 1 λ k, respectively.
A Note on Eigenvalues of Perturbed Hermitian Matrices Chi-Kwong Li Ren-Cang Li July 2004 Let ( H1 E A = E H 2 Abstract and à = ( H1 H 2 be Hermitian matrices with eigenvalues λ 1 λ k and λ 1 λ k, respectively.
Chapter 3 Transformations
 Chapter 3 Transformations An Introduction to Optimization Spring, 2014 Wei-Ta Chu 1 Linear Transformations A function is called a linear transformation if 1. for every and 2. for every If we fix the bases
Chapter 3 Transformations An Introduction to Optimization Spring, 2014 Wei-Ta Chu 1 Linear Transformations A function is called a linear transformation if 1. for every and 2. for every If we fix the bases
Sufficiency of Signed Principal Minors for Semidefiniteness: A Relatively Easy Proof
 Sufficiency of Signed Principal Minors for Semidefiniteness: A Relatively Easy Proof David M. Mandy Department of Economics University of Missouri 118 Professional Building Columbia, MO 65203 USA mandyd@missouri.edu
Sufficiency of Signed Principal Minors for Semidefiniteness: A Relatively Easy Proof David M. Mandy Department of Economics University of Missouri 118 Professional Building Columbia, MO 65203 USA mandyd@missouri.edu
On the simultaneous diagonal stability of a pair of positive linear systems
 On the simultaneous diagonal stability of a pair of positive linear systems Oliver Mason Hamilton Institute NUI Maynooth Ireland Robert Shorten Hamilton Institute NUI Maynooth Ireland Abstract In this
On the simultaneous diagonal stability of a pair of positive linear systems Oliver Mason Hamilton Institute NUI Maynooth Ireland Robert Shorten Hamilton Institute NUI Maynooth Ireland Abstract In this
Fuzhen Zhang s Publication List
 Fuzhen Zhang s Publication List Papers in peer-reviewed journals 1. Inequalities of generalized matrix functions via tensor products, with Vehbi E. Paksoy and Ramazan Turkmen, Electron. J. Linear Algebra,
Fuzhen Zhang s Publication List Papers in peer-reviewed journals 1. Inequalities of generalized matrix functions via tensor products, with Vehbi E. Paksoy and Ramazan Turkmen, Electron. J. Linear Algebra,
Fuzhen Zhang s Publication and Presentation List (updated Dec. 2007)
 Fuzhen Zhang s Publication and Presentation List (updated Dec. 2007) Papers in peer-reviewed journals 1. Revisiting Hua-Marcus-Bellman-Ando inequalities on contractive matrices, with C. Xu and Z. Xu, Lin.
Fuzhen Zhang s Publication and Presentation List (updated Dec. 2007) Papers in peer-reviewed journals 1. Revisiting Hua-Marcus-Bellman-Ando inequalities on contractive matrices, with C. Xu and Z. Xu, Lin.
On the adjacency matrix of a block graph
 On the adjacency matrix of a block graph R. B. Bapat Stat-Math Unit Indian Statistical Institute, Delhi 7-SJSS Marg, New Delhi 110 016, India. email: rbb@isid.ac.in Souvik Roy Economics and Planning Unit
On the adjacency matrix of a block graph R. B. Bapat Stat-Math Unit Indian Statistical Institute, Delhi 7-SJSS Marg, New Delhi 110 016, India. email: rbb@isid.ac.in Souvik Roy Economics and Planning Unit
Positive definite preserving linear transformations on symmetric matrix spaces
 Positive definite preserving linear transformations on symmetric matrix spaces arxiv:1008.1347v1 [math.ra] 7 Aug 2010 Huynh Dinh Tuan-Tran Thi Nha Trang-Doan The Hieu Hue Geometry Group College of Education,
Positive definite preserving linear transformations on symmetric matrix spaces arxiv:1008.1347v1 [math.ra] 7 Aug 2010 Huynh Dinh Tuan-Tran Thi Nha Trang-Doan The Hieu Hue Geometry Group College of Education,
CS 246 Review of Linear Algebra 01/17/19
 1 Linear algebra In this section we will discuss vectors and matrices. We denote the (i, j)th entry of a matrix A as A ij, and the ith entry of a vector as v i. 1.1 Vectors and vector operations A vector
1 Linear algebra In this section we will discuss vectors and matrices. We denote the (i, j)th entry of a matrix A as A ij, and the ith entry of a vector as v i. 1.1 Vectors and vector operations A vector
Conceptual Questions for Review
 Conceptual Questions for Review Chapter 1 1.1 Which vectors are linear combinations of v = (3, 1) and w = (4, 3)? 1.2 Compare the dot product of v = (3, 1) and w = (4, 3) to the product of their lengths.
Conceptual Questions for Review Chapter 1 1.1 Which vectors are linear combinations of v = (3, 1) and w = (4, 3)? 1.2 Compare the dot product of v = (3, 1) and w = (4, 3) to the product of their lengths.
MATH 423 Linear Algebra II Lecture 33: Diagonalization of normal operators.
 MATH 423 Linear Algebra II Lecture 33: Diagonalization of normal operators. Adjoint operator and adjoint matrix Given a linear operator L on an inner product space V, the adjoint of L is a transformation
MATH 423 Linear Algebra II Lecture 33: Diagonalization of normal operators. Adjoint operator and adjoint matrix Given a linear operator L on an inner product space V, the adjoint of L is a transformation
Notes on Eigenvalues, Singular Values and QR
 Notes on Eigenvalues, Singular Values and QR Michael Overton, Numerical Computing, Spring 2017 March 30, 2017 1 Eigenvalues Everyone who has studied linear algebra knows the definition: given a square
Notes on Eigenvalues, Singular Values and QR Michael Overton, Numerical Computing, Spring 2017 March 30, 2017 1 Eigenvalues Everyone who has studied linear algebra knows the definition: given a square
MATH36001 Generalized Inverses and the SVD 2015
 MATH36001 Generalized Inverses and the SVD 201 1 Generalized Inverses of Matrices A matrix has an inverse only if it is square and nonsingular. However there are theoretical and practical applications
MATH36001 Generalized Inverses and the SVD 201 1 Generalized Inverses of Matrices A matrix has an inverse only if it is square and nonsingular. However there are theoretical and practical applications
Wavelets and Linear Algebra
 Wavelets and Linear Algebra 4(1) (2017) 43-51 Wavelets and Linear Algebra Vali-e-Asr University of Rafsanan http://walavruacir Some results on the block numerical range Mostafa Zangiabadi a,, Hamid Reza
Wavelets and Linear Algebra 4(1) (2017) 43-51 Wavelets and Linear Algebra Vali-e-Asr University of Rafsanan http://walavruacir Some results on the block numerical range Mostafa Zangiabadi a,, Hamid Reza
Matrices A brief introduction
 Matrices A brief introduction Basilio Bona DAUIN Politecnico di Torino Semester 1, 2014-15 B. Bona (DAUIN) Matrices Semester 1, 2014-15 1 / 41 Definitions Definition A matrix is a set of N real or complex
Matrices A brief introduction Basilio Bona DAUIN Politecnico di Torino Semester 1, 2014-15 B. Bona (DAUIN) Matrices Semester 1, 2014-15 1 / 41 Definitions Definition A matrix is a set of N real or complex
Lecture notes: Applied linear algebra Part 1. Version 2
 Lecture notes: Applied linear algebra Part 1. Version 2 Michael Karow Berlin University of Technology karow@math.tu-berlin.de October 2, 2008 1 Notation, basic notions and facts 1.1 Subspaces, range and
Lecture notes: Applied linear algebra Part 1. Version 2 Michael Karow Berlin University of Technology karow@math.tu-berlin.de October 2, 2008 1 Notation, basic notions and facts 1.1 Subspaces, range and
CLASSIFICATION OF COMPLETELY POSITIVE MAPS 1. INTRODUCTION
 CLASSIFICATION OF COMPLETELY POSITIVE MAPS STEPHAN HOYER ABSTRACT. We define a completely positive map and classify all completely positive linear maps. We further classify all such maps that are trace-preserving
CLASSIFICATION OF COMPLETELY POSITIVE MAPS STEPHAN HOYER ABSTRACT. We define a completely positive map and classify all completely positive linear maps. We further classify all such maps that are trace-preserving
Applied Mathematics 205. Unit V: Eigenvalue Problems. Lecturer: Dr. David Knezevic
 Applied Mathematics 205 Unit V: Eigenvalue Problems Lecturer: Dr. David Knezevic Unit V: Eigenvalue Problems Chapter V.2: Fundamentals 2 / 31 Eigenvalues and Eigenvectors Eigenvalues and eigenvectors of
Applied Mathematics 205 Unit V: Eigenvalue Problems Lecturer: Dr. David Knezevic Unit V: Eigenvalue Problems Chapter V.2: Fundamentals 2 / 31 Eigenvalues and Eigenvectors Eigenvalues and eigenvectors of
SOME INEQUALITIES FOR COMMUTATORS OF BOUNDED LINEAR OPERATORS IN HILBERT SPACES. S. S. Dragomir
 Faculty of Sciences and Mathematics, University of Niš, Serbia Available at: http://www.pmf.ni.ac.rs/filomat Filomat 5: 011), 151 16 DOI: 10.98/FIL110151D SOME INEQUALITIES FOR COMMUTATORS OF BOUNDED LINEAR
Faculty of Sciences and Mathematics, University of Niš, Serbia Available at: http://www.pmf.ni.ac.rs/filomat Filomat 5: 011), 151 16 DOI: 10.98/FIL110151D SOME INEQUALITIES FOR COMMUTATORS OF BOUNDED LINEAR
Preliminary/Qualifying Exam in Numerical Analysis (Math 502a) Spring 2012
 Instructions Preliminary/Qualifying Exam in Numerical Analysis (Math 502a) Spring 2012 The exam consists of four problems, each having multiple parts. You should attempt to solve all four problems. 1.
Instructions Preliminary/Qualifying Exam in Numerical Analysis (Math 502a) Spring 2012 The exam consists of four problems, each having multiple parts. You should attempt to solve all four problems. 1.
Topics in Applied Linear Algebra - Part II
 Topics in Applied Linear Algebra - Part II April 23, 2013 Some Preliminary Remarks The purpose of these notes is to provide a guide through the material for the second part of the graduate module HM802
Topics in Applied Linear Algebra - Part II April 23, 2013 Some Preliminary Remarks The purpose of these notes is to provide a guide through the material for the second part of the graduate module HM802
