WEAK SIGNAL DETECTION BASED ON TWO DIMENSIONAL STOCHASTIC RESONANCE. Leonardo Barbini, Matthew O. T. Cole, Andrew J. Hillis, Jonathan L.
|
|
|
- Beverly Webster
- 5 years ago
- Views:
Transcription
1 WEAK SIGNAL DETECTION BASED ON TWO DIMENSIONAL STOCHASTIC RESONANCE Leonardo Barbini, Matthew O. T. Cole, Andrew J. Hillis, Jonathan L. du Bois University of Bath Department of Mechanical Engineering Claverton Down, Bath, BA2 7AY UK ABSTRACT The analysis of vibrations from rotating machines gives information about their faults. From the signal processing perspective a significant problem is the detection of weak signals embedded in strong noise. Stochastic resonance SR) is a mechanism where noise is not suppressed but exploited to trigger the synchronization of a non-linear system and in its one-dimensional form has been recently applied to vibration analysis. This paper focuses on the use of SR in a twodimensional system of gradient type for detection of weak signals submerged in Gaussian noise. Comparing the traditional one-dimensional system and the two-dimensional used here, this paper shows that the latter can offer a more sensitive means of detection. An alternative metric is proposed to assess the output signal quality, requiring no a priori knowledge of the signal to be detected, and it is shown to offer similar results to the more conventional signal-to-noise ratio. Index Terms stochastic resonance, weak signal detection, non linear signal processing 1. INTRODUCTION The response of a non-linear system to both the effects of noise and a periodic signal can result in a phenomenon of synchronization: stochastic resonance SR) [1]. In the field of mechanical engineering a problem of great importance is that under operating conditions of many mechanical equipment, signals carrying useful information are submerged by heavy background noise. Conventional methods for the enhancement of the useful signal, so that it can be detected, consist of filtering or masking the noise [2,3] while in the SR mechanism the noise is used to enhance the signal, reducing the risk of losing the information of interest. In this context the flow of the detection scheme is as follows. The sum of periodic aperiodic or impact signals [4] and an heavy noise is preprocessed [4,5] and taken as the input of the non linear system, usually a 1D double well. Then will start an algorithm for tuning the parameters of this non-linear system, in order to trigger the SR mechanism. For each combination of the parameters, the output signal will be collected and evaluated Corresponding author. address: l.barbini@bath.ac.uk with certain criteria, such as maximization of the weighted kurtosis index KC) or of the signal-to-noise ratio SNR), so that the best output is found and the signal of interest is detected [4]. The assumption of the adiabatic approximation for the SR mechanism, i.e. small values of frequency, amplitude and noise variance, can be avoided [5] hence in practical applications also high frequency-amplitude signals can be detected henceforth large parameter SR ). It is worth noticing that in the above mentioned detection scheme two key roles are the type of non linearity of the system and the optimization criteria; the former because it determines the set of variables that one is able to tune, the latter because it decides the values of those variables. In the present paper we investigate both of the above mentioned aspects, firstly we will show how switching to a non linear system in more than one dimension will allow us to tune another parameter. Barbini et al. [6] investigated the effect of the addition of another degree of freedom to the usual bistable system used for the SR mechanism. It was observed a dependence of the output signal on the coupling constant, due to a change in the transition path among the stable points. Then the number of parameters which can be tuned increases, now being: the height of the potential barrier, the position of the stable points and also the coupling constant. One is tempted to think that for the same input signal, after the tuning process of the parameters, the output of the SR will be the same in the two cases. We investigate this question, comparing the best result of the 2D non-linear system with the mono-dimensional one, for the same input signal when the parameters are tuned in the same range of values. Secondly we propose a new criterion for selecting the best values of the three tuning parameters. Instead of looking at a time-frequency transformation we evaluate the degree of synchronization of the output signal using directly the distribution of the mean residence time in the stable points of the non linear system. The paper is structured as follows. In section 2 we provide a description of the two dimensional non linear system, as well as the rescaling for extending the large parameter SR to this model. In section 3 we test the efficiency of the new tuning criteria for the parameters, detecting signals using the 1D model. In section 4 we show the dependence of the output in the 2D model on the coupling constant and comparing with
2 Fig. 1. Paths on the x y plane for different values of δ: blue 1.5, red 0.65 and green Circles and squares are respectively stable and unstable steady states the results obtained in the 1D case. Conclusions and an outlook for future development are given in the final section. 2. NORMALIZED TWO DIMENSIONAL SR Let us consider the dynamical system associated to the following potential: U x, y) = a 2 x 2 + y 2) + b 4 x 4 + y 4) δ 2 x 2 y 2) 1) where a, b, δ are real positive numbers. This potential is the generalization of the one studied in [6], where a = b = 1. Throughout the paper we will consider the inertia small compared to other dynamical components. The origin is an unstable steady point so that if we consider the effect of small fluctuations to the motionless state, i.e. noise, we will observe the system to stabilize in one of the minima, then for increasing values of the fluctuations we will have random transition between those minima symmetrically displaced in the quadrants. The system is two dimensional hence, differently from the usual double well, as a function of a, b, δ we have the possibility to have saddle points as unstable steady states and curved transition paths in the x, y) plane. Respectively a, b define the height of the potential barrier between the stable steady states and their positions; δ is the coupling. Whether transitions will take place among saddle points or the maxima as well as the rate, depend on both the height of the potential barrier and on the curvature of the potential landscape [7]. In Fig.1 we show the displacement of the steady states and the transitions paths for different values of the coupling in the case a = b = 1. In green δ = 0.65) and red δ = 0.65) stable states lie on the axes of the plane and transitions occur through an unstable steady state at 0, 1). Due to the symmetry of 1) such transitions could take place also between the I II, II III and III IV quadrants not shown). When the value of the coupling constant is lower than δ < 1 there is a change in the stability of the steady states of the potential, in Fig.1 we show in blue transitions in the case δ = 1.5. It can be noticed that unstable steady states are Fig. 2. Model of the two dimensional SR detector now situated on the axes of the plane while steady states are at 0, 1) and 1, 0) respectively. The same considerations on the symmetry apply in this case. Let us consider now the effect of a periodic forcing on the dynamical system of stochastic differential equations obtained from the potential defined in 1). We add a periodic component Acosωt), of amplitude A and frequency ω, on the first of the two equations: { dx = [ ax bx 3 + δxy 2 + Acosωt) ] dt + ε 1/2 x dw x dy = ay by 3 + δyx 2) dt + ε 1/2 y dw y 2) where dw ) are independent Wiener processes and ε ) the variances of the noise. The effect of the periodic component in the first of 2) is that of modulate the potential 1), i.e. the height of the barrier between stable states changes implying a periodicity in the transition rates [1]. This synchronization phenomenon is the result of the cooperative effect of the periodic component and the noise, hence the transition rates are a function of both A, ω, ε, as well as the parameters of the non linear system a, b, δ. The theory of stochastic differential equations provides an estimate of the mean exit time from the basins of attractions of the stable points in the limit of small parameters A, ω, ε [1,7]. Nevertheless for a good use of SR in signal detection these limitations on the characteristic of the analysed signal must be avoided. Then following [5] we extend the rescale transformation to 2). For a, b > 0 we take a constant k > 0, we let and ˆx = x b/a, ŷ = y b/a, ˆδ = δ/b, ˆt = t/k; hence 2) reduces to the following system which preserves the gradient type structure: { dˆx = T R ˆx ˆx 3 + ˆδˆxŷ ) [ 2 dˆt + S R Acos Ωˆt ) ]} dˆt + ε 1/2 x dŵ x [ dŷ = T R ŷ ŷ 3 + ˆδŷˆx ) ] 2 dˆt + S R ε 1/2 y dŵ y 3) where T R = ak is the time rescale, S R = b 1/2 a 3/2 is the spatial rescale, Ω = kω is the new signal frequency and the Wiener process dŵ keeps the statistical conditions dŵ = 0, dŵ, dŵ = δˆt ˆt ); in the following we will omit theˆ for
3 Fig. 3. a) contour plot of r τ for the 1D detector; b) three output signals obtained for the values of S R, T R giving the maxima of r τ. In black the periodic components of the input: top A 3, ω 3) = , ), middle A 2, ω 2) = , ) and bottom A 1, ω 1) = , ) Fig. 4. a) contour plot of SNR for the 1D detector; b) dependence of maximum of r τ on the amplitude γε 1/2 x of the input noise; c) amplitude spectra of input noise red) for γ = 6, ε x = ) 2, input noise plus sinusoid green) in the case A, ω) = , ), output of 1D SR detector black) simplicity. In practical application of SR as a signal detection method, the input of the nonlinear system is a noisy signal and the main objective is to analyze whether a periodic component is present or not. Referring to 3) the input is the sum of the last two terms of the first equation, with unknown A, ω, ε x. In system 3) the values of the frequency and of the amplitude of the input signal can be taken without constraints, being multiplied respectively by S R, k and the position of the stable points in the x, y) plane and the height of the potential barrier are now fixed, being now the dependence on a, b in S R a, b). The detection problem is then reduced to finding the values of T R, S R, δ providing a 2D SR mechanism giving an output signal x which shows a transition rate highly synchronized to the periodic component of the input. According to the order of magnitude expected for the frequency and amplitude of the periodic component we will decide the range of values for the parameters T R and S R. Then we will test all those for a selected range of values of the coupling constant δ, so that we will have to select the best output from a total number of n TR n SR n δ. In the present paper we propose to study directly the distribution of the transition rates τ i.e. the exit times from the basins of attraction of stable steady states of 3). Those are obtained from the array of the times of the x-mode zero crossing for each of the output signals. When the system is out of resonance, the times of the transitions between stable states are random, then the distribution of τ depicts no structure and decays exponentially. In [8] Benzi et al. showed that the moments for τ are given by: τ n n! τ n 4) In contrast, when we have SR the distribution of τ is peaked at the time being half period of the periodic forcing. In the present paper we use the ratio r τ between the square of the mean and the variance of τ in order to evaluate the degree of the SR. The control parameter r τ has to be independent from the time scale at which it is evaluated; this is why it is normalized with the mean here. According to 4) when the system shows completely random jumps r τ reaches the value 1, while in the SR case r τ for a perfect identification of the signal frequency. The detection ends finding the maximum from all the r τ, the measure of success of the procedure is that of detecting the signal carrying the useful information, for which the ratio r = A/ε x is the lowest. 3. NUMERICAL RESULTS: TEST OF R τ In this section we test the use of r τ as a control parameter for the SR, all our numerical results are taken from a Simulink model reproducing system 3), the model is shown in Fig.2, the input block models the addition of periodic signals and a Gaussian noise: Input = n A n sin ω n t) + ε 1/2 x ηt) 5) being ηt) = dw/dt, and n the number of components. Within this section we restrict our analysis to the 1D system, i.e the first equation of 3) with δ = 0. We test the model with an input signal constructed as follows: n = 3; the amplitudes and frequencies of the periodic components are chosen randomly in the ranges of values 0.01 to 1 and to 1000 Hz respectively; the variance of the noise is taken as the result of multiplication of the highest of the A i for a random number in the range 5 to 10 so that we ensure that the periodic signals are heavily buried into noise. The following values for the input signal were found: A 1, ω 1 ) = , ), A 2, ω 2 ) = , ), A 3, ω 3 ) = , ) and ε x = ) 2. The tuning parameters T R, S R are tested in the range 1 to 10 6, 0.01 to 15 respectively and we decide increment steps so that we end up in a matrix of dimensions n TR n SR = In the simulations for each T R we change both the integration time step dt = 2 6 /T R and the time length of the analyzed signals L = 10000/T R, while
4 Fig. 5. contour plot of r τ : top left 1D detector, all the others are for the 2D detector with different δ Fig. 6. maxima of r τ for the 2D detector red) as a function of δ: a)γ = 0.25, b) γ = 1, c) γ = 2, d) γ = 6; in blue 1D we keep fixed the number of samples and we sub-sample the output of 27, so that we end up with signals of 5000 samples. In Fig.3a) we show the contour plot of the values of r τ for each of the tuning parameter, we have recognized the areas, red green and purple, for the peaks corresponding to the three periodic components of the input signal. In Fig.3b) we show a comparison between the periodic components, black signals, and the three output x obtained setting S R, T R as for the maxima of r τ ; the time scales of the plots are different and after the SR we can appreciate the time decomposition of the three components of the input. We show the classical signal to noise ratio SNR) metric calculated for the output values for each of the tuning parameter in Fig.4a), SNR is defined as the ratio between the power of the spectral line at the periodic input frequency and that of the noise background [5], we notice that the areas corresponding to the three input frequencies are visible and comparable with those of r τ and that a good comparison is possible. In Fig.3a) we notice the displacement of the peaks in the S R dimension due both to the ratio r i = A i /ε x and the superposition of the signals at different frequencies. In order to quantify the dependence of r τ on the ratio r without such a superposition we test an input signal where there is only one periodic component, n = 1 in 5). Following the above mentioned construction procedure we found the following values for the amplitude and frequency A, ω) = , ) and for the variance ε x = ) 2. Then we modify the ratio r multiplying the variance for γ = 0.25, 1, 2, 6, 1, 10, 30, 60, 100 while we keep the values of the periodic component fixed: Input = Asin ωt) + γε 1/2 x ηt) 6) In Fig.4b) we show the maximum values of r τ for each of the inputs as a function of γ; in Fig.4c) we show the spectral amplitudes for the case γ = 6, black green and red are respectively the output, the input and only the noise content of the input. A dotted line is plot at the input frequency value, the presence of periodicity is completely not detectable before SR, being the difference in spectra of the noise and sine wave plus noise negligible hence the input signal before SR filtering could be characterized as white noise. 4. NUMERICAL RESULTS: THE COMPARISON In this section we use the 2D model, system 3). The value of the variance of the Gaussian noise ε y of the second degree of freedom will always be taken ε y ε x so that the motion will displace in the x, y) plane but any transition in the y-mode, being the jumps between stable states of the x-mode. Firstly we test the dependence of the 2D detector on the value of the coupling constant δ with the input signal as in equation 6). We want to compare the results of this detector with the 1D one then we use same values A, ω, ε x as in the precedent section and γ = 2. In Fig.5 we show the contour plot of r τ for each of the T R, S R parameters, top left is the 1D case while all the others are the 2D case for different values of δ, respectively δ = 5, 1.5, 0.95, 0.65, 0.25, 0.25, 0.65, We notice the dependence of the position of the peaks in the T R, S R ) space on the value of the coupling. Furthermore due to the change on the stability of the steady states of 3) as a function of δ, we notice a difference on the area of r τ over a threshold, i.e. the area covered by peaks visible in Fig.5. It increases with the coupling constant value varying from < δ < 1 then occurs the change in the position of the steady states at δ = 1 and the area covered by the peaks reaches a maximum for δ = 0.95, hence for 3) approaching the case of a dynamical hysteresis [9], while decreases for 1 < δ < 1. The same dependence on the coupling is found as well on the maximum values of r τ, in Fig.6 we show such maxima as a function of δ for different values of the ratio r, plots with different vertical scales. The input signal 6) is taken for four different values of γ, respectively γ = 0.25, 1, 2, 6, while A, ω, ε x are as in the previous simulation. We notice that the increase in the degree of synchronization of the output signal due to the 2D feature of 3) is related to the stability change in the x, y) plane and that the maxima are found for δ > 1, i.e. transitions path as in the red and green cases in Fig.1. The maxima of r τ for the 1D case are blue constant lines in Fig.6, within certain values of
5 Fig. 7. comparisons of the best outputs of the 1D blue) and 2D red) detectors, for γ = 1, input sinusoid multiplied for a factor 3 black): a) time signals b) amplitude spectra δ we notice that the 2D detector outperforms the 1D one. In order to investigate such performance we show the comparison between the output signals of the 1D and 2D detectors for the input signal taken with γ = 2 and A, ω, ε x as in the previous simulation. In Fig.7a) we show the time domain, respectively blue red and black are the outputs in the 1D, 2D case and the periodic component of the input multiplied by a factor 3. Firstly we notice that in the 2D signal the variance of the output around the stable steady states is lower in respect to the one in the 1D signal; furthermore we notice that the accordance between the jumps times and the maximum values reached by the sinusoidal component is greater in the 2D case, corresponding in a fixed phase lag. In Fig.7b) the two output signals are shown in the frequency domain, blue and red are the 1D and 2D case, dotted vertical lines are plot at the values of ω and at the first two odd harmonics. The values of the steady states in the 1D case are greater in respect to the 2D one, amplitude of output signals in Fig. 7 a), nevertheless we notice that in the output signal of the 2D detector the power in the range 20 to 40 Hz is lower, this feature is better noticed in the first odd harmonic, which is visible in the 2D case while it is not in the 1D one; at the frequency value of 5ω the peak cannot be easily observed even in the 2D case. 5. CONCLUSION This paper introduced a model based on a two dimensional SR mechanism for the detection of weak periodic signals, of random frequency and amplitude, buried in heavy background noise. A new measurement index was proposed, calculated directly from the vector of the zero crossing of the output signal without the need for a time-frequency transformation or a priori knowledge of the input signal. The new index was first shown to convey similar information to that of the signal-tonoise ratio, and was then used to evaluate the periodic content in the output signal from the SR detector. It was shown that the presence of the coupling constant δ, used as a tuning parameter in the proposed two dimensional SR model, results in a better capacity for the detection of weak signals when compared with the usual mono-dimensional model. The best results in the two dimensional detector are found when the value of the coupling is close to δ = 1 corresponding to the case of a limit cycle for the dynamics of the model. The mechanism of operation in this case appears to consist of a dynamical hysteresis where transitions occur deterministically as a function of the amplitude and frequency of the periodic forcing, and further studies are in progress to explore the nature of this mechanism. Future work will involve the experimental application of the techniques developed here in the field of condition monitoring, in particular the detection of weak fault signals in rotating machines. REFERENCES [1] R. Benzi, A. Sutera, and A. Vulpiani, The mechanism of stochastic resonance, Journal of Physics A: Mathematical and General, vol. 14, no. 11, pp. L453, Nov [2] J. Lin and M.J. Zuo, Gearbox fault diagnosis using adaptive wavelet filter, Mechanical Systems and Signal Processing, vol. 17, no. 6, pp , Nov [3] J. Hongkai, H. Zhengjia, D. Chendong, and C. Peng, Gearbox fault diagnosis using adaptive redundant lifting scheme, Mechanical Systems and Signal Processing, vol. 20, no. 8, pp , Nov [4] J. Li, X. Chen, and Z. He, Adaptive stochastic resonance method for impact signal detection based on sliding window, Mechanical Systems and Signal Processing, vol. 36, no. 2, pp , Apr [5] Q. He, J. Wang, Y. Liu, D. Dai, and F. Kong, Multiscale noise tuning of stochastic resonance for enhanced fault diagnosis in rotating machines, Mechanical Systems and Signal Processing, vol. 28, pp , Apr [6] L. Barbini, I. Bordi, K. Fraedrich, and A. Sutera, The stochastic resonance in a system of gradient type, European Physical Journal Plus, vol. 128, pp. 13, Feb [7] R. Benzi, A. Sutera, and A. Vulpiani, Stochastic resonance in the landau-ginzburg equation, Journal of Physics A: Mathematical and General, vol. 18, no. 12, pp. 2239, Aug [8] R. Benzi and A. Sutera, The mechanism of stochastic resonance in climate theory, in Proceedings of the International School of Physics E. Fermi, 1985, pp [9] Jung, Gray, Roy, and Mandel, Scaling law for dynamical hysteresis, Physical Review Letters, vol. 65, no. 15, pp , Oct
If we want to analyze experimental or simulated data we might encounter the following tasks:
 Chapter 1 Introduction If we want to analyze experimental or simulated data we might encounter the following tasks: Characterization of the source of the signal and diagnosis Studying dependencies Prediction
Chapter 1 Introduction If we want to analyze experimental or simulated data we might encounter the following tasks: Characterization of the source of the signal and diagnosis Studying dependencies Prediction
Detection and Parameter Estimation of LFM Signal Based on Stochastic Resonance
 nd International Conference on Networking and Information Technology IPCSIT vol.7 () () IACSIT Press, Singapore Detection and Parameter Estimation of LFM Signal Based on Stochastic Resonance Xiaomin Wang
nd International Conference on Networking and Information Technology IPCSIT vol.7 () () IACSIT Press, Singapore Detection and Parameter Estimation of LFM Signal Based on Stochastic Resonance Xiaomin Wang
NOISE ENHANCED ANISOTROPIC DIFFUSION FOR SCALAR IMAGE RESTORATION. 6, avenue du Ponceau Cergy-Pontoise, France.
 NOISE ENHANCED ANISOTROPIC DIFFUSION FOR SCALAR IMAGE RESTORATION Aymeric HISTACE 1, David ROUSSEAU 2 1 Equipe en Traitement d'image et du Signal UMR CNRS 8051 6, avenue du Ponceau 95014 Cergy-Pontoise,
NOISE ENHANCED ANISOTROPIC DIFFUSION FOR SCALAR IMAGE RESTORATION Aymeric HISTACE 1, David ROUSSEAU 2 1 Equipe en Traitement d'image et du Signal UMR CNRS 8051 6, avenue du Ponceau 95014 Cergy-Pontoise,
Autoregressive Models Fourier Analysis Wavelets
 Autoregressive Models Fourier Analysis Wavelets BFR Flood w/10yr smooth Spectrum Annual Max: Day of Water year Flood magnitude vs. timing Jain & Lall, 2000 Blacksmith Fork, Hyrum, UT Analyses of Flood
Autoregressive Models Fourier Analysis Wavelets BFR Flood w/10yr smooth Spectrum Annual Max: Day of Water year Flood magnitude vs. timing Jain & Lall, 2000 Blacksmith Fork, Hyrum, UT Analyses of Flood
Stochastic resonance in a monostable system driven by square-wave signal and dichotomous noise
 Stochastic resonance in a monostable system driven by square-wave signal and dichotomous noise Guo Feng( 郭锋 ) a), Luo Xiang-Dong( 罗向东 ) a), Li Shao-Fu( 李少甫 ) a), and Zhou Yu-Rong( 周玉荣 ) b) a) School of
Stochastic resonance in a monostable system driven by square-wave signal and dichotomous noise Guo Feng( 郭锋 ) a), Luo Xiang-Dong( 罗向东 ) a), Li Shao-Fu( 李少甫 ) a), and Zhou Yu-Rong( 周玉荣 ) b) a) School of
A METHOD FOR NONLINEAR SYSTEM CLASSIFICATION IN THE TIME-FREQUENCY PLANE IN PRESENCE OF FRACTAL NOISE. Lorenzo Galleani, Letizia Lo Presti
 A METHOD FOR NONLINEAR SYSTEM CLASSIFICATION IN THE TIME-FREQUENCY PLANE IN PRESENCE OF FRACTAL NOISE Lorenzo Galleani, Letizia Lo Presti Dipartimento di Elettronica, Politecnico di Torino, Corso Duca
A METHOD FOR NONLINEAR SYSTEM CLASSIFICATION IN THE TIME-FREQUENCY PLANE IN PRESENCE OF FRACTAL NOISE Lorenzo Galleani, Letizia Lo Presti Dipartimento di Elettronica, Politecnico di Torino, Corso Duca
Power Supply Quality Analysis Using S-Transform and SVM Classifier
 Journal of Power and Energy Engineering, 2014, 2, 438-447 Published Online April 2014 in SciRes. http://www.scirp.org/journal/jpee http://dx.doi.org/10.4236/jpee.2014.24059 Power Supply Quality Analysis
Journal of Power and Energy Engineering, 2014, 2, 438-447 Published Online April 2014 in SciRes. http://www.scirp.org/journal/jpee http://dx.doi.org/10.4236/jpee.2014.24059 Power Supply Quality Analysis
Basic Concepts in Data Reconciliation. Chapter 6: Steady-State Data Reconciliation with Model Uncertainties
 Chapter 6: Steady-State Data with Model Uncertainties CHAPTER 6 Steady-State Data with Model Uncertainties 6.1 Models with Uncertainties In the previous chapters, the models employed in the DR were considered
Chapter 6: Steady-State Data with Model Uncertainties CHAPTER 6 Steady-State Data with Model Uncertainties 6.1 Models with Uncertainties In the previous chapters, the models employed in the DR were considered
Vibrational resonance
 Published in J. Phys. A: Math. Gen. 33, L433 L438 (2000). LETTER TO THE EDITOR Vibrational resonance P S Landa andpvemcclintock Department of Physics, Lomonosov Moscow State University, 119899 Moscow,
Published in J. Phys. A: Math. Gen. 33, L433 L438 (2000). LETTER TO THE EDITOR Vibrational resonance P S Landa andpvemcclintock Department of Physics, Lomonosov Moscow State University, 119899 Moscow,
Systematic strategies for real time filtering of turbulent signals in complex systems
 Systematic strategies for real time filtering of turbulent signals in complex systems Statistical inversion theory for Gaussian random variables The Kalman Filter for Vector Systems: Reduced Filters and
Systematic strategies for real time filtering of turbulent signals in complex systems Statistical inversion theory for Gaussian random variables The Kalman Filter for Vector Systems: Reduced Filters and
The correlation between stochastic resonance and the average phase-synchronization time of a bistable system driven by colour-correlated noises
 Chin. Phys. B Vol. 19, No. 1 (010) 01050 The correlation between stochastic resonance and the average phase-synchronization time of a bistable system driven by colour-correlated noises Dong Xiao-Juan(
Chin. Phys. B Vol. 19, No. 1 (010) 01050 The correlation between stochastic resonance and the average phase-synchronization time of a bistable system driven by colour-correlated noises Dong Xiao-Juan(
Jinki Kim Department of Mechanical Engineering University of Michigan
 Bistable and Adaptive Piezoelectric Circuitry for Impedance-Based Structural Health Monitoring Jinki Kim Department of Mechanical Engineering University of Michigan April 20 2017 Outline of the Presentation
Bistable and Adaptive Piezoelectric Circuitry for Impedance-Based Structural Health Monitoring Jinki Kim Department of Mechanical Engineering University of Michigan April 20 2017 Outline of the Presentation
Introduction to Stochastic SIR Model
 Introduction to Stochastic R Model Chiu- Yu Yang (Alex), Yi Yang R model is used to model the infection of diseases. It is short for Susceptible- Infected- Recovered. It is important to address that R
Introduction to Stochastic R Model Chiu- Yu Yang (Alex), Yi Yang R model is used to model the infection of diseases. It is short for Susceptible- Infected- Recovered. It is important to address that R
Lecture 7: Edge Detection
 #1 Lecture 7: Edge Detection Saad J Bedros sbedros@umn.edu Review From Last Lecture Definition of an Edge First Order Derivative Approximation as Edge Detector #2 This Lecture Examples of Edge Detection
#1 Lecture 7: Edge Detection Saad J Bedros sbedros@umn.edu Review From Last Lecture Definition of an Edge First Order Derivative Approximation as Edge Detector #2 This Lecture Examples of Edge Detection
Noise-enhanced propagation in a dissipative chain of triggers
 Noise-enhanced propagation in a dissipative chain of triggers S. Morfu.C. Comte.M. Bilbault and P. Marquié Université de Bourgogne, LE2I, (F.R.E.) C.N.R.S. 2309 BP 40-210 DION cedex, FRANCE email: smorfu@u-bourgogne.fr
Noise-enhanced propagation in a dissipative chain of triggers S. Morfu.C. Comte.M. Bilbault and P. Marquié Université de Bourgogne, LE2I, (F.R.E.) C.N.R.S. 2309 BP 40-210 DION cedex, FRANCE email: smorfu@u-bourgogne.fr
IV. Covariance Analysis
 IV. Covariance Analysis Autocovariance Remember that when a stochastic process has time values that are interdependent, then we can characterize that interdependency by computing the autocovariance function.
IV. Covariance Analysis Autocovariance Remember that when a stochastic process has time values that are interdependent, then we can characterize that interdependency by computing the autocovariance function.
The Continuous-time Fourier
 The Continuous-time Fourier Transform Rui Wang, Assistant professor Dept. of Information and Communication Tongji University it Email: ruiwang@tongji.edu.cn Outline Representation of Aperiodic signals:
The Continuous-time Fourier Transform Rui Wang, Assistant professor Dept. of Information and Communication Tongji University it Email: ruiwang@tongji.edu.cn Outline Representation of Aperiodic signals:
2 Department of Physics, Saratov State University, Astrahanskaya 83, Saratov, Russia
 Experimental Studies Of The Non-Adiabatic Escape Problem M. Arrayas 1, I.A. Khovanov 2, D.G. Luchinsky 1, R. Mannella 3, P.V.E. McClintock 1, M. Greenall 1, H. Sabbagh 4 1 Department of Physics, Lancaster
Experimental Studies Of The Non-Adiabatic Escape Problem M. Arrayas 1, I.A. Khovanov 2, D.G. Luchinsky 1, R. Mannella 3, P.V.E. McClintock 1, M. Greenall 1, H. Sabbagh 4 1 Department of Physics, Lancaster
Nonlinear Stochastic Resonance with subthreshold rectangular pulses arxiv:cond-mat/ v1 [cond-mat.stat-mech] 15 Jan 2004.
![Nonlinear Stochastic Resonance with subthreshold rectangular pulses arxiv:cond-mat/ v1 [cond-mat.stat-mech] 15 Jan 2004. Nonlinear Stochastic Resonance with subthreshold rectangular pulses arxiv:cond-mat/ v1 [cond-mat.stat-mech] 15 Jan 2004.](/thumbs/72/67240881.jpg) Nonlinear Stochastic Resonance with subthreshold rectangular pulses arxiv:cond-mat/4163v1 [cond-mat.stat-mech] 15 Jan 4 Jesús Casado-Pascual, José Gómez-Ordóñez, and Manuel Morillo Física Teórica, Universidad
Nonlinear Stochastic Resonance with subthreshold rectangular pulses arxiv:cond-mat/4163v1 [cond-mat.stat-mech] 15 Jan 4 Jesús Casado-Pascual, José Gómez-Ordóñez, and Manuel Morillo Física Teórica, Universidad
Stochastic Structural Dynamics Prof. Dr. C. S. Manohar Department of Civil Engineering Indian Institute of Science, Bangalore
 Stochastic Structural Dynamics Prof. Dr. C. S. Manohar Department of Civil Engineering Indian Institute of Science, Bangalore Lecture No. # 33 Probabilistic methods in earthquake engineering-2 So, we have
Stochastic Structural Dynamics Prof. Dr. C. S. Manohar Department of Civil Engineering Indian Institute of Science, Bangalore Lecture No. # 33 Probabilistic methods in earthquake engineering-2 So, we have
WHEELSET BEARING VIBRATION ANALYSIS BASED ON NONLINEAR DYNAMICAL METHOD
 15 th November 212. Vol. 45 No.1 25-212 JATIT & LLS. All rights reserved. WHEELSET BEARING VIBRATION ANALYSIS BASED ON NONLINEAR DYNAMICAL METHOD 1,2 ZHAO ZHIHONG, 2 LIU YONGQIANG 1 School of Computing
15 th November 212. Vol. 45 No.1 25-212 JATIT & LLS. All rights reserved. WHEELSET BEARING VIBRATION ANALYSIS BASED ON NONLINEAR DYNAMICAL METHOD 1,2 ZHAO ZHIHONG, 2 LIU YONGQIANG 1 School of Computing
Autoregressive tracking of vortex shedding. 2. Autoregression versus dual phase-locked loop
 Autoregressive tracking of vortex shedding Dileepan Joseph, 3 September 2003 Invensys UTC, Oxford 1. Introduction The purpose of this report is to summarize the work I have done in terms of an AR algorithm
Autoregressive tracking of vortex shedding Dileepan Joseph, 3 September 2003 Invensys UTC, Oxford 1. Introduction The purpose of this report is to summarize the work I have done in terms of an AR algorithm
arxiv: v1 [nlin.cd] 22 Aug 2016
![arxiv: v1 [nlin.cd] 22 Aug 2016 arxiv: v1 [nlin.cd] 22 Aug 2016](/thumbs/90/103054586.jpg) The Two Dynamical States of a Driven Underdamped Classical Pendulum: An Analog Simulation Experiment Ivan Skhem Sawkmie and Mangal C. Mahato Department of Physics, North-Eastern Hill University, Shillong-793022,
The Two Dynamical States of a Driven Underdamped Classical Pendulum: An Analog Simulation Experiment Ivan Skhem Sawkmie and Mangal C. Mahato Department of Physics, North-Eastern Hill University, Shillong-793022,
Lecture 9: Introduction to Diffraction of Light
 Lecture 9: Introduction to Diffraction of Light Lecture aims to explain: 1. Diffraction of waves in everyday life and applications 2. Interference of two one dimensional electromagnetic waves 3. Typical
Lecture 9: Introduction to Diffraction of Light Lecture aims to explain: 1. Diffraction of waves in everyday life and applications 2. Interference of two one dimensional electromagnetic waves 3. Typical
Effect of Non Gaussian Noises on the Stochastic Resonance-Like Phenomenon in Gated Traps. Abstract
 Effect of Non Gaussian Noises on the Stochastic Resonance-Like Phenomenon in Gated Traps Jorge A. Revelli 1 Alejandro D. Sánchez 2, and Horacio S. Wio 1 1) Grupo de Física Estadística Centro Atómico Bariloche
Effect of Non Gaussian Noises on the Stochastic Resonance-Like Phenomenon in Gated Traps Jorge A. Revelli 1 Alejandro D. Sánchez 2, and Horacio S. Wio 1 1) Grupo de Física Estadística Centro Atómico Bariloche
Bill Scheftic Feb 2nd 2008 Atmo595c
 Bill Scheftic Feb 2nd 2008 Atmo595c Review: White Noise and Red Noise ` ` Hasselman s noise forced climate External Climate forcings: Insolation Cycles Mechanisms for continuous climate variability Stochastic/Coherence
Bill Scheftic Feb 2nd 2008 Atmo595c Review: White Noise and Red Noise ` ` Hasselman s noise forced climate External Climate forcings: Insolation Cycles Mechanisms for continuous climate variability Stochastic/Coherence
16 SUPERPOSITION & STANDING WAVES
 Chapter 6 SUPERPOSITION & STANDING WAVES 6. Superposition of waves Principle of superposition: When two or more waves overlap, the resultant wave is the algebraic sum of the individual waves. Illustration:
Chapter 6 SUPERPOSITION & STANDING WAVES 6. Superposition of waves Principle of superposition: When two or more waves overlap, the resultant wave is the algebraic sum of the individual waves. Illustration:
Efficient Algorithms for Pulse Parameter Estimation, Pulse Peak Localization And Pileup Reduction in Gamma Ray Spectroscopy M.W.Raad 1, L.
 Efficient Algorithms for Pulse Parameter Estimation, Pulse Peak Localization And Pileup Reduction in Gamma Ray Spectroscopy M.W.Raad 1, L. Cheded 2 1 Computer Engineering Department, 2 Systems Engineering
Efficient Algorithms for Pulse Parameter Estimation, Pulse Peak Localization And Pileup Reduction in Gamma Ray Spectroscopy M.W.Raad 1, L. Cheded 2 1 Computer Engineering Department, 2 Systems Engineering
Chapter Three Theoretical Description Of Stochastic Resonance 24
 Table of Contents List of Abbreviations and Symbols 5 Chapter One Introduction 8 1.1 The Phenomenon of the Stochastic Resonance 8 1.2 The Purpose of the Study 10 Chapter Two The Experimental Set-up 12
Table of Contents List of Abbreviations and Symbols 5 Chapter One Introduction 8 1.1 The Phenomenon of the Stochastic Resonance 8 1.2 The Purpose of the Study 10 Chapter Two The Experimental Set-up 12
ANTICORRELATIONS AND SUBDIFFUSION IN FINANCIAL SYSTEMS. K.Staliunas Abstract
 ANICORRELAIONS AND SUBDIFFUSION IN FINANCIAL SYSEMS K.Staliunas E-mail: Kestutis.Staliunas@PB.DE Abstract Statistical dynamics of financial systems is investigated, based on a model of a randomly coupled
ANICORRELAIONS AND SUBDIFFUSION IN FINANCIAL SYSEMS K.Staliunas E-mail: Kestutis.Staliunas@PB.DE Abstract Statistical dynamics of financial systems is investigated, based on a model of a randomly coupled
Introduction to Vibration. Professor Mike Brennan
 Introduction to Vibration Professor Mie Brennan Introduction to Vibration Nature of vibration of mechanical systems Free and forced vibrations Frequency response functions Fundamentals For free vibration
Introduction to Vibration Professor Mie Brennan Introduction to Vibration Nature of vibration of mechanical systems Free and forced vibrations Frequency response functions Fundamentals For free vibration
Approximation Approach for Timing Jitter Characterization in Circuit Simulators
 Approximation Approach for iming Jitter Characterization in Circuit Simulators MM.Gourary,S.G.Rusakov,S.L.Ulyanov,M.M.Zharov IPPM, Russian Academy of Sciences, Moscow, Russia K.K. Gullapalli, B. J. Mulvaney
Approximation Approach for iming Jitter Characterization in Circuit Simulators MM.Gourary,S.G.Rusakov,S.L.Ulyanov,M.M.Zharov IPPM, Russian Academy of Sciences, Moscow, Russia K.K. Gullapalli, B. J. Mulvaney
Frequency Resolution Effects on FRF Estimation: Cyclic Averaging vs. Large Block Size
 Frequency Resolution Effects on FRF Estimation: Cyclic Averaging vs. Large Block Size Allyn W. Phillips, PhD Andrew. Zucker Randall J. Allemang, PhD Research Assistant Professor Research Assistant Professor
Frequency Resolution Effects on FRF Estimation: Cyclic Averaging vs. Large Block Size Allyn W. Phillips, PhD Andrew. Zucker Randall J. Allemang, PhD Research Assistant Professor Research Assistant Professor
THE APPLICATION OF GREY SYSTEM THEORY TO EXCHANGE RATE PREDICTION IN THE POST-CRISIS ERA
 International Journal of Innovative Management, Information & Production ISME Internationalc20 ISSN 285-5439 Volume 2, Number 2, December 20 PP. 83-89 THE APPLICATION OF GREY SYSTEM THEORY TO EXCHANGE
International Journal of Innovative Management, Information & Production ISME Internationalc20 ISSN 285-5439 Volume 2, Number 2, December 20 PP. 83-89 THE APPLICATION OF GREY SYSTEM THEORY TO EXCHANGE
Liquid-Rocket Transverse Triggered Combustion Instability: Deterministic and Stochastic Analyses
 Liquid-Rocket Transverse Triggered Combustion Instability: Deterministic and Stochastic Analyses by W. A. Sirignano Mechanical and Aerospace Engineering University of California, Irvine Collaborators:
Liquid-Rocket Transverse Triggered Combustion Instability: Deterministic and Stochastic Analyses by W. A. Sirignano Mechanical and Aerospace Engineering University of California, Irvine Collaborators:
16. Working with the Langevin and Fokker-Planck equations
 16. Working with the Langevin and Fokker-Planck equations In the preceding Lecture, we have shown that given a Langevin equation (LE), it is possible to write down an equivalent Fokker-Planck equation
16. Working with the Langevin and Fokker-Planck equations In the preceding Lecture, we have shown that given a Langevin equation (LE), it is possible to write down an equivalent Fokker-Planck equation
Stochastic contraction BACS Workshop Chamonix, January 14, 2008
 Stochastic contraction BACS Workshop Chamonix, January 14, 2008 Q.-C. Pham N. Tabareau J.-J. Slotine Q.-C. Pham, N. Tabareau, J.-J. Slotine () Stochastic contraction 1 / 19 Why stochastic contraction?
Stochastic contraction BACS Workshop Chamonix, January 14, 2008 Q.-C. Pham N. Tabareau J.-J. Slotine Q.-C. Pham, N. Tabareau, J.-J. Slotine () Stochastic contraction 1 / 19 Why stochastic contraction?
arxiv:chao-dyn/ v1 20 May 1994
 TNT 94-4 Stochastic Resonance in Deterministic Chaotic Systems A. Crisanti, M. Falcioni arxiv:chao-dyn/9405012v1 20 May 1994 Dipartimento di Fisica, Università La Sapienza, I-00185 Roma, Italy G. Paladin
TNT 94-4 Stochastic Resonance in Deterministic Chaotic Systems A. Crisanti, M. Falcioni arxiv:chao-dyn/9405012v1 20 May 1994 Dipartimento di Fisica, Università La Sapienza, I-00185 Roma, Italy G. Paladin
Abstract: Complex responses observed in an experimental, nonlinear, moored structural
 AN INDEPENDENT-FLOW-FIELD MODEL FOR A SDOF NONLINEAR STRUCTURAL SYSTEM, PART II: ANALYSIS OF COMPLEX RESPONSES Huan Lin e-mail: linh@engr.orst.edu Solomon C.S. Yim e-mail: solomon.yim@oregonstate.edu Ocean
AN INDEPENDENT-FLOW-FIELD MODEL FOR A SDOF NONLINEAR STRUCTURAL SYSTEM, PART II: ANALYSIS OF COMPLEX RESPONSES Huan Lin e-mail: linh@engr.orst.edu Solomon C.S. Yim e-mail: solomon.yim@oregonstate.edu Ocean
Additive resonances of a controlled van der Pol-Duffing oscillator
 Additive resonances of a controlled van der Pol-Duffing oscillator This paper has been published in Journal of Sound and Vibration vol. 5 issue - 8 pp.-. J.C. Ji N. Zhang Faculty of Engineering University
Additive resonances of a controlled van der Pol-Duffing oscillator This paper has been published in Journal of Sound and Vibration vol. 5 issue - 8 pp.-. J.C. Ji N. Zhang Faculty of Engineering University
Time-Series Analysis for Ear-Related and Psychoacoustic Metrics
 Time-Series Analysis for Ear-Related and Psychoacoustic Metrics V. Mellert, H. Remmers, R. Weber, B. Schulte-Fortkamp how to analyse p(t) to obtain an earrelated parameter? general remarks on acoustical
Time-Series Analysis for Ear-Related and Psychoacoustic Metrics V. Mellert, H. Remmers, R. Weber, B. Schulte-Fortkamp how to analyse p(t) to obtain an earrelated parameter? general remarks on acoustical
Stochastic resonance in the absence and presence of external signals for a chemical reaction
 JOURNAL OF CHEMICAL PHYSICS VOLUME 110, NUMBER 7 15 FEBRUARY 1999 Stochastic resonance in the absence and presence of external signals for a chemical reaction Lingfa Yang, Zhonghuai Hou, and Houwen Xin
JOURNAL OF CHEMICAL PHYSICS VOLUME 110, NUMBER 7 15 FEBRUARY 1999 Stochastic resonance in the absence and presence of external signals for a chemical reaction Lingfa Yang, Zhonghuai Hou, and Houwen Xin
Lecture 11: Introduction to diffraction of light
 Lecture 11: Introduction to diffraction of light Diffraction of waves in everyday life and applications Diffraction in everyday life Diffraction in applications Spectroscopy: physics, chemistry, medicine,
Lecture 11: Introduction to diffraction of light Diffraction of waves in everyday life and applications Diffraction in everyday life Diffraction in applications Spectroscopy: physics, chemistry, medicine,
Which wavelet bases are the best for image denoising?
 Which wavelet bases are the best for image denoising? Florian Luisier a, Thierry Blu a, Brigitte Forster b and Michael Unser a a Biomedical Imaging Group (BIG), Ecole Polytechnique Fédérale de Lausanne
Which wavelet bases are the best for image denoising? Florian Luisier a, Thierry Blu a, Brigitte Forster b and Michael Unser a a Biomedical Imaging Group (BIG), Ecole Polytechnique Fédérale de Lausanne
Laplacian Filters. Sobel Filters. Laplacian Filters. Laplacian Filters. Laplacian Filters. Laplacian Filters
 Sobel Filters Note that smoothing the image before applying a Sobel filter typically gives better results. Even thresholding the Sobel filtered image cannot usually create precise, i.e., -pixel wide, edges.
Sobel Filters Note that smoothing the image before applying a Sobel filter typically gives better results. Even thresholding the Sobel filtered image cannot usually create precise, i.e., -pixel wide, edges.
A New Circuit for Generating Chaos and Complexity: Analysis of the Beats Phenomenon
 A New Circuit for Generating Chaos and Complexity: Analysis of the Beats Phenomenon DONATO CAFAGNA, GIUSEPPE GRASSI Diparnto Ingegneria Innovazione Università di Lecce via Monteroni, 73 Lecce ITALY Abstract:
A New Circuit for Generating Chaos and Complexity: Analysis of the Beats Phenomenon DONATO CAFAGNA, GIUSEPPE GRASSI Diparnto Ingegneria Innovazione Università di Lecce via Monteroni, 73 Lecce ITALY Abstract:
Amplitude and Phase A(0) 2. We start with the Fourier series representation of X(t) in real notation: n=1
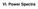 VI. Power Spectra Amplitude and Phase We start with the Fourier series representation of X(t) in real notation: A() X(t) = + [ A(n) cos(nωt) + B(n) sin(nωt)] 2 n=1 he waveform of the observed segment exactly
VI. Power Spectra Amplitude and Phase We start with the Fourier series representation of X(t) in real notation: A() X(t) = + [ A(n) cos(nωt) + B(n) sin(nωt)] 2 n=1 he waveform of the observed segment exactly
STOCHASTIC RESONANCE IN MONOSTABLE SYSTEMS
 Published in J. Phys. A: Mat. Gen. 26, L385-39 (1993). STOCHASTIC RESONANCE IN MONOSTABLE SYSTEMS N G Stocks, N D Stein and P V E McClintock School of Physics and Materials, Lancaster University, Lancaster,
Published in J. Phys. A: Mat. Gen. 26, L385-39 (1993). STOCHASTIC RESONANCE IN MONOSTABLE SYSTEMS N G Stocks, N D Stein and P V E McClintock School of Physics and Materials, Lancaster University, Lancaster,
Acoustic holography. LMS Test.Lab. Rev 12A
 Acoustic holography LMS Test.Lab Rev 12A Copyright LMS International 2012 Table of Contents Chapter 1 Introduction... 5 Chapter 2... 7 Section 2.1 Temporal and spatial frequency... 7 Section 2.2 Time
Acoustic holography LMS Test.Lab Rev 12A Copyright LMS International 2012 Table of Contents Chapter 1 Introduction... 5 Chapter 2... 7 Section 2.1 Temporal and spatial frequency... 7 Section 2.2 Time
Behaviour of synchronous machine during a short-circuit (a simple example of electromagnetic transients)
 ELEC0047 - Power system dynamics, control and stability (a simple example of electromagnetic transients) Thierry Van Cutsem t.vancutsem@ulg.ac.be www.montefiore.ulg.ac.be/~vct October 2018 1 / 25 Objectives
ELEC0047 - Power system dynamics, control and stability (a simple example of electromagnetic transients) Thierry Van Cutsem t.vancutsem@ulg.ac.be www.montefiore.ulg.ac.be/~vct October 2018 1 / 25 Objectives
SHAKING TABLE DEMONSTRATION OF DYNAMIC RESPONSE OF BASE-ISOLATED BUILDINGS ***** Instructor Manual *****
 SHAKING TABLE DEMONSTRATION OF DYNAMIC RESPONSE OF BASE-ISOLATED BUILDINGS ***** Instructor Manual ***** A PROJECT DEVELOPED FOR THE UNIVERSITY CONSORTIUM ON INSTRUCTIONAL SHAKE TABLES http://wusceel.cive.wustl.edu/ucist/
SHAKING TABLE DEMONSTRATION OF DYNAMIC RESPONSE OF BASE-ISOLATED BUILDINGS ***** Instructor Manual ***** A PROJECT DEVELOPED FOR THE UNIVERSITY CONSORTIUM ON INSTRUCTIONAL SHAKE TABLES http://wusceel.cive.wustl.edu/ucist/
New Statistical Model for the Enhancement of Noisy Speech
 New Statistical Model for the Enhancement of Noisy Speech Electrical Engineering Department Technion - Israel Institute of Technology February 22, 27 Outline Problem Formulation and Motivation 1 Problem
New Statistical Model for the Enhancement of Noisy Speech Electrical Engineering Department Technion - Israel Institute of Technology February 22, 27 Outline Problem Formulation and Motivation 1 Problem
KLT for transient signal analysis
 The Labyrinth of the Unepected: unforeseen treasures in impossible regions of phase space Nicolò Antonietti 4/1/17 Kerastari, Greece May 9 th June 3 rd Qualitatively definition of transient signals Signals
The Labyrinth of the Unepected: unforeseen treasures in impossible regions of phase space Nicolò Antonietti 4/1/17 Kerastari, Greece May 9 th June 3 rd Qualitatively definition of transient signals Signals
Stochastic Processes. M. Sami Fadali Professor of Electrical Engineering University of Nevada, Reno
 Stochastic Processes M. Sami Fadali Professor of Electrical Engineering University of Nevada, Reno 1 Outline Stochastic (random) processes. Autocorrelation. Crosscorrelation. Spectral density function.
Stochastic Processes M. Sami Fadali Professor of Electrical Engineering University of Nevada, Reno 1 Outline Stochastic (random) processes. Autocorrelation. Crosscorrelation. Spectral density function.
If the symmetry axes of a uniform symmetric body coincide with the coordinate axes, the products of inertia (Ixy etc.
 Prof. O. B. Wright, Autumn 007 Mechanics Lecture 9 More on rigid bodies, coupled vibrations Principal axes of the inertia tensor If the symmetry axes of a uniform symmetric body coincide with the coordinate
Prof. O. B. Wright, Autumn 007 Mechanics Lecture 9 More on rigid bodies, coupled vibrations Principal axes of the inertia tensor If the symmetry axes of a uniform symmetric body coincide with the coordinate
Selected Topics in Physics a lecture course for 1st year students by W.B. von Schlippe Spring Semester 2007
 Selected Topics in Physics a lecture course for st year students by W.B. von Schlippe Spring Semester 7 Lecture : Oscillations simple harmonic oscillations; coupled oscillations; beats; damped oscillations;
Selected Topics in Physics a lecture course for st year students by W.B. von Schlippe Spring Semester 7 Lecture : Oscillations simple harmonic oscillations; coupled oscillations; beats; damped oscillations;
CMPT 889: Lecture 2 Sinusoids, Complex Exponentials, Spectrum Representation
 CMPT 889: Lecture 2 Sinusoids, Complex Exponentials, Spectrum Representation Tamara Smyth, tamaras@cs.sfu.ca School of Computing Science, Simon Fraser University September 26, 2005 1 Sinusoids Sinusoids
CMPT 889: Lecture 2 Sinusoids, Complex Exponentials, Spectrum Representation Tamara Smyth, tamaras@cs.sfu.ca School of Computing Science, Simon Fraser University September 26, 2005 1 Sinusoids Sinusoids
The Approximation Problem
 EE 508 Lecture 3 The Approximation Problem Classical Approximating Functions - Thompson and Bessel Approximations Review from Last Time Elliptic Filters Can be thought of as an extension of the CC approach
EE 508 Lecture 3 The Approximation Problem Classical Approximating Functions - Thompson and Bessel Approximations Review from Last Time Elliptic Filters Can be thought of as an extension of the CC approach
Stochastic Model for Adaptation Using Basin Hopping Dynamics
 Stochastic Model for Adaptation Using Basin Hopping Dynamics Peter Davis NTT Communication Science Laboratories 2-4 Hikaridai, Keihanna Science City, Kyoto, Japan 619-0237 davis@cslab.kecl.ntt.co.jp Abstract
Stochastic Model for Adaptation Using Basin Hopping Dynamics Peter Davis NTT Communication Science Laboratories 2-4 Hikaridai, Keihanna Science City, Kyoto, Japan 619-0237 davis@cslab.kecl.ntt.co.jp Abstract
Technical note on seasonal adjustment for Capital goods imports
 Technical note on seasonal adjustment for Capital goods imports July 1, 2013 Contents 1 Capital goods imports 2 1.1 Additive versus multiplicative seasonality..................... 2 2 Steps in the seasonal
Technical note on seasonal adjustment for Capital goods imports July 1, 2013 Contents 1 Capital goods imports 2 1.1 Additive versus multiplicative seasonality..................... 2 2 Steps in the seasonal
THE problem of phase noise and its influence on oscillators
 IEEE TRANSACTIONS ON CIRCUITS AND SYSTEMS II: EXPRESS BRIEFS, VOL. 54, NO. 5, MAY 2007 435 Phase Diffusion Coefficient for Oscillators Perturbed by Colored Noise Fergal O Doherty and James P. Gleeson Abstract
IEEE TRANSACTIONS ON CIRCUITS AND SYSTEMS II: EXPRESS BRIEFS, VOL. 54, NO. 5, MAY 2007 435 Phase Diffusion Coefficient for Oscillators Perturbed by Colored Noise Fergal O Doherty and James P. Gleeson Abstract
Diagnosis of Overhead Contact Line based on Contact Force. Takahiro FUKUTANI Current Collection Laboratory, Power Supply Division
 PAPER Diagnosis of Overhead Contact Line based on Contact Force Shunichi KUSUMI Contact Line Structures Laboratory, Takahiro FUKUTANI Current Collection Laboratory, Power Supply Division Kazuyoshi NEZU
PAPER Diagnosis of Overhead Contact Line based on Contact Force Shunichi KUSUMI Contact Line Structures Laboratory, Takahiro FUKUTANI Current Collection Laboratory, Power Supply Division Kazuyoshi NEZU
Suppression of the primary resonance vibrations of a forced nonlinear system using a dynamic vibration absorber
 Suppression of the primary resonance vibrations of a forced nonlinear system using a dynamic vibration absorber J.C. Ji, N. Zhang Faculty of Engineering, University of Technology, Sydney PO Box, Broadway,
Suppression of the primary resonance vibrations of a forced nonlinear system using a dynamic vibration absorber J.C. Ji, N. Zhang Faculty of Engineering, University of Technology, Sydney PO Box, Broadway,
Vibration Control Prof. Dr. S. P. Harsha Department of Mechanical & Industrial Engineering Indian Institute of Technology, Roorkee
 Vibration Control Prof. Dr. S. P. Harsha Department of Mechanical & Industrial Engineering Indian Institute of Technology, Roorkee Module - 1 Review of Basics of Mechanical Vibrations Lecture - 2 Introduction
Vibration Control Prof. Dr. S. P. Harsha Department of Mechanical & Industrial Engineering Indian Institute of Technology, Roorkee Module - 1 Review of Basics of Mechanical Vibrations Lecture - 2 Introduction
Reliability-based Design Optimization of Nonlinear Energy Sinks
 th World Congress on Structural and Multidisciplinary Optimization 7 th - th, June, Sydney Australia Reliability-based Design Optimization of Nonlinear Energy Sinks Ethan Boroson and Samy Missoum University
th World Congress on Structural and Multidisciplinary Optimization 7 th - th, June, Sydney Australia Reliability-based Design Optimization of Nonlinear Energy Sinks Ethan Boroson and Samy Missoum University
Introduction to Biomedical Engineering
 Introduction to Biomedical Engineering Biosignal processing Kung-Bin Sung 6/11/2007 1 Outline Chapter 10: Biosignal processing Characteristics of biosignals Frequency domain representation and analysis
Introduction to Biomedical Engineering Biosignal processing Kung-Bin Sung 6/11/2007 1 Outline Chapter 10: Biosignal processing Characteristics of biosignals Frequency domain representation and analysis
AA 242B / ME 242B: Mechanical Vibrations (Spring 2016)
 AA 242B / ME 242B: Mechanical Vibrations (Spring 206) Solution of Homework #3 Control Tab Figure : Schematic for the control tab. Inadequacy of a static-test A static-test for measuring θ would ideally
AA 242B / ME 242B: Mechanical Vibrations (Spring 206) Solution of Homework #3 Control Tab Figure : Schematic for the control tab. Inadequacy of a static-test A static-test for measuring θ would ideally
These slides follow closely the (English) course textbook Pattern Recognition and Machine Learning by Christopher Bishop
 Music and Machine Learning (IFT68 Winter 8) Prof. Douglas Eck, Université de Montréal These slides follow closely the (English) course textbook Pattern Recognition and Machine Learning by Christopher Bishop
Music and Machine Learning (IFT68 Winter 8) Prof. Douglas Eck, Université de Montréal These slides follow closely the (English) course textbook Pattern Recognition and Machine Learning by Christopher Bishop
Process Damping Coefficient Identification using Bayesian Inference
 Process Damping Coefficient Identification using Bayesian Inference Jaydeep M. Karandikar, Christopher T. Tyler, and Tony L. Schmitz Mechanical Engineering and Engineering Science University of North Carolina
Process Damping Coefficient Identification using Bayesian Inference Jaydeep M. Karandikar, Christopher T. Tyler, and Tony L. Schmitz Mechanical Engineering and Engineering Science University of North Carolina
3 Mathematical modeling of the torsional dynamics of a drill string
 3 Mathematical modeling of the torsional dynamics of a drill string 3.1 Introduction Many works about torsional vibrations on drilling systems [1, 12, 18, 24, 41] have been published using different numerical
3 Mathematical modeling of the torsional dynamics of a drill string 3.1 Introduction Many works about torsional vibrations on drilling systems [1, 12, 18, 24, 41] have been published using different numerical
Adaptive Short-Time Fractional Fourier Transform Used in Time-Frequency Analysis
 Adaptive Short-Time Fractional Fourier Transform Used in Time-Frequency Analysis 12 School of Electronics and Information,Yili Normal University, Yining, 830054, China E-mail: tianlin20110501@163.com In
Adaptive Short-Time Fractional Fourier Transform Used in Time-Frequency Analysis 12 School of Electronics and Information,Yili Normal University, Yining, 830054, China E-mail: tianlin20110501@163.com In
A New Two-dimensional Empirical Mode Decomposition Based on Classical Empirical Mode Decomposition and Radon Transform
 A New Two-dimensional Empirical Mode Decomposition Based on Classical Empirical Mode Decomposition and Radon Transform Zhihua Yang and Lihua Yang Abstract This paper presents a new twodimensional Empirical
A New Two-dimensional Empirical Mode Decomposition Based on Classical Empirical Mode Decomposition and Radon Transform Zhihua Yang and Lihua Yang Abstract This paper presents a new twodimensional Empirical
DETC EXPERIMENT OF OIL-FILM WHIRL IN ROTOR SYSTEM AND WAVELET FRACTAL ANALYSES
 Proceedings of IDETC/CIE 2005 ASME 2005 International Design Engineering Technical Conferences & Computers and Information in Engineering Conference September 24-28, 2005, Long Beach, California, USA DETC2005-85218
Proceedings of IDETC/CIE 2005 ASME 2005 International Design Engineering Technical Conferences & Computers and Information in Engineering Conference September 24-28, 2005, Long Beach, California, USA DETC2005-85218
Noise and O 1 amplitude effects on heteroclinic cycles
 CHAOS VOLUME 9, NUMBER 2 JUNE 1999 Noise and O 1 amplitude effects on heteroclinic cycles Emily Stone Department of Mathematics and Statistics, Utah State University, Logan, Utah 84322-39 Dieter Armbruster
CHAOS VOLUME 9, NUMBER 2 JUNE 1999 Noise and O 1 amplitude effects on heteroclinic cycles Emily Stone Department of Mathematics and Statistics, Utah State University, Logan, Utah 84322-39 Dieter Armbruster
Vibration Testing. Typically either instrumented hammers or shakers are used.
 Vibration Testing Vibration Testing Equipment For vibration testing, you need an excitation source a device to measure the response a digital signal processor to analyze the system response Excitation
Vibration Testing Vibration Testing Equipment For vibration testing, you need an excitation source a device to measure the response a digital signal processor to analyze the system response Excitation
Supporting Information. Methods. Equations for four regimes
 Supporting Information A Methods All analytical expressions were obtained starting from quation 3, the tqssa approximation of the cycle, the derivation of which is discussed in Appendix C. The full mass
Supporting Information A Methods All analytical expressions were obtained starting from quation 3, the tqssa approximation of the cycle, the derivation of which is discussed in Appendix C. The full mass
Signal Modeling, Statistical Inference and Data Mining in Astrophysics
 ASTRONOMY 6523 Spring 2013 Signal Modeling, Statistical Inference and Data Mining in Astrophysics Course Approach The philosophy of the course reflects that of the instructor, who takes a dualistic view
ASTRONOMY 6523 Spring 2013 Signal Modeling, Statistical Inference and Data Mining in Astrophysics Course Approach The philosophy of the course reflects that of the instructor, who takes a dualistic view
Versatile, Accurate and Analytically Tractable Approximation for the Gaussian Q-function. Miguel López-Benítez and Fernando Casadevall
 Versatile, Accurate and Analytically Tractable Approximation for the Gaussian Q-function Miguel López-Benítez and Fernando Casadevall Department of Signal Theory and Communications Universitat Politècnica
Versatile, Accurate and Analytically Tractable Approximation for the Gaussian Q-function Miguel López-Benítez and Fernando Casadevall Department of Signal Theory and Communications Universitat Politècnica
Difference Resonances in a controlled van der Pol-Duffing oscillator involving time. delay
 Difference Resonances in a controlled van der Pol-Duffing oscillator involving time delay This paper was published in the journal Chaos, Solitions & Fractals, vol.4, no., pp.975-98, Oct 9 J.C. Ji, N. Zhang,
Difference Resonances in a controlled van der Pol-Duffing oscillator involving time delay This paper was published in the journal Chaos, Solitions & Fractals, vol.4, no., pp.975-98, Oct 9 J.C. Ji, N. Zhang,
PHYSICAL REVIEW LETTERS
 PHYSICAL REVIEW LETTERS VOLUME 80 1 JUNE 1998 NUMBER 22 Field-Induced Stabilization of Activation Processes N. G. Stocks* and R. Mannella Dipartimento di Fisica, Università di Pisa, and Istituto Nazionale
PHYSICAL REVIEW LETTERS VOLUME 80 1 JUNE 1998 NUMBER 22 Field-Induced Stabilization of Activation Processes N. G. Stocks* and R. Mannella Dipartimento di Fisica, Università di Pisa, and Istituto Nazionale
Pre-Calculus MATH 119 Fall Section 1.1. Section objectives. Section 1.3. Section objectives. Section A.10. Section objectives
 Pre-Calculus MATH 119 Fall 2013 Learning Objectives Section 1.1 1. Use the Distance Formula 2. Use the Midpoint Formula 4. Graph Equations Using a Graphing Utility 5. Use a Graphing Utility to Create Tables
Pre-Calculus MATH 119 Fall 2013 Learning Objectives Section 1.1 1. Use the Distance Formula 2. Use the Midpoint Formula 4. Graph Equations Using a Graphing Utility 5. Use a Graphing Utility to Create Tables
Residence-time distributions as a measure for stochastic resonance
 W e ie rstra ß -In stitu t fü r A n g e w a n d te A n a ly sis u n d S to ch a stik Period of Concentration: Stochastic Climate Models MPI Mathematics in the Sciences, Leipzig, 23 May 1 June 2005 Barbara
W e ie rstra ß -In stitu t fü r A n g e w a n d te A n a ly sis u n d S to ch a stik Period of Concentration: Stochastic Climate Models MPI Mathematics in the Sciences, Leipzig, 23 May 1 June 2005 Barbara
Generalized projective synchronization between two chaotic gyros with nonlinear damping
 Generalized projective synchronization between two chaotic gyros with nonlinear damping Min Fu-Hong( ) Department of Electrical and Automation Engineering, Nanjing Normal University, Nanjing 210042, China
Generalized projective synchronization between two chaotic gyros with nonlinear damping Min Fu-Hong( ) Department of Electrical and Automation Engineering, Nanjing Normal University, Nanjing 210042, China
Invariant Pattern Recognition using Dual-tree Complex Wavelets and Fourier Features
 Invariant Pattern Recognition using Dual-tree Complex Wavelets and Fourier Features G. Y. Chen and B. Kégl Department of Computer Science and Operations Research, University of Montreal, CP 6128 succ.
Invariant Pattern Recognition using Dual-tree Complex Wavelets and Fourier Features G. Y. Chen and B. Kégl Department of Computer Science and Operations Research, University of Montreal, CP 6128 succ.
Oscillatory Motion SHM
 Chapter 15 Oscillatory Motion SHM Dr. Armen Kocharian Periodic Motion Periodic motion is motion of an object that regularly repeats The object returns to a given position after a fixed time interval A
Chapter 15 Oscillatory Motion SHM Dr. Armen Kocharian Periodic Motion Periodic motion is motion of an object that regularly repeats The object returns to a given position after a fixed time interval A
In this lecture you will learn the following
 Module 9 : Forced Vibration with Harmonic Excitation; Undamped Systems and resonance; Viscously Damped Systems; Frequency Response Characteristics and Phase Lag; Systems with Base Excitation; Transmissibility
Module 9 : Forced Vibration with Harmonic Excitation; Undamped Systems and resonance; Viscously Damped Systems; Frequency Response Characteristics and Phase Lag; Systems with Base Excitation; Transmissibility
Dynamics of Ocean Structures Prof. Dr. Srinivasan Chandrasekaran Department of Ocean Engineering Indian Institute of Technology, Madras
 Dynamics of Ocean Structures Prof. Dr. Srinivasan Chandrasekaran Department of Ocean Engineering Indian Institute of Technology, Madras Module - 1 Lecture - 13 Undamped and Damped Systems II (Refer Slide
Dynamics of Ocean Structures Prof. Dr. Srinivasan Chandrasekaran Department of Ocean Engineering Indian Institute of Technology, Madras Module - 1 Lecture - 13 Undamped and Damped Systems II (Refer Slide
Bemidji Area Schools Outcomes in Mathematics Analysis 1. Based on Minnesota Academic Standards in Mathematics (2007) Page 1 of 5
 Understand the concept of function, and identify important features of functions and other relations using symbolic and graphical methods where appropriate. 9..1.1 9..1. 9..1.3 9..1.4 9..1.5 9..1.6 9..1.7
Understand the concept of function, and identify important features of functions and other relations using symbolic and graphical methods where appropriate. 9..1.1 9..1. 9..1.3 9..1.4 9..1.5 9..1.6 9..1.7
(a)
 Chapter 8 Subspace Methods 8. Introduction Principal Component Analysis (PCA) is applied to the analysis of time series data. In this context we discuss measures of complexity and subspace methods for
Chapter 8 Subspace Methods 8. Introduction Principal Component Analysis (PCA) is applied to the analysis of time series data. In this context we discuss measures of complexity and subspace methods for
Finite-Memory Universal Prediction of Individual Continuous Sequences
 THE IBY AND ALADAR FLEISCHMAN FACULTY OF ENGINEERING THE ZANDMAN-SLANER SCHOOL OF GRADUATE STUDIES THE SCHOOL OF ELECTRICAL ENGINEERING Finite-Memory Universal Prediction of Individual Continuous Sequences
THE IBY AND ALADAR FLEISCHMAN FACULTY OF ENGINEERING THE ZANDMAN-SLANER SCHOOL OF GRADUATE STUDIES THE SCHOOL OF ELECTRICAL ENGINEERING Finite-Memory Universal Prediction of Individual Continuous Sequences
Thesis. Wei Tang. 1 Abstract 3. 3 Experiment Background The Large Hadron Collider The ATLAS Detector... 4
 Thesis Wei Tang Contents 1 Abstract 3 2 Introduction 3 3 Experiment Background 4 3.1 The Large Hadron Collider........................... 4 3.2 The ATLAS Detector.............................. 4 4 Search
Thesis Wei Tang Contents 1 Abstract 3 2 Introduction 3 3 Experiment Background 4 3.1 The Large Hadron Collider........................... 4 3.2 The ATLAS Detector.............................. 4 4 Search
Phase Synchronization
 Phase Synchronization Lecture by: Zhibin Guo Notes by: Xiang Fan May 10, 2016 1 Introduction For any mode or fluctuation, we always have where S(x, t) is phase. If a mode amplitude satisfies ϕ k = ϕ k
Phase Synchronization Lecture by: Zhibin Guo Notes by: Xiang Fan May 10, 2016 1 Introduction For any mode or fluctuation, we always have where S(x, t) is phase. If a mode amplitude satisfies ϕ k = ϕ k
Linear Models for Regression
 Linear Models for Regression CSE 4309 Machine Learning Vassilis Athitsos Computer Science and Engineering Department University of Texas at Arlington 1 The Regression Problem Training data: A set of input-output
Linear Models for Regression CSE 4309 Machine Learning Vassilis Athitsos Computer Science and Engineering Department University of Texas at Arlington 1 The Regression Problem Training data: A set of input-output
ANNEX A: ANALYSIS METHODOLOGIES
 ANNEX A: ANALYSIS METHODOLOGIES A.1 Introduction Before discussing supplemental damping devices, this annex provides a brief review of the seismic analysis methods used in the optimization algorithms considered
ANNEX A: ANALYSIS METHODOLOGIES A.1 Introduction Before discussing supplemental damping devices, this annex provides a brief review of the seismic analysis methods used in the optimization algorithms considered
Open Access Permanent Magnet Synchronous Motor Vector Control Based on Weighted Integral Gain of Sliding Mode Variable Structure
 Send Orders for Reprints to reprints@benthamscienceae The Open Automation and Control Systems Journal, 5, 7, 33-33 33 Open Access Permanent Magnet Synchronous Motor Vector Control Based on Weighted Integral
Send Orders for Reprints to reprints@benthamscienceae The Open Automation and Control Systems Journal, 5, 7, 33-33 33 Open Access Permanent Magnet Synchronous Motor Vector Control Based on Weighted Integral
Research Article Semi-Active Pulse-Switching Vibration Suppression Using Sliding Time Window
 Smart Materials Research Volume 213, Article ID 865981, 7 pages http://dx.doi.org/1.1155/213/865981 Research Article Semi-Active Pulse-Switching Vibration Suppression Using Sliding Time Window S. Mohammadi,
Smart Materials Research Volume 213, Article ID 865981, 7 pages http://dx.doi.org/1.1155/213/865981 Research Article Semi-Active Pulse-Switching Vibration Suppression Using Sliding Time Window S. Mohammadi,
[ ], [ ] [ ] [ ] = [ ] [ ] [ ]{ [ 1] [ 2]
![[ ], [ ] [ ] [ ] = [ ] [ ] [ ]{ [ 1] [ 2] [ ], [ ] [ ] [ ] = [ ] [ ] [ ]{ [ 1] [ 2]](/thumbs/79/79554328.jpg) 4. he discrete Fourier transform (DF). Application goal We study the discrete Fourier transform (DF) and its applications: spectral analysis and linear operations as convolution and correlation. We use
4. he discrete Fourier transform (DF). Application goal We study the discrete Fourier transform (DF) and its applications: spectral analysis and linear operations as convolution and correlation. We use
DESIGN OF A NONLINEAR VIBRATION ABSORBER
 DESIGN OF A NONLINEAR VIBRATION ABSORBER Maxime Geeroms, Laurens Marijns, Mia Loccufier and Dirk Aeyels Ghent University, Department EESA, Belgium Abstract Linear vibration absorbers can only capture certain
DESIGN OF A NONLINEAR VIBRATION ABSORBER Maxime Geeroms, Laurens Marijns, Mia Loccufier and Dirk Aeyels Ghent University, Department EESA, Belgium Abstract Linear vibration absorbers can only capture certain
Output high order sliding mode control of unity-power-factor in three-phase AC/DC Boost Converter
 Output high order sliding mode control of unity-power-factor in three-phase AC/DC Boost Converter JianXing Liu, Salah Laghrouche, Maxim Wack Laboratoire Systèmes Et Transports (SET) Laboratoire SeT Contents
Output high order sliding mode control of unity-power-factor in three-phase AC/DC Boost Converter JianXing Liu, Salah Laghrouche, Maxim Wack Laboratoire Systèmes Et Transports (SET) Laboratoire SeT Contents
Chapter 14: Wave Motion Tuesday April 7 th
 Chapter 14: Wave Motion Tuesday April 7 th Wave superposition Spatial interference Temporal interference (beating) Standing waves and resonance Sources of musical sound Doppler effect Sonic boom Examples,
Chapter 14: Wave Motion Tuesday April 7 th Wave superposition Spatial interference Temporal interference (beating) Standing waves and resonance Sources of musical sound Doppler effect Sonic boom Examples,
