Fundamental Meteo Concepts
|
|
|
- Theodore Reed
- 5 years ago
- Views:
Transcription
1 Fundamental Meteo Concepts Atmos 5110 Synoptic Dynamic Meteorology I Instructor: Jim Steenburgh jim.steenburgh@utah.edu Suite 480/Office 488 INSCC Suggested reading: Lackmann (2011), sections Holton and Hakim (2013), sections These are essential meteorological concepts for success in this and other atmospheric sciences classes. To do well in this class, you must understand these concepts mathematically and physically. Geostrophic wind Horizontal momentum equation is given by DV# Dt = 1 ρ p fk. V# + Friction Acceleration PGF Coriolis Friction Assuming acceleration and friction are zero gives a balance between the PGF and Coriolis with the geostrophic wind given by V# 7 = 1 ρf k. p In component form u 7 = 1 p ρf y v 7 = 1 p ρf x The geostrophic wind is oriented parallel to the isobars with lower pressure on the left in the Northern Hemisphere 1
2 The magnitude of the geostrophic wind is: Proportional to the pressure gradient Inversely proportional to f (i.e., latitude) >V# 7 1 p Therefore: The larger the pressure gradient, the larger the geostrophic wind The lower the latitude, the stronger the geostrophic wind for a given pressure gradient The higher the latitude, the weaker the geostrophic wind for a given pressure gradient Geostrophic flow: A flow in which the actual wind and the geostrophic wind are equivalent Geostrophic approximation: Assumes the total wind can be approximated by the geostrophic wind Geostrophic wind in pressure coordinates Meteorologists typically use pressure rather than height as a vertical coordinate. The pressure gradient on a height surface is proportional to the geopotential (and geopotential height) gradient on a pressure surface. 1 ρ C p y D = C Φ y D C Z y D, where Z = geopotential height E G G The geostrophic wind in pressure coordinates is given by V# 7 = k. 1 f Φ >V# 7 > = g Q f > GZ> 2
3 The geostrophic wind is oriented parallel to the isohypses with lower heights on the left in the Northern Hemisphere The magnitude of the geostrophic wind is: Proportional to the height gradient Inversely proportional to f (i.e., latitude) >V# 7 1 > GZ> Class activity Using the IDV Supernational bundle, diagnose the 925-mb geostrophic temperature advection of over (a) Seattle, WA, (b) Salt Lake City, UT, and (c) Albany, NY. To do this, you will need to change the geopotential height level from 500 to 925 mb. Gradient wind Considers the effect of curvature with a balance between the PGF, Coriolis, and centrifugal accelerations V 7R = fr 2 ± (fw R W 4 R Φ n )Z/W R=Radius of curvature; n positive to the left of the flow (natural coordinates) In gradient wind balance, the flow is parallel to the isobars and Vgr < Vg in the trough (subgeostrophic) Vgr > Vg in the ridge (supergeostrophic) 3
4 Class activity Using the 5110>geowind-vs-totalwind bundle in IDV, identify a ridge and a trough and diagnose the total and geostrophic wind in the ridge and trough axes. Are the differences consistent with gradient wind balances? 4
5 Hydrostatic balance A balance between gravity and the vertical component of the pressure-gradient force Hydrostatic approximation p z = ρg Applicable to the synoptic scale, but not necessarily the mesoscale or smaller scales. Learn it, know it, love it. Hypsometric equation Assuming hydrostatic balance, provides a relationship between the mean temperature and the thickness of a layer (i.e., the distance between two p levels) Z = Z^ Z _ = RTb a g ln (p _ ) Z T a p^ 5
6 Critical thickness Back in the day, temperature and precipitation type forecasts were often made using the mb thickness. The critical thickness is the thickness at which there is a 50/50 chance of snow or frozen precipitation occurring. The lower the thickness, the greater the chance of snow or frozen precipitation The higher the thickness, the smaller the chance Near sea level in the northeast U.S., the critical mb thickness is ~540 dm At Denver it is ~548 dm 6
7 Problem: Critical thickness does not fully account for the influence of varied lapse rates, shallow cold pools, etc. Result: Best to use model soundings (especially BUFR soundings) when forecasting temperature and precipitation type Thermal wind The thermal wind is not an actual wind, but the name given to the vertical shear of the geostrophic wind V# f = V# 7,^GGgR V# 7,_higR = g f k. Thickness = g f k. Tb a The magnitude of the thermal wind (i.e., the shear of the geostrophic wind) is proportional to the strength of the thickness/temperature gradient A large temperature gradient yields a lot of shear The thermal wind vector (i.e., the geostrophic wind shear vector) is oriented parallel to the thickness/temperature contours with lower values on the left Cold advection is associated with backing (counterclockwise turning) winds with height and warm advection with veering (clockwise turning) winds with height 7
8 The integrated influence of horizontal temperature contrasts on thickness, height gradients, wind shear, and wind speed is shown by Figure 1.5 of Lackmann (2011): 8
9 It can also be seen in the NCEP/NCAR zonal mean temperature ( C) and wind (m s -1, note scale change) climatology ( ) for the northern hemisphere in January (top) and July (bottom) 9
10 Class activity Answer the question, have you seen the thermal wind today? Using IDV and soundings available on the web, examine the relationship between the temperature gradient and wind speed in the atmosphere, including how to diagnose temperature advection based solely on soundings. 10
Hydrostatic Equation and Thermal Wind. Meteorology 411 Iowa State University Week 5 Bill Gallus
 Hydrostatic Equation and Thermal Wind Meteorology 411 Iowa State University Week 5 Bill Gallus Hydrostatic Equation In the atmosphere, vertical accelerations (dw/dt) are normally fairly small, and we can
Hydrostatic Equation and Thermal Wind Meteorology 411 Iowa State University Week 5 Bill Gallus Hydrostatic Equation In the atmosphere, vertical accelerations (dw/dt) are normally fairly small, and we can
Dynamics of Upper-Level Waves
 Dynamics of Upper-Level Waves Atmos 5110 Synoptic Dynamic Meteorology I Instructor: Jim Steenburgh jim.steenburgh@utah.edu 801-581-8727 Suite 480/Office 488 INSCC Suggested reading: Lackman (2011) section
Dynamics of Upper-Level Waves Atmos 5110 Synoptic Dynamic Meteorology I Instructor: Jim Steenburgh jim.steenburgh@utah.edu 801-581-8727 Suite 480/Office 488 INSCC Suggested reading: Lackman (2011) section
GH = Differential temperature advection term
 QG Theory and Applications: Height Tendency Equation Atmos 5110 Synoptic Dynamic Meteorology I Instructor: Jim Steenburgh jim.steenburgh@utah.edu 801-581-8727 Suite 480/Office 488 INSCC Suggested reading:
QG Theory and Applications: Height Tendency Equation Atmos 5110 Synoptic Dynamic Meteorology I Instructor: Jim Steenburgh jim.steenburgh@utah.edu 801-581-8727 Suite 480/Office 488 INSCC Suggested reading:
The dynamics of high and low pressure systems
 The dynamics of high and low pressure systems Newton s second law for a parcel of air in an inertial coordinate system (a coordinate system in which the coordinate axes do not change direction and are
The dynamics of high and low pressure systems Newton s second law for a parcel of air in an inertial coordinate system (a coordinate system in which the coordinate axes do not change direction and are
The atmosphere in motion: forces and wind. AT350 Ahrens Chapter 9
 The atmosphere in motion: forces and wind AT350 Ahrens Chapter 9 Recall that Pressure is force per unit area Air pressure is determined by the weight of air above A change in pressure over some distance
The atmosphere in motion: forces and wind AT350 Ahrens Chapter 9 Recall that Pressure is force per unit area Air pressure is determined by the weight of air above A change in pressure over some distance
Atmospheric Pressure and Wind Frode Stordal, University of Oslo
 Chapter 4 Lecture Understanding Weather and Climate Seventh Edition Atmospheric Pressure and Wind Frode Stordal, University of Oslo Redina L. Herman Western Illinois University The Concept of Pressure
Chapter 4 Lecture Understanding Weather and Climate Seventh Edition Atmospheric Pressure and Wind Frode Stordal, University of Oslo Redina L. Herman Western Illinois University The Concept of Pressure
Synoptic Meteorology I: Other Force Balances
 Synoptic Meteorology I: Other Force Balances For Further Reading Section.1.3 of Mid-Latitude Atmospheric Dynamics by J. Martin provides a discussion of the frictional force and considerations related to
Synoptic Meteorology I: Other Force Balances For Further Reading Section.1.3 of Mid-Latitude Atmospheric Dynamics by J. Martin provides a discussion of the frictional force and considerations related to
Dynamic Meteorology 1
 Dynamic Meteorology 1 Lecture 14 Sahraei Department of Physics, Razi University http://www.razi.ac.ir/sahraei Buys-Ballot rule (Northern Hemisphere) If the wind blows into your back, the Low will be to
Dynamic Meteorology 1 Lecture 14 Sahraei Department of Physics, Razi University http://www.razi.ac.ir/sahraei Buys-Ballot rule (Northern Hemisphere) If the wind blows into your back, the Low will be to
SEVERE AND UNUSUAL WEATHER
 SEVERE AND UNUSUAL WEATHER Basic Meteorological Terminology Adiabatic - Referring to a process without the addition or removal of heat. A temperature change may come about as a result of a change in the
SEVERE AND UNUSUAL WEATHER Basic Meteorological Terminology Adiabatic - Referring to a process without the addition or removal of heat. A temperature change may come about as a result of a change in the
1/18/2011. From the hydrostatic equation, it is clear that a single. pressure and height in each vertical column of the atmosphere.
 Lecture 3: Applications of Basic Equations Pressure as Vertical Coordinate From the hydrostatic equation, it is clear that a single valued monotonic relationship exists between pressure and height in each
Lecture 3: Applications of Basic Equations Pressure as Vertical Coordinate From the hydrostatic equation, it is clear that a single valued monotonic relationship exists between pressure and height in each
Balanced Flow Geostrophic, Inertial, Gradient, and Cyclostrophic Flow
 Balanced Flow Geostrophic, Inertial, Gradient, and Cyclostrophic Flow The types of atmospheric flows describe here have the following characteristics: 1) Steady state (meaning that the flows do not change
Balanced Flow Geostrophic, Inertial, Gradient, and Cyclostrophic Flow The types of atmospheric flows describe here have the following characteristics: 1) Steady state (meaning that the flows do not change
Solution to Problems #1. I. Information Given or Otherwise Known. = 28 m/s. Heading of the ultralight aircraft!! h
 METR 520: Atmospheric Dynamics II Dr. Dave Dempsey Dept. of Geosciences, SFSU Spring 2012 Solution to Problems 1 Problem 1 An ultralight aircraft is flying. I. Information Given or Otherwise Known Horizontal
METR 520: Atmospheric Dynamics II Dr. Dave Dempsey Dept. of Geosciences, SFSU Spring 2012 Solution to Problems 1 Problem 1 An ultralight aircraft is flying. I. Information Given or Otherwise Known Horizontal
Module 9 Weather Systems
 Module 9 Weather Systems In this module the theory of atmospheric dynamics is applied to different weather phenomena. The first section deals with extratropical cyclones, low and high pressure areas of
Module 9 Weather Systems In this module the theory of atmospheric dynamics is applied to different weather phenomena. The first section deals with extratropical cyclones, low and high pressure areas of
ρ x + fv f 'w + F x ρ y fu + F y Fundamental Equation in z coordinate p = ρrt or pα = RT Du uv tanφ Dv Dt + u2 tanφ + vw a a = 1 p Dw Dt u2 + v 2
 Fundamental Equation in z coordinate p = ρrt or pα = RT Du uv tanφ + uw Dt a a = 1 p ρ x + fv f 'w + F x Dv Dt + u2 tanφ + vw a a = 1 p ρ y fu + F y Dw Dt u2 + v 2 = 1 p a ρ z g + f 'u + F z Dρ Dt + ρ
Fundamental Equation in z coordinate p = ρrt or pα = RT Du uv tanφ + uw Dt a a = 1 p ρ x + fv f 'w + F x Dv Dt + u2 tanφ + vw a a = 1 p ρ y fu + F y Dw Dt u2 + v 2 = 1 p a ρ z g + f 'u + F z Dρ Dt + ρ
p = ρrt p = ρr d = T( q v ) dp dz = ρg
 Chapter 1: Properties of the Atmosphere What are the major chemical components of the atmosphere? Atmospheric Layers and their major characteristics: Troposphere, Stratosphere Mesosphere, Thermosphere
Chapter 1: Properties of the Atmosphere What are the major chemical components of the atmosphere? Atmospheric Layers and their major characteristics: Troposphere, Stratosphere Mesosphere, Thermosphere
Quasi-Geostrophic ω-equation. 1. The atmosphere is approximately hydrostatic. 2. The atmosphere is approximately geostrophic.
 Quasi-Geostrophic ω-equation For large-scale flow in the atmosphere, we have learned about two very important characteristics:. The atmosphere is approximately hydrostatic.. The atmosphere is approximately
Quasi-Geostrophic ω-equation For large-scale flow in the atmosphere, we have learned about two very important characteristics:. The atmosphere is approximately hydrostatic.. The atmosphere is approximately
Examples of Pressure Gradient. Pressure Gradient Force. Chapter 7: Forces and Force Balances. Forces that Affect Atmospheric Motion 2/7/2019
 Chapter 7: Forces and Force Balances Forces that Affect Atmospheric Motion Fundamental force - Apparent force - Pressure gradient force Gravitational force Frictional force Centrifugal force Forces that
Chapter 7: Forces and Force Balances Forces that Affect Atmospheric Motion Fundamental force - Apparent force - Pressure gradient force Gravitational force Frictional force Centrifugal force Forces that
Precipitation and Wind AOSC 200 Tim Canty. Current Weather
 Precipitation and Wind AOSC 200 Tim Canty Class Web Site: http://www.atmos.umd.edu/~tcanty/aosc200 Topics for today: Precipitation cont. RADAR Pressure Coriolis force Lecture 12 Oct 5 2017 1 Current Weather
Precipitation and Wind AOSC 200 Tim Canty Class Web Site: http://www.atmos.umd.edu/~tcanty/aosc200 Topics for today: Precipitation cont. RADAR Pressure Coriolis force Lecture 12 Oct 5 2017 1 Current Weather
The Boundary Layer and Related Phenomena
 The Boundary Layer and Related Phenomena Jeremy A. Gibbs University of Oklahoma gibbz@ou.edu February 19, 2015 1 / 49 Overview Nocturnal Low-Level Jets Introduction Climatology of LLJs Meteorological Importance
The Boundary Layer and Related Phenomena Jeremy A. Gibbs University of Oklahoma gibbz@ou.edu February 19, 2015 1 / 49 Overview Nocturnal Low-Level Jets Introduction Climatology of LLJs Meteorological Importance
Dust devils, water spouts, tornados
 Balanced flow Things we know Primitive equations are very comprehensive, but there may be a number of vast simplifications that may be relevant (e.g., geostrophic balance). Seems that there are things
Balanced flow Things we know Primitive equations are very comprehensive, but there may be a number of vast simplifications that may be relevant (e.g., geostrophic balance). Seems that there are things
Balance. in the vertical too
 Balance. in the vertical too Gradient wind balance f n Balanced flow (no friction) More complicated (3- way balance), however, better approximation than geostrophic (as allows for centrifugal acceleration
Balance. in the vertical too Gradient wind balance f n Balanced flow (no friction) More complicated (3- way balance), however, better approximation than geostrophic (as allows for centrifugal acceleration
Lecture 1. Equations of motion - Newton s second law in three dimensions. Pressure gradient + force force
 Lecture 3 Lecture 1 Basic dynamics Equations of motion - Newton s second law in three dimensions Acceleration = Pressure Coriolis + gravity + friction gradient + force force This set of equations is the
Lecture 3 Lecture 1 Basic dynamics Equations of motion - Newton s second law in three dimensions Acceleration = Pressure Coriolis + gravity + friction gradient + force force This set of equations is the
Chapter 10 Atmospheric Forces & Winds
 Chapter 10 Atospheric Forces & Winds Chapter overview: Atospheric Pressure o Horizontal pressure variations o Station vs sea level pressure Winds and weather aps Newton s 2 nd Law Horizontal Forces o Pressure
Chapter 10 Atospheric Forces & Winds Chapter overview: Atospheric Pressure o Horizontal pressure variations o Station vs sea level pressure Winds and weather aps Newton s 2 nd Law Horizontal Forces o Pressure
Quasi-Geostrophic Implications
 Chapter 10 Quasi-Geostrophic Implications When you look at a weather chart with all its isolines and plotted data, you need a framework upon which to interpret what you see. Quasi-geostrophic theory provides
Chapter 10 Quasi-Geostrophic Implications When you look at a weather chart with all its isolines and plotted data, you need a framework upon which to interpret what you see. Quasi-geostrophic theory provides
EATS Notes 1. Some course material will be online at
 EATS 3040-2015 Notes 1 14 Aug 2015 Some course material will be online at http://www.yorku.ca/pat/esse3040/ HH = Holton and Hakim. An Introduction to Dynamic Meteorology, 5th Edition. Most of the images
EATS 3040-2015 Notes 1 14 Aug 2015 Some course material will be online at http://www.yorku.ca/pat/esse3040/ HH = Holton and Hakim. An Introduction to Dynamic Meteorology, 5th Edition. Most of the images
Dynamics Rotating Tank
 Institute for Atmospheric and Climate Science - IACETH Atmospheric Physics Lab Work Dynamics Rotating Tank Large scale flows on different latitudes of the rotating Earth Abstract The large scale atmospheric
Institute for Atmospheric and Climate Science - IACETH Atmospheric Physics Lab Work Dynamics Rotating Tank Large scale flows on different latitudes of the rotating Earth Abstract The large scale atmospheric
Lecture 25: Ocean circulation: inferences from geostrophic and thermal wind balance
 Lecture 25: Ocean circulation: inferences from geostrophic and thermal wind balance November 5, 2003 Today we are going to study vertical sections through the ocean and discuss what we can learn about
Lecture 25: Ocean circulation: inferences from geostrophic and thermal wind balance November 5, 2003 Today we are going to study vertical sections through the ocean and discuss what we can learn about
NWP Equations (Adapted from UCAR/COMET Online Modules)
 NWP Equations (Adapted from UCAR/COMET Online Modules) Certain physical laws of motion and conservation of energy (for example, Newton's Second Law of Motion and the First Law of Thermodynamics) govern
NWP Equations (Adapted from UCAR/COMET Online Modules) Certain physical laws of motion and conservation of energy (for example, Newton's Second Law of Motion and the First Law of Thermodynamics) govern
Examples of Pressure Gradient. Pressure Gradient Force. Chapter 7: Forces and Force Balances. Forces that Affect Atmospheric Motion 2/2/2015
 Chapter 7: Forces and Force Balances Forces that Affect Atmospheric Motion Fundamental force - Apparent force - Pressure gradient force Gravitational force Frictional force Centrifugal force Forces that
Chapter 7: Forces and Force Balances Forces that Affect Atmospheric Motion Fundamental force - Apparent force - Pressure gradient force Gravitational force Frictional force Centrifugal force Forces that
Problem #1: The Gradient Wind in Natural Coordinates (Due Friday, Feb. 28; 20 pts total)
 METR 50: Atmospheric Dynamics II Dr. Dave Dempsey Spring 014 Problem #1: The Gradient Wind in Natural Coordinates (Due Friday, Feb. 8; 0 pts total) In natural (s,n,p) coordinates, the synoptic-scaled,
METR 50: Atmospheric Dynamics II Dr. Dave Dempsey Spring 014 Problem #1: The Gradient Wind in Natural Coordinates (Due Friday, Feb. 8; 0 pts total) In natural (s,n,p) coordinates, the synoptic-scaled,
Part-8c Circulation (Cont)
 Part-8c Circulation (Cont) Global Circulation Means of Transfering Heat Easterlies /Westerlies Polar Front Planetary Waves Gravity Waves Mars Circulation Giant Planet Atmospheres Zones and Belts Global
Part-8c Circulation (Cont) Global Circulation Means of Transfering Heat Easterlies /Westerlies Polar Front Planetary Waves Gravity Waves Mars Circulation Giant Planet Atmospheres Zones and Belts Global
Meteorology Lecture 15
 Meteorology Lecture 15 Robert Fovell rfovell@albany.edu 1 Important notes These slides show some figures and videos prepared by Robert G. Fovell (RGF) for his Meteorology course, published by The Great
Meteorology Lecture 15 Robert Fovell rfovell@albany.edu 1 Important notes These slides show some figures and videos prepared by Robert G. Fovell (RGF) for his Meteorology course, published by The Great
ATMOSPHERIC MOTION I (ATM S 441/503 )
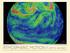 http://earth.nullschool.net/ ATMOSPHERIC MOTION I (ATM S 441/503 ) INSTRUCTOR Daehyun Kim Born in 1980 B.S. 2003 Ph.D. 2010 2010-2013 2014- Assistant Professor at Dept. of Atmospheric Sciences Office:
http://earth.nullschool.net/ ATMOSPHERIC MOTION I (ATM S 441/503 ) INSTRUCTOR Daehyun Kim Born in 1980 B.S. 2003 Ph.D. 2010 2010-2013 2014- Assistant Professor at Dept. of Atmospheric Sciences Office:
True or false: The atmosphere is always in hydrostatic balance. A. True B. False
 Clicker Questions and Clicker Quizzes Clicker Questions Chapter 7 Of the four forces that affect the motion of air in our atmosphere, which is to thank for opposing the vertical pressure gradient force
Clicker Questions and Clicker Quizzes Clicker Questions Chapter 7 Of the four forces that affect the motion of air in our atmosphere, which is to thank for opposing the vertical pressure gradient force
EAS372 Open Book Final Exam 11 April, 2013
 EAS372 Open Book Final Exam 11 April, 2013 Professor: J.D. Wilson Time available: 2 hours Value: 30% Please check the Terminology, Equations and Data section before beginning your responses. Answer all
EAS372 Open Book Final Exam 11 April, 2013 Professor: J.D. Wilson Time available: 2 hours Value: 30% Please check the Terminology, Equations and Data section before beginning your responses. Answer all
Lecture 10 March 15, 2010, Monday. Atmospheric Pressure & Wind: Part 1
 Lecture 10 March 15, 2010, Monday Atmospheric Pressure & Wind: Part 1 Speed, Velocity, Acceleration, Force, Pressure Atmospheric Pressure & Its Measurement Ideal Gas Law (Equation of State) Pressure Gradient
Lecture 10 March 15, 2010, Monday Atmospheric Pressure & Wind: Part 1 Speed, Velocity, Acceleration, Force, Pressure Atmospheric Pressure & Its Measurement Ideal Gas Law (Equation of State) Pressure Gradient
GEF 1100 Klimasystemet. Chapter 7: Balanced flow
 GEF1100 Autumn 2016 27.09.2016 GEF 1100 Klimasystemet Chapter 7: Balanced flow Prof. Dr. Kirstin Krüger (MetOs, UiO) 1 Lecture Outline Ch. 7 Ch. 7 Balanced flow 1. Motivation 2. Geostrophic motion 2.1
GEF1100 Autumn 2016 27.09.2016 GEF 1100 Klimasystemet Chapter 7: Balanced flow Prof. Dr. Kirstin Krüger (MetOs, UiO) 1 Lecture Outline Ch. 7 Ch. 7 Balanced flow 1. Motivation 2. Geostrophic motion 2.1
Lecture 12: Angular Momentum and the Hadley Circulation
 Lecture 12: Angular Momentum and the Hadley Circulation September 30, 2003 We learnt last time that there is a planetary radiative drive net warming in the tropics, cooling over the pole which induces
Lecture 12: Angular Momentum and the Hadley Circulation September 30, 2003 We learnt last time that there is a planetary radiative drive net warming in the tropics, cooling over the pole which induces
Scale Analysis of the Equations of Motion
 hen are curvature terms important? Important for GCMs and large-scale (global) weather. ere, we consider sub-global scale referred to as synoptic scale. Scale Analysis of the Equations of Motion e use
hen are curvature terms important? Important for GCMs and large-scale (global) weather. ere, we consider sub-global scale referred to as synoptic scale. Scale Analysis of the Equations of Motion e use
Atmospheric Fronts. The material in this section is based largely on. Lectures on Dynamical Meteorology by Roger Smith.
 Atmospheric Fronts The material in this section is based largely on Lectures on Dynamical Meteorology by Roger Smith. Atmospheric Fronts 2 Atmospheric Fronts A front is the sloping interfacial region of
Atmospheric Fronts The material in this section is based largely on Lectures on Dynamical Meteorology by Roger Smith. Atmospheric Fronts 2 Atmospheric Fronts A front is the sloping interfacial region of
The Behaviour of the Atmosphere
 3 The Behaviour of the Atmosphere Learning Goals After studying this chapter, students should be able to: apply the ideal gas law and the concept of hydrostatic balance to the atmosphere (pp. 49 54); apply
3 The Behaviour of the Atmosphere Learning Goals After studying this chapter, students should be able to: apply the ideal gas law and the concept of hydrostatic balance to the atmosphere (pp. 49 54); apply
1/3/2011. This course discusses the physical laws that govern atmosphere/ocean motions.
 Lecture 1: Introduction and Review Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study of motion without regard for the cause. Dynamics: On the other hand, dynamics
Lecture 1: Introduction and Review Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study of motion without regard for the cause. Dynamics: On the other hand, dynamics
MIDTERM 1: APPROXIMATE GRADES TOTAL POINTS = 45 AVERAGE = 33 HIGH SCORE = = A = B = C < 20.0 NP
 MIDTERM 1: TOTAL POINTS = 45 AVERAGE = 33 HIGH SCORE = 43 APPROXIMATE GRADES 38.0 45.0 = A 30.0 37.5 = B 20.0 29.5 = C < 20.0 NP Forces to consider: 1) Pressure Gradient Force 2) Coriolis Force 3) Centripetal
MIDTERM 1: TOTAL POINTS = 45 AVERAGE = 33 HIGH SCORE = 43 APPROXIMATE GRADES 38.0 45.0 = A 30.0 37.5 = B 20.0 29.5 = C < 20.0 NP Forces to consider: 1) Pressure Gradient Force 2) Coriolis Force 3) Centripetal
ERTH 465 Fall Lab 5. Absolute Geostrophic Vorticity. 200 points.
 Name Date ERTH 465 Fall 2015 Lab 5 Absolute Geostrophic Vorticity 200 points. 1. All labs are to be kept in a three hole binder. Turn in the binder when you have finished the Lab. 2. Show all work in mathematical
Name Date ERTH 465 Fall 2015 Lab 5 Absolute Geostrophic Vorticity 200 points. 1. All labs are to be kept in a three hole binder. Turn in the binder when you have finished the Lab. 2. Show all work in mathematical
EAS372 Open Book Final Exam 11 April, 2013
 EAS372 Open Book Final Exam 11 April, 2013 Professor: J.D. Wilson Time available: 2 hours Value: 30% Please check the Terminology, Equations and Data section before beginning your responses. Answer all
EAS372 Open Book Final Exam 11 April, 2013 Professor: J.D. Wilson Time available: 2 hours Value: 30% Please check the Terminology, Equations and Data section before beginning your responses. Answer all
ERTH 465 Fall Lab 3. Vertical Consistency and Analysis of Thickness. (300 points)
 Name Date ERTH 465 Fall 2015 Lab 3 Vertical Consistency and Analysis of Thickness (300 points) 1. All labs are to be kept in a three hole binder. Turn in the binder when you have finished the Lab. 2. Show
Name Date ERTH 465 Fall 2015 Lab 3 Vertical Consistency and Analysis of Thickness (300 points) 1. All labs are to be kept in a three hole binder. Turn in the binder when you have finished the Lab. 2. Show
g (z) = 1 (1 + z/a) = 1 1 ( km/10 4 km) 2
 1.4.2 Gravitational Force g is the gravitational force. It always points towards the center of mass, and it is proportional to the inverse square of the distance above the center of mass: g (z) = GM (a
1.4.2 Gravitational Force g is the gravitational force. It always points towards the center of mass, and it is proportional to the inverse square of the distance above the center of mass: g (z) = GM (a
7 Balanced Motion. 7.1 Return of the...scale analysis for hydrostatic balance! CSU ATS601 Fall 2015
 7 Balanced Motion We previously discussed the concept of balance earlier, in the context of hydrostatic balance. Recall that the balanced condition means no accelerations (balance of forces). That is,
7 Balanced Motion We previously discussed the concept of balance earlier, in the context of hydrostatic balance. Recall that the balanced condition means no accelerations (balance of forces). That is,
MODEL TYPE (Adapted from COMET online NWP modules) 1. Introduction
 MODEL TYPE (Adapted from COMET online NWP modules) 1. Introduction Grid point and spectral models are based on the same set of primitive equations. However, each type formulates and solves the equations
MODEL TYPE (Adapted from COMET online NWP modules) 1. Introduction Grid point and spectral models are based on the same set of primitive equations. However, each type formulates and solves the equations
+ ω = 0, (1) (b) In geometric height coordinates in the rotating frame of the Earth, momentum balance for an inviscid fluid is given by
 Problem Sheet 1: Due Thurs 3rd Feb 1. Primitive equations in different coordinate systems (a) Using Lagrangian considerations and starting from an infinitesimal mass element in cartesian coordinates (x,y,z)
Problem Sheet 1: Due Thurs 3rd Feb 1. Primitive equations in different coordinate systems (a) Using Lagrangian considerations and starting from an infinitesimal mass element in cartesian coordinates (x,y,z)
Part 4. Atmospheric Dynamics
 Part 4. Atmospheric Dynamics We apply Newton s Second Law: ma =Σ F i to the atmosphere. In Cartesian coordinates dx u = dt dy v = dt dz w = dt 1 ai = F m i i du dv dw a = ; ay = ; az = x dt dt dt 78 Coordinate
Part 4. Atmospheric Dynamics We apply Newton s Second Law: ma =Σ F i to the atmosphere. In Cartesian coordinates dx u = dt dy v = dt dz w = dt 1 ai = F m i i du dv dw a = ; ay = ; az = x dt dt dt 78 Coordinate
ERTH 465 Fall Lab 5. Absolute Geostrophic Vorticity. 200 points.
 Name Date ERTH 465 Fall 2015 Lab 5 Absolute Geostrophic Vorticity 200 points. 1. All labs are to be kept in a three hole binder. Turn in the binder when you have finished the Lab. 2. Show all work in mathematical
Name Date ERTH 465 Fall 2015 Lab 5 Absolute Geostrophic Vorticity 200 points. 1. All labs are to be kept in a three hole binder. Turn in the binder when you have finished the Lab. 2. Show all work in mathematical
Solutions to Comprehensive Final Examination Given on Thursday, 13 December 2001
 Name & Signature Dr. Droegemeier Student ID Meteorology 1004 Introduction to Meteorology Fall, 2001 Solutions to Comprehensive Final Examination Given on Thursday, 13 December 2001 BEFORE YOU BEGIN!! Please
Name & Signature Dr. Droegemeier Student ID Meteorology 1004 Introduction to Meteorology Fall, 2001 Solutions to Comprehensive Final Examination Given on Thursday, 13 December 2001 BEFORE YOU BEGIN!! Please
Homework 2: Solutions GFD I Winter 2007
 Homework : Solutions GFD I Winter 007 1.a. Part One The goal is to find the height that the free surface at the edge of a spinning beaker rises from its resting position. The first step of this process
Homework : Solutions GFD I Winter 007 1.a. Part One The goal is to find the height that the free surface at the edge of a spinning beaker rises from its resting position. The first step of this process
4. Atmospheric transport. Daniel J. Jacob, Atmospheric Chemistry, Harvard University, Spring 2017
 4. Atmospheric transport Daniel J. Jacob, Atmospheric Chemistry, Harvard University, Spring 2017 Forces in the atmosphere: Gravity g Pressure-gradient ap = ( 1/ ρ ) dp / dx for x-direction (also y, z directions)
4. Atmospheric transport Daniel J. Jacob, Atmospheric Chemistry, Harvard University, Spring 2017 Forces in the atmosphere: Gravity g Pressure-gradient ap = ( 1/ ρ ) dp / dx for x-direction (also y, z directions)
Physical Oceanography, MSCI 3001 Oceanographic Processes, MSCI Dr. Katrin Meissner Ocean Dynamics.
 Physical Oceanography, MSCI 3001 Oceanographic Processes, MSCI 5004 Dr. Katrin Meissner k.meissner@unsw.e.au Ocean Dynamics The Equations of Motion d u dt = 1 ρ Σ F dt = 1 ρ ΣF x dt = 1 ρ ΣF y dw dt =
Physical Oceanography, MSCI 3001 Oceanographic Processes, MSCI 5004 Dr. Katrin Meissner k.meissner@unsw.e.au Ocean Dynamics The Equations of Motion d u dt = 1 ρ Σ F dt = 1 ρ ΣF x dt = 1 ρ ΣF y dw dt =
Chapter 1. Introduction
 Chapter 1. Introduction In this class, we will examine atmospheric phenomena that occurs at the mesoscale, including some boundary layer processes, convective storms, and hurricanes. We will emphasize
Chapter 1. Introduction In this class, we will examine atmospheric phenomena that occurs at the mesoscale, including some boundary layer processes, convective storms, and hurricanes. We will emphasize
ERTH 465 Fall Lab 3. Vertical Consistency and Analysis of Thickness
 Name Date ERTH 465 Fall 2015 Lab 3 Vertical Consistency and Analysis of Thickness 1. All labs are to be kept in a three hole binder. Turn in the binder when you have finished the Lab. 2. Show all work
Name Date ERTH 465 Fall 2015 Lab 3 Vertical Consistency and Analysis of Thickness 1. All labs are to be kept in a three hole binder. Turn in the binder when you have finished the Lab. 2. Show all work
On side wall labeled A: we can express the pressure in a Taylor s series expansion: x 2. + higher order terms,
 Chapter 1 Notes A Note About Coordinates We nearly always use a coordinate system in this class where the vertical, ˆk, is normal to the Earth s surface and the x-direction, î, points to the east and the
Chapter 1 Notes A Note About Coordinates We nearly always use a coordinate system in this class where the vertical, ˆk, is normal to the Earth s surface and the x-direction, î, points to the east and the
Vertical Structure of Atmosphere
 ATMOS 3110 Introduction to Atmospheric Sciences Distribution of atmospheric mass and gaseous constituents Because of the earth s gravitational field, the atmosphere exerts a downward forces on the earth
ATMOS 3110 Introduction to Atmospheric Sciences Distribution of atmospheric mass and gaseous constituents Because of the earth s gravitational field, the atmosphere exerts a downward forces on the earth
Control Volume. Dynamics and Kinematics. Basic Conservation Laws. Lecture 1: Introduction and Review 1/24/2017
 Lecture 1: Introduction and Review Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study of motion without regard for the cause. Dynamics: On the other hand, dynamics
Lecture 1: Introduction and Review Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study of motion without regard for the cause. Dynamics: On the other hand, dynamics
Lecture 1: Introduction and Review
 Lecture 1: Introduction and Review Review of fundamental mathematical tools Fundamental and apparent forces Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study
Lecture 1: Introduction and Review Review of fundamental mathematical tools Fundamental and apparent forces Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study
Chapter 4: Fundamental Forces
 Chapter 4: Fundamental Forces Newton s Second Law: F=ma In atmospheric science it is typical to consider the force per unit mass acting on the atmosphere: Force mass = a In order to understand atmospheric
Chapter 4: Fundamental Forces Newton s Second Law: F=ma In atmospheric science it is typical to consider the force per unit mass acting on the atmosphere: Force mass = a In order to understand atmospheric
Temperature (T) degrees Celsius ( o C) arbitrary scale from 0 o C at melting point of ice to 100 o C at boiling point of water Also (Kelvin, K) = o C
 1 2 3 4 Temperature (T) degrees Celsius ( o C) arbitrary scale from 0 o C at melting point of ice to 100 o C at boiling point of water Also (Kelvin, K) = o C plus 273.15 0 K is absolute zero, the minimum
1 2 3 4 Temperature (T) degrees Celsius ( o C) arbitrary scale from 0 o C at melting point of ice to 100 o C at boiling point of water Also (Kelvin, K) = o C plus 273.15 0 K is absolute zero, the minimum
u g z = g T y (1) f T Margules Equation for Frontal Slope
 Margules Equation for Frontal Slope u g z = g f T T y (1) Equation (1) is the thermal wind relation for the west wind geostrophic component of the flow. For the purposes of this derivation, we assume that
Margules Equation for Frontal Slope u g z = g f T T y (1) Equation (1) is the thermal wind relation for the west wind geostrophic component of the flow. For the purposes of this derivation, we assume that
Chapter 1. Governing Equations of GFD. 1.1 Mass continuity
 Chapter 1 Governing Equations of GFD The fluid dynamical governing equations consist of an equation for mass continuity, one for the momentum budget, and one or more additional equations to account for
Chapter 1 Governing Equations of GFD The fluid dynamical governing equations consist of an equation for mass continuity, one for the momentum budget, and one or more additional equations to account for
Final Examination, MEA 443 Fall 2008, Lackmann
 Place an X here to count it double! Name: Final Examination, MEA 443 Fall 2008, Lackmann If you wish to have the final exam count double and replace your midterm score, place an X in the box above. As
Place an X here to count it double! Name: Final Examination, MEA 443 Fall 2008, Lackmann If you wish to have the final exam count double and replace your midterm score, place an X in the box above. As
Lecture 12. The diurnal cycle and the nocturnal BL
 Lecture 12. The diurnal cycle and the nocturnal BL Over flat land, under clear skies and with weak thermal advection, the atmospheric boundary layer undergoes a pronounced diurnal cycle. A schematic and
Lecture 12. The diurnal cycle and the nocturnal BL Over flat land, under clear skies and with weak thermal advection, the atmospheric boundary layer undergoes a pronounced diurnal cycle. A schematic and
CHAPTER 13 WEATHER ANALYSIS AND FORECASTING MULTIPLE CHOICE QUESTIONS
 CHAPTER 13 WEATHER ANALYSIS AND FORECASTING MULTIPLE CHOICE QUESTIONS 1. The atmosphere is a continuous fluid that envelops the globe, so that weather observation, analysis, and forecasting require international
CHAPTER 13 WEATHER ANALYSIS AND FORECASTING MULTIPLE CHOICE QUESTIONS 1. The atmosphere is a continuous fluid that envelops the globe, so that weather observation, analysis, and forecasting require international
Circulation and Vorticity
 Circulation and Vorticity Example: Rotation in the atmosphere water vapor satellite animation Circulation a macroscopic measure of rotation for a finite area of a fluid Vorticity a microscopic measure
Circulation and Vorticity Example: Rotation in the atmosphere water vapor satellite animation Circulation a macroscopic measure of rotation for a finite area of a fluid Vorticity a microscopic measure
CONVERGENCE, DIVERGENCE, AND VORTICITY
 CHAPTER 1 CONVERGENCE, DIVERGENCE, AND VORTICITY In your reading of the AG2 manual, volume 1, you became familiar with the terms convergence, divergence, and vorticity when used in relation to surface
CHAPTER 1 CONVERGENCE, DIVERGENCE, AND VORTICITY In your reading of the AG2 manual, volume 1, you became familiar with the terms convergence, divergence, and vorticity when used in relation to surface
Fixed Rossby Waves: Quasigeostrophic Explanations and Conservation of Potential Vorticity
 Fixed Rossby Waves: Quasigeostrophic Explanations and Conservation of Potential Vorticity 1. Observed Planetary Wave Patterns After upper air observations became routine, it became easy to produce contour
Fixed Rossby Waves: Quasigeostrophic Explanations and Conservation of Potential Vorticity 1. Observed Planetary Wave Patterns After upper air observations became routine, it became easy to produce contour
Class exercises Chapter 3. Elementary Applications of the Basic Equations
 Class exercises Chapter 3. Elementary Applications of the Basic Equations Section 3.1 Basic Equations in Isobaric Coordinates 3.1 For some (in fact many) applications we assume that the change of the Coriolis
Class exercises Chapter 3. Elementary Applications of the Basic Equations Section 3.1 Basic Equations in Isobaric Coordinates 3.1 For some (in fact many) applications we assume that the change of the Coriolis
Mid-Latitude Cyclones and Fronts. Lecture 12 AOS 101
 Mid-Latitude Cyclones and Fronts Lecture 12 AOS 101 Homework 4 COLDEST TEMPS GEOSTROPHIC BALANCE Homework 4 FASTEST WINDS L Consider an air parcel rising through the atmosphere The parcel expands as it
Mid-Latitude Cyclones and Fronts Lecture 12 AOS 101 Homework 4 COLDEST TEMPS GEOSTROPHIC BALANCE Homework 4 FASTEST WINDS L Consider an air parcel rising through the atmosphere The parcel expands as it
Atmospheric Thermodynamics
 Atmospheric Thermodynamics Atmospheric Composition What is the composition of the Earth s atmosphere? Gaseous Constituents of the Earth s atmosphere (dry air) Constituent Molecular Weight Fractional Concentration
Atmospheric Thermodynamics Atmospheric Composition What is the composition of the Earth s atmosphere? Gaseous Constituents of the Earth s atmosphere (dry air) Constituent Molecular Weight Fractional Concentration
PLOTTING WEATHER DATA to perform a SURFACE ANALYSIS
 PLOTTING WEATHER DATA to perform a SURFACE ANALYSIS The surface analysis permits one to identify and locate the large scale features of the sea level pressure field and the surface fronts. Isobars with
PLOTTING WEATHER DATA to perform a SURFACE ANALYSIS The surface analysis permits one to identify and locate the large scale features of the sea level pressure field and the surface fronts. Isobars with
1/25/2010. Circulation and vorticity are the two primary
 Lecture 4: Circulation and Vorticity Measurement of Rotation Circulation Bjerknes Circulation Theorem Vorticity Potential Vorticity Conservation of Potential Vorticity Circulation and vorticity are the
Lecture 4: Circulation and Vorticity Measurement of Rotation Circulation Bjerknes Circulation Theorem Vorticity Potential Vorticity Conservation of Potential Vorticity Circulation and vorticity are the
( u,v). For simplicity, the density is considered to be a constant, denoted by ρ 0
 ! Revised Friday, April 19, 2013! 1 Inertial Stability and Instability David Randall Introduction Inertial stability and instability are relevant to the atmosphere and ocean, and also in other contexts
! Revised Friday, April 19, 2013! 1 Inertial Stability and Instability David Randall Introduction Inertial stability and instability are relevant to the atmosphere and ocean, and also in other contexts
Weather, Air Masses, Fronts and Global Wind Patterns. Meteorology
 Weather, Air Masses, Fronts and Global Wind Patterns Meteorology Weather is what conditions of the atmosphere are over a short period of time. Climate is how the atmosphere "behaves" over long periods
Weather, Air Masses, Fronts and Global Wind Patterns Meteorology Weather is what conditions of the atmosphere are over a short period of time. Climate is how the atmosphere "behaves" over long periods
General Circulation. Nili Harnik DEES, Lamont-Doherty Earth Observatory
 General Circulation Nili Harnik DEES, Lamont-Doherty Earth Observatory nili@ldeo.columbia.edu Latitudinal Radiation Imbalance The annual mean, averaged around latitude circles, of the balance between the
General Circulation Nili Harnik DEES, Lamont-Doherty Earth Observatory nili@ldeo.columbia.edu Latitudinal Radiation Imbalance The annual mean, averaged around latitude circles, of the balance between the
Chapter VII. Rotating Coordinate Systems
 Chapter VII. Rotating Coordinate Systems 7.1. Frames of References In order to really look at particle dynamics in the context of the atmosphere, we must now deal with the fact that we live and observe
Chapter VII. Rotating Coordinate Systems 7.1. Frames of References In order to really look at particle dynamics in the context of the atmosphere, we must now deal with the fact that we live and observe
Synoptic Meteorology II: Petterssen-Sutcliffe Development Theory Application March 2015
 Synoptic Meteorology II: Petterssen-Sutcliffe Development Theory Application 10-12 March 2015 In our lecture on Petterssen-Sutcliffe Development Theory, we outlined the principle of selfdevelopment in
Synoptic Meteorology II: Petterssen-Sutcliffe Development Theory Application 10-12 March 2015 In our lecture on Petterssen-Sutcliffe Development Theory, we outlined the principle of selfdevelopment in
INTRODUCTION TO METEOROLOGY PART TWO SC 208 DECEMBER 2, 2014 JOHN BUSH
 INTRODUCTION TO METEOROLOGY PART TWO SC 208 DECEMBER 2, 2014 JOHN BUSH Meteorology ATMOSPHERIC SCIENCES Short term weather systems in time spans of hours, days, weeks or months Emphasis is on forecasting
INTRODUCTION TO METEOROLOGY PART TWO SC 208 DECEMBER 2, 2014 JOHN BUSH Meteorology ATMOSPHERIC SCIENCES Short term weather systems in time spans of hours, days, weeks or months Emphasis is on forecasting
Goal: Use understanding of physically-relevant scales to reduce the complexity of the governing equations
 Scale analysis relevant to the tropics [large-scale synoptic systems]* Goal: Use understanding of physically-relevant scales to reduce the complexity of the governing equations *Reminder: Midlatitude scale
Scale analysis relevant to the tropics [large-scale synoptic systems]* Goal: Use understanding of physically-relevant scales to reduce the complexity of the governing equations *Reminder: Midlatitude scale
2 Atmospheric Pressure
 2 Atmospheric Pressure METEOROLOGY 2.1 Definition and Pressure Measurement 2.1.1 Definition Pressure acts in all directions, up and sideways as well as down, but it is convenient in meteorology to regard
2 Atmospheric Pressure METEOROLOGY 2.1 Definition and Pressure Measurement 2.1.1 Definition Pressure acts in all directions, up and sideways as well as down, but it is convenient in meteorology to regard
Measurement of Rotation. Circulation. Example. Lecture 4: Circulation and Vorticity 1/31/2017
 Lecture 4: Circulation and Vorticity Measurement of Rotation Circulation Bjerknes Circulation Theorem Vorticity Potential Vorticity Conservation of Potential Vorticity Circulation and vorticity are the
Lecture 4: Circulation and Vorticity Measurement of Rotation Circulation Bjerknes Circulation Theorem Vorticity Potential Vorticity Conservation of Potential Vorticity Circulation and vorticity are the
Newton's Laws of Motion
 Newton's Laws of Motion Generally, air masses move the way they do because of the forces that act upon them. Definition: A force is something that pushes or pulls on an object, causing it to speed up,
Newton's Laws of Motion Generally, air masses move the way they do because of the forces that act upon them. Definition: A force is something that pushes or pulls on an object, causing it to speed up,
Lec 10: Interpreting Weather Maps
 Lec 10: Interpreting Weather Maps Case Study: October 2011 Nor easter FIU MET 3502 Synoptic Hurricane Forecasts Genesis: on large scale weather maps or satellite images, look for tropical waves (Africa
Lec 10: Interpreting Weather Maps Case Study: October 2011 Nor easter FIU MET 3502 Synoptic Hurricane Forecasts Genesis: on large scale weather maps or satellite images, look for tropical waves (Africa
d v 2 v = d v d t i n where "in" and "rot" denote the inertial (absolute) and rotating frames. Equation of motion F =
 Governing equations of fluid dynamics under the influence of Earth rotation (Navier-Stokes Equations in rotating frame) Recap: From kinematic consideration, d v i n d t i n = d v rot d t r o t 2 v rot
Governing equations of fluid dynamics under the influence of Earth rotation (Navier-Stokes Equations in rotating frame) Recap: From kinematic consideration, d v i n d t i n = d v rot d t r o t 2 v rot
Use of dynamical concepts in weather forecasting
 Use of dynamical concepts in weather forecasting Meteorol. Appl. 4, 345 352 (1997) E B Carroll, Meteorological Office, London Road, Bracknell, Berkshire RG12 2SZ, UK A divergence-based procedure for diagnosing
Use of dynamical concepts in weather forecasting Meteorol. Appl. 4, 345 352 (1997) E B Carroll, Meteorological Office, London Road, Bracknell, Berkshire RG12 2SZ, UK A divergence-based procedure for diagnosing
Dynamical Meteorology 1
 Dynamical Meteorology 1 Lecture 5 Sahraei Physics Department, Razi University http://www.razi.ac.ir/sahraei Structure of the Static Atmosphere جو ایستا: در صورتی که در جو هیچگونه ناپایداری وجود نداشته
Dynamical Meteorology 1 Lecture 5 Sahraei Physics Department, Razi University http://www.razi.ac.ir/sahraei Structure of the Static Atmosphere جو ایستا: در صورتی که در جو هیچگونه ناپایداری وجود نداشته
Fundamentals of Atmospheric Modelling
 M.Sc. in Computational Science Fundamentals of Atmospheric Modelling Peter Lynch, Met Éireann Mathematical Computation Laboratory (Opp. Room 30) Dept. of Maths. Physics, UCD, Belfield. January April, 2004.
M.Sc. in Computational Science Fundamentals of Atmospheric Modelling Peter Lynch, Met Éireann Mathematical Computation Laboratory (Opp. Room 30) Dept. of Maths. Physics, UCD, Belfield. January April, 2004.
Winds and Global Circulation
 Winds and Global Circulation Atmospheric Pressure Winds Global Wind and Pressure Patterns Oceans and Ocean Currents El Nino How is Energy Transported to its escape zones? Both atmospheric and ocean transport
Winds and Global Circulation Atmospheric Pressure Winds Global Wind and Pressure Patterns Oceans and Ocean Currents El Nino How is Energy Transported to its escape zones? Both atmospheric and ocean transport
Go With the Flow From High to Low Investigating Isobars
 Go With the Flow From High to Low Investigating Isobars Science 10 Mrs. Purba Air Masses The air over a warm surface can be heated, causing it to rise above more dense air. The result is the formation
Go With the Flow From High to Low Investigating Isobars Science 10 Mrs. Purba Air Masses The air over a warm surface can be heated, causing it to rise above more dense air. The result is the formation
SIO 210 Introduction to Physical Oceanography Mid-term examination November 3, 2014; 1 hour 20 minutes
 NAME: SIO 210 Introduction to Physical Oceanography Mid-term examination November 3, 2014; 1 hour 20 minutes Closed book; one sheet of your own notes is allowed. A calculator is allowed. (100 total points.)
NAME: SIO 210 Introduction to Physical Oceanography Mid-term examination November 3, 2014; 1 hour 20 minutes Closed book; one sheet of your own notes is allowed. A calculator is allowed. (100 total points.)
and 24 mm, hPa lapse rates between 3 and 4 K km 1, lifted index values
 3.2 Composite analysis 3.2.1 Pure gradient composites The composite initial NE report in the pure gradient northwest composite (N = 32) occurs where the mean sea level pressure (MSLP) gradient is strongest
3.2 Composite analysis 3.2.1 Pure gradient composites The composite initial NE report in the pure gradient northwest composite (N = 32) occurs where the mean sea level pressure (MSLP) gradient is strongest
Department of Geosciences San Francisco State University Spring Metr 201 Monteverdi Quiz #5 Key 150 pts.
 Department of Geosciences Name San Francisco State University Spring 2013 Metr 201 Monteverdi Quiz #5 Key 150 pts. 1. Definitions. (5 points each for a total of 20 points in this section). (a) Coriolis
Department of Geosciences Name San Francisco State University Spring 2013 Metr 201 Monteverdi Quiz #5 Key 150 pts. 1. Definitions. (5 points each for a total of 20 points in this section). (a) Coriolis
Meteorology 6150 Cloud System Modeling
 Meteorology 6150 Cloud System Modeling Steve Krueger Spring 2009 1 Fundamental Equations 1.1 The Basic Equations 1.1.1 Equation of motion The movement of air in the atmosphere is governed by Newton s Second
Meteorology 6150 Cloud System Modeling Steve Krueger Spring 2009 1 Fundamental Equations 1.1 The Basic Equations 1.1.1 Equation of motion The movement of air in the atmosphere is governed by Newton s Second
Dynamics of the Zonal-Mean, Time-Mean Tropical Circulation
 Dynamics of the Zonal-Mean, Time-Mean Tropical Circulation First consider a hypothetical planet like Earth, but with no continents and no seasons and for which the only friction acting on the atmosphere
Dynamics of the Zonal-Mean, Time-Mean Tropical Circulation First consider a hypothetical planet like Earth, but with no continents and no seasons and for which the only friction acting on the atmosphere
Fundamentals of Weather and Climate
 Fundamentals of Weather and Climate ROBIN McILVEEN Environmental Science Division Institute of Environmental and Biological Sciences Lancaster University CHAPMAN & HALL London Glasgow Weinheim New York
Fundamentals of Weather and Climate ROBIN McILVEEN Environmental Science Division Institute of Environmental and Biological Sciences Lancaster University CHAPMAN & HALL London Glasgow Weinheim New York
