Module 1. Probability
|
|
|
- Junior Wilkins
- 5 years ago
- Views:
Transcription
1 Module 1 Probability 1. Introduction In our daily life we come across many processes whose nature cannot be predicted in advance. Such processes are referred to as random processes. The only way to derive information about random processes is to conduct experiments. Each such experiment results in an outcome which cannot be predicted beforehand. In fact even if the experiment is repeated under identical conditions, due to presence of factors which are beyond control, outcomes of the experiment may vary from trial to trial. However we may know in advance that each outcome of the experiment will result in one of the several given possibilities. For example, in the cast of a die under a fixed environment the outcome (number of dots on the upper face of the die) cannot be predicted in advance and it varies from trial to trial. However we know in advance that the outcome has to be among one of the numbers 1, 2,, 6. Probability theory deals with the modeling and study of random processes. The field of Statistics is closely related to probability theory and it deals with drawing inferences from the data pertaining to random processes. Definition 1.1 (i) (ii) A random experiment is an experiment in which: (a) the set of all possible outcomes of the experiment is known in advance; (b) the outcome of a particular performance (trial) of the experiment cannot be predicted in advance; (c) the experiment can be repeated under identical conditions. The collection of all possible outcomes of a random experiment is called the sample space. A sample space will usually be denoted by. Example 1.1 (i) (ii) In the random experiment of casting a die one may take the sample space as = 1, 2, 3, 4, 5, 6, where indicates that the experiment results in = 1,,6 dots on the upper face of die. In the random experiment of simultaneously flipping a coin and casting a die one may take the sample space as =, 1, 2,, 6 =, :,, 1, 2,, 6, 1
2 where,, indicates that the flip of the coin resulted in head (tail) on the upper face and the cast of the die resulted in = 1, 2,, 6 dots on the upper face. (iii) (iv) Consider an experiment where a coin is tossed repeatedly until a head is observed. In this case the sample space may be taken as = 1, 2, (or = T, TH, TTH, ),where (or TT TH with 1 Ts and one H) indicates that the experiment terminates on the -th trial with first 1 trials resulting in tails on the upper face and the -th trial resulting in the head on the upper face. In the random experiment of measuring lifetimes (in hours) of a particular brand of batteries manufactured by a company one may take = 0,70,000,where we have assumed that no battery lasts for more than 70,000 hours. Definition 1.2 (i) Let be the sample space of a random experiment and let. If the outcome of the random experiment is a member of the set we say that the event has occurred. (ii) Two events and are said to be mutually exclusive if they cannot occur simultaneously, i.e., if =, the empty set. In a random experiment some events may be more likely to occur than the others. For example, in the cast of a fair die (a die that is not biased towards any particular outcome), the occurrence of an odd number of dots on the upper face is more likely than the occurrence of 2 or 4 dots on the upper face. Thus it may be desirable to quantify the likelihoods of occurrences of various events. Probability of an event is a numerical measure of chance with which that event occurs. To assign probabilities to various events associated with a random experiment one may assign a real number 0,1 to each event with the interpretation that there is a 100 % chance that the event will occur and a % chance that the event will not occur. For example if the probability of an event is 0.25 it would mean that there is a 25% chance that the event will occur and that there is a 75% chance that the event will not occur. Note that, for any such assignment of possibilities to be meaningful, one must have = 1. Now we will discuss two methods of assigning probabilities. I. Classical Method This method of assigning probabilities is used for random experiments which result in a finite number of equally likely outcomes. Let =,, be a finite sample space with N possible outcomes; here N denotes the set of natural numbers. For, let denote the number of elements in. An outcome is said to be favorable to an event 2
3 if. In the classical method of assigning probabilities, the probability of an event is given by = number of outocmes favorable to E total number of outcomes = =. Note that probabilities assigned through classical method satisfy the following properties of intuitive appeal: (i) For any event, 0; (ii) For mutually exclusive events,,, i.e., =, whenever, 1,,, = n E = E n = E = n ; (iii) = = 1. Example 1.2 Suppose that in a classroom we have 25 students (with registration numbers1, 2,, 25) born in the same year having 365 days. Suppose that we want to find the probability of the event that they all are born on different days of the year. Here an outcome consists of a sequence of 25 birthdays. Suppose that all such sequences are equally likely. Then = 365, E = = and = = The classical method of assigning probabilities has a limited applicability as it can be used only for random experiments which result in a finite number of equally likely outcomes. II. Relative Frequency Method Suppose that we have independent repetitions of a random experiment (here independent repetitions means that the outcome of one trial is not affected by the outcome of another trial) under identical conditions. Let denote the number of times an event occurs (also called the frequency of event in trials) in the first trials and let = / denote the corresponding relative frequency. Using advanced probabilistic arguments (e.g., using Weak Law of Large Numbers to be discussed in Module 7) it can be shown that, under mild conditions, the relative frequencies stabilize (in certain sense) as gets large (i.e., for any event, lim r E exists in certain sense). In the relative frequency method of assigning probabilities the probability of an event is given by 3
4 = lim lim Figure 1.1. Plot of relative frequencies ( ) of number of heads against number of trials (N) in the random experiment of tossing a fair coin (with probability of head in each trial as 0.5). In practice, to assign probability to an event, the experiment is repeated a large (but fixed) number of times (say times) and the approximation is used for assigning probability to event. Note that probabilities assigned through relative frequency method also satisfy the following properties of intuitive appeal: (i) (ii) for any event,0; for mutually exclusive events,,, (iii) 1. ; Although the relative frequency method seems to have more applicability than the classical method it too has limitations. A major problem with the relative frequency method is that it is 4
5 imprecise as it is based on an approximation. Another difficulty with relative frequency method is that it assumes that the experiment can be repeated a large number of times. This may not be always possible due to budgetary and other constraints (e.g., in predicting the success of a new space technology it may not be possible to repeat the experiment a large number of times due to high costs involved). The following definitions will be useful in future discussions. Definition 1.3 (i) (ii) (iii) (iv) (v) (vi) A set is said to be finite if either = (the empty set) or if there exists a one-one and onto function : 1,2,, or : 1,2,, for some natural number ; A set is said to be infinite if it is not finite; A set is said to be countable if either = or if there is an onto function : N, where N denotes the set of natural numbers; A set is said to be countably infinite if it is countable and infinite; A set is said to be uncountable if it is not countable; A set is said to be continuum if there is a one-one and onto function : R or : R, where R denotes the set of real numbers. The following proposition, whose proof(s) can be found in any standard textbook on set theory, provides some of the properties of finite, countable and uncountable sets. Proposition 1.1 (i) (ii) (iii) (iv) (v) (vi) (vii) (viii) (ix) (x) Any finite set is countable; If is a countable and then is countable; Any uncountable set is an infinite set; If is an infinite set and then is infinite; If is an uncountable set and then is uncountable; If is a finite set and is a set such that there exists a one-one and onto function : or : then is finite; If is a countably infinite (continuum) set and is a set such that there exists a one-one and onto function : or : then is countably infinite (continuum); A set is countable if and only if either = or there exists a one-one and onto map : N, for some N N; A set is countable if, and only if, either is finite or there exists a one-one map : N ; A set is countable if, and only if, either = or there exists a one-one map : N; 5
6 (xi) A non empty countable set can be either written as =,,, for some N, or as =,, ; (xii) Unit interval 0,1 is uncountable. Hence any interval,, where < < <, is uncountable; (xiii) N N is countable; (xiv) Let be a countable set and let : be a (countable) collection of countable sets. Then is countable. In other words, countable union of countable sets is countable; (xv) Any continuum set is uncountable. Example 1.3 (i) (ii) Define :N N by =, N. Clearly : N N is one-one and onto. Thus N is countable. Also it can be easily seen (using the contradiction method) that N is infinite. Thus N is countably infinite. Let Z denote the set of integers. Define : N Z by = 2, 1 2, if is odd if is even Clearly : N Z is one-one and onto. Therefore, using (i) above and Proportion 1.1 (vii), Z is countably infinite. Now on using Proportion 1.1 (ii) it follows that any subset of Z is countable. (iii) Using the fact that N is countably infinite and Proposition 1.1 (xiv) it is straight forward to show that Q (the set of rational numbers) is countably infinite. (iv) Define : R R and : R 0, 1 by =, R, and =, R. Then : R R and : R 0, 1 are one-one and onto functions. It follows that Rand (0, 1) are continuum (using Proposition 1.1 (vii)). Further, for < < <, let h = +, 0, 1. Clearly h: 0,1, is one-one and onto. Again using proposition 1.1 (vii) it follows that any interval, is continuum. It is clear that it may not be possible to assign probabilities in a way that applies to every situation. In the modern approach to probability theory one does not bother about how probabilities are assigned. Assignment of probabilities to various subsets of the sample space that is consistent with intuitively appealing properties (i)-(iii) of classical (or relative frequency) method is done through probability modeling. In advanced courses on probability theory it is shown that in many situations (especially when the sample space is continuum) it is not 6
7 possible to assign probabilities to all subsets of such that properties (i)-(iii) of classical (or relative frequency) method are satisfied. Therefore probabilities are assigned to only certain types of subsets of. In the following section we will discuss the modern approach to probability theory where we will not be concerned with how probabilities are assigned to suitably chosen subsets of. Rather we will define the concept of probability for certain types of subsets using a set of axioms that are consistent with properties (i)-(iii) of classical (or relative frequency) method. We will also study various properties of probability measures. 2. Axiomatic Approach to Probability and Properties of Probability Measure We begin this section with the following definitions. Definition 2.1 (i) A set whose elements are themselves set is called a class of sets. A class of sets will be usually denoted by script letters, B,,. For example = 1, 1, 3, 2, 5, 6; (ii) Let be a class of sets. A function : R is called a set function. In other words, a real-valued function whose domain is a class of sets is called a set function. As stated above, in many situations, it may not be possible to assign probabilities to all subsets of the sample space such that properties (i)-(iii) of classical (or relative frequency) method are satisfied. Therefore one begins with assigning probabilities to members of an appropriately chosen class of subsets of (e.g., if = R, then may be class of all open intervals in R; if is a countable set, then may be class of all singletons, ). We call the members of as basic sets. Starting from the basic sets in assignment of probabilities is extended, in an intuitively justified manner, to as many subsets of as possible keeping in mind that properties (i)-(iii) of classical (or relative frequency) method are not violated. Let us denote by F the class of sets for which the probability assignments can be finally done. We call the class F as event space and elements of Fare called events. It will be reasonable to assume that F satisfies the following properties: (i) F, (ii) F = F,and (iii) F, = 1,2, F. This leads to introduction of the following definition. Definition 2.2 A sigma-field (-field) of subsets of is a class F of subsets of satisfying the following properties: (i) F; (ii) F = F (closed under complements); 7
8 (iii) F, = 1, 2, F (closed under countably infinite unions). Remark 2.1 (i) (ii) We expect the event space to be a -field; Suppose that F is a -field of subsets of. Then, (a) F since = (b),, F F since = ; (c), F = F and Δ F; (d),,, F, for some N, F and F (take = = = so that = or = = = so that = ); (e) although the power set of is a -field of subsets of,in general, a field may not contain all subsets of. Example 2.1 (i) (ii) (iii) (iv) F =, is a sigma field, called the trivial sigma-field; Suppose that. Then F =,,, is a -field of subsets of. It is the smallest sigma-field containing the set ; Arbitrary intersection of -fields is a -field (see Problem 3 (i)); Let be a class of subsets of and let be the collection of all -fields that contain. Then (v) F = F is a -field and it is the smallest -field that contains class (called the -field generated by and is denoted by ) (see Problem 3 (iii)); Let = R and let be the class of all open intervals in R. Then B = is called the Borel -field on R. The Borel -field in R (denoted by B ) is the -field generated by class of all open rectangles in R. A set B is called a Borel set in R ; here R =,, : < <, = 1,, denotes the -dimensional Euclidean space; (vi) B contains all singletons and hence all countable subsets of R =, + Let be an appropriately chosen class of basic subsets of for which the probabilities can be assigned to begin with (e.g., if = R then may be class of all open intervals in R; if is a countable set then may be class of all singletons, ). It turns out (a topic for an advanced course in probability theory) that, for an appropriately chosen class of basic sets, 8
9 the assignment of probabilities that is consistent with properties (i)-(iii) of classical (or relative frequency) method can be extended in an unique manner from to, the smallest -field containing the class. Therefore, generally the domain F of a probability measure is taken to be, the -field generated by the class of basic subsets of. We have stated before that we will not care about how assignment of probabilities to various members of event space F (a -field of subsets of ) is done. Rather we will be interested in properties of probability measure defined on event space F. Let be a sample space associated with a random experiment and let F be the event space (a -field of subsets of ). Recall that members of F are called events. Now we provide a mathematical definition of probability based on a set of axioms. Definition 2.3 (i) Let F be a -field of subsets of. A probability function (or a probability measure) is a set function, defined on F, satisfying the following three axioms: (a) 0, F; (Axiom 1: Non-negativity); (b) If,, is a countably infinite collection of mutually exclusive events i. e., F, = 1, 2,, =, then = ; Axiom 2: Countably infinite additive (c) = 1 (Axiom 3: Probability of the sample space is 1). (ii) The triplet, F, is called a probability space. Remark 2.2 (i) Note that if,, is a countably infinite collection of sets in a -field Fthen F and, therefore, is well defined; (ii) In any probability space, F, we have = 1 (or = 0; see Theorem 2.1 (i) proved later) but if = 1 (or = 0), for some F, then it does not mean that = ( or = ) (see Problem 14 (ii). (iii) In general not all subsets of are events, i.e., not all subsets of are elements of F. (iv) When is countable it is possible to assign probabilities to all subsets of using Axiom 2 provided we can assign probabilities to singleton subsets of. To illustrate this let =,, or Ω =,,, for some n N and let =, = 9
10 1, 2,, so that 0 1, = 1,2, (see Theorem 2.1 (iii) below) and = = = = 1. Then, for any, =. : Thus in this case we may take F =, the power set of. It is worth mentioning here that if is countable and = (class of all singleton subsets of ) is the class of basic sets for which the assignment of the probabilities can be done, to begin with, then = (see Problem 5 (ii)). (v) Due to some inconsistency problems, assignment of probabilities for all subsets of is not possible when is continuum (e.g., if contains an interval). Theorem 2.1 Let, F, be a probability space. Then (i) = 0; (ii) F, = 1, 2,., and =, = (finite additivity); (iii) F, 0 1 and = 1 ; (iv), F and = and (monotonicity of probability measures); (v), F = +. Proof. (i) Let = and =, = 2, 3,. Then = 1, (Axiom 3) F, = 1, 2,, = and =,. Therefore, 1 = = = using Axiom 2 = 1 + = 0 10
11 0. (ii) Let, 1, 2,. Then, 1,2,,, and 0, 1,2,. Therefore,. using Axiom 2 (iii) Let. Then and. Therefore 1 (iv) 1 and 1 01 and 1. (using (ii)) (since 0,1) Let, and let. Then, and. Figure 2.1 Therefore, 11
12 = (using (ii)). As 0, it follows that. (v) Let,. Then, and. Figure 2.2 Therefore, (using(ii)) (2.1) Also and. Therefore, Figure
13 = + (using (ii) = (2.2) Using (2.1) and (2.2), we get = +. Theorem 2.2 (Inclusion-Exclusion Formula) Let, F, be a probability space and let,,, F N, 2. Then =,, where, = and, for 2, 3,,,, = 1. Proof. We will use the principle of mathematical induction. Using Theorem 2.1 (v), we have = + =, +,, where, = + and, =. Thus the result is true for = 2. Now suppose that the result is true for 2, 3,, for some positive integer 2. Then = = + using the result for = 2 = + =, + using the result for = 2.3 Let =, = 1,.. Then 13
14 = =, again using the result for =, 2.4 where, = = and, for 2, 3,,,, = 1 Using (2.4) in (2.3), we get = 1. =, + +,, + +,,,. Note that, + =,,,, =,, = 2,3,,, and, =,. Therefore, =, +, =,. Remark 2.3 (i) Let, F. Then = + +, =,, +,, + + +,, where, =,,, =, and, =,. In general, where =,, +, + 1,, 14
15 , =,, if is odd, = 1, 2,.,, if is even (ii) We have Theorem = The above inequality is known as Bonferroni s inequality. Let, F, be a probability space and let,,, F N, 2. Then, under the notations of Theorem 2.2, Proof. (i) (Boole s Inequality), +,, ; (ii) (Bonferroni s Inequality), 1. (i) We will use the principle of mathematical induction. We have = +,, =, +,,, where, = + and, = 0. Thus the result is true for = 2. Now suppose that the result is true for 2, 3,, for some positive integer 2, i.e., suppose that for arbitrary events,, F and Then, = 2, 3,, 2.5, = 2, 3,,
16 = + using 2.5 for = 2 + using 2.5 for k = m = =,. 2.7 Also, = = + using Theorem 2.2 = Using (2.5), for =, we get, 2.9 and using (2.6), for =, we get, +, Now using (2.9) and (2.10) in (2.8), we get 16
17 , +, + = =, +,. (2.11) Combining (2.7) and (2.11), we get, +,,, and the assertion follows by principle of mathematical induction. (ii) We have = 1 = 1 E 1 using Boole sinequality = 1 1 = 1. Remark 2.4 Under the notation of Theorem 2.2 we can in fact prove the following inequalities:,,, = 1,2,, 2, 17
18 where denotes the largest integer not exceeding. Corollary 2.1 Let, F, be a probability space and let,,, F be events. Then Proof. (i) = 0, = 1,, = 0; (ii) = 1, = 1,, = 1. (i) First suppose that = 0, = 1,,. Using Boole s inequality, we get 0 = 0. It follows that = 0. Conversely, suppose that = 0. Then, = 1,,, and therefore, i.e., = 0, = 1,,. 0 = 0, = 1,,, (ii) We have = 1, = 1,, = 0, = 1,, = 0 using i = 1, = 1. Definition 2.4 A countable collection : of events is said to be exhaustive if = 1. 18
19 Example 2.2 (Equally Likely Probability Models) Consider a probability space, F,. Suppose that, for some positive integer 2, =, where,,, are mutually exclusive, exhaustive and equally likely events, i.e., =, if, = = 1 and = = =.Further suppose that an event F can be written as =, where,, 1,,, =, and 2,,. Then = =. Note that here is the total number of ways in which the random experiment can terminate (number of partition sets,, ), and is the number of ways that are favorable to F. Thus, for any F, = number of cases favorable to total number of cases which is the same as classical method of assigning probabilities. Here the assumption that,, are equally likely is a part of probability modeling. For a finite sample space, when we say that an experiment has been performed at random we mean that various possible outcomes in are equally likely. For example when we say that two numbers are chosen at random, without replacement, from the set 1, 2, 3 then = 1, 2, 1, 3, 2, 3and 1, 2 = 1, 3 = 2, 3 =, where, indicates that the experiment terminates with chosen numbers as and,, 1, 2, 3,. Example 2.3 Suppose that five cards are drawn at random and without replacement from a deck of 52 cards. Here the sample space comprises of all 52 combinations of 5 cards. Thus number of 5 favorable cases= 52 5 =, say. Let,, be singleton subsets of.then = and = = =. Let be the event that each card is spade. Then Number of cases favorable to = =, 19
20 Therefore, = Now let be the event that at least one of the drawn cards is spade. Then is the event that none of the drawn cards is spade, andnumber of cases favorable to = 39 Therefore, 5 = , and = 1 = 1 Let be the event that among the drawn cards three are kings and two are queens. Then number of cases favorable to = and, therefore, 2 4 = Similarly, if is the event that among the drawn cards two are kings, two are queens and one is jack, then Example = Suppose that we have 2 letters and corresponding addressed envelopes. If these letters are inserted at random in envelopes find the probability that no letter is inserted into the correct envelope. Solution. Let us label the letters as,,, and respective envelopes as,,,. Let denote the event that letter is (correctly) inserted into envelope, = 1, 2,,. We need to find. We have 20
21 where, for 1, 2,,, = = 1 = 1,,, = 1. Note that letters can be inserted into envelopes in! ways. Also, for 1 < < <, is the event that letters,,, are inserted into correct envelopes. Clearly number of cases favorable to this event is!. Therefore, for 1 < < <, =!!, = < 2 < < = 1!! = 1! = 1 2! 1 3! + 1 4! + 1! 3. Conditional Probability and Independence of Events! Let, F, be a given probability space. In many situations we may not be interested in the whole space. Rather we may be interested in a subset F of the sample space. This may happen, for example, when we know apriori that the outcome of the experiment has to be an element of F. Example 3.1 Consider a random experiment of shuffling a deck of 52 cards in such a way that all 52! arrangements of cards (when looked from top to bottom) are equally likely..! 21
22 Here, =all 52! permutations of cards, and F = Ω. Now suppose that it is noticed that the bottom card is the king of heart. In the light of this information, sample space comprises of 51! arrangements of 52 cards with bottom card as king of heart.define the event For F, define Clearly, : top card is king. =!.! = probability of event under sample space, = probability of event under sample space. Note that = 3 50! 51! =!!!! = i. e., =. 3.1 We call the conditional probability of event given that the experiment will result in an outcome in (i.e., the experiment will result in an outcome ) and the unconditional probability of event. Example 3.1 lays ground for introduction of the concept of conditional probability. Let, F, be a given probability space. Suppose that we know in advance that the outcome of the experiment has to be an element of F, where > 0. In such situations the sample space is and natural contenders for the membership of the event space are 22
23 . This raises the question whether is an event space? i.e., whether is a sigma-field of subsets of? Theorem 3.1 Let be a -field of subsets and let. Define. Then is a field of subsets of and. Proof. Since and it is obvious that. We have and therefore. 3.2 Also, CA for same (since ) Figure 3.1, (3.3) i.e., is closed under complements with respect to. Now suppose that,1,2,.then, for some,1,2,. Therefore, since,1,2, 23
24 F, 3.4 i.e., F is closed under countable unions. Now (3.2), (3.3) and (3.4) imply that F is a -field of subsets of. Equation (3.1) suggests considering the set function : F R defined by =, F = : F. Note that, for F, is well defined as F F. Let us define another set function F R by Theorem 3.2 P =, F. Let, F, be a probability space and let F be such that > 0. Then, F, and, F, are probability spaces. Proof. Clearly 0, F. Let F, = 1, 2, be mutually exclusive.then F, = 1, 2, (since F F), and = = = =, 3.5 i.e., is countable additive on F. 24
25 Also = = 1 Thus is a probability measure on F. Note that 0, F and B B = = 1 Let F, = 1,2, be mutually exclusive. Then = F, = 1, 2, are mutually exclusive and =. using 3.5 It follows that is a probability measure on F. Note that domains of and are F and F respectively. Moreover, Definition 3.1 =, F. Let, F, be a probability space and let F be a fixed event such that > 0. Define the set function :F R by =, F. We call the conditional probability of event given that the outcome of the experiment is in or simply the conditional probability of given. Example 3.2 Six cards are dealt at random (without replacement) from a deck of 52 cards. Find the probability of getting all cards of heart in a hand (event A) given that there are at least 5 cards of heart in the hand (event B). Solution. We have, 25
26 =. Clearly, = =, and = Therefore, = Remark 3.1 For events,, F 2, and =, if > 0, = = =. If > 0 (which also guarantees that > 0, since ). Using principle of mathematical induction it can be shown that =, provided > 0 (which also guarantees that > 0, = 1, 2,, 1). 26
27 Example 3.3 An urn contains four red and six black balls. Two balls are drawn successively, at random and without replacement, from the urn. Find the probability that the first draw resulted in a red ball and the second draw resulted in a black ball. Solution. Define the events Then, : first draw results in a red ball; : second draw results in a black ball. Required probability = = = Let, F, be a probability space. For a countable collection : of mutually exclusive and exhaustive events, the following theorem provides a relationship between marginal probability of an event F and joint probabilities of events and,. Theorem 3.3 (Theorem of Total Probability) Let, F, be a probability space and let : be a countable collection of mutually exclusive and exhaustive events (i.e., =, whenever, and = 1) such that > 0,.Then, for any event F, Proof. Let = = =.. Then = 1 and = 1 = 0. Therefore, = + = 0 = 0 = s are disjoint = are disjoint 27
28 Example 3.4 =. Urn contains 4 white and 6 black balls and urn contains 6 white and 4 black balls. A fair die is cast and urn is selected if the upper face of die shows 5 or 6 dots. Otherwise urn is selected. If a ball is drawn at random from the selected urn find the probability that the drawn ball is white. Solution. Define the events: drawn ball is white; urn is selected; urn is selected. Then, is a collection of mutually exclusive and exhaustive events. Therefore = = 8 15 The following theorem provides a method for finding the probability of occurrence of an event in a past trial based on information on occurrences in future trials. Theorem 3.4 (Bayes Theorem) Let, F, be a probability space and let : be a countable collection of mutually exclusive and exhaustive events with > 0,. Then, for any event F with > 0, we have Proof. We have, for,, 28
29 = using Theorem of Total Probability. Remark 3.2 (i) (ii) Suppose that the occurrence of any one of the mutually exclusive and exhaustive events,, causes the occurrence of an event. Given that the event has occurred, Bayes theorem provides the conditional probability that the event is caused by occurrence of event,. In Bayes theorem the probabilities,, are referred to as prior probabilities and the probabilities,, are referred to as posterior probabilities. To see an application of Bayes theorem let us revisit Example 3.4. Example 3.5 Urn contains 4 white and 6 black balls and urn contains 6 white and 4 black balls. A fair die is cast and urn is selected if the upper face of die shows five or six dots. Otherwise urn is selected. A ball is drawn at random from the selected urn. (i) (ii) Given that the drawn ball is white, find the conditional probability that it came from urn ; Given that the drawn ball is white, find the conditional probability that it came from urn. Solution. Define the events: drawn ball is white; urn is selected mutually & exhaustive events urn is selected (i) We have 29
30 (ii) = 1 4 Since and are mutually exclusive and 1, we have In the above example <, i.e., and 3 4 > 2 3 =, (i) (ii) the probability of occurrence of event decreases in the presence of the information that the outcome will be an element of ; the probability of occurrence of event increases in the presence of information that the outcome will be an element of. These phenomena are related to the concept of association defined in the sequel. Note that < <, and > >. Definition 3.2 Let, F, be a probability space and let and be two events. Events and are said to be (i) (ii) (iii) negatively associated if < ; positively associated if > ; independent if =. Remark
31 (i) (ii) If = 0 then = 0 =, F, i.e., if = 0 then any event F and are independent; If > 0 then and are independent If, and only if,, i.e., if >0, then events and are independent if, and only if, the availability of the information that event has occurred does not alter the probability of occurrence of event. Now we define the concept of independence for arbitrary collection of events. Definition 3.3 Let, F, be a probability space. Let R be an index set and let : be a collection of events in F. (i) (ii) Events : are said to be pair wise independent if any pair of events and, in the collection : are independent. i.e., if =, whenever, and ; Let = 1, 2,, n, for some N, so that : =,, is a finite collection of events in F. Events,, are said to be independent if, for any sub collection,, of,, = 2,3,, =. 3.6 (iii) Let R be an arbitrary index set. Events : are said to be independent if any finite sub collection of events in : forms a collection of independent events. Remark 3.4 (i) To verify that events,, F are independent one must verify 2 1 = conditions in (3.6). For example, to conclude that three events, and are independent, the following 4 = conditions must be verified: = ; = ; 31
32 = ; =. (ii) (iv) If events,, are independent then, for any permutation,, of 1,,,the events,, are also independent. Thus the notion of independence is symmetric in the events involved. Events in any sub collection of independent events are independent. In particular independence of a collection of events implies their pair wise independence. The following example illustrates that, in general, pair wise independence of a collection of events may not imply their independence. Example 3.6 Let = 1, 2, 3, 4 and let F =, the power set of. Consider the probability space, F, P, where =, = 1, 2, 3, 4. Let = 1, 4, = 2, 4 and = 3, 4. Then, = = =, = = = 4 =, and = 4 = Clearly, = ; =, and =, i.e.,, and are pairwise independent. However, =. Thus, and are not independent. Theorem 3.5 Let, F, be a probability space and let and be independent events (, F).Then (i) and are independent events; 32
33 (ii) (iii) and are independent events; and are independent events. Proof. We have =. (i) Since = and =, we have = + = i.e., and are independent events. = = 1 =, (ii) (iii) Follows from (i) by interchanging the roles of and. Follows on using (i) and (ii) sequentially. The following theorem strengthens the results of Theorem 3.5. Theorem 3.6 Let, F, be a probability space and let,, N, 2 be independent events in F. Then, for any 1, 2,, 1 and any permutation,, of 1,,, the events,,,,, are independent. Moreover the events,, are independent. Proof. Since the notion of independence is symmetric in the events involved, it is enough to show that for any 1, 2,, 1 the events,,,,, are independent. Using backward induction and symmetry in the notion of independence the above mentioned assertion would follow if, under the hypothesis of the theorem, we show that the events,,, are independent. For this consider a sub collection,,, of,,,,, 1,, 1,where = or =, for some 1,, 1,,, depending on whether or not is a part of sub collection,,,. Thus the following two cases arise:. = Since,, are independent, we have 33
34 =, and = events and are independent = events and are independent Theorem 3.5 ii) = = =. Case II. =, for some 1,, 1,,. In this case,,, is a sub collection of independent events,, and therefore =. Now the result follows on combining the two cases. 34
35 When we say that two or more random experiments are independent (or that two or more random experiments are performed independently) it simply means that the events associated with the respective random experiments are independent. 4. Continuity of Probability Measures We begin this section with the following definition. Definition 4.1 Let, F, be a probability space and let : = 1, 2, be a sequence of events in F. (i) We say that the sequence : = 1, 2, is increasing (written as ) if, = 1,2, ; (ii) We say that the sequence : = 1, 2, is decreasing (written as ) if, = 1,2, ; (iii) We say that the sequence : = 1, 2, is monotone if either or ; (iv) If we define the limit of the sequence : = 1, 2, as and write Lim = ; (v) If we define the limit of the sequence : = 1, 2, as and write Lim =. Throughout we will denote the limit of a monotone sequence : = 1, 2, of events by Lim and the limit of a sequence : = 1, 2, of real numbers (provided it exists) by lim. Theorem 4.1 (Continuity of Probability Measures) Let : = 1, 2, be a sequence of monotone events in a probability space, F,. Then Proof. Case I. In this case, Lim = Lim = lim.. Define =, =, = 2, 3,. 35
36 Figure 4.1 Then,1,2, s are mutually exclusive and Therefore, Lim lim lim lim Lim. (using Theorem 2.1 (iv) since,1,2, ) lim lim lim. 36
37 Case II. In this case, Lim = and. Therefore, Lim = = 1 = 1 = 1 Lim = 1 lim using Case I, since = 1 lim 1 = lim. Remark 4.1 Let, F, be a probability space and let : = 1, 2, be a countably infinite collection of events in F. Define = and =, = 1,2, Then,, Lim = = and Lim = = Lim. Therefore = lim using Theorem 4.1 = lim = lim, +, + +,, 37
38 where S, s are as defined in Theorem 2.2. Moreover, = Lim = lim using Theorem 4.1 = lim Similarly, if : = 1, 2, is a collection of independent events, then. = lim = lim =. Problems 1. Let = 1, 2, 3, 4. Check which of the following is a sigma-field of subsets of : (i) F =, 1, 2, 3, 4; (ii) F =,, 1, 2, 3, 4, 1, 2, 3, 4; (iii) F =,, 1, 2, 1, 2, 3, 42, 3, 4, 1, 3, Show that a class F of subsets of is a sigma-field of subsets of if, and only if, the following three conditions are satisfied: (i) F; (ii) F = F; (iii) F, n = 1, 2, F. 3. Let F : be a collection of sigma-fields of subsets of. (i) Show that F is a sigma-field; (ii) Using a counter example show that F may not be a sigma-field; 38
39 (iii) Let be a class of subsets of and let F : be a collection of all sigma-fields that contain the class. Show that = F, where denotes the smallest sigma-field containing the class (or the sigma-field generated by class ). 4. Let be an infinite set and let = : is finite or is finite. (i) Show that is closed under complements and finite unions; (ii) Using a counter example show that may not be closed under countably infinite unions (and hence may not be a sigma-field). 5. (i) Let be an uncountable set and let F = : is countable or is countable. (a) Show that F is a sigma-field; (b) What can you say about Fwhen is countable? (ii) Let Ω be a countable set and let = : Ω. Show that =. 6. Let F = =the power set of = 0, 1, 2,. In each of the following cases, verify if, F, is a probability space: (i) =!, F, > 0; (ii) = 1, F, 0 < < 1; (iii) = 0, if has a finite number of elements, and = 1, if has infinite number of elements, F. 7. Let, F, be a probability space and let,,, F. Suppose that = 0.6, = 0.5, = 0.4, = 0.3, = 0.2, = 0.2, = 0.1, = = 0, = 0.1 and = 0.2. Find: (i) and ; (ii) and ; (iii) and ; (iv) and ; (v) and ; (vi). 8. Let, F, be a probability space and let and be two events (i.e.,, F). (i) Show that the probability that exactly one of the events or will occur is given by + 2 ; (ii) Show that = = =. 39
40 9. Suppose that 3 persons,, are made to stand in a row at random. Find the probability that there are exactly person between and ; here 1, 2,, A point, is randomly chosen on the unit square =, : 0 1, 0 1 (i.e., for any region for which the area is defined, the probability that, lies on is side does not exceed units. Find the probability that the distance from, to the nearest 11. Three numbers, and are chosen at random and with replacement from the set 1, 2,,6. Find the probability that the quadratic equation + + = 0 will have real root(s). 12. Three numbers are chosen at random from the set 1, 2,,50. Find the probability that the chosen numbers are in (i) arithmetic progression; (ii) geometric progression. 13. Consider an empty box in which four balls are to be placed (one-by-one) according to the following scheme. A fair die is cast each time and the number of dots on the upper face is noted. If the upper face shows up 2 or 5 dots then a white ball is placed in the box. Otherwise a black ball is placed in the box. Given that the first ball placed in the box was white find the probability that the box will contain exactly two black balls. 14. Let 0, 1, F, be a probability space such that Fis the smallest sigma-field containing all subintervals of = 0, 1 and, =, where 0 < 1 (such a probability measure is known to exist). (i) Show that =,, 0, 1; (ii) Show that = 0, 0, 1and 0, 1 = 1(Note that here = 0 but and 0, 1 = 1 but 0, 1 Ω) ; (iii) Show that, for any countable set F, = 0; (iv) For N, let = 0, and = +, 1. Verify that,, Lim = lim and Lim = lim. 15. Consider four coding machines,, and producing binary codes 0 and 1. The machine produces codes0 and 1 with respective probabilities and. The code produced by machine is fed into machine = 1, 2, 3 which may either leave 40
41 the received code unchanged or may change it. Suppose that each of the machines, and change the received code with probability. Given that the machine has produced code 1, find the conditional probability that the machine produced code A student appears in the examinations of four subjects Biology, Chemistry, Physics and Mathematics. Suppose that probabilities of the student clearing examinations in these subjects are,, and respectively. Assuming that the performances of the students in four subjects are independent, find the probability that the student will clear examination(s) of (i) all the subjects; (ii) no subject; (iii) exactly one subject; (iv) exactly two subjects; (v) at least one subject. 17. Let and be independent events. Show that max,, Δ 4 9, where Δ =. 18. For independent events,,, show that:. 19. Let, F, be a probability space and let,, be a sequence of events i. e., F, = 1, 2,. Define =, =, = 1,2,, = and =. Show that: (i) is the event that all but a finite number of s occur and is the event that infinitely many s occur; (ii) ; (iii) = lim = lim lim and = lim ; (iv) if < then, with probability one, only finitely many s will occur; (v) if,, are independent and < then, with probability one, infinitely many will occur. 41
42 20. Let, and be three events such that and are negatively (positively) associated and and are negatively (positively) associated. Can we conclude that, in general, and are negatively (positively) associated? 21. Let, F, be a probability space and let A and B two eventsi. e.,, F. Show that if and are positively (negatively) associated then and are negatively (positively) associated. 22. A locality has houses numbered 1,., and a terrorist is hiding in one of these houses. Let denote the event that the terrorist is hiding in house numbered, = 1,, and let = 0,1, = 1,,. During a search operation, let denote the event that search of the house number will fail to nab the terrorist there and let 0,1, = 1,,. For each, 1,,,, show that and are negatively associated but and are positively associated. Interpret these findings. 23. Let, and be three events such that > 0. Prove or disprove each of the following: (i) ; (ii) if and are independent events. 24. A -out-of- system is a system comprising of components that functions if, and only if, at least 1,2,, of the components function. A1-out-of- system is called a parallel system and an-out-of- system is called a series system. Consider components,, that function independently. At any given time the probability that the component will be functioning is 0,1 and the probability that it will not be functioning at time is 1, = 1,,. (i) Find the probability that a parallel system comprising of components,, will function at time ; (ii) Find the probability that a series system comprising of components,, will function at time ; (iii) If =, = 1,,, find the probability that a -out-of- system comprising of components,, will function at time. 42
Statistical Theory 1
 Statistical Theory 1 Set Theory and Probability Paolo Bautista September 12, 2017 Set Theory We start by defining terms in Set Theory which will be used in the following sections. Definition 1 A set is
Statistical Theory 1 Set Theory and Probability Paolo Bautista September 12, 2017 Set Theory We start by defining terms in Set Theory which will be used in the following sections. Definition 1 A set is
Axioms of Probability
 Sample Space (denoted by S) The set of all possible outcomes of a random experiment is called the Sample Space of the experiment, and is denoted by S. Example 1.10 If the experiment consists of tossing
Sample Space (denoted by S) The set of all possible outcomes of a random experiment is called the Sample Space of the experiment, and is denoted by S. Example 1.10 If the experiment consists of tossing
2. AXIOMATIC PROBABILITY
 IA Probability Lent Term 2. AXIOMATIC PROBABILITY 2. The axioms The formulation for classical probability in which all outcomes or points in the sample space are equally likely is too restrictive to develop
IA Probability Lent Term 2. AXIOMATIC PROBABILITY 2. The axioms The formulation for classical probability in which all outcomes or points in the sample space are equally likely is too restrictive to develop
Discrete Mathematics and Probability Theory Spring 2016 Rao and Walrand Note 14
 CS 70 Discrete Mathematics and Probability Theory Spring 2016 Rao and Walrand Note 14 Introduction One of the key properties of coin flips is independence: if you flip a fair coin ten times and get ten
CS 70 Discrete Mathematics and Probability Theory Spring 2016 Rao and Walrand Note 14 Introduction One of the key properties of coin flips is independence: if you flip a fair coin ten times and get ten
ELEG 3143 Probability & Stochastic Process Ch. 1 Probability
 Department of Electrical Engineering University of Arkansas ELEG 3143 Probability & Stochastic Process Ch. 1 Probability Dr. Jingxian Wu wuj@uark.edu OUTLINE 2 Applications Elementary Set Theory Random
Department of Electrical Engineering University of Arkansas ELEG 3143 Probability & Stochastic Process Ch. 1 Probability Dr. Jingxian Wu wuj@uark.edu OUTLINE 2 Applications Elementary Set Theory Random
Lecture 1: An introduction to probability theory
 Econ 514: Probability and Statistics Lecture 1: An introduction to probability theory Random Experiments Random experiment: Experiment/phenomenon/action/mechanism with outcome that is not (fully) predictable.
Econ 514: Probability and Statistics Lecture 1: An introduction to probability theory Random Experiments Random experiment: Experiment/phenomenon/action/mechanism with outcome that is not (fully) predictable.
Notes Week 2 Chapter 3 Probability WEEK 2 page 1
 Notes Week 2 Chapter 3 Probability WEEK 2 page 1 The sample space of an experiment, sometimes denoted S or in probability theory, is the set that consists of all possible elementary outcomes of that experiment
Notes Week 2 Chapter 3 Probability WEEK 2 page 1 The sample space of an experiment, sometimes denoted S or in probability theory, is the set that consists of all possible elementary outcomes of that experiment
Probability and distributions. Francesco Corona
 Probability Probability and distributions Francesco Corona Department of Computer Science Federal University of Ceará, Fortaleza Probability Many kinds of studies can be characterised as (repeated) experiments
Probability Probability and distributions Francesco Corona Department of Computer Science Federal University of Ceará, Fortaleza Probability Many kinds of studies can be characterised as (repeated) experiments
Probability Theory Review
 Cogsci 118A: Natural Computation I Lecture 2 (01/07/10) Lecturer: Angela Yu Probability Theory Review Scribe: Joseph Schilz Lecture Summary 1. Set theory: terms and operators In this section, we provide
Cogsci 118A: Natural Computation I Lecture 2 (01/07/10) Lecturer: Angela Yu Probability Theory Review Scribe: Joseph Schilz Lecture Summary 1. Set theory: terms and operators In this section, we provide
Sample Spaces, Random Variables
 Sample Spaces, Random Variables Moulinath Banerjee University of Michigan August 3, 22 Probabilities In talking about probabilities, the fundamental object is Ω, the sample space. (elements) in Ω are denoted
Sample Spaces, Random Variables Moulinath Banerjee University of Michigan August 3, 22 Probabilities In talking about probabilities, the fundamental object is Ω, the sample space. (elements) in Ω are denoted
I - Probability. What is Probability? the chance of an event occuring. 1classical probability. 2empirical probability. 3subjective probability
 What is Probability? the chance of an event occuring eg 1classical probability 2empirical probability 3subjective probability Section 2 - Probability (1) Probability - Terminology random (probability)
What is Probability? the chance of an event occuring eg 1classical probability 2empirical probability 3subjective probability Section 2 - Probability (1) Probability - Terminology random (probability)
MATH 556: PROBABILITY PRIMER
 MATH 6: PROBABILITY PRIMER 1 DEFINITIONS, TERMINOLOGY, NOTATION 1.1 EVENTS AND THE SAMPLE SPACE Definition 1.1 An experiment is a one-off or repeatable process or procedure for which (a there is a well-defined
MATH 6: PROBABILITY PRIMER 1 DEFINITIONS, TERMINOLOGY, NOTATION 1.1 EVENTS AND THE SAMPLE SPACE Definition 1.1 An experiment is a one-off or repeatable process or procedure for which (a there is a well-defined
Lecture Notes 1 Basic Probability. Elements of Probability. Conditional probability. Sequential Calculation of Probability
 Lecture Notes 1 Basic Probability Set Theory Elements of Probability Conditional probability Sequential Calculation of Probability Total Probability and Bayes Rule Independence Counting EE 178/278A: Basic
Lecture Notes 1 Basic Probability Set Theory Elements of Probability Conditional probability Sequential Calculation of Probability Total Probability and Bayes Rule Independence Counting EE 178/278A: Basic
Probability theory basics
 Probability theory basics Michael Franke Basics of probability theory: axiomatic definition, interpretation, joint distributions, marginalization, conditional probability & Bayes rule. Random variables:
Probability theory basics Michael Franke Basics of probability theory: axiomatic definition, interpretation, joint distributions, marginalization, conditional probability & Bayes rule. Random variables:
Statistical Inference
 Statistical Inference Lecture 1: Probability Theory MING GAO DASE @ ECNU (for course related communications) mgao@dase.ecnu.edu.cn Sep. 11, 2018 Outline Introduction Set Theory Basics of Probability Theory
Statistical Inference Lecture 1: Probability Theory MING GAO DASE @ ECNU (for course related communications) mgao@dase.ecnu.edu.cn Sep. 11, 2018 Outline Introduction Set Theory Basics of Probability Theory
PROBABILITY THEORY 1. Basics
 PROILITY THEORY. asics Probability theory deals with the study of random phenomena, which under repeated experiments yield different outcomes that have certain underlying patterns about them. The notion
PROILITY THEORY. asics Probability theory deals with the study of random phenomena, which under repeated experiments yield different outcomes that have certain underlying patterns about them. The notion
Lecture 8: Probability
 Lecture 8: Probability The idea of probability is well-known The flipping of a balanced coin can produce one of two outcomes: T (tail) and H (head) and the symmetry between the two outcomes means, of course,
Lecture 8: Probability The idea of probability is well-known The flipping of a balanced coin can produce one of two outcomes: T (tail) and H (head) and the symmetry between the two outcomes means, of course,
P (A B) P ((B C) A) P (B A) = P (B A) + P (C A) P (A) = P (B A) + P (C A) = Q(A) + Q(B).
 Lectures 7-8 jacques@ucsdedu 41 Conditional Probability Let (Ω, F, P ) be a probability space Suppose that we have prior information which leads us to conclude that an event A F occurs Based on this information,
Lectures 7-8 jacques@ucsdedu 41 Conditional Probability Let (Ω, F, P ) be a probability space Suppose that we have prior information which leads us to conclude that an event A F occurs Based on this information,
Probability the chance that an uncertain event will occur (always between 0 and 1)
 Quantitative Methods 2013 1 Probability as a Numerical Measure of the Likelihood of Occurrence Probability the chance that an uncertain event will occur (always between 0 and 1) Increasing Likelihood of
Quantitative Methods 2013 1 Probability as a Numerical Measure of the Likelihood of Occurrence Probability the chance that an uncertain event will occur (always between 0 and 1) Increasing Likelihood of
Properties of Probability
 Econ 325 Notes on Probability 1 By Hiro Kasahara Properties of Probability In statistics, we consider random experiments, experiments for which the outcome is random, i.e., cannot be predicted with certainty.
Econ 325 Notes on Probability 1 By Hiro Kasahara Properties of Probability In statistics, we consider random experiments, experiments for which the outcome is random, i.e., cannot be predicted with certainty.
1. Discrete Distributions
 Virtual Laboratories > 2. Distributions > 1 2 3 4 5 6 7 8 1. Discrete Distributions Basic Theory As usual, we start with a random experiment with probability measure P on an underlying sample space Ω.
Virtual Laboratories > 2. Distributions > 1 2 3 4 5 6 7 8 1. Discrete Distributions Basic Theory As usual, we start with a random experiment with probability measure P on an underlying sample space Ω.
Course: ESO-209 Home Work: 1 Instructor: Debasis Kundu
 Home Work: 1 1. Describe the sample space when a coin is tossed (a) once, (b) three times, (c) n times, (d) an infinite number of times. 2. A coin is tossed until for the first time the same result appear
Home Work: 1 1. Describe the sample space when a coin is tossed (a) once, (b) three times, (c) n times, (d) an infinite number of times. 2. A coin is tossed until for the first time the same result appear
Conditional Probability
 Conditional Probability Idea have performed a chance experiment but don t know the outcome (ω), but have some partial information (event A) about ω. Question: given this partial information what s the
Conditional Probability Idea have performed a chance experiment but don t know the outcome (ω), but have some partial information (event A) about ω. Question: given this partial information what s the
Origins of Probability Theory
 1 16.584: INTRODUCTION Theory and Tools of Probability required to analyze and design systems subject to uncertain outcomes/unpredictability/randomness. Such systems more generally referred to as Experiments.
1 16.584: INTRODUCTION Theory and Tools of Probability required to analyze and design systems subject to uncertain outcomes/unpredictability/randomness. Such systems more generally referred to as Experiments.
Topic 3: Introduction to Probability
 Topic 3: Introduction to Probability 1 Contents 1. Introduction 2. Simple Definitions 3. Types of Probability 4. Theorems of Probability 5. Probabilities under conditions of statistically independent events
Topic 3: Introduction to Probability 1 Contents 1. Introduction 2. Simple Definitions 3. Types of Probability 4. Theorems of Probability 5. Probabilities under conditions of statistically independent events
Discrete Probability
 Discrete Probability Counting Permutations Combinations r- Combinations r- Combinations with repetition Allowed Pascal s Formula Binomial Theorem Conditional Probability Baye s Formula Independent Events
Discrete Probability Counting Permutations Combinations r- Combinations r- Combinations with repetition Allowed Pascal s Formula Binomial Theorem Conditional Probability Baye s Formula Independent Events
Chapter 3 : Conditional Probability and Independence
 STAT/MATH 394 A - PROBABILITY I UW Autumn Quarter 2016 Néhémy Lim Chapter 3 : Conditional Probability and Independence 1 Conditional Probabilities How should we modify the probability of an event when
STAT/MATH 394 A - PROBABILITY I UW Autumn Quarter 2016 Néhémy Lim Chapter 3 : Conditional Probability and Independence 1 Conditional Probabilities How should we modify the probability of an event when
Lecture 9: Conditional Probability and Independence
 EE5110: Probability Foundations July-November 2015 Lecture 9: Conditional Probability and Independence Lecturer: Dr. Krishna Jagannathan Scribe: Vishakh Hegde 9.1 Conditional Probability Definition 9.1
EE5110: Probability Foundations July-November 2015 Lecture 9: Conditional Probability and Independence Lecturer: Dr. Krishna Jagannathan Scribe: Vishakh Hegde 9.1 Conditional Probability Definition 9.1
Chapter 2. Conditional Probability and Independence. 2.1 Conditional Probability
 Chapter 2 Conditional Probability and Independence 2.1 Conditional Probability Probability assigns a likelihood to results of experiments that have not yet been conducted. Suppose that the experiment has
Chapter 2 Conditional Probability and Independence 2.1 Conditional Probability Probability assigns a likelihood to results of experiments that have not yet been conducted. Suppose that the experiment has
Probability. Lecture Notes. Adolfo J. Rumbos
 Probability Lecture Notes Adolfo J. Rumbos October 20, 204 2 Contents Introduction 5. An example from statistical inference................ 5 2 Probability Spaces 9 2. Sample Spaces and σ fields.....................
Probability Lecture Notes Adolfo J. Rumbos October 20, 204 2 Contents Introduction 5. An example from statistical inference................ 5 2 Probability Spaces 9 2. Sample Spaces and σ fields.....................
Chapter 2. Conditional Probability and Independence. 2.1 Conditional Probability
 Chapter 2 Conditional Probability and Independence 2.1 Conditional Probability Example: Two dice are tossed. What is the probability that the sum is 8? This is an easy exercise: we have a sample space
Chapter 2 Conditional Probability and Independence 2.1 Conditional Probability Example: Two dice are tossed. What is the probability that the sum is 8? This is an easy exercise: we have a sample space
Chapter 2 Class Notes
 Chapter 2 Class Notes Probability can be thought of in many ways, for example as a relative frequency of a long series of trials (e.g. flips of a coin or die) Another approach is to let an expert (such
Chapter 2 Class Notes Probability can be thought of in many ways, for example as a relative frequency of a long series of trials (e.g. flips of a coin or die) Another approach is to let an expert (such
Lecture 4: Probability, Proof Techniques, Method of Induction Lecturer: Lale Özkahya
 BBM 205 Discrete Mathematics Hacettepe University http://web.cs.hacettepe.edu.tr/ bbm205 Lecture 4: Probability, Proof Techniques, Method of Induction Lecturer: Lale Özkahya Resources: Kenneth Rosen, Discrete
BBM 205 Discrete Mathematics Hacettepe University http://web.cs.hacettepe.edu.tr/ bbm205 Lecture 4: Probability, Proof Techniques, Method of Induction Lecturer: Lale Özkahya Resources: Kenneth Rosen, Discrete
Statistics for Financial Engineering Session 2: Basic Set Theory March 19 th, 2006
 Statistics for Financial Engineering Session 2: Basic Set Theory March 19 th, 2006 Topics What is a set? Notations for sets Empty set Inclusion/containment and subsets Sample spaces and events Operations
Statistics for Financial Engineering Session 2: Basic Set Theory March 19 th, 2006 Topics What is a set? Notations for sets Empty set Inclusion/containment and subsets Sample spaces and events Operations
4. Probability of an event A for equally likely outcomes:
 University of California, Los Angeles Department of Statistics Statistics 110A Instructor: Nicolas Christou Probability Probability: A measure of the chance that something will occur. 1. Random experiment:
University of California, Los Angeles Department of Statistics Statistics 110A Instructor: Nicolas Christou Probability Probability: A measure of the chance that something will occur. 1. Random experiment:
Problem # Number of points 1 /20 2 /20 3 /20 4 /20 5 /20 6 /20 7 /20 8 /20 Total /150
 Name Student ID # Instructor: SOLUTION Sergey Kirshner STAT 516 Fall 09 Practice Midterm #1 January 31, 2010 You are not allowed to use books or notes. Non-programmable non-graphic calculators are permitted.
Name Student ID # Instructor: SOLUTION Sergey Kirshner STAT 516 Fall 09 Practice Midterm #1 January 31, 2010 You are not allowed to use books or notes. Non-programmable non-graphic calculators are permitted.
Probabilistic models
 Kolmogorov (Andrei Nikolaevich, 1903 1987) put forward an axiomatic system for probability theory. Foundations of the Calculus of Probabilities, published in 1933, immediately became the definitive formulation
Kolmogorov (Andrei Nikolaevich, 1903 1987) put forward an axiomatic system for probability theory. Foundations of the Calculus of Probabilities, published in 1933, immediately became the definitive formulation
Fundamentals of Probability CE 311S
 Fundamentals of Probability CE 311S OUTLINE Review Elementary set theory Probability fundamentals: outcomes, sample spaces, events Outline ELEMENTARY SET THEORY Basic probability concepts can be cast in
Fundamentals of Probability CE 311S OUTLINE Review Elementary set theory Probability fundamentals: outcomes, sample spaces, events Outline ELEMENTARY SET THEORY Basic probability concepts can be cast in
LECTURE 1. 1 Introduction. 1.1 Sample spaces and events
 LECTURE 1 1 Introduction The first part of our adventure is a highly selective review of probability theory, focusing especially on things that are most useful in statistics. 1.1 Sample spaces and events
LECTURE 1 1 Introduction The first part of our adventure is a highly selective review of probability theory, focusing especially on things that are most useful in statistics. 1.1 Sample spaces and events
The probability of an event is viewed as a numerical measure of the chance that the event will occur.
 Chapter 5 This chapter introduces probability to quantify randomness. Section 5.1: How Can Probability Quantify Randomness? The probability of an event is viewed as a numerical measure of the chance that
Chapter 5 This chapter introduces probability to quantify randomness. Section 5.1: How Can Probability Quantify Randomness? The probability of an event is viewed as a numerical measure of the chance that
If S = {O 1, O 2,, O n }, where O i is the i th elementary outcome, and p i is the probability of the i th elementary outcome, then
 1.1 Probabilities Def n: A random experiment is a process that, when performed, results in one and only one of many observations (or outcomes). The sample space S is the set of all elementary outcomes
1.1 Probabilities Def n: A random experiment is a process that, when performed, results in one and only one of many observations (or outcomes). The sample space S is the set of all elementary outcomes
PROBABILITY VITTORIA SILVESTRI
 PROBABILITY VITTORIA SILVESTRI Contents Preface. Introduction 2 2. Combinatorial analysis 5 3. Stirling s formula 8 4. Properties of Probability measures Preface These lecture notes are for the course
PROBABILITY VITTORIA SILVESTRI Contents Preface. Introduction 2 2. Combinatorial analysis 5 3. Stirling s formula 8 4. Properties of Probability measures Preface These lecture notes are for the course
Probability COMP 245 STATISTICS. Dr N A Heard. 1 Sample Spaces and Events Sample Spaces Events Combinations of Events...
 Probability COMP 245 STATISTICS Dr N A Heard Contents Sample Spaces and Events. Sample Spaces........................................2 Events........................................... 2.3 Combinations
Probability COMP 245 STATISTICS Dr N A Heard Contents Sample Spaces and Events. Sample Spaces........................................2 Events........................................... 2.3 Combinations
Probability 1 (MATH 11300) lecture slides
 Probability 1 (MATH 11300) lecture slides Márton Balázs School of Mathematics University of Bristol Autumn, 2015 December 16, 2015 To know... http://www.maths.bris.ac.uk/ mb13434/prob1/ m.balazs@bristol.ac.uk
Probability 1 (MATH 11300) lecture slides Márton Balázs School of Mathematics University of Bristol Autumn, 2015 December 16, 2015 To know... http://www.maths.bris.ac.uk/ mb13434/prob1/ m.balazs@bristol.ac.uk
Probability Experiments, Trials, Outcomes, Sample Spaces Example 1 Example 2
 Probability Probability is the study of uncertain events or outcomes. Games of chance that involve rolling dice or dealing cards are one obvious area of application. However, probability models underlie
Probability Probability is the study of uncertain events or outcomes. Games of chance that involve rolling dice or dealing cards are one obvious area of application. However, probability models underlie
Probability, Random Processes and Inference
 INSTITUTO POLITÉCNICO NACIONAL CENTRO DE INVESTIGACION EN COMPUTACION Laboratorio de Ciberseguridad Probability, Random Processes and Inference Dr. Ponciano Jorge Escamilla Ambrosio pescamilla@cic.ipn.mx
INSTITUTO POLITÉCNICO NACIONAL CENTRO DE INVESTIGACION EN COMPUTACION Laboratorio de Ciberseguridad Probability, Random Processes and Inference Dr. Ponciano Jorge Escamilla Ambrosio pescamilla@cic.ipn.mx
Conditional Probability
 Chapter 3 Conditional Probability 3.1 Definition of conditional probability In spite of our misgivings, let us persist with the frequency definition of probability. Consider an experiment conducted N times
Chapter 3 Conditional Probability 3.1 Definition of conditional probability In spite of our misgivings, let us persist with the frequency definition of probability. Consider an experiment conducted N times
MODULE 2 RANDOM VARIABLE AND ITS DISTRIBUTION LECTURES DISTRIBUTION FUNCTION AND ITS PROPERTIES
 MODULE 2 RANDOM VARIABLE AND ITS DISTRIBUTION LECTURES 7-11 Topics 2.1 RANDOM VARIABLE 2.2 INDUCED PROBABILITY MEASURE 2.3 DISTRIBUTION FUNCTION AND ITS PROPERTIES 2.4 TYPES OF RANDOM VARIABLES: DISCRETE,
MODULE 2 RANDOM VARIABLE AND ITS DISTRIBUTION LECTURES 7-11 Topics 2.1 RANDOM VARIABLE 2.2 INDUCED PROBABILITY MEASURE 2.3 DISTRIBUTION FUNCTION AND ITS PROPERTIES 2.4 TYPES OF RANDOM VARIABLES: DISCRETE,
Formalizing Probability. Choosing the Sample Space. Probability Measures
 Formalizing Probability Choosing the Sample Space What do we assign probability to? Intuitively, we assign them to possible events (things that might happen, outcomes of an experiment) Formally, we take
Formalizing Probability Choosing the Sample Space What do we assign probability to? Intuitively, we assign them to possible events (things that might happen, outcomes of an experiment) Formally, we take
Intermediate Math Circles November 8, 2017 Probability II
 Intersection of Events and Independence Consider two groups of pairs of events Intermediate Math Circles November 8, 017 Probability II Group 1 (Dependent Events) A = {a sales associate has training} B
Intersection of Events and Independence Consider two groups of pairs of events Intermediate Math Circles November 8, 017 Probability II Group 1 (Dependent Events) A = {a sales associate has training} B
4. Conditional Probability
 1 of 13 7/15/2009 9:25 PM Virtual Laboratories > 2. Probability Spaces > 1 2 3 4 5 6 7 4. Conditional Probability Definitions and Interpretations The Basic Definition As usual, we start with a random experiment
1 of 13 7/15/2009 9:25 PM Virtual Laboratories > 2. Probability Spaces > 1 2 3 4 5 6 7 4. Conditional Probability Definitions and Interpretations The Basic Definition As usual, we start with a random experiment
TOPIC 12 PROBABILITY SCHEMATIC DIAGRAM
 TOPIC 12 PROBABILITY SCHEMATIC DIAGRAM Topic Concepts Degree of Importance References NCERT Book Vol. II Probability (i) Conditional Probability *** Article 1.2 and 1.2.1 Solved Examples 1 to 6 Q. Nos
TOPIC 12 PROBABILITY SCHEMATIC DIAGRAM Topic Concepts Degree of Importance References NCERT Book Vol. II Probability (i) Conditional Probability *** Article 1.2 and 1.2.1 Solved Examples 1 to 6 Q. Nos
Mathematical Foundations of Computer Science Lecture Outline October 18, 2018
 Mathematical Foundations of Computer Science Lecture Outline October 18, 2018 The Total Probability Theorem. Consider events E and F. Consider a sample point ω E. Observe that ω belongs to either F or
Mathematical Foundations of Computer Science Lecture Outline October 18, 2018 The Total Probability Theorem. Consider events E and F. Consider a sample point ω E. Observe that ω belongs to either F or
Probabilistic models
 Probabilistic models Kolmogorov (Andrei Nikolaevich, 1903 1987) put forward an axiomatic system for probability theory. Foundations of the Calculus of Probabilities, published in 1933, immediately became
Probabilistic models Kolmogorov (Andrei Nikolaevich, 1903 1987) put forward an axiomatic system for probability theory. Foundations of the Calculus of Probabilities, published in 1933, immediately became
Probability and Statistics Notes
 Probability and Statistics Notes Chapter One Jesse Crawford Department of Mathematics Tarleton State University (Tarleton State University) Chapter One Notes 1 / 71 Outline 1 A Sketch of Probability and
Probability and Statistics Notes Chapter One Jesse Crawford Department of Mathematics Tarleton State University (Tarleton State University) Chapter One Notes 1 / 71 Outline 1 A Sketch of Probability and
= 2 5 Note how we need to be somewhat careful with how we define the total number of outcomes in b) and d). We will return to this later.
 PROBABILITY MATH CIRCLE (ADVANCED /27/203 The likelyhood of something (usually called an event happening is called the probability. Probability (informal: We can calculate probability using a ratio: want
PROBABILITY MATH CIRCLE (ADVANCED /27/203 The likelyhood of something (usually called an event happening is called the probability. Probability (informal: We can calculate probability using a ratio: want
Preliminary Statistics Lecture 2: Probability Theory (Outline) prelimsoas.webs.com
 1 School of Oriental and African Studies September 2015 Department of Economics Preliminary Statistics Lecture 2: Probability Theory (Outline) prelimsoas.webs.com Gujarati D. Basic Econometrics, Appendix
1 School of Oriental and African Studies September 2015 Department of Economics Preliminary Statistics Lecture 2: Probability Theory (Outline) prelimsoas.webs.com Gujarati D. Basic Econometrics, Appendix
Probability Theory. Introduction to Probability Theory. Principles of Counting Examples. Principles of Counting. Probability spaces.
 Probability Theory To start out the course, we need to know something about statistics and probability Introduction to Probability Theory L645 Advanced NLP Autumn 2009 This is only an introduction; for
Probability Theory To start out the course, we need to know something about statistics and probability Introduction to Probability Theory L645 Advanced NLP Autumn 2009 This is only an introduction; for
Elementary Discrete Probability
 Elementary Discrete Probability MATH 472 Financial Mathematics J Robert Buchanan 2018 Objectives In this lesson we will learn: the terminology of elementary probability, elementary rules of probability,
Elementary Discrete Probability MATH 472 Financial Mathematics J Robert Buchanan 2018 Objectives In this lesson we will learn: the terminology of elementary probability, elementary rules of probability,
ELEG 3143 Probability & Stochastic Process Ch. 1 Experiments, Models, and Probabilities
 Department of Electrical Engineering University of Arkansas ELEG 3143 Probability & Stochastic Process Ch. 1 Experiments, Models, and Probabilities Dr. Jing Yang jingyang@uark.edu OUTLINE 2 Applications
Department of Electrical Engineering University of Arkansas ELEG 3143 Probability & Stochastic Process Ch. 1 Experiments, Models, and Probabilities Dr. Jing Yang jingyang@uark.edu OUTLINE 2 Applications
Chapter 7: Section 7-1 Probability Theory and Counting Principles
 Chapter 7: Section 7-1 Probability Theory and Counting Principles D. S. Malik Creighton University, Omaha, NE D. S. Malik Creighton University, Omaha, NE Chapter () 7: Section 7-1 Probability Theory and
Chapter 7: Section 7-1 Probability Theory and Counting Principles D. S. Malik Creighton University, Omaha, NE D. S. Malik Creighton University, Omaha, NE Chapter () 7: Section 7-1 Probability Theory and
PROBABILITY.
 PROBABILITY PROBABILITY(Basic Terminology) Random Experiment: If in each trial of an experiment conducted under identical conditions, the outcome is not unique, but may be any one of the possible outcomes,
PROBABILITY PROBABILITY(Basic Terminology) Random Experiment: If in each trial of an experiment conducted under identical conditions, the outcome is not unique, but may be any one of the possible outcomes,
1. When applied to an affected person, the test comes up positive in 90% of cases, and negative in 10% (these are called false negatives ).
 CS 70 Discrete Mathematics for CS Spring 2006 Vazirani Lecture 8 Conditional Probability A pharmaceutical company is marketing a new test for a certain medical condition. According to clinical trials,
CS 70 Discrete Mathematics for CS Spring 2006 Vazirani Lecture 8 Conditional Probability A pharmaceutical company is marketing a new test for a certain medical condition. According to clinical trials,
UNIT 5 ~ Probability: What Are the Chances? 1
 UNIT 5 ~ Probability: What Are the Chances? 1 6.1: Simulation Simulation: The of chance behavior, based on a that accurately reflects the phenomenon under consideration. (ex 1) Suppose we are interested
UNIT 5 ~ Probability: What Are the Chances? 1 6.1: Simulation Simulation: The of chance behavior, based on a that accurately reflects the phenomenon under consideration. (ex 1) Suppose we are interested
the time it takes until a radioactive substance undergoes a decay
 1 Probabilities 1.1 Experiments with randomness Wewillusethetermexperimentinaverygeneralwaytorefertosomeprocess that produces a random outcome. Examples: (Ask class for some first) Here are some discrete
1 Probabilities 1.1 Experiments with randomness Wewillusethetermexperimentinaverygeneralwaytorefertosomeprocess that produces a random outcome. Examples: (Ask class for some first) Here are some discrete
MATH2206 Prob Stat/20.Jan Weekly Review 1-2
 MATH2206 Prob Stat/20.Jan.2017 Weekly Review 1-2 This week I explained the idea behind the formula of the well-known statistic standard deviation so that it is clear now why it is a measure of dispersion
MATH2206 Prob Stat/20.Jan.2017 Weekly Review 1-2 This week I explained the idea behind the formula of the well-known statistic standard deviation so that it is clear now why it is a measure of dispersion
Lectures Conditional Probability and Independence
 Lectures 5 11 Conditional Probability and Independence Purpose: Calculate probabilities under restrictions, conditions or partial information on the random experiment. Break down complex probabilistic
Lectures 5 11 Conditional Probability and Independence Purpose: Calculate probabilities under restrictions, conditions or partial information on the random experiment. Break down complex probabilistic
CS626 Data Analysis and Simulation
 CS626 Data Analysis and Simulation Instructor: Peter Kemper R 104A, phone 221-3462, email:kemper@cs.wm.edu Today: Probability Primer Quick Reference: Sheldon Ross: Introduction to Probability Models 9th
CS626 Data Analysis and Simulation Instructor: Peter Kemper R 104A, phone 221-3462, email:kemper@cs.wm.edu Today: Probability Primer Quick Reference: Sheldon Ross: Introduction to Probability Models 9th
Sample Space: Specify all possible outcomes from an experiment. Event: Specify a particular outcome or combination of outcomes.
 Chapter 2 Introduction to Probability 2.1 Probability Model Probability concerns about the chance of observing certain outcome resulting from an experiment. However, since chance is an abstraction of something
Chapter 2 Introduction to Probability 2.1 Probability Model Probability concerns about the chance of observing certain outcome resulting from an experiment. However, since chance is an abstraction of something
1.1. MEASURES AND INTEGRALS
 CHAPTER 1: MEASURE THEORY In this chapter we define the notion of measure µ on a space, construct integrals on this space, and establish their basic properties under limits. The measure µ(e) will be defined
CHAPTER 1: MEASURE THEORY In this chapter we define the notion of measure µ on a space, construct integrals on this space, and establish their basic properties under limits. The measure µ(e) will be defined
UNIT Explain about the partition of a sampling space theorem?
 UNIT -1 1. Explain about the partition of a sampling space theorem? PARTITIONS OF A SAMPLE SPACE The events B1, B2. B K represent a partition of the sample space 'S" if (a) So, when the experiment E is
UNIT -1 1. Explain about the partition of a sampling space theorem? PARTITIONS OF A SAMPLE SPACE The events B1, B2. B K represent a partition of the sample space 'S" if (a) So, when the experiment E is
Randomized Algorithms
 Randomized Algorithms Prof. Tapio Elomaa tapio.elomaa@tut.fi Course Basics A new 4 credit unit course Part of Theoretical Computer Science courses at the Department of Mathematics There will be 4 hours
Randomized Algorithms Prof. Tapio Elomaa tapio.elomaa@tut.fi Course Basics A new 4 credit unit course Part of Theoretical Computer Science courses at the Department of Mathematics There will be 4 hours
MAT2377. Ali Karimnezhad. Version September 9, Ali Karimnezhad
 MAT2377 Ali Karimnezhad Version September 9, 2015 Ali Karimnezhad Comments These slides cover material from Chapter 1. In class, I may use a blackboard. I recommend reading these slides before you come
MAT2377 Ali Karimnezhad Version September 9, 2015 Ali Karimnezhad Comments These slides cover material from Chapter 1. In class, I may use a blackboard. I recommend reading these slides before you come
Basic Statistics and Probability Chapter 3: Probability
 Basic Statistics and Probability Chapter 3: Probability Events, Sample Spaces and Probability Unions and Intersections Complementary Events Additive Rule. Mutually Exclusive Events Conditional Probability
Basic Statistics and Probability Chapter 3: Probability Events, Sample Spaces and Probability Unions and Intersections Complementary Events Additive Rule. Mutually Exclusive Events Conditional Probability
Lecture 2: Probability. Readings: Sections Statistical Inference: drawing conclusions about the population based on a sample
 Lecture 2: Probability Readings: Sections 5.1-5.3 1 Introduction Statistical Inference: drawing conclusions about the population based on a sample Parameter: a number that describes the population a fixed
Lecture 2: Probability Readings: Sections 5.1-5.3 1 Introduction Statistical Inference: drawing conclusions about the population based on a sample Parameter: a number that describes the population a fixed
ECE353: Probability and Random Processes. Lecture 2 - Set Theory
 ECE353: Probability and Random Processes Lecture 2 - Set Theory Xiao Fu School of Electrical Engineering and Computer Science Oregon State University E-mail: xiao.fu@oregonstate.edu January 10, 2018 Set
ECE353: Probability and Random Processes Lecture 2 - Set Theory Xiao Fu School of Electrical Engineering and Computer Science Oregon State University E-mail: xiao.fu@oregonstate.edu January 10, 2018 Set
2.6 Tools for Counting sample points
 2.6 Tools for Counting sample points When the number of simple events in S is too large, manual enumeration of every sample point in S is tedious or even impossible. (Example) If S contains N equiprobable
2.6 Tools for Counting sample points When the number of simple events in S is too large, manual enumeration of every sample point in S is tedious or even impossible. (Example) If S contains N equiprobable
MASSACHUSETTS INSTITUTE OF TECHNOLOGY 6.436J/15.085J Fall 2008 Lecture 3 9/10/2008 CONDITIONING AND INDEPENDENCE
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY 6.436J/15.085J Fall 2008 Lecture 3 9/10/2008 CONDITIONING AND INDEPENDENCE Most of the material in this lecture is covered in [Bertsekas & Tsitsiklis] Sections 1.3-1.5
MASSACHUSETTS INSTITUTE OF TECHNOLOGY 6.436J/15.085J Fall 2008 Lecture 3 9/10/2008 CONDITIONING AND INDEPENDENCE Most of the material in this lecture is covered in [Bertsekas & Tsitsiklis] Sections 1.3-1.5
BASICS OF PROBABILITY CHAPTER-1 CS6015-LINEAR ALGEBRA AND RANDOM PROCESSES
 BASICS OF PROBABILITY CHAPTER-1 CS6015-LINEAR ALGEBRA AND RANDOM PROCESSES COMMON TERMS RELATED TO PROBABILITY Probability is the measure of the likelihood that an event will occur Probability values are
BASICS OF PROBABILITY CHAPTER-1 CS6015-LINEAR ALGEBRA AND RANDOM PROCESSES COMMON TERMS RELATED TO PROBABILITY Probability is the measure of the likelihood that an event will occur Probability values are
2011 Pearson Education, Inc
 Statistics for Business and Economics Chapter 3 Probability Contents 1. Events, Sample Spaces, and Probability 2. Unions and Intersections 3. Complementary Events 4. The Additive Rule and Mutually Exclusive
Statistics for Business and Economics Chapter 3 Probability Contents 1. Events, Sample Spaces, and Probability 2. Unions and Intersections 3. Complementary Events 4. The Additive Rule and Mutually Exclusive
Undergraduate Probability I. Class Notes for Engineering Students
 Undergraduate Probability I Class Notes for Engineering Students Fall 2014 Contents I Probability Laws 1 1 Mathematical Review 2 1.1 Elementary Set Operations.................... 4 1.2 Additional Rules
Undergraduate Probability I Class Notes for Engineering Students Fall 2014 Contents I Probability Laws 1 1 Mathematical Review 2 1.1 Elementary Set Operations.................... 4 1.2 Additional Rules
tossing a coin selecting a card from a deck measuring the commuting time on a particular morning
 2 Probability Experiment An experiment or random variable is any activity whose outcome is unknown or random upfront: tossing a coin selecting a card from a deck measuring the commuting time on a particular
2 Probability Experiment An experiment or random variable is any activity whose outcome is unknown or random upfront: tossing a coin selecting a card from a deck measuring the commuting time on a particular
HW2 Solutions, for MATH441, STAT461, STAT561, due September 9th
 HW2 Solutions, for MATH44, STAT46, STAT56, due September 9th. You flip a coin until you get tails. Describe the sample space. How many points are in the sample space? The sample space consists of sequences
HW2 Solutions, for MATH44, STAT46, STAT56, due September 9th. You flip a coin until you get tails. Describe the sample space. How many points are in the sample space? The sample space consists of sequences
Introduction to Probability Theory
 Introduction to Probability Theory Overview The concept of probability is commonly used in everyday life, and can be expressed in many ways. For example, there is a 50:50 chance of a head when a fair coin
Introduction to Probability Theory Overview The concept of probability is commonly used in everyday life, and can be expressed in many ways. For example, there is a 50:50 chance of a head when a fair coin
Elements of probability theory
 The role of probability theory in statistics We collect data so as to provide evidentiary support for answers we give to our many questions about the world (and in our particular case, about the business
The role of probability theory in statistics We collect data so as to provide evidentiary support for answers we give to our many questions about the world (and in our particular case, about the business
God doesn t play dice. - Albert Einstein
 ECE 450 Lecture 1 God doesn t play dice. - Albert Einstein As far as the laws of mathematics refer to reality, they are not certain; as far as they are certain, they do not refer to reality. Lecture Overview
ECE 450 Lecture 1 God doesn t play dice. - Albert Einstein As far as the laws of mathematics refer to reality, they are not certain; as far as they are certain, they do not refer to reality. Lecture Overview
Conditional Probability & Independence. Conditional Probabilities
 Conditional Probability & Independence Conditional Probabilities Question: How should we modify P(E) if we learn that event F has occurred? Definition: the conditional probability of E given F is P(E F
Conditional Probability & Independence Conditional Probabilities Question: How should we modify P(E) if we learn that event F has occurred? Definition: the conditional probability of E given F is P(E F
Chapter Learning Objectives. Random Experiments Dfiii Definition: Dfiii Definition:
 Chapter 2: Probability 2-1 Sample Spaces & Events 2-1.1 Random Experiments 2-1.2 Sample Spaces 2-1.3 Events 2-1 1.4 Counting Techniques 2-2 Interpretations & Axioms of Probability 2-3 Addition Rules 2-4
Chapter 2: Probability 2-1 Sample Spaces & Events 2-1.1 Random Experiments 2-1.2 Sample Spaces 2-1.3 Events 2-1 1.4 Counting Techniques 2-2 Interpretations & Axioms of Probability 2-3 Addition Rules 2-4
Sociology 6Z03 Topic 10: Probability (Part I)
 Sociology 6Z03 Topic 10: Probability (Part I) John Fox McMaster University Fall 2014 John Fox (McMaster University) Soc 6Z03: Probability I Fall 2014 1 / 29 Outline: Probability (Part I) Introduction Probability
Sociology 6Z03 Topic 10: Probability (Part I) John Fox McMaster University Fall 2014 John Fox (McMaster University) Soc 6Z03: Probability I Fall 2014 1 / 29 Outline: Probability (Part I) Introduction Probability
Lecture 10: Probability distributions TUESDAY, FEBRUARY 19, 2019
 Lecture 10: Probability distributions DANIEL WELLER TUESDAY, FEBRUARY 19, 2019 Agenda What is probability? (again) Describing probabilities (distributions) Understanding probabilities (expectation) Partial
Lecture 10: Probability distributions DANIEL WELLER TUESDAY, FEBRUARY 19, 2019 Agenda What is probability? (again) Describing probabilities (distributions) Understanding probabilities (expectation) Partial
Chap 1: Experiments, Models, and Probabilities. Random Processes. Chap 1 : Experiments, Models, and Probabilities
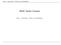 EE8103 Random Processes Chap 1 : Experiments, Models, and Probabilities Introduction Real world word exhibits randomness Today s temperature; Flip a coin, head or tail? WalkAt to a bus station, how long
EE8103 Random Processes Chap 1 : Experiments, Models, and Probabilities Introduction Real world word exhibits randomness Today s temperature; Flip a coin, head or tail? WalkAt to a bus station, how long
Chapter 6: Probability The Study of Randomness
 Chapter 6: Probability The Study of Randomness 6.1 The Idea of Probability 6.2 Probability Models 6.3 General Probability Rules 1 Simple Question: If tossing a coin, what is the probability of the coin
Chapter 6: Probability The Study of Randomness 6.1 The Idea of Probability 6.2 Probability Models 6.3 General Probability Rules 1 Simple Question: If tossing a coin, what is the probability of the coin
Axioms of Probability. Set Theory. M. Bremer. Math Spring 2018
 Math 163 - pring 2018 Axioms of Probability Definition: The set of all possible outcomes of an experiment is called the sample space. The possible outcomes themselves are called elementary events. Any
Math 163 - pring 2018 Axioms of Probability Definition: The set of all possible outcomes of an experiment is called the sample space. The possible outcomes themselves are called elementary events. Any
Introduction to Probability Theory, Algebra, and Set Theory
 Summer School on Mathematical Philosophy for Female Students Introduction to Probability Theory, Algebra, and Set Theory Catrin Campbell-Moore and Sebastian Lutz July 28, 2014 Question 1. Draw Venn diagrams
Summer School on Mathematical Philosophy for Female Students Introduction to Probability Theory, Algebra, and Set Theory Catrin Campbell-Moore and Sebastian Lutz July 28, 2014 Question 1. Draw Venn diagrams
Set theory background for probability
 Set theory background for probability Defining sets (a very naïve approach) A set is a collection of distinct objects. The objects within a set may be arbitrary, with the order of objects within them having
Set theory background for probability Defining sets (a very naïve approach) A set is a collection of distinct objects. The objects within a set may be arbitrary, with the order of objects within them having
STAT 430/510 Probability
 STAT 430/510 Probability Hui Nie Lecture 3 May 28th, 2009 Review We have discussed counting techniques in Chapter 1. Introduce the concept of the probability of an event. Compute probabilities in certain
STAT 430/510 Probability Hui Nie Lecture 3 May 28th, 2009 Review We have discussed counting techniques in Chapter 1. Introduce the concept of the probability of an event. Compute probabilities in certain
Review Basic Probability Concept
 Economic Risk and Decision Analysis for Oil and Gas Industry CE81.9008 School of Engineering and Technology Asian Institute of Technology January Semester Presented by Dr. Thitisak Boonpramote Department
Economic Risk and Decision Analysis for Oil and Gas Industry CE81.9008 School of Engineering and Technology Asian Institute of Technology January Semester Presented by Dr. Thitisak Boonpramote Department
Exercises for Unit VI (Infinite constructions in set theory)
 Exercises for Unit VI (Infinite constructions in set theory) VI.1 : Indexed families and set theoretic operations (Halmos, 4, 8 9; Lipschutz, 5.3 5.4) Lipschutz : 5.3 5.6, 5.29 5.32, 9.14 1. Generalize
Exercises for Unit VI (Infinite constructions in set theory) VI.1 : Indexed families and set theoretic operations (Halmos, 4, 8 9; Lipschutz, 5.3 5.4) Lipschutz : 5.3 5.6, 5.29 5.32, 9.14 1. Generalize
Dept. of Linguistics, Indiana University Fall 2015
 L645 Dept. of Linguistics, Indiana University Fall 2015 1 / 34 To start out the course, we need to know something about statistics and This is only an introduction; for a fuller understanding, you would
L645 Dept. of Linguistics, Indiana University Fall 2015 1 / 34 To start out the course, we need to know something about statistics and This is only an introduction; for a fuller understanding, you would
2) There should be uncertainty as to which outcome will occur before the procedure takes place.
 robability Numbers For many statisticians the concept of the probability that an event occurs is ultimately rooted in the interpretation of an event as an outcome of an experiment, others would interpret
robability Numbers For many statisticians the concept of the probability that an event occurs is ultimately rooted in the interpretation of an event as an outcome of an experiment, others would interpret
