The 2-blocking number and the upper chromatic number of PG(2, q)
|
|
|
- Anne Taylor
- 5 years ago
- Views:
Transcription
1 The 2-blocking number and the upper chromatic number of PG(2, q) Tamás Héger Joint work with Gábor Bacsó and Tamás Szőnyi Eötvös Loránd University Budapest September 18, 2012
2 The problem Color the vertices of a hypergraph H. A hyperedge is rainbow, if its vertices have pairwise distinct colors. The upper chromatic number of H, χ(h): the maximum number of colors that can be used without creating a rainbow hyperedge. Determining χ(π q ) and χ(pg(2,q)) has been of interest since the mid-1990s.
3 Example: χ(pg(2, 2)) = 3
4 Example: χ(pg(2, 2)) = 3
5 Example: χ(pg(2, 2)) = 3
6 Example: χ(pg(2, 2)) = 3
7 Example: χ(pg(2, 2)) = 3
8 Trivial coloring v := q 2 + q + 1, the number of points in Π q. τ 2 := the size of the smallest double blocking set in Π q. Then χ(π q ) v τ We call this a trivial coloring. Remark: if a coloring contains a monochromatic 2BS, it is not
9 Theorem (Bacsó, Tuza, 2007) As q, χ(π q ) v (2q + q/2)+o( q); for q square, χ(pg(2,q)) v (2q+ 2 q+ 1) = v τ 2 + 1; χ(pg(2,q)) v (2q + q)+o( q); for q non-square, χ(pg(2,q)) v (2q + Cq 2/3 )+o( q).
10 Theorem Let q = p h, p prime. Let τ 2 (PG(2,q)) = 2(q + 1)+c. Suppose that one of the following two conditions holds: c c 0 q 13, where 0 < c 0 < 1/2, q q(c 0 ) = 2(c 0 + 2)/(2/3 c 0 ) 1, and p p(c 0 ) = 50c q > 256 is a square. Then χ(pg(2,q)) = v τ 2 + 1, and equality is reached only by trivial colorings. Simpler form of the above theorem: Theorem Let q = p h, p prime. Suppose that either q > 256 is a square, or h 3 odd and p 29. Then χ(pg(2,q)) = v τ 2 + 1, and equality is reached only by trivial colorings. Remark: if τ 2 (PG(2,q)) < 8q/3, q > q(τ 2 ), then χ v τ
11 C 1,...,C n : color classes of size at least two (only these are useful) C 1 C i colors the line l iff l C i 2. All lines have to be colored, so B = n C i is a double blocking set. i=1 We use v B +n colors. B C 2 Cn To reach the trivial coloring, we must have v B +n v τ 2 +1, thus we need n B τ colors in B. Also n B /2, so B 2τ 2 6q.
12 C 1,...,C n : color classes of size at least two (only these are useful) C 1 C i colors the line l iff l C i 2. All lines have to be colored, so B = n C i is a double blocking set. i=1 We use v B +n colors. B C 2 Cn To reach the trivial coloring, we must have v B +n v τ 2 +1, thus we need n B τ colors in B. Also n B /2, so B 2τ 2 6q.
13 Eliminating color classes of size two B So there is at most one color class of size two.
14 Eliminating color classes of size two B So there is at most one color class of size two.
15 Eliminating color classes of size two B So there is at most one color class of size two.
16 Eliminating color classes of size two B So there is at most one color class of size two.
17 Eliminating color classes of size two B So there is at most one color class of size two.
18 Eliminating color classes of size two B So there is at most one color class of size two.
19 Eliminating color classes of size two B So there is at most one color class of size two.
20 B 3q ε Recall that τ 2 2.5q. Say, τ 2 2.5q. L(C i ) := the number of lines colored by C i. Then L(C i ) ( C i 2 By convexity, to satisfy q 2 + q + 1 L(C i ) ( ) C i, 2 the best is to have one giant, and many dwarf color classes. But as B C giant 0.5q B τ n 1+, 3 C g iant 3τ 2 2 B, too small. C giant 1.5q However, if C giant q + 2, we use L(Ci ) (q+1) 2 C i. ).
21 B 3q ε Recall that τ 2 2.5q. Say, τ 2 2.5q. L(C i ) := the number of lines colored by C i. Then L(C i ) ( C i 2 By convexity, to satisfy q 2 + q + 1 L(C i ) ( ) C i, 2 the best is to have one giant, and many dwarf color classes. But as B C giant 0.5q B τ n 1+, 3 C g iant 3τ 2 2 B, too small: C giant 1.5q. However, if C giant q + 2, we use L(Ci ) (q+1) 2 C i. ).
22 B 3q ε Recall that τ 2 2.5q. Say, τ 2 2.5q. L(C i ) := the number of lines colored by C i. Then L(C i ) ( C i 2 By convexity, to satisfy q 2 + q + 1 L(C i ) ( ) C i, 2 the best is to have one giant, and many dwarf color classes. But as B C giant 0.5q B τ n 1+, 3 C g iant 3τ 2 2 B, too small: C giant 1.5q. However, if C giant q + 2, we use L(Ci ) (q+1) 2 C i. ).
23 τ 2 +ε B 3q ε Lemma Let B be t-fold blocking set in PG(2, q), B = t(q + 1) + k, and P B be an essential point of B. Then there are at least (q + 1 k t) t-secants of B through P. Corollary Let B be a t-fold blocking set with B (t + 1)q points. Then there is exactly one minimal t-fold blocking set in B, namely the set of essential points. Remark Harrach has a recent result on the unique reducibility of weighted t-fold (n k)-blocking sets in the projective space PG(n,q).
24 τ 2 +ε B 3q ε Lemma Let B be t-fold blocking set in PG(2, q), B = t(q + 1) + k, and P B be an essential point of B. Then there are at least (q + 1 k t) t-secants of B through P. Corollary Let B be a t-fold blocking set with B (t + 1)q points. Then there is exactly one minimal t-fold blocking set in B, namely the set of essential points. Remark Harrach has a recent result on the unique reducibility of weighted t-fold (n k)-blocking sets in the projective space PG(n,q).
25 τ 2 +ε B 3q ε Lemma Let B be t-fold blocking set in PG(2, q), B = t(q + 1) + k, and P B be an essential point of B. Then there are at least (q + 1 k t) t-secants of B through P. Corollary Let B be a t-fold blocking set with B (t + 1)q points. Then there is exactly one minimal t-fold blocking set in B, namely the set of essential points. Remark Harrach has a recent result on the unique reducibility of weighted t-fold (n k)-blocking sets in the projective space PG(n,q).
26 τ 2 +ε B 3q ε Lemma Let B be t-fold blocking set in PG(2, q), B = t(q + 1) + k, and P B be an essential point of B. Then there are at least (q + 1 k t) t-secants of B through P. Corollary Let B be a t-fold blocking set with B (t + 1)q points. Then there is exactly one minimal t-fold blocking set in B, namely the set of essential points. Remark Harrach has a recent result on the unique reducibility of weighted t-fold (n k)-blocking sets in the projective space PG(n,q).
27 Proof of the lemma Let P B essential, and suppose to the contrary that there are more than k + t long secants through P. Let l be t-secant, P / l. t 1 R(M,B) = (M m i ) i=1 tq+k i=1 As B is a t-fold blocking set, tq+k (Mx i +B y i ) = g(m) i=1 (Mx i +B y i ). R(M,B) = (B q B) t g(m)f 0(M,B)+(M q M)h(M,b), t (M q M) j (B q j=0 where deg(f 0 ) k. Then for any m / {m 1,...,m t 1 }, {Y = mx+b} B > t (B q B) t+1 R(m,B) (B b) F 0 (m
28 Proof of the lemma Let P = (x 1,y 1 ). More than k + t long sec s on P more than k long sec s with m / {m 1,...,m t 1 }. So Mx 1 + B y 1 = 0 and F0 (M,B) = 0 have more than k common points. Thus (Mx 1 + B y 1 ) is a factor of F0 (M,B), thus the lines through P and a point of l\b are long secants. This gives a contradiction if P is essential.
29 τ 2 +ε B 3q ε Clear: if l is a 2-secant to B, then l B is monochromatic. Let B = 2(q + 1)+k. Then Proposition Every color class containing an essential point of B has at least (q k) 3q B points. B = B B, where B is the set of essential points, B τ 2. We have B τ 2 +1 n B B + B 3 q k, so 2 3 ( B τ 2)(q k) τ 2. B B B
30 B τ 2 +ε, q > 256 square (so τ 2 = 2(q + q + 1)) Blokhuis, Storme, Szőnyi: B contains two disjoint Baer subplanes, B 1 and B 2. B = B 1 B 2 can not be monochromatic. Let P B 1 be purple. There are at least (q q ε 1) 2-secants on P, so there are a lot of purple points in B 2. The same from B 2 : we have at least 2(q q ε 1) purple points. If we have brown points as well: B 4(q q ε 1)
31 B τ 2 +ε, q > 256 square (so τ 2 = 2(q + q + 1)) Blokhuis, Storme, Szőnyi: B contains two disjoint Baer subplanes, B 1 and B 2. B = B 1 B 2 can not be monochromatic. Let P B 1 be purple. There are at least (q q ε 1) 2-secants on P, so there are a lot of purple points in B 2. The same from B 2 : we have at least 2(q q ε 1) purple points. If we have brown points as well: B 4(q q ε 1)
32 B τ 2 +ε, q > 256 square (so τ 2 = 2(q + q + 1)) Blokhuis, Storme, Szőnyi: B contains two disjoint Baer subplanes, B 1 and B 2. B = B 1 B 2 can not be monochromatic. Let P B 1 be purple. There are at least (q q ε 1) 2-secants on P, so there are a lot of purple points in B 2. The same from B 2 : we have at least 2(q q ε 1) purple points. If we have brown points as well: B 4(q q ε 1)
33 B τ 2 +ε, q > 256 square (so τ 2 = 2(q + q + 1)) Blokhuis, Storme, Szőnyi: B contains two disjoint Baer subplanes, B 1 and B 2. B = B 1 B 2 can not be monochromatic. Let P B 1 be purple. There are at least (q q ε 1) 2-secants on P, so there are a lot of purple points in B 2. The same from B 2 : we have at least 2(q q ε 1) purple points. If we have brown points as well: B 4(q q ε 1)
34 B τ 2 +ε, q > 256 square (so τ 2 = 2(q + q + 1)) Blokhuis, Storme, Szőnyi: B contains two disjoint Baer subplanes, B 1 and B 2. B = B 1 B 2 can not be monochromatic. Let P B 1 be purple. There are at least (q q ε 1) 2-secants on P, so there are a lot of purple points in B 2. The same from B 2 : we have at least 2(q q ε 1) purple points. If we have brown points as well: B 4(q q ε 1)
35 B τ 2 +ε, q > 256 square (so τ 2 = 2(q + q + 1)) Blokhuis, Storme, Szőnyi: B contains two disjoint Baer subplanes, B 1 and B 2. B = B 1 B 2 can not be monochromatic. Let P B 1 be purple. There are at least (q q ε 1) 2-secants on P, so there are a lot of purple points in B 2. The same from B 2 : we have at least 2(q q ε 1) purple points. If we have brown points as well: B 4(q q ε 1)
36 B τ 2 +ε By melting color classes, we may assume n = 2, B = B r B g, and let B = B = 2(q + 1)+k < 2.5q. Theorem (Blokhuis, Lovász, Storme, Szőnyi) Let B be a minimal t-fold blocking set in PG(2,q), q = p h, h 1, B < tq +(q + 3)/2. Then every line intersects B in t (mod p) points. For a line l, let n r l = B r l, n g l = B g l, n l = n r l + ng l = B l.
37 B τ 2 +ε Define the set of red, green and balanced lines as L r = {l L: nl r > ng l }, L g = {l L: n g l > nr l }, L = = {l L: nl r = ng l }. Using double counting, we get n l = B (q + 1), hence l L l l L: n l >2n (n l 2) = B (q + 1) 2(q 2 + q + 1) kq. l L
38 B τ 2 +ε On the other hand, l L r : n l >2 l L r : n l >2 l L: n l >2 (n r l + ng l )+ 2n r l + l L g : n l >2 n l = l L g : n l >2 2n g l + (n r l + ng l )+ l L = : n l >2 l L = : n l >2 2n r l 4 (n r l + ng l ) l L r L = : n l >2 Recall B r B B g 2q + k (q k) = q + 2k < 2q. Thus for the average number of long red secants through a red point, l L r L = : n l >2 nr l B r kq 4 B r k 8. n r l.
39 B τ 2 +ε So we see: kp 16 red points on the red long secants through P, q k red points on the red two-secants through P, and q k green points. Thus 2q + k B 2q 2k + kp 16
40 Two disjoint blocking sets Let q = p h, h 3 odd, p not necessarily prime, p odd. Let m = (q 1)/(p 1) = p h 1 + p h Note that m is odd. Let f(x) = a(x p + x), a { GF(q). Then f } is GF(p)-linear, and determines the directions f(x) f(y) (x y) : x y ={f(x)/x: x 0}= {(1 : f(x)/x : 0): x 0}= {(x : f(x) : 0): x 0}. Thus B 1 = {(x : f(x) : 1)} {(x : f(x) : 0)} }{{} x 0 }{{} A 1 I 1 is a blocking set of Rédei type. Similarly, for g(x) = x p, is also a blocking set. B 2 = {(y : 1 : g(y))} {(y : 0 : g(y))} }{{} y 0 }{{} A 2 I 2
41 Two disjoint blocking sets B 1 = {(x : f(x) : 1)} {(x : f(x) : 0)} }{{} x 0 }{{} A 1 I 1 B 2 = {(y : 1 : g(y))} {(y : 0 : g(y))} }{{} y 0 }{{} A 2 I 2 f(x) = 0 iff x p + x = x(x p 1 + 1) = 0. As 1 = ( 1) m x (p 1)m = x q 1 = 1, f(x) = 0 iff x = 0. Also g(x) = 0 iff x = 0. I 2 B 1 is empty, as (0 : 0 : 1) / I 2. If (x : f(x) : 0) (y : 1 : g(y)) I 1 A 2, then g(y) = 0, hence y = 0 and x = 0, a contradiction. So I 1 A 2 =.
42 Two disjoint blocking sets B 1 = {(x : f(x) : 1)} {(x : f(x) : 0)} }{{} x 0 }{{} A 1 I 1 B 2 = {(y : 1 : g(y))} {(y : 0 : g(y))} }{{} y 0 }{{} A 2 I 2 Now we need A 1 A 2 =. (y : 1 : g(y)) (x : f(x) : 1) (x 0) iff (y;1;g(y)) = (x/f(x);1;1/f (x)), in which case 1/f(x) = g(x/f(x)) = g(x)/g(f(x)). Thus we need that g(x) = g(f(x))/f(x) = f(x) p 1 that is, x p = (a(x p + x)) p 1 = a p 1 x p 1 (x p 1 + 1) p 1 has no solution in GF(q).
43 Two disjoint blocking sets Equivalent form: 1 a p 1 = (xp 1 + 1) p 1 x should have no solutions x GF(q). = (x p 1 + 1) p 1 x q 2 =: h(x) Let D = {x m : x GF(q) } = {x (p 1) : x GF(q) }. Then 1/a p 1 D. Note that h(x) D x D. So to find an element a such that 1/a (p 1) is not in the range of h, we need that h D : D D does not permute D.
44 Permutation polynomials Theorem (Hermite-Dickson) Let f GF(q)[X], q = p h, p prime. Then f permutes GF(q) iff the following conditions hold: f has exactly one root in GF(q); for each integer t, 1 t q 2 and p t, f(x) t (mod X q X) has degree at most q 2. A variation for multiplicative subgroups of GF(q) : Theorem Suppose d q 1, and let D = {x d : x GF(q) } be the set of nonzero d th powers, m = D = (q 1)/d. Assume that g GF(q)[X] maps D into D. Then g D is a permutation of D if and only if the constant term of g(x) t (mod x m 1) is zero for all 1 t m 1, p t.
45 Two disjoint blocking sets Recall that h(x) = (X p 1 + 1) p 1 X q 2. Let t = p 1, that is, consider h p 1 (X) = (p 1) 2 k=0 ( (p 1) 2 k ) X k(p 1)+(p 1)(q 2) (mod X m 1). Since k(p 1)+(p 1)(q 2) (k 1)(p 1) (mod m), the m exponents reduced to zero have k = 1+l(m,p 1). Let r be the characteristic of the field GF(q). As ( (p 1) ) (mod r), it is enough to show that ( (p 1) 2 ) k 0 (mod r) for the other possible values of k. Suppose h 5. Then m/(m,p 1) > m/p > p h 2 > p 2, thus by k (p 1) 2, l 1 does not occur at all. The case h = 3 can also be done.
46 Thank you for your attention!
The 2-blocking number and the upper chromatic number of PG(2, q)
 The 2-blocking number and the upper chromatic number of PG(2, q) Tamás Szőnyi Joint work with Gábor Bacsó and Tamás Héger Eötvös Loránd University, MTA-ELTE GAC Research Group and Ghent University Budapest
The 2-blocking number and the upper chromatic number of PG(2, q) Tamás Szőnyi Joint work with Gábor Bacsó and Tamás Héger Eötvös Loránd University, MTA-ELTE GAC Research Group and Ghent University Budapest
Value sets of special polynomials and blocking sets
 Value sets of special polynomials and blocking sets Tamás Szőnyi Eötvös Loránd University and MTA-ELTE GAC Research Group Budapest 29th June, 2016 PhD Summer School in Discrete Mathematics, Rogla This
Value sets of special polynomials and blocking sets Tamás Szőnyi Eötvös Loránd University and MTA-ELTE GAC Research Group Budapest 29th June, 2016 PhD Summer School in Discrete Mathematics, Rogla This
Lacunary polynomials and finite geometry
 Tamás Szőnyi ELTE, CAI HAS June 24th, 2013, Lille, France Fully reducible, and lacunary polynomials Definition A polynomial over a field F is called fully reducible if it factors into linear factors over
Tamás Szőnyi ELTE, CAI HAS June 24th, 2013, Lille, France Fully reducible, and lacunary polynomials Definition A polynomial over a field F is called fully reducible if it factors into linear factors over
Two Remarks on Blocking Sets and Nuclei in Planes of Prime Order
 Designs, Codes and Cryptography, 10, 9 39 (1997) c 1997 Kluwer Academic Publishers, Boston. Manufactured in The Netherlands. Two Remarks on Blocking Sets and Nuclei in Planes of Prime Order ANDRÁS GÁCS
Designs, Codes and Cryptography, 10, 9 39 (1997) c 1997 Kluwer Academic Publishers, Boston. Manufactured in The Netherlands. Two Remarks on Blocking Sets and Nuclei in Planes of Prime Order ANDRÁS GÁCS
Some graph theoretic aspects of finite geometries
 Eötvös Loránd University Institute of Mathematics Ph.D. thesis Some graph theoretic aspects of finite geometries Tamás Héger Doctoral School: Mathematics Director: Miklós Laczkovich, D.Sc. Professor, Member
Eötvös Loránd University Institute of Mathematics Ph.D. thesis Some graph theoretic aspects of finite geometries Tamás Héger Doctoral School: Mathematics Director: Miklós Laczkovich, D.Sc. Professor, Member
1 Lacunary Polynomials over Finite Fields.
 1 Lacunary Polynomials over Finite Fields. 1.1 Introduction In 1970 Rédei published his treatise Lückenhafte Polynome über endlichen Körpern [34], soon followed by the English translation Lacunary Polynomials
1 Lacunary Polynomials over Finite Fields. 1.1 Introduction In 1970 Rédei published his treatise Lückenhafte Polynome über endlichen Körpern [34], soon followed by the English translation Lacunary Polynomials
The number of directions determined by less than q points
 The number of directions determined by less than q points arxiv:1407.5638v1 [math.co] 21 Jul 2014 Szabolcs L. Fancsali, Péter Sziklai and Marcella Takáts February 28, 2012 NOTICE: this is the author s
The number of directions determined by less than q points arxiv:1407.5638v1 [math.co] 21 Jul 2014 Szabolcs L. Fancsali, Péter Sziklai and Marcella Takáts February 28, 2012 NOTICE: this is the author s
arxiv: v1 [math.co] 23 Nov 2015
![arxiv: v1 [math.co] 23 Nov 2015 arxiv: v1 [math.co] 23 Nov 2015](/thumbs/93/111294245.jpg) arxiv:1511.0753v1 [math.co] 3 Nov 015 New results on maximal partial line spreads in PG(5, q) Maurizio Iurlo Abstract In this work, we prove the existence of maximal partial line spreads in PG(5,q) of
arxiv:1511.0753v1 [math.co] 3 Nov 015 New results on maximal partial line spreads in PG(5, q) Maurizio Iurlo Abstract In this work, we prove the existence of maximal partial line spreads in PG(5,q) of
Codewords of small weight in the (dual) code of points and k-spaces of P G(n, q)
 Codewords of small weight in the (dual) code of points and k-spaces of P G(n, q) M. Lavrauw L. Storme G. Van de Voorde October 4, 2007 Abstract In this paper, we study the p-ary linear code C k (n, q),
Codewords of small weight in the (dual) code of points and k-spaces of P G(n, q) M. Lavrauw L. Storme G. Van de Voorde October 4, 2007 Abstract In this paper, we study the p-ary linear code C k (n, q),
On the stability of small blocking sets
 J Algebr Comb (04) 40:79 9 DOI 0.007/s080-03-0487-0 On the stability of small blocking sets Tamás Szőnyi Zsuzsa Weiner Received: April 0 / Accepted: 6 November 03 / Published online: 3 December 03 Springer
J Algebr Comb (04) 40:79 9 DOI 0.007/s080-03-0487-0 On the stability of small blocking sets Tamás Szőnyi Zsuzsa Weiner Received: April 0 / Accepted: 6 November 03 / Published online: 3 December 03 Springer
Arcs and blocking sets in non-desarguesian planes
 Arcs and blocking sets in non-desarguesian planes Tamás Szőnyi Eötvös Loránd University and MTA-ELTE GAC Research Group Budapest June 3, 2016 General overview First we summarize results about arcs, blocking
Arcs and blocking sets in non-desarguesian planes Tamás Szőnyi Eötvös Loránd University and MTA-ELTE GAC Research Group Budapest June 3, 2016 General overview First we summarize results about arcs, blocking
Lacunary Polynomials over Finite Fields Course notes
 Lacunary Polynomials over Finite Fields Course notes Javier Herranz Abstract This is a summary of the course Lacunary Polynomials over Finite Fields, given by Simeon Ball, from the University of London,
Lacunary Polynomials over Finite Fields Course notes Javier Herranz Abstract This is a summary of the course Lacunary Polynomials over Finite Fields, given by Simeon Ball, from the University of London,
Bounds and spectrum results in Galois geometry and coding theory. Eötvös Loránd University
 Synopsis of the Ph.D. thesis Bounds and spectrum results in Galois geometry and coding theory Szabolcs Levente Fancsali Eötvös Loránd University Institute of Mathematics Doctoral School: Mathematics Director:
Synopsis of the Ph.D. thesis Bounds and spectrum results in Galois geometry and coding theory Szabolcs Levente Fancsali Eötvös Loránd University Institute of Mathematics Doctoral School: Mathematics Director:
Linear Point Sets and Rédei Type k-blocking
 Journal of Algebraic Combinatorics 14 (2001), 221 228 c 2001 Kluwer Academic Publishers. Manufactured in The Netherlands. Linear Point Sets and Rédei Type k-blocking Sets in PG(n, q) L. STORME ls@cage.rug.ac.be
Journal of Algebraic Combinatorics 14 (2001), 221 228 c 2001 Kluwer Academic Publishers. Manufactured in The Netherlands. Linear Point Sets and Rédei Type k-blocking Sets in PG(n, q) L. STORME ls@cage.rug.ac.be
Semiarcs with a long secant in PG(2,q)
 Innovations in Incidence Geometry Volume 14 (2015), Pages 1 26 ISSN 1781-6475 Semiarcs with a long secant in PG(2,q) Bence Csajbók Tamás Héger György Kiss Abstract At-semiarc is a point sets t with the
Innovations in Incidence Geometry Volume 14 (2015), Pages 1 26 ISSN 1781-6475 Semiarcs with a long secant in PG(2,q) Bence Csajbók Tamás Héger György Kiss Abstract At-semiarc is a point sets t with the
Some practice problems for midterm 2
 Some practice problems for midterm 2 Kiumars Kaveh November 14, 2011 Problem: Let Z = {a G ax = xa, x G} be the center of a group G. Prove that Z is a normal subgroup of G. Solution: First we prove Z is
Some practice problems for midterm 2 Kiumars Kaveh November 14, 2011 Problem: Let Z = {a G ax = xa, x G} be the center of a group G. Prove that Z is a normal subgroup of G. Solution: First we prove Z is
On the chromatic number of q-kneser graphs
 On the chromatic number of q-kneser graphs A. Blokhuis & A. E. Brouwer Dept. of Mathematics, Eindhoven University of Technology, P.O. Box 53, 5600 MB Eindhoven, The Netherlands aartb@win.tue.nl, aeb@cwi.nl
On the chromatic number of q-kneser graphs A. Blokhuis & A. E. Brouwer Dept. of Mathematics, Eindhoven University of Technology, P.O. Box 53, 5600 MB Eindhoven, The Netherlands aartb@win.tue.nl, aeb@cwi.nl
Journal of Discrete Mathematical Sciences & Cryptography Vol. 9 (2006), No. 1, pp
 Some generalizations of Rédei s theorem T. Alderson Department of Mathematical Sciences University of New Brunswick Saint John, New Brunswick Canada EL 4L5 Abstract By the famous theorems of Rédei, a set
Some generalizations of Rédei s theorem T. Alderson Department of Mathematical Sciences University of New Brunswick Saint John, New Brunswick Canada EL 4L5 Abstract By the famous theorems of Rédei, a set
Some new results on semiarcs in finite projective planes and on inverse-closed subsets in fields
 Universitá degli Studi della Basilicata Some new results on semiarcs in finite projective planes and on inverse-closed subsets in fields Dottorato di Ricerca in Matematica János Bolyai MAT 03 Coordinatore
Universitá degli Studi della Basilicata Some new results on semiarcs in finite projective planes and on inverse-closed subsets in fields Dottorato di Ricerca in Matematica János Bolyai MAT 03 Coordinatore
On two-intersection sets with respect to hyperplanes in projective spaces
 with respect to hyperplanes in projective spaces Aart Blokhuis Technische Universiteit Eindhoven, Postbox 513, 5600 MB Eindhoven, The Netherlands and Michel Lavrauw Technische Universiteit Eindhoven, Postbox
with respect to hyperplanes in projective spaces Aart Blokhuis Technische Universiteit Eindhoven, Postbox 513, 5600 MB Eindhoven, The Netherlands and Michel Lavrauw Technische Universiteit Eindhoven, Postbox
On the structure of the directions not determined by a large affine point set
 On the structure of the directions not determined by a large affine point set Jan De Beule, Peter Sziklai, and Marcella Takáts January 12, 2011 Abstract Given a point set U in an n-dimensional affine space
On the structure of the directions not determined by a large affine point set Jan De Beule, Peter Sziklai, and Marcella Takáts January 12, 2011 Abstract Given a point set U in an n-dimensional affine space
ELG 5372 Error Control Coding. Lecture 12: Ideals in Rings and Algebraic Description of Cyclic Codes
 ELG 5372 Error Control Coding Lecture 12: Ideals in Rings and Algebraic Description of Cyclic Codes Quotient Ring Example + Quotient Ring Example Quotient Ring Recall the quotient ring R={,,, }, where
ELG 5372 Error Control Coding Lecture 12: Ideals in Rings and Algebraic Description of Cyclic Codes Quotient Ring Example + Quotient Ring Example Quotient Ring Recall the quotient ring R={,,, }, where
0 Sets and Induction. Sets
 0 Sets and Induction Sets A set is an unordered collection of objects, called elements or members of the set. A set is said to contain its elements. We write a A to denote that a is an element of the set
0 Sets and Induction Sets A set is an unordered collection of objects, called elements or members of the set. A set is said to contain its elements. We write a A to denote that a is an element of the set
THE CLASSIFICATION OF PLANAR MONOMIALS OVER FIELDS OF PRIME SQUARE ORDER
 THE CLASSIFICATION OF PLANAR MONOMIALS OVER FIELDS OF PRIME SQUARE ORDER ROBERT S COULTER Abstract Planar functions were introduced by Dembowski and Ostrom in [3] to describe affine planes possessing collineation
THE CLASSIFICATION OF PLANAR MONOMIALS OVER FIELDS OF PRIME SQUARE ORDER ROBERT S COULTER Abstract Planar functions were introduced by Dembowski and Ostrom in [3] to describe affine planes possessing collineation
ARCS IN FINITE PROJECTIVE SPACES. Basic objects and definitions
 ARCS IN FINITE PROJECTIVE SPACES SIMEON BALL Abstract. These notes are an outline of a course on arcs given at the Finite Geometry Summer School, University of Sussex, June 26-30, 2017. Let K denote an
ARCS IN FINITE PROJECTIVE SPACES SIMEON BALL Abstract. These notes are an outline of a course on arcs given at the Finite Geometry Summer School, University of Sussex, June 26-30, 2017. Let K denote an
Course 212: Academic Year Section 1: Metric Spaces
 Course 212: Academic Year 1991-2 Section 1: Metric Spaces D. R. Wilkins Contents 1 Metric Spaces 3 1.1 Distance Functions and Metric Spaces............. 3 1.2 Convergence and Continuity in Metric Spaces.........
Course 212: Academic Year 1991-2 Section 1: Metric Spaces D. R. Wilkins Contents 1 Metric Spaces 3 1.1 Distance Functions and Metric Spaces............. 3 1.2 Convergence and Continuity in Metric Spaces.........
Classification of Finite Fields
 Classification of Finite Fields In these notes we use the properties of the polynomial x pd x to classify finite fields. The importance of this polynomial is explained by the following basic proposition.
Classification of Finite Fields In these notes we use the properties of the polynomial x pd x to classify finite fields. The importance of this polynomial is explained by the following basic proposition.
Homework 8 Solutions to Selected Problems
 Homework 8 Solutions to Selected Problems June 7, 01 1 Chapter 17, Problem Let f(x D[x] and suppose f(x is reducible in D[x]. That is, there exist polynomials g(x and h(x in D[x] such that g(x and h(x
Homework 8 Solutions to Selected Problems June 7, 01 1 Chapter 17, Problem Let f(x D[x] and suppose f(x is reducible in D[x]. That is, there exist polynomials g(x and h(x in D[x] such that g(x and h(x
EE 229B ERROR CONTROL CODING Spring 2005
 EE 9B ERROR CONTROL CODING Spring 005 Solutions for Homework 1. (Weights of codewords in a cyclic code) Let g(x) be the generator polynomial of a binary cyclic code of length n. (a) Show that if g(x) has
EE 9B ERROR CONTROL CODING Spring 005 Solutions for Homework 1. (Weights of codewords in a cyclic code) Let g(x) be the generator polynomial of a binary cyclic code of length n. (a) Show that if g(x) has
Inequalities for the First-Fit chromatic number
 Worcester Polytechnic Institute Digital WPI Computer Science Faculty Publications Department of Computer Science 9-007 Inequalities for the First-Fit chromatic number Zoltán Füredi Alfréd Rényi Institute,
Worcester Polytechnic Institute Digital WPI Computer Science Faculty Publications Department of Computer Science 9-007 Inequalities for the First-Fit chromatic number Zoltán Füredi Alfréd Rényi Institute,
Homework #5 Solutions
 Homework #5 Solutions p 83, #16. In order to find a chain a 1 a 2 a n of subgroups of Z 240 with n as large as possible, we start at the top with a n = 1 so that a n = Z 240. In general, given a i we will
Homework #5 Solutions p 83, #16. In order to find a chain a 1 a 2 a n of subgroups of Z 240 with n as large as possible, we start at the top with a n = 1 so that a n = Z 240. In general, given a i we will
THE GROUP OF UNITS OF SOME FINITE LOCAL RINGS I
 J Korean Math Soc 46 (009), No, pp 95 311 THE GROUP OF UNITS OF SOME FINITE LOCAL RINGS I Sung Sik Woo Abstract The purpose of this paper is to identify the group of units of finite local rings of the
J Korean Math Soc 46 (009), No, pp 95 311 THE GROUP OF UNITS OF SOME FINITE LOCAL RINGS I Sung Sik Woo Abstract The purpose of this paper is to identify the group of units of finite local rings of the
A note on the Isomorphism Problem for Monomial Digraphs
 A note on the Isomorphism Problem for Monomial Digraphs Aleksandr Kodess Department of Mathematics University of Rhode Island kodess@uri.edu Felix Lazebnik Department of Mathematical Sciences University
A note on the Isomorphism Problem for Monomial Digraphs Aleksandr Kodess Department of Mathematics University of Rhode Island kodess@uri.edu Felix Lazebnik Department of Mathematical Sciences University
Math 120. Groups and Rings Midterm Exam (November 8, 2017) 2 Hours
 Math 120. Groups and Rings Midterm Exam (November 8, 2017) 2 Hours Name: Please read the questions carefully. You will not be given partial credit on the basis of having misunderstood a question, and please
Math 120. Groups and Rings Midterm Exam (November 8, 2017) 2 Hours Name: Please read the questions carefully. You will not be given partial credit on the basis of having misunderstood a question, and please
Quasi-reducible Polynomials
 Quasi-reducible Polynomials Jacques Willekens 06-Dec-2008 Abstract In this article, we investigate polynomials that are irreducible over Q, but are reducible modulo any prime number. 1 Introduction Let
Quasi-reducible Polynomials Jacques Willekens 06-Dec-2008 Abstract In this article, we investigate polynomials that are irreducible over Q, but are reducible modulo any prime number. 1 Introduction Let
On subgraphs of large girth
 1/34 On subgraphs of large girth In Honor of the 50th Birthday of Thomas Vojtěch Rödl rodl@mathcs.emory.edu joint work with Domingos Dellamonica May, 2012 2/34 3/34 4/34 5/34 6/34 7/34 ARRANGEABILITY AND
1/34 On subgraphs of large girth In Honor of the 50th Birthday of Thomas Vojtěch Rödl rodl@mathcs.emory.edu joint work with Domingos Dellamonica May, 2012 2/34 3/34 4/34 5/34 6/34 7/34 ARRANGEABILITY AND
= 1 2x. x 2 a ) 0 (mod p n ), (x 2 + 2a + a2. x a ) 2
 8. p-adic numbers 8.1. Motivation: Solving x 2 a (mod p n ). Take an odd prime p, and ( an) integer a coprime to p. Then, as we know, x 2 a (mod p) has a solution x Z iff = 1. In this case we can suppose
8. p-adic numbers 8.1. Motivation: Solving x 2 a (mod p n ). Take an odd prime p, and ( an) integer a coprime to p. Then, as we know, x 2 a (mod p) has a solution x Z iff = 1. In this case we can suppose
Downloaded 03/01/17 to Redistribution subject to SIAM license or copyright; see
 SIAM J. DISCRETE MATH. Vol. 31, No. 1, pp. 335 382 c 2017 Society for Industrial and Applied Mathematics PARTITION CONSTRAINED COVERING OF A SYMMETRIC CROSSING SUPERMODULAR FUNCTION BY A GRAPH ATTILA BERNÁTH,
SIAM J. DISCRETE MATH. Vol. 31, No. 1, pp. 335 382 c 2017 Society for Industrial and Applied Mathematics PARTITION CONSTRAINED COVERING OF A SYMMETRIC CROSSING SUPERMODULAR FUNCTION BY A GRAPH ATTILA BERNÁTH,
Links among Finite Geometries, Graphs and Groups
 Links among Finite Geometries, Graphs and Groups Ph.D. dissertation János Ru Supervisor: György Kiss, Ph.D. Doctoral School in Mathematics and Computer Science University of Szeged Bolyai Institute 2010
Links among Finite Geometries, Graphs and Groups Ph.D. dissertation János Ru Supervisor: György Kiss, Ph.D. Doctoral School in Mathematics and Computer Science University of Szeged Bolyai Institute 2010
Groups Subgroups Normal subgroups Quotient groups Homomorphisms Cyclic groups Permutation groups Cayley s theorem Class equations Sylow theorems
 Group Theory Groups Subgroups Normal subgroups Quotient groups Homomorphisms Cyclic groups Permutation groups Cayley s theorem Class equations Sylow theorems Groups Definition : A non-empty set ( G,*)
Group Theory Groups Subgroups Normal subgroups Quotient groups Homomorphisms Cyclic groups Permutation groups Cayley s theorem Class equations Sylow theorems Groups Definition : A non-empty set ( G,*)
Information Theory. Lecture 7
 Information Theory Lecture 7 Finite fields continued: R3 and R7 the field GF(p m ),... Cyclic Codes Intro. to cyclic codes: R8.1 3 Mikael Skoglund, Information Theory 1/17 The Field GF(p m ) π(x) irreducible
Information Theory Lecture 7 Finite fields continued: R3 and R7 the field GF(p m ),... Cyclic Codes Intro. to cyclic codes: R8.1 3 Mikael Skoglund, Information Theory 1/17 The Field GF(p m ) π(x) irreducible
Definitions. Notations. Injective, Surjective and Bijective. Divides. Cartesian Product. Relations. Equivalence Relations
 Page 1 Definitions Tuesday, May 8, 2018 12:23 AM Notations " " means "equals, by definition" the set of all real numbers the set of integers Denote a function from a set to a set by Denote the image of
Page 1 Definitions Tuesday, May 8, 2018 12:23 AM Notations " " means "equals, by definition" the set of all real numbers the set of integers Denote a function from a set to a set by Denote the image of
17 Galois Fields Introduction Primitive Elements Roots of Polynomials... 8
 Contents 17 Galois Fields 2 17.1 Introduction............................... 2 17.2 Irreducible Polynomials, Construction of GF(q m )... 3 17.3 Primitive Elements... 6 17.4 Roots of Polynomials..........................
Contents 17 Galois Fields 2 17.1 Introduction............................... 2 17.2 Irreducible Polynomials, Construction of GF(q m )... 3 17.3 Primitive Elements... 6 17.4 Roots of Polynomials..........................
On sets without tangents and exterior sets of a conic
 On sets without tangents and exterior sets of a conic Geertrui Van de Voorde Abstract A set without tangents in PG(2, q) is a set of points S such that no line meets S in exactly one point. An exterior
On sets without tangents and exterior sets of a conic Geertrui Van de Voorde Abstract A set without tangents in PG(2, q) is a set of points S such that no line meets S in exactly one point. An exterior
From now on we assume that K = K.
 Divisors From now on we assume that K = K. Definition The (additively written) free abelian group generated by P F is denoted by D F and is called the divisor group of F/K. The elements of D F are called
Divisors From now on we assume that K = K. Definition The (additively written) free abelian group generated by P F is denoted by D F and is called the divisor group of F/K. The elements of D F are called
5 Set Operations, Functions, and Counting
 5 Set Operations, Functions, and Counting Let N denote the positive integers, N 0 := N {0} be the non-negative integers and Z = N 0 ( N) the positive and negative integers including 0, Q the rational numbers,
5 Set Operations, Functions, and Counting Let N denote the positive integers, N 0 := N {0} be the non-negative integers and Z = N 0 ( N) the positive and negative integers including 0, Q the rational numbers,
Cartesian product of hypergraphs: properties and algorithms
 Cartesian product of hypergraphs: properties and algorithms Alain Bretto alain.bretto@info.unicaen.fr Yannick Silvestre yannick.silvestre@info.unicaen.fr Thierry Vallée vallee@pps.jussieu.fr Université
Cartesian product of hypergraphs: properties and algorithms Alain Bretto alain.bretto@info.unicaen.fr Yannick Silvestre yannick.silvestre@info.unicaen.fr Thierry Vallée vallee@pps.jussieu.fr Université
Permutation Polynomials over Finite Fields
 Permutation Polynomials over Finite Fields Omar Kihel Brock University 1 Finite Fields 2 How to Construct a Finite Field 3 Permutation Polynomials 4 Characterization of PP Finite Fields Let p be a prime.
Permutation Polynomials over Finite Fields Omar Kihel Brock University 1 Finite Fields 2 How to Construct a Finite Field 3 Permutation Polynomials 4 Characterization of PP Finite Fields Let p be a prime.
Exercise Sheet 3 - Solutions
 Algebraic Geometry D-MATH, FS 2016 Prof. Pandharipande Exercise Sheet 3 - Solutions 1. Prove the following basic facts about algebraic maps. a) For f : X Y and g : Y Z algebraic morphisms of quasi-projective
Algebraic Geometry D-MATH, FS 2016 Prof. Pandharipande Exercise Sheet 3 - Solutions 1. Prove the following basic facts about algebraic maps. a) For f : X Y and g : Y Z algebraic morphisms of quasi-projective
Math1a Set 1 Solutions
 Math1a Set 1 Solutions October 15, 2018 Problem 1. (a) For all x, y, z Z we have (i) x x since x x = 0 is a multiple of 7. (ii) If x y then there is a k Z such that x y = 7k. So, y x = (x y) = 7k is also
Math1a Set 1 Solutions October 15, 2018 Problem 1. (a) For all x, y, z Z we have (i) x x since x x = 0 is a multiple of 7. (ii) If x y then there is a k Z such that x y = 7k. So, y x = (x y) = 7k is also
 Algebra Qualifying Exam August 2001 Do all 5 problems. 1. Let G be afinite group of order 504 = 23 32 7. a. Show that G cannot be isomorphic to a subgroup of the alternating group Alt 7. (5 points) b.
Algebra Qualifying Exam August 2001 Do all 5 problems. 1. Let G be afinite group of order 504 = 23 32 7. a. Show that G cannot be isomorphic to a subgroup of the alternating group Alt 7. (5 points) b.
Chromatic Ramsey number of acyclic hypergraphs
 Chromatic Ramsey number of acyclic hypergraphs András Gyárfás Alfréd Rényi Institute of Mathematics Hungarian Academy of Sciences Budapest, P.O. Box 127 Budapest, Hungary, H-1364 gyarfas@renyi.hu Alexander
Chromatic Ramsey number of acyclic hypergraphs András Gyárfás Alfréd Rényi Institute of Mathematics Hungarian Academy of Sciences Budapest, P.O. Box 127 Budapest, Hungary, H-1364 gyarfas@renyi.hu Alexander
MINKOWSKI THEORY AND THE CLASS NUMBER
 MINKOWSKI THEORY AND THE CLASS NUMBER BROOKE ULLERY Abstract. This paper gives a basic introduction to Minkowski Theory and the class group, leading up to a proof that the class number (the order of the
MINKOWSKI THEORY AND THE CLASS NUMBER BROOKE ULLERY Abstract. This paper gives a basic introduction to Minkowski Theory and the class group, leading up to a proof that the class number (the order of the
Lines in higgledy-piggledy arrangement
 Lines in higgledy-piggledy arrangement Szabolcs L. Fancsali MTA ELTE Geometric and Algebraic Combinatorics Research Group Budapest, Hungary nudniq@cs.elte.hu Péter Sziklai MTA ELTE Geometric and Algebraic
Lines in higgledy-piggledy arrangement Szabolcs L. Fancsali MTA ELTE Geometric and Algebraic Combinatorics Research Group Budapest, Hungary nudniq@cs.elte.hu Péter Sziklai MTA ELTE Geometric and Algebraic
Vertex colorings of graphs without short odd cycles
 Vertex colorings of graphs without short odd cycles Andrzej Dudek and Reshma Ramadurai Department of Mathematical Sciences Carnegie Mellon University Pittsburgh, PA 1513, USA {adudek,rramadur}@andrew.cmu.edu
Vertex colorings of graphs without short odd cycles Andrzej Dudek and Reshma Ramadurai Department of Mathematical Sciences Carnegie Mellon University Pittsburgh, PA 1513, USA {adudek,rramadur}@andrew.cmu.edu
The Chromatic Number of Ordered Graphs With Constrained Conflict Graphs
 The Chromatic Number of Ordered Graphs With Constrained Conflict Graphs Maria Axenovich and Jonathan Rollin and Torsten Ueckerdt September 3, 016 Abstract An ordered graph G is a graph whose vertex set
The Chromatic Number of Ordered Graphs With Constrained Conflict Graphs Maria Axenovich and Jonathan Rollin and Torsten Ueckerdt September 3, 016 Abstract An ordered graph G is a graph whose vertex set
On linear sets on a projective line
 On linear sets on a projective line M. Lavrauw G. Van de Voorde August 14, 2013 Abstract Linear sets generalise the concept of subgeometries in a projective space. They have many applications in finite
On linear sets on a projective line M. Lavrauw G. Van de Voorde August 14, 2013 Abstract Linear sets generalise the concept of subgeometries in a projective space. They have many applications in finite
Probabilistic Proofs of Existence of Rare Events. Noga Alon
 Probabilistic Proofs of Existence of Rare Events Noga Alon Department of Mathematics Sackler Faculty of Exact Sciences Tel Aviv University Ramat-Aviv, Tel Aviv 69978 ISRAEL 1. The Local Lemma In a typical
Probabilistic Proofs of Existence of Rare Events Noga Alon Department of Mathematics Sackler Faculty of Exact Sciences Tel Aviv University Ramat-Aviv, Tel Aviv 69978 ISRAEL 1. The Local Lemma In a typical
Factorization of integer-valued polynomials with square-free denominator
 accepted by Comm. Algebra (2013) Factorization of integer-valued polynomials with square-free denominator Giulio Peruginelli September 9, 2013 Dedicated to Marco Fontana on the occasion of his 65th birthday
accepted by Comm. Algebra (2013) Factorization of integer-valued polynomials with square-free denominator Giulio Peruginelli September 9, 2013 Dedicated to Marco Fontana on the occasion of his 65th birthday
About Maximal Partial 2-Spreads in PG(3m 1, q)
 Innovations in Incidence Geometry Volume 00 (XXXX), Pages 000 000 ISSN 1781-6475 About Maximal Partial 2-Spreads in PG(3m 1, q) Sz. L. Fancsali and P. Sziklai Abstract In this article we construct maximal
Innovations in Incidence Geometry Volume 00 (XXXX), Pages 000 000 ISSN 1781-6475 About Maximal Partial 2-Spreads in PG(3m 1, q) Sz. L. Fancsali and P. Sziklai Abstract In this article we construct maximal
The minimum weight of dual codes from projective planes
 The minimum weight of dual codes from projective planes J. D. Key Department of Mathematical Sciences Clemson University, University of Wales Aberystwyth, University of the Western Cape and University
The minimum weight of dual codes from projective planes J. D. Key Department of Mathematical Sciences Clemson University, University of Wales Aberystwyth, University of the Western Cape and University
Roots of Polynomials in Subgroups of F p and Applications to Congruences
 Roots of Polynomials in Subgroups of F p and Applications to Congruences Enrico Bombieri, Jean Bourgain, Sergei Konyagin IAS, Princeton, IAS Princeton, Moscow State University The decimation problem Let
Roots of Polynomials in Subgroups of F p and Applications to Congruences Enrico Bombieri, Jean Bourgain, Sergei Konyagin IAS, Princeton, IAS Princeton, Moscow State University The decimation problem Let
Codegree problems for projective geometries
 Codegree problems for projective geometries Peter Keevash Yi Zhao Abstract The codegree density γ(f ) of an r-graph F is the largest number γ such that there are F -free r-graphs G on n vertices such that
Codegree problems for projective geometries Peter Keevash Yi Zhao Abstract The codegree density γ(f ) of an r-graph F is the largest number γ such that there are F -free r-graphs G on n vertices such that
Section Properties of Rational Expressions
 88 Section. - Properties of Rational Expressions Recall that a rational number is any number that can be written as the ratio of two integers where the integer in the denominator cannot be. Rational Numbers:
88 Section. - Properties of Rational Expressions Recall that a rational number is any number that can be written as the ratio of two integers where the integer in the denominator cannot be. Rational Numbers:
COMMUTATIVE PRESEMIFIELDS AND SEMIFIELDS
 COMMUTATIVE PRESEMIFIELDS AND SEMIFIELDS ROBERT S. COULTER AND MARIE HENDERSON Abstract. Strong conditions are derived for when two commutative presemifields are isotopic. It is then shown that any commutative
COMMUTATIVE PRESEMIFIELDS AND SEMIFIELDS ROBERT S. COULTER AND MARIE HENDERSON Abstract. Strong conditions are derived for when two commutative presemifields are isotopic. It is then shown that any commutative
On q-analogues and stability theorems
 On q-analogues and stability theorems Aart Blokhuis, Andries Brouwer, Tamás Szőnyi and Zsuzsa Weiner Abstract. In this survey recent results about q-analogues of some classical theorems in extremal set
On q-analogues and stability theorems Aart Blokhuis, Andries Brouwer, Tamás Szőnyi and Zsuzsa Weiner Abstract. In this survey recent results about q-analogues of some classical theorems in extremal set
Self-Complementary Arc-Transitive Graphs and Their Imposters
 Self-Complementary Arc-Transitive Graphs and Their Imposters by Natalie Mullin A thesis presented to the University of Waterloo in fulfillment of the thesis requirement for the degree of Master of Mathematics
Self-Complementary Arc-Transitive Graphs and Their Imposters by Natalie Mullin A thesis presented to the University of Waterloo in fulfillment of the thesis requirement for the degree of Master of Mathematics
1 2n. i=1. 2m+1 i = m, while. 2m + 1 = 1. is the best possible for any odd n.
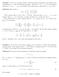 Problem 1. Let n be a positive integer. Find the largest nonnegative real number f(n) (depending on n) with the following property: whenever a 1, a,..., a n are real numbers such that a 1 + a + + a n is
Problem 1. Let n be a positive integer. Find the largest nonnegative real number f(n) (depending on n) with the following property: whenever a 1, a,..., a n are real numbers such that a 1 + a + + a n is
THE ZARANKIEWICZ PROBLEM, CAGES, AND GEOMETRIES. 1. Introduction
 THE ZARANKIEWICZ PROBLEM, CAGES, AND GEOMETRIES GÁBOR DAMÁSDI, TAMÁS HÉGER, AND TAMÁS SZŐNYI DEDICATED TO THE MEMORY OF ANDRÁS GÁCS AND ISTVÁN REIMAN Abstract. In the paper we consider some constructions
THE ZARANKIEWICZ PROBLEM, CAGES, AND GEOMETRIES GÁBOR DAMÁSDI, TAMÁS HÉGER, AND TAMÁS SZŐNYI DEDICATED TO THE MEMORY OF ANDRÁS GÁCS AND ISTVÁN REIMAN Abstract. In the paper we consider some constructions
A spectrum result on minimal blocking sets with respect to the planes of PG(3, q), q odd
 A spectrum result on minimal blocking sets with respect to the planes of PG(3, q), q odd C. Rößing L. Storme January 12, 2010 Abstract This article presents a spectrum result on minimal blocking sets with
A spectrum result on minimal blocking sets with respect to the planes of PG(3, q), q odd C. Rößing L. Storme January 12, 2010 Abstract This article presents a spectrum result on minimal blocking sets with
LECTURE 10, MONDAY MARCH 15, 2004
 LECTURE 10, MONDAY MARCH 15, 2004 FRANZ LEMMERMEYER 1. Minimal Polynomials Let α and β be algebraic numbers, and let f and g denote their minimal polynomials. Consider the resultant R(X) of the polynomials
LECTURE 10, MONDAY MARCH 15, 2004 FRANZ LEMMERMEYER 1. Minimal Polynomials Let α and β be algebraic numbers, and let f and g denote their minimal polynomials. Consider the resultant R(X) of the polynomials
MATH 361: NUMBER THEORY FOURTH LECTURE
 MATH 361: NUMBER THEORY FOURTH LECTURE 1. Introduction Everybody knows that three hours after 10:00, the time is 1:00. That is, everybody is familiar with modular arithmetic, the usual arithmetic of the
MATH 361: NUMBER THEORY FOURTH LECTURE 1. Introduction Everybody knows that three hours after 10:00, the time is 1:00. That is, everybody is familiar with modular arithmetic, the usual arithmetic of the
A Hilton-Milner Theorem for Vector Spaces
 A Hilton-Milner Theorem for ector Spaces A Blohuis, A E Brouwer, A Chowdhury 2, P Franl 3, T Mussche, B Patós 4, and T Szőnyi 5,6 Dept of Mathematics, Technological University Eindhoven, PO Box 53, 5600
A Hilton-Milner Theorem for ector Spaces A Blohuis, A E Brouwer, A Chowdhury 2, P Franl 3, T Mussche, B Patós 4, and T Szőnyi 5,6 Dept of Mathematics, Technological University Eindhoven, PO Box 53, 5600
Chapter 1 : The language of mathematics.
 MAT 200, Logic, Language and Proof, Fall 2015 Summary Chapter 1 : The language of mathematics. Definition. A proposition is a sentence which is either true or false. Truth table for the connective or :
MAT 200, Logic, Language and Proof, Fall 2015 Summary Chapter 1 : The language of mathematics. Definition. A proposition is a sentence which is either true or false. Truth table for the connective or :
Solutions 2017 AB Exam
 1. Solve for x : x 2 = 4 x. Solutions 2017 AB Exam Texas A&M High School Math Contest October 21, 2017 ANSWER: x = 3 Solution: x 2 = 4 x x 2 = 16 8x + x 2 x 2 9x + 18 = 0 (x 6)(x 3) = 0 x = 6, 3 but x
1. Solve for x : x 2 = 4 x. Solutions 2017 AB Exam Texas A&M High School Math Contest October 21, 2017 ANSWER: x = 3 Solution: x 2 = 4 x x 2 = 16 8x + x 2 x 2 9x + 18 = 0 (x 6)(x 3) = 0 x = 6, 3 but x
Axioms of separation
 Axioms of separation These notes discuss the same topic as Sections 31, 32, 33, 34, 35, and also 7, 10 of Munkres book. Some notions (hereditarily normal, perfectly normal, collectionwise normal, monotonically
Axioms of separation These notes discuss the same topic as Sections 31, 32, 33, 34, 35, and also 7, 10 of Munkres book. Some notions (hereditarily normal, perfectly normal, collectionwise normal, monotonically
PUTNAM TRAINING POLYNOMIALS. Exercises 1. Find a polynomial with integral coefficients whose zeros include
 PUTNAM TRAINING POLYNOMIALS (Last updated: December 11, 2017) Remark. This is a list of exercises on polynomials. Miguel A. Lerma Exercises 1. Find a polynomial with integral coefficients whose zeros include
PUTNAM TRAINING POLYNOMIALS (Last updated: December 11, 2017) Remark. This is a list of exercises on polynomials. Miguel A. Lerma Exercises 1. Find a polynomial with integral coefficients whose zeros include
The chromatic number of ordered graphs with constrained conflict graphs
 AUSTRALASIAN JOURNAL OF COMBINATORICS Volume 69(1 (017, Pages 74 104 The chromatic number of ordered graphs with constrained conflict graphs Maria Axenovich Jonathan Rollin Torsten Ueckerdt Department
AUSTRALASIAN JOURNAL OF COMBINATORICS Volume 69(1 (017, Pages 74 104 The chromatic number of ordered graphs with constrained conflict graphs Maria Axenovich Jonathan Rollin Torsten Ueckerdt Department
Corollary 4.2 (Pepin s Test, 1877). Let F k = 2 2k + 1, the kth Fermat number, where k 1. Then F k is prime iff 3 F k 1
 4. Primality testing 4.1. Introduction. Factorisation is concerned with the problem of developing efficient algorithms to express a given positive integer n > 1 as a product of powers of distinct primes.
4. Primality testing 4.1. Introduction. Factorisation is concerned with the problem of developing efficient algorithms to express a given positive integer n > 1 as a product of powers of distinct primes.
Section 15 Factor-group computation and simple groups
 Section 15 Factor-group computation and simple groups Instructor: Yifan Yang Fall 2006 Outline Factor-group computation Simple groups The problem Problem Given a factor group G/H, find an isomorphic group
Section 15 Factor-group computation and simple groups Instructor: Yifan Yang Fall 2006 Outline Factor-group computation Simple groups The problem Problem Given a factor group G/H, find an isomorphic group
Wilson s Theorem and Fermat s Little Theorem
 Wilson s Theorem and Fermat s Little Theorem Wilson stheorem THEOREM 1 (Wilson s Theorem): (p 1)! 1 (mod p) if and only if p is prime. EXAMPLE: We have (2 1)!+1 = 2 (3 1)!+1 = 3 (4 1)!+1 = 7 (5 1)!+1 =
Wilson s Theorem and Fermat s Little Theorem Wilson stheorem THEOREM 1 (Wilson s Theorem): (p 1)! 1 (mod p) if and only if p is prime. EXAMPLE: We have (2 1)!+1 = 2 (3 1)!+1 = 3 (4 1)!+1 = 7 (5 1)!+1 =
Coding Theory and Applications. Solved Exercises and Problems of Cyclic Codes. Enes Pasalic University of Primorska Koper, 2013
 Coding Theory and Applications Solved Exercises and Problems of Cyclic Codes Enes Pasalic University of Primorska Koper, 2013 Contents 1 Preface 3 2 Problems 4 2 1 Preface This is a collection of solved
Coding Theory and Applications Solved Exercises and Problems of Cyclic Codes Enes Pasalic University of Primorska Koper, 2013 Contents 1 Preface 3 2 Problems 4 2 1 Preface This is a collection of solved
Mathematics Course 111: Algebra I Part I: Algebraic Structures, Sets and Permutations
 Mathematics Course 111: Algebra I Part I: Algebraic Structures, Sets and Permutations D. R. Wilkins Academic Year 1996-7 1 Number Systems and Matrix Algebra Integers The whole numbers 0, ±1, ±2, ±3, ±4,...
Mathematics Course 111: Algebra I Part I: Algebraic Structures, Sets and Permutations D. R. Wilkins Academic Year 1996-7 1 Number Systems and Matrix Algebra Integers The whole numbers 0, ±1, ±2, ±3, ±4,...
REVIEW FOR THIRD 3200 MIDTERM
 REVIEW FOR THIRD 3200 MIDTERM PETE L. CLARK 1) Show that for all integers n 2 we have 1 3 +... + (n 1) 3 < 1 n < 1 3 +... + n 3. Solution: We go by induction on n. Base Case (n = 2): We have (2 1) 3 =
REVIEW FOR THIRD 3200 MIDTERM PETE L. CLARK 1) Show that for all integers n 2 we have 1 3 +... + (n 1) 3 < 1 n < 1 3 +... + n 3. Solution: We go by induction on n. Base Case (n = 2): We have (2 1) 3 =
1. Suppose that a, b, c and d are four different integers. Explain why. (a b)(a c)(a d)(b c)(b d)(c d) a 2 + ab b = 2018.
 New Zealand Mathematical Olympiad Committee Camp Selection Problems 2018 Solutions Due: 28th September 2018 1. Suppose that a, b, c and d are four different integers. Explain why must be a multiple of
New Zealand Mathematical Olympiad Committee Camp Selection Problems 2018 Solutions Due: 28th September 2018 1. Suppose that a, b, c and d are four different integers. Explain why must be a multiple of
What is a semigroup? What is a group? What is the difference between a semigroup and a group?
 The second exam will be on Thursday, July 5, 2012. The syllabus will be Sections IV.5 (RSA Encryption), III.1, III.2, III.3, III.4 and III.8, III.9, plus the handout on Burnside coloring arguments. Of
The second exam will be on Thursday, July 5, 2012. The syllabus will be Sections IV.5 (RSA Encryption), III.1, III.2, III.3, III.4 and III.8, III.9, plus the handout on Burnside coloring arguments. Of
CHAPTER 14. Ideals and Factor Rings
 CHAPTER 14 Ideals and Factor Rings Ideals Definition (Ideal). A subring A of a ring R is called a (two-sided) ideal of R if for every r 2 R and every a 2 A, ra 2 A and ar 2 A. Note. (1) A absorbs elements
CHAPTER 14 Ideals and Factor Rings Ideals Definition (Ideal). A subring A of a ring R is called a (two-sided) ideal of R if for every r 2 R and every a 2 A, ra 2 A and ar 2 A. Note. (1) A absorbs elements
9. Finite fields. 1. Uniqueness
 9. Finite fields 9.1 Uniqueness 9.2 Frobenius automorphisms 9.3 Counting irreducibles 1. Uniqueness Among other things, the following result justifies speaking of the field with p n elements (for prime
9. Finite fields 9.1 Uniqueness 9.2 Frobenius automorphisms 9.3 Counting irreducibles 1. Uniqueness Among other things, the following result justifies speaking of the field with p n elements (for prime
Immerse Metric Space Homework
 Immerse Metric Space Homework (Exercises -2). In R n, define d(x, y) = x y +... + x n y n. Show that d is a metric that induces the usual topology. Sketch the basis elements when n = 2. Solution: Steps
Immerse Metric Space Homework (Exercises -2). In R n, define d(x, y) = x y +... + x n y n. Show that d is a metric that induces the usual topology. Sketch the basis elements when n = 2. Solution: Steps
Problemen. x = 2X 3 y = 2Y 4
 Problemen NAW 5/7 nr. 3 september 2006 219 Problemen Problem Section Edition 2006/1 For Session 2006/1 We received submissions from Rik Bos, Thomas Decru, Ruud Jeurissen, Jaap Spies, B. Sury, the Fejéntaláltuka
Problemen NAW 5/7 nr. 3 september 2006 219 Problemen Problem Section Edition 2006/1 For Session 2006/1 We received submissions from Rik Bos, Thomas Decru, Ruud Jeurissen, Jaap Spies, B. Sury, the Fejéntaláltuka
APPLICATIONS OF POLYNOMIALS OVER FINITE FIELDS. Péter Sziklai
 APPLICATIONS OF POLYNOMIALS OVER FINITE FIELDS Péter Sziklai A doctoral dissertation submitted to the Hungarian Academy of Sciences Budapest, 2013 2 Foreword 3 0 Foreword A most efficient way of investigating
APPLICATIONS OF POLYNOMIALS OVER FINITE FIELDS Péter Sziklai A doctoral dissertation submitted to the Hungarian Academy of Sciences Budapest, 2013 2 Foreword 3 0 Foreword A most efficient way of investigating
Section 33 Finite fields
 Section 33 Finite fields Instructor: Yifan Yang Spring 2007 Review Corollary (23.6) Let G be a finite subgroup of the multiplicative group of nonzero elements in a field F, then G is cyclic. Theorem (27.19)
Section 33 Finite fields Instructor: Yifan Yang Spring 2007 Review Corollary (23.6) Let G be a finite subgroup of the multiplicative group of nonzero elements in a field F, then G is cyclic. Theorem (27.19)
arxiv: v1 [math.co] 14 Jan 2016
![arxiv: v1 [math.co] 14 Jan 2016 arxiv: v1 [math.co] 14 Jan 2016](/thumbs/94/119837641.jpg) The Cameron-Liebler problem for sets Maarten De Boec, Leo Storme and Andrea Švob arxiv:1601.03628v1 [math.co] 14 Jan 2016 Abstract Cameron-Liebler line classes and Cameron-Liebler -classes in PG(2 + 1,
The Cameron-Liebler problem for sets Maarten De Boec, Leo Storme and Andrea Švob arxiv:1601.03628v1 [math.co] 14 Jan 2016 Abstract Cameron-Liebler line classes and Cameron-Liebler -classes in PG(2 + 1,
MS 2001: Test 1 B Solutions
 MS 2001: Test 1 B Solutions Name: Student Number: Answer all questions. Marks may be lost if necessary work is not clearly shown. Remarks by me in italics and would not be required in a test - J.P. Question
MS 2001: Test 1 B Solutions Name: Student Number: Answer all questions. Marks may be lost if necessary work is not clearly shown. Remarks by me in italics and would not be required in a test - J.P. Question
Cases Where Finding the Minimum Entropy Coloring of a Characteristic Graph is a Polynomial Time Problem
 Cases Where Finding the Minimum Entropy Coloring of a Characteristic Graph is a Polynomial Time Problem Soheil Feizi, Muriel Médard RLE at MIT Emails: {sfeizi,medard}@mit.edu Abstract In this paper, we
Cases Where Finding the Minimum Entropy Coloring of a Characteristic Graph is a Polynomial Time Problem Soheil Feizi, Muriel Médard RLE at MIT Emails: {sfeizi,medard}@mit.edu Abstract In this paper, we
Solutions of exercise sheet 6
 D-MATH Algebra I HS 14 Prof. Emmanuel Kowalski Solutions of exercise sheet 6 1. (Irreducibility of the cyclotomic polynomial) Let n be a positive integer, and P Z[X] a monic irreducible factor of X n 1
D-MATH Algebra I HS 14 Prof. Emmanuel Kowalski Solutions of exercise sheet 6 1. (Irreducibility of the cyclotomic polynomial) Let n be a positive integer, and P Z[X] a monic irreducible factor of X n 1
Part V. Chapter 19. Congruence of integers
 Part V. Chapter 19. Congruence of integers Congruence modulo m Let m be a positive integer. Definition. Integers a and b are congruent modulo m if and only if a b is divisible by m. For example, 1. 277
Part V. Chapter 19. Congruence of integers Congruence modulo m Let m be a positive integer. Definition. Integers a and b are congruent modulo m if and only if a b is divisible by m. For example, 1. 277
Homework 9 Solutions to Selected Problems
 Homework 9 Solutions to Selected Problems June 11, 2012 1 Chapter 17, Problem 12 Since x 2 + x + 4 has degree 2 and Z 11 is a eld, we may use Theorem 17.1 and show that f(x) is irreducible because it has
Homework 9 Solutions to Selected Problems June 11, 2012 1 Chapter 17, Problem 12 Since x 2 + x + 4 has degree 2 and Z 11 is a eld, we may use Theorem 17.1 and show that f(x) is irreducible because it has
MATH 431 PART 2: POLYNOMIAL RINGS AND FACTORIZATION
 MATH 431 PART 2: POLYNOMIAL RINGS AND FACTORIZATION 1. Polynomial rings (review) Definition 1. A polynomial f(x) with coefficients in a ring R is n f(x) = a i x i = a 0 + a 1 x + a 2 x 2 + + a n x n i=0
MATH 431 PART 2: POLYNOMIAL RINGS AND FACTORIZATION 1. Polynomial rings (review) Definition 1. A polynomial f(x) with coefficients in a ring R is n f(x) = a i x i = a 0 + a 1 x + a 2 x 2 + + a n x n i=0
Saturating sets in projective planes and hypergraph covers
 Saturating sets in projective planes and hypergraph covers Zoltán Lóránt Nagy MTA ELTE Geometric and Algebraic Combinatorics Research Group H 7 Budapest, Pázmány P sétány /C, Hungary nagyzoli@cseltehu
Saturating sets in projective planes and hypergraph covers Zoltán Lóránt Nagy MTA ELTE Geometric and Algebraic Combinatorics Research Group H 7 Budapest, Pázmány P sétány /C, Hungary nagyzoli@cseltehu
