Extremal graph on normalized Laplacian spectral radius and energy

Transcription

1 Electronic Journal of Linear Algebra Volume 9 Special volume for Proceedings of the International Conference on Linear Algebra and its Applications dedicated to Professor Ravindra B. Bapat Article Extremal graph on normalized Laplacian spectral radius and energy Kinkar Chandra Das SungkyunKwan University, kinkardas003@gmail.com SHAOWEI SUN Sungkyunkwan University, sunshaowei009@16.com Follow this and additional works at: Recommended Citation Das, Kinkar Chandra and SUN, SHAOWEI. (015), "Extremal graph on normalized Laplacian spectral radius and energy", Electronic Journal of Linear Algebra, Volume 9, pp DOI: This Article is brought to you for free and open access by Wyoming Scholars Repository. It has been accepted for inclusion in Electronic Journal of Linear Algebra by an authorized editor of Wyoming Scholars Repository. For more information, please contact scholcom@uwyo.edu.

2 Volume 31, pp , December 016 EXTREMAL GRAPHS FOR NORMALIZED LAPLACIAN SPECTRAL RADIUS AND ENERGY KINKAR CH. DAS AND SHAOWEI SUN Abstract. Let G = (V, E) be a simple graph of order n and the normalized Laplacian eigenvalues ρ 1 ρ ρ ρ n = 0. The normalized Laplacian energy (or Randić energy) of G without any isolated vertex is defined as RE(G) = n ρ i 1. i=1 In this paper, a lower bound on ρ 1 of connected graph G (G is not isomorphic to complete graph) is given and the extremal graphs (that is, the second minimal normalized Laplacian spectral radius of connected graphs) are characterized. Moreover, Nordhaus-Gaddum type results for ρ 1 are obtained. Recently, Gutman et al. gave a conjecture on Randić energy of connected graph [I. Gutman, B. Furtula, Ş. B. Bozkurt, On Randić energy, Linear Algebra Appl. 44 (014) 50 57]. Here this conjecture for starlike trees is proven. Key words. Normalized Laplaican spectral radius, Randić energy, Normalized Laplacian spread, Nordhaus-Gaddum type results, Vertex cover number AMS subject classifications. 05C50, 15A18 This paper is dedicated to Professor Ravindra B. Bapat on the occasion of his 60th birthday. 1. Introduction. Let G be a simple graph with vertex set V(G) = {v 1, v,..., v n and edge set E(G). Then its order is V(G), denoted by n, and its size is E(G), denoted by m. The degree d i of a vertex v i of a graph G is the cardinality of the neighborhood N i of the vertex v i. The maximum and second maximum degrees are denoted by 1 and, respectively. If vertices v i and v j are adjacent, we denote that Received by the editors on March 8, 016. Accepted for publication on December 1, 016. Handling Editor: Manjunatha Prasad Karantha Department of Mathematics, Sungkyunkwan University, Suwon , Republic of Korea (kinkardas003@googl .com, sunshaowei009@16.com). The first author was supported by the National Research Foundation funded by the Korean government with the grant no. 013R1A1A

3 Volume 31, pp , December K. C. Das and S. Sun by v i v j E(G). Let D(G) be the diagonalmatrixof vertexdegreesof agraph G. The Laplacian matrix L(G) is defined as D(G) A(G), where A(G) is the adjacency matrix ofg. Then the normalizedlaplacianmatrix ofgraphgwithout anyisolated vertexis defined as L(G) = D 1/ (G)L(G)D 1/ (G). Let ρ 1 (G) ρ (G) ρ (G) ρ n (G) = 0 be its eigenvalues. When only one graph is under consideration, then we write ρ i instead of ρ i (G). The normalized Laplacian energy (or Randić energy) of G is defined as RE(G) = n ρ i 1. i=1 Severalbounds onrandićenergycan be found inthe literature, see[9,10, 14]. Within classes of molecular graphs, a relatively good (increasing) linear correlation between Randić energy and energy of graphs has been investigated in the recent article by Furtula and Gutman [13]. For more information on Randić energy, we refer to the reader [11, 15]. The general Randić index R α (G) of graph G is defined as the sum of (d i d j ) α over all edges v i v j of G, where α is an arbitrary real number, that is, R α (G) = The general Randić index when α = 1 is R 1 (G) = v iv j E(G) v iv j E(G) (d i d j ) α. 1 d i d j. Some basic mathematical properties of R 1 (G) can be found in [5, 18] and the references therein. Throughout this paper we use P n, C n, S n, K n and K p,q (p+q = n) to denote the path graph, the cycle graph, the star graph, the complete graph and the complete bipartite graph on n vertices, respectively. For other undefined notations and terminologies from graph theory, the readers are referred to []. The tree of odd order n( 1), containing with pendant vertices, each attached to a vertex of degree, and a vertex of degree, will be called the ( ) - sun. The tree of even order n( ), obtained from a n 4 -sun and a n 4 -sun, by connecting their central vertices, will be called a ( n 4, n 4 ) -double sun. CONJECTURE 1.1. [14] If n 1 is odd, then the connected graph of order n, having greatest Randić energy is the sun. If n is even, then the connected graph of order n, having greatest Randić energy is the balanced double sun. Thus, if n is

4 Volume 31, pp , December 016 Extremal graph on normalized Laplacian spectral radius and energy 39 odd, then the tree with maximal RE is the ( ) -sun. If n is even, then this tree is the ( n 4, n 4 ) -double sun. The paper is organized as follows. In Section, we give a list of some previously known results. In Section 3, we obtain a lower bound on ρ 1 (G) for connected graphs and characterize the extremal graphs. Using this result we present some bounds on the normalized Laplaican spread (ρ 1 ρ ) and Nordhaus-Gaddum type results for ρ 1. In Section 4, we prove Conjecture 1.1 for starlike trees.. Preliminaries. Here we recall some basic properties of the normalized Laplacian eigenvalues which will be used in next two sections. Lemma.1. [7] Let G be a connected graph of order n. Then ρ n with equality holding if and only if G = K n. If G is not the complete graph K n, then ρ 1. Lemma.. [7] Let G be a connected graph of order n. Then n ρ 1 with left equality holding if and only if G = K n, and right equality holding if and only if G = K p,q with n = p+q. Lemma.3. [7] Let G be a bipartite graph of order n. For each ρ i, the value ρ i is also an eigenvalue of G. The join G 1 G of graphs G 1 and G is the graph obtained from the disjoint union of G 1 and G by adding all edges between V(G 1 ) and V(G ). Let K r s,t = K r (Ks Kt ) with r, s, t 1. Lemma.4. [17] Let G be a connected graph with order n 3. Then G = K r s,t if and only if G is {S 4, P 4, C 4 -free. In [4], Cavers found the normalized Laplacian spectrum of G = K 1 qks with n = 1+qs: (.1) { s+1 NLS(G) = s Note that G = K 1 s,s when q =.,, s+1 s {{ sq q+1, 1 s,, 1, 0 {{ s q 1 Lemma.5. [1] Let G = (V, E) be a graph of order n. If N i = N j, i( )j = 1,,..., k, then G has at least k 1 equal normalized Laplacian eigenvalues 1. Let ρ be an eigenvalue with a corresponding eigenvector x = (x 1, x,..., x n ) T of the matrix Q(= D 1 L) with non-isolated vertices of graph G. Since the normalized Laplacian matrix L and Q are similar, then they have the same spectrum. We have.

5 Volume 31, pp , December K. C. Das and S. Sun Qx = ρx, that is, (.) ρx i = x i 1 d i x j, i = 1,,..., n. v j:v iv j E(G) By multiplying d i x i to each side of the above equation, we get (1 ρ)d i x i = x i x j, i = 1,,..., n. v j:v iv j E(G) (.3) Taking summation on the above from i = 1 to n, we get x i x j ρ = 1 From this we get the following result: v iv j E(G) n d i x i i=1 Lemma.6. [7] Let G be a graph of order n with non-isolated vertices. Then x i x j ρ 1 1 v iv j E(G) n i=1 for any non-zero vector x = (x 1, x,..., x n ) T. Lemma.7. Let K t be a complete graph on t vertices with V(K t ) = {v 1, v,..., v t. Also let H be a graph of order n t with V(H) = {v t+1, v t+,..., v n. Fix q (1 q n t), then the resultant graph G = (V, E) is as follows: V(G) = V(K t ) V(H) = {v 1, v,..., v n, d i x i E(G) = E(K t ) E(H) {v i v j : i = 1,,..., t; j = t+1, t+,..., t+q. Then G has at least t 1 equal normalized Laplacian eigenvalues Proof. From (.), we get ρx i = x i 1 q +t 1 One can easily see that ρ = t+q t+q 1 v j:v iv j E(G)., x j, i = 1,,..., t. t+q t+q 1. with corresponding eigenvectors (1, 1, 0,..., 0) T, (1, 0, 1, 0,..., 0) T,..., (1, 0,..., 1, 0,..., 0) T {{{{{{ 3 t

6 Volume 31, pp , December 016 Extremal graph on normalized Laplacian spectral radius and energy 41 satisfy the above relation. Since these eigenvectors are linearly independent, we get the required result. Lemma.8. Let G = K a Kn a (1 a n 1). Then the normalized Laplacian spectrum of graph G is { NLS(G) = 1+ a, n,, n, 1,,1, 0. {{ {{ a 1 n a 1 Proof. By Lemmas.5 and.7, we have two normalized Laplacian eigenvalues of n G are with multiplicity n a 1 and 1 with multiplicity a 1. Since ρ n = 0 and n ρ i = n, we get the required result. i=1 For a graph G = (V, E), a vertex cover of G is a set of vertices C V such that every edge of G is incident to at least one vertex in C. A minimum vertex cover is a vertex cover C such that no other vertex cover is smaller in size than C. The vertex cover number c is the size of the minimum vertex cover. Lemma.9. [6] For a tree with vertex cover number c, the multiplicity of the normalized Laplacian eigenvalue 1 is exactly n c. A matching M in G is a set of pairwise non-adjacent edges, that is, no two edges share a common vertex. A maximum matching is a matching that contains the largest possible number of edges. The matching number ν of a graph G is the size of a maximum matching. Lemma.10. (König s matching theorem) [] For any bipartite graph G, ν = c. Denoted by T(n, k, n 1, n,..., n k ), is a tree of order n formed by joining the center v i ofstar S ni to a new vertex v for i = 1,,..., k with n 1 n n k 1, that is, T(n, k, n 1, n,..., n k ) {v = S n1 S n S nk. In particular, we have T(n, k,,,..., ) = ( ) -sun, where k = and n is odd. Lemma.11. [1] Let T = (V, E) be a tree of order n 3. Also let v 1 and v be the maximum and the second maximum degree vertices of degrees 1 and, respectively. If v 1 v / E(T), then ρ (T) with equality holding if and only if T = T(n, k, n 1, n,...,n k ), n 1 = n.

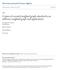
7 Volume 31, pp , December K. C. Das and S. Sun 3. Normalized Laplacian spectral radius of graphs. K 1 s,s (s+1 = n) Fig. 1: Graph K 1 s,s with s+1 = n. Several lower bounds on ρ 1 in terms of graph parameters (n, m, 1 etc.) are known, see [16] and the references therein. Moreover, it is already known that the complete graph gives the minimal normalized Laplacian spectral radius of a connected graph G of order n. In this section our aim is to find the second minimal normalized Laplacian spectral radius of a connected graph G of order n. For this we give a lower bound on ρ 1 of a connected graph G and characterize the extremal graphs. Theorem 3.1. Let G( K n ) be a connected graph of order n. Then (3.1) ρ 1 n+1 with equality holding if and only if G = K n e or Ks,s 1 with s+1 = n (see, Fig. 1). Proof. First we prove this result when P 4 or C 4 or S 4 is an induced subgraph of G. Suppose that the path P 4 : v i v j v k v l is an induced subgraph of the graph G. If d i +d j +d k +d l < 3n 3, then we set x i = 1, x j = 1, x k = 1, x l = 1 and all the other components are 0 in (.3). We have ρ > n+1 d i +d j +d k +d l. Otherwise, d i +d j +d k +d l 3n 3. Let CN = N i N j N k N l with CN = a, where 0 a n 4. Since each vertex in CN is adjacent to {v i, v j, v k, v l and CN = a, we must have d i +d j +d k +d l 3(n 4 a)+4a+6 = 3n+a 6 and hence 3 a n 4. Setting x i = x j = x k = x l = 1, x r = 4 a+1 for v r CN,

8 Volume 31, pp , December 016 Extremal graph on normalized Laplacian spectral radius and energy 43 and all the other components are 0 in (.3), we have 16a a+1 3 ρ 1 1+ d i +d j +d k +d l + vrvs E(G), vr,vs CN 16 (a+1) 16 (a+1) v r CN d r. Since vrvs E(G), vr,vs CN 16 (a+1) 8a(a 1) (a+1) and v r CN d r a(), from the above result, we have (3.) ρ a +18a 3 3a +a+3+(a 3)(a+1) /(). For 4 a n 4, we have a a 3 = (a 3)(a+1) > 0 and a+1 < and hence 5a +18a 3> 3a +a+3+(a 3)(a+1)> 3a +a+3+(a 3)(a+1) /(). Then by (3.), again we get ρ 1 > n+1. For a = 3, by (3.), we have ρ with equality holding if and only if x i = x j = x k = x l = 1, x r = 1 for v r CN, and all the other components are 0. By (.), we have 1+ = 1+ d i and hence d i = n 1, which is a contradiction with d i n 3. Therefore we get ρ 1 > n+1. Next suppose that the cycle C 4 = v i v j v k v l v i is an induced subgraph of the graph G. Then d t n, t = i, j, k, l. Setting x i = 1, x j = 1, x k = 1, x l = 1 and all the other components are 0 in (.3), we have ρ d i +d j +d k +d l 1+ n > n+1. Next suppose that the star S 4 is an induced subgraph of the graph G with vertex set V(S 4 ) = {v 1, v, v 3, v 4, where v 1 v i E(G), i =, 3, 4. First we assume that the vertices v, v 3 and v 4 have at least two common neighbors {v 1, v 5, (say). Then

9 Volume 31, pp , December K. C. Das and S. Sun d i n 3 for i =, 3, 4. Setting x 1 = 1, x = 1, x 3 = 1, x 4 = 1, x 5 = 1 and all the other components are 0 in (.3), we have if v 1 v 5 E(G) with d 1, d 5 d 1 +d +d 3 +d 4 +d 5 ρ if v 1 v 5 / E(G) with d 1, d 5 n d 1 +d +d 3 +d 4 +d ()+3(n 3) > n+1. Next we assume that v, v 3 and v 4 have exactly one common neighbor. Hence d +d 3 +d 4 (n 4)+3 = n 5. Setting x 1 = 1, x = 1, x 3 = 1, x 4 = 1 and all the other components are 0 in (.3), we have ρ d 1 +d +d 3 +d 4 +n 5 > n+1. We now consider the graph G with {S 4, P 4, C 4 -free. By Lemma.4, we have G = K r s,t (r +s+t = n) as G is connected. Then by Lemma.7, one can easily get that the normalized Laplacian eigenvalues of G are { s+r s+r 1,..., s+r t+r, {{ s+r 1 t+r 1,..., t+r, {{ t+r 1 s 1 t 1 n,..., n {{ r 1 and the remaining three eigenvalues satisfy the following equations: ρx 1 = x 1 1 ((r 1)x 1 +sx +tx 3 ) ρx = x ρx 3 = x 3 1 r+s 1 ((s 1)x +rx 1 ) 1 r+t 1 ((t 1)x 3 +rx 1 ). Therefore the remaining three normalized Laplacian eigenvalues of G satisfy the following equation xf(x) = 0,

10 Volume 31, pp , December 016 where ( f(x) = x Extremal graph on normalized Laplacian spectral radius and energy 45 r s+r 1 + s+t + + ) r x+ r+t 1 sr (r+t 1)() r (s+r 1)(r +t 1) + rt (s+r 1)(). f Now, ( ) ( n+1 n+1 = = + r n t 1 n r r n s 1 ) ( ) n+1 sr (n s 1)() + r (n t 1)(n s 1) + rt (n t 1)() ( r+1 r(n s t ) ) ( ) n+1 (n s 1)(n t 1) + n()r rst ()(n s 1)(n t 1) (3.3) = nr n r+1+(n+1)st (n 3)rst () (n s 1)(n t 1). Without loss of generality, we can assume that t s. We now consider two cases (i) r = 1, (ii) r. Case(i) : r = 1. Since s t, from (3.3), we get f ( ) n+1 = 4st () st() 0. Thus we have ρ 1 n+1 with equality holding if and only if s = t =, that is, if and only if G = Ks,s 1 with s+1 = n. Case(ii) : r. If s = t = 1, we have G = K n e. By Lemma.8, ρ 1 (G) = n+1 and hence the equality holds in (3.1). Otherwise, we consider the following two subcases: Subcase(a) : s = 1 and t. In this subcase, from (3.3), we get f ( ) n+1 = nr n r+1+(n+1)t (n 3)rt (). (n )(n t 1)

11 Volume 31, pp , December K. C. Das and S. Sun For n = 5 or 6, one can check directly that ( ) n+1 (3.4) f < 0. Otherwise, n 7. Since t and n r +3, we have t[(n 3)r (n+1)] nr+n +r 1 [(n 3)r (n+1)] nr+n +r 1 = () 4(r+1) > 0. Again (3.4) holds and hence the inequality in (3.1) is strict. Subcase(b) : t s. If n = 6, then G = K, and hence the inequality in (3.1) is strict. Otherwise, n 7. Now, st[(n 3)r (n+1)] nr+n +r 1 4[(n 3)r (n+1)] nr+n +r 1 = r(n 5)+(n ) 9 > 0. Again (3.4) holds and hence the inequality in (3.1) is strict. Using the above theorem, we can obtain a lower bound for the normalized Laplacianspread(ρ 1 ρ )ofallgraphsg( K n, K n )with fixedordernandcharacterize the extremal graphs. Theorem 3.. Let G ( K n, K n ) be a graph with order n. Then ρ 1 ρ with equality holding if and only if G = K n e. Proof. First we assume that G is a disconnected graph. Since G K n, then G has at least one edge. Thus we have ρ 1 > 1 and ρ = 0. Hence ρ 1 ρ >. Next we assume that G is a connected graph. Since G K n, by Lemma.1 and Theorem 3.1, we have ρ 1 n+1 and ρ 1. Thus ρ 1 ρ. Moreover, ρ 1 ρ = if and only if ρ = 1 and ρ 1 = n+1. Again by Theorem 3.1, we have ρ 1 = n+1 if and only if G = K n e or G = Ks,s 1 with s+1 = n. By (.1), we get ρ (Ks,s) 1 = (s + 1 = n). By Lemma.8, we have ρ (K n e) = 1. This completes the proof of the theorem. We now give the first n+ minimal normalized Laplacian spectral radius of graphs with order n. Theorem 3.3. (i) Let G / {K n, K K 1, K n K,..., K p+1 K p, K p K p+1, K n e, K 1 p,p be a graph of odd order n (= p+1). Then ρ 1 (K n ) < ρ 1 (K K 1 ) < ρ 1 (K n K ) < < ρ 1 (K p+ K p 1 )

12 Volume 31, pp , December 016 (3.5) Extremal graph on normalized Laplacian spectral radius and energy 47 < ρ 1 (K p+1 K p ) = ρ 1 (K n e) = n+1 = ρ 1(K 1 p,p ) < ρ 1(G). (ii) Let G / {K n, K K 1, K n K,..., K p+ K p, K p+1 K p 1, K n e be a graph of even order n (= p). Then ρ 1 (K n ) < ρ 1 (K K 1 ) < ρ 1 (K n K ) < < ρ 1 (K p+ K p ) (3.6) < ρ 1 (K p+1 K p 1 ) < ρ 1 (K n e) = n+1 < ρ 1(G). Proof. We have For n = p+1, we have ρ 1 (K n i K i ) = n i, i = 1,,..., n. n i 1 ρ 1 (K n ) < ρ 1 (K K 1 ) < ρ 1 (K n K ) < < ρ 1 (K p+ K p 1 ) (3.7) < ρ 1 (K p+1 K p ) = n+1. For n = p, we have ρ 1 (K n ) < ρ 1 (K K 1 ) < ρ 1 (K n K ) < < ρ 1 (K p+ K p ) (3.8) < ρ 1 (K p+1 K p 1 ) = n+ n < n+1. First we assume that G is a connected graph. For G K n, by Theorem 3.1, we have ρ 1 (G) n+1 with equality holding if and only if G = K n e or K 1 s,s with s+1 = n. From the above results, we get the required results in (3.5) and (3.6). Next we assume that G is a disconnected graph. Let G 1, G,..., G k be the k (k ) connected components in G. Also let n i be the number of vertices in G i, k i = 1,,..., k such that n i = n with n 1 n n k. If n, then by Lemma., ρ 1 (G) = max i=1 { ρ 1 (G 1 ), ρ 1 (G ),..., ρ 1 (G k ) 1+ 1 n 1 > n+1

13 Volume 31, pp , December K. C. Das and S. Sun and hence the two inequalities hold in (3.5) and (3.6). Otherwise, n = 1. Then G = G 1 K k 1. We consider the following two cases: Case(i) : n = p+1. If k p+, then ρ 1 (G) = ρ 1 (G 1 ) n 1 n k +1 = > n+1 n 1 1 n k and hence the inequality (3.5) holds. Otherwise, k p+1. For G 1 = Kn k+1, then G = K n k+1 K k 1 and hence the inequality holds in (3.7), that is, the inequality holds in (3.5). Otherwise, G 1 K n k+1. Using Theorem 3.1, we get ρ 1 (G) = ρ 1 (G 1 ) n k + n k > n+1 and hence the inequality holds in (3.5). Case(ii) : n = p. Similarly, as Case (i), we consider k p+1 and k p, and we can see that the inequality holds in (3.6). We now obtain Nordhaus-Gaddum type results on ρ 1 (G). Theorem 3.4. Let G( K n, K n ) be a graph of order n. Then (3.9) ρ 1 (G)+ρ 1 (G) + 4 with equality holding if and only if G = K K1 or G = S 3. Proof. Since G K n, K n, we have n 3. For n = 3, G = K K1 or G = S 3. Hence the equality holds in (3.9). Otherwise, n 4. One can easily see that both G and G, or one of them must be connected. Without loss of generality, we can assume that G is connected. If G is connected, by Theorem 3.1 we have ρ 1 (G)+ρ 1 (G) > + 4. Otherwise, G is disconnected. If G K i Kn i ( i ), then by Theorem 3.3, we have ρ 1 (G) > 1+ and hence ρ 1(G)+ρ 1 (G) > + 4, by Theorem 3.1. { Next we only have to consider the remaining case: G K i K n i i. Therefore ρ 1 (G) = i i 1 ( i ). By Lemma.8, we have ρ 1(G) = 1+ i ( i ) and hence ρ 1 (G)+ρ 1 (G) = + 1 i 1 + i.

14 Volume 31, pp , December 016 Extremal graph on normalized Laplacian spectral radius and energy 49 It is easy to see that the function f(x) = + 1 x 1 + x is decreasing on [, +1] and increasing on ( +1, ]. Since n 4, we have ρ 1 (G)+ρ 1 (G) f( +1) = + This completes the proof of the theorem. Theorem 3.5. Let G be a graph of order n(> ). Then + 1 > + 4. (3.10) ρ 1 (G)+ρ 1 (G) 4 with equality holding if and only if G {S 3, P 4, K,n, K Kn. Proof. One can easily check that S 3, P 4, K,n and K Kn satisfy the equality in (3.10). Otherwise, n 5 and G K,n, G K Kn. By Lemma., we can immediately get ρ 1 (G)+ρ 1 (G) 4. Suppose that equality holds in (3.10). Then by Lemma., both G and G have at least one connected bipartite component. Without loss of generality, we can assume that G is connected. Since G is a bipartite graph with n 5, then there is at least one independent vertex subset S of V(G) with S 3. Then K 3 is an induced subgraph of G. If G is connected, then G can not be a bipartite graph, a contradiction. Otherwise, G is a disconnected graph. Then G must be complete bipartite graph K p,q and hence G = K p Kq (p+q = n). Since n 5 and ρ 1 (G) =, then p = or q =, and hence G = K,n, a contradiction. This completes the proof of the theorem. 4. Normalized Laplacian energy of starlike tree. A tree is said to be starlike if exactly one of its vertices has degree greater than two. By S(n 1, n,..., n k ) we denote the starlike tree which has a vertex v 1 of degree k 3 with n 1 n n k 1 and which has the property S(n 1, n,..., n k ) v 1 = P n1 Pn Pnk. ( This treehasn 1 +n + +n k +1 = n vertices. In particular, wehaves(,,..., ) ) = -sun, where n is odd. Let s = S ( S is the cardinality of set S) be the nonnegative integer such that S = {i : n i is odd, 1 i k. Banerjee et al. [1] proved that for starlike tree T = S(n 1, n,..., n k ), T has the matching number n s+1 (s 0). This result with Lemma.10, we get the following:

15 Volume 31, pp , December K. C. Das and S. Sun Lemma 4.1. Let T = S(n 1, n,..., n k ) be a starlike tree of order n with vertex cover number c. Then s = 0, c = n+1 s s 1. Banerjee et al. [1, Theorem. (ii)] gave a result on R 1 (T) which is not true. Here we give the correct statement: Lemma 4.. Let T = S(n 1, n,..., n k ) be a starlike tree of order n and let p be the largest positive integer such that n p > 1. Then R 1 (T) = n+1 k p ( 1 ). 4 4 k Proof. Since T is a starlike tree and n 1 n n p, we have (d 1, d j ) = (k, ) for p edges v 1 v j E(T), (d 1, d j ) = (k, 1) for k p edges v 1 v j E(T), (d i, d j ) = (, 1) for p edges v i v j E(T) and (d i, d j ) = (, ) for the remaining edges v i v j E(T). Thus R 1 (T) = v i v j E(T) 1 d i d j = p k + k p + p n k p 1 + k 4 = n+1 4 k p 4 ( 1 ). k Corollary 4.3. Let T = S(n 1, n,..., n k ) be a starlike tree of order n. Then R 1 (T) n+1 4 with equality holding if and only if n k. Proof. The proof follows directly from Lemma 4.. We now obtain the Randić energy for the special kind of starlike trees. Lemma 4.4. Let T = S(,,..., ) be a starlike tree of order n. Then RE(T) = + (n 3).

16 Volume 31, pp , December 016 Extremal graph on normalized Laplacian spectral radius and energy 51 Proof. The two normalized Laplacian eigenvalues of T are 1± multiplicity n 3 [3]. Since T is bipartite with n ρ i (T) = n, we get Hence we get the required result. i=1 { NLS(T) =, 1±,..., 1±, 1, 0. {{ n 3 with the same We are now ready to prove Conjecture 1.1 for starlike trees of odd order n. Theorem 4.5. Let T = S(n 1, n,..., n k ) be a starlike tree of order n (n is odd). Then RE(T) + (n 3) (4.1) with equality holding if and only if T = S(,,..., ). Proof. Let c be the vertex cover number of T. From the matrix L, we have n ρ 1 i = n+ = n+r 1 (T). d i d j i=1 v i v j E(T) Thus we have n n (ρ i 1) = ρ i n = R 1 (T). i=1 i=1 By Lemmas.3 and.9, we have n c c (ρ i 1) = (ρ i 1) = + (ρ i 1). i=1 i=1 i= Therefore (4.) c R 1 (T) = 1+ (ρ i 1). i= Again by Lemmas.3 and.9, we conclude that ρ c > 1. Moreover, we have n c c (4.3) RE(T) = ρ i 1 = (ρ i 1) = + (ρ i 1). i=1 i=1 i=

17 Volume 31, pp , December K. C. Das and S. Sun By Cauchy-Schwartz inequality and (4.), we have c c (4.4) (ρ i 1) (c 1) (ρ i 1) = (c 1)(R 1 (T) 1) i= i= with equality holding if and only if ρ = ρ 3 = = ρ c. Since n is odd, we have s = 0 or s. By Lemma 4.1, we get c with equality holding if and only if s = 0 or s =. Using this result with Corollary 4.3, from (4.4), we get (4.5) c i= (ρ i 1) (n 3) 4. From (4.3) and (4.5), we get the required result in (4.1). The first part of the proof is done. Suppose that equality holds in (4.1). Then all the inequalities in the above proof must be equalities. In particular, from equality in (4.4), we have ρ = ρ 3 = = ρ c. Fromequalityin(4.5)withCorollary4.3,wehaven k. Moreover,wehavec =. Again from equality in (4.5) with the above result, we get ρ = ρ 3 = = ρ c = 1+. By Lemmas.3 and.9, we conclude that the normalized Laplacian spectrum is { NLS(T) =, 1, 0, 1±,..., 1±. {{ n 3 Since n k, we have k. If k =, then T = S(,,..., ). Otherwise, 3 k <. In this case n 1 3. Without loss of generality, we can assume that the second maximum degree vertex v of degree is not adjacent to the maximum degree vertex v 1 of degree k in T. Then by Lemma.11, we have ρ (T) < 1, which is a contradiction (The inequality is strict because the diameter of T is strictly greater than the diameter of T(n, n 1, n 1, n,..., n k )). Conversely. one can see easily that the equality holds in (4.1) for S(,,..., ), by

18 Volume 31, pp , December 016 Extremal graph on normalized Laplacian spectral radius and energy 53 Lemma 4.4. Acknowledgment. The authors would like to thank anonymous referee for valuable comments which have considerably improved the presentation of this paper. REFERENCES [1] A. Banerjee and R. Mehatari. Characteristics polynomial of normalized Laplacian for trees. Applied Math. Comput., 71: , 015. [] J. A. Bondy and U. S. R. Murty. Graph Theory with Applications. Macmillan Press, New York, [3] R. O. Braga, R. R. Del-Vechio, V. M. Rodrigues, and V. Trevisan. Trees with 4 or 5 distinct normalized Laplacian eigenvalues. Linear Algebra Appl., 471: , 015. [4] M. Cavers. The normalized Laplacian matrix and general Randić index of graphs. PhD dissertation, University of Regina, 010. [5] M. Cavers, S. Fallat, and S. Kirkland. On the normalized Laplacian energy and general Randić index R 1 of graphs. Linear Algebra Appl., 433:17 190, 010. [6] H. Chen and J. Jost. Minimum vertex covers and the spectrum of the normalized Laplacian on trees. Linear Algebra Appl., 437: , 01. [7] F. K. Chung. Spectral graph theory. American Mathematical Soc., [8] K. C. Das, A. D. Güngör, and Ş. B. Bozkurt. On the normalized Laplacian eigenvalues of graphs. Ars. Comb., 118: , 015. [9] K. C. Das and S. Sorgun. On Randić energy of graphs. MATCH Commun. Math. Comput. Chem., 7:7 38, 014. [10] K. C. Das, S. Sorgun, and I. Gutman. On Randić energy. MATCH Commun. Math. Comput. Chem., 73:81 9, 015. [11] K. C. Das, S. Sorgun, and K. Xu. On Randić energy of graphs. I. Gutman, X. Li (Eds.), Energies of graphs-theory and Applications, Univ. Kragujevac, Kragujevac, 016, pp [1] K. C. Das and S. Sun. Normalized Laplacian eigenvalues and energy of trees. Taiwanese Journal of Mathematics, 0 (3): , 016. [13] B. Furtula and I. Gutman. Comparing energy and Randić energy. Maced. J. Chem. Chem. Engin., 3:117 13, 013. [14] I. Gutman, B. Furtula, and Ş. B. Bozkurt. On Randić energy. Linear Algebra Appl., 44:50 57, 014. [15] I. Gutman, M. Robbiano, and B. S. Martin Upper bound on Randić energy of some graphs. Linear Algebra Appl., 478:41 55, 015. [16] J. Li, J.-M. Guo, and W. C. Shiu. Bounds on normalized Laplacian eigenvalues of graphs. Journal Inequalities Appl., 316:1 8, 014. [17] H. Lin, M. Zhai, and S. Gong. On graphs with at least three distance eigenvalues less than -1. Linear Algebra Appl., 458: , 014. [18] D. Rautenbach. A note on trees of maximum weight and restricted degrees. Discrete Math., 71:335 34, 003.