Combinatorial algorithms
|
|
|
- Sydney Woods
- 5 years ago
- Views:
Transcription
1 Combinatorial algorithms computing subset rank and unrank, Gray codes, k-element subset rank and unrank, computing permutation rank and unrank Jiří Vyskočil, Radek Mařík 2012
2 Combinatorial Generation definition: Suppose that S is a finite set. A ranking function will be a bijection rank: S {0,, S 1} and unrank function is an inverse function to rank function. definition: Given a ranking function rank, defined on S, the successor function satisfies the following rule: potential uses: successor(s) = t rank(t) = rank(s) + 1 storing combinatorial objects in the computer instead of storing a combinatorial structure which could be quite complicated generation of random objects from S ensuring equal probability 1/ S 2 / 22
3 Subsets Suppose that n is a positive integer and S = {1,, n}. Define S to consist of the 2 n subsets of S. Given a subset T S, let us define the characteristic vector of T to be the one-dimensional binary array χ T = [x n 1, x n 2,, x 0 ] where x i = 1 if (n i) T 0 if (n i) T 3 / 22
4 Subsets Example of the lexicographic ordering on subsets of S = {1,2, 3}: T χ T = [x 2, x 1, x 0 ] rank(t) [0,0,0] 0 {3} 0,0,1 1 {2} [0,1,0] 2 {2,3} [0,1,1] 3 {1} [1,0,0] 4 {1,3} [1,0,1] 5 {1,2} [1,1,0] 6 {1,2,3} [1,1,1] 7 4 / 22
5 Subsets computing the subset rank over lexicographical ordering 1) Function SUBSETLEXRANK( size n; set T ) : rank 2) r = 0 ; 3) for i = 1 to n do { 4) if i T then r = r + 2 n-i ; 5) } 6) return r ; 1) Function SUBSETLEXUNRANK( size n; rank r ) : set 2) T = ; 3) for i = n downto 1 do { 4) if r mod 2 = 1 then T = T {i} ; 5) r = 6) } r 2 ; 7) return T ; 5 / 22
6 definition: Gray Code The reflected binary code, also known as Gray code, is a binary numeral system where two successive values differ in only one bit. G n will denote the reflected binary code for 2 n binary n-tuples, and it will be written as a list of 2 n vectors, as follows: G n =[G n 0, G n n 1,, G 2 n 1] The codes G n are defined recursively: example: G 1 =[0,1] G n =[0G n 1 0, 0G n 1 1,, 0G n 1 2 n 1,1G n 1 2 n 1,,1G n 1 1, 1G n 1 0 ] G 3 =[000, 001, 011, 010, 110, 111, 101, 100] 6 / 22
7 Gray Code Example: G3 r binary representation of r r / 22
8 Gray Code lemma 1 Suppose 0 r 2 n 1 B = b n,, b 0 is a binary code of r G = g n,, g 0 is a Gray code of r Then for every j {0,1,, n 1} g j = b j + b j+1 mod 2 proof By induction on n. 8 / 22
9 Gray Code lemma 2 Suppose 0 r 2 n 1 B = b n,, b 0 is a binary code of r G = g n,, g 0 is a Gray code of r Then for every j {0,1,, n 1} b j = g j + b j+1 mod 2 proof g j = b j + b j+1 mod 2 g j b j + b j+1 (mod 2) b j g j + b j+1 mod 2 b j = g j + b j+1 mod 2 9 / 22
10 lemma 3 Gray Code Suppose 0 r 2 n 1 B = b n,, b 0 is a binary code of r G = g n,, g 0 is a Gray code of r Then for every j {0,1,, n 1} n 1 b j = g i i=j mod 2 proof n 1 g i i=j n 1 mod 2 = (b i +b i+1 ) i=j n 1 mod 2 = b j + b n + 2 b i i=j+1 mod 2 = (b j +b n ) mod 2 = b j By lemma 1. By the sum reordering. By the property of modulo. By the maximum range of r and the range of b j. 10 / 22
11 Gray Code converting to and from minimal change ordering (Gray code) 1) Function BINARYTOGRAY( binary code rank B ) : gray code rank 2) return B xor (B >> 1) ; 1) Function GRAYTOBINARY(gray code rank G ) : binary code rank 2) B = 0; 3) n = (number of bits in G) 1; 4) for i=0 to n do { 5) B = B << 1; 6) B = B or (1 and ( (B >> 1) xor (G >> n) ) ); 7) G = G << 1; 8) } 9) return B ; 11 / 22
12 Subsets Gray Code computing the subset rank over minimal change ordering 1) Function GRAYCODERANK( size n; set T ) : rank 2) r = 0 ; 3) b = 0 ; 4) for i = n 1 downto 0 do { 5) if n i T then b = 1 b ; 6) if b = 1 then r = r + 2 i ; 7) } 8) return r ; 12 / 22
13 Subsets Gray Code computing the subset unrank over minimal change ordering 1) Function GRAYCODEUNRANK( size n; rank r ) : set 2) T = ; 3) c = 0 ; 4) for i = n 1 downto 0 do { 5) b = r 2 i ; 6) if b c then T = T {n i} ; 7) c = b ; 8) r = r b 2 i ; 9) } 10) return T ; 13 / 22
14 k - Element subsets Suppose that n is a positive integer and S = {1,, n}. S k consists of all k-element subsets of S. A k-element subset T S can be represented in a natural way as a sorted one-dimensional array T = t 1, t 2,, t k where t 1 < t 2 < < t k. 14 / 22
15 k - Element subsets Example of the lexicographic ordering on k-element subsets: T T rank(t) {1,2,3} [1,2,3] 0 {1,2,4} 1,2,4 1 {1,2,5} [1,2,5] 2 {1,3,4} [1,3,4] 3 {1,3,5} [1,3,5] 4 {1,4,5} [1,4,5] 5 {2,3,4} [2,3,4] 6 {2,3,5} [2,3,5] 7 {2,4,5} [2,4,5] 8 {3,4,5} [3,4,5] 9 15 / 22
16 k - Element subsets computing the k-element subset successor with lexicographic ordering 1) Function KSUBSETLEXSUCCESOR(k-element subset as array T; 2) number n, k ) : k-element subset as array ; 3) U = T ; 4) i = k ; 5) while ( i 1 ) and ( T[i] = n k + i ) do i = i 1 ; 6) if ( i = 0 ) then 7) return undefined ; 8) else { 9) for j = i to k do U[j] = T[i] j i ; 10) return U ; 11) } 16 / 22
17 k - Element subsets computing the k-element subset rank with lexicographic ordering 1) Function KSUBSETLEXRANK(k-element subset as array T; 2) number n, k ) : rank ; 3) r = 0 ; 4) T[0] = 0 ; 5) for i = 1 to k do { 6) if ( T[i-1]+1 T[i] 1 ) then { 7) for j = T[i-1]+1 to T[i] 1 do r = r + 8) } 9) } 10) return r ; n j k i ; 17 / 22
18 k - Element subsets computing the k-element subset unrank with lexicographic ordering 1) Function KSUBSETLEXUNRANK(rank r; 2) number n, k ) : k-element subset as array ; 3) x = 1 ; 4) for i = 1 to k do { n x 5) while ( r ) do { k i n x 6) r = r ; 7) x = x + 1 ; 8) } 9) T[i] = x ; 10) x = x + 1 ; 11) } 12) return T ; k i 18 / 22
19 Permutations A permutation is a bijection from a set to itself. one possible representation of a permutation π: 1,, n 1,, n is by storing its values in a one-dimensional array as follows: index 1 2 n value π[1] π[2] π[n] 19 / 22
20 Permutations computing the permutation rank over lexicographical ordering 1) Function PERMLEXRANK( size n; permutation π ) : rank 2) r = 0 ; 3) ρ = π ; 4) for j = 1 to n do { 5) r = r + (ρ[ j ] 1) (n j)! ; 6) for i = j +1 to n do if ρ[ i ] > ρ[ j ] then ρ[ i ] = ρ[ i ] 1 ; 7) } 8) return r ; 20 / 22
21 Permutations computing the permutation unrank over lexicographical ordering 1) Function PERMLEXUNRANK( size n; rank r ) : permutation 2) π[ n ] = 1 ; 3) for j = 1 to n 1 do { 4) d = r mod j+1! j! 5) r = r d j! ; 6) π[ n j ] = d + 1 ; ; 7) for i = n j + 1 to n do if π[ i ] > d then π[ i ] = π[ i ] + 1 ; 8) } 9) return π ; 21 / 22
22 References D.L. Kreher and D.R. Stinson, Combinatorial Algorithms: Generation, Enumeration and Search, CRC press LTC, Boca Raton, Florida, / 22
Use of patterns in n-tuple combinatorial generation
 Use of patterns in n-tuple combinatorial generation Dominik Zalewski Faculty of Mathematics and Computer Science UAM Otwarte Wykłady dla Doktorantów 25-26 May 2007 Agenda 1 Applications Peer-to-peer networks
Use of patterns in n-tuple combinatorial generation Dominik Zalewski Faculty of Mathematics and Computer Science UAM Otwarte Wykłady dla Doktorantów 25-26 May 2007 Agenda 1 Applications Peer-to-peer networks
Practice Exam 1 CIS/CSE 607, Spring 2009
 Practice Exam 1 CIS/CSE 607, Spring 2009 Problem 1) Let R be a reflexive binary relation on a set A. Prove that R is transitive if, and only if, R = R R. Problem 2) Give an example of a transitive binary
Practice Exam 1 CIS/CSE 607, Spring 2009 Problem 1) Let R be a reflexive binary relation on a set A. Prove that R is transitive if, and only if, R = R R. Problem 2) Give an example of a transitive binary
A new Euler-Mahonian constructive bijection
 A new Euler-Mahonian constructive bijection Vincent Vajnovszki LE2I, Université de Bourgogne BP 47870, 21078 Dijon Cedex, France vvajnov@u-bourgogne.fr March 19, 2011 Abstract Using generating functions,
A new Euler-Mahonian constructive bijection Vincent Vajnovszki LE2I, Université de Bourgogne BP 47870, 21078 Dijon Cedex, France vvajnov@u-bourgogne.fr March 19, 2011 Abstract Using generating functions,
Generating Permutations and Combinations
 Generating Permutations and Combinations March 0, 005 Generating Permutations We have learned that there are n! permutations of {,,, n} It is important in many instances to generate a list of such permutations
Generating Permutations and Combinations March 0, 005 Generating Permutations We have learned that there are n! permutations of {,,, n} It is important in many instances to generate a list of such permutations
T Combinatorial algorithms. Combinatorial structures. T Combinatorial algorithms
 T 79.5202 Combinatorial algorithms Harri Haanpää Laboratory for Theoretical Computer Science, TKK Spring 2007 Enumerating structures Enumerating subsets Permutations and enumerating them Integer partitions
T 79.5202 Combinatorial algorithms Harri Haanpää Laboratory for Theoretical Computer Science, TKK Spring 2007 Enumerating structures Enumerating subsets Permutations and enumerating them Integer partitions
1 The Algebraic Normal Form
 1 The Algebraic Normal Form Boolean maps can be expressed by polynomials this is the algebraic normal form (ANF). The degree as a polynomial is a first obvious measure of nonlinearity linear (or affine)
1 The Algebraic Normal Form Boolean maps can be expressed by polynomials this is the algebraic normal form (ANF). The degree as a polynomial is a first obvious measure of nonlinearity linear (or affine)
Gray Codes and Overlap Cycles for Restricted Weight Words
 Gray Codes and Overlap Cycles for Restricted Weight Words Victoria Horan Air Force Research Laboratory Information Directorate Glenn Hurlbert School of Mathematical and Statistical Sciences Arizona State
Gray Codes and Overlap Cycles for Restricted Weight Words Victoria Horan Air Force Research Laboratory Information Directorate Glenn Hurlbert School of Mathematical and Statistical Sciences Arizona State
Week 4-5: Generating Permutations and Combinations
 Week 4-5: Generating Permutations and Combinations February 27, 2017 1 Generating Permutations We have learned that there are n! permutations of {1, 2,...,n}. It is important in many instances to generate
Week 4-5: Generating Permutations and Combinations February 27, 2017 1 Generating Permutations We have learned that there are n! permutations of {1, 2,...,n}. It is important in many instances to generate
SYMMETRIC (66,26,10) DESIGNS HAVING F rob 55 AUTOMORPHISM GROUP AS AN. Dean Crnković and Sanja Rukavina Faculty of Philosophy in Rijeka, Croatia
 GLASNIK MATEMATIČKI Vol. 35(55)(2000), 271 281 SYMMETRIC (66,26,10) DESIGNS HAVING F rob 55 AUTOMORPHISM GROUP AS AN Dean Crnković and Sanja Rukavina Faculty of Philosophy in Rijeka, Croatia Abstract.
GLASNIK MATEMATIČKI Vol. 35(55)(2000), 271 281 SYMMETRIC (66,26,10) DESIGNS HAVING F rob 55 AUTOMORPHISM GROUP AS AN Dean Crnković and Sanja Rukavina Faculty of Philosophy in Rijeka, Croatia Abstract.
Exploring the infinite : an introduction to proof and analysis / Jennifer Brooks. Boca Raton [etc.], cop Spis treści
![Exploring the infinite : an introduction to proof and analysis / Jennifer Brooks. Boca Raton [etc.], cop Spis treści Exploring the infinite : an introduction to proof and analysis / Jennifer Brooks. Boca Raton [etc.], cop Spis treści](/thumbs/89/97813041.jpg) Exploring the infinite : an introduction to proof and analysis / Jennifer Brooks. Boca Raton [etc.], cop. 2017 Spis treści Preface xiii I Fundamentals of Abstract Mathematics 1 1 Basic Notions 3 1.1 A
Exploring the infinite : an introduction to proof and analysis / Jennifer Brooks. Boca Raton [etc.], cop. 2017 Spis treści Preface xiii I Fundamentals of Abstract Mathematics 1 1 Basic Notions 3 1.1 A
Homework 7 Solutions, Math 55
 Homework 7 Solutions, Math 55 5..36. (a) Since a is a positive integer, a = a 1 + b 0 is a positive integer of the form as + bt for some integers s and t, so a S. Thus S is nonempty. (b) Since S is nonempty,
Homework 7 Solutions, Math 55 5..36. (a) Since a is a positive integer, a = a 1 + b 0 is a positive integer of the form as + bt for some integers s and t, so a S. Thus S is nonempty. (b) Since S is nonempty,
Pollard s Rho Algorithm for Elliptic Curves
 November 30, 2015 Consider the elliptic curve E over F 2 k, where E = n. Assume we want to solve the elliptic curve discrete logarithm problem: find k in Q = kp. Partition E into S 1 S 2 S 3, where the
November 30, 2015 Consider the elliptic curve E over F 2 k, where E = n. Assume we want to solve the elliptic curve discrete logarithm problem: find k in Q = kp. Partition E into S 1 S 2 S 3, where the
Introduction to Randomized Algorithms: Quick Sort and Quick Selection
 Chapter 14 Introduction to Randomized Algorithms: Quick Sort and Quick Selection CS 473: Fundamental Algorithms, Spring 2011 March 10, 2011 14.1 Introduction to Randomized Algorithms 14.2 Introduction
Chapter 14 Introduction to Randomized Algorithms: Quick Sort and Quick Selection CS 473: Fundamental Algorithms, Spring 2011 March 10, 2011 14.1 Introduction to Randomized Algorithms 14.2 Introduction
CDM Combinatorial Principles
 CDM Combinatorial Principles 1 Counting Klaus Sutner Carnegie Mellon University Pigeon Hole 22-in-exclusion 2017/12/15 23:16 Inclusion/Exclusion Counting 3 Aside: Ranking and Unranking 4 Counting is arguably
CDM Combinatorial Principles 1 Counting Klaus Sutner Carnegie Mellon University Pigeon Hole 22-in-exclusion 2017/12/15 23:16 Inclusion/Exclusion Counting 3 Aside: Ranking and Unranking 4 Counting is arguably
Divide-and-Conquer and Recurrence Relations: Notes on Chapter 2, Dasgupta et.al. Howard A. Blair
 Divide-and-Conquer and Recurrence Relations: Notes on Chapter 2, Dasgupta et.al. Howard A. Blair 1 Multiplication Example 1.1: Carl Friedrich Gauss (1777-1855): The multiplication of two complex numbers
Divide-and-Conquer and Recurrence Relations: Notes on Chapter 2, Dasgupta et.al. Howard A. Blair 1 Multiplication Example 1.1: Carl Friedrich Gauss (1777-1855): The multiplication of two complex numbers
Some results on the existence of t-all-or-nothing transforms over arbitrary alphabets
 Some results on the existence of t-all-or-nothing transforms over arbitrary alphabets Navid Nasr Esfahani, Ian Goldberg and Douglas R. Stinson David R. Cheriton School of Computer Science University of
Some results on the existence of t-all-or-nothing transforms over arbitrary alphabets Navid Nasr Esfahani, Ian Goldberg and Douglas R. Stinson David R. Cheriton School of Computer Science University of
De Bruijn Sequences for the Binary Strings with Maximum Density
 De Bruijn Sequences for the Binary Strings with Maximum Density Joe Sawada 1, Brett Stevens 2, and Aaron Williams 2 1 jsawada@uoguelph.ca School of Computer Science, University of Guelph, CANADA 2 brett@math.carleton.ca
De Bruijn Sequences for the Binary Strings with Maximum Density Joe Sawada 1, Brett Stevens 2, and Aaron Williams 2 1 jsawada@uoguelph.ca School of Computer Science, University of Guelph, CANADA 2 brett@math.carleton.ca
Definition: Let S and T be sets. A binary relation on SxT is any subset of SxT. A binary relation on S is any subset of SxS.
 4 Functions Before studying functions we will first quickly define a more general idea, namely the notion of a relation. A function turns out to be a special type of relation. Definition: Let S and T be
4 Functions Before studying functions we will first quickly define a more general idea, namely the notion of a relation. A function turns out to be a special type of relation. Definition: Let S and T be
BIJECTIVE PROOFS FOR FIBONACCI IDENTITIES RELATED TO ZECKENDORF S THEOREM
 BIJECTIVE PROOFS FOR FIBONACCI IDENTITIES RELATED TO ZECKENDORF S THEOREM Philip Matchett Wood Department of Mathematics, Rutgers University, Piscataway, NJ 08854 e-mail: matchett@math.rutgers.edu (Submitted
BIJECTIVE PROOFS FOR FIBONACCI IDENTITIES RELATED TO ZECKENDORF S THEOREM Philip Matchett Wood Department of Mathematics, Rutgers University, Piscataway, NJ 08854 e-mail: matchett@math.rutgers.edu (Submitted
Constant Time Generation of Set Partitions
 930 PAPER Special Section on Selected Papers from the 17th Workshop on Circuits and Systems in Karuizawa Constant Time Generation of Set Partitions Shin-ichiro KAWANO a) and Shin-ichi NAKANO b), Members
930 PAPER Special Section on Selected Papers from the 17th Workshop on Circuits and Systems in Karuizawa Constant Time Generation of Set Partitions Shin-ichiro KAWANO a) and Shin-ichi NAKANO b), Members
Mathematical Structures Combinations and Permutations
 Definitions: Suppose S is a (finite) set and n, k 0 are integers The set C(S, k) of k - combinations consists of all subsets of S that have exactly k elements The set P (S, k) of k - permutations consists
Definitions: Suppose S is a (finite) set and n, k 0 are integers The set C(S, k) of k - combinations consists of all subsets of S that have exactly k elements The set P (S, k) of k - permutations consists
Randomized Sorting Algorithms Quick sort can be converted to a randomized algorithm by picking the pivot element randomly. In this case we can show th
 CSE 3500 Algorithms and Complexity Fall 2016 Lecture 10: September 29, 2016 Quick sort: Average Run Time In the last lecture we started analyzing the expected run time of quick sort. Let X = k 1, k 2,...,
CSE 3500 Algorithms and Complexity Fall 2016 Lecture 10: September 29, 2016 Quick sort: Average Run Time In the last lecture we started analyzing the expected run time of quick sort. Let X = k 1, k 2,...,
arxiv: v1 [math.nt] 4 Mar 2014
![arxiv: v1 [math.nt] 4 Mar 2014 arxiv: v1 [math.nt] 4 Mar 2014](/thumbs/95/124152467.jpg) VARIATIONS ON A GENERATINGFUNCTIONAL THEME: ENUMERATING COMPOSITIONS WITH PARTS AVOIDING AN ARITHMETIC SEQUENCE arxiv:403.0665v [math.nt] 4 Mar 204 MATTHIAS BECK AND NEVILLE ROBBINS Abstract. A composition
VARIATIONS ON A GENERATINGFUNCTIONAL THEME: ENUMERATING COMPOSITIONS WITH PARTS AVOIDING AN ARITHMETIC SEQUENCE arxiv:403.0665v [math.nt] 4 Mar 204 MATTHIAS BECK AND NEVILLE ROBBINS Abstract. A composition
Orthogonal arrays of strength three from regular 3-wise balanced designs
 Orthogonal arrays of strength three from regular 3-wise balanced designs Charles J. Colbourn Computer Science University of Vermont Burlington, Vermont 05405 D. L. Kreher Mathematical Sciences Michigan
Orthogonal arrays of strength three from regular 3-wise balanced designs Charles J. Colbourn Computer Science University of Vermont Burlington, Vermont 05405 D. L. Kreher Mathematical Sciences Michigan
F = k Z +F k T = k Z +T k. ν(x) :=0 (x N) By the successor function one means the function σ in T 1 defined as follows: σ(x) :=x +1 (x N)
 RECURSIVE FUNCTIONS Thomas Wieting Reed College, 1996 1 Recursive Functions 2 Recursive Mappings 3 Recursively Enumerable/Decidable Sets 1 Recursive Functions 1 Let N stand for the set of all nonnegative
RECURSIVE FUNCTIONS Thomas Wieting Reed College, 1996 1 Recursive Functions 2 Recursive Mappings 3 Recursively Enumerable/Decidable Sets 1 Recursive Functions 1 Let N stand for the set of all nonnegative
Efficient random number generation on FPGA-s
 Proceedings of the 9 th International Conference on Applied Informatics Eger, Hungary, January 29 February 1, 2014. Vol. 1. pp. 313 320 doi: 10.14794/ICAI.9.2014.1.313 Efficient random number generation
Proceedings of the 9 th International Conference on Applied Informatics Eger, Hungary, January 29 February 1, 2014. Vol. 1. pp. 313 320 doi: 10.14794/ICAI.9.2014.1.313 Efficient random number generation
The constructible universe
 The constructible universe In this set of notes I want to sketch Gödel s proof that CH is consistent with the other axioms of set theory. Gödel s argument goes well beyond this result; his identification
The constructible universe In this set of notes I want to sketch Gödel s proof that CH is consistent with the other axioms of set theory. Gödel s argument goes well beyond this result; his identification
Computing Isomorphism [Ch.7, Kreher & Stinson] [Ch.3, Kaski & Östergård]
![Computing Isomorphism [Ch.7, Kreher & Stinson] [Ch.3, Kaski & Östergård] Computing Isomorphism [Ch.7, Kreher & Stinson] [Ch.3, Kaski & Östergård]](/thumbs/86/94909433.jpg) Computing Isomorphism [Ch.7, Kreher & Stinson] [Ch.3, Kaski & Östergård] Winter 2009 Introduction Isomorphism of Combinatorial Objects In general, isomorphism is an equivalence relation on a set of objects.
Computing Isomorphism [Ch.7, Kreher & Stinson] [Ch.3, Kaski & Östergård] Winter 2009 Introduction Isomorphism of Combinatorial Objects In general, isomorphism is an equivalence relation on a set of objects.
Finding the Largest Fixed-Density Necklace and Lyndon word
 Finding the Largest Fixed-Density Necklace and Lyndon word Joe Sawada Patrick Hartman April 18, 2017 Abstract We present an O(n) time algorithm for finding the lexicographically largest fixed-density necklace
Finding the Largest Fixed-Density Necklace and Lyndon word Joe Sawada Patrick Hartman April 18, 2017 Abstract We present an O(n) time algorithm for finding the lexicographically largest fixed-density necklace
Topics in Algorithms. 1 Generation of Basic Combinatorial Objects. Exercises. 1.1 Generation of Subsets. 1. Consider the sum:
 Topics in Algorithms Exercises 1 Generation of Basic Combinatorial Objects 1.1 Generation of Subsets 1. Consider the sum: (ε 1,...,ε n) {0,1} n f(ε 1,..., ε n ) (a) Show that it may be calculated in O(n)
Topics in Algorithms Exercises 1 Generation of Basic Combinatorial Objects 1.1 Generation of Subsets 1. Consider the sum: (ε 1,...,ε n) {0,1} n f(ε 1,..., ε n ) (a) Show that it may be calculated in O(n)
Additional Constructions to Solve the Generalized Russian Cards Problem using Combinatorial Designs
 Additional Constructions to Solve the Generalized Russian Cards Problem using Combinatorial Designs Colleen M. Swanson Computer Science & Engineering Division University of Michigan Ann Arbor, MI 48109,
Additional Constructions to Solve the Generalized Russian Cards Problem using Combinatorial Designs Colleen M. Swanson Computer Science & Engineering Division University of Michigan Ann Arbor, MI 48109,
Nonexistence of (9, 112, 4) and (10, 224, 5) binary orthogonal arrays
 Nonexistence of (9, 112, 4) and (10, 224, 5) binary orthogonal arrays Tanya Marinova, Maya Stoyanova Faculty of Mathematics and Informatics, Sofia University St. Kliment Ohridski, Sofia, Bulgaria 15 th
Nonexistence of (9, 112, 4) and (10, 224, 5) binary orthogonal arrays Tanya Marinova, Maya Stoyanova Faculty of Mathematics and Informatics, Sofia University St. Kliment Ohridski, Sofia, Bulgaria 15 th
Lecture 5: Fusion Trees (ctd.) Johannes Fischer
 Lecture 5: Fusion Trees (ctd.) Johannes Fischer Fusion Trees fusion tree pred/succ O(lg n / lg w) w.c. construction O(n) w.c. + SORT(n,w) space O(n) w.c. 2 2 Idea B-tree with branching factor b=w /5 b
Lecture 5: Fusion Trees (ctd.) Johannes Fischer Fusion Trees fusion tree pred/succ O(lg n / lg w) w.c. construction O(n) w.c. + SORT(n,w) space O(n) w.c. 2 2 Idea B-tree with branching factor b=w /5 b
CS1800 Discrete Structures Final Version A
 CS1800 Discrete Structures Fall 2017 Profs. Aslam, Gold, & Pavlu December 11, 2017 CS1800 Discrete Structures Final Version A Instructions: 1. The exam is closed book and closed notes. You may not use
CS1800 Discrete Structures Fall 2017 Profs. Aslam, Gold, & Pavlu December 11, 2017 CS1800 Discrete Structures Final Version A Instructions: 1. The exam is closed book and closed notes. You may not use
Data selection. Lower complexity bound for sorting
 Data selection. Lower complexity bound for sorting Lecturer: Georgy Gimel farb COMPSCI 220 Algorithms and Data Structures 1 / 12 1 Data selection: Quickselect 2 Lower complexity bound for sorting 3 The
Data selection. Lower complexity bound for sorting Lecturer: Georgy Gimel farb COMPSCI 220 Algorithms and Data Structures 1 / 12 1 Data selection: Quickselect 2 Lower complexity bound for sorting 3 The
Monotone Gray Codes and the Middle Levels Problem
 Monotone Gray Codes and the Middle Levels Problem Carla D. Savage Department of Computer Science North Carolina State University Raleigh, North Carolina 27695-8206 cds@adm.csc.ncsu.edu Peter Winkler Bellcore
Monotone Gray Codes and the Middle Levels Problem Carla D. Savage Department of Computer Science North Carolina State University Raleigh, North Carolina 27695-8206 cds@adm.csc.ncsu.edu Peter Winkler Bellcore
Relations. Binary Relation. Let A and B be sets. A (binary) relation from A to B is a subset of A B. Notation. Let R A B be a relation from A to B.
 Relations Binary Relation Let A and B be sets. A (binary) relation from A to B is a subset of A B. Notation Let R A B be a relation from A to B. If (a, b) R, we write a R b. 1 Binary Relation Example:
Relations Binary Relation Let A and B be sets. A (binary) relation from A to B is a subset of A B. Notation Let R A B be a relation from A to B. If (a, b) R, we write a R b. 1 Binary Relation Example:
Bijective proofs for Fibonacci identities related to Zeckendorf s Theorem
 Bijective proofs for Fibonacci identities related to Zeckendorf s Theorem Philip Matchett Wood Department of Mathematics, Rutgers University, Hill Center Busch Campus, 0 Frelinghuysen Rd, Piscataway, NJ
Bijective proofs for Fibonacci identities related to Zeckendorf s Theorem Philip Matchett Wood Department of Mathematics, Rutgers University, Hill Center Busch Campus, 0 Frelinghuysen Rd, Piscataway, NJ
PARTITIONS OF FINITE VECTOR SPACES INTO SUBSPACES
 PARTITIONS OF FINITE VECTOR SPACES INTO SUBSPACES S.I. EL-ZANATI, G.F. SEELINGER, P.A. SISSOKHO, L.E. SPENCE, AND C. VANDEN EYNDEN Abstract. Let V n (q) denote a vector space of dimension n over the field
PARTITIONS OF FINITE VECTOR SPACES INTO SUBSPACES S.I. EL-ZANATI, G.F. SEELINGER, P.A. SISSOKHO, L.E. SPENCE, AND C. VANDEN EYNDEN Abstract. Let V n (q) denote a vector space of dimension n over the field
A fast algorithm to generate necklaces with xed content
 Theoretical Computer Science 301 (003) 477 489 www.elsevier.com/locate/tcs Note A fast algorithm to generate necklaces with xed content Joe Sawada 1 Department of Computer Science, University of Toronto,
Theoretical Computer Science 301 (003) 477 489 www.elsevier.com/locate/tcs Note A fast algorithm to generate necklaces with xed content Joe Sawada 1 Department of Computer Science, University of Toronto,
Hanoi Graphs and Some Classical Numbers
 Hanoi Graphs and Some Classical Numbers Sandi Klavžar Uroš Milutinović Ciril Petr Abstract The Hanoi graphs Hp n model the p-pegs n-discs Tower of Hanoi problem(s). It was previously known that Stirling
Hanoi Graphs and Some Classical Numbers Sandi Klavžar Uroš Milutinović Ciril Petr Abstract The Hanoi graphs Hp n model the p-pegs n-discs Tower of Hanoi problem(s). It was previously known that Stirling
New Constructions for De Bruijn Tori
 New Constructions for De Bruijn Tori Glenn Hurlbert Garth Isaak Dedicated to the memory of Tony Brewster Abstract A De Bruijn torus is a periodic d dimensional k ary array such that each n 1 n d k ary
New Constructions for De Bruijn Tori Glenn Hurlbert Garth Isaak Dedicated to the memory of Tony Brewster Abstract A De Bruijn torus is a periodic d dimensional k ary array such that each n 1 n d k ary
MODEL ANSWERS TO THE SEVENTH HOMEWORK. (b) We proved in homework six, question 2 (c) that. But we also proved homework six, question 2 (a) that
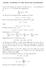 MODEL ANSWERS TO THE SEVENTH HOMEWORK 1. Let X be a finite set, and let A, B and A 1, A 2,..., A n be subsets of X. Let A c = X \ A denote the complement. (a) χ A (x) = A. x X (b) We proved in homework
MODEL ANSWERS TO THE SEVENTH HOMEWORK 1. Let X be a finite set, and let A, B and A 1, A 2,..., A n be subsets of X. Let A c = X \ A denote the complement. (a) χ A (x) = A. x X (b) We proved in homework
Generalized hyper-bent functions over GF(p)
 Discrete Applied Mathematics 55 2007) 066 070 Note Generalized hyper-bent functions over GFp) A.M. Youssef Concordia Institute for Information Systems Engineering, Concordia University, Montreal, QC, H3G
Discrete Applied Mathematics 55 2007) 066 070 Note Generalized hyper-bent functions over GFp) A.M. Youssef Concordia Institute for Information Systems Engineering, Concordia University, Montreal, QC, H3G
R ij = 2. Using all of these facts together, you can solve problem number 9.
 Help for Homework Problem #9 Let G(V,E) be any undirected graph We want to calculate the travel time across the graph. Think of each edge as one resistor of 1 Ohm. Say we have two nodes: i and j Let the
Help for Homework Problem #9 Let G(V,E) be any undirected graph We want to calculate the travel time across the graph. Think of each edge as one resistor of 1 Ohm. Say we have two nodes: i and j Let the
Iterations of sum of powers of digits
 International Journal of Computer Discovered Mathematics (IJCDM) ISSN 2367-7775 c IJCDM November 2015, Volume 0, No.0, pp.21-26. Received 18 July 2015. Published on-line 15 September 2015 web: http://www.journal-1.eu/
International Journal of Computer Discovered Mathematics (IJCDM) ISSN 2367-7775 c IJCDM November 2015, Volume 0, No.0, pp.21-26. Received 18 July 2015. Published on-line 15 September 2015 web: http://www.journal-1.eu/
Sets of MOLSs generated from a single Latin square
 Sets of MOLSs generated from a single Latin square Hau Chan and Dinesh G Sarvate Abstract The aim of this note is to present an observation on the families of square matrices generated by repeated application
Sets of MOLSs generated from a single Latin square Hau Chan and Dinesh G Sarvate Abstract The aim of this note is to present an observation on the families of square matrices generated by repeated application
Necklaces Pólya s Enumeration Theorem. Pólya Counting I. Gordon Royle. Semester 1, 2004
 Semester 1, 2004 George Pólya (1887 1985) George Polya discovered a powerful general method for enumerating the number of orbits of a group on particular configurations. This method became known as the
Semester 1, 2004 George Pólya (1887 1985) George Polya discovered a powerful general method for enumerating the number of orbits of a group on particular configurations. This method became known as the
Alternative Combinatorial Gray Codes
 Alternative Combinatorial Gray Codes Cormier-Iijima, Samuel sciyoshi@gmail.com December 17, 2010 Abstract Gray codes have numerous applications in a variety of fields, including error correction, encryption,
Alternative Combinatorial Gray Codes Cormier-Iijima, Samuel sciyoshi@gmail.com December 17, 2010 Abstract Gray codes have numerous applications in a variety of fields, including error correction, encryption,
Characterization of 2 n -Periodic Binary Sequences with Fixed 2-error or 3-error Linear Complexity
 Characterization of n -Periodic Binary Sequences with Fixed -error or 3-error Linear Complexity Ramakanth Kavuluru Department of Computer Science, University of Kentucky, Lexington, KY 40506, USA. Abstract
Characterization of n -Periodic Binary Sequences with Fixed -error or 3-error Linear Complexity Ramakanth Kavuluru Department of Computer Science, University of Kentucky, Lexington, KY 40506, USA. Abstract
Tricks of the Trade in Combinatorics and Arithmetic
 Tricks of the Trade in Combinatorics and Arithmetic Zachary Friggstad Programming Club Meeting Fast Exponentiation Given integers a, b with b 0, compute a b exactly. Fast Exponentiation Given integers
Tricks of the Trade in Combinatorics and Arithmetic Zachary Friggstad Programming Club Meeting Fast Exponentiation Given integers a, b with b 0, compute a b exactly. Fast Exponentiation Given integers
Number Theory. Modular Arithmetic
 Number Theory The branch of mathematics that is important in IT security especially in cryptography. Deals only in integer numbers and the process can be done in a very fast manner. Modular Arithmetic
Number Theory The branch of mathematics that is important in IT security especially in cryptography. Deals only in integer numbers and the process can be done in a very fast manner. Modular Arithmetic
EXHAUSTIVELY generating a class of combinatorial objects
 International Conference on Mechanical, Production and Materials Engineering (ICMPME') June 6-7,, Bangkok An Improving Scheme of Unranking t-ary Trees in Gray-code Order Ro Yu Wu, Jou Ming Chang, An Hang
International Conference on Mechanical, Production and Materials Engineering (ICMPME') June 6-7,, Bangkok An Improving Scheme of Unranking t-ary Trees in Gray-code Order Ro Yu Wu, Jou Ming Chang, An Hang
ON THE CONSTRUCTION OF ORTHOGONAL BALANCED INCOMPLETE BLOCK DESIGNS
 Hacettepe Journal of Mathematics and Statistics Volume 35 (2) (2006), 235 240 ON THE CONSTRUCTION OF ORTHOGONAL BALANCED INCOMPLETE BLOCK DESIGNS Hülya Bayrak and Hanife Bulut Received 20 : 02 : 2006 :
Hacettepe Journal of Mathematics and Statistics Volume 35 (2) (2006), 235 240 ON THE CONSTRUCTION OF ORTHOGONAL BALANCED INCOMPLETE BLOCK DESIGNS Hülya Bayrak and Hanife Bulut Received 20 : 02 : 2006 :
SIMPLE ALGORITHM FOR SORTING THE FIBONACCI STRING ROTATIONS
 SIMPLE ALGORITHM FOR SORTING THE FIBONACCI STRING ROTATIONS Manolis Christodoulakis 1, Costas S. Iliopoulos 1, Yoan José Pinzón Ardila 2 1 King s College London, Department of Computer Science London WC2R
SIMPLE ALGORITHM FOR SORTING THE FIBONACCI STRING ROTATIONS Manolis Christodoulakis 1, Costas S. Iliopoulos 1, Yoan José Pinzón Ardila 2 1 King s College London, Department of Computer Science London WC2R
Latin Squares and Orthogonal Arrays
 School of Electrical Engineering and Computer Science University of Ottawa lucia@eecs.uottawa.ca Winter 2017 Latin squares Definition A Latin square of order n is an n n array, with symbols in {1,...,
School of Electrical Engineering and Computer Science University of Ottawa lucia@eecs.uottawa.ca Winter 2017 Latin squares Definition A Latin square of order n is an n n array, with symbols in {1,...,
arxiv: v1 [math.co] 25 Apr 2013
![arxiv: v1 [math.co] 25 Apr 2013 arxiv: v1 [math.co] 25 Apr 2013](/thumbs/90/104444248.jpg) GRAHAM S NUMBER IS LESS THAN 2 6 MIKHAIL LAVROV 1, MITCHELL LEE 2, AND JOHN MACKEY 3 arxiv:1304.6910v1 [math.co] 25 Apr 2013 Abstract. In [5], Graham and Rothschild consider a geometric Ramsey problem:
GRAHAM S NUMBER IS LESS THAN 2 6 MIKHAIL LAVROV 1, MITCHELL LEE 2, AND JOHN MACKEY 3 arxiv:1304.6910v1 [math.co] 25 Apr 2013 Abstract. In [5], Graham and Rothschild consider a geometric Ramsey problem:
Ch6 Addition Proofs of Theorems on permutations.
 Ch6 Addition Proofs of Theorems on permutations. Definition Two permutations ρ and π of a set A are disjoint if every element moved by ρ is fixed by π and every element moved by π is fixed by ρ. (In other
Ch6 Addition Proofs of Theorems on permutations. Definition Two permutations ρ and π of a set A are disjoint if every element moved by ρ is fixed by π and every element moved by π is fixed by ρ. (In other
Part V. Chapter 19. Congruence of integers
 Part V. Chapter 19. Congruence of integers Congruence modulo m Let m be a positive integer. Definition. Integers a and b are congruent modulo m if and only if a b is divisible by m. For example, 1. 277
Part V. Chapter 19. Congruence of integers Congruence modulo m Let m be a positive integer. Definition. Integers a and b are congruent modulo m if and only if a b is divisible by m. For example, 1. 277
Outline. We will now investigate the structure of this important set.
 The Reals Outline As we have seen, the set of real numbers, R, has cardinality c. This doesn't tell us very much about the reals, since there are many sets with this cardinality and cardinality doesn't
The Reals Outline As we have seen, the set of real numbers, R, has cardinality c. This doesn't tell us very much about the reals, since there are many sets with this cardinality and cardinality doesn't
Harvard CS 121 and CSCI E-207 Lecture 6: Regular Languages and Countability
 Harvard CS 121 and CSCI E-207 Lecture 6: Regular Languages and Countability Salil Vadhan September 20, 2012 Reading: Sipser, 1.3 and The Diagonalization Method, pages 174 178 (from just before Definition
Harvard CS 121 and CSCI E-207 Lecture 6: Regular Languages and Countability Salil Vadhan September 20, 2012 Reading: Sipser, 1.3 and The Diagonalization Method, pages 174 178 (from just before Definition
COMBINATORIAL COUNTING
 COMBINATORIAL COUNTING Our main reference is [1, Section 3] 1 Basic counting: functions and subsets Theorem 11 (Arbitrary mapping Let N be an n-element set (it may also be empty and let M be an m-element
COMBINATORIAL COUNTING Our main reference is [1, Section 3] 1 Basic counting: functions and subsets Theorem 11 (Arbitrary mapping Let N be an n-element set (it may also be empty and let M be an m-element
arxiv: v1 [math.co] 10 Sep 2010
![arxiv: v1 [math.co] 10 Sep 2010 arxiv: v1 [math.co] 10 Sep 2010](/thumbs/85/92228468.jpg) Ranking and unranking trees with a given number or a given set of leaves arxiv:1009.2060v1 [math.co] 10 Sep 2010 Jeffery B. Remmel Department of Mathematics U.C.S.D., La Jolla, CA, 92093-0112 jremmel@ucsd.edu
Ranking and unranking trees with a given number or a given set of leaves arxiv:1009.2060v1 [math.co] 10 Sep 2010 Jeffery B. Remmel Department of Mathematics U.C.S.D., La Jolla, CA, 92093-0112 jremmel@ucsd.edu
Number Theory Basics Z = {..., 2, 1, 0, 1, 2,...} For, b Z, we say that divides b if z = b for some. Notation: b Fact: for all, b, c Z:
 Number Theory Basics Z = {..., 2, 1, 0, 1, 2,...} For, b Z, we say that divides b if z = b for some z Z Notation: b Fact: for all, b, c Z:, 1, and 0 0 = 0 b and b c = c b and c = (b + c) b and b = ±b 1
Number Theory Basics Z = {..., 2, 1, 0, 1, 2,...} For, b Z, we say that divides b if z = b for some z Z Notation: b Fact: for all, b, c Z:, 1, and 0 0 = 0 b and b c = c b and c = (b + c) b and b = ±b 1
A conjecture on the alphabet size needed to produce all correlation classes of pairs of words
 A conjecture on the alphabet size needed to produce all correlation classes of pairs of words Paul Leopardi Thanks: Jörg Arndt, Michael Barnsley, Richard Brent, Sylvain Forêt, Judy-anne Osborn. Mathematical
A conjecture on the alphabet size needed to produce all correlation classes of pairs of words Paul Leopardi Thanks: Jörg Arndt, Michael Barnsley, Richard Brent, Sylvain Forêt, Judy-anne Osborn. Mathematical
Subquadratic Space Complexity Multiplication over Binary Fields with Dickson Polynomial Representation
 Subquadratic Space Complexity Multiplication over Binary Fields with Dickson Polynomial Representation M A Hasan and C Negre Abstract We study Dickson bases for binary field representation Such representation
Subquadratic Space Complexity Multiplication over Binary Fields with Dickson Polynomial Representation M A Hasan and C Negre Abstract We study Dickson bases for binary field representation Such representation
Coloring Vertices and Edges of a Path by Nonempty Subsets of a Set
 Coloring Vertices and Edges of a Path by Nonempty Subsets of a Set P.N. Balister E. Győri R.H. Schelp April 28, 28 Abstract A graph G is strongly set colorable if V (G) E(G) can be assigned distinct nonempty
Coloring Vertices and Edges of a Path by Nonempty Subsets of a Set P.N. Balister E. Győri R.H. Schelp April 28, 28 Abstract A graph G is strongly set colorable if V (G) E(G) can be assigned distinct nonempty
Part IA Numbers and Sets
 Part IA Numbers and Sets Definitions Based on lectures by A. G. Thomason Notes taken by Dexter Chua Michaelmas 2014 These notes are not endorsed by the lecturers, and I have modified them (often significantly)
Part IA Numbers and Sets Definitions Based on lectures by A. G. Thomason Notes taken by Dexter Chua Michaelmas 2014 These notes are not endorsed by the lecturers, and I have modified them (often significantly)
Chapter 4 Mathematics of Cryptography
 Chapter 4 Mathematics of Cryptography Part II: Algebraic Structures Copyright The McGraw-Hill Companies, Inc. Permission required for reproduction or display. 4.1 Chapter 4 Objectives To review the concept
Chapter 4 Mathematics of Cryptography Part II: Algebraic Structures Copyright The McGraw-Hill Companies, Inc. Permission required for reproduction or display. 4.1 Chapter 4 Objectives To review the concept
Ranks of Hadamard Matrices and Equivalence of Sylvester Hadamard and Pseudo-Noise Matrices
 Operator Theory: Advances and Applications, Vol 1, 1 13 c 27 Birkhäuser Verlag Basel/Switzerland Ranks of Hadamard Matrices and Equivalence of Sylvester Hadamard and Pseudo-Noise Matrices Tom Bella, Vadim
Operator Theory: Advances and Applications, Vol 1, 1 13 c 27 Birkhäuser Verlag Basel/Switzerland Ranks of Hadamard Matrices and Equivalence of Sylvester Hadamard and Pseudo-Noise Matrices Tom Bella, Vadim
AN EXPLICIT UNIVERSAL CYCLE FOR THE (n 1)-PERMUTATIONS OF AN n-set
 AN EXPLICIT UNIVERSAL CYCLE FOR THE (n 1)-PERMUTATIONS OF AN n-set FRANK RUSKEY AND AARON WILLIAMS Abstract. We show how to construct an explicit Hamilton cycle in the directed Cayley graph Cay({σ n, σ
AN EXPLICIT UNIVERSAL CYCLE FOR THE (n 1)-PERMUTATIONS OF AN n-set FRANK RUSKEY AND AARON WILLIAMS Abstract. We show how to construct an explicit Hamilton cycle in the directed Cayley graph Cay({σ n, σ
Chapter 5: Integer Compositions and Partitions and Set Partitions
 Chapter 5: Integer Compositions and Partitions and Set Partitions Prof. Tesler Math 184A Winter 2017 Prof. Tesler Ch. 5: Compositions and Partitions Math 184A / Winter 2017 1 / 32 5.1. Compositions A strict
Chapter 5: Integer Compositions and Partitions and Set Partitions Prof. Tesler Math 184A Winter 2017 Prof. Tesler Ch. 5: Compositions and Partitions Math 184A / Winter 2017 1 / 32 5.1. Compositions A strict
Golomb-Lempel Construction of Costas Arrays Revisited
 International Journal of Mathematics and Computer Science, 10(2015), no. 2, 239 249 M CS Golomb-Lempel Construction of Costas Arrays Revisited Ishani Barua University of Engineering & Management Jaipur,
International Journal of Mathematics and Computer Science, 10(2015), no. 2, 239 249 M CS Golomb-Lempel Construction of Costas Arrays Revisited Ishani Barua University of Engineering & Management Jaipur,
Finite Mathematics. Nik Ruškuc and Colva M. Roney-Dougal
 Finite Mathematics Nik Ruškuc and Colva M. Roney-Dougal September 19, 2011 Contents 1 Introduction 3 1 About the course............................. 3 2 A review of some algebraic structures.................
Finite Mathematics Nik Ruškuc and Colva M. Roney-Dougal September 19, 2011 Contents 1 Introduction 3 1 About the course............................. 3 2 A review of some algebraic structures.................
TESTING FOR A SEMILATTICE TERM
 TESTING FOR A SEMILATTICE TERM RALPH FREESE, J.B. NATION, AND MATT VALERIOTE Abstract. This paper investigates the computational complexity of deciding if a given finite algebra is an expansion of a semilattice.
TESTING FOR A SEMILATTICE TERM RALPH FREESE, J.B. NATION, AND MATT VALERIOTE Abstract. This paper investigates the computational complexity of deciding if a given finite algebra is an expansion of a semilattice.
Chapter 5: Integer Compositions and Partitions and Set Partitions
 Chapter 5: Integer Compositions and Partitions and Set Partitions Prof. Tesler Math 184A Fall 2017 Prof. Tesler Ch. 5: Compositions and Partitions Math 184A / Fall 2017 1 / 46 5.1. Compositions A strict
Chapter 5: Integer Compositions and Partitions and Set Partitions Prof. Tesler Math 184A Fall 2017 Prof. Tesler Ch. 5: Compositions and Partitions Math 184A / Fall 2017 1 / 46 5.1. Compositions A strict
Classical Cryptography
 Classical Cryptography CSG 252 Fall 2006 Riccardo Pucella Goals of Cryptography Alice wants to send message X to Bob Oscar is on the wire, listening to communications Alice and Bob share a key K Alice
Classical Cryptography CSG 252 Fall 2006 Riccardo Pucella Goals of Cryptography Alice wants to send message X to Bob Oscar is on the wire, listening to communications Alice and Bob share a key K Alice
REPORT DOCUMENTATION PAGE
 REPORT DOCUMENTATION PAGE Form Approved OMB No. 0704-0188 The public reporting burden for this collection of information is estimated to average 1 hour per response, including the time for reviewing instructions,
REPORT DOCUMENTATION PAGE Form Approved OMB No. 0704-0188 The public reporting burden for this collection of information is estimated to average 1 hour per response, including the time for reviewing instructions,
Fast Sorting and Selection. A Lower Bound for Worst Case
 Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 0 Fast Sorting and Selection USGS NEIC. Public domain government image. A Lower Bound
Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 0 Fast Sorting and Selection USGS NEIC. Public domain government image. A Lower Bound
The Chinese Remainder Theorem
 The Chinese Remainder Theorem R. C. Daileda February 19, 2018 1 The Chinese Remainder Theorem We begin with an example. Example 1. Consider the system of simultaneous congruences x 3 (mod 5), x 2 (mod
The Chinese Remainder Theorem R. C. Daileda February 19, 2018 1 The Chinese Remainder Theorem We begin with an example. Example 1. Consider the system of simultaneous congruences x 3 (mod 5), x 2 (mod
Permutations with Ascending and Descending Blocks
 Permutations with Ascending and Descending Blocks Jacob Steinhardt jacob.steinhardt@gmail.com Submitted: Aug 29, 2009; Accepted: Jan 4, 200; Published: Jan 4, 200 Mathematics Subject Classification: 05A05
Permutations with Ascending and Descending Blocks Jacob Steinhardt jacob.steinhardt@gmail.com Submitted: Aug 29, 2009; Accepted: Jan 4, 200; Published: Jan 4, 200 Mathematics Subject Classification: 05A05
New quasi-symmetric designs constructed using mutually orthogonal Latin squares and Hadamard matrices
 New quasi-symmetric designs constructed using mutually orthogonal Latin squares and Hadamard matrices Carl Bracken, Gary McGuire Department of Mathematics, National University of Ireland, Maynooth, Co.
New quasi-symmetric designs constructed using mutually orthogonal Latin squares and Hadamard matrices Carl Bracken, Gary McGuire Department of Mathematics, National University of Ireland, Maynooth, Co.
Constructing c-ary Perfect Factors
 Constructing c-ary Perfect Factors Chris J. Mitchell Computer Science Department Royal Holloway University of London Egham Hill Egham Surrey TW20 0EX England. Tel.: +44 784 443423 Fax: +44 784 443420 Email:
Constructing c-ary Perfect Factors Chris J. Mitchell Computer Science Department Royal Holloway University of London Egham Hill Egham Surrey TW20 0EX England. Tel.: +44 784 443423 Fax: +44 784 443420 Email:
Generating Functions
 Semester 1, 2004 Generating functions Another means of organising enumeration. Two examples we have seen already. Example 1. Binomial coefficients. Let X = {1, 2,..., n} c k = # k-element subsets of X
Semester 1, 2004 Generating functions Another means of organising enumeration. Two examples we have seen already. Example 1. Binomial coefficients. Let X = {1, 2,..., n} c k = # k-element subsets of X
Reverse mathematics and marriage problems with unique solutions
 Reverse mathematics and marriage problems with unique solutions Jeffry L. Hirst and Noah A. Hughes January 28, 2014 Abstract We analyze the logical strength of theorems on marriage problems with unique
Reverse mathematics and marriage problems with unique solutions Jeffry L. Hirst and Noah A. Hughes January 28, 2014 Abstract We analyze the logical strength of theorems on marriage problems with unique
INEQUALITIES OF SYMMETRIC FUNCTIONS. 1. Introduction to Symmetric Functions [?] Definition 1.1. A symmetric function in n variables is a function, f,
![INEQUALITIES OF SYMMETRIC FUNCTIONS. 1. Introduction to Symmetric Functions [?] Definition 1.1. A symmetric function in n variables is a function, f, INEQUALITIES OF SYMMETRIC FUNCTIONS. 1. Introduction to Symmetric Functions [?] Definition 1.1. A symmetric function in n variables is a function, f,](/thumbs/87/97372587.jpg) INEQUALITIES OF SMMETRIC FUNCTIONS JONATHAN D. LIMA Abstract. We prove several symmetric function inequalities and conjecture a partially proved comprehensive theorem. We also introduce the condition of
INEQUALITIES OF SMMETRIC FUNCTIONS JONATHAN D. LIMA Abstract. We prove several symmetric function inequalities and conjecture a partially proved comprehensive theorem. We also introduce the condition of
A Universal Turing Machine
 A Universal Turing Machine A limitation of Turing Machines: Turing Machines are hardwired they execute only one program Real Computers are re-programmable Solution: Universal Turing Machine Attributes:
A Universal Turing Machine A limitation of Turing Machines: Turing Machines are hardwired they execute only one program Real Computers are re-programmable Solution: Universal Turing Machine Attributes:
CSE101: Design and Analysis of Algorithms. Ragesh Jaiswal, CSE, UCSD
 Greedy s Greedy s Shortest path Claim 2: Let S be a subset of vertices containing s such that we know the shortest path length l(s, u) from s to any vertex in u S. Let e = (u, v) be an edge such that 1
Greedy s Greedy s Shortest path Claim 2: Let S be a subset of vertices containing s such that we know the shortest path length l(s, u) from s to any vertex in u S. Let e = (u, v) be an edge such that 1
Andrews Curtis Groups and the Andrews Curtis Conjecture
 Andrews Curtis Groups and the Andrews Curtis Conjecture Adam Piggott adam.piggott@tufts.edu Tufts University p. 1/33 Credits and further info This work has appeared in the Journal of Group Theory 10 (2007)
Andrews Curtis Groups and the Andrews Curtis Conjecture Adam Piggott adam.piggott@tufts.edu Tufts University p. 1/33 Credits and further info This work has appeared in the Journal of Group Theory 10 (2007)
A Kruskal-Katona Type Theorem for the Linear Lattice
 A Kruskal-Katona Type Theorem for the Linear Lattice Sergei Bezrukov Department of Mathematics and Computer Science University of Paderborn Fürstenallee 11 D-33102 Paderborn, Germany Aart Blokhuis Department
A Kruskal-Katona Type Theorem for the Linear Lattice Sergei Bezrukov Department of Mathematics and Computer Science University of Paderborn Fürstenallee 11 D-33102 Paderborn, Germany Aart Blokhuis Department
Roux-type Constructions for Covering Arrays of Strengths Three
 Roux-type Constructions for Covering Arrays of Strengths Three and Four Charles J. Colbourn Computer Science and Engineering Arizona State University P.O. Box 878809, Tempe, AZ 85287, U.S.A. charles.colbourn@asu.edu
Roux-type Constructions for Covering Arrays of Strengths Three and Four Charles J. Colbourn Computer Science and Engineering Arizona State University P.O. Box 878809, Tempe, AZ 85287, U.S.A. charles.colbourn@asu.edu
Some recent results on all-or-nothing transforms, or All or nothing at all
 Some recent results on all-or-nothing transforms, or All or nothing at all Douglas R. Stinson David R. Cheriton School of Computer Science University of Waterloo Alex Rosa 80, Mikulov, June 27 30, 2017
Some recent results on all-or-nothing transforms, or All or nothing at all Douglas R. Stinson David R. Cheriton School of Computer Science University of Waterloo Alex Rosa 80, Mikulov, June 27 30, 2017
Section 11.1 Sequences
 Math 152 c Lynch 1 of 8 Section 11.1 Sequences A sequence is a list of numbers written in a definite order: a 1, a 2, a 3,..., a n,... Notation. The sequence {a 1, a 2, a 3,...} can also be written {a
Math 152 c Lynch 1 of 8 Section 11.1 Sequences A sequence is a list of numbers written in a definite order: a 1, a 2, a 3,..., a n,... Notation. The sequence {a 1, a 2, a 3,...} can also be written {a
MATH 215 Sets (S) Definition 1 A set is a collection of objects. The objects in a set X are called elements of X.
 MATH 215 Sets (S) Definition 1 A set is a collection of objects. The objects in a set X are called elements of X. Notation 2 A set can be described using set-builder notation. That is, a set can be described
MATH 215 Sets (S) Definition 1 A set is a collection of objects. The objects in a set X are called elements of X. Notation 2 A set can be described using set-builder notation. That is, a set can be described
ICT12 8. Linear codes. The Gilbert-Varshamov lower bound and the MacWilliams identities SXD
 1 ICT12 8. Linear codes. The Gilbert-Varshamov lower bound and the MacWilliams identities 19.10.2012 SXD 8.1. The Gilbert Varshamov existence condition 8.2. The MacWilliams identities 2 8.1. The Gilbert
1 ICT12 8. Linear codes. The Gilbert-Varshamov lower bound and the MacWilliams identities 19.10.2012 SXD 8.1. The Gilbert Varshamov existence condition 8.2. The MacWilliams identities 2 8.1. The Gilbert
Algorithms (II) Yu Yu. Shanghai Jiaotong University
 Algorithms (II) Yu Yu Shanghai Jiaotong University Chapter 1. Algorithms with Numbers Two seemingly similar problems Factoring: Given a number N, express it as a product of its prime factors. Primality:
Algorithms (II) Yu Yu Shanghai Jiaotong University Chapter 1. Algorithms with Numbers Two seemingly similar problems Factoring: Given a number N, express it as a product of its prime factors. Primality:
Apollonian Circle Packings: Number Theory II. Spherical and Hyperbolic Packings
 Apollonian Circle Packings: Number Theory II. Spherical and Hyperbolic Packings Nicholas Eriksson University of California at Berkeley Berkeley, CA 942 Jeffrey C. Lagarias University of Michigan Ann Arbor,
Apollonian Circle Packings: Number Theory II. Spherical and Hyperbolic Packings Nicholas Eriksson University of California at Berkeley Berkeley, CA 942 Jeffrey C. Lagarias University of Michigan Ann Arbor,
Efficient Enumeration of Regular Languages
 Efficient Enumeration of Regular Languages Margareta Ackerman and Jeffrey Shallit University of Waterloo, Waterloo ON, Canada mackerma@uwaterloo.ca, shallit@graceland.uwaterloo.ca Abstract. The cross-section
Efficient Enumeration of Regular Languages Margareta Ackerman and Jeffrey Shallit University of Waterloo, Waterloo ON, Canada mackerma@uwaterloo.ca, shallit@graceland.uwaterloo.ca Abstract. The cross-section
5. Peano arithmetic and Gödel s incompleteness theorem
 5. Peano arithmetic and Gödel s incompleteness theorem In this chapter we give the proof of Gödel s incompleteness theorem, modulo technical details treated in subsequent chapters. The incompleteness theorem
5. Peano arithmetic and Gödel s incompleteness theorem In this chapter we give the proof of Gödel s incompleteness theorem, modulo technical details treated in subsequent chapters. The incompleteness theorem
Higher Bruhat order on Weyl groups of Type B
 Mentor: Daniel Thompson Massachusetts Institute of Technology PRIMES-USA, 2013 Outline 1 Purpose 2 Symmetric Group Inversions Bruhat Graph 3 Results/Conjectures Purpose Purpose For Weyl Groups of Type
Mentor: Daniel Thompson Massachusetts Institute of Technology PRIMES-USA, 2013 Outline 1 Purpose 2 Symmetric Group Inversions Bruhat Graph 3 Results/Conjectures Purpose Purpose For Weyl Groups of Type
