1. Solve each linear system using Gaussian elimination or Gauss-Jordan reduction. The augmented matrix of this linear system is
|
|
|
- Winfred Ramsey
- 5 years ago
- Views:
Transcription
1 Solutions to Homework Additional Problems. Solve each linear system using Gaussian elimination or Gauss-Jordan reduction. (a) x + y = 8 3x + 4y = 7 x + y = 3 The augmented matrix of this linear system is The row operations r r 3, r 3r r, r 3 r r 3, r 3 + r r take the augmented 3 matrix to the matrix 0, which is in REF Using Gaussian elimination: The matrix in REF is the system x + y = 3, y =. Substituting y = into the first equation gives [ ] x = 5 so the only solution is x = 5, y =. Written as a vector this is. 5 Using Gauss-Jordan reduction: The row operation r r r will take the 0 5 matrix in REF to the matrix 0, which is in RREF. This system 0 0 [ 0 ] 5 is x = 5, y = so the only solution is. (b) x + y + z = 3 x + y z = 3 [ ] 3 The augmented matrix of this linear system is. The row 3 operations r r r, ( /3)r r take the augmented matrix to the matrix [ ], which is in REF. Using Gaussian elimination: The matrix in REF is the system x + y + z = 3, z =. Substituting z = into the first equation gives x + y =. The column corresponding to y does not have a leading, so y can be anything y and x = y. The solutions are all vectors of the y.
2 Using Gauss-Jordan reduction: [ The row operation ] r r r will take the 0 matrix in REF to the matrix, which is in RREF. This system 0 0 is x + y =, z =. The column corresponding to y does not have a leading, so y can be anything and x = y. The solutions are all vectors of the y y. (c) x + y + z = 4x 3y + z = 7 3x y + z = The augmented matrix for this system is The row operations r 3 r r 3, r r 3, r r r, r 3 4r r 3, r 3 r r 3 get the 0 matrix 0 5. This is not yet in REF, but we can see from row that there are no solutions.. Let A be an m n matrix and b be an m-vector such that Ax = b is a consistent linear system. Let x p be a solution to Ax = b and let 0 be the zero m-vector. (a) Prove that if x h is a solution to Ax = 0, then x p + x h is a solution to Ax = b. If x h is a solution to Ax = 0, then Ax h = 0. Also, since x p is a solution to Ax = b this means that Ax p = b. We want to use these facts to prove that x p + x h is a solution to Ax = b. To do this, we just need to plug in x p + x h for x in the equation Ax = b and show that the equation still holds. Using the properties of matrix operations, A(x p + x h ) = Ax p + Ax h = b + 0 = b, so x p + x h is a solution to Ax = b. (b) Prove that if x is a solution to Ax = b, then x x p is a solution to Ax = 0. If x is a solution to Ax = b, then Ax = b. As in the previous part, we know that Ax p = b. To prove that x x p is a solution to Ax = 0, we plug in x x p for x in the equation Ax = 0 and show that the equation still holds. Using the properties of matrix operations, A(x x p ) = Ax Ax p = b b = 0, so x x p is a solution to Ax = 0.
3 (c) Use the previous two parts to explain why the following statement is true: The solutions to Ax = b are exactly the vectors of the x p + x h where x h is a solution to the homogeneous linear system Ax = 0. We know from part (a) that any vector of the x p + x h where x h is a solution to the homogeneous linear system Ax = 0 is a solution to Ax = b. It remains to show that there are no other solutions that do not have this. In other words, we need to show given any solution, we can always write it in the x p + x h where x h is a solution to the homogeneous linear system Ax = 0. If x is any solution to Ax = b, then x = x p + (x x p ). By part (b), the vector x x p is a solution to Ax = 0 so we take x h = x x p and we have shown that x has the x p + x h where x h is a solution to the homogeneous linear system Ax = 0. Note: The p and h used as subscripts in this problem stand for particular and homogeneous Let A = The RREF of A is Let b = (a) Find all solutions to the homogeneous linear system Ax = 0. We will label the RREF of A as B. The augmented matrix of the homogeneous linear system looks like [A : 0]. Note that the last column is all zeros and doing row operations will not change a column of zeros. It follows that the RREF of [A : 0] is [B : 0]. Therefore the solutions to Ax = 0 are the same as the solutions to Bx = 0. Then [B : 0] = If we label the variables a, b, c, d, e we see that the columns corresponding to c, e do not contain leading ones. Therefore c, e are free variables and the other variables can be solved in terms of these variables. The fourth equation is 0 = 0 which is true but gives us no ination. The third equation is d + 4e = 0 so d = 4e. The second equation is b + c + e = 0 so b = c e. The first equation is a c + 3e = 0 so a = c 3e. Putting this all together, we get that the solutions to the homogeneous linear system are all vectors of the 3
4 c 3e c e 4e, where c, e can be any real numbers. e Note: To check this answer, you can multiply by A and make sure everything cancels to give you the zero vector. (b) Prove that is a solution to the linear system Ax = b. Plug in for x in Ax = b and see if the equation holds. A = 3 8 3() + () + ( )(0) + ( )() + ( ) = () + () + (0) + () + 8( ) 7() + ( )() + ( 9)(0) + ( 4)() + 4( ) = () + 3() + (0) + ( 5)() + ( )( ) 4 3 = b. 8 (c) Find all solutions to Ax = b. Hint: Use the result from problem c. This has augmented matrix [A : b]. The RREF is NOT going to be [B : b], because the row operations used to get from A to B will change b. If we wanted to solve this by finding RREF of [A : b], we would have to figure out the row operations used to get from A to B and do them to b. However we can avoid doing any row operations by using Problem c and the results from parts (a) and (b) of this problem. By Problem c, we know that if we have a particular solution x p to the linear system Ax = b, then the solutions to Ax = b are all vectors that look like x p + x h where x h is a solution to the 4
5 homogeneous linear system Ax = 0. By part (b), we can take x p =. By part (a), the solutions to the homogeneous system are all vectors of the c 3e c e 4e. The solutions to Ax = b are therefore all vectors of the e c 3e + c e 4e, or written as single vector, all vectors of the e + c 3e c e 4e. + e 5
Solutions to Homework 5 - Math 3410
 Solutions to Homework 5 - Math 34 (Page 57: # 489) Determine whether the following vectors in R 4 are linearly dependent or independent: (a) (, 2, 3, ), (3, 7,, 2), (, 3, 7, 4) Solution From x(, 2, 3,
Solutions to Homework 5 - Math 34 (Page 57: # 489) Determine whether the following vectors in R 4 are linearly dependent or independent: (a) (, 2, 3, ), (3, 7,, 2), (, 3, 7, 4) Solution From x(, 2, 3,
7.5 Operations with Matrices. Copyright Cengage Learning. All rights reserved.
 7.5 Operations with Matrices Copyright Cengage Learning. All rights reserved. What You Should Learn Decide whether two matrices are equal. Add and subtract matrices and multiply matrices by scalars. Multiply
7.5 Operations with Matrices Copyright Cengage Learning. All rights reserved. What You Should Learn Decide whether two matrices are equal. Add and subtract matrices and multiply matrices by scalars. Multiply
Chapter Practice Test Name: Period: Date:
 Name: Period: Date: 1. Draw the graph of the following system: 3 x+ 5 y+ 13 = 0 29 x 11 y 7 = 0 3 13 y = x 3x+ 5y+ 13= 0 5 5 29x 11y 7 = 0 29 7 y = x 11 11 Practice Test Page 1 2. Determine the ordered
Name: Period: Date: 1. Draw the graph of the following system: 3 x+ 5 y+ 13 = 0 29 x 11 y 7 = 0 3 13 y = x 3x+ 5y+ 13= 0 5 5 29x 11y 7 = 0 29 7 y = x 11 11 Practice Test Page 1 2. Determine the ordered
Section Gaussian Elimination
 Section. - Gaussian Elimination A matrix is said to be in row echelon form (REF) if it has the following properties:. The first nonzero entry in any row is a. We call this a leading one or pivot one..
Section. - Gaussian Elimination A matrix is said to be in row echelon form (REF) if it has the following properties:. The first nonzero entry in any row is a. We call this a leading one or pivot one..
9.1 - Systems of Linear Equations: Two Variables
 9.1 - Systems of Linear Equations: Two Variables Recall that a system of equations consists of two or more equations each with two or more variables. A solution to a system in two variables is an ordered
9.1 - Systems of Linear Equations: Two Variables Recall that a system of equations consists of two or more equations each with two or more variables. A solution to a system in two variables is an ordered
Sections 6.1 and 6.2: Systems of Linear Equations
 What is a linear equation? Sections 6.1 and 6.2: Systems of Linear Equations We are now going to discuss solving systems of two or more linear equations with two variables. Recall that solving an equation
What is a linear equation? Sections 6.1 and 6.2: Systems of Linear Equations We are now going to discuss solving systems of two or more linear equations with two variables. Recall that solving an equation
Homework 1 Due: Wednesday, August 27. x + y + z = 1. x y = 3 x + y + z = c 2 2x + cz = 4
 Homework 1 Due: Wednesday, August 27 1. Find all values of c for which the linear system: (a) has no solutions. (b) has exactly one solution. (c) has infinitely many solutions. (d) is consistent. x + y
Homework 1 Due: Wednesday, August 27 1. Find all values of c for which the linear system: (a) has no solutions. (b) has exactly one solution. (c) has infinitely many solutions. (d) is consistent. x + y
Review for Exam Find all a for which the following linear system has no solutions, one solution, and infinitely many solutions.
 Review for Exam. Find all a for which the following linear system has no solutions, one solution, and infinitely many solutions. x + y z = 2 x + 2y + z = 3 x + y + (a 2 5)z = a 2 The augmented matrix for
Review for Exam. Find all a for which the following linear system has no solutions, one solution, and infinitely many solutions. x + y z = 2 x + 2y + z = 3 x + y + (a 2 5)z = a 2 The augmented matrix for
Linear Algebra I Lecture 10
 Linear Algebra I Lecture 10 Xi Chen 1 1 University of Alberta January 30, 2019 Outline 1 Gauss-Jordan Algorithm ] Let A = [a ij m n be an m n matrix. To reduce A to a reduced row echelon form using elementary
Linear Algebra I Lecture 10 Xi Chen 1 1 University of Alberta January 30, 2019 Outline 1 Gauss-Jordan Algorithm ] Let A = [a ij m n be an m n matrix. To reduce A to a reduced row echelon form using elementary
Inverting Matrices. 1 Properties of Transpose. 2 Matrix Algebra. P. Danziger 3.2, 3.3
 3., 3.3 Inverting Matrices P. Danziger 1 Properties of Transpose Transpose has higher precedence than multiplication and addition, so AB T A ( B T and A + B T A + ( B T As opposed to the bracketed expressions
3., 3.3 Inverting Matrices P. Danziger 1 Properties of Transpose Transpose has higher precedence than multiplication and addition, so AB T A ( B T and A + B T A + ( B T As opposed to the bracketed expressions
Number of solutions of a system
 Roberto s Notes on Linear Algebra Chapter 3: Linear systems and matrices Section 7 Number of solutions of a system What you need to know already: How to solve a linear system by using Gauss- Jordan elimination.
Roberto s Notes on Linear Algebra Chapter 3: Linear systems and matrices Section 7 Number of solutions of a system What you need to know already: How to solve a linear system by using Gauss- Jordan elimination.
Chapter 1. Vectors, Matrices, and Linear Spaces
 1.4 Solving Systems of Linear Equations 1 Chapter 1. Vectors, Matrices, and Linear Spaces 1.4. Solving Systems of Linear Equations Note. We give an algorithm for solving a system of linear equations (called
1.4 Solving Systems of Linear Equations 1 Chapter 1. Vectors, Matrices, and Linear Spaces 1.4. Solving Systems of Linear Equations Note. We give an algorithm for solving a system of linear equations (called
Midterm 1 Review. Written by Victoria Kala SH 6432u Office Hours: R 12:30 1:30 pm Last updated 10/10/2015
 Midterm 1 Review Written by Victoria Kala vtkala@math.ucsb.edu SH 6432u Office Hours: R 12:30 1:30 pm Last updated 10/10/2015 Summary This Midterm Review contains notes on sections 1.1 1.5 and 1.7 in your
Midterm 1 Review Written by Victoria Kala vtkala@math.ucsb.edu SH 6432u Office Hours: R 12:30 1:30 pm Last updated 10/10/2015 Summary This Midterm Review contains notes on sections 1.1 1.5 and 1.7 in your
Lecture 12: Solving Systems of Linear Equations by Gaussian Elimination
 Lecture 12: Solving Systems of Linear Equations by Gaussian Elimination Winfried Just, Ohio University September 22, 2017 Review: The coefficient matrix Consider a system of m linear equations in n variables.
Lecture 12: Solving Systems of Linear Equations by Gaussian Elimination Winfried Just, Ohio University September 22, 2017 Review: The coefficient matrix Consider a system of m linear equations in n variables.
System of Linear Equations
 Chapter 7 - S&B Gaussian and Gauss-Jordan Elimination We will study systems of linear equations by describing techniques for solving such systems. The preferred solution technique- Gaussian elimination-
Chapter 7 - S&B Gaussian and Gauss-Jordan Elimination We will study systems of linear equations by describing techniques for solving such systems. The preferred solution technique- Gaussian elimination-
CHAPTER 9: Systems of Equations and Matrices
 MAT 171 Precalculus Algebra Dr. Claude Moore Cape Fear Community College CHAPTER 9: Systems of Equations and Matrices 9.1 Systems of Equations in Two Variables 9.2 Systems of Equations in Three Variables
MAT 171 Precalculus Algebra Dr. Claude Moore Cape Fear Community College CHAPTER 9: Systems of Equations and Matrices 9.1 Systems of Equations in Two Variables 9.2 Systems of Equations in Three Variables
Math 1314 Week #14 Notes
 Math 3 Week # Notes Section 5.: A system of equations consists of two or more equations. A solution to a system of equations is a point that satisfies all the equations in the system. In this chapter,
Math 3 Week # Notes Section 5.: A system of equations consists of two or more equations. A solution to a system of equations is a point that satisfies all the equations in the system. In this chapter,
SOLVING Ax = b: GAUSS-JORDAN ELIMINATION [LARSON 1.2]
![SOLVING Ax = b: GAUSS-JORDAN ELIMINATION [LARSON 1.2] SOLVING Ax = b: GAUSS-JORDAN ELIMINATION [LARSON 1.2]](/thumbs/91/104518447.jpg) SOLVING Ax = b: GAUSS-JORDAN ELIMINATION [LARSON.2 EQUIVALENT LINEAR SYSTEMS: Two m n linear systems are equivalent both systems have the exact same solution sets. When solving a linear system Ax = b,
SOLVING Ax = b: GAUSS-JORDAN ELIMINATION [LARSON.2 EQUIVALENT LINEAR SYSTEMS: Two m n linear systems are equivalent both systems have the exact same solution sets. When solving a linear system Ax = b,
Linear System Equations
 King Saud University September 24, 2018 Table of contents 1 2 3 4 Definition A linear system of equations with m equations and n unknowns is defined as follows: a 1,1 x 1 + a 1,2 x 2 + + a 1,n x n = b
King Saud University September 24, 2018 Table of contents 1 2 3 4 Definition A linear system of equations with m equations and n unknowns is defined as follows: a 1,1 x 1 + a 1,2 x 2 + + a 1,n x n = b
Quadratic Formula: - another method for solving quadratic equations (ax 2 + bx + c = 0)
 In the previous lesson we showed how to solve quadratic equations that were not factorable and were not perfect squares by making perfect square trinomials using a process called completing the square.
In the previous lesson we showed how to solve quadratic equations that were not factorable and were not perfect squares by making perfect square trinomials using a process called completing the square.
The matrix will only be consistent if the last entry of row three is 0, meaning 2b 3 + b 2 b 1 = 0.
 ) Find all solutions of the linear system. Express the answer in vector form. x + 2x + x + x 5 = 2 2x 2 + 2x + 2x + x 5 = 8 x + 2x + x + 9x 5 = 2 2 Solution: Reduce the augmented matrix [ 2 2 2 8 ] to
) Find all solutions of the linear system. Express the answer in vector form. x + 2x + x + x 5 = 2 2x 2 + 2x + 2x + x 5 = 8 x + 2x + x + 9x 5 = 2 2 Solution: Reduce the augmented matrix [ 2 2 2 8 ] to
3.4 Elementary Matrices and Matrix Inverse
 Math 220: Summer 2015 3.4 Elementary Matrices and Matrix Inverse A n n elementary matrix is a matrix which is obtained from the n n identity matrix I n n by a single elementary row operation. Elementary
Math 220: Summer 2015 3.4 Elementary Matrices and Matrix Inverse A n n elementary matrix is a matrix which is obtained from the n n identity matrix I n n by a single elementary row operation. Elementary
Exercise Sketch these lines and find their intersection.
 These are brief notes for the lecture on Friday August 21, 2009: they are not complete, but they are a guide to what I want to say today. They are not guaranteed to be correct. 1. Solving systems of linear
These are brief notes for the lecture on Friday August 21, 2009: they are not complete, but they are a guide to what I want to say today. They are not guaranteed to be correct. 1. Solving systems of linear
If A is a 4 6 matrix and B is a 6 3 matrix then the dimension of AB is A. 4 6 B. 6 6 C. 4 3 D. 3 4 E. Undefined
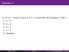 Question 1 If A is a 4 6 matrix and B is a 6 3 matrix then the dimension of AB is A. 4 6 B. 6 6 C. 4 3 D. 3 4 E. Undefined Quang T. Bach Math 18 October 18, 2017 1 / 17 Question 2 1 2 Let A = 3 4 1 2 3
Question 1 If A is a 4 6 matrix and B is a 6 3 matrix then the dimension of AB is A. 4 6 B. 6 6 C. 4 3 D. 3 4 E. Undefined Quang T. Bach Math 18 October 18, 2017 1 / 17 Question 2 1 2 Let A = 3 4 1 2 3
Matrices and Determinants
 Math Assignment Eperts is a leading provider of online Math help. Our eperts have prepared sample assignments to demonstrate the quality of solution we provide. If you are looking for mathematics help
Math Assignment Eperts is a leading provider of online Math help. Our eperts have prepared sample assignments to demonstrate the quality of solution we provide. If you are looking for mathematics help
Notes on Row Reduction
 Notes on Row Reduction Francis J. Narcowich Department of Mathematics Texas A&M University September The Row-Reduction Algorithm The row-reduced form of a matrix contains a great deal of information, both
Notes on Row Reduction Francis J. Narcowich Department of Mathematics Texas A&M University September The Row-Reduction Algorithm The row-reduced form of a matrix contains a great deal of information, both
CHAPTER 9: Systems of Equations and Matrices
 MAT 171 Precalculus Algebra Dr. Claude Moore Cape Fear Community College CHAPTER 9: Systems of Equations and Matrices 9.1 Systems of Equations in Two Variables 9.2 Systems of Equations in Three Variables
MAT 171 Precalculus Algebra Dr. Claude Moore Cape Fear Community College CHAPTER 9: Systems of Equations and Matrices 9.1 Systems of Equations in Two Variables 9.2 Systems of Equations in Three Variables
LECTURES 4/5: SYSTEMS OF LINEAR EQUATIONS
 LECTURES 4/5: SYSTEMS OF LINEAR EQUATIONS MA1111: LINEAR ALGEBRA I, MICHAELMAS 2016 1 Linear equations We now switch gears to discuss the topic of solving linear equations, and more interestingly, systems
LECTURES 4/5: SYSTEMS OF LINEAR EQUATIONS MA1111: LINEAR ALGEBRA I, MICHAELMAS 2016 1 Linear equations We now switch gears to discuss the topic of solving linear equations, and more interestingly, systems
Math 1021, Linear Algebra 1. Section: A at 10am, B at 2:30pm
 Math 1021, Linear Algebra 1. Section: A at 10am, B at 2:30pm All course information is available on Moodle. Text: Nicholson, Linear algebra with applications, 7th edition. We shall cover Chapters 1,2,3,4,5:
Math 1021, Linear Algebra 1. Section: A at 10am, B at 2:30pm All course information is available on Moodle. Text: Nicholson, Linear algebra with applications, 7th edition. We shall cover Chapters 1,2,3,4,5:
Methods for Solving Linear Systems Part 2
 Methods for Solving Linear Systems Part 2 We have studied the properties of matrices and found out that there are more ways that we can solve Linear Systems. In Section 7.3, we learned that we can use
Methods for Solving Linear Systems Part 2 We have studied the properties of matrices and found out that there are more ways that we can solve Linear Systems. In Section 7.3, we learned that we can use
Example: 2x y + 3z = 1 5y 6z = 0 x + 4z = 7. Definition: Elementary Row Operations. Example: Type I swap rows 1 and 3
 Math 0 Row Reduced Echelon Form Techniques for solving systems of linear equations lie at the heart of linear algebra. In high school we learn to solve systems with or variables using elimination and substitution
Math 0 Row Reduced Echelon Form Techniques for solving systems of linear equations lie at the heart of linear algebra. In high school we learn to solve systems with or variables using elimination and substitution
2018 Fall 2210Q Section 013 Midterm Exam I Solution
 8 Fall Q Section 3 Midterm Exam I Solution True or False questions ( points = points) () An example of a linear combination of vectors v, v is the vector v. True. We can write v as v + v. () If two matrices
8 Fall Q Section 3 Midterm Exam I Solution True or False questions ( points = points) () An example of a linear combination of vectors v, v is the vector v. True. We can write v as v + v. () If two matrices
INVERSE OF A MATRIX [2.2]
![INVERSE OF A MATRIX [2.2] INVERSE OF A MATRIX [2.2]](/thumbs/75/72004651.jpg) INVERSE OF A MATRIX [2.2] The inverse of a matrix: Introduction We have a mapping from R n to R n represented by a matrix A. Can we invert this mapping? i.e. can we find a matrix (call it B for now) such
INVERSE OF A MATRIX [2.2] The inverse of a matrix: Introduction We have a mapping from R n to R n represented by a matrix A. Can we invert this mapping? i.e. can we find a matrix (call it B for now) such
MODEL ANSWERS TO THE THIRD HOMEWORK
 MODEL ANSWERS TO THE THIRD HOMEWORK 1 (i) We apply Gaussian elimination to A First note that the second row is a multiple of the first row So we need to swap the second and third rows 1 3 2 1 2 6 5 7 3
MODEL ANSWERS TO THE THIRD HOMEWORK 1 (i) We apply Gaussian elimination to A First note that the second row is a multiple of the first row So we need to swap the second and third rows 1 3 2 1 2 6 5 7 3
Example: 2x y + 3z = 1 5y 6z = 0 x + 4z = 7. Definition: Elementary Row Operations. Example: Type I swap rows 1 and 3
 Linear Algebra Row Reduced Echelon Form Techniques for solving systems of linear equations lie at the heart of linear algebra. In high school we learn to solve systems with or variables using elimination
Linear Algebra Row Reduced Echelon Form Techniques for solving systems of linear equations lie at the heart of linear algebra. In high school we learn to solve systems with or variables using elimination
7.6 The Inverse of a Square Matrix
 7.6 The Inverse of a Square Matrix Copyright Cengage Learning. All rights reserved. What You Should Learn Verify that two matrices are inverses of each other. Use Gauss-Jordan elimination to find inverses
7.6 The Inverse of a Square Matrix Copyright Cengage Learning. All rights reserved. What You Should Learn Verify that two matrices are inverses of each other. Use Gauss-Jordan elimination to find inverses
Suggested problems solutions
 Suggested problems solutions Solving systems using Gauss-Jordan elimination P: Whih of the matries below are in redued row ehelon form? If a matrix is not in redued row ehelon form, explain where it fails,
Suggested problems solutions Solving systems using Gauss-Jordan elimination P: Whih of the matries below are in redued row ehelon form? If a matrix is not in redued row ehelon form, explain where it fails,
Math Computation Test 1 September 26 th, 2016 Debate: Computation vs. Theory Whatever wins, it ll be Huuuge!
 Math 5- Computation Test September 6 th, 6 Debate: Computation vs. Theory Whatever wins, it ll be Huuuge! Name: Answer Key: Making Math Great Again Be sure to show your work!. (8 points) Consider the following
Math 5- Computation Test September 6 th, 6 Debate: Computation vs. Theory Whatever wins, it ll be Huuuge! Name: Answer Key: Making Math Great Again Be sure to show your work!. (8 points) Consider the following
CHAPTER 8: Matrices and Determinants
 (Exercises for Chapter 8: Matrices and Determinants) E.8.1 CHAPTER 8: Matrices and Determinants (A) means refer to Part A, (B) means refer to Part B, etc. Most of these exercises can be done without a
(Exercises for Chapter 8: Matrices and Determinants) E.8.1 CHAPTER 8: Matrices and Determinants (A) means refer to Part A, (B) means refer to Part B, etc. Most of these exercises can be done without a
Matrix Solutions to Linear Equations
 Matrix Solutions to Linear Equations Augmented matrices can be used as a simplified way of writing a system of linear equations. In an augmented matrix, a vertical line is placed inside the matrix to represent
Matrix Solutions to Linear Equations Augmented matrices can be used as a simplified way of writing a system of linear equations. In an augmented matrix, a vertical line is placed inside the matrix to represent
Statistical methods. Mean value and standard deviations Standard statistical distributions Linear systems Matrix algebra
 Statistical methods Mean value and standard deviations Standard statistical distributions Linear systems Matrix algebra Statistical methods Generating random numbers MATLAB has many built-in functions
Statistical methods Mean value and standard deviations Standard statistical distributions Linear systems Matrix algebra Statistical methods Generating random numbers MATLAB has many built-in functions
MATH 2050 Assignment 6 Fall 2018 Due: Thursday, November 1. x + y + 2z = 2 x + y + z = c 4x + 2z = 2
 MATH 5 Assignment 6 Fall 8 Due: Thursday, November [5]. For what value of c does have a solution? Is it unique? x + y + z = x + y + z = c 4x + z = Writing the system as an augmented matrix, we have c R
MATH 5 Assignment 6 Fall 8 Due: Thursday, November [5]. For what value of c does have a solution? Is it unique? x + y + z = x + y + z = c 4x + z = Writing the system as an augmented matrix, we have c R
Lecture 4: Gaussian Elimination and Homogeneous Equations
 Lecture 4: Gaussian Elimination and Homogeneous Equations Reduced Row Echelon Form An augmented matrix associated to a system of linear equations is said to be in Reduced Row Echelon Form (RREF) if the
Lecture 4: Gaussian Elimination and Homogeneous Equations Reduced Row Echelon Form An augmented matrix associated to a system of linear equations is said to be in Reduced Row Echelon Form (RREF) if the
Section 5.2 Solving Recurrence Relations
 Section 5.2 Solving Recurrence Relations If a g(n) = f (a g(0),a g(1),..., a g(n 1) ) find a closed form or an expression for a g(n). Recall: nth degree polynomials have n roots: a n x n + a n 1 x n 1
Section 5.2 Solving Recurrence Relations If a g(n) = f (a g(0),a g(1),..., a g(n 1) ) find a closed form or an expression for a g(n). Recall: nth degree polynomials have n roots: a n x n + a n 1 x n 1
Definition of Equality of Matrices. Example 1: Equality of Matrices. Consider the four matrices
 IT 131: Mathematics for Science Lecture Notes 3 Source: Larson, Edwards, Falvo (2009): Elementary Linear Algebra, Sixth Edition. Matrices 2.1 Operations with Matrices This section and the next introduce
IT 131: Mathematics for Science Lecture Notes 3 Source: Larson, Edwards, Falvo (2009): Elementary Linear Algebra, Sixth Edition. Matrices 2.1 Operations with Matrices This section and the next introduce
Review Solutions for Exam 1
 Definitions Basic Theorems. Finish the definition: Review Solutions for Exam (a) A linear combination of vectors {v,..., v n } is: any vector of the form c v + c v + + c n v n (b) A set of vectors {v,...,
Definitions Basic Theorems. Finish the definition: Review Solutions for Exam (a) A linear combination of vectors {v,..., v n } is: any vector of the form c v + c v + + c n v n (b) A set of vectors {v,...,
Pre-Calculus I. For example, the system. x y 2 z. may be represented by the augmented matrix
 Pre-Calculus I 8.1 Matrix Solutions to Linear Systems A matrix is a rectangular array of elements. o An array is a systematic arrangement of numbers or symbols in rows and columns. Matrices (the plural
Pre-Calculus I 8.1 Matrix Solutions to Linear Systems A matrix is a rectangular array of elements. o An array is a systematic arrangement of numbers or symbols in rows and columns. Matrices (the plural
Name: Section Registered In:
 Name: Section Registered In: Math 125 Exam 1 Version 1 February 21, 2006 60 points possible 1. (a) (3pts) Define what it means for a linear system to be inconsistent. Solution: A linear system is inconsistent
Name: Section Registered In: Math 125 Exam 1 Version 1 February 21, 2006 60 points possible 1. (a) (3pts) Define what it means for a linear system to be inconsistent. Solution: A linear system is inconsistent
Lecture 1 Systems of Linear Equations and Matrices
 Lecture 1 Systems of Linear Equations and Matrices Math 19620 Outline of Course Linear Equations and Matrices Linear Transformations, Inverses Bases, Linear Independence, Subspaces Abstract Vector Spaces
Lecture 1 Systems of Linear Equations and Matrices Math 19620 Outline of Course Linear Equations and Matrices Linear Transformations, Inverses Bases, Linear Independence, Subspaces Abstract Vector Spaces
Lecture 22: Section 4.7
 Lecture 22: Section 47 Shuanglin Shao December 2, 213 Row Space, Column Space, and Null Space Definition For an m n, a 11 a 12 a 1n a 21 a 22 a 2n A = a m1 a m2 a mn, the vectors r 1 = [ a 11 a 12 a 1n
Lecture 22: Section 47 Shuanglin Shao December 2, 213 Row Space, Column Space, and Null Space Definition For an m n, a 11 a 12 a 1n a 21 a 22 a 2n A = a m1 a m2 a mn, the vectors r 1 = [ a 11 a 12 a 1n
Row Reduced Echelon Form
 Math 40 Row Reduced Echelon Form Solving systems of linear equations lies at the heart of linear algebra. In high school we learn to solve systems in or variables using elimination and substitution of
Math 40 Row Reduced Echelon Form Solving systems of linear equations lies at the heart of linear algebra. In high school we learn to solve systems in or variables using elimination and substitution of
Matrix multiplications that do row operations
 May 6, 204 Matrix multiplications that do row operations page Matrix multiplications that do row operations Introduction We have yet to justify our method for finding inverse matrices using row operations:
May 6, 204 Matrix multiplications that do row operations page Matrix multiplications that do row operations Introduction We have yet to justify our method for finding inverse matrices using row operations:
DM559 Linear and Integer Programming. Lecture 2 Systems of Linear Equations. Marco Chiarandini
 DM559 Linear and Integer Programming Lecture Marco Chiarandini Department of Mathematics & Computer Science University of Southern Denmark Outline 1. Outline 1. 3 A Motivating Example You are organizing
DM559 Linear and Integer Programming Lecture Marco Chiarandini Department of Mathematics & Computer Science University of Southern Denmark Outline 1. Outline 1. 3 A Motivating Example You are organizing
1 - Systems of Linear Equations
 1 - Systems of Linear Equations 1.1 Introduction to Systems of Linear Equations Almost every problem in linear algebra will involve solving a system of equations. ü LINEAR EQUATIONS IN n VARIABLES We are
1 - Systems of Linear Equations 1.1 Introduction to Systems of Linear Equations Almost every problem in linear algebra will involve solving a system of equations. ü LINEAR EQUATIONS IN n VARIABLES We are
1300 Linear Algebra and Vector Geometry Week 2: Jan , Gauss-Jordan, homogeneous matrices, intro matrix arithmetic
 1300 Linear Algebra and Vector Geometry Week 2: Jan 14 18 1.2, 1.3... Gauss-Jordan, homogeneous matrices, intro matrix arithmetic R. Craigen Office: MH 523 Email: craigenr@umanitoba.ca Winter 2019 What
1300 Linear Algebra and Vector Geometry Week 2: Jan 14 18 1.2, 1.3... Gauss-Jordan, homogeneous matrices, intro matrix arithmetic R. Craigen Office: MH 523 Email: craigenr@umanitoba.ca Winter 2019 What
Math 220: Summer Midterm 1 Questions
 Math 220: Summer 2015 Midterm 1 Questions MOST questions will either look a lot like a Homework questions This lists draws your attention to some important types of HW questions. SOME questions will have
Math 220: Summer 2015 Midterm 1 Questions MOST questions will either look a lot like a Homework questions This lists draws your attention to some important types of HW questions. SOME questions will have
Section 7.2 Solving Linear Recurrence Relations
 Section 7.2 Solving Linear Recurrence Relations If a g(n) = f (a g(0),a g(1),..., a g(n 1) ) find a closed form or an expression for a g(n). Recall: nth degree polynomials have n roots: a n x n + a n 1
Section 7.2 Solving Linear Recurrence Relations If a g(n) = f (a g(0),a g(1),..., a g(n 1) ) find a closed form or an expression for a g(n). Recall: nth degree polynomials have n roots: a n x n + a n 1
Solving Systems of Linear Equations
 LECTURE 5 Solving Systems of Linear Equations Recall that we introduced the notion of matrices as a way of standardizing the expression of systems of linear equations In today s lecture I shall show how
LECTURE 5 Solving Systems of Linear Equations Recall that we introduced the notion of matrices as a way of standardizing the expression of systems of linear equations In today s lecture I shall show how
1300 Linear Algebra and Vector Geometry
 1300 Linear Algebra and Vector Geometry R. Craigen Office: MH 523 Email: craigenr@umanitoba.ca May-June 2017 Introduction: linear equations Read 1.1 (in the text that is!) Go to course, class webpages.
1300 Linear Algebra and Vector Geometry R. Craigen Office: MH 523 Email: craigenr@umanitoba.ca May-June 2017 Introduction: linear equations Read 1.1 (in the text that is!) Go to course, class webpages.
Systems of Linear Equations. By: Tri Atmojo Kusmayadi and Mardiyana Mathematics Education Sebelas Maret University
 Systems of Linear Equations By: Tri Atmojo Kusmayadi and Mardiyana Mathematics Education Sebelas Maret University Standard of Competency: Understanding the properties of systems of linear equations, matrices,
Systems of Linear Equations By: Tri Atmojo Kusmayadi and Mardiyana Mathematics Education Sebelas Maret University Standard of Competency: Understanding the properties of systems of linear equations, matrices,
Lecture 2 Systems of Linear Equations and Matrices, Continued
 Lecture 2 Systems of Linear Equations and Matrices, Continued Math 19620 Outline of Lecture Algorithm for putting a matrix in row reduced echelon form - i.e. Gauss-Jordan Elimination Number of Solutions
Lecture 2 Systems of Linear Equations and Matrices, Continued Math 19620 Outline of Lecture Algorithm for putting a matrix in row reduced echelon form - i.e. Gauss-Jordan Elimination Number of Solutions
Math 313 Chapter 1 Review
 Math 313 Chapter 1 Review Howard Anton, 9th Edition May 2010 Do NOT write on me! Contents 1 1.1 Introduction to Systems of Linear Equations 2 2 1.2 Gaussian Elimination 3 3 1.3 Matrices and Matrix Operations
Math 313 Chapter 1 Review Howard Anton, 9th Edition May 2010 Do NOT write on me! Contents 1 1.1 Introduction to Systems of Linear Equations 2 2 1.2 Gaussian Elimination 3 3 1.3 Matrices and Matrix Operations
b for the linear system x 1 + x 2 + a 2 x 3 = a x 1 + x 3 = 3 x 1 + x 2 + 9x 3 = 3 ] 1 1 a 2 a
![b for the linear system x 1 + x 2 + a 2 x 3 = a x 1 + x 3 = 3 x 1 + x 2 + 9x 3 = 3 ] 1 1 a 2 a b for the linear system x 1 + x 2 + a 2 x 3 = a x 1 + x 3 = 3 x 1 + x 2 + 9x 3 = 3 ] 1 1 a 2 a](/thumbs/71/65559666.jpg) Practice Exercises for Exam Exam will be on Monday, September 8, 7. The syllabus for Exam consists of Sections One.I, One.III, Two.I, and Two.II. You should know the main definitions, results and computational
Practice Exercises for Exam Exam will be on Monday, September 8, 7. The syllabus for Exam consists of Sections One.I, One.III, Two.I, and Two.II. You should know the main definitions, results and computational
4 Elementary matrices, continued
 4 Elementary matrices, continued We have identified 3 types of row operations and their corresponding elementary matrices. If you check the previous examples, you ll find that these matrices are constructed
4 Elementary matrices, continued We have identified 3 types of row operations and their corresponding elementary matrices. If you check the previous examples, you ll find that these matrices are constructed
Chapter 2. Systems of Equations and Augmented Matrices. Creighton University
 Chapter Section - Systems of Equations and Augmented Matrices D.S. Malik Creighton University Systems of Linear Equations Common ways to solve a system of equations: Eliminationi Substitution Elimination
Chapter Section - Systems of Equations and Augmented Matrices D.S. Malik Creighton University Systems of Linear Equations Common ways to solve a system of equations: Eliminationi Substitution Elimination
Vector Spaces 4.4 Spanning and Independence
 Vector Spaces 4.4 and Independence Summer 2017 Goals Discuss two important basic concepts: Define linear combination of vectors. Define Span(S) of a set S of vectors. Define linear Independence of a set
Vector Spaces 4.4 and Independence Summer 2017 Goals Discuss two important basic concepts: Define linear combination of vectors. Define Span(S) of a set S of vectors. Define linear Independence of a set
Linear Algebra I Lecture 8
 Linear Algebra I Lecture 8 Xi Chen 1 1 University of Alberta January 25, 2019 Outline 1 2 Gauss-Jordan Elimination Given a system of linear equations f 1 (x 1, x 2,..., x n ) = 0 f 2 (x 1, x 2,..., x n
Linear Algebra I Lecture 8 Xi Chen 1 1 University of Alberta January 25, 2019 Outline 1 2 Gauss-Jordan Elimination Given a system of linear equations f 1 (x 1, x 2,..., x n ) = 0 f 2 (x 1, x 2,..., x n
10.3 Matrices and Systems Of
 10.3 Matrices and Systems Of Linear Equations Copyright Cengage Learning. All rights reserved. Objectives Matrices The Augmented Matrix of a Linear System Elementary Row Operations Gaussian Elimination
10.3 Matrices and Systems Of Linear Equations Copyright Cengage Learning. All rights reserved. Objectives Matrices The Augmented Matrix of a Linear System Elementary Row Operations Gaussian Elimination
Extra Problems: Chapter 1
 MA131 (Section 750002): Prepared by Asst.Prof.Dr.Archara Pacheenburawana 1 Extra Problems: Chapter 1 1. In each of the following answer true if the statement is always true and false otherwise in the space
MA131 (Section 750002): Prepared by Asst.Prof.Dr.Archara Pacheenburawana 1 Extra Problems: Chapter 1 1. In each of the following answer true if the statement is always true and false otherwise in the space
MAC1105-College Algebra. Chapter 5-Systems of Equations & Matrices
 MAC05-College Algebra Chapter 5-Systems of Equations & Matrices 5. Systems of Equations in Two Variables Solving Systems of Two Linear Equations/ Two-Variable Linear Equations A system of equations is
MAC05-College Algebra Chapter 5-Systems of Equations & Matrices 5. Systems of Equations in Two Variables Solving Systems of Two Linear Equations/ Two-Variable Linear Equations A system of equations is
4 Elementary matrices, continued
 4 Elementary matrices, continued We have identified 3 types of row operations and their corresponding elementary matrices. To repeat the recipe: These matrices are constructed by performing the given row
4 Elementary matrices, continued We have identified 3 types of row operations and their corresponding elementary matrices. To repeat the recipe: These matrices are constructed by performing the given row
Algebra & Trig. I. For example, the system. x y 2 z. may be represented by the augmented matrix
 Algebra & Trig. I 8.1 Matrix Solutions to Linear Systems A matrix is a rectangular array of elements. o An array is a systematic arrangement of numbers or symbols in rows and columns. Matrices (the plural
Algebra & Trig. I 8.1 Matrix Solutions to Linear Systems A matrix is a rectangular array of elements. o An array is a systematic arrangement of numbers or symbols in rows and columns. Matrices (the plural
Math 344 Lecture # Linear Systems
 Math 344 Lecture #12 2.7 Linear Systems Through a choice of bases S and T for finite dimensional vector spaces V (with dimension n) and W (with dimension m), a linear equation L(v) = w becomes the linear
Math 344 Lecture #12 2.7 Linear Systems Through a choice of bases S and T for finite dimensional vector spaces V (with dimension n) and W (with dimension m), a linear equation L(v) = w becomes the linear
MATH240: Linear Algebra Review for exam #1 6/10/2015 Page 1
 MATH24: Linear Algebra Review for exam # 6//25 Page No review sheet can cover everything that is potentially fair game for an exam, but I tried to hit on all of the topics with these questions, as well
MATH24: Linear Algebra Review for exam # 6//25 Page No review sheet can cover everything that is potentially fair game for an exam, but I tried to hit on all of the topics with these questions, as well
Section 6.2 Larger Systems of Linear Equations
 Section 6.2 Larger Systems of Linear Equations Gaussian Elimination In general, to solve a system of linear equations using its augmented matrix, we use elementary row operations to arrive at a matrix
Section 6.2 Larger Systems of Linear Equations Gaussian Elimination In general, to solve a system of linear equations using its augmented matrix, we use elementary row operations to arrive at a matrix
MIDTERM 1 - SOLUTIONS
 MIDTERM - SOLUTIONS MATH 254 - SUMMER 2002 - KUNIYUKI CHAPTERS, 2, GRADED OUT OF 75 POINTS 2 50 POINTS TOTAL ) Use either Gaussian elimination with back-substitution or Gauss-Jordan elimination to solve
MIDTERM - SOLUTIONS MATH 254 - SUMMER 2002 - KUNIYUKI CHAPTERS, 2, GRADED OUT OF 75 POINTS 2 50 POINTS TOTAL ) Use either Gaussian elimination with back-substitution or Gauss-Jordan elimination to solve
Introduction to Systems of Equations
 Introduction to Systems of Equations Introduction A system of linear equations is a list of m linear equations in a common set of variables x, x,, x n. a, x + a, x + Ù + a,n x n = b a, x + a, x + Ù + a,n
Introduction to Systems of Equations Introduction A system of linear equations is a list of m linear equations in a common set of variables x, x,, x n. a, x + a, x + Ù + a,n x n = b a, x + a, x + Ù + a,n
Gauss-Jordan Row Reduction and Reduced Row Echelon Form
 Gauss-Jordan Row Reduction and Reduced Row Echelon Form If we put the augmented matrix of a linear system in reduced row-echelon form, then we don t need to back-substitute to solve the system. To put
Gauss-Jordan Row Reduction and Reduced Row Echelon Form If we put the augmented matrix of a linear system in reduced row-echelon form, then we don t need to back-substitute to solve the system. To put
Solving Systems of Linear Equations Using Matrices
 Solving Systems of Linear Equations Using Matrices What is a Matrix? A matrix is a compact grid or array of numbers. It can be created from a system of equations and used to solve the system of equations.
Solving Systems of Linear Equations Using Matrices What is a Matrix? A matrix is a compact grid or array of numbers. It can be created from a system of equations and used to solve the system of equations.
Math 61CM - Solutions to homework 2
 Math 61CM - Solutions to homework 2 Cédric De Groote October 5 th, 2018 Problem 1: Let V be the vector space of polynomials of degree at most 5, with coefficients in a field F Let U be the subspace of
Math 61CM - Solutions to homework 2 Cédric De Groote October 5 th, 2018 Problem 1: Let V be the vector space of polynomials of degree at most 5, with coefficients in a field F Let U be the subspace of
Sections 1.5, 1.7. Ma 322 Fall Ma 322. Sept
 Sections 1.5, 1.7 Ma 322 Fall 213 Ma 322 Sept. 9-13 Summary ˆ Solutions of homogeneous equations AX =. ˆ Using the rank. ˆ Parametric solution of AX = B. ˆ Linear dependence and independence of vectors
Sections 1.5, 1.7 Ma 322 Fall 213 Ma 322 Sept. 9-13 Summary ˆ Solutions of homogeneous equations AX =. ˆ Using the rank. ˆ Parametric solution of AX = B. ˆ Linear dependence and independence of vectors
Partial Fraction Decomposition Honors Precalculus Mr. Velazquez Rm. 254
 Partial Fraction Decomposition Honors Precalculus Mr. Velazquez Rm. 254 Adding and Subtracting Rational Expressions Recall that we can use multiplication and common denominators to write a sum or difference
Partial Fraction Decomposition Honors Precalculus Mr. Velazquez Rm. 254 Adding and Subtracting Rational Expressions Recall that we can use multiplication and common denominators to write a sum or difference
MATH 15a: Applied Linear Algebra Practice Exam 1
 MATH 5a: Applied Linear Algebra Practice Exam Note: this practice test is NOT a guarantee of what the actual midterm will look like!. Say whether the following functions are linear. If so, write down the
MATH 5a: Applied Linear Algebra Practice Exam Note: this practice test is NOT a guarantee of what the actual midterm will look like!. Say whether the following functions are linear. If so, write down the
Perform the same three operations as above on the values in the matrix, where some notation is given as a shorthand way to describe each operation:
 SECTION 2.1: SOLVING SYSTEMS OF EQUATIONS WITH A UNIQUE SOLUTION In Chapter 1 we took a look at finding the intersection point of two lines on a graph. Chapter 2 begins with a look at a more formal approach
SECTION 2.1: SOLVING SYSTEMS OF EQUATIONS WITH A UNIQUE SOLUTION In Chapter 1 we took a look at finding the intersection point of two lines on a graph. Chapter 2 begins with a look at a more formal approach
1. (7pts) Find the points of intersection, if any, of the following planes. 3x + 9y + 6z = 3 2x 6y 4z = 2 x + 3y + 2z = 1
 Math 125 Exam 1 Version 1 February 20, 2006 1. (a) (7pts) Find the points of intersection, if any, of the following planes. Solution: augmented R 1 R 3 3x + 9y + 6z = 3 2x 6y 4z = 2 x + 3y + 2z = 1 3 9
Math 125 Exam 1 Version 1 February 20, 2006 1. (a) (7pts) Find the points of intersection, if any, of the following planes. Solution: augmented R 1 R 3 3x + 9y + 6z = 3 2x 6y 4z = 2 x + 3y + 2z = 1 3 9
Section 1.1 System of Linear Equations. Dr. Abdulla Eid. College of Science. MATHS 211: Linear Algebra
 Section 1.1 System of Linear Equations College of Science MATHS 211: Linear Algebra (University of Bahrain) Linear System 1 / 33 Goals:. 1 Define system of linear equations and their solutions. 2 To represent
Section 1.1 System of Linear Equations College of Science MATHS 211: Linear Algebra (University of Bahrain) Linear System 1 / 33 Goals:. 1 Define system of linear equations and their solutions. 2 To represent
EXAM. Exam #1. Math 2360, Second Summer Session, April 24, 2001 ANSWERS
 i i EXAM Exam #1 Math 2360, Second Summer Session, 2002 April 24, 2001 ANSWERS i 50 pts. Problem 1. In each part you are given the augmented matrix of a system of linear equations, with the coefficent
i i EXAM Exam #1 Math 2360, Second Summer Session, 2002 April 24, 2001 ANSWERS i 50 pts. Problem 1. In each part you are given the augmented matrix of a system of linear equations, with the coefficent
Sections 1.5, 1.7. Ma 322 Spring Ma 322. Jan 24-28
 Sections 1.5, 1.7 Ma 322 Spring 217 Ma 322 Jan 24-28 Summary ˆ Text: Solution Sets of Linear Systems (1.5),Linear Independence (1.7) ˆ Solutions of homogeneous equations AX =. ˆ Using the rank. ˆ Parametric
Sections 1.5, 1.7 Ma 322 Spring 217 Ma 322 Jan 24-28 Summary ˆ Text: Solution Sets of Linear Systems (1.5),Linear Independence (1.7) ˆ Solutions of homogeneous equations AX =. ˆ Using the rank. ˆ Parametric
Chapter 1 Linear Equations. 1.1 Systems of Linear Equations
 Chapter Linear Equations. Systems of Linear Equations A linear equation in the n variables x, x 2,..., x n is one that can be expressed in the form a x + a 2 x 2 + + a n x n = b where a, a 2,..., a n and
Chapter Linear Equations. Systems of Linear Equations A linear equation in the n variables x, x 2,..., x n is one that can be expressed in the form a x + a 2 x 2 + + a n x n = b where a, a 2,..., a n and
A Quick Introduction to Row Reduction
 A Quick Introduction to Row Reduction Gaussian Elimination Suppose we are asked to solve the system of equations 4x + 5x 2 + 6x 3 = 7 6x + 7x 2 + 8x 3 = 9. That is, we want to find all values of x, x 2
A Quick Introduction to Row Reduction Gaussian Elimination Suppose we are asked to solve the system of equations 4x + 5x 2 + 6x 3 = 7 6x + 7x 2 + 8x 3 = 9. That is, we want to find all values of x, x 2
Linear Systems. Math A Bianca Santoro. September 23, 2016
 Linear Systems Math A4600 - Bianca Santoro September 3, 06 Goal: Understand how to solve Ax = b. Toy Model: Let s study the following system There are two nice ways of thinking about this system: x + y
Linear Systems Math A4600 - Bianca Santoro September 3, 06 Goal: Understand how to solve Ax = b. Toy Model: Let s study the following system There are two nice ways of thinking about this system: x + y
Chapter 3. Linear Equations. Josef Leydold Mathematical Methods WS 2018/19 3 Linear Equations 1 / 33
 Chapter 3 Linear Equations Josef Leydold Mathematical Methods WS 2018/19 3 Linear Equations 1 / 33 Lineares Gleichungssystem System of m linear equations in n unknowns: a 11 x 1 + a 12 x 2 + + a 1n x n
Chapter 3 Linear Equations Josef Leydold Mathematical Methods WS 2018/19 3 Linear Equations 1 / 33 Lineares Gleichungssystem System of m linear equations in n unknowns: a 11 x 1 + a 12 x 2 + + a 1n x n
Gauss-Jordan elimination ( used in the videos below) stops when the augmented coefficient
 To review these matrix methods for solving systems of linear equations, watch the following set of YouTube videos. They are followed by several practice problems for you to try, covering all the basic
To review these matrix methods for solving systems of linear equations, watch the following set of YouTube videos. They are followed by several practice problems for you to try, covering all the basic
INVERSE OF A MATRIX [2.2] 8-1
![INVERSE OF A MATRIX [2.2] 8-1 INVERSE OF A MATRIX [2.2] 8-1](/thumbs/78/78101644.jpg) INVERSE OF A MATRIX [2.2] 8-1 The inverse of a matrix: Introduction We have a mapping from R n to R n represented by a matrix A. Can we invert this mapping? i.e. can we find a matrix (call it B for now)
INVERSE OF A MATRIX [2.2] 8-1 The inverse of a matrix: Introduction We have a mapping from R n to R n represented by a matrix A. Can we invert this mapping? i.e. can we find a matrix (call it B for now)
is Use at most six elementary row operations. (Partial
 MATH 235 SPRING 2 EXAM SOLUTIONS () (6 points) a) Show that the reduced row echelon form of the augmented matrix of the system x + + 2x 4 + x 5 = 3 x x 3 + x 4 + x 5 = 2 2x + 2x 3 2x 4 x 5 = 3 is. Use
MATH 235 SPRING 2 EXAM SOLUTIONS () (6 points) a) Show that the reduced row echelon form of the augmented matrix of the system x + + 2x 4 + x 5 = 3 x x 3 + x 4 + x 5 = 2 2x + 2x 3 2x 4 x 5 = 3 is. Use
Math 2142 Homework 5 Part 1 Solutions
 Math 2142 Homework 5 Part 1 Solutions Problem 1. For the following homogeneous second order differential equations, give the general solution and the particular solution satisfying the given initial conditions.
Math 2142 Homework 5 Part 1 Solutions Problem 1. For the following homogeneous second order differential equations, give the general solution and the particular solution satisfying the given initial conditions.
Problems for M 8/31: and put it into echelon form to see whether there are any solutions.
 Math 310, Lesieutre Problem set # September 9, 015 Problems for M 8/31: 1.3.11 Determine if b is a linear combination of a 1, a, and a 3, where 1 a 1 =, 0 a = 1, 5 a 3 = 6, b = 1. 0 8 6 We need to form
Math 310, Lesieutre Problem set # September 9, 015 Problems for M 8/31: 1.3.11 Determine if b is a linear combination of a 1, a, and a 3, where 1 a 1 =, 0 a = 1, 5 a 3 = 6, b = 1. 0 8 6 We need to form
Lecture Notes: Solving Linear Systems with Gauss Elimination
 Lecture Notes: Solving Linear Systems with Gauss Elimination Yufei Tao Department of Computer Science and Engineering Chinese University of Hong Kong taoyf@cse.cuhk.edu.hk 1 Echelon Form and Elementary
Lecture Notes: Solving Linear Systems with Gauss Elimination Yufei Tao Department of Computer Science and Engineering Chinese University of Hong Kong taoyf@cse.cuhk.edu.hk 1 Echelon Form and Elementary
Elementary Linear Algebra
 Elementary Linear Algebra Linear algebra is the study of; linear sets of equations and their transformation properties. Linear algebra allows the analysis of; rotations in space, least squares fitting,
Elementary Linear Algebra Linear algebra is the study of; linear sets of equations and their transformation properties. Linear algebra allows the analysis of; rotations in space, least squares fitting,
Roberto s Notes on Linear Algebra Chapter 4: Matrix Algebra Section 7. Inverse matrices
 Roberto s Notes on Linear Algebra Chapter 4: Matrix Algebra Section 7 Inverse matrices What you need to know already: How to add and multiply matrices. What elementary matrices are. What you can learn
Roberto s Notes on Linear Algebra Chapter 4: Matrix Algebra Section 7 Inverse matrices What you need to know already: How to add and multiply matrices. What elementary matrices are. What you can learn
