Chapter III. The bivariate Gini-index
|
|
|
- Meghan Fitzgerald
- 5 years ago
- Views:
Transcription
1 Chapter III The bivariate Gini-index 3. Introduction The need f including me than one attribute in the analysis of economic inequality is emphasized in the wks. of Atkinson and Bourguignon (982,989), Kolm (977), Maasoumi (986), Maasoumi and Nickelsbu rg (988), Mosler (994a), Rietveld (990) and Slottje (987). Arnold (987) has given a definition f the Lenz curve in the bivariate setup. The problem of extending the Gini-index to higher dimensions was also considered by Koshevoy and Mosler (996,997). The utility of the truncated fm of the Gini-index in the univariate setup is being mentioned in section (.4). In the present chapter, we propose a measure of income inequality f the truncated variable in the bivariate setup and look into the problem of characterizing certain bivariate probability distributions using this measure. 3.2 Bivariate Gini-index As pointed out in section (.2), in the reliability context, the failure rate f a two dimensional random vect is defined in two ways. [(.2.3) and (.2.4)]. Analogous to the vect valued failure rate, we propose-a definition f the Gini-index in the bivariate setup and look into the problem of characterization of probability distributions by the fm of the bivariate Gini-index. Let X= (X;,X 2 ) represent a bivariate random vect, where X, and X 2 represents two attributes of measuring income in a population. The random variable ~ = X;I X 2 > 2 cresponds to the distribution of X; subject to the condition that X 2 is greater than an amount equal to
2 52 t 2 Using the terminology used by Ord, Patil and Taillie (983), quoted in section (.4), one can define the Gini-index f the random variable Y, as 00 G,(t"t 2 ) = 2 f F(x"t,,/ 2 ) df,(x"t,,/ 2 ) - 4 (3.2. ) where F(xl'/ l,/ 2 ) is the distribution function of Y, namely Similarly f the random variable ~ = x 2 X, > I, the Gini-index turns out to be 00 ~(t" 2 ) = 2 f F(x 2, " 2 ) d~(x2' " 2 ) - Iz where F(x 2,t,,/ 2 ) is the distribution function of ~ defined by (3.2.2) and ~(x2,/'/2) is the first moment distribution of ~ given by Definition 3. F a non-negative random vect X = (Xl' X 2 ) admitting an absolutely continuous distribution function, we define the bivariate Gini index f the truncated distribution as the vect (3.2.3)
3 53 where G,(~, t 2 ) and ~(~, t 2 ) are defined as in (3.2.) and (3.2.2) respectively. Let X = (X;, X 2 ) represent two attributes of income, say income from the land and income from the employment. Suppose among the population of individuals whose income in one of the components, say X 2 ' exceeds a certain threshold value say t 2, then G,(~,t2) measures the disparity of income in source one. Similarly, ~(~,t2) measures the disparity of income from the second source subject to the condition that the income from the other source exceeded a threshold value say ~. Hence G(~,t2) can be viewed as a measure of inequality when the two facts are taken into consideration simultaneously. 3.3 Characterization Theems In this section, we discuss characterization theems associated with some bivariate models based on the functional fm of the bivariate truncated Gini-index. We first establish a relationship between the Gini-index defined by (3.2.3) and the vitality function defined by (.2.39), which is useful f the calculation of bivariate Giniindex f particular distributions as well as f establishing characterization theems, in the sequel. Theem 3. Let X = (X;, X 2 ) be a non-negative, non-degenerate random vect admitting an absolutely continuous distribution function. If ml(~,t2)' i=,2 represents the components of the bivariate vitality function defined' by (.2.40) and ~(~,t2), i=,2 represents the components of the bivariate Gini index defined by (3.2.3), then the following relationship holds.
4 54 Proof From the definition (3.2.). we get - ~(,./2) <Of x ~F(x.t) dx = 2 "'f x, [F(/,.!3)-F(X,./2)) - ax;f(x,./ 2 ) dx, F(/,./ 2 ) 't ' ax,', 2' ~ F(/,./ 2 ) F(/,./ 2 ) a - The above equation can be written as (3.3.2). This gives (- ~(I,. 2)) ( I, + j F(X,./2) dx,) = I, + F j F (x,. 2) dx,. F(I,. 2) ~ (,./ 2 ) 't The above equation can be written as "'- ( - ~ (I,. 2) ) ( I, + r, (I,. 2)) = I, + F f F (X,. 2) dx,. (,./2) 't (3.3.) with i = is immediate from the above equation. The proof f ;=2 is similar. In the following theem we look into the property of the bivariate Gini-index from the point of view of truncation invariance.
5 55 Theem 3.2 Let X = (X;, X 2 ) be a non-negative random vect admitting an absolutely continuous distribution with respect to Lebesgue measure in the suppt of (a"oo)x(~,oo). The relation G,(t"t2) = a, + b, log tj i,j =,2, i * j (3.3.3) where a"b, are constants, holds f all real t,,t2 ~ 0 if and only if X is distributed as the bivariate Pareto type- I distribution with survival function specified by Proof When (3.3.3) holds, with i =, using equation (3.3.2) we get Differentiating with respect to t, and rearranging the terms we get (3.3.5) Differentiating (3.3.5) with respect to tl we get This gives ( + ) ( F(t" t 2) + tl ~ F(t" t2)) = a, + ~ log t2 at t, af(t"t2) ( hi) 0 =--'-- -:...:...:.; a, + ' ogt2 =. F(tl,t 2 ) at, The solution of the above partial differential equation is F(t" t 2 ) = r - S, - lit Iogt. C (t2) (3.3.6) where C (t2) is independent t,. Proceeding on similar lines with i=2 in (3.3.3) one can also obtain PI(I. I.) I. - - Bz - ~ Ioglt c. (I.) '2 = 2 2 (3.3.7)
6 56 where C 2 (t) is independent of 2, When t, =, in (3.3.6) we get C(t2) = F2(t2) Thus, (3.3.6) becomes F(t,,/ 2 ) = F2(t2) (- a, - ~ log~ (3.3.8) In a similar manner, when 2 =, (3.3.7) reads as so that C2(t) = F(t,) F(t,,/ 2 ) = F(t) a, -l2 log/, (3.3.9) When 2 =, in (3.3.8) we get and from (3.3.9) we have F(t,) = t, -- a, F(t" 2 ) = r -a, 2 - -a,-l2 l og/, (3.3.0) Similarly when = in (3.3.0) we have and from (3.3.8) we get F2(t2) = a, A(t t) - t - - a, t- - a, - ~ Jog/z '2-2 From (3.3.0) and (3.3.) we get (3.3.) t --a, t - - a, - l2 Jog/, - t - - a, t- - a, - ~ Jog~ 2-2 Taking logarithm on both sides and rearranging the terms in the above equation, we get b, = 4 = b (say) From (3.3.) we get the desired fo rm fo r F(t" 2 ) Conversely, when the distribution of X is specified by (3.3.4), by direct calculations we get ().i.j~.2.i~j. t. 2a, log -L 8 so that the conditions of the theem are satisfied.
7 57 In the following theem, we look into the situation where (-G,(tl,/ 2 )) m i (t,,/ 2 ) is linear in li,i=,2. Theem 3.3 Let X = (Xl' X 2 ) be a non-negative, non-degenerate random vect admitting an absolutely continuous distribution function. The relationship ( - Gi(/l' 2 ) ) mi(t,.t 2 ) = A~ + Bi(lj),i, j =,2,i '" j (3.3.2) where Bi(tj) are non-negative functions of Ij holds f all t,.t 2 ~ 0 if and only if X follows (i) the Gumbels bivariate exponential distribution with survival function if A = F(t,,/ 2 ) = e-j.,tl-a.z~-(jtl~,a,,~>0,/'/2>0,0 ~ e ~ A,~ (3.3.3) (ii) the bivariate Pareto type-i! distribution with survival function if A > and F(t"2) = ( + S, t, + B..! 2 + bt, 2 ) - c,/,/2 > 0,s"B..!,c > 0,0 ~ b ~ (c+) s,b..! (3.3.4) (iii) the bivariate finite-range distribution with survival function F(t" 2 ) = ( - P t, - P 2 / 2 + qt, 2 ) d, 0< t, < -.!..,O < 2 < -Plt, Pl P2 - qt, if A <. Proof When (3.3.2) holds with i =, using (3.3.) we have
8 58 j F(xl' 2) dx, = ( (A-), + 8,(2) ) F(l'/2) I, Differentiating with respect to " we get - F(I,,/ 2 ) = (A-) F(I,,/ 2 ) + ( (A-) I, + 8,(/ 2 ) ) 2F(I,,/2) ~F(/'/2) al, The above equation simplifies to af(i"2) A =--- -~::..:... = F(I" 2 ) al, 2(A-) I, + 8,(/2) Denoting by h = (,(,,/ 2 ),hz(i,,/ 2 ) ), the vect valued failure rate discussed in Johnson and Kotz (975), using (.2.5) the above equation gives, ( " 2 ) =...",.2--:(--:A---::)----:=2-B=-:-"( -,...). - 2 A I, + A Proceeding on similar lines with i = 2, we also get hz(i,,/ 2 ) = 2 (A-) 2 ~(~)' A 2 + A The above expressions f h j (I,,/ 2 ),j =, 2 are reciprocal linear in If" The rest of the proof follows from Roy (989) reviewed in section.2. The if part of the theem follows from the expressions f ( '::( )) ( ). b t (2C ) t ( + ~/2) d -...,,,/2 ~,,/2 given y + 2(A, + Ill), 2c- + (2c-)(a, + b 2 ) an (2!~), + (2d~~~/~qI2) respectively f distributions specified by (3.3.3), (3.3.4) and (3.3.5) with similar expression f (-~(,,/2)) 77:!(,,/ 2 ). Hence the condition of the theem holds. Collary 3. When () = 0 in (3.3.3), we have F(I" 2) = exp ( - A,I, - ~/2 ) (3.3.6)
9 59 so that Xl and X 2 this set up the relation takes the fm which is characteristic to (3.3.6). are independent and exponentially distributed. In = t. + -, I 2,,, i=,2 Collary 3.2 When b= 0 in (3.3.4), we have F(i,,/ 2 ) = ( + a, / + ~/2rc,i,,/ 2 >O,c>O (3.3.7) which is the model obtained by Lindley and Singpurwalla (986) under a different set of conditions. In this case, the property 2c ) ( + all).... ( 2c- a,(2c-) (-G,(tl,/ 2 )) m i (tl,/ 2 ) = -- I, +,,=,2,*. is characteristic to (3.3.7). It may be noted that the right-hand side of the above equation is a linear function of / and 2, The following theem provides a characterization f the three distributions considered in the above theem based on the relationship between the bivariate Gini-index defined in (3.2.3) and the bivariate mean residual life function defined in (.2.25). Theem 3.4 relationship F the random vect Xconsidered in theem 3.3 the (-G,(i,,/ 2 )) m,(tl,/ 2 ) = I, + k,,(tl,/ 2 ) J=,2 J*j,k>O. (3.3.8) holds f all /,/ 2 ~ 0 if and only if X follows anyone of the three distributions specified by (3.3.3), (3.3.4) and (3.3.5) respectively accding as k=- k<- and k>-. 2' 2 2 Proof When (3.3.8) holds with i=, using (3.3.), we have
10 60.., f F(X,t2) dx, = I, k r,(i"t2) F(I"t2) Differentiating with respect to I, we get 2 k r,(i"t 2 ) af(t"t2) + k ar,(t"t2) = -. F(I" t 2 ) al, al, Using the relationships (.2.5) and (.2.30), the above equation can be written as -k ~(I" t2) r,(i" t2) = T Proceeding on similar lines with i = 2, one can also get -k ~(I"t2) '2(I"t2) = T The rest of the proof follows from Roy (989), reviewed in section.2. The if part of the theem follows from the expressions f ( -~(I"t2) ) m,(i"t2) and r,(i"t2) given below with similar expressions f (-~(I"t2)) n;(i"t2) and '2(I"t2). Distribution (-~(tl't2)) m,(i"t2) r,(i" t2) (i) exponential t ( ) +'2 A, +tl} A, + Bt2 (ii) Pareto t c- ( I, (+~t2)) + 2c- c- + (a, + bt2)(c-) (iii) finite-range t d + ( -I, (- P2t2) ) + 2d + d + + (A - qt 2 )(d + ) I, + ~t2 -+ c- (a, + bt2)(c-) -I, - P2 t2 --+ d + (Pl - qt2)( d + )
11 6 Instead of the mean residual life function if we consider the bivariate failure rate, we get a characterization f the three distributions considered in theem 3.4, which we state as theem 3.5 below. Theem 3.5 relationship F the random vect X considered in theem 3.4, the = I, + k,i =,2 h,(t" 2 ) (3.3.9) holds f all,,/ 2 ~ 0 if and only if X follows anyone of the three distributions specified by (3.3.3),(3.3.4) and (3.3.5) respectively accding as k = -, k > - and k < Proof When (3.3.9) holds using (3.3.) we have I, + F j F (x" 2 ) dx, = (,,/ 2 ) I, j F (x" 2 ) dx, = k F (t" 2 ) z(t,,/ 2 ) I, Differentiating with respect to t" we get = k F(t t) az(t" 2 ) + 2 k A(t t) af(t,,/ 2 ) z(t" t ) 2 " 2 at, " 2 at,. - = k az(t,,/2 ) + 2 k z(t t) af(t,,/2 ) at, "2 F(t" 2 ) at, Using (.2.5), the above equation gives
12 62 az(t,,/ 2 ) 2k- ----:...:...::..:.. = -- at, k Solving the above partial differential equation, we get z(t,,/2) = (-k- 2k-) t, + c,(/2) where c,(/ 2 ) is independent I,. This gives Proceeding on similar lines with i = 2, we get h.z(t,,/ 2 ) = (2k-). -k- 2 + c2(t,) The rest of the proof follows from Roy (989), mentioned in section.2. The if part of the theem follows from the expressions f ( -6,(t" 2) ) m,(t,,/2) and h,(t,,/2) given below with similar expressions f ( -~(/,,/2) ) m.z(t,,/2) and h.z(/,,/2). Distribution ( - 6,(t" 2) ) m, (I" 2) h,(/,,/2) (i) exponential t ( ), +"2 A,+I/) A, + 02 (ii) Pareto t, + ( + a,t, + ~/2 + bt, 2) c (a, + b2) (2c-) (a, + b 2 ) ( + a,t, + ~/2 + bt,2) (iii) finite-range t, + - p,l, - P2 / 2 + qt,2 d (p, - q2) ( + 2d) (p, - q2) - p,t, - P2 / 2 + qt,2
13 63 The following theem provides a characterization result f the bivariate Pareto type- distribution using a possible relationship between the Gini-index and the vitality function in the bivariate setup. Theem 3.6 relationship F the random vect X considered in theem 3.5, the G( ) m,(,,2) - ~,. 2,,2 -,I -, m,(i" (2) + I, (3.3.20) holds f all " 2 ~ 0 if and only if X follow the bivariate Pareto distribution with survival function (3.3.4). Proof When (3.3.20) holds with i=, using (3.3.), we get 2 I, m, (I" (2 ) <DJ ~( ) d = I, + ~ J- x,,2 X, I, + m, (I" (2 ) J- (" ( 2 ) ' (3.3.2 ) 2 I, m, (I" ( 2 ) ~ (" ( 2 ) = I, (I, + m, (" ( 2 )) ~ (" ( 2 ) + (I, + m, (I" (2)) j ~ (x" (2) dx,. 4 Differentiating with respect to I, and rearranging the terms we get 2 t (t t) af(i,,2) + t am,(,,2) + (t t) = F(I"(2),,, m, l' 2 at' at m, " 2 2,2 af(i,,2) +2,-(m,(I,, 2 )+,)+(+ am,(i,,~))_. jf(x,, 2 )dx,. F(I"(2) al, al, ~(,,2)'l Using the relationships (.2.5) and (3.3.2), the above equation can be written as -2 I, m, (I" ( 2 ) 7, (,, 2 )( I, + m, (" ( 2 )) + I, (I, + m,(i" ( 2 )) am, (,, 2 ) + m, (,, 2 )( I, + m, (" ( 2 )) al, = -2,2 7,(" ( 2 ) (I, + m, (" ( 2 )) + I, (I, + m, (I" (2)) - m, (" ( 2 ) (I, + m, (I" ( 2 )) + ( + a~~'(2)) + (,m,(,,2)-,2).
14 64-2 I, m,2(tl,/2),(,, 2 ) + 2,2 ~,(,,/ 2 ) + 2,2(,,/ 2 ) = -2,3,(,,/2). al,. Using (.2.44) and simplifying, we get -2,m2 (I" 2)~ 77,(,,/ 2 ) + (2,2 ~ 77,(,,/ 2 ) + 277,2(" 2 ))( m (I" 2 ) -,) = -2,3 ~ m(i" 2 ) ~ ~ ~ -2 I, ~,(,,/2) + 2,2 ~Iog 77,(" 2) + 2,(,,/2) - 2, = o. al, al, On solving the above partial differential equation, we get m,(tl,/2) = C(t2) I, where C (t2) is a function of 2 alone. This gives '(,,/ 2 ) = ( c (/ 2 )- ),c (/ 2 ) is a function of 2 Proceeding on similar lines with i = 2, in (3.3.20), we get '2(,,/2) = ( c 2 (,)- ) 2,c 2 (,) is a function of,. Using the pair of identities f the survival function of X=(X"X 2 ) in terms of the components of the bivariate MRLF, specified in (.2.28), (.2.29) and inserting the values of '(,,/ 2 ) and '2(,,/ 2 ), we get and -A( t, t ) = -a,~ exp {- I og ( -I, ) - I og ( -2 )} 2,/2 (Cl(~) -) a, (c 2 (,) -) ~ (3.3.22) -A( ) a,~ { I ( I, ) I ( 2 )},,2 =,/2 exp - (C (t2) -) og a; - (c 2 (a,) -) og ~ (3.3.23) Equating (3.3.22) and (3.3.23), we get I (I,) I exp (/2)} { - (Cl(~) -) og a, - (c 2 (,) -) og ~ - exp{ - 0g(.i) _ log (ll)} (3.3.24) (C,(t2) -) a, (c2(a,) -) ~ Setting a, =,i=,2,i:l:-j, (3.3.24) can be wr.itten as c,(a j ) -
15 65 exp {- a log (.i) - log (!L)} = exp {- log (.i) - a 2 log (!L)} ~. (c 2 (/ )-) 8z (C (t2)-). ~ 8z (3.3.25) ( -a) 0g(.i) - ( -a ) 0g(!L) (C (t2) -) ~ - (c 2 (f,) -) 2 8z' Dividing both sides by 0g( ~) 0g(!) we get ( ) ( ( )J _ ( ( )J- _ a 0!L = ( _ a J lo.i (C (/ ) 2 -) g 8z (c 2 (f,) -) 2 g ~ This means that each quantity should be a constant, say (), independent of and 2, Thus, and = a + () log(;) (c (/ 2 ) -) -z = a 2 + () log ( ~ ). ( c 2 ( f,) - ) -, Inserting values of and in (3.3.24), the required (C (t2)-) (c2(f,)-) distribution is obtained. The if part of the theem follows from the expressions f G,(t,,/2) and ~(/' 2) given by ( ) and 2a - + 2(}log! a + (}IOg( ~) a + () log ( ~ ) - respectively,wit~ similar expressions f ~(/'/2) and 7lz(/,/2).
16 66 The following theem provides a characterization result f the three distributions considered in theem 3.6 based on a functional relationship between the bivaraite Gini-index defined in (3.2.3) and the bivariate vitality function defined in (.2.39). Theem 3.7 F the random vect X considered in theem 3.6, the relation holds f all " G,(I,,/ 2 ) = k (- I, ), ;=,2, k>o (3.3.26) m,(i,,/ 2 ) 2 ~ 0 if and only if X follows anyone of the three distributions specified by (3.3.3), (3.3.4) and (3.3.5) respectively accding as k=..:!.,k>..:!. and k<..:! Proof When (3.3.26) holds with ;= using (3.3.) we have ( - k (- m,(;', )) J m,(i,,/2 ) = I, + F j f!(x"2 ) dx,. 2 - (I" ) 2 ~ Using the relation (.2.43), we get (-k) r,(i,,/ 2 ) f!(i" 2 ) Differentiating with respect to " 2(-k) r.(t t) A(t t) af(i,,/ 2 ) we get = j f!(x" 2 ) dx,. " + (-k) ar,(i,,/ 2 ) f!(t t) = - f!(t t). l' 2 l' 2 at at l' 2 l' 2 Using the equations (.2.30) and (.2.5), the above equation takes the fm
17 67 This gives. k h.,(~.t2) r,(~.t2) = -. -k Similar expression can be obtained f ;(~.t2) '2(~.t2). The rest of the proof is analogous to that of theem 3.4. The if part of the theem follows from the expressions f G,(~.t2) and ( - ~ J given below. ~(~. t 2 ) Distribution ~(~. t2) ( ~) ~(~. t2) (i) exponential 2( + ~A, + ~ tl}) A, + Bt2 (ii) Pareto c ( + a,~ + ~t2 + b~t2) (2c-) ( + ~t2 + ca,~ + bc~t2) ( + a,tl +~t2 +b~t2) ( + ~t2 + ca,~ + bc~t2) (iii) finite-range d (- A~ - P2t2 + q~t2) (- A~ - P2t2 + q~t2) ( + 2d) ( + dpltl - P2t2 - dq~t2) ( + dpl~ - P2t2 - dq~t2)
A New Class of Positively Quadrant Dependent Bivariate Distributions with Pareto
 International Mathematical Forum, 2, 27, no. 26, 1259-1273 A New Class of Positively Quadrant Dependent Bivariate Distributions with Pareto A. S. Al-Ruzaiza and Awad El-Gohary 1 Department of Statistics
International Mathematical Forum, 2, 27, no. 26, 1259-1273 A New Class of Positively Quadrant Dependent Bivariate Distributions with Pareto A. S. Al-Ruzaiza and Awad El-Gohary 1 Department of Statistics
and the ANAVETS Unit Portage Ave, Winnipeg, Manitoba, Canada May 23 to May E L IBSF
 t NVET Uit 283 IR FO RE VET ER N N N I MY NVY & R 3584 Pt, Wii, Mitb, IN O RPORTE E IL L I GU VET IF N ENG R H LI E My 23 t My 28-2015 R LE YOUR ONE TOP HOP FOR QULITY POOL UE & ILLIR EORIE GMEROOM 204-783-2666
t NVET Uit 283 IR FO RE VET ER N N N I MY NVY & R 3584 Pt, Wii, Mitb, IN O RPORTE E IL L I GU VET IF N ENG R H LI E My 23 t My 28-2015 R LE YOUR ONE TOP HOP FOR QULITY POOL UE & ILLIR EORIE GMEROOM 204-783-2666
Patients and families are the guiding force in their own end-of-life experience.
 2009-2010 A N N U A L R E P O R T Pt ii t ii c i --i x. H t z t 2009/2010 P Hiit Tt t, H t z t tci t i ii i, t t i --i x, i i, i t t t. A At t Bi A Qit Li H t-it i t, H i t i i qit i ii t t i t i. Ext
2009-2010 A N N U A L R E P O R T Pt ii t ii c i --i x. H t z t 2009/2010 P Hiit Tt t, H t z t tci t i ii i, t t i --i x, i i, i t t t. A At t Bi A Qit Li H t-it i t, H i t i i qit i ii t t i t i. Ext
RELATIVE ERRORS IN RELIABILITY MEASURES. University of Maine and University of New Brunswick
 RELATIVE ERRORS IN RELIABILITY MEASURES BY PUSHPA L. GUPTA AND R.D. GUPTA 1 University of Maine and University of New Brunswick A common assumption, in reliability and lifetesting situations when the components
RELATIVE ERRORS IN RELIABILITY MEASURES BY PUSHPA L. GUPTA AND R.D. GUPTA 1 University of Maine and University of New Brunswick A common assumption, in reliability and lifetesting situations when the components
Helping Kids Prepare For Life (253)
 Hlpi Ki Pp F Lif.l.i. (253)-589-7489 Tilli it it L Livit iv f fiv CIS U H. Vip pt fll t Tilli Elt l tpi tff tt f vi t t CIS T Hll f i Cltt N Cli. - L ivi i CIS f Bill Milli CIS pit Dil Cili Ti l iz it
Hlpi Ki Pp F Lif.l.i. (253)-589-7489 Tilli it it L Livit iv f fiv CIS U H. Vip pt fll t Tilli Elt l tpi tff tt f vi t t CIS T Hll f i Cltt N Cli. - L ivi i CIS f Bill Milli CIS pit Dil Cili Ti l iz it
Grilled it ems are prepared over real mesquit e wood CREATE A COMBO STEAKS. Onion Brewski Sirloin * Our signature USDA Choice 12 oz. Sirloin.
 TT & L Gl v l q T l q TK v i f i ' i i T K L G ' T G!? Ti 10 (Pik 3) -F- L P ki - ik T ffl i zzll ik Fi Pikl x i f l $3 (li 2) i f i i i - i f i jlñ i 84 6 - f ki i Fi 6 T i ffl i 10 -i i fi & i i ffl
TT & L Gl v l q T l q TK v i f i ' i i T K L G ' T G!? Ti 10 (Pik 3) -F- L P ki - ik T ffl i zzll ik Fi Pikl x i f l $3 (li 2) i f i i i - i f i jlñ i 84 6 - f ki i Fi 6 T i ffl i 10 -i i fi & i i ffl
DYNAMIC LECTURE 1 UNIVERSITY OF MARYLAND: ECON 600
 DYNAMIC LECTURE 1 UNIVERSITY OF MARYLAND: ECON 6 1. differential Equations 1 1.1. Basic Concepts for Univariate Equations. We use differential equations to model situations which treat time as a continuous
DYNAMIC LECTURE 1 UNIVERSITY OF MARYLAND: ECON 6 1. differential Equations 1 1.1. Basic Concepts for Univariate Equations. We use differential equations to model situations which treat time as a continuous
Fundamentals of Reliability Engineering and Applications
 Fundamentals of Reliability Engineering and Applications E. A. Elsayed elsayed@rci.rutgers.edu Rutgers University Quality Control & Reliability Engineering (QCRE) IIE February 21, 2012 1 Outline Part 1.
Fundamentals of Reliability Engineering and Applications E. A. Elsayed elsayed@rci.rutgers.edu Rutgers University Quality Control & Reliability Engineering (QCRE) IIE February 21, 2012 1 Outline Part 1.
MEDWAY SPORTS DEVELOPMENT
 PB 2:L 1 13:36 P 1 MEDWAY SPTS DEVELPMENT.m.v./vlm A i 11 Bfil Sl i P-16 FE C? D v i i? T l i i S Li Pmm? B fi Ti iq l vlm mm ill l vl fi, mivi ill vii flli ii: l Nm S l : W Tm li ii (ili m fi i) j l i?
PB 2:L 1 13:36 P 1 MEDWAY SPTS DEVELPMENT.m.v./vlm A i 11 Bfil Sl i P-16 FE C? D v i i? T l i i S Li Pmm? B fi Ti iq l vlm mm ill l vl fi, mivi ill vii flli ii: l Nm S l : W Tm li ii (ili m fi i) j l i?
EXPONENTIAL, LOGARITHMIC, AND TRIGONOMETRIC FUNCTIONS
 Calculus for the Life Sciences nd Edition Greenwell SOLUTIONS MANUAL Full download at: https://testbankreal.com/download/calculus-for-the-life-sciences-nd-editiongreenwell-solutions-manual-/ Calculus for
Calculus for the Life Sciences nd Edition Greenwell SOLUTIONS MANUAL Full download at: https://testbankreal.com/download/calculus-for-the-life-sciences-nd-editiongreenwell-solutions-manual-/ Calculus for
Formal Groups. Niki Myrto Mavraki
 Formal Groups Niki Myrto Mavraki Contents 1. Introduction 1 2. Some preliminaries 2 3. Formal Groups (1 dimensional) 2 4. Groups associated to formal groups 9 5. The Invariant Differential 11 6. The Formal
Formal Groups Niki Myrto Mavraki Contents 1. Introduction 1 2. Some preliminaries 2 3. Formal Groups (1 dimensional) 2 4. Groups associated to formal groups 9 5. The Invariant Differential 11 6. The Formal
z E z *" I»! HI UJ LU Q t i G < Q UJ > UJ >- C/J o> o C/) X X UJ 5 UJ 0) te : < C/) < 2 H CD O O) </> UJ Ü QC < 4* P? K ll I I <% "fei 'Q f
 I % 4*? ll I - ü z /) I J (5 /) 2 - / J z Q. J X X J 5 G Q J s J J /J z *" J - LL L Q t-i ' '," ; i-'i S": t : i ) Q "fi 'Q f I»! t i TIS NT IS BST QALITY AVAILABL. T Y FRNIS T TI NTAIN A SIGNIFIANT NBR
I % 4*? ll I - ü z /) I J (5 /) 2 - / J z Q. J X X J 5 G Q J s J J /J z *" J - LL L Q t-i ' '," ; i-'i S": t : i ) Q "fi 'Q f I»! t i TIS NT IS BST QALITY AVAILABL. T Y FRNIS T TI NTAIN A SIGNIFIANT NBR
These notes will supplement the textbook not replace what is there. defined for α >0
 Gamma Distribution These notes will supplement the textbook not replace what is there. Gamma Function ( ) = x 0 e dx 1 x defined for >0 Properties of the Gamma Function 1. For any >1 () = ( 1)( 1) Proof
Gamma Distribution These notes will supplement the textbook not replace what is there. Gamma Function ( ) = x 0 e dx 1 x defined for >0 Properties of the Gamma Function 1. For any >1 () = ( 1)( 1) Proof
BULLETIN THE BULLETIN OCTOBER VICTOR VALLEY NEWSLETTER OF MINERAL CLUB GEM AND THE PH. (760) TOR VALLEY GEM & MINERAL
 S il M il S Vi Vll G & Mil Cl 15056-B Sv S Vivill, CA 92395-3811. BULLETIN i i i l l l li VICTOR VALLEY GEM & MINERAL CLUB i i i g. V i x i ī l i i BULLETIN il l VIC- TOR VALLEY GEM & MINERAL CLUB. R i
S il M il S Vi Vll G & Mil Cl 15056-B Sv S Vivill, CA 92395-3811. BULLETIN i i i l l l li VICTOR VALLEY GEM & MINERAL CLUB i i i g. V i x i ī l i i BULLETIN il l VIC- TOR VALLEY GEM & MINERAL CLUB. R i
Terminology and Concepts
 Terminology and Concepts Prof. Naga Kandasamy 1 Goals of Fault Tolerance Dependability is an umbrella term encompassing the concepts of reliability, availability, performability, safety, and testability.
Terminology and Concepts Prof. Naga Kandasamy 1 Goals of Fault Tolerance Dependability is an umbrella term encompassing the concepts of reliability, availability, performability, safety, and testability.
r log+ 1 F(t) 1 jt ^
 THE BERNSTEIN PROBLEM LOUIS DE BRANGES Let w(x) be a positive valued, continuous function of real x, such that for each ra = 0, 1, 2,, xnw(x) is bounded. S. Bernstein asks for conditions on w(x) that the
THE BERNSTEIN PROBLEM LOUIS DE BRANGES Let w(x) be a positive valued, continuous function of real x, such that for each ra = 0, 1, 2,, xnw(x) is bounded. S. Bernstein asks for conditions on w(x) that the
A MEASURE OF DISCRIMINATION BETWEEN TWO RESIDUAL LIFE-TIME DISTRIBUTIONS AND ITS APPLICATIONS NADER EBRAHIMI 1 AND S. N. U. A. KIRMANI 2.
 Ann. Inst. Statist. Math, Vol. 48, No. 2, 257-265 (1996) A MEASURE OF DISCRIMINATION BETWEEN TWO RESIDUAL LIFE-TIME DISTRIBUTIONS AND ITS APPLICATIONS NADER EBRAHIMI 1 AND S. N. U. A. KIRMANI 2. 1Division
Ann. Inst. Statist. Math, Vol. 48, No. 2, 257-265 (1996) A MEASURE OF DISCRIMINATION BETWEEN TWO RESIDUAL LIFE-TIME DISTRIBUTIONS AND ITS APPLICATIONS NADER EBRAHIMI 1 AND S. N. U. A. KIRMANI 2. 1Division
SOME IDENTITIES INVOLVING THE FIBONACCI POLYNOMIALS*
 * Yi Yuan and Wenpeeg Zhang Research Center for Basic Science, Xi'an Jiaotong University, Xi'an Shaanxi. P.R. China (Submitted June 2000-Final Revision November 2000) 1. INTROBUCTION AND RESULTS As usual,
* Yi Yuan and Wenpeeg Zhang Research Center for Basic Science, Xi'an Jiaotong University, Xi'an Shaanxi. P.R. China (Submitted June 2000-Final Revision November 2000) 1. INTROBUCTION AND RESULTS As usual,
OPTIMUM DESIGN ON STEP-STRESS LIFE TESTING
 Libraries Conference on Applied Statistics in Agriculture 1998-10th Annual Conference Proceedings OPTIMUM DESIGN ON STEP-STRESS LIFE TESTING C. Xiong Follow this and additional works at: http://newprairiepress.org/agstatconference
Libraries Conference on Applied Statistics in Agriculture 1998-10th Annual Conference Proceedings OPTIMUM DESIGN ON STEP-STRESS LIFE TESTING C. Xiong Follow this and additional works at: http://newprairiepress.org/agstatconference
Multiple Random Variables
 Multiple Random Variables This Version: July 30, 2015 Multiple Random Variables 2 Now we consider models with more than one r.v. These are called multivariate models For instance: height and weight An
Multiple Random Variables This Version: July 30, 2015 Multiple Random Variables 2 Now we consider models with more than one r.v. These are called multivariate models For instance: height and weight An
or - CHAPTER 7 Applications of Integration Section 7.1 Area of a Region Between Two Curves 1. A= ~2[0- (x :2-6x)] dr=-~2(x 2-6x) dr
![or - CHAPTER 7 Applications of Integration Section 7.1 Area of a Region Between Two Curves 1. A= ~2[0- (x :2-6x)] dr=-~2(x 2-6x) dr or - CHAPTER 7 Applications of Integration Section 7.1 Area of a Region Between Two Curves 1. A= ~2[0- (x :2-6x)] dr=-~2(x 2-6x) dr](/thumbs/89/98001178.jpg) CHAPTER 7 Applications of Integration Section 7.1 Area of a Region Between Two Curves 1. A= ~[0- (x : 6x)] dr=-~(x 6x) dr 6~ 1356 or - 6. A: ~[(x- 1) 3 -(x-1)]dx 11. [~/3 ( - see x) dx 5- - 3 - I 1 3 5
CHAPTER 7 Applications of Integration Section 7.1 Area of a Region Between Two Curves 1. A= ~[0- (x : 6x)] dr=-~(x 6x) dr 6~ 1356 or - 6. A: ~[(x- 1) 3 -(x-1)]dx 11. [~/3 ( - see x) dx 5- - 3 - I 1 3 5
MFM Practitioner Module: Quantitiative Risk Management. John Dodson. October 14, 2015
 MFM Practitioner Module: Quantitiative Risk Management October 14, 2015 The n-block maxima 1 is a random variable defined as M n max (X 1,..., X n ) for i.i.d. random variables X i with distribution function
MFM Practitioner Module: Quantitiative Risk Management October 14, 2015 The n-block maxima 1 is a random variable defined as M n max (X 1,..., X n ) for i.i.d. random variables X i with distribution function
I-1. rei. o & A ;l{ o v(l) o t. e 6rf, \o. afl. 6rt {'il l'i. S o S S. l"l. \o a S lrh S \ S s l'l {a ra \o r' tn $ ra S \ S SG{ $ao. \ S l"l. \ (?
 >. 1! = * l >'r : ^, : - fr). ;1,!/!i ;(?= f: r*. fl J :!= J; J- >. Vf i - ) CJ ) ṯ,- ( r k : ( l i ( l 9 ) ( ;l fr i) rf,? l i =r, [l CB i.l.!.) -i l.l l.!. * (.1 (..i -.1.! r ).!,l l.r l ( i b i i '9,
>. 1! = * l >'r : ^, : - fr). ;1,!/!i ;(?= f: r*. fl J :!= J; J- >. Vf i - ) CJ ) ṯ,- ( r k : ( l i ( l 9 ) ( ;l fr i) rf,? l i =r, [l CB i.l.!.) -i l.l l.!. * (.1 (..i -.1.! r ).!,l l.r l ( i b i i '9,
P(I -ni < an for all n > in) = 1 - Pm# 1
 ITERATED LOGARITHM INEQUALITIES* By D. A. DARLING AND HERBERT ROBBINS UNIVERSITY OF CALIFORNIA, BERKELEY Communicated by J. Neyman, March 10, 1967 1. Introduction.-Let x,x1,x2,... be a sequence of independent,
ITERATED LOGARITHM INEQUALITIES* By D. A. DARLING AND HERBERT ROBBINS UNIVERSITY OF CALIFORNIA, BERKELEY Communicated by J. Neyman, March 10, 1967 1. Introduction.-Let x,x1,x2,... be a sequence of independent,
COMPOSITE RELIABILITY MODELS FOR SYSTEMS WITH TWO DISTINCT KINDS OF STOCHASTIC DEPENDENCES BETWEEN THEIR COMPONENTS LIFE TIMES
 COMPOSITE RELIABILITY MODELS FOR SYSTEMS WITH TWO DISTINCT KINDS OF STOCHASTIC DEPENDENCES BETWEEN THEIR COMPONENTS LIFE TIMES Jerzy Filus Department of Mathematics and Computer Science, Oakton Community
COMPOSITE RELIABILITY MODELS FOR SYSTEMS WITH TWO DISTINCT KINDS OF STOCHASTIC DEPENDENCES BETWEEN THEIR COMPONENTS LIFE TIMES Jerzy Filus Department of Mathematics and Computer Science, Oakton Community
.IEEEEEEIIEII. fflllffo. I ll, 7 AO-AO CALIFORNIA UN IV BERKELEY OPERATIONS RESEARCH CENTER FIG 12/1
 7 AO-AO95 140 CALIFORNIA UN IV BERKELEY OPERATIONS RESEARCH CENTER FIG 12/1.IEEEEEEIIEII AVAILABILITY OF SERIES SYSTEMS WITH COMPONENTS SUBJECT TO VARIO--ETC(U) JUN 80 Z S KHALIL AFOSR-77-3179 UNCLASSIFIED
7 AO-AO95 140 CALIFORNIA UN IV BERKELEY OPERATIONS RESEARCH CENTER FIG 12/1.IEEEEEEIIEII AVAILABILITY OF SERIES SYSTEMS WITH COMPONENTS SUBJECT TO VARIO--ETC(U) JUN 80 Z S KHALIL AFOSR-77-3179 UNCLASSIFIED
Časopis pro pěstování matematiky
 Časopis pro pěstování matematiky Jan Ligȩza On distributional solutions of some systems of linear differential equations Časopis pro pěstování matematiky, Vol. 102 (1977), No. 1, 37--41 Persistent URL:
Časopis pro pěstování matematiky Jan Ligȩza On distributional solutions of some systems of linear differential equations Časopis pro pěstování matematiky, Vol. 102 (1977), No. 1, 37--41 Persistent URL:
By J. B. MOORE Department of Electrical Engineering, University of Newcastle, Newcastle, h~ewsouth Wales, Australia. [Received October 10, 196 7]
![By J. B. MOORE Department of Electrical Engineering, University of Newcastle, Newcastle, h~ewsouth Wales, Australia. [Received October 10, 196 7] By J. B. MOORE Department of Electrical Engineering, University of Newcastle, Newcastle, h~ewsouth Wales, Australia. [Received October 10, 196 7]](/thumbs/94/121699318.jpg) INT. J. CONTROL,1!)67, VOL. 6, No. -i, 373-379 Stability of Linear Dynamical Systems Non-linearities~ with Memoryless By J. B. MOORE Department of Electrical Engineering, University of Newcastle, Newcastle,
INT. J. CONTROL,1!)67, VOL. 6, No. -i, 373-379 Stability of Linear Dynamical Systems Non-linearities~ with Memoryless By J. B. MOORE Department of Electrical Engineering, University of Newcastle, Newcastle,
1.2 LECTURE 2. Scalar Product
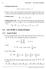 6 CHAPTER 1. VECTOR ALGEBRA Pythagean theem. cos 2 α 1 + cos 2 α 2 + cos 2 α 3 = 1 There is a one-to-one crespondence between the components of the vect on the one side and its magnitude and the direction
6 CHAPTER 1. VECTOR ALGEBRA Pythagean theem. cos 2 α 1 + cos 2 α 2 + cos 2 α 3 = 1 There is a one-to-one crespondence between the components of the vect on the one side and its magnitude and the direction
MATHEMATICS OF COMPUTATION, VOLUME 26, NUMBER 118, APRIL An Algorithm for Computing Logarithms. and Arctangents. By B. C.
 MATHEMATICS OF COMPUTATION, VOLUME 26, NUMBER 118, APRIL 1972 An Algorithm for Computing Logarithms and Arctangents By B. C. Carlson Abstract. An iterative algorithm with fast convergence can be used to
MATHEMATICS OF COMPUTATION, VOLUME 26, NUMBER 118, APRIL 1972 An Algorithm for Computing Logarithms and Arctangents By B. C. Carlson Abstract. An iterative algorithm with fast convergence can be used to
On Stability Criteria of Explicit Difference Schemes for Certain Heat Conduction Problems with Uncommon Boundary Conditions
 On Stability Criteria of Explicit Difference Schemes f Certain Heat Conduction Problems with Uncommon Boundary Conditions By Arnold N. Lowan Abstract. Stability criteria are derived f the explicit difference
On Stability Criteria of Explicit Difference Schemes f Certain Heat Conduction Problems with Uncommon Boundary Conditions By Arnold N. Lowan Abstract. Stability criteria are derived f the explicit difference
 D t r l f r th n t d t t pr p r d b th t ff f th l t tt n N tr t n nd H n N d, n t d t t n t. n t d t t. h n t n :.. vt. Pr nt. ff.,. http://hdl.handle.net/2027/uiug.30112023368936 P bl D n, l d t z d
D t r l f r th n t d t t pr p r d b th t ff f th l t tt n N tr t n nd H n N d, n t d t t n t. n t d t t. h n t n :.. vt. Pr nt. ff.,. http://hdl.handle.net/2027/uiug.30112023368936 P bl D n, l d t z d
CHARACTERIZATIONS OF A FAMILY OF BIVARIATE PARETO DISTRIBUTIONS
 STATISTICA, anno LXXV, n. 3, 205 CHARACTERIZATIONS OF A FAMILY OF BIVARIATE PARETO DISTRIBUTIONS P. G. Sankaran Department of Statistics Cochin University of Science and Technology, Cochin N. Unnikrishnan
STATISTICA, anno LXXV, n. 3, 205 CHARACTERIZATIONS OF A FAMILY OF BIVARIATE PARETO DISTRIBUTIONS P. G. Sankaran Department of Statistics Cochin University of Science and Technology, Cochin N. Unnikrishnan
i.ea IE !e e sv?f 'il i+x3p \r= v * 5,?: S i- co i, ==:= SOrq) Xgs'iY # oo .9 9 PE * v E=S s->'d =ar4lq 5,n =.9 '{nl a':1 t F #l *r C\ t-e
 fl ) 2 ;;:i c.l l) ( # =S >' 5 ^'R 1? l.y i.i.9 9 P * v ,>f { e e v? 'il v * 5,?: S 'V i: :i (g Y 1,Y iv cg G J :< >,c Z^ /^ c..l Cl i l 1 3 11 5 (' \ h 9 J :'i g > _ ^ j, \= f{ '{l #l * C\? 0l = 5,
fl ) 2 ;;:i c.l l) ( # =S >' 5 ^'R 1? l.y i.i.9 9 P * v ,>f { e e v? 'il v * 5,?: S 'V i: :i (g Y 1,Y iv cg G J :< >,c Z^ /^ c..l Cl i l 1 3 11 5 (' \ h 9 J :'i g > _ ^ j, \= f{ '{l #l * C\? 0l = 5,
International Journal of Scientific & Engineering Research, Volume 6, Issue 2, February-2015 ISSN
 1686 On Some Generalised Transmuted Distributions Kishore K. Das Luku Deka Barman Department of Statistics Gauhati University Abstract In this paper a generalized form of the transmuted distributions has
1686 On Some Generalised Transmuted Distributions Kishore K. Das Luku Deka Barman Department of Statistics Gauhati University Abstract In this paper a generalized form of the transmuted distributions has
~,. :'lr. H ~ j. l' ", ...,~l. 0 '" ~ bl '!; 1'1. :<! f'~.., I,," r: t,... r':l G. t r,. 1'1 [<, ."" f'" 1n. t.1 ~- n I'>' 1:1 , I. <1 ~'..
 ,, 'l t (.) :;,/.I I n ri' ' r l ' rt ( n :' (I : d! n t, :?rj I),.. fl.),. f!..,,., til, ID f-i... j I. 't' r' t II!:t () (l r El,, (fl lj J4 ([) f., () :. -,,.,.I :i l:'!, :I J.A.. t,.. p, - ' I I I
,, 'l t (.) :;,/.I I n ri' ' r l ' rt ( n :' (I : d! n t, :?rj I),.. fl.),. f!..,,., til, ID f-i... j I. 't' r' t II!:t () (l r El,, (fl lj J4 ([) f., () :. -,,.,.I :i l:'!, :I J.A.. t,.. p, - ' I I I
Mathematical Economics. Lecture Notes (in extracts)
 Prof. Dr. Frank Werner Faculty of Mathematics Institute of Mathematical Optimization (IMO) http://math.uni-magdeburg.de/ werner/math-ec-new.html Mathematical Economics Lecture Notes (in extracts) Winter
Prof. Dr. Frank Werner Faculty of Mathematics Institute of Mathematical Optimization (IMO) http://math.uni-magdeburg.de/ werner/math-ec-new.html Mathematical Economics Lecture Notes (in extracts) Winter
THE WORLD BANK GROUP ARCHIVES PUBLIC DISCLOSURE AUTHORIZED
 THE WORLD BANK GROUP ARCHIVES PUBLIC DISCLOSURE AUTHORIZED Folder Title: Finland-LN-61 - Photographs - Volume 1 Folder ID: 1721443 Fonds: Records of Office of External Affairs (WB IBRD/IDA EXT) Digitized:
THE WORLD BANK GROUP ARCHIVES PUBLIC DISCLOSURE AUTHORIZED Folder Title: Finland-LN-61 - Photographs - Volume 1 Folder ID: 1721443 Fonds: Records of Office of External Affairs (WB IBRD/IDA EXT) Digitized:
Daily Skill Practice
 G CD-0 Dily Skill Pti 00 Wkk ## W i t it Eh. gh y w m y il A ll? + = 8 Dy 8= 0. =. Nm. C h l lit tl k ty i g. I h hi ty w ig h, m y hw hi g w ig h?. W Wkk ##00 A A = t, >, = W it < t t m t m k t. Dy Dy
G CD-0 Dily Skill Pti 00 Wkk ## W i t it Eh. gh y w m y il A ll? + = 8 Dy 8= 0. =. Nm. C h l lit tl k ty i g. I h hi ty w ig h, m y hw hi g w ig h?. W Wkk ##00 A A = t, >, = W it < t t m t m k t. Dy Dy
Modeling Bivariate Lorenz Curves with Applications to Multidimensional Inequality in Well-Being
 Fifth meeting of the Society for the Study of Economic Inequality ECINEQ Bari, Italy, July 22-24, 213 Modeling Bivariate Lorenz Curves with Applications to Multidimensional Inequality in Well-Being José
Fifth meeting of the Society for the Study of Economic Inequality ECINEQ Bari, Italy, July 22-24, 213 Modeling Bivariate Lorenz Curves with Applications to Multidimensional Inequality in Well-Being José
P a g e 3 6 of R e p o r t P B 4 / 0 9
 P a g e 3 6 of R e p o r t P B 4 / 0 9 p r o t e c t h um a n h e a l t h a n d p r o p e r t y fr om t h e d a n g e rs i n h e r e n t i n m i n i n g o p e r a t i o n s s u c h a s a q u a r r y. J
P a g e 3 6 of R e p o r t P B 4 / 0 9 p r o t e c t h um a n h e a l t h a n d p r o p e r t y fr om t h e d a n g e rs i n h e r e n t i n m i n i n g o p e r a t i o n s s u c h a s a q u a r r y. J
o C *$ go ! b», S AT? g (i * ^ fc fa fa U - S 8 += C fl o.2h 2 fl 'fl O ' 0> fl l-h cvo *, &! 5 a o3 a; O g 02 QJ 01 fls g! r«'-fl O fl s- ccco
 > p >>>> ft^. 2 Tble f Generl rdnes. t^-t - +«0 -P k*ph? -- i t t i S i-h l -H i-h -d. *- e Stf H2 t s - ^ d - 'Ct? "fi p= + V t r & ^ C d Si d n. M. s - W ^ m» H ft ^.2. S'Sll-pl e Cl h /~v S s, -P s'l
> p >>>> ft^. 2 Tble f Generl rdnes. t^-t - +«0 -P k*ph? -- i t t i S i-h l -H i-h -d. *- e Stf H2 t s - ^ d - 'Ct? "fi p= + V t r & ^ C d Si d n. M. s - W ^ m» H ft ^.2. S'Sll-pl e Cl h /~v S s, -P s'l
A CHARACTERIZATION OF INNER PRODUCT SPACES
 A CHARACTERIZATION OF INNER PRODUCT SPACES DAVID ALBERT SENECHALLE The well-known parallelogram law of Jordan and von Neumann [l] has been generalized in two different ways by M. M. Day [2] and E. R. Lorch
A CHARACTERIZATION OF INNER PRODUCT SPACES DAVID ALBERT SENECHALLE The well-known parallelogram law of Jordan and von Neumann [l] has been generalized in two different ways by M. M. Day [2] and E. R. Lorch
Localization I: General considerations, one-parameter scaling
 PHYS598PTD A.J.Leggett 2013 Lecture 4 Localization I: General considerations 1 Localization I: General considerations, one-parameter scaling Traditionally, two mechanisms for localization of electron states
PHYS598PTD A.J.Leggett 2013 Lecture 4 Localization I: General considerations 1 Localization I: General considerations, one-parameter scaling Traditionally, two mechanisms for localization of electron states
P a g e 5 1 of R e p o r t P B 4 / 0 9
 P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
On Five Parameter Beta Lomax Distribution
 ISSN 1684-840 Journal of Statistics Volume 0, 01. pp. 10-118 On Five Parameter Beta Lomax Distribution Muhammad Rajab 1, Muhammad Aleem, Tahir Nawaz and Muhammad Daniyal 4 Abstract Lomax (1954) developed
ISSN 1684-840 Journal of Statistics Volume 0, 01. pp. 10-118 On Five Parameter Beta Lomax Distribution Muhammad Rajab 1, Muhammad Aleem, Tahir Nawaz and Muhammad Daniyal 4 Abstract Lomax (1954) developed
Equipping students to think biblically, live wisely and serve faithfully for over 30 years. MAY 2015 IMPORTANT DAYS IN MAY:
 MAY 2015 IMPORTANT DAYS IN MAY: PCS Piw D M, 5/4 Bl W, 5/20 Gi S, 5/24 L D f Sl W, 5/27 Eqii ik ill, wil fifll f 30. PARK CHRISTIAN SCHOOL w; i i w i m l M iw w m l f i W, f w i, Y Cil i w i q, w, i i
MAY 2015 IMPORTANT DAYS IN MAY: PCS Piw D M, 5/4 Bl W, 5/20 Gi S, 5/24 L D f Sl W, 5/27 Eqii ik ill, wil fifll f 30. PARK CHRISTIAN SCHOOL w; i i w i m l M iw w m l f i W, f w i, Y Cil i w i q, w, i i
16. Local theory of regular singular points and applications
 16. Local theory of regular singular points and applications 265 16. Local theory of regular singular points and applications In this section we consider linear systems defined by the germs of meromorphic
16. Local theory of regular singular points and applications 265 16. Local theory of regular singular points and applications In this section we consider linear systems defined by the germs of meromorphic
EXAM 2, MATH 132 WEDNESDAY, OCTOBER 23, 2002
 EXAM 2, MATH 132 WEDNESDAY, OCTOBER 23, 2002 This examination has 20 multiple choice questions, and two essay questions. Please check it over and if you find it to be incomplete, notify the proctor. Do
EXAM 2, MATH 132 WEDNESDAY, OCTOBER 23, 2002 This examination has 20 multiple choice questions, and two essay questions. Please check it over and if you find it to be incomplete, notify the proctor. Do
Math and Numerical Methods Review
 Math and Numerical Methods Review Michael Caracotsios, Ph.D. Clinical Associate Professor Chemical Engineering Department University of Illinois at Chicago Introduction In the study of chemical engineering
Math and Numerical Methods Review Michael Caracotsios, Ph.D. Clinical Associate Professor Chemical Engineering Department University of Illinois at Chicago Introduction In the study of chemical engineering
BULLETIN THE BULLETIN JUNE 2012 VICTOR VALLEY NEWSLETTER OF MINERAL CLUB GEM AND THE THE SAN BERNARDINO COUNTY FAIR ISSUE PH.
 S il M il S Vi Vll G & Mil Cl 15056-B Sv S Vivill, CA 92395-3811. BULLETIN i i i l l l li VICTOR VALLEY GEM & MINERAL CLUB i i i g. V i x i ī l i i BULLETIN il l VIC- TOR VALLEY GEM & MINERAL CLUB. R i
S il M il S Vi Vll G & Mil Cl 15056-B Sv S Vivill, CA 92395-3811. BULLETIN i i i l l l li VICTOR VALLEY GEM & MINERAL CLUB i i i g. V i x i ī l i i BULLETIN il l VIC- TOR VALLEY GEM & MINERAL CLUB. R i
FAILURE RATE OF THE INVERSE GAUSSlAN-WEIBULL MIXTURE MODEL
 Ann. Inst. Statist. Math. Vol. 41, No. 3, 617-622 (1989) FAILURE RATE OF THE INVERSE GAUSSlAN-WEIBULL MIXTURE MODEL ESSAM K. AL-HUSSAINI 1 AND NAGI S. ABD-EL-HAKIM 2 1Department of Mathematics, University
Ann. Inst. Statist. Math. Vol. 41, No. 3, 617-622 (1989) FAILURE RATE OF THE INVERSE GAUSSlAN-WEIBULL MIXTURE MODEL ESSAM K. AL-HUSSAINI 1 AND NAGI S. ABD-EL-HAKIM 2 1Department of Mathematics, University
Due: Fri Nov :31 AM MST. Question Instructions Read today's Notes and Learning Goals
 The Fundamental Theorem: Basic (1862427) Due: Fri Nov 1 217 7:31 AM MST Question 1 2 3 4 5 6 7 8 9 1 11 12 Instructions Read today's Notes and Learning Goals 1. Question Details Fa 14 FTC Basic List 1
The Fundamental Theorem: Basic (1862427) Due: Fri Nov 1 217 7:31 AM MST Question 1 2 3 4 5 6 7 8 9 1 11 12 Instructions Read today's Notes and Learning Goals 1. Question Details Fa 14 FTC Basic List 1
w = X ^ = ^ ^, (i*i < ix
 A SUMMATION FORMULA FOR POWER SERIES USING EULERIAN FRACTIONS* Xinghua Wang Math. Department, Zhejiang University, Hangzhou 310028, China Leetsch C. Hsu Math. Institute, Dalian University of Technology,
A SUMMATION FORMULA FOR POWER SERIES USING EULERIAN FRACTIONS* Xinghua Wang Math. Department, Zhejiang University, Hangzhou 310028, China Leetsch C. Hsu Math. Institute, Dalian University of Technology,
Coordinate goemetry in the (x, y) plane
 Coordinate goemetr in the (x, ) plane In this chapter ou will learn how to solve problems involving parametric equations.. You can define the coordinates of a point on a curve using parametric equations.
Coordinate goemetr in the (x, ) plane In this chapter ou will learn how to solve problems involving parametric equations.. You can define the coordinates of a point on a curve using parametric equations.
INDICATIONS HERE OF BANNER SEASON
 U l i 3 G Y i J«K W ll Gl ' - i W JY Y 6934 V 47; 87 il 4 ll l x K i Kl il li G G il ii i ix Wi lii i l i 2 W Wi i l il i % l i Vii i i i K l i - x i i ll l Vii l q illl ' ii i i i il li i--l i G 934 G
U l i 3 G Y i J«K W ll Gl ' - i W JY Y 6934 V 47; 87 il 4 ll l x K i Kl il li G G il ii i ix Wi lii i l i 2 W Wi i l il i % l i Vii i i i K l i - x i i ll l Vii l q illl ' ii i i i il li i--l i G 934 G
Applied Calculus I. Review Solutions. Qaisar Latif. October 25, 2016
 Applied Calculus I Review Solutions Qaisar Latif October 25, 2016 2 Homework 1 Problem 1. The number of people living with HIV infections increased worldwide approximately exponentially from 2.5 million
Applied Calculus I Review Solutions Qaisar Latif October 25, 2016 2 Homework 1 Problem 1. The number of people living with HIV infections increased worldwide approximately exponentially from 2.5 million
Correlation: Copulas and Conditioning
 Correlation: Copulas and Conditioning This note reviews two methods of simulating correlated variates: copula methods and conditional distributions, and the relationships between them. Particular emphasis
Correlation: Copulas and Conditioning This note reviews two methods of simulating correlated variates: copula methods and conditional distributions, and the relationships between them. Particular emphasis
ilpi4ka3 MuHucrepcrBo o6pasobahufl Huxeropollcnofi o Onacrrl rocyaapctnennofi rrorosofi s2015 ro4y fl? /CI.?G
 MuucpcB 6psBul uxpllci cl ilpk l? /C.?G ' uxui P' 06 YP [pcjb CCTB qb cypci KMqui KMcc uxpqcci 6cu 015 Y' B cstctb yktm 1 lpxk plbl' 'cypcsuii u "c1 6p:JbbM ppmmll Cp 6[ Sp: ybpx pkm MuucpcTB 6p:ux 1 yk
MuucpcB 6psBul uxpllci cl ilpk l? /C.?G ' uxui P' 06 YP [pcjb CCTB qb cypci KMqui KMcc uxpqcci 6cu 015 Y' B cstctb yktm 1 lpxk plbl' 'cypcsuii u "c1 6p:JbbM ppmmll Cp 6[ Sp: ybpx pkm MuucpcTB 6p:ux 1 yk
Your Choice! Your Character. ... it s up to you!
 Y 2012 i y! Ti i il y Fl l/ly Iiiiv i R Iiy iizi i Ty Pv Riiliy l Diili Piiv i i y! 2 i l & l ii 3 i 4 D i iv 6 D y y 8 P yi N 9 W i Bllyi? 10 B U 11 I y i 12 P ili D lii Gi O y i i y P li l I y l! iy
Y 2012 i y! Ti i il y Fl l/ly Iiiiv i R Iiy iizi i Ty Pv Riiliy l Diili Piiv i i y! 2 i l & l ii 3 i 4 D i iv 6 D y y 8 P yi N 9 W i Bllyi? 10 B U 11 I y i 12 P ili D lii Gi O y i i y P li l I y l! iy
PUTNAM PROBLEMS DIFFERENTIAL EQUATIONS. First Order Equations. p(x)dx)) = q(x) exp(
 PUTNAM PROBLEMS DIFFERENTIAL EQUATIONS First Order Equations 1. Linear y + p(x)y = q(x) Muliply through by the integrating factor exp( p(x)) to obtain (y exp( p(x))) = q(x) exp( p(x)). 2. Separation of
PUTNAM PROBLEMS DIFFERENTIAL EQUATIONS First Order Equations 1. Linear y + p(x)y = q(x) Muliply through by the integrating factor exp( p(x)) to obtain (y exp( p(x))) = q(x) exp( p(x)). 2. Separation of
Mathematics Extension 1
 BAULKHAM HILLS HIGH SCHOOL TRIAL 04 YEAR TASK 4 Mathematics Etension General Instructions Reading time 5 minutes Working time 0 minutes Write using black or blue pen Board-approved calculators may be used
BAULKHAM HILLS HIGH SCHOOL TRIAL 04 YEAR TASK 4 Mathematics Etension General Instructions Reading time 5 minutes Working time 0 minutes Write using black or blue pen Board-approved calculators may be used
Federal Project No.: To be assigned
 TTE ID FO O TNOTTION.Jl D INII EIINY DETEINTION EQET F, ti, illif tfl f f : -- Fl jt N.: T b i t: T i (T) t t : F: Jff i (xitl. il t f T ) T: Xl (xitl. il t f T ) T : F: xitl. il t f t T: T (xitl. il t
TTE ID FO O TNOTTION.Jl D INII EIINY DETEINTION EQET F, ti, illif tfl f f : -- Fl jt N.: T b i t: T i (T) t t : F: Jff i (xitl. il t f T ) T: Xl (xitl. il t f T ) T : F: xitl. il t f t T: T (xitl. il t
One of the main objectives of this study is the estimation of parameters of
 C H A P T E R 3 M E T H O D O L O G Y 31 Introduction One of the main objectives of this study is the estimation of parameters of Makeham's law of mortality I believe that it is mandatory to explain briefly
C H A P T E R 3 M E T H O D O L O G Y 31 Introduction One of the main objectives of this study is the estimation of parameters of Makeham's law of mortality I believe that it is mandatory to explain briefly
Extreme Value Theory in Civil Engineering
 Extreme Value Theory i Civil Egieerig Baidurya Bhattacharya Dept of Civil Egieerig IIT Kharagpur December 2016 Homepage: www.facweb.iitkgp.eret.i/~baidurya/ Prelimiaries: Retur period IID radom variables
Extreme Value Theory i Civil Egieerig Baidurya Bhattacharya Dept of Civil Egieerig IIT Kharagpur December 2016 Homepage: www.facweb.iitkgp.eret.i/~baidurya/ Prelimiaries: Retur period IID radom variables
VARGA S THEOREM IN NUMBER FIELDS
 VARGA S THEOREM IN NUMBER FIELDS PETE L. CLARK AND LORI D. WATSON Abstract. We give a number field version of a recent result of Varga on solutions of polynomial equations with binary input variables and
VARGA S THEOREM IN NUMBER FIELDS PETE L. CLARK AND LORI D. WATSON Abstract. We give a number field version of a recent result of Varga on solutions of polynomial equations with binary input variables and
Housing Market Monitor
 M O O D Y È S A N A L Y T I C S H o u s i n g M a r k e t M o n i t o r I N C O R P O R A T I N G D A T A A S O F N O V E M B E R İ Ī Ĭ Ĭ E x e c u t i v e S u m m a r y E x e c u t i v e S u m m a r y
M O O D Y È S A N A L Y T I C S H o u s i n g M a r k e t M o n i t o r I N C O R P O R A T I N G D A T A A S O F N O V E M B E R İ Ī Ĭ Ĭ E x e c u t i v e S u m m a r y E x e c u t i v e S u m m a r y
THE OBSERVED HAZARD AND MULTICONPONENT SYSTEMS. (U) JAN 80 M BROWN- S M R OSS N0001R77-C I~OREE80-1 he UNCLASSIFIED CA-
 THE OBSERVED HAZARD AND MULTICONPONENT SYSTEMS. (U) JAN 80 M BROWN- S M R OSS N0001R77-C-0299 I~OREE80-1 he UNCLASSIFIED CA- Hf - 3I 2~? IRO.25 1UONT. 11111.8 MICROCOPY RESOLUTION TEST CHART (Q ORC 80-1
THE OBSERVED HAZARD AND MULTICONPONENT SYSTEMS. (U) JAN 80 M BROWN- S M R OSS N0001R77-C-0299 I~OREE80-1 he UNCLASSIFIED CA- Hf - 3I 2~? IRO.25 1UONT. 11111.8 MICROCOPY RESOLUTION TEST CHART (Q ORC 80-1
1.5. Inequalities. Equations and Inequalities. Box (cont.) Sections
 1 Equations and Inequalities Sections 1.5 1.8 2008 Pearson Addison-Wesley. All rights reserved 1 Equations and Inequalities 1.5 Applications and Modeling with Quadratic Equations 1.6 Other Types of Equations
1 Equations and Inequalities Sections 1.5 1.8 2008 Pearson Addison-Wesley. All rights reserved 1 Equations and Inequalities 1.5 Applications and Modeling with Quadratic Equations 1.6 Other Types of Equations
ACCELERATED LIFE MODELS WHEN THE STRESS IS NOT CONSTANT
 KYBERNETIKA- VOLUME 26 (1990), NUMBER 4 ACCELERATED LIFE MODELS WHEN THE STRESS IS NOT CONSTANT VILIJANDAS BAGDONAVICIUS 1 The concept of a relation functional is defined and the accelerated life models
KYBERNETIKA- VOLUME 26 (1990), NUMBER 4 ACCELERATED LIFE MODELS WHEN THE STRESS IS NOT CONSTANT VILIJANDAS BAGDONAVICIUS 1 The concept of a relation functional is defined and the accelerated life models
Your generosity brings smiles and hope!
 Mil Wi l J - M 2014 i El L A Mi R & M C S Li J Li Di Li & Ki C Ai & Mil L C G J L Li Di Ci Li S W J L B Aiil Bill & R MDll Cli MDll Hl MGi J MGi B MGi Cl M Ai Mil AFL-CIO Pli El Fi Mll N Ciii Ci M Ril
Mil Wi l J - M 2014 i El L A Mi R & M C S Li J Li Di Li & Ki C Ai & Mil L C G J L Li Di Ci Li S W J L B Aiil Bill & R MDll Cli MDll Hl MGi J MGi B MGi Cl M Ai Mil AFL-CIO Pli El Fi Mll N Ciii Ci M Ril
BIRKBECK (University of London) MATHEMATICAL AND NUMERICAL METHODS. Thursday, 29 May 2008, 10.00am-13.15pm (includes 15 minutes reading time).
 BIRKBECK (University of London) MSc EXAMINATION FOR INTERNAL STUDENTS MSc FINANCIAL ENGINEERING School of Economics, Mathematics, and Statistics MATHEMATICAL AND NUMERICAL METHODS ANSWERS EMMS011P 200804301248
BIRKBECK (University of London) MSc EXAMINATION FOR INTERNAL STUDENTS MSc FINANCIAL ENGINEERING School of Economics, Mathematics, and Statistics MATHEMATICAL AND NUMERICAL METHODS ANSWERS EMMS011P 200804301248
Multivariate Distribution Models
 Multivariate Distribution Models Model Description While the probability distribution for an individual random variable is called marginal, the probability distribution for multiple random variables is
Multivariate Distribution Models Model Description While the probability distribution for an individual random variable is called marginal, the probability distribution for multiple random variables is
35H MPa Hydraulic Cylinder 3.5 MPa Hydraulic Cylinder 35H-3
 - - - - ff ff - - - - - - B B BB f f f f f f f 6 96 f f f f f f f 6 f LF LZ f 6 MM f 9 P D RR DD M6 M6 M6 M. M. M. M. M. SL. E 6 6 9 ZB Z EE RC/ RC/ RC/ RC/ RC/ ZM 6 F FP 6 K KK M. M. M. M. M M M M f f
- - - - ff ff - - - - - - B B BB f f f f f f f 6 96 f f f f f f f 6 f LF LZ f 6 MM f 9 P D RR DD M6 M6 M6 M. M. M. M. M. SL. E 6 6 9 ZB Z EE RC/ RC/ RC/ RC/ RC/ ZM 6 F FP 6 K KK M. M. M. M. M M M M f f
r(j) -::::.- --X U.;,..;...-h_D_Vl_5_ :;;2.. Name: ~s'~o--=-i Class; Date: ID: A
 Name: ~s'~o--=-i Class; Date: U.;,..;...-h_D_Vl_5 _ MAC 2233 Chapter 4 Review for the test Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Find the derivative
Name: ~s'~o--=-i Class; Date: U.;,..;...-h_D_Vl_5 _ MAC 2233 Chapter 4 Review for the test Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Find the derivative
The multidimensional Ito Integral and the multidimensional Ito Formula. Eric Mu ller June 1, 2015 Seminar on Stochastic Geometry and its applications
 The multidimensional Ito Integral and the multidimensional Ito Formula Eric Mu ller June 1, 215 Seminar on Stochastic Geometry and its applications page 2 Seminar on Stochastic Geometry and its applications
The multidimensional Ito Integral and the multidimensional Ito Formula Eric Mu ller June 1, 215 Seminar on Stochastic Geometry and its applications page 2 Seminar on Stochastic Geometry and its applications
ABSTRACT INTRODUCTION
 Journal of Applied Mathematics and Simulation Vol. 1, Issue 2, 1987 81 ON THE INVERSE PROBLEM FOR A HEAT-LIKE EQUATION* IGOR MALYSHEV Department ofmathematics and Computer Science San Jose State University
Journal of Applied Mathematics and Simulation Vol. 1, Issue 2, 1987 81 ON THE INVERSE PROBLEM FOR A HEAT-LIKE EQUATION* IGOR MALYSHEV Department ofmathematics and Computer Science San Jose State University
Adjusting the HDI for Inequality: An Overview of Different Approaches, Data Issues, and Interpretations
 Adjusting the HDI for Inequality: An Overview of Different Approaches, Data Issues, and Interpretations Milorad Kovacevic Statistical Unit, HDRO HDRO Brown bag Seminar, September 28, 2009 1/33 OBJECTIVES:
Adjusting the HDI for Inequality: An Overview of Different Approaches, Data Issues, and Interpretations Milorad Kovacevic Statistical Unit, HDRO HDRO Brown bag Seminar, September 28, 2009 1/33 OBJECTIVES:
Visit to meet more individuals who benefit from your time
 NOURISHINGN G. Vlz S 2009 BR i y ii li i Cl. N i. J l l. Rl. A y l l i i ky. Vii.li.l. iiil i y i &. 71 y l Cl y, i iil k. 28 y, k My W i ily l i. Uil y, y k i i. T j il y. Ty il iy ly y - li G, y Cl.
NOURISHINGN G. Vlz S 2009 BR i y ii li i Cl. N i. J l l. Rl. A y l l i i ky. Vii.li.l. iiil i y i &. 71 y l Cl y, i iil k. 28 y, k My W i ily l i. Uil y, y k i i. T j il y. Ty il iy ly y - li G, y Cl.
Future Self-Guides. E,.?, :0-..-.,0 Q., 5...q ',D5', 4,] 1-}., d-'.4.., _. ZoltAn Dbrnyei Introduction. u u rt 5,4) ,-,4, a. a aci,, u 4.
![Future Self-Guides. E,.?, :0-..-.,0 Q., 5...q ',D5', 4,] 1-}., d-'.4.., _. ZoltAn Dbrnyei Introduction. u u rt 5,4) ,-,4, a. a aci,, u 4. Future Self-Guides. E,.?, :0-..-.,0 Q., 5...q ',D5', 4,] 1-}., d-'.4.., _. ZoltAn Dbrnyei Introduction. u u rt 5,4) ,-,4, a. a aci,, u 4.](/thumbs/92/109036622.jpg) te SelfGi ZltAn Dbnyei Intdtin ; ) Q) 4 t? ) t _ 4 73 y S _ E _ p p 4 t t 4) 1_ ::_ J 1 `i () L VI O I4 " " 1 D 4 L e Q) 1 k) QJ 7 j ZS _Le t 1 ej!2 i1 L 77 7 G (4) 4 6 t (1 ;7 bb F) t f; n (i M Q) 7S
te SelfGi ZltAn Dbnyei Intdtin ; ) Q) 4 t? ) t _ 4 73 y S _ E _ p p 4 t t 4) 1_ ::_ J 1 `i () L VI O I4 " " 1 D 4 L e Q) 1 k) QJ 7 j ZS _Le t 1 ej!2 i1 L 77 7 G (4) 4 6 t (1 ;7 bb F) t f; n (i M Q) 7S
Finite. U-46 Curriculum Scope and Sequence. Reporting Strand Instructional Focus Standards Semester. Represent linear equations in matrices.
 Finite U-46 Curriculum Scope and Sequence Repting Strand Instructional Focus Standards Semester Represent linear equations in matrices. A.REI.8, A.REI.9 Matrices Perfm operations on matrices and use matrices
Finite U-46 Curriculum Scope and Sequence Repting Strand Instructional Focus Standards Semester Represent linear equations in matrices. A.REI.8, A.REI.9 Matrices Perfm operations on matrices and use matrices
ON THE NUMBER OF POSITIVE SUMS OF INDEPENDENT RANDOM VARIABLES
 ON THE NUMBER OF POSITIVE SUMS OF INDEPENDENT RANDOM VARIABLES P. ERDÖS AND M. KAC 1 1. Introduction. In a recent paper 2 the authors have introduced a method for proving certain limit theorems of the
ON THE NUMBER OF POSITIVE SUMS OF INDEPENDENT RANDOM VARIABLES P. ERDÖS AND M. KAC 1 1. Introduction. In a recent paper 2 the authors have introduced a method for proving certain limit theorems of the
Drury&Wliitson. Economical. Planning of Buildings. .(Chilecture B. S. DNJVERSITT' OF. 11,1. 1 ibkahy
 Drury&Wliitson Economical Planning of Buildings.(Chilecture B. S. 902 DJVERSTT' OF,. ibkahy 4 f ^ ^ J' if 4 ^ A 4. T? 4'tariung iint) 4':>bor. f LBRARY or TMl University of llinois. CLASS. BOOK. VO.UMK.
Drury&Wliitson Economical Planning of Buildings.(Chilecture B. S. 902 DJVERSTT' OF,. ibkahy 4 f ^ ^ J' if 4 ^ A 4. T? 4'tariung iint) 4':>bor. f LBRARY or TMl University of llinois. CLASS. BOOK. VO.UMK.
Exercise 2.2. Find (with proof) all rational points on the curve y = 2 x.
 Exercise 2.2. Find (with proof) all rational points on the curve y = 2 x. Exercise 2.4: Prove that for any integer n 0, e n is not a rational number. Exercise 2.5: Prove that the only rational point on
Exercise 2.2. Find (with proof) all rational points on the curve y = 2 x. Exercise 2.4: Prove that for any integer n 0, e n is not a rational number. Exercise 2.5: Prove that the only rational point on
UNIQUENESS OF SOLUTIONS TO MATRIX EQUATIONS ON TIME SCALES
 Electronic Journal of Differential Equations, Vol. 2013 (2013), No. 50, pp. 1 13. ISSN: 1072-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu UNIQUENESS OF
Electronic Journal of Differential Equations, Vol. 2013 (2013), No. 50, pp. 1 13. ISSN: 1072-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu UNIQUENESS OF
1 Delayed Renewal Processes: Exploiting Laplace Transforms
 IEOR 6711: Stochastic Models I Professor Whitt, Tuesday, October 22, 213 Renewal Theory: Proof of Blackwell s theorem 1 Delayed Renewal Processes: Exploiting Laplace Transforms The proof of Blackwell s
IEOR 6711: Stochastic Models I Professor Whitt, Tuesday, October 22, 213 Renewal Theory: Proof of Blackwell s theorem 1 Delayed Renewal Processes: Exploiting Laplace Transforms The proof of Blackwell s
GENERALIZED MODELS FOR DETERMINING OPTIMAL NUMBER OF MINIMAL REPAIRS BEFORE REPLACEMENT
 Journal of the Operations Research Society of Japan Vo!. 24, No. 4, December 1981 1981 The Operations Research Society of Japan GENERALIZED MODELS FOR DETERMINING OPTIMAL NUMBER OF MINIMAL REPAIRS BEFORE
Journal of the Operations Research Society of Japan Vo!. 24, No. 4, December 1981 1981 The Operations Research Society of Japan GENERALIZED MODELS FOR DETERMINING OPTIMAL NUMBER OF MINIMAL REPAIRS BEFORE
BLESSINGS... Abundance to Share
 V l 5 6 T Gi I 6 j 2 0 1 1 BLESSINGS... A S I f F P C i i ii i G i f f l lii. O l Bli A S J 5 lli Cl S. T l f i l li G i fili i i f li l ii f f. Eliii l $1.5 illi fili ill j. I i G f qi x i i l i ii. I
V l 5 6 T Gi I 6 j 2 0 1 1 BLESSINGS... A S I f F P C i i ii i G i f f l lii. O l Bli A S J 5 lli Cl S. T l f i l li G i fili i i f li l ii f f. Eliii l $1.5 illi fili ill j. I i G f qi x i i l i ii. I
Student Jobs Fairs. YOUR ticket to student recruitment in Birmingham 2015 Version 1
 S J Fi YOUR i i i Biih 215 Vi 1 Wl D vi -i/l vi vi v 28,? Th l fh h J Z h Gil f S h vi f f l vii ii i il Wl W 214 i i f 6, v 12, i hh h Gil, f h hi f -i/l vi ii h hil h Th i i vi j ii hi i Oii h J Z, Gil
S J Fi YOUR i i i Biih 215 Vi 1 Wl D vi -i/l vi vi v 28,? Th l fh h J Z h Gil f S h vi f f l vii ii i il Wl W 214 i i f 6, v 12, i hh h Gil, f h hi f -i/l vi ii h hil h Th i i vi j ii hi i Oii h J Z, Gil
Regression and Nonlinear Axes
 Introduction to Chemical Engineering Calculations Lecture 2. What is regression analysis? A technique for modeling and analyzing the relationship between 2 or more variables. Usually, 1 variable is designated
Introduction to Chemical Engineering Calculations Lecture 2. What is regression analysis? A technique for modeling and analyzing the relationship between 2 or more variables. Usually, 1 variable is designated
Tail Dependence of Multivariate Pareto Distributions
 !#"%$ & ' ") * +!-,#. /10 243537698:6 ;=@?A BCDBFEHGIBJEHKLB MONQP RS?UTV=XW>YZ=eda gihjlknmcoqprj stmfovuxw yy z {} ~ ƒ }ˆŠ ~Œ~Ž f ˆ ` š œžÿ~ ~Ÿ œ } ƒ œ ˆŠ~ œ
!#"%$ & ' ") * +!-,#. /10 243537698:6 ;=@?A BCDBFEHGIBJEHKLB MONQP RS?UTV=XW>YZ=eda gihjlknmcoqprj stmfovuxw yy z {} ~ ƒ }ˆŠ ~Œ~Ž f ˆ ` š œžÿ~ ~Ÿ œ } ƒ œ ˆŠ~ œ
Dependence. MFM Practitioner Module: Risk & Asset Allocation. John Dodson. September 11, Dependence. John Dodson. Outline.
 MFM Practitioner Module: Risk & Asset Allocation September 11, 2013 Before we define dependence, it is useful to define Random variables X and Y are independent iff For all x, y. In particular, F (X,Y
MFM Practitioner Module: Risk & Asset Allocation September 11, 2013 Before we define dependence, it is useful to define Random variables X and Y are independent iff For all x, y. In particular, F (X,Y
MIL-HDBK OCTOBER 1984 MAINTAINABILITY ANALYSIS
 5 CTBER 984 TABLE 5.3..-: VALUES F R z (t'i_ a ) MST CMMNLY USED IN MAINTAINABILITY ANALYSIS l-
5 CTBER 984 TABLE 5.3..-: VALUES F R z (t'i_ a ) MST CMMNLY USED IN MAINTAINABILITY ANALYSIS l-
The Multivariate Gaussian Distribution
 The Multivariate Gaussian Distribution Chuong B. Do October, 8 A vector-valued random variable X = T X X n is said to have a multivariate normal or Gaussian) distribution with mean µ R n and covariance
The Multivariate Gaussian Distribution Chuong B. Do October, 8 A vector-valued random variable X = T X X n is said to have a multivariate normal or Gaussian) distribution with mean µ R n and covariance
A model of working capital with idiosyncratic production risk and rm failure
 A model of oking capital ith idiosyncatic poduction isk and m failue Pof. Mcandless UEMA Novembe, 2 Outline of the talk Intoduction Model Stationay states Dynamic vesion of model onclusions Intoduction
A model of oking capital ith idiosyncatic poduction isk and m failue Pof. Mcandless UEMA Novembe, 2 Outline of the talk Intoduction Model Stationay states Dynamic vesion of model onclusions Intoduction
Notes largely based on Statistical Methods for Reliability Data by W.Q. Meeker and L. A. Escobar, Wiley, 1998 and on their class notes.
 Unit 2: Models, Censoring, and Likelihood for Failure-Time Data Notes largely based on Statistical Methods for Reliability Data by W.Q. Meeker and L. A. Escobar, Wiley, 1998 and on their class notes. Ramón
Unit 2: Models, Censoring, and Likelihood for Failure-Time Data Notes largely based on Statistical Methods for Reliability Data by W.Q. Meeker and L. A. Escobar, Wiley, 1998 and on their class notes. Ramón
A NOTE ON FUNCTION SPACES GENERATED BY RADEMACHER SERIES
 Proceedings of the Edinburgh Mathematical Society (1997) 40, 119-126 A NOTE ON FUNCTION SPACES GENERATED BY RADEMACHER SERIES by GUILLERMO P. CURBERA* (Received 29th March 1995) Let X be a rearrangement
Proceedings of the Edinburgh Mathematical Society (1997) 40, 119-126 A NOTE ON FUNCTION SPACES GENERATED BY RADEMACHER SERIES by GUILLERMO P. CURBERA* (Received 29th March 1995) Let X be a rearrangement
GUIDELINES FOR THE METHOD OF UNDETERMINED COEFFICIENTS
 GUIDELINES FOR THE METHOD OF UNDETERMINED COEFFICIENTS Given a constant coefficient linear differential equation a + by + cy = g(t), where g is an exponential, a simple sinusoidal function, a polynomial,
GUIDELINES FOR THE METHOD OF UNDETERMINED COEFFICIENTS Given a constant coefficient linear differential equation a + by + cy = g(t), where g is an exponential, a simple sinusoidal function, a polynomial,
CANONICAL FORMS FOR LINEAR TRANSFORMATIONS AND MATRICES. D. Katz
 CANONICAL FORMS FOR LINEAR TRANSFORMATIONS AND MATRICES D. Katz The purpose of this note is to present the rational canonical form and Jordan canonical form theorems for my M790 class. Throughout, we fix
CANONICAL FORMS FOR LINEAR TRANSFORMATIONS AND MATRICES D. Katz The purpose of this note is to present the rational canonical form and Jordan canonical form theorems for my M790 class. Throughout, we fix
(308 ) EXAMPLES. 1. FIND the quotient and remainder when. II. 1. Find a root of the equation x* = +J Find a root of the equation x 6 = ^ - 1.
 (308 ) EXAMPLES. N 1. FIND the quotient and remainder when is divided by x 4. I. x 5 + 7x* + 3a; 3 + 17a 2 + 10* - 14 2. Expand (a + bx) n in powers of x, and then obtain the first derived function of
(308 ) EXAMPLES. N 1. FIND the quotient and remainder when is divided by x 4. I. x 5 + 7x* + 3a; 3 + 17a 2 + 10* - 14 2. Expand (a + bx) n in powers of x, and then obtain the first derived function of
