Bifurcations of Asymmetric Vortices in Symmetric Harmonic Traps
|
|
|
- Geoffrey Price
- 5 years ago
- Views:
Transcription
1 D. E. Pelinovsky and P. G. Kevrekidis (13) Bifurcations of Asymmetric Vortices in Symmetric Harmonic Traps, Applied Mathematics Research express, Vol. 13, No. 1, pp Advance Access publication October 11, 1 doi:1.193/amrx/abs16 Bifurcations of Asymmetric Vortices in Symmetric Harmonic Traps Dmitry E. Pelinovsky 1 and Panayotis G. Kevrekidis 1 Department of Mathematics and Statistics, McMaster University, Hamilton, ON, Canada L8S K1 and Department of Mathematics and Statistics, University of Massachusetts, Amherst, MA 13, USA Correspondence to be sent to dmpeli@math.mcmaster.ca We show that, under the effect of rotation, symmetric vortices located at the center of a two-dimensional harmonic potential are subject to a pitchfork bifurcation with radial symmetry. This bifurcation leads to the family of asymmetric vortices, which precess constantly along an orbit enclosing the center of symmetry. The radius of the orbit depends monotonically on the difference between the rotation frequency and the eigenfrequency of negative Krein signature associated with the symmetric vortex. We show that both symmetric and asymmetric vortices are spectrally and orbitally stable with respect to small time-dependent perturbations for rotation frequencies exceeding the bifurcation eigenfrequency. At the same time, the symmetric vortex is a local minimizer of energy for supercritical rotation frequencies, whereas the asymmetric vortex corresponds to a saddle point of energy. For subcritical rotation frequencies, the symmetric vortex is a saddle point of the energy. 1 Introduction In the context of physics of Bose Einstein condensation, rotating vortices in symmetric harmonic traps have been reported both theoretically,, 6, 13 and experimentally 1, 7, 7. Theoretical studies in the physics literature rely on the qualitative approximation obtained from the Rayleigh Ritz variational method. These approximations have been used to predict frequencies of precession of a single vortex about the center of the Received March, 1; Revised July 3, 1; Accepted August 3, 1 c The Author(s) 1. Published by Oxford University Press. All rights reserved. For permissions, please journals.permissions@oup.com.
2 18 D. E. Pelinovsky and P. G. Kevrekidis harmonic trap as well as frequencies of the effective dynamics of dipole, tripole, and quadrupole configurations 6, 8, 31, 3. Numerical approximations of precessional frequencies for vortex configurations were obtained by Middelkamp et al. 9, 3. Similar numerical results were computed by Kollar and Pego for the spectrum of a single vortex located at the center of the harmonic potential, using shooting methods and Evans function computations. Recently, vortex-free states and vortex configurations in the symmetric harmonic traps were studied rigorously in the Thomas Fermi limit of large density states. The Painlevé-II equation for spatially uniform approximation of the vortex-free state was justified by Gallo and Pelinovsky 1. Minimization of energy was considered by Ignat and Millot 15, 16 with the method of variational calculus. These authors justified earlier computations, that the vortex-free state is the global minimizer of energy for small frequencies of the rotating Bose Einstein condensate, whereas a single vortex of charge 1 is the global minimizer of energy for a frequency above a critical value. Seiringer 36 proved that multiple vortex configurations become the global minimizers of energy for larger rotation frequencies and obtained bounds on the critical values of the rotation frequencies, when a vortex of charge (n+ 1) becomes energetically favorable to a vortex of charge n. He also proved that radially symmetric vortices cannot be global minimizers of energy for large frequencies (or for fixed frequency but in the Thomas Fermi limit), which implies that the vortex configurations of charge n break into a superposition of n individual vortices of charge 1. He refers to this case as the breakdown of the rotational symmetry, although the superposition of n individual vortices can still be rotated on the plane under any angle. Variational approximations of Castin and Dum (generalized in the anisotropic setting in 8) suggest that there exist actually two critical frequencies for a vortex of charge 1. When the frequency parameter is increased across the first critical frequency, the single vortex of charge 1 placed at the center of the harmonic potential becomes a local minimizer of energy (it is a saddle point of energy for small frequencies). This vortex becomes the global minimizer of energy when the frequency parameter is increased across the second critical frequency (which is roughly twice of the first one). Figure in also suggests that, for frequencies above the first critical value, there exists a vortex of charge 1 placed at a distance from the center of the harmonic potential, and it is a saddle point of energy. This bifurcation at the first critical frequency and the onset of the asymmetric rotating vortices are considered in the present work. In particular, we give a rigorous proof of the existence of the first critical frequency for the local bifurcation of the symmetric vortex of charge 1. This critical
3 Bifurcations of Asymmetric Vortices in Symmetric Harmonic Traps 19 frequency coincides with the nonzero eigenfrequency of negative Krein signature in the spectrum of linearization of the symmetric vortex in the absence of rotation, 9. This smallest eigenvalue gives a frequency of the vortex precession about the center of symmetry of the harmonic potential at an infinitesimal small distance, studied in our earlier work 3. It is beyond the linear approximation to decide whether this rotation is free of any radiation and is observed for infinite times. We clarify this question throughout this article, where we prove the birth of an asymmetric vortex that performs steady precession about the center of symmetry of the harmonic potential. Our results are based on the method of Lyapunov Schmidt reductions for a local bifurcation problem imposed on the family of symmetric vortices centered at the origin in the rotating coordinate frame. These results do not rely on the Thomas Fermi limit for large density states or on the variational methods used earlier. (Note that the entire bifurcation at the first critical frequency, as well as the crucial difference between symmetric and asymmetric vortices were missing in previous works, 15, 16, 36 that relied on the calculus of variations and functional analysis.) We show that the family of symmetric vortices becomes subject to a pitchfork bifurcation, where the underlying parameter is the precessional frequency. This parameter determines uniquely the radius of the orbit, which the new asymmetric vortex precesses along. The bifurcating asymmetric vortex can be placed at any point along the orbit, hence the pitchfork bifurcation exhibits a radial symmetry. We also prove that both the symmetric vortex and the new asymmetric vortex are spectrally and orbitally stable with respect to small time-dependent perturbations for supercritical rotation frequencies. This is expected on the basis of the previous theoretical and experimental observations of constantly precessing vortices in the symmetric harmonic potential. Moreover, our results agree with the previous variational approximations suggesting that the symmetric vortex is a local minimizer of energy for supercritical rotation frequencies, whereas the asymmetric vortex is a saddle point of energy (still spectrally and orbitally stable). For completeness, we also mention recent mathematical works, which are in subjects near the one of our study. The method of Lyapunov Schmidt reductions has been widely used in a series of recent works of Kapitula et al. 17, 18, devoted to similar problems. In 17, rings, multi-poles, soliton necklaces, and vortex necklaces were constructed for the Gross Pitaevskii equation with a two-dimensional radially symmetric harmonic potential in the weak interaction limit. A superposition of harmonic and small periodic potentials was considered in 18, also in the weak interaction limit. The
4 13 D. E. Pelinovsky and P. G. Kevrekidis nonradially symmetric vortices were constructed for a coupled system of two Gross Pitaevskii equations in. Another but similar bifurcation analysis was developed for a pair of rotating solitary waves in harmonic potentials by Selvitella 37. Existence and stability of both symmetric and asymmetric vortices were studied by Gallay et al. 8, 9 forthe Navier Stokes equations. A similar problem of symmetric and asymmetric vortices in two-component Ginzburg Landau energy functional was considered by Alama et al. 3. Bifurcations of periodic solutions in the system of relative equilibria of vortex configurations were considered by Garcia Azpeitia and Ize 11, 1. The paper is organized as follows. Section reviews the existence and stability of symmetric vortices of charge 1 in the stationary Gross Pitaevskii equation. In Section 3, we consider symmetric vortices of charge 1 in the rotational coordinate frame and discover a relationship between spectral stability and bifurcation problems in the rotational and nonrotational cases. Section presents the main results on the symmetry-breaking bifurcation of stable vortices of charge 1 in the rotating coordinate frame and offers some numerical illustrations. The normal form for the pitchfork bifurcation with radial symmetry is derived and justified in Section 5. Orbital stability of asymmetric vortices is proved in Section 6. Section 7 concludes the paper. We set some notations in the rest of this section. The Hilbert Sobolev space of squared integrable functions on R with square integrable derivatives up to the kth order is denoted by H k (R ).If f H k (R ) and there is m such that e imθ f(x) = ϕ(r) is radially symmetric in polar coordinates (r, θ),wesaythatϕ Hr,m k (R +). The Hilbert Lebesgue spaces of square integrable functions and their radially symmetric restrictions are denoted by L (R ) and Lr (R +), respectively. The corresponding inner products are defined by f, g L (R ) : f, g L := f, g L r (R +) : f, g L r := R f(x, y)g(x, y) dx dy, f(r)g(r)r dr. Similar notations are introduced for Lebesgue spaces L p (R ) and Lr p (R + ) for any p 1. Finally, we say that A= O(ɛ) as ɛ if there is ɛ > such that for every ɛ ( ɛ, ɛ ) there is a positive constant C such that A C ɛ. IfX is a Banach space and A X, then the notation A= O(ɛ) implies that for small ɛ, there is a positive constant C such that A X C ɛ.
5 Bifurcations of Asymmetric Vortices in Symmetric Harmonic Traps 131 Symmetric Vortex at the Center of the Harmonic Potential We consider the Gross Pitaevskii equation with the symmetric harmonic potential and repulsive nonlinear interactions, iɛu t + ɛ (u xx + u yy ) + (1 x y u )u=, (1) where parameter ɛ> is inversely proportional to the chemical potential, (x, y) R are spatial coordinates, t R + is the evolution time, and u(x, y, t) C is the wave function. Let (r, θ) be the polar coordinates on the plane (x, y) R. We denote the Laplace operator for the mth azimuthal mode by Δ m = d dr + 1 d r dr m r. () In particular, Δ = Δ m= and Δ 1 = Δ m=1. Two stationary solutions of the Gross Pitaevskii equation (1) are of our interest. One solution u(x, y, t) = η ɛ (r) is referred to as the vortex-free state if η ɛ : R + R is a radially symmetric, positive solution of the differential equation, ɛ Δ η ɛ + (1 r η ɛ )η ɛ =, η ɛ (r)>, r R +. (3) The other solution u(x, y, t) = ψ ɛ (r) e iθ is referred to as the symmetric vortex of charge 1 if ψ ɛ : R + R is a radially symmetric, positive solution of the differential equation, ɛ Δ 1 ψ ɛ + (1 r ψ ɛ )ψ ɛ =, ψ ɛ (r)>, r R +. () The vortex is symmetric because its center of symmetry is located at the origin (, ) R owing to polar coordinates (r, θ).notethatψ ɛ () = because r = is a regular singular point of the differential equation (). Let us define the Schrödinger operator for the quantum harmonic oscillator, H(ɛ) := ɛ ( x + y ) + x + y 1, (5) with the domain Dom(H(ɛ)) :={u H (R ) : x u L (R )}. The spectrum of H(ɛ) in L (R ) is purely discrete. The eigenvalues are known exactly σ(h(ɛ)) ={λ n,m (ɛ) = 1 + ɛ(n+ m + 1), (n, m) N }, (6) where N denotes the set of all natural numbers counting from.
6 13 D. E. Pelinovsky and P. G. Kevrekidis When ɛ = 1, the lowest eigenvalue λ,(ɛ) crosses and induces a local bifurcation of the vortex-free state η ɛ satisfying (3). For small ɛ 1, the ground state is close to the linear eigenmode f, = e r. When ɛ = 1, the next double eigenvalue λ 1,(ɛ) = λ,1 (ɛ) crosses and induces a local bifurcation of the symmetric vortex ψ ɛ satisfying (). For small ɛ 1, the symmetric vortex is close to the linear eigenmode f 1, + i f,1 = (x + iy) e r. This bifurcation is well known and was recently studied by Kapitula et al. 18. Standard arguments of the local bifurcation theory give the following. Lemma 1. Let μ := 1 16 ɛ. There exists a positive μ such that for all μ (, μ ), there exist a positive constant C and a solution ψ ɛ H r,1 (R +) of the differential equation () such that sup ψ ɛ (r) (18μ) 1/ r e r C μ 3/. (7) r R + The map (, μ ) μ ψ ɛ H r,1 (R +) is continuously differentiable for any μ (, μ ). Proof. We shall derive bound (7) by the standard method of Lyapunov Schmidt reductions. We rewrite the existence problem () as the local bifurcation problem (L 1 + μδ 1 )ψ ɛ = ψ 3 ɛ, ɛ = 1 16 μ, where L 1 = 1 16 Δ 1 + r 1. We note that Ker(L 1 ) = span{ψ }, where ψ (r) = r e r.using the orthogonal decomposition, ψ ɛ = μ 1/ (aψ + ϕ ɛ ), ψ, ϕ ɛ L r =, the local bifurcation problem is decoupled into a pair of two equations: ψ, Δ 1 (aψ + ϕ ɛ ) + (aψ + ϕ ɛ ) 3 L r = (8) and P L 1 P ϕ ɛ = μp (Δ 1 (aψ + ϕ ɛ ) + (aψ + ϕ ɛ ) 3 ), (9) where P is the orthogonal projection operator from L r (R +) to Ran(L 1 ) L r (R +). Bya standard application of the Implicit Function Theorem, for every a R and small μ R, there is a unique ϕ ɛ H r,1 (R +) that solves Equation (9) and satisfies the bound ϕ ɛ H r,1
7 Bifurcations of Asymmetric Vortices in Symmetric Harmonic Traps 133 C aμ for some C >. Then, the bifurcation equation (8) gives the root-finding equation: a( ψ, Δ 1 ψ L r + a ψ L + O(μ)) =. r Explicit evaluation of the inner products show that this equation is equivalent to a( a + O(μ)) =, which admits a nonzero positive root a = 18 + O(μ) as μ. These brief arguments justify bound (7) of the lemma. Let us consider the reduced energy functional, ( ) dϕ E m (ϕ) = ɛ + ɛ m ϕ + (r 1)ϕ + 1 dr r ϕ r dr. (1) Euler Lagrange equations for the reduced energy (1) yield the differential equations (3) for m = and() form = 1. The energy space is X m :={ϕ H 1 r,m (R +) : rϕ L r (R +)}. The reduced energy functional (1) can be written in the form E m (ϕ) = Q m (ϕ) + 1 ϕ L r, where Q m (ϕ) = ϕ, H(ɛ) Xm ϕ L r is the quadratic form associated with the operator H(ɛ) in (5) restricted on the space X m,thatis,h(ɛ) Xm acts on functions in the form f = ϕ(r) e imθ. Because the smallest eigenvalue of H(ɛ) is λ, (ɛ) = 1 + ɛ, the quadratic form Q (ϕ) is positive for ɛ> 1 and sign indefinite for ɛ<1. Therefore, the global minimizer of E (ϕ) in X is zero for ɛ> 1 and nonzero for ɛ<1. By Ignat and Millot 15, Theorem.1, there exists a unique nonzero global minimizer of E (ϕ) in X for every ɛ (, 1 ) and this minimizer ϕ = η ɛ is the unique classical solution of the Euler Lagrange equation (3). Similarly, because the smallest eigenvalue of H(ɛ) X1 is λ 1, = 1 + ɛ and using the similar arguments (see 36, Lemma 1), we deduce the following proposition. Proposition 1. For every ɛ (, 1 ), there exists a unique nonzero global minimizer of E 1 (ϕ) in X 1, which yields a unique classical solution ϕ = ψ ɛ of the differential equation (). Let us now define the full energy functional, E(u) = (ɛ u + ( x 1) u + 1 ) u dx, (11) in the energy space X ={u H 1 (R ) : x u L (R )}. R
8 13 D. E. Pelinovsky and P. G. Kevrekidis Theorems 1.1(i) in 15 states that the vortex-free state u= η ɛ (r) is the unique global minimizer of E(u) for ɛ (, 1 ), up to a complex multiplier of modulus 1. On the other hand, Proposition 1 implies that the vortex solution u= ψ ɛ (r) e iθ is a critical point of E(u) for ɛ (, 1 ). This critical point is actually a saddle point if the functional E(u) is not convex near the vortex solution. To study convexity of E(u) near the vortex solution, we substitute u(x, y) = ψ ɛ (r) e iθ + U(x, y), and obtain the quadratic form associated with the perturbation vector U = U, Ū T : E(u) E(ψ ɛ e iθ ) = U, H(ɛ)U L + O( U 3 H ), (1) 1 where H(ɛ) is the matrix Schrödinger operator in the form: ɛ ( x H(ɛ) = + y ) + x + y 1 + ψɛ ψɛ eiθ ψɛ e iθ ɛ ( x + y ) +. x + y 1 + ψɛ ThematrixSchrödinger operator H(ɛ) can be block-diagonalized in polar coordinates 5,. Let us consider the eigenvalue problem H(ɛ)U = ɛλu, where the spectral parameter is scaled as ɛλ for convenience of notations. Using the decomposition in normal modes, U(x, y) = V m (r) e imθ, Ū(x, y) = W m (r) e imθ, m Z m Z we obtain an uncoupled eigenvalue problem for components (V m, W m ): where Vm Vm H m (ɛ) = ɛλ, m Z, (13) W m W m ɛ Δ m + r 1 + ψɛ ψɛ H m (ɛ) =. (1) ψɛ ɛ Δ m + r 1 + ψɛ We are particularly interested in negative and zero eigenvalues of operators H m (ɛ) for m Z. The count of negative and zero eigenvalues is given in the following lemma. Lemma. There exists an ɛ (, 1 ) such that for every ɛ (ɛ, 1 ), there exists exactly one negative eigenvalue λ (ɛ) of the spectral problems (13), which has algebraic multiplicity two and is associated to the eigenvectors of H (ɛ) and H (ɛ). Moreover, λ is a
9 C 1 function of ɛ in (ɛ, 1 ) satisfying Bifurcations of Asymmetric Vortices in Symmetric Harmonic Traps 135 lim ɛ 1 λ (ɛ) = and lim λ ɛ 1 (ɛ) = 16. (15) The zero eigenvalue of the spectral problems (13) is simple and is associated with the eigenvector of H 1 (ɛ). All other eigenvalues of the spectral problems (13) are strictly positive. Proof. Proposition.3 in states that eigenvalues of H m (ɛ) are strictly positive for m 3(andm 1 by symmetry). For m = 1, the spectral problem (13) reduces further to the uncoupled eigenvalue problems for scalar Schrödinger operators: L + (ɛ)(v 1 + W 1 ) = ɛλ(v 1 + W 1 ), L (ɛ)(v 1 W 1 ) = ɛλ(v 1 W 1 ), where L + (ɛ) = ɛ Δ 1 + r 1 + 3ψɛ, L (ɛ) = ɛ Δ 1 + r 1 + ψɛ. Since L (ɛ)ψ ɛ = andψ ɛ (r)>forr >, Sturm s Oscillation Theorem implies that the operator L (ɛ) has a simple zero eigenvalue and the rest of its spectrum is strictly positive. Since L + (ɛ) = L (ɛ) + ψɛ, the operator L +(ɛ) is strictly positive. By the arguments above, negative and additional zero eigenvalues of the spectral problems (13) may only occur for m = (andm = by symmetry). For ɛ = 1, there exists only one negative eigenvalue 1 of H (ɛ), which corresponds to λ = andthe eigenvector V =, ϕ (r) = e r. (16) W ϕ The rest of the spectrum of H (ɛ) is strictly positive for ɛ = 1. The simple negative eigenvalue λ (ɛ) persists as a C 1 function of ɛ for ɛ< 1 with small ɛ 1 by the asymptotic perturbation theory 1, Section Using the asymptotic expansion (7) in Lemma 1, we write H (ɛ) = 1 16 Δ + r 1 Δ + 56ψ 18ψ 1 16 Δ + μ + O(μ ), + r 1 18ψ Δ + 56ψ
10 136 D. E. Pelinovsky and P. G. Kevrekidis where μ = 1 16 ɛ is a small positive parameter and ψ (r) = r e r. Using the orthogonal decomposition, V Ṽ = + μ, ϕ, W L r =, W ϕ W and the rescaling of the eigenvalue λ = μ λ, we obtain that for small μ R there is a positive constant C such that if and only if λ is found from the equation, Ṽ H r, + W H r, C μ ɛ λ ϕ L = ϕ, (Δ r + 56ψ )ϕ L r + O(μ). Since d dɛ = ɛ d dμ and λ (ɛ) is a C 1 function for ɛ< 1, this perturbation theory for the eigenvector (16) yields lim ɛ 1 d dɛ (ɛλ (ɛ)) = ϕ, (Δ + 56ψ )ϕ L r ϕ = 6, Lr which is equivalent to (15). The proof of the lemma is complete. By Lemma, it follows that the vortex solution is indeed a saddle point of the energy functional E(u) in the energy space X with exactly two directions, for which E(u)<E(ψ ɛ e iθ ). Note that in the Thomas Fermi limit ɛ, 3, Lemma (similar computations are reported in, ) shows that E(u x,y ) E(ψ ɛ e iθ ) = πɛω a (ɛ)(x + y )(1 + O(ɛ1/3 + x + y )), (17) where u x,y is a vortex solution ψ ɛ (r) e iθ shifted from (, ) R to the point (x, y ) R for small (x, y ). The coefficient ω a (ɛ) was found to satisfy the asymptotic expansion, ( ) 1 ω a (ɛ) = ɛ log + O(ɛ) as ɛ. (18) ɛ Finally, we address the spectral stability of symmetric vortices of charge 1 in the Gross Pitaevskii equation (1). Spectral stability is determined by eigenvalues of the non-self-adjoint spectral problem: H m (ɛ) Vm W m 1 = ɛγ 1 Vm W m, m Z, (19)
11 Bifurcations of Asymmetric Vortices in Symmetric Harmonic Traps 137 where γ is an eigenfrequency of the perturbation of the vortex. The vortex is spectrally stable if no γ exists with Im(γ ). Compared with the standard formulation of spectral stability, the spectrum of γ is rotated on the complex plane along 9. We shall prove that the eigenvalues γ of the spectral problem (19) are all real and semi-simple (i.e., they have equal algebraic and geometric multiplicities) except for the double zero eigenvalue. The main attention is drawn to a pair of real eigenvalues for m = andm = that correspond to the eigenvectors with negative values of the quadratic form associated with the operators H (ɛ) and H (ɛ). These eigenvalues are known as the eigenvalues of negative Krein signature 5, 3 (see Remark 1). The corresponding result is formulated in the following lemma. Lemma 3. There exists a ɛ (, 1 ) such that for every ɛ (ɛ, 1 ) and m Z, the spectral problem (19) admits only real eigenvalues γ of equal algebraic and geometric multiplicities, in addition to the double zero eigenvalue for m = 1. The smallest nonzero eigenvalue for m = is γ =+ω (ɛ) and for m = is γ = ω (ɛ), where ω (ɛ) >. These eigenvalues are simple and correspond to the eigenvectors V + (ɛ) = V W, V (ɛ) = such that V = W, V = W, W L r > V L r,and V W () V + (ɛ), H (ɛ)v + (ɛ) L r = V (ɛ), H (ɛ)v (ɛ) L r <. (1) Moreover, ω is a C 1 function of ɛ in (ɛ, 1 ) satisfying lim ɛ 1 ω (ɛ) = and lim ω ɛ 1 (ɛ) = 8. () The quadratic form associated with operators H m (ɛ) is strictly positive for the eigenvectors corresponding to any other eigenvalue γ of the spectral problems (19). Proof. The result follows from the negative index theory 5, 3 and the count of negative eigenvalues of operators H m (ɛ) in Lemma (see also 33, Chapter.). Because operators H m (ɛ) for m 3andm 1 are strictly positive, 5, Theorem 6 implies that the spectral stability problem (19) admits only real semi-simple eigenvalues and the quadratic form associated with these operators is strictly positive at the corresponding eigenvectors.
12 138 D. E. Pelinovsky and P. G. Kevrekidis For m = 1, the algebraic multiplicity of the zero eigenvalue of H 1 (ɛ) is at least two, because of the existence of the eigenvector V 1 and the generalized eigenvector Ṽ 1 in the form ψɛ L+ (ɛ) 1 ψ ɛ V 1 (ɛ) =, Ṽ 1 (ɛ) =, ψ ɛ L + (ɛ) 1 ψ ɛ where L + (ɛ) is strictly positive and thus invertible. We need to show that the algebraic multiplicity is exactly two, which is equivalent to the condition ψ ɛ, L + (ɛ) 1 ψ ɛ L r. To show this constraint, we let Ψ μ : R + R be a classical solution of the vortex equation Δ 1 Ψ μ + (μ r Ψ μ )Ψ μ =, Ψ μ (r)>, r R +, μ>. (3) A scaling transformation for Equation (3) implies that where ψ ɛ Proposition 1. Ψ μ (r) = μψ ɛ (R), ɛ = 1 μ, R = r μ, () is a classical solution of Equation (), existence of which is stated in Differentiating equation (3) with respect to μ, we obtain ( Δ 1 + r μ + 3Ψ μ ) μ Ψ μ = Ψ μ, which yields by the scaling transformation (): (L + (ɛ) 1 ψ ɛ )(R) = μ μψ 1 μ μ ( r μ ) = 1 ψ ɛ(r) R ψ ɛ (R) ɛ ɛ ψ ɛ(r). As a result, we have ψ ɛ, L + (ɛ) 1 ψ ɛ L r = ψ ɛ L ɛ r ɛ ψ ɛ L. r It follows from Lemma 1 that ψ ɛ L r = (8 18ɛ ) ψ L r + O(8 18ɛ ) as ɛ 1, where ψ (r) = re r. Therefore, ψ ɛ is a decreasing function of ɛ near ɛ = 1 so that Lr ψ ɛ, L + (ɛ) 1 ψ ɛ L r > at least for small ɛ 1. Hence the algebraic multiplicity of the zero eigenvalue of H 1 (ɛ) is two. Finally, for m = andm =, there is only one negative eigenvalue of operators H (ɛ) and H (ɛ) and no zero eigenvalues for small ɛ 1 (Lemma ). At ɛ = 1, the spectral stability problem (19) admits a double eigenvalue γ =+form = and a double eigenvalue γ = form = (by symmetry). We shall prove that the double eigenvalue γ = of the spectral problem (19) for m = splits for small ɛ 1 into two real eigenvalues, the smallest of which is denoted as γ = ω (ɛ). From the spectrum of the Schrödinger operator H(ɛ) in (6), we
13 Bifurcations of Asymmetric Vortices in Symmetric Harmonic Traps 139 know that the double eigenvalue γ = of the spectral problem (19) form = andɛ = 1 corresponds to the following two eigenvectors: χ1 V =, Ṽ =, χ 1 (r) = r e r, χ (r) = e r. (5) χ Therefore, the double eigenvalue γ = is semi-simple. By the asymptotic perturbation theory 1, Section 8..3, the semi-simple eigenvalues persist as real eigenvalues for ɛ< 1 with small ɛ 1 and are C 1 functions of ɛ. The actual values of these eigenvalues for small ɛ 1 can be approximated from the asymptotic expansions similar to the ones used in the proof of Lemma. Using the expansion of H (ɛ) in μ = 1 16 ɛ and the decomposition V = c 1 χ 1 (r) + μṽ, W = c χ (r) + μ W, γ = μ γ, (6) we compute the projection equations χ1 c Lr ɛ γ 1 χ1, (Δ + 56ψ = )χ 1 L 18 χ r 1, ψ χ L r χ c Lr 18 χ, ψ χ 1 L r χ, (Δ + 56ψ )χ L r Truncating this expansion, using explicitly, we obtain lim ɛ 1 d (ɛγ (ɛ)) dɛ c1 c + O(μ). d dɛ = ɛ d, and computing the inner products dμ c1 c = c1 c. (7) Two eigenvalues {, } of the reduced eigenvalue problem (7) give two slopes of the eigenvalues γ as a function of ɛ: and lim γ (ɛ) = : ɛ 1 lim γ (ɛ) = 8: ɛ 1 c1 c c1 c = 1 (8) =. (9) 1 The first eigenvalue remains at γ = for all values of ɛ< 1 by the symmetry of the spectral problem (19) form = (see, Appendix or, Equation (8)). The second eigenvalue detaches from the first eigenvalue as a simple eigenvalue γ = ω (ɛ) < forɛ< 1. This eigenvalue corresponds to the eigenvector V + (ɛ) in (). We compute ɛ = 1 : V L = r c 1 χ 1 L = 1 r 16, W L = r c χ L = 1 r 8, and hence W L r > V L r and the condition (1) are satisfied for ɛ = 1 and for small ɛ 1 by continuity. The symmetry of H (ɛ) and H (ɛ) implies that V = W and V = W.
14 1 D. E. Pelinovsky and P. G. Kevrekidis By Chugunova and Pelinovsky 5, Theorem 6 and Lemma, other eigenvalues of the spectral stability problem (19) form = andm = are real and semi-simple, whereas the quadratic form associated with these operators is strictly positive at the corresponding eigenvectors. To show that ω (ɛ) is the smallest eigenvalue of the spectral problem (19)form = and small ɛ 1, we recall again the spectrum of the Schrödinger operator H(ɛ) in (6). For ɛ = 1, the only eigenvalue that has the same absolute value as ω is the simple eigenvalue γ = that correspond to the eigenvector ˆV =, ˆχ (r) = (r 1) e r. ˆχ The same perturbation theory gives lim ɛ 1 d dɛ (ɛγ ) = ˆχ, (Δ + 56ψ ) ˆχ L r ˆχ Lr = lim γ (ɛ) =. ɛ 1 Hence, this eigenvalue also stays at γ = by the symmetry described above and γ = ω (ɛ) is the smallest eigenvalue for ɛ< 1 of the spectral problem (19) form =. The proof of the lemma is complete. Remark 1. The eigenvalue ω (ɛ) of the spectral problem (19) form = has the negative Krein signature 19, 3, which is determined by the sign of the symplectic -form V + (ɛ), V + (ɛ):= V L r W L r and it is the only positive real eigenvalue of the spectral problems (19) with a negative Krein signature. This symplectic -form vanishes when a positive eigenvalue of negative Krein signature coalesces with another eigenvalue of positive Krein signature to become the defective eigenvalue that leads ultimately to the instability bifurcations. If the eigenvalue ω (ɛ) remains the smallest eigenvalue for m = forɛ (, 1 ) and moves toasɛ, such a coalescence does not occur and V + (ɛ), V + (ɛ) < remains for all ɛ (, 1 ). (3) Numerical approximations of eigenvalues of the spectral stability problems (19) were performed in, Figure; 3, Figure. These figures illustrate that all eigenvalues γ are purely real. Among all real eigenvalues, the pair of eigenvalues ±ω (ɛ) with negative Krein signature is distinctive because this pair corresponds to the smallest nonzero eigenvalues of the spectral stability problems (19) for sufficiently small ɛ.
15 Bifurcations of Asymmetric Vortices in Symmetric Harmonic Traps 11 This pair of eigenvalues is associated with the precessional frequency of the symmetric vortex of charge 1 misplaced from (, ) R to the point (x, y ) R for small (x, y ). Using the Rayleigh Ritz variational method based on the computation (17), it was found in 3 thatω (ɛ) ω a (ɛ) as ɛ, where ω a (ɛ) satisfies the asymptotic expansion (18). We will show that the eigenvalue ω (ɛ) also determines bifurcations of asymmetric vortices from symmetric vortices of charge 1 in rotating Bose Einstein condensates. Although the results of Lemmas and 3 are applicable for small ɛ 1, we will fix the value of ɛ arbitrarily in (ɛ, 1 ) without further restrictions on ɛ. Note that because ɛ is fixed, we will not indicate the explicit dependence of the eigenvalue ω from ɛ in the remainder of this article. 3 Rotating Coordinates and the Symmetry-Breaking Bifurcation We look at the existence of vortex solutions of the Gross Pitaevskii equation (1) in the rotating coordinate frame and use the variables, x cos(ωt) sin(ωt) ξ =, (31) y sin(ωt) cos(ωt) η where ω R is the rotation frequency in the counterclockwise direction, which is favorable to the vortex compared with the rotation in the clockwise direction. In new coordinates, the Gross Pitaevskii equation (1) takes the form: iɛu t + ɛ (u ξξ + u ηη ) + (1 ξ η u )u iɛω(ξu η ηu ξ ) =. (3) In the polar coordinates (r, θ) on the plane (ξ, η) R (note that we use the same notations for polar coordinates for simplicity), the solution in the vortex form u= ϕ ω,ɛ (r) e iθ satisfies the differential equation: ɛ Δ 1 ϕ ω,ɛ + (1 + ɛω r ϕ ω,ɛ )ϕ ω,ɛ =, ϕ ω,ɛ (r)>, r R +. (33) Assuming that 1 + ɛω > and using the scaling transformation, ϕ ω,ɛ (r) = 1 + ɛωψ ν (R), r = 1 + ɛωr, ν = ɛ 1 + ɛω, (3) we can rewrite the differential equation (33) in the one-parameter form, ν ( d ψ ν dr + 1 dψ ν R dr ψ ) ν + (1 R ψ R ν )ψ ν =, ψ ν (R)>, R R +, (35)
16 1 D. E. Pelinovsky and P. G. Kevrekidis which is nothing but Equation () with the correspondence ν = ɛ and R = r. Existence of vortices of charge 1 for ν (, 1 ) is guaranteed by Proposition 1. The local bifurcation at ν = 1 corresponds to ν ɛ = 1 νω ν= 1 = 1 ω, and we require ω< to have the interval, 1 forν be mapped to the interval, 1 ω for ɛ. To study stability and bifurcations of symmetric vortices in the rotating coordinate frame, we introduce a linearization of the Gross Pitaevskii equation (3). We substitute the decomposition, u(ξ, η, t) = ϕ ω,ɛ (r) e iθ + U(ξ, η, t), and obtain the linearized evolution problem by neglecting the quadratic terms in U, iɛu t + ɛ (U ξξ + U ηη ) + (1 ξ η ϕ ω,ɛ )U ϕ ω,ɛ eiθ Ū iɛω(ξu η ηu ξ ) =. (36) Using the normal coordinates, U(ξ, η, t) = m Z V (m) (r) e imθ e iσ t, Ū(ξ, η, t) = m Z W (m) (r) e imθ e iσ t, we obtain uncoupled eigenvalue problems for components (V (m), W (m ) ), V H ω,ɛ (m) (m) 1 V (m) = ɛσ, m Z, (37) 1 W (m ) W (m ) where ɛ H ω,ɛ (m) = Δ m + r 1 ɛωm + ϕω,ɛ ϕω,ɛ. (38) ϕω,ɛ ɛ Δ m + r 1 + ɛω(m ) + ϕω,ɛ The eigenvalue problems (37) determine the spectral stability of the symmetric vortex with respect to the time-dependent perturbations. To consider the bifurcation of the symmetric vortex, we need to study the linearization of the time-independent version of the Gross Pitaevskii equation (3), which results in the self-adjoint version of the spectral problems (37), V (m) V (m) = ɛλ, m Z. (39) H (m) ω,ɛ W (m ) W (m ) Using variables (3) and the representation V (m) (r) = V m (R), W (m ) (r) = W m (R), m Z,
17 Bifurcations of Asymmetric Vortices in Symmetric Harmonic Traps 13 we rewrite the eigenvalue problems (37) and(39) in the equivalent forms: H m (ν) Vm W m = ν(σ + ω(m 1)) 1 1 Vm W m, m Z () and H m (ν) Vm W m = νλ Vm W m + νω(m 1) 1 1 Vm W m, m Z, (1) where H m (ν) is given by (1) forɛ = ν and r = R. Let us denote γ = σ + ω(m 1) and rewrite the spectral stability problems () in the form: Vm 1 Vm H m (ν) = νγ, m Z. () 1 W m W m The spectral problems () coincide with the spectral problems (19) with the correspondence ɛ = ν. By Lemma 3, all eigenvalues γ of the spectral problems () are real and semi-simple except for the double zero eigenvalue. Therefore, all eigenvalues σ of the spectral stability problems (37) are real and semi-simple, except for the double zero eigenvalue. This result implies the spectral stability of symmetric vortices of charge 1 for all values of ω, for which the transformation (3) makes sense, and hence proves the following. Proposition. Fix ω<. There exists ɛ (, 1 ) such that for every ɛ ( ɛ 1 ɛ ω, 1 ω ),the symmetric vortex of charge 1 is spectrally stable in the sense that all eigenvalues σ of the spectral stability problems (37) are real and semi-simple, except for the double zero eigenvalue. We can now address a possibility of bifurcations of the symmetric vortex u= ϕ ω,ɛ (r) e iθ in the rotating coordinate frame (31). These bifurcations are determined by zero eigenvalues λ of the self-adjoint eigenvalue problems (39). Equivalently, these bifurcations are determined by zero eigenvalues λ of the self-adjoint eigenvalue problems (1). Lemma. Let ω > be the eigenvalue defined by Lemma 3 with the correspondence ɛ ν. There exists ɛ (, 1 ) such that for every ɛ (ɛ, 1 ), the eigenvalue problem (39) for m = admits a zero eigenvalue λ = atω = ω. Moreover, the smallest eigenvalue λ is a C 1 function of ω near ω with λ (ω )>.
18 1 D. E. Pelinovsky and P. G. Kevrekidis Proof. Existence of zero eigenvalue λ = in the self-adjoint eigenvalue problem (1)for any m is equivalent to the existence of a positive eigenvalue γ = ω(m 1) in the nonself-adjoint eigenvalue problem (). By Lemma 3, the spectral problem () for m = has the smallest nonzero eigenvalue γ = ω (ν) > forν< 1 at least for small ν 1.It follows from () that lim ν 1 ω (ν) = and lim ω ν 1 (ν) = 8. (3) Using the inverse transformation (3) withω = ω (ν), thatis, we obtain ɛ(ν) = lim ɛ(ν) = 1 ν 1 ν 1 νω (ν), and lim ɛ (ν) = 6. () ν 1 The positive slope of ɛ versus ν tells us that the one-sided neighborhood ν< 1 is located for ɛ< 1 if ω = ω (ν). Therefore, there is ɛ (, 1 ) such that the self-adjoint eigenvalue problem (39) form = andω = ω (ν), admits a zero eigenvalue λ = for every ɛ (ɛ, 1 ). Once this is established, we shall now omit the argument ν in the notation for ω. Next we show that the eigenvalue λ of the eigenvalue problem (39) form = that crosses zero at ω = ω becomes positive for ω>ω. By the asymptotic perturbation theory 1, Section 8..3, λ is a C 1 function of ω near ω because the zero eigenvalue at ω = ω is simple. Differentiating the rescaled eigenvalue problem (1) form = with respect to ω at a fixed ν< 1,weobtain H (ν) d dω V W = νλ d dω + ν dλ dω V W V 1 + νω ν 1 W d dω V W V W. Projecting this derivative problem at λ = andω = ω to the eigenvector V, W ofthe eigenvalue problem (1), we obtain λ (ω )( W L + V r L ) = W r L V r L >, (5) r where the positivity follows from Lemma 3. Hence, λ (ω )> and the assertion of the lemma is proved.
19 Bifurcations of Asymmetric Vortices in Symmetric Harmonic Traps 15 Remark. On the basis of numerical evidences, we conjecture that ɛ = in Lemmas. This statement has been clearly illustrated in the numerical studies of, 9, 3 but the mathematical proof of this conjecture is beyond the scope of this article. Remark 3. Numerical approximations show that all other eigenvalues of the spectral problem () form = andm 3 are located for γ = ω(m 1) 1asν (see 3, Figure ). These eigenvalues produce a countable set of possible bifurcations in the self-adjoint eigenvalue problem (39) ifɛ = ν >. These additional bifurcations may 1 νω be related to the fact that for larger rotation frequencies ω, multiple vortex configurations become local and global minimizers of the energy (see, Figure 8; 36, Section 3). Although we do not study these possible bifurcations in this paper, we note that if these bifurcations occur, they are related with eigenvalues of positive Krein signature that become negative when the frequency parameter ω is increased. We shall mention two relevant results in connection to Lemma. First, the critical frequency ω = in the limit of weak interactions ν 1 coincides with the critical frequency of the symmetry-breaking bifurcation studied by Seiringer 36, Section 7. By Seiringer 36, Theorem (modified in our notations), for all ω (, ), there is an ɛ (, 1 ) such that for all ɛ (, ɛ ), the radially symmetric vortex cannot be a global minimizer of the energy. By Seiringer 36, Theorem 8, all vortices of charge nwith n 1 are orbitally unstable (in fact, the author conjectured that this theorem remains true for all n ). The other relevant result is a connection between the sign of λ (ω ) and the Krein signature (3) established in (5). The linear interpolation between self-adjoint and skew-adjoint spectral problems obtained in the rescaled eigenvalue problem (1) was considered long ago by Krein and Ljubarskii 5, where motion of simple eigenvalues was found to be connected to the sign of the Krein signature. Let us rewrite the full energy functional (11) in the rotating coordinate frame (31), E ω,ɛ (u) = ɛ u + ( ξ 1) u + 1 u + iɛω ξ(ūu η uū η ) iɛω η(ūu ξ uū ξ ) dξ. R (6) The symmetric vortex u= ϕ ω,ɛ (r) e iθ is a critical point of the energy E ω,ɛ (u). Eigenvalues of self-adjoint operators H ω,ɛ (m) determine convexity of E ω,ɛ (u) at the critical point. By Lemmas and, the symmetric vortex of charge 1 is a saddle point of E ω (u) for ω<ω
20 16 D. E. Pelinovsky and P. G. Kevrekidis but becomes a local minimizer of E ω (u) for ω>ω near ω. Applying the orbital stability theory 1 (see also 33, Chapter..), we obtain the following proposition. Proposition 3. For every ɛ (ɛ, 1 ),letω be the bifurcation value in Lemma. For ω> ω near ω, the symmetric vortex of charge 1 u ω,ɛ = ϕ ω,ɛ (r) e iθ is orbitally stable in the following sense: for any ε> there is a δ>, such that if u() u ω,ɛ X δ, then inf ζ R u(t) eiζ u ω,ɛ X ε, t R +, where X ={u H 1 (R ) : ξ u L (R )} is the energy space of the Gross Pitaevskii equation (3). Remark. Although the symmetric vortex is spectrally stable for ω<ω, it is a saddle point of energy and hence, we cannot conclude that it is orbitally stable for ω<ω. Main Results and Illustrations We formulate now the main results of this article. The results guarantee the existence and orbital stability of a steadily precessing vortex of charge 1 in the Gross Pitaevskii equation (1) with the precessional frequency ω slightly exceeding the bifurcation value ω. This vortex is different from the symmetric vortex u= ϕ ω,ɛ (r) e iθ, because it precesses along an orbit enclosing the center of the harmonic potential. Because of the rotational invariance, the vortex can be placed at any point along the orbit, hence it has an additional parameter α for the angle along the precessional orbit. We refer to this solution as to the asymmetric vortex because it has no symmetry about the origin (, ) R. The asymmetric vortex exists and is orbitally stable, according to the following two theorems. Theorem 1. For every ɛ (ɛ, 1 ),letω be the bifurcation value in Lemma. Besides the symmetric vortex u= ϕ ω,ɛ (r) e iθ, there exists another time-independent vortex solution u= u ω,ɛ,α (ξ) of the Gross Pitaevskii equation (3) forω>ω near ω, where u ω,ɛ,α is not radially symmetric. The center of u ω,ɛ,α is placed on the circle of radius a centered at the origin (, ) R at the angle α and there is C > such that a C ɛ(ω ω ). Theorem. Under the conditions of Theorem 1, the asymmetric vortex u ω,ɛ,α is orbitally stable in the following sense: for any ε>there is a δ>, such that if u() u ω,ɛ, X δ, then inf u(t) e iζ u ω,ɛ,α X ε, t R +. (ζ,α) R
21 Bifurcations of Asymmetric Vortices in Symmetric Harmonic Traps y y x x Fig. 1. Spatial contour plots of the amplitude (left) and phase (right) of the asymmetric vortex for ω =.365 and ɛ =.35. We shall now illustrate the results of Theorems 1 and numerically. Figure 1 shows the amplitude u and the phase arg(u) (the latter multiplied by u for clarity) of the asymmetric vortex u ω,ɛ,α as the time-independent solution of the Gross Pitaevskii equation (3) forɛ =.35 and ω =.365. We can see that the center of the asymmetric vortex is already distant from the center of the harmonic potential. Figure displays an approximate measure of the distance (through a smoothed identification of the maximum of the vorticity field) as a function of ω ω for ɛ =.35. The curve displays the characteristic supercritical pitchfork behavior. For ω>ω, both symmetric and asymmetric vortices coexist as solutions of the Gross Pitaevskii equation (3). Figure 3 shows the smallest positive eigenvalue σ of the spectral stability problems (37) as a function of ω. The positive eigenvalue for m = crosses zero at ω = ω and becomes negative for ω>ω. The negative eigenvalue for m = crosses zero at ω = ω and becomes positive for ω>ω. The smallest positive eigenvalue σ has negative Krein signature (3) forω<ω and positive Krein signature for ω>ω. Figure shows eigenvalues of the spectral stability problems (37) for all m Z associated to the symmetric vortex u= ϕ ω,ɛ (r) e iθ for ɛ =.35 and two values of ω before (left) and after (right) the pitchfork bifurcation. Note that the real eigenvalues σ are rotated to purely imaginary eigenvalues λ in the standard formulation of the spectral stability problem. It is evident that the zero crossing of the smallest eigenvalues does not lead to the creation of a pair of real unstable eigenvalues. The symmetric vortex is spectrally stable for both ω<ω and ω>ω.
22 18 D. E. Pelinovsky and P. G. Kevrekidis.8.6 a. Fig ω ω The distance a of the asymmetric vortex from the center of the trap is shown as a function of ω ω (where ω is the frequency at the bifurcation point) for ɛ =.35. Fig. 3. σ/ω ω /ω The smallest positive eigenvalue σ of the spectral stability problems (37) associated with the symmetric vortex for ɛ =.35 is shown as a function of the rotation frequency ω. Bothfrequencies are scaled by the bifurcation frequency ω. Figure 5 shows eigenvalues of a spectral stability problem associated with the asymmetric vortex u= u ω,ɛ,α for ɛ =.35 and ω =.365 past the bifurcation value. The linearization problem has no small nonzero eigenvalues, instead it has a zero eigenvalue of algebraic multiplicity four and geometric multiplicity two. This feature will be proved rigorously within the bifurcation setting in Section 6. The zero eigenvalue is induced by
23 Bifurcations of Asymmetric Vortices in Symmetric Harmonic Traps λ i /(ε) λ i /(ε) 1 1 Fig λ r /(ε) λ r /(ε) Eigenvalues λ = iσ = λ r + iλ i of the spectral stability problems (37) associated with the symmetric vortex for ɛ =.35 for two values of ω before and after the pitchfork bifurcation: ω =.11 (left) and ω =.51 (right). The axes are scaled by a factor of ɛ, so that all eigenvalues but the ones crossing zero are of O(1). λ i /(ε) λ r /(ε) Fig. 5. Eigenvalues of a spectral stability problem associated with the asymmetric vortex for ɛ =.35 and ω =.365. The zero eigenvalue has algebraic multiplicity four. the phase invariance of the Gross Pitaevskii equation (first pair) and by the rotational invariance of the position of the vortex along its precession orbit (second pair). Asymmetric vortices can be pinned at any point of their precessional orbit parametrized by the rotation frequency or, equivalently, by the distance from the center of the trap. All
24 15 D. E. Pelinovsky and P. G. Kevrekidis other eigenvalues are purely imaginary so that the asymmetric vortex is also spectrally stable with respect to the time evolution of the Gross Pitaevskii equation (3) forω>ω near ω. 5 The Birth of the Asymmetric Vortex The zero eigenvalue of the self-adjoint spectral problem (39) form = andω = ω exists by Lemma and signals a bifurcation along the family of symmetric vortex solutions. This bifurcation gives birth to the family of asymmetric vortices for ω>ω. To prove Theorem 1, we work with the local bifurcation method and study the pitchfork bifurcation at ω = ω. To develop the algorithm of Lyapunov Schmidt reductions, we rewrite the existence problem for the stationary Gross Pitaevskii equation (3) in the rotating reference frame (31) as the root-finding problem, N(u; ω) := ɛ (u ξξ + u ηη ) + (ξ + η 1 + u )u+ iɛω(ξu η ηu ξ ) =. (7) Because the root-finding problem involves ū, we need to add another equation N(u; ω) =. We will use bolded notations for -vectors, for example, N = (N, N). Note that parameter ɛ is fixed in the interval (ɛ, 1 ) to guarantee the validity of Lemmas 1,, 3, and. Therefore, we do not indicate the explicit dependence of N(u; ω) on ɛ. The Jacobian operator of N = (N, N) with respect to u = (u, ū) is given by D u N(u; ω) ɛ Δ + ξ 1 + iɛω(ξ η η ξ ) + u u =. ū ɛ Δ + ξ 1 iɛω(ξ η η ξ ) + u We note that N(ϕ ω,ɛ e iθ ; ω) = is equivalent to the differential equation (33). Let us denote ϕ ϕ ω,ɛ and H (m) H ω (m),ɛ, m Z. At the bifurcation value ω in Lemma, we know that the kernel of D u N(ϕ e iθ ; ω ) is three-dimensional thanks to the gauge invariance and the double degeneracy of the bifurcating mode of the self-adjoint problem (39) for m = andm =, { } Ker(D u N(ϕ e iθ ϕ (r) e iθ V (r) e iθ W (r) ; ω )) = span,,, (8) ϕ (r) e iθ W (r) V (r) e iθ where (V, W ) is a real-valued solution of the homogeneous system H () V =. (9) W
25 Bifurcations of Asymmetric Vortices in Symmetric Harmonic Traps 151 It follows from (7) that for every fixed ɛ>, the function N(u; ω) : H (R ) R L (R ) is smooth with respect to its arguments. We use the decomposition, u= ϕ (r) e iθ + av (r) e iθ +āw (r) + U, ω = ω + Ω, (5) where a C and Ω R are parameters of the decomposition and U = (U, Ū) satisfies the orthogonality conditions, V V, U := ( VU + WŪ) dx dy =, for every V = Ker(D u N(ϕ e iθ ; ω )). (51) R W Note that the constraint on the conjugation of a in (5) follows from representation (8) and the fact that ū is the complex conjugate of u. The root-finding problem is now decoupled into algebraic equations V V, N(ϕ e iθ + av e iθ +āw + U; ω + Ω) = for every V = Ker(D u N(ϕ e iθ ; ω )) W and a differential equation for the error term U. The system of algebraic Equations (5) gives three equations because of three eigenvectors in Ker(D u N(u ; ω )). However, because of the gauge invariance, projection to the first eigenvector in (8) is identically zero if U satisfies (51). Also projection to the third eigenvector in (8) gives a complex conjugation of the projection to the second equation. Therefore, the system of algebraic Equations (5) reduces to the scalar equation, F (U; ω, a) := ( e iθ V N(ϕ e iθ + av e iθ +āw + U; ω + Ω) R + W N(ϕ e iθ + av e iθ +āw + U; ω + Ω))dxdy =. (53) (5) We can see that F (U; ω, a) : H (R ) R C C is a smooth function with respect to its variables. As it often happens for the pitchfork bifurcation 3, 35, we need a near-identity transformation to remove nonresonant quadratic terms and to compute resonant cubic terms in amplitude a. Taking into account the decomposition for ω = ω + Ω, we set U = ɛωv 1 (r) e iθ + a V (r) e 3iθ + a V 11 (r) e iθ +ā V (r) e iθ + Ũ, (5)
26 15 D. E. Pelinovsky and P. G. Kevrekidis where Ũ is a new error term, and obtain the linear inhomogeneous equations: H (1) H (3) H (1) H ( 1) V1 W 1 V W V11 W 11 V W = ϕ By the symmetry of H (3), H (1) ( 1),andH,wehave ϕ, (55) ϕ V (V + W ) =, (56) ϕ W (W + V ) ϕ (V = + V W + W ) ϕ (V + V W + W ), (57) ϕ W (W + V ) =. (58) ϕ V (V + W ) V 1 = W 1, V = W, W = V, W 11 = V 11. (59) We note that H (3) and H ( 1) are invertible, whereas the Fredholm condition for H (1) is satisfied. Therefore, there exist unique solutions of the linear homogeneous Equations (55) (58) subject to constraints (51). Using standard fixed-point arguments, it is easy to prove that there exist positive constants a, Ω,andC such that the differential equation for Ũ admits a unique solution for all a a and Ω Ω satisfying the bound Ũ H C ( Ω + a ) a. (6) Substituting decompositions (5) and(5) into the scalar Equation (53), we obtain the normal form for the radially symmetric pitchfork bifurcation, where σ = β = a(ɛωσ + β a + F ) =, (61) ϕ V 1 (V + V W + W ) V r dr, (6) V + V W + W + ϕ (V + V W + W )V 11 + ϕ V W (V + W ) + ϕ (V V + W W )r dr, (63) and the remainder term is small F = O(Ω, a ). Nontrivial solutions of the normal-form Equation (61) for small Ω R with a exist for sign(ω) = sign(σβ). We will show in Lemmas 5 and 6 that σ>andβ<.
27 Bifurcations of Asymmetric Vortices in Symmetric Harmonic Traps 153 In this case, the nontrivial solutions of the normal-form Equation (61) exist for Ω>, that is, for ω>ω, and satisfy the expansion, a = σ β ɛω + O(Ω ). (6) If a = a e iα,thenα is an arbitrary parameter of the bifurcating solution, whereas a is uniquely determined as a =O( ɛ ω ω ). Notethat a measures the distance of the vortex center from the center of the harmonic potential, whereas α is an angle along the circle of the radius a. The new asymmetric vortex can be placed at any angle α. The proof of Theorem 1 is complete. Lemma 5. hence σ>. Proof. We prove now the claim that σ>andβ<. Under the assumptions of Lemma, the following statement holds: σ = 1 ( W L r V L r ), We look for the small eigenvalue of the self-adjoint spectral problem (39) for m = andω near ω. Using the expansion ϕ ω,ɛ = ϕ (r) + ɛωv 1 (r) + O(Ω ), we rewrite the eigenvalue problem (39) form = in the perturbation form, ( ) 1 1 V H () ɛω + ɛω ϕ V 1 + O(Ω () V () ) = ɛλ. (65) 1 Let λ(ω) be an eigenvalue of the perturbed spectral problem (65) such that λ(ω ) = at Ω =. The corresponding eigenvector at Ω = is(v (), W () ) = (V, W ) by (9). By the asymptotic perturbation theory 1, Section 8..3, λ is a C 1 function of ω near ω.writing the derivative equation, ( ) 1 1 H () ɛω + ɛω ϕ V 1 + O(Ω d V () ) 1 dω W () ( ) 1 1 V () ɛ + ɛ ϕ V 1 + O(Ω) = ɛλ d V () + ɛ dλ V (), 1 dω dω W () W () W () W () W () and computing projections to the eigenvector (9), we obtain σ = λ (ω )( V L r + W L r ) = W L r V L r, (66)
Bifurcations of Multi-Vortex Configurations in Rotating Bose Einstein Condensates
 Milan J. Math. Vol. 85 (2017) 331 367 DOI 10.1007/s00032-017-0275-8 Published online November 17, 2017 2017 Springer International Publishing AG, part of Springer Nature Milan Journal of Mathematics Bifurcations
Milan J. Math. Vol. 85 (2017) 331 367 DOI 10.1007/s00032-017-0275-8 Published online November 17, 2017 2017 Springer International Publishing AG, part of Springer Nature Milan Journal of Mathematics Bifurcations
DRIFT OF SPECTRALLY STABLE SHIFTED STATES ON STAR GRAPHS
 DRIFT OF SPECTRALLY STABLE SHIFTED STATES ON STAR GRAPHS ADILBEK KAIRZHAN, DMITRY E. PELINOVSKY, AND ROY H. GOODMAN Abstract. When the coefficients of the cubic terms match the coefficients in the boundary
DRIFT OF SPECTRALLY STABLE SHIFTED STATES ON STAR GRAPHS ADILBEK KAIRZHAN, DMITRY E. PELINOVSKY, AND ROY H. GOODMAN Abstract. When the coefficients of the cubic terms match the coefficients in the boundary
Periodic oscillations in the Gross-Pitaevskii equation with a parabolic potential
 Periodic oscillations in the Gross-Pitaevskii equation with a parabolic potential Dmitry Pelinovsky 1 and Panos Kevrekidis 2 1 Department of Mathematics, McMaster University, Hamilton, Ontario, Canada
Periodic oscillations in the Gross-Pitaevskii equation with a parabolic potential Dmitry Pelinovsky 1 and Panos Kevrekidis 2 1 Department of Mathematics, McMaster University, Hamilton, Ontario, Canada
Dmitry Pelinovsky Department of Mathematics, McMaster University, Canada
 Spectrum of the linearized NLS problem Dmitry Pelinovsky Department of Mathematics, McMaster University, Canada Collaboration: Marina Chugunova (McMaster, Canada) Scipio Cuccagna (Modena and Reggio Emilia,
Spectrum of the linearized NLS problem Dmitry Pelinovsky Department of Mathematics, McMaster University, Canada Collaboration: Marina Chugunova (McMaster, Canada) Scipio Cuccagna (Modena and Reggio Emilia,
Nonlinear instability of half-solitons on star graphs
 Nonlinear instability of half-solitons on star graphs Adilbek Kairzhan and Dmitry Pelinovsky Department of Mathematics, McMaster University, Canada Workshop Nonlinear Partial Differential Equations on
Nonlinear instability of half-solitons on star graphs Adilbek Kairzhan and Dmitry Pelinovsky Department of Mathematics, McMaster University, Canada Workshop Nonlinear Partial Differential Equations on
One Dimensional Dynamical Systems
 16 CHAPTER 2 One Dimensional Dynamical Systems We begin by analyzing some dynamical systems with one-dimensional phase spaces, and in particular their bifurcations. All equations in this Chapter are scalar
16 CHAPTER 2 One Dimensional Dynamical Systems We begin by analyzing some dynamical systems with one-dimensional phase spaces, and in particular their bifurcations. All equations in this Chapter are scalar
Diagonalization of the Coupled-Mode System.
 Diagonalization of the Coupled-Mode System. Marina Chugunova joint work with Dmitry Pelinovsky Department of Mathematics, McMaster University, Canada Collaborators: Mason A. Porter, California Institute
Diagonalization of the Coupled-Mode System. Marina Chugunova joint work with Dmitry Pelinovsky Department of Mathematics, McMaster University, Canada Collaborators: Mason A. Porter, California Institute
STATIONARY STATES OF THE CUBIC CONFORMAL FLOW ON S 3
 STATIONARY STATES OF THE CUBIC CONFORMAL FLOW ON S 3 PIOTR BIZOŃ, DOMINIKA HUNIK-KOSTYRA, AND DMITRY PELINOVSKY Abstract. We consider the resonant system of amplitude equations for the conformally invariant
STATIONARY STATES OF THE CUBIC CONFORMAL FLOW ON S 3 PIOTR BIZOŃ, DOMINIKA HUNIK-KOSTYRA, AND DMITRY PELINOVSKY Abstract. We consider the resonant system of amplitude equations for the conformally invariant
Stability of Feedback Solutions for Infinite Horizon Noncooperative Differential Games
 Stability of Feedback Solutions for Infinite Horizon Noncooperative Differential Games Alberto Bressan ) and Khai T. Nguyen ) *) Department of Mathematics, Penn State University **) Department of Mathematics,
Stability of Feedback Solutions for Infinite Horizon Noncooperative Differential Games Alberto Bressan ) and Khai T. Nguyen ) *) Department of Mathematics, Penn State University **) Department of Mathematics,
Ground state of the conformal flow on S 3
 Ground state of the conformal flow on S 3 Piotr Bizon 1 and Dmitry Pelinovsky 2 1 Department of Physics Jagiellonian University, Krakow, Poland 2 Department of Mathematics, McMaster University, Canada
Ground state of the conformal flow on S 3 Piotr Bizon 1 and Dmitry Pelinovsky 2 1 Department of Physics Jagiellonian University, Krakow, Poland 2 Department of Mathematics, McMaster University, Canada
MTH4101 CALCULUS II REVISION NOTES. 1. COMPLEX NUMBERS (Thomas Appendix 7 + lecture notes) ax 2 + bx + c = 0. x = b ± b 2 4ac 2a. i = 1.
 MTH4101 CALCULUS II REVISION NOTES 1. COMPLEX NUMBERS (Thomas Appendix 7 + lecture notes) 1.1 Introduction Types of numbers (natural, integers, rationals, reals) The need to solve quadratic equations:
MTH4101 CALCULUS II REVISION NOTES 1. COMPLEX NUMBERS (Thomas Appendix 7 + lecture notes) 1.1 Introduction Types of numbers (natural, integers, rationals, reals) The need to solve quadratic equations:
Phase Synchronization
 Phase Synchronization Lecture by: Zhibin Guo Notes by: Xiang Fan May 10, 2016 1 Introduction For any mode or fluctuation, we always have where S(x, t) is phase. If a mode amplitude satisfies ϕ k = ϕ k
Phase Synchronization Lecture by: Zhibin Guo Notes by: Xiang Fan May 10, 2016 1 Introduction For any mode or fluctuation, we always have where S(x, t) is phase. If a mode amplitude satisfies ϕ k = ϕ k
UNIQUENESS OF POSITIVE SOLUTION TO SOME COUPLED COOPERATIVE VARIATIONAL ELLIPTIC SYSTEMS
 TRANSACTIONS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 00, Number 0, Pages 000 000 S 0002-9947(XX)0000-0 UNIQUENESS OF POSITIVE SOLUTION TO SOME COUPLED COOPERATIVE VARIATIONAL ELLIPTIC SYSTEMS YULIAN
TRANSACTIONS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 00, Number 0, Pages 000 000 S 0002-9947(XX)0000-0 UNIQUENESS OF POSITIVE SOLUTION TO SOME COUPLED COOPERATIVE VARIATIONAL ELLIPTIC SYSTEMS YULIAN
Stochastic nonlinear Schrödinger equations and modulation of solitary waves
 Stochastic nonlinear Schrödinger equations and modulation of solitary waves A. de Bouard CMAP, Ecole Polytechnique, France joint work with R. Fukuizumi (Sendai, Japan) Deterministic and stochastic front
Stochastic nonlinear Schrödinger equations and modulation of solitary waves A. de Bouard CMAP, Ecole Polytechnique, France joint work with R. Fukuizumi (Sendai, Japan) Deterministic and stochastic front
Existence and Stability of PT-Symmetric Vortices in Nonlinear Two-Dimensional Square Lattices
 University of Massachusetts Amherst ScholarWorks@UMass Amherst Mathematics and Statistics Department Faculty Publication Series Mathematics and Statistics 215 Existence and Stability of PT-Symmetric Vortices
University of Massachusetts Amherst ScholarWorks@UMass Amherst Mathematics and Statistics Department Faculty Publication Series Mathematics and Statistics 215 Existence and Stability of PT-Symmetric Vortices
Finding eigenvalues for matrices acting on subspaces
 Finding eigenvalues for matrices acting on subspaces Jakeniah Christiansen Department of Mathematics and Statistics Calvin College Grand Rapids, MI 49546 Faculty advisor: Prof Todd Kapitula Department
Finding eigenvalues for matrices acting on subspaces Jakeniah Christiansen Department of Mathematics and Statistics Calvin College Grand Rapids, MI 49546 Faculty advisor: Prof Todd Kapitula Department
Symmetry breaking and restoration in the Ginzburg-Landau model of nematic liquid crystals
 Symmetry breaking and restoration in the Ginzburg-Landau model of nematic liquid crystals Micha l Kowalczyk joint project with M. Clerc and P. Smyrnelis (LAFER/DIF and LSPS/CMM). March 1, 2018 Experimental
Symmetry breaking and restoration in the Ginzburg-Landau model of nematic liquid crystals Micha l Kowalczyk joint project with M. Clerc and P. Smyrnelis (LAFER/DIF and LSPS/CMM). March 1, 2018 Experimental
1 Distributions (due January 22, 2009)
 Distributions (due January 22, 29). The distribution derivative of the locally integrable function ln( x ) is the principal value distribution /x. We know that, φ = lim φ(x) dx. x ɛ x Show that x, φ =
Distributions (due January 22, 29). The distribution derivative of the locally integrable function ln( x ) is the principal value distribution /x. We know that, φ = lim φ(x) dx. x ɛ x Show that x, φ =
The Krein signature, Krein eigenvalues, and the Krein Oscillation Theorem
 The Krein signature, Krein eigenvalues, and the Krein Oscillation Theorem Todd Kapitula Department of Mathematics and Statistics Calvin College Grand Rapids, MI 49546 June 19, 2009 Abstract. In this paper
The Krein signature, Krein eigenvalues, and the Krein Oscillation Theorem Todd Kapitula Department of Mathematics and Statistics Calvin College Grand Rapids, MI 49546 June 19, 2009 Abstract. In this paper
SPRING 2006 PRELIMINARY EXAMINATION SOLUTIONS
 SPRING 006 PRELIMINARY EXAMINATION SOLUTIONS 1A. Let G be the subgroup of the free abelian group Z 4 consisting of all integer vectors (x, y, z, w) such that x + 3y + 5z + 7w = 0. (a) Determine a linearly
SPRING 006 PRELIMINARY EXAMINATION SOLUTIONS 1A. Let G be the subgroup of the free abelian group Z 4 consisting of all integer vectors (x, y, z, w) such that x + 3y + 5z + 7w = 0. (a) Determine a linearly
Asymptotic distribution of eigenvalues of Laplace operator
 Asymptotic distribution of eigenvalues of Laplace operator 23.8.2013 Topics We will talk about: the number of eigenvalues of Laplace operator smaller than some λ as a function of λ asymptotic behaviour
Asymptotic distribution of eigenvalues of Laplace operator 23.8.2013 Topics We will talk about: the number of eigenvalues of Laplace operator smaller than some λ as a function of λ asymptotic behaviour
Uniqueness of ground state solutions of non-local equations in R N
 Uniqueness of ground state solutions of non-local equations in R N Rupert L. Frank Department of Mathematics Princeton University Joint work with Enno Lenzmann and Luis Silvestre Uniqueness and non-degeneracy
Uniqueness of ground state solutions of non-local equations in R N Rupert L. Frank Department of Mathematics Princeton University Joint work with Enno Lenzmann and Luis Silvestre Uniqueness and non-degeneracy
Understand the existence and uniqueness theorems and what they tell you about solutions to initial value problems.
 Review Outline To review for the final, look over the following outline and look at problems from the book and on the old exam s and exam reviews to find problems about each of the following topics.. Basics
Review Outline To review for the final, look over the following outline and look at problems from the book and on the old exam s and exam reviews to find problems about each of the following topics.. Basics
Separation of Variables in Linear PDE: One-Dimensional Problems
 Separation of Variables in Linear PDE: One-Dimensional Problems Now we apply the theory of Hilbert spaces to linear differential equations with partial derivatives (PDE). We start with a particular example,
Separation of Variables in Linear PDE: One-Dimensional Problems Now we apply the theory of Hilbert spaces to linear differential equations with partial derivatives (PDE). We start with a particular example,
Multi-site breathers in Klein Gordon lattices: stability, resonances and bifurcations
 IOP PUBLISHING Nonlinearity 5 () 343 345 NONLINEARITY doi:.88/95-775/5//343 Multi-site breathers in Klein Gordon lattices: stability, resonances and bifurcations Dmitry Pelinovsky and Anton Sakovich Department
IOP PUBLISHING Nonlinearity 5 () 343 345 NONLINEARITY doi:.88/95-775/5//343 Multi-site breathers in Klein Gordon lattices: stability, resonances and bifurcations Dmitry Pelinovsky and Anton Sakovich Department
Stable solitons of the cubic-quintic NLS with a delta-function potential
 Stable solitons of the cubic-quintic NLS with a delta-function potential François Genoud TU Delft Besançon, 7 January 015 The cubic-quintic NLS with a δ-potential We consider the nonlinear Schrödinger
Stable solitons of the cubic-quintic NLS with a delta-function potential François Genoud TU Delft Besançon, 7 January 015 The cubic-quintic NLS with a δ-potential We consider the nonlinear Schrödinger
Solutions for B8b (Nonlinear Systems) Fake Past Exam (TT 10)
 Solutions for B8b (Nonlinear Systems) Fake Past Exam (TT 10) Mason A. Porter 15/05/2010 1 Question 1 i. (6 points) Define a saddle-node bifurcation and show that the first order system dx dt = r x e x
Solutions for B8b (Nonlinear Systems) Fake Past Exam (TT 10) Mason A. Porter 15/05/2010 1 Question 1 i. (6 points) Define a saddle-node bifurcation and show that the first order system dx dt = r x e x
Dynamics of interacting vortices on trapped Bose-Einstein condensates. Pedro J. Torres University of Granada
 Dynamics of interacting vortices on trapped Bose-Einstein condensates Pedro J. Torres University of Granada Joint work with: P.G. Kevrekidis (University of Massachusetts, USA) Ricardo Carretero-González
Dynamics of interacting vortices on trapped Bose-Einstein condensates Pedro J. Torres University of Granada Joint work with: P.G. Kevrekidis (University of Massachusetts, USA) Ricardo Carretero-González
Ground state on the bounded and unbounded graphs
 Ground state on the bounded and unbounded graphs Dmitry Pelinovsky Department of Mathematics, McMaster University, Canada Joint work with Jeremy Marzuola, University of North Carolina, USA Workshop Mathematical
Ground state on the bounded and unbounded graphs Dmitry Pelinovsky Department of Mathematics, McMaster University, Canada Joint work with Jeremy Marzuola, University of North Carolina, USA Workshop Mathematical
MATH 205C: STATIONARY PHASE LEMMA
 MATH 205C: STATIONARY PHASE LEMMA For ω, consider an integral of the form I(ω) = e iωf(x) u(x) dx, where u Cc (R n ) complex valued, with support in a compact set K, and f C (R n ) real valued. Thus, I(ω)
MATH 205C: STATIONARY PHASE LEMMA For ω, consider an integral of the form I(ω) = e iωf(x) u(x) dx, where u Cc (R n ) complex valued, with support in a compact set K, and f C (R n ) real valued. Thus, I(ω)
Spectral stability of periodic waves in dispersive models
 in dispersive models Collaborators: Th. Gallay, E. Lombardi T. Kapitula, A. Scheel in dispersive models One-dimensional nonlinear waves Standing and travelling waves u(x ct) with c = 0 or c 0 periodic
in dispersive models Collaborators: Th. Gallay, E. Lombardi T. Kapitula, A. Scheel in dispersive models One-dimensional nonlinear waves Standing and travelling waves u(x ct) with c = 0 or c 0 periodic
Orbital stability in the cubic defocusing NLS equation: I. Cnoidal periodic waves
 Available online at www.sciencedirect.com ScienceDirect J. Differential Equations 58 15) 367 3638 www.elsevier.com/locate/jde Orbital stability in the cubic defocusing NLS equation: I. Cnoidal periodic
Available online at www.sciencedirect.com ScienceDirect J. Differential Equations 58 15) 367 3638 www.elsevier.com/locate/jde Orbital stability in the cubic defocusing NLS equation: I. Cnoidal periodic
Taylor and Laurent Series
 Chapter 4 Taylor and Laurent Series 4.. Taylor Series 4... Taylor Series for Holomorphic Functions. In Real Analysis, the Taylor series of a given function f : R R is given by: f (x + f (x (x x + f (x
Chapter 4 Taylor and Laurent Series 4.. Taylor Series 4... Taylor Series for Holomorphic Functions. In Real Analysis, the Taylor series of a given function f : R R is given by: f (x + f (x (x x + f (x
B5.6 Nonlinear Systems
 B5.6 Nonlinear Systems 5. Global Bifurcations, Homoclinic chaos, Melnikov s method Alain Goriely 2018 Mathematical Institute, University of Oxford Table of contents 1. Motivation 1.1 The problem 1.2 A
B5.6 Nonlinear Systems 5. Global Bifurcations, Homoclinic chaos, Melnikov s method Alain Goriely 2018 Mathematical Institute, University of Oxford Table of contents 1. Motivation 1.1 The problem 1.2 A
Analysis in weighted spaces : preliminary version
 Analysis in weighted spaces : preliminary version Frank Pacard To cite this version: Frank Pacard. Analysis in weighted spaces : preliminary version. 3rd cycle. Téhéran (Iran, 2006, pp.75.
Analysis in weighted spaces : preliminary version Frank Pacard To cite this version: Frank Pacard. Analysis in weighted spaces : preliminary version. 3rd cycle. Téhéran (Iran, 2006, pp.75.
Rogue periodic waves for mkdv and NLS equations
 Rogue periodic waves for mkdv and NLS equations Jinbing Chen and Dmitry Pelinovsky Department of Mathematics, McMaster University, Hamilton, Ontario, Canada http://dmpeli.math.mcmaster.ca AMS Sectional
Rogue periodic waves for mkdv and NLS equations Jinbing Chen and Dmitry Pelinovsky Department of Mathematics, McMaster University, Hamilton, Ontario, Canada http://dmpeli.math.mcmaster.ca AMS Sectional
The following definition is fundamental.
 1. Some Basics from Linear Algebra With these notes, I will try and clarify certain topics that I only quickly mention in class. First and foremost, I will assume that you are familiar with many basic
1. Some Basics from Linear Algebra With these notes, I will try and clarify certain topics that I only quickly mention in class. First and foremost, I will assume that you are familiar with many basic
Excitations and dynamics of a two-component Bose-Einstein condensate in 1D
 Author: Navarro Facultat de Física, Universitat de Barcelona, Diagonal 645, 0808 Barcelona, Spain. Advisor: Bruno Juliá Díaz Abstract: We study different solutions and their stability for a two component
Author: Navarro Facultat de Física, Universitat de Barcelona, Diagonal 645, 0808 Barcelona, Spain. Advisor: Bruno Juliá Díaz Abstract: We study different solutions and their stability for a two component
u xx + u yy = 0. (5.1)
 Chapter 5 Laplace Equation The following equation is called Laplace equation in two independent variables x, y: The non-homogeneous problem u xx + u yy =. (5.1) u xx + u yy = F, (5.) where F is a function
Chapter 5 Laplace Equation The following equation is called Laplace equation in two independent variables x, y: The non-homogeneous problem u xx + u yy =. (5.1) u xx + u yy = F, (5.) where F is a function
RANDOM PROPERTIES BENOIT PAUSADER
 RANDOM PROPERTIES BENOIT PAUSADER. Quasilinear problems In general, one consider the following trichotomy for nonlinear PDEs: A semilinear problem is a problem where the highest-order terms appears linearly
RANDOM PROPERTIES BENOIT PAUSADER. Quasilinear problems In general, one consider the following trichotomy for nonlinear PDEs: A semilinear problem is a problem where the highest-order terms appears linearly
2 Lebesgue integration
 2 Lebesgue integration 1. Let (, A, µ) be a measure space. We will always assume that µ is complete, otherwise we first take its completion. The example to have in mind is the Lebesgue measure on R n,
2 Lebesgue integration 1. Let (, A, µ) be a measure space. We will always assume that µ is complete, otherwise we first take its completion. The example to have in mind is the Lebesgue measure on R n,
Bielefeld Course on Nonlinear Waves - June 29, Department of Mathematics University of North Carolina, Chapel Hill. Solitons on Manifolds
 Joint work (on various projects) with Pierre Albin (UIUC), Hans Christianson (UNC), Jason Metcalfe (UNC), Michael Taylor (UNC), Laurent Thomann (Nantes) Department of Mathematics University of North Carolina,
Joint work (on various projects) with Pierre Albin (UIUC), Hans Christianson (UNC), Jason Metcalfe (UNC), Michael Taylor (UNC), Laurent Thomann (Nantes) Department of Mathematics University of North Carolina,
Rapidly Rotating Bose-Einstein Condensates in Strongly Anharmonic Traps. Michele Correggi. T. Rindler-Daller, J. Yngvason math-ph/
 Rapidly Rotating Bose-Einstein Condensates in Strongly Anharmonic Traps Michele Correggi Erwin Schrödinger Institute, Vienna T. Rindler-Daller, J. Yngvason math-ph/0606058 in collaboration with preprint
Rapidly Rotating Bose-Einstein Condensates in Strongly Anharmonic Traps Michele Correggi Erwin Schrödinger Institute, Vienna T. Rindler-Daller, J. Yngvason math-ph/0606058 in collaboration with preprint
University of Utrecht
 University of Utrecht Bachelor thesis The bifurcation diagram of the second nontrivial normal form of an axially symmetric perturbation of the isotropic harmonic oscillator Author: T. Welker Supervisor:
University of Utrecht Bachelor thesis The bifurcation diagram of the second nontrivial normal form of an axially symmetric perturbation of the isotropic harmonic oscillator Author: T. Welker Supervisor:
Eigenvalues and Eigenfunctions of the Laplacian
 The Waterloo Mathematics Review 23 Eigenvalues and Eigenfunctions of the Laplacian Mihai Nica University of Waterloo mcnica@uwaterloo.ca Abstract: The problem of determining the eigenvalues and eigenvectors
The Waterloo Mathematics Review 23 Eigenvalues and Eigenfunctions of the Laplacian Mihai Nica University of Waterloo mcnica@uwaterloo.ca Abstract: The problem of determining the eigenvalues and eigenvectors
Math Homework 2
 Math 73 Homework Due: September 8, 6 Suppose that f is holomorphic in a region Ω, ie an open connected set Prove that in any of the following cases (a) R(f) is constant; (b) I(f) is constant; (c) f is
Math 73 Homework Due: September 8, 6 Suppose that f is holomorphic in a region Ω, ie an open connected set Prove that in any of the following cases (a) R(f) is constant; (b) I(f) is constant; (c) f is
An introduction to Birkhoff normal form
 An introduction to Birkhoff normal form Dario Bambusi Dipartimento di Matematica, Universitá di Milano via Saldini 50, 0133 Milano (Italy) 19.11.14 1 Introduction The aim of this note is to present an
An introduction to Birkhoff normal form Dario Bambusi Dipartimento di Matematica, Universitá di Milano via Saldini 50, 0133 Milano (Italy) 19.11.14 1 Introduction The aim of this note is to present an
1 Lyapunov theory of stability
 M.Kawski, APM 581 Diff Equns Intro to Lyapunov theory. November 15, 29 1 1 Lyapunov theory of stability Introduction. Lyapunov s second (or direct) method provides tools for studying (asymptotic) stability
M.Kawski, APM 581 Diff Equns Intro to Lyapunov theory. November 15, 29 1 1 Lyapunov theory of stability Introduction. Lyapunov s second (or direct) method provides tools for studying (asymptotic) stability
1. < 0: the eigenvalues are real and have opposite signs; the fixed point is a saddle point
 Solving a Linear System τ = trace(a) = a + d = λ 1 + λ 2 λ 1,2 = τ± = det(a) = ad bc = λ 1 λ 2 Classification of Fixed Points τ 2 4 1. < 0: the eigenvalues are real and have opposite signs; the fixed point
Solving a Linear System τ = trace(a) = a + d = λ 1 + λ 2 λ 1,2 = τ± = det(a) = ad bc = λ 1 λ 2 Classification of Fixed Points τ 2 4 1. < 0: the eigenvalues are real and have opposite signs; the fixed point
The 3 dimensional Schrödinger Equation
 Chapter 6 The 3 dimensional Schrödinger Equation 6.1 Angular Momentum To study how angular momentum is represented in quantum mechanics we start by reviewing the classical vector of orbital angular momentum
Chapter 6 The 3 dimensional Schrödinger Equation 6.1 Angular Momentum To study how angular momentum is represented in quantum mechanics we start by reviewing the classical vector of orbital angular momentum
MCE693/793: Analysis and Control of Nonlinear Systems
 MCE693/793: Analysis and Control of Nonlinear Systems Systems of Differential Equations Phase Plane Analysis Hanz Richter Mechanical Engineering Department Cleveland State University Systems of Nonlinear
MCE693/793: Analysis and Control of Nonlinear Systems Systems of Differential Equations Phase Plane Analysis Hanz Richter Mechanical Engineering Department Cleveland State University Systems of Nonlinear
Linear Algebra: Matrix Eigenvalue Problems
 CHAPTER8 Linear Algebra: Matrix Eigenvalue Problems Chapter 8 p1 A matrix eigenvalue problem considers the vector equation (1) Ax = λx. 8.0 Linear Algebra: Matrix Eigenvalue Problems Here A is a given
CHAPTER8 Linear Algebra: Matrix Eigenvalue Problems Chapter 8 p1 A matrix eigenvalue problem considers the vector equation (1) Ax = λx. 8.0 Linear Algebra: Matrix Eigenvalue Problems Here A is a given
From Boltzmann Equations to Gas Dynamics: From DiPerna-Lions to Leray
 From Boltzmann Equations to Gas Dynamics: From DiPerna-Lions to Leray C. David Levermore Department of Mathematics and Institute for Physical Science and Technology University of Maryland, College Park
From Boltzmann Equations to Gas Dynamics: From DiPerna-Lions to Leray C. David Levermore Department of Mathematics and Institute for Physical Science and Technology University of Maryland, College Park
Modulated traveling fronts for a nonlocal Fisher-KPP equation: a dynamical systems approach
 Modulated traveling fronts for a nonlocal Fisher-KPP equation: a dynamical systems approach Grégory Faye 1 and Matt Holzer 2 1 CAMS - Ecole des Hautes Etudes en Sciences Sociales, 190-198 avenue de France,
Modulated traveling fronts for a nonlocal Fisher-KPP equation: a dynamical systems approach Grégory Faye 1 and Matt Holzer 2 1 CAMS - Ecole des Hautes Etudes en Sciences Sociales, 190-198 avenue de France,
Short note on compact operators - Monday 24 th March, Sylvester Eriksson-Bique
 Short note on compact operators - Monday 24 th March, 2014 Sylvester Eriksson-Bique 1 Introduction In this note I will give a short outline about the structure theory of compact operators. I restrict attention
Short note on compact operators - Monday 24 th March, 2014 Sylvester Eriksson-Bique 1 Introduction In this note I will give a short outline about the structure theory of compact operators. I restrict attention
Complex Behavior in Coupled Nonlinear Waveguides. Roy Goodman, New Jersey Institute of Technology
 Complex Behavior in Coupled Nonlinear Waveguides Roy Goodman, New Jersey Institute of Technology Nonlinear Schrödinger/Gross-Pitaevskii Equation i t = r + V (r) ± Two contexts for today: Propagation of
Complex Behavior in Coupled Nonlinear Waveguides Roy Goodman, New Jersey Institute of Technology Nonlinear Schrödinger/Gross-Pitaevskii Equation i t = r + V (r) ± Two contexts for today: Propagation of
8.1 Bifurcations of Equilibria
 1 81 Bifurcations of Equilibria Bifurcation theory studies qualitative changes in solutions as a parameter varies In general one could study the bifurcation theory of ODEs PDEs integro-differential equations
1 81 Bifurcations of Equilibria Bifurcation theory studies qualitative changes in solutions as a parameter varies In general one could study the bifurcation theory of ODEs PDEs integro-differential equations
Tangent spaces, normals and extrema
 Chapter 3 Tangent spaces, normals and extrema If S is a surface in 3-space, with a point a S where S looks smooth, i.e., without any fold or cusp or self-crossing, we can intuitively define the tangent
Chapter 3 Tangent spaces, normals and extrema If S is a surface in 3-space, with a point a S where S looks smooth, i.e., without any fold or cusp or self-crossing, we can intuitively define the tangent
On the Thomas Fermi Approximation of the Ground State in a PT-Symmetric Confining Potential
 On the Thomas Fermi Approximation of the Ground State in a PT-Symmetric Confining Potential By Clément Gallo and Dmitry Pelinovsky For the stationary Gross Pitaevskii equation with harmonic real and linear
On the Thomas Fermi Approximation of the Ground State in a PT-Symmetric Confining Potential By Clément Gallo and Dmitry Pelinovsky For the stationary Gross Pitaevskii equation with harmonic real and linear
Lecture 2: Weak Interactions and BEC
 Lecture 2: Weak Interactions and BEC Previous lecture: Ideal gas model gives a fair intuition for occurrence of BEC but is unphysical (infinite compressibility, shape of condensate...) Order parameter
Lecture 2: Weak Interactions and BEC Previous lecture: Ideal gas model gives a fair intuition for occurrence of BEC but is unphysical (infinite compressibility, shape of condensate...) Order parameter
Boulder School for Condensed Matter and Materials Physics. Laurette Tuckerman PMMH-ESPCI-CNRS
 Boulder School for Condensed Matter and Materials Physics Laurette Tuckerman PMMH-ESPCI-CNRS laurette@pmmh.espci.fr Dynamical Systems: A Basic Primer 1 1 Basic bifurcations 1.1 Fixed points and linear
Boulder School for Condensed Matter and Materials Physics Laurette Tuckerman PMMH-ESPCI-CNRS laurette@pmmh.espci.fr Dynamical Systems: A Basic Primer 1 1 Basic bifurcations 1.1 Fixed points and linear
Symmetry breaking bifurcation in Nonlinear Schrödinger /Gross-Pitaevskii Equations
 Symmetry breaking bifurcation in Nonlinear Schrödinger /Gross-Pitaevskii Equations E.W. Kirr, P.G. Kevrekidis, E. Shlizerman, and M.I. Weinstein December 23, 26 Abstract We consider a class of nonlinear
Symmetry breaking bifurcation in Nonlinear Schrödinger /Gross-Pitaevskii Equations E.W. Kirr, P.G. Kevrekidis, E. Shlizerman, and M.I. Weinstein December 23, 26 Abstract We consider a class of nonlinear
APPLIED PARTIM DIFFERENTIAL EQUATIONS with Fourier Series and Boundary Value Problems
 APPLIED PARTIM DIFFERENTIAL EQUATIONS with Fourier Series and Boundary Value Problems Fourth Edition Richard Haberman Department of Mathematics Southern Methodist University PEARSON Prentice Hall PEARSON
APPLIED PARTIM DIFFERENTIAL EQUATIONS with Fourier Series and Boundary Value Problems Fourth Edition Richard Haberman Department of Mathematics Southern Methodist University PEARSON Prentice Hall PEARSON
5.2.2 Planar Andronov-Hopf bifurcation
 138 CHAPTER 5. LOCAL BIFURCATION THEORY 5.. Planar Andronov-Hopf bifurcation What happens if a planar system has an equilibrium x = x 0 at some parameter value α = α 0 with eigenvalues λ 1, = ±iω 0, ω
138 CHAPTER 5. LOCAL BIFURCATION THEORY 5.. Planar Andronov-Hopf bifurcation What happens if a planar system has an equilibrium x = x 0 at some parameter value α = α 0 with eigenvalues λ 1, = ±iω 0, ω
Magnetic wells in dimension three
 Magnetic wells in dimension three Yuri A. Kordyukov joint with Bernard Helffer & Nicolas Raymond & San Vũ Ngọc Magnetic Fields and Semiclassical Analysis Rennes, May 21, 2015 Yuri A. Kordyukov (Ufa) Magnetic
Magnetic wells in dimension three Yuri A. Kordyukov joint with Bernard Helffer & Nicolas Raymond & San Vũ Ngọc Magnetic Fields and Semiclassical Analysis Rennes, May 21, 2015 Yuri A. Kordyukov (Ufa) Magnetic
SHORT-WAVE TRANSVERSE INSTABILITIES OF LINE SOLITONS OF THE TWO-DIMENSIONAL HYPERBOLIC NONLINEAR SCHRÖDINGER EQUATION
 Theoretical and Mathematical Physics, 179(1): 45 461 (014) SHORT-WAVE TRANSVERSE INSTABILITIES OF LINE SOLITONS OF THE TWO-DIMENSIONAL HYPERBOLIC NONLINEAR SCHRÖDINGER EQUATION D. E. Pelinovsky, E. A.
Theoretical and Mathematical Physics, 179(1): 45 461 (014) SHORT-WAVE TRANSVERSE INSTABILITIES OF LINE SOLITONS OF THE TWO-DIMENSIONAL HYPERBOLIC NONLINEAR SCHRÖDINGER EQUATION D. E. Pelinovsky, E. A.
A new integrable system: The interacting soliton of the BO
 Phys. Lett., A 204, p.336-342, 1995 A new integrable system: The interacting soliton of the BO Benno Fuchssteiner and Thorsten Schulze Automath Institute University of Paderborn Paderborn & Germany Abstract
Phys. Lett., A 204, p.336-342, 1995 A new integrable system: The interacting soliton of the BO Benno Fuchssteiner and Thorsten Schulze Automath Institute University of Paderborn Paderborn & Germany Abstract
On Some Variational Optimization Problems in Classical Fluids and Superfluids
 On Some Variational Optimization Problems in Classical Fluids and Superfluids Bartosz Protas Department of Mathematics & Statistics McMaster University, Hamilton, Ontario, Canada URL: http://www.math.mcmaster.ca/bprotas
On Some Variational Optimization Problems in Classical Fluids and Superfluids Bartosz Protas Department of Mathematics & Statistics McMaster University, Hamilton, Ontario, Canada URL: http://www.math.mcmaster.ca/bprotas
Week 2 Notes, Math 865, Tanveer
 Week 2 Notes, Math 865, Tanveer 1. Incompressible constant density equations in different forms Recall we derived the Navier-Stokes equation for incompressible constant density, i.e. homogeneous flows:
Week 2 Notes, Math 865, Tanveer 1. Incompressible constant density equations in different forms Recall we derived the Navier-Stokes equation for incompressible constant density, i.e. homogeneous flows:
154 Chapter 9 Hints, Answers, and Solutions The particular trajectories are highlighted in the phase portraits below.
 54 Chapter 9 Hints, Answers, and Solutions 9. The Phase Plane 9.. 4. The particular trajectories are highlighted in the phase portraits below... 3. 4. 9..5. Shown below is one possibility with x(t) and
54 Chapter 9 Hints, Answers, and Solutions 9. The Phase Plane 9.. 4. The particular trajectories are highlighted in the phase portraits below... 3. 4. 9..5. Shown below is one possibility with x(t) and
i=1 α i. Given an m-times continuously
 1 Fundamentals 1.1 Classification and characteristics Let Ω R d, d N, d 2, be an open set and α = (α 1,, α d ) T N d 0, N 0 := N {0}, a multiindex with α := d i=1 α i. Given an m-times continuously differentiable
1 Fundamentals 1.1 Classification and characteristics Let Ω R d, d N, d 2, be an open set and α = (α 1,, α d ) T N d 0, N 0 := N {0}, a multiindex with α := d i=1 α i. Given an m-times continuously differentiable
PART IV Spectral Methods
 PART IV Spectral Methods Additional References: R. Peyret, Spectral methods for incompressible viscous flow, Springer (2002), B. Mercier, An introduction to the numerical analysis of spectral methods,
PART IV Spectral Methods Additional References: R. Peyret, Spectral methods for incompressible viscous flow, Springer (2002), B. Mercier, An introduction to the numerical analysis of spectral methods,
Seminar 6: COUPLED HARMONIC OSCILLATORS
 Seminar 6: COUPLED HARMONIC OSCILLATORS 1. Lagrangian Equations of Motion Let consider a system consisting of two harmonic oscillators that are coupled together. As a model, we will use two particles attached
Seminar 6: COUPLED HARMONIC OSCILLATORS 1. Lagrangian Equations of Motion Let consider a system consisting of two harmonic oscillators that are coupled together. As a model, we will use two particles attached
Notes by Maksim Maydanskiy.
 SPECTRAL FLOW IN MORSE THEORY. 1 Introduction Notes by Maksim Maydanskiy. Spectral flow is a general formula or computing the Fredholm index of an operator d ds +A(s) : L1,2 (R, H) L 2 (R, H) for a family
SPECTRAL FLOW IN MORSE THEORY. 1 Introduction Notes by Maksim Maydanskiy. Spectral flow is a general formula or computing the Fredholm index of an operator d ds +A(s) : L1,2 (R, H) L 2 (R, H) for a family
Topics for the Qualifying Examination
 Topics for the Qualifying Examination Quantum Mechanics I and II 1. Quantum kinematics and dynamics 1.1 Postulates of Quantum Mechanics. 1.2 Configuration space vs. Hilbert space, wave function vs. state
Topics for the Qualifying Examination Quantum Mechanics I and II 1. Quantum kinematics and dynamics 1.1 Postulates of Quantum Mechanics. 1.2 Configuration space vs. Hilbert space, wave function vs. state
Existence of Secondary Bifurcations or Isolas for PDEs
 Existence of Secondary Bifurcations or Isolas for PDEs Marcio Gameiro Jean-Philippe Lessard Abstract In this paper, we introduce a method to conclude about the existence of secondary bifurcations or isolas
Existence of Secondary Bifurcations or Isolas for PDEs Marcio Gameiro Jean-Philippe Lessard Abstract In this paper, we introduce a method to conclude about the existence of secondary bifurcations or isolas
Solutions to Math 53 Math 53 Practice Final
 Solutions to Math 5 Math 5 Practice Final 20 points Consider the initial value problem y t 4yt = te t with y 0 = and y0 = 0 a 8 points Find the Laplace transform of the solution of this IVP b 8 points
Solutions to Math 5 Math 5 Practice Final 20 points Consider the initial value problem y t 4yt = te t with y 0 = and y0 = 0 a 8 points Find the Laplace transform of the solution of this IVP b 8 points
Functional Analysis. Franck Sueur Metric spaces Definitions Completeness Compactness Separability...
 Functional Analysis Franck Sueur 2018-2019 Contents 1 Metric spaces 1 1.1 Definitions........................................ 1 1.2 Completeness...................................... 3 1.3 Compactness......................................
Functional Analysis Franck Sueur 2018-2019 Contents 1 Metric spaces 1 1.1 Definitions........................................ 1 1.2 Completeness...................................... 3 1.3 Compactness......................................
(8.51) ẋ = A(λ)x + F(x, λ), where λ lr, the matrix A(λ) and function F(x, λ) are C k -functions with k 1,
 2.8.7. Poincaré-Andronov-Hopf Bifurcation. In the previous section, we have given a rather detailed method for determining the periodic orbits of a two dimensional system which is the perturbation of a
2.8.7. Poincaré-Andronov-Hopf Bifurcation. In the previous section, we have given a rather detailed method for determining the periodic orbits of a two dimensional system which is the perturbation of a
SPECTRAL PROPERTIES OF THE LAPLACIAN ON BOUNDED DOMAINS
 SPECTRAL PROPERTIES OF THE LAPLACIAN ON BOUNDED DOMAINS TSOGTGEREL GANTUMUR Abstract. After establishing discrete spectra for a large class of elliptic operators, we present some fundamental spectral properties
SPECTRAL PROPERTIES OF THE LAPLACIAN ON BOUNDED DOMAINS TSOGTGEREL GANTUMUR Abstract. After establishing discrete spectra for a large class of elliptic operators, we present some fundamental spectral properties
Vector Spaces. Vector space, ν, over the field of complex numbers, C, is a set of elements a, b,..., satisfying the following axioms.
 Vector Spaces Vector space, ν, over the field of complex numbers, C, is a set of elements a, b,..., satisfying the following axioms. For each two vectors a, b ν there exists a summation procedure: a +
Vector Spaces Vector space, ν, over the field of complex numbers, C, is a set of elements a, b,..., satisfying the following axioms. For each two vectors a, b ν there exists a summation procedure: a +
Studies on Lattice Systems Motivated by PT- Symmetry and Granular Crystals
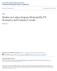 University of Massachusetts Amherst ScholarWorks@UMass Amherst Doctoral Dissertations Dissertations and Theses 6 Studies on Lattice Systems Motivated by PT- Symmetry and Granular Crystals Haitao Xu Follow
University of Massachusetts Amherst ScholarWorks@UMass Amherst Doctoral Dissertations Dissertations and Theses 6 Studies on Lattice Systems Motivated by PT- Symmetry and Granular Crystals Haitao Xu Follow
Nonlinear dynamics & chaos BECS
 Nonlinear dynamics & chaos BECS-114.7151 Phase portraits Focus: nonlinear systems in two dimensions General form of a vector field on the phase plane: Vector notation: Phase portraits Solution x(t) describes
Nonlinear dynamics & chaos BECS-114.7151 Phase portraits Focus: nonlinear systems in two dimensions General form of a vector field on the phase plane: Vector notation: Phase portraits Solution x(t) describes
Lecture 6 Positive Definite Matrices
 Linear Algebra Lecture 6 Positive Definite Matrices Prof. Chun-Hung Liu Dept. of Electrical and Computer Engineering National Chiao Tung University Spring 2017 2017/6/8 Lecture 6: Positive Definite Matrices
Linear Algebra Lecture 6 Positive Definite Matrices Prof. Chun-Hung Liu Dept. of Electrical and Computer Engineering National Chiao Tung University Spring 2017 2017/6/8 Lecture 6: Positive Definite Matrices
5. Gross-Pitaevskii theory
 5. Gross-Pitaevskii theory Outline N noninteracting bosons N interacting bosons, many-body Hamiltonien Mean-field approximation, order parameter Gross-Pitaevskii equation Collapse for attractive interaction
5. Gross-Pitaevskii theory Outline N noninteracting bosons N interacting bosons, many-body Hamiltonien Mean-field approximation, order parameter Gross-Pitaevskii equation Collapse for attractive interaction
5 Measure theory II. (or. lim. Prove the proposition. 5. For fixed F A and φ M define the restriction of φ on F by writing.
 5 Measure theory II 1. Charges (signed measures). Let (Ω, A) be a σ -algebra. A map φ: A R is called a charge, (or signed measure or σ -additive set function) if φ = φ(a j ) (5.1) A j for any disjoint
5 Measure theory II 1. Charges (signed measures). Let (Ω, A) be a σ -algebra. A map φ: A R is called a charge, (or signed measure or σ -additive set function) if φ = φ(a j ) (5.1) A j for any disjoint
Ground State on the Dumbbell Graph
 J. L. Marzuola and D. E. Pelinovsky (16) Ground State on Dumbbell Graph, Applied Mathematics Research express, Vol. 16, No. 1, pp. 98 145 Advance Access publication January 7, 16 doi:1.193/amrx/abv11 Ground
J. L. Marzuola and D. E. Pelinovsky (16) Ground State on Dumbbell Graph, Applied Mathematics Research express, Vol. 16, No. 1, pp. 98 145 Advance Access publication January 7, 16 doi:1.193/amrx/abv11 Ground
Elements of linear algebra
 Elements of linear algebra Elements of linear algebra A vector space S is a set (numbers, vectors, functions) which has addition and scalar multiplication defined, so that the linear combination c 1 v
Elements of linear algebra Elements of linear algebra A vector space S is a set (numbers, vectors, functions) which has addition and scalar multiplication defined, so that the linear combination c 1 v
Homogenization and error estimates of free boundary velocities in periodic media
 Homogenization and error estimates of free boundary velocities in periodic media Inwon C. Kim October 7, 2011 Abstract In this note I describe a recent result ([14]-[15]) on homogenization and error estimates
Homogenization and error estimates of free boundary velocities in periodic media Inwon C. Kim October 7, 2011 Abstract In this note I describe a recent result ([14]-[15]) on homogenization and error estimates
Differential Equations 2280 Sample Midterm Exam 3 with Solutions Exam Date: 24 April 2015 at 12:50pm
 Differential Equations 228 Sample Midterm Exam 3 with Solutions Exam Date: 24 April 25 at 2:5pm Instructions: This in-class exam is 5 minutes. No calculators, notes, tables or books. No answer check is
Differential Equations 228 Sample Midterm Exam 3 with Solutions Exam Date: 24 April 25 at 2:5pm Instructions: This in-class exam is 5 minutes. No calculators, notes, tables or books. No answer check is
A CONVEX-CONCAVE ELLIPTIC PROBLEM WITH A PARAMETER ON THE BOUNDARY CONDITION
 A CONVEX-CONCAVE ELLIPTIC PROBLEM WITH A PARAMETER ON THE BOUNDARY CONDITION JORGE GARCÍA-MELIÁN, JULIO D. ROSSI AND JOSÉ C. SABINA DE LIS Abstract. In this paper we study existence and multiplicity of
A CONVEX-CONCAVE ELLIPTIC PROBLEM WITH A PARAMETER ON THE BOUNDARY CONDITION JORGE GARCÍA-MELIÁN, JULIO D. ROSSI AND JOSÉ C. SABINA DE LIS Abstract. In this paper we study existence and multiplicity of
Quantum Mechanics Solutions
 Quantum Mechanics Solutions (a (i f A and B are Hermitian, since (AB = B A = BA, operator AB is Hermitian if and only if A and B commute So, we know that [A,B] = 0, which means that the Hilbert space H
Quantum Mechanics Solutions (a (i f A and B are Hermitian, since (AB = B A = BA, operator AB is Hermitian if and only if A and B commute So, we know that [A,B] = 0, which means that the Hilbert space H
Lyapunov Stability Theory
 Lyapunov Stability Theory Peter Al Hokayem and Eduardo Gallestey March 16, 2015 1 Introduction In this lecture we consider the stability of equilibrium points of autonomous nonlinear systems, both in continuous
Lyapunov Stability Theory Peter Al Hokayem and Eduardo Gallestey March 16, 2015 1 Introduction In this lecture we consider the stability of equilibrium points of autonomous nonlinear systems, both in continuous
Notes on singular value decomposition for Math 54. Recall that if A is a symmetric n n matrix, then A has real eigenvalues A = P DP 1 A = P DP T.
 Notes on singular value decomposition for Math 54 Recall that if A is a symmetric n n matrix, then A has real eigenvalues λ 1,, λ n (possibly repeated), and R n has an orthonormal basis v 1,, v n, where
Notes on singular value decomposition for Math 54 Recall that if A is a symmetric n n matrix, then A has real eigenvalues λ 1,, λ n (possibly repeated), and R n has an orthonormal basis v 1,, v n, where
Quantized Vortex Stability and Dynamics in Superfluidity and Superconductivity
 Quantized Vortex Stability and Dynamics in Superfluidity and Superconductivity Weizhu Bao Department of Mathematics National University of Singapore Email: matbaowz@nus.edu.sg URL: http://www.math.nus.edu.sg/~bao
Quantized Vortex Stability and Dynamics in Superfluidity and Superconductivity Weizhu Bao Department of Mathematics National University of Singapore Email: matbaowz@nus.edu.sg URL: http://www.math.nus.edu.sg/~bao
B5.6 Nonlinear Systems
 B5.6 Nonlinear Systems 4. Bifurcations Alain Goriely 2018 Mathematical Institute, University of Oxford Table of contents 1. Local bifurcations for vector fields 1.1 The problem 1.2 The extended centre
B5.6 Nonlinear Systems 4. Bifurcations Alain Goriely 2018 Mathematical Institute, University of Oxford Table of contents 1. Local bifurcations for vector fields 1.1 The problem 1.2 The extended centre
Linear and Nonlinear Aspects of Vortices : the Ginzburg-Landau Model. F. Pacard T. Rivière
 Linear and Nonlinear Aspects of Vortices : the Ginzburg-Landau Model F. Pacard T. Rivière January 28, 2004 Contents 1 Qualitative Aspects of Ginzburg-Landau Equations 1 1.1 The integrable case..........................
Linear and Nonlinear Aspects of Vortices : the Ginzburg-Landau Model F. Pacard T. Rivière January 28, 2004 Contents 1 Qualitative Aspects of Ginzburg-Landau Equations 1 1.1 The integrable case..........................
Stability of flow past a confined cylinder
 Stability of flow past a confined cylinder Andrew Cliffe and Simon Tavener University of Nottingham and Colorado State University Stability of flow past a confined cylinder p. 1/60 Flow past a cylinder
Stability of flow past a confined cylinder Andrew Cliffe and Simon Tavener University of Nottingham and Colorado State University Stability of flow past a confined cylinder p. 1/60 Flow past a cylinder
SYMMETRY RESULTS FOR PERTURBED PROBLEMS AND RELATED QUESTIONS. Massimo Grosi Filomena Pacella S. L. Yadava. 1. Introduction
 Topological Methods in Nonlinear Analysis Journal of the Juliusz Schauder Center Volume 21, 2003, 211 226 SYMMETRY RESULTS FOR PERTURBED PROBLEMS AND RELATED QUESTIONS Massimo Grosi Filomena Pacella S.
Topological Methods in Nonlinear Analysis Journal of the Juliusz Schauder Center Volume 21, 2003, 211 226 SYMMETRY RESULTS FOR PERTURBED PROBLEMS AND RELATED QUESTIONS Massimo Grosi Filomena Pacella S.

 ! "$# %'&'(*) +,+.-*)%0/21 3 %4/5)6#7#78 9*+287:;)
! "$# %'&'(*) +,+.-*)%0/21 3 %4/5)6#7#78 9*+287:;)