Extra Problems: Chapter 1
|
|
|
- Wilfrid Harris
- 5 years ago
- Views:
Transcription
1 MA131 (Section ): Prepared by Asst.Prof.Dr.Archara Pacheenburawana 1 Extra Problems: Chapter 1 1. In each of the following answer true if the statement is always true and false otherwise in the space provided. (a) If the reduced row-echelon form of the augmented matrix for a linear system has a row of zeros, then the system must have infinitely many solutions. Answer False (b) If A is in row-echelon form, then [A b] is in row-echelon form. Answer False (c) If A is a square matrix, then the system Ax = b has no free variable. Answer False (d) A linear system with more unknowns than equations always has infinitely many solutions. Answer False (e) Every homogeneous linear system has at least one solution. (f) If A is upper triangular and B ij is the matrix that results when the ith row and jth column of A are deleted, then B ij is upper triangular if i < j. Answer True (g) IfA = [a ij ]isn nmatrixsuchthata T = A, thena jj = 0forj = 1,2,...,n. Answer True (h) If A is upper triangular, then A T is lower triangular. (i) If A and B are matrices such that AB and BA are both defined, then A and B must be square matrices. (j) If A and B are invertible n n matrices and AB = BA, then A 1 B = BA 1. (k) If A is an invertible n n matrix and if r is a real number such that r 0, then (ra) 1 = ra 1. (l) If the product AB is defined and AB = 0, then A or B is zero matrix. (m) If A and B are invertible, then AB T is also invertible. (n) If A is an invertible matrix and B is row equivalent to A, then B is also invertible. Answer True (o) If R is reduced row-echelon form of A, then there is an invertible matrix B such that BA = R. (p) If A and B are m n matrices, then B is row equivalent to A if and only if A and B have the same reduced row-echelon form. Answer True (q) The product of two elementary matrices is an elementary matrix. (r) A is invertible if and only if the reduced row-echelon from of A is identity matrix.
2 MA131 (Section ): Prepared by Asst.Prof.Dr.Archara Pacheenburawana 2 (s) Let A be an n n matrix and let x and y be vectors in R n. If Ax = Ay and x y, then the matrix A must not be invertible. Answer True (t) If A has an LU factorization, then the LU factors are uniquely determined. 2. In each of the following fill the correct answer in the space provided. (a) Determine the value(s) of h such that the matrix is the augmented matrix of a consistent linear system. [ ] 1 3 h Answer h = 5/2 (b) Which of the following matrices are in reduced row-echelon form? (i) (ii) (iii) (iv) Answer (i) and (iii) (c) Which of the following matrices are in reduced row-echelon form? (i) 0 0 (ii) (iii) (iv) Answer (i), (ii), and (iv) (d) Which of the following matrices are in reduced row-echelon form? (i) (ii) (iii) Answer (ii) and (iii) (e) Determine whether the following matrices are in row-echelon form, reduced row-echelon form, both, or neither A = B = (c) C = D = E = (c) F = (f) Which of the following matrices have reduced row-echelon form equal to ?
3 MA131 (Section ): Prepared by Asst.Prof.Dr.Archara Pacheenburawana A = B = C = (g) Let A = Find the reduced row-echelon form of A (h) Let A = Find the reduced row-echelon form of A (i) Consider a linear system whose augmented matrix is of the form β 0 For what values of β will the system have infinitely many solutions? Answer β = 2 (j) Find all values of k for which the system of equation has infinitely many solutions. Answer k = 1 kx+ y = 1 x+ky = 1 (k) Find all values of α for which the system of equation 1 α 0 x x 2 = 4 α 0 1 x 3 7 has a unique solution. Answer α ±1 (l) For what values of b and g will the system have infinitely many solutions? Answer b = 4, g = 32 2x+by = 16 4x+8y = g (m) Find all h and k such that the system below has no solution. Answer h = 2 and k 8 x+hy = 2 4x+8y = k
4 MA131 (Section ): Prepared by Asst.Prof.Dr.Archara Pacheenburawana 4 (n) Determine the condition of a and b such that the system below is inconsistent. 6x+3y = a 2x y = b (o) Find all values of λ for which the system of equation has nontrivial solutions. Answer λ = 2, 4 (p) Let p(x) = 2x 2 3x+4 and A = [ ] 9 2 Answer 0 13 (λ 3)x+ y = 0 x+(λ 3)y = 0 [ ] 1 2. Find p(a). 0 3 (q) Find the matrix A such that x x+z A y = 0 z y z for all choices of x, y, and z? Answer A = x x z (r) Find the matrix A such that A y = 0 for all choices of x, y, and z? z y +z Answer A = (s) Let A = and B = Find the third row of AB. [ ] Answer (t) Given the following matrices [ ] A = Find tr(c 2 +AA T ). Answer 30 and C = [ ]
5 MA131 (Section ): Prepared by Asst.Prof.Dr.Archara Pacheenburawana 5 (u) Find all values of a and b such that A and B are singular. [ ] [ ] a+b A =, B = a 3b 7 Answer a = 2, b = 1 [ ] 5 1 (v) If A =, then A = (2A T ) 1. [ ] Answer [ ] 2 3 (w) If (3A) 1 =, then find A. 1 1 Answer A = 1 [ ] 1 3 = [ ] 2 1. Use the given information to find 9 5 [ (x) Find all values of x such that A 1 = A when A = Answer x = 4 (y) Find all values of x such that ] [ ] 1 2x 7 = 1 2 [ ] [ ] 3 x. 2 3 Answer x [ = 2 ] 1 3 (z) Given A =. Find the matrix X such that ( ) X 2 5 T 1 +2I 2 = A. [ ] 7 2 Answer X = In each of the following fill the correct answer in the space provided. (a) A square matrix A is symmetric if A T = A. Find a nonzero 3 3 matrix A such that A is symmetric. (b) A square matrix A is symmetric if A T = A. Determine whether ka is symmetric for any scalar k. (c) A square matrix A is called skew-symmetric if A T = A. If A and B are skew-symmetric n n matrices, determine whether A + B is skew-symmetric. Answer Yes. (d) Let A = AX = B. [ Answer X = ] and B = [ ] [ ] Find the matrix X such that (e) Solve the equation C 1 (A X)B 1 = I for X, assuming that A, B, and C are all n n invertible matrices. Answer X = CB A 1 0 [ ] (f) Find a matrix X such that = X
6 MA131 (Section ): Prepared by Asst.Prof.Dr.Archara Pacheenburawana 6 (g) Let A = and B = Find an elementary matrix E such that EA = B Answer E = (h) Find an elementary matrix E such that EA = B, where A = and B = (i) Find an elementary matrix E such that EA = B, where A = and B = Answer (j) Find an elementary matrix E such that EA = B, where A = B = (k) Given A = and B = Find an elementary matrix E such that EA = B. [ ] 2 1 (l) Let A =. Write A as a product of elementary matrices. 6 4 [ ][ ][ ] Answer A = (m) Let E be an elementary matrix such that EA = B, where A = and B = Find E Answer E 1 =
7 MA131 (Section ): Prepared by Asst.Prof.Dr.Archara Pacheenburawana 7 (n) Let E be an elementary matrix such that EA = B, where A = and B = Find E Answer E 1 = c c (o) Find two values of c such that A = c c c is singular. 8 7 c Answer 0 or 2 or (p) Find all values of a 0 such that A = 1 a 0 is noninvertible Answer a = 1 2 [ ] [ ] (q) Find matrix X such that X = [ ] Answer [ ] [ ] (r) If A = and AB =, determine the matrix B [ ] [ ] (s) If A = and AB =, then find B [ ] Answer B = (t) Let A = Evaluate ( 1 A) (u) Given A = and B = Evaluate (AB) (v) Find x, y, and z such that Answer x = 1,y = 3,z = = x 1 1. y z 1
8 MA131 (Section ): Prepared by Asst.Prof.Dr.Archara Pacheenburawana 8 (w) Let a 1 a 2 a A = a 4 a 5 a 6 and A 1 = a 7 a 8 a Solve the following system Answer x = 1, y = 2, z = 1 a 1 x+a 2 y +a 3 z = 1 a 4 x+a 5 y +a 6 z = 3 a 7 x+a 8 y +a 9 z = 2 (x) What conditions must b 1 and b 2 satisfy in order for the system of equations to be consistent? 3x 1 12x 2 = b 1 x 1 + 4x 2 = b 2 4. Solve the following system by Gaussian elimination with back substitution. x 1 +2x 2 +2x 3 +3x 4 = 4 2x 1 +4x 2 + x 3 +3x 4 = 5 3x 1 +6x 2 + x 3 +4x 4 = 7 Answer x 1 = 2 2s t, x 2 = s, x 3 = 1 t, x 4 = t 5. Solve the following system by Gaussian elimination with back substitution. w +x+2y +z = 1 w x y +z = 0 x+ y = 1 w+x +z = 2 6. Solve the given system of equations using Gauss-Jordan elimination. x 1 +2x 2 3x 3 +x 4 = 1 x 1 x 2 +4x 3 x 4 = 6 2x 1 4x 2 +7x 3 x 4 = 1 Answer x 1 = 2 6s, x 2 = 4+s, x 3 = 3 s, x 4 = s 7. Solve the given system of equations using Gauss-Jordan elimination. x 1 +2x 2 + x 3 x 4 = 2 x 1 + x 2 + x 3 = 3 3x 1 +2x 2 +3x 3 2x 4 = 1 Answer x 1 = 1 t, x 2 = 2, x 3 = t, x 4 = 3
9 MA131 (Section ): Prepared by Asst.Prof.Dr.Archara Pacheenburawana 9 8. Solve the given system of equations using Gauss-Jordan elimination. x 1 + x 2 +3x 3 +4x 4 = 12 2x 1 x 2 5x 3 7x 4 = 19 x 1 x 2 +2x 3 +2x 4 = 5 Answer x 1 = 1 3t, x 2 = 2 t, x 3 = 3, x 4 = t 9. Solve the given system of equations using Gauss-Jordan elimination. x 1 +2x 2 3x 3 + x 4 = 2 3x 1 x 2 2x 3 4x 4 = 1 2x 1 +3x 2 5x 3 + x 4 = 3 Answer x 1 = s+t, x 2 = 1+s t, x 3 = s, x 4 = t 10. Solve the given system of equations using Gauss-Jordan elimination. 2x 1 x 2 x 4 = 0 x 2 2x 3 +x 4 = 1 4x 1 + x 2 6x 3 +x 4 = 3 Answer x 1 = 1 +s, x 2 2 = 1+2s t, x 3 = s, x 4 = t 11. Solve the following system by Gauss-Jordan elimination. x 1 +2x 2 x 3 +3x 4 + x 5 = 2 x 1 2x 2 + x 3 x 4 +3x 5 = 4 2x 1 +4x 2 2x 3 +6x 4 +3x 5 = 6 Answer x 1 = 3 2s+t, x 2 = s, x 3 = t, x 4 = 1, x 5 = Solve the given system of equations using Gauss-Jordan elimination. x 1 3x 2 +4x 3 3x 4 +2x 5 = 5 3x 1 7x 2 +8x 3 5x 4 +8x 5 = 9 3x 2 6x 3 +6x 4 +4x 5 = 5 Answer x 1 = 24+2s 3t, x 2 = 7+2s 2t, x 3 = s, x 4 = t, x 5 = Solve the given system of equations using Gauss-Jordan elimination. x 1 +2x 2 +3x 3 + 4x 4 = 5 2x 1 +5x 2 +7x 3 +11x 4 = 12 x 2 + x 3 + 4x 4 = 3 Answer x 1 = 3 t, x 2 = 1 t, x 3 = t, x 4 = 1
10 MA131 (Section ): Prepared by Asst.Prof.Dr.Archara Pacheenburawana Solve the following system by Gauss-Jordan elimination. 15. Consider the system of equations x 1 +x 2 +x 3 x 4 = 4 x 1 x 2 x 3 x 4 = 2 x 1 +x 2 x 3 +x 4 = 2 x+3y + z = α 2x+βy + z = 1 2x+3y +4z = 3 (a) What conditions must α and β satisfy in order for i. the system has exactly one solution ii. the system has no solutions. iii. the system has infinitely many solutions. (b) Solve this system when α = 0 and β = A square matrix A is symmetric if A T = A. Show that A+A T is symmetric. 17. Let A = and R be the reduced row-echelon form of A. Find the elementary matrices E 1, E 2,..., E k such that E k E k 1 E 2 E 1 A = R. 18. Let A = Find the elementary matrices E 1, E 2, E 3, and E 4 such that E 4 E 3 E 2 E 1 A = A r where A r is the reduced row-echelon form of A Answer E 1 = 1 1 0, E 2 = 0 1 0, E 3 = A r = , E 4 = 0 0 1
11 MA131 (Section ): Prepared by Asst.Prof.Dr.Archara Pacheenburawana Let A = Find the elementary matrices E 1, E 2, E 3, and E 4 such that E 4 E 3 E 2 E 1 A = A r where A r is the reduced row-echelon form of A Let A = Find the elementary matrices E 1, E 2, E 3, and E 4 such that Let E 4 E 3 E 2 E 1 A = A R where A R is the reduced row-echelon form of A A = Find the elementary matrices E 1, E 2,..., E k 1, E k such that E k E k 1 E 2 E 1 A = R where R is the reduced row-echelon form of A Answer E 1 = 1 0 0, E 2 = 0 1 0, E 3 = , E 4 = R = Let A = Find the elementary matrices E 1,E 2,E 3 and E 4 such that E 4 E 3 E 2 E 1 A = R where R is the reduced row-echelon form of A Answer E 1 = 1 0 0, E 2 = 0 1 0, E 3 = 0 1 0, E 4 = 0 1 0, R =
12 MA131 (Section ): Prepared by Asst.Prof.Dr.Archara Pacheenburawana Let A = Find the elementary matrices E 1,E 2,E 3 and E 4 such that E 4 E 3 E 2 E 1 A = R where R is the reduced row-echelon form of A Answer E 1 = 2 1 0, E 2 = 0 0 1, E 3 = 0 1 0, E 4 = 0 1 2, R = Let A = Find the elementary matrices E 1,E 2,E 3 and E 4 such that E 4 E 3 E 2 E 1 A = R where R is the reduced row-echelon form of A Answer E 1 = 0 1 0, E 2 = 0 0 1, E 3 = 0 1 0, E 4 = 0 1 0, R = Let A = Find the elementary matrices E 1,E 2,E 3 and E 4 such that E 4 E 3 E 2 E 1 A = R where R is the reduced row-echelon form of A Answer E 1 = 1 0 0, E 2 = 0 1 0, E 3 = 0 1 0, E 4 = 0 1 1, R =
13 MA131 (Section ): Prepared by Asst.Prof.Dr.Archara Pacheenburawana Let A = Find the elementary matrices E 1, E 2, E 3, and E 4 such that E 4 E 3 E 2 E 1 A = R where R is the reduced row-echelon form of A Given a matrix A = Find (a) A 1. (b) Elementary matrices whose the product is A. 28. Find the inverse of A by using Gauss-Jordan elimination, where A = Find A 1 by any method of your choice when A = Let A = Find A 1 by using Gauss-Jordan elimination Let A = Find A 1 by Gauss-Jordan elimination Let Solve the following system a 1 a 2 a A = a 4 a 5 a 6 and A 1 = a 7 a 8 a a 1 x+a 2 y +a 3 z = 2 a 4 x+a 5 y +a 6 z = 1 a 7 x+a 8 y +a 9 z = Consider the system of linear equations Ax = b where x 1 5 A = 1 1 0, x = x 2, and b = x 3 5
14 MA131 (Section ): Prepared by Asst.Prof.Dr.Archara Pacheenburawana 14 (a) Find A 1 by using Gauss-Jordan elimination. (b) Solve the system Ax = b using A Answer (a) A 1 = (b) x 1 = 1,x 2 = 2,x 3 = Let A = (a) Find A 1 by using Gauss-Jordan elimination. (b) Solve the following system using A 1. (i) x+ y + z = 3 2x+3y +4z = 2 y +3z = 1 (ii) x+ y + z = 1 2x+3y +4z = 4 y +3z = 2 Answer (a) x 1 = 10, x 2 = 10, x 3 = 3 (b) x 1 = 1, x 2 = 2, x 3 = (a) Find A 1 by using Gauss-Jordan elimination when A = (b) Solve the following systems using matrix inversion. (i) x 1 + x 2 + x 3 = 2 x 1 +2x 2 +2x 3 = 1 x 1 +2x 2 +3x 3 = 1 Answer (a) A 1 = (ii) x 1 + x 2 + x 3 = 1 x 1 +2x 2 +2x 3 = 1 x 1 +2x 2 +3x 3 = 0 (b) (i) x 1 = 5, x 2 = 5, x 3 = 2 (ii) x 1 = 3, x 2 = 3, x 3 = Let A = (a) Find A 1 by using Gauss-Jordan elimination. (b) Find the elementary matrices E 1,E 2,E 3 and E 4 such that E 4 E 3 E 2 E 1 A = I Solve the following two systems of linear equations by applying the method of Gauss-Jordan elimination. (a) x 1 x 2 +3x 3 = 8 2x 1 x 2 +4x 3 = 11 x 1 +2x 2 4x 3 = 11 (b) x 1 x 2 +3x 3 = 0 2x 1 x 2 +4x 3 = 1 x 1 +2x 2 4x 3 = 2 Answer (a) x 1 = 1, x 2 = 1, x 3 = 2 (b) x 1 = 0, x 2 = 3, x 3 = 1
15 MA131 (Section ): Prepared by Asst.Prof.Dr.Archara Pacheenburawana Solve the following two systems of linear equations by applying the method of Gauss-Jordan elimination. (a) y +z = 3 x y z = 0 x z = 3 (b) y +z = 6 x y z = 0 x z = Solve the following two systems of linear equations by applying the method of Gauss-Jordan elimination. (a) x y +2z = 3 x+2y z = 3 2y 2z = 1 (b) x y +2z = 1 x+2y z = 4 2y 2z = 2 Answer (a) No solution (b) x 1 = 2 s, x 2 = 1+s, x 3 = s 40. Use Gauss-Jordan method to solve the following systems of linear equations w 42 (a) x y = z w 28 (b) x y = z Solve the following systems using matrix inversion. (Hint: First, find A 1.) (a) x 1 +x 3 = 2 x 1 x 2 = 1 2x 2 +x 3 = 1 (b) x 1 +x 3 = 1 x 1 x 2 = 3 2x 2 +x 3 = Solve the following systems using matrix inversion. (a) x 1 + x 3 = 1 3x 1 +3x 2 +4x 3 = 0 2x 1 +2x 2 +3x 3 = 1 (b) x 1 + x 3 = 3 3x 1 +3x 2 +4x 3 = 2 2x 1 +2x 2 +3x 3 = 1 Answer (a) x 1 = 4, x 2 = 0, x 3 = 3 (b) x 1 = 4, x 2 = 6, x 3 = Solve the following systems using matrix inversion. (a) x 1 +2x 2 x 3 = 1 x 2 + x 3 = 2 x 1 +4x 2 2x 3 = 1 (b) x 1 +2x 2 x 3 = 0 x 2 + x 3 = 3 x 1 +4x 2 2x 3 = 2 Answer (a) x 1 = 1, x 2 = 2, x 3 = 4 (b) x 1 = 2, x 2 = 1, x 3 = 4
16 MA131 (Section ): Prepared by Asst.Prof.Dr.Archara Pacheenburawana Solve the following systems using matrix inversion. (a) x 1 +2x 2 +3x 3 = 2 x 1 +3x 2 +2x 3 = 1 2x 1 +4x 2 +7x 3 = 3 (b) x 1 +2x 2 +3x 3 = 1 x 1 +3x 2 +2x 3 = 0 2x 1 +4x 2 +7x 3 = 2 Answer (a) x 1 = 13, x 2 = 4, x 3 = 1 (b) x 1 = 23, x 2 = 5, x 3 = Solve the following systems using matrix inversion. (a) x 1 x 2 = 2 x 1 +x 2 +x 3 = 1 x 2 +x 3 = 3 (b) x 1 x 2 = 1 x 1 +x 2 +x 3 = 2 x 2 +x 3 = 2 Answer (a) x 1 = 8, x 2 = 6, x 3 = 3 (b) x 1 = 2, x 2 = 1, x 3 = Express A = as LU-decomposition Find an LU-decomposition of A = Answer A = Find an LU-decomposition of A = Answer A = Find an LU-decomposition of A = Answer A =
17 MA131 (Section ): Prepared by Asst.Prof.Dr.Archara Pacheenburawana Find an LU-decomposition of A = Answer A = Find an LU-decomposition of A = Answer A = Find an LU-decomposition of A = Answer A = / / Find an LU-decomposition of A = Answer A = Solve the following system of linear equations by using an LU-decomposition. 2x 1 + x 2 x 3 = 1 4x 1 + x 2 4x 3 = 2 2x 1 x 2 2x 3 = Solve the following system of linear equations by using an LU-decomposition. x+4y +2z +3w = 2 x+2y + z = 2 z +4w = 2 2x+6y +3z + w = 2
18 MA131 (Section ): Prepared by Asst.Prof.Dr.Archara Pacheenburawana Solve the following system of linear equations by using an LU-decomposition. 2x 1 +3x 2 + 4x 3 = 1 6x 1 +8x 2 +10x 3 = 4 2x 1 4x 2 3x 3 = The LU-decomposition of a matrix A is given as follows: L = and U = (a) Write down the sequence of row operations which takes A to U when performing Gaussian elimination. x 1 1 (b) Solve the system Ax = b where x = x 2,b = 2 by using an LUdecomposition. x 3 3 Answer (a) r 2 +2r 1, r 3 3r 1, r 3 r 2, 1 2 r 3 (b) x 1 = 9, x 2 = 8, x 3 = 2
Systems of Linear Equations and Matrices
 Chapter 1 Systems of Linear Equations and Matrices System of linear algebraic equations and their solution constitute one of the major topics studied in the course known as linear algebra. In the first
Chapter 1 Systems of Linear Equations and Matrices System of linear algebraic equations and their solution constitute one of the major topics studied in the course known as linear algebra. In the first
Math 313 Chapter 1 Review
 Math 313 Chapter 1 Review Howard Anton, 9th Edition May 2010 Do NOT write on me! Contents 1 1.1 Introduction to Systems of Linear Equations 2 2 1.2 Gaussian Elimination 3 3 1.3 Matrices and Matrix Operations
Math 313 Chapter 1 Review Howard Anton, 9th Edition May 2010 Do NOT write on me! Contents 1 1.1 Introduction to Systems of Linear Equations 2 2 1.2 Gaussian Elimination 3 3 1.3 Matrices and Matrix Operations
Chapter 1: Systems of Linear Equations and Matrices
 : Systems of Linear Equations and Matrices Multiple Choice Questions. Which of the following equations is linear? (A) x + 3x 3 + 4x 4 3 = 5 (B) 3x x + x 3 = 5 (C) 5x + 5 x x 3 = x + cos (x ) + 4x 3 = 7.
: Systems of Linear Equations and Matrices Multiple Choice Questions. Which of the following equations is linear? (A) x + 3x 3 + 4x 4 3 = 5 (B) 3x x + x 3 = 5 (C) 5x + 5 x x 3 = x + cos (x ) + 4x 3 = 7.
Chapter 1: Systems of linear equations and matrices. Section 1.1: Introduction to systems of linear equations
 Chapter 1: Systems of linear equations and matrices Section 1.1: Introduction to systems of linear equations Definition: A linear equation in n variables can be expressed in the form a 1 x 1 + a 2 x 2
Chapter 1: Systems of linear equations and matrices Section 1.1: Introduction to systems of linear equations Definition: A linear equation in n variables can be expressed in the form a 1 x 1 + a 2 x 2
Systems of Linear Equations and Matrices
 Chapter 1 Systems of Linear Equations and Matrices System of linear algebraic equations and their solution constitute one of the major topics studied in the course known as linear algebra. In the first
Chapter 1 Systems of Linear Equations and Matrices System of linear algebraic equations and their solution constitute one of the major topics studied in the course known as linear algebra. In the first
Solving Linear Systems Using Gaussian Elimination
 Solving Linear Systems Using Gaussian Elimination DEFINITION: A linear equation in the variables x 1,..., x n is an equation that can be written in the form a 1 x 1 +...+a n x n = b, where a 1,...,a n
Solving Linear Systems Using Gaussian Elimination DEFINITION: A linear equation in the variables x 1,..., x n is an equation that can be written in the form a 1 x 1 +...+a n x n = b, where a 1,...,a n
CHAPTER 8: Matrices and Determinants
 (Exercises for Chapter 8: Matrices and Determinants) E.8.1 CHAPTER 8: Matrices and Determinants (A) means refer to Part A, (B) means refer to Part B, etc. Most of these exercises can be done without a
(Exercises for Chapter 8: Matrices and Determinants) E.8.1 CHAPTER 8: Matrices and Determinants (A) means refer to Part A, (B) means refer to Part B, etc. Most of these exercises can be done without a
Linear System Equations
 King Saud University September 24, 2018 Table of contents 1 2 3 4 Definition A linear system of equations with m equations and n unknowns is defined as follows: a 1,1 x 1 + a 1,2 x 2 + + a 1,n x n = b
King Saud University September 24, 2018 Table of contents 1 2 3 4 Definition A linear system of equations with m equations and n unknowns is defined as follows: a 1,1 x 1 + a 1,2 x 2 + + a 1,n x n = b
Review for Exam Find all a for which the following linear system has no solutions, one solution, and infinitely many solutions.
 Review for Exam. Find all a for which the following linear system has no solutions, one solution, and infinitely many solutions. x + y z = 2 x + 2y + z = 3 x + y + (a 2 5)z = a 2 The augmented matrix for
Review for Exam. Find all a for which the following linear system has no solutions, one solution, and infinitely many solutions. x + y z = 2 x + 2y + z = 3 x + y + (a 2 5)z = a 2 The augmented matrix for
Midterm 1 Review. Written by Victoria Kala SH 6432u Office Hours: R 12:30 1:30 pm Last updated 10/10/2015
 Midterm 1 Review Written by Victoria Kala vtkala@math.ucsb.edu SH 6432u Office Hours: R 12:30 1:30 pm Last updated 10/10/2015 Summary This Midterm Review contains notes on sections 1.1 1.5 and 1.7 in your
Midterm 1 Review Written by Victoria Kala vtkala@math.ucsb.edu SH 6432u Office Hours: R 12:30 1:30 pm Last updated 10/10/2015 Summary This Midterm Review contains notes on sections 1.1 1.5 and 1.7 in your
Systems of Linear Equations. By: Tri Atmojo Kusmayadi and Mardiyana Mathematics Education Sebelas Maret University
 Systems of Linear Equations By: Tri Atmojo Kusmayadi and Mardiyana Mathematics Education Sebelas Maret University Standard of Competency: Understanding the properties of systems of linear equations, matrices,
Systems of Linear Equations By: Tri Atmojo Kusmayadi and Mardiyana Mathematics Education Sebelas Maret University Standard of Competency: Understanding the properties of systems of linear equations, matrices,
Section 6.2 Larger Systems of Linear Equations
 Section 6.2 Larger Systems of Linear Equations Gaussian Elimination In general, to solve a system of linear equations using its augmented matrix, we use elementary row operations to arrive at a matrix
Section 6.2 Larger Systems of Linear Equations Gaussian Elimination In general, to solve a system of linear equations using its augmented matrix, we use elementary row operations to arrive at a matrix
MAC Module 2 Systems of Linear Equations and Matrices II. Learning Objectives. Upon completing this module, you should be able to :
 MAC 0 Module Systems of Linear Equations and Matrices II Learning Objectives Upon completing this module, you should be able to :. Find the inverse of a square matrix.. Determine whether a matrix is invertible..
MAC 0 Module Systems of Linear Equations and Matrices II Learning Objectives Upon completing this module, you should be able to :. Find the inverse of a square matrix.. Determine whether a matrix is invertible..
Gauss-Jordan Row Reduction and Reduced Row Echelon Form
 Gauss-Jordan Row Reduction and Reduced Row Echelon Form If we put the augmented matrix of a linear system in reduced row-echelon form, then we don t need to back-substitute to solve the system. To put
Gauss-Jordan Row Reduction and Reduced Row Echelon Form If we put the augmented matrix of a linear system in reduced row-echelon form, then we don t need to back-substitute to solve the system. To put
Section 1.1 System of Linear Equations. Dr. Abdulla Eid. College of Science. MATHS 211: Linear Algebra
 Section 1.1 System of Linear Equations College of Science MATHS 211: Linear Algebra (University of Bahrain) Linear System 1 / 33 Goals:. 1 Define system of linear equations and their solutions. 2 To represent
Section 1.1 System of Linear Equations College of Science MATHS 211: Linear Algebra (University of Bahrain) Linear System 1 / 33 Goals:. 1 Define system of linear equations and their solutions. 2 To represent
3.4 Elementary Matrices and Matrix Inverse
 Math 220: Summer 2015 3.4 Elementary Matrices and Matrix Inverse A n n elementary matrix is a matrix which is obtained from the n n identity matrix I n n by a single elementary row operation. Elementary
Math 220: Summer 2015 3.4 Elementary Matrices and Matrix Inverse A n n elementary matrix is a matrix which is obtained from the n n identity matrix I n n by a single elementary row operation. Elementary
MATH 2360 REVIEW PROBLEMS
 MATH 2360 REVIEW PROBLEMS Problem 1: In (a) (d) below, either compute the matrix product or indicate why it does not exist: ( )( ) 1 2 2 1 (a) 0 1 1 2 ( ) 0 1 2 (b) 0 3 1 4 3 4 5 2 5 (c) 0 3 ) 1 4 ( 1
MATH 2360 REVIEW PROBLEMS Problem 1: In (a) (d) below, either compute the matrix product or indicate why it does not exist: ( )( ) 1 2 2 1 (a) 0 1 1 2 ( ) 0 1 2 (b) 0 3 1 4 3 4 5 2 5 (c) 0 3 ) 1 4 ( 1
Problem Sheet 1 with Solutions GRA 6035 Mathematics
 Problem Sheet 1 with Solutions GRA 6035 Mathematics BI Norwegian Business School 2 Problems 1. From linear system to augmented matrix Write down the coefficient matrix and the augmented matrix of the following
Problem Sheet 1 with Solutions GRA 6035 Mathematics BI Norwegian Business School 2 Problems 1. From linear system to augmented matrix Write down the coefficient matrix and the augmented matrix of the following
GAUSSIAN ELIMINATION AND LU DECOMPOSITION (SUPPLEMENT FOR MA511)
 GAUSSIAN ELIMINATION AND LU DECOMPOSITION (SUPPLEMENT FOR MA511) D. ARAPURA Gaussian elimination is the go to method for all basic linear classes including this one. We go summarize the main ideas. 1.
GAUSSIAN ELIMINATION AND LU DECOMPOSITION (SUPPLEMENT FOR MA511) D. ARAPURA Gaussian elimination is the go to method for all basic linear classes including this one. We go summarize the main ideas. 1.
Elementary matrices, continued. To summarize, we have identified 3 types of row operations and their corresponding
 Elementary matrices, continued To summarize, we have identified 3 types of row operations and their corresponding elementary matrices. If you check the previous examples, you ll find that these matrices
Elementary matrices, continued To summarize, we have identified 3 types of row operations and their corresponding elementary matrices. If you check the previous examples, you ll find that these matrices
4 Elementary matrices, continued
 4 Elementary matrices, continued We have identified 3 types of row operations and their corresponding elementary matrices. If you check the previous examples, you ll find that these matrices are constructed
4 Elementary matrices, continued We have identified 3 types of row operations and their corresponding elementary matrices. If you check the previous examples, you ll find that these matrices are constructed
Chapter 1. Vectors, Matrices, and Linear Spaces
 1.4 Solving Systems of Linear Equations 1 Chapter 1. Vectors, Matrices, and Linear Spaces 1.4. Solving Systems of Linear Equations Note. We give an algorithm for solving a system of linear equations (called
1.4 Solving Systems of Linear Equations 1 Chapter 1. Vectors, Matrices, and Linear Spaces 1.4. Solving Systems of Linear Equations Note. We give an algorithm for solving a system of linear equations (called
Linear Algebra: Lecture notes from Kolman and Hill 9th edition.
 Linear Algebra: Lecture notes from Kolman and Hill 9th edition Taylan Şengül March 20, 2019 Please let me know of any mistakes in these notes Contents Week 1 1 11 Systems of Linear Equations 1 12 Matrices
Linear Algebra: Lecture notes from Kolman and Hill 9th edition Taylan Şengül March 20, 2019 Please let me know of any mistakes in these notes Contents Week 1 1 11 Systems of Linear Equations 1 12 Matrices
MIDTERM 1 - SOLUTIONS
 MIDTERM - SOLUTIONS MATH 254 - SUMMER 2002 - KUNIYUKI CHAPTERS, 2, GRADED OUT OF 75 POINTS 2 50 POINTS TOTAL ) Use either Gaussian elimination with back-substitution or Gauss-Jordan elimination to solve
MIDTERM - SOLUTIONS MATH 254 - SUMMER 2002 - KUNIYUKI CHAPTERS, 2, GRADED OUT OF 75 POINTS 2 50 POINTS TOTAL ) Use either Gaussian elimination with back-substitution or Gauss-Jordan elimination to solve
4 Elementary matrices, continued
 4 Elementary matrices, continued We have identified 3 types of row operations and their corresponding elementary matrices. To repeat the recipe: These matrices are constructed by performing the given row
4 Elementary matrices, continued We have identified 3 types of row operations and their corresponding elementary matrices. To repeat the recipe: These matrices are constructed by performing the given row
Applied Matrix Algebra Lecture Notes Section 2.2. Gerald Höhn Department of Mathematics, Kansas State University
 Applied Matrix Algebra Lecture Notes Section 22 Gerald Höhn Department of Mathematics, Kansas State University September, 216 Chapter 2 Matrices 22 Inverses Let (S) a 11 x 1 + a 12 x 2 + +a 1n x n = b
Applied Matrix Algebra Lecture Notes Section 22 Gerald Höhn Department of Mathematics, Kansas State University September, 216 Chapter 2 Matrices 22 Inverses Let (S) a 11 x 1 + a 12 x 2 + +a 1n x n = b
Linear Algebra. Solving Linear Systems. Copyright 2005, W.R. Winfrey
 Copyright 2005, W.R. Winfrey Topics Preliminaries Echelon Form of a Matrix Elementary Matrices; Finding A -1 Equivalent Matrices LU-Factorization Topics Preliminaries Echelon Form of a Matrix Elementary
Copyright 2005, W.R. Winfrey Topics Preliminaries Echelon Form of a Matrix Elementary Matrices; Finding A -1 Equivalent Matrices LU-Factorization Topics Preliminaries Echelon Form of a Matrix Elementary
Matrix & Linear Algebra
 Matrix & Linear Algebra Jamie Monogan University of Georgia For more information: http://monogan.myweb.uga.edu/teaching/mm/ Jamie Monogan (UGA) Matrix & Linear Algebra 1 / 84 Vectors Vectors Vector: A
Matrix & Linear Algebra Jamie Monogan University of Georgia For more information: http://monogan.myweb.uga.edu/teaching/mm/ Jamie Monogan (UGA) Matrix & Linear Algebra 1 / 84 Vectors Vectors Vector: A
22A-2 SUMMER 2014 LECTURE 5
 A- SUMMER 0 LECTURE 5 NATHANIEL GALLUP Agenda Elimination to the identity matrix Inverse matrices LU factorization Elimination to the identity matrix Previously, we have used elimination to get a system
A- SUMMER 0 LECTURE 5 NATHANIEL GALLUP Agenda Elimination to the identity matrix Inverse matrices LU factorization Elimination to the identity matrix Previously, we have used elimination to get a system
Methods for Solving Linear Systems Part 2
 Methods for Solving Linear Systems Part 2 We have studied the properties of matrices and found out that there are more ways that we can solve Linear Systems. In Section 7.3, we learned that we can use
Methods for Solving Linear Systems Part 2 We have studied the properties of matrices and found out that there are more ways that we can solve Linear Systems. In Section 7.3, we learned that we can use
Matrices and systems of linear equations
 Matrices and systems of linear equations Samy Tindel Purdue University Differential equations and linear algebra - MA 262 Taken from Differential equations and linear algebra by Goode and Annin Samy T.
Matrices and systems of linear equations Samy Tindel Purdue University Differential equations and linear algebra - MA 262 Taken from Differential equations and linear algebra by Goode and Annin Samy T.
MAT Linear Algebra Collection of sample exams
 MAT 342 - Linear Algebra Collection of sample exams A-x. (0 pts Give the precise definition of the row echelon form. 2. ( 0 pts After performing row reductions on the augmented matrix for a certain system
MAT 342 - Linear Algebra Collection of sample exams A-x. (0 pts Give the precise definition of the row echelon form. 2. ( 0 pts After performing row reductions on the augmented matrix for a certain system
MAT 2037 LINEAR ALGEBRA I web:
 MAT 237 LINEAR ALGEBRA I 2625 Dokuz Eylül University, Faculty of Science, Department of Mathematics web: Instructor: Engin Mermut http://kisideuedutr/enginmermut/ HOMEWORK 2 MATRIX ALGEBRA Textbook: Linear
MAT 237 LINEAR ALGEBRA I 2625 Dokuz Eylül University, Faculty of Science, Department of Mathematics web: Instructor: Engin Mermut http://kisideuedutr/enginmermut/ HOMEWORK 2 MATRIX ALGEBRA Textbook: Linear
Chapter 2. Systems of Equations and Augmented Matrices. Creighton University
 Chapter Section - Systems of Equations and Augmented Matrices D.S. Malik Creighton University Systems of Linear Equations Common ways to solve a system of equations: Eliminationi Substitution Elimination
Chapter Section - Systems of Equations and Augmented Matrices D.S. Malik Creighton University Systems of Linear Equations Common ways to solve a system of equations: Eliminationi Substitution Elimination
Online Exercises for Linear Algebra XM511
 This document lists the online exercises for XM511. The section ( ) numbers refer to the textbook. TYPE I are True/False. Lecture 02 ( 1.1) Online Exercises for Linear Algebra XM511 1) The matrix [3 2
This document lists the online exercises for XM511. The section ( ) numbers refer to the textbook. TYPE I are True/False. Lecture 02 ( 1.1) Online Exercises for Linear Algebra XM511 1) The matrix [3 2
Math x + 3y 5z = 14 3x 2y + 3z = 17 4x + 3y 2z = 1
 Math 210 1. Solve the system: x + y + z = 1 2x + 3y + 4z = 5 (a z = 2, y = 1 and x = 0 (b z =any value, y = 3 2z and x = z 2 (c z =any value, y = 3 2z and x = z + 2 (d z =any value, y = 3 + 2z and x =
Math 210 1. Solve the system: x + y + z = 1 2x + 3y + 4z = 5 (a z = 2, y = 1 and x = 0 (b z =any value, y = 3 2z and x = z 2 (c z =any value, y = 3 2z and x = z + 2 (d z =any value, y = 3 + 2z and x =
APPENDIX: MATHEMATICAL INDUCTION AND OTHER FORMS OF PROOF
 ELEMENTARY LINEAR ALGEBRA WORKBOOK/FOR USE WITH RON LARSON S TEXTBOOK ELEMENTARY LINEAR ALGEBRA CREATED BY SHANNON MARTIN MYERS APPENDIX: MATHEMATICAL INDUCTION AND OTHER FORMS OF PROOF When you are done
ELEMENTARY LINEAR ALGEBRA WORKBOOK/FOR USE WITH RON LARSON S TEXTBOOK ELEMENTARY LINEAR ALGEBRA CREATED BY SHANNON MARTIN MYERS APPENDIX: MATHEMATICAL INDUCTION AND OTHER FORMS OF PROOF When you are done
Linear Equations and Matrix
 1/60 Chia-Ping Chen Professor Department of Computer Science and Engineering National Sun Yat-sen University Linear Algebra Gaussian Elimination 2/60 Alpha Go Linear algebra begins with a system of linear
1/60 Chia-Ping Chen Professor Department of Computer Science and Engineering National Sun Yat-sen University Linear Algebra Gaussian Elimination 2/60 Alpha Go Linear algebra begins with a system of linear
Lecture Summaries for Linear Algebra M51A
 These lecture summaries may also be viewed online by clicking the L icon at the top right of any lecture screen. Lecture Summaries for Linear Algebra M51A refers to the section in the textbook. Lecture
These lecture summaries may also be viewed online by clicking the L icon at the top right of any lecture screen. Lecture Summaries for Linear Algebra M51A refers to the section in the textbook. Lecture
Inverting Matrices. 1 Properties of Transpose. 2 Matrix Algebra. P. Danziger 3.2, 3.3
 3., 3.3 Inverting Matrices P. Danziger 1 Properties of Transpose Transpose has higher precedence than multiplication and addition, so AB T A ( B T and A + B T A + ( B T As opposed to the bracketed expressions
3., 3.3 Inverting Matrices P. Danziger 1 Properties of Transpose Transpose has higher precedence than multiplication and addition, so AB T A ( B T and A + B T A + ( B T As opposed to the bracketed expressions
LINEAR SYSTEMS, MATRICES, AND VECTORS
 ELEMENTARY LINEAR ALGEBRA WORKBOOK CREATED BY SHANNON MARTIN MYERS LINEAR SYSTEMS, MATRICES, AND VECTORS Now that I ve been teaching Linear Algebra for a few years, I thought it would be great to integrate
ELEMENTARY LINEAR ALGEBRA WORKBOOK CREATED BY SHANNON MARTIN MYERS LINEAR SYSTEMS, MATRICES, AND VECTORS Now that I ve been teaching Linear Algebra for a few years, I thought it would be great to integrate
Linear Algebra Homework and Study Guide
 Linear Algebra Homework and Study Guide Phil R. Smith, Ph.D. February 28, 20 Homework Problem Sets Organized by Learning Outcomes Test I: Systems of Linear Equations; Matrices Lesson. Give examples of
Linear Algebra Homework and Study Guide Phil R. Smith, Ph.D. February 28, 20 Homework Problem Sets Organized by Learning Outcomes Test I: Systems of Linear Equations; Matrices Lesson. Give examples of
Lecture Notes in Linear Algebra
 Lecture Notes in Linear Algebra Dr. Abdullah Al-Azemi Mathematics Department Kuwait University February 4, 2017 Contents 1 Linear Equations and Matrices 1 1.2 Matrices............................................
Lecture Notes in Linear Algebra Dr. Abdullah Al-Azemi Mathematics Department Kuwait University February 4, 2017 Contents 1 Linear Equations and Matrices 1 1.2 Matrices............................................
System of Linear Equations
 Chapter 7 - S&B Gaussian and Gauss-Jordan Elimination We will study systems of linear equations by describing techniques for solving such systems. The preferred solution technique- Gaussian elimination-
Chapter 7 - S&B Gaussian and Gauss-Jordan Elimination We will study systems of linear equations by describing techniques for solving such systems. The preferred solution technique- Gaussian elimination-
Matrices and Matrix Algebra.
 Matrices and Matrix Algebra 3.1. Operations on Matrices Matrix Notation and Terminology Matrix: a rectangular array of numbers, called entries. A matrix with m rows and n columns m n A n n matrix : a square
Matrices and Matrix Algebra 3.1. Operations on Matrices Matrix Notation and Terminology Matrix: a rectangular array of numbers, called entries. A matrix with m rows and n columns m n A n n matrix : a square
Matrix Algebra. Matrix Algebra. Chapter 8 - S&B
 Chapter 8 - S&B Algebraic operations Matrix: The size of a matrix is indicated by the number of its rows and the number of its columns. A matrix with k rows and n columns is called a k n matrix. The number
Chapter 8 - S&B Algebraic operations Matrix: The size of a matrix is indicated by the number of its rows and the number of its columns. A matrix with k rows and n columns is called a k n matrix. The number
Finite Mathematics Chapter 2. where a, b, c, d, h, and k are real numbers and neither a and b nor c and d are both zero.
 Finite Mathematics Chapter 2 Section 2.1 Systems of Linear Equations: An Introduction Systems of Equations Recall that a system of two linear equations in two variables may be written in the general form
Finite Mathematics Chapter 2 Section 2.1 Systems of Linear Equations: An Introduction Systems of Equations Recall that a system of two linear equations in two variables may be written in the general form
6-2 Matrix Multiplication, Inverses and Determinants
 Find AB and BA, if possible. 1. A = A = ; A is a 1 2 matrix and B is a 2 2 matrix. Because the number of columns of A is equal to the number of rows of B, AB exists. To find the first entry of AB, find
Find AB and BA, if possible. 1. A = A = ; A is a 1 2 matrix and B is a 2 2 matrix. Because the number of columns of A is equal to the number of rows of B, AB exists. To find the first entry of AB, find
Section 2.2: The Inverse of a Matrix
 Section 22: The Inverse of a Matrix Recall that a linear equation ax b, where a and b are scalars and a 0, has the unique solution x a 1 b, where a 1 is the reciprocal of a From this result, it is natural
Section 22: The Inverse of a Matrix Recall that a linear equation ax b, where a and b are scalars and a 0, has the unique solution x a 1 b, where a 1 is the reciprocal of a From this result, it is natural
Solutions to Exam I MATH 304, section 6
 Solutions to Exam I MATH 304, section 6 YOU MUST SHOW ALL WORK TO GET CREDIT. Problem 1. Let A = 1 2 5 6 1 2 5 6 3 2 0 0 1 3 1 1 2 0 1 3, B =, C =, I = I 0 0 0 1 1 3 4 = 4 4 identity matrix. 3 1 2 6 0
Solutions to Exam I MATH 304, section 6 YOU MUST SHOW ALL WORK TO GET CREDIT. Problem 1. Let A = 1 2 5 6 1 2 5 6 3 2 0 0 1 3 1 1 2 0 1 3, B =, C =, I = I 0 0 0 1 1 3 4 = 4 4 identity matrix. 3 1 2 6 0
Chapter 1 Matrices and Systems of Equations
 Chapter 1 Matrices and Systems of Equations System of Linear Equations 1. A linear equation in n unknowns is an equation of the form n i=1 a i x i = b where a 1,..., a n, b R and x 1,..., x n are variables.
Chapter 1 Matrices and Systems of Equations System of Linear Equations 1. A linear equation in n unknowns is an equation of the form n i=1 a i x i = b where a 1,..., a n, b R and x 1,..., x n are variables.
Chapter 3. Linear Equations. Josef Leydold Mathematical Methods WS 2018/19 3 Linear Equations 1 / 33
 Chapter 3 Linear Equations Josef Leydold Mathematical Methods WS 2018/19 3 Linear Equations 1 / 33 Lineares Gleichungssystem System of m linear equations in n unknowns: a 11 x 1 + a 12 x 2 + + a 1n x n
Chapter 3 Linear Equations Josef Leydold Mathematical Methods WS 2018/19 3 Linear Equations 1 / 33 Lineares Gleichungssystem System of m linear equations in n unknowns: a 11 x 1 + a 12 x 2 + + a 1n x n
LINEAR ALGEBRA WITH APPLICATIONS
 SEVENTH EDITION LINEAR ALGEBRA WITH APPLICATIONS Instructor s Solutions Manual Steven J. Leon PREFACE This solutions manual is designed to accompany the seventh edition of Linear Algebra with Applications
SEVENTH EDITION LINEAR ALGEBRA WITH APPLICATIONS Instructor s Solutions Manual Steven J. Leon PREFACE This solutions manual is designed to accompany the seventh edition of Linear Algebra with Applications
OHSx XM511 Linear Algebra: Solutions to Online True/False Exercises
 This document gives the solutions to all of the online exercises for OHSx XM511. The section ( ) numbers refer to the textbook. TYPE I are True/False. Answers are in square brackets [. Lecture 02 ( 1.1)
This document gives the solutions to all of the online exercises for OHSx XM511. The section ( ) numbers refer to the textbook. TYPE I are True/False. Answers are in square brackets [. Lecture 02 ( 1.1)
Chapter 2: Matrices and Linear Systems
 Chapter 2: Matrices and Linear Systems Paul Pearson Outline Matrices Linear systems Row operations Inverses Determinants Matrices Definition An m n matrix A = (a ij ) is a rectangular array of real numbers
Chapter 2: Matrices and Linear Systems Paul Pearson Outline Matrices Linear systems Row operations Inverses Determinants Matrices Definition An m n matrix A = (a ij ) is a rectangular array of real numbers
MATH 2030: MATRICES. Example 0.2. Q:Define A 1 =, A. 3 4 A: We wish to find c 1, c 2, and c 3 such that. c 1 + c c
 MATH 2030: MATRICES Matrix Algebra As with vectors, we may use the algebra of matrices to simplify calculations. However, matrices have operations that vectors do not possess, and so it will be of interest
MATH 2030: MATRICES Matrix Algebra As with vectors, we may use the algebra of matrices to simplify calculations. However, matrices have operations that vectors do not possess, and so it will be of interest
MAC1105-College Algebra. Chapter 5-Systems of Equations & Matrices
 MAC05-College Algebra Chapter 5-Systems of Equations & Matrices 5. Systems of Equations in Two Variables Solving Systems of Two Linear Equations/ Two-Variable Linear Equations A system of equations is
MAC05-College Algebra Chapter 5-Systems of Equations & Matrices 5. Systems of Equations in Two Variables Solving Systems of Two Linear Equations/ Two-Variable Linear Equations A system of equations is
Math 4A Notes. Written by Victoria Kala Last updated June 11, 2017
 Math 4A Notes Written by Victoria Kala vtkala@math.ucsb.edu Last updated June 11, 2017 Systems of Linear Equations A linear equation is an equation that can be written in the form a 1 x 1 + a 2 x 2 +...
Math 4A Notes Written by Victoria Kala vtkala@math.ucsb.edu Last updated June 11, 2017 Systems of Linear Equations A linear equation is an equation that can be written in the form a 1 x 1 + a 2 x 2 +...
MATRIX ALGEBRA AND SYSTEMS OF EQUATIONS. + + x 1 x 2. x n 8 (4) 3 4 2
 MATRIX ALGEBRA AND SYSTEMS OF EQUATIONS SYSTEMS OF EQUATIONS AND MATRICES Representation of a linear system The general system of m equations in n unknowns can be written a x + a 2 x 2 + + a n x n b a
MATRIX ALGEBRA AND SYSTEMS OF EQUATIONS SYSTEMS OF EQUATIONS AND MATRICES Representation of a linear system The general system of m equations in n unknowns can be written a x + a 2 x 2 + + a n x n b a
is a 3 4 matrix. It has 3 rows and 4 columns. The first row is the horizontal row [ ]
![is a 3 4 matrix. It has 3 rows and 4 columns. The first row is the horizontal row [ ] is a 3 4 matrix. It has 3 rows and 4 columns. The first row is the horizontal row [ ]](/thumbs/82/86615780.jpg) Matrices: Definition: An m n matrix, A m n is a rectangular array of numbers with m rows and n columns: a, a, a,n a, a, a,n A m,n =...... a m, a m, a m,n Each a i,j is the entry at the i th row, j th column.
Matrices: Definition: An m n matrix, A m n is a rectangular array of numbers with m rows and n columns: a, a, a,n a, a, a,n A m,n =...... a m, a m, a m,n Each a i,j is the entry at the i th row, j th column.
Digital Workbook for GRA 6035 Mathematics
 Eivind Eriksen Digital Workbook for GRA 6035 Mathematics November 10, 2014 BI Norwegian Business School Contents Part I Lectures in GRA6035 Mathematics 1 Linear Systems and Gaussian Elimination........................
Eivind Eriksen Digital Workbook for GRA 6035 Mathematics November 10, 2014 BI Norwegian Business School Contents Part I Lectures in GRA6035 Mathematics 1 Linear Systems and Gaussian Elimination........................
MATH 2331 Linear Algebra. Section 2.1 Matrix Operations. Definition: A : m n, B : n p. Example: Compute AB, if possible.
 MATH 2331 Linear Algebra Section 2.1 Matrix Operations Definition: A : m n, B : n p ( 1 2 p ) ( 1 2 p ) AB = A b b b = Ab Ab Ab Example: Compute AB, if possible. 1 Row-column rule: i-j-th entry of AB:
MATH 2331 Linear Algebra Section 2.1 Matrix Operations Definition: A : m n, B : n p ( 1 2 p ) ( 1 2 p ) AB = A b b b = Ab Ab Ab Example: Compute AB, if possible. 1 Row-column rule: i-j-th entry of AB:
If A is a 4 6 matrix and B is a 6 3 matrix then the dimension of AB is A. 4 6 B. 6 6 C. 4 3 D. 3 4 E. Undefined
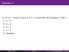 Question 1 If A is a 4 6 matrix and B is a 6 3 matrix then the dimension of AB is A. 4 6 B. 6 6 C. 4 3 D. 3 4 E. Undefined Quang T. Bach Math 18 October 18, 2017 1 / 17 Question 2 1 2 Let A = 3 4 1 2 3
Question 1 If A is a 4 6 matrix and B is a 6 3 matrix then the dimension of AB is A. 4 6 B. 6 6 C. 4 3 D. 3 4 E. Undefined Quang T. Bach Math 18 October 18, 2017 1 / 17 Question 2 1 2 Let A = 3 4 1 2 3
Steven J. Leon University of Massachusetts, Dartmouth
 INSTRUCTOR S SOLUTIONS MANUAL LINEAR ALGEBRA WITH APPLICATIONS NINTH EDITION Steven J. Leon University of Massachusetts, Dartmouth Boston Columbus Indianapolis New York San Francisco Amsterdam Cape Town
INSTRUCTOR S SOLUTIONS MANUAL LINEAR ALGEBRA WITH APPLICATIONS NINTH EDITION Steven J. Leon University of Massachusetts, Dartmouth Boston Columbus Indianapolis New York San Francisco Amsterdam Cape Town
7.6 The Inverse of a Square Matrix
 7.6 The Inverse of a Square Matrix Copyright Cengage Learning. All rights reserved. What You Should Learn Verify that two matrices are inverses of each other. Use Gauss-Jordan elimination to find inverses
7.6 The Inverse of a Square Matrix Copyright Cengage Learning. All rights reserved. What You Should Learn Verify that two matrices are inverses of each other. Use Gauss-Jordan elimination to find inverses
1 - Systems of Linear Equations
 1 - Systems of Linear Equations 1.1 Introduction to Systems of Linear Equations Almost every problem in linear algebra will involve solving a system of equations. ü LINEAR EQUATIONS IN n VARIABLES We are
1 - Systems of Linear Equations 1.1 Introduction to Systems of Linear Equations Almost every problem in linear algebra will involve solving a system of equations. ü LINEAR EQUATIONS IN n VARIABLES We are
7.5 Operations with Matrices. Copyright Cengage Learning. All rights reserved.
 7.5 Operations with Matrices Copyright Cengage Learning. All rights reserved. What You Should Learn Decide whether two matrices are equal. Add and subtract matrices and multiply matrices by scalars. Multiply
7.5 Operations with Matrices Copyright Cengage Learning. All rights reserved. What You Should Learn Decide whether two matrices are equal. Add and subtract matrices and multiply matrices by scalars. Multiply
Chapter 4. Solving Systems of Equations. Chapter 4
 Solving Systems of Equations 3 Scenarios for Solutions There are three general situations we may find ourselves in when attempting to solve systems of equations: 1 The system could have one unique solution.
Solving Systems of Equations 3 Scenarios for Solutions There are three general situations we may find ourselves in when attempting to solve systems of equations: 1 The system could have one unique solution.
Linear Algebra. Matrices Operations. Consider, for example, a system of equations such as x + 2y z + 4w = 0, 3x 4y + 2z 6w = 0, x 3y 2z + w = 0.
 Matrices Operations Linear Algebra Consider, for example, a system of equations such as x + 2y z + 4w = 0, 3x 4y + 2z 6w = 0, x 3y 2z + w = 0 The rectangular array 1 2 1 4 3 4 2 6 1 3 2 1 in which the
Matrices Operations Linear Algebra Consider, for example, a system of equations such as x + 2y z + 4w = 0, 3x 4y + 2z 6w = 0, x 3y 2z + w = 0 The rectangular array 1 2 1 4 3 4 2 6 1 3 2 1 in which the
Math 314H EXAM I. 1. (28 points) The row reduced echelon form of the augmented matrix for the system. is the matrix
 Math 34H EXAM I Do all of the problems below. Point values for each of the problems are adjacent to the problem number. Calculators may be used to check your answer but not to arrive at your answer. That
Math 34H EXAM I Do all of the problems below. Point values for each of the problems are adjacent to the problem number. Calculators may be used to check your answer but not to arrive at your answer. That
Offline Exercises for Linear Algebra XM511 Lectures 1 12
 This document lists the offline exercises for Lectures 1 12 of XM511, which correspond to Chapter 1 of the textbook. These exercises should be be done in the traditional paper and pencil format. The section
This document lists the offline exercises for Lectures 1 12 of XM511, which correspond to Chapter 1 of the textbook. These exercises should be be done in the traditional paper and pencil format. The section
Lemma 8: Suppose the N by N matrix A has the following block upper triangular form:
 17 4 Determinants and the Inverse of a Square Matrix In this section, we are going to use our knowledge of determinants and their properties to derive an explicit formula for the inverse of a square matrix
17 4 Determinants and the Inverse of a Square Matrix In this section, we are going to use our knowledge of determinants and their properties to derive an explicit formula for the inverse of a square matrix
Linear Algebra Practice Problems
 Math 7, Professor Ramras Linear Algebra Practice Problems () Consider the following system of linear equations in the variables x, y, and z, in which the constants a and b are real numbers. x y + z = a
Math 7, Professor Ramras Linear Algebra Practice Problems () Consider the following system of linear equations in the variables x, y, and z, in which the constants a and b are real numbers. x y + z = a
SECTION 3.3. PROBLEM 22. The null space of a matrix A is: N(A) = {X : AX = 0}. Here are the calculations of AX for X = a,b,c,d, and e. =
 SECTION 3.3. PROBLEM. The null space of a matrix A is: N(A) {X : AX }. Here are the calculations of AX for X a,b,c,d, and e. Aa [ ][ ] 3 3 [ ][ ] Ac 3 3 [ ] 3 3 [ ] 4+4 6+6 Ae [ ], Ab [ ][ ] 3 3 3 [ ]
SECTION 3.3. PROBLEM. The null space of a matrix A is: N(A) {X : AX }. Here are the calculations of AX for X a,b,c,d, and e. Aa [ ][ ] 3 3 [ ][ ] Ac 3 3 [ ] 3 3 [ ] 4+4 6+6 Ae [ ], Ab [ ][ ] 3 3 3 [ ]
Gaussian Elimination -(3.1) b 1. b 2., b. b n
 Gaussian Elimination -() Consider solving a given system of n linear equations in n unknowns: (*) a x a x a n x n b where a ij and b i are constants and x i are unknowns Let a n x a n x a nn x n a a a
Gaussian Elimination -() Consider solving a given system of n linear equations in n unknowns: (*) a x a x a n x n b where a ij and b i are constants and x i are unknowns Let a n x a n x a nn x n a a a
MTH501- Linear Algebra MCQS MIDTERM EXAMINATION ~ LIBRIANSMINE ~
 MTH501- Linear Algebra MCQS MIDTERM EXAMINATION ~ LIBRIANSMINE ~ Question No: 1 (Marks: 1) If for a linear transformation the equation T(x) =0 has only the trivial solution then T is One-to-one Onto Question
MTH501- Linear Algebra MCQS MIDTERM EXAMINATION ~ LIBRIANSMINE ~ Question No: 1 (Marks: 1) If for a linear transformation the equation T(x) =0 has only the trivial solution then T is One-to-one Onto Question
Lectures on Linear Algebra for IT
 Lectures on Linear Algebra for IT by Mgr Tereza Kovářová, PhD following content of lectures by Ing Petr Beremlijski, PhD Department of Applied Mathematics, VSB - TU Ostrava Czech Republic 3 Inverse Matrix
Lectures on Linear Algebra for IT by Mgr Tereza Kovářová, PhD following content of lectures by Ing Petr Beremlijski, PhD Department of Applied Mathematics, VSB - TU Ostrava Czech Republic 3 Inverse Matrix
Chapter 6 Page 1 of 10. Lecture Guide. Math College Algebra Chapter 6. to accompany. College Algebra by Julie Miller
 Chapter 6 Page 1 of 10 Lecture Guide Math 105 - College Algebra Chapter 6 to accompany College Algebra by Julie Miller Corresponding Lecture Videos can be found at Prepared by Stephen Toner & Nichole DuBal
Chapter 6 Page 1 of 10 Lecture Guide Math 105 - College Algebra Chapter 6 to accompany College Algebra by Julie Miller Corresponding Lecture Videos can be found at Prepared by Stephen Toner & Nichole DuBal
Math 1314 Week #14 Notes
 Math 3 Week # Notes Section 5.: A system of equations consists of two or more equations. A solution to a system of equations is a point that satisfies all the equations in the system. In this chapter,
Math 3 Week # Notes Section 5.: A system of equations consists of two or more equations. A solution to a system of equations is a point that satisfies all the equations in the system. In this chapter,
The matrix will only be consistent if the last entry of row three is 0, meaning 2b 3 + b 2 b 1 = 0.
 ) Find all solutions of the linear system. Express the answer in vector form. x + 2x + x + x 5 = 2 2x 2 + 2x + 2x + x 5 = 8 x + 2x + x + 9x 5 = 2 2 Solution: Reduce the augmented matrix [ 2 2 2 8 ] to
) Find all solutions of the linear system. Express the answer in vector form. x + 2x + x + x 5 = 2 2x 2 + 2x + 2x + x 5 = 8 x + 2x + x + 9x 5 = 2 2 Solution: Reduce the augmented matrix [ 2 2 2 8 ] to
Chapter 2 Notes, Linear Algebra 5e Lay
 Contents.1 Operations with Matrices..................................1.1 Addition and Subtraction.............................1. Multiplication by a scalar............................ 3.1.3 Multiplication
Contents.1 Operations with Matrices..................................1.1 Addition and Subtraction.............................1. Multiplication by a scalar............................ 3.1.3 Multiplication
1. What is the determinant of the following matrix? a 1 a 2 4a 3 2a 2 b 1 b 2 4b 3 2b c 1. = 4, then det
 What is the determinant of the following matrix? 3 4 3 4 3 4 4 3 A 0 B 8 C 55 D 0 E 60 If det a a a 3 b b b 3 c c c 3 = 4, then det a a 4a 3 a b b 4b 3 b c c c 3 c = A 8 B 6 C 4 D E 3 Let A be an n n matrix
What is the determinant of the following matrix? 3 4 3 4 3 4 4 3 A 0 B 8 C 55 D 0 E 60 If det a a a 3 b b b 3 c c c 3 = 4, then det a a 4a 3 a b b 4b 3 b c c c 3 c = A 8 B 6 C 4 D E 3 Let A be an n n matrix
MAC Learning Objectives. Learning Objectives (Cont.) Module 10 System of Equations and Inequalities II
 MAC 1140 Module 10 System of Equations and Inequalities II Learning Objectives Upon completing this module, you should be able to 1. represent systems of linear equations with matrices. 2. transform a
MAC 1140 Module 10 System of Equations and Inequalities II Learning Objectives Upon completing this module, you should be able to 1. represent systems of linear equations with matrices. 2. transform a
MATRICES. knowledge on matrices Knowledge on matrix operations. Matrix as a tool of solving linear equations with two or three unknowns.
 MATRICES After studying this chapter you will acquire the skills in knowledge on matrices Knowledge on matrix operations. Matrix as a tool of solving linear equations with two or three unknowns. List of
MATRICES After studying this chapter you will acquire the skills in knowledge on matrices Knowledge on matrix operations. Matrix as a tool of solving linear equations with two or three unknowns. List of
Linear Algebra I Lecture 10
 Linear Algebra I Lecture 10 Xi Chen 1 1 University of Alberta January 30, 2019 Outline 1 Gauss-Jordan Algorithm ] Let A = [a ij m n be an m n matrix. To reduce A to a reduced row echelon form using elementary
Linear Algebra I Lecture 10 Xi Chen 1 1 University of Alberta January 30, 2019 Outline 1 Gauss-Jordan Algorithm ] Let A = [a ij m n be an m n matrix. To reduce A to a reduced row echelon form using elementary
Extra Problems for Math 2050 Linear Algebra I
 Extra Problems for Math 5 Linear Algebra I Find the vector AB and illustrate with a picture if A = (,) and B = (,4) Find B, given A = (,4) and [ AB = A = (,4) and [ AB = 8 If possible, express x = 7 as
Extra Problems for Math 5 Linear Algebra I Find the vector AB and illustrate with a picture if A = (,) and B = (,4) Find B, given A = (,4) and [ AB = A = (,4) and [ AB = 8 If possible, express x = 7 as
A FIRST COURSE IN LINEAR ALGEBRA. An Open Text by Ken Kuttler. Matrix Arithmetic
 A FIRST COURSE IN LINEAR ALGEBRA An Open Text by Ken Kuttler Matrix Arithmetic Lecture Notes by Karen Seyffarth Adapted by LYRYX SERVICE COURSE SOLUTION Attribution-NonCommercial-ShareAlike (CC BY-NC-SA)
A FIRST COURSE IN LINEAR ALGEBRA An Open Text by Ken Kuttler Matrix Arithmetic Lecture Notes by Karen Seyffarth Adapted by LYRYX SERVICE COURSE SOLUTION Attribution-NonCommercial-ShareAlike (CC BY-NC-SA)
MODEL ANSWERS TO THE THIRD HOMEWORK
 MODEL ANSWERS TO THE THIRD HOMEWORK 1 (i) We apply Gaussian elimination to A First note that the second row is a multiple of the first row So we need to swap the second and third rows 1 3 2 1 2 6 5 7 3
MODEL ANSWERS TO THE THIRD HOMEWORK 1 (i) We apply Gaussian elimination to A First note that the second row is a multiple of the first row So we need to swap the second and third rows 1 3 2 1 2 6 5 7 3
Lecture 6 & 7. Shuanglin Shao. September 16th and 18th, 2013
 Lecture 6 & 7 Shuanglin Shao September 16th and 18th, 2013 1 Elementary matrices 2 Equivalence Theorem 3 A method of inverting matrices Def An n n matrice is called an elementary matrix if it can be obtained
Lecture 6 & 7 Shuanglin Shao September 16th and 18th, 2013 1 Elementary matrices 2 Equivalence Theorem 3 A method of inverting matrices Def An n n matrice is called an elementary matrix if it can be obtained
Fundamentals of Engineering Analysis (650163)
 Philadelphia University Faculty of Engineering Communications and Electronics Engineering Fundamentals of Engineering Analysis (6563) Part Dr. Omar R Daoud Matrices: Introduction DEFINITION A matrix is
Philadelphia University Faculty of Engineering Communications and Electronics Engineering Fundamentals of Engineering Analysis (6563) Part Dr. Omar R Daoud Matrices: Introduction DEFINITION A matrix is
ECON 186 Class Notes: Linear Algebra
 ECON 86 Class Notes: Linear Algebra Jijian Fan Jijian Fan ECON 86 / 27 Singularity and Rank As discussed previously, squareness is a necessary condition for a matrix to be nonsingular (have an inverse).
ECON 86 Class Notes: Linear Algebra Jijian Fan Jijian Fan ECON 86 / 27 Singularity and Rank As discussed previously, squareness is a necessary condition for a matrix to be nonsingular (have an inverse).
Linear Algebra March 16, 2019
 Linear Algebra March 16, 2019 2 Contents 0.1 Notation................................ 4 1 Systems of linear equations, and matrices 5 1.1 Systems of linear equations..................... 5 1.2 Augmented
Linear Algebra March 16, 2019 2 Contents 0.1 Notation................................ 4 1 Systems of linear equations, and matrices 5 1.1 Systems of linear equations..................... 5 1.2 Augmented
Linear Systems and Matrices
 Department of Mathematics The Chinese University of Hong Kong 1 System of m linear equations in n unknowns (linear system) a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1 + a 22 x 2 + + a 2n x n = b 2.......
Department of Mathematics The Chinese University of Hong Kong 1 System of m linear equations in n unknowns (linear system) a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1 + a 22 x 2 + + a 2n x n = b 2.......
Matrix operations Linear Algebra with Computer Science Application
 Linear Algebra with Computer Science Application February 14, 2018 1 Matrix operations 11 Matrix operations If A is an m n matrix that is, a matrix with m rows and n columns then the scalar entry in the
Linear Algebra with Computer Science Application February 14, 2018 1 Matrix operations 11 Matrix operations If A is an m n matrix that is, a matrix with m rows and n columns then the scalar entry in the
Math 60. Rumbos Spring Solutions to Assignment #17
 Math 60. Rumbos Spring 2009 1 Solutions to Assignment #17 a b 1. Prove that if ad bc 0 then the matrix A = is invertible and c d compute A 1. a b Solution: Let A = and assume that ad bc 0. c d First consider
Math 60. Rumbos Spring 2009 1 Solutions to Assignment #17 a b 1. Prove that if ad bc 0 then the matrix A = is invertible and c d compute A 1. a b Solution: Let A = and assume that ad bc 0. c d First consider
MTH 102A - Linear Algebra II Semester
 MTH 0A - Linear Algebra - 05-6-II Semester Arbind Kumar Lal P Field A field F is a set from which we choose our coefficients and scalars Expected properties are ) a+b and a b should be defined in it )
MTH 0A - Linear Algebra - 05-6-II Semester Arbind Kumar Lal P Field A field F is a set from which we choose our coefficients and scalars Expected properties are ) a+b and a b should be defined in it )
Elementary Linear Algebra
 Elementary Linear Algebra Linear algebra is the study of; linear sets of equations and their transformation properties. Linear algebra allows the analysis of; rotations in space, least squares fitting,
Elementary Linear Algebra Linear algebra is the study of; linear sets of equations and their transformation properties. Linear algebra allows the analysis of; rotations in space, least squares fitting,
Section Gaussian Elimination
 Section. - Gaussian Elimination A matrix is said to be in row echelon form (REF) if it has the following properties:. The first nonzero entry in any row is a. We call this a leading one or pivot one..
Section. - Gaussian Elimination A matrix is said to be in row echelon form (REF) if it has the following properties:. The first nonzero entry in any row is a. We call this a leading one or pivot one..
Chapter 5. Linear Algebra. A linear (algebraic) equation in. unknowns, x 1, x 2,..., x n, is. an equation of the form
 Chapter 5. Linear Algebra A linear (algebraic) equation in n unknowns, x 1, x 2,..., x n, is an equation of the form a 1 x 1 + a 2 x 2 + + a n x n = b where a 1, a 2,..., a n and b are real numbers. 1
Chapter 5. Linear Algebra A linear (algebraic) equation in n unknowns, x 1, x 2,..., x n, is an equation of the form a 1 x 1 + a 2 x 2 + + a n x n = b where a 1, a 2,..., a n and b are real numbers. 1
3. Replace any row by the sum of that row and a constant multiple of any other row.
 Section. Solution of Linear Systems by Gauss-Jordan Method A matrix is an ordered rectangular array of numbers, letters, symbols or algebraic expressions. A matrix with m rows and n columns has size or
Section. Solution of Linear Systems by Gauss-Jordan Method A matrix is an ordered rectangular array of numbers, letters, symbols or algebraic expressions. A matrix with m rows and n columns has size or
