Equations with Separated Variables on Time Scales
|
|
|
- Crystal Dickerson
- 5 years ago
- Views:
Transcription
1 International Journal of Difference Equations ISSN , Volume 12, Number 1, pp (217) Equations with Separated Variables on Time Scales Antoni Augustynowicz Institute of Mathematics Faculty of Mathematics, Physics and Informatics University of Gdańsk 57 Wit Stwosz str., Gdańsk, Poland antoni.augustynowicz@mat.ug.edu.pl Agata Gołaszewska Faculty of Applied Physics and Mathematics Department of Mathematics Gdańsk University of Technology 11/12 Narutowicz str., Gdańsk, Poland golaszewska@mif.pg.gda.pl, agata@gda.pl Abstract We show that the well-known theory for classical ordinary differential equations with separated variables is not valid in case of equations on time scales. Namely, the uniqueness of solutions does not depend on the convergence of appropriate integrals. AMS Subject Classifications: 26E7, 34N5, 39A1. Keywords: Dynamic equation, time scale, separated variables. 1 Introduction Dynamic equations on time scales have become very interesting for many mathematicians in recent years (see [2, 3, 5], and references for others). The main aim of this paper is to verify how the theory of dynamic equations with separated variables (see [6]) changes if we generalize classical equations to equations on time scales. We show that classical theorems are not true even under some additional assumptions. We introduce some basic definitions (see [2]). Received March 14, 216; Accepted November 22, 216 Communicated by Agnieszka Malinowska
2 2 A. Augustynowicz, A. Gołaszewska Definition 1.1. A time scale is an arbitrary nonempty closed set of the real numbers. Let T be a time scale. We denote I T := I T for an arbitrary I R. Now we define some operators. Definition 1.2. We define the forward jump operator σ : T T by σ(t) = inf {s : s T, s > t}, σ(max T) = max T if sup T <, and the backward jump operator ρ : T T by ρ(min T) = min T if inf T >. ρ(t) = sup {s : s T, s < t}, Definition 1.3. Assume that f : T R and let t T κ = T\ {sup T}. Then we define f (t) to be the number (provided it exists) with the property that for any given ɛ >, there is a neighborhood U of t such that [f(σ(t)) f] f (t)[σ(t) s] ɛ σ(t) s, for all s U T. If f (t) = g(t) for every t [a, b] T, then we denote f(b) = f(a) + b a g(t) t. Let us introduce some special class of time scales that are the most important for this paper. Definition 1.4. If there exists a sequence {t n } n=1 T such that t n and σ(t n ) > t n, then we say that T is a DNC time scale at (dense not classical). In this paper, we assume that T means a DNC time scale and let, for simplicity, min T =. Moreover, we fix the symbol {t n } for a sequence that has the property mentioned in the above definition. We study the uniqueness of solutions of the following initial value problem for equations with separated variables { x (t) = f(t)g(x(t)), t T, (1.1) x() =, where f : T R and g : R R. We say that a function z : T R is a solution of the problem (1.1) if z() = and z (t) = f(t)g(z(t)) for all t T. Rewriting from [6] the uniqueness of the zero solution of (1.1) (if g() = ) in the classical case depends on divergence of the integral ε g(x). Concerning solutions of the problem (1.1) in a local sense, all time scales can be generally divided into three following classes:
3 Equations with Separated Variables on Time Scales 3 (i) [, a] T for some a R; (ii) σ() > ; (iii) T is a DNC time scale at. In the first case (i), we are dealing with the classical theory of ordinary differential equations with separated variables. In the second case (ii), regardless of the time scale, the problem (1.1) has always exactly one solution in a local sense. The DNC time scales are very wide class of different time scales. In this paper, we find different examples of the problem (1.1), where independently from any DNC time scale and from convergence of appropriate integral it may have exactly one solution or it may have more than one solution. In some cases it may even have no solution at all. The following closed sets are some examples of DNC-time scales: {} {τ n : n N}, τ n ; {} n N [ 1 n, 1 n + 1 n 2 ] ; {} { 1 n : } { 1 n N n + 1 nk } : n, k N, k > n ; the Cantor set. In the theory of equations x (t) = F (t, x(t)) on time scales it is natural to consider not necessarily continuous but so called rd-continuous functions F. It means such functions F that for any continuous x : T R the function ϕ(t) = F (t, x(t)) has the following property: ϕ is continuous at t T if σ(t) = t and lim s t ϕ is finite if ρ(t) = t < σ(t) (see [2]). Unfortunately, the Peano type theorem is not valid for equations with rd-continuous right-hand-side (see [1, 4] for counterexample on time scale {} {1, 12, 13 },... ). We present below that for every DNC time scale T there exists a problem (1.1) without any solution, however the right-hand-side of the equation is an rd-continuous function with separated variables. Namely, for any DNC time scale T, we find an rd-continuous function of the form f(t)g(x) such that the problem (1.1) has no solution. Example 1.5. Let us define f : T R and g : R R by the formulas { t, for t = tn, f(t) =, otherwise,
4 4 A. Augustynowicz, A. Gołaszewska g(x) = { 1, for x =,, for x. It is not difficult to verify that the function given by the product of functions f and g as follows F (t, x) = f(t)g(x), is rd-continuous. Suppose that x() =, x (t) = f(t)g(x(t)) for all t [, δ) T and some δ >. Then x(t) on [, δ) T since x (t). Moreover, x(t) > for t >, because if x(t n ) =, then x (t n ) >. Hence for t >, we have x (t) =, and therefore x is a constant positive function on [, δ) T. It means that x() >. We obtain the contradiction to the assumption that x() =. We are able to prove only the following result corresponding to the classical theory of equations with separated variables. Theorem 1.6. Assume that the integral ɛ G(x) is divergent for ɛ, the function g : R R is continuous, f is integrable and nonnegative on T, xg(x) > for x and { max {g(y) : y [, x]}, for x >, G(x) = min {g(y) : y [x, ]}, for x <. Then the problem (1.1) has only a trivial solution. Proof. Suppose that z : [, δ] T R is a nonzero solution of (1.1), then the function z does not change the sign. Assume that z(t ) > for some T (, δ] T, then there exists t [, T ) T such that z(t) > for t (t, T ] T and z(t ) =. Let us assume, that σ(t ) > t. Since g() =, we have z (t ) = f(t )g(z(t )) = f(t )g() =. Consequently z(σ(t )) =. This contradicts the definition of t. If [t, h] T for some h (t, T ], then we obtain z on [t, h] from a well-known theorem for equations with separated variables (see [6], page 45) and from the fact, that ε g(x) ε G(x) = for ε >. The above result means that there exists a sequence {s n } T such that s n t and σ(s n ) > s n (T is DNC at t ). Let us define z : convt R and ρ : convt T by the formulae z(t), for t T, z(t) = z(σ t) + z(σ)(t s) σ s for t (s, σ), s T, ρ(t) = max {s T : s t}.
5 Equations with Separated Variables on Time Scales 5 For each τ T such that σ(τ) > τ, we have σ(τ) τ z σ(τ) g(z) s = τ z (τ) σ(τ) g(z(τ)) s = τ z σ(τ) g(z( ρ)) s = τ z g(z( ρ)) ds, because z is a constant function on the set (τ, σ(τ)). Suppose that y : T R is an integrable function. Let us define a new function ȳ : convt R by ȳ T = y and ȳ = y(t) for s (t, σ(t)), t T. Then Indeed, we put y s = ȳds, t T. t t F (t) = t ȳds, t convt, F (t) = y s t T, t and F = F. T For t T, we have F (t) = F +(t) = ȳ(t) = y(t) = F (t), where F + means the right-hand-side derivative of the function F. Of course F (t ) = = F (t ), so we can conclude that F (t) = F (t), for t T. Now put and Now we have y = z g(z) ȳ = for s T, z + for s convt. g(z( ρ)) t z t g(z) s = t z t + g(z( ρ)) ds = t z g(z( ρ)) ds.
6 6 A. Augustynowicz, A. Gołaszewska The last equality follows from the fact, that z can be not defined only for s T such that ρ s or s σ. The set of such s is countable. Therefore, the value of the integrand on that set does not affect the value of the Riemann integral. Then z f s = t t g(z) s = z t g(z( ρ)) ds z t G(z( ρ)) ds z z(t) G( z) ds = G(x) = t t for t (t, T ], which contradicts the integrability of function f. Analogously, we obtain a contradiction if z(t ) < for some T >. 2 Results We show that in general there is no correspondence of the uniqueness of solutions of 1 (1.1) with integrability of the function and the sign of xg(x) for x. g(x) Proposition 2.1. There exists a -integrable function f, such that any δ >, f(t), a continuous function g, such that g(x) > for x, ɛ g(x) < for ε, and the problem (1.1) has only trivial solution. δ f(t) t > for Proposition 2.2. There exists a continuous function g such that g(x) > for x > and ɛ g(x) = for ε >, but the problem (1.1) has a positive solution on T\ {} for f(t) 1. Remark 2.3. One may prove an analogous result for negative solutions in a similar manner. Proposition 2.4. There exists a continuous function g such that xg(x) < for x and the integral ɛ g(x) is divergent for ε, but the problem (1.1) for f(t) 1 has a nontrivial solution.
7 Equations with Separated Variables on Time Scales 7 3 Proofs Proof of Proposition 2.1. Let f(t) = where s 1 = 1 2, s k = s 2 k 1. Then, for t t n, s n 1 s n σ(t n ) t n, for t = t n, n = f(t) t = f(t j )(σ(t j ) t j ) = j=n+1 j=n+1 (s j 1 s j ) = s n >. Suppose that x() =, x (t) = f(t) x(t) and x(t) on [, δ) for any δ >. Then x(t) > for t >. Moreover, the function x is constant on any set [σ(t n ), t n 1 ) T, since f(t) = for t [σ(t n ), t n 1 ) T. Let us define the time scale T = {} {s n } n=1 and function z : T R by the formula z() =, z(s n ) = x(t n ). We can see, that hence z (s n ) = x(t n 1) x(t n ) s n 1 s n = x(σ(t n)) x(t n ) s n 1 s n = = x (t n ) f(t n ) = z(s n ), z(s n 1 ) = z(s n ) + (s n 1 s n ) z(s n ). Let us substitute y n = 4z(t n ). Then we obtain y n = (s n 1 s n ) 2 + yn 1 2 (s n 1 s n ) < y n 1, from the fact, that a 2 + b 2 < a + b for a, b >. Moreover y n y n+1 = y n + s n s n+1 (s n s n+1 ) 2 + y 2 n < s n s n+1, hence y n = (y j y j+1 ) < j=n (s n s n+1 ) = s n. j=n
8 8 A. Augustynowicz, A. Gołaszewska Consequently Suppose that z(s n ) < s 2 n. for all natural n and some α 2. Since s n+1 = s 2 n, we have z(s n ) < s α n (3.1) z(s n ) = z(s n+1 ) + (s n s n+1 ) z(s n+1 ) < s α n+1 + (s n s n+1 )s α/2 n+1 = = s 2α n + (s n s 2 n)s α n = s α+1 n (s α 1 n + 1 s n ) s α+1 n. This implies that (3.1) is satisfied for every α 2 and z(s n ) =, so x(t n ) =. We obtain that x(t) on [, δ] T for some δ >, and then we see, that x(t) on T. It is obvious that if T = T, then the function f is continuous, namely f(t) 1. Proof of Proposition 2.2. Let z : T R be an arbitrary -differentiable function such that z() = z () =, and z is a strictly increasing and continuous function, for example z(t) = s s. Let us define Z = z(t) { } { } z(tn ) + z(σ(t n )) x R : x > sup z (t). 2 T n N For x / Z, x >, let us define a(x) = max {y Z : y < x}, b(x) = min {y Z : y > x}. We define function g : R R as follows, for x =, z (t), for x = z(t), t T, z n, for x = z(t n) + z(σ(t n )), 2 g(x) = g(sup z (t)), for x sup z (t), T T g(a(x))(b(x) x) + g(b(x))(x a(x)) for x / Z, x >, b(x) a(x) g( x), for x <. Of course, z (t) = g(z(t)), t T, z() =. Let us suppose that z n >. Then for x, we have xg(x) >, and we can choose {z n } such that the integral is divergent for every ε. ɛ g(x)
9 Equations with Separated Variables on Time Scales 9 Proof of Proposition 2.4. Let a 1 = 1 and a k+1 = 1 k + 1 min {a k, σ(t k ) t k, σ(t k+1 ) t k+1 }, x k = ( 1) k a k. If σ(t k+1 ) = t k, then y k = x k+1, but if σ(t k+1 ) < t k, then y k is close enough to x k+1 in a such way, that A = t k σ(t k+1 ) x k x k+1 y k x k+1 σ(t k ) σ(t k+1 ) 2, and a k+3 < ( 1) k+1 y k < a k+1. We prove that there exists a continuous function z : [, t 1 ] T R, such that z() = z () =, and z(t k ) = y k, z(σ(t k )) = x k for k N. Furthermore, if σ(t k+1 ) < t k, then z is a continuous, monotonic and a sign constant function on [σ(t k+1 ), t k ] T. Let t = st k + (1 s)σ(t k+1 ), y = z(t) z(σ(t k+1)) z(t k ) z(σ(t k+1 )). (3.2) Constructing the definition of the function z on [σ(t k+1 ), t k ] T {σ(t k )}, where σ(t k ) = s t k + (1 s )σ(t k+1 ), comes down to finding a function y : [, 1] T {s } R, such that y() =, y(1) = 1, y (1) = A, where T is the image of T with the above change of variables (3.2). The following conditions for the function y are needed: the function y is continuous, monotonic, and a constant sign function on [, 1] T. If the point 1 is left-scattered in T (it means that t k is left-scattered in T), then y = s for s [, 1], y(s ) = A(s 1) + 1. Suppose that point 1 is left-dense in T. Then lim n 1 τ n τ =. Let n N be, such that 1 τ n τ < 1 A. The function y satisfying the necessary assumptions is the following y = 1 A 1 τ n τ 1 1 τ n τ s + A τ n τ s τ n τ. Let us define Z = {} conv {x k+1, y k } { } xk+3 + y k (, x 1 ] [x 2, ), 2 k N k N
10 1 A. Augustynowicz, A. Gołaszewska and a(x) = max {y Z : y < x}, b(x) = min {y Z : y > x} for x / Z. Now we define g : [x 1, x 2 ] R as g(x) = z k, z (z 1 (x)), for x conv {x k+1, y k },, for x =, g(a(x))(b(x) x) + g(b(x))(x a(x)) b(x) a(x) for x = x k+3 + y k, 2 for x / Z, where z k y k >, lim z k =. Moreover, we put g(x) = g(x 1 ) for x x 1, and k g(x) = g(x 2 ) for x x 2. Of course, the function g is continuous on R\ {} and z (t) = g(z(t)), t T\ {}. We can choose {z n }, such that the following integral ε g(x) is divergent for every ε. Moreover, for all x, we have xg(x) <. It remains to show that z () =, and that z is continuous at. If k, then from the fact, that z (t k ) = x k y k σ(t k ) t k = a k + y k σ(t k ) t k < a k + a k+1 σ(t k ) t k 2 k, we obtain Moreover lim z (t) lim z (t k ) =. t k z () = lim z(t) lim t t k x k σ(t k ) lim a k =. t σ(t k ) t k Consequently, functions z and x are solutions of the problem { x (t) = g(x(t)), t [, t 1 ] T, x() =.
11 Equations with Separated Variables on Time Scales 11 References [1] A. Augustynowicz, A. Gołaszewska, On the Peano Theorem for Some Functional Differential Equation on Time Scale, Functional Differential Equations, Vol. 21, No 3 4, 214, pp ; [2] M. Bohner, A. C. Peterson, Dynamic Equations on Time Scales, Birkhäuser, Boston 21; [3] M. Bohner, A. C. Peterson, Advances in Dynamic Equations on Time Scales, Birkhäuser, Boston 23; [4] J. Jankowski, Istnienie i jednoznaczność rozwia zań równań różniczkowych z wyprzedzonym argumentem, PhD Thesis, University of Gdańsk (29); [5] V. Lakshmikantham, S. Sivasundaram, B. Kaymakcalan, Dynamic Systems on Measure Chains, Kluwer Academic Publishers, Dordrecht 1996; [6] W. F. Trench, Elementary Differential Equations, Brooks/Cole Thomson Learning, 21 (Free Edition 1.1).
Boundary Value Problems For A Differential Equation On A Measure Chain
 Boundary Value Problems For A Differential Equation On A Measure Chain Elvan Akin Department of Mathematics and Statistics, University of Nebraska-Lincoln Lincoln, NE 68588-0323 eakin@math.unl.edu Abstract
Boundary Value Problems For A Differential Equation On A Measure Chain Elvan Akin Department of Mathematics and Statistics, University of Nebraska-Lincoln Lincoln, NE 68588-0323 eakin@math.unl.edu Abstract
Solving Third Order Three-Point Boundary Value Problem on Time Scales by Solution Matching Using Differential Inequalities
 Global Journal of Science Frontier Research Mathematics & Decision Sciences Volume 12 Issue 3 Version 1.0 Type : Double Blind Peer Reviewed International Research Journal Publisher: Global Journals Inc.
Global Journal of Science Frontier Research Mathematics & Decision Sciences Volume 12 Issue 3 Version 1.0 Type : Double Blind Peer Reviewed International Research Journal Publisher: Global Journals Inc.
International Publications (USA) PanAmerican Mathematical Journal
 International Publications (USA) PanAmerican Mathematical Journal Volume 6(2006), Number 2, 6 73 Exponential Stability of Dynamic Equations on Time Scales M. Rashford, J. Siloti, and J. Wrolstad University
International Publications (USA) PanAmerican Mathematical Journal Volume 6(2006), Number 2, 6 73 Exponential Stability of Dynamic Equations on Time Scales M. Rashford, J. Siloti, and J. Wrolstad University
Stability and Instability for Dynamic Equations on Time Scales
 PERGAMON Computers and Mathematics with Applications 0 (2005) 1 0 www.elsevier.com/locate/camwa Stability and Instability for Dynamic Equations on Time Scales J. Hoffacker Department of Mathematical Sciences,
PERGAMON Computers and Mathematics with Applications 0 (2005) 1 0 www.elsevier.com/locate/camwa Stability and Instability for Dynamic Equations on Time Scales J. Hoffacker Department of Mathematical Sciences,
A Mean Value Theorem for the Conformable Fractional Calculus on Arbitrary Time Scales
 Progr. Fract. Differ. Appl. 2, No. 4, 287-291 (2016) 287 Progress in Fractional Differentiation and Applications An International Journal http://dx.doi.org/10.18576/pfda/020406 A Mean Value Theorem for
Progr. Fract. Differ. Appl. 2, No. 4, 287-291 (2016) 287 Progress in Fractional Differentiation and Applications An International Journal http://dx.doi.org/10.18576/pfda/020406 A Mean Value Theorem for
Periodic Solutions in Shifts δ ± for a Dynamic Equation on Time Scales
 Advances in Dynamical Systems and Applications ISSN 0973-5321, Volume 9, Number 1, pp. 97 108 (2014) http://campus.mst.edu/adsa Periodic Solutions in Shifts δ ± for a Dynamic Equation on Time Scales Erbil
Advances in Dynamical Systems and Applications ISSN 0973-5321, Volume 9, Number 1, pp. 97 108 (2014) http://campus.mst.edu/adsa Periodic Solutions in Shifts δ ± for a Dynamic Equation on Time Scales Erbil
COMPLETENESS THEOREM FOR THE DISSIPATIVE STURM-LIOUVILLE OPERATOR ON BOUNDED TIME SCALES. Hüseyin Tuna
 Indian J. Pure Appl. Math., 47(3): 535-544, September 2016 c Indian National Science Academy DOI: 10.1007/s13226-016-0196-1 COMPLETENESS THEOREM FOR THE DISSIPATIVE STURM-LIOUVILLE OPERATOR ON BOUNDED
Indian J. Pure Appl. Math., 47(3): 535-544, September 2016 c Indian National Science Academy DOI: 10.1007/s13226-016-0196-1 COMPLETENESS THEOREM FOR THE DISSIPATIVE STURM-LIOUVILLE OPERATOR ON BOUNDED
Dynamic Systems and Applications 13 (2004) PARTIAL DIFFERENTIATION ON TIME SCALES
 Dynamic Systems and Applications 13 (2004) 351-379 PARTIAL DIFFERENTIATION ON TIME SCALES MARTIN BOHNER AND GUSEIN SH GUSEINOV University of Missouri Rolla, Department of Mathematics and Statistics, Rolla,
Dynamic Systems and Applications 13 (2004) 351-379 PARTIAL DIFFERENTIATION ON TIME SCALES MARTIN BOHNER AND GUSEIN SH GUSEINOV University of Missouri Rolla, Department of Mathematics and Statistics, Rolla,
BOUNDEDNESS AND EXPONENTIAL STABILITY OF SOLUTIONS TO DYNAMIC EQUATIONS ON TIME SCALES
 Electronic Journal of Differential Equations, Vol. 20062006, No. 12, pp. 1 14. ISSN: 1072-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu login: ftp BOUNDEDNESS
Electronic Journal of Differential Equations, Vol. 20062006, No. 12, pp. 1 14. ISSN: 1072-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu login: ftp BOUNDEDNESS
Research Article On the Existence of Solutions for Dynamic Boundary Value Problems under Barrier Strips Condition
 Hindawi Publishing Corporation Advances in Difference Equations Volume 2011, Article ID 378686, 9 pages doi:10.1155/2011/378686 Research Article On the Existence of Solutions for Dynamic Boundary Value
Hindawi Publishing Corporation Advances in Difference Equations Volume 2011, Article ID 378686, 9 pages doi:10.1155/2011/378686 Research Article On the Existence of Solutions for Dynamic Boundary Value
A SIMPLIFIED APPROACH TO GRONWALL S INEQUALITY ON TIME SCALES WITH APPLICATIONS TO NEW BOUNDS FOR SOLUTIONS TO LINEAR DYNAMIC EQUATIONS
 Electronic Journal of Differential Equations, Vol. 217 (217), No. 263, pp. 1 13. ISSN: 172-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu A SIMPLIFIED APPROACH TO GRONWALL S INEQUALITY
Electronic Journal of Differential Equations, Vol. 217 (217), No. 263, pp. 1 13. ISSN: 172-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu A SIMPLIFIED APPROACH TO GRONWALL S INEQUALITY
A CAUCHY PROBLEM ON TIME SCALES WITH APPLICATIONS
 ANALELE ŞTIINŢIFICE ALE UNIVERSITĂŢII AL.I. CUZA DIN IAŞI (S.N.) MATEMATICĂ, Tomul LVII, 211, Supliment A CAUCHY PROBLEM ON TIME SCALES WITH APPLICATIONS BY BIANCA SATCO Abstract. We obtain the existence
ANALELE ŞTIINŢIFICE ALE UNIVERSITĂŢII AL.I. CUZA DIN IAŞI (S.N.) MATEMATICĂ, Tomul LVII, 211, Supliment A CAUCHY PROBLEM ON TIME SCALES WITH APPLICATIONS BY BIANCA SATCO Abstract. We obtain the existence
ON THE PATHWISE UNIQUENESS OF SOLUTIONS OF STOCHASTIC DIFFERENTIAL EQUATIONS
 PORTUGALIAE MATHEMATICA Vol. 55 Fasc. 4 1998 ON THE PATHWISE UNIQUENESS OF SOLUTIONS OF STOCHASTIC DIFFERENTIAL EQUATIONS C. Sonoc Abstract: A sufficient condition for uniqueness of solutions of ordinary
PORTUGALIAE MATHEMATICA Vol. 55 Fasc. 4 1998 ON THE PATHWISE UNIQUENESS OF SOLUTIONS OF STOCHASTIC DIFFERENTIAL EQUATIONS C. Sonoc Abstract: A sufficient condition for uniqueness of solutions of ordinary
MATH 202B - Problem Set 5
 MATH 202B - Problem Set 5 Walid Krichene (23265217) March 6, 2013 (5.1) Show that there exists a continuous function F : [0, 1] R which is monotonic on no interval of positive length. proof We know there
MATH 202B - Problem Set 5 Walid Krichene (23265217) March 6, 2013 (5.1) Show that there exists a continuous function F : [0, 1] R which is monotonic on no interval of positive length. proof We know there
EXISTENCE OF POSITIVE SOLUTIONS FOR p-laplacian THREE-POINT BOUNDARY-VALUE PROBLEMS ON TIME SCALES
 Electronic Journal of Differential Equations, Vol. 28(28, No. 92, pp. 1 14. ISSN: 172-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu (login: ftp EXISTENCE
Electronic Journal of Differential Equations, Vol. 28(28, No. 92, pp. 1 14. ISSN: 172-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu (login: ftp EXISTENCE
Submitted Version to CAMWA, September 30, 2009 THE LAPLACE TRANSFORM ON ISOLATED TIME SCALES
 Submitted Version to CAMWA, September 30, 2009 THE LAPLACE TRANSFORM ON ISOLATED TIME SCALES MARTIN BOHNER AND GUSEIN SH. GUSEINOV Missouri University of Science and Technology, Department of Mathematics
Submitted Version to CAMWA, September 30, 2009 THE LAPLACE TRANSFORM ON ISOLATED TIME SCALES MARTIN BOHNER AND GUSEIN SH. GUSEINOV Missouri University of Science and Technology, Department of Mathematics
Real Analysis Math 131AH Rudin, Chapter #1. Dominique Abdi
 Real Analysis Math 3AH Rudin, Chapter # Dominique Abdi.. If r is rational (r 0) and x is irrational, prove that r + x and rx are irrational. Solution. Assume the contrary, that r+x and rx are rational.
Real Analysis Math 3AH Rudin, Chapter # Dominique Abdi.. If r is rational (r 0) and x is irrational, prove that r + x and rx are irrational. Solution. Assume the contrary, that r+x and rx are rational.
Journal of Inequalities in Pure and Applied Mathematics
 Journal of Inequalities in Pure and Applied Mathematics MONOTONE TRAJECTORIES OF DYNAMICAL SYSTEMS AND CLARKE S GENERALIZED JACOBIAN GIOVANNI P. CRESPI AND MATTEO ROCCA Université de la Vallée d Aoste
Journal of Inequalities in Pure and Applied Mathematics MONOTONE TRAJECTORIES OF DYNAMICAL SYSTEMS AND CLARKE S GENERALIZED JACOBIAN GIOVANNI P. CRESPI AND MATTEO ROCCA Université de la Vallée d Aoste
MATH 409 Advanced Calculus I Lecture 10: Continuity. Properties of continuous functions.
 MATH 409 Advanced Calculus I Lecture 10: Continuity. Properties of continuous functions. Continuity Definition. Given a set E R, a function f : E R, and a point c E, the function f is continuous at c if
MATH 409 Advanced Calculus I Lecture 10: Continuity. Properties of continuous functions. Continuity Definition. Given a set E R, a function f : E R, and a point c E, the function f is continuous at c if
TAYLOR POLYNOMIALS FOR NABLA DYNAMIC EQUATIONS ON TIME SCALES
 TAYLOR POLYNOMIALS FOR NABLA DYNAMIC EQUATIONS ON TIME SCALES DOUGLAS R. ANDERSON Abtract. We are concerned with the repreentation of polynomial for nabla dynamic equation on time cale. Once etablihed,
TAYLOR POLYNOMIALS FOR NABLA DYNAMIC EQUATIONS ON TIME SCALES DOUGLAS R. ANDERSON Abtract. We are concerned with the repreentation of polynomial for nabla dynamic equation on time cale. Once etablihed,
HOMEWORK ASSIGNMENT 6
 HOMEWORK ASSIGNMENT 6 DUE 15 MARCH, 2016 1) Suppose f, g : A R are uniformly continuous on A. Show that f + g is uniformly continuous on A. Solution First we note: In order to show that f + g is uniformly
HOMEWORK ASSIGNMENT 6 DUE 15 MARCH, 2016 1) Suppose f, g : A R are uniformly continuous on A. Show that f + g is uniformly continuous on A. Solution First we note: In order to show that f + g is uniformly
The Generalized Laplace Transform: Applications to Adaptive Control*
 The Transform: Applications to Adaptive * J.M. Davis 1, I.A. Gravagne 2, B.J. Jackson 1, R.J. Marks II 2, A.A. Ramos 1 1 Department of Mathematics 2 Department of Electrical Engineering Baylor University
The Transform: Applications to Adaptive * J.M. Davis 1, I.A. Gravagne 2, B.J. Jackson 1, R.J. Marks II 2, A.A. Ramos 1 1 Department of Mathematics 2 Department of Electrical Engineering Baylor University
Functional Differential Equations with Causal Operators
 ISSN 1749-3889 (print), 1749-3897 (online) International Journal of Nonlinear Science Vol.11(211) No.4,pp.499-55 Functional Differential Equations with Causal Operators Vasile Lupulescu Constantin Brancusi
ISSN 1749-3889 (print), 1749-3897 (online) International Journal of Nonlinear Science Vol.11(211) No.4,pp.499-55 Functional Differential Equations with Causal Operators Vasile Lupulescu Constantin Brancusi
MULTIPLE POSITIVE SOLUTIONS FOR DYNAMIC m-point BOUNDARY VALUE PROBLEMS
 Dynamic Systems and Applications 17 (2008) 25-42 MULTIPLE POSITIVE SOLUTIONS FOR DYNAMIC m-point BOUNDARY VALUE PROBLEMS ILKAY YASLAN KARACA Department of Mathematics Ege University, 35100 Bornova, Izmir,
Dynamic Systems and Applications 17 (2008) 25-42 MULTIPLE POSITIVE SOLUTIONS FOR DYNAMIC m-point BOUNDARY VALUE PROBLEMS ILKAY YASLAN KARACA Department of Mathematics Ege University, 35100 Bornova, Izmir,
Iowa State University. Instructor: Alex Roitershtein Summer Homework #5. Solutions
 Math 50 Iowa State University Introduction to Real Analysis Department of Mathematics Instructor: Alex Roitershtein Summer 205 Homework #5 Solutions. Let α and c be real numbers, c > 0, and f is defined
Math 50 Iowa State University Introduction to Real Analysis Department of Mathematics Instructor: Alex Roitershtein Summer 205 Homework #5 Solutions. Let α and c be real numbers, c > 0, and f is defined
Properties of the Generalized Laplace Transform and Transport Partial Dynamic Equation on Time Scales
 University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln Dissertations, Theses, and Student Research Papers in Mathematics Mathematics, Department of 200 Properties of the Generalized
University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln Dissertations, Theses, and Student Research Papers in Mathematics Mathematics, Department of 200 Properties of the Generalized
d(x n, x) d(x n, x nk ) + d(x nk, x) where we chose any fixed k > N
 Problem 1. Let f : A R R have the property that for every x A, there exists ɛ > 0 such that f(t) > ɛ if t (x ɛ, x + ɛ) A. If the set A is compact, prove there exists c > 0 such that f(x) > c for all x
Problem 1. Let f : A R R have the property that for every x A, there exists ɛ > 0 such that f(t) > ɛ if t (x ɛ, x + ɛ) A. If the set A is compact, prove there exists c > 0 such that f(x) > c for all x
Lecture Notes in Advanced Calculus 1 (80315) Raz Kupferman Institute of Mathematics The Hebrew University
 Lecture Notes in Advanced Calculus 1 (80315) Raz Kupferman Institute of Mathematics The Hebrew University February 7, 2007 2 Contents 1 Metric Spaces 1 1.1 Basic definitions...........................
Lecture Notes in Advanced Calculus 1 (80315) Raz Kupferman Institute of Mathematics The Hebrew University February 7, 2007 2 Contents 1 Metric Spaces 1 1.1 Basic definitions...........................
Homework 4, 5, 6 Solutions. > 0, and so a n 0 = n + 1 n = ( n+1 n)( n+1+ n) 1 if n is odd 1/n if n is even diverges.
 2..2(a) lim a n = 0. Homework 4, 5, 6 Solutions Proof. Let ɛ > 0. Then for n n = 2+ 2ɛ we have 2n 3 4+ ɛ 3 > ɛ > 0, so 0 < 2n 3 < ɛ, and thus a n 0 = 2n 3 < ɛ. 2..2(g) lim ( n + n) = 0. Proof. Let ɛ >
2..2(a) lim a n = 0. Homework 4, 5, 6 Solutions Proof. Let ɛ > 0. Then for n n = 2+ 2ɛ we have 2n 3 4+ ɛ 3 > ɛ > 0, so 0 < 2n 3 < ɛ, and thus a n 0 = 2n 3 < ɛ. 2..2(g) lim ( n + n) = 0. Proof. Let ɛ >
Tangent Space and Derivative Mapping on Time Scale
 International J.Math. Combin. Vol.2 (2009, 01-10 Tangent Space and Derivative Mapping on Time Scale Emin ÖZYILMAZ (Department of Mathematics,University of Ege, 35100, İzmir, Turkey E-mail: emin.ozyilmaz@ege.edu.tr
International J.Math. Combin. Vol.2 (2009, 01-10 Tangent Space and Derivative Mapping on Time Scale Emin ÖZYILMAZ (Department of Mathematics,University of Ege, 35100, İzmir, Turkey E-mail: emin.ozyilmaz@ege.edu.tr
Nonlinear Control Systems
 Nonlinear Control Systems António Pedro Aguiar pedro@isr.ist.utl.pt 3. Fundamental properties IST-DEEC PhD Course http://users.isr.ist.utl.pt/%7epedro/ncs2012/ 2012 1 Example Consider the system ẋ = f
Nonlinear Control Systems António Pedro Aguiar pedro@isr.ist.utl.pt 3. Fundamental properties IST-DEEC PhD Course http://users.isr.ist.utl.pt/%7epedro/ncs2012/ 2012 1 Example Consider the system ẋ = f
Economics 204 Summer/Fall 2011 Lecture 5 Friday July 29, 2011
 Economics 204 Summer/Fall 2011 Lecture 5 Friday July 29, 2011 Section 2.6 (cont.) Properties of Real Functions Here we first study properties of functions from R to R, making use of the additional structure
Economics 204 Summer/Fall 2011 Lecture 5 Friday July 29, 2011 Section 2.6 (cont.) Properties of Real Functions Here we first study properties of functions from R to R, making use of the additional structure
UNIQUENESS OF SOLUTIONS TO MATRIX EQUATIONS ON TIME SCALES
 Electronic Journal of Differential Equations, Vol. 2013 (2013), No. 50, pp. 1 13. ISSN: 1072-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu UNIQUENESS OF
Electronic Journal of Differential Equations, Vol. 2013 (2013), No. 50, pp. 1 13. ISSN: 1072-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu UNIQUENESS OF
NOTES AND ERRATA FOR RECURRENCE AND TOPOLOGY. (τ + arg z) + 1
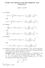 NOTES AND ERRATA FOR RECURRENCE AND TOPOLOGY JOHN M. ALONGI p.11 Replace ρ(t, z) = ρ(t, z) = p.11 Replace sin 2 z e τ ] 2 (τ + arg z) + 1 1 + z (e τ dτ. sin 2 (τ + arg z) + 1 z 2 z e τ ] 2 1 + z (e τ dτ.
NOTES AND ERRATA FOR RECURRENCE AND TOPOLOGY JOHN M. ALONGI p.11 Replace ρ(t, z) = ρ(t, z) = p.11 Replace sin 2 z e τ ] 2 (τ + arg z) + 1 1 + z (e τ dτ. sin 2 (τ + arg z) + 1 z 2 z e τ ] 2 1 + z (e τ dτ.
Economics 204 Fall 2011 Problem Set 2 Suggested Solutions
 Economics 24 Fall 211 Problem Set 2 Suggested Solutions 1. Determine whether the following sets are open, closed, both or neither under the topology induced by the usual metric. (Hint: think about limit
Economics 24 Fall 211 Problem Set 2 Suggested Solutions 1. Determine whether the following sets are open, closed, both or neither under the topology induced by the usual metric. (Hint: think about limit
ON THE BEHAVIOR OF SOLUTIONS OF LINEAR NEUTRAL INTEGRODIFFERENTIAL EQUATIONS WITH UNBOUNDED DELAY
 Georgian Mathematical Journal Volume 11 (24), Number 2, 337 348 ON THE BEHAVIOR OF SOLUTIONS OF LINEAR NEUTRAL INTEGRODIFFERENTIAL EQUATIONS WITH UNBOUNDED DELAY I.-G. E. KORDONIS, CH. G. PHILOS, I. K.
Georgian Mathematical Journal Volume 11 (24), Number 2, 337 348 ON THE BEHAVIOR OF SOLUTIONS OF LINEAR NEUTRAL INTEGRODIFFERENTIAL EQUATIONS WITH UNBOUNDED DELAY I.-G. E. KORDONIS, CH. G. PHILOS, I. K.
This exam contains 5 pages (including this cover page) and 4 questions. The total number of points is 100. Grade Table
 MAT25-2 Summer Session 2 207 Practice Final August 24th, 207 Time Limit: Hour 40 Minutes Name: Instructor: Nathaniel Gallup This exam contains 5 pages (including this cover page) and 4 questions. The total
MAT25-2 Summer Session 2 207 Practice Final August 24th, 207 Time Limit: Hour 40 Minutes Name: Instructor: Nathaniel Gallup This exam contains 5 pages (including this cover page) and 4 questions. The total
Reflected Brownian Motion
 Chapter 6 Reflected Brownian Motion Often we encounter Diffusions in regions with boundary. If the process can reach the boundary from the interior in finite time with positive probability we need to decide
Chapter 6 Reflected Brownian Motion Often we encounter Diffusions in regions with boundary. If the process can reach the boundary from the interior in finite time with positive probability we need to decide
Numerical Sequences and Series
 Numerical Sequences and Series Written by Men-Gen Tsai email: b89902089@ntu.edu.tw. Prove that the convergence of {s n } implies convergence of { s n }. Is the converse true? Solution: Since {s n } is
Numerical Sequences and Series Written by Men-Gen Tsai email: b89902089@ntu.edu.tw. Prove that the convergence of {s n } implies convergence of { s n }. Is the converse true? Solution: Since {s n } is
converges as well if x < 1. 1 x n x n 1 1 = 2 a nx n
 Solve the following 6 problems. 1. Prove that if series n=1 a nx n converges for all x such that x < 1, then the series n=1 a n xn 1 x converges as well if x < 1. n For x < 1, x n 0 as n, so there exists
Solve the following 6 problems. 1. Prove that if series n=1 a nx n converges for all x such that x < 1, then the series n=1 a n xn 1 x converges as well if x < 1. n For x < 1, x n 0 as n, so there exists
DELAY INTEGRO DIFFERENTIAL EQUATIONS OF MIXED TYPE IN BANACH SPACES. Tadeusz Jankowski Technical University of Gdańsk, Poland
 GLASNIK MATEMATIČKI Vol. 37(57)(22), 32 33 DELAY INTEGRO DIFFERENTIAL EQUATIONS OF MIXED TYPE IN BANACH SPACES Tadeusz Jankowski Technical University of Gdańsk, Poland Abstract. This paper contains sufficient
GLASNIK MATEMATIČKI Vol. 37(57)(22), 32 33 DELAY INTEGRO DIFFERENTIAL EQUATIONS OF MIXED TYPE IN BANACH SPACES Tadeusz Jankowski Technical University of Gdańsk, Poland Abstract. This paper contains sufficient
Some nonlinear dynamic inequalities on time scales
 Proc. Indian Acad. Sci. Math. Sci.) Vol. 117, No. 4, November 2007,. 545 554. Printed in India Some nonlinear dynamic inequalities on time scales WEI NIAN LI 1,2 and WEIHONG SHENG 1 1 Deartment of Mathematics,
Proc. Indian Acad. Sci. Math. Sci.) Vol. 117, No. 4, November 2007,. 545 554. Printed in India Some nonlinear dynamic inequalities on time scales WEI NIAN LI 1,2 and WEIHONG SHENG 1 1 Deartment of Mathematics,
Calculus C (ordinary differential equations)
 Calculus C (ordinary differential equations) Lesson 1: Ordinary first order differential equations Separable differential equations Autonomous differential equations Logistic growth Frank Hansen Institute
Calculus C (ordinary differential equations) Lesson 1: Ordinary first order differential equations Separable differential equations Autonomous differential equations Logistic growth Frank Hansen Institute
MAT 570 REAL ANALYSIS LECTURE NOTES. Contents. 1. Sets Functions Countability Axiom of choice Equivalence relations 9
 MAT 570 REAL ANALYSIS LECTURE NOTES PROFESSOR: JOHN QUIGG SEMESTER: FALL 204 Contents. Sets 2 2. Functions 5 3. Countability 7 4. Axiom of choice 8 5. Equivalence relations 9 6. Real numbers 9 7. Extended
MAT 570 REAL ANALYSIS LECTURE NOTES PROFESSOR: JOHN QUIGG SEMESTER: FALL 204 Contents. Sets 2 2. Functions 5 3. Countability 7 4. Axiom of choice 8 5. Equivalence relations 9 6. Real numbers 9 7. Extended
Real Analysis Problems
 Real Analysis Problems Cristian E. Gutiérrez September 14, 29 1 1 CONTINUITY 1 Continuity Problem 1.1 Let r n be the sequence of rational numbers and Prove that f(x) = 1. f is continuous on the irrationals.
Real Analysis Problems Cristian E. Gutiérrez September 14, 29 1 1 CONTINUITY 1 Continuity Problem 1.1 Let r n be the sequence of rational numbers and Prove that f(x) = 1. f is continuous on the irrationals.
Principle of Mathematical Induction
 Advanced Calculus I. Math 451, Fall 2016, Prof. Vershynin Principle of Mathematical Induction 1. Prove that 1 + 2 + + n = 1 n(n + 1) for all n N. 2 2. Prove that 1 2 + 2 2 + + n 2 = 1 n(n + 1)(2n + 1)
Advanced Calculus I. Math 451, Fall 2016, Prof. Vershynin Principle of Mathematical Induction 1. Prove that 1 + 2 + + n = 1 n(n + 1) for all n N. 2 2. Prove that 1 2 + 2 2 + + n 2 = 1 n(n + 1)(2n + 1)
Fundamental Inequalities, Convergence and the Optional Stopping Theorem for Continuous-Time Martingales
 Fundamental Inequalities, Convergence and the Optional Stopping Theorem for Continuous-Time Martingales Prakash Balachandran Department of Mathematics Duke University April 2, 2008 1 Review of Discrete-Time
Fundamental Inequalities, Convergence and the Optional Stopping Theorem for Continuous-Time Martingales Prakash Balachandran Department of Mathematics Duke University April 2, 2008 1 Review of Discrete-Time
h(x) lim H(x) = lim Since h is nondecreasing then h(x) 0 for all x, and if h is discontinuous at a point x then H(x) > 0. Denote
 Real Variables, Fall 4 Problem set 4 Solution suggestions Exercise. Let f be of bounded variation on [a, b]. Show that for each c (a, b), lim x c f(x) and lim x c f(x) exist. Prove that a monotone function
Real Variables, Fall 4 Problem set 4 Solution suggestions Exercise. Let f be of bounded variation on [a, b]. Show that for each c (a, b), lim x c f(x) and lim x c f(x) exist. Prove that a monotone function
4.6 Montel's Theorem. Robert Oeckl CA NOTES 7 17/11/2009 1
 Robert Oeckl CA NOTES 7 17/11/2009 1 4.6 Montel's Theorem Let X be a topological space. We denote by C(X) the set of complex valued continuous functions on X. Denition 4.26. A topological space is called
Robert Oeckl CA NOTES 7 17/11/2009 1 4.6 Montel's Theorem Let X be a topological space. We denote by C(X) the set of complex valued continuous functions on X. Denition 4.26. A topological space is called
f(s)ds, i.e. to write down the general solution in
 1. First order ODEs. Simplest examples. Existence and uniqueness theorem Example 1.1. Consider the equation (1.1) x (t) = 1 This is an equation because there is an unknown: the function x(t). This is a
1. First order ODEs. Simplest examples. Existence and uniqueness theorem Example 1.1. Consider the equation (1.1) x (t) = 1 This is an equation because there is an unknown: the function x(t). This is a
Existence of a Limit on a Dense Set, and. Construction of Continuous Functions on Special Sets
 Existence of a Limit on a Dense Set, and Construction of Continuous Functions on Special Sets REU 2012 Recap: Definitions Definition Given a real-valued function f, the limit of f exists at a point c R
Existence of a Limit on a Dense Set, and Construction of Continuous Functions on Special Sets REU 2012 Recap: Definitions Definition Given a real-valued function f, the limit of f exists at a point c R
QUALITATIVE ANALYSIS OF DYNAMIC EQUATIONS ON TIME SCALES
 Electronic Journal of Differential Equations, Vol. 2018 (2018), No. 51, pp. 1 13. ISSN: 1072-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu QUALITATIVE ANALYSIS OF DYNAMIC EQUATIONS
Electronic Journal of Differential Equations, Vol. 2018 (2018), No. 51, pp. 1 13. ISSN: 1072-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu QUALITATIVE ANALYSIS OF DYNAMIC EQUATIONS
Midterm 1. Every element of the set of functions is continuous
 Econ 200 Mathematics for Economists Midterm Question.- Consider the set of functions F C(0, ) dened by { } F = f C(0, ) f(x) = ax b, a A R and b B R That is, F is a subset of the set of continuous functions
Econ 200 Mathematics for Economists Midterm Question.- Consider the set of functions F C(0, ) dened by { } F = f C(0, ) f(x) = ax b, a A R and b B R That is, F is a subset of the set of continuous functions
Course 212: Academic Year Section 1: Metric Spaces
 Course 212: Academic Year 1991-2 Section 1: Metric Spaces D. R. Wilkins Contents 1 Metric Spaces 3 1.1 Distance Functions and Metric Spaces............. 3 1.2 Convergence and Continuity in Metric Spaces.........
Course 212: Academic Year 1991-2 Section 1: Metric Spaces D. R. Wilkins Contents 1 Metric Spaces 3 1.1 Distance Functions and Metric Spaces............. 3 1.2 Convergence and Continuity in Metric Spaces.........
Lecture 4: Numerical solution of ordinary differential equations
 Lecture 4: Numerical solution of ordinary differential equations Department of Mathematics, ETH Zürich General explicit one-step method: Consistency; Stability; Convergence. High-order methods: Taylor
Lecture 4: Numerical solution of ordinary differential equations Department of Mathematics, ETH Zürich General explicit one-step method: Consistency; Stability; Convergence. High-order methods: Taylor
A brief introduction to ordinary differential equations
 Chapter 1 A brief introduction to ordinary differential equations 1.1 Introduction An ordinary differential equation (ode) is an equation that relates a function of one variable, y(t), with its derivative(s)
Chapter 1 A brief introduction to ordinary differential equations 1.1 Introduction An ordinary differential equation (ode) is an equation that relates a function of one variable, y(t), with its derivative(s)
FRACTIONAL DYNAMIC INEQUALITIES HARMONIZED ON TIME SCALES
 FRACTIONAL DYNAMIC INEQUALITIES HARMONIZED ON TIME SCALES M JIBRIL SHAHAB SAHIR Accepted Mnuscript Version This is the unedited version of the rticle s it ppered upon cceptnce by the journl. A finl edited
FRACTIONAL DYNAMIC INEQUALITIES HARMONIZED ON TIME SCALES M JIBRIL SHAHAB SAHIR Accepted Mnuscript Version This is the unedited version of the rticle s it ppered upon cceptnce by the journl. A finl edited
THEOREMS, ETC., FOR MATH 515
 THEOREMS, ETC., FOR MATH 515 Proposition 1 (=comment on page 17). If A is an algebra, then any finite union or finite intersection of sets in A is also in A. Proposition 2 (=Proposition 1.1). For every
THEOREMS, ETC., FOR MATH 515 Proposition 1 (=comment on page 17). If A is an algebra, then any finite union or finite intersection of sets in A is also in A. Proposition 2 (=Proposition 1.1). For every
On perturbations in the leading coefficient matrix of time-varying index-1 DAEs
 On perturbations in the leading coefficient matrix of time-varying index-1 DAEs Institute of Mathematics, Ilmenau University of Technology Darmstadt, March 27, 2012 Institute of Mathematics, Ilmenau University
On perturbations in the leading coefficient matrix of time-varying index-1 DAEs Institute of Mathematics, Ilmenau University of Technology Darmstadt, March 27, 2012 Institute of Mathematics, Ilmenau University
Homework 11. Solutions
 Homework 11. Solutions Problem 2.3.2. Let f n : R R be 1/n times the characteristic function of the interval (0, n). Show that f n 0 uniformly and f n µ L = 1. Why isn t it a counterexample to the Lebesgue
Homework 11. Solutions Problem 2.3.2. Let f n : R R be 1/n times the characteristic function of the interval (0, n). Show that f n 0 uniformly and f n µ L = 1. Why isn t it a counterexample to the Lebesgue
Proof. We indicate by α, β (finite or not) the end-points of I and call
 C.6 Continuous functions Pag. 111 Proof of Corollary 4.25 Corollary 4.25 Let f be continuous on the interval I and suppose it admits non-zero its (finite or infinite) that are different in sign for x tending
C.6 Continuous functions Pag. 111 Proof of Corollary 4.25 Corollary 4.25 Let f be continuous on the interval I and suppose it admits non-zero its (finite or infinite) that are different in sign for x tending
arxiv: v1 [math.ap] 4 Sep 2007
![arxiv: v1 [math.ap] 4 Sep 2007 arxiv: v1 [math.ap] 4 Sep 2007](/thumbs/83/88184350.jpg) EXISENCE OF POSIIVE SOLUIONS FOR NON LOCAL p-laplacian HERMISOR PROBLEMS ON IME SCALES MOULAY RCHID SIDI AMMI AND DELFIM F. M. ORRES Abstract. We make use of the Guo-Krasnoselskii fixed point theorem on
EXISENCE OF POSIIVE SOLUIONS FOR NON LOCAL p-laplacian HERMISOR PROBLEMS ON IME SCALES MOULAY RCHID SIDI AMMI AND DELFIM F. M. ORRES Abstract. We make use of the Guo-Krasnoselskii fixed point theorem on
Solutions to Problem Set 5 for , Fall 2007
 Solutions to Problem Set 5 for 18.101, Fall 2007 1 Exercise 1 Solution For the counterexample, let us consider M = (0, + ) and let us take V = on M. x Let W be the vector field on M that is identically
Solutions to Problem Set 5 for 18.101, Fall 2007 1 Exercise 1 Solution For the counterexample, let us consider M = (0, + ) and let us take V = on M. x Let W be the vector field on M that is identically
L p Spaces and Convexity
 L p Spaces and Convexity These notes largely follow the treatments in Royden, Real Analysis, and Rudin, Real & Complex Analysis. 1. Convex functions Let I R be an interval. For I open, we say a function
L p Spaces and Convexity These notes largely follow the treatments in Royden, Real Analysis, and Rudin, Real & Complex Analysis. 1. Convex functions Let I R be an interval. For I open, we say a function
FUNDAMENTALS OF REAL ANALYSIS by. II.1. Prelude. Recall that the Riemann integral of a real-valued function f on an interval [a, b] is defined as
![FUNDAMENTALS OF REAL ANALYSIS by. II.1. Prelude. Recall that the Riemann integral of a real-valued function f on an interval [a, b] is defined as FUNDAMENTALS OF REAL ANALYSIS by. II.1. Prelude. Recall that the Riemann integral of a real-valued function f on an interval [a, b] is defined as](/thumbs/83/87136844.jpg) FUNDAMENTALS OF REAL ANALYSIS by Doğan Çömez II. MEASURES AND MEASURE SPACES II.1. Prelude Recall that the Riemann integral of a real-valued function f on an interval [a, b] is defined as b n f(xdx :=
FUNDAMENTALS OF REAL ANALYSIS by Doğan Çömez II. MEASURES AND MEASURE SPACES II.1. Prelude Recall that the Riemann integral of a real-valued function f on an interval [a, b] is defined as b n f(xdx :=
REAL VARIABLES: PROBLEM SET 1. = x limsup E k
 REAL VARIABLES: PROBLEM SET 1 BEN ELDER 1. Problem 1.1a First let s prove that limsup E k consists of those points which belong to infinitely many E k. From equation 1.1: limsup E k = E k For limsup E
REAL VARIABLES: PROBLEM SET 1 BEN ELDER 1. Problem 1.1a First let s prove that limsup E k consists of those points which belong to infinitely many E k. From equation 1.1: limsup E k = E k For limsup E
Advanced Calculus Math 127B, Winter 2005 Solutions: Final. nx2 1 + n 2 x, g n(x) = n2 x
 . Define f n, g n : [, ] R by f n (x) = Advanced Calculus Math 27B, Winter 25 Solutions: Final nx2 + n 2 x, g n(x) = n2 x 2 + n 2 x. 2 Show that the sequences (f n ), (g n ) converge pointwise on [, ],
. Define f n, g n : [, ] R by f n (x) = Advanced Calculus Math 27B, Winter 25 Solutions: Final nx2 + n 2 x, g n(x) = n2 x 2 + n 2 x. 2 Show that the sequences (f n ), (g n ) converge pointwise on [, ],
Econ Slides from Lecture 1
 Econ 205 Sobel Econ 205 - Slides from Lecture 1 Joel Sobel August 23, 2010 Warning I can t start without assuming that something is common knowledge. You can find basic definitions of Sets and Set Operations
Econ 205 Sobel Econ 205 - Slides from Lecture 1 Joel Sobel August 23, 2010 Warning I can t start without assuming that something is common knowledge. You can find basic definitions of Sets and Set Operations
Solution of the 8 th Homework
 Solution of the 8 th Homework Sangchul Lee December 8, 2014 1 Preinary 1.1 A simple remark on continuity The following is a very simple and trivial observation. But still this saves a lot of words in actual
Solution of the 8 th Homework Sangchul Lee December 8, 2014 1 Preinary 1.1 A simple remark on continuity The following is a very simple and trivial observation. But still this saves a lot of words in actual
Continuous Functions on Metric Spaces
 Continuous Functions on Metric Spaces Math 201A, Fall 2016 1 Continuous functions Definition 1. Let (X, d X ) and (Y, d Y ) be metric spaces. A function f : X Y is continuous at a X if for every ɛ > 0
Continuous Functions on Metric Spaces Math 201A, Fall 2016 1 Continuous functions Definition 1. Let (X, d X ) and (Y, d Y ) be metric spaces. A function f : X Y is continuous at a X if for every ɛ > 0
Copyright 2010 Pearson Education, Inc. Publishing as Prentice Hall.
 .1 Limits of Sequences. CHAPTER.1.0. a) True. If converges, then there is an M > 0 such that M. Choose by Archimedes an N N such that N > M/ε. Then n N implies /n M/n M/N < ε. b) False. = n does not converge,
.1 Limits of Sequences. CHAPTER.1.0. a) True. If converges, then there is an M > 0 such that M. Choose by Archimedes an N N such that N > M/ε. Then n N implies /n M/n M/N < ε. b) False. = n does not converge,
Walker Ray Econ 204 Problem Set 3 Suggested Solutions August 6, 2015
 Problem 1. Take any mapping f from a metric space X into a metric space Y. Prove that f is continuous if and only if f(a) f(a). (Hint: use the closed set characterization of continuity). I make use of
Problem 1. Take any mapping f from a metric space X into a metric space Y. Prove that f is continuous if and only if f(a) f(a). (Hint: use the closed set characterization of continuity). I make use of
Measures. Chapter Some prerequisites. 1.2 Introduction
 Lecture notes Course Analysis for PhD students Uppsala University, Spring 2018 Rostyslav Kozhan Chapter 1 Measures 1.1 Some prerequisites I will follow closely the textbook Real analysis: Modern Techniques
Lecture notes Course Analysis for PhD students Uppsala University, Spring 2018 Rostyslav Kozhan Chapter 1 Measures 1.1 Some prerequisites I will follow closely the textbook Real analysis: Modern Techniques
THE INVERSE FUNCTION THEOREM FOR LIPSCHITZ MAPS
 THE INVERSE FUNCTION THEOREM FOR LIPSCHITZ MAPS RALPH HOWARD DEPARTMENT OF MATHEMATICS UNIVERSITY OF SOUTH CAROLINA COLUMBIA, S.C. 29208, USA HOWARD@MATH.SC.EDU Abstract. This is an edited version of a
THE INVERSE FUNCTION THEOREM FOR LIPSCHITZ MAPS RALPH HOWARD DEPARTMENT OF MATHEMATICS UNIVERSITY OF SOUTH CAROLINA COLUMBIA, S.C. 29208, USA HOWARD@MATH.SC.EDU Abstract. This is an edited version of a
A Nonlinear Sturm Picone Comparison Theorem for Dynamic Equations on Time Scales
 International Journal of Difference Equations IJDE). ISSN 0973-6069 Volume 2 Number 1 2007), pp. 25 35 Research India Publications http://www.ripublication.com/ijde.htm A Nonlinear Sturm Picone Comparison
International Journal of Difference Equations IJDE). ISSN 0973-6069 Volume 2 Number 1 2007), pp. 25 35 Research India Publications http://www.ripublication.com/ijde.htm A Nonlinear Sturm Picone Comparison
Stochastic Differential Equations.
 Chapter 3 Stochastic Differential Equations. 3.1 Existence and Uniqueness. One of the ways of constructing a Diffusion process is to solve the stochastic differential equation dx(t) = σ(t, x(t)) dβ(t)
Chapter 3 Stochastic Differential Equations. 3.1 Existence and Uniqueness. One of the ways of constructing a Diffusion process is to solve the stochastic differential equation dx(t) = σ(t, x(t)) dβ(t)
Seminar In Topological Dynamics
 Bar Ilan University Department of Mathematics Seminar In Topological Dynamics EXAMPLES AND BASIC PROPERTIES Harari Ronen May, 2005 1 2 1. Basic functions 1.1. Examples. To set the stage, we begin with
Bar Ilan University Department of Mathematics Seminar In Topological Dynamics EXAMPLES AND BASIC PROPERTIES Harari Ronen May, 2005 1 2 1. Basic functions 1.1. Examples. To set the stage, we begin with
1/12/05: sec 3.1 and my article: How good is the Lebesgue measure?, Math. Intelligencer 11(2) (1989),
 Real Analysis 2, Math 651, Spring 2005 April 26, 2005 1 Real Analysis 2, Math 651, Spring 2005 Krzysztof Chris Ciesielski 1/12/05: sec 3.1 and my article: How good is the Lebesgue measure?, Math. Intelligencer
Real Analysis 2, Math 651, Spring 2005 April 26, 2005 1 Real Analysis 2, Math 651, Spring 2005 Krzysztof Chris Ciesielski 1/12/05: sec 3.1 and my article: How good is the Lebesgue measure?, Math. Intelligencer
Even Number of Positive Solutions for 3n th Order Three-Point Boundary Value Problems on Time Scales K. R. Prasad 1 and N.
 Electronic Journal of Qualitative Theory of Differential Equations 011, No. 98, 1-16; http://www.math.u-szeged.hu/ejqtde/ Even Number of Positive Solutions for 3n th Order Three-Point Boundary Value Problems
Electronic Journal of Qualitative Theory of Differential Equations 011, No. 98, 1-16; http://www.math.u-szeged.hu/ejqtde/ Even Number of Positive Solutions for 3n th Order Three-Point Boundary Value Problems
EXISTENCE OF NEUTRAL STOCHASTIC FUNCTIONAL DIFFERENTIAL EQUATIONS WITH ABSTRACT VOLTERRA OPERATORS
 International Journal of Differential Equations and Applications Volume 7 No. 1 23, 11-17 EXISTENCE OF NEUTRAL STOCHASTIC FUNCTIONAL DIFFERENTIAL EQUATIONS WITH ABSTRACT VOLTERRA OPERATORS Zephyrinus C.
International Journal of Differential Equations and Applications Volume 7 No. 1 23, 11-17 EXISTENCE OF NEUTRAL STOCHASTIC FUNCTIONAL DIFFERENTIAL EQUATIONS WITH ABSTRACT VOLTERRA OPERATORS Zephyrinus C.
The Minimum Speed for a Blocking Problem on the Half Plane
 The Minimum Speed for a Blocking Problem on the Half Plane Alberto Bressan and Tao Wang Department of Mathematics, Penn State University University Park, Pa 16802, USA e-mails: bressan@mathpsuedu, wang
The Minimum Speed for a Blocking Problem on the Half Plane Alberto Bressan and Tao Wang Department of Mathematics, Penn State University University Park, Pa 16802, USA e-mails: bressan@mathpsuedu, wang
Dynamic Systems and Applications xx (2005) pp-pp MULTIPLE INTEGRATION ON TIME SCALES
 Dynamic Systems and Applications xx (2005) pp-pp MULTIPL INTGATION ON TIM SCALS MATIN BOHN AND GUSIN SH. GUSINOV University of Missouri olla, Department of Mathematics and Statistics, olla, Missouri 65401,
Dynamic Systems and Applications xx (2005) pp-pp MULTIPL INTGATION ON TIM SCALS MATIN BOHN AND GUSIN SH. GUSINOV University of Missouri olla, Department of Mathematics and Statistics, olla, Missouri 65401,
Analysis Finite and Infinite Sets The Real Numbers The Cantor Set
 Analysis Finite and Infinite Sets Definition. An initial segment is {n N n n 0 }. Definition. A finite set can be put into one-to-one correspondence with an initial segment. The empty set is also considered
Analysis Finite and Infinite Sets Definition. An initial segment is {n N n n 0 }. Definition. A finite set can be put into one-to-one correspondence with an initial segment. The empty set is also considered
On Stability of Dynamic Equations on Time Scales Via Dichotomic Maps
 Available at http://pvamu.edu/aam Appl. Appl. Math. ISSN: 93-9466 Vol. 7, Issue (December ), pp. 5-57 Applications and Applied Mathematics: An International Journal (AAM) On Stability of Dynamic Equations
Available at http://pvamu.edu/aam Appl. Appl. Math. ISSN: 93-9466 Vol. 7, Issue (December ), pp. 5-57 Applications and Applied Mathematics: An International Journal (AAM) On Stability of Dynamic Equations
Hyers Ulam stability of first-order linear dynamic equations on time scales
 Hyers Ulam stability of first-order linear dynamic equations on time scales Douglas R. Anderson Concordia College, Moorhead, Minnesota USA April 21, 2018, MAA-NCS@Mankato Introduction In 1940, Stan Ulam
Hyers Ulam stability of first-order linear dynamic equations on time scales Douglas R. Anderson Concordia College, Moorhead, Minnesota USA April 21, 2018, MAA-NCS@Mankato Introduction In 1940, Stan Ulam
EXISTENCE AND APPROXIMATION OF SOLUTIONS OF SECOND ORDER NONLINEAR NEUMANN PROBLEMS
 Electronic Journal of Differential Equations, Vol. 2005(2005), No. 03, pp. 1 10. ISSN: 1072-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu (login: ftp) EXISTENCE
Electronic Journal of Differential Equations, Vol. 2005(2005), No. 03, pp. 1 10. ISSN: 1072-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu (login: ftp) EXISTENCE
Introductory Analysis 2 Spring 2010 Exam 1 February 11, 2015
 Introductory Analysis 2 Spring 21 Exam 1 February 11, 215 Instructions: You may use any result from Chapter 2 of Royden s textbook, or from the first four chapters of Pugh s textbook, or anything seen
Introductory Analysis 2 Spring 21 Exam 1 February 11, 215 Instructions: You may use any result from Chapter 2 of Royden s textbook, or from the first four chapters of Pugh s textbook, or anything seen
Lecture 10. Riemann-Stieltjes Integration
 Lecture 10 Riemann-Stieltjes Integration In this section we will develop the basic definitions and some of the properties of the Riemann-Stieltjes Integral. The development will follow that of the Darboux
Lecture 10 Riemann-Stieltjes Integration In this section we will develop the basic definitions and some of the properties of the Riemann-Stieltjes Integral. The development will follow that of the Darboux
MATH 117 LECTURE NOTES
 MATH 117 LECTURE NOTES XIN ZHOU Abstract. This is the set of lecture notes for Math 117 during Fall quarter of 2017 at UC Santa Barbara. The lectures follow closely the textbook [1]. Contents 1. The set
MATH 117 LECTURE NOTES XIN ZHOU Abstract. This is the set of lecture notes for Math 117 during Fall quarter of 2017 at UC Santa Barbara. The lectures follow closely the textbook [1]. Contents 1. The set
EXISTENCE OF POSITIVE SOLUTIONS FOR NON LOCAL p-laplacian THERMISTOR PROBLEMS ON TIME SCALES
 Volume 8 27, Issue 3, Article 69, 1 pp. EXISENCE OF POSIIVE SOLUIONS FOR NON LOCAL p-laplacian HERMISOR PROBLEMS ON IME SCALES MOULAY RCHID SIDI AMMI AND DELFIM F. M. ORRES DEPARMEN OF MAHEMAICS UNIVERSIY
Volume 8 27, Issue 3, Article 69, 1 pp. EXISENCE OF POSIIVE SOLUIONS FOR NON LOCAL p-laplacian HERMISOR PROBLEMS ON IME SCALES MOULAY RCHID SIDI AMMI AND DELFIM F. M. ORRES DEPARMEN OF MAHEMAICS UNIVERSIY
Prove that this gives a bounded linear operator T : X l 1. (6p) Prove that T is a bounded linear operator T : l l and compute (5p)
 Uppsala Universitet Matematiska Institutionen Andreas Strömbergsson Prov i matematik Funktionalanalys Kurs: F3B, F4Sy, NVP 2006-03-17 Skrivtid: 9 14 Tillåtna hjälpmedel: Manuella skrivdon, Kreyszigs bok
Uppsala Universitet Matematiska Institutionen Andreas Strömbergsson Prov i matematik Funktionalanalys Kurs: F3B, F4Sy, NVP 2006-03-17 Skrivtid: 9 14 Tillåtna hjälpmedel: Manuella skrivdon, Kreyszigs bok
SOME PROPERTIES ON THE CLOSED SUBSETS IN BANACH SPACES
 ARCHIVUM MATHEMATICUM (BRNO) Tomus 42 (2006), 167 174 SOME PROPERTIES ON THE CLOSED SUBSETS IN BANACH SPACES ABDELHAKIM MAADEN AND ABDELKADER STOUTI Abstract. It is shown that under natural assumptions,
ARCHIVUM MATHEMATICUM (BRNO) Tomus 42 (2006), 167 174 SOME PROPERTIES ON THE CLOSED SUBSETS IN BANACH SPACES ABDELHAKIM MAADEN AND ABDELKADER STOUTI Abstract. It is shown that under natural assumptions,
Ordinary differential equations. Recall that we can solve a first-order linear inhomogeneous ordinary differential equation (ODE) dy dt
 MATHEMATICS 3103 (Functional Analysis) YEAR 2012 2013, TERM 2 HANDOUT #1: WHAT IS FUNCTIONAL ANALYSIS? Elementary analysis mostly studies real-valued (or complex-valued) functions on the real line R or
MATHEMATICS 3103 (Functional Analysis) YEAR 2012 2013, TERM 2 HANDOUT #1: WHAT IS FUNCTIONAL ANALYSIS? Elementary analysis mostly studies real-valued (or complex-valued) functions on the real line R or
Real Analysis Comprehensive Exam Fall A(k, ε) is of Lebesgue measure zero.
 Real Analysis Comprehensive Exam Fall 2002 by XYC Good luck! [1] For ε>0andk>0, denote by A(k, ε) thesetofx Rsuch that x p q 1 for any integers p, q with q 0. k q 2+ε Show that R \ k=1 A(k, ε) is of Lebesgue
Real Analysis Comprehensive Exam Fall 2002 by XYC Good luck! [1] For ε>0andk>0, denote by A(k, ε) thesetofx Rsuch that x p q 1 for any integers p, q with q 0. k q 2+ε Show that R \ k=1 A(k, ε) is of Lebesgue
t y n (s) ds. t y(s) ds, x(t) = x(0) +
 1 Appendix Definition (Closed Linear Operator) (1) The graph G(T ) of a linear operator T on the domain D(T ) X into Y is the set (x, T x) : x D(T )} in the product space X Y. Then T is closed if its graph
1 Appendix Definition (Closed Linear Operator) (1) The graph G(T ) of a linear operator T on the domain D(T ) X into Y is the set (x, T x) : x D(T )} in the product space X Y. Then T is closed if its graph
Lebesgue Measure on R n
 CHAPTER 2 Lebesgue Measure on R n Our goal is to construct a notion of the volume, or Lebesgue measure, of rather general subsets of R n that reduces to the usual volume of elementary geometrical sets
CHAPTER 2 Lebesgue Measure on R n Our goal is to construct a notion of the volume, or Lebesgue measure, of rather general subsets of R n that reduces to the usual volume of elementary geometrical sets
arxiv: v1 [math.ca] 12 Feb 2010
![arxiv: v1 [math.ca] 12 Feb 2010 arxiv: v1 [math.ca] 12 Feb 2010](/thumbs/93/114127631.jpg) YOUNG S INTEGRAL INEQUALITY WITH UPPER AND LOWER BOUNDS DOUGLAS R. ANDERSON, STEVEN NOREN, AND BRENT PERREAULT arxiv:12.2463v1 [math.ca] 12 Feb 21 Abstract. Young s integral inequality is reformulated
YOUNG S INTEGRAL INEQUALITY WITH UPPER AND LOWER BOUNDS DOUGLAS R. ANDERSON, STEVEN NOREN, AND BRENT PERREAULT arxiv:12.2463v1 [math.ca] 12 Feb 21 Abstract. Young s integral inequality is reformulated
4th Preparation Sheet - Solutions
 Prof. Dr. Rainer Dahlhaus Probability Theory Summer term 017 4th Preparation Sheet - Solutions Remark: Throughout the exercise sheet we use the two equivalent definitions of separability of a metric space
Prof. Dr. Rainer Dahlhaus Probability Theory Summer term 017 4th Preparation Sheet - Solutions Remark: Throughout the exercise sheet we use the two equivalent definitions of separability of a metric space
Oscillation of second-order differential equations with a sublinear neutral term
 CARPATHIAN J. ATH. 30 2014), No. 1, 1-6 Online version available at http://carpathian.ubm.ro Print Edition: ISSN 1584-2851 Online Edition: ISSN 1843-4401 Oscillation of second-order differential equations
CARPATHIAN J. ATH. 30 2014), No. 1, 1-6 Online version available at http://carpathian.ubm.ro Print Edition: ISSN 1584-2851 Online Edition: ISSN 1843-4401 Oscillation of second-order differential equations
Solutions Final Exam May. 14, 2014
 Solutions Final Exam May. 14, 2014 1. Determine whether the following statements are true or false. Justify your answer (i.e., prove the claim, derive a contradiction or give a counter-example). (a) (10
Solutions Final Exam May. 14, 2014 1. Determine whether the following statements are true or false. Justify your answer (i.e., prove the claim, derive a contradiction or give a counter-example). (a) (10
