Parametric Curves You Should Know
|
|
|
- Jonas Norman
- 5 years ago
- Views:
Transcription
1 Parametric Curves You Should Know Straight Lines Let a and c be constants which are not both zero. Then the parametric equations determining the straight line passing through (b d) with slope c/a (i.e. the line y d = c/a(x b)) are: { x(t) = at + b < t <. y(t) = ct + d Note that when c = 0 the line is horizontal of the form y = d and when a = 0 the line is vertical of the form x = b x(t) = 2t + 3 y(t) = t + 4 x(t) = 3-2t y(t) = 2t + 1 x(t) = t + 2 y(t) = 3-3t x(t) = 3 y(t) = 2 + 3t x(t) = 2 + 3t y(t) = Figure 1 A collection of lines whose parametric equations are given as above. Circles Let r > 0 and let x 0 and y 0 be real numbers. Then the parametric equations determining the circle of radius r centered at (x 0 y 0 ) are: { x(t) = r cos t + x0 y(t) = r sin t + y 0 0 < t < 2π. (1) To get a circular arc instead of the full circle restrict the t-values in (1) to t 1 < t < t 2. 1
2 (3-1) -1 (3-1) (a) 0 t 2π (b) π/4 t 7π/6 Figure 2 The circle x(t) = 2 cos t + 3 y(t) = 2 sin t 1 and a circular arc thereof. Note that the center is at (3 1). Circles tangent to the x- and/or y-axes occur as special one-petal cases of the roses covered below. Ellipses Ellipses are algebraically similar to circles and so their parametric equations are qualitatively similar. In particular let r 1 r 2 > 0 and let x 0 and y 0 be real numbers. Then the parametric equations determining the ellipse of horizontal radius r 1 and vertical radius r 2 centered at (x 0 y 0 ) are: { x(t) = r1 cos t + x 0 y(t) = r 2 sin t + y 0 0 < t < 2π. (2) Obviously when r 1 = r 2 in (2) your ellipse is a circle with parametric equation (1). Spirals One way to describe a spiral qualitatively is to say that its the shape formed when the angle (cos t sin t) is proportional to the value t i.e. its parametric equations have the form: { x(t) = c1 t cos t + x 0 y(t) = c 2 t sin t + y 0 0 < t < t terminal (c 1 c 2 constants; x 1 x 2 real numbers). (3) Here the spiral will cross the horizontal line y = y 0 (e.g. the x-axis when y 0 = 0) precisely t terminal times. In the event that x 0 = y 0 = 0 and c 1 = c 2 = 1 the spiral is a circular spiral spiraling about the origin: Figure below shows how the spiral grows as t gets larger. 2
3 (3-0.1) x(t) = 0.cos(t) + 3 y(t) = 0.2sin(t) Figure 3 The ellipse x(t) = 0. cos t + 3 y(t) = 0.2 sin t t 2π. Note that the center is at (3 1) Figure 4 The spiral whose parametric equations are given by x(t) = t cos t y(t) = t sin t 0 t 6π. Cycloids Cycloids are curves traced out by a point P on the circumference of a circle as the circle rolls along a straight line. The picture below shows what this looks like with a (pink) point P on the circumference of a (blue) circle rolling along the (black) straight line (/axis). 3
4 There s a complicated procedure by which you can figure out the parametric equations producing various cycloids but the gist is this: The parametric equations defining a cycloid formed when a circle of radius r is rolled n times is { x(t) = r(t sin t) y(t) = r(1 cos t) 0 < t < nrπ. So for example a circle of radius 2 which is rolled 12 times will have the parametric equations { x(t) = 2(t sin t) y(t) = 2(1 cos t) 0 < t < 24π. The following figure shows a number of cycloids. x(t) = 2(t -sin t) y(t) = 2(1-cos t) x(t) = 4(t -sin t) y(t) = 4(1-cos t) x(t) = 8(t -sin t) y(t) = 8(1-cos t) x(t) = 12(t -sin t) y(t) = 12(1-cos t) x(t) = 24(t -sin t) y(t) = 24(1-cos t) Figure A collection of cycloids whose parametric equations are given as above all plotted for 0 < t < 24π. Notice that the number of rollings is given by 24/r for the various radii provided (so that r = 2 is rolled 12 times but r = 24 is rolled once). Related Curves Interestingly the cycloid described above is one of a number of cycloid-type parametric curves which are defined similarly and which therefore have similar parametric representations. For example the curtate cycloid is a curve traced out by a (red) point P on the interior of a given (blue) circle rolling along the (black) straight line (/axis): There s also the prolate cycloid formed by a (red) point P on the exterior of a given (blue) circle rolling along the (black) straight line (/axis): 4
5 As it happens the curtate cycloid is defined by parametric equations of the form { x(t) = at b sin t 0 < t < t y(t) = a b cos t terminal (4) for a > b while the prolate cycloid is defined by the same parametric equations (4) with a < b. Limaçons and Cardioids Curves defined by parametric equations of the form { x(t) = (1 + c sin t) cos t y(t) = (1 + c sin t) sin t 0 < t < 2π (c constant) () are called limaçons. Figure 11 below shows limaçons for various values c. When c = ±1 the equations in () become { x(t) = (1 ± sin t) cos t 0 < t < 2π (6) y(t) = (1 ± sin t) sin t and the associated curve is called a cardioid. Alternatively horizontal analogues of (6) can be obtained by replacing (1 + sin t) in (6) by (1 + cos t): { x(t) = (1 ± cos t) cos t 0 < t < 2π. (7) y(t) = (1 ± cos t) sin t The curves obtained from (6) and (7) are shown in figure 6 below. (a) x(t) = (1 ± sin t) cos t y(t) = (1 ± sin t) sin t (plus in blue minus in orange) Figure 6 Vertical and horizontal cardioids (b) x(t) = (1 ± cos t) cos t y(t) = (1 ± sin t) cos t (plus in blue minus in orange)
6 Roses Consider the parametric curves shown in the following figures: (a) Figure 7 Various roses. (b) Unsurprisingly these curves are called roses. There are four general forms for the parametric curves defining roses: The equations defining the roses in figure (7a) have the form { x(t) = ± sin(ct) cos t 0 < t < 2π (c constant) (8) y(t) = ± sin(ct) sin t (where + sin(ct) is in blue and sin(ct) is in orange) while the equations defining those in (7b) have the form { x(t) = ± sin(ct) sin t 0 < t < 2π (c constant). (9) y(t) = ± sin(ct) cos t (with + sin(ct) and sin(ct) again in blue and orange respectively). When c is odd the roses in (8) and (9) have c petals; when c is even they have 2c petals. Figure 12 below shows curves corresponding to (8) for varying values of c. In the special case that c = 1 the result is four roses with one petal i.e. circles. In contrast to the circles shown in figure 2 above the one-petal roses are tangent to the x- and y-axes. Figure 8 illustrates this case. Important Note As we saw in class replacing cos t and sin t with cos(kt) and sin(kt) respectively in (1) will yield a curve which graphically is the same as that rendered by (1) but which loops around k times instead of once. Figure 9 below demonstrates precisely that via the parametric equations x(t) = cos(kt) y(t) = sin(kt) 0 t 2π for the values k = 1 k = and k = 0. 6
7 (a) x(t) = ± sin t cos t y(t) = ± sin t sin t (plus in blue minus in orange) (b) x(t) = ± sin t sin t y(t) = ± sin t cos t (plus in blue minus in orange) Figure 8 Various one-petal roses (i.e. circles tangent to the x- and y-axes) x(t) = cos(t) y(t) = sin(t) x(t) = cos(t) y(t) = sin(t) x(t) = cos(0t) y(t) = sin(0t) Figure 9 Curves which are identical as curves but which are different as parametric curves (i.e. curves + their associated parametric equations). Note too that for these parametrizations varying the terminal value t terminal may also yield the same curve: For example x(t) = cos(kt) and y(t) = sin(kt) yield graphs which are unit circles for all k and for all parameter values 0 t 2π + c for all values c 0. This tells us that parametric curves aren t unique; even more concretely it tells us that there are often multiple parametrizations which yield the same curve. This fact will be very important when we start doing calculus (e.g. definite integration) because presumably the mechanisms we employ there should yield correct results while allowing for different parametrizations. These are ideas we ll revisit later. 7
8 0 < t < π 12 0 < t < π 6 0 < t < π < t < π 3 0 < t < π 12 0 < t < π < t < 7 π 12 0 < t < 2 π 3 0 < t < 3 π < t < π 6 0 < t < 11 π 12 0 < t < π Figure The growth of the spiral whose parametric equations are given by x(t) = t cos t y(t) = t sin t 8 for increasing values of t.
9 c = -2 c = -3 / 2 c = -1 c = -1 / 2 c = 0 c = 1 / 2 c = 1 c = 3 / 2 c = 2 Figure 11 Limaçons of the form x(t) = (1 + c sin t) cos t y(t) = (1 + c sin t) sin t for various values c. 9
10 c = -4 c = -3 c = -2 c = -1 c = 0 c = 1 c = 2 c = 3 c = 4 Figure 12 Roses of the form x(t) = ± sin(ct) cos t y(t) = ± sin(ct) sin t 0 < t < 2π for various values of c. Note that when c is even there are 2c petals and that the blue and orange curves coincide; otherwise there are c petals and the blue and orange curves are unique. Also when c = 0 x(t) = 0 = y(t).
Find the rectangular coordinates for each of the following polar coordinates:
 WORKSHEET 13.1 1. Plot the following: 7 3 A. 6, B. 3, 6 4 5 8 D. 6, 3 C., 11 2 E. 5, F. 4, 6 3 Find the rectangular coordinates for each of the following polar coordinates: 5 2 2. 4, 3. 8, 6 3 Given the
WORKSHEET 13.1 1. Plot the following: 7 3 A. 6, B. 3, 6 4 5 8 D. 6, 3 C., 11 2 E. 5, F. 4, 6 3 Find the rectangular coordinates for each of the following polar coordinates: 5 2 2. 4, 3. 8, 6 3 Given the
A different parametric curve ( t, t 2 ) traces the same curve, but this time the par-
 Parametric Curves: Suppose a particle is moving around in a circle or any curve that fails the vertical line test, then we cannot describe the path of this particle using an equation of the form y fx)
Parametric Curves: Suppose a particle is moving around in a circle or any curve that fails the vertical line test, then we cannot describe the path of this particle using an equation of the form y fx)
Section 8.4 Plane Curves and Parametric Equations
 Section 8.4 Plane Curves and Parametric Equations Suppose that x and y are both given as functions of a third variable t (called a parameter) by the equations x = f(t), y = g(t) (called parametric equations).
Section 8.4 Plane Curves and Parametric Equations Suppose that x and y are both given as functions of a third variable t (called a parameter) by the equations x = f(t), y = g(t) (called parametric equations).
10.1 Curves Defined by Parametric Equation
 10.1 Curves Defined by Parametric Equation 1. Imagine that a particle moves along the curve C shown below. It is impossible to describe C by an equation of the form y = f (x) because C fails the Vertical
10.1 Curves Defined by Parametric Equation 1. Imagine that a particle moves along the curve C shown below. It is impossible to describe C by an equation of the form y = f (x) because C fails the Vertical
8.2 Graphs of Polar Equations
 8. Graphs of Polar Equations Definition: A polar equation is an equation whose variables are polar coordinates. One method used to graph a polar equation is to convert the equation to rectangular form.
8. Graphs of Polar Equations Definition: A polar equation is an equation whose variables are polar coordinates. One method used to graph a polar equation is to convert the equation to rectangular form.
Chapter 10: Conic Sections; Polar Coordinates; Parametric Equations
 Chapter 10: Conic Sections; Polar Coordinates; Parametric Equations Section 10.1 Geometry of Parabola, Ellipse, Hyperbola a. Geometric Definition b. Parabola c. Ellipse d. Hyperbola e. Translations f.
Chapter 10: Conic Sections; Polar Coordinates; Parametric Equations Section 10.1 Geometry of Parabola, Ellipse, Hyperbola a. Geometric Definition b. Parabola c. Ellipse d. Hyperbola e. Translations f.
= 3, the vertical velocty is. (x(t), y(t)) = (1 + 3t, 2 + 4t) for t [0, 1],
![= 3, the vertical velocty is. (x(t), y(t)) = (1 + 3t, 2 + 4t) for t [0, 1], = 3, the vertical velocty is. (x(t), y(t)) = (1 + 3t, 2 + 4t) for t [0, 1],](/thumbs/88/117509611.jpg) Math 133 Parametric Curves Stewart 10.1 Back to pictures! We have emphasized four conceptual levels, or points of view on mathematics: physical, geometric, numerical, algebraic. The physical viewpoint
Math 133 Parametric Curves Stewart 10.1 Back to pictures! We have emphasized four conceptual levels, or points of view on mathematics: physical, geometric, numerical, algebraic. The physical viewpoint
Vector Functions & Space Curves MATH 2110Q
 Vector Functions & Space Curves Vector Functions & Space Curves Vector Functions Definition A vector function or vector-valued function is a function that takes real numbers as inputs and gives vectors
Vector Functions & Space Curves Vector Functions & Space Curves Vector Functions Definition A vector function or vector-valued function is a function that takes real numbers as inputs and gives vectors
Name: SOLUTIONS Date: 09/07/2017. M20550 Calculus III Tutorial Worksheet 2
 M20550 Calculus III Tutorial Worksheet 2 1. Find an equation of the plane passes through the point (1, 1, 7) and perpendicular to the line x = 1 + 4t, y = 1 t, z = 3. Solution: To write an equation of
M20550 Calculus III Tutorial Worksheet 2 1. Find an equation of the plane passes through the point (1, 1, 7) and perpendicular to the line x = 1 + 4t, y = 1 t, z = 3. Solution: To write an equation of
Unit 10 Parametric and Polar Equations - Classwork
 Unit 10 Parametric and Polar Equations - Classwork Until now, we have been representing graphs by single equations involving variables x and y. We will now study problems with which 3 variables are used
Unit 10 Parametric and Polar Equations - Classwork Until now, we have been representing graphs by single equations involving variables x and y. We will now study problems with which 3 variables are used
Calculus and Parametric Equations
 Calculus and Parametric Equations MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Given a pair a parametric equations x = f (t) y = g(t) for a t b we know how
Calculus and Parametric Equations MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Given a pair a parametric equations x = f (t) y = g(t) for a t b we know how
Calculus III. George Voutsadakis 1. LSSU Math 251. Lake Superior State University. 1 Mathematics and Computer Science
 Calculus III George Voutsadakis 1 1 Mathematics and Computer Science Lake Superior State University LSSU Math 251 George Voutsadakis (LSSU) Calculus III January 2016 1 / 76 Outline 1 Parametric Equations,
Calculus III George Voutsadakis 1 1 Mathematics and Computer Science Lake Superior State University LSSU Math 251 George Voutsadakis (LSSU) Calculus III January 2016 1 / 76 Outline 1 Parametric Equations,
Chapter 11 Parametric Equations, Polar Curves, and Conic Sections
 Chapter 11 Parametric Equations, Polar Curves, and Conic Sections ü 11.1 Parametric Equations Students should read Sections 11.1-11. of Rogawski's Calculus [1] for a detailed discussion of the material
Chapter 11 Parametric Equations, Polar Curves, and Conic Sections ü 11.1 Parametric Equations Students should read Sections 11.1-11. of Rogawski's Calculus [1] for a detailed discussion of the material
C10.4 Notes and Formulas. (a) (b) (c) Figure 2 (a) A graph is symmetric with respect to the line θ =
 C10.4 Notes and Formulas symmetry tests A polar equation describes a curve on the polar grid. The graph of a polar equation can be evaluated for three types of symmetry, as shown in Figure. Figure A graph
C10.4 Notes and Formulas symmetry tests A polar equation describes a curve on the polar grid. The graph of a polar equation can be evaluated for three types of symmetry, as shown in Figure. Figure A graph
ENGI Parametric Vector Functions Page 5-01
 ENGI 3425 5. Parametric Vector Functions Page 5-01 5. Parametric Vector Functions Contents: 5.1 Arc Length (Cartesian parametric and plane polar) 5.2 Surfaces of Revolution 5.3 Area under a Parametric
ENGI 3425 5. Parametric Vector Functions Page 5-01 5. Parametric Vector Functions Contents: 5.1 Arc Length (Cartesian parametric and plane polar) 5.2 Surfaces of Revolution 5.3 Area under a Parametric
Figure: Aparametriccurveanditsorientation
 Parametric Equations Not all curves are functions. To deal with curves that are not of the form y = f (x) orx = g(y), we use parametric equations. Define both x and y in terms of a parameter t: x = x(t)
Parametric Equations Not all curves are functions. To deal with curves that are not of the form y = f (x) orx = g(y), we use parametric equations. Define both x and y in terms of a parameter t: x = x(t)
10.1 Review of Parametric Equations
 10.1 Review of Parametric Equations Recall that often, instead of representing a curve using just x and y (called a Cartesian equation), it is more convenient to define x and y using parametric equations
10.1 Review of Parametric Equations Recall that often, instead of representing a curve using just x and y (called a Cartesian equation), it is more convenient to define x and y using parametric equations
This set of questions goes with the pages of applets and activities for Lab 09. Use the applets and activities there to answer the questions.
 Page 1 of 5 Lab 09 Name: Start time: Number of questions: 11 This set of questions goes with the pages of applets and activities for Lab 09. Use the applets and activities there to answer the questions.
Page 1 of 5 Lab 09 Name: Start time: Number of questions: 11 This set of questions goes with the pages of applets and activities for Lab 09. Use the applets and activities there to answer the questions.
Figure 10: Tangent vectors approximating a path.
 3 Curvature 3.1 Curvature Now that we re parametrizing curves, it makes sense to wonder how we might measure the extent to which a curve actually curves. That is, how much does our path deviate from being
3 Curvature 3.1 Curvature Now that we re parametrizing curves, it makes sense to wonder how we might measure the extent to which a curve actually curves. That is, how much does our path deviate from being
4 The Cartesian Coordinate System- Pictures of Equations
 4 The Cartesian Coordinate System- Pictures of Equations Concepts: The Cartesian Coordinate System Graphs of Equations in Two Variables x-intercepts and y-intercepts Distance in Two Dimensions and the
4 The Cartesian Coordinate System- Pictures of Equations Concepts: The Cartesian Coordinate System Graphs of Equations in Two Variables x-intercepts and y-intercepts Distance in Two Dimensions and the
Chapter 9 Overview: Parametric and Polar Coordinates
 Chapter 9 Overview: Parametric and Polar Coordinates As we saw briefly last year, there are axis systems other than the Cartesian System for graphing (vector coordinates, polar coordinates, rectangular
Chapter 9 Overview: Parametric and Polar Coordinates As we saw briefly last year, there are axis systems other than the Cartesian System for graphing (vector coordinates, polar coordinates, rectangular
MATH Final Review
 MATH 1592 - Final Review 1 Chapter 7 1.1 Main Topics 1. Integration techniques: Fitting integrands to basic rules on page 485. Integration by parts, Theorem 7.1 on page 488. Guidelines for trigonometric
MATH 1592 - Final Review 1 Chapter 7 1.1 Main Topics 1. Integration techniques: Fitting integrands to basic rules on page 485. Integration by parts, Theorem 7.1 on page 488. Guidelines for trigonometric
8.1 Solutions to Exercises
 Last edited 9/6/17 8.1 Solutions to Exercises 1. Since the sum of all angles in a triangle is 180, 180 = 70 + 50 + α. Thus α = 60. 10 α B The easiest way to find A and B is to use Law of Sines. sin( )
Last edited 9/6/17 8.1 Solutions to Exercises 1. Since the sum of all angles in a triangle is 180, 180 = 70 + 50 + α. Thus α = 60. 10 α B The easiest way to find A and B is to use Law of Sines. sin( )
MATH 162. Midterm 2 ANSWERS November 18, 2005
 MATH 62 Midterm 2 ANSWERS November 8, 2005. (0 points) Does the following integral converge or diverge? To get full credit, you must justify your answer. 3x 2 x 3 + 4x 2 + 2x + 4 dx You may not be able
MATH 62 Midterm 2 ANSWERS November 8, 2005. (0 points) Does the following integral converge or diverge? To get full credit, you must justify your answer. 3x 2 x 3 + 4x 2 + 2x + 4 dx You may not be able
9.4 CALCULUS AND PARAMETRIC EQUATIONS
 9.4 Calculus with Parametric Equations Contemporary Calculus 1 9.4 CALCULUS AND PARAMETRIC EQUATIONS The previous section discussed parametric equations, their graphs, and some of their uses for visualizing
9.4 Calculus with Parametric Equations Contemporary Calculus 1 9.4 CALCULUS AND PARAMETRIC EQUATIONS The previous section discussed parametric equations, their graphs, and some of their uses for visualizing
Midterm 1 Review. Distance = (x 1 x 0 ) 2 + (y 1 y 0 ) 2.
 Midterm 1 Review Comments about the midterm The midterm will consist of five questions and will test on material from the first seven lectures the material given below. No calculus either single variable
Midterm 1 Review Comments about the midterm The midterm will consist of five questions and will test on material from the first seven lectures the material given below. No calculus either single variable
CURVATURE AND RADIUS OF CURVATURE
 CHAPTER 5 CURVATURE AND RADIUS OF CURVATURE 5.1 Introduction: Curvature is a numerical measure of bending of the curve. At a particular point on the curve, a tangent can be drawn. Let this line makes an
CHAPTER 5 CURVATURE AND RADIUS OF CURVATURE 5.1 Introduction: Curvature is a numerical measure of bending of the curve. At a particular point on the curve, a tangent can be drawn. Let this line makes an
Math 32A Discussion Session Week 5 Notes November 7 and 9, 2017
 Math 32A Discussion Session Week 5 Notes November 7 and 9, 2017 This week we want to talk about curvature and osculating circles. You might notice that these notes contain a lot of the same theory or proofs
Math 32A Discussion Session Week 5 Notes November 7 and 9, 2017 This week we want to talk about curvature and osculating circles. You might notice that these notes contain a lot of the same theory or proofs
AP Calculus BC Summer Assignment. Please show all work either in the margins or on separate paper. No credit will be given without supporting work.
 AP Calculus BC Summer Assignment These problems are essential practice for AP Calculus BC. Unlike AP Calculus AB, BC students need to also be quite familiar with polar and parametric equations, as well
AP Calculus BC Summer Assignment These problems are essential practice for AP Calculus BC. Unlike AP Calculus AB, BC students need to also be quite familiar with polar and parametric equations, as well
Arc Length. Philippe B. Laval. Today KSU. Philippe B. Laval (KSU) Arc Length Today 1 / 12
 Philippe B. Laval KSU Today Philippe B. Laval (KSU) Arc Length Today 1 / 12 Introduction In this section, we discuss the notion of curve in greater detail and introduce the very important notion of arc
Philippe B. Laval KSU Today Philippe B. Laval (KSU) Arc Length Today 1 / 12 Introduction In this section, we discuss the notion of curve in greater detail and introduce the very important notion of arc
Example 2.1. Draw the points with polar coordinates: (i) (3, π) (ii) (2, π/4) (iii) (6, 2π/4) We illustrate all on the following graph:
 Section 10.3: Polar Coordinates The polar coordinate system is another way to coordinatize the Cartesian plane. It is particularly useful when examining regions which are circular. 1. Cartesian Coordinates
Section 10.3: Polar Coordinates The polar coordinate system is another way to coordinatize the Cartesian plane. It is particularly useful when examining regions which are circular. 1. Cartesian Coordinates
Worksheet 1.7: Introduction to Vector Functions - Position
 Boise State Math 275 (Ultman) Worksheet 1.7: Introduction to Vector Functions - Position From the Toolbox (what you need from previous classes): Cartesian Coordinates: Coordinates of points in general,
Boise State Math 275 (Ultman) Worksheet 1.7: Introduction to Vector Functions - Position From the Toolbox (what you need from previous classes): Cartesian Coordinates: Coordinates of points in general,
5.2 LENGTHS OF CURVES & AREAS OF SURFACES OF REVOLUTION
 5.2 Arc Length & Surface Area Contemporary Calculus 1 5.2 LENGTHS OF CURVES & AREAS OF SURFACES OF REVOLUTION This section introduces two additional geometric applications of integration: finding the length
5.2 Arc Length & Surface Area Contemporary Calculus 1 5.2 LENGTHS OF CURVES & AREAS OF SURFACES OF REVOLUTION This section introduces two additional geometric applications of integration: finding the length
9.4 Polar Coordinates
 9.4 Polar Coordinates Polar coordinates uses distance and direction to specify a location in a plane. The origin in a polar system is a fixed point from which a ray, O, is drawn and we call the ray the
9.4 Polar Coordinates Polar coordinates uses distance and direction to specify a location in a plane. The origin in a polar system is a fixed point from which a ray, O, is drawn and we call the ray the
MTHE 227 Problem Set 2 Solutions
 MTHE 7 Problem Set Solutions 1 (Great Circles). The intersection of a sphere with a plane passing through its center is called a great circle. Let Γ be the great circle that is the intersection of the
MTHE 7 Problem Set Solutions 1 (Great Circles). The intersection of a sphere with a plane passing through its center is called a great circle. Let Γ be the great circle that is the intersection of the
Module 16 : Line Integrals, Conservative fields Green's Theorem and applications. Lecture 48 : Green's Theorem [Section 48.
 Module 16 : Line Integrals, Conservative fields Green's Theorem and applications Lecture 48 : Green's Theorem [Section 48.1] Objectives In this section you will learn the following : Green's theorem which
Module 16 : Line Integrals, Conservative fields Green's Theorem and applications Lecture 48 : Green's Theorem [Section 48.1] Objectives In this section you will learn the following : Green's theorem which
Differentiation of Parametric Space Curves. Goals: Velocity in parametric curves Acceleration in parametric curves
 Block #2: Differentiation of Parametric Space Curves Goals: Velocity in parametric curves Acceleration in parametric curves 1 Displacement in Parametric Curves - 1 Displacement in Parametric Curves Using
Block #2: Differentiation of Parametric Space Curves Goals: Velocity in parametric curves Acceleration in parametric curves 1 Displacement in Parametric Curves - 1 Displacement in Parametric Curves Using
Tangent and Normal Vector - (11.5)
 Tangent and Normal Vector - (.5). Principal Unit Normal Vector Let C be the curve traced out by the vector-valued function rt vector T t r r t t is the unit tangent vector to the curve C. Now define N
Tangent and Normal Vector - (.5). Principal Unit Normal Vector Let C be the curve traced out by the vector-valued function rt vector T t r r t t is the unit tangent vector to the curve C. Now define N
Go over the illustrated examples in each section.
 Math 242 Fall 2009 Please before you start the practice problems, go over the illustrated examples in each section first. Cover up the solutions and try to work out the answers on your own. Practice Problems
Math 242 Fall 2009 Please before you start the practice problems, go over the illustrated examples in each section first. Cover up the solutions and try to work out the answers on your own. Practice Problems
Math 113 Final Exam Practice
 Math Final Exam Practice The Final Exam is comprehensive. You should refer to prior reviews when studying material in chapters 6, 7, 8, and.-9. This review will cover.0- and chapter 0. This sheet has three
Math Final Exam Practice The Final Exam is comprehensive. You should refer to prior reviews when studying material in chapters 6, 7, 8, and.-9. This review will cover.0- and chapter 0. This sheet has three
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. 3 2, 5 2 C) - 5 2
 Test Review (chap 0) Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Solve the problem. ) Find the point on the curve x = sin t, y = cos t, -
Test Review (chap 0) Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Solve the problem. ) Find the point on the curve x = sin t, y = cos t, -
9.1 (10.1) Parametric Curves ( 參數曲線 )
 9.1 (10.1) Parametric Curves ( 參數曲線 ) [Ex]Sketch and identify the curve defined by parametric equations x= 6 t, y = t, t 4 (a) Sketch the curve by using the parametric equations to plot points: (b) Eliminate
9.1 (10.1) Parametric Curves ( 參數曲線 ) [Ex]Sketch and identify the curve defined by parametric equations x= 6 t, y = t, t 4 (a) Sketch the curve by using the parametric equations to plot points: (b) Eliminate
Polar Coordinates: Graphs
 Polar Coordinates: Graphs By: OpenStaxCollege The planets move through space in elliptical, periodic orbits about the sun, as shown in [link]. They are in constant motion, so fixing an exact position of
Polar Coordinates: Graphs By: OpenStaxCollege The planets move through space in elliptical, periodic orbits about the sun, as shown in [link]. They are in constant motion, so fixing an exact position of
+ 4 Ex: y = v = (1, 4) x = 1 Focus: (h, k + ) = (1, 6) L.R. = 8 units We can have parabolas that open sideways too (inverses) x = a (y k) 2 + h
 Unit 7 Notes Parabolas: E: reflectors, microphones, (football game), (Davinci) satellites. Light placed where ras will reflect parallel. This point is the focus. Parabola set of all points in a plane that
Unit 7 Notes Parabolas: E: reflectors, microphones, (football game), (Davinci) satellites. Light placed where ras will reflect parallel. This point is the focus. Parabola set of all points in a plane that
Parametric Curves. Calculus 2 Lia Vas
 Calculus Lia Vas Parametric Curves In the past, we mostly worked with curves in the form y = f(x). However, this format does not encompass all the curves one encounters in applications. For example, consider
Calculus Lia Vas Parametric Curves In the past, we mostly worked with curves in the form y = f(x). However, this format does not encompass all the curves one encounters in applications. For example, consider
CHAPTER 6 VECTOR CALCULUS. We ve spent a lot of time so far just looking at all the different ways you can graph
 CHAPTER 6 VECTOR CALCULUS We ve spent a lot of time so far just looking at all the different ways you can graph things and describe things in three dimensions, and it certainly seems like there is a lot
CHAPTER 6 VECTOR CALCULUS We ve spent a lot of time so far just looking at all the different ways you can graph things and describe things in three dimensions, and it certainly seems like there is a lot
(1) Recap of Differential Calculus and Integral Calculus (2) Preview of Calculus in three dimensional space (3) Tools for Calculus 3
 Math 127 Introduction and Review (1) Recap of Differential Calculus and Integral Calculus (2) Preview of Calculus in three dimensional space (3) Tools for Calculus 3 MATH 127 Introduction to Calculus III
Math 127 Introduction and Review (1) Recap of Differential Calculus and Integral Calculus (2) Preview of Calculus in three dimensional space (3) Tools for Calculus 3 MATH 127 Introduction to Calculus III
4.1 Analysis of functions I: Increase, decrease and concavity
 4.1 Analysis of functions I: Increase, decrease and concavity Definition Let f be defined on an interval and let x 1 and x 2 denote points in that interval. a) f is said to be increasing on the interval
4.1 Analysis of functions I: Increase, decrease and concavity Definition Let f be defined on an interval and let x 1 and x 2 denote points in that interval. a) f is said to be increasing on the interval
1. Which of the following defines a function f for which f ( x) = f( x) 2. ln(4 2 x) < 0 if and only if
 . Which of the following defines a function f for which f ( ) = f( )? a. f ( ) = + 4 b. f ( ) = sin( ) f ( ) = cos( ) f ( ) = e f ( ) = log. ln(4 ) < 0 if and only if a. < b. < < < < > >. If f ( ) = (
. Which of the following defines a function f for which f ( ) = f( )? a. f ( ) = + 4 b. f ( ) = sin( ) f ( ) = cos( ) f ( ) = e f ( ) = log. ln(4 ) < 0 if and only if a. < b. < < < < > >. If f ( ) = (
Absolute and Local Extrema
 Extrema of Functions We can use the tools of calculus to help us understand and describe the shapes of curves. Here is some of the data that derivatives f (x) and f (x) can provide about the shape of the
Extrema of Functions We can use the tools of calculus to help us understand and describe the shapes of curves. Here is some of the data that derivatives f (x) and f (x) can provide about the shape of the
CALCULUS 3 DR JASON SAMUELS LECTURE NOTES Table of Contents: 4 Sequences and Series 4 Sequences 8 Series 8 Intro 9 Tests for Convergence 9 n-th term
 1 CALCULUS 3 DR JASON SAMUELS LECTURE NOTES Table of Contents: 4 Sequences and Series 4 Sequences 8 Series 8 Intro 9 Tests for Convergence 9 n-th term test 10 Integral test 12 Direct Comparison test (DCT)
1 CALCULUS 3 DR JASON SAMUELS LECTURE NOTES Table of Contents: 4 Sequences and Series 4 Sequences 8 Series 8 Intro 9 Tests for Convergence 9 n-th term test 10 Integral test 12 Direct Comparison test (DCT)
AP Calculus (BC) Chapter 10 Test No Calculator Section. Name: Date: Period:
 AP Calculus (BC) Chapter 10 Test No Calculator Section Name: Date: Period: Part I. Multiple-Choice Questions (5 points each; please circle the correct answer.) 1. The graph in the xy-plane represented
AP Calculus (BC) Chapter 10 Test No Calculator Section Name: Date: Period: Part I. Multiple-Choice Questions (5 points each; please circle the correct answer.) 1. The graph in the xy-plane represented
Linear Systems of ODE: Nullclines, Eigenvector lines and trajectories
 Linear Systems of ODE: Nullclines, Eigenvector lines and trajectories James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University October 6, 2013 Outline
Linear Systems of ODE: Nullclines, Eigenvector lines and trajectories James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University October 6, 2013 Outline
AP Calculus Worksheet: Chapter 2 Review Part I
 AP Calculus Worksheet: Chapter 2 Review Part I 1. Given y = f(x), what is the average rate of change of f on the interval [a, b]? What is the graphical interpretation of your answer? 2. The derivative
AP Calculus Worksheet: Chapter 2 Review Part I 1. Given y = f(x), what is the average rate of change of f on the interval [a, b]? What is the graphical interpretation of your answer? 2. The derivative
MAT 272 Test 1 Review. 1. Let P = (1,1) and Q = (2,3). Find the unit vector u that has the same
 11.1 Vectors in the Plane 1. Let P = (1,1) and Q = (2,3). Find the unit vector u that has the same direction as. QP a. u =< 1, 2 > b. u =< 1 5, 2 5 > c. u =< 1, 2 > d. u =< 1 5, 2 5 > 2. If u has magnitude
11.1 Vectors in the Plane 1. Let P = (1,1) and Q = (2,3). Find the unit vector u that has the same direction as. QP a. u =< 1, 2 > b. u =< 1 5, 2 5 > c. u =< 1, 2 > d. u =< 1 5, 2 5 > 2. If u has magnitude
The Calculus of Vec- tors
 Physics 2460 Electricity and Magnetism I, Fall 2007, Lecture 3 1 The Calculus of Vec- Summary: tors 1. Calculus of Vectors: Limits and Derivatives 2. Parametric representation of Curves r(t) = [x(t), y(t),
Physics 2460 Electricity and Magnetism I, Fall 2007, Lecture 3 1 The Calculus of Vec- Summary: tors 1. Calculus of Vectors: Limits and Derivatives 2. Parametric representation of Curves r(t) = [x(t), y(t),
Parametric Equations, Function Composition and the Chain Rule: A Worksheet
 Parametric Equations, Function Composition and the Chain Rule: A Worksheet Prof.Rebecca Goldin Oct. 8, 003 1 Parametric Equations We have seen that the graph of a function f(x) of one variable consists
Parametric Equations, Function Composition and the Chain Rule: A Worksheet Prof.Rebecca Goldin Oct. 8, 003 1 Parametric Equations We have seen that the graph of a function f(x) of one variable consists
Math 153 Calculus III Notes
 Math 153 Calculus III Notes 10.1 Parametric Functions A parametric function is a where x and y are described by a function in terms of the parameter t: Example 1 (x, y) = {x(t), y(t)}, or x = f(t); y =
Math 153 Calculus III Notes 10.1 Parametric Functions A parametric function is a where x and y are described by a function in terms of the parameter t: Example 1 (x, y) = {x(t), y(t)}, or x = f(t); y =
MTH4100 Calculus I. Week 6 (Thomas Calculus Sections 3.5 to 4.2) Rainer Klages. School of Mathematical Sciences Queen Mary, University of London
 MTH4100 Calculus I Week 6 (Thomas Calculus Sections 3.5 to 4.2) Rainer Klages School of Mathematical Sciences Queen Mary, University of London Autumn 2008 R. Klages (QMUL) MTH4100 Calculus 1 Week 6 1 /
MTH4100 Calculus I Week 6 (Thomas Calculus Sections 3.5 to 4.2) Rainer Klages School of Mathematical Sciences Queen Mary, University of London Autumn 2008 R. Klages (QMUL) MTH4100 Calculus 1 Week 6 1 /
Limits for parametric and polar curves
 Roberto s Notes on Differential Calculus Chapter : Resolving indeterminate forms Section 7 Limits for parametric and polar curves What you need to know already: How to handle limits for functions of the
Roberto s Notes on Differential Calculus Chapter : Resolving indeterminate forms Section 7 Limits for parametric and polar curves What you need to know already: How to handle limits for functions of the
Mathematics Engineering Calculus III Fall 13 Test #1
 Mathematics 2153-02 Engineering Calculus III Fall 13 Test #1 Instructor: Dr. Alexandra Shlapentokh (1) Which of the following statements is always true? (a) If x = f(t), y = g(t) and f (1) = 0, then dy/dx(1)
Mathematics 2153-02 Engineering Calculus III Fall 13 Test #1 Instructor: Dr. Alexandra Shlapentokh (1) Which of the following statements is always true? (a) If x = f(t), y = g(t) and f (1) = 0, then dy/dx(1)
Learning Objectives for Math 166
 Learning Objectives for Math 166 Chapter 6 Applications of Definite Integrals Section 6.1: Volumes Using Cross-Sections Draw and label both 2-dimensional perspectives and 3-dimensional sketches of the
Learning Objectives for Math 166 Chapter 6 Applications of Definite Integrals Section 6.1: Volumes Using Cross-Sections Draw and label both 2-dimensional perspectives and 3-dimensional sketches of the
MATH 32A: MIDTERM 1 REVIEW. 1. Vectors. v v = 1 22
 MATH 3A: MIDTERM 1 REVIEW JOE HUGHES 1. Let v = 3,, 3. a. Find e v. Solution: v = 9 + 4 + 9 =, so 1. Vectors e v = 1 v v = 1 3,, 3 b. Find the vectors parallel to v which lie on the sphere of radius two
MATH 3A: MIDTERM 1 REVIEW JOE HUGHES 1. Let v = 3,, 3. a. Find e v. Solution: v = 9 + 4 + 9 =, so 1. Vectors e v = 1 v v = 1 3,, 3 b. Find the vectors parallel to v which lie on the sphere of radius two
NIL. Let M be R 3 equipped with the metric in which the following vector. fields, U = and. are an orthonormal basis.
 NIL KEVIN WHYTE Let M be R 3 equipped with the metric in which the following vector fields: U = x + y z V = y and W = z are an orthonormal basis. 1. Preliminaries Since we re given the metric via an orthonormal
NIL KEVIN WHYTE Let M be R 3 equipped with the metric in which the following vector fields: U = x + y z V = y and W = z are an orthonormal basis. 1. Preliminaries Since we re given the metric via an orthonormal
SOLUTIONS TO SECOND PRACTICE EXAM Math 21a, Spring 2003
 SOLUTIONS TO SECOND PRACTICE EXAM Math a, Spring 3 Problem ) ( points) Circle for each of the questions the correct letter. No justifications are needed. Your score will be C W where C is the number of
SOLUTIONS TO SECOND PRACTICE EXAM Math a, Spring 3 Problem ) ( points) Circle for each of the questions the correct letter. No justifications are needed. Your score will be C W where C is the number of
Exam 1 Review SOLUTIONS
 1. True or False (and give a short reason): Exam 1 Review SOLUTIONS (a) If the parametric curve x = f(t), y = g(t) satisfies g (1) = 0, then it has a horizontal tangent line when t = 1. FALSE: To make
1. True or False (and give a short reason): Exam 1 Review SOLUTIONS (a) If the parametric curve x = f(t), y = g(t) satisfies g (1) = 0, then it has a horizontal tangent line when t = 1. FALSE: To make
Since x + we get x² + 2x = 4, or simplifying it, x² = 4. Therefore, x² + = 4 2 = 2. Ans. (C)
 SAT II - Math Level 2 Test #01 Solution 1. x + = 2, then x² + = Since x + = 2, by squaring both side of the equation, (A) - (B) 0 (C) 2 (D) 4 (E) -2 we get x² + 2x 1 + 1 = 4, or simplifying it, x² + 2
SAT II - Math Level 2 Test #01 Solution 1. x + = 2, then x² + = Since x + = 2, by squaring both side of the equation, (A) - (B) 0 (C) 2 (D) 4 (E) -2 we get x² + 2x 1 + 1 = 4, or simplifying it, x² + 2
10.3 Parametric Equations. 1 Math 1432 Dr. Almus
 Math 1432 DAY 39 Dr. Melahat Almus almus@math.uh.edu OFFICE HOURS (212 PGH) MW12-1:30pm, F:12-1pm. If you email me, please mention the course (1432) in the subject line. Check your CASA account for Quiz
Math 1432 DAY 39 Dr. Melahat Almus almus@math.uh.edu OFFICE HOURS (212 PGH) MW12-1:30pm, F:12-1pm. If you email me, please mention the course (1432) in the subject line. Check your CASA account for Quiz
698 Chapter 11 Parametric Equations and Polar Coordinates
 698 Chapter Parametric Equations and Polar Coordinates 67. 68. 69. 70. 7. 7. 7. 7. Chapter Practice Eercises 699 75. (a Perihelion a ae a( e, Aphelion ea a a( e ( Planet Perihelion Aphelion Mercur 0.075
698 Chapter Parametric Equations and Polar Coordinates 67. 68. 69. 70. 7. 7. 7. 7. Chapter Practice Eercises 699 75. (a Perihelion a ae a( e, Aphelion ea a a( e ( Planet Perihelion Aphelion Mercur 0.075
MATH 151, FALL SEMESTER 2014 COMMON EXAMINATION I - VERSION B GUIDELINES
 MATH151-14c MATH 151, FALL SEMESTER 2014 COMMON EXAMINATION I - VERSION B Time Allowed: 2 hours Last name, First name (print): Signature: Instructor s name: Section No: GUIDELINES In Part 1 (Problems 1
MATH151-14c MATH 151, FALL SEMESTER 2014 COMMON EXAMINATION I - VERSION B Time Allowed: 2 hours Last name, First name (print): Signature: Instructor s name: Section No: GUIDELINES In Part 1 (Problems 1
a k 0, then k + 1 = 2 lim 1 + 1
 Math 7 - Midterm - Form A - Page From the desk of C. Davis Buenger. https://people.math.osu.edu/buenger.8/ Problem a) [3 pts] If lim a k = then a k converges. False: The divergence test states that if
Math 7 - Midterm - Form A - Page From the desk of C. Davis Buenger. https://people.math.osu.edu/buenger.8/ Problem a) [3 pts] If lim a k = then a k converges. False: The divergence test states that if
Review Problems for the Final
 Review Problems for the Final Math -3 5 7 These problems are provided to help you study. The presence of a problem on this handout does not imply that there will be a similar problem on the test. And the
Review Problems for the Final Math -3 5 7 These problems are provided to help you study. The presence of a problem on this handout does not imply that there will be a similar problem on the test. And the
Exercise. Exercise 1.1. MA112 Section : Prepared by Dr.Archara Pacheenburawana 1
 MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 1 Exercise Exercise 1.1 1 8 Find the vertex, focus, and directrix of the parabola and sketch its graph. 1. x = 2y 2 2. 4y +x 2 = 0 3. 4x 2 =
MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 1 Exercise Exercise 1.1 1 8 Find the vertex, focus, and directrix of the parabola and sketch its graph. 1. x = 2y 2 2. 4y +x 2 = 0 3. 4x 2 =
Differential Geometry of Curves
 Differential Geometry of Curves Cartesian coordinate system René Descartes (1596-165) (lat. Renatus Cartesius) French philosopher, mathematician, and scientist. Rationalism y Ego cogito, ergo sum (I think,
Differential Geometry of Curves Cartesian coordinate system René Descartes (1596-165) (lat. Renatus Cartesius) French philosopher, mathematician, and scientist. Rationalism y Ego cogito, ergo sum (I think,
0, such that. all. for all. 0, there exists. Name: Continuity. Limits and. calculus. the definitionn. satisfying. limit. However, is the limit of its
 L Marizzaa A Bailey Multivariable andd Vector Calculus Name: Limits and Continuity Limits and Continuity We have previously defined limit in for single variable functions, but how do we generalize this
L Marizzaa A Bailey Multivariable andd Vector Calculus Name: Limits and Continuity Limits and Continuity We have previously defined limit in for single variable functions, but how do we generalize this
MATH 423/ Note that the algebraic operations on the right hand side are vector subtraction and scalar multiplication.
 MATH 423/673 1 Curves Definition: The velocity vector of a curve α : I R 3 at time t is the tangent vector to R 3 at α(t), defined by α (t) T α(t) R 3 α α(t + h) α(t) (t) := lim h 0 h Note that the algebraic
MATH 423/673 1 Curves Definition: The velocity vector of a curve α : I R 3 at time t is the tangent vector to R 3 at α(t), defined by α (t) T α(t) R 3 α α(t + h) α(t) (t) := lim h 0 h Note that the algebraic
MAC Calculus II Spring Homework #6 Some Solutions.
 MAC 2312-15931-Calculus II Spring 23 Homework #6 Some Solutions. 1. Find the centroid of the region bounded by the curves y = 2x 2 and y = 1 2x 2. Solution. It is obvious, by inspection, that the centroid
MAC 2312-15931-Calculus II Spring 23 Homework #6 Some Solutions. 1. Find the centroid of the region bounded by the curves y = 2x 2 and y = 1 2x 2. Solution. It is obvious, by inspection, that the centroid
Math 116 Second Midterm November 16, 2011
 Math 6 Second Midterm November 6, Name: EXAM SOLUTIONS Instructor: Section:. Do not open this exam until you are told to do so.. This exam has pages including this cover. There are 9 problems. Note that
Math 6 Second Midterm November 6, Name: EXAM SOLUTIONS Instructor: Section:. Do not open this exam until you are told to do so.. This exam has pages including this cover. There are 9 problems. Note that
PARAMETRIC EQUATIONS AND POLAR COORDINATES
 10 PARAMETRIC EQUATIONS AND POLAR COORDINATES PARAMETRIC EQUATIONS & POLAR COORDINATES We have seen how to represent curves by parametric equations. Now, we apply the methods of calculus to these parametric
10 PARAMETRIC EQUATIONS AND POLAR COORDINATES PARAMETRIC EQUATIONS & POLAR COORDINATES We have seen how to represent curves by parametric equations. Now, we apply the methods of calculus to these parametric
Math 116 Practice for Exam 2
 Math 6 Practice for Exam 2 Generated November 9, 206 Name: Instructor: Section Number:. This exam has 0 questions. Note that the problems are not of equal difficulty, so you may want to skip over and return
Math 6 Practice for Exam 2 Generated November 9, 206 Name: Instructor: Section Number:. This exam has 0 questions. Note that the problems are not of equal difficulty, so you may want to skip over and return
Calculus of Vector-Valued Functions
 Chapter 3 Calculus of Vector-Valued Functions Useful Tip: If you are reading the electronic version of this publication formatted as a Mathematica Notebook, then it is possible to view 3-D plots generated
Chapter 3 Calculus of Vector-Valued Functions Useful Tip: If you are reading the electronic version of this publication formatted as a Mathematica Notebook, then it is possible to view 3-D plots generated
Lecture 6, September 1, 2017
 Engineering Mathematics Fall 07 Lecture 6, September, 07 Escape Velocity Suppose we have a planet (or any large near to spherical heavenly body) of radius R and acceleration of gravity at the surface of
Engineering Mathematics Fall 07 Lecture 6, September, 07 Escape Velocity Suppose we have a planet (or any large near to spherical heavenly body) of radius R and acceleration of gravity at the surface of
= cos(cos(tan t)) ( sin(tan t)) d (tan t) = cos(cos(tan t)) ( sin(tan t)) sec 2 t., we get. 4x 3/4 f (t) 4 [ ln(f (t)) ] 3/4 f (t)
![= cos(cos(tan t)) ( sin(tan t)) d (tan t) = cos(cos(tan t)) ( sin(tan t)) sec 2 t., we get. 4x 3/4 f (t) 4 [ ln(f (t)) ] 3/4 f (t) = cos(cos(tan t)) ( sin(tan t)) d (tan t) = cos(cos(tan t)) ( sin(tan t)) sec 2 t., we get. 4x 3/4 f (t) 4 [ ln(f (t)) ] 3/4 f (t)](/thumbs/71/66031338.jpg) Tuesday, January 2 Solutions A review of some important calculus topics 1. Chain Rule: (a) Let h(t) = sin ( cos(tan t) ). Find the derivative with respect to t. Solution. d (h(t)) = d (sin(cos(tan t)))
Tuesday, January 2 Solutions A review of some important calculus topics 1. Chain Rule: (a) Let h(t) = sin ( cos(tan t) ). Find the derivative with respect to t. Solution. d (h(t)) = d (sin(cos(tan t)))
Math Test #3 Info and Review Exercises
 Math 181 - Test #3 Info and Review Exercises Fall 2018, Prof. Beydler Test Info Date: Wednesday, November 28, 2018 Will cover sections 10.1-10.4, 11.1-11.7. You ll have the entire class to finish the test.
Math 181 - Test #3 Info and Review Exercises Fall 2018, Prof. Beydler Test Info Date: Wednesday, November 28, 2018 Will cover sections 10.1-10.4, 11.1-11.7. You ll have the entire class to finish the test.
I can translate between a number line graph, an inequality, and interval notation.
 Unit 1: Absolute Value 2 I can translate between a number line graph, an inequality, and interval notation. 2 2 I can translate between absolute value expressions and English statements about numbers on
Unit 1: Absolute Value 2 I can translate between a number line graph, an inequality, and interval notation. 2 2 I can translate between absolute value expressions and English statements about numbers on
Calculus BC: Section I
 Calculus BC: Section I Section I consists of 45 multiple-choice questions. Part A contains 28 questions and does not allow the use of a calculator. Part B contains 17 questions and requires a graphing
Calculus BC: Section I Section I consists of 45 multiple-choice questions. Part A contains 28 questions and does not allow the use of a calculator. Part B contains 17 questions and requires a graphing
April 28, 2017 Geometry 11.1 Circumference and Arc Length
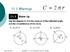 11.1 Warmup April 28, 2017 Geometry 11.1 Circumference and Arc Length 1 Geometry 11.1 Circumference and Arc Length mbhaub@mpsaz.org 11.1 Essential Question How can you find the length of a circular arc?
11.1 Warmup April 28, 2017 Geometry 11.1 Circumference and Arc Length 1 Geometry 11.1 Circumference and Arc Length mbhaub@mpsaz.org 11.1 Essential Question How can you find the length of a circular arc?
xvi xxiii xxvi Construction of the Real Line 2 Is Every Real Number Rational? 3 Problems Algebra of the Real Numbers 7
 About the Author v Preface to the Instructor xvi WileyPLUS xxii Acknowledgments xxiii Preface to the Student xxvi 1 The Real Numbers 1 1.1 The Real Line 2 Construction of the Real Line 2 Is Every Real
About the Author v Preface to the Instructor xvi WileyPLUS xxii Acknowledgments xxiii Preface to the Student xxvi 1 The Real Numbers 1 1.1 The Real Line 2 Construction of the Real Line 2 Is Every Real
The fundamental theorem of calculus for definite integration helped us to compute If has an anti-derivative,
 Module 16 : Line Integrals, Conservative fields Green's Theorem and applications Lecture 47 : Fundamental Theorems of Calculus for Line integrals [Section 47.1] Objectives In this section you will learn
Module 16 : Line Integrals, Conservative fields Green's Theorem and applications Lecture 47 : Fundamental Theorems of Calculus for Line integrals [Section 47.1] Objectives In this section you will learn
SOME PROBLEMS YOU SHOULD BE ABLE TO DO
 SOME PROBLEMS YOU SHOULD BE ABLE TO DO I ve attempted to make a list of the main calculations you should be ready for on the exam, and included a handful of the more important formulas. There are no examples
SOME PROBLEMS YOU SHOULD BE ABLE TO DO I ve attempted to make a list of the main calculations you should be ready for on the exam, and included a handful of the more important formulas. There are no examples
problem score possible Total 60
 Math 32 A: Midterm 1, Oct. 24, 2008 Name: ID Number: Section: problem score possible 1. 10 2. 10 3. 10 4. 10 5. 10 6. 10 Total 60 1 1. Determine whether the following points are coplanar: a. P = (8, 14,
Math 32 A: Midterm 1, Oct. 24, 2008 Name: ID Number: Section: problem score possible 1. 10 2. 10 3. 10 4. 10 5. 10 6. 10 Total 60 1 1. Determine whether the following points are coplanar: a. P = (8, 14,
8.2 APPLICATIONS TO GEOMETRY
 8.2 APPLICATIONS TO GEOMETRY In Section 8.1, we calculated volumes using slicing and definite integrals. In this section, we use the same method to calculate the volumes of more complicated regions as
8.2 APPLICATIONS TO GEOMETRY In Section 8.1, we calculated volumes using slicing and definite integrals. In this section, we use the same method to calculate the volumes of more complicated regions as
Linear Systems of ODE: Nullclines, Eigenvector lines and trajectories
 Linear Systems of ODE: Nullclines, Eigenvector lines and trajectories James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University October 6, 203 Outline
Linear Systems of ODE: Nullclines, Eigenvector lines and trajectories James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University October 6, 203 Outline
Exercises for Multivariable Differential Calculus XM521
 This document lists all the exercises for XM521. The Type I (True/False) exercises will be given, and should be answered, online immediately following each lecture. The Type III exercises are to be done
This document lists all the exercises for XM521. The Type I (True/False) exercises will be given, and should be answered, online immediately following each lecture. The Type III exercises are to be done
AP CALCULUS BC Syllabus / Summer Assignment 2015
 AP CALCULUS BC Syllabus / Summer Assignment 015 Name Congratulations! You made it to BC Calculus! In order to complete the curriculum before the AP Exam in May, it is necessary to do some preparatory work
AP CALCULUS BC Syllabus / Summer Assignment 015 Name Congratulations! You made it to BC Calculus! In order to complete the curriculum before the AP Exam in May, it is necessary to do some preparatory work
Parametric Functions and Vector Functions (BC Only)
 Parametric Functions and Vector Functions (BC Only) Parametric Functions Parametric functions are another way of viewing functions. This time, the values of x and y are both dependent on another independent
Parametric Functions and Vector Functions (BC Only) Parametric Functions Parametric functions are another way of viewing functions. This time, the values of x and y are both dependent on another independent
9.2 CALCULUS IN THE POLAR COORDINATE SYSTEM
 9.2 alculus In The Polar oordinate System ontemporary alculus 9.2 LULUS IN THE POLR OORINTE SYSTEM The previous section introduced the polar coordinate system and discussed how to plot points, how to create
9.2 alculus In The Polar oordinate System ontemporary alculus 9.2 LULUS IN THE POLR OORINTE SYSTEM The previous section introduced the polar coordinate system and discussed how to plot points, how to create
Index. Excerpt from "Calculus" 2013 AoPS Inc. Copyrighted Material INDEX
 Index #, 2 \, 5, 4 [, 4 - definition, 38 ;, 2 indeterminate form, 2 22, 24 indeterminate form, 22 23, see Euler s Constant 2, 2, see infinity, 33 \, 6, 3, 2 3-6-9 triangle, 2 4-dimensional sphere, 85 45-45-9
Index #, 2 \, 5, 4 [, 4 - definition, 38 ;, 2 indeterminate form, 2 22, 24 indeterminate form, 22 23, see Euler s Constant 2, 2, see infinity, 33 \, 6, 3, 2 3-6-9 triangle, 2 4-dimensional sphere, 85 45-45-9
CHAPTER 4 Trigonometry
 CHAPTER Trigonometr Section. Radian and Degree Measure You should know the following basic facts about angles, their measurement, and their applications. Tpes of Angles: (a) Acute: Measure between 0 and
CHAPTER Trigonometr Section. Radian and Degree Measure You should know the following basic facts about angles, their measurement, and their applications. Tpes of Angles: (a) Acute: Measure between 0 and
