Commutativity of -Prime Rings with Generalized Derivations
|
|
|
- Egbert Thornton
- 5 years ago
- Views:
Transcription
1 REND. SEM. MAT. UNIV. PADOVA, Vol. 125 (2011) Commutativity of -Prime Rings with Generalized Derivations MOHAMMAD ASHRAF -ALMAS KHAN ABSTRACT -LetR be a 2-torsion free -prime ring and F be a generalized derivation of R with associated derivation d. IfU is a Lie ideal of R then in the presentpaper, we shall show thatu Z(R) if R admits a generalized derivation F(with associated derivation d) satisfying any one of the properties: (i)f[u; v] ˆ [F(u); v]; (ii)f(u v) ˆ F(u) v; (iii)f[u; v] ˆ [F(u); v] [d(v); u]; (iv)f(u v) ˆ F(u) v d(v) u; (v)f(uv) uv ˆ 0 and (vi)d(u)f(v) uv ˆ 0 for all u; v 2 U 1. Introduction. Let R be an associative ring with centre Z(R). R is said to be 2-torsion free if 2x ˆ 0 implies x ˆ 0 for all x 2 R. For any x; y 2 R; [x; y] ˆ xy yx and x y ˆ xy yx will denote the Lie product and the Jordan product respectively. A ring R is prime if arb ˆf0g implies that a ˆ 0orb ˆ 0. An additive mapping x 7! x on a ring R is called an involution if (xy) ˆ y x and (x ) ˆ x hold for all x; y 2 R. A ring equipped with an involution is called a ring with involution or -ring. A ring with an involution ` 0 is said to -prime if arb ˆ arb ˆ 0ora Rb ˆ arb ˆ 0 implies that either a ˆ 0or b ˆ 0. Every prime ring with an involution is -prime butthe converse need not hold in general. An example due to Oukhtite [8] justifies the above statement that is, let R be a prime ring. Consider S ˆ R R o, where R o is the opposite ring of R. Define involution on S as (x; y) ˆ (y; x). Since (0; x)s(x; 0) ˆ 0, itfollows thats is notprime. Further, itcan be easily seen that if (a; b)s(c; d) ˆ (a; b)s(c; d) ˆ 0, then either (a; b) ˆ 0or(c; d) ˆ 0. Hence S is -prime butnotprime. The setof symmetric and skew-sym- Indirizzo degli A.: Department of Mathematics, Aligarh Muslim University, Aligarh , India mashraf80@hotmail.com almasleo@gmail.com
2 72 Mohammad Ashraf - Almas Khan metric elements of a -ring will be denoted by S (R) i.e., S (R) ˆ ˆfx 2 R j x ˆxg. An additive subgroup U of R is said to be a Lie ideal of R if [U; R] U. A Lie ideal is said to a -Lie ideal if U ˆ U. An additive mapping d : R! R is said to be a derivation of R if d(xy) ˆ d(x)y xd(y) holds for all x; y 2 R: An additive mapping F : R! R is called a generalized inner derivation if F(x) ˆ ax xb for fixed a; b 2 R. For such a mapping F, it is easy to see that F(xy) ˆ F(x)y x[y; b] ˆ F(x)y xi b (y) for all x; y 2 R: This observation leads to the following definition, given in [5]; an additive mapping F : R! R is called a generalized derivation with associated derivation d if F(xy) ˆ F(x)y xd(y) holds for all x; y 2 R: Familiar examples of generalized derivations are derivations and generalized inner derivations and the later includes left multiplier i.e., an additive map F : R! R satisfying F(xy) ˆ F(x)y for all x; y 2 R. Since the sum of two generalized derivations is a generalized derivation, every map of the form F(x) ˆ cx d(x), where c is fixed elementof R and d a derivation of R is a generalized derivation and if R has 1, all generalized derivations have this form. Recently a number of authors have studied commutativity of rings satisfying certain differential identities (see [1], [2], [4] etc. where further refrences can be found). In the present paper our objective is to extend some earlier results for Lie ideals in -prime rings involving generalized derivations. Infact, we shall show that a -Lie ideal U is central if R admits a generalized derivation F with associated derivation d satisfying any one of the following properties (i)f[u; v] ˆ [F(u); v]; (ii)f(uv) ˆ F(u) v; (iii)f[u; v] ˆ [F(u); v] [d(v); u]; (iv)f(u v) ˆ F(u)v d(v) u; (v)f(uv) uv ˆ 0; and (vi)d(u)f(v) uv ˆ 0 for all u; v 2 U: 2. Preliminary Results. We shall be frequently using the following identities without any specific mention, [xy; z] ˆ x[y; z] [x; z]y [x; yz] ˆ [x; y]z y[x; z] xo(yz) ˆ (xoy)z y[x; z] ˆ y(xoz) [x; y]z (xy)oz ˆ x(yoz) [x; z]y ˆ (xoz)y x[y; z]
3 Commutativity of -Prime Rings with Generalized Derivations 73 We begin with the following known results which shall be used throughout to prove our theorems: LEMMA 2.1 ([11], Lemma 4). If U 6 Z(R) is a -Lie ideal of a 2-torsion free -prime ring and a; b 2 R such that aub ˆ 0 ˆ a Ub then either a ˆ 0 or b ˆ 0. LEMMA 2.2 ([10], Lemma 2.3 ). Let U be a non zero -Lie ideal of a 2-torsion free -prime ring R. If [U; U] ˆ 0,then U Z(R): LEMMA 2.3 ([11], Lemma 3 ). Let U be a non zero -Lie ideal of a 2-torsion free -prime ring R. If [U; U] 6ˆ 0,then there exist a non zero -ideal M of R such that [M; R] Uand[M; R] 6 Z(R). LEMMA 2.4 ([10], Theorem 1.1 ). Let R be a 2-torsion free -prime ring, U a non zero Lie ideal of R and d a non zero derivation of R which commutes with. Ifd 2 (U) ˆ 0,then U Z(R): LEMMA 2.5 ([10], Lemma 2.4 ). Let U be a -Lie ideal of a 2-torsion free -prime ring R and d( 6ˆ 0) be derivation of R which commutes with. Ifd(U) Z(R); then U Z(R): LEMMA 2.6 ([10], Lemma 2.5 ). Let d( 6ˆ 0) be derivation of a 2-torsion free -prime ring R which commutes with. Let U 6 Z(R) be a -Lie ideal of R. If t 2 R satisfies td(u) ˆ 0 or d(u)t ˆ 0 then t ˆ 0. We shall now prove the following : LEMMA 2.7. Let R be a 2-torsion free -prime ring and U be a -Lie ideal of R. If a 2 S (R) \ R such that [a; U] Z(R) then either U Z(R) or a 2 Z(R). PROOF. Let U 6 Z(R). The given hypothesis can be written as I a (U) Z(R) where I a is the inner derivation determined by a. Hence using Lemma 2.5, I a ˆ 0 and this gives that a 2 Z(R). LEMMA 2.8. Let R be a 2-torsion free -prime ring and d be a non-zero derivation of R which commutes with. IfU6 Z(R) is a -Lie ideal of R such that [a; d(u)] ˆ 0 for some a 2 S (R) \ R,then a 2 Z(R).
4 74 Mohammad Ashraf - Almas Khan PROOF. Replacing u by [a; u] in [a; d(u)] ˆ 0 we have, 0 ˆ ˆ [a; d[a; u]] ˆ [a; [a; d(u)]] [a; [d(a); u]] ˆ [a; [d(a); u]] for all u 2 U: Hence, 0 ˆ d[a; [d(a); u]] ˆ [d(a); [d(a); u]] [a; d[d(a); u]] for all u 2 U, Now using the hypothesis 0 ˆ [d(a); [d(a); u]] for all u 2 U, by Lemma 2.4, d(a) 2 Z(R). Therefore, d[a; u] ˆ [d(a); u] [a; d(u)] ˆ 0. Replacing u by [a 2 ; u]in[a; d(u)] ˆ 0 we obtain, 0 ˆ [a; d[a 2 ; u]] ˆ [a; d(a[a; u] [a; u]a)] ˆ [a; d(a)[a; u] ad[a; u] d[a; u]a [a; u]d(a)] ˆ [a; d(a)[a; u]] [a; [a; u]d(a)] ˆ d(a)[a; [a; u]] [a; d(a)][a; u] [a; u][a; d(a)] [a; [a; u]]d(a) ˆ d(a)[a; [a; u]] [a; [a; u]]d(a) ˆ 2d(a)[a; [a; u]]: Since R is 2-torsion free, d(a)[a; [a; u]] ˆ 0 for all u 2 U. Hence 0 ˆ d(a)[a; [a; u]] ˆ d(a)u[a; [a; u]] for all u 2 U: Since, a 2 S (R) \ R so, d(a) 2 S (R) \ R. Thus, 0 ˆ d(a)u[a; [a; u]] ˆ ˆ (d(a)) U[a; [a; u]] for all u 2 U. Therefore, either [a; [a; u]] ˆ 0 for all u 2 U or d(a) ˆ 0. If [a; [a; u]] ˆ 0 for all u 2 U then a 2 Z(R): If d(a) ˆ 0, using Lemma 2.3 there exists an -ideal M of R, let[va; u] 2 U where v 2 [M; R], hence 0 ˆ [a; d[va; u]] ˆ [a; d(v)[a; u] vd[a; u] d[v; u]a [v; u]d(a)] ˆ [a; d(v)[a; u] [v; u]d(a)] ˆ d(v)[a; [a; u]] [a; d(v)][a; u] [v; u][a; d(a)] [a; [v; u]]d(a) ˆ d(v)[a; [a; u]] for all v 2 [M; R], u 2 U: Therefore, 0 ˆ d[m; R][a; [a; u]] for all u 2 U: Using Lemma 2.6, 0 ˆ [a; [a; u]] for all u 2 U. Thus, a 2 Z(R). 3. Main Results. We facilitate our discussion by proving the following theorem THEOREM 3.1. Let R be a 2-torsion free -prime ring and F : R! R be a generalized derivation with associated non zero derivation d which commutes with. If U is a -Lie ideal of R such that F[u; v] ˆ [F(u); v] for all u; v 2 U then U Z(R). have PROOF. Replacing u by [u; ru] in F[u; v] ˆ [F(u); v] for all u; v 2 U we F[[u; r]u; v] ˆ [F([u; r]u); v] for all u; v 2 U; r 2 R:
5 Commutativity of -Prime Rings with Generalized Derivations 75 This implies that F([u; r][u; v] [[u; r]; v]u) ˆ [F[u; r]u [u; r]d(u); v] for all u; v 2 U; r 2 R: Using the hypothesis we obtain [u; r]d[u; v] ˆ ˆ [u; r][d(u); v] for all u; v 2 U; r 2 R: This gives us [u; r][u; d(v)] ˆ 0 for all u; v 2 U; r 2 R: Replacing r by rs for some s in R we get (3:1) [u; R]R[u; d(v)] ˆ 0 for all u; v 2 U: If u 2 S (R) \ U, then [u; R]R[u; d(u)] ˆ [u; R] R[u; d(u)]. Thus, for some u 2 S (R) \ U either [u; R] ˆ 0 or [u; d(u)] ˆ 0. Butfor any u 2 U, u u ; u u 2 S (R) \ U. Therefore, for some u 2 U either [u u ; R] ˆ 0or[u u ; d(u)] ˆ 0. If [u u ; R] ˆ 0 then from equation (3.1) we obtain that [u; R]R[u; d(u)] ˆ [u; R] R[u; d(u)] ˆ 0 for all u 2 U hence either [u; R] ˆ 0or[u; d(u)] ˆ 0. Let L ˆfu 2 U j [u; R] ˆ 0g and K ˆfu 2 U j [u; d(u)] ˆ 0g. Then itcan be seen thatl and K are two additive subgroups of U whose union is U. Using Brauer's trick we have either L ˆ U or K ˆ U. IfL ˆ U, then [u; R] ˆ 0 for all u 2 U that is U Z(R) and if K ˆ U, then [u; d(u)] ˆ 0 for all u 2 U, which implies that U Z(R) by Lemma 2.8. If [u u ; d(u)] ˆ 0, then again by (3.1) we obtain that [u; R]R[u; d(u)] ˆ [u; R]R[u; d(u)] ˆ 0 for all u 2 U. This gives us either [u; R] ˆ 0or[u; d(u)] ˆ 0. If [u; d(u)] ˆ 0 then using Lemma 2.7 we obtain U Z(R): Hence in any case we obtain that U Z(R): THEOREM 3.2. Let R be a 2-torsion free -prime ring and F : R! Rbe a generalized derivation with associated non zero derivation d which commutes with. If U is a -Lie ideal of R such that F(u v) ˆ F(u) v for all u; v 2 U then U Z(R). PROOF. Replacing u by [u; ru] inf(u v) ˆ F(u) v for all u; v 2 U, r 2 R we have This yeilds that, F([u; r]u v) ˆ F([u; r]u) v for all u; v 2 U; r 2 R: F(([u; r] v)u [u; r][u; v]) ˆ F[u; r]uv [u; r]d(u)v for all u; v2u; r 2 R: Thus we obtain, F([u; r] v)u ([u; r] v)d(u) F[u; r][u; v] [u; r]d[u; v] ˆ (F[u; r] v)u F[u; r][u; v] ([u; r] v)d(u) [u; r][d(u); v] for all u; v 2 U; r 2 R:
6 76 Mohammad Ashraf - Almas Khan Using our hypothesis we find that [u; r]d[u; v] ˆ [u; r][d(u); v] for all u; v 2 U; r 2 R:Hence, we obtain, [u; r][u; d(v)] ˆ 0 for all u; v 2 U; r 2 R: Replacing r by rs for some s in R we get[u; R]R[u; d(v)] ˆ 0forallu; v 2 U: This leads to equation (3.1). Hence, proceeding on the same way as above, we obtain that U Z(R): THEOREM 3.3. Let R be a 2-torsion free -prime ring and F : R! Rbe a generalized derivation with associated non zero derivation d which commutes with. If U is a -Lie ideal of R such that F[u; v] ˆ ˆ [F(u); v] [d(v); u] for all u; v 2 U then U Z(R). PROOF. We have F[u; v] ˆ [F(u); v] [d(v); u] for all u; v 2 U. Now replacing u by [u; ru] we get F[[u; r]u; v] ˆ [F([u; r]u); v] [d(v); [u; r]u] for all u; v 2 U; r 2 R: This gives us F([u; r][u; v] [[u; r]; v]u) ˆ [F[u; r]u [u; r]d(u); v] [d(v); [u; r]u] Hence for all u; v 2 U; r 2 R: F[u; r][u; v] [u; r]d[u; v] F[[u; r]; v]u [[u; r]; v]d(u) ˆ F[u; r][u; v] [F[u; r]; v]u [u; r][d(u); v] [[u; r]; v]d(u) [u; r][d(v); u] [d(v); [u; r]]u for all u; v 2 U; r 2 R: Using the hypothesis we obtain, [u; r]d[u; v] ˆ [u; r][d(v); u] [u; r][d(u); v] for all u; v 2 U; r 2 R: Thisgivesus[u; r][u; d(v)] ˆ 0 for all u; v 2 U; r 2 R: This is same as equation (3.1) hence, continuing in the same manner as above we obtain that U Z(R): THEOREM 3.4. Let R be a 2-torsion free -prime ring and F : R! Rbe a generalized derivation with associated non zero derivation d which commutes with. If U is a -Lie ideal of R such that F(u v) ˆ ˆ F(u) v d(v) u for all u; v 2 U then U Z(R). PROOF. Replacing u by [u; ru] in F(u v) ˆ F(u) v d(v) u for all u; v 2 U; we obtain, F([u; r]u v) ˆ F([u; r]u) v d(v) [u; r]u for all u; v 2 U; r 2 R: This gives us, F(([u; r] v)u [u; r][u; v]) ˆ
7 Commutativity of -Prime Rings with Generalized Derivations 77 ˆ F[u; r]u v [u; r]d(u) v d(v) [u; r]u for all u; v 2 U; r 2 R: Thus, F([u; r] v)u ([u; r] v)d(u) F[u; r][u; v] [u; r]d[u; v] ˆ (F[u; r] v)u F[u; r][u; v] ([u; r] v)d(u) [u; r][d(u); v] (d(v) [u; r])u [u; r][d(v); u] for all u; v 2 U; r 2 R: Using our hypothesis [u; r]d[u; v] ˆ [u; r][d(u); v] [u; r][d(v); u] for all u; v 2 U; r 2 R: This gives us [u; r][u; d(v)] ˆ 0 for all u; v 2 U; r 2 R: Replacing r by rs for some s in R we get[u; R]R[u; d(v)] ˆ 0 for all u; v 2 U which is equation (3.1). Therefore, proceeding in the same way as above we obtain that U Z(R): THEOREM 3.5. Let R be a 2-torsion free -prime ring and U a -Lie ideal of R. If d and g are any two derivations such that both of them are non-zero which commute with. If[g(U); d(u)] ˆ 0 then U Z(R). PROOF. In view of Lemma 2.8 the proof is clear. THEOREM 3.6. Let R be a 2-torsion free -prime ring and U a -Lie ideal of R. If F is a generalized derivation with associated non zero derivation d which commutes with such that F(uv) uv ˆ 0 for all u; v 2 U then U Z(R). PROOF. Let U 6 R. WehaveF(uv) uv ˆ 0 for all u; v 2 U. This can be rewritten as (3:2) F(u)v ud(v) uv ˆ 0 for all u; v 2 U: Replacing u by [u; ru] in (3.2) and using (3.2) we get (3:3) [u; r]ud(v) ˆ 0 for all u; v 2 U; r 2 R: Substituting rs in place of r for some s 2 R in (3.3) we get[u; R]Rud(U) ˆ 0 for all u 2 U: If u 2 S (R) \ U, then either [u; R] ˆ 0orud(U) ˆ 0 for each fixed u 2 S (R) \ U. For any v 2 U we have v v 2 S (R) \ U and v v 2 S (R) \ U, thus 2v 2 S (R) \ U. Thus for some fixed v 2 U, either [2v; R] ˆ 0or2vd(U) ˆ 0. As R is 2-torsion free we have for some fixed v 2 U, either [v; R] ˆ 0orvd(U) ˆ 0: Let A ˆfv 2 U j [v; R] ˆ 0g and B ˆfv 2 U j vd(u) ˆ 0g. Itcan be easily seen thata and B are two additive subgroups of U whose union is U thus using Brauer's trick we get
8 78 Mohammad Ashraf - Almas Khan A ˆ U or B ˆ U. IfA ˆ U, then U Z(R): If B ˆ U, then using Lemma 2.6 we obtain that U Z(R) oru ˆ 0. Thus in every case we obtain that U Z(R). THEOREM 3.7. Let R be a 2-torsion free -prime ring and U a -Lie ideal of R. If F is a generalized derivation with associated non zero derivation d which commutes with such that d(u)f(v) uv ˆ 0 for all u; v 2 U then U Z(R). PROOF. We have d(u)f(v) uv ˆ 0 for all u; v 2 U. Replacing v by [v; rv], r 2 R we obtain (3:4) d(u)[v; r]d(v) ˆ 0 for all u; v 2 U; r 2 R: Using Lemma 2.6 we find that, [v; r]d(v) ˆ 0 for all v 2 U; r 2 R. Substituting rs for r where s 2 R we have (3:5) [v; R]Rd(v) ˆ 0 for all v 2 U: If v 2 S (R) \ U, then either [v; R] ˆ 0 or d(v) ˆ 0. For any u 2 U, u u 2 S (R) \ U. Thus from above [u u ; R] ˆ 0ord(u u ) ˆ 0 that is either [u; R] ˆ [u; R] or d(u) ˆ (d(u)).if[u; R] ˆ [u; R] then from (3.5) we have [u; R]Rd(u) ˆ [u; R] Rd(u) ˆ 0 for all u 2 U. Thus either [u; R] ˆ 0ord(u) ˆ 0. Now if d(u) ˆ (d(u)), then again equation (3.5) yields that [u; R] ˆ 0ord(u) ˆ 0. In both cases, by using Brauer's trick and since d 6ˆ 0, we conclude that U Z(R). REFERENCES [1] M. ASHRAF - A. ALI - S. ALI, Some commutativity theorems for rings with generalized derivations, Southeast Asian Bull. Math., 32 (2) (2007), pp [2] M. ASHRAF - N. REHMAN, On commutativity of rings with derivations, Results Math., 42 (2002), pp [3] J. BERGEN -I.N.HERSTEIN -J. W.KERR, Lie ideals and derivations of prime rings, J. Algebra, 71 (1981), pp [4] H. E. BELL, Some commutativity results involving derivations, Trends in Theory of Rings and Modules, S. T. Rizvi and S. M. A. Zaidi (Eds.), Anamaya Publishers, New Delhi, India (2005), pp [5] BRES Æ AR, On the distance of the composition of two derivations to the generalized derivations, Glasgow Math. J., 33 (1991), pp [6] P. H. LEE - T. K. LEE, Lie ideals of prime rings with derivations, Bull. Inst. Math. Acad. Sinica, 11 (1) (1983), pp
9 Commutativity of -Prime Rings with Generalized Derivations 79 [7] I. N. HERSTEIN, Topics in ring theory, Univ. Chicago Press, Chicago (1969). [8] L. OUKHTITE -S. SALHI, On generalized Derivations of s-prime rings, African Diaspora J. Math., 5 (1) (2006), pp [9] L. OUKHTITE - S. SALHI, Commutativity of s-prime rings, Glasnik Math., 41 (2006), pp [10] L. OUKHTITE -S.SALHI, Lie ideals and derivations of s prime rings, Int. J. Algebra, 1 (2007), pp [11] L. OUKHTITE - S. SALHI, Centralizing automorphisms and Jordan left derivations of s-prime rings, Advances in Algebra, 1 (1) (2008), pp Manoscritto pervenuto in redazione il 9 luglio 2010.
10
NOTES ON GENERALIZED DERIVATIONS OF -PRIME RINGS
 Miskolc Mathematical Notes HU e-issn 1787-2413 Vol. 15 (2014), No. 1, pp. 117 123 NOTES ON GENERALIZED DERIVATIONS OF -PRIME RINGS EMINE KOÇ AND NADEEM UR REHMAN Received 24 September, 2013 Abstract. Let
Miskolc Mathematical Notes HU e-issn 1787-2413 Vol. 15 (2014), No. 1, pp. 117 123 NOTES ON GENERALIZED DERIVATIONS OF -PRIME RINGS EMINE KOÇ AND NADEEM UR REHMAN Received 24 September, 2013 Abstract. Let
Generalized (α, β)-derivations on Jordan ideals in -prime rings
 Rend. Circ. Mat. Palermo (2014) 63:11 17 DOI 10.1007/s12215-013-0138-2 Generalized (α, β)-derivations on Jordan ideals in -prime rings Öznur Gölbaşi Özlem Kizilgöz Received: 20 May 2013 / Accepted: 7 October
Rend. Circ. Mat. Palermo (2014) 63:11 17 DOI 10.1007/s12215-013-0138-2 Generalized (α, β)-derivations on Jordan ideals in -prime rings Öznur Gölbaşi Özlem Kizilgöz Received: 20 May 2013 / Accepted: 7 October
Left Multipliers Satisfying Certain Algebraic Identities on Lie Ideals of Rings With Involution
 Int. J. Open Problems Comput. Math., Vol. 5, No. 3, September, 2012 ISSN 2074-2827; Copyright c ICSRS Publication, 2012 www.i-csrs.org Left Multipliers Satisfying Certain Algebraic Identities on Lie Ideals
Int. J. Open Problems Comput. Math., Vol. 5, No. 3, September, 2012 ISSN 2074-2827; Copyright c ICSRS Publication, 2012 www.i-csrs.org Left Multipliers Satisfying Certain Algebraic Identities on Lie Ideals
Lie Ideals and Generalized Derivations. in -Prime Rings - II
 International Journal of Algebra, Vol. 6, 2012, no. 29, 1419 1429 Lie Ideals and Generalized Derivations in -Prime Rings - II M. S. Khan Department of Mathematics and Statistics Faculty of Science, Sultan
International Journal of Algebra, Vol. 6, 2012, no. 29, 1419 1429 Lie Ideals and Generalized Derivations in -Prime Rings - II M. S. Khan Department of Mathematics and Statistics Faculty of Science, Sultan
Commutativity theorems for rings with differential identities on Jordan ideals
 Comment.Math.Univ.Carolin. 54,4(2013) 447 457 447 Commutativity theorems for rings with differential identities on Jordan ideals L. Oukhtite, A. Mamouni, Mohammad Ashraf Abstract. In this paper we investigate
Comment.Math.Univ.Carolin. 54,4(2013) 447 457 447 Commutativity theorems for rings with differential identities on Jordan ideals L. Oukhtite, A. Mamouni, Mohammad Ashraf Abstract. In this paper we investigate
ON 3-PRIME NEAR-RINGS WITH GENERALIZED DERIVATIONS
 Palestine Journal of Mathematics Vol. 51) 2016), 12 16 Palestine Polytechnic University-PPU 2016 ON 3-PRIME NEAR-RINGS WITH GENERALIZED DERIVATIONS A. Boua, L. Oukhtite and A. Raji Communicated by N. Mahdou
Palestine Journal of Mathematics Vol. 51) 2016), 12 16 Palestine Polytechnic University-PPU 2016 ON 3-PRIME NEAR-RINGS WITH GENERALIZED DERIVATIONS A. Boua, L. Oukhtite and A. Raji Communicated by N. Mahdou
On Generalized Derivations and Commutativity. of Prime Rings with Involution
 International Journal of Algebra, Vol. 11, 2017, no. 6, 291-300 HIKARI Ltd, www.m-hikari.com https://doi.org/10.12988/ija.2017.7839 On Generalized Derivations and Commutativity of Prime Rings with Involution
International Journal of Algebra, Vol. 11, 2017, no. 6, 291-300 HIKARI Ltd, www.m-hikari.com https://doi.org/10.12988/ija.2017.7839 On Generalized Derivations and Commutativity of Prime Rings with Involution
On generalized -derivations in -rings
 Palestine Journal of Mathematics Vol. 1 (2012), 32 37 Palestine Polytechnic University-PPU 2012 On generalized -derivations in -rings Shakir Ali Communicated by Tariq Rizvi 2000 Mathematics Subject Classification:
Palestine Journal of Mathematics Vol. 1 (2012), 32 37 Palestine Polytechnic University-PPU 2012 On generalized -derivations in -rings Shakir Ali Communicated by Tariq Rizvi 2000 Mathematics Subject Classification:
Generalized Multiplicative Derivations in Near-Rings
 Generalized Multiplicative Derivations in Near-Rings Mohammad Aslam Siddeeque Department of Mathematics Aligarh Muslim University Aligarh -222(India) E-mail : aslamsiddeeque@gmail.com Abstract: In the
Generalized Multiplicative Derivations in Near-Rings Mohammad Aslam Siddeeque Department of Mathematics Aligarh Muslim University Aligarh -222(India) E-mail : aslamsiddeeque@gmail.com Abstract: In the
PAijpam.eu GENERALIZED SEMIDERIVATIONS IN
 International Journal of Pure and Applied Mathematics Volume 109 No. 6 2016, 41-47 ISSN: 1311-8080 (printed version); ISSN: 1314-3395 (on-line version) url: http://www.ijpam.eu doi: 10.12732/ijpam.v109i6.6
International Journal of Pure and Applied Mathematics Volume 109 No. 6 2016, 41-47 ISSN: 1311-8080 (printed version); ISSN: 1314-3395 (on-line version) url: http://www.ijpam.eu doi: 10.12732/ijpam.v109i6.6
On R-Strong Jordan Ideals
 International Journal of Algebra, Vol. 3, 2009, no. 18, 897-902 On R-Strong Jordan Ideals Anita Verma Department of Mathematics University of Delhi, Delhi 1107, India verma.anitaverma.anita945@gmail.com
International Journal of Algebra, Vol. 3, 2009, no. 18, 897-902 On R-Strong Jordan Ideals Anita Verma Department of Mathematics University of Delhi, Delhi 1107, India verma.anitaverma.anita945@gmail.com
Lie Ideals in Prime Rings with (σ, τ) Derivation
 International Journal of Algebra, Vol. 3, 2009, no. 17, 857-862 Lie Ideals in Prime Rings with (σ, τ) Derivation Evrim Güven Kocaeli University Faculty of Art and Sciences Department of Mathematics, Turkey
International Journal of Algebra, Vol. 3, 2009, no. 17, 857-862 Lie Ideals in Prime Rings with (σ, τ) Derivation Evrim Güven Kocaeli University Faculty of Art and Sciences Department of Mathematics, Turkey
Jordan α-centralizers in rings and some applications
 Bol. Soc. Paran. Mat. (3s.) v. 26 1-2 (2008): 71 80. c SPM ISNN-00378712 Jordan α-centralizers in rings and some applications Shakir Ali and Claus Haetinger abstract: Let R be a ring, and α be an endomorphism
Bol. Soc. Paran. Mat. (3s.) v. 26 1-2 (2008): 71 80. c SPM ISNN-00378712 Jordan α-centralizers in rings and some applications Shakir Ali and Claus Haetinger abstract: Let R be a ring, and α be an endomorphism
Some theorems of commutativity on semiprime rings with mappings
 Some theorems of commutativity on semiprime rings with mappings S. K. Tiwari Department of Mathematics Indian Institute of Technology Delhi, New Delhi-110016, INDIA Email: shaileshiitd84@gmail.com R. K.
Some theorems of commutativity on semiprime rings with mappings S. K. Tiwari Department of Mathematics Indian Institute of Technology Delhi, New Delhi-110016, INDIA Email: shaileshiitd84@gmail.com R. K.
Multiplicative (Generalized)-(α, β)-derivations in Prime and Semiprime Rings
 Multiplicative (Generalized)-(α, β)-derivations in Prime and Semiprime Rings Chirag Garg*, R. K. Sharma Department of Mathematics, Indian Institute of Technology, Delhi-110016, India. * Corresponding author.
Multiplicative (Generalized)-(α, β)-derivations in Prime and Semiprime Rings Chirag Garg*, R. K. Sharma Department of Mathematics, Indian Institute of Technology, Delhi-110016, India. * Corresponding author.
Derivations and Reverse Derivations. in Semiprime Rings
 International Mathematical Forum, 2, 2007, no. 39, 1895-1902 Derivations and Reverse Derivations in Semiprime Rings Mohammad Samman Department of Mathematical Sciences King Fahd University of Petroleum
International Mathematical Forum, 2, 2007, no. 39, 1895-1902 Derivations and Reverse Derivations in Semiprime Rings Mohammad Samman Department of Mathematical Sciences King Fahd University of Petroleum
ON GENERALIZED DERIVATION IN RINGS AND BANACH ALGEBRAS
 Kragujevac Journal of Mathematics Volume 41(1) (2017), Pages 105 120. ON GENERALIZED DERIVATION IN RINGS AND BANACH ALGEBRAS M. A. RAZA 1 AND N. U. REHMAN 2 Abstract. Let R be a prime ring, F be a generalized
Kragujevac Journal of Mathematics Volume 41(1) (2017), Pages 105 120. ON GENERALIZED DERIVATION IN RINGS AND BANACH ALGEBRAS M. A. RAZA 1 AND N. U. REHMAN 2 Abstract. Let R be a prime ring, F be a generalized
Nadeem Ur Rehman. 1. Introduction
 J. Korean Soc. Math. Educ. Ser. B: Pure Appl. Math. ISSN(Print) 1226-0657 https://doi.org/10.7468/jksmeb.2018.25.3.181 ISSN(Online) 2287-6081 Volume 25, Number 3 (August 2018), Pages 181 191 A REMARK ON
J. Korean Soc. Math. Educ. Ser. B: Pure Appl. Math. ISSN(Print) 1226-0657 https://doi.org/10.7468/jksmeb.2018.25.3.181 ISSN(Online) 2287-6081 Volume 25, Number 3 (August 2018), Pages 181 191 A REMARK ON
On Generalized Derivations. of Semiprime Rings
 International Journal of Algebra, Vol. 4, 2010, no. 12, 591-598 On Generalized Derivations of Semiprime Rings Mehsin Jabel Atteya Al-Mustansiriyah University, College of Education Department of Mathematics,
International Journal of Algebra, Vol. 4, 2010, no. 12, 591-598 On Generalized Derivations of Semiprime Rings Mehsin Jabel Atteya Al-Mustansiriyah University, College of Education Department of Mathematics,
COMMUTATIVITY RESULTS FOR SEMIPRIME RINGS WITH DERIVATIONS. KEY WORDS AND PHRASES: Semiprime ring, derivation, commutator, and central ideal.
 Internat. J. Math. & Math. Sci. VOL. 21 NO. 3 (1998) 471-474 471 COMMUTATIVITY RESULTS FOR SEMIPRIME RINGS WITH DERIVATIONS MOHAMAD NAGY DAIF Department of Mathematics Faculty of Science AI-Azhar University
Internat. J. Math. & Math. Sci. VOL. 21 NO. 3 (1998) 471-474 471 COMMUTATIVITY RESULTS FOR SEMIPRIME RINGS WITH DERIVATIONS MOHAMAD NAGY DAIF Department of Mathematics Faculty of Science AI-Azhar University
ON COMMUTATIVITY OF SEMIPRIME RINGS WITH GENERALIZED DERIVATIONS
 Indian J. pure appl. Math., 40(3): 191-199, June 2009 c Printed in India. ON COMMUTATIVITY OF SEMIPRIME RINGS WITH GENERALIZED DERIVATIONS ÖZNUR GÖLBAŞI Cumhuriyet University, Faculty of Arts and Science,
Indian J. pure appl. Math., 40(3): 191-199, June 2009 c Printed in India. ON COMMUTATIVITY OF SEMIPRIME RINGS WITH GENERALIZED DERIVATIONS ÖZNUR GÖLBAŞI Cumhuriyet University, Faculty of Arts and Science,
ON SEMIGROUP IDEALS OF PRIME NEAR-RINGS WITH GENERALIZED SEMIDERIVATION
 Palestine Journal of Mathematics Vol. 7(1)(2018), 243 250 Palestine Polytechnic University-PPU 2018 ON SEMIGROUP IDEALS OF PRIME NEAR-RINGS WITH GENERALIZED SEMIDERIVATION Öznur Gölbaş and Emine Koç Communicated
Palestine Journal of Mathematics Vol. 7(1)(2018), 243 250 Palestine Polytechnic University-PPU 2018 ON SEMIGROUP IDEALS OF PRIME NEAR-RINGS WITH GENERALIZED SEMIDERIVATION Öznur Gölbaş and Emine Koç Communicated
2. MAIN RESULTS. derivation,
 International Journal of Scientific and Innovative Mathematical Research (IJSIMR) Volume 2, Issue 3, March 2014, PP 306-312 ISSN 2347-307X (Print) & ISSN 2347-3142 (Online) www.arcjournals.org On Generalized
International Journal of Scientific and Innovative Mathematical Research (IJSIMR) Volume 2, Issue 3, March 2014, PP 306-312 ISSN 2347-307X (Print) & ISSN 2347-3142 (Online) www.arcjournals.org On Generalized
JORDAN *-DERIVATIONS ON PRIME AND SEMIPRIME *-RINGS د.عبد الرحمن حميد مجيد وعلي عبد عبيد الطائي كلية العلوم جامعة بغداد العراق.
 JORDAN *-DERIVATIONS ON PRIME AND SEMIPRIME *-RINGS A.H.Majeed Department of mathematics, college of science, University of Baghdad Mail: ahmajeed6@yahoo.com A.A.ALTAY Department of mathematics, college
JORDAN *-DERIVATIONS ON PRIME AND SEMIPRIME *-RINGS A.H.Majeed Department of mathematics, college of science, University of Baghdad Mail: ahmajeed6@yahoo.com A.A.ALTAY Department of mathematics, college
A NOTE ON JORDAN DERIVATIONS IN SEMIPRIME RINGS WITH INVOLUTION 1
 International Mathematical Forum, 1, 2006, no. 13, 617-622 A NOTE ON JORDAN DERIVATIONS IN SEMIPRIME RINGS WITH INVOLUTION 1 Joso Vukman Department of Mathematics University of Maribor PeF, Koroška 160,
International Mathematical Forum, 1, 2006, no. 13, 617-622 A NOTE ON JORDAN DERIVATIONS IN SEMIPRIME RINGS WITH INVOLUTION 1 Joso Vukman Department of Mathematics University of Maribor PeF, Koroška 160,
ON STRUCTURE AND COMMUTATIVITY OF NEAR - RINGS
 Proyecciones Vol. 19, N o 2, pp. 113-124, August 2000 Universidad Católica del Norte Antofagasta - Chile ON STRUCTURE AND COMMUTATIVITY OF NEAR - RINGS H. A. S. ABUJABAL, M. A. OBAID and M. A. KHAN King
Proyecciones Vol. 19, N o 2, pp. 113-124, August 2000 Universidad Católica del Norte Antofagasta - Chile ON STRUCTURE AND COMMUTATIVITY OF NEAR - RINGS H. A. S. ABUJABAL, M. A. OBAID and M. A. KHAN King
International Journal of Pure and Applied Sciences and Technology
 Int. J. Pure Appl. Sci. Technol., 2(1) (2011), pp. 71-77 International Journal of Pure and Applied Sciences and Technology ISSN 2229-6107 Available online at www.ijopaasat.in Research Paper A Note on α
Int. J. Pure Appl. Sci. Technol., 2(1) (2011), pp. 71-77 International Journal of Pure and Applied Sciences and Technology ISSN 2229-6107 Available online at www.ijopaasat.in Research Paper A Note on α
Research Article On Prime Near-Rings with Generalized Derivation
 International Mathematics and Mathematical Sciences Volume 2008, Article ID 490316, 5 pages doi:10.1155/2008/490316 Research Article On Prime Near-Rings with Generalized Derivation Howard E. Bell Department
International Mathematics and Mathematical Sciences Volume 2008, Article ID 490316, 5 pages doi:10.1155/2008/490316 Research Article On Prime Near-Rings with Generalized Derivation Howard E. Bell Department
On Right α-centralizers and Commutativity of Prime Rings
 On Right α-centralizers and Commutativity of Prime Rings Amira A. Abduljaleel*, Abdulrahman H. Majeed Department of Mathematics, College of Science, Baghdad University, Baghdad, Iraq Abstract: Let R be
On Right α-centralizers and Commutativity of Prime Rings Amira A. Abduljaleel*, Abdulrahman H. Majeed Department of Mathematics, College of Science, Baghdad University, Baghdad, Iraq Abstract: Let R be
On (σ, τ) Derivations in Prime Rings
 Int. J. Contemp. Math. Sciences, Vol. 3, 2008, no. 26, 1289-1293 On (σ, τ) Derivations in Prime Rings Evrim Güven Kocaeli University evrim@kocaeli.edu.tr Abstract. Let R be a prime ring with characteristic
Int. J. Contemp. Math. Sciences, Vol. 3, 2008, no. 26, 1289-1293 On (σ, τ) Derivations in Prime Rings Evrim Güven Kocaeli University evrim@kocaeli.edu.tr Abstract. Let R be a prime ring with characteristic
Pacific Journal of Mathematics
 Pacific Journal of Mathematics INVERSION INVARIANT ADDITIVE SUBGROUPS OF DIVISION RINGS DANIEL GOLDSTEIN, ROBERT M. GURALNICK, LANCE SMALL AND EFIM ZELMANOV Volume 227 No. 2 October 2006 PACIFIC JOURNAL
Pacific Journal of Mathematics INVERSION INVARIANT ADDITIVE SUBGROUPS OF DIVISION RINGS DANIEL GOLDSTEIN, ROBERT M. GURALNICK, LANCE SMALL AND EFIM ZELMANOV Volume 227 No. 2 October 2006 PACIFIC JOURNAL
Relations of Centralizers on Semiprime Semirings
 International Journal of Mathematics Research. ISSN 0976-5840 Volume 10, Number 1 (2018), pp. 21-32 International Research Publication House http://www.irphouse.com Relations of Centralizers on Semiprime
International Journal of Mathematics Research. ISSN 0976-5840 Volume 10, Number 1 (2018), pp. 21-32 International Research Publication House http://www.irphouse.com Relations of Centralizers on Semiprime
Algebraic Sum of Unbounded Normal Operators and the Square Root Problem of Kato.
 REND. SEM. MAT. UNIV. PADOVA, Vol. 110 (2003) Algebraic Sum of Unbounded Normal Operators and the Square Root Problem of Kato. TOKA DIAGANA (*) ABSTRACT - We prove that the algebraic sum of unbounded normal
REND. SEM. MAT. UNIV. PADOVA, Vol. 110 (2003) Algebraic Sum of Unbounded Normal Operators and the Square Root Problem of Kato. TOKA DIAGANA (*) ABSTRACT - We prove that the algebraic sum of unbounded normal
SEMI-INVARIANTS AND WEIGHTS OF GROUP ALGEBRAS OF FINITE GROUPS. D. S. Passman P. Wauters University of Wisconsin-Madison Limburgs Universitair Centrum
 SEMI-INVARIANTS AND WEIGHTS OF GROUP ALGEBRAS OF FINITE GROUPS D. S. Passman P. Wauters University of Wisconsin-Madison Limburgs Universitair Centrum Abstract. We study the semi-invariants and weights
SEMI-INVARIANTS AND WEIGHTS OF GROUP ALGEBRAS OF FINITE GROUPS D. S. Passman P. Wauters University of Wisconsin-Madison Limburgs Universitair Centrum Abstract. We study the semi-invariants and weights
Subrings and Ideals 2.1 INTRODUCTION 2.2 SUBRING
 Subrings and Ideals Chapter 2 2.1 INTRODUCTION In this chapter, we discuss, subrings, sub fields. Ideals and quotient ring. We begin our study by defining a subring. If (R, +, ) is a ring and S is a non-empty
Subrings and Ideals Chapter 2 2.1 INTRODUCTION In this chapter, we discuss, subrings, sub fields. Ideals and quotient ring. We begin our study by defining a subring. If (R, +, ) is a ring and S is a non-empty
On generalized n-derivation in prime near rings
 IOSR Journal of Mathematics (IOSR-JM) e-issn: 2278-5728, p-issn: 2319-765X. Volume 11, Issue 3 Ver. I (May - Jun. 2015), PP 115-122 www.iosrjournals.org On generalized n-derivation in prime near rings
IOSR Journal of Mathematics (IOSR-JM) e-issn: 2278-5728, p-issn: 2319-765X. Volume 11, Issue 3 Ver. I (May - Jun. 2015), PP 115-122 www.iosrjournals.org On generalized n-derivation in prime near rings
Since Brešar and Vukman initiated the study of left derivations in noncom-
 JORDAN LEFT DERIVATIONS IN FULL AND UPPER TRIANGULAR MATRIX RINGS XIAO WEI XU AND HONG YING ZHANG Abstract. In this paper, left derivations and Jordan left derivations in full and upper triangular matrix
JORDAN LEFT DERIVATIONS IN FULL AND UPPER TRIANGULAR MATRIX RINGS XIAO WEI XU AND HONG YING ZHANG Abstract. In this paper, left derivations and Jordan left derivations in full and upper triangular matrix
I Results in Mathematics
 Result.Matn. 46 (2004) 123-129 1422-6383/04/020123-7 DOII0.1007/s00025-004-0135-z Birkhauser Vertag, Basel, 2004 I Results in Mathematics Skew-commuting and Commuting Mappings in Rings with Left Identity
Result.Matn. 46 (2004) 123-129 1422-6383/04/020123-7 DOII0.1007/s00025-004-0135-z Birkhauser Vertag, Basel, 2004 I Results in Mathematics Skew-commuting and Commuting Mappings in Rings with Left Identity
Polynomials of small degree evaluated on matrices
 Polynomials of small degree evaluated on matrices Zachary Mesyan January 1, 2013 Abstract A celebrated theorem of Shoda states that over any field K (of characteristic 0), every matrix with trace 0 can
Polynomials of small degree evaluated on matrices Zachary Mesyan January 1, 2013 Abstract A celebrated theorem of Shoda states that over any field K (of characteristic 0), every matrix with trace 0 can
ON (m, n) JORDAN CENTRALIZERS IN RINGS AND ALGEBRAS. Joso Vukman University of Maribor, Slovenia
 GLASNIK MATEMATIČKI Vol. 45(65)(2010), 43 53 ON (m, n) JORDAN CENTRALIZERS IN RINGS AND ALGEBRAS Joso Vukman University of Maribor, Slovenia Abstract. Let m 0, n 0 be fixed integers with m + n 0 and let
GLASNIK MATEMATIČKI Vol. 45(65)(2010), 43 53 ON (m, n) JORDAN CENTRALIZERS IN RINGS AND ALGEBRAS Joso Vukman University of Maribor, Slovenia Abstract. Let m 0, n 0 be fixed integers with m + n 0 and let
BERNARD RUSSO University of California, Irvine. Report on joint work with. Antonio M. Peralta Universidad de Granada, Spain
 TERNARY WEAKLY AMENABLE C*-ALGEBRAS BERNARD RUSSO University of California, Irvine Report on joint work with Antonio M. Peralta Universidad de Granada, Spain GPOTS XXXI ARIZONA STATE UNIVERSITY MAY 18,
TERNARY WEAKLY AMENABLE C*-ALGEBRAS BERNARD RUSSO University of California, Irvine Report on joint work with Antonio M. Peralta Universidad de Granada, Spain GPOTS XXXI ARIZONA STATE UNIVERSITY MAY 18,
On (θ, θ)-derivations in Semiprime Rings
 Gen. Math. Notes, Vol. 24, No. 1, September 2014, pp. 89-97 ISSN 2219-7184; Copyright ICSRS Publication, 2014 www.i-csrs.org Available free online at http://www.geman.in On (θ, θ)-derivations in Semiprime
Gen. Math. Notes, Vol. 24, No. 1, September 2014, pp. 89-97 ISSN 2219-7184; Copyright ICSRS Publication, 2014 www.i-csrs.org Available free online at http://www.geman.in On (θ, θ)-derivations in Semiprime
Research Article On Maps of Period 2 on Prime and Semiprime Rings
 International Mathematics and Mathematical Sciences, Article ID 140790, 4 pages http://dx.doi.org/10.1155/2014/140790 Research Article On Maps of Period 2 on Prime and Semiprime Rings H. E. Bell 1 and
International Mathematics and Mathematical Sciences, Article ID 140790, 4 pages http://dx.doi.org/10.1155/2014/140790 Research Article On Maps of Period 2 on Prime and Semiprime Rings H. E. Bell 1 and
Algebra Homework, Edition 2 9 September 2010
 Algebra Homework, Edition 2 9 September 2010 Problem 6. (1) Let I and J be ideals of a commutative ring R with I + J = R. Prove that IJ = I J. (2) Let I, J, and K be ideals of a principal ideal domain.
Algebra Homework, Edition 2 9 September 2010 Problem 6. (1) Let I and J be ideals of a commutative ring R with I + J = R. Prove that IJ = I J. (2) Let I, J, and K be ideals of a principal ideal domain.
Final Exam Review Sheet : Comments and Selected Solutions
 MATH 55 Applied Honors alculus III Winter Final xam Review heet : omments and elected olutions Note: The final exam will cover % among topics in chain rule, linear approximation, maximum and minimum values,
MATH 55 Applied Honors alculus III Winter Final xam Review heet : omments and elected olutions Note: The final exam will cover % among topics in chain rule, linear approximation, maximum and minimum values,
ON DERIVATIONS IN PRIME GAMMA-NEAR-RINGS
 GANIT J. Bangladesh Math. Soc. (ISSN 1606-3694) 32 (2012) 23-28 ON DERIVATIONS IN PRIME GAMMA-NEAR-RINGS Kalyan Kumar Dey 1 and Akhil Chandra Paul 2 Department of Mathematics University of Rajshahi, Rajshahi-6205,
GANIT J. Bangladesh Math. Soc. (ISSN 1606-3694) 32 (2012) 23-28 ON DERIVATIONS IN PRIME GAMMA-NEAR-RINGS Kalyan Kumar Dey 1 and Akhil Chandra Paul 2 Department of Mathematics University of Rajshahi, Rajshahi-6205,
x 9 or x > 10 Name: Class: Date: 1 How many natural numbers are between 1.5 and 4.5 on the number line?
 1 How many natural numbers are between 1.5 and 4.5 on the number line? 2 How many composite numbers are between 7 and 13 on the number line? 3 How many prime numbers are between 7 and 20 on the number
1 How many natural numbers are between 1.5 and 4.5 on the number line? 2 How many composite numbers are between 7 and 13 on the number line? 3 How many prime numbers are between 7 and 20 on the number
On Commutativity of Completely Prime Gamma-Rings
 alaysian Journal of athematical Sciences 7(2): 283-295 (2013) ALAYSIAN JOURNAL OF ATHEATICAL SCIENCES Journal homepage: http://einspem.upm.edu.my/journal 1,2 I. S. Rakhimov, 3* Kalyan Kumar Dey and 3 Akhil
alaysian Journal of athematical Sciences 7(2): 283-295 (2013) ALAYSIAN JOURNAL OF ATHEATICAL SCIENCES Journal homepage: http://einspem.upm.edu.my/journal 1,2 I. S. Rakhimov, 3* Kalyan Kumar Dey and 3 Akhil
Some Results of Compatible Mapping in Metric Spaces
 International Refereed Journal of Engineering and Science (IRJES) ISSN (Online) 2319-183X, (Print) 2319-1821 Volume 6, Issue 3 (March 2017), PP.38-44 Some Results of Compatible Mapping in Metric Spaces
International Refereed Journal of Engineering and Science (IRJES) ISSN (Online) 2319-183X, (Print) 2319-1821 Volume 6, Issue 3 (March 2017), PP.38-44 Some Results of Compatible Mapping in Metric Spaces
TOPOLOGY HW 2. x x ± y
 TOPOLOGY HW 2 CLAY SHONKWILER 20.9 Show that the euclidean metric d on R n is a metric, as follows: If x, y R n and c R, define x + y = (x 1 + y 1,..., x n + y n ), cx = (cx 1,..., cx n ), x y = x 1 y
TOPOLOGY HW 2 CLAY SHONKWILER 20.9 Show that the euclidean metric d on R n is a metric, as follows: If x, y R n and c R, define x + y = (x 1 + y 1,..., x n + y n ), cx = (cx 1,..., cx n ), x y = x 1 y
Continuous r.v practice problems
 Continuous r.v practice problems SDS 321 Intro to Probability and Statistics 1. (2+2+1+1 6 pts) The annual rainfall (in inches) in a certain region is normally distributed with mean 4 and standard deviation
Continuous r.v practice problems SDS 321 Intro to Probability and Statistics 1. (2+2+1+1 6 pts) The annual rainfall (in inches) in a certain region is normally distributed with mean 4 and standard deviation
LIE AND JORDAN STRUCTURE IN PRIME RINGS WITH DERIVATIONS
 PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 41, Number 1, November 1973 LIE AND JORDAN STRUCTURE IN PRIME RINGS WITH DERIVATIONS RAM AWTAR1 Abstract. In this paper Lie ideals and Jordan ideals
PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 41, Number 1, November 1973 LIE AND JORDAN STRUCTURE IN PRIME RINGS WITH DERIVATIONS RAM AWTAR1 Abstract. In this paper Lie ideals and Jordan ideals
On superalgebras. Ajda Fo²ner University of Primorska Faculty of Management Cankarjeva 5 SI-6104 Koper Slovenia
 On superalgebras Ajda Fo²ner University of Primorska Faculty of Management Cankarjeva 5 SI-6104 Koper Slovenia ajda.fosner@fm-kp.si Maja Fo²ner University of Maribor Faculty of Logistics Mariborska cesta
On superalgebras Ajda Fo²ner University of Primorska Faculty of Management Cankarjeva 5 SI-6104 Koper Slovenia ajda.fosner@fm-kp.si Maja Fo²ner University of Maribor Faculty of Logistics Mariborska cesta
Quasigroups and Related Systems 21 (2013), Introduction
 Quasigroups and Related Systems 21 (2013), 175 184 On 2-absorbing semimodules Manish Kant Dubey and Poonam Sarohe Abstract. In this paper, we introduce the concept of 2-absorbing semimodules over a commutative
Quasigroups and Related Systems 21 (2013), 175 184 On 2-absorbing semimodules Manish Kant Dubey and Poonam Sarohe Abstract. In this paper, we introduce the concept of 2-absorbing semimodules over a commutative
DERIVATIONS IN PRIME RINGS
 proceedings of the american mathematical society Volume 84, Number 1, January 1982 DERIVATIONS IN PRIME RINGS B. FELZENSZWALB1 Abstract. Let R be a ring and d =0 a. derivation of R such that d(x") = 0,
proceedings of the american mathematical society Volume 84, Number 1, January 1982 DERIVATIONS IN PRIME RINGS B. FELZENSZWALB1 Abstract. Let R be a ring and d =0 a. derivation of R such that d(x") = 0,
@FMI c Kyung Moon Sa Co.
 Annals of Fuzzy Mathematics and Informatics Volume 4, No. 2, October 2012), pp. 365 375 ISSN 2093 9310 http://www.afmi.or.kr @FMI c Kyung Moon Sa Co. http://www.kyungmoon.com On soft int-groups Kenan Kaygisiz
Annals of Fuzzy Mathematics and Informatics Volume 4, No. 2, October 2012), pp. 365 375 ISSN 2093 9310 http://www.afmi.or.kr @FMI c Kyung Moon Sa Co. http://www.kyungmoon.com On soft int-groups Kenan Kaygisiz
A note on Derivations of Commutative Rings
 A note on Derivations of Commutative Rings MICHAEL GR. VOSKOGLOU School of Technological Applications Graduate Technological Educational Institute (T. E. I.) Meg. Alexandrou 1, 26334 Patras GREECE e-mail:
A note on Derivations of Commutative Rings MICHAEL GR. VOSKOGLOU School of Technological Applications Graduate Technological Educational Institute (T. E. I.) Meg. Alexandrou 1, 26334 Patras GREECE e-mail:
Factorization of weighted EP elements in C -algebras
 Factorization of weighted EP elements in C -algebras Dijana Mosić, Dragan S. Djordjević Abstract We present characterizations of weighted EP elements in C -algebras using different kinds of factorizations.
Factorization of weighted EP elements in C -algebras Dijana Mosić, Dragan S. Djordjević Abstract We present characterizations of weighted EP elements in C -algebras using different kinds of factorizations.
Introduction to Differentials
 Introduction to Differentials David G Radcliffe 13 March 2007 1 Increments Let y be a function of x, say y = f(x). The symbol x denotes a change or increment in the value of x. Note that a change in the
Introduction to Differentials David G Radcliffe 13 March 2007 1 Increments Let y be a function of x, say y = f(x). The symbol x denotes a change or increment in the value of x. Note that a change in the
Introduction Non-uniqueness of factorization in A[x]... 66
![Introduction Non-uniqueness of factorization in A[x]... 66 Introduction Non-uniqueness of factorization in A[x]... 66](/thumbs/78/78085310.jpg) Abstract In this work, we study the factorization in A[x], where A is an Artinian local principal ideal ring (briefly SPIR), whose maximal ideal, (t), has nilpotency h: this is not a Unique Factorization
Abstract In this work, we study the factorization in A[x], where A is an Artinian local principal ideal ring (briefly SPIR), whose maximal ideal, (t), has nilpotency h: this is not a Unique Factorization
Hereditary right Jacobson radicals of type-1(e) and 2(e) for right near-rings
 An. Şt. Univ. Ovidius Constanţa Vol. 21(1), 2013, 1 14 Hereditary right Jacobson radicals of type-1(e) and 2(e) for right near-rings Ravi Srinivasa Rao and K. Siva Prasad Abstract Near-rings considered
An. Şt. Univ. Ovidius Constanţa Vol. 21(1), 2013, 1 14 Hereditary right Jacobson radicals of type-1(e) and 2(e) for right near-rings Ravi Srinivasa Rao and K. Siva Prasad Abstract Near-rings considered
Math 203A - Solution Set 1
 Math 203A - Solution Set 1 Problem 1. Show that the Zariski topology on A 2 is not the product of the Zariski topologies on A 1 A 1. Answer: Clearly, the diagonal Z = {(x, y) : x y = 0} A 2 is closed in
Math 203A - Solution Set 1 Problem 1. Show that the Zariski topology on A 2 is not the product of the Zariski topologies on A 1 A 1. Answer: Clearly, the diagonal Z = {(x, y) : x y = 0} A 2 is closed in
arxiv: v1 [math.ra] 25 May 2013
![arxiv: v1 [math.ra] 25 May 2013 arxiv: v1 [math.ra] 25 May 2013](/thumbs/81/84380444.jpg) Quasigroups and Related Systems 20 (2012), 203 209 Congruences on completely inverse AG -groupoids Wieslaw A. Dudek and Roman S. Gigoń arxiv:1305.6858v1 [math.ra] 25 May 2013 Abstract. By a completely
Quasigroups and Related Systems 20 (2012), 203 209 Congruences on completely inverse AG -groupoids Wieslaw A. Dudek and Roman S. Gigoń arxiv:1305.6858v1 [math.ra] 25 May 2013 Abstract. By a completely
Rendiconti del Seminario Matematico della Università di Padova, tome 88 (1992), p
 RENDICONTI del SEMINARIO MATEMATICO della UNIVERSITÀ DI PADOVA ANDREA LUCCHINI Generating the augmentation ideal Rendiconti del Seminario Matematico della Università di Padova, tome 88 (1992), p. 145-149
RENDICONTI del SEMINARIO MATEMATICO della UNIVERSITÀ DI PADOVA ANDREA LUCCHINI Generating the augmentation ideal Rendiconti del Seminario Matematico della Università di Padova, tome 88 (1992), p. 145-149
B 1 = {B(x, r) x = (x 1, x 2 ) H, 0 < r < x 2 }. (a) Show that B = B 1 B 2 is a basis for a topology on X.
 Math 6342/7350: Topology and Geometry Sample Preliminary Exam Questions 1. For each of the following topological spaces X i, determine whether X i and X i X i are homeomorphic. (a) X 1 = [0, 1] (b) X 2
Math 6342/7350: Topology and Geometry Sample Preliminary Exam Questions 1. For each of the following topological spaces X i, determine whether X i and X i X i are homeomorphic. (a) X 1 = [0, 1] (b) X 2
A CHARACTERIZATION OF WARPED PRODUCT PSEUDO-SLANT SUBMANIFOLDS IN NEARLY COSYMPLECTIC MANIFOLDS
 Journal of Mathematical Sciences: Advances and Applications Volume 46, 017, Pages 1-15 Available at http://scientificadvances.co.in DOI: http://dx.doi.org/10.1864/jmsaa_71001188 A CHARACTERIATION OF WARPED
Journal of Mathematical Sciences: Advances and Applications Volume 46, 017, Pages 1-15 Available at http://scientificadvances.co.in DOI: http://dx.doi.org/10.1864/jmsaa_71001188 A CHARACTERIATION OF WARPED
JORDAN HOMOMORPHISMS AND DERIVATIONS ON SEMISIMPLE BANACH ALGEBRAS
 JORDAN HOMOMORPHISMS AND DERIVATIONS ON SEMISIMPLE BANACH ALGEBRAS A. M. SINCLAIR 1. Introduction. One may construct a Jordan homomorphism from one (associative) ring into another ring by taking the sum
JORDAN HOMOMORPHISMS AND DERIVATIONS ON SEMISIMPLE BANACH ALGEBRAS A. M. SINCLAIR 1. Introduction. One may construct a Jordan homomorphism from one (associative) ring into another ring by taking the sum
RESUME PROFORMA. 4 Residential Address: Department of Mathematics, Jamia Millia Islamia, New Delhi Residential Phone :
 RESUME PROFORMA 1 Name : MOHD. RAIS KHAN 2 Designation : Professor 3 Office Address : Department of Mathematics, New Delhi 110025 Office Phone : 011-26822272 4 Residential Address: Department of Mathematics,
RESUME PROFORMA 1 Name : MOHD. RAIS KHAN 2 Designation : Professor 3 Office Address : Department of Mathematics, New Delhi 110025 Office Phone : 011-26822272 4 Residential Address: Department of Mathematics,
Algebra Exam Topics. Updated August 2017
 Algebra Exam Topics Updated August 2017 Starting Fall 2017, the Masters Algebra Exam will have 14 questions. Of these students will answer the first 8 questions from Topics 1, 2, and 3. They then have
Algebra Exam Topics Updated August 2017 Starting Fall 2017, the Masters Algebra Exam will have 14 questions. Of these students will answer the first 8 questions from Topics 1, 2, and 3. They then have
ON STRONGLY PRIME IDEALS AND STRONGLY ZERO-DIMENSIONAL RINGS. Christian Gottlieb
 ON STRONGLY PRIME IDEALS AND STRONGLY ZERO-DIMENSIONAL RINGS Christian Gottlieb Department of Mathematics, University of Stockholm SE-106 91 Stockholm, Sweden gottlieb@math.su.se Abstract A prime ideal
ON STRONGLY PRIME IDEALS AND STRONGLY ZERO-DIMENSIONAL RINGS Christian Gottlieb Department of Mathematics, University of Stockholm SE-106 91 Stockholm, Sweden gottlieb@math.su.se Abstract A prime ideal
Chapter 5. Modular arithmetic. 5.1 The modular ring
 Chapter 5 Modular arithmetic 5.1 The modular ring Definition 5.1. Suppose n N and x, y Z. Then we say that x, y are equivalent modulo n, and we write x y mod n if n x y. It is evident that equivalence
Chapter 5 Modular arithmetic 5.1 The modular ring Definition 5.1. Suppose n N and x, y Z. Then we say that x, y are equivalent modulo n, and we write x y mod n if n x y. It is evident that equivalence
Strongly Nil -Clean Rings
 Strongly Nil -Clean Rings Abdullah HARMANCI Huanyin CHEN and A. Çiğdem ÖZCAN Abstract A -ring R is called strongly nil -clean if every element of R is the sum of a projection and a nilpotent element that
Strongly Nil -Clean Rings Abdullah HARMANCI Huanyin CHEN and A. Çiğdem ÖZCAN Abstract A -ring R is called strongly nil -clean if every element of R is the sum of a projection and a nilpotent element that
Groups with many subnormal subgroups. *
 Groups with many subnormal subgroups. * Eloisa Detomi Dipartimento di Matematica, Facoltà di Ingegneria, Università degli Studi di Brescia, via Valotti 9, 25133 Brescia, Italy. E-mail: detomi@ing.unibs.it
Groups with many subnormal subgroups. * Eloisa Detomi Dipartimento di Matematica, Facoltà di Ingegneria, Università degli Studi di Brescia, via Valotti 9, 25133 Brescia, Italy. E-mail: detomi@ing.unibs.it
Research Article A Note on Jordan Triple Higher -Derivations on Semiprime Rings
 ISRN Algebra, Article ID 365424, 5 pages http://dx.doi.org/10.1155/2014/365424 Research Article A Note on Jordan Triple Higher -Derivations on Semiprime Rings O. H. Ezzat Mathematics Department, Al-Azhar
ISRN Algebra, Article ID 365424, 5 pages http://dx.doi.org/10.1155/2014/365424 Research Article A Note on Jordan Triple Higher -Derivations on Semiprime Rings O. H. Ezzat Mathematics Department, Al-Azhar
Extensions of Regular Rings
 Available online at http://ijim.srbiau.ac.ir/ Int. J. Industrial Mathematics (ISSN 2008-5621) Vol. 8, No. 4, 2016 Article ID IJIM-00782, 7 pages Research Article Extensions of Regular Rings SH. A. Safari
Available online at http://ijim.srbiau.ac.ir/ Int. J. Industrial Mathematics (ISSN 2008-5621) Vol. 8, No. 4, 2016 Article ID IJIM-00782, 7 pages Research Article Extensions of Regular Rings SH. A. Safari
A note on restricted Lie supertriple systems
 Advances in Theoretical and Applied Mathematics. ISSN 0973-4554 Volume 10, Number 1 (2015), pp. 1 13 c Research India Publications http://www.ripublication.com/atam.htm A note on restricted Lie supertriple
Advances in Theoretical and Applied Mathematics. ISSN 0973-4554 Volume 10, Number 1 (2015), pp. 1 13 c Research India Publications http://www.ripublication.com/atam.htm A note on restricted Lie supertriple
The Tensor Product of Galois Algebras
 Gen. Math. Notes, Vol. 22, No. 1, May 2014, pp.11-16 ISSN 2219-7184; Copyright c ICSRS Publication, 2014 www.i-csrs.org Available free online at http://www.geman.in The Tensor Product of Galois Algebras
Gen. Math. Notes, Vol. 22, No. 1, May 2014, pp.11-16 ISSN 2219-7184; Copyright c ICSRS Publication, 2014 www.i-csrs.org Available free online at http://www.geman.in The Tensor Product of Galois Algebras
Factorization in Polynomial Rings
 Factorization in Polynomial Rings These notes are a summary of some of the important points on divisibility in polynomial rings from 17 and 18. PIDs Definition 1 A principal ideal domain (PID) is an integral
Factorization in Polynomial Rings These notes are a summary of some of the important points on divisibility in polynomial rings from 17 and 18. PIDs Definition 1 A principal ideal domain (PID) is an integral
THE RING OF POLYNOMIALS. Special Products and Factoring
 THE RING OF POLYNOMIALS Special Products and Factoring Special Products and Factoring Upon completion, you should be able to Find special products Factor a polynomial completely Special Products - rules
THE RING OF POLYNOMIALS Special Products and Factoring Special Products and Factoring Upon completion, you should be able to Find special products Factor a polynomial completely Special Products - rules
Math 115 ( ) Yum-Tong Siu 1. Euler-Lagrange Equations for Many Functions and Variables and High-Order Derivatives
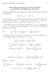 Math 115 006-007 Yum-Tong Siu 1 Euler-Lagrange Equations for Many Functions and Variables and High-Order Derivatives The Case of High-Order Derivatives. The context is to find the extremal for the functional
Math 115 006-007 Yum-Tong Siu 1 Euler-Lagrange Equations for Many Functions and Variables and High-Order Derivatives The Case of High-Order Derivatives. The context is to find the extremal for the functional
Math 10C - Fall Final Exam
 Math 1C - Fall 217 - Final Exam Problem 1. Consider the function f(x, y) = 1 x 2 (y 1) 2. (i) Draw the level curve through the point P (1, 2). Find the gradient of f at the point P and draw the gradient
Math 1C - Fall 217 - Final Exam Problem 1. Consider the function f(x, y) = 1 x 2 (y 1) 2. (i) Draw the level curve through the point P (1, 2). Find the gradient of f at the point P and draw the gradient
GLOBAL JOURNAL OF ENGINEERING SCIENCE AND RESEARCHES ON LEFT BIDERIVATIONS IN SEMIPRIME SEMIRING U. Revathy *1, R. Murugesan 2 & S.
 GLOBAL JOURNAL OF ENGINEERING SCIENCE AND RESEARCHES ON LEFT BIDERIVATIONS IN SEMIPRIME SEMIRING U. Revathy *1, R. Murugesan 2 & S. Somasundaram 3 *1 Register Number: 11829, Thiruvalluvar College, Affiliation
GLOBAL JOURNAL OF ENGINEERING SCIENCE AND RESEARCHES ON LEFT BIDERIVATIONS IN SEMIPRIME SEMIRING U. Revathy *1, R. Murugesan 2 & S. Somasundaram 3 *1 Register Number: 11829, Thiruvalluvar College, Affiliation
Houston Journal of Mathematics. c 2012 University of Houston Volume 38, No. 1, Communicated by Kenneth R. Davidson
 Houston Journal of Mathematics c 2012 University of Houston Volume 38, No. 1, 2012 JORDAN HIGHER DERIVATIONS ON SOME OPERATOR ALGEBRAS ZHANKUI XIAO AND FENG WEI Communicated by Kenneth R. Davidson Abstract.
Houston Journal of Mathematics c 2012 University of Houston Volume 38, No. 1, 2012 JORDAN HIGHER DERIVATIONS ON SOME OPERATOR ALGEBRAS ZHANKUI XIAO AND FENG WEI Communicated by Kenneth R. Davidson Abstract.
CHAPTER I. Rings. Definition A ring R is a set with two binary operations, addition + and
 CHAPTER I Rings 1.1 Definitions and Examples Definition 1.1.1. A ring R is a set with two binary operations, addition + and multiplication satisfying the following conditions for all a, b, c in R : (i)
CHAPTER I Rings 1.1 Definitions and Examples Definition 1.1.1. A ring R is a set with two binary operations, addition + and multiplication satisfying the following conditions for all a, b, c in R : (i)
On Quasi Quadratic Functionals and Existence of Related Sesquilinear Functionals
 International Mathematical Forum, 2, 2007, no. 63, 3115-3123 On Quasi Quadratic Functionals and Existence of Related Sesquilinear Functionals Mehmet Açıkgöz University of Gaziantep, Faculty of Science
International Mathematical Forum, 2, 2007, no. 63, 3115-3123 On Quasi Quadratic Functionals and Existence of Related Sesquilinear Functionals Mehmet Açıkgöz University of Gaziantep, Faculty of Science
Applicable Analysis and Discrete Mathematics available online at
 Applicable Analysis and Discrete Mathematics available online at http://pefmath.etf.bg.ac.yu Appl. Anal. Discrete Math. 3 (2009), 236 241. doi:10.2298/aadm0902236a BANACH CONTRACTION PRINCIPLE ON CONE
Applicable Analysis and Discrete Mathematics available online at http://pefmath.etf.bg.ac.yu Appl. Anal. Discrete Math. 3 (2009), 236 241. doi:10.2298/aadm0902236a BANACH CONTRACTION PRINCIPLE ON CONE
Jordan Γ * -Derivation on Semiprime Γ-Ring M with Involution
 Advances in Linear Algebra & Matrix Theory, 206, 6, 40-50 Published Online June 206 in SciRes. http://www.scirp.org/journal/alamt http://dx.doi.org/0.4236/alamt.206.62006 Jordan Γ -Derivation on Semiprime
Advances in Linear Algebra & Matrix Theory, 206, 6, 40-50 Published Online June 206 in SciRes. http://www.scirp.org/journal/alamt http://dx.doi.org/0.4236/alamt.206.62006 Jordan Γ -Derivation on Semiprime
Skew Monoid Rings over Zip Rings
 International Journal of Algebra, Vol. 4, 2010, no. 21, 1031-1036 Skew Monoid Rings over Zip Rings Amit Bhooshan Singh, M. R. Khan and V. N. Dixit Department of Mathematics Jamia Millia Islamia (Central
International Journal of Algebra, Vol. 4, 2010, no. 21, 1031-1036 Skew Monoid Rings over Zip Rings Amit Bhooshan Singh, M. R. Khan and V. N. Dixit Department of Mathematics Jamia Millia Islamia (Central
Part IX. Factorization
 IX.45. Unique Factorization Domains 1 Part IX. Factorization Section IX.45. Unique Factorization Domains Note. In this section we return to integral domains and concern ourselves with factoring (with respect
IX.45. Unique Factorization Domains 1 Part IX. Factorization Section IX.45. Unique Factorization Domains Note. In this section we return to integral domains and concern ourselves with factoring (with respect
Part 1. For any A-module, let M[x] denote the set of all polynomials in x with coefficients in M, that is to say expressions of the form
![Part 1. For any A-module, let M[x] denote the set of all polynomials in x with coefficients in M, that is to say expressions of the form Part 1. For any A-module, let M[x] denote the set of all polynomials in x with coefficients in M, that is to say expressions of the form](/thumbs/89/99263345.jpg) Commutative Algebra Homework 3 David Nichols Part 1 Exercise 2.6 For any A-module, let M[x] denote the set of all polynomials in x with coefficients in M, that is to say expressions of the form m 0 + m
Commutative Algebra Homework 3 David Nichols Part 1 Exercise 2.6 For any A-module, let M[x] denote the set of all polynomials in x with coefficients in M, that is to say expressions of the form m 0 + m
Course 311: Michaelmas Term 2005 Part III: Topics in Commutative Algebra
 Course 311: Michaelmas Term 2005 Part III: Topics in Commutative Algebra D. R. Wilkins Contents 3 Topics in Commutative Algebra 2 3.1 Rings and Fields......................... 2 3.2 Ideals...............................
Course 311: Michaelmas Term 2005 Part III: Topics in Commutative Algebra D. R. Wilkins Contents 3 Topics in Commutative Algebra 2 3.1 Rings and Fields......................... 2 3.2 Ideals...............................
Two generator 4-Engel groups
 Two generator 4-Engel groups Gunnar Traustason Centre for Mathematical Sciences Lund University Box 118, SE-221 00 Lund Sweden email: gt@maths.lth.se Using known results on 4-Engel groups one can see that
Two generator 4-Engel groups Gunnar Traustason Centre for Mathematical Sciences Lund University Box 118, SE-221 00 Lund Sweden email: gt@maths.lth.se Using known results on 4-Engel groups one can see that
EP elements and Strongly Regular Rings
 Filomat 32:1 (2018), 117 125 https://doi.org/10.2298/fil1801117y Published by Faculty of Sciences and Mathematics, University of Niš, Serbia Available at: http://www.pmf.ni.ac.rs/filomat EP elements and
Filomat 32:1 (2018), 117 125 https://doi.org/10.2298/fil1801117y Published by Faculty of Sciences and Mathematics, University of Niš, Serbia Available at: http://www.pmf.ni.ac.rs/filomat EP elements and
Strongly nil -clean rings
 J. Algebra Comb. Discrete Appl. 4(2) 155 164 Received: 12 June 2015 Accepted: 20 February 2016 Journal of Algebra Combinatorics Discrete Structures and Applications Strongly nil -clean rings Research Article
J. Algebra Comb. Discrete Appl. 4(2) 155 164 Received: 12 June 2015 Accepted: 20 February 2016 Journal of Algebra Combinatorics Discrete Structures and Applications Strongly nil -clean rings Research Article
Written Homework # 4 Solution
 Math 516 Fall 2006 Radford Written Homework # 4 Solution 12/10/06 You may use results form the book in Chapters 1 6 of the text, from notes found on our course web page, and results of the previous homework.
Math 516 Fall 2006 Radford Written Homework # 4 Solution 12/10/06 You may use results form the book in Chapters 1 6 of the text, from notes found on our course web page, and results of the previous homework.
Polynomial Rings. i=0. i=0. n+m. i=0. k=0
 Polynomial Rings 1. Definitions and Basic Properties For convenience, the ring will always be a commutative ring with identity. Basic Properties The polynomial ring R[x] in the indeterminate x with coefficients
Polynomial Rings 1. Definitions and Basic Properties For convenience, the ring will always be a commutative ring with identity. Basic Properties The polynomial ring R[x] in the indeterminate x with coefficients
On quasi-reduced rings
 Global Journal of Pure and Applied Mathematics. ISSN 0973-1768 Volume 12, Number 1 (2016), pp. 927 935 Research India Publications http://www.ripublication.com/gjpam.htm On quasi-reduced rings Sang Jo
Global Journal of Pure and Applied Mathematics. ISSN 0973-1768 Volume 12, Number 1 (2016), pp. 927 935 Research India Publications http://www.ripublication.com/gjpam.htm On quasi-reduced rings Sang Jo
AE/ME 339. Computational Fluid Dynamics (CFD) K. M. Isaac. Momentum equation. Computational Fluid Dynamics (AE/ME 339) MAEEM Dept.
 AE/ME 339 Computational Fluid Dynamics (CFD) 9//005 Topic7_NS_ F0 1 Momentum equation 9//005 Topic7_NS_ F0 1 Consider the moving fluid element model shown in Figure.b Basis is Newton s nd Law which says
AE/ME 339 Computational Fluid Dynamics (CFD) 9//005 Topic7_NS_ F0 1 Momentum equation 9//005 Topic7_NS_ F0 1 Consider the moving fluid element model shown in Figure.b Basis is Newton s nd Law which says
MATH 403 MIDTERM ANSWERS WINTER 2007
 MAH 403 MIDERM ANSWERS WINER 2007 COMMON ERRORS (1) A subset S of a ring R is a subring provided that x±y and xy belong to S whenever x and y do. A lot of people only said that x + y and xy must belong
MAH 403 MIDERM ANSWERS WINER 2007 COMMON ERRORS (1) A subset S of a ring R is a subring provided that x±y and xy belong to S whenever x and y do. A lot of people only said that x + y and xy must belong
DERIVATIONS. Introduction to non-associative algebra. Playing havoc with the product rule? BERNARD RUSSO University of California, Irvine
 DERIVATIONS Introduction to non-associative algebra OR Playing havoc with the product rule? PART VI COHOMOLOGY OF LIE ALGEBRAS BERNARD RUSSO University of California, Irvine FULLERTON COLLEGE DEPARTMENT
DERIVATIONS Introduction to non-associative algebra OR Playing havoc with the product rule? PART VI COHOMOLOGY OF LIE ALGEBRAS BERNARD RUSSO University of California, Irvine FULLERTON COLLEGE DEPARTMENT
