Chapter #3 EEE Subsea Control and Communication Systems
|
|
|
- Aubrie Mercy Taylor
- 5 years ago
- Views:
Transcription
1 EEE 87 Chter #3 EEE 87 Sube Cotrol d Commuictio Sytem Cloed loo ytem Stedy tte error PID cotrol Other cotroller Chter 3 /3
2 EEE 87 Itroductio The geerl form for CL ytem: C R ', where ' c ' H or Oe Loo (OL) TF:, c TF of cotroller, TF of lt R - Cotroller E c U Sytem C Feedbck H Feedbck TF Our Tk: DESIN c d H (if licble). OLFT: Oe loo reoe (deired outut): Chter 3 /3
3 EEE 87 Ste Reoe.8 Amlitude Time (ec) CLTF: C CL C R Cloed loo reoe (k): Chter 3 3/3
4 EEE 87 Ste Reoe.8 Amlitude Time (ec) : Ste Reoe.8 Amlitude Time (ec) Chter 3 4/3
5 EEE 87 Higher order ytem Util ow we hve ee oly t order ytem with feedbck. I thee ytem, the feedbck d the cotroller ifluece the tedy tte d the time cott. The decree of the time cott me tht we moved the ole further ito miu ifiity re. Hece we chged the -le of the ytem. Wht i it goig to he if we ue d order ytem i feedbck ytem? ( )( ).4 Ste Reoe. Amlitude Time (ec) So rt from fter ytem d mller tedy tte error we hve ocilltio! k k CL ( )( ) k 3 k Chter 3 5/3
6 EEE 87 CE: 3 k but the geerl from: ζ o ζ 3 d k d for k hece ζ ζ : d So the feedbck d the cotroller c comletely chge the loctio of the ole i the -le. Exmle: ( )( )( 3) The oe loo reoe for vriou gi i: 9 Ste Reoe Amlitude Time (ec) The oe loo ytem will be tble for ll vlue of ice they do ot ifluece the ole of the ytem. The reoe of cloed loo ytem for,, i: Chter 3 6/3
7 EEE 87 5 Ste Reoe 4 3 Amlitude Time (ec) Hece the feedbck my itroduce itbility. To udertd why we hve thee chge olve the CE. Proertie of feedbck ytem:. Miimie tedy tte error.. Fter ytem. 3. Le eitive to ytem ucertitie. 4. Itroduce itbility (eve for egtive feedbck). 5. Exeive (we eed to feedbck the igl, i.e. ue eor). Chter 3 7/3
8 EEE 87 PID cotrol Coider the ytem: () for : ( )( )( 3).9 error.8.7 outut To icree the tye of the OLTF (which i C x) we dd itegrtor: c ( ) i > OL ( ) i ( )( )( 3) (Thi i the o-clled PI cotroller). Chter 3 8/3
9 EEE 87 Itegrtor i Ste 36 6 Trfer Fc Scoe i i i Further icree of, i: Chter 3 9/3
10 EEE , i 6, i Check the derivtive of error, i.e. the rte of chge of e: De e Chter 3 /3
11 EEE 87 Mximum vlue of De jut before e. So De c cotrol the ocilltio: ( ) i d > c OL ( ) d i ( )( )( 3) Ste Itegrtor i 36 6 Trfer Fc Scoe du/dt Derivtive d Chter 3 /3
12 EEE d d 5 d Sice I hve o ocilltio I c icree little bit more to mke the ytem fter: Chter 3 /3
13 EEE P outut Outut Chter 3 3/3
14 EEE 87.5 D outut Outut I Outut Outut Chter 3 4/3
15 EEE 87 Aother wy to write the PID cotroller: CL CL i i d ( ) d ( ) Td Ti Tuig of PID cotroller. Tril d error.. Ziegler Nichol I 3. Ziegler Nichol II 4. Root locu 5. Frequecy reoe 6. Other dvced cotrol method Tril d error: P: Fter ytem, i ome ce reduce the error (c cue itbility). I: Reduce the tedy tte error, icree the umber of ocilltio. D: Reduce the ocilltio. Chter 3 5/3
16 EEE 87 Ziegler Nichol I Aume ytem with o dely (we do ot tudy thee ytem) d with o-comlex cojugte ole. It oe loo te reoe my look like (obtied exerimetlly of from imultio): Thi c be modelled : C( ) U ( ) L e T Bed o tht we hve the followig tble: Chter 3 6/3
17 EEE 87 Tye of cotroller P PI PID T i T d T L.9T L L.3.T L L.5L Ziegler Nichol II Iitilly ume i d. Icree util the ytem i mrgilly tble. Record the cr d the frequecy of ocilltio: P cr c(t) t, Chter 3 7/3
18 EEE 87 Tye of cotroller P PI PID Ti Td.5 cr.45 cr..6 cr.5pcr P cr.5pcr Thee method im t chievig overhoot of 5%. Root locu method With the RL we ecificlly trget ole loctio t the -le, i.e. we trget dmig fctor, turl d dmed frequecie. Exmle: The OLTF i ( ) ue PI cotroller. 34 OL ( ) i 34 ( 34) i CL ( ) ( 34) i i Thi i 3 rd order ytem d order x t order: Chter 3 8/3
19 EEE 87 CE: ( ) ( )( ) 34 i ζ ( ) ( ) ( ) i ζ ζ 34 i ζ ζ Aume tht the deig ec re:.5 6 ζ So: i i Homework: Fid the PID gi : the CLTF of 6 6 ) ( h.5 6 ζ d rel ole t -5. Solutio: 5, i 8, d 5. Frequecy reoe Advced method We will ot tudy thee. Chter 3 9/3
20 EEE 87 Other cotroller By uig the reviou (root locu) method we c deig more geerl cotroller. Exmle: R() ( ) ( b) C() C() b?? 6 θ 6 o 6 ζ co ( ) o 6 6 ζ.5 () ( ) b C R () () ( ) ( b) ( ) CE : CE 3 b ( )( ζ ) 3 : b Chter 3 /3
21 EEE 87 ( )( ) 3 : b CE ζ ( ) ( ) 3 3 : b CE ζ ζ b ζ ζ b Exmle: () ( )( ).5 OL, Uity feedbck d iut: r(t)5t ) If.5, fid the tedy tte error b) The ytem mut hve tedy tte error, E<. fid the vlue of C() C() ( )( ).5 5 () R () () ( )( ) R C.5 () ( )( ) C.5 5 Chter 3 /3
22 EEE 87 E ( ) R( ) C( ) E() 5 ( )(.5 ) E () 5 ( )(.5 ) ( )(.5 ) E ( )(.5 ) ( )( ).5 5 lim 5 E 5 ) E E <. > 5 b) <. Exmle: OL () (. )(. ) ) Fid the vlue of uch the ytem i mrgilly tble b) Fid the frequecy of ocilltio t tht oit Chter 3 /3
23 EEE 87 C R () () (. )(. ) (. )(. ) CE : For mrgilly tble ytem: j (. j )(. j ) CE : j 3 (.. ) (.. ) j CE : j rd / d 5 Chter 3 3/3
Chapter #5 EEE Control Systems
 Sprig EEE Chpter #5 EEE Cotrol Sytem Deig Bed o Root Locu Chpter / Sprig EEE Deig Bed Root Locu Led Cotrol (equivlet to PD cotrol) Ued whe the tedy tte propertie of the ytem re ok but there i poor performce,
Sprig EEE Chpter #5 EEE Cotrol Sytem Deig Bed o Root Locu Chpter / Sprig EEE Deig Bed Root Locu Led Cotrol (equivlet to PD cotrol) Ued whe the tedy tte propertie of the ytem re ok but there i poor performce,
Chapter #2 EEE Subsea Control and Communication Systems
 EEE 87 Chpter # EEE 87 Sube Cotrol d Commuictio Sytem Trfer fuctio Pole loctio d -ple Time domi chrcteritic Extr pole d zero Chpter /8 EEE 87 Trfer fuctio Lplce Trform Ued oly o LTI ytem Differetil expreio
EEE 87 Chpter # EEE 87 Sube Cotrol d Commuictio Sytem Trfer fuctio Pole loctio d -ple Time domi chrcteritic Extr pole d zero Chpter /8 EEE 87 Trfer fuctio Lplce Trform Ued oly o LTI ytem Differetil expreio
ELEC 372 LECTURE NOTES, WEEK 6 Dr. Amir G. Aghdam Concordia University
 ELEC 37 LECTURE NOTES, WEE 6 Dr mir G ghdm Cocordi Uiverity Prt of thee ote re dpted from the mteril i the followig referece: Moder Cotrol Sytem by Richrd C Dorf d Robert H Bihop, Pretice Hll Feedbck Cotrol
ELEC 37 LECTURE NOTES, WEE 6 Dr mir G ghdm Cocordi Uiverity Prt of thee ote re dpted from the mteril i the followig referece: Moder Cotrol Sytem by Richrd C Dorf d Robert H Bihop, Pretice Hll Feedbck Cotrol
Advanced Control Theory
 Advced Cotrol Theory Review of Cotrol Sytem chibum@eoultech.c.kr Outlie Simle feedbck cotrol Advced Cotrol Theory Feedbck Sytem U V Y m Motly H - r : the referece iut - y m : the outut of the ytem - e
Advced Cotrol Theory Review of Cotrol Sytem chibum@eoultech.c.kr Outlie Simle feedbck cotrol Advced Cotrol Theory Feedbck Sytem U V Y m Motly H - r : the referece iut - y m : the outut of the ytem - e
The Performance of Feedback Control Systems
 The Performace of Feedbac Cotrol Sytem Objective:. Secify the meaure of erformace time-domai the firt te i the deig roce Percet overhoot / Settlig time T / Time to rie / Steady-tate error e. ut igal uch
The Performace of Feedbac Cotrol Sytem Objective:. Secify the meaure of erformace time-domai the firt te i the deig roce Percet overhoot / Settlig time T / Time to rie / Steady-tate error e. ut igal uch
Chap8 - Freq 1. Frequency Response
 Chp8 - Freq Frequecy Repoe Chp8 - Freq Aged Prelimirie Firt order ytem Frequecy repoe Low-p filter Secod order ytem Clicl olutio Frequecy repoe Higher order ytem Chp8 - Freq 3 Frequecy repoe Stedy-tte
Chp8 - Freq Frequecy Repoe Chp8 - Freq Aged Prelimirie Firt order ytem Frequecy repoe Low-p filter Secod order ytem Clicl olutio Frequecy repoe Higher order ytem Chp8 - Freq 3 Frequecy repoe Stedy-tte
ROUTH-HURWITZ CRITERION
 Automti Cotrol Sytem, Deprtmet of Mehtroi Egieerig, Germ Jordi Uiverity Routh-Hurwitz Criterio ite.google.om/ite/ziydmoud 7 ROUTH-HURWITZ CRITERION The Routh-Hurwitz riterio i lytil proedure for determiig
Automti Cotrol Sytem, Deprtmet of Mehtroi Egieerig, Germ Jordi Uiverity Routh-Hurwitz Criterio ite.google.om/ite/ziydmoud 7 ROUTH-HURWITZ CRITERION The Routh-Hurwitz riterio i lytil proedure for determiig
2.Decision Theory of Dependence
 .Deciio Theoy of Depedece Theoy :I et of vecto if thee i uet which i liely depedet the whole et i liely depedet too. Coolly :If the et i liely idepedet y oepty uet of it i liely idepedet. Theoy : Give
.Deciio Theoy of Depedece Theoy :I et of vecto if thee i uet which i liely depedet the whole et i liely depedet too. Coolly :If the et i liely idepedet y oepty uet of it i liely idepedet. Theoy : Give
Week 13 Notes: 1) Riemann Sum. Aim: Compute Area Under a Graph. Suppose we want to find out the area of a graph, like the one on the right:
 Week 1 Notes: 1) Riem Sum Aim: Compute Are Uder Grph Suppose we wt to fid out the re of grph, like the oe o the right: We wt to kow the re of the red re. Here re some wys to pproximte the re: We cut the
Week 1 Notes: 1) Riem Sum Aim: Compute Are Uder Grph Suppose we wt to fid out the re of grph, like the oe o the right: We wt to kow the re of the red re. Here re some wys to pproximte the re: We cut the
System Control. Lesson #19a. BME 333 Biomedical Signals and Systems - J.Schesser
 Sytem Cotrol Leo #9a 76 Sytem Cotrol Baic roblem Say you have a ytem which you ca ot alter but it repoe i ot optimal Example Motor cotrol for exokeleto Robotic cotrol roblem that ca occur Utable Traiet
Sytem Cotrol Leo #9a 76 Sytem Cotrol Baic roblem Say you have a ytem which you ca ot alter but it repoe i ot optimal Example Motor cotrol for exokeleto Robotic cotrol roblem that ca occur Utable Traiet
Note 7 Root-Locus Techniques
 Lecture Note of Cotrol Syte I - ME 43/Alyi d Sythei of Lier Cotrol Syte - ME862 Note 7 Root-Locu Techique Deprtet of Mechicl Egieerig, Uiverity Of Sktchew, 57 Cpu Drive, Sktoo, S S7N 5A9, Cd Lecture Note
Lecture Note of Cotrol Syte I - ME 43/Alyi d Sythei of Lier Cotrol Syte - ME862 Note 7 Root-Locu Techique Deprtet of Mechicl Egieerig, Uiverity Of Sktchew, 57 Cpu Drive, Sktoo, S S7N 5A9, Cd Lecture Note
Probability and Stochastic Processes: A Friendly Introduction for Electrical and Computer Engineers Roy D. Yates and David J.
 Probbility d Stochstic Processes: A Friedly Itroductio for Electricl d Computer Egieers Roy D. Ytes d Dvid J. Goodm Problem Solutios : Ytes d Goodm,4..4 4..4 4..7 4.4. 4.4. 4..6 4.6.8 4.6.9 4.7.4 4.7.
Probbility d Stochstic Processes: A Friedly Itroductio for Electricl d Computer Egieers Roy D. Ytes d Dvid J. Goodm Problem Solutios : Ytes d Goodm,4..4 4..4 4..7 4.4. 4.4. 4..6 4.6.8 4.6.9 4.7.4 4.7.
SUTCLIFFE S NOTES: CALCULUS 2 SWOKOWSKI S CHAPTER 11
 UTCLIFFE NOTE: CALCULU WOKOWKI CHAPTER Ifiite eries Coverget or Diverget eries Cosider the sequece If we form the ifiite sum 0, 00, 000, 0 00 000, we hve wht is clled ifiite series We wt to fid the sum
UTCLIFFE NOTE: CALCULU WOKOWKI CHAPTER Ifiite eries Coverget or Diverget eries Cosider the sequece If we form the ifiite sum 0, 00, 000, 0 00 000, we hve wht is clled ifiite series We wt to fid the sum
10.2 Series. , we get. which is called an infinite series ( or just a series) and is denoted, for short, by the symbol. i i n
 0. Sere I th ecto, we wll troduce ere tht wll be dcug for the ret of th chpter. Wht ere? If we dd ll term of equece, we get whch clled fte ere ( or jut ere) d deoted, for hort, by the ymbol or Doe t mke
0. Sere I th ecto, we wll troduce ere tht wll be dcug for the ret of th chpter. Wht ere? If we dd ll term of equece, we get whch clled fte ere ( or jut ere) d deoted, for hort, by the ymbol or Doe t mke
Chapter 2 Infinite Series Page 1 of 9
 Chpter Ifiite eries Pge of 9 Chpter : Ifiite eries ectio A Itroductio to Ifiite eries By the ed of this sectio you will be ble to uderstd wht is met by covergece d divergece of ifiite series recogise geometric
Chpter Ifiite eries Pge of 9 Chpter : Ifiite eries ectio A Itroductio to Ifiite eries By the ed of this sectio you will be ble to uderstd wht is met by covergece d divergece of ifiite series recogise geometric
State space systems analysis
 State pace ytem aalyi Repreetatio of a ytem i tate-pace (tate-pace model of a ytem To itroduce the tate pace formalim let u tart with a eample i which the ytem i dicuio i a imple electrical circuit with
State pace ytem aalyi Repreetatio of a ytem i tate-pace (tate-pace model of a ytem To itroduce the tate pace formalim let u tart with a eample i which the ytem i dicuio i a imple electrical circuit with
Introduction to Modern Control Theory
 Itroductio to Moder Cotrol Theory MM : Itroductio to Stte-Spce Method MM : Cotrol Deig for Full Stte Feedck MM 3: Etitor Deig MM 4: Itroductio of the Referece Iput MM 5: Itegrl Cotrol d Rout Trckig //4
Itroductio to Moder Cotrol Theory MM : Itroductio to Stte-Spce Method MM : Cotrol Deig for Full Stte Feedck MM 3: Etitor Deig MM 4: Itroductio of the Referece Iput MM 5: Itegrl Cotrol d Rout Trckig //4
Calculus II Homework: The Integral Test and Estimation of Sums Page 1
 Clculus II Homework: The Itegrl Test d Estimtio of Sums Pge Questios Emple (The p series) Get upper d lower bouds o the sum for the p series i= /ip with p = 2 if the th prtil sum is used to estimte the
Clculus II Homework: The Itegrl Test d Estimtio of Sums Pge Questios Emple (The p series) Get upper d lower bouds o the sum for the p series i= /ip with p = 2 if the th prtil sum is used to estimte the
EECE 301 Signals & Systems Prof. Mark Fowler
 EECE 30 Sigal & Sytem Prof. Mark Fowler Note Set #8 C-T Sytem: Laplace Traform Solvig Differetial Equatio Readig Aigmet: Sectio 6.4 of Kame ad Heck / Coure Flow Diagram The arrow here how coceptual flow
EECE 30 Sigal & Sytem Prof. Mark Fowler Note Set #8 C-T Sytem: Laplace Traform Solvig Differetial Equatio Readig Aigmet: Sectio 6.4 of Kame ad Heck / Coure Flow Diagram The arrow here how coceptual flow
A New Estimator Using Auxiliary Information in Stratified Adaptive Cluster Sampling
 Ope Jourl of ttitic, 03, 3, 78-8 ttp://d.doi.org/0.436/oj.03.3403 Publied Olie eptember 03 (ttp://www.cirp.org/jourl/oj) New Etimtor Uig uilir Iformtio i trtified dptive Cluter mplig Nippor Cutim *, Moc
Ope Jourl of ttitic, 03, 3, 78-8 ttp://d.doi.org/0.436/oj.03.3403 Publied Olie eptember 03 (ttp://www.cirp.org/jourl/oj) New Etimtor Uig uilir Iformtio i trtified dptive Cluter mplig Nippor Cutim *, Moc
0 otherwise. sin( nx)sin( kx) 0 otherwise. cos( nx) sin( kx) dx 0 for all integers n, k.
 . Computtio of Fourier Series I this sectio, we compute the Fourier coefficiets, f ( x) cos( x) b si( x) d b, i the Fourier series To do this, we eed the followig result o the orthogolity of the trigoometric
. Computtio of Fourier Series I this sectio, we compute the Fourier coefficiets, f ( x) cos( x) b si( x) d b, i the Fourier series To do this, we eed the followig result o the orthogolity of the trigoometric
732 Appendix E: Previous EEE480 Exams. Rules: One sheet permitted, calculators permitted. GWC 352,
 732 Aedix E: Previous EEE0 Exams EEE0 Exam 2, Srig 2008 A.A. Rodriguez Rules: Oe 8. sheet ermitted, calculators ermitted. GWC 32, 9-372 Problem Aalysis of a Feedback System Cosider the feedback system
732 Aedix E: Previous EEE0 Exams EEE0 Exam 2, Srig 2008 A.A. Rodriguez Rules: Oe 8. sheet ermitted, calculators ermitted. GWC 32, 9-372 Problem Aalysis of a Feedback System Cosider the feedback system
SM2H. Unit 2 Polynomials, Exponents, Radicals & Complex Numbers Notes. 3.1 Number Theory
 SMH Uit Polyomils, Epoets, Rdicls & Comple Numbers Notes.1 Number Theory .1 Addig, Subtrctig, d Multiplyig Polyomils Notes Moomil: A epressio tht is umber, vrible, or umbers d vribles multiplied together.
SMH Uit Polyomils, Epoets, Rdicls & Comple Numbers Notes.1 Number Theory .1 Addig, Subtrctig, d Multiplyig Polyomils Notes Moomil: A epressio tht is umber, vrible, or umbers d vribles multiplied together.
2 SKEE/SKEU v R(t) - Figure Q.1(a) Evaluate the transfer function of the network as
 SKEE/SKEU 073 PART A Q. ) A trfer futio i ued to deribe the reltiohi betwee the iut d outut igl of ytem. Figure Q.) how RC etwork ued to form filter futio. V it) R + v Rt) - C + v t) - Figure Q.) i) ii)
SKEE/SKEU 073 PART A Q. ) A trfer futio i ued to deribe the reltiohi betwee the iut d outut igl of ytem. Figure Q.) how RC etwork ued to form filter futio. V it) R + v Rt) - C + v t) - Figure Q.) i) ii)
Chapter 7 Infinite Series
 MA Ifiite Series Asst.Prof.Dr.Supree Liswdi Chpter 7 Ifiite Series Sectio 7. Sequece A sequece c be thought of s list of umbers writte i defiite order:,,...,,... 2 The umber is clled the first term, 2
MA Ifiite Series Asst.Prof.Dr.Supree Liswdi Chpter 7 Ifiite Series Sectio 7. Sequece A sequece c be thought of s list of umbers writte i defiite order:,,...,,... 2 The umber is clled the first term, 2
Linear Open Loop Systems
 Colordo School of Me CHEN43 Trfer Fucto Ler Ope Loop Sytem Ler Ope Loop Sytem... Trfer Fucto for Smple Proce... Exmple Trfer Fucto Mercury Thermometer... 2 Derblty of Devto Vrble... 3 Trfer Fucto for Proce
Colordo School of Me CHEN43 Trfer Fucto Ler Ope Loop Sytem Ler Ope Loop Sytem... Trfer Fucto for Smple Proce... Exmple Trfer Fucto Mercury Thermometer... 2 Derblty of Devto Vrble... 3 Trfer Fucto for Proce
Last time: Ground rules for filtering and control system design
 6.3 Stochatic Etimatio ad Cotrol, Fall 004 Lecture 7 Lat time: Groud rule for filterig ad cotrol ytem deig Gral ytem Sytem parameter are cotaied i w( t ad w ( t. Deired output i grated by takig the igal
6.3 Stochatic Etimatio ad Cotrol, Fall 004 Lecture 7 Lat time: Groud rule for filterig ad cotrol ytem deig Gral ytem Sytem parameter are cotaied i w( t ad w ( t. Deired output i grated by takig the igal
G x, x E x E x E x E x. a a a a. is some matrix element. For a general single photon state. ), applying the operators.
 Topic i Qutu Optic d Qutu Ifortio TA: Yuli Mxieko Uiverity of Illioi t Urb-hpig lt updted Februry 6 Proble Set # Quetio With G x, x E x E x E x E x G pqr p q r where G pqr i oe trix eleet For geerl igle
Topic i Qutu Optic d Qutu Ifortio TA: Yuli Mxieko Uiverity of Illioi t Urb-hpig lt updted Februry 6 Proble Set # Quetio With G x, x E x E x E x E x G pqr p q r where G pqr i oe trix eleet For geerl igle
positive definite (symmetric with positive eigenvalues) positive semi definite (symmetric with nonnegative eigenvalues)
 Chter Liner Qudrtic Regultor Problem inimize the cot function J given by J x' Qx u' Ru dt R > Q oitive definite ymmetric with oitive eigenvlue oitive emi definite ymmetric with nonnegtive eigenvlue ubject
Chter Liner Qudrtic Regultor Problem inimize the cot function J given by J x' Qx u' Ru dt R > Q oitive definite ymmetric with oitive eigenvlue oitive emi definite ymmetric with nonnegtive eigenvlue ubject
AUTOMATIC CONTROL SYSTEMS
 9 HE UO ONROL SYSES OSVE SLE RELZONS OF ONNUOUS-E LNER SYSES deuz Kzore trt: he rolem for exitee d determitio of the et of oitive ymtotilly tle reliztio of roer trfer futio of lier otiuou-time ytem i formulted
9 HE UO ONROL SYSES OSVE SLE RELZONS OF ONNUOUS-E LNER SYSES deuz Kzore trt: he rolem for exitee d determitio of the et of oitive ymtotilly tle reliztio of roer trfer futio of lier otiuou-time ytem i formulted
MATH 118 HW 7 KELLY DOUGAN, ANDREW KOMAR, MARIA SIMBIRSKY, BRANDEN LASKE
 MATH 118 HW 7 KELLY DOUGAN, ANDREW KOMAR, MARIA SIMBIRSKY, BRANDEN LASKE Prt 1. Let be odd rime d let Z such tht gcd(, 1. Show tht if is qudrtic residue mod, the is qudrtic residue mod for y ositive iteger.
MATH 118 HW 7 KELLY DOUGAN, ANDREW KOMAR, MARIA SIMBIRSKY, BRANDEN LASKE Prt 1. Let be odd rime d let Z such tht gcd(, 1. Show tht if is qudrtic residue mod, the is qudrtic residue mod for y ositive iteger.
Discrete Mathematics I Tutorial 12
 Discrete Mthemtics I Tutoril Refer to Chpter 4., 4., 4.4. For ech of these sequeces fid recurrece reltio stisfied by this sequece. (The swers re ot uique becuse there re ifiitely my differet recurrece
Discrete Mthemtics I Tutoril Refer to Chpter 4., 4., 4.4. For ech of these sequeces fid recurrece reltio stisfied by this sequece. (The swers re ot uique becuse there re ifiitely my differet recurrece
ELEC 372 LECTURE NOTES, WEEK 4 Dr. Amir G. Aghdam Concordia University
 ELEC 37 LECTURE NOTES, WEE 4 Dr Amir G Aghdam Cocordia Uiverity Part of thee ote are adapted from the material i the followig referece: Moder Cotrol Sytem by Richard C Dorf ad Robert H Bihop, Pretice Hall
ELEC 37 LECTURE NOTES, WEE 4 Dr Amir G Aghdam Cocordia Uiverity Part of thee ote are adapted from the material i the followig referece: Moder Cotrol Sytem by Richard C Dorf ad Robert H Bihop, Pretice Hall
UNIT #5 SEQUENCES AND SERIES COMMON CORE ALGEBRA II
 Awer Key Nme: Dte: UNIT # SEQUENCES AND SERIES COMMON CORE ALGEBRA II Prt I Quetio. For equece defied by f? () () 08 6 6 f d f f, which of the followig i the vlue of f f f f f f 0 6 6 08 (). I the viul
Awer Key Nme: Dte: UNIT # SEQUENCES AND SERIES COMMON CORE ALGEBRA II Prt I Quetio. For equece defied by f? () () 08 6 6 f d f f, which of the followig i the vlue of f f f f f f 0 6 6 08 (). I the viul
We will look for series solutions to (1) around (at most) regular singular points, which without
 ENM 511 J. L. Baai April, 1 Frobeiu Solutio to a d order ODE ear a regular igular poit Coider the ODE y 16 + P16 y 16 + Q1616 y (1) We will look for erie olutio to (1) aroud (at mot) regular igular poit,
ENM 511 J. L. Baai April, 1 Frobeiu Solutio to a d order ODE ear a regular igular poit Coider the ODE y 16 + P16 y 16 + Q1616 y (1) We will look for erie olutio to (1) aroud (at mot) regular igular poit,
All the Laplace Transform you will encounter has the following form: Rational function X(s)
 EE G Note: Chpter Itructor: Cheug Pge - - Iverio of Rtiol Fuctio All the Lplce Trform you will ecouter h the followig form: m m m m e τ 0...... Rtiol fuctio Dely Why? Rtiol fuctio come out turlly from
EE G Note: Chpter Itructor: Cheug Pge - - Iverio of Rtiol Fuctio All the Lplce Trform you will ecouter h the followig form: m m m m e τ 0...... Rtiol fuctio Dely Why? Rtiol fuctio come out turlly from
Reversing the Arithmetic mean Geometric mean inequality
 Reversig the Arithmetic me Geometric me iequlity Tie Lm Nguye Abstrct I this pper we discuss some iequlities which re obtied by ddig o-egtive expressio to oe of the sides of the AM-GM iequlity I this wy
Reversig the Arithmetic me Geometric me iequlity Tie Lm Nguye Abstrct I this pper we discuss some iequlities which re obtied by ddig o-egtive expressio to oe of the sides of the AM-GM iequlity I this wy
Limit of a function:
 - Limit of fuctio: We sy tht f ( ) eists d is equl with (rel) umer L if f( ) gets s close s we wt to L if is close eough to (This defiitio c e geerlized for L y syig tht f( ) ecomes s lrge (or s lrge egtive
- Limit of fuctio: We sy tht f ( ) eists d is equl with (rel) umer L if f( ) gets s close s we wt to L if is close eough to (This defiitio c e geerlized for L y syig tht f( ) ecomes s lrge (or s lrge egtive
Introduction to Control Systems
 Itroductio to Cotrol Sytem CLASSIFICATION OF MATHEMATICAL MODELS Icreaig Eae of Aalyi Static Icreaig Realim Dyamic Determiitic Stochatic Lumped Parameter Ditributed Parameter Liear Noliear Cotat Coefficiet
Itroductio to Cotrol Sytem CLASSIFICATION OF MATHEMATICAL MODELS Icreaig Eae of Aalyi Static Icreaig Realim Dyamic Determiitic Stochatic Lumped Parameter Ditributed Parameter Liear Noliear Cotat Coefficiet
10.5 Power Series. In this section, we are going to start talking about power series. A power series is a series of the form
 0.5 Power Series I the lst three sectios, we ve spet most of tht time tlkig bout how to determie if series is coverget or ot. Now it is time to strt lookig t some specific kids of series d we will evetully
0.5 Power Series I the lst three sectios, we ve spet most of tht time tlkig bout how to determie if series is coverget or ot. Now it is time to strt lookig t some specific kids of series d we will evetully
3. REVIEW OF PROPERTIES OF EIGENVALUES AND EIGENVECTORS
 . REVIEW OF PROPERTIES OF EIGENVLUES ND EIGENVECTORS. EIGENVLUES ND EIGENVECTORS We hll ow revew ome bc fct from mtr theory. Let be mtr. clr clled egevlue of f there et ozero vector uch tht Emle: Let 9
. REVIEW OF PROPERTIES OF EIGENVLUES ND EIGENVECTORS. EIGENVLUES ND EIGENVECTORS We hll ow revew ome bc fct from mtr theory. Let be mtr. clr clled egevlue of f there et ozero vector uch tht Emle: Let 9
Chapter 5. Root Locus Techniques
 Chapter 5 Rt Lcu Techique Itrducti Sytem perfrmace ad tability dt determied dby cled-lp l ple Typical cled-lp feedback ctrl ytem G Ope-lp TF KG H Zer -, - Ple 0, -, - K Lcati f ple eaily fud Variati f
Chapter 5 Rt Lcu Techique Itrducti Sytem perfrmace ad tability dt determied dby cled-lp l ple Typical cled-lp feedback ctrl ytem G Ope-lp TF KG H Zer -, - Ple 0, -, - K Lcati f ple eaily fud Variati f
INFINITE SERIES. ,... having infinite number of terms is called infinite sequence and its indicated sum, i.e., a 1
 Appedix A.. Itroductio As discussed i the Chpter 9 o Sequeces d Series, sequece,,...,,... hvig ifiite umber of terms is clled ifiite sequece d its idicted sum, i.e., + + +... + +... is clled ifite series
Appedix A.. Itroductio As discussed i the Chpter 9 o Sequeces d Series, sequece,,...,,... hvig ifiite umber of terms is clled ifiite sequece d its idicted sum, i.e., + + +... + +... is clled ifite series
Chapter #4 EEE Automatic Control
 Spring 008 EEE 00 Chapter #4 EEE 00 Automatic Control Root Locu Chapter 4 /4 Spring 008 EEE 00 Introduction Repone depend on ytem and controller parameter > Cloed loop pole location depend on ytem and
Spring 008 EEE 00 Chapter #4 EEE 00 Automatic Control Root Locu Chapter 4 /4 Spring 008 EEE 00 Introduction Repone depend on ytem and controller parameter > Cloed loop pole location depend on ytem and
Graphing Review Part 3: Polynomials
 Grphig Review Prt : Polomils Prbols Recll, tht the grph of f ( ) is prbol. It is eve fuctio, hece it is smmetric bout the bout the -is. This mes tht f ( ) f ( ). Its grph is show below. The poit ( 0,0)
Grphig Review Prt : Polomils Prbols Recll, tht the grph of f ( ) is prbol. It is eve fuctio, hece it is smmetric bout the bout the -is. This mes tht f ( ) f ( ). Its grph is show below. The poit ( 0,0)
In an algebraic expression of the form (1), like terms are terms with the same power of the variables (in this case
 Chpter : Algebr: A. Bckgroud lgebr: A. Like ters: I lgebric expressio of the for: () x b y c z x y o z d x... p x.. we cosider x, y, z to be vribles d, b, c, d,,, o,.. to be costts. I lgebric expressio
Chpter : Algebr: A. Bckgroud lgebr: A. Like ters: I lgebric expressio of the for: () x b y c z x y o z d x... p x.. we cosider x, y, z to be vribles d, b, c, d,,, o,.. to be costts. I lgebric expressio
A GENERAL METHOD FOR SOLVING ORDINARY DIFFERENTIAL EQUATIONS: THE FROBENIUS (OR SERIES) METHOD
 Diol Bgoo () A GENERAL METHOD FOR SOLVING ORDINARY DIFFERENTIAL EQUATIONS: THE FROBENIUS (OR SERIES) METHOD I. Itroductio The first seprtio of vribles (see pplictios to Newto s equtios) is ver useful method
Diol Bgoo () A GENERAL METHOD FOR SOLVING ORDINARY DIFFERENTIAL EQUATIONS: THE FROBENIUS (OR SERIES) METHOD I. Itroductio The first seprtio of vribles (see pplictios to Newto s equtios) is ver useful method
Fast Fourier Transform 1) Legendre s Interpolation 2) Vandermonde Matrix 3) Roots of Unity 4) Polynomial Evaluation
 Algorithm Desig d Alsis Victor Admchi CS 5-45 Sprig 4 Lecture 3 J 7, 4 Cregie Mello Uiversit Outlie Fst Fourier Trsform ) Legedre s Iterpoltio ) Vdermode Mtri 3) Roots of Uit 4) Polomil Evlutio Guss (777
Algorithm Desig d Alsis Victor Admchi CS 5-45 Sprig 4 Lecture 3 J 7, 4 Cregie Mello Uiversit Outlie Fst Fourier Trsform ) Legedre s Iterpoltio ) Vdermode Mtri 3) Roots of Uit 4) Polomil Evlutio Guss (777
ECE-320 Linear Control Systems. Spring 2014, Exam 1. No calculators or computers allowed, you may leave your answers as fractions.
 ECE-0 Linear Control Sytem Spring 04, Exam No calculator or computer allowed, you may leave your anwer a fraction. All problem are worth point unle noted otherwie. Total /00 Problem - refer to the unit
ECE-0 Linear Control Sytem Spring 04, Exam No calculator or computer allowed, you may leave your anwer a fraction. All problem are worth point unle noted otherwie. Total /00 Problem - refer to the unit
Spherical refracting surface. Here, the outgoing rays are on the opposite side of the surface from the Incoming rays.
 Sphericl refrctig urfce Here, the outgoig ry re o the oppoite ide of the urfce from the Icomig ry. The oject i t P. Icomig ry PB d PV form imge t P. All prxil ry from P which trike the phericl urfce will
Sphericl refrctig urfce Here, the outgoig ry re o the oppoite ide of the urfce from the Icomig ry. The oject i t P. Icomig ry PB d PV form imge t P. All prxil ry from P which trike the phericl urfce will
Taylor Polynomials. The Tangent Line. (a, f (a)) and has the same slope as the curve y = f (x) at that point. It is the best
 Tylor Polyomils Let f () = e d let p() = 1 + + 1 + 1 6 3 Without usig clcultor, evlute f (1) d p(1) Ok, I m still witig With little effort it is possible to evlute p(1) = 1 + 1 + 1 (144) + 6 1 (178) =
Tylor Polyomils Let f () = e d let p() = 1 + + 1 + 1 6 3 Without usig clcultor, evlute f (1) d p(1) Ok, I m still witig With little effort it is possible to evlute p(1) = 1 + 1 + 1 (144) + 6 1 (178) =
EVALUATING DEFINITE INTEGRALS
 Chpter 4 EVALUATING DEFINITE INTEGRALS If the defiite itegrl represets re betwee curve d the x-xis, d if you c fid the re by recogizig the shpe of the regio, the you c evlute the defiite itegrl. Those
Chpter 4 EVALUATING DEFINITE INTEGRALS If the defiite itegrl represets re betwee curve d the x-xis, d if you c fid the re by recogizig the shpe of the regio, the you c evlute the defiite itegrl. Those
Chapter 10: The Z-Transform Adapted from: Lecture notes from MIT, Binghamton University Dr. Hamid R. Rabiee Fall 2013
 Sigls & Systems Chpter 0: The Z-Trsform Adpted from: Lecture otes from MIT, Bighmto Uiversity Dr. Hmid R. Rbiee Fll 03 Lecture 5 Chpter 0 Lecture 6 Chpter 0 Outlie Itroductio to the -Trsform Properties
Sigls & Systems Chpter 0: The Z-Trsform Adpted from: Lecture otes from MIT, Bighmto Uiversity Dr. Hmid R. Rbiee Fll 03 Lecture 5 Chpter 0 Lecture 6 Chpter 0 Outlie Itroductio to the -Trsform Properties
8.3 Sequences & Series: Convergence & Divergence
 8.3 Sequeces & Series: Covergece & Divergece A sequece is simply list of thigs geerted by rule More formlly, sequece is fuctio whose domi is the set of positive itegers, or turl umbers,,,3,. The rge of
8.3 Sequeces & Series: Covergece & Divergece A sequece is simply list of thigs geerted by rule More formlly, sequece is fuctio whose domi is the set of positive itegers, or turl umbers,,,3,. The rge of
APPENDIX 2 LAPLACE TRANSFORMS
 APPENDIX LAPLACE TRANSFORMS Thi ppendix preent hort introduction to Lplce trnform, the bic tool ued in nlyzing continuou ytem in the frequency domin. The Lplce trnform convert liner ordinry differentil
APPENDIX LAPLACE TRANSFORMS Thi ppendix preent hort introduction to Lplce trnform, the bic tool ued in nlyzing continuou ytem in the frequency domin. The Lplce trnform convert liner ordinry differentil
The Exponential Function
 The Epoetil Fuctio Defiitio: A epoetil fuctio with bse is defied s P for some costt P where 0 d. The most frequetly used bse for epoetil fuctio is the fmous umber e.788... E.: It hs bee foud tht oyge cosumptio
The Epoetil Fuctio Defiitio: A epoetil fuctio with bse is defied s P for some costt P where 0 d. The most frequetly used bse for epoetil fuctio is the fmous umber e.788... E.: It hs bee foud tht oyge cosumptio
FOURIER SERIES PART I: DEFINITIONS AND EXAMPLES. To a 2π-periodic function f(x) we will associate a trigonometric series. a n cos(nx) + b n sin(nx),
 FOURIER SERIES PART I: DEFINITIONS AND EXAMPLES To -periodic fuctio f() we will ssocite trigoometric series + cos() + b si(), or i terms of the epoetil e i, series of the form c e i. Z For most of the
FOURIER SERIES PART I: DEFINITIONS AND EXAMPLES To -periodic fuctio f() we will ssocite trigoometric series + cos() + b si(), or i terms of the epoetil e i, series of the form c e i. Z For most of the
EE Control Systems LECTURE 8
 Coyright F.L. Lewi 999 All right reerved Udted: Sundy, Ferury, 999 EE 44 - Control Sytem LECTURE 8 REALIZATION AND CANONICAL FORMS A liner time-invrint (LTI) ytem cn e rereented in mny wy, including: differentil
Coyright F.L. Lewi 999 All right reerved Udted: Sundy, Ferury, 999 EE 44 - Control Sytem LECTURE 8 REALIZATION AND CANONICAL FORMS A liner time-invrint (LTI) ytem cn e rereented in mny wy, including: differentil
Homework 12 Solution - AME30315, Spring 2013
 Homework 2 Solution - AME335, Spring 23 Problem :[2 pt] The Aerotech AGS 5 i a linear motor driven XY poitioning ytem (ee attached product heet). A friend of mine, through careful experimentation, identified
Homework 2 Solution - AME335, Spring 23 Problem :[2 pt] The Aerotech AGS 5 i a linear motor driven XY poitioning ytem (ee attached product heet). A friend of mine, through careful experimentation, identified
1.3 Continuous Functions and Riemann Sums
 mth riem sums, prt 0 Cotiuous Fuctios d Riem Sums I Exmple we sw tht lim Lower() = lim Upper() for the fuctio!! f (x) = + x o [0, ] This is o ccidet It is exmple of the followig theorem THEOREM Let f be
mth riem sums, prt 0 Cotiuous Fuctios d Riem Sums I Exmple we sw tht lim Lower() = lim Upper() for the fuctio!! f (x) = + x o [0, ] This is o ccidet It is exmple of the followig theorem THEOREM Let f be
LECTURE 13 SIMULTANEOUS EQUATIONS
 NOVEMBER 5, 26 Demad-upply ytem LETURE 3 SIMULTNEOUS EQUTIONS I thi lecture, we dicu edogeeity problem that arie due to imultaeity, i.e. the left-had ide variable ad ome of the right-had ide variable are
NOVEMBER 5, 26 Demad-upply ytem LETURE 3 SIMULTNEOUS EQUTIONS I thi lecture, we dicu edogeeity problem that arie due to imultaeity, i.e. the left-had ide variable ad ome of the right-had ide variable are
Root Locus Contents. Root locus, sketching algorithm. Root locus, examples. Root locus, proofs. Root locus, control examples
 Root Locu Content Root locu, ketching algorithm Root locu, example Root locu, proof Root locu, control example Root locu, influence of zero and pole Root locu, lead lag controller deign 9 Spring ME45 -
Root Locu Content Root locu, ketching algorithm Root locu, example Root locu, proof Root locu, control example Root locu, influence of zero and pole Root locu, lead lag controller deign 9 Spring ME45 -
ELECTRONICS & COMMUNICATIONS DEP. 3rd YEAR, 2010/2011 CONTROL ENGINEERING. SHEET 2 Bode Plot
 CAIRO UNIVERITY FACULTY OF ENGINEERING ELECTRONIC & COMMUNICATION DEP. 3rd YEAR, 00/0 CONTROL ENGINEERING HEET Bode Plot [] Drw the symptotic Bode plots for ech of the followig trsfer fuctios: ) ( 0.5
CAIRO UNIVERITY FACULTY OF ENGINEERING ELECTRONIC & COMMUNICATION DEP. 3rd YEAR, 00/0 CONTROL ENGINEERING HEET Bode Plot [] Drw the symptotic Bode plots for ech of the followig trsfer fuctios: ) ( 0.5
Hidden Markov Model Parameters
 .PPT 5/04/00 Lecture 6 HMM Traiig Traiig Hidde Markov Model Iitial model etimate Viterbi traiig Baum-Welch traiig 8.7.PPT 5/04/00 8.8 Hidde Markov Model Parameter c c c 3 a a a 3 t t t 3 c a t A Hidde
.PPT 5/04/00 Lecture 6 HMM Traiig Traiig Hidde Markov Model Iitial model etimate Viterbi traiig Baum-Welch traiig 8.7.PPT 5/04/00 8.8 Hidde Markov Model Parameter c c c 3 a a a 3 t t t 3 c a t A Hidde
TI-83/84 Calculator Instructions for Math Elementary Statistics
 TI-83/84 Calculator Itructio for Math 34- Elemetary Statitic. Eterig Data: Data oit are tored i Lit o the TI-83/84. If you have't ued the calculator before, you may wat to erae everythig that wa there.
TI-83/84 Calculator Itructio for Math 34- Elemetary Statitic. Eterig Data: Data oit are tored i Lit o the TI-83/84. If you have't ued the calculator before, you may wat to erae everythig that wa there.
The Reimann Integral is a formal limit definition of a definite integral
 MATH 136 The Reim Itegrl The Reim Itegrl is forml limit defiitio of defiite itegrl cotiuous fuctio f. The costructio is s follows: f ( x) dx for Reim Itegrl: Prtitio [, ] ito suitervls ech hvig the equl
MATH 136 The Reim Itegrl The Reim Itegrl is forml limit defiitio of defiite itegrl cotiuous fuctio f. The costructio is s follows: f ( x) dx for Reim Itegrl: Prtitio [, ] ito suitervls ech hvig the equl
x with A given by (6.2.1). The control ( ) ( )
 Homework 5 Sring 9 AerE33 Due 4/(F) SOLUTION PROBLEM (3t) In thi roblem we will invetigate the longitudinal dynamic of the B747 airlane a decribed in Etkin 66 The tate model i x Ax Bu where the tate vector
Homework 5 Sring 9 AerE33 Due 4/(F) SOLUTION PROBLEM (3t) In thi roblem we will invetigate the longitudinal dynamic of the B747 airlane a decribed in Etkin 66 The tate model i x Ax Bu where the tate vector
Area, Volume, Rotations, Newton s Method
 Are, Volume, Rottio, Newto Method Are etwee curve d the i A ( ) d Are etwee curve d the y i A ( y) yd yc Are etwee curve A ( ) g( ) d where ( ) i the "top" d g( ) i the "ottom" yd Are etwee curve A ( y)
Are, Volume, Rottio, Newto Method Are etwee curve d the i A ( ) d Are etwee curve d the y i A ( y) yd yc Are etwee curve A ( ) g( ) d where ( ) i the "top" d g( ) i the "ottom" yd Are etwee curve A ( y)
ON THE SCALE PARAMETER OF EXPONENTIAL DISTRIBUTION
 Review of the Air Force Academy No. (34)/7 ON THE SCALE PARAMETER OF EXPONENTIAL DISTRIBUTION Aca Ileaa LUPAŞ Military Techical Academy, Bucharet, Romaia (lua_a@yahoo.com) DOI:.96/84-938.7.5..6 Abtract:
Review of the Air Force Academy No. (34)/7 ON THE SCALE PARAMETER OF EXPONENTIAL DISTRIBUTION Aca Ileaa LUPAŞ Military Techical Academy, Bucharet, Romaia (lua_a@yahoo.com) DOI:.96/84-938.7.5..6 Abtract:
Let. Then. k n. And. Φ npq. npq. ε 2. Φ npq npq. npq. = ε. k will be very close to p. If n is large enough, the ratio n
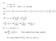 Let The m ( ) ( + ) where > very smll { } { ( ) ( + ) } Ad + + { } Φ Φ Φ Φ Φ Let, the Φ( ) lim This is lled thelw of lrge umbers If is lrge eough, the rtio will be very lose to. Exmle -Tossig oi times.
Let The m ( ) ( + ) where > very smll { } { ( ) ( + ) } Ad + + { } Φ Φ Φ Φ Φ Let, the Φ( ) lim This is lled thelw of lrge umbers If is lrge eough, the rtio will be very lose to. Exmle -Tossig oi times.
Frequency-domain Characteristics of Discrete-time LTI Systems
 requecy-domi Chrcteristics of Discrete-time LTI Systems Prof. Siripog Potisuk LTI System descriptio Previous bsis fuctio: uit smple or DT impulse The iput sequece is represeted s lier combitio of shifted
requecy-domi Chrcteristics of Discrete-time LTI Systems Prof. Siripog Potisuk LTI System descriptio Previous bsis fuctio: uit smple or DT impulse The iput sequece is represeted s lier combitio of shifted
PROGRESSIONS AND SERIES
 PROGRESSIONS AND SERIES A sequece is lso clled progressio. We ow study three importt types of sequeces: () The Arithmetic Progressio, () The Geometric Progressio, () The Hrmoic Progressio. Arithmetic Progressio.
PROGRESSIONS AND SERIES A sequece is lso clled progressio. We ow study three importt types of sequeces: () The Arithmetic Progressio, () The Geometric Progressio, () The Hrmoic Progressio. Arithmetic Progressio.
UNIVERSITY OF CALIFORNIA College of Engineering Department of Electrical Engineering and Computer Sciences
 Name [ oit]: AMIN SID: UNIESITY OF CAIFONIA College of Egieerig Deartmet of Electrical Egieerig ad Comuter Sciece Midterm EECS 05 B E BOSE Setember 8 00 FA 00 Show derivatio ad mark reult with box aroud
Name [ oit]: AMIN SID: UNIESITY OF CAIFONIA College of Egieerig Deartmet of Electrical Egieerig ad Comuter Sciece Midterm EECS 05 B E BOSE Setember 8 00 FA 00 Show derivatio ad mark reult with box aroud
ME2142/ME2142E Feedback Control Systems First half: Professor POO Aun Neow Second half: Professor V Subramaniam
 ME4/ME4E Feedbck Cotrol Sytem Firt hlf: Profeor POO Au Neow Secod hlf: Profeor V Subrmim Referece Text Cotrol Sytem Egieerig 5 th Editio by Nom S Nie. Joh Wiley & So RefereceText: Moder Cotrol Egieerig
ME4/ME4E Feedbck Cotrol Sytem Firt hlf: Profeor POO Au Neow Secod hlf: Profeor V Subrmim Referece Text Cotrol Sytem Egieerig 5 th Editio by Nom S Nie. Joh Wiley & So RefereceText: Moder Cotrol Egieerig
MTH 146 Class 16 Notes
 MTH 46 Clss 6 Notes 0.4- Cotiued Motivtio: We ow cosider the rc legth of polr curve. Suppose we wish to fid the legth of polr curve curve i terms of prmetric equtios s: r f where b. We c view the cos si
MTH 46 Clss 6 Notes 0.4- Cotiued Motivtio: We ow cosider the rc legth of polr curve. Suppose we wish to fid the legth of polr curve curve i terms of prmetric equtios s: r f where b. We c view the cos si
Remarks: (a) The Dirac delta is the function zero on the domain R {0}.
 Sectio Objective(s): The Dirc s Delt. Mi Properties. Applictios. The Impulse Respose Fuctio. 4.4.. The Dirc Delt. 4.4. Geerlized Sources Defiitio 4.4.. The Dirc delt geerlized fuctio is the limit δ(t)
Sectio Objective(s): The Dirc s Delt. Mi Properties. Applictios. The Impulse Respose Fuctio. 4.4.. The Dirc Delt. 4.4. Geerlized Sources Defiitio 4.4.. The Dirc delt geerlized fuctio is the limit δ(t)
MATRIX ALGEBRA, Systems Linear Equations
 MATRIX ALGEBRA, Systes Lier Equtios Now we chge to the LINEAR ALGEBRA perspective o vectors d trices to reforulte systes of lier equtios. If you fid the discussio i ters of geerl d gets lost i geerlity,
MATRIX ALGEBRA, Systes Lier Equtios Now we chge to the LINEAR ALGEBRA perspective o vectors d trices to reforulte systes of lier equtios. If you fid the discussio i ters of geerl d gets lost i geerlity,
Section IV.6: The Master Method and Applications
 Sectio IV.6: The Mster Method d Applictios Defiitio IV.6.1: A fuctio f is symptoticlly positive if d oly if there exists rel umer such tht f(x) > for ll x >. A cosequece of this defiitio is tht fuctio
Sectio IV.6: The Mster Method d Applictios Defiitio IV.6.1: A fuctio f is symptoticlly positive if d oly if there exists rel umer such tht f(x) > for ll x >. A cosequece of this defiitio is tht fuctio
CONTROL SYSTEMS LABORATORY ECE311 LAB 3: Control Design Using the Root Locus
 CONTROL SYSTEMS LABORATORY ECE311 LAB 3: Control Deign Uing the Root Locu 1 Purpoe The purpoe of thi lbortory i to deign cruie control ytem for cr uing the root locu. 2 Introduction Diturbnce D( ) = d
CONTROL SYSTEMS LABORATORY ECE311 LAB 3: Control Deign Uing the Root Locu 1 Purpoe The purpoe of thi lbortory i to deign cruie control ytem for cr uing the root locu. 2 Introduction Diturbnce D( ) = d
We will begin by supplying the proof to (a).
 (The solutios of problem re mostly from Jeffrey Mudrock s HWs) Problem 1. There re three sttemet from Exmple 5.4 i the textbook for which we will supply proofs. The sttemets re the followig: () The spce
(The solutios of problem re mostly from Jeffrey Mudrock s HWs) Problem 1. There re three sttemet from Exmple 5.4 i the textbook for which we will supply proofs. The sttemets re the followig: () The spce
Comments on Discussion Sheet 18 and Worksheet 18 ( ) An Introduction to Hypothesis Testing
 Commet o Dicuio Sheet 18 ad Workheet 18 ( 9.5-9.7) A Itroductio to Hypothei Tetig Dicuio Sheet 18 A Itroductio to Hypothei Tetig We have tudied cofidece iterval for a while ow. Thee are method that allow
Commet o Dicuio Sheet 18 ad Workheet 18 ( 9.5-9.7) A Itroductio to Hypothei Tetig Dicuio Sheet 18 A Itroductio to Hypothei Tetig We have tudied cofidece iterval for a while ow. Thee are method that allow
Northwest High School s Algebra 2
 Northwest High School s Algebr Summer Review Pcket 0 DUE August 8, 0 Studet Nme This pcket hs bee desiged to help ou review vrious mthemticl topics tht will be ecessr for our success i Algebr. Istructios:
Northwest High School s Algebr Summer Review Pcket 0 DUE August 8, 0 Studet Nme This pcket hs bee desiged to help ou review vrious mthemticl topics tht will be ecessr for our success i Algebr. Istructios:
lecture 16: Introduction to Least Squares Approximation
 97 lecture 16: Itroductio to Lest Squres Approximtio.4 Lest squres pproximtio The miimx criterio is ituitive objective for pproximtig fuctio. However, i my cses it is more ppelig (for both computtio d
97 lecture 16: Itroductio to Lest Squres Approximtio.4 Lest squres pproximtio The miimx criterio is ituitive objective for pproximtig fuctio. However, i my cses it is more ppelig (for both computtio d
Section 6.3: Geometric Sequences
 40 Chpter 6 Sectio 6.: Geometric Sequeces My jobs offer ul cost-of-livig icrese to keep slries cosistet with ifltio. Suppose, for exmple, recet college grdute fids positio s sles mger erig ul slry of $6,000.
40 Chpter 6 Sectio 6.: Geometric Sequeces My jobs offer ul cost-of-livig icrese to keep slries cosistet with ifltio. Suppose, for exmple, recet college grdute fids positio s sles mger erig ul slry of $6,000.
( a n ) converges or diverges.
 Chpter Ifiite Series Pge of Sectio E Rtio Test Chpter : Ifiite Series By the ed of this sectio you will be ble to uderstd the proof of the rtio test test series for covergece by pplyig the rtio test pprecite
Chpter Ifiite Series Pge of Sectio E Rtio Test Chpter : Ifiite Series By the ed of this sectio you will be ble to uderstd the proof of the rtio test test series for covergece by pplyig the rtio test pprecite
Société de Calcul Mathématique, S. A. Algorithmes et Optimisation
 Société de Calcul Mathématique S A Algorithme et Optimiatio Radom amplig of proportio Berard Beauzamy Jue 2008 From time to time we fid a problem i which we do ot deal with value but with proportio For
Société de Calcul Mathématique S A Algorithme et Optimiatio Radom amplig of proportio Berard Beauzamy Jue 2008 From time to time we fid a problem i which we do ot deal with value but with proportio For
National Quali cations AHEXEMPLAR PAPER ONLY
 Ntiol Quli ctios AHEXEMPLAR PAPER ONLY EP/AH/0 Mthemtics Dte Not pplicble Durtio hours Totl mrks 00 Attempt ALL questios. You my use clcultor. Full credit will be give oly to solutios which coti pproprite
Ntiol Quli ctios AHEXEMPLAR PAPER ONLY EP/AH/0 Mthemtics Dte Not pplicble Durtio hours Totl mrks 00 Attempt ALL questios. You my use clcultor. Full credit will be give oly to solutios which coti pproprite
 n. A Very Interesting Example + + = d. + x3. + 5x4. math 131 power series, part ii 7. One of the first power series we examined was. 2!
 mth power series, prt ii 7 A Very Iterestig Emple Oe of the first power series we emied ws! + +! + + +!! + I Emple 58 we used the rtio test to show tht the itervl of covergece ws (, ) Sice the series coverges
mth power series, prt ii 7 A Very Iterestig Emple Oe of the first power series we emied ws! + +! + + +!! + I Emple 58 we used the rtio test to show tht the itervl of covergece ws (, ) Sice the series coverges
, we would have a series, designated as + j 1
 Clculus sectio 9. Ifiite Series otes by Ti Pilchowski A sequece { } cosists of ordered set of ubers. If we were to begi ddig the ubers of sequece together s we would hve series desigted s. Ech iteredite
Clculus sectio 9. Ifiite Series otes by Ti Pilchowski A sequece { } cosists of ordered set of ubers. If we were to begi ddig the ubers of sequece together s we would hve series desigted s. Ech iteredite
Lecture 4 Recursive Algorithm Analysis. Merge Sort Solving Recurrences The Master Theorem
 Lecture 4 Recursive Algorithm Alysis Merge Sort Solvig Recurreces The Mster Theorem Merge Sort MergeSortA, left, right) { if left < right) { mid = floorleft + right) / 2); MergeSortA, left, mid); MergeSortA,
Lecture 4 Recursive Algorithm Alysis Merge Sort Solvig Recurreces The Mster Theorem Merge Sort MergeSortA, left, right) { if left < right) { mid = floorleft + right) / 2); MergeSortA, left, mid); MergeSortA,
Exponents and Radical
 Expoets d Rdil Rule : If the root is eve d iside the rdil is egtive, the the swer is o rel umber, meig tht If is eve d is egtive, the Beuse rel umber multiplied eve times by itself will be lwys positive.
Expoets d Rdil Rule : If the root is eve d iside the rdil is egtive, the the swer is o rel umber, meig tht If is eve d is egtive, the Beuse rel umber multiplied eve times by itself will be lwys positive.
1999 by CRC Press LLC
 Poulri A. D. The Melli Trform The Hdboo of Formul d Tble for Sigl Proceig. Ed. Alexder D. Poulri Boc Rto: CRC Pre LLC,999 999 by CRC Pre LLC 8 The Melli Trform 8. The Melli Trform 8. Propertie of Melli
Poulri A. D. The Melli Trform The Hdboo of Formul d Tble for Sigl Proceig. Ed. Alexder D. Poulri Boc Rto: CRC Pre LLC,999 999 by CRC Pre LLC 8 The Melli Trform 8. The Melli Trform 8. Propertie of Melli
MA123, Chapter 9: Computing some integrals (pp )
 MA13, Chpter 9: Computig some itegrls (pp. 189-05) Dte: Chpter Gols: Uderstd how to use bsic summtio formuls to evlute more complex sums. Uderstd how to compute its of rtiol fuctios t ifiity. Uderstd how
MA13, Chpter 9: Computig some itegrls (pp. 189-05) Dte: Chpter Gols: Uderstd how to use bsic summtio formuls to evlute more complex sums. Uderstd how to compute its of rtiol fuctios t ifiity. Uderstd how
Student Success Center Elementary Algebra Study Guide for the ACCUPLACER (CPT)
 Studet Success Ceter Elemetry Algebr Study Guide for the ACCUPLACER (CPT) The followig smple questios re similr to the formt d cotet of questios o the Accuplcer Elemetry Algebr test. Reviewig these smples
Studet Success Ceter Elemetry Algebr Study Guide for the ACCUPLACER (CPT) The followig smple questios re similr to the formt d cotet of questios o the Accuplcer Elemetry Algebr test. Reviewig these smples
Convergence rates of approximate sums of Riemann integrals
 Jourl of Approximtio Theory 6 (9 477 49 www.elsevier.com/locte/jt Covergece rtes of pproximte sums of Riem itegrls Hiroyuki Tski Grdute School of Pure d Applied Sciece, Uiversity of Tsukub, Tsukub Ibrki
Jourl of Approximtio Theory 6 (9 477 49 www.elsevier.com/locte/jt Covergece rtes of pproximte sums of Riem itegrls Hiroyuki Tski Grdute School of Pure d Applied Sciece, Uiversity of Tsukub, Tsukub Ibrki
Surds, Indices, and Logarithms Radical
 MAT 6 Surds, Idices, d Logrithms Rdicl Defiitio of the Rdicl For ll rel, y > 0, d ll itegers > 0, y if d oly if y where is the ide is the rdicl is the rdicd. Surds A umber which c be epressed s frctio
MAT 6 Surds, Idices, d Logrithms Rdicl Defiitio of the Rdicl For ll rel, y > 0, d ll itegers > 0, y if d oly if y where is the ide is the rdicl is the rdicd. Surds A umber which c be epressed s frctio
SUTCLIFFE S NOTES: CALCULUS 2 SWOKOWSKI S CHAPTER 11
 SUTCLIFFE S NOTES: CALCULUS SWOKOWSKI S CHAPTER Ifiite Series.5 Altertig Series d Absolute Covergece Next, let us cosider series with both positive d egtive terms. The simplest d most useful is ltertig
SUTCLIFFE S NOTES: CALCULUS SWOKOWSKI S CHAPTER Ifiite Series.5 Altertig Series d Absolute Covergece Next, let us cosider series with both positive d egtive terms. The simplest d most useful is ltertig
Systems Analysis. Prof. Cesar de Prada ISA-UVA
 Sytem Analyi Prof. Cear de Prada ISAUVA rada@autom.uva.e Aim Learn how to infer the dynamic behaviour of a cloed loo ytem from it model. Learn how to infer the change in the dynamic of a cloed loo ytem
Sytem Analyi Prof. Cear de Prada ISAUVA rada@autom.uva.e Aim Learn how to infer the dynamic behaviour of a cloed loo ytem from it model. Learn how to infer the change in the dynamic of a cloed loo ytem
Lecture 38 (Trapped Particles) Physics Spring 2018 Douglas Fields
 Lecture 38 (Trpped Prticles) Physics 6-01 Sprig 018 Dougls Fields Free Prticle Solutio Schrödiger s Wve Equtio i 1D If motio is restricted to oe-dimesio, the del opertor just becomes the prtil derivtive
Lecture 38 (Trpped Prticles) Physics 6-01 Sprig 018 Dougls Fields Free Prticle Solutio Schrödiger s Wve Equtio i 1D If motio is restricted to oe-dimesio, the del opertor just becomes the prtil derivtive
Chapter 8. Root Locus Techniques
 Chapter 8 Rt Lcu Technique Intrductin Sytem perfrmance and tability dt determined dby cled-lp l ple Typical cled-lp feedback cntrl ytem G Open-lp TF KG H Zer -, - Ple 0, -, -4 K 4 Lcatin f ple eaily fund
Chapter 8 Rt Lcu Technique Intrductin Sytem perfrmance and tability dt determined dby cled-lp l ple Typical cled-lp feedback cntrl ytem G Open-lp TF KG H Zer -, - Ple 0, -, -4 K 4 Lcatin f ple eaily fund
