Solutions of Linear Equations

Transcription

1 Lesson 14 Part 1: Introduction Solutions of Linear Equations Develop Skills and Strategies CCSS 8.EE.C.7a You ve learned how to solve linear equations and how to check your solution. In this lesson, you ll learn that not every linear equation has just one solution. Take a look at this problem. Jason and his friend Amy are arguing. Jason says that a linear equation always has just one solution. Amy says that some linear equations have more than one solution. Who s right? Amy asked Jason to eplore solutions to the following equation ( 2 2) 1 7 Eplore It Use the math you already know to solve this problem. Remember that a solution to an equation is a number that makes the equation true. To check to see if a number is a solution to this equation, replace with its value. Is 6 a solution to the equation? Show your work. Is 22 a solution to the equation? Show your work. Is 0 a solution to the equation? Show your work. Can an equation have more than one solution? Eplain. Who is right Jason or Amy? 124

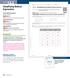
2 Part 1: Introduction Lesson 14 Find Out More Look at how you could solve Amy s equation. First, simplify each side: ( 2 2) 1 7 Use the distributive property Combine like terms Once both sides of an equation are in simplest form, you can say a lot about the solution without actually solving the equation. You can just look at the structure. Think about how you might solve this equation with pictures. Look at the pan balance below. The left pan represents So does the right pan. If you take away 3 from both sides, you end up with 1 5 1, a true statement. If you take away 1 from both sides, you end up with 3 5 3, a true statement. You can replace with any number and you will always get a true statement. The pan will remain balanced. This equation has infinitely many solutions. You ve seen that a linear equation can have one solution or, in a case like this, infinitely many solutions. You will also see that a linear equation can have no solution. Reflect 1 Once both sides of an equation are in simplest form, how can you tell if it has infinitely many solutions? 125

3 Part 2: Modeled Instruction Lesson 14 Read the problem below. Then eplore how to identify when an equation has one solution, infinitely many solutions, or no solution. Yari and her friends, Alyssa and David, were each given an equation to solve. Yari: 2( 1 10) Alyssa: ( 1 3) 2 5 David: 2( 2 3) Whose equation has one solution? Infinitely many solutions? No solution? Model It You can use properties of operations to simplify each side of Yari s equation. 2( 1 10) The variable terms and the constants are the same on both sides of the equation. No matter what value you choose for, the equation will always be true. Model It You can use properties of operations to simplify each side of Alyssa s equation ( 1 3) The variable terms are the same on both sides of the equation but the constants are different. There is no value for that will make the equation true. Model It You can use properties of operations to simplify each side of David s equation. 2( 2 3) The variable terms are different. There is only one value for that will make the equation true. 126

4 Part 2: Guided Instruction Lesson 14 Connect It Now you will use the models to solve this problem. 2 Look at Model It for Yari s equation. What do you notice about both sides of the equation? What equation do you get if you subtract 2 from both sides of the equation? 3 Look at Model It for Alyssa s equation. How is it different than Yari s equation? How is it similar? 4 Look at the pan balance for Alyssa s equation. Is there any way to balance the pan? Eplain. What equation do you get if you subtract 2 from both sides of the equation? 5 Look at the Model It for David s equation. Are the variable terms on each side of the equation the same or different? Solve David s equation. 6 Eplain how you know when an equation has one solution, no solution, or infinitely many solutions. Try It Use what you just learned about equations with one solution, no solution, or infinitely many solutions. Show your work on a separate sheet of paper. Replace c and d in the equation c 1 d with the given values. Eplain why the equation has one solution, no solution, or infinitely many solutions. 7 c 5 6 and d c 5 8 and d

5 Part 3: Guided Practice Lesson 14 Study the student model below. Then solve problems The student solved the equation to find that 0 is a solution. Student Model Michelle looks at the equation and says there is no solution. Is she correct? Eplain. Look at how you can show your work How could you convince Michelle that there is a solution to this equation? Solution: No; There is one solution to this equation, 5 0. How can you tell when a linear equation has no solution? 9 Draw lines to match each linear equation to its correct number of solutions. Show your work. 5(4 2 ) no solution 25(4 2 ) infinitely many solutions When the variable terms on both sides of an equation are the same, what does that tell you about the solution(s) to the equation? 5(5 2 ) one solution 128

6 Part 3: Guided Practice Lesson Write a number in the bo so that the equation will have the type of solution(s) shown. no solution What is the difference between an equation with no solution and an equation with infinitely many solutions? infinitely many solutions one solution What do you notice about the solution to equations that have the same variable term on each side of the equation? 11 What is the solution to the equation 3( 2 4) 5 2( 2 6)? A 5 0 B 5 1 How can you simplify this equation to justify the correct answer? C There are infinitely many solutions. D There is no solution. Brian chose D as the correct answer. How did he get that answer? How could you eplain the correct response to Brian? 129

7 Part 1: Introduction Lesson 14 AT A GLANCE Students discover that some linear equations have more than one solution. Lesson 14 Part 1: Introduction Solutions of Linear Equations Develop Skills and Strategies CCSS 8.EE.C.7a STEP BY STEP Tell students that this page models how to test whether a value is a solution to a given equation. Eplain that a solution is any value of that makes an equation true. Ask, Is the value 4 a solution to the equation ? Eplain. [No; 4 is not a solution because Þ 7.] Ask, Is the value 2 a solution to the equation? [Yes; 2 is a solution because ] Have students read the problem at the top of the page. Work through the first three parts of Eplore It as a class. Point out how the distributive property is used to epand the epression 3( 2 2) to Ask students to answer the last question on their own. Then invite volunteers to eplain their answer. SMP Tip: The last question provides an opportunity for students to refine their communication skills (SMP 6). A model response includes using appropriate terminology. As a class, develop a model response. For eample: Yes. An equation can have more than one solution. The values 6, 2, and 0 are all solutions to the equation. Concept Etension Use the distributive property to simplify. Write: 1 (2 1 4) on the board. 2 Remind students to epand the epression over addition. 1(2 1 4) 5 (2) 1 (4) Point out that the distributive property can also epand over subtraction. 1(2 2 4) 5 (2) 2 (4) Point out that the epression within the parentheses can also be viewed as 2 1 (24). 124 You ve learned how to solve linear equations and how to check your solution. In this lesson, you ll learn that not every linear equation has just one solution. Take a look at this problem. Jason and his friend Amy are arguing. Jason says that a linear equation always has just one solution. Amy says that some linear equations have more than one solution. Who s right? Amy asked Jason to eplore solutions to the following equation. Eplore It ( 2 2) 1 7 Use the math you already know to solve this problem. Remember that a solution to an equation is a number that makes the equation true. To check to see if a number is a solution to this equation, replace with its value. Is 6 a solution to the equation? Show your work. Yes. 2(6) (6 2 2) (4) Is 22 a solution to the equation? Show your work. Yes. 2(22) (22) 5 3(22 2 2) (22) 5 3(24) Is 0 a solution to the equation? Show your work. Yes. 2(0) (0 2 2) (22) Can an equation have more than one solution? Eplain. Who is right Jason or Amy? Yes, 6, 22, and 0 are all solutions to Amy s equation. She was right. Mathematical Discourse On the board, write: What is the value of in the equation? Justify your answer. 5, because 2(5) , which simplifies to Does any number other than 5 make this equation true? Eplain. Guide students to realize that any other value would make the left side of the equation greater or less than 14. Replace the right side of the equation with 2( 1 6) 2 8. Make a prediction. Is there one or more than one solution to the new equation? Support your answer. Elicit opinions from the class. Guide the discussion so students realize that because , any value could be a solution. If necessary, test different values. 138

8 Part 1: Introduction Lesson 14 AT A GLANCE Students simplify a linear equation and relate it to an image of the simplified equation on a balance scale. STEP BY STEP Read Find Out More as a class. Be certain students understand where the distributive property is applied in the first step. That is, 3( 2 2) In the net step, be sure students understand how to combine like terms. Terms with the same variable raised to the same power with numeric coefficients are like terms. Have student pairs answer the Reflect question using appropriate terminology. If necessary, define infinitely many solutions. Part 1: Introduction Find Out More Look at how you could solve Amy s equation. First, simplify each side: ( 2 2) 1 7 Use the distributive property Combine like terms Once both sides of an equation are in simplest form, you can say a lot about the solution without actually solving the equation. You can just look at the structure. Think about how you might solve this equation with pictures. Look at the pan balance below. The left pan represents So does the right pan. If you take away 3 from both sides, you end up with 1 5 1, a true statement. If you take away 1 from both sides, you end up with 3 5 3, a true statement. You can replace with any number and you will always get a true statement. The pan will remain balanced. This equation has infinitely many solutions. Lesson 14 You ve seen that a linear equation can have one solution or, in a case like this, infinitely many solutions. You will also see that a linear equation can have no solution. ELL Support Point to the balance scale. If necessary, model how it works. Eplain that the pans (areas where terms are placed) are even when both sides of the equation have the same value. Reflect 1 Once both sides of an equation are in simplest form, how can you tell if it has infinitely many solutions? If the variable terms and the constant on each side of the equation are the same, the equation has infinitely many solutions. 125 SMP Tip: The balance scale model is a way to visually represent the simplified equation in the problem (SMP 4). Hands-On Activity Model equations using a balance scale. Materials: pencil, paper, colored pencils Write the equation (2 1 2). Work as a class to simplify. [ ] Sketch the simplified equation on a balance scale. Show the variable in one color and the constants in another. Ask, How does the sketch show that the equation has infinitely many solutions? [If I take away 4 from each side, I have Since can be any value, there are infinitely many solutions.] Real-World Connection Discuss real-life situations that involve linear equations. Have volunteers share any suggestions they have. As a class, write possible equations to model the situations. Eamples: temperature conversion 1 C 5 F , length 1 ft 5 in. 12 2, travel (distance 5 rate 3 time), time (hr min), weight (lb oz), currency echange rates, cell phone plans, tips 139

9 Part 2: Modeled Instruction Lesson 14 AT A GLANCE Students eplore how to identify an equation with infinitely many solutions, no solution, or only one solution. STEP BY STEP Read the problem at the top of the page as a class. Part 2: Modeled Instruction Lesson 14 Read the problem below. Then eplore how to identify when an equation has one solution, infinitely many solutions, or no solution. Yari and her friends, Alyssa and David, were each given an equation to solve. Yari: 2( 1 10) Alyssa: ( 1 3) 2 5 David: 2( 2 3) Whose equation has one solution? Infinitely many solutions? No solution? Direct students attention to the small squares on the balance scales. Ask, What does each small square represent? [the constant 11] Relate the first Model It equation to the equation students solved in Find Out More on the previous page. If you subtract 3 from both sides, you have 2 5 2, which is true. Substituting any value for will also be true. For the second equation, point out that the variable terms are both 2, but the constants are 3 and 1. No matter what value you use for, Þ For the third equation, point out that the variable terms are 2 and. Students may find it easier to understand why this equation can have only one value for that will make it true. If so, as a class, solve for. [ 5 1] 126 Model It You can use properties of operations to simplify each side of Yari s equation. 2( 1 10) Model It You can use properties of operations to simplify each side of Alyssa s equation ( 1 3) 2 5 Model It You can use properties of operations to simplify each side of David s equation. 2( 2 3) The variable terms and the constants are the same on both sides of the equation. No matter what value you choose for, the equation will always be true. The variable terms are the same on both sides of the equation but the constants are different. There is no value for that will make the equation true. The variable terms are different. There is only one value for that will make the equation true. Mathematical Discourse ELL Support You may need to reinforce the difference between a variable term and a constant term. Point out that in the epression : 2 means a number multiplied by 2. Since the number can vary (change), 2 is a variable term. The value of 20 is always 20, so 20 is a constant. (The word constant means unchanging or always the same. ) On the board, write: Have students identify the constant and the variable in the epression. What do you notice about the balance pans in the three models? The balance pans in the first and the last models are level, but the ones in the middle model are not. If the balance pans are level, what might you conclude about the equation? Do you think you can tell if the equation has one solution or infinitely many solutions? Guide the discussion so students realize that the equation has the same value on both sides, so it has a solution. However, you cannot tell if there is one or infinitely many solutions by looking at the level of the balance pans alone. 140

10 AT A GLANCE Part 2: Guided Instruction Students revisit the problems on page 126. They answer questions that are designed to reinforce their understanding of the number of solutions a linear equation will have. STEP BY STEP Read the first sentence in Connect It with students. Refer back to the problems and the models on page 126. Have students answer problems 2 5 individually. As a class, review the answers. For problem 5, you may want to point out that when the variable terms on each side are different, you can solve the equation for, which means that there is one solution. Have pairs of students work on problem 6. Then have volunteers share their answers. Lesson 14 Part 2: Guided Instruction Lesson 14 Connect It Now you will use the models to solve this problem. 2 Look at Model It for Yari s equation. What do you notice about both sides of the equation? What equation do you get if you subtract 2 from both sides of the equation? Both sides are eactly the same Look at Model It for Alyssa s equation. How is it different than Yari s equation? How is it similar? The variable terms are the same on both sides in both Yari s and Alyssa s equation. The constant terms are the same in Yari s equation and different in Alyssa s equation. 4 Look at the pan balance for Alyssa s equation. Is there any way to balance the pan? Eplain. What equation do you get if you subtract 2 from both sides of the equation? No matter what you add or subtract on both sides of the equation, the pan will always be out of balance. If you subtract 2 from both sides, you get Look at the Model It for David s equation. Are the variable terms on each side of the equation the same or different? different Solve David s equation Eplain how you know when an equation has one solution, no solution, or infinitely many solutions. Possible answer: An equation has infinitely many solutions when you get a true sentence like An equation has no solution when you get a false statement like When the variable terms on both sides are different, the equation will have one solution. Try It Hands-On Activity Make a poster about solutions to equations. Materials: pencil, poster board or heavy paper As a class, create a poster that shows an equation with each of the following types of solutions: infinitely many solutions, no solution, and one solution. Write your own equations or use the following equations: 3( 1 6) , ( 1 2) 1 5, and 2( 2 4) On the poster, include the original three equations, the three equations simplified, and a statement that tells how many solutions each equation has, followed by an eplanation. Include any other information or drawings that may be helpful. Use what you just learned about equations with one solution, no solution, or infinitely many solutions. Show your work on a separate sheet of paper. Replace c and d in the equation c 1 d with the given values. Eplain why the equation has one solution, no solution, or infinitely many solutions. 7 c 5 6 and d 5 34 one solution 8 c 5 8 and d 5 6 no solution TRY IT SOLUTIONS 7 Solution: one solution; Students may give the following eplanation: After substituting, the equation is Combine the like terms 6 and 8. Then solve for. So there is only one value that will make the equation true. ERROR ALERT: Students who did not answer the questions correctly may have substituted into the equation incorrectly, or they may have confused the variable terms and the constant. Reviewing the three Model It eamples on page 126 may be helpful. 8 Solution: no solution; Students may give the following eplanation: The variable terms are the same but the constant terms are different. If you subtract 8 from both sides you have , which is not true. So the equation has no solution

11 Part 3: Guided Practice Lesson 14 Part 3: Guided Practice Lesson 14 Part 3: Guided Practice Lesson 14 The student solved the equation to find that 0 is a solution. Study the student model below. Then solve problems Student Model Michelle looks at the equation and says there is no solution. Is she correct? Eplain. Look at how you can show your work. 10 Write a number in the bo so that the equation will have the type of solution(s) shown. no solution any number but 5 What is the difference between an equation with no solution and an equation with infinitely many solutions? infinitely many solutions How could you convince Michelle that there is a solution to this equation? How can you tell when a linear equation has no solution? When the variable terms on both sides of an equation are the same, what does that tell you about the solution(s) to the equation? Solution: No; There is one solution to this equation, Draw lines to match each linear equation to its correct number of solutions. Show your work (4 2 ) no solution (4 2 ) infinitely many solutions (5 2 ) one solution one solution What is the solution to the equation 3( 2 4) 5 2( 2 6)? A 5 0 B 5 1 C D 5 any number but 1 3 There are infinitely many solutions. There is no solution. Brian chose D as the correct answer. How did he get that answer? Brian thought that 5 0 means that there is no solution to the equation. What do you notice about the solution to equations that have the same variable term on each side of the equation? How can you simplify this equation to justify the correct answer? How could you eplain the correct response to Brian? AT A GLANCE Students practice identifying the number of solutions for a given equation. STEP BY STEP Ask students to solve the problems individually. Some students may be able to apply a rule that they have learned. Others may need to use the work in the eample as a model. Circulate among the class as students work and give appropriate support to students who are struggling. For the second equation in problem 9, you may need to point out that 2 25 is the same as 1 5. When students have completed each problem, have them to discuss their solutions. SOLUTIONS E Michelle is not correct. There are different variable terms on each side, so there is only one solution. 9 Solution: See possible student work above. The first equation has infinitely many solutions (identical variable terms and constants), the second has one solution (different variable terms), and the third has no solution (identical variable terms but different constants. (DOK 2) 10 Solution: First equation: any number but 5. Second equation: 5. Third equation: any number but 1 3. (DOK 2) 11 Solution: A; There is one solution because there are different variable terms. Solve for ; 5 0. Eplain to students why the other two answer choices are not correct: B is not correct because if 5 1, then , which is not true. C is not correct because the constants are identical on both sides, but the variable terms are not. (DOK 3) 142

12 Differentiated Instruction Lesson 14 Assessment and Remediation Ask students to read each equation carefully and then fill in the blanks. 5(2 1 6) 5 5( 1 3) 1 2 3(6 1 ) 5 2( 1 12) [10, 30, 7, 15] [18, 3, 3, 24] The terms are different. [variable] The terms are the same, but the are different. [variable; constants] There is solution. [one] There is solution. [no] For students who are struggling, use the chart below to guide remediation. After providing remediation, check students understanding. Ask students to predict the number of solutions to the equation 2(3 1 6) 5 2( 1 6) 1 4 and eplain their reasoning. [The equation simplifies to , so any value for will be true. There are an infinite number of solutions.] If a student is still having difficulty, use Ready Instruction, Level 8, Lesson 13. If the error is... Students may... To remediate... no or infinitely many one or infinitely many not understand the relationship between the variables on each side of the equation. not understand why the same variable but different constants on each side results in no solution. Have students solve the equation for. Students should see that because can be isolated on one side of the equation, there is only one solution. Have students try to solve the equation. Students should see that while is true, is not true, so there is no solution. Hands-On Activity Use a pan balance to model equations. Materials: actual or virtual balance scale; two sizes of weights larger to represent, smaller to represent the constant 1 Organize students into pairs and provide equations for them to model. As necessary, students use the distributive property, combine like terms, and use operations with integers to simplify the equations so there is one variable term and one constant on each side of the equal sign. Then they model the epression on the balance scale. If the scale balances, have students decide if there is one or an infinite number of values of that will make the equation true. For each equation modeled, have pairs compare their results and adjust their models as necessary. Challenge Activity Develop a solutions matching game. Materials: inde cards, modified number cube with faces labeled 0, 0, 1, 1, M, and M (M stands for many) Have student pairs write three equations, each one on an inde card; each with a different number of solutions. On the back of the card students write the number of solutions and justify their answer. Encourage them to include at least one equation with negative integers. Partner pairs combine their cards and display them equation-side up. Then each pair takes a turn rolling the number cube and selecting an equation that matches their roll. (Students cannot select their own equation unless no other match is left.) Students review the answer on the back of the card and keep the card if it is a match. (Students can challenge equations if they disagree with the number of solutions stated.) When all the cards are selected, the pair with the greatest number of cards wins. 144