Bravais lattices and crystal systems
|
|
|
- Milton Carr
- 5 years ago
- Views:
Transcription
1 3 Brvis ltties nd rystl systems 3. Introdution The definitions of the motif, the repeting unit of pttern, nd the lttie, n rry of points in spe in whih eh point hs n identil environment, hold in three dimensions extly s they do in two dimensions. However, in three dimensions there re dditionl symmetry elements tht need to e onsidered: oth point symmetry elements to desrie the symmetry of the three-dimensionl motif (or indeed ny rystl or three-dimensionl ojet) nd lso trnsltionl symmetry elements, whih re required (like glide lines in the two-dimensionl se) to desrie ll the possile ptterns whih rise y omining motifs of different symmetries with their pproprite ltties. Clerly, these onsidertions suggest tht the sujet is going to e rther more omplited nd diffiult ; it is ovious tht there re going to e mny more threedimensionl ptterns (or spe groups) thn the seventeen two-dimensionl ptterns (or plne groups or the eighty two-sided ptterns Chpter ), nd to work through ll of these systemtilly would tke up mny pges! However, it is not neessry to do so; ll tht is required is n understnding of the priniples involved (Chpter ), the opertion nd signifine of the dditionl symmetry elements, nd the min results. These min results my e stted stright wy. The dditionl point symmetry elements required re entres of symmetry, mirror plnes (insted of lines) nd inversion xes; the dditionl trnsltionl symmetry elements re glide plnes (insted of lines) nd srew xes. The pplition nd permuttion of ll symmetry elements to ptterns in spe give rise to 30 spe groups (insted of seventeen plne groups) distriuted mong fourteen spe ltties (insted of five plne ltties) nd thirty-two point group symmetries (insted of ten plne point group symmetries). In this hpter the onept of spe (or Brvis) ltties nd their symmetries is disussed nd, deriving from this, the lssifition of rystls into seven systems. 3. The fourteen spe (Brvis) ltties The systemti work of desriing nd enumerting the spe ltties ws done initilly y Frnkenheim who, in 835, proposed tht there were fifteen in ll. Unfortuntely for Frnkenheim, two of his ltties were identil, ft first pointed out y Brvis in 848. It ws, to tke two-dimensionl nlogy, s if Frnkenheim hd filed to notie Denotes iogrphil notes ville in ppendix 3.
2 3. The fourteen spe (Brvis) ltties 85 (see Fig..4()) tht the rhomi or dimond nd the retngulr entred plne ltties were identil! Hene, to this dy, the fourteen spe ltties re usully, nd perhps unfirly, lled Brvis ltties. The unit ells of the Brvis ltties re shown in Fig. 3.. The different shpes nd sizes of these ells my e desried in terms of three ell edge lengths or xil distnes, ui Body-entred ui (I) Fe-entred ui (F) tetrgonl Body-entred tetrgonl (I) orthorhomi Body-entred orthorhomi (I) α α α 0 Bse-entred orthorhomi (C) Fe-entred orthorhomi (F) Rhomohedrl (R) Hexgonl β β β γ α monolini Bse-entred monolini (C) Trilini Fig. 3.. The fourteen Brvis ltties (from Elements of X-Ry Diffrtion, (nd edn), y B. D. Cullity, ddison-wesley, 978).
3 86 Brvis ltties nd rystl systems,,, or lttie vetors,, nd the ngles etween them, α, β, γ, where α is the ngle etween nd, β the ngle etween nd, nd γ the ngle etween nd. The xil distnes nd ngles re mesured from one orner to the ell, i.e. ommon origin. It does not mtter where we tke the origin ny orner will do ut, s pointed out in Chpter, it is useful onvention (nd helps to void onfusion) if the origin is tken s the k left-hnd orner of the ell, the -xis pointing forwrd (out of the pge), the -xis towrds the right nd the -xis upwrds. This onvention lso gives right-hnded xil system. If ny one of the xes is reversed (e.g. the -xis towrds the left insted of the right), then left-hnded xil system results. The distintion etween them is tht, like left nd right hnds, they re mirror imges of one nother nd nnot e rought into oinidene y rottion. The drwings of the unit ells of the Brvis ltties in Fig. 3. n e misleding euse, s shown in Chpter, it is the pttern of lttie points whih distinguishes the ltties. The unit ells simply represent ritrry, though onvenient, wys of joining up the lttie points. Consider, for exmple, the three ui ltties; ui P (for Primitive, one lttie point per ell, i.e. lttie points only t the orners of the ell), ui I (for Innenzentrierte, whih is Germn for ody-entred, n dditionl lttie point t the entre of the ell, giving two lttie points per ell) nd ui F (for Fe-entred, with dditionl lttie points t the entres of eh fe of the ell, giving four lttie points per ell). It is possile to outline lterntive primitive ells (i.e. lttie points only t the orners) for the ui I nd ui F ltties, s is shown in Fig. 3.. s mentioned in Chpter, these primitive ells re not often used () euse the inter-xil ngles re not the onvenient 90 (i.e. they re not orthogonl) nd () euse they do not revel very lerly the ui symmetry of the ui I nd ui F ltties. (The symmetry of the Brvis ltties, or rther the point group symmetries of their unit ells, will e desried in Setion 3.3.) Similr rguments onerning the use of primitive ells pply to ll the other entred ltties. Notie tht the unit ells of two of the ltties re entred on the top nd ottom fes. These re lled se-entred or C-entred euse these fes re interseted y the -xis () () Fig. 3.. () The ui I nd () the ui F ltties with the primitive rhomohedrl ells nd inter-xil ngles indited.
4 3. The fourteen spe (Brvis) ltties 87 The Brvis ltties my e thought of s eing uilt up y stking lyers of the five plne ltties, one on top of nother. The ui nd tetrgonl ltties re sed on the stking of squre lttie lyers; the orthorhomi P nd I ltties on the stking of retngulr lyers; the orthorhomi C nd F ltties on the stking of retngulr entred lyers; the rhomohedrl nd hexgonl lttie on the stking of hexgonl lyers nd the monolini nd trilini ltties on the stking of olique lyers. These reltionships etween the plne nd the Brvis ltties re esy to see, exept perhps for the rhomohedrl lttie. The rhomohedrl unit ell hs xes of equl length nd with equl ngles (α) etween them. Notie tht the lyers of lttie points, perpendiulr to the vertil diretion (shown dotted in Fig. 3.) form tringulr, or equivlently, hexgonl lyers. The hexgonl nd rhomohedrl ltties differ in the wys in whih the hexgonl lyers re stked. In the hexgonl lttie they re stked diretly one on top of the other (Fig. 3.3()) nd in the rhomohedrl lttie they re stked suh tht the next two lyers of points lie ove the tringulr hollows or intersties of the lyer elow, giving three lyer repet (Fig. 3.3()). These hexgonl nd rhomohedrl stking sequenes hve een met efore in the stking of lose-pked lyers (Chpter ); the hexgonl lttie orresponds to the simple hexgonl...sequene nd the rhomohedrl lttie orresponds to the f BCBC...sequene. Now oservnt reders will notie tht the rhomohedrl nd ui ltties re therefore relted. The primitive ells of the ui I nd ui F ltties (Fig. 3.) re rhomohedrl the xes re of equl length nd the ngles (α) etween them re equl. s in the two-dimensionl ses, wht distinguishes the ui ltties from the rhomohedrl is their symmetry. When the ngle α is 90 we hve ui P lttie, when it is 60 we hve ui F lttie nd when it is we hve ui I lttie (Fig. 3.). Or, lterntively, when the hexgonl lyers of lttie points in the rhomohedrl lttie re sped prt in suh wy tht the ngle α is 90,60 or 09.47, then ui symmetry results. Finlly, ompre the orthorhomi ltties (ll sides of the unit ell of different lengths) with the tetrgonl ltties (two sides of the ell of equl length). Why re there C B () () Fig Stking of hexgonl lyers of lttie points in () the hexgonl lttie nd () the rhomohedrl lttie.
5 88 Brvis ltties nd rystl systems P I C F () () Fig Plns of tetrgonl ltties showing () the tetrgonl P = C lttie nd () the tetrgonl I = F lttie. four orthorhomi ltties, P, C, I nd F, nd only two tetrgonl ltties, P nd I? Why re there not tetrgonl C nd F ltties s well? The nswer is tht there re tetrgonl C nd F ltties, ut y redrwing or outlining different unit ells, s shown in Fig. 3.4, it will e seen tht they re identil to the tetrgonl P nd I ltties, respetively. In short, they represent no new rrngements of lttie points. 3.3 The symmetry of the fourteen Brvis ltties: rystl systems The unit ells of the Brvis ltties my e thought of s the uilding loks of rystls, preisely s Hüy envisged (Fig..). Hene it follows tht the hit or externl shpe, or the oserved symmetry of rystls, will e sed upon the shpes nd symmetry of the Brvis ltties, nd we now hve to desrie the point symmetry of the unit ells of the Brvis ltties just s we desried the point symmetry of plne ptterns nd ltties. The sujet is fr more redily understood if simple models re used (ppendix ). First, mirror lines of symmetry eome mirror plnes in three dimensions. Seond, xes of symmetry (dids, trids, tetrds nd hexds) lso pply to three dimensions. The dditionl omplition is tht, wheres plne motif or ojet n only hve one suh xis (perpendiulr to its plne), three-dimensionl ojet n hve severl xes running in different diretions (ut lwys through point in the entre of the ojet). Consider, for exmple, ui unit ell (Fig. 3.5()). It ontins totl of nine mirror plnes, three prllel to the ue fes nd six prllel to the fe digonls. There re three tetrd (four-fold) xes perpendiulr to the three sets of ue fes, four trid (three-fold) xes running etween opposite ue orners, nd six did (two-fold) xes running etween the entres of opposite edges. This olletion of symmetry elements is lled the point group symmetry of the ue euse ll the elements plnes nd xes pss through point in the entre. Why should there e these prtiulr numers of mirror plnes nd xes? It is euse ll the vrious symmetry elements operting t or round the point must e onsistent with one nother. Self-onsisteny is fundmentl priniple, underlying ll the twodimensionl plne groups, ll the three-dimensionl point groups nd ll the spe groups
6 3.3 The symmetry of the fourteen Brvis ltties 89 () () Fig The point symmetry elements in () ue (ui unit ell) nd () n orthorhomi unit ell. tht will e disussed in Chpter 4. If there re two did xes, for exmple, then they hve to e mutully orthogonl, otherwise hos would result; y the sme token they lso must generte third did perpendiulr to oth of them. It is the neessity for selfonsisteny whih governs the onstrution of every one of the different omintions of symmetry, ontrolling the nture of eh omintion; it is this, lso, whih limits the totl numers of possile omintions to quite definite numers suh s thirty-two, in the se of the rystllogrphi point groups (the rystl lsses), the fourteen Brvis ltties, nd so on. The ui unit ell hs more symmetry elements thn ny other: its very simpliity mkes its symmetry diffiult to grsp. More esy to follow is the symmetry of n orthorhomi ell. Figure 3.5() shows the point group symmetry of n orthorhomi unit ell. It ontins, like the ue, three mirror plnes prllel to the fes of the ell ut no more mirror plnes do not exist prllel to the fe digonls. The only xes of symmetry re three dids perpendiulr to the three fes of the unit ell. In oth ses it n e seen tht the point group symmetry of these unit ells (Figs 3.5() nd 3.5()) is independent of whether the ells re entred or not. ll three ui ltties, P, I nd F, hve the sme point group symmetry; ll four orthorhomi ltties, P, I, F nd C, hve the sme point group symmetry nd so on. This simple oservtion leds to n importnt onlusion: it is not possile, from the oserved symmetry of rystl, to tell whether the underlying Brvis lttie is entred or not. Therefore, in terms of their point group symmetries, the Brvis ltties re grouped, ording to the shpes of their unit ells, into seven rystl systems. For exmple, rystls with ui P, I or F ltties elong to the ui system, rystls with orthorhomi P, I, F or C ltties elong to the orthorhomi system, nd so on. However, omplition rises in the se of rystls with hexgonl lttie. One might expet tht ll rystls with hexgonl lttie should elong to the hexgonl system, ut, s shown in Chpter 4, the externl symmetry of rystls my not e identil (nd usully is not identil) to the symmetry of the underlying Brvis lttie. Some rystls with hexgonl lttie, e.g. α-qurtz, do not show hexgonl (hexd) symmetry ut hve trid symmetry. (see Fig..33, Setion..5) Suh rystls re ssigned to the trigonl system rther thn to the hexgonl system. Hene the trigonl system inludes rystls with oth hexgonl nd rhomohedrl Brvis ltties. There is yet nother prolem whih is prtiulrly ssoited with the trigonl system, whih is tht the rhomohedrl unit ell outlined
7 90 Brvis ltties nd rystl systems in Figs 3. nd 3.3 is not lwys used lrger (non-primitive) unit ell of three times the size is sometimes more onvenient. The prolem of trnsforming xes from one unit ell to nother is ddressed in Chpter 5. The rystl systems nd their orresponding Brvis ltties re shown in Tle 3.. Notie tht there re no xes or plnes of symmetry in the trilini system. The only symmetry tht the trilini lttie possesses (nd whih is possessed y ll the other ltties) is entre of symmetry. This point symmetry element nd inversion xes of symmetry re explined in Chpter The oordintion or environments of Brvis lttie points: spe-filling polyhedr So fr we hve onsidered ltties s ptterns of points in spe in whih eh lttie point hs the sme environment in the sme orienttion. This pproh is omplete nd suffiient, ut it fils to stress, or even mke ler, the ft tht eh of these environments is distint nd hrteristi of the ltties themselves. We need therefore method of lerly nd unmiguously defining wht we men y the environment of lttie point. One pproh (whih we hve used lredy in working out the sizes of interstitil sites) is to stte this in terms of oordintion the numers nd distnes of nerest neighours. For exmple, in the simple ui (ui P) lttie eh lttie point is surrounded y six other equidistnt lttie points; in the (ui I) lttie eh lttie point is surrounded y eight equidistnt lttie points nd so on. This is stisftory, ut n lterntive nd muh more fruitful pproh is to onsider the environment or domin of eh lttie point in terms of polyhedron whose fes, edges nd verties re equidistnt etween eh lttie point nd its nerest neighours. The onstrution of suh polyhedron is illustrted in two dimensions for simpliity in Fig This is pln view of simple monolini (monolini P) lttie with the xis perpendiulr to the pge. The line lelled represents the edge or tre of plne perpendiulr to the pge nd hlf wy etween the entrl lttie point 0 nd its neighour. ll points lying in this plne (oth in the plne of the pper nd ove nd elow) re therefore equidistnt etween the two lttie points 0 nd. We now repet the proess for the other lttie points, 3, 4, et., surrounding the entrl lttie point. The plnes,, 3 et. form the six vertil fes of the polyhedron nd in three dimensions, onsidering the lttie points ove nd elow the entrl lttie point 0, the polyhedron for the monolini P lttie is losed prism, shown shded in pln in Fig Eh lttie point is surrounded y n identil polyhedron nd they ll fit together to ompletely fill spe with no gps in etween. In this exmple (of monolini P lttie) the edges of the polyhedron re where the fes interset nd represent points whih re equidistnt etween the entrl lttie point nd two other surrounding lttie points. Similrly, the verties of the polyhedron represent points whih re equidistnt etween the entrl lttie point nd three other surrounding points. However, for ltties of higher symmetry this orrespondene does not hold. If, for exmple, we onsider ui P lttie, squre in pln, nd follow the proedure outlined ove, we find tht the polyhedron is (s expeted) ue, ut the edges of whih re equidistnt etween the entrl lttie point nd three surrounding
GM1 Consolidation Worksheet
 Cmridge Essentils Mthemtis Core 8 GM1 Consolidtion Worksheet GM1 Consolidtion Worksheet 1 Clulte the size of eh ngle mrked y letter. Give resons for your nswers. or exmple, ngles on stright line dd up
Cmridge Essentils Mthemtis Core 8 GM1 Consolidtion Worksheet GM1 Consolidtion Worksheet 1 Clulte the size of eh ngle mrked y letter. Give resons for your nswers. or exmple, ngles on stright line dd up
Project 6: Minigoals Towards Simplifying and Rewriting Expressions
 MAT 51 Wldis Projet 6: Minigols Towrds Simplifying nd Rewriting Expressions The distriutive property nd like terms You hve proly lerned in previous lsses out dding like terms ut one prolem with the wy
MAT 51 Wldis Projet 6: Minigols Towrds Simplifying nd Rewriting Expressions The distriutive property nd like terms You hve proly lerned in previous lsses out dding like terms ut one prolem with the wy
1 PYTHAGORAS THEOREM 1. Given a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
 1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
Comparing the Pre-image and Image of a Dilation
 hpter Summry Key Terms Postultes nd Theorems similr tringles (.1) inluded ngle (.2) inluded side (.2) geometri men (.) indiret mesurement (.6) ngle-ngle Similrity Theorem (.2) Side-Side-Side Similrity
hpter Summry Key Terms Postultes nd Theorems similr tringles (.1) inluded ngle (.2) inluded side (.2) geometri men (.) indiret mesurement (.6) ngle-ngle Similrity Theorem (.2) Side-Side-Side Similrity
Section 1.3 Triangles
 Se 1.3 Tringles 21 Setion 1.3 Tringles LELING TRINGLE The line segments tht form tringle re lled the sides of the tringle. Eh pir of sides forms n ngle, lled n interior ngle, nd eh tringle hs three interior
Se 1.3 Tringles 21 Setion 1.3 Tringles LELING TRINGLE The line segments tht form tringle re lled the sides of the tringle. Eh pir of sides forms n ngle, lled n interior ngle, nd eh tringle hs three interior
ENERGY AND PACKING. Outline: MATERIALS AND PACKING. Crystal Structure
 EERGY AD PACKIG Outline: Crstlline versus morphous strutures Crstl struture - Unit ell - Coordintion numer - Atomi pking ftor Crstl sstems on dense, rndom pking Dense, regulr pking tpil neighor ond energ
EERGY AD PACKIG Outline: Crstlline versus morphous strutures Crstl struture - Unit ell - Coordintion numer - Atomi pking ftor Crstl sstems on dense, rndom pking Dense, regulr pking tpil neighor ond energ
THE PYTHAGOREAN THEOREM
 THE PYTHAGOREAN THEOREM The Pythgoren Theorem is one of the most well-known nd widely used theorems in mthemtis. We will first look t n informl investigtion of the Pythgoren Theorem, nd then pply this
THE PYTHAGOREAN THEOREM The Pythgoren Theorem is one of the most well-known nd widely used theorems in mthemtis. We will first look t n informl investigtion of the Pythgoren Theorem, nd then pply this
Analytical Methods for Materials
 Anlyticl Methods for Mterils Lesson 7 Crystl Geometry nd Crystllogrphy, Prt 1 Suggested Reding Chpters 2 nd 6 in Wsed et l. 169 Slt crystls N Cl http://helthfreedoms.org/2009/05/24/tble-slt-vs-unrefined-se-slt--primer/
Anlyticl Methods for Mterils Lesson 7 Crystl Geometry nd Crystllogrphy, Prt 1 Suggested Reding Chpters 2 nd 6 in Wsed et l. 169 Slt crystls N Cl http://helthfreedoms.org/2009/05/24/tble-slt-vs-unrefined-se-slt--primer/
April 8, 2017 Math 9. Geometry. Solving vector problems. Problem. Prove that if vectors and satisfy, then.
 pril 8, 2017 Mth 9 Geometry Solving vetor prolems Prolem Prove tht if vetors nd stisfy, then Solution 1 onsider the vetor ddition prllelogrm shown in the Figure Sine its digonls hve equl length,, the prllelogrm
pril 8, 2017 Mth 9 Geometry Solving vetor prolems Prolem Prove tht if vetors nd stisfy, then Solution 1 onsider the vetor ddition prllelogrm shown in the Figure Sine its digonls hve equl length,, the prllelogrm
PYTHAGORAS THEOREM WHAT S IN CHAPTER 1? IN THIS CHAPTER YOU WILL:
 PYTHAGORAS THEOREM 1 WHAT S IN CHAPTER 1? 1 01 Squres, squre roots nd surds 1 02 Pythgors theorem 1 03 Finding the hypotenuse 1 04 Finding shorter side 1 05 Mixed prolems 1 06 Testing for right-ngled tringles
PYTHAGORAS THEOREM 1 WHAT S IN CHAPTER 1? 1 01 Squres, squre roots nd surds 1 02 Pythgors theorem 1 03 Finding the hypotenuse 1 04 Finding shorter side 1 05 Mixed prolems 1 06 Testing for right-ngled tringles
Activities. 4.1 Pythagoras' Theorem 4.2 Spirals 4.3 Clinometers 4.4 Radar 4.5 Posting Parcels 4.6 Interlocking Pipes 4.7 Sine Rule Notes and Solutions
 MEP: Demonstrtion Projet UNIT 4: Trigonometry UNIT 4 Trigonometry tivities tivities 4. Pythgors' Theorem 4.2 Spirls 4.3 linometers 4.4 Rdr 4.5 Posting Prels 4.6 Interloking Pipes 4.7 Sine Rule Notes nd
MEP: Demonstrtion Projet UNIT 4: Trigonometry UNIT 4 Trigonometry tivities tivities 4. Pythgors' Theorem 4.2 Spirls 4.3 linometers 4.4 Rdr 4.5 Posting Prels 4.6 Interloking Pipes 4.7 Sine Rule Notes nd
1.3 SCALARS AND VECTORS
 Bridge Course Phy I PUC 24 1.3 SCLRS ND VECTORS Introdution: Physis is the study of nturl phenomen. The study of ny nturl phenomenon involves mesurements. For exmple, the distne etween the plnet erth nd
Bridge Course Phy I PUC 24 1.3 SCLRS ND VECTORS Introdution: Physis is the study of nturl phenomen. The study of ny nturl phenomenon involves mesurements. For exmple, the distne etween the plnet erth nd
Lecture V. Introduction to Space Groups Charles H. Lake
 Lecture V. Introduction to Spce Groups 2003. Chrles H. Lke Outline:. Introduction B. Trnsltionl symmetry C. Nomenclture nd symols used with spce groups D. The spce groups E. Derivtion nd discussion of
Lecture V. Introduction to Spce Groups 2003. Chrles H. Lke Outline:. Introduction B. Trnsltionl symmetry C. Nomenclture nd symols used with spce groups D. The spce groups E. Derivtion nd discussion of
3 Angle Geometry. 3.1 Measuring Angles. 1. Using a protractor, measure the marked angles.
 3 ngle Geometry MEP Prtie ook S3 3.1 Mesuring ngles 1. Using protrtor, mesure the mrked ngles. () () (d) (e) (f) 2. Drw ngles with the following sizes. () 22 () 75 120 (d) 90 (e) 153 (f) 45 (g) 180 (h)
3 ngle Geometry MEP Prtie ook S3 3.1 Mesuring ngles 1. Using protrtor, mesure the mrked ngles. () () (d) (e) (f) 2. Drw ngles with the following sizes. () 22 () 75 120 (d) 90 (e) 153 (f) 45 (g) 180 (h)
Lesson 2: The Pythagorean Theorem and Similar Triangles. A Brief Review of the Pythagorean Theorem.
 27 Lesson 2: The Pythgoren Theorem nd Similr Tringles A Brief Review of the Pythgoren Theorem. Rell tht n ngle whih mesures 90º is lled right ngle. If one of the ngles of tringle is right ngle, then we
27 Lesson 2: The Pythgoren Theorem nd Similr Tringles A Brief Review of the Pythgoren Theorem. Rell tht n ngle whih mesures 90º is lled right ngle. If one of the ngles of tringle is right ngle, then we
Intermediate Math Circles Wednesday 17 October 2012 Geometry II: Side Lengths
 Intermedite Mth Cirles Wednesdy 17 Otoer 01 Geometry II: Side Lengths Lst week we disussed vrious ngle properties. As we progressed through the evening, we proved mny results. This week, we will look t
Intermedite Mth Cirles Wednesdy 17 Otoer 01 Geometry II: Side Lengths Lst week we disussed vrious ngle properties. As we progressed through the evening, we proved mny results. This week, we will look t
Translation symmetry, Space groups, Bloch functions, Fermi energy
 9/7/4 Trnsltion symmetry, Spe groups, Bloh funtions, Fermi energy Roerto Orlndo Diprtimento di Chimi Università di Torino Vi ietro Giuri 5, 6 Torino, Itly roerto.orlndo@unito.it Outline The rystllogrphi
9/7/4 Trnsltion symmetry, Spe groups, Bloh funtions, Fermi energy Roerto Orlndo Diprtimento di Chimi Università di Torino Vi ietro Giuri 5, 6 Torino, Itly roerto.orlndo@unito.it Outline The rystllogrphi
CHENG Chun Chor Litwin The Hong Kong Institute of Education
 PE-hing Mi terntionl onferene IV: novtion of Mthemtis Tehing nd Lerning through Lesson Study- onnetion etween ssessment nd Sujet Mtter HENG hun hor Litwin The Hong Kong stitute of Edution Report on using
PE-hing Mi terntionl onferene IV: novtion of Mthemtis Tehing nd Lerning through Lesson Study- onnetion etween ssessment nd Sujet Mtter HENG hun hor Litwin The Hong Kong stitute of Edution Report on using
Matrices SCHOOL OF ENGINEERING & BUILT ENVIRONMENT. Mathematics (c) 1. Definition of a Matrix
 tries Definition of tri mtri is regulr rry of numers enlosed inside rkets SCHOOL OF ENGINEERING & UIL ENVIRONEN Emple he following re ll mtries: ), ) 9, themtis ), d) tries Definition of tri Size of tri
tries Definition of tri mtri is regulr rry of numers enlosed inside rkets SCHOOL OF ENGINEERING & UIL ENVIRONEN Emple he following re ll mtries: ), ) 9, themtis ), d) tries Definition of tri Size of tri
Chapter 3. Vector Spaces. 3.1 Images and Image Arithmetic
 Chpter 3 Vetor Spes In Chpter 2, we sw tht the set of imges possessed numer of onvenient properties. It turns out tht ny set tht possesses similr onvenient properties n e nlyzed in similr wy. In liner
Chpter 3 Vetor Spes In Chpter 2, we sw tht the set of imges possessed numer of onvenient properties. It turns out tht ny set tht possesses similr onvenient properties n e nlyzed in similr wy. In liner
Ellipses. The second type of conic is called an ellipse.
 Ellipses The seond type of oni is lled n ellipse. Definition of Ellipse An ellipse is the set of ll points (, y) in plne, the sum of whose distnes from two distint fied points (foi) is onstnt. (, y) d
Ellipses The seond type of oni is lled n ellipse. Definition of Ellipse An ellipse is the set of ll points (, y) in plne, the sum of whose distnes from two distint fied points (foi) is onstnt. (, y) d
Geometry of the Circle - Chords and Angles. Geometry of the Circle. Chord and Angles. Curriculum Ready ACMMG: 272.
 Geometry of the irle - hords nd ngles Geometry of the irle hord nd ngles urriulum Redy MMG: 272 www.mthletis.om hords nd ngles HRS N NGLES The irle is si shpe nd so it n e found lmost nywhere. This setion
Geometry of the irle - hords nd ngles Geometry of the irle hord nd ngles urriulum Redy MMG: 272 www.mthletis.om hords nd ngles HRS N NGLES The irle is si shpe nd so it n e found lmost nywhere. This setion
Plotting Ordered Pairs Using Integers
 SAMPLE Plotting Ordered Pirs Using Integers Ple two elsti nds on geoord to form oordinte xes shown on the right to help you solve these prolems.. Wht letter of the lphet does eh set of pirs nme?. (, )
SAMPLE Plotting Ordered Pirs Using Integers Ple two elsti nds on geoord to form oordinte xes shown on the right to help you solve these prolems.. Wht letter of the lphet does eh set of pirs nme?. (, )
Introduction to Olympiad Inequalities
 Introdution to Olympid Inequlities Edutionl Studies Progrm HSSP Msshusetts Institute of Tehnology Snj Simonovikj Spring 207 Contents Wrm up nd Am-Gm inequlity 2. Elementry inequlities......................
Introdution to Olympid Inequlities Edutionl Studies Progrm HSSP Msshusetts Institute of Tehnology Snj Simonovikj Spring 207 Contents Wrm up nd Am-Gm inequlity 2. Elementry inequlities......................
TOPIC: LINEAR ALGEBRA MATRICES
 Interntionl Blurete LECTUE NOTES for FUTHE MATHEMATICS Dr TOPIC: LINEA ALGEBA MATICES. DEFINITION OF A MATIX MATIX OPEATIONS.. THE DETEMINANT deta THE INVESE A -... SYSTEMS OF LINEA EQUATIONS. 8. THE AUGMENTED
Interntionl Blurete LECTUE NOTES for FUTHE MATHEMATICS Dr TOPIC: LINEA ALGEBA MATICES. DEFINITION OF A MATIX MATIX OPEATIONS.. THE DETEMINANT deta THE INVESE A -... SYSTEMS OF LINEA EQUATIONS. 8. THE AUGMENTED
Linear Algebra Introduction
 Introdution Wht is Liner Alger out? Liner Alger is rnh of mthemtis whih emerged yers k nd ws one of the pioneer rnhes of mthemtis Though, initilly it strted with solving of the simple liner eqution x +
Introdution Wht is Liner Alger out? Liner Alger is rnh of mthemtis whih emerged yers k nd ws one of the pioneer rnhes of mthemtis Though, initilly it strted with solving of the simple liner eqution x +
Nondeterministic Automata vs Deterministic Automata
 Nondeterministi Automt vs Deterministi Automt We lerned tht NFA is onvenient model for showing the reltionships mong regulr grmmrs, FA, nd regulr expressions, nd designing them. However, we know tht n
Nondeterministi Automt vs Deterministi Automt We lerned tht NFA is onvenient model for showing the reltionships mong regulr grmmrs, FA, nd regulr expressions, nd designing them. However, we know tht n
NON-DETERMINISTIC FSA
 Tw o types of non-determinism: NON-DETERMINISTIC FS () Multiple strt-sttes; strt-sttes S Q. The lnguge L(M) ={x:x tkes M from some strt-stte to some finl-stte nd ll of x is proessed}. The string x = is
Tw o types of non-determinism: NON-DETERMINISTIC FS () Multiple strt-sttes; strt-sttes S Q. The lnguge L(M) ={x:x tkes M from some strt-stte to some finl-stte nd ll of x is proessed}. The string x = is
A Study on the Properties of Rational Triangles
 Interntionl Journl of Mthemtis Reserh. ISSN 0976-5840 Volume 6, Numer (04), pp. 8-9 Interntionl Reserh Pulition House http://www.irphouse.om Study on the Properties of Rtionl Tringles M. Q. lm, M.R. Hssn
Interntionl Journl of Mthemtis Reserh. ISSN 0976-5840 Volume 6, Numer (04), pp. 8-9 Interntionl Reserh Pulition House http://www.irphouse.om Study on the Properties of Rtionl Tringles M. Q. lm, M.R. Hssn
The University of Nottingham SCHOOL OF COMPUTER SCIENCE A LEVEL 2 MODULE, SPRING SEMESTER MACHINES AND THEIR LANGUAGES ANSWERS
 The University of ottinghm SCHOOL OF COMPUTR SCIC A LVL 2 MODUL, SPRIG SMSTR 2015 2016 MACHIS AD THIR LAGUAGS ASWRS Time llowed TWO hours Cndidtes my omplete the front over of their nswer ook nd sign their
The University of ottinghm SCHOOL OF COMPUTR SCIC A LVL 2 MODUL, SPRIG SMSTR 2015 2016 MACHIS AD THIR LAGUAGS ASWRS Time llowed TWO hours Cndidtes my omplete the front over of their nswer ook nd sign their
m m m m m m m m P m P m ( ) m m P( ) ( ). The o-ordinte of the point P( ) dividing the line segment joining the two points ( ) nd ( ) eternll in the r
 CO-ORDINTE GEOMETR II I Qudrnt Qudrnt (-.+) (++) X X - - - 0 - III IV Qudrnt - Qudrnt (--) - (+-) Region CRTESIN CO-ORDINTE SSTEM : Retngulr Co-ordinte Sstem : Let X' OX nd 'O e two mutull perpendiulr
CO-ORDINTE GEOMETR II I Qudrnt Qudrnt (-.+) (++) X X - - - 0 - III IV Qudrnt - Qudrnt (--) - (+-) Region CRTESIN CO-ORDINTE SSTEM : Retngulr Co-ordinte Sstem : Let X' OX nd 'O e two mutull perpendiulr
Chapter 8 Roots and Radicals
 Chpter 8 Roots nd Rdils 7 ROOTS AND RADICALS 8 Figure 8. Grphene is n inredily strong nd flexile mteril mde from ron. It n lso ondut eletriity. Notie the hexgonl grid pttern. (redit: AlexnderAIUS / Wikimedi
Chpter 8 Roots nd Rdils 7 ROOTS AND RADICALS 8 Figure 8. Grphene is n inredily strong nd flexile mteril mde from ron. It n lso ondut eletriity. Notie the hexgonl grid pttern. (redit: AlexnderAIUS / Wikimedi
Trigonometry Revision Sheet Q5 of Paper 2
 Trigonometry Revision Sheet Q of Pper The Bsis - The Trigonometry setion is ll out tringles. We will normlly e given some of the sides or ngles of tringle nd we use formule nd rules to find the others.
Trigonometry Revision Sheet Q of Pper The Bsis - The Trigonometry setion is ll out tringles. We will normlly e given some of the sides or ngles of tringle nd we use formule nd rules to find the others.
HS Pre-Algebra Notes Unit 9: Roots, Real Numbers and The Pythagorean Theorem
 HS Pre-Alger Notes Unit 9: Roots, Rel Numers nd The Pythgoren Theorem Roots nd Cue Roots Syllus Ojetive 5.4: The student will find or pproximte squre roots of numers to 4. CCSS 8.EE.-: Evlute squre roots
HS Pre-Alger Notes Unit 9: Roots, Rel Numers nd The Pythgoren Theorem Roots nd Cue Roots Syllus Ojetive 5.4: The student will find or pproximte squre roots of numers to 4. CCSS 8.EE.-: Evlute squre roots
Vectors. a Write down the vector AB as a column vector ( x y ). A (3, 2) x point C such that BC = 3. . Go to a OA = a
 Streth lesson: Vetors Streth ojetives efore you strt this hpter, mrk how onfident you feel out eh of the sttements elow: I n lulte using olumn vetors nd represent the sum nd differene of two vetors grphilly.
Streth lesson: Vetors Streth ojetives efore you strt this hpter, mrk how onfident you feel out eh of the sttements elow: I n lulte using olumn vetors nd represent the sum nd differene of two vetors grphilly.
Lecture Notes No. 10
 2.6 System Identifition, Estimtion, nd Lerning Leture otes o. Mrh 3, 26 6 Model Struture of Liner ime Invrint Systems 6. Model Struture In representing dynmil system, the first step is to find n pproprite
2.6 System Identifition, Estimtion, nd Lerning Leture otes o. Mrh 3, 26 6 Model Struture of Liner ime Invrint Systems 6. Model Struture In representing dynmil system, the first step is to find n pproprite
AP Calculus BC Chapter 8: Integration Techniques, L Hopital s Rule and Improper Integrals
 AP Clulus BC Chpter 8: Integrtion Tehniques, L Hopitl s Rule nd Improper Integrls 8. Bsi Integrtion Rules In this setion we will review vrious integrtion strtegies. Strtegies: I. Seprte the integrnd into
AP Clulus BC Chpter 8: Integrtion Tehniques, L Hopitl s Rule nd Improper Integrls 8. Bsi Integrtion Rules In this setion we will review vrious integrtion strtegies. Strtegies: I. Seprte the integrnd into
CS 491G Combinatorial Optimization Lecture Notes
 CS 491G Comintoril Optimiztion Leture Notes Dvi Owen July 30, August 1 1 Mthings Figure 1: two possile mthings in simple grph. Definition 1 Given grph G = V, E, mthing is olletion of eges M suh tht e i,
CS 491G Comintoril Optimiztion Leture Notes Dvi Owen July 30, August 1 1 Mthings Figure 1: two possile mthings in simple grph. Definition 1 Given grph G = V, E, mthing is olletion of eges M suh tht e i,
SECTION A STUDENT MATERIAL. Part 1. What and Why.?
 SECTION A STUDENT MATERIAL Prt Wht nd Wh.? Student Mteril Prt Prolem n > 0 n > 0 Is the onverse true? Prolem If n is even then n is even. If n is even then n is even. Wht nd Wh? Eploring Pure Mths Are
SECTION A STUDENT MATERIAL Prt Wht nd Wh.? Student Mteril Prt Prolem n > 0 n > 0 Is the onverse true? Prolem If n is even then n is even. If n is even then n is even. Wht nd Wh? Eploring Pure Mths Are
2. There are an infinite number of possible triangles, all similar, with three given angles whose sum is 180.
 SECTION 8-1 11 CHAPTER 8 Setion 8 1. There re n infinite numer of possile tringles, ll similr, with three given ngles whose sum is 180. 4. If two ngles α nd β of tringle re known, the third ngle n e found
SECTION 8-1 11 CHAPTER 8 Setion 8 1. There re n infinite numer of possile tringles, ll similr, with three given ngles whose sum is 180. 4. If two ngles α nd β of tringle re known, the third ngle n e found
7.1 Integral as Net Change and 7.2 Areas in the Plane Calculus
 7.1 Integrl s Net Chnge nd 7. Ares in the Plne Clculus 7.1 INTEGRAL AS NET CHANGE Notecrds from 7.1: Displcement vs Totl Distnce, Integrl s Net Chnge We hve lredy seen how the position of n oject cn e
7.1 Integrl s Net Chnge nd 7. Ares in the Plne Clculus 7.1 INTEGRAL AS NET CHANGE Notecrds from 7.1: Displcement vs Totl Distnce, Integrl s Net Chnge We hve lredy seen how the position of n oject cn e
where the box contains a finite number of gates from the given collection. Examples of gates that are commonly used are the following: a b
 CS 294-2 9/11/04 Quntum Ciruit Model, Solovy-Kitev Theorem, BQP Fll 2004 Leture 4 1 Quntum Ciruit Model 1.1 Clssil Ciruits - Universl Gte Sets A lssil iruit implements multi-output oolen funtion f : {0,1}
CS 294-2 9/11/04 Quntum Ciruit Model, Solovy-Kitev Theorem, BQP Fll 2004 Leture 4 1 Quntum Ciruit Model 1.1 Clssil Ciruits - Universl Gte Sets A lssil iruit implements multi-output oolen funtion f : {0,1}
PYTHAGORAS THEOREM,TRIGONOMETRY,BEARINGS AND THREE DIMENSIONAL PROBLEMS
 PYTHGORS THEOREM,TRIGONOMETRY,ERINGS ND THREE DIMENSIONL PROLEMS 1.1 PYTHGORS THEOREM: 1. The Pythgors Theorem sttes tht the squre of the hypotenuse is equl to the sum of the squres of the other two sides
PYTHGORS THEOREM,TRIGONOMETRY,ERINGS ND THREE DIMENSIONL PROLEMS 1.1 PYTHGORS THEOREM: 1. The Pythgors Theorem sttes tht the squre of the hypotenuse is equl to the sum of the squres of the other two sides
LESSON 11: TRIANGLE FORMULAE
 . THE SEMIPERIMETER OF TRINGLE LESSON : TRINGLE FORMULE In wht follows, will hve sides, nd, nd these will e opposite ngles, nd respetively. y the tringle inequlity, nd..() So ll of, & re positive rel numers.
. THE SEMIPERIMETER OF TRINGLE LESSON : TRINGLE FORMULE In wht follows, will hve sides, nd, nd these will e opposite ngles, nd respetively. y the tringle inequlity, nd..() So ll of, & re positive rel numers.
The Ellipse. is larger than the other.
 The Ellipse Appolonius of Perg (5 B.C.) disovered tht interseting right irulr one ll the w through with plne slnted ut is not perpendiulr to the is, the intersetion provides resulting urve (oni setion)
The Ellipse Appolonius of Perg (5 B.C.) disovered tht interseting right irulr one ll the w through with plne slnted ut is not perpendiulr to the is, the intersetion provides resulting urve (oni setion)
I1 = I2 I1 = I2 + I3 I1 + I2 = I3 + I4 I 3
 2 The Prllel Circuit Electric Circuits: Figure 2- elow show ttery nd multiple resistors rrnged in prllel. Ech resistor receives portion of the current from the ttery sed on its resistnce. The split is
2 The Prllel Circuit Electric Circuits: Figure 2- elow show ttery nd multiple resistors rrnged in prllel. Ech resistor receives portion of the current from the ttery sed on its resistnce. The split is
m A 1 1 A ! and AC 6
 REVIEW SET A Using sle of m represents units, sketh vetor to represent: NON-CALCULATOR n eroplne tking off t n ngle of 8 ± to runw with speed of 6 ms displement of m in north-esterl diretion. Simplif:
REVIEW SET A Using sle of m represents units, sketh vetor to represent: NON-CALCULATOR n eroplne tking off t n ngle of 8 ± to runw with speed of 6 ms displement of m in north-esterl diretion. Simplif:
Chapter 4 State-Space Planning
 Leture slides for Automted Plnning: Theory nd Prtie Chpter 4 Stte-Spe Plnning Dn S. Nu CMSC 722, AI Plnning University of Mrylnd, Spring 2008 1 Motivtion Nerly ll plnning proedures re serh proedures Different
Leture slides for Automted Plnning: Theory nd Prtie Chpter 4 Stte-Spe Plnning Dn S. Nu CMSC 722, AI Plnning University of Mrylnd, Spring 2008 1 Motivtion Nerly ll plnning proedures re serh proedures Different
Vectors. Chapter14. Syllabus reference: 4.1, 4.2, 4.5 Contents:
 hpter Vetors Syllus referene:.,.,.5 ontents: D E F G H I J K Vetors nd slrs Geometri opertions with vetors Vetors in the plne The mgnitude of vetor Opertions with plne vetors The vetor etween two points
hpter Vetors Syllus referene:.,.,.5 ontents: D E F G H I J K Vetors nd slrs Geometri opertions with vetors Vetors in the plne The mgnitude of vetor Opertions with plne vetors The vetor etween two points
CS 573 Automata Theory and Formal Languages
 Non-determinism Automt Theory nd Forml Lnguges Professor Leslie Lnder Leture # 3 Septemer 6, 2 To hieve our gol, we need the onept of Non-deterministi Finite Automton with -moves (NFA) An NFA is tuple
Non-determinism Automt Theory nd Forml Lnguges Professor Leslie Lnder Leture # 3 Septemer 6, 2 To hieve our gol, we need the onept of Non-deterministi Finite Automton with -moves (NFA) An NFA is tuple
12.4 Similarity in Right Triangles
 Nme lss Dte 12.4 Similrit in Right Tringles Essentil Question: How does the ltitude to the hpotenuse of right tringle help ou use similr right tringles to solve prolems? Eplore Identifing Similrit in Right
Nme lss Dte 12.4 Similrit in Right Tringles Essentil Question: How does the ltitude to the hpotenuse of right tringle help ou use similr right tringles to solve prolems? Eplore Identifing Similrit in Right
6.5 Improper integrals
 Eerpt from "Clulus" 3 AoPS In. www.rtofprolemsolving.om 6.5. IMPROPER INTEGRALS 6.5 Improper integrls As we ve seen, we use the definite integrl R f to ompute the re of the region under the grph of y =
Eerpt from "Clulus" 3 AoPS In. www.rtofprolemsolving.om 6.5. IMPROPER INTEGRALS 6.5 Improper integrls As we ve seen, we use the definite integrl R f to ompute the re of the region under the grph of y =
CS311 Computational Structures Regular Languages and Regular Grammars. Lecture 6
 CS311 Computtionl Strutures Regulr Lnguges nd Regulr Grmmrs Leture 6 1 Wht we know so fr: RLs re losed under produt, union nd * Every RL n e written s RE, nd every RE represents RL Every RL n e reognized
CS311 Computtionl Strutures Regulr Lnguges nd Regulr Grmmrs Leture 6 1 Wht we know so fr: RLs re losed under produt, union nd * Every RL n e written s RE, nd every RE represents RL Every RL n e reognized
8 THREE PHASE A.C. CIRCUITS
 8 THREE PHSE.. IRUITS The signls in hpter 7 were sinusoidl lternting voltges nd urrents of the so-lled single se type. n emf of suh type n e esily generted y rotting single loop of ondutor (or single winding),
8 THREE PHSE.. IRUITS The signls in hpter 7 were sinusoidl lternting voltges nd urrents of the so-lled single se type. n emf of suh type n e esily generted y rotting single loop of ondutor (or single winding),
Maintaining Mathematical Proficiency
 Nme Dte hpter 9 Mintining Mthemtil Profiieny Simplify the epression. 1. 500. 189 3. 5 4. 4 3 5. 11 5 6. 8 Solve the proportion. 9 3 14 7. = 8. = 9. 1 7 5 4 = 4 10. 0 6 = 11. 7 4 10 = 1. 5 9 15 3 = 5 +
Nme Dte hpter 9 Mintining Mthemtil Profiieny Simplify the epression. 1. 500. 189 3. 5 4. 4 3 5. 11 5 6. 8 Solve the proportion. 9 3 14 7. = 8. = 9. 1 7 5 4 = 4 10. 0 6 = 11. 7 4 10 = 1. 5 9 15 3 = 5 +
Symmetrical Components 1
 Symmetril Components. Introdution These notes should e red together with Setion. of your text. When performing stedy-stte nlysis of high voltge trnsmission systems, we mke use of the per-phse equivlent
Symmetril Components. Introdution These notes should e red together with Setion. of your text. When performing stedy-stte nlysis of high voltge trnsmission systems, we mke use of the per-phse equivlent
Exercise 3 Logic Control
 Exerise 3 Logi Control OBJECTIVE The ojetive of this exerise is giving n introdution to pplition of Logi Control System (LCS). Tody, LCS is implemented through Progrmmle Logi Controller (PLC) whih is lled
Exerise 3 Logi Control OBJECTIVE The ojetive of this exerise is giving n introdution to pplition of Logi Control System (LCS). Tody, LCS is implemented through Progrmmle Logi Controller (PLC) whih is lled
Proving the Pythagorean Theorem
 Proving the Pythgoren Theorem W. Bline Dowler June 30, 2010 Astrt Most people re fmilir with the formul 2 + 2 = 2. However, in most ses, this ws presented in lssroom s n solute with no ttempt t proof or
Proving the Pythgoren Theorem W. Bline Dowler June 30, 2010 Astrt Most people re fmilir with the formul 2 + 2 = 2. However, in most ses, this ws presented in lssroom s n solute with no ttempt t proof or
Discrete Structures Lecture 11
 Introdution Good morning. In this setion we study funtions. A funtion is mpping from one set to nother set or, perhps, from one set to itself. We study the properties of funtions. A mpping my not e funtion.
Introdution Good morning. In this setion we study funtions. A funtion is mpping from one set to nother set or, perhps, from one set to itself. We study the properties of funtions. A mpping my not e funtion.
Spacetime and the Quantum World Questions Fall 2010
 Spetime nd the Quntum World Questions Fll 2010 1. Cliker Questions from Clss: (1) In toss of two die, wht is the proility tht the sum of the outomes is 6? () P (x 1 + x 2 = 6) = 1 36 - out 3% () P (x 1
Spetime nd the Quntum World Questions Fll 2010 1. Cliker Questions from Clss: (1) In toss of two die, wht is the proility tht the sum of the outomes is 6? () P (x 1 + x 2 = 6) = 1 36 - out 3% () P (x 1
PAIR OF LINEAR EQUATIONS IN TWO VARIABLES
 PAIR OF LINEAR EQUATIONS IN TWO VARIABLES. Two liner equtions in the sme two vriles re lled pir of liner equtions in two vriles. The most generl form of pir of liner equtions is x + y + 0 x + y + 0 where,,,,,,
PAIR OF LINEAR EQUATIONS IN TWO VARIABLES. Two liner equtions in the sme two vriles re lled pir of liner equtions in two vriles. The most generl form of pir of liner equtions is x + y + 0 x + y + 0 where,,,,,,
Chapter17. Congruence and transformations. Contents: A Transformations B Congruent figures C Congruent triangles D Proof using congruence
 hpter17 ongruene nd trnsfortions ontents: Trnsfortions ongruent figures ongruent tringles Proof using ongruene 352 ONGRUENE N TRNSFORMTIONS (hpter 17) Opening prole Jne ut two tringulr slies of heeseke,
hpter17 ongruene nd trnsfortions ontents: Trnsfortions ongruent figures ongruent tringles Proof using ongruene 352 ONGRUENE N TRNSFORMTIONS (hpter 17) Opening prole Jne ut two tringulr slies of heeseke,
Arrow s Impossibility Theorem
 Rep Voting Prdoxes Properties Arrow s Theorem Arrow s Impossiility Theorem Leture 12 Arrow s Impossiility Theorem Leture 12, Slide 1 Rep Voting Prdoxes Properties Arrow s Theorem Leture Overview 1 Rep
Rep Voting Prdoxes Properties Arrow s Theorem Arrow s Impossiility Theorem Leture 12 Arrow s Impossiility Theorem Leture 12, Slide 1 Rep Voting Prdoxes Properties Arrow s Theorem Leture Overview 1 Rep
Part I: Study the theorem statement.
 Nme 1 Nme 2 Nme 3 A STUDY OF PYTHAGORAS THEOREM Instrutions: Together in groups of 2 or 3, fill out the following worksheet. You my lift nswers from the reding, or nswer on your own. Turn in one pket for
Nme 1 Nme 2 Nme 3 A STUDY OF PYTHAGORAS THEOREM Instrutions: Together in groups of 2 or 3, fill out the following worksheet. You my lift nswers from the reding, or nswer on your own. Turn in one pket for
Tutorial Worksheet. 1. Find all solutions to the linear system by following the given steps. x + 2y + 3z = 2 2x + 3y + z = 4.
 Mth 5 Tutoril Week 1 - Jnury 1 1 Nme Setion Tutoril Worksheet 1. Find ll solutions to the liner system by following the given steps x + y + z = x + y + z = 4. y + z = Step 1. Write down the rgumented mtrix
Mth 5 Tutoril Week 1 - Jnury 1 1 Nme Setion Tutoril Worksheet 1. Find ll solutions to the liner system by following the given steps x + y + z = x + y + z = 4. y + z = Step 1. Write down the rgumented mtrix
Pythagoras Theorem. Pythagoras Theorem. Curriculum Ready ACMMG: 222, 245.
 Pythgors Theorem Pythgors Theorem Curriulum Redy ACMMG:, 45 www.mthletis.om Fill in these spes with ny other interesting fts you n find out Pythgors. In the world of Mthemtis, Pythgors is legend. He lived
Pythgors Theorem Pythgors Theorem Curriulum Redy ACMMG:, 45 www.mthletis.om Fill in these spes with ny other interesting fts you n find out Pythgors. In the world of Mthemtis, Pythgors is legend. He lived
Numbers and indices. 1.1 Fractions. GCSE C Example 1. Handy hint. Key point
 GCSE C Emple 7 Work out 9 Give your nswer in its simplest form Numers n inies Reiprote mens invert or turn upsie own The reiprol of is 9 9 Mke sure you only invert the frtion you re iviing y 7 You multiply
GCSE C Emple 7 Work out 9 Give your nswer in its simplest form Numers n inies Reiprote mens invert or turn upsie own The reiprol of is 9 9 Mke sure you only invert the frtion you re iviing y 7 You multiply
Crystal symmetry. (a) two fold (diad ) 2. (b) three fold (triad ) 3. (c) four fold (tetrad ) 4. (d) six fold (hexad ) 6. mirror
 MS2041 leture ntes fr edutinl purpses nly III Crystl symmetry 3-1 Symmetry elements (1) Rttin symmetry () tw fld (did ) 2 () three fld (trid ) 3 () fur fld (tetrd ) 4 (d) six fld (hexd ) 6 (2) Refletin
MS2041 leture ntes fr edutinl purpses nly III Crystl symmetry 3-1 Symmetry elements (1) Rttin symmetry () tw fld (did ) 2 () three fld (trid ) 3 () fur fld (tetrd ) 4 (d) six fld (hexd ) 6 (2) Refletin
A Lower Bound for the Length of a Partial Transversal in a Latin Square, Revised Version
 A Lower Bound for the Length of Prtil Trnsversl in Ltin Squre, Revised Version Pooy Htmi nd Peter W. Shor Deprtment of Mthemtil Sienes, Shrif University of Tehnology, P.O.Bo 11365-9415, Tehrn, Irn Deprtment
A Lower Bound for the Length of Prtil Trnsversl in Ltin Squre, Revised Version Pooy Htmi nd Peter W. Shor Deprtment of Mthemtil Sienes, Shrif University of Tehnology, P.O.Bo 11365-9415, Tehrn, Irn Deprtment
Non Right Angled Triangles
 Non Right ngled Tringles Non Right ngled Tringles urriulum Redy www.mthletis.om Non Right ngled Tringles NON RIGHT NGLED TRINGLES sin i, os i nd tn i re lso useful in non-right ngled tringles. This unit
Non Right ngled Tringles Non Right ngled Tringles urriulum Redy www.mthletis.om Non Right ngled Tringles NON RIGHT NGLED TRINGLES sin i, os i nd tn i re lso useful in non-right ngled tringles. This unit
Pythagoras theorem and surds
 HPTER Mesurement nd Geometry Pythgors theorem nd surds In IE-EM Mthemtis Yer 8, you lernt out the remrkle reltionship etween the lengths of the sides of right-ngled tringle. This result is known s Pythgors
HPTER Mesurement nd Geometry Pythgors theorem nd surds In IE-EM Mthemtis Yer 8, you lernt out the remrkle reltionship etween the lengths of the sides of right-ngled tringle. This result is known s Pythgors
TIME AND STATE IN DISTRIBUTED SYSTEMS
 Distriuted Systems Fö 5-1 Distriuted Systems Fö 5-2 TIME ND STTE IN DISTRIUTED SYSTEMS 1. Time in Distriuted Systems Time in Distriuted Systems euse eh mhine in distriuted system hs its own lok there is
Distriuted Systems Fö 5-1 Distriuted Systems Fö 5-2 TIME ND STTE IN DISTRIUTED SYSTEMS 1. Time in Distriuted Systems Time in Distriuted Systems euse eh mhine in distriuted system hs its own lok there is
Something found at a salad bar
 Nme PP Something found t sld r 4.7 Notes RIGHT TRINGLE hs extly one right ngle. To solve right tringle, you n use things like SOH-H-TO nd the Pythgoren Theorem. n OLIQUE TRINGLE hs no right ngles. To solve
Nme PP Something found t sld r 4.7 Notes RIGHT TRINGLE hs extly one right ngle. To solve right tringle, you n use things like SOH-H-TO nd the Pythgoren Theorem. n OLIQUE TRINGLE hs no right ngles. To solve
Identifying and Classifying 2-D Shapes
 Ientifying n Clssifying -D Shpes Wht is your sign? The shpe n olour of trffi signs let motorists know importnt informtion suh s: when to stop onstrution res. Some si shpes use in trffi signs re illustrte
Ientifying n Clssifying -D Shpes Wht is your sign? The shpe n olour of trffi signs let motorists know importnt informtion suh s: when to stop onstrution res. Some si shpes use in trffi signs re illustrte
Analytically, vectors will be represented by lowercase bold-face Latin letters, e.g. a, r, q.
 1.1 Vector Alger 1.1.1 Sclrs A physicl quntity which is completely descried y single rel numer is clled sclr. Physiclly, it is something which hs mgnitude, nd is completely descried y this mgnitude. Exmples
1.1 Vector Alger 1.1.1 Sclrs A physicl quntity which is completely descried y single rel numer is clled sclr. Physiclly, it is something which hs mgnitude, nd is completely descried y this mgnitude. Exmples
Ch. 2.3 Counting Sample Points. Cardinality of a Set
 Ch..3 Counting Smple Points CH 8 Crdinlity of Set Let S e set. If there re extly n distint elements in S, where n is nonnegtive integer, we sy S is finite set nd n is the rdinlity of S. The rdinlity of
Ch..3 Counting Smple Points CH 8 Crdinlity of Set Let S e set. If there re extly n distint elements in S, where n is nonnegtive integer, we sy S is finite set nd n is the rdinlity of S. The rdinlity of
8.3 THE HYPERBOLA OBJECTIVES
 8.3 THE HYPERBOLA OBJECTIVES 1. Define Hperol. Find the Stndrd Form of the Eqution of Hperol 3. Find the Trnsverse Ais 4. Find the Eentriit of Hperol 5. Find the Asmptotes of Hperol 6. Grph Hperol HPERBOLAS
8.3 THE HYPERBOLA OBJECTIVES 1. Define Hperol. Find the Stndrd Form of the Eqution of Hperol 3. Find the Trnsverse Ais 4. Find the Eentriit of Hperol 5. Find the Asmptotes of Hperol 6. Grph Hperol HPERBOLAS
f (x)dx = f(b) f(a). a b f (x)dx is the limit of sums
 Green s Theorem If f is funtion of one vrible x with derivtive f x) or df dx to the Fundmentl Theorem of lulus, nd [, b] is given intervl then, ording This is not trivil result, onsidering tht b b f x)dx
Green s Theorem If f is funtion of one vrible x with derivtive f x) or df dx to the Fundmentl Theorem of lulus, nd [, b] is given intervl then, ording This is not trivil result, onsidering tht b b f x)dx
Exercise sheet 6: Solutions
 Eerise sheet 6: Solutions Cvet emptor: These re merel etended hints, rther thn omplete solutions. 1. If grph G hs hromti numer k > 1, prove tht its verte set n e prtitioned into two nonempt sets V 1 nd
Eerise sheet 6: Solutions Cvet emptor: These re merel etended hints, rther thn omplete solutions. 1. If grph G hs hromti numer k > 1, prove tht its verte set n e prtitioned into two nonempt sets V 1 nd
9.1 Day 1 Warm Up. Solve the equation = x x 2 = March 1, 2017 Geometry 9.1 The Pythagorean Theorem 1
 9.1 Dy 1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 1, 2017 Geometry 9.1 The Pythgoren Theorem 1 9.1 Dy 2 Wrm Up Use the Pythgoren
9.1 Dy 1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 1, 2017 Geometry 9.1 The Pythgoren Theorem 1 9.1 Dy 2 Wrm Up Use the Pythgoren
Probability. b a b. a b 32.
 Proility If n event n hppen in '' wys nd fil in '' wys, nd eh of these wys is eqully likely, then proility or the hne, or its hppening is, nd tht of its filing is eg, If in lottery there re prizes nd lnks,
Proility If n event n hppen in '' wys nd fil in '' wys, nd eh of these wys is eqully likely, then proility or the hne, or its hppening is, nd tht of its filing is eg, If in lottery there re prizes nd lnks,
In right-angled triangles the square on the side subtending the right angle is equal to the squares on the sides containing the right angle.
 Mth 3329-Uniform Geometries Leture 06 1. Review of trigonometry While we re looking t Eulid s Elements, I d like to look t some si trigonometry. Figure 1. The Pythgoren theorem sttes tht if = 90, then
Mth 3329-Uniform Geometries Leture 06 1. Review of trigonometry While we re looking t Eulid s Elements, I d like to look t some si trigonometry. Figure 1. The Pythgoren theorem sttes tht if = 90, then
Generalization of 2-Corner Frequency Source Models Used in SMSIM
 Generliztion o 2-Corner Frequeny Soure Models Used in SMSIM Dvid M. Boore 26 Mrh 213, orreted Figure 1 nd 2 legends on 5 April 213, dditionl smll orretions on 29 My 213 Mny o the soure spetr models ville
Generliztion o 2-Corner Frequeny Soure Models Used in SMSIM Dvid M. Boore 26 Mrh 213, orreted Figure 1 nd 2 legends on 5 April 213, dditionl smll orretions on 29 My 213 Mny o the soure spetr models ville
How do we solve these things, especially when they get complicated? How do we know when a system has a solution, and when is it unique?
 XII. LINEAR ALGEBRA: SOLVING SYSTEMS OF EQUATIONS Tody we re going to tlk out solving systems of liner equtions. These re prolems tht give couple of equtions with couple of unknowns, like: 6= x + x 7=
XII. LINEAR ALGEBRA: SOLVING SYSTEMS OF EQUATIONS Tody we re going to tlk out solving systems of liner equtions. These re prolems tht give couple of equtions with couple of unknowns, like: 6= x + x 7=
= x x 2 = 25 2
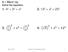 9.1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 7, 2016 Geometry 9.1 The Pythgoren Theorem 1 Geometry 9.1 The Pythgoren Theorem 9.1
9.1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 7, 2016 Geometry 9.1 The Pythgoren Theorem 1 Geometry 9.1 The Pythgoren Theorem 9.1
are coplanar. ˆ ˆ ˆ and iˆ
 SML QUSTION Clss XII Mthemtis Time llowed: hrs Mimum Mrks: Generl Instrutions: i ll questions re ompulsor ii The question pper onsists of 6 questions divided into three Setions, B nd C iii Question No
SML QUSTION Clss XII Mthemtis Time llowed: hrs Mimum Mrks: Generl Instrutions: i ll questions re ompulsor ii The question pper onsists of 6 questions divided into three Setions, B nd C iii Question No
] dx (3) = [15x] 2 0
![] dx (3) = [15x] 2 0 ] dx (3) = [15x] 2 0](/thumbs/80/81916477.jpg) Leture 6. Double Integrls nd Volume on etngle Welome to Cl IV!!!! These notes re designed to be redble nd desribe the w I will eplin the mteril in lss. Hopefull the re thorough, but it s good ide to hve
Leture 6. Double Integrls nd Volume on etngle Welome to Cl IV!!!! These notes re designed to be redble nd desribe the w I will eplin the mteril in lss. Hopefull the re thorough, but it s good ide to hve
Arrow s Impossibility Theorem
 Rep Fun Gme Properties Arrow s Theorem Arrow s Impossiility Theorem Leture 12 Arrow s Impossiility Theorem Leture 12, Slide 1 Rep Fun Gme Properties Arrow s Theorem Leture Overview 1 Rep 2 Fun Gme 3 Properties
Rep Fun Gme Properties Arrow s Theorem Arrow s Impossiility Theorem Leture 12 Arrow s Impossiility Theorem Leture 12, Slide 1 Rep Fun Gme Properties Arrow s Theorem Leture Overview 1 Rep 2 Fun Gme 3 Properties
Part 4. Integration (with Proofs)
 Prt 4. Integrtion (with Proofs) 4.1 Definition Definition A prtition P of [, b] is finite set of points {x 0, x 1,..., x n } with = x 0 < x 1
Prt 4. Integrtion (with Proofs) 4.1 Definition Definition A prtition P of [, b] is finite set of points {x 0, x 1,..., x n } with = x 0 < x 1
Math 32B Discussion Session Week 8 Notes February 28 and March 2, f(b) f(a) = f (t)dt (1)
 Green s Theorem Mth 3B isussion Session Week 8 Notes Februry 8 nd Mrh, 7 Very shortly fter you lerned how to integrte single-vrible funtions, you lerned the Fundmentl Theorem of lulus the wy most integrtion
Green s Theorem Mth 3B isussion Session Week 8 Notes Februry 8 nd Mrh, 7 Very shortly fter you lerned how to integrte single-vrible funtions, you lerned the Fundmentl Theorem of lulus the wy most integrtion
2.1 ANGLES AND THEIR MEASURE. y I
 .1 ANGLES AND THEIR MEASURE Given two interseting lines or line segments, the mount of rottion out the point of intersetion (the vertex) required to ring one into orrespondene with the other is lled the
.1 ANGLES AND THEIR MEASURE Given two interseting lines or line segments, the mount of rottion out the point of intersetion (the vertex) required to ring one into orrespondene with the other is lled the
4 VECTORS. 4.0 Introduction. Objectives. Activity 1
 4 VECTRS Chpter 4 Vectors jectives fter studying this chpter you should understnd the difference etween vectors nd sclrs; e le to find the mgnitude nd direction of vector; e le to dd vectors, nd multiply
4 VECTRS Chpter 4 Vectors jectives fter studying this chpter you should understnd the difference etween vectors nd sclrs; e le to find the mgnitude nd direction of vector; e le to dd vectors, nd multiply
Things to Memorize: A Partial List. January 27, 2017
 Things to Memorize: A Prtil List Jnury 27, 2017 Chpter 2 Vectors - Bsic Fcts A vector hs mgnitude (lso clled size/length/norm) nd direction. It does not hve fixed position, so the sme vector cn e moved
Things to Memorize: A Prtil List Jnury 27, 2017 Chpter 2 Vectors - Bsic Fcts A vector hs mgnitude (lso clled size/length/norm) nd direction. It does not hve fixed position, so the sme vector cn e moved
Algorithms & Data Structures Homework 8 HS 18 Exercise Class (Room & TA): Submitted by: Peer Feedback by: Points:
 Eidgenössishe Tehnishe Hohshule Zürih Eole polytehnique fédérle de Zurih Politenio federle di Zurigo Federl Institute of Tehnology t Zurih Deprtement of Computer Siene. Novemer 0 Mrkus Püshel, Dvid Steurer
Eidgenössishe Tehnishe Hohshule Zürih Eole polytehnique fédérle de Zurih Politenio federle di Zurigo Federl Institute of Tehnology t Zurih Deprtement of Computer Siene. Novemer 0 Mrkus Püshel, Dvid Steurer
( ) { } [ ] { } [ ) { } ( ] { }
![( ) { } [ ] { } [ ) { } ( ] { } ( ) { } [ ] { } [ ) { } ( ] { }](/thumbs/96/129291861.jpg) Mth 65 Prelulus Review Properties of Inequlities 1. > nd > >. > + > +. > nd > 0 > 4. > nd < 0 < Asolute Vlue, if 0, if < 0 Properties of Asolute Vlue > 0 1. < < > or
Mth 65 Prelulus Review Properties of Inequlities 1. > nd > >. > + > +. > nd > 0 > 4. > nd < 0 < Asolute Vlue, if 0, if < 0 Properties of Asolute Vlue > 0 1. < < > or
SECOND HARMONIC GENERATION OF Bi 4 Ti 3 O 12 FILMS
 SECOND HARMONIC GENERATION OF Bi 4 Ti 3 O 12 FILMS IN-SITU PROBING OF DOMAIN POLING IN Bi 4 Ti 3 O 12 THIN FILMS BY OPTICAL SECOND HARMONIC GENERATION YANIV BARAD, VENKATRAMAN GOPALAN Mterils Reserh Lortory
SECOND HARMONIC GENERATION OF Bi 4 Ti 3 O 12 FILMS IN-SITU PROBING OF DOMAIN POLING IN Bi 4 Ti 3 O 12 THIN FILMS BY OPTICAL SECOND HARMONIC GENERATION YANIV BARAD, VENKATRAMAN GOPALAN Mterils Reserh Lortory
Reflection Property of a Hyperbola
 Refletion Propert of Hperol Prefe The purpose of this pper is to prove nltill nd to illustrte geometrill the propert of hperol wherein r whih emntes outside the onvit of the hperol, tht is, etween the
Refletion Propert of Hperol Prefe The purpose of this pper is to prove nltill nd to illustrte geometrill the propert of hperol wherein r whih emntes outside the onvit of the hperol, tht is, etween the
A study of Pythagoras Theorem
 CHAPTER 19 A study of Pythgors Theorem Reson is immortl, ll else mortl. Pythgors, Diogenes Lertius (Lives of Eminent Philosophers) Pythgors Theorem is proly the est-known mthemticl theorem. Even most nonmthemticins
CHAPTER 19 A study of Pythgors Theorem Reson is immortl, ll else mortl. Pythgors, Diogenes Lertius (Lives of Eminent Philosophers) Pythgors Theorem is proly the est-known mthemticl theorem. Even most nonmthemticins
Section 4.4. Green s Theorem
 The Clulus of Funtions of Severl Vriles Setion 4.4 Green s Theorem Green s theorem is n exmple from fmily of theorems whih onnet line integrls (nd their higher-dimensionl nlogues) with the definite integrls
The Clulus of Funtions of Severl Vriles Setion 4.4 Green s Theorem Green s theorem is n exmple from fmily of theorems whih onnet line integrls (nd their higher-dimensionl nlogues) with the definite integrls
2. VECTORS AND MATRICES IN 3 DIMENSIONS
 2 VECTORS AND MATRICES IN 3 DIMENSIONS 21 Extending the Theory of 2-dimensionl Vectors x A point in 3-dimensionl spce cn e represented y column vector of the form y z z-xis y-xis z x y x-xis Most of the
2 VECTORS AND MATRICES IN 3 DIMENSIONS 21 Extending the Theory of 2-dimensionl Vectors x A point in 3-dimensionl spce cn e represented y column vector of the form y z z-xis y-xis z x y x-xis Most of the
