Convex functions. Definition. f : R n! R is convex if dom f is a convex set and. f ( x +(1 )y) < f (x)+(1 )f (y) f ( x +(1 )y) apple f (x)+(1 )f (y)
|
|
|
- Georgia Brown
- 5 years ago
- Views:
Transcription
1 Convex functions I basic properties and I operations that preserve convexity I quasiconvex functions I log-concave and log-convex functions IOE 611: Nonlinear Programming, Fall Convex functions Page 3 1 Definition f : R n! R is convex if dom f is a convex set and f ( x +(1 )y) apple f (x)+(1 )f (y) for all x, y 2 dom f,0apple apple1 ments (x, f(x)) (y, f(y)) I f is concave if f is convex I f is strictly convex if dom f is convex and f ( x +(1 )y) < f (x)+(1 )f (y) for x, y 2 dom f, x 6= y, 0< < 1 IOE 611: Nonlinear Programming, Fall Convex functions Page 3 2
2 Examples on R convex: I a ne: ax + b on R, foranya, b 2 R I exponential: e ax,foranya 2 R I powers: x on R ++,for 1or apple 0 I powers of absolute value: x p on R, forp 1 I negative entropy: x log x on R ++ concave: I a ne: ax + b on R, foranya, b 2 R I powers: x on R ++,for0apple apple 1 I logarithm: log x on R ++ IOE 611: Nonlinear Programming, Fall Convex functions Page 3 3 Examples on R n and R m n a ne functions are convex and concave; all norms are convex on R n I a ne function f (x) =a T x + b I norms: kxk p =( P n i=1 x i p ) 1/p for p 1; kxk 1 =max k x k on R m n (m n matrices) I a ne function f (X )=tr(a T X )+b = mx nx A ij X ij + b i=1 j=1 I spectral (maximum singular value) norm f (X )=kx k 2 = max (X )=( max (X T X )) 1/2 IOE 611: Nonlinear Programming, Fall Convex functions Page 3 4
3 Restriction of a convex function to a line f : R n! R is convex if and only if the function g : R! R, g(t) =f (x + tv), dom g = {t x + tv 2 dom f } is convex (in t) foranyx 2 dom f, v 2 R n So, can check convexity of f by checking convexity of functions of one variable example. f : S n! R with f (X ) = log det X, dom f = S n ++ g(t) = log det(x + tv ) = log det X + log det(i + tx 1/2 VX 1/2 ) nx = log det X + log(1 + t i ) i=1 where i are the eigenvalues of X 1/2 VX 1/2 g is concave in t (for any choice of X 0, V ); hence f is concave IOE 611: Nonlinear Programming, Fall Convex functions Page 3 5 First-order condition f is di erentiable if dom f is open and the (x) rf (x) n exists at each x 2 dom f 1st-order condition: di erentiable f with convex domain is convex i f (y) f (x)+rf (x) T (y x) for all x, y 2 dom f (gradient inequality) s f(y) f(x) + f(x) T (y x) (x, f(x)) first-order approximation of f is global underestimator IOE 611: Nonlinear Programming, Fall Convex functions Page 3 6
4 Second-order conditions f is twice di erentiable if dom f is open and the Hessian r 2 f (x) 2 S n, r 2 f (x) ij f j, i, j =1,...,n, exists at each x 2 dom f 2nd-order conditions: for twice di erentiable f with convex domain I f is convex if and only if r 2 f (x) 0 for all x 2 dom f I if r 2 f (x) 0forallx 2 dom f,thenf is strictly convex IOE 611: Nonlinear Programming, Fall Convex functions Page 3 7 Examples quadratic function: f (x) =(1/2)x T Px + q T x + r (with P 2 S n ) rf (x) =Px + q, r 2 f (x) =P convex i P 0 least-squares objective: f (x) =kax bk 2 2 rf (x) =2A T (Ax b), r 2 f (x) =2A T A convex (for any A) PSfrag replacements quadratic-over-linear: f (x, y) =x 2 /y r 2 f (x, y) = 2 apple y 3 convex for y > 0 y x apple y x T 0 f(x, y) y 0 2 x 0 2 IOE Convex 611: Nonlinear functions Programming, Fall Convex functions Page
5 Examples log-sum-exp: f (x) = log P n k=1 exp x k is convex r 2 f (x) = 1 1 T z diag(z) 1 (1 T z) 2 zzt (z k =expx k ) to show r 2 f (x) 0, we must verify that v T r 2 f (x)v 0forallv: v T r 2 f (x)v = (P k z kv 2 k )(P k z k) ( P k v kz k ) 2 ( P k z k) 2 0 since ( P k v kz k ) 2 apple ( P k z kv 2 k )(P k z k) (from Cauchy-Schwarz inequality) geometric mean: f (x) =( Q n k=1 x k) 1/n on R n ++ is concave (similar proof as for log-sum-exp) IOE 611: Nonlinear Programming, Fall Convex functions Page 3 9 Sublevel set and Epigraph -sublevel set of f : R n! R: C = {x 2 dom f f (x) apple } sublevel sets of convex functions are convex (converse is false) epigraph of f : R n! R: epi f = {(x, t) 2 R n+1 x 2 dom f, f (x) apple t} epi f s f f is convex if and only if epi f is a convex set IOE 611: Nonlinear Programming, Fall Convex functions Page 3 10
6 Jensen s inequality basic inequality: if f is convex, then for 0 apple apple 1, f ( x +(1 )y) apple f (x)+(1 )f (y) extension: if f is convex, then f (E z) apple E f (z) for any random variable z s.t. P(z 2 dom f )=1 basic inequality is special case with discrete distribution prob(z = x) =, prob(z = y) =1 IOE 611: Nonlinear Programming, Fall Convex functions Page 3 11 Operations that preserve convexity practical methods for establishing convexity of a function: first, show it has convex domain; then, 1. verify definition (often simplified by restricting to a line) 2. for twice di erentiable functions, show r 2 f (x) 0 8x 2 dom f 3. show that f is obtained from simple convex functions by operations that preserve convexity I nonnegative weighted sum I composition with a ne function I pointwise maximum and supremum I composition I minimization I perspective Proofs that these operations are convexity preserving are often based on analysis of epigraphs and their convexity-preserving transformations IOE 611: Nonlinear Programming, Fall Convex functions Page 3 12
7 Positive weighted sum & composition with a ne function nonnegative multiple: f is convex if f is convex, 0 sum: f 1 + f 2 convex if f 1, f 2 convex (extends to infinite sums, integrals) composition with a ne function: f (Ax + b) is convex if f is convex I log barrier for linear inequalities f (x) = mx log(b i i=1 a T i x), dom f = {x a T i x < b i, i =1,...,m} I (any) norm of a ne function: f (x) =kax + bk IOE 611: Nonlinear Programming, Fall Convex functions Page 3 13 Pointwise maximum if f 1,...,f m are convex, then f (x) =max{f 1 (x),...,f m (x)} is convex proof: epi max{f 1 (x),...,f m (x)} = \ m i=1 epi f i I piecewise-linear function: f (x) =max i=1,...,m (a T i x + b i )is convex I sum of r largest components of x 2 R n : f (x) =x [1] + x [2] + + x [r] is convex (x [i] is ith largest component of x) proof: f (x) =max{x i1 + x i2 + + x ir 1 apple i 1 < i 2 < < i r apple n} IOE 611: Nonlinear Programming, Fall Convex functions Page 3 14
8 Pointwise supremum if f (x, y) is convex in x for each y 2 A, then is convex g(x) =supf (x, y) y2a I support function of a set C: S C (x) =sup y2c y T x is convex I distance to farthest point in a set C: f (x) =supkx y2c yk I maximum eigenvalue of symmetric matrix: for X 2 S n, max(x )= sup y T Xy kyk 2 =1 IOE 611: Nonlinear Programming, Fall Convex functions Page 3 15 Extended-value extension extended-value extension of f is f : R n! R [ {1} f (x) =f (x), x 2 dom f, f (x) =1, x 62 dom f often simplifies notation; for example, the condition 0 apple apple 1 =) f ( x +(1 )y) apple f (x)+(1 ) f (y) (as an inequality in R [ {1}), means the same as the two conditions I dom f is convex I for x, y 2 dom f, 0 apple apple 1 =) f ( x +(1 )y) apple f (x)+(1 )f (y) IOE 611: Nonlinear Programming, Fall Convex functions Page 3 16
9 Composition with scalar functions composition of g : R n! R and h : R! R: f is convex if f (x) =h(g(x)) g convex, h convex, h nondecreasing g concave, h convex, h nonincreasing I note: monotonicity must hold for extended-value extension h I proof (for n = 1, twice di erentiable g, h defined everywhere) f 00 (x) =h 00 (g(x))g 0 (x) 2 + h 0 (g(x))g 00 (x) I exp g(x) is convex if g is convex I 1/g(x) is convex if g is concave and positive IOE 611: Nonlinear Programming, Fall Convex functions Page 3 17 Vector composition composition of g : R n! R k and h : R k! R: f (x) =h(g(x)) = h(g 1 (x), g 2 (x),...,g k (x)) f is convex if g i s convex, h convex, h nondecreasing in each argument g i s concave, h convex, h nonincreasing in each argument proof (for n = 1, twice di erentiable g, h defined everywhere) f 00 (x) =g 0 (x) T r 2 h(g(x))g 0 (x)+rh(g(x)) T g 00 (x) I P m i=1 log g i(x) is concave if g i are concave and positive I log P m i=1 exp g i(x) is convex if g i are convex IOE 611: Nonlinear Programming, Fall Convex functions Page 3 18
10 Minimization if f (x, y) is convex in (x, y) andc is a convex set, then is convex g(x) = inf f (x, y) y2c I f (x, y) =x T Ax +2x T By + y T Cy with apple A B B T C 0, C 0 minimizing over y gives g(x) =inf y f (x, y) =x T (A BC 1 B T )x g is convex, hence Schur complement A BC 1 B T 0 I distance to a set: dist(x, S) =inf y2s kx convex yk is convex if S is IOE 611: Nonlinear Programming, Fall Convex functions Page 3 19 Perspective the perspective of a function f : R n! R is the function g : R n R! R: g(x, t) =tf (x/t), dom g = {(x, t) x/t 2 dom f, t > 0} g is convex if f is convex I f (x) =x T x is convex on R n ;henceg(x, t) =x T x/t is convex for t > 0 I f (x) = log x is convex of R ++ ; hence relative entropy g(x, t) =t log t t log x is convex on R 2 ++ I if f is convex, then g(x) =(c T x + d)f (Ax + b)/(c T x + d) is convex on {x c T x + d > 0, (Ax + b)/(c T x + d) 2 dom f } IOE 611: Nonlinear Programming, Fall Convex functions Page 3 20
11 Quasiconvex functions f : R n! R is quasiconvex if dom f is convex and the sublevel sets S = {x 2 dom f f (x) apple } are convex for all nts β α a b c I f is quasiconcave if f is quasiconvex I f is quasilinear if it is quasiconvex and quasiconcave IOE 611: Nonlinear Programming, Fall Convex functions Page 3 21 Examples I p x is quasiconvex on R I ceil(x) =inf{z 2 Z z I log x is quasilinear on R ++ x} is quasilinear I f (x 1, x 2 )=x 1 x 2 is quasiconcave on R 2 ++ I linear-fractional function f (x) = at x + b c T x + d, dom f = {x ct x + d > 0} is quasilinear I distance ratio f (x) = kx ak 2 kx bk 2, dom f = {x kx ak 2 applekx bk 2 } is quasiconvex IOE 611: Nonlinear Programming, Fall Convex functions Page 3 22
12 Internal rate of return I cash flow x =(x 0,...,x n ); x i is payment in period i (to us if x i > 0) I we assume x 0 < 0andx 0 + x x n > 0 I present value of cash flow x, forinterestrater: PV(x, r) = nx (1 + r) i x i i=0 I internal rate of return is smallest interest rate for which PV(x, r) = 0: IRR(x) =inf{r 0 PV(x, r) =0} IRR is quasiconcave: superlevel set is intersection of halfspaces IRR(x) R () nx (1 + r) i x i 0for0apple r apple R i=0 IOE 611: Nonlinear Programming, Fall Convex functions Page 3 23 Properties modified Jensen inequality: for quasiconvex f 0 apple apple 1 =) f ( x +(1 )y) apple max{f (x), f (y)} first-order condition: di erentiable f with convex domain is quasiconvex i f (y) apple f (x) =) rf (x) T (y x) apple 0 x f(x) s sums of quasiconvex functions are not necessarily quasiconvex IOE 611: Nonlinear Programming, Fall Convex functions Page 3 24
3. Convex functions. basic properties and examples. operations that preserve convexity. the conjugate function. quasiconvex functions
 3. Convex functions Convex Optimization Boyd & Vandenberghe basic properties and examples operations that preserve convexity the conjugate function quasiconvex functions log-concave and log-convex functions
3. Convex functions Convex Optimization Boyd & Vandenberghe basic properties and examples operations that preserve convexity the conjugate function quasiconvex functions log-concave and log-convex functions
3. Convex functions. basic properties and examples. operations that preserve convexity. the conjugate function. quasiconvex functions
 3. Convex functions Convex Optimization Boyd & Vandenberghe basic properties and examples operations that preserve convexity the conjugate function quasiconvex functions log-concave and log-convex functions
3. Convex functions Convex Optimization Boyd & Vandenberghe basic properties and examples operations that preserve convexity the conjugate function quasiconvex functions log-concave and log-convex functions
Convex Functions. Daniel P. Palomar. Hong Kong University of Science and Technology (HKUST)
 Convex Functions Daniel P. Palomar Hong Kong University of Science and Technology (HKUST) ELEC5470 - Convex Optimization Fall 2017-18, HKUST, Hong Kong Outline of Lecture Definition convex function Examples
Convex Functions Daniel P. Palomar Hong Kong University of Science and Technology (HKUST) ELEC5470 - Convex Optimization Fall 2017-18, HKUST, Hong Kong Outline of Lecture Definition convex function Examples
Lecture 2: Convex functions
 Lecture 2: Convex functions f : R n R is convex if dom f is convex and for all x, y dom f, θ [0, 1] f is concave if f is convex f(θx + (1 θ)y) θf(x) + (1 θ)f(y) x x convex concave neither x examples (on
Lecture 2: Convex functions f : R n R is convex if dom f is convex and for all x, y dom f, θ [0, 1] f is concave if f is convex f(θx + (1 θ)y) θf(x) + (1 θ)f(y) x x convex concave neither x examples (on
Conve functions 2{2 Conve functions f : R n! R is conve if dom f is conve and y 2 dom f 2 [0 1] + f ( + (1 ; )y) f () + (1 ; )f (y) (1) f is concave i
![Conve functions 2{2 Conve functions f : R n! R is conve if dom f is conve and y 2 dom f 2 [0 1] + f ( + (1 ; )y) f () + (1 ; )f (y) (1) f is concave i Conve functions 2{2 Conve functions f : R n! R is conve if dom f is conve and y 2 dom f 2 [0 1] + f ( + (1 ; )y) f () + (1 ; )f (y) (1) f is concave i](/thumbs/75/71779490.jpg) ELEC-E5420 Conve functions 2{1 Lecture 2 Conve functions conve functions, epigraph simple eamples, elementary properties more eamples, more properties Jensen's inequality quasiconve, quasiconcave functions
ELEC-E5420 Conve functions 2{1 Lecture 2 Conve functions conve functions, epigraph simple eamples, elementary properties more eamples, more properties Jensen's inequality quasiconve, quasiconcave functions
Convex Functions. Wing-Kin (Ken) Ma The Chinese University of Hong Kong (CUHK)
 Convex Functions Wing-Kin (Ken) Ma The Chinese University of Hong Kong (CUHK) Course on Convex Optimization for Wireless Comm. and Signal Proc. Jointly taught by Daniel P. Palomar and Wing-Kin (Ken) Ma
Convex Functions Wing-Kin (Ken) Ma The Chinese University of Hong Kong (CUHK) Course on Convex Optimization for Wireless Comm. and Signal Proc. Jointly taught by Daniel P. Palomar and Wing-Kin (Ken) Ma
A function(al) f is convex if dom f is a convex set, and. f(θx + (1 θ)y) < θf(x) + (1 θ)f(y) f(x) = x 3
 Convex functions The domain dom f of a functional f : R N R is the subset of R N where f is well-defined. A function(al) f is convex if dom f is a convex set, and f(θx + (1 θ)y) θf(x) + (1 θ)f(y) for all
Convex functions The domain dom f of a functional f : R N R is the subset of R N where f is well-defined. A function(al) f is convex if dom f is a convex set, and f(θx + (1 θ)y) θf(x) + (1 θ)f(y) for all
1. Introduction. mathematical optimization. least-squares and linear programming. convex optimization. example. course goals and topics
 1. Introduction Convex Optimization Boyd & Vandenberghe mathematical optimization least-squares and linear programming convex optimization example course goals and topics nonlinear optimization brief history
1. Introduction Convex Optimization Boyd & Vandenberghe mathematical optimization least-squares and linear programming convex optimization example course goals and topics nonlinear optimization brief history
1. Introduction. mathematical optimization. least-squares and linear programming. convex optimization. example. course goals and topics
 1. Introduction Convex Optimization Boyd & Vandenberghe mathematical optimization least-squares and linear programming convex optimization example course goals and topics nonlinear optimization brief history
1. Introduction Convex Optimization Boyd & Vandenberghe mathematical optimization least-squares and linear programming convex optimization example course goals and topics nonlinear optimization brief history
Unconstrained minimization: assumptions
 Unconstrained minimization I terminology and assumptions I gradient descent method I steepest descent method I Newton s method I self-concordant functions I implementation IOE 611: Nonlinear Programming,
Unconstrained minimization I terminology and assumptions I gradient descent method I steepest descent method I Newton s method I self-concordant functions I implementation IOE 611: Nonlinear Programming,
Optimisation convexe: performance, complexité et applications.
 Optimisation convexe: performance, complexité et applications. Introduction, convexité, dualité. A. d Aspremont. M2 OJME: Optimisation convexe. 1/128 Today Convex optimization: introduction Course organization
Optimisation convexe: performance, complexité et applications. Introduction, convexité, dualité. A. d Aspremont. M2 OJME: Optimisation convexe. 1/128 Today Convex optimization: introduction Course organization
CSCI : Optimization and Control of Networks. Review on Convex Optimization
 CSCI7000-016: Optimization and Control of Networks Review on Convex Optimization 1 Convex set S R n is convex if x,y S, λ,µ 0, λ+µ = 1 λx+µy S geometrically: x,y S line segment through x,y S examples (one
CSCI7000-016: Optimization and Control of Networks Review on Convex Optimization 1 Convex set S R n is convex if x,y S, λ,µ 0, λ+µ = 1 λx+µy S geometrically: x,y S line segment through x,y S examples (one
A Brief Review on Convex Optimization
 A Brief Review on Convex Optimization 1 Convex set S R n is convex if x,y S, λ,µ 0, λ+µ = 1 λx+µy S geometrically: x,y S line segment through x,y S examples (one convex, two nonconvex sets): A Brief Review
A Brief Review on Convex Optimization 1 Convex set S R n is convex if x,y S, λ,µ 0, λ+µ = 1 λx+µy S geometrically: x,y S line segment through x,y S examples (one convex, two nonconvex sets): A Brief Review
Convex Optimization. Convex Analysis - Functions
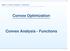 Convex Optimization Convex Analsis - Functions p. 1 A function f : K R n R is convex, if K is a convex set and x, K,x, λ (,1) we have f(λx+(1 λ)) λf(x)+(1 λ)f(). (x, f(x)) (,f()) x - strictl convex,
Convex Optimization Convex Analsis - Functions p. 1 A function f : K R n R is convex, if K is a convex set and x, K,x, λ (,1) we have f(λx+(1 λ)) λf(x)+(1 λ)f(). (x, f(x)) (,f()) x - strictl convex,
Lecture 4: Convex Functions, Part I February 1
 IE 521: Convex Optimization Instructor: Niao He Lecture 4: Convex Functions, Part I February 1 Spring 2017, UIUC Scribe: Shuanglong Wang Courtesy warning: These notes do not necessarily cover everything
IE 521: Convex Optimization Instructor: Niao He Lecture 4: Convex Functions, Part I February 1 Spring 2017, UIUC Scribe: Shuanglong Wang Courtesy warning: These notes do not necessarily cover everything
Linear and non-linear programming
 Linear and non-linear programming Benjamin Recht March 11, 2005 The Gameplan Constrained Optimization Convexity Duality Applications/Taxonomy 1 Constrained Optimization minimize f(x) subject to g j (x)
Linear and non-linear programming Benjamin Recht March 11, 2005 The Gameplan Constrained Optimization Convexity Duality Applications/Taxonomy 1 Constrained Optimization minimize f(x) subject to g j (x)
Subgradients. subgradients and quasigradients. subgradient calculus. optimality conditions via subgradients. directional derivatives
 Subgradients subgradients and quasigradients subgradient calculus optimality conditions via subgradients directional derivatives Prof. S. Boyd, EE392o, Stanford University Basic inequality recall basic
Subgradients subgradients and quasigradients subgradient calculus optimality conditions via subgradients directional derivatives Prof. S. Boyd, EE392o, Stanford University Basic inequality recall basic
Lecture 1: January 12
 10-725/36-725: Convex Optimization Fall 2015 Lecturer: Ryan Tibshirani Lecture 1: January 12 Scribes: Seo-Jin Bang, Prabhat KC, Josue Orellana 1.1 Review We begin by going through some examples and key
10-725/36-725: Convex Optimization Fall 2015 Lecturer: Ryan Tibshirani Lecture 1: January 12 Scribes: Seo-Jin Bang, Prabhat KC, Josue Orellana 1.1 Review We begin by going through some examples and key
Convex Functions and Optimization
 Chapter 5 Convex Functions and Optimization 5.1 Convex Functions Our next topic is that of convex functions. Again, we will concentrate on the context of a map f : R n R although the situation can be generalized
Chapter 5 Convex Functions and Optimization 5.1 Convex Functions Our next topic is that of convex functions. Again, we will concentrate on the context of a map f : R n R although the situation can be generalized
APPENDIX A. Background Mathematics. A.1 Linear Algebra. Vector algebra. Let x denote the n-dimensional column vector with components x 1 x 2.
 APPENDIX A Background Mathematics A. Linear Algebra A.. Vector algebra Let x denote the n-dimensional column vector with components 0 x x 2 B C @. A x n Definition 6 (scalar product). The scalar product
APPENDIX A Background Mathematics A. Linear Algebra A.. Vector algebra Let x denote the n-dimensional column vector with components 0 x x 2 B C @. A x n Definition 6 (scalar product). The scalar product
Convex optimization problems. Optimization problem in standard form
 Convex optimization problems optimization problem in standard form convex optimization problems linear optimization quadratic optimization geometric programming quasiconvex optimization generalized inequality
Convex optimization problems optimization problem in standard form convex optimization problems linear optimization quadratic optimization geometric programming quasiconvex optimization generalized inequality
8. Conjugate functions
 L. Vandenberghe EE236C (Spring 2013-14) 8. Conjugate functions closed functions conjugate function 8-1 Closed set a set C is closed if it contains its boundary: x k C, x k x = x C operations that preserve
L. Vandenberghe EE236C (Spring 2013-14) 8. Conjugate functions closed functions conjugate function 8-1 Closed set a set C is closed if it contains its boundary: x k C, x k x = x C operations that preserve
Geometric problems. Chapter Projection on a set. The distance of a point x 0 R n to a closed set C R n, in the norm, is defined as
 Chapter 8 Geometric problems 8.1 Projection on a set The distance of a point x 0 R n to a closed set C R n, in the norm, is defined as dist(x 0,C) = inf{ x 0 x x C}. The infimum here is always achieved.
Chapter 8 Geometric problems 8.1 Projection on a set The distance of a point x 0 R n to a closed set C R n, in the norm, is defined as dist(x 0,C) = inf{ x 0 x x C}. The infimum here is always achieved.
Shiqian Ma, MAT-258A: Numerical Optimization 1. Chapter 4. Subgradient
 Shiqian Ma, MAT-258A: Numerical Optimization 1 Chapter 4 Subgradient Shiqian Ma, MAT-258A: Numerical Optimization 2 4.1. Subgradients definition subgradient calculus duality and optimality conditions Shiqian
Shiqian Ma, MAT-258A: Numerical Optimization 1 Chapter 4 Subgradient Shiqian Ma, MAT-258A: Numerical Optimization 2 4.1. Subgradients definition subgradient calculus duality and optimality conditions Shiqian
The proximal mapping
 The proximal mapping http://bicmr.pku.edu.cn/~wenzw/opt-2016-fall.html Acknowledgement: this slides is based on Prof. Lieven Vandenberghes lecture notes Outline 2/37 1 closed function 2 Conjugate function
The proximal mapping http://bicmr.pku.edu.cn/~wenzw/opt-2016-fall.html Acknowledgement: this slides is based on Prof. Lieven Vandenberghes lecture notes Outline 2/37 1 closed function 2 Conjugate function
Lecture 1: Background on Convex Analysis
 Lecture 1: Background on Convex Analysis John Duchi PCMI 2016 Outline I Convex sets 1.1 Definitions and examples 2.2 Basic properties 3.3 Projections onto convex sets 4.4 Separating and supporting hyperplanes
Lecture 1: Background on Convex Analysis John Duchi PCMI 2016 Outline I Convex sets 1.1 Definitions and examples 2.2 Basic properties 3.3 Projections onto convex sets 4.4 Separating and supporting hyperplanes
Convex Optimization in Communications and Signal Processing
 Convex Optimization in Communications and Signal Processing Prof. Dr.-Ing. Wolfgang Gerstacker 1 University of Erlangen-Nürnberg Institute for Digital Communications National Technical University of Ukraine,
Convex Optimization in Communications and Signal Processing Prof. Dr.-Ing. Wolfgang Gerstacker 1 University of Erlangen-Nürnberg Institute for Digital Communications National Technical University of Ukraine,
EE Applications of Convex Optimization in Signal Processing and Communications Dr. Andre Tkacenko, JPL Third Term
 EE 150 - Applications of Convex Optimization in Signal Processing and Communications Dr. Andre Tkacenko JPL Third Term 2011-2012 Due on Thursday May 3 in class. Homework Set #4 1. (10 points) (Adapted
EE 150 - Applications of Convex Optimization in Signal Processing and Communications Dr. Andre Tkacenko JPL Third Term 2011-2012 Due on Thursday May 3 in class. Homework Set #4 1. (10 points) (Adapted
IE 521 Convex Optimization
 Lecture 5: Convex II 6th February 2019 Convex Local Lipschitz Outline Local Lipschitz 1 / 23 Convex Local Lipschitz Convex Function: f : R n R is convex if dom(f ) is convex and for any λ [0, 1], x, y
Lecture 5: Convex II 6th February 2019 Convex Local Lipschitz Outline Local Lipschitz 1 / 23 Convex Local Lipschitz Convex Function: f : R n R is convex if dom(f ) is convex and for any λ [0, 1], x, y
Subgradients. subgradients. strong and weak subgradient calculus. optimality conditions via subgradients. directional derivatives
 Subgradients subgradients strong and weak subgradient calculus optimality conditions via subgradients directional derivatives Prof. S. Boyd, EE364b, Stanford University Basic inequality recall basic inequality
Subgradients subgradients strong and weak subgradient calculus optimality conditions via subgradients directional derivatives Prof. S. Boyd, EE364b, Stanford University Basic inequality recall basic inequality
Solutions Chapter 5. The problem of finding the minimum distance from the origin to a line is written as. min 1 2 kxk2. subject to Ax = b.
 Solutions Chapter 5 SECTION 5.1 5.1.4 www Throughout this exercise we will use the fact that strong duality holds for convex quadratic problems with linear constraints (cf. Section 3.4). The problem of
Solutions Chapter 5 SECTION 5.1 5.1.4 www Throughout this exercise we will use the fact that strong duality holds for convex quadratic problems with linear constraints (cf. Section 3.4). The problem of
N. L. P. NONLINEAR PROGRAMMING (NLP) deals with optimization models with at least one nonlinear function. NLP. Optimization. Models of following form:
 0.1 N. L. P. Katta G. Murty, IOE 611 Lecture slides Introductory Lecture NONLINEAR PROGRAMMING (NLP) deals with optimization models with at least one nonlinear function. NLP does not include everything
0.1 N. L. P. Katta G. Murty, IOE 611 Lecture slides Introductory Lecture NONLINEAR PROGRAMMING (NLP) deals with optimization models with at least one nonlinear function. NLP does not include everything
EE 546, Univ of Washington, Spring Proximal mapping. introduction. review of conjugate functions. proximal mapping. Proximal mapping 6 1
 EE 546, Univ of Washington, Spring 2012 6. Proximal mapping introduction review of conjugate functions proximal mapping Proximal mapping 6 1 Proximal mapping the proximal mapping (prox-operator) of a convex
EE 546, Univ of Washington, Spring 2012 6. Proximal mapping introduction review of conjugate functions proximal mapping Proximal mapping 6 1 Proximal mapping the proximal mapping (prox-operator) of a convex
Convex Optimization Theory. Chapter 5 Exercises and Solutions: Extended Version
 Convex Optimization Theory Chapter 5 Exercises and Solutions: Extended Version Dimitri P. Bertsekas Massachusetts Institute of Technology Athena Scientific, Belmont, Massachusetts http://www.athenasc.com
Convex Optimization Theory Chapter 5 Exercises and Solutions: Extended Version Dimitri P. Bertsekas Massachusetts Institute of Technology Athena Scientific, Belmont, Massachusetts http://www.athenasc.com
A : k n. Usually k > n otherwise easily the minimum is zero. Analytical solution:
 1-5: Least-squares I A : k n. Usually k > n otherwise easily the minimum is zero. Analytical solution: f (x) =(Ax b) T (Ax b) =x T A T Ax 2b T Ax + b T b f (x) = 2A T Ax 2A T b = 0 Chih-Jen Lin (National
1-5: Least-squares I A : k n. Usually k > n otherwise easily the minimum is zero. Analytical solution: f (x) =(Ax b) T (Ax b) =x T A T Ax 2b T Ax + b T b f (x) = 2A T Ax 2A T b = 0 Chih-Jen Lin (National
Subgradient. Acknowledgement: this slides is based on Prof. Lieven Vandenberghes lecture notes. definition. subgradient calculus
 1/41 Subgradient Acknowledgement: this slides is based on Prof. Lieven Vandenberghes lecture notes definition subgradient calculus duality and optimality conditions directional derivative Basic inequality
1/41 Subgradient Acknowledgement: this slides is based on Prof. Lieven Vandenberghes lecture notes definition subgradient calculus duality and optimality conditions directional derivative Basic inequality
Exercises. Exercises. Basic terminology and optimality conditions. 4.2 Consider the optimization problem
 Exercises Basic terminology and optimality conditions 4.1 Consider the optimization problem f 0(x 1, x 2) 2x 1 + x 2 1 x 1 + 3x 2 1 x 1 0, x 2 0. Make a sketch of the feasible set. For each of the following
Exercises Basic terminology and optimality conditions 4.1 Consider the optimization problem f 0(x 1, x 2) 2x 1 + x 2 1 x 1 + 3x 2 1 x 1 0, x 2 0. Make a sketch of the feasible set. For each of the following
Examples of Dual Spaces from Measure Theory
 Chapter 9 Examples of Dual Spaces from Measure Theory We have seen that L (, A, µ) is a Banach space for any measure space (, A, µ). We will extend that concept in the following section to identify an
Chapter 9 Examples of Dual Spaces from Measure Theory We have seen that L (, A, µ) is a Banach space for any measure space (, A, µ). We will extend that concept in the following section to identify an
Optimization and Optimal Control in Banach Spaces
 Optimization and Optimal Control in Banach Spaces Bernhard Schmitzer October 19, 2017 1 Convex non-smooth optimization with proximal operators Remark 1.1 (Motivation). Convex optimization: easier to solve,
Optimization and Optimal Control in Banach Spaces Bernhard Schmitzer October 19, 2017 1 Convex non-smooth optimization with proximal operators Remark 1.1 (Motivation). Convex optimization: easier to solve,
CHAPTER 2: CONVEX SETS AND CONCAVE FUNCTIONS. W. Erwin Diewert January 31, 2008.
 1 ECONOMICS 594: LECTURE NOTES CHAPTER 2: CONVEX SETS AND CONCAVE FUNCTIONS W. Erwin Diewert January 31, 2008. 1. Introduction Many economic problems have the following structure: (i) a linear function
1 ECONOMICS 594: LECTURE NOTES CHAPTER 2: CONVEX SETS AND CONCAVE FUNCTIONS W. Erwin Diewert January 31, 2008. 1. Introduction Many economic problems have the following structure: (i) a linear function
Unconstrained minimization
 CSCI5254: Convex Optimization & Its Applications Unconstrained minimization terminology and assumptions gradient descent method steepest descent method Newton s method self-concordant functions 1 Unconstrained
CSCI5254: Convex Optimization & Its Applications Unconstrained minimization terminology and assumptions gradient descent method steepest descent method Newton s method self-concordant functions 1 Unconstrained
4. Convex optimization problems
 Convex Optimization Boyd & Vandenberghe 4. Convex optimization problems optimization problem in standard form convex optimization problems quasiconvex optimization linear optimization quadratic optimization
Convex Optimization Boyd & Vandenberghe 4. Convex optimization problems optimization problem in standard form convex optimization problems quasiconvex optimization linear optimization quadratic optimization
Lecture Note 5: Semidefinite Programming for Stability Analysis
 ECE7850: Hybrid Systems:Theory and Applications Lecture Note 5: Semidefinite Programming for Stability Analysis Wei Zhang Assistant Professor Department of Electrical and Computer Engineering Ohio State
ECE7850: Hybrid Systems:Theory and Applications Lecture Note 5: Semidefinite Programming for Stability Analysis Wei Zhang Assistant Professor Department of Electrical and Computer Engineering Ohio State
Lecture: Convex Optimization Problems
 1/36 Lecture: Convex Optimization Problems http://bicmr.pku.edu.cn/~wenzw/opt-2015-fall.html Acknowledgement: this slides is based on Prof. Lieven Vandenberghe s lecture notes Introduction 2/36 optimization
1/36 Lecture: Convex Optimization Problems http://bicmr.pku.edu.cn/~wenzw/opt-2015-fall.html Acknowledgement: this slides is based on Prof. Lieven Vandenberghe s lecture notes Introduction 2/36 optimization
Static Problem Set 2 Solutions
 Static Problem Set Solutions Jonathan Kreamer July, 0 Question (i) Let g, h be two concave functions. Is f = g + h a concave function? Prove it. Yes. Proof: Consider any two points x, x and α [0, ]. Let
Static Problem Set Solutions Jonathan Kreamer July, 0 Question (i) Let g, h be two concave functions. Is f = g + h a concave function? Prove it. Yes. Proof: Consider any two points x, x and α [0, ]. Let
1. Introduction. mathematical optimization. least-squares and linear programming. convex optimization. example. course goals and topics
 1. Introduction mathematical optimization least-squares and linear programming convex optimization example course goals and topics nonlinear optimization brief history of convex optimization 1 1 Mathematical
1. Introduction mathematical optimization least-squares and linear programming convex optimization example course goals and topics nonlinear optimization brief history of convex optimization 1 1 Mathematical
1. Introduction. mathematical optimization. least-squares and linear programming. convex optimization. example. course goals and topics
 1. Introduction Convex Optimization Boyd & Vandenberghe mathematical optimization least-squares and linear programming convex optimization example course goals and topics nonlinear optimization brief history
1. Introduction Convex Optimization Boyd & Vandenberghe mathematical optimization least-squares and linear programming convex optimization example course goals and topics nonlinear optimization brief history
1. Introduction. mathematical optimization. least-squares and linear programming. convex optimization. example. course goals and topics
 1. Introduction Convex Optimization Boyd & Vandenberghe mathematical optimization least-squares and linear programming convex optimization example course goals and topics nonlinear optimization brief history
1. Introduction Convex Optimization Boyd & Vandenberghe mathematical optimization least-squares and linear programming convex optimization example course goals and topics nonlinear optimization brief history
A : k n. Usually k > n otherwise easily the minimum is zero. Analytical solution:
 1-5: Least-squares I A : k n. Usually k > n otherwise easily the minimum is zero. Analytical solution: f (x) =(Ax b) T (Ax b) =x T A T Ax 2b T Ax + b T b f (x) = 2A T Ax 2A T b = 0 Chih-Jen Lin (National
1-5: Least-squares I A : k n. Usually k > n otherwise easily the minimum is zero. Analytical solution: f (x) =(Ax b) T (Ax b) =x T A T Ax 2b T Ax + b T b f (x) = 2A T Ax 2A T b = 0 Chih-Jen Lin (National
WHY DUALITY? Gradient descent Newton s method Quasi-newton Conjugate gradients. No constraints. Non-differentiable ???? Constrained problems? ????
 DUALITY WHY DUALITY? No constraints f(x) Non-differentiable f(x) Gradient descent Newton s method Quasi-newton Conjugate gradients etc???? Constrained problems? f(x) subject to g(x) apple 0???? h(x) =0
DUALITY WHY DUALITY? No constraints f(x) Non-differentiable f(x) Gradient descent Newton s method Quasi-newton Conjugate gradients etc???? Constrained problems? f(x) subject to g(x) apple 0???? h(x) =0
EE/ACM Applications of Convex Optimization in Signal Processing and Communications Lecture 17
 EE/ACM 150 - Applications of Convex Optimization in Signal Processing and Communications Lecture 17 Andre Tkacenko Signal Processing Research Group Jet Propulsion Laboratory May 29, 2012 Andre Tkacenko
EE/ACM 150 - Applications of Convex Optimization in Signal Processing and Communications Lecture 17 Andre Tkacenko Signal Processing Research Group Jet Propulsion Laboratory May 29, 2012 Andre Tkacenko
Lecture 3. Optimization Problems and Iterative Algorithms
 Lecture 3 Optimization Problems and Iterative Algorithms January 13, 2016 This material was jointly developed with Angelia Nedić at UIUC for IE 598ns Outline Special Functions: Linear, Quadratic, Convex
Lecture 3 Optimization Problems and Iterative Algorithms January 13, 2016 This material was jointly developed with Angelia Nedić at UIUC for IE 598ns Outline Special Functions: Linear, Quadratic, Convex
10. Unconstrained minimization
 Convex Optimization Boyd & Vandenberghe 10. Unconstrained minimization terminology and assumptions gradient descent method steepest descent method Newton s method self-concordant functions implementation
Convex Optimization Boyd & Vandenberghe 10. Unconstrained minimization terminology and assumptions gradient descent method steepest descent method Newton s method self-concordant functions implementation
Using Schur Complement Theorem to prove convexity of some SOC-functions
 Journal of Nonlinear and Convex Analysis, vol. 13, no. 3, pp. 41-431, 01 Using Schur Complement Theorem to prove convexity of some SOC-functions Jein-Shan Chen 1 Department of Mathematics National Taiwan
Journal of Nonlinear and Convex Analysis, vol. 13, no. 3, pp. 41-431, 01 Using Schur Complement Theorem to prove convexity of some SOC-functions Jein-Shan Chen 1 Department of Mathematics National Taiwan
Determinant maximization with linear. S. Boyd, L. Vandenberghe, S.-P. Wu. Information Systems Laboratory. Stanford University
 Determinant maximization with linear matrix inequality constraints S. Boyd, L. Vandenberghe, S.-P. Wu Information Systems Laboratory Stanford University SCCM Seminar 5 February 1996 1 MAXDET problem denition
Determinant maximization with linear matrix inequality constraints S. Boyd, L. Vandenberghe, S.-P. Wu Information Systems Laboratory Stanford University SCCM Seminar 5 February 1996 1 MAXDET problem denition
Constrained Optimization and Lagrangian Duality
 CIS 520: Machine Learning Oct 02, 2017 Constrained Optimization and Lagrangian Duality Lecturer: Shivani Agarwal Disclaimer: These notes are designed to be a supplement to the lecture. They may or may
CIS 520: Machine Learning Oct 02, 2017 Constrained Optimization and Lagrangian Duality Lecturer: Shivani Agarwal Disclaimer: These notes are designed to be a supplement to the lecture. They may or may
4. Convex optimization problems
 Convex Optimization Boyd & Vandenberghe 4. Convex optimization problems optimization problem in standard form convex optimization problems quasiconvex optimization linear optimization quadratic optimization
Convex Optimization Boyd & Vandenberghe 4. Convex optimization problems optimization problem in standard form convex optimization problems quasiconvex optimization linear optimization quadratic optimization
Chapter 13. Convex and Concave. Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 1 / 44
 Chapter 13 Convex and Concave Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 1 / 44 Monotone Function Function f is called monotonically increasing, if x 1 x 2 f (x 1 ) f (x 2 ) It
Chapter 13 Convex and Concave Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 1 / 44 Monotone Function Function f is called monotonically increasing, if x 1 x 2 f (x 1 ) f (x 2 ) It
Nonlinear Programming Models
 Nonlinear Programming Models Fabio Schoen 2008 http://gol.dsi.unifi.it/users/schoen Nonlinear Programming Models p. Introduction Nonlinear Programming Models p. NLP problems minf(x) x S R n Standard form:
Nonlinear Programming Models Fabio Schoen 2008 http://gol.dsi.unifi.it/users/schoen Nonlinear Programming Models p. Introduction Nonlinear Programming Models p. NLP problems minf(x) x S R n Standard form:
Extreme Abridgment of Boyd and Vandenberghe s Convex Optimization
 Extreme Abridgment of Boyd and Vandenberghe s Convex Optimization Compiled by David Rosenberg Abstract Boyd and Vandenberghe s Convex Optimization book is very well-written and a pleasure to read. The
Extreme Abridgment of Boyd and Vandenberghe s Convex Optimization Compiled by David Rosenberg Abstract Boyd and Vandenberghe s Convex Optimization book is very well-written and a pleasure to read. The
5. Duality. Lagrangian
 5. Duality Convex Optimization Boyd & Vandenberghe Lagrange dual problem weak and strong duality geometric interpretation optimality conditions perturbation and sensitivity analysis examples generalized
5. Duality Convex Optimization Boyd & Vandenberghe Lagrange dual problem weak and strong duality geometric interpretation optimality conditions perturbation and sensitivity analysis examples generalized
EE5138R: Problem Set 5 Assigned: 16/02/15 Due: 06/03/15
 EE538R: Problem Set 5 Assigned: 6/0/5 Due: 06/03/5. BV Problem 4. The feasible set is the convex hull of (0, ), (0, ), (/5, /5), (, 0) and (, 0). (a) x = (/5, /5) (b) Unbounded below (c) X opt = {(0, x
EE538R: Problem Set 5 Assigned: 6/0/5 Due: 06/03/5. BV Problem 4. The feasible set is the convex hull of (0, ), (0, ), (/5, /5), (, 0) and (, 0). (a) x = (/5, /5) (b) Unbounded below (c) X opt = {(0, x
ECON 4117/5111 Mathematical Economics
 Test 1 September 23, 2016 1. Suppose that p and q are logical statements. The exclusive or, denoted by p Y q, is true when only one of p and q is true. (a) Construct the truth table of p Y q. (b) Prove
Test 1 September 23, 2016 1. Suppose that p and q are logical statements. The exclusive or, denoted by p Y q, is true when only one of p and q is true. (a) Construct the truth table of p Y q. (b) Prove
Monotone Function. Function f is called monotonically increasing, if. x 1 x 2 f (x 1 ) f (x 2 ) x 1 < x 2 f (x 1 ) < f (x 2 ) x 1 x 2
 Monotone Function Function f is called monotonically increasing, if Chapter 3 x x 2 f (x ) f (x 2 ) It is called strictly monotonically increasing, if f (x 2) f (x ) Convex and Concave x < x 2 f (x )
Monotone Function Function f is called monotonically increasing, if Chapter 3 x x 2 f (x ) f (x 2 ) It is called strictly monotonically increasing, if f (x 2) f (x ) Convex and Concave x < x 2 f (x )
Kernel Method: Data Analysis with Positive Definite Kernels
 Kernel Method: Data Analysis with Positive Definite Kernels 2. Positive Definite Kernel and Reproducing Kernel Hilbert Space Kenji Fukumizu The Institute of Statistical Mathematics. Graduate University
Kernel Method: Data Analysis with Positive Definite Kernels 2. Positive Definite Kernel and Reproducing Kernel Hilbert Space Kenji Fukumizu The Institute of Statistical Mathematics. Graduate University
Convex Functions. Pontus Giselsson
 Convex Functions Pontus Giselsson 1 Today s lecture lower semicontinuity, closure, convex hull convexity preserving operations precomposition with affine mapping infimal convolution image function supremum
Convex Functions Pontus Giselsson 1 Today s lecture lower semicontinuity, closure, convex hull convexity preserving operations precomposition with affine mapping infimal convolution image function supremum
4. Convex Sets and (Quasi-)Concave Functions
 4. Convex Sets and (Quasi-)Concave Functions Daisuke Oyama Mathematics II April 17, 2017 Convex Sets Definition 4.1 A R N is convex if (1 α)x + αx A whenever x, x A and α [0, 1]. A R N is strictly convex
4. Convex Sets and (Quasi-)Concave Functions Daisuke Oyama Mathematics II April 17, 2017 Convex Sets Definition 4.1 A R N is convex if (1 α)x + αx A whenever x, x A and α [0, 1]. A R N is strictly convex
EE364 Review Session 4
 EE364 Review Session 4 EE364 Review Outline: convex optimization examples solving quasiconvex problems by bisection exercise 4.47 1 Convex optimization problems we have seen linear programming (LP) quadratic
EE364 Review Session 4 EE364 Review Outline: convex optimization examples solving quasiconvex problems by bisection exercise 4.47 1 Convex optimization problems we have seen linear programming (LP) quadratic
Course Notes for EE227C (Spring 2018): Convex Optimization and Approximation
 Course Notes for EE7C (Spring 018): Convex Optimization and Approximation Instructor: Moritz Hardt Email: hardt+ee7c@berkeley.edu Graduate Instructor: Max Simchowitz Email: msimchow+ee7c@berkeley.edu February
Course Notes for EE7C (Spring 018): Convex Optimization and Approximation Instructor: Moritz Hardt Email: hardt+ee7c@berkeley.edu Graduate Instructor: Max Simchowitz Email: msimchow+ee7c@berkeley.edu February
Convex Optimization. 9. Unconstrained minimization. Prof. Ying Cui. Department of Electrical Engineering Shanghai Jiao Tong University
 Convex Optimization 9. Unconstrained minimization Prof. Ying Cui Department of Electrical Engineering Shanghai Jiao Tong University 2017 Autumn Semester SJTU Ying Cui 1 / 40 Outline Unconstrained minimization
Convex Optimization 9. Unconstrained minimization Prof. Ying Cui Department of Electrical Engineering Shanghai Jiao Tong University 2017 Autumn Semester SJTU Ying Cui 1 / 40 Outline Unconstrained minimization
L p Spaces and Convexity
 L p Spaces and Convexity These notes largely follow the treatments in Royden, Real Analysis, and Rudin, Real & Complex Analysis. 1. Convex functions Let I R be an interval. For I open, we say a function
L p Spaces and Convexity These notes largely follow the treatments in Royden, Real Analysis, and Rudin, Real & Complex Analysis. 1. Convex functions Let I R be an interval. For I open, we say a function
Nonlinear Programming Algorithms Handout
 Nonlinear Programming Algorithms Handout Michael C. Ferris Computer Sciences Department University of Wisconsin Madison, Wisconsin 5376 September 9 1 Eigenvalues The eigenvalues of a matrix A C n n are
Nonlinear Programming Algorithms Handout Michael C. Ferris Computer Sciences Department University of Wisconsin Madison, Wisconsin 5376 September 9 1 Eigenvalues The eigenvalues of a matrix A C n n are
Convex Optimization Boyd & Vandenberghe. 5. Duality
 5. Duality Convex Optimization Boyd & Vandenberghe Lagrange dual problem weak and strong duality geometric interpretation optimality conditions perturbation and sensitivity analysis examples generalized
5. Duality Convex Optimization Boyd & Vandenberghe Lagrange dual problem weak and strong duality geometric interpretation optimality conditions perturbation and sensitivity analysis examples generalized
Minimizing Cubic and Homogeneous Polynomials over Integers in the Plane
 Minimizing Cubic and Homogeneous Polynomials over Integers in the Plane Alberto Del Pia Department of Industrial and Systems Engineering & Wisconsin Institutes for Discovery, University of Wisconsin-Madison
Minimizing Cubic and Homogeneous Polynomials over Integers in the Plane Alberto Del Pia Department of Industrial and Systems Engineering & Wisconsin Institutes for Discovery, University of Wisconsin-Madison
MATH MEASURE THEORY AND FOURIER ANALYSIS. Contents
 MATH 3969 - MEASURE THEORY AND FOURIER ANALYSIS ANDREW TULLOCH Contents 1. Measure Theory 2 1.1. Properties of Measures 3 1.2. Constructing σ-algebras and measures 3 1.3. Properties of the Lebesgue measure
MATH 3969 - MEASURE THEORY AND FOURIER ANALYSIS ANDREW TULLOCH Contents 1. Measure Theory 2 1.1. Properties of Measures 3 1.2. Constructing σ-algebras and measures 3 1.3. Properties of the Lebesgue measure
LMI MODELLING 4. CONVEX LMI MODELLING. Didier HENRION. LAAS-CNRS Toulouse, FR Czech Tech Univ Prague, CZ. Universidad de Valladolid, SP March 2009
 LMI MODELLING 4. CONVEX LMI MODELLING Didier HENRION LAAS-CNRS Toulouse, FR Czech Tech Univ Prague, CZ Universidad de Valladolid, SP March 2009 Minors A minor of a matrix F is the determinant of a submatrix
LMI MODELLING 4. CONVEX LMI MODELLING Didier HENRION LAAS-CNRS Toulouse, FR Czech Tech Univ Prague, CZ Universidad de Valladolid, SP March 2009 Minors A minor of a matrix F is the determinant of a submatrix
Inequality Constraints
 Chapter 2 Inequality Constraints 2.1 Optimality Conditions Early in multivariate calculus we learn the significance of differentiability in finding minimizers. In this section we begin our study of the
Chapter 2 Inequality Constraints 2.1 Optimality Conditions Early in multivariate calculus we learn the significance of differentiability in finding minimizers. In this section we begin our study of the
Lecture 15 Newton Method and Self-Concordance. October 23, 2008
 Newton Method and Self-Concordance October 23, 2008 Outline Lecture 15 Self-concordance Notion Self-concordant Functions Operations Preserving Self-concordance Properties of Self-concordant Functions Implications
Newton Method and Self-Concordance October 23, 2008 Outline Lecture 15 Self-concordance Notion Self-concordant Functions Operations Preserving Self-concordance Properties of Self-concordant Functions Implications
Symmetric Matrices and Eigendecomposition
 Symmetric Matrices and Eigendecomposition Robert M. Freund January, 2014 c 2014 Massachusetts Institute of Technology. All rights reserved. 1 2 1 Symmetric Matrices and Convexity of Quadratic Functions
Symmetric Matrices and Eigendecomposition Robert M. Freund January, 2014 c 2014 Massachusetts Institute of Technology. All rights reserved. 1 2 1 Symmetric Matrices and Convexity of Quadratic Functions
1. Gradient method. gradient method, first-order methods. quadratic bounds on convex functions. analysis of gradient method
 L. Vandenberghe EE236C (Spring 2016) 1. Gradient method gradient method, first-order methods quadratic bounds on convex functions analysis of gradient method 1-1 Approximate course outline First-order
L. Vandenberghe EE236C (Spring 2016) 1. Gradient method gradient method, first-order methods quadratic bounds on convex functions analysis of gradient method 1-1 Approximate course outline First-order
Elements of Positive Definite Kernel and Reproducing Kernel Hilbert Space
 Elements of Positive Definite Kernel and Reproducing Kernel Hilbert Space Statistical Inference with Reproducing Kernel Hilbert Space Kenji Fukumizu Institute of Statistical Mathematics, ROIS Department
Elements of Positive Definite Kernel and Reproducing Kernel Hilbert Space Statistical Inference with Reproducing Kernel Hilbert Space Kenji Fukumizu Institute of Statistical Mathematics, ROIS Department
15. Conic optimization
 L. Vandenberghe EE236C (Spring 216) 15. Conic optimization conic linear program examples modeling duality 15-1 Generalized (conic) inequalities Conic inequality: a constraint x K where K is a convex cone
L. Vandenberghe EE236C (Spring 216) 15. Conic optimization conic linear program examples modeling duality 15-1 Generalized (conic) inequalities Conic inequality: a constraint x K where K is a convex cone
Mathematical Analysis Outline. William G. Faris
 Mathematical Analysis Outline William G. Faris January 8, 2007 2 Chapter 1 Metric spaces and continuous maps 1.1 Metric spaces A metric space is a set X together with a real distance function (x, x ) d(x,
Mathematical Analysis Outline William G. Faris January 8, 2007 2 Chapter 1 Metric spaces and continuous maps 1.1 Metric spaces A metric space is a set X together with a real distance function (x, x ) d(x,
CONVEX OPTIMIZATION, DUALITY, AND THEIR APPLICATION TO SUPPORT VECTOR MACHINES. Contents 1. Introduction 1 2. Convex Sets
 CONVEX OPTIMIZATION, DUALITY, AND THEIR APPLICATION TO SUPPORT VECTOR MACHINES DANIEL HENDRYCKS Abstract. This paper develops the fundamentals of convex optimization and applies them to Support Vector
CONVEX OPTIMIZATION, DUALITY, AND THEIR APPLICATION TO SUPPORT VECTOR MACHINES DANIEL HENDRYCKS Abstract. This paper develops the fundamentals of convex optimization and applies them to Support Vector
Convex Optimization M2
 Convex Optimization M2 Lecture 3 A. d Aspremont. Convex Optimization M2. 1/49 Duality A. d Aspremont. Convex Optimization M2. 2/49 DMs DM par email: dm.daspremont@gmail.com A. d Aspremont. Convex Optimization
Convex Optimization M2 Lecture 3 A. d Aspremont. Convex Optimization M2. 1/49 Duality A. d Aspremont. Convex Optimization M2. 2/49 DMs DM par email: dm.daspremont@gmail.com A. d Aspremont. Convex Optimization
Real Analysis, 2nd Edition, G.B.Folland Elements of Functional Analysis
 Real Analysis, 2nd Edition, G.B.Folland Chapter 5 Elements of Functional Analysis Yung-Hsiang Huang 5.1 Normed Vector Spaces 1. Note for any x, y X and a, b K, x+y x + y and by ax b y x + b a x. 2. It
Real Analysis, 2nd Edition, G.B.Folland Chapter 5 Elements of Functional Analysis Yung-Hsiang Huang 5.1 Normed Vector Spaces 1. Note for any x, y X and a, b K, x+y x + y and by ax b y x + b a x. 2. It
HW1 solutions. 1. α Ef(x) β, where Ef(x) is the expected value of f(x), i.e., Ef(x) = n. i=1 p if(a i ). (The function f : R R is given.
 HW1 solutions Exercise 1 (Some sets of probability distributions.) Let x be a real-valued random variable with Prob(x = a i ) = p i, i = 1,..., n, where a 1 < a 2 < < a n. Of course p R n lies in the standard
HW1 solutions Exercise 1 (Some sets of probability distributions.) Let x be a real-valued random variable with Prob(x = a i ) = p i, i = 1,..., n, where a 1 < a 2 < < a n. Of course p R n lies in the standard
subject to (x 2)(x 4) u,
 Exercises Basic definitions 5.1 A simple example. Consider the optimization problem with variable x R. minimize x 2 + 1 subject to (x 2)(x 4) 0, (a) Analysis of primal problem. Give the feasible set, the
Exercises Basic definitions 5.1 A simple example. Consider the optimization problem with variable x R. minimize x 2 + 1 subject to (x 2)(x 4) 0, (a) Analysis of primal problem. Give the feasible set, the
13. Convex programming
 CS/ISyE/ECE 524 Introduction to Optimization Spring 2015 16 13. Convex programming Convex sets and functions Convex programs Hierarchy of complexity Example: geometric programming Laurent Lessard (www.laurentlessard.com)
CS/ISyE/ECE 524 Introduction to Optimization Spring 2015 16 13. Convex programming Convex sets and functions Convex programs Hierarchy of complexity Example: geometric programming Laurent Lessard (www.laurentlessard.com)
Linear Algebra, part 2 Eigenvalues, eigenvectors and least squares solutions
 Linear Algebra, part 2 Eigenvalues, eigenvectors and least squares solutions Anna-Karin Tornberg Mathematical Models, Analysis and Simulation Fall semester, 2013 Main problem of linear algebra 2: Given
Linear Algebra, part 2 Eigenvalues, eigenvectors and least squares solutions Anna-Karin Tornberg Mathematical Models, Analysis and Simulation Fall semester, 2013 Main problem of linear algebra 2: Given
j=1 [We will show that the triangle inequality holds for each p-norm in Chapter 3 Section 6.] The 1-norm is A F = tr(a H A).
![j=1 [We will show that the triangle inequality holds for each p-norm in Chapter 3 Section 6.] The 1-norm is A F = tr(a H A). j=1 [We will show that the triangle inequality holds for each p-norm in Chapter 3 Section 6.] The 1-norm is A F = tr(a H A).](/thumbs/88/117636161.jpg) Math 344 Lecture #19 3.5 Normed Linear Spaces Definition 3.5.1. A seminorm on a vector space V over F is a map : V R that for all x, y V and for all α F satisfies (i) x 0 (positivity), (ii) αx = α x (scale
Math 344 Lecture #19 3.5 Normed Linear Spaces Definition 3.5.1. A seminorm on a vector space V over F is a map : V R that for all x, y V and for all α F satisfies (i) x 0 (positivity), (ii) αx = α x (scale
Handout 2: Elements of Convex Analysis
 ENGG 5501: Foundations of Optimization 2018 19 First Term Handout 2: Elements of Convex Analysis Instructor: Anthony Man Cho So September 10, 2018 As briefly mentioned in Handout 1, the notion of convexity
ENGG 5501: Foundations of Optimization 2018 19 First Term Handout 2: Elements of Convex Analysis Instructor: Anthony Man Cho So September 10, 2018 As briefly mentioned in Handout 1, the notion of convexity
COM S 578X: Optimization for Machine Learning
 COM S 578X: Optimization for Machine Learning Lecture Note 4: Duality Jia (Kevin) Liu Assistant Professor Department of Computer Science Iowa State University, Ames, Iowa, USA Fall 2018 JKL (CS@ISU) COM
COM S 578X: Optimization for Machine Learning Lecture Note 4: Duality Jia (Kevin) Liu Assistant Professor Department of Computer Science Iowa State University, Ames, Iowa, USA Fall 2018 JKL (CS@ISU) COM
Equality constrained minimization
 Chapter 10 Equality constrained minimization 10.1 Equality constrained minimization problems In this chapter we describe methods for solving a convex optimization problem with equality constraints, minimize
Chapter 10 Equality constrained minimization 10.1 Equality constrained minimization problems In this chapter we describe methods for solving a convex optimization problem with equality constraints, minimize
Lecture: Duality of LP, SOCP and SDP
 1/33 Lecture: Duality of LP, SOCP and SDP Zaiwen Wen Beijing International Center For Mathematical Research Peking University http://bicmr.pku.edu.cn/~wenzw/bigdata2017.html wenzw@pku.edu.cn Acknowledgement:
1/33 Lecture: Duality of LP, SOCP and SDP Zaiwen Wen Beijing International Center For Mathematical Research Peking University http://bicmr.pku.edu.cn/~wenzw/bigdata2017.html wenzw@pku.edu.cn Acknowledgement:
Lecture 2: Convex Sets and Functions
 Lecture 2: Convex Sets and Functions Hyang-Won Lee Dept. of Internet & Multimedia Eng. Konkuk University Lecture 2 Network Optimization, Fall 2015 1 / 22 Optimization Problems Optimization problems are
Lecture 2: Convex Sets and Functions Hyang-Won Lee Dept. of Internet & Multimedia Eng. Konkuk University Lecture 2 Network Optimization, Fall 2015 1 / 22 Optimization Problems Optimization problems are
CS-E4830 Kernel Methods in Machine Learning
 CS-E4830 Kernel Methods in Machine Learning Lecture 3: Convex optimization and duality Juho Rousu 27. September, 2017 Juho Rousu 27. September, 2017 1 / 45 Convex optimization Convex optimisation This
CS-E4830 Kernel Methods in Machine Learning Lecture 3: Convex optimization and duality Juho Rousu 27. September, 2017 Juho Rousu 27. September, 2017 1 / 45 Convex optimization Convex optimisation This
Lecture: Duality.
 Lecture: Duality http://bicmr.pku.edu.cn/~wenzw/opt-2016-fall.html Acknowledgement: this slides is based on Prof. Lieven Vandenberghe s lecture notes Introduction 2/35 Lagrange dual problem weak and strong
Lecture: Duality http://bicmr.pku.edu.cn/~wenzw/opt-2016-fall.html Acknowledgement: this slides is based on Prof. Lieven Vandenberghe s lecture notes Introduction 2/35 Lagrange dual problem weak and strong
In English, this means that if we travel on a straight line between any two points in C, then we never leave C.
 Convex sets In this section, we will be introduced to some of the mathematical fundamentals of convex sets. In order to motivate some of the definitions, we will look at the closest point problem from
Convex sets In this section, we will be introduced to some of the mathematical fundamentals of convex sets. In order to motivate some of the definitions, we will look at the closest point problem from
7) Important properties of functions: homogeneity, homotheticity, convexity and quasi-convexity
 30C00300 Mathematical Methods for Economists (6 cr) 7) Important properties of functions: homogeneity, homotheticity, convexity and quasi-convexity Abolfazl Keshvari Ph.D. Aalto University School of Business
30C00300 Mathematical Methods for Economists (6 cr) 7) Important properties of functions: homogeneity, homotheticity, convexity and quasi-convexity Abolfazl Keshvari Ph.D. Aalto University School of Business
