Undulating Relativity ABSTRACT
|
|
|
- Dale Mosley
- 6 years ago
- Views:
Transcription
1 Unlaing Relaiiy h: lfe ias Meia Gaia -ail: STRCT The Speial They f Relaiiy aes s esls ha pesenly ae nsiee inepliable any enne sieniss, n: -The ilaain f ie, an -The nain f he enz engh. The slin hese hae ien he ah he eelpen f he Unlaing Relaiiy (UR) hey, hee he Tepal aiain is e he iffeenes n he e f he ligh ppagain an he lenghs ae nsans beeen lanas in nif elaie een. The Unlaing Relaiiy pies ansfains beeen he lanas ha iffes f he ansfains f enz f: Spae (,y,z), Tie (), Spee ( ), eleain ( a ), negy (), Men ( p ), e ( ), leial iel ( ), Magnei iel ( ), igh eqeny ( y ), leial Cen ( J ) an leial Chage (ρ ). he analysis f he eelpen f he Unlaing Relaiiy, he flling an be synhesize: - I is a hey ih piniples pleely n physis; - The ansfains ae linea; - eeps nhe he liian piniples; - Cnsies he Galile s ansfain isin n eah efeenial; - Ties he Spee f igh an Tie a niqe phenenn; - The enz fe an be aaine by isin ypes f ile es, an - Wih he absene f he spaial nain f enz, eah he sae lassial esls f he speial elaiiy ning is n neessay as nle n he pple effe. h, he Unlaing Relaiiy an he Speial Relaiiy f lbe insein eplain he epeiene f Mihel- Mley, he lngiinal an ansesal pple effe, an spplies ealy ienial flain : beain f zenih gα / esnel s fla ( ) n n.. Mass ( ) ih eliy ( ) [esing ass ( )]/... Men p.. Relain beeen en (p) an negy ().. p. Relain beeen he elei fiel ( ) an he agnei fiel ( V ). µο.i i-saan s fla µ..π.r is e glie s ae eqain ψ(,) a.si nπγ ; /
2 lng ih he eqains f ansfains beeen efeenes f he UR, e ge he inaiane f shape Maell s eqains, sh as: ρ i ; i. ο i. R. R µο. j ο.µο. ; R ο.µο.. We als ge he inaiane f shape he eqain f ae an eqain f niniy ne iffeenial shape: y z ρ.j. Ohe Ws: 9 plaining he Sagna ffe ih he Unlaing Relaiiy plaining he epeiene f Ies-Silell ih he Unlaing Relaiiy Tansfain f he pe f a lins ay beeen efeenials in he Speial They f Relaiiy ineaiy Riha C. Tlan. Veliies psiin 5 Inaiane 6 Tie an eqeny 7 Tansfain f. enz 8 The Mihelsn & Mley epeiene 9 Regessin f he peihelin f Mey f 7, 9 ane f Mey s peihelin f.79 Ineia ane f Mey s peihelin f.79 allae ih he Unlaing Relaiiy /
3 h: lfe ias Meia Gaia. e-ail: Unlaing Relaiiy Tansla: Rlf Mas Venâni e-ail: Tansfain spae an ie The Unlaing Relaiiy (UR) eep he piniple f he elaiiy an he piniple f Cnsany f ligh spee, ealy lie lbe insein s Speial Relaiiy They efine: a) The las, ne hih he sae f physis syses ae hange ae he sae, eihe hen efee a eeine syse f inaes any he ha has nif anslain een in elain he fis. b) ny ay f ligh es in he esing inaes syse ih a eeine eliy, ha is he sae, haee his ay is eie by a esing by by a by in een (hih eplains he epeiene f Mihel-Mley). e s iagine fis ha bsees O an O (in a), ing in nif anslain een in elain eah he, ha is, he bsee n ae elaiely eah he. In his ay, he bsee O gehe ih he ais, y, an z f a syse f a eangle Caesian inaes, sees he bsee O e ih eliy, n he psiie ais, ih he espeie paallel ais an sliing alng ih he ais hile he O, gehe ih he, y an z ais f a syse f a eangle Caesian inaes sees O ing ih eliy, in negaie iein as he ais ih he espeie paallel ais an sliing alng ih he ais. The bsee O eases he ie an he O bsee eases he ie ( ). e s ai ha bh bsees se hei ls in sh a ay ha, hen he iniene f he igin f he inae syse happens ze. In he insan ha, a ay f ligh is pjee f he n igin bh bsees. fe he ie ineal he bsee O ill nie ha his ay f ligh ha silanesly hi he inaes pin (, y, z) ih he ay f he O bsee ih eliy an ha he igin f he syse f he O bsee has n he isane alng he psiie ay f he ais, nling ha: y z... The sae ay afe he ie ineal he O bsee ill nie ha his ay f ligh silanesly hi ih he bsee O he inae pin (, y, z ) ih eliy an ha he igin f he syse f he bsee O has n he isane n he negaie ay f he ais, nling ha: y z... Maing. eqal. e hae y z y z..5 ease f he syey y y en z z, ha siplify.5 in..6 T he bsee O (.) ha applie in.6 spplies ( ) f hee..7 T he bsee O (.) ha applie in.6 spplies ( ) f hee /
4 ..8 Table I, ansfains he spae an ie.. y y.. y y.. z z.. z z he eqain syse fe by. an. e fin (nsieing > e >).9 ha ensaes he inaiane f he spae in he Unlay Relaiiy. he eqain syse fe by.7 an.8 e fin... If in. hen, ha applie in. spplies,... If in. an hen... T he bsee O he piniple f ligh spee nsany gaanees ha he pnens, y an z f he ligh spee ae als nsan alng is ais, hs y y z z, y, z. an hen e an ie.. Wih he se f.7 an.9 an. e an ie..5 iffeeniaing.9 ih nsan an, else, nly he ie aying e hae,.6 b f.5 hen eing an nsans, he eazns..7 an / in.5 s als be nsan bease f his he iffeenial f s be eqal ze f hee e nle, ha is ealy he sae as..
5 T he bsee O he piniple f Cnsany f eliy f ligh gaanees ha he pnens, y, an z f eliy f ligh ae als nsan alngsie is ais, hs y y z z, y, z,.8 an ih his e an ie,..9 Wih he se f.8,.9, an.9 e an ie.. iffeeniaing.9 ih an nsan, ha is, nly he ie aying e hae,. b f. hen eing an nsan he iisins.. an in. als hae be nsan bease f his he iffeenial f s be eqal ze f hee e nle, ha is ealy lie.8. Replaing. an.9 in. e hae... T he bsee O he e psiin f he pin f inaes (,y,z) is R i yj z,. an he e psiin f he igin f he syse f he bsee O is R..5 R i j i T he bsee O, he e psiin f he pin f inaes (,y,z ) is R i y j z,.6 an he e psiin f he igin f he syse f he bsee O is R i j R i..7 e.9,.5, an.7 e hae, R R..8 s. is eqal.5 pls.6 e hae R R R R R R..9 pplying.8 in.9 e hae, R R R.. 5/
6 6/ T he bsee O he e eliy f he igin f he syse f he bsee O is i j i R.. T he bsee O he e eliy f he igin f he syse f he bsee O is i j i R...5,.,., an. e fin he flling elains beeen an... Obseain: in he able I he flas.,.., an.. ae he pnens f he e.9 an he flas.,.., an.. ae he pnens f he e.. a f eliy ansfains an iffeeniaing.9 an iiing i by.7 e hae R R R.. iffeeniaing. an iiing i by. e hae R R R.. Table, a f eliy ansfains an.... y y.. y y.. z z.. z z
7 7/ Mliplying. by iself e hae..7 If in.7 e ae hen as i is eqie by he piniple f nsany f eliy f ligh. Mliplying. by iself e hae..8 If in.8 e ae hen as i is eqie by he piniple f nsany f eliy f ligh. If in. e ae hen as i is eqie by he piniple f nsany f eliy f ligh. If in. e ae hen as i is eqie by he piniple f nsany f eliy f ligh. Reeling.7 an.8 e hae..9.. The ie elains beeen he ies an eliies f pins in spae an be baine ih he eqaliies ing f., ha applie in.7,.,., an.5 spply,.,.,...
8 beain f he zenih T he bsee O alng ih he sa, y an z, an he bsee O alng ih he ah e hae he njn., y, z, y y z ealy as feseen by he piniple f elaiiy. T he bsee O he ligh ppagaes in a iein ha aes an angle ih he eial ais y gien by / angα.5 y. ha is he abeain fla f he zenih in he speial elaiiy. If e inee he bsees e l hae he njn., ( ) y y, z, y z ( ) / angα.6 y. ha is eqal.5, ih he negaie sign iniaing he nay iein f he angles. Cnsieing in., elain he appaas hen esnel s fla / n he eliy f ligh elaiily he ae, ill be he eliy f ligh elaiely he labay / n / n / n n Igning he e / e hae n n n n n an igning he e / n n n n n n n he eliy f ae in n e hae he esnel s fla n..7 8/
9 Maing y z an ( ) ( ) as pple effe eplaing hen, hen ( ) ( ) e ill efine y z in.5 e hae an.7 e fin ( ) ( ) hee aen he piniple f elaiiy.8 Resling in he epessin ( ) syei an inaiable beeen he bsees. T he bsee O an epessin in he fla f ψ(,) f ( ).9 epesens a e ha ppagaes in he iein f R. T he bsee O an epessin in he fla f ψ, f. epesens a e ha ppaes in he iein f pplying in.8 λ λ e R. π π,,.,.9,.,.5, an.6 e hae λ λ λ λ,. ha applie in yλ y λ spply, y y an y y.. Cnsieing he elain f Plan-insein beeen enegy ( ) an feqeny ( y ), e hae he bsee O hy an he bsee O hy ha eplae in. spply an.. If he bsee O ha sees he bsee O ing ih eliy in a psiie ay he ais, eis aes f feqeny y an eliy in a psiie ay he ais hen, aing. an bsee O ill ease he aes ih eliy an feqeny ha is ealy he lassi fla f he lngiinal pple effe. he y y,. If he bsee O ha sees he bsee O ing ih eliy in he negaie ay f he ais, eis aes f feqeny y an eliy, hen he bsee O aing. an ill ease aes f feqeny y an eliy in a pepenila plane he een f O gien by γ γ,.5 ha is ealy he fla f he ansesal pple effe in he Speial Relaiiy. iffeeniaing. an iiing i by.7 e hae Tansfains f he aeleains a an a / / a a ( ) a ( ).. iffeeniaing. an iiing i by. e hae / / a a ( ) a ( ).. 9/
10 Table, ansfains f he aeleains a an a a a a a a ( ). a ( ). a a a a a ( ). a ( ). ay a a y a a y y.. ay y az a a z a a z z.. az z a a a.8 a he ables an e an nle ha if he bsee O hen i is als he bsee O an is pepenila.a ze an y z,.a ze an y z, hs is pepenila a a as he es hey eqies. iffeeniaing.9 ih he eliies an he ies hanging e hae,, b nsieing.6 e hae,.7 Whee eplaing.5 an iiing i by.7 e hae, We an als eplae. in.7 an iie i by. eing a a..8 a a..9 The ie elains beeen he les f he aeleains a an a f pins in spae an be baine ih he a ing f., ha applie in.8 an.9 spply a a a an a a a.. Tha an als be ee f. an. if e se he sae eqaliies ing f.. a Tansfains f he Mens p an p efine as p an p hee an ( ) We ill hae he elains beeen an ( ),. syblizes he fnin asses f he les f eliies an. an he esing ass, analyzing he elasi llisin in a plane beeen he sphee s ha f he bsee es alngsie he ais y ih eliy y an he sphee s ha f he bsee O es alngsie he ais y ih eliy y -. The sphees hile bsee in elaie esing ae ienial an hae he ass. The nsiee llisin is syei in elain a paallel line he ais y an y passing by he ene f he sphees in he en f. Cllisin. efe an afe he llisin he sphees hae eliies bsee by O an O aing he flling able gen f able /
11 Sphee Obsee O Obsee O efe s s ze, ys s Cllisin s s, fe s ze Cllisin s s, ys, y s s ze, y s s, ys s ys, y s s ze, y s T he bsee O, he piniple f nseain f ens esablishes ha he ens py y p an, f he sphees s an s in elain he ais an y, eain nsan befe an afe he llisin hs f he ais e hae ( s ys ) s ( s ys ) s ( s ys ) s ( s ys )s hee eplaing he ales f he able e hae f hee e nle ha, an f he ais y ( s ys ) ys ( s ys ) ys ( s ys ) ys ( s ys )ys hee eplaing he ales f he able e hae,, siplifying e hae,, hee hen bees b is eqal he esing ass hs, ih a elaie eliy ha applie in. spplies p. Wih he sae pees e l hae f he O bsee.., /
12 ( ). p an Siplifying he siblgy e ill ap an ( ).... ha siplify he ens in p an p.. pplying. an. in.9 an. e hae an efining fe as Nen e hae inei enegy (, ) as p an.. p ( ), ih his e an efine hen.r.r ( ). ( ), an ( ).R.R ( ). ( ) Reeling. an. an iffeeniaing e hae. an, ha applie in he flas f inei enegy spplies an hee an,.5.6 ae he al enegies as in he speial elaiiy an he esing enegy..7 pplying.6 in. e hae ealy...6,.,., an. e fin p an p.8 ienial elains he Speial Relaiiy. Mliplying. an. by e ge /
13 an p p p p Table, ansfains f ens p an p p p.9 p p. p p. p p. p y py.. py p y.. p z pz.. pz p z..... ( ) p.8 p.8 Wae eqain f is e glie The bsee O assiaes a esing paile in is igin he flling ppeies:.9.. -Resing ass -Tie -Resing negy -eqeny -Wae fnin y h h ψ asenπ y ih a nsan. The bsee O assiaes a paile ih eliy he flling: -Mass -Tie -negy (f. hee ) an ) (f. ih an ) (f.7 ih /
14 -eqeny y y /h (f. ih -isane (f. ih ) -Wae fnin -Wae lengh an y y ) π ih ψ asen y asenπ y asenπ y ) yh h yλ λ (f.9 ih p p p p p T g ba he O bsee efeenial hee, e ill nsie he flling aiables: -isane (f. ih ) -Tie -eqeny -Veliy (f.8 ih ) y y (f. ih ) (e.) ha applie he ae fnin spplies ψ asenπ y asenπ y asen y π, b as an y y hen ψ ψ. 5 Tansfains f he es an iffeeniaing.9 an iiing by.7 e hae p p iffeeniaing. an iiing by. e hae (.) p p he syse fe by 5. an 5. e hae.. (. ) , 5. ha is an inaian beeen he bsees in he Unlaing.Relaiiy. /
15 Table 5, ansfains f he es an (.) 5.. (.). 5. y y/ 5.. y y / 5.5. z z/ 5.. z z / Tansfains f he ensiy f hageρ, ρ an ensiy f en J an J q Mliplying. an. by he ensiy f he esing elei hage efine as ρ e hae ρ ρ ρ ρ ρ ρ J J ρ ρ ρ ρ an ρ ρ ρ J J ρ Table 6, ansfains f he ensiy f hagesρ, ρ an ensiy f en J an J J J ρ 6. J J ρ 6. J Jρ 6. J J ρ 6. J y Jy 6.. Jy J y 6.. J z Jz 6.. Jz J z 6.. J ρ 6.5 J ρ 6.6 ρ ρ ρ ρ ρ ρ 6.9 ρ ρ Κ he syse fe by 6. an 6. e ha 6.9 an Tansfain f he elei fiels, an agnei fiels, pplying he fes f enz q( ) an q( ) q( ) q( ) [ q( ). ] an q( ) q( ) [ ] q in 5. an 5. e hae, ha siplifie bee ( ) ( ) (.) an ( ). f hee e ge he inaiane f. beeen he bsees as a nseqene f 5. an he flling pnens f eah ais 5/
16 yy zz y z z y yz zy 7. y z z [ y z z] 7.. z y y [ z y y ] 7.. y y z z yzzy y z z y 7. y z z [ y z z ] 7.. z y y [ z y y ] 7.. T he njn 7. an 7. e hae slins esibe in he ables 7 an 8. Table 7, ansfains f he elei fiels, an agnei fiels e y z y 7.. y z y 7.. z y z z y 7.. z y y z 7.5. y y z 7.6. z z y 7.5. z z y 7.6. y y 7.7 y y 7.8 z z 7.7. z z 7.8. y z 7.9 y z 7. z y 7.9. z y 7.. Table 8, ansfains f he elei fiels, an agnei fiels e (.) y ( y z) 7.. y ( y z ) 7.. z ( z y) 7.. z ( z y ) y y 7.. y y 7.. z z 7.. z z 7.. 6/
17 Relain beeen he elei fiel an agnei fiel If an elei-agnei fiel has he bsee O he nagh agnei pnen ze an he elei pnen. T he bsee O his fiel is epesene ih bh pnens, being he agnei fiel esibe by he njn 7.5 an hás as pnens ze, y ha ae eqialen z, y z, la f i-saa The bsee O assiaes a esing elei hage, nifly isibe alngsie is ais he flling elei-agnei ppeies: -inea ensiy f esing elei hage ρ q -Nagh elei en I ze -Nagh agnei fiel ze ze ρ -Raial eleial fiel f le y z a any pin f ais R πr he pnen ze. y z ih T he bsee O i elaes an elei hage nifly isibe alngsie is ais ih eliy hih i assiaes he flling elei-agnei ppeies: -inea ensiy f he elei hage ρ ρ (f 6.7 ih ) -lei en I ρ ρ -Raial eleial fiel f le (aing he njns 7. an 7.5 ih ze ze an ) -Magnei fiel f pnens ze, z y y, z an le ρ µ I hee µ, being in he eial f πr πr µ I πr 7.7 hee is a niay e pepenila he eleial fiel an angen he ifeene ha passes by he pin f ais R y z bease f he njn 7. an 7.6. ze. 7/
18 8 Tansfains f he iffeenial peas Table 9, iffeenial peas y y z z y y z z he syse fe by 8., 8., 8., an 8. an ih.5 an. e nly fin he slins / an /. 8.5 hee e nle ha nly he fnins ψ (.9) an ψ (.) ha spply he niins ψ / ψ an ψ / ψ, 8.6 an epesen he ppagain ih eliy in he Unlaing Relaiiy iniaing ha he fiel ppagaes ih efinie eliy an ih isin being applie. an.8. ease f syey e an als ie he he ais ψ y y / ψ ψ y y / ψ, an ψ z / ψ z ψ z z / ψ,. 8.7 he ansfains f spae an ie f he Unlay Relaiiy e ge Jab s hee J an (,y,z,) (, y,z,) J, 8.8 (, y,z,) (, y,z,) aiables ih an as a nseqene f he piniple f nany f he ligh eliy b ae eqal ais J J an ill be eqal ne J J hen. The ae eqain he bsee O is Inaiane f he ae eqain y z ze hee applying he flas f ables 9 an. e ge f hee e fin y z ze 8/
19 9/ ze z y ha siplifying spplies ze z y 6 hee eeing he es e fin ze z y 8.9 b f 8.5 an. e hae ze / ha applie in 8.9 spplies he ae eqain he bsee O ze z y. 8. T en he efeenial f he bsee O e ill apply 8. he flas f ables 9 an.8, geing ze z y f hee e fin ze z y ha siplifying spplies ze z y 6 hee eeing he es e fin ze z y b f 8.5 an.8 e hae ze / ha eplae in he eee eqain spplies he ae eqain he bsee O. Inaiane f he Cniniy eqain The niniy eqain in he iffeenial f he bsee O is ze z Jz y Jy J ρ ze.j ρ 8. hee eplaing he flas f ables 6, 9, an. e ge ze z Jz y Jy ρ J ρ
20 aing he peains e fin ρ ρ ρ ρ J J ρ ρ Jy y Jz z ze ha siplifying spplies ρ ρ J J Jy Jz y z ze hee applying J ρ ih nsan e ge ρ ρ J ( ρ) Jy Jz ρ J Jy Jz ze y z y z ze 8. ha is he niniy eqain in he iffeenial f he bsee O. T ge again he niniy eqain in he iffeenial f he bsee O e ill eplae he flas f ables 6, 9, an.8 in 8. geing J y J z ρ ( J ρ ) ze y z aing he peains e fin ρ ρ ρ ρ J J ρ ρ J y y J z z ze ha siplifying spplies ρ ρ J J J y J z y z hee applying J ρ ih nsan e ge ρ ρ J ( ρ ) J y J z y z ze ρ J J y J z ze y z ha is he niniy eqain in he iffeenial f he bsee O. Tha in he iffeenial f ae ien his ay Inaiane f Maell s eqains ze Wih eleial hage T he bsee O T he bsee O y z ρ y 8. y z y y z y z y z y z y y z z y z y µ Jz µ y z z z ρ y z y z y z y z y y z z y z y µ J z µ y z /
21 z y µ J µ y z z µ Jy µ z y z y z y z z Wih eleial hage ρ ρ ze an J J ze T he bsee O T he bsee O y z y z y z y z y z y z y y z z y z y z µ y z y µ y z z y µ z µ µ J µ µ J y µ y z y z y z y z y z y z y y z z y z y z µ y z y µ y z z y µ z y We ensae he inaiane f he a f Gass in he iffeenial f ha f he bsee O is y z ρ 8. y z hee eplaing he flas f he ables 6, 7, 9, an.8, an nsieing nsan, e ge z z y y y ρ Κ aing he ps, sing an sbaing he e z z y y z z y z z z z ρ, e fin y y z y y y ha eeing esls z y y z y z y z ρ /
22 hee he fis paenheses is 8.5 an bease f his eqal ze, he sen blan is eqal ρ ( µ J) µ ρ gen f 8.5 an 8.5 esling in y z ρ y z y z ρ f hee e ge y z ha is he a f Gass in he iffeenial f he bsee O. ρ ρ T ae he inese e ill eplae in 8. he flas f he ables 6, 7, 9, an., an nsieing nsan, e ge z z y y y ρ Κ aing he ps, aing an sbaing he e z z y z ha eeing esls in z z z y z z z y y y z y z, e ge y y y y ρ y z ρ y z hee he fis blan is 8.5 an bease f his eqals ze, he sen blan is eqal ρ ( µ J ) µ ρ gen f 8.6 an 8.5 esling in y y f hee e ge bsee. z z y y ρ z ρ z ρ ρ 8. ha is he a f Gass in he iffeenial f he O Peeing his ay e an pe he inaiane f f f all he he eqains f Maell. 9 plaining he Sagna ffe ih he Unlaing Relaiiy We s ansf he saigh een f he bsees O an O se in he ein f he Unlaing Relaiiy in a plain ila een ih a nsan ais. e s iagine ha he bsee O sees he bsee O ning an ih a angenial spee in a lise ay (C) eqals he psiie se f he ais f UR an ha he bsee O sees he bsee O ning an ih a angeial spee in a nlise ay (U) eqals he negaie se f he ais f he UR. In he en ze, he bsee O eis ays f ligh f he n igin bh bsees, ne in a nlise ay f a U an anhe in a lise ay f a C, heefe U C an U C, bease is he spee f he nsan ligh, an U an C he ie. /
23 In he en ze he bsee O als eis ays f ligh f he n igin bh bsees, ne in a nlise ay (seless) f a U an anhe ne in a lise ay f a C, hs U C an U C bease is he spee f he nsan ligh, an U an C he ie. Reiing he eqains.5 an. f he Unlaing Relaiiy (UR):..5.. Maing ( ay f ligh pjee alngsie he psiie ais ) an spliing he eqains e hae: When he igin f he bsee O ees he nlise ay f he bsee O, ill be a he isane f he bsee O an silanesly ill ee is lise ay f ligh a he sae pin f C U he bsee O, in a syei psiin he iaee ha ges hgh he bsee O bease U C U C an U C U C, flling he f eqains abe e hae: U πr C πr C 9.5 C πr U πr C 9.6 When he igin f he bsee O ees he lise ay f he bsee O, silanesly ill ee is n lise ay an ill be a he isane f he bsee O, hen flling he eqains,, an abe e hae: C U C πr πr C C 9.7 C πr πr C 9.8 The ie iffeene he bsee O is: πr πr πr C C 9.9 The ie iffeene he bsee O is: C C πr πr πr ( ) 9. Replaing he eqains 5 in e pe ha hey nfi he ansfains f he Unlaing Relaiiy. /
24 plaining he epeiene f Ies-Silell ih he Unlaing Relaiiy We shl eie he eqains (.) he ae lengh in he Unlaing Relaiiy: λ λ an λ λ,. Maing ( Ray f ligh pjee alngsie he psiie ais ), e hae he eqains: an λ λ λ λ,. If he bsee O, h sees he bsee O ging aay ih he eliy in he psiie ay f he ais, eis aes, penien f a esing se in is igin ih eliy an ae lengh λ in he psiie ay f he ais, hen aing he eqain. he bsee O ill ease he aes ih eliy an he ae lengh λ aing he flas: λ λ an λ λ,. If he bsee O, h sees he bsese O ging aay ih eliy in he negaie ay f he ais, eis aes, penien f a esing se in is igin ih eliy an he ae lengh λ in he psiie ay f he ais, hen aing he eqain. he bsee O ill ease aes ih eliy an ae lengh λ aing he flas: λ λ an λ λ,. The esing ses in he igin f he bsees O an O ae ienial hs λ λ. We allae he aeage ae lengh λ f he ease aes (,λ )., he lef sie in eah eqain: λ λ λ λ λ λ λ λ λ sing he eqains. an λ We allae he iffene beeen he aeage ae lengh λ an he eie ae lengh by he ses λ λ λ : λ λ λ λ λ λ λ λ λ λ /
25 λ λ λ λ. Refeene hp://.babin.ne/physis/faaj7.h Ies-Silell (ninain) The pple s effe ansesal he Unlaing Relaiiy as baine in he as flls: If he bsee O, ha sees he bsee O, es ih he spee in a negaie ay he ais, eis aes ih he feqeny y an he spee hen he bsee O aing. an ill ease aes f feqeny y an spee in a pepenila plane he een f O gien by y y.5 e ill hae ze an y y an he se feqeny y y lie his y he ansesal feqeny y ih his e an ie he elain beeen.5 Wih y λ y λ e hae he elain beeen he lengh f he ansesal ae he se ae λ λ λ an he lengh f λ.6 The aiain f he lengh f he ansesal ae in he elain he lengh f he se ae is: λ λ λ λ λ λ λ.7 ha is he sae ale gen in he They f Speial Relaiiy. pplying.7 in. e hae λ λ Wih he eqains. an. e an ge he elains.9,., an. esibe as flls λ λ.9 n f his e hae he fla f spee λ λ.8. λ λ λ λ λ. pplying. an. in.6 e hae λ λ λ λ. λ 5/
26 .8 an. e nle ha λ λ λ λ λ.. S ha e he ales f λ an λ baine f he Ies-Siell epeiene e an ealae λ, an nle hehe hee is n he spae efain peie in he They f Speial Relaiiy. Tansfain f he pe f a lins ay beeen efeenials in he Speial They f Relaiiy The elainship ihin he pe eelpe by he fes beeen efeenials is ien in he Speial They f he Relaiiy in he flling ay:.. The efiniin f he pnen f he fe alng he ais is: p. a lins ay, he piniple f ligh spee nsany gaanees ha he pnen f he ligh spee is als nsan alng is ais, hs The fla f enegy is nsan, ensaing ha in he efiniin f enegy e hae pplying 5 in e hee: λ,. ze. f hee e hae.. ha applying in an e hae..5. (. ). hee e fin ha...6 esl eqal 5. f he Unlaing Relaiiy ha an be epeienally pen, nsieing he Sn as he se. ineaiy The They f Unlaing Relaiiy has as is fnaenal ai he neessiy ha ineial efeenials be nae elsiely as hse nes in hih a ay f ligh eie in any iein f is igin speas in a saigh line, ha is aheaially esibe by he flae (.,.8, 8.6 e 8.7) f he Unlaing Relaiiy: y y z z y, z,. y y z z, y, z.8 Wlea Vig e in.887 he linea ansfain beeen he efeenials s he bsees O e O in he flling ay: 6/
27 .. Wih he espeie inee eqains:.. Whee,, an ae nsans an bease f he syey e n nsie he es ih y, z an y, z. We n ha an ae pjeins f he ays f lighs an ha spea ih Cnsan spee (e he nsany piniple f he Ray f ligh), eie in any iein f he igin f he espeie ineials efeenial a he en in hih he igins ae inien an a he en hee: ze.5 bease f his in he eqain. a he en hee ze e s hae ze s ha e als hae ze, e an asse ha hen ze, als be eqal ze, bease if he speaing happens in he plane y z e ill hae ze pls ze. We shl eie he ee eqains ( ze):.6.7 Wih he espeie ee inee eqains:.8.9 If he speaing happens in he plane y z e hae ze an iiing.6 by.7 e hae:. hee is he le f he spee in hih he bsee O sees he efeenial f he bsee O ing alngsie he ais in he psiie ay bease he sign f he eqain is psiie. If he speaing happens in he plane y z e hae ze an iiing.8 by.9 e hae:. hee is he le f he spee in hih he bsee O sees he efeenial f he bsee O ing alngsie he ais in he negaie ay bease he signal f he eqain is negaie. The eqain.6 esibes he nsany piniple f he spee f ligh ha s be asse by he eqains.6.9:.6 pplying.6 an.7 in.6 e hae: ( ) hee e hae: 7/
28 ( ) hee aing in he baes in a an in he saigh baes e hae he eqaliy beeen bh sies f he eqal signal f he eqain. ppllying in e hae. ppllying in. e hae. Tha applie in. splies: (, ). as (, ) is eqal he fnin epening f he aiables an. pplying.8 an.9 in.6 e hae: hee e hae: hee aing in he bae in a an in he saigh bae e hae he eqaliy beeen bh sies f he eqal signal f he eqain. (,). pplying an. in e hae: as (, ) is eqal he fnin epening n he aiables an. We s ae he flling naing aing.5 an.6:..5 s he eqain (, ) f. an (, ) f. s be eqal, e hae: 8/
29 .6 Ths: aly eqal...7 Reiing he eqains.6,.7,.8 an.9 aing he fnin f, an e hae:.6.7 Wih he espeie inee ee eqains:.8.9 We hae he eqains.6,.7,.8 an.9 finals eplaing by he espning flae:.6.7 Wih he espeie inee final eqains:.8.9 Tha ae ealy he eqains f he able I s an hen he elains beeen an ae..8 We ill ansf (.) fnin f he eleens,, an f (.) fnin f he eleens, an, eplaing in. he eqains.8,.9 an.8: ( ) ( ) 9/
30 Tha is ealy he eqain.. We ill ansf (.) fnin f he eleens,, an f (.) fnin f he eleens, an, eplaing in. he eqains.6,.7 an.8: ( ) Tha is ealy he eqain.. We hae allae he al ifeenial f (, ) (.): as: an.9 e hae: hee applying.8 e fin:. hee e nle ha fnin f an is a nsan. We hae allae he al ifeenial f (, ) (.): as: an. e hae:. /
31 hee applying. e fin: hee e nle ha fnin f an is a nsan. The eqains. an.8 epesen he bsees O an O he piniple f nsany f he ligh spee ali f infiniely sall he infiniely big an ean ha in he Unlaing Relaiiy he spae an ie ae ease silanesly. They shln be inepee ih a epeneny beeen spae an ie. The ie has is n inepeain ha an be nes if e analyze a eeine bsee he eissin f ays f ligh f he insan ze. If e a he ies e ge, f eah ay f ligh, e ill ge a esl ih any se f he physis. If in he insan ze, he bsee O eis ays f ligh, ne alngsie he ais an he he alngsie he ais y, afe he ineal f ie, he ays hi f he bsee O, silanesly, he pins an y he isane f he igin, alhgh f he bsee O, he pins n be hi silanesly. bh ays f lighs be silanes bh bsees, hey s hi he pins ha hae he sae ais in elain he ais an ha pie he sae ie f bh bsees ( an ), hih eans ha nly ne ay f ligh is neessay he he ie beeen he efeenials. ing, bh efeenials f he bsees O an O ae ineial, hs he ligh speas in a saigh line aing ha is eane by he fnaenal ai f he Unlaing Relaiiy, bease f his, he iffeene in eliies an is e nly a iffeene in ie beeen he efeenials... We an als elae na ineial efeenial f hih he ligh spea in a saigh line aing ha is eane by he fnaenal ai f he Unlaing Relaiiy, ih an aeleae ing efeenial f hih he ligh spea in a e line, nsieing ha in his ase he iffeene an isn e nly he iffeene f ie beeen he efeenials. ing, if he bsee O a he insan ze, eis a ay f ligh f he igin f is efeenial, afe an ineal f ie, he ay f ligh his he pin ih inaes (, y, z, ) he isane f he igin f he bsee O, hen e hae: fe hiing he pin he ay f ligh sill spea in he sae iein an in he sae ay, afe an ineal f ie, he ay f ligh his he pin ih inaes (, y y, z z, ) he isane he pin, hen e hae: an ih his e ge: ( ) ( ) ( ) ( ) The geey f spae an ie in he Unlaing Relaiiy is saize in he fige bel ha an be epane n pins an seeal bsees. /
32 In he fige he angles hae a elain ψ an ae eqal he flling segens: O O O is eqal O O O ( O O ) O O is eqal O O ( O O ( ) ( ) O O O O ) n ae paallel he flling segens: O is paallel O O is paallel O X X is paallel X X The sine f he angles f inlinain an he ays f he bsees O an O aing. an. ae: s / s sen n ih his e hae: sen s s / s / s. s /. s s / s.5
33 n ih his e hae sen sen.6 The sine f he angle ψ ih inesein f ays eqal : s s s ψ.7 n ih his e hae: The inaiane f he Unlaing Relaiiy. sen sen sen ψ.8 s ψ shs he hany f all ape hypheses f spae an ie in he The aials s s s ψ is eqal he Jabians f he ansfains f he spae an ie f he pie I, hee he an J i j ae nsiee aiables an ae eie. (,y,z, ) (,y,z, ) / ψ 8.8 J l / (,y,z, ) (,y,z, ) ψ 8.8 Riha C. Tlan The Tansfains f he Mena f Unlaing Relaiiy as eelpe base n he epeiene ne by eis an Tlan, aing he efeene []. Whee he llisin f sphees peseing he piniple f nseain f enegy an he piniple f nseain f ena, shs ha he ass is a fnin f he eliy aing : hee is he ass f he sphee hen in esing psiin an / he le f is spee. nalyzing he llisin beeen ienial sphees hen in elaie esing psiin, ha f he bsee O ae nae S an S ae ing alng he ais in he nay ay ih he flling eliies befe he llisin: Table sphee S sphee S y ze y ze z ze z ze he bsee O he sae sphees ae nae S an S an hae he eliies,, y z ze befe he llisin allae aing he able as flls: i i
34 The eliy f he sphee S is eqals :. The ansfain f aing. f Table is:. Tha applie in spplies: The eliy f he sphee S is eqal : ( ) Table Sphee S Sphee S ze y ze y ze z ze z ze ze he bsees O an O he sphees hae he sae ass hen in elaie esing psiin. n f he bsee O he sphees llie ih eliies f eqal le an ppsie iein bease f his he ena ( p p ) nll heseles ing he llisin, fing f a bief ie ( ) nly ne by f ass. ing he piniple f nseain f ena f he bsee O e ill hae ipse ha he ena befe he llisin ae eqal he ena afe he llisin, hs: ( ) Whee f he bsee O, is he abiay eliy ha sppsely f a bief ie asses nie ( ) ing. s he asses i ill als see he hae iffeen eliies an he asses ay aing hei n eliies, his eqain ann be siplifie algebaially, haing his aiain f asses: T he lef sie f he eqal sign in he eqain e hae: /
35 5/ ze ze T he igh sie f he eqal sign in he eqain e hae: pplying in he eqain f nseain f ena e hae:. hee e hae: s f he bsee O he asses nie ln e enaily alngsie he bsee O hih is neiable if e nsie ha he insans ae iffeen hee sppsely he asses l be in a esing psiin f he pin f ie f eah bsee an ha he ass aing ih eliy is bigge han he ass in esing psiin. If e peae ih hese aiables in line e l hae:.
36 hee e nle ha hih s be eqal he peis ale f, ha is: elain beeen an ha is baine f Table hen he eliy aing e he sphee in esing psiin. Refeene Millenni Relaiiy Veliies psiin UR: hp://.elaiiy.ne/miefs/vcp_si_sab_way.h ha espns f he bsee O e s ie he ansfains f eni. enz f spae an ie in he Speial They f Relaiiy:.a.a y y.b y y.b z z. z z... he e bain he eqains f eliy ansfain: y z y.5a.5b z.5 y z y.6a.6b z.6 e s nsie ha in elain he bsee O an bje es ih eliy: 5,5. / s(,5 ). 6/
37 n ha he eliy f he bsee O in elain he bsee O is: 5,5. / s(,5 ). The eliy f he bje in elain he bsee O s be allae by he fla.6a: 5 5,5.,5. 5,5..,5. 5 (,. ) 5 5,. / s(,8 ). 5 Whee e se,. / s(, ). Cnsieing ha he bje has e ing ne sen in elain he bsee O (,s ) e an hen ih. allae he ie passe he bsee O :,5., 5.,. 5 (,. ) 5 (,5. ) 5 (,. ) 5,6, 75,69s T he bsee O he bsee O is aay he isane gien by he fla: 5 5,5..,,5.. T he bsee O he bsee O is aay he isane gien by he fla: 5.,6 5,5.,9.., 75 T he isane f he bje (, ) in elain he bsees O an O is gien by he flae: O O 5 5,..,,.. O 5,6 5,5..,9.., 75 O T he bsee O he isane beeen he bje an he bsee O is gien by he fla: 5 5 5,.,5.,9.. O T he bsee O he eliy f he bje in elain he bsee O is gien by: 5,9.,9. / s,s 5 (,) Relaing he ies an sing he fla is nly pssible an elsiely hen an ze ha isn he ase abe, ae i pssible nesan his e ie he eqains. an. in he fla bel:. s. s. 7/
38 Whee s an s. The eqains abe an be ien as: f (,) e f (, ).7 In eah efeenial f he bsees O an O he ligh ppagain eaes a sphee ih ais an ha ineep eah he fing a ifeene ha ppagaes ih eliy. The ais an an he psiie ay f he ais an f he angles an nsan beeen he efeenials. If f he sae pai f efeenials e angles ee aiable he ie l be alleay an l bee seless f he Physis. In he eqain f (,) e hae ienial fnin f an, if e hae in i nsan an aies aing e ge he n elain beeen he ies an beeen efeenials, hee if e hae nsan an aies aing e ill hae f eah ale f f,. ne ale f an beeen iffeen efeenials, an his analysis is als ali f iiing.5a by e hae: s s s Whee s an s Islaing he eliy e hae:..8. ( ss ) ( ss ).9 hee e nle ha e s hae angles an nsan s ha e hae he sae eliy beeen he efeenials. This ean f nsan angles beeen he efeenials s sle he nesies f ebe ingle. 5 Inaiane The ansfains he spae an ie f able I, gp. pls.7, in he ai f is ien lie his: y y z z 5. Tha ien in he f bel epesens he sae inae ansfains: / y y z z 5. We all as: i y z /, α αij, j y z 8/ 5.
39 Tha ae he fnins i i j i i ( ) (,,, ) (, y, z, ) 5. Tha in he sybli f is ien: α. in he inee f i α j ij j i α ij j 5.5 Whee e se insein s s nenin. The ansfains he spae an ie f able I, gp. pls.8, in he ai f is ien: y y z z 5.6 Tha ien in he f bel epesens he sae inae ansfains: / y y z z 5.7 Tha e all as: y z /, α α l, l y z l Tha ae he fnins ( ) (,,, ) (, y, z, ) Tha in he sybli f is ien: α. in he inee f α l l l α eing (.7), (.8) an. (.). l l 5. The ansfain aies α α ij an α l α hae he ppeies: / / α. α αijα l αijα jl I δ j α α α jiα l α jiα i I δ i / / i l j Whee α α ji is he anspse ai f α ij δ is he nee s ela. α an α α l is he anspse ai f α α l an / / α. α α l αij α l α lj I δ j l 5. 9/
40 α α α l α ji α l α i I δ / / l i 5. Whee α α l is he anspse ai f α l an δ is he nee s ela. Obseain: he aies an α α. ij The paial eiaies l α ij an i i j elae aing ( ) nsiee nsan an eqal : l α an α α ji is he anspse ai f α α ij α α α ae inese f ne anhe b ae n hgnal, ha is: ji l i i i j f he al iffeenial f he inae pnens ha j j, hee in he ansfain ai α α ij he aial is Table, paial eiaies f he inae pnens: i j j i j j i j j i j j The al iffeenial f he inaes in he ai f is eqal : / 5.5 Tha e all as: i, i j i j /, j 5.6 i i Then e hae j j j i i j j 5.7 The paial eiaies elae aing nsiee nsan an eqal : l f he al iffeenial f he inae pnens ha l l l, hee in he ansfain ai α α l he aial is /
41 Table paial eiaies f he inae pnens: l l l l l l l l The al iffeenial f he inaes in he ai f is eqal : / 5.8 Tha e all as:, l l /, l 5.9 Then e hae: l l l l l 5. The Jabians f he ansfains 5.5 an 5.8 ae: J J l i j (,,, ) (,,, ) (,,, ) (,,, ) / / Whee (.5), (.6) an. (.). The aies f he ansfain an aies α an α. als hae he ppeies 5., 5., 5. an 5. f he l l he fnin ( ) [ ( )] hee he inaes elae in he f ( ) hae esibe as: l l e /
42 / Tha in he ai f an ih pesening he fnin bees: l Whee eplaing he ies bel: Obseain: his las elain shs ha he ie aies in an eqal f beeen he efeenials. We ge: l Tha is he gp 8. pls 8. f he able 9, iffeenial peas, in he ai f. he fnin [ ] j i i hee he inaes elae in he f j i i e hae j i i j esibe as:
43 / i i i i i i i i Tha in he ai f an ih pesening he fnin bees: j Whee eplaing he ies bel: Obseain: his las elain shs ha he ie aies in an eqal f beeen he efeenials. We ge: j Tha is he gp 8. pls 8. f he able 9, iffeenial peas in he ai f. pplying 8.5 in 8. an in 8. e siplify hese eqains in he flling ay:
44 Table 9, iffeenial peas ih he eqains 8. an 8. siplifie: ze ze The able 9, in he ai f bees: 5. / 5. / The sqae aies f he ansfains abe ae anspse f he aies an. Inaiane f he Tal iffeenial In he bsee O efeenial he al iffeenial f a fnin ( ) is eqal : ( ) 5.5 l Whee he inaes elae ih he nes f he bsee O aing ( ) ansfains 5. an 5.8 an ih pesening he fnin e hae:, eplaing he / 5.6 / The lipliain f he ile aies spplies: / / / / 5.7 Resl ha an be iie in aies: / / / / 5.8 /
45 Tha applie he al iffeenial spplies: / 5.9 / eing he peains f he sen e e hae: / Whee applying 8.5 e hae: / ( ) ze Then e hae: / / ze 5. Wih his esl e hae in 5.9 he inaiane f he al iffeenial: l l In he bsee O efeenial he al iffeenial f a fnin ( i ) is eqal : 5. i i ( ) 5. i i i j Whee he inaes elae ih he nes f he bsee O efeenial aing ( ), eplaing he ansfains 5. an 5.5 an ih pesening he fnin e hae: / i 5. i / The lipliain f he ile aies spplies: / / / / 5. Resl ha an be iie in aies: 5/
46 6/ / / / / 5.5 Tha applie he al iffeenial spplies: / / i i 5.6 eing he peains f he sen e e hae: / / Whee applying 8.5 e hae: ze Then e hae: ze / / 5.7 Wih his esl e hae in 5.6 he inaiane f he al iffeenial: j j i i 5.8 Inaiane f he Wae qain The ae eqain he bsee O is eqal : 5.9 Whee applying 5. an he anspse f 5. e hae:
47 5. The lipliain f he hee ile aies spplies: 5. Resl ha an be iie in aies: 5. Tha applie in he ae eqain spplies: 5. eing he peains f he sen e e hae: eing he peains e hae: ( ) Whee applying 8.5 e hae: ( ) Then e hae: ( ) ze ( ) 7/
48 8/ ze 5. Wih his esl e hae in 5. he inaiane f he ae eqain: 5.5 The ae eqain he bsee O is eqal : 5.6 Whee applying 5. an he anspse f 5. e hae: 5.7 The lipliain f he hee ile aies spplies: 5.8 Resl ha an be iie in aies: 5.9 Tha applie in he ae eqain spplies:
49 9/ 5.5 eing he peains f he sen e e hae: eing he peains e hae: Whee applying 8.5 e hae: ze Then e hae: ze 5.5 Then in 5.5 e hae he inaiane f he ae eqain: 5.5 Inaiane f he eqains 8.5 f linea ppagain Replaing., 8., 8. in 8.5 e hae: ze eing he peains e hae: ze
50 Tha siplifie spplies he inaiane f he eqain 8.5: ze Replaing., 8., 8. in 8.5 e hae: ze eing he peains e hae: ze Tha siplifie spplies he inaiane f he eqain 8.5: ze The able in a ai f bees: p / p p p p 5.5 p / / p / p p p p 5.5 p / / The able 6 in a ai f bees: J / J J J J J ρ ρ J / J J J J J ρ ρ Inaiane f he Cniniy qain The niniy eqain he bsee O is eqal : J ρ J J J ρ. J J ze J ρ 5.57 Whee eplaing 5. an 5.56 e hae: / J ρ. J J ze J / ρ /
51 The p f he ansfain aies is gien in 5.7 an 5.8 ih his: ρ.j / / J J J ρ 5.59 eing he peains f he sen e e hae: / ρ / J J J J ρ Whee eplaing J an 8.5 e hae: ( ) ρ ze ρ ρ Then e hae: ρ ρ / / J J J ze ρ 5.6 Wih his esl e hae in 5.59 he inaiane f he niniy eqain: ρ.j J J ρ.j J ρ 5.6 The niniy eqain he bsee O is eqal : J ρ J J J ρ. J J ze J ρ Whee eplaing 5. an 5.55 e hae: / J ρ. J J ze J / ρ The p f he ansfain aies is gien in 5. an 5.5 hen e hae: ρ J / / J J J ρ. 5.6 eing he peains f he sen e e hae: 5/
52 / J J J ρ J / ρ ρ Whee eplaing J an 8.5 e hae: ( ) ρ ze ρ ρ ρ Then e hae: / J J ze J / ρ 5.65 Wih his esl e hae in 5.6 he inaiane f he niniy eqain: ρ.j J J ρ.j J ρ 5.66 Inaiane f he line iffeenial eleen: Tha he bsee O is ien his ay: ( s ) ( ) ( ) ( ) ( ) [ ] Whee eplaing 5.8 an he anspse f 5.8 e hae: 5.67 s 5.68 [ ] The lipliain f he hee enal aies spplies: 5.69 Resl ha an be iie in aies: 5.7 Tha applie in he line iffeenial eleen spplies: 5/
53 s 5.7 [ ] eing he peains f he sen e e hae: [ ] ze Then e hae: [ ] ze 5.7 Wih his esl e hae in 5.7 he inaiane f he line iffeenial eleen: 5.7 ( s ) [ ] ( ) ( ) ( ) ( ) ( s ) T he bsee O he line iffeenial eleen is ien his ay: ( s ) ( ) ( ) ( ) ( ) [ ] Whee eplaing 5.5 an he anspse f 5.5 e hae: 5.7 s 5.75 [ ] The lipliain f he hee enal aies spplies: 5.76 Resl ha an be iie in aies: /
54 Tha applie in he line iffeenial eleen spplies: s 5.78 [ ] eing he peains f he sen e e hae: [ ] ze Then e hae: [ ] ze 5.79 Wih his esl e hae in 5.78 he inaiane f he line iffeenial eleen: 5.8 ( s ) [ ] ( ) ( ) ( ) ( ) ( s) In 7 as a nseqene f 5. e ha he inaiane f.. hee n applying 7.., 7.., 7.., 7.. an he eliy ansfain flae f able e hae ne elains beeen an isin f 7. an 7. an ih he e eie he able 7 in he f bel: Table 7 y y y y z z 7.. z z y y z y y z z z y z z y y z y z z y z y Wih he ables 7 an 9 e an hae he inaiane f all Maell s eqains. 5/
55 Inaiane f he Gass a f he eleial fiel: y z y z ρ 8. Whee applying he ables 6, 7 an 9 e hae: y z ρ ( /) y z Whee siplifying an eplaing 8.5 e hae: Tha eee spplies: y z ρ ( / ) y z y z ρ ( / ) y z Tha siplifie spplies he inaiane f he Gass a f he eleial fiel. Inaiane f he Gass a f he agnei fiel:. y z ze y z 8.6 Whee applying he ables 7 an 9 e hae: y y Tha eee spplies: z z z y z z y y z y z y Whee he e in paenhesis is he aaay-eny s a (8.9) ha is eqal ze f hee e hae he inaiane f he Gass a f he agnei fiel. Inaiane f he aaay-eny s a: y z y 8.8 Whee applying he ables 7 an 9 e hae: y y ( /) z Tha siplifie an liplie by ( /) e hae: y z y y Whee eeing he ps an eplaing 7.9. e hae: 55/
56 y z y y y s he e in paenhesis is he eqain 8.5 ha is eqal ze hen e hae he inaiane f he aaay-eny s a. Inaiane f he aaay-eny s a: z y y z 8. Whee applying he ables 7 an 9 e hae: z y y z Tha siplifie spplies he inaiane f he aaay-eny s a. Inaiane f he aaay-eny s a: z y z 8. Whee applying he ables 7 an 9 e hae: ( / ) z y z Tha siplifie an liplie by ( /) e hae: z z z y Tha siplifying an aing he peains e hae: z y z Whee applying 7.9 e hae: z y z z y z z. z z s he e in paenhesis is he eqain 8.5 ha is eqal ze hen e hae he inaiane f he aaay-eny s a. Inaiane f he pee-maell s a: y y z J z µ µ 8. Whee applying he ables 6, 7 an 9 e hae: y z µ Jz µ y z Tha siplifying an aing he peains e hae: 56/
57 57/ z y z z z z Jz y y µ µ Whee siplifying an applying 7.9 e hae: z z z z Jz y y µ µ Tha eganize spplies z z z Jz y y µ µ s he e in paenhesis is he eqain 8.5 ha is eqal ze hen e hae he inaiane f he pee-maell s a: Inaiane f he pee-maell s a: J z y y z µ µ 8.6 Whee applying he ables 6, 7 an 9 e hae: / J z y z y z y µ ρ µ Maing he peains e hae: / z z y y J z y y z µ ρ µ µ Replaing in he fis paenhesis he Gass a an liplying by e hae: J z y y z J z y y z µ µ µ Whee eplaing J ρ, 7.9., 7.9 an 8.5 e hae: z z y y J z y y z ρ µ µ µ Tha siplifie spplies: z z y y J z y y z ρ µ µ µ Replaing in he fis paenhesis he Gass a e hae: J z y y z µ µ Tha eganize aes: J z y y z µ µ
58 s he e in paenhesis is he eqain 8.5 ha is eqal ze hen e hae he inaiane f he pee-maell s a: Inaiane f he pee-maell s a: z y µ J y µ 8.8 z Whee applying he ables 6, 7 an 9 e hae: z z Maing he peains e hae: y µ Jy µ y z y µ Jy µ z y Whee siplifying an applying 7.9. e hae: z y µ Jy µ z Tha eganize aes: y z y y y µ Jy µ z y y y y z s he e in paenhesis is he eqain 8.5 ha is eqal ze hen e hae he inaiane f he pee-maell s a: Inaiane f he Gass a f he eleial fiel ih eleial hage: y y z ze y z 8. Whee applying he ables 7 an 9 e hae: ( / ) y z y z ze Whee siplifying an eplaing 8.5 e hae: ( / ) Tha eganize aes: ( / ) y z ze y z y z ze y z. Tha siplifie spplies he Gass a f he eleial fiel ih eleial hage. 58/
59 Inaiane f he pee-maell s a ih eleial hage: y y z µ 8. Whee applying he ables 7 an 9 e hae: y z µ y Maing he peains e hae: z y z µ y z Whee siplifying an applying 7.9 e hae: y z µ y Tha eganize aes: z y z z z y µ z z z z y s he e in paenhesis is he eqain 8.5 ha is eqal ze hen e hae he inaiane f he pee-maell s a ih eleial hage: Inaiane f he pee-maell s a ih eleial hage: z y y z µ z 8. Whee applying he ables 7 an 9 e hae: z y y y z z µ ( / ) Maing he peains e hae: z y y z y z y z µ ( / ) Replaing in he fis paenhesis he Gass a ih eleial hage an liplying by ( / ) hae: z y µ y z z y y z Whee eplaing 7.9, 7.9. an 8.5 e hae: z y µ y z Tha siplifie spplies: y z y z e 59/
60 6/ z z y y z y y z µ Replaing in he fis paenhesis he Gass a ih eleial hage e hae: z y y z µ Tha eganize aes: J z y y z µ µ s he e in paenhesis is he eqain 8.5 ha is eqal ze hen e hae he inaiane f he pee-maell s a ih eleial hage: Inaiane f he pee-maell s a ih eleial hage: y z z µ 8. Whee applying he ables 6, 7 an 9 e hae: y y z z µ Maing he peains e hae: y z y y y y z z µ Whee siplifying an applying 7.9. e hae: y y y y z z µ Tha eganize aes: y y y z z µ s he e in paenhesis is he eqain 8.5 ha is eqal ze hen e hae he inaiane f he pee-maell s a ih eleial hage: 5 Inaiane (ninain) fnin f f θ.9 Whee he phase is eqal θ 5.8 In e epesen an nlaing een ha ges n in ne abiay iein s ply ih he ae eqain an bease f his e hae: ze f f z y f z y θ θ θ θ θ θ 5.8 Tha esn ee ih he ae eqain bease he las eleens ge nle b he fis ne esn.
61 In e ee his pble e eflae he phase θ f he fnin in he flling ay. niay e sh as n s i sαj s β 5.8 hee s, y y s α, z z s β 5.8 has he le eqal n n n.n s s α s β Maing he p y z ( si sαj sβ )(. i yj z ) s sαy sβz n.r e hae n.r s sαy s βz Φ ( ) ( n.r ) ( s sαy s βz ) ha applie he phase θ spplies a ne phase ih he sae eaning f he peis phase θ Φ. Replaing phase in he f n.r s sαy s βz e in he phase θ liplie by e als ge anhe Φ s sαy s βz 5.88 θ. ih he sae eaning f he peis phase Φ Ths e an ie a ne fnin as: f s sαy sβz ( Φ) f 5.89 Tha eplae in he ae eqain ih he ie sine nsiee nsan spplies: f Φ ( Φ) f ( Φ) f ( Φ) f ( Φ) s s α s β ze 5.9 Φ Φ Φ ha siplifie ees he ae eqain. The psiie esl f he phase Φ in he ae eqain is an elsie nseqene f he ie sines being nsan in he paial eiaies shing ha he ae eqain eans he ppagain hae ne seay iein in he spae (plane ae). he bsee O a se lae in he igin f is efeenial pes in a an pin lae a he isane y z f he igin, an eleial fiel esibe by: i yj z 5.9 6/
62 Whee he pnens ae esibe as: y z y z. f. f. f ( Φ) ( Φ) ( Φ) 5.9 Tha applie in spplies: f f ( Φ) i f ( Φ) j f ( Φ) [ i j ] f ( Φ) ( Φ) y z ih le eqal ( ) ( ) ( ).f ( Φ). f ( Φ) eing y z y z i j 5.95 y z The ai aplie e Cnsan ih he pnens, y, z 5.96 n le y z 5.97 eing f ( Φ) a fnin ih he phase Φ eqal eiing he pnen in elain an e hae: ( Φ) Φ f ( Φ) f ( Φ) f ( Φ) f Φ Φ Φ ( Φ) Φ f ( Φ) f ( Φ) ( ) f Φ Φ Φ Φ ha applie in 8.5 spplies ( Φ) Φ / f ( Φ) Φ f ( Φ) / f Φ / Φ ze ze ze Φ Φ Φ ( Φ) f Φ / Φ Φ / Φ ze ze Φ ensaing ha i is he phase Φ ha s ply ih 8.5. Φ as / Φ ze ( ) / ( ) hen plies ih 8.5. ze / 5. ( ) ze ze s he phase is he sae f he pnens y an z hen hey als ply ih 8.5. s he phases f he bsees O an O ae eqal ( ) ( ) bsee O als ply ih 8.5. / ( ) / ( ) hen he pnens f he ze 5. 6/
63 The pnens elaiely he bsee O f he eleial fiel ae ansfe f he efeenial f he bsee O aing he ables 7, 7 an 8. pplying in 8.5 a ae fnin ien in he f: Ψ e ( ) iφ e ( ) i ( ) Φ i Φ i s sin s sin 5. hee i. eiing e hae: Ψ senφ is Φ en Ψ senφ i s Φ 5. Ψ e iφ an Ψ e iφ 5. Tha applie in 8.5 spplies: Ψ / Ψ ze / ( senφ i sφ) ( senφ i sφ) ze ha is eqal : i sin Φ i sφ ze Ψ / Ψ iφ / ze e e ze hee e s hae he effiiens eqal ze s ha e ge na ieniy, hen: ze i i ze iφ / iφ ( e ) ( e ) ze iφ Whee applying e hae: Then ee ih he eqain 8.5 e s hae a ae ppagain alng he ais ih he spee. If e apply an e hae:. esl als gen f he is e glie s ae eqain. 6/
64 Cnsieing he pple effe as a la f physis. 6 Tie an eqeny We an efine a l as any eie ha pes a feqeny f ienial eens in a seies pssible be enlise an ae in sh a ay ha a an een n f a eie ill be ienial any een in he seies f eens pe by a eplia f his eie hen he eens ae pae in a elaie esing psiin. The ylial een f a l in a esing psiin aing he bsee O efeenial ses he ie in his efeenial an he ylial een f he as f a l in a esing psiin aing he bsee O ses he ie in his efeenial. The flas f ie ansfain.7 an.8 elae he ies beeen he efeenials in elaie een hs, elae eens in elaie een. The elaie een beeen he ineial efeenials pes he pple effe ha pes ha he feqeny aies ih eliy an as he feqeny an be inepee as being he feqeny f he ylial een f he as f a l hen he ie aies in he sae ppin ha aies he feqeny ih he elaie een ha is, i is engh eplae he ie an in he flas.7 an.8 by he feqenies y an y ge he flas f feqeny ansfain, hen: y y.7 bees. y y.8 bees. The Galile s ansfain f eliies beeen ineial efeenials pesens ininsially hee efes ha an be esibe his ay: a) The Galile s ansfain f eliy he ais is. In ha ne if e hae hen an if e hae hen. s bh esls ae n silanesly pssible else e hae hen he ansfain esn all ha a ay f ligh be silanesly bsee by he bsees O an O ha shs he piilege f an bsee in elain he he bease eah bsee an nly see he ay f ligh nning in is n efeenial (ininsi efe he lassi analysis f he Sagna s effe). b) I ann als ply Nen s fis la f ineia bease a ay f ligh eie paallel he ais f he igin f he espeie ineial efeenials a he en ha he igins ae inien an a he en in hih ze ill hae by he Galile s ansfain he eliy f ligh alee by ± he efeenials, n he nay f he ineial la ha ln all he eisene f a aiain in eliy bease hee is n eenal ain aing n he ay f ligh an bease f his bh bsees shl see he ay f ligh ih eliy. ) s i nsies he ie as a nsan beeen he efeenials i esn pe he epal aiain beeen he efeenials in een as i is eqie by he pple effe. The piniple f nsany f ligh eliy is nhing b a eqieen f he Nen s fis la, he ineia la. Nen s fis la, he ineia la, is ine in Galile s ansfain hen he piniple f nsany f ligh eliy is applie in Galile s ansfain piing he eqain f ables an f he Unlaing Relaiiy ha esn hae he hee efes esibe. The ie an eliy eqains f ables an an be ien as: s.7.5 s 6/
65 s.8. s The isane beeen he efeenials is eqal he p f eliy by ie his ay:.9 I esn epen n he ppagain angle f he ay f ligh, being elsiely a fnin f eliy an ie, ha is, he ppagain angle f he ay f ligh, nly ales beeen he ineial efeenial he ppin beeen ie an eliy, eeping he isane nsan in eah en, any ppagain angle. The eqains abe in a fnin f ae ien as: (,) e (, ) e.9 (,, ) f.7 (, ) (,, ) g.5 f.8 (, ) g. Then e hae ha he isane is a fnin f aiables, he ie a fnin f hee aiables an he eliy a fnin f aiables. he efiniin f en. an enegy.6 e hae: p 6. The eleae he pe f spplies: p 6. leaing he pe f he enegy fla e hae: Whee applying 6. e hae: p p.8 hee e nle ha if he ass in esing psiin f a paile is nll ze he paile enegy is eqal p /
66 Tha applie in 6. spplies: p p 6. ( p) hee e nle ha he een f a paile ih a nll ass in esing psiin alays be a he eliy f ligh. ze ill pplying in p he elains yh an yλ e hae: yh yλp p h an in he sae ay λ p h λ 6.5 qain ha elaes he en f a paile ih a nll ass in esing psiin ih is n ay lengh. leaing he pe f he fla f en ansfain (.9) e hae: p p p p p Whee applying p an p ps p e fin: ( p) p p p p p p p p 6.6 Whee applying 6.5 esls in: h h λ λ p p λ inee λ. λ λ Whee applying yλ an yλ e hae: y y inee y y. In e hae he eqains. an. applying he piniple f elaiiy he ae phase. 7 Tansfain f. enz bsees in a elaie een, he eqain ha epesens he piniple f nsany f ligh spee f a an pin is: 7. y z y z In his eqain aneling he syei es e hae: Nesa anelan s es siéis bes: 7. Tha e an ie as: ( )( ) ( )( ) 7. If in his eqain e efine he ppin fas η an µ as: ( ) η( ) ( ) µ ( ) 66/ 7.
67 67/ hee e s hae µ η. ply 7.. The eqains 7. hee fis gen by lbe insein. When a ay f ligh es in he plane y z he bsee O e hae ze an an sh niins applie he eqain 7. spplies: 7.5 This esl ill als be spplie by he eqains an f he gp 7. ne he sae niins: µ η 7.6 hse e hae: η an µ 7.7 Whee e hae pen ha µ η.. he gp 7. e hae he Tansfains f. enz: η µ µ η 7.8 µ η η µ 7.9 µ η µ η 7. µ η µ η 7. Inees eqains µ η, η µ an µ η : µ η µ η 7. η µ η µ 7. µ η µ η 7.
68 Sagna effe When bh bsees igins ae eqal he ie is zee ( ze) in bh efeenials an ays f ligh ae eie f he n igin, ne in he psiie iein (lise ine ) f he ais an ih a ae fn an anhe in he negaie iein (ne-lise ine ) f he ais an ih a ae fn. The ppagain niins abe applie he enz eqains spply he ables an bel: Table qain Clise ay () qain Cne-lise ay () S f ays Resl Resl Cniin Cniin Table µ η µ η µ 7.9 η µ η µ η qain Clise ay () qain Cne-lise ay () S f ays Resl Resl Cniin Cniin 7. η 7. µ η µ η µ 7. η 7. µ η µ We bsee ha he ables an ae inese ne anhe. When e f he gp f he s eqains f he ays f ables an : µ η η µ 7.5 Whee he bsee O is he isane beeen he fn aes an an hee he bsee O is he isane beeen he fn aes an. f he In he eqains 7.5 abe, e he ispy f spae an ie an he fn aes ays f ligh being he sae f bh bsees, he s f ays f ligh e ies s be inaiable beeen he bsees, hih e an epess by: 7.6 This esl ha geneaes an eqain f ispy f spae an ie an be alle as he nseain f spae an ie piniple. The hee hyphesis f ppagain efine as flls ill be applie in 7.5 an ese pe he nseain f spae an ie piniple gien by 7.6: 68/
69 yphesis : If he spae an ie ae ispi an hee is n een ih n piilege f ne bsee nsiee e he he in an epy spae hen he ppagain geey f ays f ligh an be gien by: an 7.7 This hyphesis applie he eqain f he gp 7.5 plies he spae an ie nseain piniple gien by 7.6. The hyphesis 7.7 applie he ables an esls in: µ a η a yphesis : η µ C 7.8 If he spae an ie ae ispi b he bsee O is in an absle esing psiin in an epy spae hen he geey f ppagain f he ays f ligh is gien by: 7.9 Tha applie he able an esls in: a µ η η a µ µ η Sing an in 7. e hae: C η µ η µ i This esl esn ply ih he nseain f spae an ie piniple gien by 7.6 an as esls in a siain f f ays f ligh, eah bsee, an eah ay f ligh ih is espeie inepenen fn ae f he hes. yphesis C: If he spae an ie ae ispi b he bsee O is in an absle esing psiin in an epy spae hen he ppagain geey f he ays f ligh is gien: 7. Tha applie he ables an esls in: a a µ η η µ C 7. η µ /
Undulating Relativity ABSTRACT
 Unling Relii h: lfe is Mei Gi -il: li@sj.sp.g.b STRCT The Speil The f Relii es s esls h pesenl e nsiee ineplible n enne sieniss, n: -The ilin f ie, n -The nin f he enz engh. The slin hese he ien he h he
Unling Relii h: lfe is Mei Gi -il: li@sj.sp.g.b STRCT The Speil The f Relii es s esls h pesenl e nsiee ineplible n enne sieniss, n: -The ilin f ie, n -The nin f he enz engh. The slin hese he ien he h he
Undulating Relativity ABSTRACT
 Unling Relii h: lfe is Mei Gi -il: li@sj.sp.g.b STRCT The Speil The f Relii es s esls h pesenl e nsiee ineplible n enne sieniss, n: -The ilin f ie, n -The nin f he enz engh. The slin hese he ien he h he
Unling Relii h: lfe is Mei Gi -il: li@sj.sp.g.b STRCT The Speil The f Relii es s esls h pesenl e nsiee ineplible n enne sieniss, n: -The ilin f ie, n -The nin f he enz engh. The slin hese he ien he h he
5. Differential Amplifiers
 5. iffeential plifies eain: Sea & Sith: Chapte 8 MOS ptins an Chapte.. ECE, Winte, F. Najabai iffeential an Cn-Me Sinals Cnsie a linea iuit with TWO inputs By supepsitin: efine: iffeene iffeential Me Cn
5. iffeential plifies eain: Sea & Sith: Chapte 8 MOS ptins an Chapte.. ECE, Winte, F. Najabai iffeential an Cn-Me Sinals Cnsie a linea iuit with TWO inputs By supepsitin: efine: iffeene iffeential Me Cn
Coupled Mass Transport and Reaction in LPCVD Reactors
 ople Ma Tanpo an eaion in LPV eao ile A in B e.g., SiH 4 in H Sepaae eao ino o egion, inaafe & annla b - oniniy Eqn: : onveion-iffion iffion-eaion Eqn Ampion! ile peie i in majo aie ga e.g., H isih 4!
ople Ma Tanpo an eaion in LPV eao ile A in B e.g., SiH 4 in H Sepaae eao ino o egion, inaafe & annla b - oniniy Eqn: : onveion-iffion iffion-eaion Eqn Ampion! ile peie i in majo aie ga e.g., H isih 4!
ÖRNEK 1: THE LINEAR IMPULSE-MOMENTUM RELATION Calculate the linear momentum of a particle of mass m=10 kg which has a. kg m s
 MÜHENDİSLİK MEKANİĞİ. HAFTA İMPULS- MMENTUM-ÇARPIŞMA Linea oenu of a paicle: The sybol L denoes he linea oenu and is defined as he ass ies he elociy of a paicle. L ÖRNEK : THE LINEAR IMPULSE-MMENTUM RELATIN
MÜHENDİSLİK MEKANİĞİ. HAFTA İMPULS- MMENTUM-ÇARPIŞMA Linea oenu of a paicle: The sybol L denoes he linea oenu and is defined as he ass ies he elociy of a paicle. L ÖRNEK : THE LINEAR IMPULSE-MMENTUM RELATIN
Relative and Circular Motion
 Relaie and Cicula Moion a) Relaie moion b) Cenipeal acceleaion Mechanics Lecue 3 Slide 1 Mechanics Lecue 3 Slide 2 Time on Video Pelecue Looks like mosly eeyone hee has iewed enie pelecue GOOD! Thank you
Relaie and Cicula Moion a) Relaie moion b) Cenipeal acceleaion Mechanics Lecue 3 Slide 1 Mechanics Lecue 3 Slide 2 Time on Video Pelecue Looks like mosly eeyone hee has iewed enie pelecue GOOD! Thank you
IrrItrol Products 2016 catalog
 l Ps Valves 205, 200 an 2500 eies Valves M Pa Nmbe -205F 1" n-line E Valve w/ FC - se 2500 eies 3* -200 1" E n-line Valve w/ FC F x F 3-200F 1" n-line Valve w/ FC F x F -2500 1" E Valve w/ FC F x F -2500F
l Ps Valves 205, 200 an 2500 eies Valves M Pa Nmbe -205F 1" n-line E Valve w/ FC - se 2500 eies 3* -200 1" E n-line Valve w/ FC F x F 3-200F 1" n-line Valve w/ FC F x F -2500 1" E Valve w/ FC F x F -2500F
Department of Mathematics, Faculty of Education, Ain Shams University, Roxy, Cairo, Egypt b)
 Ineninl Jnl f Sienifi n Innvive Mheil Reeh (IJSIMR Vle Ie Obe 4 844-854 ISSN 347-37X (in & ISSN 347-34 (Online www.jnl.g lile Min f Nn-Newnin Fli wih He n M nfe hgh Mei in Sli Cylinil ie in he eene f Mgnei
Ineninl Jnl f Sienifi n Innvive Mheil Reeh (IJSIMR Vle Ie Obe 4 844-854 ISSN 347-37X (in & ISSN 347-34 (Online www.jnl.g lile Min f Nn-Newnin Fli wih He n M nfe hgh Mei in Sli Cylinil ie in he eene f Mgnei
A L A BA M A L A W R E V IE W
 A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
11. HAFAT İş-Enerji Power of a force: Power in the ability of a force to do work
 MÜHENDİSLİK MEKNİĞİ. HFT İş-Eneji Pwe f a fce: Pwe in he abiliy f a fce d wk F: The fce applied n paicle Q P = F v = Fv cs( θ ) F Q v θ Pah f Q v: The velciy f Q ÖRNEK: İŞ-ENERJİ ω µ k v Calculae he pwe
MÜHENDİSLİK MEKNİĞİ. HFT İş-Eneji Pwe f a fce: Pwe in he abiliy f a fce d wk F: The fce applied n paicle Q P = F v = Fv cs( θ ) F Q v θ Pah f Q v: The velciy f Q ÖRNEK: İŞ-ENERJİ ω µ k v Calculae he pwe
Classification of Equations Characteristics
 Clssiiion o Eqions Cheisis Consie n elemen o li moing in wo imensionl spe enoe s poin P elow. The ph o P is inie he line. The posiion ile is s so h n inemenl isne long is s. Le he goening eqions e epesene
Clssiiion o Eqions Cheisis Consie n elemen o li moing in wo imensionl spe enoe s poin P elow. The ph o P is inie he line. The posiion ile is s so h n inemenl isne long is s. Le he goening eqions e epesene
Fig. 1S. The antenna construction: (a) main geometrical parameters, (b) the wire support pillar and (c) the console link between wire and coaxial
 a b c Fig. S. The anenna consucion: (a) ain geoeical paaees, (b) he wie suppo pilla and (c) he console link beween wie and coaial pobe. Fig. S. The anenna coss-secion in he y-z plane. Accoding o [], he
a b c Fig. S. The anenna consucion: (a) ain geoeical paaees, (b) he wie suppo pilla and (c) he console link beween wie and coaial pobe. Fig. S. The anenna coss-secion in he y-z plane. Accoding o [], he
Algebra 2A. Algebra 2A- Unit 5
 Algeba 2A Algeba 2A- Ui 5 ALGEBRA 2A Less: 5.1 Name: Dae: Plymial fis O b j e i! I a evalae plymial fis! I a ideify geeal shapes f gaphs f plymial fis Plymial Fi: ly e vaiable (x) V a b l a y a :, ze a
Algeba 2A Algeba 2A- Ui 5 ALGEBRA 2A Less: 5.1 Name: Dae: Plymial fis O b j e i! I a evalae plymial fis! I a ideify geeal shapes f gaphs f plymial fis Plymial Fi: ly e vaiable (x) V a b l a y a :, ze a
β A Constant-G m Biasing
 p 2002 EE 532 Anal IC Des II Pae 73 Cnsan-G Bas ecall ha us a PTAT cuen efeence (see p f p. 66 he nes) bas a bpla anss pes cnsan anscnucance e epeaue (an als epenen f supply lae an pcess). Hw h we achee
p 2002 EE 532 Anal IC Des II Pae 73 Cnsan-G Bas ecall ha us a PTAT cuen efeence (see p f p. 66 he nes) bas a bpla anss pes cnsan anscnucance e epeaue (an als epenen f supply lae an pcess). Hw h we achee
Physics 140. Assignment 4 (Mechanics & Heat)
 Physis 14 Assignen 4 (Mehanis & Hea) This assignen us be handed in by 1 nn n Thursday 11h May. Yu an hand i in a he beginning f he leure n ha day r yu ay hand i yur labrary densrar befrehand if yu ish.
Physis 14 Assignen 4 (Mehanis & Hea) This assignen us be handed in by 1 nn n Thursday 11h May. Yu an hand i in a he beginning f he leure n ha day r yu ay hand i yur labrary densrar befrehand if yu ish.
( t) Steady Shear Flow Material Functions. Material function definitions. How do we predict material functions?
 Rle f aeial Funins in Rhelgial Analysis Rle f aeial Funins in Rhelgial Analysis QUALIY CONROL QUALIAIVE ANALYSIS QUALIY CONROL QUALIAIVE ANALYSIS mpae wih he in-huse daa n qualiaive basis unknwn maeial
Rle f aeial Funins in Rhelgial Analysis Rle f aeial Funins in Rhelgial Analysis QUALIY CONROL QUALIAIVE ANALYSIS QUALIY CONROL QUALIAIVE ANALYSIS mpae wih he in-huse daa n qualiaive basis unknwn maeial
T h e C S E T I P r o j e c t
 T h e P r o j e c t T H E P R O J E C T T A B L E O F C O N T E N T S A r t i c l e P a g e C o m p r e h e n s i v e A s s es s m e n t o f t h e U F O / E T I P h e n o m e n o n M a y 1 9 9 1 1 E T
T h e P r o j e c t T H E P R O J E C T T A B L E O F C O N T E N T S A r t i c l e P a g e C o m p r e h e n s i v e A s s es s m e n t o f t h e U F O / E T I P h e n o m e n o n M a y 1 9 9 1 1 E T
Control Volume Derivation
 School of eospace Engineeing Conol Volume -1 Copyigh 1 by Jey M. Seizman. ll ighs esee. Conol Volume Deiaion How o cone ou elaionships fo a close sysem (conol mass) o an open sysem (conol olume) Fo mass
School of eospace Engineeing Conol Volume -1 Copyigh 1 by Jey M. Seizman. ll ighs esee. Conol Volume Deiaion How o cone ou elaionships fo a close sysem (conol mass) o an open sysem (conol olume) Fo mass
Chapter 6: Maxwell Equations, Macroscopic Electromagnetism, Conservation Laws 6.1 Mawell s Displacement Current; Maxwell Equations
 Chape 6: Mawell Equaions, Maosopi Eleomagneism, Conseaion Laws 6. Mawell s Displaemen Cuen; Mawell Equaions The Displaemen Cuen : o fa, we hae he following se of laws : D,, fee H J fee E, an (6. Taking
Chape 6: Mawell Equaions, Maosopi Eleomagneism, Conseaion Laws 6. Mawell s Displaemen Cuen; Mawell Equaions The Displaemen Cuen : o fa, we hae he following se of laws : D,, fee H J fee E, an (6. Taking
ENGI 4430 Advanced Calculus for Engineering Faculty of Engineering and Applied Science Problem Set 9 Solutions [Theorems of Gauss and Stokes]
![ENGI 4430 Advanced Calculus for Engineering Faculty of Engineering and Applied Science Problem Set 9 Solutions [Theorems of Gauss and Stokes] ENGI 4430 Advanced Calculus for Engineering Faculty of Engineering and Applied Science Problem Set 9 Solutions [Theorems of Gauss and Stokes]](/thumbs/91/106162145.jpg) ENGI 44 Avance alculus fo Engineeing Faculy of Engineeing an Applie cience Poblem e 9 oluions [Theoems of Gauss an okes]. A fla aea A is boune by he iangle whose veices ae he poins P(,, ), Q(,, ) an R(,,
ENGI 44 Avance alculus fo Engineeing Faculy of Engineeing an Applie cience Poblem e 9 oluions [Theoems of Gauss an okes]. A fla aea A is boune by he iangle whose veices ae he poins P(,, ), Q(,, ) an R(,,
A NEW PRINCIPLE FOR ELIMINATION OF APPLIED DEFECTS IN THE RELATIVITY THEORY. Kexin Yao
 A NEW PRINIPLE FOR ELIINATION OF APPLIED DEFETS IN THE RELATIITY THEORY Kexin Yao Addess: Roo -7- Xi an Insiue of eology N0. Laodong Souh Road Xian P.R.hina 70068 ABSTRAT: This pape pus fowad he foe equilibiu
A NEW PRINIPLE FOR ELIINATION OF APPLIED DEFETS IN THE RELATIITY THEORY Kexin Yao Addess: Roo -7- Xi an Insiue of eology N0. Laodong Souh Road Xian P.R.hina 70068 ABSTRAT: This pape pus fowad he foe equilibiu
Millennium Theory Equations Original Copyright 2002 Joseph A. Rybczyk Updated Copyright 2003 Joseph A. Rybczyk Updated March 16, 2006
 Millennim heoy Eqaions Oiginal Copyigh 00 Joseph A. Rybzyk Updaed Copyigh 003 Joseph A. Rybzyk Updaed Mah 6, 006 Following is a omplee lis o he Millennim heoy o Relaiviy eqaions: Fo easy eeene, all eqaions
Millennim heoy Eqaions Oiginal Copyigh 00 Joseph A. Rybzyk Updaed Copyigh 003 Joseph A. Rybzyk Updaed Mah 6, 006 Following is a omplee lis o he Millennim heoy o Relaiviy eqaions: Fo easy eeene, all eqaions
Sections 3.1 and 3.4 Exponential Functions (Growth and Decay)
 Secions 3.1 and 3.4 Eponenial Funcions (Gowh and Decay) Chape 3. Secions 1 and 4 Page 1 of 5 Wha Would You Rahe Have... $1million, o double you money evey day fo 31 days saing wih 1cen? Day Cens Day Cens
Secions 3.1 and 3.4 Eponenial Funcions (Gowh and Decay) Chape 3. Secions 1 and 4 Page 1 of 5 Wha Would You Rahe Have... $1million, o double you money evey day fo 31 days saing wih 1cen? Day Cens Day Cens
Lecture 4. Electric Potential
 Lectue 4 Electic Ptentil In this lectue yu will len: Electic Scl Ptentil Lplce s n Pissn s Eutin Ptentil f Sme Simple Chge Distibutins ECE 0 Fll 006 Fhn Rn Cnell Univesity Cnsevtive Ittinl Fiels Ittinl
Lectue 4 Electic Ptentil In this lectue yu will len: Electic Scl Ptentil Lplce s n Pissn s Eutin Ptentil f Sme Simple Chge Distibutins ECE 0 Fll 006 Fhn Rn Cnell Univesity Cnsevtive Ittinl Fiels Ittinl
Transient Radial Flow Toward a Well Aquifer Equation, based on assumptions becomes a 1D PDE for h(r,t) : Transient Radial Flow Toward a Well
 ansien Radial Flw wad a Well Aqife Eqain, based n assmpins becmes a D PDE f h(,) : -ansien flw in a hmgenes, ispic aqife -flly peneaing pmping well & infinie, hiznal, cnfined aqife f nifm hickness, hs
ansien Radial Flw wad a Well Aqife Eqain, based n assmpins becmes a D PDE f h(,) : -ansien flw in a hmgenes, ispic aqife -flly peneaing pmping well & infinie, hiznal, cnfined aqife f nifm hickness, hs
e-hm REPAIR PARTS REPAIR PARTS ReHM R3
 e-hm REPAIR PARTS REPAIR PARTS ReHM R3 TABLE OF CONTENTS Rating Plate..........................................................................................2 A li ati n ene t an n t......................................................................3
e-hm REPAIR PARTS REPAIR PARTS ReHM R3 TABLE OF CONTENTS Rating Plate..........................................................................................2 A li ati n ene t an n t......................................................................3
dm dt = 1 V The number of moles in any volume is M = CV, where C = concentration in M/L V = liters. dcv v
 Mg: Pcess Aalyss: Reac ae s defed as whee eac ae elcy lue M les ( ccea) e. dm he ube f les ay lue s M, whee ccea M/L les. he he eac ae beces f a hgeeus eac, ( ) d Usually s csa aqueus eeal pcesses eac,
Mg: Pcess Aalyss: Reac ae s defed as whee eac ae elcy lue M les ( ccea) e. dm he ube f les ay lue s M, whee ccea M/L les. he he eac ae beces f a hgeeus eac, ( ) d Usually s csa aqueus eeal pcesses eac,
Chapter Finite Difference Method for Ordinary Differential Equations
 Chape 8.7 Finie Diffeence Mehod fo Odinay Diffeenial Eqaions Afe eading his chape, yo shold be able o. Undesand wha he finie diffeence mehod is and how o se i o solve poblems. Wha is he finie diffeence
Chape 8.7 Finie Diffeence Mehod fo Odinay Diffeenial Eqaions Afe eading his chape, yo shold be able o. Undesand wha he finie diffeence mehod is and how o se i o solve poblems. Wha is he finie diffeence
Table of C on t en t s Global Campus 21 in N umbe r s R e g ional Capac it y D e v e lopme nt in E-L e ar ning Structure a n d C o m p o n en ts R ea
 G Blended L ea r ni ng P r o g r a m R eg i o na l C a p a c i t y D ev elo p m ent i n E -L ea r ni ng H R K C r o s s o r d e r u c a t i o n a n d v e l o p m e n t C o p e r a t i o n 3 0 6 0 7 0 5
G Blended L ea r ni ng P r o g r a m R eg i o na l C a p a c i t y D ev elo p m ent i n E -L ea r ni ng H R K C r o s s o r d e r u c a t i o n a n d v e l o p m e n t C o p e r a t i o n 3 0 6 0 7 0 5
ME 3560 Fluid Mechanics
 ME3560 Flid Mechanics Fall 08 ME 3560 Flid Mechanics Analsis of Flid Flo Analsis of Flid Flo ME3560 Flid Mechanics Fall 08 6. Flid Elemen Kinemaics In geneal a flid paicle can ndego anslaion, linea defomaion
ME3560 Flid Mechanics Fall 08 ME 3560 Flid Mechanics Analsis of Flid Flo Analsis of Flid Flo ME3560 Flid Mechanics Fall 08 6. Flid Elemen Kinemaics In geneal a flid paicle can ndego anslaion, linea defomaion
Notes on Inductance and Circuit Transients Joe Wolfe, Physics UNSW. Circuits with R and C. τ = RC = time constant
 Nes n Inducance and cu Tansens Je Wlfe, Physcs UNSW cus wh and - Wha happens when yu clse he swch? (clse swch a 0) - uen flws ff capac, s d Acss capac: Acss ess: c d s d d ln + cns. 0, ln cns. ln ln ln
Nes n Inducance and cu Tansens Je Wlfe, Physcs UNSW cus wh and - Wha happens when yu clse he swch? (clse swch a 0) - uen flws ff capac, s d Acss capac: Acss ess: c d s d d ln + cns. 0, ln cns. ln ln ln
UIUC Physics 436 EM Fields & Sources II Fall Semester, 2015 Lect. Notes 14 Prof. Steven Errede LECTURE NOTES 14
 UIUC Physis 46 EM Fields & Sues II Fall Semese, 05 Le. Nes 4 Pf. Seven Eede LECTURE NOTES 4 EM RADIATION FROM AN ARBITRARY SOURCE: We nw apply he fmalism/mehdlgy ha we have develped in he pevius leues
UIUC Physis 46 EM Fields & Sues II Fall Semese, 05 Le. Nes 4 Pf. Seven Eede LECTURE NOTES 4 EM RADIATION FROM AN ARBITRARY SOURCE: We nw apply he fmalism/mehdlgy ha we have develped in he pevius leues
H STO RY OF TH E SA NT
 O RY OF E N G L R R VER ritten for the entennial of th e Foundin g of t lair oun t y on ay 8 82 Y EEL N E JEN K RP O N! R ENJ F ] jun E 3 1 92! Ph in t ed b y h e t l a i r R ep u b l i c a n O 4 1922
O RY OF E N G L R R VER ritten for the entennial of th e Foundin g of t lair oun t y on ay 8 82 Y EEL N E JEN K RP O N! R ENJ F ] jun E 3 1 92! Ph in t ed b y h e t l a i r R ep u b l i c a n O 4 1922
Sharif University of Technology - CEDRA By: Professor Ali Meghdari
 Shaif Univesiy of echnology - CEDRA By: Pofesso Ali Meghai Pupose: o exen he Enegy appoach in eiving euaions of oion i.e. Lagange s Meho fo Mechanical Syses. opics: Genealize Cooinaes Lagangian Euaion
Shaif Univesiy of echnology - CEDRA By: Pofesso Ali Meghai Pupose: o exen he Enegy appoach in eiving euaions of oion i.e. Lagange s Meho fo Mechanical Syses. opics: Genealize Cooinaes Lagangian Euaion
Codewords and Letter Logic Samples
 odewords and Letter Logic amples yndicated Puzzles Inc, 2014 odewords Numbers are substituted for letters in the crossword grid. o the right of the grid is the key with two letters solved. ry to complete
odewords and Letter Logic amples yndicated Puzzles Inc, 2014 odewords Numbers are substituted for letters in the crossword grid. o the right of the grid is the key with two letters solved. ry to complete
4/3/2017. PHY 712 Electrodynamics 9-9:50 AM MWF Olin 103
 PHY 7 Eleodnais 9-9:50 AM MWF Olin 0 Plan fo Leue 0: Coninue eading Chap Snhoon adiaion adiaion fo eleon snhoon deies adiaion fo asonoial objes in iula obis 0/05/07 PHY 7 Sping 07 -- Leue 0 0/05/07 PHY
PHY 7 Eleodnais 9-9:50 AM MWF Olin 0 Plan fo Leue 0: Coninue eading Chap Snhoon adiaion adiaion fo eleon snhoon deies adiaion fo asonoial objes in iula obis 0/05/07 PHY 7 Sping 07 -- Leue 0 0/05/07 PHY
P a g e 5 1 of R e p o r t P B 4 / 0 9
 P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
I N A C O M P L E X W O R L D
 IS L A M I C E C O N O M I C S I N A C O M P L E X W O R L D E x p l o r a t i o n s i n A g-b eanste d S i m u l a t i o n S a m i A l-s u w a i l e m 1 4 2 9 H 2 0 0 8 I s l a m i c D e v e l o p m e
IS L A M I C E C O N O M I C S I N A C O M P L E X W O R L D E x p l o r a t i o n s i n A g-b eanste d S i m u l a t i o n S a m i A l-s u w a i l e m 1 4 2 9 H 2 0 0 8 I s l a m i c D e v e l o p m e
Today - Lecture 13. Today s lecture continue with rotations, torque, Note that chapters 11, 12, 13 all involve rotations
 Today - Lecue 13 Today s lecue coninue wih oaions, oque, Noe ha chapes 11, 1, 13 all inole oaions slide 1 eiew Roaions Chapes 11 & 1 Viewed fom aboe (+z) Roaional, o angula elociy, gies angenial elociy
Today - Lecue 13 Today s lecue coninue wih oaions, oque, Noe ha chapes 11, 1, 13 all inole oaions slide 1 eiew Roaions Chapes 11 & 1 Viewed fom aboe (+z) Roaional, o angula elociy, gies angenial elociy
Electromagnetic Theory 1
 / lectomagnetic Theoy uestion : lectostatic Potential negy A sphee of adius caies a positive chage density ρ constant Obviously the spheical coodinates system is appopiate hee Take - C m - and cm τ a)
/ lectomagnetic Theoy uestion : lectostatic Potential negy A sphee of adius caies a positive chage density ρ constant Obviously the spheical coodinates system is appopiate hee Take - C m - and cm τ a)
The Special Theory of Relativity Chapter II
 The Speial Theory of Relaiiy Chaper II 1. Relaiisi Kinemais. Time dilaion and spae rael 3. Lengh onraion 4. Lorenz ransformaions 5. Paradoes? Simulaneiy/Relaiiy If one obserer sees he eens as simulaneous,
The Speial Theory of Relaiiy Chaper II 1. Relaiisi Kinemais. Time dilaion and spae rael 3. Lengh onraion 4. Lorenz ransformaions 5. Paradoes? Simulaneiy/Relaiiy If one obserer sees he eens as simulaneous,
Ch. 3: Inverse Kinematics Ch. 4: Velocity Kinematics. The Interventional Centre
 Ch. : Invee Kinemati Ch. : Velity Kinemati The Inteventinal Cente eap: kinemati eupling Apppiate f ytem that have an am a wit Suh that the wit jint ae ae aligne at a pint F uh ytem, we an plit the invee
Ch. : Invee Kinemati Ch. : Velity Kinemati The Inteventinal Cente eap: kinemati eupling Apppiate f ytem that have an am a wit Suh that the wit jint ae ae aligne at a pint F uh ytem, we an plit the invee
RESOLUTION NO OVERSIGHT BOARD FOR THE SUCCESSOR AGENCY TO THE REDEVELOPMENT AGENCY OF THE CITY OF SOUTH SAN FRANCISCO
 R. - 1 RG BR R R G RP G R PPRG RG BG P ( RP) R BG R PR 1 RG 17, PR 177( 1). R, elh fe e ei 177( 1), befe eh fil ei, he e ge ile Reeele ge i eqie ee f Regie bligi Pe hele (" RP") h li ll f he bligi h e
R. - 1 RG BR R R G RP G R PPRG RG BG P ( RP) R BG R PR 1 RG 17, PR 177( 1). R, elh fe e ei 177( 1), befe eh fil ei, he e ge ile Reeele ge i eqie ee f Regie bligi Pe hele (" RP") h li ll f he bligi h e
The Components of Vector B. The Components of Vector B. Vector Components. Component Method of Vector Addition. Vector Components
 Upcming eens in PY05 Due ASAP: PY05 prees n WebCT. Submiing i ges yu pin ward yur 5-pin Lecure grade. Please ake i seriusly, bu wha cuns is wheher r n yu submi i, n wheher yu ge hings righ r wrng. Due
Upcming eens in PY05 Due ASAP: PY05 prees n WebCT. Submiing i ges yu pin ward yur 5-pin Lecure grade. Please ake i seriusly, bu wha cuns is wheher r n yu submi i, n wheher yu ge hings righ r wrng. Due
A Cosmological Model and Modifications to Einstein s Theory of Relativity
 Open Aess Liay Jounal A osmologial odel and odifiaions o Einsein s Theoy of Relaiiy Jianheng Liu Dongfang Boile o, Ld, Zigong, hina Reeied 6 Januay 6; aeped Feuay 6; pulished 5 Feuay 6 opyigh 6 y auho
Open Aess Liay Jounal A osmologial odel and odifiaions o Einsein s Theoy of Relaiiy Jianheng Liu Dongfang Boile o, Ld, Zigong, hina Reeied 6 Januay 6; aeped Feuay 6; pulished 5 Feuay 6 opyigh 6 y auho
The Impact of the Earth s Movement through the Space on Measuring the Velocity of Light (Part Two)
 Jonal of Applied Mahemais and Phsis, 7, 5, 74-757 hp://wwwsipog/jonal/jamp ISSN Online: 7-479 ISSN Pin: 7-45 The Impa of he Eah s Movemen hogh he Spae on Measing he Veloi of Ligh (Pa Two Miloš Čojanović
Jonal of Applied Mahemais and Phsis, 7, 5, 74-757 hp://wwwsipog/jonal/jamp ISSN Online: 7-479 ISSN Pin: 7-45 The Impa of he Eah s Movemen hogh he Spae on Measing he Veloi of Ligh (Pa Two Miloš Čojanović
Mass-Spring Systems Surface Reconstruction
 Mass-Spng Syses Physally-Based Modelng: Mass-Spng Syses M. Ale O. Vasles Mass-Spng Syses Mass-Spng Syses Snake pleenaon: Snake pleenaon: Iage Poessng / Sae Reonson: Iage poessng/ Sae Reonson: Mass-Spng
Mass-Spng Syses Physally-Based Modelng: Mass-Spng Syses M. Ale O. Vasles Mass-Spng Syses Mass-Spng Syses Snake pleenaon: Snake pleenaon: Iage Poessng / Sae Reonson: Iage poessng/ Sae Reonson: Mass-Spng
2-d Motion: Constant Acceleration
 -d Moion: Consan Acceleaion Kinemaic Equaions o Moion (eco Fom Acceleaion eco (consan eloci eco (uncion o Posiion eco (uncion o The eloci eco and posiion eco ae a uncion o he ime. eloci eco a ime. Posiion
-d Moion: Consan Acceleaion Kinemaic Equaions o Moion (eco Fom Acceleaion eco (consan eloci eco (uncion o Posiion eco (uncion o The eloci eco and posiion eco ae a uncion o he ime. eloci eco a ime. Posiion
Physics 442. Electro-Magneto-Dynamics. M. Berrondo. Physics BYU
 Physis 44 Eleo-Magneo-Dynamis M. Beondo Physis BYU Paaveos Φ= V + Α Φ= V Α = = + J = + ρ J J ρ = J S = u + em S S = u em S Physis BYU Poenials Genealize E = V o he ime dependen E & B ase Podu of paaveos:
Physis 44 Eleo-Magneo-Dynamis M. Beondo Physis BYU Paaveos Φ= V + Α Φ= V Α = = + J = + ρ J J ρ = J S = u + em S S = u em S Physis BYU Poenials Genealize E = V o he ime dependen E & B ase Podu of paaveos:
Derivatives of Inverse Trig Functions
 Derivaives of Inverse Trig Fncions Ne we will look a he erivaives of he inverse rig fncions. The formlas may look complicae, b I hink yo will fin ha hey are no oo har o se. Yo will js have o be carefl
Derivaives of Inverse Trig Fncions Ne we will look a he erivaives of he inverse rig fncions. The formlas may look complicae, b I hink yo will fin ha hey are no oo har o se. Yo will js have o be carefl
The sound field of moving sources
 Nose Engneeng / Aoss -- ong Soes The son el o mong soes ong pon soes The pesse el geneae by pon soe o geneal me an The pess T poson I he soe s onenae a he sngle mong pon, soe may I he soe s I be wen as
Nose Engneeng / Aoss -- ong Soes The son el o mong soes ong pon soes The pesse el geneae by pon soe o geneal me an The pess T poson I he soe s onenae a he sngle mong pon, soe may I he soe s I be wen as
NSEP EXAMINATION
 NSE 00-0 EXAMINATION CAEE OINT INDIAN ASSOCIATION OF HYSICS TEACHES NATIONAL STANDAD EXAMINATION IN HYSICS 00-0 Tal ie : 0 inues (A-, A- & B) AT - A (Tal Maks : 80) SUB-AT A- Q. Displaceen f an scillaing
NSE 00-0 EXAMINATION CAEE OINT INDIAN ASSOCIATION OF HYSICS TEACHES NATIONAL STANDAD EXAMINATION IN HYSICS 00-0 Tal ie : 0 inues (A-, A- & B) AT - A (Tal Maks : 80) SUB-AT A- Q. Displaceen f an scillaing
Outline. Review Homework Problem. Review Homework Problem II. Review Dimensionless Problem. Review Convection Problem
 adial diffsio eqaio Febay 4 9 Diffsio Eqaios i ylidical oodiaes ay aeo Mechaical Egieeig 5B Seia i Egieeig Aalysis Febay 4, 9 Olie eview las class Gadie ad covecio boday codiio Diffsio eqaio i adial coodiaes
adial diffsio eqaio Febay 4 9 Diffsio Eqaios i ylidical oodiaes ay aeo Mechaical Egieeig 5B Seia i Egieeig Aalysis Febay 4, 9 Olie eview las class Gadie ad covecio boday codiio Diffsio eqaio i adial coodiaes
Derivation of longitudinal Doppler shift equation between two moving bodies in reference frame at rest
 Deriaion o longiudinal Doppler shi equaion beween wo moing bodies in reerene rame a res Masanori Sao Honda Eleronis Co., d., Oyamazuka, Oiwa-ho, Toyohashi, ihi 44-393, Japan E-mail: msao@honda-el.o.jp
Deriaion o longiudinal Doppler shi equaion beween wo moing bodies in reerene rame a res Masanori Sao Honda Eleronis Co., d., Oyamazuka, Oiwa-ho, Toyohashi, ihi 44-393, Japan E-mail: msao@honda-el.o.jp
The Pressure Perturbation Equation: Exposed!
 Pressre Perrbain Eqain Page f 6 The Pressre Perrbain Eqain: Esed! The rainal dnamics f sercell srms hae a l d ih he ressre errbains creaed b he air fl. I is his effec ha makes sercells secial. Phase :
Pressre Perrbain Eqain Page f 6 The Pressre Perrbain Eqain: Esed! The rainal dnamics f sercell srms hae a l d ih he ressre errbains creaed b he air fl. I is his effec ha makes sercells secial. Phase :
Exponential and Logarithmic Equations and Properties of Logarithms. Properties. Properties. log. Exponential. Logarithmic.
 Eponenial and Logaihmic Equaions and Popeies of Logaihms Popeies Eponenial a a s = a +s a /a s = a -s (a ) s = a s a b = (ab) Logaihmic log s = log + logs log/s = log - logs log s = s log log a b = loga
Eponenial and Logaihmic Equaions and Popeies of Logaihms Popeies Eponenial a a s = a +s a /a s = a -s (a ) s = a s a b = (ab) Logaihmic log s = log + logs log/s = log - logs log s = s log log a b = loga
Electric Potential. Outline. Potential Energy per Unit Charge. Potential Difference. Potential Energy Difference. Quiz Thursday on Chapters 23, 24.
 lectic otential Quiz Thusay on Chaptes 3, 4. Outline otential as enegy pe unit chage. Thi fom of Coulomb s Law. elations between fiel an potential. otential negy pe Unit Chage Just as the fiel is efine
lectic otential Quiz Thusay on Chaptes 3, 4. Outline otential as enegy pe unit chage. Thi fom of Coulomb s Law. elations between fiel an potential. otential negy pe Unit Chage Just as the fiel is efine
OH BOY! Story. N a r r a t iv e a n d o bj e c t s th ea t e r Fo r a l l a g e s, fr o m th e a ge of 9
 OH BOY! O h Boy!, was or igin a lly cr eat ed in F r en ch an d was a m a jor s u cc ess on t h e Fr en ch st a ge f or young au di enc es. It h a s b een s een by ap pr ox i ma t ely 175,000 sp ect at
OH BOY! O h Boy!, was or igin a lly cr eat ed in F r en ch an d was a m a jor s u cc ess on t h e Fr en ch st a ge f or young au di enc es. It h a s b een s een by ap pr ox i ma t ely 175,000 sp ect at
Solution: (a) C 4 1 AI IC 4. (b) IBC 4
 C A C C R A C R C R C sin 9 sin. A cuent f is maintaine in a single cicula lp f cicumfeence C. A magnetic fiel f is iecte paallel t the plane f the lp. (a) Calculate the magnetic mment f the lp. (b) What
C A C C R A C R C R C sin 9 sin. A cuent f is maintaine in a single cicula lp f cicumfeence C. A magnetic fiel f is iecte paallel t the plane f the lp. (a) Calculate the magnetic mment f the lp. (b) What
A Hallelujah for My Father
 Univeity o New Mexico UNM Digital Repoitoy New Mexico Compoe' chive Reeach Collection and Data 1312011 Hallelujah o My Fathe lan Stinge Robet Fanci Follow thi and additional wok at: http://digitalepoitoyunmedu/nm_compoe_achive
Univeity o New Mexico UNM Digital Repoitoy New Mexico Compoe' chive Reeach Collection and Data 1312011 Hallelujah o My Fathe lan Stinge Robet Fanci Follow thi and additional wok at: http://digitalepoitoyunmedu/nm_compoe_achive
2. The units in which the rate of a chemical reaction in solution is measured are (could be); 4rate. sec L.sec
 Kineic Pblem Fm Ramnd F. X. Williams. Accding he equain, NO(g + B (g NOB(g In a ceain eacin miue he ae f fmain f NOB(g was fund be 4.50 0-4 ml L - s -. Wha is he ae f cnsumpin f B (g, als in ml L - s -?
Kineic Pblem Fm Ramnd F. X. Williams. Accding he equain, NO(g + B (g NOB(g In a ceain eacin miue he ae f fmain f NOB(g was fund be 4.50 0-4 ml L - s -. Wha is he ae f cnsumpin f B (g, als in ml L - s -?
Practice Problems: Improper Integrals
 Pracice Problem: Improper Inegral Wrien by Vicoria Kala vkala@mah.cb.ed December 6, Solion o he pracice problem poed on November 3. For each of he folloing problem: a Eplain hy he inegral are improper.
Pracice Problem: Improper Inegral Wrien by Vicoria Kala vkala@mah.cb.ed December 6, Solion o he pracice problem poed on November 3. For each of he folloing problem: a Eplain hy he inegral are improper.
Doppler Effect (Text 1.3)
 Doppler Effet (et 1.3) Consider a light soure as a soure sending out a tik eery 1/ν and these tiks are traeling forward with speed. tik tik tik tik Doppler Effet (et 1.3) Case 1. Obserer oing transersely.
Doppler Effet (et 1.3) Consider a light soure as a soure sending out a tik eery 1/ν and these tiks are traeling forward with speed. tik tik tik tik Doppler Effet (et 1.3) Case 1. Obserer oing transersely.
FARADAY'S LAW dt
 FAADAY'S LAW 31.1 Faaday's Law of Induction In the peious chapte we leaned that electic cuent poduces agnetic field. Afte this ipotant discoey, scientists wondeed: if electic cuent poduces agnetic field,
FAADAY'S LAW 31.1 Faaday's Law of Induction In the peious chapte we leaned that electic cuent poduces agnetic field. Afte this ipotant discoey, scientists wondeed: if electic cuent poduces agnetic field,
Diffusivity Equation
 Perleum Enineerin 34 Reservir Perfrmane Diffusiviy Equain 13 February 008 Thmas A. lasiname, Ph.D., P.E. Dilhan Il Dearmen f Perleum Enineerin Dearmen f Perleum Enineerin Texas A&M Universiy Texas A&M
Perleum Enineerin 34 Reservir Perfrmane Diffusiviy Equain 13 February 008 Thmas A. lasiname, Ph.D., P.E. Dilhan Il Dearmen f Perleum Enineerin Dearmen f Perleum Enineerin Texas A&M Universiy Texas A&M
Physics I Keystone Institute of Technology & Management, Surajgarh Unit V. Postulates of Einstein s special theory of relativity
 Physis I Keystne Institte f Tehnlgy & Manageent, Srajgarh Unit V Pstlates f Einstein s speial thery f relativity. Priniple f Physial Eqivalene The laws f physis, (bth ehanis and eletrdynais) epressed in
Physis I Keystne Institte f Tehnlgy & Manageent, Srajgarh Unit V Pstlates f Einstein s speial thery f relativity. Priniple f Physial Eqivalene The laws f physis, (bth ehanis and eletrdynais) epressed in
AP Physics 1 MC Practice Kinematics 1D
 AP Physics 1 MC Pracice Kinemaics 1D Quesins 1 3 relae w bjecs ha sar a x = 0 a = 0 and mve in ne dimensin independenly f ne anher. Graphs, f he velciy f each bjec versus ime are shwn belw Objec A Objec
AP Physics 1 MC Pracice Kinemaics 1D Quesins 1 3 relae w bjecs ha sar a x = 0 a = 0 and mve in ne dimensin independenly f ne anher. Graphs, f he velciy f each bjec versus ime are shwn belw Objec A Objec
Deriving the Useful Expression for Time Dilation in the Presence Of the Gravitation by means of a Light Clock
 IOSR Journal of Applied Physis (IOSR-JAP) e-issn: 78-486Volue 7, Issue Ver II (Mar - Apr 5), PP 7- wwwiosrjournalsorg Deriing he Useful xpression for Tie Dilaion in he Presene Of he Graiaion by eans of
IOSR Journal of Applied Physis (IOSR-JAP) e-issn: 78-486Volue 7, Issue Ver II (Mar - Apr 5), PP 7- wwwiosrjournalsorg Deriing he Useful xpression for Tie Dilaion in he Presene Of he Graiaion by eans of
Laplace Potential Distribution and Earnshaw s Theorem
 Laplae Potential Distibution and Eanshaw s Theoem Fits F.M. de Mul Laplae and Eanshaw Pesentations: Eletomagnetism: Histoy Eletomagnetism: Elet. topis Eletomagnetism: Magn. topis Eletomagnetism: Waves
Laplae Potential Distibution and Eanshaw s Theoem Fits F.M. de Mul Laplae and Eanshaw Pesentations: Eletomagnetism: Histoy Eletomagnetism: Elet. topis Eletomagnetism: Magn. topis Eletomagnetism: Waves
Faraday s Law. To be able to find. motional emf transformer and motional emf. Motional emf
 Objecie F s w Tnsfome Moionl To be ble o fin nsfome. moionl nsfome n moionl. 331 1 331 Mwell s quion: ic Fiel D: Guss lw :KV : Guss lw H: Ampee s w Poin Fom Inegl Fom D D Q sufce loop H sufce H I enclose
Objecie F s w Tnsfome Moionl To be ble o fin nsfome. moionl nsfome n moionl. 331 1 331 Mwell s quion: ic Fiel D: Guss lw :KV : Guss lw H: Ampee s w Poin Fom Inegl Fom D D Q sufce loop H sufce H I enclose
Lecture 3. Electrostatics
 Lecue lecsics In his lecue yu will len: Thee wys slve pblems in elecsics: ) Applicin f he Supepsiin Pinciple (SP) b) Applicin f Guss Lw in Inegl Fm (GLIF) c) Applicin f Guss Lw in Diffeenil Fm (GLDF) C
Lecue lecsics In his lecue yu will len: Thee wys slve pblems in elecsics: ) Applicin f he Supepsiin Pinciple (SP) b) Applicin f Guss Lw in Inegl Fm (GLIF) c) Applicin f Guss Lw in Diffeenil Fm (GLDF) C
Provider Satisfaction
 Prider Satisfaction Prider Satisfaction [1] NOTE: if you nd to navigate away from this page, please click the "Save Draft" page at the bottom (visible to ONLY logged in users). Otherwise, your rpons will
Prider Satisfaction Prider Satisfaction [1] NOTE: if you nd to navigate away from this page, please click the "Save Draft" page at the bottom (visible to ONLY logged in users). Otherwise, your rpons will
A) N B) 0.0 N C) N D) N E) N
 Cdinat: H Bahluli Sunday, Nvembe, 015 Page: 1 Q1. Five identical pint chages each with chage =10 nc ae lcated at the cnes f a egula hexagn, as shwn in Figue 1. Find the magnitude f the net electic fce
Cdinat: H Bahluli Sunday, Nvembe, 015 Page: 1 Q1. Five identical pint chages each with chage =10 nc ae lcated at the cnes f a egula hexagn, as shwn in Figue 1. Find the magnitude f the net electic fce
I ,.,., -_ IiiiiiiiiiiiiiI ~ ... IX Gloria Patri ,...,._ "'p. f.. ~: -;..-:-:;!": ~
 '70 X Gloia Pai (Allego modeao e maesoso) 785 P"""" 1 ilje 'i UJ f (D : f,, ;J :J () () ' : ;::;!": iiiiiiiiiiiii i J [ "*,,, "'io J, :i Sop ) (j) 790 fl,, sie, i a Pa i, e Fi Lo, Glo '!l o he Fah e and
'70 X Gloia Pai (Allego modeao e maesoso) 785 P"""" 1 ilje 'i UJ f (D : f,, ;J :J () () ' : ;::;!": iiiiiiiiiiiii i J [ "*,,, "'io J, :i Sop ) (j) 790 fl,, sie, i a Pa i, e Fi Lo, Glo '!l o he Fah e and
Electric Potential Energy
 Electic Ptentil Enegy Ty Cnsevtive Fces n Enegy Cnsevtin Ttl enegy is cnstnt n is sum f kinetic n ptentil Electic Ptentil Enegy Electic Ptentil Cnsevtin f Enegy f pticle fm Phys 7 Kinetic Enegy (K) nn-eltivistic
Electic Ptentil Enegy Ty Cnsevtive Fces n Enegy Cnsevtin Ttl enegy is cnstnt n is sum f kinetic n ptentil Electic Ptentil Enegy Electic Ptentil Cnsevtin f Enegy f pticle fm Phys 7 Kinetic Enegy (K) nn-eltivistic
2 tel
 Us. Timeless, sophisticated wall decor that is classic yet modern. Our style has no limitations; from traditional to contemporar y, with global design inspiration. The attention to detail and hand- craf
Us. Timeless, sophisticated wall decor that is classic yet modern. Our style has no limitations; from traditional to contemporar y, with global design inspiration. The attention to detail and hand- craf
Physics Courseware Physics I Constant Acceleration
 Physics Curseware Physics I Cnsan Accelerain Equains fr cnsan accelerain in dimensin x + a + a + ax + x Prblem.- In he 00-m race an ahlee acceleraes unifrmly frm res his p speed f 0m/s in he firs x5m as
Physics Curseware Physics I Cnsan Accelerain Equains fr cnsan accelerain in dimensin x + a + a + ax + x Prblem.- In he 00-m race an ahlee acceleraes unifrmly frm res his p speed f 0m/s in he firs x5m as
LINEAR DIFFERENTIAL EQUATIONS OF ORDER 1. where a(x) and b(x) are functions. Observe that this class of equations includes equations of the form
 LINEAR DIFFERENTIAL EQUATIONS OF ORDER 1 We consier ifferential equations of the form y + a()y = b(), (1) y( 0 ) = y 0, where a() an b() are functions. Observe that this class of equations inclues equations
LINEAR DIFFERENTIAL EQUATIONS OF ORDER 1 We consier ifferential equations of the form y + a()y = b(), (1) y( 0 ) = y 0, where a() an b() are functions. Observe that this class of equations inclues equations
MEAN GRAVITY ALONG PLUMBLINE. University of New Brunswick, Department of Geodesy and Geomatics Engineering, Fredericton, N.B.
 MEA GRAVITY ALG PLUMBLIE Beh-Anne Main 1, Chis MacPhee, Rbe Tenze 1, Pe Vaníek 1 and Macel Sans 1 1. Inducin 1 Univesiy f ew Bunswick, Depamen f Gedesy and Gemaics Engineeing, Fedeicn,.B., E3B 5A3, Canada
MEA GRAVITY ALG PLUMBLIE Beh-Anne Main 1, Chis MacPhee, Rbe Tenze 1, Pe Vaníek 1 and Macel Sans 1 1. Inducin 1 Univesiy f ew Bunswick, Depamen f Gedesy and Gemaics Engineeing, Fedeicn,.B., E3B 5A3, Canada
Recitation PHYS 131. must be one-half of T 2
 Reitation PHYS 131 Ch. 5: FOC 1, 3, 7, 10, 15. Pobles 4, 17, 3, 5, 36, 47 & 59. Ch 5: FOC Questions 1, 3, 7, 10 & 15. 1. () The eloity of a has a onstant agnitude (speed) and dietion. Sine its eloity is
Reitation PHYS 131 Ch. 5: FOC 1, 3, 7, 10, 15. Pobles 4, 17, 3, 5, 36, 47 & 59. Ch 5: FOC Questions 1, 3, 7, 10 & 15. 1. () The eloity of a has a onstant agnitude (speed) and dietion. Sine its eloity is
Lecture 4 ( ) Some points of vertical motion: Here we assumed t 0 =0 and the y axis to be vertical.
 Sme pins f erical min: Here we assumed and he y axis be erical. ( ) y g g y y y y g dwnwards 9.8 m/s g Lecure 4 Accelerain The aerage accelerain is defined by he change f elciy wih ime: a ; In analgy,
Sme pins f erical min: Here we assumed and he y axis be erical. ( ) y g g y y y y g dwnwards 9.8 m/s g Lecure 4 Accelerain The aerage accelerain is defined by he change f elciy wih ime: a ; In analgy,
In electrostatics, the electric field E and its sources (charges) are related by Gauss s law: Surface
 Ampee s law n eletostatis, the eleti field E and its soues (hages) ae elated by Gauss s law: EdA i 4πQenl Sufae Why useful? When symmety applies, E an be easily omputed Similaly, in magnetism the magneti
Ampee s law n eletostatis, the eleti field E and its soues (hages) ae elated by Gauss s law: EdA i 4πQenl Sufae Why useful? When symmety applies, E an be easily omputed Similaly, in magnetism the magneti
Executive Committee and Officers ( )
 Gifted and Talented International V o l u m e 2 4, N u m b e r 2, D e c e m b e r, 2 0 0 9. G i f t e d a n d T a l e n t e d I n t e r n a t i o n a2 l 4 ( 2), D e c e m b e r, 2 0 0 9. 1 T h e W o r
Gifted and Talented International V o l u m e 2 4, N u m b e r 2, D e c e m b e r, 2 0 0 9. G i f t e d a n d T a l e n t e d I n t e r n a t i o n a2 l 4 ( 2), D e c e m b e r, 2 0 0 9. 1 T h e W o r
Maximum Cross Section Reduction Ratio of Billet in a Single Wire Forming Pass Based on Unified Strength Theory. Xiaowei Li1,2, a
 Inenainal Fum n Enegy, Envinmen and Susainable evelpmen (IFEES 06 Maximum Css Sein Reduin Rai f Bille in a Single Wie Fming Pass Based n Unified Sengh They Xiawei Li,, a Shl f Civil Engineeing, Panzhihua
Inenainal Fum n Enegy, Envinmen and Susainable evelpmen (IFEES 06 Maximum Css Sein Reduin Rai f Bille in a Single Wie Fming Pass Based n Unified Sengh They Xiawei Li,, a Shl f Civil Engineeing, Panzhihua
Practice Problems - Week #4 Higher-Order DEs, Applications Solutions
 Pracice Probles - Wee #4 Higher-Orer DEs, Applicaions Soluions 1. Solve he iniial value proble where y y = 0, y0 = 0, y 0 = 1, an y 0 =. r r = rr 1 = rr 1r + 1, so he general soluion is C 1 + C e x + C
Pracice Probles - Wee #4 Higher-Orer DEs, Applicaions Soluions 1. Solve he iniial value proble where y y = 0, y0 = 0, y 0 = 1, an y 0 =. r r = rr 1 = rr 1r + 1, so he general soluion is C 1 + C e x + C
Charged particle motion in magnetic field
 Chaged paticle otion in agnetic field Paticle otion in cued agnetic fieldlines We diide the equation of otion into a elocity coponent along the agnetic field and pependicula to the agnetic field. Suppose
Chaged paticle otion in agnetic field Paticle otion in cued agnetic fieldlines We diide the equation of otion into a elocity coponent along the agnetic field and pependicula to the agnetic field. Suppose
PHYS-3301 Lecture 5. Chapter 2. Announcement. Sep. 12, Special Relativity. What about y and z coordinates? (x - direction of motion)
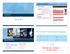 Announemen Course webpage hp://www.phys.u.edu/~slee/33/ Tebook PHYS-33 Leure 5 HW (due 9/4) Chaper, 6, 36, 4, 45, 5, 5, 55, 58 Sep., 7 Chaper Speial Relaiiy. Basi Ideas. Consequenes of Einsein s Posulaes
Announemen Course webpage hp://www.phys.u.edu/~slee/33/ Tebook PHYS-33 Leure 5 HW (due 9/4) Chaper, 6, 36, 4, 45, 5, 5, 55, 58 Sep., 7 Chaper Speial Relaiiy. Basi Ideas. Consequenes of Einsein s Posulaes
To Find Different Gravity Laws
 T Fin Diffn ai Laws Pal A Ma д Mninsa Appli Psis LLC inna A 8 Absa T a iffn ainals f plin ais ai ls T ipan is lk in spifi pis in siabl alia s ls T q is w is in iss spp l aliain In sal f s ls i is n b in
T Fin Diffn ai Laws Pal A Ma д Mninsa Appli Psis LLC inna A 8 Absa T a iffn ainals f plin ais ai ls T ipan is lk in spifi pis in siabl alia s ls T q is w is in iss spp l aliain In sal f s ls i is n b in
0# E % D 0 D - C AB
 5-70,- 393 %& 44 03& / / %0& / / 405 4 90//7-90/8/3 ) /7 0% 0 - @AB 5? 07 5 >0< 98 % =< < ; 98 07 &? % B % - G %0A 0@ % F0 % 08 403 08 M3 @ K0 J? F0 4< - G @ I 0 QR 4 @ 8 >5 5 % 08 OF0 80P 0O 0N 0@ 80SP
5-70,- 393 %& 44 03& / / %0& / / 405 4 90//7-90/8/3 ) /7 0% 0 - @AB 5? 07 5 >0< 98 % =< < ; 98 07 &? % B % - G %0A 0@ % F0 % 08 403 08 M3 @ K0 J? F0 4< - G @ I 0 QR 4 @ 8 >5 5 % 08 OF0 80P 0O 0N 0@ 80SP
A Crash Course in (2 2) Matrices
 A Cash Couse in ( ) Matices Seveal weeks woth of matix algeba in an hou (Relax, we will only stuy the simplest case, that of matices) Review topics: What is a matix (pl matices)? A matix is a ectangula
A Cash Couse in ( ) Matices Seveal weeks woth of matix algeba in an hou (Relax, we will only stuy the simplest case, that of matices) Review topics: What is a matix (pl matices)? A matix is a ectangula
Representing Knowledge. CS 188: Artificial Intelligence Fall Properties of BNs. Independence? Reachability (the Bayes Ball) Example
 C 188: Aificial Inelligence Fall 2007 epesening Knowledge ecue 17: ayes Nes III 10/25/2007 an Klein UC ekeley Popeies of Ns Independence? ayes nes: pecify complex join disibuions using simple local condiional
C 188: Aificial Inelligence Fall 2007 epesening Knowledge ecue 17: ayes Nes III 10/25/2007 an Klein UC ekeley Popeies of Ns Independence? ayes nes: pecify complex join disibuions using simple local condiional
ACCEPTS HUGE FLORAL KEY TO LOWELL. Mrs, Walter Laid to Rest Yesterday
 $ j < < < > XXX Y 928 23 Y Y 4% Y 6 -- Q 5 9 2 5 Z 48 25 )»-- [ Y Y Y & 4 j q - Y & Y 7 - -- - j \ -2 -- j j -2 - - - - [ - - / - ) ) - - / j Y 72 - ) 85 88 - / X - j ) \ 7 9 Y Y 2 3» - ««> Y 2 5 35 Y
$ j < < < > XXX Y 928 23 Y Y 4% Y 6 -- Q 5 9 2 5 Z 48 25 )»-- [ Y Y Y & 4 j q - Y & Y 7 - -- - j \ -2 -- j j -2 - - - - [ - - / - ) ) - - / j Y 72 - ) 85 88 - / X - j ) \ 7 9 Y Y 2 3» - ««> Y 2 5 35 Y
Lecture 3: Resistive forces, and Energy
 Lecure 3: Resisive frces, and Energy Las ie we fund he velciy f a prjecile ving wih air resisance: g g vx ( ) = vx, e vy ( ) = + v + e One re inegrain gives us he psiin as a funcin f ie: dx dy g g = vx,
Lecure 3: Resisive frces, and Energy Las ie we fund he velciy f a prjecile ving wih air resisance: g g vx ( ) = vx, e vy ( ) = + v + e One re inegrain gives us he psiin as a funcin f ie: dx dy g g = vx,
`Derivation of Weinberg s Relation in a Inflationary Universe
 1 `Derivain f Weinberg s Relain in a Inflainary Universe Iannis Iraklis aranas Yrk Universiy Deparen f Physis and Asrny 1A Perie Building Nrh Yrk, Onari MJ-1P CANADA e ail: iannis@yrku.a Absra We prpse
1 `Derivain f Weinberg s Relain in a Inflainary Universe Iannis Iraklis aranas Yrk Universiy Deparen f Physis and Asrny 1A Perie Building Nrh Yrk, Onari MJ-1P CANADA e ail: iannis@yrku.a Absra We prpse
A SYSTEMS-THEORETICAL REPRESENTATION OF TECHNOLOGIES AND THEIR CONNECTIONS
 A SYSTEMS-THERETCAL REPRESENTATN F TECHNLGES AN THER CNNECTNS Takehiro nohara eparmen of Vale and eision Siene, Gradae Shool of Soial and eision Siene and Tehnology, Tokyo nsie of Tehnology, 2-12-1 -okayama
A SYSTEMS-THERETCAL REPRESENTATN F TECHNLGES AN THER CNNECTNS Takehiro nohara eparmen of Vale and eision Siene, Gradae Shool of Soial and eision Siene and Tehnology, Tokyo nsie of Tehnology, 2-12-1 -okayama
PHY132 Lecture 6 02/05/2010. Lecture 6 1
 Claical Phyic II PHY3 Lectue 6 The lectic Potential ti - II /5/ Lectue 6 Wok by a Vaying Foce Wok i a cala quantity, an we can thu a little piece of wok togethe, i.e. um a eie of ot-pouct of the foce F(
Claical Phyic II PHY3 Lectue 6 The lectic Potential ti - II /5/ Lectue 6 Wok by a Vaying Foce Wok i a cala quantity, an we can thu a little piece of wok togethe, i.e. um a eie of ot-pouct of the foce F(
dp dt For the time interval t, approximately, we can write,
 PHYSICS OCUS 58 So far we hae deal only wih syses in which he oal ass of he syse, sys, reained consan wih ie. Now, we will consider syses in which ass eners or leaes he syse while we are obsering i. The
PHYSICS OCUS 58 So far we hae deal only wih syses in which he oal ass of he syse, sys, reained consan wih ie. Now, we will consider syses in which ass eners or leaes he syse while we are obsering i. The
a. Show that these lines intersect by finding the point of intersection. b. Find an equation for the plane containing these lines.
 Mah A Final Eam Problems for onsideraion. Show all work for credi. Be sure o show wha you know. Given poins A(,,, B(,,, (,, 4 and (,,, find he volume of he parallelepiped wih adjacen edges AB, A, and A.
Mah A Final Eam Problems for onsideraion. Show all work for credi. Be sure o show wha you know. Given poins A(,,, B(,,, (,, 4 and (,,, find he volume of he parallelepiped wih adjacen edges AB, A, and A.
Th e E u r o p e a n M ig r a t io n N e t w o r k ( E M N )
 Th e E u r o p e a n M ig r a t io n N e t w o r k ( E M N ) H E.R E T h em at ic W o r k sh o p an d Fin al C o n fer en ce 1 0-1 2 Ju n e, R agu sa, It aly D avid R eisen zein IO M V ien n a Foto: Monika
Th e E u r o p e a n M ig r a t io n N e t w o r k ( E M N ) H E.R E T h em at ic W o r k sh o p an d Fin al C o n fer en ce 1 0-1 2 Ju n e, R agu sa, It aly D avid R eisen zein IO M V ien n a Foto: Monika
PHYSICS 151 Notes for Online Lecture #23
 PHYSICS 5 Ntes fr Online Lecture #3 Peridicity Peridic eans that sething repeats itself. r exaple, eery twenty-fur hurs, the Earth aes a cplete rtatin. Heartbeats are an exaple f peridic behair. If yu
PHYSICS 5 Ntes fr Online Lecture #3 Peridicity Peridic eans that sething repeats itself. r exaple, eery twenty-fur hurs, the Earth aes a cplete rtatin. Heartbeats are an exaple f peridic behair. If yu
