arxiv:cond-mat/ v2 [cond-mat.str-el] 3 Nov 2006
|
|
|
- Lawrence Bridges
- 6 years ago
- Views:
Transcription
1 arxiv:cond-mat/61148v [cond-mat.str-el] 3 Nov 6 Lang-Firsov approaches to polaron physics: From variational methods to unbiased quantum Monte Carlo simulations Martin Hohenadler and Wolfgang von der Linden Institute for Theoretical and Computational Physics, TU Graz, Austria hohenadler@itp.tu-graz.ac.at, wvl@itp.tu-graz.ac.at 1 Introduction In the last decades, there has been substantial interest in simple models for electron-phonon (el-ph) interaction in condensed matter. Despite intensive theoretical efforts, it was not before the advent of numerical methods in the 198 s that a thorough understanding on the basis of exact, unbiased results was achieved. Although at the present our knowledge of the rather simple cases of a single carrier (the polaron problem) or two carriers (the bipolaron problem) in Holstein and Fröhlich models is fairly complete, this is not true for arbitrary band fillings. There is still a major desire to develop more efficient simulation techniques to tackle strongly correlated many-polaron models, which are expected to describe several aspects of real materials currently under investigation, such as quantum dots and quantum wires, high-temperature superconductors or colossal-magnetoresistance manganites. One of the principle problems in computer simulations of microscopic models is the limitation in both system size and parameter values. Whereas the former can be overcome for the polaron and the bipolaron problem in some cases, it is very difficult to obtain results of similar quality in the many-electron case. Moreover, many approaches still suffer from severe restrictions concerning the parameter regions accessible. For example, interesting materials such as the cuprates and manganites are characterized by small but finite phonon frequencies as compared to the electronic hopping integral and intermediate to strong el-ph interaction. Unfortunately, simulations turn out to be most difficult exactly for such parameters, and it is therefore highly desirable to improve existing simulation methods. In this chapter, we shall mainly review different versions of a recently developed quantum Monte Carlo (QMC) method applicable to Holstein-type models with one, two or many electrons. The appealing advantages of QMC over other numerical methods include the accessibility of rather large systems, the exact treatment of bosonic degrees of freedom (i.e., no truncation is
2 Martin Hohenadler and Wolfgang von der Linden necessary), and the possibility to consider finite temperatures to study phase transitions. The important new aspect here is the use of canonically transformed Hamiltonians, which permits the introduction of exact sampling for the phonon degrees of freedom, enabling us to carry out accurate simulations in practically all interesting parameter regimes. Additionally, based on a generalization of the Lang-Firsov transformation, we shall present a simple variational approach to the polaron and the bipolaron problem which yields surprisingly accurate results. The chapter is organized as follows. In section, we present the general model Hamiltonian. Section 3 is devoted to a discussion of the Lang-Firsov transformation, and section 4 contains the derivation of the variational approach. The QMC method is introduced in section 5. Section 6 gives a selection of results for the cases of one, two and many electrons. Finally, we summarize in section 7. Model In this paper we focus on the extended Holstein-Hubbard model defined by H = t n i n i + V n i n j ij c iσ c jσ + U ij σ i + ω ( p i + x i ) g i i n i x i. (1) Here c iσ creates an electron with spin σ at site i, and n i = σ n iσ with n iσ = c iσ c iσ. The phonon degrees of freedom at site i are described by the momentum p i and coordinate (displacement) x i of a harmonic oscillator. The microscopic parameters are the nearest-neighbour (denoted by ) hopping amplitude t, the on-site (Hubbard ) repulsion U, the nearest-neighbour Coulomb repulsion V, the Einstein phonon frequency ω and the el-ph coupling g. This model neglects both long-range Coulomb and el-ph interaction, which is often a suitable approximation for metallic systems due to screening. Two simple limiting cases of the Hamiltonian (1) are the Holstein model (U = V = ) and the Hubbard model (g = V = ). In general, the physics of the model (1) is determined by the competition of the various interactions. Depending on the choice of parameters and band filling, it describes fascinating phenomena such as (bi-)polaron formation, Mott and Peierls quantum phase transitions or superconductivity. As we shall see below, the adiabaticity ratio α = ω /t () permits us to distinguish two physically different regimes, namely the adiabatic regime α < 1 and the non-adiabatic regime α > 1. We further define the dimensionless el-ph coupling parameter λ = g /(ω W), where W = 4tD is the bare bandwidth in D dimensions. Alternatively, λ may
3 Lang-Firsov approaches to polaron physics 3 also be written as λ = E P /W, i.e., the ratio of the polaron binding energy in the atomic limit t =, E P = g /ω, and half the bare bandwidth. A useful constant in the non-adiabatic regime is g = E P /ω. We exclusively consider hypercubic lattices with linear size N and volume N D, and assume periodic boundary conditions in real space. 3 Lang-Firsov transformation The cornerstone of the methods presented here is the canonical (extended) Lang-Firsov transformation of the Hamiltonian (1). The original Lang-Firsov (LF) transformation [1] has been used extensively to study Holstein-type models. A well-known, early approximation is due to Holstein [], who replaced the hopping term by its expectation value in a zero-phonon state, neglecting emission and absorption of phonons during electron transfer. However, this approach yields reliable results only in the non-adiabatic strong-coupling (SC) limit. For λ = (or t = ), the LF transformation provides an exact solution of the single-site problem [3]. Whereas transformed Hamiltonians have been treated numerically before [4 6], the first QMC method making use of the LF transformation has been proposed in [7]. We introduce the extended LF transformation by defining the unitary operator Φ = e S, S = i γ ij n i p j (3) ij with real parameters γ ij, i, j = 1,...,N D. Φ as defined in equation (3) has the form of a translation operator, and fulfills Φ = Φ 1. Given an electron at site i, Φ mediates displacements γ ij of the harmonic oscillators at all sites j. Hence, the extended transformation is capable of describing an extended phonon cloud, important in the large-polaron or bipolaron regime. We shall use this transformation for the variational approach. However, the standard (local) LF transformation will be expedient as a basis for unbiased QMC simulations, in which the transformed Hamiltonian is treated exactly. Operators have to be transformed according to  = Φ Φ. Defining the function f(η) = e η b S Âe η bs we obtain where f f/ η. A simple calculation gives f (η) = e η bs [Ŝ, Â]e η bs, (4) [Ŝ, c iσ] = i l γ il p l c iσ, [Ŝ, c iσ ] = i l γ il p l c iσ. (5) Substitution in equation (4), integration with respect to η and setting η = 1 results in
4 4 Martin Hohenadler and Wolfgang von der Linden c iσ = c iσ ei P j γij bpj, c iσ = c iσ e i P j γij bpj. (6) For phonon operators, the relation b  = e S Âe bs =  + [Ŝ, Â] + 1 [Ŝ, [Ŝ, Â]] +, (7)! yields xi = x i + j γ ij n j, pi = p i. (8) Collecting these results, the transformation of the Hamiltonian (1) leads to H = t c iσ c P jσ ei l (γ il γ jl )bp l + ω ( p i + x i ) + ij σ i ij }{{} eh kin ( ω n i n j } {{ } eh ph H ep ph + H e ph x ) γ lj γ li g γ ij + U δ ij + V δ ij n j x i (ω γ ij g δ ij ) } {{ } eh ep + 1U ij l i }{{} eh ee n i. (9) Here the term H ep describes the coupling between electrons and phonons, whereas H ee represents an effective el-el interaction. Hamiltonian (9) will be the starting point for the variational approach in section 4. For QMC simulations, it is more suitable to require that the el-ph terms in H ep cancel. This can be achieved by setting γ ij = γδ ij with γ = λw ω. (1) The parameter γ corresponds to the distortion which minimizes the potential energy of the shifted harmonic oscillator E pot = ω x g x. This leads us to the standard LF transformation Φ = e S, S = iγ i n i p i, (11) and the familiar results for the transformed operators c iσ = c iσ eiγbpi, c iσ = c iσ e iγbpi (1) and xi = x i + γ n i, pi = p i. (13) In contrast to the non-local transformation (3), only the oscillator at the site of the electron is displaced. The transformed Hamiltonian reads
5 Lang-Firsov approaches to polaron physics 5 H = t c iσ c jσ eiγ(bpi bpj) + ω ( p i + x i ) ij σ i }{{}}{{} eh kin eh ph + ( 1 U E P) i n i + V ij n i n j 1 U i n i. (14) } {{ } eh ee As we shall discuss in detail in section 5, the difficulties encountered in QMC simulations of the original Hamiltonian (1) are to a certain extent related to (bi-)polaron effects, i.e., to the dynamic formation of spatially rather localized lattice distortions which surround the charge carriers and follow their motion in the lattice. For a single electron, the aforementioned Holstein-Lang-Firsov (HLF) approximation [] becomes exact in the non-adiabatic SC or small-polaron limit, and agrees qualitatively with exact results also in the intermediate-coupling (IC) regime [8]. Although it overestimates the shift γ of the equilibrium position of the oscillator in the presence of an electron, and does not reproduce the retardation effects when the electron hops onto a previously unoccupied site, the approximation mediates the crucial impact of el-ph interaction on the lattice. Consequently, the transformed Hamiltonian (14) can be expected to be a good starting point for QMC simulations, which then merely need to account for the rather small fluctuations around the (shifted or unshifted) equilibrium positions. In principle, it would also be possible to develop a QMC algorithm based on the Hamiltonian (9) the basis of our variational approach with the parameters γ ij determined variationally, but the local LF transformation proves to be sufficient. The Hamiltonian (14) does no longer contain a term coupling the electron density n and the lattice displacement x. By contrast, the extended transformation does not eliminate the interaction term completely. On top of that, the hopping term involves all phonon momenta p i as well as the parameters γ ij, and the el-el interaction becomes long ranged [cf equation (9)]. For spin dependent carriers with n i n i, the interaction term H ee contains a Hubbard-like attractive interaction. Whereas the latter can be treated exactly in the case of two electrons (section 5.1), the many-electron case requires the introduction of auxiliary fields which complicate simulations. However, no such difficulties arise for the spinless Holstein model considered in section 6. 4 Variational approach For simplicity, we shall restrict the following derivation to one dimension; an extension to D > 1 is straight forward. Furthermore, we only consider finite clusters with periodic boundary conditions, although infinite systems may also be treated. The results of this section have originally been presented in [7, 9].
6 6 Martin Hohenadler and Wolfgang von der Linden 4.1 One electron As noted before, the simple variational method presented here is based on the extended transformation (3), leading to the Hamiltonian (9). We treat the γ ij as variational parameters which are determined by minimizing the ground-state energy in a zero-phonon basis in which H ep =. For systems with translation invariance the displacement fields satisfy the condition γ ij = γ i j. Together with i n i = 1 for a single electron we get H ee = ω l γ l g γ. The eigenvalue problem of the transformed Hamiltonian (9) is solved by making the following ansatz for the one-electron basis states { N l = c lσ ν=1 φ (ν), l = 1,...,N }, (15) where φ (ν) denotes the ground state of the harmonic oscillator at site ν. The non-zero matrix elements of the hopping term are l H kin l = tδ ll φ (ν) ei(γ lν γ l ν )bp ν φ (ν) ν = tδ ll dxφ(x + γ lν )φ(x + γ l ν) ν = tδ ll e 1 4 P ν (γν γ ν+l l ), (16) where φ(x) denotes the real-space wavefunction of the harmonic-oscillator ground state. The Kronecker symbol δ ll forces l and l to represent nearestneighbor sites. A simple calculation gives for the other terms in equation (9) l H ph l ω = δ ll, l H ep l =, l H ee l = δ ll ( ω ) γl g γ. (17) In the zero-phonon subspace spanned by the basis states (15), the eigenstates of Hamiltonian (9) with momentum k are l ψ k = c kσ ν φ (ν) (18) with eigenvalues and the kinetic energy E(k) = E kin + Nω E kin = t δ=±1 + ω e ikδ e 1 4 γl g γ (19) l P ν (γν γ ν+δ). ()
7 Lang-Firsov approaches to polaron physics 7 Defining the Fourier transform γ q = 1 e iql γ l (1) N l and using (γ l R) γ ν γ ν+δ = ν q we may write γ q γ q e iqδ = q γ q cosqδ, () E kin = t δ e ikδ e 1 P q (1 cos qδ)γ q = ε (k)e 1 P q (1 cos q)γ q = ε(k) (3) with the tight-binding dispersion ε (k) = t cosk. Hence the ground-state energy becomes E(k) = ε(k) + Nω + ω γ q g γ q. (4) N The variational parameters γ p are determined by requiring q E γ p = γ p ε(k)(1 cosp) + ω γ p g N! =, (5) so that the optimal values γ p can be obtained from γ p = g N 1 ω + ε(k)(1 cosp). (6) Since ε(k) depends implicitly on the γ p, equation (6) has to be solved selfconsistently. It has the typical form of the random-phase approximation since a variational ansatz for the untransformed Hamiltonian may be written as q Φ ψ k = 1 e ikj c P jσ e i l γ jl bp l N ν j φ (ν), (7) with Φ as defined in equation (3). We shall also calculate the quasiparticle spectral weight for momentum k =, defined as z = c k=,σ ψ. (8) Here ψ denotes the ground state with one electron of momentum p = and the oscillators in the ground state φ. Fourier transformation and the same manipulations as in equation (16) lead to
8 8 Martin Hohenadler and Wolfgang von der Linden z = 1 φ c N iσ c jσ φ ij = 1 φ e i P k γ ik bp k φ N = e 1 4 i P q eγ q. (9) Just as the HLF approximation, the present variational method becomes exact in the non-interacting limit (λ = ) and in the non-adiabatic SC limit. Furthermore, it yields the correct results both for α = (classical phonons) and α =, and also gives accurate results for large α and finite λ, since the displacements of the oscillators only local and generally overestimated in the HLF approximation are determined variationally. 4. Two electrons As in the one-electron case, the use of a zero-phonon basis leads to H ep = and, neglecting the ground-state energy of the oscillators, we also have H ph =. Hence, H = Hkin + H ee with the transformed hopping term H kin = t eff ε(k) c kσ c kσ (3) ij σ c iσ c jσ = kσ and ε(k) = t eff cos(k). Here the effective hopping t eff = 1 δ=±1 e 1 4 P l (γ l δ γ l ), (31) where rotational invariance has been exploited. For two electrons of opposite spin (i.e., n iσ n jσ = for i j) and V =, Hee in equation (9) reduces to H ee = v U + ij v ij n i n j, v ij = ω The eigenstates of the two-electron problem have the form γ lj γ li g γ ij + 1δ iju. (3) l ψ k = p d p c k p c p, (33) suppressing the phonon component [cf equation (18)], and may be written as with the Fourier transform ψ k = 1 e ikxi d l c i c i+l, (34) N i l d = Fd, (F) lp = e ix lp / N. (35)
9 The normalization of equation (33) reads Lang-Firsov approaches to polaron physics 9 ψ k ψ k = p d p. (36) Using equation (33), we find for the expectation value of H kin ψ k H kin ψ k = d p d p ε(q) pp ( = p q c p c k p n q c k p c p }{{ } δ p,p δ q,p d p [ε(p) + ε(k p)] ) + c ck p n p q c k p c p }{{ } δ p,p δ q,k p = 4 t eff d T k d. (37) In the last step we have introduced T k = 1 F diag[cos(p) + cos(k p)] F and made use of equation (35). The expectation value of the interaction term, best computed in the realspace representation (34), takes the form ψ k H ee ψ k = (v U) l = (v U) l d l + v ij d l d N l e ik(x l xl ) d l + N ij j j ll c j +l c j n i n j c j c j +l }{{ } δ jj δ jj δ i,j+l δ l,l v j+l,j d l jl = (v U)d d + d V d, (38) with the diagonal matrix V ij = δ ij v i. The minimization of the total energy with respect to d yields the eigenvalue problem ( 4t eff T k + V )d = (E v + U)d. (39) The vector of coefficients d and thereby the ground state are found by minimizing the ground-state energy E through variation of the displacement fields γ ij. Similar to the one-electron case, this procedure takes into account displacements of the oscillators not only at the same but also at surrounding sites of the two electrons, and is therefore capable of describing extended bipolaron states (see section 6.). Note that the two-electron problem is diagonalized exactly without phonons (i.e., for λ = ).
10 1 Martin Hohenadler and Wolfgang von der Linden 5 Quantum Monte Carlo In this section, we present an overview of our recently developed QMC algorithms for Holstein-type models [7,9 11]. As mentioned before, in contrast to the variational approach, the QMC approaches discussed here, based on the local LF transformation (14) which does not contain any free parameters, are unbiased. They yield exact results with only statistical errors that can in principle be made arbitrarily small. The motivation for the development of improved QMC schemes for Holstein models stems from the fact that calculations with existing methods often suffer from strong autocorrelations, i.e., non-negligible statistical correlations between successive MC configurations [7, 1]. In fact, autocorrelations may render accurate simulations impossible within reasonable computing time. As discussed in [7], the problem becomes particularly noticeable for small phonon frequencies and low temperatures. Whereas autocorrelations can be avoided to a large extent for one or two electrons by integrating out the phonons analytically, no efficient general schemes exist for finite charge-carrier densities (see discussion in [7]). In the sequel, we present a general (i.e., applicable for all densities) solution for this problem in several steps. First, the effects due to el-ph interaction are separated from the free lattice dynamics by means of the LF transformation (14). Since the latter contains the crucial impact of the electronic degrees of freedom on the lattice, simulations may be based only on the purely phononic part of the resulting action. The fermionic degrees of freedom can then be taken into account exactly by reweighting of the probability distribution. Consequently, we may completely ignore the electronic weights in the updating process, and thereby dramatically reduce the computational effort. The principal component representation of the phonon coordinates allows exact sampling and avoids any autocorrelations. 5.1 Partition function We begin by deriving the partition function for the case of a single electron. Then we discuss the differences occurring in the cases of two or more carriers. One electron The partition function is defined as Z = Tre β e H (4) with H given by equation (14) and the inverse temperature β = (k B T) 1. For a single electron, H ee = E P becomes a constant which needs only to be considered in calculating the total energy. Using the Suzuki-Trotter decomposition [1], we obtain
11 Lang-Firsov approaches to polaron physics 11 e β eh (e τ e H kin e τ e H p ph e τ e H x ph ) L U L, (41) where τ = β/l 1. Splitting up the trace into a bosonic and a fermionic part and inserting L 1 complete sets of oscillator momentum eigenstates we find the approximation Z L = Tr f dp 1 dp dp L p 1 U p p L U p 1 (4) with dp τ i dp i,τ. Each matrix element can be evaluated by inserting a complete set of phonon coordinate eigenstates dx x x, since all x-integrals are of Gaussian form and can easily be carried out. The result is p τ e τ H ex ph pτ+1 = C ND e 1 P ω τ i (pi,τ pi,τ+1), C = π ω τ. (43) The normalization factor in front of the exponential has to be taken into account in the calculation of the total energy, but cancels when we measure other observables. With the abbreviation Dp = dp 1 dp dp L the partition function finally becomes Z L = C ND L Dp w b w f, (44) where w b = e τs b, w f = Tr f Ω, Ω = L τ=1 e τ e H (τ) kin. (45) (τ) Here H kin corresponds to H kin with the phonon operators p i, p j replaced by the momenta p i,τ, p j,τ on the τth Trotter slice, and its exponential may be written as ( e τ H e(τ) kin = Dτ κd τ, κ jj = e τt htb), (D τ ) jj = δ jj e iγpj,τ, (46) jj where h tb is the N D N D tight-binding hopping matrix. To save some computer time, we employ the checkerboard breakup [13] e τt P ij c i c j e τtc i c j. (47) Using equation (47), the numerical effort scales as N D instead of N 3D (see also section 5.6), but the error due to this additional approximation is of the same order τ as the Trotter error in equation (41). According to equation (46), we have the same matrix κ for every time slice, which is transformed by the diagonal unitary matrices D τ. The matrix Ω can be calculated in an efficient way by noting that the transformation matrices D τ and D τ+1 at time slice τ may be combined to a diagonal matrix ij
12 1 Martin Hohenadler and Wolfgang von der Linden (D τ,τ+1 ) ij = δ ij e iγ(pi,τ+1 pi,τ). (48) Due to the cyclic invariance of the fermionic trace, D 1 can be shifted to the end of the product, where it combines with D L to D L,1. Hence we can write Ω = L κ D τ,τ+1, (49) τ=1 with periodic boundary conditions in imaginary time. In the one-electron case, the fermionic weight w f = n n Ω n is given by the sum over the diagonal elements of the matrix representation of Ω in the basis of one-electron states (dropping unnecessary spin indices) n = c n. (5) The bosonic action in equation (45) contains only classical variables: S b = ω p 1 i,τ + ω τ (p i,τ p i,τ+1 ), (51) i,τ where the indices i = 1,...,N D and τ = 1,...,L run over all lattice sites and time slices, respectively, and p i,l+1 = p i,1. It may also be written as i,τ S b = i p T i Ap i (5) with p i = (p i,1,..., p i,l ) and a periodic, tridiagonal L L matrix A with non-zero elements (A) l,l = ω + 1 ω τ, (A) 1 l,l±1 = ω τ. (53) Since Z L is a trace, it follows that (A) 1,L = (A) L,1 = (ω τ ) 1. Two electrons In contrast to [9], here we also take into account nearest-neighbour Coulomb repulsion V. For two electrons, the Hamiltonian (14) simplifies to H = H kin + H ph + H ee E P, Hee = (U E P ) i n i n i +V ij n i n j. (54) Again, the constant shift can be neglected in the QMC simulation, but in contrast to the single-electron case, we have a non-trivial interaction term. The Suzuki-Trotter decomposition yields e β eh ( e τ e H kin e τ e H p ph e τ e H x ph e τ e H ee ) L U L. (55)
13 Using the same steps as above we obtain w b = e τs b, w f = Tr f Ω, Ω = Lang-Firsov approaches to polaron physics 13 L τ=1 e τ e H (τ) kin e τ e H ee, (56) with S b given by equation (51). As pointed out in [9], the numerical effort for two electrons increases substantially in higher dimensions. Therefore, we restrict ourselves to D = 1. Previously, we only considered the case of two electrons of opposite spin (forming a singlet) [9]. Here we shall also present results for the triplet state. Singlet In the singlet case we choose the two-electron basis states { l i, j c i c j, i, j = 1,...,N }, (57) where we have used a combined index l = 1,...,N. The tight-binding hopping matrix, denoted as κ, has dimension N N, and the corresponding exponential in equation (56) can again be written as e τ H e(τ) kin = D τ κd τ [cf equation (45)], where (D τ ) ll = δ ll e iγ(pi,τ+pj,τ) (58) is diagonal in the basis (57). The remaining contribution to Ω comes from the effective el-el interaction term H ee in terms of the sparse matrix (V) ll = (δ lk e τ(u EP)δij ) lk (e τv δ ij ) kl. (59) k The momenta p merely enter the diagonal matrix D; the N N matrices V and κ are fixed throughout the entire MC simulation. Finally, we have Ω = τ D τ κd τ V, (6) and the fermionic trace can be calculated as the sum over the diagonal elements of the matrix Ω in the basis (57), i.e., Tr f Ω = ij i, j Ω i, j. (61) Triplet For two electrons with parallel spin we use the basis states { l i, j c i c j, i = 1,...,N, j = i + 1,...,N }, (6) i.e., double occupation of a site is not possible. Since we can further not distinguish between the states i, j and j, i, the dimension of the electronic Hilbert space is reduced from N (singlet case) to N(N 1)/. Consequently, for the same system size, simulations for the triplet case will be much faster.
14 14 Martin Hohenadler and Wolfgang von der Linden Many-electron case The one-electron QMC algorithm can easily be extended to the spinless Holstein model with many electrons. For the latter, assuming V =, the interaction term in equation (14) reduces to H ee = E P i n i. Therefore, the grand-canonical Hamiltonian becomes H = H µ i n i = t ij c i c j eiγ(bpi bpj) + H ph (E P + µ) i n i, (63) } {{ } eh kin } {{ } eh ee where µ denotes the chemical potential. For half filling n =.5 [N/ spinless fermions on N sites, cf equation (84)], the latter is given by µ = E P, whereas for n.5, it has to be adjusted to yield the carrier density of interest. The approximation to the partition function may again be cast into the form of equation (44), with w b as defined by equations (45) and (51), respectively. The fermionic weight is given by w f = Tr f ( B 1 B B L ), Bτ = e τ e H (τ) kin e τ e H ee. (64) Following Blankenbecler et al. [14], the fermion degrees of freedom can be integrated out exactly leading to w f = det(1 + B 1 B L ) det(1 + Ω), (65) where the N D N D matrix B τ is given by Here κ and D τ are identical to equation (46), and B τ = D τ κ D τ V. (66) (V) ij = δ ij e τ(ep+µ). (67) There is a close relation to the one-electron Green function In real space and imaginary time, we have [14,15] G ij = c i c j }{{} + c i c j. (68) }{{} G a ij G b ij G a ij = c i c j = (1 + Ω) 1 ij, Gb ij = δ ij G a ij = (Ω G a ) ji. (69) At this stage, with the above results for the partition function, a QMC simulation of the transformed Holstein model would proceed as follows. In each MC step, a pair of indices (i, τ ) on the N D L lattice of phonon momenta p i,τ is chosen at random. At this site, a change p i,τ p i,τ + p of the phonon configuration is proposed. To decide upon the acceptance of
15 Lang-Firsov approaches to polaron physics 15 the new configuration using the Metropolis algorithm [1], the corresponding weights w b w f and w b w f have to be calculated. Due to the local updating process, the computation of the change of the bosonic weight w b = w b /w b is very fast, which is not the case for the fermionic weight w f = w f /w f. By varying τ sequentially from 1 to L instead of picking random values, the calculation of the ratio of the fermionic weights can be reduced to only two matrix multiplications. It turns out that a local updating as described above does not permit efficient simulations for small phonon frequencies or low temperatures. Therefore, we shall introduce an alternative global updating in terms of principal components in section Observables Using the transformed Hamiltonian (14), the expectation value O = Z 1 Tr Ô e βh = Z 1 Tr Õ e β e H (7) of an observables O is computed according to O = Z 1 Tr f dp p Õ e β eh p. (71) As a result of the analytic integration over the phonon coordinates x, interesting observables such as the correlation function n i x j are difficult to measure accurately. Other quantities such as the quasiparticle weight, and the closely related effective mass [16], can be determined from the one-electron Green function at long imaginary times [17], but results for one electron or two electrons would not be as accurate as in existing work (e.g., [18 ]). The situation is strikingly different in the many-electron case, for which many methods fail to produce results of high accuracy for large systems and physically relevant parameters. Moreover, other important observables, such as the one-electron Green function, can be calculated with our approach. One electron The electronic kinetic energy is defined as E kin = H kin = tz 1 ij Tr ( c i c j eiγ(bpi bpj) e β e H ). (7) Repeating the steps used to derive the partition function, and noting that the additional phase factors in equation (7) again lead to the same matrix Ω as in equation (49), we find
16 16 Martin Hohenadler and Wolfgang von der Linden E kin = tz 1 L Dp w b n Ωc i c j n ij n = tz 1 L Dp w b j Ω i (73) ij with the one-electron states (5). Introducing the matrix elements (Ω) ij = i Ω j and the expectation value with respect to w b, O b = Dp wb O(p) Dp wb (74) we obtain E kin = t ij Ω ji b i Ω ii b. (75) Here we have anticipated the reweighting discussed in section 5.3. The total energy can be obtained from E = (ln Z)/ β as E = E kin + ω E ph = ND τ 1 ω τ L p i + E ph E P, i i,τ (p i,τ p i,τ+1 ). (76) To compare with other work we subtract the ground-state energy of the phonons, E,ph = N D ω /. Two electrons For two electrons, exploiting spin symmetry, we have E kin = t ij σ c iσ c jσ = t c i c j eiγ(bpi bpj). (77) ij A simple calculation gives c i c j = Z 1 L Dp w b e iγ(pi,1 pj,1) Tr f (Ω c i c j ). (78) Writing out explicitly the fermionic trace we obtain Tr f (Ω c i c j ) = i j i, j Ωc i c j i, j = j j, j Ω i, j, (79) and the kinetic energy finally becomes
17 E kin = tz 1 L Lang-Firsov approaches to polaron physics 17 Dp w b ij j e iγ(pi,1 pj,1) j, j Ω i, j. (8) In addition to E kin, we shall also consider the correlation function ρ(δ) = i n i n i+δ, δ =, 1,..., N/ 1 (81) depending on the distance δ. We find ρ(δ) = Z 1 L Dp w b i, i + δ Ω i, i + δ. (8) Many-electron case The calculation of observables within the formalism presented here is similar to the standard determinant QMC method [13 15]. For an equal-time (i.e., static) observable O we have i O b = Dp wb w f Tr f (Ô B 1 B L ) Dp wb. (83) The carrier density n = 1 N D n i (84) may be calculated from G b [equation (69)] using n i = G b ii. Similarly, the modulus of the kinetic energy per site is given by E kin = t N D i ij G b ji Equal-time two-particle correlation functions such as. (85) ρ(δ) = i n i n i+δ (86) may be calculated in the same way as in [14,15]. For a given phonon configuration, Wick s Theorem [3] yields n i n j p = c i c i c j c j p = c i c i p c j c j p + c i c j p c i c j p = G b ii Gb jj + Gb ij Ga ij, (87) and n i n j is then determined by averaging over all phonon configurations. The time-dependent one-particle Green function
18 18 Martin Hohenadler and Wolfgang von der Linden G b (k, τ) = c k (τ)c k = eτ H c k e τ H c k (88) is related to the momentum and energy-dependent spectral function through A(k, ω µ) = 1 π Im Gb (k, ω µ) (89) G b (k, τ) = dω e τ(ω µ) A(k, ω µ) 1 + e β(ω µ). (9) The inversion of the above relation is ill-conditioned and requires the use of the maximum entropy method [11,1,1]. Fourier transformation leads to G b (k, τ) = 1 N D e ik (ri rj) G b ij(τ). (91) ij The allowed imaginary times are τ l = l τ, with non-negative integers l L. Within the QMC approach, we have [14,15] The one-electron density of states is given by G b ij (τ l) = (G a B 1 B l ) ji. (9) N(ω µ) = 1 Im G(ω µ), (93) π where G(ω µ) = (N D ) 1 k G(k, ω µ). It may be obtained numerically via N(τ) = G b ii(τ), (94) and subsequent analytical continuation. Suzuki-Trotter error The error associated with the approximation made in, e.g., equation (41) can be systematically reduced by using smaller values of τ. In practice, there are two strategies to handle this so-called Suzuki-Trotter error. Owing to the usually large numerical effort for QMC simulations, τ is often simply chosen such that the systematic error is smaller than the statistical errors for observables. A second, more satisfactory, but also more costly method is to run simulations at different values of τ, and to exploit the τ dependence of the results to extrapolate to τ =. For the results in section 6, we have used a scaling toward τ = based on typical values τ =.1,.75 and.5 to obtain the results for one and two electrons. In contrast, for the numerically more demanding calculations of dynamic properties in the many-electron case, τ =.1 has been chosen. This is justified by the uncertainties in the analytical continuation.
19 Lang-Firsov approaches to polaron physics Reweighting As pointed out at the end of section 5.1, the calculation of the change of the fermionic weight w f represents the most time-consuming part of the updating process. Consequently, it would be highly desirable to avoid the evaluation of w f. This may be achieved by using only the bosonic weight w b in the updating, and treating w f as part of the observables. For the expectation value of an observable O, such a reweighting requires calculation of O = O w f b w f b, (95) where the subscript b indicates that the average is computed based on w b only [cf equation (74)]. Reweighting of the probability distribution is frequently used in MC simulations if a minus-sign problem occurs [1]. Here, the splitting into the configuration weight w b and the observable Ow f is practicable provided the variance of both w f and Ow f is small, which is the case after the LF transformation. Furthermore, we require a significant overlap of the two distributions, which may be quantified using the Kullback-Leibler number [7], in order to avoid prohibitive statistical noise. In fact, our calculations show that, in general, for the untransformed model the reweighting method cannot be applied. For a detailed discussion of this point in the one-electron case see [7]. Here we merely note that no problems arise when simulating the transformed model. Apart from the significant advantage that the fermionic weight w f only has to be calculated when observables are measured, the reweighting method becomes particularly effective in the present case when combined with the principal component representation introduced in section 5.4. In this case, we will be able to perform an exact sampling of the phonons without any autocorrelations. For a reliable error analysis for observables calculated according to equation (95) the Jackknife procedure [] is applied. 5.4 Principal components The reweighting method allows us, in principle, to skip enough sweeps between measurements to reduce autocorrelations to a minimum. However, even though a single phonon update requires negligible computer time compared to the evaluation of w f, for critical parameters, an enormous number of such steps will be necessary between successive measurements [7]. On top of that, reliable results require knowledge of the longest autocorrelation times, which have to be determined in separate simulations for each set of parameters. Due to the structure of the bosonic action S b [see equation (51)], even relatively small (local) changes to the phonon momenta lead to large variations in S b and hence the weight w b. As a consequence, only minor changes may be proposed in order to reach a reasonable acceptance rate. Unfortunately, this strategy is the very origin of autocorrelations.
20 Martin Hohenadler and Wolfgang von der Linden The problem can be overcome by a transformation to the normal modes of the phonons (along the imaginary time axis), so that we can sample completely uncorrelated configurations. As the fermion degrees of freedom are treated exactly, the resulting QMC method is then indeed free of any autocorrelations. To find such a transformation, let us recall the form of the bosonic action, given by equation (5), which we write as S b = i p T i Ap i = i p T i A 1/ A 1/ p i i ξ T i ξ i (96) with the principal components ξ i = A 1/ p i, in terms of which the bosonic weight takes the simple Gaussian form w b = e τ P i ξt i ξi. (97) The sampling can now be performed directly in terms of the new variables ξ. To calculate observables we have to transform back to the physical momenta p using A 1/. Comparison with equation (5) shows that instead of the ill-conditioned matrix A we now have the ideal case that we can easily generate exact samples of a Gaussian distribution. With the new coordinates ξ, the probability distribution can be sampled exactly, e.g., by the Box-Müller method [3]. In contrast to a standard Markov chain MC simulation, every new configuration is accepted and measurements can be made at each step, so that simulation times are significantly reduced. From the definition of the principal components it is obvious that an update of a single variable ξ i,τ, say, actually corresponds to a change of all p i,τ, τ = 1,...,L. Thus, in terms of the original phonon momenta p, the updating becomes non-local. The principal component representation can be used for one, two and many electrons, since the bosonic action [equation (97)] is identical. This even holds for models including, e.g., spin-spin interactions, as long as the phonon operators enter in the same form as in the Holstein model. An important point is the combination of the principal components with the reweighting method. Using the latter, the changes to the original momenta p, which are made in the simulation, do not depend in any way on the electronic degrees of freedom. Thus we are actually sampling a set of independent harmonic oscillators, as described by S b. The crucial requirement for the success of this method is the use of the LF transformed model, in which the (bi-)polaron effects are separated from the zero-point motion of the oscillators around their current equilibrium positions. Finally, as there is no need for a warm-up phase, and owing to the statistical independence of the configurations, the present algorithm is perfectly suited for parallelization.
21 Lang-Firsov approaches to polaron physics <sign>.6.4. βt = 4 βt = 6 βt = 8 (a) N = 16, α =.4, n = λ <sign>.6.4. α =.4 α = 1. α =. α = 4. (b) N = 16, βt = 8, n = λ Fig. 1. Average sign sign in the many-electron case as a function of el-ph coupling λ in D = 1 (a) for different inverse temperatures β, and (b) for different values of the adiabaticity ratio α. Lines are guides to the eye, and errorbars are smaller than the symbols shown. The data presented in figures 1 and are for τ =.5. [Taken from [11].] 5.5 Minus-sign problem The motivation for our development of a novel QMC approach to Holstein models was to improve on the performance of existing methods, especially in the many-electron case. As pointed out in [1], the LF transformation causes a sign problem even for the pure Holstein model which, in general, may significantly affect the applicability of the method. Therefore, we briefly discuss the resulting limitations, focussing on the many-electron case. We shall see that there is a fundamental difference between simulations for one or two electrons the carrier density being zero in the thermodynamic limit and grand-canonical calculations at finite density n >. Whereas for one or two carriers the sign problem turns out to be rather uncritical the average sign approaches unity upon increasing system size, in contrast to the usual behaviour [1] restrictions are encountered in simulations of the manyelectron case. Since w b is strictly positive, we define the average sign as sign = w f b / w f b. (98) For simplicity, we first show results for n =.5, while the effect of band filling will be discussed later. The choice n =.5 is convenient since we know the chemical potential, and we shall see below that the sign problem is most pronounced for a half-filled band. Moreover, most existing QMC results for the spinless Holstein model are for half filling (see references in [7]). Figure 1(a) shows the dependence of sign on the el-ph coupling strength. It takes on a minimum near λ = 1 (for α < 1) that becomes more pronounced with decreasing temperature. At weak coupling (WC) and SC, sign 1, so that accurate simulations can be carried out. These results are quite similar to the cases of one or two electrons [4].
22 Martin Hohenadler and Wolfgang von der Linden <sign>.6.4. (a) N = 16, βt = 8, α =.4, λ = n <sign>.6.4. βt = 4 βt = 6 βt = 8 (b) α =.4, n =.5, λ = ln N 3 Fig.. Average sign in the many-electron case as a function of (a) band filling n, and (b) system size N. The dependence on phonon frequency [figure 1(b)] also bears a close resemblance to the polaron problem [4]. Whereas sign becomes very small for α 1, it increases noticeably in the non-adiabatic regime α > 1, permitting efficient and accurate simulations. As illustrated in figure (a), the average sign depends strongly on the band filling n. While it is close to one in the vicinity of n = or n = 1 (equivalent to one or two electrons), a significant reduction is visible near half filling n =.5. The minimum occurs at n =.5, and the results display particle-hole symmetry as expected. Here we have chosen βt = 8, α =.4 and λ = 1, for which the sign problem is most noticeable according to figure 1. In figure (b), we report the average sign as a function of system size, again for n =.5. The dependence is strikingly different from the one-electron case. While in the latter sign 1 as N [7,4], here the average sign decreases nearly exponentially with increasing system size, a behaviour well-known from QMC simulations of Hubbard models [1]. Obviously, this limits the applicability of our method. However, we shall see below that we can nevertheless obtain accurate results at low temperatures, small phonon frequencies, and over a large range of the el-ph coupling strength. Moreover, we would like to point out that for such parameters, other methods suffer strongly from autocorrelations, rendering simulations extremely difficult. The dependence of the sign problem on the dimension of the system is again similar to the single-electron case [4]. The minimum at intermediate λ becomes more pronounced for the same parameters N, α, βt and λ as one increases the dimension of the cluster. To conclude with, we would like to point out that, in principle, the sign problem can be compensated by performing sufficiently long QMC runs, but we have to keep in mind that the statistical errors increase proportional to sign [1], setting a practical limit to the accuracy.
23 5.6 Comparison with other approaches Lang-Firsov approaches to polaron physics 3 The QMC method presented above seems to be most advantageous as compared to other approaches in the case of the spinless Holstein model with many electrons. For the latter, other methods are severely restricted by autocorrelations, rendering accurate simulations in the physically important adiabatic, IC regime virtually impossible even at moderately low temperatures. In contrast, the present method enables us to study the single-particle spectrum on rather large clusters and for a wide range of model parameters and band filling (see section 6.3). Unfortunately, the generalization to the spinful Hubbard-Holstein model suffers severely from the sign problem. For the polaron and the bipolaron problem, our method requires more computer time than other QMC algorithms [5 8]. However, we are able to consider practically all parameter regimes on reasonably large clusters in one (polaron and bipolaron problem) and two dimensions (polaron problem). Finally, a discussion of the scaling of computer time with the system parameters can be found in [7, 9,1]. 6 Selected results We now come to a selection of results obtained with the methods discussed so far, most of which have been published before [7, 9 11]. Note that errorbars will be suppressed in the figures if smaller than the symbolsize. Moreover, lines connecting data points are guides to the eye only. 6.1 Small-polaron cross-over The Holstein model with a single electron (for a review see [9]) exhibits a cross-over from a large polaron (D = 1) or a quasi-free electron (D > 1) to a small polaron with increasing el-ph coupling strength. Quantum Monte Carlo To investigate the small-polaron cross-over, following previous work [4, 16, 18,5,3 3], we calculate the electronic kinetic energy E kin given by equation (75). As we shall compare results for different dimensions, we define the normalized quantity E kin = E kin /( td) (99) with E kin = 1 for T = and λ =. The inverse temperature will be fixed to βt = 1, low enough to identify the cross-over. Calculations at even lower temperatures can easily be done for α > 1, but α < 1 requires very large numbers of measurements to ensure satisfactorily small statistical errors. System sizes were 3 sites in 1D, a
24 4 Martin Hohenadler and Wolfgang von der Linden Ekin Ekin Ekin α =.1 α =.5 α = 1. α =. α = 3. α = 4. α = 6. α = 8. α = 1. (a) 1D, N = 3, βt = 1 α =.1, N = 6 (b) D, N = 1, βt = 1 (c) 3D, N = 6, βt = λ Fig. 3. Normalized kinetic energy E kin [equation (99)] of the Holstein model with one electron from QMC as a function of el-ph coupling λ for different adiabaticity ratios α and different dimensions D of the lattice (N denotes the linear cluster size). Here and in subsequent figures, QMC data have been extrapolated to τ = (see section 5.). [Taken from [1].] 1 1 cluster in D, and a lattice in 3D. In contrast to D = 1,, where results are well converged with respect to system size, non-negligible finite-size effects (maximal relative changes of up to % between N = 5 and N = 6 for α 1; much smaller changes otherwise) are observed in three dimensions. Moreover, for small N, effects due to thermal population of states with non-zero momentum k absent in ground-state calculations are visible, as discussed below. Nevertheless, the main characteristics are well visible already for N = 6. For a detailed study of finite-size and finite-temperature effects see [4]. Figure 3 shows E kin as a function of the el-ph coupling λ for different phonon frequencies varying over two orders of magnitude, in one to three dimensions. Generally, the kinetic energy is large at WC, where the ground state consists of a weakly dressed electron (D > 1) or a large polaron (D =
25 Lang-Firsov approaches to polaron physics 5 1). It reduces more or less strongly depending on α in the SC regime, where a small, heavy polaron exists, defined as an electron surrounded by a lattice distortion essentially localized at the same site. The finite values of E kin even for large λ are a result of undirected motion of the electron inside the surrounding phonon cloud. In contrast, the quasiparticle weight is exponentially reduced in the SC regime (see, e.g., []), whereas the effective mass becomes exponentially large. In all dimensions, the phonon frequency has a crucial influence on the behaviour of the kinetic energy. While in the adiabatic regime α < 1 the small-polaron cross-over is determined by the condition λ = E P /td > 1, the corresponding criterion for α > 1 is g = E P /ω > 1. The former condition reflects the fact that the loss in kinetic energy of the electron has to be outweighed by a gain in potential energy in order to make small-polaron formation favourable. The latter condition expresses the increasing importance of the lattice energy for α > 1, since the formation of a localized state requires a sizable lattice distortion. As a consequence, for large phonon frequencies, the critical coupling shifts to λ c > 1, whereas for α < 1 we have λ c = 1. Additionally, the decrease of E kin at λ c becomes significantly sharper with decreasing phonon frequency. Concerning the effect of dimensionality, figure 3 reveals that, for fixed α, the small-polaron cross-over becomes more abrupt in higher dimensions, with a very sharp decrease in 3D. Nevertheless, there is no real phase transition [33]. Figure 3 also contains results for N = 6 in one and two dimensions, i.e., for the same linear cluster size as in 3D (dashed lines). Clearly, for such small clusters, the spacing between the discrete allowed momenta k is too large to permit substantial thermal population, so that results are closer to the ground state [e.g., E kin (λ = ) 1], and exhibit a slightly more pronounced decrease near the critical coupling. However, the sharpening of the latter with increasing dimensionality is still well visible. Variational approach To test the validity of the variational approach of section 4 we have calculated the total energy [equation (4)] and the quasiparticle weight [equation (9)] on a cluster with N = 4 for various values of α. A comparison with exact diagonalization results [34] is depicted in figure 4. We only consider the regime α 1 where the zero-phonon approximation is expected to be justified. The overall agreement is strikingly good. Minor deviations from the exact results increase with decreasing α. For the smallest frequency shown, α = 1, the result of the HLF approximation is also reported. Clearly, the variational method represents a significant improvement over the HLF approximation, underlining the importance of taking into account non-local distortions. Similar conclusions can be drawn for larger system sizes (see figure 3 in [7]). In figure 5 we present results for the variational displacement fields γ δ, which provide a measure for the polaron size. For α =.1 we see an abrupt
26 6 Martin Hohenadler and Wolfgang von der Linden - (a) 1 (b) E / t -4 α = 1 α = α = 4 α = 8 α = 1, HLF -6 1 λ z.5 α = 8 α = 4 α = α = 1 α = 1, HLF 1 λ Fig. 4. Total energy E (a) and quasiparticle weight z (b) for N = 4 as functions of the el-ph coupling λ for different values of the adiabaticity ratio α. Symbols correspond to variational results and full lines represent exact T = data obtained with the Lanczos method [34]. Dashed lines are results of the HLF approximation. [Taken from [7].] γδ (a) α =.1 LF δ = δ = 1 δ = δ = 3 1 λ γδ 3 1 (b) α = 4 LF δ = δ = 1 δ = δ = λ Fig. 5. Polaron-size parameter γ δ for N = 16 as a function of the el-ph coupling λ for various distances δ in the (a) adiabatic and (b) anti-adiabatic regime. Also shown is the LF parameter γ [equation (1)]. [Taken from [7].] cross-over from a large to a small polaron at λ 1.. For smaller λ, the electron induces lattice distortions at neighboring sites even at a distance of more than three lattice constants. Above λ 1. we have a mobile small polaron extending over a single site only. In contrast, for the anti-adiabatic case α = 4, the cross-over is much more gradual, and γ 1 > even for λ 1. The same behaviour has been found by Marsiglio [35] who determined the correlation function n i x i+δ by exact diagonalization; within the variational approach n i x i+δ = γ δ. Although in Marsiglio s results the cross-over to a small polaron for α =.1 occurs at a smaller value of the coupling λ 1, the simple variational approach reproduces the main characteristics. 6. Bipolaron formation in the extended Holstein-Hubbard model In contrast to Cooper pairing of electrons with opposite momentum, two electrons may also form a bound state by travelling sufficiently close in real space.
arxiv:cond-mat/ v2 [cond-mat.str-el] 24 Feb 2006
![arxiv:cond-mat/ v2 [cond-mat.str-el] 24 Feb 2006 arxiv:cond-mat/ v2 [cond-mat.str-el] 24 Feb 2006](/thumbs/87/97408356.jpg) Applications of Cluster Perturbation Theory Using Quantum Monte Carlo Data arxiv:cond-mat/0512406v2 [cond-mat.str-el] 24 Feb 2006 Fei Lin, Erik S. Sørensen, Catherine Kallin and A. John Berlinsky Department
Applications of Cluster Perturbation Theory Using Quantum Monte Carlo Data arxiv:cond-mat/0512406v2 [cond-mat.str-el] 24 Feb 2006 Fei Lin, Erik S. Sørensen, Catherine Kallin and A. John Berlinsky Department
Quantum Simulation Studies of Charge Patterns in Fermi-Bose Systems
 Quantum Simulation Studies of Charge Patterns in Fermi-Bose Systems 1. Hubbard to Holstein 2. Peierls Picture of CDW Transition 3. Phonons with Dispersion 4. Holstein Model on Honeycomb Lattice 5. A New
Quantum Simulation Studies of Charge Patterns in Fermi-Bose Systems 1. Hubbard to Holstein 2. Peierls Picture of CDW Transition 3. Phonons with Dispersion 4. Holstein Model on Honeycomb Lattice 5. A New
Fermions in the unitary regime at finite temperatures from path integral auxiliary field Monte Carlo simulations
 Fermions in the unitary regime at finite temperatures from path integral auxiliary field Monte Carlo simulations Aurel Bulgac,, Joaquin E. Drut and Piotr Magierski University of Washington, Seattle, WA
Fermions in the unitary regime at finite temperatures from path integral auxiliary field Monte Carlo simulations Aurel Bulgac,, Joaquin E. Drut and Piotr Magierski University of Washington, Seattle, WA
Quantum Monte Carlo approach to the Holstein polaron problem
 phys. stat. sol. (b) 242, No. 7, 1406 1413 (2005) / DOI 10.1002/pssb.200440019 Quantum Monte Carlo approach to the Holstein polaron problem Martin Hohenadler *, Hans Gerd Evertz, and Wolfgang von der Linden
phys. stat. sol. (b) 242, No. 7, 1406 1413 (2005) / DOI 10.1002/pssb.200440019 Quantum Monte Carlo approach to the Holstein polaron problem Martin Hohenadler *, Hans Gerd Evertz, and Wolfgang von der Linden
Lecture notes for QFT I (662)
 Preprint typeset in JHEP style - PAPER VERSION Lecture notes for QFT I (66) Martin Kruczenski Department of Physics, Purdue University, 55 Northwestern Avenue, W. Lafayette, IN 47907-036. E-mail: markru@purdue.edu
Preprint typeset in JHEP style - PAPER VERSION Lecture notes for QFT I (66) Martin Kruczenski Department of Physics, Purdue University, 55 Northwestern Avenue, W. Lafayette, IN 47907-036. E-mail: markru@purdue.edu
Is a system of fermions in the crossover BCS-BEC. BEC regime a new type of superfluid?
 Is a system of fermions in the crossover BCS-BEC BEC regime a new type of superfluid? Finite temperature properties of a Fermi gas in the unitary regime Aurel Bulgac,, Joaquin E. Drut, Piotr Magierski
Is a system of fermions in the crossover BCS-BEC BEC regime a new type of superfluid? Finite temperature properties of a Fermi gas in the unitary regime Aurel Bulgac,, Joaquin E. Drut, Piotr Magierski
Diagrammatic Green s Functions Approach to the Bose-Hubbard Model
 Diagrammatic Green s Functions Approach to the Bose-Hubbard Model Matthias Ohliger Institut für Theoretische Physik Freie Universität Berlin 22nd of January 2008 Content OVERVIEW CONSIDERED SYSTEM BASIC
Diagrammatic Green s Functions Approach to the Bose-Hubbard Model Matthias Ohliger Institut für Theoretische Physik Freie Universität Berlin 22nd of January 2008 Content OVERVIEW CONSIDERED SYSTEM BASIC
3 Symmetry Protected Topological Phase
 Physics 3b Lecture 16 Caltech, 05/30/18 3 Symmetry Protected Topological Phase 3.1 Breakdown of noninteracting SPT phases with interaction Building on our previous discussion of the Majorana chain and
Physics 3b Lecture 16 Caltech, 05/30/18 3 Symmetry Protected Topological Phase 3.1 Breakdown of noninteracting SPT phases with interaction Building on our previous discussion of the Majorana chain and
Electronic structure of correlated electron systems. Lecture 2
 Electronic structure of correlated electron systems Lecture 2 Band Structure approach vs atomic Band structure Delocalized Bloch states Fill up states with electrons starting from the lowest energy No
Electronic structure of correlated electron systems Lecture 2 Band Structure approach vs atomic Band structure Delocalized Bloch states Fill up states with electrons starting from the lowest energy No
Electrons in a periodic potential
 Chapter 3 Electrons in a periodic potential 3.1 Bloch s theorem. We consider in this chapter electrons under the influence of a static, periodic potential V (x), i.e. such that it fulfills V (x) = V (x
Chapter 3 Electrons in a periodic potential 3.1 Bloch s theorem. We consider in this chapter electrons under the influence of a static, periodic potential V (x), i.e. such that it fulfills V (x) = V (x
5. Superconductivity. R(T) = 0 for T < T c, R(T) = R 0 +at 2 +bt 5, B = H+4πM = 0,
 5. Superconductivity In this chapter we shall introduce the fundamental experimental facts about superconductors and present a summary of the derivation of the BSC theory (Bardeen Cooper and Schrieffer).
5. Superconductivity In this chapter we shall introduce the fundamental experimental facts about superconductors and present a summary of the derivation of the BSC theory (Bardeen Cooper and Schrieffer).
4 Matrix product states
 Physics 3b Lecture 5 Caltech, 05//7 4 Matrix product states Matrix product state (MPS) is a highly useful tool in the study of interacting quantum systems in one dimension, both analytically and numerically.
Physics 3b Lecture 5 Caltech, 05//7 4 Matrix product states Matrix product state (MPS) is a highly useful tool in the study of interacting quantum systems in one dimension, both analytically and numerically.
Quasiparticle dynamics and interactions in non uniformly polarizable solids
 Quasiparticle dynamics and interactions in non uniformly polarizable solids Mona Berciu University of British Columbia à beautiful physics that George Sawatzky has been pursuing for a long time à today,
Quasiparticle dynamics and interactions in non uniformly polarizable solids Mona Berciu University of British Columbia à beautiful physics that George Sawatzky has been pursuing for a long time à today,
Luigi Paolasini
 Luigi Paolasini paolasini@esrf.fr LECTURE 4: MAGNETIC INTERACTIONS - Dipole vs exchange magnetic interactions. - Direct and indirect exchange interactions. - Anisotropic exchange interactions. - Interplay
Luigi Paolasini paolasini@esrf.fr LECTURE 4: MAGNETIC INTERACTIONS - Dipole vs exchange magnetic interactions. - Direct and indirect exchange interactions. - Anisotropic exchange interactions. - Interplay
Lecture 5. Hartree-Fock Theory. WS2010/11: Introduction to Nuclear and Particle Physics
 Lecture 5 Hartree-Fock Theory WS2010/11: Introduction to Nuclear and Particle Physics Particle-number representation: General formalism The simplest starting point for a many-body state is a system of
Lecture 5 Hartree-Fock Theory WS2010/11: Introduction to Nuclear and Particle Physics Particle-number representation: General formalism The simplest starting point for a many-body state is a system of
arxiv: v1 [cond-mat.str-el] 18 Jul 2007
![arxiv: v1 [cond-mat.str-el] 18 Jul 2007 arxiv: v1 [cond-mat.str-el] 18 Jul 2007](/thumbs/89/99838639.jpg) arxiv:0707.2704v1 [cond-mat.str-el] 18 Jul 2007 Determination of the Mott insulating transition by the multi-reference density functional theory 1. Introduction K. Kusakabe Graduate School of Engineering
arxiv:0707.2704v1 [cond-mat.str-el] 18 Jul 2007 Determination of the Mott insulating transition by the multi-reference density functional theory 1. Introduction K. Kusakabe Graduate School of Engineering
Numerical Studies of the 2D Hubbard Model
 arxiv:cond-mat/0610710v1 [cond-mat.str-el] 25 Oct 2006 Numerical Studies of the 2D Hubbard Model D.J. Scalapino Department of Physics, University of California, Santa Barbara, CA 93106-9530, USA Abstract
arxiv:cond-mat/0610710v1 [cond-mat.str-el] 25 Oct 2006 Numerical Studies of the 2D Hubbard Model D.J. Scalapino Department of Physics, University of California, Santa Barbara, CA 93106-9530, USA Abstract
Quantum Monte Carlo Simulations of the Half-filled Hubbard Model. Anders F. J. Gabrielsson
 Quantum Monte Carlo Simulations of the Half-filled Hubbard Model Anders F. J. Gabrielsson June 2011 Abstract A Quantum Monte Carlo method of calculating operator expectation values for the ground state
Quantum Monte Carlo Simulations of the Half-filled Hubbard Model Anders F. J. Gabrielsson June 2011 Abstract A Quantum Monte Carlo method of calculating operator expectation values for the ground state
Part III: Impurities in Luttinger liquids
 Functional RG for interacting fermions... Part III: Impurities in Luttinger liquids 1. Luttinger liquids 2. Impurity effects 3. Microscopic model 4. Flow equations 5. Results S. Andergassen, T. Enss (Stuttgart)
Functional RG for interacting fermions... Part III: Impurities in Luttinger liquids 1. Luttinger liquids 2. Impurity effects 3. Microscopic model 4. Flow equations 5. Results S. Andergassen, T. Enss (Stuttgart)
MONTE CARLO STUDIES OF HUBBARD MODELS. Helen Craig
 MONTE CARLO STUDIES OF HUBBARD MODELS Helen Craig ABSTRACT This summer, I studied two variations of the extended Hubbard model: the extended Hubbard Holstein model and the extended Hubbard model with staggered
MONTE CARLO STUDIES OF HUBBARD MODELS Helen Craig ABSTRACT This summer, I studied two variations of the extended Hubbard model: the extended Hubbard Holstein model and the extended Hubbard model with staggered
SECOND QUANTIZATION. Lecture notes with course Quantum Theory
 SECOND QUANTIZATION Lecture notes with course Quantum Theory Dr. P.J.H. Denteneer Fall 2008 2 SECOND QUANTIZATION 1. Introduction and history 3 2. The N-boson system 4 3. The many-boson system 5 4. Identical
SECOND QUANTIZATION Lecture notes with course Quantum Theory Dr. P.J.H. Denteneer Fall 2008 2 SECOND QUANTIZATION 1. Introduction and history 3 2. The N-boson system 4 3. The many-boson system 5 4. Identical
Classical Monte Carlo Simulations
 Classical Monte Carlo Simulations Hyejin Ju April 17, 2012 1 Introduction Why do we need numerics? One of the main goals of condensed matter is to compute expectation values O = 1 Z Tr{O e βĥ} (1) and
Classical Monte Carlo Simulations Hyejin Ju April 17, 2012 1 Introduction Why do we need numerics? One of the main goals of condensed matter is to compute expectation values O = 1 Z Tr{O e βĥ} (1) and
Lecture 6: Fluctuation-Dissipation theorem and introduction to systems of interest
 Lecture 6: Fluctuation-Dissipation theorem and introduction to systems of interest In the last lecture, we have discussed how one can describe the response of a well-equilibriated macroscopic system to
Lecture 6: Fluctuation-Dissipation theorem and introduction to systems of interest In the last lecture, we have discussed how one can describe the response of a well-equilibriated macroscopic system to
Identical Particles. Bosons and Fermions
 Identical Particles Bosons and Fermions In Quantum Mechanics there is no difference between particles and fields. The objects which we refer to as fields in classical physics (electromagnetic field, field
Identical Particles Bosons and Fermions In Quantum Mechanics there is no difference between particles and fields. The objects which we refer to as fields in classical physics (electromagnetic field, field
arxiv:quant-ph/ v5 10 Feb 2003
 Quantum entanglement of identical particles Yu Shi Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, United Kingdom and Theory of
Quantum entanglement of identical particles Yu Shi Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, United Kingdom and Theory of
The Quantum Heisenberg Ferromagnet
 The Quantum Heisenberg Ferromagnet Soon after Schrödinger discovered the wave equation of quantum mechanics, Heisenberg and Dirac developed the first successful quantum theory of ferromagnetism W. Heisenberg,
The Quantum Heisenberg Ferromagnet Soon after Schrödinger discovered the wave equation of quantum mechanics, Heisenberg and Dirac developed the first successful quantum theory of ferromagnetism W. Heisenberg,
Magnetism and Superconductivity in Decorated Lattices
 Magnetism and Superconductivity in Decorated Lattices Mott Insulators and Antiferromagnetism- The Hubbard Hamiltonian Illustration: The Square Lattice Bipartite doesn t mean N A = N B : The Lieb Lattice
Magnetism and Superconductivity in Decorated Lattices Mott Insulators and Antiferromagnetism- The Hubbard Hamiltonian Illustration: The Square Lattice Bipartite doesn t mean N A = N B : The Lieb Lattice
Generalization of the matrix product ansatz for integrable chains
 arxiv:cond-mat/0608177v1 [cond-mat.str-el] 7 Aug 006 Generalization of the matrix product ansatz for integrable chains F. C. Alcaraz, M. J. Lazo Instituto de Física de São Carlos, Universidade de São Paulo,
arxiv:cond-mat/0608177v1 [cond-mat.str-el] 7 Aug 006 Generalization of the matrix product ansatz for integrable chains F. C. Alcaraz, M. J. Lazo Instituto de Física de São Carlos, Universidade de São Paulo,
Physics 211B : Problem Set #0
 Physics 211B : Problem Set #0 These problems provide a cross section of the sort of exercises I would have assigned had I taught 211A. Please take a look at all the problems, and turn in problems 1, 4,
Physics 211B : Problem Set #0 These problems provide a cross section of the sort of exercises I would have assigned had I taught 211A. Please take a look at all the problems, and turn in problems 1, 4,
Preface. Preface to the Third Edition. Preface to the Second Edition. Preface to the First Edition. 1 Introduction 1
 xi Contents Preface Preface to the Third Edition Preface to the Second Edition Preface to the First Edition v vii viii ix 1 Introduction 1 I GENERAL THEORY OF OPEN QUANTUM SYSTEMS 5 Diverse limited approaches:
xi Contents Preface Preface to the Third Edition Preface to the Second Edition Preface to the First Edition v vii viii ix 1 Introduction 1 I GENERAL THEORY OF OPEN QUANTUM SYSTEMS 5 Diverse limited approaches:
where β = 1, H = H µn (3.3) If the Hamiltonian has no explicit time dependence, the Greens functions are homogeneous in time:
 3. Greens functions 3.1 Matsubara method In the solid state theory class, Greens functions were introduced as response functions; they can be used to determine the quasiparticle density of states. They
3. Greens functions 3.1 Matsubara method In the solid state theory class, Greens functions were introduced as response functions; they can be used to determine the quasiparticle density of states. They
Examination paper for TFY4210 Quantum theory of many-particle systems
 Department of Physics Examination paper for TFY4210 Quantum theory of many-particle systems Academic contact during examination: Associate Professor John Ove Fjærestad Phone: 97 94 00 36 Examination date:
Department of Physics Examination paper for TFY4210 Quantum theory of many-particle systems Academic contact during examination: Associate Professor John Ove Fjærestad Phone: 97 94 00 36 Examination date:
1 Equal-time and Time-ordered Green Functions
 1 Equal-time and Time-ordered Green Functions Predictions for observables in quantum field theories are made by computing expectation values of products of field operators, which are called Green functions
1 Equal-time and Time-ordered Green Functions Predictions for observables in quantum field theories are made by computing expectation values of products of field operators, which are called Green functions
Metal-insulator transition with Gutzwiller-Jastrow wave functions
 Metal-insulator transition with Gutzwiller-Jastrow wave functions Odenwald, July 20, 2010 Andrea Di Ciolo Institut für Theoretische Physik, Goethe Universität Frankfurt Metal-insulator transition withgutzwiller-jastrow
Metal-insulator transition with Gutzwiller-Jastrow wave functions Odenwald, July 20, 2010 Andrea Di Ciolo Institut für Theoretische Physik, Goethe Universität Frankfurt Metal-insulator transition withgutzwiller-jastrow
Tensor network simulations of strongly correlated quantum systems
 CENTRE FOR QUANTUM TECHNOLOGIES NATIONAL UNIVERSITY OF SINGAPORE AND CLARENDON LABORATORY UNIVERSITY OF OXFORD Tensor network simulations of strongly correlated quantum systems Stephen Clark LXXT[[[GSQPEFS\EGYOEGXMZMXMIWUYERXYQGSYVWI
CENTRE FOR QUANTUM TECHNOLOGIES NATIONAL UNIVERSITY OF SINGAPORE AND CLARENDON LABORATORY UNIVERSITY OF OXFORD Tensor network simulations of strongly correlated quantum systems Stephen Clark LXXT[[[GSQPEFS\EGYOEGXMZMXMIWUYERXYQGSYVWI
SSH Model. Alessandro David. November 3, 2016
 SSH Model Alessandro David November 3, 2016 Adapted from Lecture Notes at: https://arxiv.org/abs/1509.02295 and from article: Nature Physics 9, 795 (2013) Motivations SSH = Su-Schrieffer-Heeger Polyacetylene
SSH Model Alessandro David November 3, 2016 Adapted from Lecture Notes at: https://arxiv.org/abs/1509.02295 and from article: Nature Physics 9, 795 (2013) Motivations SSH = Su-Schrieffer-Heeger Polyacetylene
Magnetism and Superconductivity on Depleted Lattices
 Magnetism and Superconductivity on Depleted Lattices 1. Square Lattice Hubbard Hamiltonian: AF and Mott Transition 2. Quantum Monte Carlo 3. The 1/4 depleted (Lieb) lattice and Flat Bands 4. The 1/5 depleted
Magnetism and Superconductivity on Depleted Lattices 1. Square Lattice Hubbard Hamiltonian: AF and Mott Transition 2. Quantum Monte Carlo 3. The 1/4 depleted (Lieb) lattice and Flat Bands 4. The 1/5 depleted
Lecture 6. Fermion Pairing. WS2010/11: Introduction to Nuclear and Particle Physics
 Lecture 6 Fermion Pairing WS2010/11: Introduction to Nuclear and Particle Physics Experimental indications for Cooper-Pairing Solid state physics: Pairing of electrons near the Fermi surface with antiparallel
Lecture 6 Fermion Pairing WS2010/11: Introduction to Nuclear and Particle Physics Experimental indications for Cooper-Pairing Solid state physics: Pairing of electrons near the Fermi surface with antiparallel
Physics 127c: Statistical Mechanics. Application of Path Integrals to Superfluidity in He 4
 Physics 17c: Statistical Mechanics Application of Path Integrals to Superfluidity in He 4 The path integral method, and its recent implementation using quantum Monte Carlo methods, provides both an intuitive
Physics 17c: Statistical Mechanics Application of Path Integrals to Superfluidity in He 4 The path integral method, and its recent implementation using quantum Monte Carlo methods, provides both an intuitive
A theoretical study of the single-molecule transistor
 A theoretical study of the single-molecule transistor B. C. Friesen Department of Physics, Oklahoma Baptist University, Shawnee, OK 74804 J. K. Ingersent Department of Physics, University of Florida, Gainesville,
A theoretical study of the single-molecule transistor B. C. Friesen Department of Physics, Oklahoma Baptist University, Shawnee, OK 74804 J. K. Ingersent Department of Physics, University of Florida, Gainesville,
in-medium pair wave functions the Cooper pair wave function the superconducting order parameter anomalous averages of the field operators
 (by A. A. Shanenko) in-medium wave functions in-medium pair-wave functions and spatial pair particle correlations momentum condensation and ODLRO (off-diagonal long range order) U(1) symmetry breaking
(by A. A. Shanenko) in-medium wave functions in-medium pair-wave functions and spatial pair particle correlations momentum condensation and ODLRO (off-diagonal long range order) U(1) symmetry breaking
Computational strongly correlated materials R. Torsten Clay Physics & Astronomy
 Computational strongly correlated materials R. Torsten Clay Physics & Astronomy Current/recent students Saurabh Dayal (current PhD student) Wasanthi De Silva (new grad student 212) Jeong-Pil Song (finished
Computational strongly correlated materials R. Torsten Clay Physics & Astronomy Current/recent students Saurabh Dayal (current PhD student) Wasanthi De Silva (new grad student 212) Jeong-Pil Song (finished
(about) Polarons and Bipolarons
 (about) Polarons and Bipolarons Mona Berciu University of British Columbia Thanks: George Sawatzky Glen Goodvin, Dominic Marchand and Lucian Covaci Hadi Ebrahimnejad, Clemens Adolphs and Mirko Moeller
(about) Polarons and Bipolarons Mona Berciu University of British Columbia Thanks: George Sawatzky Glen Goodvin, Dominic Marchand and Lucian Covaci Hadi Ebrahimnejad, Clemens Adolphs and Mirko Moeller
Magnets, 1D quantum system, and quantum Phase transitions
 134 Phys620.nb 10 Magnets, 1D quantum system, and quantum Phase transitions In 1D, fermions can be mapped into bosons, and vice versa. 10.1. magnetization and frustrated magnets (in any dimensions) Consider
134 Phys620.nb 10 Magnets, 1D quantum system, and quantum Phase transitions In 1D, fermions can be mapped into bosons, and vice versa. 10.1. magnetization and frustrated magnets (in any dimensions) Consider
10 Thermal field theory
 0 Thermal field theory 0. Overview Introduction The Green functions we have considered so far were all defined as expectation value of products of fields in a pure state, the vacuum in the absence of real
0 Thermal field theory 0. Overview Introduction The Green functions we have considered so far were all defined as expectation value of products of fields in a pure state, the vacuum in the absence of real
Engineering of quantum Hamiltonians by high-frequency laser fields Mikhail Katsnelson
 Engineering of quantum Hamiltonians by high-frequency laser fields Mikhail Katsnelson Main collaborators: Sasha Itin Clément Dutreix Zhenya Stepanov Theory of Condensed Matter group http://www.ru.nl/tcm
Engineering of quantum Hamiltonians by high-frequency laser fields Mikhail Katsnelson Main collaborators: Sasha Itin Clément Dutreix Zhenya Stepanov Theory of Condensed Matter group http://www.ru.nl/tcm
Lecture contents. A few concepts from Quantum Mechanics. Tight-binding model Solid state physics review
 Lecture contents A few concepts from Quantum Mechanics Particle in a well Two wells: QM perturbation theory Many wells (atoms) BAND formation Tight-binding model Solid state physics review Approximations
Lecture contents A few concepts from Quantum Mechanics Particle in a well Two wells: QM perturbation theory Many wells (atoms) BAND formation Tight-binding model Solid state physics review Approximations
Testing the Monte Carlo - Mean Field approximation in the one-band Hubbard model
 Testing the Monte Carlo - Mean Field approximation in the one-band Hubbard model Anamitra Mukherjee 1, Niravkumar D. Patel 1, Shuai Dong 2, Steve Johnston 1, Adriana Moreo 1,3, and Elbio Dagotto 1,3 1
Testing the Monte Carlo - Mean Field approximation in the one-band Hubbard model Anamitra Mukherjee 1, Niravkumar D. Patel 1, Shuai Dong 2, Steve Johnston 1, Adriana Moreo 1,3, and Elbio Dagotto 1,3 1
Time-dependent DMRG:
 The time-dependent DMRG and its applications Adrian Feiguin Time-dependent DMRG: ^ ^ ih Ψ( t) = 0 t t [ H ( t) E ] Ψ( )... In a truncated basis: t=3 τ t=4 τ t=5τ t=2 τ t= τ t=0 Hilbert space S.R.White
The time-dependent DMRG and its applications Adrian Feiguin Time-dependent DMRG: ^ ^ ih Ψ( t) = 0 t t [ H ( t) E ] Ψ( )... In a truncated basis: t=3 τ t=4 τ t=5τ t=2 τ t= τ t=0 Hilbert space S.R.White
Quantum Cluster Methods (CPT/CDMFT)
 Quantum Cluster Methods (CPT/CDMFT) David Sénéchal Département de physique Université de Sherbrooke Sherbrooke (Québec) Canada Autumn School on Correlated Electrons Forschungszentrum Jülich, Sept. 24,
Quantum Cluster Methods (CPT/CDMFT) David Sénéchal Département de physique Université de Sherbrooke Sherbrooke (Québec) Canada Autumn School on Correlated Electrons Forschungszentrum Jülich, Sept. 24,
arxiv:cond-mat/ v1 [cond-mat.str-el] 24 Jan 2000
![arxiv:cond-mat/ v1 [cond-mat.str-el] 24 Jan 2000 arxiv:cond-mat/ v1 [cond-mat.str-el] 24 Jan 2000](/thumbs/78/77713225.jpg) The sign problem in Monte Carlo simulations of frustrated quantum spin systems Patrik Henelius and Anders W. Sandvik 2 National High Magnetic Field Laboratory, 800 East Paul Dirac Dr., Tallahassee, Florida
The sign problem in Monte Carlo simulations of frustrated quantum spin systems Patrik Henelius and Anders W. Sandvik 2 National High Magnetic Field Laboratory, 800 East Paul Dirac Dr., Tallahassee, Florida
NUMERICAL METHODS FOR QUANTUM IMPURITY MODELS
 NUMERICAL METODS FOR QUANTUM IMPURITY MODELS http://www.staff.science.uu.nl/~mitch003/nrg.html March 2015 Andrew Mitchell, Utrecht University Quantum impurity problems Part 1: Quantum impurity problems
NUMERICAL METODS FOR QUANTUM IMPURITY MODELS http://www.staff.science.uu.nl/~mitch003/nrg.html March 2015 Andrew Mitchell, Utrecht University Quantum impurity problems Part 1: Quantum impurity problems
Lecture 11: Long-wavelength expansion in the Neel state Energetic terms
 Lecture 11: Long-wavelength expansion in the Neel state Energetic terms In the last class we derived the low energy effective Hamiltonian for a Mott insulator. This derivation is an example of the kind
Lecture 11: Long-wavelength expansion in the Neel state Energetic terms In the last class we derived the low energy effective Hamiltonian for a Mott insulator. This derivation is an example of the kind
Physics 239/139 Spring 2018 Assignment 2 Solutions
 University of California at San Diego Department of Physics Prof. John McGreevy Physics 39/139 Spring 018 Assignment Solutions Due 1:30pm Monday, April 16, 018 1. Classical circuits brain-warmer. (a) Show
University of California at San Diego Department of Physics Prof. John McGreevy Physics 39/139 Spring 018 Assignment Solutions Due 1:30pm Monday, April 16, 018 1. Classical circuits brain-warmer. (a) Show
Second Quantization: Quantum Fields
 Second Quantization: Quantum Fields Bosons and Fermions Let X j stand for the coordinate and spin subscript (if any) of the j-th particle, so that the vector of state Ψ of N particles has the form Ψ Ψ(X
Second Quantization: Quantum Fields Bosons and Fermions Let X j stand for the coordinate and spin subscript (if any) of the j-th particle, so that the vector of state Ψ of N particles has the form Ψ Ψ(X
Potts And XY, Together At Last
 Potts And XY, Together At Last Daniel Kolodrubetz Massachusetts Institute of Technology, Center for Theoretical Physics (Dated: May 16, 212) We investigate the behavior of an XY model coupled multiplicatively
Potts And XY, Together At Last Daniel Kolodrubetz Massachusetts Institute of Technology, Center for Theoretical Physics (Dated: May 16, 212) We investigate the behavior of an XY model coupled multiplicatively
Quantum Physics II (8.05) Fall 2004 Assignment 3
 Quantum Physics II (8.5) Fall 24 Assignment 3 Massachusetts Institute of Technology Physics Department Due September 3, 24 September 23, 24 7:pm This week we continue to study the basic principles of quantum
Quantum Physics II (8.5) Fall 24 Assignment 3 Massachusetts Institute of Technology Physics Department Due September 3, 24 September 23, 24 7:pm This week we continue to study the basic principles of quantum
PHYSICS 219 Homework 2 Due in class, Wednesday May 3. Makeup lectures on Friday May 12 and 19, usual time. Location will be ISB 231 or 235.
 PHYSICS 219 Homework 2 Due in class, Wednesday May 3 Note: Makeup lectures on Friday May 12 and 19, usual time. Location will be ISB 231 or 235. No lecture: May 8 (I m away at a meeting) and May 29 (holiday).
PHYSICS 219 Homework 2 Due in class, Wednesday May 3 Note: Makeup lectures on Friday May 12 and 19, usual time. Location will be ISB 231 or 235. No lecture: May 8 (I m away at a meeting) and May 29 (holiday).
Superconductivity by kinetic energy saving?
 Superconductivity by kinetic energy saving? D. van der Marel, H. J. A. Molegraaf, C. Presura and I. Santoso Chapter in "Concepts in electron correlation", Edit e d by A. He ws on and V. Zlat ic, Kluwe
Superconductivity by kinetic energy saving? D. van der Marel, H. J. A. Molegraaf, C. Presura and I. Santoso Chapter in "Concepts in electron correlation", Edit e d by A. He ws on and V. Zlat ic, Kluwe
ANTIFERROMAGNETIC EXCHANGE AND SPIN-FLUCTUATION PAIRING IN CUPRATES
 ANTIFERROMAGNETIC EXCHANGE AND SPIN-FLUCTUATION PAIRING IN CUPRATES N.M.Plakida Joint Institute for Nuclear Research, Dubna, Russia CORPES, Dresden, 26.05.2005 Publications and collaborators: N.M. Plakida,
ANTIFERROMAGNETIC EXCHANGE AND SPIN-FLUCTUATION PAIRING IN CUPRATES N.M.Plakida Joint Institute for Nuclear Research, Dubna, Russia CORPES, Dresden, 26.05.2005 Publications and collaborators: N.M. Plakida,
arxiv:cond-mat/ v1 [cond-mat.str-el] 19 Sep 2001
![arxiv:cond-mat/ v1 [cond-mat.str-el] 19 Sep 2001 arxiv:cond-mat/ v1 [cond-mat.str-el] 19 Sep 2001](/thumbs/79/80145245.jpg) Many-polaron states in the Holstein-Hubbard model Laurent Proville and Serge Aubry arxiv:cond-mat/010934v1 [cond-mat.str-el] 19 Sep 001 Groupe de Physique des Solides, UMR 7588-CNRS Universités Paris 7
Many-polaron states in the Holstein-Hubbard model Laurent Proville and Serge Aubry arxiv:cond-mat/010934v1 [cond-mat.str-el] 19 Sep 001 Groupe de Physique des Solides, UMR 7588-CNRS Universités Paris 7
The Gutzwiller Density Functional Theory
 The Gutzwiller Density Functional Theory Jörg Bünemann, BTU Cottbus I) Introduction 1. Model for an H 2 -molecule 2. Transition metals and their compounds II) Gutzwiller variational theory 1. Gutzwiller
The Gutzwiller Density Functional Theory Jörg Bünemann, BTU Cottbus I) Introduction 1. Model for an H 2 -molecule 2. Transition metals and their compounds II) Gutzwiller variational theory 1. Gutzwiller
5.4 Given the basis e 1, e 2 write the matrices that represent the unitary transformations corresponding to the following changes of basis:
 5 Representations 5.3 Given a three-dimensional Hilbert space, consider the two observables ξ and η that, with respect to the basis 1, 2, 3, arerepresentedby the matrices: ξ ξ 1 0 0 0 ξ 1 0 0 0 ξ 3, ξ
5 Representations 5.3 Given a three-dimensional Hilbert space, consider the two observables ξ and η that, with respect to the basis 1, 2, 3, arerepresentedby the matrices: ξ ξ 1 0 0 0 ξ 1 0 0 0 ξ 3, ξ
Lecture 1: The Equilibrium Green Function Method
 Lecture 1: The Equilibrium Green Function Method Mark Jarrell April 27, 2011 Contents 1 Why Green functions? 2 2 Different types of Green functions 4 2.1 Retarded, advanced, time ordered and Matsubara
Lecture 1: The Equilibrium Green Function Method Mark Jarrell April 27, 2011 Contents 1 Why Green functions? 2 2 Different types of Green functions 4 2.1 Retarded, advanced, time ordered and Matsubara
Finite-temperature Field Theory
 Finite-temperature Field Theory Aleksi Vuorinen CERN Initial Conditions in Heavy Ion Collisions Goa, India, September 2008 Outline Further tools for equilibrium thermodynamics Gauge symmetry Faddeev-Popov
Finite-temperature Field Theory Aleksi Vuorinen CERN Initial Conditions in Heavy Ion Collisions Goa, India, September 2008 Outline Further tools for equilibrium thermodynamics Gauge symmetry Faddeev-Popov
Landau s Fermi Liquid Theory
 Thors Hans Hansson Stockholm University Outline 1 Fermi Liquids Why, What, and How? Why Fermi liquids? What is a Fermi liquids? Fermi Liquids How? 2 Landau s Phenomenological Approach The free Fermi gas
Thors Hans Hansson Stockholm University Outline 1 Fermi Liquids Why, What, and How? Why Fermi liquids? What is a Fermi liquids? Fermi Liquids How? 2 Landau s Phenomenological Approach The free Fermi gas
The 1+1-dimensional Ising model
 Chapter 4 The 1+1-dimensional Ising model The 1+1-dimensional Ising model is one of the most important models in statistical mechanics. It is an interacting system, and behaves accordingly. Yet for a variety
Chapter 4 The 1+1-dimensional Ising model The 1+1-dimensional Ising model is one of the most important models in statistical mechanics. It is an interacting system, and behaves accordingly. Yet for a variety
8.334: Statistical Mechanics II Problem Set # 4 Due: 4/9/14 Transfer Matrices & Position space renormalization
 8.334: Statistical Mechanics II Problem Set # 4 Due: 4/9/14 Transfer Matrices & Position space renormalization This problem set is partly intended to introduce the transfer matrix method, which is used
8.334: Statistical Mechanics II Problem Set # 4 Due: 4/9/14 Transfer Matrices & Position space renormalization This problem set is partly intended to introduce the transfer matrix method, which is used
In-class exercises. Day 1
 Physics 4488/6562: Statistical Mechanics http://www.physics.cornell.edu/sethna/teaching/562/ Material for Week 8 Exercises due Mon March 19 Last correction at March 5, 2018, 8:48 am c 2017, James Sethna,
Physics 4488/6562: Statistical Mechanics http://www.physics.cornell.edu/sethna/teaching/562/ Material for Week 8 Exercises due Mon March 19 Last correction at March 5, 2018, 8:48 am c 2017, James Sethna,
arxiv:cond-mat/ v1 [cond-mat.str-el] 25 Sep 2002
![arxiv:cond-mat/ v1 [cond-mat.str-el] 25 Sep 2002 arxiv:cond-mat/ v1 [cond-mat.str-el] 25 Sep 2002](/thumbs/93/113693780.jpg) arxiv:cond-mat/0209587v1 [cond-mat.str-el] 25 Sep 2002 The 2D Mott-Hubbard transition in presence of a parallel magnetic field A. Avella and F. Mancini Dipartimento di Fisica E.R. Caianiello - Unità INFM
arxiv:cond-mat/0209587v1 [cond-mat.str-el] 25 Sep 2002 The 2D Mott-Hubbard transition in presence of a parallel magnetic field A. Avella and F. Mancini Dipartimento di Fisica E.R. Caianiello - Unità INFM
Time Evolving Block Decimation Algorithm
 Time Evolving Block Decimation Algorithm Application to bosons on a lattice Jakub Zakrzewski Marian Smoluchowski Institute of Physics and Mark Kac Complex Systems Research Center, Jagiellonian University,
Time Evolving Block Decimation Algorithm Application to bosons on a lattice Jakub Zakrzewski Marian Smoluchowski Institute of Physics and Mark Kac Complex Systems Research Center, Jagiellonian University,
Lecture 20: Effective field theory for the Bose- Hubbard model
 Lecture 20: Effective field theory for the Bose- Hubbard model In the previous lecture, we have sketched the expected phase diagram of the Bose-Hubbard model, and introduced a mean-field treatment that
Lecture 20: Effective field theory for the Bose- Hubbard model In the previous lecture, we have sketched the expected phase diagram of the Bose-Hubbard model, and introduced a mean-field treatment that
1. Introductory Examples
 1. Introductory Examples We introduce the concept of the deterministic and stochastic simulation methods. Two problems are provided to explain the methods: the percolation problem, providing an example
1. Introductory Examples We introduce the concept of the deterministic and stochastic simulation methods. Two problems are provided to explain the methods: the percolation problem, providing an example
First Problem Set for Physics 847 (Statistical Physics II)
 First Problem Set for Physics 847 (Statistical Physics II) Important dates: Feb 0 0:30am-:8pm midterm exam, Mar 6 9:30am-:8am final exam Due date: Tuesday, Jan 3. Review 0 points Let us start by reviewing
First Problem Set for Physics 847 (Statistical Physics II) Important dates: Feb 0 0:30am-:8pm midterm exam, Mar 6 9:30am-:8am final exam Due date: Tuesday, Jan 3. Review 0 points Let us start by reviewing
Incompatibility Paradoxes
 Chapter 22 Incompatibility Paradoxes 22.1 Simultaneous Values There is never any difficulty in supposing that a classical mechanical system possesses, at a particular instant of time, precise values of
Chapter 22 Incompatibility Paradoxes 22.1 Simultaneous Values There is never any difficulty in supposing that a classical mechanical system possesses, at a particular instant of time, precise values of
Second Lecture: Quantum Monte Carlo Techniques
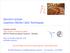 Second Lecture: Quantum Monte Carlo Techniques Andreas Läuchli, New states of quantum matter MPI für Physik komplexer Systeme - Dresden http://www.pks.mpg.de/~aml aml@pks.mpg.de Lecture Notes at http:www.pks.mpg.de/~aml/leshouches
Second Lecture: Quantum Monte Carlo Techniques Andreas Läuchli, New states of quantum matter MPI für Physik komplexer Systeme - Dresden http://www.pks.mpg.de/~aml aml@pks.mpg.de Lecture Notes at http:www.pks.mpg.de/~aml/leshouches
Phonons and lattice dynamics
 Chapter Phonons and lattice dynamics. Vibration modes of a cluster Consider a cluster or a molecule formed of an assembly of atoms bound due to a specific potential. First, the structure must be relaxed
Chapter Phonons and lattice dynamics. Vibration modes of a cluster Consider a cluster or a molecule formed of an assembly of atoms bound due to a specific potential. First, the structure must be relaxed
Any live cell with less than 2 live neighbours dies. Any live cell with 2 or 3 live neighbours lives on to the next step.
 2. Cellular automata, and the SIRS model In this Section we consider an important set of models used in computer simulations, which are called cellular automata (these are very similar to the so-called
2. Cellular automata, and the SIRS model In this Section we consider an important set of models used in computer simulations, which are called cellular automata (these are very similar to the so-called
Preface Introduction to the electron liquid
 Table of Preface page xvii 1 Introduction to the electron liquid 1 1.1 A tale of many electrons 1 1.2 Where the electrons roam: physical realizations of the electron liquid 5 1.2.1 Three dimensions 5 1.2.2
Table of Preface page xvii 1 Introduction to the electron liquid 1 1.1 A tale of many electrons 1 1.2 Where the electrons roam: physical realizations of the electron liquid 5 1.2.1 Three dimensions 5 1.2.2
Finite Temperature Field Theory
 Finite Temperature Field Theory Dietrich Bödeker, Universität Bielefeld 1. Thermodynamics (better: thermo-statics) (a) Imaginary time formalism (b) free energy: scalar particles, resummation i. pedestrian
Finite Temperature Field Theory Dietrich Bödeker, Universität Bielefeld 1. Thermodynamics (better: thermo-statics) (a) Imaginary time formalism (b) free energy: scalar particles, resummation i. pedestrian
QUANTUM FIELD THEORY IN CONDENSED MATTER PHYSICS. Wolfgang Belzig
 QUANTUM FIELD THEORY IN CONDENSED MATTER PHYSICS Wolfgang Belzig FORMAL MATTERS Wahlpflichtfach 4h lecture + 2h exercise Lecture: Mon & Thu, 10-12, P603 Tutorial: Mon, 14-16 (P912) or 16-18 (P712) 50%
QUANTUM FIELD THEORY IN CONDENSED MATTER PHYSICS Wolfgang Belzig FORMAL MATTERS Wahlpflichtfach 4h lecture + 2h exercise Lecture: Mon & Thu, 10-12, P603 Tutorial: Mon, 14-16 (P912) or 16-18 (P712) 50%
Organic Conductors and Superconductors: signatures of electronic correlations Martin Dressel 1. Physikalisches Institut der Universität Stuttgart
 Organic Conductors and Superconductors: signatures of electronic correlations Martin Dressel 1. Physikalisches Institut der Universität Stuttgart Outline 1. Organic Conductors basics and development 2.
Organic Conductors and Superconductors: signatures of electronic correlations Martin Dressel 1. Physikalisches Institut der Universität Stuttgart Outline 1. Organic Conductors basics and development 2.
MP463 QUANTUM MECHANICS
 MP463 QUANTUM MECHANICS Introduction Quantum theory of angular momentum Quantum theory of a particle in a central potential - Hydrogen atom - Three-dimensional isotropic harmonic oscillator (a model of
MP463 QUANTUM MECHANICS Introduction Quantum theory of angular momentum Quantum theory of a particle in a central potential - Hydrogen atom - Three-dimensional isotropic harmonic oscillator (a model of
Quantum Theory of Matter
 Quantum Theory of Matter Revision Lecture Derek Lee Imperial College London May 2006 Outline 1 Exam and Revision 2 Quantum Theory of Matter Microscopic theory 3 Summary Outline 1 Exam and Revision 2 Quantum
Quantum Theory of Matter Revision Lecture Derek Lee Imperial College London May 2006 Outline 1 Exam and Revision 2 Quantum Theory of Matter Microscopic theory 3 Summary Outline 1 Exam and Revision 2 Quantum
Chapter 2 Ensemble Theory in Statistical Physics: Free Energy Potential
 Chapter Ensemble Theory in Statistical Physics: Free Energy Potential Abstract In this chapter, we discuss the basic formalism of statistical physics Also, we consider in detail the concept of the free
Chapter Ensemble Theory in Statistical Physics: Free Energy Potential Abstract In this chapter, we discuss the basic formalism of statistical physics Also, we consider in detail the concept of the free
Likewise, any operator, including the most generic Hamiltonian, can be written in this basis as H11 H
 Finite Dimensional systems/ilbert space Finite dimensional systems form an important sub-class of degrees of freedom in the physical world To begin with, they describe angular momenta with fixed modulus
Finite Dimensional systems/ilbert space Finite dimensional systems form an important sub-class of degrees of freedom in the physical world To begin with, they describe angular momenta with fixed modulus
Polarons. University of Ljubljana Faculty of Mathematics and Physics. Seminar - Ib, 1. year II. cycle degrees
 University of Ljubljana Faculty of Mathematics and Physics Seminar - Ib, 1. year II. cycle degrees Polarons Author: Jaka Vodeb Advisor: prof. dr. Viktor Kabanov Kranj, 017 Abstract After the discovery
University of Ljubljana Faculty of Mathematics and Physics Seminar - Ib, 1. year II. cycle degrees Polarons Author: Jaka Vodeb Advisor: prof. dr. Viktor Kabanov Kranj, 017 Abstract After the discovery
I. QUANTUM MONTE CARLO METHODS: INTRODUCTION AND BASICS
 I. QUANTUM MONTE CARLO METHODS: INTRODUCTION AND BASICS Markus Holzmann LPMMC, UJF, Grenoble, and LPTMC, UPMC, Paris markus@lptl.jussieu.fr http://www.lptl.jussieu.fr/users/markus (Dated: January 24, 2012)
I. QUANTUM MONTE CARLO METHODS: INTRODUCTION AND BASICS Markus Holzmann LPMMC, UJF, Grenoble, and LPTMC, UPMC, Paris markus@lptl.jussieu.fr http://www.lptl.jussieu.fr/users/markus (Dated: January 24, 2012)
Some detailed information for BCS-BEC Crossover
 BCS-BEC Crossover Some detailed information for BCS-BEC Crossover BCS Theory 李泽阳 April 3, 2015 School of Physics, Peking University BCS-BEC Crossover April 3, 2015 1 / 31 BCS-BEC Crossover Table of Contents
BCS-BEC Crossover Some detailed information for BCS-BEC Crossover BCS Theory 李泽阳 April 3, 2015 School of Physics, Peking University BCS-BEC Crossover April 3, 2015 1 / 31 BCS-BEC Crossover Table of Contents
Complexity of the quantum adiabatic algorithm
 Complexity of the quantum adiabatic algorithm Peter Young e-mail:peter@physics.ucsc.edu Collaborators: S. Knysh and V. N. Smelyanskiy Colloquium at Princeton, September 24, 2009 p.1 Introduction What is
Complexity of the quantum adiabatic algorithm Peter Young e-mail:peter@physics.ucsc.edu Collaborators: S. Knysh and V. N. Smelyanskiy Colloquium at Princeton, September 24, 2009 p.1 Introduction What is
Bound states of two particles confined to parallel two-dimensional layers and interacting via dipole-dipole or dipole-charge laws
 PHYSICAL REVIEW B VOLUME 55, NUMBER 8 15 FEBRUARY 1997-II Bound states of two particles confined to parallel two-dimensional layers and interacting via dipole-dipole or dipole-charge laws V. I. Yudson
PHYSICAL REVIEW B VOLUME 55, NUMBER 8 15 FEBRUARY 1997-II Bound states of two particles confined to parallel two-dimensional layers and interacting via dipole-dipole or dipole-charge laws V. I. Yudson
Introduction to Density Functional Theory with Applications to Graphene Branislav K. Nikolić
 Introduction to Density Functional Theory with Applications to Graphene Branislav K. Nikolić Department of Physics and Astronomy, University of Delaware, Newark, DE 19716, U.S.A. http://wiki.physics.udel.edu/phys824
Introduction to Density Functional Theory with Applications to Graphene Branislav K. Nikolić Department of Physics and Astronomy, University of Delaware, Newark, DE 19716, U.S.A. http://wiki.physics.udel.edu/phys824
ICCP Project 2 - Advanced Monte Carlo Methods Choose one of the three options below
 ICCP Project 2 - Advanced Monte Carlo Methods Choose one of the three options below Introduction In statistical physics Monte Carlo methods are considered to have started in the Manhattan project (1940
ICCP Project 2 - Advanced Monte Carlo Methods Choose one of the three options below Introduction In statistical physics Monte Carlo methods are considered to have started in the Manhattan project (1940
Quantum Monte Carlo and the Holstein Model
 Quantum Monte Carlo and the Holstein Model homas Blommel North Dakota State University (Dated: January 26, 28) With the advent of increasingly fast computers and their ubiquity in society, computational
Quantum Monte Carlo and the Holstein Model homas Blommel North Dakota State University (Dated: January 26, 28) With the advent of increasingly fast computers and their ubiquity in society, computational
221B Lecture Notes Quantum Field Theory II (Fermi Systems)
 1B Lecture Notes Quantum Field Theory II (Fermi Systems) 1 Statistical Mechanics of Fermions 1.1 Partition Function In the case of fermions, we had learnt that the field operator satisfies the anticommutation
1B Lecture Notes Quantum Field Theory II (Fermi Systems) 1 Statistical Mechanics of Fermions 1.1 Partition Function In the case of fermions, we had learnt that the field operator satisfies the anticommutation
Lecture 4. Diffusing photons and superradiance in cold gases
 Lecture 4 Diffusing photons and superradiance in cold gases Model of disorder-elastic mean free path and group velocity. Dicke states- Super- and sub-radiance. Scattering properties of Dicke states. Multiple
Lecture 4 Diffusing photons and superradiance in cold gases Model of disorder-elastic mean free path and group velocity. Dicke states- Super- and sub-radiance. Scattering properties of Dicke states. Multiple
Trapped ion spin-boson quantum simulators: Non-equilibrium physics and thermalization. Diego Porras
 Trapped ion spin-boson quantum simulators: Non-equilibrium physics and thermalization Diego Porras Outline Spin-boson trapped ion quantum simulators o Rabi Lattice/Jahn-Teller models o Gauge symmetries
Trapped ion spin-boson quantum simulators: Non-equilibrium physics and thermalization Diego Porras Outline Spin-boson trapped ion quantum simulators o Rabi Lattice/Jahn-Teller models o Gauge symmetries
Lecture 4 Recap: normal metals and the clectron-phonon interaction *
 Phys. 598SC Fall 2015 Prof. A. J. Leggett Lecture 4 Recap: normal metals and the clectron-phonon interaction * 1. Normal metals: Sommerfeld-Bloch picture 2. Screening 3. Fermi liquid theory 4. Electron-phonon
Phys. 598SC Fall 2015 Prof. A. J. Leggett Lecture 4 Recap: normal metals and the clectron-phonon interaction * 1. Normal metals: Sommerfeld-Bloch picture 2. Screening 3. Fermi liquid theory 4. Electron-phonon
Ground-state properties, excitations, and response of the 2D Fermi gas
 Ground-state properties, excitations, and response of the 2D Fermi gas Introduction: 2D FG and a condensed matter perspective Auxiliary-field quantum Monte Carlo calculations - exact* here Results on spin-balanced
Ground-state properties, excitations, and response of the 2D Fermi gas Introduction: 2D FG and a condensed matter perspective Auxiliary-field quantum Monte Carlo calculations - exact* here Results on spin-balanced
Diagrammatic Monte Carlo methods for Fermions
 Diagrammatic Monte Carlo methods for Fermions Philipp Werner Department of Physics, Columbia University PRL 97, 7645 (26) PRB 74, 15517 (26) PRB 75, 8518 (27) PRB 76, 235123 (27) PRL 99, 12645 (27) PRL
Diagrammatic Monte Carlo methods for Fermions Philipp Werner Department of Physics, Columbia University PRL 97, 7645 (26) PRB 74, 15517 (26) PRB 75, 8518 (27) PRB 76, 235123 (27) PRL 99, 12645 (27) PRL
