Errata Instructor s Solutions Manual Introduction to Electrodynamics, 3rd ed Author: David Griffiths Date: September 1, 2004
|
|
|
- Eric Dawson
- 6 years ago
- Views:
Transcription
1 Errata Instructor s Solutions Manual Introduction to Electrodynamics, 3rd ed Author: David Griffiths Date: September, 004 Page 4, Prob..5 (b): last expression should read y +z +3x. Page 4, Prob..6: at the beginning, insert the following figure Page 8, Prob..6: last line should read From Prob..8: v a = 6xz ˆx +zŷ +3z ẑ ( v a )= x ( 6xz)+ y (z)+ z (3z )= 6z +6z =0. Page 8, Prob..7, in the determinant for ( f), 3rd row, nd column: change y 3 to y. Page 8, Prob..9, line : the number in the box should be - (insert minus sign). Page 9, Prob..3, line : change x 3 to z 3 ; first line of part (c): insert comma between dx and dz. Page, Probl.39, line 5: remove comma after cos θ. Page 3, Prob..4(c), last line: insert ẑ after ). Page 4, Prob..46(b): change r to a. Page 4, Prob..48, second line of J: change the upper limit on the r integral from to R. Fix the last line to read: = 4π ( e r) R 0 +4πe R =4π ( e R + e 0) +4πe R =4π. Page 5, Prob..49(a), line 3: in the box, change x to x 3.
2 Page 5, Prob..49(b), last integration constant should be l(x, z), not l(x, y). Page 7, Prob..53, first expression in (4): insert θ, soda = r sin θdrdφˆθˆθˆθ. Page 7, Prob..55: Solution should read as follows: Problem.55 () x = z =0; dx = dz =0; y :0. v dl =(yz ) dy =0; v dl =0. () x =0; z = y; dz = dy; y : 0. v dl =(yz ) dy +(3y + z) dz = y( y) dy (3y + y) dy; v dl = 0 [ ] y (y 3 4y 4 + y ) dy = 4y3 3 + y 0 y = 4 3. (3) x = y =0; dx = dy =0; z : 0. v dl =(3y + z) dz = zdz. v dl = 0 zdz= z 0 =. Total: v dl = = 8 3. Meanwhile, Stokes thereom says v dl = ( v) da. Here da = dy dz ˆx, so all we need is ( v) x = y (3y + z) z (yz )=3 yz. Therefore { } y ( v) da = (3 yz) dy dz = (3 yz) dz dy 0 0 = [ 0 3( y) y ( y)] dy = 0 ( 4y3 +8y 0y +6) dy = [ y y3 5y +6y ] = = 8 3. Page 8, Prob..56: change (3) and (4) to read as follows: (3) φ = π ; r sin θ = y =, so r = sin θ, dr = sin θ cos θdθ, θ : π θ 0 tan ( ). v dl = ( r cos θ ) ( (dr) (r cos θ sin θ)(rdθ)= cos θ cos θ ) cos θ sin θ sin θ sin dθ θ sin dθ θ ( cos 3 θ = sin 3 θ + cos θ ) dθ = cos θ ( cos θ +sin ) θ sin θ sin θ sin dθ = cos θ θ sin 3 θ dθ. Therefore v dl = θ 0 π/ cos θ sin 3 θ dθ = sin θ θ 0 π/ = (/5) () = 5 =.
3 (4) θ = θ 0,φ= π ; r : 5 0. v dl = ( r cos θ ) (dr) = 4 5 rdr. 0 v dl = 4 rdr= r 0 = =. Total: v dl =0+ 3π + = 3π. Page, Probl.6(e), line : change = z ẑ to +z ẑ. Page 5, Prob..: last line should read Since Q tot = 4 3 πr3 ρ, E = Q 4πɛ 0 R r (as in Prob..8). 3 Page 6, Prob..5: last expression in first line of (ii) should be dφ, not d phi. Page 8, Prob.., at the end, insert the following figure V(r) r In the figure, r is in units of R, and V (r) is in units of Page 30, Prob..8: remove right angle sign in the figure. q 4πɛ 0R. Page 4, Prob. 3.5: subscript on V in last integral should be 3, not. Page 45, Prob. 3.0: after the first box, add: q F = 4πɛ 0 { (a) ˆx } (b) ŷ + ( [cos θ ˆx +sin θ ŷ], a + b ) where cos θ = a/ a + b, sin θ = b/ a + b. {[ F = q a 6πɛ 0 (a + b ) ] 3/ a [ ˆx + b (a + b ) 3/ b ] } ŷ. 3
4 W = 4 4πɛ 0 [ q (a) + q (b) + q ] ( = q a + b ) 3πɛ 0 [ a + b a b Page 45, Prob. 3.0: in the second box, change and to an. Page 46, Probl 3.3, at the end, insert the following: [Comment: Technically, the series solution for σ is defective, since term-by-term differentiation has produced a (naively) non-convergent sum. More sophisticated definitions of convergence permit one to work with series of this form, but it is better to sum the series first and then differentiate (the second method).] Page 5, Prob. 3.8, midpage: the reference to Eq. 3.7 should be 3.7. Page 53, Prob. 3.(b), line 5: A should be R. σ 4ɛ 0R ; next line, insert r after Page 55, Prob. 3.3, third displayed equation: remove the first Φ. Page 58, Prob. 3.8(a), second line, first integral: R 3 should read R. Page 59, Prob. 3.3(c): change first V to W. Page 64, Prob. 3.4(a), lines and 3: remove ɛ 0 in the first factor in the expressions for E ave ; in the second expression change ρ to q. Page 69, Prob. 3.47, at the end add the following: Alternatively, start with the separable solution V (x, y) =(C sin kx + D cos kx) ( Ae ky + Be ky). Note that the configuration is symmetric in x, soc = 0, and V (x, 0) = 0 B = A, so (combining the constants) V (x, y) =A cos kx sinh ky. But V (b, y) =0,socoskb = 0, which means that kb = ±π/, ±3π/,, or k =(n )π/b α n, with n =,, 3,... (negative k does not yield a different solution the sign can be absorbed into A). The general linear combination is V (x, y) = A n cos α n x sinh α n y, n= and it remains to fit the final boundary condition: V (x, a) =V 0 = A n cos α n x sinh α n a. n= ]. 4
5 Use Fourier s trick, multiplying by cos α n x and integrating: b b V 0 cos α n xdx= A n sinh α n a cos α n x cos α n xdx b So A n = V 0 b V 0 sin α n b α n = n= b A n sinh α n a (bδ n n)=ba n sinh α n a; n= sin α n b α n sinh α n a. But sin α nb = sin V (x, y) = V 0 b ( n ( ) n sinh α ny α n sinh α n a cos α nx. n= ) π = ( ) n, so Page 74, Prob. 4.4: exponent on r in boxed equation should be 5, not 3. Page 75, Prob. 4.7: replace the (defective) solution with the following: If the potential is zero at infinity, the energy of a point charge Q is (Eq..39) W = QV (r). For a physical dipole, with q at r and +q at r+d, [ ] r+d U = qv (r + d) qv (r) =q [V (r + d) V (r)] = q E dl. For an ideal dipole the integral reduces to E d, and U = qe d = p E, since p = qd. If you do not (or cannot) use infinity as the reference point, the result still holds, as long as you bring the two charges in from the same point, r 0 (or two points at the same potential). In that case W = Q [V (r) V (r 0 )], and U = q [V (r + d) V (r 0 )] q [V (r) V (r 0 )] = q [V (r + d) V (r)], as before. Page 75, Prob. 4.0(a): r should be 3 r. Page 79, Prob. 4.9: in the upper right box of the Table (σ f for air) there is a missing factor of ɛ 0. Page 9, Problem 5.0(b): in the first line µ 0 I /π should read µ 0 I a/πs; in the final boxed equation the first should be a s. Page 9, Prob. 5.5: the signs are all wrong. The end of line should read right (ẑ), the middle of the next line should read left ( ẑ). In the first box it should be (n n ), and in the second box the minus sign does not belong. r 5
6 Page 4, Prob. 6.4: last term in second expression for F should be +ẑ Bx z (plus, not minus). Page 9, Prob. 6.(a): replace with the following: The magnetic force on the dipole is given by Eq. 6.3; to move the dipole in from infinity we must exert an opposite force, so the work done is U = r F dl = r (m B) dl = m B(r)+m B( ) (I used the gradient theorem, Eq..55). As long as the magnetic field goes to zero at infinity, then, U = m B. If the magnetic field does not go to zero at infinity, one must stipulate that the dipole starts out oriented perpendicular to the field. Page 5, Prob. 7.(b): in the box, c should be C. Page 9, Prob. 7.8: change first two lines to read: Φ= B da; B = µ 0I πs ˆφˆφˆφ; Φ= µ s+a 0Ia ds π s s = µ ( ) 0Ia s + a π ln ; s E = I loop R = dq dt R = dφ dt = µ 0a ln( + a/s)di π dt. dq = µ 0a ln( + a/s) di πr Q = µ 0aI ln( + a/s). πr Page 3, Prob. 7.7: in the second integral, r should be s. Page 3, Prob. 7.3(c), last line: in the final two equations, insert an I immediately after µ 0. Page 40, Prob. 7.47: in the box, the top equation should have a minus sign in front, and in the bottom equation the plus sign should be minus. Page 4, Prob. 7.50, final answer: R should read R. Page 43, Prob. 7.55, penultimate displayed equation: tp should be. Page 47, Prob. 8., top line, penultimate expression: change a to a 4 ;in (c), in the first box, change 6 to 8. Page 49, Prob. 8.5(c): there should be a minus sign in front of σ in the box. Page 49, Prob. 8.7: almost all the r s here should be s s. In line change a <r<r to s<r ; in the same line change dr to ds; in the next line change dr to ds (twice), and change ˆr to ŝ; in the last line change r to s, dr to ds, and ˆr to ŝ (but leave r as is). 6
7 Page 53, Prob. 8., last line of equations: in the numerator of the expression for R change.0 to.0. Page 75, Prob. 9.34, penultimate line: α = n 3 /n (not n 3 /n 3 ). Page 77, Prob. 9.38: half-way down, remove minus sign in k x + k y + k z = (ω/c). Page 8, Prob. 0.8: first line: remove. Page 84, Prob. 0.4: in the first line, change (9.98) to (0.4). Page 03, Prob..4: at beginning of second paragraph, remove. Page, Prob..5, end of first sentence: change comma to period. Page 5, Prob..3. The figure contains two errors: the slopes are for v/c = / (not 3/), and the intervals are incorrect. The correct solution is as follows: Page 7, Prob..33: first expression in third line, change c to c. 7
xy 2 e 2z dx dy dz = 8 3 (1 e 4 ) = 2.62 mc. 12 x2 y 3 e 2z 2 m 2 m 2 m Figure P4.1: Cube of Problem 4.1.
 Problem 4.1 A cube m on a side is located in the first octant in a Cartesian coordinate system, with one of its corners at the origin. Find the total charge contained in the cube if the charge density
Problem 4.1 A cube m on a side is located in the first octant in a Cartesian coordinate system, with one of its corners at the origin. Find the total charge contained in the cube if the charge density
Physics 3323, Fall 2016 Problem Set 2 due Sep 9, 2016
 Physics 3323, Fall 26 Problem Set 2 due Sep 9, 26. What s my charge? A spherical region of radius R is filled with a charge distribution that gives rise to an electric field inside of the form E E /R 2
Physics 3323, Fall 26 Problem Set 2 due Sep 9, 26. What s my charge? A spherical region of radius R is filled with a charge distribution that gives rise to an electric field inside of the form E E /R 2
Department of Physics IIT Kanpur, Semester II,
 Department of Physics IIT Kanpur, Semester II, 7-8 PHYA: Physics II Solution # 4 Instructors: AKJ & SC Solution 4.: Force with image charges (Griffiths rd ed. Prob.6 As far as force is concerned, this
Department of Physics IIT Kanpur, Semester II, 7-8 PHYA: Physics II Solution # 4 Instructors: AKJ & SC Solution 4.: Force with image charges (Griffiths rd ed. Prob.6 As far as force is concerned, this
Homework Assignment 4 Solution Set
 Homework Assignment 4 Solution Set PHYCS 442 7 February, 24 Problem (Griffiths 2.37 If the plates are sufficiently large the field near them does not depend on d. The field between the plates is zero (the
Homework Assignment 4 Solution Set PHYCS 442 7 February, 24 Problem (Griffiths 2.37 If the plates are sufficiently large the field near them does not depend on d. The field between the plates is zero (the
Corrections and Minor Revisions of Mathematical Methods in the Physical Sciences, third edition, by Mary L. Boas (deceased)
 Corrections and Minor Revisions of Mathematical Methods in the Physical Sciences, third edition, by Mary L. Boas (deceased) Updated December 6, 2017 by Harold P. Boas This list includes all errors known
Corrections and Minor Revisions of Mathematical Methods in the Physical Sciences, third edition, by Mary L. Boas (deceased) Updated December 6, 2017 by Harold P. Boas This list includes all errors known
Quantum Mechanics: A Paradigms Approach David H. McIntyre. 27 July Corrections to the 1 st printing
 Quantum Mechanics: A Paradigms Approach David H. McIntyre 7 July 6 Corrections to the st printing page xxi, last paragraph before "The End", nd line: Change "become" to "became". page, first line after
Quantum Mechanics: A Paradigms Approach David H. McIntyre 7 July 6 Corrections to the st printing page xxi, last paragraph before "The End", nd line: Change "become" to "became". page, first line after
Electrostatics. Chapter Maxwell s Equations
 Chapter 1 Electrostatics 1.1 Maxwell s Equations Electromagnetic behavior can be described using a set of four fundamental relations known as Maxwell s Equations. Note that these equations are observed,
Chapter 1 Electrostatics 1.1 Maxwell s Equations Electromagnetic behavior can be described using a set of four fundamental relations known as Maxwell s Equations. Note that these equations are observed,
Two dimensional oscillator and central forces
 Two dimensional oscillator and central forces September 4, 04 Hooke s law in two dimensions Consider a radial Hooke s law force in -dimensions, F = kr where the force is along the radial unit vector and
Two dimensional oscillator and central forces September 4, 04 Hooke s law in two dimensions Consider a radial Hooke s law force in -dimensions, F = kr where the force is along the radial unit vector and
Electromagnetism: Worked Examples. University of Oxford Second Year, Part A2
 Electromagnetism: Worked Examples University of Oxford Second Year, Part A2 Caroline Terquem Department of Physics caroline.terquem@physics.ox.ac.uk Michaelmas Term 2017 2 Contents 1 Potentials 5 1.1 Potential
Electromagnetism: Worked Examples University of Oxford Second Year, Part A2 Caroline Terquem Department of Physics caroline.terquem@physics.ox.ac.uk Michaelmas Term 2017 2 Contents 1 Potentials 5 1.1 Potential
3. Calculating Electrostatic Potential
 3. Calculating Electrostatic Potential 3. Laplace s Equation 3. The Method of Images 3.3 Separation of Variables 3.4 Multipole Expansion 3.. Introduction The primary task of electrostatics is to study
3. Calculating Electrostatic Potential 3. Laplace s Equation 3. The Method of Images 3.3 Separation of Variables 3.4 Multipole Expansion 3.. Introduction The primary task of electrostatics is to study
Integral Vector Calculus
 ontents 29 Integral Vector alculus 29.1 Line Integrals Involving Vectors 2 29.2 Surface and Volume Integrals 34 29.3 Integral Vector Theorems 54 Learning outcomes In this Workbook you will learn how to
ontents 29 Integral Vector alculus 29.1 Line Integrals Involving Vectors 2 29.2 Surface and Volume Integrals 34 29.3 Integral Vector Theorems 54 Learning outcomes In this Workbook you will learn how to
Curvilinear Coordinates
 University of Alabama Department of Physics and Astronomy PH 106-4 / LeClair Fall 2008 Curvilinear Coordinates Note that we use the convention that the cartesian unit vectors are ˆx, ŷ, and ẑ, rather than
University of Alabama Department of Physics and Astronomy PH 106-4 / LeClair Fall 2008 Curvilinear Coordinates Note that we use the convention that the cartesian unit vectors are ˆx, ŷ, and ẑ, rather than
Laplace equation in polar coordinates
 Laplace equation in polar coordinates The Laplace equation is given by 2 F 2 + 2 F 2 = 0 We have x = r cos θ, y = r sin θ, and also r 2 = x 2 + y 2, tan θ = y/x We have for the partials with respect to
Laplace equation in polar coordinates The Laplace equation is given by 2 F 2 + 2 F 2 = 0 We have x = r cos θ, y = r sin θ, and also r 2 = x 2 + y 2, tan θ = y/x We have for the partials with respect to
UNIVERSITY OF CALIFORNIA - SANTA CRUZ DEPARTMENT OF PHYSICS PHYS 110A. Homework #7. Benjamin Stahl. March 3, 2015
 UNIVERSITY OF CALIFORNIA - SANTA CRUZ DEPARTMENT OF PHYSICS PHYS A Homework #7 Benjamin Stahl March 3, 5 GRIFFITHS, 5.34 It will be shown that the magnetic field of a dipole can written in the following
UNIVERSITY OF CALIFORNIA - SANTA CRUZ DEPARTMENT OF PHYSICS PHYS A Homework #7 Benjamin Stahl March 3, 5 GRIFFITHS, 5.34 It will be shown that the magnetic field of a dipole can written in the following
PHYS 110B - HW #4 Spring 2004, Solutions by David Pace Any referenced equations are from Griffiths Problem statements are paraphrased
 PHYS 11B - HW #4 Spring 4, Solutions by David Pace Any referenced equations are from Griffiths Problem statements are paraphrased [1.] Problem 8. from Griffiths Reference problem 7.31 figure 7.43. a Let
PHYS 11B - HW #4 Spring 4, Solutions by David Pace Any referenced equations are from Griffiths Problem statements are paraphrased [1.] Problem 8. from Griffiths Reference problem 7.31 figure 7.43. a Let
UNIVERSITY OF CALIFORNIA - SANTA CRUZ DEPARTMENT OF PHYSICS PHYS 110A. Homework #6. Benjamin Stahl. February 17, 2015
 UNIVERSITY OF CALIFORNIA - SANTA CRUZ DEPARTMENT OF PHYSICS PHYS A Homework #6 Benjamin Stahl February 7, 5 GRIFFITHS, 5.9 The magnetic field at a point, P, will be found for each of the steady current
UNIVERSITY OF CALIFORNIA - SANTA CRUZ DEPARTMENT OF PHYSICS PHYS A Homework #6 Benjamin Stahl February 7, 5 GRIFFITHS, 5.9 The magnetic field at a point, P, will be found for each of the steady current
Single Particle Motion
 Single Particle Motion C ontents Uniform E and B E = - guiding centers Definition of guiding center E gravitation Non Uniform B 'grad B' drift, B B Curvature drift Grad -B drift, B B invariance of µ. Magnetic
Single Particle Motion C ontents Uniform E and B E = - guiding centers Definition of guiding center E gravitation Non Uniform B 'grad B' drift, B B Curvature drift Grad -B drift, B B invariance of µ. Magnetic
Errata for Conquering the Physics GRE, edition 2
 Errata for Conquering the Physics GRE, edition 2 March 12, 217 This document contains corrections to Conquering the Physics GRE, edition 2. It includes errata that are present in both all printings of
Errata for Conquering the Physics GRE, edition 2 March 12, 217 This document contains corrections to Conquering the Physics GRE, edition 2. It includes errata that are present in both all printings of
Electromagnetism Answers to Problem Set 9 Spring 2006
 Electromagnetism 70006 Answers to Problem et 9 pring 006. Jackson Prob. 5.: Reformulate the Biot-avart law in terms of the solid angle subtended at the point of observation by the current-carrying circuit.
Electromagnetism 70006 Answers to Problem et 9 pring 006. Jackson Prob. 5.: Reformulate the Biot-avart law in terms of the solid angle subtended at the point of observation by the current-carrying circuit.
Summary: Applications of Gauss Law
 Physics 2460 Electricity and Magnetism I, Fall 2006, Lecture 15 1 Summary: Applications of Gauss Law 1. Field outside of a uniformly charged sphere of radius a: 2. An infinite, uniformly charged plane
Physics 2460 Electricity and Magnetism I, Fall 2006, Lecture 15 1 Summary: Applications of Gauss Law 1. Field outside of a uniformly charged sphere of radius a: 2. An infinite, uniformly charged plane
SUMMARY Phys 2523 (University Physics II) Compiled by Prof. Erickson. F e (r )=q E(r ) dq r 2 ˆr = k e E = V. V (r )=k e r = k q i. r i r.
 SUMMARY Phys 53 (University Physics II) Compiled by Prof. Erickson q 1 q Coulomb s Law: F 1 = k e r ˆr where k e = 1 4π =8.9875 10 9 N m /C, and =8.85 10 1 C /(N m )isthepermittivity of free space. Generally,
SUMMARY Phys 53 (University Physics II) Compiled by Prof. Erickson q 1 q Coulomb s Law: F 1 = k e r ˆr where k e = 1 4π =8.9875 10 9 N m /C, and =8.85 10 1 C /(N m )isthepermittivity of free space. Generally,
Contents. MATH 32B-2 (18W) (L) G. Liu / (TA) A. Zhou Calculus of Several Variables. 1 Multiple Integrals 3. 2 Vector Fields 9
 MATH 32B-2 (8W) (L) G. Liu / (TA) A. Zhou Calculus of Several Variables Contents Multiple Integrals 3 2 Vector Fields 9 3 Line and Surface Integrals 5 4 The Classical Integral Theorems 9 MATH 32B-2 (8W)
MATH 32B-2 (8W) (L) G. Liu / (TA) A. Zhou Calculus of Several Variables Contents Multiple Integrals 3 2 Vector Fields 9 3 Line and Surface Integrals 5 4 The Classical Integral Theorems 9 MATH 32B-2 (8W)
SOLUTIONS TO THE FINAL EXAM. December 14, 2010, 9:00am-12:00 (3 hours)
 SOLUTIONS TO THE 18.02 FINAL EXAM BJORN POONEN December 14, 2010, 9:00am-12:00 (3 hours) 1) For each of (a)-(e) below: If the statement is true, write TRUE. If the statement is false, write FALSE. (Please
SOLUTIONS TO THE 18.02 FINAL EXAM BJORN POONEN December 14, 2010, 9:00am-12:00 (3 hours) 1) For each of (a)-(e) below: If the statement is true, write TRUE. If the statement is false, write FALSE. (Please
Physics 505 Fall 2005 Homework Assignment #7 Solutions
 Physics 505 Fall 005 Homework Assignment #7 Solutions Textbook problems: Ch. 4: 4.10 Ch. 5: 5.3, 5.6, 5.7 4.10 Two concentric conducting spheres of inner and outer radii a and b, respectively, carry charges
Physics 505 Fall 005 Homework Assignment #7 Solutions Textbook problems: Ch. 4: 4.10 Ch. 5: 5.3, 5.6, 5.7 4.10 Two concentric conducting spheres of inner and outer radii a and b, respectively, carry charges
Quiz 4 (Discussion Session) Phys 1302W.400 Spring 2018
 Quiz 4 (Discussion ession) Phys 1302W.400 pring 2018 This group quiz consists of one problem that, together with the individual problems on Friday, will determine your grade for quiz 4. For the group problem,
Quiz 4 (Discussion ession) Phys 1302W.400 pring 2018 This group quiz consists of one problem that, together with the individual problems on Friday, will determine your grade for quiz 4. For the group problem,
Problem Set #3: 2.11, 2.15, 2.21, 2.26, 2.40, 2.42, 2.43, 2.46 (Due Thursday Feb. 27th)
 Chapter Electrostatics Problem Set #3:.,.5,.,.6,.40,.4,.43,.46 (Due Thursday Feb. 7th). Coulomb s Law Coulomb showed experimentally that for two point charges the force is - proportional to each of the
Chapter Electrostatics Problem Set #3:.,.5,.,.6,.40,.4,.43,.46 (Due Thursday Feb. 7th). Coulomb s Law Coulomb showed experimentally that for two point charges the force is - proportional to each of the
Vector Integrals. Scott N. Walck. October 13, 2016
 Vector Integrals cott N. Walck October 13, 16 Contents 1 A Table of Vector Integrals Applications of the Integrals.1 calar Line Integral.........................1.1 Finding Total Charge of a Line Charge..........1.
Vector Integrals cott N. Walck October 13, 16 Contents 1 A Table of Vector Integrals Applications of the Integrals.1 calar Line Integral.........................1.1 Finding Total Charge of a Line Charge..........1.
THE UNIVERSITY OF SYDNEY FACULTY OF SCIENCE INTERMEDIATE PHYSICS PHYS 2912 PHYSICS 2B (ADVANCED) ALL QUESTIONS HAVE THE VALUE SHOWN
 CC0936 THE UNIVERSITY OF SYDNEY FACULTY OF SCIENCE INTERMEDIATE PHYSICS PHYS 91 PHYSICS B (ADVANCED) SEMESTER, 014 TIME ALLOWED: 3 HOURS ALL QUESTIONS HAVE THE VALUE SHOWN INSTRUCTIONS: This paper consists
CC0936 THE UNIVERSITY OF SYDNEY FACULTY OF SCIENCE INTERMEDIATE PHYSICS PHYS 91 PHYSICS B (ADVANCED) SEMESTER, 014 TIME ALLOWED: 3 HOURS ALL QUESTIONS HAVE THE VALUE SHOWN INSTRUCTIONS: This paper consists
Practice Final Solutions
 Practice Final Solutions Math 1, Fall 17 Problem 1. Find a parameterization for the given curve, including bounds on the parameter t. Part a) The ellipse in R whose major axis has endpoints, ) and 6, )
Practice Final Solutions Math 1, Fall 17 Problem 1. Find a parameterization for the given curve, including bounds on the parameter t. Part a) The ellipse in R whose major axis has endpoints, ) and 6, )
One side of each sheet is blank and may be used as scratch paper.
 Math 244 Spring 2017 (Practice) Final 5/11/2017 Time Limit: 2 hours Name: No calculators or notes are allowed. One side of each sheet is blank and may be used as scratch paper. heck your answers whenever
Math 244 Spring 2017 (Practice) Final 5/11/2017 Time Limit: 2 hours Name: No calculators or notes are allowed. One side of each sheet is blank and may be used as scratch paper. heck your answers whenever
Phys. 505 Electricity and Magnetism Fall 2003 Prof. G. Raithel Problem Set 1
 Phys. 505 Electricity and Magnetism Fall 2003 Prof. G. Raithel Problem Set Problem.3 a): By symmetry, the solution must be of the form ρ(x) = ρ(r) = Qδ(r R)f, with a constant f to be specified by the condition
Phys. 505 Electricity and Magnetism Fall 2003 Prof. G. Raithel Problem Set Problem.3 a): By symmetry, the solution must be of the form ρ(x) = ρ(r) = Qδ(r R)f, with a constant f to be specified by the condition
Notes 19 Gradient and Laplacian
 ECE 3318 Applied Electricity and Magnetism Spring 218 Prof. David R. Jackson Dept. of ECE Notes 19 Gradient and Laplacian 1 Gradient Φ ( x, y, z) =scalar function Φ Φ Φ grad Φ xˆ + yˆ + zˆ x y z We can
ECE 3318 Applied Electricity and Magnetism Spring 218 Prof. David R. Jackson Dept. of ECE Notes 19 Gradient and Laplacian 1 Gradient Φ ( x, y, z) =scalar function Φ Φ Φ grad Φ xˆ + yˆ + zˆ x y z We can
PHYS 110B - HW #4 Fall 2005, Solutions by David Pace Equations referenced as EQ. # are from Griffiths Problem statements are paraphrased
 PHYS B - HW #4 Fall 5, Solutions by David Pace Equations referenced as EQ. # are from Griffiths Problem statements are paraphrased [.] Problem 8. from Griffiths Reference problem 7.3 figure 7.43. a Let
PHYS B - HW #4 Fall 5, Solutions by David Pace Equations referenced as EQ. # are from Griffiths Problem statements are paraphrased [.] Problem 8. from Griffiths Reference problem 7.3 figure 7.43. a Let
University of Illinois at Chicago Department of Physics. Electricity and Magnetism PhD Qualifying Examination
 University of Illinois at Chicago Department of Physics Electricity and Magnetism PhD Qualifying Examination January 8, 216 (Friday) 9: am - 12: noon Full credit can be achieved from completely correct
University of Illinois at Chicago Department of Physics Electricity and Magnetism PhD Qualifying Examination January 8, 216 (Friday) 9: am - 12: noon Full credit can be achieved from completely correct
Queen s University at Kingston. Faculty of Arts and Science. Department of Physics PHYSICS 106. Final Examination.
 Page 1 of 5 Queen s University at Kingston Faculty of Arts and Science Department of Physics PHYSICS 106 Final Examination April 16th, 2009 Professor: A. B. McLean Time allowed: 3 HOURS Instructions This
Page 1 of 5 Queen s University at Kingston Faculty of Arts and Science Department of Physics PHYSICS 106 Final Examination April 16th, 2009 Professor: A. B. McLean Time allowed: 3 HOURS Instructions This
Integration is the reverse of the process of differentiation. In the usual notation. k dx = kx + c. kx dx = 1 2 kx2 + c.
 PHYS122 - Electricity and Magnetism Integration Reminder Integration is the reverse of the process of differentiation. In the usual notation f (x)dx = f(x) + constant The derivative of the RHS gives you
PHYS122 - Electricity and Magnetism Integration Reminder Integration is the reverse of the process of differentiation. In the usual notation f (x)dx = f(x) + constant The derivative of the RHS gives you
Chapter 27 Sources of Magnetic Field
 Chapter 27 Sources of Magnetic Field In this chapter we investigate the sources of magnetic of magnetic field, in particular, the magnetic field produced by moving charges (i.e., currents). Ampere s Law
Chapter 27 Sources of Magnetic Field In this chapter we investigate the sources of magnetic of magnetic field, in particular, the magnetic field produced by moving charges (i.e., currents). Ampere s Law
Math 350 Solutions for Final Exam Page 1. Problem 1. (10 points) (a) Compute the line integral. F ds C. z dx + y dy + x dz C
 Math 35 Solutions for Final Exam Page Problem. ( points) (a) ompute the line integral F ds for the path c(t) = (t 2, t 3, t) with t and the vector field F (x, y, z) = xi + zj + xk. (b) ompute the line
Math 35 Solutions for Final Exam Page Problem. ( points) (a) ompute the line integral F ds for the path c(t) = (t 2, t 3, t) with t and the vector field F (x, y, z) = xi + zj + xk. (b) ompute the line
Errata 1. p. 5 The third line from the end should read one of the four rows... not one of the three rows.
 Errata 1 Front inside cover: e 2 /4πɛ 0 should be 1.44 10 7 ev-cm. h/e 2 should be 25800 Ω. p. 5 The third line from the end should read one of the four rows... not one of the three rows. p. 8 The eigenstate
Errata 1 Front inside cover: e 2 /4πɛ 0 should be 1.44 10 7 ev-cm. h/e 2 should be 25800 Ω. p. 5 The third line from the end should read one of the four rows... not one of the three rows. p. 8 The eigenstate
Math Review for Exam Compute the second degree Taylor polynomials about (0, 0) of the following functions: (a) f(x, y) = e 2x 3y.
 Math 35 - Review for Exam 1. Compute the second degree Taylor polynomial of f e x+3y about (, ). Solution. A computation shows that f x(, ), f y(, ) 3, f xx(, ) 4, f yy(, ) 9, f xy(, ) 6. The second degree
Math 35 - Review for Exam 1. Compute the second degree Taylor polynomial of f e x+3y about (, ). Solution. A computation shows that f x(, ), f y(, ) 3, f xx(, ) 4, f yy(, ) 9, f xy(, ) 6. The second degree
2.20 Fall 2018 Math Review
 2.20 Fall 2018 Math Review September 10, 2018 These notes are to help you through the math used in this class. This is just a refresher, so if you never learned one of these topics you should look more
2.20 Fall 2018 Math Review September 10, 2018 These notes are to help you through the math used in this class. This is just a refresher, so if you never learned one of these topics you should look more
MP204 Electricity and Magnetism
 MATHEMATICAL PHYSICS SEMESTER 2, REPEAT 2016 2017 MP204 Electricity and Magnetism Prof. S. J. Hands, Dr. M. Haque and Dr. J.-I. Skullerud Time allowed: 1 1 2 hours Answer ALL questions MP204, 2016 2017,
MATHEMATICAL PHYSICS SEMESTER 2, REPEAT 2016 2017 MP204 Electricity and Magnetism Prof. S. J. Hands, Dr. M. Haque and Dr. J.-I. Skullerud Time allowed: 1 1 2 hours Answer ALL questions MP204, 2016 2017,
University of Illinois at Chicago Department of Physics
 University of Illinois at Chicago Department of Physics Electromagnetism Qualifying Examination January 4, 2017 9.00 am - 12.00 pm Full credit can be achieved from completely correct answers to 4 questions.
University of Illinois at Chicago Department of Physics Electromagnetism Qualifying Examination January 4, 2017 9.00 am - 12.00 pm Full credit can be achieved from completely correct answers to 4 questions.
Corrections to the First Printing: Chapter 6. This list includes corrections and clarifications through November 6, 1999.
 June 2,2 1 Corrections to the First Printing: Chapter 6 This list includes corrections and clarifications through November 6, 1999. We should have mentioned that our treatment of differential forms, especially
June 2,2 1 Corrections to the First Printing: Chapter 6 This list includes corrections and clarifications through November 6, 1999. We should have mentioned that our treatment of differential forms, especially
x + ye z2 + ze y2, y + xe z2 + ze x2, z and where T is the
 1.(8pts) Find F ds where F = x + ye z + ze y, y + xe z + ze x, z and where T is the T surface in the pictures. (The two pictures are two views of the same surface.) The boundary of T is the unit circle
1.(8pts) Find F ds where F = x + ye z + ze y, y + xe z + ze x, z and where T is the T surface in the pictures. (The two pictures are two views of the same surface.) The boundary of T is the unit circle
Written Examination. Antennas and Propagation (AA ) June 22, 2018.
 Written Examination Antennas and Propagation (AA. 7-8 June, 8. Problem ( points A circular loop of radius a = cm is positioned at a height h over a perfectly electric conductive ground plane as in figure,
Written Examination Antennas and Propagation (AA. 7-8 June, 8. Problem ( points A circular loop of radius a = cm is positioned at a height h over a perfectly electric conductive ground plane as in figure,
Final Review Worksheet
 Score: Name: Final Review Worksheet Math 2110Q Fall 2014 Professor Hohn Answers (in no particular order): f(x, y) = e y + xe xy + C; 2; 3; e y cos z, e z cos x, e x cos y, e x sin y e y sin z e z sin x;
Score: Name: Final Review Worksheet Math 2110Q Fall 2014 Professor Hohn Answers (in no particular order): f(x, y) = e y + xe xy + C; 2; 3; e y cos z, e z cos x, e x cos y, e x sin y e y sin z e z sin x;
Electric fields in matter
 Electric fields in matter November 2, 25 Suppose we apply a constant electric field to a block of material. Then the charges that make up the matter are no longer in equilibrium: the electrons tend to
Electric fields in matter November 2, 25 Suppose we apply a constant electric field to a block of material. Then the charges that make up the matter are no longer in equilibrium: the electrons tend to
Supporting Information
 Supporting Information A: Calculation of radial distribution functions To get an effective propagator in one dimension, we first transform 1) into spherical coordinates: x a = ρ sin θ cos φ, y = ρ sin
Supporting Information A: Calculation of radial distribution functions To get an effective propagator in one dimension, we first transform 1) into spherical coordinates: x a = ρ sin θ cos φ, y = ρ sin
Make sure you show all your work and justify your answers in order to get full credit.
 PHYSICS 7B, Lecture 3 Spring 5 Final exam, C. Bordel Tuesday, May, 5 8- am Make sure you show all your work and justify your answers in order to get full credit. Problem : Thermodynamic process ( points)
PHYSICS 7B, Lecture 3 Spring 5 Final exam, C. Bordel Tuesday, May, 5 8- am Make sure you show all your work and justify your answers in order to get full credit. Problem : Thermodynamic process ( points)
Integration by Substitution
 November 22, 2013 Introduction 7x 2 cos(3x 3 )dx =? 2xe x2 +5 dx =? Chain rule The chain rule: d dx (f (g(x))) = f (g(x)) g (x). Use the chain rule to find f (x) and then write the corresponding anti-differentiation
November 22, 2013 Introduction 7x 2 cos(3x 3 )dx =? 2xe x2 +5 dx =? Chain rule The chain rule: d dx (f (g(x))) = f (g(x)) g (x). Use the chain rule to find f (x) and then write the corresponding anti-differentiation
Maxwell s equations for electrostatics
 Maxwell s equations for electrostatics October 6, 5 The differential form of Gauss s law Starting from the integral form of Gauss s law, we treat the charge as a continuous distribution, ρ x. Then, letting
Maxwell s equations for electrostatics October 6, 5 The differential form of Gauss s law Starting from the integral form of Gauss s law, we treat the charge as a continuous distribution, ρ x. Then, letting
Motion of Charged Particles in Fields
 Chapter Motion of Charged Particles in Fields Plasmas are complicated because motions of electrons and ions are determined by the electric and magnetic fields but also change the fields by the currents
Chapter Motion of Charged Particles in Fields Plasmas are complicated because motions of electrons and ions are determined by the electric and magnetic fields but also change the fields by the currents
Math221: HW# 7 solutions
 Math22: HW# 7 solutions Andy Royston November 7, 25.3.3 let x = e u. Then ln x = u, x2 = e 2u, and dx = e 2u du. Furthermore, when x =, u, and when x =, u =. Hence x 2 ln x) 3 dx = e 2u u 3 e u du) = e
Math22: HW# 7 solutions Andy Royston November 7, 25.3.3 let x = e u. Then ln x = u, x2 = e 2u, and dx = e 2u du. Furthermore, when x =, u, and when x =, u =. Hence x 2 ln x) 3 dx = e 2u u 3 e u du) = e
Solution Set Eight. 1 Problem #1: Toroidal Electromagnet with Gap Problem #4: Self-Inductance of a Long Solenoid. 9
 : Solution Set Eight Northwestern University, Electrodynamics I Wednesday, March 9, 6 Contents Problem #: Toroidal Electromagnet with Gap. Problem #: Electromagnetic Momentum. 3 3 Problem #3: Type I Superconductor.
: Solution Set Eight Northwestern University, Electrodynamics I Wednesday, March 9, 6 Contents Problem #: Toroidal Electromagnet with Gap. Problem #: Electromagnetic Momentum. 3 3 Problem #3: Type I Superconductor.
Note: Each problem is worth 14 points except numbers 5 and 6 which are 15 points. = 3 2
 Math Prelim II Solutions Spring Note: Each problem is worth points except numbers 5 and 6 which are 5 points. x. Compute x da where is the region in the second quadrant between the + y circles x + y and
Math Prelim II Solutions Spring Note: Each problem is worth points except numbers 5 and 6 which are 5 points. x. Compute x da where is the region in the second quadrant between the + y circles x + y and
University of Alabama Department of Physics and Astronomy. PH 125 / LeClair Spring A Short Math Guide. Cartesian (x, y) Polar (r, θ)
 University of Alabama Department of Physics and Astronomy PH 125 / LeClair Spring 2009 A Short Math Guide 1 Definition of coordinates Relationship between 2D cartesian (, y) and polar (r, θ) coordinates.
University of Alabama Department of Physics and Astronomy PH 125 / LeClair Spring 2009 A Short Math Guide 1 Definition of coordinates Relationship between 2D cartesian (, y) and polar (r, θ) coordinates.
EECS 117 Lecture 7: Electrostatics Review
 EECS 117 Lecture 7: Electrostatics Review Prof. Niknejad University of California, Berkeley University of California, Berkeley EECS 117 Lecture 7 p. 1/19 Existence of Charge Charge, like mass, is an intrinsic
EECS 117 Lecture 7: Electrostatics Review Prof. Niknejad University of California, Berkeley University of California, Berkeley EECS 117 Lecture 7 p. 1/19 Existence of Charge Charge, like mass, is an intrinsic
Physics 7B, Speliotopoulos Final Exam, Spring 2014 Berkeley, CA
 Physics 7B, Speliotopoulos Final Exam, Spring 4 Berkeley, CA Rules: This final exam is closed book and closed notes. In particular, calculators are not allowed during this exam. Cell phones must be turned
Physics 7B, Speliotopoulos Final Exam, Spring 4 Berkeley, CA Rules: This final exam is closed book and closed notes. In particular, calculators are not allowed during this exam. Cell phones must be turned
MATH503 - HOMEWORK #2. v k. + v i. (fv i ) = f v i. + v k. ) + u j (ɛ ijk. ) u j (ɛ jik
 1 KO UNIVERITY Mon April 18, ollege of Arts and ciences Handout # Department of Physics Instructor: Alkan Kabakço lu MATH - HOMEWORK # 1 ( f) = Using Einstein notation and expressing x, y, x as e 1, e,
1 KO UNIVERITY Mon April 18, ollege of Arts and ciences Handout # Department of Physics Instructor: Alkan Kabakço lu MATH - HOMEWORK # 1 ( f) = Using Einstein notation and expressing x, y, x as e 1, e,
ECE 3209 Electromagnetic Fields Final Exam Example. University of Virginia Solutions
 ECE 3209 Electromagnetic Fields Final Exam Example University of Virginia Solutions (print name above) This exam is closed book and closed notes. Please perform all work on the exam sheets in a neat and
ECE 3209 Electromagnetic Fields Final Exam Example University of Virginia Solutions (print name above) This exam is closed book and closed notes. Please perform all work on the exam sheets in a neat and
Wave propagation in an inhomogeneous plasma
 DRAFT Wave propagation in an inhomogeneous plasma Felix I. Parra Rudolf Peierls Centre for Theoretical Physics, University of Oxford, Oxford OX NP, UK This version is of 7 February 208. Introduction In
DRAFT Wave propagation in an inhomogeneous plasma Felix I. Parra Rudolf Peierls Centre for Theoretical Physics, University of Oxford, Oxford OX NP, UK This version is of 7 February 208. Introduction In
Physics 3323, Fall 2016 Problem Set 7 due Oct 14, 2016
 Physics 333, Fll 16 Problem Set 7 due Oct 14, 16 Reding: Griffiths 4.1 through 4.4.1 1. Electric dipole An electric dipole with p = p ẑ is locted t the origin nd is sitting in n otherwise uniform electric
Physics 333, Fll 16 Problem Set 7 due Oct 14, 16 Reding: Griffiths 4.1 through 4.4.1 1. Electric dipole An electric dipole with p = p ẑ is locted t the origin nd is sitting in n otherwise uniform electric
Tutorial 3 - Solutions Electromagnetic Waves
 Tutorial 3 - Solutions Electromagnetic Waves You can find formulas you require for vector calculus at the end of this tutorial. 1. Find the Divergence and Curl of the following functions - (a) k r ˆr f
Tutorial 3 - Solutions Electromagnetic Waves You can find formulas you require for vector calculus at the end of this tutorial. 1. Find the Divergence and Curl of the following functions - (a) k r ˆr f
FORMULA SHEET FOR QUIZ 2 Exam Date: November 8, 2017
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Department Physics 8.07: Electromagnetism II November 5, 207 Prof. Alan Guth FORMULA SHEET FOR QUIZ 2 Exam Date: November 8, 207 A few items below are marked
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Department Physics 8.07: Electromagnetism II November 5, 207 Prof. Alan Guth FORMULA SHEET FOR QUIZ 2 Exam Date: November 8, 207 A few items below are marked
Topic 3. Integral calculus
 Integral calculus Topic 3 Line, surface and volume integrals Fundamental theorems of calculus Fundamental theorems for gradients Fundamental theorems for divergences! Green s theorem Fundamental theorems
Integral calculus Topic 3 Line, surface and volume integrals Fundamental theorems of calculus Fundamental theorems for gradients Fundamental theorems for divergences! Green s theorem Fundamental theorems
r r 1 r r 1 2 = q 1 p = qd and it points from the negative charge to the positive charge.
 MP204, Important Equations page 1 Below is a list of important equations that we meet in our study of Electromagnetism in the MP204 module. For your exam, you are expected to understand all of these, and
MP204, Important Equations page 1 Below is a list of important equations that we meet in our study of Electromagnetism in the MP204 module. For your exam, you are expected to understand all of these, and
7 Curvilinear coordinates
 7 Curvilinear coordinates Read: Boas sec. 5.4, 0.8, 0.9. 7. Review of spherical and cylindrical coords. First I ll review spherical and cylindrical coordinate systems so you can have them in mind when
7 Curvilinear coordinates Read: Boas sec. 5.4, 0.8, 0.9. 7. Review of spherical and cylindrical coords. First I ll review spherical and cylindrical coordinate systems so you can have them in mind when
(b) For the system in question, the electric field E, the displacement D, and the polarization P = D ɛ 0 E are as follows. r2 0 inside the sphere,
 PHY 35 K. Solutions for the second midterm exam. Problem 1: a The boundary conditions at the oil-air interface are air side E oil side = E and D air side oil side = D = E air side oil side = ɛ = 1+χ E.
PHY 35 K. Solutions for the second midterm exam. Problem 1: a The boundary conditions at the oil-air interface are air side E oil side = E and D air side oil side = D = E air side oil side = ɛ = 1+χ E.
= π + sin π = π + 0 = π, so the object is moving at a speed of π feet per second after π seconds. (c) How far does it go in π seconds?
 Mathematics 115 Professor Alan H. Stein April 18, 005 SOLUTIONS 1. Define what is meant by an antiderivative or indefinite integral of a function f(x). Solution: An antiderivative or indefinite integral
Mathematics 115 Professor Alan H. Stein April 18, 005 SOLUTIONS 1. Define what is meant by an antiderivative or indefinite integral of a function f(x). Solution: An antiderivative or indefinite integral
Evaluation of integrals
 Evaluation of certain contour integrals: Type I Type I: Integrals of the form 2π F (cos θ, sin θ) dθ If we take z = e iθ, then cos θ = 1 (z + 1 ), sin θ = 1 (z 1 dz ) and dθ = 2 z 2i z iz. Substituting
Evaluation of certain contour integrals: Type I Type I: Integrals of the form 2π F (cos θ, sin θ) dθ If we take z = e iθ, then cos θ = 1 (z + 1 ), sin θ = 1 (z 1 dz ) and dθ = 2 z 2i z iz. Substituting
Electrodynamics Exam Solutions
 Electrodynamics Exam Solutions Name: FS 215 Prof. C. Anastasiou Student number: Exercise 1 2 3 4 Total Max. points 15 15 15 15 6 Points Visum 1 Visum 2 The exam lasts 18 minutes. Start every new exercise
Electrodynamics Exam Solutions Name: FS 215 Prof. C. Anastasiou Student number: Exercise 1 2 3 4 Total Max. points 15 15 15 15 6 Points Visum 1 Visum 2 The exam lasts 18 minutes. Start every new exercise
Mathematics (Course B) Lent Term 2005 Examples Sheet 2
 N12d Natural Sciences, Part IA Dr M. G. Worster Mathematics (Course B) Lent Term 2005 Examples Sheet 2 Please communicate any errors in this sheet to Dr Worster at M.G.Worster@damtp.cam.ac.uk. Note that
N12d Natural Sciences, Part IA Dr M. G. Worster Mathematics (Course B) Lent Term 2005 Examples Sheet 2 Please communicate any errors in this sheet to Dr Worster at M.G.Worster@damtp.cam.ac.uk. Note that
Ordinary Differential Equations (ODEs)
 c01.tex 8/10/2010 22: 55 Page 1 PART A Ordinary Differential Equations (ODEs) Chap. 1 First-Order ODEs Sec. 1.1 Basic Concepts. Modeling To get a good start into this chapter and this section, quickly
c01.tex 8/10/2010 22: 55 Page 1 PART A Ordinary Differential Equations (ODEs) Chap. 1 First-Order ODEs Sec. 1.1 Basic Concepts. Modeling To get a good start into this chapter and this section, quickly
S12.1 SOLUTIONS TO PROBLEMS 12 (ODD NUMBERS)
 OLUTION TO PROBLEM 2 (ODD NUMBER) 2. The electric field is E = φ = 2xi + 2y j and at (2, ) E = 4i + 2j. Thus E = 2 5 and its direction is 2i + j. At ( 3, 2), φ = 6i + 4 j. Thus the direction of most rapid
OLUTION TO PROBLEM 2 (ODD NUMBER) 2. The electric field is E = φ = 2xi + 2y j and at (2, ) E = 4i + 2j. Thus E = 2 5 and its direction is 2i + j. At ( 3, 2), φ = 6i + 4 j. Thus the direction of most rapid
Without fully opening the exam, check that you have pages 1 through 12.
 Name: Section: Recitation Instructor: INSTRUCTIONS Fill in your name, etc. on this first page. Without fully opening the exam, check that you have pages 1 through 12. Show all your work on the standard
Name: Section: Recitation Instructor: INSTRUCTIONS Fill in your name, etc. on this first page. Without fully opening the exam, check that you have pages 1 through 12. Show all your work on the standard
PHYSICS 7B, Section 1 Fall 2013 Midterm 2, C. Bordel Monday, November 4, pm-9pm. Make sure you show your work!
 PHYSICS 7B, Section 1 Fall 2013 Midterm 2, C. Bordel Monday, November 4, 2013 7pm-9pm Make sure you show your work! Problem 1 - Current and Resistivity (20 pts) a) A cable of diameter d carries a current
PHYSICS 7B, Section 1 Fall 2013 Midterm 2, C. Bordel Monday, November 4, 2013 7pm-9pm Make sure you show your work! Problem 1 - Current and Resistivity (20 pts) a) A cable of diameter d carries a current
Maxima/minima with constraints
 Maxima/minima with constraints Very often we want to find maxima/minima but subject to some constraint Example: A wire is bent to a shape y = 1 x 2. If a string is stretched from the origin to the wire,
Maxima/minima with constraints Very often we want to find maxima/minima but subject to some constraint Example: A wire is bent to a shape y = 1 x 2. If a string is stretched from the origin to the wire,
Without fully opening the exam, check that you have pages 1 through 12.
 MTH 34 Solutions to Exam April 9th, 8 Name: Section: Recitation Instructor: INSTRUTIONS Fill in your name, etc. on this first page. Without fully opening the exam, check that you have pages through. Show
MTH 34 Solutions to Exam April 9th, 8 Name: Section: Recitation Instructor: INSTRUTIONS Fill in your name, etc. on this first page. Without fully opening the exam, check that you have pages through. Show
Final exam (practice 1) UCLA: Math 32B, Spring 2018
 Instructor: Noah White Date: Final exam (practice 1) UCLA: Math 32B, Spring 218 This exam has 7 questions, for a total of 8 points. Please print your working and answers neatly. Write your solutions in
Instructor: Noah White Date: Final exam (practice 1) UCLA: Math 32B, Spring 218 This exam has 7 questions, for a total of 8 points. Please print your working and answers neatly. Write your solutions in
No calculators, cell phones or any other electronic devices can be used on this exam. Clear your desk of everything excepts pens, pencils and erasers.
 Name: Section: Recitation Instructor: READ THE FOLLOWING INSTRUCTIONS. Do not open your exam until told to do so. No calculators, cell phones or any other electronic devices can be used on this exam. Clear
Name: Section: Recitation Instructor: READ THE FOLLOWING INSTRUCTIONS. Do not open your exam until told to do so. No calculators, cell phones or any other electronic devices can be used on this exam. Clear
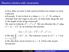
(b) g(x) = 4 + 6(x 3) (x 3) 2 (= x x 2 ) M1A1 Note: Accept any alternative form that is correct. Award M1A0 for a substitution of (x + 3).
 Paper. Answers. (a) METHOD f (x) q x f () q 6 q 6 f() p + 8 9 5 p METHOD f(x) (x ) + 5 x + 6x q 6, p (b) g(x) + 6(x ) (x ) ( + x x ) Note: Accept any alternative form that is correct. Award A for a substitution
Paper. Answers. (a) METHOD f (x) q x f () q 6 q 6 f() p + 8 9 5 p METHOD f(x) (x ) + 5 x + 6x q 6, p (b) g(x) + 6(x ) (x ) ( + x x ) Note: Accept any alternative form that is correct. Award A for a substitution
Physics 7B, Speliotopoulos Final Exam, Fall 2014 Berkeley, CA
 Physics 7B, Speliotopoulos Final Exam, Fall 4 Berkeley, CA Rules: This final exam is closed book and closed notes. In particular, calculators are not allowed during this exam. Cell phones must be turned
Physics 7B, Speliotopoulos Final Exam, Fall 4 Berkeley, CA Rules: This final exam is closed book and closed notes. In particular, calculators are not allowed during this exam. Cell phones must be turned
Math 31CH - Spring Final Exam
 Math 3H - Spring 24 - Final Exam Problem. The parabolic cylinder y = x 2 (aligned along the z-axis) is cut by the planes y =, z = and z = y. Find the volume of the solid thus obtained. Solution:We calculate
Math 3H - Spring 24 - Final Exam Problem. The parabolic cylinder y = x 2 (aligned along the z-axis) is cut by the planes y =, z = and z = y. Find the volume of the solid thus obtained. Solution:We calculate
ELECTROMAGNETIC WAVES
 Physics 4D ELECTROMAGNETIC WAVE Hans P. Paar 26 January 2006 i Chapter 1 Vector Calculus 1.1 Introduction Vector calculus is a branch of mathematics that allows differentiation and integration of (scalar)
Physics 4D ELECTROMAGNETIC WAVE Hans P. Paar 26 January 2006 i Chapter 1 Vector Calculus 1.1 Introduction Vector calculus is a branch of mathematics that allows differentiation and integration of (scalar)
THE UNIVERSITY OF SYDNEY FACULTY OF SCIENCE INTERMEDIATE PHYSICS PHYS 2912 PHYSICS 2B (ADVANCED) ALL QUESTIONS HAVE THE VALUE SHOWN
 CC0936 THE UNIVERSITY OF SYDNEY FACULTY OF SCIENCE INTERMEDIATE PHYSICS PHYS 91 PHYSICS B (ADVANCED SEMESTER, 015 TIME ALLOWED: 3 HOURS ALL QUESTIONS HAVE THE VALUE SHOWN INSTRUCTIONS: This paper consists
CC0936 THE UNIVERSITY OF SYDNEY FACULTY OF SCIENCE INTERMEDIATE PHYSICS PHYS 91 PHYSICS B (ADVANCED SEMESTER, 015 TIME ALLOWED: 3 HOURS ALL QUESTIONS HAVE THE VALUE SHOWN INSTRUCTIONS: This paper consists
r 4 r 2 q 2 r 3 V () r En dln (r) 1 q 1 Negative sign from integration of E field cancels the negative sign from the original equation.
 Question from last class Potential due to a Group of Point Charges rr V () r E dl r r 1 q 1 X rr N V () r E dl r n n N V(r) V n (r) 1 n1 4 o 1/30/2018 2 q 2 N r r N r r q n V () r En dln dr 2 n n r n r
Question from last class Potential due to a Group of Point Charges rr V () r E dl r r 1 q 1 X rr N V () r E dl r n n N V(r) V n (r) 1 n1 4 o 1/30/2018 2 q 2 N r r N r r q n V () r En dln dr 2 n n r n r
0.4. math. r r = r 2 + r 2 2r r cos(θ ) 0.5. Coordiates.
 .. Electrostatics... Multipole. F = E(r) = E(r) = S n qq i r r i 3 (r r i) i= n i= q i r r i 3 (r r i) d 3 r ρ(r ) 3 (r r ) ds E(r) = 4πQ enclosed E(r) = 4πρ(r ) E(r) = Φ(r) d 3 r ρ(r ) r dl E W = q(φ(r
.. Electrostatics... Multipole. F = E(r) = E(r) = S n qq i r r i 3 (r r i) i= n i= q i r r i 3 (r r i) d 3 r ρ(r ) 3 (r r ) ds E(r) = 4πQ enclosed E(r) = 4πρ(r ) E(r) = Φ(r) d 3 r ρ(r ) r dl E W = q(φ(r
/R = If we take the surface normal to be +ẑ, then the right hand rule gives positive flowing current to be in the +ˆφ direction.
 Problem 6.2 The loop in Fig. P6.2 is in the x y plane and B = ẑb 0 sinωt with B 0 positive. What is the direction of I (ˆφ or ˆφ) at: (a) t = 0 (b) ωt = π/4 (c) ωt = π/2 V emf y x I Figure P6.2: Loop of
Problem 6.2 The loop in Fig. P6.2 is in the x y plane and B = ẑb 0 sinωt with B 0 positive. What is the direction of I (ˆφ or ˆφ) at: (a) t = 0 (b) ωt = π/4 (c) ωt = π/2 V emf y x I Figure P6.2: Loop of
Vector analysis. 1 Scalars and vectors. Fields. Coordinate systems 1. 2 The operator The gradient, divergence, curl, and Laplacian...
 Vector analysis Abstract These notes present some background material on vector analysis. Except for the material related to proving vector identities (including Einstein s summation convention and the
Vector analysis Abstract These notes present some background material on vector analysis. Except for the material related to proving vector identities (including Einstein s summation convention and the
Errata. The following errors are known to be present in The Mechanics of Inhaled Pharmaceutical Aerosols: An Introduction:
 Errata The following errors are known to be present in The Mechanics of Inhaled Pharmaceutical Aerosols: An Introduction: p. 4, line 2: x and dx should be x and x+dx p. 6: Both sides of eqn. (2.15) should
Errata The following errors are known to be present in The Mechanics of Inhaled Pharmaceutical Aerosols: An Introduction: p. 4, line 2: x and dx should be x and x+dx p. 6: Both sides of eqn. (2.15) should
Chapter 28 Sources of Magnetic Field
 Chapter 28 Sources of Magnetic Field In this chapter we investigate the sources of magnetic field, in particular, the magnetic field produced by moving charges (i.e., currents), Ampere s Law is introduced
Chapter 28 Sources of Magnetic Field In this chapter we investigate the sources of magnetic field, in particular, the magnetic field produced by moving charges (i.e., currents), Ampere s Law is introduced
Disclaimer: This Final Exam Study Guide is meant to help you start studying. It is not necessarily a complete list of everything you need to know.
 Disclaimer: This is meant to help you start studying. It is not necessarily a complete list of everything you need to know. The MTH 234 final exam mainly consists of standard response questions where students
Disclaimer: This is meant to help you start studying. It is not necessarily a complete list of everything you need to know. The MTH 234 final exam mainly consists of standard response questions where students
MAC 2311 Calculus I Spring 2004
 MAC 2 Calculus I Spring 2004 Homework # Some Solutions.#. Since f (x) = d dx (ln x) =, the linearization at a = is x L(x) = f() + f ()(x ) = ln + (x ) = x. The answer is L(x) = x..#4. Since e 0 =, and
MAC 2 Calculus I Spring 2004 Homework # Some Solutions.#. Since f (x) = d dx (ln x) =, the linearization at a = is x L(x) = f() + f ()(x ) = ln + (x ) = x. The answer is L(x) = x..#4. Since e 0 =, and
y=1 1 J (a x ) dy dz dx dz 10 4 sin(2)e 2y dy dz sin(2)e 2y
 Chapter 5 Odd-Numbered 5.. Given the current density J = 4 [sin(x)e y a x + cos(x)e y a y ]ka/m : a) Find the total current crossing the plane y = in the a y direction in the region
Chapter 5 Odd-Numbered 5.. Given the current density J = 4 [sin(x)e y a x + cos(x)e y a y ]ka/m : a) Find the total current crossing the plane y = in the a y direction in the region
Electric Potential. David J. Starling Penn State Hazleton PHYS 212. Electricity is really just organized lightning. - George Carlin.
 Electricity is really just organized lightning. - George Carlin David J. Starling Penn State Hazleton PHYS 212 Since the electric force is so similar to gravity, might it be conservative? Yes! If we move
Electricity is really just organized lightning. - George Carlin David J. Starling Penn State Hazleton PHYS 212 Since the electric force is so similar to gravity, might it be conservative? Yes! If we move
MATHS 267 Answers to Stokes Practice Dr. Jones
 MATH 267 Answers to tokes Practice Dr. Jones 1. Calculate the flux F d where is the hemisphere x2 + y 2 + z 2 1, z > and F (xz + e y2, yz, z 2 + 1). Note: the surface is open (doesn t include any of the
MATH 267 Answers to tokes Practice Dr. Jones 1. Calculate the flux F d where is the hemisphere x2 + y 2 + z 2 1, z > and F (xz + e y2, yz, z 2 + 1). Note: the surface is open (doesn t include any of the
Ch 4 Differentiation
 Ch 1 Partial fractions Ch 6 Integration Ch 2 Coordinate geometry C4 Ch 5 Vectors Ch 3 The binomial expansion Ch 4 Differentiation Chapter 1 Partial fractions We can add (or take away) two fractions only
Ch 1 Partial fractions Ch 6 Integration Ch 2 Coordinate geometry C4 Ch 5 Vectors Ch 3 The binomial expansion Ch 4 Differentiation Chapter 1 Partial fractions We can add (or take away) two fractions only
Page Points Score Total: 210. No more than 200 points may be earned on the exam.
 Name: PID: Section: Recitation Instructor: DO NOT WRITE BELOW THIS LINE. GO ON TO THE NEXT PAGE. Page Points Score 3 18 4 18 5 18 6 18 7 18 8 18 9 18 10 21 11 21 12 21 13 21 Total: 210 No more than 200
Name: PID: Section: Recitation Instructor: DO NOT WRITE BELOW THIS LINE. GO ON TO THE NEXT PAGE. Page Points Score 3 18 4 18 5 18 6 18 7 18 8 18 9 18 10 21 11 21 12 21 13 21 Total: 210 No more than 200
Department of Physics IIT Kanpur, Semester II,
 Department of Phsics IIT Kanpur, Semester II, 7-8 PHYA: Phsics II Solutions # Instructors: AKJ & SC Solution.: (a) At the top of the hill, the gradient of the height function should be ero, that is, h(,
Department of Phsics IIT Kanpur, Semester II, 7-8 PHYA: Phsics II Solutions # Instructors: AKJ & SC Solution.: (a) At the top of the hill, the gradient of the height function should be ero, that is, h(,
