Numerical Methods in Informatics
|
|
|
- Shannon Ferguson
- 6 years ago
- Views:
Transcription
1 Numerical Methods in Informatics Lecture 2, : Nonlinear Equations in One Variable Tulin Kaman Institute of Mathematics, University of Zurich Lecture 2, T. Kaman Numerical Methods in Informatics Lecture 2, / 35
2 3. Nonlinear Equations in One Variable Goals of today To develop useful methods for a basic, simply stated problem, including such favourites as fixed point iteration and Newton s method; to develop and assess several algorithmic concepts that are prevalent throughout the field of numerical computing; to study basic algorithms for minimizing a function in one variable. T. Kaman Numerical Methods in Informatics Lecture 2, / 35
3 3. Nonlinear Equations in One Variable Outline Bisection method Fixed point iteration Newton s method and variants Minimizing a function in one variable T. Kaman Numerical Methods in Informatics Lecture 2, / 35
4 3. Nonlinear Equations in One Variable Solving nonlinear equations We want to find solutions to the scalar, nonlinear equation f (x) = 0, where the independent variable x is in an interval [a, b]. Example If x is value of x where f vanishes then x is a root or zero of f. How many roots? This depends not only on the function but also on the interval. f (x) = sin(x) has one root in [ π/2, π/2], two roots in [ π/4, 5π/4], and no roots in [π/4, 3π/4]. Why study a nonlinear problem before addressing linear ones?! One linear equation, e.g. ax = b, is too simple (solution: x = b/a, a 0), whereas a system of linear equations (Chapter 5 and 7) can have many complications. Several important general methods can be described in a simple context. Several important algorithm properties can be defined and used in a simple context. T. Kaman Numerical Methods in Informatics Lecture 2, / 35
5 3. Nonlinear Equations in One Variable Solving nonlinear equations Examples 1 f (x) = sin(x) Since sin(nπ) = 0 for any integer n, we have on the interval [a, b] = [π/2, 3π/2] one root, x = π. [a, b] = [0, 4π] five roots 2 f (x) = x 3 30x , 0 x 20. One root 3 f (x) = 10 cosh(x/4) x, x. Not every equation has a solution. No real root T. Kaman Numerical Methods in Informatics Lecture 2, / 35
6 3. Nonlinear Equations in One Variable Solving nonlinear equations Iterative methods for finding roots It is not realistic to expect to find a solution of a nonlinear equation by using a closed form formula They practically exist only for very low order polynomials We have to resort to iterative methods: Starting with an initial iterate x 0, the method generates a sequence of iterates x 1, x 2, that (hopefully) converges to a root of the function. A rough knowledge of the root s location is required. To find approximate locations of roots we can roughly plot the function we can probe the function, try to find two arguments a, b s.t. f (a)f (b) < 0. Intermediate value theorem If f C[a, b] and s is a value such that f (â) s f (ˆb) for two numbers â, ˆb [a, b], then there exists a real number c [a, b] for which f (c) = s. T. Kaman Numerical Methods in Informatics Lecture 2, / 35
7 3. Nonlinear Equations in One Variable Solving nonlinear equations Iterative methods for finding roots Generally for a nonlinear problem, must consider an iterative method: starting with initial iterate (guess) x 0, generate sequence of iterates x 1, x 2,, x k, that hopefully converge to a root x. Desirable qualities of a root finding algorithm are: Efficient: requires a small number of function evaluations. Robust: fails rarely, if ever. Announces failure if it does fail. Requires a minimal amount of additional information such as the derivative of f. Requires f to satisfy only minimal smoothness properties. Generalizes easily and naturally to many equations in many unknowns. Like many other wish-lists, this one is hard to fully satisfy... T. Kaman Numerical Methods in Informatics Lecture 2, / 35
8 3. Nonlinear Equations in One Variable Bisection method Bisection method simple safe requires minimal assumptions on the function f (x). slow hard to generalize to higher dimensions T. Kaman Numerical Methods in Informatics Lecture 2, / 35
9 3. Nonlinear Equations in One Variable Bisection method Bisection method development Given a < b such that f (a)f (b) < 0, there must be a root in [a, b]. Refer to [a, b] as the uncertainty interval. So, at each iteration, evaluate f (p) at p = a+b 2 and check the sign of f (a)f (b). If positive, set a p, if negative set b p. This reduces the length of the uncertainty interval by factor 0.5 at each iteration. So, setting x n = p, the error after n iterations satisfies x x n b a 2 2 n. Stopping criterion: given (absolute) tolerance atol, require b a 2 2 n atol. This allows a priori determination of the number of iterations n: unusual in algorithms for nonlinear problems. n = log 2 ( b a 2atol ) T. Kaman Numerical Methods in Informatics Lecture 2, / 35
10 3. Nonlinear Equations in One Variable Bisection method bisect function function [p,n] = bisect(func,a,b,fa,fb,atol) if (a >= b) (fa*fb >= 0) (atol <= 0) disp( something wrong with the input: quitting ); p = NaN; n=nan; return end n = ceil ( log2 (b-a) - log2 (2*atol)); for k=1:n p = (a+b)/2; fp = feval(func,p); if fa * fp < 0 b = p; fb = fp; else a = p; fa = fp; end end p = (a+b)/2; T. Kaman Numerical Methods in Informatics Lecture 2, / 35
11 3. Nonlinear Equations in One Variable Fixed point iteration Fixed point iteration This is an intuitively appealing approach which often leads to simple algorithms for complicated problems. 1 Write given problem f (x) = 0 as g(x) = x, so that f (x ) = 0 iff g(x ) = x. x is a fixed point of the mapping g. 2 Iterate: x k+1 = g(x k ), k = 0, 1, starting with guess x 0. It s all in the choice of the function g. T. Kaman Numerical Methods in Informatics Lecture 2, / 35
12 3. Nonlinear Equations in One Variable Fixed point iteration Choosing the function g The convergence properties of the fixed point iteration depend on the choice of the function g. There are many possible choices g for the given f : we are considering a family of methods. Examples: g(x) = x f (x), g(x) = x + 2f (x), g(x) = x f (x)/f (x) (assuming f exists and f (x) 0). The first two choices are simple, the last one has potential to yield fast convergence. We want resulting method to be simple converge do it rapidly. T. Kaman Numerical Methods in Informatics Lecture 2, / 35
13 3. Nonlinear Equations in One Variable Fixed point iteration Questions arise Suppose that we have somehow determined the continuous function g C[a, b], and let us consider the fixed point iteration. 1 Is there a fixed point x in [a, b]? 2 If yes, is it unique? 3 Does the sequence of iterates converge to a root x? 4 If yes, how fast? 5 If not, does this mean that no root exists? T. Kaman Numerical Methods in Informatics Lecture 2, / 35
14 3. Nonlinear Equations in One Variable Fixed point iteration Fixed Point Theorem Theorem If g C[a, b] and a g(x) b for all x [a, b], then there is a fixed point x in the interval [a, b]. If, in addition, the derivative g exists and there is a constant ρ < 1 such that the derivative satisfies g (x) ρ x (a, b), then the fixed point x is unique in this interval. T. Kaman Numerical Methods in Informatics Lecture 2, / 35
15 3. Nonlinear Equations in One Variable Fixed point iteration Convergence of the fixed point iteration Assuming ρ < 1 as for the fixed point theorem, obtain x k+1 x = g(x k ) g(x ) ρ x k x This is a contraction by the factor ρ. So, x k+1 x ρ x k x ρ 2 x k 1 x ρ k+1 x 0 x Since contraction factor ρ < 1, then ρ k 0 as k The smaller ρ, the faster convergence is. T. Kaman Numerical Methods in Informatics Lecture 2, / 35
16 3. Nonlinear Equations in One Variable Fixed point iteration Graphical illustration, x = e x, starting from x 0 = 1 This yields x 1 = e 1, x 2 = e e 1, T. Kaman Numerical Methods in Informatics Lecture 2, / 35
17 3. Nonlinear Equations in One Variable Fixed point iteration Example: cosh with two roots f (x) = g(x) x, g(x) = 2 cosh(x/4) The functions x and 2 cosh(x/4) meet at two locations. T. Kaman Numerical Methods in Informatics Lecture 2, / 35
18 3. Nonlinear Equations in One Variable Fixed point iteration Fixed point iteration with g = 2 cosh(x/4) There are two fixed points (roots of f ), 2 x1 4 and 8 x x , x For tolerance 1.e 8 : Starting at x 0 = 2 converge to x1 in 16 iterations. Starting at x 0 = 4 converge to x1 in 18 iterations. Starting at x 0 = 8 converge to x1 (even though x 2 is closer to x 0). Starting at x 0 = 10 obtain overflow in 3 iterations. Note: bisection yields both roots in 27 iterations. T. Kaman Numerical Methods in Informatics Lecture 2, / 35
19 3. Nonlinear Equations in One Variable Fixed point iteration Rate of convergence Suppose we want x k x 0.1 x 0 x Since x k x ρ k x 0 x, we want ρ k 0.1, k log 10 ρ 1 Definition of the rate of convergence: rate = log 10 ρ Then it takes about k = [1/rate] iterations to reduce the error by more than an order of magnitude. The higher the rate is (the faster convergence is), the smaller ρ. T. Kaman Numerical Methods in Informatics Lecture 2, / 35
20 3. Nonlinear Equations in One Variable Fixed point iteration Return to Example: cosh with two roots Bisection: ρ = 0.5 so rate = log k = 4 For the root x 1 of fixed point example, ρ 0.31 so rate = log k = 2 For the root x 2 of fixed point example, ρ > 1 so rate = log 10 ρ < 0 no convergence T. Kaman Numerical Methods in Informatics Lecture 2, / 35
21 3. Nonlinear Equations in One Variable Newton s method and variants Newton s method Not so simple Not very safe or robust Requires more than continuity on f (x). Fast Automatically generalized to systems T. Kaman Numerical Methods in Informatics Lecture 2, / 35
22 3. Nonlinear Equations in One Variable Newton s method and variants Derivation By Taylor series, f (x) = f (x k ) + f (x k )(x x k ) + f (η)(x x k ) 2 /2. So, for x = x 0 = f (x k ) + f (x k )(x x k ) + O((x x k ) 2 ). The method is obtained by neglecting nonlinear term, defining 0 = f (x k ) + f (x k )(x k+1 x k ), which gives the iteration step x k+1 = x k f (x k) f, k = 0, 1, 2, (x k ) T. Kaman Numerical Methods in Informatics Lecture 2, / 35
23 3. Nonlinear Equations in One Variable Newton s method and variants Geometric Interpretation Newtons method: the next iterate is the x-intercept of the tangent line to f at the current iterate. T. Kaman Numerical Methods in Informatics Lecture 2, / 35
24 3. Nonlinear Equations in One Variable Newton s method and variants Example: cosh with two roots f (x) = 2 cosh(x/4) x has two roots x and x in the interval [2, 10]. Newton s iteration is x k+1 = x k 2 cosh(x k/4) x k 0.5 sinh(x k /4) 1 For absolute tolerance 1.e 8 : Starting at x 0 = 2 requires 4 iterations to reach x 1. Starting at x 0 = 4 requires 5 iterations to reach x 1. Starting at x 0 = 8 requires 5 iterations to reach x 2. Starting at x 0 = 10 requires 6 iterations to reach x 2. The values of f (x k ), starting from x 0 = 8, are displayed below k f (x k ) -4.76e e e e e e-15 Note that the number of significant digits essentially doubles at each iteration (until the 5th, when roundoff error takes over). T. Kaman Numerical Methods in Informatics Lecture 2, / 35
25 3. Nonlinear Equations in One Variable Newton s method and variants Convergence theorem for Newton s method Theorem If f C 2 [a, b] and there is a root x in [a, b] such that f (x ) = 0, f (x ) 0, then there is a number δ such that, starting with x 0 from anywhere in the neighborhood [x δ, x + δ], Newton s method converges quadratically. Idea of Proof: Find the relation between e k+1 = x k+1 x and e k = x k x. Expand f (x ) in terms of Taylor series about x k ; divide by f (x k ), rearrange and replace x k f (x k) f (x k ) by x k+1; find the relation between e k+1 = x k+1 x and e k = x k x T. Kaman Numerical Methods in Informatics Lecture 2, / 35
26 3. Nonlinear Equations in One Variable Newton s method and variants Proof of convergence theorem for Newton s Method T. Kaman Numerical Methods in Informatics Lecture 2, / 35
27 3. Nonlinear Equations in One Variable Newton s method and variants Secant method (quasi-newton) One potential disadvantage of Newton s method is the need to know and evaluate the derivative of f. No derivative is needed in the secant method. Observe that near the root (assuming convergence) f (x k ) f (x k) f (x k 1 ) x k x k 1 So, Secant iteration x k x k 1 x k+1 = x k f (x k ), k = 0, 1, 2, f (x k ) f (x k 1 ) The secant method is not a fixed point method but a multi-point method. Note: the need for two initial starting iterates x 0 and x 1 : a two-step method. T. Kaman Numerical Methods in Informatics Lecture 2, / 35
28 3. Nonlinear Equations in One Variable Newton s method and variants Example: cosh with two roots f (x) = 2 cosh(x/4) x has two roots x and x in the interval [2, 10]. Secant s iteration is (2 cosh(x k /4) x k )(x k x k 1 ) x k+1 = x k (2 cosh(x k /4) x k )(2 cosh(x k 1 /4) x k 1 ) For absolute tolerance 1.e 8 : Starting at x 0 = 2 and x 1 = 4 requires 7 iterations to reach x 1. Starting at x 0 = 10 and x 1 = 8 requires 7 iterations to reach x 2. k f (x k ) e e e e e e-9 Observe superlinear convergence (convergence order ): x k+1 x c x k x 1.618, for some constant c much faster than bisection and fixed point iteration, yet not quite as fast as Newton s iteration. T. Kaman Numerical Methods in Informatics Lecture 2, / 35
29 3. Nonlinear Equations in One Variable Newton s method and variants Newton iteration for multiple roots f (x) = (x x ) m q(x) where q(x ) 0 then x is a root of multiplicity m. The fast local convergence rate of both Newton and secant methods is predicated on the assumption that f (x ) = 0. If m > 1, then f (x ) = 0 The method is linearly convergent, with the contraction factor ρ = 1 1 m. Show!!! Idea of proof: g(x) = x f (x) f (x), derive g (x). T. Kaman Numerical Methods in Informatics Lecture 2, / 35
30 3. Nonlinear Equations in One Variable Review: Convergence Definition: Speed (Rate) of Convergence Let {x k } k=0 be a sequence of in Rn that converges to x R n and assume that each x k x for each k. We say that the rate of convergence of {x k } to x is of order r and with asymptotic error constant C, if x k+1 x lim k 0 x k x r = C where r 1 and C > 0. T. Kaman Numerical Methods in Informatics Lecture 2, / 35
31 3. Nonlinear Equations in One Variable Review: Convergence Convergence rate of Methods Bisection Method: converges linearly, with asymptotic error constant 1 2 Fixed point iteration: converges at least quadratically, with asymptotic error constant g (x ) 2 Newton Method: converges quadratically, with asymptotic error constant f (x ) 2f (x ) Recommendation: Determine the convergence rate of methods T. Kaman Numerical Methods in Informatics Lecture 2, / 35
32 3. Nonlinear Equations in One Variable Review: Convergence Review: Speed (Rate) of convergence A given method is said to be linearly convergent if there is a constant ρ < 1 such that x k+1 x ρ x k x, quadratically convergent if there is a constant M such that x k+1 x M x k x 2, superlinearly convergent if there is a sequence of constant ρ k 0 such that x k+1 x ρ k x k x, for all k sufficiently large. T. Kaman Numerical Methods in Informatics Lecture 2, / 35
33 3. Nonlinear Equations in One Variable Minimizing a function in one variable Example A major source of applications giving rise to root finding is optimization. One-variable version: find an argument x = ˆx that minimizes a given objective function Find x = x that minimizes Φ(x) = 10 cosh(x/4) x This function has no zeros but has one minimizer around x = 1.6 T. Kaman Numerical Methods in Informatics Lecture 2, / 35
34 3. Nonlinear Equations in One Variable Minimizing a function in one variable Conditions for optimum and algorithms Necessary condition for an optimum: Suppose Φ C 2 and denote f (x) = Φ (x). Then a zero of f is a critical point of Φ, where Φ (x ) = 0. To be a minimizer or a maximizer, it is necessary for x to be a critical point. Sufficient condition for an optimum: A critical point x is a minimizer of Φ(x) if also Φ (x ) > 0. a maximizer of Φ(x) if also Φ (x ) < 0. further investigation is required if Φ (x ) = 0 Hence, an algorithm for finding a minimizer is obtained by using one of the methods we have learned for finding the roots of Φ (x), then checking for each such root x if also Φ (x ) > 0. T. Kaman Numerical Methods in Informatics Lecture 2, / 35
35 3. Nonlinear Equations in One Variable Minimizing a function in one variable Example To find a minimizer for Φ(x) = 10 cosh(x/4) x 1 Calculate first derivative Φ (x) = 2.5 sinh(x/4) 1 2 Find the root of Φ (x) = 0 using any of our methods, obtaining x Calculate second derivative Φ (x) = 2.5/4 cosh(x/4) > 0 x so x is a minimizer. T. Kaman Numerical Methods in Informatics Lecture 2, / 35
Lecture Notes to Accompany. Scientific Computing An Introductory Survey. by Michael T. Heath. Chapter 5. Nonlinear Equations
 Lecture Notes to Accompany Scientific Computing An Introductory Survey Second Edition by Michael T Heath Chapter 5 Nonlinear Equations Copyright c 2001 Reproduction permitted only for noncommercial, educational
Lecture Notes to Accompany Scientific Computing An Introductory Survey Second Edition by Michael T Heath Chapter 5 Nonlinear Equations Copyright c 2001 Reproduction permitted only for noncommercial, educational
Scientific Computing: An Introductory Survey
 Scientific Computing: An Introductory Survey Chapter 5 Nonlinear Equations Prof. Michael T. Heath Department of Computer Science University of Illinois at Urbana-Champaign Copyright c 2002. Reproduction
Scientific Computing: An Introductory Survey Chapter 5 Nonlinear Equations Prof. Michael T. Heath Department of Computer Science University of Illinois at Urbana-Champaign Copyright c 2002. Reproduction
3.1 Introduction. Solve non-linear real equation f(x) = 0 for real root or zero x. E.g. x x 1.5 =0, tan x x =0.
 3.1 Introduction Solve non-linear real equation f(x) = 0 for real root or zero x. E.g. x 3 +1.5x 1.5 =0, tan x x =0. Practical existence test for roots: by intermediate value theorem, f C[a, b] & f(a)f(b)
3.1 Introduction Solve non-linear real equation f(x) = 0 for real root or zero x. E.g. x 3 +1.5x 1.5 =0, tan x x =0. Practical existence test for roots: by intermediate value theorem, f C[a, b] & f(a)f(b)
CS 450 Numerical Analysis. Chapter 5: Nonlinear Equations
 Lecture slides based on the textbook Scientific Computing: An Introductory Survey by Michael T. Heath, copyright c 2018 by the Society for Industrial and Applied Mathematics. http://www.siam.org/books/cl80
Lecture slides based on the textbook Scientific Computing: An Introductory Survey by Michael T. Heath, copyright c 2018 by the Society for Industrial and Applied Mathematics. http://www.siam.org/books/cl80
Chapter 3: Root Finding. September 26, 2005
 Chapter 3: Root Finding September 26, 2005 Outline 1 Root Finding 2 3.1 The Bisection Method 3 3.2 Newton s Method: Derivation and Examples 4 3.3 How To Stop Newton s Method 5 3.4 Application: Division
Chapter 3: Root Finding September 26, 2005 Outline 1 Root Finding 2 3.1 The Bisection Method 3 3.2 Newton s Method: Derivation and Examples 4 3.3 How To Stop Newton s Method 5 3.4 Application: Division
Numerical Methods. Root Finding
 Numerical Methods Solving Non Linear 1-Dimensional Equations Root Finding Given a real valued function f of one variable (say ), the idea is to find an such that: f() 0 1 Root Finding Eamples Find real
Numerical Methods Solving Non Linear 1-Dimensional Equations Root Finding Given a real valued function f of one variable (say ), the idea is to find an such that: f() 0 1 Root Finding Eamples Find real
Outline. Scientific Computing: An Introductory Survey. Nonlinear Equations. Nonlinear Equations. Examples: Nonlinear Equations
 Methods for Systems of Methods for Systems of Outline Scientific Computing: An Introductory Survey Chapter 5 1 Prof. Michael T. Heath Department of Computer Science University of Illinois at Urbana-Champaign
Methods for Systems of Methods for Systems of Outline Scientific Computing: An Introductory Survey Chapter 5 1 Prof. Michael T. Heath Department of Computer Science University of Illinois at Urbana-Champaign
Outline. Math Numerical Analysis. Intermediate Value Theorem. Lecture Notes Zeros and Roots. Joseph M. Mahaffy,
 Outline Math 541 - Numerical Analysis Lecture Notes Zeros and Roots Joseph M. Mahaffy, jmahaffy@mail.sdsu.edu Department of Mathematics and Statistics Dynamical Systems Group Computational Sciences Research
Outline Math 541 - Numerical Analysis Lecture Notes Zeros and Roots Joseph M. Mahaffy, jmahaffy@mail.sdsu.edu Department of Mathematics and Statistics Dynamical Systems Group Computational Sciences Research
Math Numerical Analysis
 Math 541 - Numerical Analysis Lecture Notes Zeros and Roots Joseph M. Mahaffy, jmahaffy@mail.sdsu.edu Department of Mathematics and Statistics Dynamical Systems Group Computational Sciences Research Center
Math 541 - Numerical Analysis Lecture Notes Zeros and Roots Joseph M. Mahaffy, jmahaffy@mail.sdsu.edu Department of Mathematics and Statistics Dynamical Systems Group Computational Sciences Research Center
Simple Iteration, cont d
 Jim Lambers MAT 772 Fall Semester 2010-11 Lecture 2 Notes These notes correspond to Section 1.2 in the text. Simple Iteration, cont d In general, nonlinear equations cannot be solved in a finite sequence
Jim Lambers MAT 772 Fall Semester 2010-11 Lecture 2 Notes These notes correspond to Section 1.2 in the text. Simple Iteration, cont d In general, nonlinear equations cannot be solved in a finite sequence
Chapter 1. Root Finding Methods. 1.1 Bisection method
 Chapter 1 Root Finding Methods We begin by considering numerical solutions to the problem f(x) = 0 (1.1) Although the problem above is simple to state it is not always easy to solve analytically. This
Chapter 1 Root Finding Methods We begin by considering numerical solutions to the problem f(x) = 0 (1.1) Although the problem above is simple to state it is not always easy to solve analytically. This
Solution of Algebric & Transcendental Equations
 Page15 Solution of Algebric & Transcendental Equations Contents: o Introduction o Evaluation of Polynomials by Horner s Method o Methods of solving non linear equations o Bracketing Methods o Bisection
Page15 Solution of Algebric & Transcendental Equations Contents: o Introduction o Evaluation of Polynomials by Horner s Method o Methods of solving non linear equations o Bracketing Methods o Bisection
PART I Lecture Notes on Numerical Solution of Root Finding Problems MATH 435
 PART I Lecture Notes on Numerical Solution of Root Finding Problems MATH 435 Professor Biswa Nath Datta Department of Mathematical Sciences Northern Illinois University DeKalb, IL. 60115 USA E mail: dattab@math.niu.edu
PART I Lecture Notes on Numerical Solution of Root Finding Problems MATH 435 Professor Biswa Nath Datta Department of Mathematical Sciences Northern Illinois University DeKalb, IL. 60115 USA E mail: dattab@math.niu.edu
Numerical Methods I Solving Nonlinear Equations
 Numerical Methods I Solving Nonlinear Equations Aleksandar Donev Courant Institute, NYU 1 donev@courant.nyu.edu 1 MATH-GA 2011.003 / CSCI-GA 2945.003, Fall 2014 October 16th, 2014 A. Donev (Courant Institute)
Numerical Methods I Solving Nonlinear Equations Aleksandar Donev Courant Institute, NYU 1 donev@courant.nyu.edu 1 MATH-GA 2011.003 / CSCI-GA 2945.003, Fall 2014 October 16th, 2014 A. Donev (Courant Institute)
ROOT FINDING REVIEW MICHELLE FENG
 ROOT FINDING REVIEW MICHELLE FENG 1.1. Bisection Method. 1. Root Finding Methods (1) Very naive approach based on the Intermediate Value Theorem (2) You need to be looking in an interval with only one
ROOT FINDING REVIEW MICHELLE FENG 1.1. Bisection Method. 1. Root Finding Methods (1) Very naive approach based on the Intermediate Value Theorem (2) You need to be looking in an interval with only one
x 2 x n r n J(x + t(x x ))(x x )dt. For warming-up we start with methods for solving a single equation of one variable.
 Maria Cameron 1. Fixed point methods for solving nonlinear equations We address the problem of solving an equation of the form (1) r(x) = 0, where F (x) : R n R n is a vector-function. Eq. (1) can be written
Maria Cameron 1. Fixed point methods for solving nonlinear equations We address the problem of solving an equation of the form (1) r(x) = 0, where F (x) : R n R n is a vector-function. Eq. (1) can be written
Variable. Peter W. White Fall 2018 / Numerical Analysis. Department of Mathematics Tarleton State University
 Newton s Iterative s Peter W. White white@tarleton.edu Department of Mathematics Tarleton State University Fall 2018 / Numerical Analysis Overview Newton s Iterative s Newton s Iterative s Newton s Iterative
Newton s Iterative s Peter W. White white@tarleton.edu Department of Mathematics Tarleton State University Fall 2018 / Numerical Analysis Overview Newton s Iterative s Newton s Iterative s Newton s Iterative
MA 8019: Numerical Analysis I Solution of Nonlinear Equations
 MA 8019: Numerical Analysis I Solution of Nonlinear Equations Suh-Yuh Yang ( 楊肅煜 ) Department of Mathematics, National Central University Jhongli District, Taoyuan City 32001, Taiwan syyang@math.ncu.edu.tw
MA 8019: Numerical Analysis I Solution of Nonlinear Equations Suh-Yuh Yang ( 楊肅煜 ) Department of Mathematics, National Central University Jhongli District, Taoyuan City 32001, Taiwan syyang@math.ncu.edu.tw
Unit 2: Solving Scalar Equations. Notes prepared by: Amos Ron, Yunpeng Li, Mark Cowlishaw, Steve Wright Instructor: Steve Wright
 cs416: introduction to scientific computing 01/9/07 Unit : Solving Scalar Equations Notes prepared by: Amos Ron, Yunpeng Li, Mark Cowlishaw, Steve Wright Instructor: Steve Wright 1 Introduction We now
cs416: introduction to scientific computing 01/9/07 Unit : Solving Scalar Equations Notes prepared by: Amos Ron, Yunpeng Li, Mark Cowlishaw, Steve Wright Instructor: Steve Wright 1 Introduction We now
CLASS NOTES Models, Algorithms and Data: Introduction to computing 2018
 CLASS NOTES Models, Algorithms and Data: Introduction to computing 2018 Petros Koumoutsakos, Jens Honore Walther (Last update: April 16, 2018) IMPORTANT DISCLAIMERS 1. REFERENCES: Much of the material
CLASS NOTES Models, Algorithms and Data: Introduction to computing 2018 Petros Koumoutsakos, Jens Honore Walther (Last update: April 16, 2018) IMPORTANT DISCLAIMERS 1. REFERENCES: Much of the material
STOP, a i+ 1 is the desired root. )f(a i) > 0. Else If f(a i+ 1. Set a i+1 = a i+ 1 and b i+1 = b Else Set a i+1 = a i and b i+1 = a i+ 1
 53 17. Lecture 17 Nonlinear Equations Essentially, the only way that one can solve nonlinear equations is by iteration. The quadratic formula enables one to compute the roots of p(x) = 0 when p P. Formulas
53 17. Lecture 17 Nonlinear Equations Essentially, the only way that one can solve nonlinear equations is by iteration. The quadratic formula enables one to compute the roots of p(x) = 0 when p P. Formulas
SOLUTION OF ALGEBRAIC AND TRANSCENDENTAL EQUATIONS BISECTION METHOD
 BISECTION METHOD If a function f(x) is continuous between a and b, and f(a) and f(b) are of opposite signs, then there exists at least one root between a and b. It is shown graphically as, Let f a be negative
BISECTION METHOD If a function f(x) is continuous between a and b, and f(a) and f(b) are of opposite signs, then there exists at least one root between a and b. It is shown graphically as, Let f a be negative
1. Method 1: bisection. The bisection methods starts from two points a 0 and b 0 such that
 Chapter 4 Nonlinear equations 4.1 Root finding Consider the problem of solving any nonlinear relation g(x) = h(x) in the real variable x. We rephrase this problem as one of finding the zero (root) of a
Chapter 4 Nonlinear equations 4.1 Root finding Consider the problem of solving any nonlinear relation g(x) = h(x) in the real variable x. We rephrase this problem as one of finding the zero (root) of a
Introductory Numerical Analysis
 Introductory Numerical Analysis Lecture Notes December 16, 017 Contents 1 Introduction to 1 11 Floating Point Numbers 1 1 Computational Errors 13 Algorithm 3 14 Calculus Review 3 Root Finding 5 1 Bisection
Introductory Numerical Analysis Lecture Notes December 16, 017 Contents 1 Introduction to 1 11 Floating Point Numbers 1 1 Computational Errors 13 Algorithm 3 14 Calculus Review 3 Root Finding 5 1 Bisection
Numerical solutions of nonlinear systems of equations
 Numerical solutions of nonlinear systems of equations Tsung-Ming Huang Department of Mathematics National Taiwan Normal University, Taiwan E-mail: min@math.ntnu.edu.tw August 28, 2011 Outline 1 Fixed points
Numerical solutions of nonlinear systems of equations Tsung-Ming Huang Department of Mathematics National Taiwan Normal University, Taiwan E-mail: min@math.ntnu.edu.tw August 28, 2011 Outline 1 Fixed points
Solution of Nonlinear Equations
 Solution of Nonlinear Equations (Com S 477/577 Notes) Yan-Bin Jia Sep 14, 017 One of the most frequently occurring problems in scientific work is to find the roots of equations of the form f(x) = 0. (1)
Solution of Nonlinear Equations (Com S 477/577 Notes) Yan-Bin Jia Sep 14, 017 One of the most frequently occurring problems in scientific work is to find the roots of equations of the form f(x) = 0. (1)
MATH 3795 Lecture 12. Numerical Solution of Nonlinear Equations.
 MATH 3795 Lecture 12. Numerical Solution of Nonlinear Equations. Dmitriy Leykekhman Fall 2008 Goals Learn about different methods for the solution of f(x) = 0, their advantages and disadvantages. Convergence
MATH 3795 Lecture 12. Numerical Solution of Nonlinear Equations. Dmitriy Leykekhman Fall 2008 Goals Learn about different methods for the solution of f(x) = 0, their advantages and disadvantages. Convergence
Math 471. Numerical methods Root-finding algorithms for nonlinear equations
 Math 471. Numerical methods Root-finding algorithms for nonlinear equations overlap Section.1.5 of Bradie Our goal in this chapter is to find the root(s) for f(x) = 0..1 Bisection Method Intermediate value
Math 471. Numerical methods Root-finding algorithms for nonlinear equations overlap Section.1.5 of Bradie Our goal in this chapter is to find the root(s) for f(x) = 0..1 Bisection Method Intermediate value
Computational Methods CMSC/AMSC/MAPL 460. Solving nonlinear equations and zero finding. Finding zeroes of functions
 Computational Methods CMSC/AMSC/MAPL 460 Solving nonlinear equations and zero finding Ramani Duraiswami, Dept. of Computer Science Where does it arise? Finding zeroes of functions Solving functional equations
Computational Methods CMSC/AMSC/MAPL 460 Solving nonlinear equations and zero finding Ramani Duraiswami, Dept. of Computer Science Where does it arise? Finding zeroes of functions Solving functional equations
Line Search Methods. Shefali Kulkarni-Thaker
 1 BISECTION METHOD Line Search Methods Shefali Kulkarni-Thaker Consider the following unconstrained optimization problem min f(x) x R Any optimization algorithm starts by an initial point x 0 and performs
1 BISECTION METHOD Line Search Methods Shefali Kulkarni-Thaker Consider the following unconstrained optimization problem min f(x) x R Any optimization algorithm starts by an initial point x 0 and performs
Goals for This Lecture:
 Goals for This Lecture: Learn the Newton-Raphson method for finding real roots of real functions Learn the Bisection method for finding real roots of a real function Look at efficient implementations of
Goals for This Lecture: Learn the Newton-Raphson method for finding real roots of real functions Learn the Bisection method for finding real roots of a real function Look at efficient implementations of
Queens College, CUNY, Department of Computer Science Numerical Methods CSCI 361 / 761 Spring 2018 Instructor: Dr. Sateesh Mane.
 Queens College, CUNY, Department of Computer Science Numerical Methods CSCI 361 / 761 Spring 2018 Instructor: Dr. Sateesh Mane c Sateesh R. Mane 2018 3 Lecture 3 3.1 General remarks March 4, 2018 This
Queens College, CUNY, Department of Computer Science Numerical Methods CSCI 361 / 761 Spring 2018 Instructor: Dr. Sateesh Mane c Sateesh R. Mane 2018 3 Lecture 3 3.1 General remarks March 4, 2018 This
Lecture 7. Root finding I. 1 Introduction. 2 Graphical solution
 1 Introduction Lecture 7 Root finding I For our present purposes, root finding is the process of finding a real value of x which solves the equation f (x)=0. Since the equation g x =h x can be rewritten
1 Introduction Lecture 7 Root finding I For our present purposes, root finding is the process of finding a real value of x which solves the equation f (x)=0. Since the equation g x =h x can be rewritten
Motivation: We have already seen an example of a system of nonlinear equations when we studied Gaussian integration (p.8 of integration notes)
 AMSC/CMSC 460 Computational Methods, Fall 2007 UNIT 5: Nonlinear Equations Dianne P. O Leary c 2001, 2002, 2007 Solving Nonlinear Equations and Optimization Problems Read Chapter 8. Skip Section 8.1.1.
AMSC/CMSC 460 Computational Methods, Fall 2007 UNIT 5: Nonlinear Equations Dianne P. O Leary c 2001, 2002, 2007 Solving Nonlinear Equations and Optimization Problems Read Chapter 8. Skip Section 8.1.1.
1. Nonlinear Equations. This lecture note excerpted parts from Michael Heath and Max Gunzburger. f(x) = 0
 Numerical Analysis 1 1. Nonlinear Equations This lecture note excerpted parts from Michael Heath and Max Gunzburger. Given function f, we seek value x for which where f : D R n R n is nonlinear. f(x) =
Numerical Analysis 1 1. Nonlinear Equations This lecture note excerpted parts from Michael Heath and Max Gunzburger. Given function f, we seek value x for which where f : D R n R n is nonlinear. f(x) =
Bisection Method. and compute f (p 1 ). repeat with p 2 = a 2+b 2
 Bisection Method Given continuous function f (x) on the interval [a, b] with f (a) f (b) < 0, there must be a root in (a, b). To find a root: set [a 1, b 1 ] = [a, b]. set p 1 = a 1+b 1 2 and compute f
Bisection Method Given continuous function f (x) on the interval [a, b] with f (a) f (b) < 0, there must be a root in (a, b). To find a root: set [a 1, b 1 ] = [a, b]. set p 1 = a 1+b 1 2 and compute f
CHAPTER-II ROOTS OF EQUATIONS
 CHAPTER-II ROOTS OF EQUATIONS 2.1 Introduction The roots or zeros of equations can be simply defined as the values of x that makes f(x) =0. There are many ways to solve for roots of equations. For some
CHAPTER-II ROOTS OF EQUATIONS 2.1 Introduction The roots or zeros of equations can be simply defined as the values of x that makes f(x) =0. There are many ways to solve for roots of equations. For some
Lecture 8. Root finding II
 1 Introduction Lecture 8 Root finding II In the previous lecture we considered the bisection root-bracketing algorithm. It requires only that the function be continuous and that we have a root bracketed
1 Introduction Lecture 8 Root finding II In the previous lecture we considered the bisection root-bracketing algorithm. It requires only that the function be continuous and that we have a root bracketed
Root Finding: Close Methods. Bisection and False Position Dr. Marco A. Arocha Aug, 2014
 Root Finding: Close Methods Bisection and False Position Dr. Marco A. Arocha Aug, 2014 1 Roots Given function f(x), we seek x values for which f(x)=0 Solution x is the root of the equation or zero of the
Root Finding: Close Methods Bisection and False Position Dr. Marco A. Arocha Aug, 2014 1 Roots Given function f(x), we seek x values for which f(x)=0 Solution x is the root of the equation or zero of the
Numerical Methods Dr. Sanjeev Kumar Department of Mathematics Indian Institute of Technology Roorkee Lecture No 7 Regula Falsi and Secant Methods
 Numerical Methods Dr. Sanjeev Kumar Department of Mathematics Indian Institute of Technology Roorkee Lecture No 7 Regula Falsi and Secant Methods So welcome to the next lecture of the 2 nd unit of this
Numerical Methods Dr. Sanjeev Kumar Department of Mathematics Indian Institute of Technology Roorkee Lecture No 7 Regula Falsi and Secant Methods So welcome to the next lecture of the 2 nd unit of this
THE SECANT METHOD. q(x) = a 0 + a 1 x. with
 THE SECANT METHOD Newton s method was based on using the line tangent to the curve of y = f (x), with the point of tangency (x 0, f (x 0 )). When x 0 α, the graph of the tangent line is approximately the
THE SECANT METHOD Newton s method was based on using the line tangent to the curve of y = f (x), with the point of tangency (x 0, f (x 0 )). When x 0 α, the graph of the tangent line is approximately the
Spring 2015, Math 111 Lab 8: Newton s Method
 Spring 2015, Math 111 Lab 8: William and Mary April 7, 2015 Spring 2015, Math 111 Lab 8: Historical Outline Intuition Learning Objectives Today, we will be looking at applications of. Learning Objectives:
Spring 2015, Math 111 Lab 8: William and Mary April 7, 2015 Spring 2015, Math 111 Lab 8: Historical Outline Intuition Learning Objectives Today, we will be looking at applications of. Learning Objectives:
Jim Lambers MAT 460 Fall Semester Lecture 2 Notes
 Jim Lambers MAT 460 Fall Semester 2009-10 Lecture 2 Notes These notes correspond to Section 1.1 in the text. Review of Calculus Among the mathematical problems that can be solved using techniques from
Jim Lambers MAT 460 Fall Semester 2009-10 Lecture 2 Notes These notes correspond to Section 1.1 in the text. Review of Calculus Among the mathematical problems that can be solved using techniques from
Solving Non-Linear Equations (Root Finding)
 Solving Non-Linear Equations (Root Finding) Root finding Methods What are root finding methods? Methods for determining a solution of an equation. Essentially finding a root of a function, that is, a zero
Solving Non-Linear Equations (Root Finding) Root finding Methods What are root finding methods? Methods for determining a solution of an equation. Essentially finding a root of a function, that is, a zero
Nonlinear Equations. Chapter The Bisection Method
 Chapter 6 Nonlinear Equations Given a nonlinear function f(), a value r such that f(r) = 0, is called a root or a zero of f() For eample, for f() = e 016064, Fig?? gives the set of points satisfying y
Chapter 6 Nonlinear Equations Given a nonlinear function f(), a value r such that f(r) = 0, is called a root or a zero of f() For eample, for f() = e 016064, Fig?? gives the set of points satisfying y
5 Finding roots of equations
 Lecture notes for Numerical Analysis 5 Finding roots of equations Topics:. Problem statement. Bisection Method 3. Newton s Method 4. Fixed Point Iterations 5. Systems of equations 6. Notes and further
Lecture notes for Numerical Analysis 5 Finding roots of equations Topics:. Problem statement. Bisection Method 3. Newton s Method 4. Fixed Point Iterations 5. Systems of equations 6. Notes and further
Order of convergence
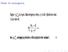 Order of convergence Linear and Quadratic Order of convergence Computing square root with Newton s Method Given a > 0, p def = a is positive root of equation Newton s Method p k+1 = p k p2 k a 2p k = 1
Order of convergence Linear and Quadratic Order of convergence Computing square root with Newton s Method Given a > 0, p def = a is positive root of equation Newton s Method p k+1 = p k p2 k a 2p k = 1
Bisection and False Position Dr. Marco A. Arocha Aug, 2014
 Bisection and False Position Dr. Marco A. Arocha Aug, 2014 1 Given function f, we seek x values for which f(x)=0 Solution x is the root of the equation or zero of the function f Problem is known as root
Bisection and False Position Dr. Marco A. Arocha Aug, 2014 1 Given function f, we seek x values for which f(x)=0 Solution x is the root of the equation or zero of the function f Problem is known as root
CHAPTER 10 Zeros of Functions
 CHAPTER 10 Zeros of Functions An important part of the maths syllabus in secondary school is equation solving. This is important for the simple reason that equations are important a wide range of problems
CHAPTER 10 Zeros of Functions An important part of the maths syllabus in secondary school is equation solving. This is important for the simple reason that equations are important a wide range of problems
Review of Classical Optimization
 Part II Review of Classical Optimization Multidisciplinary Design Optimization of Aircrafts 51 2 Deterministic Methods 2.1 One-Dimensional Unconstrained Minimization 2.1.1 Motivation Most practical optimization
Part II Review of Classical Optimization Multidisciplinary Design Optimization of Aircrafts 51 2 Deterministic Methods 2.1 One-Dimensional Unconstrained Minimization 2.1.1 Motivation Most practical optimization
Notes for Numerical Analysis Math 5465 by S. Adjerid Virginia Polytechnic Institute and State University. (A Rough Draft)
 Notes for Numerical Analysis Math 5465 by S. Adjerid Virginia Polytechnic Institute and State University (A Rough Draft) 1 2 Contents 1 Error Analysis 5 2 Nonlinear Algebraic Equations 7 2.1 Convergence
Notes for Numerical Analysis Math 5465 by S. Adjerid Virginia Polytechnic Institute and State University (A Rough Draft) 1 2 Contents 1 Error Analysis 5 2 Nonlinear Algebraic Equations 7 2.1 Convergence
Root Finding For NonLinear Equations Bisection Method
 Root Finding For NonLinear Equations Bisection Method P. Sam Johnson November 17, 2014 P. Sam Johnson (NITK) Root Finding For NonLinear Equations Bisection MethodNovember 17, 2014 1 / 26 Introduction The
Root Finding For NonLinear Equations Bisection Method P. Sam Johnson November 17, 2014 P. Sam Johnson (NITK) Root Finding For NonLinear Equations Bisection MethodNovember 17, 2014 1 / 26 Introduction The
Math 473: Practice Problems for Test 1, Fall 2011, SOLUTIONS
 Math 473: Practice Problems for Test 1, Fall 011, SOLUTIONS Show your work: 1. (a) Compute the Taylor polynomials P n (x) for f(x) = sin x and x 0 = 0. Solution: Compute f(x) = sin x, f (x) = cos x, f
Math 473: Practice Problems for Test 1, Fall 011, SOLUTIONS Show your work: 1. (a) Compute the Taylor polynomials P n (x) for f(x) = sin x and x 0 = 0. Solution: Compute f(x) = sin x, f (x) = cos x, f
Determining the Roots of Non-Linear Equations Part I
 Determining the Roots of Non-Linear Equations Part I Prof. Dr. Florian Rupp German University of Technology in Oman (GUtech) Introduction to Numerical Methods for ENG & CS (Mathematics IV) Spring Term
Determining the Roots of Non-Linear Equations Part I Prof. Dr. Florian Rupp German University of Technology in Oman (GUtech) Introduction to Numerical Methods for ENG & CS (Mathematics IV) Spring Term
CLASS NOTES Computational Methods for Engineering Applications I Spring 2015
 CLASS NOTES Computational Methods for Engineering Applications I Spring 2015 Petros Koumoutsakos Gerardo Tauriello (Last update: July 2, 2015) IMPORTANT DISCLAIMERS 1. REFERENCES: Much of the material
CLASS NOTES Computational Methods for Engineering Applications I Spring 2015 Petros Koumoutsakos Gerardo Tauriello (Last update: July 2, 2015) IMPORTANT DISCLAIMERS 1. REFERENCES: Much of the material
CS 323: Numerical Analysis and Computing
 CS 323: Numerical Analysis and Computing MIDTERM #2 Instructions: This is an open notes exam, i.e., you are allowed to consult any textbook, your class notes, homeworks, or any of the handouts from us.
CS 323: Numerical Analysis and Computing MIDTERM #2 Instructions: This is an open notes exam, i.e., you are allowed to consult any textbook, your class notes, homeworks, or any of the handouts from us.
1-D Optimization. Lab 16. Overview of Line Search Algorithms. Derivative versus Derivative-Free Methods
 Lab 16 1-D Optimization Lab Objective: Many high-dimensional optimization algorithms rely on onedimensional optimization methods. In this lab, we implement four line search algorithms for optimizing scalar-valued
Lab 16 1-D Optimization Lab Objective: Many high-dimensional optimization algorithms rely on onedimensional optimization methods. In this lab, we implement four line search algorithms for optimizing scalar-valued
Nonlinearity Root-finding Bisection Fixed Point Iteration Newton s Method Secant Method Conclusion. Nonlinear Systems
 Nonlinear Systems CS 205A: Mathematical Methods for Robotics, Vision, and Graphics Doug James (and Justin Solomon) CS 205A: Mathematical Methods Nonlinear Systems 1 / 27 Part III: Nonlinear Problems Not
Nonlinear Systems CS 205A: Mathematical Methods for Robotics, Vision, and Graphics Doug James (and Justin Solomon) CS 205A: Mathematical Methods Nonlinear Systems 1 / 27 Part III: Nonlinear Problems Not
Section 1.4 Tangents and Velocity
 Math 132 Tangents and Velocity Section 1.4 Section 1.4 Tangents and Velocity Tangent Lines A tangent line to a curve is a line that just touches the curve. In terms of a circle, the definition is very
Math 132 Tangents and Velocity Section 1.4 Section 1.4 Tangents and Velocity Tangent Lines A tangent line to a curve is a line that just touches the curve. In terms of a circle, the definition is very
Zeros of Functions. Chapter 10
 Chapter 10 Zeros of Functions An important part of the mathematics syllabus in secondary school is equation solving. This is important for the simple reason that equations are important a wide range of
Chapter 10 Zeros of Functions An important part of the mathematics syllabus in secondary school is equation solving. This is important for the simple reason that equations are important a wide range of
Midterm Review. Igor Yanovsky (Math 151A TA)
 Midterm Review Igor Yanovsky (Math 5A TA) Root-Finding Methods Rootfinding methods are designed to find a zero of a function f, that is, to find a value of x such that f(x) =0 Bisection Method To apply
Midterm Review Igor Yanovsky (Math 5A TA) Root-Finding Methods Rootfinding methods are designed to find a zero of a function f, that is, to find a value of x such that f(x) =0 Bisection Method To apply
Solving nonlinear equations
 Chapter Solving nonlinear equations Bisection Introduction Linear equations are of the form: find x such that ax + b = 0 Proposition Let f be a real-valued function that is defined and continuous on a
Chapter Solving nonlinear equations Bisection Introduction Linear equations are of the form: find x such that ax + b = 0 Proposition Let f be a real-valued function that is defined and continuous on a
Numerical Methods in Physics and Astrophysics
 Kostas Kokkotas 2 October 20, 2014 2 http://www.tat.physik.uni-tuebingen.de/ kokkotas Kostas Kokkotas 3 TOPICS 1. Solving nonlinear equations 2. Solving linear systems of equations 3. Interpolation, approximation
Kostas Kokkotas 2 October 20, 2014 2 http://www.tat.physik.uni-tuebingen.de/ kokkotas Kostas Kokkotas 3 TOPICS 1. Solving nonlinear equations 2. Solving linear systems of equations 3. Interpolation, approximation
Chapter 4. Solution of Non-linear Equation. Module No. 1. Newton s Method to Solve Transcendental Equation
 Numerical Analysis by Dr. Anita Pal Assistant Professor Department of Mathematics National Institute of Technology Durgapur Durgapur-713209 email: anita.buie@gmail.com 1 . Chapter 4 Solution of Non-linear
Numerical Analysis by Dr. Anita Pal Assistant Professor Department of Mathematics National Institute of Technology Durgapur Durgapur-713209 email: anita.buie@gmail.com 1 . Chapter 4 Solution of Non-linear
1 The best of all possible worlds
 Notes for 2017-03-18 1 The best of all possible worlds Last time, we discussed three methods of solving f(x) = 0: Newton, modified Newton, and bisection. Newton is potentially faster than bisection; bisection
Notes for 2017-03-18 1 The best of all possible worlds Last time, we discussed three methods of solving f(x) = 0: Newton, modified Newton, and bisection. Newton is potentially faster than bisection; bisection
Convergence Rates on Root Finding
 Convergence Rates on Root Finding Com S 477/577 Oct 5, 004 A sequence x i R converges to ξ if for each ǫ > 0, there exists an integer Nǫ) such that x l ξ > ǫ for all l Nǫ). The Cauchy convergence criterion
Convergence Rates on Root Finding Com S 477/577 Oct 5, 004 A sequence x i R converges to ξ if for each ǫ > 0, there exists an integer Nǫ) such that x l ξ > ǫ for all l Nǫ). The Cauchy convergence criterion
Numerical Analysis Fall. Roots: Open Methods
 Numerical Analysis 2015 Fall Roots: Open Methods Open Methods Open methods differ from bracketing methods, in that they require only a single starting value or two starting values that do not necessarily
Numerical Analysis 2015 Fall Roots: Open Methods Open Methods Open methods differ from bracketing methods, in that they require only a single starting value or two starting values that do not necessarily
Solutions of Equations in One Variable. Newton s Method
 Solutions of Equations in One Variable Newton s Method Numerical Analysis (9th Edition) R L Burden & J D Faires Beamer Presentation Slides prepared by John Carroll Dublin City University c 2011 Brooks/Cole,
Solutions of Equations in One Variable Newton s Method Numerical Analysis (9th Edition) R L Burden & J D Faires Beamer Presentation Slides prepared by John Carroll Dublin City University c 2011 Brooks/Cole,
University of Houston, Department of Mathematics Numerical Analysis, Fall 2005
 3 Numerical Solution of Nonlinear Equations and Systems 3.1 Fixed point iteration Reamrk 3.1 Problem Given a function F : lr n lr n, compute x lr n such that ( ) F(x ) = 0. In this chapter, we consider
3 Numerical Solution of Nonlinear Equations and Systems 3.1 Fixed point iteration Reamrk 3.1 Problem Given a function F : lr n lr n, compute x lr n such that ( ) F(x ) = 0. In this chapter, we consider
Numerical Optimization
 Unconstrained Optimization (II) Computer Science and Automation Indian Institute of Science Bangalore 560 012, India. NPTEL Course on Unconstrained Optimization Let f : R R Unconstrained problem min x
Unconstrained Optimization (II) Computer Science and Automation Indian Institute of Science Bangalore 560 012, India. NPTEL Course on Unconstrained Optimization Let f : R R Unconstrained problem min x
Numerical Methods Lecture 3
 Numerical Methods Lecture 3 Nonlinear Equations by Pavel Ludvík Introduction Definition (Root or zero of a function) A root (or a zero) of a function f is a solution of an equation f (x) = 0. We learn
Numerical Methods Lecture 3 Nonlinear Equations by Pavel Ludvík Introduction Definition (Root or zero of a function) A root (or a zero) of a function f is a solution of an equation f (x) = 0. We learn
Chapter III. Unconstrained Univariate Optimization
 1 Chapter III Unconstrained Univariate Optimization Introduction Interval Elimination Methods Polynomial Approximation Methods Newton s Method Quasi-Newton Methods 1 INTRODUCTION 2 1 Introduction Univariate
1 Chapter III Unconstrained Univariate Optimization Introduction Interval Elimination Methods Polynomial Approximation Methods Newton s Method Quasi-Newton Methods 1 INTRODUCTION 2 1 Introduction Univariate
Solving Nonlinear Equations
 Solving Nonlinear Equations Jijian Fan Department of Economics University of California, Santa Cruz Oct 13 2014 Overview NUMERICALLY solving nonlinear equation Four methods Bisection Function iteration
Solving Nonlinear Equations Jijian Fan Department of Economics University of California, Santa Cruz Oct 13 2014 Overview NUMERICALLY solving nonlinear equation Four methods Bisection Function iteration
Nonlinear Equations in One Variable
 Chapter 3 Nonlinear Equations in One Variable فهرست مطالب این جلسه حل معادله تک متغیره غیر خطی بروشهای نصف کردن نقطه ثابت نیوتن و سکانت آشنایی مقدماتی با مینیمم سازی تک متغیره فرض می شود تابع مورد نظر
Chapter 3 Nonlinear Equations in One Variable فهرست مطالب این جلسه حل معادله تک متغیره غیر خطی بروشهای نصف کردن نقطه ثابت نیوتن و سکانت آشنایی مقدماتی با مینیمم سازی تک متغیره فرض می شود تابع مورد نظر
Lecture 5. September 4, 2018 Math/CS 471: Introduction to Scientific Computing University of New Mexico
 Lecture 5 September 4, 2018 Math/CS 471: Introduction to Scientific Computing University of New Mexico 1 Review: Office hours at regularly scheduled times this week Tuesday: 9:30am-11am Wed: 2:30pm-4:00pm
Lecture 5 September 4, 2018 Math/CS 471: Introduction to Scientific Computing University of New Mexico 1 Review: Office hours at regularly scheduled times this week Tuesday: 9:30am-11am Wed: 2:30pm-4:00pm
1.1: The bisection method. September 2017
 (1/11) 1.1: The bisection method Solving nonlinear equations MA385/530 Numerical Analysis September 2017 3 2 f(x)= x 2 2 x axis 1 0 1 x [0] =a x [2] =1 x [3] =1.5 x [1] =b 2 0.5 0 0.5 1 1.5 2 2.5 1 Solving
(1/11) 1.1: The bisection method Solving nonlinear equations MA385/530 Numerical Analysis September 2017 3 2 f(x)= x 2 2 x axis 1 0 1 x [0] =a x [2] =1 x [3] =1.5 x [1] =b 2 0.5 0 0.5 1 1.5 2 2.5 1 Solving
Nonlinear equations. Norms for R n. Convergence orders for iterative methods
 Nonlinear equations Norms for R n Assume that X is a vector space. A norm is a mapping X R with x such that for all x, y X, α R x = = x = αx = α x x + y x + y We define the following norms on the vector
Nonlinear equations Norms for R n Assume that X is a vector space. A norm is a mapping X R with x such that for all x, y X, α R x = = x = αx = α x x + y x + y We define the following norms on the vector
Chapter 6. Nonlinear Equations. 6.1 The Problem of Nonlinear Root-finding. 6.2 Rate of Convergence
 Chapter 6 Nonlinear Equations 6. The Problem of Nonlinear Root-finding In this module we consider the problem of using numerical techniques to find the roots of nonlinear equations, f () =. Initially we
Chapter 6 Nonlinear Equations 6. The Problem of Nonlinear Root-finding In this module we consider the problem of using numerical techniques to find the roots of nonlinear equations, f () =. Initially we
CHAPTER 4 ROOTS OF EQUATIONS
 CHAPTER 4 ROOTS OF EQUATIONS Chapter 3 : TOPIC COVERS (ROOTS OF EQUATIONS) Definition of Root of Equations Bracketing Method Graphical Method Bisection Method False Position Method Open Method One-Point
CHAPTER 4 ROOTS OF EQUATIONS Chapter 3 : TOPIC COVERS (ROOTS OF EQUATIONS) Definition of Root of Equations Bracketing Method Graphical Method Bisection Method False Position Method Open Method One-Point
Numerical Methods in Physics and Astrophysics
 Kostas Kokkotas 2 October 17, 2017 2 http://www.tat.physik.uni-tuebingen.de/ kokkotas Kostas Kokkotas 3 TOPICS 1. Solving nonlinear equations 2. Solving linear systems of equations 3. Interpolation, approximation
Kostas Kokkotas 2 October 17, 2017 2 http://www.tat.physik.uni-tuebingen.de/ kokkotas Kostas Kokkotas 3 TOPICS 1. Solving nonlinear equations 2. Solving linear systems of equations 3. Interpolation, approximation
Nonlinearity Root-finding Bisection Fixed Point Iteration Newton s Method Secant Method Conclusion. Nonlinear Systems
 Nonlinear Systems CS 205A: Mathematical Methods for Robotics, Vision, and Graphics Justin Solomon CS 205A: Mathematical Methods Nonlinear Systems 1 / 24 Part III: Nonlinear Problems Not all numerical problems
Nonlinear Systems CS 205A: Mathematical Methods for Robotics, Vision, and Graphics Justin Solomon CS 205A: Mathematical Methods Nonlinear Systems 1 / 24 Part III: Nonlinear Problems Not all numerical problems
FIXED POINT ITERATION
 FIXED POINT ITERATION The idea of the fixed point iteration methods is to first reformulate a equation to an equivalent fixed point problem: f (x) = 0 x = g(x) and then to use the iteration: with an initial
FIXED POINT ITERATION The idea of the fixed point iteration methods is to first reformulate a equation to an equivalent fixed point problem: f (x) = 0 x = g(x) and then to use the iteration: with an initial
A Few Concepts from Numerical Analysis
 2 A Few Concepts from Numerical Analysis A systematic treatment of numerical methods is provided in conventional courses and textbooks on numerical analysis. But a few very common issues, that emerge in
2 A Few Concepts from Numerical Analysis A systematic treatment of numerical methods is provided in conventional courses and textbooks on numerical analysis. But a few very common issues, that emerge in
Solving nonlinear equations (See online notes and lecture notes for full details) 1.3: Newton s Method
 Solving nonlinear equations (See online notes and lecture notes for full details) 1.3: Newton s Method MA385 Numerical Analysis September 2018 (1/16) Sir Isaac Newton, 1643-1727, England. Easily one of
Solving nonlinear equations (See online notes and lecture notes for full details) 1.3: Newton s Method MA385 Numerical Analysis September 2018 (1/16) Sir Isaac Newton, 1643-1727, England. Easily one of
GENG2140, S2, 2012 Week 7: Curve fitting
 GENG2140, S2, 2012 Week 7: Curve fitting Curve fitting is the process of constructing a curve, or mathematical function, f(x) that has the best fit to a series of data points Involves fitting lines and
GENG2140, S2, 2012 Week 7: Curve fitting Curve fitting is the process of constructing a curve, or mathematical function, f(x) that has the best fit to a series of data points Involves fitting lines and
Lec7p1, ORF363/COS323
 Lec7 Page 1 Lec7p1, ORF363/COS323 This lecture: One-dimensional line search (root finding and minimization) Bisection Newton's method Secant method Introduction to rates of convergence Instructor: Amir
Lec7 Page 1 Lec7p1, ORF363/COS323 This lecture: One-dimensional line search (root finding and minimization) Bisection Newton's method Secant method Introduction to rates of convergence Instructor: Amir
Caculus 221. Possible questions for Exam II. March 19, 2002
 Caculus 221 Possible questions for Exam II March 19, 2002 These notes cover the recent material in a style more like the lecture than the book. The proofs in the book are in section 1-11. At the end there
Caculus 221 Possible questions for Exam II March 19, 2002 These notes cover the recent material in a style more like the lecture than the book. The proofs in the book are in section 1-11. At the end there
Root Finding (and Optimisation)
 Root Finding (and Optimisation) M.Sc. in Mathematical Modelling & Scientific Computing, Practical Numerical Analysis Michaelmas Term 2018, Lecture 4 Root Finding The idea of root finding is simple we want
Root Finding (and Optimisation) M.Sc. in Mathematical Modelling & Scientific Computing, Practical Numerical Analysis Michaelmas Term 2018, Lecture 4 Root Finding The idea of root finding is simple we want
Numerical Study of Some Iterative Methods for Solving Nonlinear Equations
 International Journal of Engineering Science Invention ISSN (Online): 2319 6734, ISSN (Print): 2319 6726 Volume 5 Issue 2 February 2016 PP.0110 Numerical Study of Some Iterative Methods for Solving Nonlinear
International Journal of Engineering Science Invention ISSN (Online): 2319 6734, ISSN (Print): 2319 6726 Volume 5 Issue 2 February 2016 PP.0110 Numerical Study of Some Iterative Methods for Solving Nonlinear
R x n. 2 R We simplify this algebraically, obtaining 2x n x n 1 x n x n
 Math 42 Homework 4. page 3, #9 This is a modification of the bisection method. Write a MATLAB function similar to bisect.m. Here, given the points P a a,f a and P b b,f b with f a f b,we compute the point
Math 42 Homework 4. page 3, #9 This is a modification of the bisection method. Write a MATLAB function similar to bisect.m. Here, given the points P a a,f a and P b b,f b with f a f b,we compute the point
15 Nonlinear Equations and Zero-Finders
 15 Nonlinear Equations and Zero-Finders This lecture describes several methods for the solution of nonlinear equations. In particular, we will discuss the computation of zeros of nonlinear functions f(x).
15 Nonlinear Equations and Zero-Finders This lecture describes several methods for the solution of nonlinear equations. In particular, we will discuss the computation of zeros of nonlinear functions f(x).
Figure 1: Graph of y = x cos(x)
 Chapter The Solution of Nonlinear Equations f(x) = 0 In this chapter we will study methods for find the solutions of functions of single variables, ie values of x such that f(x) = 0 For example, f(x) =
Chapter The Solution of Nonlinear Equations f(x) = 0 In this chapter we will study methods for find the solutions of functions of single variables, ie values of x such that f(x) = 0 For example, f(x) =
FIXED POINT ITERATIONS
 FIXED POINT ITERATIONS MARKUS GRASMAIR 1. Fixed Point Iteration for Non-linear Equations Our goal is the solution of an equation (1) F (x) = 0, where F : R n R n is a continuous vector valued mapping in
FIXED POINT ITERATIONS MARKUS GRASMAIR 1. Fixed Point Iteration for Non-linear Equations Our goal is the solution of an equation (1) F (x) = 0, where F : R n R n is a continuous vector valued mapping in
Homework and Computer Problems for Math*2130 (W17).
 Homework and Computer Problems for Math*2130 (W17). MARCUS R. GARVIE 1 December 21, 2016 1 Department of Mathematics & Statistics, University of Guelph NOTES: These questions are a bare minimum. You should
Homework and Computer Problems for Math*2130 (W17). MARCUS R. GARVIE 1 December 21, 2016 1 Department of Mathematics & Statistics, University of Guelph NOTES: These questions are a bare minimum. You should
8 Numerical methods for unconstrained problems
 8 Numerical methods for unconstrained problems Optimization is one of the important fields in numerical computation, beside solving differential equations and linear systems. We can see that these fields
8 Numerical methods for unconstrained problems Optimization is one of the important fields in numerical computation, beside solving differential equations and linear systems. We can see that these fields
Scientific Computing: Optimization
 Scientific Computing: Optimization Aleksandar Donev Courant Institute, NYU 1 donev@courant.nyu.edu 1 Course MATH-GA.2043 or CSCI-GA.2112, Spring 2012 March 8th, 2011 A. Donev (Courant Institute) Lecture
Scientific Computing: Optimization Aleksandar Donev Courant Institute, NYU 1 donev@courant.nyu.edu 1 Course MATH-GA.2043 or CSCI-GA.2112, Spring 2012 March 8th, 2011 A. Donev (Courant Institute) Lecture
Computational Methods. Solving Equations
 Computational Methods Solving Equations Manfred Huber 2010 1 Solving Equations Solving scalar equations is an elemental task that arises in a wide range of applications Corresponds to finding parameters
Computational Methods Solving Equations Manfred Huber 2010 1 Solving Equations Solving scalar equations is an elemental task that arises in a wide range of applications Corresponds to finding parameters
MATH 350: Introduction to Computational Mathematics
 MATH 350: Introduction to Computational Mathematics Chapter IV: Locating Roots of Equations Greg Fasshauer Department of Applied Mathematics Illinois Institute of Technology Spring 2011 fasshauer@iit.edu
MATH 350: Introduction to Computational Mathematics Chapter IV: Locating Roots of Equations Greg Fasshauer Department of Applied Mathematics Illinois Institute of Technology Spring 2011 fasshauer@iit.edu
A Review of Bracketing Methods for Finding Zeros of Nonlinear Functions
 Applied Mathematical Sciences, Vol 1, 018, no 3, 137-146 HIKARI Ltd, wwwm-hikaricom https://doiorg/101988/ams018811 A Review of Bracketing Methods for Finding Zeros of Nonlinear Functions Somkid Intep
Applied Mathematical Sciences, Vol 1, 018, no 3, 137-146 HIKARI Ltd, wwwm-hikaricom https://doiorg/101988/ams018811 A Review of Bracketing Methods for Finding Zeros of Nonlinear Functions Somkid Intep
Families of Functions, Taylor Polynomials, l Hopital s
 Unit #6 : Rule Families of Functions, Taylor Polynomials, l Hopital s Goals: To use first and second derivative information to describe functions. To be able to find general properties of families of functions.
Unit #6 : Rule Families of Functions, Taylor Polynomials, l Hopital s Goals: To use first and second derivative information to describe functions. To be able to find general properties of families of functions.
