Chapter 4 One Dimensional Kinematics

Transcription

1 Chapter 4 One Dimensional Kinematics Chapter 4 One Dimensional Kinematics 41 Introduction 4 Position, Time Interval, Displacement 3 41 Position 3 4 Time Interval 3 43 Displacement 3 43 Velocity Average Velocity Instantaneous Velocity 4 Eample 41 Determining Velocity from Position 5 44 Acceleration Average Acceleration 6 44 Instantaneous Acceleration 7 Eample 4 Determining Acceleration from Velocity 8 45 Constant Acceleration Velocity: Area Under the Acceleration vs Time Graph 9 45 Displacement: Area Under the Velocity vs Time Graph 9 Eample 43 Accelerating Car 11 Eample 44 Catching a Bus One Dimensional Kinematics Non-Constant Acceleration Change of Velocity as the Integral of Non-constant Acceleration Integral of Velocity 19 Eample 45 Non-constant Acceleration 0 Eample 46 Bicycle and Car 1 4-1

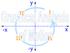
2 Chapter 4 One Dimensional Kinematics In the first place, what do we mean by time and space? It turns out that these deep philosophical questions have to be analyzed very carefully in physics, and this is not easy to do The theory of relativity shows that our ideas of space and time are not as simple as one might imagine at first sight However, for our present purposes, for the accuracy that we need at first, we need not be very careful about defining things precisely Perhaps you say, That s a terrible thing I learned that in science we have to define everything precisely We cannot define anything precisely! If we attempt to, we get into that paralysis of thought that comes to philosophers, who sit opposite each other, one saying to the other, You don t know what you are talking about! The second one says What do you mean by know? What do you mean by talking? What do you mean by you?, and so on In order to be able to talk constructively, we just have to agree that we are talking roughly about the same thing You know as much about time as you need for the present, but remember that there are some subtleties that have to be discussed; we shall discuss them later 1 41 Introduction Richard Feynman Kinematics is the mathematical description of motion The term is derived from the Greek word kinema, meaning movement In order to quantify motion, a mathematical coordinate system, called a reference frame, is used to describe space and time Once a reference frame has been chosen, we can introduce the physical concepts of position, velocity and acceleration in a mathematically precise manner Figure 41 shows a Cartesian coordinate system in one dimension with unit vector î pointing in the direction of increasing -coordinate Figure 41 A one-dimensional Cartesian coordinate system 1 Richard P Feynman, Robert B Leighton, Matthew Sands, The Feynman Lectures on Physics, Addison-Wesley, Reading, Massachusetts, (1963), p 1-4-

3 4 Position, Time Interval, Displacement 41 Position Consider an object moving in one dimension We denote the position coordinate of the center of mass of the object with respect to the choice of origin by ( t ) The position coordinate is a function of time and can be positive, zero, or negative, depending on the location of the object The position has both direction and magnitude, and hence is a vector (Figure 4),! ( t) = ( t) ˆi (41) We denote the position coordinate of the center of the mass at t = 0 by the symbol 0! ( t = 0) The SI unit for position is the meter [m] 4 Time Interval Figure 4 The position vector, with reference to a chosen origin Consider a closed interval of time [ t1, t ] We characterize this time interval by the difference in endpoints of the interval such that The SI units for time intervals are seconds [s] 43 Displacement! t = t " t1 (4) The displacement, of a body between times t 1 and t (Figure 43) is defined to be the change in position coordinate of the body!! " ( ( t ) # ( t )) ˆi "! ( t) ˆi (43) 1 Displacement is a vector quantity 4-3

4 Figure 43 The displacement vector of an object over a time interval is the vector difference between the two position vectors 43 Velocity When describing the motion of objects, words like speed and velocity are used in common language; however when introducing a mathematical description of motion, we need to define these terms precisely Our procedure will be to define average quantities for finite intervals of time and then eamine what happens in the limit as the time interval becomes infinitesimally small This will lead us to the mathematical concept that velocity at an instant in time is the derivative of the position with respect to time 431 Average Velocity The component of the average velocity, v, for a time interval! t is defined to be the displacement! divided by the time interval! t, The average velocity vector is then v! " (431)! t!! v( t) " ˆi = v ( ) ˆ t i (43)! t The SI units for average velocity are meters per second " % m$ s!1 # & 433 Instantaneous Velocity Consider a body moving in one direction We denote the position coordinate of the body by ( t ), with initial position 0 at time t = 0 Consider the time interval [ t, t +! t] The average velocity for the interval! t is the slope of the line connecting the points ( t, ( t )) and ( t, ( t +! t)) The slope, the rise over the run, is the change in position over the change in time, and is given by 4-4

5 v rise! ( t +! t) " ( t) # = = (433) run! t! t Let s see what happens to the average velocity as we shrink the size of the time interval The slope of the line connecting the points ( t, ( t )) and ( t, ( t +! t)) approaches the slope of the tangent line to the curve ( t ) at the time t (Figure 44) Figure 44 Graph of position vs time showing the tangent line at time t In order to define the limiting value for the slope at any time, we choose a time interval [ t, t +! t] For each value of! t, we calculate the average velocity As! t " 0, we generate a sequence of average velocities The limiting value of this sequence is defined to be the -component of the instantaneous velocity at the time t The -component of instantaneous velocity at time t is given by the slope of the tangent line to the curve of position vs time curve at time t :! ( t +! t) # ( t) d v( t) $ lim v = lim = lim $ (434)! t" 0! t" 0! t! t" 0! t dt The instantaneous velocity vector is then Eample 41 Determining Velocity from Position! v( t) = v ( t) ˆi (435) Consider an object that is moving along the -coordinate ais represented by the equation 1 ( t) = 0 + bt (436) 4-5

6 where 0 is the initial position of the object at t = 0 We can eplicitly calculate the -component of instantaneous velocity from Equation (434) by first calculating the displacement in the -direction,! = ( t +! t) " ( t) We need to calculate the position at time t +! t, Then the instantaneous velocity is 1 1 ( t +! t) = 0 + b( t +! t) = 0 + b( t + t! t +! t ) (437) # 1 $ # 1 $ 0 + b( t + t! t +! t ) % 0 + bt ( t +! t) % ( t) & ' & ' v ( t) = lim = lim ( ) ( ) (438)! t" 0! t! t" 0! t This epression reduces to # 1 $ v( t) = lim % bt + b! t &! t" 0' ( (439) The first term is independent of the interval! t and the second term vanishes because the limit as! t " 0 of! t is zero Thus the instantaneous velocity at time t is v ( ) t = bt (4310) In Figure 45 we graph the instantaneous velocity, v( t ), as a function of time t Figure 45 A graph of instantaneous velocity as a function of time 44 Acceleration We shall apply the same physical and mathematical procedure for defining acceleration, the rate of change of velocity We first consider how the instantaneous velocity changes over an interval of time and then take the limit as the time interval approaches zero 441 Average Acceleration Acceleration is the quantity that measures a change in velocity over a particular time interval Suppose during a time interval! t a body undergoes a change in velocity 4-6

7 !!!! v = v( t +! t) " v( t) (441) The change in the -component of the velocity,! v, for the time interval [ t, t +! t] is then! v = v ( t +! t) " v ( t) (44) The -component of the average acceleration for the time interval to be! t is defined! ˆ! v ˆ ( v( t +! t) " v( t)) ˆ! v a = a ˆ i # i = i = i (443)! t! t! t! The SI units for average acceleration are meters per second squared, [m" s ] 44 Instantaneous Acceleration On a graph of the -component of velocity vs time, the average acceleration for a time interval! t is the slope of the straight line connecting the two points ( t, v ( t )) and ( t +! t, v( t +! t)) In order to define the -component of the instantaneous acceleration at time t, we employ the same limiting argument as we did when we defined the instantaneous velocity in terms of the slope of the tangent line The -component of the instantaneous acceleration at time t is the limit of the slope of the tangent line at time t of the graph of the -component of the velocity as a function of time, ( v ( t +! t) # v ( t))! v dv a( t) $ lim a = lim = lim $! t! t dt! t" 0! t" 0! t" 0 (444) The instantaneous acceleration vector is then! a( t) = a ( t) ˆi (445) In Figure 46 we illustrate this geometrical construction Because the velocity is the derivative of position with respect to time, the -component of the acceleration is the second derivative of the position function, a = dv = d (446) dt dt 4-7

8 Figure 46 Graph of velocity vs time showing the tangent line at time t Eample 4 Determining Acceleration from Velocity Let s continue Eample 41, in which the position function for the body is given by = 0 + (1/ ) bt, and the -component of the velocity is v = bt The -component of the instantaneous acceleration at time t is the limit of the slope of the tangent line at time t of the graph of the -component of the velocity as a function of time (Figure 45) a dv v ( t +! t) # v ( t) bt + b! t # bt = = lim = lim = b (447) dt! t" 0! t! t" 0! t Note that in Equation (447), the ratio! v /! t is independent of! t, consistent with the constant slope of the graph in Figure Constant Acceleration Let s consider a body undergoing constant acceleration for a time interval! t = [0, t] When the acceleration a is a constant, the average acceleration is equal to the instantaneous acceleration Denote the -component of the velocity at time t = 0 by v,0! v( t = 0) Therefore the -component of the acceleration is given by a " v v( t)! v = a = = " t t Thus the velocity as a function of time is given by,0,0 (451) v ( t) = v + a t (45) When the acceleration is constant, the velocity is a linear function of time 4-8

9 451 Velocity: Area Under the Acceleration vs Time Graph In Figure 47, the -component of the acceleration is graphed as a function of time Figure 47 Graph of the -component of the acceleration for a constant as a function of time The area under the acceleration vs time graph, for the time interval! t = t " 0 = t, is Using the definition of average acceleration given above, Area( a, t)! a t (453),0 Area( a, t)! a t = " v = v ( t) # v (454) 45 Displacement: Area Under the Velocity vs Time Graph In Figure 48, we graph the -component of the velocity vs time curve Figure 48 Graph of velocity as a function of time for a constant The region under the velocity vs time curve is a trapezoid, formed from a rectangle and a triangle and the area of the trapezoid is given by Area(v,t) = v,0 t + 1 (v (t)! v )t (455),0 Substituting for the velocity (Equation (45)) yields 4-9

10 1 1 Area( v, t) v t ( v a t v ) t v t a t =,0 +,0 +!,0 =,0 + (456) Figure 49 The average velocity over a time interval We can then determine the average velocity by adding the initial and final velocities and dividing by a factor of two (Figure 49) 1 v = ( v ( t ) + v,0 ) (457) The above method for determining the average velocity differs from the definition of average velocity in Equation (431) When the acceleration is constant over a time interval, the two methods will give identical results Substitute into Equation (457) the -component of the velocity, Equation (45), to yield v = 1 (v (t) + v,0 ) = 1 ((v,0 + a t) + v,0 ) = v,0 + 1 a t (458) Recall Equation (431); the average velocity is the displacement divided by the time interval (note we are now using the definition of average velocity that always holds, for non-constant as well as constant acceleration) The displacement is equal to! " t # = v t (459) ( ) 0 Substituting Equation (458) into Equation (459) shows that displacement is given by 1! " ( t) # 0 = v t = v,0 t + a t (4510) Now compare Equation (4510) to Equation (456) to conclude that the displacement is equal to the area under the graph of the -component of the velocity vs time, 4-10

11 1! " ( t) # 0 = v,0 t + a t = Area( v, t), (4511) and so we can solve Equation (4511) for the position as a function of time, 1 ( t) v t a t = 0 +,0 + (451) Figure 410 shows a graph of this equation Notice that at t = 0 the slope may be in general non-zero, corresponding to the initial velocity component v,0 Figure 410 Graph of position vs time for constant acceleration Eample 43 Accelerating Car A car, starting at rest at t = 0, accelerates in a straight line for 100 m with an unknown constant acceleration It reaches a speed of 0 m! s "1 and then continues at this speed for another 10 s (a) Write down the equations for position and velocity of the car as a function of time (b) How long was the car accelerating? (c) What was the magnitude of the acceleration? (d) Plot speed vs time, acceleration vs time, and position vs time for the entire motion (e) What was the average velocity for the entire trip? Solutions: (a) For the acceleration a, the position (t) and velocity v(t) as a function of time t for a car starting from rest are (t) = (1/ )at v (t) = at (4513) b) Denote the time interval during which the car accelerated by t 1 We know that the position (t 1 ) = 100m and v(t 1 ) = 0 m!s "1 Note that we can eliminate the acceleration a between the Equations (4513) to obtain (t) = (1/ )v(t) t (4514) 4-11

12 We can solve this equation for time as a function of the distance and the final speed giving t = (t) v(t) (4515) We can now substitute our known values for the position (t 1 ) = 100m and v(t 1 ) = 0 m! s "1 and solve for the time interval that the car has accelerated t 1 = (t ) 1 v(t 1 ) = 100 m = 10s (4516) "1 0 m! s c) We can substitute into either of the epressions in Equation (4513); the second is slightly easier to use, a = v(t ) 1 0 m!s"1 = = 0m! s " (4517) t 1 10s d) The -component of acceleration vs time, -component of the velocity vs time, and the position vs time are piece-wise functions given by " a (t) = m!s- ; 0 < t < 10 s #, $% 0; 10 s < t < 0 s " $ v (t) = ( m!s- )t; 0 < t < 10 s #, %$ 0 m!s -1 ; 10 s < t < 0 s #% (t) = (1/ )( m!s- )t ; 0 < t < 10 s $ &% 100 m +(0 m!s - )(t "10 s); 10 s < t < 0 s The graphs of the -component of acceleration vs time, -component of the velocity vs time, and the position vs time are shown in Figure 411 (e) After accelerating, the car travels for an additional ten seconds at constant speed and during this interval the car travels an additional distance! = v(t 1 ) " 10s=00m (note that this is twice the distance traveled during the 10s of acceleration), so the total distance traveled is 300m and the total time is 0s, for an average velocity of v ave = 300m 0s =15m!s"1 (4518) 4-1

13 Figure 411 Graphs of the -components of acceleration, velocity and position as piecewise functions of time 4-13

14 Eample 44 Catching a Bus At the instant a traffic light turns green, a car starts from rest with a given constant acceleration, 50! 10 "1 m #s - Just as the light turns green, a bus, traveling with a given constant speed, 16! 10 1 m "s -1, passes the car The car speeds up and passes the bus some time later How far down the road has the car traveled, when the car passes the bus? Solution: In this eample we will illustrate the Polya approach to problem solving 1 Understand get a conceptual grasp of the problem Think about the problem How many objects are involved in this problem? Two, the bus and the car How many different stages of motion are there for each object? Each object has one stage of motion For each object, how many independent directions are needed to describe the motion of that object? We need only one independent direction for each object What information can you infer from the problem? The acceleration of the car, the velocity of the bus, and that the position of the car and the bus are identical when the bus just passes the car Sketch qualitatively the position of the car and bus as a function of time (Figure 41) Figure 41 Position vs time of the car and bus What choice of coordinate system best suits the problem? Cartesian coordinates with a choice of coordinate system in which the car and bus begin at the origin and travel along the positive -ais (Figure 413) Draw arrows for the position coordinate function for the car and bus Figure 413 A coordinate system for car and bus 4-14

15 Devise a Plan - set up a procedure to obtain the desired solution Write down the complete set of equations for the position and velocity functions There are two objects, the car and the bus Choose a coordinate system with the origin at the traffic light with the car and bus traveling in the positive -direction Call the position function of the car, 1 (t), and the position function for the bus, (t) In general the position and velocity functions of the car are given by 1 (t) = 1,0 + v 10 t + 1 a,1 t, v,1 (t) = v 10 + a,1 t In this eample, using both the information from the problem and our choice of coordinate system, the initial position and initial velocity of the car are both zero, 1,0 = 0 and v 10 = 0, and the acceleration of the car is non-zero a,1! 0 So the position and velocity of the car is given by 1 (t) = 1 a,1 t, v,1 (t) = a,1 t The initial position of the bus is zero,,0 = 0, the initial velocity of the bus is non-zero, ) = v,0 t v! 0, and the acceleration of the bus is zero, a a = 0 So the position,0, function for the bus is (t) = v,0 t The velocity is constant, v, (t) = v,0 Identify any specified quantities The problem states: The car speeds up and passes the bus some time later What analytic condition best epresses this condition? Let t = t a correspond to the time that the car passes the bus Then at that time, the position functions of the bus and car are equal, 1 ) = ) How many quantities need to be specified in order to find a solution? There are three independent equations at time t = t a : the equations for position and velocity of the car 1 ) = 1 a t, v,1 a,1 ) = a,1 t a, and the equation for the position of the bus, (t) = v,0 t There is one constraint condition 1 ) = ) The si quantities that are as yet unspecified are 1 ), ), v,1 ), v,0, a, t a So you need to be given at least two numerical values in order to completely specify all the quantities; for eample the distance where the car and bus meet The problem specifying the initial velocity of the bus, v,0, and the acceleration, a, of the car with given values 4-15

16 3 Carry our your plan solve the problem! The number of independent equations is equal to the number of unknowns so you can design a strategy for solving the system of equations for the distance the car has traveled in terms of the velocity of the bus v,0 and the acceleration of the car a,1, when the car passes the bus Let s use the constraint condition to solve for the time t = t a where the car and bus meet Then we can use either of the position functions to find out where this occurs Thus the constraint condition, 1 ) = ) becomes (1/ )a,1 t a = v,0 t a We can solve for this time, t a = v,0 / a,1 Therefore the position of the car at the meeting point is 1 ) = 1 a t = 1,1 a a! v $,0,1 # & = v,0 " % a,1 4 Look Back check your solution and method of solution Check your algebra Do your units agree? The units look good since in the answer the two sides agree in units,!" m# $ =! " m %s - / m%s - # $ and the algebra checks Substitute in numbers Suppose a = 50! 10 "1 m #s - and v,0 = 16! 10 1 m " s -1, Introduce your numerical values for v,0 and a, and solve numerically for the distance the car has traveled when the bus just passes the car Then a,1 t a = v,0 ( 16! 10 1 m "s ) -1 = a,1 50! 10 #1 m "s - 1 ) = v,0 = a,1 ( ) = 64! 101 s, ( ) ( 50! 10 #1 m " s ) = 10! m ( ) 16! 101 m "s -1 Check your results Once you have an answer, think about whether it agrees with your estimate of what it should be Some very careless errors can be caught at this point Is it possible that when the car just passes the bus, the car and bus have the same velocity? Then there would be an additional constraint condition at time t = t a, that the velocities are equal, v,1 ) = v,0 Thus v,1 ) = a,1 t a = v,0 implies that t a = v,0 / a,1 From our other result for the time of intersection t a = v,0 / a,1 But these two results contradict each other, so it is not possible 4-16

17 46 One Dimensional Kinematics Non-Constant Acceleration 461 Change of Velocity as the Integral of Non-constant Acceleration When the acceleration is a non-constant function, we would like to know how the - component of the velocity changes for a time interval!t = [0, t] Since the acceleration is non-constant we cannot simply multiply the acceleration by the time interval We shall calculate the change in the -component of the velocity for a small time interval!t i " [t i, t i+1 ] and sum over these results We then take the limit as the time intervals become very small and the summation becomes an integral of the -component of the acceleration For a time interval!t = [0, t], we divide the interval up into N small intervals!t i " [t i, t i+1 ], where the inde i = 1,,, N, and t 1! 0, t N! t Over the interval!t i, we can approimate the acceleration as a constant, a (t i ) Then the change in the - component of the velocity is the area under the acceleration vs time curve,!v,i " v (t i+1 ) # v (t i ) = a (t i )!t i + E i, (461) where E i is the error term (see Figure 414a) Then the sum of the changes in the - component of the velocity is!v,i " = (v (t ) # v (t 1 = 0)) + (v (t 3 ) # v (t )) +! + (v (t N = t) # v (t N #1 )) (46) In this summation pairs of terms of the form ( v (t )! v (t )) = 0 sum to zero, and the overall sum becomes Substituting Equation (461) into Equation (463), v (t)! v (0) = # "v,i (463) v (t)! v (0) = # "v,i = # a (t i ) "t i + # E i (464) We now approimate the area under the graph in Figure 414a by summing up all the rectangular area terms, Area N (a,t) = " a (t i )!t i (465) 4-17

18 Figures 414a and 414b Approimating the area under the graph of the -component of the acceleration vs time Suppose we make a finer subdivision of the time interval!t = [0, t] by increasing N, as shown in Figure 414b The error in the approimation of the area decreases We now take the limit as N approaches infinity and the size of each interval! t approaches zero For each value of N, the summation in Equation (465) gives a value for Area N (a,t), and we generate a sequence of values {Area 1 (a,t), Area (a,t),, Area N (a,t)} (466) i The limit of this sequence is the area, Area(a,t), under the graph of the -component of the acceleration vs time When taking the limit, the error term vanishes in Equation (464), lim # E i = 0 (467) N!" Therefore in the limit as N approaches infinity, Equation (464) becomes v (t)! v (0) = lim % a (t i ) $t i + lim % E i = lim % a (t i ) $t i = Area(a,t), (468) N "# N "# N "# and thus the change in the -component of the velocity is equal to the area under the graph of -component of the acceleration vs time The integral of the -component of the acceleration for the interval [0, t] is defined to be the limit of the sequence of areas, Area N (a,t), and is denoted by 4-18

19 t! =t " a ( t! ) d t! # lim & a (t i ) $t i = Area(a,t) (469) t! =0 $t i %0 Equation (468) shows that the change in the component of the velocity is the integral of the -component of the acceleration with respect to time t " =t v (t)! v (0) = # a ( t ") d t " (4610) Using integration techniques, we can in principle find the epressions for the velocity as a function of time for any acceleration 46 Integral of Velocity We can repeat the same argument for approimating the area Area(v, t) under the graph of the -component of the velocity vs time by subdividing the time interval into N intervals and approimating the area by t " =0 Area N (a, t) = " v (t i )!t i (4611) The displacement for a time interval!t = [0, t] is limit of the sequence of sums Area N (a, t), This approimation is shown in Figure 415! = (t) " (0) = lim % v (t i )!t i (461) N #$ The integral of the -component of the velocity for the interval [0, t] is the limit of the sequence of areas, Area N (a, t), and is denoted by t! =t " v ( t! ) d t! # lim & v (t i ) $t i = Area(v,t) (4613) t! =0 $t i %0 4-19

20 Figure 415 Approimating the area under the graph of the -component of the velocity vs time The displacement is then the integral of the -component of the velocity with respect to time,! = (t) " (0) = $ v ( t #) d t # (4614) Using integration techniques, we can in principle find the epressions for the position as a function of time for any acceleration Eample 45 Non-constant Acceleration Let s consider a case in which the acceleration, a (t), is not constant in time, t # =t t # =0 a (t) = b 0 + b 1 t + b t (4615) The graph of the -component of the acceleration vs time is shown in Figure 416 Figure 416 Non-constant acceleration vs time graph 4-0

21 Let s find the change in the -component of the velocity as a function of time Denote the initial velocity at t = 0 by v,0! v (t = 0) Then, t " =t v (t)! v,0 = # a ( t ") d t " = # (b o + b 1 t " + b t " ) d t" = b 0 t + b t 1 t " =0 t " =t t " =0 The -component of the velocity as a function in time is then v (t) = v,0 + b 0 t + b 1 t + b t3 3 (4616) + b t3 3 (4617) Denote the initial position by 0! (t = 0) The displacement as a function of time is the integral t " =t (t)! 0 = # v ( t ") d t " (4618) Use Equation (4617) for the -component of the velocity in Equation (4618) to find t " =0 t " =t # (t)! 0 = v,0 + b 0 t " + b t" 1 + b t" 3 & ) % ( $ 3 ' d t" = v,0 t + b t 0 + b 1 t3 6 + b t 4 1 (4619) t " =0 Finally the position is then (t) = 0 + v,0 t + b 0 t + b 1 t3 6 + b t 4 1 (460) Eample 46 Bicycle and Car A car is driving through a green light at t = 0 located at = 0 with an initial speed v c,0 = 1 m!s -1 The acceleration of the car as a function of time is given by #% a c = 0; 0 < t < t = 1 s 1 $ &%!(6 m "s -3 )(t! t 1 ); 1 s < t < t (a) Find the speed and position of the car as a function of time (b) A bicycle rider is riding at a constant speed of v b,0 and at t = 0 is 17 m behind the car The bicyclist reaches the car when the car just comes to rest Find the speed of the bicycle 4-1

22 Solution: a) We need to integrate the acceleration for both intervals The first interval is easy, the speed is constant For the second integral we need to be careful about the endpoints of the integral and the fact that the integral is the change in speed so we must subtract v c (t 1 ) = v c0 $ v c0 ; 0 < t < t 1 = 1s & t v c (t) = % & v c (t 1 ) + #!(6 m "s -3 )(t! t 1 ); 1s < t < t ' t 1 After integrating we get # v c0 ; 0 < t < t 1 = 1 s % v c (t) = $ v c0! (3 m " s -3 )(t! t 1 ) t ; 1 s < t < t & % t 1 Now substitute the endpoint so the integral to finally yield #% v c (t) = v = 1 m! c0 s-1 ; 0 < t < t 1 = 1s $ &% 1 m!s -1 " (3 m! s -3 )(t " t 1 ) ; 1s < t < t For this one-dimensional motion the change in position is the integral of the speed so Upon integration we have t $ 1 & c (0) + " (1 m! s -1 )dt; 0 < t < t 1 = 1s & 0 c (t) = % t & c (t 1 ) + " ( 1 m! s -1 # (3m! s -3 )(t # t 1 ) ) dt; 1s < t < t & ' t 1 # c (0) + (1 m! s -1 )t; 0 < t < t 1 = 1 s % c (t) = $ % c (t 1 ) + (1 m! s -1 )(t " t 1 ) " (1 m! s -3 )(t " t 1 ) 3 & t ( ) t1 ; 1s < t < t We choose our coordinate system such that c (0) = 0, therefore c (t 1 ) = (1 m! s -1 )(1s)=1 m So after substituting in the endpoints of the integration interval we have that #% c (t) = (1 m!s-1 )t; 0 < t < t 1 = 1s $ &% 1 m+(1 m!s -1 )(t " t 1 ) " (1 m!s -3 )(t " t 1 ) 3 ; 1s < t < t 4-

23 (b) We are looking for the instant that t the car has come to rest So we use our epression for the speed for the interval 1s < t < t, 0 = v c (t ) = 1 m!s -1 " (3 m! s -3 )(t " t 1 ) We can solve this for t : (t! t 1 ) = 4 s We have two solutions: (t! t 1 ) = s or (t! t 1 ) =! s The second solution t = t 1! s = 1 s! s =! 1 s does not apply to our time interval and so t = t 1 + s = 1 s + s = 3 s During the position of the car at t is then given by c (t ) = 1 m+(1 m!s -1 )(t " t 1 ) " (1m!s -3 )(t " t 1 ) 3 = 1 m+(1 m!s -1 )( s) " (1m!s -3 )( s) 3 = 8 m Because the bicycle is traveling at a constant speed with an initial position b0 =!17 m, the position of the bicycle is given by b (t) =!17 m + v b t The bicycle and car intersect at instant t = 3 s : b (t ) = c (t ) Therefore!17 m + v b (3 s) = 8 m So the speed of the bicycle is (8 m + 17 m) v b = = 15 m! s -1 (3 s) 4-3