THE M SCALE IN POLISH SKALA SLIDE RULES
|
|
|
- Aubrie Perry
- 6 years ago
- Views:
Transcription
1 THE M SCALE IN POLISH SKALA SLIDE RULES Angel Crrso (Roger) Trnslted from Spnish y: Alvro González (Teruteru34) nd José Griel F dez -Rventós (e-lento).
2 To Mrtin, she s lmost here nd we re witing her imptiently. Mdrid, My 0
3 ACKNOWLEDGEMENTS I wnt to epress my sinere grtitude to my ollegues Álvro González nd José Griel Fernández, of the Spnish Assoition Amigos de ls Regls de Cálulo (ARC), for their detiled review of the mnusript, providing lots of suggestions nd omments, tht for sure hve enrihed the doument, nd for their kind trnsltion into English. Also I wnt to thnk Gonzlo Mrtín, for mking his wonderful olletion of Frenh rules ville to everyody. In prtiulr, I hve used the slide rules from Grphople rnd ville in his we to omplete the different models omprison. And, of ourse, I wish to thnk Jorge Fáregs, the true responsile for ll this, s he reted our Assoition, sed in his we
4 CONTENT.- INTRODUCTION 5.- SCALE DESCRIPTION SCALE FOUNDATIONS SCALE PLACEMENT IN THE SLIDE RULE SCALE OPERATION 6.- EXAMPLES 7.- SOLUTIONS WITH OTHER SLIDE RULES CONCLUSIONS BIBLIOGRAPHY 5
5 The M sle in SKALA Polish slide rules.- INTRODUCTION The solution for right tringle hs mny prtil uses in ny tehnil sope, s the trnsformtion of rtesin into polr oordintes or omple numers representtion in their polr form, defining its modulus nd rgument from the rel nd imginry prts respetively. The smll sle mrked with n M letter, ppering in models ELEKTRO SLE nd SLPP from polish Brnd SKALA, llow esy nd fst solutions to right tringles. It dditionlly gives etter ury thn the one otined with trditionl trigonometri sles usge. SKALA ELEKTRO SLE SKALA SLPP In this rtile it is desried the sle M in detiled form, it s eplined its usge nd desried the right tringle solution proedures with other types of slide rules through stndrd trigonometri sles, pplying sines theorem. In the neessrily redued spes of slide rules mnuls is not possile to eplin in detil the theoretil foundtions tht llow the solution of the different mthemtil opertions, giving only in its ple series of reipes. 5
6 The M sle in SKALA Polish slide rules We intend to eplin those foundtions in the elief tht it s esier to rememer the movements nd redings sequenes needed on the slide rules sles when the orresponding theoretil se is lredy known..- SCALE DESCRIPTION The smll sle M sits on the slide, etween the sles C nd CI, nd its length is of out m. The vlues of the M sle spn from 0 to nd inrese from right to left. The vlue 0 of M sle is just over the 5 of C sle, nd the vlue of M is over the 4,4 of C. 3.- SCALE FOUNDATIONS In right tringle where its legs re nd, the vlue of the hypotenuse is esily otined through the diret pplition of the well known Pythgors theorem, s: Tht sme reltionship n e epressed in the following form: Being: M 6
7 The M sle in SKALA Polish slide rules 7 Where: M And In this quotient, s is the smller of oth legs, it is nmely lwys true: The proof tht oth epressions re relly equivlent is very simple, it s enough to ehnge the vlue of in M nd lter the M vlue in. Following the proedure would e: M And Operting: Sustituting this vlue of Δ, in the first eqution eomes: Nmely And finly
8 The M sle in SKALA Polish slide rules Whih demonstrtes the equlity of the two equtions proposed. By pplying this proedure nd using the M sle, the vlue of Δ is otined diretly nd, y simple ddition, the hypotenuse of the tringle. 4.- SCALE PLACEMENT IN THE SLIDE RULE A reltively interesting spet whih deserves some ttention is the position of the sle M in the rule. First, this is not onventionl full-length sle, ut develops from out 4.4 to 5 vlues of the C sle, hving, s lredy mentioned, length of m. As outlined elow, this position is onditioned y the minimum nd mimum vlues tht M n tke s funtion of the vlue of. The vlue of is the rtio etween the smllest nd lrgest leg or wht is the sme, the vlue of the tngent of the ngle etween the hypotenuse nd the higher leg, whih we will ll hereinfter, nd therefore n only tke vlues etween "0" nd "", sine the vlue of the ngle shll not eeed 45 degrees. The vlue = orresponds to the se where nd re equl, ie when the tringle, dditionlly to eing right is lso isoseles. In this se it s esy to see tht M vlue is: M 0.44 Wht is not so ovious is tht when the vlue of is infinitely smll, prtilly lmost zero, M = 0.5. To eplin this we need to dip into the infinitesiml lulus nd the theory of limits. Indeed, to lulte the vlue tken y M when is infinitely smll, it is neessry to lulte the limit of the funtion M, where hs vlue lose to zero, ie: lim 0 8
9 The M sle in SKALA Polish slide rules In relity this sitution would never e met nd would orrespond to the theoretil se in whih = 0. In this se it s ovious the tringle n t e onstruted, ut for very smll vlues of versus, we would otin vlues of very lose to zero. If =0 in the funtion M we otin wht in the theory of limits is known s type 0/0 indeterminy. Suh unertinties in the theory of limits, re solved y pplying the L'Hôpitl rule. This rule is nmed fter the 7th entury Frenh mthemtiin Guillume Frnçois Antoine, Mrquis de L'Hôpitl (66-704), who mde the rule known in his "Anlyse des infinement petits pour l'intelligene des lignes oures" in 69. The wording of the rule of L'Hopitl is essentilly s follows: If f() nd g() re two differentile funtions (ie, the derivtive funtion eists) in the neighorhood of point p in whih: f (p) = g (p) = 0 And dditionlly it is true tht the derivtive funtion g() t point p is not null, ie g (p) 0 9
10 The M sle in SKALA Polish slide rules Then, if it eists It lso eists f '( ) lim p g'( ) lim p f ( ) g ( ) And they re the sme, ie f '( ) lim p g'( ) = lim p f ( ) g ( ) Applying the L Hôpitl rule to funtion M, hving in this se p=0, it is: f ( ) g ( ) Their derivtive funtions re: f '( ) g' ( ) Then, dividing oth numertor nd denomintor y, finlly it omes to: f '( ) lim g'( ) In summry, the etreme vlues of the funtion M re: 0,44 for = nd 0.5 for = 0, nd this eplins the position of this sle in the rule, diretly onfronted with the vlues etween 4.4 nd 5.00, respetively, of the C sle. The et length of the sle M, for rule with sles of 50 mm is: L M = (log 5.00 log 4.4)*50 = 0.49 mm 0
11 The M sle in SKALA Polish slide rules 5.- SCALE OPERATION This setion desries in detil the proedure to e followed for the resolution of right tringle y using the sle M. In the first ple nd using sles C nd D, lulte the vlue of = tn( ), tking into ount tht orresponds to the smllest of the legs. This is done esily y pling the vlue of, on the C sle over the vlue of, on the sle D. Under the of the C sle, you n red the vlue of tn( ). The orresponding ngle α is otined diretly on the T sle, ering in mind tht these rules hve ngulr sles in minutes rther thn tenths of degrees. C D T tn If to otin the vlue of, the sle M is pled outside the rnge of the D sle, with the help of the ursor the slide should e moved ehnging the left of the C sle for the 0 to the right of the sme sle, s in ny other lultions with the rule. From here the proedure is the sme. Using the ursor nd without moving the slide, move to the vlue otined for on the sle M. On the D sle will then red the result of the produt M M Note tht in relity the funtion vlue of M is red on the C sle nd not on the M sle itself. C M tg M D M.
12 The M sle in SKALA Polish slide rules To finlly otin the vlue of, is still needed to multiply the ove result gin y. It is more onvenient to use the sle CI, ie to divide y the inverse of. To do this, without moving the ursor, move the slide to red under its min line the vlue of on the reiprol sle CI. The vlue of my e red diretly on the D sle, under the of C sle. D CI C Now we just dd to this vlue the one of, to otin the hypotenuse. When the vlue of is very smll nd therefore diffiult to ple on the M sle with some preision (sine in this re the divisions of the sle re very lose together), it n e more effiient to pproimte the vlue of Δ with the epression: Sine, s mentioned ove, the vlue of the M funtion is lose to / where is lose to zero. Furthermore, this ltter term is used, in ny se, to determine the deiml position on the vlue of, following the known rules of the estimtive lultions, s seen in the following emples. 6.- EXAMPLES Emple. To solve the tringle whose legs re: = 7,35 nd = 8,65 Solution: In the first ple we lulte the vlue of = tn α:
13 The M sle in SKALA Polish slide rules On T sle we n red the vlue of ngle α, eing in this se: α = 40º Trnsferring the result of, on the sle M, we n red on the C sle, the vlue of M, in this se: M = 0,43 On the D sle we n e red, ut only hs edutionl interest, the intermedite produt: M M 3
14 The M sle in SKALA Polish slide rules But to finlly get the vlue of, we still need to multiply the ove result gin y. It is esier, however, to divide y the inverse of, for whih, without moving the ursor, vlue is mthed, on the CI sle, with the min line of the ursor. Under the of the C sle, the vlue of Δ n e red on D sle. In this se: Δ =,7 The deiml position hs een otined y the following proimtion lultion: 7 0,8,8 As seen, it is not neessry to red the intermedite results of opertions for otining the vlues of M or M. To get the vlue of the hypotenuse it is only needed to dd the vlue of Δ to the longest leg, tht is: = Δ + =,70 + 8,65 =,35 (et vlue: =.35) 4
15 The M sle in SKALA Polish slide rules Emple. To solve the tringle whose legs re: = 7,0 y =,85 Solution: As in the previous se, we lulte the vlue of = tn α: On T sle we n red the vlue of ngle α, in this se: α = 9º 5 In this se the sle M is outside the rnge of C sle nd therefore it is neessry to trnspose the slide. To do this, without moving the ursor (whih is lredy pled on the of C sle), the slide is fully moved to mth the 0 of this sle with the min line of the ursor. 5
16 The M sle in SKALA Polish slide rules From here the proedure is etly the sme s in the previous emple, otining the following results: M = 0,466 Δ =,88 Where the deiml position hs een otined y following pproimte lultion: 7 0,5,75 And finlly: = Δ + =,88 +,85 = 4,73 (et vlue = 4.73) Emple 3. To solve the tringle whose legs re: =,86 y = 9,0 6
17 The M sle in SKALA Polish slide rules Solution: Now the vlue of = tn α is: On the T sle we n red the vlue of ngle α: α = 8º 8 Here, where the vlue of is very smll, it is diffiult to urtely ple it on the sle M. Then it is esier nd suffiiently pproimtion to lulte:,86 0,49 0,3 In this se the deimls ome diretly from this lst lultion, nd it is not neessry ny pproimte estimtion to find the deiml point position. And finlly: = Δ + = 0,3 + 9,0 = 9,43 (et vlue = 9.4) 7
18 The M sle in SKALA Polish slide rules 7.- SOLUTIONS WITH OTHER RULES The resolution of tringle with slide rule n e rried out esily y pplying rtios of sines theorem. sen sen sen Where, nd re the sides of the tringle nd, side respetively. nd re the ngles opposite eh For right tringle, with the legs nd, nd the hypotenuse, then: And so: = 90º sin = In ddition nd ngles re omplementry, ie the two of them dd up to 90 º, nd thus: sin os = os = sin Given the ove, the lw of sines for right tringle, n lso e written s follows: sen os Multiplying ll terms y sin : tn sin Although the theory disussed ove is the sme, the prtil proedure, s disussed elow, depends on where the trigonometri sles S nd T re pled in the slide rule. The resolution of tringles, s eplined so fr, is not possile when the vlues of the sle S re red ginst the sle of squres A/B insted of on the sles C/D. In some ses it will e neessry to trnspose the slide, hnging with the help of the ursor, the left inde (the of C sle) for the right one (0 of the sme sle) or vievers. 8
19 The M sle in SKALA Polish slide rules S nd T sles on the ody of the rule This rrngement is quite ommon in Europen rules, ut rules from the Frenh rnd Grphople nd some Aristo models hve these sles loted on the slide. FABER-CASTELL 5/8 ARISTO 0968 STUDIO To mke use of proportions in this type of slide rule, it is more interesting to epress the ove equtions ording to the inverse of, nd, whih would finlly give: tg sen / / / The operting proedure with the slide rule is s follows: We ple the vlue of (rememer tht is the shorter leg) on the sle CI, ove the 0 on the sle D. Move the ursor to the vlue of on the CI sle. On D sle we red the vlue of tn α nd on the T sle we n red the vlue of the ngle α. T D CI tn 9
20 The M sle in SKALA Polish slide rules In some ses it is neessry to ompletely disple the slide to reple the 0 y the on D sle. Without moving the slide, move the ursor to red the sme ngle α on the S sle, llowing to red on the CI sle the vlue of the hypotenuse. S CI S nd T sles on the slide This rrngement is quite ommon in Amerin-mde rules nd in the Frenh rnd Grphople. PICKETT N-500-ES LOG LOG KEUFFEL & ESSER DECI-LON In this se it is more onvenient to rememer tht the sines lw for right tringle n e epressed lso in its inverse form s: sin os 0
21 The M sle in SKALA Polish slide rules From this, the only eqution with prtil vlue for the resolution with slide rule is: sin Furthermore, dividing this epression y os, it gives tn os And similrly, here only the first equlity is of interest: tg To solve the tringle y suh epressions we ple the 0 of the C sle over the vlue of ( is the vlue of the longer leg) on D sle. Over the vlue of in the D sle, it n e red the vlue of tn on the C sle, nd on T sle (whih is now on the slide) the vlue of the ngle. T C tg D Without moving the ursor, move the slide to ple the vlue of from S sle elow the enter line thereof. Then under the of the C sle, we n red the vlue of the hypotenuse in D sle. In some ses it is neessry to ompletely disple the slide to reple the 0 y the of C sle. S C D S nd T sles on the k of the slide This set of sles is ommon on simple rules, in whih the only sles on the k re the trigonometri sles rrnged in the slide.
22 The M sle in SKALA Polish slide rules ARISTO 99 RIETZ GRAPHOPLEX 60 In these ses it is more prtil to write the ove reltions s follows: And tn sin With the equtions presented in this wy, the opertion proedure with the rule would e s follows: We ple the vlue of the smller leg, from the C sle, over the vlue of the longer leg, from D sle. Then, over the of the D sle, we n red the vlue of tn D C tg In this position we n e red on the k of the rule, on the T sle of the slide, the vlue of ngle. T
23 The M sle in SKALA Polish slide rules We move the slide to red the vlue of on the S sle. S Keeping this position of the slide nd turning round the rule, on the front nd elow the vlue of from C sle, you n red the vlue of the hypotenuse, on the D sle. D C 3
24 The M sle in SKALA Polish slide rules 8.- CONCLUSIONS In order to stlish riteri so tht to ompre the different sle lyouts, summry tle is inluded with the numer of movements of the ursor nd the slide needed to solve eh one of the emples shown. This tle is to evlute the effiieny of eh of the different sle lyouts presented. For ounting the movements, the folded sles hve not een onsidered, s these re not ville in ll slide rules. This type of sles, in some ses, mkes the hnge from left to right end of the sle unneessry, reduing the numer of movements. In those rules with sles in the k of the rule, models with reding windows t oth ends hve een used for the ounting of movements, so tht the reding is ville either t the right or the left. On the ontrry, some other hnge from left to right sle ends might e needed, dding to the totl numer of movements required. EXAMPLE = 7.35 =8.65 EXAMPLE = 7.0 =.85 EXAMPLE 3 =.86 = 9.0 MOVEMENTS CURSOR SLIDE TOTAL SKALA 4 6 S, T in the ody 4 6 S, T in the slide front 3 5 S, T in the slide k SKALA S, T in the ody 4 6 S, T in the slide front 3 5 S, T in the slide k 3 5 SKALA 3 5 S, T in the ody 4 6 S, T in the slide front 3 5 S, T in the slide k 3 5 As n e ppreited in the preeding tle, there re no ig differenes in the numer of movements from one sle lyout to the other. The slight differenes re due to the need to hnge of slide ends in some ses. This differene depends on the prolem initil dt rther thn on the speifi sle lyout. No sle lyout hs een found where the hnge of slide ends hd not een needed t some time. Regrding the preision of the result, s in ll slide rules, it is silly dependnt on the length of the sles nd not on their lyout. The igger the length, the greter is the distne etween sle divisions nd thus the respetive redings re esier. 4
25 The M sle in SKALA Polish slide rules All models used hve 5 m length sles (eept for M sle, oviously), nd so this does not ring ny differene in regrds to results preision. In reltion with the lultion of ngle, the proedure is the sme no mtter the sle lyout of the slide rule, tht is, first the vlue of tg is found nd, fterwrds, the vlue of the ngle is found y mens of T sle. Therefore, the preision in the lultion of rules nd is not dependnt on the sle lyout. ngle is etly the sme in ll slide The sustntil differene ppers in the lultion of the hypotenuse. In the rules without M sle, independently from the sle lyout, the net step is to trnsfer the vlue of to the S sle. The preision of the result depends on how this djustment is done. It is esy to see, in this type of slide rules, tht the preision inreses with the derese of the vlue of the ngle, s the divisions in the S sle re lrger for smll ngles. For vlues of over 5º (gin, it is onvenient to rememer tht is never greter thn 45º) it is not esy to position the vlue of the ngle in the S sle with enough preision. If the ngle hs deimls of degree, s it is usul, the diffiulty is gretly inresed. When the M sle is used, the vlue to use is not ut tg, to e pled on M sle. The preision hieved with the use of this sle is muh greter, espeilly for ig ngle vlues. For vlues of smller thn 0º the preision otined is similr oth with the trditionl trigonometri sles nd with the M sle. Also, s it hs een shown in emple numer 3, even in the ses of very low tg vlues, where it is somehow diffiult to preisely djust the M sle, the simplified method presented provides vlues very proimte to the et vlue. To sum up, the retngle tringle solving with SKALA slide rules where the M sle is inluded, the vlue otined for the ngle hs the sme preision s when otined with ny other rule, ut the differene in the preision for the lultion of the hypotenuse is igger s igger is the vlue of. 9.- BIBLIOGRAPHY.- Additionl M sle on polish SKALA SLE nd SKALA SLPP 0 inhes slide rules. Adm Entrnt Pplinski. Deemer The Slide Rule. A Complete Mnul. Alfred L. Slter. Los Angeles City College. Holt, Rinehrt nd Winston, In Aristo, Fer-Cstell nd Grphople user mnuls. 5
AP Calculus BC Chapter 8: Integration Techniques, L Hopital s Rule and Improper Integrals
 AP Clulus BC Chpter 8: Integrtion Tehniques, L Hopitl s Rule nd Improper Integrls 8. Bsi Integrtion Rules In this setion we will review vrious integrtion strtegies. Strtegies: I. Seprte the integrnd into
AP Clulus BC Chpter 8: Integrtion Tehniques, L Hopitl s Rule nd Improper Integrls 8. Bsi Integrtion Rules In this setion we will review vrious integrtion strtegies. Strtegies: I. Seprte the integrnd into
Maintaining Mathematical Proficiency
 Nme Dte hpter 9 Mintining Mthemtil Profiieny Simplify the epression. 1. 500. 189 3. 5 4. 4 3 5. 11 5 6. 8 Solve the proportion. 9 3 14 7. = 8. = 9. 1 7 5 4 = 4 10. 0 6 = 11. 7 4 10 = 1. 5 9 15 3 = 5 +
Nme Dte hpter 9 Mintining Mthemtil Profiieny Simplify the epression. 1. 500. 189 3. 5 4. 4 3 5. 11 5 6. 8 Solve the proportion. 9 3 14 7. = 8. = 9. 1 7 5 4 = 4 10. 0 6 = 11. 7 4 10 = 1. 5 9 15 3 = 5 +
1 PYTHAGORAS THEOREM 1. Given a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
 1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
Comparing the Pre-image and Image of a Dilation
 hpter Summry Key Terms Postultes nd Theorems similr tringles (.1) inluded ngle (.2) inluded side (.2) geometri men (.) indiret mesurement (.6) ngle-ngle Similrity Theorem (.2) Side-Side-Side Similrity
hpter Summry Key Terms Postultes nd Theorems similr tringles (.1) inluded ngle (.2) inluded side (.2) geometri men (.) indiret mesurement (.6) ngle-ngle Similrity Theorem (.2) Side-Side-Side Similrity
SECTION A STUDENT MATERIAL. Part 1. What and Why.?
 SECTION A STUDENT MATERIAL Prt Wht nd Wh.? Student Mteril Prt Prolem n > 0 n > 0 Is the onverse true? Prolem If n is even then n is even. If n is even then n is even. Wht nd Wh? Eploring Pure Mths Are
SECTION A STUDENT MATERIAL Prt Wht nd Wh.? Student Mteril Prt Prolem n > 0 n > 0 Is the onverse true? Prolem If n is even then n is even. If n is even then n is even. Wht nd Wh? Eploring Pure Mths Are
Trigonometry Revision Sheet Q5 of Paper 2
 Trigonometry Revision Sheet Q of Pper The Bsis - The Trigonometry setion is ll out tringles. We will normlly e given some of the sides or ngles of tringle nd we use formule nd rules to find the others.
Trigonometry Revision Sheet Q of Pper The Bsis - The Trigonometry setion is ll out tringles. We will normlly e given some of the sides or ngles of tringle nd we use formule nd rules to find the others.
Section 1.3 Triangles
 Se 1.3 Tringles 21 Setion 1.3 Tringles LELING TRINGLE The line segments tht form tringle re lled the sides of the tringle. Eh pir of sides forms n ngle, lled n interior ngle, nd eh tringle hs three interior
Se 1.3 Tringles 21 Setion 1.3 Tringles LELING TRINGLE The line segments tht form tringle re lled the sides of the tringle. Eh pir of sides forms n ngle, lled n interior ngle, nd eh tringle hs three interior
April 8, 2017 Math 9. Geometry. Solving vector problems. Problem. Prove that if vectors and satisfy, then.
 pril 8, 2017 Mth 9 Geometry Solving vetor prolems Prolem Prove tht if vetors nd stisfy, then Solution 1 onsider the vetor ddition prllelogrm shown in the Figure Sine its digonls hve equl length,, the prllelogrm
pril 8, 2017 Mth 9 Geometry Solving vetor prolems Prolem Prove tht if vetors nd stisfy, then Solution 1 onsider the vetor ddition prllelogrm shown in the Figure Sine its digonls hve equl length,, the prllelogrm
Activities. 4.1 Pythagoras' Theorem 4.2 Spirals 4.3 Clinometers 4.4 Radar 4.5 Posting Parcels 4.6 Interlocking Pipes 4.7 Sine Rule Notes and Solutions
 MEP: Demonstrtion Projet UNIT 4: Trigonometry UNIT 4 Trigonometry tivities tivities 4. Pythgors' Theorem 4.2 Spirls 4.3 linometers 4.4 Rdr 4.5 Posting Prels 4.6 Interloking Pipes 4.7 Sine Rule Notes nd
MEP: Demonstrtion Projet UNIT 4: Trigonometry UNIT 4 Trigonometry tivities tivities 4. Pythgors' Theorem 4.2 Spirls 4.3 linometers 4.4 Rdr 4.5 Posting Prels 4.6 Interloking Pipes 4.7 Sine Rule Notes nd
Lesson 2: The Pythagorean Theorem and Similar Triangles. A Brief Review of the Pythagorean Theorem.
 27 Lesson 2: The Pythgoren Theorem nd Similr Tringles A Brief Review of the Pythgoren Theorem. Rell tht n ngle whih mesures 90º is lled right ngle. If one of the ngles of tringle is right ngle, then we
27 Lesson 2: The Pythgoren Theorem nd Similr Tringles A Brief Review of the Pythgoren Theorem. Rell tht n ngle whih mesures 90º is lled right ngle. If one of the ngles of tringle is right ngle, then we
Project 6: Minigoals Towards Simplifying and Rewriting Expressions
 MAT 51 Wldis Projet 6: Minigols Towrds Simplifying nd Rewriting Expressions The distriutive property nd like terms You hve proly lerned in previous lsses out dding like terms ut one prolem with the wy
MAT 51 Wldis Projet 6: Minigols Towrds Simplifying nd Rewriting Expressions The distriutive property nd like terms You hve proly lerned in previous lsses out dding like terms ut one prolem with the wy
Numbers and indices. 1.1 Fractions. GCSE C Example 1. Handy hint. Key point
 GCSE C Emple 7 Work out 9 Give your nswer in its simplest form Numers n inies Reiprote mens invert or turn upsie own The reiprol of is 9 9 Mke sure you only invert the frtion you re iviing y 7 You multiply
GCSE C Emple 7 Work out 9 Give your nswer in its simplest form Numers n inies Reiprote mens invert or turn upsie own The reiprol of is 9 9 Mke sure you only invert the frtion you re iviing y 7 You multiply
THE PYTHAGOREAN THEOREM
 THE PYTHAGOREAN THEOREM The Pythgoren Theorem is one of the most well-known nd widely used theorems in mthemtis. We will first look t n informl investigtion of the Pythgoren Theorem, nd then pply this
THE PYTHAGOREAN THEOREM The Pythgoren Theorem is one of the most well-known nd widely used theorems in mthemtis. We will first look t n informl investigtion of the Pythgoren Theorem, nd then pply this
PYTHAGORAS THEOREM WHAT S IN CHAPTER 1? IN THIS CHAPTER YOU WILL:
 PYTHAGORAS THEOREM 1 WHAT S IN CHAPTER 1? 1 01 Squres, squre roots nd surds 1 02 Pythgors theorem 1 03 Finding the hypotenuse 1 04 Finding shorter side 1 05 Mixed prolems 1 06 Testing for right-ngled tringles
PYTHAGORAS THEOREM 1 WHAT S IN CHAPTER 1? 1 01 Squres, squre roots nd surds 1 02 Pythgors theorem 1 03 Finding the hypotenuse 1 04 Finding shorter side 1 05 Mixed prolems 1 06 Testing for right-ngled tringles
12.4 Similarity in Right Triangles
 Nme lss Dte 12.4 Similrit in Right Tringles Essentil Question: How does the ltitude to the hpotenuse of right tringle help ou use similr right tringles to solve prolems? Eplore Identifing Similrit in Right
Nme lss Dte 12.4 Similrit in Right Tringles Essentil Question: How does the ltitude to the hpotenuse of right tringle help ou use similr right tringles to solve prolems? Eplore Identifing Similrit in Right
GM1 Consolidation Worksheet
 Cmridge Essentils Mthemtis Core 8 GM1 Consolidtion Worksheet GM1 Consolidtion Worksheet 1 Clulte the size of eh ngle mrked y letter. Give resons for your nswers. or exmple, ngles on stright line dd up
Cmridge Essentils Mthemtis Core 8 GM1 Consolidtion Worksheet GM1 Consolidtion Worksheet 1 Clulte the size of eh ngle mrked y letter. Give resons for your nswers. or exmple, ngles on stright line dd up
Lecture 6: Coding theory
 Leture 6: Coing theory Biology 429 Crl Bergstrom Ferury 4, 2008 Soures: This leture loosely follows Cover n Thoms Chpter 5 n Yeung Chpter 3. As usul, some of the text n equtions re tken iretly from those
Leture 6: Coing theory Biology 429 Crl Bergstrom Ferury 4, 2008 Soures: This leture loosely follows Cover n Thoms Chpter 5 n Yeung Chpter 3. As usul, some of the text n equtions re tken iretly from those
Introduction to Olympiad Inequalities
 Introdution to Olympid Inequlities Edutionl Studies Progrm HSSP Msshusetts Institute of Tehnology Snj Simonovikj Spring 207 Contents Wrm up nd Am-Gm inequlity 2. Elementry inequlities......................
Introdution to Olympid Inequlities Edutionl Studies Progrm HSSP Msshusetts Institute of Tehnology Snj Simonovikj Spring 207 Contents Wrm up nd Am-Gm inequlity 2. Elementry inequlities......................
Math 32B Discussion Session Week 8 Notes February 28 and March 2, f(b) f(a) = f (t)dt (1)
 Green s Theorem Mth 3B isussion Session Week 8 Notes Februry 8 nd Mrh, 7 Very shortly fter you lerned how to integrte single-vrible funtions, you lerned the Fundmentl Theorem of lulus the wy most integrtion
Green s Theorem Mth 3B isussion Session Week 8 Notes Februry 8 nd Mrh, 7 Very shortly fter you lerned how to integrte single-vrible funtions, you lerned the Fundmentl Theorem of lulus the wy most integrtion
6.5 Improper integrals
 Eerpt from "Clulus" 3 AoPS In. www.rtofprolemsolving.om 6.5. IMPROPER INTEGRALS 6.5 Improper integrls As we ve seen, we use the definite integrl R f to ompute the re of the region under the grph of y =
Eerpt from "Clulus" 3 AoPS In. www.rtofprolemsolving.om 6.5. IMPROPER INTEGRALS 6.5 Improper integrls As we ve seen, we use the definite integrl R f to ompute the re of the region under the grph of y =
Math Lesson 4-5 The Law of Cosines
 Mth-1060 Lesson 4-5 The Lw of osines Solve using Lw of Sines. 1 17 11 5 15 13 SS SSS Every pir of loops will hve unknowns. Every pir of loops will hve unknowns. We need nother eqution. h Drop nd ltitude
Mth-1060 Lesson 4-5 The Lw of osines Solve using Lw of Sines. 1 17 11 5 15 13 SS SSS Every pir of loops will hve unknowns. Every pir of loops will hve unknowns. We need nother eqution. h Drop nd ltitude
MCH T 111 Handout Triangle Review Page 1 of 3
 Hnout Tringle Review Pge of 3 In the stuy of sttis, it is importnt tht you e le to solve lgeri equtions n tringle prolems using trigonometry. The following is review of trigonometry sis. Right Tringle:
Hnout Tringle Review Pge of 3 In the stuy of sttis, it is importnt tht you e le to solve lgeri equtions n tringle prolems using trigonometry. The following is review of trigonometry sis. Right Tringle:
Section 4: Integration ECO4112F 2011
 Reding: Ching Chpter Section : Integrtion ECOF Note: These notes do not fully cover the mteril in Ching, ut re ment to supplement your reding in Ching. Thus fr the optimistion you hve covered hs een sttic
Reding: Ching Chpter Section : Integrtion ECOF Note: These notes do not fully cover the mteril in Ching, ut re ment to supplement your reding in Ching. Thus fr the optimistion you hve covered hs een sttic
LESSON 11: TRIANGLE FORMULAE
 . THE SEMIPERIMETER OF TRINGLE LESSON : TRINGLE FORMULE In wht follows, will hve sides, nd, nd these will e opposite ngles, nd respetively. y the tringle inequlity, nd..() So ll of, & re positive rel numers.
. THE SEMIPERIMETER OF TRINGLE LESSON : TRINGLE FORMULE In wht follows, will hve sides, nd, nd these will e opposite ngles, nd respetively. y the tringle inequlity, nd..() So ll of, & re positive rel numers.
Trigonometry and Constructive Geometry
 Trigonometry nd Construtive Geometry Trining prolems for M2 2018 term 1 Ted Szylowie tedszy@gmil.om 1 Leling geometril figures 1. Prtie writing Greek letters. αβγδɛθλµπψ 2. Lel the sides, ngles nd verties
Trigonometry nd Construtive Geometry Trining prolems for M2 2018 term 1 Ted Szylowie tedszy@gmil.om 1 Leling geometril figures 1. Prtie writing Greek letters. αβγδɛθλµπψ 2. Lel the sides, ngles nd verties
5. Every rational number have either terminating or repeating (recurring) decimal representation.
 CHAPTER NUMBER SYSTEMS Points to Rememer :. Numer used for ounting,,,,... re known s Nturl numers.. All nturl numers together with zero i.e. 0,,,,,... re known s whole numers.. All nturl numers, zero nd
CHAPTER NUMBER SYSTEMS Points to Rememer :. Numer used for ounting,,,,... re known s Nturl numers.. All nturl numers together with zero i.e. 0,,,,,... re known s whole numers.. All nturl numers, zero nd
Chapter Gauss Quadrature Rule of Integration
 Chpter 7. Guss Qudrture Rule o Integrtion Ater reding this hpter, you should e le to:. derive the Guss qudrture method or integrtion nd e le to use it to solve prolems, nd. use Guss qudrture method to
Chpter 7. Guss Qudrture Rule o Integrtion Ater reding this hpter, you should e le to:. derive the Guss qudrture method or integrtion nd e le to use it to solve prolems, nd. use Guss qudrture method to
Mathematics Number: Logarithms
 plce of mind F A C U L T Y O F E D U C A T I O N Deprtment of Curriculum nd Pedgogy Mthemtics Numer: Logrithms Science nd Mthemtics Eduction Reserch Group Supported y UBC Teching nd Lerning Enhncement
plce of mind F A C U L T Y O F E D U C A T I O N Deprtment of Curriculum nd Pedgogy Mthemtics Numer: Logrithms Science nd Mthemtics Eduction Reserch Group Supported y UBC Teching nd Lerning Enhncement
A Study on the Properties of Rational Triangles
 Interntionl Journl of Mthemtis Reserh. ISSN 0976-5840 Volume 6, Numer (04), pp. 8-9 Interntionl Reserh Pulition House http://www.irphouse.om Study on the Properties of Rtionl Tringles M. Q. lm, M.R. Hssn
Interntionl Journl of Mthemtis Reserh. ISSN 0976-5840 Volume 6, Numer (04), pp. 8-9 Interntionl Reserh Pulition House http://www.irphouse.om Study on the Properties of Rtionl Tringles M. Q. lm, M.R. Hssn
Green s Theorem. (2x e y ) da. (2x e y ) dx dy. x 2 xe y. (1 e y ) dy. y=1. = y e y. y=0. = 2 e
 Green s Theorem. Let be the boundry of the unit squre, y, oriented ounterlokwise, nd let F be the vetor field F, y e y +, 2 y. Find F d r. Solution. Let s write P, y e y + nd Q, y 2 y, so tht F P, Q. Let
Green s Theorem. Let be the boundry of the unit squre, y, oriented ounterlokwise, nd let F be the vetor field F, y e y +, 2 y. Find F d r. Solution. Let s write P, y e y + nd Q, y 2 y, so tht F P, Q. Let
Matrices SCHOOL OF ENGINEERING & BUILT ENVIRONMENT. Mathematics (c) 1. Definition of a Matrix
 tries Definition of tri mtri is regulr rry of numers enlosed inside rkets SCHOOL OF ENGINEERING & UIL ENVIRONEN Emple he following re ll mtries: ), ) 9, themtis ), d) tries Definition of tri Size of tri
tries Definition of tri mtri is regulr rry of numers enlosed inside rkets SCHOOL OF ENGINEERING & UIL ENVIRONEN Emple he following re ll mtries: ), ) 9, themtis ), d) tries Definition of tri Size of tri
Chapter 8 Roots and Radicals
 Chpter 8 Roots nd Rdils 7 ROOTS AND RADICALS 8 Figure 8. Grphene is n inredily strong nd flexile mteril mde from ron. It n lso ondut eletriity. Notie the hexgonl grid pttern. (redit: AlexnderAIUS / Wikimedi
Chpter 8 Roots nd Rdils 7 ROOTS AND RADICALS 8 Figure 8. Grphene is n inredily strong nd flexile mteril mde from ron. It n lso ondut eletriity. Notie the hexgonl grid pttern. (redit: AlexnderAIUS / Wikimedi
Logarithms LOGARITHMS.
 Logrithms LOGARITHMS www.mthletis.om.u Logrithms LOGARITHMS Logrithms re nother method to lulte nd work with eponents. Answer these questions, efore working through this unit. I used to think: In the
Logrithms LOGARITHMS www.mthletis.om.u Logrithms LOGARITHMS Logrithms re nother method to lulte nd work with eponents. Answer these questions, efore working through this unit. I used to think: In the
Intermediate Math Circles Wednesday 17 October 2012 Geometry II: Side Lengths
 Intermedite Mth Cirles Wednesdy 17 Otoer 01 Geometry II: Side Lengths Lst week we disussed vrious ngle properties. As we progressed through the evening, we proved mny results. This week, we will look t
Intermedite Mth Cirles Wednesdy 17 Otoer 01 Geometry II: Side Lengths Lst week we disussed vrious ngle properties. As we progressed through the evening, we proved mny results. This week, we will look t
September 13 Homework Solutions
 College of Engineering nd Computer Science Mechnicl Engineering Deprtment Mechnicl Engineering 5A Seminr in Engineering Anlysis Fll Ticket: 5966 Instructor: Lrry Cretto Septemer Homework Solutions. Are
College of Engineering nd Computer Science Mechnicl Engineering Deprtment Mechnicl Engineering 5A Seminr in Engineering Anlysis Fll Ticket: 5966 Instructor: Lrry Cretto Septemer Homework Solutions. Are
Non Right Angled Triangles
 Non Right ngled Tringles Non Right ngled Tringles urriulum Redy www.mthletis.om Non Right ngled Tringles NON RIGHT NGLED TRINGLES sin i, os i nd tn i re lso useful in non-right ngled tringles. This unit
Non Right ngled Tringles Non Right ngled Tringles urriulum Redy www.mthletis.om Non Right ngled Tringles NON RIGHT NGLED TRINGLES sin i, os i nd tn i re lso useful in non-right ngled tringles. This unit
2 b. , a. area is S= 2π xds. Again, understand where these formulas came from (pages ).
 AP Clculus BC Review Chpter 8 Prt nd Chpter 9 Things to Know nd Be Ale to Do Know everything from the first prt of Chpter 8 Given n integrnd figure out how to ntidifferentite it using ny of the following
AP Clculus BC Review Chpter 8 Prt nd Chpter 9 Things to Know nd Be Ale to Do Know everything from the first prt of Chpter 8 Given n integrnd figure out how to ntidifferentite it using ny of the following
PYTHAGORAS THEOREM,TRIGONOMETRY,BEARINGS AND THREE DIMENSIONAL PROBLEMS
 PYTHGORS THEOREM,TRIGONOMETRY,ERINGS ND THREE DIMENSIONL PROLEMS 1.1 PYTHGORS THEOREM: 1. The Pythgors Theorem sttes tht the squre of the hypotenuse is equl to the sum of the squres of the other two sides
PYTHGORS THEOREM,TRIGONOMETRY,ERINGS ND THREE DIMENSIONL PROLEMS 1.1 PYTHGORS THEOREM: 1. The Pythgors Theorem sttes tht the squre of the hypotenuse is equl to the sum of the squres of the other two sides
PAIR OF LINEAR EQUATIONS IN TWO VARIABLES
 PAIR OF LINEAR EQUATIONS IN TWO VARIABLES. Two liner equtions in the sme two vriles re lled pir of liner equtions in two vriles. The most generl form of pir of liner equtions is x + y + 0 x + y + 0 where,,,,,,
PAIR OF LINEAR EQUATIONS IN TWO VARIABLES. Two liner equtions in the sme two vriles re lled pir of liner equtions in two vriles. The most generl form of pir of liner equtions is x + y + 0 x + y + 0 where,,,,,,
Calculus Cheat Sheet. Integrals Definitions. where F( x ) is an anti-derivative of f ( x ). Fundamental Theorem of Calculus. dx = f x dx g x dx
 Clulus Chet Sheet Integrls Definitions Definite Integrl: Suppose f ( ) is ontinuous Anti-Derivtive : An nti-derivtive of f ( ) on [, ]. Divide [, ] into n suintervls of is funtion, F( ), suh tht F = f.
Clulus Chet Sheet Integrls Definitions Definite Integrl: Suppose f ( ) is ontinuous Anti-Derivtive : An nti-derivtive of f ( ) on [, ]. Divide [, ] into n suintervls of is funtion, F( ), suh tht F = f.
Integration. antidifferentiation
 9 Integrtion 9A Antidifferentition 9B Integrtion of e, sin ( ) nd os ( ) 9C Integrtion reognition 9D Approimting res enlosed funtions 9E The fundmentl theorem of integrl lulus 9F Signed res 9G Further
9 Integrtion 9A Antidifferentition 9B Integrtion of e, sin ( ) nd os ( ) 9C Integrtion reognition 9D Approimting res enlosed funtions 9E The fundmentl theorem of integrl lulus 9F Signed res 9G Further
In right-angled triangles the square on the side subtending the right angle is equal to the squares on the sides containing the right angle.
 Mth 3329-Uniform Geometries Leture 06 1. Review of trigonometry While we re looking t Eulid s Elements, I d like to look t some si trigonometry. Figure 1. The Pythgoren theorem sttes tht if = 90, then
Mth 3329-Uniform Geometries Leture 06 1. Review of trigonometry While we re looking t Eulid s Elements, I d like to look t some si trigonometry. Figure 1. The Pythgoren theorem sttes tht if = 90, then
CS 573 Automata Theory and Formal Languages
 Non-determinism Automt Theory nd Forml Lnguges Professor Leslie Lnder Leture # 3 Septemer 6, 2 To hieve our gol, we need the onept of Non-deterministi Finite Automton with -moves (NFA) An NFA is tuple
Non-determinism Automt Theory nd Forml Lnguges Professor Leslie Lnder Leture # 3 Septemer 6, 2 To hieve our gol, we need the onept of Non-deterministi Finite Automton with -moves (NFA) An NFA is tuple
Proving the Pythagorean Theorem
 Proving the Pythgoren Theorem W. Bline Dowler June 30, 2010 Astrt Most people re fmilir with the formul 2 + 2 = 2. However, in most ses, this ws presented in lssroom s n solute with no ttempt t proof or
Proving the Pythgoren Theorem W. Bline Dowler June 30, 2010 Astrt Most people re fmilir with the formul 2 + 2 = 2. However, in most ses, this ws presented in lssroom s n solute with no ttempt t proof or
Generalization of 2-Corner Frequency Source Models Used in SMSIM
 Generliztion o 2-Corner Frequeny Soure Models Used in SMSIM Dvid M. Boore 26 Mrh 213, orreted Figure 1 nd 2 legends on 5 April 213, dditionl smll orretions on 29 My 213 Mny o the soure spetr models ville
Generliztion o 2-Corner Frequeny Soure Models Used in SMSIM Dvid M. Boore 26 Mrh 213, orreted Figure 1 nd 2 legends on 5 April 213, dditionl smll orretions on 29 My 213 Mny o the soure spetr models ville
2. There are an infinite number of possible triangles, all similar, with three given angles whose sum is 180.
 SECTION 8-1 11 CHAPTER 8 Setion 8 1. There re n infinite numer of possile tringles, ll similr, with three given ngles whose sum is 180. 4. If two ngles α nd β of tringle re known, the third ngle n e found
SECTION 8-1 11 CHAPTER 8 Setion 8 1. There re n infinite numer of possile tringles, ll similr, with three given ngles whose sum is 180. 4. If two ngles α nd β of tringle re known, the third ngle n e found
A Lower Bound for the Length of a Partial Transversal in a Latin Square, Revised Version
 A Lower Bound for the Length of Prtil Trnsversl in Ltin Squre, Revised Version Pooy Htmi nd Peter W. Shor Deprtment of Mthemtil Sienes, Shrif University of Tehnology, P.O.Bo 11365-9415, Tehrn, Irn Deprtment
A Lower Bound for the Length of Prtil Trnsversl in Ltin Squre, Revised Version Pooy Htmi nd Peter W. Shor Deprtment of Mthemtil Sienes, Shrif University of Tehnology, P.O.Bo 11365-9415, Tehrn, Irn Deprtment
CHENG Chun Chor Litwin The Hong Kong Institute of Education
 PE-hing Mi terntionl onferene IV: novtion of Mthemtis Tehing nd Lerning through Lesson Study- onnetion etween ssessment nd Sujet Mtter HENG hun hor Litwin The Hong Kong stitute of Edution Report on using
PE-hing Mi terntionl onferene IV: novtion of Mthemtis Tehing nd Lerning through Lesson Study- onnetion etween ssessment nd Sujet Mtter HENG hun hor Litwin The Hong Kong stitute of Edution Report on using
Chapter 9 Definite Integrals
 Chpter 9 Definite Integrls In the previous chpter we found how to tke n ntiderivtive nd investigted the indefinite integrl. In this chpter the connection etween ntiderivtives nd definite integrls is estlished
Chpter 9 Definite Integrls In the previous chpter we found how to tke n ntiderivtive nd investigted the indefinite integrl. In this chpter the connection etween ntiderivtives nd definite integrls is estlished
Pythagoras Theorem. Pythagoras Theorem. Curriculum Ready ACMMG: 222, 245.
 Pythgors Theorem Pythgors Theorem Curriulum Redy ACMMG:, 45 www.mthletis.om Fill in these spes with ny other interesting fts you n find out Pythgors. In the world of Mthemtis, Pythgors is legend. He lived
Pythgors Theorem Pythgors Theorem Curriulum Redy ACMMG:, 45 www.mthletis.om Fill in these spes with ny other interesting fts you n find out Pythgors. In the world of Mthemtis, Pythgors is legend. He lived
Similar Right Triangles
 Geometry V1.noteook Ferury 09, 2012 Similr Right Tringles Cn I identify similr tringles in right tringle with the ltitude? Cn I identify the proportions in right tringles? Cn I use the geometri mens theorems
Geometry V1.noteook Ferury 09, 2012 Similr Right Tringles Cn I identify similr tringles in right tringle with the ltitude? Cn I identify the proportions in right tringles? Cn I use the geometri mens theorems
m m m m m m m m P m P m ( ) m m P( ) ( ). The o-ordinte of the point P( ) dividing the line segment joining the two points ( ) nd ( ) eternll in the r
 CO-ORDINTE GEOMETR II I Qudrnt Qudrnt (-.+) (++) X X - - - 0 - III IV Qudrnt - Qudrnt (--) - (+-) Region CRTESIN CO-ORDINTE SSTEM : Retngulr Co-ordinte Sstem : Let X' OX nd 'O e two mutull perpendiulr
CO-ORDINTE GEOMETR II I Qudrnt Qudrnt (-.+) (++) X X - - - 0 - III IV Qudrnt - Qudrnt (--) - (+-) Region CRTESIN CO-ORDINTE SSTEM : Retngulr Co-ordinte Sstem : Let X' OX nd 'O e two mutull perpendiulr
1.3 SCALARS AND VECTORS
 Bridge Course Phy I PUC 24 1.3 SCLRS ND VECTORS Introdution: Physis is the study of nturl phenomen. The study of ny nturl phenomenon involves mesurements. For exmple, the distne etween the plnet erth nd
Bridge Course Phy I PUC 24 1.3 SCLRS ND VECTORS Introdution: Physis is the study of nturl phenomen. The study of ny nturl phenomenon involves mesurements. For exmple, the distne etween the plnet erth nd
7. Indefinite Integrals
 7. Indefinite Integrls These lecture notes present my interprettion of Ruth Lwrence s lecture notes (in Herew) 7. Prolem sttement By the fundmentl theorem of clculus, to clculte n integrl we need to find
7. Indefinite Integrls These lecture notes present my interprettion of Ruth Lwrence s lecture notes (in Herew) 7. Prolem sttement By the fundmentl theorem of clculus, to clculte n integrl we need to find
3.1 Review of Sine, Cosine and Tangent for Right Angles
 Foundtions of Mth 11 Section 3.1 Review of Sine, osine nd Tngent for Right Tringles 125 3.1 Review of Sine, osine nd Tngent for Right ngles The word trigonometry is derived from the Greek words trigon,
Foundtions of Mth 11 Section 3.1 Review of Sine, osine nd Tngent for Right Tringles 125 3.1 Review of Sine, osine nd Tngent for Right ngles The word trigonometry is derived from the Greek words trigon,
p-adic Egyptian Fractions
 p-adic Egyptin Frctions Contents 1 Introduction 1 2 Trditionl Egyptin Frctions nd Greedy Algorithm 2 3 Set-up 3 4 p-greedy Algorithm 5 5 p-egyptin Trditionl 10 6 Conclusion 1 Introduction An Egyptin frction
p-adic Egyptin Frctions Contents 1 Introduction 1 2 Trditionl Egyptin Frctions nd Greedy Algorithm 2 3 Set-up 3 4 p-greedy Algorithm 5 5 p-egyptin Trditionl 10 6 Conclusion 1 Introduction An Egyptin frction
Something found at a salad bar
 Nme PP Something found t sld r 4.7 Notes RIGHT TRINGLE hs extly one right ngle. To solve right tringle, you n use things like SOH-H-TO nd the Pythgoren Theorem. n OLIQUE TRINGLE hs no right ngles. To solve
Nme PP Something found t sld r 4.7 Notes RIGHT TRINGLE hs extly one right ngle. To solve right tringle, you n use things like SOH-H-TO nd the Pythgoren Theorem. n OLIQUE TRINGLE hs no right ngles. To solve
Mathematics. Area under Curve.
 Mthemtics Are under Curve www.testprepkrt.com Tle of Content 1. Introduction.. Procedure of Curve Sketching. 3. Sketching of Some common Curves. 4. Are of Bounded Regions. 5. Sign convention for finding
Mthemtics Are under Curve www.testprepkrt.com Tle of Content 1. Introduction.. Procedure of Curve Sketching. 3. Sketching of Some common Curves. 4. Are of Bounded Regions. 5. Sign convention for finding
Chapter 6 Techniques of Integration
 MA Techniques of Integrtion Asst.Prof.Dr.Suprnee Liswdi Chpter 6 Techniques of Integrtion Recll: Some importnt integrls tht we hve lernt so fr. Tle of Integrls n+ n d = + C n + e d = e + C ( n ) d = ln
MA Techniques of Integrtion Asst.Prof.Dr.Suprnee Liswdi Chpter 6 Techniques of Integrtion Recll: Some importnt integrls tht we hve lernt so fr. Tle of Integrls n+ n d = + C n + e d = e + C ( n ) d = ln
Reflection Property of a Hyperbola
 Refletion Propert of Hperol Prefe The purpose of this pper is to prove nltill nd to illustrte geometrill the propert of hperol wherein r whih emntes outside the onvit of the hperol, tht is, etween the
Refletion Propert of Hperol Prefe The purpose of this pper is to prove nltill nd to illustrte geometrill the propert of hperol wherein r whih emntes outside the onvit of the hperol, tht is, etween the
The Double Integral. The Riemann sum of a function f (x; y) over this partition of [a; b] [c; d] is. f (r j ; t k ) x j y k
![The Double Integral. The Riemann sum of a function f (x; y) over this partition of [a; b] [c; d] is. f (r j ; t k ) x j y k The Double Integral. The Riemann sum of a function f (x; y) over this partition of [a; b] [c; d] is. f (r j ; t k ) x j y k](/thumbs/86/94790710.jpg) The Double Integrl De nition of the Integrl Iterted integrls re used primrily s tool for omputing double integrls, where double integrl is n integrl of f (; y) over region : In this setion, we de ne double
The Double Integrl De nition of the Integrl Iterted integrls re used primrily s tool for omputing double integrls, where double integrl is n integrl of f (; y) over region : In this setion, we de ne double
H (2a, a) (u 2a) 2 (E) Show that u v 4a. Explain why this implies that u v 4a, with equality if and only u a if u v 2a.
 Chpter Review 89 IGURE ol hord GH of the prol 4. G u v H (, ) (A) Use the distne formul to show tht u. (B) Show tht G nd H lie on the line m, where m ( )/( ). (C) Solve m for nd sustitute in 4, otining
Chpter Review 89 IGURE ol hord GH of the prol 4. G u v H (, ) (A) Use the distne formul to show tht u. (B) Show tht G nd H lie on the line m, where m ( )/( ). (C) Solve m for nd sustitute in 4, otining
Ellipses. The second type of conic is called an ellipse.
 Ellipses The seond type of oni is lled n ellipse. Definition of Ellipse An ellipse is the set of ll points (, y) in plne, the sum of whose distnes from two distint fied points (foi) is onstnt. (, y) d
Ellipses The seond type of oni is lled n ellipse. Definition of Ellipse An ellipse is the set of ll points (, y) in plne, the sum of whose distnes from two distint fied points (foi) is onstnt. (, y) d
Naming the sides of a right-angled triangle
 6.2 Wht is trigonometry? The word trigonometry is derived from the Greek words trigonon (tringle) nd metron (mesurement). Thus, it literlly mens to mesure tringle. Trigonometry dels with the reltionship
6.2 Wht is trigonometry? The word trigonometry is derived from the Greek words trigonon (tringle) nd metron (mesurement). Thus, it literlly mens to mesure tringle. Trigonometry dels with the reltionship
Tutorial Worksheet. 1. Find all solutions to the linear system by following the given steps. x + 2y + 3z = 2 2x + 3y + z = 4.
 Mth 5 Tutoril Week 1 - Jnury 1 1 Nme Setion Tutoril Worksheet 1. Find ll solutions to the liner system by following the given steps x + y + z = x + y + z = 4. y + z = Step 1. Write down the rgumented mtrix
Mth 5 Tutoril Week 1 - Jnury 1 1 Nme Setion Tutoril Worksheet 1. Find ll solutions to the liner system by following the given steps x + y + z = x + y + z = 4. y + z = Step 1. Write down the rgumented mtrix
Part I: Study the theorem statement.
 Nme 1 Nme 2 Nme 3 A STUDY OF PYTHAGORAS THEOREM Instrutions: Together in groups of 2 or 3, fill out the following worksheet. You my lift nswers from the reding, or nswer on your own. Turn in one pket for
Nme 1 Nme 2 Nme 3 A STUDY OF PYTHAGORAS THEOREM Instrutions: Together in groups of 2 or 3, fill out the following worksheet. You my lift nswers from the reding, or nswer on your own. Turn in one pket for
Geometry of the Circle - Chords and Angles. Geometry of the Circle. Chord and Angles. Curriculum Ready ACMMG: 272.
 Geometry of the irle - hords nd ngles Geometry of the irle hord nd ngles urriulum Redy MMG: 272 www.mthletis.om hords nd ngles HRS N NGLES The irle is si shpe nd so it n e found lmost nywhere. This setion
Geometry of the irle - hords nd ngles Geometry of the irle hord nd ngles urriulum Redy MMG: 272 www.mthletis.om hords nd ngles HRS N NGLES The irle is si shpe nd so it n e found lmost nywhere. This setion
3 Angle Geometry. 3.1 Measuring Angles. 1. Using a protractor, measure the marked angles.
 3 ngle Geometry MEP Prtie ook S3 3.1 Mesuring ngles 1. Using protrtor, mesure the mrked ngles. () () (d) (e) (f) 2. Drw ngles with the following sizes. () 22 () 75 120 (d) 90 (e) 153 (f) 45 (g) 180 (h)
3 ngle Geometry MEP Prtie ook S3 3.1 Mesuring ngles 1. Using protrtor, mesure the mrked ngles. () () (d) (e) (f) 2. Drw ngles with the following sizes. () 22 () 75 120 (d) 90 (e) 153 (f) 45 (g) 180 (h)
Distance Measurement. Distance Measurement. Distance Measurement. Distance Measurement. Distance Measurement. Distance Measurement
 IVL 1101 Surveying - Mesuring Distne 1/5 Distne is one of the most si engineering mesurements Erly mesurements were mde in terms of the dimensions of the ody very old wooden rule - Royl Egyptin uit uits
IVL 1101 Surveying - Mesuring Distne 1/5 Distne is one of the most si engineering mesurements Erly mesurements were mde in terms of the dimensions of the ody very old wooden rule - Royl Egyptin uit uits
Pythagoras theorem and surds
 HPTER Mesurement nd Geometry Pythgors theorem nd surds In IE-EM Mthemtis Yer 8, you lernt out the remrkle reltionship etween the lengths of the sides of right-ngled tringle. This result is known s Pythgors
HPTER Mesurement nd Geometry Pythgors theorem nd surds In IE-EM Mthemtis Yer 8, you lernt out the remrkle reltionship etween the lengths of the sides of right-ngled tringle. This result is known s Pythgors
5: The Definite Integral
 5: The Definite Integrl 5.: Estimting with Finite Sums Consider moving oject its velocity (meters per second) t ny time (seconds) is given y v t = t+. Cn we use this informtion to determine the distnce
5: The Definite Integrl 5.: Estimting with Finite Sums Consider moving oject its velocity (meters per second) t ny time (seconds) is given y v t = t+. Cn we use this informtion to determine the distnce
8 THREE PHASE A.C. CIRCUITS
 8 THREE PHSE.. IRUITS The signls in hpter 7 were sinusoidl lternting voltges nd urrents of the so-lled single se type. n emf of suh type n e esily generted y rotting single loop of ondutor (or single winding),
8 THREE PHSE.. IRUITS The signls in hpter 7 were sinusoidl lternting voltges nd urrents of the so-lled single se type. n emf of suh type n e esily generted y rotting single loop of ondutor (or single winding),
Electromagnetism Notes, NYU Spring 2018
 Eletromgnetism Notes, NYU Spring 208 April 2, 208 Ation formultion of EM. Free field desription Let us first onsider the free EM field, i.e. in the bsene of ny hrges or urrents. To tret this s mehnil system
Eletromgnetism Notes, NYU Spring 208 April 2, 208 Ation formultion of EM. Free field desription Let us first onsider the free EM field, i.e. in the bsene of ny hrges or urrents. To tret this s mehnil system
I1 = I2 I1 = I2 + I3 I1 + I2 = I3 + I4 I 3
 2 The Prllel Circuit Electric Circuits: Figure 2- elow show ttery nd multiple resistors rrnged in prllel. Ech resistor receives portion of the current from the ttery sed on its resistnce. The split is
2 The Prllel Circuit Electric Circuits: Figure 2- elow show ttery nd multiple resistors rrnged in prllel. Ech resistor receives portion of the current from the ttery sed on its resistnce. The split is
QUADRATIC EQUATION. Contents
 QUADRATIC EQUATION Contents Topi Pge No. Theory 0-04 Exerise - 05-09 Exerise - 09-3 Exerise - 3 4-5 Exerise - 4 6 Answer Key 7-8 Syllus Qudrti equtions with rel oeffiients, reltions etween roots nd oeffiients,
QUADRATIC EQUATION Contents Topi Pge No. Theory 0-04 Exerise - 05-09 Exerise - 09-3 Exerise - 3 4-5 Exerise - 4 6 Answer Key 7-8 Syllus Qudrti equtions with rel oeffiients, reltions etween roots nd oeffiients,
Linear Algebra Introduction
 Introdution Wht is Liner Alger out? Liner Alger is rnh of mthemtis whih emerged yers k nd ws one of the pioneer rnhes of mthemtis Though, initilly it strted with solving of the simple liner eqution x +
Introdution Wht is Liner Alger out? Liner Alger is rnh of mthemtis whih emerged yers k nd ws one of the pioneer rnhes of mthemtis Though, initilly it strted with solving of the simple liner eqution x +
The University of Nottingham SCHOOL OF COMPUTER SCIENCE A LEVEL 2 MODULE, SPRING SEMESTER MACHINES AND THEIR LANGUAGES ANSWERS
 The University of ottinghm SCHOOL OF COMPUTR SCIC A LVL 2 MODUL, SPRIG SMSTR 2015 2016 MACHIS AD THIR LAGUAGS ASWRS Time llowed TWO hours Cndidtes my omplete the front over of their nswer ook nd sign their
The University of ottinghm SCHOOL OF COMPUTR SCIC A LVL 2 MODUL, SPRIG SMSTR 2015 2016 MACHIS AD THIR LAGUAGS ASWRS Time llowed TWO hours Cndidtes my omplete the front over of their nswer ook nd sign their
Core 2 Logarithms and exponentials. Section 1: Introduction to logarithms
 Core Logrithms nd eponentils Setion : Introdution to logrithms Notes nd Emples These notes ontin subsetions on Indies nd logrithms The lws of logrithms Eponentil funtions This is n emple resoure from MEI
Core Logrithms nd eponentils Setion : Introdution to logrithms Notes nd Emples These notes ontin subsetions on Indies nd logrithms The lws of logrithms Eponentil funtions This is n emple resoure from MEI
= x x 2 = 25 2
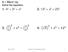 9.1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 7, 2016 Geometry 9.1 The Pythgoren Theorem 1 Geometry 9.1 The Pythgoren Theorem 9.1
9.1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 7, 2016 Geometry 9.1 The Pythgoren Theorem 1 Geometry 9.1 The Pythgoren Theorem 9.1
Goals: Determine how to calculate the area described by a function. Define the definite integral. Explore the relationship between the definite
 Unit #8 : The Integrl Gols: Determine how to clculte the re described by function. Define the definite integrl. Eplore the reltionship between the definite integrl nd re. Eplore wys to estimte the definite
Unit #8 : The Integrl Gols: Determine how to clculte the re described by function. Define the definite integrl. Eplore the reltionship between the definite integrl nd re. Eplore wys to estimte the definite
Interpreting Integrals and the Fundamental Theorem
 Interpreting Integrls nd the Fundmentl Theorem Tody, we go further in interpreting the mening of the definite integrl. Using Units to Aid Interprettion We lredy know tht if f(t) is the rte of chnge of
Interpreting Integrls nd the Fundmentl Theorem Tody, we go further in interpreting the mening of the definite integrl. Using Units to Aid Interprettion We lredy know tht if f(t) is the rte of chnge of
TOPIC: LINEAR ALGEBRA MATRICES
 Interntionl Blurete LECTUE NOTES for FUTHE MATHEMATICS Dr TOPIC: LINEA ALGEBA MATICES. DEFINITION OF A MATIX MATIX OPEATIONS.. THE DETEMINANT deta THE INVESE A -... SYSTEMS OF LINEA EQUATIONS. 8. THE AUGMENTED
Interntionl Blurete LECTUE NOTES for FUTHE MATHEMATICS Dr TOPIC: LINEA ALGEBA MATICES. DEFINITION OF A MATIX MATIX OPEATIONS.. THE DETEMINANT deta THE INVESE A -... SYSTEMS OF LINEA EQUATIONS. 8. THE AUGMENTED
Improper Integrals. The First Fundamental Theorem of Calculus, as we ve discussed in class, goes as follows:
 Improper Integrls The First Fundmentl Theorem of Clculus, s we ve discussed in clss, goes s follows: If f is continuous on the intervl [, ] nd F is function for which F t = ft, then ftdt = F F. An integrl
Improper Integrls The First Fundmentl Theorem of Clculus, s we ve discussed in clss, goes s follows: If f is continuous on the intervl [, ] nd F is function for which F t = ft, then ftdt = F F. An integrl
Factorising FACTORISING.
 Ftorising FACTORISING www.mthletis.om.u Ftorising FACTORISING Ftorising is the opposite of expning. It is the proess of putting expressions into rkets rther thn expning them out. In this setion you will
Ftorising FACTORISING www.mthletis.om.u Ftorising FACTORISING Ftorising is the opposite of expning. It is the proess of putting expressions into rkets rther thn expning them out. In this setion you will
Date Lesson Text TOPIC Homework. Solving for Obtuse Angles QUIZ ( ) More Trig Word Problems QUIZ ( )
 UNIT 5 TRIGONOMETRI RTIOS Dte Lesson Text TOPI Homework pr. 4 5.1 (48) Trigonometry Review WS 5.1 # 3 5, 9 11, (1, 13)doso pr. 6 5. (49) Relted ngles omplete lesson shell & WS 5. pr. 30 5.3 (50) 5.3 5.4
UNIT 5 TRIGONOMETRI RTIOS Dte Lesson Text TOPI Homework pr. 4 5.1 (48) Trigonometry Review WS 5.1 # 3 5, 9 11, (1, 13)doso pr. 6 5. (49) Relted ngles omplete lesson shell & WS 5. pr. 30 5.3 (50) 5.3 5.4
INTEGRATION. 1 Integrals of Complex Valued functions of a REAL variable
 INTEGRATION NOTE: These notes re supposed to supplement Chpter 4 of the online textbook. 1 Integrls of Complex Vlued funtions of REAL vrible If I is n intervl in R (for exmple I = [, b] or I = (, b)) nd
INTEGRATION NOTE: These notes re supposed to supplement Chpter 4 of the online textbook. 1 Integrls of Complex Vlued funtions of REAL vrible If I is n intervl in R (for exmple I = [, b] or I = (, b)) nd
9.1 Day 1 Warm Up. Solve the equation = x x 2 = March 1, 2017 Geometry 9.1 The Pythagorean Theorem 1
 9.1 Dy 1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 1, 2017 Geometry 9.1 The Pythgoren Theorem 1 9.1 Dy 2 Wrm Up Use the Pythgoren
9.1 Dy 1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 1, 2017 Geometry 9.1 The Pythgoren Theorem 1 9.1 Dy 2 Wrm Up Use the Pythgoren
Appendix C Partial discharges. 1. Relationship Between Measured and Actual Discharge Quantities
 Appendi Prtil dishrges. Reltionship Between Mesured nd Atul Dishrge Quntities A dishrging smple my e simply represented y the euilent iruit in Figure. The pplied lternting oltge V is inresed until the
Appendi Prtil dishrges. Reltionship Between Mesured nd Atul Dishrge Quntities A dishrging smple my e simply represented y the euilent iruit in Figure. The pplied lternting oltge V is inresed until the
(h+ ) = 0, (3.1) s = s 0, (3.2)
 Chpter 3 Nozzle Flow Qusistedy idel gs flow in pipes For the lrge vlues of the Reynolds number typilly found in nozzles, the flow is idel. For stedy opertion with negligible body fores the energy nd momentum
Chpter 3 Nozzle Flow Qusistedy idel gs flow in pipes For the lrge vlues of the Reynolds number typilly found in nozzles, the flow is idel. For stedy opertion with negligible body fores the energy nd momentum
m A 1 1 A ! and AC 6
 REVIEW SET A Using sle of m represents units, sketh vetor to represent: NON-CALCULATOR n eroplne tking off t n ngle of 8 ± to runw with speed of 6 ms displement of m in north-esterl diretion. Simplif:
REVIEW SET A Using sle of m represents units, sketh vetor to represent: NON-CALCULATOR n eroplne tking off t n ngle of 8 ± to runw with speed of 6 ms displement of m in north-esterl diretion. Simplif:
] dx (3) = [15x] 2 0
![] dx (3) = [15x] 2 0 ] dx (3) = [15x] 2 0](/thumbs/80/81916477.jpg) Leture 6. Double Integrls nd Volume on etngle Welome to Cl IV!!!! These notes re designed to be redble nd desribe the w I will eplin the mteril in lss. Hopefull the re thorough, but it s good ide to hve
Leture 6. Double Integrls nd Volume on etngle Welome to Cl IV!!!! These notes re designed to be redble nd desribe the w I will eplin the mteril in lss. Hopefull the re thorough, but it s good ide to hve
Pythagoras Theorem. The area of the square on the hypotenuse is equal to the sum of the squares on the other two sides
 Pythgors theorem nd trigonometry Pythgors Theorem The hypotenuse of right-ngled tringle is the longest side The hypotenuse is lwys opposite the right-ngle 2 = 2 + 2 or 2 = 2-2 or 2 = 2-2 The re of the
Pythgors theorem nd trigonometry Pythgors Theorem The hypotenuse of right-ngled tringle is the longest side The hypotenuse is lwys opposite the right-ngle 2 = 2 + 2 or 2 = 2-2 or 2 = 2-2 The re of the
Symmetrical Components 1
 Symmetril Components. Introdution These notes should e red together with Setion. of your text. When performing stedy-stte nlysis of high voltge trnsmission systems, we mke use of the per-phse equivlent
Symmetril Components. Introdution These notes should e red together with Setion. of your text. When performing stedy-stte nlysis of high voltge trnsmission systems, we mke use of the per-phse equivlent
QUADRATIC EQUATIONS OBJECTIVE PROBLEMS
 QUADRATIC EQUATIONS OBJECTIVE PROBLEMS +. The solution of the eqution will e (), () 0,, 5, 5. The roots of the given eqution ( p q) ( q r) ( r p) 0 + + re p q r p (), r p p q, q r p q (), (d), q r p q.
QUADRATIC EQUATIONS OBJECTIVE PROBLEMS +. The solution of the eqution will e (), () 0,, 5, 5. The roots of the given eqution ( p q) ( q r) ( r p) 0 + + re p q r p (), r p p q, q r p q (), (d), q r p q.
Continuous Random Variables Class 5, Jeremy Orloff and Jonathan Bloom
 Lerning Gols Continuous Rndom Vriles Clss 5, 8.05 Jeremy Orloff nd Jonthn Bloom. Know the definition of continuous rndom vrile. 2. Know the definition of the proility density function (pdf) nd cumultive
Lerning Gols Continuous Rndom Vriles Clss 5, 8.05 Jeremy Orloff nd Jonthn Bloom. Know the definition of continuous rndom vrile. 2. Know the definition of the proility density function (pdf) nd cumultive
Chapter 6 Notes, Larson/Hostetler 3e
 Contents 6. Antiderivtives nd the Rules of Integrtion.......................... 6. Are nd the Definite Integrl.................................. 6.. Are............................................ 6. Reimnn
Contents 6. Antiderivtives nd the Rules of Integrtion.......................... 6. Are nd the Definite Integrl.................................. 6.. Are............................................ 6. Reimnn
21.1 Using Formulae Construct and Use Simple Formulae Revision of Negative Numbers Substitution into Formulae
 MEP Jmi: STRAND G UNIT 1 Formule: Student Tet Contents STRAND G: Alger Unit 1 Formule Student Tet Contents Setion 1.1 Using Formule 1. Construt nd Use Simple Formule 1.3 Revision of Negtive Numers 1.4
MEP Jmi: STRAND G UNIT 1 Formule: Student Tet Contents STRAND G: Alger Unit 1 Formule Student Tet Contents Setion 1.1 Using Formule 1. Construt nd Use Simple Formule 1.3 Revision of Negtive Numers 1.4
Lesson 2.1 Inductive Reasoning
 Lesson 2.1 Inutive Resoning Nme Perio Dte For Eerises 1 7, use inutive resoning to fin the net two terms in eh sequene. 1. 4, 8, 12, 16,, 2. 400, 200, 100, 50, 25,, 3. 1 8, 2 7, 1 2, 4, 5, 4. 5, 3, 2,
Lesson 2.1 Inutive Resoning Nme Perio Dte For Eerises 1 7, use inutive resoning to fin the net two terms in eh sequene. 1. 4, 8, 12, 16,, 2. 400, 200, 100, 50, 25,, 3. 1 8, 2 7, 1 2, 4, 5, 4. 5, 3, 2,
Proportions: A ratio is the quotient of two numbers. For example, 2 3
 Proportions: rtio is the quotient of two numers. For exmple, 2 3 is rtio of 2 n 3. n equlity of two rtios is proportion. For exmple, 3 7 = 15 is proportion. 45 If two sets of numers (none of whih is 0)
Proportions: rtio is the quotient of two numers. For exmple, 2 3 is rtio of 2 n 3. n equlity of two rtios is proportion. For exmple, 3 7 = 15 is proportion. 45 If two sets of numers (none of whih is 0)
Lecture Notes No. 10
 2.6 System Identifition, Estimtion, nd Lerning Leture otes o. Mrh 3, 26 6 Model Struture of Liner ime Invrint Systems 6. Model Struture In representing dynmil system, the first step is to find n pproprite
2.6 System Identifition, Estimtion, nd Lerning Leture otes o. Mrh 3, 26 6 Model Struture of Liner ime Invrint Systems 6. Model Struture In representing dynmil system, the first step is to find n pproprite
