4.317 d 4 y. 4 dx d 2 y dy. 20. dt d 2 x. 21. y 3y 3y y y 6y 12y 8y y (4) y y y (4) 2y y 0. d 4 y 26.
|
|
|
- Lesley Bennett
- 6 years ago
- Views:
Transcription
1 38 CHAPTER 4 HIGHER-ORDER DIFFERENTIAL EQUATIONS sstems are also able, b means of their dsolve commands, to provide eplicit solutions of homogeneous linear constant-coefficient differential equations. In the classic tet Differential Equations b Ralph Palmer Agnew * (used b the author as a student) the following statement is made: It is not reasonable to epect students in this course to have computing skill and equipment necessar for efficient solving of equations such as 4.37 d 4 (3) d.79 d 3 4 d.46 d d d d Although it is debatable whether computing skills have improved in the intervening ears, it is a certaint that technolog has. If one has access to a computer algebra sstem, equation (3) could now be considered reasonable. After simplification and some relabeling of output, Mathematica ields the (approimate) general solution c e.7885 cos(.6865) c e.7885 sin(.6865) c 3 e cos(.7598) c 4 e sin(.7598). Finall, if we are faced with an initial-value problem consisting of, sa, a fourth-order equation, then to fit the general solution of the DE to the four initial conditions, we must solve four linear equations in four unknowns (the c, c, c 3, c 4 in the general solution). Using a CAS to solve the sstem can save lots of time. See Problems 59 and 6 in Eercises 4.3 and Problem 35 in Chapter 4 in Review. * McGraw-Hill, New York, 96. EXERCISES 4.3 In Problems 4 find the general solution of the given second-order differential equation Answers to selected odd-numbered problems begin on page ANS-4. d 3. d (4) 4. (4) 5. 6 d 4 d 4 d 9 4 d d 4 6. d 7 d 8 4 d In Problems 5 8 find the general solution of the given higher-order differential equation. 7. d 5 u dr 5 d 4 u 5 dr d 3 u 4 dr d u du 3 dr dr 5u d 3 u d u u 3 8. In Problems 9 36 solve the given initial-value problem. 9. 6, (), () 3. d 5 ds 5 7 d 4 ds 4 d 3 ds 3 8 d ds d, d 3, 3
2 4.3 HOMOGENEOUS LINEAR EQUATIONS WITH CONSTANT COEFFICIENTS d d 4 5, (), () , (), () 5 33., () () 34., () 5, () , (), (), () , () (), () In Problems 37 4 solve the given boundar-value problem , (), () 38. 4, (), (p) 39., (), 4., (), (p) In Problems 4 and 4 solve the given problem first using the form of the general solution given in (). Solve again, this time using the form given in (). FIGURE Graph for Problem FIGURE Graph for Problem , (), () 5 4., (), () In Problems each figure represents the graph of a particular solution of one of the following differential equations: (a) 34 (b) 4 (c) (d) (e) (f) 3 Match a solution curve with one of the differential equations. Eplain our reasoning. 43. π FIGURE Graph for Problem π FIGURE Graph for Problem 48 FIGURE 4.3. Graph for Problem FIGURE Graph for Problem 44 Discussion Problems 49. The roots of a cubic auiliar equation are m 4 and m m 3 5. What is the corresponding homogeneous linear differential equation? Discuss: Is our answer unique? 5. Two roots of a cubic auiliar equation with real coefficients are m and m 3 i. What is the corresponding homogeneous linear differential equation?
3 4.6 VARIATION OF PARAMETERS 6 The first n equations in this sstem, like u u in (4), are assumptions that are made to simplif the resulting equation after p u () () u n () n () is substituted in (9). In this case Cramer s rule gives u k W k, k,,..., n, W where W is the Wronskian of,,..., n and W k is the determinant obtained b replacing the kth column of the Wronskian b the column consisting of the righthand side of () that is, the column consisting of (,,..., f ()). When n, we get (5). When n 3, the particular solution is p u u u 3 3, where,, and 3 constitute a linearl independent set of solutions of the associated homogeneous DE and u, u, u 3 are determined from u W W, u W W, u 3 W 3 W, () W p f () 3 3 p, 3 W p f () 3 3 p, W 3 p 3 f () p, and W p 3 3 p. 3 See Problems 5 and 6 in Eercises 4.6. REMARKS (i) Variation of parameters has a distinct advantage over the method of undetermined coefficients in that it will alwas ield a particular solution p provided that the associated homogeneous equation can be solved. The present method is not limited to a function f () that is a combination of the four tpes listed on page 4. As we shall see in the net section, variation of parameters, unlike undetermined coefficients, is applicable to linear DEs with variable coefficients. (ii) In the problems that follow, do not hesitate to simplif the form of p. Depending on how the antiderivatives of u and u are found, ou might not obtain the same p as given in the answer section. For eample, in Problem 3 in Eercises 4.6 both p sin cos and p 4 sin cos are valid answers. In either case the general solution c p simplifies to c cos c sin cos. Wh? EXERCISES 4.6 In Problems 8 solve each differential equation b variation of parameters.. sec. tan 3. sin 4. sec u tan u 5. cos 6. sec 7. cosh 8. sinh 9. 4 e. 9 9 e 3 Answers to selected odd-numbered problems begin on page ANS e e sin e 4. e t arctan t 5. e t ln t e sec e /
4 6 CHAPTER 4 HIGHER-ORDER DIFFERENTIAL EQUATIONS In Problems 9 solve each differential equation b variation of parameters, subject to the initial conditions (), (). 9. 4e /.. 8 e e. 44 ( 6)e In Problems 3 and 4 the indicated functions are known linearl independent solutions of the associated homogeneous differential equation on (, ). Find the general solution of the given nonhomogeneous equation. 3. ( 4) 3/ ; / cos, / sin 4. sec(ln ); cos(ln ), sin(ln ) In Problems 5 and 6 solve the given third-order differential equation b variation of parameters. 5. tan 6. 4sec Discussion Problems In Problems 7 and 8 discuss how the methods of undetermined coefficients and variation of parameters can be combined to solve the given differential equation. Carr out our ideas sin e tan e 9. What are the intervals of definition of the general solutions in Problems, 7, 9, and 8? Discuss wh the interval of definition of the general solution in Problem 4 is not (, ). 3. Find the general solution of given that is a solution of the associated homogeneous equation. 3. Suppose p () u () () u () (), where u and u are defined b (5) is a particular solution of () on an interval I for which P, Q, and f are continuous. Show that p can be written as p () where and are in I, G(, t)f(t), G(, t) (t) () () (t), W(t) () (3) and W(t) W( (t), (t)) is the Wronskian. The function G(, t) in (3) is called the Green s function for the differential equation (). 3. Use (3) to construct the Green s function for the differential equation in Eample 3. Epress the general solution given in (8) in terms of the particular solution (). 33. Verif that () is a solution of the initial-value problem d Pd d d Q f(), ( ), ( ). on the interval I. [Hint: Look up Leibniz s Rule for differentiation under an integral sign.] 34. Use the results of Problems 3 and 33 and the Green s function found in Problem 3 to find a solution of the initial-value problem e, (), () using (). Evaluate the integral. 4.7 CAUCHY-EULER EQUATION REVIEW MATERIAL Review the concept of the auiliar equation in Section 4.3. INTRODUCTION The same relative ease with which we were able to find eplicit solutions of higher-order linear differential equations with constant coefficients in the preceding sections does not, in general, carr over to linear equations with variable coefficients. We shall see in Chapter 6 that when a linear DE has variable coefficients, the best that we can usuall epect is to find a solution in the form of an infinite series. However, the tpe of differential equation that we consider in this section is an eception to this rule; it is a linear equation with variable coefficients whose general solution can alwas be epressed in terms of powers of, sines, cosines, and logarithmic functions. Moreover, its method of solution is quite similar to that for constant-coefficient equations in that an auiliar equation must be solved.
5 ANS-4 ANSWERS FOR SELECTED ODD-NUMBERED PROBLEMS ANSWERS FOR SELECTED ODD-NUMBERED PROBLEMS CHAPTER 4 EXERCISES 3.3 (PAGE ). (t) e t 3. 5,, 47 das. The time when (t) and z(t) are the same makes sense because most of A and half of B are gone, so half of C should have been formed (a) 3. d t 3 t (b) (t) (t) 5; (3) 47.4 lb 5. i() i, s() n i, r() CHAPTER 3 IN REVIEW (PAGE 3). dp.5p 3. P(45) 8.99 billion (a) 9. d d (b). (t) ac e ak t c e, (t) c ak t ( c e akt ) k /k 3. c e 5. (a) (t) (e t e t ) z(t) d 3 t t L di (R R )i R i 3 e t e t L di 3 R i (R R 3 ) i 3 E(t) ln BT T B, BT T B T(t) BT T B T T B ek(b)t i(t) 4t 5 t, t, t E(t) p() r()g Kq() d (b) The ratio is increasing; the ratio is constant. Kp (d) r() gk q() d ; r() Kp B(CKp bg) EXERCISES 4. (PAGE 8). e e ln 9. (, ). (a) e (b) sinh e (e e ) sinh 3. (a) e cos e sin (b) no solution (c) e cos e p/ e sin (d) c e sin, where c is arbitrar 5. dependent 7. dependent 9. dependent. independent 3. The functions satisf the DE and are linearl independent on the interval since W(e 3, e 4 ) 7e ; c e 3 c e The functions satisf the DE and are linearl independent on the interval since W(e cos, e sin ) e ; c e cos c e sin. 7. The functions satisf the DE and are linearl independent on the interval since W( 3, 4 ) 6 ; c 3 c The functions satisf the DE and are linearl independent on the interval since W(,, ln ) 9 6 ; c c c 3 ln. 35. (b) p 3 3e ; p 6 3 e EXERCISES 4. (PAGE 3). e 3. sin 4 5. sinh 7. e / ln. 3. cos (ln ) e, p 9. e, p 5 e3 EXERCISES 4.3 (PAGE 38). c c e /4 3. c e 3 c e 5. c e 4 c e 4 7. c e /3 c e /4 9. c cos 3 c sin 3. e (c cos c sin ) 3. e /3 (c cos 5. c c e 3 c sin c 3 e 5 3 ) 7. c e c e 3 c 3 e 3 9. u c e t e t (c cos t c 3 sin t). c e c e c 3 e 3. c c e / (c 3 cos 3 c 5. c cos 3 c sin 3 4 sin 3 ) c 3 cos 3 c 4 sin 3 7. u c e r c re r c 3 e r c 4 re r c 5 e 5r 9. cos 4 3. sin 4 3 e(t) 3 e5(t) 33.
6 ANSWERS FOR SELECTED ODD-NUMBERED PROBLEMS ANS e6 6 e6 35. c e 3 c e e 5 e c c e c e c e e3 3 5 e3 ; 4. c c c 3 e c e 3 c e 4 7 e4 cosh sinh3 45. c e c e 3 e c cos 5 c sin 5 sin c e 3 c e 3 49 e4 343 e4 EXERCISES 4.4 (PAGE 48) 5. c e c e 6 3 e 4 e 4 e 5. c e c e 53. e 3 (c cos c sin ) 3 e sin 3. c e 5 c e c cos 5 c sin 5 cos c e c e e 7. c cos 3 c / c sin 3 ( )e 3 cos 3 c sin 3 9. c c e sin cos cos 3. c e / c e / e / 59. c c c 3 e c cos c sin 3 4 cos 6. c e c e c 3 e 6 3 e c cos c sin cos sin c e cos c e sin 4 e sin c e c e cos 63. c c c 3 e c 4 e e e8 5 8 e e sin 5 cos 69. cos 3 sin 8 3 cos cos. c c c 3 e cos 37 sin 7. e cos 3 64 e sin c e c e c 3 e e 5. c cos c sin c 3 cos c 4 sin 3 EXERCISES 4.6 (PAGE 6). c cos c sin sin cos ln cos 7. sin 9. e / c 3 cos c sin cos 3. e cos 9e sin 7e 4 5. c cos c sin 6 cos 33. F t F 7. c e c e sinh t cos t 9. c 35. e 9e e e c e 4 e 4t e ln e e5 t, cos 6(cot ) sin sin 3. c e c e (e e ) ln( e ) sin 3 3 cos 3 3. c e c e e sin e 4. cos 5 sin 6 3 sin, > 3 cos 5 6 sin, > EXERCISES 4.5 (PAGE 56). (3D )(3D ) sin 3. (D 6)(D ) 6 5. D(D 5) e 7. (D )(D )(D 5) e 9. D(D )(D D 4) 4 5. D 4 7. D(D ) 9. D 4. D 3 (D 6) 3. (D )(D ) 3 5. D(D D 5) 7.,,, 3, 4 9. e 6, e 3/ 3. cos 5, sin 5 33., e 5, e 5 5. c e t c te t t e t ln t 3 4 t e t 7. c e sin c e cos 3 e sin 9. 4 e/ 3 4 e/ 8 e / 4 e/. 4 9 e e 4 e 9 e 3. c / cos c / sin / 5. 3 e cos ln cos c c cos c 3 sin ln cos sin ln sec tan EXERCISES 4.7 (PAGE 68). c c 3. c c ln 5. c cos( ln ) c sin( ln ) ANSWERS FOR SELECTED ODD-NUMBERED PROBLEMS CHAPTER 4
Additional Topics in Differential Equations
 0537_cop6.qd 0/8/08 :6 PM Page 3 6 Additional Topics in Differential Equations In Chapter 6, ou studied differential equations. In this chapter, ou will learn additional techniques for solving differential
0537_cop6.qd 0/8/08 :6 PM Page 3 6 Additional Topics in Differential Equations In Chapter 6, ou studied differential equations. In this chapter, ou will learn additional techniques for solving differential
2.2 SEPARABLE VARIABLES
 44 CHAPTER FIRST-ORDER DIFFERENTIAL EQUATIONS 6 Consider the autonomous DE 6 Use our ideas from Problem 5 to find intervals on the -ais for which solution curves are concave up and intervals for which
44 CHAPTER FIRST-ORDER DIFFERENTIAL EQUATIONS 6 Consider the autonomous DE 6 Use our ideas from Problem 5 to find intervals on the -ais for which solution curves are concave up and intervals for which
INTRODUCTION TO DIFFERENTIAL EQUATIONS
 INTRODUCTION TO DIFFERENTIAL EQUATIONS. Definitions and Terminolog. Initial-Value Problems.3 Differential Equations as Mathematical Models CHAPTER IN REVIEW The words differential and equations certainl
INTRODUCTION TO DIFFERENTIAL EQUATIONS. Definitions and Terminolog. Initial-Value Problems.3 Differential Equations as Mathematical Models CHAPTER IN REVIEW The words differential and equations certainl
SEPARABLE EQUATIONS 2.2
 46 CHAPTER FIRST-ORDER DIFFERENTIAL EQUATIONS 4. Chemical Reactions When certain kinds of chemicals are combined, the rate at which the new compound is formed is modeled b the autonomous differential equation
46 CHAPTER FIRST-ORDER DIFFERENTIAL EQUATIONS 4. Chemical Reactions When certain kinds of chemicals are combined, the rate at which the new compound is formed is modeled b the autonomous differential equation
Additional Topics in Differential Equations
 6 Additional Topics in Differential Equations 6. Eact First-Order Equations 6. Second-Order Homogeneous Linear Equations 6.3 Second-Order Nonhomogeneous Linear Equations 6.4 Series Solutions of Differential
6 Additional Topics in Differential Equations 6. Eact First-Order Equations 6. Second-Order Homogeneous Linear Equations 6.3 Second-Order Nonhomogeneous Linear Equations 6.4 Series Solutions of Differential
Math 214 Spring problem set (a) Consider these two first order equations. (I) dy dx = x + 1 dy
 Math 4 Spring 08 problem set. (a) Consider these two first order equations. (I) d d = + d (II) d = Below are four direction fields. Match the differential equations above to their direction fields. Provide
Math 4 Spring 08 problem set. (a) Consider these two first order equations. (I) d d = + d (II) d = Below are four direction fields. Match the differential equations above to their direction fields. Provide
Second-Order Linear Differential Equations C 2
 C8 APPENDIX C Additional Topics in Differential Equations APPENDIX C. Second-Order Homogeneous Linear Equations Second-Order Linear Differential Equations Higher-Order Linear Differential Equations Application
C8 APPENDIX C Additional Topics in Differential Equations APPENDIX C. Second-Order Homogeneous Linear Equations Second-Order Linear Differential Equations Higher-Order Linear Differential Equations Application
Roberto s Notes on Integral Calculus Chapter 3: Basics of differential equations Section 3. Separable ODE s
 Roberto s Notes on Integral Calculus Chapter 3: Basics of differential equations Section 3 Separable ODE s What ou need to know alread: What an ODE is and how to solve an eponential ODE. What ou can learn
Roberto s Notes on Integral Calculus Chapter 3: Basics of differential equations Section 3 Separable ODE s What ou need to know alread: What an ODE is and how to solve an eponential ODE. What ou can learn
39. (a) Use trigonometric substitution to verify that. 40. The parabola y 2x divides the disk into two
 35. Prove the formula A r for the area of a sector of a circle with radius r and central angle. [Hint: Assume 0 and place the center of the circle at the origin so it has the equation. Then is the sum
35. Prove the formula A r for the area of a sector of a circle with radius r and central angle. [Hint: Assume 0 and place the center of the circle at the origin so it has the equation. Then is the sum
y sin n x dx cos x sin n 1 x n 1 y sin n 2 x cos 2 x dx y sin n xdx cos x sin n 1 x n 1 y sin n 2 x dx n 1 y sin n x dx
 SECTION 7. INTEGRATION BY PARTS 57 EXAPLE 6 Prove the reduction formula N Equation 7 is called a reduction formula because the eponent n has been reduced to n and n. 7 sin n n cos sinn n n sin n where
SECTION 7. INTEGRATION BY PARTS 57 EXAPLE 6 Prove the reduction formula N Equation 7 is called a reduction formula because the eponent n has been reduced to n and n. 7 sin n n cos sinn n n sin n where
Particular Solutions
 Particular Solutions Our eamples so far in this section have involved some constant of integration, K. We now move on to see particular solutions, where we know some boundar conditions and we substitute
Particular Solutions Our eamples so far in this section have involved some constant of integration, K. We now move on to see particular solutions, where we know some boundar conditions and we substitute
APPENDIX D Rotation and the General Second-Degree Equation
 APPENDIX D Rotation and the General Second-Degree Equation Rotation of Aes Invariants Under Rotation After rotation of the - and -aes counterclockwise through an angle, the rotated aes are denoted as the
APPENDIX D Rotation and the General Second-Degree Equation Rotation of Aes Invariants Under Rotation After rotation of the - and -aes counterclockwise through an angle, the rotated aes are denoted as the
Fitting Integrands to Basic Rules
 6_8.qd // : PM Page 8 8 CHAPTER 8 Integration Techniques, L Hôpital s Rule, and Improper Integrals Section 8. Basic Integration Rules Review proceres for fitting an integrand to one of the basic integration
6_8.qd // : PM Page 8 8 CHAPTER 8 Integration Techniques, L Hôpital s Rule, and Improper Integrals Section 8. Basic Integration Rules Review proceres for fitting an integrand to one of the basic integration
1.6 CONTINUITY OF TRIGONOMETRIC, EXPONENTIAL, AND INVERSE FUNCTIONS
 .6 Continuit of Trigonometric, Eponential, and Inverse Functions.6 CONTINUITY OF TRIGONOMETRIC, EXPONENTIAL, AND INVERSE FUNCTIONS In this section we will discuss the continuit properties of trigonometric
.6 Continuit of Trigonometric, Eponential, and Inverse Functions.6 CONTINUITY OF TRIGONOMETRIC, EXPONENTIAL, AND INVERSE FUNCTIONS In this section we will discuss the continuit properties of trigonometric
Systems of Linear Equations: Solving by Graphing
 8.1 Sstems of Linear Equations: Solving b Graphing 8.1 OBJECTIVE 1. Find the solution(s) for a set of linear equations b graphing NOTE There is no other ordered pair that satisfies both equations. From
8.1 Sstems of Linear Equations: Solving b Graphing 8.1 OBJECTIVE 1. Find the solution(s) for a set of linear equations b graphing NOTE There is no other ordered pair that satisfies both equations. From
5.6. Differential equations
 5.6. Differential equations The relationship between cause and effect in phsical phenomena can often be formulated using differential equations which describe how a phsical measure () and its derivative
5.6. Differential equations The relationship between cause and effect in phsical phenomena can often be formulated using differential equations which describe how a phsical measure () and its derivative
67. (a) Use a computer algebra system to find the partial fraction CAS. 68. (a) Find the partial fraction decomposition of the function CAS
 SECTION 7.5 STRATEGY FOR INTEGRATION 483 6. 2 sin 2 2 cos CAS 67. (a) Use a computer algebra sstem to find the partial fraction decomposition of the function 62 63 Find the area of the region under the
SECTION 7.5 STRATEGY FOR INTEGRATION 483 6. 2 sin 2 2 cos CAS 67. (a) Use a computer algebra sstem to find the partial fraction decomposition of the function 62 63 Find the area of the region under the
1.3 LIMITS AT INFINITY; END BEHAVIOR OF A FUNCTION
 . Limits at Infinit; End Behavior of a Function 89. LIMITS AT INFINITY; END BEHAVIOR OF A FUNCTION Up to now we have been concerned with its that describe the behavior of a function f) as approaches some
. Limits at Infinit; End Behavior of a Function 89. LIMITS AT INFINITY; END BEHAVIOR OF A FUNCTION Up to now we have been concerned with its that describe the behavior of a function f) as approaches some
FUNCTIONS OF ONE VARIABLE FUNCTION DEFINITIONS
 Page of 6 FUNCTIONS OF ONE VARIABLE FUNCTION DEFINITIONS 6. HYPERBOLIC FUNCTIONS These functions which are defined in terms of e will be seen later to be related to the trigonometic functions via comple
Page of 6 FUNCTIONS OF ONE VARIABLE FUNCTION DEFINITIONS 6. HYPERBOLIC FUNCTIONS These functions which are defined in terms of e will be seen later to be related to the trigonometic functions via comple
Rising HONORS Algebra 2 TRIG student Summer Packet for 2016 (school year )
 Rising HONORS Algebra TRIG student Summer Packet for 016 (school ear 016-17) Welcome to Algebra TRIG! To be successful in Algebra Trig, ou must be proficient at solving and simplifing each tpe of problem
Rising HONORS Algebra TRIG student Summer Packet for 016 (school ear 016-17) Welcome to Algebra TRIG! To be successful in Algebra Trig, ou must be proficient at solving and simplifing each tpe of problem
Introduction to Differential Equations
 Introduction to Differential Equations. Definitions and Terminolog.2 Initial-Value Problems.3 Differential Equations as Mathematical Models Chapter in Review The words differential and equations certainl
Introduction to Differential Equations. Definitions and Terminolog.2 Initial-Value Problems.3 Differential Equations as Mathematical Models Chapter in Review The words differential and equations certainl
Exact Differential Equations. The general solution of the equation is f x, y C. If f has continuous second partials, then M y 2 f
 APPENDIX C Additional Topics in Differential Equations APPENDIX C. Eact First-Order Equations Eact Differential Equations Integrating Factors Eact Differential Equations In Chapter 6, ou studied applications
APPENDIX C Additional Topics in Differential Equations APPENDIX C. Eact First-Order Equations Eact Differential Equations Integrating Factors Eact Differential Equations In Chapter 6, ou studied applications
24. x 2 y xy y sec(ln x); 1 e x y 1 cos(ln x), y 2 sin(ln x) 25. y y tan x 26. y 4y sec 2x 28.
 16 CHAPTER 4 HIGHER-ORDER DIFFERENTIAL EQUATIONS 11. y 3y y 1 4. x yxyy sec(ln x); 1 e x y 1 cos(ln x), y sin(ln x) ex 1. y y y 1 x 13. y3yy sin e x 14. yyy e t arctan t 15. yyy e t ln t 16. y y y 41x
16 CHAPTER 4 HIGHER-ORDER DIFFERENTIAL EQUATIONS 11. y 3y y 1 4. x yxyy sec(ln x); 1 e x y 1 cos(ln x), y sin(ln x) ex 1. y y y 1 x 13. y3yy sin e x 14. yyy e t arctan t 15. yyy e t ln t 16. y y y 41x
SPS Mathematical Methods
 SPS 2281 - Mathematical Methods Assignment No. 2 Deadline: 11th March 2015, before 4:45 p.m. INSTRUCTIONS: Answer the following questions. Check our answer for odd number questions at the back of the tetbook.
SPS 2281 - Mathematical Methods Assignment No. 2 Deadline: 11th March 2015, before 4:45 p.m. INSTRUCTIONS: Answer the following questions. Check our answer for odd number questions at the back of the tetbook.
Fitting Integrands to Basic Rules. x x 2 9 dx. Solution a. Use the Arctangent Rule and let u x and a dx arctan x 3 C. 2 du u.
 58 CHAPTER 8 Integration Techniques, L Hôpital s Rule, and Improper Integrals Section 8 Basic Integration Rules Review proceres for fitting an integrand to one of the basic integration rules Fitting Integrands
58 CHAPTER 8 Integration Techniques, L Hôpital s Rule, and Improper Integrals Section 8 Basic Integration Rules Review proceres for fitting an integrand to one of the basic integration rules Fitting Integrands
Math 308 Week 8 Solutions
 Math 38 Week 8 Solutions There is a solution manual to Chapter 4 online: www.pearsoncustom.com/tamu math/. This online solutions manual contains solutions to some of the suggested problems. Here are solutions
Math 38 Week 8 Solutions There is a solution manual to Chapter 4 online: www.pearsoncustom.com/tamu math/. This online solutions manual contains solutions to some of the suggested problems. Here are solutions
Section 1.2: A Catalog of Functions
 Section 1.: A Catalog of Functions As we discussed in the last section, in the sciences, we often tr to find an equation which models some given phenomenon in the real world - for eample, temperature as
Section 1.: A Catalog of Functions As we discussed in the last section, in the sciences, we often tr to find an equation which models some given phenomenon in the real world - for eample, temperature as
FIRST- AND SECOND-ORDER IVPS The problem given in (1) is also called an nth-order initial-value problem. For example, Solve: Solve:
 .2 INITIAL-VALUE PROBLEMS 3.2 INITIAL-VALUE PROBLEMS REVIEW MATERIAL Normal form of a DE Solution of a DE Famil of solutions INTRODUCTION We are often interested in problems in which we seek a solution
.2 INITIAL-VALUE PROBLEMS 3.2 INITIAL-VALUE PROBLEMS REVIEW MATERIAL Normal form of a DE Solution of a DE Famil of solutions INTRODUCTION We are often interested in problems in which we seek a solution
Engineering Mathematics I
 Engineering Mathematics I_ 017 Engineering Mathematics I 1. Introduction to Differential Equations Dr. Rami Zakaria Terminolog Differential Equation Ordinar Differential Equations Partial Differential
Engineering Mathematics I_ 017 Engineering Mathematics I 1. Introduction to Differential Equations Dr. Rami Zakaria Terminolog Differential Equation Ordinar Differential Equations Partial Differential
AP Calculus BC Chapter 8: Integration Techniques, L Hopital s Rule and Improper Integrals
 AP Calculus BC Chapter 8: Integration Techniques, L Hopital s Rule and Improper Integrals 8. Basic Integration Rules In this section we will review various integration strategies. Strategies: I. Separate
AP Calculus BC Chapter 8: Integration Techniques, L Hopital s Rule and Improper Integrals 8. Basic Integration Rules In this section we will review various integration strategies. Strategies: I. Separate
11 PARAMETRIC EQUATIONS, POLAR COORDINATES, AND CONIC SECTIONS
 PARAMETRIC EQUATIONS, POLAR COORDINATES, AND CONIC SECTIONS. Parametric Equations Preliminar Questions. Describe the shape of the curve = cos t, = sin t. For all t, + = cos t + sin t = 9cos t + sin t =
PARAMETRIC EQUATIONS, POLAR COORDINATES, AND CONIC SECTIONS. Parametric Equations Preliminar Questions. Describe the shape of the curve = cos t, = sin t. For all t, + = cos t + sin t = 9cos t + sin t =
In everyday speech, a continuous. Limits and Continuity. Critical Thinking Exercises
 062 Chapter Introduction to Calculus Critical Thinking Eercises Make Sense? In Eercises 74 77, determine whether each statement makes sense or does not make sense, and eplain our reasoning. 74. I evaluated
062 Chapter Introduction to Calculus Critical Thinking Eercises Make Sense? In Eercises 74 77, determine whether each statement makes sense or does not make sense, and eplain our reasoning. 74. I evaluated
Try It Exploration A Exploration B Open Exploration. Fitting Integrands to Basic Rules. A Comparison of Three Similar Integrals
 58 CHAPTER 8 Integration Techniques, L Hôpital s Rule, and Improper Integrals Section 8 Basic Integration Rules Review procedures for fitting an integrand to one of the basic integration rules Fitting
58 CHAPTER 8 Integration Techniques, L Hôpital s Rule, and Improper Integrals Section 8 Basic Integration Rules Review procedures for fitting an integrand to one of the basic integration rules Fitting
Finding Limits Graphically and Numerically. An Introduction to Limits
 60_00.qd //0 :05 PM Page 8 8 CHAPTER Limits and Their Properties Section. Finding Limits Graphicall and Numericall Estimate a it using a numerical or graphical approach. Learn different was that a it can
60_00.qd //0 :05 PM Page 8 8 CHAPTER Limits and Their Properties Section. Finding Limits Graphicall and Numericall Estimate a it using a numerical or graphical approach. Learn different was that a it can
2. Higher-order Linear ODE s
 2. Higher-order Linear ODE s 2A. Second-order Linear ODE s: General Properties 2A-1. On the right below is an abbreviated form of the ODE on the left: (*) y + p()y + q()y = r() Ly = r() ; where L is the
2. Higher-order Linear ODE s 2A. Second-order Linear ODE s: General Properties 2A-1. On the right below is an abbreviated form of the ODE on the left: (*) y + p()y + q()y = r() Ly = r() ; where L is the
Core Mathematics 3 A2 compulsory unit for GCE Mathematics and GCE Pure Mathematics Mathematics. Unit C3. C3.1 Unit description
 Unit C3 Core Mathematics 3 A2 compulsory unit for GCE Mathematics and GCE Pure Mathematics Mathematics C3. Unit description Algebra and functions; trigonometry; eponentials and logarithms; differentiation;
Unit C3 Core Mathematics 3 A2 compulsory unit for GCE Mathematics and GCE Pure Mathematics Mathematics C3. Unit description Algebra and functions; trigonometry; eponentials and logarithms; differentiation;
y sec 3 x dx sec x tan x y sec x tan 2 x dx y sec 3 x dx 1 2(sec x tan x ln sec x tan x ) C
 SECTION 7. TRIGONOETRIC INTEGRLS 465 Then sec 3 sec tan sec tan sec tan sec sec sec tan sec 3 sec Using ormula and solving for the required integral, we get sec 3 (sec tan ln sec tan ) C Integrals such
SECTION 7. TRIGONOETRIC INTEGRLS 465 Then sec 3 sec tan sec tan sec tan sec sec sec tan sec 3 sec Using ormula and solving for the required integral, we get sec 3 (sec tan ln sec tan ) C Integrals such
7.7. Inverse Trigonometric Functions. Defining the Inverses
 7.7 Inverse Trigonometric Functions 57 7.7 Inverse Trigonometric Functions Inverse trigonometric functions arise when we want to calculate angles from side measurements in triangles. The also provide useful
7.7 Inverse Trigonometric Functions 57 7.7 Inverse Trigonometric Functions Inverse trigonometric functions arise when we want to calculate angles from side measurements in triangles. The also provide useful
Integration Techniques for the AB exam
 For the AB eam, students need to: determine antiderivatives of the basic functions calculate antiderivatives of functions using u-substitution use algebraic manipulation to rewrite the integrand prior
For the AB eam, students need to: determine antiderivatives of the basic functions calculate antiderivatives of functions using u-substitution use algebraic manipulation to rewrite the integrand prior
TO THE STUDENT: To best prepare for Test 4, do all the problems on separate paper. The answers are given at the end of the review sheet.
 MATH TEST 4 REVIEW TO THE STUDENT: To best prepare for Test 4, do all the problems on separate paper. The answers are given at the end of the review sheet. PART NON-CALCULATOR DIRECTIONS: The problems
MATH TEST 4 REVIEW TO THE STUDENT: To best prepare for Test 4, do all the problems on separate paper. The answers are given at the end of the review sheet. PART NON-CALCULATOR DIRECTIONS: The problems
f ax ; a 0 is a periodic function b is a periodic function of x of p b. f which is assumed to have the period 2 π, where
 (a) (b) If () Year - Tutorial: Toic: Fourier series Time: Two hours π π n Find the fundamental eriod of (i) cos (ii) cos k k f a ; a is a eriodic function b is a eriodic function of of b. f is a eriodic
(a) (b) If () Year - Tutorial: Toic: Fourier series Time: Two hours π π n Find the fundamental eriod of (i) cos (ii) cos k k f a ; a is a eriodic function b is a eriodic function of of b. f is a eriodic
11.4. Differentiating ProductsandQuotients. Introduction. Prerequisites. Learning Outcomes
 Differentiating ProductsandQuotients 11.4 Introduction We have seen, in the first three Sections, how standard functions like n, e a, sin a, cos a, ln a may be differentiated. In this Section we see how
Differentiating ProductsandQuotients 11.4 Introduction We have seen, in the first three Sections, how standard functions like n, e a, sin a, cos a, ln a may be differentiated. In this Section we see how
Handout 1. Research shows that students learn when they MAKE MISTAKES and not when they get it right. SO MAKE MISTAKES, because MISTAKES ARE GOOD!
 Handout Research shows that students learn when they MAKE MISTAKES and not when they get it right. SO MAKE MISTAKES, because MISTAKES ARE GOOD! Review:. The Substitution Rule Indefinite f (g()) g ()d =
Handout Research shows that students learn when they MAKE MISTAKES and not when they get it right. SO MAKE MISTAKES, because MISTAKES ARE GOOD! Review:. The Substitution Rule Indefinite f (g()) g ()d =
1 Solution to Homework 4
 Solution to Homework Section. 5. The characteristic equation is r r + = (r )(r ) = 0 r = or r =. y(t) = c e t + c e t y = c e t + c e t. y(0) =, y (0) = c + c =, c + c = c =, c =. To find the maximum value
Solution to Homework Section. 5. The characteristic equation is r r + = (r )(r ) = 0 r = or r =. y(t) = c e t + c e t y = c e t + c e t. y(0) =, y (0) = c + c =, c + c = c =, c =. To find the maximum value
INSTRUCTOR S SOLUTIONS MANUAL SECTION 17.1 (PAGE 902)
 INSTRUCTOR S SOLUTIONS MANUAL SECTION 7 PAGE 90 CHAPTER 7 ORDINARY DIFFEREN- TIAL EQUATIONS Section 7 Classifing Differential Equations page 90 = 5: st order, linear, homogeneous d d + = : nd order, linear,
INSTRUCTOR S SOLUTIONS MANUAL SECTION 7 PAGE 90 CHAPTER 7 ORDINARY DIFFEREN- TIAL EQUATIONS Section 7 Classifing Differential Equations page 90 = 5: st order, linear, homogeneous d d + = : nd order, linear,
DIFFERENTIAL EQUATION
 MDE DIFFERENTIAL EQUATION NCERT Solved eamples upto the section 9. (Introduction) and 9. (Basic Concepts) : Eample : Find the order and degree, if defined, of each of the following differential equations
MDE DIFFERENTIAL EQUATION NCERT Solved eamples upto the section 9. (Introduction) and 9. (Basic Concepts) : Eample : Find the order and degree, if defined, of each of the following differential equations
Finding Limits Graphically and Numerically. An Introduction to Limits
 8 CHAPTER Limits and Their Properties Section Finding Limits Graphicall and Numericall Estimate a it using a numerical or graphical approach Learn different was that a it can fail to eist Stud and use
8 CHAPTER Limits and Their Properties Section Finding Limits Graphicall and Numericall Estimate a it using a numerical or graphical approach Learn different was that a it can fail to eist Stud and use
MA 113 Calculus I Fall 2009 Exam 4 December 15, 2009
 MA 3 Calculus I Fall 009 Eam December 5, 009 Answer all of the questions - 7 and two of the questions 8-0. Please indicate which problem is not to be graded b crossing through its number in the table below.
MA 3 Calculus I Fall 009 Eam December 5, 009 Answer all of the questions - 7 and two of the questions 8-0. Please indicate which problem is not to be graded b crossing through its number in the table below.
EXERCISES FOR SECTION 3.1
 174 CHAPTER 3 LINEAR SYSTEMS EXERCISES FOR SECTION 31 1 Since a > 0, Paul s making a pro t > 0 has a bene cial effect on Paul s pro ts in the future because the a term makes a positive contribution to
174 CHAPTER 3 LINEAR SYSTEMS EXERCISES FOR SECTION 31 1 Since a > 0, Paul s making a pro t > 0 has a bene cial effect on Paul s pro ts in the future because the a term makes a positive contribution to
AP Calculus (AB/BC) Prerequisite Packet Paint Branch High School Math Department
 Updated 6/015 The problems in this packet are designed to help ou review topics from previous math courses that are important to our success in AP Calculus AB / BC. It is important that ou take time during
Updated 6/015 The problems in this packet are designed to help ou review topics from previous math courses that are important to our success in AP Calculus AB / BC. It is important that ou take time during
MA 242 Review Exponential and Log Functions Notes for today s class can be found at
 MA 242 Review Exponential and Log Functions Notes for today s class can be found at www.xecu.net/jacobs/index242.htm Example: If y = x n If y = x 2 then then dy dx = nxn 1 dy dx = 2x1 = 2x Power Function
MA 242 Review Exponential and Log Functions Notes for today s class can be found at www.xecu.net/jacobs/index242.htm Example: If y = x n If y = x 2 then then dy dx = nxn 1 dy dx = 2x1 = 2x Power Function
Integration Techniques for the AB exam
 For the AB eam, students need to: determine antiderivatives of the basic functions calculate antiderivatives of functions using u-substitution use algebraic manipulation to rewrite the integrand prior
For the AB eam, students need to: determine antiderivatives of the basic functions calculate antiderivatives of functions using u-substitution use algebraic manipulation to rewrite the integrand prior
Integration Techniques, L Hôpital s Rule, and Improper Integrals
 8 Integration Techniques, L Hôpital s Rule, and Improper Integrals In previous chapters, ou studied several basic techniques for evaluating simple integrals. In this chapter, ou will stud other integration
8 Integration Techniques, L Hôpital s Rule, and Improper Integrals In previous chapters, ou studied several basic techniques for evaluating simple integrals. In this chapter, ou will stud other integration
UNDETERMINED COEFFICIENTS SUPERPOSITION APPROACH *
 4.4 UNDETERMINED COEFFICIENTS SUPERPOSITION APPROACH 19 Discussion Problems 59. Two roots of a cubic auxiliary equation with real coeffi cients are m 1 1 and m i. What is the corresponding homogeneous
4.4 UNDETERMINED COEFFICIENTS SUPERPOSITION APPROACH 19 Discussion Problems 59. Two roots of a cubic auxiliary equation with real coeffi cients are m 1 1 and m i. What is the corresponding homogeneous
2.5 CONTINUITY. a x. Notice that Definition l implicitly requires three things if f is continuous at a:
 SECTION.5 CONTINUITY 9.5 CONTINUITY We noticed in Section.3 that the it of a function as approaches a can often be found simpl b calculating the value of the function at a. Functions with this propert
SECTION.5 CONTINUITY 9.5 CONTINUITY We noticed in Section.3 that the it of a function as approaches a can often be found simpl b calculating the value of the function at a. Functions with this propert
TOTAL NAME DATE PERIOD AP CALCULUS AB UNIT 4 ADVANCED DIFFERENTIATION TECHNIQUES DATE TOPIC ASSIGNMENT /6 10/8 10/9 10/10 X X X X 10/11 10/12
 NAME DATE PERIOD AP CALCULUS AB UNIT ADVANCED DIFFERENTIATION TECHNIQUES DATE TOPIC ASSIGNMENT 0 0 0/6 0/8 0/9 0/0 X X X X 0/ 0/ 0/5 0/6 QUIZ X X X 0/7 0/8 0/9 0/ 0/ 0/ 0/5 UNIT EXAM X X X TOTAL AP Calculus
NAME DATE PERIOD AP CALCULUS AB UNIT ADVANCED DIFFERENTIATION TECHNIQUES DATE TOPIC ASSIGNMENT 0 0 0/6 0/8 0/9 0/0 X X X X 0/ 0/ 0/5 0/6 QUIZ X X X 0/7 0/8 0/9 0/ 0/ 0/ 0/5 UNIT EXAM X X X TOTAL AP Calculus
We have examined power functions like f (x) = x 2. Interchanging x
 CHAPTER 5 Eponential and Logarithmic Functions We have eamined power functions like f =. Interchanging and ields a different function f =. This new function is radicall different from a power function
CHAPTER 5 Eponential and Logarithmic Functions We have eamined power functions like f =. Interchanging and ields a different function f =. This new function is radicall different from a power function
Section B. Ordinary Differential Equations & its Applications Maths II
 Section B Ordinar Differential Equations & its Applications Maths II Basic Concepts and Ideas: A differential equation (D.E.) is an equation involving an unknown function (or dependent variable) of one
Section B Ordinar Differential Equations & its Applications Maths II Basic Concepts and Ideas: A differential equation (D.E.) is an equation involving an unknown function (or dependent variable) of one
Trigonometric. equations. Topic: Periodic functions and applications. Simple trigonometric. equations. Equations using radians Further trigonometric
 Trigonometric equations 6 sllabusref eferenceence Topic: Periodic functions and applications In this cha 6A 6B 6C 6D 6E chapter Simple trigonometric equations Equations using radians Further trigonometric
Trigonometric equations 6 sllabusref eferenceence Topic: Periodic functions and applications In this cha 6A 6B 6C 6D 6E chapter Simple trigonometric equations Equations using radians Further trigonometric
CHAPTER 3 Applications of Differentiation
 CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. Section. Rolle s Theorem and the Mean Value Theorem. 7 Section. Increasing and Decreasing Functions and the First Derivative
CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. Section. Rolle s Theorem and the Mean Value Theorem. 7 Section. Increasing and Decreasing Functions and the First Derivative
Ordinary Differential Equations
 58229_CH0_00_03.indd Page 6/6/6 2:48 PM F-007 /202/JB0027/work/indd & Bartlett Learning LLC, an Ascend Learning Compan.. PART Ordinar Differential Equations. Introduction to Differential Equations 2. First-Order
58229_CH0_00_03.indd Page 6/6/6 2:48 PM F-007 /202/JB0027/work/indd & Bartlett Learning LLC, an Ascend Learning Compan.. PART Ordinar Differential Equations. Introduction to Differential Equations 2. First-Order
3.2 LOGARITHMIC FUNCTIONS AND THEIR GRAPHS
 Section. Logarithmic Functions and Their Graphs 7. LOGARITHMIC FUNCTIONS AND THEIR GRAPHS Ariel Skelle/Corbis What ou should learn Recognize and evaluate logarithmic functions with base a. Graph logarithmic
Section. Logarithmic Functions and Their Graphs 7. LOGARITHMIC FUNCTIONS AND THEIR GRAPHS Ariel Skelle/Corbis What ou should learn Recognize and evaluate logarithmic functions with base a. Graph logarithmic
6.5 Trigonometric Equations
 6. Trigonometric Equations In this section, we discuss conditional trigonometric equations, that is, equations involving trigonometric functions that are satisfied only by some values of the variable (or
6. Trigonometric Equations In this section, we discuss conditional trigonometric equations, that is, equations involving trigonometric functions that are satisfied only by some values of the variable (or
Higher Order Linear ODEs
 im03.qxd 9/21/05 11:04 AM Page 59 CHAPTER 3 Higher Order Linear ODEs This chapter is new. Its material is a rearranged and somewhat extended version of material previously contained in some of the sections
im03.qxd 9/21/05 11:04 AM Page 59 CHAPTER 3 Higher Order Linear ODEs This chapter is new. Its material is a rearranged and somewhat extended version of material previously contained in some of the sections
CHAPTER 5 Logarithmic, Exponential, and Other Transcendental Functions
 CHAPTER 5 Logarithmic, Eponential, and Other Transcendental Functions Section 5. The Natural Logarithmic Function: Differentiation.... 9 Section 5. The Natural Logarithmic Function: Integration...... 98
CHAPTER 5 Logarithmic, Eponential, and Other Transcendental Functions Section 5. The Natural Logarithmic Function: Differentiation.... 9 Section 5. The Natural Logarithmic Function: Integration...... 98
24. ; Graph the function and observe where it is discontinuous. 2xy f x, y x 2 y 3 x 3 y xy 35. 6x 3 y 2x 4 y 4 36.
 SECTION. LIMITS AND CONTINUITY 877. EXERCISES. Suppose that, l 3, f, 6. What can ou sa about the value of f 3,? What if f is continuous?. Eplain wh each function is continuous or discontinuous. (a) The
SECTION. LIMITS AND CONTINUITY 877. EXERCISES. Suppose that, l 3, f, 6. What can ou sa about the value of f 3,? What if f is continuous?. Eplain wh each function is continuous or discontinuous. (a) The
Trigonometric integrals by basic methods
 Roberto s Notes on Integral Calculus Chapter : Integration methods Section 7 Trigonometric integrals by basic methods What you need to know already: Integrals of basic trigonometric functions. Basic trigonometric
Roberto s Notes on Integral Calculus Chapter : Integration methods Section 7 Trigonometric integrals by basic methods What you need to know already: Integrals of basic trigonometric functions. Basic trigonometric
Integration by Tables and Other Integration Techniques. Integration by Tables
 3346_86.qd //4 3:8 PM Page 56 SECTION 8.6 and Other Integration Techniques 56 Section 8.6 and Other Integration Techniques Evaluate an indefinite integral using a table of integrals. Evaluate an indefinite
3346_86.qd //4 3:8 PM Page 56 SECTION 8.6 and Other Integration Techniques 56 Section 8.6 and Other Integration Techniques Evaluate an indefinite integral using a table of integrals. Evaluate an indefinite
Introduction to Differential Equations
 Math0 Lecture # Introduction to Differential Equations Basic definitions Definition : (What is a DE?) A differential equation (DE) is an equation that involves some of the derivatives (or differentials)
Math0 Lecture # Introduction to Differential Equations Basic definitions Definition : (What is a DE?) A differential equation (DE) is an equation that involves some of the derivatives (or differentials)
Determinants. We said in Section 3.3 that a 2 2 matrix a b. Determinant of an n n Matrix
 3.6 Determinants We said in Section 3.3 that a 2 2 matri a b is invertible if and onl if its c d erminant, ad bc, is nonzero, and we saw the erminant used in the formula for the inverse of a 2 2 matri.
3.6 Determinants We said in Section 3.3 that a 2 2 matri a b is invertible if and onl if its c d erminant, ad bc, is nonzero, and we saw the erminant used in the formula for the inverse of a 2 2 matri.
13.1. For further details concerning the physics involved and animations of the trajectories of the particles, see the following websites:
 8 CHAPTER 3 VECTOR FUNCTIONS N Some computer algebra sstems provie us with a clearer picture of a space curve b enclosing it in a tube. Such a plot enables us to see whether one part of a curve passes
8 CHAPTER 3 VECTOR FUNCTIONS N Some computer algebra sstems provie us with a clearer picture of a space curve b enclosing it in a tube. Such a plot enables us to see whether one part of a curve passes
Fourier Analysis Fourier Series C H A P T E R 1 1
 C H A P T E R Fourier Analysis 474 This chapter on Fourier analysis covers three broad areas: Fourier series in Secs...4, more general orthonormal series called Sturm iouville epansions in Secs..5 and.6
C H A P T E R Fourier Analysis 474 This chapter on Fourier analysis covers three broad areas: Fourier series in Secs...4, more general orthonormal series called Sturm iouville epansions in Secs..5 and.6
Algebra/Pre-calc Review
 Algebra/Pre-calc Review The following pages contain various algebra and pre-calculus topics that are used in the stud of calculus. These pages were designed so that students can refresh their knowledge
Algebra/Pre-calc Review The following pages contain various algebra and pre-calculus topics that are used in the stud of calculus. These pages were designed so that students can refresh their knowledge
The Fundamental Theorem of Calculus Part 3
 The Fundamental Theorem of Calculus Part FTC Part Worksheet 5: Basic Rules, Initial Value Problems, Rewriting Integrands A. It s time to find anti-derivatives algebraically. Instead of saying the anti-derivative
The Fundamental Theorem of Calculus Part FTC Part Worksheet 5: Basic Rules, Initial Value Problems, Rewriting Integrands A. It s time to find anti-derivatives algebraically. Instead of saying the anti-derivative
Differential Equations
 6 Differential Equations In this chapter, ou will stu one of the most important applications of calculus differential equations. You will learn several methods for solving different tpes of differential
6 Differential Equations In this chapter, ou will stu one of the most important applications of calculus differential equations. You will learn several methods for solving different tpes of differential
In this note we will evaluate the limits of some indeterminate forms using L Hôpital s Rule. Indeterminate Forms and 0 0. f(x)
 L Hôpital s Rule In this note we will evaluate the its of some indeterminate forms using L Hôpital s Rule. Indeterminate Forms and 0 0 f() Suppose a f() = 0 and a g() = 0. Then a g() the indeterminate
L Hôpital s Rule In this note we will evaluate the its of some indeterminate forms using L Hôpital s Rule. Indeterminate Forms and 0 0 f() Suppose a f() = 0 and a g() = 0. Then a g() the indeterminate
b. Create a graph that gives a more complete representation of f.
 or Use Onl in Pilot Program F 96 Chapter Limits 6 7. Steep secant lines a. Given the graph of f in the following figures, find the slope of the secant line that passes through, and h, f h in terms of h,
or Use Onl in Pilot Program F 96 Chapter Limits 6 7. Steep secant lines a. Given the graph of f in the following figures, find the slope of the secant line that passes through, and h, f h in terms of h,
LESSON #48 - INTEGER EXPONENTS COMMON CORE ALGEBRA II
 LESSON #8 - INTEGER EXPONENTS COMMON CORE ALGEBRA II We just finished our review of linear functions. Linear functions are those that grow b equal differences for equal intervals. In this unit we will
LESSON #8 - INTEGER EXPONENTS COMMON CORE ALGEBRA II We just finished our review of linear functions. Linear functions are those that grow b equal differences for equal intervals. In this unit we will
Math098 Practice Final Test
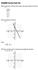 Math098 Practice Final Test Find an equation of the line that contains the points listed in the table. 1) 0-6 1-2 -4 3-3 4-2 Find an equation of the line. 2) 10-10 - 10 - -10 Solve. 3) 2 = 3 + 4 Find the
Math098 Practice Final Test Find an equation of the line that contains the points listed in the table. 1) 0-6 1-2 -4 3-3 4-2 Find an equation of the line. 2) 10-10 - 10 - -10 Solve. 3) 2 = 3 + 4 Find the
Properties of Limits
 33460_003qd //04 :3 PM Page 59 SECTION 3 Evaluating Limits Analticall 59 Section 3 Evaluating Limits Analticall Evaluate a it using properties of its Develop and use a strateg for finding its Evaluate
33460_003qd //04 :3 PM Page 59 SECTION 3 Evaluating Limits Analticall 59 Section 3 Evaluating Limits Analticall Evaluate a it using properties of its Develop and use a strateg for finding its Evaluate
Infinite Limits. Let f be the function given by. f x 3 x 2.
 0_005.qd //0 :07 PM Page 8 SECTION.5 Infinite Limits 8, as Section.5, as + f() = f increases and decreases without bound as approaches. Figure.9 Infinite Limits Determine infinite its from the left and
0_005.qd //0 :07 PM Page 8 SECTION.5 Infinite Limits 8, as Section.5, as + f() = f increases and decreases without bound as approaches. Figure.9 Infinite Limits Determine infinite its from the left and
Analytic Geometry in Three Dimensions
 Analtic Geometr in Three Dimensions. The Three-Dimensional Coordinate Sstem. Vectors in Space. The Cross Product of Two Vectors. Lines and Planes in Space The three-dimensional coordinate sstem is used
Analtic Geometr in Three Dimensions. The Three-Dimensional Coordinate Sstem. Vectors in Space. The Cross Product of Two Vectors. Lines and Planes in Space The three-dimensional coordinate sstem is used
Brief Notes on Differential Equations
 Brief Notes on Differential Equations (A) Searable First-Order Differential Equations Solve the following differential equations b searation of variables: (a) (b) Solution ( 1 ) (a) The ODE becomes d and
Brief Notes on Differential Equations (A) Searable First-Order Differential Equations Solve the following differential equations b searation of variables: (a) (b) Solution ( 1 ) (a) The ODE becomes d and
McKinney High School AP Calculus Summer Packet
 McKinne High School AP Calculus Summer Packet (for students entering AP Calculus AB or AP Calculus BC) Name:. This packet is to be handed in to our Calculus teacher the first week of school.. ALL work
McKinne High School AP Calculus Summer Packet (for students entering AP Calculus AB or AP Calculus BC) Name:. This packet is to be handed in to our Calculus teacher the first week of school.. ALL work
Exact Equations. M(x,y) + N(x,y) y = 0, M(x,y) dx + N(x,y) dy = 0. M(x,y) + N(x,y) y = 0
 Eact Equations An eact equation is a first order differential equation that can be written in the form M(, + N(,, provided that there eists a function ψ(, such that = M (, and N(, = Note : Often the equation
Eact Equations An eact equation is a first order differential equation that can be written in the form M(, + N(,, provided that there eists a function ψ(, such that = M (, and N(, = Note : Often the equation
8.3. Integration of Rational Functions by Partial Fractions. 570 Chapter 8: Techniques of Integration
 570 Chapter 8: Techniques of Integration 8.3 Integration of Rational Functions b Partial Fractions This section shows how to epress a rational function (a quotient of polnomials) as a sum of simpler fractions,
570 Chapter 8: Techniques of Integration 8.3 Integration of Rational Functions b Partial Fractions This section shows how to epress a rational function (a quotient of polnomials) as a sum of simpler fractions,
Differential Equations Practice: 2nd Order Linear: Nonhomogeneous Equations: Variation of Parameters Page 1
 Differential Equations Practice: 2nd Order Linear: Nonhomogeneous Equations: Variation of Parameters Page Questions Example (3.6.) Find a particular solution of the differential equation y 5y + 6y = 2e
Differential Equations Practice: 2nd Order Linear: Nonhomogeneous Equations: Variation of Parameters Page Questions Example (3.6.) Find a particular solution of the differential equation y 5y + 6y = 2e
Math 123 Summary of Important Algebra & Trigonometry Concepts Chapter 1 & Appendix D, Stewart, Calculus Early Transcendentals
 Math Summar of Important Algebra & Trigonometr Concepts Chapter & Appendi D, Stewart, Calculus Earl Transcendentals Function a rule that assigns to each element in a set D eactl one element, called f (
Math Summar of Important Algebra & Trigonometr Concepts Chapter & Appendi D, Stewart, Calculus Earl Transcendentals Function a rule that assigns to each element in a set D eactl one element, called f (
Fixed Point Theorem and Sequences in One or Two Dimensions
 Fied Point Theorem and Sequences in One or Two Dimensions Dr. Wei-Chi Yang Let us consider a recursive sequence of n+ = n + sin n and the initial value can be an real number. Then we would like to ask
Fied Point Theorem and Sequences in One or Two Dimensions Dr. Wei-Chi Yang Let us consider a recursive sequence of n+ = n + sin n and the initial value can be an real number. Then we would like to ask
CHAPTER 3 Applications of Differentiation
 CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. 0 Section. Rolle s Theorem and the Mean Value Theorem. 07 Section. Increasing and Decreasing Functions and the First
CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. 0 Section. Rolle s Theorem and the Mean Value Theorem. 07 Section. Increasing and Decreasing Functions and the First
MA 15800, Summer 2016 Lesson 25 Notes Solving a System of Equations by substitution (or elimination) Matrices. 2 A System of Equations
 MA 800, Summer 06 Lesson Notes Solving a Sstem of Equations b substitution (or elimination) Matrices Consider the graphs of the two equations below. A Sstem of Equations From our mathematics eperience,
MA 800, Summer 06 Lesson Notes Solving a Sstem of Equations b substitution (or elimination) Matrices Consider the graphs of the two equations below. A Sstem of Equations From our mathematics eperience,
Mathematics 309 Conic sections and their applicationsn. Chapter 2. Quadric figures. ai,j x i x j + b i x i + c =0. 1. Coordinate changes
 Mathematics 309 Conic sections and their applicationsn Chapter 2. Quadric figures In this chapter want to outline quickl how to decide what figure associated in 2D and 3D to quadratic equations look like.
Mathematics 309 Conic sections and their applicationsn Chapter 2. Quadric figures In this chapter want to outline quickl how to decide what figure associated in 2D and 3D to quadratic equations look like.
Daily Lessons and Assessments for AP* Calculus AB, A Complete Course Page 584 Mark Sparks 2012
 The Second Fundamental Theorem of Calculus Functions Defined by Integrals Given the functions, f(t), below, use F( ) f ( t) dt to find F() and F () in terms of.. f(t) = 4t t. f(t) = cos t Given the functions,
The Second Fundamental Theorem of Calculus Functions Defined by Integrals Given the functions, f(t), below, use F( ) f ( t) dt to find F() and F () in terms of.. f(t) = 4t t. f(t) = cos t Given the functions,
A.5. Complex Numbers AP-12. The Development of the Real Numbers
 AP- A.5 Comple Numbers Comple numbers are epressions of the form a + ib, where a and b are real numbers and i is a smbol for -. Unfortunatel, the words real and imaginar have connotations that somehow
AP- A.5 Comple Numbers Comple numbers are epressions of the form a + ib, where a and b are real numbers and i is a smbol for -. Unfortunatel, the words real and imaginar have connotations that somehow
Worksheet Week 7 Section
 Worksheet Week 7 Section 8.. 8.4. This worksheet is for improvement of your mathematical writing skill. Writing using correct mathematical epression and steps is really important part of doing math. Please
Worksheet Week 7 Section 8.. 8.4. This worksheet is for improvement of your mathematical writing skill. Writing using correct mathematical epression and steps is really important part of doing math. Please
TImath.com Calculus. Topic: Techniques of Integration Derive the formula for integration by parts and use it to compute integrals
 Integration by Parts ID: 985 Time required 45 minutes Activity Overview In previous activities, students have eplored the differential calculus through investigations of the methods of first principles,
Integration by Parts ID: 985 Time required 45 minutes Activity Overview In previous activities, students have eplored the differential calculus through investigations of the methods of first principles,
Chapter 1 Overview: Review of Derivatives
 Chapter Overview: Review of Derivatives The purpose of this chapter is to review the how of ifferentiation. We will review all the erivative rules learne last year in PreCalculus. In the net several chapters,
Chapter Overview: Review of Derivatives The purpose of this chapter is to review the how of ifferentiation. We will review all the erivative rules learne last year in PreCalculus. In the net several chapters,
13.1. For further details concerning the physics involved and animations of the trajectories of the particles, see the following websites:
 8 CHAPTER VECTOR FUNCTIONS N Some computer algebra sstems provide us with a clearer picture of a space curve b enclosing it in a tube. Such a plot enables us to see whether one part of a curve passes in
8 CHAPTER VECTOR FUNCTIONS N Some computer algebra sstems provide us with a clearer picture of a space curve b enclosing it in a tube. Such a plot enables us to see whether one part of a curve passes in
Increasing and Decreasing Functions and the First Derivative Test. Increasing and Decreasing Functions. Video
 SECTION and Decreasing Functions and the First Derivative Test 79 Section and Decreasing Functions and the First Derivative Test Determine intervals on which a unction is increasing or decreasing Appl
SECTION and Decreasing Functions and the First Derivative Test 79 Section and Decreasing Functions and the First Derivative Test Determine intervals on which a unction is increasing or decreasing Appl
