Applied Statistics I
|
|
|
- Camron Payne
- 6 years ago
- Views:
Transcription
1 Applied Statistics I Liang Zhang Department of Mathematics, University of Utah July 8, 2008 Liang Zhang (UofU) Applied Statistics I July 8, / 15
2 Distribution for Sample Mean Liang Zhang (UofU) Applied Statistics I July 8, / 15
3 Distribution for Sample Mean Example (Problem 54) Suppose the sediment density (g/cm) of a randomly selected specimen from a certain region is normally distributed with mean 2.65 and standard deviation.85 (suggested in Modeling Sediment and Water Column Interactions for Hydrophobic Pollutants, Water Research, 1984: ). Liang Zhang (UofU) Applied Statistics I July 8, / 15
4 Distribution for Sample Mean Example (Problem 54) Suppose the sediment density (g/cm) of a randomly selected specimen from a certain region is normally distributed with mean 2.65 and standard deviation.85 (suggested in Modeling Sediment and Water Column Interactions for Hydrophobic Pollutants, Water Research, 1984: ). a. If a random sample of 25 specimens is selected, what is the probability that the sample average sediment density is at most 3.00? Liang Zhang (UofU) Applied Statistics I July 8, / 15
5 Distribution for Sample Mean Example (Problem 54) Suppose the sediment density (g/cm) of a randomly selected specimen from a certain region is normally distributed with mean 2.65 and standard deviation.85 (suggested in Modeling Sediment and Water Column Interactions for Hydrophobic Pollutants, Water Research, 1984: ). a. If a random sample of 25 specimens is selected, what is the probability that the sample average sediment density is at most 3.00? b. How large a sample size would be required to ensure that the above probability is at least.99? Liang Zhang (UofU) Applied Statistics I July 8, / 15
6 Distribution for Sample Mean Liang Zhang (UofU) Applied Statistics I July 8, / 15
7 Distribution for Sample Mean The Central Limit Theorem (CLT) Let X 1, X 2,..., X n be a random sample from a distribution with mean value µ and standard deviation σ. Then if n is sufficiently large, X has approximately a normal distribution with mean value µ and standard deviation σ/ n, and T 0 also has approximately a normal distribution with mean value nµ and standard deviation nσ. The larger the value of n, the better the approximation. Liang Zhang (UofU) Applied Statistics I July 8, / 15
8 Distribution for Sample Mean The Central Limit Theorem (CLT) Let X 1, X 2,..., X n be a random sample from a distribution with mean value µ and standard deviation σ. Then if n is sufficiently large, X has approximately a normal distribution with mean value µ and standard deviation σ/ n, and T 0 also has approximately a normal distribution with mean value nµ and standard deviation nσ. The larger the value of n, the better the approximation. Remark: 1. As long as n is sufficiently large, CLT is applicable no matter X i s are discrete random variables or continuous random variables. Liang Zhang (UofU) Applied Statistics I July 8, / 15
9 Distribution for Sample Mean The Central Limit Theorem (CLT) Let X 1, X 2,..., X n be a random sample from a distribution with mean value µ and standard deviation σ. Then if n is sufficiently large, X has approximately a normal distribution with mean value µ and standard deviation σ/ n, and T 0 also has approximately a normal distribution with mean value nµ and standard deviation nσ. The larger the value of n, the better the approximation. Remark: 1. As long as n is sufficiently large, CLT is applicable no matter X i s are discrete random variables or continuous random variables. 2. How large should n be such that CLT is applicable? Liang Zhang (UofU) Applied Statistics I July 8, / 15
10 Distribution for Sample Mean The Central Limit Theorem (CLT) Let X 1, X 2,..., X n be a random sample from a distribution with mean value µ and standard deviation σ. Then if n is sufficiently large, X has approximately a normal distribution with mean value µ and standard deviation σ/ n, and T 0 also has approximately a normal distribution with mean value nµ and standard deviation nσ. The larger the value of n, the better the approximation. Remark: 1. As long as n is sufficiently large, CLT is applicable no matter X i s are discrete random variables or continuous random variables. 2. How large should n be such that CLT is applicable? Generally, if n > 30, CLT can be used. Liang Zhang (UofU) Applied Statistics I July 8, / 15
11 Distribution for Sample Mean Liang Zhang (UofU) Applied Statistics I July 8, / 15
12 Distribution for Sample Mean Example (Problem 49) There are 40 students in an elementary statistics class. On the basis of years of experience, the instructor knows that the time needed to grade a randomly chosen first examination paper is a random variable with an expected value of 6 min and a standard deviation of 6 min. Liang Zhang (UofU) Applied Statistics I July 8, / 15
13 Distribution for Sample Mean Example (Problem 49) There are 40 students in an elementary statistics class. On the basis of years of experience, the instructor knows that the time needed to grade a randomly chosen first examination paper is a random variable with an expected value of 6 min and a standard deviation of 6 min. a. If grading times are independent and the instructor begins grading at 6:50pm and grades continuously, what is the (approximate) probability that he is through grading before the 11:00pm TV news begins? Liang Zhang (UofU) Applied Statistics I July 8, / 15
14 Distribution for Sample Mean Example (Problem 49) There are 40 students in an elementary statistics class. On the basis of years of experience, the instructor knows that the time needed to grade a randomly chosen first examination paper is a random variable with an expected value of 6 min and a standard deviation of 6 min. a. If grading times are independent and the instructor begins grading at 6:50pm and grades continuously, what is the (approximate) probability that he is through grading before the 11:00pm TV news begins? b. If the sports report begins at 11:10pm, what is the probability that he misses part of the report if he waits unitl grading is done before turning on the TV? Liang Zhang (UofU) Applied Statistics I July 8, / 15
15 Distribution for Sample Mean Liang Zhang (UofU) Applied Statistics I July 8, / 15
16 Distribution for Sample Mean The original version of CLT The Central Limit Theorem (CLT) Let X 1, X 2,... be a sequence of i.i.d. random variables from a distribution with mean value µ and standard deviation σ. Define random variables n i=1 Y n = X i nµ for n = 1, 2,... nσ Then as n, Y n has approximately a normal distribution. Liang Zhang (UofU) Applied Statistics I July 8, / 15
17 Distribution for Sample Mean Liang Zhang (UofU) Applied Statistics I July 8, / 15
18 Distribution for Sample Mean Corollary Let X 1, X 2,..., X n be a random sample from a distribution for which only positive values are possible [P(X i > 0) = 1]. Then if n is sufficiently large, the product Y = X 1 X 2 X n has approximately a lognormal distribution. Liang Zhang (UofU) Applied Statistics I July 8, / 15
19 Distribution for Linear Combinations Liang Zhang (UofU) Applied Statistics I July 8, / 15
20 Distribution for Linear Combinations Proposition Let X 1, X 2,..., X n have mean values µ 1, µ 2,..., µ n, respectively, and variances σ 2 1, σ2 2,..., σ2 n, respectively. 1.Whether or not the X i s are independent, E(a 1 X 1 + a 2 X a n X n ) = a 1 E(X 1 ) + a 2 E(X 2 ) + + a n E(X n ) 2. If X 1, X 2,..., X n are independent, = a 1 µ 1 + a 2 µ a n µ n V (a 1 X 1 + a 2 X a n X n ) = a 2 1V (X 1 ) + a 2 2V (X 2 ) + + a 2 nv (X n ) = a 1 σ a 2 σ a n σ 2 n Liang Zhang (UofU) Applied Statistics I July 8, / 15
21 Distribution for Linear Combinations Liang Zhang (UofU) Applied Statistics I July 8, / 15
22 Distribution for Linear Combinations Proposition (Continued) Let X 1, X 2,..., X n have mean values µ 1, µ 2,..., µ n, respectively, and variances σ 2 1, σ2 2,..., σ2 n, respectively. 3. More generally, for any X 1, X 2,..., X n V (a 1 X 1 + a 2 X a n X n ) = n n a i a j Cov(X i, X j ) i=1 j=1 Liang Zhang (UofU) Applied Statistics I July 8, / 15
23 Distribution for Linear Combinations Proposition (Continued) Let X 1, X 2,..., X n have mean values µ 1, µ 2,..., µ n, respectively, and variances σ 2 1, σ2 2,..., σ2 n, respectively. 3. More generally, for any X 1, X 2,..., X n V (a 1 X 1 + a 2 X a n X n ) = n n a i a j Cov(X i, X j ) i=1 j=1 We call a 1 X 1 + a 2 X a n X n a linear combination of the X i s. Liang Zhang (UofU) Applied Statistics I July 8, / 15
24 Distribution for Linear Combinations Liang Zhang (UofU) Applied Statistics I July 8, / 15
25 Distribution for Linear Combinations Example (Problem 64) Suppose your waiting time for a bus in the morning is uniformly distributed on [0,8], whereas waiting time in the evening is uniformly distributed on [0,10] independent of morning waiting time. Liang Zhang (UofU) Applied Statistics I July 8, / 15
26 Distribution for Linear Combinations Example (Problem 64) Suppose your waiting time for a bus in the morning is uniformly distributed on [0,8], whereas waiting time in the evening is uniformly distributed on [0,10] independent of morning waiting time. a. If you take the bus each morning and evening for a week, what is your total expected waiting time? Liang Zhang (UofU) Applied Statistics I July 8, / 15
27 Distribution for Linear Combinations Example (Problem 64) Suppose your waiting time for a bus in the morning is uniformly distributed on [0,8], whereas waiting time in the evening is uniformly distributed on [0,10] independent of morning waiting time. a. If you take the bus each morning and evening for a week, what is your total expected waiting time? b. What is the variance of your total waiting time? Liang Zhang (UofU) Applied Statistics I July 8, / 15
28 Distribution for Linear Combinations Example (Problem 64) Suppose your waiting time for a bus in the morning is uniformly distributed on [0,8], whereas waiting time in the evening is uniformly distributed on [0,10] independent of morning waiting time. a. If you take the bus each morning and evening for a week, what is your total expected waiting time? b. What is the variance of your total waiting time? c. What are the expected value and variance of the difference between morning and evening waiting times on a given day? Liang Zhang (UofU) Applied Statistics I July 8, / 15
29 Distribution for Linear Combinations Example (Problem 64) Suppose your waiting time for a bus in the morning is uniformly distributed on [0,8], whereas waiting time in the evening is uniformly distributed on [0,10] independent of morning waiting time. a. If you take the bus each morning and evening for a week, what is your total expected waiting time? b. What is the variance of your total waiting time? c. What are the expected value and variance of the difference between morning and evening waiting times on a given day? d. What are the expected value and variance of the difference between total morning waiting time and total evening waiting time on a particular week? Liang Zhang (UofU) Applied Statistics I July 8, / 15
30 Distribution for Linear Combinations Liang Zhang (UofU) Applied Statistics I July 8, / 15
31 Distribution for Linear Combinations Corollary E(X 1 X 2 ) = E(X 1 ) E(X 2 ) and, if X 1 and X 2 are independent, V (X 1 X 2 ) = V (X 1 ) + V (X 2 ). Liang Zhang (UofU) Applied Statistics I July 8, / 15
32 Distribution for Linear Combinations Corollary E(X 1 X 2 ) = E(X 1 ) E(X 2 ) and, if X 1 and X 2 are independent, V (X 1 X 2 ) = V (X 1 ) + V (X 2 ). Proposition If X 1, X 2,..., X n are independent, normally distributed rv s (with possibly different means and/or variances), then any linear combination of the X i s also has a normal distribution. In particular, the difference X 1 X 2 between two independent, normally distributed variables is itself normally distributed. Liang Zhang (UofU) Applied Statistics I July 8, / 15
33 Distribution for Linear Combinations Liang Zhang (UofU) Applied Statistics I July 8, / 15
34 Distribution for Linear Combinations Example (Problem 62) Manufacture of a certain component requires three different maching operations. Machining time for each operation has a normal distribution, and the three times are independent of one another. The mean values are 15, 30, and 20min, respectively, and the standard deviations are 1, 2, and 1.5min, respectively. Liang Zhang (UofU) Applied Statistics I July 8, / 15
35 Distribution for Linear Combinations Example (Problem 62) Manufacture of a certain component requires three different maching operations. Machining time for each operation has a normal distribution, and the three times are independent of one another. The mean values are 15, 30, and 20min, respectively, and the standard deviations are 1, 2, and 1.5min, respectively. What is the probability that it takes at most 1 hour of machining time to produce a randomly selected component? Liang Zhang (UofU) Applied Statistics I July 8, / 15
36 Point Estimation Liang Zhang (UofU) Applied Statistics I July 8, / 15
37 Point Estimation Example (a variant of Problem 62, Ch5) Manufacture of a certain component requires three different maching operations. The total time for manufacturing one such component is known to have a normal distribution. However, the mean µ and variance σ 2 for the normal distribution are unknown. If we did an experiment in which we manufactured 10 components and record the operation time, and the sample time is given as following: time time What can we say about the population mean µ and population variance σ 2? Liang Zhang (UofU) Applied Statistics I July 8, / 15
38 Point Estimation Liang Zhang (UofU) Applied Statistics I July 8, / 15
39 Point Estimation Example (a variant of Problem 64, Ch5) Suppose the waiting time for a certain bus in the morning is uniformly distributed on [0, θ], where θ is unknown. If we record 10 waiting times as follwos: time time What can we say about the parameter θ? Liang Zhang (UofU) Applied Statistics I July 8, / 15
40 Point Estimation Liang Zhang (UofU) Applied Statistics I July 8, / 15
41 Point Estimation Definition A point estimate of a parameter θ is a single number that can be regarded as a sensible value for θ. A point estimate is obtained by selecting a suitable statistic and computing its value from the given sample data. The selected statistic is called the point estimator of θ. Liang Zhang (UofU) Applied Statistics I July 8, / 15
42 Point Estimation Definition A point estimate of a parameter θ is a single number that can be regarded as a sensible value for θ. A point estimate is obtained by selecting a suitable statistic and computing its value from the given sample data. The selected statistic is called the point estimator of θ. e.g. X = 10 i=1 X i/10 is a point estimator for µ for the normal distribution example. Liang Zhang (UofU) Applied Statistics I July 8, / 15
43 Point Estimation Definition A point estimate of a parameter θ is a single number that can be regarded as a sensible value for θ. A point estimate is obtained by selecting a suitable statistic and computing its value from the given sample data. The selected statistic is called the point estimator of θ. e.g. X = 10 i=1 X i/10 is a point estimator for µ for the normal distribution example. The largest sample data X 10,10 is a point estimator for θ for the uniform distribution example. Liang Zhang (UofU) Applied Statistics I July 8, / 15
44 Methods of Point Estimation Liang Zhang (UofU) Applied Statistics I July 8, / 15
45 Methods of Point Estimation Definition Let X 1, X 2,..., X n be a random sample from a distribution with pmf or pdf f (x). For k = 1, 2, 3,..., the kth population moment, or kth moment of the distribution f (x), is E(X k ). The kth sample moment is 1 n n i=1 X k i. Liang Zhang (UofU) Applied Statistics I July 8, / 15
46 Methods of Point Estimation Definition Let X 1, X 2,..., X n be a random sample from a distribution with pmf or pdf f (x). For k = 1, 2, 3,..., the kth population moment, or kth moment of the distribution f (x), is E(X k ). The kth sample moment is 1 n n i=1 X k i. Definition Let X 1, X 2,..., X n be a random sample from a distribution with pmf or pdf f (x; θ 1,..., θ m ), where θ 1,..., θ m are parameters whose values are unknown. Then the moment estimators ˆθ 1,..., ˆθ m are obtained by equating the first m sample moments to the corresponding first m population moments and solving for θ 1,..., θ m. Liang Zhang (UofU) Applied Statistics I July 8, / 15
STAT Chapter 5 Continuous Distributions
 STAT 270 - Chapter 5 Continuous Distributions June 27, 2012 Shirin Golchi () STAT270 June 27, 2012 1 / 59 Continuous rv s Definition: X is a continuous rv if it takes values in an interval, i.e., range
STAT 270 - Chapter 5 Continuous Distributions June 27, 2012 Shirin Golchi () STAT270 June 27, 2012 1 / 59 Continuous rv s Definition: X is a continuous rv if it takes values in an interval, i.e., range
Week 9 The Central Limit Theorem and Estimation Concepts
 Week 9 and Estimation Concepts Week 9 and Estimation Concepts Week 9 Objectives 1 The Law of Large Numbers and the concept of consistency of averages are introduced. The condition of existence of the population
Week 9 and Estimation Concepts Week 9 and Estimation Concepts Week 9 Objectives 1 The Law of Large Numbers and the concept of consistency of averages are introduced. The condition of existence of the population
Applied Statistics I
 Applied Statistics I Liang Zhang Department of Mathematics, University of Utah July 17, 2008 Liang Zhang (UofU) Applied Statistics I July 17, 2008 1 / 23 Large-Sample Confidence Intervals Liang Zhang (UofU)
Applied Statistics I Liang Zhang Department of Mathematics, University of Utah July 17, 2008 Liang Zhang (UofU) Applied Statistics I July 17, 2008 1 / 23 Large-Sample Confidence Intervals Liang Zhang (UofU)
6 Central Limit Theorem. (Chs 6.4, 6.5)
 6 Central Limit Theorem (Chs 6.4, 6.5) Motivating Example In the next few weeks, we will be focusing on making statistical inference about the true mean of a population by using sample datasets. Examples?
6 Central Limit Theorem (Chs 6.4, 6.5) Motivating Example In the next few weeks, we will be focusing on making statistical inference about the true mean of a population by using sample datasets. Examples?
Review. December 4 th, Review
 December 4 th, 2017 Att. Final exam: Course evaluation Friday, 12/14/2018, 10:30am 12:30pm Gore Hall 115 Overview Week 2 Week 4 Week 7 Week 10 Week 12 Chapter 6: Statistics and Sampling Distributions Chapter
December 4 th, 2017 Att. Final exam: Course evaluation Friday, 12/14/2018, 10:30am 12:30pm Gore Hall 115 Overview Week 2 Week 4 Week 7 Week 10 Week 12 Chapter 6: Statistics and Sampling Distributions Chapter
Definition A random variable X is said to have a Weibull distribution with parameters α and β (α > 0, β > 0) if the pdf of X is
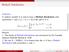 Weibull Distribution Definition A random variable X is said to have a Weibull distribution with parameters α and β (α > 0, β > 0) if the pdf of X is { α β x α 1 e f (x; α, β) = α (x/β)α x 0 0 x < 0 Remark:
Weibull Distribution Definition A random variable X is said to have a Weibull distribution with parameters α and β (α > 0, β > 0) if the pdf of X is { α β x α 1 e f (x; α, β) = α (x/β)α x 0 0 x < 0 Remark:
Statistics and Sampling distributions
 Statistics and Sampling distributions a statistic is a numerical summary of sample data. It is a rv. The distribution of a statistic is called its sampling distribution. The rv s X 1, X 2,, X n are said
Statistics and Sampling distributions a statistic is a numerical summary of sample data. It is a rv. The distribution of a statistic is called its sampling distribution. The rv s X 1, X 2,, X n are said
Continuous distributions
 CHAPTER 7 Continuous distributions 7.. Introduction A r.v. X is said to have a continuous distribution if there exists a nonnegative function f such that P(a X b) = ˆ b a f(x)dx for every a and b. distribution.)
CHAPTER 7 Continuous distributions 7.. Introduction A r.v. X is said to have a continuous distribution if there exists a nonnegative function f such that P(a X b) = ˆ b a f(x)dx for every a and b. distribution.)
Probability and Statistics Notes
 Probability and Statistics Notes Chapter Five Jesse Crawford Department of Mathematics Tarleton State University Spring 2011 (Tarleton State University) Chapter Five Notes Spring 2011 1 / 37 Outline 1
Probability and Statistics Notes Chapter Five Jesse Crawford Department of Mathematics Tarleton State University Spring 2011 (Tarleton State University) Chapter Five Notes Spring 2011 1 / 37 Outline 1
Probability Distributions Columns (a) through (d)
 Discrete Probability Distributions Columns (a) through (d) Probability Mass Distribution Description Notes Notation or Density Function --------------------(PMF or PDF)-------------------- (a) (b) (c)
Discrete Probability Distributions Columns (a) through (d) Probability Mass Distribution Description Notes Notation or Density Function --------------------(PMF or PDF)-------------------- (a) (b) (c)
Mathematical statistics
 October 18 th, 2018 Lecture 16: Midterm review Countdown to mid-term exam: 7 days Week 1 Chapter 1: Probability review Week 2 Week 4 Week 7 Chapter 6: Statistics Chapter 7: Point Estimation Chapter 8:
October 18 th, 2018 Lecture 16: Midterm review Countdown to mid-term exam: 7 days Week 1 Chapter 1: Probability review Week 2 Week 4 Week 7 Chapter 6: Statistics Chapter 7: Point Estimation Chapter 8:
CHAPTER 5. Jointly Probability Mass Function for Two Discrete Distributed Random Variables:
 CHAPTER 5 Jointl Distributed Random Variable There are some situations that experiment contains more than one variable and researcher interested in to stud joint behavior of several variables at the same
CHAPTER 5 Jointl Distributed Random Variable There are some situations that experiment contains more than one variable and researcher interested in to stud joint behavior of several variables at the same
Midterm #1. Lecture 10: Joint Distributions and the Law of Large Numbers. Joint Distributions - Example, cont. Joint Distributions - Example
 Midterm #1 Midterm 1 Lecture 10: and the Law of Large Numbers Statistics 104 Colin Rundel February 0, 01 Exam will be passed back at the end of class Exam was hard, on the whole the class did well: Mean:
Midterm #1 Midterm 1 Lecture 10: and the Law of Large Numbers Statistics 104 Colin Rundel February 0, 01 Exam will be passed back at the end of class Exam was hard, on the whole the class did well: Mean:
COMPSCI 240: Reasoning Under Uncertainty
 COMPSCI 240: Reasoning Under Uncertainty Andrew Lan and Nic Herndon University of Massachusetts at Amherst Spring 2019 Lecture 20: Central limit theorem & The strong law of large numbers Markov and Chebyshev
COMPSCI 240: Reasoning Under Uncertainty Andrew Lan and Nic Herndon University of Massachusetts at Amherst Spring 2019 Lecture 20: Central limit theorem & The strong law of large numbers Markov and Chebyshev
ST 371 (IX): Theories of Sampling Distributions
 ST 371 (IX): Theories of Sampling Distributions 1 Sample, Population, Parameter and Statistic The major use of inferential statistics is to use information from a sample to infer characteristics about
ST 371 (IX): Theories of Sampling Distributions 1 Sample, Population, Parameter and Statistic The major use of inferential statistics is to use information from a sample to infer characteristics about
Example continued. Math 425 Intro to Probability Lecture 37. Example continued. Example
 continued : Coin tossing Math 425 Intro to Probability Lecture 37 Kenneth Harris kaharri@umich.edu Department of Mathematics University of Michigan April 8, 2009 Consider a Bernoulli trials process with
continued : Coin tossing Math 425 Intro to Probability Lecture 37 Kenneth Harris kaharri@umich.edu Department of Mathematics University of Michigan April 8, 2009 Consider a Bernoulli trials process with
EXAM # 3 PLEASE SHOW ALL WORK!
 Stat 311, Summer 2018 Name EXAM # 3 PLEASE SHOW ALL WORK! Problem Points Grade 1 30 2 20 3 20 4 30 Total 100 1. A socioeconomic study analyzes two discrete random variables in a certain population of households
Stat 311, Summer 2018 Name EXAM # 3 PLEASE SHOW ALL WORK! Problem Points Grade 1 30 2 20 3 20 4 30 Total 100 1. A socioeconomic study analyzes two discrete random variables in a certain population of households
Probability Distributions for Discrete RV
 An example: Assume we toss a coin 3 times and record the outcomes. Let X i be a random variable defined by { 1, if the i th outcome is Head; X i = 0, if the i th outcome is Tail; Let X be the random variable
An example: Assume we toss a coin 3 times and record the outcomes. Let X i be a random variable defined by { 1, if the i th outcome is Head; X i = 0, if the i th outcome is Tail; Let X be the random variable
Quick Tour of Basic Probability Theory and Linear Algebra
 Quick Tour of and Linear Algebra Quick Tour of and Linear Algebra CS224w: Social and Information Network Analysis Fall 2011 Quick Tour of and Linear Algebra Quick Tour of and Linear Algebra Outline Definitions
Quick Tour of and Linear Algebra Quick Tour of and Linear Algebra CS224w: Social and Information Network Analysis Fall 2011 Quick Tour of and Linear Algebra Quick Tour of and Linear Algebra Outline Definitions
Practice Problem - Skewness of Bernoulli Random Variable. Lecture 7: Joint Distributions and the Law of Large Numbers. Joint Distributions - Example
 A little more E(X Practice Problem - Skewness of Bernoulli Random Variable Lecture 7: and the Law of Large Numbers Sta30/Mth30 Colin Rundel February 7, 014 Let X Bern(p We have shown that E(X = p Var(X
A little more E(X Practice Problem - Skewness of Bernoulli Random Variable Lecture 7: and the Law of Large Numbers Sta30/Mth30 Colin Rundel February 7, 014 Let X Bern(p We have shown that E(X = p Var(X
STAT 430/510: Lecture 16
 STAT 430/510: Lecture 16 James Piette June 24, 2010 Updates HW4 is up on my website. It is due next Mon. (June 28th). Starting today back at section 6.7 and will begin Ch. 7. Joint Distribution of Functions
STAT 430/510: Lecture 16 James Piette June 24, 2010 Updates HW4 is up on my website. It is due next Mon. (June 28th). Starting today back at section 6.7 and will begin Ch. 7. Joint Distribution of Functions
Applied Statistics I
 Applied Statistics I Liang Zhang Department of Mathematics, University of Utah June 17, 2008 Liang Zhang (UofU) Applied Statistics I June 17, 2008 1 / 22 Random Variables Definition A dicrete random variable
Applied Statistics I Liang Zhang Department of Mathematics, University of Utah June 17, 2008 Liang Zhang (UofU) Applied Statistics I June 17, 2008 1 / 22 Random Variables Definition A dicrete random variable
Distributions of linear combinations
 Distributions of linear combinations CE 311S MORE THAN TWO RANDOM VARIABLES The same concepts used for two random variables can be applied to three or more random variables, but they are harder to visualize
Distributions of linear combinations CE 311S MORE THAN TWO RANDOM VARIABLES The same concepts used for two random variables can be applied to three or more random variables, but they are harder to visualize
Chapter 4: Continuous Random Variables and Probability Distributions
 Chapter 4: and Probability Distributions Walid Sharabati Purdue University February 14, 2014 Professor Sharabati (Purdue University) Spring 2014 (Slide 1 of 37) Chapter Overview Continuous random variables
Chapter 4: and Probability Distributions Walid Sharabati Purdue University February 14, 2014 Professor Sharabati (Purdue University) Spring 2014 (Slide 1 of 37) Chapter Overview Continuous random variables
Functions of Several Random Variables (Ch. 5.5)
 (Ch. 5.5) Iowa State University Mar 7, 2013 Iowa State University Mar 7, 2013 1 / 37 Outline Iowa State University Mar 7, 2013 2 / 37 several random variables We often consider functions of random variables
(Ch. 5.5) Iowa State University Mar 7, 2013 Iowa State University Mar 7, 2013 1 / 37 Outline Iowa State University Mar 7, 2013 2 / 37 several random variables We often consider functions of random variables
Mathematical statistics
 October 4 th, 2018 Lecture 12: Information Where are we? Week 1 Week 2 Week 4 Week 7 Week 10 Week 14 Probability reviews Chapter 6: Statistics and Sampling Distributions Chapter 7: Point Estimation Chapter
October 4 th, 2018 Lecture 12: Information Where are we? Week 1 Week 2 Week 4 Week 7 Week 10 Week 14 Probability reviews Chapter 6: Statistics and Sampling Distributions Chapter 7: Point Estimation Chapter
Estimation Theory. as Θ = (Θ 1,Θ 2,...,Θ m ) T. An estimator
 Estimation Theory Estimation theory deals with finding numerical values of interesting parameters from given set of data. We start with formulating a family of models that could describe how the data were
Estimation Theory Estimation theory deals with finding numerical values of interesting parameters from given set of data. We start with formulating a family of models that could describe how the data were
Course: ESO-209 Home Work: 1 Instructor: Debasis Kundu
 Home Work: 1 1. Describe the sample space when a coin is tossed (a) once, (b) three times, (c) n times, (d) an infinite number of times. 2. A coin is tossed until for the first time the same result appear
Home Work: 1 1. Describe the sample space when a coin is tossed (a) once, (b) three times, (c) n times, (d) an infinite number of times. 2. A coin is tossed until for the first time the same result appear
Math 494: Mathematical Statistics
 Math 494: Mathematical Statistics Instructor: Jimin Ding jmding@wustl.edu Department of Mathematics Washington University in St. Louis Class materials are available on course website (www.math.wustl.edu/
Math 494: Mathematical Statistics Instructor: Jimin Ding jmding@wustl.edu Department of Mathematics Washington University in St. Louis Class materials are available on course website (www.math.wustl.edu/
Joint p.d.f. and Independent Random Variables
 1 Joint p.d.f. and Independent Random Variables Let X and Y be two discrete r.v. s and let R be the corresponding space of X and Y. The joint p.d.f. of X = x and Y = y, denoted by f(x, y) = P(X = x, Y
1 Joint p.d.f. and Independent Random Variables Let X and Y be two discrete r.v. s and let R be the corresponding space of X and Y. The joint p.d.f. of X = x and Y = y, denoted by f(x, y) = P(X = x, Y
Some Assorted Formulae. Some confidence intervals: σ n. x ± z α/2. x ± t n 1;α/2 n. ˆp(1 ˆp) ˆp ± z α/2 n. χ 2 n 1;1 α/2. n 1;α/2
 STA 248 H1S MIDTERM TEST February 26, 2008 SURNAME: SOLUTIONS GIVEN NAME: STUDENT NUMBER: INSTRUCTIONS: Time: 1 hour and 50 minutes Aids allowed: calculator Tables of the standard normal, t and chi-square
STA 248 H1S MIDTERM TEST February 26, 2008 SURNAME: SOLUTIONS GIVEN NAME: STUDENT NUMBER: INSTRUCTIONS: Time: 1 hour and 50 minutes Aids allowed: calculator Tables of the standard normal, t and chi-square
STAT 135 Lab 3 Asymptotic MLE and the Method of Moments
 STAT 135 Lab 3 Asymptotic MLE and the Method of Moments Rebecca Barter February 9, 2015 Maximum likelihood estimation (a reminder) Maximum likelihood estimation Suppose that we have a sample, X 1, X 2,...,
STAT 135 Lab 3 Asymptotic MLE and the Method of Moments Rebecca Barter February 9, 2015 Maximum likelihood estimation (a reminder) Maximum likelihood estimation Suppose that we have a sample, X 1, X 2,...,
Continuous random variables
 Continuous random variables Continuous r.v. s take an uncountably infinite number of possible values. Examples: Heights of people Weights of apples Diameters of bolts Life lengths of light-bulbs We cannot
Continuous random variables Continuous r.v. s take an uncountably infinite number of possible values. Examples: Heights of people Weights of apples Diameters of bolts Life lengths of light-bulbs We cannot
ECE302 Exam 2 Version A April 21, You must show ALL of your work for full credit. Please leave fractions as fractions, but simplify them, etc.
 ECE32 Exam 2 Version A April 21, 214 1 Name: Solution Score: /1 This exam is closed-book. You must show ALL of your work for full credit. Please read the questions carefully. Please check your answers
ECE32 Exam 2 Version A April 21, 214 1 Name: Solution Score: /1 This exam is closed-book. You must show ALL of your work for full credit. Please read the questions carefully. Please check your answers
Twelfth Problem Assignment
 EECS 401 Not Graded PROBLEM 1 Let X 1, X 2,... be a sequence of independent random variables that are uniformly distributed between 0 and 1. Consider a sequence defined by (a) Y n = max(x 1, X 2,..., X
EECS 401 Not Graded PROBLEM 1 Let X 1, X 2,... be a sequence of independent random variables that are uniformly distributed between 0 and 1. Consider a sequence defined by (a) Y n = max(x 1, X 2,..., X
Distributions of Functions of Random Variables. 5.1 Functions of One Random Variable
 Distributions of Functions of Random Variables 5.1 Functions of One Random Variable 5.2 Transformations of Two Random Variables 5.3 Several Random Variables 5.4 The Moment-Generating Function Technique
Distributions of Functions of Random Variables 5.1 Functions of One Random Variable 5.2 Transformations of Two Random Variables 5.3 Several Random Variables 5.4 The Moment-Generating Function Technique
M(t) = 1 t. (1 t), 6 M (0) = 20 P (95. X i 110) i=1
 Math 66/566 - Midterm Solutions NOTE: These solutions are for both the 66 and 566 exam. The problems are the same until questions and 5. 1. The moment generating function of a random variable X is M(t)
Math 66/566 - Midterm Solutions NOTE: These solutions are for both the 66 and 566 exam. The problems are the same until questions and 5. 1. The moment generating function of a random variable X is M(t)
ECO220Y Continuous Probability Distributions: Uniform and Triangle Readings: Chapter 9, sections
 ECO220Y Continuous Probability Distributions: Uniform and Triangle Readings: Chapter 9, sections 9.8-9.9 Fall 2011 Lecture 8 Part 1 (Fall 2011) Probability Distributions Lecture 8 Part 1 1 / 19 Probability
ECO220Y Continuous Probability Distributions: Uniform and Triangle Readings: Chapter 9, sections 9.8-9.9 Fall 2011 Lecture 8 Part 1 (Fall 2011) Probability Distributions Lecture 8 Part 1 1 / 19 Probability
STAT 135 Lab 2 Confidence Intervals, MLE and the Delta Method
 STAT 135 Lab 2 Confidence Intervals, MLE and the Delta Method Rebecca Barter February 2, 2015 Confidence Intervals Confidence intervals What is a confidence interval? A confidence interval is calculated
STAT 135 Lab 2 Confidence Intervals, MLE and the Delta Method Rebecca Barter February 2, 2015 Confidence Intervals Confidence intervals What is a confidence interval? A confidence interval is calculated
P (x). all other X j =x j. If X is a continuous random vector (see p.172), then the marginal distributions of X i are: f(x)dx 1 dx n
 JOINT DENSITIES - RANDOM VECTORS - REVIEW Joint densities describe probability distributions of a random vector X: an n-dimensional vector of random variables, ie, X = (X 1,, X n ), where all X is are
JOINT DENSITIES - RANDOM VECTORS - REVIEW Joint densities describe probability distributions of a random vector X: an n-dimensional vector of random variables, ie, X = (X 1,, X n ), where all X is are
Mathematical statistics
 October 1 st, 2018 Lecture 11: Sufficient statistic Where are we? Week 1 Week 2 Week 4 Week 7 Week 10 Week 14 Probability reviews Chapter 6: Statistics and Sampling Distributions Chapter 7: Point Estimation
October 1 st, 2018 Lecture 11: Sufficient statistic Where are we? Week 1 Week 2 Week 4 Week 7 Week 10 Week 14 Probability reviews Chapter 6: Statistics and Sampling Distributions Chapter 7: Point Estimation
MAS113 Introduction to Probability and Statistics
 MAS113 Introduction to Probability and Statistics School of Mathematics and Statistics, University of Sheffield 2018 19 Identically distributed Suppose we have n random variables X 1, X 2,..., X n. Identically
MAS113 Introduction to Probability and Statistics School of Mathematics and Statistics, University of Sheffield 2018 19 Identically distributed Suppose we have n random variables X 1, X 2,..., X n. Identically
MTMS Mathematical Statistics
 MTMS.01.099 Mathematical Statistics Lecture 12. Hypothesis testing. Power function. Approximation of Normal distribution and application to Binomial distribution Tõnu Kollo Fall 2016 Hypothesis Testing
MTMS.01.099 Mathematical Statistics Lecture 12. Hypothesis testing. Power function. Approximation of Normal distribution and application to Binomial distribution Tõnu Kollo Fall 2016 Hypothesis Testing
Class 26: review for final exam 18.05, Spring 2014
 Probability Class 26: review for final eam 8.05, Spring 204 Counting Sets Inclusion-eclusion principle Rule of product (multiplication rule) Permutation and combinations Basics Outcome, sample space, event
Probability Class 26: review for final eam 8.05, Spring 204 Counting Sets Inclusion-eclusion principle Rule of product (multiplication rule) Permutation and combinations Basics Outcome, sample space, event
Limiting Distributions
 Limiting Distributions We introduce the mode of convergence for a sequence of random variables, and discuss the convergence in probability and in distribution. The concept of convergence leads us to the
Limiting Distributions We introduce the mode of convergence for a sequence of random variables, and discuss the convergence in probability and in distribution. The concept of convergence leads us to the
Ch. 5 Joint Probability Distributions and Random Samples
 Ch. 5 Joint Probability Distributions and Random Samples 5. 1 Jointly Distributed Random Variables In chapters 3 and 4, we learned about probability distributions for a single random variable. However,
Ch. 5 Joint Probability Distributions and Random Samples 5. 1 Jointly Distributed Random Variables In chapters 3 and 4, we learned about probability distributions for a single random variable. However,
HT Introduction. P(X i = x i ) = e λ λ x i
 MODS STATISTICS Introduction. HT 2012 Simon Myers, Department of Statistics (and The Wellcome Trust Centre for Human Genetics) myers@stats.ox.ac.uk We will be concerned with the mathematical framework
MODS STATISTICS Introduction. HT 2012 Simon Myers, Department of Statistics (and The Wellcome Trust Centre for Human Genetics) myers@stats.ox.ac.uk We will be concerned with the mathematical framework
CS145: Probability & Computing
 CS45: Probability & Computing Lecture 5: Concentration Inequalities, Law of Large Numbers, Central Limit Theorem Instructor: Eli Upfal Brown University Computer Science Figure credits: Bertsekas & Tsitsiklis,
CS45: Probability & Computing Lecture 5: Concentration Inequalities, Law of Large Numbers, Central Limit Theorem Instructor: Eli Upfal Brown University Computer Science Figure credits: Bertsekas & Tsitsiklis,
FINAL EXAM: 3:30-5:30pm
 ECE 30: Probabilistic Methods in Electrical and Computer Engineering Spring 016 Instructor: Prof. A. R. Reibman FINAL EXAM: 3:30-5:30pm Spring 016, MWF 1:30-1:0pm (May 6, 016) This is a closed book exam.
ECE 30: Probabilistic Methods in Electrical and Computer Engineering Spring 016 Instructor: Prof. A. R. Reibman FINAL EXAM: 3:30-5:30pm Spring 016, MWF 1:30-1:0pm (May 6, 016) This is a closed book exam.
Partial Solutions for h4/2014s: Sampling Distributions
 27 Partial Solutions for h4/24s: Sampling Distributions ( Let X and X 2 be two independent random variables, each with the same probability distribution given as follows. f(x 2 e x/2, x (a Compute the
27 Partial Solutions for h4/24s: Sampling Distributions ( Let X and X 2 be two independent random variables, each with the same probability distribution given as follows. f(x 2 e x/2, x (a Compute the
Variance reduction. Michel Bierlaire. Transport and Mobility Laboratory. Variance reduction p. 1/18
 Variance reduction p. 1/18 Variance reduction Michel Bierlaire michel.bierlaire@epfl.ch Transport and Mobility Laboratory Variance reduction p. 2/18 Example Use simulation to compute I = 1 0 e x dx We
Variance reduction p. 1/18 Variance reduction Michel Bierlaire michel.bierlaire@epfl.ch Transport and Mobility Laboratory Variance reduction p. 2/18 Example Use simulation to compute I = 1 0 e x dx We
7 Random samples and sampling distributions
 7 Random samples and sampling distributions 7.1 Introduction - random samples We will use the term experiment in a very general way to refer to some process, procedure or natural phenomena that produces
7 Random samples and sampling distributions 7.1 Introduction - random samples We will use the term experiment in a very general way to refer to some process, procedure or natural phenomena that produces
Chapter 3 sections. SKIP: 3.10 Markov Chains. SKIP: pages Chapter 3 - continued
 Chapter 3 sections Chapter 3 - continued 3.1 Random Variables and Discrete Distributions 3.2 Continuous Distributions 3.3 The Cumulative Distribution Function 3.4 Bivariate Distributions 3.5 Marginal Distributions
Chapter 3 sections Chapter 3 - continued 3.1 Random Variables and Discrete Distributions 3.2 Continuous Distributions 3.3 The Cumulative Distribution Function 3.4 Bivariate Distributions 3.5 Marginal Distributions
SDS 321: Introduction to Probability and Statistics
 SDS 321: Introduction to Probability and Statistics Lecture 14: Continuous random variables Purnamrita Sarkar Department of Statistics and Data Science The University of Texas at Austin www.cs.cmu.edu/
SDS 321: Introduction to Probability and Statistics Lecture 14: Continuous random variables Purnamrita Sarkar Department of Statistics and Data Science The University of Texas at Austin www.cs.cmu.edu/
Homework 4 Math 11, UCSD, Winter 2018 Due on Tuesday, 13th February
 PID: Last Name, First Name: Section: Approximate time spent to complete this assignment: hour(s) Homework 4 Math 11, UCSD, Winter 2018 Due on Tuesday, 13th February Readings: Chapters 16.6-16.7 and the
PID: Last Name, First Name: Section: Approximate time spent to complete this assignment: hour(s) Homework 4 Math 11, UCSD, Winter 2018 Due on Tuesday, 13th February Readings: Chapters 16.6-16.7 and the
Lecture 3: Statistical sampling uncertainty
 Lecture 3: Statistical sampling uncertainty c Christopher S. Bretherton Winter 2015 3.1 Central limit theorem (CLT) Let X 1,..., X N be a sequence of N independent identically-distributed (IID) random
Lecture 3: Statistical sampling uncertainty c Christopher S. Bretherton Winter 2015 3.1 Central limit theorem (CLT) Let X 1,..., X N be a sequence of N independent identically-distributed (IID) random
SUFFICIENT STATISTICS
 SUFFICIENT STATISTICS. Introduction Let X (X,..., X n ) be a random sample from f θ, where θ Θ is unknown. We are interested using X to estimate θ. In the simple case where X i Bern(p), we found that the
SUFFICIENT STATISTICS. Introduction Let X (X,..., X n ) be a random sample from f θ, where θ Θ is unknown. We are interested using X to estimate θ. In the simple case where X i Bern(p), we found that the
Intro to Probability Instructor: Alexandre Bouchard
 www.stat.ubc.ca/~bouchard/courses/stat302-sp2017-18/ Intro to Probability Instructor: Alexandre Bouchard Info on midterm CALCULATOR: only NON-programmable, NON-scientific, NON-graphing (and of course,
www.stat.ubc.ca/~bouchard/courses/stat302-sp2017-18/ Intro to Probability Instructor: Alexandre Bouchard Info on midterm CALCULATOR: only NON-programmable, NON-scientific, NON-graphing (and of course,
Two hours. Statistical Tables to be provided THE UNIVERSITY OF MANCHESTER. 14 January :45 11:45
 Two hours Statistical Tables to be provided THE UNIVERSITY OF MANCHESTER PROBABILITY 2 14 January 2015 09:45 11:45 Answer ALL four questions in Section A (40 marks in total) and TWO of the THREE questions
Two hours Statistical Tables to be provided THE UNIVERSITY OF MANCHESTER PROBABILITY 2 14 January 2015 09:45 11:45 Answer ALL four questions in Section A (40 marks in total) and TWO of the THREE questions
Course information: Instructor: Tim Hanson, Leconte 219C, phone Office hours: Tuesday/Thursday 11-12, Wednesday 10-12, and by appointment.
 Course information: Instructor: Tim Hanson, Leconte 219C, phone 777-3859. Office hours: Tuesday/Thursday 11-12, Wednesday 10-12, and by appointment. Text: Applied Linear Statistical Models (5th Edition),
Course information: Instructor: Tim Hanson, Leconte 219C, phone 777-3859. Office hours: Tuesday/Thursday 11-12, Wednesday 10-12, and by appointment. Text: Applied Linear Statistical Models (5th Edition),
HW1 (due 10/6/05): (from textbook) 1.2.3, 1.2.9, , , (extra credit) A fashionable country club has 100 members, 30 of whom are
 HW1 (due 10/6/05): (from textbook) 1.2.3, 1.2.9, 1.2.11, 1.2.12, 1.2.16 (extra credit) A fashionable country club has 100 members, 30 of whom are lawyers. Rumor has it that 25 of the club members are liars
HW1 (due 10/6/05): (from textbook) 1.2.3, 1.2.9, 1.2.11, 1.2.12, 1.2.16 (extra credit) A fashionable country club has 100 members, 30 of whom are lawyers. Rumor has it that 25 of the club members are liars
STAT/MATH 395 PROBABILITY II
 STAT/MATH 395 PROBABILITY II Chapter 6 : Moment Functions Néhémy Lim 1 1 Department of Statistics, University of Washington, USA Winter Quarter 2016 of Common Distributions Outline 1 2 3 of Common Distributions
STAT/MATH 395 PROBABILITY II Chapter 6 : Moment Functions Néhémy Lim 1 1 Department of Statistics, University of Washington, USA Winter Quarter 2016 of Common Distributions Outline 1 2 3 of Common Distributions
Continuous Expectation and Variance, the Law of Large Numbers, and the Central Limit Theorem Spring 2014
 Continuous Expectation and Variance, the Law of Large Numbers, and the Central Limit Theorem 18.5 Spring 214.5.4.3.2.1-4 -3-2 -1 1 2 3 4 January 1, 217 1 / 31 Expected value Expected value: measure of
Continuous Expectation and Variance, the Law of Large Numbers, and the Central Limit Theorem 18.5 Spring 214.5.4.3.2.1-4 -3-2 -1 1 2 3 4 January 1, 217 1 / 31 Expected value Expected value: measure of
Test Problems for Probability Theory ,
 1 Test Problems for Probability Theory 01-06-16, 010-1-14 1. Write down the following probability density functions and compute their moment generating functions. (a) Binomial distribution with mean 30
1 Test Problems for Probability Theory 01-06-16, 010-1-14 1. Write down the following probability density functions and compute their moment generating functions. (a) Binomial distribution with mean 30
Chapter 5 continued. Chapter 5 sections
 Chapter 5 sections Discrete univariate distributions: 5.2 Bernoulli and Binomial distributions Just skim 5.3 Hypergeometric distributions 5.4 Poisson distributions Just skim 5.5 Negative Binomial distributions
Chapter 5 sections Discrete univariate distributions: 5.2 Bernoulli and Binomial distributions Just skim 5.3 Hypergeometric distributions 5.4 Poisson distributions Just skim 5.5 Negative Binomial distributions
Exponential Distribution and Poisson Process
 Exponential Distribution and Poisson Process Stochastic Processes - Lecture Notes Fatih Cavdur to accompany Introduction to Probability Models by Sheldon M. Ross Fall 215 Outline Introduction Exponential
Exponential Distribution and Poisson Process Stochastic Processes - Lecture Notes Fatih Cavdur to accompany Introduction to Probability Models by Sheldon M. Ross Fall 215 Outline Introduction Exponential
Gaussian vectors and central limit theorem
 Gaussian vectors and central limit theorem Samy Tindel Purdue University Probability Theory 2 - MA 539 Samy T. Gaussian vectors & CLT Probability Theory 1 / 86 Outline 1 Real Gaussian random variables
Gaussian vectors and central limit theorem Samy Tindel Purdue University Probability Theory 2 - MA 539 Samy T. Gaussian vectors & CLT Probability Theory 1 / 86 Outline 1 Real Gaussian random variables
Math 416 Lecture 2 DEFINITION. Here are the multivariate versions: X, Y, Z iff P(X = x, Y = y, Z =z) = p(x, y, z) of X, Y, Z iff for all sets A, B, C,
 Math 416 Lecture 2 DEFINITION. Here are the multivariate versions: PMF case: p(x, y, z) is the joint Probability Mass Function of X, Y, Z iff P(X = x, Y = y, Z =z) = p(x, y, z) PDF case: f(x, y, z) is
Math 416 Lecture 2 DEFINITION. Here are the multivariate versions: PMF case: p(x, y, z) is the joint Probability Mass Function of X, Y, Z iff P(X = x, Y = y, Z =z) = p(x, y, z) PDF case: f(x, y, z) is
Math 151. Rumbos Spring Solutions to Review Problems for Exam 3
 Math 151. Rumbos Spring 2014 1 Solutions to Review Problems for Exam 3 1. Suppose that a book with n pages contains on average λ misprints per page. What is the probability that there will be at least
Math 151. Rumbos Spring 2014 1 Solutions to Review Problems for Exam 3 1. Suppose that a book with n pages contains on average λ misprints per page. What is the probability that there will be at least
Joint Probability Distributions and Random Samples (Devore Chapter Five)
 Joint Probability Distributions and Random Samples (Devore Chapter Five) 1016-345-01: Probability and Statistics for Engineers Spring 2013 Contents 1 Joint Probability Distributions 2 1.1 Two Discrete
Joint Probability Distributions and Random Samples (Devore Chapter Five) 1016-345-01: Probability and Statistics for Engineers Spring 2013 Contents 1 Joint Probability Distributions 2 1.1 Two Discrete
Math 475. Jimin Ding. August 29, Department of Mathematics Washington University in St. Louis jmding/math475/index.
 istical A istic istics : istical Department of Mathematics Washington University in St. Louis www.math.wustl.edu/ jmding/math475/index.html August 29, 2013 istical August 29, 2013 1 / 18 istical A istic
istical A istic istics : istical Department of Mathematics Washington University in St. Louis www.math.wustl.edu/ jmding/math475/index.html August 29, 2013 istical August 29, 2013 1 / 18 istical A istic
Chapter 9: Hypothesis Testing Sections
 Chapter 9: Hypothesis Testing Sections 9.1 Problems of Testing Hypotheses 9.2 Testing Simple Hypotheses 9.3 Uniformly Most Powerful Tests Skip: 9.4 Two-Sided Alternatives 9.6 Comparing the Means of Two
Chapter 9: Hypothesis Testing Sections 9.1 Problems of Testing Hypotheses 9.2 Testing Simple Hypotheses 9.3 Uniformly Most Powerful Tests Skip: 9.4 Two-Sided Alternatives 9.6 Comparing the Means of Two
p. 6-1 Continuous Random Variables p. 6-2
 Continuous Random Variables Recall: For discrete random variables, only a finite or countably infinite number of possible values with positive probability (>). Often, there is interest in random variables
Continuous Random Variables Recall: For discrete random variables, only a finite or countably infinite number of possible values with positive probability (>). Often, there is interest in random variables
MAT 271E Probability and Statistics
 MAT 271E Probability and Statistics Spring 2011 Instructor : Class Meets : Office Hours : Textbook : Supp. Text : İlker Bayram EEB 1103 ibayram@itu.edu.tr 13.30 16.30, Wednesday EEB? 10.00 12.00, Wednesday
MAT 271E Probability and Statistics Spring 2011 Instructor : Class Meets : Office Hours : Textbook : Supp. Text : İlker Bayram EEB 1103 ibayram@itu.edu.tr 13.30 16.30, Wednesday EEB? 10.00 12.00, Wednesday
Statistics Ph.D. Qualifying Exam: Part I October 18, 2003
 Statistics Ph.D. Qualifying Exam: Part I October 18, 2003 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your answer
Statistics Ph.D. Qualifying Exam: Part I October 18, 2003 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your answer
Lecture 11. Multivariate Normal theory
 10. Lecture 11. Multivariate Normal theory Lecture 11. Multivariate Normal theory 1 (1 1) 11. Multivariate Normal theory 11.1. Properties of means and covariances of vectors Properties of means and covariances
10. Lecture 11. Multivariate Normal theory Lecture 11. Multivariate Normal theory 1 (1 1) 11. Multivariate Normal theory 11.1. Properties of means and covariances of vectors Properties of means and covariances
5.2 Fisher information and the Cramer-Rao bound
 Stat 200: Introduction to Statistical Inference Autumn 208/9 Lecture 5: Maximum likelihood theory Lecturer: Art B. Owen October 9 Disclaimer: These notes have not been subjected to the usual scrutiny reserved
Stat 200: Introduction to Statistical Inference Autumn 208/9 Lecture 5: Maximum likelihood theory Lecturer: Art B. Owen October 9 Disclaimer: These notes have not been subjected to the usual scrutiny reserved
The mean, variance and covariance. (Chs 3.4.1, 3.4.2)
 4 The mean, variance and covariance (Chs 3.4.1, 3.4.2) Mean (Expected Value) of X Consider a university having 15,000 students and let X equal the number of courses for which a randomly selected student
4 The mean, variance and covariance (Chs 3.4.1, 3.4.2) Mean (Expected Value) of X Consider a university having 15,000 students and let X equal the number of courses for which a randomly selected student
5.2 Continuous random variables
 5.2 Continuous random variables It is often convenient to think of a random variable as having a whole (continuous) interval for its set of possible values. The devices used to describe continuous probability
5.2 Continuous random variables It is often convenient to think of a random variable as having a whole (continuous) interval for its set of possible values. The devices used to describe continuous probability
Part IA Probability. Theorems. Based on lectures by R. Weber Notes taken by Dexter Chua. Lent 2015
 Part IA Probability Theorems Based on lectures by R. Weber Notes taken by Dexter Chua Lent 2015 These notes are not endorsed by the lecturers, and I have modified them (often significantly) after lectures.
Part IA Probability Theorems Based on lectures by R. Weber Notes taken by Dexter Chua Lent 2015 These notes are not endorsed by the lecturers, and I have modified them (often significantly) after lectures.
Masters Comprehensive Examination Department of Statistics, University of Florida
 Masters Comprehensive Examination Department of Statistics, University of Florida May 6, 003, 8:00 am - :00 noon Instructions: You have four hours to answer questions in this examination You must show
Masters Comprehensive Examination Department of Statistics, University of Florida May 6, 003, 8:00 am - :00 noon Instructions: You have four hours to answer questions in this examination You must show
8 Laws of large numbers
 8 Laws of large numbers 8.1 Introduction We first start with the idea of standardizing a random variable. Let X be a random variable with mean µ and variance σ 2. Then Z = (X µ)/σ will be a random variable
8 Laws of large numbers 8.1 Introduction We first start with the idea of standardizing a random variable. Let X be a random variable with mean µ and variance σ 2. Then Z = (X µ)/σ will be a random variable
Sampling Distributions
 Sampling Distributions Mathematics 47: Lecture 9 Dan Sloughter Furman University March 16, 2006 Dan Sloughter (Furman University) Sampling Distributions March 16, 2006 1 / 10 Definition We call the probability
Sampling Distributions Mathematics 47: Lecture 9 Dan Sloughter Furman University March 16, 2006 Dan Sloughter (Furman University) Sampling Distributions March 16, 2006 1 / 10 Definition We call the probability
Lecture 9. d N(0, 1). Now we fix n and think of a SRW on [0,1]. We take the k th step at time k n. and our increments are ± 1
![Lecture 9. d N(0, 1). Now we fix n and think of a SRW on [0,1]. We take the k th step at time k n. and our increments are ± 1 Lecture 9. d N(0, 1). Now we fix n and think of a SRW on [0,1]. We take the k th step at time k n. and our increments are ± 1](/thumbs/84/89691998.jpg) Random Walks and Brownian Motion Tel Aviv University Spring 011 Lecture date: May 0, 011 Lecture 9 Instructor: Ron Peled Scribe: Jonathan Hermon In today s lecture we present the Brownian motion (BM).
Random Walks and Brownian Motion Tel Aviv University Spring 011 Lecture date: May 0, 011 Lecture 9 Instructor: Ron Peled Scribe: Jonathan Hermon In today s lecture we present the Brownian motion (BM).
Section 9.1. Expected Values of Sums
 Section 9.1 Expected Values of Sums Theorem 9.1 For any set of random variables X 1,..., X n, the sum W n = X 1 + + X n has expected value E [W n ] = E [X 1 ] + E [X 2 ] + + E [X n ]. Proof: Theorem 9.1
Section 9.1 Expected Values of Sums Theorem 9.1 For any set of random variables X 1,..., X n, the sum W n = X 1 + + X n has expected value E [W n ] = E [X 1 ] + E [X 2 ] + + E [X n ]. Proof: Theorem 9.1
McGill University. Faculty of Science. Department of Mathematics and Statistics. Part A Examination. Statistics: Theory Paper
 McGill University Faculty of Science Department of Mathematics and Statistics Part A Examination Statistics: Theory Paper Date: 10th May 2015 Instructions Time: 1pm-5pm Answer only two questions from Section
McGill University Faculty of Science Department of Mathematics and Statistics Part A Examination Statistics: Theory Paper Date: 10th May 2015 Instructions Time: 1pm-5pm Answer only two questions from Section
Random Variables and Their Distributions
 Chapter 3 Random Variables and Their Distributions A random variable (r.v.) is a function that assigns one and only one numerical value to each simple event in an experiment. We will denote r.vs by capital
Chapter 3 Random Variables and Their Distributions A random variable (r.v.) is a function that assigns one and only one numerical value to each simple event in an experiment. We will denote r.vs by capital
STAT 512 sp 2018 Summary Sheet
 STAT 5 sp 08 Summary Sheet Karl B. Gregory Spring 08. Transformations of a random variable Let X be a rv with support X and let g be a function mapping X to Y with inverse mapping g (A = {x X : g(x A}
STAT 5 sp 08 Summary Sheet Karl B. Gregory Spring 08. Transformations of a random variable Let X be a rv with support X and let g be a function mapping X to Y with inverse mapping g (A = {x X : g(x A}
DEPARTMENT OF MATHEMATICS AND STATISTICS
 DEPARTMENT OF MATHEMATICS AND STATISTICS Memorial University of Newfoundland St. John s, Newfoundland CANADA A1C 5S7 ph. (709) 737-8075 fax (709) 737-3010 Alwell Julius Oyet, Phd email: aoyet@math.mun.ca
DEPARTMENT OF MATHEMATICS AND STATISTICS Memorial University of Newfoundland St. John s, Newfoundland CANADA A1C 5S7 ph. (709) 737-8075 fax (709) 737-3010 Alwell Julius Oyet, Phd email: aoyet@math.mun.ca
Chapter 3 sections. SKIP: 3.10 Markov Chains. SKIP: pages Chapter 3 - continued
 Chapter 3 sections 3.1 Random Variables and Discrete Distributions 3.2 Continuous Distributions 3.3 The Cumulative Distribution Function 3.4 Bivariate Distributions 3.5 Marginal Distributions 3.6 Conditional
Chapter 3 sections 3.1 Random Variables and Discrete Distributions 3.2 Continuous Distributions 3.3 The Cumulative Distribution Function 3.4 Bivariate Distributions 3.5 Marginal Distributions 3.6 Conditional
Lecture 7: Chapter 7. Sums of Random Variables and Long-Term Averages
 Lecture 7: Chapter 7. Sums of Random Variables and Long-Term Averages ELEC206 Probability and Random Processes, Fall 2014 Gil-Jin Jang gjang@knu.ac.kr School of EE, KNU page 1 / 15 Chapter 7. Sums of Random
Lecture 7: Chapter 7. Sums of Random Variables and Long-Term Averages ELEC206 Probability and Random Processes, Fall 2014 Gil-Jin Jang gjang@knu.ac.kr School of EE, KNU page 1 / 15 Chapter 7. Sums of Random
Expectations. Definition Let X be a discrete rv with set of possible values D and pmf p(x). The expected value or mean value of X, denoted by E(X ) or
 Expectations Expectations Definition Let X be a discrete rv with set of possible values D and pmf p(x). The expected value or mean value of X, denoted by E(X ) or µ X, is E(X ) = µ X = x D x p(x) Expectations
Expectations Expectations Definition Let X be a discrete rv with set of possible values D and pmf p(x). The expected value or mean value of X, denoted by E(X ) or µ X, is E(X ) = µ X = x D x p(x) Expectations
Statistics 1B. Statistics 1B 1 (1 1)
 0. Statistics 1B Statistics 1B 1 (1 1) 0. Lecture 1. Introduction and probability review Lecture 1. Introduction and probability review 2 (1 1) 1. Introduction and probability review 1.1. What is Statistics?
0. Statistics 1B Statistics 1B 1 (1 1) 0. Lecture 1. Introduction and probability review Lecture 1. Introduction and probability review 2 (1 1) 1. Introduction and probability review 1.1. What is Statistics?
Statistics, Data Analysis, and Simulation SS 2015
 Statistics, Data Analysis, and Simulation SS 2015 08.128.730 Statistik, Datenanalyse und Simulation Dr. Michael O. Distler Mainz, 27. April 2015 Dr. Michael O. Distler
Statistics, Data Analysis, and Simulation SS 2015 08.128.730 Statistik, Datenanalyse und Simulation Dr. Michael O. Distler Mainz, 27. April 2015 Dr. Michael O. Distler
Math 180A. Lecture 16 Friday May 7 th. Expectation. Recall the three main probability density functions so far (1) Uniform (2) Exponential.
 Math 8A Lecture 6 Friday May 7 th Epectation Recall the three main probability density functions so far () Uniform () Eponential (3) Power Law e, ( ), Math 8A Lecture 6 Friday May 7 th Epectation Eample
Math 8A Lecture 6 Friday May 7 th Epectation Recall the three main probability density functions so far () Uniform () Eponential (3) Power Law e, ( ), Math 8A Lecture 6 Friday May 7 th Epectation Eample
Ph.D. Preliminary Examination Statistics June 2, 2014
 Ph.D. Preliminary Examination Statistics June, 04 NOTES:. The exam is worth 00 points.. Partial credit may be given for partial answers if possible.. There are 5 pages in this exam paper. I have neither
Ph.D. Preliminary Examination Statistics June, 04 NOTES:. The exam is worth 00 points.. Partial credit may be given for partial answers if possible.. There are 5 pages in this exam paper. I have neither
FINAL EXAM PLEASE SHOW ALL WORK!
 STAT 311, Fall 015 Name Discussion Section: Please circle one! LEC 001 TR 11:00AM-1:15PM FISCHER, ISMOR LEC 00 TR 9:30-10:45AM FISCHER, ISMOR DIS 311 W 1:0-:10PM Zhang, ilin DIS 31 W 1:0-:10PM Li, iaomao
STAT 311, Fall 015 Name Discussion Section: Please circle one! LEC 001 TR 11:00AM-1:15PM FISCHER, ISMOR LEC 00 TR 9:30-10:45AM FISCHER, ISMOR DIS 311 W 1:0-:10PM Zhang, ilin DIS 31 W 1:0-:10PM Li, iaomao
Economics 520. Lecture Note 19: Hypothesis Testing via the Neyman-Pearson Lemma CB 8.1,
 Economics 520 Lecture Note 9: Hypothesis Testing via the Neyman-Pearson Lemma CB 8., 8.3.-8.3.3 Uniformly Most Powerful Tests and the Neyman-Pearson Lemma Let s return to the hypothesis testing problem
Economics 520 Lecture Note 9: Hypothesis Testing via the Neyman-Pearson Lemma CB 8., 8.3.-8.3.3 Uniformly Most Powerful Tests and the Neyman-Pearson Lemma Let s return to the hypothesis testing problem
Dennis Bricker Dept of Mechanical & Industrial Engineering The University of Iowa
 Dennis Bricker Dept of Mechanical & Industrial Engineering The University of Iowa dennis-bricker@uiowa.edu Probability Theory Results page 1 D.Bricker, U. of Iowa, 2002 Probability of simultaneous occurrence
Dennis Bricker Dept of Mechanical & Industrial Engineering The University of Iowa dennis-bricker@uiowa.edu Probability Theory Results page 1 D.Bricker, U. of Iowa, 2002 Probability of simultaneous occurrence
E X A M. Probability Theory and Stochastic Processes Date: December 13, 2016 Duration: 4 hours. Number of pages incl.
 E X A M Course code: Course name: Number of pages incl. front page: 6 MA430-G Probability Theory and Stochastic Processes Date: December 13, 2016 Duration: 4 hours Resources allowed: Notes: Pocket calculator,
E X A M Course code: Course name: Number of pages incl. front page: 6 MA430-G Probability Theory and Stochastic Processes Date: December 13, 2016 Duration: 4 hours Resources allowed: Notes: Pocket calculator,
