The Semilinear Klein-Gordon equation in two and three space dimensions
|
|
|
- Joleen Stokes
- 6 years ago
- Views:
Transcription
1 Università degli Studi Roma Tre Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea Magistrale in Matematica Tesi di Laurea Magistrale in Matematica Sintesi The Semilinear Klein-Gordon equation in two and three space dimensions Candidato Vincenzo Morinelli Relatore Prof. Giovanni Mancini Anno Accademico Luglio 2012 AMS classification: 35L05. Key words: Semilinear wave equations, defocusing wave equation, well posedness, critical power growth, exponential nonlinearity, blow up.
2 In the thesis we will discuss some recent developments for a particular semilinear defocusing wave equation: the semilinear u u p 1 Klein-Gordon equation, focusing on the two and three space dimensions cases. A semilinear wave equation (SLW) has the form u(t, x) + g(u(t, x)) = 0 (t, x) R R n. (0.1) where g : R R, the differential operator is defined := tt with the standard space Laplace operator = n i=1 2. x 2 i The Cauchy problem for the above equation on R R n has initial data: (u, u t ) t=0 = (ϕ, ψ) (0.2) We can associate to SLW, the energy: E(u)(t) = e(u)(t, x)dx (0.3) R n where e(u)(t, x) = ( u 2 + u t 2 + G(u) ),G(u) = u g(s)ds and E 0 := E(u)(0) is the initial data energy. The semilinear Klein-Gordon equation is a SLW with odd nonlinearity g(u) = u u p 1. In the last 25 years there has been considerable interest in studying hyperbolic non linear partial differential equations. They model phenomena of wave propagation in different problems arising from Physics: for instance, water waves, lasers, problems of general relativity and relativistic particle Physics. In 1920 s Physicists were looking for relativistic quantum mechanic equation for the electron. The Klein-Gordon equation was proposed by Klein and Gordon in 1927 but it did not work. Together with a positive energy solution, by the relativistic invariant E 2 = m 2 c 4 + p 2 c 2, a negative energy solution can be found and it can not be a priori discarded. The next year the equation proposed by Dirac was able to describe the spinning 1
3 electron behaviour. In 1934 the Klein-Gordon equation was re-considered together with the study of spinless particles. It was discovered that it describes the behaviour of the lightest mesons, the π-mesons particles. In the free form (without potential) the Klein-Gordon equation assumes the form: ψ 1 c 2 2 t ψ = m2 c where c is the speed of light, is the Plank constant divided by 2π, m is the mass of the particle. By the Pauli and Weisskopf interpretation, the Klein-Gordon equation is a field equation for a charged spin-0 field. It is interesting how this equation put together the relativistic constant c and the quantum mechanic one. Assuming c = 1, the equation can be rewritten in the following way: ( ) + m2 φ = 0 2 the box operator, or d Alambertian operator, emphasizes that there are no more differences between time and space variables with the Minkowski metric. The Minkowski metric is defined by the quadratic form η = for the variables(t, x 0,..., x n ) = (y 0,...y n ) R n+1. ψ = diag( 1, 1,..., 1) M m+1,m+1 (R) Under a more analytic point of view it is important to interpret the solution of a wave equation in the following sense: Definition 0.1. Let X be a Banach space and u(t, x) be a solution for the Cauchy problem (0.1)+(0.2) with (ϕ, ψ) X. 2
4 We can define U(t) : [0, T] X t (u(t, ), u t (t, )) Henceforth, for the sake of notational simplicity, we will identify U(t) with u(t). We will concentrate on defocusing semilinear wave equations. We say that a semilinear wave equation is defocusing if G(u) cooperates with the energy of the linear operator, hence if the whole energy is positive defined. For example, consider the defocusing semi linear Klein-Gordon problem with power nonlinearity: u + u u p 1 = 0 R R n. (0.4) with initial data (0.2). The associated energy is ( ) u 2 E(u)(t) = + u2 t u p+1 dx 0. p + 1 R n Generally speaking, a defocusing wave equation tends to dissipate the solution when it is concentrated. It follows that defocusing equations will tend to avoid blow up phenomena. We say that a semilinear wave equation is focusing if the energy associated is not positive defined, for example if G(u), signed defined, has the wrong sign with respect to the linear operator energy. This type of equations tend to be affected by blow-up phenomena. Changing sign to the nonlinearity we have the focusing problem: u u u p 1 = 0 R R n. (0.5) with initial data (0.2) and associated energy E(u)(t) = R n ( u u2 t u p+1 2 p+1 )dx. Note that in the latter case the primitive of the nonlinearity in the energy expression has a minus sign. It is important to focus on the main aspects and on the different issues of the SLW studies. Consider the following classical definitions of well and ill posed semilinear problems: 3
5 Definition 0.2. Consider the Cauchy problem (0.1)+(0.2). Let X be a Banach space. We say that the Cauchy problem, with (ϕ, ψ) X is locally-well posed in X if there exists T > 0, a space Y(T) and a u Y(T) such that: 1. u satisfies the equation in the sense of distributions on [0, T] R n : T 0 R n u υdz = T 0 gυ + φυ t (, 0)dx ψυ(, 0)dx (0.6) R n R n R n υ C 0 ((, T] Rn ) 2. u is unique in Y(T) 3. For any (ϕ, ψ) X there is a neighbourhood N of (ϕ, ψ) X such that the solution map (ϕ, ψ) u is a continuous function from N to Y(T). We will say that the Cauchy problem is globally well-posed in X if it is well posed and T can be taken arbitrary. We will say that the Cauchy problem is strongly well-posed in X if it is well posed and the solution map is uniformly continuous We will say that the Cauchy problem is ill-posed in X if the solution map is not continuous. We will say that the Cauchy problem is weakly ill-posed on a set Z X if the solution map is not uniformly continuous on Z. We will consider Y(T) always embedded C([0, T], X). We will see that the natural Banach space for the well-posedness for n 3 will be the energy space Ḣ 1 L 2 4
6 defined by the norm u(t) Ḣ 1 L = u(t) 2 L 2 + u t(t) L 2 and for n = 2 is the space H 1 L 2 defined by u(t) Ḣ 1 L = u(t) 2 H 1 + u t(t) L 2. Pioneers in studying the well posedness of wave equations were Strichartz [38], Peacher [29], Ginibre and Velo [11]. In the late 1980 s there were introduced tools from harmonic analysis to study the local theory of Cauchy problems (see [24],[23]). For more modern results see Tao [44], or Tataru [47],[46]. In the recent years there has been a great interest in studying dispersive wave equations, their long time behaviour, regularity and uniqueness of solutions. For the 3 space dimensions case, the results we will present are essentially due to Segal[31], Jörgens[21], Rauch[30], Strichartz[38],Struwe [39],[40]. In 2 space dimensions results of regularity and well posedness of semilinear Klein-Gordon equation are mainly provided by Struwe([43],[42],[41]) Ibrahim, Majdoub and Masmoudi ([16], [15], [18]). All these results have been provided in the last two decades, especially the 2 space dimensions problem has been developed in the last decade. We will see that although techniques are particularly developed there are completely open problems. At this point, for n 3, it is important to classify the semilinear Klein-Gordon equation introducing the critical exponent. The problem at the critical exponent heuristically comes from how the energy scales with respect to the scaling: u λ (t, x) = λ 2 p 1 u(λt, λx) p [1, + ). Let u be a classical solution of (0.4): u λ (t, x) = λ 2 p 1 +2 u(λt, λx) = λ 2 p 1 +2 u(λx, λt) u(λt, λx) p 1 = λ 2 p p 1 (p 1)( 2 p 1 ) u λ (t, x) u λ (t, x) p 1 = u λ (t, x) u λ (t, x) p 1 5
7 hence both u, u λ solve (0.4). The associated energy: ( ) ut 2 + u 2 E(u(t)) = + u p+1 dx 2 p + 1 evaluated on u λ changes: E(u λ ) = λ 2 n+ 4 p 1 R n We note that E(u λ ) = E(u),i.e. p = 2 1 where 2 = R n ( ut 2 + u 2 2 ) + u p+1 dx = λ 2 n+ p 1 4 E(u). p + 1 the energy does not change under scaling, if 2n 4. Moreover the exponent 2 n + n 2 p 1 is positive for p < 2 1 and is negative for p > 2 1. It is clear that that for λ + for p 2 1 the energy remains bounded (actually goes to zero for p > 2 1). It follows that the solution s energy concentrates at a point for p < 2 1. The concentration implies an infinite amount of energy and in this case it might be possible to prove well posendess or regularity of solutions. For n 3 and p = 2 1 the concentration requires a finite amount of energy and it should be ruled out for small energy data. Ginibre and Velo [10] show that the problem (0.4)+(0.2) is globally well posed in the energy space in the sub-critical range p < 2 1. For the critical power nonlinearity the problem was solved by Shatah and Struwe. In [33] they proved that the critical problem is well posed in the energy space for any space dimensions n 3. In the super-critical range the well-posedness is an open problem except for some partial results(for example see [5],[6],[17],[26]). In two space dimensions, power nonlinearities appear to be sub-critical with respect to H 1 norm. The critical exponent in Sobolev embedding is infinite. Hence the exponential nonlinearity seems to be a critical nonlinearity. The 2D Klein-Gordon equation we will study is the following: u + ue u2 = 0 (0.7) ( with associated energy density e(u) = 1 2 u 2 t + u 2 + e u2 1 ). The first theorems about this type of equation were due to Ibrahim Majdoub and 6
8 Masmoudi (see for example [16], [18],) and they make evidence of the relation between the considered equation and its initial energy data by the version of Moser Trudinger inequality provided by Adachi and Tanaka: Proposition 0.3. Let α (0, 4π). It exists a constant C = C(α) such that for all u H 1 (R 2 ) such that u L 2 (R 2 ) 1. If α 4π the inequality is false. R 2 ( e αu2(x) 1 ) dx C u 2 L 2 (0.8) Remark 0.4. α = 4π becomes admissible if we require u H 1 1. In particular ( sup e 4πu2 1 ) dx < + u H 1 (R 2 ) 1 R 2 and it is false for α > 4π. See [1]. It seems that problems arises when we consider large initial data energy. In fact in 2006 Ibrahim Majdoub and Masmoudi [16] proved the following theorem: Theorem 0.5. Assume ϕ L 2 < 2π. It exists a time T > 0 and a unique weak solution u(t, x) to the problem (0.7) with initial data (0.2) in H 1 L 2 in C T (H 1 (R 2 )) C 1 T (L2 (R 2 )). Furthermore u L 4 T (C 1 4 (R 2 )), t [0, T) and E(u)(t) = E(u)(0) The proof is essentially based on a contraction argument. If E(u)(0) 2π it is possible to prolong the solution for any T > 0, hence to have a global weak solution. The authors refers that the contraction argument is enough to assure global strong well-posedness in H 1 L 2 for small energy initial data, E(u)(0) 7
9 2π. In this sense we define critical the Cauchy problem (0.7) + (0.2) with initial data energy 2π, sub-critical with initial data energy less than 2π and super-critical with initial data energy larger than 2π. Asking higher regularity to initial data it is possible to remove the smallness condition on the initial data and have a local well-posedness result for strong solutions in the space H s H s 1 with s > 1. Using the last result, in 2009, Ibrahim, Majdoub and Masmoudi showed that for any initial data the problem (0.7)+(0.2) is locally well posed in H 1 L 2 (see[18]). In addition, in [17] and in [18], they proved, in the super-critical case, that the local solution does not depend on the initial data in a locally uniform continuous fashion, i.e. the problem is weakly ill posed on {E < 2π + δ} H 1 L 2, δ > 0. In [18], they consider the re-scaled equation u + ue 4πu2 = 0 with associated energy E(u)(t) = R 2 ( u t 2 + u 2 + e4πu2 1 4π The critical energy become 1 and we have the following ill-posedness theorem in {E < 1 + δ} H 1 L 2 : Theorem 0.6. Let υ > 0. It exists a sequence of positive real numbers {t k } and two sequences{u k } k N,{w k } k N solving the Klein-Gordon equation (0.7)such that t k k + 0 ) dx. (u k w k )(0) 2 H 1 + t (u k w k )(0) 2 L 2 o(1) as k + 0 < E(u k )(0) 1 e 3 υ 2, 0 < E(w k )(0) 1 υ 2 and lim inf k + t(u k w k )(t k ) 2 L 2 π 4 (e2 + e 3 8π )υ 2 8
10 It follows that the problem is weakly ill posed in the energy space in the supercritical range. In the thesis we will present the 2006 result in order to understand how the Moser Trudinger inequality implies the restriction on the initial data and we will provide the example of the ill posedness for large energy data. Other important studies we survey in the thesis strictly concern the existence and regularity of solutions for SLW. The first part of the thesis is in fact devoted to classical and modern results for general SLW always directed to the study of Klein-Gordon equation. At this point it is important to have a broad overview on some important SLW properties. We will present the Lagrangian formulation for the wave equation in order to understand the relation between invariants and conserved momenta. The SLW can be obtained by Euler-Lagrange equations for the action { A = 1 2 u2 t + 1 } 2 u 2 + G(u) dxdt. R R n The Lagrangian formulation, of these wave equations, allows us to systematically derive conserved quantities by means of Noether s theorem Theorem 0.7. If the action A is invariant under a group of diffeomorphisms, the solution u satisfies conservation laws determinated by this invariance. Another important property of SLW is the finite speed of signal s spread. It means that if the problem s solution has initial data compactly supported in a subset Ω R n, its support at the time t will be contained in the envelop Ω+B t (0), for t 0. In particular if Ω = B r (0), then Supp u K + ( r, 0) = {(t, x) x r + t, t 0}, where K + ( r, 0) is the forward truncated cone with vertex in ( r, 0). Moreover, considering the backward light cone K(z 0 ) = {(t, x) x x 0 t 0 t, 0 t t 0 } we are sure that the perturbation outside the cone will not affect the solution inside. This will make us able to reduce global problems, for instance existence 9
11 of global solution, to a local estimate of solution s norm. Segal, in [31], shows that it is possible to find global weak solutions for general SLW assuming initial data (0.2) in (H 1 L 2 )(R n ), G(ϕ) L 1 (R n ) and asking coerciveness on the nonlinearity: Theorem 0.8 (Segal s Theorem). Consider SLW. Assume g(0) = 0 and the coercive assumption on g: 0 ug(u) + C 1 u 2 CG(u) + C 2 u 2 for u + (0.9) with C, C 1, C 2 [0, + ). For any initial data (ϕ, ψ) (H 1 L 2 )(R n ), G(ϕ) L 1 (R n ), it exists a global weak solution for SLW problem u H 1 loc such that Du L (R, L 2 (R n )), G(u) L (R; L 1 (R n )) and E(u)(t) E(u)(0) = Rn ψ(t, x) ϕ(t, x) G(ϕ(t, x))dx =: E 0 (0.10) For the proof, we need to show the existence of a unique weak solution for Lipschitz nonlinearity in order to use approximated problem with globally Lipschitz nonlinearity. The Segal s result provides the existence of global weak solutions for any u u p 1 nonlinearity. On the other hand it does not work with the 2 space dimensions exponential nonlinearity considered. The main problem seems to establish regularity and uniqueness conditions on solutions. Following Shatah and Struwe [35], by using energy methods we provide uniqueness and the regularity of this solutions for 1 p n 2. Ginibre and Velo, in [10], were able to improve the uniqueness range for solutions for the problem (0.4)+(0.2) in the energy space Ḣ 1 L 2 up to the Sobolev critical exponent 2 1. Regarding existence of smooth solution Shatah and Struwe, in [33], show that a unique smooth solution of the smooth Cauchy problem can be found until n = 7. Struwe, in [35], quoted that for p 2 1 and n 9 for 10
12 smooth initial data we have a smooth solution. Concerning the focusing case, global regularity and well posedness conjecture fails. In fact H.Levine[28], for instance, shows that if (ϕ, ψ) Ḣ 1 (R n ) L 2 (R n ), the initial data energy is negative and we have a growth condition on nonlinearity, the solution has finite lifespan. Theorem 0.9 (Levine s Theorem). Consider the initial value problem (0.1)+(0.2). Assume that ug(u) (2 + ɛ)g(u) u R, ɛ > 0 (0.11) Assume that the initial data satisfies E(u)(0) = ( ) ϕ 2 + ψ2 + G(ϕ) dx < 0. Then R n 2 2 the solution of the SWE does not exists for all the time. For focusing problem we have a ground state conjecture: there exist a ground state, whose energy is a threshold for global existence. Merle and Kenig [25], [22] proved the theorem: Theorem For the focusing energy critical SLW, 3 n 5, (ϕ, ψ) Ḣ 1 (R n ) L 2 (R n ), E(ϕ, ψ) < E(W, 0), where W(x) = ( 1 + ) n 2 x 2 2 n(n 2) if ϕ Ḣ 1 < W Ḣ1, the solution exists for all the time. if ϕ Ḣ 1 > W Ḣ1, the solution has finite lifespan. Ḣ 1 we have: As we said, in the thesis we focus on the three dimensional (0.4)+(0.2) problem. In this case the critical exponent is 5 and as above we can distinguish a subcritical (p 5), a critical (p = 5) and a supercritical (p 5) equation. Following Jörgens s idea, presented in [21], we will be able to show the theorem: Theorem Let G be a closed bounded domain. Let ϕ C 3 (G), ψ C 2 (G) and g C 2 (R), g(0) = 0. Then it exists T > 0 and a unique u C 2 (K T (G)) solution of the problem (0.1)+(0.2) in K T (G). 11
13 where K T (G) = ( B G K(B)) ([0, T] R 3 ), B are R 3 balls and K(B) is the backward cone built on the ball B. It gives the existence of a local classical solution for any regular initial data and nonlinearity. We give a proof based on a converging argument of approximate solutions. Then, following [35], we will prove the existence of a unique global classical solution in the subcritical range. In particular we can observe that blow up phenomena are characterized by the loss of L norm of solution. This important result can not be generalized in higher dimensions because it heavily uses representation formula for solutions of the linear Cauchy problem. Completed the subcritical case, we consider the 3D-SLW with critical nonlinearity. Assuming small energy initial data, Rauch in [30], was able to show the existence of an L a priori bound on solutions depending only on the initial data and its support s size. It prevents the overcome of blow up at finite time and ensures the existence of a unique classical solution: Theorem It exists ɛ 0 > 0 such that the initial data problem (0.4)+(0.2) with p = 5, ϕ C 3 (R 3 ), ψ C 2 (R 3 ) such that initial data energy E(u)(0) ɛ 0 admits a unique C 2 global solution. The bound obtained comes from the explicit representation formula for solution of the linear three space dimensions problem. On every backward cone K(z 0 ) such that u(z 0 ) = sup K(z0 ) u(t, x) we have the estimate: u(z 0 ) C + u(z 0) 4π M T (z 0 ) u 4 (t, x) t 0 t dσ + CE t 0 T < T < t 0 (0.12) where M T (z 0 ) is the mantle of the cone s upper part higher than T. For small energy initial data we can choose T = 0 and have 1 4π M 0 (z 0 ) u 4 (t,x) t 0 dσ < 1. t This gives a uniform control on the L norm of the solution over every backward light cone and assure the absence of blow up. Afterwards, following Struwe 12
14 [40] we will see the existence of a unique global classical solution for any initial data by the Grillakis geometric idea presented in [13], assuring the condition: u 4 lim sup dσ 2π. z z 0,z K(z 0 ) M T (z) t 0 t We can prevent the blow up in z 0 through the above condition and (0.12): it suffices to have a uniform bound for u on K(z 0 )\{z 0 } i.e. the condition Struwe s theorem reads as follows: lim sup u(z) < +. z z 0,z K(z 0 ) Theorem Let ϕ C 3 (R 3 ), ψ C 2 (R 3 ). solution, i.e. u C 2 ([0, + ) R 3 ), of the Cauchy problem: u tt u + u 5 = 0 u t=0 = ϕ u t t=0 = ψ It exists a unique, global, classical (0.13) Note that the bound that will be obtained is not an a priori bound for the solution u on a general cone K only depending on initial data and K. Eventually we will present the pointwise decay property of the solution of the u 5 Klein-Gordon equation s as in Grillakis [13]. Theorem Let u C 2 ([0, + ) R n ) be solution of u tt u + u 5 = 0 u(a, x) = φ(x) C 3 u t (a, x) = ψ(x) C 2 Supp(ϕ) Supp(ψ) B a 2 (0) (0.14) we have the estimate: (t 2 x 2 ) u(t, x) C (0.15) where C := C(ϕ, ψ) 13
15 We notice that the above estimate gives the decay rate of 1 on characteristic t cones {t x = τ}, τ 0. For the two space dimensions case, Struwe, in 2010 ([42]), was able to show the existence of a unique smooth solution for (0.7)+(0.2) in the class of radial symmetric smooth functions, in spite of the above initial data classification. We present the result provided by Struwe the following year, in[41], where he was able to avoid the radial condition and to prove the result: Theorem For any ϕ, ψ C (R 2 ) it exists a unique smooth solution u C (R R 2 ) for the Cauchy problem (0.7)+(0.2). Struwe gives a proposition characterizing blow up phenomenon by energy concentration: Proposition There exists ɛ 0 > 0 such that if a solution u C ([0, T 0 ) R 2 ) can not be extended to a neighbourhood of z 0 = (T 0, x 0 ) there holds E(u(t), B T0 t(x 0 )) ɛ 0 t [0, T 0 ) (0.16) It means that whenever a solution of (0.7)+(0.2) blows up at a time t the energy will concentrate at the singular point. The proof of Theorem (0.15) is provided by contradiction. We will assume that the solution can not be extended in a neighbourhood of (T 0, x 0 ) and the absurd will come from the lack of energy concentration. The interesting fact comes from the absence of assumptions on the initial data energy. The smart idea comes from a clever extension of the Moser-Trudinger inequality Lemma For any E > 0, p < +, there exists ɛ = 4π2 and a constant C > 0 such p 2 E that for any ξ 0 > 0, any v H 1 0 ([0, 1]2 ) with (ξ 0 v y 2 + ξ 1 0 v x 2 )dxdy E, ξ 1 0 v x 2 dxdy ɛ 14
16 there holds epv2 dxdy C needed to prove the lemma Lemma There exists ɛ > 0 and 0 < C < + such that for T ɛ T < T 0 there holds e 4u2 dxdt C(T 0 T). K T (z 0 ) that improve the bound on the non linear term of the equation (0.7). This result, together with a decay lemma applied to estimate the energy term coming from the nonlinearity, let us reach a uniform smallness condition on the energy of solution inside backward light cone with vertex in (T 0, x 0 ) for times close to T 0, and rule out the blow up. 15
17 References [1] Shinji Adachi and Kazunaga Tanaka, Trudinger type inequalities in R N and their best exponents, Proc. Amer. Math. Soc. 128 (2000), no. 7, [2] Philip Brenner and Peter Kumlin, On wave equations with supercritical nonlinearities, Arch. Math. (Basel) 74 (2000), no. 2, MR (2001g:35162) [3] Philip Brenner and Wolf von Wahl, Global classical solutions of nonlinear wave equations, Math. Z. 176 (1981), no. 1, MR (82m:35103) [4] Felix E. Browder, On non-linear wave equations, Math. Z. 80 (1962), [5] Ibrahim S. Burque, N. and P. Gérard, Instability results for non linear s roedinger and wave equations, Preprint. [6] C. Chris, J. Colliander, and T. Tao, Ill-posedness for non linear s roedinger and wave equations, Preprint. [7] Michael Christ, James Colliander, and Terrence Tao, Asymptotics, frequency modulation, and low regularity ill-posedness for canonical defocusing equations, Amer. J. Math. 125 (2003), no. 6, [8] Emmanuele DiBenedetto, Partial differential equations, second ed., Cornerstones, Birkhäuser Boston Inc., Boston, MA, [9] Lawrence C. Evans, Partial differential equations, second ed., Graduate Studies in Mathematics, vol. 19, American Mathematical Society, Providence, RI, [10] J. Ginibre, A. Soffer, and G. Velo, The global Cauchy problem for the critical nonlinear wave equation, J. Funct. Anal. 110 (1992), no. 1,
18 [11] J. Ginibre and G. Velo, On a class of nonlinear Schrödinger equations. II. Scattering theory, general case, J. Funct. Anal. 32 (1979), no. 1, MR (82c:35058) [12], Generalized Strichartz inequalities for the wave equation, J. Funct. Anal. 133 (1995), no. 1, [13] Manoussos G. Grillakis, Regularity and asymptotic behaviour of the wave equation with a critical nonlinearity, Ann. of Math. (2) 132 (1990), no. 3, [14] Dorothee D. Haroske and Hans Triebel, Distributions, Sobolev spaces, elliptic equations, EMS Textbooks in Mathematics, European Mathematical Society (EMS), Zürich, [15] S. Ibrahim, M. Majdoub, and N. Masmoudi, Double logarithmic inequality with a sharp constant, Proc. Amer. Math. Soc. 135 (2007), no. 1, (electronic). [16] Slim Ibrahim, Mohamed Majdoub, and Nader Masmoudi, Global solutions for a semilinear, two-dimensional Klein-Gordon equation with exponential-type nonlinearity, Comm. Pure Appl. Math. 59 (2006), no. 11, [17], Ill-posedness of H 1 -supercritical waves, C. R. Math. Acad. Sci. Paris 345 (2007), no. 3, [18], Well and ill-posedness issues for energy supercritical waves, to appear in Analysis and PDE (2009). [19] Fritz John, Blow-up of solutions of nonlinear wave equations in three space dimensions, Manuscripta Math. 28 (1979), no. 1-3, [20], Partial differential equations, fourth ed., Applied Mathematical Sciences, vol. 1, Springer-Verlag, New York,
19 [21] Konrad Jörgens, Das Anfangswertproblem im Grossen für eine Klasse nichtlinearer Wellengleichungen, Math. Z. 77 (1961), [22] Carlos E. Kenig and Frank Merle, Global well-posedness, scattering and blowup for the energy-critical focusing non-linear wave equation, Acta Math. 201 (2008), no. 2, [23] Carlos E. Kenig, Gustavo Ponce, and Luis Vega, The Cauchy problem for the Korteweg-de Vries equation in Sobolev spaces of negative indices, Duke Math. J. 71 (1993), no. 1, MR (94g:35196) [24], Small solutions to nonlinear Schrödinger equations, Ann. Inst. H. Poincaré Anal. Non Linéaire 10 (1993), no. 3, MR (94h:35238) [25] C.E. Koenig, The well-posedness of non-linear dispersive equations: Some recent developments,, Contemp. Math. 411 (2006), [26] Gilles Lebeau, Non linear optic and supercritical wave equation, Bull. Soc. Roy. Sci. Liège 70 (2001), no. 4-6, (2002), Hommage à Pascal Laubin. [27] Giovanni Leoni, A first course in Sobolev spaces, Graduate Studies in Mathematics, vol. 105, American Mathematical Society, Providence, RI, [28] Howard A. Levine, Instability and nonexistence of global solutions to nonlinear wave equations of the form Pu tt = Au + F (u), Trans. Amer. Math. Soc. 192 (1974), [29] Hartmut Pecher, Ein nichtlinearer Interpolationssatz und seine Anwendung auf nichtlineare Wellengleichungen, Math. Z. 161 (1978), no. 1, MR (81i:46039) 18
20 [30] Jeffrey Rauch, I. The u 5 Klein-Gordon equation. II. Anomalous singularities for semilinear wave equations, Nonlinear partial differential equations and their applications. Collège de France Seminar, Vol. I(Paris, 1978/1979), Res. Notes in Math., vol. 53, Pitman, Boston, Mass., 1981, pp [31] I. E. Segal, The global Cauchy problem for a relativistic scalar field with power interaction, Bull. Soc. Math. France 91 (1963), MR (27 #3928) [32] Jalal Shatah, Weak solutions and development of singularities of the SU(2) σ- model, Comm. Pure Appl. Math. 41 (1988), no. 4, [33] Jalal Shatah and Michael Struwe, Regularity results for nonlinear wave equations, Ann. of Math. (2) 138 (1993), no. 3, [34], Well-posedness in the energy space for semilinear wave equations with critical growth, Internat. Math. Res. Notices (1994), no. 7, 303ff., approx. 7 pp. (electronic). [35], Geometric wave equations, Courant Lecture Notes in Mathematics, vol. 2, New York University Courant Institute of Mathematical Sciences, New York, [36] Christopher D. Sogge, Lectures on nonlinear wave equations, Monographs in Analysis, II, International Press, Boston, MA, [37] Walter A. Strauss, Nonlinear wave equations, CBMS Regional Conference Series in Mathematics, vol. 73, Published for the Conference Board of the Mathematical Sciences, Washington, DC, [38] Robert S. Strichartz, Restrictions of Fourier transforms to quadratic surfaces and decay of solutions of wave equations, Duke Math. J. 44 (1977), no. 3,
21 [39] Michael Struwe, Globally regular solutions to the u 5 Klein-Gordon equation, Ann. Scuola Norm. Sup. Pisa Cl. Sci. (4) 15 (1988), no. 3, (1989). [40], Semi-linear wave equations, Bull. Amer. Math. Soc. (N.S.) 26 (1992), no. 1, [41], The critical non linear wave equation in 2 space dimensions, Preprint (2010). [42], Global well-posedness of the Cauchy problem for a super-critical nonlinear wave equation in two space dimensions, Math. Ann. 350 (2011), no. 3, [43], A super-critical nonlinear wave equation in 2 space dimensions, Milan J. Math. 79 (2011), no. 1, MR [44] Terence Tao, Global regularity of wave maps. II. Small energy in two dimensions, Comm. Math. Phys. 224 (2001), no. 2, [45], Global regularity for a logarithmically supercritical defocusing nonlinear wave equation for spherically symmetric data, J. Hyperbolic Differ. Equ. 4 (2007), no. 2, [46] Daniel Tataru, Local and global results for wave maps. I, Comm. Partial Differential Equations 23 (1998), no. 9-10, MR (99j:58209) [47], On global existence and scattering for the wave maps equation, Amer. J. Math. 123 (2001), no. 1,
Global well-posedness for semi-linear Wave and Schrödinger equations. Slim Ibrahim
 Global well-posedness for semi-linear Wave and Schrödinger equations Slim Ibrahim McMaster University, Hamilton ON University of Calgary, April 27th, 2006 1 1 Introduction Nonlinear Wave equation: ( 2
Global well-posedness for semi-linear Wave and Schrödinger equations Slim Ibrahim McMaster University, Hamilton ON University of Calgary, April 27th, 2006 1 1 Introduction Nonlinear Wave equation: ( 2
Recent developments on the global behavior to critical nonlinear dispersive equations. Carlos E. Kenig
 Recent developments on the global behavior to critical nonlinear dispersive equations Carlos E. Kenig In the last 25 years or so, there has been considerable interest in the study of non-linear partial
Recent developments on the global behavior to critical nonlinear dispersive equations Carlos E. Kenig In the last 25 years or so, there has been considerable interest in the study of non-linear partial
SCATTERING FOR THE TWO-DIMENSIONAL NLS WITH EXPONENTIAL NONLINEARITY
 SCATTERING FOR THE TWO-DIMENSIONAL NLS WITH EXPONENTIAL NONLINEARITY S. IBRAHIM, M. MAJDOUB, N. MASMOUDI, AND K. NAKANISHI Abstract. We investigate existence and asymptotic completeness of the wave operators
SCATTERING FOR THE TWO-DIMENSIONAL NLS WITH EXPONENTIAL NONLINEARITY S. IBRAHIM, M. MAJDOUB, N. MASMOUDI, AND K. NAKANISHI Abstract. We investigate existence and asymptotic completeness of the wave operators
BLOWUP THEORY FOR THE CRITICAL NONLINEAR SCHRÖDINGER EQUATIONS REVISITED
 BLOWUP THEORY FOR THE CRITICAL NONLINEAR SCHRÖDINGER EQUATIONS REVISITED TAOUFIK HMIDI AND SAHBI KERAANI Abstract. In this note we prove a refined version of compactness lemma adapted to the blowup analysis
BLOWUP THEORY FOR THE CRITICAL NONLINEAR SCHRÖDINGER EQUATIONS REVISITED TAOUFIK HMIDI AND SAHBI KERAANI Abstract. In this note we prove a refined version of compactness lemma adapted to the blowup analysis
GLOBAL SOLUTIONS FOR A SEMILINEAR 2D KLEIN-GORDON EQUATION WITH EXPONENTIAL TYPE NONLINEARITY
 GLOBAL SOLUTIONS FOR A SEMILINEAR D KLEIN-GORDON EQUATION WITH EXPONENTIAL TYPE NONLINEARITY S. Ibrahim Department of Mathematics & Statistics, McMaster University, 180 main Street West, Hamilton, Ontario,
GLOBAL SOLUTIONS FOR A SEMILINEAR D KLEIN-GORDON EQUATION WITH EXPONENTIAL TYPE NONLINEARITY S. Ibrahim Department of Mathematics & Statistics, McMaster University, 180 main Street West, Hamilton, Ontario,
DECAY ESTIMATES FOR THE KLEIN-GORDON EQUATION IN CURVED SPACETIME
 Electronic Journal of Differential Equations, Vol. 218 218), No. 17, pp. 1 9. ISSN: 172-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu DECAY ESTIMATES FOR THE KLEIN-GORDON EQUATION
Electronic Journal of Differential Equations, Vol. 218 218), No. 17, pp. 1 9. ISSN: 172-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu DECAY ESTIMATES FOR THE KLEIN-GORDON EQUATION
DISPERSIVE EQUATIONS: A SURVEY
 DISPERSIVE EQUATIONS: A SURVEY GIGLIOLA STAFFILANI 1. Introduction These notes were written as a guideline for a short talk; hence, the references and the statements of the theorems are often not given
DISPERSIVE EQUATIONS: A SURVEY GIGLIOLA STAFFILANI 1. Introduction These notes were written as a guideline for a short talk; hence, the references and the statements of the theorems are often not given
DETERMINATION OF THE BLOW-UP RATE FOR THE SEMILINEAR WAVE EQUATION
 DETERMINATION OF THE LOW-UP RATE FOR THE SEMILINEAR WAVE EQUATION y FRANK MERLE and HATEM ZAAG Abstract. In this paper, we find the optimal blow-up rate for the semilinear wave equation with a power nonlinearity.
DETERMINATION OF THE LOW-UP RATE FOR THE SEMILINEAR WAVE EQUATION y FRANK MERLE and HATEM ZAAG Abstract. In this paper, we find the optimal blow-up rate for the semilinear wave equation with a power nonlinearity.
A REMARK ON AN EQUATION OF WAVE MAPS TYPE WITH VARIABLE COEFFICIENTS
 A REMARK ON AN EQUATION OF WAVE MAPS TYPE WITH VARIABLE COEFFICIENTS DAN-ANDREI GEBA Abstract. We obtain a sharp local well-posedness result for an equation of wave maps type with variable coefficients.
A REMARK ON AN EQUATION OF WAVE MAPS TYPE WITH VARIABLE COEFFICIENTS DAN-ANDREI GEBA Abstract. We obtain a sharp local well-posedness result for an equation of wave maps type with variable coefficients.
CUTOFF RESOLVENT ESTIMATES AND THE SEMILINEAR SCHRÖDINGER EQUATION
 CUTOFF RESOLVENT ESTIMATES AND THE SEMILINEAR SCHRÖDINGER EQUATION HANS CHRISTIANSON Abstract. This paper shows how abstract resolvent estimates imply local smoothing for solutions to the Schrödinger equation.
CUTOFF RESOLVENT ESTIMATES AND THE SEMILINEAR SCHRÖDINGER EQUATION HANS CHRISTIANSON Abstract. This paper shows how abstract resolvent estimates imply local smoothing for solutions to the Schrödinger equation.
GLOBAL EXISTENCE FOR THE ONE-DIMENSIONAL SEMILINEAR TRICOMI-TYPE EQUATIONS
 GLOBAL EXISTENCE FOR THE ONE-DIMENSIONAL SEMILINEAR TRICOMI-TYPE EQUATIONS ANAHIT GALSTYAN The Tricomi equation u tt tu xx = 0 is a linear partial differential operator of mixed type. (For t > 0, the Tricomi
GLOBAL EXISTENCE FOR THE ONE-DIMENSIONAL SEMILINEAR TRICOMI-TYPE EQUATIONS ANAHIT GALSTYAN The Tricomi equation u tt tu xx = 0 is a linear partial differential operator of mixed type. (For t > 0, the Tricomi
Dynamics of energy-critical wave equation
 Dynamics of energy-critical wave equation Carlos Kenig Thomas Duyckaerts Franke Merle September 21th, 2014 Duyckaerts Kenig Merle Critical wave 2014 1 / 22 Plan 1 Introduction Duyckaerts Kenig Merle Critical
Dynamics of energy-critical wave equation Carlos Kenig Thomas Duyckaerts Franke Merle September 21th, 2014 Duyckaerts Kenig Merle Critical wave 2014 1 / 22 Plan 1 Introduction Duyckaerts Kenig Merle Critical
BIHARMONIC WAVE MAPS INTO SPHERES
 BIHARMONIC WAVE MAPS INTO SPHERES SEBASTIAN HERR, TOBIAS LAMM, AND ROLAND SCHNAUBELT Abstract. A global weak solution of the biharmonic wave map equation in the energy space for spherical targets is constructed.
BIHARMONIC WAVE MAPS INTO SPHERES SEBASTIAN HERR, TOBIAS LAMM, AND ROLAND SCHNAUBELT Abstract. A global weak solution of the biharmonic wave map equation in the energy space for spherical targets is constructed.
arxiv:math/ v1 [math.ap] 24 Apr 2003
![arxiv:math/ v1 [math.ap] 24 Apr 2003 arxiv:math/ v1 [math.ap] 24 Apr 2003](/thumbs/95/122489725.jpg) ICM 2002 Vol. III 1 3 arxiv:math/0304397v1 [math.ap] 24 Apr 2003 Nonlinear Wave Equations Daniel Tataru Abstract The analysis of nonlinear wave equations has experienced a dramatic growth in the last ten
ICM 2002 Vol. III 1 3 arxiv:math/0304397v1 [math.ap] 24 Apr 2003 Nonlinear Wave Equations Daniel Tataru Abstract The analysis of nonlinear wave equations has experienced a dramatic growth in the last ten
ANALYTIC SMOOTHING EFFECT FOR NONLI TitleSCHRÖDINGER EQUATION IN TWO SPACE DIMENSIONS. Citation Osaka Journal of Mathematics.
 ANALYTIC SMOOTHING EFFECT FOR NONLI TitleSCHRÖDINGER EQUATION IN TWO SPACE DIMENSIONS Author(s) Hoshino, Gaku; Ozawa, Tohru Citation Osaka Journal of Mathematics. 51(3) Issue 014-07 Date Text Version publisher
ANALYTIC SMOOTHING EFFECT FOR NONLI TitleSCHRÖDINGER EQUATION IN TWO SPACE DIMENSIONS Author(s) Hoshino, Gaku; Ozawa, Tohru Citation Osaka Journal of Mathematics. 51(3) Issue 014-07 Date Text Version publisher
Nonlinear Schrödinger Equation BAOXIANG WANG. Talk at Tsinghua University 2012,3,16. School of Mathematical Sciences, Peking University.
 Talk at Tsinghua University 2012,3,16 Nonlinear Schrödinger Equation BAOXIANG WANG School of Mathematical Sciences, Peking University 1 1 33 1. Schrödinger E. Schrödinger (1887-1961) E. Schrödinger, (1887,
Talk at Tsinghua University 2012,3,16 Nonlinear Schrödinger Equation BAOXIANG WANG School of Mathematical Sciences, Peking University 1 1 33 1. Schrödinger E. Schrödinger (1887-1961) E. Schrödinger, (1887,
Presenter: Noriyoshi Fukaya
 Y. Martel, F. Merle, and T.-P. Tsai, Stability and Asymptotic Stability in the Energy Space of the Sum of N Solitons for Subcritical gkdv Equations, Comm. Math. Phys. 31 (00), 347-373. Presenter: Noriyoshi
Y. Martel, F. Merle, and T.-P. Tsai, Stability and Asymptotic Stability in the Energy Space of the Sum of N Solitons for Subcritical gkdv Equations, Comm. Math. Phys. 31 (00), 347-373. Presenter: Noriyoshi
Scattering theory for nonlinear Schrödinger equation with inverse square potential
 Scattering theory for nonlinear Schrödinger equation with inverse square potential Université Nice Sophia-Antipolis Based on joint work with: Changxing Miao (IAPCM) and Junyong Zhang (BIT) February -6,
Scattering theory for nonlinear Schrödinger equation with inverse square potential Université Nice Sophia-Antipolis Based on joint work with: Changxing Miao (IAPCM) and Junyong Zhang (BIT) February -6,
Scattering for cubic-quintic nonlinear Schrödinger equation on R 3
 Scattering for cubic-quintic nonlinear Schrödinger equation on R 3 Oana Pocovnicu Princeton University March 9th 2013 Joint work with R. Killip (UCLA), T. Oh (Princeton), M. Vişan (UCLA) SCAPDE UCLA 1
Scattering for cubic-quintic nonlinear Schrödinger equation on R 3 Oana Pocovnicu Princeton University March 9th 2013 Joint work with R. Killip (UCLA), T. Oh (Princeton), M. Vişan (UCLA) SCAPDE UCLA 1
Solutions to the Nonlinear Schrödinger Equation in Hyperbolic Space
 Solutions to the Nonlinear Schrödinger Equation in Hyperbolic Space SPUR Final Paper, Summer 2014 Peter Kleinhenz Mentor: Chenjie Fan Project suggested by Gigliola Staffilani July 30th, 2014 Abstract In
Solutions to the Nonlinear Schrödinger Equation in Hyperbolic Space SPUR Final Paper, Summer 2014 Peter Kleinhenz Mentor: Chenjie Fan Project suggested by Gigliola Staffilani July 30th, 2014 Abstract In
arxiv: v3 [math.ap] 1 Sep 2017
![arxiv: v3 [math.ap] 1 Sep 2017 arxiv: v3 [math.ap] 1 Sep 2017](/thumbs/96/127728439.jpg) arxiv:1603.0685v3 [math.ap] 1 Sep 017 UNIQUE CONTINUATION FOR THE SCHRÖDINGER EQUATION WITH GRADIENT TERM YOUNGWOO KOH AND IHYEOK SEO Abstract. We obtain a unique continuation result for the differential
arxiv:1603.0685v3 [math.ap] 1 Sep 017 UNIQUE CONTINUATION FOR THE SCHRÖDINGER EQUATION WITH GRADIENT TERM YOUNGWOO KOH AND IHYEOK SEO Abstract. We obtain a unique continuation result for the differential
Energy transfer model and large periodic boundary value problem for the quintic NLS
 Energy transfer model and large periodic boundary value problem for the quintic NS Hideo Takaoka Department of Mathematics, Kobe University 1 ntroduction This note is based on a talk given at the conference
Energy transfer model and large periodic boundary value problem for the quintic NS Hideo Takaoka Department of Mathematics, Kobe University 1 ntroduction This note is based on a talk given at the conference
Necessary Conditions and Sufficient Conditions for Global Existence in the Nonlinear Schrödinger Equation
 Necessary Conditions and Sufficient Conditions for Global Existence in the Nonlinear Schrödinger Equation Pascal Bégout aboratoire Jacques-ouis ions Université Pierre et Marie Curie Boîte Courrier 187,
Necessary Conditions and Sufficient Conditions for Global Existence in the Nonlinear Schrödinger Equation Pascal Bégout aboratoire Jacques-ouis ions Université Pierre et Marie Curie Boîte Courrier 187,
arxiv: v1 [math.ap] 28 Mar 2014
![arxiv: v1 [math.ap] 28 Mar 2014 arxiv: v1 [math.ap] 28 Mar 2014](/thumbs/85/91332009.jpg) GROUNDSTATES OF NONLINEAR CHOQUARD EQUATIONS: HARDY-LITTLEWOOD-SOBOLEV CRITICAL EXPONENT VITALY MOROZ AND JEAN VAN SCHAFTINGEN arxiv:1403.7414v1 [math.ap] 28 Mar 2014 Abstract. We consider nonlinear Choquard
GROUNDSTATES OF NONLINEAR CHOQUARD EQUATIONS: HARDY-LITTLEWOOD-SOBOLEV CRITICAL EXPONENT VITALY MOROZ AND JEAN VAN SCHAFTINGEN arxiv:1403.7414v1 [math.ap] 28 Mar 2014 Abstract. We consider nonlinear Choquard
Global unbounded solutions of the Fujita equation in the intermediate range
 Global unbounded solutions of the Fujita equation in the intermediate range Peter Poláčik School of Mathematics, University of Minnesota, Minneapolis, MN 55455, USA Eiji Yanagida Department of Mathematics,
Global unbounded solutions of the Fujita equation in the intermediate range Peter Poláčik School of Mathematics, University of Minnesota, Minneapolis, MN 55455, USA Eiji Yanagida Department of Mathematics,
NUMERICAL SIMULATIONS OF THE ENERGY-SUPERCRITICAL NONLINEAR SCHRÖDINGER EQUATION
 Journal of Hyperbolic Differential Equations Vol. 7, No. 2 (2010) 279 296 c World Scientific Publishing Company DOI: 10.1142/S0219891610002104 NUMERICAL SIMULATIONS OF THE ENERGY-SUPERCRITICAL NONLINEAR
Journal of Hyperbolic Differential Equations Vol. 7, No. 2 (2010) 279 296 c World Scientific Publishing Company DOI: 10.1142/S0219891610002104 NUMERICAL SIMULATIONS OF THE ENERGY-SUPERCRITICAL NONLINEAR
A Quasi-Linear Parabolic Partial Differential Equation with Accretive Property
 ONLINE ISSN 8-749 : Volume 3, Issue, 433-438 A Quasi-Linear Parabolic Partial Differential Equation with Accretive Property Aminu U. Bawa *, Micheal O. Egwurube and Murtala M. Ahmad 3 Department of Computer
ONLINE ISSN 8-749 : Volume 3, Issue, 433-438 A Quasi-Linear Parabolic Partial Differential Equation with Accretive Property Aminu U. Bawa *, Micheal O. Egwurube and Murtala M. Ahmad 3 Department of Computer
Global solutions for the cubic non linear wave equation
 Global solutions for the cubic non linear wave equation Nicolas Burq Université Paris-Sud, Laboratoire de Mathématiques d Orsay, CNRS, UMR 8628, FRANCE and Ecole Normale Supérieure Oxford sept 12th, 2012
Global solutions for the cubic non linear wave equation Nicolas Burq Université Paris-Sud, Laboratoire de Mathématiques d Orsay, CNRS, UMR 8628, FRANCE and Ecole Normale Supérieure Oxford sept 12th, 2012
Heat equations with singular potentials: Hardy & Carleman inequalities, well-posedness & control
 Outline Heat equations with singular potentials: Hardy & Carleman inequalities, well-posedness & control IMDEA-Matemáticas & Universidad Autónoma de Madrid Spain enrique.zuazua@uam.es Analysis and control
Outline Heat equations with singular potentials: Hardy & Carleman inequalities, well-posedness & control IMDEA-Matemáticas & Universidad Autónoma de Madrid Spain enrique.zuazua@uam.es Analysis and control
Sharp Sobolev Strichartz estimates for the free Schrödinger propagator
 Sharp Sobolev Strichartz estimates for the free Schrödinger propagator Neal Bez, Chris Jeavons and Nikolaos Pattakos Abstract. We consider gaussian extremisability of sharp linear Sobolev Strichartz estimates
Sharp Sobolev Strichartz estimates for the free Schrödinger propagator Neal Bez, Chris Jeavons and Nikolaos Pattakos Abstract. We consider gaussian extremisability of sharp linear Sobolev Strichartz estimates
Existence of a ground state and blow-up problem for a nonlinear Schrödinger equation with critical growth
 Existence of a ground state and blow-up problem for a nonlinear Schrödinger equation with critical growth Takafumi Akahori, Slim Ibrahim, Hiroaki Kikuchi and Hayato Nawa 1 Introduction In this paper, we
Existence of a ground state and blow-up problem for a nonlinear Schrödinger equation with critical growth Takafumi Akahori, Slim Ibrahim, Hiroaki Kikuchi and Hayato Nawa 1 Introduction In this paper, we
Nonlinear Schrödinger equation with combined power-type nonlinearities and harmonic potential
 Appl. Math. Mech. -Engl. Ed. 31(4), 521 528 (2010) DOI 10.1007/s10483-010-0412-7 c Shanghai University and Springer-Verlag Berlin Heidelberg 2010 Applied Mathematics and Mechanics (English Edition) Nonlinear
Appl. Math. Mech. -Engl. Ed. 31(4), 521 528 (2010) DOI 10.1007/s10483-010-0412-7 c Shanghai University and Springer-Verlag Berlin Heidelberg 2010 Applied Mathematics and Mechanics (English Edition) Nonlinear
ENERGY SCATTERING FOR THE 2D CRITICAL WAVE EQUATION
 ENERGY SCATTERING FOR THE 2D CRITICAL WAVE EQUATION S. IBRAHIM, M. MAJDOUB, N. MASMOUDI, AND K. NAKANISHI Abstract. We investigate existence and asymptotic completeness of the wave operators for nonlinear
ENERGY SCATTERING FOR THE 2D CRITICAL WAVE EQUATION S. IBRAHIM, M. MAJDOUB, N. MASMOUDI, AND K. NAKANISHI Abstract. We investigate existence and asymptotic completeness of the wave operators for nonlinear
A COUNTEREXAMPLE TO AN ENDPOINT BILINEAR STRICHARTZ INEQUALITY TERENCE TAO. t L x (R R2 ) f L 2 x (R2 )
 Electronic Journal of Differential Equations, Vol. 2006(2006), No. 5, pp. 6. ISSN: 072-669. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu (login: ftp) A COUNTEREXAMPLE
Electronic Journal of Differential Equations, Vol. 2006(2006), No. 5, pp. 6. ISSN: 072-669. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu (login: ftp) A COUNTEREXAMPLE
Long-term dynamics of nonlinear wave equations
 Long-term dynamics of nonlinear wave equations W. Schlag (University of Chicago) Recent Developments & Future Directions, September 2014 Wave maps Let (M, g) be a Riemannian manifold, and u : R 1+d t,x
Long-term dynamics of nonlinear wave equations W. Schlag (University of Chicago) Recent Developments & Future Directions, September 2014 Wave maps Let (M, g) be a Riemannian manifold, and u : R 1+d t,x
The Kato square root problem on vector bundles with generalised bounded geometry
 The Kato square root problem on vector bundles with generalised bounded geometry Lashi Bandara (Joint work with Alan McIntosh, ANU) Centre for Mathematics and its Applications Australian National University
The Kato square root problem on vector bundles with generalised bounded geometry Lashi Bandara (Joint work with Alan McIntosh, ANU) Centre for Mathematics and its Applications Australian National University
VANISHING-CONCENTRATION-COMPACTNESS ALTERNATIVE FOR THE TRUDINGER-MOSER INEQUALITY IN R N
 VAISHIG-COCETRATIO-COMPACTESS ALTERATIVE FOR THE TRUDIGER-MOSER IEQUALITY I R Abstract. Let 2, a > 0 0 < b. Our aim is to clarify the influence of the constraint S a,b = { u W 1, (R ) u a + u b = 1 } on
VAISHIG-COCETRATIO-COMPACTESS ALTERATIVE FOR THE TRUDIGER-MOSER IEQUALITY I R Abstract. Let 2, a > 0 0 < b. Our aim is to clarify the influence of the constraint S a,b = { u W 1, (R ) u a + u b = 1 } on
The Kato square root problem on vector bundles with generalised bounded geometry
 The Kato square root problem on vector bundles with generalised bounded geometry Lashi Bandara (Joint work with Alan McIntosh, ANU) Centre for Mathematics and its Applications Australian National University
The Kato square root problem on vector bundles with generalised bounded geometry Lashi Bandara (Joint work with Alan McIntosh, ANU) Centre for Mathematics and its Applications Australian National University
The Concentration-compactness/ Rigidity Method for Critical Dispersive and Wave Equations
 The Concentration-compactness/ Rigidity Method for Critical Dispersive and Wave Equations Carlos E. Kenig Supported in part by NSF 3 In these lectures I will describe a program (which I will call the
The Concentration-compactness/ Rigidity Method for Critical Dispersive and Wave Equations Carlos E. Kenig Supported in part by NSF 3 In these lectures I will describe a program (which I will call the
A GLOBAL COMPACT ATTRACTOR FOR HIGH-DIMENSIONAL DEFOCUSING NON-LINEAR SCHRÖDINGER EQUATIONS WITH POTENTIAL TERENCE TAO
 A GLOBAL COMPACT ATTRACTOR FOR HIGH-DIMENSIONAL DEFOCUSING NON-LINEAR SCHRÖDINGER EQUATIONS WITH POTENTIAL TERENCE TAO arxiv:85.1544v2 [math.ap] 28 May 28 Abstract. We study the asymptotic behavior of
A GLOBAL COMPACT ATTRACTOR FOR HIGH-DIMENSIONAL DEFOCUSING NON-LINEAR SCHRÖDINGER EQUATIONS WITH POTENTIAL TERENCE TAO arxiv:85.1544v2 [math.ap] 28 May 28 Abstract. We study the asymptotic behavior of
SYMMETRY RESULTS FOR PERTURBED PROBLEMS AND RELATED QUESTIONS. Massimo Grosi Filomena Pacella S. L. Yadava. 1. Introduction
 Topological Methods in Nonlinear Analysis Journal of the Juliusz Schauder Center Volume 21, 2003, 211 226 SYMMETRY RESULTS FOR PERTURBED PROBLEMS AND RELATED QUESTIONS Massimo Grosi Filomena Pacella S.
Topological Methods in Nonlinear Analysis Journal of the Juliusz Schauder Center Volume 21, 2003, 211 226 SYMMETRY RESULTS FOR PERTURBED PROBLEMS AND RELATED QUESTIONS Massimo Grosi Filomena Pacella S.
Note on the Chen-Lin Result with the Li-Zhang Method
 J. Math. Sci. Univ. Tokyo 18 (2011), 429 439. Note on the Chen-Lin Result with the Li-Zhang Method By Samy Skander Bahoura Abstract. We give a new proof of the Chen-Lin result with the method of moving
J. Math. Sci. Univ. Tokyo 18 (2011), 429 439. Note on the Chen-Lin Result with the Li-Zhang Method By Samy Skander Bahoura Abstract. We give a new proof of the Chen-Lin result with the method of moving
Global well-posedness for KdV in Sobolev spaces of negative index
 Electronic Journal of Differential Equations, Vol. (), No. 6, pp. 7. ISSN: 7-669. URL: http://ejde.math.swt.edu or http://ejde.math.unt.edu ftp ejde.math.swt.edu (login: ftp) Global well-posedness for
Electronic Journal of Differential Equations, Vol. (), No. 6, pp. 7. ISSN: 7-669. URL: http://ejde.math.swt.edu or http://ejde.math.unt.edu ftp ejde.math.swt.edu (login: ftp) Global well-posedness for
Partial Differential Equations
 Part II Partial Differential Equations Year 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2015 Paper 4, Section II 29E Partial Differential Equations 72 (a) Show that the Cauchy problem for u(x,
Part II Partial Differential Equations Year 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2015 Paper 4, Section II 29E Partial Differential Equations 72 (a) Show that the Cauchy problem for u(x,
COMBINED EFFECTS FOR A STATIONARY PROBLEM WITH INDEFINITE NONLINEARITIES AND LACK OF COMPACTNESS
 Dynamic Systems and Applications 22 (203) 37-384 COMBINED EFFECTS FOR A STATIONARY PROBLEM WITH INDEFINITE NONLINEARITIES AND LACK OF COMPACTNESS VICENŢIU D. RĂDULESCU Simion Stoilow Mathematics Institute
Dynamic Systems and Applications 22 (203) 37-384 COMBINED EFFECTS FOR A STATIONARY PROBLEM WITH INDEFINITE NONLINEARITIES AND LACK OF COMPACTNESS VICENŢIU D. RĂDULESCU Simion Stoilow Mathematics Institute
2 A Model, Harmonic Map, Problem
 ELLIPTIC SYSTEMS JOHN E. HUTCHINSON Department of Mathematics School of Mathematical Sciences, A.N.U. 1 Introduction Elliptic equations model the behaviour of scalar quantities u, such as temperature or
ELLIPTIC SYSTEMS JOHN E. HUTCHINSON Department of Mathematics School of Mathematical Sciences, A.N.U. 1 Introduction Elliptic equations model the behaviour of scalar quantities u, such as temperature or
NULL CONDITION FOR SEMILINEAR WAVE EQUATION WITH VARIABLE COEFFICIENTS. Fabio Catalano
 Serdica Math J 25 (999), 32-34 NULL CONDITION FOR SEMILINEAR WAVE EQUATION WITH VARIABLE COEFFICIENTS Fabio Catalano Communicated by V Petkov Abstract In this work we analyse the nonlinear Cauchy problem
Serdica Math J 25 (999), 32-34 NULL CONDITION FOR SEMILINEAR WAVE EQUATION WITH VARIABLE COEFFICIENTS Fabio Catalano Communicated by V Petkov Abstract In this work we analyse the nonlinear Cauchy problem
Strichartz Estimates in Domains
 Department of Mathematics Johns Hopkins University April 15, 2010 Wave equation on Riemannian manifold (M, g) Cauchy problem: 2 t u(t, x) gu(t, x) =0 u(0, x) =f (x), t u(0, x) =g(x) Strichartz estimates:
Department of Mathematics Johns Hopkins University April 15, 2010 Wave equation on Riemannian manifold (M, g) Cauchy problem: 2 t u(t, x) gu(t, x) =0 u(0, x) =f (x), t u(0, x) =g(x) Strichartz estimates:
Four-Fermion Interaction Approximation of the Intermediate Vector Boson Model
 Four-Fermion Interaction Approximation of the Intermediate Vector Boson odel Yoshio Tsutsumi Department of athematics, Kyoto University, Kyoto 66-852, JAPAN 1 Introduction In this note, we consider the
Four-Fermion Interaction Approximation of the Intermediate Vector Boson odel Yoshio Tsutsumi Department of athematics, Kyoto University, Kyoto 66-852, JAPAN 1 Introduction In this note, we consider the
AW -Convergence and Well-Posedness of Non Convex Functions
 Journal of Convex Analysis Volume 10 (2003), No. 2, 351 364 AW -Convergence Well-Posedness of Non Convex Functions Silvia Villa DIMA, Università di Genova, Via Dodecaneso 35, 16146 Genova, Italy villa@dima.unige.it
Journal of Convex Analysis Volume 10 (2003), No. 2, 351 364 AW -Convergence Well-Posedness of Non Convex Functions Silvia Villa DIMA, Università di Genova, Via Dodecaneso 35, 16146 Genova, Italy villa@dima.unige.it
A PHYSICAL SPACE PROOF OF THE BILINEAR STRICHARTZ AND LOCAL SMOOTHING ESTIMATES FOR THE SCHRÖDINGER EQUATION
 A PHYSICAL SPACE PROOF OF THE BILINEAR STRICHARTZ AND LOCAL SMOOTHING ESTIMATES FOR THE SCHRÖDINGER EQUATION TERENCE TAO Abstract. Let d 1, and let u, v : R R d C be Schwartz space solutions to the Schrödinger
A PHYSICAL SPACE PROOF OF THE BILINEAR STRICHARTZ AND LOCAL SMOOTHING ESTIMATES FOR THE SCHRÖDINGER EQUATION TERENCE TAO Abstract. Let d 1, and let u, v : R R d C be Schwartz space solutions to the Schrödinger
Nonlinear stabilization via a linear observability
 via a linear observability Kaïs Ammari Department of Mathematics University of Monastir Joint work with Fathia Alabau-Boussouira Collocated feedback stabilization Outline 1 Introduction and main result
via a linear observability Kaïs Ammari Department of Mathematics University of Monastir Joint work with Fathia Alabau-Boussouira Collocated feedback stabilization Outline 1 Introduction and main result
SMOOTHING ESTIMATES OF THE RADIAL SCHRÖDINGER PROPAGATOR IN DIMENSIONS n 2
 Acta Mathematica Scientia 1,3B(6):13 19 http://actams.wipm.ac.cn SMOOTHING ESTIMATES OF THE RADIAL SCHRÖDINGER PROPAGATOR IN DIMENSIONS n Li Dong ( ) Department of Mathematics, University of Iowa, 14 MacLean
Acta Mathematica Scientia 1,3B(6):13 19 http://actams.wipm.ac.cn SMOOTHING ESTIMATES OF THE RADIAL SCHRÖDINGER PROPAGATOR IN DIMENSIONS n Li Dong ( ) Department of Mathematics, University of Iowa, 14 MacLean
Piecewise Smooth Solutions to the Burgers-Hilbert Equation
 Piecewise Smooth Solutions to the Burgers-Hilbert Equation Alberto Bressan and Tianyou Zhang Department of Mathematics, Penn State University, University Park, Pa 68, USA e-mails: bressan@mathpsuedu, zhang
Piecewise Smooth Solutions to the Burgers-Hilbert Equation Alberto Bressan and Tianyou Zhang Department of Mathematics, Penn State University, University Park, Pa 68, USA e-mails: bressan@mathpsuedu, zhang
Well-posedness for the Fourth-order Schrödinger Equations with Quadratic Nonlinearity
 Well-posedness for the Fourth-order Schrödinger Equations with Quadratic Nonlinearity Jiqiang Zheng The Graduate School of China Academy of Engineering Physics P. O. Box 20, Beijing, China, 00088 (zhengjiqiang@gmail.com)
Well-posedness for the Fourth-order Schrödinger Equations with Quadratic Nonlinearity Jiqiang Zheng The Graduate School of China Academy of Engineering Physics P. O. Box 20, Beijing, China, 00088 (zhengjiqiang@gmail.com)
SCATTERING FOR THE NON-RADIAL 3D CUBIC NONLINEAR SCHRÖDINGER EQUATION
 SCATTERING FOR THE NON-RADIAL 3D CUBIC NONLINEAR SCHRÖDINGER EQUATION THOMAS DUYCKAERTS, JUSTIN HOLMER, AND SVETLANA ROUDENKO Abstract. Scattering of radial H 1 solutions to the 3D focusing cubic nonlinear
SCATTERING FOR THE NON-RADIAL 3D CUBIC NONLINEAR SCHRÖDINGER EQUATION THOMAS DUYCKAERTS, JUSTIN HOLMER, AND SVETLANA ROUDENKO Abstract. Scattering of radial H 1 solutions to the 3D focusing cubic nonlinear
Singular Limits of the Klein-Gordon Equation
 Singular Limits of the Klein-Gordon Equation Abstract Chi-Kun Lin 1 and Kung-Chien Wu 2 Department of Applied Mathematics National Chiao Tung University Hsinchu 31, TAIWAN We establish the singular limits
Singular Limits of the Klein-Gordon Equation Abstract Chi-Kun Lin 1 and Kung-Chien Wu 2 Department of Applied Mathematics National Chiao Tung University Hsinchu 31, TAIWAN We establish the singular limits
arxiv:math/ v1 [math.ap] 28 Oct 2005
![arxiv:math/ v1 [math.ap] 28 Oct 2005 arxiv:math/ v1 [math.ap] 28 Oct 2005](/thumbs/72/66322244.jpg) arxiv:math/050643v [math.ap] 28 Oct 2005 A remark on asymptotic completeness for the critical nonlinear Klein-Gordon equation Hans Lindblad and Avy Soffer University of California at San Diego and Rutgers
arxiv:math/050643v [math.ap] 28 Oct 2005 A remark on asymptotic completeness for the critical nonlinear Klein-Gordon equation Hans Lindblad and Avy Soffer University of California at San Diego and Rutgers
Equivariant self-similar wave maps from Minkowski spacetime into 3-sphere
 Equivariant self-similar wave maps from Minkowski spacetime into 3-sphere arxiv:math-ph/99126v1 17 Oct 1999 Piotr Bizoń Institute of Physics, Jagellonian University, Kraków, Poland March 26, 28 Abstract
Equivariant self-similar wave maps from Minkowski spacetime into 3-sphere arxiv:math-ph/99126v1 17 Oct 1999 Piotr Bizoń Institute of Physics, Jagellonian University, Kraków, Poland March 26, 28 Abstract
ALMOST CONSERVATION LAWS AND GLOBAL ROUGH SOLUTIONS TO A NONLINEAR SCHRÖDINGER EQUATION
 ALMOST CONSERVATION LAWS AND GLOBAL ROUGH SOLUTIONS TO A NONLINEAR SCHRÖDINGER EQUATION J. COLLIANDER, M. KEEL, G. STAFFILANI, H. TAKAOKA, AND T. TAO Abstract. We prove an almost conservation law to obtain
ALMOST CONSERVATION LAWS AND GLOBAL ROUGH SOLUTIONS TO A NONLINEAR SCHRÖDINGER EQUATION J. COLLIANDER, M. KEEL, G. STAFFILANI, H. TAKAOKA, AND T. TAO Abstract. We prove an almost conservation law to obtain
Sharp blow-up criteria for the Davey-Stewartson system in R 3
 Dynamics of PDE, Vol.8, No., 9-60, 011 Sharp blow-up criteria for the Davey-Stewartson system in R Jian Zhang Shihui Zhu Communicated by Y. Charles Li, received October 7, 010. Abstract. In this paper,
Dynamics of PDE, Vol.8, No., 9-60, 011 Sharp blow-up criteria for the Davey-Stewartson system in R Jian Zhang Shihui Zhu Communicated by Y. Charles Li, received October 7, 010. Abstract. In this paper,
M ath. Res. Lett. 15 (2008), no. 6, c International Press 2008 SCATTERING FOR THE NON-RADIAL 3D CUBIC NONLINEAR SCHRÖDINGER EQUATION
 M ath. Res. Lett. 15 (2008), no. 6, 1233 1250 c International Press 2008 SCATTERING FOR THE NON-RADIAL 3D CUBIC NONLINEAR SCHRÖDINGER EQUATION Thomas Duyckaerts, Justin Holmer, and Svetlana Roudenko Abstract.
M ath. Res. Lett. 15 (2008), no. 6, 1233 1250 c International Press 2008 SCATTERING FOR THE NON-RADIAL 3D CUBIC NONLINEAR SCHRÖDINGER EQUATION Thomas Duyckaerts, Justin Holmer, and Svetlana Roudenko Abstract.
On the Cauchy problem of 3-D energy-critical Schrödinger equations with subcritical perturbations
 J. Differential Equations 30 (006 4 445 www.elsevier.com/locate/jde On the Cauchy problem of 3-D energy-critical Schrödinger equations with subcritical perturbations Xiaoyi Zhang Academy of Mathematics
J. Differential Equations 30 (006 4 445 www.elsevier.com/locate/jde On the Cauchy problem of 3-D energy-critical Schrödinger equations with subcritical perturbations Xiaoyi Zhang Academy of Mathematics
Sharp estimates for a class of hyperbolic pseudo-differential equations
 Results in Math., 41 (2002), 361-368. Sharp estimates for a class of hyperbolic pseudo-differential equations Michael Ruzhansky Abstract In this paper we consider the Cauchy problem for a class of hyperbolic
Results in Math., 41 (2002), 361-368. Sharp estimates for a class of hyperbolic pseudo-differential equations Michael Ruzhansky Abstract In this paper we consider the Cauchy problem for a class of hyperbolic
ON STRICHARTZ ESTIMATES FOR SCHRÖDINGER OPERATORS IN COMPACT MANIFOLDS WITH BOUNDARY. 1. Introduction
 ON STRICHARTZ ESTIMATES FOR SCHRÖDINGER OPERATORS IN COMPACT MANIFOLDS WITH BOUNDARY MATTHEW D. BLAIR, HART F. SMITH, AND CHRISTOPHER D. SOGGE 1. Introduction Let (M, g) be a Riemannian manifold of dimension
ON STRICHARTZ ESTIMATES FOR SCHRÖDINGER OPERATORS IN COMPACT MANIFOLDS WITH BOUNDARY MATTHEW D. BLAIR, HART F. SMITH, AND CHRISTOPHER D. SOGGE 1. Introduction Let (M, g) be a Riemannian manifold of dimension
Hylomorphic solitons and their dynamics
 Hylomorphic solitons and their dynamics Vieri Benci Dipartimento di Matematica Applicata U. Dini Università di Pisa 18th May 2009 Vieri Benci (DMA-Pisa) Hylomorphic solitons 18th May 2009 1 / 50 Types
Hylomorphic solitons and their dynamics Vieri Benci Dipartimento di Matematica Applicata U. Dini Università di Pisa 18th May 2009 Vieri Benci (DMA-Pisa) Hylomorphic solitons 18th May 2009 1 / 50 Types
Tesi di Laurea Magistrale in Matematica presentata da. Claudia Dennetta. Symplectic Geometry. Il Relatore. Prof. Massimiliano Pontecorvo
 UNIVERSITÀ DEGLI STUDI ROMA TRE FACOLTÀ DI SCIENZE M.F.N. Tesi di Laurea Magistrale in Matematica presentata da Claudia Dennetta Symplectic Geometry Relatore Prof. Massimiliano Pontecorvo Il Candidato
UNIVERSITÀ DEGLI STUDI ROMA TRE FACOLTÀ DI SCIENZE M.F.N. Tesi di Laurea Magistrale in Matematica presentata da Claudia Dennetta Symplectic Geometry Relatore Prof. Massimiliano Pontecorvo Il Candidato
arxiv: v1 [math.ap] 5 Nov 2018
![arxiv: v1 [math.ap] 5 Nov 2018 arxiv: v1 [math.ap] 5 Nov 2018](/thumbs/89/100785953.jpg) STRONG CONTINUITY FOR THE 2D EULER EQUATIONS GIANLUCA CRIPPA, ELIZAVETA SEMENOVA, AND STEFANO SPIRITO arxiv:1811.01553v1 [math.ap] 5 Nov 2018 Abstract. We prove two results of strong continuity with respect
STRONG CONTINUITY FOR THE 2D EULER EQUATIONS GIANLUCA CRIPPA, ELIZAVETA SEMENOVA, AND STEFANO SPIRITO arxiv:1811.01553v1 [math.ap] 5 Nov 2018 Abstract. We prove two results of strong continuity with respect
CONCENTRATION COMPACTNESS FOR CRITICAL WAVE MAPS, BY JOACHIM KRIEGER AND WILHELM SCHLAG
 CONCENTRATION COMPACTNESS FOR CRITICAL WAVE MAPS, BY JOACHIM KRIEGER AND WILHELM SCHLAG Imagine a perfectly elastic d-dimensional sheet, infinite in extent, immersed (possibly with self-intersection) in
CONCENTRATION COMPACTNESS FOR CRITICAL WAVE MAPS, BY JOACHIM KRIEGER AND WILHELM SCHLAG Imagine a perfectly elastic d-dimensional sheet, infinite in extent, immersed (possibly with self-intersection) in
COMPLEX SPHERICAL WAVES AND INVERSE PROBLEMS IN UNBOUNDED DOMAINS
 COMPLEX SPHERICAL WAVES AND INVERSE PROBLEMS IN UNBOUNDED DOMAINS MIKKO SALO AND JENN-NAN WANG Abstract. This work is motivated by the inverse conductivity problem of identifying an embedded object in
COMPLEX SPHERICAL WAVES AND INVERSE PROBLEMS IN UNBOUNDED DOMAINS MIKKO SALO AND JENN-NAN WANG Abstract. This work is motivated by the inverse conductivity problem of identifying an embedded object in
THE FORM SUM AND THE FRIEDRICHS EXTENSION OF SCHRÖDINGER-TYPE OPERATORS ON RIEMANNIAN MANIFOLDS
 THE FORM SUM AND THE FRIEDRICHS EXTENSION OF SCHRÖDINGER-TYPE OPERATORS ON RIEMANNIAN MANIFOLDS OGNJEN MILATOVIC Abstract. We consider H V = M +V, where (M, g) is a Riemannian manifold (not necessarily
THE FORM SUM AND THE FRIEDRICHS EXTENSION OF SCHRÖDINGER-TYPE OPERATORS ON RIEMANNIAN MANIFOLDS OGNJEN MILATOVIC Abstract. We consider H V = M +V, where (M, g) is a Riemannian manifold (not necessarily
arxiv: v1 [math.ap] 9 Jun 2016
![arxiv: v1 [math.ap] 9 Jun 2016 arxiv: v1 [math.ap] 9 Jun 2016](/thumbs/72/66587423.jpg) Refined regularity for the blow-up set at non characteristic points for the complex semilinear wave equation arxiv:1606.0863v1 [math.ap] 9 Jun 016 Asma AZAIEZ Université de Cergy-Pontoise, AGM, CNRS (UMR
Refined regularity for the blow-up set at non characteristic points for the complex semilinear wave equation arxiv:1606.0863v1 [math.ap] 9 Jun 016 Asma AZAIEZ Université de Cergy-Pontoise, AGM, CNRS (UMR
arxiv: v2 [math.ap] 4 Dec 2013
![arxiv: v2 [math.ap] 4 Dec 2013 arxiv: v2 [math.ap] 4 Dec 2013](/thumbs/95/124164877.jpg) ON D NLS ON NON-TRAPPING EXTERIOR DOMAINS FARAH ABOU SHAKRA arxiv:04.768v [math.ap] 4 Dec 0 Abstract. Global existence and scattering for the nonlinear defocusing Schrödinger equation in dimensions are
ON D NLS ON NON-TRAPPING EXTERIOR DOMAINS FARAH ABOU SHAKRA arxiv:04.768v [math.ap] 4 Dec 0 Abstract. Global existence and scattering for the nonlinear defocusing Schrödinger equation in dimensions are
COMPARISON PRINCIPLES FOR CONSTRAINED SUBHARMONICS PH.D. COURSE - SPRING 2019 UNIVERSITÀ DI MILANO
 COMPARISON PRINCIPLES FOR CONSTRAINED SUBHARMONICS PH.D. COURSE - SPRING 2019 UNIVERSITÀ DI MILANO KEVIN R. PAYNE 1. Introduction Constant coefficient differential inequalities and inclusions, constraint
COMPARISON PRINCIPLES FOR CONSTRAINED SUBHARMONICS PH.D. COURSE - SPRING 2019 UNIVERSITÀ DI MILANO KEVIN R. PAYNE 1. Introduction Constant coefficient differential inequalities and inclusions, constraint
STRICHARTZ ESTIMATES FOR THE WAVE EQUATION ON MANIFOLDS WITH BOUNDARY. 1. Introduction
 STRICHARTZ ESTIMATES FOR THE WAVE EQUATION ON MANIFOLDS WITH BOUNDARY MATTHEW D. BLAIR, HART F. SMITH, AND CHRISTOPHER D. SOGGE. Introduction Let (M, g) be a Riemannian manifold of dimension n. Strichartz
STRICHARTZ ESTIMATES FOR THE WAVE EQUATION ON MANIFOLDS WITH BOUNDARY MATTHEW D. BLAIR, HART F. SMITH, AND CHRISTOPHER D. SOGGE. Introduction Let (M, g) be a Riemannian manifold of dimension n. Strichartz
LIFE SPAN OF BLOW-UP SOLUTIONS FOR HIGHER-ORDER SEMILINEAR PARABOLIC EQUATIONS
 Electronic Journal of Differential Equations, Vol. 21(21), No. 17, pp. 1 9. ISSN: 172-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu LIFE SPAN OF BLOW-UP
Electronic Journal of Differential Equations, Vol. 21(21), No. 17, pp. 1 9. ISSN: 172-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu LIFE SPAN OF BLOW-UP
GLOBAL EXISTENCE AND ENERGY DECAY OF SOLUTIONS TO A PETROVSKY EQUATION WITH GENERAL NONLINEAR DISSIPATION AND SOURCE TERM
 Georgian Mathematical Journal Volume 3 (26), Number 3, 397 4 GLOBAL EXITENCE AND ENERGY DECAY OF OLUTION TO A PETROVKY EQUATION WITH GENERAL NONLINEAR DIIPATION AND OURCE TERM NOUR-EDDINE AMROUN AND ABBE
Georgian Mathematical Journal Volume 3 (26), Number 3, 397 4 GLOBAL EXITENCE AND ENERGY DECAY OF OLUTION TO A PETROVKY EQUATION WITH GENERAL NONLINEAR DIIPATION AND OURCE TERM NOUR-EDDINE AMROUN AND ABBE
HARDY INEQUALITIES WITH BOUNDARY TERMS. x 2 dx u 2 dx. (1.2) u 2 = u 2 dx.
 Electronic Journal of Differential Equations, Vol. 003(003), No. 3, pp. 1 8. ISSN: 107-6691. UL: http://ejde.math.swt.edu or http://ejde.math.unt.edu ftp ejde.math.swt.edu (login: ftp) HADY INEQUALITIES
Electronic Journal of Differential Equations, Vol. 003(003), No. 3, pp. 1 8. ISSN: 107-6691. UL: http://ejde.math.swt.edu or http://ejde.math.unt.edu ftp ejde.math.swt.edu (login: ftp) HADY INEQUALITIES
arxiv: v1 [math.ap] 25 Jun 2008
![arxiv: v1 [math.ap] 25 Jun 2008 arxiv: v1 [math.ap] 25 Jun 2008](/thumbs/74/70611767.jpg) On the existence of smooth self-similar blow-up profiles for the wave-map equation arxiv:86.4148v1 [math.ap] 5 Jun 8 Pierre Germain October, 17 Abstract Consider the equivariant wave map equation from
On the existence of smooth self-similar blow-up profiles for the wave-map equation arxiv:86.4148v1 [math.ap] 5 Jun 8 Pierre Germain October, 17 Abstract Consider the equivariant wave map equation from
Complex geometrical optics solutions for Lipschitz conductivities
 Rev. Mat. Iberoamericana 19 (2003), 57 72 Complex geometrical optics solutions for Lipschitz conductivities Lassi Päivärinta, Alexander Panchenko and Gunther Uhlmann Abstract We prove the existence of
Rev. Mat. Iberoamericana 19 (2003), 57 72 Complex geometrical optics solutions for Lipschitz conductivities Lassi Päivärinta, Alexander Panchenko and Gunther Uhlmann Abstract We prove the existence of
Existence of Positive Solutions to Semilinear Elliptic Systems Involving Concave and Convex Nonlinearities
 Journal of Physical Science Application 5 (2015) 71-81 doi: 10.17265/2159-5348/2015.01.011 D DAVID PUBLISHING Existence of Positive Solutions to Semilinear Elliptic Systems Involving Concave Convex Nonlinearities
Journal of Physical Science Application 5 (2015) 71-81 doi: 10.17265/2159-5348/2015.01.011 D DAVID PUBLISHING Existence of Positive Solutions to Semilinear Elliptic Systems Involving Concave Convex Nonlinearities
arxiv:math/ v2 [math.ap] 8 Jun 2006
![arxiv:math/ v2 [math.ap] 8 Jun 2006 arxiv:math/ v2 [math.ap] 8 Jun 2006](/thumbs/73/68662045.jpg) LOW REGULARITY GLOBAL WELL-POSEDNESS FOR THE KLEIN-GORDON-SCHRÖDINGER SYSTEM WITH THE HIGHER ORDER YUKAWA COUPLING arxiv:math/0606079v [math.ap] 8 Jun 006 Changxing Miao Institute of Applied Physics and
LOW REGULARITY GLOBAL WELL-POSEDNESS FOR THE KLEIN-GORDON-SCHRÖDINGER SYSTEM WITH THE HIGHER ORDER YUKAWA COUPLING arxiv:math/0606079v [math.ap] 8 Jun 006 Changxing Miao Institute of Applied Physics and
Lectures on Non-Linear Wave Equations
 Lectures on Non-Linear Wave Equations Second Edition Christopher D. Sogge Department of Mathematics Johns Hopkins University International Press www.intlpress.com Lectures on Non-Linear Wave Equations,
Lectures on Non-Linear Wave Equations Second Edition Christopher D. Sogge Department of Mathematics Johns Hopkins University International Press www.intlpress.com Lectures on Non-Linear Wave Equations,
Non-radial solutions to a bi-harmonic equation with negative exponent
 Non-radial solutions to a bi-harmonic equation with negative exponent Ali Hyder Department of Mathematics, University of British Columbia, Vancouver BC V6TZ2, Canada ali.hyder@math.ubc.ca Juncheng Wei
Non-radial solutions to a bi-harmonic equation with negative exponent Ali Hyder Department of Mathematics, University of British Columbia, Vancouver BC V6TZ2, Canada ali.hyder@math.ubc.ca Juncheng Wei
TADAHIRO OH 0, 3 8 (T R), (1.5) The result in [2] is in fact stated for time-periodic functions: 0, 1 3 (T 2 ). (1.4)
![TADAHIRO OH 0, 3 8 (T R), (1.5) The result in [2] is in fact stated for time-periodic functions: 0, 1 3 (T 2 ). (1.4) TADAHIRO OH 0, 3 8 (T R), (1.5) The result in [2] is in fact stated for time-periodic functions: 0, 1 3 (T 2 ). (1.4)](/thumbs/95/125089959.jpg) PERIODIC L 4 -STRICHARTZ ESTIMATE FOR KDV TADAHIRO OH 1. Introduction In [], Bourgain proved global well-posedness of the periodic KdV in L T): u t + u xxx + uu x 0, x, t) T R. 1.1) The key ingredient
PERIODIC L 4 -STRICHARTZ ESTIMATE FOR KDV TADAHIRO OH 1. Introduction In [], Bourgain proved global well-posedness of the periodic KdV in L T): u t + u xxx + uu x 0, x, t) T R. 1.1) The key ingredient
SHARP BOUNDARY TRACE INEQUALITIES. 1. Introduction
 SHARP BOUNDARY TRACE INEQUALITIES GILES AUCHMUTY Abstract. This paper describes sharp inequalities for the trace of Sobolev functions on the boundary of a bounded region R N. The inequalities bound (semi-)norms
SHARP BOUNDARY TRACE INEQUALITIES GILES AUCHMUTY Abstract. This paper describes sharp inequalities for the trace of Sobolev functions on the boundary of a bounded region R N. The inequalities bound (semi-)norms
ON BOUNDEDNESS OF MAXIMAL FUNCTIONS IN SOBOLEV SPACES
 Annales Academiæ Scientiarum Fennicæ Mathematica Volumen 29, 2004, 167 176 ON BOUNDEDNESS OF MAXIMAL FUNCTIONS IN SOBOLEV SPACES Piotr Haj lasz and Jani Onninen Warsaw University, Institute of Mathematics
Annales Academiæ Scientiarum Fennicæ Mathematica Volumen 29, 2004, 167 176 ON BOUNDEDNESS OF MAXIMAL FUNCTIONS IN SOBOLEV SPACES Piotr Haj lasz and Jani Onninen Warsaw University, Institute of Mathematics
Minimization problems on the Hardy-Sobolev inequality
 manuscript No. (will be inserted by the editor) Minimization problems on the Hardy-Sobolev inequality Masato Hashizume Received: date / Accepted: date Abstract We study minimization problems on Hardy-Sobolev
manuscript No. (will be inserted by the editor) Minimization problems on the Hardy-Sobolev inequality Masato Hashizume Received: date / Accepted: date Abstract We study minimization problems on Hardy-Sobolev
EXISTENCE OF NONTRIVIAL SOLUTIONS FOR A QUASILINEAR SCHRÖDINGER EQUATIONS WITH SIGN-CHANGING POTENTIAL
 Electronic Journal of Differential Equations, Vol. 2014 (2014), No. 05, pp. 1 8. ISSN: 1072-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu EXISTENCE OF NONTRIVIAL
Electronic Journal of Differential Equations, Vol. 2014 (2014), No. 05, pp. 1 8. ISSN: 1072-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu EXISTENCE OF NONTRIVIAL
Strong uniqueness for second order elliptic operators with Gevrey coefficients
 Strong uniqueness for second order elliptic operators with Gevrey coefficients Ferruccio Colombini, Cataldo Grammatico, Daniel Tataru Abstract We consider here the problem of strong unique continuation
Strong uniqueness for second order elliptic operators with Gevrey coefficients Ferruccio Colombini, Cataldo Grammatico, Daniel Tataru Abstract We consider here the problem of strong unique continuation
OBSERVABILITY INEQUALITY AND DECAY RATE FOR WAVE EQUATIONS WITH NONLINEAR BOUNDARY CONDITIONS
 Electronic Journal of Differential Equations, Vol. 27 (27, No. 6, pp. 2. ISSN: 72-669. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu OBSERVABILITY INEQUALITY AND DECAY RATE FOR WAVE EQUATIONS
Electronic Journal of Differential Equations, Vol. 27 (27, No. 6, pp. 2. ISSN: 72-669. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu OBSERVABILITY INEQUALITY AND DECAY RATE FOR WAVE EQUATIONS
THE WAVE MAPS EQUATION. 1. The equations Let us begin with the Laplace equation, R n
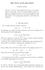 THE WAVE MAPS EQUATION DANIEL TATARU Abstract. The wave maps equation has become a very popular topic in recent years. The aim of these expository notes is to present a non-technical survey of the ideas
THE WAVE MAPS EQUATION DANIEL TATARU Abstract. The wave maps equation has become a very popular topic in recent years. The aim of these expository notes is to present a non-technical survey of the ideas
ATTRACTORS FOR SEMILINEAR PARABOLIC PROBLEMS WITH DIRICHLET BOUNDARY CONDITIONS IN VARYING DOMAINS. Emerson A. M. de Abreu Alexandre N.
 ATTRACTORS FOR SEMILINEAR PARABOLIC PROBLEMS WITH DIRICHLET BOUNDARY CONDITIONS IN VARYING DOMAINS Emerson A. M. de Abreu Alexandre N. Carvalho Abstract Under fairly general conditions one can prove that
ATTRACTORS FOR SEMILINEAR PARABOLIC PROBLEMS WITH DIRICHLET BOUNDARY CONDITIONS IN VARYING DOMAINS Emerson A. M. de Abreu Alexandre N. Carvalho Abstract Under fairly general conditions one can prove that
EXISTENCE AND REGULARITY RESULTS FOR SOME NONLINEAR PARABOLIC EQUATIONS
 EXISTECE AD REGULARITY RESULTS FOR SOME OLIEAR PARABOLIC EUATIOS Lucio BOCCARDO 1 Andrea DALL AGLIO 2 Thierry GALLOUËT3 Luigi ORSIA 1 Abstract We prove summability results for the solutions of nonlinear
EXISTECE AD REGULARITY RESULTS FOR SOME OLIEAR PARABOLIC EUATIOS Lucio BOCCARDO 1 Andrea DALL AGLIO 2 Thierry GALLOUËT3 Luigi ORSIA 1 Abstract We prove summability results for the solutions of nonlinear
Construction of concentrating bubbles for the energy-critical wave equation
 Construction of concentrating bubbles for the energy-critical wave equation Jacek Jendrej University of Chicago University of North Carolina February 13th 2017 Jacek Jendrej Energy-critical wave equations
Construction of concentrating bubbles for the energy-critical wave equation Jacek Jendrej University of Chicago University of North Carolina February 13th 2017 Jacek Jendrej Energy-critical wave equations
On Asymptotic Variational Wave Equations
 On Asymptotic Variational Wave Equations Alberto Bressan 1, Ping Zhang 2, and Yuxi Zheng 1 1 Department of Mathematics, Penn State University, PA 1682. E-mail: bressan@math.psu.edu; yzheng@math.psu.edu
On Asymptotic Variational Wave Equations Alberto Bressan 1, Ping Zhang 2, and Yuxi Zheng 1 1 Department of Mathematics, Penn State University, PA 1682. E-mail: bressan@math.psu.edu; yzheng@math.psu.edu
Asymptotic behavior of Ginzburg-Landau equations of superfluidity
 Communications to SIMAI Congress, ISSN 1827-9015, Vol. 3 (2009) 200 (12pp) DOI: 10.1685/CSC09200 Asymptotic behavior of Ginzburg-Landau equations of superfluidity Alessia Berti 1, Valeria Berti 2, Ivana
Communications to SIMAI Congress, ISSN 1827-9015, Vol. 3 (2009) 200 (12pp) DOI: 10.1685/CSC09200 Asymptotic behavior of Ginzburg-Landau equations of superfluidity Alessia Berti 1, Valeria Berti 2, Ivana
Integro-differential equations: Regularity theory and Pohozaev identities
 Integro-differential equations: Regularity theory and Pohozaev identities Xavier Ros Oton Departament Matemàtica Aplicada I, Universitat Politècnica de Catalunya PhD Thesis Advisor: Xavier Cabré Xavier
Integro-differential equations: Regularity theory and Pohozaev identities Xavier Ros Oton Departament Matemàtica Aplicada I, Universitat Politècnica de Catalunya PhD Thesis Advisor: Xavier Cabré Xavier
Explosive Solution of the Nonlinear Equation of a Parabolic Type
 Int. J. Contemp. Math. Sciences, Vol. 4, 2009, no. 5, 233-239 Explosive Solution of the Nonlinear Equation of a Parabolic Type T. S. Hajiev Institute of Mathematics and Mechanics, Acad. of Sciences Baku,
Int. J. Contemp. Math. Sciences, Vol. 4, 2009, no. 5, 233-239 Explosive Solution of the Nonlinear Equation of a Parabolic Type T. S. Hajiev Institute of Mathematics and Mechanics, Acad. of Sciences Baku,
NONLINEAR FREDHOLM ALTERNATIVE FOR THE p-laplacian UNDER NONHOMOGENEOUS NEUMANN BOUNDARY CONDITION
 Electronic Journal of Differential Equations, Vol. 2016 (2016), No. 210, pp. 1 7. ISSN: 1072-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu NONLINEAR FREDHOLM ALTERNATIVE FOR THE p-laplacian
Electronic Journal of Differential Equations, Vol. 2016 (2016), No. 210, pp. 1 7. ISSN: 1072-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu NONLINEAR FREDHOLM ALTERNATIVE FOR THE p-laplacian
