Spherical Harmonics and Related Topics. David Randall 2 S = 0, r 2 r r S 2. S = r n Y n
|
|
|
- Allyson Rich
- 6 years ago
- Views:
Transcription
1 ! Revised April 10, :32 PM! 1 Spherical Harmonics and Related Topics David Randall The spherical surface harmonics are convenient functions for representing the distribution of geophysical quantities over the surface of the spherical Earth. We look for solutions of Laplace s differential equation, which is in a three-dimensional space. The 2 2 S = 0, operator can be expanded in spherical coordinates as: (1) 2 S = 1 r 2 r r S 2 r + 2 S = 0. h Here r is the distance from the origin, and 2 hs is the Laplacian on a two-dimensional surface of constant r, i.e., on a spherical surface. We postpone showing the form of 2 hs until page 2. Inspection of (2) suggests that S should be proportional to a power of r. We write S = r n Y n. (3) Here we are assuming that the radial dependence of S is separable, in the sense that the Y n are independent of radius. They are called spherical surface harmonics of order n. The subscript n is attached to Y n to remind us that it corresponds a particular exponent in the radial dependence of S. In order for S to remain finite as r 0, we need n 0. Since n = 0 would mean that S is independent of radius, we conclude that n must be a positive integer. Using r 2 ( ) 1 r r S 2 = n n +1 S, which follows immediately from (3), we can rewrite (2) as r r 2 (2)
2 ! Revised April 10, :32 PM! 2 2 Y + n( n +1) h n Y r 2 n = 0. (4) Before continuing with the separation of variables, it is important to point out that all of the quantities appearing in (4) have meaning without the need for any particular coordinate system on the two-dimensional spherical surface. We are going to use longitude and latitude coordinates below, but we do not need them to write down (4). At this point we make an analogy with a trigonometric functions. Suppose that we have a doubly periodic function W x, y ( ) defined on a plane, with the usual Cartesian coordinates x and y. As a particular example, let W ( x, y) = Asin( kx)cos( ly), (5) where A is an arbitrary constant. In Cartesian coordinates the two-dimensional Laplacian of W is 2 h W = 2 x + 2 W 2 y 2 = ( k 2 + l 2 )W. Compare (4) and (6). They are closely analogous. In particular, n n + 1 ( k 2 + l 2 ) in (6). This shows that n n + 1 number on the sphere. We now write out the horizontal Laplacian as (6) ( ) / r 2 in (4) corresponds to ( ) / r 2 can be interpreted as a total horizontal wave 2 S = 1 S h cosϕ r 2 cosϕ ϕ ϕ S r 2 cos 2 ϕ λ, 2 (7) using the familiar spherical coordinate system in which r is the radial coordinate, λ is longitude and ϕ is latitude. Then (4) can be rewritten as 1 cosϕ ϕ cosϕ Y n ϕ Y n cos 2 ϕ λ + n( n +1)Y = 0. 2 n Factors of 1/ r 2 have cancelled out in (8), and as a result r no longer appears. Nevertheless, its exponent, n, is still visible, like the smile of the Cheshire cat. (8)
3 ! Revised April 10, :32 PM! 3 Next, we separate the longitude and latitude dependence in the Y n λ,ϕ Y n ( ϕ,λ) = Φ ( ϕ)λ λ ( ), ( ), i.e. where Φ ( ϕ) and Λ( λ) are to be determined. By substitution of (9) into (8), we find that (9) cos 2 ϕ 1 d dφ cosϕ Φ cosϕ dϕ dϕ + n( n + 1)Φ = 1 d 2 Λ Λ dλ. 2 (10) The left-hand side of (10) does not contain λ, and the right-hand side does not contain ϕ, so both sides must be a constant, c. Then the longitudinal structure of the solution is governed by d 2 Λ dλ 2 + cλ = 0. (11) It follows that Λ( λ) must be a trigonometric function of longitude, i.e. Λ = A S exp( imλ), where m = c, and A S is an arbitrary complex constant. The cyclic condition Λ( λ + 2π ) = Λ( λ) implies that c must be an integer, which we denote by m. We refer to m as the zonal wave number. Note that m is non-dimensional, and can be either positive or negative. Notice m has meaning only with respect to a particular spherical coordinate system. In this way m is less fundamental than n, which comes from the radial dependence of the three dimensional function S, and has a meaning that is independent of any particular spherical coordinate system. The equation for Φ ( ϕ), which determines the meridional structure of the solution, is 1 d dφ cosϕ cosϕ dϕ dϕ + n n +1 ( ) m2 cos 2 ϕ Φ = 0. (13) Note that the zonal wave number, m, appears in this meridional structure equation, as does the radial exponent, n. The longitude and radius dependencies have disappeared, but the zonal wave number and the radial exponent are still visible. For convenience, we define a new independent variable to measure latitude, (12)
4 ! Revised April 10, :32 PM! 4 µ sinϕ, so that dµ cosϕdϕ. Then (13) can be written as (14) d dµ 1 µ 2 ( ) dφ dµ + n n +1 ( ) m2 1 µ 2 Φ = 0. (15) Eq. (15) is simpler than (13), in that (15) does not involve trigonometric functions of the independent variable. This added simplicity is the motivation for using (14). We solve (15) subject to the boundary conditions that Φ is bounded at both poles. These boundary conditions imply that n is an integer such that n m. The solutions of (15) are called the associated Legendre functions, are denoted by P m n ( µ ), and are given by P m n ( µ ) = ( 2n)! 2 n n! ( n m)! 1 µ 2 + n m ( ) m 2 µ n m n m ( )( n m 1) ( n m 2) ( n m 3) 2 4( 2n 1) ( 2n 3) ( )( n m 1) 2( 2n 1) µ n m 4 µ n m 2 (17) The subscript n and superscript m are just markers to remind us that n and m appear as parameters in (15), denoting the radial exponent and zonal wave number, respectively, of S r,λ,ϕ ( ). The functions P m n ( µ ) are said to be of order n and rank m. The sum in (17) is continued out as far as necessary to include all non-negative powers of µ. The factor in brackets is, therefore, a polynomial of degree n m 0. In view of the leading factor of ( 1 µ 2 ) m 2 in (17), the complete function P m n ( µ ) is a polynomial in µ for even values of m, but not for odd values of m. Substitution can be used to confirm that the associated Legendre functions are indeed solutions of (15). Here we plot some examples of associated Legendre functions, which you might want to check for their consistency with (17): (16)
5 ! Revised April 10, :32 PM! Caption:
6 ! Revised April 10, :32 PM! P 0 0 ( µ ) = 1 P 1 0 ( µ ) = µ P 1 1 ( µ ) = 1 µ
7 ! Revised April 10, :32 PM! P 2 0 ( µ ) = 3 2 µ P 1 2 ( µ ) = 3µ 1 µ P 2 2 ( ) ( µ ) = 3 1 µ 2
8 ! Revised April 10, :32 PM! 8 P 3 0 ( µ ) = 5 2 µ µ - - P 1 3 ( µ ) = µ 2 µ P 3 2 ( µ ) = 15( 1 µ 2 )µ
9 ! Revised April 10, :32 PM! P 3 3 ( µ ) = 15 1 µ 2 ( 1 µ 2 ) It can be shown that the associated Legendre functions are mutually orthogonal, i.e., 1 1 P m n ( µ ) P m l ( µ )dµ = 0, for n l, and P m 2 2 n ( µ ) ( dµ = 2n +1 n + m)!. ( n m)! 1 It follows that the functions 2n +1 ( 2 n m)! ( n + m)! P n are mutually orthonormal for 1 µ 1. m µ 1 ( ), n = m, m +1, m + 2, (18) (19) Referring back to (9), we see that a particular spherical surface harmonic can be written as Y n m ( µ,λ) = P m n ( µ )exp imλ ( ). (20) It is the product of an associated Legendre function of µ with a trigonometric function of longitude. Note that the arbitrary constant has been set to unity.
10 ! Revised April 10, :32 PM! 10 Figure 1:Examples of low-resolution spherical harmonics, mapped out onto the plane. The horizontal direction in each panel represents longitude, and the vertical direction represents latitude. The numbers in parentheses in each panel are the appropriate values of n and s, in that order. Recall that the number of nodes in the meridional direction is n s. The shading in each panel represents the sign of the field (and all signs can be flipped arbitrarily). You may think of white as negative and stippled as positive. From Washington and Parkinson (1986). Fig. 1 shows examples of spherical harmonics of low order, as mapped out onto the longitude-latitude plane. Fig. 2 gives similar diagrams for n = 5 and m = 0, 1, 2,...,5, plotted out onto stretched spheres. Fig. 3 shows some low-order spherical harmonics mapped onto threedimensional pseudo-spheres, in which the local radius of the surface of the pseudo-sphere is one plus a constant times the local value of the spherical harmonic. By using the orthogonality condition (18) for the associated Legendre functions, and also the orthogonality properties of the trigonometric functions, we can show that 1 2π P m n ( µ )exp( imλ)p m l ( µ )exp( i m λ)dµ dλ = 0 unless n = 1 and m = m. 1 0 (21)
11 ! Revised April 10, :32 PM! 11 Figure 2: Alternating patterns of positives and negatives for spherical harmonics with n = 5 and m = 0,1, From Baer (1972). The mean value over the surface of a sphere of the square of a spherical surface harmonic is given by 1 2π 1 P m 2 1 n ( µ )exp( imλ) 4π dµ dλ = ( n + m)! for s 0. 2( 2n +1) ( n m)! 1 0 For the special case m = 0, the corresponding value is 1 / ( 2n + 1). (22) For a given n, the mean values given by (22) vary greatly with m, which is inconvenient for the interpretation of data. For this reason, it is customary to use, instead of P n m µ ( ), the seminormalized associated Legendre functions, denoted by P! m n ( µ ). These functions are identical with P m n ( µ ) when m = 0. For m > 0, the semi-normalized functions are defined by
12 ! Revised April 10, :32 PM! 12! nm ( µ ) = 2 ( n m )! P m ( µ ). P ( n + m )! n (23)! The mean value over the sphere of the square of P m n ( µ ) exp (imλ ) is then ( 2n + 1), for any n 1 and m. n = 2, m = 1 n = 4, m = 2 n = 4, m = 1 n = 10, m = 1 Figure 3: Selected spherical harmonics mapped onto three-dimensional pseudo-spheres, in which the local radius of the surface of the pseudo-sphere is one plus a constant times the local value of the spherical harmonic. The spherical harmonics can be shown to form a complete orthonormal basis, and so can be used to represent an arbitrary function, F ( λ,ϕ ) of latitude and longitude: F ( λ,ϕ ) = F n Yn m ( λ,ϕ ) m m= n= m (24)
13 ! Revised April 10, :32 PM! 13 Here the Y n m are the expansion coefficients. Note that the sum over ranges over both positive and negative values, and that the sum over n is taken so that n m 0. The sums in (24) range over an infinity of terms, but in practice, of course, we have to truncate after a finite number of terms, so that (24) is replaced by F = M N ( m) F m m n Y n. m= M n= m Here the overbar reminds us that the sum is truncated. The sum over n ranges up to N m (25) ( ), which has to be specified somehow. The sum over m ranges from M to M. It can be shown that this ensures that the final result is real; this is an important result that you should prove for yourself. The choice of N ( m) fixes what is called the truncation procedure. There are two commonly used truncation procedures. The first, called rhomboidal, takes The second, called triangular, takes N ( m) = M + m. (26) N ( m) = M. Triangular truncation has the following beautiful property. In order to actually perform a spherical harmonic transform, it is necessary to adopt a spherical coordinate system ( λ,ϕ). There are of course infinitely many such systems. There is no reason in principle that the coordinates have to be chosen in the conventional way, so that the poles of the coordinate system coincide with the Earth s poles of rotation. The choice of a particular spherical coordinate system is, therefore, somewhat arbitrary. Suppose that we choose two different spherical coordinate systems (tilted with respect to one another in an arbitrary way), perform a triangularly truncated expansion in both, then plot the results. It can be shown that the two maps will be identical. This means that the arbitrary orientations of the spherical coordinate systems used had no effect whatsoever on the results obtained. The coordinate system used disappears at the end. Triangular truncation is very widely used today, in part because of this nice property. (27)
14 ! Revised April 10, :32 PM! 14 Figure 4: Demonstration of the effects of various horizontal truncations of 500 m patterns of geopotential height (m) data provided originally on a 2.5 longitude-latitude grid. From Washington and Parkinson (1986). Fig. 4 shows an example based on 500 mb height data, provided originally on a 2.5 longitude-latitude grid. The figure shows how the data look when represented by just a few spherical harmonics (top left), a few more (top right), a moderate number (bottom left) and at full 2.5 resolution. The smoothing effect of severe truncation is clearly visible. References and Bibliography Baer, F., 1972: An alternate scale representation of atmospheric energy spectra. J. Atmos. Sci., 29, Jarraud, M., and A. J. Simmons, 1983: The spectral technique. Seminar on Numerical Methods for Weather Prediction, European Centre for Medium Range Weather Prediction, Reading, England, Washington, W. M., and C. L. Parkinson, 1986: An introduction to three-dimensional climate modeling. University Science Books, Mill Valley, New York, 422 pp.
Spectral transforms. Contents. ARPEGE-Climat Version 5.1. September Introduction 2
 Spectral transforms ARPEGE-Climat Version 5.1 September 2008 Contents 1 Introduction 2 2 Spectral representation 2 2.1 Spherical harmonics....................... 2 2.2 Collocation grid.........................
Spectral transforms ARPEGE-Climat Version 5.1 September 2008 Contents 1 Introduction 2 2 Spectral representation 2 2.1 Spherical harmonics....................... 2 2.2 Collocation grid.........................
( )e ikx. ( ) = ˆq k
 ! Revised December 15, 2015 6:57 PM! 1 Chapter 13: Spectral Methods Copyright 2015, David A. Randall Introduction Assume that q( x,t) is real and integrable. If the domain is periodic, with period L, we
! Revised December 15, 2015 6:57 PM! 1 Chapter 13: Spectral Methods Copyright 2015, David A. Randall Introduction Assume that q( x,t) is real and integrable. If the domain is periodic, with period L, we
Solutions to Laplace s Equations- II
 Solutions to Laplace s Equations- II Lecture 15: Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay Laplace s Equation in Spherical Coordinates : In spherical coordinates
Solutions to Laplace s Equations- II Lecture 15: Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay Laplace s Equation in Spherical Coordinates : In spherical coordinates
( u,v). For simplicity, the density is considered to be a constant, denoted by ρ 0
 ! Revised Friday, April 19, 2013! 1 Inertial Stability and Instability David Randall Introduction Inertial stability and instability are relevant to the atmosphere and ocean, and also in other contexts
! Revised Friday, April 19, 2013! 1 Inertial Stability and Instability David Randall Introduction Inertial stability and instability are relevant to the atmosphere and ocean, and also in other contexts
d 1 µ 2 Θ = 0. (4.1) consider first the case of m = 0 where there is no azimuthal dependence on the angle φ.
 4 Legendre Functions In order to investigate the solutions of Legendre s differential equation d ( µ ) dθ ] ] + l(l + ) m dµ dµ µ Θ = 0. (4.) consider first the case of m = 0 where there is no azimuthal
4 Legendre Functions In order to investigate the solutions of Legendre s differential equation d ( µ ) dθ ] ] + l(l + ) m dµ dµ µ Θ = 0. (4.) consider first the case of m = 0 where there is no azimuthal
Reynolds Averaging. Let u and v be two flow variables (which might or might not be velocity components), and suppose that. u t + x uv ( ) = S u,
 ! Revised January 23, 208 7:7 PM! Reynolds Averaging David Randall Introduction It is neither feasible nor desirable to consider in detail all of the small-scale fluctuations that occur in the atmosphere.
! Revised January 23, 208 7:7 PM! Reynolds Averaging David Randall Introduction It is neither feasible nor desirable to consider in detail all of the small-scale fluctuations that occur in the atmosphere.
Physics 221A Fall 1996 Notes 12 Orbital Angular Momentum and Spherical Harmonics
 Physics 221A Fall 1996 Notes 12 Orbital Angular Momentum and Spherical Harmonics We now consider the spatial degrees of freedom of a particle moving in 3-dimensional space, which of course is an important
Physics 221A Fall 1996 Notes 12 Orbital Angular Momentum and Spherical Harmonics We now consider the spatial degrees of freedom of a particle moving in 3-dimensional space, which of course is an important
(ii) Observational Geomagnetism. Lecture 5: Spherical harmonic field models
 (ii) Observational Geomagnetism Lecture 5: Spherical harmonic field models Lecture 5: Spherical harmonic field models 5.1 Introduction 5.2 How to represent functions on a spherical surface 5.3 Spherical
(ii) Observational Geomagnetism Lecture 5: Spherical harmonic field models Lecture 5: Spherical harmonic field models 5.1 Introduction 5.2 How to represent functions on a spherical surface 5.3 Spherical
Overview of the Numerics of the ECMWF. Atmospheric Forecast Model
 Overview of the Numerics of the Atmospheric Forecast Model M. Hortal Seminar 6 Sept 2004 Slide 1 Characteristics of the model Hydrostatic shallow-atmosphere approimation Pressure-based hybrid vertical
Overview of the Numerics of the Atmospheric Forecast Model M. Hortal Seminar 6 Sept 2004 Slide 1 Characteristics of the model Hydrostatic shallow-atmosphere approimation Pressure-based hybrid vertical
Basic Quantum Mechanics Prof. Ajoy Ghatak Department of Physics Indian Institute of Technology, Delhi
 Basic Quantum Mechanics Prof. Ajoy Ghatak Department of Physics Indian Institute of Technology, Delhi Module No. # 05 The Angular Momentum I Lecture No. # 02 The Angular Momentum Problem (Contd.) In the
Basic Quantum Mechanics Prof. Ajoy Ghatak Department of Physics Indian Institute of Technology, Delhi Module No. # 05 The Angular Momentum I Lecture No. # 02 The Angular Momentum Problem (Contd.) In the
Physics 200 Lecture 4. Integration. Lecture 4. Physics 200 Laboratory
 Physics 2 Lecture 4 Integration Lecture 4 Physics 2 Laboratory Monday, February 21st, 211 Integration is the flip-side of differentiation in fact, it is often possible to write a differential equation
Physics 2 Lecture 4 Integration Lecture 4 Physics 2 Laboratory Monday, February 21st, 211 Integration is the flip-side of differentiation in fact, it is often possible to write a differential equation
Connection to Laplacian in spherical coordinates (Chapter 13)
 Connection to Laplacian in spherical coordinates (Chapter 13) We might often encounter the Laplace equation and spherical coordinates might be the most convenient 2 u(r, θ, φ) = 0 We already saw in Chapter
Connection to Laplacian in spherical coordinates (Chapter 13) We might often encounter the Laplace equation and spherical coordinates might be the most convenient 2 u(r, θ, φ) = 0 We already saw in Chapter
20 The Hydrogen Atom. Ze2 r R (20.1) H( r, R) = h2 2m 2 r h2 2M 2 R
 20 The Hydrogen Atom 1. We want to solve the time independent Schrödinger Equation for the hydrogen atom. 2. There are two particles in the system, an electron and a nucleus, and so we can write the Hamiltonian
20 The Hydrogen Atom 1. We want to solve the time independent Schrödinger Equation for the hydrogen atom. 2. There are two particles in the system, an electron and a nucleus, and so we can write the Hamiltonian
Physics 342 Lecture 23. Radial Separation. Lecture 23. Physics 342 Quantum Mechanics I
 Physics 342 Lecture 23 Radial Separation Lecture 23 Physics 342 Quantum Mechanics I Friday, March 26th, 2010 We begin our spherical solutions with the simplest possible case zero potential. Aside from
Physics 342 Lecture 23 Radial Separation Lecture 23 Physics 342 Quantum Mechanics I Friday, March 26th, 2010 We begin our spherical solutions with the simplest possible case zero potential. Aside from
The spectral transform method
 The spectral transform method by Nils Wedi European Centre for Medium-Range Weather Forecasts wedi@ecmwf.int Advanced Numerical Methods for Earth-System Modelling Slide 1 Advanced Numerical Methods for
The spectral transform method by Nils Wedi European Centre for Medium-Range Weather Forecasts wedi@ecmwf.int Advanced Numerical Methods for Earth-System Modelling Slide 1 Advanced Numerical Methods for
Recent Developments in Numerical Methods for 4d-Var
 Recent Developments in Numerical Methods for 4d-Var Mike Fisher Slide 1 Recent Developments Numerical Methods 4d-Var Slide 2 Outline Non-orthogonal wavelets on the sphere: - Motivation: Covariance Modelling
Recent Developments in Numerical Methods for 4d-Var Mike Fisher Slide 1 Recent Developments Numerical Methods 4d-Var Slide 2 Outline Non-orthogonal wavelets on the sphere: - Motivation: Covariance Modelling
6.1 Polynomial Functions
 6.1 Polynomial Functions Definition. A polynomial function is any function p(x) of the form p(x) = p n x n + p n 1 x n 1 + + p 2 x 2 + p 1 x + p 0 where all of the exponents are non-negative integers and
6.1 Polynomial Functions Definition. A polynomial function is any function p(x) of the form p(x) = p n x n + p n 1 x n 1 + + p 2 x 2 + p 1 x + p 0 where all of the exponents are non-negative integers and
Separation of Variables in Polar and Spherical Coordinates
 Separation of Variables in Polar and Spherical Coordinates Polar Coordinates Suppose we are given the potential on the inside surface of an infinitely long cylindrical cavity, and we want to find the potential
Separation of Variables in Polar and Spherical Coordinates Polar Coordinates Suppose we are given the potential on the inside surface of an infinitely long cylindrical cavity, and we want to find the potential
CHAPTER 3 POTENTIALS 10/13/2016. Outlines. 1. Laplace s equation. 2. The Method of Images. 3. Separation of Variables. 4. Multipole Expansion
 CHAPTER 3 POTENTIALS Lee Chow Department of Physics University of Central Florida Orlando, FL 32816 Outlines 1. Laplace s equation 2. The Method of Images 3. Separation of Variables 4. Multipole Expansion
CHAPTER 3 POTENTIALS Lee Chow Department of Physics University of Central Florida Orlando, FL 32816 Outlines 1. Laplace s equation 2. The Method of Images 3. Separation of Variables 4. Multipole Expansion
MATH20411 PDEs and Vector Calculus B
 MATH2411 PDEs and Vector Calculus B Dr Stefan Güttel Acknowledgement The lecture notes and other course materials are based on notes provided by Dr Catherine Powell. SECTION 1: Introctory Material MATH2411
MATH2411 PDEs and Vector Calculus B Dr Stefan Güttel Acknowledgement The lecture notes and other course materials are based on notes provided by Dr Catherine Powell. SECTION 1: Introctory Material MATH2411
GEOMETRICAL TOOLS FOR PDES ON A SURFACE WITH ROTATING SHALLOW WATER EQUATIONS ON A SPHERE
 GEOETRICAL TOOLS FOR PDES ON A SURFACE WITH ROTATING SHALLOW WATER EQUATIONS ON A SPHERE BIN CHENG Abstract. This is an excerpt from my paper with A. ahalov [1]. PDE theories with Riemannian geometry are
GEOETRICAL TOOLS FOR PDES ON A SURFACE WITH ROTATING SHALLOW WATER EQUATIONS ON A SPHERE BIN CHENG Abstract. This is an excerpt from my paper with A. ahalov [1]. PDE theories with Riemannian geometry are
Quantum Mechanics-I Prof. Dr. S. Lakshmi Bala Department of Physics Indian Institute of Technology, Madras. Lecture - 21 Square-Integrable Functions
 Quantum Mechanics-I Prof. Dr. S. Lakshmi Bala Department of Physics Indian Institute of Technology, Madras Lecture - 21 Square-Integrable Functions (Refer Slide Time: 00:06) (Refer Slide Time: 00:14) We
Quantum Mechanics-I Prof. Dr. S. Lakshmi Bala Department of Physics Indian Institute of Technology, Madras Lecture - 21 Square-Integrable Functions (Refer Slide Time: 00:06) (Refer Slide Time: 00:14) We
4 Power Series Solutions: Frobenius Method
 4 Power Series Solutions: Frobenius Method Now the ODE adventure takes us to series solutions for ODEs, a technique A & W, that is often viable, valuable and informative. These can be readily applied Sec.
4 Power Series Solutions: Frobenius Method Now the ODE adventure takes us to series solutions for ODEs, a technique A & W, that is often viable, valuable and informative. These can be readily applied Sec.
Energy Efficiency, Acoustics & Daylighting in building Prof. B. Bhattacharjee Department of Civil Engineering Indian Institute of Technology, Delhi
 Energy Efficiency, Acoustics & Daylighting in building Prof. B. Bhattacharjee Department of Civil Engineering Indian Institute of Technology, Delhi Lecture - 05 Introduction & Environmental Factors (contd.)
Energy Efficiency, Acoustics & Daylighting in building Prof. B. Bhattacharjee Department of Civil Engineering Indian Institute of Technology, Delhi Lecture - 05 Introduction & Environmental Factors (contd.)
Supporting Information
 Supporting Information A: Calculation of radial distribution functions To get an effective propagator in one dimension, we first transform 1) into spherical coordinates: x a = ρ sin θ cos φ, y = ρ sin
Supporting Information A: Calculation of radial distribution functions To get an effective propagator in one dimension, we first transform 1) into spherical coordinates: x a = ρ sin θ cos φ, y = ρ sin
A Fast Spherical Filter with Uniform Resolution
 JOURNAL OF COMPUTATIONAL PHYSICS 136, 580 584 (1997) ARTICLE NO. CP975782 A Fast Spherical Filter with Uniform Resolution Rüdiger Jakob-Chien*, and Bradley K. Alpert *Department of Computer Science & Engineering,
JOURNAL OF COMPUTATIONAL PHYSICS 136, 580 584 (1997) ARTICLE NO. CP975782 A Fast Spherical Filter with Uniform Resolution Rüdiger Jakob-Chien*, and Bradley K. Alpert *Department of Computer Science & Engineering,
Spherical Coordinates and Legendre Functions
 Spherical Coordinates and Legendre Functions Spherical coordinates Let s adopt the notation for spherical coordinates that is standard in physics: φ = longitude or azimuth, θ = colatitude ( π 2 latitude)
Spherical Coordinates and Legendre Functions Spherical coordinates Let s adopt the notation for spherical coordinates that is standard in physics: φ = longitude or azimuth, θ = colatitude ( π 2 latitude)
example consider flow of water in a pipe. At each point in the pipe, the water molecule has a velocity
 Module 1: A Crash Course in Vectors Lecture 1: Scalar and Vector Fields Objectives In this lecture you will learn the following Learn about the concept of field Know the difference between a scalar field
Module 1: A Crash Course in Vectors Lecture 1: Scalar and Vector Fields Objectives In this lecture you will learn the following Learn about the concept of field Know the difference between a scalar field
III. TRANSFORMATION RELATIONS
 III. TRANSFORMATION RELATIONS The transformation relations from cartesian coordinates to a general curvilinear system are developed here using certain concepts from differential geometry and tensor analysis,
III. TRANSFORMATION RELATIONS The transformation relations from cartesian coordinates to a general curvilinear system are developed here using certain concepts from differential geometry and tensor analysis,
The Sommerfeld Polynomial Method: Harmonic Oscillator Example
 Chemistry 460 Fall 2017 Dr. Jean M. Standard October 2, 2017 The Sommerfeld Polynomial Method: Harmonic Oscillator Example Scaling the Harmonic Oscillator Equation Recall the basic definitions of the harmonic
Chemistry 460 Fall 2017 Dr. Jean M. Standard October 2, 2017 The Sommerfeld Polynomial Method: Harmonic Oscillator Example Scaling the Harmonic Oscillator Equation Recall the basic definitions of the harmonic
Exercises * on Linear Algebra
 Exercises * on Linear Algebra Laurenz Wiskott Institut für Neuroinformatik Ruhr-Universität Bochum, Germany, EU 4 February 7 Contents Vector spaces 4. Definition...............................................
Exercises * on Linear Algebra Laurenz Wiskott Institut für Neuroinformatik Ruhr-Universität Bochum, Germany, EU 4 February 7 Contents Vector spaces 4. Definition...............................................
Chapter 4 Sequences and Series
 Chapter 4 Sequences and Series 4.1 Sequence Review Sequence: a set of elements (numbers or letters or a combination of both). The elements of the set all follow the same rule (logical progression). The
Chapter 4 Sequences and Series 4.1 Sequence Review Sequence: a set of elements (numbers or letters or a combination of both). The elements of the set all follow the same rule (logical progression). The
Lecture 1 - Vectors. A Puzzle... Introduction. Vectors: The quest begins! TA s Information. Vectors
 Lecture 1 - Vectors Puzzle... The sum starts at 0. Players alternate by choosing an integer from 1 to 10 and then adding it to the sum. The player who gets to 100 wins. You go first. What is the winning
Lecture 1 - Vectors Puzzle... The sum starts at 0. Players alternate by choosing an integer from 1 to 10 and then adding it to the sum. The player who gets to 100 wins. You go first. What is the winning
Expansion of 1/r potential in Legendre polynomials
 Expansion of 1/r potential in Legendre polynomials In electrostatics and gravitation, we see scalar potentials of the form V = K d Take d = R r = R 2 2Rr cos θ + r 2 = R 1 2 r R cos θ + r R )2 Use h =
Expansion of 1/r potential in Legendre polynomials In electrostatics and gravitation, we see scalar potentials of the form V = K d Take d = R r = R 2 2Rr cos θ + r 2 = R 1 2 r R cos θ + r R )2 Use h =
which implies that we can take solutions which are simultaneous eigen functions of
 Module 1 : Quantum Mechanics Chapter 6 : Quantum mechanics in 3-D Quantum mechanics in 3-D For most physical systems, the dynamics is in 3-D. The solutions to the general 3-d problem are quite complicated,
Module 1 : Quantum Mechanics Chapter 6 : Quantum mechanics in 3-D Quantum mechanics in 3-D For most physical systems, the dynamics is in 3-D. The solutions to the general 3-d problem are quite complicated,
Limits of Functions (a, L)
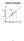 Limits of Functions f(x) (a, L) L f(x) x a x x 20 Informal Definition: If the values of can be made as close to as we like by taking values of sufficiently close to [but not equal to ] then we write or
Limits of Functions f(x) (a, L) L f(x) x a x x 20 Informal Definition: If the values of can be made as close to as we like by taking values of sufficiently close to [but not equal to ] then we write or
Classical Field Theory: Electrostatics-Magnetostatics
 Classical Field Theory: Electrostatics-Magnetostatics April 27, 2010 1 1 J.D.Jackson, Classical Electrodynamics, 2nd Edition, Section 1-5 Electrostatics The behavior of an electrostatic field can be described
Classical Field Theory: Electrostatics-Magnetostatics April 27, 2010 1 1 J.D.Jackson, Classical Electrodynamics, 2nd Edition, Section 1-5 Electrostatics The behavior of an electrostatic field can be described
The Spectral Method (MAPH 40260)
 The Spectral Method (MAPH 40260) Part 4: Barotropic Vorticity Equation Peter Lynch School of Mathematical Sciences Outline Background Rossby-Haurwitz Waves Interaction Coefficients Transform Method The
The Spectral Method (MAPH 40260) Part 4: Barotropic Vorticity Equation Peter Lynch School of Mathematical Sciences Outline Background Rossby-Haurwitz Waves Interaction Coefficients Transform Method The
Physics 6303 Lecture 11 September 24, LAST TIME: Cylindrical coordinates, spherical coordinates, and Legendre s equation
 Physics 6303 Lecture September 24, 208 LAST TIME: Cylindrical coordinates, spherical coordinates, and Legendre s equation, l l l l l l. Consider problems that are no axisymmetric; i.e., the potential depends
Physics 6303 Lecture September 24, 208 LAST TIME: Cylindrical coordinates, spherical coordinates, and Legendre s equation, l l l l l l. Consider problems that are no axisymmetric; i.e., the potential depends
LEGENDRE POLYNOMIALS AND APPLICATIONS. We construct Legendre polynomials and apply them to solve Dirichlet problems in spherical coordinates.
 LEGENDRE POLYNOMIALS AND APPLICATIONS We construct Legendre polynomials and apply them to solve Dirichlet problems in spherical coordinates.. Legendre equation: series solutions The Legendre equation is
LEGENDRE POLYNOMIALS AND APPLICATIONS We construct Legendre polynomials and apply them to solve Dirichlet problems in spherical coordinates.. Legendre equation: series solutions The Legendre equation is
Angular momentum. Quantum mechanics. Orbital angular momentum
 Angular momentum 1 Orbital angular momentum Consider a particle described by the Cartesian coordinates (x, y, z r and their conjugate momenta (p x, p y, p z p. The classical definition of the orbital angular
Angular momentum 1 Orbital angular momentum Consider a particle described by the Cartesian coordinates (x, y, z r and their conjugate momenta (p x, p y, p z p. The classical definition of the orbital angular
The discrete and fast Fourier transforms
 The discrete and fast Fourier transforms Marcel Oliver Revised April 7, 1 1 Fourier series We begin by recalling the familiar definition of the Fourier series. For a periodic function u: [, π] C, we define
The discrete and fast Fourier transforms Marcel Oliver Revised April 7, 1 1 Fourier series We begin by recalling the familiar definition of the Fourier series. For a periodic function u: [, π] C, we define
ES 111 Mathematical Methods in the Earth Sciences Lecture Outline 3 - Thurs 5th Oct 2017 Vectors and 3D geometry
 ES 111 Mathematical Methods in the Earth Sciences Lecture Outline 3 - Thurs 5th Oct 2017 Vectors and 3D geometry So far, all our calculus has been two-dimensional, involving only x and y. Nature is threedimensional,
ES 111 Mathematical Methods in the Earth Sciences Lecture Outline 3 - Thurs 5th Oct 2017 Vectors and 3D geometry So far, all our calculus has been two-dimensional, involving only x and y. Nature is threedimensional,
COMPARISON OF FINITE DIFFERENCE- AND PSEUDOSPECTRAL METHODS FOR CONVECTIVE FLOW OVER A SPHERE
 COMPARISON OF FINITE DIFFERENCE- AND PSEUDOSPECTRAL METHODS FOR CONVECTIVE FLOW OVER A SPHERE BENGT FORNBERG and DAVID MERRILL Abstract. For modeling convective flows over a sphere or within a spherical
COMPARISON OF FINITE DIFFERENCE- AND PSEUDOSPECTRAL METHODS FOR CONVECTIVE FLOW OVER A SPHERE BENGT FORNBERG and DAVID MERRILL Abstract. For modeling convective flows over a sphere or within a spherical
Summary: Curvilinear Coordinates
 Physics 2460 Electricity and Magnetism I, Fall 2007, Lecture 10 1 Summary: Curvilinear Coordinates 1. Summary of Integral Theorems 2. Generalized Coordinates 3. Cartesian Coordinates: Surfaces of Constant
Physics 2460 Electricity and Magnetism I, Fall 2007, Lecture 10 1 Summary: Curvilinear Coordinates 1. Summary of Integral Theorems 2. Generalized Coordinates 3. Cartesian Coordinates: Surfaces of Constant
1 Commutators (10 pts)
 Final Exam Solutions 37A Fall 0 I. Siddiqi / E. Dodds Commutators 0 pts) ) Consider the operator  = Ĵx Ĵ y + ĴyĴx where J i represents the total angular momentum in the ith direction. a) Express both
Final Exam Solutions 37A Fall 0 I. Siddiqi / E. Dodds Commutators 0 pts) ) Consider the operator  = Ĵx Ĵ y + ĴyĴx where J i represents the total angular momentum in the ith direction. a) Express both
Notes: Most of the material presented in this chapter is taken from Jackson, Chap. 2, 3, and 4, and Di Bartolo, Chap. 2. 2π nx i a. ( ) = G n.
 Chapter. Electrostatic II Notes: Most of the material presented in this chapter is taken from Jackson, Chap.,, and 4, and Di Bartolo, Chap... Mathematical Considerations.. The Fourier series and the Fourier
Chapter. Electrostatic II Notes: Most of the material presented in this chapter is taken from Jackson, Chap.,, and 4, and Di Bartolo, Chap... Mathematical Considerations.. The Fourier series and the Fourier
The 3 dimensional Schrödinger Equation
 Chapter 6 The 3 dimensional Schrödinger Equation 6.1 Angular Momentum To study how angular momentum is represented in quantum mechanics we start by reviewing the classical vector of orbital angular momentum
Chapter 6 The 3 dimensional Schrödinger Equation 6.1 Angular Momentum To study how angular momentum is represented in quantum mechanics we start by reviewing the classical vector of orbital angular momentum
1 Numbers. exponential functions, such as x 7! a x ; where a; x 2 R; trigonometric functions, such as x 7! sin x; where x 2 R; ffiffi x ; where x 0:
 Numbers In this book we study the properties of real functions defined on intervals of the real line (possibly the whole real line) and whose image also lies on the real line. In other words, they map
Numbers In this book we study the properties of real functions defined on intervals of the real line (possibly the whole real line) and whose image also lies on the real line. In other words, they map
8.1 The hydrogen atom solutions
 8.1 The hydrogen atom solutions Slides: Video 8.1.1 Separating for the radial equation Text reference: Quantum Mechanics for Scientists and Engineers Section 10.4 (up to Solution of the hydrogen radial
8.1 The hydrogen atom solutions Slides: Video 8.1.1 Separating for the radial equation Text reference: Quantum Mechanics for Scientists and Engineers Section 10.4 (up to Solution of the hydrogen radial
Outline. The Spectral Method (MAPH 40260) Part 4: Barotropic Vorticity Equation. Outline. Background. Rossby-Haurwitz Waves.
 Outline The Spectral Method (MAPH 40260) Part 4: Barotropic Vorticity Equation Peter Lynch School of Mathematical Sciences Outline The dynamics of non-divergent flow on a rotating sphere are described
Outline The Spectral Method (MAPH 40260) Part 4: Barotropic Vorticity Equation Peter Lynch School of Mathematical Sciences Outline The dynamics of non-divergent flow on a rotating sphere are described
is any such piece, suppose we choose a in this piece and use σ ( xk, yk, zk) . If B
 Multivariable Calculus Lecture # Notes In this lecture we look at integration over regions in space, ie triple integrals, using Cartesian coordinates, cylindrical coordinates, and spherical coordinates
Multivariable Calculus Lecture # Notes In this lecture we look at integration over regions in space, ie triple integrals, using Cartesian coordinates, cylindrical coordinates, and spherical coordinates
Recall that any inner product space V has an associated norm defined by
 Hilbert Spaces Recall that any inner product space V has an associated norm defined by v = v v. Thus an inner product space can be viewed as a special kind of normed vector space. In particular every inner
Hilbert Spaces Recall that any inner product space V has an associated norm defined by v = v v. Thus an inner product space can be viewed as a special kind of normed vector space. In particular every inner
1.1.1 Algebraic Operations
 1.1.1 Algebraic Operations We need to learn how our basic algebraic operations interact. When confronted with many operations, we follow the order of operations: Parentheses Exponentials Multiplication
1.1.1 Algebraic Operations We need to learn how our basic algebraic operations interact. When confronted with many operations, we follow the order of operations: Parentheses Exponentials Multiplication
Chapter 5. Shallow Water Equations. 5.1 Derivation of shallow water equations
 Chapter 5 Shallow Water Equations So far we have concentrated on the dynamics of small-scale disturbances in the atmosphere and ocean with relatively simple background flows. In these analyses we have
Chapter 5 Shallow Water Equations So far we have concentrated on the dynamics of small-scale disturbances in the atmosphere and ocean with relatively simple background flows. In these analyses we have
Modern Navigation. Thomas Herring
 12.215 Modern Navigation Thomas Herring Today s Class Latitude and Longitude Simple spherical definitions Geodetic definition: For an ellipsoid Astronomical definition: Based on direction of gravity Relationships
12.215 Modern Navigation Thomas Herring Today s Class Latitude and Longitude Simple spherical definitions Geodetic definition: For an ellipsoid Astronomical definition: Based on direction of gravity Relationships
SOLVING HYPERBOLIC PARTIAL DIFFERENTIAL EQUATIONS IN SPHERICAL GEOMETRY WITH RADIAL BASIS FUNCTIONS
 SOLVING HYPERBOLIC PARTIAL DIFFERENTIAL EQUATIONS IN SPHERICAL GEOMETRY WITH RADIAL BASIS FUNCTIONS NATASHA FLYER 1. Introduction Mathematical modeling of space and climate phenomena generally requires
SOLVING HYPERBOLIC PARTIAL DIFFERENTIAL EQUATIONS IN SPHERICAL GEOMETRY WITH RADIAL BASIS FUNCTIONS NATASHA FLYER 1. Introduction Mathematical modeling of space and climate phenomena generally requires
Solving the 3D Laplace Equation by Meshless Collocation via Harmonic Kernels
 Solving the 3D Laplace Equation by Meshless Collocation via Harmonic Kernels Y.C. Hon and R. Schaback April 9, Abstract This paper solves the Laplace equation u = on domains Ω R 3 by meshless collocation
Solving the 3D Laplace Equation by Meshless Collocation via Harmonic Kernels Y.C. Hon and R. Schaback April 9, Abstract This paper solves the Laplace equation u = on domains Ω R 3 by meshless collocation
Multidimensional Calculus: Mainly Differential Theory
 9 Multidimensional Calculus: Mainly Differential Theory In the following, we will attempt to quickly develop the basic differential theory of calculus in multidimensional spaces You ve probably already
9 Multidimensional Calculus: Mainly Differential Theory In the following, we will attempt to quickly develop the basic differential theory of calculus in multidimensional spaces You ve probably already
Laplace s Equation on a Sphere
 Laplace s Equation on a Sphere Pierre Simon de Laplace Domenic Scorzetti Millersville University dascorze@marauder.millersville.edu April 5, 6 Problem Outline A spherical shell has an inner radius, and
Laplace s Equation on a Sphere Pierre Simon de Laplace Domenic Scorzetti Millersville University dascorze@marauder.millersville.edu April 5, 6 Problem Outline A spherical shell has an inner radius, and
Seminar: Measurement of Stellar Parameters with Asteroseismology
 Seminar: Measurement of Stellar Parameters with Asteroseismology Author: Gal Kranjc Kušlan Mentor: dr. Andrej Prša Ljubljana, December 2017 Abstract In this seminar I introduce asteroseismology, which
Seminar: Measurement of Stellar Parameters with Asteroseismology Author: Gal Kranjc Kušlan Mentor: dr. Andrej Prša Ljubljana, December 2017 Abstract In this seminar I introduce asteroseismology, which
Vectors and Geometry
 Vectors and Geometry Vectors In the context of geometry, a vector is a triplet of real numbers. In applications to a generalized parameters space, such as the space of random variables in a reliability
Vectors and Geometry Vectors In the context of geometry, a vector is a triplet of real numbers. In applications to a generalized parameters space, such as the space of random variables in a reliability
Tutorial Exercises: Geometric Connections
 Tutorial Exercises: Geometric Connections 1. Geodesics in the Isotropic Mercator Projection When the surface of the globe is projected onto a flat map some aspects of the map are inevitably distorted.
Tutorial Exercises: Geometric Connections 1. Geodesics in the Isotropic Mercator Projection When the surface of the globe is projected onto a flat map some aspects of the map are inevitably distorted.
A Truncated Model for Finite Amplitude Baroclinic Waves in a Channel
 A Truncated Model for Finite Amplitude Baroclinic Waves in a Channel Zhiming Kuang 1 Introduction To date, studies of finite amplitude baroclinic waves have been mostly numerical. The numerical models,
A Truncated Model for Finite Amplitude Baroclinic Waves in a Channel Zhiming Kuang 1 Introduction To date, studies of finite amplitude baroclinic waves have been mostly numerical. The numerical models,
Green s Tensors for the Electromagnetic Field in Cylindrical Coordinates
 Chapter 25 Green s Tensors for the Electromagnetic Field in Cylindrical Coordinates The solutions of the vector Helmholtz equation in three dimensions can be expressed by a complete set of vector fields
Chapter 25 Green s Tensors for the Electromagnetic Field in Cylindrical Coordinates The solutions of the vector Helmholtz equation in three dimensions can be expressed by a complete set of vector fields
1 Fundamentals. 1.1 Overview. 1.2 Units: Physics 704 Spring 2018
 Physics 704 Spring 2018 1 Fundamentals 1.1 Overview The objective of this course is: to determine and fields in various physical systems and the forces and/or torques resulting from them. The domain of
Physics 704 Spring 2018 1 Fundamentals 1.1 Overview The objective of this course is: to determine and fields in various physical systems and the forces and/or torques resulting from them. The domain of
Last Update: March 1 2, 201 0
 M ath 2 0 1 E S 1 W inter 2 0 1 0 Last Update: March 1 2, 201 0 S eries S olutions of Differential Equations Disclaimer: This lecture note tries to provide an alternative approach to the material in Sections
M ath 2 0 1 E S 1 W inter 2 0 1 0 Last Update: March 1 2, 201 0 S eries S olutions of Differential Equations Disclaimer: This lecture note tries to provide an alternative approach to the material in Sections
Here are brief notes about topics covered in class on complex numbers, focusing on what is not covered in the textbook.
 Phys374, Spring 2008, Prof. Ted Jacobson Department of Physics, University of Maryland Complex numbers version 5/21/08 Here are brief notes about topics covered in class on complex numbers, focusing on
Phys374, Spring 2008, Prof. Ted Jacobson Department of Physics, University of Maryland Complex numbers version 5/21/08 Here are brief notes about topics covered in class on complex numbers, focusing on
Notes on Special Functions
 Spring 25 1 Notes on Special Functions Francis J. Narcowich Department of Mathematics Texas A&M University College Station, TX 77843-3368 Introduction These notes are for our classes on special functions.
Spring 25 1 Notes on Special Functions Francis J. Narcowich Department of Mathematics Texas A&M University College Station, TX 77843-3368 Introduction These notes are for our classes on special functions.
Light Scattering Group
 Light Scattering Inversion Light Scattering Group A method of inverting the Mie light scattering equation of spherical homogeneous particles of real and complex argument is being investigated The aims
Light Scattering Inversion Light Scattering Group A method of inverting the Mie light scattering equation of spherical homogeneous particles of real and complex argument is being investigated The aims
3 Green s functions in 2 and 3D
 William J. Parnell: MT34032. Section 3: Green s functions in 2 and 3 57 3 Green s functions in 2 and 3 Unlike the one dimensional case where Green s functions can be found explicitly for a number of different
William J. Parnell: MT34032. Section 3: Green s functions in 2 and 3 57 3 Green s functions in 2 and 3 Unlike the one dimensional case where Green s functions can be found explicitly for a number of different
Numerical Methods I Orthogonal Polynomials
 Numerical Methods I Orthogonal Polynomials Aleksandar Donev Courant Institute, NYU 1 donev@courant.nyu.edu 1 Course G63.2010.001 / G22.2420-001, Fall 2010 Nov. 4th and 11th, 2010 A. Donev (Courant Institute)
Numerical Methods I Orthogonal Polynomials Aleksandar Donev Courant Institute, NYU 1 donev@courant.nyu.edu 1 Course G63.2010.001 / G22.2420-001, Fall 2010 Nov. 4th and 11th, 2010 A. Donev (Courant Institute)
The Radiative Transfer Equation
 The Radiative Transfer Equation R. Wordsworth April 11, 215 1 Objectives Derive the general RTE equation Derive the atmospheric 1D horizontally homogenous RTE equation Look at heating/cooling rates in
The Radiative Transfer Equation R. Wordsworth April 11, 215 1 Objectives Derive the general RTE equation Derive the atmospheric 1D horizontally homogenous RTE equation Look at heating/cooling rates in
The Not-Formula Book for C2 Everything you need to know for Core 2 that won t be in the formula book Examination Board: AQA
 Not The Not-Formula Book for C Everything you need to know for Core that won t be in the formula book Examination Board: AQA Brief This document is intended as an aid for revision. Although it includes
Not The Not-Formula Book for C Everything you need to know for Core that won t be in the formula book Examination Board: AQA Brief This document is intended as an aid for revision. Although it includes
[Disclaimer: This is not a complete list of everything you need to know, just some of the topics that gave people difficulty.]
![[Disclaimer: This is not a complete list of everything you need to know, just some of the topics that gave people difficulty.] [Disclaimer: This is not a complete list of everything you need to know, just some of the topics that gave people difficulty.]](/thumbs/82/86615903.jpg) Math 43 Review Notes [Disclaimer: This is not a complete list of everything you need to know, just some of the topics that gave people difficulty Dot Product If v (v, v, v 3 and w (w, w, w 3, then the
Math 43 Review Notes [Disclaimer: This is not a complete list of everything you need to know, just some of the topics that gave people difficulty Dot Product If v (v, v, v 3 and w (w, w, w 3, then the
Numerical Investigation on Spherical Harmonic Synthesis and Analysis
 Numerical Investigation on Spherical Harmonic Synthesis and Analysis Johnny Bärlund Master of Science Thesis in Geodesy No. 3137 TRITA-GIT EX 15-006 School of Architecture and the Built Environment Royal
Numerical Investigation on Spherical Harmonic Synthesis and Analysis Johnny Bärlund Master of Science Thesis in Geodesy No. 3137 TRITA-GIT EX 15-006 School of Architecture and the Built Environment Royal
13 Spherical Coordinates
 Utah State University DigitalCommons@USU Foundations of Wave Phenomena Library Digital Monographs 8-204 3 Spherical Coordinates Charles G. Torre Department of Physics, Utah State University, Charles.Torre@usu.edu
Utah State University DigitalCommons@USU Foundations of Wave Phenomena Library Digital Monographs 8-204 3 Spherical Coordinates Charles G. Torre Department of Physics, Utah State University, Charles.Torre@usu.edu
Tidal Effects on Earth s Surface
 Tidal Effects on Earth s Surface Tom Murphy February, 1 This treatment follows the conventions of F. D. Stacey s Physics of the Earth, and is largely an elaboration on this work. 1 Tidal Potential The
Tidal Effects on Earth s Surface Tom Murphy February, 1 This treatment follows the conventions of F. D. Stacey s Physics of the Earth, and is largely an elaboration on this work. 1 Tidal Potential The
Differential Operators and the Divergence Theorem
 1 of 6 1/15/2007 6:31 PM Differential Operators and the Divergence Theorem One of the most important and useful mathematical constructs is the "del operator", usually denoted by the symbol Ñ (which is
1 of 6 1/15/2007 6:31 PM Differential Operators and the Divergence Theorem One of the most important and useful mathematical constructs is the "del operator", usually denoted by the symbol Ñ (which is
H atom solution. 1 Introduction 2. 2 Coordinate system 2. 3 Variable separation 4
 H atom solution Contents 1 Introduction 2 2 Coordinate system 2 3 Variable separation 4 4 Wavefunction solutions 6 4.1 Solution for Φ........................... 6 4.2 Solution for Θ...........................
H atom solution Contents 1 Introduction 2 2 Coordinate system 2 3 Variable separation 4 4 Wavefunction solutions 6 4.1 Solution for Φ........................... 6 4.2 Solution for Θ...........................
Lecture 13: Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay. Poisson s and Laplace s Equations
 Poisson s and Laplace s Equations Lecture 13: Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay We will spend some time in looking at the mathematical foundations of electrostatics.
Poisson s and Laplace s Equations Lecture 13: Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay We will spend some time in looking at the mathematical foundations of electrostatics.
Control Volume. Dynamics and Kinematics. Basic Conservation Laws. Lecture 1: Introduction and Review 1/24/2017
 Lecture 1: Introduction and Review Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study of motion without regard for the cause. Dynamics: On the other hand, dynamics
Lecture 1: Introduction and Review Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study of motion without regard for the cause. Dynamics: On the other hand, dynamics
Lecture 1: Introduction and Review
 Lecture 1: Introduction and Review Review of fundamental mathematical tools Fundamental and apparent forces Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study
Lecture 1: Introduction and Review Review of fundamental mathematical tools Fundamental and apparent forces Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study
Earth s flattening : which impact for meteorology and climatology?
 Earth s flattening : which impact for meteorology and climatology? Pierre Bénard Météo-France CNRM/GMAP CNRS 16 21 Aug. 2014, Montreal P. Bénard (Météo-France) Earth s flattening : which impact? 16/21
Earth s flattening : which impact for meteorology and climatology? Pierre Bénard Météo-France CNRM/GMAP CNRS 16 21 Aug. 2014, Montreal P. Bénard (Météo-France) Earth s flattening : which impact? 16/21
A Quick Introduction to Vectors, Vector Calculus, and Coordinate Systems
 Copyright 2006, David A. Randall Revised Wed, Feb 06, :36:23 A Quick Introduction to Vectors, Vector Calculus, and Coordinate Systems David A. Randall Department of Atmospheric Science Colorado State University,
Copyright 2006, David A. Randall Revised Wed, Feb 06, :36:23 A Quick Introduction to Vectors, Vector Calculus, and Coordinate Systems David A. Randall Department of Atmospheric Science Colorado State University,
Chem 3502/4502 Physical Chemistry II (Quantum Mechanics) 3 Credits Spring Semester 2006 Christopher J. Cramer. Lecture 9, February 8, 2006
 Chem 3502/4502 Physical Chemistry II (Quantum Mechanics) 3 Credits Spring Semester 2006 Christopher J. Cramer Lecture 9, February 8, 2006 The Harmonic Oscillator Consider a diatomic molecule. Such a molecule
Chem 3502/4502 Physical Chemistry II (Quantum Mechanics) 3 Credits Spring Semester 2006 Christopher J. Cramer Lecture 9, February 8, 2006 The Harmonic Oscillator Consider a diatomic molecule. Such a molecule
Vectors. January 13, 2013
 Vectors January 13, 2013 The simplest tensors are scalars, which are the measurable quantities of a theory, left invariant by symmetry transformations. By far the most common non-scalars are the vectors,
Vectors January 13, 2013 The simplest tensors are scalars, which are the measurable quantities of a theory, left invariant by symmetry transformations. By far the most common non-scalars are the vectors,
Bohr & Wheeler Fission Theory Calculation 4 March 2009
 Bohr & Wheeler Fission Theory Calculation 4 March 9 () Introduction The goal here is to reproduce the calculation of the limiting Z /A against spontaneous fission Z A lim a S. (.) a C as first done by
Bohr & Wheeler Fission Theory Calculation 4 March 9 () Introduction The goal here is to reproduce the calculation of the limiting Z /A against spontaneous fission Z A lim a S. (.) a C as first done by
Astronomy 6570 Physics of the Planets
 Astronomy 6570 Physics of the Planets Planetary Rotation, Figures, and Gravity Fields Topics to be covered: 1. Rotational distortion & oblateness 2. Gravity field of an oblate planet 3. Free & forced planetary
Astronomy 6570 Physics of the Planets Planetary Rotation, Figures, and Gravity Fields Topics to be covered: 1. Rotational distortion & oblateness 2. Gravity field of an oblate planet 3. Free & forced planetary
1 Potential due to a charged wire/sheet
 Lecture XXX Renormalization, Regularization and Electrostatics Let us calculate the potential due to an infinitely large object, e.g. a uniformly charged wire or a uniformly charged sheet. Our main interest
Lecture XXX Renormalization, Regularization and Electrostatics Let us calculate the potential due to an infinitely large object, e.g. a uniformly charged wire or a uniformly charged sheet. Our main interest
Particle in a 3 Dimensional Box just extending our model from 1D to 3D
 CHEM 2060 Lecture 20: Particle in a 3D Box; H atom L20-1 Particle in a 3 Dimensional Box just extending our model from 1D to 3D A 3D model is a step closer to reality than a 1D model. Let s increase the
CHEM 2060 Lecture 20: Particle in a 3D Box; H atom L20-1 Particle in a 3 Dimensional Box just extending our model from 1D to 3D A 3D model is a step closer to reality than a 1D model. Let s increase the
On an Eigenvalue Problem Involving Legendre Functions by Nicholas J. Rose North Carolina State University
 On an Eigenvalue Problem Involving Legendre Functions by Nicholas J. Rose North Carolina State University njrose@math.ncsu.edu 1. INTRODUCTION. The classical eigenvalue problem for the Legendre Polynomials
On an Eigenvalue Problem Involving Legendre Functions by Nicholas J. Rose North Carolina State University njrose@math.ncsu.edu 1. INTRODUCTION. The classical eigenvalue problem for the Legendre Polynomials
Mountain Torques Caused by Normal-Mode Global Rossby Waves, and the Impact on Atmospheric Angular Momentum
 1045 Mountain Torques Caused by Normal-Mode Global Rossby Waves, and the Impact on Atmospheric Angular Momentum HARALD LEJENÄS Department of Meteorology, Stockholm University, Stockholm, Sweden ROLAND
1045 Mountain Torques Caused by Normal-Mode Global Rossby Waves, and the Impact on Atmospheric Angular Momentum HARALD LEJENÄS Department of Meteorology, Stockholm University, Stockholm, Sweden ROLAND
Cauchy Integral Formula Consequences
 Cauchy Integral Formula Consequences Monday, October 28, 2013 1:59 PM Homework 3 due November 15, 2013 at 5 PM. Last time we derived Cauchy's Integral Formula, which we will present in somewhat generalized
Cauchy Integral Formula Consequences Monday, October 28, 2013 1:59 PM Homework 3 due November 15, 2013 at 5 PM. Last time we derived Cauchy's Integral Formula, which we will present in somewhat generalized
Practical Algebra. A Step-by-step Approach. Brought to you by Softmath, producers of Algebrator Software
 Practical Algebra A Step-by-step Approach Brought to you by Softmath, producers of Algebrator Software 2 Algebra e-book Table of Contents Chapter 1 Algebraic expressions 5 1 Collecting... like terms 5
Practical Algebra A Step-by-step Approach Brought to you by Softmath, producers of Algebrator Software 2 Algebra e-book Table of Contents Chapter 1 Algebraic expressions 5 1 Collecting... like terms 5
Stephen F Austin. Exponents and Logarithms. chapter 3
 chapter 3 Starry Night was painted by Vincent Van Gogh in 1889. The brightness of a star as seen from Earth is measured using a logarithmic scale. Exponents and Logarithms This chapter focuses on understanding
chapter 3 Starry Night was painted by Vincent Van Gogh in 1889. The brightness of a star as seen from Earth is measured using a logarithmic scale. Exponents and Logarithms This chapter focuses on understanding
Eigenfunctions on the surface of a sphere. In spherical coordinates, the Laplacian is. u = u rr + 2 r u r + 1 r 2. sin 2 (θ) + 1
 Eigenfunctions on the surface of a sphere In spherical coordinates, the Laplacian is u = u rr + 2 r u r + 1 r 2 [ uφφ sin 2 (θ) + 1 sin θ (sin θ u θ) θ ]. Eigenfunctions on the surface of a sphere In spherical
Eigenfunctions on the surface of a sphere In spherical coordinates, the Laplacian is u = u rr + 2 r u r + 1 r 2 [ uφφ sin 2 (θ) + 1 sin θ (sin θ u θ) θ ]. Eigenfunctions on the surface of a sphere In spherical
Week 7: Integration: Special Coordinates
 Week 7: Integration: Special Coordinates Introduction Many problems naturally involve symmetry. One should exploit it where possible and this often means using coordinate systems other than Cartesian coordinates.
Week 7: Integration: Special Coordinates Introduction Many problems naturally involve symmetry. One should exploit it where possible and this often means using coordinate systems other than Cartesian coordinates.
PHYS 404 Lecture 1: Legendre Functions
 PHYS 404 Lecture 1: Legendre Functions Dr. Vasileios Lempesis PHYS 404 - LECTURE 1 DR. V. LEMPESIS 1 Legendre Functions physical justification Legendre functions or Legendre polynomials are the solutions
PHYS 404 Lecture 1: Legendre Functions Dr. Vasileios Lempesis PHYS 404 - LECTURE 1 DR. V. LEMPESIS 1 Legendre Functions physical justification Legendre functions or Legendre polynomials are the solutions
Representation of inhomogeneous, non-separable covariances by sparse wavelet-transformed matrices
 Representation of inhomogeneous, non-separable covariances by sparse wavelet-transformed matrices Andreas Rhodin, Harald Anlauf German Weather Service (DWD) Workshop on Flow-dependent aspects of data assimilation,
Representation of inhomogeneous, non-separable covariances by sparse wavelet-transformed matrices Andreas Rhodin, Harald Anlauf German Weather Service (DWD) Workshop on Flow-dependent aspects of data assimilation,
