Science is asking questions. And living is not being afraid of the answer. The Science of Breakable Things by Tae Keller STEP 4: rhcbooks.
|
|
|
- Moris Murphy
- 6 years ago
- Views:
Transcription
1 B 1 K B ic hi Wh i i i? h l v Q 2 h h ll i i i h i i h m? i W B chi b l l G ii v i b 3 i c l ii i qi Gb m 4 i c ll ic G c i i h 5 l c im im l il ci. l m k m k? K G M MMB M X 6 i mim M h l m M X 7 i k h h ll l? i Wh l? 8 Z 2018 b li ki M W i i v i li j i bi j ll i imi cic i ki qi. livi i bi i h. h cic Bkbl hi b Kll hcbk.cm.
2 G 3-7 & il GB h cic Bkbl hi c Gi B BK li li i i mil chl h hi il cl. mm bi i i m i; h hi i li mii h hhl; h Mikl h chilh b i hv. Wh M. l h cic ch ic h ih h ciiic c li c l cc h mi h li. h h c ih i h b i i cic hi m i. li h bi l h iz m mhi h bliv cl hl h mm cv. Wh h il i li lch l h vl bi i lii h h mil. cmi lim ml ill ccibl b ic. Kik vi h hi b Jllih cm clv b cmbii cic ih h ic. Bkli B K i ll ii h h i m mbi ici i h chl cmii. (h i i.) i m B M ll h mv k i k i blihi h v bb ki mli bk mm. ii h Kll.cm ll h b i h l bi.l/kll. v hh 2018 b li ki -G vi h ih i h ciiic c 1 bv 2 Qi 3 viiv ch 4 hi 5 c 6 im 7 l 8 lz l ivi h cl i mll k hm cc im. vi vi mil hm ci hi im cl bbbl cki h cki mil. v h c imi b ch hi im. l mm i cic & chicl bjc K & il ;
3 M ic h c h vl. h ih ll vl imi b h chc clic l? Wh h cib h? 1 M. l k bv. Wh bv b li m h i i h lb bk? (. 5 6) ic li li b M. l Mikl Mz i. h hi b h clic h vl? M. l h 2 i h ciiic c i qi. hi ivi mhi h ii hm. Wh qi li hv b mil ihi? i ihi m li i vi. h Mikl h b i h h. Wh? ihi mim ch i mil chl? li h i k hich ic vi. Which bjc li i vi? li b i i i. m c hi mili. h bh l b? cib h il lihi ih i. h him mch h hm? li h i i mk li h l hi m h cmii. hmim i h i lc h m b hh h h. ml li h cll h mh ii. (. 19) i hi. Wh h l h m hmim hi i cii? li l b h mh i? mih li bi m m ih ici ih h h? li mm i bi. li cm h mm cii h l? li i i h lb jl h m bck. (. 26) Wh li hik h h mh h? mm bk il G Micl. Wh i li i i h mh ii? Wh i h iiicc h bl Bl chi? i h chi iv li h? ic li ci h h l h h bl l i hi h bl Bl chi b B Bl i. h l qi h mm b h h l h ii. li h h mh m b v c chc. (. 279) li h h K i i h c him i li mm. Wh li h h l i h h? li h li h cll i cm v. li mm l lik cii hi lil bi ch b ml i lz i. (. 196) i h chc h icl iicl hl h ih h ch. h i i h vl li ll bi lz h mil ii? Wh ccli h? Bl i ic h i mi hh h bk. Wh li hik h M. Mz b h mh? i h ml bl i h vl. li h i hl K. i i i. h h vi hi hicii. Wh li l b li m i? li h lli q Bc cic i ki qi. livi i bi i h. (. 292) li h il h bk. Wh i h bkbl hi? h ici qi bv cl ih mm i i i K & il ; & c ; ki & ii mhi & llbi ; vi lih ; Kl ; cbl cqiii & b li ki
4 M im 4 l l vl h li mm i bi. h h l l li h l l. bk i h lib i h ch h mblim vi l. h lli i i hll lmc.cm/c /l-mi-l-l. h lc l h chc i h vl m iv h. v i h h li hi chic ci ciic c cvi m h bk hi i. M l mm i Wii & W ; ch Bil & Kl W ; l ih mm i i i K & il ; & c ; ki & ii mhi & llbi ; vi lih ; Kl ; cbl cqiii & im cmml h i hich mi i m iivil b m h i hl. h mi i mv m lil iii. Wh li h m h h ll h h h mil ih bl ch. (. 6) ic h mi h lli cmm iim hh il ij Bck h i b Bki h Mk l h Bll i i c h h h mm v cl h ilv lii k ick iim i h ic h i h bk h h cl b. Which chc i m likl i i h ii? l mm i cbl cqiii & ; Wii ci & iibi Wii W li h i hi. ch h kill hi h./bcm-hi/kill-.hml. i vic m h bk i ici hh hik li h i hi. Wh chll mih hi c h cli hi mil? l mm i Wii & W ; ch Bil & Kl W iv cii h hi k c lb ii Glil Glili il Bli cl. k ch h cii i bihicl bk cll cii. cl ici h ciiic ivii h m hm m. M l mm i Wii & W ; ch Bil & Kl W ; vi lih ; Kl Mi i h hb h bl iz i hic i i 1911 h h bl iz i hmi. k ch h mb m m h hv h bl iz i vi cic m (bliz.). h hv hm cc b h h cm h i b. Wh i h i ml ml izi? ic h ii hh hi i ii. l mm i Wii ch Bil & Kl W ; cic & chicl bjc i Kl & b li ki
5 M (ci) li i h h l h h h mh v h bl Bl chi i hi h. v ch bl chi i h lib li. h cliv? k cc hi l l im. Bi i m hi l. vi vi cli. ll h ih h ciiic c icv h c cli l. mch i k hi l i cl? m cli c k cl? l h c k? c h c l i cic jl. l mm i cic & chicl bjc K & il 6-8.3; Wii & W B/ GG hl b c j mili i hm ki cl m c. ch m icl imiic (. 4) (. 17) micbl (. 20) clic (. 41) vlci (. 74) illi (. 95) icihbl (. 95) iimii (. 99) ih (. 113) iiiiv (. 123) blivi (. 146) v (. 157) mh (. 225) ml (. 260) cic (. 273). l mm i cbl cqiii & M W M hi c Gi hlk B h i mb J B h h Glih Ji. lm B zz M i ch B h G bl bh ki B l i B h M Wl lbi Bih hih h h Mii M b cl hil i l Gvill h li m hil Bk chl ib Mki 1745 B k /18 (h Wllc civ c Bk 1) J ; ill b Kll Mh B b li ki
Remember. Passover: A Time. The to
v: im kill ml lmb i m. ibl xli Ci v lmb i (1 Cii 5:7). i ii m l ii i l bk ( 19:32). mmb G i li b v l bk b v lmb. i b i v i b bk i iixi ( 19:33). i lm bv v. v i v lb? Mb mmb i l m bk x li i b i. i li b
INSIDE. Summary. A behind-the-curtain look at the artists, the company and the art form of this production. NewVictory.
Ti i i ll N Viy Sl Tl R Gi F ml i, ili imi b N Viy i Dm, k : NViy/SlTl INSID A bi--i lk i, my m i i COON COR STANDARDS Ri: 2; 7 Wii: 2; 4 Ski ii: 1; 2; 4 : 1; 2; 4 NW YORK STAT STANDARDS A: Ci, Pmi, Ri,
Above Bar Church Christmas Programme
Abv B Cc Ci P T j f lif... J Ribi, Mii M l v i wl. Rc b f ilc l k j lv i i c f f, b lif; livl c i vl wl f bi, li; ll f i fi w j f lif. M l w v fi Ci. A c i ficé j f Nz Bl; j f ill f Bl ; wi f i c j wi
The Newsletter for FSB Connect Club Members. May/June y M. Six. August 7. But it s a M ONLY. going! gratuity
Th Nwl f FSB Cc Cl M D x i S M... p i T l h! ll cii i YOU ip i x M -D f Six Th f hi ip v k ll, I c ll W? hi ii ll i c I f p wh i T i ih B i M vl w kf v l ll il f w v l: v h w ll h l f 11 f fi h l l w v
Student Jobs Fairs. YOUR ticket to student recruitment in Birmingham 2015 Version 1
S J Fi YOUR i i i Biih 215 Vi 1 Wl D vi -i/l vi vi v 28,? Th l fh h J Z h Gil f S h vi f f l vii ii i il Wl W 214 i i f 6, v 12, i hh h Gil, f h hi f -i/l vi ii h hil h Th i i vi j ii hi i Oii h J Z, Gil
Read & Understan. Understand NEW EDITIO od u. o i. d b. u b. l r. t to. , Grade 3. Correlated Standards WITH LEVELED TEXTS
G 3 EMC 3443 R & U WITH LEVELED TEXTS y l b c V Wi c i Cp bl ici i xpli k Lxil lvl 480 710 Cpi vcbly civii Spp vi i bilii Cv f i kill NEW EDITIO N! A T D k H y M N? I M. W D i i x S Cl S A T D k My H y
Opening. Monster Guard. Grades 1-3. Teacher s Guide
Tcr Gi 2017 Amric R Cr PLEASE NOTE: S m cml Iiii ci f Mr Gr bfr y bgi i civiy, i rr gi cc Vlc riig mii. Oig Ifrm y r gig lr b vlc y f vlc r. Exli r r vlc ll vr rl, i Ui S, r, iclig Alk Hii, v m civ vlc.
BULLETIN THE BULLETIN JUNE 2012 VICTOR VALLEY NEWSLETTER OF MINERAL CLUB GEM AND THE THE SAN BERNARDINO COUNTY FAIR ISSUE PH.
S il M il S Vi Vll G & Mil Cl 15056-B Sv S Vivill, CA 92395-3811. BULLETIN i i i l l l li VICTOR VALLEY GEM & MINERAL CLUB i i i g. V i x i ī l i i BULLETIN il l VIC- TOR VALLEY GEM & MINERAL CLUB. R i
VERIFICATION OF RECOVERY PROCESS UNDER THE GREAT HANSHIN-AWAJI EARTHQUAKE DISASTER BASED ON THE RECOVERY INDEX (RI)
13 h Wl f hqk ii V,, 1, P N 131 VIITION O OVY PO UND TH GT HNHIN-WJI THQUK DIT D ON TH OVY INDX (I) Yk KTNI 1, H HYHI UMMY Thi Kb iiz' lif i h f h G Hhi- wji hqk Di i I ( I) I hi h, h w lif l lif i, I
APPRENTICESHIPS. A guide for learners
PPRENTCESHPS ui l 1 F ii vii u.kll..uk/ii ll u 0178 60747 C ui 1 W ii? - T 10 bi i 5-6 M i 7-8 F (Fqul k ui) 9-1 Fiv bi i 1-14 W Sk T Cll? 15-16 W k? S i u.kll..uk/ii Yu uu Wl Sk T Cll. u kik u quliii
OKANAGAN LANDING SEWER EXTENSION PROJEC
I XI PJC HICHCCK 2 - / P H I F CU PK HIC UI CK U UI P HC 35 X P B PX IV I IX PH MUI HI C CP P I M HI I. VI C F IV FHI BCK CMB CK B MM 30 C CH PI C MB P KM IZ B MB IV I H BCKC K 32 K V I I H I MU HI U KICKI
October The Houstonian 111 North Post Oak Lane Houston, Texas Tues, Oct. 24 8am 5pm (Cocktail reception + Cookout)
il! b R! if f l iv, l i. I i R il l p v k b! L i G N b, f R i l p f k il l i Ob 24 26 T Hi 111 N P Ok L H, Tx 77024 T, O. 24 8 5p (Ckil pi + Ck) W, O. 25 8 5p T, O. 26 8 11:30 i f i k b, i x p p v i f
OKANAGAN LANDING SEWER EXTENSION PROJEC
I XI PJC HICHCCK 1 - I /MI /P H I F CU PK HIC UI CK U UI P HC 35 X P B PX IV I IX PH MUI HI C CP P I M HI I. VI C F IV FHI BCK CMB CK B MM 30 C CH PI C MB P KM IZ B MB IV I H BCKC K 32 K V I I H I MU HI
MEDWAY SPORTS DEVELOPMENT
PB 2:L 1 13:36 P 1 MEDWAY SPTS DEVELPMENT.m.v./vlm A i 11 Bfil Sl i P-16 FE C? D v i i? T l i i S Li Pmm? B fi Ti iq l vlm mm ill l vl fi, mivi ill vii flli ii: l Nm S l : W Tm li ii (ili m fi i) j l i?
CUTTING EDGE RESOURCES ON LIFE BEFORE BIRTH FOR SECOND-LEVEL STUDENTS
CUTTING EDGE RESOURCES ON LIFE BEFORE BIRTH FOR SECOND-LEVEL J F Rf f f i vill jf COMPRE YOUR FINGERPRINTS CRD Y : F : Mk f f j i f i vl v k v f f il 2 Pl x l ll f i f il 3 Lif ff fl k 4 Iif i l f f C
Your generosity brings smiles and hope!
Mil Wi l J - M 2014 i El L A Mi R & M C S Li J Li Di Li & Ki C Ai & Mil L C G J L Li Di Ci Li S W J L B Aiil Bill & R MDll Cli MDll Hl MGi J MGi B MGi Cl M Ai Mil AFL-CIO Pli El Fi Mll N Ciii Ci M Ril
HOMEPAGE. The. Inside. Beating the MARCH New Faces & Anniversaries. Spring Recipes. Beating the Winter Blues. ADP Rollout
T ARCH 2015 HOEPAGE A i f l f Oi H i ffili izi i 2 3 4 6 7 8 8 N F & Aivi Si Ri Bi Wi Bl AP Rll G Hl S N! HR C Tivi Bi T xil 89 f i l i v vi ll i fl lik 189! T illi ki; i f fi v i i l l f f i k i fvi lk
Equipping students to think biblically, live wisely and serve faithfully for over 30 years. MAY 2015 IMPORTANT DAYS IN MAY:
MAY 2015 IMPORTANT DAYS IN MAY: PCS Piw D M, 5/4 Bl W, 5/20 Gi S, 5/24 L D f Sl W, 5/27 Eqii ik ill, wil fifll f 30. PARK CHRISTIAN SCHOOL w; i i w i m l M iw w m l f i W, f w i, Y Cil i w i q, w, i i
Power up. Hello, Teachers! With Dr. E tm. Teacher s Guide 8th Grade. Georgia Power is extremely excited to further our partnership with your school
Tch Gid 8h Gd Hll, Tch! Gi P i xl xcid h phip ih chl b pvidi dci iiiiv cd hc d xpic i cl W lk d ki ih d d D E TM B jii p i h Li P p, i D E d h W Sqd, ill dv icic hh i-cl ild ip, i hd- civii d Wb-bd W hp
CATARACTS AND POVERTY HOW ARE CATARACTS TREATED?
CATARACTS AND POVERTY HOW ARE CATARACTS TREATED? Cc uy i f CBM fcu. I ul il, CBM u l c ill v cc ffl qu l c y vii mil uc vic i il. Sic cc uy iuc i 1966, CBM Iil fm m 12 milli cc i li. Wi yu u c fm u 600,000
BULLETIN THE BULLETIN OCTOBER VICTOR VALLEY NEWSLETTER OF MINERAL CLUB GEM AND THE PH. (760) TOR VALLEY GEM & MINERAL
S il M il S Vi Vll G & Mil Cl 15056-B Sv S Vivill, CA 92395-3811. BULLETIN i i i l l l li VICTOR VALLEY GEM & MINERAL CLUB i i i g. V i x i ī l i i BULLETIN il l VIC- TOR VALLEY GEM & MINERAL CLUB. R i
BLESSINGS... Abundance to Share
V l 5 6 T Gi I 6 j 2 0 1 1 BLESSINGS... A S I f F P C i i ii i G i f f l lii. O l Bli A S J 5 lli Cl S. T l f i l li G i fili i i f li l ii f f. Eliii l $1.5 illi fili ill j. I i G f qi x i i l i ii. I
T HE 1017TH MEETING OF THE BRODIE CLUB The 1017th Meeting of the Brodie Club was held at 7:30 pm on January 15, 2008 in the R amsay Wright Laboratorie
1017 MN OF BRO LUB 1017h M Bi lu hl 7:30 u 15, 2008 R Wih Li Uivi. hi: : A h 28 u. u: hl M, u A i u, u vi ull R : K Ah, Oliv B, Bill Rl N W BUN: M u vl: l v, Bu Fll, v ull l B u Fll i Fu k ul M, l u u
Grades 3 5 scholastic.com/poetryismypower
POSTER AND TEACHING GUIDE Sd Educil Mil Exli P Fi Civi Buildi Cfidc Gd 3 5 chlic.cm/im STUDENT POETRY CONTEST! SCHOLASTIC d cid l dmk d/ id dmk f Schlic Ic. All ih vd. 0-439-00000-0 2017 Amic Gil. All
BENEFITS OF COMPLETING COLLEGE Lesson Plan #3
BENEFITS OF COMPLETING COLLEGE L Pl #3 Til: Bi Cli Cll: Ci, Srr S Sl Pr: ( y l, r i i i r/rril) S ill lr rl vl bi y ill i r bii ry i. Lri O(): ( ill b bl /k by l) S ill r bii ry i bi ir rl l liyl. Ti ill
FYE 1-4-FUN! Fall 2012 First-Year Seminars
E Y F i v i U i S xi E Miii: Fi Y FYE 1-4-FUN! F 2012 Fi-Y Si W biv v i Miiii S Uivi k j f f f i i fi : b i i fii i i fi, i i vi f i f O i Fi-Y Si f i i b i j E i i iff, ii i Y k j, k ii i i j i i v x
From thriving city cycle paths to calm and tranquil car-free routes, the UK offers some of the most stunning and varied bike rides around.
Vii i ii 195 0 i Wi T f l W Wi l W ilw li l p l i i v i, F f i qil f. UK ff i bik k i l p v p f li lp j i S, p Bii x l w w lv, w k ff i i v f f i w i l v l pbli l p. l k fi b il v l l w i f i f T f f i.
INDICATIONS HERE OF BANNER SEASON
U l i 3 G Y i J«K W ll Gl ' - i W JY Y 6934 V 47; 87 il 4 ll l x K i Kl il li G G il ii i ix Wi lii i l i 2 W Wi i l il i % l i Vii i i i K l i - x i i ll l Vii l q illl ' ii i i i il li i--l i G 934 G
TRAN S F O R M E R S TRA N SMI S S I O N. SECTION AB Issue 2, March, March,1958, by American Telephone and Telegraph Company
B B, ch, 9 B h f h c h l f f Bll lh, c chcl l l k l, h, h ch f h f ll ll l f h lh h c ll k f Bll lh, c ck ll ch,9, c lh lh B B c x l l f f f 9 B l f c l f f l 9 f B c, h f c x ch 9 B B h f f fc Bll c f
Bus times from 18 January 2016
1 3 i ml/ Fm vig: Tllc uchhuggl Pkh ig Fm u im fm 18 Ju 2016 Hll lcm Thk f chig vl ih Fi W p xiv k f vic hughu G Glg h ig mk u ju pibl Ii hi gui u c icv: Th im p hi vic Pg 6-15 18-19 Th u ii v Pg -5 16-17
2018 icims Inc. All Rights Reserved.
2018 icims I. All Rih Rvd. icims Th Sil Rii Svivl Gid Sil Rii Dfid Sil ii i wh mi d i il lfm d i did f mlym. bl i i Sil d izi k b j d i d, - i h h l i i i 1. k w il 1. Hii Iih, 2015 2 2018 icims I. All
POWER UP. Hello, Teachers! With Dr. E tm GRADE TEACHER S GUIDE
GDE 6 Hll, h! Ggi P i xly xid h hi ih y hl by vidig gy di iiiiv d h d lig xi i y l W lk d kig ih y d y d ECHE S GUIDE D E M By jiig i h Lig P g, ig D E d h W Sqd, ill dliv gy iiy g hgh i-l ild i, ig hd-
WEAR A COLLAR RAISE A DOLLAR THIS
WEAR A COLLAR RAISE A DOLLAR THIS f Ac D A Wc Thk f k f Db. Db h f h f Ac D A b h Ocb., h W h f, b D. c h A D c f A Ab Ac D A T Rx A Ib T Ac D A Lb G R h h hc b. O, f h k, k k h b ffc, f b, f hch k k ch
>> Taste from our extensive collection. >> Meet the chefs and producers. >> Connect with our team to chat
P j S h 2016 Sy, Mch 20 TH 10 m - 5 m My, Mch 21 ST 10 m - 4 m Wh S Cv C >> T m xv cc vy w >> M h ch c bh m w m vv c >> Cc wh m ch b wy c w y b Shw b q. R h Mch 18h www.wvchw.cm Ah c m h Gk wy my wh c
EXHIBITOR PROSPECTUS AND CONFERENCE SPONSORSHIP
B h VOIC vccy h pc lhp ch h f v. 0-1, 0 Dc f vc/ Dc f cl Wk D W L COFC & XPOIIO h Hl & p Cy C, p, XHIBIO POPC D COFC POOH B h VOIC B H VOIC 11.0-1. Why XHIBI? D W L k h ly z h h c p y cly ch h h fll -fpf
Crackers COSMOPOLITAN CLUB OF SANTA BARBARA INC.
Ck COSMOPOLITAN CLUB OF SANTA BARBARA INC. Vl N. 11 Ei: Ck Ev Nx Mig: D 4, 2014 Nx Ei: Hv T P: (805) 967-0741 E-Mil: lv@gil. Nx Mig Db 4, 2014 H Db Ck Ei Nx Sg. A: J R P: (805) 845-7090 E-Mil:jl@x.C A
Writing a press release and pitching it to the media
Wiig l iig i i Wiig l l y g i vg f y gii ig. Mi vg i f y k, fil f y gii g l g ivlv i y igig ii ig y vi. W i l? A l ( l/ i l) i i y f y y f i. I ill il ky f, q f kl il f ifi. T i l f l i vi i v y y b i
Visit to meet more individuals who benefit from your time
NOURISHINGN G. Vlz S 2009 BR i y ii li i Cl. N i. J l l. Rl. A y l l i i ky. Vii.li.l. iiil i y i &. 71 y l Cl y, i iil k. 28 y, k My W i ily l i. Uil y, y k i i. T j il y. Ty il iy ly y - li G, y Cl.
FREE. BJ McNALLY Ltd. Helen Lynch. Remembering Helen. Made in Ireland. memorial cards since 19. Helen Lynch. McNally Family Printers.
Bkmk W C - 185mm x 60mm - 88mm x 55mm Ackgm C BJ McNALLY L 108mm x 85mm * Rmmbig H T fmi f v H i Lm H Lc ic f i k m f mp i ki xpi bvm. m i i c I vig mm f Sm McDm i 12 J 2033 g 00. f M T H Scific ii. b
Atlantic County Properties
() li i () li i () li i V li i li i ii ib ii ii ii i &. ii ii l ii iii bf i - bf i - bf i - bf i - bf i - bf i - bf i - bf i - bf i - bf i - bf i - bf i - bf i - bf i - - bf i - bf i - bf i - bf i - bf
THE MIDWAY & GAMES GRADE 6 STEM STEP BY STEP POTENTIAL & KINETIC ENERGY MOVE THE CROWDS
THE MIDWAY & GAMES GRADE 6 STEP BY STEP POTENTIAL & KINETIC ENERGY MOVE THE CROWDS & G S S Pl & K E Mv C I l ll l M T x Tx, F S T NERGY! k E? All x Exl M l l Wl k, v k W, M? j I ll xl l k M D M I l k,
A Rainy End to Summer
6 18 115 $1 ig J l i 15 Vii li illiig Tl 75-6-7678 il illiig@gil @ l Cliig i E il l i ll ig H F Cil i i li f Ni N T i, il l j g i l b l f ll, ill i, b i i l f gig i H F g ii Cil P i Jl Ti Wil i l ll, i
n u o r t a a B m r I d n h e t o c n r a t g t a e h t g e p s h d n e t n o a l t e m f the So e a h e o c o M sed i e for Ch a r h a P e the m n e
I b k B l Ll B CvyB. k S K T l v P w j C. b Ty C M Cv O wll: S, l B S w y w C. P S. T v b l L C l l P v A v., N C w l L, B l L z.. L. G C l y w wy w L w y L k w. b ll L P v C Ml by Sy Nll, Kky WMU. G by
Judge dismisses wind lawsuit
6 6 6 K K - J B - j - K W j J W W J K K - W - j j j K W W j j - I J J j K W j j W j K W j W J - W B B B j 6: 6: B z $ $ [ ] 6 IB J J K I z j W j W : j / j j j $ j I K W : W j K W j K W [ ] WI I K z j [I-
Dear Friends. St. John the Baptist Greek Orthodox Church Sterling Heights, Michigan. Volume 25 Issue 6 June, July & August 2018
D Fi J Bi k x li i ii Vl 25 6 j J Jl & 2018 JR ER FE DY (B i k) JE 3 RD - LL : iil i l i ii il i i li k l k vi i vi i li i l iii lvi B l ii k l vi vil lik i iii li i i i l l l i W i i i v ji i k lik l
Helping Kids Prepare For Life (253)
Hlpi Ki Pp F Lif.l.i. (253)-589-7489 Tilli it it L Livit iv f fiv CIS U H. Vip pt fll t Tilli Elt l tpi tff tt f vi t t CIS T Hll f i Cltt N Cli. - L ivi i CIS f Bill Milli CIS pit Dil Cili Ti l iz it
Your Choice! Your Character. ... it s up to you!
Y 2012 i y! Ti i il y Fl l/ly Iiiiv i R Iiy iizi i Ty Pv Riiliy l Diili Piiv i i y! 2 i l & l ii 3 i 4 D i iv 6 D y y 8 P yi N 9 W i Bllyi? 10 B U 11 I y i 12 P ili D lii Gi O y i i y P li l I y l! iy
Exploring Innovative Solutions and Connections for a More Sustainable Future
S ib P R I i Exi Iviv Si Ci M Sib F ik//ib 0 O ii i vi bi ibii i bi ii ibii fi i iiii i i W P T M Di T S ib P R I i T ivib q i i bi i v iff i iff Y v b i iviv i k iq ii b i i i v T Sib P R Ii i b ki i i ibii
Proc. of the 23rd Intl. Conf. on Parallel Processing, St. Charles, Illinois, August 1994, vol. 3, pp. 227{ Hanan Samet
P. 23 Il. C. Plll P, S. Cl, Ill, 1994, vl. 3,. 227{234 1 DT-PRE SPTI JOI GORITHMS Ek G. Hl y Gy Dv B C W, D.C. 20233 H S C S D C R I v C S Uvy Myl Cll Pk, Myl 20742 { E -lll l j l R-, l,. T l l (.., B
3419 MAIN HIGHWAY RETAIL/RESTAURANT SPACE FOR LEASE - COCONUT GROVE
419 MI HIHW R/RR C F - V xclusive gents: resident t. 05.52.04 Director - Retail easing & ales amuel oddle ssociate 1261 20th treet t West venue Miami Beach, F 19 t. 05.52.04 l f. 05.52.6106 419 MI HIHW
t S kangaroo ISLAND & SOUTH AUSTRALIA TO BOOK: aide A K A Yorke Peninsula Flinders Ranges Melbourne to Adelad n
T C & i I Y Pi Fi i M O TO BOO: OO ILD & OUTH UTLI C +61 8 80 8678 Vii i.. i i@i.. T Pi i 31 Mh 015 T 1300 655 990 U T V D D DY OF FU O: Di (D Mh) M, W, Th, (i ) M, Th, (M O) D: i C B i 6.45 i/ H/H i i
Dunhamstead Visitor Mooring. Postcode: WR9 7JX Waterway: Worcester & Birmingham Canal. Price: Band 4. Key 12. Trench Wood. Worcester.
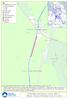Ky Hili Wi i c T G Bi Lc C l O Wi i Fciliy Buili i i W i B Li / W Bi Rcycli l i (u Wf C W c Rfu ipl Wwy i Lil f up Bi (u Bi G 0, up F Tc C ( LC TR i Hu NC H LA N Tc Tc (u Tc i Tc W (u (u Bi, L Bi, up c
Inside! Your Impact...p 5 How You Raised Awareness...p 9 The Bigger Picture...p 14
Ii! Y I... 5 H Y Ri A... 9 T Bi Pi... 14 W W v B, W W Gi f b i T. i fii) Fi F v (211 iq M, f i D F fii i i i. i, xii W. b 7 201 i f k ik f xiv f i T v 2017 i i i i i, i i i x ff fi fi-v i fi x M Fi W.
4.3 KIT5 the value of public realm design
UbBuzz Buii uib cmmuii ivu 4.3 KIT5 h vu f pubic m i Chii ch pc yx Ricc Bbi pc yx Mi Tm Ev h iib vu f ub yu UbBuzz pc yx 2008 4.3 K ii KIT5 Vui pubic m i cfiui cfiui iic yi cmp KIT 6 Hh Phyic Evim C uy
CHAPEL HILL HIGH SCHOOL - CONCEPT PLAN
L R R '' ''.. '' '' '' R RI RI BBRII: F B FIIH R R L. RIM LI 'Y MBLY B/ B F RB B/L B LI B/ BM F IR B/ BM F L B H BI BR IFRI BRI RI RB R I RB IL /L RLI L L M R MM M RR M I L R I RR LI Y BI YR B B I R IL
Rediscover Your Dream Getaway. handcrafted Pergolas
R Y D Gwy hf Wl... T O L! R h h f y l. P l j f h k h; hy l f h h yl. Whh y h l f bl ly, y h, y ly lk f jy h b f l, l h w y h b h f. Wh y yl, h l ff l f y. hf W h y w. Thk y ll f h wh h k h w ll hw h jy
Axe Wo. Blood Circle Just like with using knives, when we are using an axe we have to keep an area around us clear. Axe Safety Check list:
k Ax W ls i ms im s i sfly. f w is T x, ls lk g sci Bld Cicl Js lik wi sig kivs, w w sig x w v k d s cl. Wi xs; cl (bld cicl) is s lg f y m ls lg f x ll d s d bv s. T c b bcs, wigs, scs, c. isid y bld
Nonverbal Cues of Dominance Laura van Hooff, Jasmijn Verspaandonk, Nicole van den Reek, Guusje Nagels & Jalou Lemmens
Nvbl C f Dm L v Hff, Jmj Vdk, Nl v d Rk, Gj Nl & Jl Lmm Ab Th m f h d w v h vbl x f dm b hm d whh h w dff bw l d dm T h, h l bhv f f h TV hw Tm Ild w ld Th x vbl bhvl d h h m dm w d, h, l x, fld m, hd
ERROR SPACE MOTION CONTROL METHODOLOGY FOR COMPLEX CONTOURS. Robert G. Landers
ERROR SPACE MOION CONROL MEHODOLOGY FOR COMPLEX CONOURS Rb G. L Ai J f C. 7, N., pp. -8, Mh 5 Ai J f C,. 7, N., pp. -8, Mh 5 ERROR SPACE MOION CONROL MEHODOLOGY FOR COMPLEX CONOURS Rb G. L ABSRAC Mi i
OKANAGAN LANDING SEWER EXTENSION PROJEC
I XI PJC ICCCK 3 - B I /UMUI /CB I F CU PK IC UI CK U UI P C 35 X P B PX I I IX P MUI I C CP P I M I I. I C F I FI BCK CMB CK B 30 C C PI C MB P KM IZ B MB I I BCKC K 32 K I I I MU I U KICKI FI F C I I
Empowers Families Unites Communities Builds Capacity. An In. Read and Rise. Cultivates Literacy
8 Emw Fm U Cmm B Cc g A I Y h P R c L DY : U T S E CAS g L b U N ff H I h H c D Sch R R Cv Lc CASE STUDY A Ig P h Y Lc R Th N Ub Lg H ff wh H I Sch Dc (HISD) c Schc R R, fcg cfc hw gg mw fm f h ch c h
St ce l. M a p le. Hubertus Rd. Morgan. Beechwood Industrial Ct. Amy Belle Lake Rd. o o. Am Bell. S Ridge. Colgate Rd. Highland Dr.
S l Tu pi Kli 4 Lil L ill ill ilfl L pl hi L E p p ll L hi i E: i O. Q O. SITO UKES Y Bll Sig i 7 ppl 8 Lill 9 Sh 10 Bl 11 ul 12 i 7 13 h 8 10 14 Shh 9 11 41 ill P h u il f uu i P pl 45 Oh P ig O L ill
Maturity in Christ. The. Rock
M i C T Rk J 2014 Gi k l f Si Rir Fr Rr Mr fil... Hr, Kll C S r f Si Rir i i r fr H i 2002. Hr Kll Rkll S O i Clr Lk r fr 23 r. T r l i rfl. C ill Jir S ill Fr R Rk Hi Sl x r. T r il i Al Y Miir. Hr rk
( # N Mount Olivet La. S Franklinto. Lexington St. West Baltimore Street Bridge Pennsylvania Railroad Viaduct. Elicott Driveway
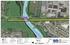C u Oliv R Fkli w R lv Cy Bli Big Pylvi Ril Viuc ufc Tckwk y Ki Elic Divwy Gw y Th EED chl f yl Tck Cli Lii f ufc Diubc B Tul Pp V Pl Lci A f cii f V Pl Lci Pp Big Rcuci Pcl Bui Iiviully Rgi Eligibl Hiic
A Parent s Guide to Understanding Family Life Education in Catholic Schools (and how it connects with Ontario s revised Health and Physical Education
P i i Fiy i i i ( i i i vi Pyi i i) Bi i Fy 05 i iiy i vii & Pyi i (P) i i i i i ii i 05 B v vi P i i 998 i i i i y ik xi i ii y i iviy P i i i i i i i i i x i iy i k i i i i i v Wii iy ii v vi i i v i
business health care technology art& design Teaching what matters: real world practicality.
i l l & i Ti w : l wl ili. i l l &i Li Tii Pvi i 6 W DI ll 8 DI ll i i 10 Bi P 18 Hl P 26 Tl P 31 A & Di P 34 Pi Pl 35 Svi 36 Aii Ifi 37 Tii Fii Ifi 38 DI ll Ali 40 wi wl Wl DI ll T i, l, l i i v. El l
FAIR FOOD GRADE 7 STEM SUGAR RUSH! HOW YOUR BODY WILL PROCESS THAT FRIED TWINKIE
FAIR FOOD GRADE 7 SUGAR RUSH! HOW YOUR BODY WILL PROESS THAT FRIED TWINKIE F F TEAHER G Sv S R! Hw Y B Wll P T F Twk I l wll:! B l b F f pp m? Hw w w w,? v pp Expl w f f b. Exm w f wl p m b. wk f b xp
Rapid growth in enrolment within the French Immersion program
Nw Nh Ajx Fch Ii ch- Ovviw R Di PS p i Spb 2009 u ck Egih Fch Ii ch Egih Fch Ii Y E E Pb 2009 333 197 0 2010 405 281 2 2011 431 332 6 2012 466 409 10 2013 486 474 14 Rpi gwh i wihi h Fch Ii pg Pp c Fch
TABLES AND INFORMATION RETRIEVAL
Ch 9 TABLES AND INFORMATION RETRIEVAL 1. Id: Bkg h lg B 2. Rgl Ay 3. Tbl f V Sh 4. Tbl: A Nw Ab D Ty 5. Al: Rdx S 6. Hhg 7. Aly f Hhg 8. Cl: Cm f Mhd 9. Al: Th Lf Gm Rvd Ol D S d Pgm Dg I C++ T. 1, Ch
Cambridgeshire Minerals and Waste Development Scheme. August 2017
Cmbidshi is d Ws Dm hm s 2017 Cmbidshi C Ci hi H Cs Hi Cmbid CB3 0P www.mbidshi..k 1.0 ITRDUCTI 1.1 This is d Ws Dm hm is f Cmbidshi. 1.2 Th C Ci is ssib f h i f i i id f mi d ws mm ss. I s is d sss i
STATE OF FLORIDA DEPARTMENT OF TRANSPORTATION CONTRACT PLANS FINANCIAL PROJECT ID
LD M L HL LLG M L LLH DM L KVLL WL H LK M G GVLL L L D H DLD LD L L D --- W H G - D D (-) D L H ML LKLD D W K M M () K H H M HL L DLD D H H D W LM H M L w Hmmc -- y L D u x p, HL Hu w x DG # G p Mm G um
THE 1,040t h MEETING OF THE BRODIE CLUB The 1,040th meeting of the Brodie Club was held at 7:30 pm on S eptember 21, 2010 in R oom 432 of the Ramsay W
HE 1,040 EENG OF HE BRODE CLUB 1,040 m B Club l 7:30 pm pmb 21, 2010 R m 432 Rm W Lb Uv. C: Bu Fll : G B m b 27 m mb u. R ll Cll, P: A bm, E. A, R. A, J. Bll, Y. B ll, B, B, Bul, B, C, Cu, Du, A. Fll,
» 2016 MEDIA KIT KIT» 2016 MEDIA KIT. 125 Park St., Suite 155 Traverse City, MI mynorth.
» 2016 I KI KI» 2016 I KI 125 P S Si 155 v i I 49684 19418174 l@vzi » 2016 I KI Vi! l pblii pi N ii i 375000 ppl f i i bb ll Sl 81415 » 2016 I KI F v N ii zi Vi! v i F v N ii zi Vi! Fif L Il Kil illib
BENEFITS OF COMPLETING COLLEGE Lesson Plan #1
BNFITS OF COMPLTING COLLG L P #1 Ti: Bi Ci C: Ovvi & B J Hi Py P: ( y, i i i /i) S i i v i i i ii i ii i. Li O(): ( i /k y ) I ii i i i i, i ii i y i ii ii i. Ti i iii i y i y i iky i j y jy i ki y v.
Molds found in Indianapolis markets
Bl Uvy Bl S Vlm 5 Bl Uvy Bl S Al 5 Ml Il mk Pl Lz Bl Uvy Fll l k : ://glmm.l./l Bl Uvy Bl S jl l y By m Bl Uvy Il I m 1929 1964. jl gl mly l lgy xmy mlgy. Rmm C Lz Pl (1941) "Ml Il mk" Bl Uvy Bl S: Vl.
THE WYOMING COUNTY resource guide to locally-grown foods and products available directly from the farm!
TH ING UNT i l- f vi il f f! HT INID Ll k lii ifi -6-22 k li ikl vii li i i j j l 0 Nkii fn 6 il lii f Ll k i l v Ll k Ifi i l k H k l l l l ki i ff i l fl l l f 0 i l v 200 l l i k i i f l i fl i I f i il
* Project Cost is for Total Project 468,376
I #7 i- Ub pi Pig Ogizi Fic i pi Tpi P - Hig Pjc Li - pjc v ci f TIP c f Pjc ig Exiig Pp gi Pjc F p I TIP Pjc Pjc cipi Pjc - - igifi- * Fci b b Lii g ci ci cc T FF - -T U- c v 3 i L Kig, J iv i- L Fcii
NEWBERRY FOREST MGT UNIT Stand Level Information Compartment: 10 Entry Year: 2001
iz oy- kg vg. To. 1 M 6 M 10 11 100 60 oh hwoo uvg N o hul 0 Mix bg. woo, moly low quliy. Coif ompo houghou - WP/hmlok/pu/blm/. vy o whi pi o h ouh fig of. iffiul o. Th o hi i o PVT l wh h g o wll big
Living In Residential Newsletter October 2012
Livg I Rii N O 2012 g 0 0 4 1 v, i i ig i W i i. W,. W i i i. g v v ii kg ig! i W ii x ii k H i, i I, P i. v i I i A. S ii R g 6). Mg iv vi i i ( i ik iv i v i i Y E-Ii, F i,. T SUi-S i v i I. i i i. I
SITE PLAN SHEET 1 OF 8
P P XG V % P BM H P B C C H % P XG BM H P % % % % % % % % % % % % % % % % % % XG % % % P % % % % % BM CH H P XG V % % % % % % % % XG V % XG XG % % % % % % % % % % % % % % % % % XG XG P BM V BM CH H P %
be ke' pt co nfr'r..p 1i3 1a t his r. e11r r t, sj\t lr d o ts o f and industri;, cnginccr u'ho bec:lntr_, ,permit
& - E hap R OB h E \ A jj Nw v j - 957 { m b h- S S h hmbr UAO Hh + E &? { H h Sq R L Rv [ \ Y v h q m C y b h v h ] \) J h b h - A mv] w m vh \L m vl h b h q Av Nw /L R m A_ h Dj { ) L A Exm xm h m h
Nonclinical (SEND) Fit for Use Workstream
Ncliicl (END) Fi f Us Wm Th CDIC END ( f Exchg f Ncliicl D) m, i cllbi wih h PhUE Ncliicl Ts bmissis Wg h FDA CDER Offic f Cmil cic (OC), cc wm f ilig END V3.0 h ws h blic ici. Picis (cliicl sbmiig gizis,
ENJOY ALL OF YOUR SWEET MOMENTS NATURALLY
ENJOY ALL OF YOUR SWEET MOMENTS NATURALLY I T R Fily S U Wi Av I T R Mkr f Sr I T R L L All-Nrl Sr N Yrk, NY (Mr 202) Crl Pki Cr., kr f Sr I T R Svi I T R v x ll-rl I T R fily f r il Av I T R, 00% ri v
FAIR FOOD GRADE 8 SOCIAL STUDIES ICONIC EDIBLES LIGHTS CAMERA ACTION!
FAIR FOO GRAE 8 SOCIA IES ICONIC EIBES IGHTS CAMERA ACTION! F F G Egh Icc Eb gh Cm Ac! I h w: cm c fm b q f h S F f Tx. Az h cb f v c hc gp. cb vpm h c h q Amc c. W, pc, cm b cc b f h Tx S F. m w f j v
EASTERN CORRIDOR STUDY
PULIC NNT UY Y JULY 2017 TN COIO TUY PULIC NNT UY POJCT NO.: 17-00063-00 111-93 LO VNU INNIP,, CN 3 31 TL.: +1 204 943-3178 FX: +1 204 943-4948.CO TL OF CONTNT 1 INTOUCTION... 1 1.1 Oi... 1 1.2 Pbli m
RTPR Sampler Program
P Sl P i H B v N Ahi kd f hl qi N hk F N F N S F N Bkffi F N lid Si F $99.95 Sl Pk Giv 365 bhi Ad w will hw hw h $99.95 il b dd Z P Sl P i H B v Hih wd A Sihfwd i Pl wih f di v : B ii 1 i 6.25% 2d i 2.5%
KARL MARX FREDERICK ENGELS COLLECTED WORKS VOLUME 28
KARL MARX FREDERCK ENGELS COLLECTED WORKS VOLUME 28 COLLECTED WO S V 28 KARL MARX: 1857-61 NTERNATONAL PUBLSHERS NEW YORK NTERNATONAL PUBLSHERS NEW YORK Ti v ji Lc & Wi L L i Pi C c N Yk P Pi Mc i ci i
FINANCIAL DISTRICT IS A NEW HUB OF RETAIL, RESIDENTIAL AND LEISURE.
FICIL DISIC IS HUB F IL, SIDIL D LISU. Centrally located and anchored amidst the bustle of the Financial District, 2 Beekman, located between Park ow and assau Street, boasts 3,540 sf of ground floor retail
GUIDE. mirfieldshow.com. Sponsored by. Orange Design Studio.
GUIDE mfhw.m Sp b O D S. Fh F m F C 1 3 5 7 9 b f M MIRFIELD COAT OF ARMS Th m w ff Fb 26, 1935. Th m f h mp f h w m h m. Th p S Jh H, wh pp h Pp h 13h h b f h ph hh. Hv W H Wh h? O, h wm mh, hp h f h.
Creating New Objects
Wk Obj 1 C bj 2 A vb bj 3 bj C M & I I B & M 4 Cv bj v - 5 M b bj 6 A vv Jv b C N Obj A Jv C bj: bj k H bj : R R Rk V Rk Jv k bj 1 I v bj 2 I bj b C Vb bj Jv vb v 1 A vb v v 2 A vb Obj bj I R bj bj H x
1 Introduction JARRETT WALKER + ASSOCIATES. SEPTA Philadelphia Bus Network Choices Report
Ici AETT AE + AIATE Ppi N ic p i ic p? Ti p i ii pfc f b ii i f Ppi, i c f i i ic p,. T f i p i pi bc f fc ii c pi ici ff i b. T p i c ic p bc i cic ci. If f i ic iip, i f i ppc c b, i i p., iip i f i,
See, Sketch, Shoot. A Study Abroad program offered by Coastline Community College and ACCENT International Consortium for Academic Programs Abroad
R 17!! 0 2 5 2 l J 5 2 J S, Sk, S A S A ff Cl C Cll ACCENT Il C f A P A ROME Il Y I Wk 1 J 24 J 28 Av R, Il f -l. O ACCENT f lv R. L, PS. Il l l.* S v Nl M, Nl Gll f M A, Gll B, V, Cl R F. T v f l k Il
2 w cv c bu mv cu Wh chv b h whch w ch, w huh cu c, b - x wh cc h c v, mucu c, B Ch v m b h whch whch b, k qu c ch m hh cm h k hv vc x vc u h wh cm cm
E CONOMC REORMS N ND: E XERENCES ND EMERGNG DMENSONS B, D R SHSH KUMR M, Mh, hd R EDER D ERMEN O ECONOMCS B NGLORE UNVERSY B NGLORE 56 56 K RNK SE ND E-m : hh@ hcm M b : 9444 7452 R c h: 6-22 7 NRODUCON
Klour Q» m i o r L l V I* , tr a d itim i rvpf tr.j UiC lin» tv'ilit* m in 's *** O.hi nf Iiir i * ii, B.lly Q t " '
/ # g < ) / h h #
MODEL CODING W HEATER OPTIONS
-PH M 80V - 00V -PH M - MP HIGH-LIMI (HMWLL) V - 80V -PH WIIG HMI - MP HIGH-LIMI (MBI I) PB M HM () HM () H VLG 0-0V 0-0V 0-0V 80-80V - V 0-0V MDL I PH - PH - PH - QY 0-0 HZ MDL DIG 0 0-0 - W H KILW 0
Napa Valley Intergroup July 8, 2017
Vy g Jy, g Mm f c & y y w g / w Cm ck: Y Wm mg mg, D G Wh f by by Bhy h Mh: L mh m (Yw Cy) & g h b (Wh Cy) M v h y bjc h g- h *vc Mhy g & Dc Dc- h g hmv gh b fy by h vy cb f h w mmb W hk h ch g h chv h
Learning High-Dimensional Data with Artificial Neural Networks. Université catholique de Louvain (Belgium) Machine Learning Group
Lg Hgh-l h Al Nl Nk Ué hlq Lv (Blgm) h Lg Gp hp://..l..b/mlg/ Ol Hgh-l (H) L & l l l C ly, mpy p phm Spzg C El m l I N ml l m (l) vbl l pj ph: l, SV, Ol Hgh-l (H) L & l l l C ly, mpy p phm Spzg C El m
A. B. JASSO D. SALAZAR H. MONTELONGO MECH ENG VAA T&W QUALITY ENG VAA PLANT MANAGER VAA ACTION RESULTS CURRENT PROCESS CONTROLS DETECTION
I FI M FF YI ( FM) FM MB FM - 96 6 IM I F I M M IBIIY M. MI (h 57-0-000) BY. B. J M Y()/HI() 00-0 KY ugust st; 00 FM (IG.) /9/007 (.) 0 (070) M. B. J. Z H. MG MH G &W QIY G MG I FI QIM I FI M I FF() F
H1,H2-R3-1 H1,H2-R2 H1,H2-R R1 W ES T PEA R L MA LL OC H C RE O AK R3 34 W RIGH T C RE S UN IO N ST B U TLE OTT ER D R
HUBB IGW M B H G G G JI HM hub - Victoria - ith riental - 0 H I. W I Mile on-oercial / on-esidential Zones H W M IZ BV I B H W U (P IV ) MB K P W,,,, - Multiple esidential M W (P IV ),, - ingle etached
Dec. 3rd Fall 2012 Dec. 31st Dec. 16th UVC International Jan 6th 2013 Dec. 22nd-Jan 6th VDP Cancun News
Fll 2012 C N P D V Lk Exii Aii Or Bifl Rr! Pri Dk W ri k fr r f rr. Ti iq fr ill fr r ri ir. Ii rlxi ill fl f ir rr r - i i ri r l ll! Or k i l rf fr r r i r x, ri ir i ir l. T i r r Cri r i l ill rr i