Official Solutions 2014 Sun Life Financial CMO Qualifying Rêpechage 1
|
|
|
- Christopher Anthony Scott
- 6 years ago
- Views:
Transcription
1 Official s 2014 Sun Life Financial CMO Qualifying Rêpechage 1 1. Let f : Z Z + be a function, and define h : Z Z Z + by h(x, y) = gcd(f(x), f(y)). If h(x, y) is a two-variable polynomial in x and y, prove that it must be constant. Since h > 0, write h(x, y) = P n (y)x n + + P 1 (y)x + P 0 (y) where n 0, {P 0, P 1,..., P n } are polynomials, and P n 0. As P n has finitely many roots, choose a y 0 > 0 with P n (y 0 ) 0. Then for every x, h(x, y 0 ) = gcd(f(x), f(y 0 )) f(y 0 ), hence h(x, y 0 ) f(y 0 ) for all x. But now as x, h(x, y 0 ) P n (y 0 )x n. Since P n (y 0 ) is constant, and h(x, y 0 ) is bounded (below by 0 and above by f(y 0 ) ), this then implies that n 1 is impossible. Hence n = 0 so h(x, y) = P 0 (y). Thus the highest power of x that occurs is x 0, i.e. h(x, y) does not depend on x. But we can switch x and y to obtain the analogous result of h(x, y) does not depend on y either, hence it is the constant polynomial.
2 Official s 2014 Sun Life Financial CMO Qualifying Rêpechage 2 2. Alphonse and Beryl play a game involving n safes. Each safe can be opened by a unique key and each key opens a unique safe. Beryl randomly shuffles the n keys, and after placing one key inside each safe, she locks all of the safes with her master key. Alphonse then selects m of the safes (where m < n), and Beryl uses her master key to open just the safes that Alphonse selected. Alphonse collects all of the keys inside these m safes and tries to use these keys to open up the other n m safes. If he can open a safe with one of the m keys, he can then use the key in that safe to try to open any of the remaining safes, repeating the process until Alphonse successfully opens all of the safes, or cannot open any more. Let P m (n) be the probability that Alphonse can eventually open all n safes starting from his initial selection of m keys. (a) Show that P 2 (3) = 2 3. (b) Prove that P 1 (n) = 1 n. (c) For all integers n 2, prove that (d) Determine a formula for P 2 (n). P 2 (n) = 2 n P 1(n 1) + n 2 n P 2(n 1). (a) All 3 safes can be open if the key for the third safe is in one of the two opened safes. This occurs with probability 2 3. (b) When we have a single key, we can open all the safes if and only if we can order the safes as s 1, s 2,..., s n, where the key inside safe s i opens safe s i+1 for each i. There are (n 1)! assignments of keys for which this can occur. There are a total of n! ways the keys can be assigned to the safes, so P 1 (n) = (n 1)! n! = 1 n. (c) Consider the key inside the first chosen safe. With probability 2 n it opens one of the 2 selected safes. In this case, there is a P 1 n 1 chance to open the remaining safes. With probabiltiy n 2 n the key opens one of the other n 2 safes. In this case, there is a P 2 n 1 chance to open the remaining safes. Thus P 2 (n) = 2 n P 1(n 1) + n 2 n P 2(n 1). (d) P 2 (n) = 2 n, which easily follows by induction from part (c).
3 Official s 2014 Sun Life Financial CMO Qualifying Rêpechage 3 3. Let 1000 n = ABCD be a positive integer whose digits ABCD satisfy the divisibilty condition: 1111 (ABCD + AB CD). Determine the smallest possible value of n. Define integers n = ABCD, x = AB and y = CD. Then n = 100x + y, is the number that we want to find. The condition that n has four decimal digit positive integer means 1000 n 9999, which is equivalent 10 x 99 and 0 y 99. Adding 100 to the the condition (3) gives the equivalent condition for some integer z n + xy = (x + 1)(y + 100) = z (1) If x = 10, then we would have z, which is impossible. Therefore x 11 and (x + 1) 12. Because n > 0 and x, y 0, it follows that 1111z = n + xy > 0, and thus z > 0. Suppose that z = 1. In this case, (x + 1)(y + 100) = 1211, and it follows that x + 1 = 1211/(y + 100) 1211/100 = Since, x + 1 is integer, we have (x + 1) 12 and from above, (x + 1) 12, which combined say that x + 1 = 12. But 12 does not divide 1211, contradicting condition (1) and supposition z = 1. Therefore z 2. Suppose that z = 2. The right hand side of condition (1) becomes z = This is even. Dividing by two gives The sum of the digits of this is 9, so it is divisible by 3 giving 387. This is again divisible by 3, giving 129, which is a factor of 2322, namely 2322/(2 3 3). Because factor 129 is between 100 and 199, try it as a candidate y The other factor = 18 can serve as x + 1, and is in the right range. This gives a possible solution satisfying (1) with x = 17 and y = 29 and n = Suppose henceforth that a smaller solution n < 1729 to condition (1) existed. Suppose that x > 17. Then n > 1729, a contradiction. Suppose x = 17. Then z 2 gives z 2322, which gives y 29, and n 1729, a contradiction. Therefore, x < 17. Consequently, (x + 1) 17 subsituted into (1) gives z = (x + 1)(y + 100) = It follows that z 3283/1111 < 3. Therefore z = 2, since z 2 was proved above. Consequently, z = 2322, whose prime factorization, started above, completes to: 2322 = (2) The number x+1 belongs to the set {12, 13, 14, 15, 16, 17} because the bounds 12 (x+1) 17 established above. Each number in this set is divisible either by 4 or by a prime strictly between 3 and 43, so it cannot divide 2322, a contradiction.
4 Official s 2014 Sun Life Financial CMO Qualifying Rêpechage 4 4. In ABC, the interior sides of which are mirrors, a laser is placed at point A 1 on side BC. A laser beam exits the point A 1, hits side AC at point B 1, and then reflects off the side. (Because this is a laser beam, every time it hits a side, the angle of incidence is equal to the angle of reflection). It then hits side AB at point C 1, then side BC at point A 2, then side AC again at point B 2, then side AB again at point C 2, then side BC again at point A 3, and finally, side AC again at point B 3. (a) Prove that B 3 A 3 C = B 1 A 1 C. (b) Prove that such a laser exists if and only if all the angles in ABC are less than 90. (a) Let a = A, b = B, c = C, α = B 1 A 1 C. AB 1 C 1 = α (1) AC 1 B 1 = π a α (2) BC 1 A 2 = π a α BA 2 C 1 = a + α b (3) CA 2 B 2 = a + α b CB 2 A 2 = π c a + b α (4) AB 2 C 3 = π c a + b α AC 3 B 2 = c b + α (5) BC 3 A 3 = c b + α BA 3 C 3 = π c α (6) CA 3 B 3 = π c α CB 3 A 3 = α (b) We observe that if the angle of incidence of the laser with the side is greater than π 2 that the laser will bounce back to the side it came from. Thus, for such a laser to exist, we must have all of the angles on the right side of the above being less than π 2. Taking lines (1) and (4), we have that π c a + b < π, which gives b < c + a. We similarly get c < a + b from (2) and (5), and a < b + c from (3) and (6), This tells us that all angles of ABC are less than 90. To see that when all angles are less than 90 such a laser must exist, we take 3 copies of ABC as shown in the figure below. We choose a point X on side AC and label Y, the same point in the last copy of the triangle. Then the line between these two points defines 3 line segments inside ABC which will give us a laser.
5 Official s 2014 Sun Life Financial CMO Qualifying Rêpechage 5
6 Official s 2014 Sun Life Financial CMO Qualifying Rêpechage 6 5. Let f(x) = x 4 + 2x 3 x 1. (a) Prove that f(x) cannot be written a the product of two non-constant polynomials with integer coefficients. (b) Find the exact values of the 4 roots of f(x). (a) If f(x) was reducible, then it factors either as a product of a linear and a cubic, or two quadratics. But for the linear and cubic case, this implies that it has a root, so we use the rational roots test and check that f(±1) 0 so this is impossible. Hence let f(x) = (x 2 + ax + b)(x 2 + cx + d) where a, b, c, d are integers. Then: x 4 + 2x 3 x 1 = x 4 + (a + c)x 3 + (b + d + ac)x 2 + (ad + bc)x + bd a + c = 2; b + d + ac = 0; ad + bc = 1; bd = 1 From bd = 1 we get b = 1,d = 1 or b = 1,d = 1. In either case b + d = 0, hence 0 = b + d + ac = ac so a = 0 or c = 0. But a + c = 2, so a = 0,c = 2 or a = 2,c = 0. But then 2 a, c so 2 ad + bc = 1, contradiction. Thus f(x) is irriducible as claimed. (b) Note that f(x 1) = x 4 2x 3 + x 1, hence f(x) = f( x 1), and so f(x 1/2) = f( x 1/2). This encourages us to look at g(x) = f(x 1/2) = x x2 9 ; this is 16 obviously a quadratic in x 2! The roots of g(x) satisfy x 2 = 3/2 ± ( 3/2) 2 + 4(9/16) = 3 ± 3 2. Hence g(x) has roots ± 4 4 that the 4 roots of f(x) are 1 3 ± ± ± 3 2, and using 0 = g(x) = f(x 1/2) we see
7 Official s 2014 Sun Life Financial CMO Qualifying Rêpechage 7 6. Given a triangle A, B, C, X is on side AB, Y is on side AC, and P and Q are on side BC such that AX = AY, BX = BP and CY = CQ. Let XP and Y Q intersect at T. Prove that AT passes through the midpoint of P Q. Let AT intersect BC at M. Let R, S be on sides AB, AC, respectively such that MR XP and MS Y Q. Then since BX = BP, BR = BM. Therefore, XR = P T. Similarly, Y S = QT. We need to show that P T = QT. It suffices to show that XR = Y S. AR Since RM XT and SM Y T, AX RX = SY, as desired. = AM AT = AS AY. Since AX = AY, AR = AS. Therefore,
8 Official s 2014 Sun Life Financial CMO Qualifying Rêpechage 8 7. A bug is standing at each of the vertices of a regular hexagon ABCDEF. At the same time each bug picks one of the vertices of the hexagon, which it is not currently in, and immediately starts moving towards that vertex. Each bug travels in a straight line from the vertex it was in originally to the vertex it picked. All bugs travel at the same speed and are of negligible size. Once a bug arrives at a vertex it picked, it stays there. In how many ways can the bugs move to the vertices so that no two bugs are ever in the same spot at the same time? Label the vertices 0, 1, 2, 3, 4, 5 in order around the hexagon and let b i be the bug starting at vertex i. We have the following restrictions on the bugs: 1. We cannot have two bugs travel to the same vertex, since they will be at the same point at the end. 2. If b i goes to vertex i + 3 then for j i bug b j does not go to vertex j If bug b i goes to vertex b i+2 then bug b i+1 cannot go to vertex b i If bug b i goes to vertex b i 2 then bug b i 3 cannot go to vertex b i 1. The first restriction tells us that the movement of the bugs must be a permutation of the vertices 0, 1, 2, 3, 4, 5. The last 3 restrictions tell us which permutations will have bugs meeting at interior points of the hexagon and dictate which permutations are valid. In the below figure, we show the permutations which will work. A There are 2 permutations that look like this. There are 2 choices for the direction of the cycle. B There are 12 permutations that look like this. There are 3 choices for which pair of 3-cycles are used, and 2 choices for the direction of each cycle. C There are 6 permutations that look like this. There are 3 rotations of the cycle, and 2 choices for the direction. D There are 2 permutations that look like this. There are 2 choices for the direction of one cycle, and the other cycle must have the same direction. E There are 12 permutations that look like this. There are 2 choices for the direction of the cycle and 6 rotations of the cycle. F There are 12 permutations that look like this. There are 2 choices for the direction of the cycle and 6 rotations of the cycle. G There are 12 permutations that look like this. There are 2 choices for the direction of the cycle and 6 rotations of the cycle. This gives a total of = 56 ways.
9 Official s 2014 Sun Life Financial CMO Qualifying Rêpechage 9
10 Official s 2014 Sun Life Financial CMO Qualifying Rêpechage For any given non-negative integer m, let f(m) be the number of 1 s in the base 2 representation of m. Let n be a positive integer. Prove that the integer 2 n 1 (( 1) f(m) 2 m) contains at least n! positive divisors. m=0 Note that every integer from 0 to 2 n 1 (inclusively) can be written uniquely as the sum of the elements of a subset of {2 0, 2 1,..., 2 n 1 }. By the definition of f(m), the summation in the problem statement is equal to Note that for each k {0, 1, 2,..., n 1}, ( 1) n (2 20 1)(2 21 1)(2 22 1) (2 2n 1 1). 2 2k 1 = (2 21 1)( )( ) (2 2k 1 + 1) = ( )( )( ) (2 2k 1 + 1). Therefore, ( 1) n (2 20 1)(2 21 1)(2 22 1) (2 2n 1 1) = ( 1) n ( ) n 1 ( ) n 2 (2 2n 2 + 1) 2 (2 2n 1 + 1). It suffices to show that this term has at least n! positive divisors. To show this, it suffices to show that these n 1 factors are pairwise relatively prime. This is because then ( 1) n ( ) n 1 ( ) n 2 (2 2n 2 +1) 2 (2 2n 1 +1) has a factor of the form p n 1 1 p n p 2 n 1 p n where p 1,..., p n are pairwise distinct primes. This factor has n(n 1)(n 2) = n! positive divisors, which will imply that ( 1) n ( ) n 1 ( ) n 2 (2 2n 2 + 1) 2 (2 2n 1 + 1) has n! positive divisors. This will complete the problem. It suffices to show that for all pairs of non-negative integers a, b satisfying a b, we have gcd(2 2a + 1, 2 2b + 1) = 1. Without loss of generality, suppose a < b. Note that ( )( ) (2 2b 1 + 1) = b 1 = 2 2b 1 = (2 2b + 1) 2. Then suppose gcd(2 2a + 1, 2 2b + 1) > 1. Let p be a prime number that divides both 2 2a + 1 and 2 2b + 1. Then p divides 2. Hence, p = 2. This is impossible since 2 2a + 1 is odd. Therefore, gcd(2 2a + 1, 2 2b + 1) = 1. This solves the problem.
Hanoi Open Mathematical Competition 2017
 Hanoi Open Mathematical Competition 2017 Junior Section Saturday, 4 March 2017 08h30-11h30 Important: Answer to all 15 questions. Write your answers on the answer sheets provided. For the multiple choice
Hanoi Open Mathematical Competition 2017 Junior Section Saturday, 4 March 2017 08h30-11h30 Important: Answer to all 15 questions. Write your answers on the answer sheets provided. For the multiple choice
USA Mathematical Talent Search Round 1 Solutions Year 27 Academic Year
 1/1/27. Fill in the spaces of the grid to the right with positive integers so that in each 2 2 square with top left number a, top right number b, bottom left number c, and bottom right number d, either
1/1/27. Fill in the spaces of the grid to the right with positive integers so that in each 2 2 square with top left number a, top right number b, bottom left number c, and bottom right number d, either
1. The sides of a triangle are in the ratio 3 : 5 : 9. Which of the following words best describes the triangle?
 UNIVERSITY OF NORTH CAROLINA CHARLOTTE 999 HIGH SCHOOL MATHEMATICS CONTEST March 8, 999 The sides of a triangle are in the ratio : 5 : 9 Which of the following words best describes the triangle? (A) obtuse
UNIVERSITY OF NORTH CAROLINA CHARLOTTE 999 HIGH SCHOOL MATHEMATICS CONTEST March 8, 999 The sides of a triangle are in the ratio : 5 : 9 Which of the following words best describes the triangle? (A) obtuse
The Advantage Testing Foundation Solutions
 The Advantage Testing Foundation 2016 Problem 1 Let T be a triangle with side lengths 3, 4, and 5. If P is a point in or on T, what is the greatest possible sum of the distances from P to each of the three
The Advantage Testing Foundation 2016 Problem 1 Let T be a triangle with side lengths 3, 4, and 5. If P is a point in or on T, what is the greatest possible sum of the distances from P to each of the three
Solution: By direct calculation, or observe that = = ( ) 2222 = =
 1 Fillins 1. Find the last 4 digits of 3333 6666. Solution: 7778. By direct calculation, or observe that 3333 6666 = 9999 2222 = (10000 1) 2222 = 22220000 2222 = 22217778. 2. How many ways are there to
1 Fillins 1. Find the last 4 digits of 3333 6666. Solution: 7778. By direct calculation, or observe that 3333 6666 = 9999 2222 = (10000 1) 2222 = 22220000 2222 = 22217778. 2. How many ways are there to
1. Suppose that a, b, c and d are four different integers. Explain why. (a b)(a c)(a d)(b c)(b d)(c d) a 2 + ab b = 2018.
 New Zealand Mathematical Olympiad Committee Camp Selection Problems 2018 Solutions Due: 28th September 2018 1. Suppose that a, b, c and d are four different integers. Explain why must be a multiple of
New Zealand Mathematical Olympiad Committee Camp Selection Problems 2018 Solutions Due: 28th September 2018 1. Suppose that a, b, c and d are four different integers. Explain why must be a multiple of
2017 ARML Local Problems Team Round (45 minutes)
 2017 ARML Local Problems Team Round (45 minutes) T-1 A fair six-sided die has faces with values 0, 0, 1, 3, 6, and 10. Compute the smallest positive integer that cannot be the sum of four rolls of this
2017 ARML Local Problems Team Round (45 minutes) T-1 A fair six-sided die has faces with values 0, 0, 1, 3, 6, and 10. Compute the smallest positive integer that cannot be the sum of four rolls of this
2008 Euclid Contest. Solutions. Canadian Mathematics Competition. Tuesday, April 15, c 2008 Centre for Education in Mathematics and Computing
 Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 008 Euclid Contest Tuesday, April 5, 008 Solutions c 008
Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 008 Euclid Contest Tuesday, April 5, 008 Solutions c 008
Sun Life Financial Canadian Open Mathematics Challenge Section A 4 marks each. Official Solutions
 Sun Life Financial Canadian Open Mathematics Challenge 2015 Official Solutions COMC exams from other years, with or without the solutions included, are free to download online. Please visit http://comc.math.ca/2015/practice.html
Sun Life Financial Canadian Open Mathematics Challenge 2015 Official Solutions COMC exams from other years, with or without the solutions included, are free to download online. Please visit http://comc.math.ca/2015/practice.html
The sum x 1 + x 2 + x 3 is (A): 4 (B): 6 (C): 8 (D): 14 (E): None of the above. How many pairs of positive integers (x, y) are there, those satisfy
 Important: Answer to all 15 questions. Write your answers on the answer sheets provided. For the multiple choice questions, stick only the letters (A, B, C, D or E) of your choice. No calculator is allowed.
Important: Answer to all 15 questions. Write your answers on the answer sheets provided. For the multiple choice questions, stick only the letters (A, B, C, D or E) of your choice. No calculator is allowed.
be any ring homomorphism and let s S be any element of S. Then there is a unique ring homomorphism
 21. Polynomial rings Let us now turn out attention to determining the prime elements of a polynomial ring, where the coefficient ring is a field. We already know that such a polynomial ring is a UFD. Therefore
21. Polynomial rings Let us now turn out attention to determining the prime elements of a polynomial ring, where the coefficient ring is a field. We already know that such a polynomial ring is a UFD. Therefore
2015 Canadian Team Mathematics Contest
 The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 205 Canadian Team Mathematics Contest April 205 Solutions 205 University of Waterloo 205 CTMC Solutions Page 2 Individual Problems.
The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 205 Canadian Team Mathematics Contest April 205 Solutions 205 University of Waterloo 205 CTMC Solutions Page 2 Individual Problems.
1 Hanoi Open Mathematical Competition 2017
 1 Hanoi Open Mathematical Competition 017 1.1 Junior Section Question 1. Suppose x 1, x, x 3 are the roots of polynomial P (x) = x 3 6x + 5x + 1. The sum x 1 + x + x 3 is (A): 4 (B): 6 (C): 8 (D): 14 (E):
1 Hanoi Open Mathematical Competition 017 1.1 Junior Section Question 1. Suppose x 1, x, x 3 are the roots of polynomial P (x) = x 3 6x + 5x + 1. The sum x 1 + x + x 3 is (A): 4 (B): 6 (C): 8 (D): 14 (E):
High School Math Contest
 High School Math Contest University of South Carolina February th, 017 Problem 1. If (x y) = 11 and (x + y) = 169, what is xy? (a) 11 (b) 1 (c) 1 (d) (e) 8 Solution: Note that xy = (x + y) (x y) = 169
High School Math Contest University of South Carolina February th, 017 Problem 1. If (x y) = 11 and (x + y) = 169, what is xy? (a) 11 (b) 1 (c) 1 (d) (e) 8 Solution: Note that xy = (x + y) (x y) = 169
= 10 such triples. If it is 5, there is = 1 such triple. Therefore, there are a total of = 46 such triples.
 . Two externally tangent unit circles are constructed inside square ABCD, one tangent to AB and AD, the other to BC and CD. Compute the length of AB. Answer: + Solution: Observe that the diagonal of the
. Two externally tangent unit circles are constructed inside square ABCD, one tangent to AB and AD, the other to BC and CD. Compute the length of AB. Answer: + Solution: Observe that the diagonal of the
Functions and Equations
 Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario Euclid eworkshop # Functions and Equations c 006 CANADIAN
Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario Euclid eworkshop # Functions and Equations c 006 CANADIAN
2018 Entrance Examination for the BSc Programmes at CMI. Read the instructions on the front of the booklet carefully!
 2018 Entrance Examination for the BSc Programmes at CMI Read the instructions on the front of the booklet carefully! Part A. Write your final answers on page 3. Part A is worth a total of (4 10 = 40) points.
2018 Entrance Examination for the BSc Programmes at CMI Read the instructions on the front of the booklet carefully! Part A. Write your final answers on page 3. Part A is worth a total of (4 10 = 40) points.
XX Asian Pacific Mathematics Olympiad
 XX Asian Pacific Mathematics Olympiad March, 008 Problem 1. Let ABC be a triangle with A < 60. Let X and Y be the points on the sides AB and AC, respectively, such that CA + AX = CB + BX and BA + AY =
XX Asian Pacific Mathematics Olympiad March, 008 Problem 1. Let ABC be a triangle with A < 60. Let X and Y be the points on the sides AB and AC, respectively, such that CA + AX = CB + BX and BA + AY =
UNC Charlotte 2005 Algebra March 7, 2005
 UNC Charlotte March 7, 2005 1. What is the y-coordinate of the vertex of the parabola y = x 2 6x + 4? (A) 5 (B) 3 (C) 3 (D) 5 (E) 9 2. The line y = x intersects the circle (x 3) 2 + (y 2) 2 = 1 in two
UNC Charlotte March 7, 2005 1. What is the y-coordinate of the vertex of the parabola y = x 2 6x + 4? (A) 5 (B) 3 (C) 3 (D) 5 (E) 9 2. The line y = x intersects the circle (x 3) 2 + (y 2) 2 = 1 in two
High School Math Contest
 High School Math Contest University of South Carolina February 4th, 017 Problem 1. If (x y) = 11 and (x + y) = 169, what is xy? (a) 11 (b) 1 (c) 1 (d) 4 (e) 48 Problem. Suppose the function g(x) = f(x)
High School Math Contest University of South Carolina February 4th, 017 Problem 1. If (x y) = 11 and (x + y) = 169, what is xy? (a) 11 (b) 1 (c) 1 (d) 4 (e) 48 Problem. Suppose the function g(x) = f(x)
Math Day at the Beach 2017
 Math Day at the Beach 017 Multiple Choice Write your name and school and mark your answers on the answer sheet. You have 0 minutes to work on these problems. No calculator is allowed. 1. How many integers
Math Day at the Beach 017 Multiple Choice Write your name and school and mark your answers on the answer sheet. You have 0 minutes to work on these problems. No calculator is allowed. 1. How many integers
1 2n. i=1. 2m+1 i = m, while. 2m + 1 = 1. is the best possible for any odd n.
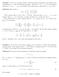 Problem 1. Let n be a positive integer. Find the largest nonnegative real number f(n) (depending on n) with the following property: whenever a 1, a,..., a n are real numbers such that a 1 + a + + a n is
Problem 1. Let n be a positive integer. Find the largest nonnegative real number f(n) (depending on n) with the following property: whenever a 1, a,..., a n are real numbers such that a 1 + a + + a n is
HMMT February 2018 February 10, 2018
 HMMT February 018 February 10, 018 Algebra and Number Theory 1. For some real number c, the graphs of the equation y = x 0 + x + 18 and the line y = x + c intersect at exactly one point. What is c? 18
HMMT February 018 February 10, 018 Algebra and Number Theory 1. For some real number c, the graphs of the equation y = x 0 + x + 18 and the line y = x + c intersect at exactly one point. What is c? 18
Mathematics Course 111: Algebra I Part I: Algebraic Structures, Sets and Permutations
 Mathematics Course 111: Algebra I Part I: Algebraic Structures, Sets and Permutations D. R. Wilkins Academic Year 1996-7 1 Number Systems and Matrix Algebra Integers The whole numbers 0, ±1, ±2, ±3, ±4,...
Mathematics Course 111: Algebra I Part I: Algebraic Structures, Sets and Permutations D. R. Wilkins Academic Year 1996-7 1 Number Systems and Matrix Algebra Integers The whole numbers 0, ±1, ±2, ±3, ±4,...
Solutions, 2004 NCS/MAA TEAM COMPETITION
 Solutions, 004 NCS/MAA TEAM COMPETITION Each problem number is followed by an 11-tuple (a 10, a 9, a 8, a 7, a 6, a 5, a 4, a 3, a, a 1, a 0 ), where a k is the number of teams that scored k points on
Solutions, 004 NCS/MAA TEAM COMPETITION Each problem number is followed by an 11-tuple (a 10, a 9, a 8, a 7, a 6, a 5, a 4, a 3, a, a 1, a 0 ), where a k is the number of teams that scored k points on
13 = m m = (C) The symmetry of the figure implies that ABH, BCE, CDF, and DAG are congruent right triangles. So
 Solutions 2005 56 th AMC 2 A 2. (D It is given that 0.x = 2 and 0.2y = 2, so x = 20 and y = 0. Thus x y = 0. 2. (B Since 2x + 7 = 3 we have x = 2. Hence 2 = bx 0 = 2b 0, so 2b = 8, and b = 4. 3. (B Let
Solutions 2005 56 th AMC 2 A 2. (D It is given that 0.x = 2 and 0.2y = 2, so x = 20 and y = 0. Thus x y = 0. 2. (B Since 2x + 7 = 3 we have x = 2. Hence 2 = bx 0 = 2b 0, so 2b = 8, and b = 4. 3. (B Let
HMMT November 2015 November 14, 2015
 HMMT November 05 November, 05 Guts round. [5] Farmer Yang has a 05 05 square grid of corn plants. One day, the plant in the very center of the grid becomes diseased. Every day, every plant adjacent to
HMMT November 05 November, 05 Guts round. [5] Farmer Yang has a 05 05 square grid of corn plants. One day, the plant in the very center of the grid becomes diseased. Every day, every plant adjacent to
HANOI OPEN MATHEMATICAL COMPETITON PROBLEMS
 HANOI MATHEMATICAL SOCIETY NGUYEN VAN MAU HANOI OPEN MATHEMATICAL COMPETITON PROBLEMS HANOI - 2013 Contents 1 Hanoi Open Mathematical Competition 3 1.1 Hanoi Open Mathematical Competition 2006... 3 1.1.1
HANOI MATHEMATICAL SOCIETY NGUYEN VAN MAU HANOI OPEN MATHEMATICAL COMPETITON PROBLEMS HANOI - 2013 Contents 1 Hanoi Open Mathematical Competition 3 1.1 Hanoi Open Mathematical Competition 2006... 3 1.1.1
2018 LEHIGH UNIVERSITY HIGH SCHOOL MATH CONTEST
 08 LEHIGH UNIVERSITY HIGH SCHOOL MATH CONTEST. A right triangle has hypotenuse 9 and one leg. What is the length of the other leg?. Don is /3 of the way through his run. After running another / mile, he
08 LEHIGH UNIVERSITY HIGH SCHOOL MATH CONTEST. A right triangle has hypotenuse 9 and one leg. What is the length of the other leg?. Don is /3 of the way through his run. After running another / mile, he
UNC Charlotte 2004 Algebra with solutions
 with solutions March 8, 2004 1. Let z denote the real number solution to of the digits of z? (A) 13 (B) 14 (C) 15 (D) 16 (E) 17 3 + x 1 = 5. What is the sum Solution: E. Square both sides twice to get
with solutions March 8, 2004 1. Let z denote the real number solution to of the digits of z? (A) 13 (B) 14 (C) 15 (D) 16 (E) 17 3 + x 1 = 5. What is the sum Solution: E. Square both sides twice to get
1 What is the area model for multiplication?
 for multiplication represents a lovely way to view the distribution property the real number exhibit. This property is the link between addition and multiplication. 1 1 What is the area model for multiplication?
for multiplication represents a lovely way to view the distribution property the real number exhibit. This property is the link between addition and multiplication. 1 1 What is the area model for multiplication?
1. Let g(x) and h(x) be polynomials with real coefficients such that
 1. Let g(x) and h(x) be polynomials with real coefficients such that g(x)(x 2 3x + 2) = h(x)(x 2 + 3x + 2) and f(x) = g(x)h(x) + (x 4 5x 2 + 4). Prove that f(x) has at least four real roots. 2. Let M be
1. Let g(x) and h(x) be polynomials with real coefficients such that g(x)(x 2 3x + 2) = h(x)(x 2 + 3x + 2) and f(x) = g(x)h(x) + (x 4 5x 2 + 4). Prove that f(x) has at least four real roots. 2. Let M be
MODEL ANSWERS TO HWK #10
 MODEL ANSWERS TO HWK #10 1. (i) As x + 4 has degree one, either it divides x 3 6x + 7 or these two polynomials are coprime. But if x + 4 divides x 3 6x + 7 then x = 4 is a root of x 3 6x + 7, which it
MODEL ANSWERS TO HWK #10 1. (i) As x + 4 has degree one, either it divides x 3 6x + 7 or these two polynomials are coprime. But if x + 4 divides x 3 6x + 7 then x = 4 is a root of x 3 6x + 7, which it
UNC Charlotte 2005 Comprehensive March 7, 2005
 March 7, 2005 1. The numbers x and y satisfy 2 x = 15 and 15 y = 32. What is the value xy? (A) 3 (B) 4 (C) 5 (D) 6 (E) none of A, B, C or D Solution: C. Note that (2 x ) y = 15 y = 32 so 2 xy = 2 5 and
March 7, 2005 1. The numbers x and y satisfy 2 x = 15 and 15 y = 32. What is the value xy? (A) 3 (B) 4 (C) 5 (D) 6 (E) none of A, B, C or D Solution: C. Note that (2 x ) y = 15 y = 32 so 2 xy = 2 5 and
Math Day at the Beach 2017 Solutions
 Math Day at the Beach 07 Solutions Mike Bao, Brendan Brzycki, Benjamin Chen, Samuel Cui, Michael Diao, Ayush Kamat, Emma Qin, Jack Sun, Jason Ye, Xuyang Yu, Beckman Math Club Individual Round Problem.
Math Day at the Beach 07 Solutions Mike Bao, Brendan Brzycki, Benjamin Chen, Samuel Cui, Michael Diao, Ayush Kamat, Emma Qin, Jack Sun, Jason Ye, Xuyang Yu, Beckman Math Club Individual Round Problem.
USA Mathematical Talent Search Round 3 Solutions Year 20 Academic Year
 1/3/20. Let S be the set of all 10-digit numbers (which by definition may not begin with 0) in which each digit 0 through 9 appears exactly once. For example, the number 3,820,956,714 is in S. A number
1/3/20. Let S be the set of all 10-digit numbers (which by definition may not begin with 0) in which each digit 0 through 9 appears exactly once. For example, the number 3,820,956,714 is in S. A number
Polynomial Rings. (Last Updated: December 8, 2017)
 Polynomial Rings (Last Updated: December 8, 2017) These notes are derived primarily from Abstract Algebra, Theory and Applications by Thomas Judson (16ed). Most of this material is drawn from Chapters
Polynomial Rings (Last Updated: December 8, 2017) These notes are derived primarily from Abstract Algebra, Theory and Applications by Thomas Judson (16ed). Most of this material is drawn from Chapters
Organization Team Team ID#
 1. [4] A random number generator will always output 7. Sam uses this random number generator once. What is the expected value of the output? 2. [4] Let A, B, C, D, E, F be 6 points on a circle in that
1. [4] A random number generator will always output 7. Sam uses this random number generator once. What is the expected value of the output? 2. [4] Let A, B, C, D, E, F be 6 points on a circle in that
Baltic Way 2003 Riga, November 2, 2003
 altic Way 2003 Riga, November 2, 2003 Problems and solutions. Let Q + be the set of positive rational numbers. Find all functions f : Q + Q + which for all x Q + fulfil () f ( x ) = f (x) (2) ( + x ) f
altic Way 2003 Riga, November 2, 2003 Problems and solutions. Let Q + be the set of positive rational numbers. Find all functions f : Q + Q + which for all x Q + fulfil () f ( x ) = f (x) (2) ( + x ) f
14 th Annual Harvard-MIT Mathematics Tournament Saturday 12 February 2011
 14 th Annual Harvard-MIT Mathematics Tournament Saturday 1 February 011 1. Let a, b, and c be positive real numbers. etermine the largest total number of real roots that the following three polynomials
14 th Annual Harvard-MIT Mathematics Tournament Saturday 1 February 011 1. Let a, b, and c be positive real numbers. etermine the largest total number of real roots that the following three polynomials
CHAPTER 2 POLYNOMIALS KEY POINTS
 CHAPTER POLYNOMIALS KEY POINTS 1. Polynomials of degrees 1, and 3 are called linear, quadratic and cubic polynomials respectively.. A quadratic polynomial in x with real coefficient is of the form a x
CHAPTER POLYNOMIALS KEY POINTS 1. Polynomials of degrees 1, and 3 are called linear, quadratic and cubic polynomials respectively.. A quadratic polynomial in x with real coefficient is of the form a x
15 th Annual Harvard-MIT Mathematics Tournament Saturday 11 February 2012
 1 th Annual Harvard-MIT Mathematics Tournament Saturday 11 February 01 1. Let f be the function such that f(x) = { x if x 1 x if x > 1 What is the total length of the graph of f(f(...f(x)...)) from x =
1 th Annual Harvard-MIT Mathematics Tournament Saturday 11 February 01 1. Let f be the function such that f(x) = { x if x 1 x if x > 1 What is the total length of the graph of f(f(...f(x)...)) from x =
PUTNAM TRAINING POLYNOMIALS. Exercises 1. Find a polynomial with integral coefficients whose zeros include
 PUTNAM TRAINING POLYNOMIALS (Last updated: December 11, 2017) Remark. This is a list of exercises on polynomials. Miguel A. Lerma Exercises 1. Find a polynomial with integral coefficients whose zeros include
PUTNAM TRAINING POLYNOMIALS (Last updated: December 11, 2017) Remark. This is a list of exercises on polynomials. Miguel A. Lerma Exercises 1. Find a polynomial with integral coefficients whose zeros include
The University of Melbourne Department of Mathematics and Statistics School Mathematics Competition, 2016 INTERMEDIATE DIVISION: SOLUTIONS
 The University of Melbourne Department of Mathematics and Statistics School Mathematics Competition, 2016 INTERMEDIATE DIVISION: SOLUTIONS (1) In the following sum substitute each letter for a different
The University of Melbourne Department of Mathematics and Statistics School Mathematics Competition, 2016 INTERMEDIATE DIVISION: SOLUTIONS (1) In the following sum substitute each letter for a different
BC Exam Solutions Texas A&M High School Math Contest October 24, p(1) = b + 2 = 3 = b = 5.
 C Exam Solutions Texas &M High School Math Contest October 4, 01 ll answers must be simplified, and If units are involved, be sure to include them. 1. p(x) = x + ax + bx + c has three roots, λ i, with
C Exam Solutions Texas &M High School Math Contest October 4, 01 ll answers must be simplified, and If units are involved, be sure to include them. 1. p(x) = x + ax + bx + c has three roots, λ i, with
45-th Moldova Mathematical Olympiad 2001
 45-th Moldova Mathematical Olympiad 200 Final Round Chişinǎu, March 2 Grade 7. Prove that y 3 2x+ x 3 2y x 2 + y 2 for any numbers x,y [, 2 3 ]. When does equality occur? 2. Let S(n) denote the sum of
45-th Moldova Mathematical Olympiad 200 Final Round Chişinǎu, March 2 Grade 7. Prove that y 3 2x+ x 3 2y x 2 + y 2 for any numbers x,y [, 2 3 ]. When does equality occur? 2. Let S(n) denote the sum of
Math 109 HW 9 Solutions
 Math 109 HW 9 Solutions Problems IV 18. Solve the linear diophantine equation 6m + 10n + 15p = 1 Solution: Let y = 10n + 15p. Since (10, 15) is 5, we must have that y = 5x for some integer x, and (as we
Math 109 HW 9 Solutions Problems IV 18. Solve the linear diophantine equation 6m + 10n + 15p = 1 Solution: Let y = 10n + 15p. Since (10, 15) is 5, we must have that y = 5x for some integer x, and (as we
The Alberta High School Mathematics Competition Solution to Part I, 2014.
 The Alberta High School Mathematics Competition Solution to Part I, 2014. Question 1. When the repeating decimal 0.6 is divided by the repeating decimal 0.3, the quotient is (a) 0.2 (b) 2 (c) 0.5 (d) 0.5
The Alberta High School Mathematics Competition Solution to Part I, 2014. Question 1. When the repeating decimal 0.6 is divided by the repeating decimal 0.3, the quotient is (a) 0.2 (b) 2 (c) 0.5 (d) 0.5
Some Basic Logic. Henry Liu, 25 October 2010
 Some Basic Logic Henry Liu, 25 October 2010 In the solution to almost every olympiad style mathematical problem, a very important part is existence of accurate proofs. Therefore, the student should be
Some Basic Logic Henry Liu, 25 October 2010 In the solution to almost every olympiad style mathematical problem, a very important part is existence of accurate proofs. Therefore, the student should be
1. Prove that for every positive integer n there exists an n-digit number divisible by 5 n all of whose digits are odd.
 32 nd United States of America Mathematical Olympiad Proposed Solutions May, 23 Remark: The general philosophy of this marking scheme follows that of IMO 22. This scheme encourages complete solutions.
32 nd United States of America Mathematical Olympiad Proposed Solutions May, 23 Remark: The general philosophy of this marking scheme follows that of IMO 22. This scheme encourages complete solutions.
2015 Hypatia Contest
 The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 015 Hypatia Contest Thursday, April 16, 015 (in North America and South America) Friday, April 17, 015 (outside of North America
The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 015 Hypatia Contest Thursday, April 16, 015 (in North America and South America) Friday, April 17, 015 (outside of North America
Mathathon Round 1 (2 points each)
 Mathathon Round ( points each). A circle is inscribed inside a square such that the cube of the radius of the circle is numerically equal to the perimeter of the square. What is the area of the circle?
Mathathon Round ( points each). A circle is inscribed inside a square such that the cube of the radius of the circle is numerically equal to the perimeter of the square. What is the area of the circle?
Permutations and Polynomials Sarah Kitchen February 7, 2006
 Permutations and Polynomials Sarah Kitchen February 7, 2006 Suppose you are given the equations x + y + z = a and 1 x + 1 y + 1 z = 1 a, and are asked to prove that one of x,y, and z is equal to a. We
Permutations and Polynomials Sarah Kitchen February 7, 2006 Suppose you are given the equations x + y + z = a and 1 x + 1 y + 1 z = 1 a, and are asked to prove that one of x,y, and z is equal to a. We
Sydney University Mathematical Society Problems Competition Solutions.
 Sydney University Mathematical Society Problems Competition 005 Solutions 1 Suppose that we look at the set X n of strings of 0 s and 1 s of length n Given a string ɛ = (ɛ 1,, ɛ n ) X n, we are allowed
Sydney University Mathematical Society Problems Competition 005 Solutions 1 Suppose that we look at the set X n of strings of 0 s and 1 s of length n Given a string ɛ = (ɛ 1,, ɛ n ) X n, we are allowed
PRMO Solution
 PRMO Solution 0.08.07. How many positive integers less than 000 have the property that the sum of the digits of each such number is divisible by 7 and the number itself is divisible by 3?. Suppose a, b
PRMO Solution 0.08.07. How many positive integers less than 000 have the property that the sum of the digits of each such number is divisible by 7 and the number itself is divisible by 3?. Suppose a, b
Solutions to Practice Final
 s to Practice Final 1. (a) What is φ(0 100 ) where φ is Euler s φ-function? (b) Find an integer x such that 140x 1 (mod 01). Hint: gcd(140, 01) = 7. (a) φ(0 100 ) = φ(4 100 5 100 ) = φ( 00 5 100 ) = (
s to Practice Final 1. (a) What is φ(0 100 ) where φ is Euler s φ-function? (b) Find an integer x such that 140x 1 (mod 01). Hint: gcd(140, 01) = 7. (a) φ(0 100 ) = φ(4 100 5 100 ) = φ( 00 5 100 ) = (
2005 Euclid Contest. Solutions
 Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 2005 Euclid Contest Tuesday, April 19, 2005 Solutions c
Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 2005 Euclid Contest Tuesday, April 19, 2005 Solutions c
Mathematical Reasoning & Proofs
 Mathematical Reasoning & Proofs MAT 1362 Fall 2018 Alistair Savage Department of Mathematics and Statistics University of Ottawa This work is licensed under a Creative Commons Attribution-ShareAlike 4.0
Mathematical Reasoning & Proofs MAT 1362 Fall 2018 Alistair Savage Department of Mathematics and Statistics University of Ottawa This work is licensed under a Creative Commons Attribution-ShareAlike 4.0
T-2 In the equation A B C + D E F = G H I, each letter denotes a distinct non-zero digit. Compute the greatest possible value of G H I.
 2016 ARML Local Problems and Solutions Team Round Solutions T-1 All the shelves in a library are the same length. When filled, two shelves side-by-side can hold exactly 12 algebra books and 10 geometry
2016 ARML Local Problems and Solutions Team Round Solutions T-1 All the shelves in a library are the same length. When filled, two shelves side-by-side can hold exactly 12 algebra books and 10 geometry
International Mathematics TOURNAMENT OF THE TOWNS
 International Mathematics TOURNAMENT OF THE TOWNS Senior A-Level Paper Fall 2008. 1. A standard 8 8 chessboard is modified by varying the distances between parallel grid lines, so that the cells are rectangles
International Mathematics TOURNAMENT OF THE TOWNS Senior A-Level Paper Fall 2008. 1. A standard 8 8 chessboard is modified by varying the distances between parallel grid lines, so that the cells are rectangles
Math1a Set 1 Solutions
 Math1a Set 1 Solutions October 15, 2018 Problem 1. (a) For all x, y, z Z we have (i) x x since x x = 0 is a multiple of 7. (ii) If x y then there is a k Z such that x y = 7k. So, y x = (x y) = 7k is also
Math1a Set 1 Solutions October 15, 2018 Problem 1. (a) For all x, y, z Z we have (i) x x since x x = 0 is a multiple of 7. (ii) If x y then there is a k Z such that x y = 7k. So, y x = (x y) = 7k is also
Baltic Way 2016 Solutions
 Baltic Way 2016 Solutions 1. Find all pairs of primes (p, q) such that p 3 q 5 =(p + q) 2. Solution. Assume first that neither of the numbers equals 3. Then, if p q mod 3, the left hand side is divisible
Baltic Way 2016 Solutions 1. Find all pairs of primes (p, q) such that p 3 q 5 =(p + q) 2. Solution. Assume first that neither of the numbers equals 3. Then, if p q mod 3, the left hand side is divisible
10! = ?
 AwesomeMath Team Contest 013 Solutions Problem 1. Define the value of a letter as its position in the alphabet. For example, C is the third letter, so its value is 3. The value of a word is the sum of
AwesomeMath Team Contest 013 Solutions Problem 1. Define the value of a letter as its position in the alphabet. For example, C is the third letter, so its value is 3. The value of a word is the sum of
2017 AMC 12A 10A Problems
 AMC 12/AHSME 2017 2017 AMC 12/AHSME 2017 AMC 12A 10A Problems A 1 Pablo buys popsicles for his friends. The store sells single popsicles for $1 each, 3-popsicle boxes for $2, and 5-popsicle boxes for $3.
AMC 12/AHSME 2017 2017 AMC 12/AHSME 2017 AMC 12A 10A Problems A 1 Pablo buys popsicles for his friends. The store sells single popsicles for $1 each, 3-popsicle boxes for $2, and 5-popsicle boxes for $3.
... z = (2x y) 2 2y 2 3y.
 1. [4] Let R be the rectangle in the Cartesian plane with vertices at (0,0),(2,0),(2,1), and (0,1). R can be divided into two unit squares, as shown. The resulting figure has 7 segments of unit length,
1. [4] Let R be the rectangle in the Cartesian plane with vertices at (0,0),(2,0),(2,1), and (0,1). R can be divided into two unit squares, as shown. The resulting figure has 7 segments of unit length,
Solutions 2017 AB Exam
 1. Solve for x : x 2 = 4 x. Solutions 2017 AB Exam Texas A&M High School Math Contest October 21, 2017 ANSWER: x = 3 Solution: x 2 = 4 x x 2 = 16 8x + x 2 x 2 9x + 18 = 0 (x 6)(x 3) = 0 x = 6, 3 but x
1. Solve for x : x 2 = 4 x. Solutions 2017 AB Exam Texas A&M High School Math Contest October 21, 2017 ANSWER: x = 3 Solution: x 2 = 4 x x 2 = 16 8x + x 2 x 2 9x + 18 = 0 (x 6)(x 3) = 0 x = 6, 3 but x
3. Applying the definition, we have 2#0 = = 5 and 1#4 = = 0. Thus, (2#0)#(1#4) = 5#0 = ( 5) 0 ( 5) 3 = 2.
 JHMMC 01 Grade 7 Solutions October 1, 01 1. There are 16 words in the sentence, and exactly 5 of them have four letters, as shown: What is the probability that a randomly chosen word of this sentence has
JHMMC 01 Grade 7 Solutions October 1, 01 1. There are 16 words in the sentence, and exactly 5 of them have four letters, as shown: What is the probability that a randomly chosen word of this sentence has
= 126 possible 5-tuples.
 19th Philippine Mathematical Olympiad 1 January, 017 JUDGES COPY EASY 15 seconds, points 1. If g (x) = x x 5 Answer: 14 Solution: Note that x x and f ( g ( x)) = x, find f (). x 6 = = x = 1. Hence f ()
19th Philippine Mathematical Olympiad 1 January, 017 JUDGES COPY EASY 15 seconds, points 1. If g (x) = x x 5 Answer: 14 Solution: Note that x x and f ( g ( x)) = x, find f (). x 6 = = x = 1. Hence f ()
International Mathematical Olympiad. Preliminary Selection Contest 2017 Hong Kong. Outline of Solutions 5. 3*
 International Mathematical Olympiad Preliminary Selection Contest Hong Kong Outline of Solutions Answers: 06 0000 * 6 97 7 6 8 7007 9 6 0 6 8 77 66 7 7 0 6 7 7 6 8 9 8 0 0 8 *See the remar after the solution
International Mathematical Olympiad Preliminary Selection Contest Hong Kong Outline of Solutions Answers: 06 0000 * 6 97 7 6 8 7007 9 6 0 6 8 77 66 7 7 0 6 7 7 6 8 9 8 0 0 8 *See the remar after the solution
Sample Question Paper Mathematics First Term (SA - I) Class X. Time: 3 to 3 ½ hours
 Sample Question Paper Mathematics First Term (SA - I) Class X Time: 3 to 3 ½ hours M.M.:90 General Instructions (i) All questions are compulsory. (ii) The question paper consists of 34 questions divided
Sample Question Paper Mathematics First Term (SA - I) Class X Time: 3 to 3 ½ hours M.M.:90 General Instructions (i) All questions are compulsory. (ii) The question paper consists of 34 questions divided
Reading Mathematical Expressions & Arithmetic Operations Expression Reads Note
 Math 001 - Term 171 Reading Mathematical Expressions & Arithmetic Operations Expression Reads Note x A x belongs to A,x is in A Between an element and a set. A B A is a subset of B Between two sets. φ
Math 001 - Term 171 Reading Mathematical Expressions & Arithmetic Operations Expression Reads Note x A x belongs to A,x is in A Between an element and a set. A B A is a subset of B Between two sets. φ
UNCC 2001 Comprehensive, Solutions
 UNCC 2001 Comprehensive, Solutions March 5, 2001 1 Compute the sum of the roots of x 2 5x + 6 = 0 (A) (B) 7/2 (C) 4 (D) 9/2 (E) 5 (E) The sum of the roots of the quadratic ax 2 + bx + c = 0 is b/a which,
UNCC 2001 Comprehensive, Solutions March 5, 2001 1 Compute the sum of the roots of x 2 5x + 6 = 0 (A) (B) 7/2 (C) 4 (D) 9/2 (E) 5 (E) The sum of the roots of the quadratic ax 2 + bx + c = 0 is b/a which,
Section September 6, If n = 3, 4, 5,..., the polynomial is called a cubic, quartic, quintic, etc.
 Section 2.1-2.2 September 6, 2017 1 Polynomials Definition. A polynomial is an expression of the form a n x n + a n 1 x n 1 + + a 1 x + a 0 where each a 0, a 1,, a n are real numbers, a n 0, and n is a
Section 2.1-2.2 September 6, 2017 1 Polynomials Definition. A polynomial is an expression of the form a n x n + a n 1 x n 1 + + a 1 x + a 0 where each a 0, a 1,, a n are real numbers, a n 0, and n is a
where c R and the content of f is one. 1
 9. Gauss Lemma Obviously it would be nice to have some more general methods of proving that a given polynomial is irreducible. The first is rather beautiful and due to Gauss. The basic idea is as follows.
9. Gauss Lemma Obviously it would be nice to have some more general methods of proving that a given polynomial is irreducible. The first is rather beautiful and due to Gauss. The basic idea is as follows.
SOLUTIONS TO ADDITIONAL EXERCISES FOR II.1 AND II.2
 SOLUTIONS TO ADDITIONAL EXERCISES FOR II.1 AND II.2 Here are the solutions to the additional exercises in betsepexercises.pdf. B1. Let y and z be distinct points of L; we claim that x, y and z are not
SOLUTIONS TO ADDITIONAL EXERCISES FOR II.1 AND II.2 Here are the solutions to the additional exercises in betsepexercises.pdf. B1. Let y and z be distinct points of L; we claim that x, y and z are not
number. However, unlike , three of the digits of N are 3, 4 and 5, and N is a multiple of 6.
 C1. The positive integer N has six digits in increasing order. For example, 124 689 is such a number. However, unlike 124 689, three of the digits of N are 3, 4 and 5, and N is a multiple of 6. How many
C1. The positive integer N has six digits in increasing order. For example, 124 689 is such a number. However, unlike 124 689, three of the digits of N are 3, 4 and 5, and N is a multiple of 6. How many
Algebra II Vocabulary Word Wall Cards
 Algebra II Vocabulary Word Wall Cards Mathematics vocabulary word wall cards provide a display of mathematics content words and associated visual cues to assist in vocabulary development. The cards should
Algebra II Vocabulary Word Wall Cards Mathematics vocabulary word wall cards provide a display of mathematics content words and associated visual cues to assist in vocabulary development. The cards should
Individual Round CHMMC November 20, 2016
 Individual Round CHMMC 20 November 20, 20 Problem. We say that d k d k d d 0 represents the number n in base 2 if each d i is either 0 or, and n d k ( 2) k + d k ( 2) k + + d ( 2) + d 0. For example, 0
Individual Round CHMMC 20 November 20, 20 Problem. We say that d k d k d d 0 represents the number n in base 2 if each d i is either 0 or, and n d k ( 2) k + d k ( 2) k + + d ( 2) + d 0. For example, 0
IMO Training Camp Mock Olympiad #2
 IMO Training Camp Mock Olympiad #2 July 3, 2008 1. Given an isosceles triangle ABC with AB = AC. The midpoint of side BC is denoted by M. Let X be a variable point on the shorter arc MA of the circumcircle
IMO Training Camp Mock Olympiad #2 July 3, 2008 1. Given an isosceles triangle ABC with AB = AC. The midpoint of side BC is denoted by M. Let X be a variable point on the shorter arc MA of the circumcircle
Unofficial Solutions
 Canadian Open Mathematics Challenge 2016 Unofficial Solutions COMC exams from other years, with or without the solutions included, are free to download online. Please visit http://comc.math.ca/2016/practice.html
Canadian Open Mathematics Challenge 2016 Unofficial Solutions COMC exams from other years, with or without the solutions included, are free to download online. Please visit http://comc.math.ca/2016/practice.html
1 Take-home exam and final exam study guide
 Math 215 - Introduction to Advanced Mathematics Fall 2013 1 Take-home exam and final exam study guide 1.1 Problems The following are some problems, some of which will appear on the final exam. 1.1.1 Number
Math 215 - Introduction to Advanced Mathematics Fall 2013 1 Take-home exam and final exam study guide 1.1 Problems The following are some problems, some of which will appear on the final exam. 1.1.1 Number
1998 IMO Shortlist BM BN BA BC AB BC CD DE EF BC CA AE EF FD
 IMO Shortlist 1998 Geometry 1 A convex quadrilateral ABCD has perpendicular diagonals. The perpendicular bisectors of the sides AB and CD meet at a unique point P inside ABCD. the quadrilateral ABCD is
IMO Shortlist 1998 Geometry 1 A convex quadrilateral ABCD has perpendicular diagonals. The perpendicular bisectors of the sides AB and CD meet at a unique point P inside ABCD. the quadrilateral ABCD is
is equal to = 3 2 x, if x < 0 f (0) = lim h = 0. Therefore f exists and is continuous at 0.
 Madhava Mathematics Competition January 6, 2013 Solutions and scheme of marking Part I N.B. Each question in Part I carries 2 marks. p(k + 1) 1. If p(x) is a non-constant polynomial, then lim k p(k) (a)
Madhava Mathematics Competition January 6, 2013 Solutions and scheme of marking Part I N.B. Each question in Part I carries 2 marks. p(k + 1) 1. If p(x) is a non-constant polynomial, then lim k p(k) (a)
x = y +z +2, y = z +x+1, and z = x+y +4. C R
 1. [5] Solve for x in the equation 20 14+x = 20+14 x. 2. [5] Find the area of a triangle with side lengths 14, 48, and 50. 3. [5] Victoria wants to order at least 550 donuts from Dunkin Donuts for the
1. [5] Solve for x in the equation 20 14+x = 20+14 x. 2. [5] Find the area of a triangle with side lengths 14, 48, and 50. 3. [5] Victoria wants to order at least 550 donuts from Dunkin Donuts for the
Algebra I. Book 2. Powered by...
 Algebra I Book 2 Powered by... ALGEBRA I Units 4-7 by The Algebra I Development Team ALGEBRA I UNIT 4 POWERS AND POLYNOMIALS......... 1 4.0 Review................ 2 4.1 Properties of Exponents..........
Algebra I Book 2 Powered by... ALGEBRA I Units 4-7 by The Algebra I Development Team ALGEBRA I UNIT 4 POWERS AND POLYNOMIALS......... 1 4.0 Review................ 2 4.1 Properties of Exponents..........
IMO Training Camp Mock Olympiad #2 Solutions
 IMO Training Camp Mock Olympiad #2 Solutions July 3, 2008 1. Given an isosceles triangle ABC with AB = AC. The midpoint of side BC is denoted by M. Let X be a variable point on the shorter arc MA of the
IMO Training Camp Mock Olympiad #2 Solutions July 3, 2008 1. Given an isosceles triangle ABC with AB = AC. The midpoint of side BC is denoted by M. Let X be a variable point on the shorter arc MA of the
UNC Charlotte 2005 Comprehensive March 7, 2005
 March 7, 2005 1 The numbers x and y satisfy 2 x = 15 and 15 y = 32 What is the value xy? (A) 3 (B) 4 (C) 5 (D) 6 (E) none of A, B, C or D 2 Suppose x, y, z, and w are real numbers satisfying x/y = 4/7,
March 7, 2005 1 The numbers x and y satisfy 2 x = 15 and 15 y = 32 What is the value xy? (A) 3 (B) 4 (C) 5 (D) 6 (E) none of A, B, C or D 2 Suppose x, y, z, and w are real numbers satisfying x/y = 4/7,
MADHAVA MATHEMATICS COMPETITION, December 2015 Solutions and Scheme of Marking
 MADHAVA MATHEMATICS COMPETITION, December 05 Solutions and Scheme of Marking NB: Part I carries 0 marks, Part II carries 30 marks and Part III carries 50 marks Part I NB Each question in Part I carries
MADHAVA MATHEMATICS COMPETITION, December 05 Solutions and Scheme of Marking NB: Part I carries 0 marks, Part II carries 30 marks and Part III carries 50 marks Part I NB Each question in Part I carries
2010 Fermat Contest (Grade 11)
 Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 010 Fermat Contest (Grade 11) Thursday, February 5, 010
Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 010 Fermat Contest (Grade 11) Thursday, February 5, 010
2007 Fermat Contest (Grade 11)
 Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 007 Fermat Contest (Grade 11) Tuesday, February 0, 007 Solutions
Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 007 Fermat Contest (Grade 11) Tuesday, February 0, 007 Solutions
BmMT 2017 Individual Round Solutions November 19, 2017
 1. It s currently 6:00 on a 12 hour clock. What time will be shown on the clock 100 hours from now? Express your answer in the form hh : mm. Answer: 10:00 Solution: We note that adding any multiple of
1. It s currently 6:00 on a 12 hour clock. What time will be shown on the clock 100 hours from now? Express your answer in the form hh : mm. Answer: 10:00 Solution: We note that adding any multiple of
Solutions Parabola Volume 52, Issue 3 (2016)
 Parabola Volume 5, Issue (06) Solutions 50 50 Q50 Find the sum of the sum of the sum of the digits for the number06 06. SOLUTION Write S(n) for the sum of the digits of a positive integer n. We wish to
Parabola Volume 5, Issue (06) Solutions 50 50 Q50 Find the sum of the sum of the sum of the digits for the number06 06. SOLUTION Write S(n) for the sum of the digits of a positive integer n. We wish to
Math Wrangle Practice Problems
 Math Wrangle Practice Problems American Mathematics Competitions December 22, 2011 ((3!)!)! 1. Given that, = k. n!, where k and n are positive integers and n 3. is as large as possible, find k + n. 2.
Math Wrangle Practice Problems American Mathematics Competitions December 22, 2011 ((3!)!)! 1. Given that, = k. n!, where k and n are positive integers and n 3. is as large as possible, find k + n. 2.
Georgia Tech High School Math Competition
 Georgia Tech High School Math Competition Multiple Choice Test February 28, 2015 Each correct answer is worth one point; there is no deduction for incorrect answers. Make sure to enter your ID number on
Georgia Tech High School Math Competition Multiple Choice Test February 28, 2015 Each correct answer is worth one point; there is no deduction for incorrect answers. Make sure to enter your ID number on
Mathematical Olympiad Training Polynomials
 Mathematical Olympiad Training Polynomials Definition A polynomial over a ring R(Z, Q, R, C) in x is an expression of the form p(x) = a n x n + a n 1 x n 1 + + a 1 x + a 0, a i R, for 0 i n. If a n 0,
Mathematical Olympiad Training Polynomials Definition A polynomial over a ring R(Z, Q, R, C) in x is an expression of the form p(x) = a n x n + a n 1 x n 1 + + a 1 x + a 0, a i R, for 0 i n. If a n 0,
Mathematical Olympiad for Girls
 UKMT UKMT UKMT United Kingdom Mathematics Trust Mathematical Olympiad for Girls Organised by the United Kingdom Mathematics Trust These are polished solutions and do not illustrate the process of failed
UKMT UKMT UKMT United Kingdom Mathematics Trust Mathematical Olympiad for Girls Organised by the United Kingdom Mathematics Trust These are polished solutions and do not illustrate the process of failed
Proofs. Chapter 2 P P Q Q
 Chapter Proofs In this chapter we develop three methods for proving a statement. To start let s suppose the statement is of the form P Q or if P, then Q. Direct: This method typically starts with P. Then,
Chapter Proofs In this chapter we develop three methods for proving a statement. To start let s suppose the statement is of the form P Q or if P, then Q. Direct: This method typically starts with P. Then,
UNDERSTANDING RULER AND COMPASS CONSTRUCTIONS WITH FIELD THEORY
 UNDERSTANDING RULER AND COMPASS CONSTRUCTIONS WITH FIELD THEORY ISAAC M. DAVIS Abstract. By associating a subfield of R to a set of points P 0 R 2, geometric properties of ruler and compass constructions
UNDERSTANDING RULER AND COMPASS CONSTRUCTIONS WITH FIELD THEORY ISAAC M. DAVIS Abstract. By associating a subfield of R to a set of points P 0 R 2, geometric properties of ruler and compass constructions
HIGH SCHOOL - PROBLEMS
 PURPLE COMET! MATH MEET April 2017 HIGH SCHOOL - PROBLEMS Copyright c Titu Andreescu and Jonathan Kane Problem 1 Paul starts at 1 and counts by threes: 1, 4, 7, 10,.... At the same time and at the same
PURPLE COMET! MATH MEET April 2017 HIGH SCHOOL - PROBLEMS Copyright c Titu Andreescu and Jonathan Kane Problem 1 Paul starts at 1 and counts by threes: 1, 4, 7, 10,.... At the same time and at the same
Which number listed below belongs to the interval 0,7; 0,8? c) 6 7. a) 3 5. b) 7 9. d) 8 9
 Problem 1 Which number listed below belongs to the interval 0,7; 0,8? a) 3 5 b) 7 9 c) 6 7 d) 8 9 2 Problem 2 What is the greatest common divisor of the numbers 3 2 3 5 and 2 3 3 5? a) 6 b) 15 c) 30 d)
Problem 1 Which number listed below belongs to the interval 0,7; 0,8? a) 3 5 b) 7 9 c) 6 7 d) 8 9 2 Problem 2 What is the greatest common divisor of the numbers 3 2 3 5 and 2 3 3 5? a) 6 b) 15 c) 30 d)
