Chapter IV Vector and Tensor Analysis IV.2 Vector and Tensor Analysis September 23,
|
|
|
- Domenic Dalton
- 6 years ago
- Views:
Transcription
1 hapte I ecto and Tenso Analyss I. ecto and Tenso Analyss eptembe, 07 47
2 hapte I ecto and Tenso Analyss I. ecto and Tenso Analyss eptembe, I. ETOR AND TENOR ANALYI I... Tenso functon th Let A n n be an n ode tenso. Then the tenso functon of a scala vaable s defned as a map n A t : n (4) The scala vaable (paamete) t can epesent tme, path, etc. Fo n 0, 0 and we have a eal-valued functon of a eal vaable: y a( t ) :I vecto functon Fo n, and we have the vecto functon of a scala vaable s a vecto-valued functon defned as a map fom the set of eal numbes to the space of vectos xt : ( t) y( t) z( t) x( t ) :I (4a) ( t ) :I (4b) 0 The vecto functon povdes a convenent method fo the defnton of cuves n space by tacng the ponts by the poston vecto t, t a,b. The change of paamete also povdes nfomaton about the poston of the pont on the cuve fo dffeent moments of tme. Ths defnton of cuves by vecto functons s equvalent to the paametc defnton of cuves: whee t [ a,b] ( t) xt y t z t [ a,b] x t,y t,z t, t [ ] x xt o y y( t) t [ a,b] (4) z z( t) ae eal valued functons. Devatve of a tenso functon The devatve of a tenso functon wth espect to a scala vaable s defned as d A t lm dt ( + ) A t t A t n n n t 0 (4) t If the lmt exsts, then the devatve s a tenso of the same ode d A ( t ) : dt n n n Repeatedly, the hghe ode devatves can be defned.
3 hapte I ecto and Tenso Analyss I. ecto and Tenso Analyss eptembe, I... Tenso feld Let be a poston vecto whch specfes a locaton n Eucldan space E A tenso feld s defned as a map In patcula, we have s ( ) v( ) Aj n ( ) A : n scala feld (tempeatue, densty, etc) vecto feld (velocty, foce, etc) tenso feld (defomaton tenso, etc) defned at all ponts of space. A non-statonay tenso feld s defned as a map n ( ) A,t : n All consdeed functons ae assumed to be contnuous: lm A 0 ( ) A ( ) n n 0 scala feld A scala feld s defned as a eal valued functon of a vecto vaable: ϕ ( ) : ϕ ϕ ( x,y,z ) : By ths functon, a scala value s specfed fo any pont of space. A scala feld can descbe dstbuton n space of tempeatue, densty, concentaton, etc. Functon ϕ ϕ x,y : defnes a scala feld on a plane. vecto feld v( ) v(,t) A vecto feld s defned as a vecto valued functon of a vecto vaable: v( ) : P( x,y,z) + Q( x,y,z) + R( x,y,z) v j By ths functon, a vecto value s specfed at any pont. A vecto feld can be descbed by a dstbuton n space of velocty, acceleaton, foce, etc. A non-statonay scala o vecto feld ae defned as tme-dependent maps (,t ) : ϕ (,t) : v All opeatons defned fo tensos can be appled fo tenso felds pont-wse.
4 hapte I ecto and Tenso Analyss I. ecto and Tenso Analyss eptembe, I... pace cuves onsde a bounded space cuve n wth the end ponts A and B. The gaph of the space cuve s taced by a vecto functon : ( t) t [ a,b] wth ( a ) A, b B (44) o n the tenso notatons: : x ( t ) t [ a,b] wth x a A, x b B (45) whch s just anothe fom of a tadtonal paametc defnton of the cuve: : x x( t) x x( t) t [ a,b] x x ( t) (46) Natual paametezaton ( s) wth the help of ac length s has some useful popetes. A dffeental element on the space cuve s tangent to the cuve: dx dt x ( t) dx x t dt (47) d d ds ds T d T ds (48) dt ds dt dt Types of some patcula space cuves: s a closed cuve f ( a) ( b) o x ( a) x ( b) s a smooth cuve f x ( t) [ a,b] (devatves ae contnuous) s a pece-wse smooth f, whee ae smooth cuves s a smple cuve f x ( t) x ( t ) f t t (w/o self-ntesecton)
5 hapte I ecto and Tenso Analyss I. ecto and Tenso Analyss eptembe, 07 5 I..4. Level cuves and sufaces f : be a scala feld, then equaton Let f c o f ( x,x) c descbes the cuves n the plane xx called the level cuves: {( x,x ) f ( x,x ) c, c } Let ϕ : be a scala feld, then equaton ϕ ( ) c o ( x,x,x ) descbes the suface n ϕ c called the level suface: {( x,x,x ) ϕ ( x,x,x ) c, c } Fo dffeent values of the constant c, we obtan the famles of un-ntesected level cuves and sufaces (why do level cuves not ntesect?). I..5. Opeato nabla, gadent and dectonal devatve nabla : s a dffeental vecto opeato defned as,, tenso notaton (49) x shot-hand tenso notaton ometmes opeato nabla s also called the Hamlton opeato. gadent Opeato nabla appled to a scala-valued vecto functon ϕ yelds a vecto called the gadent of the scala feld ϕ ϕ, ϕ, ϕ ϕ + ϕ + ϕ (50) x x x whch s a vecto othogonal to the level suface of the scala feld (o to the level cuve n the -D case). ϕ ϕ x ϕ shot-hand tenso notaton
6 hapte I ecto and Tenso Analyss I. ecto and Tenso Analyss eptembe, 07 5 Dectonal devatve of the scala feld Let functon ϕ : defnes a scala feld, and let s be a unt vecto, s. ecto hs wth a small h > 0 s an ncement n the decton s. Then a devatve of functon defned as ϕ ( ) n the decton s at the pont n space s ϕ ϕ D s ϕ ( + hs) ϕ( ) lm s h 0 h (5) It detemnes the ate of change of the scala feld decton s. ϕ ( ) at the pont n the Usng the dffeentaton ules fo the multvaable functons and the defnton of the opeato nabla, let us wte the othe epesentatons of the dectonal devatve: ϕ s ϕ x x + ϕ + ϕ x s x s x s ϕ ϕ ϕ cos, + cos, + cos, x x x ( s ) ( s ) ( s ) ϕ ϕ ϕ s+ s+ s x x x ϕ s ϕ s (5) x Theefoe, the devatve of ϕ n any decton s equal to the pojecton of the gadent ϕ onto ths decton: ϕ s ϕ s ϕ cos ( ϕ, s ) (5) It follows fom ths equaton that the maxmum value of the dectonal devatve s acheved n the decton of the gadent of the scala feld at ths pont. o we can conclude that the gadent of the scala feld s a vecto whch has a decton of the geatest ncease and ts magntude s equal to the dectonal devatve n ths decton. The opposte decton ϕ coesponds to the decton of the geatest decease. Fom equaton (5) yelds also that dϕ ϕ d. If n s the unt nomal vecto to the level suface of ϕ, then ϕ ϕ n (54) n Gadent of scala feld s othogonal to level suface.
7 hapte I ecto and Tenso Analyss I. ecto and Tenso Analyss eptembe, 07 5 Dectonal devatve of the vecto feld a : defne a vecto feld, and let s be a unt vecto, Let functon s. ecto hs wth a small h > 0 s an ncement n the decton s. Then the devatve of functon a n a decton s at the pont of space s defned as D s a s a a ( + hs) a lm h 0 h (55) povded that the lmt exsts. It detemnes the ate of change of the vecto feld a at the pont n the decton s : s a + + x s x s x s cos, + cos, + cos, x x x ( s ) ( s ) ( s ) s+ s+ s x x x ( sa ) (56) In tenso notaton, the dectonal devatve s wtten as a s (57) a s x Dectonal devatve of the nd ode tenso feld The dectonal devatve of the nd ode tenso feld s the natual genealzaton of the dectonal devatves of the scala and vecto felds n tems of tensos gven by equatons (5) and (57). A : defne a nd ode tenso feld, and let s be a unt Let functon 9 9 vecto, s. ecto hs wth a small h > 0 s an ncement n the decton. Then a devatve of tenso functon A space s defned as n a decton s at the pont of s DA s A A ( + hs) A ( ) lm s h 0 h (58) povded that the lmt exsts. onsde the components of the dectonal devatve A s A A A x A A A + + s + s + s x s x s x s x x x o as a contucton of the d ode tenso A s A s (59) j x j
8 hapte I ecto and Tenso Analyss I. ecto and Tenso Analyss eptembe, I..6. Flux onsde a vecto feld a. Let us defne a flux of a vecto feld though the suface as a suface ntegal of the vecto functon a : flux though the suface flux a d (60) Let be a suface and let a unt vecto n detemne the unt decton to suface (fo the decton of the nomal vecto, we wll agee to tae the exteo decton fo closed sufaces, and one of two dectons fo non-closed sufaces and stc to ths decton when changng poston on the suface). The dot poduct a n a cos n, a n s the magntude of the pojecton of vecto a on the nomal decton n. ubdvde suface nto subsufaces wth the aeas whch can be assumed to be flat and be chaactezed by the nomal vecto wth the magntude equal to the aea : n. Then the suface ntegal can be defned as a lmt of the sums a d lm a 0 (6) Usng the dffeental elaton d n d, we can expess a d ( an )d and ( n ) ( n ) ( n ) ax cos, ax cos, ax cos, + + d ( n ) ( n ) ( n ) ax cos, d + ax cos, d + ax cos, d a dx dx + a dx dx + a dx dx (6) x x x Then the flux of the vecto feld though the suface can be wtten n the tadtonal fom of the suface ntegal: ( x ) x x a d an d a dx dx + a dx dx + a dx dx (6) The flux of the vecto feld though the closed suface s denoted by a d an d Useful fact: the flux though any closed suface n the constant vecto feld a a s zeo (consevaton law): 0 a 0 d 0
9 hapte I ecto and Tenso Analyss I. ecto and Tenso Analyss eptembe, Flux of the nd ode tenso Let functon A : defne a nd ode tenso feld and let n be a 9 9 vaable nomal vecto to the smooth suface. Then the flux of the nd ode tenso feld though the suface s defned as a vecto f wth the components f A n d (64) Fo example, the flux of the stess tenso p n the elastc medum though the suface defnes the total stess vecto P actng on the suface whch has the components: P p n d I..7. Dvegence Dvegence of the vecto feld a at the pont of space s defned as a lmt of the aveaged flux though the suface of the abtay volume contanng pont : dva lm 0 a d (65) Use a paallelepped fo the abtay volume wth one cone located at the pont ( x,x,x), sdes x and faces pependcula to the coodnate axes, and x x x wth the sufaces x x, (see pctue). Then dva lm 0 a d an d lm 0 a lm 0 a n lm 0 ( ) x x,x,x x,x,x... lm a + a + 0 lm x x x 0 lm x x x 0 a x + x,x,x a x,x,x x x +... x x x ( ) a x + x,x,x a x,x,x +... x
10 hapte I ecto and Tenso Analyss I. ecto and Tenso Analyss eptembe, lm x x x 0 lm x x x 0 ( ) ax x + x,x,x ax x,x,x +... x ( ) ax x + x,x,x ax x,x,x +... x + + x x x x a (66) Physcal meanng of the dvegence [Z-59, K-45]: dv a a Fo ncompessble flud, the dvegence of the velocty vecto feld dv v 0 Dvegence of the nd ode tenso feld s defned as a lmt ( dva ) j lm 0 A n d jm m (67) It can be shown that the dvegence of the nd ode tenso s a vecto wth the components ( dva ) j A jm (68) x m
11 hapte I ecto and Tenso Analyss I. ecto and Tenso Analyss eptembe, I..8. ul The othe physcal chaactestc of a tenso feld s gven by the cul of the tenso feld. The cul of the vecto feld a at the pont of space s defned as a lmt of the aveaged flux though the suface of the abtay volume contanng pont cul a n a d lm 0 (69) ompae wth dvegence (equaton (66)): dva na d lm 0 a Applcaton of the opeato nabla yelds a smla epesentaton of the cul cul a a (70) Physcal meanng: cul a measues how fast vecto feld otates. Fo otatonal flud, the cul of the velocty vecto feld s zeo cul v 0 Useful fomulas: cul a a x x x a a a (7) ( cula ) j j whee ndces, j, ae a cyclc pemutaton of the numbes,, Wth the help of altenatng unt tenso, t can be wtten as cula εj j (7) In the vecto fom: cul a + j+
12 hapte I ecto and Tenso Analyss I. ecto and Tenso Analyss eptembe, I..9. OPERATOR NABLA AND RELATED DIFFERENTIAL OPERATOR nabla ( ) x x gad ϕ n ϕd lm 0 ϕ ( ϕ ) ϕ ϕ ϕ x ϕ x dv a na d lm 0 a dva x + + n a d cul a lm a ( cula) 0 ε j j j j cul a a x x x a a a x x x + j+ ϕ ϕ ϕ ϕ dv gad + + ϕ ϕ ϕ ϕ, ϕ : Laplacan of scala feld ϕ δ ϕ ϕ ϕ j j shot-hand notaton fo Laplacan notatons fo the Laplacan opeato
13 hapte I ecto and Tenso Analyss I. ecto and Tenso Analyss eptembe, Let a, b, F : be vecto felds, ϕ,u : be scala felds, c [B&T, p.68] ϕ gad ϕ a a dv a cul a ( a ) ϕ ( a ) gad dv a dv gad ϕ ϕ ϕ Laplacan opeato dv cul a 0 vanshes dentcally ϕ cul gad ϕ 0 vanshes dentcally ( a ) cul cul a. ( ϕ + ψ ) ϕ + ψ. ( ϕ+ ψ) ϕ+ ψ gad ϕ+ ψ gadϕ+ gadψ. ( a+ b) ( a) + ( b ) gad dv a+ b gad dv a+ gad dv b 7. ( ( a+ b) ) ( a) + ( b ) cul cul ( a+ b) cul cul ( a) + cul cul ( b ) ( ϕψ ) ψ ϕ + ϕ ψ 0... ( a+ b) a+ b ( ca) c a dv( ca) ( a+ b) a+ b. ( ) ( ) ( ) a a a dv a+ b dva+ dvb cdva cul a+ b cula+ culb ( a ϕ ) ( a ) cul ( cula+ gadϕ ) cul ( cula) + ( ϕa) ϕ a a ϕ + ( a b) b ( a) a ( b ) ( ϕa) ϕ( a) ϕ a + gad ϕψ ψ gadϕ + ϕ gadψ dv ϕa ϕdva+ a gadϕ dv a b b cula a culb cul ϕa ϕcula+ gadϕ a cul cula gad dva a Fo composte functons ϕ f ( ) and f dϕ df a, the chan ule s appled 4. ϕ f ( ) f ( ) 5. f ( f ) d a a a ( ) df 6. a f ( ) ( f ) a ( ) da df m ( a) εjεlm xj x a a l dϕ gad ϕ f gad f df da dv f gad f df da cul f gad f df
14 hapte I ecto and Tenso Analyss I. ecto and Tenso Analyss eptembe, atesan coodnates ( x,y,z ) ylndcal coodnates (,,z) phecal coodnates (, φ, ) x cos x cosφsn y sn y snφsn z z z cos x + y y tan x x + y + z y tanφ, x z z cos x + y + z Bass vectos (,0,0) ( 0,,0) ( 0,0,) e cos + j sn e cos φ sn + j sn φ sn + cos j e - sn + j cos e -sn + j cosφ e z eφ cosφcos + jsnφcos sn, Lne elements dx,dy,dz d,d,dz d, snd φ, d Dffeental aeas da x dydz da y dxdz da z dxdy da d dz da sndφd da ddz da φ sndφ d da z d d da ρdφd ρ φ Dffeental volume Ac length d dxdydz ds dx + dy + dz d dd dz ds d + d + dz d sndφd d ds d + sn dφ + d
15 hapte I ecto and Tenso Analyss I. ecto and Tenso Analyss eptembe, 07 6 scala feld u ( ) u( x,y,z ) u(,,z) u(, φ, ) Gadent u u u u u,, y z u u u u,, z u u u u,, sn φ u u u u u u u u u + j+ e + e + e z e + eφ + e y z z sn φ Laplacan u u u u y z u + + u u + u u + + z u u + u u + + sn sn φ sn vecto feld F( ) ( F x,f y,f z) ( F,F,Fz) ( F,F φ,f ) F Fx cos + Fy sn F Fx cosφsn + Fy snφsn + Fz cos F Fx sn + Fy cos Fφ Fx snφ + Fy cosφ F z Fz x + y z F F cosφcos F snφcos F sn F F cos F sn x x F F sn F cos F y + y z Fz z F F cosφsn F snφ + F cosφcos φ F F snφsn + F cosφ + F snφcos F F cos F sn φ Dvegence dv F F F F x y Fz + + y z F F z z ( F ) + + ( F ) Fφ + + sn φ + ( sn ) F sn cul F F j e e ez e e sne y z z sn φ F F F F F Fz F F sn F x y z F z F y + y z F F z e Fφ sn F e + sn φ z + φ φ F F z j F Fz + + z x z + + Fy F x + y F F + e φ + e ( F ) F e z F sn φ + ( Fφ ) sn e
16 hapte I ecto and Tenso Analyss I. ecto and Tenso Analyss eptembe, 07 6 Execses: ) Nave-toes equatons (govenng equaton fo flud moton): ρ + ( ) P+ ρ g + µ t Usng tenso notatons show that fo ncompessble, otatonal, steady flow ths smplfes to Benoull s equaton: ρ P+ ρg ) Maxwell s equatons [B&T, 46] Electomagnetc feld n a medum of dalectc constant ε, magnetc pemeablty µ, and conductvty σ ( ρ 0, no fee chadge nconductng medum, and j σ E (Ohm s law) ) s descbed by a system of Maxwelll s equatons: dv E 0 Gauss s law dv H 0 Gauss s law fo magnetsm µ H cul E Faaday s law c t ε E 4πσ cul H + E Maxwell-Ampee law c t c whee E E (,t) s the electc feld and (,t) H H s the magnetc feld. how that the followng wave equaton can be deved fom Maxwell s equatons: E E + c t c µε 4πµσ E t Hnt: apply opeato cul to the last two equaton.
17 hapte I ecto and Tenso Analyss I. ecto and Tenso Analyss eptembe, 07 6 I..0. Lne Integal onsde a vecto-valued functon a, whee vectos belong to the space cuve : ( t) t [ a,b] wth ( a ) A, b B (69) We wll consde a lne ntegal whch symbolcally s wtten as: a d (70) Let us see how ths ntegal s defned n ts physcal sense. et up a patton P n of the cuve nto a dscete set of n ponts: { } P a,,,..., b n 0 n and defne the ncement Defne the nom of patton as the bggest ncement n the patton: P max Denote the values of functon Fom a dot poduct n a at the ponts of patton whch has a physcal sense of the wo pefomed by the foce a ove path. Then the lne ntegal s defned smlaly to defnton of the defnte ntegal as a lmt of the Remann sum: whch physcally expesses the wo done by the foce a cuve. alculaton of the lne ntegal. Let the vecto functon a a have the followng specfcaton: j P x,x,x + Q x,x,x + R x,x,x j along the space (7) P x (7) Let the paametezaton of the cuve be defned by x t + x t + x t ( t) (7) dffeentaton of ths equaton yelds: d t x t o d ( t) x ( t) dt dx (74) dt a a a n a d lm a n Pn 0 P x,x,x + P x,x,x + P x,x,x ( t) x fom whch follows that d dx (75)
18 hapte I ecto and Tenso Analyss I. ecto and Tenso Analyss eptembe, Then the lne ntegal (5) can be tansfomed to a d P x,x,x P x,x,x P x,x,x d + + P x,x,x d P x,x,x d P x,x,x d + + P x,x,x dx + P x,x,x dx + P x,x,x dx P x,x,x dx + P x,x,x dx + P x,x,x dx ths s the tadtonal fom wthout paentheses. Then applyng dx x dt, b P( x,x,x) x P( x,x,x) x P( x,x,x) x dt (76) a + + Example Fnd a d fo vecto functon a p,q,x p,q along the space cuve t cos t + sn t + t t fom 0 to π : Identfy: x t cos t x ( t) snt x ( t) t x t snt x t cos t x t Then, usng equaton (56), one ends up wth a d π [ ] p snt + q cos t + t dt 0 t p cos t + q snt + π 0 π p+ p π p If the cuve s defned wth the natual paametezaton, then d d s ds T ds whee T s a unt vecto tangent to the cuve. dt ds dt dt Then d T ds ( s) Recall also ds dx + dx + dx x + x + x dt
19 hapte I ecto and Tenso Analyss I. ecto and Tenso Analyss eptembe, The lne ntegal then s calculated accodng to a d b a P x,x,x T+ P x,x,x T+ P x,x,x T x + x + x dt b at x + x + x dt (77) a P x,x,x P x,x,x P x,x,x d + + Theefoe, the wo s pefomed only by the tangental component of the foce. onsevatve vecto felds If a s a gadent feld of some scala feld a ϕ (78) (n ths case functon ϕ ( ) s called a potental functon fo the gadent feld a ), then a lnea ntegal along the cuve connectng two ponts and s equal to the dffeence between values of the scala functon at these end ponts: a d ϕ d dϕ ϕ ϕ (79) It means that the same esult wll occu fo any cuve connectng ponts and, and the lne ntegal s sad to be ndependent of path. Of patcula nteest ae the lnea ntegals along the closed cuves denoted by a d It s obvous that fo the gadent feld a d ϕ d 0 That s why f a vecto feld s a gadent feld of some scala feld t s sad to be consevatve. We have fo a consevatve feld that dϕ ϕ d a d ( P P P) d ( P d P d P d ) Pdx + Pdx + Pdx (80) Theefoe, Pdx + Pdx + Pdx s an exact dffeental. o, the lne ntegal P dx + P dx + P dx s ndependent of path, f Pdx + Pdx + Pdx dϕ s an exact dffeental. Test fo path ndependence Recall fom calculus that the dffeental fom Pdx + Pdx + Pdxs an exact dffeental f and only f P P It s called the test fo path ndependence of a lnea ntegal n space. (8)
20 hapte I ecto and Tenso Analyss I. ecto and Tenso Analyss eptembe, I... olume ntegal onsde a scala feld ϕ ( ) and let be a volume. ubdvde the volume nto subvolumes and constuct an ntegal of the functon ϕ ( ) ove the volume as a lmt ϕ ( ) d lm ϕ 0 (8) whee s an abtay pont n the subvolume. I... The Dvegence Theoem (the Gauss-Ostogadsy Theoem o the Dvegence Theoem) Let be a volume bounded by a closed suface. Then flux of the vecto feld a though the suface s equal to the ntegal of the dvegence of the vecto feld ove the volume : a d dvad (8) Poof: We wll show that equaton (8) s appoxmately vald wth any degee of accuacy,.e. that fo any ε > 0. a d - dvad < ε ubdvde volume nto such that a d - dv a <δ that s possble accodng to the defnton of the dvegence as a lmt (65). Multply ths nequalty by a d - dv a <δ then summaton ove all yelds a a d - dv <δ In ths esult, the suface ntegal only ove the exteo suface s left. All nteo sufaces have to be the boundaes of some adjacent volumes m and. Havng the opposte nomal vectos, n n m, the suface ntegals ove cancel each othe n the summaton: a d + a d m and m + an m d and and 0
21 hapte I ecto and Tenso Analyss I. ecto and Tenso Analyss eptembe, Let wth 0, then accodng to the volume ntegal defnton (8), lm dva 0 and dva d a d - dvad <δ. ε hoose δ, then a d - dvad < ε fo any specfed ε > 0. Recall x x x dva + + a n a cos n, a x n Then the othe foms of the Dvegence Theoem (Gauss-Ostogadsy theoem) can be wtten as a d dvad an d dvad n a a d dv d x x x a cos ( n, ) + a cos ( n, ) + a cos ( n, ) d + + d x x x Applcaton: The Dvegence Theoem has a geat mpotance n mathematcal modelng n engneeng. In devaton of the govenng equatons fo physcal pocesses n the contnuous meda, the consevaton laws ae appled to the contol volume yeldng an equaton whch contans both suface ntegals and volume ntegals. Applcaton of the Dvegence Theoem educes all ntegals to the volume ntegal whch allows combnaton of all tems n one volume ntegal and concludes wth the patal dffeental equaton whch govens the physcal pocess unde consdeaton (see example of devaton of the Heat Equaton n the ecton III..).
22 hapte I ecto and Tenso Analyss I. ecto and Tenso Analyss eptembe, 07 68
Chapter IV Vector and Tensor Analysis IV.2 Vector and Tensor Analysis September 29,
 hapte I ecto and Tenso Analyss I. ecto and Tenso Analyss eptembe 9, 08 47 hapte I ecto and Tenso Analyss I. ecto and Tenso Analyss eptembe 9, 08 48 I. ETOR AND TENOR ANALYI I... Tenso functon th Let A
hapte I ecto and Tenso Analyss I. ecto and Tenso Analyss eptembe 9, 08 47 hapte I ecto and Tenso Analyss I. ecto and Tenso Analyss eptembe 9, 08 48 I. ETOR AND TENOR ANALYI I... Tenso functon th Let A
Integral Vector Operations and Related Theorems Applications in Mechanics and E&M
 Dola Bagayoko (0) Integal Vecto Opeatons and elated Theoems Applcatons n Mechancs and E&M Ι Basc Defnton Please efe to you calculus evewed below. Ι, ΙΙ, andιιι notes and textbooks fo detals on the concepts
Dola Bagayoko (0) Integal Vecto Opeatons and elated Theoems Applcatons n Mechancs and E&M Ι Basc Defnton Please efe to you calculus evewed below. Ι, ΙΙ, andιιι notes and textbooks fo detals on the concepts
Chapter I Matrices, Vectors, & Vector Calculus 1-1, 1-9, 1-10, 1-11, 1-17, 1-18, 1-25, 1-27, 1-36, 1-37, 1-41.
 Chapte I Matces, Vectos, & Vecto Calculus -, -9, -0, -, -7, -8, -5, -7, -36, -37, -4. . Concept of a Scala Consde the aa of patcles shown n the fgue. he mass of the patcle at (,) can be epessed as. M (,
Chapte I Matces, Vectos, & Vecto Calculus -, -9, -0, -, -7, -8, -5, -7, -36, -37, -4. . Concept of a Scala Consde the aa of patcles shown n the fgue. he mass of the patcle at (,) can be epessed as. M (,
Review of Vector Algebra and Vector Calculus Operations
 Revew of Vecto Algeba and Vecto Calculus Opeatons Tpes of vaables n Flud Mechancs Repesentaton of vectos Dffeent coodnate sstems Base vecto elatons Scala and vecto poducts Stess Newton s law of vscost
Revew of Vecto Algeba and Vecto Calculus Opeatons Tpes of vaables n Flud Mechancs Repesentaton of vectos Dffeent coodnate sstems Base vecto elatons Scala and vecto poducts Stess Newton s law of vscost
Scalars and Vectors Scalar
 Scalas and ectos Scala A phscal quantt that s completel chaacteed b a eal numbe (o b ts numecal value) s called a scala. In othe wods a scala possesses onl a magntude. Mass denst volume tempeatue tme eneg
Scalas and ectos Scala A phscal quantt that s completel chaacteed b a eal numbe (o b ts numecal value) s called a scala. In othe wods a scala possesses onl a magntude. Mass denst volume tempeatue tme eneg
Set of square-integrable function 2 L : function space F
 Set of squae-ntegable functon L : functon space F Motvaton: In ou pevous dscussons we have seen that fo fee patcles wave equatons (Helmholt o Schödnge) can be expessed n tems of egenvalue equatons. H E,
Set of squae-ntegable functon L : functon space F Motvaton: In ou pevous dscussons we have seen that fo fee patcles wave equatons (Helmholt o Schödnge) can be expessed n tems of egenvalue equatons. H E,
Test 1 phy What mass of a material with density ρ is required to make a hollow spherical shell having inner radius r i and outer radius r o?
 Test 1 phy 0 1. a) What s the pupose of measuement? b) Wte all fou condtons, whch must be satsfed by a scala poduct. (Use dffeent symbols to dstngush opeatons on ectos fom opeatons on numbes.) c) What
Test 1 phy 0 1. a) What s the pupose of measuement? b) Wte all fou condtons, whch must be satsfed by a scala poduct. (Use dffeent symbols to dstngush opeatons on ectos fom opeatons on numbes.) c) What
CSJM University Class: B.Sc.-II Sub:Physics Paper-II Title: Electromagnetics Unit-1: Electrostatics Lecture: 1 to 4
 CSJM Unvesty Class: B.Sc.-II Sub:Physcs Pape-II Ttle: Electomagnetcs Unt-: Electostatcs Lectue: to 4 Electostatcs: It deals the study of behavo of statc o statonay Chages. Electc Chage: It s popety by
CSJM Unvesty Class: B.Sc.-II Sub:Physcs Pape-II Ttle: Electomagnetcs Unt-: Electostatcs Lectue: to 4 Electostatcs: It deals the study of behavo of statc o statonay Chages. Electc Chage: It s popety by
Rigid Bodies: Equivalent Systems of Forces
 Engneeng Statcs, ENGR 2301 Chapte 3 Rgd Bodes: Equvalent Sstems of oces Intoducton Teatment of a bod as a sngle patcle s not alwas possble. In geneal, the se of the bod and the specfc ponts of applcaton
Engneeng Statcs, ENGR 2301 Chapte 3 Rgd Bodes: Equvalent Sstems of oces Intoducton Teatment of a bod as a sngle patcle s not alwas possble. In geneal, the se of the bod and the specfc ponts of applcaton
Chapter 23: Electric Potential
 Chapte 23: Electc Potental Electc Potental Enegy It tuns out (won t show ths) that the tostatc foce, qq 1 2 F ˆ = k, s consevatve. 2 Recall, fo any consevatve foce, t s always possble to wte the wok done
Chapte 23: Electc Potental Electc Potental Enegy It tuns out (won t show ths) that the tostatc foce, qq 1 2 F ˆ = k, s consevatve. 2 Recall, fo any consevatve foce, t s always possble to wte the wok done
PHYS 705: Classical Mechanics. Derivation of Lagrange Equations from D Alembert s Principle
 1 PHYS 705: Classcal Mechancs Devaton of Lagange Equatons fom D Alembet s Pncple 2 D Alembet s Pncple Followng a smla agument fo the vtual dsplacement to be consstent wth constants,.e, (no vtual wok fo
1 PHYS 705: Classcal Mechancs Devaton of Lagange Equatons fom D Alembet s Pncple 2 D Alembet s Pncple Followng a smla agument fo the vtual dsplacement to be consstent wth constants,.e, (no vtual wok fo
Chapter Fifiteen. Surfaces Revisited
 Chapte Ffteen ufaces Revsted 15.1 Vecto Descpton of ufaces We look now at the vey specal case of functons : D R 3, whee D R s a nce subset of the plane. We suppose s a nce functon. As the pont ( s, t)
Chapte Ffteen ufaces Revsted 15.1 Vecto Descpton of ufaces We look now at the vey specal case of functons : D R 3, whee D R s a nce subset of the plane. We suppose s a nce functon. As the pont ( s, t)
Chapter 8. Linear Momentum, Impulse, and Collisions
 Chapte 8 Lnea oentu, Ipulse, and Collsons 8. Lnea oentu and Ipulse The lnea oentu p of a patcle of ass ovng wth velocty v s defned as: p " v ote that p s a vecto that ponts n the sae decton as the velocty
Chapte 8 Lnea oentu, Ipulse, and Collsons 8. Lnea oentu and Ipulse The lnea oentu p of a patcle of ass ovng wth velocty v s defned as: p " v ote that p s a vecto that ponts n the sae decton as the velocty
Chapter 3 Vector Integral Calculus
 hapte Vecto Integal alculus I. Lne ntegals. Defnton A lne ntegal of a vecto functon F ove a cuve s F In tems of components F F F F If,, an ae functon of t, we have F F F F t t t t E.. Fn the value of the
hapte Vecto Integal alculus I. Lne ntegals. Defnton A lne ntegal of a vecto functon F ove a cuve s F In tems of components F F F F If,, an ae functon of t, we have F F F F t t t t E.. Fn the value of the
VEKTORANALYS FLUX INTEGRAL LINE INTEGRAL. and. Kursvecka 2. Kapitel 4 5. Sidor 29 50
 VEKTORANAYS Ksecka INE INTEGRA and UX INTEGRA Kaptel 4 5 Sdo 9 5 A wnd TARGET PROBEM We want to psh a mne cat along a path fom A to B. Bt the wnd s blowng. How mch enegy s needed? (.e. how mch s the wok?
VEKTORANAYS Ksecka INE INTEGRA and UX INTEGRA Kaptel 4 5 Sdo 9 5 A wnd TARGET PROBEM We want to psh a mne cat along a path fom A to B. Bt the wnd s blowng. How mch enegy s needed? (.e. how mch s the wok?
COORDINATE SYSTEMS, COORDINATE TRANSFORMS, AND APPLICATIONS
 Dola Bagaoo 0 COORDINTE SYSTEMS COORDINTE TRNSFORMS ND PPLICTIONS I. INTRODUCTION Smmet coce of coodnate sstem. In solvng Pscs poblems one cooses a coodnate sstem tat fts te poblem at and.e. a coodnate
Dola Bagaoo 0 COORDINTE SYSTEMS COORDINTE TRNSFORMS ND PPLICTIONS I. INTRODUCTION Smmet coce of coodnate sstem. In solvng Pscs poblems one cooses a coodnate sstem tat fts te poblem at and.e. a coodnate
24-2: Electric Potential Energy. 24-1: What is physics
 D. Iyad SAADEDDIN Chapte 4: Electc Potental Electc potental Enegy and Electc potental Calculatng the E-potental fom E-feld fo dffeent chage dstbutons Calculatng the E-feld fom E-potental Potental of a
D. Iyad SAADEDDIN Chapte 4: Electc Potental Electc potental Enegy and Electc potental Calculatng the E-potental fom E-feld fo dffeent chage dstbutons Calculatng the E-feld fom E-potental Potental of a
Physics 11b Lecture #2. Electric Field Electric Flux Gauss s Law
 Physcs 11b Lectue # Electc Feld Electc Flux Gauss s Law What We Dd Last Tme Electc chage = How object esponds to electc foce Comes n postve and negatve flavos Conseved Electc foce Coulomb s Law F Same
Physcs 11b Lectue # Electc Feld Electc Flux Gauss s Law What We Dd Last Tme Electc chage = How object esponds to electc foce Comes n postve and negatve flavos Conseved Electc foce Coulomb s Law F Same
Thermodynamics of solids 4. Statistical thermodynamics and the 3 rd law. Kwangheon Park Kyung Hee University Department of Nuclear Engineering
 Themodynamcs of solds 4. Statstcal themodynamcs and the 3 d law Kwangheon Pak Kyung Hee Unvesty Depatment of Nuclea Engneeng 4.1. Intoducton to statstcal themodynamcs Classcal themodynamcs Statstcal themodynamcs
Themodynamcs of solds 4. Statstcal themodynamcs and the 3 d law Kwangheon Pak Kyung Hee Unvesty Depatment of Nuclea Engneeng 4.1. Intoducton to statstcal themodynamcs Classcal themodynamcs Statstcal themodynamcs
8 Baire Category Theorem and Uniform Boundedness
 8 Bae Categoy Theoem and Unfom Boundedness Pncple 8.1 Bae s Categoy Theoem Valdty of many esults n analyss depends on the completeness popety. Ths popety addesses the nadequacy of the system of atonal
8 Bae Categoy Theoem and Unfom Boundedness Pncple 8.1 Bae s Categoy Theoem Valdty of many esults n analyss depends on the completeness popety. Ths popety addesses the nadequacy of the system of atonal
1. Starting with the local version of the first law of thermodynamics q. derive the statement of the first law of thermodynamics for a control volume
 EN10: Contnuum Mechancs Homewok 5: Alcaton of contnuum mechancs to fluds Due 1:00 noon Fda Febua 4th chool of Engneeng Bown Unvest 1. tatng wth the local veson of the fst law of themodnamcs q jdj q t and
EN10: Contnuum Mechancs Homewok 5: Alcaton of contnuum mechancs to fluds Due 1:00 noon Fda Febua 4th chool of Engneeng Bown Unvest 1. tatng wth the local veson of the fst law of themodnamcs q jdj q t and
Energy in Closed Systems
 Enegy n Closed Systems Anamta Palt palt.anamta@gmal.com Abstact The wtng ndcates a beakdown of the classcal laws. We consde consevaton of enegy wth a many body system n elaton to the nvese squae law and
Enegy n Closed Systems Anamta Palt palt.anamta@gmal.com Abstact The wtng ndcates a beakdown of the classcal laws. We consde consevaton of enegy wth a many body system n elaton to the nvese squae law and
COMPLEMENTARY ENERGY METHOD FOR CURVED COMPOSITE BEAMS
 ultscence - XXX. mcocd Intenatonal ultdscplnay Scentfc Confeence Unvesty of skolc Hungay - pl 06 ISBN 978-963-358-3- COPLEENTRY ENERGY ETHOD FOR CURVED COPOSITE BES Ákos József Lengyel István Ecsed ssstant
ultscence - XXX. mcocd Intenatonal ultdscplnay Scentfc Confeence Unvesty of skolc Hungay - pl 06 ISBN 978-963-358-3- COPLEENTRY ENERGY ETHOD FOR CURVED COPOSITE BES Ákos József Lengyel István Ecsed ssstant
Engineering Mechanics. Force resultants, Torques, Scalar Products, Equivalent Force systems
 Engneeng echancs oce esultants, Toques, Scala oducts, Equvalent oce sstems Tata cgaw-hll Companes, 008 Resultant of Two oces foce: acton of one bod on anothe; chaacteed b ts pont of applcaton, magntude,
Engneeng echancs oce esultants, Toques, Scala oducts, Equvalent oce sstems Tata cgaw-hll Companes, 008 Resultant of Two oces foce: acton of one bod on anothe; chaacteed b ts pont of applcaton, magntude,
3.1 Electrostatic Potential Energy and Potential Difference
 3. lectostatc Potental negy and Potental Dffeence RMMR fom mechancs: - The potental enegy can be defned fo a system only f consevatve foces act between ts consttuents. - Consevatve foces may depend only
3. lectostatc Potental negy and Potental Dffeence RMMR fom mechancs: - The potental enegy can be defned fo a system only f consevatve foces act between ts consttuents. - Consevatve foces may depend only
19 The Born-Oppenheimer Approximation
 9 The Bon-Oppenheme Appoxmaton The full nonelatvstc Hamltonan fo a molecule s gven by (n a.u.) Ĥ = A M A A A, Z A + A + >j j (883) Lets ewte the Hamltonan to emphasze the goal as Ĥ = + A A A, >j j M A
9 The Bon-Oppenheme Appoxmaton The full nonelatvstc Hamltonan fo a molecule s gven by (n a.u.) Ĥ = A M A A A, Z A + A + >j j (883) Lets ewte the Hamltonan to emphasze the goal as Ĥ = + A A A, >j j M A
COMPUTATIONAL METHODS AND ALGORITHMS Vol. I - Methods of Potential Theory - V.I. Agoshkov, P.B. Dubovski
 METHODS OF POTENTIAL THEORY.I. Agoshkov and P.B. Dubovsk Insttute of Numecal Mathematcs, Russan Academy of Scences, Moscow, Russa Keywods: Potental, volume potental, Newton s potental, smple laye potental,
METHODS OF POTENTIAL THEORY.I. Agoshkov and P.B. Dubovsk Insttute of Numecal Mathematcs, Russan Academy of Scences, Moscow, Russa Keywods: Potental, volume potental, Newton s potental, smple laye potental,
UNIVERSITÀ DI PISA. Math thbackground
 UNIVERSITÀ DI ISA Electomagnetc Radatons and Bologcal l Inteactons Lauea Magstale n Bomedcal Engneeng Fst semeste (6 cedts), academc ea 2011/12 of. aolo Nepa p.nepa@et.unp.t Math thbackgound Edted b D.
UNIVERSITÀ DI ISA Electomagnetc Radatons and Bologcal l Inteactons Lauea Magstale n Bomedcal Engneeng Fst semeste (6 cedts), academc ea 2011/12 of. aolo Nepa p.nepa@et.unp.t Math thbackgound Edted b D.
V. Principles of Irreversible Thermodynamics. s = S - S 0 (7.3) s = = - g i, k. "Flux": = da i. "Force": = -Â g a ik k = X i. Â J i X i (7.
 Themodynamcs and Knetcs of Solds 71 V. Pncples of Ievesble Themodynamcs 5. Onsage s Teatment s = S - S 0 = s( a 1, a 2,...) a n = A g - A n (7.6) Equlbum themodynamcs detemnes the paametes of an equlbum
Themodynamcs and Knetcs of Solds 71 V. Pncples of Ievesble Themodynamcs 5. Onsage s Teatment s = S - S 0 = s( a 1, a 2,...) a n = A g - A n (7.6) Equlbum themodynamcs detemnes the paametes of an equlbum
Dynamics of Rigid Bodies
 Dynamcs of Rgd Bodes A gd body s one n whch the dstances between consttuent patcles s constant thoughout the moton of the body,.e. t keeps ts shape. Thee ae two knds of gd body moton: 1. Tanslatonal Rectlnea
Dynamcs of Rgd Bodes A gd body s one n whch the dstances between consttuent patcles s constant thoughout the moton of the body,.e. t keeps ts shape. Thee ae two knds of gd body moton: 1. Tanslatonal Rectlnea
CSU ATS601 Fall Other reading: Vallis 2.1, 2.2; Marshall and Plumb Ch. 6; Holton Ch. 2; Schubert Ch r or v i = v r + r (3.
 3 Eath s Rotaton 3.1 Rotatng Famewok Othe eadng: Valls 2.1, 2.2; Mashall and Plumb Ch. 6; Holton Ch. 2; Schubet Ch. 3 Consde the poston vecto (the same as C n the fgue above) otatng at angula velocty.
3 Eath s Rotaton 3.1 Rotatng Famewok Othe eadng: Valls 2.1, 2.2; Mashall and Plumb Ch. 6; Holton Ch. 2; Schubet Ch. 3 Consde the poston vecto (the same as C n the fgue above) otatng at angula velocty.
UNIT10 PLANE OF REGRESSION
 UIT0 PLAE OF REGRESSIO Plane of Regesson Stuctue 0. Intoducton Ojectves 0. Yule s otaton 0. Plane of Regesson fo thee Vaales 0.4 Popetes of Resduals 0.5 Vaance of the Resduals 0.6 Summay 0.7 Solutons /
UIT0 PLAE OF REGRESSIO Plane of Regesson Stuctue 0. Intoducton Ojectves 0. Yule s otaton 0. Plane of Regesson fo thee Vaales 0.4 Popetes of Resduals 0.5 Vaance of the Resduals 0.6 Summay 0.7 Solutons /
Physics 202, Lecture 2. Announcements
 Physcs 202, Lectue 2 Today s Topcs Announcements Electc Felds Moe on the Electc Foce (Coulomb s Law The Electc Feld Moton of Chaged Patcles n an Electc Feld Announcements Homewok Assgnment #1: WebAssgn
Physcs 202, Lectue 2 Today s Topcs Announcements Electc Felds Moe on the Electc Foce (Coulomb s Law The Electc Feld Moton of Chaged Patcles n an Electc Feld Announcements Homewok Assgnment #1: WebAssgn
4.4 Continuum Thermomechanics
 4.4 Contnuum Themomechancs The classcal themodynamcs s now extended to the themomechancs of a contnuum. The state aables ae allowed to ay thoughout a mateal and pocesses ae allowed to be eesble and moe
4.4 Contnuum Themomechancs The classcal themodynamcs s now extended to the themomechancs of a contnuum. The state aables ae allowed to ay thoughout a mateal and pocesses ae allowed to be eesble and moe
PHY126 Summer Session I, 2008
 PHY6 Summe Sesson I, 8 Most of nfomaton s avalable at: http://nngoup.phscs.sunsb.edu/~chak/phy6-8 ncludng the sllabus and lectue sldes. Read sllabus and watch fo mpotant announcements. Homewok assgnment
PHY6 Summe Sesson I, 8 Most of nfomaton s avalable at: http://nngoup.phscs.sunsb.edu/~chak/phy6-8 ncludng the sllabus and lectue sldes. Read sllabus and watch fo mpotant announcements. Homewok assgnment
Tensor. Syllabus: x x
 Tenso Sllabus: Tenso Calculus : Catesan tensos. Smmetc and antsmmetc tensos. Lev Vvta tenso denst. Pseudo tensos. Dual tensos. Dect poduct and contacton. Dads and dadc. Covaant, Contavaant and med tensos.
Tenso Sllabus: Tenso Calculus : Catesan tensos. Smmetc and antsmmetc tensos. Lev Vvta tenso denst. Pseudo tensos. Dual tensos. Dect poduct and contacton. Dads and dadc. Covaant, Contavaant and med tensos.
Mechanics Physics 151
 Mechancs Physcs 151 Lectue 18 Hamltonan Equatons of Moton (Chapte 8) What s Ahead We ae statng Hamltonan fomalsm Hamltonan equaton Today and 11/6 Canoncal tansfomaton 1/3, 1/5, 1/10 Close lnk to non-elatvstc
Mechancs Physcs 151 Lectue 18 Hamltonan Equatons of Moton (Chapte 8) What s Ahead We ae statng Hamltonan fomalsm Hamltonan equaton Today and 11/6 Canoncal tansfomaton 1/3, 1/5, 1/10 Close lnk to non-elatvstc
iclicker Quiz a) True b) False Theoretical physics: the eternal quest for a missing minus sign and/or a factor of two. Which will be an issue today?
 Clce Quz I egsteed my quz tansmtte va the couse webste (not on the clce.com webste. I ealze that untl I do so, my quz scoes wll not be ecoded. a Tue b False Theoetcal hyscs: the etenal quest fo a mssng
Clce Quz I egsteed my quz tansmtte va the couse webste (not on the clce.com webste. I ealze that untl I do so, my quz scoes wll not be ecoded. a Tue b False Theoetcal hyscs: the etenal quest fo a mssng
Some Approximate Analytical Steady-State Solutions for Cylindrical Fin
 Some Appoxmate Analytcal Steady-State Solutons fo Cylndcal Fn ANITA BRUVERE ANDRIS BUIIS Insttute of Mathematcs and Compute Scence Unvesty of Latva Rana ulv 9 Rga LV459 LATVIA Astact: - In ths pape we
Some Appoxmate Analytcal Steady-State Solutons fo Cylndcal Fn ANITA BRUVERE ANDRIS BUIIS Insttute of Mathematcs and Compute Scence Unvesty of Latva Rana ulv 9 Rga LV459 LATVIA Astact: - In ths pape we
(read nabla or del) is defined by, k. (9.7.1*)
 9.7 Gadient of a scala field. Diectional deivative Some of the vecto fields in applications can be obtained fom scala fields. This is vey advantageous because scala fields can be handled moe easily. The
9.7 Gadient of a scala field. Diectional deivative Some of the vecto fields in applications can be obtained fom scala fields. This is vey advantageous because scala fields can be handled moe easily. The
1. A body will remain in a state of rest, or of uniform motion in a straight line unless it
 Pncples of Dnamcs: Newton's Laws of moton. : Foce Analss 1. A bod wll eman n a state of est, o of unfom moton n a staght lne unless t s acted b etenal foces to change ts state.. The ate of change of momentum
Pncples of Dnamcs: Newton's Laws of moton. : Foce Analss 1. A bod wll eman n a state of est, o of unfom moton n a staght lne unless t s acted b etenal foces to change ts state.. The ate of change of momentum
Rotational Kinematics. Rigid Object about a Fixed Axis Western HS AP Physics 1
 Rotatonal Knematcs Rgd Object about a Fxed Axs Westen HS AP Physcs 1 Leanng Objectes What we know Unfom Ccula Moton q s Centpetal Acceleaton : Centpetal Foce: Non-unfom a F c c m F F F t m ma t What we
Rotatonal Knematcs Rgd Object about a Fxed Axs Westen HS AP Physcs 1 Leanng Objectes What we know Unfom Ccula Moton q s Centpetal Acceleaton : Centpetal Foce: Non-unfom a F c c m F F F t m ma t What we
Multipole Radiation. March 17, 2014
 Multpole Radaton Mach 7, 04 Zones We wll see that the poblem of hamonc adaton dvdes nto thee appoxmate egons, dependng on the elatve magntudes of the dstance of the obsevaton pont,, and the wavelength,
Multpole Radaton Mach 7, 04 Zones We wll see that the poblem of hamonc adaton dvdes nto thee appoxmate egons, dependng on the elatve magntudes of the dstance of the obsevaton pont,, and the wavelength,
Multistage Median Ranked Set Sampling for Estimating the Population Median
 Jounal of Mathematcs and Statstcs 3 (: 58-64 007 ISSN 549-3644 007 Scence Publcatons Multstage Medan Ranked Set Samplng fo Estmatng the Populaton Medan Abdul Azz Jeman Ame Al-Oma and Kamaulzaman Ibahm
Jounal of Mathematcs and Statstcs 3 (: 58-64 007 ISSN 549-3644 007 Scence Publcatons Multstage Medan Ranked Set Samplng fo Estmatng the Populaton Medan Abdul Azz Jeman Ame Al-Oma and Kamaulzaman Ibahm
The Forming Theory and the NC Machining for The Rotary Burs with the Spectral Edge Distribution
 oden Appled Scence The Fomn Theoy and the NC achnn fo The Rotay us wth the Spectal Ede Dstbuton Huan Lu Depatment of echancal Enneen, Zhejan Unvesty of Scence and Technoloy Hanzhou, c.y. chan, 310023,
oden Appled Scence The Fomn Theoy and the NC achnn fo The Rotay us wth the Spectal Ede Dstbuton Huan Lu Depatment of echancal Enneen, Zhejan Unvesty of Scence and Technoloy Hanzhou, c.y. chan, 310023,
If there are k binding constraints at x then re-label these constraints so that they are the first k constraints.
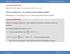 Mathematcal Foundatons -1- Constaned Optmzaton Constaned Optmzaton Ma{ f ( ) X} whee X {, h ( ), 1,, m} Necessay condtons fo to be a soluton to ths mamzaton poblem Mathematcally, f ag Ma{ f ( ) X}, then
Mathematcal Foundatons -1- Constaned Optmzaton Constaned Optmzaton Ma{ f ( ) X} whee X {, h ( ), 1,, m} Necessay condtons fo to be a soluton to ths mamzaton poblem Mathematcally, f ag Ma{ f ( ) X}, then
3. A Review of Some Existing AW (BT, CT) Algorithms
 3. A Revew of Some Exstng AW (BT, CT) Algothms In ths secton, some typcal ant-wndp algothms wll be descbed. As the soltons fo bmpless and condtoned tansfe ae smla to those fo ant-wndp, the pesented algothms
3. A Revew of Some Exstng AW (BT, CT) Algothms In ths secton, some typcal ant-wndp algothms wll be descbed. As the soltons fo bmpless and condtoned tansfe ae smla to those fo ant-wndp, the pesented algothms
Physics Exam II Chapters 25-29
 Physcs 114 1 Exam II Chaptes 5-9 Answe 8 of the followng 9 questons o poblems. Each one s weghted equally. Clealy mak on you blue book whch numbe you do not want gaded. If you ae not sue whch one you do
Physcs 114 1 Exam II Chaptes 5-9 Answe 8 of the followng 9 questons o poblems. Each one s weghted equally. Clealy mak on you blue book whch numbe you do not want gaded. If you ae not sue whch one you do
IV.3 VECTOR ANALYSIS Revisited and Enhanced
 hapte I ecto and Tenso nalsis I. ecto nalsis - Revisited eptembe 5, 7 69 I. ETOR NLYI Revisited and Enhanced hapte I ecto and Tenso nalsis I. ecto nalsis - Revisited eptembe 5, 7 7. ETOR FUNTION Let be
hapte I ecto and Tenso nalsis I. ecto nalsis - Revisited eptembe 5, 7 69 I. ETOR NLYI Revisited and Enhanced hapte I ecto and Tenso nalsis I. ecto nalsis - Revisited eptembe 5, 7 7. ETOR FUNTION Let be
Capítulo. Three Dimensions
 Capítulo Knematcs of Rgd Bodes n Thee Dmensons Mecánca Contents ntoducton Rgd Bod Angula Momentum n Thee Dmensons Pncple of mpulse and Momentum Knetc Eneg Sample Poblem 8. Sample Poblem 8. Moton of a Rgd
Capítulo Knematcs of Rgd Bodes n Thee Dmensons Mecánca Contents ntoducton Rgd Bod Angula Momentum n Thee Dmensons Pncple of mpulse and Momentum Knetc Eneg Sample Poblem 8. Sample Poblem 8. Moton of a Rgd
Chapter 3 Waves in an Elastic Whole Space. Equation of Motion of a Solid
 Chapte 3 Waves n an Elastc Whole Space Equaton of Moton of a Sold Hopefully, many of the topcs n ths chapte ae evew. Howeve, I fnd t useful to dscuss some of the key chaactestcs of elastc contnuous meda.
Chapte 3 Waves n an Elastc Whole Space Equaton of Moton of a Sold Hopefully, many of the topcs n ths chapte ae evew. Howeve, I fnd t useful to dscuss some of the key chaactestcs of elastc contnuous meda.
The Unique Solution of Stochastic Differential Equations With. Independent Coefficients. Dietrich Ryter.
 The Unque Soluton of Stochastc Dffeental Equatons Wth Independent Coeffcents Detch Ryte RyteDM@gawnet.ch Mdatweg 3 CH-4500 Solothun Swtzeland Phone +4132 621 13 07 SDE s must be solved n the ant-itô sense
The Unque Soluton of Stochastc Dffeental Equatons Wth Independent Coeffcents Detch Ryte RyteDM@gawnet.ch Mdatweg 3 CH-4500 Solothun Swtzeland Phone +4132 621 13 07 SDE s must be solved n the ant-itô sense
AE301 Aerodynamics I UNIT B: Theory of Aerodynamics
 AE301 Aeodynamics I UNIT B: Theoy of Aeodynamics ROAD MAP... B-1: Mathematics fo Aeodynamics B-2: Flow Field Repesentations B-3: Potential Flow Analysis B-4: Applications of Potential Flow Analysis AE301
AE301 Aeodynamics I UNIT B: Theoy of Aeodynamics ROAD MAP... B-1: Mathematics fo Aeodynamics B-2: Flow Field Repesentations B-3: Potential Flow Analysis B-4: Applications of Potential Flow Analysis AE301
A. Thicknesses and Densities
 10 Lab0 The Eath s Shells A. Thcknesses and Denstes Any theoy of the nteo of the Eath must be consstent wth the fact that ts aggegate densty s 5.5 g/cm (ecall we calculated ths densty last tme). In othe
10 Lab0 The Eath s Shells A. Thcknesses and Denstes Any theoy of the nteo of the Eath must be consstent wth the fact that ts aggegate densty s 5.5 g/cm (ecall we calculated ths densty last tme). In othe
Stellar Astrophysics. dt dr. GM r. The current model for treating convection in stellar interiors is called mixing length theory:
 Stella Astophyscs Ovevew of last lectue: We connected the mean molecula weght to the mass factons X, Y and Z: 1 1 1 = X + Y + μ 1 4 n 1 (1 + 1) = X μ 1 1 A n Z (1 + ) + Y + 4 1+ z A Z We ntoduced the pessue
Stella Astophyscs Ovevew of last lectue: We connected the mean molecula weght to the mass factons X, Y and Z: 1 1 1 = X + Y + μ 1 4 n 1 (1 + 1) = X μ 1 1 A n Z (1 + ) + Y + 4 1+ z A Z We ntoduced the pessue
Review: Electrostatics and Magnetostatics
 Review: Electostatics and Magnetostatics In the static egime, electomagnetic quantities do not vay as a function of time. We have two main cases: ELECTROSTATICS The electic chages do not change postion
Review: Electostatics and Magnetostatics In the static egime, electomagnetic quantities do not vay as a function of time. We have two main cases: ELECTROSTATICS The electic chages do not change postion
DYNAMICS VECTOR MECHANICS FOR ENGINEERS: Kinematics of Rigid Bodies in Three Dimensions. Seventh Edition CHAPTER
 Edton CAPTER 8 VECTOR MECANCS FOR ENGNEERS: DYNAMCS Fednand P. Bee E. Russell Johnston, J. Lectue Notes: J. Walt Ole Teas Tech Unvest Knematcs of Rgd Bodes n Thee Dmensons 003 The McGaw-ll Companes, nc.
Edton CAPTER 8 VECTOR MECANCS FOR ENGNEERS: DYNAMCS Fednand P. Bee E. Russell Johnston, J. Lectue Notes: J. Walt Ole Teas Tech Unvest Knematcs of Rgd Bodes n Thee Dmensons 003 The McGaw-ll Companes, nc.
Physics 1501 Lecture 19
 Physcs 1501 ectue 19 Physcs 1501: ectue 19 Today s Agenda Announceents HW#7: due Oct. 1 Mdte 1: aveage 45 % Topcs otatonal Kneatcs otatonal Enegy Moents of Ineta Physcs 1501: ectue 19, Pg 1 Suay (wth copason
Physcs 1501 ectue 19 Physcs 1501: ectue 19 Today s Agenda Announceents HW#7: due Oct. 1 Mdte 1: aveage 45 % Topcs otatonal Kneatcs otatonal Enegy Moents of Ineta Physcs 1501: ectue 19, Pg 1 Suay (wth copason
Physics 2A Chapter 11 - Universal Gravitation Fall 2017
 Physcs A Chapte - Unvesal Gavtaton Fall 07 hese notes ae ve pages. A quck summay: he text boxes n the notes contan the esults that wll compse the toolbox o Chapte. hee ae thee sectons: the law o gavtaton,
Physcs A Chapte - Unvesal Gavtaton Fall 07 hese notes ae ve pages. A quck summay: he text boxes n the notes contan the esults that wll compse the toolbox o Chapte. hee ae thee sectons: the law o gavtaton,
Remember: When an object falls due to gravity its potential energy decreases.
 Chapte 5: lectc Potental As mentoned seveal tmes dung the uate Newton s law o gavty and Coulomb s law ae dentcal n the mathematcal om. So, most thngs that ae tue o gavty ae also tue o electostatcs! Hee
Chapte 5: lectc Potental As mentoned seveal tmes dung the uate Newton s law o gavty and Coulomb s law ae dentcal n the mathematcal om. So, most thngs that ae tue o gavty ae also tue o electostatcs! Hee
ON THE FRESNEL SINE INTEGRAL AND THE CONVOLUTION
 IJMMS 3:37, 37 333 PII. S16117131151 http://jmms.hndaw.com Hndaw Publshng Cop. ON THE FRESNEL SINE INTEGRAL AND THE CONVOLUTION ADEM KILIÇMAN Receved 19 Novembe and n evsed fom 7 Mach 3 The Fesnel sne
IJMMS 3:37, 37 333 PII. S16117131151 http://jmms.hndaw.com Hndaw Publshng Cop. ON THE FRESNEL SINE INTEGRAL AND THE CONVOLUTION ADEM KILIÇMAN Receved 19 Novembe and n evsed fom 7 Mach 3 The Fesnel sne
As is natural, our Aerospace Structures will be described in a Euclidean three-dimensional space R 3.
 Appendix A Vecto Algeba As is natual, ou Aeospace Stuctues will be descibed in a Euclidean thee-dimensional space R 3. A.1 Vectos A vecto is used to epesent quantities that have both magnitude and diection.
Appendix A Vecto Algeba As is natual, ou Aeospace Stuctues will be descibed in a Euclidean thee-dimensional space R 3. A.1 Vectos A vecto is used to epesent quantities that have both magnitude and diection.
Part V: Velocity and Acceleration Analysis of Mechanisms
 Pat V: Velocty an Acceleaton Analyss of Mechansms Ths secton wll evew the most common an cuently pactce methos fo completng the knematcs analyss of mechansms; escbng moton though velocty an acceleaton.
Pat V: Velocty an Acceleaton Analyss of Mechansms Ths secton wll evew the most common an cuently pactce methos fo completng the knematcs analyss of mechansms; escbng moton though velocty an acceleaton.
APPLICATIONS OF SEMIGENERALIZED -CLOSED SETS
 Intenatonal Jounal of Mathematcal Engneeng Scence ISSN : 22776982 Volume Issue 4 (Apl 202) http://www.mes.com/ https://stes.google.com/ste/mesounal/ APPLICATIONS OF SEMIGENERALIZED CLOSED SETS G.SHANMUGAM,
Intenatonal Jounal of Mathematcal Engneeng Scence ISSN : 22776982 Volume Issue 4 (Apl 202) http://www.mes.com/ https://stes.google.com/ste/mesounal/ APPLICATIONS OF SEMIGENERALIZED CLOSED SETS G.SHANMUGAM,
Rotary motion
 ectue 8 RTARY TN F THE RGD BDY Notes: ectue 8 - Rgd bod Rgd bod: j const numbe of degees of feedom 6 3 tanslatonal + 3 ota motons m j m j Constants educe numbe of degees of feedom non-fee object: 6-p
ectue 8 RTARY TN F THE RGD BDY Notes: ectue 8 - Rgd bod Rgd bod: j const numbe of degees of feedom 6 3 tanslatonal + 3 ota motons m j m j Constants educe numbe of degees of feedom non-fee object: 6-p
ALL QUESTIONS ARE WORTH 20 POINTS. WORK OUT FIVE PROBLEMS.
 GNRAL PHYSICS PH -3A (D. S. Mov) Test (/3/) key STUDNT NAM: STUDNT d #: -------------------------------------------------------------------------------------------------------------------------------------------
GNRAL PHYSICS PH -3A (D. S. Mov) Test (/3/) key STUDNT NAM: STUDNT d #: -------------------------------------------------------------------------------------------------------------------------------------------
4 SingularValue Decomposition (SVD)
 /6/00 Z:\ jeh\self\boo Kannan\Jan-5-00\4 SVD 4 SngulaValue Decomposton (SVD) Chapte 4 Pat SVD he sngula value decomposton of a matx s the factozaton of nto the poduct of thee matces = UDV whee the columns
/6/00 Z:\ jeh\self\boo Kannan\Jan-5-00\4 SVD 4 SngulaValue Decomposton (SVD) Chapte 4 Pat SVD he sngula value decomposton of a matx s the factozaton of nto the poduct of thee matces = UDV whee the columns
APPENDIX A Some Linear Algebra
 APPENDIX A Some Lnear Algebra The collecton of m, n matrces A.1 Matrces a 1,1,..., a 1,n A = a m,1,..., a m,n wth real elements a,j s denoted by R m,n. If n = 1 then A s called a column vector. Smlarly,
APPENDIX A Some Lnear Algebra The collecton of m, n matrces A.1 Matrces a 1,1,..., a 1,n A = a m,1,..., a m,n wth real elements a,j s denoted by R m,n. If n = 1 then A s called a column vector. Smlarly,
Physics 207 Lecture 16
 Physcs 07 Lectue 6 Goals: Lectue 6 Chapte Extend the patcle odel to gd-bodes Undestand the equlbu of an extended object. Analyze ollng oton Undestand otaton about a fxed axs. Eploy consevaton of angula
Physcs 07 Lectue 6 Goals: Lectue 6 Chapte Extend the patcle odel to gd-bodes Undestand the equlbu of an extended object. Analyze ollng oton Undestand otaton about a fxed axs. Eploy consevaton of angula
Vector d is a linear vector function of vector d when the following relationships hold:
 Appendix 4 Dyadic Analysis DEFINITION ecto d is a linea vecto function of vecto d when the following elationships hold: d x = a xxd x + a xy d y + a xz d z d y = a yxd x + a yy d y + a yz d z d z = a zxd
Appendix 4 Dyadic Analysis DEFINITION ecto d is a linea vecto function of vecto d when the following elationships hold: d x = a xxd x + a xy d y + a xz d z d y = a yxd x + a yy d y + a yz d z d z = a zxd
2 dependence in the electrostatic force means that it is also
 lectc Potental negy an lectc Potental A scala el, nvolvng magntues only, s oten ease to wo wth when compae to a vecto el. Fo electc els not havng to begn wth vecto ssues woul be nce. To aange ths a scala
lectc Potental negy an lectc Potental A scala el, nvolvng magntues only, s oten ease to wo wth when compae to a vecto el. Fo electc els not havng to begn wth vecto ssues woul be nce. To aange ths a scala
Asymptotic Solutions of the Kinetic Boltzmann Equation and Multicomponent Non-Equilibrium Gas Dynamics
 Jounal of Appled Mathematcs and Physcs 6 4 687-697 Publshed Onlne August 6 n ScRes http://wwwscpog/jounal/jamp http://dxdoog/436/jamp64877 Asymptotc Solutons of the Knetc Boltzmann Equaton and Multcomponent
Jounal of Appled Mathematcs and Physcs 6 4 687-697 Publshed Onlne August 6 n ScRes http://wwwscpog/jounal/jamp http://dxdoog/436/jamp64877 Asymptotc Solutons of the Knetc Boltzmann Equaton and Multcomponent
Unit_III Complex Numbers: Some Basic Results: 1. If z = x +iy is a complex number, then the complex number z = x iy is
 Unt_III Comple Nmbes: In the sstem o eal nmbes R we can sole all qadatc eqatons o the om a b c, a, and the dscmnant b 4ac. When the dscmnant b 4ac
Unt_III Comple Nmbes: In the sstem o eal nmbes R we can sole all qadatc eqatons o the om a b c, a, and the dscmnant b 4ac. When the dscmnant b 4ac
2/24/2014. The point mass. Impulse for a single collision The impulse of a force is a vector. The Center of Mass. System of particles
 /4/04 Chapte 7 Lnea oentu Lnea oentu of a Sngle Patcle Lnea oentu: p υ It s a easue of the patcle s oton It s a vecto, sla to the veloct p υ p υ p υ z z p It also depends on the ass of the object, sla
/4/04 Chapte 7 Lnea oentu Lnea oentu of a Sngle Patcle Lnea oentu: p υ It s a easue of the patcle s oton It s a vecto, sla to the veloct p υ p υ p υ z z p It also depends on the ass of the object, sla
Khintchine-Type Inequalities and Their Applications in Optimization
 Khntchne-Type Inequaltes and The Applcatons n Optmzaton Anthony Man-Cho So Depatment of Systems Engneeng & Engneeng Management The Chnese Unvesty of Hong Kong ISDS-Kolloquum Unvestaet Wen 29 June 2009
Khntchne-Type Inequaltes and The Applcatons n Optmzaton Anthony Man-Cho So Depatment of Systems Engneeng & Engneeng Management The Chnese Unvesty of Hong Kong ISDS-Kolloquum Unvestaet Wen 29 June 2009
Pure infinitesimal geometry.
 Rene Infntesmalgeomete, Math. Z. 2 (1918), 384-411. Pue nfntesmal geomety. By Hemann Weyl n Züch 1. Intoducton. On the elatonshp between geomety and physcs. The eal wold n whch ou conscousness s foced
Rene Infntesmalgeomete, Math. Z. 2 (1918), 384-411. Pue nfntesmal geomety. By Hemann Weyl n Züch 1. Intoducton. On the elatonshp between geomety and physcs. The eal wold n whch ou conscousness s foced
Summer Workshop on the Reaction Theory Exercise sheet 8. Classwork
 Joned Physcs Analyss Cente Summe Wokshop on the Reacton Theoy Execse sheet 8 Vncent Matheu Contact: http://www.ndana.edu/~sst/ndex.html June June To be dscussed on Tuesday of Week-II. Classwok. Deve all
Joned Physcs Analyss Cente Summe Wokshop on the Reacton Theoy Execse sheet 8 Vncent Matheu Contact: http://www.ndana.edu/~sst/ndex.html June June To be dscussed on Tuesday of Week-II. Classwok. Deve all
Rotating Disk Electrode -a hydrodynamic method
 Rotatng Dsk Electode -a hdodnamc method Fe Lu Ma 3, 0 ente fo Electochemcal Engneeng Reseach Depatment of hemcal and Bomolecula Engneeng Rotatng Dsk Electode A otatng dsk electode RDE s a hdodnamc wokng
Rotatng Dsk Electode -a hdodnamc method Fe Lu Ma 3, 0 ente fo Electochemcal Engneeng Reseach Depatment of hemcal and Bomolecula Engneeng Rotatng Dsk Electode A otatng dsk electode RDE s a hdodnamc wokng
Physics 201 Lecture 4
 Phscs 1 Lectue 4 ltoda: hapte 3 Lectue 4 v Intoduce scalas and vectos v Peom basc vecto aleba (addton and subtacton) v Inteconvet between atesan & Pola coodnates Stat n nteestn 1D moton poblem: ace 9.8
Phscs 1 Lectue 4 ltoda: hapte 3 Lectue 4 v Intoduce scalas and vectos v Peom basc vecto aleba (addton and subtacton) v Inteconvet between atesan & Pola coodnates Stat n nteestn 1D moton poblem: ace 9.8
Lie Subalgebras and Invariant Solutions to the Equation of Fluid Flows in Toroidal Field. Lang Xia
 Le Subalgebas and Invaant Solutons to the Equaton of Flud Flows n Toodal Feld Lang a Emal: langxaog@gmalcom Abstact: Patal dffeental equatons (PDEs), patculaly coupled PDE systems, ae dffcult to solve
Le Subalgebas and Invaant Solutons to the Equaton of Flud Flows n Toodal Feld Lang a Emal: langxaog@gmalcom Abstact: Patal dffeental equatons (PDEs), patculaly coupled PDE systems, ae dffcult to solve
Hamiltonian multivector fields and Poisson forms in multisymplectic field theory
 JOURNAL OF MATHEMATICAL PHYSICS 46, 12005 Hamltonan multvecto felds and Posson foms n multsymplectc feld theoy Mchael Foge a Depatamento de Matemátca Aplcada, Insttuto de Matemátca e Estatístca, Unvesdade
JOURNAL OF MATHEMATICAL PHYSICS 46, 12005 Hamltonan multvecto felds and Posson foms n multsymplectc feld theoy Mchael Foge a Depatamento de Matemátca Aplcada, Insttuto de Matemátca e Estatístca, Unvesdade
gravity r2,1 r2 r1 by m 2,1
 Gavtaton Many of the foundatons of classcal echancs wee fst dscoveed when phlosophes (ealy scentsts and atheatcans) ted to explan the oton of planets and stas. Newton s ost faous fo unfyng the oton of
Gavtaton Many of the foundatons of classcal echancs wee fst dscoveed when phlosophes (ealy scentsts and atheatcans) ted to explan the oton of planets and stas. Newton s ost faous fo unfyng the oton of
Chapter 10 and elements of 11, 12 Rotation of Rigid Bodies
 Chapte 10 and elements of 11, 1 Rotaton of Rgd Bodes What s a Rgd Body? Rotatonal Knematcs Angula Velocty ω and Acceleaton α Rotaton wth Constant Acceleaton Angula vs. Lnea Knematcs Enegy n Rotatonal Moton:
Chapte 10 and elements of 11, 1 Rotaton of Rgd Bodes What s a Rgd Body? Rotatonal Knematcs Angula Velocty ω and Acceleaton α Rotaton wth Constant Acceleaton Angula vs. Lnea Knematcs Enegy n Rotatonal Moton:
Potential Theory. Copyright 2004
 Copyght 004 4 Potental Theoy We have seen how the soluton of any classcal echancs poble s fst one of detenng the equatons of oton. These then ust be solved n ode to fnd the oton of the patcles that copse
Copyght 004 4 Potental Theoy We have seen how the soluton of any classcal echancs poble s fst one of detenng the equatons of oton. These then ust be solved n ode to fnd the oton of the patcles that copse
2. Electrostatics. Dr. Rakhesh Singh Kshetrimayum 8/11/ Electromagnetic Field Theory by R. S. Kshetrimayum
 2. Electostatics D. Rakhesh Singh Kshetimayum 1 2.1 Intoduction In this chapte, we will study how to find the electostatic fields fo vaious cases? fo symmetic known chage distibution fo un-symmetic known
2. Electostatics D. Rakhesh Singh Kshetimayum 1 2.1 Intoduction In this chapte, we will study how to find the electostatic fields fo vaious cases? fo symmetic known chage distibution fo un-symmetic known
ECE 3318 Applied Electricity and Magnetism. Spring Prof. David R. Jackson ECE Dept. Notes 13
 ECE 338 Applied Electicity and Magnetism ping 07 Pof. David R. Jackson ECE Dept. Notes 3 Divegence The Physical Concept Find the flux going outwad though a sphee of adius. x ρ v0 z a y ψ = D nˆ d = D ˆ
ECE 338 Applied Electicity and Magnetism ping 07 Pof. David R. Jackson ECE Dept. Notes 3 Divegence The Physical Concept Find the flux going outwad though a sphee of adius. x ρ v0 z a y ψ = D nˆ d = D ˆ
The Greatest Deviation Correlation Coefficient and its Geometrical Interpretation
 By Rudy A. Gdeon The Unvesty of Montana The Geatest Devaton Coelaton Coeffcent and ts Geometcal Intepetaton The Geatest Devaton Coelaton Coeffcent (GDCC) was ntoduced by Gdeon and Hollste (987). The GDCC
By Rudy A. Gdeon The Unvesty of Montana The Geatest Devaton Coelaton Coeffcent and ts Geometcal Intepetaton The Geatest Devaton Coelaton Coeffcent (GDCC) was ntoduced by Gdeon and Hollste (987). The GDCC
Correspondence Analysis & Related Methods
 Coespondence Analyss & Related Methods Ineta contbutons n weghted PCA PCA s a method of data vsualzaton whch epesents the tue postons of ponts n a map whch comes closest to all the ponts, closest n sense
Coespondence Analyss & Related Methods Ineta contbutons n weghted PCA PCA s a method of data vsualzaton whch epesents the tue postons of ponts n a map whch comes closest to all the ponts, closest n sense
Pattern Analyses (EOF Analysis) Introduction Definition of EOFs Estimation of EOFs Inference Rotated EOFs
 Patten Analyses (EOF Analyss) Intoducton Defnton of EOFs Estmaton of EOFs Infeence Rotated EOFs . Patten Analyses Intoducton: What s t about? Patten analyses ae technques used to dentfy pattens of the
Patten Analyses (EOF Analyss) Intoducton Defnton of EOFs Estmaton of EOFs Infeence Rotated EOFs . Patten Analyses Intoducton: What s t about? Patten analyses ae technques used to dentfy pattens of the
TUTORIAL 9. Static magnetic field
 TUTOIAL 9 Static magnetic field Vecto magnetic potential Null Identity % & %$ A # Fist postulation # " B such that: Vecto magnetic potential Vecto Poisson s equation The solution is: " Substitute it into
TUTOIAL 9 Static magnetic field Vecto magnetic potential Null Identity % & %$ A # Fist postulation # " B such that: Vecto magnetic potential Vecto Poisson s equation The solution is: " Substitute it into
LINEAR MOMENTUM. product of the mass m and the velocity v r of an object r r
 LINEAR MOMENTUM Imagne beng on a skateboad, at est that can move wthout cton on a smooth suace You catch a heavy, slow-movng ball that has been thown to you you begn to move Altenatvely you catch a lght,
LINEAR MOMENTUM Imagne beng on a skateboad, at est that can move wthout cton on a smooth suace You catch a heavy, slow-movng ball that has been thown to you you begn to move Altenatvely you catch a lght,
One-dimensional kinematics
 Phscs 45 Fomula Sheet Eam 3 One-dmensonal knematcs Vectos dsplacement: Δ total dstance taveled aveage speed total tme Δ aveage veloct: vav t t Δ nstantaneous veloct: v lm Δ t v aveage acceleaton: aav t
Phscs 45 Fomula Sheet Eam 3 One-dmensonal knematcs Vectos dsplacement: Δ total dstance taveled aveage speed total tme Δ aveage veloct: vav t t Δ nstantaneous veloct: v lm Δ t v aveage acceleaton: aav t
Chapter I Vector Analysis
 . Chpte I Vecto nlss . Vecto lgeb j It s well-nown tht n vecto cn be wtten s Vectos obe the followng lgebc ules: scl s ) ( j v v cos ) ( e Commuttv ) ( ssoctve C C ) ( ) ( v j ) ( ) ( ) ( ) ( (v) he lw
. Chpte I Vecto nlss . Vecto lgeb j It s well-nown tht n vecto cn be wtten s Vectos obe the followng lgebc ules: scl s ) ( j v v cos ) ( e Commuttv ) ( ssoctve C C ) ( ) ( v j ) ( ) ( ) ( ) ( (v) he lw
Instantaneous velocity field of a round jet
 Fee shea flows Instantaneos velocty feld of a ond et 3 Aveage velocty feld of a ond et 4 Vtal ogn nozzle coe Developng egon elf smla egon 5 elf smlaty caled vaables: ~ Q ξ ( ξ, ) y δ ( ) Q Q (, y) ( )
Fee shea flows Instantaneos velocty feld of a ond et 3 Aveage velocty feld of a ond et 4 Vtal ogn nozzle coe Developng egon elf smla egon 5 elf smlaty caled vaables: ~ Q ξ ( ξ, ) y δ ( ) Q Q (, y) ( )
Contact, information, consultations
 ontact, nfomaton, consultatons hemsty A Bldg; oom 07 phone: 058-347-769 cellula: 664 66 97 E-mal: wojtek_c@pg.gda.pl Offce hous: Fday, 9-0 a.m. A quote of the week (o camel of the week): hee s no expedence
ontact, nfomaton, consultatons hemsty A Bldg; oom 07 phone: 058-347-769 cellula: 664 66 97 E-mal: wojtek_c@pg.gda.pl Offce hous: Fday, 9-0 a.m. A quote of the week (o camel of the week): hee s no expedence
Physica A 392 (2013) Contents lists available at SciVerse ScienceDirect. Physica A. journal homepage:
 Physca A 392 (2013) 1318 1335 Contents lsts avalable at ScVese ScenceDect Physca A jounal homepage: www.elseve.com/locate/physa Themodynamcs n the lmt of evesble eactons A.N. Goban a,, E.M. Mkes b, G.S.
Physca A 392 (2013) 1318 1335 Contents lsts avalable at ScVese ScenceDect Physca A jounal homepage: www.elseve.com/locate/physa Themodynamcs n the lmt of evesble eactons A.N. Goban a,, E.M. Mkes b, G.S.
PHYS Week 5. Reading Journals today from tables. WebAssign due Wed nite
 PHYS 015 -- Week 5 Readng Jounals today fom tables WebAssgn due Wed nte Fo exclusve use n PHYS 015. Not fo e-dstbuton. Some mateals Copyght Unvesty of Coloado, Cengage,, Peason J. Maps. Fundamental Tools
PHYS 015 -- Week 5 Readng Jounals today fom tables WebAssgn due Wed nte Fo exclusve use n PHYS 015. Not fo e-dstbuton. Some mateals Copyght Unvesty of Coloado, Cengage,, Peason J. Maps. Fundamental Tools
Chapter 12 Equilibrium and Elasticity
 Chapte 12 Equlbum and Elastcty In ths chapte we wll defne equlbum and fnd the condtons needed so that an object s at equlbum. We wll then apply these condtons to a vaety of pactcal engneeng poblems of
Chapte 12 Equlbum and Elastcty In ths chapte we wll defne equlbum and fnd the condtons needed so that an object s at equlbum. We wll then apply these condtons to a vaety of pactcal engneeng poblems of
MULTIPOLE FIELDS. Multipoles, 2 l poles. Monopoles, dipoles, quadrupoles, octupoles... Electric Dipole R 1 R 2. P(r,θ,φ) e r
 MULTIPOLE FIELDS Mutpoes poes. Monopoes dpoes quadupoes octupoes... 4 8 6 Eectc Dpoe +q O θ e R R P(θφ) -q e The potenta at the fed pont P(θφ) s ( θϕ )= q R R Bo E. Seneus : Now R = ( e) = + cosθ R = (
MULTIPOLE FIELDS Mutpoes poes. Monopoes dpoes quadupoes octupoes... 4 8 6 Eectc Dpoe +q O θ e R R P(θφ) -q e The potenta at the fed pont P(θφ) s ( θϕ )= q R R Bo E. Seneus : Now R = ( e) = + cosθ R = (
Groupoid and Topological Quotient Group
 lobal Jounal of Pue and Appled Mathematcs SSN 0973-768 Volume 3 Numbe 7 07 pp 373-39 Reseach nda Publcatons http://wwwpublcatoncom oupod and Topolocal Quotent oup Mohammad Qasm Manna Depatment of Mathematcs
lobal Jounal of Pue and Appled Mathematcs SSN 0973-768 Volume 3 Numbe 7 07 pp 373-39 Reseach nda Publcatons http://wwwpublcatoncom oupod and Topolocal Quotent oup Mohammad Qasm Manna Depatment of Mathematcs
