This document is stored in Documents/4C/nablaoperator.tex. Compile it with LaTex. VECTOR CALCULUS
|
|
|
- Paula Stokes
- 6 years ago
- Views:
Transcription
1 This document is stored in Documents/4C/nablaoperator.tex. Compile it with LaTex. November 12, 2014 Hans P. Paar VECTOR CALCULUS 1 Introduction sec:intro Vector calculus is a branch of mathematics that allows differentiation and integration of scalar) functions and vector function in several variables at once. It is based upon multivariable calculus. A scalar) function is a scalar whose value depends upon several variables. Examples are the temperature and pressure of the atmosphere, the densit of an inhomogeneous solid and so on. A vector function also called a vector field) is a vector whose components depend upon several variables. Examples of these are the electric and magnetic field, the velocit of a fluid, and so on. In the present case we are dealing with vectors in three-dimensional space so the have three components. The number of variables that functions and vector components can depend on is also three. In this chapter we review the formalism of the nabla operator ) and what it is used for in vector calculus. 2 The Operator We obviousl must require r 0. sec:nabla The fundamental operator we deal with in vector calculus is the operator. It is defined as = + e z eq:a1 The vectors, e, e z are three mutuall perpendicular unit vectors that 1 1)
2 form a right-handed triplet with along the positiv-axis and e along the positive -axis and e z along the positive z-axis. We do not use the notation i, j, k for these. The partial differentiations are familiar from multivariable calculus. It is seen that the operator is a vector because it is the sum of three terms that are each a vector. The order of the factors in each term does not matter because the unit vectors are constant vectors, independent of position x,, z so the partial differentiations will do nothing to them. This is all ou need to know besides some nomenclature) because everthing in vector calculus we need follows from the definition 1) of the operator. 3 The Gradient of a Scalar Function sec:grad The gradient of a scalar) function fx,,z), defined as f, is evaluated as f = + e ) z fx,, z) 2) eq:a2 Working out the parentheses in 2) we get f = f f + e f ) z eq:a3 It is seen that the gradient of a scalar) function is a vector. 4 The Divergence of a Vector Function sec:div The divergence of a vector function vx,, z), defined as v, is evaluated as v = + e ) z vx + v e + v z e z ) 4) eq:a4 Working out the parentheses in 4) we get nine terms. The three unit vectors, e, e z form a right-handed triplet of mutuall perpendicular unit vectors. So for example = 1, e = 0, etc. and we get 3) v = v x x + v + v z 5) 2
3 eq:a5 It is seen that the divergence of a vector function is a scalar as expected for the dot product of two vectors. 5 The Rotation of a Vector Function The rotation of a vector function vx,, z), defined as v, is evaluated as v = + e ) z vx + v e + v z e z ) 6) eq:a6 Working out the parentheses we get nine terms. The three unit vectors, e, e z form a right-handed triplet of mutuall perpendicular unit vectors. So for example = 0, e = e z, e z = e, etc. and we get v = v z v ) ex v z x v x ) e + v x v x ) ez 7) eq:a7 where we grouped terms according to, e, and e z. This formula is not eas to remember. It is seen that this result can also be obtained be evaluating the determinant e e z v = x 8) v x v v z eq:a6a The form of the determinant is easier to remember. It is seen that the curl of a vector function is a vector as expected for the cross product of two vectors. 6 Examples sec:ex When evaluating an expression involving the nabla operator determine ahead of time whether the result should be a scalar or vector entit. 3
4 The simplest example of a gradient is r where r = x z 2 is the length of the vector r = x + e + ze z. We get r = + e ) z x z 2 ) 1 2 9) eq:a7a Working out the parentheses in the first factor we get terms proportional to, e, and e z. The first of these can be evaluated as x x z 2 ) = 2 x z 2 ) 1 x 2 2x = r 10) eq:a7b Obviousl we must require r 0. Similar expressions hold for the other two terms. This can be seen b an explicit calculation or b replacing x b and replacing x b z respectivel in 10). It is a good idea to pick up these substitution tricks and save time. The also serve as a check if ou did the explicit calculation after all. All three expressions have a factor 1/r in common which we take outside parentheses to get r = x + e + e z z r = r r eq:a7c We expect r to be a vector and it is. The units work out too. If fx,, z) = r n then the gradient of f is 11) f = + e ) z x z 2 ) n 2 12) eq:a8 Working out the parentheses in the first factor we get terms proportional to, e, and e z. The first of these can be evaluated as x x z 2 ) n 2 = ex n 2 x z 2 ) n 2 1 2x = nx r n 2 13) eq:a9 Similar expressions hold for the other two terms. All three expressions have a factor nr n 2 in common which we take outside parentheses to get f = r n ) = x + e + e z z) nr n 2 = rnr n 2 14) 4
5 eq:a10 We expect f to be a vector and indeed it is. Obviousl we msut require r 0 when n < 2. We could have guessed the answer b using fr) = df r 15) dr eq:a10a which results in 14) as well. It is often true in vector calculus that when ou guess a relation it is often correct but it bears checking. This feature is what makes vector calculus useful. The special case n = 1 corresponds to a 1/r potential such as we encounter in electrostatics and gravit. The force is proportional to the negative of the gradient of f. Setting n = 1 in 14) we find that the force is proportional to r/r 3. The force is along r and has a magnitude proportional to 1/r 2 as expected. The proportionalit constant can be positive or negative so the direction of the force can be in the direction of r or in the direction of r. Other useful results are epressions for r and r. Using 5) with v = r = x,, z) we find r = 3 16) eq:a10aa Calculating r we find using 8) e e z r = x x z 17) which is identicall zero so eq:a6b r = 0 18) eq:a6c Next consider products of a scalar function f = fx,, z) and a vector function v = vx,, z). Examples are fv) and fv). In the first case we get fv) = + e ) z [fvx + v e + v z e z )] 19) 5
6 eq:a10b Working out the parenthese we get nine terms. The three unit vectors form a right-handed triplet of mutuall perpendicular unit vectors. So for example = 1, e = 0, etc and we get fv) = x fv x) + fv ) + fv z) 20) eq:a10c We use the chain rule of differentiation to find fv) = f x v x + f v x x + f v + f v + f v z + f v z 21) eq:a10d We regroup terms in a suggestive order as fv) = f x v x + f v + f v z + f v x x + f v + f v z 22) eq:a10e Using 3) and 5) we see that this equation can be written in a compact form as fv) = f) v + f v 23) eq:a10f You will soon be able to guess this result. It looks like the chain rule of differentiation applied to a product. Knowing that the result has to be a scalar this is the onl wa it can come out. Next consider the second case fv). e e z fv) = x fv x fv fv z eq:a10g In working out the determinant we get six terms. The first one is 24) fv z) = f v z + f v z 25) 6
7 eq:a10h where we used the chain rule of differentiation. There are no simplifications as before so we must add all two times six terms to get fv) = e f x v z + f vz f v ) f v e f x v z + f vz x f v ) x f vx + e f z x v + f v x f v ) x f vx 26) eq:a10i We regroup terms in a suggestive order b writing the odd numbered terms first followed b the even numbered terms fv) = e f x v z f v e f x v z f v x + e z f x v f e f v z x f vx v x) + f v z f ) v ) v + ez f x f ) vx 27) eq:a10j It is seen that the first six terms can be written in the form of the determinant e e z f f f x 28) v x v v z eq:a10k The second six terms can also be written as a determinant e e z f x v x v v z 29) eq:a10ka Using 3) and 8) we see that 27) can be written in a compact form as fv) = f) v + f v) 30) eq:a10m You will soon be able to guess this result. It looks like the chain rule of differentiation applied to a product. Knowing that the result has to be a vector this is the onl wa it can come out when ou realize that the onl operation that can do on the scalar function f is taking the gradient. 7
8 You might wonder whether the order of f and v on the left side of 30) matters. You might think that exchanging them would replace 30) b vf) = v f) + v)f 31) eq:a10ma If this were true that would be bad because the left hand side of 30) and 31) are the same while on the right hand side the first term has changed sign while the second term has not. Fortunatel 31) is incorrect. This can be seen be tracing the derivation of 30) for vf). One finds that the first term becomes e e z v x v v z 32) f x f f eq:a10mb while the second term remains equal to 29), it does not matter whether f is to the left or the right of the determinant. Comparing 28) and 32) we see that the second and third row are exchanged and that three minus signs appeared. We know from the theor of determinants that if two rows are exchanged the value of the determinant changes sign. Also, a prefactor multipling a determinant can be brought inside the determinant if one applies it to an entire row or column an row or column will do). These are general properties of determinants but at this stage ou can see that these properties are true when recalling the expression for the curl of two vectors in terms of a determinant. Reversing the order of the two vectors in the curl introduces a minus sign and multipling one of the vectors b a scalar is the same as having a prefactor in from of the curl. Using these two properties of determinants in 32) we see that the determinant becomes equal to the determinant 28). So even though the order of f and v on the left hand side of 30) is irrelevant the order of the factors on the right hand side of 30) is relevant. The equation should be memorized as an equation for f v) and not for vf) when guessing it in the manner indicated above. Next consider a vector function r/r n. Obviousl we must require that r 0 if n > 0. The divergence of this vector function can be calculated using 30) with f = r n and v = r. In 30) we need f = r n = r n)r n 2 33) eq:a10n where we have used 14) and replaced n n. We also need r which 8
9 equals 3 according to 16). Substituting 33) and 16) in 30) we find ) r r n = r ) 1 r n + r r n = 3 r n + r r n)r n 2 = 3 n r n 34) eq:a10p In the special case that n = 0 we get r = 3 35) eq:a17 Another special case is n = 3 and thus the vector function is v = r/r 3 and we get ) r r 3 = 0 36) eq:a17a We similarl can now evaluate 2 1/r) where 2 =. Using 14) with f = 1/r so n = 1 we find ) ) 1 r = r r 3 37) eq:a17b Appling to the left and right side of 37) and using 36) we get ) 1 2 = 0 38) r eq:a17c Next consider the curl of r/r n. Obviousl we must require that r 0 for n > 0. It can be evaluated using 30) with f = r n and v = r. In 30) we need f = r n which we take from 33) and r which is zero according to 18). Substituting these results in 30) we find r r n = 0 39) eq:a23 This is true for all n so we have in particular that r = 0 for n = 0 in agreement with 18). 9
This document is stored in Documents/4C/nablaoperator.tex. Compile it with LaTex. VECTOR CALCULUS
 This document is stored in Documents/4C/nablaoperator.tex. Compile it with LaTex. November 12, 2014 Hans P. Paar VECTOR CALCULUS 1 Introduction Vector calculus is a branch of mathematics that allows differentiation
This document is stored in Documents/4C/nablaoperator.tex. Compile it with LaTex. November 12, 2014 Hans P. Paar VECTOR CALCULUS 1 Introduction Vector calculus is a branch of mathematics that allows differentiation
ELECTROMAGNETIC WAVES
 Physics 4D ELECTROMAGNETIC WAVE Hans P. Paar 26 January 2006 i Chapter 1 Vector Calculus 1.1 Introduction Vector calculus is a branch of mathematics that allows differentiation and integration of (scalar)
Physics 4D ELECTROMAGNETIC WAVE Hans P. Paar 26 January 2006 i Chapter 1 Vector Calculus 1.1 Introduction Vector calculus is a branch of mathematics that allows differentiation and integration of (scalar)
This document is stored in Documents/4C/vectoralgebra.tex Compile it with LaTex. VECTOR ALGEBRA
 This document is stored in Documents/4C/vectoralgebra.tex Compile it with LaTex. September 23, 2014 Hans P. Paar VECTOR ALGEBRA 1 Introduction Vector algebra is necessary in order to learn vector calculus.
This document is stored in Documents/4C/vectoralgebra.tex Compile it with LaTex. September 23, 2014 Hans P. Paar VECTOR ALGEBRA 1 Introduction Vector algebra is necessary in order to learn vector calculus.
DIVERGENCE AND CURL THEOREMS
 This document is stored in Documents/4C/Gausstokes.tex. with LaTex. Compile it November 29, 2014 Hans P. Paar DIVERGENCE AND CURL THEOREM 1 Introduction We discuss the theorems of Gauss and tokes also
This document is stored in Documents/4C/Gausstokes.tex. with LaTex. Compile it November 29, 2014 Hans P. Paar DIVERGENCE AND CURL THEOREM 1 Introduction We discuss the theorems of Gauss and tokes also
Page 52. Lecture 3: Inner Product Spaces Dual Spaces, Dirac Notation, and Adjoints Date Revised: 2008/10/03 Date Given: 2008/10/03
 Page 5 Lecture : Inner Product Spaces Dual Spaces, Dirac Notation, and Adjoints Date Revised: 008/10/0 Date Given: 008/10/0 Inner Product Spaces: Definitions Section. Mathematical Preliminaries: Inner
Page 5 Lecture : Inner Product Spaces Dual Spaces, Dirac Notation, and Adjoints Date Revised: 008/10/0 Date Given: 008/10/0 Inner Product Spaces: Definitions Section. Mathematical Preliminaries: Inner
Physics 217, Fall September 2002
 Toda in Phsics 217: vector derivatives First derivatives: Gradient ( ) Divergence ( ) Curl ( ) Second derivatives: the Laplacian ( 2 ) and its relatives Vector-derivative identities: relatives of the chain
Toda in Phsics 217: vector derivatives First derivatives: Gradient ( ) Divergence ( ) Curl ( ) Second derivatives: the Laplacian ( 2 ) and its relatives Vector-derivative identities: relatives of the chain
1. FUNDAMENTAL CONCEPTS AND MATH REVIEW
 1. FUNDAMENTAL CONCEPTS AND MATH REVIEW 1.1. Introduction Here we provide for your reading pleasure a review of some of the math concepts used in part of this course. Most of this falls under the heading
1. FUNDAMENTAL CONCEPTS AND MATH REVIEW 1.1. Introduction Here we provide for your reading pleasure a review of some of the math concepts used in part of this course. Most of this falls under the heading
Review of Vector Analysis in Cartesian Coordinates
 Review of Vector Analysis in Cartesian Coordinates 1 Scalar: A quantity that has magnitude, but no direction. Examples are mass, temperature, pressure, time, distance, and real numbers. Scalars are usually
Review of Vector Analysis in Cartesian Coordinates 1 Scalar: A quantity that has magnitude, but no direction. Examples are mass, temperature, pressure, time, distance, and real numbers. Scalars are usually
Green s Theorem Jeremy Orloff
 Green s Theorem Jerem Orloff Line integrals and Green s theorem. Vector Fields Vector notation. In 8.4 we will mostl use the notation (v) = (a, b) for vectors. The other common notation (v) = ai + bj runs
Green s Theorem Jerem Orloff Line integrals and Green s theorem. Vector Fields Vector notation. In 8.4 we will mostl use the notation (v) = (a, b) for vectors. The other common notation (v) = ai + bj runs
Electromagnetic Theory Prof. D. K. Ghosh Department of Physics Indian Institute of Technology, Bombay
 Electromagnetic Theory Prof. D. K. Ghosh Department of Physics Indian Institute of Technology, Bombay Lecture -1 Element of vector calculus: Scalar Field and its Gradient This is going to be about one
Electromagnetic Theory Prof. D. K. Ghosh Department of Physics Indian Institute of Technology, Bombay Lecture -1 Element of vector calculus: Scalar Field and its Gradient This is going to be about one
. This is the Basic Chain Rule. x dt y dt z dt Chain Rule in this context.
 Math 18.0A Gradients, Chain Rule, Implicit Dierentiation, igher Order Derivatives These notes ocus on our things: (a) the application o gradients to ind normal vectors to curves suraces; (b) the generaliation
Math 18.0A Gradients, Chain Rule, Implicit Dierentiation, igher Order Derivatives These notes ocus on our things: (a) the application o gradients to ind normal vectors to curves suraces; (b) the generaliation
Vector Calculus Review
 Course Instructor Dr. Ramond C. Rumpf Office: A-337 Phone: (915) 747-6958 E-Mail: rcrumpf@utep.edu Vector Calculus Review EE3321 Electromagnetic Field Theor Outline Mathematical Preliminaries Phasors,
Course Instructor Dr. Ramond C. Rumpf Office: A-337 Phone: (915) 747-6958 E-Mail: rcrumpf@utep.edu Vector Calculus Review EE3321 Electromagnetic Field Theor Outline Mathematical Preliminaries Phasors,
Functions of Several Variables
 Chapter 1 Functions of Several Variables 1.1 Introduction A real valued function of n variables is a function f : R, where the domain is a subset of R n. So: for each ( 1,,..., n ) in, the value of f is
Chapter 1 Functions of Several Variables 1.1 Introduction A real valued function of n variables is a function f : R, where the domain is a subset of R n. So: for each ( 1,,..., n ) in, the value of f is
Solutions to Two Interesting Problems
 Solutions to Two Interesting Problems Save the Lemming On each square of an n n chessboard is an arrow pointing to one of its eight neighbors (or off the board, if it s an edge square). However, arrows
Solutions to Two Interesting Problems Save the Lemming On each square of an n n chessboard is an arrow pointing to one of its eight neighbors (or off the board, if it s an edge square). However, arrows
MATH 280 Multivariate Calculus Spring Derivatives of vector fields: divergence and curl
 MATH 280 Multivariate Calculus Spring 2011 Vector fields in the plane Derivatives of vector fields: divergence and curl Given a planar vector field F P x, y î + Qx, y ĵ, we can consider the partial derivatives.
MATH 280 Multivariate Calculus Spring 2011 Vector fields in the plane Derivatives of vector fields: divergence and curl Given a planar vector field F P x, y î + Qx, y ĵ, we can consider the partial derivatives.
Physics 225 Relativity and Math Applications. Fall Unit 8 Differential Calculus: now available in 3D
 Physics 225 Relativity and Math Applications Fall 2012 Unit 8 Differential Calculus: now available in 3D N.C.R. Makins University of Illinois at Urbana-Champaign 2010 Physics 225 8.2 8.2 Physics 225 8.3
Physics 225 Relativity and Math Applications Fall 2012 Unit 8 Differential Calculus: now available in 3D N.C.R. Makins University of Illinois at Urbana-Champaign 2010 Physics 225 8.2 8.2 Physics 225 8.3
Coordinate systems and vectors in three spatial dimensions
 PHYS2796 Introduction to Modern Physics (Spring 2015) Notes on Mathematics Prerequisites Jim Napolitano, Department of Physics, Temple University January 7, 2015 This is a brief summary of material on
PHYS2796 Introduction to Modern Physics (Spring 2015) Notes on Mathematics Prerequisites Jim Napolitano, Department of Physics, Temple University January 7, 2015 This is a brief summary of material on
18.02 Review Jeremy Orloff. 1 Review of multivariable calculus (18.02) constructs
 18.02 eview Jerem Orloff 1 eview of multivariable calculus (18.02) constructs 1.1 Introduction These notes are a terse summar of what we ll need from multivariable calculus. If, after reading these, some
18.02 eview Jerem Orloff 1 eview of multivariable calculus (18.02) constructs 1.1 Introduction These notes are a terse summar of what we ll need from multivariable calculus. If, after reading these, some
Topic 3 Notes Jeremy Orloff
 Topic 3 Notes Jerem Orloff 3 Line integrals and auch s theorem 3.1 Introduction The basic theme here is that comple line integrals will mirror much of what we ve seen for multivariable calculus line integrals.
Topic 3 Notes Jerem Orloff 3 Line integrals and auch s theorem 3.1 Introduction The basic theme here is that comple line integrals will mirror much of what we ve seen for multivariable calculus line integrals.
AP Calculus. (Mr. Surowski) Homework from Chapter 7 (and some of Chapter 8)
 AP Calculus (Mr. Surowski) Homework from Chapter 7 (and some of Chapter 8) Lesson 30 Integral as accumulation (7.):, 3, 5, 8 0, 7, 20 22, 25 (to do quadratic regression on our (TI-84 calculators, refer
AP Calculus (Mr. Surowski) Homework from Chapter 7 (and some of Chapter 8) Lesson 30 Integral as accumulation (7.):, 3, 5, 8 0, 7, 20 22, 25 (to do quadratic regression on our (TI-84 calculators, refer
- HH Why Can Light Propagate in Vacuum? Hsiu-Hau Lin (Apr 1, 2014)
 - HH0124 - Why Can Light Propagate in Vacuum? Hsiu-Hau Lin hsiuhau@phys.nthu.edu.tw (Apr 1, 2014) Sunlight is vital for most creatures in this warm and humid planet. From interference experiments, scientists
- HH0124 - Why Can Light Propagate in Vacuum? Hsiu-Hau Lin hsiuhau@phys.nthu.edu.tw (Apr 1, 2014) Sunlight is vital for most creatures in this warm and humid planet. From interference experiments, scientists
MATH The Chain Rule Fall 2016 A vector function of a vector variable is a function F: R n R m. In practice, if x 1, x n is the input,
 MATH 20550 The Chain Rule Fall 2016 A vector function of a vector variable is a function F: R n R m. In practice, if x 1, x n is the input, F(x 1,, x n ) F 1 (x 1,, x n ),, F m (x 1,, x n ) where each
MATH 20550 The Chain Rule Fall 2016 A vector function of a vector variable is a function F: R n R m. In practice, if x 1, x n is the input, F(x 1,, x n ) F 1 (x 1,, x n ),, F m (x 1,, x n ) where each
Lecture 11: Vector Calculus I
 1. Key points Scalar and vector fields Gradient and directional derivative Laplacian Maple Derivatives VectorCalculus package SetCoordinates Vector Norm DotProduct Gradient, Del, Nabla Laplacian evalvf
1. Key points Scalar and vector fields Gradient and directional derivative Laplacian Maple Derivatives VectorCalculus package SetCoordinates Vector Norm DotProduct Gradient, Del, Nabla Laplacian evalvf
February 27, 2019 LECTURE 10: VECTOR FIELDS.
 February 27, 209 LECTURE 0: VECTOR FIELDS 02 HONORS MULTIVARIABLE CALCULUS PROFESSOR RICHARD BROWN Synopsis Vector fields, as geometric objects and/or functions, provide a backbone in which all of physics
February 27, 209 LECTURE 0: VECTOR FIELDS 02 HONORS MULTIVARIABLE CALCULUS PROFESSOR RICHARD BROWN Synopsis Vector fields, as geometric objects and/or functions, provide a backbone in which all of physics
3.3.1 Linear functions yet again and dot product In 2D, a homogenous linear scalar function takes the general form:
 3.3 Gradient Vector and Jacobian Matri 3 3.3 Gradient Vector and Jacobian Matri Overview: Differentiable functions have a local linear approimation. Near a given point, local changes are determined by
3.3 Gradient Vector and Jacobian Matri 3 3.3 Gradient Vector and Jacobian Matri Overview: Differentiable functions have a local linear approimation. Near a given point, local changes are determined by
Trigonometric Functions
 TrigonometricReview.nb Trigonometric Functions The trigonometric (or trig) functions are ver important in our stud of calculus because the are periodic (meaning these functions repeat their values in a
TrigonometricReview.nb Trigonometric Functions The trigonometric (or trig) functions are ver important in our stud of calculus because the are periodic (meaning these functions repeat their values in a
Worksheet #1. A little review.
 Worksheet #1. A little review. I. Set up BUT DO NOT EVALUATE definite integrals for each of the following. 1. The area between the curves = 1 and = 3. Solution. The first thing we should ask ourselves
Worksheet #1. A little review. I. Set up BUT DO NOT EVALUATE definite integrals for each of the following. 1. The area between the curves = 1 and = 3. Solution. The first thing we should ask ourselves
In this chapter, we study the calculus of vector fields.
 16 VECTOR CALCULUS VECTOR CALCULUS In this chapter, we study the calculus of vector fields. These are functions that assign vectors to points in space. VECTOR CALCULUS We define: Line integrals which can
16 VECTOR CALCULUS VECTOR CALCULUS In this chapter, we study the calculus of vector fields. These are functions that assign vectors to points in space. VECTOR CALCULUS We define: Line integrals which can
4.7. Newton s Method. Procedure for Newton s Method HISTORICAL BIOGRAPHY
 4. Newton s Method 99 4. Newton s Method HISTORICAL BIOGRAPHY Niels Henrik Abel (18 189) One of the basic problems of mathematics is solving equations. Using the quadratic root formula, we know how to
4. Newton s Method 99 4. Newton s Method HISTORICAL BIOGRAPHY Niels Henrik Abel (18 189) One of the basic problems of mathematics is solving equations. Using the quadratic root formula, we know how to
Vector, Matrix, and Tensor Derivatives
 Vector, Matrix, and Tensor Derivatives Erik Learned-Miller The purpose of this document is to help you learn to take derivatives of vectors, matrices, and higher order tensors (arrays with three dimensions
Vector, Matrix, and Tensor Derivatives Erik Learned-Miller The purpose of this document is to help you learn to take derivatives of vectors, matrices, and higher order tensors (arrays with three dimensions
Topic 3. Integral calculus
 Integral calculus Topic 3 Line, surface and volume integrals Fundamental theorems of calculus Fundamental theorems for gradients Fundamental theorems for divergences! Green s theorem Fundamental theorems
Integral calculus Topic 3 Line, surface and volume integrals Fundamental theorems of calculus Fundamental theorems for gradients Fundamental theorems for divergences! Green s theorem Fundamental theorems
2.2 SEPARABLE VARIABLES
 44 CHAPTER FIRST-ORDER DIFFERENTIAL EQUATIONS 6 Consider the autonomous DE 6 Use our ideas from Problem 5 to find intervals on the -ais for which solution curves are concave up and intervals for which
44 CHAPTER FIRST-ORDER DIFFERENTIAL EQUATIONS 6 Consider the autonomous DE 6 Use our ideas from Problem 5 to find intervals on the -ais for which solution curves are concave up and intervals for which
Multivariable Calculus Lecture #13 Notes. in each piece. Then the mass mk. 0 σ = σ = σ
 Multivariable Calculus Lecture #1 Notes In this lecture, we ll loo at parameterization of surfaces in R and integration on a parameterized surface Applications will include surface area, mass of a surface
Multivariable Calculus Lecture #1 Notes In this lecture, we ll loo at parameterization of surfaces in R and integration on a parameterized surface Applications will include surface area, mass of a surface
Vector Operations. Vector Operations. Graphical Operations. Component Operations. ( ) ˆk
 Vector Operations Vector Operations ME 202 Multiplication by a scalar Addition/subtraction Scalar multiplication (dot product) Vector multiplication (cross product) 1 2 Graphical Operations Component Operations
Vector Operations Vector Operations ME 202 Multiplication by a scalar Addition/subtraction Scalar multiplication (dot product) Vector multiplication (cross product) 1 2 Graphical Operations Component Operations
Math (P)Review Part II:
 Math (P)Review Part II: Vector Calculus Computer Graphics Assignment 0.5 (Out today!) Same story as last homework; second part on vector calculus. Slightly fewer questions Last Time: Linear Algebra Touched
Math (P)Review Part II: Vector Calculus Computer Graphics Assignment 0.5 (Out today!) Same story as last homework; second part on vector calculus. Slightly fewer questions Last Time: Linear Algebra Touched
Conservation of Linear Momentum for a Differential Control Volume
 Conservation of Linear Momentum for a Differential Control Volume When we applied the rate-form of the conservation of mass equation to a differential control volume (open sstem in Cartesian coordinates,
Conservation of Linear Momentum for a Differential Control Volume When we applied the rate-form of the conservation of mass equation to a differential control volume (open sstem in Cartesian coordinates,
Math 123 Summary of Important Algebra & Trigonometry Concepts Chapter 1 & Appendix D, Stewart, Calculus Early Transcendentals
 Math Summar of Important Algebra & Trigonometr Concepts Chapter & Appendi D, Stewart, Calculus Earl Transcendentals Function a rule that assigns to each element in a set D eactl one element, called f (
Math Summar of Important Algebra & Trigonometr Concepts Chapter & Appendi D, Stewart, Calculus Earl Transcendentals Function a rule that assigns to each element in a set D eactl one element, called f (
2 Ordinary Differential Equations: Initial Value Problems
 Ordinar Differential Equations: Initial Value Problems Read sections 9., (9. for information), 9.3, 9.3., 9.3. (up to p. 396), 9.3.6. Review questions 9.3, 9.4, 9.8, 9.9, 9.4 9.6.. Two Examples.. Foxes
Ordinar Differential Equations: Initial Value Problems Read sections 9., (9. for information), 9.3, 9.3., 9.3. (up to p. 396), 9.3.6. Review questions 9.3, 9.4, 9.8, 9.9, 9.4 9.6.. Two Examples.. Foxes
3.0 PROBABILITY, RANDOM VARIABLES AND RANDOM PROCESSES
 3.0 PROBABILITY, RANDOM VARIABLES AND RANDOM PROCESSES 3.1 Introduction In this chapter we will review the concepts of probabilit, rom variables rom processes. We begin b reviewing some of the definitions
3.0 PROBABILITY, RANDOM VARIABLES AND RANDOM PROCESSES 3.1 Introduction In this chapter we will review the concepts of probabilit, rom variables rom processes. We begin b reviewing some of the definitions
Chapter 1. Vector Algebra and Vector Space
 1. Vector Algebra 1.1. Scalars and vectors Chapter 1. Vector Algebra and Vector Space The simplest kind of physical quantity is one that can be completely specified by its magnitude, a single number, together
1. Vector Algebra 1.1. Scalars and vectors Chapter 1. Vector Algebra and Vector Space The simplest kind of physical quantity is one that can be completely specified by its magnitude, a single number, together
+ = + + = x = + = + = 36x
 Ch 5 Alg L Homework Worksheets Computation Worksheet #1: You should be able to do these without a calculator! A) Addition (Subtraction = add the opposite of) B) Multiplication (Division = multipl b the
Ch 5 Alg L Homework Worksheets Computation Worksheet #1: You should be able to do these without a calculator! A) Addition (Subtraction = add the opposite of) B) Multiplication (Division = multipl b the
Vectors Primer. M.C. Simani. July 7, 2007
 Vectors Primer M.. Simani Jul 7, 2007 This note gives a short introduction to the concept of vector and summarizes the basic properties of vectors. Reference textbook: Universit Phsics, Young and Freedman,
Vectors Primer M.. Simani Jul 7, 2007 This note gives a short introduction to the concept of vector and summarizes the basic properties of vectors. Reference textbook: Universit Phsics, Young and Freedman,
16.3. Conservative Vector Fields
 16.3 onservative Vector Fields Review: Work F d r = FT ds = Fr '( t ) dt Mdx Nd Pdz if F Mi Nj Pk F d r is also called circulation if F represents a velocit vector field. Outward flux across a simple closed
16.3 onservative Vector Fields Review: Work F d r = FT ds = Fr '( t ) dt Mdx Nd Pdz if F Mi Nj Pk F d r is also called circulation if F represents a velocit vector field. Outward flux across a simple closed
Math-2. Lesson:1-2 Properties of Exponents
 Math- Lesson:- Properties of Eponents Properties of Eponents What is a power? Power: An epression formed b repeated multiplication of the same factor. Coefficient Base Eponent The eponent applies to the
Math- Lesson:- Properties of Eponents Properties of Eponents What is a power? Power: An epression formed b repeated multiplication of the same factor. Coefficient Base Eponent The eponent applies to the
1.1 The Equations of Motion
 1.1 The Equations of Motion In Book I, balance of forces and moments acting on an component was enforced in order to ensure that the component was in equilibrium. Here, allowance is made for stresses which
1.1 The Equations of Motion In Book I, balance of forces and moments acting on an component was enforced in order to ensure that the component was in equilibrium. Here, allowance is made for stresses which
Physics Gravitational force. 2. Strong or color force. 3. Electroweak force
 Phsics 360 Notes on Griffths - pluses and minuses No tetbook is perfect, and Griffithsisnoeception. Themajorplusisthat it is prett readable. For minuses, see below. Much of what G sas about the del operator
Phsics 360 Notes on Griffths - pluses and minuses No tetbook is perfect, and Griffithsisnoeception. Themajorplusisthat it is prett readable. For minuses, see below. Much of what G sas about the del operator
Major Ideas in Calc 3 / Exam Review Topics
 Major Ideas in Calc 3 / Exam Review Topics Here are some highlights of the things you should know to succeed in this class. I can not guarantee that this list is exhaustive!!!! Please be sure you are able
Major Ideas in Calc 3 / Exam Review Topics Here are some highlights of the things you should know to succeed in this class. I can not guarantee that this list is exhaustive!!!! Please be sure you are able
Mathematical Statistics. Gregg Waterman Oregon Institute of Technology
 Mathematical Statistics Gregg Waterman Oregon Institute of Technolog c Gregg Waterman This work is licensed under the Creative Commons Attribution. International license. The essence of the license is
Mathematical Statistics Gregg Waterman Oregon Institute of Technolog c Gregg Waterman This work is licensed under the Creative Commons Attribution. International license. The essence of the license is
Experimental Uncertainty Review. Abstract. References. Measurement Uncertainties and Uncertainty Propagation
 Experimental Uncertaint Review Abstract This is intended as a brief summar of the basic elements of uncertaint analsis, and a hand reference for laborator use. It provides some elementar "rules-of-thumb"
Experimental Uncertaint Review Abstract This is intended as a brief summar of the basic elements of uncertaint analsis, and a hand reference for laborator use. It provides some elementar "rules-of-thumb"
Chapter 2 Basic Conservation Equations for Laminar Convection
 Chapter Basic Conservation Equations for Laminar Convection Abstract In this chapter, the basic conservation equations related to laminar fluid flow conservation equations are introduced. On this basis,
Chapter Basic Conservation Equations for Laminar Convection Abstract In this chapter, the basic conservation equations related to laminar fluid flow conservation equations are introduced. On this basis,
Autonomous Equations / Stability of Equilibrium Solutions. y = f (y).
 Autonomous Equations / Stabilit of Equilibrium Solutions First order autonomous equations, Equilibrium solutions, Stabilit, Longterm behavior of solutions, direction fields, Population dnamics and logistic
Autonomous Equations / Stabilit of Equilibrium Solutions First order autonomous equations, Equilibrium solutions, Stabilit, Longterm behavior of solutions, direction fields, Population dnamics and logistic
220A Solutions. Assignment 5.
 4-40. Draw the free-bod diagram. 220A Solutions Assignment 5. - cos sin here are two stumbling points. he first is to resist the temptation to draw a force pointing down the inclined plane. he onl forces
4-40. Draw the free-bod diagram. 220A Solutions Assignment 5. - cos sin here are two stumbling points. he first is to resist the temptation to draw a force pointing down the inclined plane. he onl forces
CONQUERING CALCULUS POST-SECONDARY PREPARATION SOLUTIONS TO ALL EXERCISES. Andrijana Burazin and Miroslav Lovrić
 CONQUERING CALCULUS POST-SECONDARY PREPARATION SOLUTIONS TO ALL EXERCISES Andrijana Burazin and Miroslav Lovrić c 7 Miroslav Lovrić. This is an open-access document. You are allowed to download, print
CONQUERING CALCULUS POST-SECONDARY PREPARATION SOLUTIONS TO ALL EXERCISES Andrijana Burazin and Miroslav Lovrić c 7 Miroslav Lovrić. This is an open-access document. You are allowed to download, print
Main topics for the First Midterm Exam
 Main topics for the First Midterm Exam The final will cover Sections.-.0, 2.-2.5, and 4.. This is roughly the material from first three homeworks and three quizzes, in addition to the lecture on Monday,
Main topics for the First Midterm Exam The final will cover Sections.-.0, 2.-2.5, and 4.. This is roughly the material from first three homeworks and three quizzes, in addition to the lecture on Monday,
VECTORS, TENSORS AND INDEX NOTATION
 VECTORS, TENSORS AND INDEX NOTATION Enrico Nobile Dipartimento di Ingegneria e Architettura Università degli Studi di Trieste, 34127 TRIESTE March 5, 2018 Vectors & Tensors, E. Nobile March 5, 2018 1 /
VECTORS, TENSORS AND INDEX NOTATION Enrico Nobile Dipartimento di Ingegneria e Architettura Università degli Studi di Trieste, 34127 TRIESTE March 5, 2018 Vectors & Tensors, E. Nobile March 5, 2018 1 /
43.1 Vector Fields and their properties
 Module 15 : Vector fields, Gradient, Divergence and Curl Lecture 43 : Vector fields and their properties [Section 43.1] Objectives In this section you will learn the following : Concept of Vector field.
Module 15 : Vector fields, Gradient, Divergence and Curl Lecture 43 : Vector fields and their properties [Section 43.1] Objectives In this section you will learn the following : Concept of Vector field.
We have examined power functions like f (x) = x 2. Interchanging x
 CHAPTER 5 Eponential and Logarithmic Functions We have eamined power functions like f =. Interchanging and ields a different function f =. This new function is radicall different from a power function
CHAPTER 5 Eponential and Logarithmic Functions We have eamined power functions like f =. Interchanging and ields a different function f =. This new function is radicall different from a power function
Mathematics 309 Conic sections and their applicationsn. Chapter 2. Quadric figures. ai,j x i x j + b i x i + c =0. 1. Coordinate changes
 Mathematics 309 Conic sections and their applicationsn Chapter 2. Quadric figures In this chapter want to outline quickl how to decide what figure associated in 2D and 3D to quadratic equations look like.
Mathematics 309 Conic sections and their applicationsn Chapter 2. Quadric figures In this chapter want to outline quickl how to decide what figure associated in 2D and 3D to quadratic equations look like.
Review! Kinematics: Free Fall, A Special Case. Review! A Few Facts About! Physics 101 Lecture 3 Kinematics: Vectors and Motion in 1 Dimension
 Phsics 101 Lecture 3 Kinematics: Vectors and Motion in 1 Dimension What concepts did ou find most difficult, or what would ou like to be sure we discuss in lecture? Acceleration vectors. Will ou go over
Phsics 101 Lecture 3 Kinematics: Vectors and Motion in 1 Dimension What concepts did ou find most difficult, or what would ou like to be sure we discuss in lecture? Acceleration vectors. Will ou go over
CHAPTER 7 DIV, GRAD, AND CURL
 CHAPTER 7 DIV, GRAD, AND CURL 1 The operator and the gradient: Recall that the gradient of a differentiable scalar field ϕ on an open set D in R n is given by the formula: (1 ϕ = ( ϕ, ϕ,, ϕ x 1 x 2 x n
CHAPTER 7 DIV, GRAD, AND CURL 1 The operator and the gradient: Recall that the gradient of a differentiable scalar field ϕ on an open set D in R n is given by the formula: (1 ϕ = ( ϕ, ϕ,, ϕ x 1 x 2 x n
11.1 Double Riemann Sums and Double Integrals over Rectangles
 Chapter 11 Multiple Integrals 11.1 ouble Riemann Sums and ouble Integrals over Rectangles Motivating Questions In this section, we strive to understand the ideas generated b the following important questions:
Chapter 11 Multiple Integrals 11.1 ouble Riemann Sums and ouble Integrals over Rectangles Motivating Questions In this section, we strive to understand the ideas generated b the following important questions:
Dr. Allen Back. Sep. 8, 2014
 in R 3 Dr. Allen Back Sep. 8, 2014 in R 3 in R 3 Def: For f (x, y), the partial derivative with respect to x at p 0 = (x 0, y 0 ) is f x = lim f (x 0 + h, y 0 ) f (x 0, y 0 ) h 0 h or f x = lim f (p 0
in R 3 Dr. Allen Back Sep. 8, 2014 in R 3 in R 3 Def: For f (x, y), the partial derivative with respect to x at p 0 = (x 0, y 0 ) is f x = lim f (x 0 + h, y 0 ) f (x 0, y 0 ) h 0 h or f x = lim f (p 0
9.4 Radical Expressions
 Section 9.4 Radical Expressions 95 9.4 Radical Expressions In the previous two sections, we learned how to multiply and divide square roots. Specifically, we are now armed with the following two properties.
Section 9.4 Radical Expressions 95 9.4 Radical Expressions In the previous two sections, we learned how to multiply and divide square roots. Specifically, we are now armed with the following two properties.
Vector Basics. Lecture 1 Vector Basics
 Lecture 1 Vector Basics Vector Basics We will be using vectors a lot in this course. Remember that vectors have both magnitude and direction e.g. a, You should know how to find the components of a vector
Lecture 1 Vector Basics Vector Basics We will be using vectors a lot in this course. Remember that vectors have both magnitude and direction e.g. a, You should know how to find the components of a vector
Chapter 2. Vector Calculus. 2.1 Directional Derivatives and Gradients. [Bourne, pp ] & [Anton, pp ]
![Chapter 2. Vector Calculus. 2.1 Directional Derivatives and Gradients. [Bourne, pp ] & [Anton, pp ] Chapter 2. Vector Calculus. 2.1 Directional Derivatives and Gradients. [Bourne, pp ] & [Anton, pp ]](/thumbs/76/74158055.jpg) Chapter 2 Vector Calculus 2.1 Directional Derivatives and Gradients [Bourne, pp. 97 104] & [Anton, pp. 974 991] Definition 2.1. Let f : Ω R be a continuously differentiable scalar field on a region Ω R
Chapter 2 Vector Calculus 2.1 Directional Derivatives and Gradients [Bourne, pp. 97 104] & [Anton, pp. 974 991] Definition 2.1. Let f : Ω R be a continuously differentiable scalar field on a region Ω R
Physics 225 Relativity and Math Applications. Fall Unit 10 The Line Element and Grad, Div, Curl
 Physics 225 Relativity and Math Applications Fall 2012 Unit 10 The Line Element and Grad, Div, Curl N.C.R. Makins University of Illinois at Urbana-Champaign 2010 Physics 225 10.2 10.2 Physics 225 10.3
Physics 225 Relativity and Math Applications Fall 2012 Unit 10 The Line Element and Grad, Div, Curl N.C.R. Makins University of Illinois at Urbana-Champaign 2010 Physics 225 10.2 10.2 Physics 225 10.3
5. Zeros. We deduce that the graph crosses the x-axis at the points x = 0, 1, 2 and 4, and nowhere else. And that s exactly what we see in the graph.
 . Zeros Eample 1. At the right we have drawn the graph of the polnomial = ( 1) ( 2) ( 4). Argue that the form of the algebraic formula allows ou to see right awa where the graph is above the -ais, where
. Zeros Eample 1. At the right we have drawn the graph of the polnomial = ( 1) ( 2) ( 4). Argue that the form of the algebraic formula allows ou to see right awa where the graph is above the -ais, where
1.1 Basic Algebra. 1.2 Equations and Inequalities. 1.3 Systems of Equations
 1. Algebra 1.1 Basic Algebra 1.2 Equations and Inequalities 1.3 Systems of Equations 1.1 Basic Algebra 1.1.1 Algebraic Operations 1.1.2 Factoring and Expanding Polynomials 1.1.3 Introduction to Exponentials
1. Algebra 1.1 Basic Algebra 1.2 Equations and Inequalities 1.3 Systems of Equations 1.1 Basic Algebra 1.1.1 Algebraic Operations 1.1.2 Factoring and Expanding Polynomials 1.1.3 Introduction to Exponentials
18.02 Multivariable Calculus Fall 2007
 MIT OpenCourseWare http://ocw.mit.edu 18.02 Multivariable Calculus Fall 2007 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. V7. Laplace's Equation and
MIT OpenCourseWare http://ocw.mit.edu 18.02 Multivariable Calculus Fall 2007 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. V7. Laplace's Equation and
Culminating Review for Vectors
 Culminating Review for Vectors 0011 0010 1010 1101 0001 0100 1011 An Introduction to Vectors Applications of Vectors Equations of Lines and Planes 4 12 Relationships between Points, Lines and Planes An
Culminating Review for Vectors 0011 0010 1010 1101 0001 0100 1011 An Introduction to Vectors Applications of Vectors Equations of Lines and Planes 4 12 Relationships between Points, Lines and Planes An
Chapter -1: Di erential Calculus and Regular Surfaces
 Chapter -1: Di erential Calculus and Regular Surfaces Peter Perry August 2008 Contents 1 Introduction 1 2 The Derivative as a Linear Map 2 3 The Big Theorems of Di erential Calculus 4 3.1 The Chain Rule............................
Chapter -1: Di erential Calculus and Regular Surfaces Peter Perry August 2008 Contents 1 Introduction 1 2 The Derivative as a Linear Map 2 3 The Big Theorems of Di erential Calculus 4 3.1 The Chain Rule............................
3.7 InveRSe FUnCTIOnS
 CHAPTER functions learning ObjeCTIveS In this section, ou will: Verif inverse functions. Determine the domain and range of an inverse function, and restrict the domain of a function to make it one-to-one.
CHAPTER functions learning ObjeCTIveS In this section, ou will: Verif inverse functions. Determine the domain and range of an inverse function, and restrict the domain of a function to make it one-to-one.
Today in Physics 217: begin electrostatics
 Today in Physics 217: begin electrostatics Fields and potentials, and the Helmholtz theorem The empirical basis of electrostatics Coulomb s Law At right: the classic hand-to-thevan-de-graaf experiment.
Today in Physics 217: begin electrostatics Fields and potentials, and the Helmholtz theorem The empirical basis of electrostatics Coulomb s Law At right: the classic hand-to-thevan-de-graaf experiment.
nm nm
 The Quantum Mechanical Model of the Atom You have seen how Bohr s model of the atom eplains the emission spectrum of hdrogen. The emission spectra of other atoms, however, posed a problem. A mercur atom,
The Quantum Mechanical Model of the Atom You have seen how Bohr s model of the atom eplains the emission spectrum of hdrogen. The emission spectra of other atoms, however, posed a problem. A mercur atom,
Cumulative Review of Vectors
 Cumulative Review of Vectors 1. For the vectors a! 1, 1, and b! 1, 4, 1, determine the following: a. the angle between the two vectors! the scalar and vector projections of a! on the scalar and vector
Cumulative Review of Vectors 1. For the vectors a! 1, 1, and b! 1, 4, 1, determine the following: a. the angle between the two vectors! the scalar and vector projections of a! on the scalar and vector
1 GSW Gaussian Elimination
 Gaussian elimination is probabl the simplest technique for solving a set of simultaneous linear equations, such as: = A x + A x + A x +... + A x,,,, n n = A x + A x + A x +... + A x,,,, n n... m = Am,x
Gaussian elimination is probabl the simplest technique for solving a set of simultaneous linear equations, such as: = A x + A x + A x +... + A x,,,, n n = A x + A x + A x +... + A x,,,, n n... m = Am,x
Lecture 4: Exact ODE s
 Lecture 4: Exact ODE s Dr. Michael Doughert Januar 23, 203 Exact equations are first-order ODE s of a particular form, and whose methods of solution rel upon basic facts concerning partial derivatives,
Lecture 4: Exact ODE s Dr. Michael Doughert Januar 23, 203 Exact equations are first-order ODE s of a particular form, and whose methods of solution rel upon basic facts concerning partial derivatives,
Class 4 : Maxwell s Equations for Electrostatics
 Class 4 : Maxwell s Equations for Electrostatics Concept of charge density Maxwell s 1 st and 2 nd Equations Physical interpretation of divergence and curl How do we check whether a given vector field
Class 4 : Maxwell s Equations for Electrostatics Concept of charge density Maxwell s 1 st and 2 nd Equations Physical interpretation of divergence and curl How do we check whether a given vector field
9.7 Gradient of a Scalar Field. Directional Derivative. Mean Value Theorem. Special Cases
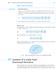 SEC. 9.7 Gradient of a Scalar Field. Directional Derivative 395 Mean Value Theorems THEOREM Mean Value Theorem Let f(x, y, z) be continuous and have continuous first partial derivatives in a domain D in
SEC. 9.7 Gradient of a Scalar Field. Directional Derivative 395 Mean Value Theorems THEOREM Mean Value Theorem Let f(x, y, z) be continuous and have continuous first partial derivatives in a domain D in
Math Divergence and Curl
 Math 23 - Divergence and Curl Peter A. Perry University of Kentucky November 3, 28 Homework Work on Stewart problems for 6.5: - (odd), 2, 3-7 (odd), 2, 23, 25 Finish Homework D2 due tonight Begin Homework
Math 23 - Divergence and Curl Peter A. Perry University of Kentucky November 3, 28 Homework Work on Stewart problems for 6.5: - (odd), 2, 3-7 (odd), 2, 23, 25 Finish Homework D2 due tonight Begin Homework
Random Vectors, Random Matrices, and Matrix Expected Value
 Random Vectors, Random Matrices, and Matrix Expected Value James H. Steiger Department of Psychology and Human Development Vanderbilt University James H. Steiger (Vanderbilt University) 1 / 16 Random Vectors,
Random Vectors, Random Matrices, and Matrix Expected Value James H. Steiger Department of Psychology and Human Development Vanderbilt University James H. Steiger (Vanderbilt University) 1 / 16 Random Vectors,
Section 4.3 Vector Fields
 Section 4.3 Vector Fields DEFINITION: A vector field in R n is a map F : A R n R n that assigns to each point x in its domain A a vector F(x). If n = 2, F is called a vector field in the plane, and if
Section 4.3 Vector Fields DEFINITION: A vector field in R n is a map F : A R n R n that assigns to each point x in its domain A a vector F(x). If n = 2, F is called a vector field in the plane, and if
Section 5.3, Exercise 22
 The Legendre equation is where α is a constant. Section 5.3, Exercise 22 (1 x 2 ) 2x + α(α + 1) 0 Determine two linearl independent solutions in powers of x for x < 1. Assume (x) a n x n and substitute
The Legendre equation is where α is a constant. Section 5.3, Exercise 22 (1 x 2 ) 2x + α(α + 1) 0 Determine two linearl independent solutions in powers of x for x < 1. Assume (x) a n x n and substitute
Parameter estimation Conditional risk
 Parameter estimation Conditional risk Formalizing the problem Specify random variables we care about e.g., Commute Time e.g., Heights of buildings in a city We might then pick a particular distribution
Parameter estimation Conditional risk Formalizing the problem Specify random variables we care about e.g., Commute Time e.g., Heights of buildings in a city We might then pick a particular distribution
3. Maxwell's Equations and Light Waves
 3. Maxwell's Equations and Light Waves Vector fields, vector derivatives and the 3D Wave equation Derivation of the wave equation from Maxwell's Equations Why light waves are transverse waves Why is the
3. Maxwell's Equations and Light Waves Vector fields, vector derivatives and the 3D Wave equation Derivation of the wave equation from Maxwell's Equations Why light waves are transverse waves Why is the
Math 123, Week 9: Separable, First-Order Linear, and Substitution Methods. Section 1: Separable DEs
 Math 123, Week 9: Separable, First-Order Linear, and Substitution Methods Section 1: Separable DEs We are finally to the point in the course where we can consider how to find solutions to differential
Math 123, Week 9: Separable, First-Order Linear, and Substitution Methods Section 1: Separable DEs We are finally to the point in the course where we can consider how to find solutions to differential
Math 216 Calculus 3 Directional derivatives. Math 216 Calculus 3 Directional derivatives 1 / 6
 Math 216 Calculus 3 Directional derivatives Math 216 Calculus 3 Directional derivatives 1 / 6 How fast does f (x, y) change if you change (x, y) in the direction v The partial derivatives f x and f y measure
Math 216 Calculus 3 Directional derivatives Math 216 Calculus 3 Directional derivatives 1 / 6 How fast does f (x, y) change if you change (x, y) in the direction v The partial derivatives f x and f y measure
Fluid Mechanics II. Newton s second law applied to a control volume
 Fluid Mechanics II Stead flow momentum equation Newton s second law applied to a control volume Fluids, either in a static or dnamic motion state, impose forces on immersed bodies and confining boundaries.
Fluid Mechanics II Stead flow momentum equation Newton s second law applied to a control volume Fluids, either in a static or dnamic motion state, impose forces on immersed bodies and confining boundaries.
Physics 141 Energy 1 Page 1. Energy 1
 Physics 4 Energy Page Energy What I tell you three times is true. Lewis Carroll The interplay of mathematics and physics The mathematization of physics in ancient times is attributed to the Pythagoreans,
Physics 4 Energy Page Energy What I tell you three times is true. Lewis Carroll The interplay of mathematics and physics The mathematization of physics in ancient times is attributed to the Pythagoreans,
LECTURE 10: REVIEW OF POWER SERIES. 1. Motivation
 LECTURE 10: REVIEW OF POWER SERIES By definition, a power series centered at x 0 is a series of the form where a 0, a 1,... and x 0 are constants. For convenience, we shall mostly be concerned with the
LECTURE 10: REVIEW OF POWER SERIES By definition, a power series centered at x 0 is a series of the form where a 0, a 1,... and x 0 are constants. For convenience, we shall mostly be concerned with the
Theoretical Physics Prof. Ruiz, UNC Asheville, doctorphys on YouTube Chapter E Notes. Differential Form for the Maxwell Equations
 Theoretical Physics Prof Rui, UNC sheville, doctorphys on YouTube Chapter Notes Differential Form for the Maxwell quations 1 The Divergence Theorem We are going to derive two important theorems in vector
Theoretical Physics Prof Rui, UNC sheville, doctorphys on YouTube Chapter Notes Differential Form for the Maxwell quations 1 The Divergence Theorem We are going to derive two important theorems in vector
VECTOR DIFFERENTIAL CALCULUS
 VECTOR DIFFERENTIAL CALCULUS INTRODUCTION: Vector calculus is a branch of mathematics concerned with differential and integration of vector field, primarily in 3-dimensional space R3. It was developed
VECTOR DIFFERENTIAL CALCULUS INTRODUCTION: Vector calculus is a branch of mathematics concerned with differential and integration of vector field, primarily in 3-dimensional space R3. It was developed
Lines and Planes 1. x(t) = at + b y(t) = ct + d
 1 Lines in the Plane Lines and Planes 1 Ever line of points L in R 2 can be epressed as the solution set for an equation of the form A + B = C. Will we call this the ABC form. Recall that the slope-intercept
1 Lines in the Plane Lines and Planes 1 Ever line of points L in R 2 can be epressed as the solution set for an equation of the form A + B = C. Will we call this the ABC form. Recall that the slope-intercept
MATHEMATICS 200 December 2014 Final Exam Solutions
 MATHEMATICS 2 December 214 Final Eam Solutions 1. Suppose that f,, z) is a function of three variables and let u 1 6 1, 1, 2 and v 1 3 1, 1, 1 and w 1 3 1, 1, 1. Suppose that at a point a, b, c), Find
MATHEMATICS 2 December 214 Final Eam Solutions 1. Suppose that f,, z) is a function of three variables and let u 1 6 1, 1, 2 and v 1 3 1, 1, 1 and w 1 3 1, 1, 1. Suppose that at a point a, b, c), Find
Introduction and Vectors Lecture 1
 1 Introduction Introduction and Vectors Lecture 1 This is a course on classical Electromagnetism. It is the foundation for more advanced courses in modern physics. All physics of the modern era, from quantum
1 Introduction Introduction and Vectors Lecture 1 This is a course on classical Electromagnetism. It is the foundation for more advanced courses in modern physics. All physics of the modern era, from quantum
Image Registration Lecture 2: Vectors and Matrices
 Image Registration Lecture 2: Vectors and Matrices Prof. Charlene Tsai Lecture Overview Vectors Matrices Basics Orthogonal matrices Singular Value Decomposition (SVD) 2 1 Preliminary Comments Some of this
Image Registration Lecture 2: Vectors and Matrices Prof. Charlene Tsai Lecture Overview Vectors Matrices Basics Orthogonal matrices Singular Value Decomposition (SVD) 2 1 Preliminary Comments Some of this
6. Linear transformations. Consider the function. f : R 2 R 2 which sends (x, y) (x, y)
 Consider the function 6 Linear transformations f : R 2 R 2 which sends (x, ) (, x) This is an example of a linear transformation Before we get into the definition of a linear transformation, let s investigate
Consider the function 6 Linear transformations f : R 2 R 2 which sends (x, ) (, x) This is an example of a linear transformation Before we get into the definition of a linear transformation, let s investigate
Lecture 3 BRANCHES AND NODES
 Lecture 3 Definitions: Circuits, Nodes, Branches Kirchoff s Voltage Law (KVL) Kirchoff s Current Law (KCL) Examples and generalizations RC Circuit Solution 1 Branch: BRANCHES AND NODES elements connected
Lecture 3 Definitions: Circuits, Nodes, Branches Kirchoff s Voltage Law (KVL) Kirchoff s Current Law (KCL) Examples and generalizations RC Circuit Solution 1 Branch: BRANCHES AND NODES elements connected
University of Waterloo Faculty of Mathematics. MATH 227: Calculus 3 for Honours Physics
 Universit of Waterloo Facult of Mathematics MATH 227: Calculus 3 for Honours Phsics Fall 2010 Lecture Notes E.R. Vrsca Department of Applied Mathematics c E.R. Vrsca 2010 1 Lecture 1 (Relevant sections
Universit of Waterloo Facult of Mathematics MATH 227: Calculus 3 for Honours Phsics Fall 2010 Lecture Notes E.R. Vrsca Department of Applied Mathematics c E.R. Vrsca 2010 1 Lecture 1 (Relevant sections
LESSON 35: EIGENVALUES AND EIGENVECTORS APRIL 21, (1) We might also write v as v. Both notations refer to a vector.
 LESSON 5: EIGENVALUES AND EIGENVECTORS APRIL 2, 27 In this contet, a vector is a column matri E Note 2 v 2, v 4 5 6 () We might also write v as v Both notations refer to a vector (2) A vector can be man
LESSON 5: EIGENVALUES AND EIGENVECTORS APRIL 2, 27 In this contet, a vector is a column matri E Note 2 v 2, v 4 5 6 () We might also write v as v Both notations refer to a vector (2) A vector can be man
