Yimin Math Centre. 4 Unit Math Homework for Year 12 (Worked Answers) 4.1 Further Geometric Properties of the Ellipse and Hyperbola...
|
|
|
- Gillian McDaniel
- 6 years ago
- Views:
Transcription
1 4 Uni Mah Homework for Year 12 (Worked Answers) Suden Name: Grade: Dae: Score: Table of conens 4 Topic 2 Conics (Par 4) Furher Geomeric Properies of he Ellipse and Hyperbola The Recangular Hyperbola Caresian Equaion of he Recangular Hyperbola Parameric Equaions of he Recangular Hyperbola Equaion of a Chord of he Hyperbola xy = c Equaions of Tangens and Normals o he hyperbola xy = c Equaion of he Chord of Conac of Tangen from an Exernal Poin Furher geomeric properies of he recangular hyperbola Locus Problem and he Recangular Hyperbola This ediion was prined on June 17, Camera ready copy was prepared wih he L A TEX2e ypeseing sysem. Copyrigh ( 4 Uni Mah Homework for Year 12
2 Year 12 Topic 4 Worked Answers Page 1 of 13 4 Topic 2 Conics (Par 4) 4.1 Furher Geomeric Properies of he Ellipse and Hyperbola Definiion: 1. The segmen of he angen o an ellipse or hyperbola beween he poin of he conac and he direcrix subends a righ angle a he corresponding focus. (P S ST ) 2. The angen a a poin P on he ellipse or hyperbola is equally inclines o he focal chords hrough P. ( SP T = S P T ) 3. The normal a a poin P on he ellipse or hyperbola is equally inclined o he focal chords hrough P. Copyrigh (
3 Year 12 Topic 4 Worked Answers Page 2 of 13 Example P (a sec θ, b an θ) lies on he hyperbola x2 y2 = 1. The angen a P mees he a 2 b 2 angens a he ends of he major axis a Q and R. Show ha QR subends a righ angle a eiher focus. Deduce ha if P is he poin 5, 4 x2 on he hyperbola 3 9 y2 = 1, wih foci S and S, hen Q, S, S, S are concyclic and find he equaion of he circle hrough hese poins. Soluion: Le he angen a P mee x = a, x = a in he Q, R respecively. Le QR mee he y-axis in C. Tangen PR has equaion x sec θ = 1. a b Hence Q has coordinaes [ b a, (sec θ 1)] and R has coordinaes [ a, b an θ b(sec θ 1 Gradien QS.gradien RS = b(secθ+1 y an θ a an θ(1 e) a an θ(1+e) = b2 (sec2 θ 1). a 2 (1 e 2 ) an 2 θ Then b 2 = a 2 (e 2 1) gradien QS gradien RS = 1, QS RS Similarly, replacing e by e, QS RS. an θ (sec θ + 1)] Hence QR subends angles of 90 a each of S and S, and Q, S, R, S are noncyclic, wih QR he diameer of he circle hrough he poins. The y-axis is he perpendicular bisecor of he chord SS, Hence he cenre of his circle is he poin C where he diameer QR mees he y-axis. If P (5, 4 x2 lies in he hyperbola y = 1, hen QR has equaion 5x 4y he y-axis in C ( 3 0, 4). Also b 2 = a 2 (e 2 1) gives e = 10, and S ahs coordinaes ( 10, 0). 9 Hence CS 2 = and he circle hrough Q, R, S, S has equaion x 2 + ( y = 1 and mees ) 2 = Copyrigh (
4 Year 12 Topic 4 Worked Answers Page 3 of The Recangular Hyperbola Caresian Equaion of he Recangular Hyperbola Definiion: A hyperbola is called recangular if is asympoes mee a righ angles. The asympoes of x2 y2 = 1 have equaions y = ± b x. a 2 b 2 a Hence asympoes perpendicular ( b ) ( b = 1), a = b. a a Then b 2 = a 2 (e 2 1), e = (1 + b2 ), e = 2. a 2 Hence a recangular hyperbola, wih major axis along he x-axis, has equaion x 2 y 2 = a 2, eccenriciy e = 2 and asympoes y = ±x Parameric Equaions of he Recangular Hyperbola Definiion: The sandard parameric from of he recangular hyperbola xy = c 2 is x = c and y = c, where he value of parameer depends on he posiion of P (c, c ) on he curve as in he figure shown below: Copyrigh (
5 Year 12 Topic 4 Worked Answers Page 4 of 13 Exercise For he recangular hyperbola xy = 4, find he parameric equaion. Soluion: For he hyperbola yxy = 4 we have c 2 = 4, c = 2. Hence he hyperbola equaion xy = 4 has parameric equaions x = c, y = c, x = 2, y = For he recangular hyperbola x = 4, y = 4, find he Caresian equaion. Soluion: The hyperbola x = 4, y = 4 has Caresian equaion xy = 4, xy = Find he parameric equaion of he recangular hyperbola xy = 25. Soluion: For he hyperbola xy = 25 we have c 2 = 25 c = 5 Hence he hyperbola xy = 25 has parameric equaions x = c, y = c, x = 5, y = Find he Caresian equaion of he recangular hyperbola x = 3, y = 3. Soluion: The hyperbola x = 3, y = 3 has Caresian equaion xy = 3 3, xy = 9. Copyrigh (
6 Year 12 Topic 4 Worked Answers Page 5 of Equaion of a Chord of he Hyperbola xy = c 2 Caresian form: Le P (x 1, y 1 ), Q(x 2, y 2 ) lie on he ( hyperbola) xy = c 2. The gradien of PQ is y 2 y 1 x 2 x 1 = 1 c 2 x 2 x 1 c2 = c2 x 2 x 2 1 x 1 x 2 chord PQ has equaion c 2 x + x 1 x 2 y = k, k is consan. k = c 2 (x 1 + x 2 ). The chord from P (x 1, y 1 ) o Q(x 2, y 2 ) on xy = c 2 has equaion c 2 x + x 1 x 2 y = c 2 (x 1 + x 2 ). Parameric form: ( ) ( ) Le P cp, c, Q cq, c lie on he hyperbola xy = c 2. p q The gradien of PQ is c( 1 q 1 p ) = 1 c(q p) pq chord PQ has equaion x + pqy = k, k is consan. c P (cp, ) lies on P Q k = c(p + q). p The chord from P (cp, c) o Q(cq, c ) on xy = c2 p q has equaion x + pqy = c(p + q). Example The poins P (cp, c p ) and Q(cq, c q ) lie on he recangula hyperbola xy = c2. The chord PQ subends a righ angle a he anoher poin R(cr, c ) on he hyperbola. Show he he r normal a R is parallel o PQ. Soluion: The gradien of PR is c( 1 p 1 r ) = 1, c(p r) pr he gradien of QR is c( 1 q 1 r ) c(q r) = 1 qr. Therefore P Q QR, gradien P R gradien QR = 1, 1 pqr 2 = 1 r 2 = 1 pq. The normal a he poin R(cr, c r ) has gradien of r2, he gradien of PQ is c( 1 p 1 q = 1. c(p q) pq Since r 2 = 1, hen gradien of he normal a R equal o gradien of PQ. pq Thus he normal a he poin R is parallel o he chord PR. Copyrigh (
7 Year 12 Topic 4 Worked Answers Page 6 of Equaions of Tangens and Normals o he hyperbola xy = c 2 Caresian from of equaion of angen: By implici differeniaion, xy = c 2, y + x dy dx = 0 dy dx = y x Gradien of angen a P (x 1, y 1 ) on he hyperbola is y 1 x 1 angen a P has equaion y 1 x + x 1 y = k, k is consan. By P lies on angen k = 2x 1 y 1 = 2c 2. The angen o xy = c 2 ap (x 1, y 1 ) has equaion xy 1 + yx 1 = 2c 2 Caresian from of equaion of normal: Also he normal a P (x 1, y 1 ) and equaion y y 1 = x 1 y 1 (x x 1 ). The normal o xy = c 2 a P (x 1, y 1 ) has equaion xx 1 yy 1 = x 2 1 y 2. Parameric form of equaion of angen: x = c, dx = c, and y = c, dy = c d d dy = 1 dx 2 Gradien of angen a P (cp, c ) on he hyperbola is 1, p p 2 angen a P has equaion x + p 2 y = k, k is consan. Bu P lies on angen k = ( 2cp. ) The angen o xy = c 2 a P cp, c has equaion x + p 2 y = 2cp. p Parameric form of equaion ( of normal: ) Also he normal a P cp, c has gradien P 2 and equaion y c = p P p2 (x cp). ( ) ( The normal o xy = c 2 a P cp, c has equaion px 1y = c p 2 ). 1 p p p 2 Example Find he equaion of he angen and he normal o he recangular hyperbola x = 2, y = 2 a he poin where = 4. 2, Soluion: For he hyperbola x = 2, y = 2, where we have c = 2. Hence he angen o he hyperbola x = 2, y = 2 a poin where = 4 has equaion x + 2 y = 2c, x + 16y = 16 and he normal has equaion x 1 y = c ( ) 32x 2y = 255. Copyrigh (
8 Year 12 Topic 4 Worked Answers Page 7 of 13 Exercise Find he equaions of he angen and he normal o he recangular hyperbola xy = 12 a he poin (-3, -4). Soluion: For he hyperbola xy = 12 we have c 2 = 12. Hence he angen o he hyperbola xy = 12 a he poin P ( 3, 4) has equaion xy 1 + yx 1 = 2c 2 4x + 3y = 24 and he normal has equaion xx 1 yy 1 = x 2 1 y1, 2 3x 4y = Find he equaions of he angen and he normal o he recangular hyperbola x = 3, y = 3 a he poin = 1. Soluion: For he hyperbola x = 3, y = 3, we have c = 3. Hence he angen o he hyperbola x = 3, y = 3 a he poin where = 1 has equaion x + 2 y = 2c, x + y = 6, and he normal has equaion x y = c ( ) x = y. 3. Find he equaion of chord of conac of angen from he poin (1, -2) ro he hyperbola xy = 6. Soluion: For he hyperbola xy = 6, c 2 = 6. Hence he chord of anac of angens from he poin T (x 0, y 0 ) = T (1, 2) o he hyperbola xy = 6 has equaion xy 0 + yx 0 = 2c 2 2x y = Find he equaion of he angen and he noram o he recangular hyperbola xy = 8 a he poin (4, 2). Soluion: For he hyperbola xy = 8 we have c 2 = 8. Hence he angen o he hyperbola xy = 8 a he poin P (x 1, y 1 ) = P (4, 2) has equaion xy 1 + yx 1 = 2c 2 x + 2y = 8 and he normal has equaion xx 1 yy 1 = x 2 1 y1 2 2x y = 6. Copyrigh (
9 Year 12 Topic 4 Worked Answers Page 8 of Equaion of he Chord of Conac of Tangen from an Exernal Poin Definiion: T lies on he angen PT and QT, x 0 y 1 +y 0 x 1 = 2x 2 and x 0 y 2 +y 0 x 2 = 2c 2. Hence P (x 1, y 1 ) and Q(x 2, y 2 ) boh saisfy x 0 y + y 0 x = 2c 2. his linear equaion mus be he equaion of PQ. The chord conac of angen from an exernal poin T (x 0, y 0 ) o he hyperbola xy = c has equaion xy 0 + yx 0 = 2c 2. Example Find he equaion of he chord of conac of angen from he poin (2, 1) o xy = 10. Soluion: For he hyperbola xy = 10, we have c 2 = 10. Hence he chord of conac of angens from he poin T (x 0, y 0 ) = T (2, 1) o he hyperbola xy = 10 has equaion xy 0 + yx 0 = 2c 2 x + 2y = 20. Exercise Find he equaion of he chord of conac of angens from he poin ( 1, 3) o he recangular hyperbola xy = 4. Hence find he coordinaed of heir poins of conac and he equaions of hese angens. Soluion: The chord of conac of angen from he poin (-1, -3) o he hyperbola xy = 4 has equaion xy 0 + yx 0 = 2c 2, 3x + y = 8 Le T (x 0, y 0 ) be a poin of conac. Then T lies on he chord 3x 0 + y 0 = 8, T lies on he hyperbola x 0 y 0 = 4. Hence x 0 ( 8 3x 0 ) = 4 3x x = 0 (3x + 2)(x + 2) = 0 x 0 = 2, y 3 0 = 8 3x 0 = 6 or x 0 = 2, y 0 = 8 3x 0 = 2. Equaion of angen a he poin T (x 0, y) 0 ) is xy 0 + yx 0 = 2c 2. he angen form he poin ( 1, 3) o he hyperbola xy = 4 are y = x 4, wih poin of conac P ( 2, 2) and y = 9x 12, wih poin of conac P ( 2, 6). 3 Copyrigh (
10 Year 12 Topic 4 Worked Answers Page 9 of Furher geomeric properies of he recangular hyperbola Definiion: 1. The area of he riangle bounded by a angen and he asympoes is a consan. Le he angen a P (c, c on xy = c2 mee he x-axes and y-axes in R and T respecively. The angen has equaion x + 2 y = 2c. A T, x = 0, y = 2c Area OT R = 1 2 2c 2c = 2c The lengh of he inercep cu off a angen by he asympoes is wice he disance from he poin of he inersecion of he asympoes o he poin of he conac of he angen. T R 2 = ( 2c2 ) + (2c)= 4c 2 ( ), and OP 2 (c) 2 + ( c )2 = c 2 ( ). T R 2 = 4OP 2, T R = 2OP. 3. The produc of he focal disance of a poin P on a recangular hyperbola is equal o he square of he disance from P o he poin of inersecion of he asympoes. Le xy = c 2 have foci S and S, and direcrices m and m. Le M, M be he fee of he perpendiculars from P (c, c o m, m respecively. Then P S P S = ep M ep M = 2P M P M (since e = 2), P S P S = 2 c+ c 2c 2 c+ c + 2c 2 = (c + c )2 ( 2c) 2 P S P S = (c) 2 + ( c )2 = OP 2. Copyrigh (
11 Year 12 Topic 4 Worked Answers Page 10 of 13 Example For he recangular hyperbola xy = 16, find (a) he eccenriciy; (b) he coordinaes if he foci; (c) he equaion s of he direcrices; (d) he equaions of he asympoes. Skech he hyperbola. Soluion: For he hyperbola xy = 16 we have c 2 = 16 c = 4. Hence he hyperbola xy = 16 has eccenriciy e = 2 Foci: S(c 2, c 2), S(4 2, 4 2) and S ( c 2, c 2), S ( 4 2, 4 2), Dircires: x + y = ±c 2, x + y = ±4 2, Asympoes: x = 0 and y = 0. Exercise The poin P (c, c ), where = -1 lies on he recangular hyperbola xy = c2. The angen and normal a P mee he line y = x a T and N respecively. Show ha OT ON = 4c 2. Soluion: The angen o he hyperbola xy = c 2 a he poin P (c, c ) has equaion x + 2 y = 2c. As y = x he poin T has coordinaes ( 2c 1+ 2, 2c 1+ 2 ). The normal o he hyperbola xy = c 2 a he poin P (c, c ) has equaion x y = c(2 1 ). 2 Therefore he poin N has coordinaes ( c(2 +1), c(2 +1) ). OT = 2c 2, ON = c(2 +1) 2, OT ON = 4c Copyrigh (
12 Year 12 Topic 4 Worked Answers Page 11 of Locus Problem and he Recangular Hyperbola Example P (c, c) is a poin on he recangular hyperbola xy = c2. N is he foo of he perpendicular from P o he x-axis and M is he midpoin of P N. Find he Caresian equaion of he locus of M as he posiion of P varies. and describe his locus geomerically. Soluion: M has coordinaes (c, c 2 ). Hence he locus of M has parameric equaions x = c, and y = c 2 and Caresian equaion xy = 1 2 c2. M races a recangular hyperbola as he posiion of P varies. Example P (3p, 3) and Q(3q, 3 ) are poin on differen branches of he hyperbola xy = 9. p q Find he coordinaes of he poin of inersecion T of he angens a P and Q. Find he locus of T if he posiions of P and Q very so ha he chord P Q passes hrough (0, 4). { x + p 2 y = 6p (1) Soluion: T lies on he angen a P and Q. A T, x + q 2 y = 6q (2) (1) (2) (p 2 q 2 )y = 6(p q), p q y = ( ) 6 p+q Then (1) x = 6pq, T has coordinaes 6pq, 6. p+q p+q p+q If (0, 4) lies on chord PQ, wih equaion ( ) x + pqy = 3(p + q), 9 hen 4pq = 3(p + q) and T is T, pq P, Q on differen branches pq < 0, locus of T is x = 9, y < 0 2 Copyrigh (
13 Year 12 Topic 4 Worked Answers Page 12 of 13 Exercise P and Q are variable poins on he recangular hyperbola xy = 9. The angens a P and Q mee a R. If P Q passes hrough he poin (6, 2). find he equaion of he locus of R. Soluion: Le R has coordinaes (x 0, y 0 ). PQ is he chord of conac of angens from R o hyperbola xy = 9. Hence PQ has equaion xx 0 + yy 0 = 18. The poin (6, 2) lies on P Q. Therefore x 0 + 3y 0 = 9. Thus he locus of R has equaion x + 3y = The poin P (c, c ) lies on he recangular hyperbola xy = c2. The angen a P cus he x-axis a X and he y-axis a Y. Show ha he area of Y OX is independen of. Soluion: The angen o he hyperbola xy = c 2 a he poin P ( c, c has equaion x + 2 y = 2c. Hence he poin X has coordinaes (2c, 0) and he poin Y has coordinaes ( 0, 2c The area of Y OX = 1 OX OY = 1 2c 2c = 2c Thus he area of Y OX is independen of. 3. On he recangular hyperbola xy = c 2 here are variable poins P and Q. The angens a P and Q mee a R. Find he equaion of he locus of R if PQ passes hrough he poin (a, 0). Soluion: Le R has coordinaes (x 0, y 0 ). PQ is he chord of conac of angens from R o he hyperbola xy = c 2. Hence PQ has equaion xy 0 + yx 0 = 2c 2. Then (a, 0) lies on PQ. herefore xy 0 + yx 0 = 2c 2, ay)o = ac 2. Thus he locus of R has equaion y = 2c2 a. ) ). 4. The poin P (c, c ) lies on he recangular hyperbola xy = c2. The angen a P cus he x-axis a X and he y-axis a Y. Show ha PX = PY. Soluion: The angen o he hyperbola xy = c 2 a he poin P (c, c ) has equaion x + 2 y = ac. Hence he poin x has coordinaes xy = c 2 and he poin Y has coordinaes (0, 2c ). P X 2 = (c 2c) 2 + ( c )2 = c 2 ( ) and P X 2 = (c) 2 + ( c 2c )2 = c 2 ( ). Therefore P X = P Y. Copyrigh (
14 Year 12 Topic 4 Worked Answers Page 13 of 13 Exercise The poin P (c, c ) lies on he recangular hyperbola xy = c2. Show ha he normal a P cus he hyperbola again a he poin Q wih coordinaes ( c 3, c 3 ). Hence find he coordinaes of he poin R where he normal a Q cus he hyperbola again. Soluion: The normal o he hyperbola xy = c 2 a poin P (c, c ) has equaion x y = c ( ) ( ) The poin Q cq, c lies on he normal. q Hence cq c = q c(2 1 ). ( 2 ) Therefore (q 2 ) = 0. 3 q Since Q P, hen q. Thus q = 1 and Q has coordinaes ( c, c 3). 3 3 Similarly he normal a Q cus he hyperbola again a R(cr, c) wih r = 1 = 9. r q 3 So R has coordinaes ( ) c 9 c, The poin P (c, c ) lies on he recangular hyperbola xy = c2. The normal a P mees he x-axis a A and he angen a P mees he y-axis a B. M is he midpoin of AB. Find he equaion of he locus of M as P moves on he hyperbola. Soluion: The normal o he hyperbola xy = c 2 a he poin P (c, c ) has he equaion x y = c ( ). The normal a P mees he x-axis a A( c (2 1 2 ), 0). The angen o he hyperbola xy = c 2 a he P (c, c ) has equaion x + 2 y = 2c. Hence he angen mees he y-axis a B(0, 2c). If M(x, y) is he midpoin of AB, hen x = c 2 (2 1 ) and y = c. 2 Thus = c and consequenly, x = y ( c2 y2 ). y 2 y 2 c 2 Therefore he locus of N has equaion 2c 2 xy = c 4 y 4. Copyrigh (
PARABOLA. moves such that PM. = e (constant > 0) (eccentricity) then locus of P is called a conic. or conic section.
 wwwskshieducioncom PARABOLA Le S be given fixed poin (focus) nd le l be given fixed line (Direcrix) Le SP nd PM be he disnce of vrible poin P o he focus nd direcrix respecively nd P SP moves such h PM
wwwskshieducioncom PARABOLA Le S be given fixed poin (focus) nd le l be given fixed line (Direcrix) Le SP nd PM be he disnce of vrible poin P o he focus nd direcrix respecively nd P SP moves such h PM
Check in: 1 If m = 2(x + 1) and n = find y when. b y = 2m n 2
 7 Parameric equaions This chaer will show ou how o skech curves using heir arameric equaions conver arameric equaions o Caresian equaions find oins of inersecion of curves and lines using arameric equaions
7 Parameric equaions This chaer will show ou how o skech curves using heir arameric equaions conver arameric equaions o Caresian equaions find oins of inersecion of curves and lines using arameric equaions
Teaching parametric equations using graphing technology
 Teaching parameric equaions using graphing echnology The session will sar by looking a problems which help sudens o see ha parameric equaions are no here o make life difficul bu are imporan and give rise
Teaching parameric equaions using graphing echnology The session will sar by looking a problems which help sudens o see ha parameric equaions are no here o make life difficul bu are imporan and give rise
!!"#"$%&#'()!"#&'(*%)+,&',-)./0)1-*23)
 "#"$%&#'()"#&'(*%)+,&',-)./)1-*) #$%&'()*+,&',-.%,/)*+,-&1*#$)()5*6$+$%*,7&*-'-&1*(,-&*6&,7.$%$+*&%'(*8$&',-,%'-&1*(,-&*6&,79*(&,%: ;..,*&1$&$.$%&'()*1$$.,'&',-9*(&,%)?%*,('&5
"#"$%&#'()"#&'(*%)+,&',-)./)1-*) #$%&'()*+,&',-.%,/)*+,-&1*#$)()5*6$+$%*,7&*-'-&1*(,-&*6&,7.$%$+*&%'(*8$&',-,%'-&1*(,-&*6&,79*(&,%: ;..,*&1$&$.$%&'()*1$$.,'&',-9*(&,%)?%*,('&5
Parametrics and Vectors (BC Only)
 Paramerics and Vecors (BC Only) The following relaionships should be learned and memorized. The paricle s posiion vecor is r() x(), y(). The velociy vecor is v(),. The speed is he magniude of he velociy
Paramerics and Vecors (BC Only) The following relaionships should be learned and memorized. The paricle s posiion vecor is r() x(), y(). The velociy vecor is v(),. The speed is he magniude of he velociy
BEng (Hons) Telecommunications. Examinations for / Semester 2
 BEng (Hons) Telecommunicaions Cohor: BTEL/14/FT Examinaions for 2015-2016 / Semeser 2 MODULE: ELECTROMAGNETIC THEORY MODULE CODE: ASE2103 Duraion: 2 ½ Hours Insrucions o Candidaes: 1. Answer ALL 4 (FOUR)
BEng (Hons) Telecommunicaions Cohor: BTEL/14/FT Examinaions for 2015-2016 / Semeser 2 MODULE: ELECTROMAGNETIC THEORY MODULE CODE: ASE2103 Duraion: 2 ½ Hours Insrucions o Candidaes: 1. Answer ALL 4 (FOUR)
The equation to any straight line can be expressed in the form:
 Sring Graphs Par 1 Answers 1 TI-Nspire Invesigaion Suden min Aims Deermine a series of equaions of sraigh lines o form a paern similar o ha formed by he cables on he Jerusalem Chords Bridge. Deermine he
Sring Graphs Par 1 Answers 1 TI-Nspire Invesigaion Suden min Aims Deermine a series of equaions of sraigh lines o form a paern similar o ha formed by he cables on he Jerusalem Chords Bridge. Deermine he
Solutionbank Edexcel AS and A Level Modular Mathematics
 Page of 4 Soluionbank Edexcel AS and A Level Modular Mahemaics Exercise A, Quesion Quesion: Skech he graphs of (a) y = e x + (b) y = 4e x (c) y = e x 3 (d) y = 4 e x (e) y = 6 + 0e x (f) y = 00e x + 0
Page of 4 Soluionbank Edexcel AS and A Level Modular Mahemaics Exercise A, Quesion Quesion: Skech he graphs of (a) y = e x + (b) y = 4e x (c) y = e x 3 (d) y = 4 e x (e) y = 6 + 0e x (f) y = 00e x + 0
EXERCISE - 01 CHECK YOUR GRASP
 UNIT # 09 PARABOLA, ELLIPSE & HYPERBOLA PARABOLA EXERCISE - 0 CHECK YOUR GRASP. Hin : Disnce beween direcri nd focus is 5. Given (, be one end of focl chord hen oher end be, lengh of focl chord 6. Focus
UNIT # 09 PARABOLA, ELLIPSE & HYPERBOLA PARABOLA EXERCISE - 0 CHECK YOUR GRASP. Hin : Disnce beween direcri nd focus is 5. Given (, be one end of focl chord hen oher end be, lengh of focl chord 6. Focus
Math 116 Practice for Exam 2
 Mah 6 Pracice for Exam Generaed Ocober 3, 7 Name: SOLUTIONS Insrucor: Secion Number:. This exam has 5 quesions. Noe ha he problems are no of equal difficuly, so you may wan o skip over and reurn o a problem
Mah 6 Pracice for Exam Generaed Ocober 3, 7 Name: SOLUTIONS Insrucor: Secion Number:. This exam has 5 quesions. Noe ha he problems are no of equal difficuly, so you may wan o skip over and reurn o a problem
1 d Solving xy = 12 and. 2 a Solving xy = 9 and y= or x= 3 and y = 3 (point P)
 Coni Seions D a d Solving y and + + 6 + 6 y + b Solving y and y + 5 + 5 + 5 + 5 ( )( ) So y or y So he oordinaes are, Q, P and Using he quadrai formula: ± 6 ± 5 ± ± a Solving y 9 and y 9 So and y (poin
Coni Seions D a d Solving y and + + 6 + 6 y + b Solving y and y + 5 + 5 + 5 + 5 ( )( ) So y or y So he oordinaes are, Q, P and Using he quadrai formula: ± 6 ± 5 ± ± a Solving y 9 and y 9 So and y (poin
Answers to 1 Homework
 Answers o Homework. x + and y x 5 y To eliminae he parameer, solve for x. Subsiue ino y s equaion o ge y x.. x and y, x y x To eliminae he parameer, solve for. Subsiue ino y s equaion o ge x y, x. (Noe:
Answers o Homework. x + and y x 5 y To eliminae he parameer, solve for x. Subsiue ino y s equaion o ge y x.. x and y, x y x To eliminae he parameer, solve for. Subsiue ino y s equaion o ge x y, x. (Noe:
THE 2-BODY PROBLEM. FIGURE 1. A pair of ellipses sharing a common focus. (c,b) c+a ROBERT J. VANDERBEI
 THE 2-BODY PROBLEM ROBERT J. VANDERBEI ABSTRACT. In his shor noe, we show ha a pair of ellipses wih a common focus is a soluion o he 2-body problem. INTRODUCTION. Solving he 2-body problem from scrach
THE 2-BODY PROBLEM ROBERT J. VANDERBEI ABSTRACT. In his shor noe, we show ha a pair of ellipses wih a common focus is a soluion o he 2-body problem. INTRODUCTION. Solving he 2-body problem from scrach
2.7. Some common engineering functions. Introduction. Prerequisites. Learning Outcomes
 Some common engineering funcions 2.7 Inroducion This secion provides a caalogue of some common funcions ofen used in Science and Engineering. These include polynomials, raional funcions, he modulus funcion
Some common engineering funcions 2.7 Inroducion This secion provides a caalogue of some common funcions ofen used in Science and Engineering. These include polynomials, raional funcions, he modulus funcion
Differentiation 9G. 1 a. 2t 1 2t 1 dx 2 dy 2 t(2t 1) 2t. t 3t. d 2 2. dx 2(1 t ) 4t 2(1 t ) y t t t t t d 2 (1 ) 2 (1 ) 4.
 Differeniaion 9G a c d e x, y, x, y 6, 6 d 6 6 x, y 6, d 6 5 x, y, 5 d 5 5, x y, 6 d 6 f x, y ( ), d ( ) d ( ) ( ) y d ( ) d g x, y ( ) ( ) d ( ) ( ) d ( ) ( ) y d ( ) ( ) ( ) h x e, y e e, d e e ( )e
Differeniaion 9G a c d e x, y, x, y 6, 6 d 6 6 x, y 6, d 6 5 x, y, 5 d 5 5, x y, 6 d 6 f x, y ( ), d ( ) d ( ) ( ) y d ( ) d g x, y ( ) ( ) d ( ) ( ) d ( ) ( ) y d ( ) ( ) ( ) h x e, y e e, d e e ( )e
Let ( α, β be the eigenvector associated with the eigenvalue λ i
 ENGI 940 4.05 - Sabiliy Analysis (Linear) Page 4.5 Le ( α, be he eigenvecor associaed wih he eigenvalue λ i of he coefficien i i) marix A Le c, c be arbirary consans. a b c d Case of real, disinc, negaive
ENGI 940 4.05 - Sabiliy Analysis (Linear) Page 4.5 Le ( α, be he eigenvecor associaed wih he eigenvalue λ i of he coefficien i i) marix A Le c, c be arbirary consans. a b c d Case of real, disinc, negaive
10.1 EXERCISES. y 2 t 2. y 1 t y t 3. y e
 66 CHAPTER PARAMETRIC EQUATINS AND PLAR CRDINATES SLUTIN We use a graphing device o produce he graphs for he cases a,,.5,.,,.5,, and shown in Figure 7. Noice ha all of hese curves (ecep he case a ) have
66 CHAPTER PARAMETRIC EQUATINS AND PLAR CRDINATES SLUTIN We use a graphing device o produce he graphs for he cases a,,.5,.,,.5,, and shown in Figure 7. Noice ha all of hese curves (ecep he case a ) have
Lecture 17. Implicit differentiation. Making y the subject: If xy =1,y= x 1 & dy. changed to the subject of y. Note: Example 1.
 Implicit differentiation. Lecture 17 Making y the subject: If xy 1,y x 1 & dy dx x 2. But xy y 2 1 is harder to be changed to the subject of y. Note: d dx (f(y)) f (y) dy dx Example 1. Find dy dx given
Implicit differentiation. Lecture 17 Making y the subject: If xy 1,y x 1 & dy dx x 2. But xy y 2 1 is harder to be changed to the subject of y. Note: d dx (f(y)) f (y) dy dx Example 1. Find dy dx given
3, so θ = arccos
 Mahemaics 210 Professor Alan H Sein Monday, Ocober 1, 2007 SOLUTIONS This problem se is worh 50 poins 1 Find he angle beween he vecors (2, 7, 3) and (5, 2, 4) Soluion: Le θ be he angle (2, 7, 3) (5, 2,
Mahemaics 210 Professor Alan H Sein Monday, Ocober 1, 2007 SOLUTIONS This problem se is worh 50 poins 1 Find he angle beween he vecors (2, 7, 3) and (5, 2, 4) Soluion: Le θ be he angle (2, 7, 3) (5, 2,
Solutions from Chapter 9.1 and 9.2
 Soluions from Chaper 9 and 92 Secion 9 Problem # This basically boils down o an exercise in he chain rule from calculus We are looking for soluions of he form: u( x) = f( k x c) where k x R 3 and k is
Soluions from Chaper 9 and 92 Secion 9 Problem # This basically boils down o an exercise in he chain rule from calculus We are looking for soluions of he form: u( x) = f( k x c) where k x R 3 and k is
AP CALCULUS BC 2016 SCORING GUIDELINES
 6 SCORING GUIDELINES Quesion A ime, he posiion of a paricle moving in he xy-plane is given by he parameric funcions ( x ( ), y ( )), where = + sin ( ). The graph of y, consising of hree line segmens, is
6 SCORING GUIDELINES Quesion A ime, he posiion of a paricle moving in he xy-plane is given by he parameric funcions ( x ( ), y ( )), where = + sin ( ). The graph of y, consising of hree line segmens, is
Math 23 Spring Differential Equations. Final Exam Due Date: Tuesday, June 6, 5pm
 Mah Spring 6 Differenial Equaions Final Exam Due Dae: Tuesday, June 6, 5pm Your name (please prin): Insrucions: This is an open book, open noes exam. You are free o use a calculaor or compuer o check your
Mah Spring 6 Differenial Equaions Final Exam Due Dae: Tuesday, June 6, 5pm Your name (please prin): Insrucions: This is an open book, open noes exam. You are free o use a calculaor or compuer o check your
Additional Exercises for Chapter What is the slope-intercept form of the equation of the line given by 3x + 5y + 2 = 0?
 ddiional Eercises for Caper 5 bou Lines, Slopes, and Tangen Lines 39. Find an equaion for e line roug e wo poins (, 7) and (5, ). 4. Wa is e slope-inercep form of e equaion of e line given by 3 + 5y +
ddiional Eercises for Caper 5 bou Lines, Slopes, and Tangen Lines 39. Find an equaion for e line roug e wo poins (, 7) and (5, ). 4. Wa is e slope-inercep form of e equaion of e line given by 3 + 5y +
AP Calculus BC Chapter 10 Part 1 AP Exam Problems
 AP Calculus BC Chaper Par AP Eam Problems All problems are NO CALCULATOR unless oherwise indicaed Parameric Curves and Derivaives In he y plane, he graph of he parameric equaions = 5 + and y= for, is a
AP Calculus BC Chaper Par AP Eam Problems All problems are NO CALCULATOR unless oherwise indicaed Parameric Curves and Derivaives In he y plane, he graph of he parameric equaions = 5 + and y= for, is a
Module MA1132 (Frolov), Advanced Calculus Tutorial Sheet 1. To be solved during the tutorial session Thursday/Friday, 21/22 January 2016
 Module MA113 (Frolov), Advanced Calculus Tuorial Shee 1 To be solved during he uorial session Thursday/Friday, 1/ January 16 A curve C in he xy-plane is represened by he equaion Ax + Bxy + Cy + Dx + Ey
Module MA113 (Frolov), Advanced Calculus Tuorial Shee 1 To be solved during he uorial session Thursday/Friday, 1/ January 16 A curve C in he xy-plane is represened by he equaion Ax + Bxy + Cy + Dx + Ey
Math 221: Mathematical Notation
 Mah 221: Mahemaical Noaion Purpose: One goal in any course is o properly use he language o ha subjec. These noaions summarize some o he major conceps and more diicul opics o he uni. Typing hem helps you
Mah 221: Mahemaical Noaion Purpose: One goal in any course is o properly use he language o ha subjec. These noaions summarize some o he major conceps and more diicul opics o he uni. Typing hem helps you
1 1 + x 2 dx. tan 1 (2) = ] ] x 3. Solution: Recall that the given integral is improper because. x 3. 1 x 3. dx = lim dx.
![1 1 + x 2 dx. tan 1 (2) = ] ] x 3. Solution: Recall that the given integral is improper because. x 3. 1 x 3. dx = lim dx. 1 1 + x 2 dx. tan 1 (2) = ] ] x 3. Solution: Recall that the given integral is improper because. x 3. 1 x 3. dx = lim dx.](/thumbs/71/65799522.jpg) . Use Simpson s rule wih n 4 o esimae an () +. Soluion: Since we are using 4 seps, 4 Thus we have [ ( ) f() + 4f + f() + 4f 3 [ + 4 4 6 5 + + 4 4 3 + ] 5 [ + 6 6 5 + + 6 3 + ]. 5. Our funcion is f() +.
. Use Simpson s rule wih n 4 o esimae an () +. Soluion: Since we are using 4 seps, 4 Thus we have [ ( ) f() + 4f + f() + 4f 3 [ + 4 4 6 5 + + 4 4 3 + ] 5 [ + 6 6 5 + + 6 3 + ]. 5. Our funcion is f() +.
AP Calculus BC - Parametric equations and vectors Chapter 9- AP Exam Problems solutions
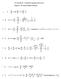 AP Calculus BC - Parameric equaions and vecors Chaper 9- AP Exam Problems soluions. A 5 and 5. B A, 4 + 8. C A, 4 + 4 8 ; he poin a is (,). y + ( x ) x + 4 4. e + e D A, slope.5 6 e e e 5. A d hus d d
AP Calculus BC - Parameric equaions and vecors Chaper 9- AP Exam Problems soluions. A 5 and 5. B A, 4 + 8. C A, 4 + 4 8 ; he poin a is (,). y + ( x ) x + 4 4. e + e D A, slope.5 6 e e e 5. A d hus d d
3 at MAC 1140 TEST 3 NOTES. 5.1 and 5.2. Exponential Functions. Form I: P is the y-intercept. (0, P) When a > 1: a = growth factor = 1 + growth rate
 1 5.1 and 5. Eponenial Funcions Form I: Y Pa, a 1, a > 0 P is he y-inercep. (0, P) When a > 1: a = growh facor = 1 + growh rae The equaion can be wrien as The larger a is, he seeper he graph is. Y P( 1
1 5.1 and 5. Eponenial Funcions Form I: Y Pa, a 1, a > 0 P is he y-inercep. (0, P) When a > 1: a = growh facor = 1 + growh rae The equaion can be wrien as The larger a is, he seeper he graph is. Y P( 1
Be able to sketch a function defined parametrically. (by hand and by calculator)
 Pre Calculus Uni : Parameric and Polar Equaions (7) Te References: Pre Calculus wih Limis; Larson, Hoseler, Edwards. B he end of he uni, ou should be able o complee he problems below. The eacher ma provide
Pre Calculus Uni : Parameric and Polar Equaions (7) Te References: Pre Calculus wih Limis; Larson, Hoseler, Edwards. B he end of he uni, ou should be able o complee he problems below. The eacher ma provide
dy dx = xey (a) y(0) = 2 (b) y(1) = 2.5 SOLUTION: See next page
 Assignmen 1 MATH 2270 SOLUTION Please wrie ou complee soluions for each of he following 6 problems (one more will sill be added). You may, of course, consul wih your classmaes, he exbook or oher resources,
Assignmen 1 MATH 2270 SOLUTION Please wrie ou complee soluions for each of he following 6 problems (one more will sill be added). You may, of course, consul wih your classmaes, he exbook or oher resources,
Evolute and involute (evolvent)
 Evolue and involue (evolven Ineracive soluions o problem s of differenial geomery S.N Nosulya, V.V Shelomovskii. Topical ses for geomery, 1. D.V. Shelomovskii. GInMA, 1. hp://www.deoma-cmd.ru/ Maerials
Evolue and involue (evolven Ineracive soluions o problem s of differenial geomery S.N Nosulya, V.V Shelomovskii. Topical ses for geomery, 1. D.V. Shelomovskii. GInMA, 1. hp://www.deoma-cmd.ru/ Maerials
AP CALCULUS AB 2003 SCORING GUIDELINES (Form B)
 SCORING GUIDELINES (Form B) Quesion A blood vessel is 6 millimeers (mm) long Disance wih circular cross secions of varying diameer. x (mm) 6 8 4 6 Diameer The able above gives he measuremens of he B(x)
SCORING GUIDELINES (Form B) Quesion A blood vessel is 6 millimeers (mm) long Disance wih circular cross secions of varying diameer. x (mm) 6 8 4 6 Diameer The able above gives he measuremens of he B(x)
ADDITIONAL MATHEMATICS PAPER 1
 000-CE A MATH PAPER HONG KONG EXAMINATIONS AUTHORITY HONG KONG CERTIFICATE OF EDUCATION EXAMINATION 000 ADDITIONAL MATHEMATICS PAPER 8.0 am 0.0 am ( hours This paper mus be answered in English. Answer
000-CE A MATH PAPER HONG KONG EXAMINATIONS AUTHORITY HONG KONG CERTIFICATE OF EDUCATION EXAMINATION 000 ADDITIONAL MATHEMATICS PAPER 8.0 am 0.0 am ( hours This paper mus be answered in English. Answer
AP Calculus BC 2004 Free-Response Questions Form B
 AP Calculus BC 200 Free-Response Quesions Form B The maerials included in hese files are inended for noncommercial use by AP eachers for course and exam preparaion; permission for any oher use mus be sough
AP Calculus BC 200 Free-Response Quesions Form B The maerials included in hese files are inended for noncommercial use by AP eachers for course and exam preparaion; permission for any oher use mus be sough
Rectangular Hyperbola Conics HSC Maths Extension 2
 Rectangular Hyperbola HSC Maths Etension Question For the y, find: (c) (d) (e) the eccentricity the coordinates of the foci the equations of the directrices the equations of the asymptotes sketch the hyperbola.
Rectangular Hyperbola HSC Maths Etension Question For the y, find: (c) (d) (e) the eccentricity the coordinates of the foci the equations of the directrices the equations of the asymptotes sketch the hyperbola.
10.6 Parametric Equations
 0_006.qd /8/05 9:05 AM Page 77 Secion 0.6 77 Parameric Equaions 0.6 Parameric Equaions Wha ou should learn Evaluae ses of parameric equaions for given values of he parameer. Skech curves ha are represened
0_006.qd /8/05 9:05 AM Page 77 Secion 0.6 77 Parameric Equaions 0.6 Parameric Equaions Wha ou should learn Evaluae ses of parameric equaions for given values of he parameer. Skech curves ha are represened
Some Basic Information about M-S-D Systems
 Some Basic Informaion abou M-S-D Sysems 1 Inroducion We wan o give some summary of he facs concerning unforced (homogeneous) and forced (non-homogeneous) models for linear oscillaors governed by second-order,
Some Basic Informaion abou M-S-D Sysems 1 Inroducion We wan o give some summary of he facs concerning unforced (homogeneous) and forced (non-homogeneous) models for linear oscillaors governed by second-order,
Math Week 14 April 16-20: sections first order systems of linear differential equations; 7.4 mass-spring systems.
 Mah 2250-004 Week 4 April 6-20 secions 7.-7.3 firs order sysems of linear differenial equaions; 7.4 mass-spring sysems. Mon Apr 6 7.-7.2 Sysems of differenial equaions (7.), and he vecor Calculus we need
Mah 2250-004 Week 4 April 6-20 secions 7.-7.3 firs order sysems of linear differenial equaions; 7.4 mass-spring sysems. Mon Apr 6 7.-7.2 Sysems of differenial equaions (7.), and he vecor Calculus we need
Mark Scheme (Results) January 2011
 Mark (Resuls) January 0 GCE GCE Furher Pure Mahemaics FP (6667) Paper Edexcel Limied. Regisered in England and Wales No. 4496750 Regisered Office: One90 High Holborn, London WCV 7BH Edexcel is one of he
Mark (Resuls) January 0 GCE GCE Furher Pure Mahemaics FP (6667) Paper Edexcel Limied. Regisered in England and Wales No. 4496750 Regisered Office: One90 High Holborn, London WCV 7BH Edexcel is one of he
Distance Between Two Ellipses in 3D
 Disance Beween Two Ellipses in 3D David Eberly Magic Sofware 6006 Meadow Run Cour Chapel Hill, NC 27516 eberly@magic-sofware.com 1 Inroducion An ellipse in 3D is represened by a cener C, uni lengh axes
Disance Beween Two Ellipses in 3D David Eberly Magic Sofware 6006 Meadow Run Cour Chapel Hill, NC 27516 eberly@magic-sofware.com 1 Inroducion An ellipse in 3D is represened by a cener C, uni lengh axes
u(x) = e x 2 y + 2 ) Integrate and solve for x (1 + x)y + y = cos x Answer: Divide both sides by 1 + x and solve for y. y = x y + cos x
 . 1 Mah 211 Homework #3 February 2, 2001 2.4.3. y + (2/x)y = (cos x)/x 2 Answer: Compare y + (2/x) y = (cos x)/x 2 wih y = a(x)x + f(x)and noe ha a(x) = 2/x. Consequenly, an inegraing facor is found wih
. 1 Mah 211 Homework #3 February 2, 2001 2.4.3. y + (2/x)y = (cos x)/x 2 Answer: Compare y + (2/x) y = (cos x)/x 2 wih y = a(x)x + f(x)and noe ha a(x) = 2/x. Consequenly, an inegraing facor is found wih
Available Online :
 fo/u fopjr Hh# u] ugh vjehs de] foifr ns[ NsMs rqjr e/;e eu dj ';ea iq#" flg ldyi dj] lgrs foifr vusd] ^cu^ u NsMs /;s; ds] j?qcj j[s VsdAA jfpr% euo /ez iz.sr ln~xq# Jh j.nsmnlh egj STUDY PACKAGE Subjec
fo/u fopjr Hh# u] ugh vjehs de] foifr ns[ NsMs rqjr e/;e eu dj ';ea iq#" flg ldyi dj] lgrs foifr vusd] ^cu^ u NsMs /;s; ds] j?qcj j[s VsdAA jfpr% euo /ez iz.sr ln~xq# Jh j.nsmnlh egj STUDY PACKAGE Subjec
1. VELOCITY AND ACCELERATION
 1. VELOCITY AND ACCELERATION 1.1 Kinemaics Equaions s = u + 1 a and s = v 1 a s = 1 (u + v) v = u + as 1. Displacemen-Time Graph Gradien = speed 1.3 Velociy-Time Graph Gradien = acceleraion Area under
1. VELOCITY AND ACCELERATION 1.1 Kinemaics Equaions s = u + 1 a and s = v 1 a s = 1 (u + v) v = u + as 1. Displacemen-Time Graph Gradien = speed 1.3 Velociy-Time Graph Gradien = acceleraion Area under
From Particles to Rigid Bodies
 Rigid Body Dynamics From Paricles o Rigid Bodies Paricles No roaions Linear velociy v only Rigid bodies Body roaions Linear velociy v Angular velociy ω Rigid Bodies Rigid bodies have boh a posiion and
Rigid Body Dynamics From Paricles o Rigid Bodies Paricles No roaions Linear velociy v only Rigid bodies Body roaions Linear velociy v Angular velociy ω Rigid Bodies Rigid bodies have boh a posiion and
CHAPTER 2: Mathematics for Microeconomics
 CHAPTER : Mahemaics for Microeconomics The problems in his chaper are primarily mahemaical. They are inended o give sudens some pracice wih he conceps inroduced in Chaper, bu he problems in hemselves offer
CHAPTER : Mahemaics for Microeconomics The problems in his chaper are primarily mahemaical. They are inended o give sudens some pracice wih he conceps inroduced in Chaper, bu he problems in hemselves offer
(1) (2) Differentiation of (1) and then substitution of (3) leads to. Therefore, we will simply consider the second-order linear system given by (4)
 Phase Plane Analysis of Linear Sysems Adaped from Applied Nonlinear Conrol by Sloine and Li The general form of a linear second-order sysem is a c b d From and b bc d a Differeniaion of and hen subsiuion
Phase Plane Analysis of Linear Sysems Adaped from Applied Nonlinear Conrol by Sloine and Li The general form of a linear second-order sysem is a c b d From and b bc d a Differeniaion of and hen subsiuion
QUESTION BANK ON. CONIC SECTION (Parabola, Ellipse & Hyperbola)
 QUESTION BANK ON CONIC SECTION (Parabola, Ellipse & Hyperbola) Question bank on Parabola, Ellipse & Hyperbola Select the correct alternative : (Only one is correct) Q. Two mutually perpendicular tangents
QUESTION BANK ON CONIC SECTION (Parabola, Ellipse & Hyperbola) Question bank on Parabola, Ellipse & Hyperbola Select the correct alternative : (Only one is correct) Q. Two mutually perpendicular tangents
15. Vector Valued Functions
 1. Vecor Valued Funcions Up o his poin, we have presened vecors wih consan componens, for example, 1, and,,4. However, we can allow he componens of a vecor o be funcions of a common variable. For example,
1. Vecor Valued Funcions Up o his poin, we have presened vecors wih consan componens, for example, 1, and,,4. However, we can allow he componens of a vecor o be funcions of a common variable. For example,
SYSTEM OF CIRCLES OBJECTIVES (a) Touch each other internally (b) Touch each other externally
 SYSTEM OF CIRCLES OBJECTIVES. A circle passes through (0, 0) and (, 0) and touches the circle x + y = 9, then the centre of circle is (a) (c) 3,, (b) (d) 3,, ±. The equation of the circle having its centre
SYSTEM OF CIRCLES OBJECTIVES. A circle passes through (0, 0) and (, 0) and touches the circle x + y = 9, then the centre of circle is (a) (c) 3,, (b) (d) 3,, ±. The equation of the circle having its centre
Applications of the Basic Equations Chapter 3. Paul A. Ullrich
 Applicaions of he Basic Equaions Chaper 3 Paul A. Ullrich paullrich@ucdavis.edu Par 1: Naural Coordinaes Naural Coordinaes Quesion: Why do we need anoher coordinae sysem? Our goal is o simplify he equaions
Applicaions of he Basic Equaions Chaper 3 Paul A. Ullrich paullrich@ucdavis.edu Par 1: Naural Coordinaes Naural Coordinaes Quesion: Why do we need anoher coordinae sysem? Our goal is o simplify he equaions
Chapters 6 & 7: Trigonometric Functions of Angles and Real Numbers. Divide both Sides by 180
 Algebra Chapers & : Trigonomeric Funcions of Angles and Real Numbers Chapers & : Trigonomeric Funcions of Angles and Real Numbers - Angle Measures Radians: - a uni (rad o measure he size of an angle. rad
Algebra Chapers & : Trigonomeric Funcions of Angles and Real Numbers Chapers & : Trigonomeric Funcions of Angles and Real Numbers - Angle Measures Radians: - a uni (rad o measure he size of an angle. rad
DIFFERENTIAL GEOMETRY HW 5
 DIFFERENTIAL GEOMETRY HW 5 CLAY SHONKWILER 3. Le M be a complee Riemannian manifold wih non-posiive secional curvaure. Prove ha d exp p v w w, for all p M, all v T p M and all w T v T p M. Proof. Le γ
DIFFERENTIAL GEOMETRY HW 5 CLAY SHONKWILER 3. Le M be a complee Riemannian manifold wih non-posiive secional curvaure. Prove ha d exp p v w w, for all p M, all v T p M and all w T v T p M. Proof. Le γ
Let us start with a two dimensional case. We consider a vector ( x,
 Roaion marices We consider now roaion marices in wo and hree dimensions. We sar wih wo dimensions since wo dimensions are easier han hree o undersand, and one dimension is a lile oo simple. However, our
Roaion marices We consider now roaion marices in wo and hree dimensions. We sar wih wo dimensions since wo dimensions are easier han hree o undersand, and one dimension is a lile oo simple. However, our
From String Art to Caustic Curves: Envelopes in Symbolic Geometry
 From Sring r o ausic urves: nvelopes in Symbolic eomery Philip Todd phil@salire.com Salire Sofware, PO 565, eaveron, OR 97223, U.S.. bsrac: In his paper, we use he symbolic geomery program eomery xpressions
From Sring r o ausic urves: nvelopes in Symbolic eomery Philip Todd phil@salire.com Salire Sofware, PO 565, eaveron, OR 97223, U.S.. bsrac: In his paper, we use he symbolic geomery program eomery xpressions
23.5. Half-Range Series. Introduction. Prerequisites. Learning Outcomes
 Half-Range Series 2.5 Inroducion In his Secion we address he following problem: Can we find a Fourier series expansion of a funcion defined over a finie inerval? Of course we recognise ha such a funcion
Half-Range Series 2.5 Inroducion In his Secion we address he following problem: Can we find a Fourier series expansion of a funcion defined over a finie inerval? Of course we recognise ha such a funcion
556: MATHEMATICAL STATISTICS I
 556: MATHEMATICAL STATISTICS I INEQUALITIES 5.1 Concenraion and Tail Probabiliy Inequaliies Lemma (CHEBYCHEV S LEMMA) c > 0, If X is a random variable, hen for non-negaive funcion h, and P X [h(x) c] E
556: MATHEMATICAL STATISTICS I INEQUALITIES 5.1 Concenraion and Tail Probabiliy Inequaliies Lemma (CHEBYCHEV S LEMMA) c > 0, If X is a random variable, hen for non-negaive funcion h, and P X [h(x) c] E
MA 214 Calculus IV (Spring 2016) Section 2. Homework Assignment 1 Solutions
 MA 14 Calculus IV (Spring 016) Secion Homework Assignmen 1 Soluions 1 Boyce and DiPrima, p 40, Problem 10 (c) Soluion: In sandard form he given firs-order linear ODE is: An inegraing facor is given by
MA 14 Calculus IV (Spring 016) Secion Homework Assignmen 1 Soluions 1 Boyce and DiPrima, p 40, Problem 10 (c) Soluion: In sandard form he given firs-order linear ODE is: An inegraing facor is given by
Differential Equations
 Mah 21 (Fall 29) Differenial Equaions Soluion #3 1. Find he paricular soluion of he following differenial equaion by variaion of parameer (a) y + y = csc (b) 2 y + y y = ln, > Soluion: (a) The corresponding
Mah 21 (Fall 29) Differenial Equaions Soluion #3 1. Find he paricular soluion of he following differenial equaion by variaion of parameer (a) y + y = csc (b) 2 y + y y = ln, > Soluion: (a) The corresponding
Homework sheet Exercises done during the lecture of March 12, 2014
 EXERCISE SESSION 2A FOR THE COURSE GÉOMÉTRIE EUCLIDIENNE, NON EUCLIDIENNE ET PROJECTIVE MATTEO TOMMASINI Homework shee 3-4 - Exercises done during he lecure of March 2, 204 Exercise 2 Is i rue ha he parameerized
EXERCISE SESSION 2A FOR THE COURSE GÉOMÉTRIE EUCLIDIENNE, NON EUCLIDIENNE ET PROJECTIVE MATTEO TOMMASINI Homework shee 3-4 - Exercises done during he lecure of March 2, 204 Exercise 2 Is i rue ha he parameerized
a. Show that these lines intersect by finding the point of intersection. b. Find an equation for the plane containing these lines.
 Mah A Final Eam Problems for onsideraion. Show all work for credi. Be sure o show wha you know. Given poins A(,,, B(,,, (,, 4 and (,,, find he volume of he parallelepiped wih adjacen edges AB, A, and A.
Mah A Final Eam Problems for onsideraion. Show all work for credi. Be sure o show wha you know. Given poins A(,,, B(,,, (,, 4 and (,,, find he volume of he parallelepiped wih adjacen edges AB, A, and A.
Position, Velocity, and Acceleration
 rev 06/2017 Posiion, Velociy, and Acceleraion Equipmen Qy Equipmen Par Number 1 Dynamic Track ME-9493 1 Car ME-9454 1 Fan Accessory ME-9491 1 Moion Sensor II CI-6742A 1 Track Barrier Purpose The purpose
rev 06/2017 Posiion, Velociy, and Acceleraion Equipmen Qy Equipmen Par Number 1 Dynamic Track ME-9493 1 Car ME-9454 1 Fan Accessory ME-9491 1 Moion Sensor II CI-6742A 1 Track Barrier Purpose The purpose
4.5 Constant Acceleration
 4.5 Consan Acceleraion v() v() = v 0 + a a() a a() = a v 0 Area = a (a) (b) Figure 4.8 Consan acceleraion: (a) velociy, (b) acceleraion When he x -componen of he velociy is a linear funcion (Figure 4.8(a)),
4.5 Consan Acceleraion v() v() = v 0 + a a() a a() = a v 0 Area = a (a) (b) Figure 4.8 Consan acceleraion: (a) velociy, (b) acceleraion When he x -componen of he velociy is a linear funcion (Figure 4.8(a)),
Phys 221 Fall Chapter 2. Motion in One Dimension. 2014, 2005 A. Dzyubenko Brooks/Cole
 Phys 221 Fall 2014 Chaper 2 Moion in One Dimension 2014, 2005 A. Dzyubenko 2004 Brooks/Cole 1 Kinemaics Kinemaics, a par of classical mechanics: Describes moion in erms of space and ime Ignores he agen
Phys 221 Fall 2014 Chaper 2 Moion in One Dimension 2014, 2005 A. Dzyubenko 2004 Brooks/Cole 1 Kinemaics Kinemaics, a par of classical mechanics: Describes moion in erms of space and ime Ignores he agen
Narayana IIT Academy
 INDIA XI_IC_SPARK ime : 3 Hours JEE-MAIN CP -5 Date: 5-0-8 Max Marks : 360 KEY SHEE PHYSICS.. 3. 4. 5. 6. 7. 8. 9. 0... 3. 4. 5. 6. 7. 8. 9. 0... 3. 4. 5. 6. 7. 8. 9. 30. CHEMISRY 3. 3. 33. 34. 35. 36.
INDIA XI_IC_SPARK ime : 3 Hours JEE-MAIN CP -5 Date: 5-0-8 Max Marks : 360 KEY SHEE PHYSICS.. 3. 4. 5. 6. 7. 8. 9. 0... 3. 4. 5. 6. 7. 8. 9. 0... 3. 4. 5. 6. 7. 8. 9. 30. CHEMISRY 3. 3. 33. 34. 35. 36.
Non-uniform circular motion *
 OpenSax-CNX module: m14020 1 Non-uniform circular moion * Sunil Kumar Singh This work is produced by OpenSax-CNX and licensed under he Creaive Commons Aribuion License 2.0 Wha do we mean by non-uniform
OpenSax-CNX module: m14020 1 Non-uniform circular moion * Sunil Kumar Singh This work is produced by OpenSax-CNX and licensed under he Creaive Commons Aribuion License 2.0 Wha do we mean by non-uniform
2.1: What is physics? Ch02: Motion along a straight line. 2.2: Motion. 2.3: Position, Displacement, Distance
 Ch: Moion along a sraigh line Moion Posiion and Displacemen Average Velociy and Average Speed Insananeous Velociy and Speed Acceleraion Consan Acceleraion: A Special Case Anoher Look a Consan Acceleraion
Ch: Moion along a sraigh line Moion Posiion and Displacemen Average Velociy and Average Speed Insananeous Velociy and Speed Acceleraion Consan Acceleraion: A Special Case Anoher Look a Consan Acceleraion
NAME: Date: HOMEWORK: C1. Question Obtained. Total/100 A 80 B 70 C 60 D 50 E 40 U 39
 NAME: Date: HOMEWORK: C1 Question Obtained 1 2 3 4 5 6 7 8 9 10 Total/100 A 80 B 70 C 60 D 50 E 40 U 39 1. Figure 2 y A(1, 7) B(20, 7) D(8, 2) O x C(p, q) The points A(1, 7), B(20, 7) and C(p, q) form
NAME: Date: HOMEWORK: C1 Question Obtained 1 2 3 4 5 6 7 8 9 10 Total/100 A 80 B 70 C 60 D 50 E 40 U 39 1. Figure 2 y A(1, 7) B(20, 7) D(8, 2) O x C(p, q) The points A(1, 7), B(20, 7) and C(p, q) form
Kinematics Vocabulary. Kinematics and One Dimensional Motion. Position. Coordinate System in One Dimension. Kinema means movement 8.
 Kinemaics Vocabulary Kinemaics and One Dimensional Moion 8.1 WD1 Kinema means movemen Mahemaical descripion of moion Posiion Time Inerval Displacemen Velociy; absolue value: speed Acceleraion Averages
Kinemaics Vocabulary Kinemaics and One Dimensional Moion 8.1 WD1 Kinema means movemen Mahemaical descripion of moion Posiion Time Inerval Displacemen Velociy; absolue value: speed Acceleraion Averages
Math 116 Second Midterm March 21, 2016
 Mah 6 Second Miderm March, 06 UMID: EXAM SOLUTIONS Iniials: Insrucor: Secion:. Do no open his exam unil you are old o do so.. Do no wrie your name anywhere on his exam. 3. This exam has pages including
Mah 6 Second Miderm March, 06 UMID: EXAM SOLUTIONS Iniials: Insrucor: Secion:. Do no open his exam unil you are old o do so.. Do no wrie your name anywhere on his exam. 3. This exam has pages including
DIFFERENTIAL EQUATIONS
 DIFFERENTIAL EQUATIONS PAGE # An equaion conaining independen variable, dependen variable & differenial coeffeciens of dependen variables wr independen variable is called differenial equaion If all he
DIFFERENTIAL EQUATIONS PAGE # An equaion conaining independen variable, dependen variable & differenial coeffeciens of dependen variables wr independen variable is called differenial equaion If all he
Concourse Math Spring 2012 Worked Examples: Matrix Methods for Solving Systems of 1st Order Linear Differential Equations
 Concourse Mah 80 Spring 0 Worked Examples: Marix Mehods for Solving Sysems of s Order Linear Differenial Equaions The Main Idea: Given a sysem of s order linear differenial equaions d x d Ax wih iniial
Concourse Mah 80 Spring 0 Worked Examples: Marix Mehods for Solving Sysems of s Order Linear Differenial Equaions The Main Idea: Given a sysem of s order linear differenial equaions d x d Ax wih iniial
HOMEWORK # 2: MATH 211, SPRING Note: This is the last solution set where I will describe the MATLAB I used to make my pictures.
 HOMEWORK # 2: MATH 2, SPRING 25 TJ HITCHMAN Noe: This is he las soluion se where I will describe he MATLAB I used o make my picures.. Exercises from he ex.. Chaper 2.. Problem 6. We are o show ha y() =
HOMEWORK # 2: MATH 2, SPRING 25 TJ HITCHMAN Noe: This is he las soluion se where I will describe he MATLAB I used o make my picures.. Exercises from he ex.. Chaper 2.. Problem 6. We are o show ha y() =
VISUALIZING SPECIAL FUNCTIONS AND APPLICATIONS IN CALCULUS 1
 VISUALIZING SPECIAL FUNCTIONS AND APPLICATIONS IN CALCULUS 1 Rober E. Kowalczk and Adam O. Hausknech Universi of Massachuses Darmouh Mahemaics Deparmen, 85 Old Wespor Road, N. Darmouh, MA 747-3 rkowalczk@umassd.edu
VISUALIZING SPECIAL FUNCTIONS AND APPLICATIONS IN CALCULUS 1 Rober E. Kowalczk and Adam O. Hausknech Universi of Massachuses Darmouh Mahemaics Deparmen, 85 Old Wespor Road, N. Darmouh, MA 747-3 rkowalczk@umassd.edu
9231 FURTHER MATHEMATICS
 CAMBRIDGE INTERNATIONAL EXAMINATIONS GCE Advanced Level MARK SCHEME for he May/June series 9 FURTHER MATHEMATICS 9/ Paper, maximum raw mark This mark scheme is published as an aid o eachers and candidaes,
CAMBRIDGE INTERNATIONAL EXAMINATIONS GCE Advanced Level MARK SCHEME for he May/June series 9 FURTHER MATHEMATICS 9/ Paper, maximum raw mark This mark scheme is published as an aid o eachers and candidaes,
Instructor: Barry McQuarrie Page 1 of 5
 Procedure for Solving radical equaions 1. Algebraically isolae one radical by iself on one side of equal sign. 2. Raise each side of he equaion o an appropriae power o remove he radical. 3. Simplify. 4.
Procedure for Solving radical equaions 1. Algebraically isolae one radical by iself on one side of equal sign. 2. Raise each side of he equaion o an appropriae power o remove he radical. 3. Simplify. 4.
After the completion of this section the student. Theory of Linear Systems of ODEs. Autonomous Systems. Review Questions and Exercises
 Chaper V ODE V.5 Sysems of Ordinary Differenial Equaions 45 V.5 SYSTEMS OF FIRST ORDER LINEAR ODEs Objecives: Afer he compleion of his secion he suden - should recall he definiion of a sysem of linear
Chaper V ODE V.5 Sysems of Ordinary Differenial Equaions 45 V.5 SYSTEMS OF FIRST ORDER LINEAR ODEs Objecives: Afer he compleion of his secion he suden - should recall he definiion of a sysem of linear
Review Exercises for Chapter 3
 60_00R.qd //0 :9 M age CHATER Applicaions of Differeniaion Review Eercises for Chaper. Give he definiion of a criical number, and graph a funcion f showing he differen pes of criical numbers.. Consider
60_00R.qd //0 :9 M age CHATER Applicaions of Differeniaion Review Eercises for Chaper. Give he definiion of a criical number, and graph a funcion f showing he differen pes of criical numbers.. Consider
x i v x t a dx dt t x
 Physics 3A: Basic Physics I Shoup - Miderm Useful Equaions A y A sin A A A y an A y A A = A i + A y j + A z k A * B = A B cos(θ) A B = A B sin(θ) A * B = A B + A y B y + A z B z A B = (A y B z A z B y
Physics 3A: Basic Physics I Shoup - Miderm Useful Equaions A y A sin A A A y an A y A A = A i + A y j + A z k A * B = A B cos(θ) A B = A B sin(θ) A * B = A B + A y B y + A z B z A B = (A y B z A z B y
Homework 10 (Stats 620, Winter 2017) Due Tuesday April 18, in class Questions are derived from problems in Stochastic Processes by S. Ross.
 Homework (Sas 6, Winer 7 Due Tuesday April 8, in class Quesions are derived from problems in Sochasic Processes by S. Ross.. A sochasic process {X(, } is said o be saionary if X(,..., X( n has he same
Homework (Sas 6, Winer 7 Due Tuesday April 8, in class Quesions are derived from problems in Sochasic Processes by S. Ross.. A sochasic process {X(, } is said o be saionary if X(,..., X( n has he same
Area A 0 level is h 0, assuming the pipe flow to be laminar. D, L and assuming the pipe flow to be highly turbulent.
 Pipe Flows (ecures 5 o 7). Choose he crec answer (i) While deriving an expression f loss of head due o a sudden expansion in a pipe, in addiion o he coninuiy and impulse-momenum equaions, one of he following
Pipe Flows (ecures 5 o 7). Choose he crec answer (i) While deriving an expression f loss of head due o a sudden expansion in a pipe, in addiion o he coninuiy and impulse-momenum equaions, one of he following
The Arcsine Distribution
 The Arcsine Disribuion Chris H. Rycrof Ocober 6, 006 A common heme of he class has been ha he saisics of single walker are ofen very differen from hose of an ensemble of walkers. On he firs homework, we
The Arcsine Disribuion Chris H. Rycrof Ocober 6, 006 A common heme of he class has been ha he saisics of single walker are ofen very differen from hose of an ensemble of walkers. On he firs homework, we
Hamilton- J acobi Equation: Explicit Formulas In this lecture we try to apply the method of characteristics to the Hamilton-Jacobi equation: u t
 M ah 5 2 7 Fall 2 0 0 9 L ecure 1 0 O c. 7, 2 0 0 9 Hamilon- J acobi Equaion: Explici Formulas In his lecure we ry o apply he mehod of characerisics o he Hamilon-Jacobi equaion: u + H D u, x = 0 in R n
M ah 5 2 7 Fall 2 0 0 9 L ecure 1 0 O c. 7, 2 0 0 9 Hamilon- J acobi Equaion: Explici Formulas In his lecure we ry o apply he mehod of characerisics o he Hamilon-Jacobi equaion: u + H D u, x = 0 in R n
Mathematics Paper- II
 R Prerna Tower, Road No -, Conracors Area, Bisupur, Jamsedpur - 8, Tel - (65789, www.prernaclasses.com Maemaics Paper- II Jee Advance PART III - MATHEMATICS SECTION - : (One or more opions correc Type
R Prerna Tower, Road No -, Conracors Area, Bisupur, Jamsedpur - 8, Tel - (65789, www.prernaclasses.com Maemaics Paper- II Jee Advance PART III - MATHEMATICS SECTION - : (One or more opions correc Type
18 Biological models with discrete time
 8 Biological models wih discree ime The mos imporan applicaions, however, may be pedagogical. The elegan body of mahemaical heory peraining o linear sysems (Fourier analysis, orhogonal funcions, and so
8 Biological models wih discree ime The mos imporan applicaions, however, may be pedagogical. The elegan body of mahemaical heory peraining o linear sysems (Fourier analysis, orhogonal funcions, and so
Differential Geometry: Revisiting Curvatures
 Differenial Geomery: Reisiing Curaures Curaure and Graphs Recall: hus, up o a roaion in he x-y plane, we hae: f 1 ( x, y) x y he alues 1 and are he principal curaures a p and he corresponding direcions
Differenial Geomery: Reisiing Curaures Curaure and Graphs Recall: hus, up o a roaion in he x-y plane, we hae: f 1 ( x, y) x y he alues 1 and are he principal curaures a p and he corresponding direcions
SOLUTIONS TO ECE 3084
 SOLUTIONS TO ECE 384 PROBLEM 2.. For each sysem below, specify wheher or no i is: (i) memoryless; (ii) causal; (iii) inverible; (iv) linear; (v) ime invarian; Explain your reasoning. If he propery is no
SOLUTIONS TO ECE 384 PROBLEM 2.. For each sysem below, specify wheher or no i is: (i) memoryless; (ii) causal; (iii) inverible; (iv) linear; (v) ime invarian; Explain your reasoning. If he propery is no
MECHANICS OF MATERIALS Poisson s Ratio
 Poisson s Raio For a slender bar subjeced o axial loading: ε x x y 0 The elongaion in he x-direcion i is accompanied by a conracion in he oher direcions. Assuming ha he maerial is isoropic (no direcional
Poisson s Raio For a slender bar subjeced o axial loading: ε x x y 0 The elongaion in he x-direcion i is accompanied by a conracion in he oher direcions. Assuming ha he maerial is isoropic (no direcional
Lecture #31, 32: The Ornstein-Uhlenbeck Process as a Model of Volatility
 Saisics 441 (Fall 214) November 19, 21, 214 Prof Michael Kozdron Lecure #31, 32: The Ornsein-Uhlenbeck Process as a Model of Volailiy The Ornsein-Uhlenbeck process is a di usion process ha was inroduced
Saisics 441 (Fall 214) November 19, 21, 214 Prof Michael Kozdron Lecure #31, 32: The Ornsein-Uhlenbeck Process as a Model of Volailiy The Ornsein-Uhlenbeck process is a di usion process ha was inroduced
UCLA: Math 3B Problem set 3 (solutions) Fall, 2018
 UCLA: Mah 3B Problem se 3 (soluions) Fall, 28 This problem se concenraes on pracice wih aniderivaives. You will ge los of pracice finding simple aniderivaives as well as finding aniderivaives graphically
UCLA: Mah 3B Problem se 3 (soluions) Fall, 28 This problem se concenraes on pracice wih aniderivaives. You will ge los of pracice finding simple aniderivaives as well as finding aniderivaives graphically
Physics 235 Chapter 2. Chapter 2 Newtonian Mechanics Single Particle
 Chaper 2 Newonian Mechanics Single Paricle In his Chaper we will review wha Newon s laws of mechanics ell us abou he moion of a single paricle. Newon s laws are only valid in suiable reference frames,
Chaper 2 Newonian Mechanics Single Paricle In his Chaper we will review wha Newon s laws of mechanics ell us abou he moion of a single paricle. Newon s laws are only valid in suiable reference frames,
Applicable Mathematics 2A
 Applicable Mahemaics A Lecure Noes Revised: Augus 00 Please noe ha hese are my lecure noes: hey are no course noes. So I will be following hese noes very closely, supplemened by he homework eamples ec
Applicable Mahemaics A Lecure Noes Revised: Augus 00 Please noe ha hese are my lecure noes: hey are no course noes. So I will be following hese noes very closely, supplemened by he homework eamples ec
Topic 2 [312 marks] The rectangle ABCD is inscribed in a circle. Sides [AD] and [AB] have lengths
![Topic 2 [312 marks] The rectangle ABCD is inscribed in a circle. Sides [AD] and [AB] have lengths Topic 2 [312 marks] The rectangle ABCD is inscribed in a circle. Sides [AD] and [AB] have lengths](/thumbs/86/93150791.jpg) Topic 2 [312 marks] 1 The rectangle ABCD is inscribed in a circle Sides [AD] and [AB] have lengths [12 marks] 3 cm and (\9\) cm respectively E is a point on side [AB] such that AE is 3 cm Side [DE] is
Topic 2 [312 marks] 1 The rectangle ABCD is inscribed in a circle Sides [AD] and [AB] have lengths [12 marks] 3 cm and (\9\) cm respectively E is a point on side [AB] such that AE is 3 cm Side [DE] is
WEEK-3 Recitation PHYS 131. of the projectile s velocity remains constant throughout the motion, since the acceleration a x
 WEEK-3 Reciaion PHYS 131 Ch. 3: FOC 1, 3, 4, 6, 14. Problems 9, 37, 41 & 71 and Ch. 4: FOC 1, 3, 5, 8. Problems 3, 5 & 16. Feb 8, 018 Ch. 3: FOC 1, 3, 4, 6, 14. 1. (a) The horizonal componen of he projecile
WEEK-3 Reciaion PHYS 131 Ch. 3: FOC 1, 3, 4, 6, 14. Problems 9, 37, 41 & 71 and Ch. 4: FOC 1, 3, 5, 8. Problems 3, 5 & 16. Feb 8, 018 Ch. 3: FOC 1, 3, 4, 6, 14. 1. (a) The horizonal componen of he projecile
MEI STRUCTURED MATHEMATICS 4758
 OXFORD CAMBRIDGE AND RSA EXAMINATIONS Advanced Subsidiary General Cerificae of Educaion Advanced General Cerificae of Educaion MEI STRUCTURED MATHEMATICS 4758 Differenial Equaions Thursday 5 JUNE 006 Afernoon
OXFORD CAMBRIDGE AND RSA EXAMINATIONS Advanced Subsidiary General Cerificae of Educaion Advanced General Cerificae of Educaion MEI STRUCTURED MATHEMATICS 4758 Differenial Equaions Thursday 5 JUNE 006 Afernoon
Conic section. Ans: c. Ans: a. Ans: c. Episode:43 Faculty: Prof. A. NAGARAJ. 1. A circle
 Episode:43 Faculty: Prof. A. NAGARAJ Conic section 1. A circle gx fy c 0 is said to be imaginary circle if a) g + f = c b) g + f > c c) g + f < c d) g = f. If (1,-3) is the centre of the circle x y ax
Episode:43 Faculty: Prof. A. NAGARAJ Conic section 1. A circle gx fy c 0 is said to be imaginary circle if a) g + f = c b) g + f > c c) g + f < c d) g = f. If (1,-3) is the centre of the circle x y ax
t is a basis for the solution space to this system, then the matrix having these solutions as columns, t x 1 t, x 2 t,... x n t x 2 t...
 Mah 228- Fri Mar 24 5.6 Marix exponenials and linear sysems: The analogy beween firs order sysems of linear differenial equaions (Chaper 5) and scalar linear differenial equaions (Chaper ) is much sronger
Mah 228- Fri Mar 24 5.6 Marix exponenials and linear sysems: The analogy beween firs order sysems of linear differenial equaions (Chaper 5) and scalar linear differenial equaions (Chaper ) is much sronger
t + t sin t t cos t sin t. t cos t sin t dt t 2 = exp 2 log t log(t cos t sin t) = Multiplying by this factor and then integrating, we conclude that
 ODEs, Homework #4 Soluions. Check ha y ( = is a soluion of he second-order ODE ( cos sin y + y sin y sin = 0 and hen use his fac o find all soluions of he ODE. When y =, we have y = and also y = 0, so
ODEs, Homework #4 Soluions. Check ha y ( = is a soluion of he second-order ODE ( cos sin y + y sin y sin = 0 and hen use his fac o find all soluions of he ODE. When y =, we have y = and also y = 0, so
Biol. 356 Lab 8. Mortality, Recruitment, and Migration Rates
 Biol. 356 Lab 8. Moraliy, Recruimen, and Migraion Raes (modified from Cox, 00, General Ecology Lab Manual, McGraw Hill) Las week we esimaed populaion size hrough several mehods. One assumpion of all hese
Biol. 356 Lab 8. Moraliy, Recruimen, and Migraion Raes (modified from Cox, 00, General Ecology Lab Manual, McGraw Hill) Las week we esimaed populaion size hrough several mehods. One assumpion of all hese
Physics 3A: Basic Physics I Shoup Sample Midterm. Useful Equations. x f. x i v x. a x. x i. v xi v xf. 2a x f x i. y f. a r.
 Physics 3A: Basic Physics I Shoup Sample Miderm Useful Equaions A y Asin A A x A y an A y A x A = A x i + A y j + A z k A * B = A B cos(θ) A x B = A B sin(θ) A * B = A x B x + A y B y + A z B z A x B =
Physics 3A: Basic Physics I Shoup Sample Miderm Useful Equaions A y Asin A A x A y an A y A x A = A x i + A y j + A z k A * B = A B cos(θ) A x B = A B sin(θ) A * B = A x B x + A y B y + A z B z A x B =
