November 2000 Course 1. Society of Actuaries/Casualty Actuarial Society
|
|
|
- Wilfrid Jenkins
- 6 years ago
- Views:
Transcription
1 November 2000 Course 1 Society of Actuaries/Casualty Actuarial Society
2 1. A recent study indicates that the annual cost of maintaining and repairing a car in a town in Ontario averages 200 with a variance of 260. If a tax of 20% is introduced on all items associated with the maintenance and repair of cars (i.e., everything is made 20% more expensive), what will be the variance of the annual cost of maintaining and repairing a car? (A) 208 (B) 260 (C) 270 (D) 312 (E) 374 November Course 1
3 2. An investor purchases two assets, each having an initial value of The value V n of the first asset after n years can be modeled by the relationship: V n = 1.10V n 1 for n = 1, 2, 3,... The value W n of the second asset after n years can be modeled by the relationship: W n = W n W 0 for n = 1, 2, 3,... According to these models, by how much will the value of the first asset exceed the value of the second asset after 25 years? (A) 4050 (B) 4835 (C) 5035 (D) 5718 (E) 6000 Course 1 2 Form 00B
4 3. An auto insurance company has 10,000 policyholders. Each policyholder is classified as (i) (ii) (iii) young or old; male or female; and married or single. Of these policyholders, 3000 are young, 4600 are male, and 7000 are married. The policyholders can also be classified as 1320 young males, 3010 married males, and 1400 young married persons. Finally, 600 of the policyholders are young married males. How many of the company s policyholders are young, female, and single? (A) 280 (B) 423 (C) 486 (D) 880 (E) 896 November Course 1
5 4. A diagnostic test for the presence of a disease has two possible outcomes: 1 for disease present and 0 for disease not present. Let X denote the disease state of a patient, and let Y denote the outcome of the diagnostic test. The joint probability function of X and Y is given by: P(X = 0, Y = 0) = P(X = 1, Y = 0) = P(X = 0, Y = 1) = P(X = 1, Y = 1) = Calculate Var( YX= 1). (A) 0.13 (B) 0.15 (C) 0.20 (D) 0.51 (E) 0.71 Course 1 4 Form 00B
6 5. An equation of the line tangent to the graph of a differentiable function f at x = 0 is y = 3x + 4. Determine xf( x) lim x 0 sin(2 x ). (A) 0 (B) 1 (C) 2 (D) 4 (E) The limit does not exist. November Course 1
7 6. An insurance company issues 1250 vision care insurance policies. The number of claims filed by a policyholder under a vision care insurance policy during one year is a Poisson random variable with mean 2. Assume the numbers of claims filed by distinct policyholders are independent of one another. What is the approximate probability that there is a total of between 2450 and 2600 claims during a one-year period? (A) 0.68 (B) 0.82 (C) 0.87 (D) 0.95 (E) 1.00 Course 1 6 Form 00B
8 7. A group insurance policy covers the medical claims of the employees of a small company. The value, V, of the claims made in one year is described by V = 100,000Y where Y is a random variable with density function k y < y< f( y) = 0 otherwise, 4 (1 ) for 0 1 where k is a constant. What is the conditional probability that V exceeds 40,000, given that V exceeds 10,000? (A) 0.08 (B) 0.13 (C) 0.17 (D) 0.20 (E) 0.51 November Course 1
9 8. An insurance company can sell 20 auto insurance policies per month if it charges 40 per policy. Moreover, for each decrease or increase of 1 in the price per policy, the company can sell 1 more or 1 less policy, respectively. Fixed costs are 100. Variable costs are 32 per policy. What is the maximum monthly profit that the insurance company can achieve from selling auto insurance policies? (A) 96 (B) 196 (C) 296 (D) 400 (E) 900 Course 1 8 Form 00B
10 9. An insurance company sells an auto insurance policy that covers losses incurred by a policyholder, subject to a deductible of 100. Losses incurred follow an exponential distribution with mean 300. What is the 95 th percentile of actual losses that exceed the deductible? (A) 600 (B) 700 (C) 800 (D) 900 (E) 1000 November Course 1
11 10. Let S be a solid in 3-space and f a function defined on S such that: S f( x, y, z) dv = 5 S (4 f( x, y, z) + 3) dv = 47 Calculate the volume of S. (A) 2 (B) 5 (C) 7 (D) 9 (E) 14 Course 1 10 Form 00B
12 11. An actuary determines that the claim size for a certain class of accidents is a random variable, X, with moment generating function M X (t) = 1 ( t) 4. Determine the standard deviation of the claim size for this class of accidents. (A) 1,340 (B) 5,000 (C) 8,660 (D) 10,000 (E) 11,180 November Course 1
13 12. An actuary studied the likelihood that different types of drivers would be involved in at least one collision during any one-year period. The results of the study are presented below. Type of driver Percentage of all drivers Teen 8% Young adult 16% Midlife 45% Senior 31% Total 100% Probability of at least one collision Given that a driver has been involved in at least one collision in the past year, what is the probability that the driver is a young adult driver? (A) 0.06 (B) 0.16 (C) 0.19 (D) 0.22 (E) 0.25 Course 1 12 Form 00B
14 13. An actuary believes that the demand for life insurance, L, and the demand for health insurance, H, can be modeled as functions of time, t: L(t) = t 3 + 9t for 0 t 4 H(t) = 6t for 0 t 4 During the time period 0 t 4, the greatest absolute difference between the two demands occurs n times. Determine n. (A) 1 (B) 2 (C) 3 (D) 4 (E) 5 November Course 1
15 14. A piece of equipment is being insured against early failure. The time from purchase until failure of the equipment is exponentially distributed with mean 10 years. The insurance will pay an amount x if the equipment fails during the first year, and it will pay 0.5x if failure occurs during the second or third year. If failure occurs after the first three years, no payment will be made. At what level must x be set if the expected payment made under this insurance is to be 1000? (A) 3858 (B) 4449 (C) 5382 (D) 5644 (E) 7235 Course 1 14 Form 00B
16 15. Let C be the curve in R 3 defined by x = t 2, y = 4t 3/2, z = 9t, for t 0. Calculate the distance along C from (1, 4, 9) to (16, 32, 36). (A) 6 (B) 33 (C) 42 (D) 52 (E) 597 November Course 1
17 16. The total cost of manufacturing n microchips consists of a positive fixed set-up cost of k plus a constant positive cost j per microchip manufactured. Which of the following most closely represents the graph of V, the average cost per microchip? V V (A) j n (B) k n V (C) (D) k n V (E) k j n Course 1 16 Form 00B
18 A stock market analyst has recorded the daily sales revenue for two companies over the last year and displayed them in the histograms below. Company A Company B Number of occurrences Number of occurrences Daily sales revenue Daily sales revenue The analyst noticed that a daily sales revenue above 100 for Company A was always accompanied by a daily sales revenue below 100 for Company B, and vice versa. Let X denote the daily sales revenue for Company A and let Y denote the daily sales revenue for Company B, on some future day. Assuming that for each company the daily sales revenues are independent and identically distributed, which of the following is true? (A) Var(X) > Var(Y) and Var(X + Y) > Var(X) + Var(Y). (B) Var(X) > Var(Y) and Var(X + Y) < Var(X) + Var(Y). (C) Var(X) > Var(Y) and Var(X + Y) = Var(X) + Var(Y). (D) Var(X) < Var(Y) and Var(X + Y) > Var(X) + Var(Y). (E) Var(X) < Var(Y) and Var(X + Y) < Var(X) + Var(Y). November Course 1
19 18. Due to decreasing business, the amount an insurer expects to pay for claims will decrease at a constant rate of 5% per month indefinitely. This month the insurer paid 1000 in claims. What is the insurer s total expected amount of claims to be paid over the 30-month period that began this month? (A) 13,922 (B) 14,707 (C) 14,922 (D) 15,707 (E) 15,922 Course 1 18 Form 00B
20 19. Claims filed under auto insurance policies follow a normal distribution with mean 19,400 and standard deviation 5,000. What is the probability that the average of 25 randomly selected claims exceeds 20,000? (A) 0.01 (B) 0.15 (C) 0.27 (D) 0.33 (E) 0.45 November Course 1
21 20. The future lifetimes (in months) of two components of a machine have the following joint density function: 6 (50 x y) for 0 < x< 50 y< 50 f( x, y) = 125,000 0 otherwise. What is the probability that both components are still functioning 20 months from now? (A) (B) (C) (D) (E) 6 125, , , , , x x y x x y (50 x y) dydx (50 x y) dydx (50 x y) dydx (50 x y) dydx (50 x y) dydx Course 1 20 Form 00B
22 21. A consumer has 100 to spend on x units of product X and y units of product Y. The price per unit is 10 for X and 5 for Y. The consumer prefers quantities (including fractional quantities) x 1 and y 1 over x 2 and y 2 if f(x 1,y 1 ) > f(x 2, y 2 ), where f(x,y) = x 0.75 y 0.25 for x, y 0. What is the maximum value of f(x,y) that can be achieved given the consumer s spending constraint? (A) 6.78 (B) 7.50 (C) 8.41 (D) 9.58 (E) November Course 1
23 22. The probability that a randomly chosen male has a circulation problem is Males who have a circulation problem are twice as likely to be smokers as those who do not have a circulation problem. What is the conditional probability that a male has a circulation problem, given that he is a smoker? (A) (B) (C) (D) (E) Course 1 22 Form 00B
24 23. A company buys a policy to insure its revenue in the event of major snowstorms that shut down business. The policy pays nothing for the first such snowstorm of the year and 10,000 for each one thereafter, until the end of the year. The number of major snowstorms per year that shut down business is assumed to have a Poisson distribution with mean 1.5. What is the expected amount paid to the company under this policy during a one-year period? (A) 2,769 (B) 5,000 (C) 7,231 (D) 8,347 (E) 10,578 November Course 1
25 24. Let f be a function such that f (x + h) f (x) = 6xh + 3h 2 and f (1) = 5. Determine f (2) - f (2). (A) 0 (B) 2 (C) 3 (D) 5 (E) 6 Course 1 24 Form 00B
26 25. A manufacturer s annual losses follow a distribution with density function (0.6) for x > f( x) = x 0 otherwise. To cover its losses, the manufacturer purchases an insurance policy with an annual deductible of 2. What is the mean of the manufacturer s annual losses not paid by the insurance policy? (A) 0.84 (B) 0.88 (C) 0.93 (D) 0.95 (E) 1.00 November Course 1
27 26. The price of gasoline changes over time. Over a period of three years, the rate of change in price increases for the first year, remains constant for the second year, and declines for the third year. The rate of change in price is never negative over this time. Which of the following graphs best represents price graphed against time? Price (A) (B) Time (C) (D) (E) Course 1 26 Form 00B
28 27. Let X 1, X 2, X 3 be a random sample from a discrete distribution with probability function 1 for x 0 3 = px ( ) = 2 for x = otherwise Determine the moment generating function, M(t), of Y = X 1 X 2 X 3. (A) e t (B) 1+ 2e t (C) (D) (E) 1 2 t + e e e 3 3 3t 3 3t November Course 1
29 28. A doctor is studying the relationship between blood pressure and heartbeat abnormalities in her patients. She tests a random sample of her patients and notes their blood pressures (high, low, or normal) and their heartbeats (regular or irregular). She finds that: (i) (ii) (iii) (iv) (v) 14% have high blood pressure. 22% have low blood pressure. 15% have an irregular heartbeat. Of those with an irregular heartbeat, one-third have high blood pressure. Of those with normal blood pressure, one-eighth have an irregular heartbeat. What portion of the patients selected have a regular heartbeat and low blood pressure? (A) 2% (B) 5% (C) 8% (D) 9% (E) 20% Course 1 28 Form 00B
30 29. Insurance losses are not always reported in the year they occur. In fact, some losses are reported many years later. The year in which a loss occurs is called the occurrence year. For a given occurrence year, let R n denote the total number of losses reported in the occurrence year and the following n years. An actuary determines that R n can be modeled by the sequence: R n n = 2 R for n = 0, 1, 2,... n For occurrence year 1999, 250 losses were reported during In other words, R 0 = 250. How many more occurrence year 1999 losses does the model predict will be reported in years subsequent to 1999? (A) 1750 (B) 2000 (C) 3172 (D) 3422 (E) 3750 November Course 1
31 30. An actuary studying the insurance preferences of automobile owners makes the following conclusions: (i) (ii) (iii) An automobile owner is twice as likely to purchase collision coverage as disability coverage. The event that an automobile owner purchases collision coverage is independent of the event that he or she purchases disability coverage. The probability that an automobile owner purchases both collision and disability coverages is What is the probability that an automobile owner purchases neither collision nor disability coverage? (A) 0.18 (B) 0.33 (C) 0.48 (D) 0.67 (E) 0.82 Course 1 30 Form 00B
32 31. Let 2 3x for 0 x 1 f( x) = 4 x for 1 x 4. Let R be the region bounded by the graph of f, the x-axis, and the lines x = b and x = b + 2, where 0 b 1. Determine the value of b that maximizes the area of R. (A) 0 (B) (C) (D) (E) 1 November Course 1
33 32. The monthly profit of Company I can be modeled by a continuous random variable with density function f. Company II has a monthly profit that is twice that of Company I. Determine the probability density function of the monthly profit of Company II. (A) (B) 1 x f 2 2 x f 2 x (C) 2 f 2 (D) 2 f( x) (E) 2 f(2 x) Course 1 32 Form 00B
34 33. Let C be the curve defined by the polar function r = 2 + cos ( θ ). The vertices of triangle PQR are the points on C corresponding to q = 0, q = p, and q = 3 π. Calculate the area of triangle PQR. (A) 2 (B) (C) (D) 4 (E) November Course 1
35 34. The number of days that elapse between the beginning of a calendar year and the moment a high-risk driver is involved in an accident is exponentially distributed. An insurance company expects that 30% of high-risk drivers will be involved in an accident during the first 50 days of a calendar year. What portion of high-risk drivers are expected to be involved in an accident during the first 80 days of a calendar year? (A) 0.15 (B) 0.34 (C) 0.43 (D) 0.57 (E) 0.66 Course 1 34 Form 00B
36 35. A company s value at time t is growing at a rate proportional to the difference between 20 and its value at t. At t = 0, the value is 2. At t = 1, the value is 3. Calculate the value at t = 3. (A) 4.84 (B) 5.00 (C) 5.87 (D) 6.39 (E) 6.75 November Course 1
37 36. An insurance company insures a large number of drivers. Let X be the random variable representing the company s losses under collision insurance, and let Y represent the company s losses under liability insurance. X and Y have joint density function 2x+ 2 y for 0 < x< 1 and 0 < y< 2 f( x, y) = 4 0 otherwise. What is the probability that the total loss is at least 1? (A) 0.33 (B) 0.38 (C) 0.41 (D) 0.71 (E) 0.75 Course 1 36 Form 00B
38 37. The level of prices, P, is determined by the level of employment, E, and the cost of raw materials, M, as follows: P = 160 E 3/4 M 2/5 Which of the following statements is true? (A) (B) (C) (D) (E) P increases at a constant rate as either E or M increases. P increases at a decreasing rate as E increases, but increases at an increasing rate as M increases. P increases at an increasing rate as E increases, but increases at a decreasing rate as M increases. P increases at an increasing rate as either E or M increases. P increases at a decreasing rate as either E or M increases. November Course 1
39 38. The profit for a new product is given by Z = 3X Y - 5. X and Y are independent random variables with Var(X) = 1 and Var(Y) = 2. What is the variance of Z? (A) 1 (B) 5 (C) 7 (D) 11 (E) 16 Course 1 38 Form 00B
40 39. In a certain town, the number of deaths in year t due to a particular disease is modeled by 90, 000 ( t + ) 3 3 for t = 1, 2, 3... Let N be the total number of deaths that the model predicts will occur in the town after the end of the 27 th year. Which of the following intervals contains N? (A) 39.5 N < 43.0 (B) 43.0 N < 46.5 (C) 46.5 N < 50.0 (D) 50.0 N < 53.5 (E) 53.5 N < 57.0 November Course 1
41 40. A device contains two circuits. The second circuit is a backup for the first, so the second is used only when the first has failed. The device fails when and only when the second circuit fails. Let X and Y be the times at which the first and second circuits fail, respectively. X and Y have joint probability density function x 2 y 6e e for 0 < x< y< f( x, y) = 0 otherwise. What is the expected time at which the device fails? (A) 0.33 (B) 0.50 (C) 0.67 (D) 0.83 (E) 1.50 Course 1 40 Form 00B
42 Course 1 November 2000 Answer Key 1 E 21 A 2 B 22 C 3 D 23 C 4 C 24 B 5 C 25 C 6 B 26 A 7 B 27 A 8 A 28 E 9 E 29 E 10 D 30 B 11 B 31 C 12 D 32 A 13 D 33 E 14 D 34 C 15 C 35 A 16 A 36 D 17 E 37 E 18 D 38 D 19 C 39 C 20 B 40 D Course 1 1 November 2000
43 1. E Let X and Y denote the annual cost of maintaining and repairing a car before and after the 20% tax, respectively. Then Y = 1.2X and Var[Y] = Var[1.2X] = (1.2) 2 Var[X] = (1.2) 2 (260) = B Note that V 25 = 1.10 V 24 = (1.10) 2 V 23 =... = (1.10) 25 V 0 = (1.10) = 10,835 while W 25 = W W 0 = W 23 + (2)(0.20) W 0 =... = W 0 + (25)(0.20)W 0 = (0.20)(1000) = Therefore, V 25 W 25 = 10,835 6,000 = D Let N(C) denote the number of policyholders in classification C. Then N(Young «Female «Single) = N(Young «Female) N(Young «Female «Married) = N(Young) N(Young «Male) [N(Young «Married) N(Young «Married «Male)] = ( ) = C Note that PX ( = 1, Y= 0) PX ( = 1, Y= 0) 0.05 P(Y = 0ΩX = 1) = = = PX ( = 1) PX ( = 1, Y= 0) + PX ( = 1, Y= 1) = P(Y = 1ΩX=1) = 1 P(Y = 0 Ω X = 1) = = Therefore, E(YΩX = 1) = (0) P(Y = 0ΩX = 1) + (1) P(Y = 1ΩX = 1) = (1)(0.714) = E(Y 2 ΩX = 1) = (0) 2 P(Y = 0ΩX = 1) + (1) 2 P(Y = 1ΩX = 1) = Var(YΩX = 1) = E(Y 2 ΩX = 1) [E(YΩX = 1)] 2 = (0.714) 2 = C Note that f(0) = 3(0) + 4 = 4 since y = 3x + 4 is tangent to f at x = 0. Moreover, lim f(x) = f(0) = 4 since f is differentiable at x = 0. x 0 sin x Finally, from the fact that lim = 1, it follows that x 0 x xf ( x) 2 xf ( x) 1 sin(2 x) 4 lim = lim = lim f( x) lim = = 2. x 0 sin(2 x ) x 0 2sin(2 x ) 2 x 0 x 0 2 x 2 Course 1. 2 November 2000
44 6. B Let X 1,..., X 1250 be the number of claims filed by each of the 1250 policyholders. We are given that each X i follows a Poisson distribution with mean 2. It follows that E[X i ] = Var[X i ] = 2. Now we are interested in the random variable S = X X Assuming that the random variables are independent, we may conclude that S has an approximate normal distribution with E[S] = Var[S] = (2)(1250) = Therefore P[2450 < S < 2600] = S S 2500 P < < = P < < 50 S 2500 S 2500 = P < 2 P < S 2500 Then using the normal approximation with Z =, we have P[2450 < S < 2600] 50 P[Z < 2] P[Z > 1] = P[Z < 2] + P[Z < 1] = B To determine k, note that 1 4 k 5 1 = ( 1 ) ( 1 ) 1 k k y dy = y = k = 5 We next need to find P[V > 10,000] = P[100,000 Y > 10,000] = P[Y > 0.1] = (0.9) 5 = 0.59 and P[V > 40,000] 0.1 = 51 ( y ) dy = ( 1 y ) = (0.6) 5 = = P[100,000 Y > 40,000] = P[Y > 0.4] = 51 ( y ) dy = ( 1 y ) It now follows that P[V > 40,000ΩV > 10,000] PV [ > 40,000 V > 10, 000] PV [ > 40, 000] = = = = PV [ > 10, 000] PV [ > 10, 000] A Let x be the number of policies sold per month. Then the price function p(x) satisfies the relationship x = 20 + [40 p(x)]. Therefore, p(x) = 60 x. Next, define R(x), C(x), and P(x) to be the company s respective revenue, cost, and profit functions. Then R(x) = x p(x) = x(60 x) = 60x x 2 C(x) = 32x P(x) = R(x) C(x) = 60x x 2 32x 100 = -x x 100. Now since the quadratic P(x) is clearly maximized at x such that P (x) = 0, we see 0 = P (x) = -2x x = 28 or x = 14. Finally, P(14) = -(14) (14) 100 = 96 is the maximum profit the company can achieve. Course 1. 3 November 2000
45 9. E Let X denote actual losses incurred. We are given that X follows an exponential distribution with mean 300, and we are asked to find the 95 th percentile of all claims that exceed 100. Consequently, we want to find p 95 such that Pr[100 < x< p95] F( p95) F(100) 0.95 = = where F(x) is the distribution function of X. PX [ > 100] 1 F(100) Now F(x) = 1 e x/300. p95 / /300 1/3 p95 /300 1 e (1 e ) e e 1/3 p95 /300 Therefore, 0.95 = = = 1 e e 100/300 1/3 1 (1 e ) e p 95 /300 e = 0.05 e 1/3 p 95 = -300 ln(0.05 e 1/3 ) = D We zzz are given that: f(x,y,z)dv = 5 and S S zzz [4f(x,y,z) + 3]dV = 47 Using these two equalities, we can solve for the volume of S, 47 = zzz zzz zzz [4f(x,y,z) + 3]dV = 4 f(x,y,z)dv + 3 dv S zzz S S dv S 47 = 4(5) + 3 zzz S dv = (1/3) (47 20) = 9. zzz S dv, as follows: 11. B 1 We are given that M x (t) = for the claim size X in a certain class of accidents. 4 ( t) ( 4)( 2500) 10, 000 First, compute M x (t) = = 5 5 ( t) ( t) (10, 000)( 5)( 2500) 125, 000, 000 M x (t) = = 6 6 ( t) ( t) Then E[X] = M x (0) = 10,000 E[X 2 ] = M x (0) = 125,000,000 Var[X] = E[X 2 ] {E[X]} 2 = 125,000,000 (10,000) 2 = 25,000,000 Var[ X ] = 5,000. Course 1. 4 November 2000
46 12. D Let C = Event of a collision T = Event of a teen driver Y = Event of a young adult driver M = Event of a midlife driver S = Event of a senior driver Then using Bayes Theorem, we see that PCY [ ] PY [ ] P[YΩC] = PCT [ ] PT [ ] + PCY [ ] PY [ ] + PCM [ ] PM [ ] + PCS [ ] PS [ ] (0.08)(0.16) = = (0.15)(0.08) + (0.08)(0.16) + (0.04)(0.45) + (0.05)(0.31) 13. D In order to determine n, we need to determine the extreme values of D(t) = L(t) - H(t) = t 3 + 9t t = t 3 6t 2 + 9t 2, 0 t 4. Note: D (t) = 3t 2 12t + 9 = 3(t 2 4t + 3) = 3(t 1)(t 3) and recall that extreme values of D(t) occur either at t such that D (t) = 0 or at endpoints of the interval 0 t 4 on which D(t) is defined. Extreme values can thus occur at t = 0, 1, 3, or 4. The table below provides the remaining information we need in order to determine n: t D(t) ΩD(t)Ω We conclude that n = D Let T be the time from purchase until failure of the equipment. We are given that T is exponentially distributed with parameter l = 10 since 10 = E[T] = l. Next define the payment x for 0 T 1 x P under the insurance contract by P= for 1< T for T > 3 We want to find x such that 1 3 x 1000 = E[P] = 10 e t/10 x 1 dt + e t/10 1 t/10 x t/10 3 dt = xe e = -x e 1/10 + x (x/2) e 3/10 + (x/2) e 1/10 = x(1 ½ e 1/10 ½ e 3/10 ) = x. We conclude that x = Course 1. 5 November 2000
47 15. C First, observe that the point (1,4,9) corresponds to t = 1 while the point (16,32,36) corresponds to t = 4. Next, let L denote the distance along C from (1,4,9) to (16,32,36). Then: dx dy dz 1/ L = ( ) ( ) ( ) + + dt = 2t + 6t + 9 dt = 4t + 36t + 81dt dt dt dt t + 9 dt = 2 t + 9 dt = t + 9 t = ( ) ( ) ( ) = (1 + 9) = A Let C(n) denote the total cost of manufacturing n widgets, and let V(n) denote the average cost of manufacturing n widgets. We are given that C(n) = jn + k, from which it follows that V(n) = (1/n) C(n) = j + k/n. Next note that lim V(n) = j and lim V(n) = +. The graph that most closely reflects n n 0 these characteristics of V is A. 17. E The histograms imply that Var(X) < Var(Y) because Company A s share price X is less dispersed about the mean share price of 100 than Company B s share price Y. Moreover, we can deduce that Cov(X,Y) < 0 from the fact that a share price above 100 for Company A is always accompanied by a share price less than 100 for Company B. Since Var(X + Y) = Var(X) + Var(Y) + 2 Cov(X,Y) we conclude that Var(X + Y) < Var(X) + Var(Y). 18. D Let C be expected claims. Then C = (0.95) (0.95) (0.95) 29 = 1000 [ (0.95) (0.95) (0.95) ] = 1000 = 15, C 1 Let X 1,..., X 25 denote the 25 collision claims, and let X = (X X 25 ). We are 25 given that each X i (i = 1,..., 25) follows a normal distribution with mean 19,400 and standard deviation As a result X also follows a normal distribution with mean 1 19,400 and standard deviation (5000) = We conclude that P[ X > 20,000] 25 X 19, , , 400 X 19, 400 = P P > = > = 1 - F(0.6) = = Course 1. 6 November 2000
48 20. B 6 (50 x y) for 0 < x< 50 y< 50 We are given that f( x, y) = 125,000 0 otherwise and we want to determine P[X > 20 «Y > 20]. In order to determine integration limits, consider the following diagram: y 50 We conclude that P[X > 20 «Y > 20] = x>20 y>20 (20, 30) (30, 20) x x 6 (50 x y) 125, 000 dy dx A The consumer s spending constraints are characterized by the equation 10x + 5y = 100 or y = 20 2x. The constrained maximum value of f(x,y) can thus be found by focusing on g(x) = f(x, 20 2x) = x 0.75 (20 2x) 0.25, 0 x 10. Given this restriction of x to the closed interval [0,10], a maximum for g(x) clearly exists and occurs at the interval s endpoints or at x such that 0 = g (x) = 0.75 x 0.25 (20 2x) (0.25) x 0.75 (20 2x) 0.75 = 0.25 x 0.25 (20 2x) 0.75 [3(20 2x) 2x] = 0.25 x 0.25 (20 2x) 0.75 (60 8x). This condition is satisfied when 0 = 60 8x or x = 7.5. Therefore, the constrained maximum of f(x,y) occurs at x = 0, 7.5, or 10. Since g(0) = g(10) = 0, we conclude that g(7.5) = (7.5) 0.75 [20 2(7.5)] 0.25 = (7.5) 0.75 (5) 0.25 = 6.78 is the maximum value of f(x,y) subject to the consumer s spending constraints. 22. C Let: S = Event of a smoker C = Event of a circulation problem Then we are given that P[C] = 0.25 and P[SΩC] = 2 P[SΩC C ] PSCPC [ ] [ ] Now applying Bayes Theorem, we find that P[CΩS] = C C PSCPC [ ] [ ] + PSC [ ]( PC [ ]) = C 2 PSC [ ] PC [ ] 2(0.25) 2 2 C C 2 PSC [ ] PC [ ] PSC [ ](1 PC [ ]) = 2(0.25) 0.75 = 2 3 = Course 1. 7 November 2000
49 23. C Let N be the number of major snowstorms per year, and let P be the amount paid to 3/2 (3/ 2) n e the company under the policy. Then Pr[N = n] =, n = 0, 1, 2,... and n! 0 for N = 0 P =. 10, 000( N 1) for N 1 n 3/2 (3/ 2) e Now observe that E[P] = 10, 000( n 1) n! n= 1 = 10,000 e 3/2 n 3/2 (3/ 2) e + 10, 000( n 1) = 10,000 e 3/2 + E[10,000 (N 1)] n= 0 n! = 10,000 e 3/2 + E[10,000N] E[10,000] = 10,000 e 3/2 + 10,000 (3/2) 10,000 = 7, B f( x+ h) f( x) First rewrite the equation as = 6x + 3h. Then, taking the limit as h Æ 0, h f( x+ h) f( x) we see that f (x) = lim = 6x. It follows that f(x) = Ú 6x dx = 3x 2 + C h 0 h and, since f(1) = 5, we have 5 = 3(1) 2 + C or C = 2. Therefore, f(x) = 3x and f(2) f (2) = 3(2) (2) = C Let Y denote the manufacturer s retained annual losses. x for 0.6 < x 2 Then Y = 2 for x > (0.6) 2.5(0.6) 2.5(0.6) 2(0.6) and E[Y] = x dx 2 dx dx x + = x x x = (0.6) 2 2(0.6) 2.5(0.6) 2.5(0.6) (0.6) + = + + = x (2) 1.5(2) 1.5(0.6) A Let p denote price, and let t denote time. We are given: i) d 2 p/dt 2 > 0 during the first year (i.e., the price curve is concave up for 0 < t < 1); ii) d 2 p/dt 2 = 0 during the second year (i.e., the price curve is linear for 1 < t < 2); iii) d 2 p/dt 2 < 0 during the third year (i.e., the price curve is concave down for 2 < t < 3); and iv) dp/dt 0 during all three years (i.e., the price curve is nondecreasing for 0 t 3). Only graph A is consistent with the above requirements. Course 1. 8 November 2000
50 27. A Let g(y) be the probability function for Y = X 1 X 2 X 3. Note that Y = 1 if and only if X 1 = X 2 = X 3 = 1. Otherwise, Y = 0. Since P[Y = 1] = P[X 1 = 1 «X 2 = 1 «X 3 = 1] = P[X 1 = 1] P[X 2 = 1] P[X 3 = 1] = (2/3) 3 = 8/ for y = We conclude that g( y) = for y = otherwise y 19 8 t t and M(t) = E e = + e E Boxed numbers in the table below were computed. High BP Low BP Norm BP Total Regular heartbeat Irregular heartbeat Total From the table, we can see that 20% of patients have a regular heartbeat and low blood pressure. 29. E We first need to determine lim R n. To do this, observe that n R 0 = 250 R 1 = 2 R 0 = 2(250) R 2 = R 1 = (2)( )(250) R 3 = R 2 = (2)( )( ) 2 (250) = (0.75) (250) R n = n 1 (0.75) 2 n (0.75) (0.75) (250) = 2 (250) Therefore, lim n R n = 2 1/(1 0.75) (250) = 2 4 (250) = 4000 Finally, we are asked to find lim R n R 0 = = n Course 1. 9 November 2000
51 30. B Let C = Event that a policyholder buys collision coverage D = Event that a policyholder buys disability coverage Then we are given that P[C] = 2P[D] and P[C «D] = By the independence of C and D, it therefore follows that 0.15 = P[C «D] = P[C] P[D] = 2P[D] P[D] = 2(P[D]) 2 (P[D]) 2 = 0.15/2 = P[D] = and P[C] = 2P[D] = Now the independence of C and D also implies the independence of C C and D C. As a result, we see that P[C C «D C ] = P[C C ] P[D C ] = (1 P[C]) (1 P[D]) = ( ) ( ) = C The graph of f(x) is shown below: y Note that for 0 b 1, Area(R) = 4 (1, 3) 4 - x 3x 2 b R b+2 1 b+ 2 b b b 3 xdx+ (4 xdx ) = 3 xdx+ (4 xdx ) By the Fundamental Theorem of Calculus, d/db [Area(R)] = -3b 2 + [4 (b + 2)] d/db [b + 2] = -3b b = -(3b 2 + b 2) = -(3b 2)(b + 1). Also, d 2 /db 2 [Area(R)] = -6b 1 < 0 for 0 b 1. It follows that Area(R) is concave down as a function of b on the interval 0 b 1. Since d/db [Area(R)] = 0 at b = 2/3, the concavity of Area(R) implies that b = 2/3 maximizes Area(R) on the interval 0 b A Let X and Y be the monthly profits of Company I and Company II, respectively. We are given that the pdf of X is f. Let us also take g to be the pdf of Y and take F and G to be the distribution functions corresponding to f and g. Then G(y) = Pr[Y y] = P[2X y] = P[X y/2] = F(y/2) and g(y) = G (y) = d/dy F(y/2) = ½ F (y/2) = ½ f(y/2). 4 x Course November 2000
52 33. E We will first find the vertex corresponding to each q. I. q = 0 r = 2 + cos(0) = 3, cos(0) = 1, sin(0) = 0 vertex: (r cos q, r sin q) = (3, 0) II. q = p r = 2 + cos(p) = 1, cos(p) = -1, sin(p) = 0 vertex: (r cos q, r sin q) = (-1, 0) III. q = p/3 r = 2 + cos(p/3) = 5/2, cos(p/3) = ½, sin(p/3) = 3/2 vertex: (r cos q, r sin q) = (5/4, (5 3/4) The diagram below shows triangle PQR and thus summarizes the work above. y (-1,0) (5/4,5 3/4) (3,0) It follows from the diagram that Area of Triangle = ½ (base)(height) = ½ (4)(5 3 /4) = (5 3 /2). 34. C Let T denote the number of days that elapse before a high-risk driver is involved in an accident. Then T is exponentially distributed with unknown parameter l. Now we are given that 0.3 = P[T 50] = 50 λt λt 50 λe dt = e = 1 e 50l 0 0 Therefore, e 50l = 0.7 or l = - (1/50) ln(0.7) It follows that P[T 80] = = 1 e (80/50) ln(0.7) = 1 (0.7) 80/50 = λt λt 80 λe dt = e = 1 e 80l 0 0 x Course November 2000
53 35. A Let y(t) denote the company s value at time t. We are given that y (t) = k[20 y(t)], y(0) = 2, y(1) = 3, k is constant. The solution to this differential equation may be found as follows: dy() t = kdt 20 yt ( ) -ln [20 y(t)] = kt + C (C is a constant) 20 y(t) = e kt C y(t) = 20 e kt - C = 20 e C e kt Now using the fact that y(0) = 2, we see that 2 = y(0) = 20 e C e C = 18 It follows that y(t) = e kt Then using the fact that y(1) = 3, we see that 3 = y(1) = e k 18e k = 17 e k = 17/18 k = ln (17/18) It follows that y(t) = e t ln(17/18) = 20-18(17/18) t We conclude that y(3) = (17/18) 3 = D We want to find P[X + Y > 1]. To this end, note that P[X + Y > 1] = = = x+ 2 y dydx xy y y dx 4 = x 0 1 x x+ 1 x(1 x) (1 x) + (1 x) dx = x + x+ dx = x + x + x = = x+ x + x+ x dx 37. E The first and second partial derivatives of P with respect to E and M are given below: P = 160 E 3/4 M 2/5, E > 0, M > 0 P/ E = 120 E ¼ M 2/5 > 0 P/ M = 64 E ¾ M 3/5 > 0 2 P/ E 2 = -30 E 5/4 M 2/5 < 0 2 P/ M 2 = E ¾ M 8/5 < 0 It follows that P increases at a decreasing rate as either E or M increases. 38. D Note that due to the independence of X and Y Var(Z) = Var(3X - Y - 5) = Var(3X) + Var(Y) = 3 2 Var(X) + Var(Y) = 9(1) + 2 = 11. Course November 2000
54 39. C Consider the following two diagrams: Diagram 1 90,000 /(t+3) 3 Diagram 2 90,000 /(t+3) 3 t t 40. D 90, ,000 90, , 000 Note that Diagram 1 shows that > dt = = t= 28 ( t+ 3) ( t+ 3) 2( t+ 3) 2(28 + 3) 28 = , , , , 000 while Diagram 2 shows that < = = = t= 28 ( t+ 3) ( t+ 3) 2( t+ 3) 2(27 + 3) 27 90, 000 It follows that 46.8 < N = < ( t + 3) t= 28 The marginal distribution of Y is given by f 2 (y) = = -6 e 2y e y + 6e 2y = 6 e 2y 6 e 3y, 0 < y < 0 y 6 0 2y 3y (6ye 6 ye ) 0 Therefore, E(Y) = y f 2 (y) dy = dy = = 2 2 ye 2y dy y e 3y dy But 0 2 y e 2y dy and y e x e x e 2y dx = 6 e 2y dx 0 2 y ye dy y e 3y dy y e 3y dy are equivalent to the means of exponential random variables with parameters 1/2 and 1/3, respectively. In other words, and 3 2 y e 2y dy = 1/2 y e 3y dy = 1/3. We conclude that E(Y) = (6/2) (1/2) (6/3) (1/3) = 3/2 2/3 0 = 9/6-4/6 = 5/6 = Course November 2000
Notes for Math 324, Part 19
 48 Notes for Math 324, Part 9 Chapter 9 Multivariate distributions, covariance Often, we need to consider several random variables at the same time. We have a sample space S and r.v. s X, Y,..., which
48 Notes for Math 324, Part 9 Chapter 9 Multivariate distributions, covariance Often, we need to consider several random variables at the same time. We have a sample space S and r.v. s X, Y,..., which
Course 1 Solutions November 2001 Exams
 Course Solutions November Exams . A For i =,, let R = event that a red ball is drawn form urn i i B = event that a blue ball is drawn from urn i. i Then if x is the number of blue balls in urn, ( R R)
Course Solutions November Exams . A For i =,, let R = event that a red ball is drawn form urn i i B = event that a blue ball is drawn from urn i. i Then if x is the number of blue balls in urn, ( R R)
SOCIETY OF ACTUARIES/CASUALTY ACTUARIAL SOCIETY EXAM P PROBABILITY P SAMPLE EXAM SOLUTIONS
 SOCIETY OF ACTUARIES/CASUALTY ACTUARIAL SOCIETY EXAM P PROBABILITY P SAMPLE EXAM SOLUTIONS Copyright 9 by the Society of Actuaries and the Casualty Actuarial Society Some of the questions in this study
SOCIETY OF ACTUARIES/CASUALTY ACTUARIAL SOCIETY EXAM P PROBABILITY P SAMPLE EXAM SOLUTIONS Copyright 9 by the Society of Actuaries and the Casualty Actuarial Society Some of the questions in this study
SOCIETY OF ACTUARIES EXAM P PROBABILITY EXAM P SAMPLE SOLUTIONS
 SOCIETY OF ACTUARIES EXAM P PROBABILITY EXAM P SAMPLE SOLUTIONS Copyright 8 by the Society of Actuaries Some of the questions in this study note are taken from past examinations. Some of the questions
SOCIETY OF ACTUARIES EXAM P PROBABILITY EXAM P SAMPLE SOLUTIONS Copyright 8 by the Society of Actuaries Some of the questions in this study note are taken from past examinations. Some of the questions
Notes for Math 324, Part 20
 7 Notes for Math 34, Part Chapter Conditional epectations, variances, etc.. Conditional probability Given two events, the conditional probability of A given B is defined by P[A B] = P[A B]. P[B] P[A B]
7 Notes for Math 34, Part Chapter Conditional epectations, variances, etc.. Conditional probability Given two events, the conditional probability of A given B is defined by P[A B] = P[A B]. P[B] P[A B]
Errata for the ASM Study Manual for Exam P, Fourth Edition By Dr. Krzysztof M. Ostaszewski, FSA, CFA, MAAA
 Errata for the ASM Study Manual for Exam P, Fourth Edition By Dr. Krzysztof M. Ostaszewski, FSA, CFA, MAAA (krzysio@krzysio.net) Effective July 5, 3, only the latest edition of this manual will have its
Errata for the ASM Study Manual for Exam P, Fourth Edition By Dr. Krzysztof M. Ostaszewski, FSA, CFA, MAAA (krzysio@krzysio.net) Effective July 5, 3, only the latest edition of this manual will have its
Math 151. Rumbos Fall Solutions to Review Problems for Final Exam
 Math 5. Rumbos Fall 23 Solutions to Review Problems for Final Exam. Three cards are in a bag. One card is red on both sides. Another card is white on both sides. The third card in red on one side and white
Math 5. Rumbos Fall 23 Solutions to Review Problems for Final Exam. Three cards are in a bag. One card is red on both sides. Another card is white on both sides. The third card in red on one side and white
ACTEX Seminar Exam P
 ACTEX Seminar Exam P Written & Presented by Matt Hassett, ASA, PhD 1 Remember: 1 This is a review seminar. It assumes that you have already studied probability. This is an actuarial exam seminar. We will
ACTEX Seminar Exam P Written & Presented by Matt Hassett, ASA, PhD 1 Remember: 1 This is a review seminar. It assumes that you have already studied probability. This is an actuarial exam seminar. We will
Notes for Math 324, Part 17
 126 Notes for Math 324, Part 17 Chapter 17 Common discrete distributions 17.1 Binomial Consider an experiment consisting by a series of trials. The only possible outcomes of the trials are success and
126 Notes for Math 324, Part 17 Chapter 17 Common discrete distributions 17.1 Binomial Consider an experiment consisting by a series of trials. The only possible outcomes of the trials are success and
Math438 Actuarial Probability
 Math438 Actuarial Probability Jinguo Lian Department of Math and Stats Jan. 22, 2016 Continuous Random Variables-Part I: Definition A random variable X is continuous if its set of possible values is an
Math438 Actuarial Probability Jinguo Lian Department of Math and Stats Jan. 22, 2016 Continuous Random Variables-Part I: Definition A random variable X is continuous if its set of possible values is an
ASM Study Manual for Exam P, First Edition By Dr. Krzysztof M. Ostaszewski, FSA, CFA, MAAA Errata
 ASM Study Manual for Exam P, First Edition By Dr. Krzysztof M. Ostaszewski, FSA, CFA, MAAA (krzysio@krzysio.net) Errata Effective July 5, 3, only the latest edition of this manual will have its errata
ASM Study Manual for Exam P, First Edition By Dr. Krzysztof M. Ostaszewski, FSA, CFA, MAAA (krzysio@krzysio.net) Errata Effective July 5, 3, only the latest edition of this manual will have its errata
ASM Study Manual for Exam P, Second Edition By Dr. Krzysztof M. Ostaszewski, FSA, CFA, MAAA Errata
 ASM Study Manual for Exam P, Second Edition By Dr. Krzysztof M. Ostaszewski, FSA, CFA, MAAA (krzysio@krzysio.net) Errata Effective July 5, 3, only the latest edition of this manual will have its errata
ASM Study Manual for Exam P, Second Edition By Dr. Krzysztof M. Ostaszewski, FSA, CFA, MAAA (krzysio@krzysio.net) Errata Effective July 5, 3, only the latest edition of this manual will have its errata
Fall 2009 Math 113 Final Exam Solutions. f(x) = 1 + ex 1 e x?
 . What are the domain and range of the function Fall 9 Math 3 Final Exam Solutions f(x) = + ex e x? Answer: The function is well-defined everywhere except when the denominator is zero, which happens when
. What are the domain and range of the function Fall 9 Math 3 Final Exam Solutions f(x) = + ex e x? Answer: The function is well-defined everywhere except when the denominator is zero, which happens when
STA 256: Statistics and Probability I
 Al Nosedal. University of Toronto. Fall 2017 My momma always said: Life was like a box of chocolates. You never know what you re gonna get. Forrest Gump. There are situations where one might be interested
Al Nosedal. University of Toronto. Fall 2017 My momma always said: Life was like a box of chocolates. You never know what you re gonna get. Forrest Gump. There are situations where one might be interested
MATH/STAT 3360, Probability Sample Final Examination Model Solutions
 MATH/STAT 3360, Probability Sample Final Examination Model Solutions This Sample examination has more questions than the actual final, in order to cover a wider range of questions. Estimated times are
MATH/STAT 3360, Probability Sample Final Examination Model Solutions This Sample examination has more questions than the actual final, in order to cover a wider range of questions. Estimated times are
Extrema and the First-Derivative Test
 Extrema and the First-Derivative Test MATH 151 Calculus for Management J. Robert Buchanan Department of Mathematics 2018 Why Maximize or Minimize? In almost all quantitative fields there are objective
Extrema and the First-Derivative Test MATH 151 Calculus for Management J. Robert Buchanan Department of Mathematics 2018 Why Maximize or Minimize? In almost all quantitative fields there are objective
MATH 236 ELAC FALL 2017 CA 9 NAME: SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
 MATH 236 ELAC FALL 207 CA 9 NAME: SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. ) 27 p 3 27 p 3 ) 2) If 9 t 3 4t 9-2t = 3, find t. 2) Solve the equation.
MATH 236 ELAC FALL 207 CA 9 NAME: SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. ) 27 p 3 27 p 3 ) 2) If 9 t 3 4t 9-2t = 3, find t. 2) Solve the equation.
Online Math 1314 Final Exam Review
 Online Math 1314 Final Exam Review 1. The following table of values gives a company s annual profits in millions of dollars. Rescale the data so that the year 2003 corresponds to x = 0. Year 2003 2004
Online Math 1314 Final Exam Review 1. The following table of values gives a company s annual profits in millions of dollars. Rescale the data so that the year 2003 corresponds to x = 0. Year 2003 2004
Math 142 Week-in-Review #11 (Final Exam Review: All previous sections as well as sections 6.6 and 6.7)
 Math 142 Week-in-Review #11 (Final Exam Review: All previous sections as well as sections 6.6 and 6.7) Note: This review is intended to highlight the topics covered on the Final Exam (with emphasis on
Math 142 Week-in-Review #11 (Final Exam Review: All previous sections as well as sections 6.6 and 6.7) Note: This review is intended to highlight the topics covered on the Final Exam (with emphasis on
Math Want to have fun with chapter 4? Find the derivative. 1) y = 5x2e3x. 2) y = 2xex - 2ex. 3) y = (x2-2x + 3) ex. 9ex 4) y = 2ex + 1
 Math 160 - Want to have fun with chapter 4? Name Find the derivative. 1) y = 52e3 2) y = 2e - 2e 3) y = (2-2 + 3) e 9e 4) y = 2e + 1 5) y = e - + 1 e e 6) y = 32 + 7 7) y = e3-1 5 Use calculus to find
Math 160 - Want to have fun with chapter 4? Name Find the derivative. 1) y = 52e3 2) y = 2e - 2e 3) y = (2-2 + 3) e 9e 4) y = 2e + 1 5) y = e - + 1 e e 6) y = 32 + 7 7) y = e3-1 5 Use calculus to find
8.4 Application to Economics/ Biology & Probability
 8.4 Application to Economics/ Biology & 8.5 - Probability http://classic.hippocampus.org/course_locat or?course=general+calculus+ii&lesson=62&t opic=2&width=800&height=684&topictitle= Costs+&+probability&skinPath=http%3A%2F%
8.4 Application to Economics/ Biology & 8.5 - Probability http://classic.hippocampus.org/course_locat or?course=general+calculus+ii&lesson=62&t opic=2&width=800&height=684&topictitle= Costs+&+probability&skinPath=http%3A%2F%
Mathematics for Economics ECON MA/MSSc in Economics-2017/2018. Dr. W. M. Semasinghe Senior Lecturer Department of Economics
 Mathematics for Economics ECON 53035 MA/MSSc in Economics-2017/2018 Dr. W. M. Semasinghe Senior Lecturer Department of Economics MATHEMATICS AND STATISTICS LERNING OUTCOMES: By the end of this course unit
Mathematics for Economics ECON 53035 MA/MSSc in Economics-2017/2018 Dr. W. M. Semasinghe Senior Lecturer Department of Economics MATHEMATICS AND STATISTICS LERNING OUTCOMES: By the end of this course unit
STAT 430/510 Probability Lecture 12: Central Limit Theorem and Exponential Distribution
 STAT 430/510 Probability Lecture 12: Central Limit Theorem and Exponential Distribution Pengyuan (Penelope) Wang June 15, 2011 Review Discussed Uniform Distribution and Normal Distribution Normal Approximation
STAT 430/510 Probability Lecture 12: Central Limit Theorem and Exponential Distribution Pengyuan (Penelope) Wang June 15, 2011 Review Discussed Uniform Distribution and Normal Distribution Normal Approximation
Re: January 27, 2015 Math 080: Final Exam Review Page 1 of 6
 Re: January 7, 015 Math 080: Final Exam Review Page 1 of 6 Note: If you have difficulty with any of these problems, get help, then go back to the appropriate sections and work more problems! 1. Solve for
Re: January 7, 015 Math 080: Final Exam Review Page 1 of 6 Note: If you have difficulty with any of these problems, get help, then go back to the appropriate sections and work more problems! 1. Solve for
Math 211 Business Calculus TEST 3. Question 1. Section 2.2. Second Derivative Test.
 Math 211 Business Calculus TEST 3 Question 1. Section 2.2. Second Derivative Test. p. 1/?? Math 211 Business Calculus TEST 3 Question 1. Section 2.2. Second Derivative Test. Question 2. Section 2.3. Graph
Math 211 Business Calculus TEST 3 Question 1. Section 2.2. Second Derivative Test. p. 1/?? Math 211 Business Calculus TEST 3 Question 1. Section 2.2. Second Derivative Test. Question 2. Section 2.3. Graph
1. If X has density. cx 3 e x ), 0 x < 0, otherwise. Find the value of c that makes f a probability density. f(x) =
 1. If X has density f(x) = { cx 3 e x ), 0 x < 0, otherwise. Find the value of c that makes f a probability density. 2. Let X have density f(x) = { xe x, 0 < x < 0, otherwise. (a) Find P (X > 2). (b) Find
1. If X has density f(x) = { cx 3 e x ), 0 x < 0, otherwise. Find the value of c that makes f a probability density. 2. Let X have density f(x) = { xe x, 0 < x < 0, otherwise. (a) Find P (X > 2). (b) Find
A random variable is said to have a beta distribution with parameters (a, b) ifits probability density function is equal to
 224 Chapter 5 Continuous Random Variables A random variable is said to have a beta distribution with parameters (a, b) ifits probability density function is equal to 1 B(a, b) xa 1 (1 x) b 1 x 1 and is
224 Chapter 5 Continuous Random Variables A random variable is said to have a beta distribution with parameters (a, b) ifits probability density function is equal to 1 B(a, b) xa 1 (1 x) b 1 x 1 and is
Study Guide - Part 2
 Math 116 Spring 2015 Study Guide - Part 2 1. Which of the following describes the derivative function f (x) of a quadratic function f(x)? (A) Cubic (B) Quadratic (C) Linear (D) Constant 2. Find the derivative
Math 116 Spring 2015 Study Guide - Part 2 1. Which of the following describes the derivative function f (x) of a quadratic function f(x)? (A) Cubic (B) Quadratic (C) Linear (D) Constant 2. Find the derivative
Section 11.3 Rates of Change:
 Section 11.3 Rates of Change: 1. Consider the following table, which describes a driver making a 168-mile trip from Cleveland to Columbus, Ohio in 3 hours. t Time (in hours) 0 0.5 1 1.5 2 2.5 3 f(t) Distance
Section 11.3 Rates of Change: 1. Consider the following table, which describes a driver making a 168-mile trip from Cleveland to Columbus, Ohio in 3 hours. t Time (in hours) 0 0.5 1 1.5 2 2.5 3 f(t) Distance
STA 584 Supplementary Examples (not to be graded) Fall, 2003
 Page 1 of 8 Central Michigan University Department of Mathematics STA 584 Supplementary Examples (not to be graded) Fall, 003 1. (a) If A and B are independent events, P(A) =.40 and P(B) =.70, find (i)
Page 1 of 8 Central Michigan University Department of Mathematics STA 584 Supplementary Examples (not to be graded) Fall, 003 1. (a) If A and B are independent events, P(A) =.40 and P(B) =.70, find (i)
FACULTY OF ARTS AND SCIENCE University of Toronto FINAL EXAMINATIONS, APRIL 2016 MAT 133Y1Y Calculus and Linear Algebra for Commerce
 FACULTY OF ARTS AND SCIENCE University of Toronto FINAL EXAMINATIONS, APRIL 206 MAT YY Calculus and Linear Algebra for Commerce Duration: Examiners: hours N. Hoell A. Igelfeld D. Reiss L. Shorser J. Tate
FACULTY OF ARTS AND SCIENCE University of Toronto FINAL EXAMINATIONS, APRIL 206 MAT YY Calculus and Linear Algebra for Commerce Duration: Examiners: hours N. Hoell A. Igelfeld D. Reiss L. Shorser J. Tate
INSTITUTE AND FACULTY OF ACTUARIES. Curriculum 2019 SPECIMEN SOLUTIONS
 INSTITUTE AND FACULTY OF ACTUARIES Curriculum 09 SPECIMEN SOLUTIONS Subject CSA Risk Modelling and Survival Analysis Institute and Faculty of Actuaries Sample path A continuous time, discrete state process
INSTITUTE AND FACULTY OF ACTUARIES Curriculum 09 SPECIMEN SOLUTIONS Subject CSA Risk Modelling and Survival Analysis Institute and Faculty of Actuaries Sample path A continuous time, discrete state process
Math 115 Final Exam December 19, 2016
 EXAM SOLUTIONS Math 115 Final Exam December 19, 2016 1. Do not open this exam until you are told to do so. 2. Do not write your name anywhere on this exam. 3. This exam has 14 pages including this cover.
EXAM SOLUTIONS Math 115 Final Exam December 19, 2016 1. Do not open this exam until you are told to do so. 2. Do not write your name anywhere on this exam. 3. This exam has 14 pages including this cover.
Math Final Solutions - Spring Jaimos F Skriletz 1
 Math 160 - Final Solutions - Spring 2011 - Jaimos F Skriletz 1 Answer each of the following questions to the best of your ability. To receive full credit, answers must be supported by a sufficient amount
Math 160 - Final Solutions - Spring 2011 - Jaimos F Skriletz 1 Answer each of the following questions to the best of your ability. To receive full credit, answers must be supported by a sufficient amount
MATH 2070 Test 3 (Sections , , & )
 Multiple Choice: Use a #2 pencil and completely fill in each bubble on your scantron to indicate the answer to each question. Each question has one correct answer. If you indicate more than one answer,
Multiple Choice: Use a #2 pencil and completely fill in each bubble on your scantron to indicate the answer to each question. Each question has one correct answer. If you indicate more than one answer,
Practice Questions for Math 131 Exam # 1
 Practice Questions for Math 131 Exam # 1 1) A company produces a product for which the variable cost per unit is $3.50 and fixed cost 1) is $20,000 per year. Next year, the company wants the total cost
Practice Questions for Math 131 Exam # 1 1) A company produces a product for which the variable cost per unit is $3.50 and fixed cost 1) is $20,000 per year. Next year, the company wants the total cost
Math 1314 Final Exam Review. Year Profits (in millions of dollars)
 Math 1314 Final Exam Review 1. The following table of values gives a company s annual profits in millions of dollars. Rescale the data so that the year 2003 corresponds to x = 0. Year 2003 2004 2005 2006
Math 1314 Final Exam Review 1. The following table of values gives a company s annual profits in millions of dollars. Rescale the data so that the year 2003 corresponds to x = 0. Year 2003 2004 2005 2006
Answer Key for M. A. Economics Entrance Examination 2017 (Main version)
 Answer Key for M. A. Economics Entrance Examination 2017 (Main version) July 4, 2017 1. Person A lexicographically prefers good x to good y, i.e., when comparing two bundles of x and y, she strictly prefers
Answer Key for M. A. Economics Entrance Examination 2017 (Main version) July 4, 2017 1. Person A lexicographically prefers good x to good y, i.e., when comparing two bundles of x and y, she strictly prefers
f X (x) = λe λx, , x 0, k 0, λ > 0 Γ (k) f X (u)f X (z u)du
 11 COLLECTED PROBLEMS Do the following problems for coursework 1. Problems 11.4 and 11.5 constitute one exercise leading you through the basic ruin arguments. 2. Problems 11.1 through to 11.13 but excluding
11 COLLECTED PROBLEMS Do the following problems for coursework 1. Problems 11.4 and 11.5 constitute one exercise leading you through the basic ruin arguments. 2. Problems 11.1 through to 11.13 but excluding
Question 1. (8 points) The following diagram shows the graphs of eight equations.
 MAC 2233/-6 Business Calculus, Spring 2 Final Eam Name: Date: 5/3/2 Time: :am-2:nn Section: Show ALL steps. One hundred points equal % Question. (8 points) The following diagram shows the graphs of eight
MAC 2233/-6 Business Calculus, Spring 2 Final Eam Name: Date: 5/3/2 Time: :am-2:nn Section: Show ALL steps. One hundred points equal % Question. (8 points) The following diagram shows the graphs of eight
Probability and Probability Distributions. Dr. Mohammed Alahmed
 Probability and Probability Distributions 1 Probability and Probability Distributions Usually we want to do more with data than just describing them! We might want to test certain specific inferences about
Probability and Probability Distributions 1 Probability and Probability Distributions Usually we want to do more with data than just describing them! We might want to test certain specific inferences about
3 Continuous Random Variables
 Jinguo Lian Math437 Notes January 15, 016 3 Continuous Random Variables Remember that discrete random variables can take only a countable number of possible values. On the other hand, a continuous random
Jinguo Lian Math437 Notes January 15, 016 3 Continuous Random Variables Remember that discrete random variables can take only a countable number of possible values. On the other hand, a continuous random
Math 151. Rumbos Fall Solutions to Review Problems for Final Exam
 Math 5. Rumbos Fall 7 Solutions to Review Problems for Final Exam. Three cards are in a bag. One card is red on both sides. Another card is white on both sides. The third card is red on one side and white
Math 5. Rumbos Fall 7 Solutions to Review Problems for Final Exam. Three cards are in a bag. One card is red on both sides. Another card is white on both sides. The third card is red on one side and white
Discussion 03 Solutions
 STAT Discussion Solutions Spring 8. A new flavor of toothpaste has been developed. It was tested by a group of people. Nine of the group said they liked the new flavor, and the remaining indicated they
STAT Discussion Solutions Spring 8. A new flavor of toothpaste has been developed. It was tested by a group of people. Nine of the group said they liked the new flavor, and the remaining indicated they
Stat 366 A1 (Fall 2006) Midterm Solutions (October 23) page 1
 Stat 366 A1 Fall 6) Midterm Solutions October 3) page 1 1. The opening prices per share Y 1 and Y measured in dollars) of two similar stocks are independent random variables, each with a density function
Stat 366 A1 Fall 6) Midterm Solutions October 3) page 1 1. The opening prices per share Y 1 and Y measured in dollars) of two similar stocks are independent random variables, each with a density function
Final Exam Review. MATH Intuitive Calculus Fall 2013 Circle lab day: Mon / Fri. Name:. Show all your work.
 MATH 11012 Intuitive Calculus Fall 2013 Circle lab day: Mon / Fri Dr. Kracht Name:. 1. Consider the function f depicted below. Final Exam Review Show all your work. y 1 1 x (a) Find each of the following
MATH 11012 Intuitive Calculus Fall 2013 Circle lab day: Mon / Fri Dr. Kracht Name:. 1. Consider the function f depicted below. Final Exam Review Show all your work. y 1 1 x (a) Find each of the following
Math 120 Final Exam Practice Problems, Form: A
 Math 120 Final Exam Practice Problems, Form: A Name: While every attempt was made to be complete in the types of problems given below, we make no guarantees about the completeness of the problems. Specifically,
Math 120 Final Exam Practice Problems, Form: A Name: While every attempt was made to be complete in the types of problems given below, we make no guarantees about the completeness of the problems. Specifically,
1 Cost, Revenue and Profit
 MATH 104 - SECTION 101 FIN AL REVIEW 1 Cost, Revenue and Profit C(x), R(x), and P(x); marginal cost MC(x), marginal revenue MR(x), and marginal profit M P(x). 1. Profit is the difference between cost and
MATH 104 - SECTION 101 FIN AL REVIEW 1 Cost, Revenue and Profit C(x), R(x), and P(x); marginal cost MC(x), marginal revenue MR(x), and marginal profit M P(x). 1. Profit is the difference between cost and
THE USE OF A CALCULATOR, CELL PHONE, OR ANY OTHER ELECTRONIC DEVICE IS NOT PERMITTED IN THIS EXAMINATION.
 MATH 110 FINAL EXAM SPRING 2008 FORM A NAME STUDENT NUMBER INSTRUCTOR SECTION NUMBER This examination will be machine processed by the University Testing Service. Use only a number 2 pencil on your scantron.
MATH 110 FINAL EXAM SPRING 2008 FORM A NAME STUDENT NUMBER INSTRUCTOR SECTION NUMBER This examination will be machine processed by the University Testing Service. Use only a number 2 pencil on your scantron.
Functions. A function is a rule that gives exactly one output number to each input number.
 Functions A function is a rule that gives exactly one output number to each input number. Why it is important to us? The set of all input numbers to which the rule applies is called the domain of the function.
Functions A function is a rule that gives exactly one output number to each input number. Why it is important to us? The set of all input numbers to which the rule applies is called the domain of the function.
Introductory Mathematics and Statistics Summer Practice Questions
 University of Warwick Introductory Mathematics and Statistics Summer Practice Questions Jeremy Smith Piotr Z. Jelonek Nicholas Jackson This version: 22nd August 2017 Please find below a list of warm-up
University of Warwick Introductory Mathematics and Statistics Summer Practice Questions Jeremy Smith Piotr Z. Jelonek Nicholas Jackson This version: 22nd August 2017 Please find below a list of warm-up
Homework 10 (due December 2, 2009)
 Homework (due December, 9) Problem. Let X and Y be independent binomial random variables with parameters (n, p) and (n, p) respectively. Prove that X + Y is a binomial random variable with parameters (n
Homework (due December, 9) Problem. Let X and Y be independent binomial random variables with parameters (n, p) and (n, p) respectively. Prove that X + Y is a binomial random variable with parameters (n
Math 116: Business Calculus Chapter 4 - Calculating Derivatives
 Math 116: Business Calculus Chapter 4 - Calculating Derivatives Instructor: Colin Clark Spring 2017 Exam 2 - Thursday March 9. 4.1 Techniques for Finding Derivatives. 4.2 Derivatives of Products and Quotients.
Math 116: Business Calculus Chapter 4 - Calculating Derivatives Instructor: Colin Clark Spring 2017 Exam 2 - Thursday March 9. 4.1 Techniques for Finding Derivatives. 4.2 Derivatives of Products and Quotients.
TABLE OF CONTENTS. 1. Survival Multiple Lives Multiple Decrements Daniel Markov Daniel Poisson
 TABLE OF CONTENTS 1. Survival 1 2. Multiple Lives 95 3. Multiple Decrements 135 4. Daniel Markov 1 169 5. Daniel Poisson 185 6. Insurance 279 7. Annuities 367 8. Premiums 449 9. Reserves 517 10. Insurances/Annuities
TABLE OF CONTENTS 1. Survival 1 2. Multiple Lives 95 3. Multiple Decrements 135 4. Daniel Markov 1 169 5. Daniel Poisson 185 6. Insurance 279 7. Annuities 367 8. Premiums 449 9. Reserves 517 10. Insurances/Annuities
Final Exam Study Guide
 Final Exam Study Guide Final Exam Coverage: Sections 10.1-10.2, 10.4-10.5, 10.7, 11.2-11.4, 12.1-12.6, 13.1-13.2, 13.4-13.5, and 14.1 Sections/topics NOT on the exam: Sections 10.3 (Continuity, it definition
Final Exam Study Guide Final Exam Coverage: Sections 10.1-10.2, 10.4-10.5, 10.7, 11.2-11.4, 12.1-12.6, 13.1-13.2, 13.4-13.5, and 14.1 Sections/topics NOT on the exam: Sections 10.3 (Continuity, it definition
STAT/MA 416 Answers Homework 6 November 15, 2007 Solutions by Mark Daniel Ward PROBLEMS
 STAT/MA 4 Answers Homework November 5, 27 Solutions by Mark Daniel Ward PROBLEMS Chapter Problems 2a. The mass p, corresponds to neither of the first two balls being white, so p, 8 7 4/39. The mass p,
STAT/MA 4 Answers Homework November 5, 27 Solutions by Mark Daniel Ward PROBLEMS Chapter Problems 2a. The mass p, corresponds to neither of the first two balls being white, so p, 8 7 4/39. The mass p,
STA 256: Statistics and Probability I
 Al Nosedal. University of Toronto. Fall 2017 My momma always said: Life was like a box of chocolates. You never know what you re gonna get. Forrest Gump. Experiment, outcome, sample space, and sample point
Al Nosedal. University of Toronto. Fall 2017 My momma always said: Life was like a box of chocolates. You never know what you re gonna get. Forrest Gump. Experiment, outcome, sample space, and sample point
Chapter 1: Revie of Calculus and Probability
 Chapter 1: Revie of Calculus and Probability Refer to Text Book: Operations Research: Applications and Algorithms By Wayne L. Winston,Ch. 12 Operations Research: An Introduction By Hamdi Taha, Ch. 12 OR441-Dr.Khalid
Chapter 1: Revie of Calculus and Probability Refer to Text Book: Operations Research: Applications and Algorithms By Wayne L. Winston,Ch. 12 Operations Research: An Introduction By Hamdi Taha, Ch. 12 OR441-Dr.Khalid
Midterm Study Guide and Practice Problems
 Midterm Study Guide and Practice Problems Coverage of the midterm: Sections 10.1-10.7, 11.2-11.6 Sections or topics NOT on the midterm: Section 11.1 (The constant e and continuous compound interest, Section
Midterm Study Guide and Practice Problems Coverage of the midterm: Sections 10.1-10.7, 11.2-11.6 Sections or topics NOT on the midterm: Section 11.1 (The constant e and continuous compound interest, Section
IEOR 3106: Introduction to Operations Research: Stochastic Models. Professor Whitt. SOLUTIONS to Homework Assignment 2
 IEOR 316: Introduction to Operations Research: Stochastic Models Professor Whitt SOLUTIONS to Homework Assignment 2 More Probability Review: In the Ross textbook, Introduction to Probability Models, read
IEOR 316: Introduction to Operations Research: Stochastic Models Professor Whitt SOLUTIONS to Homework Assignment 2 More Probability Review: In the Ross textbook, Introduction to Probability Models, read
MATH 2070 Test 3 (Sections , , & )
 Multiple Choice: Use a #2 pencil and completely fill in each bubble on your scantron to indicate the answer to each question. Each question has one correct answer. If you indicate more than one answer,
Multiple Choice: Use a #2 pencil and completely fill in each bubble on your scantron to indicate the answer to each question. Each question has one correct answer. If you indicate more than one answer,
Brief Review of Probability
 Maura Department of Economics and Finance Università Tor Vergata Outline 1 Distribution Functions Quantiles and Modes of a Distribution 2 Example 3 Example 4 Distributions Outline Distribution Functions
Maura Department of Economics and Finance Università Tor Vergata Outline 1 Distribution Functions Quantiles and Modes of a Distribution 2 Example 3 Example 4 Distributions Outline Distribution Functions
Ch 2: Probability. Contents. Fall 2017 UAkron Dept. of Stats [3470 : 451/551] Theoretical Statistics I
![Ch 2: Probability. Contents. Fall 2017 UAkron Dept. of Stats [3470 : 451/551] Theoretical Statistics I Ch 2: Probability. Contents. Fall 2017 UAkron Dept. of Stats [3470 : 451/551] Theoretical Statistics I](/thumbs/87/97208267.jpg) Fall 2017 UAkron Dept. of Stats [3470 : 451/551] Theoretical Statistics I Ch 2: Probability Contents 1 Preliminaries 3 1.1 Interpretation of Probability (2.2)......................................................
Fall 2017 UAkron Dept. of Stats [3470 : 451/551] Theoretical Statistics I Ch 2: Probability Contents 1 Preliminaries 3 1.1 Interpretation of Probability (2.2)......................................................
Definition: A random variable X is a real valued function that maps a sample space S into the space of real numbers R. X : S R
 Random Variables Definition: A random variable X is a real valued function that maps a sample space S into the space of real numbers R. X : S R As such, a random variable summarizes the outcome of an experiment
Random Variables Definition: A random variable X is a real valued function that maps a sample space S into the space of real numbers R. X : S R As such, a random variable summarizes the outcome of an experiment
Section K MATH 211 Homework Due Friday, 8/30/96 Professor J. Beachy Average: 15.1 / 20. ), and f(a + 1).
 Section K MATH 211 Homework Due Friday, 8/30/96 Professor J. Beachy Average: 15.1 / 20 # 18, page 18: If f(x) = x2 x 2 1, find f( 1 2 ), f( 1 2 ), and f(a + 1). # 22, page 18: When a solution of acetylcholine
Section K MATH 211 Homework Due Friday, 8/30/96 Professor J. Beachy Average: 15.1 / 20 # 18, page 18: If f(x) = x2 x 2 1, find f( 1 2 ), f( 1 2 ), and f(a + 1). # 22, page 18: When a solution of acetylcholine
x C) y = - A) $20000; 14 years B) $28,000; 14 years C) $28,000; 28 years D) $30,000; 15 years
 Dr. Lee - Math 35 - Calculus for Business - Review of 3 - Show Complete Work for Each Problem MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find
Dr. Lee - Math 35 - Calculus for Business - Review of 3 - Show Complete Work for Each Problem MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find
MATH 236 ELAC FALL 2017 TEST 3 NAME: SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
 MATH 6 ELAC FALL 7 TEST NAME: SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. Evaluate the integral using integration by parts. ) 9x ln x dx ) ) x 5 -
MATH 6 ELAC FALL 7 TEST NAME: SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. Evaluate the integral using integration by parts. ) 9x ln x dx ) ) x 5 -
Final Exam 2011 Winter Term 2 Solutions
 . (a Find the radius of convergence of the series: ( k k+ x k. Solution: Using the Ratio Test, we get: L = lim a k+ a k = lim ( k+ k+ x k+ ( k k+ x k = lim x = x. Note that the series converges for L
. (a Find the radius of convergence of the series: ( k k+ x k. Solution: Using the Ratio Test, we get: L = lim a k+ a k = lim ( k+ k+ x k+ ( k k+ x k = lim x = x. Note that the series converges for L
MATH 142 Business Mathematics II. Spring, 2015, WEEK 1. JoungDong Kim
 MATH 142 Business Mathematics II Spring, 2015, WEEK 1 JoungDong Kim Week 1: A8, 1.1, 1.2, 1.3 Chapter 1. Functions Section 1.1 and A.8 Definition. A function is a rule that assigns to each element x in
MATH 142 Business Mathematics II Spring, 2015, WEEK 1 JoungDong Kim Week 1: A8, 1.1, 1.2, 1.3 Chapter 1. Functions Section 1.1 and A.8 Definition. A function is a rule that assigns to each element x in
3. Find the slope of the tangent line to the curve given by 3x y e x+y = 1 + ln x at (1, 1).
 1. Find the derivative of each of the following: (a) f(x) = 3 2x 1 (b) f(x) = log 4 (x 2 x) 2. Find the slope of the tangent line to f(x) = ln 2 ln x at x = e. 3. Find the slope of the tangent line to
1. Find the derivative of each of the following: (a) f(x) = 3 2x 1 (b) f(x) = log 4 (x 2 x) 2. Find the slope of the tangent line to f(x) = ln 2 ln x at x = e. 3. Find the slope of the tangent line to
Math Practice Final - solutions
 Math 151 - Practice Final - solutions 2 1-2 -1 0 1 2 3 Problem 1 Indicate the following from looking at the graph of f(x) above. All answers are small integers, ±, or DNE for does not exist. a) lim x 1
Math 151 - Practice Final - solutions 2 1-2 -1 0 1 2 3 Problem 1 Indicate the following from looking at the graph of f(x) above. All answers are small integers, ±, or DNE for does not exist. a) lim x 1
Economics th April 2011
 Economics 401 8th April 2011 Instructions: Answer 7 of the following 9 questions. All questions are of equal weight. Indicate clearly on the first page which questions you want marked. 1. Answer both parts.
Economics 401 8th April 2011 Instructions: Answer 7 of the following 9 questions. All questions are of equal weight. Indicate clearly on the first page which questions you want marked. 1. Answer both parts.
Week 04 Discussion. a) What is the probability that of those selected for the in-depth interview 4 liked the new flavor and 1 did not?
 STAT Wee Discussion Fall 7. A new flavor of toothpaste has been developed. It was tested by a group of people. Nine of the group said they lied the new flavor, and the remaining 6 indicated they did not.
STAT Wee Discussion Fall 7. A new flavor of toothpaste has been developed. It was tested by a group of people. Nine of the group said they lied the new flavor, and the remaining 6 indicated they did not.
MATH/STAT 3360, Probability
 MATH/STAT 3360, Probability Sample Final Examination This Sample examination has more questions than the actual final, in order to cover a wider range of questions. Estimated times are provided after each
MATH/STAT 3360, Probability Sample Final Examination This Sample examination has more questions than the actual final, in order to cover a wider range of questions. Estimated times are provided after each
Math 1325 Final Exam Review
 Math 1325 Final Exam Review 1. The following table of values gives a company s annual profits in millions of dollars. Rescale the data so that the year 2003 corresponds to x = 0. Year 2003 2004 2005 2006
Math 1325 Final Exam Review 1. The following table of values gives a company s annual profits in millions of dollars. Rescale the data so that the year 2003 corresponds to x = 0. Year 2003 2004 2005 2006
2 Functions and Their
 CHAPTER Functions and Their Applications Chapter Outline Introduction The Concept of a Function Types of Functions Roots (Zeros) of a Function Some Useful Functions in Business and Economics Equilibrium
CHAPTER Functions and Their Applications Chapter Outline Introduction The Concept of a Function Types of Functions Roots (Zeros) of a Function Some Useful Functions in Business and Economics Equilibrium
Introductory Mathematics and Statistics Summer Practice Questions
 University of Warwick Introductory Mathematics and Statistics Summer Practice Questions Jeremy Smith Piotr Z. Jelonek Nicholas Jackson This version: 15th August 2018 Please find below a list of warm-up
University of Warwick Introductory Mathematics and Statistics Summer Practice Questions Jeremy Smith Piotr Z. Jelonek Nicholas Jackson This version: 15th August 2018 Please find below a list of warm-up
1 Basic continuous random variable problems
 Name M362K Final Here are problems concerning material from Chapters 5 and 6. To review the other chapters, look over previous practice sheets for the two exams, previous quizzes, previous homeworks and
Name M362K Final Here are problems concerning material from Chapters 5 and 6. To review the other chapters, look over previous practice sheets for the two exams, previous quizzes, previous homeworks and
Notes for Math 324, Part 12
 72 Notes for Math 324, Part 12 Chapter 12 Definition and main properties of probability 12.1 Sample space, events We run an experiment which can have several outcomes. The set consisting by all possible
72 Notes for Math 324, Part 12 Chapter 12 Definition and main properties of probability 12.1 Sample space, events We run an experiment which can have several outcomes. The set consisting by all possible
Find all points where the function is discontinuous. 1) Find all vertical asymptotes of the given function. x(x - 1) 2) f(x) =
 Math 90 Final Review Find all points where the function is discontinuous. ) Find all vertical asymptotes of the given function. x(x - ) 2) f(x) = x3 + 4x Provide an appropriate response. 3) If x 3 f(x)
Math 90 Final Review Find all points where the function is discontinuous. ) Find all vertical asymptotes of the given function. x(x - ) 2) f(x) = x3 + 4x Provide an appropriate response. 3) If x 3 f(x)
Intro to Probability
 Intro to Probability Al Nosedal. University of Toronto. Summer 2017 Al Nosedal. University of Toronto. Intro to Probability Summer 2017 1 / 56 My momma always said: Life was like a box of chocolates. You
Intro to Probability Al Nosedal. University of Toronto. Summer 2017 Al Nosedal. University of Toronto. Intro to Probability Summer 2017 1 / 56 My momma always said: Life was like a box of chocolates. You
Doug Clark The Learning Center 100 Student Success Center learningcenter.missouri.edu Overview
 Math 1400 Final Exam Review Saturday, December 9 in Ellis Auditorium 1:00 PM 3:00 PM, Saturday, December 9 Part 1: Derivatives and Applications of Derivatives 3:30 PM 5:30 PM, Saturday, December 9 Part
Math 1400 Final Exam Review Saturday, December 9 in Ellis Auditorium 1:00 PM 3:00 PM, Saturday, December 9 Part 1: Derivatives and Applications of Derivatives 3:30 PM 5:30 PM, Saturday, December 9 Part
SECTION 5.1: Polynomials
 1 SECTION 5.1: Polynomials Functions Definitions: Function, Independent Variable, Dependent Variable, Domain, and Range A function is a rule that assigns to each input value x exactly output value y =
1 SECTION 5.1: Polynomials Functions Definitions: Function, Independent Variable, Dependent Variable, Domain, and Range A function is a rule that assigns to each input value x exactly output value y =
UNIT 2 DERIVATIVES 2.1 EXPONENTIAL AND LOGARITHMIC FUNCTION APPLICATIONS. Pre-Class:
 1830 UNIT 2 DERIVATIVES 2.1 EXPONENTIAL AND LOGARITHMIC FUNCTION APPLICATIONS Pre-Class: Take notes on the videos and readings (use the space below). Work and check problem #1 in the 2.1 NOTES section.
1830 UNIT 2 DERIVATIVES 2.1 EXPONENTIAL AND LOGARITHMIC FUNCTION APPLICATIONS Pre-Class: Take notes on the videos and readings (use the space below). Work and check problem #1 in the 2.1 NOTES section.
MATH 115 SECOND MIDTERM EXAM
 MATH 115 SECOND MIDTERM EXAM November 22, 2005 NAME: SOLUTION KEY INSTRUCTOR: SECTION NO: 1. Do not open this exam until you are told to begin. 2. This exam has 10 pages including this cover. There are
MATH 115 SECOND MIDTERM EXAM November 22, 2005 NAME: SOLUTION KEY INSTRUCTOR: SECTION NO: 1. Do not open this exam until you are told to begin. 2. This exam has 10 pages including this cover. There are
3 Conditional Expectation
 3 Conditional Expectation 3.1 The Discrete case Recall that for any two events E and F, the conditional probability of E given F is defined, whenever P (F ) > 0, by P (E F ) P (E)P (F ). P (F ) Example.
3 Conditional Expectation 3.1 The Discrete case Recall that for any two events E and F, the conditional probability of E given F is defined, whenever P (F ) > 0, by P (E F ) P (E)P (F ). P (F ) Example.
Increasing/Decreasing Test. Extreme Values and The First Derivative Test.
 Calculus 1 Lia Vas Increasing/Decreasing Test. Extreme Values and The First Derivative Test. Recall that a function f(x) is increasing on an interval if the increase in x-values implies an increase in
Calculus 1 Lia Vas Increasing/Decreasing Test. Extreme Values and The First Derivative Test. Recall that a function f(x) is increasing on an interval if the increase in x-values implies an increase in
Partial derivatives, linear approximation and optimization
 ams 11b Study Guide 4 econ 11b Partial derivatives, linear approximation and optimization 1. Find the indicated partial derivatives of the functions below. a. z = 3x 2 + 4xy 5y 2 4x + 7y 2, z x = 6x +
ams 11b Study Guide 4 econ 11b Partial derivatives, linear approximation and optimization 1. Find the indicated partial derivatives of the functions below. a. z = 3x 2 + 4xy 5y 2 4x + 7y 2, z x = 6x +
Creating New Distributions
 Creating New Distributions Section 5.2 Stat 477 - Loss Models Section 5.2 (Stat 477) Creating New Distributions Brian Hartman - BYU 1 / 18 Generating new distributions Some methods to generate new distributions
Creating New Distributions Section 5.2 Stat 477 - Loss Models Section 5.2 (Stat 477) Creating New Distributions Brian Hartman - BYU 1 / 18 Generating new distributions Some methods to generate new distributions
Math Final Exam Review. 1. The following equation gives the rate at which the angle between two objects is changing during a game:
 Math 131 Spring 2008 c Sherry Scarborough and Heather Ramsey Page 1 Math 131 - Final Exam Review 1. The following equation gives the rate at which the angle between two objects is changing during a game:
Math 131 Spring 2008 c Sherry Scarborough and Heather Ramsey Page 1 Math 131 - Final Exam Review 1. The following equation gives the rate at which the angle between two objects is changing during a game:
Name of the Student: Problems on Discrete & Continuous R.Vs
 SUBJECT NAME : Probability & Random Processes SUBJECT CODE : MA645 MATERIAL NAME : Additional Problems MATERIAL CODE : JM08AM004 REGULATION : R03 UPDATED ON : March 05 (Scan the above QR code for the direct
SUBJECT NAME : Probability & Random Processes SUBJECT CODE : MA645 MATERIAL NAME : Additional Problems MATERIAL CODE : JM08AM004 REGULATION : R03 UPDATED ON : March 05 (Scan the above QR code for the direct
UNIVERSITY OF KWA-ZULU NATAL
 UNIVERSITY OF KWA-ZULU NATAL EXAMINATIONS: June 006 Solutions Subject, course and code: Mathematics 34 MATH34P Multiple Choice Answers. B. B 3. E 4. E 5. C 6. A 7. A 8. C 9. A 0. D. C. A 3. D 4. E 5. B
UNIVERSITY OF KWA-ZULU NATAL EXAMINATIONS: June 006 Solutions Subject, course and code: Mathematics 34 MATH34P Multiple Choice Answers. B. B 3. E 4. E 5. C 6. A 7. A 8. C 9. A 0. D. C. A 3. D 4. E 5. B
Random Variable And Probability Distribution. Is defined as a real valued function defined on the sample space S. We denote it as X, Y, Z,
 Random Variable And Probability Distribution Introduction Random Variable ( r.v. ) Is defined as a real valued function defined on the sample space S. We denote it as X, Y, Z, T, and denote the assumed
Random Variable And Probability Distribution Introduction Random Variable ( r.v. ) Is defined as a real valued function defined on the sample space S. We denote it as X, Y, Z, T, and denote the assumed
1 Functions And Change
 1 Functions And Change 1.1 What Is a Function? * Function A function is a rule that takes certain numbers as inputs and assigns to each a definite output number. The set of all input numbers is called
1 Functions And Change 1.1 What Is a Function? * Function A function is a rule that takes certain numbers as inputs and assigns to each a definite output number. The set of all input numbers is called
Marginal Propensity to Consume/Save
 Marginal Propensity to Consume/Save The marginal propensity to consume is the increase (or decrease) in consumption that an economy experiences when income increases (or decreases). The marginal propensity
Marginal Propensity to Consume/Save The marginal propensity to consume is the increase (or decrease) in consumption that an economy experiences when income increases (or decreases). The marginal propensity
ANSWERS, Homework Problems, Fall 2014: Lectures Now You Try It, Supplemental problems in written homework, Even Answers. 24x + 72 (x 2 6x + 4) 4
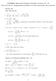 ANSWERS, Homework Problems, Fall 014: Lectures 19 35 Now You Try It, Supplemental problems in written homework, Even Answers Lecture 19 1. d [ 4 ] dx x 6x + 4) 3 = 4x + 7 x 6x + 4) 4. a) P 0) = 800 b)
ANSWERS, Homework Problems, Fall 014: Lectures 19 35 Now You Try It, Supplemental problems in written homework, Even Answers Lecture 19 1. d [ 4 ] dx x 6x + 4) 3 = 4x + 7 x 6x + 4) 4. a) P 0) = 800 b)
STAT515, Review Worksheet for Midterm 2 Spring 2019
 STAT55, Review Worksheet for Midterm 2 Spring 29. During a week, the proportion of time X that a machine is down for maintenance or repair has the following probability density function: 2( x, x, f(x The
STAT55, Review Worksheet for Midterm 2 Spring 29. During a week, the proportion of time X that a machine is down for maintenance or repair has the following probability density function: 2( x, x, f(x The
Social Science/Commerce Calculus I: Assignment #10 - Solutions Page 1/15
 Social Science/Commerce Calculus I: Assignment #10 - Solutions Page 1/15 1. Consider the function f (x) = x - 8x + 3, on the interval 0 x 8. The global (absolute) maximum of f (x) (on the given interval)
Social Science/Commerce Calculus I: Assignment #10 - Solutions Page 1/15 1. Consider the function f (x) = x - 8x + 3, on the interval 0 x 8. The global (absolute) maximum of f (x) (on the given interval)
Name of the Student: Problems on Discrete & Continuous R.Vs
 Engineering Mathematics 08 SUBJECT NAME : Probability & Random Processes SUBJECT CODE : MA645 MATERIAL NAME : University Questions REGULATION : R03 UPDATED ON : November 07 (Upto N/D 07 Q.P) (Scan the
Engineering Mathematics 08 SUBJECT NAME : Probability & Random Processes SUBJECT CODE : MA645 MATERIAL NAME : University Questions REGULATION : R03 UPDATED ON : November 07 (Upto N/D 07 Q.P) (Scan the
Actuarial Science Exam 1/P
 Actuarial Science Exam /P Ville A. Satopää December 5, 2009 Contents Review of Algebra and Calculus 2 2 Basic Probability Concepts 3 3 Conditional Probability and Independence 4 4 Combinatorial Principles,
Actuarial Science Exam /P Ville A. Satopää December 5, 2009 Contents Review of Algebra and Calculus 2 2 Basic Probability Concepts 3 3 Conditional Probability and Independence 4 4 Combinatorial Principles,
