Translational Motion Rotational Motion Equations Sheet
|
|
|
- Timothy Foster
- 6 years ago
- Views:
Transcription
1 PHYSICS 01 Translational Motion Rotational Motion Equations Sheet LINEAR ANGULAR Time t t Displacement x; (x = rθ) θ Velocity v = Δx/Δt; (v = rω) ω = Δθ/Δt Acceleration a = Δv/Δt; (a = rα) α = Δω/Δt ( r v ) a c = ω = Kinematic Equations v = v 0 + at ω = ω 0 + αt x = ½(v + v 0 )t θ = ½(ω + ω 0 )t x = v 0 t + ½ at θ = ω 0 t + ½ αt v = v 0 + ax ω = ω 0 + αθ Inertia m = mass I = Rotational inertia; I = m i r i To create force = F torque = τ = LA F Newton's second law of ΣF = ma Στ = Iα motion ΣF = Δp/Δt Στ = ΔL/Δt Work F x τ θ Kinetic Energy Translational Kinetic Energy = TKE = ½ mv Momentum p = m V L = I ω Conservation of Σm i v i = Σm f v f ΣI i ω i = ΣI f ω f momentum Pressure = Force/Area P abs = P atm + P G Density = Mass/Volume Pressure (P) due to depth h of fluid of density ρ; P = ρgh. 1 atm = x 10 5 N/m = 76 cm.hg = 760 mm.hg The density of the air is 1.9 kg/m 3 ; Density of water = 1000 kg/m 3 = 1 g/cm 3 ; Acceleration due to gravity = g = 9.8 m/s. Rotational Kinetic Energy = RKE = ½ Iω Area of a circle of radius r, A circle = π r.area of a rectangle of length l, and width w, A rec =l x w; Area of a triangle, A triangle = 0.5 x base x height. Volume of a cylinder of radius r and height h; V= π r h; Volume of a sphere = (4/3) π r 3. r Hooke s law: F = kx Elastic PE = EPE = 1 kx KE = 1 mv GGG = mmh 1
2 PHYS 01 Fall 014 Test #3 Name: I. For the following multiple choice questions, write your answer in the line next to the question number. 1. Express the diastolic pressure 85 mm.hg in Pa. a b x 10 4 c x 10 5 d x 10 4 e x What is the angular speed in rad/s of the hour hand of an analog watch? a x 10-3 b c x 10-3 d x 10-3 e x During a spin dry cycle of a washing machine, the motor speeds from 30 rad/s to 95 rad/s while turning the drum through an angle of 40 radians. How long it took to spin this angle? a s b. 3.1 s c. 4.3 s d s e. 6.5 s 4. A ball of radius 0.00 m is given an initial angular velocity of 15 rad/s. The ball rolls along a straight line for 5 seconds until it comes to rest. How far the ball travels during this time? a. 7.5 m b m c. 3 m d. 75 m e. 15 m f. 1.0 m 5-6) Five hockey pucks are sliding across frictionless ice. The drawing shows a top view of the pucks and the three forces that act on each one. The forces can have different magnitudes (F, F, or 3F), and can be applied at different points on the puck. The radius of the puck is R. 5. Which one of the five pucks is in Equilibrium? 6. Which one of the five pucks has a net torque of 5FR? a. b. c. d. e. 7-8) The drawing shows three containers of circular cross-section, filled to the same height with the same fluid. 7. In which container, is the pressure at the bottom the greatest? 8. In which container, is the force at the bottom the greatest? Answers for a. Container A b. Container B c. Container C d. All three containers experience the same
3 9. Sit-ups are more difficult to do with your hands placed behind your head instead of on your stomach. This is because, a. The mass is greater when the hands are placed behind the head instead on the stomach. b. The mass is smaller when the hands are placed behind the head instead on the stomach. c. The moment of inertia is greater when the hands are placed behind the head instead on the stomach. d. The moment of inertia is smaller when the hands are placed behind the head instead on the stomach. 10. For the motion graphed below, what are the instantaneous angular velocity and angular acceleration at 1 second? a. 6 rad/s, 6 rad/s b. -6 rad/s, 6 rad/s c. 6 rad/s, 3 rad/s d. -6 rad/s, 3 rad/s e. -6 rad/s, 1. rad/s 11. A force, F = 1-N is applied to a brake pedal as shown below. The length of the brake pedal is 1-cm and the master-cylinder piston is attached 3-cm from the axis, to the brake pedal. Calculate the force exerted to the master cylinder. a. 3 N b. 8 N c. 1 N d. 4 N e. 48 N 1. The purpose of a water tower is to provide storage capacity and to provide sufficient pressure in the pipes that deliver the water to customers. The drawing shows a spherical reservoir, which is vented to the atmosphere at the top and full. What height must be used to find the gauge pressure at the faucet in house B? a. 15 m b. 7 m c. 7.3 m d m e m 3
4 13. A mercury barometer is used to measure the atmospheric pressure as shown in the figure to the right. What is the absolute pressure at point C shown in the diagram? a. 0 b. 76 cm. Hg c. 760 mm.hg d. 1 atm e x 10 5 N/m 14. Resonance occurs in harmonic motion when, a. The system is over-damped. b. The system is critically damped. c. The energy in the system is a minimum. d. The driving frequency is the same as the natural frequency of the system. e. The energy in the system is proportional to the square of the motion's amplitude. 15. The drawing shows a graph of displacement x versus time t for simple harmonic motion of an object on a horizontal spring. Which one of the following answers correctly gives the magnitude v of the velocity and the magnitude a of the acceleration at points A and B in the graph? a. v A = maximum, a A = maximum, v B = 0 m/s, a B = 0 m/s b. v A = maximum, a A = 0 m/s, v B = 0 m/s, a B = maximum c. v A = 0 m/s, a A = 0 m/s, v B = maximum, a B = maximum d. v A = 0 m/s, a A = maximum, v B = maximum, a B = 0 m/s e. v A = maximum, a A = maximum, v B = 0 m/s, a B = maximum end of MC questions. II. State Pascal s principle and identify a practical application of the principle. III. The spring loaded gun in a ballistic pendulum is compressed by 5. cm and released. The 54 gram steel ball leaves the gun with a velocity of 6.3 m/s. Calculate the spring constant of the spring. 4
5 IV. A 150-N uniform horizontal beam is hinged to a vertical wall at one end and is supported by a cable at the other end as shown below. Draw a free-body diagram for the beam and find the tension in the cable. V. The drawing shows a model for the motion of the human forearm in throwing a dart. Because of the force applied by the triceps muscle, the forearm can rotate about an axis at the elbow joint. Assume that the forearm has the dimensions shown in the drawing and a moment of inertia of kg.m (including the effect of the dart) relative to the axis at the elbow. Assume also that the force acts perpendicular to the forearm. Ignoring the effect of gravity and any frictional forces, determine the magnitude of the force needed to give the dart a tangential speed of in 0.10 s, starting from rest. 5
We define angular displacement, θ, and angular velocity, ω. What's a radian?
 We define angular displacement, θ, and angular velocity, ω Units: θ = rad ω = rad/s What's a radian? Radian is the ratio between the length of an arc and its radius note: counterclockwise is + clockwise
We define angular displacement, θ, and angular velocity, ω Units: θ = rad ω = rad/s What's a radian? Radian is the ratio between the length of an arc and its radius note: counterclockwise is + clockwise
Final Exam Spring 2014 May 05, 2014
 95.141 Final Exam Spring 2014 May 05, 2014 Section number Section instructor Last/First name Last 3 Digits of Student ID Number: Answer all questions, beginning each new question in the space provided.
95.141 Final Exam Spring 2014 May 05, 2014 Section number Section instructor Last/First name Last 3 Digits of Student ID Number: Answer all questions, beginning each new question in the space provided.
Momentum Circular Motion and Gravitation Rotational Motion Fluid Mechanics
 Momentum Circular Motion and Gravitation Rotational Motion Fluid Mechanics Momentum Momentum Collisions between objects can be evaluated using the laws of conservation of energy and of momentum. Momentum
Momentum Circular Motion and Gravitation Rotational Motion Fluid Mechanics Momentum Momentum Collisions between objects can be evaluated using the laws of conservation of energy and of momentum. Momentum
Chapter 8 Lecture Notes
 Chapter 8 Lecture Notes Physics 2414 - Strauss Formulas: v = l / t = r θ / t = rω a T = v / t = r ω / t =rα a C = v 2 /r = ω 2 r ω = ω 0 + αt θ = ω 0 t +(1/2)αt 2 θ = (1/2)(ω 0 +ω)t ω 2 = ω 0 2 +2αθ τ
Chapter 8 Lecture Notes Physics 2414 - Strauss Formulas: v = l / t = r θ / t = rω a T = v / t = r ω / t =rα a C = v 2 /r = ω 2 r ω = ω 0 + αt θ = ω 0 t +(1/2)αt 2 θ = (1/2)(ω 0 +ω)t ω 2 = ω 0 2 +2αθ τ
Welcome back to Physics 211
 Welcome back to Physics 211 Today s agenda: Moment of Inertia Angular momentum 13-2 1 Current assignments Prelecture due Tuesday after Thanksgiving HW#13 due next Wednesday, 11/24 Turn in written assignment
Welcome back to Physics 211 Today s agenda: Moment of Inertia Angular momentum 13-2 1 Current assignments Prelecture due Tuesday after Thanksgiving HW#13 due next Wednesday, 11/24 Turn in written assignment
Circular Motion, Pt 2: Angular Dynamics. Mr. Velazquez AP/Honors Physics
 Circular Motion, Pt 2: Angular Dynamics Mr. Velazquez AP/Honors Physics Formulas: Angular Kinematics (θ must be in radians): s = rθ Arc Length 360 = 2π rads = 1 rev ω = θ t = v t r Angular Velocity α av
Circular Motion, Pt 2: Angular Dynamics Mr. Velazquez AP/Honors Physics Formulas: Angular Kinematics (θ must be in radians): s = rθ Arc Length 360 = 2π rads = 1 rev ω = θ t = v t r Angular Velocity α av
43. A person sits on a freely spinning lab stool that has no friction in its axle. When this person extends her arms,
 43. A person sits on a freely spinning lab stool that has no friction in its axle. When this person extends her arms, A) her moment of inertia increases and her rotational kinetic energy remains the same.
43. A person sits on a freely spinning lab stool that has no friction in its axle. When this person extends her arms, A) her moment of inertia increases and her rotational kinetic energy remains the same.
Your Name: PHYSICS 101 MIDTERM. Please circle your section 1 9 am Galbiati 2 10 am Kwon 3 11 am McDonald 4 12:30 pm McDonald 5 12:30 pm Kwon
 1 Your Name: PHYSICS 101 MIDTERM October 26, 2006 2 hours Please circle your section 1 9 am Galbiati 2 10 am Kwon 3 11 am McDonald 4 12:30 pm McDonald 5 12:30 pm Kwon Problem Score 1 /13 2 /20 3 /20 4
1 Your Name: PHYSICS 101 MIDTERM October 26, 2006 2 hours Please circle your section 1 9 am Galbiati 2 10 am Kwon 3 11 am McDonald 4 12:30 pm McDonald 5 12:30 pm Kwon Problem Score 1 /13 2 /20 3 /20 4
Physics 202 Exam 1. May 1, 2013
 Name: Physics 202 Exam 1 May 1, 2013 Word Problems Show all your work and circle your final answer. (Ten points each.) 1. If 2.4 m 3 of a gas initially at STP is compressed to 1.6 m 3 and its temperature
Name: Physics 202 Exam 1 May 1, 2013 Word Problems Show all your work and circle your final answer. (Ten points each.) 1. If 2.4 m 3 of a gas initially at STP is compressed to 1.6 m 3 and its temperature
A Ferris wheel in Japan has a radius of 50m and a mass of 1.2 x 10 6 kg. If a torque of 1 x 10 9 Nm is needed to turn the wheel when it starts at
 Option B Quiz 1. A Ferris wheel in Japan has a radius of 50m and a mass of 1. x 10 6 kg. If a torque of 1 x 10 9 Nm is needed to turn the wheel when it starts at rest, what is the wheel s angular acceleration?
Option B Quiz 1. A Ferris wheel in Japan has a radius of 50m and a mass of 1. x 10 6 kg. If a torque of 1 x 10 9 Nm is needed to turn the wheel when it starts at rest, what is the wheel s angular acceleration?
31 ROTATIONAL KINEMATICS
 31 ROTATIONAL KINEMATICS 1. Compare and contrast circular motion and rotation? Address the following Which involves an object and which involves a system? Does an object/system in circular motion have
31 ROTATIONAL KINEMATICS 1. Compare and contrast circular motion and rotation? Address the following Which involves an object and which involves a system? Does an object/system in circular motion have
AP Pd 3 Rotational Dynamics.notebook. May 08, 2014
 1 Rotational Dynamics Why do objects spin? Objects can travel in different ways: Translation all points on the body travel in parallel paths Rotation all points on the body move around a fixed point An
1 Rotational Dynamics Why do objects spin? Objects can travel in different ways: Translation all points on the body travel in parallel paths Rotation all points on the body move around a fixed point An
Chapter 9 TORQUE & Rotational Kinematics
 Chapter 9 TORQUE & Rotational Kinematics This motionless person is in static equilibrium. The forces acting on him add up to zero. Both forces are vertical in this case. This car is in dynamic equilibrium
Chapter 9 TORQUE & Rotational Kinematics This motionless person is in static equilibrium. The forces acting on him add up to zero. Both forces are vertical in this case. This car is in dynamic equilibrium
Wiley Plus. Final Assignment (5) Is Due Today: Before 11 pm!
 Wiley Plus Final Assignment (5) Is Due Today: Before 11 pm! Final Exam Review December 9, 009 3 What about vector subtraction? Suppose you are given the vector relation A B C RULE: The resultant vector
Wiley Plus Final Assignment (5) Is Due Today: Before 11 pm! Final Exam Review December 9, 009 3 What about vector subtraction? Suppose you are given the vector relation A B C RULE: The resultant vector
Rotational Dynamics, Moment of Inertia and Angular Momentum
 Rotational Dynamics, Moment of Inertia and Angular Momentum Now that we have examined rotational kinematics and torque we will look at applying the concepts of angular motion to Newton s first and second
Rotational Dynamics, Moment of Inertia and Angular Momentum Now that we have examined rotational kinematics and torque we will look at applying the concepts of angular motion to Newton s first and second
Slide 1 / 37. Rotational Motion
 Slide 1 / 37 Rotational Motion Slide 2 / 37 Angular Quantities An angle θ can be given by: where r is the radius and l is the arc length. This gives θ in radians. There are 360 in a circle or 2π radians.
Slide 1 / 37 Rotational Motion Slide 2 / 37 Angular Quantities An angle θ can be given by: where r is the radius and l is the arc length. This gives θ in radians. There are 360 in a circle or 2π radians.
Uniform Circular Motion
 Uniform Circular Motion Motion in a circle at constant angular speed. ω: angular velocity (rad/s) Rotation Angle The rotation angle is the ratio of arc length to radius of curvature. For a given angle,
Uniform Circular Motion Motion in a circle at constant angular speed. ω: angular velocity (rad/s) Rotation Angle The rotation angle is the ratio of arc length to radius of curvature. For a given angle,
Department of Physics
 Department of Physics PHYS101-051 FINAL EXAM Test Code: 100 Tuesday, 4 January 006 in Building 54 Exam Duration: 3 hrs (from 1:30pm to 3:30pm) Name: Student Number: Section Number: Page 1 1. A car starts
Department of Physics PHYS101-051 FINAL EXAM Test Code: 100 Tuesday, 4 January 006 in Building 54 Exam Duration: 3 hrs (from 1:30pm to 3:30pm) Name: Student Number: Section Number: Page 1 1. A car starts
Figure 1 Answer: = m
 Q1. Figure 1 shows a solid cylindrical steel rod of length =.0 m and diameter D =.0 cm. What will be increase in its length when m = 80 kg block is attached to its bottom end? (Young's modulus of steel
Q1. Figure 1 shows a solid cylindrical steel rod of length =.0 m and diameter D =.0 cm. What will be increase in its length when m = 80 kg block is attached to its bottom end? (Young's modulus of steel
PHYSICS 221, FALL 2011 EXAM #2 SOLUTIONS WEDNESDAY, NOVEMBER 2, 2011
 PHYSICS 1, FALL 011 EXAM SOLUTIONS WEDNESDAY, NOVEMBER, 011 Note: The unit vectors in the +x, +y, and +z directions of a right-handed Cartesian coordinate system are î, ĵ, and ˆk, respectively. In this
PHYSICS 1, FALL 011 EXAM SOLUTIONS WEDNESDAY, NOVEMBER, 011 Note: The unit vectors in the +x, +y, and +z directions of a right-handed Cartesian coordinate system are î, ĵ, and ˆk, respectively. In this
UNIVERSITY OF MANITOBA. All questions are of equal value. No marks are subtracted for wrong answers.
 (3:30 pm 6:30 pm) PAGE NO.: 1 of 7 All questions are of equal value. No marks are subtracted for wrong answers. Record all answers on the computer score sheet provided. USE PENCIL ONLY! Black pen will
(3:30 pm 6:30 pm) PAGE NO.: 1 of 7 All questions are of equal value. No marks are subtracted for wrong answers. Record all answers on the computer score sheet provided. USE PENCIL ONLY! Black pen will
Pleeeeeeeeeeeeeease mark your UFID, exam number, and name correctly. 20 problems 3 problems from exam 2
 Pleeeeeeeeeeeeeease mark your UFID, exam number, and name correctly. 20 problems 3 problems from exam 1 3 problems from exam 2 6 problems 13.1 14.6 (including 14.5) 8 problems 1.1---9.6 Go through the
Pleeeeeeeeeeeeeease mark your UFID, exam number, and name correctly. 20 problems 3 problems from exam 1 3 problems from exam 2 6 problems 13.1 14.6 (including 14.5) 8 problems 1.1---9.6 Go through the
On my honor, I have neither given nor received unauthorized aid on this examination.
 Instructor(s): Profs. D. Reitze, H. Chan PHYSICS DEPARTMENT PHY 2053 Exam 2 April 2, 2009 Name (print, last first): Signature: On my honor, I have neither given nor received unauthorized aid on this examination.
Instructor(s): Profs. D. Reitze, H. Chan PHYSICS DEPARTMENT PHY 2053 Exam 2 April 2, 2009 Name (print, last first): Signature: On my honor, I have neither given nor received unauthorized aid on this examination.
. d. v A v B. e. none of these.
 General Physics I Exam 3 - Chs. 7,8,9 - Momentum, Rotation, Equilibrium Oct. 28, 2009 Name Rec. Instr. Rec. Time For full credit, make your work clear to the grader. Show the formulas you use, the essential
General Physics I Exam 3 - Chs. 7,8,9 - Momentum, Rotation, Equilibrium Oct. 28, 2009 Name Rec. Instr. Rec. Time For full credit, make your work clear to the grader. Show the formulas you use, the essential
1.1. Rotational Kinematics Description Of Motion Of A Rotating Body
 PHY 19- PHYSICS III 1. Moment Of Inertia 1.1. Rotational Kinematics Description Of Motion Of A Rotating Body 1.1.1. Linear Kinematics Consider the case of linear kinematics; it concerns the description
PHY 19- PHYSICS III 1. Moment Of Inertia 1.1. Rotational Kinematics Description Of Motion Of A Rotating Body 1.1.1. Linear Kinematics Consider the case of linear kinematics; it concerns the description
b) (6) With 10.0 N applied to the smaller piston, what pressure force F 2 (in newtons) is produced on the larger piston?
 General Physics I Exam 4 - Chs. 10,11,12 - Fluids, Waves, Sound Nov. 17, 2010 Name Rec. Instr. Rec. Time For full credit, make your work clear to the grader. Show formulas used, essential steps, and results
General Physics I Exam 4 - Chs. 10,11,12 - Fluids, Waves, Sound Nov. 17, 2010 Name Rec. Instr. Rec. Time For full credit, make your work clear to the grader. Show formulas used, essential steps, and results
Chapters 10 & 11: Rotational Dynamics Thursday March 8 th
 Chapters 10 & 11: Rotational Dynamics Thursday March 8 th Review of rotational kinematics equations Review and more on rotational inertia Rolling motion as rotation and translation Rotational kinetic energy
Chapters 10 & 11: Rotational Dynamics Thursday March 8 th Review of rotational kinematics equations Review and more on rotational inertia Rolling motion as rotation and translation Rotational kinetic energy
1 MR SAMPLE EXAM 3 FALL 2013
 SAMPLE EXAM 3 FALL 013 1. A merry-go-round rotates from rest with an angular acceleration of 1.56 rad/s. How long does it take to rotate through the first rev? A) s B) 4 s C) 6 s D) 8 s E) 10 s. A wheel,
SAMPLE EXAM 3 FALL 013 1. A merry-go-round rotates from rest with an angular acceleration of 1.56 rad/s. How long does it take to rotate through the first rev? A) s B) 4 s C) 6 s D) 8 s E) 10 s. A wheel,
UNIVERSITY OF MANITOBA
 PAGE NO.: 1 of 6 + Formula Sheet Equal marks for all questions. No marks are subtracted for wrong answers. Record all answers on the computer score sheet provided. USE PENCIL ONLY! Black pen will look
PAGE NO.: 1 of 6 + Formula Sheet Equal marks for all questions. No marks are subtracted for wrong answers. Record all answers on the computer score sheet provided. USE PENCIL ONLY! Black pen will look
The... of a particle is defined as its change in position in some time interval.
 Distance is the. of a path followed by a particle. Distance is a quantity. The... of a particle is defined as its change in position in some time interval. Displacement is a.. quantity. The... of a particle
Distance is the. of a path followed by a particle. Distance is a quantity. The... of a particle is defined as its change in position in some time interval. Displacement is a.. quantity. The... of a particle
Chapter 10. Rotation
 Chapter 10 Rotation Rotation Rotational Kinematics: Angular velocity and Angular Acceleration Rotational Kinetic Energy Moment of Inertia Newton s nd Law for Rotation Applications MFMcGraw-PHY 45 Chap_10Ha-Rotation-Revised
Chapter 10 Rotation Rotation Rotational Kinematics: Angular velocity and Angular Acceleration Rotational Kinetic Energy Moment of Inertia Newton s nd Law for Rotation Applications MFMcGraw-PHY 45 Chap_10Ha-Rotation-Revised
All questions are of equal value. No marks are subtracted for wrong answers.
 (1:30 PM 4:30 PM) Page 1 of 6 All questions are of equal value. No marks are subtracted for wrong answers. Record all answers on the computer score sheet provided. USE PENCIL ONLY! Black pen will look
(1:30 PM 4:30 PM) Page 1 of 6 All questions are of equal value. No marks are subtracted for wrong answers. Record all answers on the computer score sheet provided. USE PENCIL ONLY! Black pen will look
( ) Physics 201, Final Exam, Fall 2006 PRACTICE EXAMINATION Answer Key. The next three problems refer to the following situation:
 Physics 201, Final Exam, Fall 2006 PRACTICE EXAMINATION Answer Key The next three problems refer to the following situation: Two masses, m 1 and m 2, m 1 > m 2, are suspended by a massless rope over a
Physics 201, Final Exam, Fall 2006 PRACTICE EXAMINATION Answer Key The next three problems refer to the following situation: Two masses, m 1 and m 2, m 1 > m 2, are suspended by a massless rope over a
First Name: Last Name: Section: 22 December, :25 2:25 PM Physics 207 FINAL EXAM
 1 First Name: Last Name: Section: 22 December, 2009 12:25 2:25 PM Physics 207 FINAL EXAM Please print your name and section number (or TA s name) clearly on the first page. Show all your work in the space
1 First Name: Last Name: Section: 22 December, 2009 12:25 2:25 PM Physics 207 FINAL EXAM Please print your name and section number (or TA s name) clearly on the first page. Show all your work in the space
b) (6) What is the volume of the iron cube, in m 3?
 General Physics I Exam 4 - Chs. 10,11,12 - Fluids, Waves, Sound Nov. 14, 2012 Name Rec. Instr. Rec. Time For full credit, make your work clear to the grader. Show formulas used, essential steps, and results
General Physics I Exam 4 - Chs. 10,11,12 - Fluids, Waves, Sound Nov. 14, 2012 Name Rec. Instr. Rec. Time For full credit, make your work clear to the grader. Show formulas used, essential steps, and results
Chapter 9. Rotational Dynamics
 Chapter 9 Rotational Dynamics In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination of translation and rotation. 1) Torque Produces angular
Chapter 9 Rotational Dynamics In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination of translation and rotation. 1) Torque Produces angular
Chapter 9. Rotational Dynamics
 Chapter 9 Rotational Dynamics In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination of translation and rotation. 1) Torque Produces angular
Chapter 9 Rotational Dynamics In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination of translation and rotation. 1) Torque Produces angular
Chapter 8. Rotational Equilibrium and Rotational Dynamics
 Chapter 8 Rotational Equilibrium and Rotational Dynamics Wrench Demo Torque Torque, τ, is the tendency of a force to rotate an object about some axis τ = Fd F is the force d is the lever arm (or moment
Chapter 8 Rotational Equilibrium and Rotational Dynamics Wrench Demo Torque Torque, τ, is the tendency of a force to rotate an object about some axis τ = Fd F is the force d is the lever arm (or moment
SCHOOL OF COMPUTING, ENGINEERING AND MATHEMATICS SEMESTER 1 EXAMINATIONS 2012/2013 XE121. ENGINEERING CONCEPTS (Test)
 s SCHOOL OF COMPUTING, ENGINEERING AND MATHEMATICS SEMESTER EXAMINATIONS 202/203 XE2 ENGINEERING CONCEPTS (Test) Time allowed: TWO hours Answer: Attempt FOUR questions only, a maximum of TWO questions
s SCHOOL OF COMPUTING, ENGINEERING AND MATHEMATICS SEMESTER EXAMINATIONS 202/203 XE2 ENGINEERING CONCEPTS (Test) Time allowed: TWO hours Answer: Attempt FOUR questions only, a maximum of TWO questions
AP Physics. Harmonic Motion. Multiple Choice. Test E
 AP Physics Harmonic Motion Multiple Choice Test E A 0.10-Kg block is attached to a spring, initially unstretched, of force constant k = 40 N m as shown below. The block is released from rest at t = 0 sec.
AP Physics Harmonic Motion Multiple Choice Test E A 0.10-Kg block is attached to a spring, initially unstretched, of force constant k = 40 N m as shown below. The block is released from rest at t = 0 sec.
PHYSICS 221 SPRING 2015
 PHYSICS 221 SPRING 2015 EXAM 2: April 2, 2015 8:15-10:15pm Name (printed): Recitation Instructor: Section # INSTRUCTIONS: This exam contains 25 multiple-choice questions plus 2 extra credit questions,
PHYSICS 221 SPRING 2015 EXAM 2: April 2, 2015 8:15-10:15pm Name (printed): Recitation Instructor: Section # INSTRUCTIONS: This exam contains 25 multiple-choice questions plus 2 extra credit questions,
On my honor as a Texas A&M University student, I will neither give nor receive unauthorized help on this exam.
 Physics 201, Exam 3 Name (printed) On my honor as a Texas A&M University student, I will neither give nor receive unauthorized help on this exam. Name (signed) The multiple-choice problems carry no partial
Physics 201, Exam 3 Name (printed) On my honor as a Texas A&M University student, I will neither give nor receive unauthorized help on this exam. Name (signed) The multiple-choice problems carry no partial
Assessment Schedule 2016 Physics: Demonstrate understanding of mechanical systems (91524)
 NCEA Level 3 Physics (91524) 2016 page 1 of 6 Assessment Schedule 2016 Physics: Demonstrate understanding of mechanical systems (91524) Evidence Statement NØ N1 N2 A3 A4 M5 M6 E7 E8 No response; no relevant
NCEA Level 3 Physics (91524) 2016 page 1 of 6 Assessment Schedule 2016 Physics: Demonstrate understanding of mechanical systems (91524) Evidence Statement NØ N1 N2 A3 A4 M5 M6 E7 E8 No response; no relevant
= o + t = ot + ½ t 2 = o + 2
 Chapters 8-9 Rotational Kinematics and Dynamics Rotational motion Rotational motion refers to the motion of an object or system that spins about an axis. The axis of rotation is the line about which the
Chapters 8-9 Rotational Kinematics and Dynamics Rotational motion Rotational motion refers to the motion of an object or system that spins about an axis. The axis of rotation is the line about which the
Physics for Scientists and Engineers 4th Edition, 2017
 A Correlation of Physics for Scientists and Engineers 4th Edition, 2017 To the AP Physics C: Mechanics Course Descriptions AP is a trademark registered and/or owned by the College Board, which was not
A Correlation of Physics for Scientists and Engineers 4th Edition, 2017 To the AP Physics C: Mechanics Course Descriptions AP is a trademark registered and/or owned by the College Board, which was not
Chapter 8 continued. Rotational Dynamics
 Chapter 8 continued Rotational Dynamics 8.6 The Action of Forces and Torques on Rigid Objects Chapter 8 developed the concepts of angular motion. θ : angles and radian measure for angular variables ω :
Chapter 8 continued Rotational Dynamics 8.6 The Action of Forces and Torques on Rigid Objects Chapter 8 developed the concepts of angular motion. θ : angles and radian measure for angular variables ω :
Rotational Dynamics continued
 Chapter 9 Rotational Dynamics continued 9.4 Newton s Second Law for Rotational Motion About a Fixed Axis ROTATIONAL ANALOG OF NEWTON S SECOND LAW FOR A RIGID BODY ROTATING ABOUT A FIXED AXIS I = ( mr 2
Chapter 9 Rotational Dynamics continued 9.4 Newton s Second Law for Rotational Motion About a Fixed Axis ROTATIONAL ANALOG OF NEWTON S SECOND LAW FOR A RIGID BODY ROTATING ABOUT A FIXED AXIS I = ( mr 2
Chapter 12. Recall that when a spring is stretched a distance x, it will pull back with a force given by: F = -kx
 Chapter 1 Lecture Notes Chapter 1 Oscillatory Motion Recall that when a spring is stretched a distance x, it will pull back with a force given by: F = -kx When the mass is released, the spring will pull
Chapter 1 Lecture Notes Chapter 1 Oscillatory Motion Recall that when a spring is stretched a distance x, it will pull back with a force given by: F = -kx When the mass is released, the spring will pull
Solution Only gravity is doing work. Since gravity is a conservative force mechanical energy is conserved:
 8) roller coaster starts with a speed of 8.0 m/s at a point 45 m above the bottom of a dip (see figure). Neglecting friction, what will be the speed of the roller coaster at the top of the next slope,
8) roller coaster starts with a speed of 8.0 m/s at a point 45 m above the bottom of a dip (see figure). Neglecting friction, what will be the speed of the roller coaster at the top of the next slope,
UNIVERSITY OF MANITOBA. All questions are of equal value. No marks are subtracted for wrong answers.
 (1:30 pm 4:30 pm) PAGE NO.: 1 of 7 All questions are of equal value. No marks are subtracted for wrong answers. Record all answers on the computer score sheet provided. USE PENCIL ONLY! Black pen will
(1:30 pm 4:30 pm) PAGE NO.: 1 of 7 All questions are of equal value. No marks are subtracted for wrong answers. Record all answers on the computer score sheet provided. USE PENCIL ONLY! Black pen will
Unit 8 Notetaking Guide Torque and Rotational Motion
 Unit 8 Notetaking Guide Torque and Rotational Motion Rotational Motion Until now, we have been concerned mainly with translational motion. We discussed the kinematics and dynamics of translational motion
Unit 8 Notetaking Guide Torque and Rotational Motion Rotational Motion Until now, we have been concerned mainly with translational motion. We discussed the kinematics and dynamics of translational motion
Write your name legibly on the top right hand corner of this paper
 NAME Phys 631 Summer 2007 Quiz 2 Tuesday July 24, 2007 Instructor R. A. Lindgren 9:00 am 12:00 am Write your name legibly on the top right hand corner of this paper No Books or Notes allowed Calculator
NAME Phys 631 Summer 2007 Quiz 2 Tuesday July 24, 2007 Instructor R. A. Lindgren 9:00 am 12:00 am Write your name legibly on the top right hand corner of this paper No Books or Notes allowed Calculator
Oscillatory Motion SHM
 Chapter 15 Oscillatory Motion SHM Dr. Armen Kocharian Periodic Motion Periodic motion is motion of an object that regularly repeats The object returns to a given position after a fixed time interval A
Chapter 15 Oscillatory Motion SHM Dr. Armen Kocharian Periodic Motion Periodic motion is motion of an object that regularly repeats The object returns to a given position after a fixed time interval A
Solution to phys101-t112-final Exam
 Solution to phys101-t112-final Exam Q1. An 800-N man stands halfway up a 5.0-m long ladder of negligible weight. The base of the ladder is.0m from the wall as shown in Figure 1. Assuming that the wall-ladder
Solution to phys101-t112-final Exam Q1. An 800-N man stands halfway up a 5.0-m long ladder of negligible weight. The base of the ladder is.0m from the wall as shown in Figure 1. Assuming that the wall-ladder
PHYSICS 221 SPRING 2015
 PHYSICS 221 SPRING 2015 EXAM 2: April 2, 2015 8:15-10:15pm Name (printed): Recitation Instructor: Section # INSTRUCTIONS: This exam contains 25 multiple-choice questions plus 2 extra credit questions,
PHYSICS 221 SPRING 2015 EXAM 2: April 2, 2015 8:15-10:15pm Name (printed): Recitation Instructor: Section # INSTRUCTIONS: This exam contains 25 multiple-choice questions plus 2 extra credit questions,
Chapter 8. Rotational Equilibrium and Rotational Dynamics. 1. Torque. 2. Torque and Equilibrium. 3. Center of Mass and Center of Gravity
 Chapter 8 Rotational Equilibrium and Rotational Dynamics 1. Torque 2. Torque and Equilibrium 3. Center of Mass and Center of Gravity 4. Torque and angular acceleration 5. Rotational Kinetic energy 6. Angular
Chapter 8 Rotational Equilibrium and Rotational Dynamics 1. Torque 2. Torque and Equilibrium 3. Center of Mass and Center of Gravity 4. Torque and angular acceleration 5. Rotational Kinetic energy 6. Angular
Rotation. PHYS 101 Previous Exam Problems CHAPTER
 PHYS 101 Previous Exam Problems CHAPTER 10 Rotation Rotational kinematics Rotational inertia (moment of inertia) Kinetic energy Torque Newton s 2 nd law Work, power & energy conservation 1. Assume that
PHYS 101 Previous Exam Problems CHAPTER 10 Rotation Rotational kinematics Rotational inertia (moment of inertia) Kinetic energy Torque Newton s 2 nd law Work, power & energy conservation 1. Assume that
Kinematics (special case) Dynamics gravity, tension, elastic, normal, friction. Energy: kinetic, potential gravity, spring + work (friction)
 Kinematics (special case) a = constant 1D motion 2D projectile Uniform circular Dynamics gravity, tension, elastic, normal, friction Motion with a = constant Newton s Laws F = m a F 12 = F 21 Time & Position
Kinematics (special case) a = constant 1D motion 2D projectile Uniform circular Dynamics gravity, tension, elastic, normal, friction Motion with a = constant Newton s Laws F = m a F 12 = F 21 Time & Position
Rotational Kinetic Energy
 Lecture 17, Chapter 10: Rotational Energy and Angular Momentum 1 Rotational Kinetic Energy Consider a rigid body rotating with an angular velocity ω about an axis. Clearly every point in the rigid body
Lecture 17, Chapter 10: Rotational Energy and Angular Momentum 1 Rotational Kinetic Energy Consider a rigid body rotating with an angular velocity ω about an axis. Clearly every point in the rigid body
Physics 201 Midterm Exam 3
 Physics 201 Midterm Exam 3 Information and Instructions Student ID Number: Section Number: TA Name: Please fill in all the information above. Please write and bubble your Name and Student Id number on
Physics 201 Midterm Exam 3 Information and Instructions Student ID Number: Section Number: TA Name: Please fill in all the information above. Please write and bubble your Name and Student Id number on
Rotational Motion What is the difference between translational and rotational motion? Translational motion.
 Rotational Motion 1 1. What is the difference between translational and rotational motion? Translational motion Rotational motion 2. What is a rigid object? 3. What is rotational motion? 4. Identify and
Rotational Motion 1 1. What is the difference between translational and rotational motion? Translational motion Rotational motion 2. What is a rigid object? 3. What is rotational motion? 4. Identify and
CEE 271: Applied Mechanics II, Dynamics Lecture 25: Ch.17, Sec.4-5
 1 / 36 CEE 271: Applied Mechanics II, Dynamics Lecture 25: Ch.17, Sec.4-5 Prof. Albert S. Kim Civil and Environmental Engineering, University of Hawaii at Manoa Date: 2 / 36 EQUATIONS OF MOTION: ROTATION
1 / 36 CEE 271: Applied Mechanics II, Dynamics Lecture 25: Ch.17, Sec.4-5 Prof. Albert S. Kim Civil and Environmental Engineering, University of Hawaii at Manoa Date: 2 / 36 EQUATIONS OF MOTION: ROTATION
Energy Conservation AP
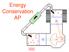 Energy Conservation AP Manicouagan Reservoir seen from space shuttle; formed almost 1 million years ago when a large meteorite hit Earth Earth did work on meteorite to change its kinetic energy energy
Energy Conservation AP Manicouagan Reservoir seen from space shuttle; formed almost 1 million years ago when a large meteorite hit Earth Earth did work on meteorite to change its kinetic energy energy
Sample Physics Placement Exam
 Sample Physics 130-1 Placement Exam A. Multiple Choice Questions: 1. A cable is used to take construction equipment from the ground to the top of a tall building. During the trip up, when (if ever) is
Sample Physics 130-1 Placement Exam A. Multiple Choice Questions: 1. A cable is used to take construction equipment from the ground to the top of a tall building. During the trip up, when (if ever) is
PHYSICS 149: Lecture 21
 PHYSICS 149: Lecture 21 Chapter 8: Torque and Angular Momentum 8.2 Torque 8.4 Equilibrium Revisited 8.8 Angular Momentum Lecture 21 Purdue University, Physics 149 1 Midterm Exam 2 Wednesday, April 6, 6:30
PHYSICS 149: Lecture 21 Chapter 8: Torque and Angular Momentum 8.2 Torque 8.4 Equilibrium Revisited 8.8 Angular Momentum Lecture 21 Purdue University, Physics 149 1 Midterm Exam 2 Wednesday, April 6, 6:30
CHAPTER 6 WORK AND ENERGY
 CHAPTER 6 WORK AND ENERGY ANSWERS TO FOCUS ON CONCEPTS QUESTIONS (e) When the force is perpendicular to the displacement, as in C, there is no work When the force points in the same direction as the displacement,
CHAPTER 6 WORK AND ENERGY ANSWERS TO FOCUS ON CONCEPTS QUESTIONS (e) When the force is perpendicular to the displacement, as in C, there is no work When the force points in the same direction as the displacement,
AP Physics QUIZ Chapters 10
 Name: 1. Torque is the rotational analogue of (A) Kinetic Energy (B) Linear Momentum (C) Acceleration (D) Force (E) Mass A 5-kilogram sphere is connected to a 10-kilogram sphere by a rigid rod of negligible
Name: 1. Torque is the rotational analogue of (A) Kinetic Energy (B) Linear Momentum (C) Acceleration (D) Force (E) Mass A 5-kilogram sphere is connected to a 10-kilogram sphere by a rigid rod of negligible
PHYSICS 221 SPRING 2014
 PHYSICS 221 SPRING 2014 EXAM 2: April 3, 2014 8:15-10:15pm Name (printed): Recitation Instructor: Section # INSTRUCTIONS: This exam contains 25 multiple-choice questions plus 2 extra credit questions,
PHYSICS 221 SPRING 2014 EXAM 2: April 3, 2014 8:15-10:15pm Name (printed): Recitation Instructor: Section # INSTRUCTIONS: This exam contains 25 multiple-choice questions plus 2 extra credit questions,
= y(x, t) =A cos (!t + kx)
 A harmonic wave propagates horizontally along a taut string of length L = 8.0 m and mass M = 0.23 kg. The vertical displacement of the string along its length is given by y(x, t) = 0. m cos(.5 t + 0.8
A harmonic wave propagates horizontally along a taut string of length L = 8.0 m and mass M = 0.23 kg. The vertical displacement of the string along its length is given by y(x, t) = 0. m cos(.5 t + 0.8
Physics Final Exam Formulas
 INSTRUCTIONS: Write your NAME on the front of the blue exam booklet. The exam is closed book, and you may have only pens/pencils and a calculator (no stored equations or programs and no graphing). Show
INSTRUCTIONS: Write your NAME on the front of the blue exam booklet. The exam is closed book, and you may have only pens/pencils and a calculator (no stored equations or programs and no graphing). Show
Periodic Motion. Periodic motion is motion of an object that. regularly repeats
 Periodic Motion Periodic motion is motion of an object that regularly repeats The object returns to a given position after a fixed time interval A special kind of periodic motion occurs in mechanical systems
Periodic Motion Periodic motion is motion of an object that regularly repeats The object returns to a given position after a fixed time interval A special kind of periodic motion occurs in mechanical systems
Physics 207 Lecture 25. Lecture 25. HW11, Due Tuesday, May 6 th For Thursday, read through all of Chapter 18. Angular Momentum Exercise
 Lecture 5 Today Review: Exam covers Chapters 14-17 17 plus angular momentum, rolling motion & torque Assignment HW11, Due Tuesday, May 6 th For Thursday, read through all of Chapter 18 Physics 07: Lecture
Lecture 5 Today Review: Exam covers Chapters 14-17 17 plus angular momentum, rolling motion & torque Assignment HW11, Due Tuesday, May 6 th For Thursday, read through all of Chapter 18 Physics 07: Lecture
Exam II Difficult Problems
 Exam II Difficult Problems Exam II Difficult Problems 90 80 70 60 50 40 30 20 10 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 Two boxes are connected to each other as shown. The system is released
Exam II Difficult Problems Exam II Difficult Problems 90 80 70 60 50 40 30 20 10 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 Two boxes are connected to each other as shown. The system is released
Chapter 14 Oscillations. Copyright 2009 Pearson Education, Inc.
 Chapter 14 Oscillations Oscillations of a Spring Simple Harmonic Motion Energy in the Simple Harmonic Oscillator Simple Harmonic Motion Related to Uniform Circular Motion The Simple Pendulum The Physical
Chapter 14 Oscillations Oscillations of a Spring Simple Harmonic Motion Energy in the Simple Harmonic Oscillator Simple Harmonic Motion Related to Uniform Circular Motion The Simple Pendulum The Physical
Chapter 8. Rotational Equilibrium and Rotational Dynamics
 Chapter 8 Rotational Equilibrium and Rotational Dynamics 1 Force vs. Torque Forces cause accelerations Torques cause angular accelerations Force and torque are related 2 Torque The door is free to rotate
Chapter 8 Rotational Equilibrium and Rotational Dynamics 1 Force vs. Torque Forces cause accelerations Torques cause angular accelerations Force and torque are related 2 Torque The door is free to rotate
Answers to test yourself questions
 Answers to test yourself questions Option B B Rotational dynamics ( ω + ω )t Use 0 ( +.).0 θ to get θ 46. 46 rad. Use ω ω0 + αθ to get ω.0 +. 4 and so ω 7.8 7 rad s. Use ω ω0 + αθ to get.4. + α 0 π. Hence
Answers to test yourself questions Option B B Rotational dynamics ( ω + ω )t Use 0 ( +.).0 θ to get θ 46. 46 rad. Use ω ω0 + αθ to get ω.0 +. 4 and so ω 7.8 7 rad s. Use ω ω0 + αθ to get.4. + α 0 π. Hence
Chapter 9. Rotational Dynamics
 Chapter 9 Rotational Dynamics 9.1 The Action of Forces and Torques on Rigid Objects In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination
Chapter 9 Rotational Dynamics 9.1 The Action of Forces and Torques on Rigid Objects In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination
The graph shows how an external force applied to an object of mass 2.0 kg varies with time. The object is initially at rest.
 T2-2 [195 marks] 1. The graph shows how an external force applied to an object of mass 2.0 kg varies with time. The object is initially at rest. What is the speed of the object after 0.60 s? A. 7.0 ms
T2-2 [195 marks] 1. The graph shows how an external force applied to an object of mass 2.0 kg varies with time. The object is initially at rest. What is the speed of the object after 0.60 s? A. 7.0 ms
Chapter 10. Rotation of a Rigid Object about a Fixed Axis
 Chapter 10 Rotation of a Rigid Object about a Fixed Axis Angular Position Axis of rotation is the center of the disc Choose a fixed reference line. Point P is at a fixed distance r from the origin. A small
Chapter 10 Rotation of a Rigid Object about a Fixed Axis Angular Position Axis of rotation is the center of the disc Choose a fixed reference line. Point P is at a fixed distance r from the origin. A small
General Physics Contest 2012
 General Physics Contest May 6, (9:am-:5am), Total of 5 pages. Some useful constants: Gas constant R = 8.34 J/mol K Electron mass m e = 9.9-3 kg Electron charge e =.6-9 C Electric constant (permittivity)
General Physics Contest May 6, (9:am-:5am), Total of 5 pages. Some useful constants: Gas constant R = 8.34 J/mol K Electron mass m e = 9.9-3 kg Electron charge e =.6-9 C Electric constant (permittivity)
FALL TERM EXAM, PHYS 1211, INTRODUCTORY PHYSICS I Thursday, 11 December 2014, 6 PM to 9 PM, Field House Gym
 FALL TERM EXAM, PHYS 1211, INTRODUCTORY PHYSICS I Thursday, 11 December 2014, 6 PM to 9 PM, Field House Gym NAME: STUDENT ID: INSTRUCTION 1. This exam booklet has 13 pages. Make sure none are missing 2.
FALL TERM EXAM, PHYS 1211, INTRODUCTORY PHYSICS I Thursday, 11 December 2014, 6 PM to 9 PM, Field House Gym NAME: STUDENT ID: INSTRUCTION 1. This exam booklet has 13 pages. Make sure none are missing 2.
SAMPLE FINAL EXAM (Closed Book)
 PHYS 111-01 SAMPLE FINAL EXAM (Closed Book) 1. DO NOT OPEN THE EXAM UNTIL TOLD TO DO SO. NAME: (Given) (Family) 2. For the problems, write clearly and neatly and be sure to show your work. Answers without
PHYS 111-01 SAMPLE FINAL EXAM (Closed Book) 1. DO NOT OPEN THE EXAM UNTIL TOLD TO DO SO. NAME: (Given) (Family) 2. For the problems, write clearly and neatly and be sure to show your work. Answers without
Q1. Which of the following is the correct combination of dimensions for energy?
 Tuesday, June 15, 2010 Page: 1 Q1. Which of the following is the correct combination of dimensions for energy? A) ML 2 /T 2 B) LT 2 /M C) MLT D) M 2 L 3 T E) ML/T 2 Q2. Two cars are initially 150 kilometers
Tuesday, June 15, 2010 Page: 1 Q1. Which of the following is the correct combination of dimensions for energy? A) ML 2 /T 2 B) LT 2 /M C) MLT D) M 2 L 3 T E) ML/T 2 Q2. Two cars are initially 150 kilometers
PHYS 1114, Lecture 33, April 10 Contents:
 PHYS 1114, Lecture 33, April 10 Contents: 1 This class is o cially cancelled, and has been replaced by the common exam Tuesday, April 11, 5:30 PM. A review and Q&A session is scheduled instead during class
PHYS 1114, Lecture 33, April 10 Contents: 1 This class is o cially cancelled, and has been replaced by the common exam Tuesday, April 11, 5:30 PM. A review and Q&A session is scheduled instead during class
Physics 23 Exam 3 April 2, 2009
 1. A string is tied to a doorknob 0.79 m from the hinge as shown in the figure. At the instant shown, the force applied to the string is 5.0 N. What is the torque on the door? A) 3.3 N m B) 2.2 N m C)
1. A string is tied to a doorknob 0.79 m from the hinge as shown in the figure. At the instant shown, the force applied to the string is 5.0 N. What is the torque on the door? A) 3.3 N m B) 2.2 N m C)
is acting on a body of mass m = 3.0 kg and changes its velocity from an initial
 PHYS 101 second major Exam Term 102 (Zero Version) Q1. A 15.0-kg block is pulled over a rough, horizontal surface by a constant force of 70.0 N acting at an angle of 20.0 above the horizontal. The block
PHYS 101 second major Exam Term 102 (Zero Version) Q1. A 15.0-kg block is pulled over a rough, horizontal surface by a constant force of 70.0 N acting at an angle of 20.0 above the horizontal. The block
Chapter 8 continued. Rotational Dynamics
 Chapter 8 continued Rotational Dynamics 8.4 Rotational Work and Energy Work to accelerate a mass rotating it by angle φ F W = F(cosθ)x x = s = rφ = Frφ Fr = τ (torque) = τφ r φ s F to s θ = 0 DEFINITION
Chapter 8 continued Rotational Dynamics 8.4 Rotational Work and Energy Work to accelerate a mass rotating it by angle φ F W = F(cosθ)x x = s = rφ = Frφ Fr = τ (torque) = τφ r φ s F to s θ = 0 DEFINITION
FALL TERM EXAM, PHYS 1211, INTRODUCTORY PHYSICS I Monday, 14 December 2015, 6 PM to 9 PM, Field House Gym
 FALL TERM EXAM, PHYS 111, INTRODUCTORY PHYSICS I Monday, 14 December 015, 6 PM to 9 PM, Field House Gym NAME: STUDENT ID: INSTRUCTION 1. This exam booklet has 13 pages. Make sure none are missing. There
FALL TERM EXAM, PHYS 111, INTRODUCTORY PHYSICS I Monday, 14 December 015, 6 PM to 9 PM, Field House Gym NAME: STUDENT ID: INSTRUCTION 1. This exam booklet has 13 pages. Make sure none are missing. There
PHY131H1S - Class 20. Pre-class reading quiz on Chapter 12
 PHY131H1S - Class 20 Today: Gravitational Torque Rotational Kinetic Energy Rolling without Slipping Equilibrium with Rotation Rotation Vectors Angular Momentum Pre-class reading quiz on Chapter 12 1 Last
PHY131H1S - Class 20 Today: Gravitational Torque Rotational Kinetic Energy Rolling without Slipping Equilibrium with Rotation Rotation Vectors Angular Momentum Pre-class reading quiz on Chapter 12 1 Last
Final Mock Exam PH 221-1D
 Final Mock Exam PH 221-1D April 18, 2015 You will have 2 hours to complete this exam. You must answer 8 questions to make a perfect score of 80. 1 Chapter Concept Summary Equations: Cutnell & Johnson
Final Mock Exam PH 221-1D April 18, 2015 You will have 2 hours to complete this exam. You must answer 8 questions to make a perfect score of 80. 1 Chapter Concept Summary Equations: Cutnell & Johnson
Chapter 9. Rotational Dynamics
 Chapter 9 Rotational Dynamics 9.1 The Action of Forces and Torques on Rigid Objects In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination
Chapter 9 Rotational Dynamics 9.1 The Action of Forces and Torques on Rigid Objects In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination
Midterm 3 Review (Ch 9-14)
 Midterm 3 Review (Ch 9-14) PowerPoint Lectures for University Physics, Twelfth Edition Hugh D. Young and Roger A. Freedman Lectures by James Pazun Copyright 2008 Pearson Education Inc., publishing as Pearson
Midterm 3 Review (Ch 9-14) PowerPoint Lectures for University Physics, Twelfth Edition Hugh D. Young and Roger A. Freedman Lectures by James Pazun Copyright 2008 Pearson Education Inc., publishing as Pearson
Concept Question: Normal Force
 Concept Question: Normal Force Consider a person standing in an elevator that is accelerating upward. The upward normal force N exerted by the elevator floor on the person is 1. larger than 2. identical
Concept Question: Normal Force Consider a person standing in an elevator that is accelerating upward. The upward normal force N exerted by the elevator floor on the person is 1. larger than 2. identical
Do not fill out the information below until instructed to do so! Name: Signature: Student ID: Section Number:
 Do not fill out the information below until instructed to do so! Name: Signature: Student ID: E-mail: Section Number: Formulae are provided on the last page. You may NOT use any other formula sheet. You
Do not fill out the information below until instructed to do so! Name: Signature: Student ID: E-mail: Section Number: Formulae are provided on the last page. You may NOT use any other formula sheet. You
A) 1 gm 2 /s. B) 3 gm 2 /s. C) 6 gm 2 /s. D) 9 gm 2 /s. E) 10 gm 2 /s. A) 0.1 kg. B) 1 kg. C) 2 kg. D) 5 kg. E) 10 kg A) 2:5 B) 4:5 C) 1:1 D) 5:4
 1. A 4 kg object moves in a circle of radius 8 m at a constant speed of 2 m/s. What is the angular momentum of the object with respect to an axis perpendicular to the circle and through its center? A)
1. A 4 kg object moves in a circle of radius 8 m at a constant speed of 2 m/s. What is the angular momentum of the object with respect to an axis perpendicular to the circle and through its center? A)
Final Review, Day 1. Announcements: Web page:
 Announcements: Final Review, Day 1 Final exam next Wednesday (5/9) at 7:30am in the Coors Event Center. Recitation tomorrow is a review. Please feel free to ask the TA any questions on the course material.
Announcements: Final Review, Day 1 Final exam next Wednesday (5/9) at 7:30am in the Coors Event Center. Recitation tomorrow is a review. Please feel free to ask the TA any questions on the course material.
Translational vs Rotational. m x. Connection Δ = = = = = = Δ = = = = = = Δ =Δ = = = = = 2 / 1/2. Work
 Translational vs Rotational / / 1/ Δ m x v dx dt a dv dt F ma p mv KE mv Work Fd / / 1/ θ ω θ α ω τ α ω ω τθ Δ I d dt d dt I L I KE I Work / θ ω α τ Δ Δ c t s r v r a v r a r Fr L pr Connection Translational
Translational vs Rotational / / 1/ Δ m x v dx dt a dv dt F ma p mv KE mv Work Fd / / 1/ θ ω θ α ω τ α ω ω τθ Δ I d dt d dt I L I KE I Work / θ ω α τ Δ Δ c t s r v r a v r a r Fr L pr Connection Translational
AP Physics B Summer Assignment
 BERGEN COUNTY TECHNICAL SCHOOL AP Physics B Summer Assignment 2011 Solve all problems on separate paper. This will be due the first week of school. If you need any help you can e-mail Mr. Zavorotniy at
BERGEN COUNTY TECHNICAL SCHOOL AP Physics B Summer Assignment 2011 Solve all problems on separate paper. This will be due the first week of school. If you need any help you can e-mail Mr. Zavorotniy at
Chapter 8- Rotational Kinematics Angular Variables Kinematic Equations
 Chapter 8- Rotational Kinematics Angular Variables Kinematic Equations Chapter 9- Rotational Dynamics Torque Center of Gravity Newton s 2 nd Law- Angular Rotational Work & Energy Angular Momentum Angular
Chapter 8- Rotational Kinematics Angular Variables Kinematic Equations Chapter 9- Rotational Dynamics Torque Center of Gravity Newton s 2 nd Law- Angular Rotational Work & Energy Angular Momentum Angular
Physics 201. Professor P. Q. Hung. 311B, Physics Building. Physics 201 p. 1/1
 Physics 201 p. 1/1 Physics 201 Professor P. Q. Hung 311B, Physics Building Physics 201 p. 2/1 Rotational Kinematics and Energy Rotational Kinetic Energy, Moment of Inertia All elements inside the rigid
Physics 201 p. 1/1 Physics 201 Professor P. Q. Hung 311B, Physics Building Physics 201 p. 2/1 Rotational Kinematics and Energy Rotational Kinetic Energy, Moment of Inertia All elements inside the rigid
