Cyclic inclusion/exclusion
|
|
|
- Alexandra Newton
- 6 years ago
- Views:
Transcription
1 Cyclic inclusion/exclusion Valentin Féray LaBRI, CNRS, Bordeaux Journées Combinatoire Algébrique du GDR-IM, Rouen Valentin Féray (LaBRI, CNRS) Cyclic inclusion/exclusion Rouen, / 16
2 Introduction Context What is this talk about? To a bipartite graph, we will associate a formal series: i,j p i p j q max(i,j) Valentin Féray (LaBRI, CNRS) Cyclic inclusion/exclusion Rouen, / 16
3 Introduction Context What is this talk about? To a bipartite graph, we will associate a formal series: i,j p i p j q max(i,j) Question: which linear combination of graphs are sent to 0? Example : + 0. Valentin Féray (LaBRI, CNRS) Cyclic inclusion/exclusion Rouen, / 16
4 Introduction Context What is this talk about? To a bipartite graph, we will associate a formal series: i,j p i p j q max(i,j) Question: which linear combination of graphs are sent to 0? Example : + 0. Motivation : computation of irreducible character values of symmetric groups. Valentin Féray (LaBRI, CNRS) Cyclic inclusion/exclusion Rouen, / 16
5 Introduction Context Definition of N Let p, q be two infinite set of variables. G = N(G) = General formula: N(G) = Q[p,q], Valentin Féray (LaBRI, CNRS) Cyclic inclusion/exclusion Rouen, / 16
6 Introduction Context Definition of N Let p, q be two infinite set of variables. G = N(G) = General formula: N(G) = Q[p,q], Valentin Féray (LaBRI, CNRS) Cyclic inclusion/exclusion Rouen, / 16
7 Introduction Context Definition of N Let p, q be two infinite set of variables. G = i j N(G) = i,j p i p j General formula: N(G) = p ϕ( ) ϕ:v N V Q[p,q], Valentin Féray (LaBRI, CNRS) Cyclic inclusion/exclusion Rouen, / 16
8 Introduction Context Definition of N Let p, q be two infinite set of variables. max(i, j) j G = i N(G) = i,j j p i p j q j q max(i,j) General formula: N(G) = p ϕ( ) q ψ( ) ϕ:v N V V Q[p,q], with ψ( ) = max ϕ( ). Valentin Féray (LaBRI, CNRS) Cyclic inclusion/exclusion Rouen, / 16
9 Kernel of our algebra morphism N as an algebra morphism Let BG be the Q vector space of linear combination of bipartite graphs. It is an algebra G G = G G. N defines a morphism of algebra BG Q[p,q] G p ϕ( ) ϕ:v N V V q ψ( ), Question What is the kernel of N? Valentin Féray (LaBRI, CNRS) Cyclic inclusion/exclusion Rouen, / 16
10 Kernel of our algebra morphism Cyclic inclusion/exclusion Consider a bipartite graph G endowed with an oriented cycle C. We define the following element of BG: A G,C = ( 1) E G \ E Example : E E (C) + Valentin Féray (LaBRI, CNRS) Cyclic inclusion/exclusion Rouen, / 16
11 Kernel of our algebra morphism Kernel of N Proposition N(A G,C ) = 0. Valentin Féray (LaBRI, CNRS) Cyclic inclusion/exclusion Rouen, / 16
12 Kernel of our algebra morphism Kernel of N Proposition N(A G,C ) = 0. Sketch of proof. We look at the contribution of a fixed function ϕ : V (G) N Valentin Féray (LaBRI, CNRS) Cyclic inclusion/exclusion Rouen, / 16
13 Kernel of our algebra morphism Kernel of N Proposition N(A G,C ) = 0. Sketch of proof. We look at the contribution of a fixed function ϕ : V (G) N Valentin Féray (LaBRI, CNRS) Cyclic inclusion/exclusion Rouen, / 16
14 Kernel of our algebra morphism Kernel of N Proposition N(A G,C ) = 0. Sketch of proof. We look at the contribution of a fixed function ϕ : V (G) N Valentin Féray (LaBRI, CNRS) Cyclic inclusion/exclusion Rouen, / 16
15 Kernel of our algebra morphism Presentation of the next few slides We will show that N defines an injective morphism BG/ A G,C Z[[p,q]]. Method: Construct a family of graphs G I. Show that G I is a generating family in the quotient BG/ A G,C. Prove that N(G I ) is linearly independant in Z[[p,q]]. Valentin Féray (LaBRI, CNRS) Cyclic inclusion/exclusion Rouen, / 16
16 Kernel of our algebra morphism A generating family Definition Let I = (i 1,i,...,i r ) be a composition. Define G I as the following bipartite graph: i1-1 black vertices i -1 black vertices i_r -1 black vertices Valentin Féray (LaBRI, CNRS) Cyclic inclusion/exclusion Rouen, / 16
17 Kernel of our algebra morphism A generating family Definition Let I = (i 1,i,...,i r ) be a composition. Define G I as the following bipartite graph: i1-1 black vertices i -1 black vertices i_r -1 black vertices Valentin Féray (LaBRI, CNRS) Cyclic inclusion/exclusion Rouen, / 16
18 Kernel of our algebra morphism A generating family Definition Let I = (i 1,i,...,i r ) be a composition. Define G I as the following bipartite graph: i1-1 black vertices i -1 black vertices i_r -1 black vertices Proposition {G I,I composition} is a linear generating set of BG/I. Valentin Féray (LaBRI, CNRS) Cyclic inclusion/exclusion Rouen, / 16
19 Kernel of our algebra morphism Idea of proof Proposition {G I,I composition} is a linear generating set of BG/I. graph G I Valentin Féray (LaBRI, CNRS) Cyclic inclusion/exclusion Rouen, / 16
20 Kernel of our algebra morphism Idea of proof Proposition {G I,I composition} is a linear generating set of BG/I. Consider a graph G G I Valentin Féray (LaBRI, CNRS) Cyclic inclusion/exclusion Rouen, / 16
21 Kernel of our algebra morphism Idea of proof Proposition {G I,I composition} is a linear generating set of BG/I. There is a graph G 0 with an oriented cycle C such that G 0 \E (C) = G Valentin Féray (LaBRI, CNRS) Cyclic inclusion/exclusion Rouen, / 16
22 Kernel of our algebra morphism Idea of proof Proposition {G I,I composition} is a linear generating set of BG/I. Consider a graph G G I. Lemma: There is a graph G 0 with an oriented cycle C such that: G 0 \E (C) = G Consequence : in BG/I, G = linear combination of bigger graphs. we iterate until we obtain a linear combination of G I s. Valentin Féray (LaBRI, CNRS) Cyclic inclusion/exclusion Rouen, / 16
23 Kernel of our algebra morphism Independence Lemma The N(G I ), where I runs over all compositions are linearly independent. Gradation: N(G I ) is a homogenous polynomial of degree r = l(i) in p and of total degree n = I. Valentin Féray (LaBRI, CNRS) Cyclic inclusion/exclusion Rouen, / 16
24 Kernel of our algebra morphism Independence Lemma The N(G I ), where I runs over compositions of length r and size n are linearly independent. Consider M GI (p 1,p,...,p r,q 1,q,...,q r ) (we truncate the alphabets to r = l(i) = V (G I ) variables) Valentin Féray (LaBRI, CNRS) Cyclic inclusion/exclusion Rouen, / 16
25 Kernel of our algebra morphism Independence Lemma The N(G I ), where I runs over compositions of length r and size n are linearly independent. Consider M GI (p 1,p,...,p r,q 1,q,...,q r ) (we truncate the alphabets to r = l(i) = V (G I ) variables) We will consider only p-square free monomials. As total degree in p is r, they are: T J = p 1 q j p q j 1 p r q jr 1 r, where J is a composition of n and length r. In N(G I ), they correspond to bijections ϕ : V (G I ) {1,...,r}. Valentin Féray (LaBRI, CNRS) Cyclic inclusion/exclusion Rouen, / 16
26 Kernel of our algebra morphism Independence Lemma The N(G I ), where I runs over compositions of length r and size n are linearly independent. 1 r 1 1 r 1 r M GI = T I Valentin Féray (LaBRI, CNRS) Cyclic inclusion/exclusion Rouen, / 16
27 Kernel of our algebra morphism Independence Lemma The N(G I ), where I runs over compositions of length r and size n are linearly independent M GI = T I + J = I =n, l(j)=l(i)=r J I c I,J T J + non-p-square-free terms stands for the right-dominance order. Valentin Féray (LaBRI, CNRS) Cyclic inclusion/exclusion Rouen, / 16
28 Other contexts One set of variables We considered a morphism BG Q[[p,q]] Valentin Féray (LaBRI, CNRS) Cyclic inclusion/exclusion Rouen, / 16
29 Other contexts One set of variables It factorizes via BG BG/ A G,C Q[[p,q]] Valentin Féray (LaBRI, CNRS) Cyclic inclusion/exclusion Rouen, / 16
30 Other contexts One set of variables Same kernel if we identify p i and q i! BG BG/ A G,C Q[[p,q]] p i x i q i x i Q[[x]] Valentin Féray (LaBRI, CNRS) Cyclic inclusion/exclusion Rouen, / 16
31 Other contexts One set of variables We can describe the image BG BG/ A G,C Q[[p,q]] QSym(x) Q[[x]] p i x i q i x i QSym(x): ring of quasi-symmetric function in x. Example: M 1, (x 1,x,x 3 ) = x 1 x + x 1x 3 + x x 3. Valentin Féray (LaBRI, CNRS) Cyclic inclusion/exclusion Rouen, / 16
32 Other contexts One set of variables We can describe the image BG BG/ A G,C Q[[p,q]] QSym(x) Q[[x]] p i x i q i x i QSym(x): ring of quasi-symmetric function in x. Example: M 1, (x 1,x,x 3 ) = x 1 x + x 1x 3 + x x 3. BG QSym is a Hopf algebra morphism! Valentin Féray (LaBRI, CNRS) Cyclic inclusion/exclusion Rouen, / 16
33 Other contexts Coproduct on BG = Valentin Féray (LaBRI, CNRS) Cyclic inclusion/exclusion Rouen, / 16
34 Other contexts Some variants N (G) := ϕ:v G N (, ) E G ϕ( ) ϕ( ) v V G x ϕg. Then Ker(N ) = Ker(N). Valentin Féray (LaBRI, CNRS) Cyclic inclusion/exclusion Rouen, / 16
35 Other contexts Some variants N (G) := ϕ:v G N (, ) E G ϕ( ) ϕ( ) v V G x ϕg. Then Ker(N ) = Ker(N). The definition above is naturally extended to acyclic directed graphs. Valentin Féray (LaBRI, CNRS) Cyclic inclusion/exclusion Rouen, / 16
36 Other contexts Some variants N (G) := ϕ:v G N (, ) E G ϕ( ) ϕ( ) v V G x ϕg. Then Ker(N ) = Ker(N). The definition above is naturally extended to acyclic directed graphs. One can also consider labeled graphs and polynomials in non-commutative variables (QSym is replaced by WQSym). N(G) = a f(1)... a f(n), f:[n] G f ր where the a s are non-commutative variables. Valentin Féray (LaBRI, CNRS) Cyclic inclusion/exclusion Rouen, / 16
37 Other contexts Does cyclic inclusion/exclusion always span the kernel? Same method as before: 1 Construct a family of (labelled/unlabelled) (bipartite/directed acyclic) graphs. Show that it is a generating family in the quotient G / A G,C. 3 Prove that the corresponding functions are linearly independant. 3 is hard in non-commutative setting. Valentin Féray (LaBRI, CNRS) Cyclic inclusion/exclusion Rouen, / 16
38 Other contexts The family of graphs in the bipartite labelled setting We consider set compositions (or ordered set-partitions) I. Example: I = We associate the following graph G I : Valentin Féray (LaBRI, CNRS) Cyclic inclusion/exclusion Rouen, / 16
39 Other contexts The family of graphs in the bipartite labelled setting We consider set compositions (or ordered set-partitions) I. Example: I = We associate the following graph G I : Valentin Féray (LaBRI, CNRS) Cyclic inclusion/exclusion Rouen, / 16
40 Other contexts The family of graphs in the bipartite labelled setting We consider set compositions (or ordered set-partitions) I. Example: I = We associate the following graph G I : Valentin Féray (LaBRI, CNRS) Cyclic inclusion/exclusion Rouen, / 16
41 Other contexts I need some help here! Proposition The graphs G I generate the quotient G / A G,C Valentin Féray (LaBRI, CNRS) Cyclic inclusion/exclusion Rouen, / 16
42 Other contexts I need some help here! Proposition The graphs G I generate the quotient G / A G,C Conjecture N(G I ), where I runs over all set compositions, is a basis of WQSym. Equivalently, the A G,C span the kernel of N. Valentin Féray (LaBRI, CNRS) Cyclic inclusion/exclusion Rouen, / 16
43 Other contexts I need some help here! Proposition The graphs G I generate the quotient G / A G,C Conjecture N(G I ), where I runs over all set compositions, is a basis of WQSym. Equivalently, the A G,C span the kernel of N. Thanks for listening! Valentin Féray (LaBRI, CNRS) Cyclic inclusion/exclusion Rouen, / 16
Quasisymmetric functions and Young diagrams
 Quasisymmetric functions and Young diagrams Valentin Féray joint work with Jean-Christophe Aval (LaBRI), Jean-Christophe Novelli and Jean-Yves Thibon (IGM) LaBRI, CNRS, Bordeaux Séminaire Lotharingien
Quasisymmetric functions and Young diagrams Valentin Féray joint work with Jean-Christophe Aval (LaBRI), Jean-Christophe Novelli and Jean-Yves Thibon (IGM) LaBRI, CNRS, Bordeaux Séminaire Lotharingien
Shifted symmetric functions II: expansions in multi-rectangular coordinates
 Shifted symmetric functions II: expansions in multi-rectangular coordinates Valentin Féray Institut für Mathematik, Universität Zürich Séminaire Lotharingien de Combinatoire Bertinoro, Italy, Sept. 11th-12th-13th
Shifted symmetric functions II: expansions in multi-rectangular coordinates Valentin Féray Institut für Mathematik, Universität Zürich Séminaire Lotharingien de Combinatoire Bertinoro, Italy, Sept. 11th-12th-13th
arxiv: v2 [math.co] 23 Jul 2014
![arxiv: v2 [math.co] 23 Jul 2014 arxiv: v2 [math.co] 23 Jul 2014](/thumbs/94/119220904.jpg) QUASI-SYMMETRIC FUNCTIONS AS POLYNOMIAL FUNCTIONS ON YOUNG DIAGRAMS arxiv:1312.2727v2 [math.co] 23 Jul 2014 JEAN-CHRISTOPHE AVAL, VALENTIN FÉRAY, JEAN-CHRISTOPHE NOVELLI, AND JEAN-YVES THIBON Abstract.
QUASI-SYMMETRIC FUNCTIONS AS POLYNOMIAL FUNCTIONS ON YOUNG DIAGRAMS arxiv:1312.2727v2 [math.co] 23 Jul 2014 JEAN-CHRISTOPHE AVAL, VALENTIN FÉRAY, JEAN-CHRISTOPHE NOVELLI, AND JEAN-YVES THIBON Abstract.
Honors Algebra 4, MATH 371 Winter 2010 Assignment 4 Due Wednesday, February 17 at 08:35
 Honors Algebra 4, MATH 371 Winter 2010 Assignment 4 Due Wednesday, February 17 at 08:35 1. Let R be a commutative ring with 1 0. (a) Prove that the nilradical of R is equal to the intersection of the prime
Honors Algebra 4, MATH 371 Winter 2010 Assignment 4 Due Wednesday, February 17 at 08:35 1. Let R be a commutative ring with 1 0. (a) Prove that the nilradical of R is equal to the intersection of the prime
NOTES IN COMMUTATIVE ALGEBRA: PART 2
 NOTES IN COMMUTATIVE ALGEBRA: PART 2 KELLER VANDEBOGERT 1. Completion of a Ring/Module Here we shall consider two seemingly different constructions for the completion of a module and show that indeed they
NOTES IN COMMUTATIVE ALGEBRA: PART 2 KELLER VANDEBOGERT 1. Completion of a Ring/Module Here we shall consider two seemingly different constructions for the completion of a module and show that indeed they
15. Polynomial rings Definition-Lemma Let R be a ring and let x be an indeterminate.
 15. Polynomial rings Definition-Lemma 15.1. Let R be a ring and let x be an indeterminate. The polynomial ring R[x] is defined to be the set of all formal sums a n x n + a n 1 x n +... a 1 x + a 0 = a
15. Polynomial rings Definition-Lemma 15.1. Let R be a ring and let x be an indeterminate. The polynomial ring R[x] is defined to be the set of all formal sums a n x n + a n 1 x n +... a 1 x + a 0 = a
Exercise Sheet 8 Linear Algebra I
 Fachbereich Mathematik Martin Otto Achim Blumensath Nicole Nowak Pavol Safarik Winter Term 2008/2009 (E8.1) [Morphisms] Exercise Sheet 8 Linear Algebra I Let V be a finite dimensional F-vector space and
Fachbereich Mathematik Martin Otto Achim Blumensath Nicole Nowak Pavol Safarik Winter Term 2008/2009 (E8.1) [Morphisms] Exercise Sheet 8 Linear Algebra I Let V be a finite dimensional F-vector space and
AN EXACT SEQUENCE FOR THE BROADHURST-KREIMER CONJECTURE
 AN EXACT SEQUENCE FOR THE BROADHURST-KREIMER CONJECTURE FRANCIS BROWN Don Zagier asked me whether the Broadhurst-Kreimer conjecture could be reformulated as a short exact sequence of spaces of polynomials
AN EXACT SEQUENCE FOR THE BROADHURST-KREIMER CONJECTURE FRANCIS BROWN Don Zagier asked me whether the Broadhurst-Kreimer conjecture could be reformulated as a short exact sequence of spaces of polynomials
Formal power series rings, inverse limits, and I-adic completions of rings
 Formal power series rings, inverse limits, and I-adic completions of rings Formal semigroup rings and formal power series rings We next want to explore the notion of a (formal) power series ring in finitely
Formal power series rings, inverse limits, and I-adic completions of rings Formal semigroup rings and formal power series rings We next want to explore the notion of a (formal) power series ring in finitely
Fields and Galois Theory. Below are some results dealing with fields, up to and including the fundamental theorem of Galois theory.
 Fields and Galois Theory Below are some results dealing with fields, up to and including the fundamental theorem of Galois theory. This should be a reasonably logical ordering, so that a result here should
Fields and Galois Theory Below are some results dealing with fields, up to and including the fundamental theorem of Galois theory. This should be a reasonably logical ordering, so that a result here should
A polynomial realization of the Hopf algebra of uniform block permutations.
 FPSAC 202, Nagoya, Japan DMTCS proc AR, 202, 93 204 A polynomial realization of the Hopf algebra of uniform block permutations Rémi Maurice Institut Gaspard Monge, Université Paris-Est Marne-la-Vallée,
FPSAC 202, Nagoya, Japan DMTCS proc AR, 202, 93 204 A polynomial realization of the Hopf algebra of uniform block permutations Rémi Maurice Institut Gaspard Monge, Université Paris-Est Marne-la-Vallée,
GEOMETRIC CONSTRUCTIONS AND ALGEBRAIC FIELD EXTENSIONS
 GEOMETRIC CONSTRUCTIONS AND ALGEBRAIC FIELD EXTENSIONS JENNY WANG Abstract. In this paper, we study field extensions obtained by polynomial rings and maximal ideals in order to determine whether solutions
GEOMETRIC CONSTRUCTIONS AND ALGEBRAIC FIELD EXTENSIONS JENNY WANG Abstract. In this paper, we study field extensions obtained by polynomial rings and maximal ideals in order to determine whether solutions
12. Hilbert Polynomials and Bézout s Theorem
 12. Hilbert Polynomials and Bézout s Theorem 95 12. Hilbert Polynomials and Bézout s Theorem After our study of smooth cubic surfaces in the last chapter, let us now come back to the general theory of
12. Hilbert Polynomials and Bézout s Theorem 95 12. Hilbert Polynomials and Bézout s Theorem After our study of smooth cubic surfaces in the last chapter, let us now come back to the general theory of
MATH 8253 ALGEBRAIC GEOMETRY WEEK 12
 MATH 8253 ALGEBRAIC GEOMETRY WEEK 2 CİHAN BAHRAN 3.2.. Let Y be a Noetherian scheme. Show that any Y -scheme X of finite type is Noetherian. Moreover, if Y is of finite dimension, then so is X. Write f
MATH 8253 ALGEBRAIC GEOMETRY WEEK 2 CİHAN BAHRAN 3.2.. Let Y be a Noetherian scheme. Show that any Y -scheme X of finite type is Noetherian. Moreover, if Y is of finite dimension, then so is X. Write f
ABSTRACT. Department of Mathematics. interesting results. A graph on n vertices is represented by a polynomial in n
 ABSTRACT Title of Thesis: GRÖBNER BASES WITH APPLICATIONS IN GRAPH THEORY Degree candidate: Angela M. Hennessy Degree and year: Master of Arts, 2006 Thesis directed by: Professor Lawrence C. Washington
ABSTRACT Title of Thesis: GRÖBNER BASES WITH APPLICATIONS IN GRAPH THEORY Degree candidate: Angela M. Hennessy Degree and year: Master of Arts, 2006 Thesis directed by: Professor Lawrence C. Washington
One-sided shift spaces over infinite alphabets
 Reasoning Mind West Coast Operator Algebra Seminar October 26, 2013 Joint work with William Ott and Mark Tomforde Classical Construction Infinite Issues New Infinite Construction Shift Spaces Classical
Reasoning Mind West Coast Operator Algebra Seminar October 26, 2013 Joint work with William Ott and Mark Tomforde Classical Construction Infinite Issues New Infinite Construction Shift Spaces Classical
JORDAN NORMAL FORM. Contents Introduction 1 Jordan Normal Form 1 Conclusion 5 References 5
 JORDAN NORMAL FORM KATAYUN KAMDIN Abstract. This paper outlines a proof of the Jordan Normal Form Theorem. First we show that a complex, finite dimensional vector space can be decomposed into a direct
JORDAN NORMAL FORM KATAYUN KAMDIN Abstract. This paper outlines a proof of the Jordan Normal Form Theorem. First we show that a complex, finite dimensional vector space can be decomposed into a direct
The Segre Embedding. Daniel Murfet May 16, 2006
 The Segre Embedding Daniel Murfet May 16, 2006 Throughout this note all rings are commutative, and A is a fixed ring. If S, T are graded A-algebras then the tensor product S A T becomes a graded A-algebra
The Segre Embedding Daniel Murfet May 16, 2006 Throughout this note all rings are commutative, and A is a fixed ring. If S, T are graded A-algebras then the tensor product S A T becomes a graded A-algebra
Section III.6. Factorization in Polynomial Rings
 III.6. Factorization in Polynomial Rings 1 Section III.6. Factorization in Polynomial Rings Note. We push several of the results in Section III.3 (such as divisibility, irreducibility, and unique factorization)
III.6. Factorization in Polynomial Rings 1 Section III.6. Factorization in Polynomial Rings Note. We push several of the results in Section III.3 (such as divisibility, irreducibility, and unique factorization)
2a 2 4ac), provided there is an element r in our
 MTH 310002 Test II Review Spring 2012 Absractions versus examples The purpose of abstraction is to reduce ideas to their essentials, uncluttered by the details of a specific situation Our lectures built
MTH 310002 Test II Review Spring 2012 Absractions versus examples The purpose of abstraction is to reduce ideas to their essentials, uncluttered by the details of a specific situation Our lectures built
Linear Algebra. Chapter 5
 Chapter 5 Linear Algebra The guiding theme in linear algebra is the interplay between algebraic manipulations and geometric interpretations. This dual representation is what makes linear algebra a fruitful
Chapter 5 Linear Algebra The guiding theme in linear algebra is the interplay between algebraic manipulations and geometric interpretations. This dual representation is what makes linear algebra a fruitful
FILTERED RINGS AND MODULES. GRADINGS AND COMPLETIONS.
 FILTERED RINGS AND MODULES. GRADINGS AND COMPLETIONS. Let A be a ring, for simplicity assumed commutative. A filtering, or filtration, of an A module M means a descending sequence of submodules M = M 0
FILTERED RINGS AND MODULES. GRADINGS AND COMPLETIONS. Let A be a ring, for simplicity assumed commutative. A filtering, or filtration, of an A module M means a descending sequence of submodules M = M 0
Representations and Linear Actions
 Representations and Linear Actions Definition 0.1. Let G be an S-group. A representation of G is a morphism of S-groups φ G GL(n, S) for some n. We say φ is faithful if it is a monomorphism (in the category
Representations and Linear Actions Definition 0.1. Let G be an S-group. A representation of G is a morphism of S-groups φ G GL(n, S) for some n. We say φ is faithful if it is a monomorphism (in the category
Combinatorial Hopf algebras in particle physics I
 Combinatorial Hopf algebras in particle physics I Erik Panzer Scribed by Iain Crump May 25 1 Combinatorial Hopf Algebras Quantum field theory (QFT) describes the interactions of elementary particles. There
Combinatorial Hopf algebras in particle physics I Erik Panzer Scribed by Iain Crump May 25 1 Combinatorial Hopf Algebras Quantum field theory (QFT) describes the interactions of elementary particles. There
A multivariate interlace polynomial
 A multivariate interlace polynomial Bruno Courcelle LaBRI, Université Bordeaux 1 and CNRS General objectives : Logical descriptions of graph polynomials Application to their computations Systematic construction
A multivariate interlace polynomial Bruno Courcelle LaBRI, Université Bordeaux 1 and CNRS General objectives : Logical descriptions of graph polynomials Application to their computations Systematic construction
(Permutations Arising from) Hook Coefficients of Chromatic Symmetric Functions
 (Permutations Arising from) Hook Coefficients of Chromatic Symmetric Functions Ryan Kaliszewski Drexel University rlk72@drexel.edu July 17, 2014 Ryan Kaliszewski (Drexel University) Hook Coefficients July
(Permutations Arising from) Hook Coefficients of Chromatic Symmetric Functions Ryan Kaliszewski Drexel University rlk72@drexel.edu July 17, 2014 Ryan Kaliszewski (Drexel University) Hook Coefficients July
Combinatorial Hopf Algebras. YORK
 Combinatorial Hopf Algebras. YORK Nantel Bergeron York Research Chair in Applied Algebra www.math.yorku.ca/bergeron [with J.Y. Thibon...... and many more] U N I V E R S I T É U N I V E R S I T Y Ottrott
Combinatorial Hopf Algebras. YORK Nantel Bergeron York Research Chair in Applied Algebra www.math.yorku.ca/bergeron [with J.Y. Thibon...... and many more] U N I V E R S I T É U N I V E R S I T Y Ottrott
MATH 101B: ALGEBRA II PART A: HOMOLOGICAL ALGEBRA
 MATH 101B: ALGEBRA II PART A: HOMOLOGICAL ALGEBRA These are notes for our first unit on the algebraic side of homological algebra. While this is the last topic (Chap XX) in the book, it makes sense to
MATH 101B: ALGEBRA II PART A: HOMOLOGICAL ALGEBRA These are notes for our first unit on the algebraic side of homological algebra. While this is the last topic (Chap XX) in the book, it makes sense to
EXTERIOR AND SYMMETRIC POWERS OF MODULES FOR CYCLIC 2-GROUPS
 EXTERIOR AND SYMMETRIC POWERS OF MODULES FOR CYCLIC 2-GROUPS FRANK IMSTEDT AND PETER SYMONDS Abstract. We prove a recursive formula for the exterior and symmetric powers of modules for a cyclic 2-group.
EXTERIOR AND SYMMETRIC POWERS OF MODULES FOR CYCLIC 2-GROUPS FRANK IMSTEDT AND PETER SYMONDS Abstract. We prove a recursive formula for the exterior and symmetric powers of modules for a cyclic 2-group.
Simply connected gradings of complex matrix algebra
 of matrix algebras Simply connected gradings of complex matrix algebra 04.07.2013 of matrix algebras Table of contents 1 2 of matrix algebras 3 of matrix algebras A grading of an algebra A by a group G
of matrix algebras Simply connected gradings of complex matrix algebra 04.07.2013 of matrix algebras Table of contents 1 2 of matrix algebras 3 of matrix algebras A grading of an algebra A by a group G
Math 210B:Algebra, Homework 2
 Math 210B:Algebra, Homework 2 Ian Coley January 21, 2014 Problem 1. Is f = 2X 5 6X + 6 irreducible in Z[X], (S 1 Z)[X], for S = {2 n, n 0}, Q[X], R[X], C[X]? To begin, note that 2 divides all coefficients
Math 210B:Algebra, Homework 2 Ian Coley January 21, 2014 Problem 1. Is f = 2X 5 6X + 6 irreducible in Z[X], (S 1 Z)[X], for S = {2 n, n 0}, Q[X], R[X], C[X]? To begin, note that 2 divides all coefficients
ABSTRACT NONSINGULAR CURVES
 ABSTRACT NONSINGULAR CURVES Affine Varieties Notation. Let k be a field, such as the rational numbers Q or the complex numbers C. We call affine n-space the collection A n k of points P = a 1, a,..., a
ABSTRACT NONSINGULAR CURVES Affine Varieties Notation. Let k be a field, such as the rational numbers Q or the complex numbers C. We call affine n-space the collection A n k of points P = a 1, a,..., a
NOTES ON FINITE FIELDS
 NOTES ON FINITE FIELDS AARON LANDESMAN CONTENTS 1. Introduction to finite fields 2 2. Definition and constructions of fields 3 2.1. The definition of a field 3 2.2. Constructing field extensions by adjoining
NOTES ON FINITE FIELDS AARON LANDESMAN CONTENTS 1. Introduction to finite fields 2 2. Definition and constructions of fields 3 2.1. The definition of a field 3 2.2. Constructing field extensions by adjoining
CHEAT SHEET: PROPERTIES OF MORPHISMS OF SCHEMES
 CHEAT SHEET: PROPERTIES OF MORPHISMS OF SCHEMES BRIAN OSSERMAN The purpose of this cheat sheet is to provide an easy reference for definitions of various properties of morphisms of schemes, and basic results
CHEAT SHEET: PROPERTIES OF MORPHISMS OF SCHEMES BRIAN OSSERMAN The purpose of this cheat sheet is to provide an easy reference for definitions of various properties of morphisms of schemes, and basic results
ALGEBRAIC GROUPS J. WARNER
 ALGEBRAIC GROUPS J. WARNER Let k be an algebraically closed field. varieties unless otherwise stated. 1. Definitions and Examples For simplicity we will work strictly with affine Definition 1.1. An algebraic
ALGEBRAIC GROUPS J. WARNER Let k be an algebraically closed field. varieties unless otherwise stated. 1. Definitions and Examples For simplicity we will work strictly with affine Definition 1.1. An algebraic
Math 120 HW 9 Solutions
 Math 120 HW 9 Solutions June 8, 2018 Question 1 Write down a ring homomorphism (no proof required) f from R = Z[ 11] = {a + b 11 a, b Z} to S = Z/35Z. The main difficulty is to find an element x Z/35Z
Math 120 HW 9 Solutions June 8, 2018 Question 1 Write down a ring homomorphism (no proof required) f from R = Z[ 11] = {a + b 11 a, b Z} to S = Z/35Z. The main difficulty is to find an element x Z/35Z
Skew row-strict quasisymmetric Schur functions
 Journal of Algebraic Combinatorics manuscript No. (will be inserted by the editor) Skew row-strict quasisymmetric Schur functions Sarah K. Mason Elizabeth Niese Received: date / Accepted: date Abstract
Journal of Algebraic Combinatorics manuscript No. (will be inserted by the editor) Skew row-strict quasisymmetric Schur functions Sarah K. Mason Elizabeth Niese Received: date / Accepted: date Abstract
The uniqueness problem for chromatic symmetric functions of trees
 The uniqueness problem for chromatic symmetric functions of trees Jeremy L. Martin (University of Kansas) AMS Western Sectional Meeting UNLV, April 18, 2015 Colorings and the Chromatic Polynomial Throughout,
The uniqueness problem for chromatic symmetric functions of trees Jeremy L. Martin (University of Kansas) AMS Western Sectional Meeting UNLV, April 18, 2015 Colorings and the Chromatic Polynomial Throughout,
A zoo of Hopf algebras
 Non-Commutative Symmetric Functions I: A zoo of Hopf algebras Mike Zabrocki York University Joint work with Nantel Bergeron, Anouk Bergeron-Brlek, Emmanurel Briand, Christophe Hohlweg, Christophe Reutenauer,
Non-Commutative Symmetric Functions I: A zoo of Hopf algebras Mike Zabrocki York University Joint work with Nantel Bergeron, Anouk Bergeron-Brlek, Emmanurel Briand, Christophe Hohlweg, Christophe Reutenauer,
Math 762 Spring h Y (Z 1 ) (1) h X (Z 2 ) h X (Z 1 ) Φ Z 1. h Y (Z 2 )
 Math 762 Spring 2016 Homework 3 Drew Armstrong Problem 1. Yoneda s Lemma. We have seen that the bifunctor Hom C (, ) : C C Set is analogous to a bilinear form on a K-vector space, : V V K. Recall that
Math 762 Spring 2016 Homework 3 Drew Armstrong Problem 1. Yoneda s Lemma. We have seen that the bifunctor Hom C (, ) : C C Set is analogous to a bilinear form on a K-vector space, : V V K. Recall that
38 Irreducibility criteria in rings of polynomials
 38 Irreducibility criteria in rings of polynomials 38.1 Theorem. Let p(x), q(x) R[x] be polynomials such that p(x) = a 0 + a 1 x +... + a n x n, q(x) = b 0 + b 1 x +... + b m x m and a n, b m 0. If b m
38 Irreducibility criteria in rings of polynomials 38.1 Theorem. Let p(x), q(x) R[x] be polynomials such that p(x) = a 0 + a 1 x +... + a n x n, q(x) = b 0 + b 1 x +... + b m x m and a n, b m 0. If b m
Lecture 7.3: Ring homomorphisms
 Lecture 7.3: Ring homomorphisms Matthew Macauley Department of Mathematical Sciences Clemson University http://www.math.clemson.edu/~macaule/ Math 4120, Modern Algebra M. Macauley (Clemson) Lecture 7.3:
Lecture 7.3: Ring homomorphisms Matthew Macauley Department of Mathematical Sciences Clemson University http://www.math.clemson.edu/~macaule/ Math 4120, Modern Algebra M. Macauley (Clemson) Lecture 7.3:
The combinatorics of binomial ideals
 The combinatorics of binomial ideals Thomas Kahle (MSRI) (joint with Ezra Miller, Duke) December 6, 2012 No Theorem Let k be a field. Every binomial ideal in k[x 1,..., x n ] is an intersection of primary
The combinatorics of binomial ideals Thomas Kahle (MSRI) (joint with Ezra Miller, Duke) December 6, 2012 No Theorem Let k be a field. Every binomial ideal in k[x 1,..., x n ] is an intersection of primary
The orbit algebra of an oligomorphic permutation group with polynomial profile is Cohen-Macaulay
 Séminaire Lotharingien de Combinatoire XX (2018) Article #YY, 12 pp. Proceedings of the 30 th Conference on Formal Power Series and Algebraic Combinatorics (Hanover) The orbit algebra of an oligomorphic
Séminaire Lotharingien de Combinatoire XX (2018) Article #YY, 12 pp. Proceedings of the 30 th Conference on Formal Power Series and Algebraic Combinatorics (Hanover) The orbit algebra of an oligomorphic
CHAPTER 1. AFFINE ALGEBRAIC VARIETIES
 CHAPTER 1. AFFINE ALGEBRAIC VARIETIES During this first part of the course, we will establish a correspondence between various geometric notions and algebraic ones. Some references for this part of the
CHAPTER 1. AFFINE ALGEBRAIC VARIETIES During this first part of the course, we will establish a correspondence between various geometric notions and algebraic ones. Some references for this part of the
Kiddie Talk - The Diamond Lemma and its applications
 Kiddie Tal - The Diamond Lemma and its applications April 22, 2013 1 Intro Start with an example: consider the following game, a solitaire. Tae a finite graph G with n vertices and a function e : V (G)
Kiddie Tal - The Diamond Lemma and its applications April 22, 2013 1 Intro Start with an example: consider the following game, a solitaire. Tae a finite graph G with n vertices and a function e : V (G)
10. Smooth Varieties. 82 Andreas Gathmann
 82 Andreas Gathmann 10. Smooth Varieties Let a be a point on a variety X. In the last chapter we have introduced the tangent cone C a X as a way to study X locally around a (see Construction 9.20). It
82 Andreas Gathmann 10. Smooth Varieties Let a be a point on a variety X. In the last chapter we have introduced the tangent cone C a X as a way to study X locally around a (see Construction 9.20). It
Descents, Peaks, and Shuffles of Permutations and Noncommutative Symmetric Functions
 Descents, Peaks, and Shuffles of Permutations and Noncommutative Symmetric Functions Ira M. Gessel Department of Mathematics Brandeis University Workshop on Quasisymmetric Functions Bannf International
Descents, Peaks, and Shuffles of Permutations and Noncommutative Symmetric Functions Ira M. Gessel Department of Mathematics Brandeis University Workshop on Quasisymmetric Functions Bannf International
Chapter 2 Linear Transformations
 Chapter 2 Linear Transformations Linear Transformations Loosely speaking, a linear transformation is a function from one vector space to another that preserves the vector space operations. Let us be more
Chapter 2 Linear Transformations Linear Transformations Loosely speaking, a linear transformation is a function from one vector space to another that preserves the vector space operations. Let us be more
Notes on tensor products. Robert Harron
 Notes on tensor products Robert Harron Department of Mathematics, Keller Hall, University of Hawai i at Mānoa, Honolulu, HI 96822, USA E-mail address: rharron@math.hawaii.edu Abstract. Graduate algebra
Notes on tensor products Robert Harron Department of Mathematics, Keller Hall, University of Hawai i at Mānoa, Honolulu, HI 96822, USA E-mail address: rharron@math.hawaii.edu Abstract. Graduate algebra
School of Mathematics and Statistics. MT5836 Galois Theory. Handout 0: Course Information
 MRQ 2017 School of Mathematics and Statistics MT5836 Galois Theory Handout 0: Course Information Lecturer: Martyn Quick, Room 326. Prerequisite: MT3505 (or MT4517) Rings & Fields Lectures: Tutorials: Mon
MRQ 2017 School of Mathematics and Statistics MT5836 Galois Theory Handout 0: Course Information Lecturer: Martyn Quick, Room 326. Prerequisite: MT3505 (or MT4517) Rings & Fields Lectures: Tutorials: Mon
Periods, Galois theory and particle physics
 Periods, Galois theory and particle physics Francis Brown All Souls College, Oxford Gergen Lectures, 21st-24th March 2016 1 / 29 Reminders We are interested in periods I = γ ω where ω is a regular algebraic
Periods, Galois theory and particle physics Francis Brown All Souls College, Oxford Gergen Lectures, 21st-24th March 2016 1 / 29 Reminders We are interested in periods I = γ ω where ω is a regular algebraic
Educjatipnal. L a d ie s * COBNWALILI.S H IG H SCHOOL. I F O R G IR L S A n B k i n d e r g a r t e n.
 - - - 0 x ] - ) ) -? - Q - - z 0 x 8 - #? ) 80 0 0 Q ) - 8-8 - ) x ) - ) -] ) Q x?- x - - / - - x - - - x / /- Q ] 8 Q x / / - 0-0 0 x 8 ] ) / - - /- - / /? x ) x x Q ) 8 x q q q )- 8-0 0? - Q - - x?-
- - - 0 x ] - ) ) -? - Q - - z 0 x 8 - #? ) 80 0 0 Q ) - 8-8 - ) x ) - ) -] ) Q x?- x - - / - - x - - - x / /- Q ] 8 Q x / / - 0-0 0 x 8 ] ) / - - /- - / /? x ) x x Q ) 8 x q q q )- 8-0 0? - Q - - x?-
Generalized Alexander duality and applications. Osaka Journal of Mathematics. 38(2) P.469-P.485
 Title Generalized Alexander duality and applications Author(s) Romer, Tim Citation Osaka Journal of Mathematics. 38(2) P.469-P.485 Issue Date 2001-06 Text Version publisher URL https://doi.org/10.18910/4757
Title Generalized Alexander duality and applications Author(s) Romer, Tim Citation Osaka Journal of Mathematics. 38(2) P.469-P.485 Issue Date 2001-06 Text Version publisher URL https://doi.org/10.18910/4757
SHIFTED K-THEORETIC POIRIER-REUTENAUER BIALGEBRA
 SHIFTED K-THEORETIC POIRIER-REUTENAUER BIALGEBRA ADAM KEILTHY, REBECCA PATRIAS, LILLIAN WEBSTER, YINUO ZHANG, SHUQI ZHOU Abstract We use shifted K-theoretic jeu de taquin to show that the weak K-Knuth
SHIFTED K-THEORETIC POIRIER-REUTENAUER BIALGEBRA ADAM KEILTHY, REBECCA PATRIAS, LILLIAN WEBSTER, YINUO ZHANG, SHUQI ZHOU Abstract We use shifted K-theoretic jeu de taquin to show that the weak K-Knuth
MATH 196, SECTION 57 (VIPUL NAIK)
 TAKE-HOME CLASS QUIZ: DUE MONDAY NOVEMBER 25: SUBSPACE, BASIS, DIMENSION, AND ABSTRACT SPACES: APPLICATIONS TO CALCULUS MATH 196, SECTION 57 (VIPUL NAIK) Your name (print clearly in capital letters): PLEASE
TAKE-HOME CLASS QUIZ: DUE MONDAY NOVEMBER 25: SUBSPACE, BASIS, DIMENSION, AND ABSTRACT SPACES: APPLICATIONS TO CALCULUS MATH 196, SECTION 57 (VIPUL NAIK) Your name (print clearly in capital letters): PLEASE
Commutative Algebra MAS439 Lecture 3: Subrings
 Commutative Algebra MAS439 Lecture 3: Subrings Paul Johnson paul.johnson@sheffield.ac.uk Hicks J06b October 4th Plan: slow down a little Last week - Didn t finish Course policies + philosophy Sections
Commutative Algebra MAS439 Lecture 3: Subrings Paul Johnson paul.johnson@sheffield.ac.uk Hicks J06b October 4th Plan: slow down a little Last week - Didn t finish Course policies + philosophy Sections
MAS439 Lecture 9 k-algebras. October 25th
 MAS439 Lecture 9 k-algebras October 25th Feedback Only two people filled in the early questionaires One blandly positive One really didn t like lectures, depended on the notes Response to that: This is
MAS439 Lecture 9 k-algebras October 25th Feedback Only two people filled in the early questionaires One blandly positive One really didn t like lectures, depended on the notes Response to that: This is
Linear and Bilinear Algebra (2WF04) Jan Draisma
 Linear and Bilinear Algebra (2WF04) Jan Draisma CHAPTER 3 The minimal polynomial and nilpotent maps 3.1. Minimal polynomial Throughout this chapter, V is a finite-dimensional vector space of dimension
Linear and Bilinear Algebra (2WF04) Jan Draisma CHAPTER 3 The minimal polynomial and nilpotent maps 3.1. Minimal polynomial Throughout this chapter, V is a finite-dimensional vector space of dimension
JOSEPH ALFANO* Department of Mathematics, Assumption s y i P (x; y) = 0 for all r; s 0 (with r + s > 0). Computer explorations by
 A BASIS FOR THE Y SUBSPACE OF DIAGONAL HARMONIC POLYNOMIALS JOSEPH ALFANO* Department of Mathematics, Assumption College 500 Salisbury Street, Worcester, Massachusetts 065-0005 ABSTRACT. The space DH n
A BASIS FOR THE Y SUBSPACE OF DIAGONAL HARMONIC POLYNOMIALS JOSEPH ALFANO* Department of Mathematics, Assumption College 500 Salisbury Street, Worcester, Massachusetts 065-0005 ABSTRACT. The space DH n
Visual Abstract Algebra. Marcus Pivato
 Visual Abstract Algebra Marcus Pivato March 25, 2003 2 Contents I Groups 1 1 Homomorphisms 3 1.1 Cosets and Coset Spaces............................... 3 1.2 Lagrange s Theorem.................................
Visual Abstract Algebra Marcus Pivato March 25, 2003 2 Contents I Groups 1 1 Homomorphisms 3 1.1 Cosets and Coset Spaces............................... 3 1.2 Lagrange s Theorem.................................
On the centre of the generic algebra of M 1,1
 On the centre of the generic algebra of M 1,1 Thiago Castilho de Mello University of Campinas PhD grant from CNPq, Brazil F is a field of characteristic zero; F X = F x 1, x 2,... is the free associative
On the centre of the generic algebra of M 1,1 Thiago Castilho de Mello University of Campinas PhD grant from CNPq, Brazil F is a field of characteristic zero; F X = F x 1, x 2,... is the free associative
Transcendental Numbers and Hopf Algebras
 Transcendental Numbers and Hopf Algebras Michel Waldschmidt Deutsch-Französischer Diskurs, Saarland University, July 4, 2003 1 Algebraic groups (commutative, linear, over Q) Exponential polynomials Transcendence
Transcendental Numbers and Hopf Algebras Michel Waldschmidt Deutsch-Französischer Diskurs, Saarland University, July 4, 2003 1 Algebraic groups (commutative, linear, over Q) Exponential polynomials Transcendence
Operads. Spencer Liang. March 10, 2015
 Operads Spencer Liang March 10, 2015 1 Introduction The notion of an operad was created in order to have a well-defined mathematical object which encodes the idea of an abstract family of composable n-ary
Operads Spencer Liang March 10, 2015 1 Introduction The notion of an operad was created in order to have a well-defined mathematical object which encodes the idea of an abstract family of composable n-ary
Picard-Vessiot theory, algebraic groups and group schemes
 Picard-Vessiot theory, algebraic groups and group schemes Jerald J. Kovacic Department of Mathematics The City College of The City University of New York New York, NY 003 email: jkovacic@verizon.net URL:
Picard-Vessiot theory, algebraic groups and group schemes Jerald J. Kovacic Department of Mathematics The City College of The City University of New York New York, NY 003 email: jkovacic@verizon.net URL:
An example of generalization of the Bernoulli numbers and polynomials to any dimension
 An example of generalization of the Bernoulli numbers and polynomials to any dimension Olivier Bouillot, Villebon-Georges Charpak institute, France C.A.L.I.N. team seminary. Tuesday, 29 th March 26. Introduction
An example of generalization of the Bernoulli numbers and polynomials to any dimension Olivier Bouillot, Villebon-Georges Charpak institute, France C.A.L.I.N. team seminary. Tuesday, 29 th March 26. Introduction
Symbolic integration of multiple polylogarithms
 Symbolic integration of multiple polylogarithms Erik Panzer Institute des Hautes E tudes Scientifiques Applications of Computer Algebra July 22nd, 215 Kalamata, Greece Problem: Multiple integrals of rational
Symbolic integration of multiple polylogarithms Erik Panzer Institute des Hautes E tudes Scientifiques Applications of Computer Algebra July 22nd, 215 Kalamata, Greece Problem: Multiple integrals of rational
Math 121 Homework 4: Notes on Selected Problems
 Math 121 Homework 4: Notes on Selected Problems 11.2.9. If W is a subspace of the vector space V stable under the linear transformation (i.e., (W ) W ), show that induces linear transformations W on W
Math 121 Homework 4: Notes on Selected Problems 11.2.9. If W is a subspace of the vector space V stable under the linear transformation (i.e., (W ) W ), show that induces linear transformations W on W
Dependence of logarithms on commutative algebraic groups
 INTERNATIONAL CONFERENCE on ALGEBRA and NUMBER THEORY Hyderabad, December 11 16, 2003 Dependence of logarithms on commutative algebraic groups Michel Waldschmidt miw@math.jussieu.fr http://www.math.jussieu.fr/
INTERNATIONAL CONFERENCE on ALGEBRA and NUMBER THEORY Hyderabad, December 11 16, 2003 Dependence of logarithms on commutative algebraic groups Michel Waldschmidt miw@math.jussieu.fr http://www.math.jussieu.fr/
A correction to Conducteur des Représentations du groupe linéaire
 A correction to Conducteur des Représentations du groupe linéaire Hervé Jacquet December 5, 2011 Nadir Matringe has indicated to me that the paper Conducteur des Représentations du groupe linéaire ([JPSS81a],
A correction to Conducteur des Représentations du groupe linéaire Hervé Jacquet December 5, 2011 Nadir Matringe has indicated to me that the paper Conducteur des Représentations du groupe linéaire ([JPSS81a],
On finitely presented expansions of semigroups, algebras, and gr
 On finitely presented expansions of semigroups, algebras, and groups Computer Science Department, The University of Auckland, New Zealand In collaboration with D. Hirschfeldt, and independently A. Miasnikov
On finitely presented expansions of semigroups, algebras, and groups Computer Science Department, The University of Auckland, New Zealand In collaboration with D. Hirschfeldt, and independently A. Miasnikov
2. Intersection Multiplicities
 2. Intersection Multiplicities 11 2. Intersection Multiplicities Let us start our study of curves by introducing the concept of intersection multiplicity, which will be central throughout these notes.
2. Intersection Multiplicities 11 2. Intersection Multiplicities Let us start our study of curves by introducing the concept of intersection multiplicity, which will be central throughout these notes.
MATH32062 Notes. 1 Affine algebraic varieties. 1.1 Definition of affine algebraic varieties
 MATH32062 Notes 1 Affine algebraic varieties 1.1 Definition of affine algebraic varieties We want to define an algebraic variety as the solution set of a collection of polynomial equations, or equivalently,
MATH32062 Notes 1 Affine algebraic varieties 1.1 Definition of affine algebraic varieties We want to define an algebraic variety as the solution set of a collection of polynomial equations, or equivalently,
Shifted symmetric functions I: the vanishing property, skew Young diagrams and symmetric group characters
 I: the vanishing property, skew Young diagrams and symmetric group characters Valentin Féray Institut für Mathematik, Universität Zürich Séminaire Lotharingien de Combinatoire Bertinoro, Italy, Sept. 11th-12th-13th
I: the vanishing property, skew Young diagrams and symmetric group characters Valentin Féray Institut für Mathematik, Universität Zürich Séminaire Lotharingien de Combinatoire Bertinoro, Italy, Sept. 11th-12th-13th
INTRO TO TENSOR PRODUCTS MATH 250B
 INTRO TO TENSOR PRODUCTS MATH 250B ADAM TOPAZ 1. Definition of the Tensor Product Throughout this note, A will denote a commutative ring. Let M, N be two A-modules. For a third A-module Z, consider the
INTRO TO TENSOR PRODUCTS MATH 250B ADAM TOPAZ 1. Definition of the Tensor Product Throughout this note, A will denote a commutative ring. Let M, N be two A-modules. For a third A-module Z, consider the
MATH 221 NOTES BRENT HO. Date: January 3, 2009.
 MATH 22 NOTES BRENT HO Date: January 3, 2009. 0 Table of Contents. Localizations......................................................................... 2 2. Zariski Topology......................................................................
MATH 22 NOTES BRENT HO Date: January 3, 2009. 0 Table of Contents. Localizations......................................................................... 2 2. Zariski Topology......................................................................
Q(x n+1,..., x m ) in n independent variables
 Cluster algebras of geometric type (Fomin / Zelevinsky) m n positive integers ambient field F of rational functions over Q(x n+1,..., x m ) in n independent variables Definition: A seed in F is a pair
Cluster algebras of geometric type (Fomin / Zelevinsky) m n positive integers ambient field F of rational functions over Q(x n+1,..., x m ) in n independent variables Definition: A seed in F is a pair
Notes on p-divisible Groups
 Notes on p-divisible Groups March 24, 2006 This is a note for the talk in STAGE in MIT. The content is basically following the paper [T]. 1 Preliminaries and Notations Notation 1.1. Let R be a complete
Notes on p-divisible Groups March 24, 2006 This is a note for the talk in STAGE in MIT. The content is basically following the paper [T]. 1 Preliminaries and Notations Notation 1.1. Let R be a complete
Lecture Notes Math 371: Algebra (Fall 2006) by Nathanael Leedom Ackerman
 Lecture Notes Math 371: Algebra (Fall 2006) by Nathanael Leedom Ackerman October 17, 2006 TALK SLOWLY AND WRITE NEATLY!! 1 0.1 Integral Domains and Fraction Fields 0.1.1 Theorems Now what we are going
Lecture Notes Math 371: Algebra (Fall 2006) by Nathanael Leedom Ackerman October 17, 2006 TALK SLOWLY AND WRITE NEATLY!! 1 0.1 Integral Domains and Fraction Fields 0.1.1 Theorems Now what we are going
Algebra Review. Instructor: Laszlo Babai Notes by Vincent Lucarelli and the instructor. June 15, 2001
 Algebra Review Instructor: Laszlo Babai Notes by Vincent Lucarelli and the instructor June 15, 2001 1 Groups Definition 1.1 A semigroup (G, ) is a set G with a binary operation such that: Axiom 1 ( a,
Algebra Review Instructor: Laszlo Babai Notes by Vincent Lucarelli and the instructor June 15, 2001 1 Groups Definition 1.1 A semigroup (G, ) is a set G with a binary operation such that: Axiom 1 ( a,
BEZOUT S THEOREM CHRISTIAN KLEVDAL
 BEZOUT S THEOREM CHRISTIAN KLEVDAL A weaker version of Bézout s theorem states that if C, D are projective plane curves of degrees c and d that intersect transversally, then C D = cd. The goal of this
BEZOUT S THEOREM CHRISTIAN KLEVDAL A weaker version of Bézout s theorem states that if C, D are projective plane curves of degrees c and d that intersect transversally, then C D = cd. The goal of this
The Proj Construction
 The Proj Construction Daniel Murfet May 16, 2006 Contents 1 Basic Properties 1 2 Functorial Properties 2 3 Products 6 4 Linear Morphisms 9 5 Projective Morphisms 9 6 Dimensions of Schemes 11 7 Points of
The Proj Construction Daniel Murfet May 16, 2006 Contents 1 Basic Properties 1 2 Functorial Properties 2 3 Products 6 4 Linear Morphisms 9 5 Projective Morphisms 9 6 Dimensions of Schemes 11 7 Points of
A Little Beyond: Linear Algebra
 A Little Beyond: Linear Algebra Akshay Tiwary March 6, 2016 Any suggestions, questions and remarks are welcome! 1 A little extra Linear Algebra 1. Show that any set of non-zero polynomials in [x], no two
A Little Beyond: Linear Algebra Akshay Tiwary March 6, 2016 Any suggestions, questions and remarks are welcome! 1 A little extra Linear Algebra 1. Show that any set of non-zero polynomials in [x], no two
Limits of Functions (a, L)
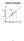 Limits of Functions f(x) (a, L) L f(x) x a x x 20 Informal Definition: If the values of can be made as close to as we like by taking values of sufficiently close to [but not equal to ] then we write or
Limits of Functions f(x) (a, L) L f(x) x a x x 20 Informal Definition: If the values of can be made as close to as we like by taking values of sufficiently close to [but not equal to ] then we write or
DIVISORS ON NONSINGULAR CURVES
 DIVISORS ON NONSINGULAR CURVES BRIAN OSSERMAN We now begin a closer study of the behavior of projective nonsingular curves, and morphisms between them, as well as to projective space. To this end, we introduce
DIVISORS ON NONSINGULAR CURVES BRIAN OSSERMAN We now begin a closer study of the behavior of projective nonsingular curves, and morphisms between them, as well as to projective space. To this end, we introduce
HILBERT FUNCTIONS. 1. Introduction
 HILBERT FUCTIOS JORDA SCHETTLER 1. Introduction A Hilbert function (so far as we will discuss) is a map from the nonnegative integers to themselves which records the lengths of composition series of each
HILBERT FUCTIOS JORDA SCHETTLER 1. Introduction A Hilbert function (so far as we will discuss) is a map from the nonnegative integers to themselves which records the lengths of composition series of each
Lecture 4.1: Homomorphisms and isomorphisms
 Lecture 4.: Homomorphisms and isomorphisms Matthew Macauley Department of Mathematical Sciences Clemson University http://www.math.clemson.edu/~macaule/ Math 4, Modern Algebra M. Macauley (Clemson) Lecture
Lecture 4.: Homomorphisms and isomorphisms Matthew Macauley Department of Mathematical Sciences Clemson University http://www.math.clemson.edu/~macaule/ Math 4, Modern Algebra M. Macauley (Clemson) Lecture
The varieties of e-th powers
 The varieties of e-th powers M.A. Bik Master thesis Thesis advisors: dr. R.M. van Luijk dr. R.I. van der Veen Date master exam: 25 July 2016 Mathematisch Instituut, Universiteit Leiden Acknowledgements
The varieties of e-th powers M.A. Bik Master thesis Thesis advisors: dr. R.M. van Luijk dr. R.I. van der Veen Date master exam: 25 July 2016 Mathematisch Instituut, Universiteit Leiden Acknowledgements
The algebra of multiple divisor functions and applications to multiple zeta values
 The algebra of multiple divisor functions and applications to multiple zeta values ESF Workshop: New Approaches To Multiple Zeta Values ICMAT Madrid - 30th September 2013 joint work: H.B., Ulf Kühn, arxiv:1309.3920
The algebra of multiple divisor functions and applications to multiple zeta values ESF Workshop: New Approaches To Multiple Zeta Values ICMAT Madrid - 30th September 2013 joint work: H.B., Ulf Kühn, arxiv:1309.3920
Definition : We refer to Ψ as the associated presentation complex.
 7.3. Back to group presentations. Let Γ be a group with generating set S, and let = (Γ, S) be the Cayley graph. Recall that /Γ is a finite wedge of circles one for each generators. Suppose that Γ is finitely
7.3. Back to group presentations. Let Γ be a group with generating set S, and let = (Γ, S) be the Cayley graph. Recall that /Γ is a finite wedge of circles one for each generators. Suppose that Γ is finitely
Graph invariants in the spin model
 Graph invariants in the spin model Alexander Schrijver 1 Abstract. Given a symmetric n n matrix A, we define, for any graph G, f A (G) := a φ(u),φ(v). φ:v G {1,...,n} uv EG We characterize for which graph
Graph invariants in the spin model Alexander Schrijver 1 Abstract. Given a symmetric n n matrix A, we define, for any graph G, f A (G) := a φ(u),φ(v). φ:v G {1,...,n} uv EG We characterize for which graph
MATH 101A: ALGEBRA I PART C: TENSOR PRODUCT AND MULTILINEAR ALGEBRA. This is the title page for the notes on tensor products and multilinear algebra.
 MATH 101A: ALGEBRA I PART C: TENSOR PRODUCT AND MULTILINEAR ALGEBRA This is the title page for the notes on tensor products and multilinear algebra. Contents 1. Bilinear forms and quadratic forms 1 1.1.
MATH 101A: ALGEBRA I PART C: TENSOR PRODUCT AND MULTILINEAR ALGEBRA This is the title page for the notes on tensor products and multilinear algebra. Contents 1. Bilinear forms and quadratic forms 1 1.1.
Polynomials, Ideals, and Gröbner Bases
 Polynomials, Ideals, and Gröbner Bases Notes by Bernd Sturmfels for the lecture on April 10, 2018, in the IMPRS Ringvorlesung Introduction to Nonlinear Algebra We fix a field K. Some examples of fields
Polynomials, Ideals, and Gröbner Bases Notes by Bernd Sturmfels for the lecture on April 10, 2018, in the IMPRS Ringvorlesung Introduction to Nonlinear Algebra We fix a field K. Some examples of fields
Abstract Algebra II Groups ( )
 Abstract Algebra II Groups ( ) Melchior Grützmann / melchiorgfreehostingcom/algebra October 15, 2012 Outline Group homomorphisms Free groups, free products, and presentations Free products ( ) Definition
Abstract Algebra II Groups ( ) Melchior Grützmann / melchiorgfreehostingcom/algebra October 15, 2012 Outline Group homomorphisms Free groups, free products, and presentations Free products ( ) Definition
BASIC GROUP THEORY : G G G,
 BASIC GROUP THEORY 18.904 1. Definitions Definition 1.1. A group (G, ) is a set G with a binary operation : G G G, and a unit e G, possessing the following properties. (1) Unital: for g G, we have g e
BASIC GROUP THEORY 18.904 1. Definitions Definition 1.1. A group (G, ) is a set G with a binary operation : G G G, and a unit e G, possessing the following properties. (1) Unital: for g G, we have g e
Motivic Periods, Coleman Functions, and the Unit Equation
 Motivic Periods, Coleman Functions, and the Unit Equation An Ongoing Project D. Corwin 1 I. Dan-Cohen 2 1 MIT 2 Ben Gurion University of the Negev April 10, 2018 Corwin, Dan-Cohen Motivic Periods, Coleman
Motivic Periods, Coleman Functions, and the Unit Equation An Ongoing Project D. Corwin 1 I. Dan-Cohen 2 1 MIT 2 Ben Gurion University of the Negev April 10, 2018 Corwin, Dan-Cohen Motivic Periods, Coleman
3 Universal enveloping algebras
 3 UNIVERSAL ENVELOPING ALGEBRAS 26 3 Universal enveloping algebras 3.1 Definition and first properties In this section, k will be an arbitrary field, not necessarily of characteristic zero. The idea is
3 UNIVERSAL ENVELOPING ALGEBRAS 26 3 Universal enveloping algebras 3.1 Definition and first properties In this section, k will be an arbitrary field, not necessarily of characteristic zero. The idea is
The Major Problems in Group Representation Theory
 The Major Problems in Group Representation Theory David A. Craven 18th November 2009 In group representation theory, there are many unsolved conjectures, most of which try to understand the involved relationship
The Major Problems in Group Representation Theory David A. Craven 18th November 2009 In group representation theory, there are many unsolved conjectures, most of which try to understand the involved relationship
Linear Algebra. Paul Yiu. Department of Mathematics Florida Atlantic University. Fall 2011
 Linear Algebra Paul Yiu Department of Mathematics Florida Atlantic University Fall 2011 Linear Algebra Paul Yiu Department of Mathematics Florida Atlantic University Fall 2011 1A: Vector spaces Fields
Linear Algebra Paul Yiu Department of Mathematics Florida Atlantic University Fall 2011 Linear Algebra Paul Yiu Department of Mathematics Florida Atlantic University Fall 2011 1A: Vector spaces Fields
