Massachusetts Institute of Technology Computational Evolutionary Biology, Fall, 2005 Notes for November 7: Molecular evolution
|
|
|
- Valerie Jean Owens
- 6 years ago
- Views:
Transcription
1 Massachusetts Institute of Technology Computational Evolutionary Biology, Fall, 2005 Notes for November 7: Molecular evolution 1. Rates of amino acid replacement The initial motivation for the neutral theory came from observations on the rate of amino acid replacements in proteins. When extrapolated to the entire genome, the inferred rate of evolution was several nucleotide substitutions per year. This rate was regarded as much to high to result from natural selection, because the intensity of selection must be limited by the total amount of differential survival and reproduction that occurs in the organism. Direct DNA sequencing later revealed that rates of nucleotide substitution vary according to the function or presumed absence of function of the nucleotides. The first 18 amino acids in the amino terminal end of the human and mouse gamma interferon proteins are a signal peptide that is used in the secretion of molecules. The sequences are: Hum: Met Lys Try Thr Ser Tyr Ile Leu Ala Phe Gln Leu Cys Ile Val Leu Gly Ser Mou: Met Asn Ala Thr His Tyr Cys Leu Ala Leu Gln Leu Phe Leu Met Ala Val Ser We could simply count the number of sites that differ in the two sequences: there are 10/18 that differ, or To interpret this, let us assume that amino acid replacements occur at the rate λ per unit time. Consider two independently evolving sequences, initially identical, which at time t are found to differ in proportion D t of their amino acids. After the next time interval, the proportion of differences is just D t+1 = (1 D t )(2λ)+D t, so we add to the already existing proportion of differences those that might have arisen in the current time interval. The factor of 2 is present because the total time for evolution is 2t time units (t units in each lineage). The equation ignores the unlikely possibility of an amino acid replacement making two previously different sites identical. If λ is the rate of amino acid replacement per unit time, then the probability that a particular site remains unsubstituted for t consecutive intervals along each of two independent lineages is (1-λ) 2t which is approximately e 2λt if λt is not too large. So, the probability of 1 or more replacements is just 1 minus this quantity, or about (1 e 2λt ). Since λ is the rate of amino acid replacement per unit time, the expected proportion of differences between two sequences at any time t is K=2λt. Substituting and rearranging gives the estimate of K from the observed differences K = ln(1 D t ). This quantity is used in preference to D because it takes multiple substitutions into account, especially over a long period of time. Rates of amino acid substitution vary over a 500-fold range in different proteins. The rate of amino acid replacement in gamma interferon is one of the largest rates known.
2 Among the slowest rates is that of histone H4, for which the substitution rate λ is 0.01 x per year. The average rate for many proteins is very close to the rate found in hemoglobin, which is about 1 x 10-9 amino acid replacement per amino acid site per year. So far we have done our computations on polymorphism sequences based on just the observed counts, all on the assumption that we were looking at individuals from the same species. However, when we look across species, or even within species, if the time since common divergence is long enough, there is always the possibility that the same nucleotide site position could have changed more than once. For example, position 1, say, could first be an A; then be substituted with a T; and then once more back to A. In this case, we would not see any change from the ancestral state even though a change had occurred. We call this a multiple hit. (So in a way this relaxes the constraint of the infinite sites model.) In general then, the number of nucleotide substitutions that we observe, and that we have been calling mutations, are always an undercount of the true number. There are many models of nucleotide substitutions that have been proposed to provide a correction factor for this possibility. Nucleotide sequences are analyzed in the same manner as amino acid sequences, but we have to correct for cases where a substitution makes two previously different nucleotide sites identical. This is significant because an expected 1/3 of random substitutions will make two previously different nucleotides identical, while the chance is only 1/19 for amino acids. Many models of nucleotide substitution have been proposed, which differ mostly in the assumptions about rates of mutations between pairs of nucleotides. The simplest model for nucleotide substitution assumes that mutation occurs at a constant rate, and each nucleotide is equally likely to mutate to any other, the Jukes-Cantor model. If α is the rate of mutating from one nucleotide to another, then in any time interval, A mutates to C with probability α, A mutates to T with probability α, and A mutates to G with probability α. The probability that it does not mutate in this time interval is therefore (1 3α), The probability that a particular site is A at time t+1 is the probability of having been A at time t and not mutating, plus the probability of being at any other nucleotide an mutating to A: P A(t+1) = (1 3α)P A(t) +α(1 P A(t) ). From this we can obtain a simple differential equation: dp A(t ) =!4"P A(t ) + " which as we know show has the solution: P A(t ) = e!4"t To solve this, we can use an integrating factor, multiplying both sides by f(t):
3 f (t)4!p A(t ) + f (t) dp A(t ) =! f (t) we need f (t) = f (t)4! so that we can use integration by parts so if f (t) = f (t)4!, then f (t) = e 4!t Substitution this value for f, we get: dp e 4!t 4!P A(t ) + e 4!t A(t ) =!e 4!t d ( e 4!t P A(t ) ) =!e 4!t d " e 4!t P A(t ) =!e 4!t + C ( e 4!t P A(t ) ) = "!e 4!t =!e 4!t + C To find the value of C, we use the fact that at time t=0, P A (0)=1 (we start at A). This gives us: 1 = Ce!4" 0 or C = 3 4 If we observe two sequences that have been separated for time t, then the probability that they continue to carry the same nucleotide at a particular site is: P AA = e!8"t The proportion of sites that differ between the two sequences is just 1 minus this, or D=(1 P AA ). Therefore, D == 3 4 ( 1! e!8"t ) In our previous symbols, λ is the rate of mutation to a nucleotide different from the current nucleotide, so relating this to α, we have λ=3α. This implies that K=2λt=2(3α)=6αt. Taking logs of both sides of the equation above, we get: and since K=3/4(8αt), # 8!t = " ln 1" 4 $ % 3 D & ( K =! 3 4 ln " 1! 4 # $ 3 D % & This is the Jukes-Cantor correction factor. If one lets t go to infinity, the divergence will approach ¾, which makes sense: after enough time, the common ancestry of the two sequences has been erased, and ¼ of all sites will match by chance.
4 Example 1. If 25% of observed sites are different, D=0.25, then plugging this into the formula, the actual number of substitutions is K=0.3404, higher, as expected. Felsenstein s intuitive picture. To construct a more general picture, we can posit a 4x4 transition probability matrix, whose entries give the probability that a particular site will change to another site in one time-step. Let u be the mutation rate per unit per site; P ij = the probability that base i changes to base j in one generation. If t is large and u is small, we can approximate the process as a Poisson, on a continuous scale, with a constant risk of mutation. Note that if we had a type of mutation that changed a base to any one of the four bases chosen at random, with equal probability of the four outcomes, it would almost be like Jukes- Cantor, except that ¼ of the time it would make no change at all (it would do nothing, i.e., no event would occur at all). Now we imagine that we alter this new model by increasing the mutation rate to 4/3u. In this (rescaled) model, the mutations that change the bases occur at rate u, continuously in time (this includes the events that change, e.g., a base A to the same base A). Now this is just a Poisson model with mean rate of change 4/3u, so we can write the probability that k mutations occur, given that time t has passed, as follows: k " 4 Pr[k t] = e! 4 3 ut # $ 3 u % & k! Now we can easily compute the probability that we wind up with base j having started with a base i. The probability that zero base-changing events occur at all during time t is j just the 0 th term of the Poisson, which is just exp( 4/3ut) (The (4/3u) term drops out when j=0, as usual.). Therefore, the probability that there is at least one event that picks a base ¼ at random is 1 this probability, or (1 exp( 4/3ut)). ¼ of the time this change will be to some particular base. Putting this all together, we have: P ij = 1 4 (1! e! 4 3 ut ) (for i " j) P ij = 1 4 (1! e! 4 3 ut ) + e! 4 3 ut (for i = j) because in the second case we must add the probability that no base-changing event has happened at all, leaving us at base i. Thus, if we add up the expected proportion of sites that two sequences will differ after time t, it is just 3 times the first case above, giving us the expected fraction of sites that differing: D == 3 " 4 4 1! e! 3 ut # $ % & Note that the re-parameterization via the ut term is meant to replace the parameter K in the earlier derivation: the value of t here is actually the time 2t (total divergence time since common ancestor) given earlier.
5 The Kimura 2-parameter model. The Jukes-Cantor model suffers from several biological inaccuracies. For one thing, all transitions are assumed equal. However, it is well known that the rate of mutations between the two chemically similar purine bases (Adenine and Guanine, A and G) or between the two chemically similar pyrimidine bases (Cytosine and Thymine, C and T), is much higher (generally more than double) the rate of mutations between a purine and a pyrimidine (e.g., from an A to a T). This is particularly true, e.g., in mammals. The purine-purine or pyrimidine-pyrimidine mutations are called transitions and the purinepyrimidine mutations, transversions. If there were only one mutation parameter, as in the JC model, we would expect a 2:1 ration of transversions to transitions. Estimates from mammalian sequences, however, show that 57% of changes are actually transitions. There are two possible transition pairs (A-G and C-T) and four possible transversion pairs (A-T, A-C, G-T, G-C), discounting self-loops. So, in all there are 4 possible transitions, 8 transversions, and 4 self-loops. This suggests that one ought to move from a one parameter, single rate model to at least a 2 parameter rate model, one for the transition mutation rate (often denoted t s ) and one parameter for the transversion mutation rate (often denoted t v ). This is what Kimura suggested; this model is known as K2P. In the formulations of this model, we will often see the difference between the transition mutation rate and the transversion mutation rate expressed as a ratio, R= transition/transversion rates, or R=t s /t v. We can set up a differential equation as before to solve for the K2P model and its correction factor. If the time divergence is not too great, this will be close to Jukes- Cantor. We can also solve this model using general methods for continuous time Markov chains, as shown later for a slightly different model. Or, one can do the same sort of reparameterizing trick as with the Jukes-Cantor model, which we also defer to the next section. For now, we simply give the solution. If P denotes the total frequency of transitions and Q the total probability of transversions then the K2P says that: P = (1/ 4)(1! 2e!4(" +# )t + e!#t ) Q = (1/ 2)(1! e!8#t ) K = 2$t = 2"t + 4#t =!(1/ 2)ln(1! 2P! Q)! (1/ 4)(1! 2Q) For the Kimura model, we can show that the equilibrium frequency for all bases is ¼, irrespective of their initial frequency this follows from the symmetry of the model, as in Jukes-Cantor. However, turning this around, also like Jukes-Cantor, the formulas are applicable irrespective of the initial base frequency, so the model is applicable to a wider range of cases than many other models that are more complex. Further, the more complex models require one to estimate more parameters. We ll probe this further a bit later.
6 Example. You are given two sequences (50 bp each) of the homologous pseudogene in two species of yeast. (Pseudogene: non-transcribed gene that has decayed and is subject to purely neutral evolution.) The alignment is shown below: Species 1: CCTCGACGGCTTAGATCTGATCTGACCTAATGCTGCAATCGTTACAAAGT Species 2: CCTCCACGAGTAAGAGTTGATCCGACTTAGTCCTGCGATCGTTAGATAAT Note that Jukes-Cantor isn t exactly applicable here because there are 7 transitions and 7 transversions, 14 substitutions out of 50 base pairs. However, the Jukes-Cantor model assumes that there are twice as many transversions as transitions. To apply the Kimura correction, if we knew, say, that the two species diverged 10 million years ago, and there are 50 generations per year, the divergence time is 2 x 500 million or 10 9, but we d also have to get estimates of the transition/transversion ratio. In this data, it looks to be 1. The Jukes-Cantor correction would proceed as follows: There are 14 substitutions in 50 bp. D = 14/50 = K = (3/4)*ln(1-(4/3)*D)=0.35. You should figure out what the difference is for the Kimura model, given R=1. Finally, notice that if we have these figures, we can determine the mutation rate (assuming that it is equal for the two species): K = 2t (years)*μ(mutations per bp per year) μ = 0.35/20 Myr = mutations per bp per year Forthcoming: the matrix method of solution for estimating substitution corrections.
Lecture Notes: Markov chains
 Computational Genomics and Molecular Biology, Fall 5 Lecture Notes: Markov chains Dannie Durand At the beginning of the semester, we introduced two simple scoring functions for pairwise alignments: a similarity
Computational Genomics and Molecular Biology, Fall 5 Lecture Notes: Markov chains Dannie Durand At the beginning of the semester, we introduced two simple scoring functions for pairwise alignments: a similarity
Understanding relationship between homologous sequences
 Molecular Evolution Molecular Evolution How and when were genes and proteins created? How old is a gene? How can we calculate the age of a gene? How did the gene evolve to the present form? What selective
Molecular Evolution Molecular Evolution How and when were genes and proteins created? How old is a gene? How can we calculate the age of a gene? How did the gene evolve to the present form? What selective
Sequence Analysis 17: lecture 5. Substitution matrices Multiple sequence alignment
 Sequence Analysis 17: lecture 5 Substitution matrices Multiple sequence alignment Substitution matrices Used to score aligned positions, usually of amino acids. Expressed as the log-likelihood ratio of
Sequence Analysis 17: lecture 5 Substitution matrices Multiple sequence alignment Substitution matrices Used to score aligned positions, usually of amino acids. Expressed as the log-likelihood ratio of
Lecture 27. Phylogeny methods, part 4 (Models of DNA and protein change) p.1/26
 Lecture 27. Phylogeny methods, part 4 (Models of DNA and protein change) Joe Felsenstein Department of Genome Sciences and Department of Biology Lecture 27. Phylogeny methods, part 4 (Models of DNA and
Lecture 27. Phylogeny methods, part 4 (Models of DNA and protein change) Joe Felsenstein Department of Genome Sciences and Department of Biology Lecture 27. Phylogeny methods, part 4 (Models of DNA and
Lecture 4: Evolutionary Models and Substitution Matrices (PAM and BLOSUM)
 Bioinformatics II Probability and Statistics Universität Zürich and ETH Zürich Spring Semester 2009 Lecture 4: Evolutionary Models and Substitution Matrices (PAM and BLOSUM) Dr Fraser Daly adapted from
Bioinformatics II Probability and Statistics Universität Zürich and ETH Zürich Spring Semester 2009 Lecture 4: Evolutionary Models and Substitution Matrices (PAM and BLOSUM) Dr Fraser Daly adapted from
7.36/7.91 recitation CB Lecture #4
 7.36/7.91 recitation 2-19-2014 CB Lecture #4 1 Announcements / Reminders Homework: - PS#1 due Feb. 20th at noon. - Late policy: ½ credit if received within 24 hrs of due date, otherwise no credit - Answer
7.36/7.91 recitation 2-19-2014 CB Lecture #4 1 Announcements / Reminders Homework: - PS#1 due Feb. 20th at noon. - Late policy: ½ credit if received within 24 hrs of due date, otherwise no credit - Answer
Reading for Lecture 13 Release v10
 Reading for Lecture 13 Release v10 Christopher Lee November 15, 2011 Contents 1 Evolutionary Trees i 1.1 Evolution as a Markov Process...................................... ii 1.2 Rooted vs. Unrooted Trees........................................
Reading for Lecture 13 Release v10 Christopher Lee November 15, 2011 Contents 1 Evolutionary Trees i 1.1 Evolution as a Markov Process...................................... ii 1.2 Rooted vs. Unrooted Trees........................................
Sequence Alignments. Dynamic programming approaches, scoring, and significance. Lucy Skrabanek ICB, WMC January 31, 2013
 Sequence Alignments Dynamic programming approaches, scoring, and significance Lucy Skrabanek ICB, WMC January 31, 213 Sequence alignment Compare two (or more) sequences to: Find regions of conservation
Sequence Alignments Dynamic programming approaches, scoring, and significance Lucy Skrabanek ICB, WMC January 31, 213 Sequence alignment Compare two (or more) sequences to: Find regions of conservation
Bio 1B Lecture Outline (please print and bring along) Fall, 2007
 Bio 1B Lecture Outline (please print and bring along) Fall, 2007 B.D. Mishler, Dept. of Integrative Biology 2-6810, bmishler@berkeley.edu Evolution lecture #5 -- Molecular genetics and molecular evolution
Bio 1B Lecture Outline (please print and bring along) Fall, 2007 B.D. Mishler, Dept. of Integrative Biology 2-6810, bmishler@berkeley.edu Evolution lecture #5 -- Molecular genetics and molecular evolution
Evolutionary Analysis of Viral Genomes
 University of Oxford, Department of Zoology Evolutionary Biology Group Department of Zoology University of Oxford South Parks Road Oxford OX1 3PS, U.K. Fax: +44 1865 271249 Evolutionary Analysis of Viral
University of Oxford, Department of Zoology Evolutionary Biology Group Department of Zoology University of Oxford South Parks Road Oxford OX1 3PS, U.K. Fax: +44 1865 271249 Evolutionary Analysis of Viral
Lecture 24. Phylogeny methods, part 4 (Models of DNA and protein change) p.1/22
 Lecture 24. Phylogeny methods, part 4 (Models of DNA and protein change) Joe Felsenstein Department of Genome Sciences and Department of Biology Lecture 24. Phylogeny methods, part 4 (Models of DNA and
Lecture 24. Phylogeny methods, part 4 (Models of DNA and protein change) Joe Felsenstein Department of Genome Sciences and Department of Biology Lecture 24. Phylogeny methods, part 4 (Models of DNA and
Mutation models I: basic nucleotide sequence mutation models
 Mutation models I: basic nucleotide sequence mutation models Peter Beerli September 3, 009 Mutations are irreversible changes in the DNA. This changes may be introduced by chance, by chemical agents, or
Mutation models I: basic nucleotide sequence mutation models Peter Beerli September 3, 009 Mutations are irreversible changes in the DNA. This changes may be introduced by chance, by chemical agents, or
The neutral theory of molecular evolution
 The neutral theory of molecular evolution Introduction I didn t make a big deal of it in what we just went over, but in deriving the Jukes-Cantor equation I used the phrase substitution rate instead of
The neutral theory of molecular evolution Introduction I didn t make a big deal of it in what we just went over, but in deriving the Jukes-Cantor equation I used the phrase substitution rate instead of
POPULATION GENETICS Winter 2005 Lecture 17 Molecular phylogenetics
 POPULATION GENETICS Winter 2005 Lecture 17 Molecular phylogenetics - in deriving a phylogeny our goal is simply to reconstruct the historical relationships between a group of taxa. - before we review the
POPULATION GENETICS Winter 2005 Lecture 17 Molecular phylogenetics - in deriving a phylogeny our goal is simply to reconstruct the historical relationships between a group of taxa. - before we review the
Phylogenetics: Distance Methods. COMP Spring 2015 Luay Nakhleh, Rice University
 Phylogenetics: Distance Methods COMP 571 - Spring 2015 Luay Nakhleh, Rice University Outline Evolutionary models and distance corrections Distance-based methods Evolutionary Models and Distance Correction
Phylogenetics: Distance Methods COMP 571 - Spring 2015 Luay Nakhleh, Rice University Outline Evolutionary models and distance corrections Distance-based methods Evolutionary Models and Distance Correction
Taming the Beast Workshop
 Workshop David Rasmussen & arsten Magnus June 27, 2016 1 / 31 Outline of sequence evolution: rate matrices Markov chain model Variable rates amongst different sites: +Γ Implementation in BES2 2 / 31 genotype
Workshop David Rasmussen & arsten Magnus June 27, 2016 1 / 31 Outline of sequence evolution: rate matrices Markov chain model Variable rates amongst different sites: +Γ Implementation in BES2 2 / 31 genotype
EVOLUTIONARY DISTANCE MODEL BASED ON DIFFERENTIAL EQUATION AND MARKOV PROCESS
 August 0 Vol 4 No 005-0 JATIT & LLS All rights reserved ISSN: 99-8645 wwwjatitorg E-ISSN: 87-95 EVOLUTIONAY DISTANCE MODEL BASED ON DIFFEENTIAL EUATION AND MAKOV OCESS XIAOFENG WANG College of Mathematical
August 0 Vol 4 No 005-0 JATIT & LLS All rights reserved ISSN: 99-8645 wwwjatitorg E-ISSN: 87-95 EVOLUTIONAY DISTANCE MODEL BASED ON DIFFEENTIAL EUATION AND MAKOV OCESS XIAOFENG WANG College of Mathematical
Quantitative Understanding in Biology Module III: Linear Difference Equations Lecture I: Introduction to Linear Difference Equations
 Quantitative Understanding in Biology Module III: Linear Difference Equations Lecture I: Introduction to Linear Difference Equations Introductory Remarks This section of the course introduces dynamic systems;
Quantitative Understanding in Biology Module III: Linear Difference Equations Lecture I: Introduction to Linear Difference Equations Introductory Remarks This section of the course introduces dynamic systems;
Some of these slides have been borrowed from Dr. Paul Lewis, Dr. Joe Felsenstein. Thanks!
 Some of these slides have been borrowed from Dr. Paul Lewis, Dr. Joe Felsenstein. Thanks! Paul has many great tools for teaching phylogenetics at his web site: http://hydrodictyon.eeb.uconn.edu/people/plewis
Some of these slides have been borrowed from Dr. Paul Lewis, Dr. Joe Felsenstein. Thanks! Paul has many great tools for teaching phylogenetics at his web site: http://hydrodictyon.eeb.uconn.edu/people/plewis
Using Higher Calculus to Study Biologically Important Molecules Julie C. Mitchell
 Using Higher Calculus to Study Biologically Important Molecules Julie C. Mitchell Mathematics and Biochemistry University of Wisconsin - Madison 0 There Are Many Kinds Of Proteins The word protein comes
Using Higher Calculus to Study Biologically Important Molecules Julie C. Mitchell Mathematics and Biochemistry University of Wisconsin - Madison 0 There Are Many Kinds Of Proteins The word protein comes
Early History up to Schedule. Proteins DNA & RNA Schwann and Schleiden Cell Theory Charles Darwin publishes Origin of Species
 Schedule Bioinformatics and Computational Biology: History and Biological Background (JH) 0.0 he Parsimony criterion GKN.0 Stochastic Models of Sequence Evolution GKN 7.0 he Likelihood criterion GKN 0.0
Schedule Bioinformatics and Computational Biology: History and Biological Background (JH) 0.0 he Parsimony criterion GKN.0 Stochastic Models of Sequence Evolution GKN 7.0 he Likelihood criterion GKN 0.0
Nucleotide substitution models
 Nucleotide substitution models Alexander Churbanov University of Wyoming, Laramie Nucleotide substitution models p. 1/23 Jukes and Cantor s model [1] The simples symmetrical model of DNA evolution All
Nucleotide substitution models Alexander Churbanov University of Wyoming, Laramie Nucleotide substitution models p. 1/23 Jukes and Cantor s model [1] The simples symmetrical model of DNA evolution All
Introduction to Polymer Physics
 Introduction to Polymer Physics Enrico Carlon, KU Leuven, Belgium February-May, 2016 Enrico Carlon, KU Leuven, Belgium Introduction to Polymer Physics February-May, 2016 1 / 28 Polymers in Chemistry and
Introduction to Polymer Physics Enrico Carlon, KU Leuven, Belgium February-May, 2016 Enrico Carlon, KU Leuven, Belgium Introduction to Polymer Physics February-May, 2016 1 / 28 Polymers in Chemistry and
Probabilistic modeling and molecular phylogeny
 Probabilistic modeling and molecular phylogeny Anders Gorm Pedersen Molecular Evolution Group Center for Biological Sequence Analysis Technical University of Denmark (DTU) What is a model? Mathematical
Probabilistic modeling and molecular phylogeny Anders Gorm Pedersen Molecular Evolution Group Center for Biological Sequence Analysis Technical University of Denmark (DTU) What is a model? Mathematical
Amira A. AL-Hosary PhD of infectious diseases Department of Animal Medicine (Infectious Diseases) Faculty of Veterinary Medicine Assiut
 Amira A. AL-Hosary PhD of infectious diseases Department of Animal Medicine (Infectious Diseases) Faculty of Veterinary Medicine Assiut University-Egypt Phylogenetic analysis Phylogenetic Basics: Biological
Amira A. AL-Hosary PhD of infectious diseases Department of Animal Medicine (Infectious Diseases) Faculty of Veterinary Medicine Assiut University-Egypt Phylogenetic analysis Phylogenetic Basics: Biological
Bioinformatics. Scoring Matrices. David Gilbert Bioinformatics Research Centre
 Bioinformatics Scoring Matrices David Gilbert Bioinformatics Research Centre www.brc.dcs.gla.ac.uk Department of Computing Science, University of Glasgow Learning Objectives To explain the requirement
Bioinformatics Scoring Matrices David Gilbert Bioinformatics Research Centre www.brc.dcs.gla.ac.uk Department of Computing Science, University of Glasgow Learning Objectives To explain the requirement
Properties of amino acids in proteins
 Properties of amino acids in proteins one of the primary roles of DNA (but not the only one!) is to code for proteins A typical bacterium builds thousands types of proteins, all from ~20 amino acids repeated
Properties of amino acids in proteins one of the primary roles of DNA (but not the only one!) is to code for proteins A typical bacterium builds thousands types of proteins, all from ~20 amino acids repeated
Lecture 4. Models of DNA and protein change. Likelihood methods
 Lecture 4. Models of DNA and protein change. Likelihood methods Joe Felsenstein Department of Genome Sciences and Department of Biology Lecture 4. Models of DNA and protein change. Likelihood methods p.1/36
Lecture 4. Models of DNA and protein change. Likelihood methods Joe Felsenstein Department of Genome Sciences and Department of Biology Lecture 4. Models of DNA and protein change. Likelihood methods p.1/36
Quantifying sequence similarity
 Quantifying sequence similarity Bas E. Dutilh Systems Biology: Bioinformatic Data Analysis Utrecht University, February 16 th 2016 After this lecture, you can define homology, similarity, and identity
Quantifying sequence similarity Bas E. Dutilh Systems Biology: Bioinformatic Data Analysis Utrecht University, February 16 th 2016 After this lecture, you can define homology, similarity, and identity
How Molecules Evolve. Advantages of Molecular Data for Tree Building. Advantages of Molecular Data for Tree Building
 How Molecules Evolve Guest Lecture: Principles and Methods of Systematic Biology 11 November 2013 Chris Simon Approaching phylogenetics from the point of view of the data Understanding how sequences evolve
How Molecules Evolve Guest Lecture: Principles and Methods of Systematic Biology 11 November 2013 Chris Simon Approaching phylogenetics from the point of view of the data Understanding how sequences evolve
Evolutionary Models. Evolutionary Models
 Edit Operators In standard pairwise alignment, what are the allowed edit operators that transform one sequence into the other? Describe how each of these edit operations are represented on a sequence alignment
Edit Operators In standard pairwise alignment, what are the allowed edit operators that transform one sequence into the other? Describe how each of these edit operations are represented on a sequence alignment
Computational Biology: Basics & Interesting Problems
 Computational Biology: Basics & Interesting Problems Summary Sources of information Biological concepts: structure & terminology Sequencing Gene finding Protein structure prediction Sources of information
Computational Biology: Basics & Interesting Problems Summary Sources of information Biological concepts: structure & terminology Sequencing Gene finding Protein structure prediction Sources of information
Maximum Likelihood Until recently the newest method. Popularized by Joseph Felsenstein, Seattle, Washington.
 Maximum Likelihood This presentation is based almost entirely on Peter G. Fosters - "The Idiot s Guide to the Zen of Likelihood in a Nutshell in Seven Days for Dummies, Unleashed. http://www.bioinf.org/molsys/data/idiots.pdf
Maximum Likelihood This presentation is based almost entirely on Peter G. Fosters - "The Idiot s Guide to the Zen of Likelihood in a Nutshell in Seven Days for Dummies, Unleashed. http://www.bioinf.org/molsys/data/idiots.pdf
Similarity or Identity? When are molecules similar?
 Similarity or Identity? When are molecules similar? Mapping Identity A -> A T -> T G -> G C -> C or Leu -> Leu Pro -> Pro Arg -> Arg Phe -> Phe etc If we map similarity using identity, how similar are
Similarity or Identity? When are molecules similar? Mapping Identity A -> A T -> T G -> G C -> C or Leu -> Leu Pro -> Pro Arg -> Arg Phe -> Phe etc If we map similarity using identity, how similar are
BMI/CS 776 Lecture 4. Colin Dewey
 BMI/CS 776 Lecture 4 Colin Dewey 2007.02.01 Outline Common nucleotide substitution models Directed graphical models Ancestral sequence inference Poisson process continuous Markov process X t0 X t1 X t2
BMI/CS 776 Lecture 4 Colin Dewey 2007.02.01 Outline Common nucleotide substitution models Directed graphical models Ancestral sequence inference Poisson process continuous Markov process X t0 X t1 X t2
Lecture 4: Evolutionary models and substitution matrices (PAM and BLOSUM).
 1 Bioinformatics: In-depth PROBABILITY & STATISTICS Spring Semester 2011 University of Zürich and ETH Zürich Lecture 4: Evolutionary models and substitution matrices (PAM and BLOSUM). Dr. Stefanie Muff
1 Bioinformatics: In-depth PROBABILITY & STATISTICS Spring Semester 2011 University of Zürich and ETH Zürich Lecture 4: Evolutionary models and substitution matrices (PAM and BLOSUM). Dr. Stefanie Muff
Proteins: Characteristics and Properties of Amino Acids
 SBI4U:Biochemistry Macromolecules Eachaminoacidhasatleastoneamineandoneacidfunctionalgroupasthe nameimplies.thedifferentpropertiesresultfromvariationsinthestructuresof differentrgroups.thergroupisoftenreferredtoastheaminoacidsidechain.
SBI4U:Biochemistry Macromolecules Eachaminoacidhasatleastoneamineandoneacidfunctionalgroupasthe nameimplies.thedifferentpropertiesresultfromvariationsinthestructuresof differentrgroups.thergroupisoftenreferredtoastheaminoacidsidechain.
Dr. Amira A. AL-Hosary
 Phylogenetic analysis Amira A. AL-Hosary PhD of infectious diseases Department of Animal Medicine (Infectious Diseases) Faculty of Veterinary Medicine Assiut University-Egypt Phylogenetic Basics: Biological
Phylogenetic analysis Amira A. AL-Hosary PhD of infectious diseases Department of Animal Medicine (Infectious Diseases) Faculty of Veterinary Medicine Assiut University-Egypt Phylogenetic Basics: Biological
Amino Acid Side Chain Induced Selectivity in the Hydrolysis of Peptides Catalyzed by a Zr(IV)-Substituted Wells-Dawson Type Polyoxometalate
 Amino Acid Side Chain Induced Selectivity in the Hydrolysis of Peptides Catalyzed by a Zr(IV)-Substituted Wells-Dawson Type Polyoxometalate Stef Vanhaecht, Gregory Absillis, Tatjana N. Parac-Vogt* Department
Amino Acid Side Chain Induced Selectivity in the Hydrolysis of Peptides Catalyzed by a Zr(IV)-Substituted Wells-Dawson Type Polyoxometalate Stef Vanhaecht, Gregory Absillis, Tatjana N. Parac-Vogt* Department
Other Methods for Generating Ions 1. MALDI matrix assisted laser desorption ionization MS 2. Spray ionization techniques 3. Fast atom bombardment 4.
 Other Methods for Generating Ions 1. MALDI matrix assisted laser desorption ionization MS 2. Spray ionization techniques 3. Fast atom bombardment 4. Field Desorption 5. MS MS techniques Matrix assisted
Other Methods for Generating Ions 1. MALDI matrix assisted laser desorption ionization MS 2. Spray ionization techniques 3. Fast atom bombardment 4. Field Desorption 5. MS MS techniques Matrix assisted
Major Types of Association of Proteins with Cell Membranes. From Alberts et al
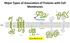 Major Types of Association of Proteins with Cell Membranes From Alberts et al Proteins Are Polymers of Amino Acids Peptide Bond Formation Amino Acid central carbon atom to which are attached amino group
Major Types of Association of Proteins with Cell Membranes From Alberts et al Proteins Are Polymers of Amino Acids Peptide Bond Formation Amino Acid central carbon atom to which are attached amino group
Get started on your Cornell notes right away
 UNIT 10: Evolution DAYSHEET 100: Introduction to Evolution Name Biology I Date: Bellringer: 1. Get out your technology and go to www.biomonsters.com 2. Click the Biomonsters Cinema link. 3. Click the CHS
UNIT 10: Evolution DAYSHEET 100: Introduction to Evolution Name Biology I Date: Bellringer: 1. Get out your technology and go to www.biomonsters.com 2. Click the Biomonsters Cinema link. 3. Click the CHS
7.012 Problem Set 1. i) What are two main differences between prokaryotic cells and eukaryotic cells?
 ame 7.01 Problem Set 1 Section Question 1 a) What are the four major types of biological molecules discussed in lecture? Give one important function of each type of biological molecule in the cell? b)
ame 7.01 Problem Set 1 Section Question 1 a) What are the four major types of biological molecules discussed in lecture? Give one important function of each type of biological molecule in the cell? b)
"Nothing in biology makes sense except in the light of evolution Theodosius Dobzhansky
 MOLECULAR PHYLOGENY "Nothing in biology makes sense except in the light of evolution Theodosius Dobzhansky EVOLUTION - theory that groups of organisms change over time so that descendeants differ structurally
MOLECULAR PHYLOGENY "Nothing in biology makes sense except in the light of evolution Theodosius Dobzhansky EVOLUTION - theory that groups of organisms change over time so that descendeants differ structurally
Advanced Topics in RNA and DNA. DNA Microarrays Aptamers
 Quiz 1 Advanced Topics in RNA and DNA DNA Microarrays Aptamers 2 Quantifying mrna levels to asses protein expression 3 The DNA Microarray Experiment 4 Application of DNA Microarrays 5 Some applications
Quiz 1 Advanced Topics in RNA and DNA DNA Microarrays Aptamers 2 Quantifying mrna levels to asses protein expression 3 The DNA Microarray Experiment 4 Application of DNA Microarrays 5 Some applications
Translation. A ribosome, mrna, and trna.
 Translation The basic processes of translation are conserved among prokaryotes and eukaryotes. Prokaryotic Translation A ribosome, mrna, and trna. In the initiation of translation in prokaryotes, the Shine-Dalgarno
Translation The basic processes of translation are conserved among prokaryotes and eukaryotes. Prokaryotic Translation A ribosome, mrna, and trna. In the initiation of translation in prokaryotes, the Shine-Dalgarno
Lecture 4. Models of DNA and protein change. Likelihood methods
 Lecture 4. Models of DNA and protein change. Likelihood methods Joe Felsenstein Department of Genome Sciences and Department of Biology Lecture 4. Models of DNA and protein change. Likelihood methods p.1/39
Lecture 4. Models of DNA and protein change. Likelihood methods Joe Felsenstein Department of Genome Sciences and Department of Biology Lecture 4. Models of DNA and protein change. Likelihood methods p.1/39
MATHEMATICAL MODELS - Vol. III - Mathematical Modeling and the Human Genome - Hilary S. Booth MATHEMATICAL MODELING AND THE HUMAN GENOME
 MATHEMATICAL MODELING AND THE HUMAN GENOME Hilary S. Booth Australian National University, Australia Keywords: Human genome, DNA, bioinformatics, sequence analysis, evolution. Contents 1. Introduction:
MATHEMATICAL MODELING AND THE HUMAN GENOME Hilary S. Booth Australian National University, Australia Keywords: Human genome, DNA, bioinformatics, sequence analysis, evolution. Contents 1. Introduction:
Molecular Evolution and Comparative Genomics
 Molecular Evolution and Comparative Genomics --- the phylogenetic HMM model 10-810, CMB lecture 5---Eric Xing Some important dates in history (billions of years ago) Origin of the universe 15 ±4 Formation
Molecular Evolution and Comparative Genomics --- the phylogenetic HMM model 10-810, CMB lecture 5---Eric Xing Some important dates in history (billions of years ago) Origin of the universe 15 ±4 Formation
Phylogeny Estimation and Hypothesis Testing using Maximum Likelihood
 Phylogeny Estimation and Hypothesis Testing using Maximum Likelihood For: Prof. Partensky Group: Jimin zhu Rama Sharma Sravanthi Polsani Xin Gong Shlomit klopman April. 7. 2003 Table of Contents Introduction...3
Phylogeny Estimation and Hypothesis Testing using Maximum Likelihood For: Prof. Partensky Group: Jimin zhu Rama Sharma Sravanthi Polsani Xin Gong Shlomit klopman April. 7. 2003 Table of Contents Introduction...3
O 3 O 4 O 5. q 3. q 4. Transition
 Hidden Markov Models Hidden Markov models (HMM) were developed in the early part of the 1970 s and at that time mostly applied in the area of computerized speech recognition. They are first described in
Hidden Markov Models Hidden Markov models (HMM) were developed in the early part of the 1970 s and at that time mostly applied in the area of computerized speech recognition. They are first described in
5. DISCRETE DYNAMICAL SYSTEMS
 5 DISCRETE DYNAMICAL SYSTEMS In Chapter 5, we considered the dynamics of systems consisting of a single quantity in either discrete or continuous time Here we consider the dynamics of certain systems consisting
5 DISCRETE DYNAMICAL SYSTEMS In Chapter 5, we considered the dynamics of systems consisting of a single quantity in either discrete or continuous time Here we consider the dynamics of certain systems consisting
The translation machinery of the cell works with triples of types of RNA bases. Any triple of RNA bases is known as a codon. The set of codons is
 Relations Supplement to Chapter 2 of Steinhart, E. (2009) More Precisely: The Math You Need to Do Philosophy. Broadview Press. Copyright (C) 2009 Eric Steinhart. Non-commercial educational use encouraged!
Relations Supplement to Chapter 2 of Steinhart, E. (2009) More Precisely: The Math You Need to Do Philosophy. Broadview Press. Copyright (C) 2009 Eric Steinhart. Non-commercial educational use encouraged!
C.DARWIN ( )
 C.DARWIN (1809-1882) LAMARCK Each evolutionary lineage has evolved, transforming itself, from a ancestor appeared by spontaneous generation DARWIN All organisms are historically interconnected. Their relationships
C.DARWIN (1809-1882) LAMARCK Each evolutionary lineage has evolved, transforming itself, from a ancestor appeared by spontaneous generation DARWIN All organisms are historically interconnected. Their relationships
Some of these slides have been borrowed from Dr. Paul Lewis, Dr. Joe Felsenstein. Thanks!
 Some of these slides have been borrowed from Dr. Paul Lewis, Dr. Joe Felsenstein. Thanks! Paul has many great tools for teaching phylogenetics at his web site: http://hydrodictyon.eeb.uconn.edu/people/plewis
Some of these slides have been borrowed from Dr. Paul Lewis, Dr. Joe Felsenstein. Thanks! Paul has many great tools for teaching phylogenetics at his web site: http://hydrodictyon.eeb.uconn.edu/people/plewis
CSE 549: Computational Biology. Substitution Matrices
 CSE 9: Computational Biology Substitution Matrices How should we score alignments So far, we ve looked at arbitrary schemes for scoring mutations. How can we assign scores in a more meaningful way? Are
CSE 9: Computational Biology Substitution Matrices How should we score alignments So far, we ve looked at arbitrary schemes for scoring mutations. How can we assign scores in a more meaningful way? Are
Week 5: Distance methods, DNA and protein models
 Week 5: Distance methods, DNA and protein models Genome 570 February, 2016 Week 5: Distance methods, DNA and protein models p.1/69 A tree and the expected distances it predicts E A 0.08 0.05 0.06 0.03
Week 5: Distance methods, DNA and protein models Genome 570 February, 2016 Week 5: Distance methods, DNA and protein models p.1/69 A tree and the expected distances it predicts E A 0.08 0.05 0.06 0.03
Molecular evolution 2. Please sit in row K or forward
 Molecular evolution 2 Please sit in row K or forward RBFD: cat, mouse, parasite Toxoplamsa gondii cyst in a mouse brain http://phenomena.nationalgeographic.com/2013/04/26/mind-bending-parasite-permanently-quells-cat-fear-in-mice/
Molecular evolution 2 Please sit in row K or forward RBFD: cat, mouse, parasite Toxoplamsa gondii cyst in a mouse brain http://phenomena.nationalgeographic.com/2013/04/26/mind-bending-parasite-permanently-quells-cat-fear-in-mice/
Sara C. Madeira. Universidade da Beira Interior. (Thanks to Ana Teresa Freitas, IST for useful resources on this subject)
 Bioinformática Sequence Alignment Pairwise Sequence Alignment Universidade da Beira Interior (Thanks to Ana Teresa Freitas, IST for useful resources on this subject) 1 16/3/29 & 23/3/29 27/4/29 Outline
Bioinformática Sequence Alignment Pairwise Sequence Alignment Universidade da Beira Interior (Thanks to Ana Teresa Freitas, IST for useful resources on this subject) 1 16/3/29 & 23/3/29 27/4/29 Outline
Energy Minimization of Protein Tertiary Structure by Parallel Simulated Annealing using Genetic Crossover
 Minimization of Protein Tertiary Structure by Parallel Simulated Annealing using Genetic Crossover Tomoyuki Hiroyasu, Mitsunori Miki, Shinya Ogura, Keiko Aoi, Takeshi Yoshida, Yuko Okamoto Jack Dongarra
Minimization of Protein Tertiary Structure by Parallel Simulated Annealing using Genetic Crossover Tomoyuki Hiroyasu, Mitsunori Miki, Shinya Ogura, Keiko Aoi, Takeshi Yoshida, Yuko Okamoto Jack Dongarra
Lecture 15: Realities of Genome Assembly Protein Sequencing
 Lecture 15: Realities of Genome Assembly Protein Sequencing Study Chapter 8.10-8.15 1 Euler s Theorems A graph is balanced if for every vertex the number of incoming edges equals to the number of outgoing
Lecture 15: Realities of Genome Assembly Protein Sequencing Study Chapter 8.10-8.15 1 Euler s Theorems A graph is balanced if for every vertex the number of incoming edges equals to the number of outgoing
EVOLUTIONARY DISTANCES
 EVOLUTIONARY DISTANCES FROM STRINGS TO TREES Luca Bortolussi 1 1 Dipartimento di Matematica ed Informatica Università degli studi di Trieste luca@dmi.units.it Trieste, 14 th November 2007 OUTLINE 1 STRINGS:
EVOLUTIONARY DISTANCES FROM STRINGS TO TREES Luca Bortolussi 1 1 Dipartimento di Matematica ed Informatica Università degli studi di Trieste luca@dmi.units.it Trieste, 14 th November 2007 OUTLINE 1 STRINGS:
C CH 3 N C COOH. Write the structural formulas of all of the dipeptides that they could form with each other.
 hapter 25 Biochemistry oncept heck 25.1 Two common amino acids are 3 2 N alanine 3 2 N threonine Write the structural formulas of all of the dipeptides that they could form with each other. The carboxyl
hapter 25 Biochemistry oncept heck 25.1 Two common amino acids are 3 2 N alanine 3 2 N threonine Write the structural formulas of all of the dipeptides that they could form with each other. The carboxyl
Natural selection on the molecular level
 Natural selection on the molecular level Fundamentals of molecular evolution How DNA and protein sequences evolve? Genetic variability in evolution } Mutations } forming novel alleles } Inversions } change
Natural selection on the molecular level Fundamentals of molecular evolution How DNA and protein sequences evolve? Genetic variability in evolution } Mutations } forming novel alleles } Inversions } change
Markov Chains. Sarah Filippi Department of Statistics TA: Luke Kelly
 Markov Chains Sarah Filippi Department of Statistics http://www.stats.ox.ac.uk/~filippi TA: Luke Kelly With grateful acknowledgements to Prof. Yee Whye Teh's slides from 2013 14. Schedule 09:30-10:30 Lecture:
Markov Chains Sarah Filippi Department of Statistics http://www.stats.ox.ac.uk/~filippi TA: Luke Kelly With grateful acknowledgements to Prof. Yee Whye Teh's slides from 2013 14. Schedule 09:30-10:30 Lecture:
Molecular Population Genetics
 Molecular Population Genetics The 10 th CJK Bioinformatics Training Course in Jeju, Korea May, 2011 Yoshio Tateno National Institute of Genetics/POSTECH Top 10 species in INSDC (as of April, 2011) CONTENTS
Molecular Population Genetics The 10 th CJK Bioinformatics Training Course in Jeju, Korea May, 2011 Yoshio Tateno National Institute of Genetics/POSTECH Top 10 species in INSDC (as of April, 2011) CONTENTS
Packing of Secondary Structures
 7.88 Lecture Notes - 4 7.24/7.88J/5.48J The Protein Folding and Human Disease Professor Gossard Retrieving, Viewing Protein Structures from the Protein Data Base Helix helix packing Packing of Secondary
7.88 Lecture Notes - 4 7.24/7.88J/5.48J The Protein Folding and Human Disease Professor Gossard Retrieving, Viewing Protein Structures from the Protein Data Base Helix helix packing Packing of Secondary
How should we go about modeling this? Model parameters? Time Substitution rate Can we observe time or subst. rate? What can we observe?
 How should we go about modeling this? gorilla GAAGTCCTTGAGAAATAAACTGCACACACTGG orangutan GGACTCCTTGAGAAATAAACTGCACACACTGG Model parameters? Time Substitution rate Can we observe time or subst. rate? What
How should we go about modeling this? gorilla GAAGTCCTTGAGAAATAAACTGCACACACTGG orangutan GGACTCCTTGAGAAATAAACTGCACACACTGG Model parameters? Time Substitution rate Can we observe time or subst. rate? What
Introduction to Comparative Protein Modeling. Chapter 4 Part I
 Introduction to Comparative Protein Modeling Chapter 4 Part I 1 Information on Proteins Each modeling study depends on the quality of the known experimental data. Basis of the model Search in the literature
Introduction to Comparative Protein Modeling Chapter 4 Part I 1 Information on Proteins Each modeling study depends on the quality of the known experimental data. Basis of the model Search in the literature
 Tree of Life iological Sequence nalysis Chapter http://tolweb.org/tree/ Phylogenetic Prediction ll organisms on Earth have a common ancestor. ll species are related. The relationship is called a phylogeny
Tree of Life iological Sequence nalysis Chapter http://tolweb.org/tree/ Phylogenetic Prediction ll organisms on Earth have a common ancestor. ll species are related. The relationship is called a phylogeny
Bustamante et al., Supplementary Nature Manuscript # 1 out of 9 Information #
 Bustamante et al., Supplementary Nature Manuscript # 1 out of 9 Details of PRF Methodology In the Poisson Random Field PRF) model, it is assumed that non-synonymous mutations at a given gene are either
Bustamante et al., Supplementary Nature Manuscript # 1 out of 9 Details of PRF Methodology In the Poisson Random Field PRF) model, it is assumed that non-synonymous mutations at a given gene are either
Substitution = Mutation followed. by Fixation. Common Ancestor ACGATC 1:A G 2:C A GAGATC 3:G A 6:C T 5:T C 4:A C GAAATT 1:G A
 GAGATC 3:G A 6:C T Common Ancestor ACGATC 1:A G 2:C A Substitution = Mutation followed 5:T C by Fixation GAAATT 4:A C 1:G A AAAATT GAAATT GAGCTC ACGACC Chimp Human Gorilla Gibbon AAAATT GAAATT GAGCTC ACGACC
GAGATC 3:G A 6:C T Common Ancestor ACGATC 1:A G 2:C A Substitution = Mutation followed 5:T C by Fixation GAAATT 4:A C 1:G A AAAATT GAAATT GAGCTC ACGACC Chimp Human Gorilla Gibbon AAAATT GAAATT GAGCTC ACGACC
Phylogenetic Trees. What They Are Why We Do It & How To Do It. Presented by Amy Harris Dr Brad Morantz
 Phylogenetic Trees What They Are Why We Do It & How To Do It Presented by Amy Harris Dr Brad Morantz Overview What is a phylogenetic tree Why do we do it How do we do it Methods and programs Parallels
Phylogenetic Trees What They Are Why We Do It & How To Do It Presented by Amy Harris Dr Brad Morantz Overview What is a phylogenetic tree Why do we do it How do we do it Methods and programs Parallels
Genomics and bioinformatics summary. Finding genes -- computer searches
 Genomics and bioinformatics summary 1. Gene finding: computer searches, cdnas, ESTs, 2. Microarrays 3. Use BLAST to find homologous sequences 4. Multiple sequence alignments (MSAs) 5. Trees quantify sequence
Genomics and bioinformatics summary 1. Gene finding: computer searches, cdnas, ESTs, 2. Microarrays 3. Use BLAST to find homologous sequences 4. Multiple sequence alignments (MSAs) 5. Trees quantify sequence
Cladistics and Bioinformatics Questions 2013
 AP Biology Name Cladistics and Bioinformatics Questions 2013 1. The following table shows the percentage similarity in sequences of nucleotides from a homologous gene derived from five different species
AP Biology Name Cladistics and Bioinformatics Questions 2013 1. The following table shows the percentage similarity in sequences of nucleotides from a homologous gene derived from five different species
Molecular Evolution and Phylogenetic Analysis
 Molecular Evolution and Phylogenetic Analysis David Pollock and Richard Goldstein Introduction All of biology is based on evolution. Evolution is the organizing principle for understanding the shared history
Molecular Evolution and Phylogenetic Analysis David Pollock and Richard Goldstein Introduction All of biology is based on evolution. Evolution is the organizing principle for understanding the shared history
Any protein that can be labelled by both procedures must be a transmembrane protein.
 1. What kind of experimental evidence would indicate that a protein crosses from one side of the membrane to the other? Regions of polypeptide part exposed on the outside of the membrane can be probed
1. What kind of experimental evidence would indicate that a protein crosses from one side of the membrane to the other? Regions of polypeptide part exposed on the outside of the membrane can be probed
Q1) Explain how background selection and genetic hitchhiking could explain the positive correlation between genetic diversity and recombination rate.
 OEB 242 Exam Practice Problems Answer Key Q1) Explain how background selection and genetic hitchhiking could explain the positive correlation between genetic diversity and recombination rate. First, recall
OEB 242 Exam Practice Problems Answer Key Q1) Explain how background selection and genetic hitchhiking could explain the positive correlation between genetic diversity and recombination rate. First, recall
Endowed with an Extra Sense : Mathematics and Evolution
 Endowed with an Extra Sense : Mathematics and Evolution Todd Parsons Laboratoire de Probabilités et Modèles Aléatoires - Université Pierre et Marie Curie Center for Interdisciplinary Research in Biology
Endowed with an Extra Sense : Mathematics and Evolution Todd Parsons Laboratoire de Probabilités et Modèles Aléatoires - Université Pierre et Marie Curie Center for Interdisciplinary Research in Biology
Lab 2A--Life on Earth
 Lab 2A--Life on Earth Geology 1402 Chapters 3 & 7 in the textbook 1 A comment Many people including professional scientist are skeptical of evolution or outright reject it. I am not attempting to change
Lab 2A--Life on Earth Geology 1402 Chapters 3 & 7 in the textbook 1 A comment Many people including professional scientist are skeptical of evolution or outright reject it. I am not attempting to change
Peptides And Proteins
 Kevin Burgess, May 3, 2017 1 Peptides And Proteins from chapter(s) in the recommended text A. Introduction B. omenclature And Conventions by amide bonds. on the left, right. 2 -terminal C-terminal triglycine
Kevin Burgess, May 3, 2017 1 Peptides And Proteins from chapter(s) in the recommended text A. Introduction B. omenclature And Conventions by amide bonds. on the left, right. 2 -terminal C-terminal triglycine
π b = a π a P a,b = Q a,b δ + o(δ) = 1 + Q a,a δ + o(δ) = I 4 + Qδ + o(δ),
 ABC estimation of the scaled effective population size. Geoff Nicholls, DTC 07/05/08 Refer to http://www.stats.ox.ac.uk/~nicholls/dtc/tt08/ for material. We will begin with a practical on ABC estimation
ABC estimation of the scaled effective population size. Geoff Nicholls, DTC 07/05/08 Refer to http://www.stats.ox.ac.uk/~nicholls/dtc/tt08/ for material. We will begin with a practical on ABC estimation
Bioinformatics 1. Sepp Hochreiter. Biology, Sequences, Phylogenetics Part 4. Bioinformatics 1: Biology, Sequences, Phylogenetics
 Bioinformatics 1 Biology, Sequences, Phylogenetics Part 4 Sepp Hochreiter Klausur Mo. 30.01.2011 Zeit: 15:30 17:00 Raum: HS14 Anmeldung Kusss Contents Methods and Bootstrapping of Maximum Methods Methods
Bioinformatics 1 Biology, Sequences, Phylogenetics Part 4 Sepp Hochreiter Klausur Mo. 30.01.2011 Zeit: 15:30 17:00 Raum: HS14 Anmeldung Kusss Contents Methods and Bootstrapping of Maximum Methods Methods
C3020 Molecular Evolution. Exercises #3: Phylogenetics
 C3020 Molecular Evolution Exercises #3: Phylogenetics Consider the following sequences for five taxa 1-5 and the known outgroup O, which has the ancestral states (note that sequence 3 has changed from
C3020 Molecular Evolution Exercises #3: Phylogenetics Consider the following sequences for five taxa 1-5 and the known outgroup O, which has the ancestral states (note that sequence 3 has changed from
Ranjit P. Bahadur Assistant Professor Department of Biotechnology Indian Institute of Technology Kharagpur, India. 1 st November, 2013
 Hydration of protein-rna recognition sites Ranjit P. Bahadur Assistant Professor Department of Biotechnology Indian Institute of Technology Kharagpur, India 1 st November, 2013 Central Dogma of life DNA
Hydration of protein-rna recognition sites Ranjit P. Bahadur Assistant Professor Department of Biotechnology Indian Institute of Technology Kharagpur, India 1 st November, 2013 Central Dogma of life DNA
Introduction to the Ribosome Overview of protein synthesis on the ribosome Prof. Anders Liljas
 Introduction to the Ribosome Molecular Biophysics Lund University 1 A B C D E F G H I J Genome Protein aa1 aa2 aa3 aa4 aa5 aa6 aa7 aa10 aa9 aa8 aa11 aa12 aa13 a a 14 How is a polypeptide synthesized? 2
Introduction to the Ribosome Molecular Biophysics Lund University 1 A B C D E F G H I J Genome Protein aa1 aa2 aa3 aa4 aa5 aa6 aa7 aa10 aa9 aa8 aa11 aa12 aa13 a a 14 How is a polypeptide synthesized? 2
Biol478/ August
 Biol478/595 29 August # Day Inst. Topic Hwk Reading August 1 M 25 MG Introduction 2 W 27 MG Sequences and Evolution Handouts 3 F 29 MG Sequences and Evolution September M 1 Labor Day 4 W 3 MG Database
Biol478/595 29 August # Day Inst. Topic Hwk Reading August 1 M 25 MG Introduction 2 W 27 MG Sequences and Evolution Handouts 3 F 29 MG Sequences and Evolution September M 1 Labor Day 4 W 3 MG Database
Maximum Likelihood Tree Estimation. Carrie Tribble IB Feb 2018
 Maximum Likelihood Tree Estimation Carrie Tribble IB 200 9 Feb 2018 Outline 1. Tree building process under maximum likelihood 2. Key differences between maximum likelihood and parsimony 3. Some fancy extras
Maximum Likelihood Tree Estimation Carrie Tribble IB 200 9 Feb 2018 Outline 1. Tree building process under maximum likelihood 2. Key differences between maximum likelihood and parsimony 3. Some fancy extras
Phylogenetic inference
 Phylogenetic inference Bas E. Dutilh Systems Biology: Bioinformatic Data Analysis Utrecht University, March 7 th 016 After this lecture, you can discuss (dis-) advantages of different information types
Phylogenetic inference Bas E. Dutilh Systems Biology: Bioinformatic Data Analysis Utrecht University, March 7 th 016 After this lecture, you can discuss (dis-) advantages of different information types
Physiochemical Properties of Residues
 Physiochemical Properties of Residues Various Sources C N Cα R Slide 1 Conformational Propensities Conformational Propensity is the frequency in which a residue adopts a given conformation (in a polypeptide)
Physiochemical Properties of Residues Various Sources C N Cα R Slide 1 Conformational Propensities Conformational Propensity is the frequency in which a residue adopts a given conformation (in a polypeptide)
Processes of Evolution
 15 Processes of Evolution Forces of Evolution Concept 15.4 Selection Can Be Stabilizing, Directional, or Disruptive Natural selection can act on quantitative traits in three ways: Stabilizing selection
15 Processes of Evolution Forces of Evolution Concept 15.4 Selection Can Be Stabilizing, Directional, or Disruptive Natural selection can act on quantitative traits in three ways: Stabilizing selection
Chapter 9 DNA recognition by eukaryotic transcription factors
 Chapter 9 DNA recognition by eukaryotic transcription factors TRANSCRIPTION 101 Eukaryotic RNA polymerases RNA polymerase RNA polymerase I RNA polymerase II RNA polymerase III RNA polymerase IV Function
Chapter 9 DNA recognition by eukaryotic transcription factors TRANSCRIPTION 101 Eukaryotic RNA polymerases RNA polymerase RNA polymerase I RNA polymerase II RNA polymerase III RNA polymerase IV Function
Lecture 10: Cyclins, cyclin kinases and cell division
 Chem*3560 Lecture 10: Cyclins, cyclin kinases and cell division The eukaryotic cell cycle Actively growing mammalian cells divide roughly every 24 hours, and follow a precise sequence of events know as
Chem*3560 Lecture 10: Cyclins, cyclin kinases and cell division The eukaryotic cell cycle Actively growing mammalian cells divide roughly every 24 hours, and follow a precise sequence of events know as
Videos. Bozeman, transcription and translation: https://youtu.be/h3b9arupxzg Crashcourse: Transcription and Translation - https://youtu.
 Translation Translation Videos Bozeman, transcription and translation: https://youtu.be/h3b9arupxzg Crashcourse: Transcription and Translation - https://youtu.be/itsb2sqr-r0 Translation Translation The
Translation Translation Videos Bozeman, transcription and translation: https://youtu.be/h3b9arupxzg Crashcourse: Transcription and Translation - https://youtu.be/itsb2sqr-r0 Translation Translation The
-1- HO H O H. β-d-galactopyranose (A) OMe CH 3 I. MeO. Ag 2 O. O Me HNO 3. OAc (CH 3 CO) 2 O. AcO. pyridine. O Ac. NaBH 4 H 2 O. MeOH. dry HCl.
 -1-1. Draw structures for the products you would expect to obtain from reaction of β-dgalactopyranose () with each of the reagents below. Be sure to include all relevant stereochemistry. (40 pts). β-d-galactopyranose
-1-1. Draw structures for the products you would expect to obtain from reaction of β-dgalactopyranose () with each of the reagents below. Be sure to include all relevant stereochemistry. (40 pts). β-d-galactopyranose
Protein structure. Protein structure. Amino acid residue. Cell communication channel. Bioinformatics Methods
 Cell communication channel Bioinformatics Methods Iosif Vaisman Email: ivaisman@gmu.edu SEQUENCE STRUCTURE DNA Sequence Protein Sequence Protein Structure Protein structure ATGAAATTTGGAAACTTCCTTCTCACTTATCAGCCACCT...
Cell communication channel Bioinformatics Methods Iosif Vaisman Email: ivaisman@gmu.edu SEQUENCE STRUCTURE DNA Sequence Protein Sequence Protein Structure Protein structure ATGAAATTTGGAAACTTCCTTCTCACTTATCAGCCACCT...
Supplementary Figure 3 a. Structural comparison between the two determined structures for the IL 23:MA12 complex. The overall RMSD between the two
 Supplementary Figure 1. Biopanningg and clone enrichment of Alphabody binders against human IL 23. Positive clones in i phage ELISA with optical density (OD) 3 times higher than background are shown for
Supplementary Figure 1. Biopanningg and clone enrichment of Alphabody binders against human IL 23. Positive clones in i phage ELISA with optical density (OD) 3 times higher than background are shown for
BINF6201/8201. Molecular phylogenetic methods
 BINF60/80 Molecular phylogenetic methods 0-7-06 Phylogenetics Ø According to the evolutionary theory, all life forms on this planet are related to one another by descent. Ø Traditionally, phylogenetics
BINF60/80 Molecular phylogenetic methods 0-7-06 Phylogenetics Ø According to the evolutionary theory, all life forms on this planet are related to one another by descent. Ø Traditionally, phylogenetics
Module: Sequence Alignment Theory and Applications Session: Introduction to Searching and Sequence Alignment
 Module: Sequence Alignment Theory and Applications Session: Introduction to Searching and Sequence Alignment Introduction to Bioinformatics online course : IBT Jonathan Kayondo Learning Objectives Understand
Module: Sequence Alignment Theory and Applications Session: Introduction to Searching and Sequence Alignment Introduction to Bioinformatics online course : IBT Jonathan Kayondo Learning Objectives Understand
Molecular Evolution & Phylogenetics Traits, phylogenies, evolutionary models and divergence time between sequences
 Molecular Evolution & Phylogenetics Traits, phylogenies, evolutionary models and divergence time between sequences Basic Bioinformatics Workshop, ILRI Addis Ababa, 12 December 2017 1 Learning Objectives
Molecular Evolution & Phylogenetics Traits, phylogenies, evolutionary models and divergence time between sequences Basic Bioinformatics Workshop, ILRI Addis Ababa, 12 December 2017 1 Learning Objectives
