Singapore International Mathematical Olympiad 2008 Senior Team Training. Take Home Test Solutions. 15x 2 7y 2 = 9 y 2 0 (mod 3) x 0 (mod 3).
|
|
|
- Merryl Hutchinson
- 6 years ago
- Views:
Transcription
1 Singapore International Mathematical Olympiad 2008 Senior Team Training Take Home Test Solutions. Show that the equation 5x 2 7y 2 = 9 has no solution in integers. If the equation has a solution in integer, then 5x 2 7y 2 = 9 y 2 0 (mod 3) y 0 (mod 3). Hence y = 3y for some integer y. This implies that 5x 2 7(3y ) 2 = 9 5x 2 2y 2 = 3 2x 2 0 (mod 3) x 0 (mod 3). Hence x = 3x for some integer x. This implies that 5(3x ) 2 7(3y ) 2 = 9 5x 2 7y 2 = y 2 (mod 3) y 2 2 (mod 3). The last congruence is impossible. Hence the given equation has no solution in integers. 2. Let n and k be positive integers. Prove that is divisible by n 5 +. We prove by induction on k: When k =, we have (n 4 )(n 3 n 2 + n ) k + (n + )n 4k (n 4 )(n 3 n 2 + n ) + (n + )n 3 = n 7 n 6 + n 5 + n 2 n + = n 2 (n 5 + ) n(n 5 + ) + n 5 + = (n 5 + )(n 2 n + ).
2 2 So the statement is true for k =. Now assume that the statement is true for k and consider the case k +, we have (n 4 )(n 3 n 2 + n ) k+ + (n + )n 4(k+) = (n 4 )(n 3 n 2 + n ) k (n 3 n 2 + n ) + (n + )n 4k n 4 = [(n 4 )(n 3 n 2 + n ) k (n 3 n 2 + n ) + (n + )n 4k (n 3 n 2 + n )] + [(n + )n 4k n 4 (n + )n 4k (n 3 n 2 + n )] = (n 3 n 2 + n )[(n 4 )(n 3 n 2 + n ) k + (n + )n 4k ] + n 4k (n + )(n 4 n 3 + n 2 n + ) = (n 3 n 2 + n )[(n 4 )(n 3 n 2 + n ) k + (n + )n 4k ] + n 4k (n 5 + ). This is divisible by n 5 + by induction hypothesis. Hence the statement is true for k +. This completes the induction. 3. Let f(x) = (x + ) p (x 3) q where p and q are positive integers. = x n + a x n + a 2 x n a n x + a n, () Given that a = a 2, prove that 3n is a perfect square. (2) (b) Prove that there exist infinitely many pairs (p, q) of positive integers p and q such that the equality a = a 2 is valid for the polynomial p(x). (Belarussian 2003) (a) Since (x + ) p = x p + px p p(p ) + x p (x 3) q = x q 3qx q 9q(q ) + x q 2 +, 2 we have n = p + q, a = p 3q, a 2 = 9q2 9q+p 2 p 6pq 2. Therefore a = a 2 Since n = p + q, we are done. 2p 6q = 9q 2 9q + p 2 p 6pq (3q p) 2 = 3(p + q). (b) This is equivalent to showing that the equation (3q p) 2 = 3(p + q) has an infinite family of solutions in positive integers. Treating this as a
3 quadratic equation in p, 9p 2 (6q + 3)p + (9q 2 3q) = 0 we have 48q + 9 p = 6q + 3 ±. 2 Thus 48q + 9 is an odd square. Hence 48q + 9 = (2k + ) 2, or q = k2 + k 2 2 Let k = 2t +, then q = 2t 2 + 3t and p = 36t 2 3t, where t N is the required infinite family. 4. Show that if m < n, then 2 2m + divides 2 2n. Hence deduce that 2 2m + and 2 2n + are relatively prime. Conclude that there are infinitely many primes. If m < n then n = m + k for some integer k, so we have 2 2n = 2 2m 2 k = (2 2m + )(2 2m (2 k ) 2 2m (2 k 2) m ). Hence 2 2m + divides 2 2n. Let d = gcd(2 2m +, 2 2n + ). By above, we have 3 2 2n + = (2 2n ) + 2 = l(2 2m + ) + 2 for some integer l d 2 (since d (2 2m + ) and d (2 2n + )) d = or d = 2 d = (since 2 2m + is odd) Thus gcd(2 2m +, 2 2n + ) =, i.e. 2 2m + and 2 2n + are relatively prime. For any positive integer n, let p n be a prime divisor of 2 2n +. For any m, n with n m, we have p n p m since 2 2n + and 2 2m + are relatively prime. Hence {p, p 2, p 3...} is an infinite set of primes. 5. Let x, y, z be positive numbers so that xyz =. Prove that x + y + z 3 z x + 3 x y + 3 y z. By AM-GM inequality, y + z + z 3 3 yz 2 = 3 3 z x, x + x + z 3 3 x 2 z = 3 3 x y,
4 4 and x + y + y 3 3 xy 2 = 3 3 y z. Summing the three inequalities gives the desired result. 6. Let p, p 2,..., p n (n 2) be any rearrangement of, 2,... n. Show that p + p 2 + p 2 + p > n p n + p n n + 2. Since AM HM, Thus n [(p + p 2 ) + (p 2 + p 3 ) + + (p n + p n )] { [ ]}. + + n p + p 2 p n + p n + + p + p 2 p n + p n (n ) 2 2(p + + p n ) p p n (n )2 n(n + ) 3 = (n ) 2 (n )(n + 2) (n ) 2 > (n )(n + 2) = n n + 2.
5 7. From a point P outside a circle, tangent lines P A and P B are drawn with A and B on the circle. A third line P CD meets the circle at C and D, with C lying in between P and D. A point Q is chosen on the chord CD so that DAQ = P BC. Show that DBQ = P AC. 5 Since ABC = ADQ BAC = P BC = DAQ, ADQ ABC. Thus BC AD = AB DQ. Also, P CA P AD. Hence P C P A = AC AD. Similarly, P C P B = BC BD. But P A = P B. So we have AC AD = BC BD, and thus AC BD = BC AD = AB DQ. By Ptolemy s Theorem, AC BD + BC AD = AB CD. Therefore, AB CD = 2AB DQ, or DQ = 2CD. So Q is the midpoint of CD. Now AD AB = DQ BC = CQ BC and BCQ = BAD. It follows that CBQ ABD. Hence CBQ = ABD. Thus DBQ = ABC = P AC.
6 6 8. In triangle ABC, A = 60 and AB > AC. The altitudes BE and CF intersect at H. Points M and N are chosen on the segments BH and HF so that BM = CN. If O is the circumcircle of ABC, find the ratio MH + NH. OH Note that BOC = 2 A = 20 and BHC = 80 A = 20 (since A, E, H, F are concyclic). Hence B, O, H, C are concyclic. Thus OBH = OCH. As BO = CO and BM = CN as well, OBM is congruent to OCN. Hence OM = ON and BM O = CN O. It follows that O, M, H, N are concyclic. Therefore, NOM = NHE = 20. Also, ONM = OHM = OHB = OCB = 30. Thus MN sin 20 = OM sin 30 = 3. Finally, from Ptolemy s Theorem, we have Therefore, MH ON + NH OM = OH MN. MH + NH OH = MN OM = 3.
7 7 9. On the plane, there are 3 mutually and externally disjoint circles Γ, Γ 2 and Γ 3 centred at X, X 2 and X 3 respectively. The two internal common tangents of Γ 2 and Γ 3, (Γ 3 and Γ, Γ and Γ 2 ) meet at P, (Q, R respectively). Prove that X P, X 2 Q and X 3 Z are concurrent. Let the radii of Γ, Γ 2 and Γ 3 be r, r 2 and r 3 respectively. Then X R : RX 2 := r : r 2, X 2 P : P X 3 := r 2 : r 3 and X 3 Q : QX := r 3 : r. Thus X R X2P X3Q =. RX 2 P X 3 QX By the converse of Ceva s Theorem, X P, X 2 Q and X 3 Z are concurrent.
8 8 0. The excircle centred at I a with respect to A of ABC touches the sides AB, BC and AC or their extensions at E, D and F respectively. Let H be the foot of the perpendicular from B onto I a C. Prove that E, H, F are collinear. Join EH, F H, DH, EI a, BI a. Then E, I a, H, B are concylic. Also D, B, E, I a are concylic. Thus B, E, I a, H, D all lie on a circle with diameter BI a. As BD = BE, we have BHD = BHE. On the other hand, DHC is congruent to CHF so that DHC = CHF. As BHC = 90, we have DHE + DHF = 2 BHC = 80. Therefore, E, H, F are collinear.
IMO Training Camp Mock Olympiad #2 Solutions
 IMO Training Camp Mock Olympiad #2 Solutions July 3, 2008 1. Given an isosceles triangle ABC with AB = AC. The midpoint of side BC is denoted by M. Let X be a variable point on the shorter arc MA of the
IMO Training Camp Mock Olympiad #2 Solutions July 3, 2008 1. Given an isosceles triangle ABC with AB = AC. The midpoint of side BC is denoted by M. Let X be a variable point on the shorter arc MA of the
Singapore International Mathematical Olympiad Training Problems
 Singapore International athematical Olympiad Training Problems 18 January 2003 1 Let be a point on the segment Squares D and EF are erected on the same side of with F lying on The circumcircles of D and
Singapore International athematical Olympiad Training Problems 18 January 2003 1 Let be a point on the segment Squares D and EF are erected on the same side of with F lying on The circumcircles of D and
IMO Training Camp Mock Olympiad #2
 IMO Training Camp Mock Olympiad #2 July 3, 2008 1. Given an isosceles triangle ABC with AB = AC. The midpoint of side BC is denoted by M. Let X be a variable point on the shorter arc MA of the circumcircle
IMO Training Camp Mock Olympiad #2 July 3, 2008 1. Given an isosceles triangle ABC with AB = AC. The midpoint of side BC is denoted by M. Let X be a variable point on the shorter arc MA of the circumcircle
2013 Sharygin Geometry Olympiad
 Sharygin Geometry Olympiad 2013 First Round 1 Let ABC be an isosceles triangle with AB = BC. Point E lies on the side AB, and ED is the perpendicular from E to BC. It is known that AE = DE. Find DAC. 2
Sharygin Geometry Olympiad 2013 First Round 1 Let ABC be an isosceles triangle with AB = BC. Point E lies on the side AB, and ED is the perpendicular from E to BC. It is known that AE = DE. Find DAC. 2
International Mathematical Olympiad. Preliminary Selection Contest 2017 Hong Kong. Outline of Solutions 5. 3*
 International Mathematical Olympiad Preliminary Selection Contest Hong Kong Outline of Solutions Answers: 06 0000 * 6 97 7 6 8 7007 9 6 0 6 8 77 66 7 7 0 6 7 7 6 8 9 8 0 0 8 *See the remar after the solution
International Mathematical Olympiad Preliminary Selection Contest Hong Kong Outline of Solutions Answers: 06 0000 * 6 97 7 6 8 7007 9 6 0 6 8 77 66 7 7 0 6 7 7 6 8 9 8 0 0 8 *See the remar after the solution
Hanoi Open Mathematical Olympiad
 HEXAGON inspiring minds always Let x = 6+2 + Hanoi Mathematical Olympiad 202 6 2 Senior Section 20 Find the value of + x x 7 202 2 Arrange the numbers p = 2 2, q =, t = 2 + 2 in increasing order Let ABCD
HEXAGON inspiring minds always Let x = 6+2 + Hanoi Mathematical Olympiad 202 6 2 Senior Section 20 Find the value of + x x 7 202 2 Arrange the numbers p = 2 2, q =, t = 2 + 2 in increasing order Let ABCD
Baltic Way 2008 Gdańsk, November 8, 2008
 Baltic Way 008 Gdańsk, November 8, 008 Problems and solutions Problem 1. Determine all polynomials p(x) with real coefficients such that p((x + 1) ) = (p(x) + 1) and p(0) = 0. Answer: p(x) = x. Solution:
Baltic Way 008 Gdańsk, November 8, 008 Problems and solutions Problem 1. Determine all polynomials p(x) with real coefficients such that p((x + 1) ) = (p(x) + 1) and p(0) = 0. Answer: p(x) = x. Solution:
45-th Moldova Mathematical Olympiad 2001
 45-th Moldova Mathematical Olympiad 200 Final Round Chişinǎu, March 2 Grade 7. Prove that y 3 2x+ x 3 2y x 2 + y 2 for any numbers x,y [, 2 3 ]. When does equality occur? 2. Let S(n) denote the sum of
45-th Moldova Mathematical Olympiad 200 Final Round Chişinǎu, March 2 Grade 7. Prove that y 3 2x+ x 3 2y x 2 + y 2 for any numbers x,y [, 2 3 ]. When does equality occur? 2. Let S(n) denote the sum of
1. Suppose that a, b, c and d are four different integers. Explain why. (a b)(a c)(a d)(b c)(b d)(c d) a 2 + ab b = 2018.
 New Zealand Mathematical Olympiad Committee Camp Selection Problems 2018 Solutions Due: 28th September 2018 1. Suppose that a, b, c and d are four different integers. Explain why must be a multiple of
New Zealand Mathematical Olympiad Committee Camp Selection Problems 2018 Solutions Due: 28th September 2018 1. Suppose that a, b, c and d are four different integers. Explain why must be a multiple of
XX Asian Pacific Mathematics Olympiad
 XX Asian Pacific Mathematics Olympiad March, 008 Problem 1. Let ABC be a triangle with A < 60. Let X and Y be the points on the sides AB and AC, respectively, such that CA + AX = CB + BX and BA + AY =
XX Asian Pacific Mathematics Olympiad March, 008 Problem 1. Let ABC be a triangle with A < 60. Let X and Y be the points on the sides AB and AC, respectively, such that CA + AX = CB + BX and BA + AY =
(D) (A) Q.3 To which of the following circles, the line y x + 3 = 0 is normal at the point ? 2 (A) 2
 CIRCLE [STRAIGHT OBJECTIVE TYPE] Q. The line x y + = 0 is tangent to the circle at the point (, 5) and the centre of the circles lies on x y = 4. The radius of the circle is (A) 3 5 (B) 5 3 (C) 5 (D) 5
CIRCLE [STRAIGHT OBJECTIVE TYPE] Q. The line x y + = 0 is tangent to the circle at the point (, 5) and the centre of the circles lies on x y = 4. The radius of the circle is (A) 3 5 (B) 5 3 (C) 5 (D) 5
Classical Theorems in Plane Geometry 1
 BERKELEY MATH CIRCLE 1999 2000 Classical Theorems in Plane Geometry 1 Zvezdelina Stankova-Frenkel UC Berkeley and Mills College Note: All objects in this handout are planar - i.e. they lie in the usual
BERKELEY MATH CIRCLE 1999 2000 Classical Theorems in Plane Geometry 1 Zvezdelina Stankova-Frenkel UC Berkeley and Mills College Note: All objects in this handout are planar - i.e. they lie in the usual
11 th Philippine Mathematical Olympiad Questions, Answers, and Hints
 view.php3 (JPEG Image, 840x888 pixels) - Scaled (71%) https://mail.ateneo.net/horde/imp/view.php3?mailbox=inbox&inde... 1 of 1 11/5/2008 5:02 PM 11 th Philippine Mathematical Olympiad Questions, Answers,
view.php3 (JPEG Image, 840x888 pixels) - Scaled (71%) https://mail.ateneo.net/horde/imp/view.php3?mailbox=inbox&inde... 1 of 1 11/5/2008 5:02 PM 11 th Philippine Mathematical Olympiad Questions, Answers,
CIRCLES. ii) P lies in the circle S = 0 s 11 = 0
 CIRCLES 1 The set of points in a plane which are at a constant distance r ( 0) from a given point C is called a circle The fixed point C is called the centre and the constant distance r is called the radius
CIRCLES 1 The set of points in a plane which are at a constant distance r ( 0) from a given point C is called a circle The fixed point C is called the centre and the constant distance r is called the radius
HANOI OPEN MATHEMATICAL COMPETITON PROBLEMS
 HANOI MATHEMATICAL SOCIETY NGUYEN VAN MAU HANOI OPEN MATHEMATICAL COMPETITON PROBLEMS HANOI - 2013 Contents 1 Hanoi Open Mathematical Competition 3 1.1 Hanoi Open Mathematical Competition 2006... 3 1.1.1
HANOI MATHEMATICAL SOCIETY NGUYEN VAN MAU HANOI OPEN MATHEMATICAL COMPETITON PROBLEMS HANOI - 2013 Contents 1 Hanoi Open Mathematical Competition 3 1.1 Hanoi Open Mathematical Competition 2006... 3 1.1.1
INVERSION IN THE PLANE BERKELEY MATH CIRCLE
 INVERSION IN THE PLANE BERKELEY MATH CIRCLE ZVEZDELINA STANKOVA MILLS COLLEGE/UC BERKELEY SEPTEMBER 26TH 2004 Contents 1. Definition of Inversion in the Plane 1 Properties of Inversion 2 Problems 2 2.
INVERSION IN THE PLANE BERKELEY MATH CIRCLE ZVEZDELINA STANKOVA MILLS COLLEGE/UC BERKELEY SEPTEMBER 26TH 2004 Contents 1. Definition of Inversion in the Plane 1 Properties of Inversion 2 Problems 2 2.
QUESTION BANK ON STRAIGHT LINE AND CIRCLE
 QUESTION BANK ON STRAIGHT LINE AND CIRCLE Select the correct alternative : (Only one is correct) Q. If the lines x + y + = 0 ; 4x + y + 4 = 0 and x + αy + β = 0, where α + β =, are concurrent then α =,
QUESTION BANK ON STRAIGHT LINE AND CIRCLE Select the correct alternative : (Only one is correct) Q. If the lines x + y + = 0 ; 4x + y + 4 = 0 and x + αy + β = 0, where α + β =, are concurrent then α =,
Pre RMO Exam Paper Solution:
 Paper Solution:. How many positive integers less than 000 have the property that the sum of the digits of each such number is divisible by 7 and the number itself is divisible by 3? Sum of Digits Drivable
Paper Solution:. How many positive integers less than 000 have the property that the sum of the digits of each such number is divisible by 7 and the number itself is divisible by 3? Sum of Digits Drivable
2011 Olympiad Solutions
 011 Olympiad Problem 1 Let A 0, A 1, A,..., A n be nonnegative numbers such that Prove that A 0 A 1 A A n. A i 1 n A n. Note: x means the greatest integer that is less than or equal to x.) Solution: We
011 Olympiad Problem 1 Let A 0, A 1, A,..., A n be nonnegative numbers such that Prove that A 0 A 1 A A n. A i 1 n A n. Note: x means the greatest integer that is less than or equal to x.) Solution: We
2018 LEHIGH UNIVERSITY HIGH SCHOOL MATH CONTEST
 08 LEHIGH UNIVERSITY HIGH SCHOOL MATH CONTEST. A right triangle has hypotenuse 9 and one leg. What is the length of the other leg?. Don is /3 of the way through his run. After running another / mile, he
08 LEHIGH UNIVERSITY HIGH SCHOOL MATH CONTEST. A right triangle has hypotenuse 9 and one leg. What is the length of the other leg?. Don is /3 of the way through his run. After running another / mile, he
21. Prove that If one side of the cyclic quadrilateral is produced then the exterior angle is equal to the interior opposite angle.
 21. Prove that If one side of the cyclic quadrilateral is produced then the exterior angle is equal to the interior opposite angle. 22. Prove that If two sides of a cyclic quadrilateral are parallel, then
21. Prove that If one side of the cyclic quadrilateral is produced then the exterior angle is equal to the interior opposite angle. 22. Prove that If two sides of a cyclic quadrilateral are parallel, then
1 Hanoi Open Mathematical Competition 2017
 1 Hanoi Open Mathematical Competition 017 1.1 Junior Section Question 1. Suppose x 1, x, x 3 are the roots of polynomial P (x) = x 3 6x + 5x + 1. The sum x 1 + x + x 3 is (A): 4 (B): 6 (C): 8 (D): 14 (E):
1 Hanoi Open Mathematical Competition 017 1.1 Junior Section Question 1. Suppose x 1, x, x 3 are the roots of polynomial P (x) = x 3 6x + 5x + 1. The sum x 1 + x + x 3 is (A): 4 (B): 6 (C): 8 (D): 14 (E):
13 = m m = (C) The symmetry of the figure implies that ABH, BCE, CDF, and DAG are congruent right triangles. So
 Solutions 2005 56 th AMC 2 A 2. (D It is given that 0.x = 2 and 0.2y = 2, so x = 20 and y = 0. Thus x y = 0. 2. (B Since 2x + 7 = 3 we have x = 2. Hence 2 = bx 0 = 2b 0, so 2b = 8, and b = 4. 3. (B Let
Solutions 2005 56 th AMC 2 A 2. (D It is given that 0.x = 2 and 0.2y = 2, so x = 20 and y = 0. Thus x y = 0. 2. (B Since 2x + 7 = 3 we have x = 2. Hence 2 = bx 0 = 2b 0, so 2b = 8, and b = 4. 3. (B Let
Baltic Way 2003 Riga, November 2, 2003
 altic Way 2003 Riga, November 2, 2003 Problems and solutions. Let Q + be the set of positive rational numbers. Find all functions f : Q + Q + which for all x Q + fulfil () f ( x ) = f (x) (2) ( + x ) f
altic Way 2003 Riga, November 2, 2003 Problems and solutions. Let Q + be the set of positive rational numbers. Find all functions f : Q + Q + which for all x Q + fulfil () f ( x ) = f (x) (2) ( + x ) f
HANOI OPEN MATHEMATICS COMPETITON PROBLEMS
 HANOI MATHEMATICAL SOCIETY NGUYEN VAN MAU HANOI OPEN MATHEMATICS COMPETITON PROBLEMS 2006-2013 HANOI - 2013 Contents 1 Hanoi Open Mathematics Competition 3 1.1 Hanoi Open Mathematics Competition 2006...
HANOI MATHEMATICAL SOCIETY NGUYEN VAN MAU HANOI OPEN MATHEMATICS COMPETITON PROBLEMS 2006-2013 HANOI - 2013 Contents 1 Hanoi Open Mathematics Competition 3 1.1 Hanoi Open Mathematics Competition 2006...
The sum x 1 + x 2 + x 3 is (A): 4 (B): 6 (C): 8 (D): 14 (E): None of the above. How many pairs of positive integers (x, y) are there, those satisfy
 Important: Answer to all 15 questions. Write your answers on the answer sheets provided. For the multiple choice questions, stick only the letters (A, B, C, D or E) of your choice. No calculator is allowed.
Important: Answer to all 15 questions. Write your answers on the answer sheets provided. For the multiple choice questions, stick only the letters (A, B, C, D or E) of your choice. No calculator is allowed.
PRMO Solution
 PRMO Solution 0.08.07. How many positive integers less than 000 have the property that the sum of the digits of each such number is divisible by 7 and the number itself is divisible by 3?. Suppose a, b
PRMO Solution 0.08.07. How many positive integers less than 000 have the property that the sum of the digits of each such number is divisible by 7 and the number itself is divisible by 3?. Suppose a, b
LLT Education Services
 8. The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle. (a) 4 cm (b) 3 cm (c) 6 cm (d) 5 cm 9. From a point P, 10 cm away from the
8. The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle. (a) 4 cm (b) 3 cm (c) 6 cm (d) 5 cm 9. From a point P, 10 cm away from the
Inversion. Contents. 1 General Properties. 1 General Properties Problems Solutions... 3
 c 007 The Author(s) and The IMO Compendium Group Contents Inversion Dušan Djukić 1 General Properties................................... 1 Problems........................................ 3 Solutions........................................
c 007 The Author(s) and The IMO Compendium Group Contents Inversion Dušan Djukić 1 General Properties................................... 1 Problems........................................ 3 Solutions........................................
Calgary Math Circles: Triangles, Concurrency and Quadrilaterals 1
 Calgary Math Circles: Triangles, Concurrency and Quadrilaterals 1 1 Triangles: Basics This section will cover all the basic properties you need to know about triangles and the important points of a triangle.
Calgary Math Circles: Triangles, Concurrency and Quadrilaterals 1 1 Triangles: Basics This section will cover all the basic properties you need to know about triangles and the important points of a triangle.
CAREER POINT. PRMO EXAM-2017 (Paper & Solution) Sum of number should be 21
 PRMO EXAM-07 (Paper & Solution) Q. How many positive integers less than 000 have the property that the sum of the digits of each such number is divisible by 7 and the number itself is divisible by 3? Sum
PRMO EXAM-07 (Paper & Solution) Q. How many positive integers less than 000 have the property that the sum of the digits of each such number is divisible by 7 and the number itself is divisible by 3? Sum
Hanoi Open Mathematical Competition 2017
 Hanoi Open Mathematical Competition 2017 Junior Section Saturday, 4 March 2017 08h30-11h30 Important: Answer to all 15 questions. Write your answers on the answer sheets provided. For the multiple choice
Hanoi Open Mathematical Competition 2017 Junior Section Saturday, 4 March 2017 08h30-11h30 Important: Answer to all 15 questions. Write your answers on the answer sheets provided. For the multiple choice
Pre-Regional Mathematical Olympiad Solution 2017
 Pre-Regional Mathematical Olympiad Solution 07 Time:.5 hours. Maximum Marks: 50 [Each Question carries 5 marks]. How many positive integers less than 000 have the property that the sum of the digits of
Pre-Regional Mathematical Olympiad Solution 07 Time:.5 hours. Maximum Marks: 50 [Each Question carries 5 marks]. How many positive integers less than 000 have the property that the sum of the digits of
1. (A) Factor to get (2x+3)(2x 10) = 0, so the two roots are 3/2 and 5, which sum to 7/2.
 Solutions 00 53 rd AMC 1 A 1. (A) Factor to get (x+3)(x 10) = 0, so the two roots are 3/ and 5, which sum to 7/.. (A) Let x be the number she was given. Her calculations produce so x 9 3 = 43, x 9 = 19
Solutions 00 53 rd AMC 1 A 1. (A) Factor to get (x+3)(x 10) = 0, so the two roots are 3/ and 5, which sum to 7/.. (A) Let x be the number she was given. Her calculations produce so x 9 3 = 43, x 9 = 19
This class will demonstrate the use of bijections to solve certain combinatorial problems simply and effectively.
 . Induction This class will demonstrate the fundamental problem solving technique of mathematical induction. Example Problem: Prove that for every positive integer n there exists an n-digit number divisible
. Induction This class will demonstrate the fundamental problem solving technique of mathematical induction. Example Problem: Prove that for every positive integer n there exists an n-digit number divisible
2013 IMO Shortlist. a b c d 1
 IMO Shortlist 2013 Algebra A1 A2 Letnbeapositiveintegerandleta 1,...,a n 1 bearbitraryrealnumbers. Define the sequences u 0,...,u n and v 0,...,v n inductively by u 0 = u 1 = v 0 = v 1 = 1, and u k+1 =
IMO Shortlist 2013 Algebra A1 A2 Letnbeapositiveintegerandleta 1,...,a n 1 bearbitraryrealnumbers. Define the sequences u 0,...,u n and v 0,...,v n inductively by u 0 = u 1 = v 0 = v 1 = 1, and u k+1 =
INTERNATIONAL MATHEMATICAL OLYMPIADS. Hojoo Lee, Version 1.0. Contents 1. Problems 1 2. Answers and Hints References
 INTERNATIONAL MATHEMATICAL OLYMPIADS 1990 2002 Hojoo Lee, Version 1.0 Contents 1. Problems 1 2. Answers and Hints 15 3. References 16 1. Problems 021 Let n be a positive integer. Let T be the set of points
INTERNATIONAL MATHEMATICAL OLYMPIADS 1990 2002 Hojoo Lee, Version 1.0 Contents 1. Problems 1 2. Answers and Hints 15 3. References 16 1. Problems 021 Let n be a positive integer. Let T be the set of points
10. Show that the conclusion of the. 11. Prove the above Theorem. [Th 6.4.7, p 148] 4. Prove the above Theorem. [Th 6.5.3, p152]
![10. Show that the conclusion of the. 11. Prove the above Theorem. [Th 6.4.7, p 148] 4. Prove the above Theorem. [Th 6.5.3, p152] 10. Show that the conclusion of the. 11. Prove the above Theorem. [Th 6.4.7, p 148] 4. Prove the above Theorem. [Th 6.5.3, p152]](/thumbs/94/121826807.jpg) foot of the altitude of ABM from M and let A M 1 B. Prove that then MA > MB if and only if M 1 A > M 1 B. 8. If M is the midpoint of BC then AM is called a median of ABC. Consider ABC such that AB < AC.
foot of the altitude of ABM from M and let A M 1 B. Prove that then MA > MB if and only if M 1 A > M 1 B. 8. If M is the midpoint of BC then AM is called a median of ABC. Consider ABC such that AB < AC.
The 3rd Olympiad of Metropolises
 The 3rd Olympiad of Metropolises Day 1. Solutions Problem 1. Solve the system of equations in real numbers: (x 1)(y 1)(z 1) xyz 1, Answer: x 1, y 1, z 1. (x )(y )(z ) xyz. (Vladimir Bragin) Solution 1.
The 3rd Olympiad of Metropolises Day 1. Solutions Problem 1. Solve the system of equations in real numbers: (x 1)(y 1)(z 1) xyz 1, Answer: x 1, y 1, z 1. (x )(y )(z ) xyz. (Vladimir Bragin) Solution 1.
2007 Shortlist JBMO - Problems
 Chapter 1 007 Shortlist JBMO - Problems 1.1 Algebra A1 Let a be a real positive number such that a 3 = 6(a + 1). Prove that the equation x + ax + a 6 = 0 has no solution in the set of the real number.
Chapter 1 007 Shortlist JBMO - Problems 1.1 Algebra A1 Let a be a real positive number such that a 3 = 6(a + 1). Prove that the equation x + ax + a 6 = 0 has no solution in the set of the real number.
37th United States of America Mathematical Olympiad
 37th United States of America Mathematical Olympiad 1. Prove that for each positive integer n, there are pairwise relatively prime integers k 0, k 1,..., k n, all strictly greater than 1, such that k 0
37th United States of America Mathematical Olympiad 1. Prove that for each positive integer n, there are pairwise relatively prime integers k 0, k 1,..., k n, all strictly greater than 1, such that k 0
10! = ?
 AwesomeMath Team Contest 013 Solutions Problem 1. Define the value of a letter as its position in the alphabet. For example, C is the third letter, so its value is 3. The value of a word is the sum of
AwesomeMath Team Contest 013 Solutions Problem 1. Define the value of a letter as its position in the alphabet. For example, C is the third letter, so its value is 3. The value of a word is the sum of
USA Aime 1983: Problems & Solutions 1
 USA Aime 1983: Problems & Solutions 1 1 Problems 1. Let x,y, and z all exceed 1, and let w be a positive number such that log x w = 4, log y w = 40, and log xyz w = 1. Find log z w.. Let f(x) = x p + x
USA Aime 1983: Problems & Solutions 1 1 Problems 1. Let x,y, and z all exceed 1, and let w be a positive number such that log x w = 4, log y w = 40, and log xyz w = 1. Find log z w.. Let f(x) = x p + x
Q.1 If a, b, c are distinct positive real in H.P., then the value of the expression, (A) 1 (B) 2 (C) 3 (D) 4. (A) 2 (B) 5/2 (C) 3 (D) none of these
 Q. If a, b, c are distinct positive real in H.P., then the value of the expression, b a b c + is equal to b a b c () (C) (D) 4 Q. In a triangle BC, (b + c) = a bc where is the circumradius of the triangle.
Q. If a, b, c are distinct positive real in H.P., then the value of the expression, b a b c + is equal to b a b c () (C) (D) 4 Q. In a triangle BC, (b + c) = a bc where is the circumradius of the triangle.
NEW YORK CITY INTERSCHOLASTIC MATHEMATICS LEAGUE Senior A Division CONTEST NUMBER 1
 Senior A Division CONTEST NUMBER 1 PART I FALL 2011 CONTEST 1 TIME: 10 MINUTES F11A1 Larry selects a 13-digit number while David selects a 10-digit number. Let be the number of digits in the product of
Senior A Division CONTEST NUMBER 1 PART I FALL 2011 CONTEST 1 TIME: 10 MINUTES F11A1 Larry selects a 13-digit number while David selects a 10-digit number. Let be the number of digits in the product of
= 0 1 (3 4 ) 1 (4 4) + 1 (4 3) = = + 1 = 0 = 1 = ± 1 ]
![= 0 1 (3 4 ) 1 (4 4) + 1 (4 3) = = + 1 = 0 = 1 = ± 1 ] = 0 1 (3 4 ) 1 (4 4) + 1 (4 3) = = + 1 = 0 = 1 = ± 1 ]](/thumbs/74/71228184.jpg) STRAIGHT LINE [STRAIGHT OBJECTIVE TYPE] Q. If the lines x + y + = 0 ; x + y + = 0 and x + y + = 0, where + =, are concurrent then (A) =, = (B) =, = ± (C) =, = ± (D*) = ±, = [Sol. Lines are x + y + = 0
STRAIGHT LINE [STRAIGHT OBJECTIVE TYPE] Q. If the lines x + y + = 0 ; x + y + = 0 and x + y + = 0, where + =, are concurrent then (A) =, = (B) =, = ± (C) =, = ± (D*) = ±, = [Sol. Lines are x + y + = 0
1. SETS AND FUNCTIONS
 . SETS AND FUNCTIONS. For two sets A and B, A, B A if and only if B A A B A! B A + B z. If A B, then A + B is B A\ B A B\ A. For any two sets Pand Q, P + Q is " x : x! P or x! Q, " x : x! P and x b Q,
. SETS AND FUNCTIONS. For two sets A and B, A, B A if and only if B A A B A! B A + B z. If A B, then A + B is B A\ B A B\ A. For any two sets Pand Q, P + Q is " x : x! P or x! Q, " x : x! P and x b Q,
Olympiad Correspondence Problems. Set 3
 (solutions follow) 1998-1999 Olympiad Correspondence Problems Set 3 13. The following construction and proof was proposed for trisecting a given angle with ruler and Criticizecompasses the arguments. Construction.
(solutions follow) 1998-1999 Olympiad Correspondence Problems Set 3 13. The following construction and proof was proposed for trisecting a given angle with ruler and Criticizecompasses the arguments. Construction.
Chapter (Circle) * Circle - circle is locus of such points which are at equidistant from a fixed point in
 Chapter - 10 (Circle) Key Concept * Circle - circle is locus of such points which are at equidistant from a fixed point in a plane. * Concentric circle - Circle having same centre called concentric circle.
Chapter - 10 (Circle) Key Concept * Circle - circle is locus of such points which are at equidistant from a fixed point in a plane. * Concentric circle - Circle having same centre called concentric circle.
Pre-REGIONAL MATHEMATICAL OLYMPIAD, 2017
 P-RMO 017 NATIONAL BOARD FOR HIGHER MATHEMATICS AND HOMI BHABHA CENTRE FOR SCIENCE EDUCATION TATA INSTITUTE OF FUNDAMENTAL RESEARCH Pre-REGIONAL MATHEMATICAL OLYMPIAD, 017 TEST PAPER WITH SOLUTION & ANSWER
P-RMO 017 NATIONAL BOARD FOR HIGHER MATHEMATICS AND HOMI BHABHA CENTRE FOR SCIENCE EDUCATION TATA INSTITUTE OF FUNDAMENTAL RESEARCH Pre-REGIONAL MATHEMATICAL OLYMPIAD, 017 TEST PAPER WITH SOLUTION & ANSWER
Solutions for November. f(x + f(y)) = f(x) + y
 Solutions for November 647. Find all continuous functions f : R R such that for every x, y R. f(x + f(y)) = f(x) + y Solution 1. Setting (x, y) = (t, 0) yields f(t + f(0)) = f(t) for all real t. Setting
Solutions for November 647. Find all continuous functions f : R R such that for every x, y R. f(x + f(y)) = f(x) + y Solution 1. Setting (x, y) = (t, 0) yields f(t + f(0)) = f(t) for all real t. Setting
2017 Harvard-MIT Mathematics Tournament
 Team Round 1 Let P(x), Q(x) be nonconstant polynomials with real number coefficients. Prove that if P(y) = Q(y) for all real numbers y, then P(x) = Q(x) for all real numbers x. 2 Does there exist a two-variable
Team Round 1 Let P(x), Q(x) be nonconstant polynomials with real number coefficients. Prove that if P(y) = Q(y) for all real numbers y, then P(x) = Q(x) for all real numbers x. 2 Does there exist a two-variable
2003 AIME2 SOLUTIONS (Answer: 336)
 1 (Answer: 336) 2003 AIME2 SOLUTIONS 2 Call the three integers a, b, and c, and, without loss of generality, assume a b c Then abc = 6(a + b + c), and c = a + b Thus abc = 12c, and ab = 12, so (a, b, c)
1 (Answer: 336) 2003 AIME2 SOLUTIONS 2 Call the three integers a, b, and c, and, without loss of generality, assume a b c Then abc = 6(a + b + c), and c = a + b Thus abc = 12c, and ab = 12, so (a, b, c)
2010 Shortlist JBMO - Problems
 Chapter 1 2010 Shortlist JBMO - Problems 1.1 Algebra A1 The real numbers a, b, c, d satisfy simultaneously the equations abc d = 1, bcd a = 2, cda b = 3, dab c = 6. Prove that a + b + c + d 0. A2 Determine
Chapter 1 2010 Shortlist JBMO - Problems 1.1 Algebra A1 The real numbers a, b, c, d satisfy simultaneously the equations abc d = 1, bcd a = 2, cda b = 3, dab c = 6. Prove that a + b + c + d 0. A2 Determine
Non-standard MMC problems
 Non-standard MMC problems Carl Joshua Quines 1 Algebra 1. (15S/9B/E6) A quadratic function f(x) satisfies f(0) = 30 and f(2) = 0. Determine all the zeros of f(x). [2 and 15] 2. (15S/IVB/E6) What is the
Non-standard MMC problems Carl Joshua Quines 1 Algebra 1. (15S/9B/E6) A quadratic function f(x) satisfies f(0) = 30 and f(2) = 0. Determine all the zeros of f(x). [2 and 15] 2. (15S/IVB/E6) What is the
1 2n. i=1. 2m+1 i = m, while. 2m + 1 = 1. is the best possible for any odd n.
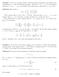 Problem 1. Let n be a positive integer. Find the largest nonnegative real number f(n) (depending on n) with the following property: whenever a 1, a,..., a n are real numbers such that a 1 + a + + a n is
Problem 1. Let n be a positive integer. Find the largest nonnegative real number f(n) (depending on n) with the following property: whenever a 1, a,..., a n are real numbers such that a 1 + a + + a n is
27th Russian Mathematics Olympiad
 27th Russian Mathematics Olympiad 10 April 2001 (Communicated by Fedor Petrov) 9 FORM 1. The integers from 1 to 999999 are partioned into two groups: those integers for which the nearest perfect square
27th Russian Mathematics Olympiad 10 April 2001 (Communicated by Fedor Petrov) 9 FORM 1. The integers from 1 to 999999 are partioned into two groups: those integers for which the nearest perfect square
41st International Mathematical Olympiad
 41st International Mathematical Olympiad Taejon, Korea, July 2000 1 Two circles Γ 1 and Γ 2 intersect at M and N Let l be the common tangent to Γ 1 and Γ 2 so that M is closer to l than N is Let l touch
41st International Mathematical Olympiad Taejon, Korea, July 2000 1 Two circles Γ 1 and Γ 2 intersect at M and N Let l be the common tangent to Γ 1 and Γ 2 so that M is closer to l than N is Let l touch
Solutions of APMO 2016
 Solutions of APMO 016 Problem 1. We say that a triangle ABC is great if the following holds: for any point D on the side BC, if P and Q are the feet of the perpendiculars from D to the lines AB and AC,
Solutions of APMO 016 Problem 1. We say that a triangle ABC is great if the following holds: for any point D on the side BC, if P and Q are the feet of the perpendiculars from D to the lines AB and AC,
VAISHALI EDUCATION POINT (QUALITY EDUCATION PROVIDER)
 BY:Prof. RAHUL MISHRA Class :- X QNo. VAISHALI EDUCATION POINT (QUALITY EDUCATION PROVIDER) CIRCLES Subject :- Maths General Instructions Questions M:9999907099,9818932244 1 In the adjoining figures, PQ
BY:Prof. RAHUL MISHRA Class :- X QNo. VAISHALI EDUCATION POINT (QUALITY EDUCATION PROVIDER) CIRCLES Subject :- Maths General Instructions Questions M:9999907099,9818932244 1 In the adjoining figures, PQ
6 CHAPTER. Triangles. A plane figure bounded by three line segments is called a triangle.
 6 CHAPTER We are Starting from a Point but want to Make it a Circle of Infinite Radius A plane figure bounded by three line segments is called a triangle We denote a triangle by the symbol In fig ABC has
6 CHAPTER We are Starting from a Point but want to Make it a Circle of Infinite Radius A plane figure bounded by three line segments is called a triangle We denote a triangle by the symbol In fig ABC has
Topic 2 [312 marks] The rectangle ABCD is inscribed in a circle. Sides [AD] and [AB] have lengths
![Topic 2 [312 marks] The rectangle ABCD is inscribed in a circle. Sides [AD] and [AB] have lengths Topic 2 [312 marks] The rectangle ABCD is inscribed in a circle. Sides [AD] and [AB] have lengths](/thumbs/86/93150791.jpg) Topic 2 [312 marks] 1 The rectangle ABCD is inscribed in a circle Sides [AD] and [AB] have lengths [12 marks] 3 cm and (\9\) cm respectively E is a point on side [AB] such that AE is 3 cm Side [DE] is
Topic 2 [312 marks] 1 The rectangle ABCD is inscribed in a circle Sides [AD] and [AB] have lengths [12 marks] 3 cm and (\9\) cm respectively E is a point on side [AB] such that AE is 3 cm Side [DE] is
2007 Mathematical Olympiad Summer Program Tests
 2007 Mathematical Olympiad Summer Program Tests Edited by Zuming Feng Mathematics Olympiad Summer Program 2007 Tests 1 Practice Test 1 1.1. In triangle ABC three distinct triangles are inscribed, similar
2007 Mathematical Olympiad Summer Program Tests Edited by Zuming Feng Mathematics Olympiad Summer Program 2007 Tests 1 Practice Test 1 1.1. In triangle ABC three distinct triangles are inscribed, similar
1998 IMO Shortlist BM BN BA BC AB BC CD DE EF BC CA AE EF FD
 IMO Shortlist 1998 Geometry 1 A convex quadrilateral ABCD has perpendicular diagonals. The perpendicular bisectors of the sides AB and CD meet at a unique point P inside ABCD. the quadrilateral ABCD is
IMO Shortlist 1998 Geometry 1 A convex quadrilateral ABCD has perpendicular diagonals. The perpendicular bisectors of the sides AB and CD meet at a unique point P inside ABCD. the quadrilateral ABCD is
VKR Classes TIME BOUND TESTS 1-7 Target JEE ADVANCED For Class XI VKR Classes, C , Indra Vihar, Kota. Mob. No
 VKR Classes TIME BOUND TESTS -7 Target JEE ADVANCED For Class XI VKR Classes, C-9-0, Indra Vihar, Kota. Mob. No. 9890605 Single Choice Question : PRACTICE TEST-. The smallest integer greater than log +
VKR Classes TIME BOUND TESTS -7 Target JEE ADVANCED For Class XI VKR Classes, C-9-0, Indra Vihar, Kota. Mob. No. 9890605 Single Choice Question : PRACTICE TEST-. The smallest integer greater than log +
CMO 2007 Solutions. 3. Suppose that f is a real-valued function for which. f(xy) + f(y x) f(y + x) for all real numbers x and y.
 CMO 2007 Solutions 1 What is the maximum number of non-overlapping 2 1 dominoes that can be placed on an 8 9 checkerboard if six of them are placed as shown? Each domino must be placed horizontally or
CMO 2007 Solutions 1 What is the maximum number of non-overlapping 2 1 dominoes that can be placed on an 8 9 checkerboard if six of them are placed as shown? Each domino must be placed horizontally or
Geometry. Class Examples (July 3) Paul Yiu. Department of Mathematics Florida Atlantic University. Summer 2014
 Geometry lass Examples (July 3) Paul Yiu Department of Mathematics Florida tlantic University c b a Summer 2014 Example 11(a): Fermat point. Given triangle, construct externally similar isosceles triangles
Geometry lass Examples (July 3) Paul Yiu Department of Mathematics Florida tlantic University c b a Summer 2014 Example 11(a): Fermat point. Given triangle, construct externally similar isosceles triangles
SOLVED SUBJECTIVE EXAMPLES
 Example 1 : SOLVED SUBJECTIVE EXAMPLES Find the locus of the points of intersection of the tangents to the circle x = r cos, y = r sin at points whose parametric angles differ by /3. All such points P
Example 1 : SOLVED SUBJECTIVE EXAMPLES Find the locus of the points of intersection of the tangents to the circle x = r cos, y = r sin at points whose parametric angles differ by /3. All such points P
Concurrency and Collinearity
 Concurrency and Collinearity Victoria Krakovna vkrakovna@gmail.com 1 Elementary Tools Here are some tips for concurrency and collinearity questions: 1. You can often restate a concurrency question as a
Concurrency and Collinearity Victoria Krakovna vkrakovna@gmail.com 1 Elementary Tools Here are some tips for concurrency and collinearity questions: 1. You can often restate a concurrency question as a
( 1 ) Show that P ( a, b + c ), Q ( b, c + a ) and R ( c, a + b ) are collinear.
 Problems 01 - POINT Page 1 ( 1 ) Show that P ( a, b + c ), Q ( b, c + a ) and R ( c, a + b ) are collinear. ( ) Prove that the two lines joining the mid-points of the pairs of opposite sides and the line
Problems 01 - POINT Page 1 ( 1 ) Show that P ( a, b + c ), Q ( b, c + a ) and R ( c, a + b ) are collinear. ( ) Prove that the two lines joining the mid-points of the pairs of opposite sides and the line
Berkeley Math Circle, May
 Berkeley Math Circle, May 1-7 2000 COMPLEX NUMBERS IN GEOMETRY ZVEZDELINA STANKOVA FRENKEL, MILLS COLLEGE 1. Let O be a point in the plane of ABC. Points A 1, B 1, C 1 are the images of A, B, C under symmetry
Berkeley Math Circle, May 1-7 2000 COMPLEX NUMBERS IN GEOMETRY ZVEZDELINA STANKOVA FRENKEL, MILLS COLLEGE 1. Let O be a point in the plane of ABC. Points A 1, B 1, C 1 are the images of A, B, C under symmetry
Australian Intermediate Mathematics Olympiad 2016
 Australian Intermediate Mathematics Olympiad 06 Questions. Find the smallest positive integer x such that x = 5y, where y is a positive integer. [ marks]. A 3-digit number in base 7 is also a 3-digit number
Australian Intermediate Mathematics Olympiad 06 Questions. Find the smallest positive integer x such that x = 5y, where y is a positive integer. [ marks]. A 3-digit number in base 7 is also a 3-digit number
1966 IMO Shortlist. IMO Shortlist 1966
 IMO Shortlist 1966 1 Given n > 3 points in the plane such that no three of the points are collinear. Does there exist a circle passing through (at least) 3 of the given points and not containing any other
IMO Shortlist 1966 1 Given n > 3 points in the plane such that no three of the points are collinear. Does there exist a circle passing through (at least) 3 of the given points and not containing any other
The 33 rd Balkan Mathematical Olympiad Tirana, May 7, 2016
 Language: English The 33 rd Balkan Mathematical Olympiad Tirana, May 7, 2016 Problem 1. Find all injective functions f : R R such that for every real number x and every positive integer n, n i f(x + i
Language: English The 33 rd Balkan Mathematical Olympiad Tirana, May 7, 2016 Problem 1. Find all injective functions f : R R such that for every real number x and every positive integer n, n i f(x + i
SOLVED PROBLEMS. 1. The angle between two lines whose direction cosines are given by the equation l + m + n = 0, l 2 + m 2 + n 2 = 0 is
 SOLVED PROBLEMS OBJECTIVE 1. The angle between two lines whose direction cosines are given by the equation l + m + n = 0, l 2 + m 2 + n 2 = 0 is (A) π/3 (B) 2π/3 (C) π/4 (D) None of these hb : Eliminating
SOLVED PROBLEMS OBJECTIVE 1. The angle between two lines whose direction cosines are given by the equation l + m + n = 0, l 2 + m 2 + n 2 = 0 is (A) π/3 (B) 2π/3 (C) π/4 (D) None of these hb : Eliminating
SUMMATIVE ASSESSMENT-1 SAMPLE PAPER (SET-2) MATHEMATICS CLASS IX
 SUMMATIVE ASSESSMENT-1 SAMPLE PAPER (SET-) MATHEMATICS CLASS IX Time: 3 to 3 1 hours Maximum Marks: 80 GENERAL INSTRUCTIONS: 1. All questions are compulsory.. The question paper is divided into four sections
SUMMATIVE ASSESSMENT-1 SAMPLE PAPER (SET-) MATHEMATICS CLASS IX Time: 3 to 3 1 hours Maximum Marks: 80 GENERAL INSTRUCTIONS: 1. All questions are compulsory.. The question paper is divided into four sections
Definitions, Axioms, Postulates, Propositions, and Theorems from Euclidean and Non-Euclidean Geometries by Marvin Jay Greenberg ( )
 Definitions, Axioms, Postulates, Propositions, and Theorems from Euclidean and Non-Euclidean Geometries by Marvin Jay Greenberg (2009-03-26) Logic Rule 0 No unstated assumptions may be used in a proof.
Definitions, Axioms, Postulates, Propositions, and Theorems from Euclidean and Non-Euclidean Geometries by Marvin Jay Greenberg (2009-03-26) Logic Rule 0 No unstated assumptions may be used in a proof.
40th International Mathematical Olympiad
 40th International Mathematical Olympiad Bucharest, Romania, July 999 Determine all finite sets S of at least three points in the plane which satisfy the following condition: for any two distinct points
40th International Mathematical Olympiad Bucharest, Romania, July 999 Determine all finite sets S of at least three points in the plane which satisfy the following condition: for any two distinct points
Objective Mathematics
 . In BC, if angles, B, C are in geometric seq- uence with common ratio, then is : b c a (a) (c) 0 (d) 6. If the angles of a triangle are in the ratio 4 : :, then the ratio of the longest side to the perimeter
. In BC, if angles, B, C are in geometric seq- uence with common ratio, then is : b c a (a) (c) 0 (d) 6. If the angles of a triangle are in the ratio 4 : :, then the ratio of the longest side to the perimeter
Isogonal Conjugates. Navneel Singhal October 9, Abstract
 Isogonal Conjugates Navneel Singhal navneel.singhal@ymail.com October 9, 2016 Abstract This is a short note on isogonality, intended to exhibit the uses of isogonality in mathematical olympiads. Contents
Isogonal Conjugates Navneel Singhal navneel.singhal@ymail.com October 9, 2016 Abstract This is a short note on isogonality, intended to exhibit the uses of isogonality in mathematical olympiads. Contents
Figure 1: Problem 1 diagram. Figure 2: Problem 2 diagram
 Geometry A Solutions 1. Note that the solid formed is a generalized cylinder. It is clear from the diagram that the area of the base of this cylinder (i.e., a vertical cross-section of the log) is composed
Geometry A Solutions 1. Note that the solid formed is a generalized cylinder. It is clear from the diagram that the area of the base of this cylinder (i.e., a vertical cross-section of the log) is composed
Objective Mathematics
 . A tangent to the ellipse is intersected by a b the tangents at the etremities of the major ais at 'P' and 'Q' circle on PQ as diameter always passes through : (a) one fied point two fied points (c) four
. A tangent to the ellipse is intersected by a b the tangents at the etremities of the major ais at 'P' and 'Q' circle on PQ as diameter always passes through : (a) one fied point two fied points (c) four
High School Math Contest
 High School Math Contest University of South Carolina February th, 017 Problem 1. If (x y) = 11 and (x + y) = 169, what is xy? (a) 11 (b) 1 (c) 1 (d) (e) 8 Solution: Note that xy = (x + y) (x y) = 169
High School Math Contest University of South Carolina February th, 017 Problem 1. If (x y) = 11 and (x + y) = 169, what is xy? (a) 11 (b) 1 (c) 1 (d) (e) 8 Solution: Note that xy = (x + y) (x y) = 169
First selection test. a n = 3n + n 2 1. b n = 2( n 2 + n + n 2 n),
 First selection test Problem. Find the positive real numbers a, b, c which satisfy the inequalities 4(ab + bc + ca) a 2 + b 2 + c 2 3(a 3 + b 3 + c 3 ). Laurenţiu Panaitopol Problem 2. Consider the numbers
First selection test Problem. Find the positive real numbers a, b, c which satisfy the inequalities 4(ab + bc + ca) a 2 + b 2 + c 2 3(a 3 + b 3 + c 3 ). Laurenţiu Panaitopol Problem 2. Consider the numbers
nx + 1 = (n + 1)x 13(n + 1) and nx = (n + 1)x + 27(n + 1).
 1. (Answer: 630) 001 AIME SOLUTIONS Let a represent the tens digit and b the units digit of an integer with the required property. Then 10a + b must be divisible by both a and b. It follows that b must
1. (Answer: 630) 001 AIME SOLUTIONS Let a represent the tens digit and b the units digit of an integer with the required property. Then 10a + b must be divisible by both a and b. It follows that b must
UNC Charlotte 2005 Comprehensive March 7, 2005
 March 7, 2005 1 The numbers x and y satisfy 2 x = 15 and 15 y = 32 What is the value xy? (A) 3 (B) 4 (C) 5 (D) 6 (E) none of A, B, C or D 2 Suppose x, y, z, and w are real numbers satisfying x/y = 4/7,
March 7, 2005 1 The numbers x and y satisfy 2 x = 15 and 15 y = 32 What is the value xy? (A) 3 (B) 4 (C) 5 (D) 6 (E) none of A, B, C or D 2 Suppose x, y, z, and w are real numbers satisfying x/y = 4/7,
2017 China Team Selection Test
 China Team Selection Test 2017 TST 1 1 Find out the maximum value of the numbers of edges of a solid regular octahedron that we can see from a point out of the regular octahedron.(we define we can see
China Team Selection Test 2017 TST 1 1 Find out the maximum value of the numbers of edges of a solid regular octahedron that we can see from a point out of the regular octahedron.(we define we can see
Theorem 1.2 (Converse of Pythagoras theorem). If the lengths of the sides of ABC satisfy a 2 + b 2 = c 2, then the triangle has a right angle at C.
 hapter 1 Some asic Theorems 1.1 The ythagorean Theorem Theorem 1.1 (ythagoras). The lengths a b < c of the sides of a right triangle satisfy the relation a + b = c. roof. b a a 3 b b 4 b a b 4 1 a a 3
hapter 1 Some asic Theorems 1.1 The ythagorean Theorem Theorem 1.1 (ythagoras). The lengths a b < c of the sides of a right triangle satisfy the relation a + b = c. roof. b a a 3 b b 4 b a b 4 1 a a 3
Problems First day. 8 grade. Problems First day. 8 grade
 First day. 8 grade 8.1. Let ABCD be a cyclic quadrilateral with AB = = BC and AD = CD. ApointM lies on the minor arc CD of its circumcircle. The lines BM and CD meet at point P, thelinesam and BD meet
First day. 8 grade 8.1. Let ABCD be a cyclic quadrilateral with AB = = BC and AD = CD. ApointM lies on the minor arc CD of its circumcircle. The lines BM and CD meet at point P, thelinesam and BD meet
Note that Todd can only move north or west. After this point, Allison executes the following strategy based on Todd s turn.
 1. First, note that both Todd and Allison place exactly one blue stone in each of their turns. Also, it will take Todd at least eight moves to get from the center to a corner. Therefore, as Todd would
1. First, note that both Todd and Allison place exactly one blue stone in each of their turns. Also, it will take Todd at least eight moves to get from the center to a corner. Therefore, as Todd would
The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca Euclid Contest. Wednesday, April 15, 2015
 The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 015 Euclid Contest Wednesday, April 15, 015 (in North America and South America) Thursday, April 16, 015 (outside of North America
The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 015 Euclid Contest Wednesday, April 15, 015 (in North America and South America) Thursday, April 16, 015 (outside of North America
2. (i) Find the equation of the circle which passes through ( 7, 1) and has centre ( 4, 3).
 Circle 1. (i) Find the equation of the circle with centre ( 7, 3) and of radius 10. (ii) Find the centre of the circle 2x 2 + 2y 2 + 6x + 8y 1 = 0 (iii) What is the radius of the circle 3x 2 + 3y 2 + 5x
Circle 1. (i) Find the equation of the circle with centre ( 7, 3) and of radius 10. (ii) Find the centre of the circle 2x 2 + 2y 2 + 6x + 8y 1 = 0 (iii) What is the radius of the circle 3x 2 + 3y 2 + 5x
OLYMON. Produced by the Canadian Mathematical Society and the Department of Mathematics of the University of Toronto. Issue 7:2.
 OLYMON Produced by the Canadian Mathematical Society and the Department of Mathematics of the University of Toronto. Please send your solution to Ms. Valeria Pandelieva 64 Kirkwood Avenue Ottawa, ON KZ
OLYMON Produced by the Canadian Mathematical Society and the Department of Mathematics of the University of Toronto. Please send your solution to Ms. Valeria Pandelieva 64 Kirkwood Avenue Ottawa, ON KZ
It is known that the length of the tangents drawn from an external point to a circle is equal.
 CBSE -MATHS-SET 1-2014 Q1. The first three terms of an AP are 3y-1, 3y+5 and 5y+1, respectively. We need to find the value of y. We know that if a, b and c are in AP, then: b a = c b 2b = a + c 2 (3y+5)
CBSE -MATHS-SET 1-2014 Q1. The first three terms of an AP are 3y-1, 3y+5 and 5y+1, respectively. We need to find the value of y. We know that if a, b and c are in AP, then: b a = c b 2b = a + c 2 (3y+5)
International Mathematics TOURNAMENT OF THE TOWNS
 International Mathematics TOURNAMENT OF THE TOWNS Senior A-Level Paper Fall 2008. 1. A standard 8 8 chessboard is modified by varying the distances between parallel grid lines, so that the cells are rectangles
International Mathematics TOURNAMENT OF THE TOWNS Senior A-Level Paper Fall 2008. 1. A standard 8 8 chessboard is modified by varying the distances between parallel grid lines, so that the cells are rectangles
Singapore Mathematical Society
 Singapore Mathematical Society Interschool Mathematical Competition 1990 Part A Saturday, 23 June 1990 100Q-1100 Attempt as many questions as you can. No calculators are allowed. Circle your answers on
Singapore Mathematical Society Interschool Mathematical Competition 1990 Part A Saturday, 23 June 1990 100Q-1100 Attempt as many questions as you can. No calculators are allowed. Circle your answers on
1 / 23
 CBSE-XII-017 EXAMINATION CBSE-X-008 EXAMINATION MATHEMATICS Series: RLH/ Paper & Solution Code: 30//1 Time: 3 Hrs. Max. Marks: 80 General Instuctions : (i) All questions are compulsory. (ii) The question
CBSE-XII-017 EXAMINATION CBSE-X-008 EXAMINATION MATHEMATICS Series: RLH/ Paper & Solution Code: 30//1 Time: 3 Hrs. Max. Marks: 80 General Instuctions : (i) All questions are compulsory. (ii) The question
Syllabus. + + x + n 1 n. + x + 2
 1. Special Functions This class will cover problems involving algebraic functions other than polynomials, such as square roots, the floor function, and logarithms. Example Problem: Let n be a positive
1. Special Functions This class will cover problems involving algebraic functions other than polynomials, such as square roots, the floor function, and logarithms. Example Problem: Let n be a positive
Review exercise 2. 1 The equation of the line is: = 5 a The gradient of l1 is 3. y y x x. So the gradient of l2 is. The equation of line l2 is: y =
 Review exercise The equation of the line is: y y x x y y x x y 8 x+ 6 8 + y 8 x+ 6 y x x + y 0 y ( ) ( x 9) y+ ( x 9) y+ x 9 x y 0 a, b, c Using points A and B: y y x x y y x x y x 0 k 0 y x k ky k x a
Review exercise The equation of the line is: y y x x y y x x y 8 x+ 6 8 + y 8 x+ 6 y x x + y 0 y ( ) ( x 9) y+ ( x 9) y+ x 9 x y 0 a, b, c Using points A and B: y y x x y y x x y x 0 k 0 y x k ky k x a
Exercises for Unit I I I (Basic Euclidean concepts and theorems)
 Exercises for Unit I I I (Basic Euclidean concepts and theorems) Default assumption: All points, etc. are assumed to lie in R 2 or R 3. I I I. : Perpendicular lines and planes Supplementary background
Exercises for Unit I I I (Basic Euclidean concepts and theorems) Default assumption: All points, etc. are assumed to lie in R 2 or R 3. I I I. : Perpendicular lines and planes Supplementary background
